MATEMATICA con quadernodegli esercizi
F. Lama • G. Tricerri Il piacere di apprendere
Editoriale ELi Oltre l’insegnamento Educ Ability
Gruppo
Il piacere di apprendere Gruppo Editoriale ELi Oltre l’insegnamento Educ Ability
MATEMATICA con quadernodegli esercizi Nome Cognome
N UMERI
4 Da 0 a 100
5 Il sistema decimale
6 Il valore posizionale delle cifre
7 Da 0 a 999
8 Comporre e scomporre fino a 999
9 Confrontare e ordinare fino a 999
10 Il migliaio
12 Comporre e scomporre fino a 9 999
13 Confrontare e ordinare fino a 9 999
40 Le proprietà della moltiplicazione
42 Moltiplicazioni in colonna
44 Moltiplicare per 10, 100, 1000
45 VERSO L’INVALSI
46 La moltiplicazione
47 PAGINE STELLA
48 La divisione
49 La tabella della divisione
50 La proprietà invariantiva
51 Moltiplicazione e divisione: operazioni inverse
14 I numeri fino a 9 999
15 PAGINE STELLA
16 L’addizione
17 La tabella dell’addizione
18 Le proprietà dell’addizione
19 Addizioni in colonna
20 Addizionare velocemente
22 Addizioni con il cambio
23 Addizioni con le migliaia
52 Divisioni in colonna
53 Divisioni in colonna con il resto
54 Ancora divisioni
55 Dividere per 10, 100, 1000
57 VERSO L’INVALSI
58 La divisione
59 PAGINE STELLA
P ROBLEMI
24 L’addizione
25 PAGINE STELLA
26 La sottrazione
27 La tabella della sottrazione
28 La proprietà invariantiva
29 Addizione e sottrazione: operazioni inverse
30 Sottrarre velocemente
Con le STEM posso… CALCOLARE
32 Sottrazioni in colonna
33 Sottrazioni con un cambio
34 Sottrazioni con più cambi
35 VERSO L’INVALSI
60 I problemi
62 Come risolvere i problemi?
63 I quantificatori
64 I dati
65 I dati inutili
66 I dati nascosti
67 I dati mancanti
68 La domanda giusta
69 Problemi e diagrammi
70 Due domande, due operazioni
Con le STEM posso… CALCOLARE
72 La domanda nascosta
36 La sottrazione
37 PAGINE STELLA
38 La moltiplicazione
39 La tabella della moltiplicazione
74 Problemi a più soluzioni
76 VERSO L’INVALSI
78 I problemi
79 PAGINE STELLA
INDICE 2
80 Frazionare
81 L’unità frazionaria
82 Le frazioni
84 Le frazioni
85 PAGINE STELLA
86 Le frazioni decimali
87 Dalle frazioni decimali ai numeri decimali
88 I decimi
89 I centesimi
90 I millesimi
91 VERSO L’INVALSI
119 Dalle figure piane alle linee
120 La linea retta
121 Rette parallele, incidenti, perpendicolari
122 Gli angoli
124 Solidi, linee e angoli
125 PAGINE STELLA
126 Poligoni e non poligoni
127 I poligoni
128 Classificare i poligoni
129 Il perimetro
92 I numeri decimali
93 PAGINE STELLA
M ISURE
94 Le unità di misura
95 Le misure di lunghezza
96 I sottomultipli del metro
98 I multipli del metro
100 Le equivalenze
102 Le misure di capacità
103 Le misure di massa o peso
105 Peso netto, peso lordo e tara
106 Le misure di valore: l’euro
108 Costo unitario e costo totale
109 Problemi con l’euro
Con le STEM posso… RISOLVERE
110 Le misure di tempo
130 L’area
131 VERSO L’INVALSI
132 La simmetria
134 I poligoni
135 PAGINE STELLA
R ELAZIONI , DATI E PREVISIONI
136 Classificare
137 Rappresentare con i diagrammi
138 Le relazioni
139 Le indagini
140 Certo, possibile, impossibile
141 Probabilità
142 Relazioni, dati e previsioni
143 PAGINE STELLA
144 VERSO L’INVALSI
112 Le misure
113 PAGINE STELLA
114 Quanta acqua siamo?
S PAZIO E FIGURE
116 I solidi
117 Tanti solidi
118 Dai solidi alle figure piane
QUADERNO DEGLI ESERCIZI
146 I miei schemi
157 I miei esercizi
188 Laboratorio STEM
Le avventure della capitana Tilly
LIBRO DIGITALE: www.gruppoeli.it/libridigitali
INDICE
3
DA 0 A 100
1 Scrivi il numero precedente e il numero successivo.
2 Confronta le coppie di numeri con i segni <, > oppure = .
3 Scomponi i numeri. Segui l’esempio.
3 da, 8 u
4 Componi i numeri. Segui l’esempio.
3 da, 4 u =
4 da, 5 u =
da, 9 u =
u, 5 da =
da, 0 u =
da, 1 u = 1 da, 1 u =
u, 9 da =
5 Riscrivi i numeri in ordine crescente (dal minore al maggiore).
6 Riscrivi i numeri in ordine decrescente (dal maggiore al minore).
da, 9 u =
NUMERI
19 60 91 31 99 75
28 80 37 42 36 10 27 90 64 63 54 45 74 47 22 22
38
............................................ 71
............................................ 89 = ............................................ 25
50 = 28 = 15
67
44
=
=
=
=
=
=
2
8
6
7
9
2
65 • 48 • 7 • 11 • 89 • 90 • 61 • 84
14 • 57 • 13 • 90 • 73 • 41 • 27 • 72
4
34
IL SISTEMA DECIMALE
Quando conti, usi il sistema decimale, cioè raggruppi le quantità per 10. Ogni volta che formi gruppi da 10, devi fare un cambio.
cambio cambio
10 unità 1 decina
10 unità formano 1 decina
10 u = 1 da
PROVO IO
10 decine 1 centinaio
10 decine formano 1 centinaio
10 da = 1 h
Conta i fiori e registra le quantità sull’abaco e in tabella.
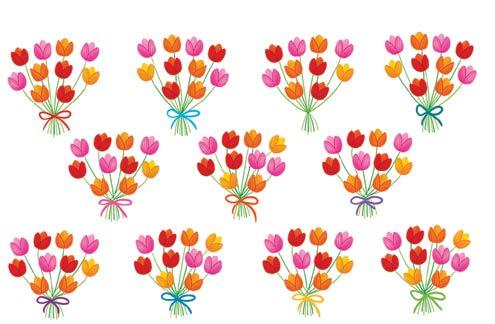
u u h
da da NUMERI 5
IL VALORE POSIZIONALE DELLE CIFRE
Osserva, registra in tabella e rispondi.
da da u h
• La cifra 2 ha lo stesso valore nei numeri 27 e 270? Sì NO
• Quanto vale la cifra 2 nel numero 27? ............................................
• Quanto vale la cifra 2 nel numero 270?
• La cifra 7 ha lo stesso valore nei numeri 27 e 270? Sì NO
• Quanto vale la cifra 7 nel numero 27?
• Quanto vale la cifra 7 nel numero 270?
• Per il posto vuoto quale cifra hai usato?
• In base a che cosa cambia il valore di una cifra in un numero? Alla posizione. Alla grandezza.
! ?
Il sistema di numerazione che utilizzi è un sistema posizionale, perché il valore di ciascuna cifra dipende dalla posizione che occupa nel numero.
In ciascun numero, cerchia la cifra che vale di più.
PROVO IO 1 3
u
2
9 9 0 4 5 3
NUMERI 6
4
0
3 7
DA 0 A 999
1 Completa per formare 100
2 Colora e indica con una X solo il centinaio.
70 + 30
1 h
1 da 100
99
3 Completa.
4
5
30 + 7 10 da
centodue
10 u cento
2 centinaia = decine = unità
1 centinaio = decine = unità
4 centinaia = decine = unità
3 centinaia = decine = unità
8 centinaia = decine = unità
5 centinaia = decine = unità
cento
Scrivi in lettere. 76 99 999 ............................................................................................. 560 601 817 .............................................................................................
Scrivi in cifre.
50 + .......................
100 30 +
100 80 + .......................
100 60 +
100 95 + ....................... = 100 10 + = 100 da
h da u h 20 I MIEI ESERCIZI PAGINA 157 NUMERI 7
centocinque trecentoquaranta ............................................................. novantasette ottocentoquarantadue settecentoventisei ...........................................................
=
=
=
=
u
COMPORRE E SCOMPORRE FINO A 999
1 Scrivi in cifre e in lettere le quantità rappresentate.
2 Scrivi in cifre e in lettere le quantità rappresentate sull’abaco.
3
Componi. 1 h, 7 da, 0 u = ................................................................. 5 h, 3 da, 1 u = 3 h, 9 u = ............................................................................... 9 h, 6 da =
Scomponi. 208 = ....................................................................................... 730 = 625 = ....................................................................................... 472 = da u h da u h da u h da u h da u h NUMERI 8
4
E ORDINARE FINO A 999 1 Confronta le coppie di numeri con i segni < oppure >. 127 217 199 299 221 211 704 470 409 410 371 307 450 540 899 99 307 95 726 421 710 199 249 429 110 924 770 520 771 709 519 – 1 + 1 109 460 991 389 201 – 1 + 1 503 899 669 909 166
Scrivi il numero precedente (– 1) e il numero successivo (+ 1).
Riscrivi i numeri in ordine crescente (dal minore al maggiore). 230 • 203 • 79 • 97 • 444 • 443 678 • 45 • 409 • 990 • 99 • 375 .......................................................................................................................................................... 4 Riscrivi i numeri in ordine decrescente (dal maggiore al minore). 568 • 685 • 211 • 770 • 303 • 330 109 • 345 • 609 • 969 • 346 • 111
CONFRONTARE
2
3
In
numero
e di azzurro
numero minore NUMERI 9
5
ciascun gruppo, cerchia di rosso il
maggiore
il
IL MIGLIAIO
Un gruppo di 10 centinaia forma 1 migliaio ( k ).
10 centinaia formano 1 migliaio
cambio
• Osserva che cosa succede quando si aggiunge 1 u al numero 999
La cifra delle migliaia va separata con un piccolo spazio dalle cifre di centinaia, decine e unità.
10 centinaia 1 migliaio PROVO
k 1 k = 10 h = 100 da = 1 000 u
10 h = 1
8 3 6 7 20 972 5 6 81 + = ! ?
IO 1 Forma il numero 1 000. 100 + = 1 000 350 + = 1 000 500 + = 1 000 670 + = 1 000 750 + = 1 000 990 + = 1 000 k h da u 1 0 0 0 u 1 k h da u k h da u 9 9 9 NUMERI 10
2 Completa le tabelle scrivendo in cifre le quantità rappresentate, come nell’esempio.
1
5 u
da u h h
da u h h
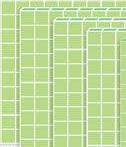
3 Completa gli abachi con i numeri o con le palline.
3 da NUMERI 11
2
da u h h 7 da 0 u 5 1 h k da u h k 0 da 8 u 2 1 h k da u h k
h h
COMPORRE E SCOMPORRE FINO A 9 999
1 Completa gli abachi con i numeri o con le palline. 7 da 5 u 9 2 h k da u h k da u h k
2 Colora nello stesso modo il numero e la sua scomposizione.
3 Scrivi il valore della cifra colorata.
4 Scomponi e scrivi i numeri in lettere, come nell’esempio.
8 213 = 6 054 =
3 128 = 4 950 =
8 k, 2 h, 1 da, 3 u = 8000 + 200 + 10 + 3 = ottomiladuecentotredici
1 0 87 3 154 5 29 6 8 13 4 4 3 56 9 24 5 7 428 2 168
2 k, 6 h, 1 da, 8 u
5 k, 5 h, 0 da, 4 u 3 k, 1 h, 8 da, 0 u 2 k, 8h, 3 da, 5 u 1 k, 0 h, 9 da, 7 u
1
3 180 5 504 2
2 835
097
618
NUMERI 12
CONFRONTARE E ORDINARE FINO A 9 999
1 Completa le sequenze.
3
1 998 2 006 5 200 5 209
con una
il confronto tra le coppie di numeri è vero ( V ) o falso (F ). 2 390 < 2 900 V F 1 569 > 1 560 V F 3 099 = 3 990 V F 8 200 > 8 200 V F 6 435 < 6 543 V F 7 182 > 7 281 V F 5 001 = 5 001 V F 9 290 > 9 920 V F 4 138 < 4 140 V F 5 Riscrivi i numeri in ordine crescente. 2 098 • 7 654 • 3 146 • 7 564 • 990 6 Riscrivi i numeri in ordine decrescente. 6 801 • 8 600 • 3 010 • 3 100 • 4 651 ...................................................................................................... 1 209 2 091 3 190 1 930 4 135 6 001 5 314 4 145 9 125 7 326 7 236 8 752
2 Indica
X se
Scrivi il numero precedente e il numero successivo. 2 100 3 890 7 295 .................... 4 689 .................... .................... 6 609 .................... .................... 8 999 .................... 3 000 4 001 5 098 I MIEI ESERCIZI PAGINA 158 NUMERI 13
In ciascuna zucca, cerchia di arancione il numero maggiore e di verde il numero minore. 4
MAPPA
I NUMERI FINO A 9999
Completa la mappa con i simboli e i numeri che mancano.
IN UN LAMPO 1 u 1 000 1 1 800 8 8 4 4 4 70 7 7 1 k = h = da = u 1 h = da = u 1 da = u k h da u
RIPASSO
14
numero maggiore: ......................... numero maggiore: .........................
numero minore: numero minore:
7 562 =
3 Scomponi e scrivi i numeri in lettere, come nell’esempio.
1 Usa tutte le cifre di ogni gruppo per formare il numero maggiore e minore possibile.2 986 1 986 4 856 4 857 5 092 5 102 3 066 3 670 9 201 9 200 8 320 8 330 2 150 2 120 7 000 7 001 5 045 5 005
2
Confronta
le coppie di numeri con i segni < oppure >
1 10 100 1 000 120 1 950 5 400 1 10 100 1 000 9 900 4 500 2 010
Riscrivi
2 015 • 2 536 • 2 563 • 2 236 • 2 010 6 Riscrivi i numeri in ordine decrescente. 7 067 • 7 176 • 7 076 • 7 167 • 7 157
+
+ 60
+ –8 0 5
. 3 7 1 6 VERIFICA 15
STELLA TUTTO OK?
3 205 = 5 681 = 2 437 = 4 Completa
le tabelle.
5
i numeri in ordine crescente.
7 k, 5 h, 6 da, 2 u = 7 000
500
+ 2 = settemilacinquecentosessantadue
4
PAGINE
L’ADDIZIONE
A Marco piace giocare con le costruzioni. Oggi ha realizzato una torre con 12 mattoncini rossi e 12 mattoncini blu. Quanti mattoncini ha utilizzato in tutto?
Per risolvere questo problema bisogna eseguire una:
ADDIZIONE
È l’operazione che permette di mettere insieme due o più quantità o di aggiungere una quantità a un’altra.
PROVO IO
Il segno è + e si legge più.
Leggi, rifletti, completa e risolvi.
I termini sono: 12 + 12 = 24 addendo addendo somma o totale
Per realizzare un cartellone gli alunni della classe terza hanno a disposizione due barattoli di pennarelli. Nel primo ce ne sono 20, nel secondo 36. Quanti pennarelli possono usare gli alunni?
• La domanda ti chiede:
il numero dei pennarelli rimasti.
il numero totale dei pennarelli.
il numero dei pennarelli in un barattolo.
• Scrivi l’operazione e risolvi.
• Devi eseguire: un’addizione. una sottrazione. una moltiplicazione.
• Scrivi la risposta.
I MIEI ESERCIZI PAGINA 160 NUMERI 16
LA TABELLA DELL’ADDIZIONE
Completa la tabella dell’addizione, rispondi alle domande e scopri alcune regole. addendo addendo
• Hai completato tutta la tabella? Sì NO
È sempre possibile eseguire una
Osserva la riga e la colonna colorate di verde. Che cosa noti?
Osserva la riga e la colonna colorate di giallo. Che cosa noti?
0 è l’elemento neutro dell’addizione: ciascun numero sommato a 0 non cambia.
Se a qualsiasi numero si somma 1, si ottiene il numero intero successivo.
PROVO IO
Esegui le addizioni con lo 0. 53 + 0 = 30 + 0 = 27 + 0 = 49 + 0 = 14 + 0 = 81 + 0 =
1
Esegui le addizioni con 1. 38 + 1 = 30 + 1 = 50 + 1 = 19 + 1 = 128 + 1 = 156 + 1 =
2
0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10 +
ADDIZIONE E SOTTRAZIONE 17
LE PROPRIETÀ DELL’ADDIZIONE
LA PROPRIETÀ COMMUTATIVA
1 Osserva e completa.
18 + 6 = 24
6 + 18 = 24
Abbiamo applicato la proprietà commutativa dell’addizione.
Puoi utilizzare la proprietà commutativa come prova dell’addizione, per verificare che il risultato sia corretto.
LA PROPRIETÀ ASSOCIATIVA
2 Osserva e rispondi.
29 + 13 + 7 = 49
29 + 20 = 49
• Nelle due addizioni: sono cambiati gli addendi. è cambiato l’ordine degli addendi.
Il risultato è cambiato? Sì NO
Se si cambia l’ordine degli addendi, il risultato non cambia.
• Che cosa è successo nella seconda addizione?
• Il risultato è cambiato? Sì NO
Abbiamo applicato la proprietà associativa dell’addizione.
PROVO IO
Se si sostituiscono due o più addendi con la loro somma , il risultato non cambia.
1 Applica la proprietà commutativa ed esegui le addizioni.
14 + 25 = .........................................
9 + 80 = ...........................................
2 Applica la proprietà associativa ed esegui le addizioni.
35
12 + 36 = ........................................
+ 2 8
9 2 8 + 7 1 = 9 9
7 1
= 9
14
+
+ 27 + 5 = 51 + 9 +
= 4
26 + 52 =
NUMERI 18
ADDIZIONI IN COLONNA
Al Museo di Scienze Naturali in un giorno sono stati venduti 154 biglietti interi e 113 biglietti ridotti. Quanti biglietti sono stati venduti in tutto?
Per risolvere questo problema
bisogna fare un’................................................................
Per rendere più semplici i calcoli, puoi eseguire l’addizione in colonna Segui le istruzioni.
• Scrivi gli addendi uno sotto l’altro: le unità sotto le u, le decine sotto le da , le centinaia sotto le h
PROVO IO
1 Metti in colonna le addizioni ed esegui.
• Addiziona: prima le unità , dopo le decine, infine le centinaia .
2 Esegui le addizioni in colonna sul quaderno e verifica i risultati con la prova. 143 + 205 = 321 +
..................... + ..................... = .....................
h da u 1 5 4 + 1 1 3 = h da u 1 5 4 + 1 1 3 = 2 6 7
h
+ = ........ ........ ........ 305 + 173
h
+ = ........ ........ ........ 162 + 25 = h
+ = ........ ........ ........ 240 +
da u
=
da u
da u
135 =
48
240 + 548
521 + 307 = 608 + 391 = 842 + 136 = 370 + 24
103
+ 451 +
75 + 603 + 20
421 + 36 + 740 =
I MIEI ESERCIZI PAGINA 161 ADDIZIONE E SOTTRAZIONE 19
= 86 + 302 = 52 + 37 =
=
+
= 406
2 =
=
a b c
ADDIZIONARE VELOCEMENTE
Per eseguire velocemente le addizioni puoi utilizzare alcune strategie. Leggi con attenzione le indicazioni, segui gli esempi e calcola.
a Scomponi gli addendi, poi applica la proprietà associativa e risolvi.
35 + 23 =
(30 + 5) + (20 + 3) =
50 + 8 = 58
18 + 34 = (10 + 8) + (30 + 4) = =
39 + 17 =
b Fai tappa alla decina o al centinaio successivi.
57 + 16 =
(57+ 3) + (16 – 3) =
60 + 13 = 73
38 + 27 = (38 – 3) + (27 + 3) = + =
65 + 19 =
c Per sommare 9, 99, 999, aggiungi 1 da, 1 h, 1 k e poi togli 1 u.
74 + 9 =
74 + 10 – 1 =
84 – 1 = 83
92 + 99 =
92 + 100 – 1 =
192 – 1 = 191
75 + 9 = (75 + 10) – 1 = ............... – .............. =
63 + 99 =
d Per sommare 11, 21, 31…, prima aggiungi 10, 20, 30…, poi ancora 1 u.
68 + 11 =
68 + 10 + 1 =
78 + 1 = 79
87 + 11 = (87 + 10) + 1 =
94 + 21 =
146 + 51 =
146 + 50 + 1 =
196 + 1 = 197
.................
..............
.................
............... –
=
NUMERI 20
PROVO IO
1 Esegui le addizioni velocemente. Usa la strategia che ritieni più adatta.
72 + 15 =
44 + 48 =
174 + 58 =
240 + 95 =
385 + 99 =
1280 + 999 =
245 + 41 = ...............................................................................................................................................
478 + 51 =
58 + 42 =
47 + 16 =
35 + 19 =
63 + 31 = .........................
26 + 99 =
134 + 9 =
a b c
380 + 45 =
219 + 99 =
108 + 11 = ........................
563 + 99 =
2 Calcola velocemente e completa le tabelle.
185 + 29 =
714 + 9 =
636 + 41 =
1 257 + 999 = ......................
1 508 + 999 =
6 u 5 da 3 h 74 148 2 705 9 11 51 99 58 136 1 249
+ 8 + 21 + 99 + 3 da + 12 50 + 21 + 16 + 132 + 3 h + 99 534
3 Completa le catene di addizioni.
+ +
ADDIZIONE E SOTTRAZIONE 21
ADDIZIONI CON IL CAMBIO
Quando la somma di due o più cifre è uguale a 10 o maggiore di 10, è necessario fare il cambio. Metti in colonna le cifre e segui le istruzioni per procedere ai calcoli.
Addizione con un cambio 248 + 127 =
• Somma le unità :
8 + 7 = 15 = 1 da e 5 u
• Scrivi 5 nella colonna delle u e riporta 1 nella colonna delle da
• Somma le decine:
1 + 4 + 2 = 7
• Scrivi 7 nella colonna delle da
Addizione con due cambi 379 + 148 =
• Somma le unità :
9 + 8 = 17 = 1 da e 7 u
• Scrivi 7 nella colonna delle u e riporta 1 nella colonna delle decine.
• Somma le decine:
1 + 7 + 4 = 12 da = 1 h e 2 da
• Scrivi 2 nella colonna delle da e riporta 1 nella colonna delle h.
• Somma le centinaia :
2 + 1 = 3
• Scrivi 3 nella colonna delle h
• Somma le centinaia :
1 + 3 + 1 = 5
• Scrivi 5 nella colonna delle h.
PROVO IO
Esegui le addizioni in colonna sul quaderno e verifica i risultati con la prova.
167 + 129 = 491 + 136 =
+ 237 = 340 + 293 =
+ 94 = 85 + 428 + 134 = a b
285 + 259 = 346 +
2 4 8 + 1 2 7 = 5 +1 1 h da u 2 4 8 + 1 2 7 = 7 5 +1 h da u 2 4 8 + 1 2 7 = 3 7 5 +1
h da u
h da u 3 7 9 + 1 4 8 = 2 7 +1 +1 1 h da u 3 7 9 + 1 4 8 = 7 +1 1 h da u 3 7 9 + 1 4 8 = 5 2 7 +1 +1
545
576
54 + 127 =
NUMERI 22
ADDIZIONI CON LE MIGLIAIA
1 Metti in colonna ed esegui le addizioni senza cambio.
1 426 + 1 532 =
k h da u + ........ ........ ........ ........ =
2 360 + 428 =
k h da u + ........ ........ ........ ........ =
2 Metti in colonna ed esegui le addizioni con un cambio.
2 507 + 274 =
k h da u + =
629 + 3 157 =
k h da u + =
3 Metti in colonna ed esegui le addizioni con più cambi.
1 758 + 1 426 =
k h da u + =
7 084 + 359 =
k h da u + =
5 172 + 1 614 =
k h da u + ........ ........ ........ ........ =
3 475 + 1 283 =
k h da u + =
4 578 + 1 637 =
k h da u + =
4 Esegui le addizioni in colonna sul quaderno e verifica i risultati con la prova.
1 347 + 1 421 =
3 905 + 278 =
2 890 + 3 726 =
763 + 2 438 =
4 925 + 715 =
a b c
89 + 3 279 =
5 038 + 436 =
864 + 2 508 =
2 039 + 27 + 451 =
1 925 + 438 + 75 =
4 937 + 27 + 815 =
742 + 1 506 + 39 =
ADDIZIONE E SOTTRAZIONE 23
L’ADDIZIONE
Completa la mappa, inserendo le parole che seguono:
cambio • più • addendi • successivo • somma • decine
Addizionare vuol dire…
mettere insieme due o più quantità oppure aggiungere una quantità a un’altra. Il segno dell’addizione è + ( )
COMMUTATIVA
Le proprietà
I termini sono: 12 + 12 = 24
addendo addendo somma o totale
In colonna
Se cambio l’ordine degli , il risultato non cambia.
ASSOCIATIVA
Se sostituisco due addendi con la loro , il risultato non cambia.
Devo sommare prima le unità (u ), poi le (da ), le centinaia ( h ) e le migliaia ( k ).
18 + 6 = 24
6
29 + 13 + 7 = 49
29 + 20 = 49
Quando la somma è superiore al 9, faccio il .
Addizioni con 0 e con 1
• Se aggiungo 0 a un numero qualunque, la somma è il numero stesso.
• Se aggiungo 1 a un numero qualunque, la somma è il numero .
RIPASSO IN UN LAMPO
k h da
1 1 5 4 + 1 1 3 = 1 2 6 7
+ 18 =
u
da h da u 1 2 4 8 + 1 2 7 = 1 3 7 5 +1 1
MAPPA 24
I MIEI SCHEMI PAGINA 146
1 Calcola velocemente e completa le tabelle.
2 Completa le addizioni con i numeri mancanti.
150 + ................... = 200 ................... + 100 = 350
+ .................................... = 1 000 380 + = 400 + 90 = 490
+ = 1 200 245
3 Esegui a mente le addizioni e collega con una al risultato corretto.
+ 0 =
=
+ 180 + 15 =
4 Esegui le addizioni in colonna sul quaderno e verifica i risultati con la prova. 917
=
=
=
950
800
+
1
+
430 + 10
3
650 + = 800 + 250
750 4 999
= 5 000 1 10 100 1 000 74 308 752 1 540 9 11 51 99 37 82 103 560 a senza cambi c con più cambi
= 250 + 400 = 800
900 + = 2 000 412
=
= 270
995 + = 4 000
=
+
+
465
+ 125
62 =
+ 231 = 702 + 184 = 31
+ 2
+
31
b con un cambio
+ 159
590 + 346
+ 284
458 + 127
5 394 + 1 245
187 +
305 + 827
472 + 98
094 + 756
894 + 326 + 73
1 065
402 +
728
=
= 372
= 1
=
=
294 =
=
= 2
=
=
250
180
250
150
380
150 + 150
100
10 + 175
65
200 + 175
25
350
125 + 125
195
55
250 375 400 + + VERIFICA 25
TUTTO OK?
+
+ 20 =
+
=
+
=
=
+
=
+
=
PAGINE STELLA
LA SOTTRAZIONE
All’inizio della giornata il fruttivendolo Arturo ha messo sullo scaffale 38 cestini di fragole.
Durante la mattinata ne ha venduti 23.
Quanti cestini sono rimasti?
Per risolvere questo problema bisogna eseguire una:
SOTTRAZIONE
È l’operazione che:
• toglie una quantità da un’altra;
• calcola quanto manca per completare una quantità;
• calcola la differenza tra due quantità.
PROVO IO
Il segno è –e si legge meno.
Leggi, rifletti, completa e risolvi.
I termini sono: 38 – 23 = 15
minuendo sottraendo resto o differenza
In una postazione di biciclette a noleggio ci sono a disposizione 45 biciclette. Oggi sono già state noleggiate 24 biciclette. Quante biciclette sono ancora disponibili?
• La domanda ti chiede:
• Devi eseguire:
il numero delle biciclette noleggiate. un’addizione.
il numero totale delle biciclette. una sottrazione.
il numero delle biciclette che possono una moltiplicazione. ancora essere utilizzate.
• Scrivi l’operazione e risolvi.
• Scrivi la risposta.
......................................................................................................
I MIEI ESERCIZI PAGINA 162 NUMERI 26
LA TABELLA DELLA SOTTRAZIONE
Completa la tabella della sottrazione, rispondi alle domande e scopri alcune regole.
sottraendo minuendo Esegui le sottrazioni a mente e cerchia quelle che non sono possibili.
–
0
Hai completato tutta la tabella? Sì NO
• Osserva i numeri delle caselle colorate di verde. Che cosa noti? ..........................................................................................
0 è l’elemento neutro della sottrazione: se a un numero si sottrae 0, il numero non cambia.
• Osserva i numeri delle caselle colorate di giallo. Che cosa noti?
Se a un numero si sottrae 1, si ottiene il numero precedente.
• Osserva i numeri delle caselle colorate di azzurro. Che cosa noti?
6 – 0 =
15 – 15 =
29 – 0 = .........................
18 – 0 =
0 – 47 =
83 – 0 =
18 – 18 =
35 – 1 =
20 – 23 = ......................
41 – 1 = 6 – 7 =
95 – 1 =
Se a un numero si sottrae il numero stesso, si ottiene 0
ADDIZIONE E SOTTRAZIONE 27
..........................................................................................
! ?
È possibile eseguire la sottrazione solo quando il minuendo è maggiore o uguale al sottraendo. 0 1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
PROVO IO
LA PROPRIETÀ INVARIANTIVA
• Osserva e rispondi.
25 – 18 = 7
+ 2
27 – 20 = 7
• Che cosa è successo?
• Il risultato è cambiato? Sì NO
49 – 14 = 35
45 – 10 = 35 – 4 – 4
• Che cosa è successo?
• Il risultato è cambiato? Sì NO
Abbiamo applicato la proprietà invariantiva della sottrazione.
Se si aggiunge o si toglie lo stesso numero al minuendo e al sottraendo, il risultato della sottrazione non cambia.
1 Applica la proprietà invariantiva e calcola.
48 – 30
2 Applica la proprietà invariantiva ed esegui le sottrazioni sul quaderno.
+ 2
– 5 + 4 – 5 + 4
– 27 = 29 – 15 = 82 – 34 = 71 – 16 = = = = = 85 – 29 = 126 – 34 = 108 – 19 = 139 – 27 = .............................. = ............. ................................. = ............. ................................. = ............. ................................. = .............
45
17
8 = 81 – 34 = 108 – 27 = 123 – 18 = 24 – 19 = 96 – 29 = 137 – 28 = 251 – 45 = 42 – 25 = 73 – 48 = 102 – 16 = 305 – 56 = + 3 + 3 – 2 – 2
b NUMERI 28
–
PROVO IO a
ADDIZIONE E SOTTRAZIONE: OPERAZIONI INVERSE
Osserva, leggi e completa.
Sul lago ci sono 5 barche a vela e 8 barche senza vela.
Quante barche ci sono sul lago?
=
Addizione e sottrazione sono operazioni inverse.
Sul lago ci sono 13 barche. 8 barche non hanno le vele.
Quante sono le barche con le vele?
PROVO IO
Segui le frecce e completa le operazioni.
• Per verificare se la sottrazione è corretta, fai la prova con l’operazione inversa, cioè con l’addizione: aggiungi il resto al sottraendo e ottieni il minuendo.
+
–
=
+ 6 –405 + 5 999 + 10 283 + 8 – 8 132
+
– 8 5 13 7 8 –2 5 = 5 3 5 3 + 2 5 = 7 8
8
ADDIZIONE E SOTTRAZIONE 29
SOTTRARRE VELOCEMENTE
1 Per eseguire velocemente le sottrazioni puoi utilizzare alcune strategie. Leggi con attenzione le indicazioni, segui gli esempi e calcola.
a
Scomponi il sottraendo e sottrai dal minuendo prima le decine e poi le unità.
88 – 36 = (88 – 30) – 6 =
58 – 6 = 52
49 – 25 = (49 – 20) – 5 = – =
54 – 33 =
97 – 42 = ...................................................................................................................................................
79 – 24 =
b c
Scomponi il minuendo e il sottraendo, poi sottrai prima le centinaia, poi le decine e le unità. Infine, componi o somma i risultati ottenuti.
98 – 74 = (90 + 8) – (70 + 4) = (90 – 70) + (8 – 4) =
286 – 145 =
65 – 32 =
184 – 53 =
376 – 125 =
Per togliere 9, 99, 999, togli 1 da, 1 h, 1 k e poi aggiungi 1 u.
375 – 9 =
(200 + 80 + 6) – (100 + 40 + 5) =
(200 – 100) + (80 – 40) + (6 – 5) =
100 + 40 + 1 = 141
37 – 9 =
37 – 10 + 1 =
27 + 1 = 28
92 – 9 = (92 – 10) + 1 = + =
264 – 99 =
264 – 100 + 1 =
164 + 1 = 165
824 – 99 = ................................................................................................................................................
631 – 999 =
NUMERI 30
Per togliere 11, 21, 31… togli prima 10, 20, 30… poi togli ancora 1 u.
80 – 11 =
80 – 10 – 1 =
70 – 1 = 69
52 – 21 = (52 – 20) – 1 = – =
d b c
328 – 61 =
328 – 60 – 1 =
268 – 1 = 267
96 – 41 = .............................................................................................................................................
284 – 61 =
190 – 31 =
2 Esegui le sottrazioni velocemente. Usa la strategia che ritieni più adatta.
a
39 – 15 =
47 – 23 = .........................
65 – 9 =
58 – 41 =
25 – 9 =
146 – 75 =
280 – 99 = ......................
435 – 51 =
206 – 9 =
632 – 21 =
3 Completa le catene di sottrazioni. – 3 da – 99
249 – 74 =
861 – 9 = ...........................
568 – 41 =
1 346 – 999 =
2 308 – 999 =
– 9 – 2 da – 31 – 8 u – 18
375 49 350 100
Con le STEM posso… CALCOLARE
Devi eseguire la sottrazione: 685 – 243. Completa le istruzioni.
1. Scomponi il minuendo:
685 = ........... + ...........
2. Scomponi il : 243 = + +
3. Ora sottrai le centinaia:
4. Poi sottrai
5. Infine sottrai le unità:
120
+
...........
–
=
–
...........
........... = ...........
– =
+ + =
6. Somma i risultati ottenuti: ADDIZIONE E SOTTRAZIONE 31
SOTTRAZIONI IN COLONNA
In un autosilo ci sono 287 posti per le auto. Oggi sono già state parcheggiate 125 auto.
Quanti sono i posti ancora vuoti?
Per risolvere questo problema bisogna fare una .............................................................. – =
Per rendere più semplici i calcoli, puoi eseguire una sottrazione in colonna . Segui le istruzioni.
• Scrivi il minuendo sopra e il sottraendo sotto: le unità sotto le u, le decine sotto le da , le centinaia sotto le h.
PROVO IO
1 Metti in colonna le sottrazioni ed esegui.
• Sottrai: prima le unità , dopo le decine, infine le centinaia .
2 Esegui le sottrazioni in colonna sul quaderno e verifica i risultati con la prova.
185 –
274 –
3
h da u 2 8 7 –1 2 5 = h da u 2 8 7 –1 2 5 = 1 6 2
h da u –= 375 – 241 = ............. h da u –= 694 – 72 = ............. k h da u –= 2 786 – 1 206 = .............
123 =
61
=
8
563 – 132 = 938 – 705 = 189 – 72 = 674 – 230 =
908
306 =
193 – 170 = 519 –
=
1
–
287
43
519
408 = 6 893
5 291 = a
c I MIEI ESERCIZI PAGINA 163 NUMERI 32
–
= 4
– 1
–
b
SOTTRAZIONI CON UN CAMBIO
Metti in colonna le cifre e segui le istruzioni per eseguire le sottrazioni con un cambio.
Sottrazione con un cambio 382 – 154 =
• Sottrai le unità:
2 – 4 = non si può fare!
• Dalle decine prendi 1 da , fai il cambio in 10 u e aggiungile a
2 u, che diventano 12
• Esegui: 12 – 4 = 8
• Scrivi 8 nella colonna delle u
• Sottrai le decine. Poiché hai preso 1 da , 8 è diventato 7: 7 – 5 = 2
• Scrivi 2 nella colonna delle da . h da u 3
• Sottrai le centinaia: 3 – 1 = 2
• Scrivi 2 nella colonna delle h.
PROVO IO
1 Metti in colonna le sottrazioni ed esegui.
2 618 – 452 =
2 Esegui le sottrazioni in colonna sul quaderno e verifica i risultati con la prova.
853 – 215 =
5
2 2 8 7
h da u 3 8 2 –1
4 =
1
1 5 4
2 8 7
2
1 5 4
8 1 7
8 2 –
=
1 h da u 3 8
–
=
h
........ ........ ........ –=
h
........ ........ ........ –
k
........ ........ ........ ........ –=
da u
563 – 127 =
da u
= 891 – 243 =
h da u
537
ADDIZIONE E SOTTRAZIONE 33
634 – 108 = 270 – 46 = 408 – 163 = 352 – 94 = 714 – 382 = 1 864 – 249 = 3 580 – 325 = 2
– 182 = 2 506 – 1 271 = 4 274 – 1 830 = 3 628 – 2 054 = a b
SOTTRAZIONI CON PIÙ CAMBI
Metti in colonna le cifre e segui le istruzioni per eseguire le sottrazioni con più cambi.
Sottrazione con due cambi 473 – 195 =
• Sottrai le unità : 3 – 5 = non si può fare!
• Dalle decine prendi 1 da , fai il cambio in 10 u e aggiungile a 3 u che diventano 13.
• Esegui: 13 – 5 = 8
• Scrivi 8 nella colonna delle u.
• Sottrai le decine. Poiché hai preso 1 da , 7 è diventato 6: 6 – 9 = non si può fare!
• Dalle centinaia prendi 1 h, fai il cambio in 10 da e aggiungile a 6, che diventa 16.
• Esegui: 16 – 9 = 7
• Scrivi 7 nella colonna delle da
• Sottrai le centinaia
Poiché hai preso 1 h,
4 è diventato 3. 3 – 1 = 2
• Scrivi 2 nella colonna delle h.
PROVO IO
Metti in colonna le sottrazioni ed esegui.
u ........ ........ ........ –= 423 – 156 = h da u ........ ........ ........ –= 515 – 96 = k h da u ........ ........ ........ ........ –=
h da
=
3 482 – 635
h da u 4 7 3 –1 9 5 = 2 7 8 1 16 3 h da u 4 7 3 –1 9 5 = 8 1 6 h da u 4 7 3 –1 9 5 = 7 8 1 16 3
I MIEI ESERCIZI PAGINA 164, 166 NUMERI 34
Risolvi questi problemi completando i disegni.
1. Giada ha 9 anni. Lucia ha 3 anni in più di Giada. Marco ha 6 anni in meno di Lucia.
Quanti anni ha Lucia?
Quanti anni ha Marco?
GIADA
LUCIA MARCO
2. Su un autobus salgono, all’inizio del viaggio, 12 persone. Alla prima fermata ne scendono 5.
Alla seconda fermata ne salgono 8.
Quante persone ci sono ora sull’autobus?
INIZIO VIAGGIO 1° FERMATAVERSO L’INVALSI 35
2° FERMATA
LA SOTTRAZIONE
Completa la mappa, inserendo le parole che seguono:
sottraggo • meno • cambio • precedente • minuendo • decine
Sottrarre vuol dire…
togliere una quantità più piccola da una quantità più grande, calcolare la differenza tra due quantità o quanto manca per completare una quantità.
La proprietà
I termini sono:
38 – 23 = 15
minuendo sottraendo resto o differenza
Il segno della sottrazione è – (.................)
INVARIANTIVA
Se aggiungo o lo stesso numero a entrambi i termini della sottrazione, il risultato non cambia.
25 – 18 = 7
In colonna k h da u
Devo sottrarre prima le unità (u ), poi le (da ), le centinaia ( h ) e le migliaia ( k ).
27 – 20 = 7 + 2 + 2 h da u
Quando il sottraendo è maggiore del minuendo, faccio il .
Sottrazioni con 0 e con 1
• Se sottraggo 0 a un numero qualunque, ottengo il numero stesso.
• Se sottraggo 1 a un numero qualunque, ottengo il numero
L’addizione e la sottrazione sono operazioni inverse. Posso usare l’addizione per fare la prova della sottrazione: se il mio calcolo è esatto, sommando il resto al sottraendo, otterrò il
Operazioni inverse RIPASSO IN UN LAMPO
3 2 8 7 –1 1 2 5 = 2 1 6 2
3 8
1 5 4
2 2 8 7
2 –
=
1
MAPPA 36 I MIEI SCHEMI PAGINA 147
PAGINE STELLA
1 Calcola velocemente solo le sottrazioni possibili e completa le tabelle.
457
903
3 509
709
1 350
5 028
2 Completa le sottrazioni con i numeri mancanti.
320 – = 100
470 – = 430
150 – = 145
706 – = 6
– 100 = 50
– 90 = 200
– 8 = 302
– 250 = 500
2 800 – = 2 000
– 1 000 = 4 782
1 750 – = 1 250
– 800 = 4 200
3 Esegui a mente le sottrazioni e collega con una al risultato corretto.
182 – 40 =
258 – 11 =
109 – 25 =
175 – 9 =
2
430 – 5 da =
1 749 – 2 h =
1 836 – 1 k =
2 500 – 8 u =
4 Esegui le sottrazioni in colonna sul quaderno e verifica i risultati con la prova.
a senza cambi c con più cambi b con un cambio
849 – 207 =
395 – 182 =
783 – 51 =
1 870 – 340 =
2 598 – 1 207 =
4 763 – 521 =
394 – 158 =
780 – 435 =
547 – 96 =
1 638 – 254 =
3 057 – 623 =
6 947 – 2 554 =
647 – 89 =
731 – 256 =
560 – 183 =
1 394 – 816 =
5 724 – 2 389 =
4 285 – 1 726 =
10 100 1000
1
195
1 10 100 1 000
80
492 247 380 166 142 1 549 836 84
– –
VERIFICA 37
TUTTO OK?
LA MOLTIPLICAZIONE
Nel parco giochi ci sono 3 giostre per i bambini. Su ciascuna giostra ci sono 5 bambini.
Quanti bambini sono sulle giostre?
Per risolvere questo problema bisogna eseguire una:
MOLTIPLICAZIONE
È l’operazione che ripete più volte la stessa quantità .
Il segno è e si legge per.
PROVO IO
Leggi, rifletti, completa e risolvi.
I termini sono:
5 3 = 15
moltiplicando fattori moltiplicatore prodotto
Per la Festa dello Sport organizzata in una Scuola Primaria vengono consegnate 18 confezioni di acqua minerale. In ciascuna confezione ci sono 6 bottiglie di acqua.
Quante bottiglie di acqua vengono consegnate in tutto?
•
• La domanda ti chiede: Devi eseguire:
il numero delle bottiglie in ciascuna confezione. un’addizione.
il numero delle confezioni. una sottrazione.
il numero di tutte le bottiglie consegnate. una moltiplicazione.
• Scrivi l’operazione e risolvi.
• Scrivi la risposta.
..................................................................................................
I MIEI ESERCIZI PAGINA 167 NUMERI 38
LA TABELLA DELLA MOLTIPLICAZIONE
Completa la tabella della moltiplicazione, rispondi alle domande e scopri alcune regole.
Hai completato tutta la tabella? Sì NO È sempre possibile eseguire una
! ?
• Osserva i numeri della riga e della colonna colorate di verde. Che cosa noti?
0 è l’elemento annullante della moltiplicazione: ciascun numero moltiplicato per 0 dà come risultato 0.
• Osserva i numeri della riga e della colonna colorate di giallo. Che cosa noti? .........................................................................................
1 è l’elemento neutro della moltiplicazione: ciascun numero moltiplicato per 1 dà come risultato il numero stesso.
0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10 fattore fattore
IO Esegui le moltiplicazioni a mente. 5 0 = ..................... 1 0 = ..................... 7 1 = 8 1 = 4 0 = 2 0 = 3 1 = 0 1 = 9 0 = 10 0 = 6 1 = ..................... 10 1 = ..................
PROVO
MOLTIPLICAZIONE E DIVISIONE 39
LE PROPRIETÀ DELLA MOLTIPLICAZIONE
LA PROPRIETÀ COMMUTATIVA
Osserva e completa.
7 5 = 35
5 7 = 35
Abbiamo applicato la proprietà commutativa della moltiplicazione.
Puoi utilizzare la proprietà commutativa come prova della moltiplicazione.
LA PROPRIETÀ ASSOCIATIVA
Osserva e rispondi.
3 5 4 = 60
3 20 = 60
• Nelle due moltiplicazioni: sono cambiati i fattori. è cambiato l’ordine dei fattori.
• Il risultato è cambiato? Sì NO
Se cambia l’ordine dei fattori, il risultato non cambia.
4 8 =
• Che cosa è successo nella seconda moltiplicazione?
• Il risultato è cambiato? Sì NO
Abbiamo applicato la proprietà associativa della moltiplicazione.
PROVO IO
Se si sostituisce a due o più fattori il loro prodotto, il risultato non cambia.
Calcola e verifica il risultato applicando la proprietà commutativa.
9 5 = 5 =
2 6 = =
8 4 = =
4
3 2 8
= 3 2
3 8 = = NUMERI 40
LA PROPRIETÀ DISTRIBUTIVA
Osserva e rispondi.
12 3 = 36
(10 + 2) 3 =
(10 3) + (2 3) =
• Che cosa è successo? .......................................................................................................
• Il risultato è cambiato? Sì NO
30 + 6 = 36 Abbiamo applicato la proprietà distributiva della moltiplicazione.
PROVO IO
Se scomponi un fattore in una addizione, poi moltiplichi ciascun addendo per l’altro fattore e sommi i prodotti, il risultato non cambia.
1 Applica la proprietà associativa ed esegui le moltiplicazioni.
6 2 3 =
5
2 Applica la proprietà distributiva ed esegui le moltiplicazioni.
23 4 = (20 + 3) 4 = ( ) + ( ) =
16 3 =
18 6 =
27 2 =
48 5 =
3 Esegui le moltiplicazioni e scrivi quale proprietà hai applicato.
3 9 = 9 3 =
5
24 8 = (20 +
9 7 2
=
2 8 4 =
4 5 = 10 9 2 =
7 2 =
8
........................................................................................................................................................................................
7
7 4 = (5 4)
=
8
4)
=
10
................................. ...........................................................................................
2 10 9 = (2 9)
=
MOLTIPLICAZIONE E DIVISIONE 41
MOLTIPLICAZIONI IN COLONNA
Per realizzare un cartellone Leo e i suoi amici hanno a disposizione 2 barattoli di pennarelli.
In ciascun barattolo ci sono 24 pennarelli.
Quanti pennarelli hanno in tutto?
Per risolvere questo problema bisogna fare una =
MOLTIPLICATORE CON UNA CIFRA
Per rendere più semplici i calcoli, puoi eseguire una moltiplicazione in colonna Segui le istruzioni.
Moltiplicazione senza cambio 24 2 =
• Moltiplica le unità:
2 4 = 8
• Scrivi 8 nella colonna delle u
• Moltiplica le decine:
2 2 = 4
• Scrivi 4 nella colonna delle da
Segui le istruzioni per eseguire le moltiplicazioni in colonna con un cambio.
Moltiplicazione con un cambio 37 2 =
• Moltiplica le unità:
2 7 = 14, cioè 1 da e 4 u.
• Scrivi 4 nella colonna delle u e riporta 1 nella colonna delle da .
• Moltiplica le decine: 2 3 = 6
• Aggiungi il riporto: 6 + 1 = 7
• Scrivi 7 nella colonna delle da
h da u 3 7 2 = 7 4 +1 h da u 3 7 2 = 4 +1 1
h da u 2 4 2 = 8 h da u 2 4 2 = 4 8
NUMERI 42
MOLTIPLICATORE CON DUE CIFRE
Segui le istruzioni per eseguire le moltiplicazioni con due cifre al moltiplicatore.
Moltiplicazione senza cambio 21 14 =
• Moltiplica le unità del moltiplicatore (4) per le unità e poi per le decine del moltiplicando (prima 1 e poi 2): 4 1 = 4, 4 2 = 8. 84 è il primo prodotto parziale.
• Prima di moltiplicare le decine, aggiungi uno 0 segnaposto nella
colonna delle u
• Moltiplica le da dal moltiplicatore (1) per le unità e poi per le decine del moltiplicando (prima 1 e poi 2):
1 1 = 1 1 2 = 2 210 è il secondo prodotto parziale.
• Somma in colonna i due prodotti parziali e ottieni il prodotto finale: 84 + 210 = 294
Moltiplicazione con il cambio 26 13 =
h da u 2 1 1 4 = 8 4 + = h da u 2 1 1 4 = 8 4 + 2 1 0 = h da u 2 1 1 4 = 8 4 + 2 1 0 = 2 9 4
h da u 2 6 1 3 = 7 8 + = +1 a h da u 2 6 1 3 = 7 8 + 0 = b h da u 2 6 1 3 = 7 8 + 2 6 0 = c h da u 2 6 1 3 = 7 8 + 2 6 0 = 3 3 8 +1 d I MIEI ESERCIZI PAGINA 168, 169 MOLTIPLICAZIONE E DIVISIONE 43
MOLTIPLICARE PER 10, 100, 1 000
Moltiplicare un numero per 10 significa aumentare di 10 volte il suo valore, per 100 aumentare di 100 volte il suo valore, per 1 000 aumentare di 1 000 volte il suo valore.
k h da u
2 4 2 4 0 10
k h da u
3 7
3 7 0 0
k h da u
9
9 0 0 0 1 000
24 10 = ..............
Se moltiplichi per 10, le unità diventano , le decine diventano
Il posto vuoto delle u viene occupato dallo ............. .
37 100 =
Se moltiplichi per 100, le unità diventano , le decine diventano .
I posti vuoti delle u e delle da vengono occupati dagli
9 1 000 =
Se moltiplichi per 1 000, le unità diventano .
I posti vuoti delle u, delle da e delle h vengono occupati dagli .
Quando moltiplichi un numero per 10, per 100, per 1 000, aggiungi a destra uno, due, tre zeri.
PROVO IO
Esegui
le moltiplicazioni.
10 = ................................ 8 100 = 14 10 = 258 10 = 34 100 = .................................... 15 1 000 = 319 10 = 9 1 000 = 123 10 = .................................... 6 1 000 = 47 100 = 139 100 =
7
100
NUMERI 44
1 Osserva i numeri nel riquadro, poi, per ciascuna affermazione, indica V (vero) o F (falso).
18 • 6 • 49 • 85 • 28 • 37 • 5 • 53 • 60 • 32
• Tutti i numeri sono maggiori di 10.
V F
• Alcuni numeri appartengono alla tabellina del 7. V F
• Qualche numero è pari.
• Nessun numero è a una cifra.
• Ciascun numero è minore di 70.
V F
V F
V F
• Almeno un numero è minore di 29. V F
• Solo un numero è superiore a 8 decine.
V F
2 Leggi, poi, per ciascuna affermazione, indica V (vero) o F (falso).
In 3 a B alcuni bambini giocano con i numeri della tombola estraendo a turno due numeri dal sacchetto:
• Marco ha estratto 25 e 36.
• Lisa ha estra tto 48 e 82.
• Sofia ha estratto 35 e 40.
• Marta ha estratto 50 e 70.
• Matteo ha estratto 21 e 9.
• Mario ha estratto 22 e 18.
Alla fine del gioco l’insegnante scrive alla lavagna queste frasi.
• Marco ha estratto due numeri pari.
V F
• Lisa ha estratto due numeri mag giori di 54. V F
• Sofia ha estratto due numeri della tabellina del 5. V F
• Marta ha estratto due numeri con 0 unità. V F
• Matteo ha estratto due numeri dispari.
• Mario ha estratto due numeri dis pari.
V F
V F
L’INVALSI 45
VERSO
LA MOLTIPLICAZIONE
Completa la mappa, inserendo le parole che seguono:
fattori • prodotto • stesso • somma • prodotti • per
Moltiplicare vuol dire…
ripetere più volte la stessa quantità.
Il segno
della moltiplicazione è ( )
COMMUTATIVA
Le proprietà
In colonna
Moltiplicazioni con 0 e con 1
I termini sono:
5 3 = 15
moltiplicando fattori
Se cambio l’ordine dei , il risultato non cambia.
ASSOCIATIVA
Se sostituisco due fattori con il loro , il risultato non cambia.
DISTRIBUTIVA
Il risultato non cambia se scompongo un fattore in una , poi moltiplico ogni addendo per l’altro fattore e sommo i loro prodotti.
(10
(10
Moltiplico le unità del moltiplicatore per il moltiplicando. Aggiungo uno 0 segnaposto nella colonna delle unità, quindi moltiplico le decine del moltiplicatore per il moltiplicando. Infine sommo i parziali.
• Se moltiplico un numero qualunque per 0, il prodotto è 0 .
• Se moltiplico un numero qualunque per 1 , il prodotto è il numero .
RIPASSO IN UN LAMPO
7
60 20 3
60 12 3
36
7 5 = 35 5
= 35 5 4 3 =
=
=
3
+ 2)
=
30
6
3) + (2 3) =
+
= 36
h da u 2 1 1 4
8 4 2 1 0
2 9 4
=
=
moltiplicatore prodotto MAPPA 46 I MIEI SCHEMI PAGINA 148
1 Controlla le moltiplicazioni e indica con una X se sono vere ( V ) o false (F ).
4 4 = 16 V F
6 8 = 58 V F
2 6 = 14 V F
2 Completa le moltiplicazioni per
100, 1 000.
4
3 Esegui le moltiplicazioni sul quaderno applicando la proprietà indicata.
7 4 = 28 V
9 6
3 5 = 18 V F
F
= 54 V F
0 8
8
5 7
=
V F
= 35 V F
3 9
8 9
= 36 V F
= 72 V F
8 5
V
7 6
6 4
V
8 8
F
= 30
F
= 42 V F 9 9 = 18 V F
= 24
F
= 54 V
3 9 = 4 8 = 7 2 = 9 6 = 5 8 = 5 9 2 = 6 6 5 = 8 3 10 = 27 2 5 = 4 15 5 = 32 6 = 28 4 = 71 5 = 19 3 = 48 7 =
39 5 = 85 7 = 317 5 = 139 4 = 47 4 = 59 3 = 508 2 = 341 6 = 72 6 = 96 8 = 264 9 = 728 8 = 34 25 = 67 34 = 135 36 = 409 28 = 46 18 = 39 16 = 268 62 = 173 89 = 76 26 = 40 29 = 514 47 = 385 56 =
Esegui le moltiplicazioni in colonna sul quaderno.
10,
45 = 450 7 1 000 = 10 = 600 286 10 = 100 = 6 700 38 = 38 000 100 = 900 24 = 240 72 100 = 38 ......................... = 380 ............................ 1 000 = 3 000 ............................. 100 = 2 000 74 100 = 35 = 3 500 10 = 5 600 a b a commutativa c distributiva b associativa moltiplicazioni con una cifra al moltiplicatore c d moltiplicazioni con due cifre al moltiplicatore
47
VERIFICA
TUTTO OK?
PAGINE STELLA
LA DIVISIONE
Per un gioco in palestra i 24 alunni della classe 3ª A si sono organizzati in squadre da 6 bambini. Quante squadre hanno formato?
Per risolvere questo problema bisogna eseguire una:
DIVISIONE
È l’operazione che permette di dividere o distribuire una quantità in parti uguali o raggruppare una quantità in parti uguali.
PROVO IO
Il segno è : e si legge diviso.
I termini sono:
24 : 6 = 4
dividendo divisore quoto (resto 0)
Quando c’è il resto, il risultato si chiama quoziente.
a b
Leggi, rifletti, completa e risolvi. Il nonno ha comperato 12 bustine di figurine e le distribuisce in parti uguali ai suoi 3 nipotini. Quante bustine di figurine riceve ciascun bambino?
• La domanda ti chiede: di distribuire in parti uguali. di raggruppare in parti uguali.
• Scrivi l’operazione e risolvi.
Irene ha 15 pupazzetti di plastica e li vuole sistemare in alcune scatolette. Ciascuna scatoletta può contenere 5 pupazzetti. Quante scatolette le servono?
• La domanda ti chiede: di distribuire in parti uguali. di raggruppare in parti uguali.
• Scrivi l’operazione e risolvi.
• Scrivi la risposta.
• Scrivi la risposta.
I MIEI ESERCIZI PAGINA 170 NUMERI 48
LA TABELLA DELLA DIVISIONE
Completa la tabella della divisione: scrivi solo i risultati delle divisioni che non hanno resto. Poi rispondi alle domande e scopri alcune regole. Fai attenzione: la X indica che in quei casi la divisione è impossibile.
divisore dividendo
:
0 0 0 0 0 0 0 0 0 0
1 X X X X X X X X X X
2 X X X X X X X X X
3 X X X X X X X X
4 X X X X X X X
5 X X X X X X
6 X X X X X
7 X X X X
8 X X X
9 X X 9 X
• Segui l’esempio e osserva la colonna arancione.
5 : 0 = è impossibile perché non esiste un numero che moltiplicato per 0 dia come risultato 5.
Dividere un numero per è ................................................................................
! ?
10 X
• Osserva i numeri della riga verde. Che cosa noti?
Se si divide 0 per qualsiasi numero, il risultato è sempre 0.
• Osserva i numeri della colonna gialla. Che cosa noti?
1 è l’elemento neutro della divisione: ciascun numero diviso per 1 dà come risultato il numero stesso.
5
divisioni.
4 : 0 = 8
• Osserva i numeri delle caselle colorate di azzurro. Che cosa noti? ....................................................
MOLTIPLICAZIONE E DIVISIONE 49
: 5 = 47 : 47 =
0 : 3 = 9 : 1 =
: 1
........................... 68 : 0 = ..............................
= 26 : 1 =
Se si divide un numero per se stesso, il risultato è sempre 1. 0 1 2 3 4 5 6 7 8 9 10
0 X
PROVO IO
LA PROPRIETÀ INVARIANTIVA
Osserva e rispondi.
• Che cosa è successo?
• Il risultato è cambiato? Sì NO
Abbiamo applicato la proprietà invariantiva della divisione.
PROVO IO
• Che cosa è successo?
• Il risultato è cambiato? Sì NO
Se dividi o moltiplichi per lo stesso numero (diverso da 0) il dividendo e il divisore, il risultato della divisione non cambia.
1 Applica la proprietà invariantiva ed esegui le divisioni.
2 Applica la proprietà invariantiva ed esegui le divisioni sul quaderno.
24 : 12 = 2 8 : 4 = 2 : 3 : 3 15 : 5 = 3 30 : 10 = 3 2 2
10 : 2 = : = 3 3 32 : 8 = : = 16 4 : 2 : 2 45 : 15 = : = : 5 : 5 20 : 5 = : = 2 2
18 : 6 = 72 : 18 = 96 : 16 = 240 : 20 = 24 : 8 = 48 : 12 = 105 : 15 = 195 : 5 = 81 : 9 = 42 : 14 = 108 : 18 = 600 : 30 = 96 : 16 = : = 36 : 18 = : = 105 : 5 = : = 140 : 70 = : = a b NUMERI 50
MOLTIPLICAZIONE E DIVISIONE: OPERAZIONI INVERSE
Il trenino del parco è composto da 6 vagoni.
Su ciascun vagone c’è posto per 9 bambini.
Quanti bambini possono salire sul trenino?
Osserva, leggi e completa. : =
Sul trenino del parco possono salire 54 bambini.
Su ciascun vagone c’è posto per 9 bambini.
................... ................... = ...................
• Per verificare se la divisione è corretta, fai la prova con l’operazione inversa, cioè con la moltiplicazione.
Moltiplica il quoto per il divisore e ottieni il dividendo.
• Se la divisione ha resto, moltiplica il quoziente per il divisore, poi aggiungi il resto.
9 54 divisione prova
:
Segui le frecce e completa le operazioni.
MOLTIPLICAZIONE E DIVISIONE 51
4 7 ......... : 3 27 5 6 7
32
4 = 8 resto 0 45
7 = 6 resto 3 8 4
32 6 7 = 42 + 3
Moltiplicazione e divisione sono operazioni inverse. 6 : 6 45
:
=
=
PROVO IO
Da quanti vagoni è composto il trenino?
DIVISIONI IN COLONNA
Un fiorista ha ricevuto 69 rose che suddivide in parti uguali in 3 vasi.
Quanti fiori mette in ciascun vaso?
Per risolvere questo problema bisogna fare una
Per rendere più semplici i calcoli, puoi eseguire una divisione in colonna . Segui le istruzioni.
Divisione senza resto 68 : 2 =
• Disegna lo schema della divisione. Con un prendi la prima cifra del dividendo, partendo da quella che vale di più: in questo caso le da .
• Aiutandoti con le tabelline, conta quante volte il divisore è contenuto nel dividendo: il 2 è contenuto 3 volte nel 6.
• Scrivi 3 sotto al divisore e 6 sotto al dividendo, nella colonna delle da . Fai la sottrazione in colonna: 6 – 6 = 0.
PROVO IO
• A fianco al risultato della sottrazione, abbassa la cifra successiva del dividendo: le u. Stavolta, il 2 è contenuto 4 volte nell’8.
• Scrivi 4 sotto al divisore e 8 sotto al dividendo, nella colonna delle u. Fai la sottrazione in colonna: 8 – 8 = 0. Il risultato della divisione è 34 con resto 0.
Esegui le divisioni in colonna sul quaderno e verifica i risultati con la prova.
a b
d
6 8 2 – 6 3 0 6 8 2 – 6 3 4 0 8 – 8 0
84 : 4 = 248 : 2 = 3 690 : 3 = 4 286 : 2 = 93 : 3 = 336 : 3 = 5 050 : 5 = 6 093 : 3 = 55 : 5 = 488 : 4 = 2 840 : 2 = 6 480 : 2 = 28 : 2 = 666 : 6 = 4 840 : 4 = 2 648 : 2 = 36 : 3 = 826 : 2 = 8 628 : 2 = 8 484 : 4 = 86 : 2 = 696 : 3 = 5 500 : 5 = 7 070 : 7 = : =
c
NUMERI 52
DIVISIONI IN COLONNA CON IL RESTO
Segui le istruzioni per eseguire le divisioni in colonna con il resto.
Divisione con il resto 837 : 6 =
• Disegna lo schema della divisione. Con un consideri la prima cifra del dividendo, le h.
• Il 6 è contenuto 1 volta nell’8. Facendo la sottrazione 8 – 6, calcoli il resto che è 2.
• A fianco al risultato della sottrazione, abbassa la cifra successiva del dividendo: le da. Ottieni così 23.
• Il 6 è contenuto 3 volte nel 23. Facendo la sottrazione 23 – 18, calcoli il resto che è 5.
• A fianco al risultato della sottrazione, abbassa ora le u. Ottieni così il 57.
• Il 6 è contenuto 9 volte nel 57. Facendo la sottrazione 57 – 54, calcoli il resto che è 3. Leggi ora il risultato: 139 con resto 3.
8 3 7 6 – 6 1 3 9 2 3 – 1 8 5 7 – 5 4 3 8 3 7 6 – 6 1 3 2 3 – 1 8 5 8 3 7 6 – 6 1 2
45 : 2 = 87 : 5 = 79 : 6 = 94 : 7 = 603 : 4 = 824 : 6 = 469 : 3 = 825 : 6 = 971 : 2 = 590 : 3 = 750 : 4 = 358 : 2 = 4 380 : 3 = 7 348 : 5 = 9 527 : 7 = 5 094 : 3 = 2 947 : 2 = 6 318 : 4 = 9 645 : 8 = 9 072 : 6 = divisioni in colonna 68 : 4 = 53 : 3 = 58 : 3 = 69 : 4 = a b c MOLTIPLICAZIONE E DIVISIONE 53
PROVO IO Esegui le sul quaderno e verifica i risultati con la prova.
ANCORA DIVISIONI
Quando la prima cifra del dividendo è minore del divisore, bisogna considerare due cifre del dividendo.
347 : 4 = .............
Segui le istruzioni.
• La prima cifra del dividendo, 3, è minore del divisore, 4. Allora devi usare il per prendere due cifre, cioè il 34.
• Ora procedi come sai: il 34 è contenuto 8 volte nel 4, con resto 2.
• A fianco al risultato della sottrazione, abbassa la cifra successiva del dividendo: le u. Ottieni così 27.
• Il 4 è contenuto 6 volte nel 27 e il resto finale è 3.
Per essere sicuri che la divisione sia esatta si può fare la prova:
86 4 = 344 + 3 = 347
PROVO IO
Esegui le divisioni in colonna sul quaderno e verifica i risultati con la prova.
! ?
132
4 = 437 : 7 = 1 839 : 4 = 3 076 : 6 = 329 : 7 = 519 : 9 = 2 073 : 6 = 1 890 : 7 = 450 : 8 = 187 : 2 = 4 618 : 5 = 6 503 : 8 = 109 : 3 = 273 : 5 = 5 972 : 9 = 1 920 : 6 = 781 : 9 = 620 : 8 = 7 364 : 8 = 2 508 : 3 = 293 : 5 = 304 : 4 = 1 637 : 9 = 4 971 : 5 = 491 : 6 = 735 : 9 = 3 806 : 7 = 5 372 : 9 = a b c d 3 4 7 4 – 3 2 8 2 3 4 7 4 – 3 2 8 6 2 7 – 2 4 3 NUMERI 54
:
DIVIDERE PER 10, 100, 1 000
Dividere un numero per 10 significa diminuire di 10 volte il suo valore, per 100 diminuire di 100 volte il suo valore, per 1 000 diminuire di 1 000 volte il suo valore.
k h da u
2 6 0
2 6 : 10
k h da u
1 4 0 0
1 4 : 100
k h da u
260 : 10 = ..............
• Se dividi per 10, le decine diventano , le centinaia diventano .
1 400 : 100 =
• Se dividi per 100, le centinaia diventano ........................................, le migliaia diventano .
3 000 : 1 000 =
3 0 0 0 3 : 1 000 PROVO
• Se dividi per 1 000, le migliaia diventano .........................................
Quando dividi un numero per 10, per 100, per 1 000, togli a destra uno, due, tre zeri.
IO Esegui le divisioni. 40 : 10 = 9 000 : 1 000 = 350 : 10 = ........................................ 600 : 100 = .................................... 600 : 10 = 7 000 : 100 = 3 480 : 10 = 6 200 : 100 = 4 000 : 1 000 = 900 : 100 = 8 000 : 100 = 12 000 : 1 000 = 1 700 : 10 = 2 300 : 100 = MOLTIPLICAZIONE E DIVISIONE 55
4
Completa le divisioni. Utilizza le tabelline. 27 : ............ = 9 42 : ............ = 6 81 : ............ = 9 54 : ............ = 6 : 8 = 5 : 7 = 9 : 4 = 7 : 3 = 8 35 : = 7 48 : = 8 72 : = 9 36 : = 6 : 2 = 8 : 6 = 10 : 5 = 4 : 9 = 3
Esegui le divisioni sul quaderno e verifica i risultati con la prova. 480 : 7 = 674 : 8 = 1 328 : 7 = 5 036 : 9 = 938 : 4 = 805 : 5 = 2 075 : 6 = 3 219 : 3 = 526 : 9 = 718 : 2 = 4 938 : 8 = 5 007 : 4 =
2
5
Esegui le divisioni. 89 : 3 = h da u 8 9 3 72 : 6 = h da u 7 2 6 124 : 7 = h da u 1 2 4 7
Calcola velocemente e completa le tabelle. 5 000 5 50 2 000 20 200 7 000 7 700 10 100 1 000 1 000 8 000 13 000 : : I MIEI ESERCIZI PAGINA 171, 172 NUMERI 56
3
1 Quale operazione dà lo stesso risultato di quella nel riquadro?
324 : 6 =
A. 304 + 10 =
B. 9 6 =
C. 162 : 2 =
D. 324 – 300 =
2 Quale di queste divisioni dà un risultato maggiore di 50 e minore di 100?
A. 74 : 2 =
B. 180 : 3 =
C. 420 : 4 =
D. 324 : 3 =
3 Indica con una X se le uguaglianze sono vere ( V ) o false (F ).
V F
4 8 = 8 340 – 6
150 : 5 = 10 3
39 + 9 = 50 – 2
6 7 = 7 6
72 : 8 = 8 3
80 – 11 = 9 7
99 + 1 = 100 : 10
90 : 2 = 50 – 5
4 Qual è il segno mancante?
186 39 = 147
A. + B. –
C.
D. :
5 Quale operazione dà come risultato il numero formato da 1 h e 8 u?
A. 36 3 =
B. 58 + 58 =
C. 128 – 18 =
D. 208 : 2 =
6 Quale numero si nasconde sotto la macchia?
14 : 7 = 20
A. 7
B. 1
C. 4
D. 0
7 Una di queste operazioni è sbagliata. Quale?
A. 284 : 4 = 71
B. 5 4 8 = 150
C. 6 3 2 = 36
D. 175 : 7 = 25
8 Quale di queste operazioni dà il risultato minore?
A. 345 : 5 =
B. 6 9 =
C. 1 128 – 39 =
D. 48 + 42 =
9 Il risultato di questa moltiplicazione:
34 15
A. sarà un numero di due cifre.
B. sarà minore di 500.
C. sarà compreso fra 500 e 520.
D. sarà uguale a 500.
VERSO L’INVALSI 57
LA DIVISIONE
Completa la mappa, inserendo le parole che seguono:
moltiplico • tabelline • diviso • cappellino • numero stesso
Dividere vuol dire…
distribuire oppure raggruppare una quantità in parti uguali. Il segno della divisione è : ( )
La proprietà INVARIANTIVA
In colonna
Divisioni con 0 e con 1
Operazioni inverse
I termini sono:
24 : 6 = 4 dividendo divisore quoto (resto 0)
quoziente (resto diverso da 0)
Se divido o moltiplico per lo stesso numero il dividendo e il divisore, il risultato non cambia.
Abbasso col ........................... ogni cifra del dividendo, poi, aiutandomi con le , conto quante volte il divisore è contenuto nel dividendo.
Facendo la sottrazione, calcolo il resto.
Se la prima cifra del dividendo è minore del divisore, considero anche la cifra successiva.
15 : 5 = 3
30 : 10 = 3 2 2
6 8 2 – 6 3 4 0 8 – 8 0
• Se divido un numero qualunque per 1 (5 : 1) il risultato è il
• Se divido 0 per un qualunque numero (0 : 5), il risultato è 0.
• Dividere un qualunque numero per 0 (5 : 0), invece, è impossibile.
La moltiplicazione e la divisione sono operazioni inverse. Con la moltiplicazione posso fare la prova della divisione: otterrò il dividendo se il quoto per il divisore, oppure se moltiplico il quoziente per il divisore e poi sommo il resto.
RIPASSO IN UN LAMPO
MAPPA 58 I MIEI SCHEMI PAGINA 149
1 Completa le divisioni con i numeri mancanti. 32 : 4 = ................. ................. : 2 = 9 54 : ................. = 6 24 : = 4 48 : = 6 70 : 10 = : 3 = 7 : 7 = 8 : 5 = 9 25 : = 5 81 : 9 = : 7 = 4 : 8 = 4 49 : = 7 72 : = 8 : 9 = 6 : 8 = 3 36 : = 6 2 Esegui solo le divisioni possibili. Poi cerchia quelle impossibili. 15 : 3 = ................... 27 : 9 = .................. 18 : 0 = .................. 26 : 26 = 35 : 1 = 40 : 8 = 47 : 0 = ................... 49 : 7 = .................. 56 : 1 = .................. 50 : 10 = 38 : 38 = 0 : 6 = 48 : 8 = 19 : 0 = 17 : 17 = 0 : 15 = 72 : 9 = 28 : 0 = 3 Completa le divisioni per 10, 100, 1 000. 180 : = 18 2 400 : 100 = : 100 = 6 300 : 100 = : 100 = 52 23 000 : = 23 : 10 = 140 800 : = 80 5 400 : = 540 3 500 : = 350 : 1 000 = 29 : 10 = 8 7 000 : 1 000 = 840 : = 84 : 100 = 390 : = 675 : 100 = 30 6 700 : = 670 a b c d 4 Esegui le divisioni in colonna sul quaderno. 69 : 3 = 438 : 2 = 184 : 4 = 390 : 6 = 45 : 2 = 705 : 3 = 378 : 5 = 281 : 3 = 73 : 6 = 692 : 4 = 409 : 7 = 618 : 7 = 94 : 8 = 815 : 6 = 714 : 9 = 284 : 9 = 79 : 5 = 838 : 9 = 576 : 8 = 492 : 4 = VERIFICA 59
TUTTO OK?
PAGINE STELLA
PROBLEMI
I PROBLEMI
Un problema è una situazione che richiede di intervenire per trovare una soluzione.
Giulia va in edicola per comprare il suo giornalino settimanale, che costa 4 euro. Ma questa volta c’è qualcosa in più che attira la sua attenzione...
Mamma, il giornalino costa € 4.
Vorrei anche il gioco delle perline da € 9.
Va bene, ma sai quanto spendiamo?
• Per risolvere questo problema, Giulia deve eseguire un’addizione:
€ 4 + € 9 = € 13
Quando il problema presenta dei numeri e per risolvere la situazione
è necessario usare le operazioni, si parla di problema matematico.
I problemi matematici sono composti da 3 elementi fondamentali:
• il testo, che presenta la situazione
• i dati numerici, che indicano le quantità con cui bisogna operare
• la domanda , a cui bisogna rispondere
Giulia è in edicola con la mamma. Vuole comperare un giornalino che costa € 4 e le perline da € 9.
€ 4 = costo del giornalino
€ 9 = costo delle perline
Quanto spende in tutto Giulia?
60
PROVO IO
1 Leggi il testo del problema con attenzione.
In un vivaio la signora Lucia ha comperato 24 piantine di ciclamini. Ha già sistemato
nelle aiuole del suo giardino 18 piantine.
Quante piantine deve ancora sistemare?
Cerchia di verde i dati numerici.
Sottolinea di arancione la domanda.
Leggi le affermazioni e indica con una X se sono vere ( V ) o false (F ).
• La signora Lucia ha comperato 18 piantine di ciclamini. V F
• La signora Lucia ha sistemato tutte le piantine acquistate. V F
• La signora Lucia deve ancora sistemare alcune piantine. V F
• Il testo del problema dice quante piantine sono state comperate. V F
• La domanda ti chiede quante piantine devono essere ancora piantate. V F
2 Colora nello stesso modo il dato e il suo significato.
24
numero delle piantine acquistate
numero delle piantine già sistemate
18
numero delle piantine acquistate
3 Colora l’operazione giusta per risolvere il problema.
24 + 18 24 – 18 24 18
numero delle piantine già sistemate
24 : 18
61 PROBLEMI
COME RISOLVERE I PROBLEMI?
Per risolvere un problema matematico è necessario eseguire i passaggi con ordine.
Leggi e completa.
Durante una passeggiata nel bosco
Marco raccoglie 25 castagne e 18 noci.
Quanti frutti raccoglie in tutto?
1 Leggere il testo e capire le informazioni che fornisce.
• Di chi si parla? ....................................................................................................................................................................
• Che cosa fa Marco?
2 Individuare e capire la domanda .
• La domanda è:
3 Cercare nel testo i dati utili e analizzarli.
• 25 =
• 18 = .............................................................................................................................................................................................
4 Scoprire l’operazione necessaria per poter rispondere.
• Per rispondere alla domanda si deve eseguire l’operazione:
5 Eseguire i calcoli
=
6 Rispondere alla domanda.
• La risposta è:
PROBLEMI 62
.........................................................................................................................................................................................................
I QUANTIFICATORI
Nel testo dei problemi ci sono spesso delle parole particolari che danno informazioni importanti. Sono i quantificatori: ogni, ognuno, ciascuno, tutti, tutto…
A queste parole bisogna attribuire il corretto significato per capire bene il testo e poter risolvere il problema.
PROVO IO
1 Leggi i problemi, indica con una X se le affermazioni sono vere ( V ) o false (F ), poi risolvi.
a
Matteo compera dal cartolaio 4 quaderni. Ogni quaderno costa € 2,00.
Quanto spende in tutto?
• Un quaderno costa € 2,00. V F
• 4 quaderni costano € 2,00. V F
• Matteo spende € 2,00. V F
• Il costo di ciascun quaderno è di € 2,00. V F
• Per sapere quanto spende in tutto Matteo bisogna fare una =
b Nel carrello della spesa di Livio ci sono 3 vaschette di carote. Ciascuna vaschetta contiene 12 carote. Quante carote ha comprato in tutto Livio?
• Ogni vaschetta contiene 12 carote. V F
• Il contenuto di una vaschetta è di 12 carote. V F
• Le 3 vaschette contengono 12 carote in tutto. V F
• Per sapere quante carote ci sono in tutto bisogna fare una
c
La signora Lucia compera 3 bambole per le sue nipotine e spende in tutto € 75,00.
Quanto costa ogni bambola?
• Una bambola costa € 75,00. V F
• Le 3 bambole costano € 75,00. V F
• Tutte le bambole costano € 75,00. V F
• Il prezzo di ciascuna bambola è di € 75,00. V F
• Per sapere quanto costa una bambola bisogna fare una
PROBLEMI 63
..........................................................................................................
......................... ......................... = .........................
.........................
......................... = .........................
I DATI
I dati sono le informazioni, contenute nel testo, necessarie a risolvere il problema. Se espressi in cifre, sono dati numerici.
Leggi il testo del problema e rispondi.
Sul tavolo della maestra ci sono 12 quaderni rossi e 13 quaderni blu.
Quanti sono in tutto i quaderni sul tavolo?
• Che cosa ti chiede la domanda?
Il numero totale dei ................................................................................
Nel testo del problema, quali sono le informazioni utili per poter rispondere alla domanda?
• Rileggi con attenzione il testo, prova a immaginare la situazione concretamente: concentrati e visualizza l’aula, il tavolo, i quaderni rossi, i quaderni blu…
• Poi completa i dati.
PROVO IO
DATI: ........................................................... quaderni blu
12
Operazione (che ti permette di rispondere alla domanda):
Risposta:
Risolvi i problemi sul quaderno con i passaggi indicati in questa pagina.
La maestra Paola porta in classe 72 pastelli. A ciascun alunno dà 3 pastelli. Quanti sono gli alunni della maestra Paola?
a b
Anna compera in libreria un libro di 65 pagine. Ne legge subito 24. Quante pagine deve ancora leggere per finire il libro?
PROBLEMI 64
I DATI INUTILI
Nel testo di alcuni problemi possono essere presenti dei cioè dati che non servono per rispondere alla domanda.
Leggi il testo del problema e segui le indicazioni.
Nel parco pubblico ci sono 45 bambini e 27 adulti.
18 bambini giocano a calcio.
Quanti bambini non giocano a calcio?
• Sottolinea la domanda
• Analizza i dati:
45 .....................................................................................................
27
18
dati inutili,
• La domanda ti chiede quanti bambini non giocano a calcio.
Quale dato è inutile? ..................................................................................................................................................
• Scrivi ed esegui l’operazione
• Rispondi.
PROVO IO
Sottolinea di blu il dato inutile e risolvi i problemi sul quaderno.
a b
Un gruppo di 52 studenti parte con il pullman per una gita d’istruzione.
Il viaggio fino alla loro meta è di 145 km.
Hanno percorso finora 89 km.
Quanti chilometri mancano per arrivare a destinazione?
Federica ha acquistato in cartoleria un astuccio da € 18,00, un quadernone da € 2,00 e una scatola di colori da € 3,00.
In tasca aveva € 35,00.
Quanto spende Federica in cartoleria?
PROBLEMI 65
I DATI NASCOSTI
Nel testo di alcuni problemi ci possono essere dei dati nascosti, cioè dei dati espressi non con numeri ma con parole, oppure dati ricavabili dal contesto, come il numero di ruote di una bici o quello delle zampe di un animale.
Leggi il testo del problema e segui le indicazioni.
Beatrice ha un sacchetto con 64 perline colorate. Ne ha già utilizzate la metà per preparare dei braccialetti. Quante perline le rimangono per preparare una collana?
• Sottolinea la domanda .
• Analizza i dati: 64
• Qual è la parola che fornisce un’indicazione numerica? .....................................
• Che cosa significa?
• Scrivi ed esegui l’operazione.
• Rispondi.
! ?
Queste parole sostituiscono un dato numerico: rifletti e completa.
• una settimana = giorni
• un mese = giorni
• un anno = giorni
• un anno = .............................................................. mesi
• un’ora = minuti
• una decina vale
• un centinaio vale
• una dozzina vale
PROVO IO
• il doppio significa
• il triplo significa
• il quadruplo significa
• la metà significa ............................................................
• la terza parte significa
• un paio significa
• una coppia significa
Cerchia di arancione il dato nascosto, traducilo in un valore numerico e risolvi i problemi sul quaderno.
a
Nella famiglia di Roberta si consumano in media 6 panini al giorno. Quanti panini si consumano in un mese?
PROBLEMI 66
Per preparare i dolci di Carnevale il signor Carlo compera 3 dozzine di uova. Quante uova compera in tutto? b
I DATI MANCANTI
In alcuni problemi può capitare che ci siano dei dati mancanti, cioè dei dati che non sono presenti nel testo, ma senza i quali non si può risolvere il problema.
Leggi il testo del problema e segui le indicazioni.
Sul pullman in partenza per Torino sono già salite 39 persone.
Quante persone possono ancora salire?
• Sottolinea la domanda .
• Analizza i dati: 39
• È possibile risolvere questo problema con solo questo dato? Sì NO
• Quale altra informazione è necessaria per la soluzione?
• Inventa e scrivi tu il dato mancante
• Scrivi ed esegui l’operazione.
• Rispondi.
PROVO IO
Scopri il dato mancante, aggiungilo tu e risolvi i problemi sul quaderno.
a b c d
I nonni di Tommaso si chiamano Mariuccia e Antonio. Il signor Antonio ha 64 anni.
Qual è la differenza di età fra Mariuccia e Antonio?
Dato mancante: ................................................................................................................................................................
L a signora Daniela ha acquistato un paio di pantaloni da € 45,00, una maglietta da € 39,00 e un golfino da € 52,00.
Quanti soldi le sono rimasti dopo gli acquisti?
Dato mancante:
La nonna ha regalato ai suoi nipotini un sacchetto con 24 caramelle che i bambini devono dividersi in parti uguali. Quante caramelle avrà ciascun bambino?
Dato mancante: ................................................................................................................................................................
G abriella ha deciso di trascorrere alcuni giorni al mare. Per l’albergo spende € 58,00 al giorno. Qual è la spesa per l’albergo per tutto il soggiorno?
Dato mancante: PROBLEMI 67
LA DOMANDA GIUSTA
Per domanda giusta si intende quella a cui è possibile rispondere con i dati a disposizione.
1 Leggi con attenzione i problemi e indica con una X la domanda giusta. Poi spiega a voce il perché delle tue scelte.
Nella fattoria di Marco ci sono 45 animali. Le galline sono 22.
Quanti animali ci sono nella fattoria di Marco?
Quante uova raccoglie Marco ogni giorno?
Quanti sono gli altri animali?
b
c d
Il nonno Luca ha 67 anni. La nonna Elisabetta ha 4 anni meno del nonno.
Quanti anni di differenza ci sono fra il nonno e la nonna?
Quanti anni ha la nonna Elisabetta?
Quanti anni ha il nonno Luca?
La segretaria della scuola ha ricevuto 24 risme di carta per le fotocopie. Ciascuna risma contiene 300 fogli.
Quante fotocopie si potranno fare in tutto?
Quanti fogli riceverà ciascun insegnante?
Quanti fogli contiene ciascuna risma?
Il Comune ha comperato 208 piantine di viole per le aiuole del parco giochi. Le viole saranno distribuite in parti uguali fra le 8 aiuole.
Quante viole ha comperato il Comune?
Quanti giorni impiegherà il giardiniere a sistemarle tutte?
Quante viole saranno sistemate in ciascuna aiuola?
PROVO IO
La domanda ti aiuta a comprendere quale operazione devi eseguire per trovare la soluzione del problema.
Dopo aver individuato la domanda giusta , risolvi i problemi di questa pagina sul quaderno.
PROBLEMI 68
a
PROBLEMI E DIAGRAMMI
Per visualizzare le relazioni fra i dati del problema può essere utile schematizzarli con un diagramma , che rappresenta il percorso per arrivare alla soluzione del problema.
1 Leggi il testo del problema e segui le indicazioni.
Il libro che sta leggendo Laura è formato da 125 pagine. Laura ha già letto 85 pagine.
Quante pagine deve ancora leggere?
• Sottolinea la domanda
• Analizza i dati:
125 85
• Scopri l’operazione.
Rappresenta con il diagramma il percorso che devi seguire per giungere alla soluzione.
• Esegui l’operazione in colonna.
• Rispondi.
Per visualizzare le relazioni fra i dati del problema può essere utile
in colonna
125 85
2 Partendo dall’osservazione di un diagramma è possibile costruire il testo di un problema e risolverlo.
Un giardiniere deve abbellire le 3 aiuole della piazza del paese. Decide di piantare in ciascuna aiuola
. Quante
• Analizza i dati: 24 3
• Esegui l’operazione in colonna.
• Rispondi.
PROBLEMI 69
24 3
.............................................................................................................................
? in colonna
–
...............................................................................................................
DUE DOMANDE, DUE OPERAZIONI
Leggi il testo del problema e fai attenzione alle domande.
Il signor Franco compera per il suo bar
8 confezioni di gelato, ciascuna con 12 gelati. Quanti gelati compera Franco in tutto?
Dopo qualche settimana si accorge che gli sono rimasti solo 24 gelati. Quanti gelati ha già venduto?
Questo problema è come una storia in due puntate: non puoi passare alla seconda puntata se non hai risolto la prima. Segui le indicazioni.
• Leggi il testo.
• Sottolinea le due domande con due colori diversi.
• Concentrati sulla prima domanda e risolvi.
Calcola quanti gelati ha comperato il signor Franco in tutto.
• Rispondi. Il signor Franco ha comperato in tutto gelati.
• Dopo aver risposto alla prima domanda, concentrati sulla seconda domanda del problema e risolvi.
Calcola quanti gelati ha venduto il signor Franco.
• Rispondi. Il signor Franco ha venduto gelati.
• Puoi rappresentare la soluzione delle due domande del problema con un diagramma
PROBLEMI
12 8 24 1 2 × 8 = 1 2 × 8 = 9 6 – 2 4 = 9 6 –2 4 =
PROVO IO
Leggi il testo del problema, completa il diagramma e risolvi sul quaderno.
Emma acquista 6 quaderni che costano € 2,00 ciascuno.
Quanto spende per tutti i quaderni?
Compera anche una penna stilo che costa € 8,00.
Quanto spende in tutto Emma?
Con le STEM posso… CALCOLARE
Risolvi il problema con il diagramma e rifletti sul percorso che devi seguire.
In pizzeria 4 amici spendono € 27,00 per le pizze, € 13,00 per le bibite e € 16,00 per i dolci.
Quanto spendono in tutto?
Da buoni amici dividono la spesa in parti uguali.
Quanto spendono a testa?
1. Scegli la prima fase del percorso:
• calcolare la spesa totale
addizione
sottrazione
• calcolare quanto spende
moltiplicazione ciascuno dei 4 amici
divisione
2. Scegli la seconda fase del percorso:
• calcolare quanto spende
moltiplicazione ciascuno dei 4 amici
divisione
addizione
• calcolare la spesa totale
sottrazione
PROBLEMI 71
LA DOMANDA NASCOSTA
Nel testo di alcuni problemi c’è una domanda nascosta , cioè non espressa chiaramente, ma alla quale è necessario rispondere per risolvere il problema.
Leggi il testo del problema ed esegui tutti i passaggi utili per giungere alla soluzione.
• Analizza i dati. 234
450
139
Per la festa del paese sono stati preparati 234 panini al formaggio e 450 panini al pomodoro. Alla fine della giornata sono rimasti 139 panini. Quanti panini sono stati consumati?
• Per rispondere alla domanda del problema, serve un dato che non è espresso nel testo, ma che è possibile trovare con i dati a disposizione.
• L’informazione che manca è sapere il numero totale dei panini preparati. La domanda nascosta , quindi, è: “ Quanti panini sono stati preparati in tutto? ”.
Per rispondere a questa domanda devi eseguire una:
• Ora che hai questo dato, per rispondere alla domanda del problema devi proseguire con una:
Per rispondere a questa domanda devi eseguire una:
• Rispondi.
PROBLEMI 72
...............................................................................
=
=
.................. .................. ..................
I MIEI ESERCIZI PAGINA 174
PROVO IO
1 Leggi il testo dei problemi, individua la domanda nascosta e risolvi sul quaderno.
I libri della biblioteca sono sistemati su 8 scaffali.
Su ciascuno scaffale ce ne sono 25. Domani arriveranno altri 43 libri.
Quanti saranno tutti i libri della biblioteca?
b c d
Marta compera 6 pasticcini da € 2,00 ognuno e una torta da € 14,00.Quanto spende Marta in pasticceria?
Samuel sta leggendo un libro di 162 pagine. La prima settimana ha letto 38 pagine, la seconda ne ha lette 25. Quante pagine deve ancora leggere?
La maestra porta in classe 3 risme di carta da 350 fogli ciascuna.
Per realizzare il primo numero del giornalino, vengono usati 298 fogli. Quanti fogli rimangono?
Un contadino raccoglie 8 dozzine di mele. Al mercato vende 67 mele. Quante mele gli restano?
2 Osserva i diagrammi. Sul quaderno, inventa e scrivi il testo dei problemi con la domanda nascosta , poi risolvi.
PROBLEMI 73 6 270 18 : –8 16 86 +
a
e
a b
PROBLEMI A PIÙ SOLUZIONI
Alcune situazioni problematiche non hanno una sola soluzione: possono presentare soluzioni diverse
Leggi il testo del problema e osserva le immagini.
Giorgio ha una banconota da € 20,00.
Va in cartoleria ed ecco che cosa vede in vetrina. Che cosa potrebbe acquistare Giorgio con i suoi € 20,00?
Queste sono solo alcune delle possibili combinazioni di acquisti. Completa.
Calcola quanto riceverebbe Giorgio di resto.
1° acquisto resto:
2° acquisto resto:
3° acquisto resto:
Rifletti e rispondi.
Perché?
Quanto?
• Giorgio potrebbe acquistare tutto ciò che c’è in vetrina? Sì NO
• Riceverebbe il resto o gli mancherebbe del denaro?
PROBLEMI 74
€ 4,00
€ 5,00
€ 3,00
€ 8,00
€ 2,00
4 5 6
Trova altre possibili scelte di Giorgio.
+ + =
1° acquisto
+ + =
2° acquisto
+ + =
3° acquisto
€ 9,00
1 Leggi, osserva le immagini e completa.
Corinna vuole rinnovare il suo guardaroba. Ha in borsetta € 225,00 ed entra nel negozio “Tutto da Ornella”. a
Controlla i prezzi degli oggetti esposti, poi verifica se Corinna può effettuare i seguenti acquisti.
2 3
2 Sul quaderno, inventa tu un problema a più soluzioni ambientato, per esempio, in pasticceria oppure in un negozio di articoli sportivi.
PROBLEMI 75
PROVO IO
€ € € Sì NO € ...................... € ...................... € ...................... Sì NO € € € Sì NO
Trova altre possibili scelte per Corinna.
1
b
VERSO L’INVALSI
1 Leggi il testo del problema e indica con una X se le affermazioni
nella tabella sono vere ( V ) o false (F ).
Per il suo compleanno Lorenzo riceve dal nonno 20 euro.
Compera un libro che costa 12 euro e spende i soldi rimanenti per comperare dei pacchetti di figurine che costano 2 euro ciascuno.
Quanti pacchetti di figurine compera?
V F
Il libro costa 20 euro.
Un pacchetto di figurine costa 3 euro.
Compera 2 pacchetti di figurine.
Sai quanto costa il libro. Per risolvere il problema devi fare due operazioni.
Il problema ti dice quanti pacchetti di figurine compera.
2 Leggi e completa.
Una pasticciera ha preparato 45 pasticcini alla crema, che vuole disporre in parti uguali su alcuni vassoi.
Quanti vassoi potrebbe utilizzare?
Trova tu le varie possibilità.
a)
b) c)
3 Quale operazione risolve il problema?
Alice ha 37 gommine profumate, Sandro ne ha 43. Quante gommine ha in più Sandro?
A. 37 + 43
B. 43 – 37
4 Leggi e rispondi.
C. 37 – 43
D. 43 + 37
Per un rinfresco un cuoco ha preparato 65 pizzette al pomodoro, 58 al prosciutto e 47 al formaggio. Quante pizzette rimangono alla fine della festa?
Puoi risolvere questo problema?
Sì NO
Perché?
5 Quali operazioni sono necessarie per risolvere il problema?
Questa mattina nel parcheggio davanti alla stazione c’erano 48 automobili.
Durante la giornata ne sono arrivate altre 24. Alla sera ne sono andate via 56. Quante automobili sono rimaste nel parcheggio?
A. Prima la moltiplicazione, dopo la sottrazione.
B. Prima l’addizione, dopo la divisione.
C. Prima la sottrazione, dopo l’addizione.
D. Prima l’addizione, dopo la sottrazione.
..........................................................................................
76
6 Leggi il testo dei problemi, scrivi le domande adatte e risolvi sul quaderno.
Umberto percorre ogni giorno lo stesso percorso in bicicletta, tranne la domenica. In una settimana ha pedalato per 240 km. ?
Il lunedì al magazzino del supermercato sono arrivati 30 scatoloni da 25 confezioni di fazzoletti ciascuno. ................................................................................................................................................................
Alla fine della settimana sugli scaffali si trovano ancora 390 confezioni. ........................................... ?
Un teatro ha 124 posti. Per lo spettacolo pomeridiano sono rimasti liberi 85 posti.
Se il costo del biglietto è di € 4,00,
Un libraio ha ricevuto 12 scatole con 16 libri ciascuna.
Sistema i libri in parti uguali su 8 scaffali del suo negozio.
7 Leggi il testo del problema, scopri la domanda nascosta, poi risolvi sul quaderno con il diagramma.
Leonardo compera 4 cartucce per la stampante che costano ciascuna € 16,00.
Alla cassa paga con una banconota da € 100,00. Quanto riceve di resto?
8 Leggi il testo del problema, osserva le immagini e risolvi.
Marco va in gelateria per comperare dei gelati per 4 persone.
Ha in tasca 10 euro. Quali gelati può comperare?
• Scrivi le soluzioni possibili.
a b c d cono piccolo € 1,00
1a soluz.:
2 a soluz.:
3 a soluz.:
coppa € 3,00 coppetta € 1,50
VERSO L’INVALSI 77
bicchiere € 4,00
?
?
?
?
?
?
4 a soluz.: cono grande € 2,00
I PROBLEMI
Completa la mappa, inserendo le parole che seguono:
soluzione • dati • domande • mancanti • risposta
Le parti del problema
La risoluzione del problema
Ogni problema è composto da un testo, che contiene una o più
. Il testo del problema fornisce tutti i che sono necessari per arrivare alla .......................................
1) Leggere attentamente il testo:
Nella cameretta di Rosa ci sono 7 ripiani dedicati ai giocattoli. Su ogni ripiano ci sono 5 robot e 2 peluche. Quanti giochi ha Rosa in tutto?
2) Individuare e capire la domanda:
Devo riuscire a capire il numero dei giochi totali.
3) Trovare e analizzare i dati:
5 + 2: giochi su ogni ripiano;
7: numero di tutti i ripiani
4) Scoprire se ci sono domande nascoste, dati , dati inutili o dati nascosti.
Domanda nascosta: quanti giochi ci sono in tutto su ogni ripiano?
5) Scoprire le operazioni da eseguire: prima un’addizione, poi una moltiplicazione.
6) Eseguire le operazioni
7) Verificare di aver trovato una a tutte le domande.
RIPASSO IN UN LAMPO
MAPPA 78 I MIEI SCHEMI PAGINA 150
PAGINE STELLA
1 Risolvi i problemi sul quaderno.
a. A una manifestazione sportiva prendono parte 7 società, ciascuna con 13 atleti.
Quanti sono tutti i partecipanti?
Di questi, 48 sono donne. Quanti sono gli atleti maschi?
b. Un ristorante ha 25 tavoli da 6 posti ciascuno. Quanti clienti può ospitare in tutto?
Per una cerimonia viene aggiunto un tavolo da 16 posti. Quanti posti saranno disponibili?
c. Un rifugio alpino ha una camerata con 24 posti letto e una stanza con 6 letti a castello da 3 posti l’uno. Quanti posti per dormire ha in tutto il rifugio?
e. Un grattacielo di 27 piani ha 12 finestre per piano. Questa sera le finestre illuminate sono 289. Quante sono le finestre non illuminate?
d. Un teatro ha 162 posti, disposti in 9 file uguali. Quanti posti ci sono per ciascuna fila? Se sono complete solo 7 file, quanti sono gli spettatori presenti?
f. Silvia sta leggendo un libro che ha 764 pagine. Ne ha già lette 308 e vuole leggere quelle che mancano per finirlo in 8 giorni. Quante pagine deve leggere ogni giorno?
2 Sottolinea il dato inutile e risolvi il problema sul quaderno. Marco decide di spendere € 8,00 dei suoi risparmi per comperare dei fumetti. Ogni settimana Marco riceve dai suoi genitori € 12,00.
Quanto riceve Marco in 6 settimane?
VERIFICA 79
TUTTO OK?
FRAZIONARE
Osserva e rispondi indicando con una X.
È una pera intera?
Sì NO
È una torta intera?
Sì NO
L’intero è qualsiasi elemento al quale non manca nessuna parte.
• Un intero può essere diviso in tante parti in modo diverso.
Osserva e indica con X gli interi divisi in parti uguali.
È un cocomero intero?
Sì NO
In matematica, dividere l’intero in parti uguali si dice frazionare.
PROVO IO
Indica con una X gli elementi che sono stati frazionati.
NUMERI 80
L’UNITÀ FRAZIONARIA
• Marianna ha diviso il foglio in due parti uguali.
Ciascuna parte corrisponde a 1 2 del foglio e si legge “un mezzo”.
• Riccardo, invece, ha diviso il foglio in quattro parti uguali.
Ciascuna parte corrisponde a 1 4 del foglio e si legge “un quarto”. 1
delle unità frazionarie.
Ciascuna parte uguale in cui viene diviso l’intero si chiama unità frazionaria .
PROVO IO
1 Collega l’unità frazionaria in cifre e in parole al disegno corrispondente.
4
2 e 1
sono
1 2 1 2
1 4 1 4 1 4 1 4
frazionarie
1 1 1 1 un mezzo un decimo un quinto un settimo 1 7 1 10 1 5 1 2 81 FRAZIONI E NUMERI DECIMALI
2 Osserva le figure e completa le unità
.
LE FRAZIONI
• Beatrice ha preparato una splendida pizza!
Ha diviso la pizza in 5 fette uguali.
La frazione corrispondente a ciascuna fetta è 1 5 e si legge “ un quinto”.
• Ha dato una fetta alla sua amica Gaia, una fetta
al suo amico Teo e una fetta l’ha messa nel suo piatto.
La frazione corrispondente alle fette distribuite è 3 5 e si legge “ tre quinti ”.
3 5 significa: • l’intero è stato diviso in 5 parti;
• di queste 5 parti ne sono state prese 3.
I termini della frazione hanno dei nomi precisi:
3 5
numeratore: indica quante parti dell’intero sono state considerate l inea di frazione: indica che l’intero è stato frazionato denominatore: indica in quante parti è stato diviso l’intero
PROVO IO
1 Scrivi in cifre e in parole le frazioni corrispondenti alla parte colorata, come nell’esempio.
2 5 due quinti
2 Indica con una X se le frazioni relative alla parte colorata sono vere ( V ) o false (F ).
......... ......... ......... ......... 5 6 2 7 9 10
V F V F V F NUMERI 82
3 Scrivi in cifre e in parole le frazioni corrispondenti alla parte colorata, come nell’esempio.
4 Colora la parte indicata dalla frazione.
5 Dividi ogni intero nelle parti indicate dal denominatore; poi colora le parti indicate dal numeratore.
2 5
............................................. ............................................. .............................................
due quinti
5 6 1 6 1 3 3 4 1 4 7 10 9 10 9 12 11 12 1 3 5 6 4 6 1 2 1 4 7 12 83 FRAZIONI E NUMERI DECIMALI
LE FRAZIONI
Completa la mappa, inserendo le parole che seguono:
numeratore • diviso • frazionaria • denominatore • su • linea di frazione
Frazionare vuol dire…
dividere l’intero in parti uguali.
Ciascuna parte in cui viene diviso l’intero si chiama unità ............................................
I termini
Come si scrive e come si legge una frazione
Il ............................................ indica quante parti dell’intero sono state considerate.
La vuol dire che l’intero è stato “frazionato”, cioè in parti uguali.
Il indica in quante parti è stato diviso l’intero.
L’intero è stato diviso in 5 parti: ognuna di queste parti è “un quinto”.
Di queste, vengono prese in considerazione 3 parti, quindi “ tre quinti”.
“Tre quinti” vuol dire anche “tre cinque”.
numeratore
linea di frazione
3 5
RIPASSO IN UN LAMPO
denominatore MAPPA 84 I MIEI SCHEMI PAGINA 151
1 Osserva l’immagine e indica con una X se le affermazioni sono vere ( V ) o false (F ).
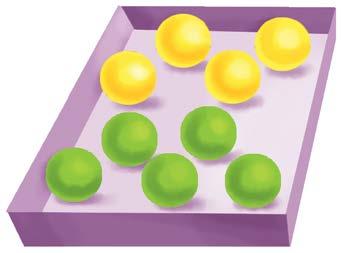
• Il totale, cioè l’intero, è di 9 biglie. V F
• La frazione che rappresenta le biglie gialle è 4 5 V F
• La frazione che rappresenta le biglie verdi è 5 9 . V F
2 Collega con una ogni elemento della frazione al suo nome e al suo significato.
linea di frazione denominatore numeratore
5 6
parti in cui è diviso l’intero parti dell’intero considerate linea che indica il frazionamento
3 Osserva le figure e scrivi la frazione della parte colorata in lettere e in numero.
4 Colora la parte indicata dalla frazione.
4 9 7 12 3 8 2 5 5 6 VERIFICA 85 PAGINE STELLA TUTTO OK?
LE FRAZIONI DECIMALI
Osserva e completa.
• L’intero è stato diviso in parti.
Ciascuna parte è 1 10 (un decimo) dell’intero.
• L’intero è stato diviso in ................................................ parti. Ciascuna parte è 1 100 (un centesimo) dell’intero.
• L’intero è stato diviso in parti. Ciascuna parte è 1 1 000 (un millesimo) dell’intero.
Le frazioni che hanno come denominatore 10, 100, 1 000 sono definite frazioni decimali.
PROVO IO
1 Scrivi la frazione decimale corrispondente alla parte colorata.
2 Cerchia le frazioni decimali.
3 10 4 9 7 10 14 100 6 15 2 7 1 10 4 5 4 10
NUMERI 86
DALLE FRAZIONI DECIMALI AI NUMERI DECIMALI
Michela vuole fare un collage. Prende un foglio di carta, lo divide in 10 rettangolini tutti uguali per colorarne ciascuno con un colore diverso.
Ha colorato di rosso il primo rettangolino.
Il foglio rappresenta l’intero, cioè l’unità.
• È stato colorato tutto il foglio? Sì NO
• Che cosa è stato colorato?
• Scrivi la frazione corrispondente alla parte colorata:
Come già sai, 1 10 è una frazione decimale.
Una frazione decimale può essere scritta anche come numero decimale.
Il foglio rappresenta l’unità.
• Quante unità sono state colorate? 0
Il rettangolino rappresenta un decimo.
• Quanti decimi sono stati colorati? 1
• Osserva le cifre nella tabella e come sono formati i numeri decimali.
PROVO IO
u d 0 1 , parte intera
parte decimale
la virgola separa la parte intera dalla parte decimale
1 I numeri decimali possono essere rappresentati anche sulla linea dei numeri. Scrivi i numeri che mancano.
2 Completa come nell’esempio.
3 10 = 0,3 ......... = 0 0,1 0,4 0,5 0,7 0,9 1 1,1 1,4 1,5 1,8 2
......... = 87 FRAZIONI E NUMERI DECIMALI
I DECIMI
Un decimo può essere scritto:
• come frazione decimale: 1 10
PROVO IO
L’intero può essere diviso in 10 parti uguali. Ciascuna parte corrisponde a un decimo dell’intero.
• come numero decimale
PARTE INTERA u unità d decimi c centesimi m millesimi 0 1 , PARTE DECIMALE
0,1
:
0,3 • 1,2 • 0,9 • 2,5 • 0,4 • 3,8 • 0,7 0 1 2 3 4
1 Scrivi i numeri decimali in ordine crescente sulla linea dei numeri.
da u d
da u d
3,2 12,5 0,4 7,1 16,9 8,7 da u d , da u d , da u d , da u d , NUMERI 88
2 Inserisci i numeri decimali nelle tabelle.
,
,
I CENTESIMI
L’intero può essere diviso in 100 parti uguali. Ciascuna parte corrisponde a un centesimo dell’intero.
Un centesimo può essere scritto:
• come frazione decimale: 1 100
• come numero decimale: 0,01
Completa. 0,06 0,07 0,08 0,50 1,01 – 0,01 + 0,01 0,11 0,69 1,09 – 0,01 + 0,01 0,19 0,99 1,99 – 0,01 + 0,01
PROVO IO 2
5 100 = 15 100 = 9 100 = 38 100 = PARTE INTERA u unità d decimi c centesimi m millesimi 0 0 1 , PARTE DECIMALE 89 FRAZIONI E NUMERI DECIMALI
1 Colora le parti indicate dalla frazione, poi scrivi il numero decimale
corrispondente.
I MILLESIMI
L’intero può essere diviso in 1000 parti uguali.
Ciascuna parte corrisponde a un millesimo dell’intero.
Un millesimo può essere scritto:
• come frazione decimale: 1 1 000
• come numero decimale: 0,001
0
PROVO IO
1 Trasforma la frazione decimale in numero decimale.
2 Scrivi il numero decimale.
3 Cerchia di rosso la parte intera e di blu la parte decimale dei seguenti numeri, poi inseriscili in tabella.
5 1 000 = 16 1 000 = 38 1 000 = 101 1 000 = .............................. 159 1 000 = .............................. 224 1 000 = ..............................
0
2 u, 3
5
m
u, 3 d, 0 c, 9 m
......................................... 3 u, 0 d, 0 c, 5 m = ...........................................
u, 7 d, 1 c, 5 m =
u, 9 d, 9 c, 9 m = 0 u, 0 d, 1 c, 1 m =
d,
c, 1
= 1
=
h
,
, h da u d c m , , ,
da u d c m
,
0,3 • 0,39 • 5,347 138,09 • 1,724 • 0,182
PARTE INTERA u unità d decimi c centesimi m millesimi 0 0 0 1 , PARTE DECIMALE a b NUMERI 90 I MIEI ESERCIZI PAGINA 175, 176
1 Quale tavoletta di cioccolato è stata frazionata?
5 Indica con una X la frazione decimale.
A. B.
2 Frazionare significa:
C. D.
A. dividere l’intero in due parti.
B. dividere l’intero in modo casuale.
C. dividere l’intero in parti uguali.
D. non dividere l’intero.
3 Osserva:
La frazione corrispondente alla parte colorata è:
A. 5 8
B. 8 3
C. 8 8
D. 3 8
4 Osserva la figura precedente e indica con una X l’affermazione NON vera.
A. L’intero è stato frazionato.
B. La parte colorata corrisponde all’unità frazionaria.
C. La parte non colorata corrisponde a 5 8
D. L’intero corrisponde a 8 8 .
A. 3 4
B. 2 5
C. 7 10
D. 10 12
6 A quale numero decimale corrisponde la frazione 2 10 ?
A. 0,2
B. 0,02
C. 2,1
D. 1,2
7 Quale uguaglianza è sbagliata?
A. 1 u, 4 d, 7 c = 1,47
B. 3 c = 0,03
C. 5 d, 4 m = 0,54
D. 7 c, 1 m = 0,071
8 Partendo dal numero 1,14 quanto manca per arrivare all’unità successiva?
A. 0,8
B. 0,06
C. 0,86
D. 1,6
9 Qual è la scomposizione corretta del numero nel riquadro?
3,09
A. 3 u, 9 d
B. 3 u, 9 c
C. 3 h, 9 u
D. 3 d, 9 m
VERSO L’INVALSI 91
I NUMERI DECIMALI
Completa la mappa, inserendo le parole che seguono:
virgola • decimale • denominatore
Frazione decimale vuol dire… Numero decimale vuol dire…
una frazione che ha come 10, 100, 1000.
un numero con la : in un numero decimale la virgola separa la parte intera dalla parte .............................................
Frazioni decimali e numeri decimali
Decimi
• frazione decimale: 1 10
Centesimi
• frazione decimale: 1 100
• numero decimale: 0,01 PARTE INTERA PARTE DECIMALE
Millesimi
• frazione decimale: 1 1 000
• numero decimale: 0,001 PARTE INTERA PARTE DECIMALE
u unità d decimi c centesimi m millesimi 0 0 1 , MAPPA 92 I MIEI SCHEMI PAGINA 152
u unità d decimi c centesimi m millesimi 0 1 ,
RIPASSO IN UN LAMPO
• numero decimale: 0,1 PARTE INTERA PARTE DECIMALE
u unità d decimi c centesimi m millesimi 0 0 0 1 ,
1 Conta e completa l’intero.
2
5 10 = 7 10 = 12 10 = 8 100 = 45 100 =
Trasforma la frazione decimale in numero decimale.
3
Scrivi
il numero decimale.
0 u, 7 d, 1 c, 4 m = ............................. 0,67 = ................................................................................................ 1 u, 5 d, 3 c = 0,159 = 2 u, 5 c, 1 m = 1,324 = 2 u, 3 m = 5,031 = 6 u, 2 d, 1 m = 3,802 = 1 2 0 1 1,4 • 1,1 • 1,7 • 1,9 • 1,6
4 Indica il valore di ogni cifra.
0,1 • 0,7 • 0,3 • 0,8 • 0,5 0,7 + = 1 0,201 + = 1 0,28 + = 1 + = 2 0,90 + = 1 VERIFICA 93 PAGINE STELLA TUTTO OK?
5 Scrivi i numeri decimali in ordine crescente sulla linea dei numeri.
LE UNITÀ DI MISURA
Misurare una grandezza vuol dire confrontare la misura campione con la grandezza da misurare e registrare quante volte vi è contenuta.
• Misura la lunghezza, l’altezza e la larghezza di alcuni oggetti presenti in palestra.
Prima di fare le misurazioni è necessario scegliere l’unità di misura o misura campione, come per esempio un bastone o una corda.
Stabilisci quante volte la misura campione è contenuta nella grandezza da misurare e registra i dati in tabella.
oggetti da misurare misura campione altezza spalliera lunghezza asse di equilibrio lunghezza tappetino larghezza campo da gioco bastone corda MISURE MISURE
L’utilizzo di unità di misura arbitrarie, cioè che dipendono da una singola persona, porta a risultati diversi. Per questo motivo, il Sistema Internazionale di unità di misura (SI) ha stabilito delle unità di misura convenzionali, cioè uguali per tutti.
Le principali unità di misura sono:
• per la lunghezza, il metro (m);
• per il peso, il chilogrammo ( kg);
La scrittura delle unità di misura segue alcune regole.
• L’unità di misura si scrive sempre dopo il numero a cui è riferita e con la lettera minuscola.
• per la capacità, il litro (ℓ ).
• Il simbolo dell’unità di misura non è mai seguito dal punto 12 kg 2 ℓ
• Si può scrivere prima del numero solo l’unità di misura del denaro € 25,00 ! ? 94
LE MISURE DI LUNGHEZZA
L’unità di misura fondamentale della lunghezza è il metro e il simbolo è m.
Il metro ha i suoi multipli e i suoi sottomultipli.
Ciascuna unità di misura è 10 volte più grande di quella che si trova
alla sua destra e 10 volte più piccola di quella che si trova alla sua sinistra.
Con le misure di lunghezza è possibile misurare l’altezza, la lunghezza, la larghezza, la distanza tra due punti…
PROVO IO
Procurati un nastro lungo 1 metro, usalo come unità campione per misurare gli oggetti elencati in tabella e completa con una X, come nell’esempio.
oggetti misura – di 1 m misura 1 m misura + di 1 m
lunghezza matita X
altezza banco
lunghezza cattedra
larghezza porta
altezza zaino
larghezza aula
altezza sedia
MULTIPLI
DI MISURA SOTTOMULTIPLI km
hm
dam decametro m metro dm decimetro cm centimetro mm millimetro 1 000 m 100 m 10 m 1 m 1 10 di m 1 100 di m 1 1 000 di m
UNITÀ
chilometro
ettometro
95 MISURE
I SOTTOMULTIPLI DEL METRO
cm mm MISURE
1 dm
1 decimetro è la decima parte di 1 metro.
1 cm
1 centimetro è la centesima parte di 1 metro.
Per misurare lunghezze inferiori al metro, si utilizzano i sottomultipli del metro: il decimetro (dm), il centimetro ( ) e il millimetro ( ). 1 mm
1 metro è formato da 10 decimetri.
1 m = 10 dm
1 dm = 1 10 di 1 m 1 dm = 0 m, e 1 dm 1 dm = 0,1 m
1 metro è formato da 100 centimetri.
1 m = 100 cm
1 cm = 1 100 di 1 m 1 cm = 0 m, 0 dm e 1 cm 1 cm = 0,01 m
1 millimetro è la millesima parte di 1 metro
1 metro è formato da 1 000 millimetri.
1 m = 1 000 mm
1 mm = 1 1 000 di 1 m 1 mm = 0 m, 0 dm, 0 cm e 1 mm 1 mm = 0,001 m
PROVO IO
cm ........................ mm cm ........................ mm cm ........................
mm
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
1 Misura con il righello i seguenti oggetti e riporta le misure. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 96
2 Osserva la misura di ogni oggetto e completa.
Per misurare lunghezze minori di 1 metro, si usano i
I sottomultipli del metro nella realtà
3 Osserva la misura di ogni oggetto e completa.
• La penna è lunga: dm = cm = mm
• La gomma è lunga: dm = cm = mm
• La punta del pennarello è lunga: dm = cm = mm
UNITÀ DI MISURA SOTTOMULTIPLI m 1 m 1 ....... di m 1 di m 1 ............... di m 97 MISURE
I MULTIPLI DEL METRO
Per misurare lunghezze superiori al metro, si utilizzano i multipli del metro:
• il decametro (dam), che è 10 volte più grande del metro
• l’ettometro ( hm), che è 100 volte più grande del metro
• il chilometro ( km), che è 1000 volte più grande del metro
PROVO IO
1 dam = 10 m
1 hm = 100 m
1 km = 1 000 m
1 Indica con una X gli elementi che si possono misurare con i multipli del metro.
2 Osserva le immagini e indica con una X la misura più adatta per ciascun elemento.
Un campo da calcio è lungo: alcuni metri. alcuni decametri. 1 chilometro.
3 Completa.
6 m + = 1 dam
85 m + = 1 hm
Un’autostrada si misura in: metri. decametri. chilometri.
25
100
m + = 1 hm
m + = 1 km
250
3
m + = 1 km
m + = 1 dam
98 MISURE
100 m = 10 = 1
10 m = ....................... dam = ....................... dm
8 km = ....................... hm = ....................... dam = ....................... m
99 MISURE
4 Osserva e completa.
LE EQUIVALENZE
Per esprimere una grandezza con unità di misura diverse, senza modificarne il valore, bisogna eseguire un’equivalenza
Osserva la tabella, leggi e completa.
Quando passi da una unità di misura maggiore a una di valore minore, devi:
• moltiplicare per 10 se ti sposti di una sola marca;
• moltiplicare per 100 se ti sposti di due marche;
• moltiplicare per 1000 se ti sposti di tre marche.
Quando passi da una unità di misura minore a una di valore maggiore, devi:
• dividere per 10 se ti sposti di una sola marca;
• dividere per 100 se ti sposti di due marche;
• dividere per 1000 se ti sposti di tre marche.
Il simbolo dell’unità di misura, la marca , si riferisce alla cifra dell’unità.
10 5 m dm 100 2 hm m 1 000 3 km m
: 10 10 m dam : 100 400 m hm : 1 000 3 000 m km
216 m = 2 hm, 1 dam, 6 m
km chilometro hm ettometro dam decametro m metro dm decimetro cm centimetro mm millimetro 10 10 10 10 10 10
10
10
10
10
10
10
? 100 MISURE
:
:
:
:
:
:
!
1 Inserisci le misure in tabella, come nell’esempio.
1
375 dm
9 012 mm
85 hm
461 cm
2 Esegui le equivalenze.
3 Cancella con una X le misure che non sono equivalenti a quella data. 40
4 Scrivi il valore della cifra colorata, come nell’esempio.
2 km = ................................. m 1 hm = ................................. dam 230 hm = .................... km 800 m = hm 4 500 cm = m 58 m = dm 570 m = cm 6 000 mm = m 380 m = dam
m 400
dam 400 mm 70 dm 700 mm 7 m 700 hm 50 hm 5 km 500 m 5 000 mm 7 km 700 m 7 000 dam 70 hm 500 cm 5 dm 5 m 50 mm 2 dam 20 m 2 000 cm 200 mm
dm 4
4 5 m 4 dam 1 742 m 2 3 hm 13 4 mm 2 85 cm 4 6 dm
3
km hm dam m dm cm mm
248
1 2 4 8
m
101 MISURE
347 m PROVO IO
LE MISURE DI CAPACITÀ
L’unità di misura fondamentale della capacità , cioè la quantità di liquido contenuta da un recipiente, è il litro e il simbolo è ℓ. Il litro ha i suoi multipli e i suoi sottomultipli
UNITÀ DI
PROVO IO
1 Inserisci le misure in tabella, come nell’esempio.
467
1 065 ml
17 dal
254 cl
9 hl
643 dl
2 Indica con X l’unità di misura adatta per indicare la capacità di questi recipienti.
MULTIPLI
SOTTOMULTIPLI hℓ ettolitro daℓ decalitro ℓ litro dℓ decilitro cℓ centilitro mℓ millilitro 100 l 10 l 1 ℓ 1 10 di l 1 100 di l 1 1 000 di l
MISURA
h ℓ daℓ ℓ dℓ c ℓ m ℓ
l 4 6 7
cℓ ℓ ℓ hℓ daℓ ℓ ℓ mℓ
102 MISURE
LE MISURE DI MASSA O PESO
L’unità di misura fondamentale di peso o massa è il chilogrammo e il simbolo è kg. Il chilogrammo ha i suoi multipli e i suoi sottomultipli.
MULTIPLI
UNITÀ DI MISURA
Mg megagrammo h di kg da di kg kg chilogrammo hg ettogrammo dag decagrammo g grammo
Per misurare il peso di oggetti molto piccoli si usano i sottomultipli del grammo Sono unità di misura utilizzate solo in alcuni settori specifici, come la farmacia, l’oreficeria…
PROVO IO
Farina
UNITÀ DI MISURA
1 Secondo te, quale unità di misura è più adatta a indicare il peso di questi oggetti? Indica con una X.
SOTTOMULTIPLI
1 000 kg 100 kg 10 kg 1 kg 1 10 di kg 1 100 di kg 1 1 000 di kg
SOTTOMULTIPLI g grammo dg decigrammo cg centigrammo mg milligrammo 1 g 1 10 di g 1 100 di g 1 1 000 di g g kg g kg kg g kg g
I MIEI ESERCIZI PAGINA 179 103 MISURE
PROVO IO
2 Inserisci le misure in tabella, come nell’esempio.
kg hg dag g dg cg mg
150 g
1 367 mg
91 dag
40 hg
2 098 g
1 5 0
3 Un megagrammo è equivalente a 1 000 kg. Scrivi quanto manca per formare 1 Mg.
350 kg + ................................... kg = 1 Mg 450 kg + ................................... kg = 1 Mg
699 kg + kg = 1 Mg 999 kg + kg = 1 Mg
710 kg + kg = 1 Mg
4 Esegui le equivalenze.
625 kg + kg = 1 Mg
6 kg = g 75 g = mg 3 400 g = hg
12 hg = dag 2 000 g = kg 2 500 cg = g
450 g = dag 500 dg = g 5 kg = hg
5 Scomponi le misure, come nell’esempio.
6 Componi le misure, come nell’esempio.
1 678 g = ...................................................................................
354 cg =
1 kg, 6 hg, 7 dag, 8 g
1 296 mg =
78 hg = 763 dg =
7 Risolvi i problemi sul quaderno.
2 kg, 4 hg, 1 dag, 5 g =
2 415 g
6 hg, 7 g = g
4 g, 5 dg, 3 cg = cg
5 dg, 9 cg, 1 mg = ................................................ mg
3 dag, 2 g, 7 mg = mg
Luca compera 1 hg di prosciutto crudo e 200 g di prosciutto cotto. Quanti grammi di prosciutto compera Luca in tutto?
a b
Un corriere consegna un pacco di 250 g e un pacco di 1 kg. Quanti grammi pesano i due pacchi insieme?
104 MISURE
PESO NETTO, PESO LORDO E TARA
Il peso complessivo della merce e del contenitore della merce si chiama peso lordo
Il peso della sola merce si chiama peso netto.
tara tara
Il peso del solo contenitore si chiama tara .
–
+ peso lordo +
515 g 500 g 250 g 50 g 23 kg .................................... 3 kg
1 Completa la tabella. peso lordo peso netto tara
Spesso i prodotti sono acquistati con il contenitore ed è importante conoscere il peso di ciascuna singola parte. –peso netto
tara
peso lordo peso lordo peso netto peso netto
105 MISURE
PROVO IO
LE MISURE DI VALORE: L’EURO
Per misurare il costo degli oggetti si usa il denaro.
L’euro è la moneta ufficiale usata in Italia e in molti Paesi d’Europa.
Il suo simbolo è €.
L’euro ha un solo sottomultiplo: il centesimo o cent.
1 cent vale 1 100 di euro e si può scrivere come numero decimale: 1 cent = € 0,01.
Gli euro che puoi trovare in circolazione sono i seguenti:
2 euro = € 2,00
1 euro = € 1,00
50 centesimi = € 0,50
20 centesimi = € 0,20
10 centesimi = € 0,10
5 centesimi = € 0,05
2 centesimi = € 0,02
1 centesimo = € 0,01
500 euro = € 500,00
200 euro = € 200,00
100 euro = € 100,00
50 euro = € 50,00
20 euro = € 20,00
10 euro = € 10,00
5 euro = € 5,00
1 Scrivi quanto manca per formare 1 euro.
20 cent + .............. cent = € 1 35 cent + .............. cent = € 1 70 cent + .............. cent = € 1
95 cent + cent = € 1 81 cent + cent = € 1 12 cent + cent = € 1
106 MISURE
PROVO IO
2 A quanto corrispondono? Completa.
3 Completa come nell’esempio.
7 euro e 20 centesimi = € 7,20
4 Completa.
Marco osserva una vetrina di articoli sportivi.
Che cosa può acquistare se ha a disposizione € 75,00? €
€ €
€ €
€
€ € resto €
€ resto € €
resto
€ € I MIEI ESERCIZI PAGINA 177, 178, 180 107 MISURE
COSTO UNITARIO E COSTO TOTALE
Osserva, leggi e rifletti.
3 = quantità
€ 2 = costo unitario
5 = quantità
€ 15 = costo totale
€ 5 = costo unitario
€ 30 = costo totale
PROVO IO
Completa la tabella.
Beatrice compera 3 coni gelato.
Ciascun cono costa € 2,00. Quanto spende in tutto Beatrice?
€ 2 x 3 = € 6
costo unitario x quantità = costo totale
Matilde compera 5 vasetti di yogurt e spende in tutto € 15,00. Quanto costa ciascun vasetto di yogurt?
€ 15 : 5 = € 3 costo totale : quantità = costo unitario
Anna e Marta comperano un vassoio di pasticcini spendendo € 30,00.
Ciascun pasticcino costa € 5,00.
Quanti pasticcini contiene il vassoio?
€ 30 : € 5 = 6 costo totale : costo unitario = quantità
costo unitario costo totale quantità operazione € € 64,00 4 € 8,00 € 104,00 € 67,00 € ................................. 3
108 MISURE
PROBLEMI CON L’EURO
Risolvi i problemi sul quaderno.
• Samuela spende € 12,00 per il parcheggio di 6 ore della sua auto.
Quanto spende per un’ora?
• Nella vetrina di un negozio sono esposte 5 palline da tennis che costano in tutto € 25,00.
Quanto costa ciascuna pallina?
• Al supermercato Giacomo spende € 126,00 per la spesa settimanale.
Alla cassa paga con una banconota da € 200,00.
Quanto riceve di resto?
Con le STEM posso… RISOLVERE
• La nonna compera 4 astucci per i suoi nipoti. Ciascun astuccio costa € 7,00.
Quanto spende in tutto?
• Betti, per il suo cane, spende € 4,00 per le crocchette e € 12,00 per un guinzaglio.
Quanto spende in tutto Betti?
• Luca compera 3 hg di formaggio che costa € 2,00 all’ettogrammo e del pane che costa € 4,00.
Quanto spende in tutto Luca?
Risolvi il problema e rifletti sul percorso che devi seguire.
Francesca compera 3 libri che costano € 17,00 ciascuno.
Alla cassa paga con una banconota da € 50,00 e una da € 20,00. Quanto riceve di resto?
Per risolvere questo problema sono necessarie 3 operazioni: una sottrazione, un’addizione e una moltiplicazione.
Scrivi l’ordine in cui vanno eseguite le operazioni e svolgile. 1.
109 MISURE
2. 3.
LE MISURE DI TEMPO
Il tempo è una grandezza misurabile e l’unità di misura fondamentale è il secondo (s).
• I multipli del secondo sono: minuti, ore, giorni, settimane, mesi, anni
s secondo minuto min ora h giorno d settimana mese anno
1 min = 60 s 1 h = 60 min 1 d = 24 h 1 settimana = 7 d 1 mese = 30 d 1 anno = 12 mesi
Lo strumento più usato per misurare il tempo è l’orologio. Con questo strumento misuriamo il tempo di una giornata.
PROVO IO
Osserva e completa.
• In un orologio la lancetta più corta segna le
• La lancetta più lunga segna i
• La lancetta più sottile segna i .....................................................................................................
1 Osserva gli orologi e scrivi le ore indicate. Poi disegna le lancette sugli orologi sotto, secondo le indicazioni, e scrivi le ore ottenute.
12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11
12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 dopo h 1 e mezza 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 dopo 55 m 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 dopo 15 m 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 dopo 20 m 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 dopo 1 h 10 m 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11
110 MISURE
2 Colora nello stesso modo i riquadri che indicano la stessa durata.
mezz’ora
90 minuti
15 minuti
un’ora e mezza
45 minuti
30 minuti un quarto d’ora tre quarti d’ora
3 Leggi il cartello e rispondi alle domande.
Orari di apertura
Lunedì: dalle 8:00 alle 12:30
Dal martedì al sabato:
8:00 – 12:30 / 16:00 – 19:30
Domenica chiuso
Alla porta della panetteria di Rocco è appeso il cartello degli orari.
• Quante ore è aperta la panetteria lunedì?
• Quante ore è aperta mercoledì?
• Quante ore dura l’intervallo di pranzo?
• Quante ore alla settimana è aperta la panetteria?
4 Leggi, rifletti e completa.
Nella città di Como, un biglietto del bus urbano ha la durata di 90 minuti.
• Un turista ha timbrato il biglietto alle 11:50. Il biglietto scade alle ore
• Una signora timbra il biglietto alle ore 16:30. Il biglietto scade alle ore
• Un signore timbra il biglietto alle ore 20:15. Il biglietto scade alle ore
5 Leggi, disegna le lancette e completa.
La maestra Laura entra a scuola alle ore 8:30. Fa lezione per tre ore e mezza, poi va a casa. Che ore sono?
Rientra alle 14:30 e lavora 2 ore. A che ora esce?
• In tutta la giornata la maestra Laura ha effettuato ore di lezione.
111 MISURE
LE MISURE
Completa le tabelle inserendo i simboli giusti.
Lunghezza
MULTIPLI UNITÀ DI MISURA SOTTOMULTIPLI
km
chilometro hm ettometro decametro m metro dm decimetro cm centimetro mm millimetro
1 000 m 100 m 10 m 1 m 1 10 di m 1 100 di m 1 1 000 di m
Capacità
MULTIPLI UNITÀ
DI
MISURA SOTTOMULTIPLI hℓ ettolitro daℓ decalitro ℓ litro dℓ decilitro cℓ centilitro .............. millilitro
100 ℓ 10 ℓ 1 ℓ 1 10 di ℓ 1 100 di ℓ 1 1 000 di ℓ
Peso
MULTIPLI UNITÀ DI MISURA SOTTOMULTIPLI
megagrammo h di kg da di kg kg chilogrammo hg ettogrammo dag decagrammo g grammo
1 000 kg 100 kg 10 kg 1 kg 1 10 di kg 1 100 di kg 1 1 000 di kg
UNITÀ DI MISURA
SOTTOMULTIPLI
g grammo dg decigrammo centigrammo mg milligrammo 1 g 1 10 di g 1 100 di g 1 1 000 di g
Le misure di valore
Per misurare il valore degli oggetti si usa il denaro. L’euro è la moneta ufficiale usata in Italia e in molti Paesi d’Europa. Il suo simbolo è €. L’euro ha un solo sottomultiplo: il centesimo o cent.
Le misure di tempo
s secondo minuto min ora h giorno d settimana mese anno
1 min = 60 s 1 h = 60 min 1 d = 24 1 settimana = 7 d 1 mese = 30 d 1 anno = 12 mesi
RIPASSO IN UN LAMPO
MAPPA 112 I MIEI SCHEMI PAGINA 153
1 Quanto misurano gli elementi disegnati? Colora la misura che consideri corretta.
2 Esegui le equivalenze.
100 m = hm
25 dag = g
12 l = d l 6 kg = g
8 h l = l 15 g = dg
70 hm = km 500 l = da l 4 hg = g
6 m = dm 2 l = c l 8 g = cg
7 000 mm = m 200 m l = d l 200 g = dag
3 Completa la tabella.
hℓ daℓ ℓ dℓ c ℓ mℓ
240 cl
1 850 ml
0,02 hl
310 dl
4 l
5 Risolvi i problemi sul quaderno.
La corsa campestre si svolge su un percorso lungo 800 m. Dopo 10 giri, quanti chilometri ha percorso Davide?
a PAGINE STELLA TUTTO OK?
4 Cerchia le monete che servono per comperare la bibita.
€ 1,90
b VERIFICA 113
2 dm 2 m 20 cm 2 cm 4 km 4 m 10 m 10 km
Giorgio effettua un viaggio in aereo che dura 3 ore e 40 minuti. Se è partito alle 7:45, a che ora arriva a destinazione?
QUANTA ACQUA SIAMO?
1. Se dividiamo l’intera superficie del pianeta Terra in 100 quadratini , scopriremo che solo 30 di questi sono costituiti dalle terre emerse dei diversi continenti.
Quante parti di acqua ci sono sulla superficie totale del pianeta?
Colora di marrone le parti costituite da terra e di azzurro quelle costituite da acqua, poi completa le frazioni.
Il nostro pianeta è formato per 30/100 (trenta ) da terre e per /100 (........................................................................) da acqua.
2. Ora invece dividiamo il nostro corpo in dieci parti: per una persona adulta, fino a 6 di queste parti sono costituite da acqua. Quando siamo neonati, quasi 8 parti del nostro corpo sono costituite da acqua!
Colora i disegni secondo le indicazioni e completa le frazioni.
Il corpo di una persona adulta è costituito da /10 di acqua.
Il corpo di un neonato è costituito da /10 di acqua.
114 educazione civica
educazione civica
3. Secondo gli studi di Legambiente (l’associazione per la tutela dell’ambiente), il consumo di ogni abitante delle maggiori città italiane è sempre superiore ai 100 litri di acqua al giorno!
Completa la tabella con i dati richiesti, poi esegui le moltiplicazioni per conoscere il consumo di acqua:
Comunità Numero di persone Consumo di acqua totale
I membri della mia famiglia, compresa/o me ...................
Tutte le persone che vivono nel mio stesso edificio ...................
x 100= litri di acqua al giorno
x 100= litri di acqua al giorno
Con l’aiuto dell’insegnante, completa la tabella con i dati richiesti e poi esegui le moltiplicazioni per conoscere il consumo di acqua di questi gruppi di persone:
Comunità
Numero di persone Consumo di acqua totale
Gli alunni e le alunne della nostra classe ............... x 100= litri di acqua al giorno
Alunni e alunne della nostra classe + i membri di tutte le loro famiglie
Tutti gli alunni e le alunne della nostra scuola ...................
x 100= litri di acqua al giorno
x 100= litri di acqua al giorno
4. Ora ispirati ai consigli seguenti per risparmiare quanta più acqua possibile nelle tue abitudini giornaliere: cercane un altro, poi condividilo con la classe.
1. Non lasciare che l’acqua scorra inutilmente mentre ti lavi i denti o ti insaponi.
2. Verifica che non ci siano in casa rubinetti che “perdono”.
3. Chiedi ai genitori di lavare frutta e verdura in una bacinella piuttosto che sotto l’acqua corrente.
4. ..............................................................................................................................................................................................................................
115
I SOLIDI
Guardati intorno mentre sei in classe! Lo spazio dell’aula è occupato da tanti oggetti. Osserva solo la loro forma e considerali dal punto di vista geometrico: ricordano le figure geometriche solide o solidi.
Collega ciascun oggetto alla sua forma.
I solidi sono figure geometriche tridimensionali, che hanno cioè un’altezza , una larghezza e una lunghezza
PROVO IO
Sul quaderno, trasforma con un disegno ciascun solido in un oggetto di uso quotidiano.
parallelepipedo cubo cono cilindro sferaSPAZIO E FIGURE 116 SPAZIO E FIGURE
TANTI SOLIDI
Osserva questi solidi. Classificali in base alle indicazioni e scrivi il loro nome.
1. Solidi che rotolano: I solidi che rotolano si chiamano solidi rotondi
spigolo vertice faccia
2. Solidi che non rotolano: piramide, I solidi che non rotolano si chiamano poliedri
• I confini di un poliedro si chiamano facce.
• L’incontro di due facce dà origine a uno spigolo
• Il punto di incontro di tre spigoli è un vertice.
Un poliedro è caratterizzato da tre elementi: le facce, gli spigoli e i vertici.
PROVO IO
Per ciascuna figura, ripassa di rosso i vertici, di viola gli spigoli e colora di verde una faccia. Poi completa.
• È un
• Facce: n.
• Spigoli: n. ......................................
• Vertici: n.
• È un
• Facce: n.
• Spigoli: n. ......................................
• Vertici: n.
SPAZIO E FIGURE 117
DAI SOLIDI ALLE FIGURE PIANE
Segui le istruzioni e rifletti.
2. Con la matita segui il contorno della faccia appoggiata sul foglio.
3. Togli la scatola. Sul foglio è rimasta l’impronta dell’oggetto.
1. Prendi un oggetto di uso quotidiano, come per esempio una scatola di pasta, e appoggialo su un foglio.
L’impronta dell’oggetto è una figura piana a due dimensioni: lunghezza e larghezza
PROVO IO
1 Scrivi il nome del solido e della figura piana corrispondente.
2 Scrivi il nome di oggetti che richiamano le figure piane disegnate.
................................................. ................................................. ................................................. ................................................. SPAZIO E FIGURE 118
DALLE FIGURE PIANE ALLE LINEE
Le figure geometriche sono delimitate da linee chiuse Una linea può essere retta o curva, aperta o chiusa, semplice o intrecciata, spezzata o mista.
Osserva.
La linea retta mantiene sempre la stessa direzione.
Nella linea aperta l’inizio e la fine non coincidono.
La linea curva cambia sempre direzione.
Nella linea chiusa l’inizio e la fine coincidono.
PROVO IO
La linea è un insieme infinito e continuo di punti e ha una sola dimensione: la lunghezza a b c
La linea semplice non si sovrappone in alcun punto.
La linea spezzata è formata solo da tratti di linea retta.
La linea intrecciata si sovrappone in uno o più punti.
Segna con una X le caratteristiche di ciascuna linea disegnata.
La linea mista è formata da tratti di linea retta e da tratti di linea curva.
d e f
Retta Curva Aperta Chiusa Semplice Intrecciata Spezzata Mista
a b c d e f
SPAZIO E FIGURE 119
LA LINEA RETTA
La linea retta è una linea illimitata, che non ha né inizio né fine.
Viene indicata con una lettera minuscola.
Se dividi una retta con un punto, ottieni due semirette.
La semiretta è una linea che ha un inizio ma non una fine.
Il punto (O) si chiama origine della semiretta.
Una parte di retta compresa fra due punti si chiama segmento.
Il segmento ha un inizio e una fine.
Gli estremi del segmento si indicano con le lettere maiuscole (AB).
Rispetto alla sua posizione sul piano, una retta può essere:
orizzontale verticale obliqua
PROVO IO
1 Osserva le linee e scrivi il loro nome.
2 Completa.
• Una parte di retta compresa tra due punti si chiama
• Il punto da cui parte una semiretta si chiama
a
O
A B
O H
I
SPAZIO E FIGURE 120
RETTE PARALLELE, INCIDENTI, PERPENDICOLARI
Su un piano due rette, tra loro, possono essere:
• parallele, quando mantengono sempre la stessa distanza e non si incontrano mai;
• incidenti, quando si incontrano in un punto e dividono il piano in quattro parti;
• incidenti perpendicolari, quando due rette incidenti dividono il piano in quattro parti uguali.
a b c d e f
PROVO IO
1 Per ciascuna retta , disegnane un’altra, in modo da ottenere rette: incidenti perpendicolari incidenti parallele
2 Disegna due rette parallele, due rette incidenti perpendicolari, due rette incidenti.
SPAZIO E FIGURE 121
GLI ANGOLI
Giulia
Lucia
Osserva il percorso di Giulia per andare a casa della sua amica Lucia. Giulia cambia spesso direzione.
In geometria ciascun cambio di direzione forma un angolo.
L’angolo è la parte di piano compresa fra due semirette che hanno la stessa origine.
• Le semirette sono i lati dell’angolo.
• Il punto di origine è il vertice dell’angolo.
lato ampiezza
• Lo spazio compreso tra i due lati è l’ampiezza dell’angolo. vertice
Gli angoli prendono nomi diversi secondo la loro ampiezza .
Osserva l’orologio: la rotazione delle lancette corrisponde a un angolo di ampiezza diversa.
Un quarto di giro forma un angolo retto.
Un angolo con l’ampiezza minore dell’angolo retto si chiama acuto.
Mezzo giro forma un angolo piatto.
Un giro intero forma un angolo giro.
Un angolo con l’ampiezza maggiore dell’angolo retto e minore dell’angolo piatto si chiama ottuso.
SPAZIO E FIGURE 122
PROVO IO
1 Scrivi il nome di ciascun angolo.
angolo ............................................. angolo ............................................. angolo ...................................................
2 Colora di rosso gli angoli retti, di viola quelli ottusi e di verde quelli acuti.
3 Completa.
• Per formare un angolo piatto occorrono angoli retti.
• Per formare un angolo giro occorrono .................... angoli retti.
• Un angolo acuto è dell’angolo retto.
• Un angolo ottuso è dell’angolo retto.
4 Metti in ordine crescente i seguenti angoli, in base alla loro ampiezza. angolo giro • angolo retto • angolo acuto • angolo ottuso • angolo piatto
1.
2. .............................................................................................
3.
4. 5. ...........................................................................................
5 Per ciascun angolo, indica se è acuto o ottuso.
I MIEI ESERCIZI PAGINA 181 SPAZIO E FIGURE 123
SOLIDI, LINEE E ANGOLI
Completa la mappa, inserendo le parole che seguono:
semplice • incidenti • origine • ottuso • inizio • spigolo • vertice • punti
I solidi
La linea
Linea retta, semiretta, segmento
hanno 3 dimensioni: altezza, larghezza, lunghezza.
• I confini di un poliedro si chiamano facce;
• l’incontro di 2 facce dà origine a uno ;
• il punto di incontro di 3 spigoli dà origine a un .....................................
è un insieme infinito e continuo di e ha una sola dimensione: la lunghezza. Ogni linea può essere:
• retta o curva;
• aperta o chiusa;
Due rette possono
essere:
L’angolo
• o intrecciata;
• spezzata o mista.
La linea retta è una linea illimitata, che non ha né inizio né fine. Si indica con una lettera minuscola.
La semiretta è una linea che ha un ma non ha una fine. Il punto O è l’ della semiretta. Il segmento è una parte di retta compresa tra due punti, dunque ha un inizio e una fine. Gli estremi si indicano con lettere maiuscole.
• parallele , quando mantengono sempre la stessa distanza e non si incontrano mai;
• , quando si incontrano in un punto e dividono il piano in quattro parti;
• perpendicolari , quando sono incidenti e dividono il piano in quattro parti uguali.
è una parte di piano compresa tra due semirette che hanno la stessa origine. A seconda della sua ampiezza, un angolo può essere:
• acuto; • retto; • ; • piatto; • giro.
RIPASSO IN UN LAMPO
MAPPA 124 I MIEI SCHEMI PAGINA 154
PAGINE STELLA
1 Completa.
Spigoli n.
Vertici n.
Facce n. ...............................................
2 Collega ciascun nome alla sua definizione.
retta segmento semiretta
Linea che ha un inizio ma non una fine.
Linea che ha un inizio e una fine.
Linea che non ha né un inizio né una fine.
3 Disegna le linee richieste. linea aperta curva linea aperta spezzata linea chiusa curva linea chiusa spezzata
4 Definisci le rette.
5 Disegna gli angoli richiesti. angolo retto angolo giro angolo piatto angolo ottuso angolo acuto
................................................
VERIFICA 125
TUTTO OK?
POLIGONI E NON POLIGONI
Osserva le figure sotto e completa.
• Le figure sono delimitate da: linee aperte. linee chiuse.
Collega ciascuna figura alla sua definizione.
Figura piana racchiusa da una linea curva chiusa.
Figura piana racchiusa da una linea mista chiusa.
Figura piana racchiusa da una linea spezzata chiusa.
Una figura piana racchiusa da una linea spezzata chiusa è un poligono.
Una figura piana racchiusa da una linea curva o mista è un non poligono
PROVO IO
Cerchia in rosso i poligoni e in blu i non poligoni.
SPAZIO E FIGURE 126
I POLIGONI
I poligoni sono figure piane racchiuse da una linea spezzata chiusa.
C
• I segmenti che formano il confine di un poligono si chiamano lati.
• La parte di piano racchiusa dai lati si chiama superficie.
• Il punto in cui due lati si incontrano si chiama vertice. I vertici di un poligono si indicano con le lettere maiuscole A, B, C, D…
A
D B
PROVO IO
• La parte di piano delimitata da due lati si chiama angolo.
1 Osserva l’immagine e scrivi i nomi al posto giusto. vertice angolo lato superficie .................................... .................................... A
2 Completa le definizioni.
• Il poligono è
D B
C
• L’angolo è ...............................................................................................................................................................................
• Il lato è
• Il vertice è
• La superficie è
3 Indica con una X se le affermazioni sono vere ( V ) o false (F ).
• I poligoni sono figure geometriche piane. V F
• I segmenti che delimitano un poligono si chiamano lati. V F
• Il punto d’incontro di due lati si chiama vertice. V F
• I vertici di un poligono si indicano con i numeri. V F
• La parte di piano racchiusa dai lati si chiama angolo. V F
SPAZIO E FIGURE 127
CLASSIFICARE I POLIGONI
I poligoni si classificano e prendono il nome in base al numero dei lati, dei vertici e degli angoli.
1 Completa la tabella dei poligoni, come nell’esempio. Poi rispondi. nome forma numero lati numero angoli numero vertici
triangolo 3 3 3
quadrilatero
pentagono
esagono
2 Che cosa noti? In un poligono, il numero dei vertici e degli angoli è sempre:
uguale al numero dei lati. non uguale al numero dei lati.
PROVO IO
Completa, poi colora i poligoni secondo le indicazioni.
triangoli ( lati) quadrilateri ( lati)
pentagoni ( lati) esagoni ( lati)
SPAZIO E FIGURE 128
IL PERIMETRO
Il perimetro è la misura del contorno di un poligono
Il perimetro si indica con la lettera P. Il perimetro di un poligono si calcola sommando la misura dei suoi lati.
PROVO IO
1 Calcola il perimetro (P) di ciascuna figura. Prendi come unità di misura il lato del quadretto. unità di misura =
2 Per ciascuna figura, misura la lunghezza dei lati con il righello, poi calcola il perimetro (P).
P = AB + BC + CD + DA A B D C
P = ........... + ........... + ........... + ........... = ............ cm
P
P
P = ........... + ........... + ........... + ........... + ........... = ............ cm SPAZIO E FIGURE 129
P =
=
=
L ’ AREA
L’area di un poligono è la misura della sua superficie, cioè della parte di piano racchiusa dal contorno.
L’area si indica con la lettera A
Per calcolare l’area di un poligono è necessario utilizzare come unità di misura una figura piana, per esempio un quadrato di piccole dimensioni, e calcolare quante figure occorrono per ricoprire tutta la superficie.
Osserva, conta i quadretti e completa.
L’area del quadrilatero misura
1 Calcola l’area (A) di ciascun poligono. unità di misura =
L’area del triangolo misura
A = A = A = A =
2 Per ciascun poligono, colora di verde la superficie e ripassa di rosso il contorno.
A B C
I MIEI ESERCIZI PAGINA 184, 185 SPAZIO E FIGURE 130
PROVO IO
1 Quale tra questi è un angolo acuto?
1 2 3
A. L’angolo 1.
B. L’angolo 2.
C. Nessuno dei tre.
D. L’angolo 3.
2 Osserva le figure: quali sono poligoni?
a b c d e
A. Le figure a, b, c.
B. Le figure a, c, e.
C. Le figure a, c, d.
D. Le figure c, d, e.
3 Osserva le figure. Quanti sono i quadrilateri?
VERSO L’INVALSI
4 Quale operazione ti permette di calcolare il perimetro di questa figura?
AB = 6 cm
AD = 4 cm
A
D C B
A. 6 x 4
B. 6 + 6 + 4 + 4
C. 6 + 4
D. 6 – 4
5 L’area della figura disegnata è:
A. 30
B. 32
C. 29
D. 31
6 Per calcolare il perimetro di una figura, Leo ha scritto:
12 + 12 + 12 Di quale poligono si tratta?
A. B. D. C.
7 Osserva le altre 3 figure dell’esercizio precedente: a quale di esse si possono riferire le seguenti misure?
8 + 8 + 15 + 10
9 + 9 + 6 + 6
13 x 5
131
4
A. 2 B. 3 C.
D. 5
LA SIMMETRIA
La simmetria è il ribaltamento di una figura rispetto a una retta, che è l’asse di simmetria .
• Se pieghi il foglio lungo la linea rossa, il piano viene diviso in due parti perfettamente sovrapponibili.
La linea rossa è l’asse di simmetria ed è interno alla figura.
• Se pieghi il foglio lungo l’asse di simmetria, le due figure sono perfettamente sovrapponibili.
La linea rossa è l’asse di simmetria ed è esterno alla figura.
• L’asse di simmetria può essere interno o esterno alla figura e in posizione: orizzontale verticale obliqua
I poligoni possono avere uno o più assi di simmetria. Disegna gli assi mancanti.
SPAZIO E FIGURE 132
PROVO IO
1 Dove possibile, disegna nelle figure uno o più assi di simmetria interni.
2 Disegna la figura simmetrica a quella data.
3 Osserva le figure e per ognuna scrivi se l’asse di simmetria è interno o esterno.
asse asse asse asse
I MIEI ESERCIZI PAGINA 182 SPAZIO E FIGURE 133
I POLIGONI
Completa la mappa, inserendo le parole che seguono:
vertice • asse • lati • superficie • angolo
Il poligono
è una figura piana racchiusa da una linea spezzata chiusa.
• I segmenti che formano il confine di un poligono si chiamano ;
• la parte di piano racchiusa dai lati si chiama superficie;
• il punto in cui due lati si incontrano si chiama e si indica con una lettera maiuscola;
• la parte di piano che si trova all’incontro di due lati forma un . angolo lato
Perimetro e area
D B
C
vertice superficie A
Il perimetro è la misura del contorno di un poligono.
L’area è la misura della occupata da un poligono, cioè la parte di piano racchiusa dal suo contorno.
La simmetria è il ribaltamento di una figura rispetto a una retta, che è il suo di simmetria.
RIPASSO IN UN LAMPO
MAPPA 134 I MIEI SCHEMI PAGINA 155
PAGINE STELLA
1 Colora di rosso i poligoni e di verde i non poligoni.
2 Collega con una ciascun elemento del poligono alla sua definizione. lato superficie angolo vertice
Parte di piano delimitata da due lati.
Punto d’incontro di due lati.
Segmento del confine del poligono.
Parte di piano racchiusa dai lati del poligono.
3 Per ciascun poligono, misura la lunghezza dei lati con il righello e calcola il perimetro.
4 Solo una figura è simmetrica rispetto a quella disegnata nel riquadro. Quale? Indicala con una X.
P
P
P = cm
= cm
= cm
VERIFICA 135
TUTTO OK?
CLASSIFICARE
Classificare significa raggruppare elementi secondo una o più caratteristiche comuni.
Classifica i bambini scrivendo i loro nomi negli insiemi in base alla caratteristica indicata. Poi rispondi.
insieme dei bambini al parco
• Chi non appartiene all’insieme dei bambini al parco?
• Perché Tommy non può entrare nel sottoinsieme?
• Perché Anna appartiene all’insieme, ma non al sottoinsieme?
• Perché Sara appartiene all’insieme e anche al sottoinsieme?
sottoinsieme dei bambini con i jeans
La situazione è stata rappresentata con un diagramma: il diagramma di Venn
136 DATI E PREVISIONI
Anna
Chiara
Marco
Sara Tommy
Fabio Luca
........................................................................................................................................................................................................................
DATI E PREVISIONI
RELAZIONI,
RAPPRESENTARE CON I DIAGRAMMI
1 Osserva la rappresentazione. Poi completa e rispondi. Se non ricordi i nomi dei bambini, guarda a pagina 136.
bambini con
bambini con bambini con
Questo è l’insieme intersezione
• Marco appartiene all’insieme intersezione? Sì NO Perché? .............................................................
• Sara appartiene all’insieme intersezione? Sì NO Perché?
• Tommy appartiene all’insieme intersezione? Sì NO Perché?
2 Per rappresentare la situazione puoi usare anche altri diagrammi.
• Il diagramma di Carroll bambini con maglietta a maniche corte bambini senza maglietta a maniche corte bambini con jeans bambini senza jeans
• Il diagramma ad albero con jeans
con maglietta a maniche corte
senza maglietta a maniche corte
senza jeans
con maglietta a maniche corte
senza maglietta a maniche corte
I MIEI ESERCIZI PAGINA 186 137 RELAZIONI, DATI E PREVISIONI
LE RELAZIONI
Lorenza e Sebastian hanno alcune figurine di animali e vogliono sapere in quali ambienti vivono questi animali.
1 Aiuta i due amici a stabilire le relazioni giuste: collega con delle frecce ciascun animale al suo ambiente di vita.
bosco savana mare montagna deserto
2 Le relazioni fra gli animali e il loro ambiente di vita sono state rappresentate con un diagramma sagittale, in cui ciascuna freccia vuol dire: “vive in…”.
Una relazione è un legame tra due o più elementi secondo una regola
3 Le relazioni fra gli elementi di due insiemi possono essere rappresentate anche con una tabella a doppia entrata.
4 Completa la tabella come nell’esempio.
vive in bosco savana mare montagna deserto zebra X volpe
stambecco
cammello pesce
138 RELAZIONI, DATI E PREVISIONI
LE INDAGINI
Gli alunni di una classe 3ª devono effettuare un’indagine fra di loro per sapere dove vorrebbero trascorrere una settimana di vacanza.
I bambini iniziano subito il lavoro dopo aver definito, insieme all’insegnante, i punti che si devono seguire per svolgere un’indagine.
1. Definire l’argomento dell’indagine.
• “Dove vorresti trascorrere una settimana di vacanze?”
2. Stabilire qual è la popolazione a cui rivolgere la domanda.
• I bambini della classe 3ª.
3. Rivolgere la domanda a ciascun elemento della popolazione considerata e raccogliere le risposte in una tabella .
4. Rappresentare le informazioni ottenute con un grafico
al mare in un campo sportivo in un agriturismo in una città d’arte in montagna
Luoghi Preferenze al mare x x x x in un campo sportivo x x x x x x x x x in un agriturismo x x x x x x in una città d’arte x in montagna x x
• Per leggere in modo corretto il grafico, è necessario fornire la legenda , che indica il significato di ciascun riquadro.
Legenda = 1 preferenza
Il numero di preferenze per ciascun dato si chiama frequenza . Il dato che si presenta con maggior frequenza si chiama moda .
5. Ricavare le conclusioni.
Dall’indagine effettuata, i bambini hanno dedotto che:
• la moda, cioè il dato che si presenta con maggior frequenza, è il campo sportivo;
• il dato che si presenta con minor frequenza è la città d’arte.
I MIEI ESERCIZI PAGINA 187 139 RELAZIONI, DATI E PREVISIONI
1 2 3 4 5 6 7 8 9
CERTO, POSSIBILE, IMPOSSIBILE
È possibile che esca il numero 5.
È impossibile che esca il 95.
Un evento è certo quando sicuramente si verificherà .
Un evento è possibile quando può verificarsi oppure può non verificarsi
Un evento è impossibile quando sicuramente non si verificherà .
PROVO IO
È certo che uscirà un numero fra l’1 e il 90!
1 Osserva la situazione e indica con una X se le affermazioni sono vere ( V ) o false (F ).
In un sacchetto ci sono 6 caramelle all’arancia e 4 caramelle alla menta.
Manuela deve prendere una caramella a occhi chiusi.
• È certo che prenderà una caramella all’arancia. V F
• È possibile che prenderà una caramella all’arancia. V F
• È possibile che prenderà una caramella alla fragola. V F
• È certo che prenderà una caramella. V F
• È possibile che prenderà una caramella alla menta. V F
• È impossibile che prenderà una caramella alla crema. V F
• È possibile che prenderà un cioccolatino. V F
2 Disegna il contenuto di questo cassetto in modo che, se prendi a occhi chiusi quello che contiene:
• è certo che tu prenda un pastello;
• è possibile che tu prenda un pastello verde;
• è possibile che tu prenda un pastello rosso;
• è impossibile che tu prenda un pastello giallo.
140 RELAZIONI, DATI E PREVISIONI
PROBABILITÀ
Tra gli eventi possibili, alcuni hanno più probabilità di altri di verificarsi.
1 Leggi, osserva e rispondi.
Per la festa della loro nonna, Michele e Clara mettono in tavola un vassoio di pasticcini: alcuni alla frutta, altri al cioccolato, altri alla crema, altri alla panna.
• Quanti pasticcini ci sono sul vassoio?
• Quanti sono quelli alla frutta?
• Quanti sono quelli al cioccolato? ...........................................
• Quanti sono quelli alla panna?
• Quanti sono quelli alla crema?
• Secondo te, se la nonna prende un pasticcino senza guardare, quale è più probabile che possa prendere?
• Perché?
2 Rappresenta la situazione nella tabella. Colora un riquadro per ciascun pasticcino.
141 RELAZIONI, DATI E PREVISIONI
RELAZIONI, DATI E PREVISIONI
Completa la mappa, inserendo le parole che seguono:
diagramma di Venn • popolazione • diagramma ad albero • grafico • diagramma di Carroll
La classificazione
è mettere insieme elementi con una o più caratteristiche comuni. Una classificazione può essere rappresentata in vari modi:
Compiere un’indagine
1) Definire l’argomento dell’indagine;
2) stabilire qual è la a cui rivolgere la domanda;
3) raccogliere le risposte;
4) ordinare le informazioni in un
Le previsioni si fanno per esprimersi sulla possibilità che un evento si realizzi.
L’evento può essere:
• certo, cioè si verificherà di sicuro;
• possibile , cioè potrebbe verificarsi;
• impossibile , cioè non si verificherà mai.
RIPASSO IN UN LAMPO MAPPA 142 I MIEI SCHEMI PAGINA 156
A B C D ..................................................................................
PAGINE STELLA
1 Leggi e completa il diagramma di Carroll.
Luca e Marta hanno l’ombrello e gli stivali.
Marco e Alice hanno solo l’ombrello.
Omar e Ivan hanno solo gli stivali. Roberto non ha ombrello e non ha stivali.
ombrello non ombrello stivali non stivali
2 Agli alunni della 3ª A è stato chiesto qual è il loro primo piatto preferito. Le risposte sono state registrate nell’ideogramma. Completa la tabella e l’istogramma. Poi rispondi.
Legenda
= 1 preferenza
risotto
pasta in bianco
pasta al pomodoro
lasagne
minestrone
ravioli
primi piatti preferenze
risotto
pasta in bianco
pasta al pomodoro
lasagne
minestrone
ravioli
Legenda = 1 preferenza
• Quanti bambini sono stati intervistati?
• Quale piatto ha avuto più preferenze?
• Quale piatto ha avuto meno preferenze?
• Qual è la moda?
VERIFICA 143
TUTTO OK?
.......................................................................
8 7 6 5 4 3 2 1
VERSO L’INVALSI
1 Osserva: chi è l’intruso?
Luca Simona Arianna
Silvia
A. Silvia.
B. Luca.
C. Arianna.
D. Simona.
2 Carola, Marta e Daniele giocano al gioco dell’oca con un solo dado.
Carola dice: – Uscirà un numero minore di 7.
Daniele dice: – Uscirà un numero pari.
Marta dice: – Uscirà lo 0.
Chi esprime un evento certo?
A. Marta.
B. Daniele.
C. Carola.
D. Nessuno dei tre.
3 Il grafico rappresenta il numero di alunni delle classi terze che praticano sport di squadra.
3 a A
3 a B
3 a C
Quanti sono i bambini che praticano sport di squadra?
A. 11
B. 9
C. 12
D. 32
4 A una gara di corsa partecipano
4 ragazzi di 3ª A, 6 ragazzi di 3ª B e 5 ragazzi di 3ª C. Qual è la probabilità che arrivi primo un ragazzo di 3a A?
A. 7 su 15
B. 4 su 15
C. 5 su 15
D. 7 su 14
5 Osserva il diagramma di Carroll: con quale altro animale inseriresti il gatto?
domestico non domestico con 2 zampe gallina canarino aquila gufo con 4 zampe criceto cane tigre elefante
A. Con gallina e canarino.
B. Con tigre ed elefante.
C. Con criceto e cane.
D. Con aquila e gufo.
6 Osserva i due gruppi. Quale può essere il significato delle frecce?
A. “ È il doppio di”.
B. “ È la metà di”.
C. “ È il triplo di”.
D. “ È la terza parte di”.
144
30 12 25 75 90 36
QUADERNO DEGLI ESERCIZI
I MIEI SCHEMI
146 L’addizione
147 La sottrazione
148 La moltiplicazione
149 La divisione
150 I problemi
151 Le frazioni
I MIEI ESERCIZI
157 I numeri fino a 999
158 I numeri da 0 a 9 999
160 L’addizione
161 Addizioni in riga e in colonna
162 La sottrazione
163 Sottrazioni in riga e in colonna
164 Addizioni e sottrazioni
166 Addizione o sottrazione?
167 La moltiplicazione
168 Tante moltiplicazioni
169 Moltiplicazioni in colonna
170 La divisione
171 Moltiplicazioni e divisioni
172 Ancora moltiplicazioni e divisioni
152 I numeri decimali
153 Le misure
154 Solidi, linee e angoli
155 I poligoni
156 Relazioni, dati e previsioni
174 Problemi: al lavoro con Amanda!
175 Frazioni e numeri decimali
176 Ancora frazioni e numeri decimali
177 L’euro: acquisti e alla posta
178 Tante misure
179 Lunghezza, peso, capacità
180 Ancora misure
181 Figure geometriche
182 Figure geometriche e simmetrie
184 Angoli e poligoni
185 I poligoni
186 Gli insiemi
187 Relazioni, dati e previsioni
LABORATORIO STEM 188 Le avventure della capitana Tilly
L’ADDIZIONE
Completa testo e operazioni.
Addizionare vuol dire…
mettere insieme due o più oppure una quantità a un’altra.
Il segno dell’addizione è
Le proprietà
COMMUTATIVA
Se cambio , il risultato .
ASSOCIATIVA
Se sostituisco
I termini sono:
40 + 13 =
, il risultato non cambia.
Devo sommare prima le ( ), poi le ( ), le ( ) e le ( ).
25 + 16 =
=
60 + 18 + 12 =
=
Quando la somma è superiore al , faccio il ............................................
I MIEI SCHEMI 146 Consulta la MAPPA pag. 24
+
+
In colonna k h da u 2 3 2 5 + 1 1 7 3 =
da h da u 3 4 3 5 + 3 2 6 7 = ........... ........... ........... ...........
LA SOTTRAZIONE
Completa testo e operazioni.
Sottrarre vuol dire…
togliere una quantità più da una quantità più , calcolare la ............................... tra due quantità o quanto per completare una quantità.
Il segno della sottrazione è
La proprietà
I termini sono:
67 – 22 =
INVARIANTIVA
Se aggiungo o sottraggo lo stesso
............................... a entrambi i ............................... della sottrazione, il risultato .
38 – 23 =
In colonna k h da u
Devo sottrarre prima le ( ), poi le ........................... (.........), le ........................... (.........) e le ( )
– = h da u
Quando il è maggiore del , faccio il cambio.
........... ........... ...........
L’addizione e la sottrazione sono operazioni inverse. Se la mia sottrazione è stata esatta, sommando ...................................................... otterrò
I MIEI SCHEMI 147 Consulta la MAPPA pag. 36
Operazioni inverse
2 6 7 9
1 5 1 4
–
=
3 5
1 5 4
4
–
=
LA MOLTIPLICAZIONE
Completa testo e operazioni.
Moltiplicare vuol dire…
ripetere più volte la stessa
I termini sono:
9 8 = fattori
Le proprietà
COMMUTATIVA
. Il segno della moltiplicazione è 15 3 =
Se cambio l’ordine dei , il risultato .
ASSOCIATIVA
Se sostituisco due con il loro prodotto, il risultato .
DISTRIBUTIVA
Il risultato non cambia se scompongo un in un’addizione, poi ogni addendo per l’altro fattore e ........................................... i loro prodotti.
In
I MIEI SCHEMI 148 Consulta la MAPPA pag. 46
.........
6 5 3 = 3 = 28 4 = ( + ) = ( ) + ( ) = + =
......... = .........
Infine
h da u 7 2 1 5 = = .......... .......... ..........
colonna Moltiplico per . Aggiungo , quindi moltiplico ...................................................................... per
.
LA DIVISIONE
Completa testo e operazioni.
Dividere vuol dire… distribuire oppure una
quantità in parti .
Il segno della divisione è .
La proprietà INVARIANTIVA
In colonna
I termini sono:
27 : 3 = resto 0
Quando c’è il resto, il risultato si definisce
Se divido o moltiplico per lo stesso numero il e il
, il risultato
.
Abbasso col cappellino ogni cifra del ........................................... poi, aiutandomi con le tabelline, conto quante volte il è contenuto nel
Facendo la , ottengo .
Se la prima cifra del dividendo è .......................................... del divisore, considero anche la cifra successiva.
100 : 20 = ......... : ......... = .........
...... ......
Operazioni inverse
Se la mia divisione è stata esatta, moltiplicando ...................................................................................... otterrò .
7 2 3 ––
I MIEI SCHEMI 149 Consulta la MAPPA pag. 58
I PROBLEMI
Completa e inventa un problema.
Le parti del problema
La risoluzione del problema
Ogni problema è composto da un che contiene una o più . Il testo del problema fornisce tutti i che sono necessari per arrivare alla soluzione.
1) Leggere attentamente il testo: ?
2) Individuare e capire la domanda: Devo riuscire a .................................................................................................................
3) Trovare e analizzare i dati:
4) Scoprire se ci sono domande nascoste, dati , dati inutili o dati nascosti.
Domanda nascosta: .......................................................................................................
5) Scoprire le operazioni da eseguire: .........................................................................................................................................................
6) Eseguire le operazioni:
7) Verificare di aver trovato una tutte le risposte necessarie:
I MIEI SCHEMI 150 Consulta la MAPPA pag. 78
LE FRAZIONI
Completa e inventa una frazione.
Frazionare vuol dire…
dividere l’intero in parti .
Ciascuna parte in cui viene diviso si chiama unità .
I termini
Come si scrive e come si legge una frazione
Il numeratore indica quante dell’intero sono state considerate.
La linea di frazione vuol dire che l’ è stato diviso in parti .
Il denominatore indica in quante ............................................ è stato diviso l’intero.
L’intero è stato diviso in parti:
ognuna di queste parti è “............................................”.
Di queste, vengono prese in considerazione parti, quindi “ ”.
La frazione “ ” vuol dire anche “ volte ............................................”.
I MIEI SCHEMI 151 Consulta la MAPPA pag. 84
I MIEI SCHEMI
I NUMERI DECIMALI
Completa e inventa alcune frazioni decimali con i corrispondenti numeri decimali.
Frazione decimale vuol dire… Numero decimale vuol dire…
una frazione che ha come denominatore , , .
un numero con la virgola: in un numero decimale la virgola separa la parte dalla parte .
Frazioni decimali e numeri decimali
Decimi
• frazione decimale:
• numero decimale:
Centesimi
• frazione decimale:
• numero decimale:
Millesimi
• frazione decimale:
• numero decimale:
PARTE INTERA PARTE DECIMALE
u unità d decimi c centesimi m millesimi ,
PARTE INTERA PARTE DECIMALE
u unità d decimi c centesimi m millesimi
,
......... ......... .........
PARTE INTERA PARTE DECIMALE
u unità d decimi c centesimi m millesimi ,
152 Consulta la MAPPA pag. 92
LE MISURE
Completa.
Lunghezza
MULTIPLI UNITÀ DI MISURA SOTTOMULTIPLI
chilometro ettometro decametro metro decimetro centimetro millimetro
1 000 m 100 m 10 m 1 m 1 10 di m 1 100 di m 1 1 000 di m
Capacità
MULTIPLI UNITÀ
DI MISURA
SOTTOMULTIPLI hℓ ettolitro daℓ decalitro ℓ litro dℓ decilitro cℓ centilitro mℓ millilitro ℓ ℓ 1 ℓ 1 ...... di ℓ 1 di ℓ 1 di ℓ
Peso
MULTIPLI UNITÀ
DI
MISURA SOTTOMULTIPLI h di kg da di kg
1 000 kg 100 kg 10 kg 1 kg 1 10 di kg 1 100 di kg 1 1 000 di kg
UNITÀ DI MISURA
SOTTOMULTIPLI
g grammo decigrammo centigrammo .............. milligrammo 1 g
Le misure di valore
Per misurare il valore degli oggetti si usa il denaro. L’ è la moneta ufficiale usata in Italia e in molti Paesi d’Europa. Il suo simbolo è .............. L’euro ha un solo sottomultiplo: il .
Le misure di tempo
s secondo minuto ora ..............
I MIEI SCHEMI 153 Consulta la MAPPA pag. 112
= 60
= 60
= 24
1
=
=
giorno .............. settimana mese anno
s
min
h
settimana
7 1 mese
30 1 anno = 12
SOLIDI, LINEE E ANGOLI Completa.
Hanno 3 dimensioni: altezza, larghezza,
I solidi
La linea
Linea retta, semiretta, segmento
• I confini di un poliedro si chiamano ;
• l’incontro di 2 da’ origine a uno spigolo;
• il punto di incontro di 3 spigoli
è un insieme infinito e continuo di .................................................... e ha una sola
dimensione: la . Una linea può essere:
• retta o ;
• aperta o ; • o intrecciata; • o mista.
La linea retta è una linea , che non ha né inizio né fine. Si indica con una lettera .
La semiretta è una linea che ha un inizio ma non ha una .................................
Il punto O è .
Il segmento è una parte di
Gli estremi si indicano .
Due rette possono essere:
• parallele , quando mantengono sempre la stessa e non si incontrano mai;
• incidenti, quando si incontrano in un punto e dividono il piano in ;
• perpendicolari , quando sono e dividono il piano in quattro .
L’angolo è una parte di compresa tra due che hanno la stessa ............................................. A seconda della sua ampiezza un angolo può essere:
• ;
• retto;
• ....................................................;
• ; • .
I MIEI SCHEMI 154 Consulta la MAPPA pag. 124
I POLIGONI
Completa e disegna un poligono.
Il poligono
è una figura piana delimitata da una .........................................................................................
• I lati sono i che formano il di un poligono;
• la superficie è la parte di racchiusa dai .
• il vertice è il in cui due si incontrano e si indica con una ;
• l’angolo è ................................................................................................................................................................
Perimetro e area
Il perimetro è la misura del .................................................................................................................... L’area è la misura della cioè la parte di piano
La simmetria è il ribaltamento di una figura , che è il suo ..................................................................................................................................................................
155 Consulta la MAPPA pag. 134
I MIEI SCHEMI
RELAZIONI, DATI E PREVISIONI
Completa e disegna i diagrammi richiesti.
La classificazione
è mettere insieme .
Una classificazione può essere rappresentata in vari modi:
DIAGRAMMA DI VENN:
DIAGRAMMA DI CARROLL:
DIAGRAMMA AD ALBERO:
Compiere un’indagine
1) Definire l’ dell’indagine;
2) stabilire qual è la popolazione a cui rivolgere la ;
3) raccogliere le ;
4) ordinare le ......................................... in un grafico.
Le previsioni si fanno per esprimersi sulla ......................................... che un evento si realizzi. L’evento può essere:
• , cioè si verificherà di sicuro;
• , cioè potrebbe verificarsi;
• , cioè non si verificherà mai.
I MIEI SCHEMI 156 Consulta la MAPPA pag. 142
I NUMERI FINO A 999
1 Completa come nell’esempio. trecentoventuno duecentocinquanta seicentonove settecentododici novecentodiciotto cinquecentoventi
2 Completa le sequenze in ordine crescente o in ordine decrescente.
• numero maggiore:
• numero minore:
• numero maggiore:
• numero minore:
197 • • • • • • • • • • 207 429 • • • • • • • • • • 439 534 • • • • • • • • • • 524 902 • • • • • • • • • • 892
+ 1 u + 1 da + 1 h 19 138 240 588 799 – 1 u – 1 da – 1 h 120 271 409 550 891
3 Completa le tabelle.
321 300 + 20 + 1 h da u 3 2 1 1 7 6 4 0 8
4 Per ciascun gruppo di cifre, forma il numero maggiore e minore possibile.
I MIEI ESERCIZI 157
I NUMERI DA 0 A 9 999
1 Confronta le coppie di numeri con i segni <, = oppure >.
4 da 46 u 20 da 2 h 9 h 8 da 599 u 60 da
750 u 75 da 100 u 9 h 99 da 9 h 65 da 7 h
2 Riscrivi i numeri in ordine crescente.
702 • 910 • 358 • 77 • 538 • 184 • 190
3 Riscrivi i numeri in ordine decrescente.
473 • 601 • 990 • 19 • 72 • 27 • 909
4 In ciascun gruppo, cerchia di blu il numero maggiore e di verde il numero minore.
5 Completa le tabelle.
6 Scrivi il precedente e il successivo. Segui le frecce.
–1 +1
10 da 5 h 1 k
400 3 120 2101
005 10 da 5 h 1 k 1 349 1 901 2 490 3 015
4
1
3 089 3 999 6 000 4 679 1 001 5 600 2 010 7 885 9 000 6 100 543 250 520 764 875 790 709 568 865 194 934 589 321 471 765 + –I MIEI ESERCIZI 158
7 Leggi questi numeri scritti in lettere e scrivili in cifre, ordinandoli dal maggiore al minore.
milleduecentotre • cinquecento • duemilacentotrentasette • tremilacentocinquanta • millequattrocento • cinquemilacentosettanta • milleduecentosette • quattromilacinquecentouno
8 Componi i numeri.
9 Scomponi i numeri.
3258 792 4998 2102 ............................................................................................................................... ..................................................................................... 3823 8949 316 1004 5050 6281
1 k, 8 h, 3 da
9 da, 5 h, 1 k
2 k, 7 da, 5 u
6 u, 2 k, 3 da
4 k, 8 u 2 h, 2 k, 4 u
1 k, 6 h, 1 u
I MIEI ESERCIZI 159
3 k, 8 u, 9 da
1 Segna con una X l’affermazione non vera.
L’elemento neutro dell’addizione è lo 0.
Se cambio l’ordine degli addendi il risultato cambia.
Gli addendi sono i termini dell’addizione.
È sempre possibile eseguire un’addizione.
2 Qual è il risultato corretto di questa addizione? 1295 + 3da
3 Calcola a mente e collega ogni addizione al risultato corrispondente.
4 Verifica se le addizioni sono giuste o sbagliate, poi correggi quelle sbagliate.
3482 + 827 =
906 + 874 =
L’ADDIZIONE
4318
1780
1503
1582 1807 + 203 = 2000 2094 + 1501 = 3595 5009 + 374 = 5383 250 + 25 1200 + 400 240 4000 308 + 12 2050 + 150 1000 1200 120 + 120 2000 + 2450 275 2200 400 + 37 3900 + 100 700 1600 590 + 110 4999 + 1001 320 4450 855 + 145 1180 + 20 437 6000
179 +
=
1330 1298 1595 1325 I MIEI ESERCIZI 160
ADDIZIONI IN RIGA E IN COLONNA
1 Segui i segni <, >, = e completa nel modo opportuno.
A. 20 + 5 > 20 +
50 + 8 < 50 +
35 + 15 = +
40 + = 30 +
74 + > +
82 + < +
B. 125 + 25 > 125 +
200 + = 180 +
320 + 80 < +
408 + > +
500 + = +
750 + < 750 +
2 Esegui velocemente le addizioni e cerchia di rosso quelle con il risultato > di 1 000.
600 + 280 = 250 + 758 = 390 + 430 =
850 + 400 = 585 + 505 = 320 + 80 =
950 + 50 = 730 + 275 = 892 + 110 =
3 Completa le addizioni in colonna.
4 Esegui le addizioni sul quaderno e indica con una X se i risultati sono veri (V) o falsi (F). 1
758 + 394 = 2 152 V F 875 + 2 489 + 6 = 3
V F
906 + 2 785 = 8 619 V F 3 642 + 875 + 72 = 4 589 V F
512 + 1 487 = 5 927 V F 24 + 5 608 + 795 = 5 429 V F
058 + 973 = 7 031 V F 607 + 93 + 1 879 = 2 579 V F
730
5
4
6
k h da
3 8 + 1 4 2 = 3 9 9 k h da u 1 3 0 5 + 2 = 4 1 8 k h da u 1 5 8 + 4 1 = 3 8 4 k h da u 9 4 + 4 7 = 6 0 4 k h da u 4 4 9 + 2 5 = 1 1 k h da u 7 0 4 + 7 = 9 0 6 0
u
I MIEI ESERCIZI 161
LA SOTTRAZIONE
1 Completa la regola e poi applica la proprietà invariantiva per risolvere le sottrazioni.
Se aggiungo o tolgo lo a entrambi della , il risultato non cambia.
47
47
2 Qual è il sottraendo misterioso? Osserva i risultati e completa, poi verifica facendo la prova sul quaderno.
da u –........ ........ = da u –........ ........ = 89 – = 23 h da u –= h da u –= 77 – = 61 381 – = 364 260 – = 70 h da u –........ ........ ........ = h da u –= 100 – = 45 415 – = 359
12
– 2 – 2
–
=
– 17
................................. – 7 – 7
=
9
+ 1 + 1
– 7
................................. +3 +3 24 – 19
................................. – 4 – 4
17
– 5 – 5
14 –
=
21
=
=
47 –
=
12
– 2 – 2
– 24
................................. +1 +1 I MIEI ESERCIZI 162
37 –
=
39
=
SOTTRAZIONI IN RIGA E IN COLONNA
1 Esegui le sottrazioni, poi riscrivi i risultati dal maggiore al minore.
249 – 19 = 209 – 11 =
568 – 31 = 365 – 42 =
137 – 9 = 485 – 29 =
426 – 50 = 300 – 65 =
2 Esegui le sottrazioni. Poi segui le indicazioni.
350 – 125 = 2 h – 7 u =
184 – 39 =
3 h – 4 da = 475 – 215 = 462 – 128 =
• Cerchia di rosso le operazioni con lo stesso risultato.
• Cerchia di viola la sottrazione con il risultato maggiore
• Cerchia di verde la sottrazione con il risultato minore.
3 Scopri il segreto di questo “gioco” e poi proponilo ai tuoi amici o alle tue amiche.
Luca pensa un numero, aggiunge 17 e ottiene 39.
• Quale numero ha pensato Luca?
• Quale operazione hai fatto per scoprirlo?
4 Completa le sottrazioni con i numeri mancanti.
h da u
.
k
7 5 8 –1 9 = 1 4 5 k h da u 6 5 2 –0 8 = 1 8 7 k
3 2 8 –5 4 = 1 6 2
ESERCIZI 163
h da u
I MIEI
MIEI
ADDIZIONI E SOTTRAZIONI
1 Applica la proprietà associativa dell’addizione e calcola a mente.
26 + 5 + 4 =
71 + 13 + 9 =
8 + 42 + 7 =
15 + 90 + 10 =
300 + 200 + 88 =
250 + 15 + 50 =
2 Esegui le addizioni sul quaderno e verifica i risultati con la prova.
349 + 257 = 126 + 67 = 384 + 759 = 1 095 + 699 = 1 378 + 746 =
1 908 + 2 364 = 573 + 867 = 2 548 + 863 = 924 + 3 785 = 29 + 457 + 398 =
1 654 + 583 = 427 + 698 = 965 + 1 099 = 2 176 + 1 953 = 175 + 308 + 999 =
3 Completa le tabelle.
+ –
4 Collega con una ciascuna sottrazione al risultato corrispondente.
– 135 =
5 Esegui le sottrazioni con la prova sul quaderno.
438 – 125 = 985 – 362 =
760 – 459 = 829 – 568 =
904 – 381 = 756 – 228 =
1 761 – 925 = 1 803 – 724 =
6 Risolvi i problemi sul quaderno.
A. Al bar, Ernesto prepara 8 panini al tonno, 15 panini al formaggio e 13 panini al pomodoro.
Quanti panini prepara in tutto Ernesto?
1 u 1 da 1 h 99 120 586
1 u 1 da 1 h 101 190 500
1 010
1 011
418 235 122 1044 257
803
1 920
876 =
186
951
I
B. Al ristorante, Edoardo prepara 192 tramezzini. Quelli al tonno sono 105. Quanti sono i tramezzini con altri gusti? ESERCIZI 164
– 385 =
–
1
–
=
I MIEI ESERCIZI
7 Completa la tabella.
Usa le proprietà dell’addizione e le tecniche per il calcolo veloce.
8 Completa la tabella.
Usa la proprietà della sottrazione e le tecniche per il calcolo veloce.
+ –
50 32 160 205
125
180
309
471
9 Completa le operazioni con il numero mancante.
456 + = 656 + 11 = 839 375 – 125 = + 49 = 369 2 340 + = 2 451 890 – = 805
510 + 75 = 109 – = 90 – 500 = 2 100
1 038 + = 1 650 – 200 = 341 3 040 – = 2 940
10 Esegui le addizioni in colonna sul quaderno.
1 397 + 185 = 683 + 1 849 =
2 035 + 1 496 = 4 729 + 2 395 =
1 904 + 958 = 78 + 4 587 =
11 Esegui le sottrazioni in colonna sul quaderno.
3 925 – 1 468 = 1 005 – 638 =
4 307 – 2 851 = 2 490 – 723 =
2 500 – 1 947 = 1 580 – 1 294 =
12 Indica con una X se le seguenti affermazioni sono vere (V) o false (F).
• Addizionare significa unire due o più quantità. V F
• I termini dell’addizione si chiamano fattori. V F
• Lo zero è l’elemento neutro dell’addizione. V F
• L’addizione e la sottrazione sono due operazioni inverse. V F
• È sempre possibile eseguire una sottrazione. V F
• Il primo termine della sottrazione si chiama minuendo. V F
• Per calcolare la differenza si deve eseguire un’addizione. V F
174
35 70 109
180 300 498 509
165
ADDIZIONE O SOTTRAZIONE?
1 Leggi attentamente i problemi e poi colora il pulsante “+” o “–” per scegliere l’operazione da utilizzare. Quindi risolvi le operazioni e scrivi la risposta.
a In un parcheggio sostano 250 automobili, 15 motociclette e 3 camper. Quanti veicoli sono presenti in tutto nel parcheggio?
+ –
OPERAZIONE:
RISPOSTA:
b In un parcheggio sostano 250 automobili e 15 motociclette. Quante sono le automobili in più rispetto alle motociclette?
+ –
OPERAZIONE:
RISPOSTA:
c L’arciera Joella ha 21 frecce nella sua faretra. Stamattina ne ha scoccate 15 per esercitarsi. Quante frecce le sono rimaste?
+ –
OPERAZIONE:
RISPOSTA:
d Dopo essersi esercitata con l’arco, Joella riceve in regalo da sua madre, la regina Sandra, altre 100 frecce. Quante frecce ha ora Joella?
+ –
OPERAZIONE:
RISPOSTA:
ESERCIZI 166
I MIEI
LA MOLTIPLICAZIONE
1 Completa le tabelle.
2 Calcola a mente associando i fattori, come nell’esempio.
4 x 3 x 5 = 4 x 5 x 3 = 20 x 3 = 60
6 x 10 x 5 =
4 x 6 x 5 =
15 x 5 x 2 =
9 x 2 x 100 =
15 x 6 x 2 =
3 Qual è il risultato corretto di questa moltiplicazione? 36 x 18
748
4 Esegui in colonna. 49 x 9 =
658
648
x 2 4 5 7 8 1 7 8 x 2 4 5 6 8 0 3 9
108
87
59
19
69
200
I MIEI ESERCIZI 167
x 4 =
x 13 =
x 76 =
x 18 =
x 42 = 712 x 87 =
x 70 =
TANTE MOLTIPLICAZIONI
1 Indica con una X se le seguenti uguaglianze sono vere (V) o false (F).
3
2 Completa le moltiplicazioni con i numeri mancanti.
3 Le seguenti moltiplicazioni non sono corrette. Controlla e spiega l’errore, poi esegui correttamente sul quaderno.
4
6 2 V F 6 6 = (5 7) + 1 V F 7 7 = (2 5 5) – 1 V F
6 = 8 9 V F 7 4 = (9 3) + 3 V F 8 6 = 4 4 3 V F
9 = 8 8 V F 9 9 = (9 10) – 9 V F 5 9 = (7 7) – 2 V F 4 5 = 3 7 V F 4 8 = (5 6) + 2 V F 3 6 = (2 9) + 4 V F 3 3 = 9 0 V F 7 9 = (8 9) – 8 V F 6 5 = (5 7) – 5 V F
=
7
6
h
u 4 6 8 = 6 8 h da u 7 3 4 = 2 9 h da u 2 6 3 = 6 4 8 h da u 4 9 6 = 8 4 h da u 3 5 1 7 = 2 5 + 3 5 = 5 5 k h da u 4 9 8 = 8 + 3 9 2 0 = 0 k h da u 2 6 7 8 = 8 + 1 8 2 = 0 2 k h da u 8 6 3 4 = 3 2 4 + 2 4 8 0 = 2 8 0 4 k h da u 9 3 4 5 = 4 6 5 + 3 7 2 = 8 3 7 k h da u 6 7 4 9 = 5 4 3 + 2 4 8 0 = 2 9 2 3 I MIEI ESERCIZI 168
da
MOLTIPLICAZIONI IN COLONNA
1 Esegui in colonna la seguente moltiplicazione: Rifletti e completa il percorso che hai seguito.
1. Metto in colonna i numeri.
2. Moltiplico
3. Scrivo
4. Moltiplico
5. Aggiungo
6. Scrivo
2 Metti in colonna le moltiplicazioni e calcola.
3 Esegui le moltiplicazioni in colonna sul quaderno.
4 Esegui le moltiplicazioni sul quaderno e verifica i risultati con la prova.
A. 23 3 = 34 2 = 21 4 = 32 2 = 124 2 = 231 3 = B. 28 2 = 26 4 = 35 5 = 42 6 = 14 7 = 15 8 = C. 127 3 = 238 2 = 326 4 = 106 6 = 124 8 = 324 3 =
A. senza cambio 23 12 = 41 22 = 13 23 = 21 14 = B. con un cambio 38 12 = 17 15 = 92 18 = 43 27 = C. con più cambi 39 32 = 342 28 = 67 35 = 127 35 = 56 46 = 209 36 = 84 58 = 564 43 =
h da u = 35 8 = h da u = 93 5 = h da u = 107 4 = h da u = 136 7 = h da u =
37
I MIEI ESERCIZI 169
4 =
LA DIVISIONE
1 Indica con una X se le seguenti uguaglianze sono vere (V) o false (F).
24 : 6 = 28 : 7 V F 49 : 7 = 63 : 9 V F 99 : 9 = 66 : 6 V F
64 : 8 = 63 : 9 V F 84 : 7 = 72 : 9 V F 84 : 7 = 28 : 2 V F
45 : 5 = 81 : 9 V F 128 : 4 = 192 : 6 V F 306 : 6 = 304 : 4 V F
72 : 6 = 48 : 4 V F 145 : 5 = 161 : 7 V F 135 : 3 = 225 : 5 V F
2 Leggi i problemi, rifletti e risolvi sul quaderno.
A. Oggi nonna Sofia compie 65 anni. Poiché 65 candeline sono tante, il nipotino Carlo decide che ciascuna candelina che verrà messa sulla torta avrà il valore di 5 anni.
Quante candeline ci saranno sulla torta di nonna Sofia?
• Scrivi il tuo ragionamento per arrivare alla soluzione.
3 Continua queste divisioni.
B. Quale soluzione si potrebbe trovare per l’altra nonna di Carlo, che fra qualche giorno compirà 68 anni?
• Scrivi il tuo ragionamento per arrivare alla soluzione.
7 4 8 6 9 3 7 5 4 3 6 7 3 9 4 8
170
I MIEI ESERCIZI
MOLTIPLICAZIONI E DIVISIONI
1 Esegui le moltiplicazioni sul quaderno e riporta il risultato.
24 3 =
37 5 =
2 Esegui le divisioni sul quaderno e riporta il risultato.
204 : 6 =
341 : 8 =
198 : 5 =
: 4 =
3 Esegui le operazioni sul quaderno e poi sottolinea in rosso quelle sbagliate e in verde quelle corrette.
357 7 = 2 499
284 6 = 1 704
79 23 = 1 870
4 Calcola in riga le moltiplicazioni e le divisioni con 10, 100, 1000.
48
55 9
135 4 = 37 16 = 49 24 = 85 14 = 26 15 = 72 61 = 83 16 = 45 60 =
2 =
=
564
718
9
345
5 = 682
7 = 386
3 = 814
7 = 903 : 8 = 745 : 5 = 864
6 =
:
=
:
:
:
:
:
45 58
448
8 = 54 972 : 6 = 162 675
5 = 130 882
7 = 126 561
3 = 187
= 2 006
:
:
:
:
7 10 = 40 : 10 = 52 10 = 600 : 100 = 7 100 = 3500 : 10 = 52 1000 = 2000 : 1000 = I MIEI ESERCIZI 171
ANCORA MOLTIPLICAZIONI E DIVISIONI
1 Calcola velocemente le moltiplicazioni e colora il risultato corretto.
2 Esegui le moltiplicazioni in colonna sul quaderno.
3 Indica con una X se i risultati delle seguenti divisioni sono veri (V) o falsi (F).
4 Esegui le divisioni sul quaderno, poi cerchia di rosso quelle che hanno come risultato un quoto e di verde quelle che hanno come risultato un quoziente.
5 Risolvi i problemi sul quaderno.
A. Marco ha disegnato un albero con 6 rami. Vuole attaccare su ciascun ramo lo stesso numero di foglie. Ha ritagliato 36 foglie. Quante foglie ci saranno su ciascun ramo?
B. Sul trenino del parco possono salire 18 bambini. In un pomeriggio il trenino ha fatto 6 volte il percorso stabilito. Quanti bambini sono saliti in tutto sul trenino?
7 3 = 24 21 6 4 = 24 32 2 9 = 16 18 5 8 = 40 45 9 7 = 36 63 8 3 = 24 32 6 6 = 42 36 3 6 = 18 15 9 4 = 45 36
74 5 = 48 7 = 138 7 = 1 067 4 = 39 4 = 61 9 = 409 2 = 3 750 3 = 95 6 = 57 8 = 395 8 = 6 182 6 = 28 3 = 19 2 = 174 9 = 2 804 5 =
28 : 4 = 7 resto 0 V F 38 : 6 = 6 resto 0 V F 60 : 9 = 10 resto 0 V F 36 : 7 = 5 resto 1 V F 30 : 4 = 7 resto 2 V F 52 : 8 = 6 resto 4 V F 20 : 3 = 6 resto 1 V F 72 : 9 = 8 resto 0 V F 53 : 7 = 6 resto 2 V F
75 : 4 = 58 : 3 = 53 : 2 = 308 : 2 = 128 : 3 = 81 : 9 = 48 : 7 = 72 : 6 = 104 : 4 = 948 : 6 = 86 : 2 = 95 : 5 = 450 : 5 = 428 : 7 = 240 : 8 =
MIEI ESERCIZI 172
I
6 Osserva e scrivi l’operatore sulle frecce.
7 Esegui le moltiplicazioni. Usa la proprietà distributiva.
16 4 =
37 5 =
24 3 =
13 7 =
26 8 =
9 Esegui le moltiplicazioni in colonna sul quaderno.
24 36 = 308 14 =
53 18 = 427 36 =
19 24 = 194 28 =
72 15 = 295 63 =
48 27 = 104 25 =
39 43 = 812 28 =
8 Esegui le divisioni sul quaderno. Usa la proprietà invariantiva.
32 : 4 =
96 : 6 =
48 : 8 =
75 : 15 =
96 : 12 =
10 Esegui le divisioni in colonna sul quaderno.
870 : 5 = 1 248 : 6 =
129 : 7 = 3 087 : 8 =
306 : 4 = 2 750 : 7 =
295 : 8 = 1 302 : 9 =
938 : 6 = 8 472 : 5 =
294 : 3 = 6 048 : 9 =
11 Per ciascuna affermazione, scrivi se si riferisce alla moltiplicazione o alla divisione.
• Significa distribuire in parti uguali.
• I suoi termini si chiamano fattori.
• Il risultato è il prodotto.
• Può avere il resto.
• Il primo termine è il dividendo.
• Se non ha il resto, il suo risultato si chiama quoto.
• Uno dei due termini si chiama moltiplicatore.
85 850 14 1 400 90 9 7 200 72 5 000 50 17 1 700
49 125 12 500 8 000 8
49 0
I MIEI ESERCIZI 173
PROBLEMI: AL LAVORO CON AMANDA!
1 Leggi il testo dei problemi, scrivi le domande adatte e risolvi sul quaderno.
A. Amanda gestisce una palestra. Nel mese di gennaio Amanda ha incassato 50 euro da ognuno dei suoi 75 iscritti.
Domanda: ?
B. Amanda tiene per i suoi iscritti 5 lezioni a settimana, ma nel mese di febbraio ha dovuto saltare le ultime 2 lezioni.
Domanda: ?
C. Amanda decide di invitare degli esperti a tenere delle lezioni di danza. A queste lezioni speciali si presentano tutti gli iscritti della palestra più altre due dozzine di partecipanti.
Domanda: ?
2 Leggi il problema, scopri le domande nascoste e risolvi sul quaderno.
La dottoressa Rossi consiglia ad Amanda di tenere sempre, all’ingresso della palestra, una cesta con della buona frutta fresca da offrire a tutti. Oggi ci sono 4 banane, una dozzina di mele, una decina di pere e 20 arance.
Domanda: .............................................................................................................................................................................................. ?
Alla fine della giornata, nella cesta ci sono solo 1 banana e 1 arancia.
Domanda: ?
Se ogni persona che si è allenata oggi ha mangiato 2 frutti, quanti iscritti erano presenti in palestra?
I MIEI ESERCIZI 174
FRAZIONI E NUMERI DECIMALI
1 Scrivi in cifre e in parole le frazioni corrispondenti alla parte colorata, come nell’esempio.
5 un quinto
2 Colora la parte indicata dalla frazione.
3 Cerchia le frazioni decimali.
4 Collega con una ciascuna frazione decimale al numero decimale corrispondente.
5 Scrivi il numero decimale corrispondente alla scomposizione.
1
1 6 3 3 2 4 4 10 5 12
2 11 3 10 25 100 12 1 000 69 100 10 13 4 1 000 5 10
3 10 20 100 12 1 000 4 100 50 100 9 10 6 1 000 0,012 0,04 0,2 0,3 0,006 0,5 0,9
u, 6
3
= 1 u, 3 d, 5 c, 7 m = 3 u, 2 d, 1 m = 5 u, 5 c, 3 m = I MIEI ESERCIZI 175
0
d,
c
ANCORA FRAZIONI E NUMERI DECIMALI
1 Scrivi la frazione corrispondente alla parte colorata.
2 Rappresenta le frazioni con il disegno, come nell’esempio.
3 Collega con una ciascuna rappresentazione alla frazione in cifre e in parole corrispondente.
un decimo
nove decimi
sette decimi
cinque decimi
4 Completa la tabella.
8 10 3 8 4 8 7 12 3 5
9 10 7 10 1 10 5 10
numero k h da u , d c m 2,976 1 389,2 75,124 I MIEI ESERCIZI 176
L’EURO: ACQUISTI E ALLA POSTA
1 Leggi e risolvi.
Acquisti
Quattro amici decidono di fare acquisti con i loro risparmi e contano quanti euro ha ciascuno di loro:
• Luca ha due euro;
• Marco ha il triplo degli euro di Luca;
• Nicolò ha la metà degli euro di Luca;
• Paola ha il doppio degli euro di Nicolò.
Quanti euro possono spendere in tutto i quattro amici?
Euro
Marco
Luca
Nicolò ..........................................
Paola
Alla posta
A. Il signor Fabrizio deve spedire per posta dei documenti suddivisi in 4 buste. Il peso delle buste è il seguente:
• la prima busta pesa 16 g;
• la seconda busta pesa 245 g;
• la terza pesa 10 g più della prima.
Il peso totale delle buste è di 300 g.
• Quanto pesa la quarta busta?
Grammi
1a busta
2a busta
3a busta
B. Spedire una busta del peso inferiore a 100 g costa 1 euro; spedire una busta del peso superiore a 100 g costa 3 euro.
Quanto spende il signor Fabrizio per spedire le 4 buste?
I MIEI ESERCIZI 177
4a busta
TANTE MISURE
1 Leggi che cosa dicono questi bambini e indica con una X l’affermazione NON corretta.
A. Omar
B. Marta
Il ruscello è lungo 300 m, cioè 30 dam.
La mia cartella pesa 2 500 g, cioè più di 2 chili.
C. Alice
D. Luca
Questo bicchiere contiene 20 cℓ di succo, cioè 20 dℓ.
Ho in tasca
10 monete da 20 cent, cioè 2 euro.
2 Per arrivare a casa della sua amica, Anna deve fare un percorso di 500 metri. Se ha già fatto 400 metri, quanta strada deve ancora percorrere?
A. 10 metri
B. 100 decimetri
C. 10 decametri
D. 1 chilometro
3 Kevin ha comperato una cassetta piena di arance che pesa 12 chilogrammi. La cassetta vuota pesa 2 chilogrammi. Quanto pesano le arance?
A. 100 hg
B. 1 000 g
4 Quale capacità può avere questa lattina?
A. 3 l
B. 3 d l
C. 3 c l
D. 3 m l
5 – Che ore sono? – chiede Lucia.
– Sono le 17 e 35 – risponde Paolo. Qual è l’orologio che indica quest’ora?
C. 100 kg
D. 10 dag
A.
C.
B.
D.
6 Marco ha in tasca queste monete:
Vorrebbe acquistare un libro a fumetti che costa € 7,50. Quanto gli manca?
A. 1 euro e 30 centesimi
B. 2 euro
C. 2 euro e 30 centesimi
D. 2 euro e 50 centesimi
12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 I MIEI ESERCIZI 178
LUNGHEZZA, PESO, CAPACITÀ
1 In ciascuna riga della tabella, colora solo la misura superiore a quella in verde.
70 m 7 dm 4 m 700 cm 30 dam
4 dam 40 m 4 m 400 mm 44 dam
10 km 10 m 1 hm 90 km 101 m
5 hm 20 mm 400 m 7 000 dam 100 cm
200 dm 100 cm 2 000 mm 1 dam 200 m
250 m 30 cm 4 dm 40 hm 1 dam
2 Esegui le equivalenze.
12 g = dg = cg
400 g = dag = hg
50 hg = kg = g
2 000 cg = g = dg
30 dg = g = mg
10 dag = hg = g
300 mg = dg = cg
150 g = dg = hg
3 Osserva le immagini e scrivi il peso delle torte sulla bilancia.
4 Osserva le immagini e completa le equivalenze. 1
l h l da l d l c l m l
l h l da l d l c l m l
5
l h l da l l d l m l
100 c
I MIEI ESERCIZI 179
La torta pesa g La torta pesa g La torta pesa g
ANCORA MISURE
1 Risolvi i problemi sul quaderno.
A. Un cesto vuoto pesava 2 hg. Adesso che è pieno di frutta pesa 2 500 g. Quanto pesa solo la frutta?
B. Ogni giorno, tranne la domenica, Sara corre per 3 000 m.
Quanti chilometri percorre in una settimana?
C. Su un banco del pasticciere c’è una confezione di amaretti al pistacchio che costa € 18,00. Ciascun amaretto costa € 2,00. Quanti amaretti ci sono nella confezione?
D. Dal pasticciere Susanna compera 15 meringhe che costano ciascuna € 2,00.
Quanto spende in tutto? Se paga con una banconota da € 50,00, quanto riceve di resto?
E. Davide prepara la macedonia con 2,5 hg di pere, 100 g di mele,
8 dag di banane e 500 dg di fragole. Quanti grammi di frutta utilizza in tutto?
2 Osserva le immagini e prova a fare la spesa.
Che cosa puoi comperare con € 20,00 e solo 5 pezzi al massimo?
Scrivi quattro possibili soluzioni.
1a soluzione:
2 a
3 a soluzione:
:
4 a
:
3 Leggi il problema, risolvi e rispondi.
In una settimana Alex va tre volte in piscina: il lunedì è in vasca dalle 17:45 alle 18:45; il mercoledì dalle 18:15 alle 19:30; il venerdì dalle 18:30 alle 19:45. Quante ore e quanti minuti è in vasca Alex in una settimana?
Risposta:
soluzione
€ 1,50 € 2,00 € 8,50 € 3,50 € 6,00 € 7,00
soluzione
180
I MIEI ESERCIZI
FIGURE GEOMETRICHE
1 Collega ciascun oggetto alla figura solida di riferimento.
cubo sfera
parallelepipedo
2 Ripassa di verde le linee curve chiuse, di azzurro le linee spezzate chiuse, di rosso le linee miste chiuse, di viola le linee aperte.
piramide
3 Ripassa di rosso le rette parallele, di viola le rette incidenti, di verde le rette incidenti perpendicolari.
4 Indica con una X solo gli angoli retti.
I MIEI ESERCIZI 181
FIGURE GEOMETRICHE E SIMMETRIE
1 Completa la tabella. solido nome numero facce numero spigoli numero vertici
2 Completa le definizioni.
• Le rette che si incontrano in un punto si chiamano rette
• Le rette che non si incontrano in nessun punto e mantengono sempre la stessa direzione si chiamano rette
• Le rette che si incontrano in un punto e dividono il piano in quattro parti uguali si chiamano rette
3 Disegna un angolo retto, un angolo acuto e un angolo ottuso.
4 Completa le definizioni.
L’angolo
è il doppio di un angolo
.
L’angolo
è il doppio di un angolo .
I MIEI ESERCIZI 182
I MIEI ESERCIZI
5 Osserva e scrivi al posto giusto: retta, semiretta, segmento.
A B A
6 Osserva e ripassa di rosso gli angoli retti, di rosa gli angoli acuti, di verde gli angoli ottusi.
7 Disegna le figure simmetriche a quelle date.
183
I MIEI ESERCIZI
ANGOLI E POLIGONI
1 Tieni d’occhio l’orologio! Disegna qui 5 momenti della giornata in cui le lancette disegnano i seguenti tipi di angoli, poi riporta l’orario corrispondente.
angolo acuto • angolo retto • angolo piatto • angolo ottuso • angolo giro
Confronta i tuoi orari con quelli di compagni e compagne. Avete disegnato le stesse ore? L’ampiezza degli angoli è cambiata?
2 Misura con il righello i lati dei poligoni e calcola il loro perimetro.
P = cm P = cm P = cm 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11 12 6 3 2 10 4 8 5 7 1 11 12 6 3 9 2 10 4 8 5 7 1 11
184
I POLIGONI
1 Colora solo i poligoni.
2 Colora nello stesso modo il termine e la definizione corrispondente.
Segmenti che formano il confine di un poligono.
Figura racchiusa da linea spezzata chiusa. lati angolo poligono vertice
Punto in cui due lati si incontrano.
3 Misura con il righello i lati dei poligoni e calcola il loro perimetro.
Parte di piano delimitata da due lati.
4 Calcola l’area dei poligoni. Usa come unità di misura un .
A
A =
=
P = cm P = cm P = cm I MIEI ESERCIZI 185
I MIEI ESERCIZI
GLI INSIEMI
1 Scrivi nell’insieme 8 parole, tenendo presente che:
• Ciascuna parola ha 5 lettere;
• alcune parole finiscono con E;
• non tutte le parole terminano per vocale;
• nessuna parola inizia con M;
• soltanto una parola è un nome di persona.
Simone e Daniela hanno risolto il problema in questo modo:
Simone Daniela fiore Lucia super
torre robot caffè libro penne
2 Rispondi.
• Quale dei due bambini ha sbagliato?
• Quali sono i tre errori che ha commesso?
1.
2.
3.
perle film Paolo
Inter merce aceto Sofia leone
186
RELAZIONI, DATI E PREVISIONI
1 Scegli un criterio e raggruppa i seguenti numeri. Poi completa i cartellini.
2 Collega con una . La freccia significa: “lavora con…”.
3 A casa di Igor si gioca a tombola. La tombola prevede l’estrazione di numeri da 1 a 90. Per ciascun evento, scrivi se è certo (C), possibile (P) o impossibile (I).
• Uscirà un numero dispari.
• Uscirà un numero minore di 90.
• Uscirà il numero 0.
• Uscirà il numero 99.
• Uscirà il numero 1.
• Uscirà un numero pari.
4 In classe 3ª B è stata fatta un’indagine per scoprire qual è lo sport preferito. Ecco i risultati raccolti in un grafico. Osserva e rispondi.
nuoto calcio
pallavolo basket
Legenda
1 bambino/a
• Quanti hanno partecipato all’indagine?
• Qual è lo sport preferito in 3ª B?
7 12 19 24 10 13 15 30 11 4
ESERCIZI 187
I MIEI
LE AVVENTURE DELLA CAPITANA TILLY
Analizzo, programmo e costruisco con le STEM
La capitana Tilly ha ricevuto l’incarico di consegnare a Città Grande ogni giorno 12 casse di legname, navigando lungo il fiume.
1 PROBLEMA:
L’unica barca grande abbastanza per trasportare 12 casse al momento è in riparazione. Come fare per trasportare il legname?
PROGRAMMO:
La capitana Tilly deve portare a destinazione ogni giorno tutte le casse di legname previste. Compila il suo programma per i primi 4 giorni.
GIORNO 1: 12 casse
GIORNO 2:
ANALIZZO:
GIORNO 3:
GIORNO 4:
Ti starai chiedendo allora quante barche abbia a disposizione Tilly… Beh, che domande! Tutti stimano la capitana Tilly! Immediatamente gli abitanti dei villaggi vicini mettono a disposizione di Tilly le proprie imbarcazioni.
• Nel villaggio Stellabianca ci sono barche che possono portare ognuna 2 casse di legname.
• Nel villaggio Polpoblù ci sono barche che possono portare ognuna 4 casse di legname.
• E nel villaggio Algaverde ci sono barche grandi abbastanza da portare ognuna 6 casse di legname!
2 VINCOLO:
Tilly può usare quante barche vuole ma da un solo villaggio alla volta: i marinai dei vari villaggi, infatti, non vanno molto d’accordo tra loro e non vogliono viaggiare insieme nello stesso giorno !
Ma fare tutto da soli è molto stancante, e quindi i marinai di ogni equipaggio, dopo aver viaggiato per un giorno, prendono almeno un giorno di riposo.
ANALIZZO, PROGRAMMO, COSTRUISCO:
Ogni giorno dunque Tilly dovrà scegliere da quale villaggio servirsi.
Laboratorio STEM
188
Laboratorio STEM
Aiutati con i mattoncini da costruzioni: ogni mattoncino è una cassa di legname.
Dividili in gruppi contando quante casse possono portare le barche di cui Tilly ha deciso di servirsi. Poi, schematizza nei riquadri le soluzioni che hai trovato.
Ricorda i vincoli:
• ogni giorno un equipaggio diverso, quindi nessun equipaggio si mescola con gli altri;
• nessun equipaggio viaggia per due giorni consecutivi.
GIORNO 1:
… barche di Algaverde
GIORNO 2
… barche …
GIORNO 3
… barche …
GIORNO 4
… barche…
189
ANALIZZO:
Ottimo, procedi con la prossima analisi!
Grazie alle tue soluzioni, la capitana Tilly riuscirà ogni giorno a consegnare 12 casse, non di più né di meno?
ANALIZZO, PROGRAMMO, COSTRUISCO:
Che cosa puoi cambiare per risolvere il problema?
Torna indietro, rileggi i vincoli e riprova con altre soluzioni!
A partire dal quinto giorno, gli equipaggi fanno pace e decidono di viaggiare insieme mescolando le loro barche nei modi più diversi.
Aiutati con i mattoncini da costruzione per visualizzare le possibili soluzioni, poi rappresenta le soluzioni nel riquadro sotto e in altri riquadri sul tuo quaderno.
Ricorda i vincoli:
• ogni giorno devono viaggiare 12 casse totali, non di più né di meno;
• ora gli equipaggi possono viaggiare mescolati e anche in giorni consecutivi.
Per ogni soluzione trovata, fai il controllo usando lo schema di sopra.
ESEMPIO GIORNO 5:
… barche del villaggio…
… barche…
… barche…
Laboratorio STEM
SÌ NO
190
ANALIZZO E PROGRAMMO:
Una volta giunta a Città Grande, la capitana Tilly deve fare in modo che le casse di legname siano consegnate al magazzino, e per fare questo i marinai incaricati della consegna dovranno partire dal porto ed evitare sia le pozzanghere che le bancarelle del mercato.
Aiuta Tilly a scrivere le istruzioni per i marinai.
Laboratorio STEM
AVANTI – MAGAZZINO
191
PORTO –
MAGAZZINO PORTO
CLASSE 3 a
• Letture
• Riflessione linguistica
• Matematica • Ed. civica
• Scienze e Tecnologia • Ed. civica
• Storia • Ed. civica
• Geografia • Ed. civica
• Quaderno per la valutazione e l’autovalutazione
CONFIGURAZIONI CLASSE 1 a
A) Stampato
• Quaderno dei primi giorni
• Metodo stampato
• Letture
• Quaderno dello stampato e del corsivo
• Matematica con quaderno degli esercizi
• Storia • Geografia • Scienze e Tecnologia • Ed. civica
• Quaderno per la valutazione e l’autovalutazione
B) Quattro caratteri
• Quaderno dei primi giorni
• Metodo quattro caratteri
• Quaderno di scrittura nei 4 caratteri
• Letture
• Matematica con quaderno degli esercizi
• Storia • Geografia • Scienze e Tecnologia • Ed. civica
• Quaderno per la valutazione e l’autovalutazione
CLASSE 2 a
• Letture
• Riflessione linguistica
• Matematica con quaderno degli esercizi
• Storia • Geografia • Scienze e Tecnologia • Ed. civica
• Quaderno per la valutazione e l’autovalutazione
• KIT DOCENTE guida per lʼinsegnante, percorsi semplificati, risorse didattiche online.
• LIBRO DIGITALE (scaricalo subito seguendo le istruzioni all’interno della copertina) volumi sfogliabili, esercizi interattivi, audiolibri, tracce audio, libro liquido accessibile e percorsi semplificati stampabili. (www.gruppoeli.it/libridigitali)
a NUOVA FESTA A SORPRESA
Non vendibile
www.gruppoeli.it
Sistema Digitale Accessibile
Allegato
3
separatamente
#PROGETTOPARITÀ equilibri
altuofianco
NE E L AUTOVALUTAZIONE ity
#
3