

BeyondNeutrosophic Graphs Ideas|Approaches|Accessibility|Availability Dr.HenryGarrett Report|Exposition|References|Research#222022
E-publishing: Educational Publisher
1091 West 1st Ave Grandview Heights, Ohio 43212 United States
E-mail: info@edupublisher.com Website: www.EduPublisher.com
ISBN 978-1-59973-725 6
Abstract
Inthisoutlet,ajourneyamidthreemodelsaredesigned.Graphs,fuzzygraphs andneutrosophicgraphsarethreemodelswhichformmainparts.Assigningone specificnumberwithsomeconditionstoverticesandedgesofgraphsmakethem tobetitledasfuzzygraphsandassigningthreespecificnumberswithsome conditionstoverticesandedgesofgraphsmakethemtobetitledasneutrosophic graphs.Inotherviewpoint,neutrosophicgraphsare3-arrayfuzzygraphswhich everythingsaretriple.Tomakemoresense,thewell-knowngraphsaredefined innewways.Forexample,crispcomplete,fuzzycompleteandneutrosophic completewhenthecontextisaboutbeingcompleteineverymodel.Newnotions aredefinedinthecomparablestructuresonthesethreemodelstounderstand thebehaviorsofthesemodelsaccordingtothenotions.Differentedgesdefine newformofconnectionsamidvertices.Thusdefiningnewnotionofcoloringis possiblewhentheconnectionsofverticeswhichdeterminenewcolorandit’s deciderwhetherusingnewcolorornot,havebeenconsideredifthey’vespecial edges.Thetoolstodefinespecificedgesarestudied.Onenotionistousethe connectednesstohavetwodifferenttypesofnumberswhichareneutrosophic chromaticnumberandchromaticnumber.Othernotionistousetheideaof neutrosophicstrongtogetspecificedgeswhichareeligibletodefinenewnumbers. Someclassesofneutrosophicgraphsarestudiedinthethetermsofdifferent typesofchromaticnumbersandneutrosophicchromaticnumbers.Thisbookis basedonneutrosophicgraphtheorywhichisdesignedtostudydifferenttypes ofcoloringinthatgraphstogetnewideasandnewresults.Theresultsconcern specificclassesofneutrosophicgraphs.Inthisbook,ideaofneutrosophicis appliedintothesettingofhypergraphsandn-SuperHyperGraphs.Newsetting hasthenameneutrosophichypergraphsandneutrosophicn-SuperHyperGraphs. Also,ideaofclosenumbersandsuper-closenumbersareappliedtostudy.The ideaofclosingnumbersandsuper-closingnumbersaresomenamesfor(dual) super-coloringand(dual)super-resolvingalongside(dual)super-dominating whichgiveusasetandnumberarisingfromhyper-verticesandsuper-vertices alongsidetheirrelationsinneutrosophichypergraphsandneutrosophicnSuperHyperGraphs.Whenhyper-verticesandsuper-verticesaretooclose, ideaof(dual)super-coloringand(dual)super-resolvingalongside(dual)superdominatingareintroducedtostudythebehaviorsoftooclosehyper-verticesand super-vertices.Inthisbook,ideaofneutrosophicisappliedintothesettingof hypergraphsandn-SuperHyperGraphs.Newsettinghasthenameneutrosophic hypergraphsandneutrosophicn-SuperHyperGraphs.Also,ideaofclosenumbers andsuper-closenumbersareappliedtostudy.Theideaofclosingnumbers i
andsuper-closingnumbersaresomenamesfor(dual)super-coloringand(dual) super-resolvingalongside(dual)super-dominatingwhichgiveusasetand numberarisingfromhyper-verticesandsuper-verticesalongsidetheirrelations inneutrosophichypergraphsandneutrosophicn-SuperHyperGraphs.When hyper-verticesandsuper-verticesaretooclose,ideaof(dual)super-coloring and(dual)super-resolvingalongside(dual)super-dominatingareintroducedto studythebehaviorsoftooclosehyper-verticesandsuper-vertices.Newsettingis introducedtostudythealliances.Alliancesareaboutasetofverticeswhichare appliedintothesettingofneutrosophicgraphs.Neighborhoodhasthekeyrole todefinethesenotions.Also,neighborhoodisdefinedbasedontheedges,strong edgesandsomeedgeswhicharecomingfromconnectedness.Thesethreetypes ofedgesgetaframeworkasneighborhoodandafterthat,toocloseverticeshave keyroletodefineoffensivealliance,defensivealliance,t-offensivealliance,andtdefensivealliancebasedonthreetypesofedges,commonedges,strongedgesand someedgeswhicharecomingfromconnectedness.Thestructureofsetisstudied andgeneralresultsareobtained.Also,someclassesofneutrosophicgraphs containingcomplete,empty,path,cycle,bipartite,t-partite,starandwheelare investigatedinthetermsofset,minimalset,number,andneutrosophicnumber. Inthisstudy,there’sanopenwaytoextendtheseresultsintothefamilyofthese classesofneutrosophicgraphs.Thefamilyofneutrosophicgraphsaren’tstudy butitseemsthatanalogousresultsaredetermined.There’saquestion.How canberelatedtoeachother,twosetspartitioningthevertexsetofagraph?The ideasofneighborhoodandneighborsbasedondifferentedgesillustrateopen waytogetresults.Asetisalliancewhentwosetspartitioningvertexsethave uniformstructure.Allmembersofsethavedifferentamountofneighborsinthe setandoutofset.Itleadsustothenotionofoffensiveanddefensive.Newideas, offensivealliance,defensivealliance,t-offensivealliance,t-defensivealliance, strongoffensivealliance,strongdefensivealliance,strongt-offensivealliance, strongt-defensivealliance,connectedoffensivealliance,connecteddefensive alliance,connectedt-offensivealliance,andconnectedt-defensiveallianceare introduced.Twonumbersconcerningcardinalityandneutrosophiccardinalityof alliancesareintroduced.Asetisalliancewhenitscomplementmakearelation inthetermsofneighborhood.Differentedgesmakedifferentneighborhoods. Threetypesofedgesareappliedtodefinethreestylesofneighborhoods.General edges,strongedgesandconnectededgesareusedwhereconnectededgesare theedgesarisingfromconnectednessamidtwoendpointsoftheedges.These notionsareappliedintoneutrosophicgraphsasindividualsandfamilyofthem. Independentsetasanallianceisaspecialsetwhichhasnoneighborinside anditimpliessomedrawbacksforthisnotions.Findingspecialsetswhichare well-known,isanopenwaytopursethisstudy.Specialsetwhichitsmembers haveonlyoneneighborinside,characterizetheconnectedcomponentswhere thecardinalityofitscomplementisthenumberofconnectedcomponents.Some problemsareproposedtopursuethisstudy.Basicfamiliaritieswithgraph theoryandneutrosophicgraphtheoryareproposedforthisbook.Newsetting isintroducedtostudytheglobaloffensivealliance.Globaloffensiveallianceis aboutasetofverticeswhichareappliedintothesettingofneutrosophicgraphs. Neighborhoodhasthekeyroletodefinethisnotion.Also,neighborhoodis definedbasedonstrongedges.Strongedgegetsaframeworkasneighborhood andafterthat,toocloseverticeshavekeyroletodefineglobaloffensivealliance basedonstrongedges.Thestructureofsetisstudiedandgeneralresultsare
ii
Abstract
obtained.Also,someclassesofneutrosophicgraphscontainingcomplete,empty, path,cycle,star,andwheelareinvestigatedinthetermsofset,minimalset, number,andneutrosophicnumber.Neutrosophicnumberisdefinedinnewway. It’sfirsttimetodefinethistypeofneutrosophicnumberinthewaythat,three valuesofavertexareusedandthey’vesamesharetoconstructthisnumber. It’scalled“modifiedneutrosophicnumber”.Summationofthreevaluesofvertex makesonenumberandapplyingittoasetmakesneutrosophicnumberofset. Thisapproachfacilitatesidentifyingminimalsetandoptimalsetwhichforms minimal-global-offensive-alliancenumberandminimal-global-offensive-allianceneutrosophicnumber.Twodifferenttypesofsetsnamelyglobal-offensive allianceandminimal-global-offensivealliancearedefined.Global-offensive allianceidentifiesthesetsingeneralvisionbutminimal-global-offensivealliance takesfocusonthesetswhichdeletingavertexisimpossible.Minimal-globaloffensive-alliancenumberisaboutminimumcardinalityamidthecardinalities ofallminimal-global-offensivealliancesinagivenneutrosophicgraph.New notionsareappliedinthesettingsbothindividualandfamily.Familyof neutrosophicgraphsisstudiedinthewaythat,thefamilyonlycontainssame classesofneutrosophicgraphs.Threetypesoffamilyofneutrosophicgraphs includingm-familyofneutrosophicstarswithcommonneutrosophicvertexset, m-familyofoddcompletegraphswithcommonneutrosophicvertexset,and m-familyofoddcompletegraphswithcommonneutrosophicvertexsetare studied.Theresultsareaboutminimal-global-offensivealliance,minimal-globaloffensive-alliancenumberanditscorrespondedsets,minimal-global-offensivealliance-neutrosophicnumberanditscorrespondedsets,andcharacterizingall minimal-global-offensivealliances.Theconnectionofglobal-offensive-alliances withdominatingsetandchromaticnumberareobtained.Thenumberof connectedcomponentshassomerelationswiththisnewconceptanditgets someresults.Someclassesofneutrosophicgraphsbehavedifferentlywhen theparityofverticesaredifferentandinthiscase,path,cycle,andcomplete illustratethesebehaviors.Twoapplicationsconcerningcompletemodelas individualandfamily,underthetitlesoftimetableandschedulingconclude theresultsandtheygivemoreclarifications.Inthisstudy,there’sanopenway toextendtheseresultsintothefamilyoftheseclassesofneutrosophicgraphs. Thefamilyofneutrosophicgraphsaren’tstudydeeplyandwithmoreresults butitseemsthatanalogousresultsaredetermined.Slightprogressisobtained inthefamilyofthesemodelsbutthereareopenavenuestostudyfamilyof othermodelsassamemodelsanddifferentmodels.There’saquestion.How canberelatedtoeachother,twosetspartitioningthevertexsetofagraph? Theideasofneighborhoodandneighborsbasedonstrongedgesillustrateopen waytogetresults.Asetisglobaloffensivealliancewhentwosetspartitioning vertexsethaveuniformstructure.Allmembersofsethavemoreamountof neighborsinthesetthanoutofset.Itleadsustothenotionofglobaloffensive alliance.Differentedgesmakedifferentneighborhoodsbutit’susedonestyle edgetitledstrongedge.Thesenotionsareappliedintoneutrosophicgraphsas individualsandfamilyofthem.Independentsetasanallianceisaspecialset whichhasnoneighborinsideanditimpliessomedrawbacksforthesenotions. Findingspecialsetswhicharewell-known,isanopenwaytopursethisstudy. Specialsetwhichitsmembershaveonlyoneneighborinside,characterizethe connectedcomponentswherethecardinalityofitscomplementisthenumberof connectedcomponents.Someproblemsareproposedtopursuethisstudy.Basic
iii
Abstract
familiaritieswithgraphtheoryandneutrosophicgraphtheoryareproposedfor thisbook.
Newnotionsaredefinedinthecomparablestructuresonthesethreemodelsto understandthebehaviorsofthesemodelsaccordingtothenotions.Thisbookisbased onneutrosophicgraphtheorywhichisdesignedtostudydifferenttypesofcoloringin thatgraphstogetnewideasandnewresults.Theresultsconcernspecificclassesof neutrosophicgraphs.Newnotionsaredefinedinthecomparablestructuresonthese threemodelstounderstandthebehaviorsofthesemodelsaccordingtothenotions.This bookisbasedonneutrosophicgraphtheorywhichisdesignedtostudydifferenttypes ofcoloringinthatgraphstogetnewideasandnewresults.Theresultsconcernspecific classesofneutrosophicgraphs.
iv
Acknowledgements
Theauthorisgoingtosayhisgratitudeandhisappreciationaboutthebrains andtheirhandswhichareshowingtheimportanceofwordsintheframework ofeverywisdom,knowledge,artsandemotionswhicharestreaming inthelines Thewordsofmindandthe mindsofwords,aretoo eligibletobeinthestage ofaknowledgements fromthewords,notions,ideasandapproachestohavethematerialwhichis onlythewaytoflourishtheminds,thegrowingthenotions,advancingways andmakingthestablewaystobeamidtheeventsandstormsofmindsfor survivingfromthemandmakingtheoutstandingexperiencesaboutthetools andideastobeonthestarlinesofwordsandshininglikestars,forever.
v
Contents
Abstracti Acknowledgementsv Contentsvii ListofFiguresxi ListofTablesxiii
1NeutrosophicGraphs1 1.1Definitions.............................1 1.2NewIdeas.............................20 1.3Abstract..............................20 1.4Background............................21 1.5Definitions.............................24 1.6Fuzzy(Neutrosophic)TwinVertices...............26 1.7AntipodalVertices........................29 1.8ExtendedResults.........................32 1.9Applications............................37 1.10OpenProblems..........................40 1.11ConclusionandClosingRemarks................41 Bibliography43 2NeutrosophicChromaticNumber45 2.1Definitions.............................45 2.2ChromaticNumberandNeutrosophicChromaticNumber..46 2.3Abstract..............................46 2.4MotivationandContributions..................47 2.5ChromaticNumberandNeutrosophicChromaticNumber..47 2.6ApplicationsinTimeTableandScheduling..........52 2.7OpenProblems..........................53 2.8ConclusionandClosingRemarks................54 2.9NeutrosophicChromaticNumberBasedonConnectedness..54 2.10Abstract..............................54 2.11MotivationandContributions..................55 vii
2.12DefinitionsandClarification...................55
2.13BasicProperties..........................56 2.14VitalChromaticNumber.....................59
2.15LargestVitalChromaticNumber................59 2.16SmallestVitalChromaticNumber................59 2.17n-VitalChromaticNumber....................61
2.18Largestn-VitalChromaticNumber...............61 2.19Smallestn-VitalChromaticNumber...............62
2.20ApplicationsinTimeTableandScheduling..........66 2.21OpenProblems..........................67 2.22ConclusionandClosingRemarks................68 2.23NewIdeas.............................68
2.24DifferentTypesofNeutrosophicChromaticNumber......68 2.25Abstract..............................69
2.26MotivationandContributions..................69 2.27NewIdeas.............................70 2.28NewResults............................74 2.29DifferentTypesofNeutrosophicChromaticNumber......74 2.30NewResults............................74
2.31ApplicationsinTimeTableandScheduling...........97 2.32OpenProblems..........................99 2.33ConclusionandClosingRemarks................99 Bibliography101
3NeutrosophicHypergraphs103 3.1NumbersandSets.........................103
3.2 PreliminariesForSettingofNeutrosophicn-SuperHyperGraph andSettingofNeutrosophicHypergraphs............103 3.3 DimensionandColoringalongsideDominationinNeutrosophic Hypergraphs............................107 3.4Abstract..............................107 3.5MotivationandContributions..................108 3.6NewIdeasForNeutrosophicHypergraphs...........108 3.7OptimalNumbersForNeutrosophicHypergraphs.......111 3.8OptimalSetsForNeutrosophicHypergraphs..........114 3.9 OptimalSetsandNumbersForFamilyofNeutrosophic Hypergraphs............................116 3.10ApplicationsinTimeTableandScheduling...........119 3.11OpenProblems..........................120 3.12ConclusionandClosingRemarks................121 3.13ClassesOfNeutrosophicHypergraphs..............121 3.14Co-degreeandDegreeofclassesofNeutrosophicHypergraphs121 3.15Abstract..............................121 3.16MotivationandContributions..................122 3.17NewIdeasForNeutrosophicHypergraphs...........123 3.18ApplicationsinTimeTableandScheduling...........132 3.19OpenProblems..........................133 3.20ConclusionandClosingRemarks................134 3.21BeyondNeutrosophicHypergraphs...............134 viii
Contents
3.22 ClosingNumbersandSuper-ClosingNumbersas(Dual)Resolving and(Dual)Coloringalongside(Dual)Dominatingin (Neutrosophic)n-SuperHyperGraph...............135 3.23Abstract..............................135 3.24NewIdeasForSettingofNeutrosophicn-SuperHyperGraph.136 3.25NewIdeasForn-SuperHyperGraph...............141 3.26OptimalNumbersForn-SuperHyperGraph...........142 3.27OptimalSetsForn-SuperHyperGraph.............146 3.28OptimalSetsandNumbersForFamilyofn-SuperHyperGraph147 3.29TwinSuper-verticesinn-SuperHyperGraph..........150 3.30Antipodalsuper-verticesinn-SuperHyperGraph........152 3.31ExtendedResultsForn-SuperHyperGraph...........155 3.32Optimal-super-coloringNumberinn-SuperHyperGraph....160 3.33 ApplicationsinTimeTableandSchedulinginNeutrosophic n-SuperHyperGraph........................163 3.34OpenProblems..........................166 3.35ConclusionandClosingRemarks................167 Bibliography169
4NeutrosophicAlliances171 4.1DifferentNeutrosophicAlliances.................171 4.2 ThreeTypesofNeutrosophicAlliancesbasedonConnectedness and(Strong)Edges........................171 4.3Abstract..............................171 4.4MotivationandContributions..................172 4.5Preliminaries............................173 4.6IntheSettingofSet.......................175 4.7ClassesofNeutrosophicGraphs.................179 4.8IntheSettingofNumber.....................183 4.9ClassesofNeutrosophicGraphs.................187 4.10ApplicationsinTimeTableandScheduling...........190 4.11OpenProblems..........................190 4.12ConclusionandClosingRemarks................191 4.13GlobalOffensiveAlliances....................191 4.14GlobalOffensiveAllianceinStrongNeutrosophicGraphs...191 4.15Abstract..............................191 4.16MotivationandContributions..................193 4.17Preliminaries............................194 4.18GeneralResultsForNeutrosophicGraphs...........196 4.19ClassesofNeutrosophicGraphs.................199 4.20FamilyofNeutrosophicGraphs.................212 4.21ApplicationsinTimeTableandScheduling...........217 4.22Case1:CompleteModelasIndividual.............218 4.23Case2:FamilyofCompleteModels...............219 4.24OpenProblems..........................221 4.25ConclusionandClosingRemarks................221 4.26GlobalPowerfulAllianceinStrongNeutrosophicGraphs...221 4.27Abstract..............................222 4.28MotivationandContributions..................223 ix
Contents
Contents
4.29Preliminaries............................224
4.30r-Regular-Strong-NeutrosophicGraph..............227
4.31ApplicationsinTimeTableandScheduling...........235
4.32Case1:CompleteModelasIndividual.............236
4.33Case2:FamilyofCompleteModels...............237 4.34OpenProblems..........................238 4.35ConclusionandClosingRemarks................239 Bibliography241
x
ListofFigures
1.1NeutrosophicGraph, N1 ........................2
1.2NeutrosophicComplete, N1 ......................2
1.3NeutrosophicStrong, N1 ........................3
1.4 NeutrosophicCycle, N1, hassameneutrosophicvaluesfortwo vertices..................................5
1.5NeutrosophicCycle, N1, hassameneutrosophicvaluesforvertices.6
1.6 Neutrosophicpath, N1, hassameneutrosophicvaluesforvertices. It’salsoNeutrosophicstrongandNeutrosophiccomplete......8
1.7 NeutrosophicPath, N1, hassameneutrosophicvaluesforvertices. It’salsoNeutrosophicstrongandNeutrosophiccomplete......8
1.8 Blackvertex {f6} isonlyfuzzy(neutrosophic)-metricsetamidall setsofverticesforfuzzy(neutrosophic)graph G. ..........25
1.9 Blackvertex {f4} andthesetofvertices {f2} aresimultaneously fuzzy(neutrosophic)-metricsetamidallsetsofverticesforfamily offuzzy(neutrosophic)graphs G ...................26
1.10 Blackvertex {s1} isonlyfuzzy(neutrosophic)-metricsetamidall setsofverticesforfuzzy(neutrosophic)graph T. ...........38
1.11 Blackvertices {i1,i2} areonlyfuzzy(neutrosophic)-metricsetamid allsetsofverticesforfuzzy(neutrosophic)graph T. Blackvertices V \{c1,c2} areonlyfuzzy(neutrosophic)-metricsetamidallsetsof verticesforfuzzy(neutrosophic)graph T ..............40
2.1NeutrosophicGraph,
2.2Blackverticesaresuspicionsaboutchoosingthem.........52 2.3
2.4Blackverticesaresuspicionsaboutchoosingthem.........67 2.5Twoedgesaren’ttype-I........................70 2.6
2.7Blackverticesaresuspicionsaboutchoosingthem.........98 3.1
3.2
N1 ........................48
Neutrosophicgraph N1 isconsideredwithrespecttofirstorder. It’scompletebutitisn’tneutrosophiccomplete.It’scyclebutit isn’tneutrosophiccycle.It’sneutrosophic3-partitebutitisn’t neutrosophiccomplete3-partite....................56
Neutrosophicgraphwhichisfixed-edgebutnotstrongfixed-vertex. 71
Therearethreeneutrosophichyperedgesandtwoneutrosophic vertices.................................104
NHG =(V,E,σ,µ) isneutrosophicedge 3 regularhypergraph..105 xi
ListofFigures
3.3 NHG =(V,E,σ,µ) isneutrosophicstronghypergraph.......105
3.4 NHG =(V,E,σ,µ) isneutrosophicstronghypergraph.......106
3.5Verticesaresuspicionsaboutchoosingthem.............119
3.6 NHG3 4 =(V,E,σ,µ) isneutrosophic (3, 4) regularhypergraph..124
3.7 NHG3 3,3,3 =(V,E,σ,µ) isneutrosophiccomplete 3 partite hypergraph................................125
3.8Verticesaresuspicionsaboutchoosingthem.............132
3.9 NHG3 4 =(V,E,σ,µ) isneutrosophic (3, 4) regularhypergraph..137
3.10 NHG3 3,3,3 =(V,E,σ,µ) isneutrosophiccomplete 3 partite hypergraph................................138
3.11super-verticesaresuspicionsaboutchoosingthem..........164
3.12Verticesaresuspicionsaboutchoosingthem.............165
4.1Thesetofblackcirclesisminimal-global-offensivealliance.....196
4.2Thesetofblackcirclesisminimal-global-offensivealliance.....201
4.3Thesetofblackcirclesisminimal-global-offensivealliance.....203
4.4Thesetofblackcirclesisminimal-global-offensivealliance.....205
4.5Thesetofblackcirclesisminimal-global-offensivealliance.....207
4.6Thesetofblackcirclesisminimal-global-offensivealliance.....208
4.7Thesetofblackcirclesisminimal-global-offensivealliance.....210
4.8Thesetofblackcirclesisminimal-global-offensivealliance.....211
4.9Thesetofblackcirclesisminimal-global-offensivealliance.....213
4.10Thesetofblackcirclesisminimal-global-offensivealliance.....214
4.11Thesetofblackcirclesisminimal-global-offensivealliance.....216
4.12Thesetofblackcirclesisminimal-global-offensivealliance.....217
4.13Thesetofblackcirclesisminimal-global-offensivealliance.....219
4.14Thesetofblackcirclesisminimal-global-offensivealliance.....220
4.15Blackcirclesformasetwhichis1-powerfulalliance.........232
4.16Blackcirclesformasetwhichis1-powerfulalliance.........235
4.17Thesetofblackcirclesisminimal-global-offensivealliance.....237
4.18Thesetofblackcirclesisminimal-global-offensivealliance.....239
xii
ListofTables
1.1Crisp-fying,Fuzzy-fyingandNeutrosophic-fying..........3
1.2Crisp-fying,Fuzzy-fyingandNeutrosophic-fying..........18
1.3Crisp-fying,Fuzzy-fyingandNeutrosophic-fying..........23
1.4Crisp-fying,Fuzzy-fyingandNeutrosophic-fying..........23
1.5 DistancesofVerticesfromsetsofvertices {f6} and {f4} in fuzzy(neutrosophic)Graph G. .....................24
1.6 DistancesofVerticesfromsetofvertices {f6} inFamilyof fuzzy(neutrosophic)Graphs G. ....................25
1.7 ATrainconcerningitsStationsanditsConnectionsasaFuzzy GraphinaModel............................39
1.8 AnInfectedPersonconcerninghistwoselectiveConnectionsand hisPartnersWiththeirtwoselectiveConnectionsasaFuzzyGraph T inaModel...............................40
1.9 AnInfectedPersonconcerninghisConnectionsandhisPartnersas aFuzzyGraph T inaModel......................40
1.10ABriefOverviewaboutAdvantagesandLimitationsofthisstudy42
2.1
SchedulingconcernsitsSubjectsanditsConnectionsasaNeutrosophicGraphinaModel........................53
2.2ABriefOverviewaboutAdvantagesandLimitationsofthisstudy54
2.3
SchedulingconcernsitsSubjectsanditsConnectionsasaNeutrosophicGraphinaModel........................66
2.4ABriefOverviewaboutAdvantagesandLimitationsofthisstudy68
2.5
SchedulingconcernsitsSubjectsanditsConnectionsasaNeutrosophicGraphinaModel........................98
2.6ABriefOverviewaboutAdvantagesandLimitationsofthisstudy100
3.1
SchedulingconcernsitsSubjectsanditsConnectionsasaNeutrosophicHypergraphinaModel.....................119
3.2ABriefOverviewaboutAdvantagesandLimitationsofthisstudy121
3.3
SchedulingconcernsitsSubjectsanditsConnectionsasaNeutrosophicHypergraphinaModel.....................132
3.4ABriefOverviewaboutAdvantagesandLimitationsofthisstudy134
3.5
SchedulingconcernsitsSubjectsanditsConnectionsasanSuperHyperGraphinaModel.....................164 xiii
3.6
SchedulingconcernsitsSubjectsanditsConnectionsasaNeutrosophicHypergraphinaModel.....................166
3.7ABriefOverviewaboutAdvantagesandLimitationsofthisstudy167
4.1
SchedulingconcernsitsSubjectsanditsConnectionsasaneutrosophicgraphsanditsalliancesinaModel...............190
4.2ABriefOverviewaboutAdvantagesandLimitationsofthisstudy191
4.3
SchedulingconcernsitsSubjectsanditsConnectionsasaneutrosophicgraphanditsalliancesinaModel...............218
4.4ABriefOverviewaboutAdvantagesandLimitationsofthisstudy222
4.5
SchedulingconcernsitsSubjectsanditsConnectionsasaneutrosophicgraphanditsalliancesinaModel...............236
4.6ABriefOverviewaboutAdvantagesandLimitationsofthisstudy240
ListofTables
xiv
Toclarifyabout thedefinitions, Iusesome examplesandin thisway, exemplifyinghas keyroletomake senseaboutthe definitionsand tointroducenew waystouseon thesemodelsin thetermsofnew notions.
NeutrosophicGraphs
Akrametal.[1]introducebipolarneutrosophicgraphs.Heetal.[2]also proposeoperationsonsingle-valuedneutrosophicgraphs.Broumietal.[3] elicitanintroductiontobipolarsinglevaluedneutrosophicgraphtheory.He etal.alsointroduceIntervalvaluedneutrosophicgraphs[4],Isolatedsingle valuedneutrosophicgraphs[5],onbipolarsinglevaluedneutrosophicgraphs [6],Singlevaluedneutrosophicgraphs[7],singlevaluedneutrosophicgraphs: degree,orderandsize[8].Kandasamyetal.[11]illustrateNeutrosophicgraphs: anewdimensiontographtheoryin2015.In2017,Operationsonsinglevalued neutrosophicgraphswithapplicationwasintroducedbyNazetal.[12].
1.1Definitions
Theconceptofcompleteisusedtoclassifyspecificgraphineveryenvironment. Todifferentiate,Iuseanadjectiveorprefixineverydefinition.Twoadjectives “fuzzy”and“neutrosophic”areusedtodistinguisheverygraphorclassesof graphoranynotiononthem.
Thereference[9; 10]isusedtowritethecontentsofthischapter.
Definition1.1.1. G :(V,E) iscalleda crispgraph where V isasetofobjects and E isasubsetof V × V suchthatthissubsetissymmetric.
Definition1.1.2. Acrispgraph G :(V,E) iscalleda fuzzygraph G :(σ,µ) where σ : V → [0, 1] and µ : E → [0, 1] suchthat µ(xy) ≤ σ(x) ∧ σ(y) forall xy ∈ E.
Definition1.1.3. Acrispgraph G :(V,E) iscalleda neutrosophicgraph G :(σ,µ) where σ =(σ1,σ2,σ3): V → [0, 1] and µ =(µ1,µ2.µ3): E → [0, 1] suchthat µ(xy) ≤ σ(x) ∧ σ(y) forall xy ∈ E.
Definition1.1.4. Acrispgraph G :(V,E) iscalleda crispcomplete where ∀x ∈ V, ∀y ∈ V,xy ∈ E.
Definition1.1.5. Afuzzygraph G :(σ,µ) iscalled fuzzycomplete whereit’s completeand µ(xy)= σ(x) ∧ σ(y) forall xy ∈ E.
Definition1.1.6. Aneutrosophicgraph G :(σ,µ) iscalleda neutrosophic complete whereit’scompleteand µ(xy)= σ(x) ∧ σ(y) forall xy ∈ E.
Definition1.1.7. Acrispgraph G :(V,E) iscalleda crispstrong
CHAPTER1
1
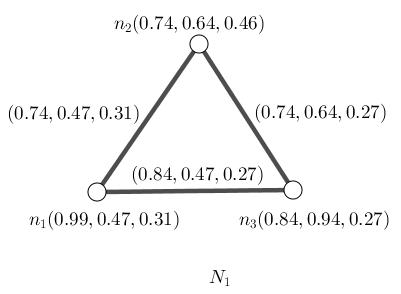
Figure1.1:NeutrosophicGraph, N1 nsc1
Figure1.2:NeutrosophicComplete, N1 nsc2
Definition1.1.8. Afuzzygraph G :(σ,µ) iscalled fuzzystrong where µ(xy)= σ(x) ∧ σ(y) forall xy ∈ E.
Definition1.1.9. Aneutrosophicgraph G :(σ,µ) iscalleda neutrosophic strong where µ(xy)= σ(x) ∧ σ(y) forall xy ∈ E.
Definition1.1.10. Adistinctsequenceofvertices v0,v1, ··· ,vn inacrisp graph G :(V,E) iscalled crisppath withlength n from v0 to vn where vivi+1 ∈ E,i =0, 1, ,n 1

1.NeutrosophicGraphs
2
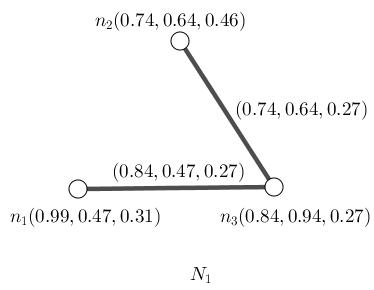
Figure1.3:NeutrosophicStrong, N1 nsc3
Definition1.1.11. Apath v0,v1, ,vn iscalled fuzzypath where µ(vivi+1) > 0,i =0, 1, ,n 1
Definition1.1.12. Apath v0,v1, ,vn iscalled neutrosophicpath where µ(vivi+1) > 0,i =0, 1, ··· ,n 1
Definition1.1.13. Apath v0,v1, ,vn withexceptionof v0 and vn inacrisp graph G :(V,E) iscalled crispcycle withlength n for v0 where v0 = vn and theorderisthree.
Definition1.1.14. Acrispcycle v0,v1, ··· ,vn,v0 iscalled fuzzycycle wheretherearetwoedges xy and uv suchthat µ(xy)= µ(uv)= i=0,1, ,n 1 µ(vivi+1)
Definition1.1.15. Acrispcycle v0,v1, ,vn,v0 iscalled neutrosophic cycle wheretherearetwoedges xy and uv suchthat µ(xy)= µ(uv)= i=0,1, ,n 1 µ(vivi+1)
Table1.1:Crisp-fying,Fuzzy-fyingandNeutrosophic-fying tbl1
CrispGraphs FuzzyGraphs NeutrosophicGraphs
CrispComplete FuzzyComplete NeutrosophicComplete
CrispStrong FuzzyStrong NeutrosophicStrong
CrispPath FuzzyPath NeutrosophicPath
CrispCycle FuzzyCycle NeutrosophicCycle
Newdefinitionsareintroducedinthetermsofneutrosophictype.Thereare somequestionsabouttherelationsamidthesenotions. Thenotionofstrongistooclosetothenotionsofcomplete.
1.1.Definitions
3
(1). Isneutrosophicstrong,neutrosophiccomplete? No.
Example1.1.16. ConsiderFigure (1.3) N1 isaneutrosophicstrong whichisn’talsoneutrosophiccomplete.
(2). Doesneutrosophicstrongimplyneutrosophiccomplete? Sometimes.
Example1.1.17. ConsiderFigure (1.3) N1 isaneutrosophicstrong whichisn’tneutrosophiccomplete.
Example1.1.18. ConsiderFigure (1.2). N1 isaneutrosophicstrong whichisalsoneutrosophiccomplete.
(3) Doesneutrosophiccompleteimplyneutrosophicstrong? Yes.Allneutrosophiccompletefromorder 1, 2, 3, areneutrosophic strong.Allneutrosophiccompletefromanyorderareneutrosophicstrong.
Example1.1.19. ConsiderFigure (1.2) N1 isaneutrosophiccomplete whichisalsoneutrosophicstrong.
(4) Whendoesneutrosophiccompleteimplyneutrosophicstrong? Always.
Example1.1.20. ConsiderFigure (1.2) N1 isaneutrosophiccomplete whichisalsoneutrosophicstrong.
(5) Whenneutrosophicstrongimplyneutrosophiccomplete? Whenneutrosophicgraphiscrispcomplete.
Example1.1.21. ConsiderFigure (1.2) N1 isaneutrosophicstrong whichisalsoneutrosophiccomplete.Sinceit’sneutrosophicstrongand crispcomplete.
(6) Whichneutrosophicgraphsarebothneutrosophiccompleteandneutrosophicstrong?
Allneutrosophicgraphs,whichareneutrosophiccomplete,areneutrosophicstrong.Inotherwords,neutrosophicgraphs,whichareneutrosophic strongandcrispcomplete,areneutrosophiccomplete.Neutrosophiccompletemeansthatneutrosophicgraphisneutrosophicstrongandcrisp complete.
Example1.1.22. ConsiderFigure (1.2). N1 isaneutrosophicstrong whichisalsoneutrosophiccomplete.
(7) Whichneutrosophicgraphsareeitherneutrosophiccompleteorneutrosophicstrong?
Neutrosophicgraphs,whichareneutrosophicstrongbutnotcrispcomplete,aren’tneutrosophiccomplete.
Example1.1.23. ConsiderFigure (1.3) N1 isaneutrosophicstrong whichisn’talsoneutrosophiccomplete.
1.NeutrosophicGraphs
4
(8). Whichneutrosophicgraphsareneitherneutrosophiccompletenor neutrosophicstrong?
Neutrosophicgraphs,whicharen’tneutrosophicstrong,areneithter neutrosophiccomplete.
Example1.1.24. ConsiderFigure (2.1) N1 isneitheraneutrosophic strongnorneutrosophiccomplete.
Thenotionofcyclewhentheorderisthree,istooclosetothenotionsof complete.Thustherearesomenaturalquestionsaboutthem.
(1). Isneutrosophiccycle,neutrosophiccomplete?
Whentheorderisthreeandit’sneutrosophicstrong.Forinstance,there’s apossibilitytohaveneutrosophiccycleandneutrosophiccomplete.In theseExamples,atleasttheneutrosophicvaluesoftwoverticeshavetobe sameandminimumtohavetwoedgeswhichhaveminimumneutrosophic values.Inthiscase,allthreeedgeshavesameneutrosophicvalues.ThusI representthreetypesneutrosophicgraphs,whichareneutrosophiccyclein thetermsofnon-isomorphic.Firstly,twoverticeshavesameneutrosophic valuesandthirdvertexhasneutrosophicvaluewhichisgreaterthanthem.
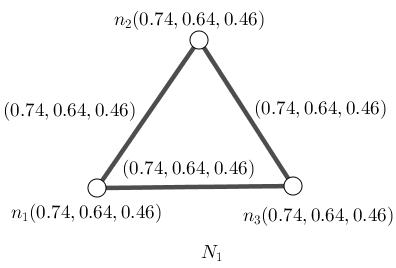
Example1.1.25. ConsiderFigure (1.4). N1 isaneutrosophiccycleand neutrosophiccomplete.
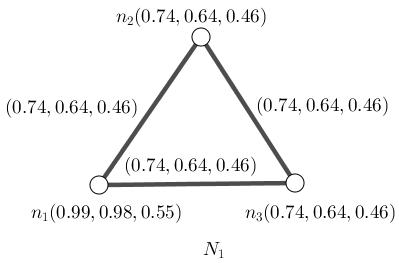
Figure1.4:NeutrosophicCycle, N1, hassameneutrosophicvaluesfortwo vertices. nsc4
Secondly,threeverticeshavesameneutrosophicvalues.
Example1.1.26. ConsiderFigure (1.4) N1 isbothaneutrosophic completeandneutrosophiccycle.
Thirdly,threeverticeshavedifferentneutrosophicvalues.
1.1.Definitions
5
1.NeutrosophicGraphs
Example1.1.27. ConsiderFigure (1.2). N1 isbothaneutrosophic completeandneutrosophiccycle.
Figure1.5:NeutrosophicCycle, N1, hassameneutrosophicvaluesforvertices. nsc5
(2) Doesneutrosophiccycleimplyneutrosophiccomplete? Whentheorderisthreeandit’sneutrosophicstrong.
(3). Doesneutrosophiccompleteimplyneutrosophiccycle? Whentheorderisthree.
(4). Whendoesneutrosophiccompleteimplyneutrosophiccycle? Whentheorderisthree.
(5) Whenneutrosophiccycleimplyneutrosophiccomplete? Whentheorderisthreeandit’sneutrosophicstrong.
(6) Whichneutrosophicgraphsarebothneutrosophiccompleteandneutrosophiccycle?
OnlythreetypesofneutrosophicgraphswhichareinFigures (1.2),(1.4) and(1.5).Theorderhastobethreeandit’sneutrosophicstrong.
Firstly,twoverticeshavesameneutrosophicvaluesandthirdvertexhas neutrosophicvaluewhichisgreaterthanthem.
Secondly,threeverticeshavesameneutrosophicvalues. Thirdly,threeverticeshavedifferentneutrosophicvalues.
(7) Whichneutrosophicgraphsareeitherneutrosophiccompleteorneutrosophiccycle?
Eitherneutrosophiccompleteorneutrosophiccyclewhichdon’thavethe orderisthreeforneutrosophiccompleteandiftheyhave,thentheyaren’t neutrosophicstrong.
(8) Whichneutrosophicgraphsareneitherneutrosophiccyclenorneutrosophic strong?
Neutrosophicgraphswhicharen’tneutrosophicstrong.
6
Proposition1.1.28. Aneutrosophiccycleisneutrosophiccompleteifandonly ifit’sneutrosophicstrongandorderisthree.
Proof. Let N isneutrosophiccycle.
(⇒) If N isneutrosophiccomplete,then,byit’sneutrosophiccomplete,it’s neutrosophicstrong.Byit’scrispcycleandcrispcomplete,orderisthree.Thus N isneutrosophicstrongandorderisthree.
(⇐) Ifit’sneutrosophicstrongandorderisthree,then,byorderisthreeandit’s crispcycle,it’scrispcomplete.Byit’sneutrosophicstrong, N isneutrosophic complete.
Proposition1.1.29. Aneutrosophiccompleteisneutrosophiccycleifandonly ifit’sorderisthree.
Proof. Let N isneutrosophiccomplete.
(⇒) If N isneutrosophiccycle,then,byit’scrispcycleandit’scrispcomplete, orderisthree.
(⇐) Iforderisthree,then,byorderisthreeandit’scrispcomplete,it’scrisp cycle.Byit’sneutrosophiccomplete, N isneutrosophiccycle.
Proposition1.1.30. Aneutrosophicpathisneutrosophiccompleteifandonly ifit’sneutrosophicstrongandorderistwo.
Proof. Let N isneutrosophicpath.
(⇒) If N isneutrosophiccomplete,then,byit’scrisppathandit’scrisp complete,orderistwo.Byit’scrispcomplete,it’sneutrosophicstrong.Thus it’sneutrosophicstrongandorderistwo.
(⇐) Iforderistwo,then,byorderistwo,it’scrispconnectedandit’s neutrosophicstrong, N isneutrosophiccomplete.
Proposition1.1.31. Aneutrosophiccompleteisneutrosophicpathifandonly ifit’sorderistwo.
Proof. Let N isneutrosophiccomplete.
(⇒) Consider N isneutrosophicpath.Then,byit’scrisppathandit’scrisp complete,orderistwo.
(⇐) Supposeorderistwo,then,byorderistwoandit’scrispcomplete,it’s crisppath.Byit’sneutrosophiccomplete,it’sneutrosophicpath.Thus N is neutrosophicpath.
Example1.1.32. Uptoisomorphictherearetwoneutrosophicgraphswhich areneutrosophicpath,neutrosophiccompleteandneutrosophicstrong.
• Firstly,twoverticeshavesameneutrosophicvaluesasFigure(1.6).
• Secondly,twoverticeshavedifferentneutrosophicvaluesasFigure (1.7)
Numbersarecreatedbysometoolsarisingfromattributesconcerningdifferent modelsofgraphs.
Definition1.1.33. Let G :(V,E) beacrispgraph.Foranygivensubset N of V, Σn∈N 1 iscalled crispcardinality of N andit’sdenotedby |N |c
1.1.Definitions
7
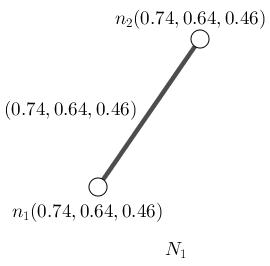
Figure1.6:Neutrosophicpath, N1, hassameneutrosophicvaluesforvertices. It’salsoNeutrosophicstrongandNeutrosophiccomplete. nsc6
Figure1.7:NeutrosophicPath, N1, hassameneutrosophicvaluesforvertices. It’salsoNeutrosophicstrongandNeutrosophiccomplete. nsc7
Definition1.1.34. Let G :(V,E) beacrispgraph.Crispcardinalityof V is called crisporder of G andit’sdenotedby Oc(G)
Definition1.1.35. Let G :(σ,µ) beafuzzygraph.Foranygivensubset N of V, Σn∈N σ(n) iscalled fuzzycardinality of N andit’sdenotedby |N |f
Definition1.1.36. Let G :(σ,µ) beafuzzygraph.Fuzzycardinalityof V is called fuzzyorder of G andit’sdenotedby Of (G)
Definition1.1.37. Let G :(σ,µ) beaneutrosophicgraph.Foranygivensubset N of V, Σn∈N σ(n) iscalled neutrosophiccardinality of N andit’sdenoted by |N |n
Definition1.1.38. Let G :(σ,µ) beaneutrosophicgraph.Neutrosophic cardinalityof V iscalled neutrosophicorder of G andit’sdenotedby On(G) exm39
Example1.1.39.
• ConsiderFigure (2.1).Neutrosophicorderof N1,On(N1) is (2 57, 2 05, 1 04) Thus On(N1)=(2 57, 2 05, 1 04)
1.NeutrosophicGraphs
8
1.1.Definitions
• ConsiderFigure (1.2).Neutrosophicorderof N1,On(N1) is (2 57, 2 05, 1 04) Thus On(N1)=(2 57, 2 05, 1 04)
• ConsiderFigure (1.3).Neutrosophicorderof N1,On(N1) is (2 57, 2 05, 1 04) Thus On(N1)=(2 57, 2 05, 1 04)
• ConsiderFigure (1.4).Neutrosophicorderof N1,On(N1) is (2 47, 2 26, 1 47) Thus On(N1)=(2 47, 2 26, 1 47)
• ConsiderFigure (1.5).Neutrosophicorderof N1,On(N1) is (2 22, 1 92, 1 47) Thus On(N1)=(2 47, 2 26, 1 38)
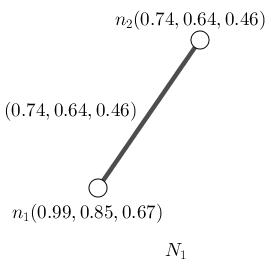
• ConsiderFigure (1.6).Neutrosophicorderof N1,On(N1) is (1 48, 1 28, 0 92) Thus On(N1)=(1 48, 1 28, 0 92)
• ConsiderFigure (1.7).Neutrosophicorderof N1,On(N1) is (1 73, 1 49, 1 13) Thus On(N1)=(1 73, 1 49, 1 13) prp40 Proposition1.1.40. |N |n ≤ (|N |c, |N |c, |N |c) Proof. |N |n =Σn∈N σ(n)=Σn=(n1,n2,n3)∈N (σ(n1),σ(n2),σ(n3)) ≤ Σn=(n1,n2,n3)∈N (1, 1, 1)=(|N |c, |N |c, |N |c)
cor41 Corollary1.1.41. On(N ) ≤ (Oc(N ),Oc(N ),Oc(N )) Proof. ByProposition (1.1.40), Oc(N )= |V |c and On(N )= |V |n, theresultis straightforward.Since On(N )= |V |n =Σv∈V σ(v)=Σv=(v1,v2,v3)∈V (σ(v1),σ(v2),σ(v3)) ≤ Σn=(v1,v2,v3)∈V (1, 1, 1)=(|V |c, |V |c, |V |c)=(Oc(N ),Oc(N ),Oc(N ))
prp42 Proposition1.1.42. |N |n =(|N |f , |N |f , |N |f ) Proof. |N |n =Σn∈N σ(n)=Σn=(n1,n2,n3)∈N (σ(n1),σ(n2),σ(n3)) =(|N |f , |N |f , |N |f )
InExample (1.1.39),thecomputationsofthisnotionwhentheycometo neutrosophicorder,aredone.There’ssametype-resultwithanalogousto Corollary(1.1.41). Corollary1.1.43. On(N )=(Of (N ),Of (N ),Of (N ))
9
1.NeutrosophicGraphs
Proof. ByProposition (1.1.42), Of (N )= |V |f and On(N )= |V |n, theresultis straightforward.Since On(N )= |V |n =Σv∈V σ(v)=Σv=(v1,v2,v3)∈V (σ(v1),σ(v2),σ(v3)) =(|V |f , |V |f , |V |f )=(Of (N ),Of (N ),Of (N )) prp44 Proposition1.1.44. Let N =(σ,µ) beaneutrosophicgraphand S,S ⊆ V. If S ⊆ S , then |S|n ≤|S |n Proof. |S|n =Σs∈S σ(s)=Σs∈S⊆S σ(s) ≤ Σs ∈S σ(s )= |S |n
TheconverseofProposition (1.1.44),doesn’thold.SinceinFigure (1.6), S = {n1},S = {n2}⊆ V = {n1,n2} |S|n =(0 74, 0 64, 0 46)= (0 74, 0 64, 0 46)= |S |n Thus |S|n ≤|S |n but S ⊆ S cor45 Corollary1.1.45. Let N =(σ,µ) beaneutrosophicgraph. S ⊆ V ifandonly if |S|n ≤|V |n Proof. (⇒) By S ⊆ V andProposition(1.1.44), |S|n ≤|V |n Inotherwords, |S|n =Σs∈S σ(s)=Σs∈S⊆V σ(s) ≤ Σv∈V σ(v)= |V |n. (⇐) Thiscaseisobvious.
Corollary1.1.46. Let N =(σ,µ) beaneutrosophicgraphand S ⊆ V. |S|n = On(N ) ifandonlyif S = V.
Proof. (⇒) Suppose |S|n = On(N ) Hence |S|n = On(N )= |V |n Thus |S|n = |V |n ByCorollary(1.1.45),weget S = V. (⇐) Consider S = V. Thus |V |n = |S|n By On(N )= |V |n, |S|n = On(N )
Definition1.1.47. Let C =(V,E) beacrispgraph.It’scalled crisp connected ifforeverygivencoupleofvertices,there’satleastonepath amidthem.
Definition1.1.48. Let F =(σ,µ) beafuzzygraph.It’scalled fuzzy connected ifforeverygivencoupleofvertices,there’satleastonepath amidthem.
Definition1.1.49. Let N =(σ,µ) beaneutrosophicgraph.It’scalled neutrosophicconnected ifforeverygivencoupleofvertices,there’sat leastonepathamidthem.
Example1.1.50. Neutrosophiccomplete,neutrosophicpathandneutrosophic cycle,areonlyneutrosophicconnectedbutneutrosophicstrongcouldbeeither neutrosophicconnectedornot.Inotherwords,ifneutrosophicgraphis neutrosophicstrong,thenit’sneutrosophicconnectedornotbutifneutrosophic graphiseitherofneutrosophiccomplete,neutrosophicpathandneutrosophic cycle,thenit’sforeverneutrosophicconnected.
10
1.1.Definitions
Definition1.1.51. Let C =(V,E) beacrispgraph.Supposeapath P : v0,v1, ,vn 1,vn from v0 to vn mini=0,1,2, ,n 1 1 iscalled crispstrength of P andit’sdenotedby Sc(P )
Definition1.1.52. Let F =(σ,µ) beafuzzygraph.Supposeapath P : v0,v1, ,vn 1,vn from v0 to vn mini=0,1,2, ,n 1 µ(vivi+1) iscalled fuzzy strength of P andit’sdenotedby Sf (P ).
Definition1.1.53. Let N =(σ,µ) beaneutrosophicgraph.Supposeapath P : v0,v1, ,vn 1,vn from v0 to vn mini=0,1,2, ,n 1 µ(vivi+1) iscalled neutrosophicstrength of P andit’sdenotedby Sn(P ) i-pathisapathwith i edges,it’salsocalled length ofpath.
Example1.1.54. InFigures (2.1), (1.2), (1.3), (1.4), (1.5), (1.6), (1.7), neutrosophicstrengthsarecomputedforallpossiblepaths.
(a): ConsiderFigure(2.1).
(i): An 1-path P1 : n1,n2 hasneutrosophicstrength (0.74, 0.47, 0.31).
(ii): An 1-path P2 : n1,n3 hasneutrosophicstrength (0 55, 0 64, 0 26)
(iii): An 1-path P3 : n2,n3 hasneutrosophicstrength (0 37, 0 46, 0 24)
(iv): An 2-path P4 : n1,n2,n3 hasneutrosophicstrength (0 37, 0 46, 0 24) (v): Thereareonlyfourdistinctpaths.
(vi): Thereareonlythreeneutrosophicstrengths.
(vii): Thereareonlytwosameneutrosophicstrengths.
(b): ConsiderFigure(1.2).
(i): An 1-path P1 : n1,n2 hasneutrosophicstrength (0 74, 0 47, 0 31) (ii): An 1-path P2 : n1,n3 hasneutrosophicstrength (0 84, 0 47, 0 27) (iii): An 1-path P3 : n2,n3 hasneutrosophicstrength (0 74, 0 64, 0 27)
(iv): An 2-path P4 : n1,n2,n3 hasneutrosophicstrength (0 74, 0 47, 0 27)
(v): Thereareonlyfourdistinctpaths.
(vi): Thereareonlyfourdifferentneutrosophicstrengths. (vii): Thereisnosameneutrosophicstrengths.
(c): ConsiderFigure(1.3).
(i): An 1-path P1 : n1,n3 hasneutrosophicstrength (0 84, 0 47, 0 27)
(ii): An 1-path P2 : n2,n3 hasneutrosophicstrength (0 74, 0 64, 0 27)
(iii): An 2-path P3 : n1,n3,n2 hasneutrosophicstrength (0 74, 0 47, 0 27)
(iv): Thereareonlythreedistinctpaths.
(v): Thereareonlythreedifferentneutrosophicstrengths.
(vii): Thereisnosameneutrosophicstrengths.
(d): ConsiderFigure(1.4).
(i): An 1-path P1 : n1,n2 hasneutrosophicstrength (0 74, 0 64, 0 46)
11
(ii): An 1-path P2 : n1,n3 hasneutrosophicstrength (0.74, 0.64, 0.46).
(iii): An 1-path P3 : n2,n3 hasneutrosophicstrength (0 74, 0 64, 0 46)
(iv): An 2-path P4 : n1,n2,n3 hasneutrosophicstrength (0 74, 0 64, 0 46)
(v): Thereareonlyfourdistinctpaths.
(vi): Thereareonlyfourdifferentneutrosophicstrengths.
(vii): Thereareonlyfoursameneutrosophicstrengths.
(e): ConsiderFigure(1.5).
(i): An 1-path P1 : n1,n2 hasneutrosophicstrength (0 74, 0 64, 0 46)
(ii): An 1-path P2 : n1,n3 hasneutrosophicstrength (0.74, 0.64, 0.46).
(iii): An 1-path P3 : n2,n3 hasneutrosophicstrength (0 74, 0 64, 0 46)
(iv): An 2-path P4 : n1,n2,n3 hasneutrosophicstrength (0 74, 0 64, 0 46)
(v): Thereareonlyfourdistinctpaths.
(vi): Thereareonlyfourdifferentneutrosophicstrengths. (vii): Thereareonlyfoursameneutrosophicstrengths.
(f ): ConsiderFigure(1.6).
(i): An 1-path P1 : n1,n2 hasneutrosophicstrength (0 74, 0 64, 0 46)
(ii): Thereisonlyonedifferentneutrosophicstrengths. (iii): Thereisnosameneutrosophicstrengths.
(g): ConsiderFigure(1.7).
(i): An 1-path P1 : n1,n2 hasneutrosophicstrength (0 74, 0 64, 0 46)
(ii): Thereisonlyonedifferentneutrosophicstrengths.
(iii): Thereisnosameneutrosophicstrengths.
prp55 Proposition1.1.55. Let N =(σ,µ) beaneutrosophiccycle.Thenthenumber ofdistinctneutrosophicpathis 2n n 1.
Proof. Thenumberofsubsetsofnumber n is 2n.Thevertexof 1-setcouldn’t beconsideredaspath.Thenumberof 1-setis n. Thusitremains 2n n. Also, thevertexof 0-setcouldn’tbeconsideredaspath.Thenumberof 0-setis 1 Thusitfinallyremains 2n n 1
Corollary1.1.56. Let N =(σ,µ) beaneutrosophiccycle.Thenthenumberof distinctneutrosophicpathis 2n n 1
Proof. neutrosophicpathimplieshavingdistinctverticesinaconsecutive sequenceofvertices.Thusneutrosophiccycleisassamecaseasneutrosophic path.SobyapplyingProposition (1.1.55),theresultisstraightforward.In otherway,there’sdirectproofasfollows.Thenumberofsubsetsofnumber n is 2n.Thevertexof 1-setcouldn’tbeconsideredaspath.Thenumberof 1-set is n. Thusitremains 2n n. Also,thevertexof 0-setcouldn’tbeconsideredas path.Thenumberof 0-setis 1 Thusitfinallyremains 2n n 1
1.NeutrosophicGraphs
12
1.1.Definitions
Definition1.1.57. Let C =(V,E) beacrispgraphwhichisn’tcrisppath.For anygivencoupleofvertices v0 and vn,
(i): max{P isapathfrom v0 to vn} Sc(P ) isdenotedby C(v0,vn) andit’scalled t-connectedness amid v0 and vn in C.
(ii): max{P isapathfrom v0 to vn}\{P :v0vn} Sc(P ) isdenotedby Cα(v0,vn) it’s called α connectedness v0 and vn in C where v0vn isanedge,if Cα(v0,vn) >µ(v0vn).
(iii): max{P isapathfrom v0 to vn}\{P :v0vn} Sc(P ) isdenotedby Cα(v0,vn) it’s called β connectedness v0 and vn in C where v0vn isanedge,if Cα(v0,vn)= µ(v0vn)
(iv): max{P isapathfrom v0 to vn}\{P :v0vn} Sc(P ) isdenotedby Cα(v0,vn) it’s called δ connectedness v0 and vn in C where v0vn isanedge,if Cα(v0,vn) <µ(v0vn).
Definition1.1.58. Let C =(V,E) beacrispgraphwhichisn’tcrisppath.For anygivencoupleofvertices v0 and vn,
(i): max{P isapathfrom v0 to vn} Sc(P )= c ∈ Q isdenotedby Ct andit’scalled t-crisp
(ii): max{P isapathfrom v0 to vn}\{P :v0vn} Sc(P ) >µ(v0vn) isdenotedby Cα it’scalled α crisp where v0vn isanedge.
(iii): max{P isapathfrom v0 to vn}\{P :v0vn} Sc(P )= µ(v0vn) isdenotedby Cβ it’scalled β crisp where v0vn isanedge.
(iv): max{P isapathfrom v0 to vn}\{P :v0vn} Sc(P ) <µ(v0vn) isdenotedby Cδ it’scalled δ crisp where v0vn isanedge.
Definition1.1.59. Let F =(σ,µ) beafuzzygraphwhichisn’tfuzzypath.For anygivencoupleofvertices v0 and vn,
(i): max{P isapathfrom v0 to vn} Sf (P ) isdenotedby F (v0,vn) andit’scalled t-connectedness amid v0 and vn in F.
(ii): max{P isapathfrom v0 to vn}\{P :v0vn} Sf (P ) isdenotedby Fα(v0,vn) it’s called α connectedness v0 and vn in F where v0vn isanedge,if Fα(v0,vn) >µ(v0vn)
(iii): max{P isapathfrom v0 to vn}\{P :v0vn} Sf (P ) isdenotedby Fα(v0,vn) it’s called β connectedness v0 and vn in F where v0vn isanedge,if Fα(v0,vn)= µ(v0vn)
(iv): max{P isapathfrom v0 to vn}\{P :v0vn} Sf (P ) isdenotedby Fα(v0,vn) it’s called δ connectedness v0 and vn in F where v0vn isanedge,if Fα(v0,vn) <µ(v0vn)
Definition1.1.60. Let F =(σ,µ) beafuzzygraphwhichisn’tfuzzypath.For anygivencoupleofvertices v0 and vn,
(i): max{P isapathfrom v0 to vn} Sf (P )= c ∈ Q isdenotedby Ft andit’s called t-fuzzy
13
(ii): max{P isapathfrom v0 to vn}\{P :v0vn} Sf (P ) >µ(v0vn) isdenotedby Fα it’scalled α fuzzy where v0vn isanedge.
(iii): max{P isapathfrom v0 to vn}\{P :v0vn} Sf (P )= µ(v0vn) isdenotedby Fβ it’scalled β fuzzy where v0vn isanedge.
(iv): max{P isapathfrom v0 to vn}\{P :v0vn} Sf (P ) <µ(v0vn) isdenotedby Fδ it’scalled δ fuzzy where v0vn isanedge.
Definition1.1.61. Let N =(σ,µ) beaneutrosophicgraphwhichisn’t neutrosophicpath.Foranygivencoupleofvertices v0 and vn,
(i): max{P isapathfrom v0 to vn} Sn(P ) isdenotedby N (v0,vn) andit’scalled t-connectedness amid v0 and vn in N.
(ii): max{P isapathfrom v0 to vn}\{P :v0vn} Sn(P ) isdenotedby Nα(v0,vn) it’s called α connectedness v0 and vn in N where v0vn isanedge,if Nα(v0,vn) >µ(v0vn)
(iii): max{P isapathfrom v0 to vn}\{P :v0vn} Sn(P ) isdenotedby Nα(v0,vn) it’s called β connectedness v0 and vn in N where v0vn isanedge,if Nα(v0,vn)= µ(v0vn)
(iv): max{P isapathfrom v0 to vn}\{P :v0vn} Sn(P ) isdenotedby Nα(v0,vn) it’s called δ connectedness v0 and vn in N where v0vn isanedge,if Nα(v0,vn) <µ(v0vn)
Definition1.1.62. Let N =(σ,µ) beaneutrosophicgraphwhichisn’t neutrosophicpath.Foranygivencoupleofvertices v0 and vn,
(i): max{P isapathfrom v0 to vn} Sn(P )= c ∈ Q. Then N =(σ,µ) isdenoted by Nt andit’scalled t-neutrosophic
(ii): max{P isapathfrom v0 to vn}\{P :v0vn} Sn(P ) >µ(v0vn). Then N =(σ,µ) isdenotedby Nα it’scalled α neutrosophic where v0vn isanedge.
(iii): max{P isapathfrom v0 to vn}\{P :v0vn} Sn(P )= µ(v0vn) Then N =(σ,µ) isdenotedby Nβ it’scalled β neutrosophic where v0vn isanedge.
(iv): max{P isapathfrom v0 to vn}\{P :v0vn} Sn(P ) <µ(v0vn) Then N =(σ,µ) isdenotedby Nδ it’scalled δ neutrosophic where v0vn isanedge.
Example1.1.63. InFigures (2.1), (1.2), (1.3), (1.4), (1.5), (1.6), (1.7), neutrosophicgraphsandallpossibleedgesarecharacterized.
(a): ConsiderFigure(2.1).
(i): Theedge n1n2 is α connectednessand Nα(v0,vn)= (0.74, 0.47, 0.31).
(ii): Theedge n1n3 is α connectednessand Nα(v0,vn)= (0 55, 0 64, 0 26)
1.NeutrosophicGraphs
14
1.1.Definitions
(iii): Theedge n2n3 isneitherof t connectedness α connectedness β connectednessand δ connectedness.Sinceforpath P : n2,n1,n3, Sn(P ) isn’tcomputable.So max {P isapathfrom v2 to v3}\{P :v2v3} Sn(P ) isn’tcomputable.
(iv): N =(σ,µ) isneitherof t neutrosophic, Nt,α neutrosophic, Nα, β neutrosophic, Nβ , and δ connectedness, Nδ.
(b): ConsiderFigure(1.2).
(i): Theedge n1n2 isneitherof t connectedness, α connectedness, β connectednessand δ connectedness.Sinceforpath P : n1,n2,n2, Sn(P ) isn’tcomputable.So max {P isapathfrom v1 to v2}\{P :v1v2} Sn(P ) isn’tcomputable.
(ii): Theedge n1n3 isneitherof t connectedness, α connectedness, β connectednessand δ connectedness.Sinceforpath P : n1,n2,n3, Sn(P ) isn’tcomputable.So max {P isapathfrom v1 to v3}\{P :v1v3} Sn(P ) isn’tcomputable.
(iii): Theedge n2n3 isneitherof t connectedness, α connectedness, β connectednessand δ connectedness.Sinceforpath P : n2,n1,n3, Sn(P ) isn’tcomputable.So max {P isapathfrom v2 to v3}\{P :v2v3} Sn(P ) isn’tcomputable.
(iv): N =(σ,µ) isneitherof t neutrosophic, Nt,α neutrosophic, Nα,β neutrosophic, Nβ and δ connectedness, Nδ.
(c): ConsiderFigure(1.3).
(i): It’sneutrosophicpath.Thusthenotioncouldn’tbeapplied.
(d): ConsiderFigure(1.4).
(i): Theedge n1n2 is t connectednessand α connectednessand Nα(v1,v2)=(0 74, 0 64, 0 46)
(ii): Theedge n1n3 is t connectednessand α connectednessand Nα(v1,v3)=(0 74, 0 64, 0 46)
(iii): Theedge n1n3 is t connectednessand α connectednessand Nα(v1,v3)=(0.74, 0.64, 0.46).
(iv): N =(σ,µ) isneitherof α neutrosophic, Nα, and δ connectedness, Nδ
15
(v): N =(σ,µ) isboth t neutrosophic, Nt, and β neutrosophic, Nβ .
(e): ConsiderFigure(1.5).
(i): Theedge n1n2 is t connectednessand α connectednessand Nα(v1,v2)=(0.74, 0.64, 0.46).
(ii): Theedge n1n3 is t connectednessand α connectednessand Nα(v1,v3)=(0.74, 0.64, 0.46).
(iii): Theedge n1n3 is t connectednessand α connectednessand Nα(v1,v3)=(0.74, 0.64, 0.46).
(iv): N =(σ,µ) isneitherof α neutrosophic, Nα, and δ connectedness, Nδ.
(v): N =(σ,µ) isboth t neutrosophic, Nt, and β neutrosophic, Nβ
(f ): ConsiderFigure(1.6).
(i): It’sneutrosophicpath.Thusthenotioncouldn’tbeapplied.
(g): ConsiderFigure(1.7).
(i): It’sneutrosophicpath.Thusthenotioncouldn’tbeapplied.
Proposition1.1.64. Let N =(σ,µ) beaneutrosophiccomplete.Thenit’s β neutrosophic.
Proof. Suppose xy isagivenneutrosophicedge.Foranygivenneutrosophicpath P : x = v0,v1, ,vn = y, neutrosophicstrength is min{σ(x),σ(v1), ,σ(y)}≤ min{σ(x),σ(y)} Itimplies Sn(P ) ≤ min{σ(x),σ(y)} Inotherhand,by xy isanedge, P : x,y isapaththus Sn(P ) ≥ min{σ(x),σ(y)} Thus Sn(P )= min{σ(x),σ(y)} Itmeanseveryedge is β neutrosophic.Itinduces N =(σ,µ) is β neutrosophic.So N =(σ,µ) is Nβ .
Proposition1.1.65. Let N =(σ,µ) beaneutrosophicgraphsuchthatforevery neutrosophicedges xy and uv,µ(xy)= µ(uv). Thenit’s β neutrosophic.
Proof. Suppose xy isagivenneutrosophicedge.Consider µ(xy)= c,c ∈ Q. For anygivenneutrosophicpath P : x = v0,v1, ··· ,vn = y, neutrosophicstrength is min{µ(xv1),µ(v1v2), ,µ(vn 1y)} = min{c,c, ,c} Itimplies Sn(P ) ≤ c. Inotherhand,by xy isanedge, P : x,y isapaththus Sn(P ) ≥ µ(xy)= c. Thus Sn(P )= c. Itmeanseveryedgeis β neutrosophic.Itinduces N =(σ,µ) is β neutrosophic.So N =(σ,µ) is Nβ .
Proposition1.1.66. Let N =(σ,µ) beaneutrosophicgraph.Thenit’sneither α neutrosophicnor δ neutrosophic.
Proof. Ifalledgeshavesamevalues,theneverygivenedgeisn’tneither α neutrosophicnor δ neutrosophic.Otherwise,ifthere’sanedgewhich hasdifferentvalue,thenthere’soneedgewhichhasminimumvaluesoitisn’t neither α neutrosophicnor δ neutrosophic.
1.NeutrosophicGraphs
16
Definition1.1.67. Let N =(σ,µ) beaneutrosophicgraph. Coloringnumber isminimumnumberofdistinctcolorswhichareusedtocolortheverticeswhich areneighbors.
Example1.1.68. InFigures (2.1), (1.2), (1.3), (1.4), (1.5), (1.6), (1.7), neutrosophicgraphsandallpossibleedgesarecharacterized.
(a): ConsiderFigure(2.1).Coloringnumberisthree.
(b): ConsiderFigure(1.2).Coloringnumberisthree.
(c): ConsiderFigure(1.3).Coloringnumberistwo.
(d): ConsiderFigure(1.4).Coloringnumberisthree.
(e): ConsiderFigure(1.5).Coloringnumberisthree.
(f ): ConsiderFigure(1.6).Coloringnumberistwo.
(g): ConsiderFigure(1.7).Coloringnumberistwo.
Proposition1.1.69. Incompleteneutrosophic,coloringnumberis n.
Proof. Everyvertexhas n 1 neighbors.Thusthenumberofcolorsare n. Proposition1.1.70. Inpathneutrosophic,coloringnumberis 2.
Proof. Everyvertexhastwodifferentneighbors.Thuscoloringnumberis 2 Proposition1.1.71. Inevencycleneutrosophic,coloringnumberis 2
Proof. Everyvertexhastwodifferentneighbors.Thuscoloringnumberis 2 Proposition1.1.72. Inoddcycleneutrosophic,coloringnumberis 3.
Proof. Everyvertexhastwodifferentneighborsbutonevertexhastwoneighbors whichhavedifferentcolors.Thuscoloringnumberis 3.
Definition1.1.73. Afuzzy(neutrosophic)graphiscalled fuzzy(neutrosophic) t-partite if V ispartitionedto t parts, V1,V2, ,Vt andtheedge xy implies x ∈ Vi and y ∈ Vj where i = j. Ifit’sfuzzy(neutrosophic)complete,then it’sdenotedby Kσ1,σ2, ,σt where σi is σ on Vi instead V whichmean x ∈ Vi induces σi(x)=0 If t =2, thenit’scalled fuzzy(neutrosophic)complete bipartite andit’sdenotedby Kσ1,σ2 especially,if |V1| =1, thenit’scalled fuzzy(neutrosophic)star andit’sdenotedby S1,σ2 Inthiscase,thevertex in V1 iscalled center andifavertexjoinstoallverticesoffuzzy(neutrosophic), it’scalled fuzzy(neutrosophic)wheel andit’sdenotedby W1,σ2
Example1.1.74. InFigures (2.1), (1.2), (1.3), (1.4), (1.5), (1.6), (1.7), neutrosophicgraphsandallpossibleedgesarecharacterized.
(a): ConsiderFigure(2.1).
(i): Neutrosophicgraphisneutrosophicwheel.
(b): ConsiderFigure(1.2).
1.1.Definitions
17
Table1.2:Crisp-fying,Fuzzy-fyingandNeutrosophic-fying
CrispGraphs FuzzyGraphs NeutrosophicGraphs CrispComplete FuzzyComplete NeutrosophicComplete CrispStrong FuzzyStrong NeutrosophicStrong CrispPath FuzzyPath NeutrosophicPath CrispCycle FuzzyCycle NeutrosophicCycle Crispt-partite Fuzzyt-partite Neutrosophict-partite CrispBipartite FuzzyBipartite NeutrosophicBipartite CrispStar FuzzyStar NeutrosophicStar CrispWheel FuzzyWheel NeutrosophicWheel
(i): Neutrosophicgraphisneutrosophicwheel.
(c): ConsiderFigure(1.3).
(i): Neutrosophicgraphisneutrosophicstar. (ii): Neutrosophicgraphisneutrosophicbipartite.
(iii): Neutrosophicgraphisneutrosophict-partite. (iv): Neutrosophicgraphisneutrosophiccomplete.
(d): ConsiderFigure(1.4).
(i): Neutrosophicgraphisneutrosophicwheel. (e): ConsiderFigure(1.5).
(i): Neutrosophicgraphisneutrosophicwheel.
(f ): ConsiderFigure(1.6).
(i): Neutrosophicgraphisneutrosophicwheel. (ii): Neutrosophicgraphisneutrosophicstar.
(iii): Neutrosophicgraphisneutrosophicbipartite.
(iv): Neutrosophicgraphisneutrosophict-partite. (v): Neutrosophicgraphisneutrosophiccomplete.
(g): ConsiderFigure(1.7).
(i): Neutrosophicgraphisneutrosophicwheel.
(ii): Neutrosophicgraphisneutrosophicstar. (iii): Neutrosophicgraphisneutrosophicbipartite. (iv): Neutrosophicgraphisneutrosophict-partite.
(v): Neutrosophicgraphisneutrosophiccomplete.
Proposition1.1.75. Instarneutrosophic,coloringnumberis 2
Proof. Thecenterhas n 1 differentneighborsanditsneighborshaveno neighborinsteadofcenter.Sotheneighborshavesamecolorandcenterhas differentcolor.Thuscoloringnumberis 2
1.NeutrosophicGraphs
tbl2
18
1.1.Definitions
Proposition1.1.76. Inwheelneutrosophic,coloringnumberis 4.
Proof. Thecenterhas n 1 differentneighborsanditsneighborshavetwo neighborswhicharedistinctfromcenter.Sotheneighborshavesamecolorand centerhasdifferentcolor.Thuscoloringnumberis 4.
Proposition1.1.77. Inbipartiteneutrosophicsuchthatit’sneutrosophic complete,coloringnumberis 2
Proof. Therearetwopartsandineverypart,there’snoneighbor.Thuscoloring numberis 2.
Proposition1.1.78. Int-partiteneutrosophicsuchthatit’sneutrosophic complete,coloringnumberis t.
Proof. Therearetpartsandineverypart,there’snoneighbor.Thuscoloring numberis t.
Definition1.1.79. Let N =(σ,µ) beaneutrosophicgraph. Dominating number isminimumnumberofverticeswhichhasatleastoneedgewiththe verticesoutofthisset.
Example1.1.80. InFigures (2.1), (1.2), (1.3), (1.4), (1.5), (1.6), (1.7), neutrosophicgraphsandallpossibleedgesarecharacterized.
(a): ConsiderFigure(2.1).Dominatingnumberisone.
(b): ConsiderFigure(1.2).Dominatingnumberisone.
(c): ConsiderFigure(1.3).Dominatingnumberisone.
(d): ConsiderFigure(1.4).Dominatingnumberisone.
(e): ConsiderFigure(1.5).Dominatingnumberisone.
(f ): ConsiderFigure(1.6).Dominatingnumberisone.
(g): ConsiderFigure(1.7).Dominatingnumberisone.
Proposition1.1.81. Incompleteneutrosophic,dominatingnumberis 1
Proof. Everyvertexhas n 1 neighbors.Thusdominatingnumberofis 1.
Proposition1.1.82. Inpathneutrosophic,dominatingnumberis n 3 .
Proof. Everyvertexhastwodifferentneighbors.Onevertexhasedgewithits neighborsandthenextvertexisthevertexhastwoverticesamiditselfandthe lastvertexintheset.Sincetheminimumnumberisondemand,onevertex dominatesitsneighborsandeveryoftheseneighborshasoneneighborwhichis dominatedbythevertexwhichiscomingupafterit.Thusdominatingnumber is n 3
Proposition1.1.83. Incycleneutrosophic,dominatingnumberis n 3
19
Newideasare appliedonthese modelsto explore behaviorsof thesemodelsin themathematical perspective. Anotherwaysto makesenseabout them,areused byrelatively comparable resultsto conclude analysis.
1.NeutrosophicGraphs
Proof. Everyvertexhastwodifferentneighbors.Onevertexhasedgewithits neighborsandthenextvertexisthevertexhastwoverticesamiditselfandthe lastvertexintheset.Sincetheminimumnumberisondemand,onevertex dominatesitsneighborsandeveryoftheseneighborshasoneneighborwhichis dominatedbythevertexwhichiscomingupafterit.Thusdominatingnumber is n 3 .
Proposition1.1.84. Instarneutrosophic,dominatingnumberis 1
Proof. Thecenterhas n 1 differentneighborsanditsneighborshaveno neighborinsteadofcenter.Sotheneighborsareonlydominatedbycenteras singleton.Sincetheminimumnumberisondemand,centeris1-setwhichison demand.Thusdominatingnumberis 1
Proposition1.1.85. Inwheelneutrosophic,dominatingnumberis 1
Proof. Thecenterhas n 1 differentneighborsanditsneighborsbutneighbors havetwoneighborsinsteadofcenter.Sotheneighborsareonlydominatedby centerassingleton.Sincetheminimumnumberisondemand,centeris1-set whichisondemand.Thusdominatingnumberis 1
Proposition1.1.86. Inbipartiteneutrosophicsuchthatit’sneutrosophic complete,dominatingnumberis 2
Proof. Therearetwopartsandineverypart,there’snoneighbor.Everyvertex fromonepart,dominatesallvertexfromdifferentpart.Thusdominating numberis 2.
Proposition1.1.87. Int-partiteneutrosophicsuchthatit’sneutrosophic complete,dominatingnumberis 2
Proof. Thereare t partsandineverypart,there’snoneighbor.Everyvertex fromonepart,dominatesallverticesfromdifferentparts.Sinceminimum numberisondemand,onevertex x, dominatesallverticesfromotherpartsand onevertex y, fromdifferentpart,dominatesallverticeswhichhavecommon partwithfirstvertex x. Thusdominatingnumberis 2
1.2NewIdeas
Thereference[9; 10]isusedtowritethecontentsofthischapterandnext chapter.
1.3Abstract
Newnotionofdimensionasset,astwooptimalnumbersincludingmetric number,dimensionnumberandasoptimalsetareintroducedinindividual frameworkandinformationoffamily.Behaviorsoftwinandantipodalare exploredinfuzzy(neutrosophic)graphs.Fuzzy(neutrosophic)graphs,under conditions,fixed-edges,fixed-vertexandstrongfixed-vertexarestudied.Some classesaspath,cycle,complete,strong,t-partite,bipartite,starandwheelin theformationofindividualcaseandinthecase,theyformafamilyarestudied
20
inthetermofdimension.Fuzzification(neutrosofication)oftwinvertices butusingcrispconceptofantipodalverticesareanotherapproachesofthis study.Thusdefiningtwonotionsconcerningverticeswhichoneofthemis fuzzy(neutrosophic)titledtwinandanotheriscrisptitledantipodaltostudy thebehaviorsofcycleswhicharepartitionedintoevenandodd,areconcluded. Classesofcyclesaccordingtoantipodalverticesaredividedintotwoclasses asevenandodd.Parityofthenumberofedgesincyclecausestohavetwo subsectionsunderthesectionisentitledtoantipodalvertices.Inthisstudy, thetermdimensionisintroducedonfuzzy(neutrosophic)graphs.Thelocations ofobjectsbyasetofsomejunctionswhichhavedistinctdistancefromany coupleofobjectsoutoftheset,aredetermined.Thusit’spossibletohave thelocationsofobjectsoutsideofthissetbyassigningpartialnumbertoany objects.Theclassesofthesespecificgraphsarechosentoobtainsomeresults basedondimension.Thetypesofcrispnotionsandfuzzy(neutrosophic)notions areusedtomakesenseaboutthematerialofthisstudyandtheoutlineofthis studyusessomenewnotionswhicharecrispandfuzzy(neutrosophic).Some questionsandproblemsareposedconcerningwaystodofurtherstudieson thistopic.Basicfamiliaritieswithfuzzy(neutrosophic)graphtheoryandgraph theoryareproposedforthisarticle.
Keywords: FuzzyGraphs,NeutrosophicGraphs,Dimension
AMSSubjectClassification: 05C17,05C22,05E45
1.4Background
Fuzzyset,neutrosophicset,relateddefinitionsofothersets,graphsandnew notionsonthem,neutrosophicgraphs,studiesonneutrosophicgraphs,relevant definitionsofothergraphsbasedonfuzzygraphs,relateddefinitionsofother graphsbasedonneutrosophicgraphs,areproposed.
Inthissection,Iusetwosubsectionstoillustrateaperspectiveaboutthe backgroundofthisstudy.
MotivationandContributions
Inthisstudy,there’sanideawhichcouldbeconsideredasamotivation. Question1.4.1. Isitpossibletousemixedversionsofideasconcerning “crisp”,“fuzzy”and“neutrosophic”todefinesomenotionswhichareappliedto fuzzy(neutrosophic)graphs?
It’smotivationtofindnotionstouseinanyclassesoffuzzy(neutrosophic) graphs.Real-worldapplicationsaboutlocatingtheitem,areanotherthoughts whichleadtobeconsideredasmotivation.Distanceandpathamidtwoitems havekeyrolestolocate.Thusthey’reusedtodefinenewideaswhichconclude tothestructureofmetricdimension.Theconceptofconnectednessinspire tostudythebehaviorofpathanddistanceinthewaythat,bothindividual fuzzy(neutrosophic)graphsandfamilyofthemarethecasesofstudy. Theframeworkofthisstudyisasfollows.Insection (3.32),Iintroducemain definitionsalongsidesomeexamplestoclarifyaboutthem.Insection (3.29),one ideatitledfuzzy(neutrosophic)twinaboutspecificfuzzy(neutrosophic)vertices, isusedtoformtheresultsforfuzzy(neutrosophic)graphsandfamilyofthem
1.4.Background
21
butinthissection,there’resomeresultsconcerninglargestmetricnumbersince fuzzy(neutrosophic)twinformslargestmetricnumberaspossible.Insection (3.30),oneideatitledantipodalverticesaboutspecificcrispvertices,isusedto formtheresultsforfuzzy(neutrosophic)graphsandfamilyofthemespecially fuzzy(neutrosophic)cyclesastwosubsections.Fuzzy(neutrosophic)cyclesform smallestmetricnumberbutInsection (3.31),theresultsareextendedand they’reinclusiveandespecificforfuzzy(neutrosophic)graphsandfamilyof theminthewaythat,theclassificationisdoneinthetermsofsmallestmetric numberandlargestmetricnumber.Insection (??),twoapplicationsareposed forfuzzy(neutrosophic)graphsandfamilyofthem.Insection (1.10),some problemsandquestionsforfurtherstudiesareproposed.Insection (1.11), gentlediscussionaboutresultsandapplicationsarefeatured.Insection (1.11), abriefoverviewconcerningadvantagesandlimitationsofthisstudyalongside conclusionsareformed.
Preliminaries
Toclarifyaboutthemodels,Iusesomedefinitionsandresults,andinthisway, resultshaveakeyroletomakesenseaboutthedefinitionsandtointroduce newwaystouseonthesemodelsinthetermsofnewnotions.Forinstance, theconceptofcompleteisusedtospecializeagraphineveryenvironment.To differentiate,Iuseanadjectiveorprefixineverydefinition.Twoadjectives “fuzzy”and“neutrosophic”areusedtodistinguisheverygraphorclassesof graphoranynotiononthem.
G :(V,E) iscalleda crispgraph where V isasetofobjectsand E isa subsetof V × V suchthatthissubsetissymmetric.Acrispgraph G :(V,E) is calleda fuzzygraph G :(σ,µ) where σ : V → [0, 1] and µ : E → [0, 1] such that µ(xy) ≤ σ(x) ∧ σ(y) forall xy ∈ E. Acrispgraph G :(V,E) iscalled a neutrosophicgraph G :(σ,µ) where σ =(σ1,σ2,σ3): V → [0, 1] and µ =(µ1,µ2,µ3): E → [0, 1] suchthat µ(xy) ≤ σ(x)∧σ(y) forall xy ∈ E. Acrisp graph G :(V,E) iscalleda crispcomplete where ∀x ∈ V, ∀y ∈ V,xy ∈ E. Afuzzygraph G :(σ,µ) iscalled fuzzycomplete whereit’scompleteand µ(xy)= σ(x) ∧ σ(y) forall xy ∈ E. Aneutrosophicgraph G :(σ,µ) iscalled a neutrosophiccomplete whereit’scompleteand µ(xy)= σ(x) ∧ σ(y) for all xy ∈ E. An N whichisasetofvertices,iscalled fuzzy(neutrosophic) cardinality andit’sdenotedby |N | suchthat |N | =Σn∈N σ(n). Acrispgraph
G :(V,E) iscalleda crispstrong.Afuzzygraph G :(σ,µ) iscalled fuzzy strong where µ(xy)= σ(x)∧σ(y) forall xy ∈ E. Aneutrosophicgraph G :(σ,µ) iscalleda neutrosophicstrong where µ(xy)= σ(x) ∧ σ(y) forall xy ∈ E. A distinctsequenceofvertices v0,v1, ,vn inacrispgraph G :(V,E) iscalled crisppath withlength n from v0 to vn where vivi+1 ∈ E,i =0, 1, ,n 1. If oneedgeisincidenttoavertex,thevertexiscalled leaf.Apath v0,v1, ,vn is called fuzzypath where µ(vivi+1) > 0,i =0, 1, ··· ,n 1 Apath v0,v1, ··· ,vn iscalled neutrosophicpath where µ(vivi+1) > 0,i =0, 1, ,n 1 Let P : v0,v1, ,vn befuzzy(neutrosophic)pathfrom v0 to vn suchthatit hasminimumnumberofverticesaspossible,then d(v0,vn) isdefinedas Σn i=0µ(vi 1vi) Apath v0,v1, ,vn withexceptionof v0 and vn inacrisp graph G :(V,E) iscalled crispcycle withlength n for v0 where v0 = vn Acycle v0,v1, ,v0 iscalled fuzzycycle wheretherearetwoedges xy and uv suchthat µ(xy)= µ(uv)= i=0,1, ,n 1 µ(vivi+1) Acycle v0,v1, ,v0 is
1.NeutrosophicGraphs
22
1.4.Background
called neutrosophiccycle wheretherearetwoedges xy and uv suchthat µ(xy)= µ(uv)= i=0,1, ,n 1 µ(vivi+1) Afuzzy(neutrosophic)cycleiscalled odd ifthenumberofitsverticesisodd.Similarly,afuzzy(neutrosophic)cycle iscalled even ifthenumberofitsverticesiseven.Afuzzy(neutrosophic) graphiscalled fuzzy(neutrosophic)t-partite if V ispartitionedto t parts, V1,V2, ,Vt andtheedge xy implies x ∈ Vi and y ∈ Vj where i = j. Ifit’s fuzzy(neutrosophic)complete,thenit’sdenotedby Kσ1,σ2, ,σt where σi is σ on Vi instead V whichmean x ∈ Vi induces σi(x)=0 If t =2, thenit’s called fuzzy(neutrosophic)completebipartite andit’sdenotedby Kσ1,σ2 especially,if |V1| =1, thenit’scalled fuzzy(neutrosophic)star andit’s denotedby S1,σ2 . Inthiscase,thevertexin V1 iscalled center andifavertex joinstoallverticesoffuzzy(neutrosophic),it’scalled fuzzy(neutrosophic) wheel andit’sdenotedby W1,σ2 Asetis n-set ifitscardinalityis n. A
Table1.3:Crisp-fying,Fuzzy-fyingandNeutrosophic-fying T1
CrispGraphs FuzzyGraphs NeutrosophicGraphs
CrispComplete FuzzyComplete NeutrosophicComplete
CrispStrong FuzzyStrong NeutrosophicStrong
CrispPath FuzzyPath NeutrosophicPath
CrispCycle FuzzyCycle NeutrosophicCycle
Crispt-partite Fuzzyt-partite Neutrosophict-partite
CrispBipartite FuzzyBipartite NeutrosophicBipartite
CrispStar FuzzyStar NeutrosophicStar
CrispWheel FuzzyWheel NeutrosophicWheel
fuzzyvertexset isthesubsetofvertexsetof(neutrosophic)fuzzygraph suchthatthevaluesoftheseverticesareconsidered.A fuzzyedgeset is thesubsetofedgesetof(neutrosophic)fuzzygraphsuchthatthevaluesof theseedgesareconsidered.Let G beafamilyoffuzzygraphsorneutrosophic graphs.Thisfamilyhave fuzzy(neutrosophic)common vertexsetifall graphshavesamevertexsetanditsvaluesbutedgessetissubsetoffuzzyedge set.A(neutrosophic)fuzzygraphiscalled fixed-edgefuzzy(neutrosophic) graph ifalledgeshavesamevalues.A(neutrosophic)fuzzygraphiscalled fixed-vertexfuzzy(neutrosophic)graph ifallverticeshavesamevalues.A coupleofvertices x and y iscalled crisptwin verticesifeither N (x)= N (y) or N [x]= N [y] where ∀x ∈ V,N (x)= {y| xy ∈ E},N [x]= N (x) ∪{x} Two vertices t and t arecalled fuzzy(neutrosophic)twin verticesif N (t)= N (t ) and µ(ts)= µ(t s), forall s ∈ N (t)= N (t ) maxx,y∈V (G) |E(P (x,y))| iscalled
Table1.4:Crisp-fying,Fuzzy-fyingandNeutrosophic-fying T1
CrispVertexSet FuzzyVertexSet NeutrosophicVertexSet
23
CrispEdgeSet FuzzyEdgeSet NeutrosophicEdgeSet CrispCommon FuzzyCommon NeutrosophicCommon CrispFixed-edge FuzzyFixed-edge NeutrosophicFixed-edge CrispFixed-vertex FuzzyFixed-vertex NeutrosophicFixed-vertex CrispTwin FuzzyTwin NeutrosophicTwin
sec2
1.NeutrosophicGraphs
diameter of G andit’sdenotedby D(G) where |E(P (x,y))| isthenumberof edgesonthepathfrom x to y. Foranygivenvertex x ifthere’sexactlyone vertex y suchthat minP (x,y) |E(P (x,y))| = D(G), thenacoupleofvertices x and y arecalled antipodal vertices.
1.5Definitions
Iusethenotionofvertexinfuzzy(neutrosophic)graphstodefinenewnotions whichstatetherelationamidvertices.Inthisway,thesetofverticesare distinguishedbyanothersetofvertices.
Definition1.5.1. Let G =(V,σ,µ) beafuzzy(neutrosophic)graph.Avertex m fuzzy(neutrosophic)-resolves vertices f1 and f2 if d(m,f1) = d(m,f2) Aset M is fuzzy(neutrosophic)-resolvingset ifforeverycoupleofvertices f1,f2 ∈ V \ M, there’savertex m ∈ M suchthat m fuzzy(neutrosophic)-resolves f1 and f2 |M | iscalled fuzzy(neutrosophic)-metricnumber of G and min S isfuzzy(neutrosophic)-resolvingset Σs∈S σ(s)=Σm∈M σ(m) iscalled fuzzy(neutrosophic)-metricdimension of G andif min S isfuzzy(neutrosophic)-resolvingset Σs∈S σ(s)=Σm∈M σ(m)
where M isfuzzy(neutrosophic)-resolvingset,then M iscalled fuzzy(neutrosophic)-metricset of G.
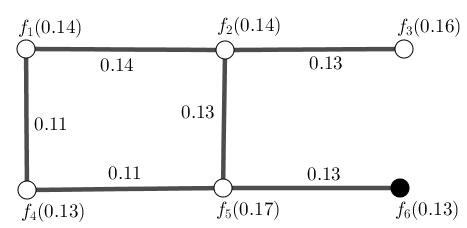
Example1.5.2. Let G beafuzzy(neutrosophic)graphasfigure (1.8).By applyingTable (1.5),the1-setisexploredwhichitscardinalityisminimum. {f6} and {f4} are1-setwhichhasminimumcardinalityamidallsetsofvertices but {f4} isn’tfuzzy(neutrosophic)-resolvingsetand {f6} isfuzzy(neutrosophic)resolvingset.Thusthere’snofuzzy(neutrosophic)-metricsetbut {f6}.f6 fuzzy(neutrosophic)-resolvesallgivencoupleofvertices.Thereforeoneis fuzzy(neutrosophic)-metricnumberof G and 0 13 isfuzzy(neutrosophic)-metric dimensionof G. ByusingTable (1.5), f4 doesn’tfuzzy(neutrosophic)-resolve f2 and f6 f4 doesn’tfuzzy(neutrosophic)-resolve f1 and f5,too.
Table1.5:DistancesofVerticesfromsetsofvertices {f6} and {f4} in fuzzy(neutrosophic)Graph G. T1
Vertices f1 f2 f3 f4 f5 f6 f6 0.22 0.26 0.39 0.24 0.13 0 Vertices f1 f2 f3 f4 f5 f6 f4 0.11 0.24 0.37 0 0.11 0.24
Definition1.5.3. Consider G asafamilyoffuzzy(neutrosophic)graphson afuzzy(neutrosophic)commonvertexset V. Avertex m simultaneously fuzzy(neutrosophic)-resolves vertices f1 and f2 if dG(m,f1) = dG(m,f2), forall G ∈G Aset M is simultaneouslyfuzzy(neutrosophic)-resolvingset ifforevery coupleofvertices f1,f2 ∈ V \ M, there’savertex m ∈ M suchthat m resolves
24
Figure1.8:Blackvertex {f6} isonlyfuzzy(neutrosophic)-metricsetamidall setsofverticesforfuzzy(neutrosophic)graph G. F1
f1 and f2, forall G ∈G |M | iscalled simultaneouslyfuzzy(neutrosophic)-metric number of G and min S isfuzzy(neutrosophic)-resolvingset Σs∈S σ(s)=Σm∈M σ(m) iscalled simultaneouslyfuzzy(neutrosophic)-metricdimension of G andif min S isfuzzy(neutrosophic)-resolvingset Σs∈S σ(s)=Σm∈M σ(m) where M isfuzzy(neutrosophic)-resolvingset,then M iscalled simultaneously fuzzy(neutrosophic)-metricset of G
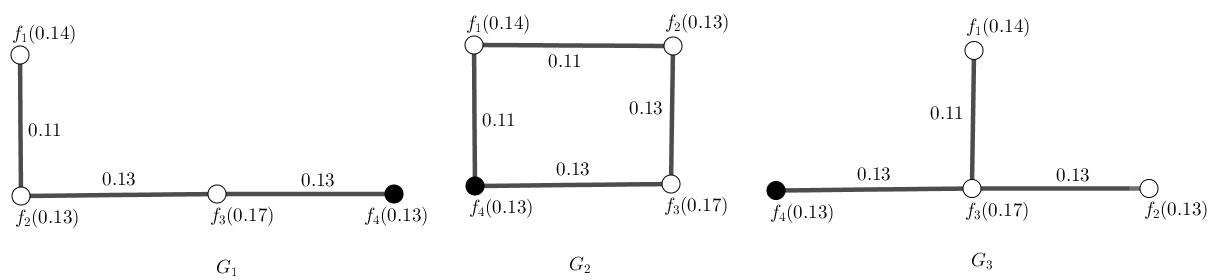
Example1.5.4. Let G = {G1,G2,G3} beacollectionoffuzzy(neutrosophic) graphswithcommonfuzzy(neutrosophic)vertexsetandasubsetof fuzzy(neutrosophic)edgesetasfigure (1.9).ByapplyingTable (1.6),the1-set isexploredwhichitscardinalityisminimum. {f2} and {f4} are1-setwhichhas minimumcardinalityamidallsetsofvertices. {f4} isasfuzzy(neutrosophic)resolvingsetas {f6} is.Thusthere’snofuzzy(neutrosophic)-metricsetbut {f4} and {f6}.f6 asfuzzy(neutrosophic)-resolvesallgivencoupleofverticesas f4 Thereforeoneisfuzzy(neutrosophic)-metricnumberof G and 0 13 isfuzzy(neutrosophic)-metricdimensionof G ByusingTable (1.6), f4 fuzzy(neutrosophic)-resolvesallgivencoupleofvertices.
Table1.6:DistancesofVerticesfromsetofvertices {f6} inFamilyof fuzzy(neutrosophic)Graphs G T2
Verticesof G1 f1 f2 f3 f4 f4 0.37 0.26 0.13 0
Verticesof G2 f1 f2 f3 f4 f4 0.11 0.22 0.13 0
Verticesof G3 f1 f2 f3 f4 f4 0.24 0.26 0.13 0
1.5.Definitions
25
sec4
Figure1.9:Blackvertex {f4} andthesetofvertices {f2} aresimultaneouslyfuzzy(neutrosophic)-metricsetamidallsetsofverticesforfamilyof fuzzy(neutrosophic)graphs G F2
1.6Fuzzy(Neutrosophic)TwinVertices
prp2 Proposition1.6.1. Let G beafuzzy(neutrosophic)graph.An (k 1)-setfrom ank-setoffuzzy(neutrosophic)twinverticesissubsetofafuzzy(neutrosophic)resolvingset.
Proof. If t and t arefuzzy(neutrosophic)twinvertices,then N (t)= N (t ) and µ(ts)= µ(t s), forall s ∈ N (t)= N (t )
cor2 Corollary1.6.2. Let G beafuzzy(neutrosophic)graph.Thenumberof fuzzy(neutrosophic)twinverticesis n 1. Thenfuzzy(neutrosophic)-metric numberis n 2
Proof. Let f and f betwovertices.Bysupposition,thecardinalityofsetof fuzzy(neutrosophic)twinverticesis n 2. Thustherearetwocases.Ifboth arefuzzy(neutrosophic)twinvertices,then N (f )= N (f ) and µ(fs)= µ(f s ), ∀s ∈ N (f ), ∀s ∈ N (f ) Itimplies d(f,t)= d(f,t) forall t ∈ V. Thussuppose ifnot,thenlet f beavertexwhichisn’tfuzzy(neutrosophic)twinvertices withanygivenvertexandlet f beavertexwhichisfuzzy(neutrosophic)twin verticeswithanygivenvertexbutnot f. Bysupposition,it’spossibleandthis isonlycase.Therefore,anygivendistinctvertexfuzzy(neutrosophic)-resolves f and f Then V \{f,f } isfuzzy(neutrosophic)-resolvingset.Itimplies fuzzy(neutrosophic)-metricnumberis n 2
Corollary1.6.3. Let G beafuzzy(neutrosophic)graph.Thenumberof fuzzy(neutrosophic)twinverticesis n. Then G isfixed-edgefuzzy(neutrosophic) graph.
Proof. Suppose f and f aretwogivenedges.Bysupposition,everycouple ofverticesarefuzzy(neutrosophic)twinvertices.Itimplies µ(f )= µ(f ).f and f arearbitrarysoeverycoupleofedgeshavesamevalues.Itinduces G is fixed-edgefuzzy(neutrosophic)graph.
cor1
Corollary1.6.4. Let G beafixed-vertexfuzzy(neutrosophic)graph.Thenumber offuzzy(neutrosophic)twinverticesis n 1 Thenfuzzy(neutrosophic)-metric numberis n 2, fuzzy(neutrosophic)-metricdimensionis (n 2)σ(m) where m isfuzzy(neutrosophic)twinvertexwithavertex.Every (n 2)-setincluding fuzzy(neutrosophic)twinverticesisfuzzy(neutrosophic)-metricset.
1.NeutrosophicGraphs
26
prp3
1.6.Fuzzy(Neutrosophic)TwinVertices
Proof. ByCorollary (3.29.2),fuzzy(neutrosophic)-metricnumberis n 2. By G isafixed-vertexfuzzy(neutrosophic)graph,fuzzymetricdimensionis (n 2)σ(m) where m isfuzzy(neutrosophic)twinvertexwithavertex.Onevertexdoesn’t belongtosetoffuzzy(neutrosophic)twinverticesandavertexfromthatset,are outoffuzzymetricset.Itinducesevery (n 2)-setincludingfuzzy(neutrosophic) twinverticesisfuzzymetricset.
Proposition1.6.5. Let G beafixed-vertexfuzzy(neutrosophic)graphsuchthat it’sfuzzy(neutrosophic)complete.Thenfuzzy(neutrosophic)-metricnumberis n 1, fuzzy(neutrosophic)-metricdimensionis (n 1)σ(m) where m isagiven vertex.Every (n 1)-setisfuzzy(neutrosophic)-metricset.
Proof. Infuzzy(neutrosophic)complete,everycoupleofverticesaretwinvertices. By G isafixed-vertexfuzzy(neutrosophic)graphandit’sfuzzy(neutrosophic) complete,everycoupleofverticesarefuzzy(neutrosophic)twinvertices.Thus byProposition(3.29.1),theresultfollows.
Proposition1.6.6. Let G beafamilyoffuzzy(neutrosophic)graphs withfuzzy(neutrosophic)commonvertexset.Thensimultaneously fuzzy(neutrosophic)-metricnumberof G is n 1
Proof. Consider (n 1)-set.Thusthere’snocoupleofverticestobe fuzzy(neutrosophic)-resolved.Therefore,every (n 1)-setisfuzzy(neutrosophic)resolvingsetforanygivenfuzzy(neutrosophic)graph.Thenitholdsforany fuzzy(neutrosophic)graph.Itimpliesit’sfuzzy(neutrosophic)-resolvingset anditscardinalityisfuzzy(neutrosophic)-metricnumber. (n 1)-sethas thecardinality n 1. Thenitholdsforanyfuzzy(neutrosophic)graph.It inducesit’ssimultaneouslyfuzzy(neutrosophic)-resolvingsetanditscardinality issimultaneouslyfuzzy(neutrosophic)-metricnumber.
prp4 Proposition1.6.7. Let G beafamilyoffuzzy(neutrosophic)graphs withfuzzy(neutrosophic)commonvertexset.Thensimultaneously fuzzy(neutrosophic)-metricnumberof G isgreaterthanthemaximum fuzzy(neutrosophic)-metricnumberof G ∈G.
Proof. Suppose t and t aresimultaneouslyfuzzy(neutrosophic)-metricnumberof G andfuzzy(neutrosophic)-metricnumberof G ∈G Thus t is fuzzy(neutrosophic)-metricnumberforany G ∈G Hence, t ≥ t Sosimultaneouslyfuzzy(neutrosophic)-metricnumberof G isgreaterthanthemaximum fuzzy(neutrosophic)-metricnumberof G ∈G
prp5 Proposition1.6.8. Let G beafamilyoffuzzy(neutrosophic)graphs withfuzzy(neutrosophic)commonvertexset.Thensimultaneously fuzzy(neutrosophic)-metricnumberof G isgreaterthansimultaneously fuzzy(neutrosophic)-metricnumberof H⊆G
Proof. Suppose t and t aresimultaneouslyfuzzy(neutrosophic)-metricnumber of G and H Thus t isfuzzy(neutrosophic)-metricnumberforany G ∈G It implies t isfuzzy(neutrosophic)-metricnumberforany G ∈H. So t issimultaneouslyfuzzy(neutrosophic)-metricnumberof H ByapplyingDefinitionabout beingtheminimumnumber, t ≥ t Sosimultaneouslyfuzzy(neutrosophic)metricnumberof G isgreaterthansimultaneouslyfuzzy(neutrosophic)-metric numberof H⊆G
27
thm1 Theorem1.6.9. Fuzzy(neutrosophic)twinverticesaren’tfuzzy(neutrosophic)resolvedinanygivenfuzzy(neutrosophic)graph.
Proof. Let t and t befuzzy(neutrosophic)twinvertices.Then N (t)= N (t ) and µ(ts)= µ(t s), forall s,s ∈ V suchthat ts,t s ∈ E. Thusforeverygiven vertex s ∈ V,dG(s ,t)= dG(s,t) where G isagivenfuzzy(neutrosophic)graph. Itmeansthat t and t aren’tresolvedinanygivenfuzzy(neutrosophic)graph. t and t arearbitrarysofuzzy(neutrosophic)twinverticesaren’tresolvedinany givenfuzzy(neutrosophic)graph.
prp6 Proposition1.6.10. Let G beafixed-vertexfuzzy(neutrosophic)graph. If G isfuzzy(neutrosophic)complete,theneverycoupleofverticesare fuzzy(neutrosophic)twinvertices.
Proof. Let t and t becoupleofgivenvertices.By G isfuzzy(neutrosophic) complete, N (t)= N (t ) By G isafixed-vertexfuzzy(neutrosophic)graph, µ(ts)= µ(t s), foralledges ts,t s ∈ E. Thus t and t arefuzzy(neutrosophic) twinvertices. t and t arearbitrarycoupleofvertices,henceeverycoupleof verticesarefuzzy(neutrosophic)twinvertices.
thm17 Theorem1.6.11. Let G beafamilyoffuzzy(neutrosophic)graphswith fuzzy(neutrosophic)commonvertexsetand G ∈G isafixed-vertex fuzzy(neutrosophic)graphsuchthatit’sfuzzy(neutrosophic)complete.Then simultaneouslyfuzzy(neutrosophic)-metricnumberis n 1, simultaneously fuzzy(neutrosophic)-metricdimensionis (n 1)σ(m) where m isagivenvertex. Every (n 1)-setissimultaneouslyfuzzy(neutrosophic)-metricsetfor G.
Proof. G isfixed-vertexfuzzy(neutrosophic)graphandit’sfuzzy(neutrosophic) complete.SobyTheorem (3.29.9),Igeteverycoupleofverticesin fuzzy(neutrosophic)completearefuzzy(neutrosophic)twinvertices.Soevery coupleofvertices,byTheorem(3.29.8),aren’tresolved.
Corollary1.6.12. Let G beafamilyoffuzzy(neutrosophic)graphswith fuzzy(neutrosophic)commonvertexsetand G ∈G isafuzzy(neutrosophic) complete.Thensimultaneouslyfuzzy(neutrosophic)-metricnumberis n 1, simultaneouslyfuzzy(neutrosophic)-metricdimensionis (n 1)σ(m) where m is agivenvertex.Every (n 1)-setissimultaneouslyfuzzy(neutrosophic)-metric setfor G.
Proof. Byfuzzy(neutrosophic)graphswithfuzzy(neutrosophic)commonvertex set, G isfixed-vertexfuzzy(neutrosophic)graph.It’sfuzzy(neutrosophic) complete.SobyTheorem(3.29.10),Igetintendedresult.
Theorem1.6.13. Let G beafamilyoffuzzy(neutrosophic)graphswith fuzzy(neutrosophic)commonvertexsetandforeverygivencoupleofvertices, there’sa G ∈G suchthatinthat,they’refuzzy(neutrosophic)twinvertices. Thensimultaneouslyfuzzy(neutrosophic)-metricnumberis n 1, simultaneously fuzzy(neutrosophic)-metricdimensionis (n 1)σ(m) where m isagivenvertex. Every (n 1)-setissimultaneouslyfuzzy(neutrosophic)-metricsetfor G
1.NeutrosophicGraphs
28
thm19
Proof. ByProposition (3.29.5),simultaneouslyfuzzy(neutrosophic)-metric numberis n 1 ByTheorem (3.29.8),simultaneouslyfuzzy(neutrosophic)metricdimensionis (n 1)σ(m) where m isagivenvertex.Also,every (n 1)-set issimultaneouslyfuzzy(neutrosophic)-metricsetfor G
Theorem1.6.14. Let G beafamilyoffuzzy(neutrosophic)graphswith fuzzy(neutrosophic)commonvertexset.If G containsthreefixedvertexfuzzy(neutrosophic)starswithdifferentcenter,thensimultaneously fuzzy(neutrosophic)-metricnumberis n 2, simultaneouslyfuzzy(neutrosophic)metricdimensionis (n 2)σ(m) where m isagivenvertex.Every (n 2)-set issimultaneouslyfuzzy(neutrosophic)-metricsetfor G.
Proof. Thecardinalityofsetoffuzzy(neutrosophic)twinverticesis n 1 Thus byCorollary(3.29.3),theresultfollows.
Corollary1.6.15. Let G beafamilyoffuzzy(neutrosophic)graphswith fuzzy(neutrosophic)commonvertexset.If G containsthreefuzzy(neutrosophic) starswithdifferentcenter,thensimultaneouslyfuzzy(neutrosophic)-metric numberis n 2, simultaneouslyfuzzy(neutrosophic)-metricdimensionis (n 2)σ(m) where m isagivenvertex.Every (n 2)-setissimultaneously fuzzy(neutrosophic)-metricsetfor G.
Proof. Byfuzzy(neutrosophic)graphswithfuzzy(neutrosophic)commonvertex set, G isfixed-vertexfuzzy(neutrosophic)graph.It’sfuzzy(neutrosophic) complete.SobyTheorem(3.29.13),Igetintendedresult.
1.7AntipodalVertices
EvenFuzzy(Neutrosophic)Cycle
prp5.1 Proposition1.7.1. Considertwoantipodalvertices x and y inanygivenfixededgeevenfuzzy(neutrosophic)cycle.Let u and v begivenvertices.Then d(x,u) = d(x,v) ifandonlyif d(y,u) = d(y,v).
Proof. (⇒) Consider d(x,u) = d(x,v) By d(x,u)+ d(u,y)= d(x,y)= D(G),D(G) d(x,u) = D(G) d(x,v) Itimplies d(y,u) = d(y,v) (⇐). Consider d(y,u) = d(y,v). By d(y,u)+ d(u,x)= d(x,y)= D(G),D(G) d(y,u) = D(G) d(y,v) Itimplies d(x,u) = d(x,v)
Proposition1.7.2. Considertwoantipodalvertices x and y inanygivenfixededgeevenfuzzy(neutrosophic)cycle.Let u and v begivenvertices.Then d(x,u)= d(x,v) ifandonlyif d(y,u)= d(y,v)
Proof. (⇒) Consider d(x,u)= d(x,v) By d(x,u)+ d(u,y)= d(x,y)= D(G),D(G) d(x,u)= D(G) d(x,v) Itimplies d(y,u)= d(y,v) (⇐) Consider d(y,u)= d(y,v) By d(y,u)+ d(u,x)= d(x,y)= D(G),D(G) d(y,u)= D(G) d(y,v). Itimplies d(x,u)= d(x,v).
Proposition1.7.3. Thesetcontainstwoantipodalvertices,isn’t fuzzy(neutrosophic)-metricsetinanygivenfixed-edgeevenfuzzy(neutrosophic) cycle.
1.7.AntipodalVertices
sec5
29
1.NeutrosophicGraphs
Proof. Let x and y betwogivenantipodalverticesinanygiveneven fuzzy(neutrosophic)cycle.ByProposition (3.30.1), d(x,u) = d(x,v) ifand onlyif d(y,u) = d(y,v) Itimpliesthatif x fuzzy(neutrosophic)-resolvesa coupleofvertices,then y fuzzy(neutrosophic)-resolvesthem,too.Thuseither x isinfuzzy(neutrosophic)-metricsetor y is.Itinducesthesetcontains twoantipodalvertices,isn’tfuzzy(neutrosophic)-metricsetinanygiveneven fuzzy(neutrosophic)cycle.
Proposition1.7.4. Considertwoantipodalvertices x and y inanygivenfixededgeevenfuzzy(neutrosophic)cycle. x fuzzy(neutrosophic)-resolvesagiven coupleofvertices, z and z ,ifandonlyif y does.
Proof. (⇒).x fuzzy(neutrosophic)-resolvesagivencoupleofvertices, z and z , then d(x,z) = d(x,z ) ByProposition (3.30.1), d(x,z) = d(x,z ) ifandonlyif d(y,z) = d(y,z ) Thus y fuzzy(neutrosophic)-resolvesagivencoupleofvertices z and z . (⇐).y fuzzy(neutrosophic)-resolvesagivencoupleofvertices, z and z ,then d(y,z) = d(y,z ) ByProposition (3.30.1), d(y,z) = d(y,z ) ifandonlyif d(x,z) = d(x,z ) Thus x fuzzy(neutrosophic)-resolvesagivencoupleofvertices z and z
Proposition1.7.5. Therearetwoantipodalverticesaren’tfuzzy(neutrosophic)resolvedbyothertwoantipodalverticesinanygivenfixed-edgeeven fuzzy(neutrosophic)cycle.
Proof. Suppose x and y areacoupleofvertices.Itimplies d(x,y)= D(G). Consider u and v areanothercoupleofverticessuchthat d(x,u)= D(G) 2 Itimplies d(y,u)= D(G) 2 Thus d(x,u)= d(y,u) Therefore, u doesn’t fuzzy(neutrosophic)-resolveagivencoupleofvertices x and y. By D(G)= d(u,v)= d(u,x)+ d(x,v)= D(G) 2 + d(x,v),d(x,v)= D(G) 2 Itimplies d(y,v)= D(G) 2 Thus d(x,v)= d(y,v) Therefore, v doesn’tfuzzy(neutrosophic)resolveagivencoupleofvertices x and y.
Proposition1.7.6. Foranytwoantipodalverticesinanygivenfixed-edge evenfuzzy(neutrosophic)cycle,thereareonlytwoantipodalverticesdon’t fuzzy(neutrosophic)-resolvethem
Proof. Suppose x and y areacoupleofverticessuchthatthey’reantipodal vertices.Let u beavertexsuchthat d(x,u)= D(G) 2 Itimplies d(y,u)= D(G) 2 Thus d(x,u)= d(y,u). Therefore, u doesn’tfuzzy(neutrosophic)-resolveagiven coupleofvertices x and y. Let v beaantipodalvertexfor u suchthat u and v areantipodalvertices.Thus vd(x,v)= D(G) 2 Itimplies d(y,v)= D(G) 2 Therefore, v doesn’tfuzzy(neutrosophic)-resolveagivencoupleofvertices x and y. If u isavertexsuchthat d(x,u) = D(G) 2 and v isavertexsuchthat u and v areantipodalvertices.Thus d(x,v) = D(G) 2 Itinduceseither d(x,u) = d(y,u) or d(x,v) = d(y,v) Itmeanseither u fuzzy(neutrosophic)-resolvesagivencouple ofvertices x and y or v fuzzy(neutrosophic)-resolvesagivencoupleofvertices x and y.
Proposition1.7.7. Inanygivenfixed-edgeevenfuzzy(neutrosophic)cycle,for anyvertex,there’sonlyonevertexsuchthatthey’reantipodalvertices.
30
prp5.8
cor5.9
cor5.10
cor4.11
prp5.11
prp5.12
1.7.AntipodalVertices
Proof. If d(x,y)= D(G), then x and y areantipodalvertices.
Proposition1.7.8. Let G beafixed-edgeevenfuzzy(neutrosophic)cycle.Then everycoupleofverticesarefuzzy(neutrosophic)-resolvingsetifandonlyifthey aren’tantipodalvertices.
Proof. If x and y areantipodalvertices,thentheydon’tfuzzy(neutrosophic)resolveagivencoupleofvertices u and v suchthatthey’reantipodalvertices and d(x,u)= D(G) 2 Since d(x,u)= d(x,v)= d(y,u)= d(y,v)= D(G) 2
Corollary1.7.9. Let G beafixed-edgeevenfuzzy(neutrosophic)cycle.Then fuzzy(neutrosophic)-metricnumberistwo.
Proof. Asetcontainsonevertex x isn’tfuzzy(neutrosophic)-resolvingset.Since itdoesn’tfuzzy(neutrosophic)-resolveagivencoupleofvertices u and v such that d(x,u)= d(x,v)=1 Thusfuzzy(neutrosophic)-metricnumber ≥ 2 By Proposition (3.30.8),everycoupleofverticessuchthattheyaren’tantipodal vertices,arefuzzy(neutrosophic)-resolvingset.Therefore,fuzzy(neutrosophic)metricnumberis 2
Corollary1.7.10. Let G beafixed-edgeevenfuzzy(neutrosophic)cycle.Then fuzzy(neutrosophic)-metricsetcontainscoupleofverticessuchthattheyaren’t antipodalvertices.
Proof. ByCorollary (3.30.9),fuzzy(neutrosophic)-metricnumberistwo.By Proposition (3.30.8),everycoupleofverticessuchthattheyaren’tantipodal vertices,arefuzzy(neutrosophic)-resolvingset.Therefore,fuzzy(neutrosophic)metricsetcontainscoupleofverticessuchthattheyaren’tantipodalvertices.
Corollary1.7.11. Let G beafamilyoffixed-edgeoddfuzzy(neutrosophic) cycleswithfuzzy(neutrosophic)commonvertexset.Thensimultaneously fuzzy(neutrosophic)-metricsetcontainscoupleofverticessuchthattheyaren’t antipodalverticesandfuzzy(neutrosophic)-metricnumberistwo.
OddFuzzy(Neutrosophic)Cycle
Proposition1.7.12. Inanygivenfixed-edgeoddfuzzy(neutrosophic)cycle,for anyvertex,there’snovertexsuchthatthey’reantipodalvertices.
Proof. Let G beafixed-edgeoddfuzzy(neutrosophic)cycle.if x isagiven vertex.Thentherearetwovertices u and v suchthat d(x,u)= d(x,v)= D(G) Itimpliestheyaren’tantipodalvertices.
Proposition1.7.13. Let G beafixed-edgeoddfuzzy(neutrosophic)cycle.Then everycoupleofverticesarefuzzy(neutrosophic)-resolvingset.
Proof. Let l and l becoupleofvertices.Thus,byProposition (3.30.12), l and l aren’tantipodalvertices.Itimpliesforeverygivencoupleofvertices fi and fj ,Igeteither d(l,fi) = d(l,fj ) or d(l ,fi) = d(l ,fj ) Therefore, fi and fj arefuzzy(neutrosophic)-resolvedbyeither l or l .Itinducestheset {l,l } is fuzzy(neutrosophic)-resolvingset.
31
prp5.13 Proposition1.7.14. Let G beafixed-edgeoddfuzzy(neutrosophic)cycle.Then fuzzy(neutrosophic)-metricnumberistwo.
Proof. Let l and l becoupleofvertices.Thus,byProposition (3.30.12), l and l aren’tantipodalvertices.Itimpliesforeverygivencoupleofvertices fi and fj ,Igeteither d(l,fi) = d(l,fj ) or d(l ,fi) = d(l ,fj ) Therefore, fi and fj arefuzzy(neutrosophic)-resolvedbyeither l or l .Itinducestheset {l,l } is fuzzy(neutrosophic)-resolvingset.
Corollary1.7.15. Let G beafixed-edgeoddfuzzy(neutrosophic)cycle.Then fuzzy(neutrosophic)-metricsetcontainscoupleofvertices.
Proof. ByProposition (3.30.14),fuzzy(neutrosophic)-metricnumberistwo.By Proposition (3.30.13),everycoupleofverticesarefuzzy(neutrosophic)-resolving set.Therefore,fuzzy(neutrosophic)-metricsetcontainscoupleofvertices.
Corollary1.7.16. Let G beafamilyoffixed-edgeoddfuzzy(neutrosophic) cycleswithfuzzy(neutrosophic)commonvertexset.Thensimultaneouslyfuzzy(neutrosophic)-metricsetcontainscoupleofverticesand fuzzy(neutrosophic)-metricnumberistwo.
1.8ExtendedResults
sec6
SmallestMetricNumber
prp1 Proposition1.8.1. Let G beafuzzy(neutrosophic)path.Theneveryleafis fuzzy(neutrosophic)-resolvingset.
Proof. Let l bealeaf.Foreverygivenacoupleofvertices fi and fj ,Iget d(l,fi) = d(l,fj ) SinceifIreassignindexestoverticessuchthateveryvertex fi and l have i verticesamidthemselves,then d(l,fi)=Σj≤iµ(fj fi) ≤ i.Thus j ≤ i implies Σt≤j µ(ftfj )+Σj≤s≤iµ(fsfi) > Σj≤iµ(ffi) ≡ d(l,fj )+c = d(l,fi) ≡ d(l,fj ) <d(l,fi)
Therefore,by d(l,fj ) <d(l,fi), Iget d(l,fi) = d(l,fj ).fi and fj arearbitrary so l fuzzy(neutrosophic)-resolvesanygivencoupleofvertices fi and fj which implies {l} isafuzzy(neutrosophic)-resolvingset.
Corollary1.8.2. Let G beafixed-edgefuzzy(neutrosophic)path.Thenevery leafisfuzzy(neutrosophic)-resolvingset.
Proof. Let l bealeaf.Foreverygivencoupleofvertices, fi and fj , Iget d(l,fi)= ci = d(l,fj )= cj. Itimplies l fuzzy(neutrosophic)-resolvesanygiven coupleofvertices fi and fj whichimplies {l} isafuzzy(neutrosophic)-resolving set.
Corollary1.8.3. Let G beafixed-vertexfuzzy(neutrosophic)path.Thenevery leafisfuzzy(neutrosophic)-metricset,fuzzy(neutrosophic)-metricnumberisone andfuzzy(neutrosophic)-metricdimensionis c where c = σ(f ),f ∈ V.
1.NeutrosophicGraphs
32
prp7
Proof. ByProposition (3.31.1),everyleafisfuzzy(neutrosophic)-resolving set.By c = σ(f ), ∀f ∈ V, everyleafisfuzzy(neutrosophic)-metricset, fuzzy(neutrosophic)-metricnumberisoneandfuzzy(neutrosophic)-metric dimensionis c.
Proposition1.8.4. Let G beafuzzy(neutrosophic)path.Thenasetincluding everycoupleofverticesisfuzzy(neutrosophic)-resolvingset.
Proof. Let f and f beacoupleofvertices.Foreverygivenacoupleofvertices fi and fj ,Igeteither d(f,fi) = d(f,fj ) or d(f ,fi) = d(f ,fj ).
Corollary1.8.5. Let G beafixed-edgefuzzy(neutrosophic)path.Thenevery setcontainingcoupleofverticesisfuzzy(neutrosophic)-resolvingset.
Proof. Consider G isafuzzy(neutrosophic)path.ThusbyProposition (3.31.2), everysetcontainingcoupleofverticesisfuzzy(neutrosophic)-resolvingset.So itholdsforanygivenfixed-edgepathfuzzy(neutrosophic)graph.
Proposition1.8.6. IfIusefixed-vertexstrongfuzzy(neutrosophic)cyclesinstead offixed-edgefuzzy(neutrosophic)cycles,thenallresultsofSection (3.30) hold.
Proof. Let G beafixed-vertexstrongfuzzy(neutrosophic)cycles.By G isfuzzy(neutrosophic)strongandit’sfixed-vertex, G isfixed-edge fuzzy(neutrosophic).
prp6.2
Proposition1.8.7. Let G beafixed-vertexstrongfuzzy(neutrosophic)path. Thenan 1-setcontainsleaf,isfuzzy(neutrosophic)-resolvingset.An 1-set containsleaf,isfuzzy(neutrosophic)-metricset.Fuzzy(neutrosophic)-metric numberisone.Fuzzy(neutrosophic)-metricdimensionis σ(m) where m isa givenvertex.
Proof. Therearetwoleaves.Consider l isagivenleaf.By G isafixed-vertex strongfuzzy(neutrosophic)path,there’sonlyonenumbertobeseen.Thusif v and e areagivenvertexandgivenedge,then σ(v)= σ(e)= c where c ∈ [0, 1] Further,foreverygivenvertices v and v ,σ(v)= σ(v ) Withanalogous,for everygivenedges e and e ,σ(e)= σ(e ).Withrearrangingtheindexesof vertices, d(l,vi)= ci. Furthermore, d(l,vi)= ci = cj = d(l,vj ). Therefore, l fuzzy(neutrosophic)-resolveseverygivencoupleofvertices x and v. Itinduces 1-setcontainingleaf,isfuzzy(neutrosophic)-resolvingset.By G isafixed-vertex, foreverygivenvertices v and v ,σ(v)= σ(v ) Itimplies 1-setcontainingleaf, isfuzzy(neutrosophic)-metricset.Also,fuzzy(neutrosophic)-metricnumberis one.Hence,fuzzy(neutrosophic)-metricdimensionis σ(m) where m isagiven vertex.
cor6.3 Corollary1.8.8. Let G beafamilyoffuzzy(neutrosophic)pathswith fuzzy(neutrosophic)commonvertexsetsuchthatthey’veacommonleaf. Thensimultaneouslyfuzzy(neutrosophic)-metricnumberis 1, simultaneously fuzzy(neutrosophic)-metricdimensionis σ(m) where m isagivenvertex. 1-set containscommonleaf,issimultaneouslyfuzzy(neutrosophic)-metricsetfor G
1.8.ExtendedResults
33
1.NeutrosophicGraphs
Proof. ByProposition (3.31.3),commonleaffuzzy(neutrosophic)-resolvesevery givencoupleofvertices x and v, simultaneously.Thus 1-setcontaining commonleaf,issimultaneouslyfuzzy(neutrosophic)-metricset.Also,simultaneouslyfuzzy(neutrosophic)-metricnumberisone.Hence,simultaneously fuzzy(neutrosophic)-metricdimensionis σ(m) where m isagivenvertex.
prp6.4 Proposition1.8.9. Let G beafixed-vertexstrongfuzzy(neutrosophic)path. Thenan 2-setcontainseverycoupleofvertices,isfuzzy(neutrosophic)-resolving set.An 2-setcontainseverycoupleofvertices,isfuzzy(neutrosophic)-metric set.Fuzzy(neutrosophic)-metricnumberistwo.Fuzzy(neutrosophic)-metric dimensionis 2σ(m) where m isagivenvertex.
Proof. Suppose v isagivenvertex.Iftherearetwovertices x and y such that d(x,v) = d(y,v), then x fuzzy(neutrosophic)-resolves x and y andthe proofisdone.Ifnot, d(x,v)= d(y,v), butforeverygivenvertex v , d(x,v ) = d(y,v )
Corollary1.8.10. Let G beafamilyoffuzzy(neutrosophic)pathswith fuzzy(neutrosophic)commonvertexsetsuchthatthey’venocommonleaf.Then an 2-setissimultaneouslyfuzzy(neutrosophic)-resolvingset,simultaneously fuzzy(neutrosophic)-metricnumberis 2, simultaneouslyfuzzy(neutrosophic)metricdimensionis minm,m ∈V σ(m)+ σ(m ) Every 2-setissimultaneously fuzzy(neutrosophic)-metricsetfor G
Proof. ByCorollary (3.31.4),commonleafformsasimultaneously fuzzy(neutrosophic)-resolvingsetbutinthiscase,there’snocommonleaf. ThusbyProposition (3.31.5),an 2-setisfuzzy(neutrosophic)-resolvingsetfor anyfuzzy(neutrosophic).Thenan 2-setissimultaneouslyfuzzy(neutrosophic)resolvingset.Itinducessimultaneouslyfuzzy(neutrosophic)-metricnumber is 2 Italsoimpliessimultaneouslyfuzzy(neutrosophic)-metricdimensionis minm,m ∈V σ(m)+ σ(m ) Soevery 2-setissimultaneouslyfuzzy(neutrosophic)metricsetfor G.
LargestMetricNumber
Fuzzy(neutrosophic) t-partite(bipartite/star/wheel)isalsostudiedbutby addingonerestrictiononthesemodels.Fuzzy(neutrosophic) t-partitegets ustworesultsasindividualandfamilywhenthey’reeitherfixed-edgeorstrong fixed-vertex.
prp55.11 Proposition1.8.11. Let G beafixed-edgefuzzy(neutrosophic) t-partite.Then everysetexcludingcoupleofverticesindifferentpartswhosecardinalitiesof themarestrictlygreaterthanone,isfuzzy(neutrosophic)-resolvingset.
Proof. Considertwovertices x and y. Suppose m hassamepartwitheither x or y. Withoutloosingthegenerality,suppose m hassamepartwith x thusit doesn’thavecommonpartwith y. Therefore, d(m,x)=2 =1= d(m,y)
cor55.12
Corollary1.8.12. Let G beafixed-vertexstrongfuzzy(neutrosophic) t-partite. Let n ≥ 3 Thenevery (n 2)-setexcludestwoverticesfromdifferentparts whosecardinalitiesofthemarestrictlygreaterthanone,isfuzzy(neutrosophic)resolvingset.Every (n 2)-setexcludestwoverticesfromdifferentpartswhose
34
cor55.13
cor55.14
1.8.ExtendedResults
cardinalitiesofthemarestrictlygreaterthanone,isfuzzy(neutrosophic)-metric set.Fuzzy(neutrosophic)-metricnumberis n 2 Fuzzy(neutrosophic)-metric dimensionis (n 2)σ(m) where m isagivenvertex.
Proof. ByProposition (3.31.7),every (n 2)-setexcludestwoverticesfrom differentpartswhosecardinalitiesofthemarestrictlygreaterthanone,is fuzzy(neutrosophic)-resolvingset.Itmeansthatevery (n 2)-setexcludestwo verticesfromdifferentpartswhosecardinalitiesofthemarestrictlygreaterthan one,isfuzzy(neutrosophic)-metricset.Sinceif x and y areeitherinsamepart orindifferentparts,then,byanygivenvertex w,d(w,x)= d(w,y). Thus 1-set isn’tfuzzy(neutrosophic)-resolvingset.Therearesameargumentsforasetwith cardinality ≤ n 3 whenpigeonholeprincipleimpliesatleasttwoverticeshave sameconditionsconcerningeitherbeinginsamepartorindifferentparts.
Corollary1.8.13. Let G beafixed-vertexstrongfuzzy(neutrosophic)bipartite. Let n ≥ 3 Thenevery (n 2)-setexcludestwoverticesfromdifferentparts,is fuzzy(neutrosophic)-resolvingset.Every (n 2)-setexcludestwoverticesfrom differentparts,isfuzzy(neutrosophic)-metricset.Fuzzy(neutrosophic)-metric numberis n 2 Fuzzy(neutrosophic)-metricdimensionis (n 2)σ(m) where m isagivenvertex.
Proof. Consider x and y areexcludedbya (n 2)-set.Let m beagiven vertexwhichisdistinctfromthem.By G isbipartite, m hasacommonpart witheither x or y andnotwithbothofthem.Itimplies d(x,m) = d(y,m). Sinceif m hasacommonpartwith x, then d(x,m)=1 =2= d(y,m) And if m hasacommonpartwith y, then d(x,m)=2 =1= d(y,m) Thus m fuzzy(neutrosophic)-resolves x and y. If w isanothervertexwhichisdistinct fromthem,thenpigeonholeprincipleinducesatleasttwoverticeshavesame conditionsconcerningeitherbeinginsamepartorindifferentparts.Itimplies (n 3)-setisn’tfuzzy(neutrosophic)-resolvingset.Therefore,every (n 2)-set excludestwoverticesfromdifferentparts,isfuzzy(neutrosophic)-metricset. Fuzzy(neutrosophic)-metricnumberis n 2 By G isfixed-vertex,foranygiven vertices m and m ,σ(m)= σ(m ). Sofuzzy(neutrosophic)-metricdimensionis (n 2)σ(m) where m isagivenvertex.
Corollary1.8.14. Let G beafixed-vertexstrongfuzzy(neutrosophic)star.Then every (n 2)-setexcludescenterandagivenvertex,isfuzzy(neutrosophic)resolvingset.An (n 2)-setexcludescenterandagivenvertex,is fuzzy(neutrosophic)-metricset.Fuzzy(neutrosophic)-metricnumberis (n 2) Fuzzy(neutrosophic)-metricdimensionis (n 2)σ(m) where m isagivenvertex.
Proof. Consider x and y areexcludedbya (n 2)-set.Let m beagiven vertexwhichisdistinctfromthem.By G isstar, m hasacommonpart witheither x or y andnotwithbothofthem.Itimplies d(x,m) = d(y,m) Sinceif m hasacommonpartwith x, then d(x,m)=1 =2= d(y,m) And if m hasacommonpartwith y, then d(x,m)=2 =1= d(y,m) Thus m fuzzy(neutrosophic)-resolves x and y. If w isanothervertexwhichisdistinct fromthem,thenpigeonholeprincipleinducesatleasttwoverticeshavesame conditionsconcerningeitherbeinginsamepartorindifferentparts.Itimplies (n 3)-setisn’tfuzzy(neutrosophic)-resolvingset.Therefore,every (n 2)-set excludestwoverticesfromdifferentparts,isfuzzy(neutrosophic)-metricset.
35
cor55.15
Fuzzy(neutrosophic)-metricnumberis n 2. By G isfixed-vertex,foranygiven vertices m and m ,σ(m)= σ(m ) Sofuzzy(neutrosophic)-metricdimensionis (n 2)σ(m) where m isagivenvertex.
Corollary1.8.15. Let G beafixed-vertexstrongfuzzy(neutrosophic)wheel. Let n ≥ 3 Thenevery (n 2)-setexcludescenterandagivenvertex,is fuzzy(neutrosophic)-resolvingset.Every (n 2)-setexcludescenterandagiven vertex,isfuzzy(neutrosophic)-metricset.Fuzzy(neutrosophic)-metricnumber is n 2. Fuzzy(neutrosophic)-metricdimensionis (n 2)σ(m) where m isa givenvertex.
Proof. Consider x and y areexcludedbya (n 2)-set.Let m beagiven vertexwhichisdistinctfromthem.By G iswheel, m hasacommonpart witheither x or y andnotwithbothofthem.Itimplies d(x,m) = d(y,m) Sinceif m hasacommonpartwith x, then d(x,m)=1 =2= d(y,m) And if m hasacommonpartwith y, then d(x,m)=2 =1= d(y,m). Thus m fuzzy(neutrosophic)-resolves x and y. If w isanothervertexwhichisdistinct fromthem,thenpigeonholeprincipleinducesatleasttwoverticeshavesame conditionsconcerningeitherbeinginsamepartorindifferentparts.Itimplies (n 3)-setisn’tfuzzy(neutrosophic)-resolvingset.Therefore,every (n 2)-set excludestwoverticesfromdifferentparts,isfuzzy(neutrosophic)-metricset. Fuzzy(neutrosophic)-metricnumberis n 2 By G isfixed-vertex,foranygiven vertices m and m ,σ(m)= σ(m ) Sofuzzy(neutrosophic)-metricdimensionis (n 2)σ(m) where m isagivenvertex.
Fuzzy(neutrosophic) t-partite(bipartite/star/wheel)isalsostudiedbutby addingonerestrictiononthesemodels.Fuzzy(neutrosophic) t-partitegetsus oneresultinvolvingfamilyofthemwhenthey’reeitherfixed-edgeorstrong fixed-vertex.
Corollary1.8.16. Let G beafamilyoffixed-vertexstrongfuzzy(neutrosophic) t-partitewithfuzzy(neutrosophic)commonvertexset.Let n ≥ 3. Then simultaneouslyfuzzy(neutrosophic)-metricnumberis n 2, simultaneously fuzzy(neutrosophic)-metricdimensionis (n 2)σ(m) Every (n 2)-setexcludes twoverticesfromdifferentparts,issimultaneouslyfuzzy(neutrosophic)-resolving setfor G There’san (n 2)-setwhichissimultaneouslyfuzzy(neutrosophic)metricsetfor G.
Proof. ByCorollary (3.31.8),everyresultholdforanygivenfixed-vertexstrong fuzzy(neutrosophic) t-partite.Thuseveryresultholdforanygivenfixed-vertex strongfuzzy(neutrosophic) t-partite,simultaneously.Therefore,simultaneously fuzzy(neutrosophic)-metricnumberis n 2, simultaneouslyfuzzy(neutrosophic)metricdimensionis (n 2)σ(m) Every (n 2)-setexcludestwoverticesfrom differentparts,issimultaneouslyfuzzy(neutrosophic)-resolvingsetfor G. There’s an (n 2)-setwhichissimultaneouslyfuzzy(neutrosophic)-metricsetfor G
Corollary1.8.17. Let G beafamilyoffixed-vertexstrongfuzzy(neutrosophic) bipartitewithfuzzy(neutrosophic)commonvertexset.Let n ≥ 3 Then simultaneouslyfuzzy(neutrosophic)-metricnumberis n 2, simultaneously fuzzy(neutrosophic)-metricdimensionis (n 2)σ(m) Every (n 2)-setexcludes twoverticesfromdifferentparts,issimultaneouslyfuzzy(neutrosophic)-resolving
1.NeutrosophicGraphs
36
Inthischapter, Iintroducesome applications concerningnew ideasandin thisways,the resultsmake sensemoreabout theirimpactson different models.
setfor G. There’san (n 2)-setwhichissimultaneouslyfuzzy(neutrosophic)metricsetfor G
Proof. ByCorollary (3.31.9),everyresultholdforanygivenfixed-vertexstrong fuzzy(neutrosophic)bipartite.Thuseveryresultholdforanygivenfixed-vertex strongfuzzy(neutrosophic)bipartite,simultaneously.Therefore,simultaneously fuzzy(neutrosophic)-metricnumberis n 2, simultaneouslyfuzzy(neutrosophic)metricdimensionis (n 2)σ(m) Every (n 2)-setexcludestwoverticesfrom differentparts,issimultaneouslyfuzzy(neutrosophic)-resolvingsetfor G. There’s an (n 2)-setwhichissimultaneouslyfuzzy(neutrosophic)-metricsetfor G.
Corollary1.8.18. Let G beafamilyoffixed-vertexstrongfuzzy(neutrosophic) starwithfuzzy(neutrosophic)commonvertexset.Let n ≥ 3 Then simultaneouslyfuzzy(neutrosophic)-metricnumberis n 2, simultaneously fuzzy(neutrosophic)-metricdimensionis (n 2)σ(m) Every (n 2)-setexcludes centerandagivenvertex,issimultaneouslyfuzzy(neutrosophic)-resolvingset for G There’san (n 2)-setwhichissimultaneouslyfuzzy(neutrosophic)-metric setfor G
Proof. ByCorollary (3.31.10),everyresultholdforanygivenfixed-vertexstrong fuzzy(neutrosophic)star.Thuseveryresultholdforanygivenfixed-vertex strongfuzzy(neutrosophic)star,simultaneously.Therefore,simultaneously fuzzy(neutrosophic)-metricnumberis n 2, simultaneouslyfuzzy(neutrosophic)metricdimensionis (n 2)σ(m). Every (n 2)-setexcludestwoverticesfrom differentparts,issimultaneouslyfuzzy(neutrosophic)-resolvingsetfor G There’s an (n 2)-setwhichissimultaneouslyfuzzy(neutrosophic)-metricsetfor G
Corollary1.8.19. Let G beafamilyoffixed-vertexstrongfuzzy(neutrosophic) wheelwithfuzzy(neutrosophic)commonvertexset.Let n ≥ 3 Then simultaneouslyfuzzy(neutrosophic)-metricnumberis n 2, simultaneously fuzzy(neutrosophic)-metricdimensionis (n 2)σ(m) Every (n 2)-setexcludes centerandagivenvertex,issimultaneouslyfuzzy(neutrosophic)-resolvingset for G There’san (n 2)-setwhichissimultaneouslyfuzzy(neutrosophic)-metric setfor G
Proof. ByCorollary (3.31.11),everyresultholdforanygivenfixed-vertexstrong fuzzy(neutrosophic)wheel.Thuseveryresultholdforanygivenfixed-vertex strongfuzzy(neutrosophic)wheel,simultaneously.Therefore,simultaneously fuzzy(neutrosophic)-metricnumberis n 2, simultaneouslyfuzzy(neutrosophic)metricdimensionis (n 2)σ(m) Every (n 2)-setexcludestwoverticesfrom differentparts,issimultaneouslyfuzzy(neutrosophic)-resolvingsetfor G There’s an (n 2)-setwhichissimultaneouslyfuzzy(neutrosophic)-metricsetfor G
1.9Applications
Twoapplicationsareposedasfollow.
1.9.Applications
37
LocatedPlaces
Aprogramisdevisedforarobottolocateeverycoupleofgivenplaces,separately.Thenumberwhichthisprogramassignstoanyplacefromagivencouple ofplacesareunique.Thuseveryplacehasanuniquenumberwhenacouple ofplacesaregiven.Threenumbersareassignedtoaplace.Firstnumberis aboutamodelconcerningattributeswhichtitledtobeobstacleforlocating theplace,secondnumberisaboutamodelconcerningattributeswhichtitled tobeindeterminateforlocatingtheplaceandsometimes,they’reobstaclebut sometimes,they’redeterminatetolocatethatplace.Thirdnumberisabout amodelconcerningattributeswhichtitledtobedeterminateforlocatingthe place.Forexample, (0 2, 0 5, 0 8) isassignedtoaplace v asinformationabout itslocation.Thisisabriefoutlineofthisapplication.Togetitmoreprecisely, Iusesomestepstoclarifyaboutthem.
Step1.(Definition) Locatedplaceisatermtocategorizeplacesintotwo classes.Applicationsforthisfunctionaretoomanybutthey’venoticed tosomeparameterslikedecreasingcosts,preciseanalysis,decreasingthe rangesofanalysis,restrictionsoncases,lowamountofselectivedataas possible,etcetera.Selectivepointsaspossibletodistinguishaboutevery coupleofpointsoutofthem,areoptimalcaseaspossibilitiesallow.
Step2.(Issue) Atrainhassomestopswhicheverystophassomeattributes. Acoupleofstopsaregivenbutthey’reimpossibletolocatebytheir attributes.
Step3.(Model) Iuseattributesofstopstogetamodelwiththreenumbers chosenfromrealnumbersamidzeroandone.Everynumberillustrates everyaspectoftheirattributes.Thefirstnumberisobstaclemeans badattributes,thesecondnumberisindeterminateandthirdnumberis determinatemeansgoodattributes.Buttousesensibleclarification,Iuse afuzzymodelasFigure (1.10).Togetitmoreprecisely,considerTable (1.7) asafuzzymodelwhichassignstoeverystationsandconnectionsa value,separately.Infact,setofstationsandsetofconnectionsareused tomakefuzzysetsfromthem.

Figure1.10:Blackvertex {s1} isonlyfuzzy(neutrosophic)-metricsetamidall setsofverticesforfuzzy(neutrosophic)graph T.
Step4.(Solution) Asfigure (1.10) shows,Istudythisfuzzymodel.By Proposition (3.31.1),thestop s1 locateseverygivencoupleofstations. Togetbeyondthisresult,IfI’veafamilyoffuzzy(neutrosophic)paths excerptfromfamilyoftrainswithfuzzy(neutrosophic)commonand s1 incommon,thenbyCorollary (3.31.4),thestop s1 locateseverygiven
1.NeutrosophicGraphs
F3
38
Table1.7:ATrainconcerningitsStationsanditsConnectionsasaFuzzy GraphinaModel. T3
Stationsof T s1 s2 s3 s4 s5 s6 s7 s8 s9,s10
Values 0.10.80.70.80.10.30.60.50.2
Connectionsof T s1s2 s2s3 s3s4 s4s5 s5s6 s6s7 s7s8 s8s9 s9s10
Values 0 10 60 40 10 10 20 40 20 1
coupleofstationsineveryfuzzy(neutrosophic)graphexcerptfromany trains,simultaneously.
Covid-19andIdentifyingInfectedPeople
Darknetworkisdescriptionforinfectedpeoplewhoareanonymousinthe matterofCovid-19.Virusanditsanonymouslystyletotransmitthevirusfrom onepersontoanotherperson,couldmakeadarknetworkinvolvingpeople. Considereveryoneasnetworktitledfuzzy(neutrosophic).Itmeansthatthe personandhisnetworkscontaininghisconnectionsmaketwomodels,fixed-edge fuzzy(neutrosophic)andfixed-vertexstrongfuzzy(neutrosophic).Now,Ihavea familyofpeoplewhicheveryoneisamodelinthetermsofCovid-19.
Step1.(Definition) Covid-19iswell-knowndiseasewhichlikeeverydisease hasgeneralparameters.Parametersareintensityofsymptom,decreasing impacts,relativelytreatments,completetreatmentsandetcetera.But Covid-19hasspecificwayswhichtheytransmitthisdisease.It’scoming upwithfindingimpressivenetworksofpeopletoidentifyinfectedpeople. Peopleandtheirconnectionsareimportantcasestodevelopthisnotion.
Step2.(Issue) ApersonhasbeeninfectedandItrytofindtheconnections andthepeoplewhichtransmitthisdisease.
Step3.(Model) Apersonandhisconnectionsareanetworkwhichareafuzzy model.Twonumbersareassignedtoapersonandhisconnections.Todo this,Ineedtoidentifyacoupleofpeoplewhicharegiveninanetwork ofthisperson.Iproposedtwofuzzymodels.Firstly,asFigure (1.11),a fuzzygraphcontainingthepeoplewhoconnecttothisperson,isproposed inTable (1.8).Secondly,asFigure (1.11),afuzzymodelincludingperson withhistwoselectiveconnectionsandotherpeoplewithtwoselective connectionsofthem,isposedinTable (1.9).Theattributesarelikethe iterationsofconnections,theintensityofinfectedpeople,serioussymptom, locationsofpeopleandetcetera,areusedtohavecoupleofpeoplewho areselected.Capableforbeinginfectedandinfectedpeopleareusedto makethesemodels.
Step4.(Solution) ByCorollary (3.30.10),aperson i1 andhispartner i2 identifyeverygivencoupleofpartnerswhichareinFigure (1.11) as T .To getbeyondthisresult,ifaperson i1 andthepartner i2 aren’tantipodal verticesineveryfuzzycyclesarecontainedinafamilyofperson’snetworks, thenbyCorollary (3.30.11),aperson i1 andthepartner i2 identifyevery givencoupleofpartnersineveryfuzzycycles,simultaneously.ByCorollary
1.9.Applications
39
sec8
Figure1.11:Blackvertices {i1,i2} areonlyfuzzy(neutrosophic)-metricset amidallsetsofverticesforfuzzy(neutrosophic)graph T. Blackvertices V \{c1,c2} areonlyfuzzy(neutrosophic)-metricsetamidallsetsofverticesfor fuzzy(neutrosophic)graph T F4

Table1.8:AnInfectedPersonconcerninghistwoselectiveConnectionsandhis PartnersWiththeirtwoselectiveConnectionsasaFuzzyGraph T inaModel. T4
Peopleof T i1 i2 c1 c2 c3 i3 Values 0 70 80 60 80 60 9 Connectionsof T i1i2 i2c1 c1c2 c2c3 c3i3 i3i1 Values 0.60.60.60.60.60.6
Table1.9:AnInfectedPersonconcerninghisConnectionsandhisPartnersas aFuzzyGraph T inaModel. T5
Peopleof T i1 c1 c2 c3 Values 0.70.70.80.9 Connectionsof T i1c1 i1c2 i1c3 c3i1 Values 0 60 60 60 6
(3.31.10), {c1,c2} identifycoupleofperson i1 andhispartner c3, inFigure (1.11)as T inoptimalwayandthissetisunique.
1.10OpenProblems
Thecrispnotionofdimensionisdefinedonfuzzy(neutrosophic)graphs.Thus
Question1.10.1. Isitpossibletodefinefuzzy(neutrosophic)notionofdimensiononfuzzy(neutrosophic)graphs?
Therearetoomanylimitationsontheclassesoffuzzy(neutrosophic) graphsbyusingfixed-edgefuzzy(neutrosophic)graphsandfixed-vertexstrong fuzzy(neutrosophic)graphs.
1.NeutrosophicGraphs
40
1.11.ConclusionandClosingRemarks
Question1.10.2. Isanapproachexistedtocomputecurrentdimensionfor specificclassesoffuzzy(neutrosophic)graphs?
Question1.10.3. Whatarebasicattributesofcurrentdimensionforgeneral classesoffuzzy(neutrosophic)graphs?
Findingotherclassesoffuzzy(neutrosophic)graphshasanordinaryapproach todevelopthisstudy.
Question1.10.4. Whichnewclassesoffuzzy(neutrosophic)graphsareexisted todevelopthisnotionofcurrentdimension?
Question1.10.5. Whichnewclassesoffuzzy(neutrosophic)graphsareexisted tocomputethisnotionofcurrentdimension?
Question1.10.6. Whichgeneralapproachesareexistedtostudythisnotionof currentdimensioninfuzzy(neutrosophic)graphs?
Question1.10.7. Whichspecificapproachesareexistedtostudythisnotionof currentdimensioninfuzzy(neutrosophic)graphs?
Problem1.10.8. Aretherespecialcrispsetsofvertices,e.g.antipodalvertices forfuzzy(neutrosophic)cycles,whichhavekeyroletostudythisnotionofcurrent dimensioninfuzzy(neutrosophic)graphs?
Problem1.10.9. Aretherefuzzy(neutrosophic)specialsetsofvertices,e.g. fuzzy(neutrosophic)twinverticesforgeneralclasses,whichhavekeyroleto studythisnotionofcurrentdimensioninfuzzy(neutrosophic)graphs?
1.11ConclusionandClosingRemarks
Thisstudyusesmixedcombinationsoffuzzyconceptsandcrispconceptsto explorenewnotionofcrispdimensioninfuzzy(neutrosophic)graphsasindividual andasfamily.Inthisway,somecrispnotionslikeantipodalverticesaredefined touseasatooltostudyfuzzy(neutrosophic)cyclesasindividualandasfamily. Also,somefuzzy(neutrosophic)notionslikefuzzy(neutrosophic)twinvertices aredefinedtouseasatooltostudygeneralclassesoffuzzy(neutrosophic) graphsasindividualandasfamily.Mixedfamilyoffuzzy(neutrosophic)graphs areslightlystudiedbyusingfuzzy(neutrosophic)twinverticesandotherideas asindividualandasfamily.InTable (1.10),Imentionsomeadvantagesand limitationsconcerningthisarticleanditsproposednotions.
sec10
41
Table1.10:ABriefOverviewaboutAdvantagesandLimitationsofthisstudy tbl5
Advantages
Limitations
1. Usingcrispandfuzzy(neutrosophic) 1. Themostusagesoffixed-edge notionsinoneframework fuzzy(neutrosophic)graphs togethersimultaneously. andfixed-vertexstrong
2. Studyonfuzzy(neutrosophic) fuzzy(neutrosophic)graphs. asindividualandasfamily.
3. Involvedclassesascomplete, 2. Studyonfamilyofdifferentmodels strong,path,cycle,t-partite, bipartite,star,wheel.
4. Characterizingclassesof 3. Characterizingclassesof fuzzy(neutrosophic)graphs fuzzy(neutrosophic)graphs withsmallestmetricnumber withsmallestdimensionnumber andlargestmetricnumber. andlargestdimensionnumber.
1.NeutrosophicGraphs
42
Bibliography
1 [1] AkramM.,ShahzadiG.(2019)“BipolarNeutrosophicGraphs”.In: KahramanC.,Otayİ.(eds)FuzzyMulti-criteriaDecision-MakingUsing NeutrosophicSets.StudiesinFuzzinessandSoftComputing,vol369. Springer,Cham.
2 [2] Akram,Muhammad,andGulfamShahzadi.“Operationsonsingle-valued neutrosophicgraphs.”InfiniteStudy,2017.
3 [3] Broumi,Said,etal.“Anintroductiontobipolarsinglevaluedneutrosophic graphtheory.”AppliedMechanicsandMaterials.Vol.841.TransTech PublicationsLtd,2016.
4 [4] Broumi,Said,etal.“Intervalvaluedneutrosophicgraphs.”CriticalReview, XII2016(2016):5-33.
5 [5] Broumi,Said,etal.“Isolatedsinglevaluedneutrosophicgraphs.”Infinite Study,2016.
6 [6] Broumi,Said,etal."“Onbipolarsinglevaluedneutrosophicgraphs.” JournalofNewTheory11(2016):84-102.
7 [7] Broumi,Said,etal.“Singlevaluedneutrosophicgraphs.”JournalofNew theory10(2016):86-101.
8 [8] Broumi,Said,etal.“Singlevaluedneutrosophicgraphs:degree,orderand size.”2016IEEEinternationalconferenceonfuzzysystems(FUZZ-IEEE). IEEE,2016.
9 [9] HenryGarrett,”MetricDimensioninfuzzy(neutrosophic)Graphs-VII ”, Preprints2021,2021110142(doi:10.20944/preprints202111.0142.v7).
10 [10] HenryGarrett,“MetricDimensioninfuzzy(neutrosophic)Graphs#12 ”, ResearchGate2021(doi:10.13140/RG.2.2.20690.48322).
11 [11] Kandasamy,Vasantha,K.Ilanthenral,andFlorentinSmarandache. “Neutrosophicgraphs:anewdimensiontographtheory”InfiniteStudy, 2015.
12 [12] Naz,Sumera,HosseinRashmanlou,andM.AslamMalik.“Operationson singlevaluedneutrosophicgraphswithapplication”JournalofIntelligent &FuzzySystems
43
Toclarifyabout thedefinitions, Iusesome examplesandin thisway, exemplifyinghas keyroletomake senseaboutthe definitionsand tointroducenew waystouseon thesemodelsin thetermsofnew notions.
NeutrosophicChromaticNumber
Rohinietal.[4]introducesinglevaluedneutrosophiccoloring.Heetal.[5] alsoproposeoperationsofsinglevaluedneutrosophiccoloring.Rohinietal.[6] studyonsinglevaluedneutrosophicirregularvertexcoloring.
2.1Definitions
Thereference[1]isusedtowritethecontentsofthischapter.
Definition2.1.1. G :(V,E) iscalleda crispgraph where V isasetofobjects and E isasubsetof V × V suchthatthissubsetissymmetric.
Definition2.1.2. Acrispgraph G :(V,E) iscalleda neutrosophicgraph G :(σ,µ) where σ =(σ1,σ2,σ3): V → [0, 1] and µ =(µ1,µ2.µ3): E → [0, 1] suchthat µ(xy) ≤ σ(x) ∧ σ(y) forall xy ∈ E.
Definition2.1.3. Aneutrosophicgraphiscalled neutrosophicempty ifit hasnoedge.It’salsocalled neutrosophictrivial.Aneutrosophicgraph whichisn’tneutrosophicempty,iscalled neutrosophicnontrivial
Definition2.1.4. Aneutrosophicgraph G :(σ,µ) iscalleda neutrosophic complete whereit’scompleteand µ(xy)= σ(x) ∧ σ(y) forall xy ∈ E.
Definition2.1.5. Aneutrosophicgraph G :(σ,µ) iscalleda neutrosophic strong where µ(xy)= σ(x) ∧ σ(y) forall xy ∈ E.
Definition2.1.6. Apath v0,v1, ,vn iscalled neutrosophicpath where µ(vivi+1) > 0,i =0, 1, ··· ,n 1.i-pathisapathwith i edges,it’salsocalled length ofpath.
Definition2.1.7. Acrispcycle v0,v1, ··· ,vn,v0 iscalled neutrosophic cycle wheretherearetwoedges xy and uv suchthat µ(xy)= µ(uv)= i=0,1, ,n 1 µ(vivi+1)
Definition2.1.8. Aneutrosophicgraphiscalled neutrosophict-partite if V ispartitionedto t parts, V1,V2, ,Vt andtheedge xy implies x ∈ Vi and y ∈ Vj where i = j. Ifit’sneutrosophiccomplete,thenit’sdenotedby Kσ1,σ2, ,σt where σi is σ on Vi instead V whichmean x ∈ Vi induces σi(x)=0 If t =2, thenit’scalled neutrosophiccompletebipartite andit’sdenoted by Kσ1,σ2 especially,if |V1| =1, thenit’scalled neutrosophicstar andit’s denotedby S1,σ2 Inthiscase,thevertexin V1 iscalled center andifavertex
CHAPTER2
45
joinstoallverticesofneutrosophiccycle,it’scalled neutrosophicwheel and it’sdenotedby W1,σ2
Definition2.1.9. Let G :(σ,µ) beaneutrosophicgraph.Foranygivensubset N of V, Σn∈N σ(n) iscalled neutrosophiccardinality of N andit’sdenoted by |N |n.
Definition2.1.10. Let G :(σ,µ) beaneutrosophicgraph.Neutrosophic cardinalityof V iscalled neutrosophicorder of G andit’sdenotedby On(G)
Definition2.1.11. Let G :(σ,µ) beaneutrosophicgraph.Thenumberof verticesisdenotedby n andthenumberofedgesisdenotedby m.
Definition2.1.12. Let N =(σ,µ) beaneutrosophicgraph.It’scalled neutrosophicconnected ifforeverygivencoupleofvertices,there’sat leastoneneutrosophicpathamidthem.
Definition2.1.13. Let N =(σ,µ) beaneutrosophicgraph.Supposeapath P : v0,v1, ··· ,vn 1,vn from v0 to vn mini=0,1,2, ,n 1 µ(vivi+1) iscalled neutrosophicstrength of P andit’sdenotedby Sn(P )
Definition2.1.14. Let N =(σ,µ) beaneutrosophicgraph.Thenumberof maximumedgesforavertex,amidallvertices,isdenotedby ∆(N ).
Firstcaseforthecontentsistousethearticlefrom[1].Thecontentsareused inthewaythat,usagesofnewcontentsarepreferencesandthepreliminaries arepassedinthebeginningofthischapter.
2.2ChromaticNumberandNeutrosophicChromatic Number
2.3Abstract
Newsettingisintroducedtostudychromaticnumber.Neutrosophicchromatic numberandchromaticnumberareproposedinthisway,someresultsare obtained.Classesofneutrosophicgraphsareusedtoobtainsthesenumbers andtherepresentativesofthecolors.Usingcolorstoassigntothevertices ofneutrosophicgraphsisapplied.Somequestionsandproblemsareposed concerningwaystodofurtherstudiesonthistopic.Usingstrongedgetodefine therelationamidverticeswhichimplieshavingdifferentcolorsamidthemand asconsequences,choosingonevertexasarepresentativeofeachcolortouse theminasetofrepresentativesandfinally,usingneutrosophiccardinalityof thissettocomputeneutrosophicchromaticnumber.Thisspecificrelationamid edgesisnecessarytocomputebothchromaticnumberconcerningthenumberof representativeinthesetofrepresentativesandneutrosophicchromaticnumber concerningneutrosophiccardinalityofsetofrepresentatives.Iftwovertices havenostrongedge,thentheycanbeassignedtosamecoloreventhey’ve commonedge.Basicfamiliaritieswithneutrosophicgraphtheoryandgraph theoryareproposedforthisarticle.
Keywords: NeutrosophicStrong,NeutrosophicGraphs,ChromaticNumber
AMSSubjectClassification: 05C17,05C22,05E45
2.NeutrosophicChromaticNumber
46
sec2
2.4MotivationandContributions
Inthisstudy,there’sanideawhichcouldbeconsideredasamotivation. Question2.4.1. Isitpossibletousemixedversionsofideasconcerning “neutrosophicstrongedges”,“neutrosophicgraphs”and“neutrosophiccoloring” todefinesomenotionswhichareappliedtoneutrosophicgraphs?
It’smotivationtofindnotionstouseinanyclassesofneutrosophicgraphs. Real-worldapplicationsabouttimetableandschedulingareanotherthoughts whichleadtobeconsideredasmotivation.Connectionsamidtwoitemshave keyrolestoassigncolors.Thusthey’reusedtodefinenewideaswhichconclude tothestructureofcoloring.Theconceptofhavingstrongedgeinspiresto studythebehaviorofstrongedgeinthewaythat,bothneutrosophicchromatic numberandchromaticnumberarethecasesofstudy.
Theframeworkofthisstudyisasfollows.Inthebeginningofchapter,I introducedbasicdefinitionstoclarifyaboutpreliminaries.Insubsection “ChromaticNumberandNeutrosophicChromaticNumber”,newnotionof coloringisappliedtotheverticesofneutrosophicgraphs.Neutrosophicstrong edgehasthekeyroleinthisway.Classesofneutrosophicgraphsarestudiedwhen theedgesareneutrosophicstrong.Insubsection“ApplicationsinTimeTable andScheduling”,oneapplicationisposedforneutrosophicgraphsconcerning timetableandschedulingwhenthesuspicionsareaboutchoosingsomesubjects. Insubsection“OpenProblems”,someproblemsandquestionsforfurther studiesareproposed.Insubsection“ConclusionandClosingRemarks”,gentle discussionaboutresultsandapplicationsarefeatured.Insubsection“Conclusion andClosingRemarks”,abriefoverviewconcerningadvantagesandlimitations ofthisstudyalongsideconclusionsareformed.
2.5ChromaticNumberandNeutrosophicChromatic Number
Definition2.5.1. Let N =(σ,µ) beaneutrosophicgraph. Chromatic number isminimumnumberofdistinctcolorswhichareusedtocolorthe verticeswhichhaveneutrosophicstrongedge.Neutrosophiccardinalityofthe setofthesedistinctcolorswhenit’sminimumamidallofthesesets,iscalled neutrosophicchromaticnumber withrespectwithfirstorder.
Example2.5.2. ConsiderFigure (2.1).Thechromaticnumberisthreeand neutrosophicchromaticnumberis 2 57 withrespecttofirstorder.
Neutrosophicchromaticnumberofsomeclassesofneutrosophicgraphsare computed.
Proposition2.5.3. Let N =(σ,µ) beaneutrosophiccomplete.Thenchromatic numberis n andneutrosophicchromaticnumberisneutrosophicorder.
Proof. Alledgesareneutrosophicstrong.Everyvertexhasedgewith n 1 vertices.Thus n ischromaticnumber.Sinceanygivenvertexhasdifferentcolor incomparisontoanothervertex,neutrosophiccardinalityof V isneutrosophic chromaticnumber.Therefore,neutrosophicchromaticnumberisneutrosophic order.
2.4.MotivationandContributions
47
Figure2.1:NeutrosophicGraph, N1 nsc1
Proposition2.5.4. Let N =(σ,µ) beaneutrosophicstrongpath.Then chromaticnumberistwoandneutrosophicchromaticnumberis min x and y havedifferentcolors{σ(x)+ σ(y)}
Proof. Withalternativecolors,neutrosophicstrongpathhasdistinctcolor foreveryverticeswhichhaveoneedgeincommon.Thusif x and y aretwo verticeswhichhaveoneedgeincommon,then x and y havedifferentcolor. Therefore,chromaticnumberistwo.Therepresentativeofcolorsareavertex withminimumvalueamidallverticeswhichhavesamecolorwithit.Thus, min x and y havedifferentcolors{σ(x)+ σ(y)}
Proposition2.5.5. Let N =(σ,µ) beanevenneutrosophicstrongcycle.Then chromaticnumberistwoandneutrosophicchromaticnumberis min x and y havedifferentcolors{σ(x)+ σ(y)}
Proof. Alledgesareneutrosophicstrong.Sincethecyclehasevenvertices, withalternativecoloringofvertices,theverticeswhichhavecommonedge,have differentcolors.Sochromaticnumberistwo.Witheverycolor,thevertexwhich hasminimumvalueamidverticeswithsamecolorwithit,isrepresentativeof thatcolor.Thus, min x and y havedifferentcolors{σ(x)+ σ(y)}

2.NeutrosophicChromaticNumber
48
2.5.ChromaticNumberandNeutrosophicChromaticNumber
Proposition2.5.6. Let N =(σ,µ) beanoddneutrosophicstrongcycle.Then chromaticnumberisthreeandneutrosophicchromaticnumberis min x,y and z havedifferentcolors{σ(x)+ σ(y)+ σ(z)}
Proof. Withalternativecoloringonvertices,atend,twoverticeshavesame color,andthey’vesameedge.So,chromaticnumberisthree.Sincethecolors arethree,theverticeswithminimumvaluesineverycolor,arerepresentatives. Hence, min x,y and z havedifferentcolors{σ(x)+ σ(y)+ σ(z)}
Proposition2.5.7. Let N =(σ,µ) beaneutrosophicstrongstarwith c as center.Thenchromaticnumberistwoandneutrosophicchromaticnumberis min x isnon-centervertex{σ(c)+ σ(x)}.
Proof. Alledgesareneutrosophicstrong.Centervertexhascommonedgewith everygivenvertex.Soithasdifferentcolorincomparisontoothervertices.So onecolorhasonlyonevertexwhichhasthatcolor.Allnon-centerverticeshave nocommonedgeamideachother.Thenthey’vesamecolor.Therepresentative ofthiscolorisanon-centervertexwhichhasminimumvalueamidallnon-center vertices.Hence, min x isnon-centervertex{σ(c)+ σ(x)}
Proposition2.5.8. Let N =(σ,µ) beaneutrosophicstrongwheelwith c as center.Thenchromaticnumberisthreewhereneutrosophiccyclehaseven numberasitslengthandneutrosophicchromaticnumberis min
x,y arenon-centerverticesandhavedifferentcolors{σ(c)+ σ(x)+ σ(y)}
Proof. Centervertexhasuniquecolor.Soit’sonlyrepresentativeofthiscolor. Non-centerverticesformaneutrosophiccyclewhichhavedistinctcolorsforthe verticeswhichhavecommonedgewitheachotherwhenthenumberofcolorsis two.Soacolorforcentervertexandtwocolorsfornon-centervertices,make neutrosophicstrongwheelhasdistinctcolorsforverticeswhichhavecommon edge.Hence,chromaticnumberisthreewhenthenon-centerverticesformodd cycle.Therefore, min
x,y arenon-centerverticesandhavedifferentcolors{σ(c)+ σ(x)+ σ(y)}.
Proposition2.5.9. Let N =(σ,µ) beaneutrosophicstrongwheelwith c as center.Thenchromaticnumberisfourwhereneutrosophiccyclehasoddnumber asitslengthandneutrosophicchromaticnumberis min
x,y,z arenon-centerverticesandhavedifferentcolors{σ(c)+ σ(x)+ σ(y)+ σ(z)}
49
2.NeutrosophicChromaticNumber
Proof. Alledgesareneutrosophicstrongandnon-centerverticesformodd neutrosophicstrongcycles.Oddneutrosophicstrongcyclehavechromatic numberwhichisthree.Non-centervertexhassameedgeswithallnon-center vertices.Thusnon-centervertexhasdifferentcolorswithnon-centervertices. Therefore,chromaticnumberisfour.Fourrepresentativesofcolorsform neutrosophicchromaticnumberwhereonerepresentativeiscentervertexand otherthreerepresentativesarenon-centervertices.So, min x,y,z arenon-centerverticesandhavedifferentcolors{σ(c)+ σ(x)+ σ(y)+ σ(z)}.
Proposition2.5.10. Let N =(σ,µ) beaneutrosophiccompletebipartite.Then chromaticnumberistwoandneutrosophicchromaticnumberis min x and y areindifferentparts{σ(x)+ σ(y)}
Proof. Everygivenvertexhasneutrosophicstrongedgewithallverticesfrom anotherpart.Sothecolorofeveryvertexwhichisinasamepartissame. Hence,twopartsimpliestwodifferentcolors.Itinduceschromaticnumberis two.Theminimumvalueofavertexamidallverticesineverypart,identify therepresentativeofeverycolor.Therefore, min x and y areindifferentparts{σ(x)+ σ(y)}.
Proposition2.5.11. Let N =(σ,µ) beaneutrosophiccomplete t partite.Then chromaticnumberis t andneutrosophicchromaticnumberis min x1,x2 , ,xt areindifferentparts{σ(x1)+ σ(x2)+ + σ(xt)}
Proof. Everyparthassamecolorforitsvertices.Sochromaticnumberis t. Everypartintroducesonevertexasarepresentativeofitscolor.Thus, neutrosophicchromaticnumberis min x1,x2 , ,xt areindifferentparts{σ(x1)+ σ(x2)+ + σ(xt)}
Proposition2.5.12. Let N =(σ,µ) beaneutrosophicstrong.Thenchromatic numberis 1 ifandonlyif N =(σ,µ) isneutrosophicempty.
Proof. (⇒) Letchromaticnumberbe 1 Itimpliesthere’snovertexwhich hassameedgewithavertex.Sothere’snoneutrosophicstrongedge.Since N =(σ,µ) isaneutrosophicstrong, N =(σ,µ) isaneutrosophicempty. (⇐). Let N =(σ,µ) beneutrosophicemptyandneutrosophicstrong.Hence there’snoedge.Itimpliesforeverygivenvertex,there’snocommon neutrosophicstrongedge.Itinducesthere’sonlyonecolorforvertices.Hence therepresentativeofthiscolorischosenfrom n vertices.Thuschromatic numberis 1 50
2.5.ChromaticNumberandNeutrosophicChromaticNumber
Proposition2.5.13. Let N =(σ,µ) beaneutrosophicstrong.Thenchromatic numberis 2 ifandonlyif N =(σ,µ) isneutrosophiccompletebipartite.
Proof. (⇒) Letchromaticnumberbetwo.Soeveryvertexhaseitherone vertexortwoverticeswithacommonedge.Thenumberofcolorsaretwoso therearetwosetswhicheachsethastheverticeswhichsamecolor.Iftwo verticeshavesamecolor,thentheydon’thaveacommonedge.Soeverysetis apartinthat,novertexhascommonedge.Thenumberofthesesetsistwo. Hencetherearetwopartsineachofthem,everyvertexhasnocommonedge withothervertices.Since N =(σ,µ) isaneutrosophicstrong, N =(σ,µ) is neutrosophiccompletebipartite.
(⇐). Assume N =(σ,µ) isneutrosophiccompletebipartite.Thenalledges areneutrosophicstrong.Everyparthastheverticeswhichhavenoedgein common.Sothey’reassignedtohavesamecolor.Therearetwoparts.Thus therearetwocolorstoassigntotheverticesinthat,theverticeswithcommon edge,havedifferentcolors.Itinduceschromaticnumberis 2.
Proposition2.5.14. Let N =(σ,µ) beaneutrosophicstrong.Thenchromatic numberis n ifandonlyif N =(σ,µ) isneutrosophiccomplete.
Proof. (⇒) Letchromaticnumberbe n. Soanygivenvertexhas n vertices whichhavecommonedgewiththemandeveryofthemhavecommonedgewith eachother.Itimplieseveryvertexhas n verticeswhichhavecommonedgewith them.Since N =(σ,µ) isaneutrosophicstrong, N =(σ,µ) isneutrosophic complete.
(⇐) Suppose N =(σ,µ) isneutrosophiccomplete.Everyvertexhas n vertices whichhavecommonedgewiththem.Sincealledgesareneutrosophicstrong, theminimumnumberofcolorsare n. Thuschromaticnumberis n.
Generalboundsforneutrosophicchromaticnumberarecomputed.
Proposition2.5.15. Let N =(σ,µ) beaneutrosophicgraph.Thenchromatic numberisatmostthenumberofverticesandneutrosophicchromaticnumberis atmostneutrosophicorder.
Proof. Wheneveryvertexisarepresentativeofeachcolor,chromaticnumber isthenumberofverticesandithappensinchromaticnumberofneutrosophic completewhichis n. Whenallverticeshavedistinctcolors,neutrosophic chromaticnumberisneutrosophicorderandit’ssharpforneutrosophic complete.
Therelationamidneutrosophicchromaticnumberandmainparametersof neutrosophicgraphsiscomputed.
Proposition2.5.16. Let N =(σ,µ) beaneutrosophicstrong.Thenchromatic numberisatmost ∆+1 andatleast 2
Proof. Neutrosophicstrongisneutrosophicnontrivial.Soitisn’tneutrosophic emptywhichinducesthere’snoedge.Itimplieschromaticnumberistwo.Since chromaticnumberisoneifandonlyif N =(σ,µ) isneutrosophicemptyif andonlyif N =(σ,µ) isneutrosophictrivial.Avertexwithdegree ∆, has ∆ verticeswhichhavecommonedgeswiththem.Iftheseverticeshavenoedge amideachother,thenchromaticnumberistwoespecially,neutrosophicstar.If
51
sec3
2.NeutrosophicChromaticNumber
not,theninthecase,allverticeshaveedgeamideachother,chromaticnumber is ∆+1, especially,neutrosophiccomplete.
Proposition2.5.17. Let N =(σ,µ) beaneutrosophic r regular.Then chromaticnumberisatmost r +1.
Proof. N =(σ,µ) isaneutrosophic r regular.Soanyofvertexhas r vertices whichhavecommonedgewithit.Iftheseverticeshavenocommonedgewith eachother,forinstanceneutrosophicstar,chromaticnumberistwo.Butsince theverticeshavecommonedgewitheachother,chromaticnumberis r +1, for instance,neutrosophiccomplete.
2.6ApplicationsinTimeTableandScheduling
Designingtheprogramstoachievesomegoalsisgeneralapproachtoapplyon someissuestofunctionproperly.Separationhaskeyroleinthecontextofthis style.Separatingthedurationofworkwhichareconsecutive,isthematterand ithasimportanttoavoidmixingup.
Step1.(Definition) Timetableisanapproachtogetsomeattributestodo theworkfastandproper.Thestyleofschedulingimpliesspecialattention tothetaskswhichareconsecutive.
Step2.(Issue) schedulingofprogramhasfacedwithdifficultiestodifferamid consecutivesection.Beyondthat,sometimessectionsarenotthesame.
Step3.(Model) AsFigure (2.2),thesituationisdesignedasamodel.The modelusesdatatoassigneverysectionandtoassigntorelationamid section,threenumbersbelongunitintervaltostateindeterminacy, possibilitiesanddeterminacy.There’sonerestrictioninthat,thenumbers amidtwosectionisatleastthenumberoftherelationamidthem.Table (2.1),clarifiesabouttheassignednumberstothesesituation.
Figure2.2:Blackverticesaresuspicionsaboutchoosingthem.

fgr1 52
sec4
Table2.1:SchedulingconcernsitsSubjectsanditsConnectionsasa NeutrosophicGraphinaModel. tbl1
Sectionsof T s1 s2 s3 s4 s5 s6 s7 s8 s9,s10
Values 0.10.80.70.80.10.30.60.50.2
Connectionsof T s1s2 s2s3 s3s4 s4s5 s5s6 s6s7 s7s8 s8s9 s9s10
Values 0 10 60 40 10 10 20 40 20 1
Step4.(Solution) AsFigure (2.2) shows,neutrosophicmodel,proposetouse chromaticnumber 2 inthecasewithistitled T Inthiscase, i1 and c1 arerepresentativeofthesetwocolorsandneutrosophicchromatic numberis 1.4. Theset {i1,c1} containsrepresentativesofcolorswhich posechromaticnumberandneutrosophicchromaticnumber.Thusthe decisionamidchoosingthesubject c1 an c2 isconcludedtochoose c1 To getbriefoverview,neutrosophicmodelusesonenumberforeveryarray so 0.9 means (0.9, 0.9, 0.9). InFigure (2.2),theneutrosophicmodel T introducethecommonsituation.Therepresentativesofcolorsare i2 and c1 Thuschromaticnumberistwoandneutrosophicchromaticnumberis 1 4 Thussuspicionaboutchoosing i1 and i2 isdeterminedtobe i2 The setsofrepresentativeforcolorsare {i2,c1}
2.7OpenProblems
Thetwonotionsofcoloringofverticesconcerningneutrosophicchromatic numberandchromaticnumberaredefinedonneutrosophicgraphswhen neutrosophicstrongedgeshavekeyroletohavethesenotions.Thus
Question2.7.1. Isitpossibletouseothertypesedgestodefinechromatic numberandneutrosophicchromaticnumber?
Question2.7.2. Isitpossibletouseothertypesofwaystomakenumberto definechromaticnumberandneutrosophicchromaticnumber?
Question2.7.3. Whichclassesofneutrosophicgraphshavetheeligibilityto pursueindependentstudyinthisway?
Question2.7.4. Whichapplicationsdomakeanindependentstudytodefine chromaticnumberandneutrosophicchromaticnumber?
Problem2.7.5. Whichapproachesdoworktoconstructclassesofneutrosophic graphstocontinuethisstudy?
Problem2.7.6. Whichapproachesdoworktoconstructapplicationstocreate independentstudy?
Problem2.7.7. Whichapproachesdoworktoconstructdefinitionswhichuse allthreearraysandtherelationsamidtheminsteadofonearrayofthreearrays tocreateindependentstudy?
2.7.OpenProblems
53
sec5
2.8ConclusionandClosingRemarks
Thisstudyusesmixedcombinationsofneutrosophicchromaticnumberand chromaticnumbertostudyonneutrosophicgraphs.Theconnectionsofvertices whichareclarifiedbyneutrosophicstrongedges,differthemfromeachother andandputthemindifferentcategoriestorepresentonerepresentativefor eachcolor.Furtherstudiescouldbeaboutchangesinthesettingstocompare thisnotionamiddifferentsettingsofgraphtheory.Onewayisfindingsome relationsamidarrayofverticestomakesensibledefinitions.InTable (2.2), somelimitationsandadvantagesofthisstudyispointedout.Secondcasefor Table2.2:ABriefOverviewaboutAdvantagesandLimitationsofthisstudy tbl2
thecontentsistousethearticlefrom[3].Thecontentsareusedintheway that,usagesofnewcontentsarepreferencesandthepreliminariesarepassedin thebeginningofthischapter.
Newsettingisintroducedtostudychromaticnumber.vitalchromaticnumber andn-vitalchromaticnumberareproposedinthisway,someresultsare obtained.Classesofneutrosophicgraphsareusedtoobtainsthesenumbers andtherepresentativesofthecolors.Usingcolorstoassigntothevertices ofneutrosophicgraphsisapplied.Somequestionsandproblemsareposed concerningwaystodofurtherstudiesonthistopic.Usingvitaledgefrom connectednesstodefinetherelationamidverticeswhichimplieshavingdifferent colorsamidthemandasconsequences,choosingonevertexasarepresentativeof eachcolortousetheminasetofrepresentativesandfinally,usingneutrosophic cardinalityofthissettocomputevitalchromaticnumber.Thisspecificrelation amidedgesisnecessarytocomputebothvitalchromaticnumberconcerning thenumberofrepresentativeinthesetofrepresentativesandn-vitalchromatic numberconcerningneutrosophiccardinalityofsetofrepresentatives.Iftwo verticeshavenovitaledge,thentheycanbeassignedtosamecoloreventhey’ve commonedge.Basicfamiliaritieswithneutrosophicgraphtheoryandgraph theoryareproposedforthisarticle.
2.NeutrosophicChromaticNumber
Limitations 1. Usingneutrosophicstrongedges 1. Usingonlyonearrayofthreearrays 2. Usingneutrosophiccardinality 3. Usingcardinality 2. Studyonafewclasses 4. Characterizingsmallestnumber 5. Characterizingbiggestnumber 3. QualityofResults
2.9NeutrosophicChromaticNumberBasedon Connectedness
Advantages
2.10Abstract
54
Keywords: NeutrosophicConnctedness,NeutrosophicGraphs,Chromatic
Number
AMSSubjectClassification: 05C17,05C22,05E45
2.11MotivationandContributions
Inthisstudy,there’sanideawhichcouldbeconsideredasamotivation. Question2.11.1. Isitpossibletousemixedversionsofideasconcerning “connectedness”,“neutrosophicgraphs”and“neutrosophiccoloring”todefine somenotionswhichareappliedtoneutrosophicgraphs?
It’smotivationtofindnotionstouseinanyclassesofneutrosophicgraphs. Real-worldapplicationsabouttimetableandschedulingareanotherthoughts whichleadtobeconsideredasmotivation.Connectionsamidtwoitemshavekey rolestoassigncolors.Thusthey’reusedtodefinenewideaswhichconcludeto thestructureofcoloring.Theconceptofhavingvitaledgefromconnectedness inspiresmetostudythebehaviorofvitaledgeinthewaythat,bothvital chromaticnumberandn-vitalnumberarethecasesofstudy. Theframeworkofthisstudyisasfollows.Inthebeginningofchapter,I introducedbasicdefinitionstoclarifyaboutpreliminaries.Insubsection “DefinitionsandClarification”,newnotionofcoloringisappliedtothevertices ofneutrosophicgraphs.Vitaledgefromconnectednesshasthekeyrole inthisway.Classesofneutrosophicgraphsarestudiedinthetermsof vitaledges.Insubsection“ApplicationsinTimeTableandScheduling”, oneapplicationisposedforneutrosophicgraphsconcerningtimetableand schedulingwhenthesuspicionsareaboutchoosingsomesubjects.Insubsection “OpenProblems”,someproblemsandquestionsforfurtherstudiesareproposed. Insubsection“ConclusionandClosingRemarks”,gentlediscussionaboutresults andapplicationsarefeatured.Insubsection“ConclusionandClosingRemarks”, abriefoverviewconcerningadvantagesandlimitationsofthisstudyalongside conclusionsareformed.
2.12DefinitionsandClarification
Definition2.12.1. Let N =(σ,µ) beaneutrosophicgraph.Aneutrosophic edge xy iscalled vital ifdeletionof xy hasnochangeonits connectedness whichisamaximumstrengthofpathsamidthem.
Definition2.12.2. Let N =(σ,µ) beaneutrosophicgraph.Avertexwhichhas commonvitaledgewithanothervertex,hasassigneddifferentcolorfromthat vertex.Thenumberofdifferentcolors,iscalled vitalchromaticnumber and itsneutrosophiccardinalityiscalled n-vitalchromaticnumber
Example2.12.3. AssumeFigure(2.3)withrespecttofirstorder.
(i): Onlyvitaledgeis n2n3 Otheredgesaren’tvital.
(ii): Thevertices n2 and n3 havedifferentcolors.
(iii): Thevertex n1 couldgetanycolor.
2.11.MotivationandContributions
55
2.NeutrosophicChromaticNumber
(iv): Thevertex n1 hasnovitaledgewithanygivenvertex.
(v): Thesetofrepresentativesofcolorsis {n1,n2}.
(vi): Amid n2 and n3,n2 hasminimumvalue.

(vii): Deletionofedge n1n2 hasnochangeintheconnectednessofobtained neutrosophicgraph.
(viii): Thevitalnumberistwo.
(ix): n-vitalchromaticnumberis 2 57
Figure2.3:Neutrosophicgraph N1 isconsideredwithrespecttofirstorder.It’s completebutitisn’tneutrosophiccomplete.It’scyclebutitisn’tneutrosophic cycle.It’sneutrosophic3-partitebutitisn’tneutrosophiccomplete3-partite. nsc1b
2.13BasicProperties
prp5b Proposition2.13.1. Let N =(σ,µ) beaneutrosophiccycle.Thenalledges arevital.
Proof. Consider N =(σ,µ) beaneutrosophiccycle.Hence,thereareatleast twoedgeswhichareweakest,itmeansthereare xy,uv ∈ E suchthat µ(uv)= µ(xy)=min e∈E µ(e).
Inotherhand,foreverygivenvertices x and y, therearetwopathsfrom x to y. Soforeverygivenpath, S(P )=min e∈E µ(e)
56
Thusforevery x,y ∈ V,xy ∈ E, thevalue µ(xy) formstheconnectednessamid x to y. Thereforeconnectednessamidanygivencoupleofvertices,doesn’t changewhentheyformanedgeandthey’redeleted.Itinduceseveryedgeis vital.
prp6b Proposition2.13.2. Let N =(σ,µ) beaneutrosophiccompletewhichisneither neutrosophicemptynorneutrosophicpath.Thenalledgesarevital.
Proof. Suppose N =(σ,µ) isaneutrosophiccompletewhichisneither neutrosophicemptynorneutrosophicpath.If x,y ∈ V, then xy ∈ E. Thus P : x,y isapathforeverygivencoupleofvertices.Hence
S(P )= µ(xy)
Therefore,connectedness ≥ µ(xy) Inotherhands,assume P : x, ,y isan arbitrarypathfrom x to y. By N =(σ,µ) isaneutrosophiccomplete, N =(σ,µ) isaneutrosophicstrong.By N =(σ,µ) isaneutrosophicstrong,
S(P ) ≤ µ(xy)
Thenconnectedness ≤ S(P ) Itimpliesconnectedness ≤ µ(xy) Tosumitup, connectedness = µ(xy). Itinduces xy isvital.
Proposition2.13.3. Let N =(σ,µ) beaneutrosophicgraphwhichisfixed-edge andwhichisneitherneutrosophicemptynorneutrosophicpath.Thenalledges arevital.
Proof. Assume N =(σ,µ) isaneutrosophicgraphwhichisfixed-edgeand whichisneitherneutrosophicemptynorneutrosophicpath.ByN =(σ,µ) isa fixed-edge,
∀e,e ∈ E,µ(e)= µ(e )
Itinducesforeverygivenedge e andeverygivenpaths P,P
S(P )= S(P )= µ(e)
Itimpliesconnectednessisfixedanditequalsto µ(e) where e ∈ E. Therefore, thedeletionof e hasnochangeonconnectednessamideverycoupleofvertices. Itmeanseveryedgeisvital.
prp8b Proposition2.13.4. Let N =(σ,µ) beaneutrosophicgraphwhichisneither neutrosophicemptynorneutrosophicpath.Thenthere’satleastonevitaledge.
Proof. Consider N =(σ,µ) isaneutrosophicgraphwhichisneither neutrosophicemptynorneutrosophicpath.Assume N =(σ,µ) isaneutrosophic graphwhichiseitherfixed-edgeorfixed-vertexandneutrosophicstrong.Hence, alledgeshavesamevalue.Itmeans
∀e,e ∈ E,µ(e)= µ(e ).
Itinducesforeverygivenedge e andeverygivenpaths P,P
S(P )= S(P )= µ(e)
2.13.BasicProperties
57
Itimpliesconnectednessisfixedanditequalsto µ(e) where e ∈ E. Therefore, thedeletionof e hasnochangeonconnectednessamideverycoupleofvertices. Itmeanseveryedgeisvital.Inotherhand,supposeotherwise.Soby |E| > 2, there’soneedge e suchthatforeveryedge e = e, µ(e) >µ(e )
Letanumber µ(e ) be min e∈E µ(e)
Thenconnectednessis ≥ µ(e ). Butthere’sacyclewhichimplies |E| > 3. Itinducesthereareatleasttwopathscorrespondedto e By µ(e) >µ(e ), connectedness ≥ µ(e ) Itimpliescorrespondedconnectednessto e isn’tchanged whenthedeletionof e isdone.Thustheedge e ∈ E isvital.
prp9b Proposition2.13.5. Let N =(σ,µ) beaneutrosophicstrongwhichisfixedvertexandwhichisneitherneutrosophicemptynorneutrosophicpath.Then alledgesarevital.
Proof. Assume N =(σ,µ) isaneutrosophicstrongwhichisfixed-vertexand whichisneitherneutrosophicemptynorneutrosophicpath.Thusby N =(σ,µ) isaneutrosophicfixed-vertex,forall v,v ∈ V, σ(v)= σ(v ).
By N =(σ,µ) isaneutrosophicstrong,forall e,e ∈ V, µ(e)= µ(e ).
Itinducesforeverycoupleofverticeswhichformanedge,connectednessamid themissameandequals µ(e) where e isagivenedge.Itimpliesatleastthere aretwopathswithstrength µ(e).Thusdeletionofeveryedgehasnochange onconnectednessamiditsvertices.Therefore,everyedgeisvital.
Proposition2.13.6. Let N =(σ,µ) beaneutrosophicgraphwhichisfixedvertexandcomplete.Thenalledgesarevital.
Proof. By N =(σ,µ) isneutrosophiccomplete, N =(σ,µ) isneutrosophic strong.By N =(σ,µ) isaneutrosophicgraphwhichisfixed-vertex,complete andapplyingProposition(2.13.5),alledgesarevital.
prp11b
Proposition2.13.7. Let N =(σ,µ) beaneutrosophicgraphwhichisfixed-edge. Thenalledgesarevital.
Proof. Suppose N =(σ,µ) isaneutrosophicgraphwhichisfixed-edge.Then foreveryedges e and e , µ(e)= µ(e ).
Itmeansallpathshassamestrengthwhichisthevalueofanedgesinceall edgeshavesamevalues.Itmeanstheconnectednessamidallgivencoupleof verticesisthesame.Thereareatleasttwopaths.Sodeletionanyedgehasno changeontheconnectednessamidallgivencoupleofvertices.
2.NeutrosophicChromaticNumber
58
2.14VitalChromaticNumber
Proposition2.14.1. Let N =(σ,µ) beaneutrosophicgraphwhichisneither neutrosophicemptynorneutrosophicpath.Thenvitalchromaticnumberisat most n andatleast 1
Proof. Theseboundsaresharpandtightasthey’llbeshowninupcoming results.Ifthere’snoedge,thenvitalchromaticnumberis 1 butifthenumberof verticesare n andthey’reconnectedtoeachother,thenvitalchromaticnumber is n.
2.15LargestVitalChromaticNumber
Proposition2.15.1. Let N =(σ,µ) beaneutrosophiccompletewhichisneither neutrosophicemptynorneutrosophicpath.Thenvitalchromaticnumberis n.
Proof. Consider N =(σ,µ) isaneutrosophiccompletewhichisneither neutrosophicemptynorneutrosophicpath.ByProposition (2.13.2),alledges arevital.By N =(σ,µ) isn’taneutrosophicpath,thereareatleasttwopath amidtwogivenedges.Inotherwords,thereisatleastonecycle.By N =(σ,µ) isaneutrosophiccomplete,allverticesareconnectedtoeachother.Itimplies, ∀v,v ∈ V,vv ∈ E.
Itinducesallverticeshavedifferentcolors.Thenumberofverticesare n. So vitalchromaticnumberis n.
Proposition2.15.2. Let N =(σ,µ) beaneutrosophicpath.Thenvital chromaticnumberaren’tcomputable.
Proof. Assume N =(σ,µ) isaneutrosophicpath.Thenthere’sonlyonepath amidtwogivenvertices.Sodeletionofanedgemakestheconnectednessamid itsvertices,tobeincomputable.
Proposition2.15.3. Let N =(σ,µ) beaneutrosophicstar.Thenvital chromaticnumberaren’tcomputable.
Proof. Consider N =(σ,µ) isaneutrosophicstar.Hencethere’sonlyonepath amidtwogivenvertices.Thusdeletionofanedgemakestheconnectedness amiditsvertices,tobeincomputable.
2.16SmallestVitalChromaticNumber
Proposition2.16.1. Let N =(σ,µ) beaneutrosophicempty.Thenvital chromaticnumberis 1.
Proof. Let N =(σ,µ) beaneutrosophicempty.Thenthere’snoedge.It impliesallverticeshavesamecolorswheretheminimumnumberofcolorsare applied.Thusvitalchromaticnumberis 1. prp17b
Proposition2.16.2. Let N =(σ,µ) beaneutrosophicgraphwhichisneither neutrosophicemptynorneutrosophicpath.Thenvitalchromaticnumberisn’t 1
2.14.VitalChromaticNumber
59
prp21b
2.NeutrosophicChromaticNumber
Proof. Assume N =(σ,µ) isaneutrosophicgraphwhichisneitherneutrosophic emptynorneutrosophicpath.ByProposition (2.13.4),there’satleastonevital edge.
Proposition2.16.3. Let N =(σ,µ) beaneutrosophiccycle.Thenvital chromaticnumberisatleast 2 andatmost 3
Proof. Suppose N =(σ,µ) isaneutrosophiccycle.There’satleastamidtwo vertices.ByProposition (2.13.1),alledgesarevital.Soatleastthecolors oftwoverticesaredifferent.Itimpliesvitalchromaticnumberisatleast 2 Byapplyingcolorsonverticesinalternativeways,atmosttwoverticeshave commonedgeswithsamecolor.Hencevitalchromaticnumberisatmost 3
Proposition2.16.4. Let N =(σ,µ) beanevenneutrosophiccycle.Thenvital chromaticnumberis 2
Proof. Assume N =(σ,µ) isanevenneutrosophiccycle.ByProposition (2.16.2),vitalchromaticnumberisatleast 2 Byapplyingcoloringonvertices inalternativeways,twoverticeswithcommonedge,hasdifferentcolors.Since thecyclehasevennumberofedges.Thusvitalchromaticnumberis 2
Proposition2.16.5. Let N =(σ,µ) beanoddneutrosophiccycle.Thenvital chromaticnumberis 3
Proof. Consider N =(σ,µ) isanoddneutrosophiccycle.ByProposition (2.13.1),alledgesarevital.Sobyusingcoloringinalternativeway,there aretwoverticeswhichhavecommonedgeandhavesamecolor.Thusvital chromaticnumberis 3.
Proposition2.16.6. Let N =(σ,µ) beaneutrosophicbipartitewhichisfixededgeandcomplete.Thenvitalchromaticnumberis 2
Proof. Suppose N =(σ,µ) isaneutrosophicbipartitewhichisfixed-edgeand complete.Thusstrengthofeverypathisassameasconnectednessamidtwo verticesis.Thusalledgesarevital.By N =(σ,µ) iscomplete,allvertices fromonepartareconnectedtoallverticesofanotherpart.Everyparthasno connectionamiditsverticessoallverticesfromeverypart,havesamecolor. Therearetwoparts.Thusvitalchromaticnumberis 2
Proposition2.16.7. Let N =(σ,µ) beaneutrosophicbipartitewhichisfixedvertexandcomplete.Thenvitalchromaticnumberis 2
Proof. By N =(σ,µ) isfixed-vertexandcomplete, N =(σ,µ) isfixed-edgeand complete.Therefore,byProposition (2.16.6),vitalchromaticnumberis 2 prp23b
Proposition2.16.8. Let N =(σ,µ) beaneutrosophic t partitewhichisfixededgeandcomplete.Thenvitalchromaticnumberis t.
Proof. By N =(σ,µ) isfixed-edge,alledgeshavesamevalue.Thusallpaths havesamestrength.Soconnectednessamidtwogivenverticesaresame. Thereforealledgesarevital.Insideeverypart,there’snoedgeamidtwo vertices.Itinducestheverticesofeveryparthavesamecolor.Thereare t parts. Itimplies t differentcolorsareapplied.Thereforevitalchromaticnumberis t. 60
2.17.n-VitalChromaticNumber
Proposition2.16.9. Let N =(σ,µ) beaneutrosophic t partitewhichisfixedvertexandcomplete.Thenvitalchromaticnumberis t.
Proof. It’sfixed-vertexandcomplete.SoIt’sfixed-edgeandcomplete.By Proposition(2.16.8),vitalchromaticnumberis t.
Proposition2.16.10. Let N =(σ,µ) beaneutrosophicwheelwhichisfixedvertexandneutrosophicstrong.Thenvitalchromaticnumberis 3 or 4.
Proof. Consider N =(σ,µ) isaneutrosophicwheelwhichisfixed-vertexand neutrosophicstrong.Byit’sfixed-vertexandneutrosophicstrong,it’sfixed-edge. Everyedgeshavesamevalue.Sostrengthofpathsandconnectednessaresame andequaltoeachother.Thusalledgesarevital.Thenthecenterhasone colorandsinceit’sconnectedtoallothervertices,thecolorofcenterisunique. Therefore,vitalchromaticnumberisatleast 2 Non-centerverticesformapath whicharecoloredbytwocolorswhenapplyingcolorsareinalternativeways. Thusvitalchromaticnumberis 3 ifthenon-centerverticesformevencolorand vitalchromaticnumberis 4 ifthenon-centerverticesformoddcolor.
Proposition2.16.11. Let N =(σ,µ) beaneutrosophicwheelwhichisfixed-edge andneutrosophicstrong.Thenvitalchromaticnumberis 3 or 4
Proof. Consider N =(σ,µ) isaneutrosophicwheelwhichisfixed-vertexand neutrosophicstrong.It’sfixed-edge.Everyedgeshavesamevalue.Sostrength ofpathsandconnectednessaresameandequaltoeachother.Thusalledges arevital.Thenthecenterhasonecolorandsinceit’sconnectedtoallother vertices,thecolorofcenterisunique.Therefore,vitalchromaticnumberisat least 2 Non-centerverticesformapathwhicharecoloredbytwocolorswhen applyingcolorsareinalternativeways.Thusvitalchromaticnumberis 3 if thenon-centerverticesformevencolorandvitalchromaticnumberis 4 ifthe non-centerverticesformoddcolor.
2.17n-VitalChromaticNumber
Proposition2.17.1. Let N =(σ,µ) beaneutrosophicgraphwhichisneither neutrosophicemptynorneutrosophicpath.Thenn-vitalchromaticnumberisat mostorderof N whichisneutrosophiccardinalityof V.
Proof. Assume N =(σ,µ) isaneutrosophicgraphwhichisneitherneutrosophic emptynorneutrosophicpath.Ifalledgesarevitalandallverticesareconnected toeachother,thenvitalchromaticnumberis n. Thusn-vitalchromaticnumber isatmostorderof N whichisneutrosophiccardinalityof V.
2.18Largestn-VitalChromaticNumber
Proposition2.18.1. Let N =(σ,µ) beaneutrosophiccompletewhichisneither neutrosophicemptynorneutrosophicpath.Thenn-vitalchromaticnumberis orderof N whichisneutrosophiccardinalityof V.
61
2.NeutrosophicChromaticNumber
Proof. Suppose N =(σ,µ) isaneutrosophiccompletewhichisneither neutrosophicemptynorneutrosophicpath.Byit’scomplete,thenallvertices areconnectedtoeachotherandalledgesarevital.Thus n colorsareused.It meansn-vitalchromaticnumberisorderof N whichisneutrosophiccardinality of V.
Proposition2.18.2. Let N =(σ,µ) beaneutrosophicpath.Thenn-vital chromaticnumberaren’tcomputable.
Proof. Deletionofoneedge,make N =(σ,µ) beinthesituationwheren-vital chromaticnumberaren’tcomputable.Sincethere’sneedtohaveatleasttwo pathstocomputen-vitalchromaticnumber.Inotherwords,thisnotionis computableinneutrosophicgraphwhichhasatleastonecycle.
Proposition2.18.3. Let N =(σ,µ) beaneutrosophicstar.Thenn-vital chromaticnumberaren’tcomputable.
Proof. Assume N =(σ,µ) isaneutrosophicstar.Thenthere’sonlyonepath amidtwogivenvertices.Deletiononeedgecausestheconnectednesstobe incomputable.Thusn-vitalchromaticnumberaren’tcomputable.
2.19Smallestn-VitalChromaticNumber
Proposition2.19.1. Let N =(σ,µ) beaneutrosophicempty.Thenn-vital chromaticnumberis min x∈V σ(x)
Proof. Suppose N =(σ,µ) isaneutrosophicempty.Thenthere’snoedge.It inducesthere’snovitaledge.Soallverticesarecoloredbyonecolor.Hence allverticeshavesamecolor.Itmeansthenumberofcolorisone.Itinduces thecardinalityofsetincludestherepresentativeofcolorisone.Tofindthe representativeofcolor,wehave 1 choicefrom n options.Thusn-vitalchromatic numberis min x∈V σ(x).
Proposition2.19.2. Let N =(σ,µ) beaneutrosophicgraphwhichisneither neutrosophicemptynorneutrosophicpath.Thenn-vitalchromaticnumberisn’t min x∈V σ(x)
Proof. Consider N =(σ,µ) isaneutrosophicgraphwhichisneither neutrosophicemptynorneutrosophicpath.Thenthere’satleastoneedge.By Proposition (2.13.4),there’satleastonevitaledge.Itinducesthenumberof colorisatleasttwo.Therefore,thecardinalityofsetofrepresentativeisat leasttwo.Itimpliesn-vitalchromaticnumberisn’t min x∈V σ(x)
62
2.19.Smallestn-VitalChromaticNumber
Proposition2.19.3. Let N =(σ,µ) beaneutrosophiccycle.Thenn-vital chromaticnumberisatleast min x,y∈V,xy∈E σ(x)+ σ(y)
Andatmost min x,y,z∈V,xy,yz,xz∈E σ(x)+ σ(y)+ σ(z)
Proof. Suppose N =(σ,µ) isaneutrosophiccycle.Byusingalternativecoloring ofvertices,twoorthreenumbersofcolorsareused.Sothecardinalityofset ofrepresentativeistwoorthree.Thereareonlythesepossibilities.Therefore n-vitalchromaticnumberisatleast min x,y∈V,xy∈E σ(x)+ σ(y)
Andatmost min x,y,z∈V,xy,yz,xz∈E σ(x)+ σ(y)+ σ(z)
Proposition2.19.4. Let N =(σ,µ) beanevenneutrosophiccycle.Thenn-vital chromaticnumberis min x,y∈V,xy∈E σ(x)+ σ(y).
Proof. Assume N =(σ,µ) isanevenneutrosophiccycle.Ifcolorsareapplied onverticesinalternativewayswhichcausetwoverticeswithacommonedge, havedifferentcolors,thenbyit’sevenneutrosophiccycle,therepresentativesof colorsaretwo.SincethereareevenedgeswhichbyProposition (2.13.1),allare vital.Itinducesthecardinalityofsetofrepresentativesistwo.Thusn-vital chromaticnumberisn-vitalchromaticnumberis
min x,y∈V,xy∈E σ(x)+ σ(y)
Proposition2.19.5. Let N =(σ,µ) beanoddneutrosophiccycle.Thenn-vital chromaticnumberis min x,y,z∈V,xy∈E σ(x)+ σ(y)+ σ(z)
Proof. Consider N =(σ,µ) isanoddneutrosophiccycle.Thennumberofedges areodd.ByProposition (2.13.1),alledgesarevital.Usingdifferentcolorson theverticeswhichhavecommonedges,impliesusageofthreecolors.Hencethe setofrepresentativeshasthecardinalitythree.Tochoose,therepresentatives, ineverycolor,minimumvalueofvertices,introducestherepresentativeof specificcolor.Thenn-vitalchromaticnumberis
min x,y,z∈V,xy∈E σ(x)+ σ(y)+ σ(z)
63
prp36b Proposition2.19.6. Let N =(σ,µ) beneutrosophicbipartitewhichisfixed-edge andcomplete.Thenn-vitalchromaticnumberis min x,y∈V,xy∈E σ(x)+ σ(y)
Proof. Assume N =(σ,µ) isneutrosophicbipartitewhichisfixed-edgeand complete.It’sfixed-edgesoalledgeshavesamevalueandasitsconsequences, allpathshavesamestrengthandallconnectednessaresame.Hencealledges arevital.Byit’scomplete,allverticesfromonepartareconnectedtoall verticesfromanotherpart.Byit’sbipartite,therearetwocolorstouseon verticessuchthateveryparthassamecolor.Sothesetofrepresentativeshas thecardinalitytwowhichimpliesn-vitalchromaticnumberis min x,y∈V,xy∈E σ(x)+ σ(y)
Proposition2.19.7. Let N =(σ,µ) beneutrosophicbipartitewhichisfixedvertexandcomplete.Thenn-vitalchromaticnumberis min x,y∈V,xy∈E σ(x)+ σ(y)
Proof. Assume N =(σ,µ) isneutrosophicbipartitewhichisfixed-vertexand complete.Byit’sfixed-vertexandcomplete,it’sfixed-edgeandcomplete.By Proposition(2.19.6),n-vitalchromaticnumberis min x,y∈V,xy∈E σ(x)+ σ(y)
prp38b Proposition2.19.8. Let N =(σ,µ) beneutrosophic t partitewhichisfixededgeandcomplete.Thenn-vitalchromaticnumberis min x1,x2, ,xt∈V,xixj ∈E σ(x1)+ σ(x2)+ + σ(xt).
Proof. Assume N =(σ,µ) isneutrosophic t partitewhichisfixed-edgeand complete.Allpartshavesamecolorontheirvertices.Byit’sfixed-edgeand applyingProposition (2.13.7),alledgesarevital.Thusminimumnumberof colorsis t. Andthesetofrepresentativeshasthecardinality t. Itmeansn-vital chromaticnumberis min x1,x2, ,xt∈V,xixj ∈E σ(x1)+ σ(x2)+ ··· + σ(xt)
Proposition2.19.9. Let N =(σ,µ) beneutrosophic t partitewhichisfixedvertexandcomplete.Thenn-vitalchromaticnumberis min x1,x2, ,xt∈V,xixj ∈E σ(x1)+ σ(x2)+ + σ(xt)
2.NeutrosophicChromaticNumber
64
2.19.Smallestn-VitalChromaticNumber
Proof. Assume N =(σ,µ) isneutrosophic t partitewhichisfixed-vertexand complete.Thenbyit’sfixed-vertexandcomplete,it’sit’sfixed-edgeand complete.ByProposition(2.19.8),n-vitalchromaticnumberis min x1,x2, ,xt∈V,xixj ∈E σ(x1)+ σ(x2)+ + σ(xt).
prp40b Proposition2.19.10. Let N =(σ,µ) beneutrosophicwheelwhichisfixed-vertex andneutrosophicstrong.Thenn-vitalchromaticnumberis
min y,z∈V,yz∈E σ(c)+ σ(y)+ σ(z)
Or min y,z∈V,yz,zt∈E σ(c)+ σ(y)+ σ(z)+ σ(t)
Proof. Consider N =(σ,µ) isneutrosophicwheelwhichisfixed-vertexand neutrosophicstrong.Byfixed-vertexandneutrosophicstrong,it’sfixed-edge. Byit’sfixed-edgeandapplyingProposition (2.13.7),alledgesarevital.Center isconnectedtonon-centervertices.Socenterusesuniquecolor.Non-center verticesformacycle.Ifthecycleiseven,thenn-vitalchromaticnumberis min y,z∈V,yz∈E σ(c)+ σ(y)+ σ(z)
Ifit’sodd,thenn-vitalchromaticnumberis min y,z∈V,yz∈E σ(c)+ σ(y)+ σ(z)
Or min y,z∈V,yz,zt∈E σ(c)+ σ(y)+ σ(z)+ σ(t)
Proposition2.19.11. Let N =(σ,µ) beneutrosophicwheelwhichisfixed-edge andneutrosophicstrong.Thenn-vitalchromaticnumberis min y,z∈V,yz∈E σ(c)+ σ(y)+ σ(z).
Proof. Assume N =(σ,µ) isneutrosophicwheelwhichisfixed-edgeand neutrosophicstrong.Byit’sfixed-edgeandneutrosophicstrong,it’sfixedvertexandneutrosophicstrong.ByProposition(2.19.10), min y,z∈V,yz∈E σ(c)+ σ(y)+ σ(z)
Or min y,z∈V,yz,zt∈E σ(c)+ σ(y)+ σ(z)+ σ(t).
Therelationamidneutrosophicchromaticnumberandmainparametersof neutrosophicgraphsiscomputed.
65
sec3b
2.NeutrosophicChromaticNumber
Proposition2.19.12. Let N =(σ,µ) beaneutrosophicstrong.Thenvital chromaticnumberisatmost ∆+1 andatleast 2
Proof. Neutrosophicstrongisneutrosophicnontrivial.Soitisn’tneutrosophic emptywhichinducesthere’snoedge.Itimplieschromaticnumberistwo.Since chromaticnumberisoneifandonlyif N =(σ,µ) isneutrosophicemptyif andonlyif N =(σ,µ) isneutrosophictrivial.Avertexwithdegree ∆, has ∆ verticeswhichhavecommonedgeswiththem.Iftheseverticeshavenoedge amideachother,thenchromaticnumberistwoespecially,neutrosophicstar.If not,theninthecase,allverticeshaveedgeamideachother,chromaticnumber is ∆+1, especially,neutrosophiccomplete.
Proposition2.19.13. Let N =(σ,µ) beaneutrosophic r regular.Thenvital chromaticnumberisatmost r +1.
Proof. N =(σ,µ) isaneutrosophic r regular.Soanyofvertexhas r vertices whichhavecommonedgewithit.Iftheseverticeshavenocommonedgewith eachother,forinstanceneutrosophicstar,chromaticnumberistwo.Butsince theverticeshavecommonedgewitheachother,chromaticnumberis r +1, for instance,neutrosophiccomplete.
2.20ApplicationsinTimeTableandScheduling
Designingtheprogramstoachievesomegoalsisgeneralapproachtoapplyon someissuestofunctionproperly.Separationhaskeyroleinthecontextofthis style.Separatingthedurationofworkwhichareconsecutive,isthematterand ithasimportanttoavoidmixingup.
Step1.(Definition) Timetableisanapproachtogetsomeattributestodo theworkfastandproper.Thestyleofschedulingimpliesspecialattention tothetaskswhichareconsecutive.
Step2.(Issue) Schedulingofprogramhasfacedwithdifficultiestodifferamid consecutivesection.Beyondthat,sometimessectionsarenotthesame.
Step3.(Model) AsFigure (2.4),thesituationisdesignedasamodel.The modelusesdatatoassigneverysectionandtoassigntorelationamid section,threenumbersbelongunitintervaltostateindeterminacy, possibilitiesanddeterminacy.There’sonerestrictioninthat,thenumbers amidtwosectionsareatleastthenumberoftherelationamidthem. Table(2.3),clarifiesabouttheassignednumberstothesesituation.
Table2.3:SchedulingconcernsitsSubjectsanditsConnectionsasa NeutrosophicGraphinaModel. tbl1b Sectionsof
s1 s2 s3 s4 s5 s6 s7 s8 s9
10
.
.
.10.30.
.
s1s2 s2s3 s3s4 s4s5 s5s6 s6s7 s7s8 s8s9 s9
66
T
,s
Values 0.10.80
70
80
60
50.2 Connectionsof T
s10 Values 0 10 60 40 10 10 20 40 20 1
sec4b
Figure2.4:Blackverticesaresuspicionsaboutchoosingthem. fgr1b

Step4.(Solution) AsFigure (2.4) shows,neutrosophicmodel,proposesto usevitalchromaticnumberwhichisincomputableinthecasewhichis titled T Inthiscase, i1 and c1 aren’trepresentativeofthesetwocolors andn-vitalchromaticnumberisincomputable.Theset {i1,c1} doesn’t containrepresentativesofcolorswhichposevitalchromaticnumberand n-vitalchromaticnumber.Thusthedecisionamidchoosingthesubject c1 an c2 isn’tconcludedtochoose c1. Togetbriefoverview,neutrosophic modelusesonenumberforeveryarrayso 0 9 means (0 9, 0 9, 0 9) In Figure (2.4),theneutrosophicmodel T introducesthecommonsituation. Therepresentativesofcolorsare i2 and c1 Thusvitalchromaticnumber istwoandn-vitalchromaticnumberis 1 4 Thussuspicionaboutchoosing i1 and i2 isdeterminedtobe i2. Thesetsofrepresentativeforcolorsare {i2,c1}
2.21OpenProblems
Thetwonotionsofcoloringofverticesconcerningvitalchromaticnumberandnvitalchromaticnumberaredefinedonneutrosophicgraphswhenconnectedness andasitsconsequences,vitaledgeshavekeyroletohavethesenotions.Thus
Question2.21.1. Isitpossibletouseothertypesedgesviaconnectednessto definevitalchromaticnumberandn-vitalchromaticnumber?
Question2.21.2. Areexistedsomeconnectionsamidthecoloringfrom connectednessinsidethisconceptandexternalconnectionswithothertypes ofcoloringfromothernotions?
Question2.21.3. Isitpossibletoconstructsomeclassesneutrosophicgraphs whichhave“nice”behavior?
Question2.21.4. Whichapplicationsdomakeanindependentstudytoapply vitalchromaticnumberandn-vitalchromaticnumber?
Problem2.21.5. Whichparametersarerelatedtothisparameter?
2.21.OpenProblems
67
sec5b
2.NeutrosophicChromaticNumber
Problem2.21.6. Whichapproachesdoworktoconstructapplicationstocreate independentstudy?
Problem2.21.7. Whichapproachesdoworktoconstructdefinitionswhichuse allthreearraysandtherelationsamidtheminsteadofonearrayofthreearrays tocreateindependentstudy?
2.22ConclusionandClosingRemarks
Thisstudyusesmixedcombinationsofvitalchromaticnumberandn-vital chromaticnumbertostudyonneutrosophicgraphs.Theconnectionsofvertices whichareclarifiedbyvitaledgesfromconnectedness,differthemfromeach otherandandputthemindifferentcategoriestorepresentonerepresentativefor eachcolor.Furtherstudiescouldbeaboutchangesinthesettingstocompare thisnotionamiddifferentsettingsofgraphtheory.Onewayisfindingsome relationsamidarrayofverticestomakesensibledefinitions.InTable (2.4), somelimitationsandadvantagesofthisstudyispointedout.
Table2.4:ABriefOverviewaboutAdvantagesandLimitationsofthisstudy tbl2b
Newideasare appliedonthis modeltoexplore behaviorsof thesemodelsin themathematical perspective. Anotherwaysto makesenseabout them,areused byrelatively comparable resultsto conclude analysis.
2.23NewIdeas
Havingdifferentcolorswhentwoverticeshavecommon“connection”.Common connectioncanonlybeanedge.Anedgewithspecialattributecanbecommon “connection”.Usingneutrosophicattributesareexpectedtomakesenseabout thestudyinthisframework.Inwhatfollows,somedefinitionsareintroduced tobeintheformofcommon“connection”.
2.24DifferentTypesofNeutrosophicChromaticNumber
Thirdcaseforthecontentsistousethearticlefrom[2].Thecontentsareused inthewaythat,usagesofnewcontentsarepreferencesandthepreliminaries arepassedinthebeginningofthischapter.
Limitations 1. Usingconnectednessforvitaledges 1. Acyclicneutrosophicgraphs 2. Usingneutrosophiccardinality 3. Usingcardinality 2. Connectionswithparameters 4. Characterizingsmallestnumber 5. Characterizingbiggestnumber 3. Starandpath
Advantages
68
2.25.Abstract
2.25Abstract
Newsettingisintroducedtostudychromaticnumber.Differenttypesof chromaticnumbersandneutrosophicchromaticnumberareproposedinthis way,someresultsareobtained.Classesofneutrosophicgraphsareusedto obtainsthesenumbersandtherepresentativesofthecolors.Usingcolorsto assigntotheverticesofneutrosophicgraphsisapplied.Somequestionsand problemsareposedconcerningwaystodofurtherstudiesonthistopic.Using differenttypesofedgesfromconnectednessinsameneutrosophicgraphsandin modifiedneutrosophicgraphstodefinetherelationamidverticeswhichimplies havingdifferentcolorsamidthemandasconsequences,choosingonevertexas arepresentativeofeachcolortousetheminasetofrepresentativesandfinally, usingneutrosophiccardinalityofthissettocomputetypesofchromaticnumbers. Thisspecificrelationamidedgesisnecessarytocomputebothtypesofchromatic numberconcerningthenumberofrepresentativeinthesetofrepresentativesand typesofneutrosophicchromaticnumberconcerningneutrosophiccardinality ofsetofrepresentatives.Iftwoverticeshavenointendededge,thentheycan beassignedtosamecoloreventhey’vecommonedge.Basicfamiliaritieswith neutrosophicgraphtheoryandgraphtheoryareproposedforthisarticle. Keywords: NeutrosophicConnctedness,NeutrosophicGraphs,Chromatic Number
AMSSubjectClassification: 05C17,05C22,05E45
2.26MotivationandContributions
Inthisstudy,there’sanideawhichcouldbeconsideredasamotivation.
Question2.26.1. Isitpossibletousemixedversionsofideasconcerning “connectedness”,“neutrosophicgraphs”and“neutrosophiccoloring”todefine somenotionswhichareappliedtoneutrosophicgraphs?
It’smotivationtofindnotionstouseinanyclassesofneutrosophicgraphs. Real-worldapplicationsabouttimetableandschedulingareanotherthoughts whichleadtobeconsideredasmotivation.Connectionsamidtwoitemshavekey rolestoassigncolors.Thusthey’reusedtodefinenewideaswhichconcludeto thestructureofcoloring.Theconceptofhavingspecificedgefromconnectedness inspiresmetostudythebehaviorofspecificedgeinthewaythat,bothtypesof chromaticnumbersandtypesofneutrosophicchromaticnumbersarethecases ofstudy.
Theframeworkofthisstudyisasfollows.Inthebeginning,Iintroducedbasic definitionstoclarifyaboutpreliminaries.Insection“NewIdeas”,newnotion ofcoloringisappliedtotheverticesofneutrosophicgraphs.Specificedgefrom connectednesshasthekeyroleinthisway.Classesofneutrosophicgraphs arestudiedinthetermsofdifferenttypesofedgesinsection“NewResults”. Insection“ApplicationsinTimeTableandScheduling”,oneapplicationis posedforneutrosophicgraphsconcerningtimetableandschedulingwhenthe suspicionsareaboutchoosingsomesubjects.Insection“OpenProblems”,some problemsandquestionsforfurtherstudiesareproposed.Insection“Conclusion andClosingRemarks”,gentlediscussionaboutresultsandapplicationsare featured.Insection“ConclusionandClosingRemarks”,abriefoverview
69
2.NeutrosophicChromaticNumber
concerningadvantagesandlimitationsofthisstudyalongsideconclusionsare formed.
2.27NewIdeas
Question2.27.1. What-ifthecommon“connection”isbeyondhavingone commonedge?
Thefirststepisthedefinitionofcommon“connection”.
Definition2.27.2. Let N =(σ,µ) beaneutrosophicgraph.Aneutrosophic edge xy iscalled type-I ifvalueof xy is connectedness whichisamaximum strengthofpathsamidthem.
Example2.27.3. ConsiderFigure(2.5).
(i): From n1 to n2, there’snoedgewhichistype-Ibut n2n3 (ii): From n2 to n3, there’snoedgewhichistype-Ibut n2n3 (iii): From n1 to n3, there’snoedgewhichistype-Ibut n1n3.
Figure2.5:Twoedgesaren’ttype-I. ncs1c2
There’sacuriousquestion.
Question2.27.4. Isthereaneutrosophicgraphwhoseedgesaretype-I?
Yesbutonlyoneclass.TwoupcomingPropositionsgivesimpleanswers aboutaclassofneutrosophicgraphs.Otherclassesofneutrosophicgraphshave atleastoneedgewhichisn’ttype-I.
Proposition2.27.5. Let N =(σ,µ) beaneutrosophicgraphwhichisfixed-edge. Thenalledgesaretype-I.
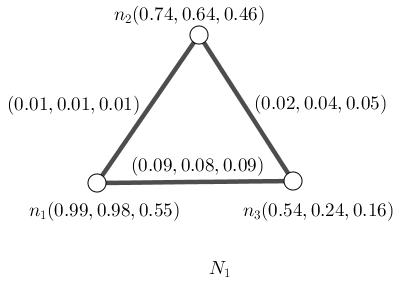
70
Proposition2.27.6. Let N =(σ,µ) beaneutrosophicgraphwhichisstrong fixed-vertex.Then N =(σ,µ) isfixed-edge.
Proposition2.27.7. Let N =(σ,µ) beaneutrosophicgraphwhichisstrong fixed-vertex.Thenalledgesaretype-I.

Example2.27.8. ConsiderFigure(2.6).Alledgesaretype-I.
Figure2.6:Neutrosophicgraphwhichisfixed-edgebutnotstrongfixed-vertex. ncs2c2
Definition2.27.9. Let N =(σ,µ) beaneutrosophicgraph.Aneutrosophic edge xy iscalled type-II ifvalueof xy islowerthan connectedness whichis amaximumstrengthofpathsamidthem.
Example2.27.10. Thecomparisonamidthevariantofedgeswhichareeither type-Iortype-II,ispossiblewhencommonneutrosophicgraphsarestudied.
(a): ConsiderFigure(2.5).
(i): From n1 to n2, there’snoedgewhichistype-IIbut n1n2 (ii): From n2 to n3, there’snoedgewhichistype-IIbut n1n2 (iii): From n1 to n3, there’snoedgewhichistype-IIbut n1n2 and n2n3
(b): ConsiderFigure(2.6).There’snoedgewhichistype-II.
Definition2.27.11. Let N =(σ,µ) beaneutrosophicgraph.Aneutrosophic edge xy iscalled type-III ifvalueof xy istheonlyvaluewhichis connectedness whichisamaximumstrengthofpathsamidthem.
Example2.27.12. Thecomparisonamidthevariantofedgeswhichareeither type-Iortype-IIortype-III,ispossiblewhencommonneutrosophicgraphsare studied.
(a): ConsiderFigure(2.5).
2.27.NewIdeas
71
(i): From n1 to n2, there’snoedgewhichistype-IIIbut n2n3.
(ii): From n2 to n3, there’snoedgewhichistype-IIIbut n2n3.
(iii): From n1 to n3, there’snoedgewhichistype-IIIbut n1n3 and n2n3.
(b): ConsiderFigure(2.6).There’snoedgewhichistype-III.
Definition2.27.13. Let N =(σ,µ) beaneutrosophicgraph.Aneutrosophic edge xy iscalled type-IV ifvalueof xy is connectedness whichisamaximum strengthofpathsamidthembutin N =(σ,µ) doesn’thave xy
Example2.27.14. Thecomparisonamidthevariantofedgeswhichareeither type-Ior...ortype-IV,ispossiblewhencommonneutrosophicgraphsarestudied.
(a): ConsiderFigure(2.5).
(i): From n1 to n2, there’snoedgewhichistype-IV.
(ii): From n2 to n3, there’snoedgewhichistype-IV.
(iii): From n1 to n3, there’snoedgewhichistype-IV.
(b): ConsiderFigure(2.6).Alledgesaretype-IV.
Definition2.27.15. Let N =(σ,µ) beaneutrosophicgraph.Aneutrosophic edge xy iscalled type-V ifvalueof xy islowerthan connectedness whichis amaximumstrengthofpathsamidthembutin N =(σ,µ) doesn’thave xy
Example2.27.16. Thecomparisonamidthevariantofedgeswhichareeither type-Ior...ortype-V,ispossiblewhencommonneutrosophicgraphsarestudied.
(a): ConsiderFigure(2.5).
(i): From n1 to n2, edge n1n2 istype-V.
(ii): From n2 to n3, there’snoedgewhichistype-V.
(iii): From n1 to n3, there’snoedgewhichistype-V.
(b): ConsiderFigure(2.6).There’snoedgewhichistype-V.
Definition2.27.17. Let N =(σ,µ) beaneutrosophicgraph.Aneutrosophic edge xy iscalled type-VI ifvalueof xy isgreaterthan connectedness which isamaximumstrengthofpathsamidthembutin N =(σ,µ) doesn’thave xy.
Example2.27.18. Thecomparisonamidthevariantofedgeswhichareeither type-Ior...ortype-VI,ispossiblewhencommonneutrosophicgraphsarestudied.
(a): ConsiderFigure(2.5).
(i): From n1 to n2, there’snoedgewhichistype-VI.
(ii): From n2 to n3, edges n2n3 and n1n3 aretype-VI.
(iii): From n1 to n3, edges n2n3 and n1n3 aretype-VI.
(b): ConsiderFigure(2.6).There’snoedgewhichistype-VI.
Definition2.27.19. Let N =(σ,µ) beaneutrosophicgraph.Aneutrosophic edge xy iscalled type-VII ifvalueof xy istheonlyvaluewhichis connectedness whichisamaximumstrengthofpathsamidthembutin N =(σ,µ) doesn’thave xy
2.NeutrosophicChromaticNumber
72
Example2.27.20. Thecomparisonamidthevariantofedgeswhichareeither type-Ior...ortype-VII,ispossiblewhencommonneutrosophicgraphsare studied.
(a): ConsiderFigure(2.5).
(i): From n1 to n2, there’snoedgewhichistype-VII.
(ii): From n2 to n3, there’snoedgewhichistype-VII.
(iii): From n1 to n3, there’snoedgewhichistype-VII.
(b): ConsiderFigure(2.6).There’snoedgewhichistype-VII.
Commonwaytodefinethenumber,couldbetwofold.Oneisaboutthe cardinalityandanotherisaboutneutrosophiccardinality.
Definition2.27.21. Let N =(σ,µ) beaneutrosophicgraph.Avertexwhich hascommontypeedgewithanothervertex,hasassigneddifferentcolorfrom thatvertex.Thecardinalityofthesetofrepresentativesofcolors,iscalled typechromaticnumber anditsneutrosophiccardinalityconcerningtheset ofrepresentativesofcolorsiscalled n-typechromaticnumber
Definition2.27.22. It’sworthytonotethattherearetwotypesofdefinitions. Oneisaboutthecomparisonamidedgesandconnectedness.Anotherisabout oneedgewhenit’sdeleted,newconnectednessiscomparedtodeletededge. Thusinfirsttype,alledgesarecomparedtoconnectednessbutinsecondtype, foreveryedge,there’sacomputationtohaveconnectedness.Soinfirsttype, connectednessisuniqueandthere’sonenumberforalledgesasconnectedness butinsecondtype,foreveryedge,there’sanewconnectednesstodecideabout theedgewhetherhasintendedattributeornot.Toavoidconfusion,chromatic numberiscomputedwithrespectto n1 and n2 wheresecondstyleisusedand alledgesarelabelledeventhey’renotdeletededgesso thirdtype isintroduced whendeletionofoneedge,isenoughtolabelalledges.Alsofirstorderisused tohavetheseconcepts.
Infollowingexample,thirdtypeofdefinitionswhichareexceptfromtypeIV,V,VI,VII,arestudied.
Example2.27.23. Thecomparisonamidthevariantofnumberswhichare eithertype-Ior...ortype-VII,ispossiblewhencommonneutrosophicgraphs arestudied.Chromaticnumberiscomputedwithrespectto n1 and n2. Also firstorderisusedtohavetheseconcepts.
(a): ConsiderFigure(2.5).
(i): Thesetofrepresentativesofcolorsis {n1,n2} Thustype-Ichromatic numberis 2 andn-type-Ichromaticnumberis 1 73
(ii): Thesetofrepresentativesofcolorsis {n1,n2} Thustype-IIchromatic numberis 2 andn-type-IIchromaticnumberis 1.73.
(iii): Thesetofrepresentativesofcolorsis {n2,n3} Thustype-III chromaticnumberis 2 andn-type-IIIchromaticnumberis 1 28
(iv): Thesetofrepresentativesofcolorsis {n2,n3} Thustype-IV chromaticnumberis 2 andn-type-IVchromaticnumberis 1 28
2.27.NewIdeas
73
Inthischapter, Iintroducesome results concerningnew ideasandin thisways,the resultsmake sensemoreabout theirimpactson different models.
2.NeutrosophicChromaticNumber
(v): Thesetofrepresentativesofcolorsis {n1,n2}. Thustype-Vchromatic numberis 2 andn-type-Vchromaticnumberis 1 73
(vi): Thesetofrepresentativesofcolorsis {n2,n3}. Thustype-VI chromaticnumberis 2 andn-type-VIchromaticnumberis 1.28.
(vii): Thesetofrepresentativesofcolorsis {n2,n3} Thustype-VII chromaticnumberis 2 andn-type-VIIchromaticnumberis 1.28.
(b): ConsiderFigure(2.6).
(i): Thesetofrepresentativesofcolorsis {n1,n2,n3}. Thustype-I chromaticnumberis 3 andn-type-Ichromaticnumberis 3 01
(ii): Thesetofrepresentativesofcolorsis {}. Thustype-IIchromatic numberis 0 andn-type-IIchromaticnumberis 0.
(iii): Thesetofrepresentativesofcolorsis {} Thustype-IIIchromatic numberis 0 andn-type-IIIchromaticnumberis 0.
(iv): Thesetofrepresentativesofcolorsis {} Thustype-IVchromatic numberis 0 andn-type-IVchromaticnumberis 0.
(v): Thesetofrepresentativesofcolorsis {} Thustype-Vchromatic numberis 0 andn-type-Vchromaticnumberis 0
(vi): Thesetofrepresentativesofcolorsis {} Thustype-VIchromatic numberis 0 andn-type-VIchromaticnumberis 0
(vii): Thesetofrepresentativesofcolorsis {} Thustype-VIIchromatic numberis 0 andn-type-VIIchromaticnumberis 0
2.28NewResults
2.29DifferentTypesofNeutrosophicChromaticNumber
Thirdcaseforthecontentsistousethearticlefrom[Ref12].Thecontents areusedinthewaythat,usagesofnewcontentsarepreferencesandthe preliminariesarepassedinthebeginningofthischapter.
2.30NewResults
Proposition2.30.1. Let N =(σ,µ) beaneutrosophicgraphwhichiscomplete. Ifit’sfixed-edge,then
(i): Thesetofrepresentativesofcolorsis {v1,v2, ··· ,vn} Thustype-I chromaticnumberis n andn-type-Ichromaticnumberisneutrosophic cardinalityof V.
(ii): Thesetofrepresentativesofcolorsis {}. Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0
(iii): Thesetofrepresentativesofcolorsis {} Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0.
(iv): Thesetofrepresentativesofcolorsis {v1,v2, ··· ,vn} Thustype-IV chromaticnumberis n andn-type-IVchromaticnumberisneutrosophic cardinalityof V.
74
(v): Thesetofrepresentativesofcolorsis {}. Thustype-Vchromaticnumber is 0 andn-type-Vchromaticnumberis 0
(vi): Thesetofrepresentativesofcolorsis {}. Thustype-VIchromaticnumber is 0 andn-type-VIchromaticnumberis 0
(vii): Thesetofrepresentativesofcolorsis {}. Thustype-VIIchromaticnumber is 0 andn-type-VIIchromaticnumberis 0
Proof. (i) Alledgeshavesameamountsotheconnectednessamidtwogiven edgesisthesame.Alledgesaretype-I.Byit’sneutrosophiccomplete,every vertexhas n 1 verticeswhichhavecommonedgeswhicharetype-I.Thusthe setofrepresentativesofcolorsis {v1,v2, ,vn} Thetype-Ichromaticnumber is n andn-type-Ichromaticnumberisneutrosophiccardinalityof V.
(ii) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-II.Byit’sneutrosophiccomplete,everyvertex has n 1 verticeswhichhavecommonedgeswhicharen’ttype-II.Thusthe setofrepresentativesofcolorsis {} Thetype-IIchromaticnumberis 0 and n-type-IIchromaticnumberis 0
(iii) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’sneutrosophiccomplete,everyvertex has n 1 verticeswhichhavecommonedgeswhicharen’ttype-III.Thusthe setofrepresentativesofcolorsis {} Thetype-IIIchromaticnumberis 0 and n-type-IIIchromaticnumberis 0
(iv) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaretype-IV.Byit’sneutrosophiccomplete,everyvertex has n 1 verticeswhichhavecommonedgeswhicharetype-IV.Thustheset ofrepresentativesofcolorsis {v1,v2, ,vn} Thetype-IVchromaticnumber is n andn-type-IVchromaticnumberisneutrosophiccardinalityof V. (v). Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-V.Byit’sneutrosophiccomplete,everyvertex has n 1 verticeswhichhavecommonedgeswhicharen’ttype-V.Thusthe setofrepresentativesofcolorsis {} Thetype-Vchromaticnumberis 0 and n-type-Vchromaticnumberis 0
(vi). Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-VI.Byit’sneutrosophiccomplete,everyvertex has n 1 verticeswhichhavecommonedgeswhicharen’ttype-VI.Thusthe setofrepresentativesofcolorsis {} Thetype-VIchromaticnumberis 0 and n-type-VIchromaticnumberis 0
(vii). Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-VII.Byit’sneutrosophiccomplete,every vertexhas n 1 verticeswhichhavecommonedgeswhicharen’ttype-VII.Thus thesetofrepresentativesofcolorsis {} Thetype-VIIchromaticnumberis 0 andn-type-VIIchromaticnumberis 0
Proposition2.30.2. Let N =(σ,µ) beaneutrosophicgraphwhichiscomplete. Ifit’sfixed-vertex,then
(i): Thesetofrepresentativesofcolorsis {v1,v2, ,vn} Thustype-I chromaticnumberis n andn-type-Ichromaticnumberis nσ(vi)
2.30.NewResults
75
(ii): Thesetofrepresentativesofcolorsis {}. Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0
(iii): Thesetofrepresentativesofcolorsis {} Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0.
(iv): Thesetofrepresentativesofcolorsis {v1,v2, ,vn} Thustype-IV chromaticnumberis n andn-type-IVchromaticnumberis nσ(vi)
(v): Thesetofrepresentativesofcolorsis {} Thustype-Vchromaticnumber is 0 andn-type-Vchromaticnumberis 0
(vi): Thesetofrepresentativesofcolorsis {}. Thustype-VIchromaticnumber is 0 andn-type-VIchromaticnumberis 0
(vii): Thesetofrepresentativesofcolorsis {}. Thustype-VIIchromaticnumber is 0 andn-type-VIIchromaticnumberis 0.
Proof. (i) Byit’sfixed-vertexandit’sneutrosophiccomplete,alledgeshave sameamountsotheconnectednessamidtwogivenedgesisthesame.Alledges aretype-I.Byit’sneutrosophiccomplete,everyvertexhas n 1 verticeswhich havecommonedgeswhicharetype-I.Thusthesetofrepresentativesofcolors is {v1,v2, ,vn}. Thetype-Ichromaticnumberis n andn-type-Ichromatic numberis nσ(vi)
(ii) Byit’sfixed-vertexandit’sneutrosophiccomplete,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’t type-II.Byit’sneutrosophiccomplete,everyvertexhas n 1 verticeswhich havecommonedgeswhicharen’ttype-II.Thusthesetofrepresentativesof colorsis {} Thetype-IIchromaticnumberis 0 andn-type-IIchromaticnumber is 0
(iii) Byit’sfixed-vertexandit’sneutrosophiccomplete,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledges aren’ttype-III.Byit’sneutrosophiccomplete,everyvertexhas n 1 vertices whichhavecommonedgeswhicharen’ttype-III.Thusthesetofrepresentatives ofcolorsis {} Thetype-IIIchromaticnumberis 0 andn-type-IIIchromatic numberis 0
(iv) Byit’sfixed-vertexandit’sneutrosophiccomplete,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesare type-IV.Byit’sneutrosophiccomplete,everyvertexhas n 1 verticeswhich havecommonedgeswhicharetype-IV.Thusthesetofrepresentativesofcolors is {v1,v2, ,vn} Thetype-IVchromaticnumberis n andn-type-IVchromatic numberis nσ(vi)
(v). Byit’sfixed-vertexandit’sneutrosophiccomplete,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’t type-V.Byit’sneutrosophiccomplete,everyvertexhas n 1 verticeswhich havecommonedgeswhicharen’ttype-V.Thusthesetofrepresentativesof colorsis {} Thetype-Vchromaticnumberis 0 andn-type-Vchromaticnumber is 0.
(vi) Byit’sfixed-vertexandit’sneutrosophiccomplete,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledges aren’ttype-VI.Byit’sneutrosophiccomplete,everyvertexhas n 1 vertices whichhavecommonedgeswhicharen’ttype-VI.Thusthesetofrepresentatives
2.NeutrosophicChromaticNumber
76
2.30.NewResults
ofcolorsis {}. Thetype-VIchromaticnumberis 0 andn-type-VIchromatic numberis 0
(vii) Byit’sfixed-vertexandit’sneutrosophiccomplete,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’t type-VII.Byit’sneutrosophiccomplete,everyvertexhas n 1 verticeswhich havecommonedgeswhicharen’ttype-VII.Thusthesetofrepresentativesof colorsis {} Thetype-VIIchromaticnumberis 0 andn-type-VIIchromatic numberis 0
Proposition2.30.3. Let N =(σ,µ) beaneutrosophicgraphwhichisstrong.If it’sfixed-edge,then
(i): Thesetofrepresentativesofcolorsis {v1,v2, ··· ,vt} where t =∆(N ) Thustype-Ichromaticnumberis t andn-type-Ichromaticnumberis neutrosophiccardinalityof {v1,v2, ,vt}
(ii): Thesetofrepresentativesofcolorsis {} Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0
(iii): Thesetofrepresentativesofcolorsis {}. Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0
(iv): Thesetofrepresentativesofcolorsis {v1,v2, ,vt} where t =∆(N ) Thustype-IVchromaticnumberis t andn-type-IVchromaticnumberis neutrosophiccardinalityof {v1,v2, ··· ,vt}
(v): Thesetofrepresentativesofcolorsis {} Thustype-Vchromaticnumber is 0 andn-type-Vchromaticnumberis 0.
(vi): Thesetofrepresentativesofcolorsis {} Thustype-VIchromaticnumber is 0 andn-type-VIchromaticnumberis 0
(vii): Thesetofrepresentativesofcolorsis {} Thustype-VIIchromaticnumber is 0 andn-type-VIIchromaticnumberis 0
Proof. (i) Alledgeshavesameamountsotheconnectednessamidtwogiven edgesisthesame.Alledgesaretype-I.Byit’sneutrosophicstrong,there’s avertexhas t =∆(N ) verticeswhichhavecommonedgeswhicharetype-I. Thusthesetofrepresentativesofcolorsis {v1,v2, ,vt} Thetype-Ichromatic numberis t andn-type-Ichromaticnumberisneutrosophiccardinalityof {v1,v2, ,vt}
(ii) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-II.Byit’sneutrosophicstrong,there’savertex has t =∆(N ) verticeswhichhavecommonedgeswhicharen’ttype-II.Thus thesetofrepresentativesofcolorsis {} Thetype-IIchromaticnumberis 0 and n-type-IIchromaticnumberis 0
(iii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-III.Byit’sneutrosophicstrong,there’sa vertexhas t =∆(N ) verticeswhichhavecommonedgeswhicharen’ttype-III. Thusthesetofrepresentativesofcolorsis {} Thetype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0
(iv) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis
77
thesame.Alledgesaretype-IV.Byit’sneutrosophicstrong,there’savertex has t =∆(N ) verticeswhichhavecommonedgeswhicharetype-IV.Thus thesetofrepresentativesofcolorsis {v1,v2, ··· ,vt} Thetype-IVchromatic numberis t andn-type-IVchromaticnumberisneutrosophiccardinalityof {v1,v2, ,vt}
(v). Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-V.Byit’sneutrosophicstrong,there’savertex has t =∆(N ) verticeswhichhavecommonedgeswhicharen’ttype-V.Thus thesetofrepresentativesofcolorsis {} Thetype-Vchromaticnumberis 0 and n-type-Vchromaticnumberis 0
(vi). Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-VI.Byit’sneutrosophicstrong,there’savertex has t =∆(N ) verticeswhichhavecommonedgeswhicharen’ttype-VI.Thus thesetofrepresentativesofcolorsis {} Thetype-VIchromaticnumberis 0 andn-type-VIchromaticnumberis 0
(vii). Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-VII.Byit’sneutrosophicstrong,there’sa vertexhas t =∆(N ) verticeswhichhavecommonedgeswhicharen’ttype-VII. Thusthesetofrepresentativesofcolorsis {} Thetype-VIIchromaticnumber is 0 andn-type-VIIchromaticnumberis 0
Proposition2.30.4. Let N =(σ,µ) beaneutrosophicgraphwhichisstrong.If it’sfixed-vertex,then
(i): Thesetofrepresentativesofcolorsis {v1,v2, ,vt} where t =∆(N ) Thustype-Ichromaticnumberis t andn-type-Ichromaticnumberis tσ(vi)
(ii): Thesetofrepresentativesofcolorsis {} Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0
(iii): Thesetofrepresentativesofcolorsis {}. Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0
(iv): Thesetofrepresentativesofcolorsis {v1,v2, ,vt} where t =∆(N ) Thustype-IVchromaticnumberis t andn-type-IVchromaticnumberis tσ(vi)
(v): Thesetofrepresentativesofcolorsis {} Thustype-Vchromaticnumber is 0 andn-type-Vchromaticnumberis 0.
(vi): Thesetofrepresentativesofcolorsis {} Thustype-VIchromaticnumber is 0 andn-type-VIchromaticnumberis 0
(vii): Thesetofrepresentativesofcolorsis {} Thustype-VIIchromaticnumber is 0 andn-type-VIIchromaticnumberis 0
Proof. (i) Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesare type-I.Byit’sneutrosophicstrong,there’savertexhas t =∆(N ) verticeswhich havecommonedgeswhicharetype-I.Thusthesetofrepresentativesofcolors is {v1,v2, ··· ,vt} Thetype-Ichromaticnumberis t andn-type-Ichromatic numberis tσ(vi)
(ii) Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesameamount
2.NeutrosophicChromaticNumber
78
2.30.NewResults
sotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’ttype-II. Byit’sneutrosophicstrong,there’savertexhas t =∆(N ) verticeswhichhave commonedgeswhicharen’ttype-II.Thusthesetofrepresentativesofcolorsis {} Thetype-IIchromaticnumberis 0 andn-type-IIchromaticnumberis 0
(iii) Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’t type-III.Byit’sneutrosophicstrong,there’savertexhas t =∆(N ) vertices whichhavecommonedgeswhicharen’ttype-III.Thusthesetofrepresentatives ofcolorsis {} Thetype-IIIchromaticnumberis 0 andn-type-IIIchromatic numberis 0
(iv).
Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesare type-IV.Byit’sneutrosophicstrong,there’savertexhas t =∆(N ) vertices whichhavecommonedgeswhicharetype-IV.Thusthesetofrepresentatives ofcolorsis {v1,v2, ,vt} Thetype-IVchromaticnumberis t andn-type-IV chromaticnumberis tσ(vi). (v) Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesameamount sotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’ttype-V. Byit’sneutrosophicstrong,there’savertexhas t =∆(N ) verticeswhichhave commonedgeswhicharen’ttype-V.Thusthesetofrepresentativesofcolorsis {}. Thetype-Vchromaticnumberis 0 andn-type-Vchromaticnumberis 0. (vi) Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’t type-VI.Byit’sneutrosophicstrong,there’savertexhas t =∆(N ) vertices whichhavecommonedgeswhicharen’ttype-VI.Thusthesetofrepresentatives ofcolorsis {}. Thetype-VIchromaticnumberis 0 andn-type-VIchromatic numberis 0
(vii) Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’t type-VII.Byit’sneutrosophicstrong,there’savertexhas t =∆(N ) vertices whichhavecommonedgeswhicharen’ttype-VII.Thusthesetofrepresentatives ofcolorsis {} Thetype-VIIchromaticnumberis 0 andn-type-VIIchromatic numberis 0
Proposition2.30.5. Let N =(σ,µ) beaneutrosophicgraphwhichisstrong andpath.Ifit’sfixed-edge,then
(i):
(ii):
(iii):
(iv):
(v):
Thesetofrepresentativesofcolorsis {vi,vj } Thustype-Ichromatic numberis 2 andn-type-Ichromaticnumberis σ(vi)+ σ(vj )
Thesetofrepresentativesofcolorsis {} Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0
Thesetofrepresentativesofcolorsis {}. Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0
Thesetofrepresentativesofcolors,type-IVchromaticnumberandn-typeIVchromaticnumberaren’tdefined.
Thesetofrepresentativesofcolors,type-Vchromaticnumberandn-type-V chromaticnumberaren’tdefined.
79
(vi): Thesetofrepresentativesofcolors,type-VIchromaticnumberandn-typeVIchromaticnumberaren’tdefined.
(vii): Thesetofrepresentativesofcolors,type-VIIchromaticnumberandntype-VIIchromaticnumberaren’tdefined.
Proof. (i) Alledgeshavesameamountsotheconnectednessamidtwogiven edgesisthesame.Alledgesaretype-I.Byit’sneutrosophicstrong,there’sa vertexhas 2 verticeswhichhavecommonedgeswhicharetype-I.Thustheset ofrepresentativesofcolorsis {vi,vj } Thetype-Ichromaticnumberis 2 and n-type-Ichromaticnumberisneutrosophiccardinalityof {vi,vj }.
(ii) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-II.Byit’sneutrosophicstrong,there’savertex has 2 verticeswhichhavecommonedgeswhicharen’ttype-II.Thusthesetof representativesofcolorsis {} Thetype-IIchromaticnumberis 0 andn-type-II chromaticnumberis 0.
(iii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-III.Byit’sneutrosophicstrong,there’sa vertexhas 2 verticeswhichhavecommonedgeswhicharen’ttype-III.Thusthe setofrepresentativesofcolorsis {} Thetype-IIIchromaticnumberis 0 and n-type-IIIchromaticnumberis 0.
(iv) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-IV.Sinceit’simpossibletodefinewhenthere’s nocycleinneutrosophicgraph.
(v) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-V.Sinceit’simpossibletodefinewhenthere’s nocycleinneutrosophicgraph.
(vi) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-VI.Sinceit’simpossibletodefinewhenthere’s nocycleinneutrosophicgraph.
(vii). Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-VII.Sinceit’simpossibletodefinewhenthere’s nocycleinneutrosophicgraph.
Proposition2.30.6. Let N =(σ,µ) beaneutrosophicgraphwhichisstrong andpath.Ifit’sfixed-vertex,then
(i):
Thesetofrepresentativesofcolorsis {vi,vj } Thustype-Ichromatic numberis 2 andn-type-Ichromaticnumberis 2σ(vi)
(ii): Thesetofrepresentativesofcolorsis {} Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0
(iii):
(iv):
Thesetofrepresentativesofcolorsis {} Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0
Thesetofrepresentativesofcolors,type-IVchromaticnumberandn-typeIVchromaticnumberaren’tdefined.
(v): Thesetofrepresentativesofcolors,type-Vchromaticnumberandn-type-V chromaticnumberaren’tdefined.
2.NeutrosophicChromaticNumber
80
(vi): Thesetofrepresentativesofcolors,type-VIchromaticnumberandn-typeVIchromaticnumberaren’tdefined.
(vii): Thesetofrepresentativesofcolors,type-VIIchromaticnumberandntype-VIIchromaticnumberaren’tdefined.
Proof. (i) Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesare type-I.Byit’sneutrosophicstrong,there’savertexhas 2 verticeswhichhave commonedgeswhicharetype-I.Thusthesetofrepresentativesofcolorsis {vi,vj } Thetype-Ichromaticnumberis 2 andn-type-Ichromaticnumberis 2σ(vi)
(ii) Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesameamount sotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’ttype-II. Byit’sneutrosophicstrong,there’savertexhas 2 verticeswhichhavecommon edgeswhicharen’ttype-II.Thusthesetofrepresentativesofcolorsis {} The type-IIchromaticnumberis 0 andn-type-IIchromaticnumberis 0 (iii) Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’t type-III.Byit’sneutrosophicstrong,there’savertexhas 2 verticeswhichhave commonedgeswhicharen’ttype-III.Thusthesetofrepresentativesofcolorsis {} Thetype-IIIchromaticnumberis 0 andn-type-IIIchromaticnumberis 0 (iv) Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’t type-IV.Sinceit’simpossibletodefinewhenthere’snocycleinneutrosophic graph.
(v) Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesameamount sotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’ttype-V. Sinceit’simpossibletodefinewhenthere’snocycleinneutrosophicgraph.
(vi). Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’t type-VI.Sinceit’simpossibletodefinewhenthere’snocycleinneutrosophic graph.
(vii) Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’t type-VII.Sinceit’simpossibletodefinewhenthere’snocycleinneutrosophic graph.
Proposition2.30.7. Let N =(σ,µ) beanevencycle.Ifit’sfixed-edge,then
(i):
Thesetofrepresentativesofcolorsis {vi,vj } Thustype-Ichromatic numberis 2 andn-type-Ichromaticnumberis σ(vi)+ σ(vj )
(ii): Thesetofrepresentativesofcolorsis {}. Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0
(iii): Thesetofrepresentativesofcolorsis {} Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0.
(iv):
Thesetofrepresentativesofcolorsis {vi,vj } Thustype-IVchromatic numberis 2 andn-type-IVchromaticnumberis σ(vi)+ σ(vj )
2.30.NewResults
81
(v): Thesetofrepresentativesofcolorsis {}. Thustype-Vchromaticnumber is 0 andn-type-Vchromaticnumberis 0
(vi): Thesetofrepresentativesofcolorsis {}. Thustype-VIchromaticnumber is 0 andn-type-VIchromaticnumberis 0
(vii): Thesetofrepresentativesofcolorsis {}. Thustype-VIIchromaticnumber is 0 andn-type-VIIchromaticnumberis 0
Proof. (i) Alledgeshavesameamountsotheconnectednessamidtwogiven edgesisthesame.Alledgesaretype-I.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharetype-I.Thusthesetofrepresentatives ofcolorsis {vi,vj } Thetype-Ichromaticnumberis 2 andn-type-Ichromatic numberisneutrosophiccardinalityof {vi,vj }
(ii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-II.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-II.Thusthesetofrepresentatives ofcolorsis {} Thetype-IIchromaticnumberis 0 andn-type-IIchromatic numberis 0
(iii) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-III.Thusthesetofrepresentatives ofcolorsis {} Thetype-IIIchromaticnumberis 0 andn-type-IIIchromatic numberis 0
(iv) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaretype-IV.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharetype-IV.Bydeletionofoneedge,it’s possibletocomputeconnectedness.Thusthesetofrepresentativesofcolorsis {vi,vj } Thetype-IVchromaticnumberis 2 andn-type-IVchromaticnumber isneutrosophiccardinalityof {vi,vj }.
(v). Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-III.Thusthesetofrepresentatives ofcolorsis {} Thetype-IIIchromaticnumberis 0 andn-type-IIIchromatic numberis 0.
(vi). Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-III.Thusthesetofrepresentatives ofcolorsis {} Thetype-IIIchromaticnumberis 0 andn-type-IIIchromatic numberis 0.
(vii). Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-III.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-III.Thusthesetofrepresentatives ofcolorsis {} Thetype-IIIchromaticnumberis 0 andn-type-IIIchromatic numberis 0.
Proposition2.30.8. Let N =(σ,µ) beaneutrosophicgraphwhichisstrong andevencycle.Ifit’sfixed-vertex,then
(i): Thesetofrepresentativesofcolorsis {vi,vj } Thustype-Ichromatic numberis 2 andn-type-Ichromaticnumberis 2σ(vi)
2.NeutrosophicChromaticNumber
82
2.30.NewResults
(ii): Thesetofrepresentativesofcolorsis {}. Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0
(iii): Thesetofrepresentativesofcolorsis {} Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0.
(iv): Thesetofrepresentativesofcolorsis {vi,vj } Thustype-IVchromatic numberis 2 andn-type-IVchromaticnumberis 2σ(vi)
(v): Thesetofrepresentativesofcolorsis {} Thustype-Vchromaticnumber is 0 andn-type-Vchromaticnumberis 0
(vi): Thesetofrepresentativesofcolorsis {}. Thustype-VIchromaticnumber is 0 andn-type-VIchromaticnumberis 0
(vii): Thesetofrepresentativesofcolorsis {}. Thustype-VIIchromaticnumber is 0 andn-type-VIIchromaticnumberis 0.
Proof. (i) Alledgeshavesameamountsotheconnectednessamidtwogiven edgesisthesame.Alledgesaretype-I.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharetype-I.Thusthesetofrepresentatives ofcolorsis {vi,vj } Thetype-Ichromaticnumberis 2 andn-type-Ichromatic numberisneutrosophiccardinalityof {vi,vj } whichis 2σ(vi).
(ii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-II.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-II.Thusthesetofrepresentatives ofcolorsis {} Thetype-IIchromaticnumberis 0 andn-type-IIchromatic numberis 0.
(iii) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-III.Thusthesetofrepresentatives ofcolorsis {} Thetype-IIIchromaticnumberis 0 andn-type-IIIchromatic numberis 0.
(iv) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaretype-IV.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharetype-IV.Bydeletionofoneedge,it’s possibletocomputeconnectedness.Thusthesetofrepresentativesofcolorsis {vi,vj }. Thetype-IVchromaticnumberis 2 andn-type-IVchromaticnumber isneutrosophiccardinalityof {vi,vj } whichis 2σ(vi)
(v) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-III.Thusthesetofrepresentatives ofcolorsis {}. Thetype-IIIchromaticnumberis 0 andn-type-IIIchromatic numberis 0
(vi) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-III.Thusthesetofrepresentatives ofcolorsis {}. Thetype-IIIchromaticnumberis 0 andn-type-IIIchromatic numberis 0
(vii)
Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-III.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-III.Thusthesetofrepresentatives
83
ofcolorsis {}. Thetype-IIIchromaticnumberis 0 andn-type-IIIchromatic numberis 0
Proposition2.30.9. Let N =(σ,µ) beaneutrosophicgraphwhichisanodd cycle.Ifit’sfixed-edge,then
(i): Thesetofrepresentativesofcolorsis {vi,vj ,vk}. Thustype-Ichromatic numberis 2 andn-type-Ichromaticnumberis σ(vi)+ σ(vj )+ σ(vk)
(ii): Thesetofrepresentativesofcolorsis {} Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0.
(iii): Thesetofrepresentativesofcolorsis {} Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0
(iv): Thesetofrepresentativesofcolorsis {vi,vj ,vk} Thustype-IVchromatic numberis 2 andn-type-IVchromaticnumberis σ(vi)+ σ(vj )+ σ(vk)
(v): Thesetofrepresentativesofcolorsis {}. Thustype-Vchromaticnumber is 0 andn-type-Vchromaticnumberis 0
(vi): Thesetofrepresentativesofcolorsis {} Thustype-VIchromaticnumber is 0 andn-type-VIchromaticnumberis 0. (vii): Thesetofrepresentativesofcolorsis {} Thustype-VIIchromaticnumber is 0 andn-type-VIIchromaticnumberis 0
Proof. (i) Alledgeshavesameamountsotheconnectednessamidtwogiven edgesisthesame.Alledgesaretype-I.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharetype-I.Thusthesetofrepresentatives ofcolorsis {vi,vj } Thetype-Ichromaticnumberis 2 andn-type-Ichromatic numberisneutrosophiccardinalityof {vi,vj ,vk} whichis σ(vi)+ σ(vj )+ σ(vk)
(ii) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-II.Byit’sneutrosophicstrong,there’savertex has 2 verticeswhichhavecommonedgeswhicharen’ttype-II.Thusthesetof representativesofcolorsis {} Thetype-IIchromaticnumberis 0 andn-type-II chromaticnumberis 0
(iii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-III.Byit’sneutrosophicstrong,there’sa vertexhas 2 verticeswhichhavecommonedgeswhicharen’ttype-III.Thusthe setofrepresentativesofcolorsis {} Thetype-IIIchromaticnumberis 0 and n-type-IIIchromaticnumberis 0
(iv) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaretype-IV.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharetype-IV.Thusthesetofrepresentativesof colorsis {vi,vj } Thetype-IVchromaticnumberis 2 andn-type-IVchromatic numberisneutrosophiccardinalityof {vi,vj ,vk} whichis σ(vi)+ σ(vj )+ σ(vk)
(v) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-V.Byit’sneutrosophicstrong,there’savertex has 2 verticeswhichhavecommonedgeswhicharen’ttype-V.Thusthesetof representativesofcolorsis {} Thetype-Vchromaticnumberis 0 andn-type-V chromaticnumberis 0
(vi) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis
2.NeutrosophicChromaticNumber
84
2.30.NewResults
thesame.Alledgesaren’ttype-VI.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-VI.Thusthesetofrepresentatives ofcolorsis {} Thetype-VIchromaticnumberis 0 andn-type-VIchromatic numberis 0
(vii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-VII.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-VII.Thusthesetofrepresentatives ofcolorsis {} Thetype-VIIchromaticnumberis 0 andn-type-VIIchromatic numberis 0
Proposition2.30.10. Let N =(σ,µ) beaneutrosophicgraphwhichisstrong andoddcycle.Ifit’sfixed-vertex,then
(i): Thesetofrepresentativesofcolorsis {vi,vj ,vk} Thustype-Ichromatic numberis 2 andn-type-Ichromaticnumberis 3σ(vi)
(ii): Thesetofrepresentativesofcolorsis {} Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0
(iii): Thesetofrepresentativesofcolorsis {}. Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0.
(iv): Thesetofrepresentativesofcolorsis {vi,vj ,vk} Thustype-IVchromatic numberis 2 andn-type-IVchromaticnumberis 3σ(vi)
(v): Thesetofrepresentativesofcolorsis {} Thustype-Vchromaticnumber is 0 andn-type-Vchromaticnumberis 0
(vi): Thesetofrepresentativesofcolorsis {} Thustype-VIchromaticnumber is 0 andn-type-VIchromaticnumberis 0
(vii): Thesetofrepresentativesofcolorsis {}. Thustype-VIIchromaticnumber is 0 andn-type-VIIchromaticnumberis 0.
Proof. (i) Alledgeshavesameamountsotheconnectednessamidtwogiven edgesisthesame.Alledgesaretype-I.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharetype-I.Thusthesetofrepresentatives ofcolorsis {vi,vj } Thetype-Ichromaticnumberis 2 andn-type-Ichromatic numberisneutrosophiccardinalityof {vi,vj ,vk} whichis 3σ(vi).
(ii) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-II.Byit’sneutrosophicstrong,there’savertex has 2 verticeswhichhavecommonedgeswhicharen’ttype-II.Thusthesetof representativesofcolorsis {} Thetype-IIchromaticnumberis 0 andn-type-II chromaticnumberis 0.
(iii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-III.Byit’sneutrosophicstrong,there’sa vertexhas 2 verticeswhichhavecommonedgeswhicharen’ttype-III.Thusthe setofrepresentativesofcolorsis {} Thetype-IIIchromaticnumberis 0 and n-type-IIIchromaticnumberis 0.
(iv) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaretype-IV.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharetype-IV.Thusthesetofrepresentativesof colorsis {vi,vj } Thetype-IVchromaticnumberis 2 andn-type-IVchromatic
85
numberisneutrosophiccardinalityof {vi,vj ,vk} whichis 3σ(vi).
(v) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-V.Byit’sneutrosophicstrong,there’savertex has 2 verticeswhichhavecommonedgeswhicharen’ttype-V.Thusthesetof representativesofcolorsis {} Thetype-Vchromaticnumberis 0 andn-type-V chromaticnumberis 0.
(vi) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-VI.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-VI.Thusthesetofrepresentatives ofcolorsis {} Thetype-VIchromaticnumberis 0 andn-type-VIchromatic numberis 0.
(vii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-VII.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-VII.Thusthesetofrepresentatives ofcolorsis {} Thetype-VIIchromaticnumberis 0 andn-type-VIIchromatic numberis 0.
Proposition2.30.11. Let N =(σ,µ) beanevenwheel.Ifit’sfixed-edge,then
(i): Thesetofrepresentativesofcolorsis {vi,vj ,vk} Thustype-Ichromatic numberis 2 andn-type-Ichromaticnumberis σ(vi)+ σ(vj )+ σ(vk)
(ii): Thesetofrepresentativesofcolorsis {} Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0
(iii): Thesetofrepresentativesofcolorsis {}. Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0
(iv): Thesetofrepresentativesofcolorsis {vi,vj ,vk} Thustype-IVchromatic numberis 3 andn-type-IVchromaticnumberis σ(vi)+ σ(vj )+ σ(vk).
(v): Thesetofrepresentativesofcolorsis {} Thustype-Vchromaticnumber is 0 andn-type-Vchromaticnumberis 0
(vi): Thesetofrepresentativesofcolorsis {} Thustype-VIchromaticnumber is 0 andn-type-VIchromaticnumberis 0
(vii): Thesetofrepresentativesofcolorsis {}. Thustype-VIIchromaticnumber is 0 andn-type-VIIchromaticnumberis 0
Proof. (i) Alledgeshavesameamountsotheconnectednessamidtwogiven edgesisthesame.Alledgesaretype-I.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharetype-I.Thusthesetofrepresentativesof colorsis {vi,vj ,vk}. Thetype-Ichromaticnumberis 3 andn-type-Ichromatic numberisneutrosophiccardinalityof {vi,vj ,vk} whichis σ(vi)+ σ(vj )+ σ(vk)
(ii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-II.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-II.Thusthesetofrepresentatives ofcolorsis {}. Thetype-IIchromaticnumberis 0 andn-type-IIchromatic numberis 0
(iii) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-III.Thusthesetofrepresentatives
2.NeutrosophicChromaticNumber
86
2.30.NewResults
ofcolorsis {}. Thetype-IIIchromaticnumberis 0 andn-type-IIIchromatic numberis 0
(iv) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaretype-IV.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharetype-IV.Bydeletionofoneedge,it’s possibletocomputeconnectedness.Thusthesetofrepresentativesofcolors is {vi,vj ,vk} Thetype-IVchromaticnumberis 3 andn-type-IVchromatic numberisneutrosophiccardinalityof {vi,vj ,vk} whichis σ(vi)+ σ(vj )+ σ(vk)
(v) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-III.Thusthesetofrepresentatives ofcolorsis {} Thetype-IIIchromaticnumberis 0 andn-type-IIIchromatic numberis 0
(vi) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-III.Thusthesetofrepresentatives ofcolorsis {} Thetype-IIIchromaticnumberis 0 andn-type-IIIchromatic numberis 0
(vii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-III.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-III.Thusthesetofrepresentatives ofcolorsis {} Thetype-IIIchromaticnumberis 0 andn-type-IIIchromatic numberis 0
Proposition2.30.12. Let N =(σ,µ) beaneutrosophicgraphwhichisstrong andevenwheel.Ifit’sfixed-vertex,then
(i): Thesetofrepresentativesofcolorsis {vi,vj ,vk} Thustype-Ichromatic numberis 3 andn-type-Ichromaticnumberis 3σ(vi)
(ii): Thesetofrepresentativesofcolorsis {}. Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0
(iii): Thesetofrepresentativesofcolorsis {} Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0.
(iv): Thesetofrepresentativesofcolorsis {vi,vj ,vk} Thustype-IVchromatic numberis 3 andn-type-IVchromaticnumberis 3σ(vi)
(v): Thesetofrepresentativesofcolorsis {} Thustype-Vchromaticnumber is 0 andn-type-Vchromaticnumberis 0
(vi): Thesetofrepresentativesofcolorsis {}. Thustype-VIchromaticnumber is 0 andn-type-VIchromaticnumberis 0
(vii): Thesetofrepresentativesofcolorsis {} Thustype-VIIchromaticnumber is 0 andn-type-VIIchromaticnumberis 0.
Proof. (i). Alledgeshavesameamountsotheconnectednessamidtwogiven edgesisthesame.Alledgesaretype-I.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharetype-I.Thusthesetofrepresentativesof colorsis {vi,vj ,vk} Thetype-Ichromaticnumberis 3 andn-type-Ichromatic numberisneutrosophiccardinalityof {vi,vj ,vk} whichis 3σ(vi)
87
(ii). Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-II.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-II.Thusthesetofrepresentatives ofcolorsis {} Thetype-IIchromaticnumberis 0 andn-type-IIchromatic numberis 0
(iii). Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-III.Thusthesetofrepresentatives ofcolorsis {} Thetype-IIIchromaticnumberis 0 andn-type-IIIchromatic numberis 0
(iv). Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaretype-IV.Byit’scycle,allverticeshave 3 vertices whichhavecommonedgeswhicharetype-IV.Bydeletionofoneedge,it’s possibletocomputeconnectedness.Thusthesetofrepresentativesofcolors is {vi,vj ,vk} Thetype-IVchromaticnumberis 3 andn-type-IVchromatic numberisneutrosophiccardinalityof {vi,vj ,vk} whichis 3σ(vi).
(v) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-III.Thusthesetofrepresentatives ofcolorsis {} Thetype-IIIchromaticnumberis 0 andn-type-IIIchromatic numberis 0.
(vi) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-III.Thusthesetofrepresentatives ofcolorsis {} Thetype-IIIchromaticnumberis 0 andn-type-IIIchromatic numberis 0.
(vii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-III.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-III.Thusthesetofrepresentatives ofcolorsis {} Thetype-IIIchromaticnumberis 0 andn-type-IIIchromatic numberis 0.
Proposition2.30.13. Let N =(σ,µ) beaneutrosophicgraphwhichisanodd wheel.Ifit’sfixed-edge,then
(i): Thesetofrepresentativesofcolorsis {vi,vj ,vk,vs} Thustype-Ichromatic numberis 4 andn-type-Ichromaticnumberis σ(vi)+σ(vj )+σ(vk)+σ(vs)
(ii): Thesetofrepresentativesofcolorsis {} Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0.
(iii): Thesetofrepresentativesofcolorsis {} Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0
(iv): Thesetofrepresentativesofcolorsis {vi,vj ,vk,vs} Thustype-IV chromaticnumberis 2 andn-type-IVchromaticnumberis σ(vi)+ σ(vj )+ σ(vk)+ σ(vs).
(v): Thesetofrepresentativesofcolorsis {} Thustype-Vchromaticnumber is 0 andn-type-Vchromaticnumberis 0
(vi): Thesetofrepresentativesofcolorsis {} Thustype-VIchromaticnumber is 0 andn-type-VIchromaticnumberis 0
2.NeutrosophicChromaticNumber
88
(vii): Thesetofrepresentativesofcolorsis {}. Thustype-VIIchromaticnumber is 0 andn-type-VIIchromaticnumberis 0
Proof. (i) Alledgeshavesameamountsotheconnectednessamidtwogiven edgesisthesame.Alledgesaretype-I.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharetype-I.Thusthesetofrepresentatives ofcolorsis {vi,vj ,vk,vs} Thetype-Ichromaticnumberis 4 andn-typeIchromaticnumberisneutrosophiccardinalityof {vi,vj ,vk,vs} whichis σ(vi)+ σ(vj )+ σ(vk)+ σ(vs)
(ii) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-II.Byit’sneutrosophicstrong,there’savertex has 2 verticeswhichhavecommonedgeswhicharen’ttype-II.Thusthesetof representativesofcolorsis {} Thetype-IIchromaticnumberis 0 andn-type-II chromaticnumberis 0
(iii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-III.Byit’sneutrosophicstrong,there’sa vertexhas 2 verticeswhichhavecommonedgeswhicharen’ttype-III.Thusthe setofrepresentativesofcolorsis {} Thetype-IIIchromaticnumberis 0 and n-type-IIIchromaticnumberis 0
(iv) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaretype-IV.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharetype-IV.Thusthesetofrepresentatives ofcolorsis {vi,vj ,vk,vs} Thetype-IVchromaticnumberis 4 andn-typeIVchromaticnumberisneutrosophiccardinalityof {vi,vj ,vk,vs} whichis σ(vi)+ σ(vj )+ σ(vk)+ σ(vs)
(v). Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-V.Byit’sneutrosophicstrong,there’savertex has 2 verticeswhichhavecommonedgeswhicharen’ttype-V.Thusthesetof representativesofcolorsis {} Thetype-Vchromaticnumberis 0 andn-type-V chromaticnumberis 0
(vi). Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-VI.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-VI.Thusthesetofrepresentatives ofcolorsis {} Thetype-VIchromaticnumberis 0 andn-type-VIchromatic numberis 0
(vii). Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-VII.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-VII.Thusthesetofrepresentatives ofcolorsis {} Thetype-VIIchromaticnumberis 0 andn-type-VIIchromatic numberis 0
Proposition2.30.14. Let N =(σ,µ) beaneutrosophicgraphwhichisstrong andoddwheel.Ifit’sfixed-vertex,then
(i): Thesetofrepresentativesofcolorsis {vi,vj ,vk,vs} Thustype-Ichromatic numberis 4 andn-type-Ichromaticnumberis 4σ(vi)
(ii): Thesetofrepresentativesofcolorsis {}. Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0
(iii): Thesetofrepresentativesofcolorsis {} Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0
2.30.NewResults
89
(iv): Thesetofrepresentativesofcolorsis {vi,vj ,vk,vs}. Thustype-IV chromaticnumberis 4 andn-type-IVchromaticnumberis 4σ(vi)
(v): Thesetofrepresentativesofcolorsis {}. Thustype-Vchromaticnumber is 0 andn-type-Vchromaticnumberis 0
(vi): Thesetofrepresentativesofcolorsis {}. Thustype-VIchromaticnumber is 0 andn-type-VIchromaticnumberis 0.
(vii): Thesetofrepresentativesofcolorsis {} Thustype-VIIchromaticnumber is 0 andn-type-VIIchromaticnumberis 0.
Proof. (i) Alledgeshavesameamountsotheconnectednessamidtwogiven edgesisthesame.Alledgesaretype-I.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharetype-I.Thusthesetofrepresentativesof colorsis {vi,vj ,vk,vs}. Thetype-Ichromaticnumberis 4 andn-type-Ichromatic numberisneutrosophiccardinalityof {vi,vj ,vk,vs} whichis 4σ(vi).
(ii) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-II.Byit’sneutrosophicstrong,there’savertex has 2 verticeswhichhavecommonedgeswhicharen’ttype-II.Thusthesetof representativesofcolorsis {}. Thetype-IIchromaticnumberis 0 andn-type-II chromaticnumberis 0.
(iii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-III.Byit’sneutrosophicstrong,there’sa vertexhas 2 verticeswhichhavecommonedgeswhicharen’ttype-III.Thusthe setofrepresentativesofcolorsis {}. Thetype-IIIchromaticnumberis 0 and n-type-IIIchromaticnumberis 0.
(iv) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaretype-IV.Byit’scycle,allverticeshave 2 verticeswhich havecommonedgeswhicharetype-IV.Thusthesetofrepresentativesofcolors is {vi,vj ,vk,vs}. Thetype-IVchromaticnumberis 4 andn-type-IVchromatic numberisneutrosophiccardinalityof {vi,vj ,vk,vs} whichis 4σ(vi).
(v) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-V.Byit’sneutrosophicstrong,there’savertex has 2 verticeswhichhavecommonedgeswhicharen’ttype-V.Thusthesetof representativesofcolorsis {}. Thetype-Vchromaticnumberis 0 andn-type-V chromaticnumberis 0.
(vi) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-VI.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-VI.Thusthesetofrepresentatives ofcolorsis {}. Thetype-VIchromaticnumberis 0 andn-type-VIchromatic numberis 0.
(vii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-VII.Byit’scycle,allverticeshave 2 vertices whichhavecommonedgeswhicharen’ttype-VII.Thusthesetofrepresentatives ofcolorsis {}. Thetype-VIIchromaticnumberis 0 andn-type-VIIchromatic numberis 0.
Proposition2.30.15. Let N =(σ,µ) beaneutrosophicgraphwhichiscomplete t partite.Ifit’sfixed-edge,then 90
2.NeutrosophicChromaticNumber
(i): Thesetofrepresentativesofcolorsis {v1,v2, ,vt}. Thustype-I chromaticnumberis t andn-type-Ichromaticnumberis σ(v1)+ σ(v2)+ ··· + σ(vt)
(ii): Thesetofrepresentativesofcolorsis {} Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0
(iii): Thesetofrepresentativesofcolorsis {}. Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0
(iv): Thesetofrepresentativesofcolorsis {v1,v2, ··· ,vt} Thustype-IV chromaticnumberis t andn-type-IVchromaticnumberis σ(v1)+ σ(v2)+ + σ(vt)
(v): Thesetofrepresentativesofcolorsis {}. Thustype-Vchromaticnumber is 0 andn-type-Vchromaticnumberis 0.
(vi): Thesetofrepresentativesofcolorsis {} Thustype-VIchromaticnumber is 0 andn-type-VIchromaticnumberis 0
(vii): Thesetofrepresentativesofcolorsis {} Thustype-VIIchromaticnumber is 0 andn-type-VIIchromaticnumberis 0
Proof. (i) Alledgeshavesameamountsotheconnectednessamidtwogiven edgesisthesame.Alledgesaretype-I.Byit’sneutrosophiccomplete,there’sa vertexhas t 1 whichhavecommonedgeswhicharetype-I.Thusthesetof representativesofcolorsis {v1,v2, ,vt} Thetype-Ichromaticnumberis t andn-type-Ichromaticnumberisneutrosophiccardinalityof {v1,v2, ,vt} whichis σ(v1)+ σ(v2)+ + σ(vt)
(ii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-II.Byit’sneutrosophiccomplete,there’sa vertexhas t 1 verticeswhichhavecommonedgeswhicharen’ttype-II.Thus thesetofrepresentativesofcolorsis {}. Thetype-IIchromaticnumberis 0 and n-type-IIchromaticnumberis 0
(iii) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’sneutrosophiccomplete,there’sa vertexhas t 1 verticeswhichhavecommonedgeswhicharen’ttype-III.Thus thesetofrepresentativesofcolorsis {}. Thetype-IIIchromaticnumberis 0 andn-type-IIIchromaticnumberis 0
(iv) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaretype-IV.Byit’sneutrosophiccomplete,there’savertex has t 1 verticeswhichhavecommonedgeswhicharetype-IV.Thusthesetof representativesofcolorsis {v1,v2, ,vt}. Thetype-IVchromaticnumberis t andn-type-IVchromaticnumberisneutrosophiccardinalityof {v1,v2, ,vt} whichis σ(v1)+ σ(v2)+ ··· + σ(vt)
(v) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-V.Byit’sneutrosophiccomplete,there’sa vertexhas t 1 verticeswhichhavecommonedgeswhicharen’ttype-V.Thus thesetofrepresentativesofcolorsis {} Thetype-Vchromaticnumberis 0 and n-type-Vchromaticnumberis 0
(vi) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-VI.Byit’sneutrosophiccomplete,there’sa
2.30.NewResults
91
vertexhas t 1 verticeswhichhavecommonedgeswhicharen’ttype-VI.Thus thesetofrepresentativesofcolorsis {} Thetype-VIchromaticnumberis 0 andn-type-VIchromaticnumberis 0
(vii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-VII.Byit’sneutrosophiccomplete,there’sa vertexhas t 1 verticeswhichhavecommonedgeswhicharen’ttype-VII.Thus thesetofrepresentativesofcolorsis {} Thetype-VIIchromaticnumberis 0 andn-type-VIIchromaticnumberis 0
Proposition2.30.16. Let N =(σ,µ) beaneutrosophicgraphwhichiscomplete t partite.Ifit’sfixed-vertex,then
(i): Thesetofrepresentativesofcolorsis {v1,v2, ,vt} Thustype-I chromaticnumberis t andn-type-Ichromaticnumberis tσ(vi)
(ii): Thesetofrepresentativesofcolorsis {}. Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0
(iii): Thesetofrepresentativesofcolorsis {} Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0.
(iv): Thesetofrepresentativesofcolorsis {v1,v2, ··· ,vt} Thustype-IV chromaticnumberis t andn-type-IVchromaticnumberis tσ(vi)
(v): Thesetofrepresentativesofcolorsis {} Thustype-Vchromaticnumber is 0 andn-type-Vchromaticnumberis 0
(vi): Thesetofrepresentativesofcolorsis {}. Thustype-VIchromaticnumber is 0 andn-type-VIchromaticnumberis 0
(vii): Thesetofrepresentativesofcolorsis {} Thustype-VIIchromaticnumber is 0 andn-type-VIIchromaticnumberis 0.
Proof. (i). Alledgeshavesameamountsotheconnectednessamidtwogiven edgesisthesame.Alledgesaretype-I.Byit’sneutrosophiccomplete,there’sa vertexhas t 1 verticeswhichhavecommonedgeswhicharetype-I.Thustheset ofrepresentativesofcolorsis {v1,v2, ,vt} Thetype-Ichromaticnumberis t andn-type-Ichromaticnumberisneutrosophiccardinalityof {v1,v2, ,vt} whichis tσ(vi).
(ii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-II.Byit’sneutrosophiccomplete,there’sa vertexhas t 1 verticeswhichhavecommonedgeswhicharen’ttype-II.Thus thesetofrepresentativesofcolorsis {} Thetype-IIchromaticnumberis 0 and n-type-IIchromaticnumberis 0.
(iii) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’sneutrosophiccomplete,there’sa vertexhas t 1 verticeswhichhavecommonedgeswhicharen’ttype-III.Thus thesetofrepresentativesofcolorsis {} Thetype-IIIchromaticnumberis 0 andn-type-IIIchromaticnumberis 0.
(iv) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaretype-IV.Byit’sneutrosophiccomplete,there’savertex has t 1 verticeswhichhavecommonedgeswhicharetype-IV.Thusthesetof representativesofcolorsis {v1,v2, ,vt} Thetype-IVchromaticnumberis t
2.NeutrosophicChromaticNumber
92
andn-type-IVchromaticnumberisneutrosophicc{v1,v2, ,vt}.{vi,vj ,vk,vs} whichis tσ(vi)
(v)
Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-V.Byit’sneutrosophiccomplete,there’sa vertexhas t 1 verticeswhichhavecommonedgeswhicharen’ttype-V.Thus thesetofrepresentativesofcolorsis {}. Thetype-Vchromaticnumberis 0 and n-type-Vchromaticnumberis 0
(vi) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-VI.Byit’sneutrosophiccomplete,there’sa vertexhas t 1 verticeswhichhavecommonedgeswhicharen’ttype-VI.Thus thesetofrepresentativesofcolorsis {}. Thetype-VIchromaticnumberis 0 andn-type-VIchromaticnumberis 0
(vii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-VII.Byit’sneutrosophiccomplete,there’sa vertexhas t 1 verticeswhichhavecommonedgeswhicharen’ttype-VII.Thus thesetofrepresentativesofcolorsis {}. Thetype-VIIchromaticnumberis 0 andn-type-VIIchromaticnumberis 0
Corollary2.30.17. Let N =(σ,µ) beaneutrosophicgraphwhichiscomplete bipartite.Ifit’sfixed-edge,then
(i): Thesetofrepresentativesofcolorsis {v1,v2}. Thustype-Ichromatic numberis 2 andn-type-Ichromaticnumberis σ(v1)+ σ(v2)
(ii): Thesetofrepresentativesofcolorsis {} Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0.
(iii): Thesetofrepresentativesofcolorsis {} Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0
(iv): Thesetofrepresentativesofcolorsis {v1,v2} Thustype-IVchromatic numberis 2 andn-type-IVchromaticnumberis σ(v1)+ σ(v2)
(v): Thesetofrepresentativesofcolorsis {}. Thustype-Vchromaticnumber is 0 andn-type-Vchromaticnumberis 0
(vi): Thesetofrepresentativesofcolorsis {} Thustype-VIchromaticnumber is 0 andn-type-VIchromaticnumberis 0.
(vii): Thesetofrepresentativesofcolorsis {} Thustype-VIIchromaticnumber is 0 andn-type-VIIchromaticnumberis 0
Proof. (i) Alledgeshavesameamountsotheconnectednessamidtwogiven edgesisthesame.Alledgesaretype-I.Byit’sneutrosophiccomplete,there’s avertexhas 1 whichhavecommonedgeswhicharetype-I.Thusthesetof representativesofcolorsis {v1,v2} Thetype-Ichromaticnumberis 2 and n-type-Ichromaticnumberisneutrosophiccardinalityof {v1,v2} whichis σ(v1)+ σ(v2)
(ii). Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-II.Byit’sneutrosophiccomplete,there’sa vertexhas 1 verticeswhichhavecommonedgeswhicharen’ttype-II.Thusthe setofrepresentativesofcolorsis {} Thetype-IIchromaticnumberis 0 and n-type-IIchromaticnumberis 0
2.30.NewResults
93
(iii). Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’sneutrosophiccomplete,there’sa vertexhas 1 verticeswhichhavecommonedgeswhicharen’ttype-III.Thusthe setofrepresentativesofcolorsis {} Thetype-IIIchromaticnumberis 0 and n-type-IIIchromaticnumberis 0
(iv). Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaretype-IV.Byit’sneutrosophiccomplete,there’sa vertexhas 1 verticeswhichhavecommonedgeswhicharetype-IV.Thusthe setofrepresentativesofcolorsis {v1,v2} Thetype-IVchromaticnumberis 2 andn-type-IVchromaticnumberisneutrosophiccardinalityof {v1,v2} which is σ(v1)+ σ(v2).
(v) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-V.Byit’sneutrosophiccomplete,there’sa vertexhas 1 verticeswhichhavecommonedgeswhicharen’ttype-V.Thusthe setofrepresentativesofcolorsis {} Thetype-Vchromaticnumberis 0 and n-type-Vchromaticnumberis 0.
(vi) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-VI.Byit’sneutrosophiccomplete,there’sa vertexhas 1 verticeswhichhavecommonedgeswhicharen’ttype-VI.Thusthe setofrepresentativesofcolorsis {} Thetype-VIchromaticnumberis 0 and n-type-VIchromaticnumberis 0.
(vii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-VII.Byit’sneutrosophiccomplete,there’sa vertexhas 1 verticeswhichhavecommonedgeswhicharen’ttype-VII.Thus thesetofrepresentativesofcolorsis {} Thetype-VIIchromaticnumberis 0 andn-type-VIIchromaticnumberis 0.
Corollary2.30.18. Let N =(σ,µ) beaneutrosophicgraphwhichiscomplete bipartite.Ifit’sfixed-vertex,then
(i): Thesetofrepresentativesofcolorsis {v1,v2} Thustype-Ichromatic numberis 2 andn-type-Ichromaticnumberis 2σ(vi).
(ii): Thesetofrepresentativesofcolorsis {} Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0
(iii): Thesetofrepresentativesofcolorsis {} Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0
(iv): Thesetofrepresentativesofcolorsis {v1,v2}. Thustype-IVchromatic numberis t andn-type-IVchromaticnumberis 2σ(vi)
(v): Thesetofrepresentativesofcolorsis {} Thustype-Vchromaticnumber is 0 andn-type-Vchromaticnumberis 0.
(vi): Thesetofrepresentativesofcolorsis {} Thustype-VIchromaticnumber is 0 andn-type-VIchromaticnumberis 0
(vii): Thesetofrepresentativesofcolorsis {} Thustype-VIIchromaticnumber is 0 andn-type-VIIchromaticnumberis 0
Proof. (i) Alledgeshavesameamountsotheconnectednessamidtwogiven edgesisthesame.Alledgesaretype-I.Byit’sneutrosophiccomplete,there’s
2.NeutrosophicChromaticNumber
94
avertexhas 1 verticeswhichhavecommonedgeswhicharetype-I.Thusthe setofrepresentativesofcolorsis {v1,v2} Thetype-Ichromaticnumberis 2 andn-type-Ichromaticnumberisneutrosophiccardinalityof {v1,v2} whichis 2σ(vi)
(ii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-II.Byit’sneutrosophiccomplete,there’sa vertexhas 1 verticeswhichhavecommonedgeswhicharen’ttype-II.Thusthe setofrepresentativesofcolorsis {} Thetype-IIchromaticnumberis 0 and n-type-IIchromaticnumberis 0
(iii) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’sneutrosophiccomplete,there’sa vertexhas 1 verticeswhichhavecommonedgeswhicharen’ttype-III.Thusthe setofrepresentativesofcolorsis {} Thetype-IIIchromaticnumberis 0 and n-type-IIIchromaticnumberis 0
(iv) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaretype-IV.Byit’sneutrosophiccomplete,there’sa vertexhas 1 verticeswhichhavecommonedgeswhicharetype-IV.Thusthe setofrepresentativesofcolorsis {v1,v2} Thetype-IVchromaticnumberis 2 andn-type-IVchromaticnumberisneutrosophic {v1,v2} whichis 2σ(vi)
(v) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-V.Byit’sneutrosophiccomplete,there’sa vertexhas 1 verticeswhichhavecommonedgeswhicharen’ttype-V.Thusthe setofrepresentativesofcolorsis {} Thetype-Vchromaticnumberis 0 and n-type-Vchromaticnumberis 0
(vi) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-VI.Byit’sneutrosophiccomplete,there’sa vertexhas 1 verticeswhichhavecommonedgeswhicharen’ttype-VI.Thusthe setofrepresentativesofcolorsis {} Thetype-VIchromaticnumberis 0 and n-type-VIchromaticnumberis 0
(vii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-VII.Byit’sneutrosophiccomplete,there’sa vertexhas 1 verticeswhichhavecommonedgeswhicharen’ttype-VII.Thus thesetofrepresentativesofcolorsis {} Thetype-VIIchromaticnumberis 0 andn-type-VIIchromaticnumberis 0
Corollary2.30.19. Let N =(σ,µ) beaneutrosophicgraphwhichisstar.Ifit’s fixed-edge,then
(i): Thesetofrepresentativesofcolorsis {c,v2} Thustype-Ichromatic numberis 2 andn-type-Ichromaticnumberis σ(c)+ σ(v2)
(ii):
(iii):
(iv):
Thesetofrepresentativesofcolorsis {} Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0
Thesetofrepresentativesofcolorsis {}. Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0
Thesetofrepresentativesofcolors,type-IVchromaticnumberandn-typeIVchromaticnumberaren’tdefined.
(v): Thesetofrepresentativesofcolors,type-Vchromaticnumberandn-type-V chromaticnumberaren’tdefined.
2.30.NewResults
95
(vi): Thesetofrepresentativesofcolors,type-VIchromaticnumberandn-typeVIchromaticnumberaren’tdefined.
(vii): Thesetofrepresentativesofcolors,type-VIIchromaticnumberandntype-VIIchromaticnumberaren’tdefined.
Proof. (i) Alledgeshavesameamountsotheconnectednessamidtwogiven edgesisthesame.Alledgesaretype-I.Byit’sneutrosophiccomplete,there’s avertexhas 1 whichhavecommonedgeswhicharetype-I.Thusthesetof representativesofcolorsis {v1,v2}. Thetype-Ichromaticnumberis 2 and n-type-Ichromaticnumberisneutrosophiccardinalityof {v1,v2} whichis σ(v1)+ σ(v2)
(ii) Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-II.Byit’sneutrosophiccomplete,there’sa vertexhas 1 verticeswhichhavecommonedgeswhicharen’ttype-II.Thusthe setofrepresentativesofcolorsis {} Thetype-IIchromaticnumberis 0 and n-type-IIchromaticnumberis 0
(iii) Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’sneutrosophiccomplete,there’sa vertexhas 1 verticeswhichhavecommonedgeswhicharen’ttype-III.Thusthe setofrepresentativesofcolorsis {} Thetype-IIIchromaticnumberis 0 and n-type-IIIchromaticnumberis 0
(iv) Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’t type-IV.Sinceit’simpossibletodefinewhenthere’snocycleinneutrosophic graph.
(v) Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesameamount sotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’ttype-V. Sinceit’simpossibletodefinewhenthere’snocycleinneutrosophicgraph.
(vi). Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’t type-VI.Sinceit’simpossibletodefinewhenthere’snocycleinneutrosophic graph.
(vii) Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’t type-VII.Sinceit’simpossibletodefinewhenthere’snocycleinneutrosophic graph.
Corollary2.30.20. Let N =(σ,µ) beaneutrosophicgraphwhichisstar.Ifit’s fixed-vertex,then
(i): Thesetofrepresentativesofcolorsis {v1,c} Thustype-Ichromatic numberis 2 andn-type-Ichromaticnumberis 2σ(c)
(ii): Thesetofrepresentativesofcolorsis {} Thustype-IIchromaticnumber is 0 andn-type-IIchromaticnumberis 0
(iii): Thesetofrepresentativesofcolorsis {} Thustype-IIIchromaticnumber is 0 andn-type-IIIchromaticnumberis 0
2.NeutrosophicChromaticNumber
96
(iv): Thesetofrepresentativesofcolors,type-IVchromaticnumberandn-typeIVchromaticnumberaren’tdefined.
(v): Thesetofrepresentativesofcolors,type-Vchromaticnumberandn-type-V chromaticnumberaren’tdefined.
(vi): Thesetofrepresentativesofcolors,type-VIchromaticnumberandn-typeVIchromaticnumberaren’tdefined.
(vii): Thesetofrepresentativesofcolors,type-VIIchromaticnumberandntype-VIIchromaticnumberaren’tdefined.
Proof. (i). Alledgeshavesameamountsotheconnectednessamidtwogiven edgesisthesame.Alledgesaretype-I.Byit’sneutrosophiccomplete,there’s avertexhas 1 verticeswhichhavecommonedgeswhicharetype-I.Thusthe setofrepresentativesofcolorsis {c,v2} Thetype-Ichromaticnumberis 2 and n-type-Ichromaticnumberisneutrosophiccardinalityof {c,v2} whichis 2σ(c)
(ii). Alledgeshavesameamountsotheconnectednessamidtwogivenedges isthesame.Alledgesaren’ttype-II.Byit’sneutrosophiccomplete,there’sa vertexhas 1 verticeswhichhavecommonedgeswhicharen’ttype-II.Thusthe setofrepresentativesofcolorsis {} Thetype-IIchromaticnumberis 0 and n-type-IIchromaticnumberis 0
(iii). Alledgeshavesameamountsotheconnectednessamidtwogivenedgesis thesame.Alledgesaren’ttype-III.Byit’sneutrosophiccomplete,there’sa vertexhas 1 verticeswhichhavecommonedgeswhicharen’ttype-III.Thusthe setofrepresentativesofcolorsis {} Thetype-IIIchromaticnumberis 0 and n-type-IIIchromaticnumberis 0
(iv). Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’t type-IV.Sinceit’simpossibletodefinewhenthere’snocycleinneutrosophic graph.
(v) Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesameamount sotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’ttype-V. Sinceit’simpossibletodefinewhenthere’snocycleinneutrosophicgraph.
(vi) Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’t type-VI.Sinceit’simpossibletodefinewhenthere’snocycleinneutrosophic graph.
(vii) Byit’sfixed-vertexandit’sneutrosophicstrong,alledgeshavesame amountsotheconnectednessamidtwogivenedgesisthesame.Alledgesaren’t type-VII.Sinceit’simpossibletodefinewhenthere’snocycleinneutrosophic graph.
2.31ApplicationsinTimeTableandScheduling
Designingtheprogramstoachievesomegoalsisgeneralapproachtoapplyon someissuestofunctionproperly.Separationhaskeyroleinthecontextofthis style.Separatingthedurationofworkwhichareconsecutive,isthematterand ithasimportanttoavoidmixingup.
2.31.ApplicationsinTimeTableandScheduling
97
Step1.(Definition) Timetableisanapproachtogetsomeattributestodo theworkfastandproper.Thestyleofschedulingimpliesspecialattention tothetaskswhichareconsecutive.
Step2.(Issue) Schedulingofprogramhasfacedwithdifficultiestodifferamid consecutivesection.Beyondthat,sometimessectionsarenotthesame.
Step3.(Model) AsFigure (2.7),thesituationisdesignedasamodel.The modelusesdatatoassigneverysectionandtoassigntorelationamid section,threenumbersbelongunitintervaltostateindeterminacy, possibilitiesanddeterminacy.There’sonerestrictioninthat,thenumbers amidtwosectionsareatleastthenumberoftherelationamidthem. Table(4.5),clarifiesabouttheassignednumberstothesesituation.

Figure2.7:Blackverticesaresuspicionsaboutchoosingthem. fgr1c
Table2.5:SchedulingconcernsitsSubjectsanditsConnectionsasa NeutrosophicGraphinaModel. tbl1c
Sectionsof T s1 s2 s3 s4 s5 s6 s7 s8 s9,s10
Values 0 10 80 70 80 10 30 60 50 2 Connectionsof T s1s2 s2s3 s3s4 s4s5 s5s6 s6s7 s7s8 s8s9 s9s10 Values 0 10 60 40 10 10 20 40 20 1
Step4.(Solution) AsFigure (2.7) shows,neutrosophicmodel,proposesto usedifferenttypesofchromaticnumberwhichisincomputablefortypes IV,V,VI,VIIinthecasewhichistitled T Inthiscase, i1 and c1 aren’t representativeofthesetwocolorsanddifferenttypesofchromaticnumber isincomputablefortypesIV,V,VI,VII.Theset {i1,c1} doesn’tcontain representativesofcolorswhichposedifferenttypesofchromaticnumber anddifferenttypesofchromaticnumberfortypesIV,V,VI,VII.Thusthe decisionamidchoosingthesubject c1 an c2 isn’tconcludedtochoose c1 fortypesIV,V,VI,VII.Togetbriefoverview,neutrosophicmodel usesonenumberforeveryarrayso 0 9 means (0 9, 0 9, 0 9) InFigure (2.7),theneutrosophicmodel T introducesthecommonsituation.The
2.NeutrosophicChromaticNumber
98
representativesofcolorsare i2 and c1. Thusdifferenttypesofchromatic numbersistwofortypesIandIVanddifferenttypesofneutrosophic chromaticnumberis 1 4 fortypesIandIV.Thussuspicionaboutchoosing i1 and i2 isdeterminedtobe i2 Thesetsofrepresentativeforcolors are {i2,c1} fortypesIandIV.Thusthecomparativestudiesbasedon differenttypesofchromaticnumberandneutrosophicchromaticnumber areconcluded.
2.32OpenProblems
Thetwonotionsofcoloringofverticesconcerningdifferenttypesofchromatic numberanddifferenttypesofneutrosophicchromaticnumberaredefinedon neutrosophicgraphswhenconnectednessandasitsconsequences,differenttypes ofedgeshavekeyroletohavethesenotions.Thus
Question2.32.1. Isitpossibletouseothertypesedgesviaconnectednessto definedifferenttypesofchromaticnumberanddifferenttypesofneutrosophic chromaticnumber?
Question2.32.2. Areexistedsomeconnectionsamidthecoloringfrom connectednessinsidethisconceptandexternalconnectionswithothertypes ofcoloringfromothernotions?
Question2.32.3. Isitpossibletoconstructsomeclassesneutrosophicgraphs whichhave“nice”behavior?
Question2.32.4. Whichapplicationsdomakeanindependentstudytoapply differenttypesofchromaticnumberanddifferenttypesofneutrosophicchromatic number?
Problem2.32.5. Whichparametersarerelatedtothisparameter?
Problem2.32.6. Whichapproachesdoworktoconstructapplicationstocreate independentstudy?
Problem2.32.7. Whichapproachesdoworktoconstructdefinitionswhichuse allthreearraysandtherelationsamidtheminsteadofonearrayofthreearrays tocreateindependentstudy?
2.33ConclusionandClosingRemarks
Thisstudyusesmixedcombinationsofdifferenttypesofchromaticnumber anddifferenttypesofneutrosophicchromaticnumbertostudyonneutrosophic graphs.Theconnectionsofverticeswhichareclarifiedbyspecialedgesand differentedgesfromconnectedness,differthemfromeachotherandandput themindifferentcategoriestorepresentonerepresentativeforeachcolor. Furtherstudiescouldbeaboutchangesinthesettingstocomparethisnotion amiddifferentsettingsofgraphtheory.Onewayisfindingsomerelationsamid arrayofverticestomakesensibledefinitions.InTable (2.4),somelimitations andadvantagesofthisstudyispointedout.
2.32.OpenProblems
99
2.NeutrosophicChromaticNumber
Advantages Limitations 1.
1.
2. Usingneutrosophiccardinality 3. Usingcardinality 2. Connectionswithparameters 4. ApplyingDifferentTypesofEdges 5. DifferentTypesofChromaticNotions 3. ConnectionsofResults 100
Table2.6:ABriefOverviewaboutAdvantagesandLimitationsofthisstudy tbl2c
Usingconnectednessforlabellingedges
GeneralResults
Bibliography
1 [1] HenryGarrett,“ChromaticNumberandNeutrosophicChromaticNumber”,Preprints2021,2021110142(doi:10.20944/preprints202112.0177.v1).
2 [2] HenryGarrett,“DifferentTypesofNeutrosophicChromaticNumber ”, Preprints2021(doi:10.20944/preprints202112.0335.v1).
3 [3] HenryGarrett,“NeutrosophicChromaticNumberBasedonConnectedness”,Preprints2021(doi:10.20944/preprints202112.0226.v1).
4 [4] Rohini,A.,etal.“SingleValuedNeutrosophicColoring”.InfiniteStudy, 2019.
5 [5] Rohini,A.,etal.“OperationsofSingleValuedNeutrosophicColoring”. InfiniteStudy,2019.
6 [6] ROHINI,A.,etal.“SingleValuedNeutrosophicirregularvertexcoloring” ActaElectrotehnica61(2020).
101
Basedonsome ideas,numbers andsetsare definedinthe waysthat,some resultsare obtained.Thus it’sanopenway tohavewellunderstandable structuresand well-defined ideasfrom neutrosophic hypergraphs.
NeutrosophicHypergraphs
Akrametal.introduceAnewdecision-makingmethodbasedonbipolar neutrosophicdirectedhypergraphs[1],Bipolarneutrosophichypergraphswith applications[2],Certainnetworksmodelsusingsingle-valuedneutrosophic directedhypergraphs[3].Also,Akrametal.inFuzzyhypergraphsandrelated extensions[4],getsomedirectionstothistopic.Hamidietal.[8]propose single-valuedneutrosophicdirected(hyper)graphsandapplications[9]poses generalizedneutrosophichypergraphs.Luqmanetal.[10]introducecomplex neutrosophichypergraphs:newsocialnetworkmodels.Maliketalpropose Isomorphismofsinglevaluedneutrosophichypergraphs[11]andregularsingle valuedneutrosophichypergraphs[12].
3.1NumbersandSets
3.2PreliminariesForSettingofNeutrosophic n-SuperHyperGraphandSettingofNeutrosophic Hypergraphs
Definition3.2.1. (Graph).
G =(V,E) iscalleda graph if V isasetofobjectsand E isasubsetof V × V (E isasetof2-subsetsof V )where V iscalled vertexset and E iscalled edgeset.Everytwoverticeshavebeencorrespondedtoatmostoneedge.
Definition3.2.2. (Hypergraph).
H =(V,E) iscalleda hypergraph if V isasetofobjectsandforevery nonnegativeinteger t ≤ n,E isasetof t subsetsof V where V iscalled vertexset and E iscalled hyperedgeset
Definition3.2.3. (NeutrosophicHypergraph).
NHG =(V,E,σ =(σ1,σ2,σ3),µ =(µ1,µ2,µ3)) iscalleda neutrosophic hypergraph ifit’shypergraph, σi : V → [0, 1],µi : E → [0, 1], andforevery v1v2 vt ∈ E, µ(v1v2 ··· vt) ≤ σ(v1) ∧ σ(v2) ∧··· σ(vt)
(i): σ iscalled neutrosophicvertexset
(ii): µ iscalled neutrosophichyperedgeset
CHAPTER3
103
(iii): |V | iscalled order ofNHGandit’sdenotedby O(NHG).
(iv): Σv∈V σ(v) iscalled neutrosophicorder ofNHGandit’sdenotedby On(NHG)
(vi): |E| iscalled size ofNHGandit’sdenotedby S(NHG)
(vii): Σe∈E µ(e) iscalled neutrosophicsize ofNHGandit’sdenotedby Sn(NHG)
Example3.2.4. AssumeFigure(3.11).
(i): Neutrosophichyperedge n1n2n3 hasthreeneutrosophicvertices.
(ii): Neutrosophichyperedge n3n4n5n6 hasfourneutrosophicvertices.
(iii): Neutrosophichyperedge n1n7n8n9n5n6 hassixneutrosophicvertices.
(iv): σ = {(n1, (0.99, 0.98, 0.55)), (n2, (0.74, 0.64, 0.46)), (n3, (0.99, 0.98, 0.55)), (n4, (0 54, 0 24, 0 16)), (n5, (0 99, 0 98, 0 55)), (n6, (0 99, 0 98, 0 55)), (n7, (0 99, 0 98, 0 55)), (n8, (0 99, 0 98, 0 55)), (n9, (0 99, 0 98, 0 55))}) is neutrosophicvertexset.
(v): µ = {(e1, (0 01, 0 01, 0 01)), (e2, (0 01, 0 01, 0 01)), (e3, (0 01, 0 01, 0 01))}) isneutrosophichyperedgeset.
(vi): O(NHG)=9.
(vii): On(NHG)=(8.21, 7.74, 4.47).
(viii): S(NHG)=3
(ix): Sn(NHG)=(0 03, 0 03, 0 03)
Figure3.1:Therearethreeneutrosophichyperedgesandtwoneutrosophic vertices. nhg1
Definition3.2.5. (NeutrosophicEdge t RegularHypergraph). Aneutrosophichypergraph NHG =(V,E,σ,µ) iscalleda neutrosophic edge t regularhypergraph ifeveryneutrosophichyperedgehasonly t neutrosophicvertices.
Question3.2.6. What-ifallneutrosophichypergraphsareeitheredge t regular ornot?

3.NeutrosophicHypergraphs
104
3.2.PreliminariesForSettingofNeutrosophicn-SuperHyperGraphand SettingofNeutrosophicHypergraphs
Figure3.2: NHG =(V,E,σ,µ) isneutrosophicedge 3 regularhypergraph nhg2

Inthefollowing,therearesomedirectionswhichclarifytheexistenceof someneutrosophichypergraphswhichareeitheredge t regularornot.
Example3.2.7. Twoneutrosophichypergraphsarepresentedsuchthatoneof themisedge t regularandanotherisn’t.
(i): AssumeFigure(3.11).Itisn’tneutrosophicedge t regularhypergraph.
(ii): SupposeFigure(3.2).It’sneutrosophicedge 3 regularhypergraph.
Definition3.2.8. (Neutrosophicvertex t RegularHypergraph). Aneutrosophichypergraph NHG =(V,E,σ,µ) iscalleda neutrosophic vertex t regularhypergraph ifeveryneutrosophicvertexisincidentto only t neutrosophichyperedges.

Example3.2.9. Threeneutrosophichypergraphsarepresentedsuchthatone ofthemisvertex t regularandanothersaren’t.
(i): ConsiderFigure (3.11).Itisn’tneutrosophicedge t regularhypergraph.
(ii): SupposeFigure (3.2).It’sneutrosophicedge 3 regularhypergraphbut Itisn’tneutrosophicvertex 3 regularhypergraph.
(iii): AssumeFigure (3.3).It’sneutrosophicvertex 2 regularhypergraphbut Itisn’tneutrosophicedge t regularhypergraph.
Figure3.3: NHG =(V,E,σ,µ) isneutrosophicstronghypergraph. nhg3
105
Definition3.2.10. (NeutrosophicStrongHypergraph). Aneutrosophichypergraph NHG =(V,E,σ,µ) iscalleda neutrosophic stronghypergraph ifit’shypergraphandforevery v1v2 ··· vt ∈ E, µ(v1v2 vt)= σ(v1) ∧ σ(v2) ∧··· σ(vt).
Figure3.4: NHG =(V,E,σ,µ) isneutrosophicstronghypergraph. nhg4
Example3.2.11. Threeneutrosophichypergraphsarepresentedsuchthatone ofthemisneutrosophicstronghypergraphandothersaren’t.
(i): ConsiderFigure(3.11).Itisn’tneutrosophicstronghypergraph.
(ii): AssumeFigure(3.2).Itisn’tneutrosophicstronghypergraph.
(iii): SupposeFigure(3.3).Itisn’tneutrosophicstronghypergraph.
(iv): AssumeFigure (3.4).It’sneutrosophicstronghypergraph.It’salso neutrosophicedge 3 regularhypergraphbutitisn’tneutrosophicvertex t regularhypergraph.

Definition3.2.12. (NeutrosophicStrongHypergraph). Assumeneutrosophichypergraph NHG =(V,E,σ,µ.) Aneutrosophic hyperedge v1v2 vt ∈ E iscalleda neutrosophicstronghyperedge if µ(v1v2 vt)= σ(v1) ∧ σ(v2) ∧··· σ(vt)
Proposition3.2.13. Assumeneutrosophicstronghypergraph NHG = (V,E,σ,µ.) Thenallneutrosophichyperedgesareneutrosophicstrong.
Definition3.2.14. (NeutrosophicHyperpath). Apath v0,E0,v1,v1,E1,v2, ··· ,vt 1,Et 1,vt, iscalled neutrosophichyperpath suchthat vi 1 and vi haveincidentto Ei 1 forallnonnegativeintegers 0 ≤ i ≤ t. Inthiscase, t 1 iscalled length ofneutrosophichyperpath.Also,if x and y aretwoneutrosophicvertices,thenmaximumlengthofneutrosophichyperpathsfrom x to y, iscalled neutrosophichyperdistance andit’sdenoted by d(x,y) If v0 = vt,thenit’scalled neutrosophichypercycle
Example3.2.15. AssumeFigure(3.11).
(i): n1,E1,n3,E2,n6,E3,n1 isaneutrosophichypercycle.
3.NeutrosophicHypergraphs
106
3.3.DimensionandColoringalongsideDominationinNeutrosophic Hypergraphs
(ii): n1,E1,nn,E2,n6,E3,n1 isn’tneitherneutrosophichypercyclenorneutrosophichyperpath.
(iii): n1E1n3E2n6E3n1 isn’tneitherneutrosophichypercyclenorneutrosophic hyperpath.
(iv): n1,n3,n6,n1 isn’tneitherneutrosophichypercyclenorneutrosophic hyperpath.
(v): n1E1,n3,E2,n6,E3,n1 isn’tneitherneutrosophichypercyclenorneutrosophichyperpath.
(vi): n1,E1,n3,E2,n6,E3,n7 isaneutrosophichyperpath.
(vii): Neutrosophichyperdistanceamid n1 and n4 istwo.
(viii): Neutrosophichyperdistanceamid n1 and n7 isone.
(ix): Neutrosophichyperdistanceamid n1 and n2 isone.
(x): Neutrosophichyperdistanceamidtwogivenneutrosophicverticesiseither oneortwo.
Firstcaseforthecontentsistousethearticlefrom[7].Thecontentsareused inthewaythat,usagesofnewcontentsarepreferencesandthepreliminaries arepassedinthebeginningofthischapter.
3.3DimensionandColoringalongsideDominationin NeutrosophicHypergraphs
3.4Abstract
Newsettingisintroducedtostudyresolvingnumberandchromaticnumber alongsidedominatingnumber.Differenttypesofproceduresincludingset, optimalset,andoptimalnumberalongsidestudyonthefamilyofneutrosophic hypergraphsareproposedinthisway,someresultsareobtained.General classesofneutrosophichypergraphsareusedtoobtainsthesenumbersand therepresentativesofthecolors,dominatingsetsandresolvingsets.Using colorstoassigntotheverticesofneutrosophichypergraphsandcharacterizing resolvingsetsanddominatingsetsareapplied.Somequestionsandproblems areposedconcerningwaystodofurtherstudiesonthistopic.Usingdifferent waysofstudyonneutrosophichypergraphstogetnewresultsaboutnumbers andsetsinthewaythatsomenumbersgetunderstandableperspective.Family ofneutrosophichypergraphsarestudiedtoinvestigateaboutthenotions, dimensionandcoloringalongsidedominationinneutrosophichypergraphs. Inthisway,setsofrepresentativesofcolors,resolvingsetsanddominating setshavekeyrole.Optimalsetsandoptimalnumbershavekeypointstoget newresultsbutinsomecases,thereareusagesofsetsandnumbersinstead ofoptimalones.Simultaneously,threenotionsareappliedintoneutrosophic hypergraphstogetsensibleresultsabouttheirstructures.Basicfamiliarities withneutrosophichypergraphstheoryandhypergraphtheoryareproposedfor thisarticle.
107
3.NeutrosophicHypergraphs
Keywords: Dimension,Coloring,Domination
AMSSubjectClassification: 05C17,05C22,05E45
3.5MotivationandContributions
Inthisstudy,there’sanideawhichcouldbeconsideredasamotivation. Question3.5.1. Isitpossibletousemixedversionsofideasconcerning“neutrosophicdomination”,“neutrosophicdimension”and“neutrosophiccoloring” todefinesomenotionswhichareappliedtoneutrosophichypergraphs?
It’smotivationtofindnotionstouseinanyclassesofneutrosophic hypergraphs.Real-worldapplicationsabouttimetableandschedulingare anotherthoughtswhichleadtobeconsideredasmotivation.Connectionsamid twoitemshavekeyrolestoassigncolors,dominatinganddomination.Thus they’reusedtodefinenewideaswhichconcludetothestructureofcoloring, dominatinganddomination.Theconceptofhavinggeneralneutrosophic hyperedgeinspiresmetostudythebehaviorofgeneralneutrosophichyperedge inthewaythat,threetypesofcoloringnumbers,dominatingnumberand resolvingsetarethecasesofstudyinindividualsandfamilies. Theframeworkofthisstudyisasfollows.Inthebeginning,Iintroducedbasic definitionstoclarifyaboutpreliminaries.Insection“NewIdeasForNeutrosophic Hypergraphs”,newnotionsofcoloring,dominatinganddominationareapplied toneutrosophicverticesofneutrosophicgraphsasindividuals.Insection “OptimalNumbersForNeutrosophicHypergraphs”,specificnumbershavethe keyroleinthisway.Classesofneutrosophicgraphsarestudiedinthetermsof differentnumbersinsection“OptimalNumbersForNeutrosophicHypergraphs” asindividuals.Inthesection“OptimalSetsForNeutrosophicHypergraphs”, usagesofgeneralneutrosophicsetsandspecialneutrosophicsetshavekeyrole inthisstudyasindividuals.Insection“OptimalSetsandNumbersForFamily ofNeutrosophicHypergraphs”,bothsetsandnumbershaveappliedintothe familyofneutrosophichypergraphs.Insection“ApplicationsinTimeTableand Scheduling”,oneapplicationisposedforneutrosophichypergraphsconcerning timetableandschedulingwhenthesuspicionsareaboutchoosingsomesubjects. Insection“OpenProblems”,someproblemsandquestionsforfurtherstudies areproposed.Insection“ConclusionandClosingRemarks”,gentlediscussion aboutresultsandapplicationsarefeatured.Insection“ConclusionandClosing Remarks”,abriefoverviewconcerningadvantagesandlimitationsofthisstudy alongsideconclusionsareformed.
3.6NewIdeasForNeutrosophicHypergraphs
Definition3.6.1. (Dominating,ResolvingandColoring). Assumeneutrosophichypergraph NHG =(V,E,σ,µ).
(a): Neutrosophic-dominatingsetandnumberaredefinedasfollows.
(i): Aneutrosophicvertex x neutrosophic-dominates avertex y if there’satleastoneneutrosophicstronghyperedgewhichhavethem.
108
(ii): Aset S iscalled neutrosophic-dominatingset ifforevery y ∈ V \ S, there’satleastonevertex x whichneutrosophic-dominates vertex y.
(iii): If S issetofallneutrosophic-dominatingsets,then Σx∈X σ(x)=min S∈S Σx∈S σ(x)
iscalled optimal-neutrosophic-dominatingnumber and X is called optimal-neutrosophic-dominatingset.
(b): Neutrosophic-resolvingsetandnumberaredefinedasfollows.
(i): Aneutrosophicvertex x neutrosophic-resolves vertices y,w if d(x,y) = d(x,w)
(ii): Aset S iscalled neutrosophic-resolvingset ifforevery y ∈ V \ S, there’satleastonevertex x whichneutrosophic-resolvesvertices y,w.
(iii): If S issetofallneutrosophic-resolvingsets,then Σx∈X σ(x)=min S∈S Σx∈S σ(x)
iscalled optimal-neutrosophic-resolvingnumber and X is called optimal-neutrosophic-resolvingset.
(c): Neutrosophic-coloringsetandnumberaredefinedasfollows.
(i): Aneutrosophicvertex x neutrosophic-colors avertex y differently withitselfifthere’satleastoneneutrosophicstronghyperedgewhich havethem.
(ii): Aset S iscalled neutrosophic-coloringset ifforevery y ∈ V \ S, there’satleastonevertex x whichneutrosophic-colorsvertex y.
(iii): If S issetofallneutrosophic-coloringsets,then Σx∈X σ(x)=min S∈S Σx∈S σ(x) iscalled optimal-neutrosophic-coloringnumber and X iscalled optimal-neutrosophic-coloringset.
Example3.6.2. ConsiderFigure (3.11) wheretheimprovementsonits hyperedgestohaveneutrosophicstronghypergraph.
(a): Thenotionsofdominatingareclarified.
(i): n1 neutrosophic-dominateseveryvertexfromthesetofvertices {n7,n8,n9,n2,n3}.n4 neutrosophic-dominateseveryvertexfrom thesetofvertices {n6,n5,n3}.n4 doesn’tneutrosophic-dominate everyvertexfromthesetofvertices {n1,n2,n7,n8,n9}
(ii): {n1,n3} isneutrosophic-coloringsetbut {n1,n4} isoptimalneutrosophic-dominatingset.
3.6.NewIdeasForNeutrosophicHypergraphs
109
(iii): (1.53, 1.22, 0.71) isoptimal-neutrosophic-dominatingnumber.
(b): Thenotionsofresolvingareclarified.
(i): n1 neutrosophic-resolvestwovertices n4 and n6.
(ii): V \{n1,n4} isneutrosophic-resolvessetbut V \{n2,n4,n9} isoptimalneutrosophic-resolvingset.
(iii): (5, 94, 6.36, 3.3) isoptimal-neutrosophic-resolvingnumber.
(c): Thenotionsofcoloringareclarified.
(i): n1 neutrosophic-colorseveryvertexfromthesetofvertices {n7,n8,n9,n2,n3}.n4 neutrosophic-colorseveryvertexfromthe setofvertices {n6,n5,n3}.n4 doesn’tneutrosophic-dominateevery vertexfromthesetofvertices {n1,n2,n7,n8,n9}
(ii): {n1,n5,n7,n8,n9,n6,n4} isneutrosophic-coloringsetbut {n1,n5,n7,n8,n2,n4} isoptimal-neutrosophic-coloringset.
(iii): (5 24, 4 8, 2 82) isoptimal-neutrosophic-coloringnumber.
Example3.6.3. ConsiderFigure(3.3).
(a): Thenotionsofdominatingareclarified.
(i): n1 neutrosophic-dominateseveryvertexfromthesetofvertices {n5,n6,n2,n3}.n4 neutrosophic-dominateseveryvertexfromtheset ofvertices {n5,n3}.n4 doesn’tneutrosophic-dominateeveryvertex fromthesetofvertices {n1,n2,n6}
(ii): {n1,n3} isneutrosophic-dominatingsetbut {n1,n4} isoptimalneutrosophic-dominatingset.
(iii): (1 53, 1 22, 0 71) isoptimal-neutrosophic-dominatingnumber.
(b): Thenotionsofresolvingareclarified.
(i): n1 neutrosophic-resolvestwovertices n4 and n6
(ii): V \{n1,n4} isneutrosophic-resolvessetbut V \{n2,n4,n6} isoptimalneutrosophic-resolvingset.
(iii): (5, 94, 6 36, 3 3) isoptimal-neutrosophic-resolvingnumber.
(c): Thenotionsofcoloringareclarified.
(i): n1 neutrosophic-colorseveryvertexfromthesetofvertices {n5,n6,n2,n3}.n4 neutrosophic-colorseveryvertexfromtheset ofvertices {n5,n3}.n4 doesn’tneutrosophic-dominateeveryvertex fromthesetofvertices {n1,n2,n6}
(ii): {n1,n5,n6} isneutrosophic-coloringsetbut {n5,n2,n4} isoptimalneutrosophic-coloringset.
(iii): (2 27, 1 86, 1 17) isoptimal-neutrosophic-coloringnumber.
110
3.NeutrosophicHypergraphs
3.7.OptimalNumbersForNeutrosophicHypergraphs
3.7OptimalNumbersForNeutrosophicHypergraphs
Proposition3.7.1. Assumeneutrosophichypergraph NHG =(V,E,σ,µ).S is maximumsetofverticeswhichformahyperedge.Thenoptimal-neutrosophiccoloringsethasascardinalityas S has.
Proof. Assumeneutrosophichypergraph NHG =(V,E,σ,µ). Everyneutrosophichyperedgehasneutrosophicverticeswhichhavecommonneutrosophic hyperedge.Thuseveryneutrosophicvertexhasdifferentcolorwithotherneutrosophicverticeswhichareincidentwithaneutrosophichyperedge.Itinduces aneutrosophichyperedgewiththemostnumberofneutrosophicverticesdeterminesoptimal-neutrosophic-coloringset. S ismaximumsetofverticeswhich formahyperedge.Thusoptimal-neutrosophic-coloringsethasascardinalityas S has.
Proposition3.7.2. Assumeneutrosophichypergraph NHG =(V,E,σ,µ).S is maximumsetofverticeswhichformahyperedge.Thenoptimal-neutrosophiccoloringnumberis Σs∈S σ(s).
Proof. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) Everyneutrosophichyperedgehasneutrosophicverticeswhichhavecommonneutrosophic hyperedge.Thuseveryneutrosophicvertexhasdifferentcolorwithotherneutrosophicverticeswhichareincidentwithaneutrosophichyperedge.Itinduces aneutrosophichyperedgewiththemostnumberofneutrosophicverticesdeterminesoptimal-neutrosophic-coloringset. S ismaximumsetofverticeswhich formahyperedge.Thusoptimal-neutrosophic-coloringnumberis Σs∈S σ(s)
Proposition3.7.3. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) If optimal-neutrosophic-coloringnumberis Σv∈V σ(v),
thenthere’satleastonehyperedgewhichcontains n verticeswhere n isthe cardinalityoftheset V.
Proof. Supposeneutrosophichypergraph NHG =(V,E,σ,µ) Consider optimal-neutrosophic-coloringnumberis Σv∈V σ(v).
Itimpliesthere’soneneutrosophichyperedgewhichhasallneutrosophicvertices. Sinceifallneutrosophicverticesareincidenttoaneutrosophichyperedge,then allhavedifferentcolors.
Proposition3.7.4. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) If there’satleastonehyperedgewhichcontains n verticeswhere n isthecardinality oftheset V, thenoptimal-neutrosophic-coloringnumberis Σv∈V σ(v)
111
Proof. Considerneutrosophichypergraph NHG =(V,E,σ,µ). Supposethere’s atleastonehyperedgewhichcontains n verticeswhere n isthecardinalityofthe set V. Itimpliesthere’soneneutrosophichyperedgewhichhasallneutrosophic vertices.Ifallneutrosophicverticesareincidenttoaneutrosophichyperedge, thenallhavedifferentcolors.So V isoptimal-neutrosophic-coloringset.It inducesoptimal-neutrosophic-coloringnumberis
Proposition3.7.5. Assumeneutrosophichypergraph NHG =(V,E,σ,µ). If optimal-neutrosophic-dominatingnumberis
thenthere’satleastoneneutrosophicvertexwhichdoesn’thaveincidenttoany neutrosophichyperedge.
Proof. Supposeneutrosophichypergraph NHG =(V,E,σ,µ) Consider optimal-neutrosophic-dominatingnumberis
Ifforallgivenneutrosophicvertex,there’satleastoneneutrosophichyperedge whichtheneutrosophicvertexhasincidenttoit,thenthere’saneutrosophic vertex x suchthatoptimal-neutrosophic-dominatingnumberis
Itinducescontradictionwithhypothesis.Itimpliesthere’satleastone neutrosophicvertexwhichdoesn’thaveincidenttoanyneutrosophichyperedge.
Proposition3.7.6. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) Then optimal-neutrosophic-dominatingnumberis < Σv∈V σ(v)
Proof. Considerneutrosophichypergraph NHG =(V,E,σ,µ) Thus V −{x} isaneutrosophic-dominatingset.Sinceifnot, x isn’tincidenttoanygiven neutrosophichyperedge.Thisiscontradictionwithsupposition.Itinducesthat x belongstoaneutrosophichyperedgewhichhasanothervertex s. Itimplies s neutrosophic-dominates x. Thus V −{x} isaneutrosophic-dominatingset.It inducesoptimal-neutrosophic-dominatingnumberis < Σv∈V σ(v).
Proposition3.7.7. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) If optimal-neutrosophic-resolvingnumberis
theneverygivenvertexdoesn’thaveincidenttoanyhyperedge.
3.NeutrosophicHypergraphs
Σv∈V σ(v)
Σv∈V σ(v),
Σv∈V σ(v)
Σv∈V −{x}σ(v).
Σv∈V σ(v),
112
Proof. Considerneutrosophichypergraph NHG =(V,E,σ,µ). Letoptimalneutrosophic-resolvingnumberbe
Σv∈V σ(v).
Itimplieseveryneutrosophicvertexisn’tneutrosophic-resolvedbyaneutrosophicvertex.It’scontradictionwithhypothesis.Soeverygivenvertexdoesn’t haveincidenttoanyhyperedge.
Proposition3.7.8. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) Then optimal-neutrosophic-resolvingnumberis < Σv∈V σ(v)
Proof. Considerneutrosophichypergraph NHG =(V,E,σ,µ) Ifoptimalneutrosophic-resolvingnumberis Σv∈V σ(v),
thenthere’sacontradictiontohypothesis.Sincetheset V \{x} isneutrosophicresolvingset.Itimpliesoptimal-neutrosophic-resolvingnumberis < Σv∈V σ(v)
Proposition3.7.9. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) If optimal-neutrosophic-coloringnumberis Σv∈V σ(v),
thenallneutrosophicvertieswhichhaveincidenttoatleastoneneutrosophic hyperedge.
Proof. Supposeneutrosophichypergraph NHG =(V,E,σ,µ) Consider optimal-neutrosophic-coloringnumberis Σv∈V σ(v)
Ifforallgivenneutrosophicvertices,there’snoneutrosophichyperedgewhich theneutrosophicverticeshaveincidenttoit,thenthere’sneutrosophicvertex x suchthatoptimal-neutrosophic-coloringnumberis Σv∈V −{x}σ(v)
Itinducescontradictionwithhypothesis.Itimpliesallneutrosophicvertices haveincidenttoatleastoneneutrosophichyperedge.
Proposition3.7.10. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) Thenoptimal-neutrosophic-coloringnumberisn’t < Σv∈V σ(v)
3.7.OptimalNumbersForNeutrosophicHypergraphs
113
Proof. Considerneutrosophichypergraph NHG =(V,E,σ,µ). Thus V −{x} isn’taneutrosophic-coloringset.Sinceifnot, x isn’tincidenttoanygiven neutrosophichyperedge.Thisiscontradictionwithsupposition.Itinducesthat x belongstoaneutrosophichyperedgewhichhasanothervertex s. Itimplies s neutrosophic-colors x. Thus V −{x} isn’taneutrosophic-coloringset.It inducesoptimal-neutrosophic-coloringnumberisn’t < Σv∈V σ(v)
Proposition3.7.11. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) Thenoptimal-neutrosophic-dominatingsethascardinalitywhichisgreaterthan n 1 where n isisthecardinalityoftheset V.
Proof. Considerneutrosophichypergraph NHG =(V,E,σ,µ). Theset V is neutrosophic-dominatingset.Sooptimal-neutrosophic-dominatingsethas cardinalitywhichisgreaterthan n where n isisthecardinalityoftheset V. But theset V \{x}, foreverygivenneutrosophicvertexisoptimal-neutrosophicdominatingsethascardinalitywhichisgreaterthan n 1 where n isisthe cardinalityoftheset V. Theresultisobtained.
Proposition3.7.12. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) S ismaximumsetofverticeswhichformahyperedge.Then S isoptimalneutrosophic-coloringsetand Σs∈S σ(S) isoptimal-neutrosophic-coloringnumber.
Proof. Supposeneutrosophichypergraph NHG =(V,E,σ,µ) Consider S is maximumsetofverticeswhichformahyperedge.Thusallverticesof S have incidenttohyperedge.Itimpliesthenumberofdifferentcolorsequalsto cardinalityof S. Therefore,optimal-neutrosophic-coloringnumber ≥ Σs∈S σ(S)
Inotherhand, S ismaximumsetofverticeswhichformahyperedge.Itinduces optimal-neutrosophic-coloringnumber ≤ Σs∈S σ(S).
So S isneutrosophic-coloringset.Hence S isoptimal-neutrosophic-coloringset and Σs∈S σ(S) isoptimal-neutrosophic-coloringnumber.
3.8OptimalSetsForNeutrosophicHypergraphs
Proposition3.8.1. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) If S isneutrosophic-dominatingset,then D contains S isneutrosophic-dominating set. 114
3.NeutrosophicHypergraphs
Proof. Considerneutrosophichypergraph NHG =(V,E,σ,µ). Suppose S is neutrosophic-dominatingset.Thenallneutrosophicverticesareneutrosophicdominated.Thus D contains S isneutrosophic-dominatingset.
Proposition3.8.2. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) If S isneutrosophic-resolvingset,then D contains S isneutrosophic-resolvingset.
Proof. Supposeneutrosophichypergraph NHG =(V,E,σ,µ) Consider S is neutrosophic-resolvingset.HenceAlltwogivenneutrosophicverticesare neutrosophic-resolvedbyatleastoneneutrosophicvertexof S. Itinduces D contains S isneutrosophic-resolvingset.
Proposition3.8.3. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) If S isneutrosophic-coloringset,then D contains S isneutrosophic-coloringset.
Proof. Supposeneutrosophichypergraph NHG =(V,E,σ,µ). Consider S is neutrosophic-coloringset.Soallneutrosophicverticeswhichhaveacommon neutrosophichyperedgehavedifferentcolors.Thuseveryneutrosophicvertex neutrosophic-coloredbyaneutrosophicvertexof S. Itinduceseveryneutrosophic vertexwhichhasacommonneutrosophichyperedgehasdifferentcolorswith otherneutrosophicverticesbelongtothatneutrosophichyperedge.then D contains S isneutrosophic-coloringset.
Proposition3.8.4. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) Then V isneutrosophic-dominatingset.
Proof. Supposeneutrosophichypergraph NHG =(V,E,σ,µ) Since V \{x} isneutrosophic-dominatingset.Then V contains V \{x} isneutrosophicdominatingset.
Proposition3.8.5. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) Then V isneutrosophic-resolvingset.
Proof. Supposeneutrosophichypergraph NHG =(V,E,σ,µ) Ifthere’sno neutrosophicvertex,thenallneutrosophicverticesareneutrosophic-resolved. HenceifIchoose V, thenthere’snoneutrosophicvertexsuchthatneutrosophic vertexisneutrosophic-resolved.Itimplies V isneutrosophic-resolvingsetbut V isn’toptimal-neutrosophic-resolvingset.SinceifIconstructonesetfrom V suchthatonlyoneneutrosophicvertexisoutof S, then S isneutrosophicresolvingset.Itimplies V isn’toptimal-neutrosophic-resolvingset.Thus V is neutrosophic-resolvingset.
Proposition3.8.6. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) Then V isneutrosophic-coloringset.
Proof. Supposeneutrosophichypergraph NHG =(V,E,σ,µ). Allneutrosophic verticesbelongtoaneutrosophichyperedgehavetocolordifferently.If V is chosen,thenallneutrosophicverticeshavedifferentcolors.Itinducesthat n colorsareusedwhere n isthenumberofneutrosophicvertices.Every neutrosophicvertexhasuniquecolor.Thus V isneutrosophic-coloringset.
3.8.OptimalSetsForNeutrosophicHypergraphs
115
3.9OptimalSetsandNumbersForFamilyofNeutrosophic Hypergraphs
Proposition3.9.1. Assume G isafamilyofneutrosophichypergraphs.Then V isneutrosophic-dominatingsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofneutrosophichypergraphs.Thus V is neutrosophic-dominatingsetforeverygivenneutrosophichypergraphof G Itimplies V isneutrosophic-dominatingsetforallmembersof G, simultaneously.
Proposition3.9.2. Assume G isafamilyofneutrosophichypergraphs.Then V isneutrosophic-resolvingsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofneutrosophichypergraphs.Thus V is neutrosophic-resolvingsetforeverygivenneutrosophichypergraphof G It implies V isneutrosophic-resolvingsetforallmembersof G, simultaneously.
Proposition3.9.3. Assume G isafamilyofneutrosophichypergraphs.Then V isneutrosophic-coloringsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofneutrosophichypergraphs.Thus V is neutrosophic-coloringsetforeverygivenneutrosophichypergraphof G It implies V isneutrosophic-coloringsetforallmembersof G, simultaneously.
Proposition3.9.4. Assume G isafamilyofneutrosophichypergraphs.Then V \{x} isneutrosophic-dominatingsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofneutrosophichypergraphs.Thus V \{x} is neutrosophic-dominatingsetforeverygivenneutrosophichypergraphof G One neutrosophicvertexisoutof V \{x}. It’sneutrosophic-dominatedfromany neutrosophicvertexin V \{x} Henceeverygiventwoneutrosophicvertices areneutrosophic-dominatedfromanyneutrosophicvertexin V \{x} Itimplies V \{x} isneutrosophic-dominatingsetforallmembersof G, simultaneously.
Proposition3.9.5. Assume G isafamilyofneutrosophichypergraphs.Then V \{x} isneutrosophic-resolvingsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofneutrosophichypergraphs.Thus V \{x} is neutrosophic-resolvingsetforeverygivenneutrosophichypergraphof G One neutrosophicvertexisoutof V \{x} It’sneutrosophic-resolvedfromany neutrosophicvertexin V \{x} Henceeverygiventwoneutrosophicvertices areneutrosophic-resolvedfromanyneutrosophicvertexin V \{x}. Itimplies V \{x} isneutrosophic-resolvingsetforallmembersof G, simultaneously.
Proposition3.9.6. Assume G isafamilyofneutrosophichypergraphs.Then V \{x} isn’tneutrosophic-coloringsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofneutrosophichypergraphs.Thus V \{x} isn’t neutrosophic-coloringsetforeverygivenneutrosophichypergraphof G. One neutrosophicvertexisoutof V \{x} Itisn’tneutrosophic-coloredfromany neutrosophicvertexin V \{x} Henceeverygiventwoneutrosophicvertices aren’tneutrosophic-coloredfromanyneutrosophicvertexin V \{x} Itimplies V \{x} isn’tneutrosophic-coloringsetforallmembersof G, simultaneously.
3.NeutrosophicHypergraphs
116
Proposition3.9.7. Assume G isafamilyofneutrosophichypergraphs.Then unionofneutrosophic-dominatingsetsfromeachmemberof G isneutrosophicdominatingsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofneutrosophichypergraphs.Foreverychosen neutrosophichypergraph,there’soneneutrosophic-dominatingsetinthe unionofneutrosophic-dominatingsetsfromeachmemberof G. Thusunionof neutrosophic-dominatingsetsfromeachmemberof G isneutrosophic-dominating setforeverygivenneutrosophichypergraphof G Evenoneneutrosophicvertex isn’toutoftheunion.It’sneutrosophic-dominatedfromanyneutrosophicvertex intheunion.Henceeverygiventwoneutrosophicverticesareneutrosophicdominatedfromanyneutrosophicvertexinunionofneutrosophic-coloringsets. Itimpliesunionofneutrosophic-coloringsetsisneutrosophic-dominatingset forallmembersof G, simultaneously.
Proposition3.9.8. Assume G isafamilyofneutrosophichypergraphs.Then unionofneutrosophic-resolvingsetsfromeachmemberof G isneutrosophicresolvingsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofneutrosophichypergraphs.Foreverychosen neutrosophichypergraph,there’soneneutrosophic-resolvingsetintheunionof neutrosophic-resolvingsetsfromeachmemberof G Thusunionofneutrosophicresolvingsetsfromeachmemberof G isneutrosophic-resolvingsetforevery givenneutrosophichypergraphof G Evenoneneutrosophicvertexisn’tout oftheunion.It’sneutrosophic-resolvedfromanyneutrosophicvertexinthe union.Henceeverygiventwoneutrosophicverticesareneutrosophic-resolved fromanyneutrosophicvertexinunionofneutrosophic-coloringsets.Itimplies unionofneutrosophic-coloringsetsisneutrosophic-resolvedsetforallmembers of G, simultaneously.
Proposition3.9.9. Assume G isafamilyofneutrosophichypergraphs.Then unionofneutrosophic-coloringsetsfromeachmemberof G isneutrosophiccoloringsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofneutrosophichypergraphs.Foreverychosen neutrosophichypergraph,there’soneneutrosophic-coloringsetintheunionof neutrosophic-coloringsetsfromeachmemberof G Thusunionofneutrosophiccoloringsetsfromeachmemberof G isneutrosophic-coloringsetforeverygiven neutrosophichypergraphof G Evenoneneutrosophicvertexisn’toutofthe union.It’sneutrosophic-coloredfromanyneutrosophicvertexintheunion. Henceeverygiventwoneutrosophicverticesareneutrosophic-coloredfromany neutrosophicvertexinunionofneutrosophic-coloringsets.Itimpliesunion ofneutrosophic-coloringsetsisneutrosophic-coloredsetforallmembersof G, simultaneously.
Proposition3.9.10. Assume G isafamilyofneutrosophichypergraphs.For everygivenneutrosophicvertex,there’soneneutrosophichypergraphsuchthat thevertexhasanotherneutrosophicvertexwhichareincidenttoaneutrosophic hyperedge.Ifforgivenneutrosophicvertex,allneutrosophicverticeshavea commonneutrosophichyperedgeinthisway,then V \{x} isoptimal-neutrosophicdominatingsetforallmembersof G, simultaneously.
3.9.OptimalSetsandNumbersForFamilyofNeutrosophicHypergraphs
117
Proof. Suppose G isafamilyofneutrosophichypergraphs.Forallneutrosophic hypergraphs,there’snoneutrosophic-dominatingsetfromanyofmemberof G Thus V \{x} isneutrosophic-dominatingsetforeverygivenneutrosophic hypergraphof G Foreverygivenneutrosophicvertex,there’soneneutrosophic hypergraphsuchthatthevertexhasanotherneutrosophicvertexwhichare incidenttoaneutrosophichyperedge.Onlyoneneutrosophicvertexisout of V \{x} It’sneutrosophic-dominatedfromanyneutrosophicvertexinthe V \{x} Henceeverygiventwoneutrosophicverticesareneutrosophic-dominated fromanyneutrosophicvertexin V \{x} Itimplies V \{x} isneutrosophicdominatingsetforallmembersof G, simultaneously.Ifforgivenneutrosophic vertex,allneutrosophicverticeshaveacommonneutrosophichyperedgeinthis way,then V \{x} isoptimal-neutrosophic-dominatingsetforallmembersof G, simultaneously.
Proposition3.9.11. Assume G isafamilyofneutrosophichypergraphs.For everygivenneutrosophicvertex,there’soneneutrosophichypergraphsuchthat theneutrosophicvertexhasanotherneutrosophicvertexwhichareincidentto aneutrosophichyperedge.Ifforgivenneutrosophicvertex,allneutrosophic verticeshaveacommonneutrosophichyperedgeinthisway,then V \{x} is optimal-neutrosophic-resolvingsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofneutrosophichypergraphs.Forallneutrosophic hypergraphs,there’snoneutrosophic-resolvingsetfromanyofmemberof G Thus V \{x} isneutrosophic-resolvingsetforeverygivenneutrosophic hypergraphof G Foreverygivenneutrosophicvertex,there’soneneutrosophic hypergraphsuchthatthevertexhasanotherneutrosophicvertexwhichare incidenttoaneutrosophichyperedge.Onlyoneneutrosophicvertexisout of V \{x} It’sneutrosophic-resolvedfromanyneutrosophicvertexinthe V \{x} Henceeverygiventwoneutrosophicverticesareneutrosophic-resolving fromanyneutrosophicvertexin V \{x} Itimplies V \{x} isneutrosophicresolvedsetforallmembersof G, simultaneously.Ifforgivenneutrosophic vertex,allneutrosophicverticeshaveacommonneutrosophichyperedgeinthis way,then V \{x} isoptimal-neutrosophic-resolvingsetforallmembersof G, simultaneously.
Proposition3.9.12. Assume G isafamilyofneutrosophichypergraphs.For everygivenneutrosophicvertex,there’soneneutrosophichypergraphsuchthat theneutrosophicvertexhasanotherneutrosophicvertexwhichareincidentto aneutrosophichyperedge.Ifforgivenneutrosophicvertex,allneutrosophic verticeshaveacommonneutrosophichyperedgeinthisway,then V isoptimalneutrosophic-coloringsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofneutrosophichypergraphs.Forallneutrosophic hypergraphs,there’snoneutrosophic-coloringsetfromanyofmemberof G Thus V isneutrosophic-coloringsetforeverygivenneutrosophichypergraphsof G For everygivenneutrosophicvertex,there’soneneutrosophichypergraphsuchthat thevertexhasanotherneutrosophicvertexwhichareincidenttoaneutrosophic hyperedge.Noneutrosophicvertexisoutof V. It’sneutrosophic-coloredfrom anyneutrosophicvertexinthe V. Henceeverygiventwoneutrosophicvertices areneutrosophic-coloredfromanyneutrosophicvertexin V. Itimplies V is neutrosophic-coloringsetforallmembersof G, simultaneously.Ifforgiven
3.NeutrosophicHypergraphs
118
neutrosophicvertex,allneutrosophicverticeshaveacommonneutrosophic hyperedgeinthisway,then V isoptimal-neutrosophic-coloringsetforall membersof G, simultaneously.
3.10ApplicationsinTimeTableandScheduling
Designingtheprogramstoachievesomegoalsisgeneralapproachtoapplyon someissuestofunctionproperly.Separationhaskeyroleinthecontextofthis style.Separatingthedurationofworkwhichareconsecutive,isthematterand ithasimportanttoavoidmixingup.
Step1.(Definition) Timetableisanapproachtogetsomeattributestodo theworkfastandproper.Thestyleofschedulingimpliesspecialattention tothetaskswhichareconsecutive.
Step2.(Issue) Schedulingofprogramhasfacedwithdifficultiestodifferamid consecutivesection.Beyondthat,sometimessectionsarenotthesame.
Step3.(Model) AsFigure (3.11),thesituationisdesignedasamodel.The modelusesdatatoassigneverysectionandtoassigntorelationamid section,threenumbersbelongunitintervaltostateindeterminacy, possibilitiesanddeterminacy.There’sonerestrictioninthat,thenumbers amidtwosectionsareatleastthenumberoftherelationamidthem. Table(4.5),clarifiesabouttheassignednumberstothesesituation.
Figure3.5:Verticesaresuspicionsaboutchoosingthem. nhg1

Table3.1:SchedulingconcernsitsSubjectsanditsConnectionsasa NeutrosophicHypergraphinaModel. tbl1c
Sectionsof NHG n1 n2 n9 Values (0 99, 0 98, 0 55)(0 74, 0 64, 0 46) (0 99, 0 98, 0 55) Connectionsof NHG E1 E2 E3 Values (0.01, 0.01, 0.01)(0.01, 0.01, 0.01)(0.01, 0.01, 0.01)
Step4.(Solution) AsFigure (3.11) shows,neutrosophichypergraphasmodel, proposestousedifferenttypesofcoloring,resolvinganddominatingas numbers,sets,optimalnumbers,optimalsetsandetcetera.
3.10.ApplicationsinTimeTableandScheduling
119
(a): Thenotionsofdominatingareapplied.
(i): n1 neutrosophic-dominateseveryvertexfromthesetofvertices {n7,n8,n9,n2,n3}.n4 neutrosophic-dominateseveryvertexfrom thesetofvertices {n6,n5,n3}.n4 doesn’tneutrosophic-dominate everyvertexfromthesetofvertices {n1,n2,n7,n8,n9}
(ii): {n1,n3} isneutrosophic-coloringsetbut {n1,n4} isoptimalneutrosophic-dominatingset.
(iii): (1 53, 1 22, 0 71) isoptimal-neutrosophic-dominatingnumber.
(b): Thenotionsofresolvingareapplied.
(i): n1 neutrosophic-resolvestwovertices n4 and n6.
(ii): V \{n1,n4} isneutrosophic-resolvessetbut V \{n2,n4,n9} is optimal-neutrosophic-resolvingset.
(iii): (5, 94, 6.36, 3.3) isoptimal-neutrosophic-resolvingnumber.
(c): Thenotionsofcoloringareapplied.
(i): n1 neutrosophic-colorseveryvertexfromthesetofvertices {n7,n8,n9,n2,n3}.n4 neutrosophic-colorseveryvertexfromthe setofvertices {n6,n5,n3}.n4 doesn’tneutrosophic-dominate everyvertexfromthesetofvertices {n1,n2,n7,n8,n9}.
(ii): {n1,n5,n7,n8,n9,n6,n4} isneutrosophic-coloringsetbut {n1,n5,n7,n8,n2,n4} isoptimal-neutrosophic-coloringset.
(iii): (5 24, 4 8, 2 82) isoptimal-neutrosophic-coloringnumber.
3.11OpenProblems
Thethreenotionsofcoloring,resolvinganddominatingareintroducedon neutrosophichypergraphs.Thus,
Question3.11.1. Isitpossibletouseothertypesneutrosophichyperedgesto definedifferenttypesofcoloring,resolvinganddominatingonneutrosophic hypergraphs?
Question3.11.2. Areexistedsomeconnectionsamidthecoloring,resolving anddominatinginsidethisconceptandexternalconnectionswithothertypesof coloring,resolvinganddominatingonneutrosophichypergraphs?
Question3.11.3. Isitpossibletoconstructsomeclassesonneutrosophic hypergraphswhichhave“nice”behavior?
Question3.11.4. Whichapplicationsdomakeanindependentstudyto applythesethreetypescoloring,resolvinganddominatingonneutrosophic hypergraphs?
Problem3.11.5. Whichparametersarerelatedtothisparameter?
Problem3.11.6. Whichapproachesdoworktoconstructapplicationstocreate independentstudy?
Problem3.11.7. Whichapproachesdoworktoconstructdefinitionswhichuse allthreedefinitionsandtherelationsamidtheminsteadofseparatedefinitions tocreateindependentstudy?
3.NeutrosophicHypergraphs
120
3.12ConclusionandClosingRemarks
Thisstudyusesmixedcombinationsofdifferenttypesofdefinitions,including coloring,resolvinganddominatingtostudyonneutrosophichypergraphs.The connectionsofneutrosophicverticeswhichareclarifiedbygeneralhyperedges differthemfromeachotherandandputthemindifferentcategoriestorepresent onerepresentativeforeachcolor,resolveranddominator.Furtherstudiescould beaboutchangesinthesettingstocomparethisnotionamiddifferentsettings ofneutrosophichypergraphstheory.Onewayisfindingsomerelationsamid threedefinitionsofnotionstomakesensibledefinitions.InTable (4.6),some limitationsandadvantagesofthisstudyarepointedout.
3.13ClassesOfNeutrosophicHypergraphs
Secondcaseforthecontentsistousethearticlefrom[6].Thecontentsareused inthewaythat,usagesofnewcontentsarepreferencesandthepreliminaries arepassedinthebeginningoffirstchapter.
3.14Co-degreeandDegreeofclassesofNeutrosophic Hypergraphs
3.15Abstract
Newsettingisintroducedtostudytypesofcoloringnumbers,degreeofvertices, degreeofhyperedges,co-degreeofvertices,co-degreeofhyperedges,neutrosophicdegreeofvertices,neutrosophicdegreeofhyperedges,neutrosophic co-degreeofvertices,neutrosophicco-degreeofhyperedges,neutrosophicnumberofvertices,neutrosophicnumberofhyperedgesinneutrosophichypergraphs. Differenttypesofproceduresincludingneutrosophic (r,n) regularhypergraphs andneutrosophiccomplete r partitehypergraphsareproposedinthisway, someresultsareobtained.Generalclassesofneutrosophichypergraphsare usedtoobtainchromaticnumber,therepresentativesofthecolors,degreeof vertices,degreeofhyperedges,co-degreeofvertices,co-degreeofhyperedges, neutrosophicdegreeofvertices,neutrosophicdegreeofhyperedges,neutrosophic co-degreeofvertices,neutrosophicco-degreeofhyperedges,neutrosophicnum-
3.12.ConclusionandClosingRemarks
1. DefiningDimension 1.
2. DefiningDomination 3. DefiningColoring 2. ConnectionsAmidNewNotions 4. ApplyingonIndividuals 5. ApplyingonFamily 3. ConnectionsofResults
Table3.2:ABriefOverviewaboutAdvantagesandLimitationsofthisstudy tbl2c Advantages Limitations
GeneralResults
121
berofvertices,neutrosophicnumberofhyperedgesinneutrosophichypergraphs. Usingcolorstoassigntotheverticesofneutrosophichypergraphsandcharacterizingrepresentativesofthecolorsareappliedinneutrosophic (r,n) regular hypergraphsandneutrosophiccomplete r partitehypergraphs.Somequestions andproblemsareposedconcerningwaystodofurtherstudiesonthistopic. Usingdifferentwaysofstudyonneutrosophichypergraphstogetnewresults aboutnumber,degreeandco-degreeinthewaythatsomenumber,degree andco-degreegetunderstandableperspective.Neutrosophic (r,n) regular hypergraphsandneutrosophiccomplete r partitehypergraphsarestudied toinvestigateaboutthenotions,coloring,therepresentativesofthecolors, degreeofvertices,degreeofhyperedges,co-degreeofvertices,co-degreeof hyperedges,neutrosophicdegreeofvertices,neutrosophicdegreeofhyperedges, neutrosophicco-degreeofvertices,neutrosophicco-degreeofhyperedges,neutrosophicnumberofvertices,neutrosophicnumberofhyperedgesinneutrosophic (r,n) regularhypergraphsandneutrosophiccomplete r partitehypergraphs. Inthisway,setsofrepresentativesofcolors,degreeofvertices,degreeof hyperedges,co-degreeofvertices,co-degreeofhyperedges,neutrosophicdegree ofvertices,neutrosophicdegreeofhyperedges,neutrosophicco-degreeofvertices,neutrosophicco-degreeofhyperedges,neutrosophicnumberofvertices, neutrosophicnumberofhyperedgeshavekeypointstogetnewresultsbut insomecases,thereareusagesofsetsandnumbersinsteadofoptimalones. Simultaneously,notionschromaticnumber,therepresentativesofthecolors, degreeofvertices,degreeofhyperedges,co-degreeofvertices,co-degreeof hyperedges,neutrosophicdegreeofvertices,neutrosophicdegreeofhyperedges, neutrosophicco-degreeofvertices,neutrosophicco-degreeofhyperedges,neutrosophicnumberofvertices,neutrosophicnumberofhyperedgesareappliedinto neutrosophichypergraphs,especially,neutrosophic (r,n) regularhypergraphs andneutrosophiccomplete r partitehypergraphstogetsensibleresultsabout theirstructures.Basicfamiliaritieswithneutrosophichypergraphstheoryand hypergraphtheoryareproposedforthisarticle.
Keywords: Degree,Coloring,Co-degree
AMSSubjectClassification: 05C17,05C22,05E45
3.16MotivationandContributions
Inthisstudy,there’sanideawhichcouldbeconsideredasamotivation.
Question3.16.1. Isitpossibletousemixedversionsofideasconcerning “neutrosophicdegree”,“neutrosophicco-degree”and“neutrosophiccoloring”to definesomenotionswhichareappliedtoneutrosophichypergraphs?
It’smotivationtofindnotionstouseinanyclassesofneutrosophic hypergraphs.Real-worldapplicationsabouttimetableandschedulingare anotherthoughtswhichleadtobeconsideredasmotivation.Connectionsamid twoitemshavekeyrolestoassigncolorsandintroducingdifferenttypesofdegree ofvertices,degreeofhyperedges,co-degreeofvertices,co-degreeofhyperedges, neutrosophicdegreeofvertices,neutrosophicdegreeofhyperedges,neutrosophic co-degreeofvertices,neutrosophicco-degreeofhyperedges,neutrosophicnumber
3.NeutrosophicHypergraphs
122
3.17.NewIdeasForNeutrosophicHypergraphs
ofvertices,neutrosophicnumberofhyperedgesinneutrosophichypergraphs. Thusthey’reusedtodefinenewideaswhichconcludetothestructureof coloring,degreeandco-degree.Theconceptofhavinggeneralneutrosophic hyperedgeinspiresmetostudythebehaviorofgeneralneutrosophichyperedge inthewaythat,typesofcoloringnumbers,degreeofvertices,degreeof hyperedges,co-degreeofvertices,co-degreeofhyperedges,neutrosophicdegree ofvertices,neutrosophicdegreeofhyperedges,neutrosophicco-degreeof vertices,neutrosophicco-degreeofhyperedges,neutrosophicnumberofvertices, neutrosophicnumberofhyperedgesinneutrosophichypergraphsareintroduced. Theframeworkofthisstudyisasfollows.Inthebeginning,Iintroduced basicdefinitionstoclarifyaboutpreliminaries.Insection“NewIdeasFor NeutrosophicHypergraphs”,newnotionsofcoloring,degreeofvertices,degree ofhyperedges,co-degreeofvertices,co-degreeofhyperedges,neutrosophic degreeofvertices,neutrosophicdegreeofhyperedges,neutrosophicco-degreeof vertices,neutrosophicco-degreeofhyperedges,neutrosophicnumberofvertices, neutrosophicnumberofhyperedgesinneutrosophichypergraphsareintroduced. Insection“ApplicationsinTimeTableandScheduling”,oneapplicationisposed forneutrosophichypergraphsconcerningtimetableandschedulingwhenthe suspicionsareaboutchoosingsomesubjects.Insection“OpenProblems”,some problemsandquestionsforfurtherstudiesareproposed.Insection“Conclusion andClosingRemarks”,gentlediscussionaboutresultsandapplicationsare featured.Insection“ConclusionandClosingRemarks”,abriefoverview concerningadvantagesandlimitationsofthisstudyalongsideconclusionsare formed.
3.17NewIdeasForNeutrosophicHypergraphs
Question3.17.1. What-ifthenotionofcompleteproposessomeclassesof neutrosophichypergraphs?
Inthesettingofneutrosophichypergraphs,thenotionofcompletehave introducedsomeclasses.Sincethevertexcouldhaveanynumberofarbitrary hyperedges.Thisnotionistooclosetothenotionofregularity.Thustheidea ofcompletehasanobviousstructureinthat,everyhyperedgehas n verticesso there’sonlyonehyperedge.
Definition3.17.2. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) It’s denotedby NHGr n andit’s (r,n) regular ifeveryhyperedgehasexactly r verticesinthewaythat,all r subsetsoftheverticeshaveanuniquehyperedge where r ≤ n and |V | = n.
Example3.17.3. InFigure(3.9), NHG3 4 isshown.
Definition3.17.4. Assumeneutrosophichypergraph NHG =(V,E,σ,µ)
(i): Maximumnumber ismaximumnumberofhyperedgeswhichare incidenttoavertexandit’sdenotedby ∆(NHG);
(ii): Minimumnumber isminimumnumberofhyperedgeswhichareincident toavertexandit’sdenotedby δ(NHG);
(iii): Maximumvalue ismaximumvalueofverticesandit’sdenotedby ∆n(NHG);
123
Figure3.6: NHG3 4 =(V,E,σ,µ) isneutrosophic (3, 4) regularhypergraph. nhg6 (iv): Minimumvalue isminimumvalueofverticesandit’sdenotedby δn(NHG)

Example3.17.5. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) as Figure(3.9).
(i): ∆(NHG)=3;
(ii): δ(NHG)=3;
(iii): ∆n(NHG)=(0 99, 0 98, 0 55);
(iv): δn(NHG)=(0 99, 0 98, 0 55)
Proposition3.17.6. Assumeneutrosophichypergraph NHGr n =(V,E,σ,µ) whichis (r,n) regular.Then ∆(NHG)= δ(NHG)
Proof. Considerneutrosophichypergraph NHGr n =(V,E,σ,µ) whichis (r,n) regular.Everyhyperedgehassamenumberofvertices.Hyperedgesaredistinct. Itimpliesthenumberofhyperedgeswhichareincidenttoeveryvertexisthe same.
Proposition3.17.7. Assumeneutrosophichypergraph NHGr n =(V,E,σ,µ) whichis (r,n) regular.Thenthenumberofhyperedgesequalsto n choose r.
Proof. Supposeneutrosophichypergraph NHGr n =(V,E,σ,µ) whichis (r,n) regular.Everyhyperedgehas r vertices.Thus r subsetsof n formhyperedges. Itinduces n choose r.
Proposition3.17.8. Assumeneutrosophichypergraph NHGr n =(V,E,σ,µ) whichis (r,n) regular.Then
(i): Chromaticnumberisatleast r;
(ii): Chromaticnumberisatmost ∆r;
(iii): Neutrosophicchromaticnumberisatmost ∆nr.
3.NeutrosophicHypergraphs
124
Proof. (i). Suppose NHGr n =(V,E,σ,µ). Everyhyperedgehas r vertices.It impliesthesetofrepresentativeshasatleast r members.Hencechromatic numberisatleast r.
(ii) Suppose NHGr n =(V,E,σ,µ) Everyhyperedgehas r vertices.Itimplies thesetofrepresentativeshasatleast r members.Ifallverticeshaveatleast onecommonhyperedge,thenchromaticnumberisatmost ∆r. Thuschromatic numberisatmost ∆r.
(iii) Consider NHGr n =(V,E,σ,µ) Everyhyperedgehas r vertices.Itimplies thesetofrepresentativeshasatleast r members.Ifallverticeshaveatleast onecommonhyperedge,thenneutrosophicchromaticnumberisatmost ∆nr. Thusneutrosophicchromaticnumberisatmost ∆nr.
Question3.17.9. What-ifthenotionofcompleteproposessomeclassesof neutrosophichypergraphswithsomeparts?
Inthesettingofneutrosophichypergraphs,wheneveryparthasspecific attributeinsideandoutside,thenotionofcompleteisappliedtopartstoform theideaofcompleteness.
Definition3.17.10. Assumeneutrosophichypergraph NHG =(V,E,σ,µ). It’sdenotedby NHGr n1,n2, ,nr andit’s complete r partite if V canbe partitionedinto r non-emptyparts, Vi, andeveryhyperedgehasonlyonevertex fromeachpartwhere ni isthenumberofverticesinpart Vi
Example3.17.11. InFigure(3.10), NHG3 3,3,3 =(V,E,σ,µ) isshown.
Figure3.7: NHG3 3,3,3 =(V,E,σ,µ) isneutrosophiccomplete 3 partite hypergraph. nhg7
Proposition3.17.12. Foranygiven r, thenumberofneutrosophiccomplete r partitehypergraph NHGr p1,p2, ,pr =(V,E,σ,µ) isatmost p1 × p2, ×···× pr

3.17.NewIdeasForNeutrosophicHypergraphs
125
Proof. Assume r isgiven.Consider NHGr p1,p2, ,pr =(V,E,σ,µ) isneutrosophiccomplete r partitehypergraph.Anypossiblehyperedgehasto chooseexactlyonevertexfromeverypart.Firstparthas p1 vertices.Thus thereare p1 choices.Secondparthas p2 verticesandetcetera.Thusfor anygiven r, thenumberofneutrosophiccomplete r partitehypergraph NHGr p1,p2, ,pr =(V,E,σ,µ) isatmost p1 × p2 ×···× pr.
Proposition3.17.13. Assumeneutrosophiccomplete r partitehypergraph NHGr n1,n2, ,nr =(V,E,σ,µ) Then (i): Chromaticnumberisatleast r; (ii): Neutrosophicchromaticnumberisatleast min X⊆V and X isr-subset Σx∈X σ(x).
Proof. (i). Supposeneutrosophiccomplete r partitehypergraph NHGr n1,n2, ,nr . Everyhyperedgehas r vertices.Itimpliesthesetofrepresentativeshas r members.Hencechromaticnumberisleast r. (ii) Considerneutrosophiccomplete r partitehypergraph NHGr n1,n2, ,nr Everyhyperedgehas r vertices.Itimpliesthesetofrepresentativeshas r members.Ifallverticeshaveatleastonecommonhyperedge,thenneutrosophic chromaticnumberisatleast minX⊆V and X isr-subset Σx∈X σ(x)
Definition3.17.14. Assumeneutrosophichypergraph NHG =(V,E,σ,µ).
(i): A neutrosophicnumber ofvertices x1,x2, ··· ,xn is Σn i=1σ(xi) (ii): A neutrosophicnumber ofhyperedges e1,e2, ,en is Σn i=1µ(ei)
Example3.17.15. Igetsomeclarificationsaboutnewdefinitions.
(i): InFigure(3.9), NHG3 4 isshown.
(a): Aneutrosophicnumberofvertices n1,n2,n3 is Σ3 i=1σ(ni)=(2 97, 2 94, 1 65)
(b): Aneutrosophicnumberofhyperedges e1,e2,e3 is Σ3 i=1σ(ei)=(1 82, 1 12, 0 78) where e1 =(0 54, 0 24, 0 16),e2 =(0 74, 0 64, 0 46),e3 = (0 54, 0 24, 0 16)
(ii): InFigure(3.10), NHG3 3,3,3 =(V,E,σ,µ) isshown. 126
3.NeutrosophicHypergraphs
(a): Aneutrosophicnumberofvertices n1,n2,n3 is Σ3 i=1σ(ni)=(2 97, 2 94, 1 65)
(b): Aneutrosophicnumberofhyperedges e1,e2,e3 is Σ3 i=1σ(ei)=(1.82, 1.12, 0.78). where e1 =(0 54, 0 24, 0 16),e2 =(0 74, 0 64, 0 46),e3 = (0 54, 0 24, 0 16)
Proposition3.17.16. Assumeneutrosophichypergraph NHG =(V,E,σ,µ). A neutrosophicnumberofverticesisatleast δn andatmost On
Proof. Supposeneutrosophichypergraph NHG =(V,E,σ,µ) Let v beagiven vertex.Then σ(v) ≥ minv∈V σ(v) Thus σ(v) ≥ δn Soaneutrosophicnumber ofverticesisatleast δn.σ(v) ≤ Σv∈V σ(v) Thus σ(v) ≤On Soaneutrosophic numberofverticesisatmost On. Henceaneutrosophicnumberofverticesis atleast δn andatmost On
Proposition3.17.17. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) Aneutrosophicnumberofhyperedgesisatleast δe n andatmost Sn where δe n =mine∈E µ(e)
Proof. Supposeneutrosophichypergraph NHG =(V,E,σ,µ) Let e beagiven hyperedge.Then µ(e) ≥ mine∈E µ(e) Thus µ(v) ≥ δe n Soaneutrosophic numberofhyperedgesisatleast δe n.µ(e) ≤ Σe∈E µ(e). Thus µ(e) ≤Sn. Soa neutrosophicnumberofhyperedgesisatmost Sn Henceaneutrosophicnumber ofhyperedgesisatleast δe n andatmost Sn Definition3.17.18. Assumeneutrosophichypergraph NHG =(V,E,σ,µ)
(i): A degree ofvertex x isthenumberofhyperedgeswhichareincidentto x.
(ii): A neutrosophicdegree ofvertex x istheneutrosophicnumberof hyperedgeswhichareincidentto x.
(iii): A degree ofhyperedge e isthenumberofverticeswhich e isincidentto them.
(iv): A neutrosophicdegree ofhyperedge e istheneutrosophicnumberof verticeswhich e isincidenttothem.
(v): A co-degree ofvertices x1,x2, ,xn isthenumberofhyperedgeswhich areincidentto x1,x2, ,xn
(vi): A neutrosophicco-degree ofvertices x1,x2, ··· ,xn istheneutrosophic numberofhyperedgeswhichareincidentto x1,x2, ··· ,xn
(vii): A co-degree ofhyperedges e1,e2, ,en isthenumberofverticeswhich e1,e2, ,en areincidenttothem.
(viii): A neutrosophicco-degree ofhyperedges e1,e2, ,en istheneutrosophicnumberofverticeswhich e1,e2, ,en areincidenttothem.
3.17.NewIdeasForNeutrosophicHypergraphs
127
Example3.17.19. Igetsomeclarificationsaboutnewdefinitions.
(i): InFigure(3.9), NHG3 4 isshown.
(a): Adegreeofanyvertexis 3.
(b): Aneutrosophicdegreeofvertex n1 is (2.07, 1.46, 0.87).
(c): Adegreeofhyperedge e where µ(e)=(0.99, 0.98, 0.55) is 3.
(d): Aneutrosophicdegreeofhyperedge e where µ(e)=(0.99, 0.98, 0.55) is (2 97, 2 94, 1 65)
(e): Aco-degreeofvertices n1,n3 is 2
(f ): Aneutrosophicco-degreeofvertices n1,n3 is (1 53, 1 22, 0 71)
(g): Aco-degreeofhyperedges e1,e2 where µ(e1)=(0 99, 0 98, 0 55) and µ(e2)=(0 54, 0 24, 0 16) is 2
(h): Aneutrosophicco-degreeofhyperedges e1,e2 where µ(e1)= (0 99, 0 98, 0 55) and µ(e2)=(0 54, 0 24, 0 16) is (1 98, 1 96, 1 1)
(ii): InFigure(3.10), NHG3 3,3,3 =(V,E,σ,µ) isshown.
(a): Adegreeofanyvertex n1,n2,n4,n6,n8,n9 is 1 anddegreeofany vertex n3,n5,n7 is 2
(b): Aneutrosophicdegreeofvertex n1,n2,n4,n6,n8,n9 is (0 99, 0 98, 0 55) anddegreeofanyvertex n3,n5,n7 is (1 98, 1 96, 1 1)
(c): Adegreeofanyhyperedgeis 3
(d): Aneutrosophicdegreeofhyperedgeis (2 97, 2 94, 1 65)
(e): Aco-degreeofvertices n1,n4 is 1
(f ): Aneutrosophicco-degreeofvertices n1,n4 is (0 54, 0 24, 0 16)
(g): Aco-degreeofhyperedges e1,e2 where µ(e1)=(0 99, 0 98, 0 55) and µ(e2)=(0.54, 0.24, 0.16) is 1.
(h): Aneutrosophicco-degreeofhyperedges e1,e2 where µ(e1)= (0.99, 0.98, 0.55) and µ(e2)=(0.54, 0.24, 0.16) is (0.99, 0.98, 0.55).
Proposition3.17.20. Assumeneutrosophiccomplete r partitehypergraph NHGr p1,p2, ,pr =(V,E,σ,µ)
(i): Adegreeofvertex x isatmost p2 ×···× pr.
(ii): Adegreeofhyperedge e is r.
(iii): Aco-degreeofvertices x1,x2, ,xt isatmost pt+1 ×···× pr.
(iv): Aco-degreeofhyperedges e1,e2, ,et is r t.
3.NeutrosophicHypergraphs
128
Proof. (i). Supposeneutrosophiccomplete r partitehypergraph NHGr p1,p2, ,pr = (V,E,σ,µ) Vertex x belongstopartfirstpart. x ischosensoforsecondpart, thereare p2 choicesandetcetera.Byit’sneutrosophiccomplete r partite hypergraph NHGr p1,p2, ,pr =(V,E,σ,µ), possiblechoicefromeverypartis exactlyonevertex.Itinducesforsecondpart,onevertexhastobechosenand etcetera.Thereforethenumberofneutrosophiccomplete r partitehypergraph NHGr p1,p2, ,pr =(V,E,σ,µ), when x ischosen,introducesbiggestpossible numberofdegreeof x whichis p2 ×···× pr Henceadegreeofvertex x isat most p2 ×···× pr
(ii) Considerneutrosophiccomplete r partitehypergraph NHGr p1,p2, ,pr = (V,E,σ,µ). Vertex x belongstopartfirstpart. x ischosensoforsecondpart, thereisonechoiceandetcetera.Byit’sneutrosophiccomplete r partite hypergraph NHGr p1,p2, ,pr =(V,E,σ,µ), possiblechoicefromeverypart isexactlyonevertex.Itinducesforsecondpart,onevertexhastobe chosenandetcetera.Thereforeneutrosophiccomplete r partitehypergraph NHGr p1,p2, ,pr =(V,E,σ,µ) introducesexactnumberofdegreeof e whichis r. Henceadegreeofhyperedge e is r.
(iii) Supposeneutrosophiccomplete r partitehypergraph NHGr p1,p2, ,pr = (V,E,σ,µ) Vertices x1,x2, ··· ,xt belongtopartfirstpart,secondpart,....,and part t.x1,x2, ,xt arechosensoforpart t +1,thereare pt+1 choicesandet cetera.Byit’sneutrosophiccomplete r partitehypergraph NHGr p1,p2, ,pr = (V,E,σ,µ), possiblechoicefromeverypartisexactlyonevertex.Itinducesfor part t +1, onevertexhastobechosenandetcetera.Thereforethenumberof neutrosophiccomplete r partitehypergraph NHGr p1,p2, ,pr =(V,E,σ,µ), when x1,x2, ,xt arechosen,introducesbiggestpossiblenumberofcodegreeof x1,x2, ,xt whichis pt+1 ×···× pr Henceaco-degreeofvertices x1,x2, ,xt isatmost pt+1 ×···× pr
(iv) Considerneutrosophiccomplete r partitehypergraph NHGr p1,p2, ,pr = (V,E,σ,µ) Vertex x belongstopartfirstpart. x ischosensoforsecond part,thereisonechoiceandetcetera.Byit’sneutrosophiccomplete r partitehypergraph NHGr p1,p2, ,pr =(V,E,σ,µ), possiblechoicefrom everypartisexactlyonevertex.Itinducesforsecondpart,onevertex hastobechosenandetcetera.Thereforeneutrosophiccomplete r partite hypergraph NHGr p1,p2, ,pr =(V,E,σ,µ) introducesexactnumberofco-degree of e1,e2, ,et whichis r t. Henceaco-degreeofhyperedges e1,e2, ,et is r t.
Proposition3.17.21. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) where E ispowersetof V. Thenthenumberofhyperedgesis 2n
3.17.NewIdeasForNeutrosophicHypergraphs
129
3.NeutrosophicHypergraphs
Proof. Considerneutrosophichypergraph NHG =(V,E,σ,µ) where E ispower setof V. Thecardinalityof E is 2n Thenumberofhyperedgesis 2n
Proposition3.17.22. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) where E ispowersetof V. Then (i): Adegreeofvertex x is 2n 1 (ii): Adegreeofhyperedge e isatmost O andatleast 0 (iii): Aco-degreeofvertices x1,x2, ,xt isatmost 2n t (iv): Aco-degreeofhyperedges e1,e2, ··· ,et isatmost O− t andatleast 0.
Proof. (i) Supposeneutrosophichypergraph NHG =(V,E,σ,µ) where E is powersetof V. Vertex x ischosen.Thusallhyperedgeshavetohave x. It induces E ispowersetof V \{x} Thecardinalityof E is 2n 1 Sothenumber ofhyperedgeswhichareincidentto x, is 2n 1 . Itimpliesadegreeofvertex x is 2n 1 .
(ii) Considerneutrosophichypergraph NHG =(V,E,σ,µ) where E ispower setof V. Hyperedge e ischosen.Thusahyperedgehaseitherallverticesor novertex.Itinducesforhyperedge e, thenumberofverticesiseither O or 0 Thenadegreeofhyperedge e isatmost O andatleast 0
(iii) Supposeneutrosophichypergraph NHG =(V,E,σ,µ) where E ispower setof V. Vertices x1,x2, ,xt arechosen.Thusallhyperedgeshavetohave x1,x2, ,xt Itinduces E ispowersetof V \{x1,x2, ,xt} Thecardinality
130
3.17.NewIdeasForNeutrosophicHypergraphs
of E is 2n t . Sothenumberofhyperedgeswhichareincidentto x1,x2, ,xt, is 2n t Itimpliesaco-degreeofvertices x1,x2, ,xt is 2n t
(iv) Considerneutrosophichypergraph NHG =(V,E,σ,µ) where E ispower setof V. Hyperedges e1,e2, ,et arechosen.Thushyperedges e1,e2, ,et don’thaveallvertices.Sinceoneedgeisincidenttoallverticesandthere’sno secondedgetobeincidenttoallvertices.Itimplieshyperedges e1,e2, ,et haveallverticesexcludingonly t verticesornovertex.Itinducesforhyperedges e1,e2, ··· ,et, thenumberofverticesiseither O− t or 0 Henceaco-degreeof hyperedges e1,e2, ,et isatmost O− t andatleast 0. Proposition3.17.23. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) where E ispowersetof V. Then (i): Chromaticnumberis O;
(ii): Neutrosophicchromaticnumberis On.
Proof. (i) Supposeneutrosophichypergraph NHG =(V,E,σ,µ) where E is powersetof V. Everyhyperedgehaseitherof 0, 1, 2, , O verticesbutfor anyoftwovertices,there’satleastonehyperedgewhichisincidenttothem. Furthermore,allverticeshaveatleastonecommonhyperedgewhichis V..Since V ∈ E and V isalsoahyperedge.Itimpliesthesetofrepresentativeshas O members.Hencechromaticnumberis O
(ii) Considerneutrosophichypergraph NHG =(V,E,σ,µ) where E ispower setof V. Everyhyperedgehaseitherof 0, 1, 2, , O verticesbutforanyoftwo vertices,there’satleastonehyperedgewhichisincidenttothem.Furthermore, allverticeshaveatleastonecommonhyperedgewhichis V..Since V ∈ E and V isalsoahyperedge.Itimpliesthesetofrepresentativeshas O members. Henceneutrosophicchromaticnumberis On
131
3.18ApplicationsinTimeTableandScheduling
Designingtheprogramstoachievesomegoalsisgeneralapproachtoapplyon someissuestofunctionproperly.Separationhaskeyroleinthecontextofthis style.Separatingthedurationofworkwhichareconsecutive,isthematterand ithasimportanttoavoidmixingup.
Step1.(Definition) Timetableisanapproachtogetsomeattributestodo theworkfastandproper.Thestyleofschedulingimpliesspecialattention tothetaskswhichareconsecutive.
Step2.(Issue) Schedulingofprogramhasfacedwithdifficultiestodifferamid consecutivesection.Beyondthat,sometimessectionsarenotthesame.
Step3.(Model) AsFigure (3.12),thesituationisdesignedasamodel.The modelusesdatatoassigneverysectionandtoassigntorelationamid section,threenumbersbelongunitintervaltostateindeterminacy, possibilitiesanddeterminacy.There’sonerestrictioninthat,thenumbers amidtwosectionsareatleastthenumberoftherelationamidthem. Table(4.5),clarifiesabouttheassignednumberstothesesituation.
Figure3.8:Verticesaresuspicionsaboutchoosingthem. nhg8

3.NeutrosophicHypergraphs
n1 n2 n9 Values (0
, 0
, 0 55)(0 74, 0
, 0 46)··· (0
E
E
132
Table3.3:SchedulingconcernsitsSubjectsanditsConnectionsasa NeutrosophicHypergraphinaModel. tbl1c Sectionsof NHG
99
98
64
99, 0 98, 0 55) Connectionsof NHG E1,E2
3
4 Values (0 54, 0 24, 0 16)(0 99, 0 98, 0 55)(0 74, 0 64, 0 46)
Step4.(Solution) AsFigure (3.12) shows, NHG3 3,3,3 =(V,E,σ,µ) isneutrosophiccomplete 3 partitehypergraphasmodel,proposestousedifferent typesofdegreeofvertices,degreeofhyperedges,co-degreeofvertices, co-degreeofhyperedges,neutrosophicnumberofvertices,neutrosophic numberofhyperedgesandetcetera.
(i): Thenotionsofneutrosophicnumberareappliedonverticesand hyperedges.
(a): Aneutrosophicnumberofvertices n1,n2,n3 is Σ3 i=1σ(ni)=(2 97, 2 94, 1 65)
(b): Aneutrosophicnumberofhyperedges e1,e2,e3 is Σ3 i=1σ(ei)=(1.82, 1.12, 0.78).
where e1 =(0.54, 0.24, 0.16),e2 =(0.74, 0.64, 0.46),e3 = (0 54, 0 24, 0 16)
(ii): Thenotionsofdegree,co-degree,neutrosophicdegreeandneutrosophicco-degreeareappliedonverticesandhyperedges.
(a): Adegreeofanyvertex n1,n2,n4,n6,n8,n9 is 1 anddegreeof anyvertex n3,n5,n7 is 2
(b): Aneutrosophicdegreeofvertex n1,n2,n4,n6,n8,n9 is (0 99, 0 98, 0 55) anddegreeofanyvertex n3,n5,n7 is (1 98, 1 96, 1 1)
(c): Adegreeofanyhyperedgeis 3.
(d): Aneutrosophicdegreeofhyperedgeis (2 97, 2 94, 1 65)
(e): Aco-degreeofvertices n1,n4 is 1
(f ): Aneutrosophicco-degreeofvertices n1,n4 is (0 54, 0 24, 0 16)
(g): Aco-degreeofhyperedges e1,e2 where µ(e1)=(0 99, 0 98, 0 55) and µ(e2)=(0 54, 0 24, 0 16) is 1
(h): Aneutrosophicco-degreeofhyperedges e1,e2 where µ(e1)=(0 99, 0 98, 0 55) and µ(e2)=(0 54, 0 24, 0 16) is (0 99, 0 98, 0 55)
3.19OpenProblems
Thedifferenttypesofdegreeofvertices,degreeofhyperedges,co-degreeof vertices,co-degreeofhyperedges,neutrosophicnumberofvertices,neutrosophic numberofhyperedgesareintroducedonneutrosophichypergraphs.Thus,
Question3.19.1. Isitpossibletouseothertypesneutrosophichyperedgesto definedifferenttypesofdegreeandco-degreeinneutrosophichypergraphs?
Question3.19.2. Areexistedsomeconnectionsamiddegreeandco-degreeinside thisconceptandexternalconnectionswithothertypesofneutrosophicdegree andneutrosophicco-degreeinneutrosophichypergraphs?
Question3.19.3. Isitpossibletoconstructsomeclassesonneutrosophic hypergraphswhichhave“nice”behavior?
3.19.OpenProblems
133
Question3.19.4. Whichapplicationsdomakeanindependentstudytoapply thesetypesdegree,co-degree,neutrosophicdegreeandneutrosophicco-degreein neutrosophichypergraphs?
Problem3.19.5. Whichparametersarerelatedtothisparameter?
Problem3.19.6. Whichapproachesdoworktoconstructapplicationstocreate independentstudy?
Problem3.19.7. Whichapproachesdoworktoconstructdefinitionswhichuse alldefinitionsandtherelationsamidtheminsteadofseparatedefinitionsto createindependentstudy?
3.20ConclusionandClosingRemarks
Thisstudyintroducesdifferenttypesofdegreeofvertices,degreeofhyperedges, co-degreeofvertices,co-degreeofhyperedges,neutrosophicdegreeofvertices, neutrosophicdegreeofhyperedges,neutrosophicco-degreeofvertices,neutrosophicco-degreeofhyperedges,neutrosophicnumberofvertices,neutrosophic numberofhyperedgesinneutrosophichypergraphs.Theconnectionsofneutrosophicverticeswhichareclarifiedbygeneralhyperedgesdifferthemfromeach otherandandputthemindifferentcategoriestorepresentonerepresentativefor eachcolor.Furtherstudiescouldbeaboutchangesinthesettingstocompare thisnotionamiddifferentsettingsofneutrosophichypergraphstheory.One wayisfindingsomerelationsamidthesedefinitionsofnotionstomakesensible definitions.InTable (4.6),somelimitationsandsomeadvantagesofthisstudy arepointedout.
3.NeutrosophicHypergraphs
Table3.4:ABriefOverviewaboutAdvantagesandLimitationsofthisstudy
Advantages Limitations 1. Definingdegree 1. GeneralResults 2. Definingco-degree 3. Definingneutrosophicdegree 2. ConnectionsWithParameters 4. Applyingcolortring 5. Definingneutrosophicco-degree 3. ConnectionsofResults
tbl2c
3.21BeyondNeutrosophicHypergraphs
ideas.
5].Thecontentsareused
134
Extended settingsare usedtoapply Neutrosophic
Thirdcaseforthecontentsistousethearticlefrom[
inthewaythat,usagesofnewcontentsarepreferencesandthepreliminaries arepassedinthebeginningoffirstchapter.
3.22.ClosingNumbersandSuper-ClosingNumbersas(Dual)Resolvingand (Dual)Coloringalongside(Dual)Dominatingin (Neutrosophic)n-SuperHyperGraph3.22ClosingNumbersandSuper-ClosingNumbersas (Dual)Resolvingand(Dual)Coloringalongside (Dual)Dominatingin (Neutrosophic)n-SuperHyperGraph
3.23Abstract
Newsettingisintroducedtostudy“closingnumbers”and“super-closing numbers”asoptimal-super-resolvingnumber,optimal-super-coloringnumber andoptimal-super-dominatingnumber.Inthisway,someapproachesare appliedtogetsomesetsfrom(Neutrosophic)n-SuperHyperGraphandafter that,someideasareappliedtogetdifferenttypesofsuper-closingnumbers whicharecalledbyoptimal-super-resolvingnumber,optimal-super-coloring numberandoptimal-super-dominatingnumber.Thenotionofdualisanother newideawhichiscoveredbythesenotionsandresults.Inthesetting ofdual,thesetofsuper-verticesisexchangedwiththesetofsuper-edges. Thustheseresultsanddefinitionsholdinthesettingofdual.Settingof neutrosophicn-SuperHyperGraphisusedtogetsomeexamplesandsolutions fortwoapplicationswhichareproposed.BothsettingofSuperHyperGraph andneutrosophicn-SuperHyperGrapharesimultaneouslystudiedbutthe resultsareaboutthesettingofn-SuperHyperGraphs.Settingofneutrosophic n-SuperHyperGraphgetsomeexampleswhereneutrosophichypergraphsas specialcaseofneutrosophicn-SuperHyperGraphareused.Theclarifications useneutrosophicn-SuperHyperGraphandtheoreticalstudyistousenSuperHyperGraphbuttheseresultsarealsoapplicableintoneutrosophicnSuperHyperGraph.Specialusagefromdifferentattributesofneutrosophic n-SuperHyperGraphareappropriatetohaveopenwaystopursuethisstudy. Differenttypesofproceduresincludingoptimal-super-set,andoptimal-supernumberalongsidestudyonthefamilyof(neutrosophic)n-SuperHyperGraph areproposedinthisway,someresultsareobtained.Generalclassesof (neutrosophic)n-SuperHyperGraphareusedtoobtainstheseclosingnumbers andsuper-closingnumbersandtherepresentativesoftheoptimal-super-coloring sets,optimal-super-dominatingsetsandoptimal-super-resolvingsets.Using colorstoassigntothesuper-verticesofn-SuperHyperGraphandcharacterizing optimal-super-resolvingsetsandoptimal-super-dominatingsetsareapplied. Somequestionsandproblemsareposedconcerningwaystodofurtherstudies onthistopic.Usingdifferentwaysofstudyonn-SuperHyperGraphtoget newresultsaboutclosingnumbersandsuper-closingnumbersalongsidesetsin thewaythatsomeclosingnumberssuper-closingnumbersgetunderstandable perspective.Familyofn-SuperHyperGrapharestudiedtoinvestigateabout thenotions,super-resolvingandsuper-coloringalongsidesuper-dominating inn-SuperHyperGraph.Inthisway,setsofrepresentativesofoptimal-supercolors,optimal-super-resolvingsetsandoptimal-super-dominatingsetshave keyrole.Optimal-supersetsandoptimal-supernumbershavekeypoints togetnewresultsbutinsomecases,thereareusagesofsetsandnumbers insteadofoptimal-superones.Simultaneously,threenotionsareapplied into(neutrosophic)n-SuperHyperGraphtogetsensibleresultsabouttheir structures.Basicfamiliaritieswithn-SuperHyperGraphtheoryandneutrosophic n-SuperHyperGraphtheoryareproposedforthisarticle.
135
Keywords: ColoringNumbers,ResolvingNumbers,DominatingNumbers
AMSSubjectClassification: 05C17,05C22,05E45
MotivationandContributions
Inthisstudy,there’sanideawhichcouldbeconsideredasamotivation. Question3.23.1. Isitpossibletousemixedversionsofideasconcerning“superdomination”,“super-dimension”and“super-coloring”todefinesomesupernotionswhichareappliedton-SuperHyperGraph?
It’smotivationtofindnotionstouseinanyclassesofn-SuperHyperGraph. Real-worldapplicationsabouttimetableandschedulingareanotherthoughts whichleadtobeconsideredasmotivation.Connectionsamidtwoitemshave keyrolestoassignsuper-colors,super-dominationandsuper-dimension.Thus they’reusedtodefinenewsuper-ideaswhichconcludetothestructureofsupercoloring,super-dominatingandsuper-resolving.Theconceptofhavinggeneral super-edgeinspiresmetostudythebehaviorofgeneralsuper-edgeintheway that,threetypesof“super-closing”numbers,e.g.,super-coloringnumbers, super-dominatingnumbersandsuper-resolvingnumbersarethecasesofstudy inthesettingsofindividualsandinsettingsoffamilies.
Theframeworkofthisstudyisasfollows.Inthebeginning,Iintroduced basicdefinitionstoclarifyaboutpreliminaries.Insection“NewIdeasFornSuperHyperGraph”,newnotionsofsuper-coloring,super-dominatingandsuperresolvingareappliedtosuper-verticesofSuperHyperGraphasindividuals.In section“OptimalNumbersForn-SuperHyperGraph”,specificclosingnumbers havethekeyroleinthisway.Classesofn-SuperHyperGrapharestudied inthetermsofdifferentclosingnumbersinsection“OptimalNumbersFor n-SuperHyperGraph”asindividuals.Inthesection“OptimalSetsFornSuperHyperGraph”,usagesofgeneralsetsandspecialsetshavekeyrolein thisstudyasindividuals.Insection“OptimalSetsandNumbersForFamily ofn-SuperHyperGraph”,bothsetsandclosingnumbershaveappliedintothe familyofn-SuperHyperGraph.Insection“ApplicationsinTimeTableand Scheduling”,twoapplicationsareposedforn-SuperHyperGraphconcerning timetableandschedulingwhenthesuspicionsareaboutchoosingsomesubjects. Insection“OpenProblems”,someproblemsandquestionsforfurtherstudies areproposed.Insection“ConclusionandClosingRemarks”,gentlediscussion aboutresultsandapplicationsarefeatured.Insection“ConclusionandClosing Remarks”,abriefoverviewconcerningadvantagesandlimitationsofthisstudy alongsideconclusionsareformed.
Inthesettingofneutrosophichypergraphs,thenotionofcompletehave introducedsomeclasses.Sincethevertexcouldhaveanynumberofarbitrary hyperedges.Thisnotionistooclosetothenotionofregularity.Thustheidea
3.NeutrosophicHypergraphs
3.24NewIdeasForSettingofNeutrosophic n-SuperHyperGraph
What-ifthenotionofcompleteproposessomeclassesof neutrosophichypergraphs?
Question3.24.1.
136
3.24.NewIdeasForSettingofNeutrosophicn-SuperHyperGraph
ofcompletehasanobviousstructureinthat,everyhyperedgehas n verticesso there’sonlyonehyperedge.
Definition3.24.2. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) It’s denotedby NHGr n andit’s (r,n) regular ifeveryhyperedgehasexactly r verticesinthewaythat,all r subsetsoftheverticeshaveanuniquehyperedge where r ≤ n and |V | = n.
Example3.24.3. InFigure(3.9), NHG3 4 isshown.
Figure3.9: NHG3 4 =(V,E,σ,µ) isneutrosophic (3, 4) regularhypergraph. nhg6

Definition3.24.4. Assumeneutrosophichypergraph NHG =(V,E,σ,µ)
(i): Maximumnumber ismaximumnumberofhyperedgeswhichare incidenttoavertexandit’sdenotedby ∆(NHG);
(ii): Minimumnumber isminimumnumberofhyperedgeswhichareincident toavertexandit’sdenotedby δ(NHG);
(iii): Maximumvalue ismaximumvalueofverticesandit’sdenotedby ∆n(NHG);
(iv): Minimumvalue isminimumvalueofverticesandit’sdenotedby δn(NHG)
Example3.24.5. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) as Figure(3.9).
(i): ∆(NHG)=3;
(ii): δ(NHG)=3;
(iii): ∆n(NHG)=(0 99, 0 98, 0 55);
(iv): δn(NHG)=(0 99, 0 98, 0 55)
Question3.24.6. What-ifthenotionofcompleteproposessomeclassesof neutrosophichypergraphswithsomeparts?
137
Inthesettingofneutrosophichypergraphs,wheneveryparthasspecific attributeinsideandoutside,thenotionofcompleteisappliedtopartstoform theideaofcompleteness.
Definition3.24.7. Assumeneutrosophichypergraph NHG =(V,E,σ,µ) It’sdenotedby NHGr n1,n2, ,nr andit’s complete r partite if V canbe partitionedinto r non-emptyparts, Vi, andeveryhyperedgehasonlyonevertex fromeachpartwhere ni isthenumberofverticesinpart Vi
Example3.24.8. InFigure(3.10), NHG3 3,3,3 =(V,E,σ,µ) isshown.
Figure3.10: NHG3 3,3,3 =(V,E,σ,µ) isneutrosophiccomplete 3 partite hypergraph. nhg7

Definition3.24.9. Assumeneutrosophichypergraph NHG =(V,E,σ,µ)
(i): A neutrosophicnumber ofvertices x1,x2, ,xn is Σn i=1σ(xi)
(ii): A neutrosophicnumber ofhyperedges e1,e2, ,en is Σn i=1µ(ei)
Example3.24.10. Igetsomeclarificationsaboutnewdefinitions.
(i): InFigure(3.9), NHG3 4 isshown.
(a): Aneutrosophicnumberofvertices n1,n2,n3 is Σ3 i=1σ(ni)=(2 97, 2 94, 1 65)
(b): Aneutrosophicnumberofhyperedges e1,e2,e3 is Σ3 i=1σ(ei)=(1 82, 1 12, 0 78)
where e1 =(0 54, 0 24, 0 16),e2 =(0 74, 0 64, 0 46),e3 = (0 54, 0 24, 0 16)
3.NeutrosophicHypergraphs
138
(ii): InFigure(3.10), NHG3 3,3,3 =(V,E,σ,µ) isshown.
(a): Aneutrosophicnumberofvertices n1,n2,n3 is
Σ3 i=1σ(ni)=(2 97, 2 94, 1 65)
(b): Aneutrosophicnumberofhyperedges e1,e2,e3 is Σ3 i=1σ(ei)=(1 82, 1 12, 0 78)
where e1 =(0 54, 0 24, 0 16),e2 =(0 74, 0 64, 0 46),e3 = (0 54, 0 24, 0 16)
Definition3.24.11. Assumeneutrosophichypergraph NHG =(V,E,σ,µ)
(i): A degree ofvertex x isthenumberofhyperedgeswhichareincidentto x.
(ii): A neutrosophicdegree ofvertex x istheneutrosophicnumberof hyperedgeswhichareincidentto x.
(iii): A degree ofhyperedge e isthenumberofverticeswhich e isincidentto them.
(iv): A neutrosophicdegree ofhyperedge e istheneutrosophicnumberof verticeswhich e isincidenttothem.
(v): A co-degree ofvertices x1,x2, ,xn isthenumberofhyperedgeswhich areincidentto x1,x2, ··· ,xn
(vi): A neutrosophicco-degree ofvertices x1,x2, ,xn istheneutrosophic numberofhyperedgeswhichareincidentto x1,x2, ,xn
(vii): A co-degree ofhyperedges e1,e2, ,en isthenumberofverticeswhich e1,e2, ··· ,en areincidenttothem.
(viii): A neutrosophicco-degree ofhyperedges e1,e2, ,en istheneutrosophicnumberofverticeswhich e1,e2, ,en areincidenttothem.
Example3.24.12. Igetsomeclarificationsaboutnewdefinitions.
(i): InFigure(3.9), NHG3 4 isshown.
(a): Adegreeofanyvertexis 3.
(b): Aneutrosophicdegreeofvertex n1 is (2 07, 1 46, 0 87)
(c): Adegreeofhyperedge e where µ(e)=(0 99, 0 98, 0 55) is 3
(d): Aneutrosophicdegreeofhyperedge e where µ(e)=(0 99, 0 98, 0 55) is (2 97, 2 94, 1 65)
(e): Aco-degreeofvertices n1,n3 is 2.
(f ): Aneutrosophicco-degreeofvertices n1,n3 is (1 53, 1 22, 0 71)
(g): Aco-degreeofhyperedges e1,e2 where µ(e1)=(0 99, 0 98, 0 55) and µ(e2)=(0 54, 0 24, 0 16) is 2
3.24.NewIdeasForSettingofNeutrosophicn-SuperHyperGraph
139
(h): Aneutrosophicco-degreeofhyperedges e1,e2 where µ(e1)= (0 99, 0 98, 0 55) and µ(e2)=(0 54, 0 24, 0 16) is (1 98, 1 96, 1 1)
(ii): InFigure(3.10), NHG3 3,3,3 =(V,E,σ,µ) isshown.
(a): Adegreeofanyvertex n1,n2,n4,n6,n8,n9 is 1 anddegreeofany vertex n3,n5,n7 is 2
(b): Aneutrosophicdegreeofvertex n1,n2,n4,n6,n8,n9 is (0 99, 0 98, 0 55) anddegreeofanyvertex n3,n5,n7 is (1 98, 1 96, 1 1)
(c): Adegreeofanyhyperedgeis 3
(d): Aneutrosophicdegreeofhyperedgeis (2 97, 2 94, 1 65)
(e): Aco-degreeofvertices n1,n4 is 1
(f ): Aneutrosophicco-degreeofvertices n1,n4 is (0 54, 0 24, 0 16)
(g): Aco-degreeofhyperedges e1,e2 where µ(e1)=(0 99, 0 98, 0 55) and µ(e2)=(0 54, 0 24, 0 16) is 1
(h): Aneutrosophicco-degreeofhyperedges e1,e2 where µ(e1)= (0 99, 0 98, 0 55) and µ(e2)=(0 54, 0 24, 0 16) is (0 99, 0 98, 0 55)
Example3.24.13. ConsiderFigure (3.11) wheretheimprovementsonitssuperedgestohavesuperstronghypergraph.
(a): Thenotionsofdominatingareclarified.
(i): n1 super-dominateseverysuper-vertexfromthesetofsuper-vertices {n7,n8,n9,n2,n3}.n4 super-dominateseverysuper-vertexfromthe setofsuper-vertices {n6,n5,n3}.n4 doesn’tsuper-dominateevery super-vertexfromthesetofsuper-vertices {n1,n2,n7,n8,n9}
(ii): {n1,n3} issuper-coloringsetbut {n1,n4} isoptimal-superdominatingset.
(iii): (1 53, 1 22, 0 71) isoptimal-super-dominatingnumber.
(b): Thenotionsofresolvingareclarified.
(i): n1 super-resolvestwosuper-vertices n4 and n6.
(ii): V \{n1,n4} issuper-resolvessetbut V \{n2,n4,n9} isoptimal-superresolvingset.
(iii): (5, 94, 6.36, 3.3) isoptimal-super-resolvingnumber.
(c): Thenotionsofcoloringareclarified.
(i): n1 super-colorseverysuper-vertexfromthesetofsuper-vertices {n7,n8,n9,n2,n3}.n4 super-colorseverysuper-vertexfromtheset ofsuper-vertices {n6,n5,n3}.n4 doesn’tsuper-dominateeverysupervertexfromthesetofsuper-vertices {n1,n2,n7,n8,n9}.
(ii): {n1,n5,n7,n8,n9,n6,n4} issuper-coloringsetbut {n1,n5,n7,n8,n2,n4} isoptimal-super-coloringset.
(iii): (5.24, 4.8, 2.82) isoptimal-super-coloringnumber.
Example3.24.14. ConsiderFigure(3.3).
3.NeutrosophicHypergraphs
140
3.25.NewIdeasForn-SuperHyperGraph
(a): Thenotionsofdominatingareclarified.
(i): n1 super-dominateseverysuper-vertexfromthesetofsuper-vertices {n5,n6,n2,n3}.n4 super-dominateseverysuper-vertexfromtheset ofsuper-vertices {n5,n3}.n4 doesn’tsuper-dominateeverysupervertexfromthesetofsuper-vertices {n1,n2,n6}
(ii): {n1,n3} issuper-dominatingsetbut {n1,n4} isoptimal-superdominatingset.
(iii): (1 53, 1 22, 0 71) isoptimal-super-dominatingnumber.
(b): Thenotionsofresolvingareclarified.
(i): n1 super-resolvestwosuper-vertices n4 and n6
(ii): V \{n1,n4} issuper-resolvessetbut V \{n2,n4,n6} isoptimal-superresolvingset.
(iii): (5, 94, 6 36, 3 3) isoptimal-super-resolvingnumber.
(c): Thenotionsofcoloringareclarified.
(i): n1 super-colorseverysuper-vertexfromthesetofsuper-vertices {n5,n6,n2,n3}.n4 super-colorseverysuper-vertexfromthesetof super-vertices {n5,n3}.n4 doesn’tsuper-dominateeverysuper-vertex fromthesetofsuper-vertices {n1,n2,n6}
(ii): {n1,n5,n6} issuper-coloringsetbut {n5,n2,n4} isoptimal-supercoloringset.
(iii): (2.27, 1.86, 1.17) isoptimal-super-coloringnumber.
PreliminariesForSettingofn-SuperHyperGraph
Definition3.24.15. (n-SuperHyperGraph). Agraph (Gn ⊆ P n(V ),En ⊆ P n(V )) iscalledby n-SuperHyperGraph and it’sdenotedbyn-SHG.
3.25NewIdeasForn-SuperHyperGraph
Definition3.25.1. (Dominating,ResolvingandColoring). Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )).
(a): Super-dominatingsetandnumberaredefinedasfollows.
(i): Asuper-vertex Xn super-dominates asuper-vertex Yn ifthere’s atleastonesuper-edgewhichhavethem.
(ii): Aset S iscalled super-dominatingset ifforevery Yn ∈ Gn \ S, there’satleastonesuper-vertex Xn whichsuper-dominatessupervertex Yn
(iii): If S issetofallsetsofsuper-dominatingsets,then |X| =min S∈S |{∪Xn|Xn ∈ S}|
iscalled optimal-super-dominatingnumber and X iscalled optimal-super-dominatingset.
141
(b): Super-resolvingsetandnumberaredefinedasfollows.
(i): Asuper-vertex x super-resolves super-vertices y,w if d(x,y) = d(x,w)
(ii): Aset S iscalled super-resolvingset ifforevery Yn ∈ Gn \ S, there’satleastonesuper-vertex Xn whichsuper-resolvessupervertices Yn,Wn
(iii): If S issetofallsetsofsuper-resolvingsets,then |X| =min S∈S |{∪Xn|Xn ∈ S}|
iscalled optimal-super-resolvingnumber and X iscalled optimal-super-resolvingset.
(c): Super-coloringsetandnumberaredefinedasfollows.
(i): Asuper-vertex Xn super-colors asuper-vertex Yn differentlywith itselfifthere’satleastonesuper-edgewhichisincidenttothem.
(ii): Aset Sn iscalled super-coloringset ifforevery y ∈ Gn \ Sn, there’satleastonesuper-vertex Xn whichsuper-colorssuper-vertex Yn
(iii): If Sn issetofallsetsofsuper-coloringsets,then |X| =min Sn∈Sn |{∪Xn|Xn ∈ Sn}| iscalled optimal-super-coloringnumber and X iscalled optimal-super-coloringset.
3.26OptimalNumbersForn-SuperHyperGraph
Proposition3.26.1. Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )).S ismaximumsetofsuper-verticeswhichforma super-edge.Thenoptimal-super-coloringsethasascardinalityas S has.
Proof. Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) Everysuper-edgehassuper-verticeswhichhavecommonsuper-edge.Thusevery super-vertexhasdifferentcolorwithothersuper-verticeswhichareincidentwith asuper-edge.Itinducesasuper-edgewiththemostnumberofsuper-vertices determinesoptimal-super-coloringset. S ismaximumsetofsuper-vertices whichformasuper-edge.Thusoptimal-super-coloringsethasascardinalityas S has.
Proposition3.26.2. Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )). Ifoptimal-super-coloringnumberis |V |,
thenforeverysuper-vertexthere’satleastonesuper-edgewhichcontainshas allmembersof V.
3.NeutrosophicHypergraphs
142
3.26.OptimalNumbersForn-SuperHyperGraph
Proof. Supposen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )). Consideroptimal-super-coloringnumberis
|V |
Itimpliesthere’sonesuper-edgewhichhasallmembersof V. Sinceifallmembers of V areincidenttoasuper-edgeviaasuper-vertex,thenallhavedifferent colors.
Proposition3.26.3. Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )). Ifthere’satleastonesuper-edgewhichhasallmembers of V, thenoptimal-super-coloringnumberis
|V |
Proof. Considern-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )). Supposethere’satleastonesuper-edgewhichhasallmembersof V. Itimplies there’sonesuper-edgewhichhassomesuper-verticesbutallmembersof V. If allsuper-verticesareincidenttoasuper-edge,thenallhavedifferentcolors.It meansifsomesuper-verticeshaveallmembersof V, inthewaythat,forevery memberof V, there’sadistinctsuper-vertexwhichhasitandallsuchthese super-verticesareincidenttoasuper-edge,thenallhavedifferentcolors.So thesetofthesesuper-verticesare V, isoptimal-super-coloringset.Itinduces optimal-super-coloringnumberis
|V |
Proposition3.26.4. Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )). Ifoptimal-super-dominatingnumberis |V |,
thenthere’sonememberof V, iscontainedin,atleastonesuper-vertexwhich doesn’thaveincidenttoanysuper-edge.
Proof. Supposen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) Consideroptimal-super-dominatingnumberis |V |
Ifforallgivensuper-vertexandallmembersof V, there’satleastonesuper-edge, whichthesuper-vertexhasincidenttoit,thenthere’sasuper-vertex Xn such thatoptimal-super-dominatingnumberis
|V |−|Xn|.
Itinducescontradictionwithhypothesis.Itimpliesthere’sonememberof V, iscontainedin,atleastonesuper-vertexwhichdoesn’thaveincidenttoany super-edge.
Proposition3.26.5. Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) Thenoptimal-super-dominatingnumberis < |V |
143
Proof. Considern-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )). Thus Gn −{Xn}, isasuper-dominatingsetwhere Xn ∈ Gn .Sinceifnot, Xn isn’tincidenttoanygivensuper-edge.Thisiscontradictionwithsupposition. Itinducesthat Xn belongstoasuper-edgewhichhasanothersuper-vertex Xn Itimplies Xn super-dominates Xn Thus Gn −{Xn} isasuper-dominatingset. Itinducesoptimal-super-dominatingnumberis < |V |
Proposition3.26.6. Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) Ifoptimal-super-resolvingnumberis |V |
theneverygivensuper-vertexdoesn’thaveincidenttoanysuper-edge.
Proof. Considern-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )). Letoptimal-super-resolvingnumberbe |V |
Ifitimpliesthere’sasuper-vertexissuper-resolvedbyasuper-vertex,then it’scontradictionwithhypothesis.Soeverygivensuper-vertexdoesn’thave incidenttoanysuper-edge.
Proposition3.26.7. Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) Thenoptimal-super-resolvingnumberis < |V |
Proof. Considern-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) Ifoptimal-super-resolvingnumberis |V |,
thenthere’sacontradictiontohypothesis.Sincetheset Gn −{Xn}, issuperresolvingset.Itimpliesoptimal-super-resolvingnumberis < |V |.
Proposition3.26.8. Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) Ifoptimal-super-coloringnumberis
|V |,
thenallsuper-verticeswhichhaveincidenttoatleastonesuper-edge.
3.NeutrosophicHypergraphs
144
3.26.OptimalNumbersForn-SuperHyperGraph
Proof. Supposen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )). Consideroptimal-super-coloringnumberis
|V |−|Xn|
Ifforallgivensuper-vertices,there’snosuper-edgewhichthesuper-verticeshave incidenttoit,thenthere’ssuper-vertex Xn suchthatoptimal-super-coloring numberis
|V |−|Xn|.
Itinducescontradictionwithhypothesis.Itimpliesallsuper-verticeshave incidenttoatleastonesuper-edge.
Proposition3.26.9. Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )). Thenoptimal-super-coloringnumberisn’t < |V |.
Proof. Considern-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )). Thus Gn −{Xn} isn’tasuper-coloringset.Sinceifnot, Xn isn’tincident toanygivensuper-edge.Thisiscontradictionwithsupposition.Itinduces that Xn belongstoasuper-edgewhichhasanothersuper-vertex Sn Itimplies Sn super-colors Xn. Thus Gn −{Xn} isn’tasuper-coloringset.Itinduces optimal-super-coloringnumberisn’t < |V |
Proposition3.26.10. Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) Thenoptimal-super-dominatingsethascardinality whichisgreaterthan n 1 where n isthecardinalityoftheset V. Proof. Considern-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) Theset Gn issuper-dominatingset.Sooptimal-super-dominatingsethas cardinalitywhichisgreaterthan n 1 where n isthecardinalityoftheset V. Buttheset Gn \{Xn}, foreverygivensuper-vertex Xn isoptimal-superdominatingsethascardinalitywhichisgreaterthan n 1 where n isisthe cardinalityoftheset V. Theresultisobtained.
Proposition3.26.11. Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )).S ismaximumsetofsuper-verticeswhichforma super-edge.Then S isoptimal-super-coloringsetand |{∪Xn | Xn ∈ S}|
isoptimal-super-coloringnumber.
Proof. Supposen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) Consider S ismaximumsetofsuper-verticeswhichformasuper-edge.Thusall super-verticesof S haveincidenttosuper-edge.Itimpliesthenumberofdifferent colorsequalstoacardinalitybasedon S. Therefore,optimal-super-coloring number ≥ |{∪Xn | Xn ∈ S}|
145
Inotherhand, S ismaximumsetofsuper-verticeswhichformasuper-edge.It inducesoptimal-super-coloringnumber ≤
|{∪Xn | Xn ∈ S}|
So S issuper-coloringset.Hence S isoptimal-super-coloringsetand |{∪Xn | Xn ∈ S}| isoptimal-super-coloringnumber.
3.27OptimalSetsForn-SuperHyperGraph
Proposition3.27.1. Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )). If S issuper-dominatingset,then D contains S is super-dominatingset.
Proof. Considern-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) Suppose S issuper-dominatingset.Thenallsuper-verticesaresuper-dominated. Thus D contains S issuper-dominatingset.
Proposition3.27.2. Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) If S issuper-resolvingset,then D contains S is super-resolvingset.
Proof. Supposen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )). Consider S issuper-resolvingset.HenceAlltwogivensuper-verticesare super-resolvedbyatleastonesuper-vertexof S. Itinduces D contains S is super-resolvingset.
Proposition3.27.3. Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) If S issuper-coloringset,then D contains S issupercoloringset.
Proof. Supposen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) Consider S issuper-coloringset.Soallsuper-verticeswhichhaveacommon super-edgehavedifferentcolors.Thuseverysuper-vertexsuper-coloredbya super-vertexof S. Itinduceseverysuper-vertexwhichhasacommonsuper-edge hasdifferentcolorswithothersuper-verticesbelongtothatsuper-edge.Then D contains S issuper-coloringset.
Proposition3.27.4. Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) Then Gn issuper-dominatingset.
Proof. Supposen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) Since Gn \{Xn} issuper-dominatingset.Then Gn contains Gn \{Xn} is super-dominatingset.
Proposition3.27.5. Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) Then Gn issuper-resolvingset.
3.NeutrosophicHypergraphs
146
Proof. Supposen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )). If there’snosuper-vertex,thenallsuper-verticesaresuper-resolved.HenceifI choose Gn, thenthere’snosuper-vertexsuchthatsuper-vertexissuper-resolved. Itimplies Gn issuper-resolvingsetbut Gn isn’toptimal-super-resolvingset. SinceifIconstructonesetfrom Gn suchthatonlyonesuper-vertexisoutof S, then S issuper-resolvingset.Itimplies Gn isn’toptimal-super-resolvingset. Thus Gn issuper-resolvingset.
Proposition3.27.6. Assumen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) Then Gn issuper-coloringset.
Proof. Supposen-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )). Allsuper-verticesbelongtoasuper-edgehavetocolordifferently.If Gn is chosen,thenallsuper-verticeshavedifferentcolors.Itinducesthat t colorsare usedwhere t isthenumberofsuper-vertices.Everysuper-vertexhasunique color.Thus Gn issuper-coloringset.
3.28OptimalSetsandNumbersForFamilyof n-SuperHyperGraph
Proposition3.28.1. Assume G isafamilyofn-SuperHyperGraph.Then Gn is super-dominatingsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofn-SuperHyperGraph.Thus Gn issuperdominatingsetforeverygivenn-SuperHyperGraphof G. Itimplies Gn is super-dominatingsetforallmembersof G, simultaneously.
Proposition3.28.2. Assume G isafamilyofn-SuperHyperGraph.Then Gn is super-resolvingsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofn-SuperHyperGraph.Thus Gn issuper-resolving setforeverygivenn-SuperHyperGraphof G Itimplies Gn issuper-resolving setforallmembersof G, simultaneously.
Proposition3.28.3. Assume G isafamilyofn-SuperHyperGraph.Then Gn is super-coloringsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofn-SuperHyperGraph.Thus Gn issuper-coloring setforeverygivenn-SuperHyperGraphof G Itimplies Gn issuper-coloringset forallmembersof G, simultaneously.
Proposition3.28.4. Assume G isafamilyofn-SuperHyperGraph.Then Gn \{Xn} issuper-dominatingsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofn-SuperHyperGraph.Thus Gn \{Xn} issuperdominatingsetforeverygivenn-SuperHyperGraphof G. Onesuper-vertexis outof Gn \{Xn} It’ssuper-dominatedfromanysuper-vertexin Gn \{Xn} Henceeverygiventwosuper-verticesaresuper-dominatedfromanysuper-vertex in Gn \{Xn} Itimplies Gn \{Xn} issuper-dominatingsetforallmembersof G, simultaneously.
3.28.OptimalSetsandNumbersForFamilyofn-SuperHyperGraph
147
Proposition3.28.5. Assume G isafamilyofn-SuperHyperGraph.Then Gn \{Xn} issuper-resolvingsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofn-SuperHyperGraph.Thus Gn \{Xn} issuperresolvingsetforeverygivenn-SuperHyperGraphof G. Onesuper-vertexis outof Gn \{Xn} It’ssuper-resolvedfromanysuper-vertexin Gn \{Xn} Henceeverygiventwosuper-verticesaresuper-resolvedfromanysuper-vertex in Gn \{Xn} Itimplies Gn \{Xn} issuper-resolvingsetforallmembersof G, simultaneously.
Proposition3.28.6. Assume G isafamilyofn-SuperHyperGraph.Then Gn \{Xn} isn’tsuper-coloringsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofn-SuperHyperGraph.Thus Gn \{Xn} isn’t super-coloringsetforeverygivenn-SuperHyperGraphof G. Onesuper-vertex isoutof Gn \{Xn} Itisn’tsuper-coloredfromanysuper-vertexin Gn \{Xn} Henceeverygiventwosuper-verticesaren’tsuper-coloredfromanysuper-vertex in Gn \{Xn} Itimplies Gn \{Xn} isn’tsuper-coloringsetforallmembersof G, simultaneously.
Proposition3.28.7. Assume G isafamilyofn-SuperHyperGraph.Thenunion ofsuper-dominatingsetsfromeachmemberof G issuper-dominatingsetforall membersof G, simultaneously.
Proof. Suppose G isafamilyofn-SuperHyperGraph.ForeverychosennSuperHyperGraph,there’sonesuper-dominatingsetintheunionofsuperdominatingsetsfromeachmemberof G Thusunionofsuper-dominating setsfromeachmemberof G issuper-dominatingsetforeverygivennSuperHyperGraphof G Evenonesuper-vertexisn’toutoftheunion.It’s super-dominatedfromanysuper-vertexintheunion.Henceeverygiventwo super-verticesaresuper-dominatedfromanysuper-vertexinunionofsupercoloringsets.Itimpliesunionofsuper-coloringsetsissuper-dominatingsetfor allmembersof G, simultaneously.
Proposition3.28.8. Assume G isafamilyofn-SuperHyperGraph.Thenunion ofsuper-resolvingsetsfromeachmemberof G issuper-resolvingsetforall membersof G, simultaneously.
Proof. Suppose G isafamilyofn-SuperHyperGraph.ForeverychosennSuperHyperGraph,there’sonesuper-resolvingsetintheunionofsuper-resolving setsfromeachmemberof G Thusunionofsuper-resolvingsetsfromeach memberof G issuper-resolvingsetforeverygivenn-SuperHyperGraphof G Evenonesuper-vertexisn’toutoftheunion.It’ssuper-resolvedfromanysupervertexintheunion.Henceeverygiventwosuper-verticesaresuper-resolved fromanysuper-vertexinunionofsuper-coloringsets.Itimpliesunionofsupercoloringsetsissuper-resolvedsetforallmembersof G, simultaneously.
Proposition3.28.9. Assume G isafamilyofn-SuperHyperGraph.Thenunion ofsuper-coloringsetsfromeachmemberof G issuper-coloringsetforall membersof G, simultaneously.
3.NeutrosophicHypergraphs
148
3.28.OptimalSetsandNumbersForFamilyofn-SuperHyperGraph
Proof. Suppose G isafamilyofn-SuperHyperGraph.ForeverychosennSuperHyperGraph,there’sonesuper-coloringsetintheunionofsuper-coloring setsfromeachmemberof G Thusunionofsuper-coloringsetsfromeachmember of G issuper-coloringsetforeverygivenn-SuperHyperGraphof G Evenone super-vertexisn’toutoftheunion.It’ssuper-coloredfromanysuper-vertex intheunion.Henceeverygiventwosuper-verticesaresuper-coloredfromany super-vertexinunionofsuper-coloringsets.Itimpliesunionofsuper-coloring setsissuper-coloredsetforallmembersof G, simultaneously.
Proposition3.28.10. Assume G isafamilyofn-SuperHyperGraph.Forevery givensuper-vertex,there’sonen-SuperHyperGraphsuchthatthesuper-vertex hasanothersuper-vertexwhichareincidenttoasuper-edge.Ifforgivensupervertex,allsuper-verticeshaveacommonsuper-edgeinthisway,then Gn \{Xn} isoptimal-super-dominatingsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofn-SuperHyperGraph.ForallnSuperHyperGraph,there’snosuper-dominatingsetfromanyofmemberof G Thus Gn \{Xn} issuper-dominatingsetforeverygivenn-SuperHyperGraphof G Foreverygivensuper-vertex,there’sonen-SuperHyperGraphsuchthatthe super-vertexhasanothersuper-vertexwhichareincidenttoasuper-edge.Only onesuper-vertexisoutof V \{x}. It’ssuper-dominatedfromanysuper-vertexin the V \{x} Henceeverygiventwosuper-verticesaresuper-dominatedfromany super-vertexin Gn \{Xn} Itimplies Gn \{Xn} issuper-dominatingsetforall membersof G, simultaneously.Ifforgivensuper-vertex,allsuper-verticeshave acommonsuper-edgeinthisway,then Gn \{Xn} isoptimal-super-dominating setforallmembersof G, simultaneously.
Proposition3.28.11. Assume G isafamilyofn-SuperHyperGraph.Forevery givensuper-vertex,there’sonen-SuperHyperGraphsuchthatthesuper-vertex hasanothersuper-vertexwhichareincidenttoasuper-edge.Ifforgivensupervertex,allsuper-verticeshaveacommonsuper-edgeinthisway,then Gn \{Xn} isoptimal-super-resolvingsetforallmembersof G, simultaneously.
Proof. Suppose G isafamilyofn-SuperHyperGraph.ForallnSuperHyperGraph,there’snosuper-resolvingsetfromanyofmemberof G Thus Gn \{Xn} issuper-resolvingsetforeverygivenn-SuperHyperGraphof G Foreverygivensuper-vertex,there’sonen-SuperHyperGraphsuchthatthe super-vertexhasanothersuper-vertexwhichareincidenttoasuper-edge.Only onesuper-vertexisoutof Gn \{Xn} It’ssuper-resolvedfromanysuper-vertex inthe Gn \{Xn}. Henceeverygiventwosuper-verticesaresuper-resolvingfrom anysuper-vertexin Gn \{Xn} Itimplies Gn \{Xn} issuper-resolvedsetforall membersof G, simultaneously.Ifforgivensuper-vertex,allsuper-verticeshave acommonsuper-edgeinthisway,then Gn \{Xn} isoptimal-super-resolving setforallmembersof G, simultaneously.
Proposition3.28.12. Assume G isafamilyofn-SuperHyperGraph.Forevery givensuper-vertex,there’sonen-SuperHyperGraphsuchthatthesuper-vertex hasanothersuper-vertexwhichareincidenttoasuper-edge.Ifforgivensupervertex,allsuper-verticeshaveacommonsuper-edgeinthisway,then Gn is optimal-super-coloringsetforallmembersof G, simultaneously.
149
sec4
prp2
Proof. Suppose G isafamilyofn-SuperHyperGraph.ForallnSuperHyperGraph,there’snosuper-coloringsetfromanyofmemberof G Thus Gn issuper-coloringsetforeverygivenn-SuperHyperGraphof G Foreverygivensuper-vertex,there’sonen-SuperHyperGraphsuchthatthe super-vertexhasanothersuper-vertexwhichareincidenttoasuper-edge.No super-vertexisoutof Gn. It’ssuper-coloredfromanysuper-vertexinthe Gn. Henceeverygiventwosuper-verticesaresuper-coloredfromanysuper-vertexin Gn Itimplies Gn issuper-coloringsetforallmembersof G, simultaneously.If forgivensuper-vertex,allsuper-verticeshaveacommonsuper-edgeinthisway, then Gn isoptimal-super-coloringsetforallmembersof G, simultaneously.
3.29TwinSuper-verticesinn-SuperHyperGraph
Proposition3.29.1. Letn-SHG bean-SuperHyperGraph.An (k 1)-setfrom ank-setoftwinsuper-verticesissubsetofasuper-resolvingset.
Proof. If Xn and Xn aretwinsuper-vertices,then N (Xn)= N (Xn). Itimplies d(Xn,Tn)= d(Xn,Tn) forall Tn ∈ Gn
cor2
Corollary3.29.2. Letn-SHG bean-SuperHyperGraph.Thenumberoftwin super-verticesis n 1. Thensuper-resolvingnumberis n 2.
Proof. Let Xn and Xn betwosuper-vertices.Bysupposition,thecardinality ofsetoftwinsuper-verticesis n 2 Thustherearetwocases.Ifbotharetwin super-vertices,then N (Xn)= N (Xn). Itimplies d(Xn,Tn)= d(Xn,Tn) forall Tn ∈ Gn Thussupposeifnot,thenlet Xn beasuper-vertexwhichisn’ttwin super-verticeswithanygivensuper-vertexandlet Xn beasuper-vertexwhich istwinsuper-verticeswithanygivensuper-vertexbutnot Xn Bysupposition, it’spossibleandthisisonlycase.Therefore,anygivendistinctsuper-vertex super-resolves Xn and Xn. Then Gn \{Xn,Xn} issuper-resolvingset.Itimplies -super-resolvingnumberis n 2
cor1
Corollary3.29.3. Letn-SHG ben-SuperHyperGraph.Thenumberoftwin super-verticesis n 1 Thensuper-resolvingnumberis n 2 Every (n 2)-set includingtwinsuper-verticesissuper-resolvingset.
Proof. ByCorollary (3.29.2),super-resolvingnumberis n 2 Byn-SHG isnSuperHyperGraph,onesuper-vertexdoesn’tbelongtosetoftwinsuper-vertices andavertexfromthatset,areoutofsuper-resolvingset.Itinducesevery (n 2)-setincludingtwinsuper-verticesissuper-resolvingset.
Proposition3.29.4. Letn-SHG ben-SuperHyperGraphsuchthatit’scomplete. Thensuper-resolvingnumberis n 1. Every (n 1)-setissuper-resolvingset.
Proof. Incomplete,everycoupleofsuper-verticesaretwinsuper-vertices.By n-SHG iscomplete,everycoupleofsuper-verticesaretwinsuper-vertices.Thus byProposition(3.29.1),theresultfollows.
prp3
Proposition3.29.5. Let G beafamilyofn-SuperHyperGraphswithcommon supervertexset Gn Thensimultaneouslysuper-resolvingnumberof G is |V |− 1
3.NeutrosophicHypergraphs
150
prp4
3.29.TwinSuper-verticesinn-SuperHyperGraph
Proof. Consider (|V |− 1)-set.Thusthere’snocoupleofsuper-verticestobe super-resolved.Therefore,every (|V |− 1)-setissuper-resolvingsetforanygiven n-SuperHyperGraph.Thenitholdsforanyn-SuperHyperGraph.Itimpliesit’s super-resolvingsetanditscardinalityissuper-resolvingnumber. (|V |−1)-sethas thecardinality|V |− 1 Thenitholdsforanyn-SuperHyperGraph.Itinduces it’ssimultaneouslysuper-resolvingsetanditscardinalityissimultaneously super-resolvingnumber.
Proposition3.29.6. Let G beafamilyofn-SuperHyperGraphswithcommon super-vertexset Gn Thensimultaneouslysuper-resolvingnumberof G isgreater thanthemaximumsuper-resolvingnumberofn-SHG ∈G
Proof. Suppose t and t aresimultaneouslysuper-resolvingnumberof G and super-resolvingnumberofn-SHG ∈G Thus t issuper-resolvingnumberfor anyn-SHG ∈G Hence, t ≥ t Sosimultaneouslysuper-resolvingnumberof G isgreaterthanthemaximumsuper-resolvingnumberofn-SHG ∈G.
prp5 Proposition3.29.7. Let G beafamilyofn-SuperHyperGraphswithcommon super-vertexset Gn Thensimultaneouslysuper-resolvingnumberof G isgreater thansimultaneouslysuper-resolvingnumberof H⊆G
Proof. Suppose t and t aresimultaneouslysuper-resolvingnumberof G and H Thus t is-super-resolvingnumberforanyn-SHG ∈G Itimplies t issuperresolvingnumberforanyn-SHG ∈H So t issimultaneouslysuper-resolving numberof H. ByapplyingDefinitionaboutbeingtheminimumnumber, t ≥ t . Sosimultaneouslysuper-resolvingnumberof G isgreaterthansimultaneously super-resolvingnumberof H⊆G
thm1
Theorem3.29.8. Twinsuper-verticesaren’tsuper-resolvedinanygivennSuperHyperGraph.
Proof. Let Xn and Xn betwinsuper-vertices.Then N (Xn)= N (Xn) Thusfor everygivensuper-vertex Sn ∈ Gn,dn-SHG(s ,t)= dn-SHG(s,t) wheren-SHG isagivenn-SuperHyperGraph.Itmeansthat t and t aren’tsuper-resolvedin anygivenn-SuperHyperGraph. t and t arearbitrarysotwinsuper-vertices aren’tsuper-resolvedinanygivenn-SuperHyperGraph.
prp6
Proposition3.29.9. Letn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beanSuperHyperGraph.Ifn-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) iscomplete,theneverycoupleofsuper-verticesaretwinsuper-vertices.
Proof. Let Xn and Xn becoupleofgivensuper-vertices.Byn-SHG iscomplete, N (Xn)= N (Xn) Thus Xn and Xn aretwinsuper-vertices. Xn and Xn are arbitrarycoupleofsuper-vertices,henceeverycoupleofsuper-verticesaretwin super-vertices.
thm17
Theorem3.29.10. Let G beafamilyofn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) withsuper-vertexset Gn andn-SHG ∈G iscomplete. Thensimultaneouslysuper-resolvingnumberis |V |− 1 Every (n 1)-setis simultaneouslysuper-resolvingsetfor G
151
Proof. Supposen-SHG ∈G isSuperHyperGraphandit’scomplete.So byTheorem (3.29.9),Igeteverycoupleofsuper-verticesincomplete SuperHyperGrapharetwinsuper-vertices.Soeverycoupleofsuper-vertices,by Theorem(3.29.8),aren’tsuper-resolved.
Corollary3.29.11. Let G beafamilyofn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) withsuper-vertexset Gn andn-SHG ∈G iscomplete. Thensimultaneouslysuper-resolvingnumberis |V |− 1. Every (|V |− 1)-setis simultaneouslysuper-resolvingsetfor G
Proof. It’scomplete.SobyTheorem(3.29.10),Igetintendedresult.
Theorem3.29.12. Let G beafamilyofn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) withsuper-vertexset Gn andforeverygivencoupleof super-vertices,there’san-SHG ∈G suchthatinthat,they’retwinsuper-vertices. Thensimultaneouslysuper-resolvingnumberis |V |− 1 Every (|V |− 1)-setis simultaneouslysuper-resolvingsetfor G
Proof. ByProposition (3.29.5),simultaneouslysuper-resolvingnumberis |V |−1 Also,every (|V |− 1)-setissimultaneouslysuper-resolvingsetfor G. thm19
Theorem3.29.13. Let G beafamilyofn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) withsuper-vertexset Gn If G containsthreesuper-stars withdifferentsuper-centers,thensimultaneouslysuper-resolvingnumberis |V |− 2 Every (|V |− 2)-setissimultaneouslysuper-resolvingsetfor G
Proof. Thecardinalityofsetoftwinsuper-verticesis |V |− 1. ThusbyCorollary (3.29.3),theresultfollows.
Corollary3.29.14. Let G beafamilyofn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) withsuper-vertexset Gn If G containsthreesuper-stars withdifferentsuper-centers,thensimultaneouslysuper-resolvingnumberis |V |− 2. Every (|V |− 2)-setissimultaneouslysuper-resolvingsetfor G.
Proof. G beafamilyofn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) withsuper-vertexset Gn It’scomplete.SobyTheorem (3.29.13),I getintendedresult.
3.30Antipodalsuper-verticesinn-SuperHyperGraph
sec5
Evensuper-cycle
prp5.1 Proposition3.30.1. Considertwoantipodalsuper-vertices Xn and Yn in anygivenevensuper-cycle.Let Un and Vn begivensuper-vertices.Then d(Xn,Un) = d(Xn,Vn) ifandonlyif d(Yn,Un) = d(Yn,Vn)
Proof. (⇒) Consider d(Xn,Un) = d(Xn,Vn) By d(Xn,Un)+ d(Un,Yn)= d(Xn,Yn)= D(n-SHG),D(n-SHG) d(Xn,Un) = D(n-SHG) d(Xn,Vn). Itimplies d(Yn,Un) = d(Yn,Vn) (⇐) Consider d(Yn,Un) = d(Yn,Vn) By d(Yn,Un)+ d(Un,Xn)= d(Xn,Yn)= D(n-SHG),D(n-SHG) d(Yn,Un) = D(n-SHG) d(Yn,Vn) Itimplies d(Xn,Un) = d(Xn,Vn)
3.NeutrosophicHypergraphs
152
3.30.Antipodalsuper-verticesinn-SuperHyperGraph
Proposition3.30.2. Considertwoantipodalsuper-vertices Xn and Yn inany givenevencycle.Let Un and Vn begivensuper-vertices.Then d(Xn,Un)= d(Xn,Vn) ifandonlyif d(Yn,Un)= d(Yn,Vn)
Proof. (⇒) Consider d(Xn,Un)= d(Xn,Vn) By d(Xn,Un)+ d(Un,Yn)= d(Xn,Yn)= D(n-SHG),D(n-SHG) d(Xn,Un)= D(n-SHG) d(Xn,Vn) Itimplies d(Yn,Un)= d(Yn,Vn) (⇐) Consider d(Yn,Un)= d(Yn,Vn) By d(Yn,Un)+ d(Un,Xn)= d(Xn,Yn)= D(n-SHG),D(n-SHG) d(Yn,Un)= D(n-SHG) d(Yn,Vn). Itimplies d(Xn,Un)= d(Xn,Vn)
Proposition3.30.3. Thesetcontainstwoantipodalsuper-vertices,isn’tsuperresolvingsetinanygivenevensuper-cycle.
Proof. Let Xn and Yn betwogivenantipodalsuper-verticesinanygiveneven super-cycle.ByProposition (3.30.1), d(Xn,Un) = d(Xn,Vn) ifandonlyif d(Yn,Un) = d(Yn,Vn) Itimpliesthatif Xn super-resolvesacoupleofsupervertices,then Yn super-resolvesthem,too.Thuseither Xn isinasuper-resolving setor Yn isin.Itinducesthesetcontainstwoantipodalsuper-vertices,isn’t super-resolvingsetinanygivenevensuper-cycle.
Proposition3.30.4. Considertwoantipodalsuper-vertices Xn and Yn inany givenevensuper-cycle. Xn super-resolvesagivencoupleofsuper-vertices, Zn and Zn,ifandonlyif Yn does.
Proof. (⇒).Xn super-resolvesagivencoupleofsuper-vertices, Zn and Zn, then d(Xn,Zn) = d(Xn,Zn). ByProposition (3.30.1), d(Xn,Zn) = d(Xn,Zn) ifandonlyif d(Yn,Zn) = d(Yn,Zn) Thus Yn super-resolvesagivencoupleof super-vertices Zn and Zn (⇐).Yn super-resolvesagivencoupleofsuper-vertices, Zn and Zn,then d(Yn,Zn) = d(Yn,Zn) ByProposition (3.30.1), d(Yn,Zn) = d(Yn,Zn) ifand onlyif d(Xn,Zn) = d(Xn,Zn). Thus Xn super-resolvesagivencoupleofsupervertices Zn and Zn
Proposition3.30.5. Therearetwoantipodalsuper-verticesaren’tsuper-resolved byothertwoantipodalsuper-verticesinanygivenevensuper-cycle.
Proof. Suppose Xn and Yn areacoupleofsuper-vertices.Itimplies d(Xn,Yn)= D(n-SHG) Consider Un and Vn areanothercoupleofsuper-verticessuchthat d(Xn,Un)= D(n-SHG) 2 Itimplies d(Yn,Un)= D(n-SHG) 2 Thus d(Xn,Un)= d(Yn,Un) Therefore, Un doesn’tsuper-resolveagivencoupleofsuper-vertices Xn and Yn. By D(n-SHGG)= d(Un,Vn)= d(Un,Xn)+ d(Xn,Vn)= D(n-SHG) 2 + d(Xn,Vn),d(Xn,Vn)= D(n-SHG) 2 Itimplies d(Yn,Vn)= D(n-SHG) 2 Thus d(Xn,Vn)= d(Yn,Vn) Therefore, Vn doesn’tsuper-resolveagivencouple ofsuper-vertices Xn and Yn
Proposition3.30.6. Foranytwoantipodalsuper-verticesinanygiveneven super-cycle,thereareonlytwoantipodalsuper-verticesdon’tsuper-resolvethem.
153
3.NeutrosophicHypergraphs
Proof. Suppose Xn and Yn areacoupleofsuper-verticessuchthatthey’re antipodalsuper-vertices.Let Un beasuper-vertexsuchthat d(Xn,Un)= D(n-SHG) 2 Itimplies d(Yn,Un)= D(n-SHG) 2 Thus d(Xn,Un)= d(Yn,Un) Therefore, Un doesn’tsuper-resolveagivencoupleofsuper-vertices Xn and Yn Let Vn beaantipodalvertexfor Un suchthat Un and Vn areantipodalsupervertices.Thus Vn d(Xn,Vn)= D(n-SHG) 2 . Itimplies d(Yn,Vn)= D(n-SHG) 2 . Therefore, Vn doesn’tsuper-resolveagivencoupleofsuper-vertices Xn and Yn If Un isasuper-vertexsuchthat d(Xn,Un) = D(n-SHG) 2 and Vn isasuper-vertex suchthat Un and Vn areantipodalsuper-vertices.Thus d(Xn,Vn) = D(n-SHG) 2 Itinduceseither d(Xn,Un) = d(Yn,Un) or d(Xn,Vn) = d(Yn,Vn) Itmeans either Un super-resolvesagivencoupleofsuper-vertices Xn and Yn or Vn super-resolvesagivencoupleofsuper-vertices Xn and Yn
Proposition3.30.7. Inanygivenevensuper-cycle,foranysuper-vertex,there’s onlyonesuper-vertexsuchthatthey’reantipodalsuper-vertices.
Proof. If d(Xn,Yn)= D(n-SHG), then Xn and Yn areantipodalsupervertices.
prp5.8 Proposition3.30.8. Letn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beanevensuper-cycle.Theneverycoupleofsuper-verticesaresuperresolvingsetifandonlyiftheyaren’tantipodalsuper-vertices.
Proof. If Xn and Yn areantipodalsuper-vertices,thentheydon’tsuper-resolve agivencoupleofsuper-vertices Un and Vn suchthatthey’reantipodalsuperverticesand d(Xn,Un)= D(n-SHG) 2 Since d(Xn,Un)= d(Xn,Vn)= d(Yn,u)= d(Yn,Vn)= D(n-SHG) 2
cor5.9
Corollary3.30.9. Letn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beanevensuper-cycle.Thensuper-resolvingnumberistwo.
Proof. Asetcontainsonesuper-vertex Xn isn’tsuper-resolvingset.Sinceit doesn’tsuper-resolveagivencoupleofsuper-vertices Un and Vn suchthat d(Xn,Un)= d(Xn,Vn)=1 Thussuper-resolvingnumber ≥ 2 ByProposition (3.30.8),everycoupleofsuper-verticessuchthattheyaren’tantipodalsupervertices,aresuper-resolvingset.Therefore,super-resolvingnumberis 2.
cor5.10
Corollary3.30.10. Letn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beanevensuper-cycle.Thensuper-resolvingsetcontainscoupleof super-verticessuchthattheyaren’tantipodalsuper-vertices.
Proof. ByCorollary (3.30.9),super-resolvingnumberistwo.ByProposition (3.30.8),everycoupleofsuper-verticessuchthattheyaren’tantipodalsupervertices,formsuper-resolvingset.Therefore,super-resolvingsetcontainscouple ofsuper-verticessuchthattheyaren’tantipodalsuper-vertices.
cor4.11
Corollary3.30.11. Let G beafamilyn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beanoddsuper-cyclewithcommonsuper-vertexset Gn Thensimultaneouslysuper-resolvingsetcontainscoupleofsuper-verticessuch thattheyaren’tantipodalsuper-verticesandsuper-resolvingnumberistwo.
154
prp5.11
Oddsuper-cycle
Proposition3.30.12. Inanygivenn-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) whichisoddsuper-cycle,foranysuper-vertex,there’sno super-vertexsuchthatthey’reantipodalsuper-vertices.
Proof. if Xn isagivensuper-vertex.Thentherearetwosuper-vertices Un and Vn suchthat d(Xn,Un)= d(Xn,Vn)= D(n-SHG) Itimpliestheyaren’t antipodalsuper-vertices.
prp5.12
Proposition3.30.13. Letn-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beanoddsuper-cycle.Theneverycoupleofsuper-verticesaresuperresolvingset.
Proof. Let Xn and Xn becoupleofsuper-vertices.Thus,byProposition (3.30.12), Xn and Xn aren’tantipodalsuper-vertices.Itimpliesforeverygiven coupleofsuper-vertices Tn and Tn,Igeteither d(Xn,Tn) = d(Xn,Tn) or d(Xn,Tn) = d(Xn,Tn) Therefore, Tn and Tn aresuper-resolvedbyeither Xn or Xn.Itinducestheset {Xn,Xn} issuper-resolvingset.
prp5.13 Proposition3.30.14. Letn-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beanoddcycle.Thensuper-resolvingnumberistwo.
Proof. Let Xn and Xn becoupleofsuper-vertices.Thus,byProposition (3.30.12), Xn and Xn aren’tantipodalsuper-vertices.Itimpliesforeverygiven coupleofsuper-vertices Tn and Tn,Igeteither d(Xn,Tn) = d(Xn,Tn) or d(Xn,Tn) = d(Xn,Tn) Therefore, Tn and Tn aresuper-resolvedbyeither Xn or Xn.Itinducestheset {Xn,Xn} issuper-resolvingset.
Corollary3.30.15. Letn-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beanoddcycle.Thensuper-resolvingsetcontainscoupleofsupervertices.
Proof. ByProposition (3.30.14),super-resolvingnumberistwo.ByProposition (3.30.13),everycoupleofsuper-verticesformsuper-resolvingset.Therefore, super-resolvingsetcontainscoupleofsuper-vertices.
Corollary3.30.16. Let G beafamilyofn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) whichareoddsuper-cycleswithcommonsuper-vertexset Gn Thensimultaneouslysuper-resolvingsetcontainscoupleofsuper-vertices andsuper-resolvingnumberistwo.
prp1
Proposition3.31.1. Letn-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beasuper-path.Theneverysuper-leafformssuper-resolvingset.
3.31.ExtendedResultsForn-SuperHyperGraph
3.31ExtendedResultsForn-SuperHyperGraph sec6 SmallestSuper-resolvingNumber
155
Proof. Let Ln beasuper-leaf.Foreverygivenacoupleofsuper-vertices Xn and Xn,Iget d(Ln,Xn) = d(Ln,Xn) SinceifIreassignindexestosuper-vertices suchthateverysuper-vertex Xn and Ln have i super-verticesamidthemselves. Thus j ≤ i implies d(Ln,Xn)+ c = d(Ln,Xn) ≡ d(Ln,Xn) <d(Ln,Xn)
Therefore,by d(Ln,Xn) <d(Ln,Xn), Iget d(Ln,Xn) = d(Ln,Xn).Xn and Xn arearbitraryso Ln super-resolvesanygivencoupleofsuper-vertices Xn and Xn whichimplies {Ln} isasuper-resolvingset.
prp7 Proposition3.31.2. Letn-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beasuper-path.Thenasetincludingeverycoupleofsuper-verticesis super-resolvingset.
Proof. Let Xn and Xn beacoupleofsuper-vertices.Foreverygivenacouple ofsuper-vertices Yn and Yn,Igeteither d(Xn,Yn) = d(Xn,Yn) or d(Xn,Yn) = d(Xn,Yn)
prp6.2 Proposition3.31.3. Letn-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beasuper-path.Thenan 1-setcontainsleafissuper-resolvingsetand super-resolvingnumberisone.
Proof. Therearetwosuper-leaves.Consider Ln isagivensuper-leaf.By n-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) isasuper-path, there’sonlyonenumbertobeseen.Withrearrangingtheindexesofsupervertices, d(Ln,Vn)= i. Furthermore, d(Ln,Vn)= i = j = d(Ln,Vn) Therefore, Ln super-resolveseverygivencoupleofsuper-vertices Vn and Vn Itinduces 1-setcontainingleafissuper-resolvingset.Also,super-resolvingnumberis one.
cor6.3
Corollary3.31.4. Let G beafamilyofn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) aresuper-pathswithcommonsuper-vertexset Gn such thatthey’veacommonsuper-leaf.Thensimultaneouslysuper-resolvingnumber is 1, 1-setcontainscommonleaf,issimultaneouslysuper-resolvingsetfor G.
Proof. ByProposition (3.31.3),commonsuper-leafsuper-resolveseverygiven coupleofsuper-vertices Xn and Xn, simultaneously.Thus 1-setcontaining commonsuper-leaf,issimultaneouslysuper-resolvingset.Also,simultaneously super-resolvingnumberisone.
prp6.4 Proposition3.31.5. Let G beafamilyofn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) aresuper-pathswithcommonsuper-vertexset Gn such thatforeverysuper-leaf Ln fromn-SHG, there’sanothern-SHG ∈G such that Ln isn’tsuper-leaf.Thenan 2-setcontainseverycoupleofsuper-vertices, issuper-resolvingset.An 2-setcontainseverycoupleofsuper-vertices,is optimal-super-resolvingset.Optimal-super-resolvingnumberistwo.
3.NeutrosophicHypergraphs
156
prp55.11
3.31.ExtendedResultsForn-SuperHyperGraph
Proof. Suppose Vn isagivensuper-vertex.Iftherearetwosuper-vertices Xn and Yn suchthat d(Xn,Vn) = d(Yn,Vn), then Xn super-resolves Xn and Yn andtheproofisdone.Ifnot, d(Xn,Vn)= d(Yn,Vn), butforeverygiven super-vertex Vn, d(Xn,Vn) = d(Yn,Vn)
Corollary3.31.6. Let G beafamilyofn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) aresuper-pathswithcommonsuper-vertexset Gn such thatthey’venocommonsuper-leaf.Thenan 2-setissimultaneouslyoptimalsuper-resolvingsetandsimultaneouslyoptimal-super-resolvingnumberis 2.
Proof. ByCorollary (3.31.4),commonsuper-leafformsasimultaneously optimal-super-resolvingsetbutinthiscase,there’snocommonsuper-leaf. ThusbyProposition (3.31.5),an 2-setisoptimal-super-resolvingsetforany n-SHG ∈G. Thenan 2-setissimultaneouslyoptimal-super-resolvingset.It inducessimultaneouslyoptimal-super-resolvingnumberis 2 Soevery 2-setis simultaneouslyoptimal-super-resolvingsetfor G
LargestOptimal-super-resolvingNumber
Super-t-partite,super-bipartite,super-star,super-wheelarealsostudiedand theygetustwotype-resultsasindividualandfamily.
Proposition3.31.7. Letn-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beasuper-t-partite.Theneverysetexcludingcoupleofsuper-vertices indifferentpartswhosecardinalitiesofthemarestrictlygreaterthanone,is optimal-super-resolvingset.
Proof. Considertwosuper-vertices Xn and Yn. Supposesuper-vertex Mn has samepartwitheither Xn or Yn. Withoutloosingthegenerality,suppose Mn hassamepartwith Xn thusitdoesn’thavecommonpartwith Yn Therefore, d(Mn,Xn)=2 =1= d(Mn,Yn)
cor55.12
Corollary3.31.8. Letn-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beasuper-t-partite.Let |V |≥ 3 Thenevery (|V |− 2)-setexcludestwo super-verticesfromdifferentpartswhosecardinalitiesofthemarestrictlygreater thanone,isoptimal-super-resolvingsetandoptimal-super-resolvingnumberis |V |− 2.
Proof. ByProposition (3.31.7),every (|V |− 2)-setexcludestwosuper-vertices fromdifferentpartswhosecardinalitiesofthemarestrictlygreaterthanone,is optimal-super-resolvingset.Sinceif Xn and Yn areeitherinsamepartorin differentparts,then,byanygivensuper-vertex Wn,d(Wn,Xn)= d(Wn,Yn). Thus 1-setisn’tsuper-resolvingset.Therearesameargumentsforaset withcardinality ≤|V |− 3 whenpigeonholeprincipleimpliesatleasttwosuperverticeshavesameconditionsconcerningeitherbeinginsamepartorindifferent parts.
157
cor55.13
Corollary3.31.9. Letn-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beasuper-bipartite.Let |V |≥ 3 Thenevery (|V |− 2)-setexcludestwo super-verticesfromdifferentparts,isoptimal-super-resolvingsetandoptimalsuper-resolvingnumberis |V |− 2
Proof. Consider Xn and Yn areexcludedbya (|V |− 2)-set.Let Mn be agivensuper-vertexwhichisdistinctfromthem.Byn-SuperHyperGraph n-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) isasuper-bipartite, Mn hasa commonpartwitheither Xn or Yn andnotwithbothofthem.Itimplies d(Xn,Mn) = d(Yn,Mn). Sinceif Mn hasacommonpartwith Xn, then d(Xn,Mn)=2 =1= d(Yn,Mn) Andif Mn hasacommonpartwith Yn, then d(Xn,Mn)=1 =2= d(Yn,Mn) Thus Mn super-resolves Xn and Yn If Wn isanothersuper-vertexwhichisdistinctfromthem,thenpigeonhole principleinducesatleasttwosuper-verticeshavesameconditionsconcerning eitherbeinginsamepartorindifferentparts.Itimplies (|V |− 3)-setisn’tsuperresolvingset.Itimplies (|V |− 2)-setexcludestwosuper-verticesfromdifferent parts,isoptimal-super-resolvingsetandoptimal-super-resolvingnumberis |V |− 2
cor55.14
Corollary3.31.10. Letn-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beasuper-star.Thenevery (|V |− 2)-setexcludessuper-centeranda givensuper-vertex,isoptimal-super-resolvingsetandoptimal-super-resolving numberis (|V |− 2)
Proof. Consider Xn and Yn areexcludedbya (|V |− 2)-set.Let Mn bea givensuper-vertexwhichisdistinctfromthem.Byn-SuperHyperGraphnSHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) issuper-star, Mn hasacommonpartwith either Xn or Yn andnotwithbothofthem.Itimplies d(Xn,Mn) = d(Yn,Mn).
Sinceif Mn hasacommonpartwith Xn, then d(Xn,Mn)=2 =1= d(Yn,Mn). Andif Mn hasacommonpartwith Yn, then d(Xn,Mn)=1 =2= d(Yn,Mn) Thus Mn -resolves Xn and Yn If Wn isanothersuper-vertexwhichisdistinct fromthem,thenpigeonholeprincipleinducesatleasttwosuper-verticeshave sameconditionsconcerningeitherbeinginsamepartorindifferentparts.It implies (|V |− 3)-setisn’tsuper-resolvingset.Therefore,every (|V |− 2)-set excludestwosuper-verticesfromdifferentparts,isoptimal-super-resolvingset andoptimal-super-resolvingnumberis |V |− 2
cor55.15
Corollary3.31.11. Letn-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beasuper-wheel.Let |V |≥ 3 Thenevery (|V |− 2)-setexcludessupercenterandagivensuper-vertex,isoptimal-super-resolvingsetandoptimalsuper-resolvingnumberis |V |− 2
Proof. Consider Xn and Yn areexcludedbya (|V |− 2)-set.Let Mn beagiven super-vertexwhichisdistinctfromthem.Byn-SuperHyperGraphn-SHG = (Gn ⊆ P n(V ),En ⊆ P n(V )) isasuper-wheel., Mn hasacommonpartwith either Xn or Yn andnotwithbothofthem.Itimplies d(Xn,Mn) = d(Yn,Mn) Sinceif Xn issuper-center,then d(Xn,Mn)=1 =2= d(Yn,Mn). Andif Yn is super-center,then d(Xn,Mn)=2 =1= d(Yn,Mn) Thus Mn super-resolves Xn and Yn If Wn isanothersuper-vertexwhichisdistinctfromthem,then pigeonholeprincipleinducesatleasttwosuper-verticeshavesameconditions concerningeitherbeinginsamepart(non-centersuper-vertices)orindifferent
3.NeutrosophicHypergraphs
158
3.31.ExtendedResultsForn-SuperHyperGraph
parts.Itimplies (|V |−3)-setisn’tsuper-resolvingset.Therefore,every (|V |−2) setsuper-centerandagivensuper-vertex,isoptimal-super-resolvingsetand optimal-super-resolvingnumberis |V |− 2
Super-t-partite,super-bipartite,super-star,super-wheelarealsostudiedbut theygetusonetype-resultinvolvingfamilyofthem.
Corollary3.31.12. Let G beafamilyofn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) whicharesuper-t-partitewithcommonsuper-vertexset Gn Let |V |≥ 3 Thensimultaneouslyoptimal-super-resolvingnumberis |V |− 2 andevery (|V |− 2)-setexcludestwosuper-verticesfromdifferentparts,is simultaneouslyoptimal-super-resolvingsetfor G.
Proof. ByCorollary (3.31.8),everyresultholdforanygivennSuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) whichare super-t-partite.Thuseveryresultholdforanygivenn-SuperHyperGraph n-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) whicharesuper-t-partite,simultaneously.Therefore,simultaneouslysuper-resolvingnumberis |V |− 2 andevery (|V |− 2)-setexcludestwosuper-verticesfromdifferentparts,issimultaneously optimal-super-resolvingsetfor G
Corollary3.31.13. Let G beafamilyofn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) whicharesuper-bipartitewithcommonsuper-vertexset Gn Let |V |≥ 3 Thensimultaneouslyoptimal-super-resolvingnumberis |V |− 2 andevery (|V |− 2)-setexcludestwosuper-verticesfromdifferentparts,is simultaneouslyoptimal-super-resolvingsetfor G
Proof. ByCorollary (3.31.9),everyresultholdforanygivennSuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) whichare super-bipartite.Thuseveryresultholdforanygivenn-SuperHyperGraph n-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) whicharesuper-bipartite,simultaneously.Therefore,simultaneouslysuper-resolvingnumberis |V |− 2 andevery (|V |− 2)-setexcludestwosuper-verticesfromdifferentparts,issimultaneously optimal-super-resolvingsetfor G
Corollary3.31.14. Let G beafamilyofn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) whicharesuper-starwithcommonsuper-vertexset Gn. Let |V |≥ 3. Thensimultaneouslyoptimal-super-resolvingnumberis |V |−2 andevery (|V |− 2)-setexcludessuper-centerandagivensuper-vertex,issimultaneously optimal-super-resolvingsetfor G
Proof. ByCorollary (3.31.10),everyresultholdforanygivennSuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) whichare super-star.Thuseveryresultholdforanygivenn-SuperHyperGraphnSHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) whicharesuper-star,simultaneously. Therefore,simultaneouslysuper-resolvingnumberis |V |− 2 andevery (|V |− 2) setexcludessuper-centerandagivensuper-vertex,issimultaneouslyoptimalsuper-resolvingsetfor G.
Corollary3.31.15. Let G beafamilyofn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) whicharesuper-wheelwithcommonsuper-vertexset Gn Let |V |≥ 3 Thensimultaneouslyoptimal-super-resolvingnumberis |V |− 2
159
sec2
andevery (|V |− 2)-setexcludessuper-centerandagivensuper-vertex,is simultaneouslyoptimal-super-resolvingsetfor G
Proof. ByCorollary (3.31.11),everyresultholdforanygivennSuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) whichare super-star.Thuseveryresultholdforanygivenn-SuperHyperGraphnSHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) whicharesuper-star,simultaneously. Therefore,simultaneouslysuper-resolvingnumberis |V |− 2 andevery (|V |− 2) setexcludessuper-centerandagivensuper-vertex,issimultaneouslyoptimalsuper-resolvingsetfor G
3.32Optimal-super-coloringNumberin
n-SuperHyperGraph
Proposition3.32.1. Letn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beasuper-complete.Thenoptimal-super-coloringnumberis |V |.
Proof. It’scomplete.Itmeansforanytwomembersof V, there’satleasttwo distinctsuper-verticescontainthem.Everysuper-vertexhasedgewithatleast |V |− 1 super-vertices.Thus |V | isoptimal-super-coloringnumber.Sinceany givenmemberof V hasdifferentcolorincomparisontoanothermemberof V. Thenoptimal-super-coloringnumberis |V |.
Proposition3.32.2. Letn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beasuper-path.Thenoptimal-super-coloringnumberistwo.
Proof. Withalternativecolors,super-pathhasdistinctcolorforeverysuperverticeswhichhaveonesuper-edgeincommon.Thusif Xn and Yn aretwosuperverticeswhichhaveonesuper-edgeincommon,then Xn and Yn havedifferent color.Therefore,optimal-super-coloringnumberistwo.Therepresentative ofcolorsaretwogivensuper-verticeswhichhaveatleastonesuper-edgein common.
Proposition3.32.3. Letn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beanevensuper-cycle.Thenoptimal-super-coloringnumberistwo.
Proof. Sinceevensuper-cyclehasevensuper-vertices,withalternativecoloring ofsuper-vertices,thesuper-verticeswhichhavecommonsuper-edge,have differentcolors.Sooptimal-super-coloringnumberistwo.
Proposition3.32.4. Letn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beanoddsuper-cycle.Thenoptimal-super-coloringnumberisthree.
Proof. Withalternativecoloringonsuper-vertices,atend,twosuper-vertices havesamecolor,andthey’vesamesuper-edge.So,optimal-super-coloring numberisthree.
Proposition3.32.5. Letn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beasuper-star.Thenoptimal-super-coloringnumberistwo.
3.NeutrosophicHypergraphs
160
3.32.Optimal-super-coloringNumberinn-SuperHyperGraph
Proof. Super-centerhascommonsuper-edgewitheveryothersuper-vertex.So ithasdifferentcolorincomparisontoothersuper-vertices.Soonecolorhasonly onesuper-vertexwhichhasthatcolor.Allothersuper-verticeshavenocommon super-edgeamideachother.Thenthey’vesamecolor.Therepresentativeof thiscolorisasuper-vertexwhichisdistinctfromsuper-center.Thesetof representativeofcolorshastworepresentativeswhicharesuper-centeranda givensuper-vertexwhichisn’tsuper-center.Optimal-super-coloringnumberis two.
Proposition3.32.6. Letn-SuperHyperGraphsn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beasuper-wheelsuchthatithasevensuper-cycle.Thenoptimal-supercoloringnumberisThree.
Proof. Super-centerhasuniquecolor.Soit’sonlyrepresentativeofthiscolor. Othersuper-verticesformasuper-cyclewhichassignsdistinctcolorstothe super-verticeswhichhavecommonsuper-edgewitheachotherwhenthenumber ofcolorsistwo.Soacolorforsuper-centerandtwocolorsforothersupervertices,makesuper-wheelhasdistinctcolorsforsuper-verticeswhichhave commonsuper-edge.Hence,optimal-super-coloringnumberisThree.
Proposition3.32.7. Letn-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beasuper-wheelsuchthatithasoddsuper-cycle.Thenoptimal-supercoloringnumberisfour.
Proof. Withoutsuper-center,othersuper-verticesformoddsuper-cycle.Odd super-cyclehasoptimal-super-coloringnumberwhichisthree.Super-center hascommonsuper-edgeswithallothersuper-vertices.Thussuper-centerhas differentcolorswithallothersuper-vertices.Therefore,optimal-super-coloring numberisfour.Fourrepresentativesofcolorsformoptimal-super-coloring numberwhereonerepresentativeissuper-centerandotherthreerepresentatives arefromallothersuper-vertices.So,optimal-super-coloringnumberisfour.
Proposition3.32.8. Letn-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beasuper-completeandsuper-bipartite.Thenoptimal-super-coloring numberistwo.
Proof. Everygivensuper-vertexhassuper-edgewithallsuper-verticesfrom anotherpart.Sothecolorofeverysuper-vertexwhichisinasamepartis same.Hence,twopartsimpliestwodifferentcolors.Itinducesoptimal-supercoloringnumberistwo.Theanyofallsuper-verticesineverypart,identifythe representativeofeverycolor.
Proposition3.32.9. Letn-SuperHyperGraphn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) beasuper-completeandsuper-t-partite.Thenoptimal-super-coloring numberis t.
Proof. Everyparthassamecolorforitssuper-vertices.Optimal-super-coloring numberis t. Everypartintroducesonesuper-vertexasarepresentativeofits color.
Proposition3.32.10. Letn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) benSuperHyperGraph.Thenoptimal-super-coloringnumberis 1 ifandonlyif n-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) issuper-empty.
161
Proof. (⇒). Letoptimal-super-coloringnumberbe 1. Itimpliesthere’sno super-vertexwhichhassameedgewithavertex.Sothere’snosuper-edge. Sincen-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) isn-SuperHyperGraphandnSHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) issuper-empty. (⇐) Letn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) ben-SuperHyperGraphand super-empty.Hencethere’snosuper-edge.Itimpliesforeverygivensupervertex,there’snocommonsuper-edge.Itinducesthere’sonlyonecolorfor super-vertices.Hencetherepresentativeofthiscolorischosenfrom |Gn| super-vertices.Thusoptimal-super-coloringnumberis 1
Proposition3.32.11. Letn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) benSuperHyperGraph.Thenoptimal-super-coloringnumberis 2 ifandonlyif n-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) isbothsuper-completeandsuperbipartite.
Proof. (⇒) Letoptimal-super-coloringnumberbetwo.Soeverysuper-vertex haseitheronesuper-vertexortwosuper-verticeswithacommonsuper-edge. Thenumberofcolorsaretwosotherearetwosetswhicheachsethasthe super-verticeswhichhavesamecolor.Iftwosuper-verticeshavesamecolor, thentheydon’thaveacommonedge.Soeverysetisapartinthat,nosupervertexhascommonsuper-edge.Thenumberofthesesetsistwo.Hencethere aretwopartsineachofthem,everysuper-vertexhasnocommonsuper-edge withothersuper-vertices.Sincen-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) is n-SuperHyperGraph,n-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) isbothsupercompleteandsuper-bipartite. (⇐) Assumen-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) isn-SuperHyperGraph, n-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) isbothsuper-completeandsuperbipartite.Thenallsuperedgesareamidtwoparts.Everyparthasthe super-verticeswhichhavenosuper-edgeincommon.Sothey’reassignedto havesamecolor.Therearetwoparts.Thustherearetwocolorstoassignto thesuper-verticesinthat,thesuper-verticeswithcommonsuper-edge,have differentcolors.Itinducesoptimal-super-coloringnumberis 2.
Proposition3.32.12. Letn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) benSuperHyperGraph.Thenoptimal-super-coloringnumberis |V | ifandonly ifn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) issuper-complete.
Proof. (⇒). Letoptimal-super-coloringnumberbe |V |. Thus |Gn| colorsare available.Soanygivensuper-vertexhas |Gn| super-verticeswhichhavecommon super-edgewiththemandeveryofthemhavecommonsuper-edgewitheach other.Itimplieseverysuper-vertexhas |Gn| super-verticeswhichhavecommon super-edgewiththem.Sincen-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) isnSuperHyperGraph, SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) issuper-complete. (⇐) Supposen-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) issuper-complete.Every vertexhas |Gn| super-verticeswhichhavecommonsuper-edgewiththem.Since allpossiblesuper-edgesareavailable,theminimumnumberofcolorsare |Gn| Thusoptimal-super-coloringnumberis |V |.
Generalboundsforoptimal-super-coloringnumberarecomputed.
3.NeutrosophicHypergraphs
162
3.33.ApplicationsinTimeTableandSchedulinginNeutrosophic n-SuperHyperGraph
Proposition3.32.13. Letn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) benSuperHyperGraph.Thenoptimal-super-coloringnumberisobtainedfromthe numberofsuper-verticeswhichis |Gn| andoptimal-super-coloringnumberisat most |V |
Proof. Wheneverysuper-vertexisarepresentativeofeachcolor,optimal-supercoloringnumberistheunionofnumberofmembersofallsuper-verticesand ithappensinoptimal-super-coloringnumberofsuper-completewhichis |V |. Whenallsuper-verticeshavedistinctcolors,optimal-super-coloringnumberis |V | andit’ssharpforsuper-complete.
Therelationamidoptimal-super-coloringnumberandmainparametersof n-SuperHyperGraphiscomputed.
Proposition3.32.14. Letn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) benSuperHyperGraph.Thenoptimal-super-coloringnumberisatmost ∆+1 and atleast 2
Proof. n-SuperHyperGraphissuper-nontrivial.Soitisn’tsuper-emptywhich inducesthere’snosuper-edge.Itimpliesoptimal-super-coloringnumberis two.Sinceoptimal-super-coloringnumberisoneifandonlyifn-SHG = (Gn ⊆ P n(V ),En ⊆ P n(V )) issuper-emptyifandonlyifn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) issuper-trivial.Asuper-vertexwithdegree ∆, has ∆ super-verticeswhichhavecommonsuper-edgeswiththem.Ifthesesuper-vertices havenosuper-edgeamideachother,thenoptimal-super-coloringnumberis twoespecially,super-star.Ifnot,theninthecase,allsuper-verticeshave super-edgeamideachother,optimal-super-coloringnumberis ∆+1, especially, super-complete.
Proposition3.32.15. Letn-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) benSuperHyperGraphandsuper-r-regular.Thenoptimal-super-coloringnumberis atmost r +1
Proof. n-SHG =(Gn ⊆ P n(V ),En ⊆ P n(V )) issuper-r-regular.Soanyof super-vertexhas r super-verticeswhichhavecommonsuper-edgewithit.If thesesuper-verticeshavenocommonsuper-edgewitheachother,forinstance super-star,optimal-super-coloringnumberistwo.Butsincethesuper-vertices havecommonsuper-edgewitheachother,optimal-super-coloringnumberis r +1, forinstance,super-complete.
3.33ApplicationsinTimeTableandSchedulingin
Designingtheprogramstoachievesomegoalsisgeneralapproachtoapplyon someissuestofunctionproperly.Separationhaskeyroleinthecontextofthis style.Separatingthedurationofworkwhichareconsecutive,isthematterand ithasimportanttoavoidmixingup.
Step1.(Definition) Timetableisanapproachtogetsomeattributestodo theworkfastandproper.Thestyleofschedulingimpliesspecialattention tothetaskswhichareconsecutive.
Neutrosophicn-SuperHyperGraph
163
Step2.(Issue) Schedulingofprogramhasfacedwithdifficultiestodifferamid consecutivesection.Beyondthat,sometimessectionsarenotthesame.
FirstCase
Step3.(Model) AsFigure (3.11),thesituationisdesignedasamodel.The modelusesdatatoassigneverysectionandtoassigntorelationamid section,threenumbersbelongunitintervaltostateindeterminacy, possibilitiesanddeterminacy.There’sonerestrictioninthat,thenumbers amidtwosectionsareatleastthenumberoftherelationamidthem. Table(4.5),clarifiesabouttheassignednumberstothesesituation.
Figure3.11:super-verticesaresuspicionsaboutchoosingthem. nhg1

Table3.5:SchedulingconcernsitsSubjectsanditsConnectionsasanSuperHyperGraphinaModel. tbl1c
Sectionsof NHG n1 n2 n9 Values (0 99, 0 98, 0 55)(0 74, 0 64, 0 46) (0 99, 0 98, 0 55) Connectionsof NHG E1 E2 E3 Values (0.01, 0.01, 0.01)(0.01, 0.01, 0.01)(0.01, 0.01, 0.01)
Step4.(Solution) AsFigure (3.11) shows,superhypergraphasmodel, proposestousedifferenttypesofcoloring,resolvinganddominating asnumbers,sets,optimalnumbers,optimalsetsandetcetera.
(a): Thenotionsofdominatingareapplied.
(i): n1 super-dominateseverysuper-vertexfromthesetofsupervertices {n7,n8,n9,n2,n3}.n4 super-dominateseverysupervertexfromthesetofsuper-vertices {n6,n5,n3}.n4 doesn’t super-dominateeverysuper-vertexfromthesetofsuper-vertices {n1,n2,n7,n8,n9}
(ii): {n1,n3} issuper-coloringsetbut {n1,n4} isoptimal-superdominatingset.
(iii): (1 53, 1 22, 0 71) isoptimal-super-dominatingnumber.
(b): Thenotionsofresolvingareapplied.
(i): n1 super-resolvestwosuper-vertices n4 and n6
3.NeutrosophicHypergraphs
164
3.33.ApplicationsinTimeTableandSchedulinginNeutrosophic n-SuperHyperGraph
(ii): V \{n1,n4} issuper-resolvessetbut V \{n2,n4,n9} isoptimalsuper-resolvingset.
(iii): (5, 94, 6.36, 3.3) isoptimal-super-resolvingnumber.
(c): Thenotionsofcoloringareapplied.
(i): n1 super-colorseverysuper-vertexfromthesetofsupervertices {n7,n8,n9,n2,n3}.n4 super-colorseverysuper-vertex fromthesetofsuper-vertices {n6,n5,n3}.n4 doesn’tsuperdominateeverysuper-vertexfromthesetofsuper-vertices {n1,n2,n7,n8,n9}
(ii): {n1,n5,n7,n8,n9,n6,n4} issuper-coloringsetbut {n1,n5,n7,n8,n2,n4} isoptimal-super-coloringset.
(iii): (5 24, 4 8, 2 82) isoptimal-super-coloringnumber.
SecondCase
Step3.(Model) AsFigure (3.12),thesituationisdesignedasamodel.The modelusesdatatoassigneverysectionandtoassigntorelationamid section,threenumbersbelongunitintervaltostateindeterminacy, possibilitiesanddeterminacy.There’sonerestrictioninthat,thenumbers amidtwosectionsareatleastthenumberoftherelationamidthem. Table(4.5),clarifiesabouttheassignednumberstothesesituation.
Figure3.12:Verticesaresuspicionsaboutchoosingthem. nhg8

Step4.(Solution) AsFigure (3.12) shows, NHG3 3,3,3 =(V,E,σ,µ) isneutrosophiccomplete 3 partitehypergraphasmodel,proposestousedifferent typesofdegreeofvertices,degreeofhyperedges,co-degreeofvertices, co-degreeofhyperedges,neutrosophicnumberofvertices,neutrosophic numberofhyperedgesandetcetera.
(i): Thenotionsofneutrosophicnumberareappliedonverticesand hyperedges.
165
Table3.6:SchedulingconcernsitsSubjectsanditsConnectionsasa NeutrosophicHypergraphinaModel. tbl1c
Sectionsof NHG n1 n2··· n9 Values (0.99, 0.98, 0.55)(0.74, 0.64, 0.46) (0.99, 0.98, 0.55) Connectionsof NHG E1,E2 E3 E4 Values (0 54, 0 24, 0 16)(0 99, 0 98, 0 55)(0 74, 0 64, 0 46)
(a): Aneutrosophicnumberofvertices n1,n2,n3 is Σ3 i=1σ(ni)=(2 97, 2 94, 1 65)
(b): Aneutrosophicnumberofhyperedges e1,e2,e3 is Σ3 i=1σ(ei)=(1 82, 1 12, 0 78) where e1 =(0 54, 0 24, 0 16),e2 =(0 74, 0 64, 0 46),e3 = (0 54, 0 24, 0 16)
(ii): Thenotionsofdegree,co-degree,neutrosophicdegreeandneutrosophicco-degreeareappliedonverticesandhyperedges.
(a): Adegreeofanyvertex n1,n2,n4,n6,n8,n9 is 1 anddegreeof anyvertex n3,n5,n7 is 2. (b): Aneutrosophicdegreeofvertex n1,n2,n4,n6,n8,n9 is (0 99, 0 98, 0 55) anddegreeofanyvertex n3,n5,n7 is (1.98, 1.96, 1.1).
(c): Adegreeofanyhyperedgeis 3 (d): Aneutrosophicdegreeofhyperedgeis (2 97, 2 94, 1 65) (e): Aco-degreeofvertices n1,n4 is 1 (f ): Aneutrosophicco-degreeofvertices n1,n4 is (0 54, 0 24, 0 16)
(g): Aco-degreeofhyperedges e1,e2 where µ(e1)=(0 99, 0 98, 0 55) and µ(e2)=(0.54, 0.24, 0.16) is 1.
(h): Aneutrosophicco-degreeofhyperedges e1,e2 where µ(e1)=(0 99, 0 98, 0 55) and µ(e2)=(0 54, 0 24, 0 16) is (0.99, 0.98, 0.55).
3.34OpenProblems
Thethreenotionsofcoloring,resolvinganddominatingareintroducedon n-SuperHyperGraph.Thus,
Question3.34.1. Isitpossibletouseothertypessuper-edgestodefinedifferent typesofcoloring,resolvinganddominatingonn-SuperHyperGraph?
Question3.34.2. Areexistedsomeconnectionsamidthecoloring,resolving anddominatinginsidethisconceptandexternalconnectionswithothertypesof coloring,resolvinganddominatingonn-SuperHyperGraph?
Question3.34.3. Isitpossibletoconstructsomeclassesonn-SuperHyperGraph whichhave“nice”behavior?
3.NeutrosophicHypergraphs
166
3.35.ConclusionandClosingRemarks
Question3.34.4. Whichapplicationsdomakeanindependentstudytoapply thesethreetypescoloring,resolvinganddominatingonn-SuperHyperGraph?
Problem3.34.5. Whichparametersarerelatedtothisparameter?
Problem3.34.6. Whichapproachesdoworktoconstructapplicationstocreate independentstudy?
Problem3.34.7. Whichapproachesdoworktoconstructdefinitionswhichuse allthreedefinitionsandtherelationsamidtheminsteadofseparatedefinitions tocreateindependentstudy?
3.35ConclusionandClosingRemarks
Thisstudyusesmixedcombinationsofdifferenttypesofdefinitions,including coloring,resolvinganddominatingtostudyonn-SuperHyperGraph.The connectionsofsuper-verticeswhichareclarifiedbygeneralsuper-edgesdiffer themfromeachotherandputthemindifferentcategoriestorepresentone representativeforeachcolor,resolveranddominator.Furtherstudiescouldbe aboutchangesinthesettingstocomparethisnotionamiddifferentsettingsof n-SuperHyperGraphtheory.Onewayisfindingsomerelationsamidthree definitionsofnotionstomakesensibledefinitions.InTable (4.6),some limitationsandadvantagesofthisstudyispointedout.
Table3.7:ABriefOverviewaboutAdvantagesandLimitationsofthisstudy tbl2c
Advantages Limitations 1. Defining(Dual)Dimension 1. GeneralResults 2. Defining(Dual)Domination 3. Defining(Dual)Coloring 2. ConnectionsAmidNewNotions 4. ApplyingonIndividuals 5. ApplyingonFamily 3. ConnectionsofResults 167
Bibliography
1 [1] Akram,Muhammad,andAnamLuqman.“Anewdecision-makingmethod basedonbipolarneutrosophicdirectedhypergraphs.”JournalofApplied MathematicsandComputing57.1(2018):547-575.
2 [2] Akram,Muhammad,andAnamLuqman.“Bipolarneutrosophichypergraphswithapplications.”JournalofIntelligent&FuzzySystems33.3 (2017):1699-1713.
3 [3] Akram,Muhammad,andAnamLuqman.“Certainnetworksmodelsusing single-valuedneutrosophicdirectedhypergraphs.”JournalofIntelligent& FuzzySystems33.1(2017):575-588.
4 [4] Akram,Muhammad,andAnamLuqman.“Fuzzyhypergraphsandrelated extensions.”SpringerSingapore,2020.
5 [5] HenryGarrett,“ClosingNumbersandSuper-ClosingNumbersas (Dual)Resolvingand(Dual)Coloringalongside(Dual)Dominating in(Neutrosophic)n-SuperHyperGraph”,ResearchGate2022(doi: 10.13140/RG.2.2.18909.54244).
6 [6] HenryGarrett,“Co-degreeandDegreeofclassesofNeutrosophic Hypergraphs”,ResearchGate2022(doi:10.13140/RG.2.2.32672.10249).
7 [7] HenryGarrett,“DimensionandColoringalongsideDominationinNeutrosophicHypergraphs”,ResearchGate2021(doi: 10.13140/RG.2.2.13070.28483).
8 [8] Hamidi,Mohammad,andFlorentinSmarandache.“Single-valuedneutrosophicdirected(hyper)graphsandapplicationsinnetworks.”Journalof Intelligent&FuzzySystems37.2(2019):2869-2885.
9 [9] Hassan,A.,andM.A.Malik.“Generalizedneutrosophichypergraphs.” InfiniteStudy,2016.
10 [10] Luqman,Anam,MuhammadAkram,andFlorentinSmarandache.“Complexneutrosophichypergraphs:newsocialnetworkmodels.”Algorithms 12.11(2019):234.
11 [11] Malik,MuhammadAslam,etal.“Isomorphismofsinglevaluedneutrosophichypergraphs.”APublicationofSocietyforMathematicsofUncertainty13(2016):19.
169
12 [12] Malik,MuhammadAslam,etal.“Regularsinglevaluedneutrosophic hypergraphs.”InfiniteStudy,2016.
Bibliography
170
NeutrosophicAlliances
4.1DifferentNeutrosophicAlliances
Thefollowingsectionsarecitedas[3].
4.2ThreeTypesofNeutrosophicAlliancesbasedon Connectednessand(Strong)Edges
4.3Abstract
Newsettingisintroducedtostudythealliances.Alliancesareaboutasetof verticeswhichareappliedintothesettingofneutrosophicgraphs.Neighborhood hasthekeyroletodefinethesenotions.Also,neighborhoodisdefinedbasedon theedges,strongedgesandsomeedgeswhicharecomingfromconnectedness. Thesethreetypesofedgesgetaframeworkasneighborhoodandafterthat, toocloseverticeshavekeyroletodefineoffensivealliance,defensivealliance,toffensivealliance,andt-defensivealliancebasedonthreetypesofedges,common edges,strongedgesandsomeedgeswhicharecomingfromconnectedness.The structureofsetisstudiedandgeneralresultsareobtained.Also,someclasses ofneutrosophicgraphscontainingcomplete,empty,path,cycle,bipartite,tpartite,starandwheelareinvestigatedinthetermsofset,minimalset,number, andneutrosophicnumber.Inthisstudy,there’sanopenwaytoextendthese resultsintothefamilyoftheseclassesofneutrosophicgraphs.Thefamily ofneutrosophicgraphsaren’tstudybutitseemsthatanalogousresultsare determined.There’saquestion.Howcanberelatedtoeachother,twosets partitioningthevertexsetofagraph?Theideasofneighborhoodandneighbors basedondifferentedgesillustrateopenwaytogetresults.Asetisalliance whentwosetspartitioningvertexsethaveuniformstructure.Allmembers ofsethavedifferentamountofneighborsinthesetandoutofset.Itleads ustothenotionofoffensiveanddefensive.Newideas,offensivealliance, defensivealliance,t-offensivealliance,t-defensivealliance,strongoffensive alliance,strongdefensivealliance,strongt-offensivealliance,strongt-defensive alliance,connectedoffensivealliance,connecteddefensivealliance,connected t-offensivealliance,andconnectedt-defensiveallianceareintroduced.Two numbersconcerningcardinalityandneutrosophiccardinalityofalliancesare introduced.Asetisalliancewhenitscomplementmakearelationintheterms ofneighborhood.Differentedgesmakedifferentneighborhoods.Threetypesof
CHAPTER4
171
4.NeutrosophicAlliances
edgesareappliedtodefinethreestylesofneighborhoods.Generaledges,strong edgesandconnectededgesareusedwhereconnectededgesaretheedgesarising fromconnectednessamidtwoendpointsoftheedges.Thesenotionsareapplied intoneutrosophicgraphsasindividualsandfamilyofthem.Independentsetas anallianceisaspecialsetwhichhasnoneighborinsideanditimpliessome drawbacksforthisnotions.Findingspecialsetswhicharewell-known,isan openwaytopursethisstudy.Specialsetwhichitsmembershaveonlyone neighborinside,characterizetheconnectedcomponentswherethecardinality ofitscomplementisthenumberofconnectedcomponents.Someproblems areproposedtopursuethisstudy.Basicfamiliaritieswithgraphtheoryand neutrosophicgraphtheoryareproposedforthisarticle.
Keywords: Alliance,OffensiveAlliance,DefensiveAlliance
AMSSubjectClassification: 05C17,05C22,05E45Inthissection,Iuse twosubsectionstoillustrateaperspectiveaboutthebackgroundofthisstudy.
4.4MotivationandContributions
Inthisstudy,there’sanideawhichcouldbeconsideredasamotivation. Question4.4.1. Isitpossibletousemixedversionsofideasconcerning “alliance”,“offensive”and“defensive”todefinesomenotionswhichareapplied toneutrosophicgraphs?
It’smotivationtofindnotionstouseinanyclassesofneutrosophicgraphs. Real-worldapplicationsabouttimetableandschedulingareanotherthoughts whichleadtobeconsideredasmotivation.Connectionsamidtwovertices havekeyrolestoassignalliances,defensivealliancesandoffensivealliances. Thusthey’reusedtodefinenewideaswhichconcludetothestructurealliances, defensivealliancesandoffensivealliances.Theconceptofhavinggeneraledge inspiresmetostudythebehaviorofgeneral,strongedgesandconnectededgein thewaythat,threetypesofnumbersandset,e.g.,alliances,defensivealliances andoffensivealliancesarethecasesofstudyinthesettingsofindividualsand insettingsoffamilies.Also,therearesomeextensionsintoalliances,t-defensive alliancesandt-offensivealliances.
Theframeworkofthisstudyisasfollows.Inthebeginning,Iintroducedbasic definitionstoclarifyaboutpreliminaries.Insubsection“Preliminaries”,new notionsof(strong/connected)alliances,(strong/connected)t-defensivealliances and(strong/connected)t-offensivealliancesareappliedtosetofverticesof neutrosophicgraphsasindividuals.Insection“IntheSettingofSet”,specific setshavethekeyroleinthisway.Classesofneutrosophicgraphsarestudied inthetermsofdifferentsetsinsection“ClassesofNeutrosophicGraphs”as individuals.Inthesection“IntheSettingofNumber”,usagesofgeneral numbershavekeyroleinthisstudyasindividuals.Insection“Classesof NeutrosophicGraphs”,bothnumbershaveappliedintoindividuals.Andas aconcludingresult,there’sonestatementaboutthefamilyofneutrosophic graphsinthissection.Insection“ApplicationsinTimeTableandScheduling”, someapplicationsareposedforalliancesconcerningtimetableandscheduling whenthesuspicionsareaboutchoosingsomesubjects.Insection“Open Problems”,someproblemsandquestionsforfurtherstudiesareproposed.In
172
section“ConclusionandClosingRemarks”,gentlediscussionaboutresultsand applicationsarefeatured.Insection“ConclusionandClosingRemarks”,a briefoverviewconcerningadvantagesandlimitationsofthisstudyalongside conclusionsareformed.
4.5Preliminaries
Definition4.5.1. (Graph).
G =(V,E) iscalleda graph if V isasetofobjectsand E isasubsetof V × V (E isasetof2-subsetsof V )where V iscalled vertexset and E iscalled edgeset.Everytwoverticeshavebeencorrespondedtoatmostoneedge.
Definition4.5.2. (NeutrosophicGraph).
NTG =(V,E,σ =(σ1,σ2,σ3),µ =(µ1,µ2,µ3)) iscalleda neutrosophic graph ifit’sgraph, σi : V → [0, 1],µi : E → [0, 1], andforevery vivj ∈ E, µ(vivj ) ≤ σ(vi) ∧ σ(vj ).
(i): σ iscalled neutrosophicvertexset
(ii): µ iscalled neutrosophicedgeset.
(iii): |V | iscalled order ofNTGandit’sdenotedby O(NTG)
(iv): Σv∈V σ(v) iscalled neutrosophicorder ofNTGandit’sdenotedby On(NTG)
(v): |E| iscalled size ofNTGandit’sdenotedby S(NTG)
(vi): Σe∈E µ(e) iscalled neutrosophicsize ofNTGandit’sdenotedby Sn(NTG)
Definition4.5.3. Let NTG :(V,E,σ,µ) beaneutrosophicgraph.Then
(i): asequenceofvertices P : x0,x1, ··· ,xn iscalleda path where xixi+1 ∈ E,i =0, 1, ··· ,n 1;
(ii): strength ofpath P : x0,x1, ··· ,xn is i=0, ,n 1 µ(xixi+1);
(iii): connectedness amidvertices x0 and xn is µ∞(x,y)= P :x0,x1, ,xn i=0, ,n 1 µ(xixi+1)
(iv): asequenceofvertices P : x0,x1, ,xn iscalleda path where xixi+1 ∈ E,i =0, 1, ··· ,n 1 andtherearetwoedges xy and uv suchthat µ(xy)= µ(uv)= i=0,1, ,n 1 µ(vivi+1);
(v): it’sa t-partite where V ispartitionedto t parts, V1,V2, ··· ,Vt andthe edge xy implies x ∈ Vi and y ∈ Vj where i = j. Ifit’scomplete,thenit’s denotedby Kσ1,σ2, ,σt where σi is σ on Vi instead V whichmean x ∈ Vi induces σi(x)=0.
(v): ant-partiteis completebipartite If t =2, andit’sdenotedby Kσ1,σ2
4.5.Preliminaries
173
(vi): acompletebipartiteis star if |V1| =1, andit’sdenotedby S1,σ2 .
(vii): avertexin V is center ifthevertexjoinstoallverticesofacycle.Then it’s wheel andit’sdenotedby W1,σ2
(viii): it’sa complete where ∀uv ∈ V,µ(uv)= σ(u) ∧ σ(v).
(ix): it’sa strong where ∀uv ∈ E,µ(uv)= σ(u) ∧ σ(v)
Basedondifferentedges,it’spossibletodefinedifferentneighborsasfollows.
Definition4.5.4. (DifferentNeighbors). Let NTG :(V,E,σ,µ) beaneutrosophicgraph.Suppose x ∈ V.
(i): N (x)= {y ∈ V | xy ∈ E};
(ii): Ns(x)= {y ∈ N (x) | µ(xy)= σ(x) ∧ σ(y)};
(iii): Nc(x)= {y ∈ N (x) | µ(xy)= µ∞(x,y)}
Definition4.5.5. Let NTG :(V,E,σ,µ) beaneutrosophicgraph.Aset S is called
(i): offensivealliance if ∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|; (ii): defensivealliance if ∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|;
(iii): t-offensivealliance if ∀a ∈ S, |(N (a) ∩ S) (N (a) ∩ (V \ S))| >t;
(iv): t-defensivealliance if ∀a ∈ S, |(N (a) ∩ S) (N (a) ∩ (V \ S))| <t.
Definition4.5.6. Let NTG :(V,E,σ,µ) beaneutrosophicgraph.Aset S is called
(i): strongoffensivealliance if ∀a ∈ S, |Ns(a) ∩ S| > |Ns(a) ∩ (V \ S)|; (ii): strongdefensivealliance if ∀a ∈ S, |Ns(a) ∩ S| < |Ns(a) ∩ (V \ S)|;
(iii): strongt-offensivealliance if ∀a ∈ S, |(Ns(a)∩S) (Ns(a)∩(V \S))| > t;
(iv): strongt-defensivealliance if ∀a ∈ S, |(Ns(a)∩S) (Ns(a)∩(V \S))| < t.
Definition4.5.7. Let NTG :(V,E,σ,µ) beaneutrosophicgraph.Aset S is called
(i): connectedoffensivealliance if ∀a ∈ S, |Nc(a) ∩ S| > |Nc(a) ∩ (V \ S)|; (ii): connecteddefensivealliance if ∀a ∈ S, |Nc(a)∩ S| < |Nc(a)∩(V \S)|; (iii): connectedt-offensivealliance if ∀a ∈ S, |(Nc(a) ∩ S) (Nc(a) ∩ (V \ S))| >t;
(iv): connectedt-defensivealliance if ∀a ∈ S, |(Nc(a) ∩ S) (Nc(a) ∩ (V \ S))| <t.
Definition4.5.8. Let NTG :(V,E,σ,µ) beaneutrosophicgraph.Then
(i): number of NTG is S isalliance |S|; (ii): neutrosophicnumber of NTG is S isalliance Σs∈S σ(s)
4.NeutrosophicAlliances
174
4.6IntheSettingofSet
Proposition4.6.1. Let NTG :(V,E,σ,µ) beaneutrosophicgraph.Then V is
(i): offensivealliance;
(ii): strongoffensivealliance;
(iii): connectedoffensivealliance;
(iv): δ-offensivealliance;
(v): strong δ-offensivealliance;
(vi): connected δ-offensivealliance.
Proof. Suppose NTG :(V,E,σ,µ) isaneutrosophicgraph.Consider V. All membersof V haveatleastoneneighborinsidethesetmorethanneighborout ofset.Thus, (i).V isoffensivealliancesincethefollowingstatementsareequivalent.
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡ ∀a ∈ V, |N (a) ∩ V | > |N (a) ∩ (V \ V )|≡ ∀a ∈ V, |N (a) ∩ V | > |N (a) ∩∅|≡ ∀a ∈ V, |N (a) ∩ V | > |∅|≡ ∀a ∈ V, |N (a) ∩ V | > 0 ≡ ∀a ∈ V,δ> 0
(ii).V isstrongoffensivealliancesincethefollowingstatementsareequivalent.
∀a ∈ S, |Ns(a) ∩ S| > |Ns(a) ∩ (V \ S)|≡
∀a ∈ V, |Ns(a) ∩ V | > |Ns(a) ∩ (V \ V )|≡
∀a ∈ V, |Ns(a) ∩ V | > |Ns(a) ∩∅|≡ ∀a ∈ V, |Ns(a) ∩ V | > |∅|≡ ∀a ∈ V, |Ns(a) ∩ V | > 0 ≡ ∀a ∈ V,δ> 0
(iii).V isconnectedoffensivealliancesincethefollowingstatementsare equivalent.
∀a ∈ S, |Nc(a) ∩ S| > |Nc(a) ∩ (V \ S)|≡
∀a ∈ V, |Nc(a) ∩ V | > |Nc(a) ∩ (V \ V )|≡ ∀a ∈ V, |Nc(a) ∩ V | > |Nc(a) ∩∅|≡ ∀a ∈ V, |Nc(a) ∩ V | > |∅|≡ ∀a ∈ V, |Nc(a) ∩ V | > 0 ≡ ∀a ∈ V,δ> 0.
(iv).V isoffensivealliancesincethefollowingstatementsareequivalent.
∀a ∈ S, |(N (a) ∩ S) (N (a) ∩ (V \ S))| >δ≡
∀a ∈ V, |(N (a) ∩ V ) (N (a) ∩ (V \ V ))| >δ≡
∀a ∈ V, |(N (a) ∩ V ) (N (a) ∩ (∅))| >δ≡ ∀a ∈ V, |(N (a) ∩ V ) (∅)| >δ≡ ∀a ∈ V, |(N (a) ∩ V )| >δ.
(v).V isstrongoffensivealliancesincethefollowingstatementsareequivalent.
4.6.IntheSettingofSet
175
∀a ∈ S, |(Ns(a) ∩ S) (Ns(a) ∩ (V \ S))| >δ≡ ∀a ∈ V, |(Ns(a) ∩ V ) (Ns(a) ∩ (V \ V ))| >δ≡
∀a ∈ V, |(Ns(a) ∩ V ) (Ns(a) ∩ (∅))| >δ≡ ∀a ∈ V, |(Ns(a) ∩ V ) (∅)| >δ≡ ∀a ∈ V, |(Ns(a) ∩ V )| >δ.
(vi).V isconnectedoffensivealliancesincethefollowingstatementsare equivalent.
∀a ∈ S, |(Nc(a) ∩ S) (Nc(a) ∩ (V \ S))| >δ≡ ∀a ∈ V, |(Nc(a) ∩ V ) (Nc(a) ∩ (V \ V ))| >δ≡ ∀a ∈ V, |(Nc(a) ∩ V ) (Nc(a) ∩ (∅))| >δ≡ ∀a ∈ V, |(Nc(a) ∩ V ) (∅)| >δ≡ ∀a ∈ V, |(Nc(a) ∩ V )| >δ.
Proposition4.6.2. Let NTG :(V,E,σ,µ) beaneutrosophicgraph.Then ∅ is (i): defensivealliance; (ii): strongdefensivealliance; (iii): connecteddefensivealliance; (iv): δ-defensivealliance; (v): strong δ-defensivealliance; (vi): connected δ-defensivealliance.
Proof. Suppose NTG :(V,E,σ,µ) isaneutrosophicgraph.Consider ∅. All membersof ∅ havenoneighborinsidethesetlessthanneighboroutofset. Thus, (i) ∅ isdefensivealliancesincethefollowingstatementsareequivalent.
∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡ ∀a ∈∅, |N (a) ∩∅| < |N (a) ∩ (V \∅)|≡ ∀a ∈∅, |∅| < |N (a) ∩ (V \∅)|≡ ∀a ∈∅, 0 < |N (a) ∩ V |≡ ∀a ∈∅, 0 < |N (a) ∩ V |≡ ∀a ∈ V,δ> 0 (ii) ∅ isstrongdefensivealliancesincethefollowingstatementsareequivalent.
∀a ∈ S, |Ns(a) ∩ S| < |Ns(a) ∩ (V \ S)|≡ ∀a ∈∅, |Ns(a) ∩∅| < |Ns(a) ∩ (V \∅)|≡ ∀a ∈∅, |∅| < |Ns(a) ∩ (V \∅)|≡ ∀a ∈∅, 0 < |Ns(a) ∩ V |≡ ∀a ∈∅, 0 < |Ns(a) ∩ V |≡ ∀a ∈ V,δ> 0
(iii) ∅ isconnecteddefensivealliancesincethefollowingstatementsare equivalent.
4.NeutrosophicAlliances
176
∀a ∈ S, |Nc(a) ∩ S| < |Nc(a) ∩ (V \ S)|≡
∀a ∈∅, |Nc(a) ∩∅| < |Nc(a) ∩ (V \∅)|≡ ∀a ∈∅, |∅| < |Nc(a) ∩ (V \∅)|≡ ∀a ∈∅, 0 < |Nc(a) ∩ V |≡ ∀a ∈∅, 0 < |Nc(a) ∩ V |≡ ∀a ∈ V,δ> 0.
(iv) ∅ isdefensivealliancesincethefollowingstatementsareequivalent.
∀a ∈ S, |(N (a) ∩ S) (N (a) ∩ (V \ S))| <δ≡
∀a ∈∅, |(N (a) ∩∅) (N (a) ∩ (V \∅))| <δ≡ ∀a ∈∅, |(N (a) ∩∅) (N (a) ∩ (V ))| <δ≡ ∀a ∈∅, |∅| <δ≡ ∀a ∈ V, 0 <δ.
(v). ∅ isstrongdefensivealliancesincethefollowingstatementsareequivalent.
∀a ∈ S, |(Ns(a) ∩ S) (Ns(a) ∩ (V \ S))| <δ≡ ∀a ∈∅, |(Ns(a) ∩∅) (Ns(a) ∩ (V \∅))| <δ≡ ∀a ∈∅, |(Ns(a) ∩∅) (Ns(a) ∩ (V ))| <δ≡ ∀a ∈∅, |∅| <δ≡ ∀a ∈ V, 0 <δ.
(vi) ∅ isconnecteddefensivealliancesincethefollowingstatementsare equivalent.
∀a ∈ S, |(Nc(a) ∩ S) (Nc(a) ∩ (V \ S))| <δ≡ ∀a ∈∅, |(Nc(a) ∩∅) (Nc(a) ∩ (V \∅))| <δ≡ ∀a ∈∅, |(Nc(a) ∩∅) (Nc(a) ∩ (V ))| <δ≡ ∀a ∈∅, |∅| <δ≡ ∀a ∈ V, 0 <δ.
Proposition4.6.3. Let NTG :(V,E,σ,µ) beaneutrosophicgraph.Thenan independentsetis
(i): defensivealliance; (ii): strongdefensivealliance; (iii): connecteddefensivealliance; (iv): δ-defensivealliance; (v): strong δ-defensivealliance; (vi): connected δ-defensivealliance.
Proof. Suppose NTG :(V,E,σ,µ) isaneutrosophicgraph.Consider ∅. All membersof ∅ havenoneighborinsidethesetlessthanneighboroutofset. Thus, (i) Anindependentsetisdefensivealliancesincethefollowingstatementsare equivalent.
4.6.IntheSettingofSet
177
∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡ ∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡ ∀a ∈ S, |∅| < |N (a) ∩ (V \ S)|≡ ∀a ∈ S, 0 < |N (a) ∩ V |≡ ∀a ∈ S, 0 < |N (a)|≡ ∀a ∈ V,δ> 0.
(ii) Anindependentsetisstrongdefensivealliancesincethefollowing statementsareequivalent.
∀a ∈ S, |Ns(a) ∩ S| < |Ns(a) ∩ (V \ S)|≡ ∀a ∈ S, |Ns(a) ∩ S| < |Ns(a) ∩ (V \ S)|≡ ∀a ∈ S, |∅| < |Ns(a) ∩ (V \ S)|≡ ∀a ∈ S, 0 < |Ns(a) ∩ V |≡ ∀a ∈ S, 0 < |Ns(a)|≡ ∀a ∈ V,δ> 0
(iii) Anindependentsetisconnecteddefensivealliancesincethefollowing statementsareequivalent.
∀a ∈ S, |Nc(a) ∩ S| < |Nc(a) ∩ (V \ S)|≡ ∀a ∈ S, |Nc(a) ∩ S| < |Nc(a) ∩ (V \ S)|≡ ∀a ∈ S, |∅| < |Nc(a) ∩ (V \ S)|≡ ∀a ∈ S, 0 < |Nc(a) ∩ V |≡ ∀a ∈ S, 0 < |Nc(a)|≡ ∀a ∈ V,δ> 0
(iv) Anindependentsetisdefensivealliancesincethefollowingstatementsare equivalent.
∀a ∈ S, |(N (a) ∩ S) (N (a) ∩ (V \ S))| <δ≡ ∀a ∈ S, |(N (a) ∩ S) (N (a) ∩ (V \ S))| <δ≡ ∀a ∈ S, |(N (a) ∩ S) (N (a) ∩ (V ))| <δ≡ ∀a ∈ S, |∅| <δ≡ ∀a ∈ V, 0 <δ.
(v). Anindependentsetisstrongdefensivealliancesincethefollowing statementsareequivalent.
∀a ∈ S, |(Ns(a) ∩ S) (Ns(a) ∩ (V \ S))| <δ≡ ∀a ∈ S, |(Ns(a) ∩ S) (Ns(a) ∩ (V \ S))| <δ≡ ∀a ∈ S, |(Ns(a) ∩ S) (Ns(a) ∩ (V ))| <δ≡ ∀a ∈ S, |∅| <δ≡ ∀a ∈ V, 0 <δ. (vi) Anindependentsetisconnecteddefensivealliancesincethefollowing statementsareequivalent.
∀a ∈ S, |(Nc(a) ∩ S) (Nc(a) ∩ (V \ S))| <δ≡ ∀a ∈ S, |(Nc(a) ∩ S) (Nc(a) ∩ (V \ S))| <δ≡ ∀a ∈ S, |(Nc(a) ∩ S) (Nc(a) ∩ (V ))| <δ≡ ∀a ∈ S, |∅| <δ≡ ∀a ∈ V, 0 <δ.
4.NeutrosophicAlliances
178
4.7ClassesofNeutrosophicGraphs
Proposition4.7.1. Let NTG :(V,E,σ,µ) beaneutrosophicgraphwhichis cycle/path/wheel.Then V isminimal
(i): offensivealliance;
(ii): strongoffensivealliance;
(iii): connectedoffensivealliance;
(iv): O(NTG)-offensivealliance;
(v): strong O(NTG)-offensivealliance;
(vi): connected O(NTG)-offensivealliance.
Proof. Suppose NTG :(V,E,σ,µ) isaneutrosophicgraphwhichis cycle/path//wheel.
(i) Consideronevertexisoutof S whichisalliance.Thisvertexhasone neighborin S,i.e,Suppose x ∈ V \ S suchthat y,z ∈ N (x). Byit’scycle, |N (x)| = |N (y)| = |N (z)| =2 Thus
∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡
∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡ ∃y ∈ V \{x}, |N (y) ∩ S| < |N (y) ∩ (V \ (V \{x}))|≡
∃y ∈ V \{x}, |N (y) ∩ S| < |N (y) ∩{x})|≡ ∃y ∈ V \{x}, |{z}| < |{x})|≡ ∃y ∈ S, 1 < 1
Thusit’scontradiction.Itimpliesevery V \{x} isn’toffensiveallianceina givencycle.
Consideronevertexisoutof S whichisalliance.Thisvertexhasoneneighbor in S,i.e,Suppose x ∈ V \ S suchthat y,z ∈ N (x) Byit’spath, |N (x)| = |N (y)| = |N (z)| =2 Thus
∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡
∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡
∃y ∈ V \{x}, |N (y) ∩ S| < |N (y) ∩ (V \ (V \{x}))|≡ ∃y ∈ V \{x}, |N (y) ∩ S| < |N (y) ∩{x})|≡ ∃y ∈ V \{x}, |{z}| < |{x})|≡ ∃y ∈ S, 1 < 1
Thusit’scontradiction.Itimpliesevery V \{x} isn’toffensiveallianceina givenpath.
Consideronevertexisoutof S whichisalliance.Thisvertexhasoneneighbor in S,i.e,Suppose x ∈ V \ S suchthat y,z ∈ N (x) Byit’swheel, |N (x)| = |N (y)| = |N (z)| =2 Thus
∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡
∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡
∃y ∈ V \{x}, |N (y) ∩ S| < |N (y) ∩ (V \ (V \{x}))|≡
∃y ∈ V \{x}, |N (y) ∩ S| < |N (y) ∩{x})|≡ ∃y ∈ V \{x}, |{z}| < |{x})|≡ ∃y ∈ S, 1 < 1
4.7.ClassesofNeutrosophicGraphs
179
Thusit’scontradiction.Itimpliesevery V \{x} isn’toffensiveallianceina givenwheel. (ii), (iii) areobviousby (i) (iv) By (i), |V | isminimalandit’soffensivealliance.Thusit’s |V |-offensive alliance. (v), (vi) areobviousby (iv).
Proposition4.7.2. Let NTG :(V,E,σ,µ) beaneutrosophicgraphwhichis cycle/path/wheel.Then V isonly (i): offensivealliance; (ii): strongoffensivealliance; (iii): connectedoffensivealliance; (iv): O(NTG)-offensivealliance; (v): strong O(NTG)-offensivealliance; (vi): connected O(NTG)-offensivealliance.
Proof. Suppose NTG :(V,E,σ,µ) isaneutrosophicgraphwhichis cycle/path//wheel. (i) Consideronevertexisoutof S whichisalliance.Thisvertexhasone neighborin S,i.e,Suppose x ∈ V \ S suchthat y,z ∈ N (x) Byit’scycle, |N (x)| = |N (y)| = |N (z)| =2. Thus
∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡ ∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡ ∃y ∈ V \{x}, |N (y) ∩ S| < |N (y) ∩ (V \ (V \{x}))|≡ ∃y ∈ V \{x}, |N (y) ∩ S| < |N (y) ∩{x})|≡ ∃y ∈ V \{x}, |{z}| < |{x})|≡ ∃y ∈ S, 1 < 1.
Thusit’scontradiction.Itimpliesevery V \{x} isn’toffensiveallianceina givencycle. Consideronevertexisoutof S whichisalliance.Thisvertexhasoneneighbor in S,i.e,Suppose x ∈ V \ S suchthat y,z ∈ N (x) Byit’spath, |N (x)| = |N (y)| = |N (z)| =2. Thus ∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡ ∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡ ∃y ∈ V \{x}, |N (y) ∩ S| < |N (y) ∩ (V \ (V \{x}))|≡ ∃y ∈ V \{x}, |N (y) ∩ S| < |N (y) ∩{x})|≡ ∃y ∈ V \{x}, |{z}| < |{x})|≡ ∃y ∈ S, 1 < 1
Thusit’scontradiction.Itimpliesevery V \{x} isn’toffensiveallianceina givenpath.
Consideronevertexisoutof S whichisalliance.Thisvertexhasoneneighbor in S,i.e,Suppose x ∈ V \ S suchthat y,z ∈ N (x) Byit’swheel, |N (x)| = |N (y)| = |N (z)| =2 Thus
4.NeutrosophicAlliances
180
∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡
∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡ ∃y ∈ V \{x}, |N (y) ∩ S| < |N (y) ∩ (V \ (V \{x}))|≡
∃y ∈ V \{x}, |N (y) ∩ S| < |N (y) ∩{x})|≡ ∃y ∈ V \{x}, |{z}| < |{x})|≡ ∃y ∈ S, 1 < 1.
Thusit’scontradiction.Itimpliesevery V \{x} isn’toffensiveallianceina givenwheel.
(ii), (iii) areobviousby (i)
(iv) By (i),V isminimalandit’soffensivealliance.Thusit’s O(NTG)-offensivealliance. (v), (vi) areobviousby (iv)
Proposition4.7.3. Let NTG :(V,E,σ,µ) beaneutrosophicgraphwhichis star/completebipartite/completet-partite.Thencenterand n half+1vertices isminimal
(i): offensivealliance;
(ii): strongoffensivealliance;
(iii): connectedoffensivealliance;
(iv): O(NTG) 2 +1-offensivealliance;
(v): strong O(NTG) 2 +1-offensivealliance;
(vi): connected O(NTG) 2 +1-offensivealliance.
Proof. (i). Consider n half +1 verticesareoutof S whichisalliance.This vertexhas n halfneighborin S. Ifthevertexisnon-center,then
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡ ∀a ∈ S, 1 > 0. Ifthevertexiscenter,then
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡
∀a ∈ S, n 2 > n 2 1.
Thusit’sproved.Itimpliesevery S isoffensiveallianceinagivenstar. Consider n half +1 verticesareoutof S whichisalliance.Thisvertexhas n halfneighborin S.
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡
∀a ∈ S, n 2 > n 2 1
Thusit’sproved.Itimpliesevery S isoffensiveallianceinagivencomplete bipartitewhichisn’tastar.
Consider n half +1 verticesareoutof S whichisallianceandtheyarechosen fromdifferentparts,equallyoralmostequallyaspossible.Thisvertexhas n halfneighborin S.
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡
∀a ∈ S, n 2 > n 2 1
Thusit’sproved.Itimpliesevery S isoffensiveallianceinagivencomplete t-partitewhichisn’tneitherastarnorcompletebipartite.
4.7.ClassesofNeutrosophicGraphs
181
(ii), (iii) areobviousby (i).
(iv) By (i), {xi} O(NTG) 2 +1 i=1 isminimalandit’soffensivealliance.Thusit’s O(NTG) 2 +1-offensivealliance.
(v), (vi) areobviousby (iv)
Proposition4.7.4. Let NTG :(V,E,σ,µ) beaneutrosophicgraphwhichis star/completebipartite/completet-partite.Thencenterand n half+1vertices isonly
(i): offensivealliance;
(ii): strongoffensivealliance;
(iii): connectedoffensivealliance;
(iv): δ-offensivealliance;
(v): strong δ-offensivealliance; (vi): connected δ-offensivealliance.
Proof. (i) Consider n half +1 verticesareoutof S whichisalliance.This vertexhas n halfneighborin S. Ifthevertexisnon-center,then
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡ ∀a ∈ S, 1 > 0 Ifthevertexiscenter,then
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡ ∀a ∈ S, n 2 > n 2 1
Thusit’sproved.Itimpliesevery S isoffensiveallianceinagivenstar. Consider n half +1 verticesareoutof S whichisalliance.Thisvertexhas n halfneighborin S.
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡ ∀a ∈ S, n 2 > n 2 1
Thusit’sproved.Itimpliesevery S isoffensiveallianceinagivencomplete bipartitewhichisn’tastar.
Consider n half +1 verticesareoutof S whichisallianceandtheyarechosen fromdifferentparts,equallyoralmostequallyaspossible.Thisvertexhas n halfneighborin S.
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡ ∀a ∈ S, n 2 > n 2 1
Thusit’sproved.Itimpliesevery S isoffensiveallianceinagivencomplete t-partitewhichisn’tneitherastarnorcompletebipartite. (ii), (iii) areobviousby (i)
(iv) By (i), {xi} O(NTG) 2 +1 i=1 isminimalandit’soffensivealliance.Thusit’s O(NTG) 2 +1-offensivealliance.
(v), (vi) areobviousby (iv)
4.NeutrosophicAlliances
182
4.8IntheSettingofNumber
Proposition4.8.1. Let NTG :(V,E,σ,µ) beaneutrosophicgraph.Thenumber ofconnectedcomponentis |V S| ifthere’sasetwhichis
(i): offensivealliance;
(ii): strongoffensivealliance;
(iii): connectedoffensivealliance;
(iv): 1-offensivealliance;
(v): strong1-offensivealliance;
(vi): connected1-offensivealliance.
Proof. (i) Considersomeverticesareoutof S whichisalliance.Thisvertex has n halfneighborin S butnovertexoutof S. Thus
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡ ∀a ∈ S, 1 > 0
Thusit’sproved.Itimpliesevery S isoffensiveallianceandnumberof connectedcomponentis |V S|
Considersomeverticesareoutof S whichisalliance.Thisvertexhas n half neighborin S butnovertexoutof S. Thus
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡ ∀a ∈ S, 1 > 0
Thusit’sproved.Itimpliesevery S isoffensiveallianceandnumberof connectedcomponentis |V S|
Considersomeverticesareoutof S whichisalliance.Thisvertexhas n half neighborin S butnovertexoutof S. Thus
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡ ∀a ∈ S, 1 > 0
Thusit’sproved.Itimpliesevery S isoffensiveallianceandnumberof connectedcomponentis |V S| (ii), (iii) areobviousby (i) (iv) By (i), {x} isminimalandit’soffensivealliance.Thusit’s 1-offensive alliance.
(v), (vi) areobviousby (iv).
Proposition4.8.2. Let NTG :(V,E,σ,µ) beaneutrosophicgraph.Thenthe numberisatmost O(NTG) andtheneutrosophicnumberisatmost On(NTG)
Proof. Suppose NTG :(V,E,σ,µ) isaneutrosophicgraph.Consider V. All membersof V haveatleastoneneighborinsidethesetmorethanneighborout ofset.Thus, V isoffensivealliancesincethefollowingstatementsareequivalent.
4.8.IntheSettingofNumber
183
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡ ∀a ∈ V, |N (a) ∩ V | > |N (a) ∩ (V \ V )|≡ ∀a ∈ V, |N (a) ∩ V | > |N (a) ∩∅|≡ ∀a ∈ V, |N (a) ∩ V | > |∅|≡ ∀a ∈ V, |N (a) ∩ V | > 0 ≡ ∀a ∈ V,δ> 0.
V isstrongoffensivealliancesincethefollowingstatementsareequivalent.
∀a ∈ S, |Ns(a) ∩ S| > |Ns(a) ∩ (V \ S)|≡ ∀a ∈ V, |Ns(a) ∩ V | > |Ns(a) ∩ (V \ V )|≡ ∀a ∈ V, |Ns(a) ∩ V | > |Ns(a) ∩∅|≡ ∀a ∈ V, |Ns(a) ∩ V | > |∅|≡ ∀a ∈ V, |Ns(a) ∩ V | > 0 ≡ ∀a ∈ V,δ> 0
V isconnectedoffensivealliancesincethefollowingstatementsareequivalent.
∀a ∈ S, |Nc(a) ∩ S| > |Nc(a) ∩ (V \ S)|≡ ∀a ∈ V, |Nc(a) ∩ V | > |Nc(a) ∩ (V \ V )|≡ ∀a ∈ V, |Nc(a) ∩ V | > |Nc(a) ∩∅|≡ ∀a ∈ V, |Nc(a) ∩ V | > |∅|≡ ∀a ∈ V, |Nc(a) ∩ V | > 0 ≡ ∀a ∈ V,δ> 0
V isoffensivealliancesincethefollowingstatementsareequivalent.
∀a ∈ S, |(N (a) ∩ S) (N (a) ∩ (V \ S))| >δ≡ ∀a ∈ V, |(N (a) ∩ V ) (N (a) ∩ (V \ V ))| >δ≡ ∀a ∈ V, |(N (a) ∩ V ) (N (a) ∩ (∅))| >δ≡ ∀a ∈ V, |(N (a) ∩ V ) (∅)| >δ≡ ∀a ∈ V, |(N (a) ∩ V )| >δ.
V isstrongoffensivealliancesincethefollowingstatementsareequivalent.
∀a ∈ S, |(Ns(a) ∩ S) (Ns(a) ∩ (V \ S))| >δ≡ ∀a ∈ V, |(Ns(a) ∩ V ) (Ns(a) ∩ (V \ V ))| >δ≡ ∀a ∈ V, |(Ns(a) ∩ V ) (Ns(a) ∩ (∅))| >δ≡ ∀a ∈ V, |(Ns(a) ∩ V ) (∅)| >δ≡ ∀a ∈ V, |(Ns(a) ∩ V )| >δ.
V isconnectedoffensivealliancesincethefollowingstatementsareequivalent.
∀a ∈ S, |(Nc(a) ∩ S) (Nc(a) ∩ (V \ S))| >δ≡ ∀a ∈ V, |(Nc(a) ∩ V ) (Nc(a) ∩ (V \ V ))| >δ≡ ∀a ∈ V, |(Nc(a) ∩ V ) (Nc(a) ∩ (∅))| >δ≡ ∀a ∈ V, |(Nc(a) ∩ V ) (∅)| >δ≡ ∀a ∈ V, |(Nc(a) ∩ V )| >δ. Thus V isallianceand V isthebiggestsetin NTG. Thenthenumberisat most O(NTG) andtheneutrosophicnumberisatmost On(NTG) Proposition4.8.3. Let NTG :(V,E,σ,µ) beaneutrosophicgraphwhich iscomplete.Thenumberis O(NTG) 2 +1 andtheneutrosophicnumberis minΣv∈{v1,v2, ,vt}t> O(NTG) 2 ⊆V σ(v), inthesettingof (i): offensivealliance; (ii): strongoffensivealliance;
4.NeutrosophicAlliances
184
(iii): connectedoffensivealliance;
(iv): ( O(NTG) 2 +1)-offensivealliance;
(v): strong ( O(NTG) 2 +1)-offensivealliance;
(vi): connected ( O(NTG) 2 +1)-offensivealliance.
Proof. (i) Consider n half +1 verticesareoutof S whichisalliance.This vertexhas n halfneighborin S.
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡ ∀a ∈ S, n 2 > n 2 1 Thusit’sproved.Itimpliesevery S isoffensiveallianceinagivencomplete graph.Thusthenumberis O(NTG) 2 +1 andtheneutrosophicnumberis minΣv∈{v1,v2, ,vt}t> O(NTG) 2 ⊆V σ(v), inthesettingofoffensivealliance.
(ii). Consider n half +1 verticesareoutof S whichisalliance.Thisvertexhas n halfneighborin S.
∀a ∈ S, |Ns(a) ∩ S| > |Ns(a) ∩ (V \ S)|≡ ∀a ∈ S, n 2 > n 2 1. Thusit’sproved.Itimpliesevery S isstrongoffensiveallianceinagiven completegraph.Thusthenumberis O(NTG) 2 +1 andtheneutrosophicnumber is min Σv∈{v1,v2, ,vt}t> O(NTG) 2 ⊆V σ(v), inthesettingofstrongoffensivealliance.
(iii) Consider n half +1 verticesareoutof S whichisalliance.Thisvertexhas n halfneighborin S.
∀a ∈ S, |Nc(a) ∩ S| > |Nc(a) ∩ (V \ S)|≡ ∀a ∈ S, n 2 > n 2 1 Thusit’sproved.Itimpliesevery S isconnectedoffensiveallianceinagiven completegraph.Thusthenumberis O(NTG) 2 +1 andtheneutrosophicnumber is minΣv∈{v1,v2, ,vt}t> O(NTG) 2 ⊆V σ(v), inthesettingofconnectedoffensive alliance.
(iv). Consider n half +1 verticesareoutof S whichisalliance.Thisvertexhas n halfneighborin S.
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡ ∀a ∈ S, n 2 > n 2 1. Thusit’sproved.Itimpliesevery S is ( O(NTG) 2 +1)-offensiveallianceina givencompletegraph.Thusthenumberis O(NTG) 2 +1 andtheneutrosophic numberis minΣv∈{v1,v2, ,vt}t> O(NTG) 2 ⊆V σ(v), inthesettingof ( O(NTG) 2 +1)-offensivealliance.
(v) Consider n half +1 verticesareoutof S whichisalliance.Thisvertexhas n halfneighborin S.
∀a ∈ S, |Ns(a) ∩ S| > |Ns(a) ∩ (V \ S)|≡ ∀a ∈ S, n 2 > n 2 1
Thusit’sproved.Itimpliesevery S isstrong ( O(NTG) 2 +1)-offensivealliancein agivencompletegraph.Thusthenumberis O(NTG) 2 +1 andtheneutrosophic
4.8.IntheSettingofNumber
185
numberis minΣv∈{v1,v2, ,vt}t> O(NTG) 2 ⊆V σ(v), inthesettingofstrong ( O(NTG) 2 +1)-offensivealliance.
(vi) Consider n half +1 verticesareoutof S whichisalliance.Thisvertexhas n halfneighborin S.
∀a ∈ S, |Nc(a) ∩ S| > |Nc(a) ∩ (V \ S)|≡ ∀a ∈ S, n 2 > n 2 1
Thusit’sproved.Itimpliesevery S isconnected ( O(NTG) 2 +1)-offensive allianceinagivencompletegraph.Thusthenumberis O(NTG) 2 +1 andthe neutrosophicnumberis minΣv∈{v1,v2, ,vt}t> O(NTG) 2 ⊆V σ(v), inthesettingof connected ( O(NTG) 2 +1)-offensivealliance.
Proposition4.8.4. Let NTG :(V,E,σ,µ) beaneutrosophicgraphwhichis ∅ Thenumberis 0 andtheneutrosophicnumberis 0, foranindependentsetin thesettingof
(i): offensivealliance;
(ii): strongoffensivealliance;
(iii): connectedoffensivealliance; (iv): 0-offensivealliance;
(v): strong 0-offensivealliance; (vi): connected 0-offensivealliance.
Proof. Suppose NTG :(V,E,σ,µ) isaneutrosophicgraph.Consider ∅ All membersof ∅ havenoneighborinsidethesetlessthanneighboroutofset. Thus, (i) ∅ isdefensivealliancesincethefollowingstatementsareequivalent.
∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡ ∀a ∈∅, |N (a) ∩∅| < |N (a) ∩ (V \∅)|≡ ∀a ∈∅, |∅| < |N (a) ∩ (V \∅)|≡ ∀a ∈∅, 0 < |N (a) ∩ V |≡ ∀a ∈∅, 0 < |N (a) ∩ V |≡ ∀a ∈ V,δ> 0.
Thenumberis 0 andtheneutrosophicnumberis 0, foranindependentsetin thesettingofoffensivealliance.
(ii) ∅ isstrongdefensivealliancesincethefollowingstatementsareequivalent.
∀a ∈ S, |Ns(a) ∩ S| < |Ns(a) ∩ (V \ S)|≡ ∀a ∈∅, |Ns(a) ∩∅| < |Ns(a) ∩ (V \∅)|≡ ∀a ∈∅, |∅| < |Ns(a) ∩ (V \∅)|≡ ∀a ∈∅, 0 < |Ns(a) ∩ V |≡ ∀a ∈∅, 0 < |Ns(a) ∩ V |≡ ∀a ∈ V,δ> 0.
Thenumberis 0 andtheneutrosophicnumberis 0, foranindependentsetin thesettingofstrongoffensivealliance.
(iii) ∅ isconnecteddefensivealliancesincethefollowingstatementsare equivalent.
4.NeutrosophicAlliances
186
∀a ∈ S, |Nc(a) ∩ S| < |Nc(a) ∩ (V \ S)|≡
∀a ∈∅, |Nc(a) ∩∅| < |Nc(a) ∩ (V \∅)|≡ ∀a ∈∅, |∅| < |Nc(a) ∩ (V \∅)|≡
∀a ∈∅, 0 < |Nc(a) ∩ V |≡ ∀a ∈∅, 0 < |Nc(a) ∩ V |≡ ∀a ∈ V,δ> 0.
Thenumberis 0 andtheneutrosophicnumberis 0, foranindependentsetin thesettingofconnectedoffensivealliance.
(iv) ∅ isdefensivealliancesincethefollowingstatementsareequivalent.
∀a ∈ S, |(N (a) ∩ S) (N (a) ∩ (V \ S))| <δ≡
∀a ∈∅, |(N (a) ∩∅) (N (a) ∩ (V \∅))| <δ≡
∀a ∈∅, |(N (a) ∩∅) (N (a) ∩ (V ))| <δ≡ ∀a ∈∅, |∅| <δ≡ ∀a ∈ V, 0 <δ.
Thenumberis 0 andtheneutrosophicnumberis 0, foranindependentsetin thesettingof 0-offensivealliance.
(v) ∅ isstrongdefensivealliancesincethefollowingstatementsareequivalent.
∀a ∈ S, |(Ns(a) ∩ S) (Ns(a) ∩ (V \ S))| <δ≡ ∀a ∈∅, |(Ns(a) ∩∅) (Ns(a) ∩ (V \∅))| <δ≡ ∀a ∈∅, |(Ns(a) ∩∅) (Ns(a) ∩ (V ))| <δ≡ ∀a ∈∅, |∅| <δ≡ ∀a ∈ V, 0 <δ.
Thenumberis 0 andtheneutrosophicnumberis 0, foranindependentsetin thesettingofstrong 0-offensivealliance.
(vi) ∅ isconnecteddefensivealliancesincethefollowingstatementsare equivalent.
∀a ∈ S, |(Nc(a) ∩ S) (Nc(a) ∩ (V \ S))| <δ≡ ∀a ∈∅, |(Nc(a) ∩∅) (Nc(a) ∩ (V \∅))| <δ≡ ∀a ∈∅, |(Nc(a) ∩∅) (Nc(a) ∩ (V ))| <δ≡ ∀a ∈∅, |∅| <δ≡ ∀a ∈ V, 0 <δ.
Thenumberis 0 andtheneutrosophicnumberis 0, foranindependentsetin thesettingofconnected 0-offensivealliance.
Proposition4.8.5. Let NTG :(V,E,σ,µ) beaneutrosophicgraphwhichis complete.Thenthere’snoindependentset.
4.9ClassesofNeutrosophicGraphs
Proposition4.9.1. Let NTG :(V,E,σ,µ) beaneutrosophicgraphwhichis cycle/path/wheel.Thenumberis O(NTG) andtheneutrosophicnumberis On(NTG), inthesettingof
(i): offensivealliance;
(ii): strongoffensivealliance; (iii): connectedoffensivealliance; (iv): O(NTG)-offensivealliance;
4.9.ClassesofNeutrosophicGraphs
187
(v): strong O(NTG)-offensivealliance;
(vi): connected O(NTG)-offensivealliance.
Proof. Suppose NTG :(V,E,σ,µ) isaneutrosophicgraphwhichis cycle/path/wheel.
(i). Consideronevertexisoutof S whichisalliance.Thisvertexhasone neighborin S,i.e,Suppose x ∈ V \ S suchthat y,z ∈ N (x). Byit’scycle, |N (x)| = |N (y)| = |N (z)| =2 Thus
∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡ ∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡ ∃y ∈ V \{x}, |N (y) ∩ S| < |N (y) ∩ (V \ (V \{x}))|≡ ∃y ∈ V \{x}, |N (y) ∩ S| < |N (y) ∩{x})|≡ ∃y ∈ V \{x}, |{z}| < |{x})|≡ ∃y ∈ S, 1 < 1.
Thusit’scontradiction.Itimpliesevery V \{x} isn’toffensiveallianceina givencycle.
Consideronevertexisoutof S whichisalliance.Thisvertexhasoneneighbor in S,i.e,Suppose x ∈ V \ S suchthat y,z ∈ N (x) Byit’spath, |N (x)| = |N (y)| = |N (z)| =2. Thus
∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡ ∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡ ∃y ∈ V \{x}, |N (y) ∩ S| < |N (y) ∩ (V \ (V \{x}))|≡ ∃y ∈ V \{x}, |N (y) ∩ S| < |N (y) ∩{x})|≡ ∃y ∈ V \{x}, |{z}| < |{x})|≡ ∃y ∈ S, 1 < 1
Thusit’scontradiction.Itimpliesevery V \{x} isn’toffensiveallianceina givenpath. Consideronevertexisoutof S whichisalliance.Thisvertexhasoneneighbor in S,i.e,Suppose x ∈ V \ S suchthat y,z ∈ N (x) Byit’swheel, |N (x)| = |N (y)| = |N (z)| =2 Thus ∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡ ∀a ∈ S, |N (a) ∩ S| < |N (a) ∩ (V \ S)|≡ ∃y ∈ V \{x}, |N (y) ∩ S| < |N (y) ∩ (V \ (V \{x}))|≡ ∃y ∈ V \{x}, |N (y) ∩ S| < |N (y) ∩{x})|≡ ∃y ∈ V \{x}, |{z}| < |{x})|≡ ∃y ∈ S, 1 < 1
Thusit’scontradiction.Itimpliesevery V \{x} isn’toffensiveallianceina givenwheel. (ii), (iii) areobviousby (i) (iv) By (i),V isminimalandit’soffensivealliance.Thusit’s O(NTG)-offensivealliance. (v), (vi) areobviousby (iv) Thusthenumberis O(NTG) andtheneutrosophicnumberis On(NTG), in thesettingofalltypesofalliance.
Proposition4.9.2. Let NTG :(V,E,σ,µ) beaneutrosophicgraphwhichis star/completebipartite/completet-partite.Thenumberis O(NTG) 2 +1 andthe neutrosophicnumberis minΣv∈{v1,v2, ,vt}t> O(NTG) 2 ⊆V σ(v), inthesettingof
4.NeutrosophicAlliances
188
(i): offensivealliance;
(ii): strongoffensivealliance;
(iii): connectedoffensivealliance;
(iv): ( O(NTG) 2 +1)-offensivealliance;
(v): strong ( O(NTG) 2 +1)-offensivealliance;
(vi): connected ( O(NTG) 2 +1)-offensivealliance.
Proof. (i) Consider n half +1 verticesareoutof S whichisalliance.This vertexhas n halfneighborin S. Ifthevertexisnon-center,then
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡ ∀a ∈ S, 1 > 0. Ifthevertexiscenter,then
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡
∀a ∈ S, n 2 > n 2 1
Thusit’sproved.Itimpliesevery S isoffensiveallianceinagivenstar. Consider n half +1 verticesareoutof S whichisalliance.Thisvertexhas n halfneighborin S.
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡ ∀a ∈ S, n 2 > n 2 1.
Thusit’sproved.Itimpliesevery S isoffensiveallianceinagivencomplete bipartitewhichisn’tastar.
Consider n half +1 verticesareoutof S whichisallianceandtheyarechosen fromdifferentparts,equallyoralmostequallyaspossible.Thisvertexhas n halfneighborin S.
∀a ∈ S, |N (a) ∩ S| > |N (a) ∩ (V \ S)|≡ ∀a ∈ S, n 2 > n 2 1.
Thusit’sproved.Itimpliesevery S isoffensiveallianceinagivencomplete t-partitewhichisn’tneitherastarnorcompletebipartite. (ii), (iii) areobviousby (i)
(iv) By (i), {xi} O(NTG) 2 +1 i=1 isminimalandit’soffensivealliance.Thusit’s O(NTG) 2 +1-offensivealliance. (v), (vi) areobviousby (iv). Thusthenumberis O(NTG) 2 +1 andtheneutrosophicnumberis minΣv∈{v1,v2, ,vt}t> O(NTG) 2 ⊆V σ(v), inthesettingofallalliances.
Proposition4.9.3. Let G beafamilyof NTGs :(V,E,σ,µ) neutrosophicgraphs whicharefromone-typeclasswhichtheresultisobtainedforindividual.Then resultsalsoholdforfamily G ofthesespecificclassesofneutrosophicgraphs.
Proof. Thereareneitherconditionsnorrestrictionsonthevertices.Thusthe resultonindividualisextendedtotheresultonfamily.
4.9.ClassesofNeutrosophicGraphs
189
4.10ApplicationsinTimeTableandScheduling
Designingtheprogramstoachievesomegoalsisgeneralapproachtoapplyon someissuestofunctionproperly.Separationhaskeyroleinthecontextofthis style.Separatingthedurationofworkwhichareconsecutive,isthematterand ithasimportanttoavoidmixingup.
Step1.(Definition) Timetableisanapproachtogetsomeattributestodo theworkfastandproper.Thestyleofschedulingimpliesspecialattention tothetaskswhichareconsecutive.
Step2.(Issue) Schedulingofprogramhasfacedwithdifficultiestodifferamid consecutivesection.Beyondthat,sometimessectionsarenotthesame.
Step3.(Model) Thesituationisdesignedasamodel.Themodelusesdatato assigneverysectionandtoassigntorelationamidsection,threenumbers belongunitintervaltostateindeterminacy,possibilitiesanddeterminacy. There’sonerestrictioninthat,thenumbersamidtwosectionsareatleast thenumberoftherelationamidthem.Table (4.5),clarifiesaboutthe assignednumberstothesesituation.
Table4.1:SchedulingconcernsitsSubjectsanditsConnectionsasaneutrosophic graphsanditsalliancesinaModel. tbl1c
Sectionsof NTG n1 n2 n9 Values (0 99, 0 98, 0 55)(0 74, 0 64, 0 46) (0 99, 0 98, 0 55) Connectionsof NTG E1 E2 E3 Values (0.01, 0.01, 0.01)(0.01, 0.01, 0.01)(0.01, 0.01, 0.01)
Step4.(Solution) Theneutrosophicgraphsanditsalliancesasmodel,propose tousedifferenttypesofsets.Iftheconfigurationmakescomplete,theset isdifferent.Also,itholdsforothertypessuchthatstar,wheel,path,and cycle.
4.11OpenProblems
14notionsconcerningalliancesaredefinedinneutrosophicgraphs.Thus,
Question4.11.1. Isitpossibletouseothertypesneighborhoodarisingfrom differenttypesofedgestodefinenewalliances?
Question4.11.2. Areexistedsomeconnectionsamiddifferenttypesofalliances inneutrosophicgraphs?
Question4.11.3. Isitpossibletoconstructsomeclassesofwhichhave“nice” behavior?
Question4.11.4. Whichmathematicalnotionsdomakeanindependentstudy toapplythesetypesinneutrosophicgraphs?
Problem4.11.5. Whichparametersarerelatedtothisparameter?
4.NeutrosophicAlliances
190
Problem4.11.6. Whichapproachesdoworktoconstructapplicationstocreate independentstudy?
Problem4.11.7. Whichapproachesdoworktoconstructdefinitionswhichuse alldefinitionsandtherelationsamidtheminsteadofseparatedefinitionsto createindependentstudy?
4.12ConclusionandClosingRemarks
Thisstudyusesmixedcombinationsofdifferenttypesofdefinitionsconcerning alliancestostudyneutrosophicgraphs.Theconnectionsofverticeswhich areclarifiedbygeneraledgesdifferthemfromeachotherandputthem indifferentcategoriestorepresentasetwhichiscalled.Furtherstudies couldbeaboutchangesinthesettingstocomparethisnotionamiddifferent settingsofneutrosophicgraphstheory.Onewayisfindingsomerelationsamid alldefinitionsofnotionstomakesensibledefinitions.InTable (4.6),some limitationsandadvantagesofthisstudyarepointedout.
Table4.2:ABriefOverviewaboutAdvantagesandLimitationsofthisstudy tbl2c
Newsettingisintroducedtostudytheglobaloffensivealliance.Globaloffensiveallianceisaboutasetofverticeswhichareappliedintothesettingof neutrosophicgraphs.Neighborhoodhasthekeyroletodefinethisnotion.Also, neighborhoodisdefinedbasedonstrongedges.Strongedgegetsaframework asneighborhoodandafterthat,toocloseverticeshavekeyroletodefine globaloffensivealliancebasedonstrongedges.Thestructureofsetisstudied andgeneralresultsareobtained.Also,someclassesofneutrosophicgraphs containingcomplete,empty,path,cycle,star,andwheelareinvestigatedinthe
4.12.ConclusionandClosingRemarks
Advantages Limitations 1. DefiningAlliances 1. SpecificResults 2. DefiningStrongAlliances 3. DefiningConnectedAlliances 2. SpecificConnections 4. ApplyingonIndividuals 5. ApplyingonFamily 3. ConnectionsofResults 4.13GlobalOffensiveAlliances Thefollowingsectionsarecitedas[1]. 4.14GlobalOffensiveAllianceinStrongNeutrosophic Graphs 4.15Abstract
191
termsofset,minimalset,number,andneutrosophicnumber.Neutrosophic numberisdefinedinnewway.It’sfirsttimetodefinethistypeofneutrosophic numberinthewaythat,threevaluesofavertexareusedandthey’vesame sharetoconstructthisnumber.It’scalled“modifiedneutrosophicnumber”. Summationofthreevaluesofvertexmakesonenumberandapplyingittoaset makesneutrosophicnumberofset.Thisapproachfacilitatesidentifyingminimal setandoptimalsetwhichformsminimal-global-offensive-alliancenumberand minimal-global-offensive-alliance-neutrosophicnumber.Twodifferenttypes ofsetsnamelyglobal-offensiveallianceandminimal-global-offensivealliance aredefined.Global-offensiveallianceidentifiesthesetsingeneralvisionbut minimal-global-offensivealliancetakesfocusonthesetswhichdeletingavertex isimpossible.Minimal-global-offensive-alliancenumberisaboutminimum cardinalityamidthecardinalitiesofallminimal-global-offensivealliancesin agivenneutrosophicgraph.Newnotionsareappliedinthesettingsboth individualandfamily.Familyofneutrosophicgraphsisstudiedintheway that,thefamilyonlycontainssameclassesofneutrosophicgraphs.Three typesoffamilyofneutrosophicgraphsincludingm-familyofneutrosophic starswithcommonneutrosophicvertexset,m-familyofoddcompletegraphs withcommonneutrosophicvertexset,andm-familyofoddcompletegraphs withcommonneutrosophicvertexsetarestudied.Theresultsareabout minimal-global-offensivealliance,minimal-global-offensive-alliancenumberand itscorrespondedsets,minimal-global-offensive-alliance-neutrosophicnumber anditscorrespondedsets,andcharacterizingallminimal-global-offensive alliances.Theconnectionofglobal-offensive-allianceswithdominatingsetand chromaticnumberareobtained.Thenumberofconnectedcomponentshas somerelationswiththisnewconceptanditgetssomeresults.Someclassesof neutrosophicgraphsbehavedifferentlywhentheparityofverticesaredifferent andinthiscase,path,cycle,andcompleteillustratethesebehaviors.Two applicationsconcerningcompletemodelasindividualandfamily,underthe titlesoftimetableandschedulingconcludetheresultsandtheygivemore clarifications.Inthisstudy,there’sanopenwaytoextendtheseresultsinto thefamilyoftheseclassesofneutrosophicgraphs.Thefamilyofneutrosophic graphsaren’tstudydeeplyandwithmoreresultsbutitseemsthatanalogous resultsaredetermined.Slightprogressisobtainedinthefamilyofthesemodels butthereareopenavenuestostudyfamilyofothermodelsassamemodels anddifferentmodels.There’saquestion.Howcanberelatedtoeachother, twosetspartitioningthevertexsetofagraph?Theideasofneighborhood andneighborsbasedonstrongedgesillustrateopenwaytogetresults.Aset isglobaloffensivealliancewhentwosetspartitioningvertexsethaveuniform structure.Allmembersofsethavemoreamountofneighborsinthesetthan outofset.Itleadsustothenotionofglobaloffensivealliance.Differentedges makedifferentneighborhoodsbutit’susedonestyleedgetitledstrongedge. Thesenotionsareappliedintoneutrosophicgraphsasindividualsandfamilyof them.Independentsetasanallianceisaspecialsetwhichhasnoneighbor insideanditimpliessomedrawbacksforthesenotions.Findingspecialsets whicharewell-known,isanopenwaytopursethisstudy.Specialsetwhichits membershaveonlyoneneighborinside,characterizetheconnectedcomponents wherethecardinalityofitscomplementisthenumberofconnectedcomponents. Someproblemsareproposedtopursuethisstudy.Basicfamiliaritieswith graphtheoryandneutrosophicgraphtheoryareproposedforthisarticle.
4.NeutrosophicAlliances
192
Keywords: ModifiedNeutrosophicNumber,GlobalOffensiveAlliance, CompleteNeutrosophicGraph
AMSSubjectClassification: 05C17,05C22,05E45
4.16MotivationandContributions
Inthisstudy,there’sanideawhichcouldbeconsideredasamotivation. Question4.16.1. Isitpossibletousemixedversionsofideasconcerning “GlobalOffensiveAlliance”,“ModifiedNeutrosophicNumber”and“Complete NeutrosophicGraph”todefinesomenotionswhichareappliedtoneutrosophic graphs?
It’smotivationtofindnotionstouseinanyclassesofneutrosophicgraphs. Real-worldapplicationsabouttimetableandschedulingareanotherthoughts whichleadtobeconsideredasmotivation.Connectionsamidtwoverticeshave keyrolestoassignglobal-offensivealliance,minimal-global-offensivealliance, minimal-global-offensive-alliancenumber,andminimal-global-offensive-allianceneutrosophicnumber.Thusthey’reusedtodefinenewideaswhichconclude tothestructureglobaloffensivealliance.Theconceptofhavingstrongedge inspiresmetostudythebehaviorofstrongedgesinthewaythat,twotypesof numbersandset,e.g.,global-offensivealliance,minimal-global-offensivealliance, minimal-global-offensive-alliancenumber,andminimal-global-offensive-allianceneutrosophicnumberarethecasesofstudyinthesettingsofindividualsandin settingsoffamilies.Also,therearesomeavenuestoextendthesenotions. Theframeworkofthisstudyisasfollows.Inthebeginning,Iintroduce basicdefinitionstoclarifyaboutpreliminaries.Insubsection“Preliminaries”, newnotionsofglobal-offensivealliance,minimal-global-offensivealliance, minimal-global-offensive-alliancenumber,andminimal-global-offensive-allianceneutrosophicnumberareintroducedandareclarifiedasindividuals.Insection “GeneralResultsForNeutrosophicGraphs”,generalsetshavethekeyrole inthisway.Generalresultsareobtainedandalso,theresultsaboutthe connectionsbetweendominatingsetandchromaticnumberwiththenotion ofglobal-offensiveallianceareelicited.Classesofneutrosophicgraphsare studiedinthetermsofglobal-offensivealliance,minimal-global-offensivealliance, minimal-global-offensive-alliancenumber,andminimal-global-offensive-allianceneutrosophicnumberinsection“ClassesofNeutrosophicGraphs”asindividuals. Insection“ClassesofNeutrosophicGraphs”,bothnumbershaveapplied intoindividuals.Asaconcludingresult,therearethreestatementsabout thefamilyofneutrosophicgraphsasm-familyofneutrosophicstarswith commonneutrosophicvertexset,m-familyofoddcompletegraphswithcommon neutrosophicvertexset,andm-familyofevencompletegraphswithcommon neutrosophicvertexsetinsection“FamilyofNeutrosophicGraphs.”The clarificationsarealsopresentedinsection“FamilyofNeutrosophicGraphs”for introducedresults.Insection“ApplicationsinTimeTableandScheduling”, twoapplicationsareposedforglobal-offensiveallianceconcerningtimetable andschedulingwhenthesuspicionsareaboutchoosingsomesubjectsandthe mentionedmodelsarecompleteasindividualanduniformfamily.Insection
4.16.MotivationandContributions
193
4.NeutrosophicAlliances
“OpenProblems”,someproblemsandquestionsforfurtherstudiesareproposed. Insection“ConclusionandClosingRemarks”,gentlediscussionaboutresults andapplicationsisfeatured.Insection“ConclusionandClosingRemarks”,a briefoverviewconcerningadvantagesandlimitationsofthisstudyalongside conclusionsisformed.
4.17Preliminaries
Inthissubsection,basicmaterialwhichisusedinthisarticle,ispresented. Also,newideasandtheirclarificationsareelicited. Basicideaisaboutthemodelwhichisused.Firstdefinitionintroducesbasic model.
Definition4.17.1. (Graph). G =(V,E) iscalleda graph if V isasetofobjectsand E isasubsetof V × V (E isasetof2-subsetsof V )where V iscalled vertexset and E iscalled edgeset.Everytwoverticeshavebeencorrespondedtoatmostoneedge.
Neutrosophicgraphisthefoundationofresultsinthispaperwhichisdefined asfollows.Also,somerelatednotionsaredemonstrated.
Definition4.17.2. (NeutrosophicGraph). NTG =(V,E,σ =(σ1,σ2,σ3),µ =(µ1,µ2,µ3)) iscalleda neutrosophic graph ifit’sgraph, σi : V → [0, 1],µi : E → [0, 1], andforevery vivj ∈ E, µ(vivj ) ≤ σ(vi) ∧ σ(vj )
(i): σ iscalled neutrosophicvertexset
(ii): µ iscalled neutrosophicedgeset
(iii): |V | iscalled order ofNTGandit’sdenotedby O(NTG)
(iv): Σv∈V σ(v) iscalled neutrosophicorder ofNTGandit’sdenotedby On(NTG)
(v): |E| iscalled size ofNTGandit’sdenotedby S(NTG)
(vi): Σe∈E Σ3 i=1µi(e) iscalled neutrosophicsize ofNTGandit’sdenotedby Sn(NTG).
Someclassesofwell-knownneutrosophicgraphsaredefined.Theseclasses ofneutrosophicgraphsareusedtoformthisstudyandthemostresultsare aboutthem.
Definition4.17.3. Let NTG :(V,E,σ,µ) beaneutrosophicgraph.Then
(i): asequenceofvertices P : x0,x1, ,xn iscalled path where xixi+1 ∈ E,i =0, 1, ,n 1;
(ii): strength ofpath P : x0,x1, ,xn is i=0, ,n 1 µ(xixi+1); (iii): connectedness amidvertices x0 and xn is µ∞(x,y)= P :x0,x1, ,xn i=0, ,n 1 µ(xixi+1);
194
(iv): asequenceofvertices P : x0,x1, ,xn iscalled cycle where xixi+1 ∈ E,i =0, 1, ,n 1 andtherearetwoedges xy and uv suchthat µ(xy)= µ(uv)= i=0,1, ,n 1 µ(vivi+1);
(v): it’s t-partite where V ispartitionedto t parts, V1,V2, ,Vt andthe edge xy implies x ∈ Vi and y ∈ Vj where i = j. Ifit’scomplete,thenit’s denotedby Kσ1,σ2, ,σt where σi is σ on Vi instead V whichmean x ∈ Vi induces σi(x)=0;
(vi): t-partiteis completebipartite if t =2, andit’sdenotedby Kσ1,σ2 ;
(vii): completebipartiteis star if |V1| =1, andit’sdenotedby S1,σ2 ;
(viii): avertexin V is center ifthevertexjoinstoallverticesofacycle.Then it’s wheel andit’sdenotedby W1,σ2 ;
(ix): it’s complete where ∀uv ∈ V,µ(uv)= σ(u) ∧ σ(v);
(x): it’s strong where ∀uv ∈ E,µ(uv)= σ(u) ∧ σ(v).
Thenotionsofneighborandneighborhoodareaboutsomeverticeswhich haveoneedgewithafixedvertex.Thesenotionspresentsverticeswhichare closetoafixedvertexaspossible.Basedonstrongedge,it’spossibletodefine differentneighborhoodasfollows.
Definition4.17.4. (StrongNeighborhood). Let NTG :(V,E,σ,µ) beaneutrosophicgraph.Suppose x ∈ V. Then Ns(x)= {y ∈ N (x) | µ(xy)= σ(x) ∧ σ(y)}.
Newnotionisdefinedbetweentwotypesofneighborhoodsforafixedvertex. Aminimalsetandsomenumbersareintroducedinthisway.Thenextdefinition hasmainroleineveryresultswhicharegiveninthisessay.
Definition4.17.5. Let NTG :(V,E,σ,µ) beaneutrosophicgraph.Then
(i) aset S iscalled global-offensivealliance if ∀a ∈ V \ S, |Ns(a) ∩ S| > |Ns(a) ∩ (V \ S)|;
(ii) ∀S ⊆ S,S isglobaloffensivealliancebut S isn’tglobaloffensivealliance. Then S iscalled minimal-global-offensivealliance;
(iii) minimal-global-offensive-alliancenumber of NTG is S isaminimal-global-offensivealliance. |S| andit’sdenotedby Γ;
(iv) minimal-global-offensive-alliance-neutrosophicnumber of NTG is S isaminimal-global-offensivealliance. Σs∈S Σ3 i=1σi(s) andit’sdenotedby Γs
4.17.Preliminaries
195
Figure4.1:Thesetofblackcirclesisminimal-global-offensivealliance. NTG1
Someclarificationsaregivenfornewdefinitionwhichispresentedinthe paperasfirsttime.Usingnewnotionstomakefamiliaritywithmainpartof thisarticle.
Example4.17.6. ConsiderFigure(4.1).
(i) S1 = {s1,s2},S2 = {s3,s5},S3 = {s3,s4},S4 = {s4,s5} areonlyminimalglobal-offensivealliancesbutonly S3 = {s3,s4} isoptimalsuchthat formsminimal-global-offensive-alliance-neutrosophicnumberandminimalglobal-offensive-alliancenumber;
(ii) N = {s2,s5} isn’tglobal-offensivealliance.Since ∃s1 ∈ V \ N, |Ns(s1) ∩ N | =1 < 2= |Ns(s1) ∩ (V \ N )| ∃s1 ∈ V \ N, |Ns(s1) ∩ N | =1 > 2= |Ns(s1) ∩ (V \ N )| ∃s1 ∈ V \ N, |Ns(s1) ∩ N | > |Ns(s1) ∩ (V \ N )|;
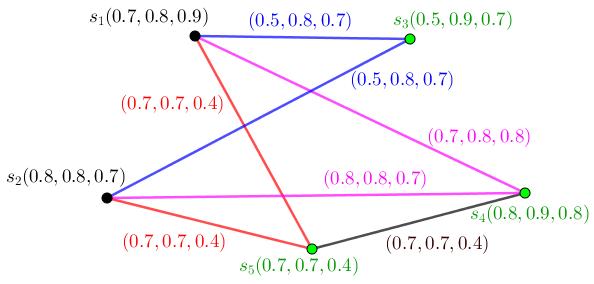
(iii) Γs =4.6;
(iv) Γ=2
4.18GeneralResultsForNeutrosophicGraphs
Inthissection,generalresultsaregivenbasedonnewdefinition.Somerelations betweennewdefinitionwithdominatingsetandchromaticnumberareprovided. Therelationamidthesetwotypesofnewnumberswithfundamentalnumbers ofneutrosophicgraphsasorderandneutrosophicorderareclarifiedintheterms ofvertices.
Proposition4.18.1. Let NTG :(V,E,σ,µ) beastrongneutrosophicgraph.If S isglobal-offensivealliance,then ∀v ∈ V \ S, ∃x ∈ S suchthat (i) v ∈ Ns(x); (ii) vx ∈ E.
Proof. (i) Suppose NTG :(V,E,σ,µ) isastrongneutrosophicgraph.Consider v ∈ V \ S. Since S isglobal-offensivealliance,
4.NeutrosophicAlliances
196
∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \ S, |Ns(v) ∩ S| > |Ns(v) ∩ (V \ S)| v ∈ V \ S, ∃x ∈ S,v ∈ Ns(x)
(ii). Suppose NTG :(V,E,σ,µ) isastrongneutrosophicgraph.Consider v ∈ V \ S. Since S isglobal-offensivealliance,
∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \ S, |Ns(v) ∩ S| > |Ns(v) ∩ (V \ S)| v ∈ V \ S, ∃x ∈ S : v ∈ Ns(x) v ∈ V \ S, ∃x ∈ S : vx ∈ E,µ(vx)= σ(v) ∧ σ(x) v ∈ V \ S, ∃x ∈ S : vx ∈ E.
Definition4.18.2. Let NTG :(V,E,σ,µ) beastrongneutrosophicgraph. Suppose S isasetofvertices.Then
(i) S iscalled dominatingset if ∀v ∈ V \ S, ∃s ∈ S suchthateither v ∈ Ns(s) or vs ∈ E;
(ii) |S| iscalled chromaticnumber if ∀v ∈ V, ∃s ∈ S suchthateither v ∈ Ns(s) or vs ∈ E implies s and v havedifferentcolors.
Example4.18.3. ConsiderFigure(4.1).
(i) S = {s3,s4} isminimaldominatingset; (ii) S = {s3,s4} isminimal-global-offensivealliance; (iii) chromaticnumberisthree.
Proposition4.18.4. Let NTG :(V,E,σ,µ) beastrongneutrosophicgraph.If S isglobal-offensivealliance,then
(i) S isdominatingset;
(ii) there’s S ⊆ S suchthat |S | ischromaticnumber.
Proof. (i) Suppose NTG :(V,E,σ,µ) isastrongneutrosophicgraph.Consider v ∈ V \ S. Since S isglobal-offensivealliance,either ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \ S, |Ns(v) ∩ S| > |Ns(v) ∩ (V \ S)| v ∈ V \ S, ∃x ∈ S,v ∈ Ns(x) or ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \ S, |Ns(v) ∩ S| > |Ns(v) ∩ (V \ S)| v ∈ V \ S, ∃x ∈ S : v ∈ Ns(x) v ∈ V \ S, ∃x ∈ S : vx ∈ E,µ(vx)= σ(v) ∧ σ(x) v ∈ V \ S, ∃x ∈ S : vx ∈ E.
Itimplies S isdominatingset.
(ii) Suppose NTG :(V,E,σ,µ) isastrongneutrosophicgraph.Consider v ∈ V \ S. Since S isglobal-offensivealliance,either
4.18.GeneralResultsForNeutrosophicGraphs
197
or
∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \ S, |Ns(v) ∩ S| > |Ns(v) ∩ (V \ S)| v ∈ V \ S, ∃x ∈ S,v ∈ Ns(x)
∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \ S, |Ns(v) ∩ S| > |Ns(v) ∩ (V \ S)| v ∈ V \ S, ∃x ∈ S : v ∈ Ns(x) v ∈ V \ S, ∃x ∈ S : vx ∈ E,µ(vx)= σ(v) ∧ σ(x) v ∈ V \ S, ∃x ∈ S : vx ∈ E.
Thuseveryvertex v ∈ V \ S, hasatleastoneneighborin S. Theonlycase isabouttherelationamidverticesin S inthetermsofneighbors.Itimplies there’s S ⊆ S suchthat |S | ischromaticnumber.
Proposition4.18.5. Let NTG :(V,E,σ,µ) beastrongneutrosophicgraph. Then (i) Γ ≤O; (ii) Γs ≤On.
Proof. (i) Suppose NTG :(V,E,σ,µ) isastrongneutrosophicgraph.Let S = V.
∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \ V, |Ns(v) ∩ V | > |Ns(v) ∩ (V \ V )| v ∈∅, |Ns(v) ∩ V | > |Ns(v) ∩∅| v ∈∅, |Ns(v) ∩ V | > |∅| v ∈∅, |Ns(v) ∩ V | > 0
Itimplies V isglobal-offensivealliance.Forallsetofvertices S,S ⊆ V. Thus forallsetofvertices S, |S|≤|V |. Itimpliesforallsetofvertices S, |S|≤O. Soforallsetofvertices S, Γ ≤O (ii) Suppose NTG :(V,E,σ,µ) isastrongneutrosophicgraph.Let S = V.
∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \ V, |Ns(v) ∩ V | > |Ns(v) ∩ (V \ V )| v ∈∅, |Ns(v) ∩ V | > |Ns(v) ∩∅| v ∈∅, |Ns(v) ∩ V | > |∅| v ∈∅, |Ns(v) ∩ V | > 0
Itimplies V isglobal-offensivealliance.Forallsetofneutrosophicvertices S,S ⊆ V. Thusforallsetofneutrosophicvertices S, Σs∈S Σ3 i=1σi(s) ≤ Σv∈V Σ3 i=1σi(v) Itimpliesforallsetofneutrosophic vertices S, Σs∈S Σ3 i=1σi(s) ≤On Soforallsetofneutrosophicvertices S, Γs ≤On
Proposition4.18.6. Let NTG :(V,E,σ,µ) beastrongneutrosophicgraph whichisconnected.Then (i) Γ ≤O− 1; (ii) Γs ≤On Σ3 i=1σi(x)
Proof. (i) Suppose NTG :(V,E,σ,µ) isastrongneutrosophicgraph.Let S = V −{x} where x isarbitraryand x ∈ V.
4.NeutrosophicAlliances
198
∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \ V −{x}, |Ns(v) ∩ (V −{x})| > |Ns(v) ∩ (V \ (V −{x}))| |Ns(x) ∩ (V −{x})| > |Ns(x) ∩{x}| |Ns(x) ∩ (V −{x})| > |∅|
|Ns(x) ∩ (V −{x})| > 0
Itimplies V −{x} isglobal-offensivealliance.Forallsetofvertices S = V,S ⊆ V −{x} Thusforallsetofvertices S = V, |S|≤|V −{x}| It impliesforallsetofvertices S = V, |S|≤O− 1 Soforallsetofvertices S, Γ ≤O− 1 (ii) Suppose NTG :(V,E,σ,µ) isastrongneutrosophicgraph.Let S = V −{x} where x isarbitraryand x ∈ V.
∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \ V −{x}, |Ns(v) ∩ (V −{x})| > |Ns(v) ∩ (V \ (V −{x}))| |Ns(x) ∩ (V −{x})| > |Ns(x) ∩{x}|
|Ns(x) ∩ (V −{x})| > |∅|
|Ns(x) ∩ (V −{x})| > 0
Itimplies V −{x} isglobal-offensivealliance.Forallsetofneutrosophic vertices S = V,S ⊆ V −{x} Thusforallsetofneutrosophicvertices S = V, Σs∈S Σ3 i=1σi(s) ≤ Σv∈V −{x}Σ3 i=1σi(v) Itimpliesforallsetof neutrosophicvertices S = V, Σs∈S Σ3 i=1σi(s) ≤On Σ3 i=1σi(x). Soforall setofneutrosophicvertices S, Γs ≤On Σ3 i=1σi(x).
4.19ClassesofNeutrosophicGraphs
Inthissection,behaviorsofsomeclassesofneutrosophicgraphsareanalyzed whennewdefinitionisapplied.Inthisway,theparityofnumberofvertices differentiatetheresultsaboutsomeclassesofneutrosophicgraphs.Paths, cyclesandcompletearesomeclassesofneutrosophicgraphswhichtheparity ofnumberofverticesgetdifferentresults.
Proposition4.19.1. Let NTG :(V,E,σ,µ) beanoddpath.Then (i) theset S = {v2,v4, ,vn 1} isminimal-global-offensivealliance; (ii) Γ= n 2 +1 andcorrespondedsetis S = {v2,v4, ··· ,vn 1}; (iii) Γs =min{Σs∈S={v2,v4, ,vn 1}Σ3 i=1σi(s), Σs∈S={v1,v3, ,vn 1}Σ3 i=1σi(s)}; (iv) thesets S1 = {v2,v4, ,vn 1} and S2 = {v1,v3, ,vn 1} areonly minimal-global-offensivealliances.
Proof. (i). Suppose NTG :(V,E,σ,µ) isanoddpath.Let S = {v2,v4, ,vn 1} whereforall vi,vj ∈{v2,v4, ,vn 1},vivj ∈ E and vi,vj ∈ V. v ∈{v1,v3, ,vn}, |Ns(v) ∩{v2,v4, .vn 1}| =2 > 0= |Ns(v) ∩{v1,v3, ,vn}|∀z ∈ V \ S, |Ns(z) ∩ S| =2 > 0= |Ns(z) ∩ (V \ S)| ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \{v2,v4, ,vn 1}, |Ns(v) ∩{v2,v4, .vn 1}| > |Ns(v) ∩ (V \{v2,v4, ··· .vn 1})| Itimplies S = {v2,v4, ,vn 1} isglobal-offensivealliance.If S = {v2,v4, ,vn 1}−{vi} where vi ∈{v2,v4, ,vn 1}, then
4.19.ClassesofNeutrosophicGraphs
199
∃vi+1 ∈ V \ S, |Ns(z) ∩ S| =1=1= |Ns(z) ∩ (V \ S)| ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| =1 > 1= |Ns(z) ∩ (V \ S)| ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)|
So {v2,v4, ,vn 1}−{vi} where vi ∈{v2,v4, ,vn 1} isn’tglobaloffensivealliance.Itinduces S = {v2,v4, ··· ,vn 1} isminimal-global-offensive alliance.
(ii) and (iii) aretrivial.
(iv). By (i),S1 = {v2,v4, ,vn 1} isminimal-global-offensivealliance.Thus it’senoughtoshowthat S2 = {v1,v3, ,vn 1} isminimal-global-offensive alliance.Suppose NTG :(V,E,σ,µ) isanoddpath.Let S = {v1,v3, ··· ,vn 1} whereforall vi,vj ∈{v1,v3, ,vn 1},vivj ∈ E and vi,vj ∈ V.
v ∈{v2,v4, ··· ,vn}, |Ns(v) ∩{v1,v3, ··· .vn 1}| =2 > 0= |Ns(v) ∩{v2,v4, ,vn}|∀z ∈ V \ S, |Ns(z) ∩ S| =2 > 0= |Ns(z) ∩ (V \ S)| ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \{v1,v3, ,vn 1}, |Ns(v) ∩{v1,v3, .vn 1}| > |Ns(v) ∩ (V \{v1,v3, .vn 1})|
Itimplies S = {v1,v3, ,vn 1} isglobal-offensivealliance.If S = {v1,v3, ,vn 1}−{vi} where vi ∈{v1,v3, ,vn 1}, then ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| =1=1= |Ns(z) ∩ (V \ S)| ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| =1 > 1= |Ns(z) ∩ (V \ S)| ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)|
So {v1,v3, ,vn 1}−{vi} where vi ∈{v1,v3, ,vn 1} isn’tglobaloffensivealliance.Itinduces S = {v1,v3, ··· ,vn 1} isminimal-global-offensive alliance.
Example4.19.2. ConsiderFigure(4.2).
(i) S1 = {s1,s3,s4} and S2 = {s2,s4} areonlyminimal-global-offensive alliances;
(ii) S1 = {s1,s3,s4} isoptimalsuchthatonlyformsminimal-global-offensivealliance-neutrosophicnumberbutnotminimal-global-offensive-alliance number;
(iii) S2 = {s2,s4} isoptimalsuchthatonlyformsminimal-global-offensivealliancenumberbutnotminimal-global-offensive-alliance-neutrosophic number;
(iv) N = {s1,s3} isn’tglobal-offensivealliance.Sincetherearetwoinstances butonlyoneofthemisenough;
(a) Firstcounterexampleforthestatement“N = {s1,s3} isglobaloffensivealliance.”;
∃s4 ∈ V \ N, |Ns(s4) ∩ N | =1=1= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | =1 > 1= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | > |Ns(s4) ∩ (V \ N )|;
(b) secondcounterexampleforthestatement“N = {s1,s3} isglobaloffensivealliance.”.
4.NeutrosophicAlliances
200
Figure4.2:Thesetofblackcirclesisminimal-global-offensivealliance. NTG2
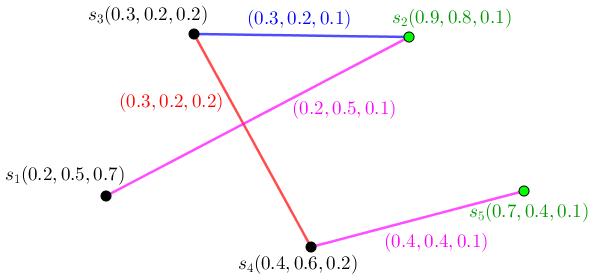
∃s5 ∈ V \ N, |Ns(s5) ∩ N | =0 < 1= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | =0 > 1= |Ns(s5) ∩ (V \ N )|
∃s5 ∈ V \ N, |Ns(s5) ∩ N | > |Ns(s5) ∩ (V \ N )|
(v) Γs =3 1 andcorrespondedsetis S1 = {s1,s3,s4};
(vi) Γ=2 andcorrespondedsetis S2 = {s2,s4}
Proposition4.19.3. Let NTG :(V,E,σ,µ) beanevenpath.Then
(i) theset S = {v2,v4, .vn} isminimal-global-offensivealliance; (ii) Γ= n 2 andcorrespondedsetsare {v2,v4, .vn} and {v1,v3, .vn 1}; (iii) Γs =min{Σs∈S={v2,v4, ,vn}Σ3 i=1σi(s), Σs∈S={v1,v3, .vn 1}Σ3 i=1σi(s)};
(iv) thesets S1 = {v2,v4, ··· .vn} and S2 = {v1,v3, ··· .vn 1} areonly minimal-global-offensivealliances.
Proof. (i). Suppose NTG :(V,E,σ,µ) isanevenpath.Let S = {v2,v4, ,vn} whereforall vi,vj ∈{v2,v4, ,vn},vivj ∈ E and vi,vj ∈ V. v ∈{v1,v3, ,vn 1}, |Ns(v) ∩{v2,v4, .vn}| =2 > 0= |Ns(v) ∩{v1,v3, ,vn 1}|∀z ∈ V \ S, |Ns(z) ∩ S| =2 > 0= |Ns(z) ∩ (V \ S)| ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \{v2,v4, ··· ,vn}, |Ns(v) ∩{v2,v4, ··· .vn}| > |Ns(v) ∩ (V \{v2,v4, ··· .vn})|
Itimplies S = {v2,v4, ,vn} isglobal-offensivealliance.If S = {v2,v4, ,vn}−{vi} where vi ∈{v2,v4, ,vn}, then ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| =1=1= |Ns(z) ∩ (V \ S)| ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| =1 > 1= |Ns(z) ∩ (V \ S)| ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| So {v2,v4, ,vn}−{vi} where vi ∈{v2,v4, ,vn} isn’tglobal-offensive alliance.Itinduces S = {v2,v4, ,vn} isminimal-global-offensivealliance. (ii) and (iii) aretrivial. (iv) By (i),S1 = {v2,v4, ,vn} isminimal-global-offensivealliance.Thusit’s enoughtoshowthat S2 = {v1,v3, ,vn 1} isminimal-global-offensivealliance.
4.19.ClassesofNeutrosophicGraphs
201
Suppose NTG :(V,E,σ,µ) isanevenpath.Let S = {v1,v3, ,vn 1} where forall vi,vj ∈{v1,v3, ,vn 1},vivj ∈ E and vi,vj ∈ V. v ∈{v2,v4, ,vn}, |Ns(v) ∩{v1,v3, .vn 1}| =2 > 0= |Ns(v) ∩{v2,v4, ,vn}|∀z ∈ V \ S, |Ns(z) ∩ S| =2 > 0= |Ns(z) ∩ (V \ S)| ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \{v1,v3, ,vn 1}, |Ns(v) ∩{v1,v3, .vn 1}| > |Ns(v) ∩ (V \{v1,v3, ··· .vn 1})| Itimplies S = {v1,v3, ,vn 1} isglobal-offensivealliance.If S = {v1,v3, ,vn 1}−{vi} where vi ∈{v1,v3, ,vn 1}, then
∃vi+1 ∈ V \ S, |Ns(z) ∩ S| =1=1= |Ns(z) ∩ (V \ S)| ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| =1 > 1= |Ns(z) ∩ (V \ S)| ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| So {v1,v3, ,vn 1}−{vi} where vi ∈{v1,v3, ,vn 1} isn’tglobaloffensivealliance.Itinduces S = {v1,v3, ,vn 1} isminimal-global-offensive alliance.
Example4.19.4. ConsiderFigure(4.3).
(i) S1 = {s1,s3,s5} and S2 = {s2,s4,s6} areonlyminimal-global-offensive alliances;
(ii) S2 = {s2,s4,s6} isoptimalsuchthatformsbothminimal-global-offensivealliance-neutrosophicnumberandminimal-global-offensive-alliancenumber;
(iii) S1 = {s1,s3,s5} isoptimalsuchthatonlyformsminimal-global-offensivealliancenumberbutnotminimal-global-offensive-alliance-neutrosophic number;
(iv) N = {s1,s3} isn’tglobal-offensivealliance.Sincetherearethreeinstances butonlyoneofthemisenough;
(a) Firstcounterexampleforthestatement“N = {s1,s3} isglobaloffensivealliance.”;
∃s4 ∈ V \ N, |Ns(s4) ∩ N | =1=1= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | =1 > 1= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | > |Ns(s4) ∩ (V \ N )|.
(b) secondcounterexampleforthestatement“N = {s1,s3} isglobaloffensivealliance.”;
∃s5 ∈ V \ N, |Ns(s5) ∩ N | =0 < 1= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | =0 > 1= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | > |Ns(s5) ∩ (V \ N )|;
(c) thirdcounterexampleforthestatement“N = {s1,s3} isglobaloffensivealliance.”;
∃s6 ∈ V \ N, |Ns(s6) ∩ N | =0 < 1= |Ns(s6) ∩ (V \ N )| ∃s6 ∈ V \ N, |Ns(s6) ∩ N | =0 > 1= |Ns(s6) ∩ (V \ N )| ∃s6 ∈ V \ N, |Ns(s6) ∩ N | > |Ns(s6) ∩ (V \ N )| (v) Γs =4 5 andcorrespondedsetis S2 = {s2,s4,s6};
4.NeutrosophicAlliances
202
Figure4.3:Thesetofblackcirclesisminimal-global-offensivealliance. NTG3

(vi) Γ=3 andcorrespondedsetsare S1 = {s1,s3,s5} and S2 = {s2,s4,s6}.
Proposition4.19.5. Let NTG :(V,E,σ,µ) beanevencycle.Then
(i) theset S = {v2,v4, ··· ,vn} isminimal-global-offensivealliance; (ii) Γ= n 2 andcorrespondedsetsare {v2,v4, ,vn} and {v1,v3, ,vn 1}; (iii) Γs =min{Σs∈S={v2,v4, ,vn}σ(s), Σs∈S={v1,v3, ,vn 1}σ(s)};
(iv) thesets S1 = {v2,v4, ,vn} and S2 = {v1,v3, ,vn 1} areonly minimal-global-offensivealliances.
Proof. (i) Suppose NTG :(V,E,σ,µ) isanevencycle.Let S = {v2,v4, ,vn} whereforall vi,vj ∈{v2,v4, ,vn},vivj ∈ E and vi,vj ∈ V.
v ∈{v1,v3, ,vn 1}, |Ns(v) ∩{v2,v4, .vn}| =2 > 0= |Ns(v) ∩{v1,v3, ,vn 1}|∀z ∈ V \ S, |Ns(z) ∩ S| =2 > 0= |Ns(z) ∩ (V \ S)| ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \{v2,v4, ,vn}, |Ns(v) ∩{v2,v4, .vn}| > |Ns(v) ∩ (V \{v2,v4, ··· .vn})| Itimplies S = {v2,v4, ··· ,vn} isglobal-offensivealliance.If S = {v2,v4, ,vn}−{vi} where vi ∈{v2,v4, ,vn}, then ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| =1=1= |Ns(z) ∩ (V \ S)| ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| =1 > 1= |Ns(z) ∩ (V \ S)| ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)|
So {v2,v4, ,vn}−{vi} where vi ∈{v2,v4, ,vn} isn’tglobal-offensive alliance.Itinduces S = {v2,v4, ,vn} isminimal-global-offensivealliance. (ii) and (iii) aretrivial. (iv) By (i),S1 = {v2,v4, ,vn} isminimal-global-offensivealliance.Thusit’s enoughtoshowthat S2 = {v1,v3, ··· ,vn 1} isminimal-global-offensivealliance. Suppose NTG :(V,E,σ,µ) isanoddpath.Let S = {v1,v3, ,vn 1} where forall vi,vj ∈{v1,v3, ,vn 1},vivj ∈ E and vi,vj ∈ V.
4.19.ClassesofNeutrosophicGraphs
203
v ∈{v2,v4, ,vn}, |Ns(v) ∩{v1,v3, .vn 1}| =2 > 0= |Ns(v) ∩{v2,v4, ,vn}|∀z ∈ V \ S, |Ns(z) ∩ S| =2 > 0= |Ns(z) ∩ (V \ S)| ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \{v1,v3, ,vn 1}, |Ns(v) ∩{v1,v3, .vn 1}| > |Ns(v) ∩ (V \{v1,v3, .vn 1})|
Itimplies S = {v1,v3, ,vn 1} isglobal-offensivealliance.If S = {v1,v3, ,vn 1}−{vi} where vi ∈{v1,v3, ,vn 1}, then ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| =1=1= |Ns(z) ∩ (V \ S)| ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| =1 > 1= |Ns(z) ∩ (V \ S)| ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)|. So {v1,v3, ,vn 1}−{vi} where vi ∈{v1,v3, ,vn 1} isn’tglobaloffensivealliance.Itinduces S = {v1,v3, ··· ,vn 1} isminimal-global-offensive alliance.
Example4.19.6. ConsiderFigure(4.4).
(i) S1 = {s1,s3,s5} and S2 = {s2,s4,s6} areonlyminimal-global-offensive alliances;
(ii) S2 = {s2,s4,s6} isoptimalsuchthatformsbothminimal-global-offensivealliance-neutrosophicnumberandminimal-global-offensive-alliancenumber;
(iii) S1 = {s1,s3,s5} isoptimalsuchthatonlyformsminimal-global-offensivealliancenumberbutnotminimal-global-offensive-alliance-neutrosophic number;
(iv) N = {s1,s3} isn’tglobal-offensivealliance.Sincetherearethreeinstances butonlyoneofthemisenough;
(a) Firstcounterexampleforthestatement“N = {s1,s3} isglobaloffensivealliance.”;
∃s4 ∈ V \ N, |Ns(s4) ∩ N | =1=1= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | =1 > 1= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | > |Ns(s4) ∩ (V \ N )|
(b) secondcounterexampleforthestatement“N = {s1,s3} isglobaloffensivealliance.”;
∃s5 ∈ V \ N, |Ns(s5) ∩ N | =0 < 1= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | =0 > 1= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | > |Ns(s5) ∩ (V \ N )|; (c) thirdcounterexampleforthestatement“N = {s1,s3} isglobaloffensivealliance.”;
∃s6 ∈ V \ N, |Ns(s6) ∩ N | =0 < 1= |Ns(s6) ∩ (V \ N )| ∃s6 ∈ V \ N, |Ns(s6) ∩ N | =0 > 1= |Ns(s6) ∩ (V \ N )| ∃s6 ∈ V \ N, |Ns(s6) ∩ N | > |Ns(s6) ∩ (V \ N )|
(v) Γs =3.2 andcorrespondedsetis S2 = {s2,s4,s6}; (vi) Γ=3 andcorrespondedsetsare S1 = {s1,s3,s5} and S2 = {s2,s4,s6}
4.NeutrosophicAlliances
204
Figure4.4:Thesetofblackcirclesisminimal-global-offensivealliance. NTG4
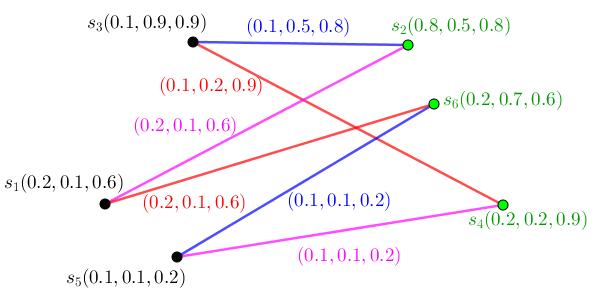
Proposition4.19.7. Let NTG :(V,E,σ,µ) beanoddcycle.Then (i) theset S = {v2,v4, ,vn 1} isminimal-global-offensivealliance; (ii) Γ= n 2 +1 andcorrespondedsetis S = {v2,v4, ,vn 1}; (iii) Γs =min{Σs∈S={v2,v4, .vn 1}Σ3 i=1σi(s), Σs∈S={v1,v3, .vn 1}Σ3 i=1σi(s)}; (iv) thesets S1 = {v2,v4, ··· .vn 1} and S2 = {v1,v3, ··· .vn 1} areonly minimal-global-offensivealliances.
Proof. (i) Suppose NTG :(V,E,σ,µ) isanoddcycle.Let S = {v2,v4, ,vn 1} whereforall vi,vj ∈{v2,v4, ,vn 1},vivj ∈ E and vi,vj ∈ V. v ∈{v1,v3, ,vn}, |Ns(v) ∩{v2,v4, .vn 1}| =2 > 0= |Ns(v) ∩{v1,v3, ,vn}|∀z ∈ V \ S, |Ns(z) ∩ S| =2 > 0= |Ns(z) ∩ (V \ S)| ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \{v2,v4, ,vn 1}, |Ns(v) ∩{v2,v4, .vn 1}| > |Ns(v) ∩ (V \{v2,v4, ··· .vn 1})| Itimplies S = {v2,v4, ,vn 1} isglobal-offensivealliance.If S = {v2,v4, ,vn 1}−{vi} where vi ∈{v2,v4, ,vn 1}, then ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| =1=1= |Ns(z) ∩ (V \ S)| ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| =1 > 1= |Ns(z) ∩ (V \ S)| ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| So {v2,v4, ,vn 1}−{vi} where vi ∈{v2,v4, ,vn 1} isn’tglobaloffensivealliance.Itinduces S = {v2,v4, ,vn 1} isminimal-global-offensive alliance.
(ii) and (iii) aretrivial. (iv) By (i),S1 = {v2,v4, ,vn 1} isminimal-global-offensivealliance.Thus it’senoughtoshowthat S2 = {v1,v3, ,vn 1} isminimal-global-offensive alliance.Suppose NTG :(V,E,σ,µ) isanoddcycle.Let S = {v1,v3, ,vn 1} whereforall vi,vj ∈{v1,v3, ··· ,vn 1},vivj ∈ E and vi,vj ∈ V. v ∈{v2,v4, ,vn}, |Ns(v) ∩{v1,v3, .vn 1}| =2 > 0= |Ns(v) ∩{v2,v4, ,vn}|∀z ∈ V \ S, |Ns(z) ∩ S| =2 > 0= |Ns(z) ∩ (V \ S)|
4.19.ClassesofNeutrosophicGraphs
205
∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \{v1,v3, ,vn 1}, |Ns(v) ∩{v1,v3, .vn 1}| > |Ns(v) ∩ (V \{v1,v3, ··· .vn 1})|
Itimplies S = {v1,v3, ,vn 1} isglobal-offensivealliance.If S = {v1,v3, ,vn 1}−{vi} where vi ∈{v1,v3, ,vn 1}, then ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| =1=1= |Ns(z) ∩ (V \ S)| ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| =1 > 1= |Ns(z) ∩ (V \ S)| ∃vi+1 ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| So {v1,v3, ,vn 1}−{vi} where vi ∈{v1,v3, ,vn 1} isn’tglobaloffensivealliance.Itinduces S = {v1,v3, ,vn 1} isminimal-global-offensive alliance.
Example4.19.8. ConsiderFigure(4.5).
(i) S1 = {s1,s3,s4} and S2 = {s2,s4} areonlyminimal-global-offensive alliances;
(ii) S2 = {s2,s4} isoptimalsuchthatformsbothminimal-global-offensivealliance-neutrosophicnumberandminimal-global-offensive-alliancenumber;
(iii) S1 = {s1,s3,s5} isoptimalsuchthatnotonlydoesn’tformminimalglobal-offensive-alliancenumberbutalsodoesn’tformminimal-globaloffensive-alliance-neutrosophicnumber;
(iv) N = {s1,s3} isn’tglobal-offensivealliance.Sincetherearetwoinstances butonlyoneofthemisenough;
(a) Firstcounterexampleforthestatement“N = {s1,s3} isglobaloffensivealliance.”;
∃s4 ∈ V \ N, |Ns(s4) ∩ N | =1=1= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | =1 > 1= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | > |Ns(s4) ∩ (V \ N )|;
(b) secondcounterexampleforthestatement“N = {s1,s3} isglobaloffensivealliance.”;
∃s5 ∈ V \ N, |Ns(s5) ∩ N | =0 < 1= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | =0 > 1= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | > |Ns(s5) ∩ (V \ N )|
(v) Γs =3.5 andcorrespondedsetis S2 = {s2,s4}; (vi) Γ=2 andcorrespondedsetis S2 = {s2,s4}
Proposition4.19.9. Let NTG :(V,E,σ,µ) bestar.Then
(i) theset S = {c} isminimal-global-offensivealliance; (ii) Γ=1; (iii) Γs =Σ3 i=1σi(c); (iv) thesets S = {c} and S ⊂ S areonlyglobal-offensivealliances.
4.NeutrosophicAlliances
206
Figure4.5:Thesetofblackcirclesisminimal-global-offensivealliance. NTG5
Proof. (i) Suppose NTG :(V,E,σ,µ) isastar.
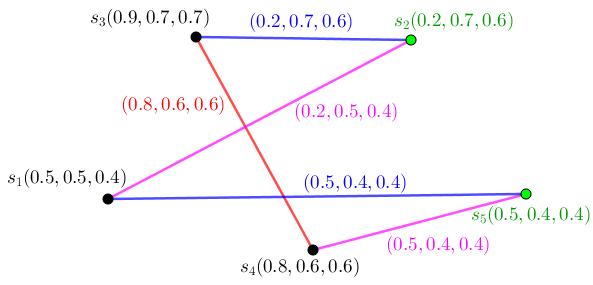
∀v ∈ V \{c}, |Ns(v) ∩{c}| =1 > 0= |Ns(v) ∩ (V \{c})| ∀z ∈ V \ S, |Ns(z) ∩ S| =1 > 0= |Ns(z) ∩ (V \ S)| ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \{c}, |Ns(v) ∩{c}| > |Ns(v) ∩ (V \{c})| Itimplies S = {c} isglobal-offensivealliance.If S = {c}−{c} = ∅, then ∃v ∈ V \ S, |Ns(z) ∩ S| =0=0= |Ns(z) ∩ (V \ S)| ∃v ∈ V \ S, |Ns(z) ∩ S| =0 > 0= |Ns(z) ∩ (V \ S)| ∃v ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)|.
So S = {c}−{c} = ∅ isn’tglobal-offensivealliance.Itinduces S = {c} is minimal-global-offensivealliance. (ii) and (iii) aretrivial. (iv). By (i),S = {c} isminimal-global-offensivealliance.Thusit’senough toshowthat S ⊆ S isminimal-global-offensivealliance.Suppose NTG : (V,E,σ,µ) isastar.Let S ⊆ S ∀v ∈ V \{c}, |Ns(v) ∩{c}| =1 > 0= |Ns(v) ∩ (V \{c})| ∀z ∈ V \ S , |Ns(z) ∩ S | =1 > 0= |Ns(z) ∩ (V \ S )| ∀z ∈ V \ S , |Ns(z) ∩ S | > |Ns(z) ∩ (V \ S )|
Itimplies S ⊆ S isglobal-offensivealliance.
Example4.19.10. ConsiderFigure(4.6).
(i) S = {s1} isonlyminimal-global-offensivealliance;
(ii) S = {s1} isoptimalsuchthatformsbothminimal-global-offensive-allianceneutrosophicnumberandminimal-global-offensive-alliancenumber;
(iii) S including S = {s1} onlyformsglobal-offensive-alliancebutnotminimalglobal-offensive-alliance;
(iv) N = {s3,s4} isn’tglobal-offensivealliance.Sincetherearethreeinstances butonlyoneofthemisenough;
(a) Firstcounterexampleforthestatement“N = {s3,s4} isglobaloffensivealliance.”;
4.19.ClassesofNeutrosophicGraphs
207
Figure4.6:Thesetofblackcirclesisminimal-global-offensivealliance. NTG6
∃s1 ∈ V \ N, |Ns(s1) ∩ N | =2=2= |Ns(s1) ∩ (V \ N )| ∃s1 ∈ V \ N, |Ns(s1) ∩ N | =2 > 2= |Ns(s1) ∩ (V \ N )| ∃s1 ∈ V \ N, |Ns(s1) ∩ N | > |Ns(s1) ∩ (V \ N )|; (b) secondcounterexampleforthestatement“N = {s3,s4} isglobaloffensivealliance.”;
∃s2 ∈ V \ N, |Ns(s2) ∩ N | =0 < 1= |Ns(s2) ∩ (V \ N )| ∃s2 ∈ V \ N, |Ns(s2) ∩ N | =0 > 1= |Ns(s2) ∩ (V \ N )| ∃s2 ∈ V \ N, |Ns(s2) ∩ N | > |Ns(s2) ∩ (V \ N )|; (c) thirdcounterexampleforthestatement“N = {s3,s4} isglobaloffensivealliance.”;
∃s5 ∈ V \ N, |Ns(s5) ∩ N | =0 < 1= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | =0 > 1= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | > |Ns(s5) ∩ (V \ N )|
(v) Γs =1 9 andcorrespondedsetis S = {s1};
(vi) Γ=1 andcorrespondedsetis S = {s1}
Proposition4.19.11. Let NTG :(V,E,σ,µ) bewheel.Then
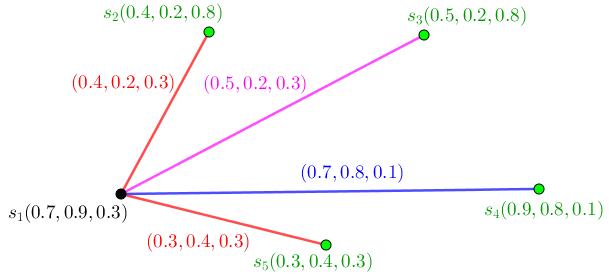
(i) theset S = {v1,v3}∪{v6,v9 ,vi+6, ,vn}6+3(i 1)≤n i=1 isminimalglobal-offensivealliance;
(ii) Γ= |{v1,v3}∪{v6,v9 ··· ,vi+6, ··· ,vn}6+3(i 1)≤n i=1 |;
(iii) Γs =Σ{v1,v3}∪{v6,v9 ,vi+6, ,vn}6+3(i 1)≤n i=1 Σ3 i=1σi(s);
(iv) theset {v1,v3}∪{v6,v9 ,vi+6, ,vn}6+3(i 1)≤n i=1 isonlyminimalglobal-offensivealliance.
Proof. (i) Suppose NTG :(V,E,σ,µ) isawheel.Let S = {v1,v3}∪ {v6,v9 ,vi+6, ,vn}6+3(i 1)≤n i=1 . Thereareeither ∀z ∈ V \ S, |Ns(z) ∩ S| =2 > 1= |Ns(z) ∩ (V \ S)| ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| or 208
4.NeutrosophicAlliances
∀z ∈ V \ S, |Ns(z) ∩ S| =3 > 0= |Ns(z) ∩ (V \ S)|
∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)|
Itimplies S = {v1,v3}∪{v6,v9 ,vi+6, ,vn}6+3(i 1)≤n i=1 isglobaloffensivealliance.If S = {v1,v3}∪{v6,v9 ,vi+6, ,vn}6+3(i 1)≤n i=1 −{z} where z ∈ S = {v1,v3}∪{v6,v9 ··· ,vi+6, ··· ,vn}6+3(i 1)≤n i=1 , thenThereare either
∀z ∈ V \ S , |Ns(z) ∩ S | =1 < 2= |Ns(z) ∩ (V \ S )| ∀z ∈ V \ S , |Ns(z) ∩ S | < |Ns(z) ∩ (V \ S )| ∀z ∈ V \ S , |Ns(z) ∩ S | > |Ns(z) ∩ (V \ S )| or
∀z ∈ V \ S , |Ns(z) ∩ S | =1=1= |Ns(z) ∩ (V \ S )| ∀z ∈ V \ S , |Ns(z) ∩ S | = |Ns(z) ∩ (V \ S )| ∀z ∈ V \ S , |Ns(z) ∩ S | > |Ns(z) ∩ (V \ S )|
So S = {v1,v3}∪{v6,v9 ,vi+6, ,vn}6+3(i 1)≤n i=1 −{z} where z ∈ S = {v1,v3}∪{v6,v9 ,vi+6, ,vn}6+3(i 1)≤n i=1 isn’tglobal-offensivealliance.It induces S = {v1,v3}∪{v6,v9 ,vi+6, ,vn}6+3(i 1)≤n i=1 isminimal-globaloffensivealliance. (ii), (iii) and (iv) areobvious.
Example4.19.12. ConsiderFigure(4.7).
(i) S = {s1,s3,s5} isonlyminimal-global-offensivealliance;
(ii) S = {s1,s3,s5} isoptimalsuchthatformsbothminimal-global-offensivealliance-neutrosophicnumberandminimal-global-offensive-alliancenumber;
(iii) S including S = {s2.s4,s5} onlyformsglobal-offensive-alliancebutnot minimal-global-offensive-alliance;
(iv) N = {s1,s3} isn’tglobal-offensivealliance.Sincethereisoneinstance andonlyoneinstanceisenough;
(a) Firstcounterexampleforthestatement“N = {s1,s3} isglobaloffensivealliance.”; ∃s5 ∈ V \ N, |Ns(s5) ∩ N | =1=1= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | =1 > 1= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | > |Ns(s5) ∩ (V \ N )|;
(v) Γs =4 9 andcorrespondedsetis S = {s1,s3,s5};
(vi) Γ=3 andcorrespondedsetis S = {s1,s3,s5}
Proposition4.19.13. Let NTG :(V,E,σ,µ) beanoddcomplete.Then
(i) theset S = {vi} n 2 +1 i=1 isminimal-global-offensivealliance;
(ii) Γ= n 2 +1;
(iii) Γs =min{Σs∈S Σ3 i=1σi(s)}S={vi} n 2 +1 i=1 ;
4.19.ClassesofNeutrosophicGraphs
209
Figure4.7:Thesetofblackcirclesisminimal-global-offensivealliance. NTG7 (iv) theset S = {vi} n 2 +1 i=1 isonlyminimal-global-offensivealliances. Proof. (i) Suppose NTG :(V,E,σ,µ) isoddcomplete.Let S = {vi} n 2 +1 i=1 Thus
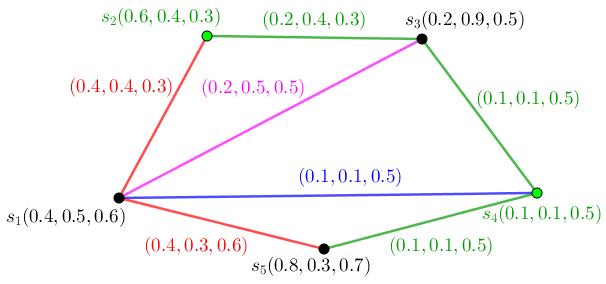
∀z ∈ V \ S, |Ns(z) ∩ S| = n 2 +1 > n 2 − 1= |Ns(z) ∩ (V \ S)| ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| Itimplies S = {vi} n 2 +1 i=1 isglobal-offensivealliance.If S = {vi} n 2 +1 i=1 −{z} where z ∈ S = {vi} n 2 +1 i=1 , then ∀z ∈ V \ S, |Ns(z) ∩ S| = n 2 = n 2 = |Ns(z) ∩ (V \ S)| ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| So S = {vi} n 2 +1 i=1 −{z} where z ∈ S = {vi} n 2 +1 i=1 isn’tglobal-offensive alliance.Itinduces S = {vi} n 2 +1 i=1 isminimal-global-offensivealliance. (ii), (iii) and (iv) areobvious.
Example4.19.14. ConsiderFigure(4.8).
(i) S1 = {s1,s2,s3},S2 = {s1,s2,s4},S3 = {s1,s2,s5},S4 = {s1,s3,s4},S5 = {s1,s3,s5},S6 = {s2,s3,s4},S7 = {s2,s3,s5},S8 = {s3,s4,s5} areonlyminimal-global-offensivealliances;
(ii) S6 = {s2,s3,s4} isoptimalsuchthatformsbothminimal-global-offensivealliance-neutrosophicnumberandminimal-global-offensive-alliancenumber;
(iii) S = {s3,s4,s5} onlyformsminimal-global-offensive-alliancenumberbut notminimal-global-offensive-alliance-neutrosophic;
(iv) N = {s3,s4} isn’tglobal-offensivealliance.Sincethereisthreeinstances andonlyoneinstanceisenough;
(a) Firstcounterexampleforthestatement“N = {s3,s4} isglobaloffensivealliance.”;
∃s1 ∈ V \ N, |Ns(s1) ∩ N | =2=2= |Ns(s1) ∩ (V \ N )| ∃s1 ∈ V \ N, |Ns(s1) ∩ N | =2 > 2= |Ns(s1) ∩ (V \ N )| ∃s1 ∈ V \ N, |Ns(s1) ∩ N | > |Ns(s1) ∩ (V \ N )|;
4.NeutrosophicAlliances
210
Figure4.8:Thesetofblackcirclesisminimal-global-offensivealliance. NTG10
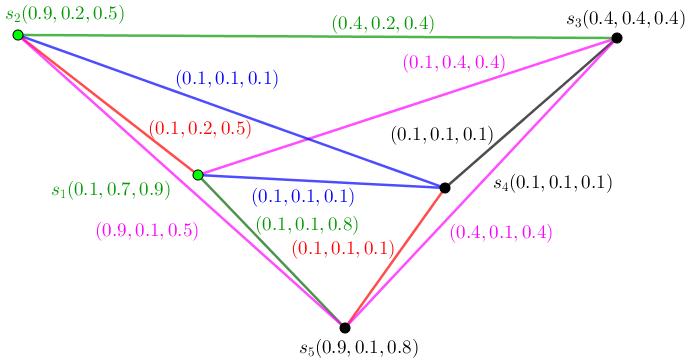
(b) secondcounterexampleforthestatement“N = {s3,s4} isglobaloffensivealliance.”;
∃s2 ∈ V \ N, |Ns(s2) ∩ N | =2=2= |Ns(s2) ∩ (V \ N )| ∃s2 ∈ V \ N, |Ns(s2) ∩ N | =2 > 2= |Ns(s2) ∩ (V \ N )| ∃s2 ∈ V \ N, |Ns(s2) ∩ N | > |Ns(s2) ∩ (V \ N )|;
(c) thirdcounterexampleforthestatement“N = {s3,s4} isglobaloffensivealliance.”.
∃s5 ∈ V \ N, |Ns(s5) ∩ N | =2=2= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | =2 > 2= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | > |Ns(s5) ∩ (V \ N )|;
(v) Γs =3 3 andcorrespondedsetis S6 = {s2,s3,s4};
(vi) Γ=3 andcorrespondedsetsare S1 = {s1,s2,s3},S2 = {s1,s2,s4},S3 = {s1,s2,s5},S4 = {s1,s3,s4},S5 = {s1,s3,s5},S6 = {s2,s3,s4},S7 = {s2,s3,s5},S8 = {s3,s4,s5} whichareonlyminimal-global-offensive alliances.
Proposition4.19.15. Let NTG :(V,E,σ,µ) beanevencomplete.Then (i) theset S = {vi} n 2 i=1 isminimal-global-offensivealliance; (ii) Γ= n 2 ; (iii) Γs =min{Σs∈S Σ3 i=1σi(s)}S={vi} n 2 i=1 ;
(iv) theset S = {vi} n 2 i=1 isonlyminimal-global-offensivealliances.
Proof. (i) Suppose NTG :(V,E,σ,µ) isevencomplete.Let S = {vi} n 2 i=1 Thus ∀z ∈ V \ S, |Ns(z) ∩ S| = n 2 > n 2 − 1= |Ns(z) ∩ (V \ S)| ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| Itimplies S = {vi} n 2 i=1 isglobal-offensivealliance.If S = {vi} n 2 i=1 −{z} where z ∈ S = {vi} n 2 i=1 , then
4.19.ClassesofNeutrosophicGraphs
211
∀z ∈ V \ S, |Ns(z) ∩ S| = n 2 − 1 < n 2 +1= |Ns(z) ∩ (V \ S)|
∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)|
So S = {vi} n 2 i=1 −{z} where z ∈ S = {vi} n 2 i=1 isn’tglobal-offensivealliance. Itinduces S = {vi} n 2 i=1 isminimal-global-offensivealliance. (ii), (iii) and (iv) areobvious.
Example4.19.16. ConsiderFigure(4.17).
(i) S1 = {s1,s2},S2 = {s1,s3},S3 = {s1,s4},S4 = {s2,s3},S5 = {s2,s4},S6 = {s3,s4} areonlyminimal-global-offensivealliances;
(ii) S6 = {s3,s4} isoptimalsuchthatformsbothminimal-global-offensivealliance-neutrosophicnumberandminimal-global-offensive-alliancenumber;
(iii) S = {s1,s3} onlyformsminimal-global-offensive-alliancenumberbutnot minimal-global-offensive-alliance-neutrosophic;
(iv) N = {s1} isn’tglobal-offensivealliance.Sincethereisthreeinstancesand onlyoneinstanceisenough;
(a) Firstcounterexampleforthestatement“N = {s1} isglobal-offensive alliance.”;
∃s2 ∈ V \ N, |Ns(s2) ∩ N | =1 < 2= |Ns(s2) ∩ (V \ N )| ∃s2 ∈ V \ N, |Ns(s2) ∩ N | =1 > 2= |Ns(s2) ∩ (V \ N )| ∃s2 ∈ V \ N, |Ns(s2) ∩ N | > |Ns(s2) ∩ (V \ N )|;
(b) secondcounterexampleforthestatement“N = {s1} isglobaloffensivealliance.”;
∃s3 ∈ V \ N, |Ns(s3) ∩ N | =1 < 2= |Ns(s3) ∩ (V \ N )| ∃s3 ∈ V \ N, |Ns(s3) ∩ N | =1 > 2= |Ns(s3) ∩ (V \ N )| ∃s3 ∈ V \ N, |Ns(s3) ∩ N | > |Ns(s3) ∩ (V \ N )|;
(c) thirdcounterexampleforthestatement“N = {s1} isglobal-offensive alliance.”.
∃s4 ∈ V \ N, |Ns(s4) ∩ N | =1 < 2= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | =1 > 2= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | > |Ns(s4) ∩ (V \ N )|;
(v) Γs =2 3 andcorrespondedsetis S6 = {s3,s4}; (vi) Γ=2 andcorrespondedsetis S6 = {s3,s4}
4.20FamilyofNeutrosophicGraphs
Inthissection,newdefinitionisappliedintofamilyofsomeclassesof neutrosophicgraphswhichinthisfamily,allneutrosophicgraphshavecommon neutrosophicvertexset.Inthecaseofcompletemodel,theparityofnumberof verticesconcludestohavedifferentresults.Clarificationsanddemonstrations aregivenforeveryresultasusual.
4.NeutrosophicAlliances
212
Figure4.9:Thesetofblackcirclesisminimal-global-offensivealliance. NTG8

Proposition4.20.1. Let G bea m-familyofneutrosophicstarswithcommon neutrosophicvertexset.Then
(i) theset S = {c1,c2, ,cm} isminimal-global-offensivealliancefor G; (ii) Γ= m for G; (iii) Γs =Σm i=1Σ3 j=1σj (ci) for G;
(iv) thesets S = {c1,c2, ,cm} and S ⊂ S areonlyminimal-global-offensive alliancesfor G
Proof. (i). Suppose NTG :(V,E,σ,µ) isastar.
∀v ∈ V \{c}, |Ns(v) ∩{c}| =1 > 0= |Ns(v) ∩ (V \{c})| ∀z ∈ V \ S, |Ns(z) ∩ S| =1 > 0= |Ns(z) ∩ (V \ S)| ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| v ∈ V \{c}, |Ns(v) ∩{c}| > |Ns(v) ∩ (V \{c})|
Itimplies S = {c1,c2, ,cm} isglobal-offensiveallianceor G If S = {c}−{c} = ∅, then ∃v ∈ V \ S, |Ns(z) ∩ S| =0=0= |Ns(z) ∩ (V \ S)| ∃v ∈ V \ S, |Ns(z) ∩ S| =0 > 0= |Ns(z) ∩ (V \ S)| ∃v ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)|
So S = {c}−{c} = ∅ isn’tglobal-offensivealliancefor G Itinduces S = {c1,c2, ,cm} isminimal-global-offensivealliancefor G (ii) and (iii) aretrivial.
(iv). By (i),S = {c1,c2, ,cm} isminimal-global-offensivealliancefor G.
Thusit’senoughtoshowthat S ⊆ S isminimal-global-offensivealliancefor G. Suppose NTG :(V,E,σ,µ) isastar.Let S ⊆ S
∀v ∈ V \{c}, |Ns(v) ∩{c}| =1 > 0= |Ns(v) ∩ (V \{c})| ∀z ∈ V \ S , |Ns(z) ∩ S | =1 > 0= |Ns(z) ∩ (V \ S )| ∀z ∈ V \ S , |Ns(z) ∩ S | > |Ns(z) ∩ (V \ S )|
Itimplies S ⊆ S isglobal-offensivealliancefor G
Example4.20.2. ConsiderFigure(4.10). (i) S = {s1} isonlyminimal-global-offensivealliancefor G;
4.20.FamilyofNeutrosophicGraphs
213
Figure4.10:Thesetofblackcirclesisminimal-global-offensivealliance. NTG9
(ii) S = {s1} isoptimalsuchthatformsbothminimal-global-offensive-allianceneutrosophicnumberandminimal-global-offensive-alliancenumberfor G;
(iii) S including S = {s1} onlyformsglobal-offensive-alliancebutnotminimalglobal-offensive-alliancefor G;
(iv) N = {s3,s4} isn’tglobal-offensivealliancefor G Sincetherearetwo instancesforeverymemberof G butonlyoneofthemisenough;forevery memberof G, wehavesamefollowinginstances;
(a) Firstcounterexampleforthestatement“N = {s3,s4} isglobaloffensivealliancefor G ”;
∃s1 ∈ V \ N, |Ns(s1) ∩ N | =2=2= |Ns(s1) ∩ (V \ N )| ∃s1 ∈ V \ N, |Ns(s1) ∩ N | =2 > 2= |Ns(s1) ∩ (V \ N )| ∃s1 ∈ V \ N, |Ns(s1) ∩ N | > |Ns(s1) ∩ (V \ N )|;
(b) secondcounterexampleforthestatement“N = {s3,s4} isglobaloffensivealliancefor G.”;
∃s2 ∈ V \ N, |Ns(s2) ∩ N | =0 < 1= |Ns(s2) ∩ (V \ N )| ∃s2 ∈ V \ N, |Ns(s2) ∩ N | =0 > 1= |Ns(s2) ∩ (V \ N )| ∃s2 ∈ V \ N, |Ns(s2) ∩ N | > |Ns(s2) ∩ (V \ N )|;
(v) Γs =0 7 andcorrespondedsetis S = {s1};
(vi) Γ=1 andcorrespondedsetis S = {s1}.
Proposition4.20.3. Let G bea m-familyofoddcompletegraphswithcommon neutrosophicvertexset.Then
(i) theset S = {vi} n 2 +1 i=1 isminimal-global-offensivealliancefor G; (ii) Γ= n 2 +1 for G;
(iii) Γs =min{Σs∈S Σ3 i=1σi(s)}S={vi} n 2 +1 i=1 for G;
(iv) thesets S = {vi} n 2 +1 i=1 areonlyminimal-global-offensivealliancesfor G
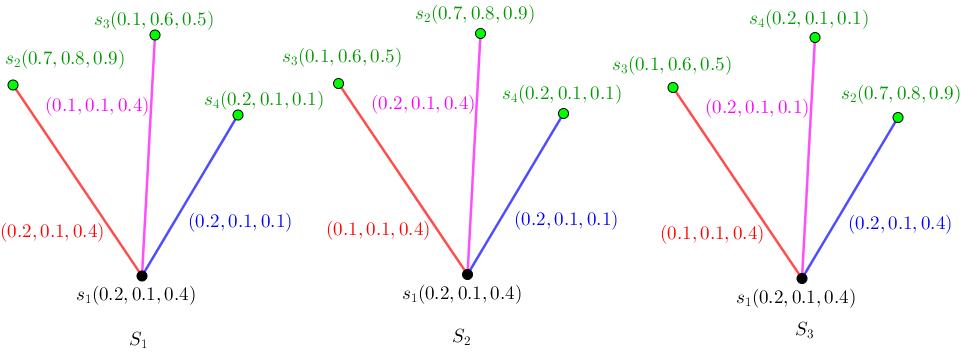
4.NeutrosophicAlliances
214
Proof. (i) Suppose NTG :(V,E,σ,µ) isoddcomplete.Let S = {vi} n 2 +1 i=1 Thus ∀z ∈ V \ S, |Ns(z) ∩ S| = n 2 +1 > n 2 − 1= |Ns(z) ∩ (V \ S)| ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)|
Itimplies S = {vi} n 2 +1 i=1 isglobal-offensivealliancefor G If S = {vi} n 2 +1 i=1 −{z} where z ∈ S = {vi} n 2 +1 i=1 , then ∀z ∈ V \ S, |Ns(z) ∩ S| = n 2 = n 2 = |Ns(z) ∩ (V \ S)| ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| So S = {vi} n 2 +1 i=1 −{z} where z ∈ S = {vi} n 2 +1 i=1 isn’tglobal-offensive alliancefor G Itinduces S = {vi} n 2 +1 i=1 isminimal-global-offensivealliancefor G. (ii), (iii) and (iv) areobvious.
Example4.20.4. ConsiderFigure(4.18).
(i) S1 = {s1,s2,s3},S2 = {s1,s2,s4},S3 = {s1,s2,s5},S4 = {s1,s3,s4},S5 = {s1,s3,s5},S6 = {s2,s3,s4},S7 = {s2,s3,s5},S8 = {s3,s4,s5} areonlyminimal-global-offensivealliances;
(ii) S3 = {s1,s2,s5} isoptimalsuchthatformsbothminimal-global-offensivealliance-neutrosophicnumberandminimal-global-offensive-alliancenumberfor G;
(iii) S8 = {s3,s4,s5} onlyformsminimal-global-offensive-alliancenumberbut notminimal-global-offensive-alliance-neutrosophicfor G;
(iv) N = {s1,s2} isn’tglobal-offensivealliance.Sincethereisthreeinstances andonlyoneinstanceisenoughfor G;
(a) Firstcounterexampleforthestatement“N = {s1,s2} isglobaloffensivealliance.”for G; ∃s3 ∈ V \ N, |Ns(s3) ∩ N | =2=2= |Ns(s3 ∩ (V \ N )| ∃s3 ∈ V \ N, |Ns(s3) ∩ N | =2 > 2= |Ns(s3) ∩ (V \ N )| ∃s3 ∈ V \ N, |Ns(s3) ∩ N | > |Ns(s3) ∩ (V \ N )|;
(b) secondcounterexampleforthestatement“N = {s1,s2} isglobaloffensivealliance.”for G;
∃s4 ∈ V \ N, |Ns(s4) ∩ N | =2=2= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | =2 > 2= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | > |Ns(s4) ∩ (V \ N )|;
(c) thirdcounterexampleforthestatement“N = {s1,s2} isglobaloffensivealliance.”for G
∃s5 ∈ V \ N, |Ns(s5) ∩ N | =2=2= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | =2 > 2= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | > |Ns(s5) ∩ (V \ N )|;
(v) Γs =4 andcorrespondedsetis S3 = {s1,s2,s5} for G;
4.20.FamilyofNeutrosophicGraphs
215
Figure4.11:Thesetofblackcirclesisminimal-global-offensivealliance. NTG11

(vi) Γ=3 andcorrespondedsetsare S1 = {s1,s2,s3},S2 = {s1,s2,s4},S3 = {s1,s2,s5},S4 = {s1,s3,s4},S5 = {s1,s3,s5},S6 = {s2,s3,s4},S7 = {s2,s3,s5},S8 = {s3,s4,s5} whichareonlyminimal-global-offensive alliancesfor G
Proposition4.20.5. Let G bea m-familyofevencompletegraphswithcommon neutrosophicvertexset.Then
(i) theset S = {vi} n 2 i=1 isminimal-global-offensivealliancefor G;
(ii) Γ= n 2 for G; (iii) Γs =min{Σs∈S Σ3 i=1σi(s)}S={vi} n 2 i=1 for G;
(iv) thesets S = {vi} n 2 i=1 areonlyminimal-global-offensivealliancesfor G Proof. (i) Suppose NTG :(V,E,σ,µ) isevencomplete.Let S = {vi} n 2 i=1 Thus
∀z ∈ V \ S, |Ns(z) ∩ S| = n 2 > n 2 − 1= |Ns(z) ∩ (V \ S)| ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)|
Itimplies S = {vi} n 2 i=1 isglobal-offensivealliancefor G If S = {vi} n 2 i=1 −{z} where z ∈ S = {vi} n 2 i=1 , then ∀z ∈ V \ S, |Ns(z) ∩ S| = n 2 − 1 < n 2 +1= |Ns(z) ∩ (V \ S)| ∀z ∈ V \ S, |Ns(z) ∩ S| > |Ns(z) ∩ (V \ S)| So S = {vi} n 2 i=1 −{z} where z ∈ S = {vi} n 2 i=1 isn’tglobal-offensivealliance for G. Itinduces S = {vi} n 2 i=1 isminimal-global-offensivealliancefor G. (ii), (iii) and (iv) areobvious.
Example4.20.6. ConsiderFigure(4.12).
(i) S1 = {s1,s2},S2 = {s1,s3},S3 = {s1,s4},S4 = {s2,s3},S5 = {s2,s4},S6 = {s3,s4} areonlyminimal-global-offensivealliancesfor G;
(ii) S1 = {s1,s2} isoptimalsuchthatformsbothminimal-global-offensivealliance-neutrosophicnumberandminimal-global-offensive-alliancenumberfor G;
(iii) S = {s1,s3} onlyformsminimal-global-offensive-alliancenumberbutnot minimal-global-offensive-alliance-neutrosophicfor G;
4.NeutrosophicAlliances
216
Figure4.12:Thesetofblackcirclesisminimal-global-offensivealliance. NTG12

(iv) N = {s1} isn’tglobal-offensivealliance.Sincethereisthreeinstancesand onlyoneinstanceisenoughfor G;
(a) Firstcounterexampleforthestatement“N = {s1} isglobal-offensive alliance.”for G;
∃s2 ∈ V \ N, |Ns(s2) ∩ N | =1 < 2= |Ns(s2) ∩ (V \ N )| ∃s2 ∈ V \ N, |Ns(s2) ∩ N | =1 > 2= |Ns(s2) ∩ (V \ N )| ∃s2 ∈ V \ N, |Ns(s2) ∩ N | > |Ns(s2) ∩ (V \ N )|;
(b) secondcounterexampleforthestatement“N = {s1} isglobaloffensivealliance.”for G;
∃s3 ∈ V \ N, |Ns(s3) ∩ N | =1 < 2= |Ns(s3) ∩ (V \ N )| ∃s3 ∈ V \ N, |Ns(s3) ∩ N | =1 > 2= |Ns(s3) ∩ (V \ N )| ∃s3 ∈ V \ N, |Ns(s3) ∩ N | > |Ns(s3) ∩ (V \ N )|;
(c) thirdcounterexampleforthestatement“N = {s1} isglobal-offensive alliance.”for G
∃s4 ∈ V \ N, |Ns(s4) ∩ N | =1 < 2= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | =1 > 2= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | > |Ns(s4) ∩ (V \ N )|;
(v) Γs =2 6 andcorrespondedsetis S1 = {s1,s2} for G; (vi) Γ=2 andcorrespondedsetsare S1 = {s1,s2},S2 = {s1,s3},S3 = {s1,s4},S4 = {s2,s3},S5 = {s2,s4},S6 = {s3,s4} for G
4.21ApplicationsinTimeTableandScheduling
Inthissection,twoapplicationsfortimetableandschedulingareprovided wherethemodelsarecompletemodelswhichmeancompleteconnectionsare formedasindividualandfamilyofcompletemodelswithcommonneutrosophic vertexset.
Designingtheprogramstoachievesomegoalsisgeneralapproachtoapplyon someissuestofunctionproperly.Separationhaskeyroleinthecontextofthis style.Separatingthedurationofworkwhichareconsecutive,isthematterand ithasimportantancetoavoidmixingup.
Step1.(Definition) Timetableisanapproachtogetsomeattributestodo theworkfastandproper.Thestyleofschedulingimpliesspecialattention tothetaskswhichareconsecutive.
Step2.(Issue) Schedulingofprogramhasfacedwithdifficultiestodifferamid consecutivesection.Beyondthat,sometimessectionsarenotthesame.
4.21.ApplicationsinTimeTableandScheduling
217
Step3.(Model) Thesituationisdesignedasamodel.Themodelusesdatato assigneverysectionandtoassigntorelationamidsection,threenumbers belongunitintervaltostateindeterminacy,possibilitiesanddeterminacy. There’sonerestrictioninthat,thenumbersamidtwosectionsareatleast thenumberoftherelationamidthem.Table (4.5),clarifiesaboutthe assignednumberstothesesituation.
Table4.3:SchedulingconcernsitsSubjectsanditsConnectionsasaneutrosophic graphanditsalliancesinaModel. tbl1c
Sectionsof NTG n1 n2 n9 Values (0 99, 0 98, 0 55)(0 74, 0 64, 0 46) (0 99, 0 98, 0 55)
Connectionsof NTG E1 E2 E3 Values (0 01, 0 01, 0 01)(0 01, 0 01, 0 01)(0 01, 0 01, 0 01)
4.22Case1:CompleteModelasIndividual
Step4.(Solution) Theneutrosophicgraphanditsglobaloffensiveallianceas model,proposetousespecificset.Everysubjecthasconnectionwith everygivensubject.Thustheconnectionisappliedaspossibleandthe modeldemonstratesfullconnectionsaspossible.Usingthenotionof strongontheconnectionamidsubjects,causestheimportanceofsubject goesinthehighestlevelsuchthatthevalueamidtwoconsecutivesubjects, isdeterminedbythosesubjects.Iftheconfigurationiscomplete,theset isdifferent.Also,itholdsforothertypessuchthatstar,wheel,path, andcycle.Thecollectionofsituationsisanotherapplicationofglobal offensivealliancewhenthenotionoffamilyisappliedinthewaythat allmembersoffamilyarefromsameclassesofneutrosophicgraphs.As follows,TherearefoursubjectswhicharerepresentedasFigure (4.17). Thismodelisstrong.Andthestudyproposesusingspecificsetofobjects whichiscalledminimal-global-offensivealliance.Therearealsosome analysesonothersetsinthewaythat,theclarificationisgainedabout beingspecialsetornot.Also,inthelastpart,therearetwonumbersto assigntothismodelandsituationtocomparethemwithsamesituations togetmoreprecise.ConsiderFigure(4.17).
(i) S1 = {s1,s2},S2 = {s1,s3},S3 = {s1,s4},S4 = {s2,s3},S5 = {s2,s4},S6 = {s3,s4} areonlyminimal-global-offensivealliances;
(ii) S6 = {s3,s4} isoptimalsuchthatformsbothminimal-globaloffensive-alliance-neutrosophicnumberandminimal-global-offensivealliancenumber;
(iii) S = {s1,s3} onlyformsminimal-global-offensive-alliancenumberbut notminimal-global-offensive-alliance-neutrosophic;
(iv) N = {s1} isn’tglobal-offensivealliance.Sincethereisthreeinstances andonlyoneinstanceisenough;
(a) Firstcounterexampleforthestatement“N = {s1} isglobaloffensivealliance.”;
4.NeutrosophicAlliances
218
Figure4.13:Thesetofblackcirclesisminimal-global-offensivealliance. NTG8

∃s2 ∈ V \ N, |Ns(s2) ∩ N | =1 < 2= |Ns(s2) ∩ (V \ N )| ∃s2 ∈ V \ N, |Ns(s2) ∩ N | =1 > 2= |Ns(s2) ∩ (V \ N )| ∃s2 ∈ V \ N, |Ns(s2) ∩ N | > |Ns(s2) ∩ (V \ N )|; (b) secondcounterexampleforthestatement“N = {s1} isglobaloffensivealliance.”;
∃s3 ∈ V \ N, |Ns(s3) ∩ N | =1 < 2= |Ns(s3) ∩ (V \ N )| ∃s3 ∈ V \ N, |Ns(s3) ∩ N | =1 > 2= |Ns(s3) ∩ (V \ N )| ∃s3 ∈ V \ N, |Ns(s3) ∩ N | > |Ns(s3) ∩ (V \ N )|; (c) thirdcounterexampleforthestatement“N = {s1} isglobaloffensivealliance.”.
∃s4 ∈ V \ N, |Ns(s4) ∩ N | =1 < 2= |Ns(s4) ∩ (V \ N )|
∃s4 ∈ V \ N, |Ns(s4) ∩ N | =1 > 2= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | > |Ns(s4) ∩ (V \ N )|; (v) Γs =2 3 andcorrespondedsetis S6 = {s3,s4}; (vi) Γ=2 andcorrespondedsetis S6 = {s3,s4}
4.23Case2:FamilyofCompleteModels
Step4.(Solution) Theneutrosophicgraphanditsglobaloffensiveallianceas model,proposetousespecificset.Everysubjecthasconnectionwith everygivensubject.Thustheconnectionisappliedaspossibleandthe modeldemonstratesfullconnectionsaspossible.Usingthenotionof strongontheconnectionamidsubjects,causestheimportanceofsubject goesinthehighestlevelsuchthatthevalueamidtwoconsecutivesubjects, isdeterminedbythosesubjects.Iftheconfigurationiscomplete,theset isdifferent.Also,itholdsforothertypessuchthatstar,wheel,path, andcycle.Thecollectionofsituationsisanotherapplicationofglobal offensivealliancewhenthenotionoffamilyisappliedinthewaythat allmembersoffamilyarefromsameclassesofneutrosophicgraphs.As follows,Therearefivesubjectswhicharerepresentedintheformationof familyofmodelsasFigure (4.17).Thesemodelsarestronginfamily.And thestudyproposesusingspecificsetofobjectswhichiscalledminimalglobal-offensiveallianceforthisfamilyofmodels.Therearealsosome analysesonothersetsinthewaythat,theclarificationisgainedabout
4.23.Case2:FamilyofCompleteModels
219
Figure4.14:Thesetofblackcirclesisminimal-global-offensivealliance. NTG11

beingspecialsetornot.Also,inthelastpart,therearetwonumbersto assigntothisfamilyofmodelsandcollectionofsituationstocompare themwithcollectionofsituationstogetmoreprecise.ConsiderFigure (4.18).
(i) S1 = {s1,s2,s3},S2 = {s1,s2,s4},S3 = {s1,s2,s5},S4 = {s1,s3,s4},S5 = {s1,s3,s5},S6 = {s2,s3,s4},S7 = {s2,s3,s5},S8 = {s3,s4,s5} areonlyminimal-global-offensivealliances;
(ii) S3 = {s1,s2,s5} isoptimalsuchthatformsbothminimal-globaloffensive-alliance-neutrosophicnumberandminimal-global-offensivealliancenumberfor G;
(iii) S8 = {s3,s4,s5} onlyformsminimal-global-offensive-alliancenumber butnotminimal-global-offensive-alliance-neutrosophicfor G;
(iv) N = {s1,s2} isn’tglobal-offensivealliance.Sincethereisthree instancesandonlyoneinstanceisenoughfor G;
(a) Firstcounterexampleforthestatement“N = {s1,s2} isglobaloffensivealliance.”for G;
∃s3 ∈ V \ N, |Ns(s3) ∩ N | =2=2= |Ns(s3 ∩ (V \ N )| ∃s3 ∈ V \ N, |Ns(s3) ∩ N | =2 > 2= |Ns(s3) ∩ (V \ N )| ∃s3 ∈ V \ N, |Ns(s3) ∩ N | > |Ns(s3) ∩ (V \ N )|; (b) secondcounterexampleforthestatement“N = {s1,s2} isglobaloffensivealliance.”for G;
∃s4 ∈ V \ N, |Ns(s4) ∩ N | =2=2= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | =2 > 2= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | > |Ns(s4) ∩ (V \ N )|; (c) thirdcounterexampleforthestatement“N = {s1,s2} isglobaloffensivealliance.”for G
∃s5 ∈ V \ N, |Ns(s5) ∩ N | =2=2= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | =2 > 2= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | > |Ns(s5) ∩ (V \ N )|; (v) Γs =4 andcorrespondedsetis S3 = {s1,s2,s5} for G; (vi) Γ=3 andcorrespondedsetsare S1 = {s1,s2,s3},S2 = {s1,s2,s4},S3 = {s1,s2,s5},S4 = {s1,s3,s4},S5 = {s1,s3,s5},S6 = {s2,s3,s4},S7 = {s2,s3,s5},S8 = {s3,s4,s5} whichareonly minimal-global-offensivealliancesfor G
4.NeutrosophicAlliances
220
4.24OpenProblems
Inthissection,somequestionsandproblemsareproposedtogivesomeavenues topursuethisstudy.Thestructuresofthedefinitionsandresultsgivesome ideastomakenewsettingswhichareeligibletoextendandtocreatenewstudy. Notionconcerningallianceisdefinedinneutrosophicgraphs.Neutrosophic numberisalsointroduced.Thus,
Question4.24.1. Isitpossibletouseothertypesneighborhoodarisingfrom differenttypesofedgestodefinenewalliances?
Question4.24.2. Areexistedsomeconnectionsamiddifferenttypesofalliances inneutrosophicgraphs?
Question4.24.3. Isitpossibletoconstructsomeclassesofwhichhave“nice” behavior?
Question4.24.4. Whichmathematicalnotionsdomakeanindependentstudy toapplythesetypesinneutrosophicgraphs?
Problem4.24.5. Whichparametersarerelatedtothisparameter?
Problem4.24.6. Whichapproachesdoworktoconstructapplicationstocreate independentstudy?
Problem4.24.7. Whichapproachesdoworktoconstructdefinitionswhichuse alldefinitionsandtherelationsamidtheminsteadofseparatedefinitionsto createindependentstudy?
4.25ConclusionandClosingRemarks
Inthissection,concludingremarksandclosingremarksarerepresented.The drawbacksofthisarticleareillustrated.Somebenefitsandadvantagesofthis studyarehighlighted.
Thisstudyusesonedefinitionconcerningglobaloffensivealliancetostudy neutrosophicgraphs.Newneutrosophicnumberisintroducedwhichistooclose tothenotionofneutrosophicnumberbutit’sdifferentsinceitusesallvalues astype-summationonthem.Theconnectionsofverticeswhichareclarifiedby generaledgesdifferthemfromeachotherandputthemindifferentcategories torepresentasetwhichiscalledglobaloffensivealliance.Furtherstudies couldbeaboutchangesinthesettingstocomparethisnotionamiddifferent settingsofneutrosophicgraphstheory.Onewayisfindingsomerelationsamid alldefinitionsofnotionstomakesensibledefinitions.InTable (4.6),some limitationsandadvantagesofthisstudyarepointedout.
4.26GlobalPowerfulAllianceinStrongNeutrosophic Graphs
Thefollowingsectionsarecitedas[2]. 221
4.24.OpenProblems
Newsettingisintroducedtostudytheglobalpowerfulalliance.Global powerfulallianceisaboutasetofverticeswhichareappliedintothesettingof neutrosophicgraphs.Neighborhoodhasthekeyroletodefinethisnotion.Also, neighborhoodisdefinedbasedonstrongedges.Strongedgegetsaframework asneighborhoodandafterthat,toocloseverticeshavekeyroletodefine globalpowerfulalliancebasedonstrongedges.Thestructureofsetisstudied andgeneralresultsareobtained.Also,someclassesofneutrosophicgraphs excludingempty,path,star,andwheelandcontainingcomplete,cycleand r-regular-strongareinvestigatedinthetermsofset,minimalset,number,and neutrosophicnumber.Neutrosophicnumberisusedinthisway.It’sappliedto usethetypeofneutrosophicnumberinthewaythat,threevaluesofavertex areusedandthey’vesamesharetoconstructthisnumber.It’scalled“modified neutrosophicnumber”.Summationofthreevaluesofvertexmakesonenumber andapplyingittoasetmakesneutrosophicnumberofset.Thisapproach facilitatesidentifyingminimalsetandoptimalsetwhichformsminimal-globalpowerful-alliancenumberandminimal-global-powerful-alliance-neutrosophic number.Twodifferenttypesofsetsnamelyglobal-powerfulallianceandminimalglobal-powerfulalliancearedefined.Global-powerfulallianceidentifiesthesets ingeneralvisionbutminimal-global-powerfulalliancetakesfocusonthesets whichdeletingavertexisimpossible.Minimal-global-powerful-alliancenumber isaboutminimumcardinalityamidthecardinalitiesofallminimal-globalpowerfulalliancesinagivenneutrosophicgraph.Newnotionsareappliedinthe settingsbothindividualandfamily.Familyofneutrosophicgraphshasanopen avenue,inthewaythat,thefamilyonlycontainssameclassesofneutrosophic graphs.Theresultsareaboutminimal-global-powerfulalliance,minimal-globalpowerful-alliancenumberanditscorrespondedsets,minimal-global-powerfulalliance-neutrosophicnumberanditscorrespondedsets,andcharacterizing allminimal-global-powerfulalliances,minimal-t-powerfulalliance,minimal-tpowerful-alliancenumberanditscorrespondedsets,minimal-t-powerful-allianceneutrosophicnumberanditscorrespondedsets,andcharacterizingallminimalt-powerfulalliances.Theconnectionsamidt-powerful-alliancesareobtained. Thenumberofconnectedcomponentshassomerelationswiththisnewconcept anditgetssomeresults.Someclassesofneutrosophicgraphsbehavedifferently whentheparityofverticesaredifferentandinthiscase,cycle,andcomplete
4.NeutrosophicAlliances
1. DefiningGlobalOffensiveAlliances 1. GeneralResults 2. ApplyingonStrongNeutrosophicGraphs 3. StudyonCompleteModels 2. DeeplyMoreConnections 4. ApplyingonIndividuals 5. ApplyingonFamily 3. SameModelsinFamily
Table4.4:ABriefOverviewaboutAdvantagesandLimitationsofthisstudy tbl2c Advantages Limitations
4.27Abstract
222
illustratethesebehaviors.Twoapplicationsconcerningcompletemodelas individualandfamily,underthetitlesoftimetableandschedulingconclude theresultsandtheygivemoreclarificationsandclosingremarks.Inthisstudy, there’sanopenwaytoextendtheseresultsintothefamilyoftheseclassesof neutrosophicgraphs.Thefamilyofneutrosophicgraphsaren’tstudydeeply andwithmoreresultsbutitseemsthatanalogousresultsaredetermined.Slight progressisobtainedinthefamilyofthesemodelsbutthereareopenavenuesto studyfamilyofothermodelsassamemodelsanddifferentmodels.There’sa question.Howcanberelatedtoeachother,twosetspartitioningthevertexset ofagraph?Theideasofneighborhoodandneighborsbasedonstrongedges illustrateopenwaytogetresults.Asetisglobalpowerfulalliancewhentwosets partitioningvertexsethaveuniformstructure.Allmembersofsethavemore amountofneighborsinthesetthanoutofsetandreverselyfornon-members ofsetwithlessmembersinthewaythatthesetissimultaneouslyt-offensive and(t-2)-defensive.Asetisglobalift=0.Itleadsustothenotionofglobal powerfulalliance.Differentedgesmakedifferentneighborhoodsbutit’sused onestyleedgetitledstrongedge.Thesenotionsareappliedintoneutrosophic graphsasindividualsandfamilyofthem.Independentsetasanallianceis aspecialsetwhichhasnoneighborinsideanditimpliessomedrawbacksfor thesenotions.Findingspecialsetswhicharewell-known,isanopenwayto pursethisstudy.Specialsetwhichitsmembershaveonlyoneneighborinside, characterizetheconnectedcomponentswherethecardinalityofitscomplement isthenumberofconnectedcomponents.Someproblemsareproposedtopursue thisstudy.Basicfamiliaritieswithgraphtheoryandneutrosophicgraphtheory areproposedforthisarticle.
Keywords: ModifiedNeutrosophicNumber,GlobalPowerfulAlliance,RRegular-Strong AMSSubjectClassification: 05C17,05C22,05E45
4.28MotivationandContributions
Inthisstudy,there’sanideawhichcouldbeconsideredasamotivation.
Question4.28.1. Isitpossibletousemixedversionsofideasconcerning “GlobalPowerfulAlliance”,“ModifiedNeutrosophicNumber”and“Complete NeutrosophicGraph”todefinesomenotionswhichareappliedtoneutrosophic graphs?
It’smotivationtofindnotionstouseinanyclassesofneutrosophicgraphs. Real-worldapplicationsabouttimetableandschedulingareanotherthoughts whichleadtobeconsideredasmotivation.Connectionsamidtwoverticeshave keyrolestoassignglobal-powerfulalliance,minimal-global-powerfulalliance, minimal-global-powerful-alliancenumber,andminimal-global-powerful-allianceneutrosophicnumber.Thusthey’reusedtodefinenewideaswhichconclude tothestructureglobalpowerfulalliance.Theconceptofhavingstrongedge inspiresmetostudythebehaviorofstrongedgesinthewaythat,twotypesof numbersandset,e.g.,global-powerfulalliance,minimal-global-powerfulalliance, minimal-global-powerful-alliancenumber,andminimal-global-powerful-allianceneutrosophicnumberarethecasesofstudyinthesettingsofindividualsandin
4.28.MotivationandContributions
223
settingsoffamilies.Also,therearesomeavenuestoextendthesenotions. Theframeworkofthisstudyisasfollows.Inthebeginning,Iintroduce basicdefinitionstoclarifyaboutpreliminaries.Insubsection“Preliminaries”, newnotionsofglobal-powerfulalliance,minimal-global-powerfulalliance, minimal-global-powerful-alliancenumber,andminimal-global-powerful-allianceneutrosophicnumberareintroducedandareclarifiedasindividuals.Insection “Preliminaries”,generalsetshavethekeyroleinthisway.Generalresults areobtainedandalso,theresultsaboutthebasicnotionsofglobal-powerful allianceareelicited.Twoclassesofneutrosophicgraphsarestudiedintheterms ofglobal-powerfulalliance,minimal-global-powerfulalliance,minimal-globalpowerful-alliancenumber,andminimal-global-powerful-alliance-neutrosophic numberinsection“r-Regular-Strong-NeutrosophicGraph’asindividuals.In section“r-Regular-Strong-NeutrosophicGraph”,bothnumbershaveapplied intoindividuals.Asaconcludingresult,therearethreestatementsandremarks aboutr-regular-strong-neutrosophicgraphswhichareeithercycleorcomplete. Theclarificationsarealsopresentedinsection“r-Regular-Strong-Neutrosophic Graph”forintroducedresults.Insection“ApplicationsinTimeTableand Scheduling”,twoapplicationsareposedforglobal-powerfulallianceconcerning timetableandschedulingwhenthesuspicionsareaboutchoosingsomesubjects andthementionedmodelsarecompleteasindividualanduniformfamily.In section“OpenProblems”,someproblemsandquestionsforfurtherstudies areproposed.Insection“ConclusionandClosingRemarks”,gentlediscussion aboutresultsandapplicationsisfeatured.Insection“ConclusionandClosing Remarks”,abriefoverviewconcerningadvantagesandlimitationsofthisstudy alongsideconclusionsisformed.
4.29Preliminaries
Inthissubsection,basicmaterialwhichisusedinthisarticle,ispresented. Also,newideasandtheirclarificationsareelicited. Basicideaisaboutthemodelwhichisused.Firstdefinitionintroducesbasic model.
Definition4.29.1. (Graph).
G =(V,E) iscalleda graph if V isasetofobjectsand E isasubsetof V × V (E isasetof2-subsetsof V )where V iscalled vertexset and E iscalled edgeset.Everytwoverticeshavebeencorrespondedtoatmostoneedge.
Neutrosophicgraphisthefoundationofresultsinthispaperwhichisdefined asfollows.Also,somerelatednotionsaredemonstrated.
Definition4.29.2. (NeutrosophicGraphAndItsSpecialCase).
NTG =(V,E,σ =(σ1,σ2,σ3),µ =(µ1,µ2,µ3)) iscalleda neutrosophic graph ifit’sgraph, σi : V → [0, 1],µi : E → [0, 1] Weaddoneconditionon itandweuse specialcase ofneutrosophicgraphbutwithsamename.The addedconditionisasfollows,forevery vivj ∈ E, µ(vivj ) ≤ σ(vi) ∧ σ(vj ).
(i): σ iscalled neutrosophicvertexset (ii): µ iscalled neutrosophicedgeset
4.NeutrosophicAlliances
224
4.29.Preliminaries
(iii): |V | iscalled order ofNTGandit’sdenotedby O(NTG).
(iv): Σv∈V σ(v) iscalled neutrosophicorder ofNTGandit’sdenotedby On(NTG)
(v): |E| iscalled size ofNTGandit’sdenotedby S(NTG)
(vi): Σe∈E Σ3 i=1µi(e) iscalled neutrosophicsize ofNTGandit’sdenotedby Sn(NTG)
Someclassesofwell-knownneutrosophicgraphsaredefined.Theseclasses ofneutrosophicgraphsareusedtoformthisstudyandthemostresultsare aboutthem.
Definition4.29.3. Let NTG :(V,E,σ,µ) beaneutrosophicgraph.Then
(i): asequenceofvertices P : x0,x1, ,xn iscalled path where xixi+1 ∈ E,i =0, 1, ··· ,n 1;
(ii): strength ofpath P : x0,x1, ,xn is i=0, ,n 1 µ(xixi+1);
(iii): connectedness amidvertices x0 and xn is µ∞(x,y)= P :x0,x1, ,xn i=0, ,n 1 µ(xixi+1);
(iv): asequenceofvertices P : x0,x1, ,xn iscalled cycle where xixi+1 ∈ E,i =0, 1, ,n 1 andtherearetwoedges xy and uv suchthat µ(xy)= µ(uv)= i=0,1, ,n 1 µ(vivi+1);
(v): it’s t-partite where V ispartitionedto t parts, V1,V2, ··· ,Vt andthe edge xy implies x ∈ Vi and y ∈ Vj where i = j. Ifit’scomplete,thenit’s denotedby Kσ1,σ2, ,σt where σi is σ on Vi instead V whichmean x ∈ Vi induces σi(x)=0;
(vi): t-partiteis completebipartite if t =2, andit’sdenotedby Kσ1,σ2 ;
(vii): completebipartiteis star if |V1| =1, andit’sdenotedby S1,σ2 ;
(viii): avertexin V is center ifthevertexjoinstoallverticesofacycle.Then it’s wheel andit’sdenotedby W1,σ2 ;
(ix): it’s complete where ∀uv ∈ V,µ(uv)= σ(u) ∧ σ(v);
(x): it’s strong where ∀uv ∈ E,µ(uv)= σ(u) ∧ σ(v)
Thenotionsofneighborandneighborhoodareaboutsomeverticeswhich haveoneedgewithafixedvertex.Thesenotionspresentverticeswhichare closetoafixedvertexaspossible.Basedonstrongedge,it’spossibletodefine differentneighborhoodasfollows.
Definition4.29.4. (StrongNeighborhood).
Let NTG :(V,E,σ,µ) beaneutrosophicgraph.Suppose x ∈ V. Then Ns(x)= {y ∈ N (x) | µ(xy)= σ(x) ∧ σ(y)}
225
Newnotionisdefinedbetweentwotypesofneighborhoodsforafixedvertex. Aminimalsetandsomenumbersareintroducedinthisway.Thenextdefinition hasmainroleineveryresultswhicharegiveninthisessay.
Definition4.29.5. Let NTG :(V,E,σ,µ) beaneutrosophicgraph.Then
(i) aset S ofverticesiscalled t-offensivealliance if ∀a ∈ V \ S, |Ns(a) ∩ S|−|Ns(a) ∩ (V \ S)| >t;
(ii) at-offensiveallianceiscalled global-offensivealliance if t =0; (iii) aset S ofverticesiscalled t-defensivealliance if ∀a ∈ S, |Ns(a) ∩ S|−|Ns(a) ∩ (V \ S)| <t;
(iv) at-defensiveallianceiscalled global-defensivealliance if t =0;
(v) aset S ofverticesiscalled t-powerfulalliance ifit’sbotht-offensive allianceand(t-2)-defensivealliance;
(vi) at-powerfulallianceiscalled global-powerfulalliance if t =0;
(vii) ∀S ⊆ S,S isglobal-powerfulalliancebut S isn’tglobal-powerfulalliance. Then S iscalled minimal-global-powerfulalliance;
(viii) minimal-global-powerful-alliancenumber of NTG is S isaminimal-global-powerfulalliance. |S| andit’sdenotedby Γ;
(ix) minimal-global-powerful-alliance-neutrosophicnumber of NTG is
S isaminimal-global-offensivealliance. Σs∈S Σ3 i=1σi(s) andit’sdenotedby Γs
Inthenextresult,thenotionsoft-defensiveallianceandt-offensivealliance havebeenextendedtopresenttheclassesofdefensiveallianceandoffensive alliancewhichholdwhenonetypeofthemholdsforagivensetofvertices.
Proposition4.29.6. Let NTG :(V,E,σ,µ) beastrongneutrosophicgraph. Thenfollowingstatementshold;
(i) if s ≥ t andaset S ofverticesist-defensivealliance,then S iss-defensive alliance;
(ii) if s ≤ t andaset S ofverticesist-offensivealliance,then S iss-offensive alliance.
Proof. (i) Suppose NTG :(V,E,σ,µ) isastrongneutrosophicgraph.Consider aset S ofverticesist-defensivealliance.Then
4.NeutrosophicAlliances
226
4.30.r-Regular-Strong-NeutrosophicGraph
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| <t;
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| <t ≤ s;
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| <s.
Thus S iss-defensivealliance.
(ii) Suppose NTG :(V,E,σ,µ) isastrongneutrosophicgraph.Consideraset S ofverticesist-offensivealliance.Then
∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| >t;
∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| >t ≥ s;
∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| >s. Thus S iss-offensivealliance.
Asaconsequenceofpreviousresult,therelationsamidasetwhichisbothtoffensiveallianceandt-defensiveallianceleadustowardthenotionoft-powerful alliance.
Proposition4.29.7. Let NTG :(V,E,σ,µ) beastrongneutrosophicgraph. Thenfollowingstatementshold;
(i) if s ≥ t +2 andaset S ofverticesist-defensivealliance,then S is s-powerfulalliance;
(ii) if s ≤ t andaset S ofverticesist-offensivealliance,then S ist-powerful alliance.
Proof. (i) Suppose NTG :(V,E,σ,µ) isastrongneutrosophicgraph.Consider aset S ofverticesist-defensivealliance.Then
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| <t; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| <t ≤ t +2 ≤ s;
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| <s. Thus S is(t+2)-defensivealliance.By S iss-defensiveallianceand S is (s+2)-offensivealliance, S iss-powerfulalliance.
(ii) Suppose NTG :(V,E,σ,µ) isastrongneutrosophicgraph.Consideraset S ofverticesist-offensivealliance.Then
∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| >t; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| >t ≥ s>s 2; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| >s 2. Thus S is(s-2)-defensivealliance.By S is(s-2)-defensiveallianceand S is s-offensivealliance, S iss-powerfulalliance.
4.30r-Regular-Strong-NeutrosophicGraph
r-regularisanattribute.Thispropertyfacilitatestheresultswhenthecondition isabouttheneighborsinsidefixedsettodetermine2-defensiveallianceand 2-offensivealliance.Also,aconditionabouttheneighborsoutsideoffixedset determinessomeresultsaboutr-defensiveallianceandr-offensivealliance.
Proposition4.30.1. Let NTG :(V,E,σ,µ) bear-regular-strong-neutrosophic graph.Thenfollowingstatementshold;
227
(i) if ∀a ∈ S, |Ns(a) ∩ S| < r 2 +1, then NTG :(V,E,σ,µ) is2-defensive alliance;
(ii) if ∀a ∈ V \ S, |Ns(a) ∩ S| > r 2 +1, then NTG :(V,E,σ,µ) is2-offensive alliance;
(iii) if ∀a ∈ S, |Ns(a) ∩ V \ S| =0, then NTG :(V,E,σ,µ) isr-defensive alliance;
(iv) if ∀a ∈ V \ S, |Ns(a) ∩ V \ S| =0, then NTG :(V,E,σ,µ) isr-offensive alliance.
Proof. (i). Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph. Then
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < r 2 +1 ( r 2 − 1); ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < r 2 +1 ( r 2 − 1) < 2; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < 2
Thus S is2-defensivealliance.
(ii) Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph.Then
∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > r 2 +1 ( r 2 − 1); ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > r 2 +1 ( r 2 − 1) > 2; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > 2 Thus S is2-offensivealliance.
(iii) Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph.Then
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| <r 0; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| <r 0= r; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| <r. Thus S isr-defensivealliance.
(iv) Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph.Then
∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| >r 0; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| >r 0= r; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| >r. Thus S isr-offensivealliance.
2-defensiveallianceand2-offensivealliancegetsomeresultsaboutthe neighborsinsidefixedset.Also,r-defensiveallianceandr-offensiveallianceget someresultsabouttheneighborsoutsideoffixedset.
Proposition4.30.2. Let NTG :(V,E,σ,µ) bear-regular-strong-neutrosophic graph.Thenfollowingstatementshold;
(i) ∀a ∈ S, |Ns(a) ∩ S| < r 2 +1 if NTG :(V,E,σ,µ) is2-defensivealliance;
(ii) ∀a ∈ V \ S, |Ns(a) ∩ S| > r 2 +1 if NTG :(V,E,σ,µ) is2-offensive alliance;
(iii) ∀a ∈ S, |Ns(a) ∩ V \ S| =0 if NTG :(V,E,σ,µ) isr-defensivealliance;
(iv) ∀a ∈ V \S, |Ns(a)∩V \S| =0 if NTG :(V,E,σ,µ) isr-offensivealliance.
4.NeutrosophicAlliances
228
4.30.r-Regular-Strong-NeutrosophicGraph
Proof. (i). Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph and2-defensivealliance.Then
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < 2; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < 2= r 2 +1 ( r 2 − 1); ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < r 2 +1 ( r 2 − 1); ∀t ∈ S, |Ns(t) ∩ S| = r 2 +1, |Ns(t) ∩ (V \ S)| = r 2 − 1.
(ii) Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph and2-offensivealliance.Then
∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > 2; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > 2= r 2 +1 ( r 2 − 1); ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > r 2 +1 ( r 2 − 1); ∀t ∈ V \ S, |Ns(t) ∩ S| = r 2 +1, |Ns(t) ∩ (V \ S)= r 2 − 1 (iii) Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph andr-defensivealliance.
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| <r;
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| <r = r 0; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| <r 0; ∀t ∈ S, |Ns(t) ∩ S| = r, |Ns(t) ∩ (V \ S)| =0
(iv). Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph andr-offensivealliance.Then
∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| >r; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| >r = r 0; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| >r 0; ∀t ∈ V \ S, |Ns(t) ∩ S| = r, |Ns(t) ∩ (V \ S)| =0.
Asaspecialcase,completeneutrosophicgraphgetsspecificresultexcerpt fromr-regularneutrosophicgraph.2-defensiveallianceand2-offensivealliance getsomeresultsabouttheneighborsinsidefixedsetdependingonorder.Also, (O− 1)-defensiveallianceand(O− 1)-offensivealliancegetsomeresultsabout theneighborsoutsideoffixedsetdependingonorder.
Proposition4.30.3. Let NTG :(V,E,σ,µ) bear-regular-strong-neutrosophic graphwhichiscomplete.Thenfollowingstatementshold;
(i) ∀a ∈ S, |Ns(a) ∩ S| < O−1 2 +1 if NTG :(V,E,σ,µ) is2-defensive alliance;
(ii) ∀a ∈ V \ S, |Ns(a) ∩ S| > O−1 2 +1 if NTG :(V,E,σ,µ) is2-offensive alliance;
(iii) ∀a ∈ S, |Ns(a) ∩ V \ S| =0 if NTG :(V,E,σ,µ) is (O− 1)-defensive alliance;
(iv) ∀a ∈ V \ S, |Ns(a) ∩ V \ S| =0 if NTG :(V,E,σ,µ) is (O− 1)-offensive alliance.
Proof. (i) Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph and2-defensivealliance.Then
229
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < 2;
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < 2= O−1 2 +1 ( O−1 2 − 1);
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < O−1 2 +1 ( O−1 2 − 1);
∀t ∈ S, |Ns(t) ∩ S| = O−1 2 +1, |Ns(t) ∩ (V \ S)| = O−1 2 − 1
(ii) Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph and2-offensivealliance.Then
∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > 2; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > 2= O−1 2 +1 ( O−1 2 − 1);
∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > O−1 2 +1 ( O−1 2 − 1); ∀t ∈ V \ S, |Ns(t) ∩ S| = O−1 2 +1, |Ns(t) ∩ (V \ S)= O−1 2 − 1 (iii) Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph and(O− 1)-defensivealliance.
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < O− 1; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < O− 1= O− 1 0; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < O− 1 0; ∀t ∈ S, |Ns(t) ∩ S| = O− 1, |Ns(t) ∩ (V \ S)| =0. (iv). Suppose NTG :(V,E,σ,µ) isa(O− 1)-regular-strong-neutrosophic graphandr-offensivealliance.Then
∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > O− 1; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > O− 1= O− 1 0; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > O− 1 0; ∀t ∈ V \ S, |Ns(t) ∩ S| = O− 1, |Ns(t) ∩ (V \ S)| =0
Asaspecialcaseofr-regular,completeisanattribute.Thisproperty facilitatestheresultswhentheconditionisabouttheneighborsinsidefixed settodetermine2-defensiveallianceand2-offensivealliance.Also,acondition abouttheneighborsoutsideoffixedsetdeterminessomeresultsabout (O− 1) defensiveallianceand (O− 1)-offensivealliance.
Proposition4.30.4. Let NTG :(V,E,σ,µ) bear-regular-strong-neutrosophic graphwhichiscomplete.Thenfollowingstatementshold;
(i) if ∀a ∈ S, |Ns(a) ∩ S| < O−1 2 +1, then NTG :(V,E,σ,µ) is2-defensive alliance;
(ii) if ∀a ∈ V \ S, |Ns(a) ∩ S| > O−1 2 +1, then NTG :(V,E,σ,µ) is 2-offensivealliance;
(iii) if ∀a ∈ S, |Ns(a)∩V \S| =0, then NTG :(V,E,σ,µ) is (O−1)-defensive alliance;
(iv) if ∀a ∈ V \ S, |Ns(a) ∩ V \ S| =0, then NTG :(V,E,σ,µ) is (O− 1) offensivealliance.
Proof. (i) Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph. Then
4.NeutrosophicAlliances
230
4.30.r-Regular-Strong-NeutrosophicGraph
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < O−1 2 +1 ( O−1 2 − 1); ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < O−1 2 +1 ( O−1 2 − 1) < 2; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < 2 Thus S is2-defensivealliance.
(ii) Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph.Then ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > O−1 2 +1 ( O−1 2 − 1); ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > O−1 2 +1 ( O−1 2 − 1) > 2; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > 2 Thus S is2-offensivealliance.
(iii) Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph.Then
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < O− 1 0; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < O− 1 0= O− 1; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < O− 1 Thus S is(O− 1)-defensivealliance.
(iv). Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph.Then
∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > O− 1 0; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > O− 1 0= O− 1; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > O− 1 Thus S is(O− 1)-offensivealliance.
Innextexample,theconceptofr-defensiveallianceandr-offensivealliance areappliedintoar-regular-strong-neutrosophicgraphwhichiscompleteand itsorderisfive,itmeans O =5.
Example4.30.5. ConsiderFigure (4.15).Inthissection,1-powerfulallianceis studiedinthewaythatmoreclarificationsarerepresented.
(i) Every3-setofvertices,e.g.,
S1 = {s1,s2,s3},S2 = {s1,s3,s5},S3 = {s2,s3,s4},S4 = {s3,s4,s5} isminimal-1-powerfulallianceanditformsaminimal-1-powerful-alliance numberbutonly S3 = {s3,s4,s5} isoptimalsuchthatformsbothminimal1-powerful-alliance-neutrosophicnumberandminimal-1-powerful-alliance number;
(ii) N = {s2,s5} isn’t1-powerfulalliance.Since
∃s1 ∈ V \ N, |Ns(s1) ∩ N |−|Ns(s1) ∩ (V \ N )| =2 2=0 < 1 ∃s1 ∈ V \ N, |Ns(s1) ∩ N |−|Ns(s1) ∩ (V \ N )| =2 2=0 > 1 ∃s1 ∈ V \ N, |Ns(s1) ∩ N |−|Ns(s1) ∩ (V \ N )| > 1; itimplies N = {s2,s5} isn’t1-offensivealliance.So N = {s2,s5} isn’t 1-powerfulalliance.Also,
∃s2 ∈ N, |Ns(s1) ∩ N |−|Ns(s1) ∩ (V \ N )| =1 3= 2 < 1 ∃s2 ∈ N, |Ns(s1) ∩ N |−|Ns(s1) ∩ (V \ N )| =1 3= 2 < 1 ∃s2 ∈ N, |Ns(s1) ∩ N |−|Ns(s1) ∩ (V \ N )| < 1; itimplies N = {s2,s5} 1-defensivealliancebut N = {s2,s5} isn’t1powerfulalliance.
231
Figure4.15:Blackcirclesformasetwhichis1-powerfulalliance. NTG13
(iii) Γs =3 3; (iv) Γ=3
Asaspecialcase,cycleneutrosophicgraphgetsspecificresultexcerptfrom 2-regularneutrosophicgraph.2-defensiveallianceand2-offensiveallianceget someresultsabouttheneighborsinsidefixedsetwhichtheirnumberisatmost 2.Also,2-defensiveallianceand2-offensivealliancegetsomeresultsaboutthe neighborsoutsideoffixedsetwhichtheirnumberisatmost2.
Proposition4.30.6. Let NTG :(V,E,σ,µ) bear-regular-strong-neutrosophic graphwhichiscycle.Thenfollowingstatementshold;
(i) ∀a ∈ S, |Ns(a) ∩ S| < 2 if NTG :(V,E,σ,µ) is2-defensivealliance;
(ii) ∀a ∈ V \ S, |Ns(a) ∩ S| > 2 if NTG :(V,E,σ,µ) is2-offensivealliance; (iii) ∀a ∈ S, |Ns(a) ∩ V \ S| =0 if NTG :(V,E,σ,µ) is2-defensivealliance; (iv) ∀a ∈ V \ S, |Ns(a) ∩ V \ S| =0 if NTG :(V,E,σ,µ) is2-offensive alliance.

Proof. (i) Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph and2-defensivealliance.Then
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < 2; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < 2=2 0; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < 2; ∀t ∈ S, |Ns(t) ∩ S| < 2, |Ns(t) ∩ (V \ S)| =0
(ii). Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph and2-offensivealliance.Then
∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > 2;
∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > 2=2 0; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > 2;
∀t ∈ V \ S, |Ns(t) ∩ S| > 2, |Ns(t) ∩ (V \ S)=0
(iii) Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph and2-defensivealliance.
4.NeutrosophicAlliances
232
4.30.r-Regular-Strong-NeutrosophicGraph
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < 2; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < 2=2 0; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < 2 0; ∀t ∈ S, |Ns(t) ∩ S| < 2, |Ns(t) ∩ (V \ S)| =0
(iv). Suppose NTG :(V,E,σ,µ) isa2-regular-strong-neutrosophicgraph andr-offensivealliance.Then
∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > 2; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > 2=2 0; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > 2 0; ∀t ∈ V \ S, |Ns(t) ∩ S| > 2, |Ns(t) ∩ (V \ S)| =0.
Asaspecialcaseofr-regular,cycleisanattribute.Thispropertyfacilitates theresultswhentheconditionisabouttheneighborsinsidefixedsetto determine2-defensiveallianceand2-offensivealliance.Also,aconditionabout theneighborsoutsideoffixedsetdeterminessomeresultsabout2-defensive allianceand2-offensivealliance.
Proposition4.30.7. Let NTG :(V,E,σ,µ) bear-regular-strong-neutrosophic graphwhichiscycle.Thenfollowingstatementshold;
(i) if ∀a ∈ S, |Ns(a) ∩ S| < 2, then NTG :(V,E,σ,µ) is2-defensivealliance;
(ii) if ∀a ∈ V \ S, |Ns(a) ∩ S| > 2, then NTG :(V,E,σ,µ) is2-offensive alliance;
(iii) if ∀a ∈ S, |Ns(a) ∩ V \ S| =0, then NTG :(V,E,σ,µ) is2-defensive alliance;
(iv) if ∀a ∈ V \ S, |Ns(a) ∩ V \ S| =0, then NTG :(V,E,σ,µ) is2-offensive alliance.
Proof. (i) Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph. Then
∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < 2 0; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < 2 0=2; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < 2. Thus S is2-defensivealliance.
(ii) Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph.Then ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > 2 0; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > 2 0=2; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > 2 Thus S is2-offensivealliance.
(iii) Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph.Then ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < 2 0; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < 2 0=2; ∀t ∈ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| < 2 Thus S is2-defensivealliance.
(iv) Suppose NTG :(V,E,σ,µ) isar-regular-strong-neutrosophicgraph.Then
233
∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > 2 0; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > 2 0=2; ∀t ∈ V \ S, |Ns(t) ∩ S|−|Ns(t) ∩ (V \ S)| > 2 Thus S is2-offensivealliance.
Example4.30.8. ConsiderFigure (4.16).Inthissection,3-powerfulallianceis studiedinthewaythatmoreclarificationsarerepresented.
(i) Every3-setofvertices,e.g.,
S1 = {s1,s2,s3},S2 = {s1,s3,s5},S3 = {s2,s3,s4},S4 = {s3,s4,s5}
isminimal-3-powerfulallianceanditformsaminimal-3-powerful-alliance numberbutonly S3 = {s3,s4,s5} isoptimalsuchthatformsbothminimal3-powerful-alliance-neutrosophicnumberandminimal-3-powerful-alliance number;since
∃s3 ∈ S4, |Ns(s3) ∩ S4|−|Ns(s3) ∩ (V \ S4)| =1 1=0 < 3 ∃s3 ∈ S4, |Ns(s3) ∩ S4|−|Ns(s3) ∩ (V \ S4)| =1 1=0 < 3 ∃s3 ∈ S4, |Ns(s3) ∩ S4|−|Ns(s3) ∩ (V \ S4)| < 3;
∃s5 ∈ S4, |Ns(s5) ∩ S4|−|Ns(s5) ∩ (V \ S4)| =1 1=0 < 3 ∃s5 ∈ S4, |Ns(s5) ∩ N |−|Ns(s5) ∩ (V \ S4)| =1 1=0 < 3 ∃s5 ∈ S4, |Ns(s5) ∩ S4|−|Ns(s5) ∩ (V \ S4)| < 3;
∃s4 ∈ S4, |Ns(s4) ∩ S4|−|Ns(s4) ∩ (V \ S4)| =2 0=2 < 3 ∃s4 ∈ S4, |Ns(s4) ∩ S4|−|Ns(s4) ∩ (V \ S4)| =2 0=2 < 3 ∃s4 ∈ S4, |Ns(s4) ∩ S4|−|Ns(s4) ∩ (V \ N )| < 3; Itimplies S4 is3-defensivealliance.Also,
∃s1 ∈ V \ S4, |Ns(s1) ∩ S4|−|Ns(s1) ∩ (V \ S4)| =1 1=0 > 1 ∃s1 ∈ V \ S4, |Ns(s1) ∩ S4|−|Ns(s1) ∩ (V \ S4)| =1 1=0 > 1 ∃s1 ∈ V \ S4, |Ns(s1) ∩ S4|−|Ns(s1) ∩ (V \ S4)| > 1; ∃s2 ∈ S4, |Ns(s2) ∩ N |−|Ns(s2) ∩ (V \ N )| =1 1=0 > 1 ∃s2 ∈ N, |Ns(s2) ∩ N |−|Ns(s2) ∩ (V \ N )| =1 1=0 > 1 ∃s2 ∈ N, |Ns(s2) ∩ N |−|Ns(s2) ∩ (V \ N )| > 1;
Itimplies S4 is(-1)-offensivealliance. S4 isn’t(-1)-powerfulalliance.
(ii) Every4-setofvertices,e.g.,
S1 = {s1,s2,s3,s4},S2 = {s1,s2,s3,s5},S3 = {s2,s3,s4,s5} isminimal-3-powerfulallianceanditformsaminimal-3-powerful-alliance numberbutonly S = {s2,s3,s4,s5} isoptimalsuchthatformsboth minimal-3-powerful-alliance-neutrosophicnumberandminimal-3-powerfulalliancenumber;since ∃s3 ∈ S, |Ns(s3) ∩ S|−|Ns(s3) ∩ (V \ S)| =2 0=2 < 3 ∃s3 ∈ S, |Ns(s3) ∩ S|−|Ns(s3) ∩ (V \ S)| =2 0=0 < 3 ∃s3 ∈ S, |Ns(s3) ∩ S|−|Ns(s3) ∩ (V \ S)| < 3;
4.NeutrosophicAlliances
234
Figure4.16:Blackcirclesformasetwhichis1-powerfulalliance. NTG14
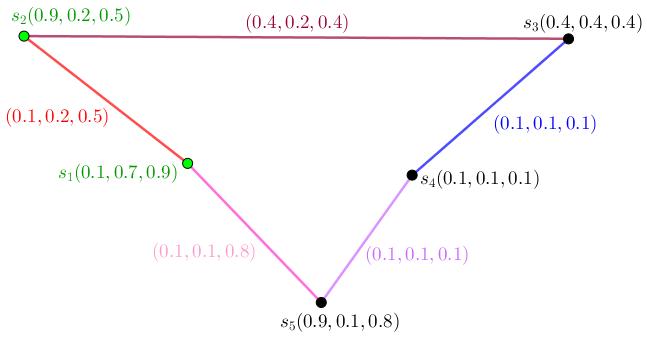
∃s4 ∈ S, |Ns(s4) ∩ S|−|Ns(s4) ∩ (V \ S)| =2 0=2 < 3 ∃s4 ∈ S, |Ns(s4) ∩ S|−|Ns(s4) ∩ (V \ S)| =2 0=2 < 3 ∃s4 ∈ S, |Ns(s4) ∩ S|−|Ns(s4) ∩ (V \ S)| < 3;
∃s5 ∈ S, |Ns(s5) ∩ S|−|Ns(s5) ∩ (V \ S)| =1 1=0 < 3 ∃s5 ∈ S, |Ns(s5) ∩ S|−|Ns(s5) ∩ (V \ S)| =1 1=0 < 3 ∃s5 ∈ S, |Ns(s5) ∩ S|−|Ns(s5) ∩ (V \ S)| < 3;
∃s2 ∈ S, |Ns(s2) ∩ S|−|Ns(s2) ∩ (V \ S)| =1 1=0 < 3 ∃s2 ∈ S, |Ns(s2) ∩ S|−|Ns(s2) ∩ (V \ S)| =1 1=0 < 3 ∃s2 ∈ S, |Ns(s2) ∩ S|−|Ns(s2) ∩ (V \ S)| < 3; itimplies S is3-defensivealliance.Also, ∃s1 ∈ V \ S, |Ns(s1) ∩ S|−|Ns(s1) ∩ (V \ S)| =2 0=2 > 1 ∃s1 ∈ V \ S, |Ns(s1) ∩ S|−|Ns(s1) ∩ (V \ S)| =2 0=2 > 1 ∃s1 ∈ V \ S, |Ns(s1) ∩ S|−|Ns(s1) ∩ (V \ S)| > 1; itimplies S4 is1-offensivealliance. S4 isn’t1-powerfulalliance. (iii) Γs isn’twell-defined; (iv) Γ isn’twell-defined.
4.31ApplicationsinTimeTableandScheduling
Inthissection,twoapplicationsfortimetableandschedulingareprovided wherethemodelsarecompletemodelswhichmeancompleteconnectionsare formedasindividualandfamilyofcompletemodelswithcommonneutrosophic vertexset.
Designingtheprogramstoachievesomegoalsisgeneralapproachtoapplyon someissuestofunctionproperly.Separationhaskeyroleinthecontextofthis style.Separatingthedurationofworkwhichareconsecutive,isthematterand ithasimportantancetoavoidmixingup.
4.31.ApplicationsinTimeTableandScheduling
235
4.NeutrosophicAlliances
Step1.(Definition) Timetableisanapproachtogetsomeattributestodo theworkfastandproper.Thestyleofschedulingimpliesspecialattention tothetaskswhichareconsecutive.
Step2.(Issue) Schedulingofprogramhasfacedwithdifficultiestodifferamid consecutivesection.Beyondthat,sometimessectionsarenotthesame.
Step3.(Model) Thesituationisdesignedasamodel.Themodelusesdatato assigneverysectionandtoassigntorelationamidsection,threenumbers belongunitintervaltostateindeterminacy,possibilitiesanddeterminacy. There’sonerestrictioninthat,thenumbersamidtwosectionsareatleast thenumberoftherelationamidthem.Table (4.5),clarifiesaboutthe assignednumberstothesesituation.
Table4.5:SchedulingconcernsitsSubjectsanditsConnectionsasaneutrosophic graphanditsalliancesinaModel. tbl1c
Sectionsof NTG n1 n2··· n9
Values (0.99, 0.98, 0.55)(0.74, 0.64, 0.46) (0.99, 0.98, 0.55) Connectionsof NTG E1 E2 E3 Values (0 01, 0 01, 0 01)(0 01, 0 01, 0 01)(0 01, 0 01, 0 01)
4.32Case1:CompleteModelasIndividual
Step4.(Solution) Theneutrosophicgraphanditsglobaloffensiveallianceas model,proposetousespecificset.Everysubjecthasconnectionwith everygivensubject.Thustheconnectionisappliedaspossibleandthe modeldemonstratesfullconnectionsaspossible.Usingthenotionof strongontheconnectionamidsubjects,causestheimportanceofsubject goesinthehighestlevelsuchthatthevalueamidtwoconsecutivesubjects, isdeterminedbythosesubjects.Iftheconfigurationiscomplete,theset isdifferent.Also,itholdsforothertypessuchthatstar,wheel,path, andcycle.Thecollectionofsituationsisanotherapplicationofglobal offensivealliancewhenthenotionoffamilyisappliedinthewaythat allmembersoffamilyarefromsameclassesofneutrosophicgraphs.As follows,TherearefoursubjectswhicharerepresentedasFigure (4.17) Thismodelisstrong.Andthestudyproposesusingspecificsetofobjects whichiscalledminimal-global-offensivealliance.Therearealsosome analysesonothersetsinthewaythat,theclarificationisgainedabout beingspecialsetornot.Also,inthelastpart,therearetwonumbersto assigntothismodelandsituationtocomparethemwithsamesituations togetmoreprecise.ConsiderFigure(4.17).
(i) S1 = {s1,s2},S2 = {s1,s3},S3 = {s1,s4},S4 = {s2,s3},S5 = {s2,s4},S6 = {s3,s4} areonlyminimal-global-offensivealliances; (ii) S6 = {s3,s4} isoptimalsuchthatformsbothminimal-globaloffensive-alliance-neutrosophicnumberandminimal-global-offensivealliancenumber;
236
Figure4.17:Thesetofblackcirclesisminimal-global-offensivealliance. NTG8

(iii) S = {s1,s3} onlyformsminimal-global-offensive-alliancenumberbut notminimal-global-offensive-alliance-neutrosophic;
(iv) N = {s1} isn’tglobal-offensivealliance.Sincethereisthreeinstances andonlyoneinstanceisenough;
(a) Firstcounterexampleforthestatement“N = {s1} isglobaloffensivealliance.”;
∃s2 ∈ V \ N, |Ns(s2) ∩ N | =1 < 2= |Ns(s2) ∩ (V \ N )| ∃s2 ∈ V \ N, |Ns(s2) ∩ N | =1 > 2= |Ns(s2) ∩ (V \ N )| ∃s2 ∈ V \ N, |Ns(s2) ∩ N | > |Ns(s2) ∩ (V \ N )|;
(b) secondcounterexampleforthestatement“N = {s1} isglobaloffensivealliance.”;
∃s3 ∈ V \ N, |Ns(s3) ∩ N | =1 < 2= |Ns(s3) ∩ (V \ N )| ∃s3 ∈ V \ N, |Ns(s3) ∩ N | =1 > 2= |Ns(s3) ∩ (V \ N )| ∃s3 ∈ V \ N, |Ns(s3) ∩ N | > |Ns(s3) ∩ (V \ N )|; (c) thirdcounterexampleforthestatement“N = {s1} isglobaloffensivealliance.”.
∃s4 ∈ V \ N, |Ns(s4) ∩ N | =1 < 2= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | =1 > 2= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | > |Ns(s4) ∩ (V \ N )|; (v) Γs =2 3 andcorrespondedsetis S6 = {s3,s4}; (vi) Γ=2 andcorrespondedsetis S6 = {s3,s4}
4.33Case2:FamilyofCompleteModels
Step4.(Solution) Theneutrosophicgraphanditsglobaloffensiveallianceas model,proposetousespecificset.Everysubjecthasconnectionwith everygivensubject.Thustheconnectionisappliedaspossibleandthe modeldemonstratesfullconnectionsaspossible.Usingthenotionof strongontheconnectionamidsubjects,causestheimportanceofsubject goesinthehighestlevelsuchthatthevalueamidtwoconsecutivesubjects, isdeterminedbythosesubjects.Iftheconfigurationiscomplete,theset isdifferent.Also,itholdsforothertypessuchthatstar,wheel,path, andcycle.Thecollectionofsituationsisanotherapplicationofglobal offensivealliancewhenthenotionoffamilyisappliedinthewaythat
4.33.Case2:FamilyofCompleteModels
237
allmembersoffamilyarefromsameclassesofneutrosophicgraphs.As follows,Therearefivesubjectswhicharerepresentedintheformationof familyofmodelsasFigure (4.17).Thesemodelsarestronginfamily.And thestudyproposesusingspecificsetofobjectswhichiscalledminimalglobal-offensiveallianceforthisfamilyofmodels.Therearealsosome analysesonothersetsinthewaythat,theclarificationisgainedabout beingspecialsetornot.Also,inthelastpart,therearetwonumbersto assigntothisfamilyofmodelsandcollectionofsituationstocompare themwithcollectionofsituationstogetmoreprecise.ConsiderFigure (4.18).
(i) S1 = {s1,s2,s3},S2 = {s1,s2,s4},S3 = {s1,s2,s5},S4 = {s1,s3,s4},S5 = {s1,s3,s5},S6 = {s2,s3,s4},S7 = {s2,s3,s5},S8 = {s3,s4,s5} areonlyminimal-global-offensivealliances;
(ii) S3 = {s1,s2,s5} isoptimalsuchthatformsbothminimal-globaloffensive-alliance-neutrosophicnumberandminimal-global-offensivealliancenumberfor G;
(iii) S8 = {s3,s4,s5} onlyformsminimal-global-offensive-alliancenumber butnotminimal-global-offensive-alliance-neutrosophicfor G;
(iv) N = {s1,s2} isn’tglobal-offensivealliance.Sincethereisthree instancesandonlyoneinstanceisenoughfor G;
(a) Firstcounterexampleforthestatement“N = {s1,s2} isglobaloffensivealliance.”for G; ∃s3 ∈ V \ N, |Ns(s3) ∩ N | =2=2= |Ns(s3 ∩ (V \ N )| ∃s3 ∈ V \ N, |Ns(s3) ∩ N | =2 > 2= |Ns(s3) ∩ (V \ N )| ∃s3 ∈ V \ N, |Ns(s3) ∩ N | > |Ns(s3) ∩ (V \ N )|; (b) secondcounterexampleforthestatement“N = {s1,s2} isglobaloffensivealliance.”for G;
∃s4 ∈ V \ N, |Ns(s4) ∩ N | =2=2= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | =2 > 2= |Ns(s4) ∩ (V \ N )| ∃s4 ∈ V \ N, |Ns(s4) ∩ N | > |Ns(s4) ∩ (V \ N )|; (c) thirdcounterexampleforthestatement“N = {s1,s2} isglobaloffensivealliance.”for G.
∃s5 ∈ V \ N, |Ns(s5) ∩ N | =2=2= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | =2 > 2= |Ns(s5) ∩ (V \ N )| ∃s5 ∈ V \ N, |Ns(s5) ∩ N | > |Ns(s5) ∩ (V \ N )|; (v) Γs =4 andcorrespondedsetis S3 = {s1,s2,s5} for G; (vi) Γ=3 andcorrespondedsetsare S1 = {s1,s2,s3},S2 = {s1,s2,s4},S3 = {s1,s2,s5},S4 = {s1,s3,s4},S5 = {s1,s3,s5},S6 = {s2,s3,s4},S7 = {s2,s3,s5},S8 = {s3,s4,s5} whichareonly minimal-global-offensivealliancesfor G.
4.34OpenProblems
Inthissection,somequestionsandproblemsareproposedtogivesomeavenues topursuethisstudy.Thestructuresofthedefinitionsandresultsgivesome ideastomakenewsettingswhichareeligibletoextendandtocreatenewstudy.
4.NeutrosophicAlliances
238
Figure4.18:Thesetofblackcirclesisminimal-global-offensivealliance. NTG11

Notionconcerningallianceisdefinedinneutrosophicgraphs.Neutrosophic numberisalsointroduced.Thus,
Question4.34.1. Isitpossibletouseothertypesneighborhoodarisingfrom differenttypesofedgestodefinenewalliances?
Question4.34.2. Areexistedsomeconnectionsamiddifferenttypesofalliances inneutrosophicgraphs?
Question4.34.3. Isitpossibletoconstructsomeclassesofwhichhave“nice” behavior?
Question4.34.4. Whichmathematicalnotionsdomakeanindependentstudy toapplythesetypesinneutrosophicgraphs?
Problem4.34.5. Whichparametersarerelatedtothisparameter?
Problem4.34.6. Whichapproachesdoworktoconstructapplicationstocreate independentstudy?
Problem4.34.7. Whichapproachesdoworktoconstructdefinitionswhichuse alldefinitionsandtherelationsamidtheminsteadofseparatedefinitionsto createindependentstudy?
4.35ConclusionandClosingRemarks
Inthissection,concludingremarksandclosingremarksarerepresented.The drawbacksofthisarticleareillustrated.Somebenefitsandadvantagesofthis studyarehighlighted.
Thisstudyusesonedefinitionconcerningglobalpowerfulalliancetostudy neutrosophicgraphs.Newneutrosophicnumberisintroducedwhichistooclose tothenotionofneutrosophicnumberbutit’sdifferentsinceitusesallvalues astype-summationonthem.Theconnectionsofverticeswhichareclarifiedby generaledgesdifferthemfromeachotherandputthemindifferentcategories torepresentasetwhichiscalledglobalpowerfulalliance.Furtherstudies couldbeaboutchangesinthesettingstocomparethisnotionamiddifferent settingsofneutrosophicgraphstheory.Onewayisfindingsomerelationsamid alldefinitionsofnotionstomakesensibledefinitions.InTable (4.6),some limitationsandadvantagesofthisstudyarepointedout.
4.35.ConclusionandClosingRemarks
239
4.NeutrosophicAlliances
Advantages Limitations 1. DefiningGlobalPowerfulAlliances 1. GeneralResults 2. ApplyingonStrongNeutrosophicGraphs 3. StudyonCompleteModels 2. StudyOnClasses 4. ApplyingonIndividuals 5. ApplyingonFamily 3. SameModelsinFamily 240
Table4.6:ABriefOverviewaboutAdvantagesandLimitationsofthisstudy tbl2c
Bibliography
1 [1] HenryGarrett,“GlobalOffensiveAllianceinStrongNeutrosophicGraphs”, Preprints2022,2022010429(doi:10.20944/preprints202201.0429.v1).
2 [2] HenryGarrett,“GlobalPowerfulAllianceinStrongNeutrosophicGraphs”, Preprints2022,2022010442(doi:10.20944/preprints202201.0442.v1).
3 [3] HenryGarrett,“ThreeTypesofNeutrosophicAlliancesbasedonConnectednessand(Strong)Edges”,Preprints2022,2022010239(doi: 10.20944/preprints202201.0239.v1).
241
This book is based on neutrosophic graph theory which is designed to studydifferenttypesofcoloringinthat graphs to get new ideas and new results. The results concern specific classes of neutrosophic graphs. New notions are defined in the comparable structures on these models to understand the behaviors of these modelsaccordingtothenotions.







































