SECONDARY EDUCATION



1. Organise the information and follow a plan
2. Represent the data in a diagram
3. Estimate
4. Work systematically Problems
CHALLENGES THAT LEAVE AN IMPRINT Arithmetics
1. The set of natural numbers
2. The relationship of divisibility
3. Prime and composite numbers
4. Lowest common multiple
5. Greatest common divisor
6. The Z set of integers
7. Operating with integers
8. Powers of integers
9. Roots of integers
Exercises and problems
Maths workshop
Self-assessment
1. Decimal numbers
2. Operating with decimal numbers
3. Decimal and sexagesimal numbers
4. The square root of a decimal number
5. Fractions
6. Fractions and decimal numbers
Exercises and problems
Maths workshop
Self-assessment
1. Adding and subtracting fractions
2. Multiplying and dividing fractions
3. Problems with fractions
4. Powers and fractions
Exercises and problems
Maths workshop
Self-assessment
Hours of sleep
CHALLENGES THAT LEAVE AN IMPRINT Proportionality
1. Ratios and proportions
2. Directly proportional magnitudes
3. Inversely proportional magnitudes
4. Problems of compound proportionality
5. Problems of proportional distribution
Exercises and problems
Maths workshop
Self-assessment
1. Percentages. Concept
2. Problems with percentages
3. Bank interest
4. Other arithmetic problems
Exercises and problems
Maths workshop
Self-assessment
1. Algebra: why do we use it?
2. Algebraic expressions
3. Polynomials
4. Notable products
Exercises and problems
Maths workshop
Self-assessment
Parcel variables
CHALLENGES THAT LEAVE AN IMPRINT
Algebra
1. Equations: meaning and use
2. Equations: elements and names
3. Transposing terms
4. Solving simple equations
5. Equations with denominators
6. The general method for solving first-degree equations
7. Solving problems with equations
8. Second-degree equations
9. Solving second-degree equations
Exercises and problems
Maths workshop
Self-assessment
1. First-degree equations with two unknowns
2. Systems of linear equations
3. Methods for solving linear systems
4. Solving problems with systems of equations
Exercises and problems
Maths workshop
Self-assessment
Calculating a maths grade
CHALLENGES THAT LEAVE AN IMPRINT
Geometry
1. Pythagorean theorem
2. Calculating one side when two are known
3. Applications of the Pythagorean theorem
Exercises and problems
Maths workshop
Self-assessment
1. Similar shapes
2. Plans, maps and models
3. How to build similar shapes
4. Thales’ theorem
5. Similarity between right-angled triangles
6. Applications of the similarity of triangles
Exercises and problems
Maths workshop
Self-assessment
1. Prisms
2. Pyramids
3. Truncated pyramids
4. Regular polyhedral
5. Cross-sections of polyhedra
6. Cylinders
7. Cones
8. Truncated cones
9. Spheres
10. Cross-sections of spheres, cylinders and cones
Exercises and problems
Maths workshop
Self-assessment
1. Units of volume
2. Cavalieri’s principle
3. Volume of a prism and a cylinder
4. Volume of a pyramid and a truncated pyramid
5. Volume of a cone and a truncated cone
6. Volume of a sphere
Exercises and problems
Maths workshop
Self-assessment
Hermitage restoration project
CHALLENGES THAT LEAVE AN IMPRINT
Functions and probability
1. The concept of a function
2. Increases, decreases, maximums and minimums
3. Functions given as tables of values
4. Functions given as equations
5. Proportionality functions: y = mx
6. The slope of a line
7. Linear functions: y = mx + n
8. Constant functions: y = k
Exercises and problems
Maths workshop
Self-assessment
1. Random events
2. Probability of an event
3. Assigning probabilities to regular experiments
4. Some strategies for calculating probabilities
Exercises and problems
Maths workshop
Self-assessment
Gema is going on a trip

Natural numbers have been used since ancient times by all civilisations. The most ancient societies used them to count objects, while the ancient Greeks also theorised about them, just for the joy of it.

Pythagoras (6TH century BC) and his disciples attributed divine, mystical powers to numbers. They believed that numbers governed everything: music, the movements of the planets, geometry, etc.
They investigated their properties and the relationships between them, as well as classifying them. This knowledge was later collected in Book 7 of Euclides' Elements.

Negative numbers arrived long after natural numbers, in order to meet the needs of commerce, and following the integration of the number zero, which was essential to their existence.
Negative numbers were not systematised until the 7TH century in Indian writings about everyday questions such as what people had compared to what they owed 'A debt subtracted from nothing becomes an asset.’. 'An asset subtracted from nothing becomes a debt.’.
Statements like this demonstrate that they used the concept of zero and the rule of sign.
The introduction of negative numbers to Europe, via the Arabs, was slow and uneven. A number of mathematicians theorised about them from the 17TH, century, but it was not until the end of the 19TH century that the set of negative integers was accepted and recognised as a mathematical object in its own right.

A group of friends are collecting NBA stickers, with 18 teams. Each team takes up a double-page spread in the album and includes 16 stickers of the players, one of the coach and one of the club logo.

1 Yesterday Marcos had 73 stickers in his album and 27 duplicates to swap. Today he bought three packs of 5 stickers, which contained six that he already had. Later on he swapped 13 of his duplicates with Marta for missing stickers. Answer the following questions in the order they appear, and join each one to the equations on the right.
a) How many stickers are in the collection?
b) How many pages does the album have if the first page is the table of contents and the last page the credits?
c) By how many more stickers has Marcos increased his collection today?
d) How many non-duplicates does he have now?
e) How many duplicates does he have?
f) How many stickers does he still need to complete his collection?
2 Rodrigo has 42 duplicates and wants to sort them in equal piles, each with between 5 and 10 stickers. How many different ways can he do this?
3 Alberto says that when he has 250 stickers, without duplicates, he will have filled 13 pages of his album. Adela does not agree, saying that he might not have filled a single one. Ramiro thinks that he might have filled three of four pages, but probably not any more. Who do you think has the most possibility of being right? Explain your answer.
4 Noemí has 310 stickers and only needs a few more to complete her collection. What is the minimum number of pages of the album she has completed? And the maximum?
Mayan numerals
Investigate the characteristics and rules of the Mayan numeral system.

8 238
The numbers we use to count objects one by one are called natural numbers. The set of natural numbers is represented with the letter N. It has a beginning and an order, but it has no end.
N = {0, 1, 2, 3, 4, …}
Natural numbers are represented and ordered on a number line.
Since the dawn* of civilisation, different cultures have devised different ways of expressing natural numbers. We call these numeral systems. H
Focus on English dawn: the beginning of a period of time.
We usually use the decimal numeral system (DNS). It was invented in India and brought to the Mediterranean by the Arabs during the expansion of the Arabic world, in the 8th century.
The decimal numeral system is a positional system, which means that each digit has a place value.
The use of 10 as the basis for the decimal numeral system is derived from the primitive method of counting with the fingers.
It is a decimal system because ten units of any place value make one unit of the place value immediately above.
Therefore, a number can be decomposed as shown in the following example (polynomial decomposition):
In the same way that we count in 10s (decimal system), other cultures throughout history have counted in 60s (sexagesimal system).
The number 60 was probably adopted as a way of counting with the 12 phalanges of the index, middle, ring and little fingers, using the thumb as a guide, and the other hand for keeping count.

➜ measuring time and angles
Nowadays, we use the sexagesimal system to measure time and angles. In these magitudes, each place value is divided into 60 units of the place value immediately below.
anayaeducacion.es
Express magnitudes in simple and complex form.
Notice that the symbols used for the minutes and seconds are different for each magnitude.
➜ complex and simple expressions
Remember that the measurement of amounts associated with a magnitude can be expressed simultaneously in several units (complex form) or in a single unit (simple form).
Copy and complete in your notebook.
1 Express in complex form:
2 Express 2 hours and 24 minutes in simple form (first in minutes and then in seconds).
a) In minutes: 2 h 24 min 8 (2 · 60 + 24) min = (… + …) min = … min
b) In seconds: 2 h 24 min 8 (2 · 3 600 + 24 · …) s = … s

Two numbers are related through the relation of divisibility when their quotient is exact.
Multiples and divisors of a number
anayaeducacion.es
Review the concept of multiples and divisors. anayaeducacion.es
• The multiples of a number contain that number an exact number of times. They are the result of multiplying that number by another natural number.
Remember
• Zero can be considered a multiple of any number.
• Zero has only one multiple: itself.
• A number has an infinite number of multiples.
• Every number is a multiple of itself and one.
multiple
• The divisors of a number are contained in that number an exact number of times. They divide it with an exact quotient.
Let’s calculate the divisors of 12:
Find multiples and divisors of a number.
The divisors of 12 are: 1
Note that they are grouped in pairs.
• A number has a finite number of divisors.
• A number has at least two divisors: the number itself and one.
Remember
A number with several digits can always be decomposed into a multiple of 2 plus the units place digit: 128 = 120 + 8
Observe that if we add two multiples of 12 together, we get another multiple of 12: 36 + 60 = 12 · 3 + 12 · 5 = 12 · (3 + 5) = 12 · 8 = 96
The sum of two multiples of a number, a, is another multiple of a.
Divisibility criteria are a set of practical rules which allow us to find out quickly if a number is a multiple of 2, 3, 5, 11…
➜ divisibility by 2, 5 and 10
You already know that:
• A number is a multiple of 2 if it ends in 0, 2, 4, 6, or 8.
• A number is a multiple of 5 if it ends in 0 or 5.
• A number is a multiple of 10 if it ends in 0.
➜ divisibility by 3 and 9
A number with several digits can always be decomposed into a multiple of 3, plus the sum of its digits.
multiple of 3 sum of the digits
The first addend is a multiple of 3. As we have seen in the property above, for the number to be a multiple of 3, its second summand must also be a multiple of 3. This reasoning also applies for multiples of 9.
• A number is a multiple of 3 if the sum of its digits is a multiple of 3.
• A number if a multiple of 9 if the sum of its digits is a multiple of 9.
➜ divisibility by 11
A number with several digits can always be decomposed into a multiple of 11, plus the result of adding and subtracting its digits alternatively.
649 = 600 = 594 + 6 40 = 44 – 4 9 = 9
All the numbers in the boxes are multiples of 11. Check it!
anayaeducacion.es
Practise the divisibility criteria.
multiple of 11 alternate addition and subtraction of digits
The first addend is a multiple of 11. In order for a number to be a multiple of 11, its second summand must also be a multiple of 11.
A number is a multiple of 11 if the sum of the odd place digits minus the sum of the even place digits (or vice versa), is a multiple of 11.
Copy and complete in your notebook.
1 Divide, observe and answer.
a) Is 173 a multiple of 19? And 228?
b) Is 43 a divisor of 516? And of 743?
2 Write the first eight multiples of 13.
3
4 Find all the multiples of 14 between 250 and 300.
The multiples of 14 between 250 and 300 are:
Let's practise!
1 Write:
a) The first five multiples of 20.
b) All the divisors of 20.
2 Draw all the ways of representing 36 as a rectangular number.
36 = 3 · 12
What is the relationship with the divisors of 36?
3 Write all the pairs of numbers whose product is 60.
4 Find:
a) All the multiples of 7 between 100 and 150.
b) The first multiple of 13 after 1 000.
5 Copy, circle the even numbers and cross out the multiples of 3.
45 - 67 - 74 - 96 - 143 - 138 - 251 - 309 - 488
6 What must the value of a be for the number to be:
5 6 a
a) A multiple of 2. b) A multiple of 3.
c) A multiple of 5. d) A multiple of 9.
7 Which of the numbers below are multiples of 11?
286 611 913 1 804 2 444 3 333
8 Observe, copy and complete in your notebook.
a) n = 2 · 3 · k = 6 · k 8 If a number, n, is a multiple of 2 and 3, it is also a multiple of 6.
b) m = 2 · 5 · k = 10 · k 8 If a number, m, is a multiple of 2 and 5, it is also a multiple of ...
c) p = 15 · k = 3 · 5 · k 8 If a number, p, is a multiple of 15, it is also a multiple of ... and ...
These are all the prime numbers smaller than 100:
• Some numbers can be decomposed into a product of factors: 40 = 8 · 5 = 2 · 2 · 2 · 5
We say that 40 is a composite number.
• Other numbers, like 13, only have two divisors, 13 and 1, and cannot be decomposed into a product.
13 = 13 · 1 8 cannot be decomposed
We say that 13 is a prime number.
• A prime number is a number that cannot be decomposed into factors.
• A prime number only has two divisors: the number itself and one.
• Numbers that are not prime are called composite numbers.
Classify numbers as prime or composite.
You reach the highest level of a number’s factorial decomposition when all the factors are prime numbers.
To decompose a number into prime factors, you need to take into account the divisibility criteria.
When decomposing a number into prime factors, we should do it systematically. Look at how we decompose 594:
Remember how to decompose a number into prime factors.
1 Separate the prime numbers from the composite numbers.
3 Decompose the following numbers into prime factors:
a) 84 b) 130 c) 160 d) 594
e) 720 f ) 975 g) 2 340 h) 5 220
4 Write, factorised, without doing any operations:
a) Three multiples of 12 = 22 · 3.
2 Copy and complete the decomposition processes.
b) All the divisors of 75 = 3 · 5 · 5.
5 Bearing in mind that m = 22 · 3 · 5 and n = 23 · 3, write:
a) Three common multiples of m and n.
b) Three common divisors of m and n
Let's practise!
1 Calculate mentally.
The lowest common multiple (LCM) of several numbers, a, b, c, … is the smallest of their common multiples, and is usually written like this:
LCM (a, b, c, …)
To calculate the LCM of a, b, c, … we find all the prime factors of a, all the prime factors of b, all the prime factors of c, … and then select the ones we need.
Example
Let’s calculate the lowest common multiple of 200 and 240.
• First, we decompose the numbers into prime factors:
200 = 23 · 52 240 = 24 · 3 · 5
• Then, we take all the required factors of 200 and 240:
To calculate the lowest common multiple of several numbers:
• We decompose the numbers into prime factors.
• We take all the prime factors, both common and non-common, raised to the highest exponent with which they appear.
A sports shoe factory manufactures trainers with 100 cm laces (200 cm per pair) and boots with 120 cm laces (240 cm per pair).
What length of shoelace must be wound on a reel to provide shoelaces for an exact number of pairs of trainers or an exact number of pairs of shoes?
LCM (200, 240) = 1 200
Solution: There must be 1 200 cm (12 m) or a multiple of that amount.
a) LCM (3, 5) b) LCM (6, 11)
c) LCM (10, 15) d) LCM (10, 25)
e) LCM (30, 40) f) LCM (50, 100)
2 Calculate.
a) LCM (18, 24) b) LCM (21, 35)
c) LCM (72, 90) d) LCM (90, 120)
e) LCM (60, 72, 90) f) LCM (50, 75, 100)
3 A supermarket does an inventory every 36 days and rearranges the shelves every 24 days. How often do both tasks happen on the same day?
4 A gear system is made up of two gears, one with 24 teeth and another with 32. How many rotations will each gear have to make before they are both back in their original position?

The greatest common divisor (GCD) of several numbers, a, b, c, … is the largest of their common divisors, and is usually written like this: GCD (a, b, c, …)
To calculate the GCD of (a, b, c, …) we find all the prime factors that a, b, c, … have in common. Example
Let’s calculate the greatest common divisor of 200 and 240.
• First, we decompose the numbers into prime factors: 200 = 23 · 52 240 = 24 · 3 · 5
• Then, we take the common factors:
To calculate the greatest common divisor of several numbers:
• First, we decompose the numbers into prime factors.
• Then, we take the common prime factors, each raised to the smallest exponent with which they appear.
Problem solved
A carpenter wants to split two boards, which are 200 cm and 240 cm long respectively, into equal pieces that are as long as possible, without having any wood left over. How long should each piece be?
GCD (200, 240) = 40
Solution: Each piece should be 40 cm long.
Let's practise!
1 Calculate mentally.
a) GCD (4, 6) b) GCD (6, 8)
c) GCD (5, 10) d) GCD (15, 20)
e) GCD (18, 24) f ) GCD (50, 75)
2 A gardener decides to use a rectangular plot measuring 248 cm Ò 250 cm as a flowerbed. She wants to divide it into uniform squares of the biggest size possible. What will the dimensions of each section be?
3 Calculate.
a) GCD (24, 36) b) GCD (28, 42)
c) GCD (63, 99) d) GCD (90, 126)
e) GCD (165, 275) f ) GCD (360, 450)
4 A warehouse operative needs to store 885 litres of olive oil and 705 litres of sunflower oil in identical containers that are as big as possible. What should the capacity of each container be so that each one is completely full and no oil is left over?
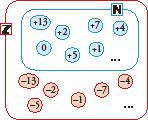
If we take the N set of natural numbers and, for each number other than zero, +a, we add another with the negative sign, –a, the result is what is known in mathematics as the set of integers. It is represented by the letter Z.
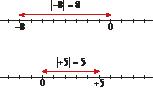
• The absolute value of an integer is the natural number that we get from taking away the sign. It is written between bars.
The absolute value of a number is equal to its distance from zero on the number line.
anayaeducacion.es
Order from smallest to highest.
Examples
(–7) < 0 < (+1)
(–12) < (–9) < (–2)
Let's practise!
8 absolute value of a
Example |+7| = 7 |–7| = 7
• The opposite of an integer is another integer of identical absolute value, but with the opposite sign.
Example
The opposite of (+7) 8 (–7) The opposite of (–7) 8 (+7)
To represent integers, we write them in order on a number line.
This way, we can see that a number is bigger than any number to its left, and smaller than any number to its right.
• Any positive number is greater than zero, and zero is greater than any negative number.
• Negative numbers are ordered backwards compared to positive numbers. In a group of negative numbers, the biggest number is the one with the smallest absolute value.
1 Write the absolute value and the opposite of each number.
a) –3 b) +8 c) –11 d) +23 e) –37 f ) +60
2 Order these numbers from smallest to biggest: –7, –13, +8, –1, +1, +5, 0, +10, –24
3 True or false?
a) Any integer is also a natural number.
b) Any natural number is an integer.
c) Only negative numbers have opposites.
d) Two opposite integers have the same absolute value.
anayaeducacion.es Activities for practising addition and subtraction.
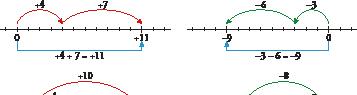



Let’s review some basic rules for solving expressions with integers.
To add (or subtract) two numbers:
same sign, we add their absolute values and keep the sign +4 + 7 = +11 –6 – 3 = –9
different signs, we subtract their absolute values and use the sign of the number with the biggest absolute value. – 4 + 10 = +6 +3 – 8 = –5
In operations with more than two integers, we have two options:


• Operate step by step, in the order in which they appear.
• Group the positive numbers on one side and the negative ones on the other. Then, proceed with the operations.
1 Read, consider and complete in your notebook.
a) If I am given €5 and then another €3, I will have €8 more than I started with: +5 + 3 = …
c) If I am given €10 and then €3 are taken from me, I will have €... ... than I started with: +10 – 3 = …
b) If I spend €4 and then spend another €2, I will have € less than I started with: –4 – 2 = …
d) If I am given €3 and then I spend €7, I will have €... ... than I started with: +3 – 7 = …
2 Copy and complete to solve the same expression in two different ways.
7 – 5 + 8 = – 5 + 8 = + 8 = …
Let's practise!
1 Calculate mentally.
a) 5 – 7 b) 2 – 9 c) –1 – 9
d) –12 + 17 e) –22 + 10 f) –12 – 13
2 Solve.
a) 10 – 3 + 5 b) 2 – 9 + 1 c) 16 – 4 – 6
d) 7 – 10 – 3 e) –7 – 8 + 5 f) –5 + 8 + 4
g) –8 + 2 + 3 h) –1 – 2 – 3 i) –7 – 3 – 4
3 Calculate.
a) 3 – 7 + 2 – 5
b) 2 – 6 + 9 – 3 + 4
c) 7 – 10 – 5 + 4 + 6 – 1
d) – 6 + 4 – 3 – 2 – 8 + 5
e) 12 + 5 – 17 – 11 + 20 – 13
f ) 16 – 22 + 24 – 31 + 12 – 15
Focus on English
withdraw: to take money out of a bank account.
Consider the following statements about a bank account:
• If I deposit €25, there will be €25 more in my account. 8 +(+25) = +25
• If I pay a bill for €18, there will be €18 less in my account. 8 +(–18) = –18
• If I withdraw* €55, there will be €55 less in my account. 8 –(+55) = –55
• If I cancel a €60 bill, there will be €60 more in my account. 8 –(–60) = +60
• When we remove brackets preceded by a plus sign, the signs inside do not change.
• When we remove brackets preceded by a minus sign, the signs inside change: plus to minus, and minus to plus.
anayaeducacion.es
Operations with integers.
3 Copy and complete to solve the same expression in two different ways.
a) Removing the brackets first.
(7 – 10) – (2 – 5 + 4 – 9) = 7 – – 2 + – + = 7 + 5 + 9 – – – = 21 – = …
b) Doing the operations in the brackets first.
(7 – 10) – (2 – 5 + 4 – 9) = (–3) – ( – ) = (–3) – (– ) = …
Let's practise!
4 Remove the brackets and calculate.
a) (–3) – (+4) – (–8)
b) –(–5) + (–6) – (–3)
c) (+8) – (+6) + (–7) – (–4)
d) –(–3) – (+2) + (–9) + (+7)
5 Solve by removing the brackets first.
a) (4 – 9) – (5 – 8)
b) –(1 – 6) + (4 – 7)
c) 4 – (8 + 2) – (3 – 13)
d) 12 + (8 – 15) – (5 + 8)
e) 22 – (7 – 11 – 3) – 13
6 Solve by doing the operations in the brackets first.
a) (2 – 6) + (4 – 8)
b) (8 – 10) – (12 – 7)
c) 15 – (2 – 5 + 8) + (6 – 9)
d) (8 – 6) – (3 – 7 – 2) + (1 – 8 + 2)
e) (5 – 16) – (7 – 3 – 6) – (9 – 13 – 5)
7 Solve in two ways, like in the example.
• 10 – (13 – 7) = 10 – (+6) = 10 – 6 = 4 10 – (13 – 7) = 10 – 13 + 7 = 17 – 13 = 4
a) 15 – (12 – 8)
c) 8 – (15 – 12)
b) 9 – (20 – 6)
d) 6 – (13 – 2)
e) 15 – (6 – 9 + 5) f) 21 – (3 – 10 + 11 + 6)
8 Calculate.
a) 7 – [1 + (9 – 13)] b) –9 + [8 – (13 – 4)]
c) 12 – [6 – (15 – 8)] d) –17 + [9 – (3 – 10)]
e) 2 + [6 – (4 – 2 + 9)] f) 15 – [9 – (5 – 11 + 7)]
9 Solve.
a) (2 – 9) – [5 + (8 – 12) – 7]
b) 13 – [15 – (6 – 8) + (5 – 9)]
c) 8 – [(6 – 11) + (2 – 5) – (7 – 10)]
d) (13 – 21) – [12 + (6 – 9 + 2) – 15]
e) [4 + (6 – 9 – 13)] – [5 – (8 + 2 – 18)]
f) [10 – (21 – 14)] – [5 + (17 – 11 + 6)]
anayaeducacion.es
Practise multiplying and dividing integers.
When calculating the product of two integers, remember that a multiplication is a sum of identical summands.
(+3) · (– 6) = We add (–6) three times:
+(– 6) + (– 6) + (– 6) = – 6 – 6 – 6 = –18
(–3) · (– 6) = We subtract (–6) three times:
–(– 6) – (– 6) – (– 6) = +6 + 6 + 6 = +18
However, to multiply quickly, we apply the following rule:
rule of signs
The product of two integers is:
• Positive, if the factors have the same sign.
• Negative, if the factors have different signs.
Let's (+) : (+) = + (-) : (-) = + (+) : (-) =(-) : (+) = -
10 Multiply.
The relationship between dividing integers and multiplying integers is the same as with natural numbers.
6 (–24) : (– 6) = +4
In divisions, the rule of signs is applied in the same way as in multiplications.
a) (+10) · (–2) b) (– 4) · (–9)
c) (–7) · (+5) d) (+11) · (+7)
11 Look at the examples and multiply in the two ways shown.
• (–3) · (+2) · (–5) = (– 6) · (–5) = +30
(–3) · (+2) · (–5) = (–3) · (–10) = +30
a) (–2) · (–3) · (+4) b) (–1) · (+2) · (–5)
c) (+4) · (–3) · (+2) d) (– 6) · (–2) · (–5)
12 Divide.
a) (–18) : (+3) b) (–15) : (–5)
c) (+36) : (–9) d) (–30) : (–10)
e) (–52) : (+13) f ) (+22) : (+11)
13 Copy, complete and compare. What do you notice?
(+60) : [(–30) : (–2)] = (+60) : [+15] = [(+60) : (–30)] : (–2) = [ ] : (–2) =
14 Calculate the value of x in each case:
a) (–18) : x = +6 b) (+4) · x = –36

anayaeducacion.es Activities for practising combined operations.
Observe the order we should follow to calculate the value of the combined operation below: (–18) : (11 – 9 – 5) + 5 · (6 – 8)
9
• First, the operations inside the brackets. 8 (–18) : (–3) + 5 · (–2)
9
• Next, the multiplications and divisions. 8 (+6) + (–10)
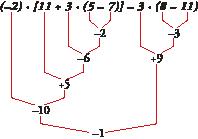
9
• Finally, the additions and subtractions. 8 6 – 10 = – 4
4 Copy and complete to find the value of the following expression:
Let's practise!
15 Calculate like in the examples.
• 15 – 8 · 3 = 15 – 24 = –9
• 18 : 6 – 5 = 3 – 5 = –2
a) 18 – 5 · 3
c) 7 · 2 – 16
e) 5 – 30 : 6
6 – 4 · 2
18 – 15 : 3
) 20 : 2 – 11
16 Calculate like in the example.
• 21 – 4 · 6 + 12 : 3 = 21 – 24 + 4 = 25 – 24 = 1
a) 20 – 4 · 7 + 11 b) 12 – 6 · 5 + 4 · 2
c) 15 – 20 : 5 – 3 d) 6 – 10 : 2 – 14 : 7
e) 5 · 3 – 4 · 4 + 2 · 6 f ) 7 · 3 – 5 · 4 + 18 : 6
17 Look at the example and calculate.
• (–3) · (– 4) + (– 6) · 3 = (+12) + (–18) = 12 – 18 = – 6
a) 5 · (–8) – (+9) · 4
b) 32 : (–8) – (–20) : 5
c) (–2) · (–9) + (–5) · (+4)
d) (+25) : (–5) + (–16) : (+4)
e) (+6) · (–7) + (–50) : (–2)
f ) (+56) : (–8) – (–12) · (+3)
18 Problem solved
= (–2) · [11 + 3 · (–2)] – 3 · (–3) = = (–2) · [11 – 6] + 9 = (–2) · [+5] + 9 = –10 + 9 = –1
19 Calculate.
a) 28 : (–7) – (–6) · [23 – 5 · (9 – 4)]
b) (–2) · (7 – 11) – [12 – (6 – 8)] : (–7)
20 Target 3.8. Write arithmetic expressions to show the difference between the maximum and minimum number of recommended hours of sleep for a 14 year old according to WHO guidelines, and solve it. The WHO recommends between 9 and 11 hours of sleep a day for a 14 year old.
Remember
Remember that a power is a multiplication of identical factors.
Examples
• (+4)2 = (+4) · (+4) = +16
• (–3)4 = (–3) · (–3) · (–3) · (–3) = +81
• (–3)5 = (–3) · (–3) · (–3) · (–3) · (–3) = –243
With successive powers of a negative number, we get positive and negative results alternatively.
(–3)1 = –3 (–3)2 = +9 (–3)3 = –27 (–3)4 = +81
When raising a negative number to a power:
• If the exponent is even, the result is positive.
(– a)n (even) 8 positive
• If the exponent is odd, the result is negative.
(– a)n (odd) 8 negative
The following properties are fundamental to calculating powers. Memorise them and carefully analyse each example below.
➜ power of a product
Remember
[(–2) + (–3)]2 = [–5]2 = +25
(–2)2 + (–3)2 = 4 + 9 = +13
The power of an addition (or subtraction) is not equal to the sum of the powers of the addends.
The power of a product is equal to the product of the powers of the factors.
[(–2) · (+5)]3 = (–2)3 · (+5)3
[–10]3 (–8) (+125)
–1 000 –1 000
➜ power of a quotient
The power of a quotient is equal to the quotient of the powers of the dividend and the divisor.
[(–10) : (+5)]3 = (–10)3 : (+5)3
(–2)3 (–1 000) : (+125)
–8
➜ product of powers with the same base
To multiply two powers with the same base, we add the exponents. (–10)2 · (–10)3 = (–10)2 + 3 = (–10)5 (+100) · (–1 000)
➜ quotient of powers with the same base
To divide two powers with the same base, we subtract the exponents.
(–10)3
➜ power of another power
To raise one power to another power, we multiply the exponents.
Let's practise!
1 Write as a product and calculate.
a) (–5)2 b) (–10)5 c) (–8)3
2 Calculate using a calculator, like in the example.
• 125 8 12**==== 8 {∫“¢°°«“}
a) (–11)3 b) 175 c) (–27)4
3 Reduce to a single power like in the example.
• 25 · (–3)5 = [2 · (–3)]5 = (– 6)5
• (–15)4 : (+3)4 = [(–15) : (+3)]4 = (–5)4 = 54
a) 32 · 42 b) (–2)3 · 43
c) (–5)2 · (+3)2 d) (+15)3 : (–5)3
e) (–20)2 : (– 4)2 f) (–18)4 : (+6)4
4 Apply the property a m · a n = a m + n, and reduce.
a) x 2 · x 3 b) a 4 · a 4 c) z 5 · z
5 Express as a single power.
a) (–2)5 · 27 b) (–2)3 · (+2)6
c) (–12)2 · (+12)2 d) (+9)4 · (–9)2
6 Apply the property a m : a n = a m – n, and reduce.
a) x 7 : x 4 b) a 7 : a 2 c) z 8 : z 3
7 Reduce to a single power.
a) (–7)8 : (–7)5 b) 109 : (–10)4
c) 124 : (–12) d) (– 4)10 : (+4)6
8 Apply the property (a m)n = a m · n, and reduce.
a) (x 3)2 b) (a 3)3 c) (z 6)3
9 Copy and complete in your notebook.
a) (32)4 = 3 b) [(–2)4]3 = (–2)
c) [(+5)2]2 = (+5) d) [(– 6)3]5 = (– 6)
10 Reduce like in the example.
• (a 6 · a 4) : a 7 = a 10 : a 7 = a 3
a) (x 5 · x 2) : x 4 b) m 7 : (m 2 · m 3)
c) (a · a 6) : (a 2 · a 4) d) (z 5 · z 3) : (z 4 · z 2)
11 Calculate.
a) 106 : (54 · 24) b) (–12)7 : [(–3)5 · 45]
c) [(–9)5 . (–2)5] : 184 d) [57 · (– 4)7] : 204
• The square root is the opposite of raising to the power of two (squaring). a = b ï b 2 = a
• Numbers that have an integer square root are called perfect squares.
Examples
anayaeducacion.es
Practise calculating square roots of integers.
ï
ï 49 77 49 400 20 20 400 2 2 == == 4 49 and 400 are perfect squares
Positive numbers have two square roots, one negative and one positive. The square roots of 16 are 4 and –4.
+4 8 because 42 = +16
– 4 8 because (– 4)2 = +16 Remember that when we write 16 , we mean the positive solution. If we mean the negative solution, we write the negative sign before the root. 16 = +4 – 16 = – 4
Negative numbers do not have a square root.
() –16 = x ï x 2 = –16 8 Impossible
() –16 8 Does not exist, because there is no number whose square is negative.
In addition to the square root, there are roots with indices greater than 2. In general:
1 Calculate the following square roots if they exist.
a) () +1 b) () –1 c) () 25 +
d) () –36 e) () +100 f ) () –100
g) () –169 h) () 400 + i ) () –900
2 Think and calculate if they exist.
a) 27 3 b) –27 3 c) 16 4
d) –16 4 e) 32 5 f ) –32 4
g) –1 7 h) –1 8 i ) 64 6 +
Numeral systems
1 Look at this number, which is written using two different numeral systems: Egyptian numeral system.

Mayan numeral system.
a) Explain the meaning of the symbols in each case.
b) Write the previous number and the next one in both numeral systems.
2 Copy and complete.
a) 2 300 UM = … C b) 4 800 D = … UM
c) 2 CM = ….. UM d) 700 UM = … DM
3 Copy, calculate and complete.
a) 1 h 13 min 27 s 8 … s
b) 587 min 8 … h … min
c) 6 542 s 8 … h … min … s
Multiples and divisors
4 Answer and explain your answers.
a) Is 132 a multiple of 11? Is 11 a divisor of 132?
b) Is 574 a multiple of 14? Is 27 a divisor of 1 542?
5 Calculate.
a) The first five multiples of 10.
b) The first five multiples of 31.
c) All the divisors of 23.
d) All the divisors of 32.
6 Think and answer.
a) The three biggest divisors of a number are 20, 30 and 60. Which number is it?
a) The three smallest divisors of a number are 12, 24 and 36. Which number is it?
Prime and composite numbers
7 Write:
a) The first ten prime numbers.
b) The biggest two-digit prime number and the smallest three-digit prime number.
8 Copy and complete to decompose the following numbers into prime factors.
1 400 = 2 · · 1 485 = · · 11
9 Decompose into the maximum number of factors.
a) 378 b) 1 144 c) 1 872
Lowest common multiple and greatest common divisor
10 Calculate mentally.
a) LCM (2, 3) b) LCM (6, 9)
c) LCM (4, 10) d) LCM (6, 10)
e) LCM (6, 12) f ) LCM (12, 18)
11 Calculate mentally.
a) GCD (4, 8) b) GCD (6, 9)
c) GCD (10, 15) d) GCD (12, 16)
e) GCD (16, 24) f ) GCD (18, 24)
12 Calculate.
a) LCM (24, 36) b) GCD (24, 36)
c) LCM (28, 42) d) GCD (28, 42)
e) LCM (45, 75) f ) GCD (45, 75)
Integers
13 Order from smallest to biggest. – 6, +8, –16, –3, +12, –7, +4, +15, –11
Adding and subtracting integers
14 Calculate.
a) 5 – 8 – 4 + 3 – 6 + 9
b) 10 – 11 + 7 – 13 + 15 – 6
c) 9 – 2 – 7 – 11 + 3 + 18 – 10
d) –7 – 15 + 8 + 10 – 9 – 6 + 11
15 Calculate.
a) 15 + (8 – 6) c) 6 + (2 – 8) – (1 + 7)
b) 11 – (2 + 8) d) (13 – 11) – (10 + 7) – (2 – 10)
Multiplying and dividing integers
16 Solve using the rule of signs.
a) (– 4) · (+7) b) (–21) : (+3)
c) (– 6) · (–8) d) (+30) : (+5)
e) (+10) · (+5) f ) (– 63) : (–9)
g) (–9) · (–5) h) (+112) : (–14)
17 Copy and complete.
a) (–3) · (…) = –15 b) (– 28) : (…) = –4
c) (…) · (– 4) = +32 d) (…) : (+5) = +10
e) (+20) · (…) = +60 f) (…) : (–7) = +8
Combined operations with integers
18 Calculate.
a) 5 – 4 · 3 b) 2 · 9 – 7
c) 4 · 5 – 6 · 3 d) 2 · 8 – 4 ·
e)
19 Calculate.
a) 7 · (6 – 4) b) (7 – 10) · 2
c) (– 3) · (7 – 6) d) (10 – 4) · (– 2)
e) 6 · (5 – 3) + 2 · (2 – 7) f) 5 · (–3 – 1) – 4 · (9 – 7)
Powers of integers
20 Calculate.
a) (–5)4 b) (+4)5 c) (– 6)3
d) (+7)3 e) (–8)2 f ) (–10)7
g) (+3)0 h) (–6)0 i) (–10)0
21 Express as the power of a single number.
a) 104 : 54 b) 127 : (– 4)7
c) (–9)6 : 36 d) 26 · 26
e) (– 4)5 · (–2)5 f ) 24 · (–5)4
22 Reduce to a single power.
a) x2 · x4 b) m4 · m3 c) x6 · x
d) m8 : m5 e) x3 : x f) m5 : m5
g) (x3)2 h) (m5)2 i) (x 2)2
Square roots of integers
23 Calculate, if they exist.
a) 49 b) 7 2 c) 49 –
d) 15 2 e) 225 f ) –225
g) 2 500 h) 50 2 i ) 2 500 –
24 The following series of numbers are the first ten natural numbers written in the binary system (it consists exclusively of the numbers 1 and 0).
0 - 1 - 10 - 11 - 100 - 101 - 110 - 111 - 1000 - 1001 Write the next ten numbers.
25 Copy these numbers and identify:
1 000 2 007 4 829 5 511 6 005
a) The multiples of 2. b) The multiples of 3.
c) The multiples of 5. d) The multiples of 11.
26 Write:
a) The prime numbers between 50 and 60.
b) The prime numbers between 80 and 100.
c) The first three prime numbers greater than 100.
27 Calculate.
a) LCM (12, 15) b) LCM (24, 60)
c) LCM (48, 54) d) LCM (90, 150)
e) LCM (6, 10, 15) f ) LCM (8, 12, 18)
28 Calculate.
a) GCD (36, 45) b) GCD (48, 72)
c) GCD (105, 120) d) GCD (135, 180)
e) GCD (8, 12, 16) f ) GCD (45, 60, 105)
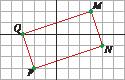
29 Write the coordinates of the vertices of this rectangle and draw another one like it, with its vertex M at point (1, 0).
30 Calculate.
a) 16 + [3 – 9 – (11 – 4)]
b) 8 – [(6 – 9) – (7 – 13)]
c) (6 – 15) – [1 – (1 – 5 – 4)]
d) (2 – 12 + 7) – [(4 – 10) – (5 – 15)]
e) [9 – (5 – 17)] – [11 – (6 – 13)]
31 Calculate.
a) (–2) · [(+3) · (–2)] b) [(+5) · (–3)] · (+2)
c) (+6) : [(–30) : (–15)] d) [(+40) : (– 4)] : (–5)
e) (–5) · [(–18) : (– 6)] f ) [(–8) · (+3)] : (– 4)
g) [(–21) : 7] · [8 : (– 4)] h) [6 · (–10)] : [(–5) · 6]
32 Calculate and note that the result changes depending on the position of the brackets.
a) 17 – 6 · 2 b) (17 – 6) · 2
c) (–10) – 2 · (–3) d) [(–10) – 2] · (–3)
e) (–3) · (+5) + (–2) f ) (–3) · [(+5) + (–2)]
33 Calculate.
a) 5 · [11 – 4 · (11 – 7)]
b) (– 4) · [12 + 3 · (5 – 8)]
c) 6 · [18 + (– 4) · (9 – 4)] – 13
d) 4 – (–2) · [–8 – 3 · (5 – 7)]
e) 6 · (7 – 11) + (–5) · [5 · (8 – 2) – 4 · (9 – 4)]
34 Reduce to a single power.
a) (x 2)5 b) (m 4)3
c) [a 10 : a 6]2 d) (a · a 3)3
e) (x 5 : x 2) · x 4 f ) (x 6 · x 4) : x 7
35 Look at the example and reduce as shown. • () xx x · 63 23 2 == = x 3
a) () x 22 b) () m 32 c) () a 42
d) x 4 e) m 6 f ) a 8
36 Find a divisor of 427 with two digits.
37 A number less than 50 is a multiple of 6 and 7. Which number is it?
38 A group of 20 people can be arranged into an exact number of rows and columns. For example, four rows and five columns. However, we cannot do the same thing with a group of 13 people. We can only arrange them into a single row.
A three-digit number is a multiple of 150 and a divisor of 2100. Which number could it be?
Problems with natural numbers
39 The WHO recommends that a 14 year old sleep between 9 and 11 hours a day, and a 40 year old between 7 and 9 hours a day. What is the difference between the annual hours of sleep of a 14 year old and a 40 year old?
40 A dance company with 156 dancers is rehearsing a routine that involves rows and columns. In one row there are 20 more dancers than in a column. How many rows and columns are there?
41 You want to divide a piece of card measuring 50 cm × 65 cm into the smallest squares possible. What is the length of the sides of each square?
42 Wooden cubes weighing 30 grams are placed on one side of a weighing scale and glass marbles weighing 36 grams on the other. If the scale is balanced and there is a total of 15 cubes and marbles:
a) How much does each side weigh?
b) How many wooden cubes and how many marbles are there?
43 Two lorries transporting identical fridges leave a factory. The first is carrying a load of 481 kilos, and the second 555 kilos. How much does each fridge weigh and how many fridges are there in each lorry?
44 A roll of cable is longer than 150 m, but shorter than 200 m. Exactly, how long is the cable if it can be divided into sections of 15 m, and also into sections of 18 m, without any cable left over?
45 The council is offering people allotment sites. For this purpose, a square piece of land has been divided into 15 m × 20 m rectangular plots. If there are almost 50 plots, what were the measurements of the piece of land?
Find all the numbers between 150 and 170 that can only be arranged in a single row.
46 This week, a bakery wants to sell 2 400 muffins and 2 640 biscuits in bags with the same number of units, but without mixing the products. How many muffins or how many biscuits can be put into each bag, taking into account that the number must be larger than 10 but smaller than 15?
47 Draw a coordinate system and represent the points A (–2, 0) and B (4, 2).

Draw all the squares that have their vertices at these points (there are three different squares).

Finally, write the coordinates of the vertices of each of the squares.
50 The sum of two integers is 3 and their difference 7. What are the two numbers?
51 The sum of two integers is –22, and the sum of their absolute values is 70. What are the two numbers?
52 A local bakery makes cupcakes every morning. They pack them into bags of half a dozen cupcakes, with two left over.
If they packed them into bags of 5, 3 cupcakes would be left over. If they packed them into bags of 8, no cupcakes would be left over.
48 If you write all the integers from –50 to +50, how many times will you use the number 7? And 5? And 5? And 3?
49
The sum of two integers is (–5) and their difference is (+19). What are the two numbers?
Let’s try with a very simple example
We take the numbers 6 and 4:
64 10 64 2 –+= = 3
8 10 – 2 = 8 8 8 : 2 = 4 6 (the smaller number)
If we subtract the difference from the sum of the two numbers, we get double the smaller number.
Now let’s solve the original problem
– The sum is (–5) and the difference is (+19).
– The sum minus the difference is double the smaller number:
(–5) – (+19) = –5 – 19 = –24
(double the smaller number)
The smaller number is: (–24) : 2 = –12
The larger number is: –12 + 19 = 7
Now check the answer.
If we know that they pack just over 40 bags, how many cupcakes do they make?
53 The members of an athletics club have decided to give their coach a stopwatch that costs €130.
‘It is a shame the shot put, discus and javelin throwers are not taking part,’ says the team captain, ‘with three more people we would each pay €3 less.’
How many people are contributing to the gift for the coach if each person pays an exact amount in Euros?
54 I am going with my brother to buy a gift that we have chosen for our mother. My brother says that after paying for his share of the gift, he still has €10. I borrow €5 from him to pay my share.
How much is the gift if we have €85 between us?
55 I have two accounts at the same bank. In the first one there are €200 more than in the second one. If I transfer money from one to the other so they both have the same balance, there will be €20 in each account.
How much money is there in each account?
You can refer to this graph:
You can also look back to problem 50 and ask: What is the sum of both accounts and what is the difference?

Ancient prime numbers
Ancient civilisations were fascinated by prime numbers. We can see evidence of this in the work of Eratosthenes, who was born nearly three hundred years before Christ. Well, that’s nothing! It turns out that even longer ago, about 20 000 years ago in Zaire, a primitive man carved some numbers on a bone.

We have no idea what they mean, but the ones on the picture are the prime numbers between 10 and 20! What do you think about that?
According to the Pythagoreans, a number is perfect if it coincides with the sum of its own divisors. For example, let’s take 6. The divisors of 6 are 1, 2 and 3 (6 is a divisor of 6, but it is not a proper divisor).
1 + 2 + 3 = 6
• There is another perfect number between 25 and 30. Can you find it?
Pythagoras called two numbers amicable when the sum of the divisors of each one was the same. A B
Sum of the divisors of B
Sum of the divisors of A
• The number 220 is amicable with another number. Can you find it?

• Amelia has stuck a number of stickers in her album that is three times the number of duplicates she needs to swap. If she manages to swap all of her duplicates for new ones she would have stuck a number of stickers in the album that is three times the empty spaces, which are more than 15 but less than 20. How many stickers are in the collection?
1 Write:
a) The first four multiples of 17.
b) All the divisors of 72.
2 Find:
a) The first multiple of 17 after 1 000.
b) A two-digit number that is a divisor of 415.




3 Write the prime numbers between 20 and 40.
4 Indicate which of the following numbers are multiples of 2, 3, 5 and 10:

897 - 765 - 990 - 2 713 - 6 077 - 6 324 - 7 005
5 Decompose the numbers 150 and 225 into prime factors. 150 = 2 · · · 225 = 3 · · ·
6 Calculate.
a) GCD (150, 225) b) LCM (150, 225)
7 Calculate.
a) 6 – 11 + (9 – 13) b) 2 – (5 – 8)
c) (7 – 15) – (6 – 2)
8 Calculate.
5 – [2 – (3 – 2)]
a) 4 · 5 – 3 · (–2) + 5 · (–8) – 4 · (–3)
b) (10 – 3 · 6) – 2 · [5 + 3 · (4 – 7)]
c) 10 – 10 · [– 6 + 5 · (– 4 + 7 – 3)]
9 Reduce to a single power.
(x 3)3 f) (–5)7 : (–5)5
10 A clothes shop puts a batch of t-shirts on sale, all at the same price. The first day they sell t-shirts with a total value of €221, and on the second day they sell even more t-shirts, with a value of €272 . What is the price of one t-shirt?

anayaeducacion.es Solutions to these problems.
11 You want to divide a rectangular plot, which is 100 m wide and 120 m long, into square plots that are as large as possible. What length should the sides of each plot be?
12 In a factory, a gas valve can be heard every 45 seconds, and an industrial hammer every 60 seconds. If you just heard the two sounds simultaneously, when will they coincide again?
13 A tower is built using wooden cubes with 45 cm edges. Next to it, another tower is built with plastic cubes with 60 cm edges. At what height will both towers be the same size?

14 The sum of two integers is 4, and the sum of their absolute values is 16. Which numbers are they?
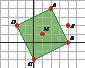
15 Look at the square.
a) Write the coordinates of the vertices, A, B, C, D and of its centre, M.
b) Imagine you rotate it, around M, so that A is on A l (4, 2). Write the coordinates of the new vertices, A l , B l , C l and D

LEARNING SITUATION
THINK
Look back at the content you have worked on and plan solutions to the problems that you may find. To do this, download the corresponding rubric from anayaeducacion.es, think individually and share in groups.
TEST YOUR SKILLS
Now you can do the skills self-evaluation included in anayaeducacion.es.

As humanity has evolved in terms of culture, commerce, science and daily life, we have had to develop the mathematical tools to respond to new challenges. In ancient civilisations, this cultural progress created the need for numbers that could represent parts of the unit.
In ancient Mesopotamia, they used a sexagesimal positional numeral system, which allowed them to write integers and fractions using only a few signs:
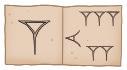


= 1 = 10 = 0
→ 1 + 15 60 → 1,25
In Europe, for several centuries, integers were expressed using the decimal system and fractions were expressed using the sexagesimal system. How complicated! But they did not know how to do it any other way.
This system, which now seems so inconvenient, was inherited from the ancient Babylonians. It survived for a long time because people were slow to accept the decimal system, which was brought from India by the Arabs, towards the 8th century.
By the mid-16th century, some Europeans, such as the Flemish mathematician Simon Stevin, began to replace sexagesimal fractions with decimal ones, as this made calculations much easier.
Over time, decimal fractions ended up completely replacing sexagesimal fractions for expressing incomplete units. The decimal system continued to evolve and its notation was further simplified, until, by the early 17th century, we arrived at the notation we use today.
Despite the adoption and widespread use of the decimal system, the sexagesimal is still with us today in the measurement and expression of two magnitudes: time and angles.

Viki has arranged to meet her friends tomorrow to play tennis. She is checking her sports bag to make sure it is not too heavy.




She calculates how much each of the items will roughly weigh.
Bread: 125 g


0.1 kg
1 Write the weight of each of the above items in grams.
RemembeR: a litre of water weighs one kilogram.

2 Look at the different ways of writing the weight of the bag of balls and explain how we arrive at each one.
⎯→ 6 · 60 g = 360 g
3 Do the same for the sandwich. ⎯→ … g
4 Now do the same for all of the other items in Viki's bag. In other words, write their weight in grams and in kilos as a decimal number and as a fraction.
5 Which form do you think is the easiest to understand in each case?

anayaeducacion.es
Revise how to read and write decimal numbers.
To express quantities in between two integers, we use decimal numbers
The decimal part represents an amount smaller than the unit. The decimal place values have the same structure as that of the integer part.
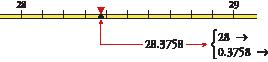
A unit of any place value is divided into ten units of the place value immediately below.
thousandshundredstens units tenthshundredthsthousandthstenthousandthshundredthousandthsmillionths
Twenty-eight units and three thousand, seven hundred and fifty-eight ten thousandths
It is important to be able to differentiate between different types of decimal numbers, as you will find them in measurements, results of operations and problems.
• Terminating decimals have a limited number of decimal places. 4.75
two decimal places
• Recurring decimals have an infinite number of decimal places which are repeated periodically. There are two types:
Pure recurring decimals: Mixed recurring decimals: 7.151515… = 7. 15 # 8.24666… = 8.24
• Non-terminating and non-recurring decimals have an infinite number of decimal places which do not repeat periodically.
2 = 1.4124135…
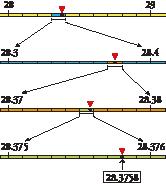
To compare two decimal numbers, we compare the corresponding decimal places, one by one, starting from the left.
Each decimal number is represented with a point on the number line. Each point on the line can be located by a decimal number.
–1.263 < –0.4 < 0.6751 < 1.55 < 2.753
Decimal numbers are ordered on the number line. If we choose any two numbers, the smaller of the two is on the left and the bigger is on the right.
1 Write the quantities in the table as words:
2 Write the following quantities as words:
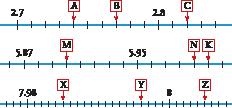
6 Look at the number line below. The red dot represents life expectancy in Spain in the year 2019. The yellow dot represents life expectancy in 2020.
3 Write in figures.
a) Three units and five hundredths.
b) Forty-three thousandths.
c) Eight thousandths.
d) Two hundred and nineteen millionths.
e) Twenty-three millionths.
f) Fourteen ten millionths.
4 Look at the following decimal numbers: 1.292929… 3 = 1.7320508…
a) Which ones are terminating decimals?
b) Which ones are pure recurring decimals?
c) Which ones are mixed recurring decimals?
d) Which ones are neither terminating nor recurring?
82 years 83 years 84 years
a) Write this data to two decimal places.
b) Did it improve or worsen from 2019 to 2020? What do you think the cause was?
7 Put these numbers in order, from lowest to highest.
a) 7.4; 6.9; 7.09; 7.11; 5.88
b) 3.9; 4.04; 3.941; 3.906; 4.001
c) 0.039; 0.01; 0.06; 0.009; 0.075
d) 11.99; 11.909; 11.009; 12.01; 11.91
8 Copy and complete the boxes in your notebook with the signs <, > or =, as appropriate. a)
meaningful: useful, important.

Calculations sometimes result in numbers with too many decimals. These are difficult to work with and provide little meaningful* information. In these cases, we take a smaller number of decimal places. This gives an approximate value, which is easier to work with.
Practise rounding decimal numbers.
When rounding off, if the first deleted digit is 5, we round up by adding one to the digit before it. Rounding
The result 1.8333… is closer to 1.83 than to 1.84.
Rounding off: Each jar of jam costs €1.83.
The result 1.8375 is closer to 1.84 than to 1.83.
Rounding off: Each packet of coffee costs €1.84
Rounding off involves deleting decimal figures from a certain decimal place value, and adding one unit to the last digit when the first one we delete is 5 or greater than 5.
When we round off we give an approximate value, so we are making an error on purpose.
The error made in rounding off is less than half a unit of the place value we have rounded to.
In both cases, we have rounded off to the nearest hundredths, and the error made is less than five thousandths; in other words, less than half a hundredth.
We say that the error bound is half a hundredth.
Practical rule
To find decimal numbers between two given decimals, we increase the number of decimal places by adding zeros to the right of the last digit.
5.09 < … < 5.1
5.090 < 5.095 < 5.100
• Let’s take any two decimals, for example 5.5 and 5.9. Obviously, there are other numbers between the two.
• Now we take two consecutive decimals from between the previous ones, for example, 5.5 and 5.6.
The difference between the two numbers is one tenth, which is divided into ten hundredths.
This reasoning can continue indefinitely and repeat for any other pair of numbers. Between two decimal numbers there are an infinite number of other decimals.
1 In your notebook, round off the number 2.83516:
a) To the nearest unit. 8 b) To the nearest tenths. 8
c) To the nearest hundredths. 8 … d) To the nearest thousandths. 8 …
2 Copy and complete.
a) Find three numbers between 2.58 and 2.59.
2.580 < … < … < … < 2.590
b) Find three numbers between 3.4 and 3.41.
3. … < … < … < … < 3. …
c) Find three numbers between 0.59 and 0.6. 0.59… < … < … < … < 0.6…
Let's practise!
9 Round off the number . 682 # :
a) To the nearest unit. b) To the nearest tenths.
c) To the nearest d) To the nearest hundredths. thousandths.
10 Round off to the nearest tenths.
a) 5.48 b) 2.8346 c) 3.057
2 Find a number between 4.09 and 4.1: 4.09 4.1
11 Round off to the nearest hundredths.
a) 6.284
b) 1.53369 c) 0.79462
12 Find a decimal number between:
a) 2.2 and 2.3
c) 1.59 and 1.6
b) 4.01 and 4.02
d) 8 and 8.1
There are always other decimals between two decimal
You already know how to add, subtract and multiply with decimals. Let’s review the operations in this water bill, as well as the rounding off of the results.

Practise calculating with decimal numbers in your head.
The calculations are shown in the margin and are summarised in these expressions:
• To add or subtract decimal numbers, we put them in a column matching the corresponding decimal places.
• To multiply decimal numbers, we multiply them as if they were integers. We then separate as many decimal places in the product as the sum of the number of decimal places of the two factors.
anayaeducacion.es Practise dividing with decimal numbers.
We will now review the different types of divisions with decimal numbers. For each one, we will start with a problem that will make the operation more meaningful.
➜ divisions with an integer divisor
Problem 1
A 70-litre can of oil is filled using 16 bottles, which are all the same size. How much oil is in each bottle?
Solution: Each bottle contains 4.375 litres of oil.
Problem 2
Remember
When rounding off, if the first deleted digit is 5 or greater, we round up by adding one to the digit before it. 1.19666… rounding off
A bag of oranges weighing 3 kilos costs €3.59. What is the price per kilo?
One kilo costs 1196 ! 8 Rounding off: €1.20
To get decimal places in the quotient:
• When we lower the tenths digit of the dividend, we put the decimal point in the quotient and then continue the division.
• If we do not have enough decimal places in the dividend, we add zeros to get to the desired approximation.
➜ divisions with a decimal divisor
Problem 3
Remember
If we multiply the dividend and the divisor by the same number, the quotient does not change. 6 :
Target 5.2. We pay €6 for 2.5 m of fabric to make a banner demanding gender equality.
How much does a metre of the fabric cost?
Solution: One meter of the fabric costs €2.40.
Problem 4
A 1.25 m2 sheet of chipboard weighs 8 kilos and 100 grams.
How much does one square metre weigh?
Solution: A square metre weighs 6.48 kg.
When there are decimals in the divisor:
• We multiply both the dividend and the divisor by the unit followed by as many zeros as there are decimal places in the divisor.
• The new division has the same quotient and an integer divisor.
In expressions involving decimal numbers with brackets and combined operations, we follow the same rules as we do with integers with regard to the priority of operations, the rule of signs, etc.
Priority of operations:
• First, brackets.
• Then, multiplications and divisions.
• Finally, additions and subtractions.
1 Copy and complete to get an equivalent division, but without decimals in the divisor. Then, do the operations.
Help
1 Example:
2 Look at the result a calculator gives when we divide 2.5 : 6. Then, copy and complete the problems in your notebook, rounding off the answers as appropriate.
2.5 / 6 = 8 {∫≠Ÿ¢‘\\\\\}
a) 2.5 kg of silver is used to make six trophies.
Each trophy contains … kilos of silver. 8 Rounding off: … grams
b) 2.5 kg of potatoes are used to make six tortillas
Each tortilla contains … kilos of potatoes. 8 Rounding off: … grams
3 Look at the combined operation, copy and complete. 3 – (1.5 + 1.54) : (4.23 – 2.33)
2 Example:
• 4.75 kg of flour makes 16 cakes.
• 4.75 kg of gold makes 16 bars. We solve using a calculator: 4.75 / 16 = 8 {∫≠Ÿ“£\°|∞‚}
• Each cake contains 0.3 kg of flour.
• Each bar contains 0.297 kg of gold.
3 Example: (3 – 1.9) · (1.43 + 1.07) – 1.15 1.1 · 2.5 – 1.15 2.75 – 1.15 1.6
4 Look at the bill from page 38 again. Copy and complete.
a) The total in section A for a consumption of 40 m3 would be: 10 · 0.03 + … · 0.65 + … · 1.93 = …. + … + … = …
b) Calculate the ‘total due’ from the bill above for a family with a consumption of 40 m3 that does not get any discount.
c) Does all the water consumed cost the same? Why do you think this is?
4 A water consumption of 55 m3 is divided as follows:
Up to 10 m3 8 10 m3
From 11 to 30 m3 8 19 m3
From 31 to 60 m3 8 26 m3
Total 8 55m3
decimal numbers.
Let's practise!
1 Calculate mentally.
a) 0.75 + 0.25 b) 0.75 – 0.25
c) 1.80 + 1.20 d) 1.80 – 1.20
e) 2.30 + 1.80 f ) 2.30 – 1.80
g) 3.50 + 1.75 h) 3.50 – 1.75
2 Calculate.
a) 2.37 + 0.356 b) 5.86 – 1.749
c) 13.2 + 4.08 + 2.635 d) 15.4 – 6.843
e) 7.04 + 12.283 + 0.05 f ) 0.35 – 0.0648
3 Remind yourself how to multiply and divide by the unit followed by zeros and complete.
a) 2.6 · 100 b) 5.4 : 10
c) 0.83 · 10 d) 12 : 100
e) 0.0048 · 1 000 f ) 350 : 1 000
4 Calculate.
a) 6.3 · 1.24 b) 0.44 · 2.375
c) 0.016 · 0.0025 d) 143 · 0.068
e) 5.48 · 2.63 f ) 0.15 · 1.01
5 Copy and complete so that each equality is true.
a) 5.2 : 0.8 = 52 : … b) 3 : 0.004 = … : 4
c) 6.31 : 2.5 = … : 25 d) 2.4 : 1.638 = 2 400 : …
e) 0.005 : 0.02 = 5 : … f) 0.12 : 0.0012 = 1 200 : …
6 Calculate the exact quotient or to a maximum of three decimal places.
a) 8 : 6 b) 218 : 16 c) 3 : 4
d) 12 : 536 e) 149.04 : 23 f ) 2.58 : 15
7 Replace each division with one that is equivalent, but has an integer divisor. Then, calculate the exact quotient or to a maximum of three decimal places.
a) 6 : 0.2 b) 13 : 0.75
c) 53 : 4.11 d) 4 : 0.009
e) 45.6 : 3.8 f ) 23.587 : 5.1
g) 2.549 : 8.5 h) 6.23 : 0.011
8 Round off each quotient to the nearest hundredths.
a) 5 : 6 b) 7 : 9 c) 6 : 3.5 d) 2.7 : 5.9
9 Solve.
a) 2.37 – 1.26 + 0.8 – 0.35
b) 2.50 – 1.25 – 1.75 – 0.20
c) 13.48 – 10.7 + 5.328 – 6.726
d) 5.6 – 8.42 – 4.725 + 1.48
10 Calculate.
a) 6.2 – (7.2 – 4.63)
b) (12.85 – 7.9) – (6.2 + 3.28)
c) 5.6 – [4.23 – (5.2 + 1.75)]
11 Do the operations and solve.
a) 3.6 – 1.2 · 0.6 – 4.5 : 1.8
b) 3.6 – 0.5 · (4 – 2.26)
c) 0.75 : (2.65 – 1.15) – 1.1
d) (0.5 + 0.1) · (0.5 – 0.1) – (0.6 – 0.4) · (0.6 + 0.4)
e) 5.4 – 1.5 · [3.2 + 10 · (0.63 – 1.25)]
12 Experiment, think of some examples, and then copy and complete in your notebook.
a) Multiplying by 0.1 is the same as dividing by...
b) Dividing by 0.1 is the same as multiplying by...
c) Multiplying by 0.5 is the same as...
d) Dividing by 0.5 is the same as...
e) Multiplying by 0.25 is the same as...
f) Dividing by 0.25 is the same as...
13 Calculate mentally.
14 Estimate mentally, without using decimals, and then check with a calculator.
a) 25.197 · 9.86 b) 142.36 · 0.49
c) 181.046 : 6.16 d) 33.44 : 0.511
You should make an error of 2 units or less.
15 Solve with a calculator and round off to the place value that you consider appropriate.
a) A packet of 500 sheets of paper weighs 652 g. What does one sheet of paper weigh?
b) A chicken costs €3.49/kg. How much will a chicken that weighs one kilo and 850 grams cost?
c) A 2-metre-long piece of wood is cut into seven equal pieces. What is the length of each piece?
d) A car consumes 50 litres of petrol over 837 km. How much does it consume per 100 kilometres?
You already know that the sexagesimal numeral system is used to measure time and angles.
Here we look at some processes that we should bear in mind when working with these magnitudes.
Also…
To get the result directly in the sexagesimal system:
4
We multiply the remainder of the hours (14) by 60 and continue dividing to get the minutes.
To solve a problem whose solution is an amount of time, we do the operations in the decimal system. However, the solution has to be given in traditional units of time, in other words, in the sexagesimal system.
Example
A cyclist covers the 49 kilometres of a time trial at an average speed of 35 km/h. What was the cyclist’s time?
Distance (km) : Speed (km/h) = Time (h)
The solution, one and four tenths of an hour, must be expressed in the sexagesimal system (hours and minutes).
To convert 0.4 hours into minutes, we multiply it by 60:
Also… 24 minutes are 60 24 of an hour:
h = 24 : 60 = 0.4 h
When we are solving a problem, the data we use must be compatible, that is, expressed in the same units. This means that we sometimes have to convert quantities from the sexagesimal to the decimal system. Example
A cyclist covers the 49 kilometres of a time trial in one hour and twenty-four minutes. What was the cyclist’s average speed in km/h?
Distance (km) : Time (h) = Speed (km/h)
For the data to be compatible we have to express the time in hours.
To convert 24 minutes into hours, we divide it by 60:
1 h 24 min = (1 + 24 : 60) h = (1 + 0.4) h = 1.4 h
We calculate the speed:
anayaeducacion.es
Remember conversions with units of time.
Let's practise!
1 A tap fills an 80-litre tank in 3 minutes and 12 seconds. How many litres does the tap supply per second?
2 A tap supplies 25 litres per minute. How long will it take to fill an 80-litre tank?
3 A shopping centre plays a music recording that lasts 5 minutes and 15 seconds on a loop for 7 hours. How many times does the recording play during this time?
Convert the data into minutes.
You already know that calculating the square root is the opposite of squaring.
How to calculate the length of the side of a square given its area:

025 = 0.5
0.52 = 0.25
= 1.2 ï 1.22 = 1.44
You also know that there are many numbers which do not have an exact root. In such cases, we can approximate to as many decimal places as we want. As an example, we will calculate successive approximations of . 72 .
We calculate the square root of a decimal using the same method that we use to calculate the square root of a natural number. From the decimal point, we lower the decimal places in twos, adding zeros until we get to the desired approximation.
Normally, to calculate the square root we use a calculator ($ key), which gives us the solution with many decimal places. We then round off that solution to as many decimal places as we need.

Let's practise! anayaeducacion.es Calculate and round off the roots of decimal numbers.
1 Calculate the following exact roots:
a) 004 b) 049 c) 081
d) 0 0001 e) 0 0121 f ) 0 1125
2 Find the solution to one decimal place using trial and error.
a) 8 b) 11.5 c) 150
3 Calculate on paper using the algorithm. If the result is not exact, find the solution to two decimal places.
a) 784 b) 56 c) 39 0625
4 Using a calculator, round off to the nearest thousandths.
a) 10 b) 254 c) 76 38
We already know what fractions are. Let’s review some important concepts before we carry on with the unit.
anayaeducacion.es
Review the concept of equivalent fractions.
Two fractions are equivalent when they express the same portion of a unit. 5
Two equivalent fractions have the same numerical value.
Remember
How can we recognise equivalent fractions?
b a d c = 5 a · d = b · c
In equivalent fractions, the cross products are the same.
If we multiply the two parts of a fraction by the same number, we get an equivalent fraction.
➜ simPliFYing Fractions
As a result of the above property, we can say that:
If we divide the two parts of a fraction by the same number, we get an equivalent fraction.
=
This transformation is called simplifying fractions. A fraction that cannot be fimplified is called an irreducible fraction.
anayaeducacion.es
Practise simplifying fractions.
Let's practise!
UNDERSTAND AND APPLY IN THE CHALLENGE
1 On average, a person sleeps seventy-five thousand hours before they reach the age of 20, one hundred and twenty-five thousand hours between the ages of 20 and 60 and fifty thousand hours after the age of 60. Write the portion of the hours of sleep for each stage of life as an irreducible fraction
2 Divide, express in decimal form and check that the fractions , 4 1 8 2 12 3 and are equivalent.
3 Find the irreducible fraction of:
a) 18 15
b) 54 30
c)
To calculate the lowest common multiple of several numbers:
• We decompose them into prime factors.
• We take the common and noncommon prime factors with the highest exponent.
Comparing, adding and subtracting fractions is very simple when they all have the same denominator. When they do not, we substitute them for equivalent fractions which have the same denominator. The example below demonstrates the process that we should follow.
Example
We want to order the fractions ,and 12 7 14 9 21 11 from lowest to highest. To do so, we first reduce them to a common denominator.
• We take the lowest common multiple of the denominators as the denominator:
• In each fraction, we multiply the numerator and denominator by the same number to get 84 in the denominator:
anayaeducacion.es
Reduce to a common denominator and compare.
Let's practise!
Now, we can put the fractions in order: 21 11 12 7 14 9 <<
To reduce fractions to a common denominator:
• We calculate the lowest common multiple of the denominators.
• We multiply the two parts of each fraction by the number that we get from dividing the lowest common multiple by the corresponding denominator.
4 Copy and complete to get equivalent fractions with the same denominator. 2, 4 3 , 10 7 8 · 20 220 , · 20 3 4 , · 20 7 4
5 Reduce to the common denominator indicated in each case.
a) 2 1 , 1 4 , 1 8 8 Common denominator: 8
b) 3 2 , 6 1 , 9 5 8 Common denominator: 18
c) 4 3 , 6 5 , 2 9 8 Common denominator: 36
d) 4 1 , 5 3 , 10 3 8 Common denominator: 20
6 Reduce to a common denominator.
7 Reduce to a common denominator. Then, order the fractions from lowest to highest.
Fractional and decimal notations are numerical forms and, as you will now see, many quantities can be expressed in both.
We already know that a fraction is an indicated division whose result is a terminating or a recurring decimal.
The irreducible fraction that results in a decimal is called the corresponding fraction of that number.
Corresponding fraction of 1. 2 ! = 9 11 : 9 11 = 11 : 9 = 1. 2 !
Any fraction can be converted into decimal form. To do this, the numerator is divided by the denominator. However, the opposite is not true: we cannot convert all decimals into fractions. We can only convert terminating and recurring decimals into fractions.
A terminating decimal can be converted into a fraction by removing the decimal point and dividing it by the unit followed by as many zeros as the original number had decimal places.
Look at the examples below which demonstrate the method for finding the corresponding fraction of a pure recurring decimal and a mixed recurring decimal.
• We want to convert 1. 2 ! into a fraction.
Let’s say A = 1.222…
We multiply it by 10 and subtract the number itself:
• We want to convert 0.7 2 ! into a fraction.
Let’s say B = 0.7222…
We multiply it by 100 and subtract 10 times the number itself:
• We say that a number is rational when we can express it in fractional form.
rational number = Integer Integer
• The set of rational numbers is represented by the letter Q
• A rational number can be expressed in many different ways. For example: 0.2 = 10 2 5 1 15 3 20 4 250 50 = === = = …
• All integers and, therefore, all natural numbers are rational. So, any integer can be expressed as a fraction: 3 = 1 3 2 6 = = … –3 = 1 3 2 6 – –=
• Terminating and recurring decimals are also rational numbers. As we have seen, these numbers can always be expressed in a fractional form: 0.35 = 20 7 . 14 9 13 = ! . 02 15 330 71 = #
• Decimals with infinite, non-recurring decimal places are not rational. For example: 2 = 1.414213… π = 3.141592… 5 = 2.236067… These numbers cannot be expressed in fractional form. All the above can be summarised in the following diagram:
DO YOU KNOW THE BASICS?
Decimal numeral system

1 Copy and complete.
a) 5 tenths = … thousandths
b) 2 thousandths = … millionths
c) 6 hundred thousandths = … hundredths

c) 8 millionths = … thousandths
2 Order these numbers from lowest to highest.
a) 5.1 - 5.099 - 4.83 - 4.9 - 4.99
b) 0.21 - 0.03 - 0.15 - 0,209 - 0.101 - 0.121
3 Write the number associated with each letter.
8 Calculate.
a) 5.8 – 3.2 · 1.6 – 0.29
b) (5.8 – 3.2) · 1.6 – 0.29
c) 5.8 – 3.2 · (1.6 – 0.29)
d) 5.8 – (3.2 · 1.6 – 0.29)
9 In your notebook, complete the operations by finding the decimal number that goes in each box.
a) · 4.8 = 9 b) 0.2 · = 0.002
c) 7 : = 5 d) : 0.25 = 1.2
10 Calculate Julián’s average grade in each subject to two decimal places.
a) English: 8 - 6 - 7 - 7 - 6 - 7
b) Mathematics: 5.2 - 6 - 5.8 - 4.5 - 7.1 - 5.7
4 Copy and complete the table in your notebook.
11 In 2020, the life expectancy in Spain was 79.59 years for men and 82.33 years for women. If there was the same number of men as women, calculate the life expectancy for the population as a whole.
Operations using the sexagesimal system
12 Express in complex form.
a) 12 639'' b) 756.25' c) 45.15°
d) 8.42 h e) 123.45 min f) 12 746 s
UNDERSTAND
Operating with decimal numbers
5 Calculate.
a) 3.2 – 1.63 – 0.528
b) 0.85 + 1.23 – 0.638 – 0.4
c) 3.458 – (6.7 – 4.284)
d) 5.2 – (2.798 + 1.36)
6 Use a calculator and give each result rounded off to the nearest hundredth.
a) 2.63 · 0.84 b) 0.27 · 0.086
c) 62.35 : 12 d) 5.27 : 153
e) 851 f ) 13, 29
7 To multiply by 0.1 we can divide by ten, as you can see in the example.
• 80 · 0.1 = 80 : 10 = 8
Which number must we divide by to...
a) Multiply by 0.01. b) Multiply by 0.001.
13 A sleep clinic studies the sleep habits of an elderly person, which shows that they sleep between 5.3 and 5.4 hours a day. Calculate the average and express all quantities in hours and minutes.
14 PROBLEM SOLVED
a) Add → 14° 27' 54" + 16° 42'18"
14° 27' 54" + 16° 42' 18"
30° 69' 72" → 31° 10' 12" +1 +1 –60 –60
b) Subtract → 31° 10' 12" – 14° 27' 54"
–1 –1 +60 +60
31° 10' 12" → 30° 69' 72"
– 14° 27' 54" → – 14° 27' 54"
16° 42' 18"
15 Calculate.
a)37° 50' 18'' + 25° 39'
b)53° 27' 46'' + 39° 43' 32''
c)(3 h 13 min) – (1 h 52 min 28 s)
d)(4 h 16 min 24 s) – (2 h 39 min 51 s)
16 Calculate.
a)(14 min 16 s) · 8b) (26° 52' 10") · 5
c)(59° 46' 18") : 6d)(2 h 25 min 36 s) : 12
Fractions. Applying concepts
17 In a bag there are 7 black balls, 11 white and 7 red.
a)What fraction of the balls are white?
b)What fraction of the balls are black and white?
c)What fraction of the balls are not white?
18 Five out of eight pupils in a class have lunch in the school canteen.
What fraction of the class has lunch at home?
19 What fraction of an hour are...?
a)5 minutes b) 24 minutesc)360 seconds
20 Calculate mentally. a) 3 2 of 60 b) 10 1 of 90c) 4 3 of 120
21
How many grams are? a) 4 3 of a kilo b) 5 3 of a kiloc) 20 7 of a kilo
22 Copy and complete this table in your notebook.
a) 4 1 of = 10 b) 4 3 of = 15
c) 3 2 of = 20 d) 5 3 of = 9
Equivalent fractions


23 Find pairs of equivalent fractions. 55
25 These two pieces of fabric are the same size:
Which of the two has a larger blue part? Explain the transformation shown in the following diagrams to answer the question:
26 Reduce to a common denominator.
a) , 6 5 9 1 b) 1, 12 3 , 8 5
c) ,, 3 2 2 1 7 1 d) ,, 9 4 33 17 99 52
27 Calculate the value of x in each case.
a) x 22 6 15 = b) x 49 21 35 =
c) x 13 99 11 = d) x 78 169 91 =
28 Write:
a)A fraction equivalent to 4/10 which has 6 as the numerator.
b)An equivalent fraction to 15/45 which has 12 as the denominator.
c)An equivalent fraction to 35/45 which has 91 as the numerator.
Fractions and decimal numbers
29 Express in decimal form:
a) 2 7 b) 50 27 c) 125 13
d) 6 7 e) 9 4 f ) 11 5
30 Convert into fractional form. a)1.1 b)0.13c)0.008
d)0. 8 ! e)1. 8 ! f ) 0.2 8 !
g)0. 24 #
31 Express in hours as a decimal number and a fraction.
a)48 minb)66 minc)6 120 s
32 Copy and complete the table in your notebook.
2. 7 ! 5. 29 # 4.6 51 #
33 Using a calculator, round off to the nearest hundredths.
a) 8.73 : 1.7 – 3.42 : 2.1
b) (8.73 : 1.7 – 3.42) : 2.1
34 Amaya weighs 54 kg and 400 g. Ana weighs 54.5 kg. Abel weighs more than Amaya, but less than Ana.
a) What can you say about the error in estimating Abel’s weight at 54.5 kilos?
b) What if you estimate his weight at 54 kilos and 450 grams?
35 Continue each sequence with three more terms.
a) 5 - 1 - 0.2 - 0.04 - …
b) 0.24 - 1.2 - 6 - 30 - …
36 Copy and complete this magic square in your notebook.
The sum of the numbers in each row, column and diagonal must be the same.
37 Calculate with pen and paper using the algorithm. Then, check your answer with a calculator
a) , 524 b) 12 c) 73, 96
38 True or false?
a) The product of a decimal number multiplied by an integer is always a decimal.

b) Dividing two decimal numbers never gives an integer result.

c) The square root of a decimal number is always less than the number.
d) The square root of a decimal number is never a terminating decimal.
39 To divide by 0.2 we can multiply by ten and divide by two. Check the answer.
• 8 : 0.2 = 40 ↔ 8 · 10 = 80 → 80 : 2 = 40 Calculate mentally.
a) 6 : 0.2 b) 15 : 0.2 c) 45 : 0.2
d) 9 : 0.3 e) 12 : 0.3 f ) 33 : 0.3
g) 6 : 0.6 h) 18 : 0.6 i ) 45 : 0.6

40 How many minutes are there in..?
a) 6 5 of an hour b) 12 3 of an hour c) 5 4 of an hour
41 Copy and complete with irreducible fractions.
42 Copy this table and complete the empty boxes following the logic of the data shown.
43 Studies show that a person sleeps some 250 000 hours in their lifetime, around 5 000 hours of which are in their first year.

a) Take the hours of sleep during their lifetime as the unit and express the portion of sleep during the first year in decimal and fractional form.
b) Represent this on a number line.

Can you use this one?

44 Each of the 30 students in a class plays one of the following sports. Look at the graph:

Football Basketball
Volleyball
Athletics
Swimming
Dance
Which fraction of the class…
a) … play football?
b) … play basketball?
c) … do not play basketball?
d) … do not play football or basketball?
45 To produce 3 500 doses of a certain medicine, we need 1.96 kg of the active ingredient.
How many grams of this ingredient is contained in each dose?
46 How much do two kilos and eight hundred grams of apples cost at €1.65 a kilo?
47 How much will I pay if I buy 1.083 kg of salmon at €9.75/kg?
Take care when rounding off.
48 A watermelon that weighs 2 kilos and 625 grams costs €4.20. What is the price per kilo?
49 Rosa buys three quarters of a kilo of cherries at €2.80/kg and 2.25 kg of apples at €1.40/kg.
How much will she pay in total?
50 Karla bought 340 grams of ham and paid with a €10 note. She received €3.88 in change. How much is a kilo of ham?
51 A film has a duration of 1h 53 min 23 s, but with advert breaks it lasts 2 h 12 min 15 s.
What was the total duration of the advert break?
52 To celebrate a party, thirteen friends buy:
✓ 6 bottles of cola at €1.65 a bottle.
✓ 1.120 kg of ham at €27.75/kg.
✓ 5 loaves of bread at €0.85 a loaf.
✓ 350 g of peanuts at €9.60/kg.
✓ 0.8 kg of crisps at €5.80/kg.
How much should each friend pay?
53 At 18 h 45 min 13 s a radio station starts broadcasting a pre-recorded music programme with a duration of 1 h 16 min 52 s. What time will the programme finish?
54 Marcelo buys a melon that weighs two kilos and four hundred grams. If the melon is sold at €1.99/kg, which of the following amounts will he pay?
55 A spinner is divided into 27 equal sections where the needle can land.
What angle does each section cover? 56 The barrel of a telescope has rotated clockwise from its initial position (North), and it is now at an angle of 158° 53' 20". What angle would it have to rotate anticlockwise from its initial position to reach the same point?
57 A van transports 250 dozen eggs which cost €0.98 a dozen. While the van is going around a curve, a box falls off and 60 eggs get broken. How much will they have to increase the price of a dozen eggs to make the same profit?
58 A tank containing 600 litres of water is two thirds full. How long would it take to fill it using a tap with a flow rate of 2.25 litres per minute?
59 PROBLEM SOLVED
A marathon runner has covered the 42.195 km in 2 h 54 min. What was her average speed in km/h?

66
A marathon runner has covered the 42.195 km at a speed of 14.55 km/h. How long did she take to complete the race?
We solve the problems with a division:
Time (h) = Distance (km) : Speed (km/h)
42.195 : 14.55 = 2.9 h
We solve the problems with a division:
Speed (km/h) = Distance (km) : Time (h)
To make the data compatible, we have to express the time in hours:
2 h 54 min = (2 + 54 : 60) h = (2 + 0.9) h = 2.9 h
Answer: 42.195 : 2.9 = 14.55 km/h
60 A lorry makes a journey of 169.29 kilometres in 2h 42 min. What is its average speed?
61 In a city, a bus completes its route every hour and twelve minutes. How many times will it complete the route in the 12 hours it is in service?
62 A van has travelled for 4 hours and 36 minutes at an average speed of 65 kilometres per hour. What distance has it travelled?
63 A bus has taken seven hours and twelve minutes to complete the journey between Barcelona and Bilbao. What was the average speed during the journey?
If there is any information missing you must search for it.
64 A cyclist trains on a circuit that is 3.2 km long with the intention of completing 10 laps. What fraction of the total distance will he have completed after 20 minutes if he cycles at an average speed of 24 km/h?
65 A water bottling machine has taken one hour and 36 minutes to fill one thousand bottles. How many bottles will it fill during an eight-hour day?
We have to express the solution as an amount of time using the sexagesimal system. So, we calculate the integer quotient (hours), multiply the rest by 60 and continue dividing to get the minutes.
4 2 , 1 9 5 1 4 , 5 5
1 3 0 9 5 2 h 54 min × 60
7 8 5 7 0 0 5 8 2 0
Answer: 42.195 : 14.55 = 2 h 54 min
67 A goods train has travelled 187 km at 55 km/h. How long did it take to complete the journey?
68 A ship sails between two islands in one hour and 24 minutes, travelling at an average speed of 5 knots. What distance did it cover?
What does 'at a speed of 5 knots' mean?
69 An oil tanker has covered the distance between the oil rig and the port in 12 hours and three quarters, travelling at an average speed of 18 knots. What distance did it cover?
70 Investigate.
a) Which decimal number do I have to multiply a quantity by to reduce it by one quarter?
b) What about to reduce it by three quarters??
c) What about to increase it by one quarter?
71 Consider and calculate.
a) If you multiply a number n by 0.1 and then by a, the final result is n. What is the value of a ?
b) If you multiply a number n by 0.2 and then by b, the final result is n. What is the value of b ?
72 Think of examples and answer.
a) A number increases if you multiply it by a What can you say about a?
a) A number decreases if you multiply it by a.
What can you say about b ?
73 Describe the different ways in which the following problem has been solved. Can you see any errors?
A lorry travels along a motorway at 90 kilometres per hour. How long does it take to travel 300 km?
74 Scientists have detected a new planet at a distance of 4.3 parsecs from our solar system. How long would a spacecraft of the future, travelling at the speed of light, take to reach that planet?
First you need to find out what a parsec is.
75 A jeans factory manager analyses the following information:
• The water tanks in the stone wash workshop need to provide a fixed water flow of 15 litres a minute, at 85°C during the working day (6:00 h - 20:00 h).
• To increase the temperature by one degree for a cubic metre of water, they need 0.65 litres of fuel, which costs €1.08 per litre.
• During the month of March, they measured the temperature of the water supplied by the network ten times. In July, they measured it another ten times:
The lorry takes 3 h 33 min.
Solution 3
300 = 90 + 90 + 90 + 30
Solution 4
90 km/h = (90 000 : 60) m/min = 1 500 m/min
300 km = 300 000 m
300 000 m : 1 500 m/min = 200 min = = 180 min + 20 min = 3 h 20 min
The lorry takes 3 h 20 min.
Solution 5
0.33 h → 0.33 · 60 = 19.8 min = 19 min + 0.8 min
0.8 min → 0.8 · 60 = 48 s
The lorry takes 3.33 h = 3 h 19 min 48 s.
With this information, estimate the fuel savings during the month of July, compared to March, and its value in Euros.
76 PROBLEM SOLVED
What angle do both hands of a clock form at 3 h 12 min?
3 h 12 min = 3 + (12 : 60) h = 3.2 h
• The hour hand covers an angle of 360 : 12 = 30° in one hour. If we start at twelve o’clock, at 3 h 12 min the hour hand will have advanced by an angle α = 3.2 · 30° = 96°.
• In one minute, the minute hand covers an angle of 360 : 60 = 6°. In twelve minutes, the minute hand will advance by an angle of β = 12 · 6 = 72°.
• The angle formed by both hands at 3 h 12 min is: 96° – 72° = 24°
77 Calculate the angle formed by the hands of a clock at the following times:
a) 2 h 24 min b) 7 h 42 min c) 13 h 18 min
• The first person to devise a way of writing decimal numbers was the Dutch mathematician Simon Stevin in the 16th century. This method was not very successful.

• In the 17th century, after successive attempts, the Scottish mathematician Napier proposed the current form of notation. He separated the integer part from the decimal part using a point or a comma, and used zeros to give every figure the desired place value.
3 + 47 100 8 347 8 3|47 8 3.47
• In Spain, and in other European countries, the comma was adopted for writing decimal numbers.
• However, in the English-speaking world a point is used.
8.5 5 {∫∫∫∫∫°…∞}
This is why calculators and computers also use a point.
Use a calculator to check these divisions whose results are numbers with infinite decimal places:
1 : 9 = 0.111...
2 : 9 = 0.222...
3 : 9 = 0.333...
4 : 9 = 0.444...
Based on these results, 9 : 9 should be 0.99999… = 0. 9 ! .
However, we know that 9 : 9 = 1. 0.999... 5 {∫∫∫∫∫‘}
• Are these results different? Would you be able to calculate their difference?
Squares
Note how the diagonal of these four squares coincides with the side of the next square.
1 2
1 2 5 4 meant 12,54
2
8 6 meant 8,06
Help
• What is the area of each one?
• How long is each diagonal?
1 Write as words.
a) 1.07 b) 0.0023 c) 0.000234
2 Write in figures.
a) Eighteen hundredths.
b) Thirteen hundred thousandths.
c) Two hundred and thirty-five millionths.
3 Round off to the nearest hundredths.
a) 5.052 b) 0.55555 c) 0.7481
4 Calculate. a) 0.25 · 11.48 b) 23 : 4.5
c) 0.08 : 1.6 d) 10.2 : 0.034
5 Calculate.
a) 1.4 – 1.8 · 0.2 – 0.4 : 1.6
b) 2.024 – 0.3 · (7.1 – 4.02)
c) 0.5 – 2.7 : [1.2 – 0.1 · (0.25 – 1.75)]
6 Express in decimal form.





12 15
7 Express each decimal with an irreducible fraction.
8 Simplify.
9 Reduce these fractions to a common denominator.
anayaeducacion.es Solutions to these problems.
12 You have spent €5.61 on a piece of cheese which is on sale for €12.75/kg. How much does the piece of cheese you bought weigh?
13 A van makes a 76 km journey along a motorway travelling at a constant speed of 95 km/h. How long does the journey take?
14 A cyclist has covered 39 km of a timed race in one hour and 19 minutes.

What was her average speed in km/h?
15 A wholesaler buys 12 400 litres of cooking oil at €1.60 /litre to be bottled in 0.75 l bottles for a supermarket chain. She does not bottle the last tenth to avoid the sediment.
How much profit will she make if she receives €2.10 for each bottle, sells the remainder to a soap factory at €0.45 /litre and estimates the storage costs to total €2 350?
LEARNING
10 A car makes a round trip. On the way there, it uses 13/15 of the total capacity of the fuel tank. Before setting off again, it fills up with petrol, and it uses 17/20 of the tank on the journey home. In which of the two journeys has more fuel been used?
11 You get the following result when you use a calculator to find the square root of 7. 7 → {∫∫∫∫∫“Ÿ\¢∞|∞‘«}


What can you say about the following rounding errors?
a) 7 = 3 b) 7 = 2.6 c) 7 = 2.646
Look back at the content you have worked on and plan solutions to the problems that you may find. To do this, download the corresponding rubric from anayaeducacion.es, think individually and share in groups.
TEST YOUR SKILLS
Now you can do the skills self-evaluation included in anayaeducacion.es.