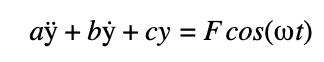
7 minute read
Resonance Mike Tsoi
Mike Tsoi (Year 13, Peel) 1 INTRODUCTION
When designing structures, one of the most important issues to consider is resonance. What is resonance? In layman’s terms, resonance describes the gradual increase in the oscillation amplitude of an object over time. When designing a bridge, engineers take resonance into account - if resonance occurs, then the bridge would sway back and forth with increasing amplitude and the oscillation would get more violent. Inevitably, the bridge would snap, as was the case for the Tacoma Narrows Bridge on November 7th 1940. Also, relatively recently in 2016, jumping fans made a football stadium resonate [1]. Fortunately, it didn’t collapse.
2 HOW DOES RESONANCE OCCUR?
When the frequency of a periodically applied force (which will now be referred to as the driving frequency) is equal to the natural frequency of the object, the force is most efficient at transferring energy to the object. The energy the object receives is converted to kinetic energy, so the oscillation amplitude increases over time.
3 THE MATHS BEHIND RESONANCE
The oscillation follows a linear second order non-homogeneous differential equation:
(1)
where a, b, c, F and ω are constants such that a > 0, b ≥ 0,c > 0,F> 0, ω > 0. ω is the driving frequency, ÿ is the acceleration at any given time, ẏ is the velocity at any given time, y is the displacement at any given time, and t is the time since the oscillation started.
We can solve (1) completely, but the solution - and hence the behaviour of the oscillation - depends on b. b is the damping coefficient. Let’s say that the system is undamped, i.e. b = 0.
Thus, (1) becomes

(2) For convenience, define
where ω 0 is the natural frequency of the oscillating object. To solve (2), we must consider two cases: when ω ≠ ω 0 and ω = ω 0
3.1 FIRST CASE (ω ≠ ω 0 )
When ω ≠ ω 0 , the auxiliary equation is
am 2 + c = 0
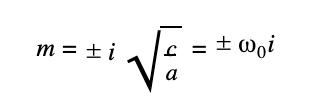
The solutions to the auxiliary equation are imaginary.
y = Asin(ω 0 t) + Bcos(ω 0 t)
where A and B are arbitrary constants.
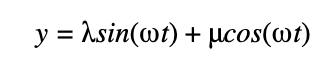
The particular integral takes the form
After solving for l and μ, we get l = 0, and
∴ The general solution to (2) is
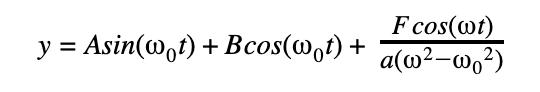
Consider y(0) = 0, then

Consider ẏ(0) = 0, then
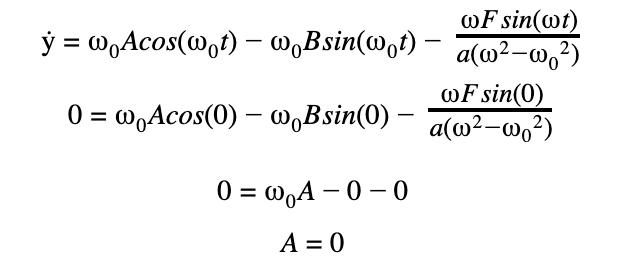
∴ The particular solution is (3)
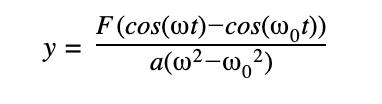
(4)
Using Desmos, by fixing a, F, and ω 0 at a value and varying ω, we can see that as ω approaches ω 0 , the amplitude (the maximum value of y) increases.
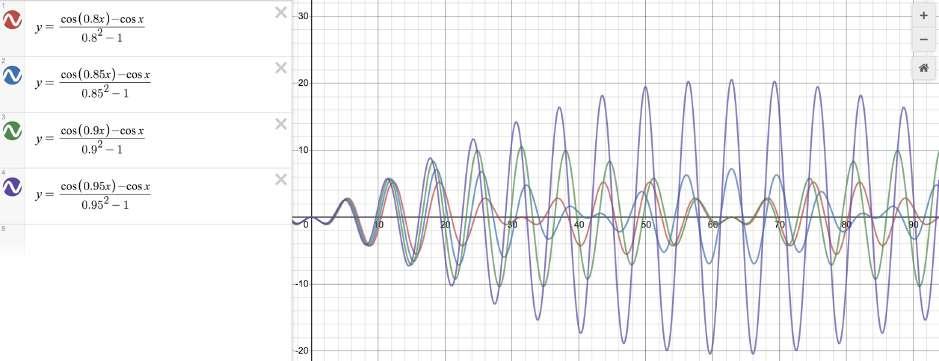
In Figure 1: 1. The red curve is where ω = 0.8 2. The blue curve is where ω = 0.85 3. The green curve is where ω = 0.9 4. The purple curve is where ω = 0.95
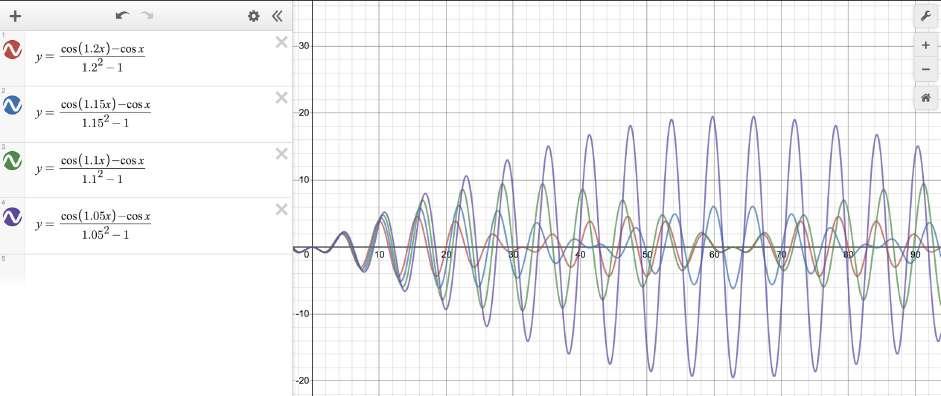
Figure 2: Graphs of the equation given by (4) for several values of ω. F = a = ω 0 = 1 In Figure 2: 1. 2. 3. 4. The red curve is where ω = 1.2 The blue curve is where ω = 1.15 The green curve is where ω = 1.1 The purple curve is where ω = 1.05
Why does the amplitude increase as ω approaches ω 0 ? Consider the denominator of the function .
As ω approaches ω 0 , the denominator becomes smaller, so the output becomes bigger.
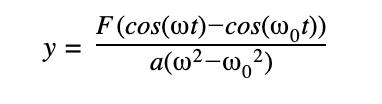
3.2 SECOND CASE (ω = ω 0 ) In (4), we couldn’t directly substitute ω = ω 0 , as the denominator would be zero, meaning the output would be undefined. This problem arises because the general solution (3) is only valid for ω ≠ ω 0 . When ω = ω 0 , we use the same method in the first case, but this time the particular integral takes the form


We see that there is a factor of t. ∴ The amplitude of the oscillation increases linearly with time. Resonance is achieved.
Figure 3: Graph of the equation given by (6) with = 1. The straight line is plotted to show the amplitude increasing linearly over time.

4 HOW TO PREVENT RESONANCE
In the introduction, we discussed the harmful effects of resonance. As we saw in the previous chapter, resonance only occurs when the driving frequency is equal to the natural frequency. Engineers can use this fact to prevent resonance. Damping a system (which means taking energy away from the oscillator, such as by friction) reduces the natural frequency and the amplitude. Reducing the natural frequency means the driving frequency will no longer be equal to the natural frequency, thus resonance is avoided. Reducing the amplitude makes the oscillation less violent, so even if the driving frequency somehow decreased and resonance occurred, the amplitude would still be significantly lower. Hence, damping allows structures to withstand the oscillation.

5.1 THE GENERAL SOLUTION
Consider the graph of y = e -x
Figure 4: A graph to show the behaviour of y = e -x over time
Either way, due to the e -lt and
e-μt term, all of the possible complementary functions tend to zero (thus resulting in the behaviour of the system being unchanging) as t tends to infinity. For this reason, the complementary function is referred to as the transient solution [2], which describes the behaviour of an oscillator from the start of oscillation to a state when the behaviour of the system is unchanging, which is called the steady state [2].

As mentioned before, the complementary function tends to zero as t tends to infinity. After a certain amount of time has passed, the complementary function becomes negligible, hence the remaining part of the general solution, the particular integral, is referred to as the steady state solution (the state when the behaviour of the system is unchanging).
5.2 THE AMPLITUDE OF THE STEADY STATE SOLUTION
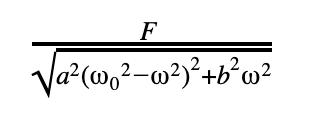
Consider (8). The amplitude of the steady state is
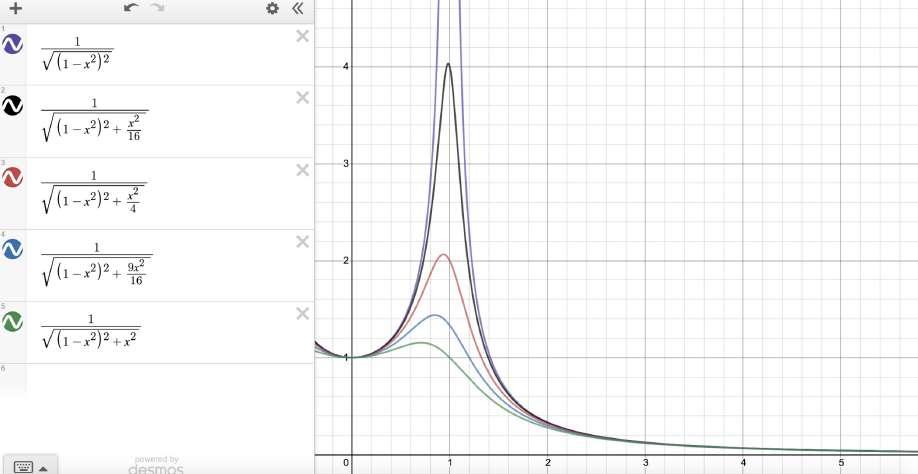
Using Desmos, by fixing a, F, and ω 0 at a value and varying b, we can see that as bincreases, the maximum amplitude decreases and the maximum amplitude occurs at a lower frequency.
Figure 5: graphs showing the amplitude of the steady state solution as a function of ωfor values of b. F = a = ω 0 = 1

6 CONCLUSION
To conclude, resonance has a very destructive effect on structures, such as bridges and stadiums. The collapse of bridges in the 20th century revealed the destructive effect of resonance, but even now engineers are sometimes careless with resonance. For example, the Millenium Bridge had to be closed 2 days after it opened because of the large number of people [4] were walking in synchrony with a frequency that matched the resonant frequency, thus causing it to sway dangerously. Engineers had taken into account the driving frequency from the wind and prevented resonance due to wind, but they hadn’t taken into account the frequency of people’s footsteps [5]. Hence, we can never be too careful with resonance.
BIBLIOGRAPHY
[1] Hunter, Matt. “Stands Shake as Thousands of German Football Fans Jump up and down to Celebrate Goal .” Daily Mail Online, Associated Newspapers, 25 May 2016, https://www.dailymail.co.uk/news/ article-3607671/Rocking-stadium-Stands-shake-thousands-German-football-fans-jump-celebrate-teams-goal.html.
[2] Yaseen, Farhan. “What Is the Difference between the Steady-State Solution and the Transient Solution? - Bayt.com Specialties.” Bayt.com, 5 June 2016, https://specialties.bayt.com/en/specialties/q/294816/ what-is-the-difference-between-the-steady-state-solution-and-the-transient-solution/.
[3] Weckesser, W. (2003). Notes on the Periodically Forced Harmonic Oscillator. Retrieved from Colgate University.
[4] “Swaying Millennium Bridge to Close after Two Days.” The Guardian, Guardian News and Media, 12 June 2000, https://www.theguardian.com/uk/2000/jun/12/2.
5] Strogatz, Steven. “Explaining Why The Millennium Bridge Wobbled.” ScienceDaily, ScienceDaily, 3 Nov. 2005, Strogatz, Steven. “Explaining Why The Millennium Bridge Wobbled.” ScienceDaily, ScienceDaily, 3 Nov. 2005, https://www.sciencedaily.com/releases/2005/11/051103080801.htm.
'SMELL AND THE MEMORIES IT BRINGS Hoikiu Wong (Year 12, Wu)











