
Besit en gepubliseer deur Optimi, deel van Optimi Central Services (Edms) Bpk. Impalalaan 7, Doringkloof, Centurion, 0157 info@optimi.co.za www.optimi.co.za
© Optimi
Afgesien van enige billike gebruik vir die doel van navorsing, kritiek of resensie soos toegelaat onder die Wet op Outeursreg, mag geen gedeelte van hierdie boek in enige vorm of op enige manier elektronies of meganies, insluitend fotokopiëring, bandopname, of enige inligtingstoring-en-herwinningstelsel, gereproduseer of versend word sonder die uitgewer se skriftelike toestemming nie.
Die uitgewer dra geen verantwoordelikheid vir die voortbestaan of akkuraatheid van URL’e van eksterne webwerwe of webwerwe van derde partye waarna daar in hierdie publikasie verwys word nie, en waarborg nie dat enige inhoud op sulke webwerwe akkuraat of toepaslik is, of sal bly nie.
Daar is gevalle waar ons nie die kopiereghouer kon kontak of opspoor nie. Die uitgewer is bereid om enige foute of weglatings so gou as moontlik reg te stel indien die saak onder ons aandag gebring word.
Reg.nr.: 2011/011959/07

Fasiliteerdersgids G07 ~ Wiskunde
INHOUDSOPGAWE
Studiebrief
1. Algemeen ................................................................................................................
2. Handleiding met aktiwiteite en oefeninge ................................................................ ii
3. Jaarpuntopdragte ....................................................................................................
4.1 Leeruitkomste.........................................................................................................
4.2 Moeilikheidsvlakke .................................................................................................
5. Jaarbeplanner ........................................................................................................
6. Meer inligting .........................................................................................................
Memorandum van handleiding
Tema 1: Getallestelsels ....................................................................................................... 4
Tema 2: Eksponente.......................................................................................................... 80
Tema 3: Algebra ................................................................................................................ 97
Tema 4: Getalpatrone en -verwantskappe .......................................................................
Tema 5.1: Meetkunde ......................................................................................................
Tema 5.2: Meetkunde: Oppervlakte, omtrek en volumes ................................................
Tema 6: Transformasiemeetkunde ..................................................................................
Tema 7: Verhouding en koers..........................................................................................
Tema 8: Finansies ...........................................................................................................
Tema 9: Statistiek ............................................................................................................
Tema 10: Waarskynlikheid...............................................................................................
Let op dat die bladsynommers van die handleiding se memorandum weer by bl. 1 begin. Gebruik die memorandum se inhoudsopgawe om die temas maklik op te spoor.
INHOUDSOPGAWE
Riglyne vir fasiliteerders
1. Algemeen
4.1
4.2
5.
Jaarbeplanner: Verkorte weergawe
1. Algemeen
1.1 Maak seker dat die volgende stukke in jou besit is:
Die handleiding
Die fasiliteerdersgids, insluitend:
Inligtingsbrief
Jaarprogram vir graad 7
Die handleiding se memorandum waarin al die antwoorde van die vrae in die handleiding uiteengesit is.
Portefeuljeboek wat die volgende bevat:
Assesseringsbeplanning
Alle toetse en take met memorandums
Sperdatums
Die eksamenvraestelle sal later aan jou gestuur word.
1.2 Hierdie brief dien as riglyn aan fasiliteerders oor:
Watter werk gedoen moet word.
Jaarbeplanning.
Die leeruitkomste soos deur die nasionale kurrikulum voorgeskryf.
Die vyf moeilikheidsvlakke en wat elkeen beteken.
Hoe om die handleiding te gebruik.
2. Handleiding met aktiwiteite en oefeninge
Die handleiding bevat verwysings en oefeninge om konsepte, begrippe, vaardighede en kennis van Wiskunde te ontwikkel. Alle verwysings na bladsynommers en die manier waarop afdelings ingedeel is, is volgens die voorgeskrewe handleiding gedoen.
Hoe om die handleiding te gebruik:
Bestudeer die teorie, voorbeelde en verduidelikings.
Doen ’n paar somme en merk dit deur na die antwoorde in die memorandum te kyk.
Enige ander bron kan vir hersiening en hulp aangewend word. Wees net bedag daarop dat KABV gevolg word en nuwe onderwerpe bemeester moet word. Sekere ou sillabuswerk is nie meer van toepassing nie en moet nie onnodige tyd opneem ten koste van dit wat belangrik is nie. Daar is geen verandering in standaard nie; inteendeel, die nuwe kurrikulum bied in meer as een opsig groter uitdagings as die ou sillabus.
Aanbevole sakrekenaar: CASIO fx-82ES (Plus)
3. Jaarpuntopdragte
Verwys na die portefeuljeboek vir volledige inligting rakende werkstukke, toetse en take.
G07 ~ Wiskunde
4.1 Leeruitkomste
Die uiteensetting van die leeruitkomste wat in graad 7, 8 en 9 vereis word.
Leeruitkoms 1 LU1 Getalle, bewerkings en verwantskappe 30%
Leeruitkoms 2 LU2 Patrone, funksies en algebra 25%
Leeruitkoms 3 LU3 Ruimte en vorm 25%
Leeruitkoms 4 LU4 Algemene meetkunde 10%
Leeruitkoms 5 LU5 Datahantering 10%
4.2 Moeilikheidsvlakke
Hierdie vlakke word in al die toetse en eksamens gehandhaaf en is ook in die handleiding as maatstaf aangedui. Die sterre by elke som dui die moeilikheidsvlak aan.
Gebruik wiskundige feite en woordeskat
Vlak
1 *
Vlak 2 **
Gebruik korrekte formules
Skat en rond waardes af
Teoretiese kennis
Voer bekende prosedures uit
Pas begrippe toe wat uit verskeie stappe bestaan
Maak afleidings uit gegewe inligting
Basiese bewerkings soos aangeleer uit voorbeelde en oefening
Komplekse berekeninge en hoëorderedenasie
Euklidiese meetkunde
Vlak 3 ***
Vlak 4 ****
Geen duidelike pad na die oplossing nie
Aandui van verbande, ooreenkomste en verskille tussen voorstellings
Vereis konseptuele en holistiese begrip
Ongesiene nieroetineprobleme wat nie noodwendig moeilik is nie
Probleme moet dikwels in verskillende dele opgelos word
Dikwels op praktiese probleme in die alledaagse lewe gerig
Hoëordebegrip en -prosesse
Vlak 5 ***** Verryking
Dikwels as versnelling in kurrikulum beskou. Word nie in toetse en eksamens ingesluit nie.
Fasiliteerdersgids
G07 ~ Wiskunde
5. Jaarbeplanner
Kwartaal 1 Getallestelsels
Eksponente
Konstruksies van meetkundige figure
Meetkunde van 2D figure
Meetkunde van reguit lyne
Kwartaal 2 Breuke
Patrone en verwantskappe
Oppervlaktes, omtrek en volume
Kwartaal 3 Algebra
Grafieke
Transformasies
Verhouding en eweredighede
Finansies
Kwartaal 4 Statistiek
Waarskynlikheid
Alle vorige werk
Jaarbeplanner graad 7: Wiskunde
Kwartaal 1 Oefening
Tema 1
Inhoud
Die oefeninge kan as leseenhede gebruik word
dae
Die getal dae dien slegs as riglyn en hoef nie slaafs nagevolg te word nie. Moet egter nie tyd mors nie. Die tweede kwartaal se sillabus is net so vol.
Kwartaal 4 Oefening
oefeninge kan as leseenhede gebruik
Hersiening
6. Meer inligting
Kontak die kontaksentrum vir meer inligting of ondersteuning. Fasiliteerdersgids
Doen die gemengde oefeninge by elke tema. Onthou dat die Novembereksamen oor die hele jaar se werk handel.
INHOUDSOPGAWE
Tema 1: Getallestelsels...................................................................................................3
Oefening 1: Waar kom getallestelsels vandaan?...........................................................3
Oefening 2: Natuurlike getalle.......................................................................................5
Oefening 3: Telgetalle..................................................................................................26
Oefening 4: Heelgetalle...............................................................................................29
Oefening 5: Breuke (rasionale getalle)........................................................................33
Oefening 6: Wortels (irrasionale getalle)......................................................................52
Oefening 7: Eienskappe van bewerkings.....................................................................58
Oefening 8: Persentasies............................................................................................63
Oefening 9: Sakrekenaarwerk.....................................................................................68
Oefening 10: Gemengde oefeninge.............................................................................72
Bibliografie...................................................................................................................77

Vereenvoudig beteken ... Fasiliteerdersgids

Vermenigvuldiging
Moeilikheidsvlakke
Hierdie vlakke word in al die toetse en eksamens gehandhaaf en is ook in die handleiding as maatstaf aangedui. Die sterre by elke som dui die moeilikheidsvlak aan.
Vlak 1 *
Vlak 2 **
Gebruik wiskundige feite en woordeskat
Gebruik korrekte formules
Skat en rond waardes af
Teoretiese kennis
Voer bekende prosedures uit
Pas begrippe toe wat uit verskeie stappe bestaan
Maak afleidings uit gegewe inligting
Basiese bewerkings soos aangeleer uit voorbeelde en oefening
Komplekse berekeninge en hoëorderedenasie
Euklidiese meetkunde
Vlak 3 ***
Geen duidelike pad na die oplossing nie
Aandui van verbande, ooreenkomste en verskille tussen voorstellings
Vereis konseptuele en holistiese begrip


Vlak 4 ****
Vlak 5 *****
Ongesiene nieroetineprobleme wat nie noodwendig moeilik is nie
Probleme moet dikwels in verskillende dele opgelos word
Dikwels op praktiese probleme in die alledaagse lewe gerig
Hoëordebegrip en -prosesse
Verryking
Dikwels as versnelling in kurrikulum beskou. Word nie in toetse en eksamens ingesluit nie.
Tema 1: Getallestelsels
Onderwerpe
Waar kom getallestelsels vandaan?
Natuurlike getalle
Telgetalle
Heelgetalle
Breuke (rasionale getalle)
Wortels (irrasionale getalle)
Eienskappe van getallestelsels. Assosiatiewe, kommutatiewe en distributiewe eienskappe
Oefening 1: Waar kom getallestelsels vandaan?
Daar is bewyse dat die Ishango-mense van die Demokratiese Republiek van die Kongo (DRK) merkies op bene gemaak het om hul beeste of familielede te tel. Die oudste been wat al gevind is om hierdie beweringe te staaf, is meer as 20 000 jaar oud.
Die getallestelsel wat ons vandag gebruik, is die Hindoe-Arabiese stelsel en is meer as 1 000 jaar gelede deur die Hindoe-Arabiese wiskundiges ontwikkel. Die Egiptiese getallestelsel het uit simbole bestaan. Kyk na die twee getallestelsels hieronder.
1.1*
Skryf die Egiptiese syfer vir 3 516 neer.
Antwoord
1.2*
Skryf die Egiptiese syfer vir 2 182 neer.
Antwoord
1.3*** Skryf die Hindoe-Arabiese syfer vir neer.
Antwoord 1 Miljoene + 2 Duisende + 2 Tiene + 3 Ene 1 002 023
1.4*
Beskou die getal 234 654 365 123 987 341 236 687.
Skryf die getal neer wat 10 000 meer is as hierdie getal.
Antwoord
234 654 356 123 987 341 246 687
1.5*** Ondersoek: Vir die pret Teken die volgende tabel oor en skryf die begrippe optel, aftrek, vermenigvuldig en deel in enige ander twee tale neer. + – ×
Afrikaans Optel Aftrek Vermenigvuldiging Deling Engels Addition Subtraction Multiplication Division Sepedi Go hlakantšha Ntšha Katišo Karolo
Oefening2: Natuurlike getalle
Natuurlikegetalle is getalle van1 tot oneindig.Die simbool hiervoor is N. As ek dit tabuleer,lyk dit so:N ={1;2;3;4;5...}.
Indien ons alle getallestelsels saam gaan voorstel,sal A die sirkel met die natuurlike getalle wees.
Onthou die krulhakies en die kommapunt tussen elke getal.
A is die natuurlike getalle. Soos die tema aangaan sal B, C, D en E aan jou verduidelik word.
Elke syfer in ’n natuurlike getal het ’n ander betekenis.
Voorbeeld
Diewoord miljard en biljoendui op dieselfde getal.Miljard word byna nooit in Amerika en Brittanje gebruik nie, maar gereeld in Kontinentale Europa.
Desimalegetallestelsel
1 miljoen
= 1000 000 = 106
Ses nulle
1 miljard
= 1000 000000 = 109
Nege nulle
1 biljoen
=1000 000000000 =1012
Twaalf nulle
1 triljoen
Agtiennulle


Duisendmiljoen (1000 000)2

= 1000000000000000 000 = 1018

(1 000 000)3 (1 000)2
2.1Voltooi die tabel deur elke keer die plekwaarde van die 7te beskryf.
Getal Beskrywing
Voorbeeld 345278 Tiene
2.1.1* 34527823
2.1.2* 2782
2.1.3** 5278254
2.1.4** 7254164
2.1.5*** 952754123
2.1.6* 12334527
2.1.7** 34527825455
2.1.8* 782
2.1.9**** 34784556723
Antwoord
Getal Beskrywing
Voorbeeld 345278 Tiene
2.1.1* 34527823 Duisende
2.1.2* 2782 Honderde
2.1.3** 5278254 Tienduisende
2.1.4** 7254164 Miljoene
2.1.5*** 952754123 Honderdduisende
2.1.6* 12 334 527 Ene
2.1.7** 34 527 825 455 Miljoene
2.1.8* 782 Honderde
2.1.9**** 34 784 556 723 Honderdmiljoene
2.2 Skryf die volgende getalle in die tabel. Beskrywing Getal
Voorbeeld 4 Honderdduisende 400 000
2.2.1* 6 Tiene
2.2.2* 12 Duisende
2.2.3** 876 Miljoene
2.2.4* 9 Ene
2.2.5** 47 Honderde
2.2.6*** 639 Tienduisende
2.2.7**** 32 456 Honderde
Antwoord Beskrywing Getal
Voorbeeld 4 Honderdduisende 400 000
2.2.1* 6 Tiene
2.2.2* 12 Duisende
2.2.3** 876 Miljoene 876 000 000
2.2.4* 9 Ene 9
2.2.5** 47 Honderde 4 700
2.2.6*** 639 Tienduisende 6 390 000
2.2.7**** 32 456 Honderde 3 245 600
2.3 Tel 10 by elkeen van die volgende getalle. Skryf die antwoord in die tabel. Getal Antwoord
2.3.1* 65 382
2.3.2* 1 234
2.3.3** 87 592
2.3.4*** 96 795
2.3.5**** 9 328 999
2.3.1* 65 382 65 392
2.3.2* 1 234 1 244
2.3.3** 87 592
2.3.4*** 96 795
2.3.5**** 9 328 999 9 329 009
2.4 Doen die bewerking met elke getal.
Getal Bewerking Antwoord
Voorbeeld 3 761 Tel 400 by. 4 161
2.4.1** 676 767 Tel 1 miljoen by.
2.4.2* 78 493 Trek 50 af.
2.4.3** 78 493 Tel 9 000 by.
2.4.4** 12 121 212 Trek 1 miljoen af.
2.4.5**** 875 462 867 Tel 4 honderdduisend by.
2.4.6** 444 444 Tel 5 000 by. Antwoord Getal Bewerking Antwoord
Voorbeeld 3 761 Tel 400 by. 4 161
2.4.1** 676 767 Tel 1 miljoen by. 1 676 767
2.4.2* 78 493 Trek 50 af. 78 443
78 493 Tel 9 000 by. 87 493
12 121 212 Trek 1 miljoen af. 11 121 212 2.4.5**** 875 462 867 Tel 4 honderdduisend by. 875 862 867 2.4.6** 444 444 Tel 5 000 by. 449 444
2.5 Breek die volgende natuurlike getalle op soos in die voorbeeld.
Getal Antwoord
Voorbeeld 1 234 567 = 1 000 000 + 200 000 + 30 000 + 4 000 + 500 + 60 + 7
2.5.1* 648
2.5.2* 33 333
2.5.3**** 54 545 454
2.5.4** 5 678
2.5.5* 6
2.5.6** 765 432 Antwoord
Getal Antwoord
Voorbeeld 123 4567 = 1 000 000 + 200 000 + 30 000 + 4 000 + 500 + 60 + 7
2.5.1* 648 = 600 + 40 + 8
2.5.2* 33 333 = 30 000 + 3 000 + 300 + 30 + 3
2.5.3**** 54 545 454 = 50 000 000 + 4 000 000 + 500 000 + 40 000 + 5 000 + 400 + 50 + 4
2.5.4** 5 678 = 5 000 + 600 + 70 + 8
2.5.5* 6 = 6
2.5.6** 765 432 = 700 000 + 60 000 + 5 000 + 400 + 30 + 2
Fasiliteerdersgids
2.6** Rangskik die volgende natuurlike getalle van klein na groot.
{2 542; 154; 2 441; 2 523; 2 509}
Antwoord
{2 542; 2 523; 2 509; 2 441; 154}
= {154; 2 441; 2 509; 2 523; 2 542}
2.7** Rangskik die volgende natuurlike getalle van groot na klein.
{592; 523; 2 600; 2 699}
Antwoord
{592; 523; 2 600; 2 699}
= {2 699; 2 600; 592; 523}
In Wiskunde gebruik ons simbole om groter as en kleiner as aan te dui.
Indien ons van links na regs kyk, kan ons die volgende sê:
Groter as
Kleiner as
Voorbeeld
234 > 233
345 < 346
2.8** Vul ’n < of ’n > tussen die getalle in.
Getal 1 < of > Getal 2
546 124
12 65
3 232 6 756
437 436 112 233 112 234
4 356 11 111
Antwoord
Getal 1 < of > Getal 2 546 > 124
12 < 65
3 232 < 6 756
437 > 436 112 233 < 112 234
4 356 < 11 111
Fasiliteerdersgids
~ Wiskunde
Wanneer jy natuurlike getalle optel en aftrek, toon genoeg stappe as bewys dat jy nie ’n sakrekenaar gebruik het om die antwoord te bepaal nie.
Voorbeelde
2 379 + 6 666
= 2 379 + 6 666
9 045
Kyk mooi waar die = geplaas word.
Leer hoe en waar om die teken te plaas.
Vereenvoudig die volgende. Toon jou stappe. Jy mag nie ’n sakrekenaar gebruik nie.
2.9* 17 + 25
Antwoord
17 + 25 = 17 + 25
42
9 370 – 6 666 = 9 379 – 6 666
2 713

2.10** Gebruik nou jou antwoord en skryf die antwoord van 17 honderd plus 25 honderd neer.
Antwoord
1 700 + 2 500 = 1 700 + 2 500
4 200
Die strepie is dieselfde as die =
2.11** Gebruik nou jou antwoord en skryf die antwoord van 17 miljoen plus 25 miljoen neer.
Antwoord
17 000 000 + 25 000 000
= 17 000 000
+ 25 000 000
42 000 000
Oppas vir al die nulle.
Fasiliteerdersgids
Wiskunde
2.12****Bepaal die som van 17 Honderdduisende en 25 Tienduisende.
Antwoord
1 700000 + 250 000 = 170 000 + 250 000 1950 000 Oppas vir al die nulle.
Berekeninge met natuurlike getalle kan slegs een van die volgende vier wees: optel aftrek vermenigvuldig deel
Voorbeeldvan bewerkings met natuurlike getalle
Kort deling

25863 ÷8
3232 res 7 = 8 ) 25 863 Lang deling
Optel
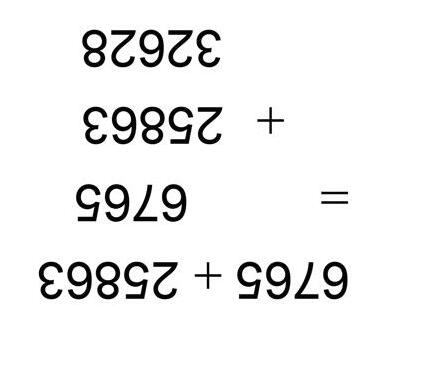

Vermenigvuldiging

Aftrek

Gebruik die voorgeskrewe metodes en doen die volgende berekeninge.Jy mag nie ’n sakrekenaargebruik nie.
2.13**2345 + 999
Antwoord
2345 + 999 =2345 +999 3 344 Skryf die getalle altyd mooi onder mekaar. Ene onder Ene Tiene onder Tiene Honderde onder Honderde, ens.
Fasiliteerdersgids
Wiskunde
2.14**2345 –999
Antwoord
2345 –999 =2345 –999 1 346
Toon genoeg stappe as bewys dat jy nie ’n sakrekenaar gebruik het nie.


2.15** 2345 ×99 Antwoord
2345 ×99 = 2345 ×99 21105 + 211050 232 155

Onthou die nul.

2.16***2345 9deur middel vanlangdeling.
Twee getalle onder mekaar sonder ’n +, –, ×of tussen-in beteken niks nie. Hier is dit ’n minus.


Antwoord 5 res 0 05 54 54 18 260 2345 9 9 2345
Fasiliteerdersgids
2.17***2345 99 deur middel vanlangdeling.
Antwoord
2.18****2345 999 deur middel vanlangdeling.
Antwoord 347 res 1998 2 2345999 999 2345
Afrikaanse sinne moet na Wiskundesinne herlei word omwoordprobleme op te los. Die volgende woorde vir bewerkings kan voorkom.Leer dit en gebruik dit reg.
Simbool Betekenis Ander Afrikaanse woorde
Vermenigvuldig Produk van Deel Kwosiënt van – Aftrek Verskil tussen + Optel Som van
Skryf die volgende Afrikaanse sinne oor in Wiskundesinne en vereenvoudig dit. Jy mag nie ’n sakrekenaar gebruik nie.
2.19**Wat is die som van 12 en 56?
Antwoord
Kan jy maklike getalle al vinnig bymekaar tel?
Indien nie, kan die getalle onder mekaar geskryf word.
Fasiliteerdersgids
G07~ Wiskunde
2.20**Bereken die produk van 12 en 56.
Antwoord 12 ×56 = 12 ×56 72 +600 672



By hierdie somme kry jy altyd ’n punt vir die Wiskundesin en punte vir die vereenvoudiging:
1 punt vir die Wiskundesin
1 punt vir 72 + 600
1 punt vir die antwoord


2.21**Wat is die kwosiënt indien 56 deur 12 gedeel word?Gee ook die res.
Antwoord
Die res word gevra.
Jy het dus nie ’n keuse nie en moet lang deling gebruik.
Ons gaan later met desimale werk. Vir eers is die antwoord en die resalbeinatuurlike getalle.
2.22***’nDrukkery druk 1 436 boeke per dag.
Hoeveel boeke het hulle in Julie 2013 gedruk as hulle nie naweke gewerk het nie?

Antwoord
Daar was23werksdae in Julie 2013. 1436 boeke per dag 1436×23virdie maand = 1436 ×23 4308 + 28720 33 028


Fasiliteerdersgids
2.23**** ’n Seiljag vaar 275 km in dieselfde rigting op die eerste dag, en dan elke dag 35 km verder as die vorige dag.
Hoe ver is die seiljag van die hawe aan die einde van die derde dag?
Dag 1 = 275 km Dag 2 Dag 3

Antwoord
Eerste dag = 275 km
Tweede dag 275 + 35 km = 310 km
Derde dag 275 + 35 + 35 km = 345 km
Totaal aan die einde van die derde dag = 275 + 310 + 345 = 930 km
2.24*** Juan ry 1 035 meter na ’n spesifieke winkel toe.
John ry 2 285 meter na dieselfde winkel toe.
Hoeveel verder bly John van die winkel af as Juan?
Antwoord
Juan 1 035
John 2 285
Verskil = 2 285 – 1 035 = 2 285 – 1 035 1 250 meter

Fasiliteerdersgids
2.25 Sandra moet 34 rompies vir dogters in ’n toneelstuk maak.
Sy koop 2 rolle materiaal met 44 meter materiaal op elke rol.
Elke rompie benodig 3 meter materiaal.
Jy mag nie ’n sakrekenaar gebruik nie.



2.25.1*** Toon al jou berekeninge en bepaal hoeveel materiaal sy kort.
Antwoord
34 dogters wat elk 3 meter benodig: 34 x 3 = 102 meter.
Daar is 88 meter materiaal gekoop.
2.25.2*** Daar moet telkens 3 meter materiaal aaneenlopend wees om die rompies te maak. Die materiaal kan nie gelas word nie.
Verduidelik hoeveel rolle materiaal sy moet koop en hoeveel materiaal op elke rol gaan oorbly sodat 34 stukke van 3 meter elk afgesny kan word.
Antwoord
Elke rol het 44 meter materiaal. 2 res 12 14 3 14 44 3
Elke rol gee net 14 stukke van 3 meter elk. 6 res 28 2 34 14
Om 34 stukke te kan kry, moet sy 3 rolle materiaal koop 14 stukke 2 rolle
Elke rol het 44 meter materiaal
Aantal stukke van 3 meter elk
Aantal meter wat gaan oorbly
Rol 1 14 stukke 2 meter
Rol 2 14 stukke 2 meter
Rol 3 6 stukke 26 meter
Totaal: 34 stukke
Wiskunde
Rondnatuurlike getalle af tot die naaste 10, 100 en 1 000. Voorbeeld
Vraag: Getal Tot die naaste... Antwoord Rede
1234 10 1230 4 is kleiner as 5.
1234 100 1200 34 is kleiner as 50.
1234 1000 1000 234 is kleiner as 500.
8795 10 8800 5 is halfpad na 10.
8795 100 8800 95 is meer as 50.
8795 1000 9000 795 is meer as 500.
Rond af tot 10.
(Dit beteken 10 moet daarin kan deel sonder ’n res).
Rond af tot100.
(Dit beteken 100 moet daarin kan deel sonder ’n res).
Rond af tot1000.
(Dit beteken 1000 moet daarin kan deel sonder ’n res).
Kyk na die Ene.
Indien minder as 5 rond af na onder Indien 5 of meer rond af na bo
Kyk na die Tiene en Ene(laaste 2 getalle).
Indien minder as 50,rond af na onder.
Indien 50 of meer,rond af na bo.
Kyk na die laaste 3 syfers.
Indien minder as 500,rond af na onder.
Indien 500 of meer,rond af na bo.
2.26**Rond die getalle af en voltooi die tabel.
Vraag: Getal Tot die naaste... Antwoord Rede
7766 10
7766 100
7719 1000 7371 10 890 100
1 miljoen1000
Antwoord
Vraag: Getal Tot die naaste... Antwoord Rede
7766 10 7770 6 is groter as 5.
7766 100 7800 66 is groter as 50.
7719 1000 8000 719 is meer as 500.
7371 10 7370 1 is kleiner as 5. 890 100 900 90 is meer as 50. 1 miljoen1000 1000 000Ons moet na die laaste
3 syfers kyk. Dit is nulle, daaromis ditnie nodig om te benader nie.
Fasiliteerdersgids
2.27***Benader 123456 tot die naaste 5.
Antwoord
123456 123455 tot die naaste 5.
Onthou,die getal moet deur 5 deelbaar wees. Dit sal dus 123455 of 123460 kan wees. Omdatdie 6 in 56 nader is aan 55 as aan 60,benader ons na 55.
2.28****Benader 74 tot die naaste 7.
Antwoord
Veelvoude van 7 ... 63;70;77 ...almal deelbaar deur 7.
Tussen 70 en 77 is waar die middelste een tussen 73 en 74 gaan wees. 71;72;73; 74;75;76
Benader na onder

Benader na bo

2.29***Shaun koop ’n broek vir R243 en ’n baadjie vir R679.
74 benader tot die naaste 7 sal dus 77 wees.
2.29.1*Benader elkeen tot die naaste R10en gee dan die bedrag wat gesamentlik vir die broek en baadjie betaal is.
Antwoord
R243 R240 tot die naaste R10. R679 R680 tot die naaste R10.
Gesamentlik: = 240 + 680
R920

Prys R243 Prys R679
Eers benader en dan bymekaar getel.

2.29.2**Indien Shaun die getalle eers opgetel het en dan benader het, wat soudie bedrag danwees?
Antwoord
R243 + R679
R920 R922 679 243
Tel eers bymekaar, en benader dan.
2.29.3***Wat is die verskil tussen die antwoorde van die vorige twee vrae?
Dink jy dat ’n mens altyd dieselfde antwoorde gaan kry?
Antwoord
Die antwoord is in albei gevalle dieselfde.
Dit lyk nie of daar ’n verskil in die twee metodes gaan wees nie.
Fasiliteerdersgids
Volgordevan bewerkings
Indien ’n vraag’nkombinasievan optel, aftrek, vermenigvuldigingen delingvereis, is daar ’n paar reëls wat jy moet volg om die bewerking te doen.

Onthou:+,–, en moet in ’n seker volgorde geskied.
Dié volgorde geld tot graad 12. Leer dit nou sodat jy nooit weer hieroor hoef te bekommer nie.
Volgorde van bewerkings:
1.Hakies(…)
2.Eksponente
3.“van” wat vermenigvuldig beteken
4.Vermenigvuldig en deel van linksna regs
5.Optelen aftrekvan links na regs
Vereenvoudig die volgende deur slegs eenbewerking per stap te doen.
Voorbeeld 1
Onthou,as jy klaar diehakie uitgewerk het, valdie hakieweg.
Vereenvoudig die volgende uitdrukking deur slegs een bewerking per stap te doen. 2.30*1324
Antwoord
Doen een bewerking per stap.


Dit sal jou die volgorde van bewerkings leer en ook die gebruik van die =.
Onthou, die getal voor en ná die = moet altyd dieselfde wees.


×en dra ewe veel gewig. Die een wat eerste staan, word eerste gedoen.


2.32** )8 12 (9
Antwoord 5 49 )8 12 (9
2.33**3333
Antwoord 9 3 12 393 3333
2.34** )26()23( Antwoord 20 4x5 )26(x5 )26()23(


Hakies eerste. Sodra jy die antwoord skryf, val die hakies weg.
Die opdrag is om een bewerking per reëlte doen. Hou daarby!


2.35** )22(22222
Antwoord 6 42 424 4 222 42242 4222x22 )22(22222
2.36** )15(6328
Antwoord 4 48 462 4668 463x28)15(6328
2.37** 3)13(4 10
Antwoord
2.38**0203
Antwoord 0 00 0x20 0203
2.39**(6 –2+7) +(3 –2 + 12)
Antwoord (6 –2+7) +(3 –2 + 12) =(4 +7)+(3 –2 + 12) =11+(1 + 12) =11 + 13 =24
Al die 2’s kan ’n mens verwar. Werk stelselmatig ... een bewerking per stap.
Fasiliteerdersgids
2.40***Vereenvoudig deur slegs een bewerking per stap te doen.
2x)8 (16 8)4 1612 x5(
Antwoord 2x)8 (16 8)4 1612 x5( = 2x)8 (16 168)4 (60 = 2x)8 (16 (608)4
Die lyn by deelsomme is soos twee groot hakies.
Die teller en die noemer moet afsonderlik vereenvoudig word.
Dan moet die teller met die noemer gedeel word.
Dit is maklik om met 0 te vermenigvuldig, die antwoord bly nul.
Voorbeeld (0)4 = 0en nie 4 nie 6×0 = 0 en nie 6 nie
Faktore
Dit is ’nalgemene term vir getallewat in ’ngroter getal kan deel met ’nheelgetal as antwoord.
So sal 10 ’nfaktor van 20 wees,want 10 kan in 20 deel.
Priemfaktore
’nPriemgetal het NET twee faktore, die getal 1 en die getal self. Dit beteken daar kan net 2 getalle in ’n geen formule om hulle te bepaal nie.
Die versameling priemgetalle = {2;3;5;7;11;13;17;19;...}
Die getal 1
1 is nie ’npriemgetal nie en ook nie ’nsaamgestelde getal nie.
Saamgestelde faktore
Getalle wat deur meer as 2 getalle gedeel kan word, word saamgestelde getallegenoem.
Bv. 24 is ’n saamgestelde getal,want dit kan deur 1, 2, 3, 4, 6, 8, 12 en 24 gedeel word.
Saamgestelde getalle het drie of meer faktore.
Voorbeeld
Faktore van 24 = {1;2;3;4;6;8;12;24}
={die getal 1} + {priemgetalle}+ {saamgestelde getalle}
={1} + {2;3} + {4;6;8;12;24}
4 is saamgestel uit2×2
6 is saamgesteluit 2 ×3
12 is saamgestel uit 2 ×2 ×3
24 is saamgestel uit 2×2×2×2×3
Priemgetalle wat met mekaar vermenigvuldig word, word saamgestelde faktore genoem.


Skryf elke getal as versamelings van 1, priemgetalle en saamgestelde faktore.
2.41* 12
Antwoord
Faktore van 12 = {1; 2; 3; 4; 6; 12}
= {1} + {2; 3} + {4; 6; 12}
2.42* 30
Antwoord
Faktore van 30 = {1; 2; 3; 5; 6; 10; 15; 30}
= {1} + {2; 3; 5} + {6; 10; 15; 30}
2.43** 36
Antwoord
Faktore van 36 = {1; 2; 3; 4; 6; 9; 12; 18; 36}
= {1} + {2; 3} + {4; 6; 9; 12; 18; 36}
2.44** 35
Antwoord
Faktore van 35 = {1; 5; 7; 35}
= {1} + {5; 7} + {35}
Hoe om die leertjiemetode te gebruik om priemfaktore te kry.
Voorbeeld
360
Skryf die volgende getalle as die produk van hul priemgetalle. Gebruik die leertjiemetode.
Dit beteken dieselfde as om die getalle in priemfaktore te ontbind.
Deel die getal deur die eerste priemgetal wat daarin kan deel. Gaan voort met die getal totdat dit nie meer kan indeel sonder ’n res nie. Doen nou dieselfde met die volgende priemgetal. Priemgetalle = {2; 3; 5; 7; 11; 13 ...}

Fasiliteerdersgids
2.50* 24
Antwoord
2.51** 68
Antwoord
2.52* Bepaal die grootste priemgetal wat in 39 600 kan indeel.
Grootste priemgetal is 11.
Ken eers die volgende:
Veelvoude: Dit is getalle waarin die gegewe getal kan deel.
Bv. veelvoude van 6 is {6; 12; 18; 24; 30; ...}
Faktore: Dit is getalle wat in die gegewe getal kan indeel.
Bv. faktore van 12 is {1; 2; 3; 4; 6; 12}
Voorbeeld
Faktore van 8 = {1; 2; 4; 8}
Veelvoude van 8 = {8; 16; 24; 32; ...}
Veelvoude is groot getalle. Faktore is klein getalle.
Bepaal die faktore en veelvoude van die volgende getalle.
2.53* 6
Antwoord
Faktore van 6 = {1; 2; 3; 6}
Veelvoude van 6 = {6; 12; 18; 24; ...}
2.54*12
Antwoord
Faktore van 12 = {1; 2; 3;4; 6; 12}
Veelvoude van 12 ={12;24; 36;...}
2.55*18
Antwoord
Faktore van 18 = {1; 2; 3; 6; 9;18}
Veelvoude van 18 ={18; 36; 54;...}
2.56*24
Antwoord
Faktore van 24 = {1; 2; 3; 4; 6;8;12; 24}
Veelvoude van 24 ={24;48; 72;...}
Bepaaldie GGD (grootste gemene deler) en KGV (kleinste gemene veelvoud) van twee of meer heelgetalle.
Voorbeeld
Bepaal die GGD en KGV van 6 en 8.
Faktore van 6 = {1; 2; 3; 6}
Faktore van 8 = {1; 2; 4; 8}
Gemeenskaplike faktore = {1;2}
GGD = 2
(Grootste gemene deler. Dus die grootste faktor wat in albei voorkom).
Veelvoude van 6 = {6; 12; 18; 24;...}
Veelvoude van 8 = {8; 16; 24; 32;40;...}
KGV =24
(Kleinste gemene veelvoud. Die kleinste getal waarin 6 en 8 kan deel.)
2.57**Bepaal die GGDvan 16 en 24.
Antwoord
Faktore van 16 = {1; 2; 4; 8; 16}
Faktore van 24= {1; 2; 3; 4; 6; 8; 12; 24}
GGD = 8
2.58**Bepaal die GGDvan 20 en 30.
Antwoord
Faktore van 20 = {1; 2; 4; 5; 10; 20}
Faktore van 30= {1; 2; 3; 5; 6; 10; 15; 30}
GGD = 10
2.59***Bepaal die KGV van9 en 12.
Antwoord
Veelvoude van 9 = {9;18; 27; 36; …}
Veelvoude van 12 = {12; 24; 36; 48;...}
KGV =36
Fasiliteerdersgids G07~ Wiskunde
2.60***Bepaal die KGVvan 5, 6, en 15.
Antwoord
Veelvoude van 5= {5; 10; 15; 20; 25; 30;...}
Veelvoude van 6= {6; 12; 18; 24; 30; 36;...}
Veelvoude van 15 = {15; 30; 45;...}
KGV =30
2.61***Bepaal die KGVvan7,9en 21.
Antwoord
Veelvoude van 7 = {7; 14; 21; 28; 35; 42; 49; 56; 63;70;…}
Veelvoude van 9 = {9;18; 27; 36; 45; 54; 63; 72;…}
Veelvoude van 21 = {21; 42; 63; ...}
KGV = 63
Oefening 3: Telgetalle



EDie afkorting vir die versameling telgetalle is N0
’nDeler is’nfaktor.
GGD = GGF
Telgetalle B sluit ook die natuurlike getalle in.
B = {0; 1; 2; 3; 4; 5; 6;...}
Nul word bygevoeg.

Natuurlike getalle A = {1; 2; 3; 4; 5; 6;...}

Net die nul het bygekom.

Onthou: 0 2 = 0
2 0 = ongedefinieerd

3.1**(2 + 0 –1)+(3 –0)
Antwoord
(2 + 0 –1)+(3 –0)
=(2 –1)+(3 –0)
=1+(3 –0)
=1 + 3
= 4
3.2** 22 ×0+4 –0+(10 –0)
Antwoord
×0 + 4 –0 +(10 –0) =22 ×0 + 4 –0 + 10
Onthou: Jy mag nie met 0 deel nie. Dit maak nie saak as die teller 0 is nie. Solank die noemer net nie 0 is nie.



3.5* )43( 12 )43(2 Antwoord eer ongedefini 0 14 1212 12 2 )43( 12 )43(2 ongedefinieerd ongedefinieerd


Moenie bang wees vir nul nie.

ongedefinieerd
3.9****Die temperatuur in Sutherland was Saterdag -9°C en Sondag -5°C. Wat was die verandering in temperatuur?
Antwoord
Bestudeer die temperatuur op ’ngetallelyn. -10-9-8-7-6-5-4-3-2-101
Regs is + Links is
Saterdag Sondag
Van -9 tot -5 is 4 eenhede na regs. Die verandering is positief en 4 °C.
3.10****Verondersteldie temperatuur in Sutherland was Saterdag -5°C en Sondag-9°C. Wat was die verandering in temperatuur?
Antwoord
Bestudeer die temperatuur op ’ngetallelyn. -10-9-8-7-6-5-4-3-2-101
Regs is + Links is
Sondag Saterdag
Van -5 tot -9 is 4 eenhede na links. Die verandering is negatief en -4 °C.
Oefening 4: Heelgetalle
Die simbool vir heelgetalle is ’nZ.

Heelgetalle C sluit ook die telgetalle in.

C = {... -3; -2; -1; 0; 1; 2; 3;...}
Fasiliteerdersgids
Wiskunde
Meer oor negatiewe getalle
Bestudeer die getallelyn. Wanneerons optel,beweeg ons regsop die getallelyn, en wanneer ons aftrek, beweeg ons links op die getallelyn.
Voorbeeld1: 2 –5 = -3 Begin by 2 en beweeg 5 eenhede na links.


Telgetalle B sluit ook die natuurlike getalle in.

B = {0; 1; 2; 3; 4; 5; 6;...} Nul word bygevoeg.

Natuurlike getalle A = {1; 2; 3; 4; 5; 6;...}

5 eenhede links
-4-3-2-1012345
Voorbeeld 2:-2 + 6= 4 Begin by -2 en beweeg 6 eenhede na regs.
6 eenhede regs
Heelgetalle







Positiewe heelgetalle Nul

=++ + + +

Negatiewe heelgetalle


= {1;2;3;4;5;...} {0} {-1;-2;-3;-4;-5;...}
Die minusvooraan’nheelgetal beteken dit werk soos skuld.
Telnegatiewe getalleop
Bv.-2–3
=-5
Treknegatiewe getalleaf
Bv.(-2)–(-3) =-2+3 =1
Vermenigvuldig negatiewe getalle
Bv.(-2)( -3)
=+ 6
Deelnegatiewe getalle
Bv.
-4-3-2-1012345
Voorbeeld 3:-2 –4= -6 Begin by -2 en beweeg 4 eenhede na links.
4 eenhede links


Lees dit as: Skuld 2 en skuld dan nog 3. Dit beteken jy skuld 5.
Maak skuld minder, beteken dat jy moet bytel.
Tekens moet ook vermenigvuldig word.
Tekens moet ook gedeel word.
-8-7-6-5-4-3-2-1012
Voorbeeld 4:-8 –(-4)
= -8 + 4... vermenigvuldig die twee tekens–x –= + Begin by -8 en beweeg 4 eenhede na regs. =-4
4 eenhede regs
-8-7-6-5-4-3-2 -1 012
Die getallelynmetode is slegs om te verduidelik hoe om op te tel en af te treken nie nodig om elke keer te skets nie. Indien jy sukkel met negatiewe en positiewe getalle, gebruik ’n getallelyn en maak seker dat jy die werk kan doen.
Om te vermenigvuldig,gee ook somtyds probleme.





Voorbeeld 5
50 +(-10)
= 50 –10 = 40
Voorbeeld 6 -30 +(+2)
= -30 + 2
= -28
Voorbeeld 7
40 –(-3)
= 40 + 3 = 43
Voorbeeld 8
-30 –-8
= -30 + 8
= -22
Voorbeeld 9
(-2)(-3) –-5
= 6 + 5
= 11
