How does the gardener's greenhouse work?

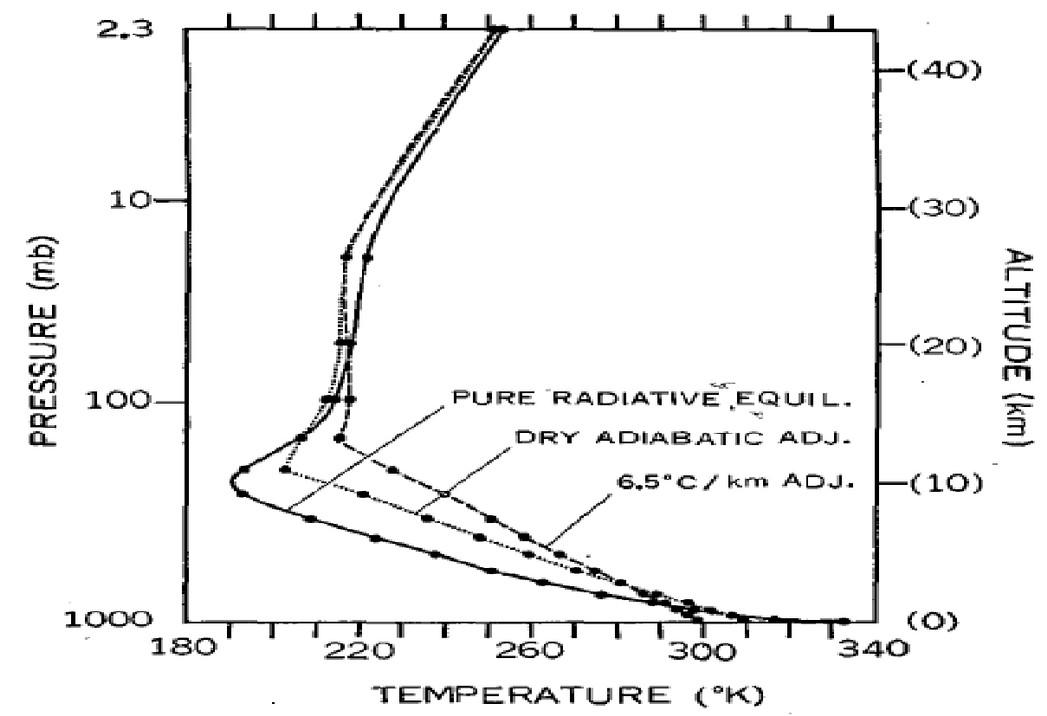
The temperature gradient is much higher than is physically possible and the temperature reaches 332.3 K at ground level,

more than 59 °C instead of the measured 15 °C. The other two curves are obtained for the convective-adiabatic model in dry air (dry adiabatic) and in humid air (6.5 °C/km with condensation taken into account). They correspond to the measured values. The

greenhouse theory, on the other hand,

contradicts the measurements.

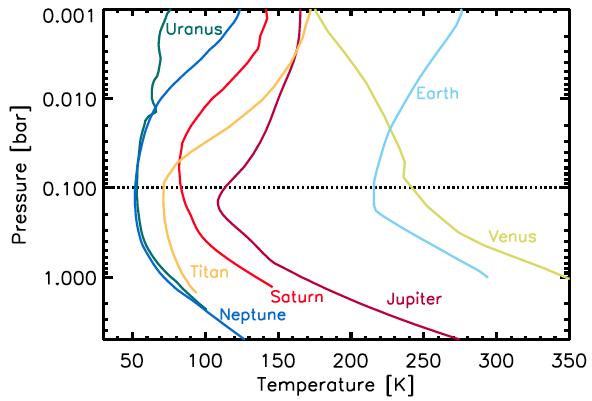
14. With the convective-adiabatic model one can calculate the temperatures on all planets

The graph from a NASA publication shows the temperature profile of all planets and moons with dense atmospheres as a function of pressure (Robinson and Catling, https://arxiv.org/pdf/1312.6859). Mars with its thin atmosphere is not one of them. Below the tropopause (that is the dashed line with a pressure of 0.1 bar) the temperature becomes higher with increasing pressure, independent of whether the atmosphere consists of nitrogen and oxygen (Earth), carbon dioxide (Venus) or hydrogen and helium (Jupiter). This relation can be calculated with the following formula, which is valid for the temperatures on all planets with dense

atmosphere:

T ̴ p(γ-1)/γ

This means: The temperature T is proportional to the pressure p to the power of an exponent that depends on the heat capacity ratio γ of the atmospheric gases. For air (nitrogen, oxygen and 1 % argon), γ has a value of 1.402.

The formula comes from the book "Theory of Heat" by James Clerk Maxwell (book version by Lord Rayleigh, https://archive.org/details/theoryofheat00maxwrich/page/n349/mode/2up/search/, page 331) and is based on the adiabatic equations of Siméon Poisson from 1822. It is used for temperature calculations in mines for more than 100 years and by NASA for all planets, also outside the solar system. With Maxwell's formula and the radiative equilibrium at the top of the clouds, one can

calculate absolute temperatures on all planets with dense atmospheres. The greenhouse theory cannot do that.

Taking the example of the calculation of the surface temperature of Venus it becomes clear (at least to those who have enjoyed a sound physical and mathematical education; to the others I apologize at this point for the many formulas). According to NASA, the intensity of solar radiation on Venus has a value of has a value of Smax = 2601 W/m² (https://nssdc.gsfc.nasa.gov/planetary/factsheet/venusfact.html). The closed cloud cover, the dense atmosphere and the high cloud speeds of more than 350 km/h ensure that the surface temperatures are very balanced. The variation is only a few percent, compared 10