KonteXt+ 2b, Lærervejledning/Web

mat e mat i k l ær e rv ej le d ning/web

2b

helle nicola je n se n · be n t lindh ardt marie t egl h us møller aline a

KonteXt+ 2b, Lærervejledning/web

© Alinea 2016

Forfattere: Helle Nicola Jensen, Bent Lindhardt, Marie Teglhus Møller

Ekstern redaktør: Bent Lindhardt

Redaktion: Susanne Schulian

Design: Jesper Frederiksen

Illustrationer: Jesper Frederiksen

Trykt hos: ScandinavianBook

1. udgave, 8. oplag 2022

ISBN: 9788723512901

ISBN overnummer: 9788723524232

Svanemærket tryksag

5041 0826

Scandinavian Print Group

Kopiering fra denne bog må kun finde sted på institutioner, der har indgået aftale med Copydan Tekst & Node.

Alinea støtter børn og unge

Alinea er en del af Egmont, der som Danmarks største mediekoncern har bragt historier til live i mere end 100 år. Egmont er en dansk fond, som hvert år uddeler 150 millioner kroner til børn og unge, der har det svært.

alinea.dk

Indhold

4Elementer i KonteXt+ 2b

6Om www.kontextplus.dk

Side til side-vejledning

9Data og chance

29Tegning og figurer

51Regn med tallene

79 Måling

KonteXt i 2. klasse består af:

•2a og 2b Elevbøger/web

•2a og 2b Tavlebøger

•2a og 2b Lærervejledninger/web inkl. digital kopimappe

•www.kontextplus.dk

Elementer i KonteXt+ 2b 2b

Elevbøgerne er engangsbøger på 72 sider. Det er elevernes fællesbog, som indeholder kernestoffet til matematikundervisningen i 2. klasse.

Elevbog a og b består hver af fire selvstændige faglige hovedemner. Hvert af disse faglige hovedemner er selvstændige matematiske forløb struktureret efter læringshjulet – se senere.

Ved køb af elevbog får eleverne adgang til forskellige materialer på www.kontextplus.dk, se næste opslag.

Elevbog 2b

Data og chance

Tegning og figurer

Regn med tallene

Måling

Tavlebog

Elevbogen udgives også som tavlebog, der er et selvstændigt materiale. Det er en pdf-udgave af bogen til brug på IWB.

Digital kopimappe

Den tidligere kopimappe vil fremover kun ligge på hjemmesiden – se næste opslag. Den er en nødvendig del af lærebogssystemet. Den digitale kopimappe 2b indeholder 106 arbejdsark.

Man får adgang til den digitale kopimappe, når man køber lærervejledningen.

1

Lærervejledningerne falder i to dele: De praktiske, faglige og pædagogiske problemstillinger, som ligger bag systemet, og en side til side-vejledning, som grundigt kommenterer hvert af de fire faglige hovedemner.

Side til side-vejledningen består af:

•Et opslag, som gennemgår det faglige grundlag for kapitlet, herunder en klar reference til de Fælles Mål.

•En grundig gennemgang af hvert af de fire værksteder.

•Familien Tal-historier til oplæsning med tilhørende klassespørgsmål.

•Forslag til klassesamtale og intro-aktiviteter, som kan spore eleverne ind på det faglige stofområde.

•Gennemgang af elevbogens opgaver og de tilhørende arbejdsark fra webdelen.

•Mange gode ideer og supplerende aktiviteter (findes på www.kontextplus.dk).

Ved køb af lærervejledning/web får læreren adgang til de forskellige materialer på www.kontextplus.dk – se næste opslag.

matematik lærervejledning/web alinea helle nicola jensen bent lindhardt marie teglhus møller

matematik lærervejledning/web alinea helle nicola jensen bent lindhardt marie teglhus møller

Om www.kontextplus.dk

På www.kontextplus.dk findes forskellige materialer til brug i undervisningen. Der er en elevadgang, der følger en elevbog, og en læreradgang, der følger en lærervejledning. Læreren har adgang til det samme som eleverne, samt EVA-ark, aktivitetssider, serviceark, facitliste m.m.

Webdelen er dynamisk og vil løbende blive suppleret med nye elementer. Eksempelvis findes følgende i webdelen, der følger bogens fire hovedemner:

Arbejdsark

1 Hvilken farve kugle er der størst chance for?

indgå i det faglige arbejde. De supplerende aktiviteter er kun tilgængelige for læreren.

Serviceark

2 Farv kuglerne, så der er størst chance for …

1 Hvor mange i alt?

2 Hvor meget koster frugten?

På www.kontextplus.dk findes også de forskellige typer af serviceark, som man får brug for i 2. klasse. Det er ark som prikpapir, udklipsark, skolepenge, talkort mm.

EVA-ark

Den tidligere kopimappe til elevbøgerne er erstattet af pdf-filer på www.kontextplus.dk. Der er arbejdsark til elevbogens to værksteder og til de to supplerende værksteder. Desuden er der supplerende opgaver og aktiviteter til elevbogen. Arbejdsarkene er placeret under de hovedemner, hvortil de skal anvendes.

Aktiviteter og spil

På www.kontextplus.dk har vi samlet alle supplerende aktiviteter og spil for 1.-3. kl. Undervejs i de enkelte kapitler giver vi forslag til, hvilke aktiviteter og spil der kan

Hvert kapitel afsluttes med en evaluering. Hertil findes en række ark, som kan bruges i forbindelse med denne evaluering, kaldet EVA-ark. Hvordan disse anvendes er

beskrevet generelt her i indledningen. Den konkrete anvendelse af de enkelte EVA-ark kan man finde oplæg til på www.kontextplus.dk. EVA-arkene er kun tilgængelige for læreren.

Observationsark og tegn på læring

Hvert kapitel har et observationsark med forslag til tegn på læring samt kommentarer til opgaverne på EVA-arket. Forventet facit vil ligeledes fremgå, og der vil være en omtale af, hvorfor opgaven er valgt til at teste elevens læring.

Samtalebillede

Der er ekstra fotos at finde, som kan anvendes til brug i klassesamtalen ved indledningen af hvert af de fire faglige hovedemner. Disse kan fx anvendes ved brug af IWB.

Værkstedsfilm

Der er til hver bog 16 værksteder, hvor de otte vises i elevbogen. Disse otte værksteder vises i otte videofilm

á 2-3 minutters varighed, som viser elever, der arbejder med værkstederne.

Forældrevideoer

Ved hvert af delforløbene i hver elevbog er der en QR-kode nederst på siden. Den viser hen til en forældrevideo, som på få minutter sætter forældrene ind i ideen bag opgaverne, og som indeholder hints til måder at hjælpe på, vanskeligheder og løsninger.

GeoGebrafiler

Eleverne kan gå direkte ind på www.kontextplus.dk og arbejde med små enkle opgaver, som leger funktioner i GeoGebra ind i undervisningen, og som understøtter det faglige indhold i elevbogens opgaver.

Filerne er enten øve-, demo- eller værkstedsfiler.

Facitlister

På www.kontextplus.dk findes desuden facitlister til elevbøgerne. Disse er kun tilgængelige for læreren.

Oversigt over læringsmål

På hjemmesiden er der en samlet oversigt over de læringsmål, som indgår i elevbog 2b. Arkene kan bruges til planlægning og dokumentation.

Er det den samme hund?

Hunden skal tegnes i de andre net, der er trukket, drejet osv. Herved fremkommer hunden på nye, besynderlige måder.

Arbejdsark 1-3

På arbejdsark 1-3 kan der arbejdes videre med denne type opgave.

Arbejdsark 1 er en mus, der skal tegnes på de forskellige net. På arbejdsark 2 og 3 kan eleverne selv tegne figurer, som så tegnes over på de andre net. Eleverne kan vælge at lave én figur på arbejdsark 2 og en anden figur på arbejdsark 3, eller de kan vælge at tegne én figur, som både overføres til nettene på arbejdsark 2 og 3. Eleverne kan også lave opgaver til hinanden.

Man kan også arbejde den anden vej, dvs. man kan tegne en figur på et af de ændrede net og så overføre figuren til det almindelige net, dvs. udgangspunktet. Kommer den ’normale’ figur til at se ud som ventet?

Man kan opfordre eleverne til at farvelægge deres figurer og lave en udstilling i klassen. Resultaterne kan blive ret flotte og sjove.

Data og chance

Data og chance

Fælles Mål

Eleven kan gennemføre statistiske undersøgelser med enkle data

Eleven kan udtrykke intuitive chancestørrelser i hverdagssituationer og enkle spil

Data

Eleven har viden om enkle metoder til at indsamle, ordne og beskrive enkle data

Eleven har viden om chancebegrebet

Vi arbejder i dette kapitel mere systematisk med diagrammer, tabeller og kurver. Det foregår med udgangspunkt i emnet hvaler, som vi erfaringsmæssigt oplever fanger mange elever. Vi har tilstræbt, at de valgte data er så troværdige som muligt, men ind imellem har vi dog måtte ”justere” tallene, så opgaverne ikke blev for svære. Der er lagt vægt på, at der præsenteres forskellige typer af tabeller og diagrammer - samt opgaver som omhandler overgange fra tabel til diagram og omvendt.

Diagrammerne omtales som søjlediagrammer som en fællesbetegnelse for markering af et antal inden for en kategori. Man vil kunne se betegnelsen pindediagrammer nogle steder, men da der i vores visuelle verden i dag sjældent udformes pinde, men snarere søjler, har vi valgt denne betegnelse. Vær opmærksom på, at førsteaksen her er en kategoriakse (som i regnearket) og ikke en tallinje. Man ville kunne bytte rundt på kategorierne, uden det har nogen betydning. Førsteaksen er således her en slags basislinje, så søjlerne står på den samme grund og dermed kan sammenlignes i højden. Andenaksen er derimod en tallinje som i koordinatsystemet.

Der indgår både aflæsning af kurver og markering af punkter ud fra tabel, som traditionelt hører til stoffet på senere klassetrin, men da det er en ikke uvæsentlig del af ”at beskrive data” og også en del af elevernes hverdag, tænker vi, at det er passende at begynde tidligt. Opgaverne er typisk aflæsningsopgaver, hvor eleverne skal afkode de enheder, som er valgt på henholdsvis før-

steaksen og andenaksen. Vi tænker ikke, at man beskriver koordinatsystemet dybere, men kun tænker i at det svarer til et ”skema”, hvor man har særlige ”kolonner og rækker”, som i koordinatsystemet bliver til punkter.

Hvor stor er chancen?

I 2. klasse indgår også stofområdet sandsynlighed - ikke som beregning, men som relativ vurdering af, om der er størst eller mindst sandsynlighed for noget - eller evt. lige stor sandsynlighed. Vi bruger i 2. klasse ordet chance som synonym for sandsynlighed. Det har den fordel, at det er en del af hverdagssproget og dermed nemmere for eleven at ”tage i sin mund”. Problemet med ordet chance er imidlertid, at det kan udlægges som en positiv hændelse modsat ordet risiko, som står for en negativ hændelse. Vi mener dog, at relationerne til hverdagen i den indledende fase er mere passende end behovet for korrekt matematisk sprog. Det kan komme på senere klassetrin.

Emnet sandsynlighed opleves traditionelt som svært stof. Her bør dog skelnes mellem beregning af sandsynligheder og så relative vurderinger af sandsynlighed. Måske er sandsynlighed i den sidste sammenhæng et af de mest anvendte matematiske stofområder vi overhovedet beskæftiger os med, idet vi dagligt vurderer chance og risiko:

•Hvad er chancen for, at vi vinder i dag?

•Hvad er risikoen for, at jeg bliver syg?

•Hvad er chancen for, at min lærer roser mig i dag?

•Gad vide om hun kommer for sent?

•Mon vi skal have min livret i aften?

Disse og mange andre lignende spørgsmål farer gennem hver af elevernes hoveder – som de vurderer på og handler efter. De oparbejder derigennem en intuition i dette felt, som er styret efter en række kontekstfyldte parametre i deres hverdag. Det kan fx være: ”Peter og Henrik er ikke på holdet. De plejer at score vores mål. Det andet hold ligger på førstepladsen og har ikke tabt endnu, men deres træner er blevet syg. Vi har måske en lille chance for at vinde.” Tanker som disse må kunne anvendes i den første indsigt i sandsynlighed.

Indledende klassesamtale

Med udgangspunkt i fotoet på side 2 kan man spørge eleverne om, de har oplevet et sådan lykkehjul. Måske har nogen vundet eller spillet på det? Var det svært?

Måske nævner eleverne ordet ”chance”. Hvor stor er chancen egentlig for at vinde en bamse i sådan en tombola?

Man kan se på, om der er nogle farver, som har større chance end andre. Bemærk fx, at farven grøn kommer oftere end farven orange. Kig også på tallene - er der lige stor chance eller forskellig chance?

Det sidste tal på lykkehjulet er 60. Se på forskellen mellem hvide og sorte felter - hvad er det for nogle tal - de lige og ulige tal. Hvis man skal spille på et tal, er der så større chance for ulige end lige eller …? Hvorfor?

Hvis en tager alle tallene fra 1-10, og en anden tager alle tallene fra 51-60, er der så lige stor chance eller forskellig chance?

Man kan evt. tegne nogle lykkehjul og spørge, hvad der størst chance for og lige stor chance for - se senere i elevbogen.

Man kan fremstille en tabel, som viser noget statistik fra en spillesituation, hvor en har spillet hundrede gange.

Lige talUlige tal

53 47

Hvis jeg skulle lave et søjlediagram, som viser dette her, hvordan skulle jeg så lave det?

Værksteder

1 Undersøg

Vælg noget, som I vil tælle. I kan fx undersøge, hvor mange der har tabt én tand, to tænder, tre tænder osv. Vis klassen, hvad I fandt ud af.

VÆRKSTED 1 Undersøg

Materialer

•Arbejdsark 4-6

Beskrivelser og kommentarer

Du skal bruge

Arbejdsark

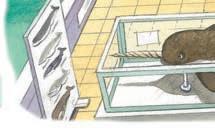
Målet med værkstedet er, at eleverne i dette værksted får erfaringer med indsamling af data og ordning af disse.

Værkstedet hedder ”Undersøg”, og kun fantasien sætter grænser for, hvad man kan undersøge. Dog er undersøgelser med ja/nej-svar som regel en for begrænset opgave.

På illustration er der vist elever, som undersøger, hvor mange tænder de har tabt. Denne illustration har vi valgt som inspiration, idet eleverne ofte er optaget af dette spørgsmål og vil kunne svare på, hvor mange tænder de har tabt, hvis de bliver spurgt. Der er selvfølgelig meget andet, der kan undersøges. Eleverne kan både være optaget af at lave en undersøgelse, hvor de spørger forskellige mennesker om noget, men der kan også laves en optælling af noget eksisterende. Hvis man endnu ikke har arbejdet med optælling af cykler, er dette værd at overveje, idet der på de fleste skoler findes et større antal cykler. Andre ting kan selvfølgelig være mere relevante at undersøge nærmere på jeres skole. Hvis man vælger at undersøge rokketænder/tabte tænder, skal eleverne rundt og spørge fx klassekammeraterne om,

hvor mange tænder de har tabt, hvor mange rokketænder de har, og hvad de ellers kan finde på mht. til tænder.

Hvis man vælger at undersøge cykler, er der mange ting, man kan undersøge: Hvilke farver har cyklerne? Hvor mange cykler har 0, 1, 2, 3 osv. gear? Hvilket mærke er cyklerne? Hvilken farve har ringklokken? Hvor mange har reflekser foran? Bagpå? På pedalerne? I hjulene?

Arbejdsarkene 4-6 anvendes til dataindsamlingen. Øverst skriver gruppen, hvad de har valgt at tælle samt gruppens medlemmer. Eleverne udvælger også, hvilke af arbejdsarkene der er mest velegnede til deres optælling.

Eleverne kan fremlægge deres undersøgelse for klassen. De kan fortælle om, hvad de har undersøgt, hvordan de har undersøgt det, og hvad de er kommet frem til. Læreren kan stille eleverne spørgsmål ud fra deres diagrammer. Dette gælder også, selvom eleverne ikke fremlægger deres arbejde. Det er vigtigt at få dialogen med gruppen af elever, så de forholder sig til det, de har undersøgt, så det ikke bare bliver en ligegyldig undersøgelse uden nogen form for overvejelser omkring observationerne.

Det kan være spørgsmål som: ”Hvad er den største værdi? Den mindste værdi? Er resultatet af undersøgelsen, som I havde forventet? Kunne I have lavet andre undersøgelser inden for emnet? Kunne I tænke jer at lave andre undersøgelser? Hvad ville I undersøge?

2 Kast tændstikæsker

En tændstikæske kan stå på tre forskellige måder.

VÆRKSTED 2 Kast tændstikæsker

Kast på skift en tændstikæske. Gør det cirka 50 gange.

Undersøg, hvor mange gange den lander på de tre måder.

Materialer

•Tændstikæske

Bestem, hvor mange point man får, når æsken lander på de tre måder.

•Evt. kuber

•Arbejdsark 7-10

Op nd et spil med en tændstikæske, hvor man får point.

Prøv også med kuber.

Beskrivelser og kommentarer

Målet med værkstedet er, at eleverne får erfaringer med sandsynligheder og anvender sandsynligheder til retfærdig pointgivning i et spil.

I dette værksted skal eleverne først gøre sig nogle erfaringer med, hvordan en tændstikæske lander, når man kaster den, og dernæst skal disse erfaringer medtages, når regler for et spil skal udformes.

Eleverne skal først kaste med en tændstikæske ca. 50 gange. Kast æsken ved at lægge den på kanten af bordet, så den rækker lidt ud over kasten, og vip så æsken op i luften med pegefingeren som vist på arbejdsark 8. På arbejdsark 7 skal eleverne registrere, hvordan æsken lander. De tre måder, den kan lande på - på fladen, på svovlet og på toppen - er vist på arket. Disse resultater skal eleverne bruge til at bestemme, hvor mange point hvert kast skal give i et spil. Eleverne skal altså bruge resultaterne til at argumentere for, hvorfor en æske, der lander på fx

toppen, skal give fx 10 point. Eleverne skal argumentere med deres undersøgelse. Et argument kunne være, at en æske, der lander på fladen, ikke skal give så mange point, fordi æsken oftest lander på denne måde. Derved inddrages vurderinger af sandsynligheder.

Når eleverne er blevet enige om pointene, skal de spille spillet på arbejdsark 8, hvor de ti gange hver kaster med en tændstikæske og får point ud fra, hvordan æsken landede. Øverst på arket noteres det, hvor mange point hver type af kast udløser. Efter spillet skal elever drøfte, om pointene var rimeligt fastsat, eller om spillet har givet anledning til ændringer i pointenes størrelser. Hvis der ændres i pointene, skal eleverne spille endnu en runde med tændstikæsken.

Herefter kan eleverne lave samme øvelse med kast med kuber og registrering af, hvordan de lander. Igen er det centrale i værkstedet, at eleverne drøfter deres resultater og med udgangspunkt i disse argumenterer for pointgivningen.

Nogle elever vil måske genkende disse spil som spillet Kastegris, hvor der skal kastes med en gris, der kan lande på tre forskellige måder. Hvis man har adgang til dette spil, er det fint at inddrage dette også.

3 Skal vi klunse?

Det er bedst, hvis I spiller 3-5 sammen. Tag tre tændstikker hver.

Hver spiller vælger, om de vil gemme nul, en, to eller tre tændstikker i hånden.

VÆRKSTED 3 Skal vi klunse?

En starter med at sige, hvor mange tændstikker han tror, der er i alt. Så er det den næstes tur, indtil alle har gættet.

Man må ikke gætte på det samme tal. Den spiller, der siger det rigtige antal, må erne en tændstik.

i deres hånd. På skift gætter eleverne, hvor mange tændstikker de tror, der er i alt i de fremviste hænder. Der må ikke gættes på det samme antal tændstikker af to eller flere spillere.

Beskrivelser og kommentarer

Vinderen af spillet er den, der først kommer af med alle sine tændstikker.

Målet med værkstedet er, at eleverne får erfaringer med sandsynlighed.

I dette værksted skal eleverne overveje, hvor stor sandsynlighed der er for et antal tændstikker, når der findes et bestemt antal tændstikker i gruppen af spillere, og jeg selv har så mange i min hånd. Man skal hele tiden have med i sine overvejelser, at der efter hver runde bliver lagt en tændstik fra.

Det optimale antal spillere til dette spil er 3 til 5 personer.

Alle begynder med at have tre tændstikker til rådighed. Hver elev vælger det antal tændstikker, som han vil gemme i hånden i første runde. Det kan være alt fra nul til tre tændstikker. Antallet af valgte tændstikker gemmes i hånden, og hånden holdes frem mod de andre spillere, som også har valgt et antal tændstikker, som de gemmer

Når alle har gættet, åbnes hænderne, og det samlede antal tændstikker tælles. Vinderen af runden er den, der gætter det rigtige antal af tændstikker eller kommer tættest på. Denne spiller må fjerne en tændstik. Den spiller, der først kommer af med alle sine tændstikker, har vundet spillet. Derefter kan man vælge at spille om andenpladsen, tredjepladsen osv.

Eleverne kan efterhånden vælge at begynde med flere end tre tændstikker.

Når eleverne har klunset et tilpas antal gange, kan man lære dem spillet Tænkeboks, som også spilles i grupper. Man skal helst være mindst tre elever. I Tænkeboks indgår også vurderinger af sandsynligheder, men i lidt mere avanceret form. Tænkeboks er beskrevet som en selvstændig aktivitet på www.kontextplus.dk.

VÆRKSTED 4 Spil Cykelløbet

Materialer

•Terninger

•Arbejdsark 11-12

Beskrivelser og kommentarer

Målet med dette værksted er, at eleverne bliver i stand til at vurdere, om et spil er retfærdigt eller ej. Hvad er retfærdigt og uretfærdigt? - ikke blot i dette spil, men også i spil, som de i fremtiden skal spille. Hvor stor er chancen for at vinde et spil som Cykelløbet?

I værkstedet skal eleverne spille Cykelløbet. Det optimale er tre spillere om en plade, idet spillerne således hver har en bane. Men der kan også spilles i hold á to eller flere spillere, hvor hvert hold så har en bane. Man kan også godt være to om et spil. Der vil i så fald være en bane i overskud.

Til spillet skal arbejdsark 11 anvendes. Hver spiller skal have en spillebrik, som stilles ved start. Inden cykelløbet går i gang, trækkes der lod om, hvilken bane de forskellige spillere kører på. Der slås på skift med en terning. Det antal øjne, terningen viser, rykkes frem på pladen. Det felt, man lander på, kan enten være blankt eller der kan stå + eller – efterfulgt af et tal. Hvis feltet, man lander på, har plus som fortegn, rykkes det antal felter frem. Hvis

fortegnet er minus, rykkes det antal felter tilbage. Det gælder om at være den, der først kører seks runder på cykelbanen.

Når eleverne har spillet det første spil, tales der indbyrdes eller med læreren om de forskellige baner. Hvilken bane er bedst og hvorfor? Er nogle baner langsommere end andre og hvorfor? Hvilken bane er længst? Hvilken bane har flest felter? Hvordan er fordelingen af plus og minus? Bed eleverne om at spille med en firesidet terning. Er banen mere retfærdig nu?

Man bør spørge eleverne om, hvordan man bedst vurderer banerne ift. hinanden. Led evt. eleverne ind på, at man kan tælle antallet af plusfelter og antallet af minusfelter og undersøge, hvor mange hop man tager i hver retning på de forskellige baner.

Lad eleverne lave nye baner på arbejdsark 12, hvor de selv udfylder felterne med plus og minus. Lad dem både prøve at lave baner, der er lige retfærdige, og baner der er uretfærdige. Hvis man forsøger at lave baner, der er lige retfærdige, kan det være en god regel, at man ikke selv skal spille på den bane, man laver. Det kan forebygge eventuelt snyd. Siden hen kan grupperne bytte baner, så eleverne prøver at spille forskellige cykelløb.

Hvilken hval er den største?

elevbogen side 4-13 samt arbejdsark 13-19

Læringsmål

Eleven kan

•lave en systematisk optælling ved en statistisk undersøgelse

•løse en problemstilling gennem en statistisk undersøgelse

•finde relevante data ud fra tekst og præsentere dem grafisk

•aflæse forskellige diagrammer og enkle grafer

Historie om Familien Tal

Talby havde fået et nyt museum. Det hed ”Hvalcentret”. Her kunne man se alt muligt om hvalernes liv lige fra de mindste marsvin til de største blåhvaler.

Det var Moster Million, der havde fået ideen til et hvalmuseum i Talby. Hun ville nemlig gøre noget for sin elskede fødeby, så der kunne komme flere turister til byen.

Hele Familien Tal var med, da ”Hvalcentret” blev åbnet for publikum. En rigtig prinsesse klippede en blå silkesnor over med en gylden saks, og der blev holdt taler, spillet musik og råbt hurra.

Det var en sjov dag, men museet var endnu sjovere, og talbørnene gik tit derhen for at se på udstillingerne.

Sådan var det også den dag, da Nysgerrige Ni og Friske Fem havde fået en opgave i skolen. De skulle fortælle deres klasse om hvaler, og nu stod de i ”Hvalcentret” for at få noget at vide, men det var ikke let at få styr på al den viden.

Der var fyldt med billeder af store og små hvaler. Under loftet hang et kæmpe dyr på størrelse med et lokomotiv.

”Den er udstoppet,” sagde Friske Fem. ”Det er kun skindet, der er fra en rigtig hval.”

”Hm,” sagde Nysgerrige Ni. ”Det ved jeg godt. Moster million har en udstoppet guldfisk på sit badeværelse. Den hedder Gulli. Det var hendes kæledyr, men en nat sprang den ud af akvariet og døde.”

De to talbørn gik lidt rundt og kiggede på udstillingen. Rundt omkring var der skilte og plakater med alle mulige oplysninger om hvaler. Der var også computere, hvor man kunne se billeder og læse om hvalernes liv.

Nysgerrige Ni og Friske Fem blev enige om at skrive nogle af oplysningerne ned på papir. Heldigvis var Nysgerrige Ni rigtig god til at læse og skrive.

”Se her,” sagde hun og pegede på en væg, hvor der hang en masse skilte og billeder. ”Her kan vi se, hvor store de forskellige hvaler kan blive. En blåhval kan blive 25 meter lang og veje 125 tons.”

Friske Fem vidste, at 1 tons var det samme som 1000 kilo, og at 1 kilo f.eks. kunne være en almindelig pose mel eller sukker. Der skulle altså 125.000 poser mel til at veje det samme som en blåhval.

På et af skiltene kunne man se hvalernes længde. Den mindste var en grindehval, og den var kun 5 meter lang.

”Vi kunne lave sådan et skilt til klassen,” sagde Nysgerrige Ni. ”På den måde er det nemt at se forskellen på hvalernes størrelse. Det er smart.”

Nysgerrige Ni læste højt for Friske Fem om spækhuggeren: ”6 til 10 meter lang tandhval,” stod der. ”Spækhuggeren lever i flokke, der overfalder andre hvaler, større fisk og sæler.”

”Det lyder som en rigtig rovfisk,” sagde Nysgerrige Ni.

Find blåhvalen i skemaet på side 4. Hvor længe kan blåhvalen være nede i vandet uden at trække vejret?

”Hvaler er ikke fisk,” sagde Friske Fem. ”Hvaler er pattedyr. De føder levende unger. Og de kan ikke trække vejret under vandet, sådan som fisk kan. Hvalerne skal op og have luft i lungerne engang imellem.”

”Ah, ha,” sagde Nysgerrige Ni. ”Det må være det, der hedder dykketid. Altså

Hvad er et søjlediagram?

Hvad bruger man et søjlediagram til?

hvor lang tid en hval kan være under vandet, før den skal op. Det har jeg lige set i et søjlediagram.”

Friske Fem var ikke helt klar over, hvad Nysgerrige Ni mente med søjlediagram.

”Jo,” forklarede Nysgerrige Ni. ”Et søjlediagram er en slags billede, hvor man kan se forskellige oplysninger.”

”Det forstår jeg ikke,” sagde Friske Fem.

”Jo, du gør da,” kom det overrasket fra Nysgerrige Ni. ”Det er ikke spor svært. En søjle er ligesom en tyk streg, og ude til venstre på tegningen er der nogle tal. Det kan f.eks. være nogle tal, der viser, hvor mange år de forskellige hvaler er om at blive voksne.”

”Det forstår jeg ikke,” sagde Friske Fem.

”Jo, du gør altså,” sagde Nysgerrige Ni. ”Hver hval har sin egen søjle i diagrammet. Hvis det tager fem år, så går søjlen op til femtallet. Hvis det tager ni år, så går søjlen op til nitallet.”

”Hvorfor kan man ikke bare skrive, hvor lang tid det tager?” spurgte Friske Fem. ”Det lyder indviklet.”

”Nej, det er smart,” sagde Nysgerrige Ni. ”Og det er meget fin matematik. Kom her, så skal jeg vise dig et søjlediagram. Man kan simpelthen ikke være et ordentligt talbarn uden at vide den slags.”

”Ok,” sagde Friske Fem og fulgte efter sin søster.

Oplæg til samtale efter oplæsningen

•Hvorfor tror I, at Nysgerrige Ni mener, at et søjlediagram er smart? Hvad kan det bruges til?

•Hvor har I set søjlediagrammer?

•Hvis vi skulle lave et søjlediagram i klassen, hvad kunne diagrammet så handle om?

Faglige og metodiske kommentarer

I dette afsnit arbejder vi med indledende statistik. Eleverne skal lære nogle få diagramtyper at kende, og de skal vide, hvordan de kan bruges, og i hvilke sammenhænge de kan være nyttige. Vi fokuserer på søjlediagrammet, som kan være en fordel at bruge, når større mængder af data skal sammenlignes. Derudover introducerer vi en simpel linjekurve, som er anvendelig, når man vil undersøge en udvikling over tid. Eleverne skal desuden få erfaringer med at orientere sig i forskellige tabeller. Vi tager udgangspunkt i data om hvaler, som mange elever har en naturlig interesse for.

For at give eleverne flere erfaringer med søjlediagrammer, og hvordan og hvornår disse med fordel kan bruges, kan man i fællesskab lave en lille undersøgelse i klassen. Man kan sige til eleverne: ”Forestil jer, at I vil undersøge, i hvilken måned (eller på hvilken årstid) der er flest, der har fødselsdag. Hvordan vil I gøre? Hvad nu, hvis I gerne vil vide, hvor mange der har fødselsdag hver måned?” Led eleverne ind på, at et søjlediagram kan give overblik fremfor bare at have data noteret på et papir. Prøv gerne at lave undersøgelsen i fællesskab i klassen ved almindelig håndsoprækning, og saml elevernes data i søjler, fx en søjle pr. årstid. På den måde kan eleverne få en oplevelse af, at data nemmere kan overskues og ikke mindst sammenlignes.

Opgaver og arbejdsark

Opgave 1-2 samt arbejdsark 13-14

Med udgangspunkt i data på side 4 udfylder eleverne skemaet i opgave 1 og tegner søjlerne i opgave 2, hvor det skal registreres, hvornår hvalerne betragtes som fuldvoksne.

På arbejdsark 13 og 14 skal eleverne ligeledes tegne søjlediagrammer med hvalers længde og vægt. Ved begge søjlediagrammer vil blåhvalen markant skille sig ud. Især når søjler for vægt skal tegnes, er søjlen for blåhvalen markant højere. Tal gerne med eleverne om, at det her er tydeligt, hvordan søjlediagrammet kan give et andet og mere helstøbt billede af data, end man umiddelbart får fra data opstillet i et skema. Derudover skal eleverne notere største- og mindsteværdi samt variationsbredde,

når de skal svare på, hvilken hval der vejer mest, og hvilken hval der vejer mindst, samt hvad forskellen er i vægt på den tungeste og den letteste vægt. De skal ikke kende fagordene, men bare gøre sig erfaringerne.

Opgave 3-4

I opgave 3 og 4 skal data bruges til at tegne søjlediagrammet for dykketid og for tiden, hvalerne er drægtige. Vær opmærksom på, at det ikke er alle elever, der kender ordet ”drægtig”. Igen er søjlediagrammet i især opgave 3 et godt eksempel på, hvordan sådan et diagram er anvendeligt, når data skal sammenlignes, idet det tydeligt ses, at kaskelothvalen skiller sig ud, hvad angår dykketid.

Hvis man ønsker at inddrage regneark i arbejdet med statistik i 2. klasse, har vi til disse opgaver, hvor der skal tegnes diagrammer, lavet et oplæg til brug af Excel. Det er at finde på www.kontextplus.dk.

Opgave 5-6

I opgave 5 kan eleverne forestille sig, at de er på hvalkiggertur. Hver hval har sin egen farve, og én helt farvet hval i registreringsskemaet er det samme som, at ti hvaler er blevet observeret. En hval, der er farvet gul, illustrerer altså, at der er observeret ti grindehvaler på turen. Eleverne skal tænke sig ud på den mest fantastiske tur på havet, hvor de har set seks forskellige hvaler i et større antal. Antallet af hvaler er blevet registreret ved hjælp af farvede hvaler som vist i opgaven. Elevernes opgave er at finde ud af, hvor mange hvaler de har set på turen.

I opgave 6 er opgaven vendt om således, at eleverne skal forestille sig, at de har set eksempelvis 100 grindehvaler. Hvis 100 grindehvaler skal registreres ved hjælp af farvede hvaler, hvor mange af de hvide hvaler skal så farves gule? Eleverne farver de hvide hvaler, så det passer med antal og farvekoder.

Opgave 7-9 samt arbejdsark 16

I historien om Familien Tal hørte vi om åbningen af det nye hvalcenter i Talby. På side 8 skal eleverne forestille sig, at Hvalcentret har talt, hvor mange der besøger Hvalcentret i løbet af en uge. De besøgende er kategoriseret i tre grupper: børn, unge og voksne. Eleverne skal i opgave 7 ved hjælp af aflæsning i diagrammet bestemme, hvor mange besøgende der var fra de tre grupper på en uge. Der er tale om en ren aflæsningsopgave, hvor udfordringen er at afkode diagrammet og at skelne de forskellige søjler fra hinanden.

I opgave 8 og 9 skal data fra side 8 anvendes, idet eleverne i opgave 8 skal tælle sammen, hvor mange besø-

gende der var på Hvalcentret hver dag, og i opgave 9 hvor mange besøgende inden for hver gruppe der var der på en uge. Der skal i opgaven primært fokuseres på afbildningen i et søjlediagram, og i mindre grad på additionen, så eleverne bør tilbydes en lommeregner som hjælpemiddel.

På arbejdsark 16 kan eleverne arbejde videre med søjlediagrammer, der viser antallet af besøgende i Hvalcentret under en ferie.

For både diagrammet i elevbogen og diagrammet på arbejdsarket gælder det, at eleverne gerne må forsøge at fortolke diagrammerne. Hvorfor er der få voksne besøgende i hverdagene og mange voksne besøgende i weekenden? En forklaring kunne være, at der i hverdagen kommer mange skoleklasser, hvor antallet af børn og unge langt overstiger antallet af voksne, mens der i weekenden kommer flere familier og dermed altså også flere voksne. Det samme gælder for diagrammet på arbejdsark 16, hvor besøgstallene for en ferie er vist.

Opgave 10-11 samt arbejdsark 17

På side 10 introduceres en ny diagramtype: linjekurvereller bare kurver, om man vil. Eleverne skal aflæse de to kurver, der viser en nyfødt blåhvals vækst i længde og vægt de første ti dage af dens liv.

Man bør drøfte denne diagramtype, inden eleverne skal arbejde med dem. Tal med eleverne om, hvad diagrammerne viser, og hvordan man aflæser. Hvor lang er en blåhval, når den bliver født? Hvor aflæses dette på kurven? Hvor lang er den efter en uge? Hvor mange centimeter vokser den hver dag? Tror I den bliver ved med at vokse på den måde? Spørgsmålene kan blive meget avancerede, men nogle elever vil blive fanget af dette: Hvis blåhvalen bliver ved med at vokse så meget, hvor lang er den så efter et år? Læreren kan fortælle, at blåhvalen så vil være mere end to kilometer lang, og det er vel nok grobund for at konkludere, at denne vækst ikke fortsætter. I skemaet på side 4 kan vi jo se, at blåhvalen cirka bliver 25 meter lang. Hvis væksten ikke fortsætter med denne stigning, hvordan kommer kurven så til at se ud? Det er avancerede spørgsmål i 2. klasse, men ikke desto mindre er det væsentligt, at eleverne allerede nu ikke kun aflæser og registrerer, men også forholder sig til data og forsøger at give en simpel fortolkning,

De samme spørgsmål kan stilles til blåhvalens vægt. Hvor mange kilogram vejer en blåhval, når den bliver født? Hvor mange kilogram vejer den efter en uge? Hvor mange kilogram tager den på et døgn? Hvis blåhvalen fortsætter denne vækst, hvor meget vejer blåhvalen efter et år? Læreren kan fortælle, at den så vejer omkring 40.000 kg, dvs. 40 tons, og at den som fuldvoksen ifølge skemaet på side 4 vejer ca. 125 tons, så den skal stadig tage flere kilogram på, men den eksplosive vækst vil aftage. Igen - det kan hurtigt blive kompliceret stof for en 2.-klasse, men snyd ikke eleverne for muligheden for at fortolke data i det omfang, det giver mening.

Data om blåhvalen er tillempet, så tallene passer godt til den faglige opgave, vi har ønsket at lave. Ved søgning på nettet kan man bl.a. læse, at en nyfødt blåhval tager 90 kg på om dagen de første syv måneder, og at den drikker mere end 600 liter mælk dagligt.

På arbejdsark 17 kan eleverne arbejde videre med aflæsning af linjekurver, hvor der er kurver for en elefant og en studs’ vægt.

Opgave 12-13 samt arbejdsark 18

På side 11 skal eleverne selv tegne linjekurver. Der er til højre i hver opgave opgivet, hvor mange grønlandshvaler og blåhvaler der var i verden på forskellige årstal. Eleverne skal markere punkter og forbinde punkterne, så der opstår en kurve. Igen er fortolkningen ligeledes central. Hvad betyder det, at kurven ser ud, som den gør? Den er faldende; hvad fortæller det os om udviklingen i antallet af hvaler i løbet af de sidste 100 år? I opgave 13 ses det, at kurven vipper opad til sidst. Hvordan kan det være? Hvordan tror I kurven ville se ud, hvis vi kunne indtegne data fra fremtiden?

På arbejdsark 18 skal eleverne arbejde videre med at indtegne kurver. To børn, William og Sofia, har fået målt deres højde hvert år på deres fødselsdag. Først indtegnes kurven, der viser Williams vækst, og derefter indtegnes Sofias kurve. Igen er fortolkningen central. Hvor meget målte de to børn, da de blev født? Hvor meget målte de, da de var 10 år? Hvor stor var forskellen på deres højde, da de var hhv. 0 og 10 år? Hvorfor er forskellen ikke den samme? Hvordan kan man på kurverne se, at det er William, der er vokset mest? Man kan også tale om, hvorvidt der er tidspunkter i livet, man vokser mere end man ellers gør, fx fra man er 0 til 1 år. Hvordan kan man se det på kurven? Man kan også omvendt spørge om, hvorfor kur-

ven stiger mest det første år. Det gør den jo netop, fordi det er den periode af ens liv, hvor man vokser mest.

Opgave 14-18

Når man arbejder med statistik, er det helt centralt, at eleverne får erfaringer med at deltage i og gennemføre undersøgelser. På side 12 og 13 lægger vi derfor op til en fælles undersøgelse i klassen. Alle elever skal finde ud af, hvor mange kuber de kan have i en hånd. De skal i opgave 14 prøve at tage en håndfuld kuber fem gange. Herefter skal de vælge det antal kuber, de med størst sandsynlighed vil have i deres hånd, hvis de prøver en sjette gang.

I opgave 15 skal hver elev registrere, hvor mange kuber hver elev fra klassen kan have i hånden. Det er et større, men nødvendigt registreringsarbejde, som bedst organiseres i fællesskab på tavlen.

I opgave 16 skal eleverne sammentælle, hvor mange der har under 35 kuber i hånden, hvor mange der har 35 kuber i hånden, 36 kuber i hånden, 37, 38 osv. I opgave 17 skal data fra opgave 16 overføres til et søjlediagram.

Til sidst skal undersøgelsen sammenlignes med en anden klasses undersøgelse; dog ikke mere end at den anden klasses resultater skal føres fra søjlediagram ind i tabel.

Grubler samt arbejdsark 19

I grubleren er vist ni forskellige huse, som kan sorteres på forskellig vis. Grubleren handler altså her om at organisere data. Ofte kan det gøre på flere forskellige måder. Eleverne skal have arbejdsark 19 udleveret, hvorpå de ni huse findes. Disse klippes ud, og eleverne undersøger, på hvor mange forskellige måder husene kan sorteres. De kan kigge på dørenes farver, tagenes farver, højden af husene, antallet af vinduer, tagets størrelse mv.

Excelfiler

På www.kontextplus.dk giver vi en helt kort introduktion til regneark (Excel) og nogle af de muligheder, et sådan program tilbyder. Der er to introduktionsvideoer og to konkrete opgaver, eleverne kan arbejde med. Det skal ses som et tilbud til de, der gerne vil i gang med at inddrage sådanne hjælpemidler. En mere omfattende introduktion til regneark er at finde i Kontext+ til 3. klasse.

Supplerende aktiviteter

Arbejdsark 15

Hvis der er elever, der har brug for at få flere erfaringer med optælling og brug af søjlediagram i forbindelse af optælling, kan der arbejdes på arbejdsark 15, hvor eleverne skal tælle, hvor mange der er af hver hval og indsætte data i et diagram. Opgaven er forholdsvis let og er tænkt til de elever, der kunne have brug for en konkret tælling og en gentagelse af konstruktion af søjlediagram.

Først til taget

På www.kontextplus.dk kan man finde spillet ”Først til taget”. Her slår eleverne med to terninger, lægger øjentallene sammen og registrerer summen i et slags søjlediagram kamufleret som et hus. Eleverne kan sagtens spille dette lille spil, som samtidig er en lille undersøgelse af, hvilken sum der oftest kommer op, når man kaster med to terninger. Derved er vi omkring sandsynlighed også, her statistisk sandsynlighed. Eleverne kan selv komme med forslag til små undersøgelser med terninger. De kan undersøge summen af tre terninger, differensen mellem to terninger, hvor mange gange man får to ens, og hvad de ellers kan finde på.