
mat e mat i k l ær e rv ej le d ning/web
helle nicola je n se n · be n t lindh ardt marie t egl h us møller aline a
2a
KonteXt+ 2a, Lærervejledning/web
© Alinea 2015
Forfattere: Helle Nicola Jensen, Bent Lindhardt, Marie Teglhus Møller
Ekstern redaktør: Bent Lindhardt
Redaktion: Susanne Schulian
Grafisk tilrettelægning: Susanne Gamsgaard og Jesper Frederiksen
Omslag: Jesper Frederiksen
Illustrationer: Jesper Frederiksen
Trykt hos: ScandinavianBook
1. udgave, 14. oplag 2022
ISBN: 978 872351 291 8
ISBN Overnummer: 978 872352 424 9
Svanemærket tryksag 5041 0826
Scandinavian Print Group
Kopiering fra denne bog må kun finde sted på institutioner, der har indgået aftale med Copydan Tekst & Node.
Alinea støtter børn og unge
Alinea er en del af Egmont, der som Danmarks største mediekoncern har bragt historier til live i mere end 100 år. Egmont er en dansk fond, som hvert år uddeler 150 millioner kroner til børn og unge, der har det svært.
alinea.dk
Indhold
4Elementer i KonteXt+ 2a
6Om www.kontextplus.dk
8Læringshjulet
10Mål og undervisning
12De matematiske kompetencer
14Anbefalinger til undervisningen
Side til side-vejledning
19Tal til 1000
41 Plus
67Spejling og figurer
87Minus
3
Elementer i KonteXt+ 2a

KonteXt i 2. klasse består af:



•2a og 2b Elevbøger/web
•2a og 2b Tavlebøger
•2a og 2b Lærervejledninger/web inkl. digital kopimappe •www.kontextplus.dk
Elevbog/web
2a
Elevbøgerne er engangsbøger på 72 sider. Det er elevernes fællesbog, som indeholder færdigheds- og vidensmål til matematikundervisningen i 2. klasse.
Elevbog a og b består hver af fire selvstændige faglige hovedemner. Hvert af disse faglige hovedemner er selvstændige matematiske forløb struktureret efter læringshjulet – se senere.
Ved køb af elevbog får eleverne adgang til forskellige materialer på www.kontextplus.dk, se næste opslag.
Elevbog 2a
Tal til 1000 Plus
Spejling og figurer Minus
Tavlebog

Elevbogen udgives også som tavlebog, der er et selvstændigt materiale. Det er en pdf-udgave af bogen til brug på IWB.
Digital kopimappe
Den tidligere kopimappe vil fremover kun ligge på hjemmesiden – se næste opslag. Den er en nødvendig del af lærebogssystemet. Den digitale kopimappe 2a indeholder 161 arbejdsark.
Man får adgang til den digitale kopimappe, når man køber lærervejledningen.
4 elementer i kontext+
matematik elevbog helle nicola je ISBN 978-872351-186-7 matematik elevbog 2a alinea indholdet er skrevet ud fra de undervisning. eleverne kommer dybden med de aktiviteter og spil, et omhyggeligt af elevpræstationer. værkstedsforløb og kontext-historier hvert har legende og eksperimentelle erfaringer frem en klassesamtale modellering, ræsonnement og på siderne. Det er små korte man kan være opmærksom på. lærer/elev/forældre adgang til eleverne ekstra opgaver til print eller til værkstedsfiler og øvefiler supplement lærervejledning og giver læreren en www.kontextplus.dk.: læring, observationsskema og misopfattelser Lærervejledning/web navn alinea arbejdsark 40 Hvad koster det cirka? ELEVBOG 2A SIDE 16-18 1 Sæt streg til nærmeste 10'er. 2 Afrund. 3 Køb for cirka 300 kr. Skriv eller tegn og regn. 38 kr. 39kr. 28 kr. 49 kr. 25 kr. 53 kr. 77 kr. 090100110120130 140 150160170180190200210 108kr. 99 kr. 91 kr. 195 kr. 111kr. 145kr. 76 kr. 205kr. 213 kr. 69kr.
Lærervejledning/web


1

2a
Lærervejledningerne falder i to dele: De praktiske, faglige og pædagogiske problemstillinger, som ligger bag systemet, og en side til side-vejledning, som grundigt kommenterer hvert af de fire faglige hovedemner.
Side til side-vejledningen består af •Et opslag, som gennemgår det faglige grundlag for kapitlet, herunder en klar reference til de forenklede Fælles Mål.
•En grundig gennemgang af hvert af de fire værksteder.
•Familien Tal-historier til oplæsning med tilhørende klassespørgsmål.
•Forslag til klassesamtale og intro-aktiviteter, som kan spore eleverne ind på det faglige stofområde.
•Gennemgang af elevbogens opgaver og de tilhørende arbejdsark fra webdelen.
•Mange gode ideer og supplerende aktiviteter (findes på www.kontextplus.dk).
Ved køb af lærervejledning/web får læreren adgang til de forskellige materialer på www.kontextplus.dk – se næste opslag.
elementer i kontext+ 5
matematik lærervejledning/web alinea helle nicola jensen ben lindhardt marie teglhus møller
matematik lærervejledning/web helle nicola je us møller
På www.kontextplus.dk findes forskellige materialer til brug i undervisningen. Der er en elevadgang, der følger en elevbog, og en læreradgang, der følger en lærervejledning. Læreren har adgang til det samme som eleverne, samt EVA-ark, aktivitetssider, serviceark, facitliste m.m.
Webdelen er dynamisk og vil løbende blive suppleret med nye elementer. Eksempelvis findes følgende i webdelen, der følger bogens fire hovedemner:
Arbejdsark
kapitler giver vi forslag til, hvilke aktiviteter og spil der kan indgå i det faglige arbejde. De supplerende aktiviteter er kun tilgængelige for læreren.
Serviceark
2 Hvor mange symmetrimønstre kan du vise?
På www.kontextplus.dk findes også de forskellige typer af serviceark, som man får brug for i 2. klasse. Det er ark som prikpapir, udklipsark, skolepenge, talkort mm.








EVA-ark
Den tidligere kopimappe til elevbøgerne er erstattet af pdf-filer på www.kontextplus.dk. Der er arbejdsark til elevbogens to værksteder og til de to supplerende værksteder. Desuden er der et stort antal ark med supplerende opgaver og aktiviteter til elevbogen. Arbejdsarkene er placeret under de hovedemner, hvortil de skal anvendes.
Aktiviteter og spil
På www.kontextplus.dk har vi samlet alle supplerende aktiviteter og spil for 1.-3. kl. Undervejs i de enkelte
Hvert kapitel afsluttes med en evaluering. Hertil findes en række ark, som kan bruges i forbindelse med denne evaluering, kaldet EVA-ark. Hvordan disse anvendes er beskrevet generelt her i indledningen. Den konkrete anvendelse af de enkelte EVA-ark kan man finde oplæg til på www.kontextplus.dk, hvor man ligeledes kan læse om
6 om www.kontextplus.dk
Prikpapir 1 cm Prikpapir 1 cm 159 Kontext 3B Kopimappe ISBN 978-87-7988-421-2 Alinea ark eva Måling 1 2 B C D 3 4 Togturen tager timer. 5 kl. kl. cm 6 Tæl rundt om. 7 Hvor langt er dette lys? 8 Tegn viserne på uret. 9 kl. 11.00 kl. 14.00 kl. 19.00 Hvad er klokken om tre timer? 10 Tegn forskellige ting, og skriv hvad de vejer. arbejdsark 43 1 Køb legetøj Legetøjs- katalog Legetøjs- katalog Legetøjs- katalogLegetøjs- katalog Legetøjs- katalog Legetøjs-Legetøjs-katalogkatalog Legetøjs- katalog Legetøjs- katalog Legetøjs- katalog Legetøjs-katalog alinea arbejdsark 47 1 Køb legetøj Du har kr. Dato: kr. kr. kr. kr. kr. kr. alt Legetøjskatalog Legetøjskatalog Du har kr. Dato: Antal Vare Pris kr. kr. kr. kr. kr. kr. alt Legetøjskatalog Legetøjskatalog arbejdsark 73 Plus med veksling ELEVBOG 2A SIDE 28-35 28 + 36 = 48 + 35 = 58 + 35 = 38 + 36 = 46 + 25 = 59 + 23 = 49 + 33 = 45 + 49 = 38 + 44 = 47 + 15 = 58 + 33 = 61 + 29 = alinea arbejdsark 106 1 Sæt en så guren bliver symmetrisk.
Prøv også
felter. Grubler ELEVBOG 2A SIDE 45
Om www.kontextplus.dk
med 16
generelle fejltyper, og hvad man i øvrigt skal være opmærksom på. EVA-arkene er kun tilgængelige for læreren.
EVA-vejledning:
Observationsark og tegn på læring
Hvert kapitel har et observationsark med forslag til tegn på læring samt kommentarer til opgaverne på EVA-arket. Forventet facit vil ligeledes fremgå, og der vil være en omtale af, hvorfor opgaven er valgt til at teste elevens læring. Der findes desuden en omtale af forskellige fejltyper og misopfattelser i besvarelserne.
Samtalebillede
Der er ekstra fotos at finde, som kan anvendes til brug i klassesamtalen ved indledningen af hvert af de fire faglige hovedemner. Disse kan fx anvendes ved brug af IWB.
Værkstedsfilm
Der er til hver bog 16 værksteder, hvor de otte vises i elevbogen. Disse otte værksteder vises i otte videofilm á 2-3 minutters varighed, som viser elever, der arbejder med værkstederne.

Forældrevideoer
video, som på få minutter sætter forældrene ind i ideen bag opgaverne, og som indeholder hints til måder at hjælpe på, vanskeligheder og løsninger.
GeoGebrafiler

Ved hvert af delforløbene i hver elevbog er der en QR-kode nederst på siden. Den viser hen til en forældre-
Eleverne kan gå direkte ind på www.kontextplus.dk og arbejde med små enkle opgaver, som leger funktioner i GeoGebra ind i undervisningen, og som understøtter det faglige indhold i elevbogens opgaver.
Filerne er enten øve-, demo- eller værkstedsfiler.
Facitlister
På www.kontextplus.dk findes desuden facitlister til elevbøgerne.
Disse er kun tilgængelige for læreren.
Oversigt over læringsmål og tegn på læring
På hjemmesiden findes der en samlet oversigt over de læringsmål, som indgår i Elevbog 2a. Til læringsmålene er knyttet mulige tegn på læring.
Arkene kan bruges til planlægning og dokumentation.
om www.kontextplus.dk 7
Læringshjulet
Førtanken, læringsmål og værksteder
Tænk efter og evaluering Opgaveløsning Matematik i en kontekst
Hver af elevbøgerne er opdelt i fire faglige emner fx tal til 1000, plus, spejling og figurer osv. Hvert af disse hovedemner er struktureret ud fra ovenstående læringshjul, som gennemløber en række progressive faser:
Fase 1: Førtanken, læringsmål og værksteder: Klassesamtale, målsættelse og forhåndserfaringer gennem værkstedsarbejde
Fase 2: Matematik i en kontekst: Kontekstforståelse gennem oplæste og diskuterede historier om Familien Tal samt opgaver, som er knyttet til


Fase 3: Opgaveløsning: Matematisk fordybelse og træning
Fase 4: Tænk efter og evaluering: Repetition og evaluering af det faglige stof fra kapitlet

Fase 1: Førtanken, læringsmål og værksteder
mål, som knytter sig til hvert af de fire hovedemner. Der ligger en samlet udgave på hjemmesiden til inspiration.

I fase 1 får eleverne lejlighed til at skabe personlige, praktiske og eksperimentelle erfaringer med matematikken. Gennem spil, undersøgelser, målinger, brug af konkrete materialer osv. får eleverne en forforståelse for det matematiske emne. Værkstederne skal således betragtes som en ”forfilm” til det kommende arbejde – ikke med forventning om, at eleverne her opnår de endelige færdigheder i stoffet, men de skal have ”snuset” til det. Dette arbejde tænkes udført i grupper á to-fire elever. Undervejs gennem det faglige hovedemne vil man som lærer kunne referere tilbage til disse praksiserfaringer. I Kontext+ er der kun præsenteret to værksteder i elevbogen. Hvis man vil supplere og bruge mere tid på dette arbejde, er der yderligere to værksteder på www.kontextplus.dk med tilhørende arbejdsark.
Til hvert værksted er der tilknyttet to elevevalueringer: En glad og sur smiley, hvor eleverne tager stilling til, om de kunne lide eller ikke lide værkstedet. De giver således udtryk for deres holdning til aktiviteten typisk med bemærkninger som ”det var sjovt/kedeligt” el.lign. En fjer og et lod, som skal symbolisere henholdsvis en svær eller nem aktivitet. Her får eleverne lejlighed til at tage stilling til grad af udfordring i aktiviteten. Eleverne vil typisk bruge bemærkninger som ”det var svært/let” el.lign.

Det anbefales, at hvert hovedemne indledes med en klassesamtale evt. med klasseaktiviteter. Med klassesamtaler tænkes på elevinvolvering gennem spørgsmål og aktiviteter, som kan skabe en orientering for eleverne mod de centrale faglige pointer, emnet vil omhandle. I lærervejledningen er der oplæg til klassesamtale til hvert kapitel. Derudover er der anvisninger på de lærings-
Til hvert hovedemne er der 2-4 delforløb, som gennemløber fase 2 og 3 med hvert sit faglige emne.








8 læringshjulet
Fase 2: Matematik i en kontekst
Værksted 3: Regn og afrund. Værksted 4: Læg penge bunker. 1 Find talkort 2 Hop på tallinjer Du skal bruge Saks Arbejdsark 5 6 7 8 9 Du skal bruge Saks Tisidede terninger Limstift Arbejdsark Tal til 1000 KG KG 15 16 17 18 19 4 Skriv, hvor mange knapper børnene Familien Tal har hver. 1 1 knap 10 knapper 100 knapper 1000 knapper Hvor mange er der? Hvor mange knapper? 2 Hvor mange knapper? 3 Skriv antallet. 3 = 30 6 2 1 = 2 = 9 = 5 = 8 = = = 50 = 700 4000 3000 200 50 4 3 2 5 4
Delforløbet indledes med en illustration og et fagligt spørgsmål, som præsenteres gennem den oplæste historie om Familien Tal. Omfanget af oplæsning svarer til ca. fem minutter. Spørgsmål til den efterfølgende dialog med eleverne findes i lærervejledningen. Eleverne har lært Familien Tal at kende i Elevbog 1a, hvor familien introduceres.
Fase 4: Evaluering







Siderne efter historien om Familien Tal og de tilhørende opgaver er et delforløb af opgaver, som giver eleverne træning og forståelse for matematikken. Den første delopgave i hver opgave er som hovedregel besvaret, så eleverne har lettere ved at afkode, hvad ideen i opgaven er. Opgaverne har ofte en tanke i sig, som udfordrer eleverne, så de ikke blot udfører rutinearbejde. Bemærk, at der er QR-koder nederst i tekstfeltet, som henviser til forældrevideoer, som på få minutter kan give et overblik over opgaver og mulige vanskeligheder. De kan også ses på www.kontextplus.dk.
Fasen afsluttes som noget nyt i Kontext+ med en grubler til de elever, som søger flere udfordringer.
På den sidste side henvises der i nederste hjørne til supplerende arbejdsark, der hentes på www.kontextplus.dk til ekstraopgaver. Dette kan foregå som individuelt arbejde eller evt. som makkerarbejde.
Udover de supplerende arbejdsark er der også forslag til supplerende aktiviteter og spil. De er samlet på www.kontextplus.dk.
Hovedemnet afsluttes med en evalueringsprocedure, som består af tre elementer:
•Den sidste side i hvert af de fire hovedemner, som i Kontext+ er omdøbt til ”Tænk efter”. I 2. klasse afslutter vi med mere kompetenceorienterede opgaver med fokus på ræsonnement, modellering og problembehandling. De beskrives særskilt under hvert kapitel.
•Særlige EVA-ark, som kan downloades fra www.kontextplus.dk. Et EVA-ark består af forside og en bagside. Forsiden indeholder spørgsmål og opgaver, som læses op af læreren. Bagsiden består af opgaver, som eleverne kan arbejde med i deres eget tempo. På www.kontextplus.dk er der beskrivelser af, hvad der kan læses ud af mulige fejl hos eleverne.
•Observationsark med udvalgte 3-4 tegn på læring til at vurdere graden af målopfyldelse hos de enkelte elever.

læringshjulet 9
Fase 3: Opgaveløsning – fordybelse og træning
7 9 8 Skriv tallet. Skriv tallet. Hvad sker der med tallet? 4783 2126 4561 1000 +1 +10+100+1000 7429 7429 4784 47944894 5894 10 Plus med 10, 100 eller 1000. 128 + 10 = 68 + 100 = 789 + 10 = 3010 + 1000 = 1387 + 1000 = 4705 + 10 = 138 11 12 13 Tæl og tegn point. Minus med 10, 100 eller 1000. Hvad sker der med tallet? 2544 4783 2126 4561 –1 –10–100–1000 238 – = 604 – 100 = 318 – 10 = 1017 – = 727 – 10 = 429 – 100 = 3719 – 10 = 1258 – 1 = 235 – 10 = 1017 – 10 = 3414 – 10 = 615 – 100 = 237 2543 25332433 1433 2659 3424450010305005 1 2 Tænk efter Hvor mange cykler? Når Noah tæller Hvor mange cykler er der cirka på skolen dag? Find en god måde at tælle dem på. biblen er der en fortælling om Noah. Noah byggede et stort skib og samlede dyrene. En dag har han talt til 18, men han har kun talt dyrenes ben. Hvilke dyr kan det være? Giv forskellige forslag.
Mål og undervisning
Læringsmål
Ved hvert af de fire hovedemner er der en indledning, som trækker nogle generelle, stofdidaktiske problemstillinger op – ikke mindst til de lærere, som ikke føler sig hjemme i aldersgruppen og stoffet. Der er altså mulighed for en faglig opdatering. Oplægget tager udgangspunkt i udvalgte målpar fra Fælles Mål og uddyber dem. Det kan derfor ses som vores forsøg på at tolke læseplanerne indholdsmæssigt og dermed orientere læreren i
Delforløb i kapitel 1Fælles Mål
Færdighedsmål
Hvor mange er der?
Hvad er rækkefølgen?
Hvordan afrunder man?
Eleven kan anvende flercifrede naturlige tal til at beskrive antal og rækkefølge
Vidensmål
Eleven har viden om naturlige tals opbygning i titalssystemet

såvel vores erfaringer med stoffet som de fagdidaktiske forskningsresultater, som synes relevante at inddrage.
Under hvert delforløb præciserer vi, hvilke læringsmål som indgår, fx som vist nederst med udgangspunkt i det første kapitel i elevbog 2a:
Læringsmål Eleven kan …
identificere tal mellem 0 og 10 000 bestemme et tal fra 0 og 10 000 ud fra forskellige repræsentationer af enere, tiere, hunderede og tusinder
bestemme rækkefølgen af tal fra 0 til 10 000
afrunde et tal til nærmeste tier foretage simple overslag ved handel
10 mål og undervisning
Vi overlader til læreren at omsætte de valgte læringsmål til elevsprog, idet det kan variere meget, hvordan det skal siges/skrives.
Vi anbefaler, at man inddrager eksempler på, hvilke problemstillinger eleverne kan håndtere, når de har været gennem forløbet. For eksempel: ”Når I er færdige, vil mange af jer kunne … ”.
Man vil på hjemmesiden www.kontextplus.dk kunne downloade disse læringsmål i samlet udgave til brug i planlægningen af undervisningen.
Undervisningsaktiviteter
Beskrivelsen af de afledte undervisningsaktiviteter foregår i beskrivelsen af fase 2 og 3. Undervejs er der omhyggelige beskrivelser af hensigten med opgaverne, og der gives gode råd til, hvordan eleverne kan hjælpes og vejledes i arbejdet med at få opgaverne løst.
Tegn på læring
Det giver for os mening at se efter tegn på læring forstået sådan, at der ses efter det, eleverne kan kommunikere, færdigheder, de kan demonstrere i praksis, eller produkter, de kan skabe.
Eksempler på samspillet mellem mål og tegn på læring kunne være:
Læringsmål: Eleverne kan identificere tal mellem
0 og 10 000.
Tegn på læring: Eleverne identificerer tal mellem
0 og 10 000.
Vi har valgt at indtænke Tegn på læring som observationspunkter, vi finder væsentlige for en forståelsesfaktor. Det er ikke det samme som, at tegnene er nok til den løbende evaluering, men indikatorer. De kan således ikke stå alene. Vi henter nogle af disse observationspunkter fra den forskningsviden, der er om elevers misopfattelser, og de faser, man ofte gennemløber ved erkendelsen af de matematiske emner og sammenhænge.
Eksempler på udvalgte Tegn på læring til førnævnte læringsmål kunne være:
Tegn på læring
Eleven …
• tæller frem og tilbage fra vilkårlige tal mellem 10 og 1000
• skriver efter anvisning tal fra 0 til 10 000
• udpeger tal fra 0 til 10 000 efter anvisning
• veksler enere til tiere, tiere til hundreder, hundreder til tusinder
• bestemmer et antal ud fra bundtning i tusinder, hundreder, tiere og enere
• optæller mønter og sedler og angiver beløbets størrelse
• placerer talkort fra 0 til 10 000 korrekt på tallinjen
• angiver tal før og efter et vilkårligt tal fra 1 til 10 000
• afrunder pengebeløb ved handel
Evaluering
Evaluering er det afsluttende element i planlægningsmodellen. Læreren skal løbende med udgangspunkt i læringsmålene for det konkrete undervisningsforløb evaluere, hvor eleverne er lige nu i forhold til læringsmålene, og hvordan de kan støttes og udfordres i at komme videre i retning af målene.
I dette arbejde indgår såvel formative som summative evalueringer.
De løbende formative evalueringer har vi koblet til lærerens observation af eleverne og undervisningen. Heri indgår elevernes matematiske begrebsdannelse – de forståelsesfaser de skal igennem, og de misopfattelser de ofte tilegner sig. Det gennemgår vi i de indledende tekster til hvert kapitel og uddyber i de observationsark, der hører til hvert kapitel.
Til den afsluttende summative evaluering kan man anvende EVA-arkene, hvor vi har trukket nogle centrale opgaver frem for at undersøge elevernes præstationsniveau. Det kan ofte være nødvendigt at have en samtale med nogle af eleverne for at sikre, at resultaterne er rimelige udtryk for, hvad eleverne er i stand til at præstere.
mål og undervisning 11
De matematiske kompetencer
Den viden og de færdigheder, eleverne skal opnå for at leve op til Fælles Mål, kan beskrives som et samspil mellem de læringsmål, der er knyttet til kompetenceområdet ”Matematiske kompetencer,” og de læringsmål, der er knyttet til stofområderne ”Tal og algebra,” ”Geometri og måling” samt ”Statistik og sandsynlighed.”
Elevernes udvikling og udøvelse af matematiske kompetencer finder sted i deres arbejde med faglige stofområder, og elevernes arbejde med stofområderne bliver meningsfuldt, når det forbindes med de processer og arbejdsmåder, der er beskrevet i de matematiske kompetencer.
I læseplanen til forenklede Fælles Mål indgår der en arbejds- og planlægningsmodel, som beskriver denne samhørighed mellem de matematiske kompetencer og det matematiske stof.
Hvordan håndterer vi det?
I Kontext+ tænker vi, at kapitlerne er udtryk for et undervisningsforløb, hvor det faglige stof fordeles gennem færdigheds- og vidensmål, som er udvalgt til klassetrinnet. Det kan ses under delforløbene i de enkelte kapitler og i oversigten over læringsmålene på hjemmesiden. At gøre det med de matematiske emner har mange års traditioner og fagdidaktisk forskning bag sig, og er derfor mere enkelt og også ofte i overensstemmelse med, hvad mange lærere tænker.
De mere kompetenceorienterede mål er derimod relativt nye og dermed uden større erfaring og tradition tilknyttet. Til forskel fra de stoflige læringsmål er kompetencelæringsmål vanskeligere at nedbryde, idet de ofte får en atomiseret og forsimplet form, som ikke er i harmoni med kompetencebegrebet. Der er således en vanskelig balance mellem at bevare en mere overordnet målbeskrivelse og så behovet for at gøre det til noget præcist og undervisningsnært.
Vi har på de yngre årgange valgt at sprede kompetencetanken ud over de enkelte kapitler, således at der almindeligvis indgår en blanding af opgaver, som i forskellige grader kan omtales som matematiske kompetenceopgaver. De kompetenceorientede mål lapper meget over hinanden og indgår i en eller anden mængde i de fleste matematiske processer. Symbolbehandling er med i de fleste arbejdsprocesser, når vi skriver tal og tegn på papir, hjælpemiddelskompetencen er med, når vi anvender it,
konkrete materialer og måleinstrumenter, problembehandling og ræsonnements-/tankegangskompetencen indgår naturligt sammen i mere åbne opgaver osv.
Opgaver orienteret mod de matematiske kompetencer

Kompetenceområdet matematiske kompetencer omfatter seks færdigheds- og vidensområder:
Problembehandling vedrører løsning og opstilling af matematiske problemer, dvs. matematiske spørgsmål, der ikke kan besvares udelukkende med rutinemetoder.
Eksempel
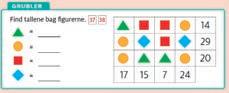
Hvert delforløb afsluttes med en grubler, som netop appellerer til problemløsning. Disse opgaver er ikkerutineprægede og lægger op til eksperimenterende virksomhed – koblet til en ræsonnementskompetence.
Modellering vedrører dels processer, hvor matematik anvendes til behandling af situationer og problemstillinger uden for matematikken, dels analyse og vurdering af matematiske modeller, som beskriver forhold i virkeligheden.
Eksempel
Hvert af de fire kapitler afsluttes med en Tænk efter-side, hvor den første opgave orienterer sig mod en modelleringsproces. Eleverne skal her vælge de kategorier, der skal tælles i og en metode at tælle på. De skal omsætte det store komplekse spørgsmål til spørgsmål i matematikkens verden.
12 de matematiske kompetencer
Ræsonnement og tankegang vedrører matematisk argumentation og karakteristika ved matematisk tankegang.

Eksempel
Den anden opgave på Tænk efter-siden er orienteret mod problembehandling- og ræsonnementskompetencen.
Der gøres meget ud af, at eleverne oplever mange repræsentationsformer, så de kan generalisere viden ud fra, at det samme princip, samme indsigt kan anvendes i nye sammenhænge. Derudover har eleverne ved gengivelse fx flere regnemetoder at vælge mellem, når de skal forme deres egen måde.
Kommunikation vedrører det at udtrykke sig med og om matematik og at sætte sig ind i og fortolke andres udtryk med og om matematik.
Eksempler

Generelt pejler vi i lærervejledningen mod dialoger med eleverne, hvor de skal svare på ”hvorfor”-spørgsmål fra læreren eller sidemakkeren.

Tankegangskompetencen er bl.a. karakteriseret ved evnen til at kunne stille et matematisk spørgsmål. Det sker løbende, men kan eksemplificeres ved klassesamtalen omkring det indledende foto.
Eleverne opfordres jævnligt til at gengive egen viden gennem løsning af forskellige opgaver. Der sættes ved flere værksteder fokus på den kommunikative del.
Repræsentation og symbolbehandling vedrører anvendelse og forståelse af repræsentationer i matematik, herunder matematisk symbolsprog.
Eksempel
Hele elevbogen er en omsættelse af sproglige, episodiske og visuelle erfaringer til matematik i form af tegning, tal og tegn.


Hjælpemidler vedrører kendskab til samt anvendelse og valg af relevante hjælpemidler i matematik.
Eksempel
Der indgår ca. 50 demo-, øve- og værkstedsfiler i 2a. Eleverne oplever digitale værktøjer som visualiserings-, konstruktions- og undersøgelsesmiddel. Dette i kombination med brugen af laborative midler typisk i værkstederne.
Vi lægger op til, at den enkelte lærer i nogle forløb gør mere ud af en kompetence frem for en anden fx ved at bruge særlig meget tid på grublerne i et af kapitlerne frem for andre.

de matematiske kompetencer 13
Anbefalinger til undervisningen
At arbejde med værksteder
Værkstederne anvendes som introduktion til de forskellige emner for, at eleverne kan få en indføring i disse på en meningsfuld måde gennem en social erfaringsdannelse. Dette sker i form af aktiviteter, der lægger op til hands on-opgaver, der indeholder undersøgende og eksperimenterende elementer. Ved at arbejde undersøgende og eksperimenterende tilgodeses flere vigtige aspekter ved læring, som ikke kan tilgodeses ved en undervisning, der traditionelt bygger på ”papir og blyant”. Praktisk matematik eller hands on-matematik kan give grundlag for en erfaringsdannelse om det, eleverne observerer og eksperimenterer.
Værkstederne giver eleverne mulighed for:
•At opleve, at matematik ikke kun er et teoretisk fag, men at faget også kan bestå af spil og lege, der kan relateres til deres hverdagserfaringer.
•At arbejde med matematikken på en anden måde end den traditionelle rutineprægede klasseundervisning.
•At udvikle individuelle og forskellige repræsentationer hos de enkelte elever for de matematiske begreber, der skal dannes.
•At kunne danne alternative repræsentationer og at kunne skifte mellem dem er en af de væsentligste kompetencer ved udviklingen af matematisk viden og kunnen.
Værkstedernes indhold er valgt således, at eleverne får mulighed for at arbejde dynamisk med begreberne, der i tillæg giver dem muligheder for at samtale i og om matematik. Lærerens observationer kan i denne arbejdsproces give ham et anderledes indblik i de forståelser, opfattelser og holdninger, den enkelte elev har i relation til matematik.
Organisationen af værkstederne
Hvert værksted i KonteXt+ er berammet til ca. 45 minutter. Der kan arbejdes med værkstederne på forskellig vis: Man kan vælge at lade hele klassen arbejde i det samme værksted. Det vil betyde, at alle elever skal have den samme instruktion, den samme forklaring. Det kan være lettere i begyndelsen at overskue værkstedsarbejdet på denne måde. I nogle værksteder skal der anvendes kon-
krete materialer, så hvis man lader alle elever arbejde i det samme værksted på en gang, skal der være flere materialer til rådighed. Man kan vælge at sætte flere værksteder i gang på samme tid. Det skaber et utroligt fagligt liv, og eleverne er tit både optagede af det, de selv laver, samt af det, der foregår i de andre grupper. Det kan kræve mere forberedelse i begyndelsen, men mindre i længden for læreren. Da meget skal ”sættes i gang” på samme tid, kræver det en arbejdsfacon, hvor eleverne accepterer, at læreren ikke kan være ”alle vegne på samme tid” – man lærer således eleverne en form for hjælp til selvhjælp. Der er desuden værksteder, der kræver mere støtte fra læreren end andre. Man kan derfor med fordel vælge at arbejde i fx to værksteder, hvor det ene værksted er mere selvkørende, hvilket frigiver tid til støtte i det andet værksted.
Ved hvert værksted i elevbogen er der som tidligere nævnt i nederste højre hjørne et felt med en glad og sur smiley, samt en vægt og en fjer, hvor eleverne tager stilling om de kunne lide at arbejde i værkstedet, og om hvor svært det var. Elevernes krydser kan man tage udgangspunkt i, når man taler med klassen om, hvordan værkstedsarbejdet er forløbet. Hvis en elev konsekvent sætter kryds over det sure ansigt, kan det også indikere, at her er der noget at tale om.
Matematik og it
Vi har i Kontext+ primært fokuseret på to centrale digitale værktøjer: regneark og dynamiske geometriprogrammer. I 2. klasse kører vi videre med GeoGebra og udvider i 2b med kendskab til regneark.
Der findes en forenklet version af GeoGebra – GeoGebraPrim – til de yngste.
Programmet også downloades til andre platforme end pc, fx iPad.
Geogebra kan downloades på www.geogebra.org. Klik på knappen download og vælg mellem:
•Webstart: Henter seneste version af programmet ned på din computer.
•Applet start: Kører programmet på Geogebras hjemme side. Fordel: der skal ikke installeres noget på computeren, og man benytter altid seneste version af
14 anbefalinger til undervisningen
programmet. Ulempe: Det virker langsommere, end hvis man har valgt Webstart og installeret programmet på sin computer, og det kræver, at man har adgang til internettet.
Der vil være adgang til GeoGebra-filerne knyttet til KonteXt+ på www.kontextplus.dk.
Der skelnes mellem tre anvendelser af programmerne
1) Demofil, som kan anvendes i klassen fx gennem brug af IWB.
2) Øvefiler, som er supplerende opgaver til elevbogen og den digitale kopimappe.
3) Værkstedsfiler, som viser programmerne som digitalt værkstøj til bl.a. undersøgelser, konstruktioner, tabellægning osv.
I 2. klasse er der primært valgt en legende og undervisningstøttende tilgang til brugen af programmet, så eleven får ”snuset” til det. Der vil indgå brug af enkle og overskuelige funktioner. Vi vil gradvist øge elevens anvendelse af programmet til at eksperimentere og konstruere med former og figurer.
Brug af lommeregner eller lignende digitale værktøjer
Lommeregneren opfattes på lige fod med alle andre hjælpemidler. Det vil gøre det muligt at håndtere svære regnesituationer på dette klassetrin, som eleverne endnu ikke kan klare med blyant og papir eller i hovedet. I sådanne situationer vil elevernes mulighed for at anvende en lommeregner ofte være mere motiverende og lærerig end en henvendelse til læreren med udsagnet: “Det kan jeg ikke finde ud af”.
Endvidere kan lommeregneren anvendes til træning og forståelse af simpel addition, subtraktion, multiplikation og division på begyndertrinnet. Lad eleverne bruge lommeregneren til dette formål fra starten af. Man kan desuden opfordre dem til at stille opgaver til hinanden og at kontrollere svarene ved hjælp af lommeregneren.
Det bør derfor være et meget tidligt mål at lære eleverne at anvende lommeregneren. Dette hjælpemiddel kan styrke både elevernes talopfattelse, og anvendt som ovennævnt vil den også fremme elevernes “hovedregning”. Så i stedet for at vente med at bruge lommeregneren til eleverne kan det elementære og så tillade lommeregneren, vil det for langt de fleste elever være mere lærerigt og motiverende at gå den anden vej. Altså lære det elementære ved brug af lommeregneren og dermed senere overflødiggør den ved de simple beregninger.
I kompetencemålene for 1.-3. klasse er netop beskrevet under hjælpemiddelkompetencen, at eleven kan anvende enkle hjælpemidler til tegning, beregning og undersøgelse.
Gruppesammensætning
Når man lader eleverne arbejde sammen om forskellige opgaver, skal man selvfølgelig overveje, hvilke elever der skal arbejde sammen. Skal alle arbejde med én, de er på niveau med, eller skal de arbejde med én, der er på et andet fagligt niveau?
Vi kan anbefale, at man laver makkerpar i klassen. Makkerparrene er lavet af læreren og bruges, når eleverne skal arbejde sammen to og to om forskellige opgaver, og også her skal man naturligvis overveje, hvordan parrene skal sammensættes. Faste makkerpar har bl.a. den fordel, at eleverne ikke skal bruge tid og energi på at finde en, der vil samarbejde. Læreren kan danne nye makkerpar, når hun fornemmer, at det er tid til luftforandring.
Der findes flere metoder til samarbejdsstrukturer fx inden for Cooperativ Learning, som kan indgå i arbejdet, hvor man finder det passende.
Hvad gør man ved elever, som skal have ekstra udfordringer?
Når eleverne arbejder i klassen – det kan være både med værksteder og i elevbogen – vil man ofte opleve, at der kan være nogle, der er hurtigt færdige med arbejdet. Til disse elever er der til sidst i hvert delforløb Grubleren, som stadig er opgaver inden for emnet men med større faglig udfordring. Det skal dog pointeres, at det ikke nødvendigvis skal forbeholdes ”de hurtigste” at løse grubleropgaverne. Opgaverne er ofte formuleret, så der kan være flere dybder og muligheder i måder at svare på.
Herudover henvises der til supplerende arbejdsark på www.kontextplus.dk. Vi har også i denne lærervejledning beskrevet spil, lege eller andre aktiviteter, man kan inddrage i undervisningen. Alle aktiviteter og spil er at finde samlet for 1.-3. kl. på www.kontextplus.dk.
Derudover vil vi opfordre til, at man arbejder med at lade eleverne udarbejde opgaver til hinanden.
Når en elev har udarbejdet en opgave, skrives den under og sættes i mappen med klassens opgaver. Andre elever kan vælge at løse en sådan elevopgave. Hvis eleverne ikke kan finde ud af opgaven, henvender han sig til den, der har lavet opgaven for at få hjælp. Denne elev skal
anbefalinger til undervisningen 15
så forklare opgaven. Når opgaven er løst, kontrollerer ophavsmanden resultatet. Man kan evt. aftale, at man altid udarbejder en opgave, før man løser en. Således løber man aldrig tør for opgaver.
Konkrete materialer og spil til 2. klasse
Der er materialer, som vi anvender ofte, og som vi derfor anbefaler, at man har til rådighed i klassen. Det drejer sig om følgende:
Centicubes
Centicubes går i materialet under det mere børnevenlige navn ”kuber”. De bruges ofte som spillebrikker, de kan tælles og sorteres mv. De er gode altid at have ved hånden, så hav gerne en mindre portion tilgængelig i klassen.
Terninger
Almindelige, sekssidede terninger inddrages jævnligt; særligt i aktiviteterne som ligger beskrevet på hjemmesiden. Hav gerne i klassen, hvad der svarer til to terninger pr. elev.
Tisidede terninger
Tisidede terninger er meget anvendelige, fordi de kan bruges til at konstruere tallene 0-99. Vi bruger dem både i værksteder og i aktiviteter, så hav gerne, hvad der svarer til 1-2 terninger pr. elev. Eleverne skal tit bruge to terninger i en gruppe.
Talkort
Vi lægger løbende i op til en del aktiviteter med talkort. Talkortene findes som serviceark på hjemmesiden. Der er en stor version af tallene 0-20 og kort i en lidt mindre størrelse med tallene 0-100. Talkortene kan lamineres, så de kan genbruges. Man kan lade eleverne have deres eget sæt hver, som de også kan arbejde med hjemme, eller man kan have sæt til rådighed, så man har, hvad der svarer til talkort til hveranden elev.
Skolepenge
Mønter og sedler anvendes jævnligt i materialet. Der findes mønter og sedler som serviceark, der kan kopieres og lamineres - se hjemmesiden. Hvis man ønsker et mere
holdbart materiale, kan man købe skolepenge i plastik, som flere klasser evt. kan dele. Se fx www.gongedanmark.dk eller www.spf-herning.dk.
Spillekort
På hjemmesiden er en del aktiviteter med spillekort beskrevet. Hvis man vil anvende disse aktiviteter i undervisningen, skal man selvfølgelig have spillekort til rådighed (ét sæt pr. to elever). Det kan være en fordel, at alle sæt spillekort har sin egen bagside, så man, når man finder et tabt spillekort, nemt kan finde ud af, hvilket sæt kort spillekortet hører til.
Sakse og limstifte og også gerne lommeregnere
Anvendes jævnligt og er gode altid at have ved hånden. Hav, hvad der svarer til et halvt klassesæt af hver.
Derudover er der en række materialer, som vi anvender i bestemte kapitler. De er oplistet nedenfor.
•Mønsterbrikker (findes som serviceark, der kan kopieres og lamineres, men det er også muligt at købe et mere holdbart materiale. Se fx hos gongedanmark.dk eller spf-herning.dk.
•Spejle.
•Sømbræt og elastikker hertil.
Vi anbefaler desuden, at man inddrager spil i sin undervisning. Det at spille rummer utrolig mange kvaliteter, som matematikundervisningen kan drage fordel af. Mange elever er automatisk motiveret, når spilleelementet inddrages. Der arbejdes ligeledes med kommunikation og problemløsning. Der er en social gevinst ved det at spille, men også vanskeligheder knyttet til at vinde og tabe. Der skal muligvis ske en tilvænning fra elevernes side til, at man nogle gange kan tabe, uden man taber ansigt. I denne sammenhæng kan det være godt, at spillene ikke tager for lang tid, så det ikke drejer sig om at finde én vinder og én taber, men at man vinder nogle gange og taber nogle gange.
Den bedste måde at lære et spil på er ved selv at spille spillet, helst sammen med en, der kender reglerne i forvejen. Næstbedst er det at se andre spille. Det kan være svært at lære et spil bare ved at få det forklaret. De fleste
16 anbefalinger til undervisningen
siger undervejs i forklaringen: Lad os nu bare komme i gang, så kan vi tage reglerne undervejs. Derfor vil vi gerne anbefale, at man fx lærer en mindre gruppe elever at spille spillet. Disse ”eksperter” kan så senere blive fordelt i andre grupper, hvor de så skal lære en ny gruppe spillet. Vi har selv rigtig gode erfaringer med denne arbejdsmetode. Der er også en sproglig sidegevinst med metoden, særligt for den elev der skal lære andre spillet. Her skal man selvfølgelig være opmærksom på, at man giver opgaven til de elever, der magter den.
Vi har på www.kontextplus.dk samlet en del spil, lege og andre aktiviteter, som med fordel kan anvendes i undervisningen. Undervejs i side til side-vejledningen refererer vi til spilleaktiviteter der, hvor vi tænker, de naturligt vil ligge i god forlængelse af emnet. Denne ”spillebank” kan også anvendes, hvis der er et fagligt emne, man gerne vil finde et spil til.
anbefalinger til undervisningen 17
Tegn fra prik til prik
Elevbogen indledes med en prik-til-prik tegning; en aktivitet som mange elever godt kan lide. Det er således et forsøg på en faglig venlig start. Eleverne skal her flytte sig i trin af ti, fx fra 240 til 250.
Arbejdsark 1-2
På arbejdsarkene kan eleverne få lejlighed til at tegne sig til en kamel og Dracula.

18 side til side-vejledning·tegn fra prik til prik 1 Tegn fra prik til prik 2 20 80 200 280 300 400 450 640 740 750 770 820 880 920 950 1000
ARBEJDSARK alinea arbejdsark 1 Tegn fra prik til prik 1 arbejdsark 2 Tegn fra prik til prik 2
Tal til 1000
Fælles Mål
Eleven kan anvende flercifrede naturlige tal til at beskrive antal og rækkefølge
Eleven har viden om naturlige tals opbygning i titalssystemet
Vi indleder 2. klasses matematik med positionssystemet. Et emne, vi opfatter som centralt for elevers talforståelse og ikke mindst som baggrund for deres senere udvikling af regnestrategier. Tallene udvides med flere positioner, så der nu arbejdes i talområdet 0-10 000. Vi har dog kaldt kapitlet Tal til 1000, men det skal blot opfattes som et forsøg på at skrive en forenklet titel. Eleverne skal arbejde med hundreder og tusinder.
Forudsætningen for, at eleverne erkender ideen bag positionssystemet, er indsigten i, at en mængde med et antal elementer kan bundtes, når man skal bestemme det. Disse bundter kan have mange forskellige størrelser, men da vi i vores kulturkreds har valgt titalssystemet som det bærende, er det altså bundter a 10 stk. Det er der arbejdet en del med i 1. klasse, men det kan være en god observation at afprøve, hvordan eleverne fx vil bestemme antallet af en pose med 200-300 genstande. Om de blot tæller fortløbende, eller om de systematiserer tællingen i enheder af ti. Ser man på forskellige matematiktest’ afprøvning af elevernes viden om positionssystemet, bemærker man opgaver af typen:
134 – Skriv, hvor mange tiere der er i tallet.
Mange elever er opgavetypevante, så de vil ofte svare, som vi gerne vil have det, nemlig 3 tiere, men dybest set rummer svaret flere refleksioner, idet der ligesåvel kan svares 13.
I arbejdet med positionssystemet ligger også elevernes færdigheder og viden om, hvordan man veksler til tiere, hundreder og tusinder. Har eleverne 12 tikroner, skal de være i stand til at omsætte det til 1 hundreder og 2 tiere.
Indsigten i positionsystemet styrkes gennem brug af forskellige repræsentationsformer. Disse repræsentationer kan bl.a. falde inden for nedenstående kategorier og blandinger af disse.
Konkret Symbolsk Model Hverdag
Den konkrete repræsentation kan ske gennem materialer som Base 10 eller lignende laborative materialer. Det centrale er her en indsigt i, at tallet 235 er opbygget ikke af to, tre og fem, men af 200 + 30 + 5. Der kan stadig indgå ting, som kan tælles, fx ved indsamling af mælkelåg op til 1000, hvor man laver bundter af hundreder, tiere og enere.
Modellerne er repræsenteret ved talkort, hvor eleverne danner tal, fx talkortene 6000, 800 og 7 ved at lade talkortene lappe over. Se værksted 1.
Her kan også anvendes talhuset, som senere kan udvides til venstre og til højre, når decimaltallene kommer til.
hundreder tusinder tiereenere
Symbolsk repræsentation er anvendelse af de ti cifre i en position, altså at skrive et antal som tretusinde og femoghalvfjerds som 3075. Bemærk i øvrigt, at eleverne kan have vanskeligt ved at placere ”nullet” i talnavne som det foregående.
Hverdagsrepræsentation er bedst gengivet gennem pengebeløb. Det skal dog siges, at elevernes kendskab til penge er vigende, idet voksne langt oftere anvender elektroniske betalingsmidler end sedler og mønter. Vores oplevelse er dog, at det stadigt virker interessant. Gennem pengene får eleverne en værdirepræsentation, som er anderledes end genstande/konkrete materialer, hvor en tier faktisk er ti enere. En tikrone er således defineret
20 side til side-vejledning·tal til 1000
Tal til 1000
6000800 7 6807
til at være ti. Man kan ikke tælle sig til ti enere, når man har den i hånden.
Om tallene fra 0 til 10 000
Hvis man kan anvende tallene fra 0 til 100 og dermed styre, at fx seksoghalvtreds er 56, vil det ofte være let for eleverne at kunne læse, skrive og bruge tallene over 1000. Der kan dog stadig være elever, som har brug for hjælp til at lære de tocifrede tal. Det kan anbefales, at man med dem bruger nogle af de lege og spil, som ligger på kontext+ hjemmeside, og som vi har refereret til i 1. klasse.
Der skal også ledes opmærksomhed hen mod hundredeovergange, fx at se på, hvordan eleverne klarer at nævne eller skrive tallene fra 205, 204, 203 osv. baglæns og iagttage, hvordan eleverne tæller.
Indledende klassesamtale
Det indledende foto på side 2 i elevbogen er tænkt som et oplæg til samtale i klassen, så eleverne ledes ind på det matematiske indhold i kapitlet. Pengene skal forestille at være tømt fra en indsamlingsbøtte, og nu skal de sorteres, så det er nemt at tælle dem. Det kan være lidt svært at se i bundtet med hundredekroner, at der er 9 sedler og en seddel, som omslutter de andre – altså 1000 kr. i alt.
Spørg fx:
•Hvor mange penge tror I, der er i alt? I skal bare gætte og skrive ned.
•Hvilke mønter kan I se på fotoet? Hvilke sedler er der?
•Hvordan vil I finde ud af, hvor mange penge der er i alt?
•Er der brug for at veksle?
Brug ord som ”10’er-bunker” og ”100-bunker.” Lad eleverne italesætte, at der arbejdes med at tælle bunker a 10. Indgå i samtaler om at veksle – og om hvordan der kan veksles.
Prøv evt. at introducere nogle beløb som fx 1205 kr. og bed dem overveje forskellige løsninger på, hvad der kunne ligge på bordet af mønter og sedler.
side til side-vejledning·tal til 1000 21
Værksteder
VÆRKSTED 1 Find talkort
Materialer

•Saks
•Arbejdsark 3-9
Beskrivelser og kommentarer
Målet med dette værksted er, at eleverne opdager, at tallene er bygget op i positioner; at 5397 er det samme som 5000 og 300 og 90 og 7 tilsammen. Til dette anvender vi en slags talkort. Disse talkort kan ses på arbejdsark 3 og

4. Kortene skal klippes ud, inden eleverne kan gå i gang med værkstedet. Eleverne kan i begyndelsen arbejde sammen to og to om et sæt talkort.
Når talkortene er klippet ud, lægges de til side for en stund. Eleverne skal nu i gang med den første opgave. Til den skal man anvende arbejdsark 5 og 6. Arbejdsark 5 og 6 består af kort med en talværdi på. På arbejdsark 5 arbejders der med værdier på hundreder og på arbejdsark 6 med tusinder. Kortene på arbejdsark 5 og 6 skal klippes ud. Dette giver mulighed for elevdifferentiering, således at elever, som ikke har hundrederne på plads endnu, kan begynde med arbejdsark 5, mens andre elever fra begyndelsen kan arbejde med tusinder. Kortene lægges med bagsiden opad og eleverne trækker herefter et kort med en talværdi. Denne talværdi skal nu bygges af talkortene. Hvis en elev fx trækker talværdien 8452, skal eleven bygge tallet, dvs. talkortene 8000, 400, 50 og 2 findes og placeres oven på hinanden. Når eleven har bygget
tallet, skal det skrives på arbejdsark 8, som er en slags registreringsark. Herefter trækker eleven et nyt kort med en talværdi. Således fortsætter man, indtil arbejdsark 8 er udfyldt.
Hvis en elev trækker kortet 6607, skal han finde 6000, 600 og 7. Han skal ikke finde et kort med en værdi på tierens plads, da der ikke er nogen tiere i tallet 6607. Det bliver meget tydeligt, når tallet deles op på denne måde.
Til værkstedet hører også et spil, ”Tårnet” på arbejdsark 9, som eleverne kan spille, hvis de når igennem værkstedet. Spillet kan spilles af to til tre elever. Eleverne skal anvende talkortene. Kortene lægges i hver sine bunker med tusinder, hundreder, tiere og enere. Eleverne skiftes til at trække en tusinder, hundreder, tier og en ener. Disse talkort samles til en talværdi, som skrives i tårnet, hvorefter talkortene lægges tilbage i de rigtige bunker. Herefter er det næste spillers tur til at trække en tusinder, hundreder, tier eller ener og disse kort. Disse kort samles igen til en talværdi og skrives i tårnet, men således at tallene i tårnet er skrevet i rækkefølge med det mindste tal nederst og det største tal øverst. Eleverne skiftes til at trække talkort indtil man får et tal, som ikke kan placeres. Denne spiller har tabt.
Hvis der er elever, der når helt igennem værkstedet, kan man opfordre dem til at lave talkort, så de kan lave større tal (titusinder, hundredtusinder osv.).
ARBEJDSARK Talværdikort 6 1 Find talkort 6547 9381 6377 8124 9583 7241 3917 7276 5718 8923 4718 8452 7960 6607 2619 4799 1931 3059 5070 1036 2005 8 1 Find talkort 43924000300902+++= +++= +++= +++= +++= +++= +++= +++= +++= +++= arbejdsark 5 Talværdikort 1 Find talkort 348 655 405 310 806 400 888 217 736 608 260 530 804 600 493 126 703 570 950 702 666 3 1 Find talkort 1000 100 10 1 2000 200 20 2 3000 300 30 3 4000 400 40 4 5000 500 50 5 22 side til side-vejledning·tal til 1000
arbejdsark 9 Spil Tårnet 1 Find talkort arbejdsark 4 1 Find talkort 6000 600 60 6 7000 700 70 7 8000 800 80 8 9000 900 90 9 arbejdsark 7 1 Find talkort 714700104 ++ ++ = ++ = ++ ++ ++ ++ ++ = ++ = ++
VÆRKSTED 2 Hop på tallinjer
Materialer
•Saks og lim
•Tosidede terninger

•Arbejdsark 10-14
Beskrivelser og kommentarer
Målet med dette værksted er, at eleverne bliver fortrolige med tallenes rækkefølge på tallinjen. Derudover skal eleverne springe frem og tilbage på tallinjen i spring på 1, 10 og 100. Her vil de opdage, hvorledes tallenes udseende ændres i et bestemt mønster.
Værkstedet er egentlig et spil, men for at eleverne forstår, hvad spillet går ud på, foreslår vi, at eleverne først løser opgaverne på arbejdsark 11-13. I den første opgave på værkstedsarket, som er løst, skal eleverne hoppe fra 0 til 27. Man må hoppe 1, 10 eller 100. Et hop på 1 eller 10 tæller for det samme, altså ét hop. Det gælder om at hoppe fra 0 til 27 med så få hop som muligt. Man kan hoppe således: 10, 20, 21, 22, 23, 24, 25, 26, og 27, men det kræver ti hop. Det kan bedre betale sig at hoppe op til 30 og derefter bagud til 27. Her bruger man kun seks hop. Tallet 6 skrives i boksen under tallinjen.
På de tre arbejdsark med opgaver er progressionen stigende. Vi indleder på arbejdsark 11 med at hoppe fra 0 hver gang. På arbejdsark 12 hoppes der fra et etcifret tal, og på arbejdsark 13 fra et tocifret tal.
I den næste opgave på værkstedsarket skal man hoppe fra 5 til 24. Her kan det bedst betale sig at hoppe til 25 og derefter et hop baglæns. Her bruger man altså 3 hop og dette skrives i kassen. Når man skal fra 5 til 24, får eleverne øvelse i at hoppe 10 op, dvs. fra 5 til 15 til 25 osv.
Inden eleverne kan gå i gang med spillet, skal tallinjen på arbejdsark 10 klippes ud og sættes sammen. Der kan være mellem to og fire elever om hver tallinje. Når tallinjen er sat sammen, skriver eleverne tal på tallinjen.
Inden spillet går i gang vælger eleverne om deres sluttal skal være to eller trecifret. Spiller 1 finder starttallet ved at slå med én tisidet terning. Herefter findes sluttallet ved at slå med to eller tre tisidede terninger. Eleverne skal nu hoppe fra starttal til sluttal med så få hop som muligt. Når eleverne har besluttet sig for, hvordan de vil hoppe, tælles hoppene sammen, og hoppene noteres i regnskabstavlen. Herefter er det den næste spillers tur. Når alle elever har prøvet 6 gange, tælles spillernes point sammen, og den spiller, der har brugt det mindste antal hop, har vundet.
Det kan være et lidt svært spil for nogle elever at overskue, så man bør overveje at starte ud med, at alle elever starter på nul og dernæst hopper frem til det sluttal, der er fundet med de to terninger. At have et andet starttal end nul kan så passende være udvidelsen af spillet.
ARBEJDSARK 2 Hop på tallinjer arbejdsark 14 RundeNavnNavnNavnNavn 2 3 4 6 Hop alt RundeNavnNavnNavnNavn 3 4 6 Hop alt alinea 2 Hop på tallinjer arbejdsark 11 Hop fra 0 til 37 Hop fra 0 til 49 Hop fra 2 til 38 Hop fra 5 til 47 Hop fra 0 til 86 Hop fra 0 til 91 Hop fra 3 til 95 Hop fra 7 til 93 2. Tallinjen 12 t b 5 F I K l Kontext Kopimappe Bestillingsnr.: 9024203 forlag Malling Beck hop hop hop hop hop hop hop hop Hop fra 0 til 37 Hop fra 0 til 49 Hop fra Hop fra Hop fra Hop fra Hop fra Hop fra 2. Tallinjen 12 t b 5 F I K l Kontext Kopimappe Bestillingsnr.: 9024203 forlag Malling Beck 10 20 30 40 50 hop hop hop hop hop Kopimappe 2A/5. korr 06/07/05 14:12 Side 24 Hop fra 2. Tallinjen 12 t b 5 F I K l Kontext Kopimappe Bestillingsnr.: 9024203 forlag Malling Beck hop hop hop 0102030 90100 4050607080 110 fra 0 til 37 hop hop hop hop hop hop hop hop fra 0 til 49 Hop fra 0 til 56 fra 0 til 85 fra 0 til 73 Hop fra 0 til 81 fra 0 til 91 Hop fra 0 til 95 arbejdsark 10 2 Hop på tallinjer 2. Tallinjen 13 t b 5 F I K l Kontext Kopimappe Bestillingsnr.: 9024203 forlag Malling Beck 2 Hop på tallinjer 12 Hop fra 3 til 43 Hop fra 0 til 37 Hop fra 0 til 49 Hop fra 2 til 38 Hop fra 5 til 47 Hop fra 0 til 86 Hop fra 0 til 91 Hop fra 3 til 95 Hop fra 7 til 93 2. Tallinjen 12 t b 5 F I K l ARBEJDSARK Kontext Kopimappe Bestillingsnr.: 9024203 forlag Malling Beck 10 20 30 4037 50 hop hop hop hop hop hop hop hop hop hop hop hop hop hop hop hop Hop fra 5 til 69 Hop fra 7 til 65 Hop fra 8 til 76 Hop fra 4 til 75 Hop fra 3 til 92 Hop fra 2 til 90 Hop fra 3 til 95 Hop fra 0 til 37 Hop fra 0 til 49 Hop fra 2 til 38 Hop fra 5 til 47 Hop fra 0 til 86 til 91 Hop fra 3 til 95 til 93 2. Tallinjen 12 t b 5 F I K l Kontext 2A Kopimappe Bestillingsnr.: 9024203 forlag Malling Beck hop hop hop hop hop hop til 38 til 86 til 95 til 93 2. Tallinjen 12 t b 5 F I K l Kontext Kopimappe Bestillingsnr.: 9024203 forlag Malling Beck hop 0102030 90100 4050607080 110 hop Hop fra 0 til 37 2. Tallinjen 12 t b 5 F I K l Kontext Kopimappe Bestillingsnr.: 9024203 forlag Malling Beck hop hop hop Hop fra 0 til 37 Hop fra 0 til 91 til 93 2. Tallinjen 12 t b 5 F I K l ARBEJDSARK Kontext Kopimappe Bestillingsnr.: 9024203 forlag Malling Beck 10 20 30 4037 50 hop side til side-vejledning·tal til 1000 23
arbejdsark 13 2 Hop på tallinjer Hop fra 0 til 37 Hop fra 0 til 49 Hop fra 2 til 38 Hop fra 5 til 47 Hop fra 0 til 86 Hop fra 0 til 91 Hop fra 3 til 95 Hop fra 7 til 93 2. Tallinjen 12 t b 5 F I K l hop hop hop hop hop hop 0102030 90100 4050607080 110 hop hop hop hop hop hop hop hop hop hop Hop fra 15 til 97 Hop 10 Hop 12 102 Hop fra 14 til 94 Hop 11 til 110 Hop 10 110 Hop 13 106 Hop 11 til 100 Hop fra 0 til 37 Hop fra 0 til 49 Hop fra 2 til 38 Hop fra 5 til 47 fra fra fra fra 2. Tallinjen 12 t b 5 F I K l Kontext Kopimappe Bestillingsnr.: 9024203 forlag Malling Beck hop hop hop hop hop hop Hop fra 0 til 37 Hop fra 2 til 38 Hop fra 5 47 Hop fra 0 fra fra 2. Tallinjen 12 t b 5 F I K l Kontext Kopimappe Bestillingsnr.: 9024203 forlag Malling Beck 10 20 30 40 50 hop hop hop Kopimappe 2A/5. korr 06/07/05 14:12 Side 24 2. Tallinjen 12 t b 5 F I K l Kontext Kopimappe Bestillingsnr.: 9024203 forlag Malling Beck hop hop Hop fra 0 til 37 Hop fra 5 til 47 Hop fra 3 til 95 Hop fra 7 til 93 2. Tallinjen 12 t b 5 F I K l Kontext Kopimappe Bestillingsnr.: 9024203 forlag Malling Beck hop 0102030 90100 4050607080 110 hop














































