DetTænkend e Klasserum
Håndbog
Matematik · Håndbog · Web
Adrian Rau Bull, Nick Hougaard og Tina Fuglsig Lauridsen
Indledning
Det Tænkende Klasserum i matematik har det formål at understøtte eleverne i at blive mere engagerede i matematikundervisningen og få dem til at tænke matematisk i længere tid. Det handler om at støtte eleverne til at forstå og forholde sig vurderende til matematikken og dens anvendelse samt kvalificere elevernes matematik i de fællesskaber, som de indgår i.
Bogen henvender sig især til dig, der gerne vil have ideer til – og erfaringer med – hvordan man i 4.-9. klasse kan styrke elevers optagethed af matematik og engagement i matematikundervisningen.
Ved at læse denne bog kan du få inspiration til, hvordan man kan afprøve forskellige relevante praksisser i matematikundervisningen. Praksisser der dels kan få eleverne til at engagere sig i matematikken, så de kan opdage dens muligheder, og dels kan få eleverne til at være ansvarsfulde og kreative med matematikken også udenfor matematiktimerne. Dette sker ikke af sig selv. For de fleste elever sker det heller ikke nødvendigvis ved den måde, matematikundervisningen klassisk er foregået på, nemlig ved at de har regnet en masse matematikopgaver i en bog, på computeren eller foran klassen.
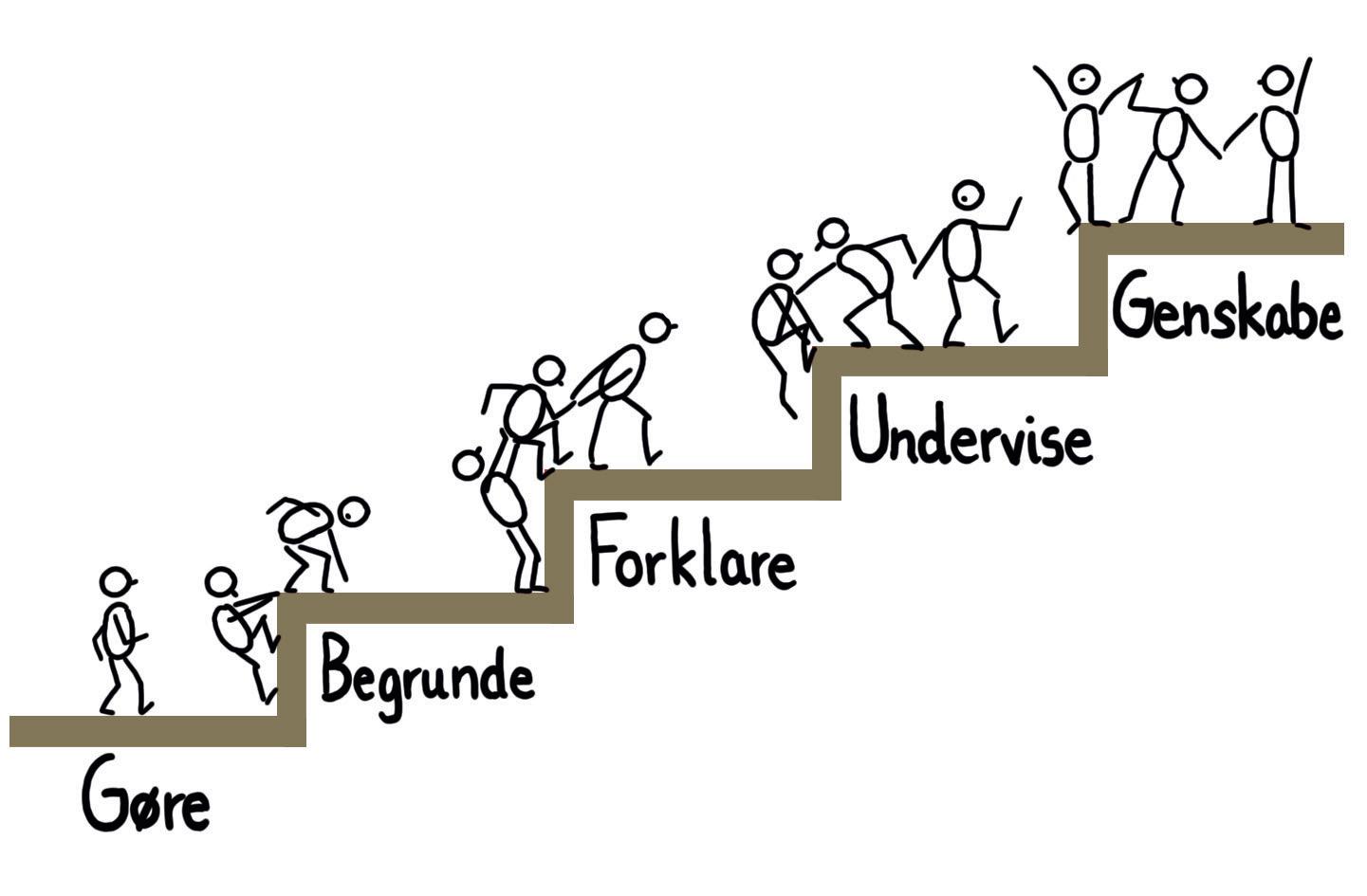
At gøre matematik ved fx at regne matematikopgaver er kun første trin i en proces, der har til formål at øge elevernes engagement i matematik og udfordre dem til at forstå de måder, matematikken bliver brugt på i samfundet omkring dem.
Peter Liljedahls forskning viser, at der findes en særlig tilgang og en dertil knyttet taksonomi, der trinvist kan udbygge elevernes engagement i matematik. Taksonomien starter med, at eleverne gør matematik, hvorefter de begrunder matematik, som de har arbejdet med. Herefter forklarer de matematik, og de underviser de andre elever i matematik Efterhånden som de trinvist gennem matematikundervisningen kommer igennem disse første fire trin af engagementstrappen, bliver eleverne støttet til at kunne genskabe matematik. Dette betyder, at de bliver i stand til at se, hvordan de kan bruge matematikken i nye situationer, eller at de bliver i stand til selv at skabe nye matematiske udfordringer.
Engagementstrappen, der har fokus på, hvordan elevernes kompetencer udvikles trinvist, er helt central for denne bog, fordi hver praksis i bogen kan bidrage til den trinvise udvikling af elevernes engagement, samarbejde, ansvar og kompetencer i matematik. Se næste side.
2 DET TÆNKENDE KLASSERUM I PRAKSIS INDLEDNING
Peter Liljedahl opererer med i alt fire værktøjssæt, som i alt indeholder 14 praksisser. Praksisserne støtter læreren i at hjælpe grupperne op ad engagementstrappen. Dermed støtter de altså eleverne i at selv at genskabe matematik, så de kan bruge den i nye situationer i deres hverdag og i deres liv i det hele taget.
Det 1. værktøjssæt, der inkluderer tre praksisser, danner grundlaget for DTK. Dette værktøjssæt er både med til at få eleverne hurtigere i gang med at gøre matematik og at støtte eleverne i at komme højere op i engagementsmodellen gennem et samarbejde, hvor eleverne bliver sat i situationer, hvor de kommer til at begrunde og forklare matematikken for hinanden.
Den 1. praksis handler om at finde og give opgaver, der kan engagere eleverne. Sådanne opgaver vil give anledning til, at eleverne bliver nødt til at begrunde den matematik, de har gjort. I et klasserum med tænkning vil det altid give anledning til forskellige forklaringer af problemet og den relaterede matematik.
Den 2. praksis handler om at opdele eleverne i offentligt tilfældige grupper på tre elever. Denne opdeling støtter yderligere eleverne i at have fokus på matematikken og i begrundelser og forklaringer af matematikken indbyrdes i grupperne.
I den 3. praksis indfører man i grupperne en vertikal tavle og én tusch med ikke-permanent skrift. Dette vil ofte være med til at engagere eleverne til at prøve sig frem, fordi det ikke er helt så farligt at skrive noget forkert her. De vil også blive opmærksomme på, hvordan andre elever arbejder med og argumenterer for problemerne. På denne måde kommer eleverne til at få fokus på begrundelserne og forklaringerne og ikke nødvendigvis kun på svarene.
3 INDLEDNING
Det 2. værktøjssæt skal yderligere støtte elevernes engagement og matematiske tænkning og bygger videre på praksissen fra 1. værktøjssæt. I dette værktøjssæt har læreren fokus på at ændre sin matematikundervisning gennem fem praksisser. Disse handler blandt andet om, hvordan rummet indrettes til matematisk tænkning, hvordan undervisningen initieres mundtligt, og hvordan læreren besvarer elevernes mange spørgsmål, så de fortsætter elevernes tænkning. Alle praksisser i værktøjssæt 2 har dermed til formål at støtte elevernes vej endnu højere op ad engagementstrappen startende med, at eleverne gør matematik, og fortsættende med, at de endnu hurtigere kommer til at begrunde og forklare og i nogle tilfælde undervise andre elever i matematik.
I 3. værktøjssæt er det bærende element at arbejde i et flow. Det handler for læreren om at kunne give hints og forlænge opgaver asynkront, så undervisningen er differentieret for hver gruppe af elever, men også om at støtte samarbejde imellem grupperne. Når eleverne selv skal tage noter, og når grupperne bliver støttet til at arbejde selvstændigt, men også bruge hinanden til at få bearbejdet problematikkerne og få konsolideret dagens konkrete arbejde og problemstillinger, vil det indebære, at eleverne kan undervise hinanden i matematik. Undervisning i matematik er mere end en forklaring, idet man, når man underviser, både skal have styr på den matematik, der skal undervises i, samt de retninger, der kan blive nødvendige i undervisningen, og have viden om dem, der skal undervises, inkl. deres matematiske forståelser. Det er meningen, at undervisningen bliver endnu mere formaliseret grupperne imellem, ved at læreren sørger for, at grupperne får tid og mulighed for at begrunde, forklare og undervise undervejs i matematiktimerne. I 3. værktøjssæt skal læreren sørge for, at eleverne arbejder med en fornuftig kombination af grublere, strukturerede sekvenser af opgaver og problemløsende opgaver. 3. værktøjssæt handler således også om at genskabe en hensigtsmæssig årsplan i matematik, som ikke nødvendigvis er særlig anderledes end dine tidligere årsplaner. Til gengæld kan årsplanen gennemføres i Det Tænkende Klasserum, således at eleverne kan opbygge deres engagement, arbejde problemløsende og være kommunikerende med hinanden omkring matematikken.
Det 4. og sidste værktøjssæt i Det Tænkende Klasserum handler primært om, hvordan læreren evaluerer og værdsætter det, som bidrager til elevernes tænkning i matematik. Det handler også om, hvordan læreren styrker de personlige og sociale kompetencer, der har betydning for, om eleverne får adgang til det faglige i matematik, og hvordan læreren giver eleverne formativ feedback, så den støtter eleverne til at få overblik over et emne, samtidig med at der skabes forståelighed for emnets kompleksitet. Der er også fokus på, hvordan der kan gives standpunktskarakterer til elever i Det Tænkende Klasserum.
4 DET TÆNKENDE KLASSERUM I PRAKSIS
INDLEDNING
En ny kontrakt mellem læreren og eleverne
Når du bruger denne bog til at skabe Det Tænkende Klasserum i din matematikundervisning, vil du forhåbentlig opdage, at du samtidig ændrer matematikundervisningen, så dine elever bliver mere deltagende og kommer til at tænke mere over matematikken. Derfor er det muligt, at du og dine elever vil opleve, at der arbejdes efter en ny didaktisk kontrakt. Det tager tid at ændre en didaktisk kontrakt, og det er naturligvis sværest at ændre en didaktisk kontrakt for de elever og måske også de lærere, der er trygge ved den gamle didaktiske kontrakt.
Hvis du i din undervisning kan genkende dele af den gamle didaktiske kontrakt, som vi har beskrevet i det næste afsnit, så synes vi, at du skal prøve at implementere DTK i din matematikundervisning.
Den gamle didaktiske kontrakt i megen matematikundervisning Den gamle didaktiske kontrakt, der kan forekomme i megen matematikundervisning, handler om, hvordan eleverne og læreren (og forældre) forventer, at matematikundervisningen skal foregå. Denne gamle kontrakt indbefatter blandt andet, at det er læreren, der har det fulde ansvar for planlægningen og forløbet af matematikundervisningen, at det er læreren, der starter matematikken, og at det er læreren, der afgør, hvornår den er færdig. Det er læreren, der bestemmer, hvordan grupperne formes, og det er læreren, der viser og forklarer metoderne, som eleverne skal bruge i den konkrete time. Det kan desværre betyde, at det ofte er læreren, der taler og tænker mest i de fleste matematikundervisningstimer, og at det ofte er læreren, der begrunder, forklarer og underviser. Derfor er det ifølge Liljedahls model ofte læreren, som udvikler sin egen matematik mest i den type undervisning, der kommer af den gamle didaktiske kontrakt. For mange af eleverne kan det betyde, at de ikke udvikler deres matematik tilstrækkeligt, når der arbejdes efter denne kontrakt.
Elevernes del i den gamle didaktiske kontrakt vil ofte primært gå ud på, at de ikke skal forstyrre undervisningen, altså at de ikke skal være forstyrrende for læreren, og at de skal gå i gang med det arbejde, som læreren beder dem om at lave. Eleverne skal være foretagsomme og opmærksomme, når læreren har afsat tid til det. Det kan dog hurtigt komme til at betyde, at eleverne vænner sig til, at de ikke skal tænke selvstændigt i matematikundervisningen, og at det ofte kan være uhensigtsmæssigt eller forstyrrende (og dermed et brud på kontrakten), hvis de er alt for talende eller selvstændigt tænkende i deres foretagsomhed. For nogle elever kan det også betyde, at de vænner sig til at nedtone deres energi på matematikken, og derfor kan nogle af de elementer i den gamle kontrakt, som de får fokus på, være, at matematik handler om at være hurtig til at gøre det, som læreren viser, og dermed arbejder eleverne kun med metoder, som læreren umiddelbart har
5
INDLEDNING
vist dem. Nogle af eleverne bliver gode til at bruge tiden (uden at forstyrre) til at tale med deres klassekammerater eller tænke over noget uden for matematikundervisningen. Der kan derfor let være meget af matematikken, som eleverne hurtigt glemmer, når matematikundervisningen er slut.
DTK – en ny didaktisk kontrakt for matematikundervisningen Den tydeligste forskel, som læreren helst skal opleve, når man bruger DTK i matematikundervisningen, er, at den enkelte elev i hver time kommer til at begrunde mere og forklare mere. Ja, måske endda undervise nogle andre elever i noget matematik. Altså at eleverne bevæger sig op ad trinene i engagementstrappen. Det er også hensigten, at læreren kommer til at tale mindre, både fordi introerne til elevernes arbejde bliver kortet ned til et minimum, og fordi læreren skal undgå at besvare de spørgsmål, der ikke hjælper eleverne videre eller måske endda kan stoppe elevernes tænkning. Læreren skal ikke bruge tid på at forklare alle metoder i detaljer, umiddelbart før eleverne skal anvende dem i undervisningen. Læreren skal i højere grad lære at være stille fremfor talende og spørgende fremfor opklarende samt udfordrende fremfor afsluttende.
Liljedahls forskning og vores påstand er, at denne nye didaktiske kontrakt kan bidrage til, at eleverne bliver mere tænkende i matematikundervisningen. Du skal dog hverken tage vores eller Peter Liljedahls ord for pålydende. Du skal selv i gang med at afprøve Det Tænkende Klasserum i din egen matematikundervisning.
Vi vil med denne bog hjælpe dig til at komme i gang med Det Tænkende Klasserum i dansk skolesammenhæng.
6 DET TÆNKENDE KLASSERUM I PRAKSIS
INDLEDNING
Forord – ved Peter Liljedahl
Indholdsfortegnelse
Indledning
Værktøjssæt 1
Praksis 1: De tre opgavetyper
Praksis 2: Tilfældige grupper
Praksis 3: Stående arbejde
Værktøjssæt 2
Praksis 4: Indretning af klasselokalet
Praksis 5: Hvordan læreren besvarer spørgsmål
Praksis 6: Måden læreren giver opgaver på
Praksis 7: Undersøg din forståelse - den nye lektietype
Praksis 8: Elevernes selvstændighed
Værktøjssæt 3
Praksis 9: Differentiering med hints og udvidelser
Praksis 10: Sådan konsolideres forståelse
Praksis 11: Noter i grupper og individuelt
Værktøjssæt 4
Praksis 12: Understøt de personlige og sociale kompetencer
Praksis 13: Formativ evaluering med elevinddragelse
Praksis 14: Hvordan gives de tre standpunktskarakterer?
Det tænkende klasserum i hverdagen
7 INDHOLDSFORTEGNELSE
Om værktøjssæt 2
Det første værktøjssæt har fokus på, hvordan eleverne kommer i tænkning. Dette andet værktøjssæt har fokus på at ændre lærerens undervisningspraksis. Det er målet, at lærerens praksis skal understøtte elevernes måder at arbejde på fra værktøjssæt 1, så de i højere grad kan få mulighed for at blive i tænkning i matematikundervisningen. Det er en forudsætning, at praksis 1-3 i værktøjssæt 1 er implementeret.
I dette sæt er det ikke vigtigt, i hvilken rækkefølge læreren vælger at implementere de fem praksisser. Flere praksisser kan godt implementeres på samme tid, eller læreren kan vælge at indføre dem én ad gangen i den rækkefølge, der synes mest hensigtsmæssig. Dog er det vigtigt, at der ikke indføres så mange ændringer på én gang, at læreren eller eleverne mister overblikket og ikke kan forblive i tænkning.
Dette værktøjssæt giver læreren mulighed for at undersøge sin egen praksis og finde ud af, hvordan denne praksis kan støtte elevernes arbejde med tænkning. Derfor er det hensigtsmæssigt, hvis læreren i arbejdet med dette sæt er fejlmodig og undersøgende omkring de fem nye praksisser. Det kan kræve flere afprøvninger end først forventet, og derfor må læreren være forberedt på at vende tilbage til de praksisser, der ikke umiddelbart fungerer, og undersøge dem igen.
Det vil være individuelt, hvilke praksisser det tager længst tid at implementere i egen praksis, men vi har erfaring for, at mange lærere med fordel kan bruge ekstra tid på at implementere praksis 5 og 6. Derfor anbefaler vi, at disse to praksisser undersøges, når læreren har mest overskud til at starte på noget nyt.
Tre ting vil afgøre, hvor gode vi er til at skabe ændringen:
• Vaner og rutiner
• Elevers (og forældres) forventninger til lærerens undervisningspraksis
• Lærerens forventninger til, hvordan elever støttes bedst.
Her er det vigtigt at holde fokus på at støtte elever i at tænke
10 DET TÆNKENDE KLASSERUM I PRAKSIS
VÆRKTØJSSÆT 2
Praksis 4 • Indretning af klasselokalet
Hvornår er et klasselokale et tænkende klasserum? Og er det overhovedet afgørende, hvordan klasselokalet ser ud, for at eleverne kan tænke i matematik? Det er selvfølgelig muligt for eleverne at tænke matematisk, uanset hvordan klasselokalet er indrettet, men indretningen har alligevel stor betydning for, hvordan de aflæser rummet. Elevernes afkodning af lokalet har indflydelse på, hvilke forventninger de har til den undervisning, der skal foregå, og hvordan de tror, at de skal agere i klasselokalet. Derfor har indretningen stor betydning for elevernes adfærd i klasselokalet.
Det har vist sig, at for at få de mest optimale betingelser for tænkning i et klasserum er der nogle særlige elementer i indretningen, der er hensigtsmæssige.
Det handler om tre ting:
• Læreren og eleverne skal være dynamisk placeret i lokalet, så det er let at bevæge sig mellem grupperne.
• Eleverne skal have plads til at stå foran de vertikale tavler, så alle kan komme til.
• Bord- og stoleopstilling skal vende i mange forskellige retninger, men der må ikke være kaotisk rodet i lokalet.
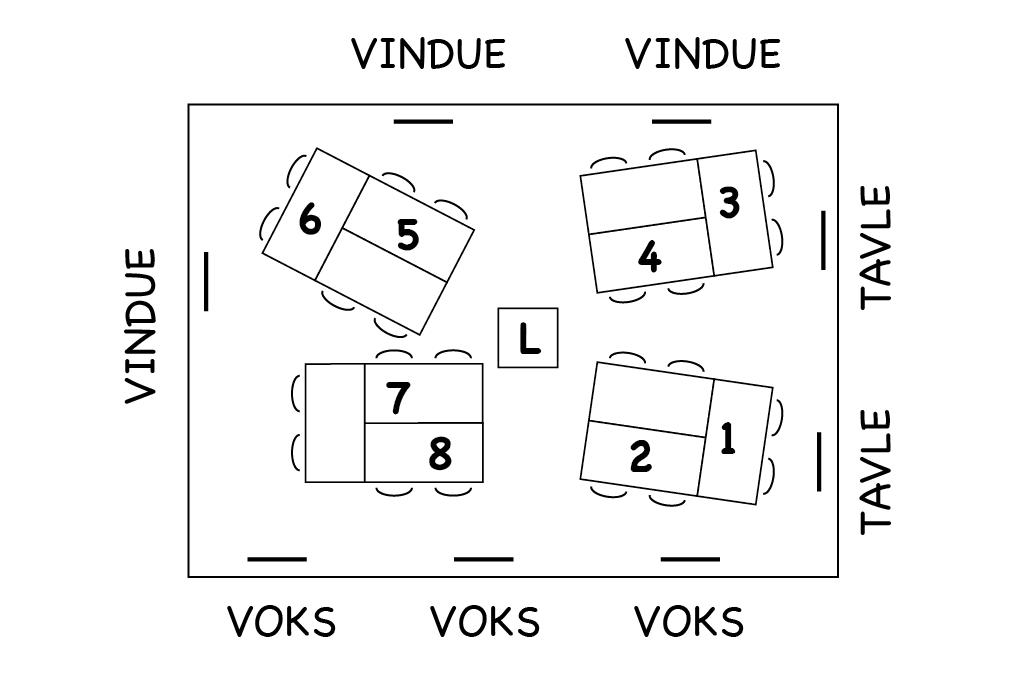
TAVLE L L TAVLE VIN D UE VIN D UE VIN D UE VINDUE 1 1 2 2 6 6 3 3 4 4 T A VLE 8 8 T A VLE 7 7 5 5 Du kan se det her på tegningen. Hvor skal vi sætte bordet? 11 PRAKSIS 4
Indretningen af det tænkende klasserum skal, så vidt det er muligt, give plads til, at eleverne har en vis bevægelsesfrihed. Der er ikke et særligt lærerområde (lærerens bord), og retningen i lokalet er ikke vendt mod en bestemt tavle, hvor læreren styrer undervisningen fra. Eleverne bevæger sig frit mellem de lodrette tavler og gruppeborde, der vender i flere retninger.
Eleverne bliver mere betydningsfulde
I den nye indretning vil eleverne opleve, at deres rolle i undervisningen bliver mere betydningsfuld. De byder mere ind med noget, alene fordi de er mere aktive, når de står op og kan bevæge sig frit rundt. Indretningen af lokalet kan derved understøtte både lærerens forventning, planlægning af selve undervisningen og elevernes tænkning. Elever med fastlåst tankesæt går mod et mere åbent tankesæt om deres egen rolle i matematikundervisningen. Ved at lave en dynamisk placering af læreren i rummet neutraliseres noget af lærerens vidensautoritet, og det giver alle i rummet medansvar for tænkning. Det er lærerens opgave at lede elevers og gruppers tanker i den retning, læreren har tænkt for lektionen, uden direkte at overlevere sine egne tanker til gruppen.
Rum for, at lærer og elever deler matematiske tanker
Eleverne i en gruppe kan hurtigt opdage, at andre grupper er i gang med nye tiltag i en opgave, fordi de kan se hen på deres tavler. Det giver de optimale betingelser for, at eleverne lader sig inspirere til at bruge de andre gruppers tavler, og det støtter dem i at generere tænkning. De tre praksisser i værktøjssæt 1 og ændret indretning i klasselokalet giver nye muligheder for læreren. Det, at læreren bevæger sig frit mellem grupperne, og at der ikke er siddepladser foran de tavler, hvor eleverne foretager deres udregninger, giver læreren mulighed for at blive opmærksom på elever, der ikke er med i det matematiske arbejde, og for at handle på det.
Risikovillighed øges
Bordopstillingen understøtter også elevernes lyst til at afprøve og dermed fejle. Da læreren ikke har en fast plads, kan man tale om, at lærerområdet er i hele lokalet. Den let ”rodede” bordopstilling og en neutralisering af et lærerområde i lokalet understreger vigtigheden af, at alle udfører tænkningen, ikke bare dem, der befinder sig i nærheden af læreren.
Da tænkning er lidt rodet og indeholder vildspor i alle mulige retninger, har vi altså nu kodet rummet til, at eleverne kan fejle og prøve igen. Fejlmodighed handler om at turde prøve alle mulige veje i den matematik, en elev måtte kende på nuværende tidspunkt. Gruppen kan derefter blive enige om, hvorvidt vejen er tættere på en løsning, eller om en ny skal afprøves. Alle de veje, der afprøves, er en del af en matematisk undersøgelse og er vigtige trin for at kunne besvare problemløsende opgaver, men er også vigtige for at blive i tænkning.
12 DET TÆNKENDE KLASSERUM I PRAKSIS
VÆRKTØJSSÆT 2
Balance mellem rod og orden
I andre fag er indretningen af klasserummet helt klassisk, fx kan nævnes idræts- og håndværk & design-lokaler, hvor indretningen – eller man kunne sige kodningen – typisk vil pege i retning af, at der skal foregå noget helt bestemt i lokalet. I matematik er der ikke stærke traditioner for at kode rummet til faget. Det er mere en undtagelse, når skoler arbejder med kodning af matematiklokaler. Typisk vil man ikke gøre det, fordi man vægter klasselokalet højere end faglokalet i matematik.
Bordopstillingen i DTK-klasselokalet er bundet til, hvordan eleverne kommer i og er i tænkning. Tænkningen har mange forgreninger, der ikke nødvendigvis giver en lineær retning, hvilket ofte afspejles i arbejdet på tavlerne i klassen, hvor grupper er i tænkning.
Når vi indretter lokalet lidt uordentligt, koder vi altså rummet til, at her er det helt i orden at tænke, og at tænkning er lidt ”rodet”. Læreren kan derved signalere til eleverne, at de gerne må fejle i dette rum, det er der plads til. Hvis lokalet til gengæld er kaotisk og meget rodet, kan det være svært at tænke, eller man har måske bare lyst til at få det ordnet, så målet er ikke at skabe fuldstændig uorden. Der skal være en balance, hvor der ikke er mere rodet, end at man kan tænke over matematikken og bevæge sig rundt i lokalet uden at skulle undvige diverse tasker og stole.
13
PRAKSIS 4
Tag dine teamkollegaer med i beslutningen om bordopstilling Du kan havne i en situation, hvor dine kollegaer ikke kan se nødvendigheden af at ændre indretningen.
I sådanne situationer kan det blive nødvendigt at ændre på indretningen både i starten og slutningen af lektionen. I de tilfælde vil det være mere fair, hvis I bliver enige om, at lokalet afleveres, så det er klar til undervisning i næste lektion. Herved opnår du, at det kun er sidst i lektionen, at du skal flytte rundt. Her kan man med fordel drage eleverne ind i opgaven, og det gøres nemmest ved at have to synlige bordplaner i klassen.
Kort sagt handler alt i denne omorganisering om at tænke kreativt og konstruktivt i løsningsmodeller, der tilgodeser alle, og med villighed til at afprøve de forskellige idéer. Det kan også være en mulighed, at borde placeres forskelligt i løbet af året, og én af disse placeringer kunne være DTK-opstillingen, som hele teamet anvender i alle lektioner, ligesom andre indretninger af lokalet benyttes i andre perioder.
Til venstre et eksempel på en bordopstilling, vi ofte ser i klasser.
Til højre et eksempel på, hvordan klasserummet kodes til DTK ved at ændre på bordplacering og arbejdsflader. Der er gruppenumre på billedet. Projektoren kan dog ikke flyttes og bruges fra vanlig placering, når det er nødvendigt.

• Gå i dialog med det team, der underviser i samme lokale som dig. Måske kan I i fællesskab blive enige om en ny indretning, der egner sig til dit mål om DTK.
• Hvis der er for store forskelle på jeres indretningsønsker, så lav en plan for, hvordan indretningen af klasselokalet skal være til de forskellige fag – og lad eleverne være med til at rykke rundt på borde og stole. Hos de største elever kan det fint være en del af en dukseordning at flytte borde.
• Når du laver indretningen om til DTK, så overvej, om du behøver et lærerbord. Måske kan du vælge et nyt bord, hver gang du er i lokalet? På den måde kan du undgå at flytte lærerbordet fra den plads, dine kollegaer ønsker, det skal have.
14 DET TÆNKENDE KLASSERUM I PRAKSIS
Fif
VÆRKTØJSSÆT 2
Denne praksis handler om, hvordan man besvarer elevernes spørgsmål. Hvordan og hvornår kan læreren styrke elevernes læring i sin respons? Hvornår virker det bedst ikke at svare eller at svare anderledes, end eleverne forventer?
Det mest ideelle er, at læreren kun besvarer spørgsmål, der får eleverne til at fortsætte deres tænkning. Den langtidsholdbare læring kræver, at eleven opbygger læringen gennem sine egne tankebaner, mønstre og forståelser. Lærerens opgave er derfor primært at igangsætte, støtte og udfordre i arbejdet med matematiske udfordringer. Dette arbejde kræver tænkning, udholdenhed, samarbejde og tålmodighed, til gengæld er der bundet forståelse og langtidsholdbar læring til processen.
Grundlæggende kan alle spørgsmål fra eleverne til læreren i matematikundervisningen ifølge Peter Liljedahl opdeles i disse tre typer af spørgsmål:
• Stop tænkningen-spørgsmål
• Fortsæt tænkningen-spørgsmål
PRAKSIS 5
Forklar mig, hvilke rkanter I har fundet. 15
Vi får 17. Vi er færdige nu.
Praksis 5 • Hvordan læreren besvarer spørgsmål
• Nærheds-spørgsmål.
Hvordan besvarer man spørgsmålene fra eleverne?
Vi vil vise, hvordan læreren kan agere, når eleverne stiller de tre typer af spørgsmål.
Vi har valgt at tage udgangspunkt i en opgave, der går ud på, at eleverne undersøger, hvor mange kvadrater der kan findes i figuren herunder:
Stop tænkningen-spørgsmål
De fleste elever kommer typisk hurtigt frem til, at der er 17 kvadrater i figuren: De seksten små (1x1-kvadrater) og det store (4x4-kvadratet). Herefter kan det ske, at eleverne stopper deres undersøgelse for at spørge læreren på en af følgende måder:
”Så – nu har vi fundet alle kvadraterne. Der er ikke flere … vel?”
”Vi er færdige nu. Der er 17 kvadrater i alt. Er det ikke rigtigt?”
Denne type spørgsmål kan karakteriseres som stop tænkningen-spørgsmål, fordi de ofte kan besvares med et kort svar, fx ”Rigtigt” eller ”Forkert”. Hvis læreren svarer ”Rigtigt”, er der fare for, at eleverne vil tænke: ”Jamen, så har vi klaret vores del, så kan vi bare slappe af, til de andre er færdige” – og dermed stoppe deres tænkning.
I stedet kunne læreren forsøge at fortsætte deres tænkning ved fx at svare:
Har I overvejet, om der er nogle kvadrater, der har en størrelse, der er mellem det store og de små.”
Læreren drejer om på hælen og går direkte efter spørgsmålet, men vender tilbage når gruppen viser tegn på at de har arbejdet videre og spørger:
Kan I forklare mig, hvilke firkanter I har fundet nu.”
Når eleverne viser den store og alle de små firkanter, som de har fundet, kan læreren stille et nyt spørgsmål, hvis det er nødvendigt. Rækkefølgen for disse 2 spørgsmål er vigtig, der kan du læse mere om i praksis 9.
Ved hvert af de nye spørgsmål, som læreren stiller, skal det overvejes, om læreren kommer til at tænke sammen med gruppen eller ligefrem i stedet for gruppen. Når en lærer opholder sig lang tid ved en enkelt gruppe for at besvare spørgsmål, kan læreren let overtage elevernes tænkning eller komme til at stille alt for ledende spørgsmål.
16 DET TÆNKENDE KLASSERUM I PRAKSIS
VÆRKTØJSSÆT 2
I de fleste situationer vil det være mere effektivt for elevernes tænkning hurtigt at stille et spørgsmål med passende åbningsgrad, bede gruppen om at arbejde videre og så vende tilbage til gruppen, når de har nye svar. Læreren kan næsten altid svare:
Undersøg, om der er en af de andre grupper, der har fundet andre kvadrater end jer.”
De fleste lærere vil naturligvis helst kun give dette svar, hvis de ved, at en af de andre grupper har et andet svar, men det er generelt en god idé at få grupperne til at tale sammen. Alternativt kan man bare sige: ”Prøv at undersøge, om de andre grupper har samme svar som jer.”
Læreren kan også spørge eleverne:
Er I så sikre, at I tør vædde med mig?”
Læreren skal dog kende sine elever rigtigt godt for at være i stand til at besvare et spørgsmål på denne måde, så ikke også dette svar kommer til at stoppe elevernes tænkning. Hvis eleverne med det samme siger “Ja”, giver svaret jo ikke anledning til, at de tænker videre over opgaven. Hør evt. en podcast om emnet på vores hjemmeside.
I nogle tilfælde kan man bare undlade at besvare gruppens spørgsmål eller komme med et kontrasvar:
Det tror jeg nu godt, at I kan finde ud af. Prøv igen.”
Hvis læreren besvarer gruppens spørgsmål med et nyt spørgsmål, fx: Okay, har I overvejet, om der er andre typer firkanter?”, kan det være hensigtsmæssigt, at læreren i samme øjeblik bevæger sig væk fra gruppen, da det oftest afføder flere spørgsmål rettet til læreren. Her kan den såkaldte ”smil-og-smut-manøvre” (udøves præcis, som det skrives) benyttes.
Til usikre grupper, der har brug for støtte til at forblive i tænkning, kan man udvide smil-smut og benytte ros/berolig – smil-smut, der kan foregå på denne måde: “Det har jeg tillid til, at I både selv kan undersøge og vurdere, men der kan være noget, som I har overset.”
Denne type ikke-svar kan med tiden få den virkning, at eleverne fortsætter deres tænkning, når de stiller læreren stop tænkningen-spørgsmål. Det kan også betyde, at eleverne faktisk hen ad vejen stiller færre af disse spørgsmål.
Efterhånden som lærere får erfaringer med at arbejde med DTK, vil de ofte blive bedre til at vide, hvilken taktik der er mest hensigtsmæssig til at få eleverne til at tænke videre i situationen.
17
PRAKSIS 5
Fortsæt tænkningen-spørgsmål
Der er selvfølgelig også spørgsmål, der bliver stillet, fordi eleverne reelt sidder fast i opgaven og ikke kan komme videre med den. Disse spørgsmål kaldes fortsæt tænkningen-spørgsmål. De vil ofte være kendetegnet ved en form for frustration eller panik, fordi gruppen reelt er frustreret over, at de ikke kan komme videre i deres matematiske tænkning.
”Vi har fundet de 16 små kvadrater, det store, 4 mellemstore, det mellemstore i midten. Vi kan ikke finde flere.”
Hertil kan læreren svare:
Prøv at tælle kvadraterne på en anden måde, så opdager I måske flere kvadrater.”
I kan også forklare en af de andre grupper, hvad I har gjort. Så finder I måske frem til flere kvadrater – altså hvis der er flere.”
Måske siger eleverne:
”Vi har fundet alle kvadraterne på nær et enkelt, og vi kan ikke finde ud af, hvilket der mangler.”
Her er det selvfølgelig interessant, hvordan gruppen ved, at der mangler et kvadrat. Det kan være, at de har fundet det på nettet, eller at de har fundet ud af det fra en anden gruppe. Uanset hvad det skyldes, vil det ofte være hensigtsmæssigt at få gruppen til at gennemgå deres løsninger. Derfor vil det som regel være en god idé at få gruppen til at vise deres løsninger til en anden gruppe. Dette kan både få dem op på et højere engagementsniveau og få dem til at tænke grundigere over matematikken og måske endda få dem til at finde det sidste kvadrat, hvis der rent faktisk er et kvadrat, der mangler.
Et eksempel på fortsæt tænkningen-spørgsmål kunne også være en gruppe, der har fundet alle kvadraterne og er sikre på disse og derfor ikke kommer videre med deres matematiske tænkning.
”Vi har fundet alle 30 kvadrater, og vi er helt hundrede procent sikre på, at der ikke er flere.” Til det kan læreren svare:
Så vil jeg ikke vædde med jer, jeg ændrer reglerne. I får en ny opgave.”
Denne gruppe kunne naturligvis også bruges til vise deres løsninger til en anden gruppe. Det er lærerens job at mærke efter, hvad der kan forstærke gruppernes matematiske tænkning i situationen. Læs mere i praksis 9.
18 DET TÆNKENDE KLASSERUM I PRAKSIS
VÆRKTØJSSÆT 2
Nærheds-spørgsmål
Når klasser arbejder med DTK og med opgaven om antallet af kvadrater, kan læreren hurtigt opdage, hvis der er en eller flere af eleverne, der ser ud, som om de ikke deltager i opgaven. I disse situationer vil den naturlige reaktion være, at læreren nærmer sig eleverne for at finde ud af, hvorfor de ikke er i gang med opgaven.
I sådanne situationer kan nogle elever finde på at stille spørgsmål til læreren for at vise, at de faktisk er i gang med opgaven (selvom det ikke altid er tilfældet). Det kan også være, at en elev gerne vil give op (holde op med selv at tænke) og gå videre til næste opgave, ved at læreren tænker for eleven og giver eleven svaret. I opgaven med kvadraterne kunne det være spørgsmål som:
”Kan vi bare finde de forskellige firkanter og så tælle, hvor mange der er?”
”Må jeg gerne tegne firkanterne og bruge dem til modellen?”
”Vi har tænkt på at dele opgaven op, så vi tager en firkant hver, er det okay?”
Denne type spørgsmål kan være nærheds-spørgsmål, der er karakteriseret ved, at det er spørgsmål, som eleverne typisk ikke ville stille, hvis ikke det var, fordi læreren pludselig var i nærheden. Læreren kan kende disse spørgsmål på, at eleverne bemærker lærerens tilstedeværelse og vupti – så var der lige et spørgsmål. Spørgsmålene bliver dog først nærheds-spørgsmål, hvis de ikke fører til, at eleverne bruger dem til at tænke på matematikken. Derfor er det centralt, at læreren får fulgt op på spørgsmålene og derved får undersøgt, om det er nærheds-spørgsmål. Det kunne eksempelvis ske med følgende svar:
Ja, det er er en god idé , hent mig, når I har undersøgt idéen.”
Hvis læreren svarer på denne måde, er det naturligvis afgørende, at der bliver fulgt op på, om de fortsætter tænkningen ud fra deres spørgsmål. Det er derfor vigtigt at vende tilbage senere, så læreren får understøttet elevernes deltagelse.
Det kan også være en mulighed at følge op på et potentielt nærheds-spørgsmål ved at sige:
Ja, lad mig se, hvordan I har tænkt.”
19
PRAKSIS 5
Herved sikrer læreren sig, at de går i gang med den foreslåede tænkning, men her skal man være opmærksom på, om dette fortsætter, efter at man har forladt gruppen igen. I denne situation skal læreren også være opmærksom på, at der er risiko for at komme til at møde nye stop tænkningen-spørgsmål eller komme ind i et spørgsmåls-loop, hvor læreren kan komme til at overtage elevernes tænkning.
Målet med matematikundervisningen er både at skabe vilkår for tænkning og holde elever i tænkning i gang. Det giver derfor god mening at sætte fokus på, hvordan læreren svarer på disse forskelligartede spørgsmål, og hvilken effekt det har på elevernes selvstændige tænkning. Selv den bedste tænkeopgave kan reduceres til det stik modsatte, hvis læreren besvarer alle de spørgsmål, eleverne måtte stille. Og det er da også lige præcis denne praksis, som udfordrer de fleste lærere, og som kræver øvelse at mestre. Det skyldes bl.a. disse faktorer:
• De fleste lærere har et grundlæggende ønske om og behov for at hjælpe eleverne videre eller forbi forhindringer.
• Mange elever er ikke særligt fejlmodige og tør derfor ikke at afprøve metoder eller tænke over matematikken uden at sikre sig, at de er på rette vej.
• Eleverne har for vane at spørge læreren, men mange lærere har også for vane at besvare alt for mange af de spørgsmål, der kan stoppe elevernes tænkning.
De tre faktorer forstærker hinanden og medvirker til, at denne ændring er svær at praktisere og tager lang tid at lære for de fleste lærere. Forventningen om, hvordan spørgsmål fra eleverne håndteres i et klasserum, er bundet til både forventninger fra eleven, læreren og forældrene. Det er denne uskrevne kontrakt, der skal omskrives. Bedste råd er god tålmodighed og forklaringer undervejs.
• Besvar ikke spørgsmål, der stopper elevernes tænkning.
• Besvar de spørgsmål, der er nødvendige for, at eleverne kan komme til at tænke yderligere over matematikken.
• Hvis du får en fornemmelse af, at et spørgsmål er et nærheds-spørgsmål, så undersøg, om besvarelse af spørgsmålet fører til, at eleverne tænker over matematikken.
20 VÆRKTØJSSÆT 2 DET TÆNKENDE KLASSERUM I PRAKSIS
Fif
Praksis 6 • Måden læreren giver opgaver på
Denne praksis handler om de første 5 minutter af matematikundervisningen. Lærerens mål er at motivere eleverne og få gang i deres tænkning. Hvilket betyder at skabe et godt udgangspunkt for, at eleverne kan involvere sig i de matematiske aktiviteter og kommer til at tænke aktivt selv. I forskning foretaget af Peter Liljedahl viser det sig, at mange elever har svært ved at lytte i mere end 5 minutter, så det er vigtigt, at læreren højst bruger 5 minutter til at starte lektionen. Forskningen viser også, at jo længere intro, des sværere er det for elever at komme i tænkning.
Peter Liljedahls undersøgelser viser, at der er fire grundlæggende pejlemærker, som har betydning for en god start på en undervisningslektion, der understøtter selvstændig tænkning i grupper:
• Introducer den første aktivitet inden for de første 3-5 minutter af timen.
• Introducer aktiviteten med eleverne stående omkring læreren.
• Introducer aktiviteten mundtligt.
• Skriv så lidt som overhovedet muligt på en vertikal flade i din intro.
21 PRAKSIS 6
Det er det, I skal arbejde med. Gå ud i jeres grupper...



