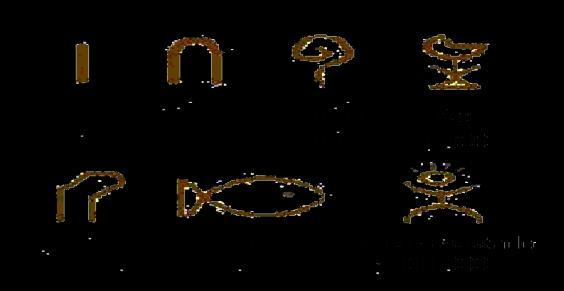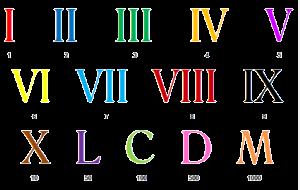El Sistema de Numeración Griego
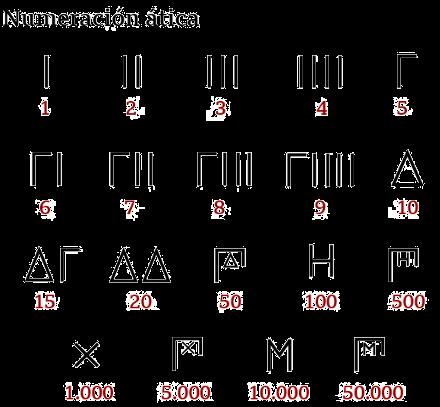
El sistema de numeración másantiguo que usa el alfabeto griego fue la numeración ática, de tipo acrofónico, que funcionaba de forma parecida al romano, que deriva de este sistema a través del etrusco. El primer sistema de numeración griego se desarrolló hacia el 600 A.C.
Para representar la unidad y los números hasta el 4 se usaban trazos verticales.
Para el 5, 10 y 100 las letras correspondientes a la inicial de la palabra cinco (pente), diez (deka) y mil (khiloi). Por este motivo se llama a este sistema acrofónico.
El Sistema de Numeración chino
Era un sistema de carácter decimal. Disponía denueve signosdistintosparalos nueve primeros números, careciendo durante todo el período estudiado de un signo específico para el cero. La forma clásica de escritura de los números en China se empezó a usar desde el 1500 A.C. aproximadamente.
Es un sistema decimal estricto que usa las unidades y los distintas potencias de 10. Utiliza ideogramas, se usa la combinación de los números hasta el diez con la decena, centena, millar y decena de millar, para según el principio multiplicativo, representar 50, 700 ó 3000.
Su numeración está formada por 14 signosfundamentales que designan las nueve unidades y las primeras cinco potencias de 10. Los números se obtienen combinado estos números.
El Sistema de Numeración
Babilónico
El sistema de numeración babilónico era el sistema de numeración sexagesimal (base-60). De aquí se deriva el uso moderno de 60 segundos en un minuto, 60 minutos en una hora, 360 grados en un círculo. En el sistema decimal babilónico, las reglas para representar una cantidad son las siguientes:
a. La cuña con valor 1 se podía repetir hasta un total de nueve veces.
b. Cuando se repiten símbolos se suman sus valores. A la izquierda se escriben los símbolos mayores.
El Sistema de Numeración Maya
Los mayas idearon un sistema de base 20 con el 5 cómo base auxiliar. La unidad se representaba por un punto. El 5 era una raya horizontal, a la que se añadían los puntos necesarios para representar 6, 7, 8 y 9. Para el 10 se usaban dos rayas, y de la misma forma se continúa hasta el 19.
Para representar el 20 se debe de subir un nivel, los números mayas se escriben en una tablita dividida en diversos niveles los cualesvan subiendo de valormientrasmás arriba esté anotado el símbolo.
Así el 20 es representado por un punto, pero en el segundo nivel.
Sistema decimal
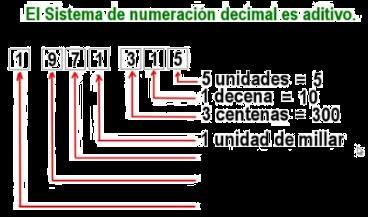
El sistema de numeración decimal es un sistema posicional. Su base es 10, y los símbolos que se utilizan son 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9, que se les llama dígitos. Es el más utilizado. Las operaciones que en él se pueden dar son las aritméticas (suma, resta, multiplicación, división, etc.) y lógicas (Unión - disyunción, Intersecciónconjunción, negación,Diferencia, etc.).Las relaciones entre los números del sistema decimal son mayor que, menor que, igual y a nivel lógico son pertenencia y contenencia.
Cada número decimal consta de una parte entera y una parte decimal que van separadas de una coma. La parte entera va a laizquierda delacoma,ypuedeincluir el cero. La parte decimal va a la derecha de la coma.
Por ejemplo, en el número decimal 1.3 la parte entera es 1 y la parte decimal es 3.
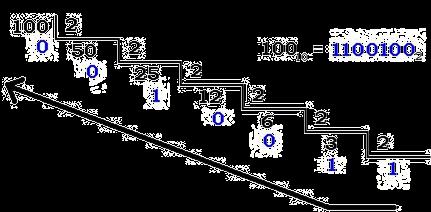
Sistema binario
El sistema de numeración Binario es el conjunto de elementos formado por el 0 y el 1, con operaciones aritméticas (suma, resta, multiplicación) y lógicas (OR, AND y NOT)yademássuspropiasrelacionesque por intermedio de reglas propias permite establecer el papel de tales relaciones y operaciones entre sus dos elementos.
El sistema binario o sistema diádico es un sistema de numeración fundamental en la computación e informática, en el cual la totalidad de los números pueden representarse empleando cifras compuestas por combinaciones de dos únicos dígitos. En el caso del código binario, los dígitos utilizados son ceros (0) y unos (1).
Sistema octal
El sistema octal es el sistema de numeración posicional cuya base es igual 8, utilizando los dígitos indio arábigos: 0, 1, 2, 3, 4, 5, 6, 7. En informática a veces se utiliza la numeración octal en vez de la hexadecimal. Tiene la ventaja de que no requiere utilizar otros símbolos diferentes de los dígitos.
Cuando se cuenta en este sistema, la secuencia es desde 0 hasta 7. Las operaciones aritméticas son las mismas de cualquier sistema numérico.
Para indicar que un número está escrito en base 8, usamos el subíndice (8), y para indicar que un número está escrito en base 10, usamos el subíndice (10).
Ejemplos: 13(8) = 11(10). 25(8) = 21(10)
Los números octales se denotan mediante el subíndice 8 o la letra o.
Sistema hexadecimal
Hexaprovienedelgriegoysignifica“seis”, mientras que decem es la palabra latina para“diez”.Elsistemahexadecimales,por lo tanto, un sistema de numeración posicional que tiene como base el 16. Esto quiere decir que el sistema hexadecimal utiliza 16 dígitos diferentes.
El sistema de numeración hexadecimal es el conjunto de elementos formado por los números del 0 al 9 y las letras A, B, C, D, E y F, siendo este último el de mayor valor (representando el 15 decimal) y el de menor valor el 0, el conteo se hace en la secuencia de 0 a F.
Ejemplo:
El sistema de numeración azteca
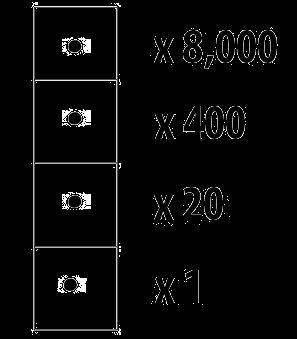
Para los aztecas la forma de contar consistıa en representar a la unidad mediante un punto; con una raya se agrupan los puntos de cinco en cinco. En cada posición o bloque se encontraban hasta 20 y con la ayuda de una bandera, el cabello o la bolsa colocados a la izquierda se agrupaban cantidades mayores.
Propio del imperio mexica, tenía la veintena como base (20) y empleaba objetos concretos como símbolos: una bandera equivalía a 20 unidades, una pluma o unos cabellos equivalían a 400, una bolsa o costal a 8000, entre otros.
Números racionales
Los números racionales se simbolizan por el símbolo ℚ, derivado de la palabra «quotient», que significa cociente en latín. Por lo tanto, cualquier número que pueda escribirse en la forma (a/b), donde (a) y (b) son enteros y b es diferente de 0, es considerado un número racional.
El conjunto de los números racionales se denota por, que significa «cociente». Este conjuntodenúmerosincluye a losnúmeros enteros decimales y a las fracciones. Una fracción s un cociente entre dos números enteros, a y b, llamados numerador y denominador, respectivamente.
Los números racionales incluyen fracciones propias e impropias, números mixtos y decimales finitos o periódicos.
Ejemplos:
Sistema de numeración romana
Los números romanos son un grupo de símbolos formado por letras mayúsculas que idearon los antiguos romanos para representar valores y cantidades.
Cada cifra está representada con una letra o combinación de letras que, dependiendo de la posición en la que se encuentren, añadirá o restará valor al monto total.
Los números se escriben como combinaciones de letras.
Por ejemplo:
El año actual, 2024, se escribe numéricamente como MMXXIV, en donde cada M representa mil unidades, cada X representa diez unidades y, finalmente, IV representa 4 unidades más (al ser V, que representa el 5, precedido por I, que representa el 1).
Los números cardinales
Un número cardinal o cardinal es una generalización de los números naturales para contar el número de elementos, la cardinalidad, de cualquier conjunto, finito o infinito. El cardinal de un conjunto finito es un número natural ordinario.
Cuando usamos los números naturales para contar los elementos de un determinado conjunto los llamamos números cardinales.
La Numeración Arábiga
El sistema arábigo de numeración cuenta con diez signos llamados dígitos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), cuyo valor se determina por la posición que ocupan dentro del número representado. Así, en 776 el primer dígito equivale a 700; el segundo, a 70, y el tercero, a 6.
Es el sistema más extendido y utilizado en laactualidad,ya que presenta laventajade poder generar con muy pocos signos, de forma inequívoca y concisa, una serie ilimitada de números. Las cifras que componen un número se escriben seguidas, formando un solo grupo: 12 (doce), 127 (ciento veintisiete), 3479 (tres mil cuatrocientos setenta y nueve).
Números ordinales
En matemática, un ordinal es un número que denota la posición de un elemento perteneciente a una sucesión ordenada. En muchas ocasiones es necesario dar un orden a las cosas: lasposicionesfinalesde una carrera o los pisos de un edificio son algunos ejemplos.
Cuando usamos los números naturales para este ordenar los llamamos ordinales.
Los números ordinales se escriben mediante un signo que los acompaña y distingue de los cardinales: el signo de grados (°). Así, por ejemplo, el número uno (1) pasa a ser el primero (1°). Es posible que dicho símbolo sea sustituido por una letra“a”envoladita (a) cuando haga falta distinguir el género femenino del referente: primera (1a).
Por otro lado, los nombres de los números ordinales se forman a través del uso de sufijos específicos, que sirven para expresar una noción de cantidad determinada. Estos sufijos cambiaron mucho a lo largo de la historia del idioma y por eso hoy en día pueden resultarnos extraños. Los principales sufijos son:
ero/era, empleado en los primeros de los ordinales, como en primero (1°) o tercero(3°).
to/ta,elmáscomúndelossufijosentre los ordinales, como en quinto (5°) o sexto(6°).
eno/ena, incorporado en el español medieval pero perdido excepto en el casodenoveno(9°).
avo/ava, utilizado únicamente para los númerosfraccionarios.Porejemplo:un catorceavo(1/14).
ésimo/ésima, empleado únicamente para las decenas ordinales: décimo (10°),vigésimo(20°),etcétera.
El hombre siempre se ha visto en la necesidad de cuantificar las cosas para llevar un control sobre estas, desde entonces se han creado numerosas formas de hacerlo. En la actualidad el sistema numérico decimal es el más usado en la vida diaria para resolver cualquier problema matemático debido a su simplicidad y su agrupación de grandes cantidades en pocos espacios.
Al hablar de los sistemas numéricos, tenemos claro que son cualquier sistema puramente compuesto por números o símbolos que representan números, y que son útiles en nuestra vida diaria. Sin embargo, hay momentos donde utilizaremos como base cierto sistema, pero que al aplicarlo en diferentes áreas de nuestra vida y en especial en la tecnología necesitamos convertir nuestro sistema numérico base a otro sistema que quizás no conocemos del todo.
Es por ello, que en este trabajo se investigó y se plasmó la información más importante que caracteriza a cada sistema, para que al momento de necesitar utilizar cualquiera de ellos, podamos implementarlo a nuestra vida de la manera correcta y así obtener resultados satisfactorios.
RIFFRAN, Natalia. Abril 1999. “Sistemas numéricos”. Monografías.com. México. [Publicación electrónica]. Disponible desde internet en: <http://www.monografias.com/trabajos3/sistnumer/sistnumer.shtml
CASADO,Santiago.10demayodel2000.“Lossitemasdenumeraciónalolargode lahistoria”.Redtelemáticadeeducaciónenandalucia.España(Andalucia)[Revistae electrónica]. Disponible desde internet en: <http://thales.cica.es/rd/Recursos/rd97/Otros/SISTNUM.html#G>
https://www.sutori.com/es/historia/los-sistemas-de-numeracion-a-lo-largo-de-lahistoria 4Mtg35nmK8EgeJ8Fa5BJL51w
GOMEZ, Virgilio. 1999. “Sistemas numéricos” Hecho en Mexico [Publicación electrónica]. Disponible desde internet en: <http://www.modelo.edu.mx/univ/virtech/prograc/cbyn01.htm>
FLOYD,Thomas.Fundamentosdesistemasdigitales.7ªediciónPrenticeHall.Santa FédeBogotá.2000.
MANO,Morris.DiseñoDigital.PrenticeHall.México.1987.
https://www3.gobiernodecanarias.org/medusa/edublog/aulacentroconvivencialparam enorescongravesproble/2020/05/13/