Europese temperatuurreeksen: homogenisatie, onzekerheid en impact op de trend

Europese temperatuurreeksen: homogenisatie, onzekerheid en effecten voor trends

Antonello Squintu (WUR, KNMI), Gerard van der Schrier (KNMI), Else van den Besselaar (KNMI), Eveline van der Linden (KNMI), Albert Klein Tank (WUR, Hadley Centre)

Warmt Europa overal even snel op? Hoe bijzonder zijn de temperatuurextremen die we de afgelopen jaren hebben gezien, en hoe betrouwbaar is de schatting in de afname van het aantal vorstdagen in heel Europa? Om deze vragen te beantwoorden, moeten we gebruik maken van lange en betrouwbare temperatuurreeksen. In dit artikel wordt beschreven hoe de meetreeksen in de Europese dataset ECA&D homogeen gemaakt worden, wat de betrouwbaarheid van deze aanpassing is en wat de impact is op trendberekeningen.

Inleiding

Alle lange meetreeksen kennen inhomogeniteiten. Verplaatsingen van een station, verandering in de meetapparatuur of in de methode waarop een meting gedaan wordt, of veranderingen in de directe omgeving van het station zoals de bouw van een naburig huis of een groeiende bomenrij, introduceren breuken in een meetreeks. Soms leiden deze inhomogeniteiten tot herkenbare sprongen in de temperatuur, maar vaak betreft het vrij subtiele verstoringen van de reeks. Het is bijvoorbeeld mogelijk dat de verstoring alleen een deel van jaar herkenbaar is, of alleen in de minimum- of maximumtemperatuur, of zelfs afhankelijk is van de temperatuur zelf! Het punt is dat een betrouwbaar historisch perspectief van temperatuurvariaties zoveel mogelijk vrij moet zijn van dit soort verstoringen; het is immers niet de bedoeling om in een analyse van klimaatverandering het klimaatsignaal te verwarren met bijvoorbeeld een stationsverplaatsing. In dit artikel nemen we een grote verzameling Europese Figuur 1. Temperatuurreeksen in ECA&D. De kleurcodering geeft de lengreeksen met dagwaarden van temperatuur onder de loep. te van de reeks aan. Daarvan bepalen we óf en wanneer er inhomogeniteiten in de reeksen zitten om vervolgens de reeksen aan te passen en ze het station en op welk soort oppervlak het meetstation staat. homogeen te maken. Nog interessanter wordt het als er gegevens bekend zijn over veranderingen in de omgeving en in bijvoorbeeld de meetapEuropean Climate Assessment & Dataset (ECA&D) paratuur. Op basis van zulke gegevens is vast te stellen of een De one-stop-shop voor meetreeksen voor temperatuur (en inhomogeniteit in de data kan worden verwacht. De meest andere variabelen) uit geheel Europa is ECA&D. Alle Eurobasale metadata zijn vaak direct en makkelijk te verkrijgen, pese meteodiensten leveren dagwaarden aan ECA&D, en maar hoe specialistischer de metadata wordt, des te moeilijker deze worden, mits de eigenaar toestemming heeft gegeven, het wordt om de gegevens boven water te krijgen. De praktijk beschikbaar gesteld voor wetenschappelijk onderzoek. Deze is dat veel meteodiensten deze specialistische metadata wel database bevat gegevens van grofweg 19.000 stations, waarhebben, maar vaak niet in gedigitaliseerde vorm. En als deze van ongeveer 7500 temperatuurgegevens leveren. Figuur 1 informatie al digitaal bestaat, dan is het vaak alleen van de geeft de verdeling van de reeksen over Europa samen met een meest recente periode of alleen van een kleine selectie van indicatie van de lengte van de reeks. Deze kaart geeft al direct stations. aan wat een complicatie is bij deze dataset: er is geen gelijke Vanwege de grootte van de dataset en het vrijwel ontbrebedekking van de stations over Europa. Ook de verdeling van ken van de meer specialistische metadata, zijn we gedwongen lange en korte reeksen is niet netjes gespreid over Europa. een methode te ontwikkelen die op basis van statistische testen Hoe dan ook: de temperatuurreeksen van ECA&D zijn de één of meerdere inhomogeniteiten in een reeks herkent en de basis voor het werk dat hier gepresenteerd wordt. meest waarschijnlijke aanpassingen voor die inhomogeniteiten toepast.

Ontbreken van metadata

Van essentieel belang bij deze meetreeksen zijn de januari 1863 – december 1883 Gymnasium Altes Borromäum 424m metadata: gegevens over de data. De meest basale metadata betreffen natuurlijk de positie, de hoogte januari 1884 – juli 1903 Oberrealschule 419m en de naam van het station. Handig is natuurlijk ook augustus 1903 – 28 februari 1941 Studiengebäude- Lehrerbildungsanstalt 423m een stationsnummer waaronder het station bekend 1 maart 1939 – 15 juni 1996 Luchthaven, locatie 1 434m staat. Verder is het voor de interpretatie van de sinds 16 juni 1996 Luchthaven, locatie 2 437m meting van belang om iets te weten over de omgeTabel 1. Beschikbare metadata voor het weerstation Salzburg, Oostenrijk. De rechterving, het landgebruik in de directe nabijheid van kolom geeft de hoogte van het station boven zeeniveau.

Figuur 2. Het meteorologisch station Salzburg in de tuin van de bibliotheek. In 1938 is dit station verplaatst naar het naburige vliegveld.

Hoe het testen in zijn werk gaat aan de hand van het station Salzburg

Een mooi voorbeeld om de werking van de homogenisatie procedure te illustreren is de meetreeks van Salzburg (Figuur 2). Via de Oostenrijkse weerdienst ZAMG is een deel van de meer specialistische metadata bekend die we gebruiken om de statistische testen te valideren. Tabel 1 geeft de beschikbare metadata van Salzburg weer.

Breukdetectie De eerste stap is om eventuele breuken in de reeks op te sporen; de meest gebruikte test hiervoor is de Standard Normal Homogeneity Test (SNHT). Het principe achter deze test is eenvoudig: om te testen of de reeks van jaargemiddelde temperatuur een breuk heeft in jaar k wordt de reeks in de twee delen rondom dit jaar gesplitst waarbij jaar k in het eerste deel valt. De cumulatieve afwijking ten opzichte van het gemiddelde van de hele reeks wordt berekend voor beide delen en gedeeld door de standaarddeviatie van de reeks en de lengte van de deelreeks (dus k voor het eerste deel en n-k voor het tweede deel). Als de breuk in jaar k valt dan zal de eerste som veel groter zijn dan de tweede, en dit gegeven wordt gebruikt om de breuk te detecteren. Het nadeel van deze aanpak is duidelijk: een reeks met een trend wordt al snel als inhomogeen gekwalificeerd. De voor de hand liggende aanpassing is om een relatieve test te doen waarbij het verschil tussen de te testen reeks en een homogene referentiereeks door de SNHT gehaald wordt. Met het gebruik van een referentiereeks wordt het klimaatsignaal weggefilterd en is een mogelijke breuk eenvoudiger te herkennen. Merk op dat een elegante alternatieve aanpak is om jaar k uit te sluiten van de analyse (zoals gedaan is in een studie van De Bilt temperaturen, zie Meteorologica nr. 4, 2019). De methode die we hier gebruiken is gebaseerd op het werk van Kuglitsch et al. (2012) die drie geavanceerdere testen dan de SNHT toepassen en vervolgens overeenstemming tussen twee van de drie testen als criterium gebruiken voor een mogelijke breuk. De testen worden toegepast op jaarlijks gemiddelden, maar ook op gemiddelde temperaturen voor het winter- en zomerhalfjaar. Onze automatische breukdetectie detecteert alle breuken in de reeks van Salzburg die veroorzaakt zijn door verplaatsingen, behalve de meest recente die waarschijnlijk een erg kleine breuk veroorzaakt heeft (vanwege slechts 3 m hoogteverschil). Er worden wel een paar extra breuken gedetecteerd waarvoor de bekende metadata geen aanleiding geven. De gebruikte testen zijn vrij conservatief, wat betekent dat deze metadata waarschijnlijk onvolledig zijn. Voor het vervolg van dit voorbeeld richten we ons op de breuk rond 1938 die gerelateerd is aan het continueren van het station op 1 maart 1939 op het nabijgelegen vliegveld.

Referentiereeksen Voor het bepalen van de aanpassingen in de temperatuur rondom een breuk zijn referentiereeksen (homogene reeksen van naburige stations) noodzakelijk. Aangenomen wordt dat het statistische karakter van de verschilreeks tussen de kandidaatreeks (de reeks die gehomogeniseerd moet worden) en de referentiereeks aan beide zijden van de breuk na correctie gelijk moet zijn. Bij het zoeken naar homogene referentiereeksen worden de resultaten van de breukdetectie gebruikt. Elke temperatuurreeks is dan te verdelen in homogene sub-reeksen, gescheiden door de gedetecteerde breuken. Zo’n sub-reeks wordt pas gebruikt voor het aanpassen van de kandidaatreeks als er ten minste vijf jaar overlap is (aan beide zijden van de breuk). Elke kandidaatreeks wordt zo door een groot aantal referentiereeksen omgeven, waarbij we alleen de homogene delen van een reeks gebruiken (de delen tussen de breuken) als de correlatie R tussen kandidaat en referentie groter is dan 0.6 én als het hoogteverschil beperkt is én als de horizontale afstand tussen de stations van de referentie- en kandidaatreeks niet groter is dan 1000 km. Voor de 1938-breuk in Salzburg vinden we op deze manier 12 geschikte referentiereeksen. Merk op dat deze criteria vrij ruim zijn; het is niet te verwachten dat de

Figuur 3. Histogram en waarschijnlijkheidsverdeling van de aangepaste minimumtemperatuur in mei voor de 20 jaar voorafgaand aan 1938 (blauw) en de 20 jaar volgend op 1938 (rood). De lichtblauwe en lichtrode lijnen geven de originele verdeling. Het onderste deel van de figuur geeft de kwantielfuncties gerelateerd aan de verdelingen van het hoofdfiguur.

Figuur 4. Schattingen van de aanpassingen voor mei voor het station Salzburg voor de breuk in 1938, als functie van het kwantiel. De inzet geeft de ligging van Salzburg (rode stip) en de omliggende stations (met hun ID-nummer) die gebruikt zijn om de aanpassing te berekenen.

referentiereeks een getrouwe kopie is van de kandidaatreeks. De methode gebruikt de verwachting dat het verschil tussen de reeksen, in statistische zin, stationair in de tijd is.

Quantile-matching Figuur 3 illustreert de aanpak om de 1938-breuk in de reeks van Salzburg te corrigeren. Voor elke maand afzonderlijk worden de waarschijnlijkheidsverdelingen gemaakt van de temperatuurwaarnemingen voor en na de breuk. Aan de hand van het verschil voor elk kwantiel tussen de kandidaatreeks en de mediaan van de referentiereeksen wordt een aanpassing van het deel van de kandidaatreeks voor de breuk bepaald. Het oudere deel van de reeks wordt dus aangepast. Het aanpassen

c

Figuur 5. Jaarlijks gemiddelde minimumtemperatuur te Salzburg. De zwarte lijn geeft de originele reeks, de blauwe lijn geeft de eerste iteratie in het homogenisatieproces, de rode lijn geeft de tweede iteratie. De verticale lijnen geven de breukdetecties in de eerste (blauw) en tweede iteratie (rood).

van de reeks naar het meest recente deel is geïnspireerd door de verwachting dat de moderne metingen preciezer zijn dan de oude, maar deze benadering maakt vooral het aanvullen van de reeks met nieuw binnenkomende data veel gemakkelijker. In het geval van meerdere breuken in een reeks, wat meer regel dan uitzondering is, wordt begonnen met het aanpassen bij de meest recente breuk en wordt stapsgewijs terug in de tijd gewerkt door de eerdere stappen (breukdetectie, referentiereeksen) te herhalen. Figuur 3 maakt duidelijk dat de waarschijnlijkheidsverdeling van de kandidaatreeksen voor en na de breuk – dus nadat de aanpassing is toegepast – veel meer op elkaar lijken. Het bepalen van de aanpassingen van de reeks voor elke maand en elk kwantiel afzonderlijk is gevoelig voor

e

d

f

Figuur 6. Kaarten met trend in jaarlijks gemiddelde minimumtemperatuur (boven: a, c, e) en maximumtemperatuur (onder: b, d, f) over de periode 1961 – 2010. De kolom links (a, b) geeft de originele trends, voor de homogenisatie, de middelste kolom (c, d) geeft de trends na de homogenisatie en de rechterkolom (e, f) geeft het verschil (na minus voor). Blauwe cirkels staan voor een negatieve waarde, rode voor een positieve waarde en de grootte van de cirkel relateert aan de grootte van het signaal. Dikgerande cirkels staan voor trends die het significantieniveau van 95% halen.

Figuur 7. Geografische verdeling van de benchmark en testdata (groene stippen), de verstoorde reeksen (zwarte stippen) en de homogene referentie reeksen (paarse stippen). Voor de Europese situatie liggen de zwarte stippen onder de groene (en zijn niet zichtbaar).

ruis. Om dit te onderdrukken worden de aanpassingen, voor toepassing op de reeks, gefilterd door een eenvoudig gemiddelde te nemen van de aanpassing zelf, en van de twee aanpassingen van naburige maanden en van naburige kwantielen. Figuur 4 geeft de grootte van de kwantielaanpassingen voor de 1938-breuk voor elk van de 12 referentiereeksen. Voor deze breuk geldt blijkbaar dat de aanpassingen voor elk kwantiel ongeveer gelijk zijn. Voor elk kwantiel en voor elke maand wordt de mediaanwaarde van de referentiereeksen genomen in de aanpassingen van de kandidaatreeks. Hierdoor heeft de homogeniteitsaanpassing ook een seizoenscyclus. Door deze aanpassingen zullen er langere homogene sub-reeksen ontstaan die als referentiereeks kunnen dienen voor andere stations. Bij een tweede iteratie van breukdetectie en homogenisatie zullen vooral in het vroegere deel van de dataset, wanneer de stationsdichtheid lager is, meer breuken gedetecteerd en aangepast kunnen worden. Dit effect is goed te zien in Figuur 5 voor de originele reeks (zwart), na de eerste iteratie (blauw) en na de tweede iteratie (rood). De tweede iteratie geeft twee nieuwe breuken in het vroege deel van de reeks.

Toepassing op de hele dataset

Het effect van het toepassen van deze procedure op de hele Europese dataset is te zien in Figuur 6. Deze figuur laat de trends zien in de jaarlijks gemiddelde minimum- en maximumtemperatuur over de periode 1961 – 2010. De trend is berekend met Sen's slope (dit is een meer robuuste manier van trend bepaling dan de standaard lineaire regressie doordat het veel minder gevoelig is voor outliers). Breuken in reeksen zullen direct effect hebben op de grootte van de trend, en de verwachting is dus dat de homogenisering vooral zichtbaar wordt in trends. De Figuren 6a en 6b laten de trends zien voor de homogenisering, waarbij duidelijk een aantal stations zichtbaar zijn met een (veel) grotere of kleinere trend dan omliggende stations of zelfs met een negatieve trend. Na homogenisatie (panelen c en d) is dit beeld veel gelijkmatiger, wat conform de verwachting is bij het beoordelen van trends – zij het dat een aantal stations nog steeds enigszins uit de toon vallen. De twee rechterpanelen van Figuur 6 (e, f) geven het verschil tussen de trends voor en na de homogenisatie. De twee rechterpanelen geven duidelijk aan dat stations aangepast worden zowel naar een situatie met een grotere temperatuurtrend (de rode cirkels) als een kleinere temperatuurtrend (de blauwe cirkels).

Figuur 8. Scatterdichtheid plot van de parameter. Op de x-as staat de homogenisatie-index voor de trend in jaargemiddelde 10 e percentiel van minimumtemperatuur. Op de y-as de homogenisatie index voor jaargemiddelde trends in de minimumtemperatuur. Bij het punt (1, 1) worden beide trends juist ingeschat. Bij (1, 0) is de trend over jaargemiddelde Tmin goed, maar die in de koude nachten niet. Bij punt (0, 1) is het omgekeerde het geval. De gekleurde punten geven de resultaten van de verschillende meetreeksen en de gekleurde lijnen omcirkelen het gebied waar de helft van de reeksen zich bevinden. De kleurcodering relateert aan de quantile-matching methode (de rode contour) en de vijf alternatieven. De linkerfiguur heeft betrekking op de Tsjechische benchmark dataset, het rechter op de Europese benchmark dataset.

b

d

f

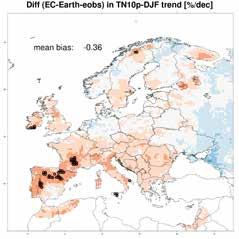
Figuur 9. Vergelijking tussen resultaten van het EC-Earth klimaatmodel op T799 resolutie met E-OBSv19.0eHOM. De bovenste rij (a, c, e) geeft resultaten voor de minimumtemperatuur in de winter (DJF), de onderste rij (b, d, f) voor de maximumtemperatuur in de zomer (JJA). De linkerkolom (a, b) geeft de bias van het model weer, de middelste kolom (c, d) geeft het verschil in trend (over de periode 1961 – 2010) van seizoensgemiddelde minimum- en maximumtemperatuur, en de rechterkolom (e, f) geeft de trend (over 1961-2010) in het aantal koude nachten of warme dagen. De zwart omrande cirkels zijn de plaatsen waar het trendverschil significant is tot op het 95% niveau.

Hoe goed is deze methode? de gerelateerd aan de benchmark (het beoogde doel) en tst is Hoe vergelijkt deze methode om temperatuurreeksen te homohet startpunt (de test-dataset). Als homind = 0, dan heeft de geniseren met andere methoden? Om dit uit te zoeken hebben homogenisatie geen enkel effect gehad. Als homind = 1, dan we een vergelijking gemaakt tussen deze quantile-matching is de homogenisatie perfect. Is de waarde groter dan 1, dan is methode en vijf andere populaire methoden. Hiervoor is er een overshoot in de aanpassingen, en waarden tussen 0 en 1 gebruik gemaakt van twee datasets, een voor Europa en een geven een undershoot aan. Negatieve waarden geven aan dat voor Tsjechië, waarvan we precies weten welke inhomogede breuk alleen maar erger is geworden door de aanpassing. niteiten deze bevatten, de zogenaamde benchmark datasets. Het succes van de verschillende methodes kan gevisualiDe Tsjechische dataset is een bijna-ideale situatie waar de seerd worden door de testdatasets voor Tsjechië en Europa te stationsdichtheid erg hoog is en de set uit homogene reeksen homogeniseren en voor elke gecorrigeerde reeks de parameter bestaat. Bij een klein percentage van de dataset (willekeurig te berekenen. In dit geval worden de trendwaarden gebruiken gekozen en minder dan 10%) is een inhomogeniteit geïntrovoor de berekening van homind. Figuur 8 laat de vergelijking duceerd. Dit is gedaan door het recente deel van de reeks zien voor op basis van trends in de jaargemiddelde minimumte verwisselen met een naburige reeks (de zwarte stippen in temperatuur en voor homind op basis van trends in het 10 e Figuur 7). Meer dan 200 homogene reeksen zijn beschikbaar percentiel van de dagelijkse minimumtemperatuur. Deze twee (de paarse stippen) om de homogenisatie mogelijk te maken. -waarden worden geplot in een scatterplot en de hoop is nu Een grotere uitdaging vormt de Europese benchmark dataset: dat de scatterpunten rondom het punt (1, 1) gegroepeerd zijn. hier is de stationsdichtheid veel lager gehouden wat beter De dichtheid van de wolk scatterpunten zal afnemen verder overeenkomt met de werkelijkheid. weg van het punt (1, 1), en de contourlijn geeft de grens van De methode die gebruikt wordt om het succes van de het gebied waarbinnen de meeste scatterpunten liggen (en de homogenisatie te kwantificeren is de “homogenisatie indidichtheid gehalveerd is). catie”; een eenvoudige methode om het verschil tussen de Figuur 8 laat zien dat voor de Tsjechische dataset alle aanpassingen en het beoogde doel in een getal te vangen: populaire homogenisatiemethoden erg goed presteren. De contourlijnen van de verdeling liggen allemaal dicht rondom hom������������=1− ℎ��������−������������ (1, 1). Blijkbaar maakt het niet zoveel uit welke methode je ������������−������������ gebruikt als de dataset die je wilt homogeniseren een hoge stationsdichtheid heeft. Voor de Europese dataset is dat anders. Hierbij is hom Hierbij is hom de gehomogeniseerde waarde, ben is de waarDe verdeling wordt veel vlakker en voor een aantal methoden de gehomogeniseerde waarde, ben is de waarde gerelateerd aan de benchmark (het beoogde doel) en tst is het startpunt (de test-dataset). Als hom������������ = 0, dan heeft de homogenisatie Meteorologica 3 - 20208 geen enkel effect gehad. Als hom������������ = 1, dan is de homogenisatie perfect. Is de waarde groter dan 1, dan is er een overshoot in de aanpassingen, en waarden tussen 0 en 1 geven een undershoot aan.

verschuift de verdeling sterk naar het punt (0, 0) wat aangeeft dat de homogenisatie weinig effect heeft. Er zijn methoden te onderscheiden die het beter doen dan andere, maar de belangrijkste opmerking die te maken is, is dat in een situatie waarin de dichtheid van homogene referentiereeksen laag is, alle methodes in meer of mindere mate moeite hebben om een betrouwbare homogenisatie uit te voeren.

Toepassing van homogene reeksen

Een belangrijke toepassing van een dataset als ECA&D is om een dataset op een regelmatig rooster gebaseerd op alleen stationswaarnemingen te maken (E-OBS). In deze vorm is het namelijk makkelijk om uitkomsten van een klimaatmodel te vergelijken met waarnemingen, om aldus het model te valideren. In een eerdere studie zijn trends in extreme temperaturen van klimaatmodellen vergeleken met E-OBS (Min et al., 2013). De conclusie was dat klimaatmodellen de trend in de toename van extreme temperaturen sterk onderschatten. Er zijn twee opmerkingen die gemaakt kunnen worden in die vergelijking. De metriek die gekozen is om de extreme temperaturen te kwantificeren, de temperatuur van de heetste dag van het jaar, is heel gevoelig voor toevalligheden tijdens het meten en zijn alleen geldig voor een klein gebied. Het is dan ook te verwachten dat grootschalige modellen deze variabele niet goed kunnen reproduceren. Bovendien is de temperatuur van de heetste dag van het jaar sterk afhankelijk is van de homogeniteit van de meetreeks. De E-OBS versie die Min et al. gebruikt hebben is niet gebaseerd op homogene temperatuurreeksen, waardoor trends in extreme temperatuur niet de correcte reflectie van klimaatverandering is die werd aangenomen. Op basis van de technieken beschreven in deze studie is een nieuwe versie van E-OBS gemaakt. Deze versie interpoleert de gehomogeniseerde temperatuurreeksen van alleen die Europese weerstations die grotendeels ononderbroken zijn over de hele tijdsperiode van E-OBS (1950 – 2019). Deze dataset heet E-OBSv19.0eHOM. De trends in minimum- en maximumtemperatuur van simulaties van het huidige klimaat door de nieuwste generatie hoge resolutie klimaatmodellen zijn vergeleken met de trends uit deze gehomogeniseerde versie van E-OBS. Hierbij vergelijken we niet de trend in de temperatuur van de warmste dag, maar kijken we naar het aantal dagen waarbij de maximumtemperatuur boven het 90 e percentiel (warme dagen) komt (waarbij de drempelwaarde bepaald wordt uit de klimatologische 1981 – 2010 periode). Ook wordt gekeken naar het aantal dagen waarbij de minimumtemperatuur onder het 10 e percentiel zakt (koude nachten). Deze grootheden zijn vanwege het gebruik van de plaatselijke klimatologie niet afhankelijk van de locatie. Figuur 9 geeft de verschillen weer tussen de modelsimulatie van EC-Earth op T799 resolutie (~ 25 km x 25 km) en E-OBSv19.0eHOM, voor de bias in minimum- en maximumtemperatuur, de trend in jaarlijks gemiddelde minimum- en maximumtemperatuur en de trend in het aantal warme dagen en koude nachten. Wat deze vergelijking laat zien, is dat het model overwegend te koud is, dat de trends in seizoensgemiddelde minimum- en maximumtemperatuur eigenlijk vrij goed zijn, maar dat er nog steeds een onderschatting is van trends in de extreme temperaturen in de modellen. Het aantal koude modelnachten in de winter neemt te langzaam af, zeker in Zuid-Europa, en in de zomer wordt de toename in het aantal warme dagen over geheel Europa onderschat.

Ten slotte

Het homogeniseren van de temperatuurreeksen van ECA&D moet, vanwege het ontbreken van relevante metadata ‘blind’ gebeuren en de grootte van de dataset maakt dat het zoeken naar breuken en geschikte referentiereeksen geautomatiseerd moet worden. Dit zijn twee belangrijke handicaps vergeleken met de aanpak die verschillende meteodiensten binnen en buiten Europa gebruiken, waar toegang tot nationale metadata en aandacht voor het uitzoeken van referentiereeksen groter is. Warmt Europa overal even snel op? Het homogeniseren van temperatuurreeksen in Europa leert ons dat de ruimtelijke variatie in trends voor een deel verklaard kan worden door problemen met de reeksen. Heel sterk opwarmende stations bleken onbetrouwbaar, net als stations die opmerkelijk koel bleven in vergelijking met omringende stations. Maar er blijven verschillen – verschillen die wellicht te relateren zijn aan terugkoppelingen binnen het klimaatsysteem en minder samenhangen met veranderingen in opstelling, apparatuur of stationslocatie. Er zijn belangrijke verbeterpunten te maken bij deze studie. Hoewel de gehomogeniseerde dataset de gebruiker minder snel op het verkeerde been zal zetten bij het kwantificeren van klimaatverandering, zou een inschatting van de onzekerheid van de homogeniteitsaanpassing een mooie aanvulling zijn. Het onderzoek hoe zo’n inschatting te maken is, staat nog maar in de kinderschoenen. Ook de keuze van de referentiereeksen is te verbeteren. In een recent afstudeeronderzoek (Bierman, 2019) is geëxperimenteerd met het gebruik van een regionale heranalyse die gedownscaled is naar een ruimteschaal van ongeveer honderd meter. Deze simulatie bleek goed te gebruiken als referentie bij een nagespeelde verplaatsing van een meting uit het Amsterdamse Vondelpark naar het naburige Schiphol, ondanks de bias in de heranalyse-data. Het is dus goed mogelijk dat modellen onmisbaar gaan worden bij het waarborgen van kwaliteit in waargenomen data!

Dankbetuiging

Deze studie is gebaseerd op het promotiewerk van Antonello Squintu, die daarbij geholpen is door Yuri Brugnara (Universiteit Bern), Richard Cornes (Southampton Oceanography Centre), Petr Štěpánek en Pavel Zahradníček (Czech Academy of Sciences) en collega’s uit het PRIMAVERA project.

Literatuur

Biermann, J. (2019), High-resolution reanalysis as reference for homogenization studies – The Amsterdam case -, WUR/KNMI internship report, 23p. Min, E., Hazeleger, W., Van Oldenborgh, G. J., & Sterl, A. (2013). Evaluation of trends in high temperature extremes in north-western Europe in regional climate models.

Environmental Research Letters, 8(1), 014011. Kuglitsch, F. G., Toreti, A., Xoplaki, E., Della‐Marta, P. M., Luterbacher, J., & Wanner, H. (2009). Homogenization of daily maximum temperature series in the Mediterranean.

Journal of Geophysical Research: Atmospheres, 114(D15). Squintu, A. A., van der Schrier, G., Brugnara, Y., & Klein Tank, A.M.G. (2019). Homogenization of daily temperature series in the European Climate Assessment & Dataset.

International journal of climatology, 39(3), 1243-1261. Squintu, A. A., van der Schrier, G., van den Besselaar, E. J., Cornes, R. C., & Klein Tank, A.

M.G. (2020). Building long homogeneous temperature series across Europe: a new approach for the blending of neighboring series. Journal of Applied Meteorology and

Climatology, 59(1), 175-189. Squintu, A. A., van der Schrier, G., Štěpánek, P., Zahradníček, P., & Klein Tank, A.M.G. (2020). Comparison of homogenization methods for daily temperature series against an observation-based benchmark dataset. Theoretical and Applied Climatology, 1-17. Squintu, A. A. van der Schrier, G., van den Besselaar, E.J.M., van der Linden, E., Scoccimarro, E., Roberts, C. and Klein Tank, A.M.G. (2020) Evaluation of trends in extreme temperatures simulated by HighResMIP models across Europe, International journal of climatology (submitted).