MAT. PEDRO DANIEL LARA MALDONADO <@unadmexico.mx>

RV:
Presentación
de la alumna Mercedes Rodríguez Robles Domingo 27 de noviembre del 2022 a las 17:00 pm 1 mensaje
Pedro Daniel Lara Maldonado <@hotmail.com>
18 de diciembre de 2022, 22:06 Para: <@unadmexico.mx>
De: MÓNICA ZAIMA VÍQUEZ CANO <@nube.unadmexico.mx> Enviado: domingo, 27 de noviembre de 2022 06:53 a. m.
Para: PEDRO DANIEL LARA MALDONADO <@nube.unadmexico.mx>; <@hotmail.com>; ALEJANDRA ZAMORA MEDINA <@nube.unadmexico.mx>; Carlos Alberto Serrato Hernández <@nube.unadmexico.mx>; CLAUDIA ISELA ALVAREZ CHAVERO <@nube.unadmexico.mx>;
MANUEL LOPEZ MATEOS<@nube.unadmexico.mx>; MÓNICA ZAIMA VÍQUEZ CANO <@nube.unadmexico.mx>
CC: MERCEDES RODRIGUEZ ROBLES <@nube.unadmexico.mx>
Asunto: Presentación de la alumna Mercedes Rodríguez Robles Domingo 27 de noviembre del 2022 a las 17:00 pm
Estimados miembros del comité evaluador, los convoco a la presentación de la alumna Mercedes Rodríguez Robles
de Proyecto Terminal 1. Dicho proyecto es el resultado de un semestre de trabajo, la alumna dispondrá de un semestre más para concluirlo, por lo que no se espera que aún tenga resultados contundentes, pero sí todo el andamiaje del trabajo, en particular, una buena fundamentación. Les pido lo revisen y hagan los comentarios, observaciones y correcciones que consideren adecuados, podrán hacérmelos llegar a mi correo.
Nos vemos en el seminario de la alumna, el Domingo 27 de noviembre del 2022 a las 17:00 pm. la presentación se llevará a cabo en la plataforma Teams, Enlace de la presentación https://teams.microsoft.com/
Título del trabajo: Uso de modelo estocástico de Cadenas Markovianas para la predicción del rendimiento estudiantil del Cedart "Ignacio Mariano de las Casas" Institución donde se realiza Proyecto: Cedart "Ignacio Mariano de las Casas"
Bienvenida y presentación del comité revisor. Presentación del alumno. 20 minutos de Exposición por parte del alumno. 15 minutos de preguntas. Despedida al comité Evaluador.
…
f%3A17526138594…1/3
19/12/22, 10:21 Correo de Universidad Abierta y a Distancia de Mexico - RV: Presentación de la alumna Mercedes Rodriguez Robles Domingo 27
https://mail.google.com/mail/u/0/?ik=1ce9153c3c&view=pt&search=all&permthid=thread-f%3A1752613859406150792&simpl=msg-
Durante este semestre se requiere que el alumno avance en los siguientes requerimientos, de acuerdo con la plantilla institucional
ÍNDICE Resumen
Contexto y planteamiento del problema Justificación
Objetivos General Específicos
Marco investigativo Marco teórico Metodología
Desarrollo capitular Cronograma Referencias Anexos
Lista de Figuras
Lista de tablas
También se debe de considerar que por indicaciones de la Coordinación Académica y de Investigación, y de conformidad con la Ley General de Educación Superior, los proyectos terminales y prácticas profesionales deberán apegarse a alguno de los siete enfoques de la visión social enlistados a continuación.
• Perspectiva de género
• Atención a la diversidad
• Fortalecimiento de la ciudadanía
• Fomento a la cultura de la legalidad
• Uso racional de los recursos naturales
• Economía naranja
• Promoción ética-eficiente de las tecnologías de la comunicación e información y redes sociales Por lo anterior, se debe revisar que el proyecto tenga una justificación de los enfoques antes enlistados.
19/12/22, 10:21 Correo de Universidad Abierta y a Distancia de Mexico
Mercedes Rodriguez Robles Domingo 27 …
f%3A17526138594…2/3
- RV: Presentación de la alumna
https://mail.google.com/mail/u/0/?ik=1ce9153c3c&view=pt&search=all&permthid=thread-f%3A1752613859406150792&simpl=msg-
19/12/22, 10:21 Correo de Universidad Abierta y a Distancia de Mexico - RV: Presentación de la alumna Mercedes Rodriguez Robles Domingo 27
Comité Evaluador
Alejandra Zamora Medina
Asesor externo: Lic. Matemático Pedro Daniel Lara Maldonado
Agradezco su disposición y compromiso con la revisión de este proyecto terminal. Cualquier duda quedo atenta. Saludos cordiales
Docente en Línea: Mónica Zaima Víquez Cano Proyecto Terminal I Carrera matemáticas
Universidad Abierta Y A Distancia De México. Anteproyecto_MPTE1_Etapa3_MERR (1).pdf 10537K
f%3A17526138594…3/3
… https://mail.google.com/mail/u/0/?ik=1ce9153c3c&view=pt&search=all&permthid=thread-f%3A1752613859406150792&simpl=msg-
Universidad Abierta y a Distancia de México Coordinación Académica y de Investigación
División de Ciencias Exactas, Ingeniería y Tecnología Programa educativo
PROYECTO TERMINAL

INFORME GENERAL DE RESULTADOS
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
Universidad Abierta y a Distancia de México
Rectora
Lilian Kravzov Appel
Coordinadora Académico y de Investigación Edgar Alcantar Corchado
Dirección de Ciencias Exactas, Ingeniería y Tecnología Dolores Alejandra Vasquez Carbajal
Responsable del Programa Educativo Carlos Alberto Serrato Hernández
Docente en línea Mónica Zaima Víquez Cano
Autor del proyecto Mercedes Rodríguez Robles
IMPORTANTE
Excepto donde el contenido así lo especifique, esta obra está bajo una Licencia de Creative Commons
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
Material desarrollado y/orecopilado con fines educativos por académicos externos a la Institución, perteneciente a la DCEIT de la Universidad Abiertay a Distancia de México (UnADM) Ciudad de México, 2022.
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1 DIVISIÓN DE CIENCIAS EXACTAS, INGENIERÍA Y TECNOLOGÍA Proyectoterminal I Uso del modelo estocástico de Cadenas Markovianas para la predicción de rendimiento estudiantil del Organización: Mercedes Rodríguez Robles ES1821016580 Nivel educativo:Licenciaturaen Matemáticas Asesor externo: Lic. Matemático Pedro Daniel Lara Maldonado Periodo de realización: Mes año de inicio: julio 2022 Mes año final: diciembre 2022 Santiago de Querétaro, Qro. Diciembre 2022
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1 ÍNDICE ÍNDICE....................................................................................................................5 RESUMEN..............................................................................................................7 CAPÍTULO 1...........................................................................................................8 Introducción....................................................................................................................................8 1.1 Contexto y planteamiento del problema..................................................................................9 1.2 Objetivos...................................... ........................................13 1.2.1 General.............................................................................................................................13 1.2.2 Específicos.................................. ...................................13 CAPÍTULO 2 Marco Investigativo..........................................................................14 2.1 Rendimiento Escolar...............................................................................................................14 2.2 Institución de la investigación.................................................................................................15 2.2.1 Prueba Planea................................ ...............................16 2.2.2 Resultados planea de rendimiento escolar......................................................................24 2.3 Cadenas de Markov.................................................................................................................25 2.3.1 Antecedentes................................. ...............................25 2.3.2 Definición.........................................................................................................................26 2.3.3 Desarrollo de las cadenas de Markov.......... .................27 2.3.4 Clasificación de estados de las cadenas de Markov.........................................................31 2.3.5 Teoría de grafos................................................................................................................33 2.3.6 Software de Aplicación....................... ...........................38 2.4 Metodología............................................................................................................................38 2.4.1 Investigación cuantitativa................................................................................................38 2.4.2 Diseño de la investigación................... ..........................39 2.4.3 Participantes.....................................................................................................................39 2.4.4 Variables de estudio......................... .............................39 CAPÍTULO 3 Resultados......................................................................................42 3.1 Actividades desarrolladas...................... ...............................43 3.1.1 Materiales y métodos......................................................................................................43 3.1.2 Cronograma................................... ................................43
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1 3.2 Resultados...............................................................................................................................43 CAPÍTULO 4 Conclusiones...................................................................................44 4.1 Relación con el Programa Educativo.......................................................................................45 4.2 Beneficios para la institución o empresa....... ......................45 4.3 Aprendizajes obtenidos...........................................................................................................45 Referencias...........................................................................................................46 Anexos..................................................................................................................48 Anexo 1. Lista de Ilustraciones......................................................................................................48 Anexo 2. Lista de tablas............................ ..................................48 Anexo 3. Lista de Gráficas.............................................................................................................48 Anexo 4. Informes mensuales.......................................................................................................49
RESUMEN
El propósito de esta investigación fue generar predicciones acerca del rendimiento escolar de alumnos de nivel media superior, específicamente bachillerato a una institución de tipo en este caso, cadenas de Markov, para la generación de un modelomatemáticodel fenómeno presentadoy la creación de este para su uso posterior para pronosticar y con este, la toma de decisiones.
Palabras Clave: rendimientoescolar; Educación Media Superior; Querétaro; Cadenas de Markov.
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
CAPÍTULO 1
Introducción
Podemos decir que el rendimiento escolar es el valor numérico que se le da al estudiante tras haber cursado un ciclo escolar, donde se considera que se refleja la cantidad de conocimientos adquiridos en contra punto de los que le fueron impartidos, partiendo de aquí podríamos ver este rendimientocomo un cúmulo de conocimientos, pero la realidad nos muestra que no siempre es así.
Desde la perspectiva de génerosabemos que este rendimiento no siempre va relacionado con el aprovechamiento, se ha observado que este nivel es más fácil de obtenerlo por el géneromasculino y se presionamásal femenino, prueba de esto es cuando los estudiantes egresan del nivel básico y se integranlaboralmentedonde se ve la preferencia al género masculino, no importando el recinto donde son contratados, mostrando gran diferencia en salarios y niveles jerárquicos de responsabilidades
Desde el punto de vista de las instituciones, elrendimiento escolar cataloga a las mismas y posiciona en niveles altos o bajos a los estudiantes egresados, pruebas como enlace, que miden el rendimiento escolar, pueden acabar con la reputación de una institución o ponerla como una entre las mejores, aunque esa no sea su realidad.
La predicción del rendimiento escolar, por tanto, toma un gran importancia en nuestros tiempo que permite medir el nivel de aprovechamiento en los alumnos lo cual redundará en mejores profesionistas y por ende un mejor avance de nuestro país.
En esta investigación se realiza una predicción matemática mediante las teorías de los procesos estocásticos de las cadenas de Markov, mostrando con él el rendimiento escolar a futuro para el análisis y comprensión del fenómeno a corto, mediano y largo plazo,
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
teniendo como principal objetivo un pronósticodonde muestre la realidad del desempeño escolar. La investigación se llevó a cabo en el CEDART1 ciudad de Querétaro que depende del INBAL2 y a su vez de la USEBEQ3 y la SEP4 ubicado en circuito plan vida # 116, col Centro sur, en la ciudadde Santiago de Querétaro, Qro.
1.1 Contexto y planteamiento del problema
El artículo tercero de la Constitución Política de los Estados Unidos Mexicanos indica que: Toda persona tiene derecho a la educación. El Estado -Federación, Estados, Ciudad de México y Municipios-impartirá y garantizará la educación inicial, preescolar, primaria, secundaria, media superior y superior. La educación inicial, preescolar, primaria y secundaria,conforman la educación básica; ésta y la media superior serán obligatorias, la educación superior lo será en términos de la fracción X del presente artículo. La educación inicial es un derecho de la niñez y será responsabilidad del Estado concientizar sobre su importancia .(Constitución Política de los Estados Unidos Mexicanos, s.f.)
Además, Los planes y programas de estudio tendrán perspectiva de género y una orientación integral,por lo que se incluirá el conocimiento de las ciencias y humanidades: la enseñanza de las matemáticas, la lecto-escritura, la literacidad, la historia, la geografía, el civismo, la filosofía, la tecnología, la innovación, las lenguas indígenas de nuestro país, las
Pl1 Centro de Educación Artística, institución del INBAL como modelo educativo integral deformación de secundaria y bachillerato general con el estudio de asignaturas provenientes de cuatro áreas artísticas, música, danza, artes plásticas, literatura y teatro.
2Instituto Nacional de las Bellas Artes y Literatura
3 Unidas de Servicios para la educación básica del estado de Querétaro.
4 Secretaria de Educación Pública.
UNADM |DCEIT| PT1
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS
lenguas extranjeras, la educación física, el deporte, las artes, en especial la música, la promoción de estilos de vida saludables, la educación sexual y reproductiva y el cuidado al medio ambiente, entre otras .(Constitución Política de los Estados Unidos Mexicanos, s.f.)
Será de excelencia, entendida como el mejoramiento integral constante que promueve el máximo logro de aprendizaje de los educandos, para el desarrollo de su pensamientocrítico y el fortalecimiento de los lazos entre escuela y comunidad . (Constitución Política de los Estados Unidos Mexicanos, s.f.)
En el inciso IX indica que: , se crea el Sistema Nacional de Mejora Continua de la Educación, que será coordinado por un organismo público descentralizado, con autonomía técnica, operativa, presupuestaria, de decisión y de gestión, con personalidad jurídica y patrimonio propios, no sectorizado, al que le corresponderá:
a) Realizar estudios, investigaciones especializadas y evaluaciones diagnósticas, formativas e integrales del Sistema Educativo Nacional; b) Determinar indicadores de resultados de la mejora continua de la educación; c)Establecer los criterios que deben cumplir las instancias evaluadoras para los procesos valorativos, cualitativos, continuos y formativos de la mejora continua de la educación; d) Emitir lineamientos relacionados con el desarrollo del magisterio, el desempeño escolar, los resultados de aprendizaje; así como de la mejora de las escuelas, organización y profesionalización de la gestión escolar; e) Proponer mecanismos de coordinación entre las autoridades educativas federal y de las entidades federativas parala atención de las necesidades de las personas en la materia;
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
f) Sugerir elementos que contribuyan a la mejora de los objetivos de la educación inicial, de los planes y programas de estudio de educación básica y media superior, así como para la educación inclusiva y de adultos, y
g) Generar y difundir información que contribuya a la mejora continua del Sistema . (Constitución Política de los Estados Unidos Mexicanos, s.f.)
Con base en esta última parte expresada del artículo 3ro de la Constituciónse establece la importancia de un grupo de indicadores que aporten los resultados de mejora continua en la educación, mismos que deberán ser medidos bajo especificas características, pero realmente no hay instrumentos que recolecten como tal este rendimiento, se usa para ello normalmente las calificaciones u otros indicadores que asientan las distintas instituciones a los diferentes estudiantes dependiendo de los niveles académicos en que se encuentren.
Ciertamente las evaluaciones emitidas al final de los ciclos escolares describen de manera ambigua, en algunos casos, el desempeño de los estudiantes, pero eso no implica que este rendimiento, expresado por un número, carezca de importancia, ya que cataloga al estudiante, a un determinado nivel de conocimientos.
Este nivel de conocimiento muestra a las instituciones, de manera poco clara, como se han impartido los conocimientos y por ende, la calidad académica que esta tiene, misma que será reflejada en sus estudiantes como un promedio de los conocimientos que obtendrán los alumnos al finalizar cualquiera de los ciclos escolares, por ello motivo de reflexión y búsqueda de mejora continua, como lo indica el artículo 3ro de la Constitución, para lograr cada vez undesempeñomás adecuadoen los alumnos y que este se vea reflejado en un estilo devida adecuado de acuerdo a las condiciones económicas y sociales en que este se desenvuelve.
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
La toma de decisiones que se deben de llevar a cabo para la mejora del rendimiento escolar no deja de ser un evento que implique riesgos, no se puede predecir el futuro de ninguna forma, pero si podemos hacer uso de las diferentes herramientas matemáticas que se tienen al alcance para logran un adecuado yasertivo cambio, estas nos permiten pronosticar y reducir los riesgos de la toma decisiones.
El uso de herramientas matemáticas que muestrena futuro los esfuerzos realizados por las entidades académicas y lespermitanacceder a la realización de adecuaciones que promuevan una mejora en la calidad que hoy por hoy imparten los llevaráal logro delos máximos objetivos académicos, por ello una herramienta que ayude a las predicciones de dichos rendimientosrepresentan acciones de vital importancia para la promoción de la calidad académicade cualquier institución.
Las herramientas matemáticas han sido utilizadas para el pronóstico de diferentes fenómenos como son los naturales, con respecto al clima o la probabilidad de lluvia de acuerdo a ciertos parámetros, financieramente hablando podemos predecir como es que se moverán ciertas divisas de acuerdo a como ha estado fluctuando en los últimos periodos de tiempo o de acuerdo a cambios políticos o sociales, por ello la utilización de las matemáticas representa la herramienta clave en el pronósticode eventos de cualquier índole.
Las herramientas matemáticas estocásticas,aquellas cuyo comportamiento no es determinista, es decir, es un proceso que depende sólo del estado anterior, por ello su utilización nos permite pronosticar los fenómenos a partir de estados iniciales, en esta investigación se utilizaron las cadenas de Markovquerepresentan modelos simplificados creados para la toma de decisiones.
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
Los modelos de Markov se han utilizado con éxito en los problemas donde se pretende generar pronósticos a partir de un evento inicial, esto es, las acciones iniciales determinan la acción inmediata a seguir o el que se le llama el siguiente estado, además de la forma en que se deberán de tomar los siguientes valores, entonces con cada valor obtenido generamos una cadena de valores que nos permite llegar a cualquier valor futuro arbitrariamente lejano.
1.2Objetivos
1.2.1 General
Planteamiento de un modelo estocástico de cadenas de Markov para predecir el Querétaro.
1.2.2 Específicos
Analizar las causas que llevan a cabo en la medición del rendimiento escolar de los Creación de la cadena de Markov que represente el rendimiento escolar de los
Analizar las asignaturas que implican cambios radicales en el rendimiento escolar de los
Creación de la cadena de Markov que represente el rendimiento escolar por asignaturas
Comparación de los niveles de rendimiento escolar con otras instituciones de igual índole.
MATEMÁTICAS UNADM |DCEIT| PT1
SÉPTIMOSEMESTRE | LICENCIATURA EN
CAPÍTULO 2Marco Investigativo
2.1 Rendimiento Escolar
Una de las dimensiones más importantes en la educación es el rendimiento académico, pero también es una de las más complejas ya que se trata de evaluar los conocimientosy revisar los factores buenos y malos que llevaron al dicho logro, por tanto, demuestra el éxito o fracaso del proceso educativo del estudiante.
El rendimiento escolar puede ser expresado como aquel número que se le da al estudiante, bajo los números de 5 al 10, donde 5 es reprobado y del 6 al 10 representa la aprobación, para establecer el dominio de los saberes, este puede ser de un bloque del curso o simplemente del curso completo, en esta investigación al referirnos al rendimiento escolar tomaremos aquellos valores que obtuvo el estudiante al finalizar el curso escolar.
hablan de este como: Nivel de conocimientos demostrado en un área omateria comparado con la norma de edad y nivel (Jimenez, 2000).
Joaquín Cano, el rendimiento escolares una dimensión del rendimiento académicoy es un índice de valoración de la calidadglobal de la educación. (Morales Sánchez, Morales Sánchez, & Holguín Quiñones, ISSN 2007-1957).
Antonio González define alrendimiento escolar como la verificación dela adquisición del conjunto de valores,actitudes, conductas y conocimientosseñalados como deseables por los actoressociales autorizados (Morales Sánchez, Morales Sánchez, & Holguín Quiñones, ISSN 2007-1957).
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
Para esta investigación definiremos el rendimiento escolar como el nivel de conocimientos demostrado en un área omateriaal final de su ciclo escolar donde se evaluó tanto el desempeño académico como de valores, actitudes y conductas
2.2 Institución de la investigación
La institución donde se llevó a cabo la investigación de nombre Centro de Educación , Cedart,es unadependencia de laSecretaría de Cultura/INBA/Subdirección General de Educación e Investigación Artísticas (SGEIA)cuya oferta educativa esde secundaria y bachillerato de Artes y Humanidades, con domicilio en circuito. Plan Vida 116, Colonia Centro Sur, Cp07690, Querétaro, Querétaro, Tels.: 442 153 19 70 al 79.
Cuenta con una población estudiantil de 300 estudiantes que incluyen los dos niveles, básico y media superior, siendo de importancia su enfoque cultural ya que permite maneja la especialidad de Arte y Humanidades con talleres de: Danza folclórica, contemporánea y clásica, Música, Literatura, Teatroy Artes plásticas, otorgando la documentación al término deCertificado.
Este modelo educativo integra la formación del bachillerato general con el estudio de asignaturas provenientes de cincoáreas artísticas. Por su carácter propedéutico, proporciona las bases y los conocimientos necesarios para continuar estudios de nivel superior, tanto en el campo de las artes como en las ciencias y las humanidades. El propósito de este bachillerato no es formar artistas. No obstante, a partir de la integración de saberes de la danza, la música, el teatro, literaturay las artes plásticas, contribuye en el desarrollo de habilidades cognitivas, afectivas, sociales y expresivas que redundan en una auténtica formación integral de sus egresados.
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
El ingreso a este modelo educativo implica conciencia de que los estudios artísticos son rigurosos y que requieren de una mayor certidumbre vocacional y total disposición para cursarlos en armonía con el resto de las asignaturas del bachillerato. Por el mismo motivo, el proceso de admisión busca comprobar estas condiciones en los aspirantes a efecto de que se cumplan las expectativas institucionales y personales.
2.2.1 PruebaPlanea
La Secretaría de Educación Pública en coordinación con la Comisión Nacional para la Mejora Continua de la Educación y las autoridades educativas de las entidades federativas, aplica la prueba Planea en Educación Media Superior a estudiantesdel último grado en poco más de 18,000 escuelas de Educación Media Superior del país de carácter público, federal y estatal, en los planteles particulares con Reconocimiento de Validez Oficial de Estudios (REVOE) otorgado por la SEP o por las entidades federativas, así como en las instituciones autónomas y en sus escuelas particulares incorporadas.
Esta prueba tiene el propósito de conocer en qué medida el estudiantado logra dominar un conjunto de aprendizajes esenciales al término de la Educación Media Superior, en dos campos de formación: Lenguaje y Comunicación y Matemáticas.
PLANEA5,agrupa los resultados obtenidos por los estudiantesen cuatro niveles de logro los cuales informan acerca de los aprendizajes clave que deben ser adquiridos por el estudiantado y en qué medida se han apropiado de ellos. Es importante señalar que estos niveles van del I al IV en orden progresivo, es decir, el nivel más bajo es el I y el más alto es el IV. Además, son acumulativos, ya que los estudiantes que se ubican en el nivel II cuentan con los aprendizajes del nivel previo (NI) y así sucesivamente.
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
5 El Plan Nacional para la Evaluación de los Aprendizajes
A continuación, se presenta la descripción genérica de los niveles de logro:
Nivel I: El estudiantado que se ubica en este nivel tiene un conocimiento insuficiente de los aprendizajes clave incluidos en los referentes curriculares. Esto refleja mayores dificultades para continuar con su trayectoria académica.
Nivel II: El estudiantado que se ubica en este nivel tiene un conocimiento elemental de los aprendizajes clave incluidos en los referentes curriculares.
Nivel III: El estudiantado que se ubica en este nivel tiene un conocimiento satisfactorio de los aprendizajes clave incluidos en los referentes curriculares.
Nivel IV: El estudiantado que se ubica en este nivel tiene un conocimiento sobresaliente de los aprendizajes clave incluidos en los referentes curriculares.
PLANEA Educación Media Superior está diseñada para ofrecer a padres y madres de familia, al estudiantado, al profesorado, la dirección, autoridades educativas y sociedad en general, información específica sobre el logro académico de las escuelas y, utilizada adecuadamente, constituye un potente instrumento que puede contribuir a mejorar la calidad de la educación.
2.2.1.1 Características de la prueba planea
Es una prueba objetiva y estandarizada.
Está alineada al Marco Curricular Común, en particular a los campos de formación asociados con las competencias de Lenguaje y Comunicación y Matemáticas.
Está conformada por 100 reactivos de opción múltiple, 50 que evalúan Lenguaje y Comunicación y 50 de Matemáticas.
Es una prueba criterial que NO está diseñada para derivar conclusiones al respecto del desempeño de las escuelas o las y los docentes.
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
Sus resultados NO deben tener consecuencias académicas o de otro tipo para el estudiantado, el profesorado o sus escuelas.
Es una prueba de diagnóstico, NO es una prueba de selección para el ingreso a instituciones de Educación Superior.
Ofrece información pertinente y oportuna a las escuelas y al profesorado, contribuyendo así al desarrollo de directrices para la mejora del sistema.
2.2.1.2 Resultados Planea 2015
Los resultados obtenidos por el Cedart en la prueba Planea en el 2015 Lenguaje y Comunicación I II III IV
% de alumnos de la escuela en cada nivel de logro7.5%10.0%37.5%45.0%
Porcentaje de alumnos de escuelas parecidas en cada nivel de logroS/RS/RS/RS/R
Porcentaje de alumnos en todas las escuelas de México en cada nivel de logro 23.1%20.2%34.7%21.9% TABLA 1:PLANEA2015:LENGUAJE Y COMUNICACIÓN, CREACIÓN PROPIA
SÉPTIMOSEMESTRE
EN MATEMÁTICAS UNADM |DCEIT| PT1
| LICENCIATURA
20
10
0
2015 Lenguaje y comunicación Porcentajes de logro por nivel CedartSimilarNacional
GRAFICA 1:PLANEA2015:LENGUAJE Y COMUNICACIÓN, CREACIÓN PROPIA
Matemáticas I II III IV
% de alumnos de la escuela en cada nivel de logro7.3%43.9%39%9.8%
Porcentaje de alumnos de escuelas parecidas en cada nivel de logroS/RS/RS/RS/R
Porcentaje de alumnos en todas las escuelas de México en cada nivel de logro 46.3%36.9%14.0%2.8%
TABLA 2:PLANEA2015:MATEMÁTICAS, CREACIÓN PROPIA
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
30 40 50 IIIIIIIV
40
30
20
10
0
2015 Matemáticas Porcentaje de logro por nivel CedartSimilarNacional
50 IIIIIIIV
GRAFICA 2:PLANEA2015MATEMÁTICAS, CREACIÓN PROPIA
2.2.1.3 Resultados Planea 2016
Los resultados obtenidos por el Cedart en la prueba Planea en el 2016 Lenguaje y Comunicación I II III IV
% de alumnos de la escuela en cada nivel de logro2.7%10.8%37.8%48.6%
Porcentaje de alumnos de escuelas parecidas en cada nivel de logro2.7%10.8%37.8%48.6%
Porcentaje de alumnos en todas las escuelas de México en cada nivel de logro 18.1%21.8%36.5%23.6% TABLA 3:PLANEA2016:LENGUAJE Y COMUNICACIÓN, CREACIÓN PROPIA
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
2016 Lenguaje y comunicación Porcentajes de logro por nivel
Matemáticas I II III IV
% de alumnos de la escuela en cada nivel de logro5.3%39.5%47.4%7.9%
Porcentaje de alumnos de escuelas parecidas en cada nivel de logro5.3%39.5%47.4%7.9%
Porcentaje de alumnos en todas las escuelas de México en cada nivel de logro 32.6%42.1%21.0%4.4%
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
GRAFICA 3:PLANEA2016:LENGUAJE Y COMUNICACIÓN, CREACIÓN PROPIA
10 20 30 40 50 60 IIIIIIIV
TABLA 4:PLANEA2016:MATEMÁTICAS, CREACIÓN PROPIA 0
CedartSimilarNacional
40
30
20
10
0
2016 Matemáticas Porcentaje de logro por nivel CedartSimilarNacional
50 IIIIIIIV
GRAFICA 4:PLANEA2016:MATEMÁTICAS, CREACIÓN PROPIA
2.2.1.4 Resultados Planea 2017
Los resultados obtenidos por el Cedart en la prueba Planea en el 2017
Lenguaje y Comunicación I II III IV
% de alumnos de la escuela en cada nivel de logro5.9%0.0%44.1%50.0%
Porcentaje de alumnos de escuelas parecidas en cada nivel de logro22.9%29.9%35.4%11.8%
Porcentaje de alumnos en todas las escuelas de México en cada nivel de logro 33.9%28.1%28.7%9.2%
TABLA 5:PLANEA2017:LENGUAJE Y COMUNICACIÓN, CREACIÓN PROPIA
SÉPTIMOSEMESTRE |
EN MATEMÁTICAS UNADM |DCEIT| PT1
LICENCIATURA
2017 Lenguaje y comunicación Porcentajes de logro por nivel
GRAFICA 5:PLANEA2017:LENGUAJE Y COMUNICACIÓN, CREACIÓN PROPIA Matemáticas I II III IV
% de alumnos de la escuela en cada nivel de logro21.4%25.0%25.0%28.6%
Porcentaje de alumnos de escuelas parecidas en cada nivel de logro48.6%31.8%14.2%5.3%
Porcentaje de alumnos en todas las escuelas de México en cada nivel de logro 66.2%23.3%8.0%2.5%
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
IIIIIIIV
TABLA 6:PLANEA2017:MATEMÁTICAS, CREACIÓN PROPIA 0 10 20 30 40 50 60
CedartSimilarNacional




















SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
G
0 10 20 30 40 50 60 70 IIIIIIIV 2017
0 10 20 30 40 50 60 Cedart2015NacionalCedart2016NacionalCedart2017Nacional
IIIIIIIV
GRAFICA 6:PLANEA2017:MATEMÁTICAS, CREACIÓN PROPIA 2.2.2 Resultados planea de rendimiento escolar
RAFICA 7:PLANEALENGUAJE Y COMUNICACIÓN, CREACIÓN PROPIA
Matemáticas Porcentaje de logro por nivel CedartSimilarNacional
Lenguaje y Comunicación
Matemáticas
GRAFICA 8:PLANEAMATEMÁTICAS, CREACIÓN PROPIA
2.3Cadenas de Markov








2.3.1 Antecedentes














Las cadenas de Markov fueron introducidas por el matemático ruso 1922) alrededor de 1905, con el objetivo decrear un modelo probabilístico parara analizar la frecuencia con laque aparecen las vocales en poemas y textos literarios.Las cadenas de Markov pueden aplicarse a una amplia gama defenómenos científicosy sociales. Andrei Markov fue alumno de la universidad de SanPetersburgo, discípulode Chebyshev como Liapunov, despuésde su doctorado en 1886 accedió como adjunto a la Academiade Ciencias de San Petersburgo, a propuesta del propioChebyshev.
En 1989, cuando Chebyshev dejó la universidad, le sustituyóen los cursos de teoría de probabilidad. En 1925 AndreiMarkov dejó definitivamente la universidad.Aparte de su perfil académico, Andrei Markov fue un activista político oponiéndosea los privilegios de la
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
0 10 20 30 40 50 60 70 Cedart2015NacionalCedart2016NacionalCedart2017Nacional
IIIIIIIV
nobleza zarista, llegando a rechazar las condecoracionesdelzar en protesta por decisiones políticas relacionadas con la Academia de Ciencias.
Andrei Markov influyó sobre diversos campos de las matemáticas, sobresaliendocon la teoría de la probabilidad.En 1887 completó la prueba que permitía generalizar el teorema central del límiteque ya había avanzado Chebyshev, aunque su aportación más conocida se encuentra en los procesos estocásticos, elaborando un instrumento matemáticoque actualmente se conoce como cadena de Markov, instrumento que, hoy en día,se consideran una herramienta esencial en disciplinas como la economía, laingeniería, la investigación de operaciones y muchas otras.
2.3.2 Definición
Un proceso estocástico o proceso aleatorio es un concepto matemático que se utiliza para usar magnitudes aleatorias que varían con el tiempo o para caracterizar una sucesión de variables aleatorias o estocásticas que varían en función de otra variable, generalmente el tiempo.Cada variable o conjunto de variables sometidas a influencias o efectos aleatorios constituyen un proceso estocástico.
En teoría de la probabilidad, una Cadena de Markov en tiempo discreto (CMTD) es un tipo especial de proceso estocástico discreto en el que la probabilidad de que ocurra un suceso depende solamente del suceso inmediatamente anterior. Esta característica de falta de memoria se conoce como propiedad de Markov (recibe el nombre del matemático ruso Andrei Markov, que introdujo en 1907).
Definimos entonces a una cadena de Markov como:
Sea una variable aleatoria que caracteriza el estado del sistema en puntos discretosen el tiempo . La familia de variables aleatorias { } forma un proceso estocástico con una cantidad finita o infinita de estados. (Taha, 2012)
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
2.3.3
Desarrollo de las cadenas de Markov

UnaCadena de Markov es una secuencia de variables aleatorias, el dominio de estas variables es el llamado Espacio Estado. El valor es el estado del proceso en el tiempo .
La distribución de la probabilidad condicionada de en estados pasados es una función de por sí sola, siendo Para cualesquiera
Si se dice que la Cadena de Markov es finita, en caso contrario se dice que es infinita.
2.3.3.1 Cadena homogénea y no homogénea
Una Cadena de Markov se dice homogénea si la probabilidad de ir del estado al estado en un paso no depende del tiempo en el que se encuentra la cadena: Cadena homogénea: para todo nodo
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
ILUSTRACIÓN 1:EJEMPLO DE CADENA DE MARKOV, CREACIÓN PROPIA
Si para alguna pareja de estados y para algún tiempo la propiedad mencionada no se cumple se dice que la Cadena de Markov es no homogénea.
2.3.3.2
Probabilidad y matriz de transición
Si una Cadena de Markov está en el estado hay una probabilidad de pasar al próximo estado a esta probabilidad se la llama probabilidad de Transición.
La probabilidad de pasar del estado al estado en un paso se llama probabilidad de transición de a : .
Las probabilidades de transición conforman la matriz de transición P, que es conrigor una matriz (finita) sólo para cadenas de Markov finitas, aunque también seconserva el nombre y la notación para cadenas de Markov infinitas.
Cada fila de la matriz de transición debe sumar 1 por las propiedades básicas de probabilidad.
El modelo para redes se puede considerar una cadena de Markov donde son losvértices del grafo dirigido y es el inverso del número de aristas salientes desde cuando hay una arista de a y cero en otro caso.
La matriz de transición en un solo paso, dada una cadena de Markov con estadosposibles y probabilidades de transición estacionarias, vienedada por la expresión:
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
SÉPTIMOSEMESTRE
2.3.3.3 Matriz de transición
El Vector distribución es un vector fila no negativo con una entrada para cada estado del sistema.
Vector probabilidad es un vector con entradas no negativas, de forma que se agregan hasta llegar a 1. Las entradas pueden representar las probabilidades de encontrar un sistema en cada uno de los estados.
El vector de distribución y la matriz de transición P determinanla probabilidad para el estado de la cadena en el segundo instante de tiempo, dicha probabilidad viene dada por el vector ( ).
Distribución después del 1 paso: Distribución después del 2 paso: ( ) = Distribución después del 3 paso: ( ) = Y así sucesivamente llegamos a Distribución después del n paso: ( ) =
Una notación conveniente para representar las probabilidades de transición de pasos es la matriz de transición de pasos:
La probabilidad de transición en una fila y columna dadas es la transición del estadoen esa fila al estado en la columna. Cuando el superíndice no se escribe y sehace referencia a ésta como una matriz de transición.
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
SÉPTIMOSEMESTRE
Las probabilidades de transición en pasos son las probabilidades de transicióndel estado al estado en pasos, denotándose como:
Las cadenas de Markov que se analizan tienen las propiedades:
2.3.3.4
Vector de Probabilidad Estacionario
Un vector de probabilidad ya sea finito oinfinito numerable se dice estacionario para una cadena de Markov en tiempodiscreto (CMTD) si cualquier transición de acuerdo con la matriz verifica:
Al vector de probabilidad estacionario también se le denomina distribuciónestacionaria o distribución de equilibrio.
Cuando la cadena de Markov se va aproximando de estado en estado hacia un estado de equilibrio se le llama estado estable, que se determina por
|
EN MATEMÁTICAS
SÉPTIMOSEMESTRE
LICENCIATURA
UNADM |DCEIT| PT1
Un vector de probabilidades
De una cadena de Markov en tiempo discreto se le llama límite si:
El vector de probabilidades de de una cadena de Markov es tiempo discreto se dice el único vector de probabilidades en equilibrio de la cadena sí convergen independientemente de la distribución , cada probabilidad es mayor estrictamente que cero.
2.3.4 Clasificación de estados de las cadenas de Markov
Estado alcanzable:
Dados dos estados y , una trayectoria de a es una secuencia de transiciones que comienza en y termina en , tal que cada transición en la secuencia tiene una probabilidad positiva de ocurrir. Un estado es alcanzable desde el estado si hay una trayectoria que conduzca de a
Estados que se comunican: Se dice que dos estados y se comunican si es alcanzable desde , y de igual manera es alcanzable desde . Conjunto cerrado: Un conjunto de estados de una Cadena de Markov es cerrado si ningún estado fuera de es alcanzable desde algún estado en .
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
Estado absorbente: Es un estado en el que Siempre que se entra en un estado absorbente, no se sale de él; un estado absorbente es un conjunto cerrado que contiene sólo un estado.
ILUSTRACIÓN 2EJEMPLO:EL ESTADO 3 ES ABSORBENTE.CREACIÓN PROPIA.TOMADO DE IMÁGENES WIKIPEDIA


Estado transitorio: Un estado es transitorio si existe un estado que es alcanzable desde , pero el estado no es alcanzable desde el estado
ILUSTRACIÓN 3EJEMPLO:EL ESTADO 2 ES TRANSITORIO.CREACIÓN PROPIA.TOMADO DE IMÁGENES WIKIPEDIA
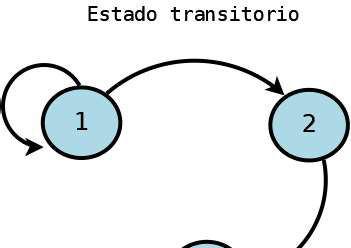
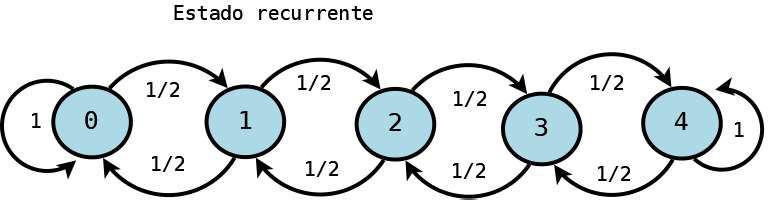
Estado recurrente:
Es un estado que no es transitorio.
UNADM |DCEIT| PT1
MATEMÁTICAS
SÉPTIMOSEMESTRE | LICENCIATURA EN
Estado periódico:
Un estado es periódico con periodo si es el número más pequeño tal que las trayectorias que conducen al estado de regreso al estado tienen una longitud que es un múltiplo de . Si un estado recurrente no es periódico, se conoce como aperiódico (Winston, 2008).
2.3.5 Teoría de grafos
Un grafo es una estructura matemática que consta de vérticesy aristas que conectan estos vértices; En términos elementales podríamos definir un grafo como un conjunto de puntos (llamados elementos, vértices, nudos o nodos) con líneas que unen pares de vértice de ellas; en algunos libros se usa red como sinónimo degrafo. (Álvarez Núñez & Parra Muñoz, 2013)

SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
ILUSTRACIÓN 4EJEMPLO:LOS ESTADOS 1,2 Y 3 SON RECURRENTES.CREACIÓN PROPIA.TOMADO DE IMÁGENES WIKIPEDIA
ILUSTRACIÓN 5EJEMPLO:CADENA DE PERÍODO 3.CREACIÓN PROPIA.TOMADO DE IMÁGENES WIKIPEDIA
2.3.5.1 Definición
Un grafo es una abstracción matemática que designaremos por Donde es el conjunto devértices opuntos y es el conjunto de líneas que unen dos puntos de puede ser vacío llamado conjunto de las aristas que están relacionadas mediante la aplicación
A cualquier arista de un grafo se le puede asociar una pareja de vértices de este. Si son dos vértices de un grafo y la arista a está asociada con este par, escribiremos
Un grafo se representa mediante un diagrama en el cual a cada vértice le corresponde un punto y si dos vértices son adyacentes se unen sus puntos correspondientes mediante una línea.
Ejemplo:
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
Entonces el grafo sería:

ILUSTRACIÓN 6:EJEMPLO DE GRAFO,TOMADO DE:(ÁLVAREZ NÚÑEZ &PARRA MUÑOZ,2013)
En el diagrama geométrico los nudos o vértices estarán indicados por pequeños círculos y las conexiones mediante arcos,líneas o rectas, los cuales pueden tener dirección o no, de donde se generan dos clasificaciones de grafos: Los dirigidos y los no dirigidos, donde llamaremos arco a la relación de dirección que existe entre 2 nodos.



2.3.5.1 Grafos no Dirigidos

Los grafos no dirigidos espropiamente aquel grafo que no considera dirección, esto es, lasaristas no tienen sentido, luego la relación existente es simétrica.
ILUSTRACIÓN 7:GRAFO NO DIRIGIDO, TOMADO DE: (ÁLVAREZNÚÑEZ&PARRAMUÑOZ,2013)
2.3.5.2 Grafos Dirigidos
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS
UNADM |DCEIT| PT1
Grafo dirigido es aquel grafo en el cual la relación existente entre los elementos considera su dirección, Se puede recalcar que si es un dígrafo, o grafo dirigido,entonces la relación T, en general no es simétrica; es decir
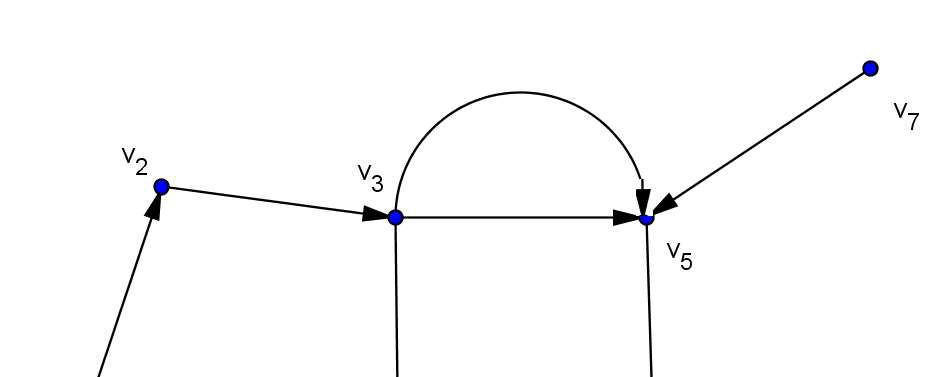

2.3.5.3 Camino

Es una ruta que se debe seguir para llegar de un punto a otro. Lo representaremos por , sabiendo que entre un punto y otro puede haber más de un camino.
Ejemplo: si trazamos el camino de este pasa por lospuntos entonces
MATEMÁTICAS
SÉPTIMOSEMESTRE | LICENCIATURA EN
UNADM |DCEIT| PT1
ILUSTRACIÓN 8:GRAFO DIRIGIDO, TOMADO DE: (ÁLVAREZNÚÑEZ&PARRAMUÑOZ,2013)
ILUSTRACIÓN 9:EJEMPLO DE CAMINO,TOMADO DE: (ÁLVAREZNÚÑEZ&PARRAMUÑOZ,2013)
2.3.5.4 Vértices Adyacentes

Se dice que dos vértices son adyacentes si estánconectados por una arista o por un arco. Ejemplo: losvértices son adyacentes, los vértices no lo son ILUSTRACIÓN 10:VÉRTICES ADYACENTES,T

2.3.5.5 Matriz de Adyacencia
Sea un grupo cuyo conjunto de vértices es , llamaremos matriz de adyacencia del grafo a la matriz de -filas y -columnas,donde Ejemplo: Utilizando el grafo: ILUSTRACIÓN 11:G
Su matriz de adyacencia está dada por
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT|
PT1
OMADO DE:(CIENCIAS.MEDELLIN.UNAL.EDU.CO, S.F.)
RAFO EJEMPLO MATRIZ DE ADYACENCIA,TOMADO DE:(CIENCIAS.MEDELLIN.UNAL.EDU.CO, S.F.)
Donde, todos los ceros de la matriz A significan que no hay ningún camino entre los vértices correspondientes; todos los unos de la matriz A significan que existe un camino entre los vértices correspondientes.
2.3.6 Software de Aplicación
Para la realización de los procesos decálculo de las matrices se utilizará el software POM QM para Windowsque es un programa para la gestión de producción/operaciones, métodos cuantitativos, ciencia de la gestión e investigación de operaciones; mismo que al ser una herramienta de software libren nos permite utilizarlo sin necesidad de pago; de igual forma para la generación de grafos se utilizará la aplicación DIA que de la misma forma es software libre.
2.4Metodología
En esta parte se hace un análisis de los que constituye la fundamentación metodológica de la investigación que abarca los temas relacionados con la investigación cuantitativa, así como la metodología empleada y el diseño de la investigación
2.4.1Investigación cuantitativa.
La presente investigación se realizó de tipo cuantitativa de abstracción aplicada ya que se buscó la solución a un problema práctico de un grupo de estudiantes, en este caso una institución pública de educación básica del nivel secundaria y bachillerato situado en la
UNADM |DCEIT| PT1
| LICENCIATURA EN MATEMÁTICAS
SÉPTIMOSEMESTRE
ciudad de Querétaro. De forma deductiva ya que partió de una premisa inicial para llegar a una conclusión general del problema. A manera correlacional debido a que partimos de hechos establecidos con una relación causa efecto para la solución de una problemática. Tratando de establecer una generalización fundamental ya que se realizó a una pequeña muestra para generalizar el fenómeno. Buscando un estudio de naturaleza descriptivocausal, debido a que se buscó visualizar a través de una amplitud de datos numéricos la relación causativa entre las variables independientes y dependiente. Se mencionauna técnica conjunta para correlacionar los resultados y determinar una conclusión. Finalmente, con la metodología cuantitativa, se llevaron a cabo mediciones sistemáticas de los eventos, así como un análisis estadístico resultante.
2.4.2Diseño de la investigación
El diagrama que ilustra el diseño metodológico que dirige la realización de este estudio fue:
G1X101
2.4.3Participantes
La población está constituida por150alumnos que cursan la educación básica en el nivel secundaria y medio superior de la institución donde se llevó a cabo la investigación, todos ellos cursaron un ciclo escolar competo,esto es, cumplieron con los 6 semestres de nivel bachillerato y obtuvieron una calificación aprobatoriafinal de rendimiento escolar.
2.4.4Variables de estudio
|
EN MATEMÁTICAS UNADM |DCEIT| PT1
SÉPTIMOSEMESTRE
LICENCIATURA
Establecemos lavariable como:
Estos datos nos representan un proceso estocástico con espacios discretos. La caminata que representanlas generaciones es: ILUSTRACIÓN 12:CAMINATA Y GRAFO DE GENERACIONES, CREACIÓN PROPIA

La matriz de incidencia está dada por

EN MATEMÁTICAS
SÉPTIMOSEMESTRE | LICENCIATURA
UNADM |DCEIT| PT1
UNADM |DCEIT| PT1
9.99.89.79.69.4 9.91 9.80.50.5 9.71 9.6 9.41
MATEMÁTICAS
SÉPTIMOSEMESTRE | LICENCIATURA EN
CAPÍTULO 3Resultados
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
3.1Actividades desarrolladas
3.1.1 Materiales y métodos
3.1.2 Cronograma
3.2Resultados
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
CAPÍTULO 4Conclusiones
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
4.1Relación con el Programa Educativo 4.2Beneficios para la institución o empresa 4.3 Aprendizajes obtenidos
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
Referencias
Álvarez Núñez, M. F., & Parra Muñoz, J. A. (2013). Teoría de Grafos. Obtenido de Universidad del Bio Bio, Chile: http://repobib.ubiobio.cl/jspui/bitstream/123456789/1953/3/Alvarez_Nunez_Marcelino. pdf
Anónimo. (s.f.). Cadenas de Markov finitas. Fenómenos de espera. Obtenido de http://www.estadistica.net/INVESTIGACION/CADENAS-MARKOV.pdf
Camarena Ibarrola, J. A. (s.f.). Cadenas de Markov. Obtenido de http://dep.fie.umich.mx/~camarena/Cadenas%20de%20Markov.pdf
ciencias.medellin.unal.edu.co. (s.f.). 3. Aplicación: Grafos y dígrafos. Obtenido de Universidad Nacional de Colombia: https://ciencias.medellin.unal.edu.co/cursos/algebralineal/clases/8-clases/40-clase-2parte3.html#:~:text=Un%20grafo%20consiste%20de%20un,est%C3%A1n%20conectados% 20por%20una%20arista.
Claverol, M., Simó, E., & Zaragozá, M. (s.f.). Teoría de grafos. Obtenido de Departamento de Matemática aplicada IV EPSEVG -UPC: https://docplayer.es/50364694-Matematicadiscreta-teoria-de-grafos-ester-simo-marisa-zaragoza-departamento-matematicaaplicada-iv-epsevg-upc.html
Constitución Política de los Estados Unidos Mexicanos. (s.f.). Obtenido de Justia México: https://mexico.justia.com/federales/constitucion-politica-de-los-estados-unidosmexicanos/titulo-primero/capitulo-i/#articulo-3o
Cuaya Simbro, G. (s.f.). Procesos de Decisión de Markov aplicados a la locomoción de robots hexápodos. Obtenido de https://inaoe.repositorioinstitucional.mx/jspui/bitstream/1009/588/1/CuayaSG.pdf
INBAL. (s.f.). Obtenido de https://inba.gob.mx/ Jimenez, M. (2000). Infancia y Sociedad. Competencia social: intervención preventiva en la escuela. Morales Sánchez, L. A., Morales Sánchez, V., & Holguín Quiñones, S. (ISSN 2007-1957). Rendimiento Escolar. Humanidades, Tecnología y Ciencia del Instituto Politécnico Nacional Navarro, R. E. (2003). El rendimiento académico: concepto, investigación y desarrollo. REICE: Revista Iberoamericana sobre Calidad, Eficacia y Cambio en Educación, 1(2), 0. Obtenido de https://www.redalyc.org/pdf/551/55110208.pdf
Pérez Lázaro, J. (s.f.). Cadenas de Markov (en tiempos discretos con estados discretos). Obtenido de Universidad de Rioja: https://www.unirioja.es/cu/franpere/ModyOptfiles/Tema6.pdf
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
Planea. (s.f.). Planea. Obtenido de http://planea.sep.gob.mx/ms/ Taha, H. A. (2012). Investigación de Operaciones (Novena Edición ed.). México: PEARSON EDUCACIÓN,. Winston, W. (2008). Investigacion de operaciones, aplicaciones y algoritmos 4a. ediccion . Mexico D.f: Cengage Learning.
EN MATEMÁTICAS
SÉPTIMOSEMESTRE | LICENCIATURA
UNADM |DCEIT| PT1
Anexos
Anexo 1. Lista de Ilustraciones
Ilustración 1: Ejemplo de Cadena de Markov, creación propia........................................................27
Ilustración 2 Ejemplo: El estado 3 es absorbente. Creación propia. Tomado de imágenes Wikipedia ...........................................................................................................................................................32
Ilustración 3 Ejemplo: El estado 2 es transitorio. Creación propia. Tomado de imágenes Wikipedia ...........................................................................................................................................................32
Ilustración 4 Ejemplo: Los estados 1, 2 y 3 son recurrentes. Creación propia. Tomado de imágenes Wikipedia.......................................... ..............................................33
Ilustración 5 Ejemplo: Cadena de período 3. Creación propia. Tomado de imágenes Wikipedia....33 Ilustración 6: Ejemplo de Grafo, Tomado de:(Álvarez Núñez & Parra Muñoz, 2013).....................35
Ilustración 7: Grafo no Dirigido, tomado de: (ÁLVAREZ NÚÑEZ & PARRA MUÑOZ, 2013)...............35
Ilustración 8: Grafo dirigido, tomado de: (ÁLVAREZ NÚÑEZ & PARRA MUÑOZ, 2013)....................36
Ilustración 9: Ejemplo de camino, Tomado de: (ÁLVAREZ NÚÑEZ & PARRA MUÑOZ, 2013)...........36
Ilustración 10: Vértices adyacentes, Tomado de: (ciencias.medellin.unal.edu.co, s.f.)...................37
Ilustración 11: Grafo ejemplo matriz de adyacencia, Tomado de: (ciencias.medellin.unal.edu.co, s.f.).....................................................................................................................................................37
Ilustración 12: Caminata y grafo de generaciones, creación propia.................................................40
Anexo 2. Lista de tablas
Tabla 1: PLANEA 2015: Lenguaje y Comunicación, creación propia.................................................18
Tabla 2: PLANEA 2015: Matemáticas, creación propia.....................................................................19
Tabla 3: PLANEA 2016: Lenguaje y Comunicación, creación propia.................................................20
Tabla 4: PLANEA 2016: Matemáticas, creación propia.. ................21
Tabla 5: PLANEA 2017: Lenguaje y Comunicación, creación propia.................................................22
Tabla 6: PLANEA2017: Matemáticas, creación propia.....................................................................23
Anexo 3. Lista de Gráficas
Grafica 1: PLANEA 2015: Lenguaje y Comunicación, creación propia..............................................19
Grafica 2: PLANEA 2015 Matemáticas, creación propia...................................................................20
Grafica 3: PLANEA 2016: Lenguaje y Comunicación, creación propia..............................................21
Grafica 4: PLANEA 2016: Matemáticas, creación propia ...............22
Grafica 5: PLANEA 2017: Lenguaje y Comunicación, creación propia..............................................23
Grafica 6: PLANEA 2017: Matemáticas, creación propia .................................................................24
Grafica 7: PLANEA Lenguaje y Comunicación, creación propia........................................................24
Grafica 8: PLANEA Matemáticas, creación propia....... ..................25
SÉPTIMOSEMESTRE | LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
Anexo 4. Informes mensuales
LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT1
SÉPTIMOSEMESTRE |
División de Ciencias Exactas, Ingeniería y Tecnología Práctica profesional/Proyecto terminal Informe mensual de actividades Organización: Estudiante: Mercedes Rodríguez Robles Matrícula: ES1821016580 Área de conocimiento: Matemáticas Número de reporte: 1 Asesor externo: Lic. Pedro Daniel Lara Maldonado
Santiago de Querétaro, 30 de septiembre de 2022.
Tabla de especificaciones del Informe
Actividad presentada Objetivo de la actividad Observaciones
Se recabo la información y se elaboraron los formatosA y B.
Formatos
Recabar la información y elaboración de los formatos A y B.
Se revisaron por el asesor externo y se firmaron de acuerdo con lo solicitado.
Se subieron a la plataforma para su revisión y aprobación del docente en línea.
Se entregaron de forma correcto.
Carta de presentación
Entregar al director académico del la carta dela UnADM para su recepción con firma, fecha y sello de recibido.
Se recibió de la UnADM la carta de presentación y envío aldirector académico
informaciónsobre la estudiante, las horas de servicio socialy consideraciones delproyecto de la UnADM que se va a realizaren su institución.
Carta de aceptación
Recibir y verificar los datos (firma y sello) de lacarta del CEDART paraentregarlo en laUnADM.
Bibliografía
Identificar la bibliografía que se vaa utilizar para el proyecto.
carta de aceptación.
Se subióa la plataforma para su revisión y aprobación del docente en línea.
Se entregóde forma correcta.
Se elaboró un listado con los libros, sitios webs, artículos de revistas y tesis a revisar para identificar cual de estos se va a usaren el proyecto.
Planeación Seleccionar título del Elaboración del documento con título,
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
del proyecto
Elaboración del Resumen
proyecto y realizar el plan delanteproyecto ybibliografía.
Redacción del resumen del anteproyecto
bibliografía y cronograma de actividades como parte del archivo de nombre anteproyecto.
Elaboración del texto del resumen del anteproyecto.Envío al asesor externo para su primera revisión.
Elaboración del texto del capítulo 1 del anteproyecto.
Elaboración del capítulo 1
Redacción del capítulo 1 del anteproyecto
1.Contexto y planteamiento del problema 2.Objetivos a.Generales b.Específicos Envío al asesor externo para su primera revisión.
Elaboración del texto del capítulo 1 del anteproyecto.
Elaboración del capítulo 2
Redacción del capítulo 2 del anteproyecto
1.Rendimiento Escolar 2.Cadenas de Markov a.Antecedentes b.Definición c.Desarrollo de las cadenas d.Clasificación de los estados 3.Metodología a.Investigación cualitativa b.Diseño de la investigación c.Participantes
Envío al asesor externo para su primera revisión.
Captura de calificaciones Capturar en un archivo de Excel las calificaciones para su
UNADM
PT|
Se recibieron documentos en fotografía y PDF que contienen las calificaciones por periodo escolar (semestre) y se diseño en Excel el
| LICENCIATURA EN MATEMÁTICAS
|DCEIT|
posterior análisis formato de captura y la captura de cada una de las calificaciones de los estudiantes a lo largo de los pasados 5 años. En este formato se incluyen las calificaciones de los exámenes extraordinarios.
Tabla de descripción de la o las problemáticas identificadas
Actividad presentada
Formatos
Carta depresentación
Problemática identificada
Fue necesario la elaboración y entrega varias veces de los documentos ya que la institución tiene ciertas reglas para la recepción de servicio social a lo cual nos tuvimos que adaptar para estos dos formatos
Tardo mucho tiempo la UNADM en entregarnos esta carta y fue complicado el iniciar con los horas de servicio sin el documento.
Carta de aceptación Sin problemas
Bibliografía
Este análisis fue muy tardado, aunque se tenían varios libros que hablaran del tema, fue complicado encontrar bibliografía que se apoyara en la elaboración de cadenas de Markov para la elaboración de pronósticos, algunas tesis fueron de ayuda para poder establecer el resumen y la problemática
Planeación del anteproyecto Sin problemas
Elaboración del Resumen Sin problemas por el momento
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Elaboración del capítulo
1
Sin problemas, pero el asesor me indica que deboenfocarlo a una asignatura en específico, me ayudo con bibliografía del tema para el enfoque.
Elaboración del capítulo 2 Sin problemas por el momento
Captura de calificaciones
Actividad realizada
La obtención de la información ha sido rápida, me han entregado por partes archivos en PDF y fotos, es complicado ya que se tiene que capturar número por número y en algunos archivos estos son poco legibles.
Tabla de resultados
Acción correctiva
Experiencia obtenida
Observaciones
Formatos
Ninguna
Paciencia y labor de convencimiento para ser aceptada.
El lograr incorporarse a una institución para el servicio social y la elaboraciones del proyecto terminal I y II es complicado, así como las condiciones de las instituciones que debes cumplir para tu incorporación.
Carta de presentación
Carta de aceptación
NingunaPacienciaRealización de trámites
Las fechas de los periodos de cada uno de los semestres de proyecto terminal I y II para ajustarlas a
Las horas de servicio social deben de ser 250 para cada semestre
Realización de trámites
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
las necesidades de la institución.
Bibliografía Ninguna por el momento
Planeación del anteproyecto Ninguna por el momento
Elaboración del Resumen Ninguna por el momento
Elaboración de lista de bibliografía
Determinar y planificar el anteproyecto
Buscar información científica en internet y uso del formato Apa para documentarla
Seleccionar el tema y planificar tiempos para la realización del anteproyecto.
Elaboración del anteproyecto
Poco a poco y con la bibliografía se ha había leído se redactó el documento para el envío a su primera revisión con el asesor externo.
Elaboración del capítulo 1
Debo enfocarlo a una asignatura en específico, me ayudo con bibliografía del tema para el enfoque.
Elaboración del capítulo 2
Ninguna por el momento
Elaboración del anteproyecto
Poco a poco y con la bibliografía se ha había leído se redactó el documento para el envío a su primera revisión con el asesor externo.
Elaboración del anteproyecto
Poco a poco y con la bibliografía se ha había leído se redactó el documento para el envío a su primera revisión con el asesor externo.
Captura de calificaciones
Ninguna por el momento
Creación y diseño de varios archivos en Excel con la captura de las calificaciones por semestre
Este proceso que todavía no se ha terminado ha resultado ser muy tardado.
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|











| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT| Servicio social presentado Periodos de impartición 75 horas Se presentó servicio por una cantidad de 3 horas diarias de lunes a viernes en el trayecto de 5 semanas que contemplan del 29 de agosto del 2022 al 30 de septiembre del 2022. Anexos: Evidencia de cada actividad. Asesor externo Estudiante Lic. Pedro Daniel Lara Maldonado
Cartas: Formato A












| LICENCIATURA EN MATEMÁTICAS
UNADM |DCEIT| PT| Evidencia de cada actividad.





| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Formato B







| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Carta de presentación











| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|





| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Carta de aceptación

| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|






| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Bibliografía
Anónimo. (s.f.). Cadenas de Markov finitas. Fenómenos de espera. Obtenido de http://www.estadistica.net/INVESTIGACION/CADENAS-MARKOV.pdf
Camarena Ibarrola, J. A. (s.f.). Cadenas de Markov. Obtenido de http://dep.fie.umich.mx/~camarena/Cadenas%20de%20Markov.pdf
Constitución Política de los Estados Unidos Mexicanos. (s.f.). Obtenido de Justia México: https://mexico.justia.com/federales/constitucion-politica-de-los-estados-unidosmexicanos/titulo-primero/capitulo-i/#articulo-3o
Cuaya Simbro, G. (s.f.). Procesos de Decisión de Markov aplicados a la locomociónde robots hexápodos. Obtenido de https://inaoe.repositorioinstitucional.mx/jspui/bitstream/1009/588/1/CuayaSG.pdf
INBAL. (s.f.). Obtenido de https://inba.gob.mx/
Jimenez, M. (2000). Infancia y Sociedad. Competencia social: intervención preventiva en la escuela. Morales Sánchez, L. A., Morales Sánchez, V., & Holguín Quiñones, S. (ISSN 2007-1957). Rendimiento Escolar. Humanidades, Tecnología y Ciencia del Instituto Politécnico Nacional. Navarro, R. E. (2003). El rendimiento académico: concepto, investigación y desarrollo. REICE: Revista Iberoamericana sobre Calidad, Eficacia y Cambio en Educación, 1(2), 0. Obtenido de https://www.redalyc.org/pdf/551/55110208.pdf
Pérez Lázaro, J. (s.f.). Cadenas de Markov (en tiempos discretos con estados discretos). Obtenido de Universidad de Rioja: https://www.unirioja.es/cu/franpere/ModyOptfiles/Tema6.pdf
Taha, H. A. (2012). Investigación de Operaciones (Novena Edición ed.). México: PEARSON EDUCACIÓN,.
Winston, W. (2008). Investigacion de operaciones, aplicaciones y algoritmos 4a. ediccion . Mexico D.f: Cengage Learning.
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Cronograma
Anteproyecto
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Universidad Abierta y a Distancia de México Coordinación Académica y de Investigación
División de Ciencias Exactas, Ingeniería y Tecnología Programa educativo
PROYECTO TERMINAL
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
INFORME GENERAL DE RESULTADOS
| LICENCIATURA EN MATEMÁTICAS
|DCEIT| PT|
UNADM
Universidad Abierta y a Distancia de México
Rectora Lilian Kravzov Appel
Coordinadora Académico y de Investigación Edgar Alcantar Corchado
Dirección de Ciencias Exactas, Ingeniería y Tecnología Dolores Alejandra Vasquez Carbajal
Responsable del Programa Educativo Carlos Alberto Serrato Hernández
Docente en línea Mónica Zaima Víquez Cano
Autor del proyecto Mercedes Rodríguez Robles
IMPORTANTE
Excepto donde el contenido así lo especifique, esta obra está bajo una Licencia de Creative Commons
| LICENCIATURA EN MATEMÁTICAS
UNADM |DCEIT| PT|
Material desarrollado y/orecopilado con fines educativos por académicos externos a la Institución, perteneciente a la DCEIT de la Universidad Abierta y a Distancia de México (UnADM) Ciudad de México, 2022.
| LICENCIATURA EN MATEMÁTICAS UNADM
|DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT| DIVISIÓN DE CIENCIAS EXACTAS, INGENIERÍA Y TECNOLOGÍA Proyectoterminal I Uso del modelo estocástico de Cadenas Markovianas para la predicción de rendimiento estudiantil del Organización: Mercedes Rodríguez Robles ES1821016580 Nivel educativo:Licenciatura en Matemáticas Asesor externo: Lic. Matemático Pedro Daniel Lara Maldonado Periodo de realización: Mes año de inicio: julio 2022 Mes año final: diciembre 2022 Santiago de Querétaro, Qro. Diciembre 2022
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT| ÍNDICE ÍNDICE..................................................................................................................22 RESUMEN............................................................................................................24 CAPÍTULO 1.........................................................................................................25 Introducción..................................................................................................................................25 1.1 Contexto y planteamiento del problema................................................................................26 1.2 Objetivos.................................................................................................................................30 1.2.1 General.............................................................................................................................30 1.2.2 Específicos.................................. ...................................30 CAPÍTULO 2 Marco Investigativo..........................................................................32 2.1 Rendimiento Escolar...............................................................................................................32 2.2 Cadenas de Markov.................................................................................................................33 2.2.1 Antecedentes................................. ...............................33 2.2.2 Definición.........................................................................................................................34 2.2.3 Desarrollo de las cadenas de Markov..............................................................................35 2.2.4 Clasificación de estados de las cadenas de Markov.........................................................39 2.3 Metodología............................................................................................................................42 2.3.1 Investigación cuantitativa................... ..........................42 2.3.2 Diseño de la investigación................................................................................................43 2.3.3 Participantes.....................................................................................................................43 2.3.4 Variables de estudio......................... .............................43 CAPÍTULO 3 Resultados......................................................................................44 3.1 Actividades desarrolladas........................................................................................................44 3.1.1 Materiales y métodos......................................................................................................44 3.1.2 Cronograma................................... ................................44 3.2 Resultados...............................................................................................................................44 CAPÍTULO 4 Conclusiones.............................. ..45 4.1 Relación con el Programa Educativo.......................................................................................45 4.2 Beneficios para la institución o empresa....... ......................45 4.3 Aprendizajes obtenidos...........................................................................................................45
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT| Referencias...........................................................................................................46 Anexos..................................................................................................................47 Anexo 1. Lista de figuras........................... .................................47 Anexo 2. Lista de tablas.................................................................................................................47 Anexo 2 A.......................................... .....................................47 Anexo 3. Informes mensuales.......................................................................................................47
RESUMEN
El propósito de esta investigación fue generar predicciones acerca del rendimiento escolar de alumnos de nivel básico y media superior, específicamente de secundaria y bachillerato ediante el uso de modelos estocásticos, en este caso, cadenas de Markov, para la descripción matemática del fenómeno presentado.
Palabras Clave: rendimientoescolar; Educación Secundaria;Educación Media Superior; Querétaro; Cadenas de Markov.
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
CAPÍTULO 1
Introducción
Podemos decir que el rendimiento escolar es el valor numérico que se le da al estudiante tras haber cursado un ciclo escolar, donde se considera que se refleja la cantidad de conocimientos adquiridos en contra punto de los que le fueron impartidos, partiendo de aquí podríamos ver este rendimiento como un cúmulo de conocimientos, pero la realidad nos muestra que no siempre es así.
Desde la perspectiva de genero sabemos que este rendimiento no siempre va relacionado con el aprovechamiento, se ha observado que este nivel es más fácil de obtenerlo por el género masculino y se presiona mas al femenino, prueba de esto es cuando los estudiantes egresan del nivel básico y se integran laboralmente donde se ve la preferencia al género masculino, no importando el recinto donde son contratados, mostrando gran diferencia en salarios y niveles jerárquicos de responsabilidades.
Desde el punto de vista de las instituciones, el rendimiento escolar cataloga a las mismas y posiciona en niveles altos o bajos a los estudiantes egresados, pruebas como enlace, que miden el rendimiento escolar, pueden acabar con la reputación de una institución o ponerla como una entre las mejores, aunque esa no sea su realidad.
La predicción del rendimiento escolar, por tanto, toma un gran importancia en nuestros tiempo que permite medir el nivel de aprovechamiento en los alumnos lo cual redundará en mejores profesionistas y por ende un mejor avance de nuestro país.
En esta investigación se realiza una predicción matemática mediante las teorías de los procesos estocásticos de las cadenas de Markov, mostrando con él el rendimiento escolar a futuro para el análisis y comprensión del fenómeno a corto, mediano y largo plazo,
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
teniendo como principal objetivo un pronósticodonde muestre la realidad del desempeño escolar. La investigación se llevó a cabo en el CEDART1 la ciudad de Querétaro que depende del INBAL2 y a su vez de la USEBEQ3 y la SEP4 ubicado en circuito plan vida # 116, col Centro sur, en la ciudad de Santiago de Querétaro, Qro.
1.1 Contexto y planteamiento del problema
El artículo tercero de la Constitución Política de los Estados Unidos Mexicanos indica que: Toda persona tiene derecho a la educación. El Estado -Federación, Estados, Ciudad de México y Municipios-impartirá y garantizará la educación inicial, preescolar, primaria, secundaria, media superior y superior. La educación inicial, preescolar, primaria y secundaria,conforman la educación básica; ésta y la media superior serán obligatorias, la educación superior lo será en términos de la fracción X del presente artículo. La educación inicial es un derecho de la niñez y será responsabilidad del Estado concientizar sobre su importancia (Constitución Política de los Estados Unidos Mexicanos, s.f.)
Los planes y programas de estudio tendrán perspectiva de género y una orientación integral, por lo que se incluirá el conocimiento de las ciencias y humanidades: la enseñanza de las matemáticas, la lecto-escritura, la literacidad, la historia, la geografía, el civismo, la filosofía, la tecnología, la innovación, las lenguas indígenas de nuestro país,
Pl1 Centro de Educación Artística, institución del INBAL como modelo educativo integral deformación de secundaria y bachillerato general con el estudio de asignaturas provenientes de cuatro áreas artísticas, música, danza, artes plásticas, literatura y teatro.
2Instituto Nacional de las Bellas Artes y Literatura
3 Unidas de Servicios para la educación básica del estado de Querétaro.
4 Secretaria de Educación Pública.
UNADM |DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS
las lenguas extranjeras, la educación física, el deporte, las artes, en especial la música, la promoción de estilos de vida saludables, la educación sexual y reproductiva y el cuidado al medio ambiente, entre otras (Constitución Política de los Estados Unidos Mexicanos, s.f.)
Será de excelencia, entendida como el mejoramiento integral constante que promueve el máximo logro de aprendizaje de los educandos, para el desarrollo de su pensamiento crítico y el fortalecimiento de los lazos entre escuela y comunidad (Constitución Política de los Estados Unidos Mexicanos, s.f.)
En el inciso IX indica que: Nacional de Mejora Continua de la Educación, que será coordinado por un organismo público descentralizado, con autonomía técnica, operativa,presupuestaria, de decisión y de gestión, con personalidad jurídica y patrimonio propios, no sectorizado, al que le corresponderá:
a) Realizar estudios, investigaciones especializadas y evaluaciones diagnósticas, formativas e integrales del Sistema Educativo Nacional;
b) Determinar indicadores de resultados de la mejora continua de la educación; c) Establecer los criterios que deben cumplir las instancias evaluadoras para los procesos valorativos, cualitativos, continuos y formativos de la mejora continua de la educación;
d) Emitir lineamientos relacionados con el desarrollo del magisterio, el desempeño escolar, los resultados de aprendizaje; así como de la mejora de las escuelas, organización y profesionalización de la gestión escolar; e) Proponer mecanismos de coordinación entre las autoridades educativas federal y de las entidades federativas para la atención de las necesidades de las personas en la materia;
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
f) Sugerir elementos que contribuyan a la mejora de los objetivos de la educación inicial, de los planes y programas de estudio de educación básica y media superior, así como para la educación inclusiva y de adultos, y g) Generar y difundir información que contribuya a la mejora continua del Sistema (Constitución Política de los Estados Unidos Mexicanos, s.f.)
Con base en esta última parte expresada del artículo 3ro de la Constitución se establece la importancia de un grupo de indicadores que aporten los resultados de mejora continua en la educación, mismos que deberán ser medidos bajo especificas características, pero realmente no hay instrumentos que recolecten como tal este rendimiento, se usa para ello normalmente las calificaciones u otros indicadores que asientan las distintas instituciones a los diferentes estudiantes dependiendo de los niveles académicos en que se encuentren.
Ciertamente las evaluaciones emitidas al final de los ciclos escolares describen de manera ambigua, en algunos casos, el desempeño de los estudiantes, pero eso no implica queeste rendimiento, expresado por un número, carezca de importancia, ya que cataloga al estudiante, a un determinado nivel de conocimientos.
Este nivel de conocimiento muestra a las instituciones, de manera poco clara, como se han impartido los conocimientos y por ende, la calidad académica que esta tiene, misma que será reflejada en sus estudiantes como un promedio de los conocimientos que obtendrán los alumnos al finalizar cualquiera de los ciclos escolares, por ello motivo de reflexión y búsqueda de mejora continua, como lo indica el artículo 3ro de la Constitución, para lograr cada vez un desempeño más adecuado en los alumnos y que este se vea reflejado en un estilo de vida adecuado de acuerdo a las condiciones económicas y sociales en que este se desenvuelve.
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
La toma de decisiones que se deben de llevar a cabo para la mejora del rendimiento escolar no deja de ser un evento que implique riesgos, no se puede predecir el futuro de ninguna forma, pero si podemos hacer uso de las diferentes herramientas matemáticas que se tienen al alcance para logran un adecuado y asertivo cambio, estas nos permiten pronosticar y reducir los riesgos de la toma decisiones.
El uso de herramientas matemáticas que muestren a futuro los esfuerzos realizados por las entidades académicas y les permitan acceder a la realización de adecuaciones que promuevan una mejora en la calidad que hoy por hoy imparten los llevará al logro de los máximos objetivos académicos, por ello una herramienta que ayude a las predicciones de dichos rendimientos representan acciones de vital importancia para la promoción de la calidad académica de cualquier institución.
Las herramientas matemáticas han sido utilizadas para el pronóstico de diferentes fenómenos como son los naturales, con respecto al climao la probabilidad de lluvia de acuerdo a ciertos parámetros, financieramente hablando podemos predecir como es que se moverán ciertas divisas de acuerdo a como ha estado fluctuando en los últimos periodos de tiempo o de acuerdo a cambios políticos o sociales, por ello la utilización de las matemáticas representa la herramienta clave en el pronóstico de eventos de cualquier índole.
Las herramientas matemáticas estocásticas, aquellas cuyo comportamiento no es determinista, es decir, es un proceso que depende sólo del estado anterior, por ello su utilización nos permite pronosticar los fenómenos a partir de estados iniciales, en esta investigación se utilizaron las cadenas de Markov que representan modelos simplificados creados para la toma de decisiones.
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Los modelos de Markov se han utilizado con éxito en los problemas donde se pretende generar pronósticos a partir de un evento inicial, esto es, las acciones iniciales determinan la acción inmediata a seguir o el que se le llama el siguiente estado, además dela forma en que se deberán de tomar los siguientes valores, entonces con cada valor obtenido generamos una cadena de valores que nos permite llegar a cualquier valor futuro arbitrariamente lejano.
1.2Objetivos
1.2.1
General
Planteamiento de un modelo estocástico de cadenas de Markov para predecir el Querétaro.
1.2.2
Específicos
Analizar las causas que llevan a cabo en la medición del rendimiento escolar de los Creación de la cadena de Markov que represente el rendimiento escolar de los
Analizar las asignaturas que implican cambios radicales en el rendimiento escolar de Creación de la cadena de Markov que represente el rendimiento escolar por
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Comparación de los niveles de rendimiento escolar con otras instituciones de igual índole.
UNADM |DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS
CAPÍTULO 2 MARCO INVESTIGATIVO
2.1 Rendimiento Escolar
Una de las dimensiones más importantes en la educación es el rendimiento académico, pero también es una de las más complejas ya que se trata de evaluar los conocimientos y revisar los factores buenos y malos que llevaron al dicho logro, por tanto, demuestra el éxito o fracaso del proceso educativo del estudiante.
El rendimiento escolar puede ser expresado como aquel número que se le da al estudiante, bajo los números de 5 al 10, donde 5 es reprobado y del 6 al 10 representa la aprobación, para establecer el dominio de los saberes, este puede ser de un bloque del curso o simplemente del curso completo, en esta investigación al referirnos al rendimiento escolar tomaremos aquellos valores que obtuvo el estudiante al finalizar el curso escolar. hablan de este como: Nivel de conocimientos demostrado en un área omateria comparado con la norma de edad y nivel (Jimenez, 2000).
Joaquín Cano, el rendimiento escolares una dimensión del rendimiento académico y es un índice de valoración de la calidadglobal de la educación. (Morales Sánchez, Morales Sánchez, & Holguín Quiñones, ISSN 2007-1957).
Antonio González define alrendimiento escolar como la verificación dela adquisición del conjunto de valores,actitudes, conductas y conocimientosseñalados como deseables por
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
los actoressociales autorizados (Morales Sánchez, Morales Sánchez, & Holguín Quiñones, ISSN 2007-1957).
Para esta investigación definiremos el rendimiento esco ivel de conocimientos demostrado en un área omateriaal final de su ciclo escolar donde se evaluó tanto el desempeño académico como de valores, actitudes y conductas del
2.2 Cadenas de Markov
2.2.1 Antecedentes
Las cadenas de Markov fueron introducidas por el matemático rusoAndrei Markov ( crear un modelo probabilístico parara analizar la frecuencia con laque aparecen las vocales en poemas y textos literarios.Las cadenas de Markov pueden aplicarse a una amplia gama defenómenos científicos y sociales.
Andrei Markov fue alumno de la universidad de SanPetersburgo, discípulo de Chebyshev como Liapunov, despuésde su doctorado en 1886 accedió como adjunto a la Academiade Ciencias de San Petersburgo, a propuesta del propioChebyshev.
En 1989, cuando Chebyshev dejó la universidad, le sustituyóen los cursos de teoría de probabilidad. En 1925 AndreiMarkov dejó definitivamente la universidad.Aparte de su perfil académico, Andrei Markov fue un activista político oponiéndosea los privilegios de la nobleza zarista, llegando a rechazar las condecoraciones delzar en protesta por decisiones políticas relacionadas con la Academia de Ciencias.
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT|
PT|
Andrei Markov influyó sobre diversos campos de las matemáticas, sobresaliendocon la teoría de la probabilidad.En 1887 completó la prueba que permitía generalizar el teorema central del límiteque ya había avanzado Chebyshev, aunque su aportación más conocida seencuentra en los procesos estocásticos, elaborando un instrumento matemáticoque actualmente se conoce como cadena de Markov, instrumento que, hoy en día,se consideran una herramienta esencial en disciplinas como la economía, laingeniería, la investigación de operaciones y muchas otras.
2.2.2 Definición
Un proceso estocástico o proceso aleatorio es un concepto matemático que se utiliza para usar magnitudes aleatorias que varían con el tiempo o para caracterizar una sucesión de variables aleatorias o estocásticas que varían en función de otra variable, generalmente el tiempo. Cada variable o conjunto de variables sometidas a influencias o efectos aleatorios constituyen un proceso estocástico.
En teoría de la probabilidad, una Cadena de Markov en tiempo discreto (CMTD) es un tipo especial de proceso estocástico discreto en el que la probabilidad de que ocurra un suceso depende solamente del suceso inmediatamente anterior. Esta característica de falta de memoria se conoce como propiedad de Markov (recibe el nombre del matemático ruso Andrei Markov, que introdujo en 1907).
Definimos entonces a una cadena de Markov como:
Sea una variable aleatoria que caracteriza el estado del sistema en puntos discretosen el tiempo . La familia de variables aleatorias { } forma un proceso estocástico con una cantidad finita o infinita de estados. (Taha, 2012)
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Ilustración 1: Ejemplo de Cadena de Markov, creación propia
2.2.3 Desarrollo de las cadenas de Markov

UnaCadena de Markov es una secuencia de variables aleatorias, el dominio de estas variables es el llamado Espacio Estado. El valor es el estado del proceso en el tiempo .
La distribución de la probabilidad condicionada de en estados pasados es una función de por sí sola, siendo Para cualesquiera
Si se dice que la Cadena de Markov es finita, en caso contrario se dice que es infinita.
2.2.3.1
Cadena homogénea y no homogénea
Una Cadena de Markov se dice homogénea si la probabilidad de ir del estado al estado en un paso no depende del tiempo en el que se encuentra la cadena: Cadena homogénea:
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
para todo nodo
Si para alguna pareja de estados y para algún tiempo la propiedad mencionada no se cumple se dice que la Cadena de Markov es no homogénea.
2.2.3.2 Probabilidad y matriz de transición
Si una Cadena de Markov está en el estado hay una probabilidad de pasar al próximo estado a esta probabilidad se la llama probabilidad de Transición.
La probabilidad de pasar del estado al estado en un paso se llama probabilidad de transición de a : .
Las probabilidades de transición conforman la matriz de transición P, que es conrigor una matriz (finita) sólo para cadenas de Markov finitas, aunque también seconserva el nombre y la notación para cadenas de Markov infinitas.
Cada fila de la matriz de transición debe sumar 1 por las propiedades básicas de probabilidad.
El modelo para redes se puede considerar una cadena de Markov donde son losvértices del grafo dirigido y es el inverso del número de aristas salientes desde cuando hay una arista de a y cero en otro caso.
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
La matriz de transición en un solo paso, dada una cadena de Markov con estados posibles y probabilidades de transición estacionarias, vienedada por la expresión:
2.2.3.3 Matriz de transición
El Vector distribución es un vector fila no negativo con una entrada para cada estado del sistema.
Vector probabilidad es un vector con entradas no negativas, de forma que se agregan hasta llegar a 1. Las entradas pueden representar las probabilidades de encontrar un sistema en cada uno de los estados.
El vector de distribución y la matriz de transición P determinan la probabilidad para el estado de la cadena en el segundo instante de tiempo, dicha probabilidad viene dada por el vector ( ).
Distribución después del 1 paso:
Distribución después del 2 paso: ( ) = Distribución después del 3 paso: ( ) = Y así sucesivamente llegamos a
Distribución después del n paso: ( ) =
| LICENCIATURA EN MATEMÁTICAS
UNADM |DCEIT| PT|
Una notación conveniente para representar las probabilidades de transición de pasos es la matriz de transición de pasos:
La probabilidad de transición en una fila y columna dadas es la transición del estadoen esa fila al estado en la columna. Cuando el superíndice no se escribe y sehace referencia a ésta como una matriz de transición.
Las probabilidades de transición en pasos son las probabilidades de transicióndel estado al estado en pasos, denotándose como:
Las cadenas de Markov que se analizan tienen las propiedades:
2.2.3.4
Vector de Probabilidad Estacionario
Un vector de probabilidad ya sea finito oinfinito numerable se dice estacionario para una cadena de Markov en tiempodiscreto (CMTD) si cualquier transición de acuerdo con la matriz verifica:
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Al vector de probabilidad estacionario también se le denomina distribuciónestacionaria o distribución de equilibrio.
Cuando la cadena de Markov se va aproximando de estado en estado hacia un estado de equilibrio se le llama estado estable, que se determina por
Un vector de probabilidades
De una cadena de Markov en tiempo discreto se le llama límite si:
El vector de probabilidades de de una cadena de Markov es tiempo discreto se dice el único vector de probabilidades en equilibrio de la cadena sí convergen independientemente de la distribución , cada probabilidad es mayor estrictamente que cero.
2.2.4 Clasificación de estados de las cadenas de Markov
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Estado alcanzable:
Dados dos estados y , una trayectoria de a es una secuencia de transiciones que comienza en y termina en , tal que cada transición en la secuencia tiene una probabilidad positiva de ocurrir. Un estado es alcanzable desde el estado si hay una trayectoria que conduzca de a
Estados que se comunican:
Se dice que dos estados y se comunican si es alcanzable desde , y de igual manera es alcanzable desde .
Conjunto cerrado: Un conjunto de estados de una Cadena de Markov es cerrado si ningún estado fuera de es alcanzable desde algún estado en .
Estado absorbente: Es un estado en el que Siempre que se entra en un estado absorbente, no se sale de él; un estado absorbente es un conjunto cerrado que contiene sólo un estado.
Ilustración 2Ejemplo: El estado 3 es absorbente. Creación propia. Tomado de imágenes Wikipedia

Estado transitorio:
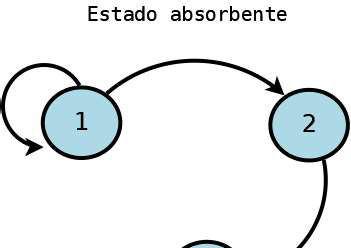
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Un estado es transitorio si existe un estado que es alcanzable desde , pero el estado no es alcanzable desde el estado
Ilustración 3Ejemplo: El estado 2es transitorio. Creación propia. Tomado de imágenes Wikipedia Estado recurrente: Es un estado que no es transitorio.
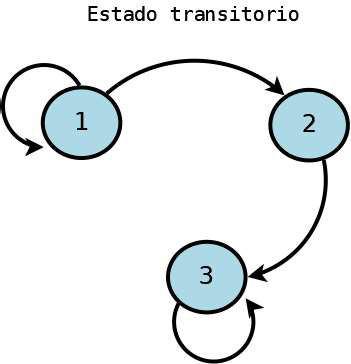
Ilustración 4Ejemplo: Los estados 1, 2 y 3 son recurrentes. Creación propia. Tomado de imágenes Wikipedia Estado periódico:
Un estado es periódico con periodo si es el número más pequeño tal que las trayectorias que conducen al estado de regreso al estado tienen una longitud que es un múltiplo de . Si un estado recurrente no es periódico, se conoce como aperiódico (Winston, 2008).

| LICENCIATURA EN MATEMÁTICAS
UNADM |DCEIT| PT|
2.3Metodología

En esta parte se hace un análisis de los que constituye la fundamentación metodológica de la investigación que abarca los temas relacionados con la investigación cuantitativa, así como la metodología empleada y el diseño de la investigación
2.3.1
Investigación cuantitativa.
La presente investigación se realizó de tipo cuantitativa de abstracción aplicada ya que se buscó la solución a un problema práctico de un grupo de estudiantes, en este caso una institución pública de educación básica del nivel secundaria y bachillerato situado en la ciudad de Querétaro. De forma deductiva ya que partió de una premisa inicial para llegar a una conclusión general del problema. A manera correlacional debido a que partimos de hechos establecidos con una relación causa efecto para la solución de una problemática. Tratando de establecer una generalización fundamental ya que se realizó a una pequeña
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Ilustración 5Ejemplo: Cadena de período 3. Creación propia. Tomado de imágenes Wikipedia
muestra para generalizar el fenómeno. Buscando un estudio de naturalezadescriptivocausal, debido a que se buscó visualizar a través de una amplitud de datos numéricos la relación causativa entre las variables independientes y dependiente. Se menciona una técnica conjunta para correlacionar los resultados y determinar una conclusión. Finalmente, con la metodología cuantitativa, se llevaron a cabo mediciones sistemáticas de los eventos, así como un análisis estadístico resultante.
2.3.2 Diseño de la investigación
El diagrama que ilustra el diseño metodológico que dirige la realización de este estudio fue: G1X101
2.3.3 Participantes
La población está constituida por ###alumnos que cursan la educación básica en el nivel secundaria y medio superior de la institución donde se llevó a cabo la investigación, todos ellos cursaron un ciclo escolar competo, obteniendo una calificación final de rendimiento escolar.
2.3.4 Variables de estudio
| LICENCIATURA EN MATEMÁTICAS
UNADM |DCEIT| PT|
CAPÍTULO 3 RESULTADOS
3.1Actividades desarrolladas
3.1.1 Materiales y métodos
3.1.2 Cronograma
3.2Resultados
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
CAPÍTULO 4 CONCLUSIONES
4.1Relación con el Programa Educativo
4.2Beneficios para la institución o empresa
4.3 Aprendizajes obtenidos
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
REFERENCIAS
Anónimo. (s.f.). Cadenas de Markov finitas. Fenómenos de espera. Obtenido de http://www.estadistica.net/INVESTIGACION/CADENAS-MARKOV.pdf
Camarena Ibarrola, J. A. (s.f.). Cadenas de Markov. Obtenido de http://dep.fie.umich.mx/~camarena/Cadenas%20de%20Markov.pdf
Constitución Política de los Estados Unidos Mexicanos. (s.f.). Obtenido de Justia México: https://mexico.justia.com/federales/constitucion-politica-de-los-estados-unidosmexicanos/titulo-primero/capitulo-i/#articulo-3o
Cuaya Simbro, G. (s.f.). Procesos de Decisión de Markov aplicados a la locomoción de robots hexápodos. Obtenido de https://inaoe.repositorioinstitucional.mx/jspui/bitstream/1009/588/1/CuayaSG.pdf
INBAL. (s.f.). Obtenido de https://inba.gob.mx/
Jimenez, M. (2000). Infancia y Sociedad. Competencia social: intervención preventiva en la escuela
Morales Sánchez, L. A., Morales Sánchez, V., & Holguín Quiñones, S. (ISSN 2007-1957). Rendimiento Escolar. Humanidades, Tecnología y Ciencia del Instituto Politécnico Nacional
Navarro, R. E. (2003). El rendimiento académico: concepto, investigación y desarrollo. REICE: Revista Iberoamericana sobre Calidad, Eficacia y Cambio en Educación, 1(2), 0. Obtenido de https://www.redalyc.org/pdf/551/55110208.pdf
Pérez Lázaro, J. (s.f.). Cadenas de Markov (en tiempos discretos con estados discretos). Obtenido de Universidad de Rioja: https://www.unirioja.es/cu/franpere/ModyOptfiles/Tema6.pdf
Taha, H. A. (2012). Investigación de Operaciones (Novena Edición ed.). México: PEARSON EDUCACIÓN,.
Winston, W. (2008). Investigacion de operaciones, aplicaciones y algoritmos 4a. ediccion . Mexico D.f: Cengage Learning.
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
ANEXOS
Anexo 1. Lista de figuras
Ilustración 1: Ejemplo de Cadena de Markov, creación propia........................................................35
Ilustración 2 Ejemplo: El estado 3 es absorbente. Creación propia. Tomado de imágenes Wikipedia ..40
Ilustración 3 Ejemplo: El estado 2 es transitorio. Creación propia. Tomado de imágenes Wikipedia ...........................................................................................................................................................41
Ilustración 4 Ejemplo: Los estados 1, 2 y 3 son recurrentes. Creación propia. Tomado de imágenes Wikipedia.......................................... ..............................................41
Ilustración 5 Ejemplo: Cadena de período 3. Creación propia. Tomado de imágenes Wikipedia....42
Anexo 2. Lista de tablas
Anexo 2 A Anexo 3. Informes mensuales
| LICENCIATURA EN MATEMÁTICAS UNADM
|DCEIT| PT|
Captura de Calificaciones


| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
División de Ciencias Exactas, Ingeniería y Tecnología Práctica profesional/Proyecto terminal Informe mensual de actividades Organización: Estudiante: Mercedes Rodríguez Robles Matrícula: ES1821016580 Área de conocimiento: Matemáticas Número de reporte: 2 Asesor externo: Lic. Pedro Daniel Lara Maldonado
Santiago de Querétaro, 14de octubrede 2022.
Tabla de especificaciones del Informe
Actividad presentada Objetivo de la actividad
Presentación del proyecto
Revisión de tesis
Realizar una presentación de la parte primera del proyecto
Revisióndel capítulo 1
Realizar una lectura de tesis entregada por el asesor externo
Corrección de retroalimentación del asesor externo
Revisióndel capítulo 2
Captura de calificaciones
Corrección de retroalimentación del asesor externo
Capturar en un archivo de Excel las calificaciones para su posterior análisis
Observaciones
La presentación contiene los siguientes datos: Identificación
Resumen Contexto y planteamiento del problema Justificación Objetivos generales y específicos Marco investigativo Marco teórico Metodología Cronograma Bibliografía
Se revisa una tesis entregada por el asesor externo para lograr cambios en la tesis de acuerdo a la forma en que trabajan las asignaturas en la investigación
Elaboración del texto corregido de acuerdo con las especificaciones del asesor externo, en el capítulo 1.
Elaboración del texto corregido de acuerdo con las especificaciones del asesor externo, en el capítulo 2.
Se continua con la captura de calificaciones
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Tabla de descripción de la o las problemáticas identificadas
Actividad presentada
Problemática identificada
Presentación del proyecto Sin problemas por el momento
Revisión de tesis Sin problemas por el momento
Revisión del capítulo 1 Sin problemas por el momento
Revisión del capítulo 2 Sin problemas por el momento
Captura de calificaciones Sin problemas por el momento
Tabla de resultados
Actividad realizada
Presentación del proyecto
Revisión de tesis
Revisión del capítulo 1
Acción correctiva Experiencia obtenida
Ninguna por el momento Muestra del anteproyecto
Ninguna por el momento Mayor entendimiento del tema a investigar
Ninguna por el momento
Revisión del capítulo 2
Captura de calificaciones
Ninguna por el momento
Ninguna por el momento
Elaboración de anteproyecto
Observaciones
Se realiza resumen que contenga lo más importante para la presentación
Aplicar el conocimiento adquirido en mi proyecto
Generar las modificaciones necesarias y enviarlo a revisión con el asesor externo.
Elaboración de anteproyecto
Captura de las calificaciones por semestre
Generar las modificaciones necesarias y enviarlo a revisión con el asesor externo.
Este proceso que todavía no se ha terminado ha resultado ser muy tardado.
| LICENCIATURA EN MATEMÁTICAS
|DCEIT|
UNADM
PT|




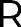

| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT| Servicio social presentado Periodos de impartición 30 horas Se presentó servicio por una cantidad de 3 horas diarias de lunes a viernes en el trayecto de 5 semanas que contemplan del 1de octubredel 2022 al 14de octubre del 2022. Anexos: Evidencia de cada actividad. Asesor externo Estudiante Lic. Pedro Daniel Lara Maldonado Mercedes Rodríguez Robles
Evidencia de cada actividad. Presentación del proyecto

| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|



| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|



| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|



| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|



| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|



| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Universidad Abierta y a Distancia de México Coordinación Académica y de Investigación
División de Ciencias Exactas, Ingeniería y Tecnología Programa educativo
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
PROYECTO TERMINAL INFORME GENERAL DE RESULTADOS
Universidad Abierta y a Distancia de México
Rectora Lilian Kravzov Appel
Coordinadora Académico y de Investigación Edgar Alcantar Corchado
Dirección de Ciencias Exactas, Ingeniería y Tecnología Dolores Alejandra Vasquez Carbajal
Responsable del Programa Educativo Carlos Alberto Serrato Hernández
Docente en línea Mónica Zaima Víquez Cano
Autor del proyecto Mercedes Rodríguez Robles
IMPORTANTE
Excepto donde el contenido así lo especifique, esta obra está bajo una Licencia de Creative Commons
| LICENCIATURA EN MATEMÁTICAS
UNADM |DCEIT| PT|
Material desarrollado y/orecopilado con fines educativos por académicos externos a la Institución, perteneciente a la DCEIT de la Universidad Abierta y a Distancia de México (UnADM) Ciudad de México, 2022.
| LICENCIATURA EN MATEMÁTICAS UNADM
|DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT| DIVISIÓN DE CIENCIAS EXACTAS, INGENIERÍA Y TECNOLOGÍA Proyectoterminal I Uso del modelo estocástico de Cadenas Markovianas para la predicción de rendimiento estudiantil del Organización: Mercedes Rodríguez Robles ES1821016580 Nivel educativo:Licenciatura en Matemáticas Asesor externo: Lic. Matemático Pedro Daniel Lara Maldonado Periodo de realización: Mes año de inicio: julio 2022 Mes año final: diciembre 2022 Santiago de Querétaro, Qro. Diciembre 2022
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT| ÍNDICE ÍNDICE..................................................................................................................19 RESUMEN............................................................................................................21 CAPÍTULO 1.........................................................................................................22 Introducción..................................................................................................................................22 1.1 Contexto y planteamiento del problema................................................................................23 1.2 Objetivos.................................................................................................................................27 1.2.1 General.............................................................................................................................27 1.2.2 Específicos.................................. ...................................27 CAPÍTULO 2 Marco Investigativo..........................................................................29 2.1 Rendimiento Escolar...............................................................................................................29 2.2 Cadenas de Markov.................................................................................................................30 2.2.1 Antecedentes................................. ...............................30 2.2.2 Definición.........................................................................................................................31 2.2.3 Desarrollo de las cadenas de Markov..............................................................................32 2.2.4 Clasificación de estados de las cadenas de Markov.........................................................36 2.3 Metodología............................................................................................................................39 2.3.1 Investigación cuantitativa................... ..........................39 2.3.2 Diseño de la investigación................................................................................................40 2.3.3 Participantes.....................................................................................................................40 2.3.4 Variables de estudio......................... .............................40 CAPÍTULO 3 Resultados......................................................................................41 3.1 Actividades desarrolladas........................................................................................................41 3.1.1 Materiales y métodos......................................................................................................41 3.1.2 Cronograma................................... ................................41 3.2 Resultados...............................................................................................................................41 CAPÍTULO 4 Conclusiones.............................. ..42 4.1 Relación con el Programa Educativo.......................................................................................42 4.2 Beneficios para la institución o empresa....... ......................42 4.3 Aprendizajes obtenidos...........................................................................................................42
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT| Referencias...........................................................................................................43 Anexos..................................................................................................................44 Anexo 1. Lista de figuras........................... .................................44 Anexo 2. Lista de tablas.................................................................................................................44 Anexo 2 A.......................................... .....................................44 Anexo 3. Informes mensuales.......................................................................................................44
RESUMEN
El propósito de esta investigación fue generar predicciones acerca del rendimiento escolar de alumnos de nivel media superior, específicamente bachillerato a una institución de tipo en este caso, cadenas de Markov, para la generación de un modelo matemático del fenómeno presentado y la creación de este para su uso posterior para pronosticar y con este, la toma de decisiones.
Palabras Clave: rendimientoescolar; Educación Media Superior; Querétaro; Cadenas de Markov.
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
CAPÍTULO 1
Introducción
Podemos decir que el rendimiento escolar es el valor numérico que se le da al estudiante tras haber cursado un ciclo escolar, donde se considera que se refleja la cantidad de conocimientos adquiridos en contra punto de los que le fueron impartidos, partiendo de aquí podríamos ver este rendimiento como un cúmulo de conocimientos, pero la realidad nos muestra que no siempre es así.
Desde la perspectiva de generosabemos que este rendimiento no siempre va relacionado con el aprovechamiento, se ha observado que este nivel es más fácil de obtenerlo por el género masculino y se presiona mas al femenino, prueba de esto es cuando los estudiantes egresan del nivel básico y se integran laboralmente donde se ve la preferencia al género masculino, no importando el recinto donde son contratados, mostrando gran diferencia en salarios y niveles jerárquicos de responsabilidades.
Desde el punto de vista de las instituciones, elrendimiento escolar cataloga a las mismas y posiciona en niveles altos o bajos a los estudiantes egresados, pruebas como enlace, que miden el rendimiento escolar, pueden acabar con la reputación de una institución o ponerla como una entre las mejores, aunque esa no sea su realidad.
La predicción del rendimiento escolar, por tanto, toma un gran importancia en nuestros tiempo que permite medir el nivel de aprovechamiento en los alumnos lo cual redundará en mejores profesionistas y por ende un mejor avance de nuestro país.
En esta investigación se realiza una predicción matemática mediante las teorías de los procesos estocásticos de las cadenas de Markov, mostrando con él el rendimiento escolar a futuro para el análisis y comprensión del fenómeno a corto, mediano y largo plazo,
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
teniendo como principal objetivo un pronósticodonde muestre la realidad del desempeño escolar. La investigación se llevó a cabo en el CEDART1 la ciudad de Querétaro que depende del INBAL2 y a su vez de la USEBEQ3 y la SEP4 ubicado en circuito plan vida # 116, col Centro sur, en la ciudad de Santiago de Querétaro, Qro.
1.1 Contexto y planteamiento del problema
El artículo tercero de la Constitución Política de los Estados Unidos Mexicanos indica que:
Toda persona tiene derecho a la educación. El Estado -Federación, Estados, Ciudad de México y Municipios-impartirá y garantizará la educación inicial, preescolar, primaria, secundaria, media superior y superior. La educación inicial, preescolar, primaria y secundaria,conforman la educación básica; ésta y la media superior serán obligatorias, la educación superior lo será en términos de la fracción X del presente artículo. La educación inicial es un derecho de la niñez y será responsabilidad del Estado concientizar sobre su importancia (Constitución Política de los Estados Unidos Mexicanos, s.f.)
Los planes y programas de estudio tendrán perspectiva de género y una orientación integral, por lo que se incluirá el conocimiento de las ciencias y humanidades: la enseñanza de las matemáticas, la lecto-escritura, la literacidad, la historia, la geografía, el civismo, la filosofía, la tecnología, la innovación, las lenguas indígenas de nuestro país,
Pl1 Centro de Educación Artística, institución del INBAL como modelo educativo integral deformación de secundaria y bachillerato general con el estudio de asignaturas provenientes de cuatro áreas artísticas, música, danza, artes plásticas, literatura y teatro.
2Instituto Nacional de las Bellas Artes y Literatura
3 Unidas de Servicios para la educación básica del estado de Querétaro.
4 Secretaria de Educación Pública.
UNADM |DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS
las lenguas extranjeras, la educación física, el deporte, las artes, en especial la música, la promoción de estilos de vida saludables, la educación sexual y reproductiva y el cuidado al medio ambiente, entre otras (Constitución Política de los Estados Unidos Mexicanos, s.f.)
Será de excelencia, entendida como el mejoramiento integral constante que promueve el máximo logro de aprendizaje de los educandos, para el desarrollo de su pensamiento crítico y el fortalecimiento de los lazos entre escuela y comunidad (Constitución Política de los Estados Unidos Mexicanos, s.f.)
En el inciso IX indica que: istema Nacional de Mejora Continua de la Educación, que será coordinado por un organismo público descentralizado, con autonomía técnica, operativa, presupuestaria, de decisión y de gestión, con personalidad jurídica y patrimonio propios, no sectorizado, alque le corresponderá:
a) Realizar estudios, investigaciones especializadas y evaluaciones diagnósticas, formativas e integrales del Sistema Educativo Nacional; b) Determinar indicadores de resultados de la mejora continua de la educación; c) Establecer los criterios que deben cumplir las instancias evaluadoras para los procesos valorativos, cualitativos, continuos y formativos de la mejora continua de la educación; d) Emitir lineamientos relacionados con el desarrollo del magisterio, el desempeño escolar, los resultados de aprendizaje; así como de la mejora de las escuelas, organización y profesionalización de la gestión escolar; e) Proponer mecanismos de coordinación entre las autoridades educativas federal y de las entidades federativas para la atención de las necesidades de las personas en la materia;
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
f) Sugerir elementos que contribuyan a la mejora de los objetivos de la educación inicial, de los planes y programas de estudio de educación básica y media superior, así como para la educación inclusiva y de adultos, y g) Generar y difundir información que contribuya a la mejora continua del Sistema (Constitución Política de los Estados Unidos Mexicanos, s.f.)
Con base en esta última parte expresada del artículo 3ro de la Constitución se establece la importancia de un grupo de indicadores que aporten los resultados de mejora continua en la educación, mismos que deberán ser medidos bajo especificas características, pero realmente no hay instrumentosque recolecten como tal este rendimiento, se usa para ello normalmente las calificaciones u otros indicadores que asientan las distintas instituciones a los diferentes estudiantes dependiendo de los niveles académicos en que se encuentren.
Ciertamente las evaluaciones emitidas al final de los ciclos escolares describen de manera ambigua, en algunos casos, el desempeño de los estudiantes, pero eso no implica que este rendimiento, expresado por un número, carezca de importancia, ya que cataloga al estudiante, a un determinado nivel de conocimientos.
Este nivel de conocimiento muestra a las instituciones, de manera poco clara, como se han impartido los conocimientos y por ende, la calidad académica que esta tiene, misma que será reflejada en sus estudiantes como un promedio de los conocimientos que obtendrán los alumnos al finalizar cualquiera de los ciclos escolares, por ello motivo de reflexión y búsqueda de mejora continua, como lo indica el artículo 3ro de la Constitución, para lograr cada vez un desempeño más adecuado en los alumnos y que este se vea reflejado en un estilo de vida adecuado de acuerdo a las condiciones económicas y sociales en que este se desenvuelve.
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
La toma de decisiones que se deben de llevar a cabo para la mejora del rendimiento escolar no deja de ser un evento que implique riesgos, no se puede predecir el futuro de ninguna forma, pero si podemos hacer uso de las diferentes herramientas matemáticas que se tienen al alcance para logran un adecuado y asertivo cambio, estas nos permiten pronosticar y reducir los riesgos de la toma decisiones.
El uso de herramientas matemáticas que muestren a futuro los esfuerzos realizados por las entidades académicas y les permitan acceder a la realización de adecuaciones que promuevan una mejora en la calidad que hoy por hoy imparten los llevará al logro de los máximos objetivos académicos, por ello una herramienta que ayude a las predicciones de dichos rendimientos representan acciones de vital importancia para la promoción de la calidad académica de cualquier institución.
Las herramientas matemáticas han sido utilizadas para el pronóstico de diferentes fenómenos como son los naturales, con respecto al clima o la probabilidad de lluvia de acuerdo a ciertos parámetros, financieramente hablando podemos predecir como es que se moverán ciertas divisas de acuerdo a como ha estado fluctuando en los últimos periodos de tiempo o de acuerdo a cambios políticos o sociales, por ello la utilización de las matemáticas representa la herramienta clave en el pronósticode eventos de cualquier índole.
Las herramientas matemáticas estocásticas, aquellas cuyo comportamiento no es determinista, es decir, es un proceso que depende sólo del estado anterior, por ello su utilización nos permite pronosticar los fenómenos a partir de estados iniciales, en esta investigación se utilizaron las cadenas de Markov que representan modelos simplificados creados para la toma de decisiones.
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Los modelos de Markov se han utilizado con éxito en los problemas donde se pretende generar pronósticos a partir de un evento inicial, esto es, las acciones iniciales determinan la acción inmediata a seguir o el que se le llama el siguiente estado, además de la forma en que se deberán de tomar los siguientes valores, entonces con cada valor obtenido generamos una cadena de valores que nos permite llegar a cualquier valor futuro arbitrariamente lejano.
1.2Objetivos
1.2.1 General
Planteamiento de un modelo estocástico de cadenas de Markov para predecir el rendimiento escolar en los Querétaro.
1.2.2 Específicos
Analizar las causas que llevan a cabo en la medición del rendimiento escolar de los Creación de la cadena de Markovque represente el rendimiento escolar de los
Analizar las asignaturas que implican cambios radicales en el rendimiento escolar de Creación dela cadena de Markov que represente el rendimiento escolar por
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Comparación de los niveles de rendimiento escolar con otras instituciones de igual índole.
UNADM |DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS
CAPÍTULO 2 MARCO INVESTIGATIVO
2.1 Rendimiento Escolar
Una de las dimensiones más importantes en la educación es el rendimiento académico, pero también es una de las más complejas ya que se trata de evaluar los conocimientos y revisar los factores buenos y malos que llevaron al dicho logro, por tanto, demuestra el éxito o fracaso del proceso educativo del estudiante.
El rendimiento escolar puede ser expresado como aquel número que se le da al estudiante, bajo los números de 5 al 10, donde 5 es reprobado y del 6 al 10 representa la aprobación, para establecer el dominio de los saberes, este puede ser de un bloque del curso o simplemente del curso completo, en esta investigación al referirnos al rendimiento escolar tomaremos aquellos valores que obtuvo el estudiante al finalizar el curso escolar. hablan de este como: Nivel de conocimientos demostrado en un área omateria comparado con la norma de edad y nivel (Jimenez, 2000).
Joaquín Cano, el rendimiento escolares una dimensión del rendimiento académico y es un índice de valoración de la calidadglobal de la educación. (Morales Sánchez, Morales Sánchez, & Holguín Quiñones, ISSN 2007-1957).
Antonio González define alrendimiento escolar como la verificación dela adquisición del conjunto de valores,actitudes, conductas y conocimientosseñalados como deseables por
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
los actoressociales autorizados (Morales Sánchez, Morales Sánchez, & Holguín Quiñones, ISSN 2007-1957).
ivel de conocimientos demostrado en un área omateriaal final de su ciclo escolar donde se evaluó tanto el desempeño académico como de valores, actitudes y conductas del
2.2 Cadenas de Markov
2.2.1 Antecedentes
Las cadenas de Markov fueron introducidas por el matemático rusoAndrei Markov crear un modelo probabilístico parara analizar la frecuencia con laque aparecen las vocales en poemas y textos literarios.Las cadenas de Markov pueden aplicarse a una amplia gama defenómenos científicos y sociales.
Andrei Markov fue alumno de la universidad de SanPetersburgo, discípulo de Chebyshev como Liapunov, despuésde su doctorado en 1886 accedió como adjunto a la Academiade Ciencias de San Petersburgo, a propuesta del propioChebyshev.
En 1989, cuando Chebyshev dejó la universidad, le sustituyóen los cursos de teoría de probabilidad. En 1925 AndreiMarkov dejó definitivamente la universidad.Aparte de su perfil académico, Andrei Markov fue un activista político oponiéndosea los privilegios de la nobleza zarista, llegando a rechazar las condecoraciones delzar en protesta por decisiones políticas relacionadas con la Academia de Ciencias.
| LICENCIATURA EN MATEMÁTICAS
UNADM |DCEIT| PT|
Andrei Markov influyó sobre diversos campos de las matemáticas, sobresaliendocon la teoría de la probabilidad.En 1887 completó la prueba que permitía generalizar el teorema central del límiteque ya había avanzado Chebyshev, aunque su aportación más conocida seencuentra en los procesos estocásticos, elaborando uninstrumento matemáticoque actualmente se conoce como cadena de Markov, instrumento que, hoy en día,se consideran una herramienta esencial en disciplinas como la economía, laingeniería, la investigación de operaciones y muchas otras.
2.2.2 Definición
Un proceso estocástico o proceso aleatorio es un concepto matemático que se utiliza para usar magnitudes aleatorias que varían con el tiempo o para caracterizar una sucesión de variables aleatorias o estocásticas que varían en función de otra variable, generalmente el tiempo. Cada variable o conjunto de variables sometidas a influencias o efectos aleatorios constituyen un proceso estocástico.
En teoría de la probabilidad, una Cadena de Markov en tiempo discreto (CMTD) es un tipo especial de proceso estocástico discreto en el que la probabilidad de que ocurra un suceso depende solamente del suceso inmediatamente anterior. Esta característica de falta de memoria se conoce como propiedad de Markov (recibe el nombre del matemático ruso Andrei Markov, que introdujo en 1907).
Definimos entonces a una cadena de Markov como:
Sea una variable aleatoria que caracteriza el estado del sistema en puntos discretosen el tiempo . La familia de variables aleatorias { } forma un proceso estocástico con una cantidad finita o infinita de estados. (Taha, 2012)
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Ilustración 1: Ejemplo de Cadena de Markov, creación propia
2.2.3 Desarrollo de las cadenas de Markov

UnaCadena de Markov es una secuencia de variables aleatorias, el dominio de estas variables es el llamado Espacio Estado. El valor es el estado del proceso en el tiempo .
La distribución de la probabilidad condicionada de en estados pasados es una función de por sí sola, siendo Para cualesquiera
Si se dice que la Cadena de Markov es finita, en caso contrario se dice que es infinita.
2.2.3.1
Cadena homogénea y no homogénea
Una Cadena de Markov se dice homogénea si la probabilidad de ir del estado al estado en un paso no depende del tiempo en el que se encuentra la cadena: Cadena homogénea:
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
para todo nodo
Si para alguna pareja de estados y para algún tiempo la propiedad mencionada no se cumple se dice que la Cadena de Markov es no homogénea.
2.2.3.2 Probabilidad y matriz de transición
Si una Cadena de Markov está en el estado hay una probabilidad de pasar al próximo estado a esta probabilidad se la llama probabilidad de Transición.
La probabilidad de pasar del estado al estado en un paso se llama probabilidad de transición de a : .
Las probabilidades de transición conforman la matriz de transición P, que es conrigor una matriz (finita) sólo para cadenas de Markov finitas, aunque también seconserva el nombre y la notación para cadenas de Markov infinitas.
Cada fila de la matriz de transición debe sumar 1 por las propiedades básicas de probabilidad.
El modelo para redes se puede considerar una cadena de Markov donde son losvértices del grafo dirigido y es el inverso del número de aristas salientes desde cuando hay una arista de a y cero en otro caso.
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
La matriz de transición en un solo paso, dada una cadena de Markov con estados posibles y probabilidades de transición estacionarias, vienedada por la expresión:
2.2.3.3 Matriz de transición
El Vector distribución es un vector fila no negativo con una entrada para cada estado del sistema.
Vector probabilidad es un vector con entradas no negativas, de forma que se agregan hasta llegar a 1. Las entradas pueden representar las probabilidades de encontrar un sistema en cada uno de los estados.
El vector de distribución y la matriz de transición P determinan la probabilidad para el estado de la cadena en el segundo instante de tiempo, dicha probabilidad viene dada por el vector ( ).
Distribución después del 1 paso:
Distribución después del 2 paso: ( ) = Distribución después del 3 paso: ( ) = Y así sucesivamente llegamos a
Distribución después del n paso: ( ) =
| LICENCIATURA EN MATEMÁTICAS
UNADM |DCEIT| PT|
Una notación conveniente para representar las probabilidades de transición de pasos es la matriz de transición de pasos:
La probabilidad de transición en una fila y columna dadas es la transición del estadoen esa fila al estado en la columna. Cuando el superíndice no se escribe y sehace referencia a ésta como una matriz de transición.
Las probabilidades de transición en pasos son las probabilidades de transicióndel estado al estado en pasos, denotándose como:
Las cadenas de Markov que se analizan tienen las propiedades:
2.2.3.4
Vector de Probabilidad Estacionario
Un vector de probabilidad ya sea finito oinfinito numerable se dice estacionario para una cadena de Markov en tiempodiscreto (CMTD) si cualquier transición de acuerdo con la matriz verifica:
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Al vector de probabilidad estacionario también se le denomina distribuciónestacionaria o distribución de equilibrio.
Cuando la cadena de Markov se va aproximando de estado en estado hacia un estado de equilibrio se le llama estado estable, que se determina por
Un vector de probabilidades
De una cadena de Markov en tiempo discreto se le llama límite si:
El vector de probabilidades de de una cadena de Markov es tiempo discreto se dice el único vector de probabilidades en equilibrio de la cadena sí convergen independientemente de la distribución , cada probabilidad es mayor estrictamente que cero.
2.2.4 Clasificación de estados de las cadenas de Markov
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Estado alcanzable:
Dados dos estados y , una trayectoria de a es una secuencia de transiciones que comienza en y termina en , tal que cada transición en la secuencia tiene una probabilidad positiva de ocurrir. Un estado es alcanzable desde el estado si hay una trayectoria que conduzca de a
Estados que se comunican:
Se dice que dos estados y se comunican si es alcanzable desde , y de igual manera es alcanzable desde .
Conjunto cerrado: Un conjunto de estados de una Cadena de Markov es cerrado si ningún estado fuera de es alcanzable desde algún estado en .
Estado absorbente: Es un estado en el que Siempre que se entra en un estado absorbente, no se sale de él; un estado absorbente es un conjunto cerrado que contiene sólo un estado.
Ilustración 2Ejemplo: El estado 3 es absorbente. Creación propia. Tomado de imágenes Wikipedia

Estado transitorio:

| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Un estado es transitorio si existe un estado que es alcanzable desde , pero el estado no es alcanzable desde el estado
Ilustración 3Ejemplo: El estado 2es transitorio. Creación propia. Tomado de imágenes Wikipedia Estado recurrente: Es un estado que no es transitorio.

Ilustración 4Ejemplo: Los estados 1, 2 y 3 son recurrentes. Creación propia. Tomado de imágenes Wikipedia Estado periódico:
Un estado es periódico con periodo si es el número más pequeño tal que las trayectorias que conducen al estado de regreso al estado tienen una longitud que es un múltiplo de . Si un estado recurrente no es periódico, se conoce como aperiódico (Winston, 2008).

| LICENCIATURA EN MATEMÁTICAS
UNADM |DCEIT| PT|
2.3Metodología

En esta parte se hace un análisis de los que constituye la fundamentación metodológica de la investigación que abarca los temas relacionados con la investigación cuantitativa, así como la metodología empleada y el diseño de la investigación
2.3.1
Investigación cuantitativa.
La presente investigación se realizó de tipo cuantitativa de abstracción aplicada ya que se buscó la solución a un problema práctico de un grupo de estudiantes, en este caso una institución pública de educación básica del nivel secundaria y bachillerato situado en la ciudad de Querétaro. De forma deductiva ya que partió de una premisa inicial para llegar a una conclusión general del problema. A manera correlacional debido a que partimos de hechos establecidos con una relación causa efecto para la solución de una problemática. Tratando de establecer una generalización fundamental ya que se realizó a una pequeña
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Ilustración 5Ejemplo: Cadena de período 3. Creación propia. Tomado de imágenes Wikipedia
muestra para generalizar el fenómeno. Buscando un estudio de naturaleza descriptivocausal, debido a que se buscó visualizar a través de una amplitudde datos numéricos la relación causativa entre las variables independientes y dependiente. Se menciona una técnica conjunta para correlacionar los resultados y determinar una conclusión.
Finalmente, con la metodología cuantitativa, se llevaron a cabo mediciones sistemáticas de los eventos, así como un análisis estadístico resultante.
2.3.2 Diseño de la investigación
El diagrama que ilustra el diseño metodológico que dirige la realización de este estudio fue: G1X101
2.3.3 Participantes
La población está constituida por ###alumnos que cursan la educación básica en el nivel secundaria y medio superior de la institución donde se llevó a cabo la investigación, todos ellos cursaron un ciclo escolar competo, obteniendo una calificación final de rendimiento escolar.
2.3.4 Variables de estudio
| LICENCIATURA EN MATEMÁTICAS
UNADM |DCEIT| PT|
CAPÍTULO 3 RESULTADOS
3.1Actividades desarrolladas
3.1.1 Materiales y métodos
3.1.2 Cronograma
3.2Resultados
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
CAPÍTULO 4 CONCLUSIONES
4.1Relación con el Programa Educativo
4.2Beneficios para la institución o empresa
4.3 Aprendizajes obtenidos
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
REFERENCIAS
Anónimo. (s.f.). Cadenas de Markov finitas. Fenómenos de espera. Obtenido de http://www.estadistica.net/INVESTIGACION/CADENAS-MARKOV.pdf
Camarena Ibarrola, J. A. (s.f.). Cadenas de Markov. Obtenido de http://dep.fie.umich.mx/~camarena/Cadenas%20de%20Markov.pdf
Constitución Política de los Estados Unidos Mexicanos. (s.f.). Obtenido de Justia México: https://mexico.justia.com/federales/constitucion-politica-de-los-estados-unidosmexicanos/titulo-primero/capitulo-i/#articulo-3o
Cuaya Simbro, G. (s.f.). Procesos de Decisión de Markov aplicados a la locomoción de robots hexápodos. Obtenido de https://inaoe.repositorioinstitucional.mx/jspui/bitstream/1009/588/1/CuayaSG.pdf
INBAL. (s.f.). Obtenido de https://inba.gob.mx/
Jimenez, M. (2000). Infancia y Sociedad. Competencia social: intervención preventiva en la escuela
Morales Sánchez, L. A., Morales Sánchez, V., & Holguín Quiñones, S. (ISSN 2007-1957). Rendimiento Escolar. Humanidades, Tecnología y Ciencia del Instituto Politécnico Nacional
Navarro, R. E. (2003). El rendimiento académico: concepto, investigación y desarrollo. REICE: Revista Iberoamericana sobre Calidad, Eficacia y Cambio en Educación, 1(2), 0. Obtenido de https://www.redalyc.org/pdf/551/55110208.pdf
Pérez Lázaro, J. (s.f.). Cadenas de Markov (en tiempos discretos con estados discretos). Obtenido de Universidad de Rioja: https://www.unirioja.es/cu/franpere/ModyOptfiles/Tema6.pdf
Taha, H. A. (2012). Investigación de Operaciones (Novena Edición ed.). México: PEARSON EDUCACIÓN,.
Winston, W. (2008). Investigacion de operaciones, aplicaciones y algoritmos 4a. ediccion . Mexico D.f: Cengage Learning.
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
ANEXOS
Anexo 1. Lista de figuras
Ilustración 1: Ejemplo de Cadena de Markov, creación propia........................................................32
Ilustración 2 Ejemplo: El estado 3 es absorbente. Creación propia. Tomado de imágenes Wikipedia ..37
Ilustración 3 Ejemplo: El estado 2 es transitorio. Creación propia. Tomado de imágenes Wikipedia ...........................................................................................................................................................38
Ilustración 4 Ejemplo: Los estados 1, 2 y 3 son recurrentes. Creación propia. Tomado de imágenes Wikipedia.......................................... ..............................................38
Ilustración 5 Ejemplo: Cadena de período 3. Creación propia. Tomado de imágenes Wikipedia....39
Anexo 2. Lista de tablas
Anexo 2 A Anexo 3. Informes mensuales
| LICENCIATURA EN MATEMÁTICAS UNADM
|DCEIT| PT|
Captura de Calificaciones
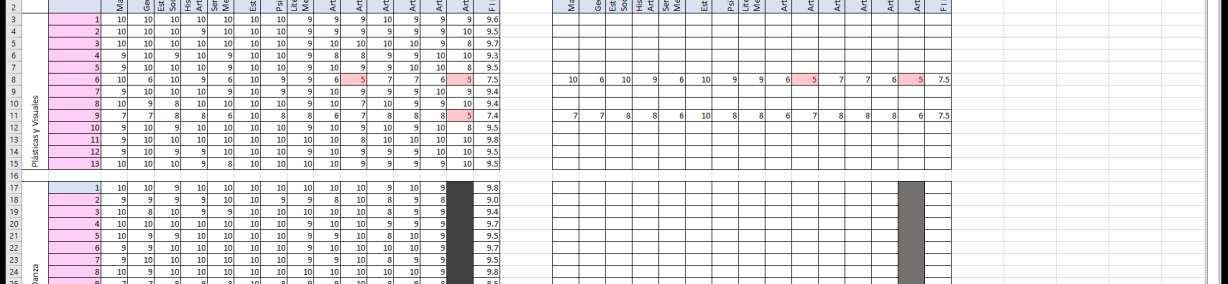

| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
División de Ciencias Exactas, Ingeniería y Tecnología Práctica profesional/Proyecto terminal Informe mensual de actividades Organización: Estudiante: Mercedes Rodríguez Robles Matrícula: ES1821016580 Área de conocimiento: Matemáticas Número de reporte: 3 Asesor externo: Lic. Pedro Daniel Lara Maldonado
Santiago de Querétaro, 21 Noviembrede 2022.
Tabla de especificaciones del Informe
Actividad presentada
Presentación del proyecto
Objetivo de la actividad Observaciones
Corrección de retroalimentación del asesor externo
Marco investigativo Marco teórico Fundamento Matemático Metodología
Elaboración del capítulo 2 Redaccióndel capítulo 2
Elaboración del texto del capítulo 2 del anteproyecto: 2.2 Institución de Investigación a) Prueba PLANEA b) Resultados de prueba PLANEA 2.3.5 Teoría de Grafos 2.3.6 Software de Aplicación 2.4 Metodología
Captura de calificaciones
Capturar en un archivo de Excel las calificaciones para su posterior análisis
Se continua con la captura de calificaciones, ya se tienen dos generaciones completas capturadas
Tabla de descripción de la o las problemáticas identificadas
Actividad presentada
Problemática identificada
Presentación del proyecto Sin problemas por el momento
Elaboración del capítulo 2 Sin problemas por el momento
Captura de calificaciones Sin problemas por el momento
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Actividad realizada
Presentación del proyecto
Revisión del capítulo 2

Captura de calificaciones
Tabla de resultados
Acción correctiva Experiencia obtenida


Ninguna por el momento Muestra del anteproyecto
Ninguna por el momento Elaboración de anteproyecto

Ninguna por el momento
Captura de las calificaciones por semestre
Observaciones
Se realiza resumen que contenga lo más importante para la presentación
Generar las modificaciones necesarias y enviarlo a revisión con el asesor externo.
Este proceso que todavía no se ha terminado ha resultado ser muy tardado.
Servicio social presentado Periodos de impartición
Se presentó servicio por una cantidad de 3 horas diarias de lunes a viernes en el trayecto de 6semanas que contemplan del 17de octubredel 2022 al 30de noviembredel 2022 y 3 días. Anexos: Evidencia de cada actividad. Asesor externo Estudiante
99 horas
Lic. Pedro Daniel Lara Maldonado
Mercedes Rodríguez Robles
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Evidencia de cada actividad. Presentación del Proyecto




| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|



| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|



| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|



| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|



| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Revisión del capítulo 2
2.2 Institución de la investigación
La institución donde se llevó a cabo la investigación de nombre Centro de Educación Secretaría de Cultura/INBA/Subdirección General de Educación e Investigación Artísticas (SGEIA)cuya oferta educativa es de secundaria y bachillerato de Artes y Humanidades, con domicilio en circuito. Plan Vida 116, Colonia Centro Sur, Cp07690, Querétaro, Querétaro, Tels.: 442 153 19 70 al 79.
Cuenta con una población estudiantil de 300 estudiantes que incluyen los dos niveles, básico y media superior, siendo de importancia su enfoque cultural ya que permite maneja la especialidad de Arte y Humanidades con talleres de: Danza folclórica, contemporánea y clásica, Música, Literatura, Teatroy Artes plásticas, otorgando la documentación al términodeCertificado.
Estemodelo educativo integra la formación del bachillerato general con el estudio de asignaturas provenientes de cincoáreas artísticas. Por su carácter propedéutico, proporciona las bases y los conocimientos necesarios para continuar estudios de nivel superior, tanto en el campo de las artes como en las ciencias y las humanidades. El propósito de este bachillerato no es formar artistas. No obstante, a partir de la integración de saberes de la danza, la música, el teatro, literaturay las artes plásticas, contribuye en el desarrollo de habilidades cognitivas, afectivas, sociales y expresivas que redundan en una auténtica formación integral de sus egresados.
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
El ingreso a este modelo educativo implica conciencia de que los estudios artísticos son rigurosos y querequieren de una mayor certidumbre vocacional y total disposición para cursarlos en armonía con el resto de las asignaturas del bachillerato. Por el mismo motivo, el proceso de admisión busca comprobar estas condiciones en los aspirantes a efecto de que se cumplan las expectativas institucionales y personales.
2.2.1 Prueba Planea
La Secretaría de Educación Pública en coordinación con la Comisión Nacional para la Mejora Continua de la Educación y las autoridades educativas de las entidades federativas, aplica la prueba Planea en Educación Media Superior a estudiantesdel último grado en poco más de 18,000 escuelas de Educación Media Superior del país de carácter público, federal y estatal, en los planteles particulares con Reconocimiento de Validez Oficial de Estudios (REVOE) otorgado por la SEP o por las entidades federativas, así como en las instituciones autónomas y en sus escuelas particulares incorporadas. Esta prueba tiene el propósito de conocer en qué medida el estudiantado logra dominar un conjunto de aprendizajes esenciales al término de la Educación Media Superior, en dos campos de formación: Lenguaje y Comunicación y Matemáticas.
PLANEA1,agrupa los resultados obtenidos por los estudiantesen cuatro niveles de logro los cuales informan acerca de los aprendizajes clave que deben ser adquiridos por el estudiantado y en qué medida se han apropiado de ellos. Es importante señalar que estos niveles van del I al IV en orden progresivo, es decir, el nivel más bajo es el I y el más alto es el IV. Además, son acumulativos, ya que los estudiantes que se ubican en el nivel II cuentan con los aprendizajes del nivel previo (NI) y así sucesivamente.
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
1 El Plan Nacional para la Evaluación de los Aprendizajes
A continuación, se presenta la descripción genérica de los niveles de logro:
Nivel I: El estudiantado que se ubica en este nivel tiene un conocimiento insuficiente de los aprendizajes clave incluidos en los referentes curriculares. Esto refleja mayores dificultades para continuar con su trayectoria académica.
Nivel II: El estudiantado que se ubica en este nivel tiene un conocimiento elemental de los aprendizajes clave incluidos en los referentes curriculares.
Nivel III: El estudiantado que se ubica en este nivel tiene un conocimiento satisfactorio de los aprendizajes clave incluidos en los referentes curriculares.
Nivel IV: El estudiantado que se ubica en este nivel tiene un conocimiento sobresaliente de los aprendizajes clave incluidos en los referentes curriculares.
PLANEA Educación Media Superior está diseñada para ofrecer a padres y madres de familia, al estudiantado, al profesorado, la dirección, autoridades educativas y sociedad en general, información específica sobre el logro académico de las escuelas y, utilizada adecuadamente, constituye un potente instrumento que puede contribuir a mejorar la calidad de la educación.
2.2.1.1 Características de la prueba planea
Es una prueba objetiva y estandarizada.
Está alineada al Marco Curricular Común, en particular a los campos de formación asociados con las competencias de Lenguaje y Comunicación y Matemáticas. Está conformada por 100 reactivos de opción múltiple, 50 que evalúan Lenguaje y Comunicación y 50 de Matemáticas.
Es una prueba criterial que NO está diseñada para derivar conclusiones al respecto del desempeño de las escuelas o las y los docentes.
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Sus resultados NO deben tener consecuencias académicas o de otro tipo para el estudiantado, el profesorado o sus escuelas.
Es una prueba de diagnóstico, NO es una prueba de selección para el ingreso a instituciones de Educación Superior.
Ofrece información pertinente y oportuna a las escuelas y al profesorado, contribuyendo así al desarrollo de directrices para la mejora del sistema.
2.2.1.2 Resultados Planea 2015
Los resultados obtenidos por el Cedart en laprueba Planea en el 2015
Lenguaje y Comunicación
I II III IV
% de alumnos de la escuela en cada nivel de logro7.5%10.0%37.5%45.0%
Porcentaje de alumnos de escuelas parecidas en cada nivel de logroS/RS/RS/RS/R
Porcentaje de alumnos en todas las escuelas de México en cada nivel de logro 23.1%20.2%34.7%21.9%
Tabla 1: PLANEA 2015: Lenguaje y Comunicación, creación propia
| LICENCIATURA EN MATEMÁTICAS
UNADM |DCEIT| PT|
2015 Lenguaje y comunicación Porcentajes de logro por nivel
40
30
20
10
0
50 IIIIIIIV
Grafica 1: PLANEA 2015: Lenguaje y Comunicación, creación propia Matemáticas I II III IV
% de alumnos de la escuela en cada nivel de logro7.3%43.9%39%9.8%
Porcentaje de alumnos de escuelas parecidas en cada nivel de logroS/RS/RS/RS/R
Porcentaje de alumnos en todas las escuelas de México en cada nivel de logro 46.3%36.9%14.0%2.8%
Tabla 2: PLANEA2015: Matemáticas,creación propia
| LICENCIATURA EN MATEMÁTICAS
UNADM |DCEIT| PT|
CedartSimilarNacional
2015 Matemáticas
Porcentaje de logro por nivel
50
40
30
20
10
0
Grafica 2: PLANEA 2015 Matemáticas, creación propia 2.2.1.3 Resultados Planea 2016
Los resultados obtenidos por el Cedart en la prueba Planea en el 2016 Lenguaje y Comunicación
I II III IV
% de alumnos de la escuela en cada nivel de logro2.7%10.8%37.8%48.6%
Porcentaje de alumnos de escuelas parecidas en cada nivel de logro2.7%10.8%37.8%48.6%
Porcentaje de alumnos en todas las escuelas de México en cada nivel de logro 18.1%21.8%36.5%23.6%
Tabla 3: PLANEA 2016: Lenguaje y Comunicación, creación propia
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
IIIIIIIV
CedartSimilarNacional
2016 Lenguaje y comunicación
Porcentajes de logro por nivel
50
40
30
20
10
0
60 IIIIIIIV
Grafica 3: PLANEA 2016: Lenguaje y Comunicación, creación propia Matemáticas I II III IV
% de alumnos de la escuela en cada nivel de logro5.3%39.5%47.4%7.9%
Porcentaje de alumnos de escuelas parecidas en cada nivel de logro5.3%39.5%47.4%7.9%
Porcentaje de alumnos en todas las escuelas de México en cada nivel de logro 32.6%42.1%21.0%4.4%
Tabla 4: PLANEA2016: Matemáticas, creación propia
| LICENCIATURA EN MATEMÁTICAS
UNADM |DCEIT| PT|
CedartSimilarNacional
2016 Matemáticas
Porcentaje de logro por nivel
50
40
30
20
10
0
Grafica 4: PLANEA 2016: Matemáticas, creación propia 2.2.1.4 Resultados Planea 2017
Los resultados obtenidos por el Cedart en la prueba Planea en el 2017 Lenguaje y Comunicación I II III IV
% de alumnos de la escuela en cada nivel de logro5.9%0.0%44.1%50.0%
Porcentaje de alumnos de escuelas parecidas en cada nivel de logro22.9%29.9%35.4%11.8%
Porcentaje de alumnos en todas las escuelas de México en cada nivel de logro 33.9%28.1%28.7%9.2%
Tabla 5: PLANEA 2017: Lenguaje y Comunicación, creación propia
| LICENCIATURA EN MATEMÁTICAS
|DCEIT| PT|
UNADM
IIIIIIIV
CedartSimilarNacional
2017 Lenguaje y comunicación Porcentajes de logro por nivel
50
40
30
20
10
0
60 IIIIIIIV
Grafica 5: PLANEA 2017: Lenguaje y Comunicación, creación propia Matemáticas I II III IV
% de alumnos de la escuela en cada nivel de logro21.4%25.0%25.0%28.6%
Porcentaje de alumnos de escuelas parecidas en cada nivel de logro48.6%31.8%14.2%5.3%
Porcentaje de alumnos en todas las escuelas de México en cada nivel de logro 66.2%23.3%8.0%2.5%
Tabla 6: PLANEA2017: Matemáticas, creación propia
| LICENCIATURA EN MATEMÁTICAS
UNADM |DCEIT| PT|
CedartSimilarNacional




















| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT|
10 20 30 40 50 60 70
0 10 20 30 40 50 60 Cedart2015NacionalCedart2016NacionalCedart2017Nacional
PT| Grafica 6: PLANEA 2017: Matemáticas, creación propia 2.2.2 Resultados planea de rendimiento escolar Grafica 7: PLANEA Lenguaje y Comunicación, creación propia 0
IIIIIIIV 2017 Matemáticas Porcentaje de logro por nivel CedartSimilarNacional
Lenguaje y Comunicación IIIIIIIV
60


50
40
30
20
10
0
70 Cedart2015NacionalCedart2016NacionalCedart2017Nacional
Grafica 8: PLANEA Matemáticas, creación propia
2.3.5 Teoría de grafos



Un grafo es una estructura matemática que consta de vértices y aristas que conectan estos vértices; En términos elementales podríamos definir un grafo como un conjunto de puntos (llamados elementos, vértices, nudos o nodos) con líneas que unen pares de vértice de ellas; en algunos libros se usa red como sinónimo de grafo.(Álvarez Núñez & Parra Muñoz, 2013)



2.3.5.1 Definición















Un grafo es una abstracción matemática que designaremos por
Donde es el conjunto de vértices o puntos y es el conjunto de líneas que unen dos puntos de
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Matemáticas IIIIIIIV
puede ser vacío llamado conjunto de las aristas que están relacionadas mediante la aplicación .
A cualquier arista de un grafo se le puede asociar una pareja de vértices de este. Si son dos vértices de un grafo y la arista a está asociada con este par, escribiremos
Un grafo se representa mediante un diagrama en el cual a cada vértice le corresponde un punto y si dos vértices son adyacentes se unen sus puntos correspondientes mediante una línea.
Ejemplo:
Entonces el grafo sería:
UNADM |DCEIT| PT|
| LICENCIATURA EN MATEMÁTICAS
Ilustración 1: Ejemplo de Grafo,Tomado de:(Álvarez Núñez & Parra Muñoz, 2013)
En el diagrama geométrico los nudos o vértices estarán indicados por pequeños círculos y las conexiones mediante arcos,líneas o rectas, los cuales pueden tener dirección o no, de donde se generan dos clasificaciones de grafos: Los dirigidos y los no dirigidos, donde llamaremos arco a la relación de dirección que existe entre 2 nodos.




2.3.5.1 Grafos no Dirigidos

Los grafos no dirigidos espropiamente aquel grafo que no considera dirección, esto es, las aristas no tienen sentido, luego la relación existente es simétrica.
2.3.5.2
Ilustración 2: Grafo no Dirigido, tomado de: (ÁLVAREZ NÚÑEZ & PARRA MUÑOZ, 2013)
Grafos Dirigidos
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Grafo dirigido es aquel grafo en el cual la relación existente entre los elementos considera su dirección, Se puede recalcar que si es un dígrafo, o grafo dirigido,entonces la relación T, en general no es simétrica; es decir
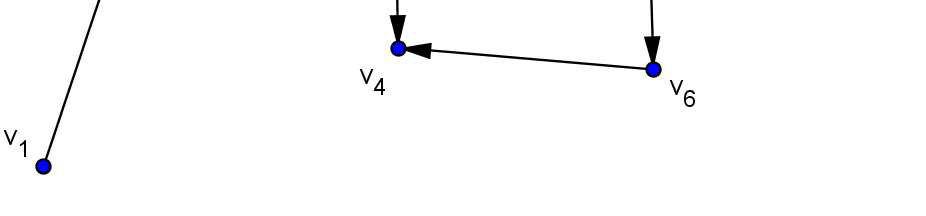
Ilustración 3: Grafo dirigido, tomado de: (ÁLVAREZ NÚÑEZ & PARRA MUÑOZ, 2013) 2.3.5.3 Camino

Es una ruta que se debe seguir para llegar de un punto a otro. Lo representaremos por , sabiendo que entre un punto y otro puede haber más de un camino.
Ejemplo: si trazamos el camino de este pasa por los puntos entonces
Ilustración 4: Ejemplo de camino, Tomado de: (ÁLVAREZ NÚÑEZ & PARRA MUÑOZ, 2013)
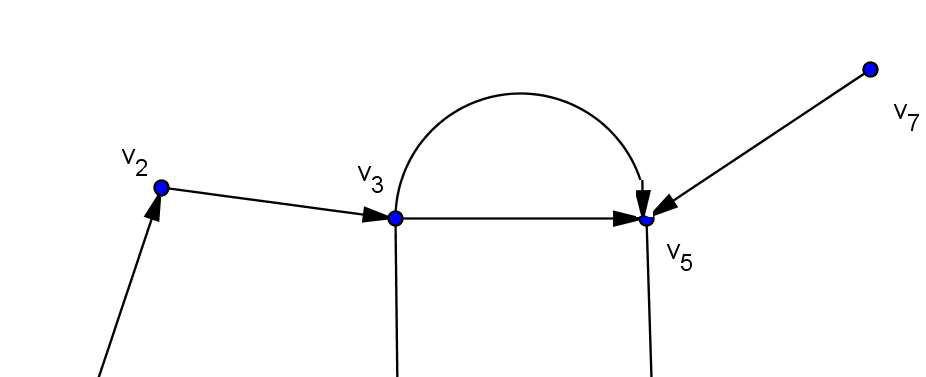
| LICENCIATURA EN MATEMÁTICAS
UNADM |DCEIT| PT|
2.3.5.4 Vértices Adyacentes

Se dice que dos vértices son adyacentes si están conectados por una arista o por un arco. Ejemplo: los vértices son adyacentes, los vértices no lo son Ilustración 5: Vértices adyacentes, Tomado de:(ciencias.medellin.unal.edu.co, s.f.)
2.3.5.5 Matriz de Adyacencia
Sea un grupo cuyo conjunto de vértices es , llamaremos matriz de adyacencia del grafo a la matriz de -filas y -columnas,donde Ejemplo: Utilizando el grafo:
Ilustración 6: Grafo ejemplo matriz de adyacencia, Tomado de:(ciencias.medellin.unal.edu.co, s.f.)

| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
Su matriz de adyacencia está dada por
Donde, todos los ceros de la matriz A significan que no hay ningún camino entre los vértices correspondientes; todos los unos de la matriz A significan que existe un camino entre los vértices correspondientes
2.3.6 Software de Aplicación
Para la realización de los procesos de cálculo de las matrices se utilizará el software POM QM para Windows que es un programa para la gestión de producción/operaciones, métodos cuantitativos, ciencia de la gestión e investigación de operaciones; mismo queal ser una herramienta de software libren nos permite utilizarlo sin necesidad de pago; de igual forma para la generación de grafos se utilizará la aplicación DIA que de la misma forma es software libre.
2.4Metodología
En esta parte se hace un análisis de los que constituye la fundamentación metodológica de la investigación que abarca los temas relacionados con la investigación cuantitativa, así como la metodología empleada y el diseño de la investigación
2.4.1 Investigación cuantitativa.
| LICENCIATURA EN MATEMÁTICAS
|DCEIT| PT|
UNADM
La presente investigación se realizó de tipo cuantitativa de abstracción aplicada ya que se buscó la solución a un problema práctico de un grupo de estudiantes, en este caso una institución pública de educación básica del nivel secundaria y bachillerato situado en la ciudad de Querétaro. De forma deductiva ya que partió de una premisa inicial para llegar a una conclusión general del problema. A manera correlacional debido a que partimos de hechos establecidos con una relación causa efecto para la solución de una problemática. Tratando de establecer una generalización fundamental ya que se realizó a una pequeña muestra para generalizar el fenómeno. Buscando un estudio de naturaleza descriptivocausal, debido a que se buscó visualizar a través de una amplitud dedatos numéricos la relación causativa entre las variables independientes y dependiente. Se menciona una técnica conjunta para correlacionar los resultados y determinar una conclusión. Finalmente, con la metodología cuantitativa, se llevaron a cabo mediciones sistemáticas de los eventos, así como un análisis estadístico resultante.
2.4.2 Diseño de la investigación
El diagrama que ilustra el diseño metodológico que dirige la realización de este estudio fue:
G1X101
2.4.3
Participantes
La población está constituida por 150alumnos que cursan la educación básica en el nivel secundaria y medio superior de la institución donde se llevó a cabo la investigación, todos ellos cursaron un ciclo escolar competo, esto es, cumplieron con los 6 semestres de nivel bachillerato y obtuvieron una calificación aprobatoriafinal de rendimiento escolar.
| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
2.4.4 Variables de estudio
Establecemos la variable como:
Estos datos nos representan un proceso estocástico con espacios discretos.
La caminata que representan las generaciones es:

Ilustración 7: Caminata y grafo de generaciones, creación propia

| LICENCIATURA EN MATEMÁTICAS UNADM |DCEIT| PT|
9.99.89.79.69.4 9.91 9.80.50.5 9.71 9.6 9.41
La matriz de incidencia está dada por Captura de calificaciones



| LICENCIATURA EN MATEMÁTICAS
UNADM |DCEIT| PT|



































































































