Xevex - Ramaz Math Publication - Spring 2024

XEVEX

Spring 2024

e Ramaz Mathematics Publication

Sarah Silverman ‘24

Grace Kollander ‘25

TABLE OF CONTENTS

62862089986280348253421170679821480865132823066470938446095505822317253594081284811174502 84102701938521105559644622948954930381964428810975665933446128475648233786783165271201909 14564856692346034861045432664821339360726024914127372458700660631558817488152092096282925 40917153643678925903600113305305488204665213841469519415116094330572703657595919530921861 17381932611793105118548074462379962749567351885752724891227938183011949129833673362440656 64308602139494639522473719070217986094370277053921717629317675238467481846766940513200056 81271452635608277857713427577896091736371787214684409012249534301465495853710507922796892 58923542019956112129021960864034418159813629774771309960518707211349999998372978049951059 73173281609631859502445945534690830264252230825334468503526193118817101000313783875288658 75332083814206171776691473035982534904287554687311595628638823537875937519577818577805321 71226806613001927876611195909216420198938095257201065485863278865936153381827968230301952 03530185296899577362259941389124972177528347913151557485724245415069595082953311686172785 58890750983817546374649393192550604009277016711390098488240128583616035637076601047101819 42955596198946767837449448255379774726847104047534646208046684259069491293313677028989152 10475216205696602405803815019351125338243003558764024749647326391419927260426992279678235

The History of Banking and its Direct Connection to Math

Morris Cohen ’26 ...3

Earning a PhD in Mathematics: Insights from Dr. Nironi

Morris Cohen ’26 ...3

Basic Understanding of the World of NFTs

Adam Schwartz ‘27 ...5

Basic Calculator Programming: A Student’s Guide

Morris Cohen ’26 ...5

The Complexities of Auto Racing

Adam Schwartz ’27 ...7

Understanding the Eruv Through Math

Saul Beroukhim ’27

The Power of Misleading Statistics

Caroline Kollander ’27

The History of Euler’s Number

Ezra Gonen ’27 ...9

The Greatest Unsolved Mystery of Our Time

Sylvie Raab ’26 ...10

What Really is the Fibonacci Sequence?

Si Heyman ’26 ...11

Utilization of Financial mathematics Within the Stock Market Landscape

Si Heyman ’26 ...12

The Math Behind Psychology

Leon Kremer ’27 ...14

85233239073941433345477624168625189835694855620992192221842725502542568876717904946016534 66804988627232791786085784383827967976681454100953883786360950680064225125205117392984896 08412848862694560424196528502221066118630674427862203919494504712371378696095636437191728 74677646575739624138908658326459958133904780275900994657640789512694683983525957098258226 20522489407726719478268482601476990902640136394437455305068203496252451749399651431429809 19065925093722169646151570985838741059788595977297549893016175392846813826868386894277415

Probability Theory in Risk Assessment

Caroline Kollander ’27 ...15

Mathematics of Taylor Swift’s Music

Caroline Kollander ’27 ...16

Math in Gemara

Tory Doft ’27 ...16

Background to Complex Numbers

Leo Eigen ’25 ...17

Hilbert’s Problems

Grace Kollander ’25 ...18

Digital Square Roots

Olivia Saar ’26 ...19

The History of Topos Theory

David Daniell ’27 ...20

Math in the Middle East

Aryeh Goldstein ’27 ...21

Fractal Geometry: A Critical Tool In Understanding The Natural World

Jack Friedman ’26 ...22

The Math Behind Piano Tuning

Ben Rubinchik ’27 ...24

Dissecting Divisibility Tricks: The Math Hidden Behind the Scenes

Benjamin Title ’27 ...26

The History of Banking and its Direct Connection to Math

Morris Cohen

Many students studying pure math often end up working in finance. This might seem like a strange path—after all, pure math is about abstract ideas and theories, right? But there’s a really practical reason why math majors lean toward finance. It’s all about numbers and problem-solving, skills at the heart of both fields. Finance, at its core, is about money management. Whether it’s setting interest rates, pricing securities, managing risk, or developing investment strategies, each aspect of finance relies heavily on mathematical principles. The predictive nature of mathematics, especially through statistical models and algorithms, is crucial for making informed financial decisions. The history of banking itself offers insights into why mathematics is so integral to the field. Early bankers in medieval Italy, such as the famous Medici family, were among the first to use arithmetic and algebra to manage their lives, including lending and exchanging currencies. A big step in banking came with something called double-entry bookkeeping. This method, which involves recording debits and credits to keep finances balanced, was put into practice by Luca Pacioli in 1494. Pacioli was not just a mathematician; he was a mathematician who showed the world how useful math could be in everyday business. Another instance was in the 17th century, mathematicians Blaise Pascal and Pierre de Fermat laid the groundwork for probability theory. Imagine trying to predict life expectancy for insurance purposes or

determining the risks involved in lending money without any mathematical tools. Early bankers and insurers faced these exact challenges. Pascal and Fermat’s work helped banks and financial institutions develop better ways to manage these uncertainties. They could now calcullate the likelihood of various outcomes, which meant they could offer more reliable insurance policies and make smarter lending decisions. Thanks to these early innovators, banks could handle risk more effectively , leading to greater stability and trust in financial operations. Another example is the Black-Scholes model, a formula used to help price options in the stock market. Economists and mathematicians developed it in the 1970s, and is still used today. This model shows how high-level math can directly impact financial decisions in big ways. Fast-forward to today, and you’ll see why math majors are still in demand in finance. Take risk management, which is a huge part of finance. Companies always want to avoid losing money, and they need people who can predict and calculate risks accurately. Math majors are trained to think critically and solve complex problems, skills that are perfect for this. In conclusion, math majors are essential in finance because their skills match the industry’s needs. As finance evolves, these abilities will remain valuable, guaranteeing that math majors will always have a role in shaping the future of finance.

Earning a PhD in Mathematics: Insights from Dr. Nironi

Morris Cohen

Have you ever wondered what it’s like to get a PhD in math? Meet Dr. Nironi, who went through the whole process

and came out on the other side. He’s here to share his story, from the long hours of study (and not so long hours of sleep) to the moments of breakthrough that make it all worthwhile. It’s not just about numbers and complex theories; it’s about a journey of persistence, learning, and discovery. Dr. Nironi gives us a peek into the life of someone who has tackled some of the toughest challenges in mathematics.

So, let’s begin…

Question: Dr. Nironi, many people are intrigued by what it takes to earn a PhD in mathematics. Could you start by telling us what motivated you to pursue this path?

Dr Nironi: Hm, so for me it started at around your age (15) that I realized that I really enjoyed math AND physics. At the time I wasn’t really sure which career I would pursue but I knew that ideally it would be both. I actually started with physics, and then like many people in theoretical physics, over time, I drifted more and more towards the theoretical and eventually ended up back in Algebra and Geometry.

Question: Can you describe your research focus or area of specialization during your PhD?

Dr Nironi: Uh… can I say no? Okay so here’s the deal: It’s algebra and geometry, but more specifically, I’ve been working with Algebraic Stack. There was a time when I was an expert in “Gerbe” , whatever that is. So basically, math has blown up so much during the last century that people are ultra-specialized. And when you do research, you spend a number of years so that you can get close to the boundaries of what is known

and what is unknown, and then you start investigating the specifics at that boundary. But the frontier is so broad so you need to pick a specific place. And so you’ll see a lot of the time it’s difficult for mathematicians to talk to each other because of the specificity of the research area. For example, if you ask a random mathematician what he knows about algebra stacks, he may not know anything.

Question: How did you balance your coursework research and other responsibilities during your PhD?

Dr. Nironi: I didn’t. Usually people who do research don’t know anything about balance. Yeah so people do research usually JUST do research. I would have dinner sometimes with my friends and maybe see a movie once in a while but don’t imagine that I had much else in my life at the time. I had some very good friends during my PhD, but they were also researchers, so our conversations were also mostly about research. So typically if you do research, that’ll be the center of your life- maybe you’ll have room for a hobby or two.

Question: Oh, I forgot to ask, where did you study?

Dr. Nironi: I did my undergrad studies in Bologna, the oldest university in Europe, with a focus in Physics. Then I moved on to graduate research school in Trieste, Italy where I got my PhD in math. After that, I was at the Max-Planck Institute as a postdoc, and then later again as a postdoc at Columbia University for 4 years.

Question: What was the most challenging part of earning your PhD?

Dr. Nironi: It’s scary. Look, imag-

ine this: your advisor comes to you one day and says: okay, I have a very vague idea about this problem that is not quite well defined. Go figure it out, you got 3-4 years to think about it. You typically are given a poorly or barely defined problem that you want to solve. That’s it. You’re given a generous amount of time- but it’s finite. So you must complete your work within that time limit. And you’ll pray that the problem is solvable. So it’s scary; it gives you a lot of anxiety because again, the time is ticking and you hope you can figure it out. And to clarify, no one has a solution- you just have to figure it out on your own.

Question: Have you ever met someone who hasn’t finished their problem?

Dr. Nironi: Oh yes it’s a common thing. First of all, if your problem doesn’t go anywhere, it could be that the problem itself you don’t complete, but through your failure you may learn something about something else and that might give you your next target. So you might not solve your original problem, but you end up solving something that’s equally interesting.

Question: Did you solve your problem?

Dr. Nironi: I actually did solve my original problem. But, it’s not necessarily better than solving other things which are also perfectly okay.

Question: What advice would you give to someone thinking about pursuing a PhD in math?

Dr. Nironi: Hm. That’s a tough one. You have to decide what level of commitment you have in mind. Are you going to be ready to be fully committed

to it for a number of years? It’s very difficult, for example, to start a family during a PhD. Is it possible? Yes. Is it common? Definitely not. Same thing goes for having kids. Professionally, it may not help you so much. From a learning perspective it is a fantastic opportunity. You get to spend a number of years learning deeply about a very specific subject and ultimately it gives you a fantastic gift: the ability of being able to learn anything very quickly. So once you complete the PhD, you are an exceptionally advanced learner, more than anything else. Even with things unrelated to math and physics: things such as coding and languages are able to be picked up very quickly.

Basic Understanding of the World of NFTs

Adam Schwartz

A Non-Fungible Token, more commonly referred to as an NFT, is similar to a specific trading card in that there is no other like it after you return or trade that exact one. They are non-fungible as they do not have a particular monetary value, meaning their value is unique, and if it is exchanged for another, there is no even swap. NFTs come in many forms, not just images. They are video games, Art, videos, Music, collectibles, and so much more.

Why would a person spend millions on something you can see for free?

The images people spend millions of dollars on are available for everyday people to view. People spend so much money on them because owning an NFT allows you to be the sole owner and buy an original. The NFT also has built-in authentication, letting

you know you are purchasing an original copy. Another reason people buy them is to have the “bragging rights” to them, which collectors value very highly.

How NFTs work

NFTs exist on a blockchain, showing every transaction made readily available to the public. The blockchain that is typically used for this is the Ethereum blockchain. A blockchain is helpful as it is a way to store information without having to trust a single computer or a corporation. The blockchain also protects your purchase as when you buy it you are aware you have bought the original, using a specific code for each individual NFT. The blockchain makes it virtually impossible to steal NFTs from it as it keeps records of every transaction. However, many have stolen NFTs by deceiving the original owner of the piece. They do this by sending a phishing link to the owner’s email address and can gain access to his virtual wallet. Another way this happens is people exploit the virtually unhackable system by finding minor errors in the code of one’s wallet or website and sell the NFT to themselves for free.

Beginners guide to purchase an NFT

1)Buy a cryptocurrency

2)Add the cryptocurrency to your crypto wallet

3)Venture to one of many sites where NFTs can be purchasesd. Some large ones are open-sea, Rarible, and Foundation.

4)Make an account, after this, there should be a button that says “Buy Now.” you press that button, and your NFT should appear in your wallet.

After you have completed these steps,

you will find that you own an NFT!

Basic Calculator Programming: A Student’s Guide

Morris Cohen

In the digital age, calculators remain necessary tools for students, not just for simple calculations but also for solving complex mathematical problems efficiently. Basic calculator programming is a skill that enhances problem-solving speed and introduces the fundamentals of programming logic. This short guide aims to make calculator programming for high school students easier, emphasizing its practicality and accessibility.

The Importance of Calculator Programming

Programming your calculator can automate repetitive tasks, quickly solve equations, and save time during tests. It’s an excellent introduction to programming concepts, showing that coding is not exclusive to computer science but a universal tool for problem-solving in STEM fields.

Getting Started

Popular calculators with programming capabilities include the TI-84 Plus, Casio fx-9750GII, and HP Prime. These devices often use TI-Basic, a user-friendly programming language suitable for beginners.

Basic Programming with TI-Basic

•Access the Program Editor: Use the “PRGM” or “PROGRAM” button on your calculator to start writing code.

•Create Simple Programs: Begin with

basic programs, like solving the quadratic equation. Use commands such as Input for entering values, Disp for displaying results, and standard arithmetic operations for calculations.

•Practice and Debug: Test your programs with various values to ensure accuracy, and debug as needed to correct any errors.

Sample Program:

A simple program to solve the quadratic equation ax^2 + bx + c = 0 could look like this: You can name your program anything, I named mine “QUAD”

1st Step: Since our program needs to solve for real and imaginary solutions, we need to start with the step “a+bi”. To do this hit “2nd”→ “catalog”→ scroll down to “a+bi”.

2nd Step: We have 3 values in the quadratic and the next step accounts for that. To do this, again hit “2nd”→ “catalog” → Hit “Alpha→P” 2 times→ Scroll down to prompt. Then you want to choose Alpha: A, B, C

3rd Step: (negative NOT minus)

(-B+√(B^2-4AC)) / (2A). Then hit the “sto→” key and write “D”

4th Step: (negative NOT minus) (-B-√(B^2-4AC)) / (2A). Then hit the “sto→” key and write “E”

5th Step: “2nd”→ “catalog” → Hit “Alpha→D” 2 times→ Scroll down to Disp. Then write: “D, E” - After this, hit 2nd→ quit

To test it, Hit “prgm” → TI- Basic→ (Under EXEC) → QUAD→ Enter That’s it!

Your code should look like this:

PROGRAM: QUAD :a+bi

:Prompt, A, B, C :(-B+√(B^2-4AC)) / (2A)→D :(-B-√(B^2-4AC)) / (2A)→E

:Disp D, E

Starting with simple projects and progressively challenging yourself can unlock the full potential of your calculator, turning it into a powerful academic tool.

The Complexities of Auto Racing

Adam Schwartz

Recently, Auto racing, especially Formula One, has grown exponentially in popularity.

Most people do not look at the details of auto racing but instead just enjoy watching it; today, we are going to dive into the details of Formula One. The Air-to-Fuel Ratio of a racecar is crucial to the car’s performance, as in racing, every millisecond counts. In the majority of gasoline-powered racecars, the perfect ratio is 14.7:1, meaning 14.7 kgs of air to one kg of fuel.

Although engineers often fix the ratios to be richer or leaner depending on the racing conditions.

Richer Mixtures- (A lower air-to-fuel ratio, adding more fuel) Usually used when engine power is more important than fuel efficiency, such as when navigating through tight turns or shorter races.

Leaner Mixtures- (A higher air-tofuel ratio, less fuel) Leaner mixtures have much better fuel efficiency, but they generate more heat, which can increase the possibility of damaging the engine.

It may seem that in racing, the larger the engine, the more powerful the car, but this often depends more on how the space is optimized rather than the size of the engine. A larger engine

may be more powerful but, at the same time, heavier, slowing down the car, which is why it is imperative to find the perfect balance.

Gear ratios are crucial because they directly influence the acceleration and top speed of a vehicle. They act as a lever, allowing the engine’s power to be adapted to different racing situations.

Lower Gear Ratios (smaller gear to larger gear)- Faster accelerations but results in a lower top speed, used in tracks with tighter turns.

Higher gear ratios (larger gear to smaller gear)- Slower acceleration but results in faster top speeds, ideal for tracks with long straight shots.

Teams usually bring a variety of gear ratios to a race as they are also changed quite often, due the conditions of one track to another, and the weather. The conditions of a track are a difficulty for the the racers team but through precautions they are able to plan for the best. There are a multitude of steps that go into this complex sport that many love to watch but never genuinely think about the inner workings of.

Understanding the Eruv Through Math

Saul Beroukhim

In Judaism there’s a certain law regarding the boundaries of areas during special holidays. It is called in Eruv, and it is meant to separate private and public domains. The Eruv is really interesting be-

cause it combines both religious legal concepts and modern day Halachic mathematics. Imagine your playing a game where certain areas are off limits. An Eruv is like drawing a circle around the area in order to make it so it’s not off limits anymore. But drawing the circle isn’t so simple and it requires mathematical precision to be able to make the circle. Then, there’s the math of measuring. In the eruv, certain heights and distances have to be just right. These measurements come from old units like the “handbreadth” and the “cubit” which are like the inches and feet we use today. Imagine having to use these old measurements to make sure everything in the eruv is set up correctly. It’s a bit like following a recipe that uses units you’re not used to.

The Eruv is measured geometrically, (usually like walls, fences, and utility poles) and can require the addition of doorways (symbolically represented by poles and wires that create a “doorframe” around the area). Mathematically, this involves mapping and geometry to ensure the area is fully enclosed. Specific halachic (Jewish legal) measurements are used to determine the validity of the eruv. For example, the height of the poles and the wires must meet certain criteria. Measurements such as a “tefach” (handbreadth) and an “amah” (cubit) are used, with a tefach being approximately 8–9.6 cm (3.15–3.78 inches) and an amah being around 48–58 cm (18.9–22.8 inches). Calculations involving these units are essential for constructing an eruv according to halachic standards. In some cases, the size of the enclosed area may be considered, especially in terms of practicality for the community. While there’s no explicit upper limit to the size of an eruv, very large eruvin might be

subject to additional scrutiny regarding their practicality and the continuity of the community within the area. The calculation of the area, although not strictly a halachic concern, involves basic principles of geometry.

The Power of Misleading Statistics

Caroline Kollander

Statistics are a powerful tool often used to prove controversial points. Statistics are brought up in cases of debate where people can’t come to an agreement without providing numbers, percentages, etc. While these statistics can be very helpful in many ways, there are also many problems that may arise.

Focusing on certain statistics and not others is a common cause of misconception. Studying just one group of people and creating a statistic categorized as a general population, leads to false understanding.

Averages hide important details. If a class reports an average test score of 80% for students, it might seem like most students performed well as a whole. However, this average could be the result of a few high achievers balancing out the scores of many who performed below average. In 2007 the toothpaste company, Colgate, sent out a statement that 80% of dentists recommend their toothpaste. This resulted in high sales for the company. In reality, the dentists were actually asked to create a list of toothpastes they would recommend. Colgate didn’t include this information in their statistics. Therefore, the public was convinced 80% of dentists primarily suggest that they use Colgate.

Leading an argument with, “studies

show” or “statistics prove” is a simple way to ensure the other person believes what you are saying. This can be used against anyone and is used against everyone. Unreliable sources online claim unrealistic things using these terms and due to the gravity of saying them, people are likely to fall for it.

Similar to lying about a study in general, statistics are often altered/ changed to boost one’s argument in their favor. An example of this is countries lying about the death rate during war to gain sympathy from the media.

Statistics that don’t benefit the one who founded them, may go unpublished or even discarded. This leaves an unfair advantage to the opposing side.

Statistics are an extremely useful tool when it comes to arguments and gaining a clearer understanding of complex things. They can also be extremely misleading. The key lies in how statistics are collected, analyzed, and interpreted. Once you have gone through this process, you are ensured to be gaining only truthful information.

The History of Euler’s Number

Ezra Gonen

Euler’s number, more commonly seen as e^x, is one of the most well known mathematical constants. It has many uses in calculus and trigonometry, but the most well known reason for the use of Euler’s number is compound interest. Along with it being the most well known use of Euler’s number, compound interest is the reason Euler’s number was discovered.

In Scotland, in 1614, while trying trying to find the logarithms of

numbers, John Napier and William Oughtred recorded the first written reference to the constant e, in their book, Mirifici: Logarithmorum: Canonis Descriptio.

Later in Switzerland in 1683, while studying compound interest, a graduate of the University of Basel Jacob Bernoulli, discovered the formula, x∞(1+1n)n, where n is the rate at which you compound the interest. At the time, Bernoulli did not assign a symbol to represent the formula, but today we know that x∞(1+1n)n=e.

Later a Swiss mathematician, who studied at the University of Basel, the same place where Jacob Bernoulli studied, Leonhard Euler, began to use Bernoulli’s formula. Euler is credited with assigning the equation to the letter e after he published his work, Mechanica in 1736. Aside from assigning Bernoulli’s equation to the letter e, Euler is also credited with contributing to ⅓ of the mathematical research done in the 18th century. Overall, through the contributions of Jacob Bernoulli and Leonhard Euler, one of the most famous mathematical concepts came into existence and is still used throughout the world today.

The Greatest Unsolved Mystery of Our Time

Sylvie Raab

The Riemann Hypothesis -- known as the greatest unknown mystery of our time -- is the oldest of the Clay Institute Millenium problems, a list of seven unsolved mathematical

hypotheses that “record some of the most difficult problems with which mathematicians were grappling at the turn of the second millennium.”

The prize for solving one of these problems is $1 million.

The Riemann Hypothesis deals with predicting when prime numbers will occur. Since the pattern of prime numbers is seemingly random, many mathematicians have tried to find and predict their location. Carl Friedrich Gauss, Riemann’s teacher, found prime numbers up to 3,000,000 and plotted their location on the Prime Counting Function, whose y-value remains constant until x reaches a prime number and then increases by one. He then noticed that the graph’s overall behavior mimicked that of the function y = 1/logx and that at any point x, the proportion of prime numbers that would be around it would be roughly the same as 1/logx. This is called Gauss’s Conjecture.

Bernhard Riemann was able to take the Prime Counting Function and find a better representation of it using the Zeta Function. The Zeta Function is 1/1^s+½^s+⅓^s+¼^s…1/n^s, and while Swiss mathematician Leonhard Euler claimed that the Zeta Function converged when s>1, Riemann experimented with the function on the imaginary plane and there, he was able to extend it through analytical continuation to the entire plane. This new function is called the Riemann Zeta Function. Now, the Zeta Function was able to pass through the origin and all other zeros. When he applied the imaginary transformation to the function, he was able to prove that all of the non-trivial zeros, meaning all infinitely many of the positive zeros, exist in the critical

strip, 0≤s≤1. He made He made the claim that all of the zeros would lie on the line s=1 ⁄ 2, the critical line. This is what is known as the Riemann Hypothesis. Using this hypothesis and a modified version of Gauss’s Conjecture, where the function would increase by log(p) at each prime number, he discovered a wave that corresponds to the Zeta Function s=1 and showed that his modified Gauss’s Conjecture would follow along this curve as long as this curve is the fundamental frequency. He used the zeta zeros to adjust this wave so that every time that the function approaches a zeta zero, the zero contributes a harmonic (the wave of a point converted into a wave through the Riemann converter). The more harmonics you add, the closer it gets to the graph of Gauss’s Conjecture which shows the frequency of prime numbers.

The Math Behind Psychology

Leon Kremer

In the world of psychology, math isn’t just about crunching numbers; it’s about understanding how we think and behave. Let’s explore how math influences not just decision-making, but also problem-solving and measurement in psychology.

Making Choices

We make decisions every day, big and small. Whether it’s choosing what to wear or what to eat, our decisions are influenced by the value we attach to different options. Sometimes, we use probabilities to help us decide. For example, when deciding whether

to buy something, we might consider how likely we are to use it. But here’s the thing: humans aren’t always rational when making decisions. Emotions, biases, and social pressures can all affect our choices. The small signals our brains send out make huge differences every single day.

Solving Problems

When faced with a problem, our minds kick into gear to find a solution. And to find the best solution, we often need data. That’s where statistics come in. By analyzing data, psychologists can better understand the situations we face. Statistics are vital in psychological experiments too, helping researchers make sense of their findings. For example, they might use probabilities to see how effective a health campaign is likely to be. Math also helps in other areas, like politics and understanding natural phenomena.

Measuring Things

Psychologists use math to measure all sorts of things, from intelligence to behavior. Take IQ tests, for example. They’re based on mathematical concepts. And as our understanding of intelligence grows, so do the formulas we use to measure it. Math also helps psychologists figure out if certain traits are subjective or objective.

In conclusion, math isn’t just a tool for psychologists; it’s woven into the very fabric of their work. By understanding the role of math in decision-making, problem-solving, and

we can better understand the complexities of human behavior. And as they continue to explore these connections, new discoveries await, offering fresh insights into the mysteries of the human mind.

Probability Theory in Risk Assessment

Caroline Kollander

Probability is a mathematical term for how likely something is to happen. The equation often used to calculate probability is the number of favorable outcomes over the number of possible outcomes. Psychologists use probability in risk assessment. In short, how likely is it for the patient to do something they would regret.

The most possible scenario where this would be necessary is a patient’s likelihood of committing self-harm. For the psychologist to assess this probability they have to consider many variables. Some of these are genetics, nurture, and current exposure. Psychologists need to be able to predict the activity of their patient in order to stop it before it’s begun. One way they do this is the “Decision Tree”. This is used primarily for complex cases. It is a graphical representation of the decision-making process. Different branches of the tree represent possible activities of the patient and their outcomes. The tree can be presented to the patient or kept separately, but the goal of it is to make an educated guess of which branch of activity the patient is most likely to follow. Another way of detecting the prob-

ability of risk is the “Bayesian Probability” method. This method is used when there are constant additional observations/changes being added to the formula: P(AIB)=P(BIA) xP(A)/P(B). P(AIB) means the probability of the scenario occurring given both A and B. P(BIA) is the probability of the event with evidence B if evidence A is also true. P(A) means the probability of the event given A without the evidence of B. P(B) is in the event that evidence A doesn’t occur, B is the one that most likely will. It is very complicated to assess the possibility of risk for a patient; However, these formulas serve as a simpler way to lay out the information you have, and see what can be drawn from them. world. Besides basic arithmetic, which has stood as a useful guidepost since early times, Geometry is the oldest math we come across in our 1-12 education. But students have only been learning the concept in the United States school system since 1844, so to put that in perspective, not many students, taking in the scope of history, have sat in the same seat as you.

added to the formula: P(AIB)=P(BIA) xP(A)/P(B). P(AIB) means the probability of the scenario occurring given both A and B. P(BIA) is the probability of the event with evidence B if evidence A is also true. P(A) means the probability of the event given A without the evidence of B. P(B) is in the event that evidence A doesn’t occur, B is the one that

It is very complicated to assess the possibility of risk for a patient; However, these formulas serve as a

tion you have, and see what can be drawn from them.

Mathematics of Taylor Swift’s Music

Caroline Kollander

Taylor Swift, while widely recog nized for her pop hits, is also a very brilliant composer. Each of her eleven albums focuses on a different instrument to highlight throughout the songs. These instruments consist of guitar, piano, ukulele, banjo and many more. Swift also helps in the process of composing music for the instruments she doesn’t play in her songs. Most of her fans would say that her piano-composed songs are her most impressive. Composing piano very obviously requires complex mathematical structure.

Take one of her hit songs from the evermore album, “Champagne Problems”. She uses chord progressions to create harmonic sequences. She is famously known for her predictable note patterns built from intervals. Her rhythm is always steady using time signatures, rhythmic subdivisions and syncopa-

tion. The tempo of this song is one hundred seventy one beats per minute and is written in C major. A popular misconception about Taylor Swift is that all of her songs sound the same. It is actually possible to mathematically prove that they are or are not. All of her music from 2006 to 2024 presents different mathematical formulas called “entropy”.

To use entropy you have to take every song that she has written and tally which words have repeatedly been said, and which have not. Entropy calculates the amount of information/content that you get out of a song. The more repetitive the lyrics are, the lower the score they will receive.

Once you do this to all of her songs, you can tell by the scores, which ones sound similar. If two songs have a comparable score, they probably do sound the same. If the scores vary, her songs are all/ mostly unique.

Taylor Swift’s songs utilize mathematics both when the calculations don’t occur within the notes of her music, and when they do.

Math in Gemara

Tory Doft

I asked Rabbi Freid to talk about how various concepts of mathematics appear in the Gemara. Rabbi Freid has a Bachelor of Arts and Master of Science in Math along with teaching Talmud. He explained that basic math concepts are used in the Gemara in order to solve problems and explain laws. He said, “One cannot learn Gemara without basic knowledge of Arithmetic… [for example] if a thief has to pay back double what they stole, you need to

be able to multiply by 2.” He also said that there are examples in Gemara that involve geometric concepts, explaining that “this comes up extensively in Masechet Sukkah. A minimum size sukkah is 7 x 7 square tefachim. If a sukkah is a different shape, it needs to be able to contain a square of this size, so the Gemara needs to calculate things like how large a circle needs to be to circumscribe a 7 x 7 square.”

Beyond just specific circumstances of math appearing in the Gemara, the Gemara also often deals with calculations of time. For example, Rabbi Fried explained that “Halachic times are determined by taking the daylight hours (or the nighttime hours if we’re talking about a nighttime Mitzvah), and dividing them into 12 equal segments that we call ‘hours.’ Thus the length of a Halachic hour will differ based on the time of year.” Additionally, numbers are used to discuss legal limits and requirements as they help to make sure you can fulfill mitzvot in a precise manner and also make them not too difficult. As well as how the Gemara incorporates aspects of numerology, and joked that “The funny thing is that when people hear I’m into math and Gemara, the first thing they ask about is Gematria, and Gematria is probably the least

Background to Complex Numbers

Leo Eigen

The idea of i—the square root of negative one—is not intuitive, yet the complex, or imaginary number, is one of the most intriguing concepts in mathematics.

During the Renaissance, Italian mathematician Nicolo Tartaglia was

perhaps the first figure to work with imaginary numbers. Working with cubic equations, Tartaglia recognized the importance of these complex numbers and, to advance his work, shared his findings with fellow mathematician Girolamo Cardano. Cardano, per many accounts, stole Tartaglia’s findings and included them in his book Ars Magna, one of the most significant works in the study of algebra, Cardano included complex numbers as a means of solving questions involving the roots of numbers. Cardano, though, failed to recognize the importance of complex members beyond abstract theory, and wrote in Ars Magna that they were “sophistic” and claimed that his application of complex numbers was “as subtle as it is useless,” according to a translation by T. Richard Witmer.

Rafael Bombelli—an Italian who had trained in design and sculpting, not specifically mathematics—built on Cardano’s Ars Magna and developed a system for operations with complex numbers. Cardono left many of his questions unsolved and Bombelli worked to provide answers, even with “irreducible” cases of functions where many others had given up. Gottfried Wilhelm Leibniz praised Bombelli as “an outstanding master of the analytical art.”

In the seventeenth century, René Descartes first thought of calling these complex quantities “imaginary numbers.” In his mind, however, this label was meant to degrade their applicability to mathematics, and he wrote that they were “sometimes only imaginary, that is one can imagine as many as I said in each equation, but sometimes there exists no quantity that matches that which we imagine.” Leibniz, on

the other hand, believed that there was a value in understanding complex numbers, as he was strongly influenced by Bombelli.

Leonhard Euler was the first mathematical voice to describe the square root of negative one as i, a symbol still used today. Euler included imaginary numbers in his famous work Elements of Algebra, and although he and many other mathematicians had examined imaginary numbers to an extent, the belief that they were truly applicable was not widespread. Abraham de Moivre, a French mathematician, linked complex numbers to trigonometry and discovered what is now known as “de Moivre’s theorem.” Carl Friedrich Gauss was instrumental in finally pushing the idea of imaginary numbers into the mathematical world, as he derived a proof for the fundamental theorem of algebra, and, with it, substantial support for the importance of complex numbers. G.H. Hardy, a British mathematician, argued that Gauss, like no other before him, worked with complex numbers in “a really confident and scientific way.”

By the turn of the twentieth century, complex numbers were seen as central to the mathematical field. Their applications are broad, ranging from quantum mechanics to theories of relativity to fractals. So while i is certainly imaginary, it is also quite necessary, as well.

Utilization of Financial mathematics within the Stock Market landscape

Si Heyman

We all alike understand quite well the fact of financial risk. It is the ones who sit at home while the

stock market drops, interest rate rises, oil prices increase who lose money. Financial planning in general was driven in part by events that occurred decades ago, to be a good defense against such situations. Perhaps, they can be referred to as financial instruments in my opinion, which give the investor a chance to reduce his risks to occurences like evil in the investment sector. Different from home fire insurance which can be readily priced by merely looking into history and statistics, they are inherently difficult to price; and, in fact, making a price on them is a complex problem from the beginning whose solution even won a Nobel prize last year for Myron Scholes and Robert Merton. This is the field where financial engineering would attribute.

The recent area of complex derivatives pricing, risk management and information technology have forced the fast-paced adoption of mathematical methods of an ever-increasing level of sophistication. Currently, the financial services industry (FSI) is undergoing structural changes as a result of globalization and the digitization of information that entered market as new technologies. Acquisitions and mergers are also changing its outlook, whereas internal system overhauls are changing the way financial institutions conduct their operations.

Instability that hit firms like Baring, Sumitomo, Orange County, and LTCM and subsequently all FSI concerning the large scale changes is one consequence of drastic changes in the FSI. The crash of Baring illustrates that all companies risk the same problem. The general public most probably will likewise believe that these events proved that

that all of the zeros would lie on the line s=1 ⁄ 2, the critical line. This is what is known as the Riemann Hypothesis. Using this hypothesis and a modified version of Gauss’s Conjecture, where the function would increase by log(p) at each prime number, he discovered a wave that corresponds to the Zeta Function s=1 and showed that his modified Gauss’s Conjecture would follow along this curve as long as this curve is the fundamental frequency. He used the zeta zeros to adjust this wave so that every time that the function approaches a zeta zero, the zero contributes a harmonic (the wave of a point converted into a wave through the Riemann converter). The more harmonics you add, the closer it gets to the graph of Gauss’s Conjecture which shows the frequency of prime numbers.

What really is the Fibonacci Sequence?

Si Heyman

The Fibonacci sequence is like a number party where each number is the cool sum of the two that came before it. So, you start with 0 and 1, the first ten numbers are 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 and it keeps going on and on. There is this math concept to describe it, but I don’t want to bore you with the details.People talk about it all the time as nature’s secret recipe for creating amazing things like the Great Pyramid at Giza or those intricate seashells. Apparently it’s not as simple as that, and the real story is far more grounded in reality.The man we now call Leonardo Fibonacci wasn’t even called that then. He was known as

Leonardo of Pisa and lived around 1170. In 19th century, some smart people called him Fibonacci (which means ‘son of the Bonacci’) to tell him apart from another Leonardo of Pisa. The math god, Keith Devlin of Stanford, outed everyone on the subject.Guess what? Leonardo of Pisa did not discover the sequence at all! The ancient Sanskrit texts from 200 B.C. pipped him to it. Well, what do you know! Keith Devlin, the author of the book “Finding Fibonacci,” was the one to spill the tea on this.In 1202, Leonardo of Pisa published a large math book called “ Liber Abaci.” It is like a cookbook for math, meant for trade people. In one rabbit-infested section, he presents the sequence. Imagine this: a rabbit soap opera with mating and that sort of thing. The answer for the question “How many rabbits after a year?” is 144, and bam, the Fibonacci sequence is created!However, the twist in the plot, Leonardo of Pisa forgets the sequence after that rabbit chaos. It was not seen until the 19th century when a French math wizard, Edouard Lucas, gave it the name the Fibonacci sequence. Now, these numbers are called the Fibonacci sequence by people, but Keith Devlin says, “Stop! This is not the universe’s blueprint.” Yes, it’s related to the fancy number called the golden ratio (phi), but it’s not the only rule for growing things. Some plants do the golden ratio dance as well, like leaves that are in the spiral arrangement or pinecones that do a golden spiral. However, loads of plants are not bothered with this rule.The well-known seashell, the nautilus, is not preparing cells in the Fibonacci way. And when people connect it to human body, art, and architecture, those links are more the

fiction than fact.The fault lies with this person Adolf Zeising in 1855. He said that the human body’s proportions were about the golden ratio, and everyone was obsessed with finding it everywhere. Spoiler alert: The majority of these claims fail when tested. We people just love patterns, even if they’re not really there. Thus, the Fibonacci sequence is like a math celebrity, but not the blueprint of the universe. It is just a cool math trick that bunny farming made popular.so is squaring and square rooting. Although you may not need to multiply numbers close to 100 very often, it is still pretty cool to be able to do those problems in your head very quickly.

Hilbert’s Problems

Grace Kollander

Hilbert’s Problems are a set of twenty-three unsolved mathematical problems that were proposed by David Hilbert in 1900. David Hilbert was a German mathematician, in fact, he was one of the most influential mathematicians of the 19th and early 20th centuries. These twenty-three unsolved problems span numerous areas of mathematics and had an incredible impact on the math world in the 20th century and shaped the direction of mathematical research for the future. Hilbert’s 23 problems include:

1) Cantor’s problem of the cardinal number of the continuum.

2) The compatibility of the arithmetical axioms.

3) The equality of the volumes of two tetrahedra of equal bases and equal altitudes.

4) Problem of the straight line as

the shortest distance between two points.

5) Lie’s concept of a continuous group of transformations without the assumption of the differentiability of the functions defining the group.

6) Mathematical treatment of the axioms of physics.

Irrationality and transcendence of certain numbers.

7)Problems of prime numbers (The “Riemann Hypothesis”).

8)Proof of the most general law of reciprocity in any number field.

9) Determination of the solvability of a Diophantine equation.

10) Quadratic forms with any algebraic numerical coefficients

11) Extensions of Kronecker’s theorem on Abelian fields to any algebraic realm of rationality

12) Impossibility of the solution of the general equation of 7th degree by means of functions of only two arguments.

13) Proof of the finiteness of certain complete systems of functions.

14) Rigorous foundation of Schubert’s enumerative calculus. Problem of the topology of algebraic curves and surfaces.

Expression of definite forms by squares.

Building up of space from congruent polyhedra.

Are the solutions of regular problems in the calculus of variations always necessarily analytic?

The general problem of boundary values (Boundary value problems in PDE’s).

Proof of the existence of linear differential equations having a prescribed monodromy group. Uniformization of analytic relations by means of automorphic functions.

Further development of the methods of the calculus of variations.

of Schubert’s enumerative calculus.

16) Problem of the topology of algebraic curves and surfaces.

17) Expression of definite forms by squares.

18) Building up of space from congruent polyhedra.

19) Are the solutions of regular problems in the calculus of variations always necessarily analytic?

20) The general problem of boundary values (Boundary value problems in PDE’s).

21) Proof of the existence of linear differential equations having a prescribed monodromy group.

22) Uniformization of analytic relations by means of automorphic functions.

23) Further development of the methods of the calculus of variations.

Eight of Hilbert’s problems, 3, 7, 10, 14, 17, 18, 19, and 20, have solutions that are widely accepted within the mathematical community. Whereas others, 1, 2, 5, 6, 9, 11, 12, 15, 21, and 22 are only partially accepted. Finally, problems 8, 13, and 16 remain unsolved and 4 and 23 are too vague rendering them unsolvable. Ultimately, Hilbert’s problems continue to push mathematicians to address the most fundamental and challenging questions in their field.

Digital Square Roots

Olivia Saar

Numbers have always held a fascination for humanity. From ancient Greece to the present, the study of numbers has uncovered secretive patterns and relationships. This essay discusses digital roots, an intriguing numerical concept that is accessible and enjoyable for

anyone, regardless of their math background.

Digital Roots Basics:

Digital roots simplify any number to its core, a single digit. The process is straightforward: Begin with any positive integer. Sum the individual digits of this number. If the sum is a single digit, it is the digital root. If not, repeat step 2 until a single-digit number is obtained.

For example, the digital root of 123 is 6, calculated as 1 + 2 + 3. Digital roots have an ancient lineage, not being a new concept but rather an age-old practice passed through various cultures and traditions. Pythagoras, the Greek mathematician and philosopher, is often credited with the notion of reducing numbers to their core essence. The idea of digital roots, therefore, dates back thousands of years. The mathematical significance of digital roots includes their interesting properties and applications. For instance, they offer a quick way to test for divisibility by 3 or 9—if the digital root is 3 or 9, so is the number. Observing sequences of numbers and their digital roots can reveal intriguing patterns and connections, adding a layer of fun to numerical exploration. In computing, digital roots ensure data integrity during storage or transmission, aiding in error detection and confirming data accuracy.

Beyond mathematics, digital roots find applications in encryption techniques, enhancing data security. Cryptographic systems employ digital roots to strengthen data protection. Additionally, digital roots are used in computer science algorithms to optimize operations like data hashing and checksums, thus increasing efficiency and aid-

ing in software error detection.Digital roots can be appreciated by anyone, not just for their mathematical basis but for the sheer curiosity they evoke, even in those with minimal math knowledge. They offer a simple yet engaging way to explore numbers, patterns, and the essence of different quantities. In our digital age, understanding digital roots helps us appreciate the hidden beauty and structure of numbers that shape our lives. Next time you encounter a number, consider its digital root; you might uncover hidden connections and patterns.

The History of Topos Theory

David Daniell

Topos theory, an advanced and highly abstract branch of mathematics, generalizes topology and provides a framework for understanding various algebraic and geometric concepts under a unified theory. Developed primarily in the 1960s, topos theory has roots in algebraic geometry and category theory and has profound implications in logic, topology, and theoretical physics. This section of the article will outline the history of topos theory, highlighting key figures and milestones that shaped its development. The story of topos theory begins with the foundational work in category theory by mathematicians Saunders Mac Lane and Samuel Eilenberg in the 1940s. Category theory, with its focus on morphisms between objects rather than the objects themselves, set the stage for the conceptual framework necessary for topos theory. It wasn’t until the 1960s, however, that topos theory began to take its modern form.

The French mathematician Alexander Grothendieck, while working on algebraic geometry, introduced the

concept of a “topos” in the early 1960s. His initial idea was to generalize sheaf theory—a method used in geometry to systematically track locally defined data attached to open subsets of a topological space. Grothendieck’s insight was to treat these sheaves as sorts of “generalized spaces” or “topoi” (plural for topos), which could then be studied using the tools of category theory.

Grothendieck’s foundational work, particularly in the context of his efforts to reformulate algebraic geometry, led him to define what are now known as Grothendieck topoi. These are categories of sheaves that satisfy certain axioms similar to those satisfied by sets in classical set theory.

Following Grothendieck, other mathematicians expanded on these ideas. Notably, Myles Tierney and William Lawvere in the late 1960s and early 1970s developed the concept of “elementary topos,” simplifying Grothendieck’s ideas to make them applicable in a broader mathematical context. An elementary topos is a category that behaves much like the category of sets and includes a subobject classifier, which captures the logical structure within the topos.

Since its inception, topos theory has had a wide-ranging impact on both pure and applied mathematics. It has enriched the understanding of logical foundations through its relationship to intuitionistic logic and has implications in theoretical physics, particularly in quantum theory and general relativity. Topos theory represents a significant leap in mathematical thinking, providing a powerful framework that extends beyond the traditional boundaries of mathematics. From Grothendieck’s initial ab-

-stract concepts to the comprehensive framework now in place, topos theory continues to influence many areas of research, underscoring its importance and the creativity of those who contributed to its development. In conclusion, the history of topos theory is a testament to the evolution of mathematical thought, reflecting both the unification of existing ideas and the advent of new, revolutionary perspectives in understanding the structure of mathematical theories.

Math in the Middle East

Aryeh Goldstein

Math is a universal language that transcends societal boundaries, with many different civilizations and cultures contributing to its development. One of the greatest of these contributors, the Islamic culture, stands out as a pioneer to the fundamentals of math as we know it. But what are the origins and what contributions has Islamic math made?

The Islamic culture began developing mathematics during the peak of the Islamic empire, from the 8th century to the 14th century, and built on various types of existing mathematics including from ancient Perisa, Greece, India, and Mesopotamia. Islamic mathematics was developed by scholars known as “Muhasibun” or “mathematicians,” who pioneered its advancement. Firstly, one of the most important contributions of Islamic mathematics was their development of algebra. The word “algebra” itself actually comes from the Arabic word “Al-Jabr,” (probably messed up how that’s said) which refers to the process of completing the square to find the roots of quadratic equations, a formula devel-

oped by the Islamic mathematician Al-Khwarizmi. Al-Khwarizmi’s work, along with other Islamic mathematicians, helped introduce systematic methods for solving linear, quadratic and more complicated algebraic equations as well as other algebraic techniques and theorems. Islamic mathematics also made great additions to arithmetic. For example, Islamic mathematics standardized the Hindu-Arabic numerals we use to represent numbers to this day. Overall, these contributions laid the groundwork for algebra and arithmetic as well as set the foundation for more advanced algebra later on, including abstract and linear algebra.

Secondly, the achievements of Islamic mathematics also have many practical applications. For example, Islamic scholars were pretty much the only ones preserving and transmitting mathematical knowledge from ancient works, translating and organizing works from Greek, Sanskrit, and Syriac sources into Arabic. Islamic mathematician Ali Qushji even translated over 20 ancient Greek mathematical manuscripts in order to preserve them! These translations not only preserved the mathematical heritage of ancient civilizations but also allowed for global exchange of mathematical knowledge and ideas. Lastly, Islamic mathematicians made significant contributions in facilitating mathematical education. For example, Islamic mathematics institutions such as the Bayt al-Ḥikmah (House of Wisdom) in Baghdad became centers for mathematical learning. Many scholars and students from around the world were able to come together at these centers to discuss and learn math. The topics discussed included a wide range of math subjects, including arithimet-

ic algebra, and geometry, which created a comprehensive math discussion. In conclusion, Islamic mathematics represents a crucial culture in the global understanding of mathematics. Through their hard work and creativity, Islamic mathematicians made incredible contributions to algebra, arithmetic, and math education, shaping the course of mathematics for generations to come. By recognizing and celebrating Islamic mathematics, we can both honor their contributions to mathematics and also inspire the next generation with the endless possibilities of mathematical advancement.

Fractal Geometry: A Critical Tool In Understanding The Natural World

Jack Friedman

We imagine that the natural world is ideal, with every figure perfectly defined and simple. However, this assumption is far from the truth. In many cases, the differentiable curves and easily definable shapes of Euclidian geometry are the exception in nature, not the norm. Countless aspects of the natural world are irregular and best explained by a complex type of geometry: fractal geometry. The word ‘fractal’ was coined in 1975 by Benoit Mandelbrot to describe non-Euclidian shapes and curves that have non-integer dimensions and are non-differentiable, meaning movements from point to point result in abrupt changes in the curve’s direction.

Fractal geometry provides a framework to better understand the function and properties of these complex figures. These fractal shapes

not only have interesting properties, but are also abundantly present throughout the natural world. Therefore, studying fractals helps us better understand the world we live in and provides practical applications for science, medicine and economics, among other areas of study.

Fractals are typically characterized by five major properties: First, they have structures with very fine details that are only visible when zoomed in, and these fine details continue no matter how much they are zoomed in on. Second, fractals are too irregular to be defined by Euclidian geometry. Third, fractals are self-similar, that is, each zoomed-in-on section has the same structure as the whole, and they continue to be self-similar even if zoomed in infinitely. Fourth, although fractals appear to be complex, they are usually defined simply and recursively, by iterating a specific transformation infinitely many times (that is performing the same transformation over and over). Lastly, fractals have a “fractal” dimension, which can be any real number, as opposed to a “topological” dimension (what we normally think of when we think of dimension), which is always an integer that is less than a fractal’s fractal dimension. One simple example of this complex idea is the Cantor Set.

The Cantor Set is constructed by starting with a line of length one, splitting it into thirds, and then deleting the middle thirds, re-

sulting in two line segments, each of length one-third, with a gap of length one-third in between (the first iteration). Both of the line segments are then split into thirds and the middle third segment of each line is eliminated. What is left (the second iteration) is four line segments, each of length one-ninth, with each pair of line segments being similar to the whole of the first iteration. If we keep iterating infinitely many times, the result will be a self-similar figure, which dimension-wise is a series of zero-dimensional points that is approaching a one-dimensional line. For this reason, the Cantor Set has a topological dimension of zero - since it is essentially just an infinite number of infinitesimally small zero-dimensional points with gaps between them. However, because these points approach a one-dimensional line, we consider the Cantor Set as having a fractal dimension of between zero and one. The exact dimension is calculated by taking the log of the number of self-similar parts in the fractal, and dividing that number by the log of the length of each self-similar part. In the Cantor Set, there are two self-similar parts, each of length one-third, so the exact dimension is calculated as log 2 / log 3, which is approximately 0.63. Mandelbrot defines a fractal as any shape whose fractal dimension exceeds its topological dimension. The Cantor Set’s fractal dimension (~0.63) is greater than its topological dimension (zero) and thus meets this definition.

Another basic and well-known example of a fractal is the Koch Curve.

The Koch Curve is constructed by again starting with a line of length one, splitting it into thirds, and eliminating the middle third. In place of the eliminated middle third, two

line segments of length one-third are added at 60° angles to each other. This results in four line segments, each of length one-third (the first iteration). The four segments are then split into thirds, and the middle third of each part is again deleted and replaced with two line segments at a 60° angle to one another. The result (the second iteration) is sixteen line segments, each of length one-ninth, with each group of four segments being similar to the whole of the first iteration. If we keep iterating infinitely many times, we will be left with a self-similar figure of an infinite number of infinitely small one-dimensional line segments arranged in a curve called the Koch Curve.

A variation on the Koch Curve is the Koch Snowflake, which is a three-sided figure where each side is a Koch Curve.

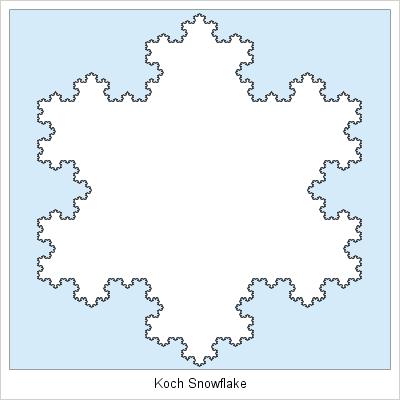
This figure has a topological dimension of one, since it is essentially just a one-dimensional curve. However because it juts out slightly into the second dimension but without filling up the two-dimensional plane, the fractal dimension of the Koch Snowflake is described as between one and two. In the Koch Snowflake, there are four self-similar parts, each of length one-third, so the exact dimension is calculated as log 4 / log 3, which is approximately 1.26. Thus, the Koch Snowflake fits

Mandelbrot’s definition of a fractal, with its fractal dimension of ~1.26, which is greater than its topological dimension of one.

An interesting and important characteristic of the Koch Snowflake is that its perimeter increases after every iteration until it approaches infinity, while its area stays finite. This property (an infinite perimeter or surface area but a finite area or volume), which is found in many fractals, is a big reason that they are so useful and prevalent throughout nature.

an octave. For example, the method that would be used to tune a piano based on looking at the ratio of an octave and fifths would be as follows:

The Math Behind Piano Tuning

Ben Rubinchik Introduction

Introduction

Piano notes (and any notes) are characterized by their frequency. Note = Frequency. For example, middle C (C4) has a frequency of about 260hz. An Octave, which is an interval of 8 white keys on a piano, is a ratio of 2:1. For example, if middle C (C4) is a frequency of 260hz, the C one octave above (C5) has a frequency of 520. Another important interval is a fifth, which has a ratio of 3:2. The fifth to C is G, which is five notes apart; the G would have a frequency of 390. However, here lies a problem. It is impossible to tune a piano based on looking at the ratio of an octave and subdividing it for every note. This is because we would end up with an infinite amount of frequencies that would need to fit inside

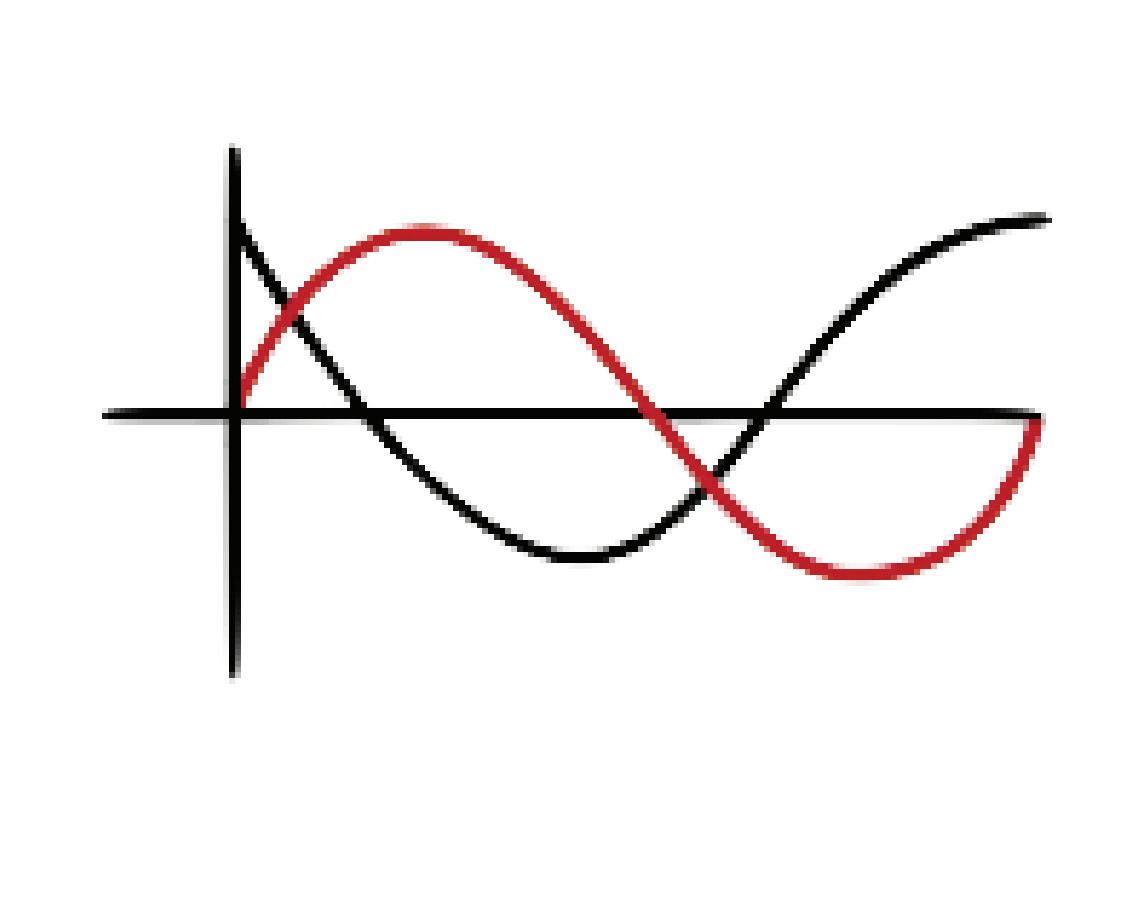
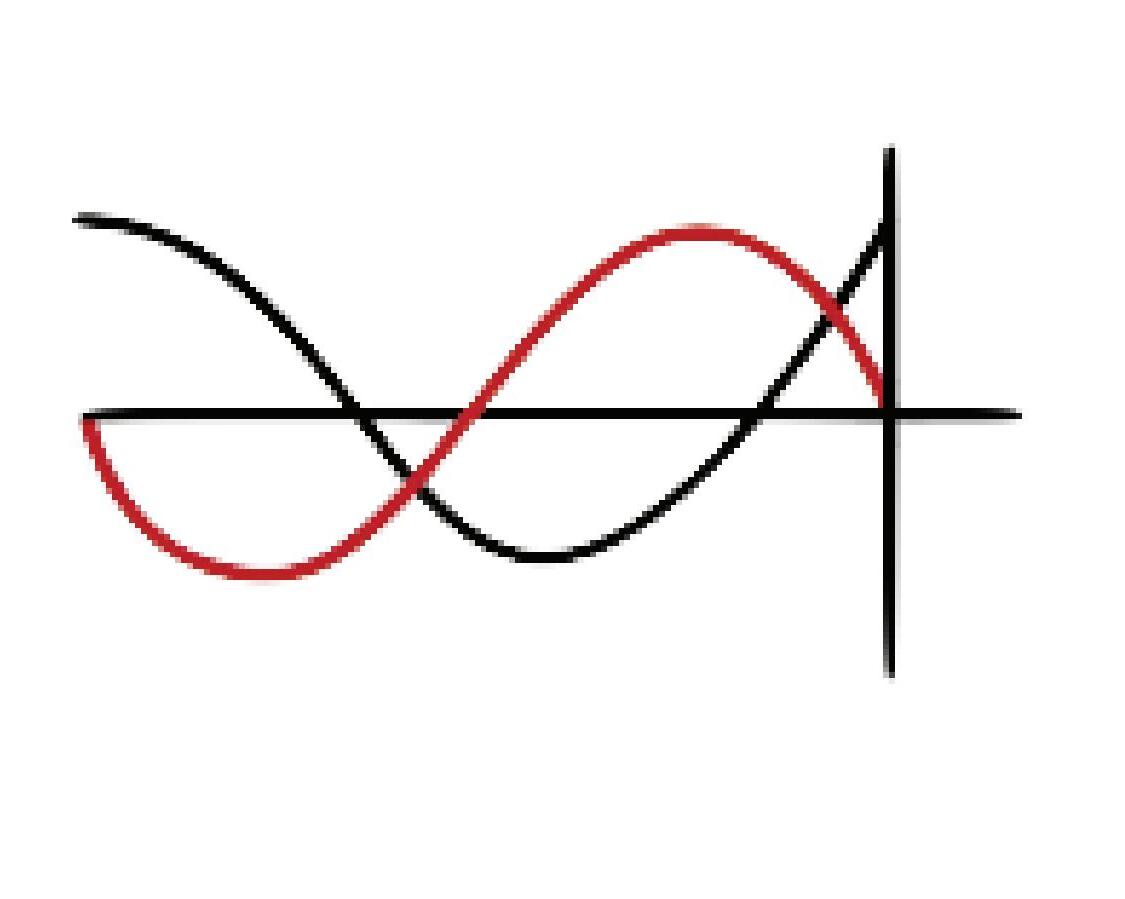
For this example, we are using 260hz as the first note in the octave. To find the frequency an octave above, we multiply 260 by 2 to get to 520. To find the fifth of 260, we would use 2:3 to find 390. Then, we will go up by another fifth from 390 to 585; however, 585hz is more than an octave above the original 260. To find the next frequency, we can go an octave down from 585: 292.5. We can repeat this pattern of going up by a fifth until exceeding an octave and going down an octave to find the frequencies of the notes in the scale. This is what the beginning of the equation would look like on a line graph:

We can use the mathematical equa tion

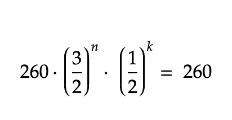
to prove by contradiction that this method doesn’t work. n = no. of times went up by a fifth. k = no. of times went up down an octave. Using this method, we cannot come back to 260 or 520 when repeating this pattern. This equation proves that if we want a piano that can play octaves and fifths, we will need a piano with infinitely many keys.

There are many solutions that musicians and scientists have come up with to solve the problem of accurately tuning a piano.

Use octaves in fifths just enough to play a simple melody: In this example, we will denote the lower note in the octave by 1 and the higher one by 2. To get specific values of the frequencies multiply the values by 260. Using this method, we will fill the range of the octaves with 7 notes.

Now we will repeat the previous process for a few steps. A fifth above the lower note is 3/2

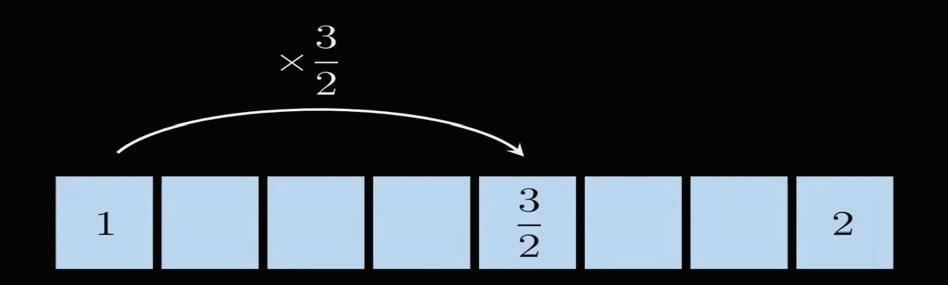
Another fifth up and one octave down will give us another note.

After repeating this process we end up with a scale of simple notes.

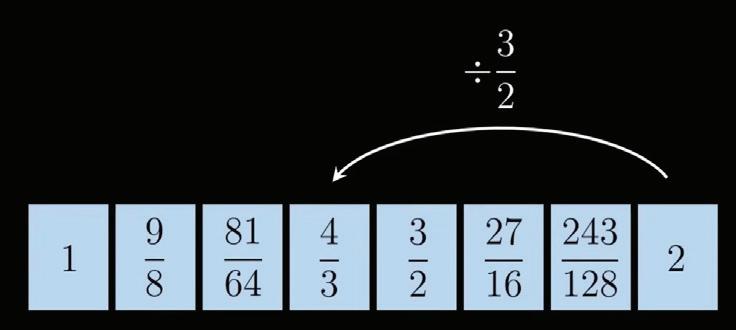
These frequencies and ratios would be valid for a basic melody. One of the flaws of this tuning is transposition. If you wanted to play a melody in 2 different keys, it may be problematic as this tuning is in only 1

scale.

Just Intonation

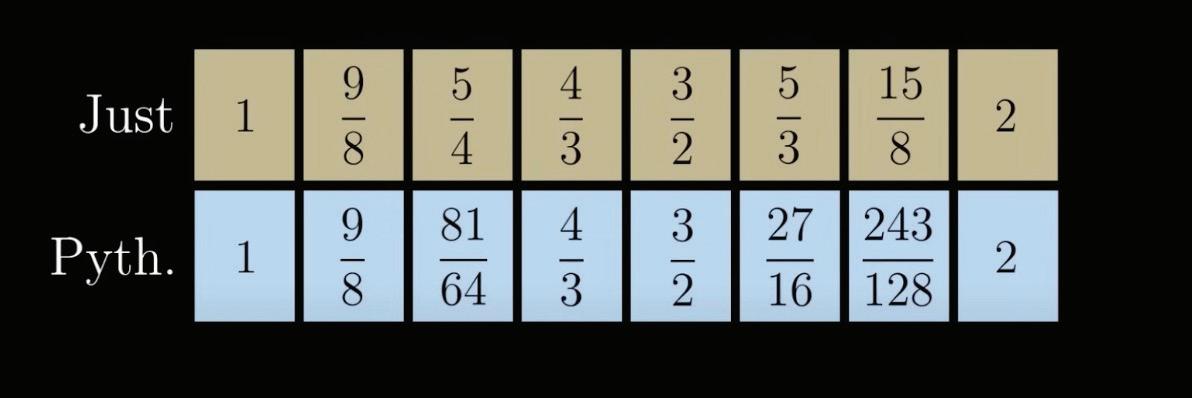
Just Intonation is a tuning system where the frequencies of notes are derived from simple, whole-number ratios, closely adhering to the natural harmonic series. This approach ensures that musical intervals such as thirds, fifths, and octaves are perfectly consonant or harmonic, resonating with the vibrations of the string. The fundamental difference from Pythagorean tuning is its basis for interval construction. While Pythagorean tuning relies on the perfect fifth, building intervals through a series of 3:2 ratios, Just Intonation considers a broader range of harmonic relationships. This leads to a tuning where major thirds are pure (in a 5:4 ratio), unlike Pythagorean tuning, where they are slightly sharper due to its exclusive focus on stacking fifths. As a result, Just Intonation offers a richness and depth of harmony that closely matches the natural order of overtones. Still, it also shares the limitation of fixed tuning, making modulation between keys challenging without returning.

Equal temperament formula. What we use now

Equal temperament, precisely the 12tone equal temperament (12TET) system, revolutionized musical tuning

equally spaced semitones. Each semitone is separated by the twelfth root of two (approximately 1.05946) in terms of frequency ratio. This uniform division allows for consistent interval spacing across all keys, enabling musicians to modulate freely between them without encountering the tuning discrepancies characteristic of just intonation or Pythagorean tuning. For instance, to calculate the frequency of an A# that is one semitone above A440 in this system, one would multiply 440 Hz by approximately 1.05946, yielding a frequency of about 466.163 Hz for A#. This approach ensures that each note’s frequency is a fixed ratio away from its neighbors, facilitating the composition and performance of music in a variety of keys without the need for retuning instruments, a significant advantage over earlier tuning systems.

Modern Music is out of tune. By standardizing the distance between notes to facilitate key modulation, equal temperament slightly alters the natural harmonic frequencies, leading to mathematically precise intervals but acoustically impure. This adjustment results in a tempering of the pure intervals found in just intonation, causing the harmonics to align less perfectly than they naturally would. The most noticeable effect of this compromise is on the thirds, sixths, and sevenths, which, in equal temperament, cannot achieve the same degree of consonance as their justly tuned counterparts. This subtle but definitive “out-oftuneness” is a flaw that musicians and composers often work around but cannot completely eliminate within the current music theory and prac-

tice framework.

Dissecting Divisibility Tricks: The Math Hidden Behind the Scenes

Benjamin Title

Have you ever heard of those number divisibility tricks and wondered why they work? Why is it that if the digits in the number add up to a multiple of 9 then the number is a multiple of 9? Why do all numbers divisible by 5 ends in a 0 or a 5? By looking at the math acting behind the scenes, we can figure out why these tricks work.

Before we can explain the magic behind these simple number tricks, we must understand a few concepts.

What is a number base? The ancient Mayans used a number system base 20, the Sumerians base 12, and the Babylonians, base 60, but what does this mean?

A number base is a unique way of writing down numbers. We were all taught that the first digit in a number is in the one’s place, followed by the ten’s place, then the hundredths, and so on. Each of these “places” is ten times that of the one before it. This is because we use a base 10 system. Algebraically, if we want to express the number 324 in this way, we could write 3 * 10^2 + 2 * 10^1 + 4 * 10^0. More generally, any number abcd… can be expressed as the sum of all its digits times some power of ten depending on its position (placement) in the number. In a different base, for example base 11, the first digit would b of large

base 11, the first digit would be the units digit, but the following digit would be the 11nth, then the 11*11nth, and so on, where instead of a 10, there is an 11.

Let’s look at some numbers in different bases and see how they compare to their base 10 representations:

What would 19 be in base 7?

It is 25, because the 2 is in the “sevenths” place, so 25 in base 7 is really 2*7 + 5 in base 10, which is just 25!

What about 5 in base 2?

It is 101, because the leftmost spot is in the “fours’’ place (2^2) and the rightmost digit is in the “ones” place, and 4 + 1 = 5! This string of 1’s and 0’s may look familiar, as base 2 is also known as binary.

There is one more concept that we must know to finally uncover the secrets of these divisibility tricks; we must know what modular arithmetic is.

While this may sound complex at first, it is really a fancy name for something we all learned a while ago; remainders! If you don’t remember what a remainder is, it is the amount left over after dividing a number by some value, representing what’s left that couldn’t be evenly divided. For example, the remainder when 19 is divided by 5 is 4, because

the biggest multiple of 5 less than 19 is 15, which is 4 away from 19. To write this in proper notation, you would say that 19 = 4 (mod 5). The “mod” just means when divided by, and 4 is the remainder (the leftover stuff).

An important thing to know is that for a number to be a multiple of another, the remainder has to be 0, meaning that it leaves nothing behind.

One more idea that you need to know is that if you want to find the remainder of a number, you can break down a number into any combination of its factors, where the factors multiply to yield the original number, find the remainder when each factor is divided by the same divisor, and multiply the remainders. For example, if we want to find the remainder when 110 is divided by 9, we can take its factors 11 and 10, and find the remainder of both factors when divided by 9, 11 = 2 (mod 9), and 10 = 1 (mod 9), and then multiply those remainders together, 2 * 1, to obtain the final remainder of 2.

This can be expressed more properly as:

11 = 2 (mod 9) and 10 = 1 (mod 9), so 110 = 11 * 10 = 2 * 1 = 2 (mod 9).

Therefore, if we want to find the remainder when a number is divided by 9, we first write it out algebraically:

abc = a*10^2 + b*10^1 + c*10^0

We can look at each term separately and find its remainder mod 9:

a*10^2 = a * 10 * 10 = a * 1 * 1 = a (mod 9)

b*10^1 = b * 10 = b * 1 = b (mod 9)

c*10^0 = c * 1 = c (mod 9)

Adding these together gives us:

abc = a + b + c (mod 9)

Therefore, the remainder of a number abc when divided by 9 is the remainder when a + b + c is divided by 9. And this works for a number of any length, not just three digits. This shows us that if we want the number to be divisible by 9, the sum of its digits must leave a remainder of 0 when divided by 9, and this is the divisibility trick with 9.

What about the 5 divisibility trick, that if the number ends in a 0 or 5 then it’s divisible by 5?

Again, we write our number out algebraically:

abc = a*10^2 + b*10^1 + c*10^0

We can look at each term separately and find its remainder mod 5:

a*10^2 = a * 10 * 10 = a * 0 * 0 = 0 (mod 10)

b*10^1 = b * 10 = b * 0 = 0 (mod 5)

c*10^0 = c * 1 = c (mod 5)

Therefore, the remainder of a number when divided by 5 is c, its units digit. And c is divisible by

5 only if it is 0 or 5.

Now that we understand why these divisibility tricks work with 9 and 5, we can come up with a divisibility trick for ANY number. But since that would require more background information, we will dive into that in the next Xevex journal.

59918559252459539594310499725246808459872736446958486538367362226260991246080512438843904 51244136549762780797715691435997700129616089441694868555848406353422072225828488648158456 02850601684273945226746767889525213852254995466672782398645659611635488623057745649803559 36345681743241125150760694794510965960940252288797108931456691368672287489405601015033086 17928680920874760917824938589009714909675985261365549781893129784821682998948722658804857 56401427047755513237964145152374623436454285844479526586782105114135473573952311342716610 21359695362314429524849371871101457654035902799344037420073105785390621983874478084784896 83321445713868751943506430218453191048481005370614680674919278191197939952061419663428754 44064374512371819217999839101591956181467514269123974894090718649423196156794520809514655 02252316038819301420937621378559566389377870830390697920773467221825625996615014215030680 38447734549202605414665925201497442850732518666002132434088190710486331734649651453905796 26856100550810665879699816357473638405257145910289706414011097120628043903975951567715770 04203378699360072305587631763594218731251471205329281918261861258673215791984148488291644 70609575270695722091756711672291098169091528017350671274858322287183520935396572512108357 91513698820914442100675103346711031412671113699086585163983150197016515116851714376576183 51556508849099898599823873455283316355076479185358932261854896321329330898570642046752590 70915481416549859461637180270981994309924488957571282890592323326097299712084433573265489 38239119325974636673058360414281388303203824903758985243744170291327656180937734440307074 69211201913020330380197621101100449293215160842444859637669838952286847831235526582131449 57685726243344189303968642624341077322697802807318915441101044682325271620105265227211166 03966655730925471105578537634668206531098965269186205647693125705863566201855810072936065 98764861179104533488503461136576867532494416680396265797877185560845529654126654085306143 44431858676975145661406800700237877659134401712749470420562230538994561314071127000407854 73326993908145466464588079727082668306343285878569830523580893306575740679545716377525420 21149557615814002501262285941302164715509792592309907965473761255176567513575178296664547 79174501129961489030463994713296210734043751895735961458901938971311179042978285647503203 19869151402870808599048010941214722131794764777262241425485454033215718530614228813758504 30633217518297986622371721591607716692547487389866549494501146540628433663937900397692656 72146385306736096571209180763832716641627488880078692560290228472104031721186082041900042 29661711963779213375751149595015660496318629472654736425230817703675159067350235072835405 67040386743513622224771589150495309844489333096340878076932599397805419341447377441842631 29860809988868741326047215695162396586457302163159819319516735381297416772947867242292465 43668009806769282382806899640048243540370141631496589794092432378969070697794223625082216 88957383798623001593776471651228935786015881617557829735233446042815126272037343146531977 77416031990665541876397929334419521541341899485444734567383162499341913181480927777103863 87734317720754565453220777092120190516609628049092636019759882816133231666365286193266863 3606273567630354477w628035045077723554710585954870279081435624014517180624643626794561275 31813407833033625423278394497538243720583531147711992606381334677687969597030983391307710 98704085913374641442822772634659470474587847787201927715280731767907707157213444730605700 73349243693113835049316312840425121925651798069411352801314701304781643788518529092854520 11658393419656213491434159562586586557055269049652098580338507224264829397285847831630577 77560688876446248246857926039535277348030480290058760758251047470916439613626760449256274 20420832085661190625454337213153595845068772460290161876679524061634252257719542916299193 06455377991403734043287526288896399587947572917464263574552540790914513571113694109119393 25191076020825202618798531887705842972591677813149699009019211697173727847684726860849003 37702424291651300500516832336435038951702989392233451722013812806965011784408745196012122 85993716231301711444846409038906449544400619869075485160263275052983491874078668088183385 10228334508504860825039302133219715518430635455007668282949304137765527939751754613953984 68339363830474611996653858153842056853386218672523340283087112328278921250771262946322956 39898989358211674562701021835646220134967151881909730381198004973407239610368540664319395 09790190699639552453005450580685501956730229219139339185680344903982059551002263535361920 41994745538593810234395544959778377902374216172711172364343543947822181852862408514006660 44332588856986705431547069657474585503323233421073015459405165537906866273337995851156257 84322988273723198987571415957811196358330059408730681216028764962867446047746491599505497 37425626901049037781986835938146574126804925648798556145372347867330390468838343634655379 49864192705638729317487233208376011230299113679386270894387993620162951541337142489283072 20126901475466847653576164773794675200490757155527819653621323926406160136358155907422020 20318727760527721900556148425551879253034351398442532234157623361064250639049750086562710 95359194658975141310348227693062474353632569160781547818115284366795706110861533150445212 74739245449454236828860613408414863776700961207151249140430272538607648236341433462351897 57664521641376796903149501910857598442391986291642193994907236234646844117394032659184044 37805133389452574239950829659122850855582157250310712570126683024029295252201187267675622 04154205161841634847565169998116141010029960783869092916030288400269104140792886215078424 51670908700069928212066041837180653556725253256753286129104248776182582976515795984703562 22629348600341587229805349896502262917487882027342092222453398562647669149055628425039127 Thank you to everyone who contributed to this issue of Xevex! Interested in becoming a writer?

Faculty Advisor: Dr. Fabio Nironi (nironif@ramaz.org)