FAVORIT MATEMATIK 3A
Lärarpaket – Tryckt + Digitalt



LÄS OCH PROVA
LÄRARPAKETETS
SAMTLIGA DELAR




LÄS OCH PROVA
LÄRARPAKETETS
SAMTLIGA DELAR
Ett lärarpaket innehåller en tryckt lärarhandledning, lärarens digitala resurs och tryckta facit till elevböckerna. Tre lärare kan dela på ett lärarpaket via egna inloggningar. Det uppskattade och välfyllda lärarpaketet innehåller allt du behöver i form av inspiration och konkreta verktyg för en kommunikativ matematikundervisning. Använd lärarpaketet som ett smörgåsbord och välj det som passar bäst i din klass.

I Favorit matematik är varje lektion viktig och har ett tydligt mål. Författarna ger dig förslag på arbetsgång men du väljer! Alla lektioner har likadana resurser och i den tryckta lärarhandledningen finns länkar som visar att det finns mer innehåll i lärarens digitala resurs. Bläddra och se här i smakprovet.
Interaktiv version av lärarmaterialet, där det går att söka, stryka under, anteckna och länka.
Lärarens digitala resurs är en uppskattad del av lärarpaketet. Här finns bland mycket annat, förberedda presentationer av lektionens matematiska innehåll, ramberättelser, samtalsbilder och problemlösning som ger ingång till viktiga matematiska samtal. Blir du extra nyfiken på något moment kan du ta del av fortbildande texter med forskning och filmer om digital kompetens och programmering.

I lärarpaketet ingår tryckta facit. Du får ett tryckt facit till Favorit och ett till Mera Favorit. Du kan dessutom ladda ner facit från lärarpaketets digitala resurs. Vill du ha fler tryckta facit finns de att köpa i 5-pack.
Här hittar du filmer, presentationer, kopieringsunderlag, facit, prov och mycket mer.
Studentlitteratur AB
Box 141
221 00 LUND
Besöksadress: Åkergränden 1
Telefon 046-31 20 00
studentlitteratur.se
Kopieringsförbud
Otavan asiakaspalvelu Puh. 0800 17117 asiakaspalvelu@otava.fi
Tilaukset
Kirjavälitys Oy Puh. 010 345 1520 Faksi 010 345 1454 kvtilaus@kirjavalitys.fi 1. painos
© 2007 Katariina Asikainen, Kimmo Nyrhinen, Pekka Rokka, Päivi Vehmas ja Kustannusosakeyhtiö Otava
Detta verk är skyddat av upphovsrättslagen. Kopiering, utöver lärares begränsade rätt att kopiera för undervisningsbruk enligt Bonus Copyright Access skolkopieringsavtal, är förbjuden. Kopieringsunderlag får dock kopieras under förutsättning att kopiorna delas ut endast i den egna undervisningsgruppen. För information om avtalet hänvisas till utbildningsanordnarens huvudman eller Bonus Copyright Access.
Toimitus: Mervi Korhonen
Piirrokset: Tarja Ilola
Kansi: Mirella Mäkilä
Vid utgivning av detta verk som e-bok, är e-boken kopieringsskyddad.
Graafinen suunnittelu: Mirella Mäkilä Taitto: Mervi Salokangas
Användning av detta verk för text- och datautvinningsändamål medges ej.
Kopiointiehdot
Tämä teos on vastauskirja. Teos on suojattu tekijänoikeuslailla (404/61). Tätä teosta ei saa valokopioida lainkaan. Myös teoksen tai sen osan digitaalinen kopioiminen tai muuntelu on ehdottomasti kielletty.
Den som bryter mot lagen om upphovsrätt kan åtalas av allmän åklagare och dömas till böter eller fängelse i upp till två år samt bli skyldig att erlägga ersättning till upphovsman eller rättsinnehavare.
Lisätietoja antaa Kopiosto ry, www.kopiosto.fi/.
Studentlitteraturs trycksaker är miljöanpassade, både när det gäller papper och tryckprocess.
Painopaikka: Otavan Kirjapaino Oy Keuruu 2008
Art.nr 37316
ISBN 978-91-44-17612-3
Upplaga 2:2
ISBN 978-951-1-22493-8
© Författarna och Studentlitteratur 2013, 2019
Originalets titel: Tuhattaituri Opettajan opas
© Otava Publishing Company Ltd, Helsingfors 2008
Översättare: Cilla Heinonen
Illustratör: Tarja Ilola
Printed by Eurographic Group, 2024

1. JAKSO

Kom igång med Favorit matematik .......... 4
KAPITEL 1
1. Vi repeterar tiotalsövergång ................ 6
2. Vi repeterar addition och subtraktion .............................................. 10
3. Addition med hjälp av hundratavlan. 14
4. Subtraktion med hjälp av hundratavlan ........................................... 18
5. Talen 0 till 1 000 22
6. Att jämföra talen 0 till 1 000 ............... 26
7. Favoritsidor – laborativ övning .......... 30
on suojattu tekijänei saa valokopioida osan digitaalinen ehdottomasti kielletty.
8. Addition med uppställning och växling .............................................. 34
KAPITEL 3
1. Kertaamme kymmenylitystä .............6
2. Kertaamme yhteen- ja vähennyslaskua ..................................10
3. Yhteenlaskua satataulun avulla .....14
4. Vähennyslaskua satataulun avulla 18
5. Luvut 0–1000.......................................22
6. Suuruusvertailua luvuilla 0–1000 ..26
7. Toimintatunti .......................................30
8. Yhteenlasku allekkain .......................34
9. Vähennyslasku allekkain ..................38
10. Nollan yli lainaaminen .....................42
11. Vihkotyöskentely ................................46
12. Monta laskua peräkkäin ..................50
13. Mitä osaan? .........................................54
2. JAKSO
14. Yhteenlaskun ja kertolaskun yhteys....................................................58
15. 5:n ja 10:n kertotaulut ......................62
3. JAKSO
28. Laskujärjestys ...................................114
29. Muodostamme lausekkeen
30. Ratkaisemme sanallisia
31. Harjoittelemme ................................126
32. Kertolasku allekkain muistinumeroa ..................................130
33. Muistinumero kertolaskussa
34. Toimintatunti .....................................138
35. Kaksi muistinumeroa kertolaskussa.....................................142
36. Harjoittelemme ................................146
37. Mitä osaan .........................................150
4. JAKSO
38. Jako yhtä suuriin
39. Jako yhtä suuriin
40. Jakolaskun merkitseminen
41. Jakolaskun ja kertolaskun yhteys..................................................166
9. Subtraktion med uppställning och växling .............................................. 38
10. Att växla över noll................................. 42
11. Vi övar 46
12. Att räkna med tre termer ................... 50
13. Vad har jag lärt mig? ........................... 54
KAPITEL 2
14. Från addition till multiplikation 58
15. Multiplikation med 5 och 10 ............... 62
16. Multiplikation med 10 och 100 ...........

17. Multiplikation med 2 och 4 ..................
18. Kommutativa lagen vid multiplikation ..........................................
19. Multiplikation med 4 och 8 ..................
16. 10 ja 100 kertolaskussa....................66
KAPITEL
17. 2:n ja 4:n kertotaulut ........................70
18. Kertolaskun vaihdannaisuus ...........74
19. 4:n ja 8:n kertotaulut ........................78
20. Harjoittelemme ..................................82
21. 3:n ja 6:n kertotaulut ........................86
22. 9:n kertotaulu .....................................90
23. Harjoittelemme ..................................94
24. 7:n kertotaulu .....................................98
25. Toimintatunti .....................................102
26. Harjoittelemme ................................106
27. Mitä osaan? .......................................110
42. Kuinka monta kertaa sisältyy toiseen lukuun?
43. Harjoittelemme ................................174
44. Jakojäännös .......................................178
45. Sanallisia tehtäviä
46. Jakajana kymmenen
47. Laskujärjestys ...................................190
48. Mitä osaan? .......................................194
49. Harjoittelemme ................................198
50. Mitä osaan? .......................................202
51. Kertaamme........................................206
52. Kertaamme........................................210
En stor författargrupp med olika kompetenser har tillsammans arbetat fram Favorit matematik som ursprungligen kommer från Finland. Det unika fyrsidessystemet håller klassen samlad kring ett gemensamt matematiskt moment samtidigt som eleverna får möjlighet att arbeta med olika uppgifter för att stimulera och utmana den matematiska utvecklingen.
Det matematiska innehållet är av hög kvalitet och eleverna får lära sig att använda ett matematiskt språk.
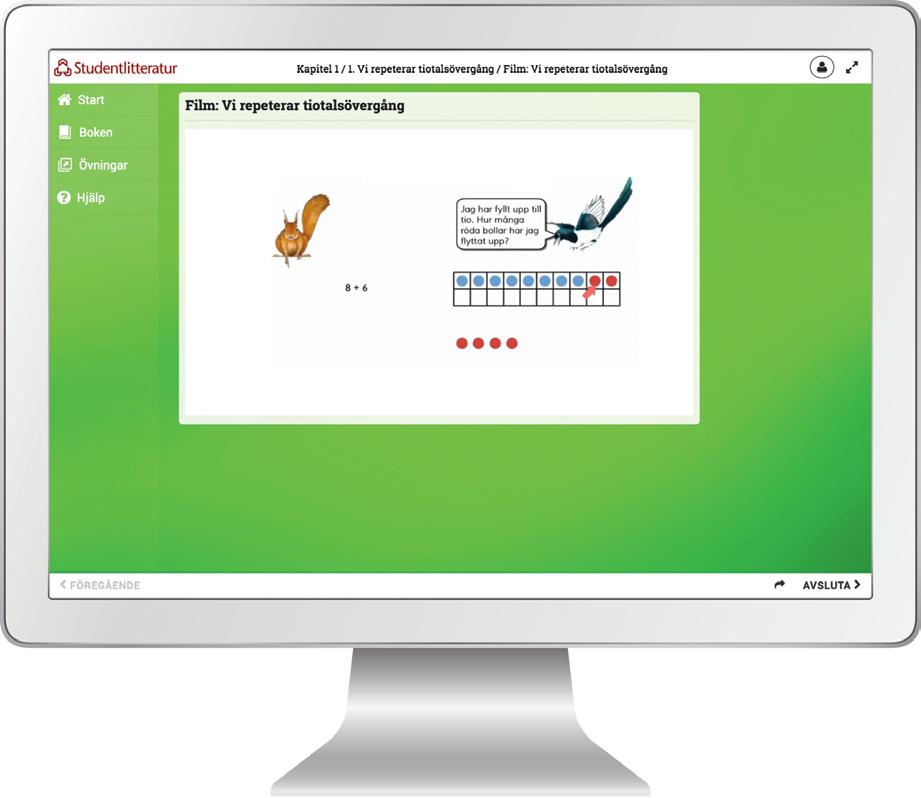
Titta på filmen* som visar den tydliga fyrsidesstrukturen och vad som ingår i ett kapitel i elevboken.
1. Lektionens innehåll
2. Lektionens mål
3. Läroplan
4. Frågor till samtalsbilden
5. Huvudräkningsuppgifter
6. Förslag på arbetsgång
7. Ramberättelse
8. Tavlan
9. Presentationer
10. Elevböcker
Fördjupad information s. 237–243























11. Problemlösning
12. Tips
13. Kunskapsbank
14. Forskning om
15. Favorit kopieringsunderlag
16. Träna digitalt (och Film)
17. Matteordlista
* Den här symbolen visar att det finns en klickbar länk i lärarens digitala resurs. Inloggningsuppgifter till lärarens digitala resurs finns på omslagets insida.




Under en vecka bör du hålla fyra stycken lektioner. Tre av dessa lektioner är genomgångslektioner och en lektion är av problemlösningskaraktär. Det kan vara bra att känna till att i Finland är det vanligt med 45-minuterslektioner. En genomgångslektion har fyra sidor i elevboken.
EN VECKA MED FAVORIT
GENOMGÅNG
GENOMGÅNG
Du kan använda terminsplaneringen som finns längst bak i lärarhandledningen. Genom att planera veckorna för hela terminen, ser du vilka lektioner som ingår i veckans matematikundervisning. Reflektera över det matematiska innehållet i relation till den information du har om dina elevers kunskaper.
PROBLEMLÖSNING ELEVBOK ELEVBOK ELEVBOK LEKTION 1
GENOMGÅNG
GENOMGÅNGS LEKTION (3 st/vecka)
Från lektionens olika resurser väljer DU vad som passar dig och din klass bäst. Följ ”Förslag på arbetsgång” eller planera och gör ett eget urval från resurserna: Elevboken • Frågor till samtalsbilden • Huvudräkningsuppgifter • Ramberättelse • Tavlan Presentationer • Tips • Matteordlista
TRÄNA PÅ LEKTIONENS INNEHÅLL






























Det första uppslaget är en genomgång av nytt innehåll. Här får eleverna öva på lektionens matematiska moment. De här två sidorna ska alla elever arbeta med.
ARBETA MED EXTRAUPPGIFTER
På det andra uppslaget finns extrauppgifter.
TRÄNA-rutan används som läxa i Finland. Eleverna gör inte uppgifterna på lektionen utan tar hem boken och repeterar lektionens innehåll. Om du inte vill skicka hem boken så finns uppgifterna som självrättande uppgifter i elevens digitala läromedel.
ÖVA-sidan med repetition och
PRÖVA-sidan med ny tillämpning och mera utmanande uppgifter.
Låt eleverna välja bland dessa uppgifter – alla behöver inte göra allt.


PROBLEMLÖSNINGSLEKTION (1 st/vecka)
Klassrumsdialogen i helklass är viktig. Du hittar de flesta kommunikativa övningarna i lärarhandledningen, inte som enskilda uppgifter i elevboken. I Favorit matematik finns det problemlösningsuppgifter till varje lektion. De finns förberedda både i den tryckta lärarhandledningen i den digitala resursen. Använd dessa och arbeta gemensamt med problemlösning en lektion i veckan. Du kan också utgå från uppgifterna på PRÖVAsidan och låta eleverna lösa dem enskilt eller i mindre grupper.
Lektionens innehåll
• repetition av tiotalsövergång vid addition och subtraktion
• repetition av sambandet mellan addition och subtraktion (så kallade räknefamiljer)
• repetition av begreppen addition, subtraktion, term, summa och differens
Lektionens mål
• att uttrycka kunskaper om sambanden mellan de olika räknesätten
• att använda utvecklingsbara metoder för att utföra beräkningar vid huvudräkning
Läroplan
Frågor till samtalsbilden
På bilden ser du Isa, Charlie, Kurre och Sally. Karaktärerna är bekanta för eleverna från Favorit Matematikböckerna 1 och 2. Ramberättelsen anknyter alltid till samtalsbilden.
1. Vad kallas talen 8 och 6 i additionen 8 + 6? (termer)
2. Berätta hur du tänker när du räknar 8 + 6 via tiotalet.
3. På vilket annat sätt kan du räkna ut summan? (t.ex. genom att räkna upp 6 tal framåt från talet 8)
4. I uppgiften 14 – 6, vad kallas a. det första talet, 14? (term) b. uppgiftens andra tal, 6? (term)
5. Berätta hur du räknar 14 – 6 via tiotalet.
6. På vilket annat sätt kan du räkna ut differensen? (t.ex. genom att räkna sex tal bakåt från talet 14, eller räkna från talet 6 upp till 14)
Huvudräkningsuppgifter
De tal som ingår i huvudräkningsuppgifterna kan skrivas upp på tavlan. Eleverna skriver svaren i de rutor som finns bredvid rubriken i elevboken.

Addition
term + term = summa
8 + 6
= 8 + 2 + 4
= 10 + 4 = 14
Addera först till tiotalet. Addera sedan resten.
1. Räkna.

Subtraktion
term – term = differens 14 – 6
= 14 – 4 – 2
= 10 – 2 = 8
Subtrahera först till tiotalet. Subtrahera sedan resten.
Taluppfattning och tals användning – grundläggande kunskaper om de fyra räknesätten och naturliga tal, hur man delar upp tal Lyssna på berättelsen. Öva begreppen. Film
978-91-44-16686-5_10_book.indb 6 2024-02-22 12:22
Förslag på arbetsgång
1. Ramberättelse
2. Frågor till samtalsbilden
3. Huvudräkningsuppgifter
Elevböcker
Favorit
Mera Favorit
Mera Favorit facit
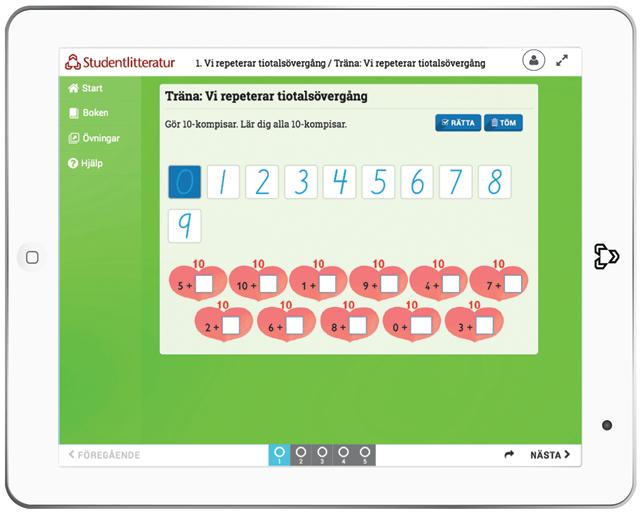
Efter huvudräkningsuppgifterna kan du låta eleverna öva på att automatisera uppgifter med tiotalsövergång. (se räknebank s. 8)
4. Repetition av ”tiokompisar”, genom att du säger den ena termen och eleverna den andra, t.ex. säger du 4 och eleverna svarar 6.
5. Arbete på tavlan
Repetition av att räkna via tiotal. Istället för att använda tavelbilden kan du använda den digitala elevboken och de rutsystem som finns på s. 6.
6. Elevbokens uppgifter
7. Favorits repetitionstest (kopieringsunderlag 1b) Med hjälp av testet kan du hitta de elever som behöver extra stöd. (se även Kunskapsbank s. 9)
Huvudräkningsuppgifter, forts.
1. 9 + 7 (16)
2. Den första termen är 14 och den andra termen som ska subtraheras är 8. Vad är differensen? (6)
3. Från talet 14 subtraherar du först 7 och sedan adderar du 6. Vad är svaret? (13)



4. Fortsätt talföljden.







Ramberättelse Bild
Skolstart!
Charlie och Isa var nervösa. Det var sista dagen på sommarlovet och skolan skulle börja i morgon. De skulle börja tredje klass, de skulle få en ny lärare och några nya klasskompisar. Charlie och Isa hade träffats många gånger under sommaren, för de brukade spela brännboll i en park i närheten. De hade också en gemensam hemlighet. I parken bodde nämligen en rolig skata och en kvick ekorre. Charlie och Isa hade döpt dem till Sally och Kurre. Charlies, Isas, Sallys och Kurres vänskap hade pågått i många år. Barnen och djuren kunde prata med varandra. Charlie och Isa nämnde inte detta för någon, för de anade att ingen ändå skulle tro dem.
– Det känns som om jag inte kommer ihåg någonting av matematiken. Jag har bara njutit av sommaren och av att spela, suckade Charlie.
– Oroa dig inte. Så länge du kommer ihåg tiotalsövergång ska du nog klara av att komma igång, tröstade Isa.
– Ja precis, i addition räknar jag först upp till tio och sedan resten. I subtraktion subtraherar jag först till tio och sedan resten, instruerade skatan Sally.
– Det är en bra minnesregel, konstaterade Charlie nöjt.
– Har ni sett Kurre den här morgonen? frågade Isa.
– Där kommer han hoppande, svarade Charlie. Samtidigt klättrade Kurre upp på Isas axel och så var kvartetten åter samlad.
Genomgång steg för steg 1
Genomgång steg för steg 2
Uppdelningen av talet 10 repeteras med hjälp av 10kompisar. I Finland kallas dessa för ”hjärtepar” så det är därför 10kompisarna skrivs i röda hjärtan i uppgiften. Uppgiftstypen är bekant från elevböckerna 1 och 2.
Problemlösningsuppgifter
Eleverna kan ha hjälp av en tallinje när de löser uppgiften.
1. Grodan och gräshoppan hoppar på stenar. Grodan hoppar framåt fem stenar i taget. Gräshoppan hoppar framåt tre stenar i taget. Grodan startar på den första stenen och gräshoppan startar på den andra. Vilken är den första sten som båda landar på? (11, 11 = 1+5+5, 11 = 2+3+3+3)
2. Grodan hoppar framåt fyra stenar i taget. Gräshoppan hoppar framåt fem stenar i taget. Grodan startar på den första stenen och gräshoppan startar på den andra. Vilken är den första sten som båda landar på?
(17, 17 = 1+4+4+4+4, 17 = 2+5+5+5)
Räknebank
1. 7 + 8 (15)
2. 6 + 9 (15)
3. 4 + 8 (13)
4. 6 + 7 (13)
5. 5 + 8 (7)
6. 15 – 8 (7)
7. 16 – 9 (7)
8. 13 – 4 (9)
9. 12 – 6 (6)
10. 11 – 4 (7)
1. Fingrar och tår
Läs uppgifter där den första termen är 11, t.ex. 11 – 5. Eleverna visar uppgiften; vi vet att vi har tio tår och så håller vi upp ett finger också (10 + 1 = 11). Vi subtraherar fem genom att först ta ner ett finger och sedan fundera på hur många tår vi ska ta bort (4). Vi räknar 10 – 4 i huvudet och får svaret 6.
Träna digitalt
Träna Favorit
Träna Mera Favorit Film

TRÄNA 1. Skriv 10-kompisar. Lär dig alla 10-kompisar.











Räkna.
3. Addera.
Räkna.
2024-02-22 12:22
978-91-44-16686-5_10_book.indb 8
2. Talkort
Eleverna har talkorten 1 och 10 (bredare kort). Alla bildar talet 11 på sin bänk genom att lägga kortet 1 på nollan på tiokortet. Öva på att subtrahera från 11, t.ex. 11 – 3. Först tar du bort ettan från nollan, du subtraherar alltså till tio. Sedan tar du bort resten, funderar alltså på hur mycket du måste subtrahera från tio? (2) Hur mycket är 11 – 3? (8)
3. Klossar: Att dela upp talen 11-19
Lägg t.ex. 11 klossar i en påse och berätta för eleverna hur många klossar det är i påsen. En av eleverna kommer fram och tar ett antal klossar ur påsen och berättar för de andra hur många klossar han eller hon tog upp. De andra berättar hur många klossar som är kvar i påsen.
4. Tallek två och två
Den ena eleven börjar med att säga talet 1 eller 2. Den andra lägger till talet 1 eller 2 och säger svaret på additionen. Om den första eleven säger t.ex. 2 så säger den andra 3 eller 4. Eleverna fortsätter så här fram till den ena säger 20 och därmed vinner. Efter leken kan du låta eleverna fundera på vilken strategi de bör ha för att ha större chans att vinna och vilket tal de bör säga näst sist (17) för att de ska kamma hem vinsten. (Vinnaren säger talen 2, 5, 8, 11, 14 och 17. Du vinner alltså genom att börja med att säga 2, eftersom du då med säkerhet kan säga talen ovan.)
Måla.







7. Fortsätt talföljden.
8. Varje bild motsvarar ett tal. Skriv talet.









Favorit kopieringsunderlag
Kopieringsunderlag 1a: Tiotalsövergång
Kopieringsunderlag 1b: Favorits repetitionstest
När man har utrett matematiksvårigheter hos elever i åk 6 har man upptäckt att svårigheterna ofta börjar redan vid addition och subtraktion i talområdet 0–20. I början av årskurs tre är det viktigt att försäkra sig om att eleven har koll på tiokompisar och tiotalsövergång. Många elever har inte det, och dessa elever behöver också konkreta övningar, t.ex. med hjälp av klossar, för att nå förståelse. Kopieringsunderlaget 1b är Favorits repetitionstest. Med hjälp av testet är det möjligt att hitta de elever som behöver stödundervisning i tiotalsövergång i addition och subtraktion. I början är det bra om du försäkrar dig om att eleverna behärskar tiokompisarna och bildandet av talen 11 till 20 (11 = 10 + 1, 12 = 10 + 2 osv.) samt uppdelning av talen 2 till 9. Det är meningen att man gör testet flera gånger så att tiotalsövergången automatiseras. Eleverna jämför sina egna testresultat med de resultat de fått tidigare och ser att de utvecklas. Den tid eleven behöver för testet kan skrivas upp med t.ex. en minuts noggrannhet.
Summa och differens
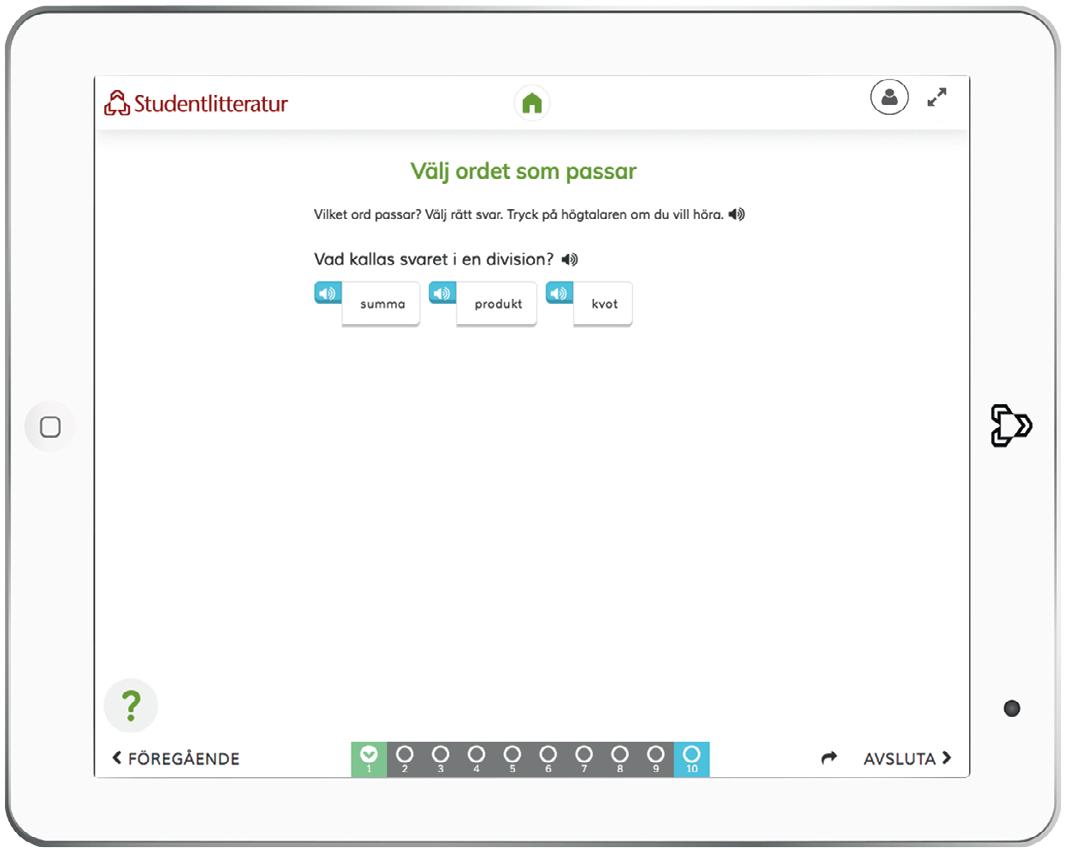
I additionen 6 + 8 = 14 är 6 + 8 den utskrivna summan eller summan och 14 är den uträknade summan, summans värde eller bara summan. I subtraktionen 14 – 8 = 6 är subtraktionen 14 – 8 den utskrivna differensen eller differensen och 6 är den uträknade differensen, differensens värde eller bara differens. I Favorit Matematikböckerna lär man sig begreppen summa, differens, produkt och kvot.
2. Vi repeterar addition och subtraktion
Lektionens innehåll
• repetition av tiotalsövergång i talområdet 0–100, ensiffrig andra term vid subtraktion
• att skriva in enhet i ett uttryck (Mera Favorit 3A)
Lektionens mål
• att visa och använda kunskaper om att beräkningar i ett talområde kan utnyttjas i ett utökat talområde
Läroplan
Frågor till samtalsbilden
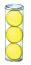
1. Hur många blå bollar finns det på bilden? (38)
2. Hur många gröna bollar finns det på bilden? (5)
3. Berätta med hjälp av bilden hur du räknar 38 + 5.
4. Hur många bollar finns det sammanlagt på bilden? (43)
5. Berätta med hjälp av bilden hur du räknar 43 – 5.
Huvudräkningsuppgifter
Eleverna skriver svaren på huvudräkningsuppgifterna i de tomma rutorna bredvid rubriken.
1. 38 + 7 (45)
2. 68 + 7 (75)
3. 43 – 9 (34)
UPPGIFT 1
Bilden anger starttalet. Eleverna kan vid behov rita fler bollar i rutsystemet vid uppgift a och dra streck över bollar i uppgift b.


Förslag på arbetsgång
1. Frågor till samtalsbilden
2. Huvudräkningsuppgifter
Efter huvudräkningsuppgifterna kan du låta eleverna öva på att automatisera uppgifter med tiotalsövergång (se räknebank s. 12).
3. Ramberättelse
4. Arbete på tavlan
Tavelbilden anger hur du kan börja. Istället för tavlan kan du använda t.ex. projektor för att visa sidan i den digitala elevboken och gå igenom uträkningarna. Repetera användning av enheter med hjälp av räkneexemplet.
5. Elevbokens uppgifter
Det kan vara bra att läsa problemuppgifterna högt tillsammans eller parvis. Det här underlättar märkbart förståelsen av uppgiften och det hjälper speciellt elever med läs och skrivsvårigheter. Det går också att använda den digitala elevboken och låta de elever som behöver höra uppgiften. Mera Favorit facit
2. Skriv






3. Räkna. Ringa in svaret i rutan.


4. Dra streck mellan de tal som tillsammans är lika med

Tiotalsövergång
Trilla omkull
På cykelloppisen fanns det många fina, begagnade cykelhjälmar. Isa valde snabbt. Hon ville ha en blå hjälm som kostade 38 kronor. Hon ville också köpa en säkerhetsvimpel till sin cykel, den kostade 5 kronor. Snabbt räknade Isa ut vad inköpen kostade sammanlagt.
– Även här räknar jag: först upp till tiotalet och sedan resten: 38 kr + 5 kr = 38 kr + 2 kr + 3 kr = 40 kr + 3 kr = 43kr. Mina pengar räcker för att köpa det här. Nu är det bara att betala, tänkte Isa nöjt.
Nästa dag satt Sally uppe i en trädtopp och såg på alla barn som cyklade till skolan. Isa skulle precis cykla nerför backen när hon upptäckte Sally:
– Hej! Hur mår min favoritskata? ropade Isa.
Innan Sally hann svara hände det någonting hemskt. Isas cykel välte och Isa flög av cykeln. Det såg illa ut. Sally flög genast dit för att se hur Isa mådde. Isa höll om sitt knä som hade fått ett otäckt sår, men förutom det var hon oskadd.
– Tur att jag hade cykelhjälm! sa Isa och höll om sitt onda knä. Hon tog ett groblad från vägkanten och tryckte det mot sitt knä som ett plåster. Sally såg så uppskärrad ut att Isa bestämde sig för att ge henne någonting annat att tänka på. – Igår köpte jag den här hjälmen och säkerhetsvimpeln. De kostade sammanlagt 43 kronor. Vimpeln kostade 5 kronor. Hur mycket kostade hjälmen?
– Ingen aning, konstaterade Sally. Kan du berätta hur du räknar ut det?
Presentationer
Favorit Mera Favorit TAVLAN
Genomgång steg för steg 1
Genomgång steg för steg 2
Elevböcker
Problemlösningsuppgifter
1. Utgå från bilden nedan. Gör en egen magisk kvadrat. Välj ett tal mellan 25 och 100. Skriv i kvadraten så att summan i alla rader både våg och lodrätt är det tal du valt. På det här sättet kan eleverna till exempel göra ett födelsedagskort till någon vuxen vän, om de vet hur många år han eller hon fyller nästa gång.
8 11 1
2 7 12
3 9 6
10 5 4
Räknebank
1. 23 + 7 (30)
2. 45 + 6 (51)
3. 76 + 8 (84)
4. 67 + 7 (74)
5. 39 + 6 (45)
6. 35 – 6 (29)
7. 45 – 7 (38)
8. 62 – 3 (59)
9. 100 – 5 (95)
10. 100 – 8 (92)
Tips
1. Att hitta på egna problemlösningsuppgifter
Skriv 65 – 30 och 60 + 12 på tavlan. Låt eleverna hitta på problemlösningsuppgifter till uttrycken. Ni kan göra en uppgift tillsammans som exempel först. Använd humor och fantasi.
2. Tallek två och två
Den ena eleven börjar med att säga ett tal mellan 1 och 10. Den andra adderar ett tal mellan 1 och 10 till det första talet och säger summan. Om den första eleven t.ex. säger 5 så ska den andra säga ett tal mellan 6 och 15. Eleverna fortsätter så här en åt gången tills någon säger 100 och därmed vinner. Efter leken låter du eleverna fundera på vilka tal de bör säga näst sist för att vinna spelet (89).

Räkna.
Skriv 10-kompisar.




978-91-44-16686-5_10_book.indb 12
3. Romerska siffror, ental och tiotal

2024-02-22 12:22
Det romerska talsystemet är bekant för eleverna från Favorit matematik åk 1 och 2. Repetera hur det romerska talsystemet fungerar. Sju elever ställer sig på rad framför klassen. Du säger tal och eleverna bildar det genom att de som föreställer tiotal står i ett X och de som är ental står som ”streck”. I talet 34, till exempel, står de tre eleverna till vänster som X och fyra elever står som ett streck. Andra lämpliga tal för sju elever är 16, 25, 43, 52, 61 och 70.
UPPGIFT 7 Mera Favorit 3A
I samband med uppgiften är det bra om du diskuterar med eleverna hur de ska sätta igång med att lösa den. Ofta är det bra att börja med att räkna antalet bokstäver i namnet. Efter detta kan eleverna hitta olika namn med hjälp av att namnet till exempel innehåller två likadana bokstäver.

6. Vid vilka tal finns djuren? Skriv.




















7. Visa hur du löser uppgiften. Skriv svar.
a. En klass har 32 elever. En dag är 8 elever hemma för att de är sjuka. Hur många elever är det i klassen den dagen?
32 – 8 = 24
Svar: 24 barn
b. I klass 3A är det 17 elever i klassen en dag. 8 elever är hemma för att de är sjuka. Hur många elever är det i klassen när alla är friska?
17 + 8 = 25
Svar: 25 barn
Film Träna Favorit Träna Mera Favorit
Favorit kopieringsunderlag
Kopieringsunderlag 2a: Addition och subtraktion på tallinjen
Kopieringsunderlag 2b: Samlad problemlösning 1
Kopieringsunderlag 2b: Samlad problemlösning 1 1. a. Grodan Sammy och gräshoppan Hoppy hoppar på stenar. Sammy hoppar framåt sju stenar i taget. Hoppy hoppar framåt tre stenar taget. Sammy startar på den första stenen och Hoppy startar på den andra. Vilken är den första sten som båda landar på?
b. Sammy hoppar framåt fyra stenar i taget. Hoppy hoppar framåt fem stenar taget. Sammy startar på den första stenen och Hoppy startar på den andra. Vilken är den första sten som båda landar på?
2. Gör en magisk kvadrat. Välj ett tal mellan 25 och 100. Skriv kvadraten med tal så att oberoende om du adderar talen vågrätt eller lodrätt är summan alltid den samma. På det här sättet kan du t.ex. göra ett födelsedagskort åt en vuxen vän, om du vet vad han eller hon fyller nästa gång.
4. Du hjälper till med olika saker och för det får du en lön. Du får en krona den första dagen, två kronor den andra dagen, 4 kronor den tredje dagen – det vill säga varje dag den dubbla lönen
Det romerska talsystemet användes av romarna från 300 f.Kr.
I det romerska talsystemet används I för talet 1, V för talet 5, X för 10, L för 50, C för 100, D för 500 och M för 1000. Romarnas talsystem är inte ett positionssystem utan kan liknas med det äldre egyptiska talsystemet. För att bilda tal adderas de romerska siffrorna. Talet 3 skrivs III, talet 7 VII, talet 27 XXVII osv. Siffrans position i talet saknar i princip betydelse. Det finns dock undantag. Om I skrivs före V innebär det en subtraktion av I. IV betyder 5 – 1 = 4. På motsvarande sätt innebär IX, 10 – 1 = 9, XC, 100 – 10 = 90 och CM, 1000 – 100 = 900.
Årtalet 2013 skrivs MMXIII och 2014, MMXIV. Det romerska talsystemet används sparsamt fortfarande, mest för numrering.
Forskning om Matematikdidaktik och missuppfattningar Progression och samband
3. Addition med hjälp av hundratavlan
Tillbehör: hundratavla
Kopieringsunderlag 2c: Tavelbilder för lektion 2, 6 och 12
Lektionens innehåll
• att använda hundratavlan som hjälpmedel vid addition med huvudräkning
• att räkna stegvis i additioner där den ena termen är tvåsiffrig
Lektionens mål
• att använda hundratavlan i beräkningar med addition
Läroplan
Frågor till samtalsbilden
1. Hur har hundratavlan fått sitt namn? (Den innehåller talen upp till hundra.)
2. Hur många tal finns det i en rad i hundratavlan? (10)
3. Säg de hela tiotalen från hundratavlan. (10, 20… 100)
4. Vi övar på addition med hjälp av hundratavlan.
a. Hitta talet 23 och lägg fingret på det. Addera tre tiotal. Vilket tal hamnar du på? (53) Addera fyra ental till talet 53. Vilket tal hamnar du nu på? (57)
b. Hitta talet 39 och lägg fingret på det. Addera två tiotal. Vilket tal hamnar du på? (59) Addera fyra ental till talet 59. Vilket tal hamnar du nu på? (63)
Huvudräkningsuppgifter
1. I Favoritskolan finns två tredjeklasser. I klass A går 19 elever och i klass B 20 elever. Hur många tredjeklassare går det på skolan? (39)
2. I matsalen finns 27 elever. 9 elever till kommer in i matsalen. Hur många elever är det där då? (36)
Vid addition använder du hundratavlan så här:
tiotalen entalen

41 + 4 = 45 62 + 3 = 65 34 + 6 = 40 24 + 2 = 26 83 + 5 = 88 71 + 2 = 73 72 + 7 = 79 19 + 3 = 22 89 + 6 = 95 28 + 3 = 31 87 + 5 = 92
Taluppfattning och tals användning – metoder för beräkningar med naturliga tal, metodernas användning i olika situationer

Mera Favorit facit
Förslag på arbetsgång
1. Huvudräkningsuppgifter
2. Ramberättelse
3. Lär känna hundratavlan
Repetera talen 1 till 100 genom att visa hundratavlan (kopieringsunderlag 3a) digitalt med projektorn och gömma tal från tavlan eller använd den digitala elevboken och projektor. Eleverna berättar vilket tal du gömt. Repetera hur hundratavlan är uppbyggd, alltså att entalen ökar mot höger och att tiotalen ökar neråt. På en rad går det tio ental och hela tavlan består av tio tiotal.
4. Frågor till samtalsbilden
I räknebanken finns det fler förslag på hur du kan använda hundratavlan tillsammans med eleverna.
5. Elevbokens uppgifter
Huvudräkningsuppgifter, forts. 3. 39 sjätteklassare är faddrar åt 39 förstaklassare och tar med dem till gymnastiksalen. Hur många elever är det då sammanlagt i gymnastiksalen? (78)
2. Addera. Måla summan i hundratavlan.

3. Addera. Ringa in summan i rutan.
4. Visa hur du löser uppgiften. Skriv svar. På en skola är det 27 pojkar och 31 flickor i årskurs 3. Hur många tredjeklassare är det sammanlagt på skolan?
Ramberättelse Bild
Räknemaskinen hundratavlan
Sally och Kurre hade redan hört många historier om Charlies och Isas nya lärare. Den nya läraren var speciellt intresserad av matematik. Idag hade Charlie kommit i god tid till skolan. Han kikade in genom klassrummets fönster med Kurre på axeln. Läraren höll som bäst på att fästa en affisch på väggen. Affischen visade talen från ett till hundra.
– Den där hundratavlan har jag sett förut! Man kan använda den som en miljövänlig räknemaskin, för den använder varken batterier eller el, konstaterade Kurre ivrigt.
– Ja, men hjärnenergi kräver den, viskade Charlie.
– Varför viskar du? undrade Kurre.
– Jag vill inte att läraren hör mig prata med en ekorre.
– Jag kan prata med dig istället, läraren tycker kanske att det är mindre konstigt, sa Kurre och fortsatte:
Kommunikation – använder hundratavlan i beräkningar med addition
TAVLAN
Kopieringsunderlag 3a Hundratavla och hundrarutsystem
– Det där med hundratavlan: När jag räknar additionen 23 + 34 så placerar jag fingret på talet 23. Först adderar jag tiotalen, då flyttar jag tre rutor neråt, alltså till ruta 53. Sedan adderar jag entalen, då flyttar jag fyra steg till höger och då hamnar jag på ruta 57, som är summan.
Liite3a:Satataulujasataruudukko
– Ja, så går det till, sa Charlie tyst.
– Så småningom kan du göra samma sak i huvudet utan hundratavla.
Presentation
Genomgång steg för steg
Elevböcker
Favorit
Mera Favorit
Problemlösningsuppgifter
1. a. Hur kan du på ett enkelt sätt addera talen 1 till 10, alltså 1 + 2 + 3… 10? (55)
b. Använd regeln du kom på och addera talen 1 till 20. (210)
I problem 1.a. är det bra att addera det första och sista talet (11), det andra och näst sista talet (11) och så vidare. Det blir fem par, 5 • 11 = 55.
I problem 1.b. finns det tio par och ett pars summa är 20 + 1 = 21. Då är summan av talen 1 till 20, 10 • 21.
Det var den tyska matematikern Gauss som upptäckte formeln för den aritmetiska talföljdens summa (t.ex. 1 + 2 + 3 + 4 +… + n)/ S = (1 + n) • n/2. Läraren gav den nioårige Gauss och hans klasskompisar i uppgift att addera talen 0 till 100 och tänkte att han kunde koncentrera sig på sitt eget arbete medan eleverna räknade och funderade på det. Gauss formulerade en formel för uppgiften redan då och löste uppgiften på nolltid.
Räknebank
1. 20 + 31 (51)
2. 31 + 31 (62)
3. 62 + 31 (93)
4. 44 + 54 (98)
5. 55 + 23 (78)
6. 35 + 36 (71)
7. 26 + 36 (62)
8. 57 + 34 (91)
9. 39 + 24 (63)
10. 47 + 27 (74)
UPPGIFT 4 Mera Favorit 3A
Uppmärksamma eleverna på att de kan försäkra sig om att de räknat rätt vid talen i mitten och vid slutet.

TRÄNA
1. Addera.
32 + 30 =
52 + 30 =
40 + 28 =
20 + 48 =
2. Skriv uppgiften och räkna.
21 + 48
Charlie gillar att spela fotboll. Han gör 36 mål på hösten och 12 mål på våren. Hur många mål gör han totalt den säsongen?
Svar:
36 + 12 = 48 48 mål 48 + 8 = 56 56 gånger
Isa gillar att simma. Hon simmar i sjön 48 gånger och i havet 8 gånger. Hur många gånger simmar hon i sjön och havet sammanlagt?
Svar:
5. Dra streck mellan uttrycket och summan på tallinjen.
2024-02-22 12:22
978-91-44-16686-5_10_book.indb 16
1. Rävens ”hänga gubbe”
Du tänker på ett uttryck, t.ex. 26 + 15 = 41, och skriver ett streck istället för varje siffra och tecken på tavlan. I stil med att hänga gubbe så gissar eleverna på vilka siffror och tecken som ska stå på strecken. Om eleven gissar rätt skrivs det på strecket, men om eleven gissar fel så ritas det ett streck till på räven. Om räven blir klar innan uttrycket så vinner läraren.
2. Hundratavla och talkort
a. Täck över ett tal på hundratavlan. Eleverna använder sina talkort och lägger det övertäckta talet på sin bänk.
b. Täck över två tal på hundratavlan. Eleverna skriver de övertäckta talen och en storleksjämförelse i sina häften eller på lösblad, t.ex. 34 < 68 eller 68 > 34.
3. Hundratavlan och klossar
Eleverna delas in i tre lag. Ett par från varje lag ställer sig framför klassen. Visa eller täck över ett tal på hundratavlan. Paret ska så snabbt som möjligt lägga talet med hjälp av tiobasmaterial; tiotal och ental. Det par som först lagt rätt tal vinner en poäng till sitt lag. Byt par och visa/täck över ett nytt tal.

Tiosystemet
6. Vilket tal?
I mitt tal är entalen och tiotalen lika många. Mitt tal är 8 mindre än Olles tal.

Annas tal är

Mitt tal är hälften så stort som det största talet i hundratavlan.
Alex tal är

Mitt tal har lika många tiotal som Alex och Olles tiotal sammanlagt. Entalen är 5 fler än i Annas tal.

Yasins tal är
7. Varje bild motsvarar ett tal. Skriv talet.






Mitt tal är tre hela tiotal.
Olles tal är






978-91-44-16686-5_10_book.indb 17












Människan har sedan länge använt fingrarna som hjälp när hon räknar. Tack vare det blev tio ett centralt tal när man räknar. Man räknade i serier om tio. Dessa tio tal fick speciella namn och senare kom man på att skriva dem med siffrorna 0 till 9. Talet tio började man skriva med två siffror: 1 och 0.
Hundratavlan
Eftersom tiotalssystemet bygger på att nästa större enhet alltid består av tio stycken av den mindre enheten, består hundratavlan av tio tiotal. Det är bra att illustrera tiotalsövergång med hjälp av hundratavlan. När ett tiotal överskrids flyttar man på ett konkret sätt till nästa tiotal, alltså till en ny rad. Hundratavlan är bekant för eleverna från elevböckerna Favorit Matematik 1 och 2.
Forskning om
Matematikdidaktik och missuppfattningar
Begrepp och fakta
Favorit kopieringsunderlag
Kopieringsunderlag 3a: Hundratavla och hundrarutsystem
Kopieringsunderlag 3b: Mirakelmaskiner
2024-02-22 12:22 Träna digitalt
Träna Favorit
Träna Mera Favorit
NÄSTA LEKTION
4. Subtraktion med hjälp av hundratavlan
Tillbehör: hundratavla
Kopieringsunderlag 3a
Lektionens innehåll
• att öva på subtraktion med huvudräkning stegvis, tvåsiffriga termer
Lektionens mål
• att använda hundratavlan i beräkningar med subtraktion
Läroplan
Frågor till samtalsbilden
1. Åt vilket håll pekar du på hundratavlan när
a. tiotalen minskar? (uppåt)
b. entalen minskar? (åt vänster)
2. Vi övar på subtraktion med hjälp av hundratavlan.
a. Hitta talet 56 och lägg fingret på det. Subtrahera två tiotal. Vilket tal hamnar du på? (36) Subtrahera 3 ental från talet 36. Vilket tal hamnar du på? (33)
b. Hitta talet 41 och lägg fingret på det. Subtrahera två tiotal. Vilket tal hamnar du på? (21) Subtrahera 4 ental från talet 21. Vilket tal hamnar du på? (17)
Huvudräkningsuppgifter
1. I matsalen sitter 53 elever. 7 går ut på rast. Hur många elever är kvar i matsalen? (46)
2. På gården är det 99 elever. 33 av dem går in. Hur många elever är kvar på gården? (66)
3. På gården är det 66 elever. Läraren ropar in 27 elever till klassrummet. Hur många elever är det kvar på gården? (39)
Vid subtraktion använder du hundratavlan så här:

– 20 = 36 41 –

1. Subtrahera. Hitta bokstaven i hundratavlan.
– 30 – 7 =
– 20 – 1 =
– 20 – 2 =
– 10 – 5 =
– 10 – 4 =
– 30 – 6 =
– 50 – 1 =
– 30 – 2 =
– 10 – 3 =
– 20 – 3 =
– 10 – 3 =
– 10 – 5 =
– 30 – 6 =
– 50 – 2 =
– 7 = 1
– 1 = 43
– 2 = 18
– 5 = 55 27 – 4 = 23 69 – 6 = 63 6 – 1 = 5 69 – 2 = 67 73 – 3 = 70 12 – 3 = 9 82 – 3 = 79 41 – 5 = 36 29 – 6 = 23 11 – 2 = 9 978-91-44-16686-5_10_book.indb 18

Taluppfattning och tals användning – metoder för beräkningar med naturliga tal, metodernas användning i olika situationer
Förslag på arbetsgång
1. Ramberättelse
2. Frågor till samtalsbilden och övning i att använda hundratavlan Öva på att använda hundratavlan med hjälp av projektor och kopierings underlag 3a eller med hjälp av den digitala elevboken. Fler gemen samma exempel där eleverna kan använda hundratavlan som räknemaskin finns i räknebanken.
3. Huvudräkningsuppgifter
4. Elevbokens uppgifter 18
2. Subtrahera. Måla differensen i hundratavlan.

3. Subtrahera. Ringa in differensen i rutan.
4. Visa hur du löser uppgiften. Skriv svar. Viktoria och Rebecka samlar på stenar.Viktoria har 51 stenar. Rebecka har 15 färre. Hur många stenar har Rebecka?
Kommunikation – använder hundratavlan i beräkningar med subtraktion
Ramberättelse Bild
Räknemaskinen hundratavla
Charlie och Kurre tittade in genom klassrumsfönstret och såg vad den nya läraren höll på med. På tavlan fanns en energisnål räknemaskin, hundratavlan. Sally kom flygande och var lika förtjust över att se hundratavlan som Kurre:
– Hör här, jag kan berätta för er hur man räknar subtraktion med den där. Jag tar till exempel uppgiften 56 – 23. Jag placerar min vingfjäder vid talet 56. Först subtraherar jag två tiotal, alltså flyttar jag två rutor uppåt. Jag hamnar då på ruta 36. Sedan subtraherar jag också de tre entalen, alltså flyttar jag tre rutor till vänster. Jag hamnar på talet 33, som är differensen. Lätt! utropade Sally.
– Ja, det är det! sa Kurre och delade Sallys glädje.
Samtidigt öppnade läraren klassrumsfönstret.
– God morgon, Charlie. Jag tyckte att jag hörde någonting. Vem pratade du med? Jag ser inga andra än en ekorre och en skata som rusar över skolgården.
– Eh… muttrade Charlie förvirrat. Sedan såg han läraren i ögonen och sa:
– Jag pratade med skatan Sally och ekorren Kurre.
– Jaså, svarade läraren och fortsatte glatt: – Jag pratar också goja ibland, släpper grodor ur munnen och ritar kråksparkar på tavlan. Dessutom har jag en stor grand danois hemma, jag berättar det mesta för den. Så jag förstår dig. Skolgården börjar fyllas av dina klasskompisar. Snart får vi börja jobba igen. Du skulle kunna förbereda dig på att i början av lektionen berätta för de andra hur du räknar med en hundratavla.
– Det ska nog gå bra! sa Charlie nöjt.
Presentation
Genomgång steg för steg
Problemlösningsuppgifter
1. Du hjälper till med olika saker och för det får du en lön. Du får en krona den första dagen, två kronor den andra dagen, 4 kronor den tredje dagen – det vill säga varje dag den dubbla lönen från föregående dag. Hur mycket tjänar du på den tionde dagen? (512 kronor)
1 krona 2 kronor 4 kronor
dag 1 dag 2 dag 3
2. Räkna med hjälp av räknare ut hur mycket du tjänar den 20:e dagen efter att du börjat jobba. (524 288 kronor)
Räknebank
1. 33 – 3 (30)
2. 33 – 4 (29)
3. 33 – 13 (20)
4. 33 – 14 (19)
5. 33 – 24 (9)
6. 33 – 29 (4)
7. 52 – 2 – 3 (47)
8. 52 – 5 (47)
9. 52 – 15 (37)
10. 52 – 25 (27)
UPPGIFT 4 Mera Favorit 3A
Uppmärksamma eleverna på att de kan försäkra sig om att de räknat rätt vid talen i mitten och vid slutet.

TRÄNA
1. Subtrahera. 23 – 10 =
2. Skriv uppgiften och räkna.
Det finns 32 hopprep i utelådan. 13 elever hoppar hopprep på rasten. Hur många hopprep ligger det då kvar i lådan?
=
Svar:
5. Räkna. Hitta bokstaven i hundrarutan.
Det finns 62 vindruvor i skålen. Isa äter 23 stycken. Hur många vindruvor till kan hon äta innan de är slut?
Svar:

978-91-44-16686-5_10_book.indb 20
Tips
1. Varje bild motsvarar ett tal Eleverna hittar på likadana uppgifter som uppgift 6 i Mera Favorit 3A och gör egna uppgifter i sina häften eller på lösblad. Låt eleverna byta uppgifter med varandra och försök lösa vilket tal som bilden motsvarar.
2. Tallek två och två
Den ena eleven börjar genom att säga 100. Den andra subtraherar ett tal mellan 1 och 10 från hundra och säger subtraktionens differens, ett tal mellan 99 och 90. Så här subtraherar man en åt gången tills någon av eleverna säger 0 och därmed vinner. Efter leken funderar eleverna på vilket tal det är bäst att säga näst sist (11) för att de ska vinna.
3. Romerska siffror, ental och tiotal
Sex elever ställer sig på rad framför klassen. Eleverna bildar tal genom att de som föreställer tiotal står i ett X och de som är ental står som ”streck”. I talet 42, till exempel, står de fyra eleverna längst till vänster som X och två elever står som ett streck. De andra eleverna säger tal som sex elever kan bilda. Fundera på vilka tal som är möjliga (15, 24, 33, 51 och 60) och leta fram dem på hundratavlan.
6. Dra streck mellan uttrycket och differensen på tallinjen.



7. Varje bild motsvarar ett tal. Skriv talet. 20 33 66 58 0














978-91-44-16686-5_10_book.indb 21
Favorit kopieringsunderlag
Kopieringsunderlag 4: Problemlösning
Kopieringsunderlag 4: Problemlösning 1. Dra streck mellan text, bild och uttryck. Räkna de uttryck som passar ihop med bilderna. Kurre har 26 kusiner. Sally har 13 kusiner. Hur många kusiner har de sammanlagt?
Charlie har 16 kusiner. Isa har 15 kusiner. Hur många kusiner har de sammanlagt?
I ingång A bor det 43 personer. I ingång B bor det 38 personer. Hur många personer bor det sammanlagt huset?
I ingångarna A och B bor det sammanlagt 82 personer. I A-ingången bor det 40 personer. Hur många personer bor det i B-ingången?
I A- och B-ingången bor det sammanlagt 79 personer. I A-ingången bor det 35 personer. Hur många personer bor det i B-ingången?
På parkeringsplatsen finns det 38 bilar. Ytterligare 35 bilar kommer dit. Hur många bilar finns det då där?
2024-02-22 12:22
I Favorit Matematik används hundratavlan som stöd vid huvudräkning, inte vid uppställning. Därför adderar eller subtraherar eleverna först tiotalen och därefter entalen, inte tvärtom som vid uppställning. Att komma fram till ett mellanled (t.ex. 25 + 36 = 25 + 30 + 6 = 55 + 6 = 61) är en viktig del i processen för att så småningom komma från den konkreta hundratavlan till en automatiserad huvudräkning. Det finns såklart även andra huvudräkningsstrategier (t.ex. 25 + 36 = 20 + 30 + 11) och dessa kan du gå igenom med eleverna utan hundratavla. Fråga också om det finns elever som har ytterligare andra sätt att lösa denna typ av uppgifter.
Forskning om Matematikdidaktik och missuppfattningar
Begrepp och fakta
Träna digitalt
Träna Favorit
Träna Mera Favorit
Film
NÄSTA LEKTION
5. Talen 0 till 1000 Tillbehör: talkort
Lektionens innehåll
• repetition av addition med uppställning och minnessiffra
• att addera ihop många termer på samma gång
• att räkna problemuppgifter med uppställning
Lektionens mål
• att använda skriftliga och fungerande metoder för att utföra beräkningar i addition med uppställning och växling
Läroplan
Frågor till samtalsbilden
Läs uppgiften högt för eleverna: Det finns 263 grå stenar, 38 vita stenar och 101 svarta stenar. Hur många stenar finns det i stensamlingen?
1. Vad är det vi ska räkna? (263 + 38 + 101)
2. Varför är det bra att räkna ut det med uppställning istället för i huvudet? (Det är lättare att räkna med uppställning.)
3. Hur skriver du talen under varandra? (Talenheterna hundratal, tiotal och ental under varandra så att uträkningens högra kant är jämn.)
4. Var börjar du räkna? (från entalen)
5. Berätta hur du tänker och räknar.
6. Varför ska du skriva svar? (I problemuppgifter ska du alltid skriva ut svaret.)
Huvudräkningsuppgifter
1. Isa uppskattar att summan i en addition är 220. Det exakta svaret var 202. Hur mycket skilde det mellan Isas uppskattning och det riktiga svaret? (18)
8. Addition med uppställning och växling

Additionsalgoritm:
• Skriv talen under varandra enligt positionssystemet.
• Addera entalen.
• Placera minnessiffran ovanför tiotalen.
• Addera tiotalen.
• Placera minnessiffran ovanför hundratalen.
• Addera hundratalen.

1. Addera. Ringa in summan i rutan längst ner.

Taluppfattning och tals användning – centrala metoder för beräkningar med skriftliga räknemetoder
Förslag på arbetsgång
1. Huvudräkningsuppgifter
2. Ramberättelse
3. Frågor till samtalsbilden
4. Arbete på tavlan
Observera speciellt exempel b. Minnessiffran behöver inte skrivas utan man skriver direkt in 18 i svaret.
5. Elevbokens uppgifter
6. Tips: 3. Makaronburkar
Huvudräkningsuppgifter, forts.
2. Charlie uppskattar att summan i en addition är 500. Det exakta svaret var 486. Hur mycket skilde det mellan Charlies uppskattning och det riktiga svaret? (14)
3. Isa har två hundrakronorssedlar, två femtiokronorssedlar och tre tiokronor. Hur mycket pengar är det sammanlagt? (330 kr) Mera Favorit facit
2. Addera. Ringa in summan i rutan längst ner.
3. Skriv uttrycket och räkna. Ringa in svaret i rutan.
a. På skolans vind finns 116 trästolar och 246 plaststolar. Hur många stolar finns det sammanlagt?
Svar:
c. I förrådet finns 99 röda linjaler, 153 gula linjaler och 87 gröna linjaler. Hur många linjaler finns det sammanlagt?
b. I skolans förråd finns det 267 blå häften och 375 gröna häften. Hur många häften finns det sammanlagt?
Svar:
d. I skåpet finns 159 gula pennor, 189 gröna pennor och 19 röda pennor. Hur många pennor finns det sammanlagt?
Ramberättelse Bild
Den glömska läraren
Läraren steg in i klassrummet och såg orolig ut.
– Jag skulle lära er någonting viktigt, men jag kan verkligen inte komma ihåg vad det var. Men låt oss börja lektionen i alla fall. Vi ska jobba med addition med uppställning ifall jag kommer ihåg rätt. Först får ni räkna ut hur många stenar jag har i min stensamling, för jag kommer inte ihåg det heller. Vad jag däremot kommer ihåg är att i addition kan jag skriva flera tal under varandra. Jag börjar räkna från entalen. Om summan av entalen är tvåsiffrig, skriver jag tiotalet som minnessiffra ovanför de andra tiotalen, sa läraren och blev tyst för en stund.
– Och nu minns jag ju vad det viktiga jag skulle berätta för er var: – Det var ju såklart att ni måste komma ihåg minnessiffran!
Svar:
Svar:
– använder skriftliga och fungerande metoder för att utföra beräkningar i addition
Presentation
Genomgång steg för steg
Elevböcker
Favorit
Mera Favorit
Problemlösningsuppgifter
1. Vilket tal tänker jag på?
a. Talet har 30 tiotal och inga ental. (300)
b. Talet har 45 tiotal och 2 ental. (452)
Räknebank
Räknebanken kan kopieras från kopieringsunderlag 12a, del A.
1. 500 + 34 (534)
2. 80 + 400 + 2 (482)
3. 6 + 700 + 40 (746)
4. 430 + 52 (482)
5. 520 + 35 (555)
6. 45 + 245 (290)
7. 210 + 67 (277)
8. 333 + 565 (898)
9. 191 + 202 (393)
10. 899 + 5 (904)

TRÄNA
1. Addera.
Tips
1. Problemuppgifter med uppställning
Eleverna skriver problemlösningsuppgifter till varandra. Lös uppgifterna med uppställning. Gör bara additioner. Talområdet är 0 till 1000.
2. Varje bild motsvarar ett tal Eleverna hittar på egna uppgifter i stil med uppgift 6. Låt eleverna först göra uppgifter utan minnessiffra. Eleverna byter uppgifter med varandra.
2. Visa hur du löser uppgiften. Skriv svar. 134 + 25
I idrottsförrådet finns 78 röda band, 143 gula band och 87 gröna band. Hur många band finns det sammanlagt?
64
I biblioteket finns 235 serietidningar, 112 Kamratposten och 19 dagstidningar. Hur många tidningar finns det sammanlagt?
Svar:
4. Addera. Ringa in summan i Kurres påse.
Svar:

978-91-44-16686-5_10_book.indb
3. Makaroner i burkar
Lägg makaroner i två genomskinliga burkar med lock. Den ena burken märks med ett A och den andra med ett B. Låt eleverna uppskatta antalet sammanlagda makaroner i bägge burkarna och skriva ner sin uppskattning på ett papper. Några elever får i uppgift att räkna antalet makaroner i burkarna. Fundera på hur det är bäst att räkna makaronerna (att dela in dem i grupper om tio makaroner). A+B adderas med hjälp av uppställning. Vem av eleverna hade den uppskattning som var närmast den riktiga summan?
T.ex. Burk A Burk B Summa
5. Varje bild motsvarar ett tal. Skriv talet.







6. Addera. Använd räknaren om du behöver. a. 145 + 55 = 321 + 43 = 667 + 11 = 882 + 91 = 284 + 32 =








Algoritm
De uppställningar för addition, subtraktion och multiplikation som har lärts ut är exempel på matematiska algoritmer. En algoritm består av en begränsad mängd instruktioner som inom ett ändligt antal steg löser en viss klass av uppgifter.
7. Måla så att ödlan är symmetrisk.

978-91-44-16686-5_10_book.indb 37 2024-02-22 12:22
Favorit kopieringsunderlag
Kopieringsunderlag 8:
Träna digitalt
Träna Favorit
Addition med uppställning och växling NÄSTA LEKTION
Film Film för kompetensutveckling
Algoritmer steg för steg
Träna Mera Favorit
9. Subtraktion med uppställning och växling
Lektionens innehåll
• öva analog programmering med kod
• beskriver och förstår begreppen kod och bugg
Lektionens mål
• att tolka skriftlig information med matematiskt innehåll

• att använda olika uttrycksformer t.ex. symboler
Läroplan
Huvudräkningsuppgifter
1. Sally har 3 mynthögar, varje hög består av 9 mynt. Hur många mynt har hon sammanlagt? (27)
2. Kurre har 5 mynthögar, varje hög består av 6 mynt. Dessutom har han ytterligare 3 mynt. Hur många mynt har han sammanlagt? (33)
3. Isa har 3 mynthögar som alla består av 8 mynt. Hon ger 5 mynt till Charlie. Hur många mynt har hon kvar? (19)
Instruktioner kan uttryckas som kod.
Förklaringar till kartans symboler genomfart förbjuden enkelriktad väg Idéhuset
Instruktioner:
1 = Gå en ruta framåt.
2 = Sväng höger.
3 = Sväng vänster.
a. Den gula roboten startar utanför Fabriken på Muttergatan. Vart går roboten med koden 1 1 1 2 1 1 2 1?
Roboten går till verkstaden.
b. Den gula roboten startar utanför Fabriken på Muttergatan. Vart går roboten med koden 1 1 1 2 1 1 1 1 3 1?
Roboten går till laddningscentralen.
Taluppfattning och tals användning – hur entydiga stegvisa instruktioner kan konstrueras, beskrivas och följas som grund för programmering. Symbolers användning vid stegvisa instruktioner
978-91-44-16686-5_10_book.indb 146 2024-02-22 12:24
Förslag på arbetsgång
1. Huvudräkningsuppgifter
2. Arbete på tavlan
3. Kör försiktigt (Se Tips)
4. Elevbokens uppgifter
Mera Favorit facit
2.
Olika lösningar.
a. Den blå roboten går från Minneshuset till Fabriken. Vilken väg tycker du den ska gå? Rita vägen. Roboten är framme när den står vid ingången till målet.
Idéhuset
Muttergatan
Maskinrummet
Robotverkstaden
Fabriken
Laddnings-centralen
Minneshuset
Fjädervägen
Förklaringar till kartans symboler genomfart förbjuden enkelriktad väg
Instruktioner:
1 = Gå en ruta framåt.
2 = Sväng höger.
3 = Sväng vänster.
Lektionen kan upplevas som svår, och kan därför kräva extra instruktioner. Uppgiften kräver att eleverna kan tänka sig in i hur roboten står när den ska svänga höger eller vänster. Det är viktigt att påpeka att roboten står stilla när den svänger. Gå igenom vilken kod som motsvarar varje instruktion. Gå med hjälp av tavelbilden igenom vad som menas med ”genomfart förbjuden” (här får du inte köra) och ”enkelriktad väg” (du får bara köra åt det håll som pilen visar).
b. Skriv koden som den blå roboten är progammerad med för att gå vägen som du har ritat.
Ex. 12112113113111121121 11121111211211311111
c. Den röda roboten går från Maskinrummet till Idéhuset med programkoden 1 1 1 2 1 1 1 1 2 1 1 2 1 1 2 1 1 1 1 1. Koden innehåller ett fel. Ringa in felet. Skriv den rätta koden.
En bugg betyder att något är fel i koden. För att hitta felet felsöker du programmet. När koden är rättad är buggen fixad.


Elevböcker
Favorit
Mera Favorit
Problemlösningsuppgifter
1. Fyra basketlag (a, b, c och d) spelar en turnering. Varje lag möter alla andra lag en gång. Hur många matcher spelar man i turneringen?
(6; ab, ac, ad, bc, bd och cd)
2. Hur många tresiffriga tal kan du bilda med siffrorna 2, 5 och 8?
(6; talen 258, 285, 528, 582, 825 och 852.)
Räknebank
Uppgifterna räknas med uppställning i mattehäfte.
1. 3 • 10 + 9 (39)
2. 8 • 9 – 8 (64)
3. 11 + 7 • 7 (60)
4. 6 + 10 • 6 (66)
5. 7 • 9 + 21 (84)
6. 18 – 3 • 2 (12)
7. 9 • 5 – 2 • 5 (35)
8. 4 • 10 + 3 • 4 (52)
9. 3 • 9 + 5 • 6 (57)
10. 6 • 1 + 6 • 4 (84)

1. Vilken kod följer roboten för att gå till kaninerna? Dra streck.
Instruktioner: 1 = Gå en ruta framåt 2 = Sväng höger 3 = Sväng vänster
2024-02-22 12:24
Tips
1. Kör försiktigt!
Dela in eleverna i par. Genomför aktiviteten på ett ställe med extra stor plats exempelvis skolgården eller idrottshallen. Den ena eleven är instruktör och den andra är chaufför. Chauffören ska blunda eller ha förbundna ögon. Instruktören ger instruktioner till chauffören: till höger, till vänster, framåt, bakåt. Till exempel: Gå 5 steg framåt. Sväng till höger och gå 8 steg framåt. Gå två steg bakåt. Sväng till vänster och gå 6 steg framåt. Bestäm hur lång tid leken ska pågå, till exempel 5 minuter. Till sist frågar instruktören chauffören var hen tror att de är. Chauffören svarar och öppnar sedan ögonen eller tar bort ögonbindeln. Låt därefter eleverna byta roller och börja om från början.
978-91-44-16686-5_10_book.indb 148
2. Symbolspråk
Vi kan beskriva vanliga händelser med naturligt språk steg för steg. Vi kan också använda oss av symboler. Bestäm gemensamt eller i mindre grupper någonting som eleverna ska beskriva. Det kan till exempel vara i vilken ordning man tar på sig kläderna, vad som händer under en skoldag eller hur det går till i matsalen. Vilka symboler behövs för att beskriva händelsen?
3. Bugg
Låt eleverna arbeta i par eller mindre grupper. Fundera på vad som händer om det blir en bugg i ett program? Finns det olika allvarliga buggar? Vilka? Varför?
4. Program
Låt eleverna arbeta i par eller mindre grupper. Fundera på vilka program som ännu inte finns och som du skulle vilja använda.

4. Lista ut.
a. Roboten får bara gå på de vita rutorna. Rita vägen.
b. Programmera roboten så att den går vägen som du har ritat. Skriv koden.
2132231423142
423142413141 3142323142
Varje 2:a kan bytas ut mot två stycken 1:or. Ex.
På slutet kan man skriva:
1 = stannar inom rutsystemet
2 = går utanför rutsystemet
Favorit kopieringsunderlag
Kopieringsunderlag 36:
Fixa buggen
Instruktioner:
1 = Gå en ruta framåt.
2 = Gå två rutor framåt.
3 = Sväng höger.
4 = Sväng vänster.
Ett program byggs upp av instruktioner. Även om det känns mest naturligt att ge instruktioner med naturligt språk så kan vi lika väl använda oss av olika typer av symboler. Det är viktigt att visa att ordningen spelar roll och vad som händer om vi inte gör instruktionerna i rätt följd. Den största nackdelen med naturligt språk är att det är svårt att vara tillräckligt exakt. Genom att använda symbolspråk kan vi undvika en del problem. Men då är det viktigt att ge varje symbol en exakt betydelse.
Fel i program kallas ofta buggar När du letar efter dessa fel kallas det att buggfixa, felsöka eller avlusa programmet. Felsökning är en viktig del av programmeringsprocessen och det är viktigt att lära eleverna att upptäcka, förändra och förbättra olika typer av fel – det är en del av att programmera. Prata också med eleverna om att varje fel (bugg) är en möjlighet och ett viktigt lärtillfälle som hjälper oss att bli bättre.
Filmer för kompetensutveckling
Stegvisa instruktioner – programmering
Algoritmer steg för steg
Visuella programmeringsmiljöer
Träna digitalt
Träna Favorit
Träna Mera Favorit
NÄSTA LEKTION
37. Vad har jag lärt mig?
Planera ...............................................................................


Lektionsplanering – varje lektion är viktig
Favorit matematik har en elevbok per termin. Dessutom finns samma lektionsinnehåll i två versioner, Favorit matematik och Mera Favorit matematik. En tydlig struktur med fyra sidor till varje lektion underlättar både för dig och för dina elever när de arbetar i boken. Uppgiftstyperna återkommer vilket gör det lätt för eleven att fokusera på den nya matematiken i uppgiften. Fördela bokens lektioner över terminen. Varje vecka är det lämpligt att ha fyra matematiklektioner, tre genomgångslektioner då ni arbetar med bokens lektioner och en problemlösningslektion. Läs mer på sida 5.
Terminsplanering
AUGUSTI
SEPTEMBER
OKTOBER
NOVEMBER
DECEMBER
KAPITEL 1 TALUPPFATTNING, ADDITION OCH SUBTRAKTION
13 lektioner. Prov 1 finns i lärarhandledningen på s. 216
KAPITEL 2 MULTIPLIKATION
14 lektioner. Prov 2 finns i lärarhandledningen på s. 220
KAPITEL 3 MULTIPLIKATION, PROBLEMLÖSNING OCH DATALOGISKT TÄNKANDE
10 lektioner. Prov 3 finns i lärarhandledningen på s. 224
KAPITEL 4 DIVISION OCH PROPORTIONALITET
13 lektioner och 2 Vi repeterarlektioner. Prov 4 finns i lärarhandledningen på s. 228
Elevboken – tillsammans men ändå individualiserat
Elevboken är en del av elevpaketet. Ett elevpaket innehåller elevbok, digitalt läromedel, laborativt material och häftet Mitt lärande.
Det är samma lektionsinnehåll i Favorit matematik och Mera Favorit matematik men utmaningarna ökar i svårighet i Mera Favorit matematik. Det är flera grundläggande uppgifter i Favorit matematik. Du som lärare har samma lärarpaket, kan gå igenom lektionens innehåll gemensamt med hela klassen och eleverna arbetar sedan med ett individualiserat innehåll.
Förmågor och färdigheter tränas regelbundet
En samtalsbild och ramberättelse ger möjlighet att kommunicera och resonera kring lektionens matematiska innehåll. Stöd finns i lärarpaketet. Elevernas förmågor utvecklas och du kan göra en formativ bedömning inför det fortsatta arbetet. Det första uppslaget i elevboken är en genomgång av det nya innehållet. Det andra uppslaget innehåller extrauppgifterna ÖVA med repetition och PRÖVA med utmaning.
På Favoritsidorna lär sig eleverna matematik med hjälp av spel, lekar och laborativt material. Alla kapitel i elevboken avslutas med ”Vad har jag lärt mig?”.



















































1. Det första uppslaget är genomgång av nytt innehåll.

2. På det andra uppslaget finns extra-uppgifter. ÖVA-sidan innehåller repetition och PRÖVA-sidan innehåller ny tillämpning och mera utmanande uppgifter.

Elevens digitala läromedel
3. Genomgångsfilmer – direkt i det digitala läromedlet.
4. TRÄNA-rutor som självrättande övningar.
Elevens digitala läromedel är en del av elevpaketet. Elevpaket innehåller elevbok, digitalt läromedel, laborativt material och häftet Mitt lärande
I elevens digitala läromedel finns hela boken inläst med textföljning. Eleven har också tillgång till ramberättelser och genomgångsfilmer till de flesta lektionerna. Genomgångsfilmerna kan användas inför lektionen eller som repetition och träning.
Elevbokens TRÄNA rutor finns som interaktiva, självrättande övningar i det digitala läromedlet. TRÄNA rutan kan användas som läxa och kan med andra ord göras antingen i boken eller digitalt.
Till övningar i statistik finns ett digitalt verktyg för stapel, cirkel och linjediagram. Med hjälp av verktyget kan eleverna upptäcka sambandet mellan talen i tabellen och förhållandet mellan staplar och cirkelsektorer i diagrammen.
I det digitala läromedlet finns också illustrerade matteordlistor som låter eleven läsa, lyssna och träna viktiga matematiska begrepp från varje kapitel. Till matteordlistorna finns interaktiva övningar som låter eleven öva och repetera i egen takt.
Laborativt material
Det laborativa materialet finns i ett kuvert som medföljer elevpaketet. Aktiviteter där det laborativa materialet används hittar du både i lärarhandledningen och i elevboken.

Häftet Mitt lärande
Häftet Mitt lärande är ett stöd för dig som vill ge återkoppling och göra eleverna medvetna om sitt eget lärande. I Mitt lärande finns proven med koppling till kunskapsmål, matriser och lärardokumentation.

Lärarhandledningen – rikligt lärarstöd ger de bästa förutsättningarna I lärarpaketet ingår lärarhandledning, digitala resurser, elevens digitala läromedel och tryckta facit. I lärarhandledningen ingår tre koder. Genom att aktivera en kod har du tillgång till de digitala resurserna.
Du väljer vad som passar dig och din klass bäst. Genom att reflektera över det matematiska innehållet i relation till den information du har om dina elevers kunskaper kan du planera en varierad matematikundervisning.
TRÄNA LEKTIONENS INNEHÅLL – FÖRSTA UPPSLAGET
Lektionens innehåll räkneordningen för multiplikationer, additioner och subtraktioner inom samma uttryck
Lektionens mål att beskriva och förstå begreppet prioriteringsregel att använda enkla prioriteringsregler
Läroplan
Frågor till samtalsbilden
1. Hur många rör med tennisbollar finns det på bilden? (3)
2. Hur många tennisbollar finns det sammanlagt rören? (9) Hur räknar du för att få reda på antalet bollar? (med multiplikationen 3 3)
3. Hur många bollar leker Sally med? (4)
4. Hur räknar du för att få reda på det sammanlagda antalet bollar på bilden? (3 • 3 + 4 eller 3 + 3 + 3 + 4)
5. Vilka räknesätt ingår i uttrycket bredvid bilden? (multiplikation och addition)
6. Titta på alla uttryck samtalsbilden. Vilket räknesätt räknar du alltid först? (multiplikation)
Huvudräkningsuppgifter I ett rör får det plats 3 bollar. 1. Hur många bollar finns det fyra fulla rör? (12)
2. På golvet ligger 5 fulla rör och en lös boll. Hur många bollar ligger det sammanlagt på golvet? (16)
3. Charlie har 3 fulla rör men två bollar försvinner under tennismatchen. Hur många bollar finns kvar efter matchen? (7)
114
1. Lektionens innehåll
2. Lektionens mål
28. Prioriteringsregler Hur många bollar är det på bilden? 3 3 + 4 = 9 + 4 = 13 Prioriteringsregler: 1. Räkna bollarna.

Multiplikation och division ska räknas före addition och subtraktion.

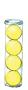





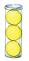













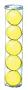





Förslag på arbetsgång 1. Ramberättelse 2. Frågor till samtalsbilden 3. Huvudräkningsuppgifter 4. Arbete på tavlan Skriv uttryck som innehåller två olika räknesätt (multiplikation, addition eller subtraktion) på tavlan och fråga eleverna vilka räknesätt uttrycken innehåller. Eleverna lär sig vilken ordning de ska räkna när det finns olika räknesätt i ett uttryck. 5. Elevbokens uppgifter 114
Visar vad lektionen handlar om och vad som är lektionens matematiska moment.
Visar mot vilka kunskapsmål eleverna arbetar med hjälp av lektionens innehåll.
3. Läroplan
Text från aktuell läroplan.
4. Frågor till samtalsbilden
Samtalsbilden fungerar som ett bra hjälpmedel för att introducera den matematik som ni ska arbeta med under lektionen. Syftet med frågorna är att uppmärksamma eleverna på lektionens innehåll. När du ställer frågor till samtalsbilden har du möjlighet att bedöma elevernas kunskaper och förmågor. Eleverna ska exempelvis kunna redogöra för och samtala om hur de tänker och räknar ut olika uppgifter.
5. Huvudräkningsuppgifter
Till varje lektion finns det huvudräkningsuppgifter. De har antingen anknytning till det eleverna ska lära sig under lektionen eller så är det repetition av tidigare innehåll. Ovanför samtalsbilden i elevboken finns tre rutor där eleven kan skriva svaren.
Prioriteringsregler

6. Förslag på arbetsgång
Det finns ett färdigt förslag på arbetsgång som du kan använda. I arbetsgången hittar du övningar som hjälper eleverna att förstå lektionens innehåll.
7. Ramberättelse
Ramberättelsens syfte är att uppmärksamma eleverna på lektionens innehåll. Ramberättelsen anknyter till det som händer på samtalsbilden. Den sätter också lektionen matematiska innehåll i en vardaglig kontext. Berättelserna handlar om skatan Sally, ekorren Kurre och de båda barnen Isa och Charlie.
Ramberättelsen finns inläst och du har tillgång till den både i din digitala resurs och i elevens digitala läromedel.
8. Tavla
Visar en förberedd tavelbild som du kan använda.
9. Presentationer
En förberedd digital genomgång som steg för steg visar och förklarar lektionens innehåll.
10. Elevböcker
Du har tillgång till elevens digitala läromedel. Om du vill samtala om lektionens innehåll och visa någon speciell uppgift, kan du visa sidor från elevboken.
ARBETA MED EXTRAUPPGIFTER – ANDRA UPPSLAGET
Problemlösningsuppgifter
1. Läraren har ritat tre streck i sanden: ett 5 meter, ett 10 meter och ett 20 meter ifrån eleverna. Eleverna springer fram och tillbaka till det närmaste strecket två gånger, tre gånger till det mittersta och fyra gånger till det längst bort. Hur många meter springer eleverna sammanlagt? (240 m)
2. Hur långt springer Isa när hon först springer till det andra strecket, sedan till det första strecket och därifrån till det tredje strecket och sedan tillbaka till början? (50 m) Räknebank
Uppgifterna kan kopieras från kopieringsunderlag 37a, del 1.
3 6 + 4 (22)
5 8
6 (34)
32 – 5 6 (2) 4. 47 + 7 7 (96) 5. 7 3 + 9 6 (75) 6. 8 7 – 7 8 (0) 7. 4 9 + 4 10 (76)
100 9 – 9 1 (891)
0 9 + 17 (17) 10. 1 + 2 3 – 4 (3)
UPPGIFT 5 Mera Favorit 3A Eleverna delar först upp faktorerna i mindre faktorer och till sist delar de upp faktorerna i primfaktorer. Att dela upp faktorer har stor betydelse senare matematikundervisningen. Att t.ex. förkorta, förlänga och lösa ekvationer kräver att eleverna kan dela in i faktorer. Medvetet finns inte faktorn 1 på den nedersta raden. Ordningen på faktorerna spelar ingen roll.

Visa hur du löser uppgiften. Skriv svar. a. Hanna har 4 påsar med 5 bullar varje och 2 bullar handen. Hur många bullar har Hanna sammanlagt? b. Einar har 3 påsar med 10 kakor varje och 6 kakor handen.

Tips 1. Bilda uttrycken Dela in eleverna två lag. Skriv ett uttryck, t.ex. 2 3 + 2, på tavlan. Lagen ska så fort som möjligt bilda grupper av sina medlemmar som motsvarar uttrycket. Det snabbaste laget får poäng. Andra lämpliga uttryck är t.ex.:
3 2 + 1, 3 3 + 2, 2 4 + 3, 4 2 + 1, 5 + 2 3, 1 + 2 3. 2. Prioriteringsregler Eleverna arbetar parvis och skriver uppgifter där prioriteringsregler ska tillämpas till varandra: Den ena eleven skriver tre tal i varannan ruta och uttryckets svar. Den andra eleven skriver rätt tecken, +, – eller , så att uttrycket är rätt. T.ex. 4 3 5 1 9 , som den andra eleven skriver i med 4 + 3 5 = 19. Skriv i mattehäfte eller på löst blad.
978-91-44-17612-3_02_book.indb 116 2024-08-09 15:16
11. Problemlösningsuppgifter
Till varje lektion finns det problemlösningsuppgifter. Uppgifterna kräver ofta tålmodigt funderande och passar därför extra bra för att lösa i en gemensam diskussion. För att underlätta för gemensam problemlösning finns uppgifterna förberedda i lärarens digitala resurs.
12. Tips
Tips ger förslag på lekar, aktiviteter och laborativt arbete som du kan använda i matematikundervisningen. Det finns även tips på aktiviteter som ni kan göra utomhus eller i en idrottshall.
13. Kunskapsbank
Kunskapsbanken innehåller fakta och information som kan vara värdefull för lektionens matematiska område.
14. Forskning om
Svenska, verksamma forskare har tillfört texter som handlar om matematik och matematikundervisning. Du får kompetensutvecklande möjligheter när du läser mer om den aktuella lektionens matematik. Här hittar du fortbildning när du själv väljer att du behöver den.
Favorit kopieringsunderlag
Kopieringsunderlag 28a: Prioriteringsregler

Kunskapsbank Prioriteringsregler är en överenskommelse som möjliggör att olika personer kan tolka ett givet aritmetiskt uttryck på samma sätt. Ibland får du frågor från eleverna som är svåra att besvara. Prioriteringsreglerna är ett exempel. Varför måste man multiplicera innan man adderar? När sådana frågor kommer upp kan det vara lämpligt att prata om vad matematik egentligen är. För att det ska fungera krävs att vi har gemensamma överenskommelser om hur vi ska räkna, så att alla som är bekanta med matematiken gör

Kopieringsunderlag 28b: Tavelbilder för lektionerna 28, 30 och 31.
NÄSTA LEKTION 29. Vi bildar ett uttryck
15. Favorit kopieringsunderlag
Kopieringsunderlagen kan du använda när dina elever behöver mer träning eller repetition. Alla kopieringsunderlag finns för nedladdning i den digitala resursen.
16. Träna digitalt (och film)
I Finland använder man TRÄNArutan som finns i elevboken vid varje lektion som läxa. Eleverna gör inte uppgifterna på lektionen utan tar hem boken och repeterar lektionens innehåll. Om du inte vill skicka hem boken så finns uppgifterna som digitala, självrättande uppgifter i elevens digitala läromedel. Du kan också visa och gå igenom dem med hjälp av din digitala resurs.
Under rubriken ”Träna digitalt” hittar du också en filmad genomgång med bild och ljud som förklarar lektionens innehåll. Filmen finns både i lärarens digitala resurs och i elevens digitala läromedel
17. Matteordlista
Till varje kapitel finns ett antal ord som är utvalda och förklarade med både ord och bild. Till Matteordlistan finns självrättande, digitala övningar. Matteordlistan finns inläst och du har tillgång till allt material både i den digitala resursen och i elevens digitala läromedel.
Lärarens digitala resurs
Lärarens digitala resurs är en del av lärarpaketet. Det finns förberedda presentationer av lektionens matematiska innehåll som du kan använda i klassrummet. Här finns bland annat ramberättelser, samtalsbilder och problemlösning som ger ingångar till viktiga matematiska samtal.
Det matematiska samtalet i klassrummet
Matematik är ett kommunikationsämne. I Favorit matematik möter eleverna genomgående korrekta matematiska ord och begrepp. Eleverna uppmanas att använda dessa när de resonerar och kommunicerar. Genom de förberedda lektionerna som du har som digitala resurser får du förutsättningar att hålla en klassrumsdialog. I elevens digitala läromedel finns språkutvecklande övningar och en matteordlista där matematiska ord och begrepp förklaras.
Den digitala resursen är ett kraftfullt stöd i din kommunikativa undervisning.
Den kan kompletteras med lärorika uppgifter från elevpaketet.
Med stöd av den digitala resursen kan du variera din undervisning inte bara innehållsmässigt utan det förberedda, digitala materialet underlättar även för variation mellan enskilt arbete och arbete såväl i mindre grupper som i helklass. Klassrumsdialogen i helklass lyfts fram i forskning och du hittar därför de flesta kommunikativa övningarna i lärarpaketet, inte som enskilda uppgifter i elevboken. 1
1. Problemlösning, resonemang och kommunikation utvecklas i problemlösningsuppgifter för arbete, exempelvis med EPA-metoden (ensam, par, alla).

2. Matteordlistan är inläst och har textföljning.
3. Till varje matteordlista finns övningar som låter eleven öva, befästa och repetera.
Matteordlistor
I den digitala lärarresursen och i elevens digitala läromedel finns rikt illustrerade matteordlistor på viktiga, matematiska begrepp från varje kapitel. Till matteordlistorna finns interaktiva självrättande övningar.
Till varje lektion finns det kopieringsunderlag. Kopieringsunderlagen innehåller varierade uppgifter som en ytterligare möjlighet för eleven att träna på lektionens innehåll. Alla kopieringsunderlag finns digitalt i ditt lärarpaket, för nedladdning.
I lärarpaketet ingår tryckta facit. Du får ett tryckt facit till Favorit och ett till Mera Favorit. Du kan dessutom ladda ner facit från lärarens digitala resurs. Vill du ha fler häften så finns facit att köpa i 5pack.


Favorit matematik är ett basläromedel i matematik med en gedigen, välfungerande och tydlig struktur. Materialet kommer från Finland där det är uppskattat för strukturen och de goda resultaten hos eleverna.
Den tryckta lärarhandledningen ingår i lärarpaketet tillsammans med lärarens digitala resurs och tryckta facit.
Det uppskattade och välfyllda lärarpaketet innehåller allt du behöver i form av inspiration och konkreta verktyg för en kommunikativ och varierad matematikundervisning.
Favorit matematik för skolår 3 består av elevböckerna 3A och 3B i två nivåer. Till varje elevbok medföljer laborativt material samt häftet Mitt lärande med prov, matriser och lärardokumentation. Lärarhandledningarna 3A och 3B kan kompletteras med Favorit matematik – Utökat stöd för klasslärare och Favorit matematik – Special för speciallärare.