FAVORIT MATEMATIK 7-9
REPETITION
Elevpaket – Tryckt + Digitalt
FAVORIT MATEMATIK 7-9 REPETITION
Elevpaket – Tryckt + Digitalt
Favorit matematik 7-9 repetition är ett elevpaket som består av två delar: elevbok och digitalt läromedel. På följande sidor kan du provläsa och bilda dig en uppfattning om såväl det digitala läromedlet som den tryckta delen.
ELEVBOK
Favorit Matematik 7-9 Repetition innehåller repetitionsuppgifter, räkneexempel, begreppförklaringar och mycket mer. Uppgifterna är uppdelade efter svårighetsgrad som följer de betygskriterier som används vid nationella prov.
DIGITALT LÄROMEDEL
Interaktiv bok med ljud och textföljning, interaktiva övningar och cirka 100 filmade förklaringar och räkneexempel.
Interaktiv version av boken, inläst med autentiskt tal och textföljning.
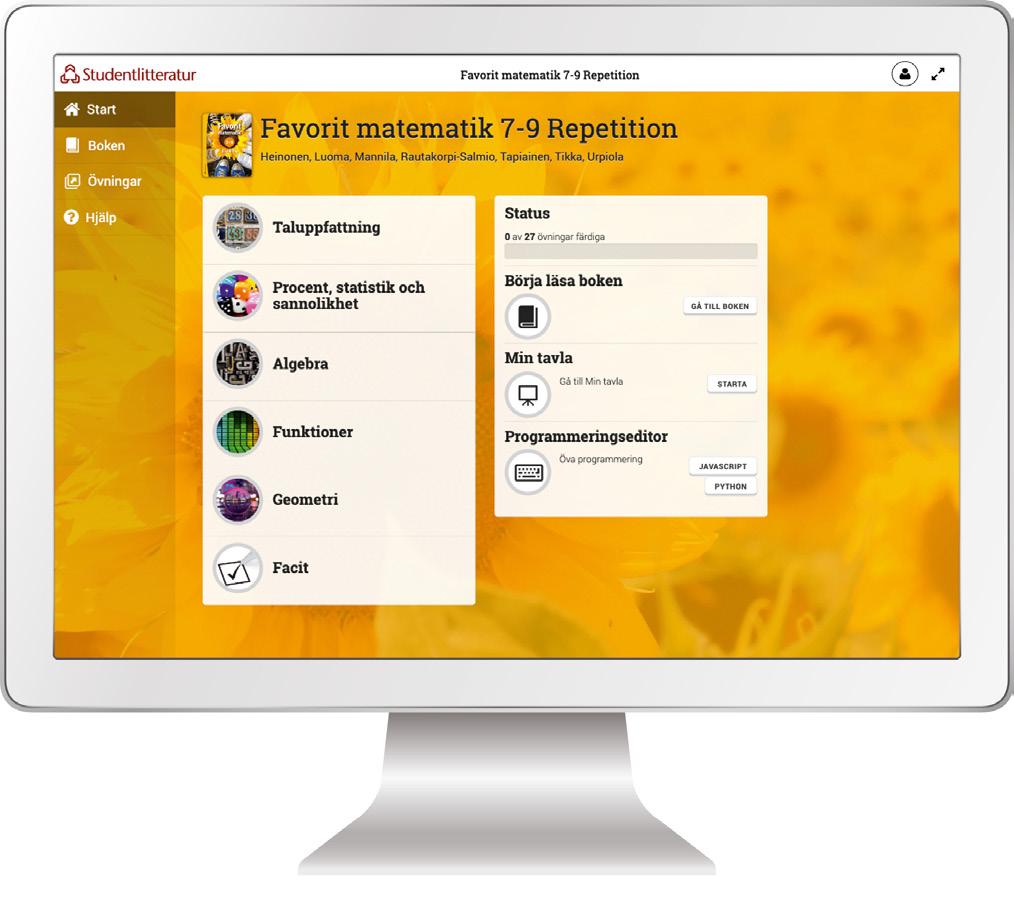
Interaktiva övningar och filmer.
Fungerar på dator, surfplatta och mobiltelefon.
Studentlitteratur AB
Box 141
221 00 LUND
Besöksadress Åkergränden 1
Telefon 046-31 20 00
studentlitteratur.se
KOPIERINGSFÖRBUD
Detta verk är skyddat av upphovsrättslagen. Kopiering, utöver lärares begränsade rätt att kopiera för undervisningsändamål enligt Bonus Copyright Access skolkopieringsavtal, är förbjuden. För information om avtalet hänvisas till utbildningsanordnarens huvudman eller Bonus Copyright Access.
Vid utgivning av detta verk som e-bok, är e-boken kopieringsskyddad.
Användning av detta verk för text- och datautvinningsändamål medges ej.
Den som bryter mot lagen om upphovsrätt kan åtalas av allmän åklagare och dömas till böter eller fängelse i upp till två år samt bli skyldig att erlägga ersättning till upphovsman eller rättsinnehavare.
Studentlitteraturs trycksaker är miljöanpassade, både när det gäller papper och tryckprocess.
Art.nr 45944
ISBN 978-91-44-19352-6
Upplaga 1:2
© Författarna och Studentlitteratur 2022
Originalets titel: Pi 9 Matematik
© Publishing Company Otava, Helsingfors 2019
Heinonen, Luoma, Mannila, Rautakorpi-Salmio, Tapiainen, Tikka, Urpiola
Redaktion: Ingeli Jönsson Stegmark, Tommy Lundahl
Anpassning av uppgifter: Per Berggren, Maria Lindroth, Nafi Zanjani
Översättning: Cilla Heinonen
Omslag: Francisco Ortega
Omslagsbild: Shutterstock
Printed by Eurographic Group, 2024
Problemlösning
Arbeta med Favorit matematik i
Välkommen till Favorit matematik! Här får du en snabb introduktion till elevpaketet så att du kan lära dig så mycket som möjligt.
Elevpaketet består av en tryckt bok och en mycket omfattande digital del. Du aktiverar den med hjälp av instruktionerna och koden på omslagets insida. I den digitala delen finns bland annat cirka 100 filmer som stöd för inlärningen.
Bokens upplägg
I Favorit matematik Repetition 7–9 får du lära dig ett matematiskt område i taget. Området är indelat i avsnitt. Avsnitten bygger oftast på varandra och kommer i en viss ordning för att det ska bli så lätt som möjligt att förstå.
Lektionerna inleds med förklaringar och räkneexempel. Dessa finns i den digitala delen som filmer, där erfarna matematiklärare förklarar och räknar igenom alla exempel. Efter förklaringarna kommer uppgifter som är ordnade efter svårighetsgrad och märkta med förmågor.
Repetitionsuppgifterna är på E/C-nivå och finns även som interaktiva uppgifter i den digitala delen. Vill du träna mer på lektionens moment, finns det länkar till många extra uppgifter: Öva mer E, Öva mer E/C och Öva mer C/A.
Filmer
Alla förklaringar och räkneexempel finns som filmer i den digitala delen. En erfaren matematiklärare går igenom lektionens innehåll. Du kan lyssna i din egen takt, så många gånger du vill. Även alla räkneexempel finns som filmer där en annan lärare räknar exemplet och förklarar lugnt och metodiskt. Totalt finns det cirka 100 filmer som handlar om precis det som står i boken.
Du har varit sjuk och missade matematiklektionerna förra veckan. Vad ska du göra?
Lösning:
Läs förklaringarna i boken. Om du inte förstår, logga in i den digitala delen, öppna den digitala boken och klicka på symbolen i marginalen med texten Förklara!
Precis som stora tal kan små tal skrivas om med tiopotenser.
2
Förklara!
Positiva tal mindre än noll har negativ exponent i tiopotensen, till exempel 0,01 = 10−2.
Klicka på den röda symbolen för att starta filmen där en matematiklärare förklarar precis det som står i boken.
Du var med på lektionen, men du förstod inte riktigt när läraren räknade och förklarade. Du läser räkneexemplet, men förstår inte riktigt ändå. Du behöver någon som förklarar en gång till. Vad ska du göra?
Lösning:
Logga in i den digitala delen, öppna den digitala boken och klicka på symbolen i marginalen vid räkneexemplet (under den första i varje lektion står det Räkna!). En lärare räknar igenom exemplet och förklarar. Lyssna i din egen takt, så många gånger du vill.
Räkna! EXEMPEL 3
Skriv talet 12,036 i utvecklad form.
Lösning och svar:
12,036 = 1 ∙ 10 + 2 ∙ 1 + 0 ∙ 0,1 + 3 ∙ 0,01 + 6 ∙ 0,001
Klicka på den röda symbolen för att starta filmen där en matematiklärare räknar och förklarar exemplet i boken.
Det finns mycket mer i den digitala delen, till exempel hela boken i digital form, inläst med textföljning (klicka på texten för att få den uppläst). Klicka på symbolen för att se en film om hur den digitala delen fungerar.
Bokens olika uppgifter
Det finns en kursplan som beskriver vad du ska kunna i matematik. För att det ska bli rättvist och tydligt gör alla elever i Sverige ett nationellt prov i årskurs 9. Du får då göra uppgifter som är på olika nivå och som testar olika förmågor.
I Favorit matematik Repetition 7–9 är alla uppgifter indelade i grupper utifrån svårighetsgrad. Vi använder samma bokstäver som för betygen: E och C. E-uppgifter är de som du måste klara för att få godkänt. C-uppgifterna är svårare.
Det finns olika typer av E- och C-uppgifter, som testar olika förmågor att lösa matematiska problem:
• Begrepp (B) – testar om du förstår matematiska ord och begrepp, samt kan använda dem.
• Metod (M) – testar om du kan metoder för beräkningar.
• Problemlösning (P) – testar om du kan lösa olika problem som presenteras för dig, och att du kan begreppen och metoderna som krävs för att kunna lösa problemet.
• Kommunikation (K) – testar om du med ord, bilder och symboler kan förklara ett matematiskt problem.
Begrepp och metod är en förutsättning för att du ska klara problemlösning och kommunikation. Därför läggs stor vikt vid de förmågorna i början.
I boken finns även många andra typer av uppgifter: Diskutera, Laborera, Resonera, Fördjupningar, Historiska nedslag och Programmeringsuppgifter.
Märkning av uppgifter
Det är tydligt i boken hur svår uppgiften är och vilken förmåga den tränar. E/C-uppgifter kommer först, under en egen rubrik. Uppgifterna är ordnade efter svårighetsgrad, med den lättaste först.
E/C-UPPGIFTER
Uppgift 1 tränar framförallt förmågan Begrepp medan uppgift 9 framförallt tränar förmågan Metod.
1 Granska talet 67,103. Vilken är talets a) heltalsdel b) decimaldel?
9 Räkna utan miniräknare.
B M
a) 13 ∙ 2,4 b) 5,04 ∙ 3,9 c) 13,6 / 8 d) 6 / 0,2
Den streckade linjen visar gränsen mellan E- och C-uppgifter.
Under uppgiftsnumret ser du vilken eller vilka förmågor den uppgiften huvudsakligen handlar om:
B = Begrepp, M = Metod, P = Problemlösning, K = Kommunikation.
A-uppgifterna är inte så många, men svårare. Du bör först vara säker på att du kan alla grunder på E- och C-nivå innan du går vidare med utmaningarna i A-uppgifterna och Resonera-/Laborera-uppgifterna. Försök först klara uppgifterna på egen hand innan du ber någon om hjälp. Det är viktigt att du verkligen förstår uppgifterna så att du klarar av att lösa liknande uppgifter själv på proven.
Det blir tydligt vad du kan och vad du behöver träna mer på
Till varje kapitel hör ett prov. Det ser ut precis som det nationella provet. När du får tillbaka provet finns en tabell, där du kan se vilka olika typer av uppgifter du har klarat.
Du kan titta på tabellen och se vilka typer av uppgifter du behöver träna mer på i fortsättningen.
Lycka till!
UPPGIFTER
1 Bläddra i boken och hitta exempel på
a) E-uppgifter, C-uppgifter och extra E- , C- och A-uppgifter
b) uppgifter som tränar problemlösning, metod, begrepp och kommunikation.
2 Vad är det för skillnad på en förklaring och ett räkneexempel?
3 Läs instruktionerna på omslagets insida och aktivera den digitala delen.
4 Öppna den digitala boken och gå till sidan 5. Titta på filmen om den digitala delen genom att klicka på länken längst ned på sidan.
5 Klicka runt i boken och hitta minst fem olika saker du kan göra. Jämför med de andra i klassen och se om ni har hittat olika saker.
6 Fundera på hur du vill använda de olika delarna som finns i den digitala delen. Tänk igenom vad du tror passar dig bäst!
Förklara!
De fyra räknesätten
I ett tal avgörs en siffras värde av vilken position den har i talet. Ett decimaltal består av en heltalsdel och en decimaldel.
25,306
tusendelar hundradelar tiondelar ental tiotal
1
Räkna!
Tiotal Ental, Tiondelar Hundradelar Tusendelar
2 5 , 3 0 6 heltalsdel decimaldel
Skriv talet som en summa av de platsvärden som ingår i talet.
a) 4 125 b) 5,93 c) 608,007
Lösning och svar:
a) 4 125 = 4 ∙ 1 000 + 1 ∙ 100 + 2 ∙ 10 + 5 ∙ 1 b) 5,93 = 5 ∙ 1 + 9 ∙ 0,1 + 3 ∙ 0,01
c) 608,007 = 6 ∙ 100 + 8 ∙ 1 + 7 ∙ 0,001
Tusendelar, hundradelar och tiondelar är exempel på platsvärden.
De naturliga talen 0, 1, 2, 3, … är de positiva heltalen och noll. De används för att ange antal. Det finns oändligt många naturliga tal.
Det finns fyra räknesätt: addition, subtraktion, multiplikation och division
• Vid addition adderas termer med varandra och svaret heter summa.
• Vid subtraktion subtraheras termer och svaret heter differens.
• Vid multiplikation multipliceras faktorer med varandra och svaret heter produkt.
• Vid division divideras täljaren med nämnaren och svaret heter kvot.
HELSINGBORG 84 LANDSKRONA 90 LUND 100 MALMÖ 11 6
136
term + term = summa term – term = differens faktor ∙ faktor = produkt täljare nämnare = kvot
Hur många 5-kronor går det på 200 kr?
Hur många mil går det på 100 km?
Hur många sekunder går det på 5 minuter?
Beräkna
a) summan av 4 och 9
Lösning:
b) differensen av 10 och 3.
Lösning: 4 + 9 = 13 10 − 3 = 7
Svar: Summan är 13.
Svar: Differensen är 7.
Skriv talet 25 som en a) produkt b) kvot.
Lösning:
Det finns flera lösningar på uppgiften. Du kan tänka att du ska multiplicera två tal med varandra så att svaret blir 25, till exempel 1 ∙ 25 eller 5 ∙ 5.
Svar: 5 ∙ 5 = 25 eller 2 ∙ 12,5 = 25.
E-UPPGIFTER
1 Vilka siffror ingår i talet?
a) 15
b) 255
c) 30,26
d) 19 023
2 Skriv som ett tal.
a) trehundrasjuttiotvå
b) tvåhundrasex
c) fem hela och tjugosju hundradelar
d) sexhundranio tusendelar
Lösning:
Det finns även här flera lösningar på uppgiften. Du kan tänka att du ska dividera ett tal med ett annat så att svaret blir 25, till exempel 75 dividerat med 3.
Svar:
75 3 = 25 eller 200 8 = 25.
E3 Ringa in heltalsdelen i talet.
a) 53,746 b) 1 325,9
c) 785,6 d) 34,91
4 Ringa in decimalerna i talet.
a) 13,4 b) 53,746
c) 657,98 d) 0,62
5 Vilken talsort har siffran?
a) 5 i talet 235
b) 0 i talet 2 073
c) 1 i talet 2,317
d) 6 i talet 0,62
6 Skriv talet i utvecklad form med varje
platsvärde för sig.
a) 392
b) 15,47
7 Skriv talet i utvecklad form med varje
platsvärde för sig.
a) 0,305
b) 5,006
8 Vilket är talet?
a) 5 ∙ 10 + 3 ∙ 1 + 6 ∙ 0,1
b) 3 ∙ 0,1 + 4 ∙ 0,01
c) 5 ∙ 1 000 000 + 7 ∙ 10 000 + 3 ∙ 1 000 + 2 ∙ 100
d) 3 ∙ 100 + 8 ∙ 1 + 2 ∙ 0,001
9 Beräkna.
a) summan av 25 och 38
b) kvoten av 95 och 5
10 Beräkna.
a) differensen av 80 och 23
b) produkten av 15 och 4
11 Addera först 9 och 37, subtrahera
sedan med 10 och multiplicera
slutligen med 3. Vad får du?
12 Beskriv delarna med rätt ord.
a) 5 + 6 +
b) 19 7
c) 8 ∙ 8
d) 18 − 5 −
13 Amanda och Siri plockar sammanlagt 68 liter jordgubbar. Beräkna hur mycket var och en plockar, då Amanda plockar 12 liter mer än Siri.
14 Leo går hemifrån till sina träningar kl. 16.40 och är tillbaka hemma igen kl. 19.25. Hur länge är Leo borta hemifrån?
16 Beräkna hur lång dagen är i Malmö, Stockholm och Kiruna.
7.39
15 Vilken är tidsskillnaden mellan klockslagen? a) b) c) d)
C-UPPGIFTER
17 Använd alla siffrorna 8, 0 och 2 minst en gång och bilda
a) ett så stort tresiffrigt naturligt tal som möjligt
b) ett så litet tresiffrigt naturligt tal som möjligt
c) ett tal så nära 200 som möjligt.
18 Använd alla siffrorna 8, 0 och 2 minst en gång och bilda
a) ett så stort fyrsiffrigt naturligt tal som möjligt
b) ett så litet fyrsiffrigt naturligt tal som möjligt.
19 Av de 50 anställda på en arbetsplats kan 19 svenska, 26 engelska och 10 både svenska och engelska. Hur många av de anställda kan varken svenska eller engelska?
22 Bilda det största och minsta möjliga talet med tre decimaler av siffrorna 5, 9, 1, 8 och 4. Varje siffra ska användas en gång i båda talen. Beräkna summan av talen.
20 Skriv det största och minsta
decimaltalet av siffrorna 2, 0, 6, 9. Du väljer själv antalet decimaler. Varje siffra ska användas en gång i båda talen.
21 Ge bokstäverna A och B siffervärden så att uttrycket stämmer.
A,07 + 4,B4 = 6,41
Resonera
Bilda fem uttryck av siffrorna 1, 2, 3, 4 och 5 som alla har värdet 31. Varje siffra får bara användas en gång och alla uttrycken ska innehålla alla fem siffrorna.
23 Från stationen går det en buss söderut med 40 minuters mellanrum och en österut med 45 minuters mellanrum. Bussarna börjar trafikera kl. 5.00.
a) Vilket är följande klockslag då bussarna avgår samtidigt?
b) Hur många gånger avgår bussarna samtidigt under en dag, då den sista bussen österut avgår kl. 23.00 och den sista söderut kl. 23.40?
REPETITION
24 Vilka siffror ingår i talet?
a) 404
b) 0,73
c) 10,206
d) 379 150
25 Vilken talsort är siffran?
a) 7 i talet 5,753
b) 9 i talet 9,27
c) 4 i talet 0,045
d) 2 i talet 25,735
26 Vilket är talet?
a) 7 ∙ 1 000 + 6 ∙ 100 + 3 ∙ 10 + 8 ∙ 1
28 Skriv talet.
a) Heltalsdelen är femtiosex och decimaldelen tolv hundradelar.
b) Talet utläses ”sextusenfem hela och fyrtionio tusendelar”.
c) Talets utvecklade form är
7 ∙ 10 + 3 ∙ 0,1 + 9 ∙ 0,001.
29 Skriv talet i utvecklad form med varje platsvärde för sig.
a) 270
b) 31,02
c) 5,089
b) 5 ∙ 1 000 + 8 ∙ 10 + 3 ∙ 1
c) 4 ∙ 100 + 5 ∙ 1 + 8 ∙ 0,1
d) 3 ∙ 1 + 9 ∙ 0,1 + 2 ∙ 0,001
27 Lena går till skolan kl. 8.20 på morgonen och är hemma igen kl. 15.10. Hur länge är Lena hemifrån?
d) 0,0203
30 Familjen Norberg kör sammanlagt 634 km under sina två första semesterdagar. Den första dagen kör familjen 92 km längre än under den andra dagen. Beräkna hur långt de kör varje dag.
Talföljder
Många problem kan lösas genom att ordna och studera tal i en följd som beskriver problemet. Talmönster är ett matematiskt mönster där tal till exempel kan öka eller minska med samma värde.
1
Lista med hjälp av de tre första figurerna ut hur många stickor den tionde figuren består av.
Lösning:
1
2
Antalet stickor i figurerna är 6, 10, 14 …
Figur 1: 1 ∙ 4 + 2 = 6
Figur 2: 2 ∙ 4 + 2 = 10
Figur 3: 3 ∙ 4 + 2 = 14
Figur 4: 4 ∙ 4 + 2 = 18
Figur 10: 10 ∙ 4 + 2 = 42
Svar: Den tionde figuren består av 42 stickor.
3
Diskutera
En vanligt förekommande talföljd i naturen är Fibonaccis talföljd som börjar så här: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 ... Hur kan du beskriva sambandet mellan talen i följden?
Figur
Figur
Figur
Förklara!
Räkna!
En talföljd är en ändlig eller oändlig följd av tal. Talen i talföljden kallas element och skiljs åt med kommatecken. Är det decimaltal i talföljden skiljs elementen åt med semikolon.
En talföljd som är oändlig skrivs med tre punkter i slutet. Den talföljd som bildas av de naturliga talen 0, 1, 2, 3, … är oändlig.
En ändlig talföljd har ett bestämt antal element. Talföljden 1, 3, 5, 7, 9 har fem tal.
I många fall kan nästa element i talföljden räknas ut genom att ett mönster hittas för de föregående elementen.
Regeln för en talföljd
Vilket tal som ska stå på en bestämd plats i talföljden räknas ut med hjälp av elementets ordningstal, om elementen i talföljderna bestäms efter en regel. Ordningstalet anger på vilken plats elementet finns i talföljden.
2
Skriv de fyra första elementen i talföljden, när elementen bestäms av följande regel:
3 ∙ elementets ordningstal − 5
Lösning:
Ordningstal Elementets värde
1 3 ∙ 1 − 5 = −2
2 3 ∙ 2 −
Du multiplicerar elementets ordningstal med talet 3, sedan subtraherar du 5 från produkten.
Svar: De fyra första elementen i talföljden är −2, 1, 4 och 7.
Utifrån några av de första elementen i en talföljd är det möjligt att formulera olika regler för talföljden. Det är viktigt att alltid kontrollera regeln. Regeln måste gälla för alla element i talföljden.
3
Enligt vilken regel är det fjärde elementet i talföljden 1, 2, 3 …
a) 4 b) 5?
Lösning och svar:
a) Till exempel: Följande tal är alltid ett större än föregående.
b) Till exempel: Följande tal är alltid (från och med talet tre) summan av de två föregående talen.
EXEMPEL
E-UPPGIFTER
1 Hur många stjärnor finns det på det femte kortet?
4 Skriv de tre följande elementen i talföljden.
a) 27, 25, 23, 21, , , ,
b) 55, 50, 45, 40, , , , …
c) 9, 7, 5, 3, , , ,
Kort 1 Kort 2 Kort 3 Kort 4 Kort 5
Kort 1: =
Kort 2: =
Kort 3: =
Kort 4: =
Kort 5: =
2 Hur många stickor består figurerna av?
Figur 1 Figur 2 Figur 3
Figur 1: =
Figur 2: =
Figur 3: = Figur 4: =
Figur 5: =
3 Hitta ett mönster och skriv de tre följande elementen i talföljden.
a) 0, 3, 6, 9, , , , …
b) 1, 4, 7, 10, , , , …
c) 5, 10, 15, , , , …
d) 2, 13, 24, 35, , , , …
d) −10, −20, −30, , , , …
5 Skriv de fyra första elementen i talföljden.
a) Det första elementet är 3, och följande element är alltid 5 större än det föregående.
3, , och
b) Det första elementet är 42, och följande element är alltid 6 mindre än det föregående.
42, , och
6 Skriv de fyra första elementen i talföljden.
a) Det första elementet är 1, och följande tal är alltid fem gånger större än det föregående.
1, , och
b) Det första elementet är 120, och följande tal är alltid 20 mindre än det föregående.
120, , och
7 En talföljd följer regeln
2 ∙ talets ordningstal + 1. Vilket är det
a) första elementet
b) femte elementet
c) sjunde elementet?
8 Skriv de fyra första elementen i talföljden, när talföljden följer regeln
a) 2 − elementets ordningstal
b) 5 ∙ elementets ordningstal + 50.
9 Vilket tal saknas i talföljden?
a) 1, 2, , 4, 5
b) 4, 2, 0, , −4
c) 200, , 50, 25, …
d) , 2, 4, 8, …
Resonera
Vilket tal ska stå i sista rutan?
Vilken regel följer talföljden?
199, 19, 10,
10 Hur många små kvadrater finns det i figur
Figur 1
Figur 2
Figur 3
a) fem
b) tio
c) femton?
Figur 4
11 Hur många tändstickor finns det i figurerna?
Figur 1 Figur 2 Figur 3
12 Hur många stickor finns det i figurerna?
Figur 1 Figur 2 Figur 3 Figur 4
a) Figur 5:
b) Figur 10:
REPETITION
13 Hur många stickor finns det i figurerna?
Figur 1 Figur 2 Figur 3
a) Figur 10:
b) Figur 20:
14 Hur många stickor finns det i figurerna?
Figur 1 Figur 2 Figur 3
Figur 1:
Figur 2:
Figur 3:
a) Figur 5:
b) Figur 10:
15 Skriv de tre följande elementen i talföljden.
a) 6, 13, 20, 27, , , , …
b) −16, −13, −10, −7, , , , …
c) 41, 30, 19, 8, , , , …
d) −10, −23, −36, , , , …
16 Skriv de tre följande elementen i talföljden.
a) 3, 6, 12, , , , …
b) 800, 400, 200, , , , …
c) −2, −4, −8, , , , …
d) 1, −1, 1, −1, , , , …
17 Regeln för talföljden är
6 ∙ talets ordningstal − 5.
Vilket är det
a) andra elementet i talföljden
b) femte elementet i talföljden
c) elfte elementet i talföljden?
18 Skriv de fyra första elementen i en talföljd, när det första elementet är 3, och du får följande element genom att
a) multiplicera föregående element med talet 2
b) subtrahera 7 från föregående element.
19 Skriv en talföljd, som beskriver
a) icke-negativa heltal
b) multipler av talet 11
c) positiva tal som är delbara med talet 25.
<Python: Talföljder>
Med programmering kan talföljder enkelt skapas för att kunna räkna ut ett bestämt värde på ett visst element eller snabbt lista de 100 första elementen i en talföljd. Om detta görs i Python finns det några kommandon som är bra att kunna.
Kommandon i Python
int(variabel) omvandlar en textsträng till ett heltal. print en metod för att bland annat skriva ut en text input en metod som ber användaren att mata in data.
Skapa ett program som beräknar ett visst element i talföljden a n = 3n + 8, där a n
är elementet med ordningstalet n. Programmet ska fråga dig för vilket n du vill räkna ut ett element.
Lösning:
print(”Räkna ut ett element i talföljd enligt detta mönster: 3 * n + 8”)
answer = input(”Vilket ordningstal ska elementet ha som du vill räkna ut? ”)
n = int(answer)
value = 3 * n + 8
print(value)
value är en variabel som beräknar elementet.
UPPGIFTER
1 Lös uppgifterna utifrån programmet i exempel 4. Ersätt talföljden med 2x + 1. Beräkna
a) det första elementet
b) det femte elementet
c) det tionde elementet
d) det tjugonde elementet
e) det hundrade elementet.
2 Lös uppgifterna utifrån programmet och beräkna det tionde elementet i
a) 4 − n b) 5n − 50
c) 8 + 6n d) −1 + 3x.
3 Skriv ett program som räknar ut Fibonaccis talföljd. Beräkna
a) den 12:e termen
b) den 20:e termen
c) den 100:e termen.
Problemlösning
Det här kapitlet innehåller sex större uppgifter som kan beröra de olika matematiska områden som behandlas iden här boken.
Tänk på det här när du löser och redovisar uppgifterna
Det är viktigt att du visar:
• vilka matematiska kunskaper du har
• att du på ett utförligt sätt redovisar hur du löser uppgiften
• hur du motiverar dina slutsatser.
Centralt innehåll
Uppgifterna behandlar framför allt dessa delar:
• Strategier för att lösa matematiska problem i olika situationer och inom olika ämnesområden samt värdering av valda strategier och metoder.
• Formulering av matematiska frågeställningar utifrån olika situationer och ämnesområden.
• Enkla matematiska modeller och hur de kan användas i olika situationer.
Varför är det bra att kunna lösa matematiska problem och när kan du använda dessa färdigheter?
UPPGIFT ECA
I Talpar
Om du har talserien 1 – 5 dvs. talen 1, 2, 3, 4 och 5 så kan du använda dem för att bilda olika summor.
Om villkoret för summorna är att de ska bestå av två efterföljande tal och att summan inte får vara större än det största av talen i talserien så är summorna 1 + 2 = 3 och 2 + 3 = 5. Alla andra summor blir högre än de tal som ingår i serien.
a) Hur många olika möjliga summor av två tal som följer på varandra kan du få av talen 1 – 15?
b) Hur många olika summor av två tal som följer på varandra kan du få av talen 1 – 53?
c) Hur många olika summor av tre tal som följer på varandra kan du få av talen 1 – 35?
d) Kommer summorna av två på varandra följande tal att vara ett udda tal, jämt tal eller båda? Kommer det att vara samma för tre tal, fyra tal, fem tal…?
e) Hur många olika summor av två tal som följer på varandra kan du få av talen 1–x? Visa en generell regel.
Favorit matematik 7–9
Repetition
Favorit matematik 7–9 Repetition sammanfattar högstadiets matematik i en bok. Läromedlet passar som repetition eller sammanfattning på högstadiet eller på introduktionsprogrammet.
Boken behandlar alla delar av det centrala innehållet i matematik för högstadiet. Boken består av 27 avsnitt samt programmeringsuppgifter och ett avsnitt med större problemlösningsuppgifter. Genomgångar följs av räkneexempel och uppgifter för eleven att arbeta med. Uppgifterna är uppdelade i E/C-uppgifter i stigande svårighetsgrad och repetitionsuppgifter. Alla uppgifter är markerade med vilka förmågor som i huvudsak tränas.
Favorit matematik 7–9 Repetition är en förbrukningsbok med tillhörande tryckt facit som bilaga samt digital del med bland annat en mängd filmer, digitala övningar och extramaterial.
När eleverna skriver direkt i boken blir det enklare att fokusera på matematiken.
Serien Favorit matematik för högstadiet bygger på den beprövade, finska matematikserien Pii, och är bearbetad för svenska förhållanden. studentlitteratur.se
Art.nr 45944