Manual Parte 4



Dra.MaríaTeresa
AliciaSilvayOrtiz 4

Dedicatoria
Paratiorientadorquequieresformarteparapoderguiaraotrosenel caminodelavidaparaaprovecharsuspotencialidadesydarlomejorde símismos.


1. Programas de matemáticas para personas con problemas de aprendizaje
1.1 Programas comerciales
¿Son útiles los programas comerciales?
Los programas comerciales ayudan a enseñar habilidades matemáticas. En particular, dado el objeto de este trabajo, a continuación, enunciamos algunos que son útiles para personas con trastornos de aprendizaje.
• Computional Arithmetic Program: para alumnos de sexto grado que necesiten aprender y dominar las habilidades básicas de cálculo de los números enteros.
• Corrective Mathematics Program: para alumnos de los cursos del 3 al12 y para adultos que no dominan las habilidades básicas.
• Cuisènaire Rods (regletas): son material de soporte para enseñar matemáticas desde preescolar hasta sexto curso. Los cubos Cuisenaire no son un programa completo y se utilizan básicamente para completar otros programas matemáticos.
• Equipos DISTAR de aritmética: ponen énfasis en la instrucción directa en un marco muy sistematizado y extensivo. Son ampliamente reconocidos y su calidad está comprobada.
• Key Math Early Steps Programs: enseña los primeros pasos matemáticos con actividades manuales con material para llevarlas a cabo.
• Key Math Teach and Practice: está ideado para identificar y corregir dificultades específicas de cálculo.
1.2 Programas de computadora
¿Son útiles los programas de computadora?
Este tipo de programas, por su parte, le permiten al alumno realizar ejercicios de práctica para el desarrollo de habilidades anteriormente adquiridas
• Academic Skill Builders in Math: este programa está ideado para motivar a los alumnos de todas las edades a asimilar las habilidades matemáticas fundamentales gracias a la rápida acción y los gráficos de color de los juegos de arcada. Seis programas individuales proporcionan preguntas y práctica de las cuatro operaciones matemáticas básicas de combinaciones de operaciones.
• Basic Skills in Math: identifica las áreas problemáticas específicas del alumno en funciones matemáticas básicas y proporciona práctica basada en las necesidades individuales.
• Math Sequences: consiste en 12 disquetes que proporcionan un programa matemático basado en objetivos con preguntas y prácticas estructuradas ideado para alumnos de primer a octavo grado o como un curso correctivo para alumnos mayores.
• Math Skills Elementary Level / Math Skills Junior High Level: estos dos programas proporcionan ejercicios y practica de conceptos matemáticos, de operaciones, y de procesos básicos.
1.3 Ejercicios para la corrección de la discalculia escolar
A continuación, se listan algunos ejercicios que se pueden realizar para atender la discalculia escolar teniendo en cuenta las funciones de maduración afectadas.
MaríaTeresaAliciaSilvayOrtiz. Paradigma cognoscitivo y las DAM. Manual. Parte 4
1.3.1 Ejercicios de memoria y percepción auditiva
A. Repetición de números. Aplaudir y decir el número correspondiente. Poner el número de pinzas que representa cada tarjeta. Meter las tarjetas en una bolsa y sacar una a una diciendo qué número es. Jugar memoria…



Actividad # 1 Banda numérica
Instrucciones. Utiliza las barajas para hacer distintos juegos y reforzar el conocimiento básico de los números.




B. Tirar dados. Decir qué número es. Variante: tener tarjetas con números y con puntos por separado para que las pueda aparear.







Actividad # 2 Números y dados
Instrucciones. Aparear números y tarjetas con puntos.
Mira el video: Canta los números. https://youtu.be/SKX5AkLTz9c


C. Discriminación auditiva. Reconocimiento de ruidos: de animales, del medio, del hogar, aparatos eléctricos, instrumentos musicales, del cuerpo


Actividad # 3 Discriminación auditiva
Instrucciones. Identificar los ruidos y sonidos de distintas fuentes: hogar, el cuerpo, el medio, animales, la calle, entre otros. Aprovechar los enlaces de los videos que se sugieren a continuación para reforzar esta área.
MaríaTeresaAliciaSilvayOrtiz. Paradigma cognoscitivo y las DAM. Manual. Parte 4
Mira los videos:

• Sonidos del cuerpo humano. https://www.youtube.com/watch?v=-7BQ6UQ0Zs



• Sonidos de los animales. https://www.youtube.com/watch?v=YxOrQM2lM-0
• Sonidos de instrumentos musicales.
https://www.youtube.com/watch?v=boCQpqAkuRs
• Sonidos del transporte. https://www.youtube.com/watch?v=k9D_-KgeSv8
• Sonidos de la casa. https://www.youtube.com/watch?v=8fpEHLGlCag
• Sonidos cotidianos. https://www.youtube.com/watch?v=xnWc0AfpigY
• Adivina cuál hace el sonido, parte 1.
https://www.youtube.com/watch?v=zDvsffsAE4s
• Adivina cuál hace el sonido, parte 2. https://www.youtube.com/watch?v=kFOUeCOWcY
• Sonidos de onomatopeyas.
https://www.youtube.com/watch?v=FubHJR3cpJw
1.3.2 Memoria y percepción visual

A. Agrupación de objetos por su forma, color y tamaño.
Actividad # 4 Memoria y de percepción visual
Instrucciones. Pon encima de cada tarjeta los objetos que son del mismo color.



B. Dictado de determinados números sin un orden y el alumno debe hacer notar los que faltan, ejemplo: 3-4-7-8-10 Faltan 1-2-5-6-9.
números faltan?
MaríaTeresaAliciaSilvayOrtiz. Paradigma cognoscitivo y las DAM. Manual. Parte 4
C. Ordena los coches. Ponerlos de menor a mayor.
siete tres ocho cinco uno cero dos cuatro seis nueve
6. Ordena los coches. Mira los videos:










• Aprendamos los colores. https://www.youtube.com/watch?v=PczrkyAZZJ4
• Los colores y los números. https://www.youtube.com/watch?v=_MBwv0g1EIo
1.3.3 Ritmo y Seriación


A. Control de movimientos. Detención de la marcha después de 2 o 3 pasos.
Actividad # 5 Ritmo y seriación
Instrucciones. Da el número de pasos que se te diga y detente. Variante: camina libremente por el salón y detente al oír el sonido del pandero.
2 pasos 4 pasos 6 pasos
2 pasos







• Video: Clap, clap sound musicograma: https://www.youtube.com/watch?v=6UYnHJqo7_4&t=14s
• Ejercicio de coordinación y gimnasia cerebral.
https://www.youtube.com/watch?v=-CIbtmVcA_w
B. Cuentos que tengan objetos de distintos tamaños
Actividad # 6
El cuento
Instrucciones. Contar cuentos que involucren cantidad, tamaños, series, por ejemplo, enfatizando la secuencia.
Ricitos de oro y los tres ositos
Ir contando el cuento de manera que los niños puedan ir mostrando los objetos que se van diciendo según su tamaño.
Agrupar cada objeto con el oso correspondiente.

Video: Ricitos de oro y los tres ositos
https://www.youtube.com/watch?v=50LpU-ZgxMg


C. Agrupación de objetos según su tamaño de menor a mayor y viceversa.
Actividad # 7

Ordenamiento por tamaño
Instrucciones. Revolver las barajas y colocarlas bocabajo. Ir volteando cada una de manera que permita ir ordenándolas según su tamaño.
1.3.4 Abstracción

A. Describir algo sin verlo. Poder describir cada escena con claridad.





Actividad # 8
Descripción de objetos
Instrucciones. El jugador en turno saca un dibujo para describirlo al grupo. Quien lo identifique será el que sacará la siguiente tarjeta y la describirá.

B. Adivina qué es. Ofrecer las características de algún objeto para que lo reconozcan.
Actividad # 9 Adivina qué es
Instrucciones. Escucha con cuidado lo que te voy a decir, pues si eres buen mago, podrás descubrir lo que te acabo de describir.
Lo traigo en mi mano Para llamar y jugar Todo el tiempo lo miro Y le puedo hablar cuando deja de sonar

Me sonríes, y sonrío. Si yo te miro, tú me ves Y todo lo que te digo Te lo digo al revés.
Entramos y salimos De nuestro agujero marchando todas juntas Somos rojas o negras Trabajadoras y fuertes
Mi cuerpo es de papel y mi colita de trapo. Subo y subo amarrada, pero no me sueltes, o me escapo.

2 Ejercicios de esquema corporal.
A. Reconocer partes de su cuerpo. Poner las tarjetas bocabajo
Actividad # 10
Las partes del cuerpo
Instrucciones. Identifica la parte del cuerpo que está en la tarjeta y muestra en dónde se ubica tanto en tu cuerpo como en el muñeco.
B. Armar el cuerpo. Empleo de rompecabezas con la figura de un niño o un muñeco desarticulado, que se debe armar.
Actividad # 11
Armado de muñecos
Instrucciones. Después de haber identificado las distintas partes del cuerpo, colorea y recorta los muñecos. Une sus partes con broches alemanes para que los puedas mover según lo vayan sugiriendo los participantes.



3 Ejercicio de direccionalidad y noción derecha – izquierda.

A. Reconocer su mano derecha e izquierda.
B. Saltar en un solo pie.
C. Ejercicios de lateralidad cruzada (con la mano derecha tocar el ojo izquierdo)
Nota: Lateralidad: lado preferente del cuerpo.
Actividad # 12
Noción derecha e izquierda
Instrucciones. Distingue hacia dónde va cada figura y señala según sea la muestra.


a) Colorea las figuras que van hacia el mismo lado que la muestra
b) Poner un círculo rojo a los coches que van hacia la derecha y uno azul a los que van a la izquierda

1.3.5 Atención
A. Serie numérica. Tachar o subrayar un número determinado en una serie. Encierra en un círculo el doble de cada número que señalas.



Actividad # 13 Atención y concentración
Instrucciones. Ve señalando el doble del número que has circulado primero.
MaríaTeresaAliciaSilvayOrtiz. Paradigma cognoscitivo y las DAM. Manual. Parte 4
B. Ritmo. Golpear el pupitre tantas veces como lo hace el maestro y con el mismo dedo. Eco rítmico con el lápiz. Combinar aplausos y pies.
Video Clap clap sound. Percusión corporal. Seguir el ritmo con distintas partes del cuerpo. https://www.youtube.com/watch?v=6UYnHJqo7_4

C. Noción de cantidad. Poner la pinza en la cifra que represente la cantidad en cada tarjeta.
Actividad # 14


Correspondencia número-objeto

Instrucciones. Ve señalando el doble del número que has circulado


D. El tren numérico. Ir subiendo y bajando los números de los vagones según se diga.


Corre trenecito


Corre trenecito, corre por el campo;, que llegas y te paras cerca de la estación. Aló, aló, que suba el número 2 y que baje el 5.




Video: Corre trenecito (adaptar la letra). Poner y quitar números en los vagones. https://www.youtube.com/watch?v=s2mSNQYDjcg
1.3.6 Ejercicio de maduración prenumérica

A. Ejercicios de mucho o poco. Señala dónde hay muchos y dónde pocos. Mete en este frasco muchos dulces y en este otro frasco pocos dulces.
Actividad # 15 Maduración prenumérica




Instrucciones. Resolver los ejercicios de maduración prenumérica.



s
B. Tomar varios objetos y decir cuál pesa más. Señala ¿cuál pesa más?

¿Cuál pesa menos?
C. Colocar el 1 delante del 2, etc. Sigue el orden de los números para terminar el dibujo y colorea



Consulta otras actividades: https://www.imageneseducativas.com/fichaspara-trabajar-los-numeros-en-infantil-y-preescolar/

1.3.7 Numeración y seriación

Actividad # 16 Numeración y seriación
Instrucciones. Llevar a cabo los distintos ejercicios que permitan reforzar la numeración y la comprensión de la seriación.
A. Sigue la serie. ¿Qué color sigue?


MaríaTeresaAliciaSilvayOrtiz. Paradigma cognoscitivo y las DAM. Manual. Parte 4
B. Noción de cantidad. Cuenta y colorea.
C. Percepción de la forma. Números básicos.


1.3.8 Operaciones

Cuadros geométricos. Ir colocando debajo de cada botón o figurita distribuida horizontalmente, otros elementos formando hileras verticales. Repetir lo mismo utilizando números.


Actividad # 17 Tabla de doble entrada
Instrucciones. Coloca las figuras geométricas de acuerdo con las indicaciones del cuadro de doble entrada. Después, sustitúyelos con los números de colores.


Nota:
Se recomienda poner en práctica los ejercicios sugeridos en los videos de mi canal en YouTube:

https://www.youtube.com/channel/UCMM3ooyNO8QDDllBrEv3Rbg
Actividad # 18 Multiplicación

Instrucciones. Localiza las operaciones que están en los muñecos en la tabla pitagórica. Ve comprobando los resultados y la lógica que tiene.

1.4 El método ABN y la suma
El aprendizaje de la tabla de sumar es el primer paso para la construcción del algoritmo de la suma, ya que la realización de sumas mentalmente agilizará y facilitará el aprendizaje progresivo de esta operación. este aprendizaje no se hará a partir de la tabla ya completada, si no mediante su construcción progresiva como aquí se expone. Junto a esta construcción y progresiva memorización se deben acompañar ejercicios de numeración en los cuales no se trate únicamente la simple memorización del resultado de dos sumandos, sino de todos los caminos que pueden llegar a ese mismo resultado. Es decir, además de saber que 8 + 7 son 15, también deben trabajar (y a esto nos va a ir ayudando la construcción de la tabla de sumar) que también es a la inversa 7 + 8, el doble de 7 +1, el doble de 8 – 1, la suma de 10 + 5, el resultado de contar 6 a partir de 9, o de retroceder 3 desde 18.
Pasos para la construcción de la tabla de sumar
1.- A cada niño se le dará una ficha con la tabla de sumar vacía y se pondrá una grande en la clase
2.- Los casilleros de la tabla de doble entrada, tanto en la tabla del alumnado como de clase, se hará una vez aprendida la familia correspondiente.

3.-Empezamos por construir la fila y columna del cero donde uno de los sumandos es el cero, ya que no les ofrecerá ninguna dificultad (21 combinaciones posibles dentro de la tabla).
4.- Seguimos con las combinaciones con el número uno (19 combinaciones dentro de la tabla). Para ello conviene que el número mayor sea el primero y se les indique que sumar uno es el siguiente al que hemos puesto en primer lugar; y una vez conocido y practicado, realizar las sumas a la inversa.
5.- Continuamos con las combinaciones el número diez (17 combinaciones dentro de la tabla). Conviene poner el 10 como primer sumando y seguir el orden 6, 7, 8, 9, 1, 2, 3, 4, 5 y 10 y posteriormente la operación conmutativa.

Con estos tres números se ha completado casi la mitad de la tabla.
6.- El siguiente conviene que sean las combinaciones el número nueve ya que es lo mismo que sumar 10 y quitar 1 (15 combinaciones dentro de la tabla). También aquí el nueve será el primer número y luego a la inversa.
7.- Para las combinaciones del dos podemos recordar el contar salteado (13 combinaciones dentro de la tabla). El orden de presentación igual al del uno.
8.- La que sigue es la familia de los dobles, a la cual sólo le faltan 6 combinaciones posibles en la tabla, las que corresponden a los números 3, 4, 5, 6, 7, 8.
9.- Seguiremos con los vecinos de los dobles, (10 combinaciones). Este tiene un pequeño truco que le explicaremos a los niños, ya que se trata de parejas que se diferencia en 1 unidad (5+4, 6+7…) y consiste el buscar el doble del mayor de los dos y quitándole 1 (Ya han hecho algo similar con el 9).
10.- Los próximos son el número misterioso, (8 combinaciones). Se trata de los sumandos con diferencia de dos unidades entre ellos (7 + 5, 6 + 4…) y el truco es el doble del número que no aparece entre medias.
11.- El siguiente grupo es sencillo ya que se trata de los complementos del diez (2 combinaciones, el resto ya han aparecido) pero que completan el grupo.
12.- Por último, nos quedan 5 combinaciones (10 con la propiedad conmutativa) que no tienen truco sencillo como las anteriores, pero que se pueden memorizar simplemente al tratarse de pocas. Son 8+3, 8+4, 8+5, 7+4 y 6+3. Para este caso podemos enseñarles un pequeño truco Consiste en descomponer el mayor en dos números, un igual al que vamos a sumar y el otro un resto que sumaremos al calcular el doble que nos ha salido. Ejemplo: 8 + 5 = 3 + 5 + 5= 3 + 10 = 13

Actividad # 19 Iniciar la construcción

Instrucciones. Inicia la construcción de la suma empezando por el primer cuadrante. Llena los espacios utilizando los palillos. Después, sustitúyelos con la cifra correspondiente.












Actividad # 20

Identifica unidades y decenas
Instrucciones. Identifica las unidades y decenas en la siguiente lámina y une la columna de la izquierda con la de la derecha utilizando este criterio.


2. Las matemáticas y sus dificultades de aprendizaje bajo el paradigma cognoscitivo

Introducción
Las matemáticas son de los conocimientos más antiguos que ha estudiado el ser humano. Su origen se encuentra en las grandes civilizaciones antiguas (Egipto, Grecia, China y Arabia).



Las matemáticas se encuentran en todos los ambientes de la vida cotidiana. Se requiere en la participación inteligente en la sociedad. Con ellas se desarrollan las aptitudes intelectuales. Aprenderlas es de gran relevancia pues son muy útiles para muchas cosas, como:


a) Son un poderoso medio de comunicación.
b) Son importantes para otros campos de conocimiento.
c) Contribuyen al desarrollo del pensamiento lógico y a la precisión y visión espacial.
d) Suscitan un interés intrínseco en muchas personas.
Las matemáticas son difíciles de enseñar y de aprender. Los estudiosos de la materia afirman que los índices de fracaso en matemáticas son muy altos, sobre todo en los últimos años de la escolaridad.
Las primeras dificultades surgen con la adquisición de las nociones básicas para la comprensión del número: clasificación, seriación, correspondencia, valor cardinal, reversibilidad, etc. El niño necesita experimentar y manipular activamente y adquirir el lenguaje matemático.
No existe una definición operativa universal de las dificultades de aprendizaje (DA), pero la mayoría suelen contar con tres elementos esenciales.

• Especificidad: las dificultades están limitadas a un número restringido de dominios académicos y cognoscitivos.
• Discrepancia: se determina que los rendimientos no miden el potencial del alumno.
• Exclusión: las DA son distinguidas de otras condiciones de impedimento o desventaja.
En el sistema educativo se suele emplear como criterio de discrepancia la presencia de “dos o más años de retraso” (Blanco y Bermejo, 2004; Rivière, 1991) y aunque en principio parece el más fácil de aplicar en el contexto escolar, a edades tempranas no resulta adecuado pues las unidades de medida de la competencia curricular no son iguales y el crecimiento no es constante a lo largo de la escolaridad.
La mayoría de los investigadores prefieren determinar el retraso mediante criterios estadísticos, pero no parece lógico asumir que un 25% de la población infantil tiene dificultades de aprendizaje en matemáticas (DAM). Blanco y Bermejo (2008) observaron que los niños DAM de 1º, a pesar de tener una ejecución matemática por debajo la media de sus pares sin dificultades, presentaban tan sólo un año de retraso. Sin embargo, este retraso no se compensaba con el paso de los años, sino que iba en aumento, de forma que al incorporarse a 3º su retraso era de casi dos años y, al iniciar 5º, de más de dos años. Si se establece el criterio de que un niño debe tener 2 años de retraso para intervenir sería necesario esperar a que estén escolarizados en 4º o 5º y por tanto se está ante un modelo de “esperar a que falle”.
En contraste, desde el punto de vista psicopedagógico, se considera que estas dificultades deben ser detectadas precozmente y sometidas a intervención temprana. Es pues el momento de que los responsables educativos valoren la mejor forma de definir las dificultades específicas de aprendizaje (DEA) y de establecer procedimientos de detección. Además, sería conveniente tener en cuenta que más de un año de retraso es estadísticamente significativo en 1º, por tanto, los niños que lo presentan deberían ser considerados con necesidades educativas específicas y, de forma precoz, beneficiarse de los recursos personales y materiales complementarios.
En algunos estados americanos se ha implementado el sistema de detección "respuesta a la intervención", el cual consta de tres fases:
• 1ª Se seleccionan los niños que en 1º presentan bajo rendimiento (por debajo del percentil 25) y no parece justificado por la presencia de una discapacidad.
• 2ª Se le somete a un periodo de instrucción por parte del especialista. De esta forma se comprueba que el bajo rendimiento no se debe a una incorrecta escolarización.
• 3ª Se les vuelve a evaluar tras la intervención y se determina que los que sigan presentando un nivel de ejecución muy bajo (normalmente por debajo del percentil 10) son niños con DEA por lo tanto se emplea con ellos los recursos de Educación Especial.
Se pretende así prevenir dificultades en toda la población empleando los recursos con los que se cuentan en las escuelas y se dejan los complementarios para los niños que realmente lo necesitan.
Desafortunadamente, el estudio de las Dificultades de Aprendizaje Específicas en Matemáticas (DAM) está menos extendido que el de las dificultades lectoras, por lo que es difícil conocer su verdadera prevalencia (Ansari y Karmiloff-Smith, 2002; Jordan, Hanich y Uberti, 2003).
La mayoría de los profesores se preocupan por el aprendizaje de las matemáticas en los orientados de educación primaria debido al nuevo lenguaje simbólico, al uso de las reglas que ocasionan dificultades para el aprendizaje, parecido al proceso de aprendizaje del lenguaje maternal.
Se ha considerado que algunos orientados tienen dificultades para el aprendizaje de las matemáticas porque no pueden aplicarlas como lo imaginó el docente, pero éstos dentro del contexto en el cual se desarrollan, pueden resolver situaciones problemáticas, como compras y ventas sin necesidad de recurrir a pasos sistematizados.


El reto está en considerar la siguiente pregunta: ¿en realidad son ellos los que tienen dificultades? Cuando se trabaja con matemáticas en las escuelas, casi siempre se hace de manera tradicional y autoritaria, limitando al niño en muchas cosas que podría experimentar directamente, dificultando su aprendizaje debido a que no responde a sus intereses.
Los orientados son el reflejo sus maestros en el aula. Quien tiene desconocimiento del número, aunque sepa cómo se escribe el signo, no lo puede manejar en su contexto, porque le faltó pasar por un proceso de adquisición pues no lo experimenta, ya que sólo se le suele enseñar de manera verbal y repetitiva. Las dificultades no están en el orientado, sino que éstas se presentan cuando tiene que resolver situaciones que implican el uso de la suma o de la resta, porque para resolverlas tiene que seguir ciertos pasos de forma sistemática, que le fueron enseñados de manera verbal, no permitiéndole hacer manipulaciones, ni aplicar su curiosidad; porque las matemáticas es saber hacer, resolviendo problemas.
Tiene dificultad para aprender un contenido de manera superficial, donde el único apoyo del maestro es proponer actividades del libro, prohibiéndole trabajar con sus compañeros, que le permitan superar sus dificultades, perdiendo la oportunidad de relacionarlo con su contexto.
El docente ha de ser consciente de que éste es un mundo nuevo, donde se le obliga al orientado a relacionarse con números, que no solamente son abstractos, sino que le resultan imprescindibles; prohibiéndole formular, probar, construir e intercambiar sus ideas o adoptar nuevas, a partir de sus propias hipótesis.
Con base en las ideas de Vygotsky, se puede afirmar que el orientado no tiene dificultades con las matemáticas per se, ésta se presenta cuando se quiere que él aprenda el lenguaje propio de la materia, sin darle la guía y el apoyo que requiere; imponiendo los intereses del docente.
El maestro, al no correlacionar esta asignatura con las demás, hace que el niño pierda el interés, impidiéndosele buscar otras alternativas. Los teóricos
cognoscitivistas afirman que las matemáticas no deben ser enseñadas de forma aislada, sino dentro de un contexto significativo, de lo contrario no es posible su enseñanza.
Dentro de las aulas los docentes, continúan impartiendo paso por paso el currículo oficial, sin alterar el orden, sin aportar innovaciones propias a las actividades propuestas, dosifica los contenidos por mes, eso lo lleva a trabajar de manera sistemática, como consecuencia, los niños que no van a ese ritmo se van rezagando dentro del aula.
Muchas de las funciones que realiza el profesor con serias limitaciones se deben a la falta de una concepción pluridisciplinar que demanda el aprendizaje las matemáticas, diferente de la manera cómo él las aprendió.
Los múltiples cursos de actualización que se les brindan a los profesores no resuelven el problema debido a la superficialidad con que se imparten generalmente, pues no llegan a la raíz del problema por no entenderlo a fondo.
Quienes los imparten necesitan comprender lo que los estudiosos de la materia han encontrado sobre las características y condiciones de aprendizaje de tal forma puedan ofrecer una manera más eficaz al tener presente cómo es la estructura del pensamiento infantil. Este conocimiento les permitiría identificar estrategias y procedimientos adecuados a los intereses de los niños, en contraste con el uso y el abuso de la repetición y la mecanización que generalmente suele emplearse por los profesores. Es el orientado quien debe aprender a resolver cualquier situación que se le presenta por sí solo, y aprender a partir de lo social a lo individual, esto es, el docente es su guía en el proceso de aprendizaje de manera que pueda ir resolviendo cada vez más situaciones por sí mismo. Al convivir con su grupo de iguales podrá contrastar y explicar sus ideas.
Hoy en día se resalta la transmisión de los procesos del pensamiento matemático como una transferencia de contenidos. Por eso, se ha considerado a la psicología cognoscitiva como una guía adecuada para ayudar a desarrollar los procesos mentales de resolución de problemas, en vez del enfoque tradicional que se centra en la transmisión de recetas específicas. Se retoma la idea de Vygotsky de que el docente debe conocer a sus niños, para que pueda potenciar sus habilidades, y utilizar el trabajo colectivo y el juego como medios y de acuerdo con sus intereses
2.1 Teorías generales
Una teoría que ha intentado explicar el aprendizaje de las matemáticas es el Cognoscitivismo Aporta cuatro modelos explicativos de gran importancia:

a) Modelos de comprensión: analizan cómo se traducen los enunciados de un problema en representaciones internas.
b) Modelos de procesos: identifican los pasos que da la persona para resolver una operación cognoscitiva bien definida, como la división.
c) Modelos de estrategias: estudian la forma de escoger, controlar y alcanzar las metas en la resolución de actividades cognoscitivas complejas, como un problema de geometría.
d) Modelos de esquemas: describen el modo de seleccionar e integrar la información de representaciones coherentes. Los aprendizajes matemáticos están ligados a las operaciones del pensamiento. Según Piaget, el desarrollo del pensamiento matemático pasa por distintas etapas, evolucionando desde un pensamiento ilógico e intuitivo a un pensamiento lógico.
1. Dificultades en la numeración: la noción de número comprende un aspecto cardinal y otro ordinal. Para la construcción del número y la adquisición de su valor posicional, el niño deberá realizar operaciones de identidad, clasificación, conservación de la cantidad, seriación, transformación e inclusión.
• Identificación de números: para el reconocimiento y comprensión del número es básica la habilidad de reconocer y discriminar entre varias formas. El niño puede confundir los números en la lectura o en la escritura. También hay que tener en cuenta el componente auditivo, ya que es necesario establecer la asociación auditivo-visual en la identificación de números.
• Correspondencia recíproca: el niño con problemas para el aprendizaje tiene dificultad para entender que cada objeto está representado con su notación numérica. Así, un niño contar los bloques en voz alta (decir los números) a una velocidad, y tocarlos a otra. L falta de coordinación le impide establecer la correspondencia uno a uno.
• Escasa habilidad para contar comprensivamente: el niño no comprende el número, no recuerda los números en el orden correcto, le cuesta saltar de decena…En el conteo ordinal le cuesta determinar la posición de un elemento en un conjunto.
• Dificultad en la comprensión de conjuntos: el entendimiento de la propiedad del número es esencial para comprender el concepto de conjunto, pudiendo diferenciar dos conjuntos por el número de elementos que lo componen. También son importantes los conceptos comparativos o cuantitativos (más, menos, grande, pequeño…).
• Dificultad en la conservación: para los niños con dificultades, más piezas significan más cantidad total. También les cuesta comprender la propiedad conmutativa de la suma y de la multiplicación.
• Dificultad para entender el valor según la ubicación de un número: en ocasiones, los niños presentan dificultades para comprender el valor de un número según su ubicación, especialmente con aquellos que contienen la cifra 0.
• Dificultades en el cálculo: muchos niños aprenden las operaciones básicas por rutina y presentan dificultades, unas veces por falta de memoria y otras por inadecuación en la presentación de las operaciones a realizar, en la presentación del problema o por confusiones de direccionalidad al operar.
• Dificultades en la comprensión del concepto de medida: están relacionadas con la incapacidad de hacer estimaciones acertadas de algo cuando no están disponibles las medidas en unidades precisas.
• Dificultad para aprender la hora: los niños suelen tener problemas para diferenciar entre la manecilla de las horas y la de los minutos. También les
resulta difícil decir las horas intermedias, siendo más sencillo aprender las horas en punto y las medias horas.
• Dificultad en la comprensión del valor de las monedas: pueden tener problemas en la adquisición de la conservación de la materia, y a la hora de reconocer el valor de cada moneda.
2. Dificultades en los algoritmos de las operaciones: Las operaciones aritméticas exigen la comprensión del concepto de número, el conocimiento del conteo y del valor del número según su ubicación. Por tanto, es necesario que el niño domine estos conceptos antes de iniciarse su instrucción. Los errores más frecuentes que cometen los niños al realizar los algoritmos escritos de suma y resta son los siguientes:
a) De colocación de los números: justifican los números a la derecha en vez de hacerlo a la izquierda o no hacen coincidir las columnas de las cifras del primer número con las columnas del segundo.
b) De orden de obtención de los hechos numéricos básicos: empieza a sumar o restar por la columna de la izquierda y avanzan hacia la derecha.
c) De obtención de los hechos numéricos básicos: se equivocan en los resultados de la tabla de sumar o restar.
d) De resta de la cifra menor de la mayor: restan la cifra menor de la mayor sin fijarse si corresponde al minuendo o sustraendo.
e) De colocación de un cero: cuando la cifra del minuendo es menor que la cifra del sustraendo pone como resultado el número cero.
f) De lugar vacío: ante un lugar vació, no completan la operación u olvidan la llevada.
g) De olvido de la llevada: no incorporan la llevada a la columna siguiente.
h) De escritura del resultado completo: cuando al operar una columna obtienen un número de dos cifras lo escriben completo en el resultado.
3. Dificultades en la resolución de problemas: Los niños con deficiencias de decodificación y de comprensión en el proceso lector, suelen tener dificultades para interpretar correctamente los problemas. Muchas veces el déficit está relacionado con el vocabulario, y otras, la dificultad radica en el ordenamiento temporal o espacial.
• Algunas de las variables relacionadas con esta dificultad son: la longitud del enunciado, la formulación complicada o desordenada del enunciado, la aportación de información innecesaria, los términos técnicos poco comprensibles, las palabras con significa-do múltiple y la puntuación confusa.
• Una posible estrategia para trabajar la dificultad en la comprensión de problemas podría ser el seguimiento de estos pasos:
1. Sacar la idea general sobre la estructura del problema.
2. Plantearse qué se pide en el problema.
3. Analizar los datos.
4. Plantearse qué se debe hacer y cuál sería el orden correcto.
5. Realizar cálculos y operaciones.
6. Responder a la pregunta con unidades de medida.
7. Observar si la respuesta es lógica y comprobar el resultado obtenido. La didáctica de la resolución de problemas debe contemplar que la acción sea significativa dentro del contexto real vivido por el niño y de su estado evolutivo. Además, se debería enseñar a los niños a leer detenidamente el problema, repetirlo con sus propias palabras, verbalizar y reproducir la situación del problema.
2.2 Campos del conocimiento matemático
Las matemáticas ofrecen un conjunto organizado de conocimientos jerarquizados, respetando una minuciosa lógica interna y coherente. Sus tres campos principales son:
a) La numeración.
b) La aritmética.
c) La resolución de problemas.
Portellano (1991) ofrece el siguiente esquema sobre los campos del conocimiento matemático:
Resolución de problemas
Operaciones Aritméticas básicas
Concepto de número Procesos cognoscitivos:
- Atención
- Memoria
- Razonamiento
- Percepción
Lenguaje Conceptos básicos:
- Tamaño
- Forma
- Cantidad
- Orden
- Posición
Cuadro # 1. Campos del conocimiento matemático.
Al parecer, la enseñanza tradicional no se adapta a las exigencias cognoscitivas necesarias para el dominio de esta disciplina.
2.2.1 Concepto de número
Las investigaciones de Piaget han tenido gran relevancia en la enseñanza del número. Éste es una abstracción que se forma lentamente en el niño a través de diversas experiencias. Piaget y Szeminska (1941) señalan que se necesitan dos condiciones psicológicas para su elaboración:
• La conservación del todo: el todo es un conjunto de partes que se puede distribuir como se quiera. Tiene que haber reversibilidad del pensamiento para que haya conservación.
• La seriación de los elementos. El número se construye en la medida que los elementos de la serie son concebidos a la vez como equivalentes y no equivalentes.
o Equivalente: se pueden agrupar en una misma clase, caracterizada por un cardinal.
o No equivalente: pueden ser seriados, siendo cada término de la serie semejante a los demás y diferente por el lugar que ocupa en la serie. El conteo prepara para adquirir habilidades numéricas posteriores. Gelman y Gallistel (1978) señalan cinco componentes de la habilidad de contar:
a) Correspondencia uno a uno: se da un emparejamiento biunívoco entre cada uno de los objetos y su etiqueta.
b) Orden estable de la secuencia numeral: 1, 2, 3, 4, 5, etc.
c) Principio de cardinalidad: el último número de la secuencia representa no sólo el elemento situado en la última posición, sino también el conjunto formado por todos los elementos.
d) Orden irrelevante: se pueden contar los objetos de izquierda a derecha o de derecha a izquierda sin afectar el resultado del conteo.
e) Principio de abstracción: permite contar tantos objetos homogéneos como heterogéneos, sin que se altere el resultado.
Cuando el niño ha adquirido la conservación y la seriación puede abordar la numeración. Para establecer la correspondencia cantidad-símbolo, debe ser capaz de percibir visualmente una cantidad, de evocar el símbolo correspondiente a dicha cantidad y de realizar el grafismo de dicho símbolo. El cuadro representa la correspondencia entre los objetos y su número.
s s s s s s s s s s
Fig. # 38. Correspondencia objeto y su número

La grafía de los números no es tan arbitraria como pudiera parecer. Se representa por un signo cuyo número de ángulos es igual a la cantidad que representa. El cero es redondo, sin ángulos. El uno tiene un ángulo, etc. Con el siguiente cuadro, Feliz y González (2002) representan el significado del grafismo de los números:
Para aprender la numeración debe comprenderse el valor posicional de los números dentro de las cifras. Por ello, antes de la representación gráfica hay que manipular diferentes materiales: fichas, palitos, bolitas, de modo que el niño comprenda cómo 10 unidades forman la decena.
2.2.2 Operaciones aritméticas básicas
Para aprenderlas se debe interiorizar previamente las nociones básicas, la numeración, las relaciones espaciales y temporales, etc., pero especialmente el vocabulario, como juntar y separar primero; sumar y restar, después. El aprendizaje de las operaciones debe seguir el orden de dificultad que presenta cada una de ellas. Primero se suman las unidades, después decenas sin llevar, llevando, etc. Después se pasa a la resta, luego a la multiplicación y se termina con la división. Éstas no se comprenden si no se realizan. El niño debe entender que:
• La suma es esencialmente una operación de unión.
• La resta se caracteriza por su complejidad: sirve para calcular una diferencia, una comparación y la parte desconocida de una suma (contrario de sumar).
• La multiplicación es una suma abreviada de números iguales.
• La división corresponde a dos acciones diferentes: una partición (“Tenía 6 lápices, he hecho 2 partes: tengo 3 lápices en cada parte”) y una distribución (“tenía 6 lápices, he hecho grupos de 3; tengo 2 grupos”).
El mecanismo de las operaciones implica: noción de espacio y de orientación. Los números se escriben de izquierda a derecha, pero las operaciones se calculan de derecha a izquierda. La resta y la división presentan dificultades específicas.
Según Vergnaud (1985), la principal dificultad está en traducir una situación del mundo real a una operación, pues exige dominar dos tipos de cálculo:
• Cálculo de relación: lo forman las operaciones de pensamiento para manejar las relaciones que intervienen en la situación, y que se expresan como teoremas o inferencias en acción, no necesariamente explícitos.
• El cálculo numérico: incluye operaciones de suma, resta, multiplicación y división.
2.2.3 Resolución de problemas
Según Bermejo (1998), se identifican distintos tipos de problemas matemáticos, el conocimiento que entra en juego en los mismos y las fases sucesivas en su resolución. Es importante cómo se representa.
Problemas de cambio
Estado inicial Cambio Estado final
Problemas de combinación
Problemas de comparación Parte Parte Todo
Cuadro # 2. Problemas de cambio.
• El esquema de los problemas de cambio consta: estado inicial-cambio-estado final. Ejemplo: Alberto tiene 7 caramelos. María le da 3 más. ¿Cuántos tiene caramelos tiene ahora Alberto?
• El de los problemas de combinación: parte-parte-todo. Antonio tiene 5 caramelos y María 8. ¿Cuántos caramelos tienen entre los dos?
• En los problemas de comparación: conjunto grande-conjunto pequeño-conjunto diferencia. Elena tiene 6 caramelos. Sergio tiene 3 caramelos más que Elena. ¿Cuántos caramelos tiene Sergio?
Las cantidades aparecidas en los problemas se escriben en el interior de los dibujos, decidiéndose después si hay que sumar o restar.
La representación de los problemas proporciona una base para su comprensión y facilita el establecimiento de relaciones entre los términos del enunciado y la selección del procedimiento para resolverlo. Esto evita que los problemas se asocien a la idea de número, de operación, pero no al de búsqueda. Lo más importante de los problemas no está en los datos, sino en la relación que hay que establecer entre ellos para llegar a la solución correcta.
En el conocimiento para solucionar problemas se diferencian los siguientes:
a) Conocimiento lingüístico: Interviene en la fase de traducción del problema.
b) Conocimiento general: acerca del mundo y conocimiento de esquemas o representación mental de la estructura semántica que subyace al problema. Interviene en la fase de integración de los datos del problema.
MaríaTeresaAliciaSilvayOrtiz. Paradigma cognoscitivo y las DAM. Manual. Parte 4
c) Conocimiento estratégico: o análisis de medios-fines. Es necesario para la fase de planificar la solución.
d) Conocimiento operativo: procedimiento necesario para resolver el problema, cómo sumar, se precisa en la fase de ejecución.
Las fases de resolución de problemas y conocimientos implicados en las mismas, según Santiuste y González Pérez (2005) se representan en el siguiente esquema:
Fase de resolución Conocimiento implicado
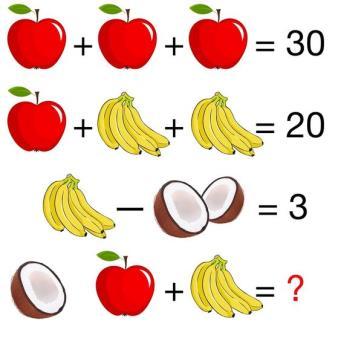
Traducción
Integración de los datos

Planificación

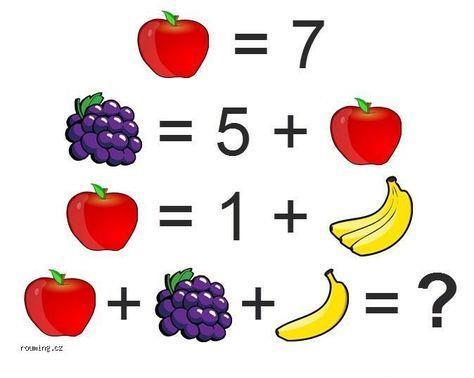
Ejecución

Lingüístico
• Conocimiento del mundo
• Conocimiento de esquemas
Estratégico
Operativo
Cuadro # 3. Fases de resolución de problemas y conocimiento implicado

Actividad # 21

Encuentra el valor de cada objeto
Instrucciones. Encuentra el valor de cada figura.
3. Dificultades en el aprendizaje de las matemáticas
Según Rivière, 1990), las dificultades en las matemáticas se basan en conceptos muy discutidos y de dudosa consistencia. Tradicionalmente se habla de la discalculia para referirse a los niños que presentan un trastorno de estructura que les dificulta aprender matemáticas.
Todavía no se cuenta con una definición clara, operativa y rigurosa para esto, por tanto, aquí se emplea el término dificultades en el aprendizaje de las matemáticas (DAM) para referirse a las personas que no logran el dominio de ciertas formas de pensamiento matemático, o que encuentran grandes dificultades para alcanzar los objetivos establecidos en el currículo escolar. No se sabe con precisión cuál es la etiología de esta dificultad, pero parce ser multifactorial. Los más importantes son:
a) No establecer la asociación número-objeto.
b) No comprender que un sistema de numeración está formado por grupos iguales de unidades que dan lugar a unidades de orden superior.
c) No comprender el valor posicional de las cifras dentro de una cantidad.
d) No descubrir la relación de los números en una serie.

e) Mostrar alteraciones en la escritura de los números (omisiones, confusiones, reiteraciones, números en espejo o invertidos, etc.).
f) Manifestar dificultades en la estructura espacial de las operaciones o en la comprensión de las acciones correctas que debe realizar.
g) Confundir los signos.
h) No conocer las operaciones necesarias para resolver un problema.
i) No considerar todos los datos de un problema u operar con ellos sin tener en cuenta el resultado., etc.
3.1 Dificultades en áreas específicas
Es importante identificar las DAM en las primeras etapas de la escolaridad, pues su aprendizaje pasa por un largo proceso de desarrollo en el que las dificultades iniciales pueden llegar a ser mayores.
Fernández, Llopis y Pablo (1991) identifican ocho áreas en las DAM: numeración, cálculo, álgebra, resolución de problemas, geometría, gráficas, fracciones y uso del lenguaje matemático.
1) Numeración. Conocimiento y memorización de los números generalmente no tiene dificultad, excepto con los números grandes, pero sí: La asociación número-objeto y la concepción del número como la unión de las operaciones de clasificar y seriar.
a. Los fundamentos del sistema decimal.
b. La escritura de los números, debido a problemas de espacio o de lateralidad, o a la comprensión del valor posicional de las cifras.
c. El establecimiento de la clave para seguir una seriación, especialmente si es descendente.

2) Cálculo. La comprensión y la mecánica de las cuatro operaciones básicas es la principal DAM. Con frecuencia se falla por déficits cognoscitivos, afectivos, grafomotores y perceptivos Estos niños necesitan mayor apoyo manipulativo. Mayer (2002) ilustra algunos fallos de la resta en el siguiente recuadro.
Cuando resta de una columna cuyo número superior es 0, el niño escribe 5, pero no sigue restando de la columna de la izquierda del 0.
El niño resta el dígito menor en cada columna del mayor, sin tener en cuenta cuál está arriba.
0
21 121
Cuando el dígito superior en una columna es 0, el niño escribe el dígito inferior como respuesta 0
Cuando el dígito superior en una columna es 0, el niño escribe como respuesta el dígito que está debajo. Cuando el niño necesita restar de una columna cuyo dígito superior es 0, se salta la columna y resta de la siguiente. Cuadro # 4. Fallos en la resta.
Multiplicación y resta


¿Cuál es el valor de cada objeto? Clave once once

nueve diez y seis ? = 176


con multiplicación y


Tabla de multiplicar

¿Cuál es el valor de cada objeto?
Clave uno tres seis dos diez y ocho
Colores
¿Cuál es el valor de cada color?
3) Álgebra. Con frecuencia no comprende que las letras simbolizan números, y que pueden tener un único valor (como en X + 5 = 9) o infinitos valores (como en X + Y = 0); tienden a sustituir expresiones aditivas (3 + X) por multiplicaciones (3x); no respetan ni comprenden el significado de los paréntesis. Los errores más comunes en secundaria son:




a. Interpretación incorrecta de la jerarquía operatoria.
b. Mala utilización de las reglas para quitar paréntesis.
c. Operaciones incorrectas con los números negativos.
d. Interferencia de reglas en las operaciones con potencias y raíces.
e. Preponderancia del número sobre la letra al operar.
f. Incorrecta interpretación algebraica del enunciado de un problema.
g. Desprecio de datos, etc.
Parece ser que estos errores se deben a factores tales como:
• Memorización de reglas, que se utilizan erróneamente por analogía con otras reglas conocidas.
• Generalización abusiva de reglas.

• Uso del signo igual como una acción que debe llevar a un resultado, en lugar de como un equilibrio manipulable en ambos sentidos.

• Omisión de algunas condiciones.
• Necesidad de reducir las situaciones a términos más simples; traducción literal de enunciados, etc.
4) Resolución de problemas. Se observa que los niños con trastornos de lenguaje tienen particulares dificultades para comprender el texto; los que padecen desorientación espaciotemporal, falta de estructuración mental o atención inestable, no ordenan bien las partes del problema.


5) Geometría. Presenta muchas dificultades debido a la aridez y abstracción de algunas nociones (línea, plano…) y a la terminología (pentágono, polígono…). Por formarse ideas equivocadas sobre el espacio debido a una enseñanza inadecuada al centrar su atención sobre conceptos erróneos; como llegar a creer que si una forma geométrica cambia de posición, también cambia su forma o su tamaño. Dickson, Brown y Gibson (1991) advierten que el aprender el concepto


de área en el contexto de medida, ligado a fórmulas, antes de poder experimentarlo prácticamente, induce al alumno a confundirlo con el perímetro o a calcularla midiendo un solo lado de la figura.

6) Gráficas. Suele confundirla con el dibujo de una situación; al no entenderla muestra una relación entre dos variables, confunde los intervalos con puntos particulares, o se centra en uno o dos factores que excluyen el resto al construir la gráfica.



7) Fracciones. Este concepto es difícil de entender. Lo más difícil es tener que sumar o restar la fracción con un número entero, pues considera que el numerador y denominador son elementos independientes, por lo que opera con ellos aisladamente; no interpreta adecuadamente el valor del 0 en la fracción.

MaríaTeresaAliciaSilvayOrtiz. Paradigma cognoscitivo y las DAM. Manual. Parte 4
8) Lenguaje matemático. El niño debe aprender a expresarse con lenguaje específico y preciso, lo cual es más complicado que su lenguaje natural. Debe acostumbrarse a la abstracción de los signos, símbolos y formulas utilizados. Según Orton (1990), las complicaciones están:
• Debe asimilar una gran cantidad de vocabulario teórico novedoso.
• El significado distinto de estos términos respecto al uso habitual.
• El uso del texto en relación con el léxico, sintaxis, diagramas, tablas, gráficos, etc.

• Los símbolos matemáticos que aparecen.
11.4.2 Dificultades en la resolución de problemas
Las habilidades que Mayer (2002) considera necesarias para resolver los problemas requieren transformar cada paso en una representación interna, por lo tanto, se necesita comprender el lenguaje (conocimiento lingüístico) y del mundo (conocimiento semántico).

• Primer paso: dominar las categorías del problema. Para este autor, los componentes de la resolución de problemas se resumen en el siguiente cuadro:
Componentes
Traducción del problema
Integración del problema
Planificación de la solución y supervisión
Ejecución de la solución
Tipos de conocimiento
• Conocimiento lingüístico
• Conocimiento semántico
• Conocimiento esquemático
• Conocimiento estratégico
• Conocimiento de procedimiento Cuadro # 5. Componentes de la resolución de problemas.
• Segundo paso: la integración del problema. Requiere más de una transformación, por ejemplo: si un libro cuesta 6 pesos, ¿Cuántos libros podría comprar Alberto con 24 pesos? Para tener éxito en su resolución hay que poseer conocimientos sobre las categorías del problema (cambio, combinación y comparación), reconocer la información relevante de la irrelevante y determinar qué información es necesaria para a resolución del problema. El conocimiento esquemático ayuda a integrar la información en una representación coherente.
• Tercer paso: planificación y supervisión de la solución. Para resolverlo hay que establecer un plan, preguntándose primero “¿conozco algún problema parecido?” El conocimiento estratégico ayuda para llevar a cabo los cálculos requeridos en el plan.
Hay tres pasos en el proceso de transformación analógica:
a) Reconocimiento. Se identifica un problema parecido (llamado base) que se puede realizar.
b) Abstracción. Se abstrae el método de solución o principio.
c) Trazado de un plan. Se aplica el método o principio al objetivo.
• Cuarto paso: la puesta en práctica de la solución Una vez que se cuenta con el plan, hay que llevarlo a cabo: realizar los cálculos. El conocimiento del procedimiento adquirido con la práctica produce una progresión de los procedimientos básicos a procedimientos más sofisticados y automáticos.
La resolución de problemas se deriva de diferentes tipos de conocimiento implicados en su resolución:
a) Conocimiento lingüístico: hay una deficiente comprensión y dificultad para decodificar textos a menudo abstractos o ambiguos.
b) Conocimiento esquemático: representación deficiente del problema o verse influido por los modelos intuitivos que se mantienen sobre las operaciones.
c) Conocimiento estratégico: no establecer las metas que faciliten la solución, no estar familiarizado con los procedimientos necesarios para resolver el problema o ser incapaz de elaborar un plan, seguirlo y corregirlo cuando sea necesario.
d) Conocimiento del procedimiento: puede desconocer el algoritmo de resolución apropiado.
Es necesario considerar los siguientes aspectos:
• Dificultades de lectura en matemáticas. Es importante que el profesor utilice técnicas especializadas para leer materiales aritméticos (Terry, 1921) ayude al alumnado a que domine el vocabulario y comprenda la complejidad sintáctica de los enunciados (Langford, 1989), pueda transcribir el enunciado verbal a una forma simbólica. Si se le deja al niño utilizar materiales concretos, como contar con los dedos, es capaz de resolver problemas típicos, como “un granjero tenía 7 vacas y vendió 3, ¿cuántas le quedan?”
• Estrategias matemáticas Realmente no se requiere de estrategias poderosas o sofisticadas, sino al contrario, sencillas para representar el problema, en forma gráfica o figurativa. El reto está cuando el problema no es fácil de representarse figurativamente.
• Los problemas de comparación. Según Lewis y Mayer (1989), algunos niños les es difícil resolver los problemas de comparación, en especial si el término de relación es inconsistente con la operación aritmética requerida, como cuando se emplea la palabra más y su respuesta exige la sustracción. “Alberto tiene 20 canicas; si tiene 8 más que Luis, ¿cuántas canicas tiene Luis?” Esto es el efecto de consistencia: se le dificulta representar las afirmaciones de relación del problema y traducirlas en un plan de solución.
• Los problemas inconsistentes: son difíciles aún para quienes los resuelven bien, pues exige un tiempo de procesamiento adicional: construir un modelo mental para estructurar un plan de solución. Quienes fallan hacen una traducción directa y derivan el plan de solución de claves lingüísticas únicamente. Hegaty, Mayer y Green (1992) señalan que la construcción del modelo mental hace que los alumnos exitosos dediquen más tiempo a leer los problemas inconsistentes que los consistentes, y los que fracasan dedican el mismo tiempo a la lectura de ambos tipos de problemas.
3.2 Causas de las dificultades en el aprendizaje de las matemáticas
Pocas personas logran formarse un pensamiento matemático al terminar la escolaridad obligatoria. ¿Cuáles son las causas del elevado índice de fracaso en las matemáticas? Es posible que, según Beltrán y otros (1987) se deba a:
• Su alto grado de abstracción.
• Su carácter acumulativo de contenidos.
• Su notación simbólica que las hace ser un medio de comunicación preciso.
• No se adquieren en un medio natural.
• No se utilizan de manera constante.
• Su carácter jerárquico, su naturaleza lógica y su complejidad.
Las causas de las DAM son muy variadas y por múltiples factores que interactúan para obstaculizar su aprendizaje, entre los cuales destacan:
A. Factores contextuales: se refiere a los procesos, contenidos y estrategias de enseñanza, como su metodología, la organización de la clase, el estilo del profesor, recursos materiales y temporales, el contenido que debe aprenderse, etc Según Stodolsky (1991) están:
a. Métodos homogéneos: contenidos, formas de enseñanza, metas cognoscitivas y comportamiento de los alumnos
b. La enseñanza de temas sigue un orden estándar: suma, resta, multiplicación y división.
c. Comportamiento uniforme del alumnado: trabajo individual en el pupitre con poca o nula interacción entre sí.
d. Metas: exclusivamente de tipo cognoscitivo.
e. Materiales comunes: libros de texto, ejercicios y fichas de trabajo.
f. Dos patrones mayoritarios de trabajo: sus objetivos en ambos métodos son comunes: la adquisición de determinados métodos y destrezas, transmitiendo la idea de que el conocimiento válido está fuera de él y deben transferírselo.
i. El profesor enseña. Trabajo de pupitre, sesiones de preguntas y respuestas y correcciones y controles.
ii. Los materiales enseñan. Enseñanza individualizada para resolver tareas con materiales diversos, según su propio ritmo.
g. Otros factores: menor énfasis a la lectura, agrupamiento de alumnos por niveles de habilidad, currículo repetitivo, distintas oportunidades de aprendizaje, actitudes del profesorado.
h. Perfiles del profesor (Hafner, 1993): según sus estrategias y estilos:
i. Proporcionan definiciones y dan información sobre hechos.
ii. Establecen comparaciones ente conceptos.
iii. Utilizan dibujos y ejemplos, promueven el razonamiento inductivo a partir de las intuiciones de los alumnos.
iv. Resuelven ecuaciones, multiplicaciones, etc., utilizando sobre todo métodos de ensayo y error.
v. Memorizan reglas, justifican los pasos de cada procedimiento y explican el significado de las fórmulas.
i. Factores de instrucción: según Engelmann, Carnine y Steely (1991), se gasta mucho tiempo en enseñar habilidades de cálculo a expensas de la comprensión de conceptos y la solución de problemas.
i. La mayoría de los temas reciben muy poco tiempo de instrucción.
ii. Hay exceso de repetición, presentación y gradación.
iii. Introducción muy rápida de conceptos sin asegurarse si el alumnado dispone del conocimiento previo necesario.
iv. Uso incoherente de estrategias.
v. No se provee al alumnado de herramientas para que revisen lo aprendido, dificultando la práctica guiada a su trabajo autónomo.
B. Factores socioculturales: nivel socioeconómico y cultural, sexo, etc.
C. Factores cognoscitivos: se refiere a los procesos mentales que subyacen a los errores en los aprendizajes de las matemáticas, como recursos de atención, recuperación de la información de la memoria a largo plazo, conservación de la información en la memoria de trabajo, conocimientos previos y automatización de procesos y operaciones básicas; esto es, estrategias, lenguaje, velocidad de procesamiento, atención, memoria, elaboración de modelos mentales, etc.
a. Según Deaño (1994), la dificultad para resolver problemas se debe a:
i. Falta de conocimientos previos.
ii. Desconocimiento de estrategias informales para usarse en su resolución o por deficiencia estratégica relacionada con la identificación del objetivo o los procedimientos adecuados, la aplicación del algoritmo conveniente o la revisión de los resultados obtenidos.
b. Según Rivière (1990), el alumno debe enfrentarse de manera activa y constructiva a las matemáticas. Muchos de los errores provienen de:
i. La aplicación de algoritmos inventados.
ii. Algoritmos que implican, en sí mismos, la posesión de cierta competencia lógicomatemática.
c. Según Brown y Burton (1978) los errores se deben a dos factores básicos:
i. Sobrecarga de la memoria de trabajo: incapacita hacerles frente a los requisitos de ciertas tareas matemáticas.
ii. Carencia de conocimientos previos para afrontar las tareas.
d. González Penda (1998): afirma que los niños con DAM pueden presentar dos tipos de perfiles cognoscitivos:
1. Problemas en la memoria a corto plazo.
2. Dificultades en el perfil psicomotor especialmente en la coordinación óculo-manual.
3. Dificultades en las habilidades visoespaciales.
4. Lentitud en los trabajos escritos y en el ritmo de adquisición de los conceptos matemáticos.
5. Puntuaciones bajas en la subprueba de códigos del WISC-R
6. Frecuentes errores en las subpruebas de aritmética
7. Dificultades con el significado de las operaciones que realizan, por lo que les incapacita aplicarlas para resolver problemas.
D. Factores afectivos: ansiedad, motivación, actitudes, sentimientos de autoeficacia, etc.
E. Factores neurológicos: las alteraciones neurológicas son causas internas de las DAM, como posibles lesiones cerebrales que en algunos sujetos tendrían repercusión en lo cognoscitivo y afectivo. Todavía hay muchas controversias al respecto, debido a su debilidad metodológica, pues, como dice Rivière (1990) hay niños con dificultad matemáticas a pesar de que son normales sus funciones intelectuales, perceptivas y emocionales, así que aunque padecer lesiones cerebrales llega a afectar esta área, no es la causa de todas o la mayor parte de este problema. De cualquier manera, sobresalen los estudios de:
• Henschen (1920) fue el primero en utilizar el término acalculia para designar un trastorno del cálculo producido por una lesión cerebral, pudiéndose emparentar con la dislexia y/o por un trastorno específico del cálculo manifestado por la dificultad para realizar operaciones.
• Luria (1977) asocia las lesiones cerebrales en zonas del lóbulo parietal inferior, parieto-occipital, sectores frontales, etcétera, producen alteraciones de la representación numérica y del cálculo.
• Money (1973) considera que las dificultades aritméticas se deben a alteraciones en el hemisferio derecho y las de lectura con el hemisferio izquierdo.
• Rourke (1993) encontró dos perfiles neuropsicológicos asociados con el bajo rendimiento aritmético al presentar marcadas diferencias en los potenciales evocados (en aritmética, lectura y ortografía) y en el funcionamiento socioemocional (pobre rendimiento aritmético, pero no en lectura, pues no está
afecta su organización perceptivo-visual ni el análisis visoespacial de orden superior).

3.3Estrategias cognoscitivas y metacognoscitivas
Estas estrategias son clave en las distintas fases de resolución de problemas Según Ashman y Conway (1990), las estrategias requeridas en las fases de resolución de problemas son: Comprensión del problema

¿Funciona el plan?
Cuadro # 6 Estrategias metacognoscitivas
Montague (1992) y Woodward (1991) afirman que quien carece de estrategias generales de solución de problemas:
• No procesa la información que aparece ni utiliza el conocimiento de modo eficaz.
• Tiene dificultades para seleccionar y aplicar estrategias adecuadas.
• No dispone de procesos de autorregulación.
• Aunque conoce y utiliza estrategias similares a las de sus pares cuando lee, calcula y verifica problemas verbales, difiere en su capacidad para representar dichos problemas, es decir tienen deficiencias para parafrasearlos, visualizarlos por medio de ilustraciones o imágenes mentales y establecer hipótesis, metas y planes de solución.
• No integra de forma correcta los subcomponentes de una habilidad, fallando cuando encuentra los detalles más elementales, como un signo de operación o un paso difícil en un algoritmo.
• En general, manifiesta un menor conocimiento metacognoscitivo respecto a sus propias destrezas de resolución.
• Es menos exacto a la hora de predecir cuántos problemas podrá resolver.
• Es menos preciso en identificar qué problemas están resueltos y cuáles no, esto es, carece de regulación metacognoscitiva.
Según Woodward (1991), los niños con DAM necesitan ayuda para automatizar sus procedimientos y para aprender a reconocer cuándo se necesita realizar un determinado cálculo y qué relación guarda con otros problemas.
• No realizan las actividades propuestas porque no sabe qué hacer.
• Aunque parece que aprenden los componentes cognoscitivos y metacognoscitivos de las estrategias con relativa facilidad, no mantienen su uso a lo largo del tiempo.
• Requieren entrenamiento en técnicas de generalización.
3.4 Evaluación de las dificultades en el aprendizaje de las matemáticas
Cualquier intervención educativa debe ser precedida de un diagnóstico diferencial en que se identifiquen las DAM.
Velasco y Jabonero (1984) señalan que la evaluación tradicional examinaba variables como:
• Nivel de desarrollo del razonamiento: conservación, clasificación, seriación, etc.
• La realización de cálculos aritméticos: numeración y operaciones.
• Conceptos matemáticos que posee, su comprensión y expresión verbal.
• Planteamiento de problemas y modo de resolverlos.
• Los elementos gnosopráxicos: estructuración espaciotemporal y dominio del espacio gráfico.
El enfoque cognoscitivo se centra especialmente en los procesos de aprendizaje:
• Conceptos correctos o erróneos.
• Estrategias adecuadas o no para afrontar las tareas.
• Examina tanto conocimiento formal como informal, pues puede ser insuficiente y dificultar el acceso a las matemáticas.
• Detallar los puntos fuertes y débiles del niño.
• La precisión y eficacia de las técnicas matemáticas básicas.
• Su grado de automatización.
• Estrategias seguidas para llegar a una solución.
• Los errores sistemáticos que comete.
• Conocer las insuficiencias de los conocimientos subyacentes.
Los instrumentos que se pueden emplear para el diagnóstico diferencial pueden apoyarse en pruebas estandarizadas, muy útiles por su solidez en su construcción (fiabilidad y validez), estandarización y baremación, pues permite comparaciones con grupos de pares. En general no se usan pruebas aisladas sino una batería de pruebas específicas para identificar los factores que intervienen.
3.4.1 Pruebas psicológicas
Finalidad: identificar déficits de aptitudes específicas asociadas con el rendimiento matemático, la inteligencia general, memoria, hábitos de estudio, autoconcepto académico, comprensión lectora y resolución de problemas. Entre las pruebas que hay en el mercado se toman las subpruebas que se relacionan directamente con este tema. Algunos ejemplos son:
Pruebas Edad/aplicación Objetivo
Escalas de inteligencia
Wechsler
WPPSI: 4 a 6 ½ años
WISC-R: 6 a 16 años
WAIS: 16 en adelante Aplicación individual
Muy utilizadas en la evaluación psicopedagógica
• Subtests: aritmética, memoria auditiva inmediata (dígitos)
• Perfil: puede ayudar en la interpretación neurológica.
Escalas McCarthy de aptitudes y psicomotricidad
MSCA: 2 ½ a 8 ½ años Aplicación individual
Escala numérica con tres subpruebas:
• Recuento y distribución
• Cálculo
• Memoria numérica
Pruebas de factor g: Factor g de Cattell
Matrices progresivas de Raven
DAT: test de aptitudes diferenciales
A partir de los 4 años Aplicación colectiva
• Miden inteligencia general
A partir de los 14 años Aplicación colectiva
Algunos aspectos de inteligencia general:
• Razonamiento abstracto
• Razonamiento verbal
• Aptitud numérica
• Rapidez y precisión perceptiva
• Razonamiento mecánico
• Relaciones espaciales.
Prueba de desarrollo de la percepción visual de Frostig
3 a 7 años
Relevante para el diagnóstico de geometría
• Coordinación visomotora
• Discriminación figura – fondo
• Constancia de forma
• Posición en el espacio
• Relaciones espaciales
Prueba gestáltica visomotora de Bender
Batería Luria –DNI
4 años hasta adultos
A partir de los 7 años
• Valora la integración visomotora
• Alteraciones neurológicas
Evalúa trastornos neuropsicológicos
• Escritura numérica: pide escribir y leer números de izquierda a derecha y de arriba hacia abajo, decidir qué número de entre arios que lee o escucha es mayor.
• Operaciones aritméticas: resolver sumas, restas, multiplicaciones, completar operaciones en las que falta un número o el signo y contar hacia atrás de tres en tres.
Cuestionario de personalidad
Cattell (ESPQ, CPQ y HSPQ)
De 6 años hasta adultos Aplicación individual
Es importante conocer la personalidad del niño y su forma de reaccionar, pues puede influir en su rendimiento académico.
Cuadro # 7. Pruebas psicológicas.
3.4.2 Pruebas pedagógicas
Finalidad: ayudan a determinar el grado de dominio de la diversidad de conceptos y procedimientos propios de las matemáticas.
a) Habilidad para comprender y usar los conceptos de cantidad, combinaciones, número, forma, tamaño, posición y medida.
b) Habilidad para sumar, restar, multiplicar y dividir números naturales, enteros y fracciones.

c) Habilidad para aplicar los conceptos matemáticos a la solución de problemas en situaciones personales y sociales: comprar y vender, calcular diferencias de tiempo, pesar y medir.
d) Habilidad para clasificar y categorizar datos y hechos matemáticos.
e) Adquisición de nociones e información específicamente matemática.
No difieren en mucho de las pruebas que elabora el profesor, pero están más estandarizadas, lo que permite comparar resultados obtenidos con los baremos disponibles del mismo nivel educativo. Algunos ejemplos son:
Pruebas Nivel/edad Objetivo EAP de Terrasa, 1989. Pruebas pedagógicas graduadas para pre-escolar y ciclo inicial
Montesinos y otros (1991). Pruebas psicopedagógicas de evaluación individual
Palomino y Crespo Pruebas de cálculo y nivel matemático
Preescolar Primero de primaria
• Reactivos graduados para distintos niveles de educación infantil y primer ciclo de primaria.
• Reactivos de lógica, cálculo y grafía de números, medida y geometría.
Preescolar Primaria
• Conocimiento de las cantidades
• Operaciones
• Problemas y otros contenidos
7 a 12 años Serie A: nociones previas:
• Conservación
• Seriación
• Previsión
• Clasificación
• Inclusión
Serie B: conocimiento de simbolización matemática:
• Dictado y lectura de números
• Concepto de valor
• Concepto de signos
• Conocimiento de figuras geométricas
• Conocimiento de cuerpos geométricos Serie C: disposición para el cálculo y resolución de problemas:
• Repartición y resta
• Resolución de problemas con elementos concretos, con dificultad en el enunciado
• Problemas abstractos
Cuadro # 8. Pruebas pedagógicas.
3.5 La evaluación informal
La evaluación informal de las necesidades matemáticas, según Jean Gross y Pablo Manzano (2004), se puede realizar también a través de:
a) La observación: mientras el niño trabaja se puede uno dar cuenta de sus patrones de atención y concentración o la falta de ellos, la frecuencia con que pide ayuda, su forma de realizar la selección de los enfoques y los materiales que usa en las tareas prácticas, el lenguaje matemático que emplea y su capacidad para hacer generalizaciones y predicciones.
b) El análisis de errores: revisar con cuidado el tipo de faltas que comete el niño en los cálculos escritos con el fin de entender su forma de pensar.
c) Utilizar materiales de evaluación informal: diseñados para comprobar la comprensión de determinados objetivos básicos que logra conseguir el niño, su progreso mensual o trimestral, para involucrarlo en la supervisión y el establecimiento de sus objetivos
d) Apoyarse de la entrevista informal: para sondear la comprensión del niño preguntándole cómo llega a determinadas conclusiones o como verificación rápida de los conceptos que ha dominado. Por ejemplo, elaborar un formato que permita evaluar en 15 minutos lo que el niño comprende acerca del tiempo, dinero, la medida, el valor posicional, el cálculo y el uso de la calculadora.
e) Combinar con las pruebas estandarizadas: con el fin de hacer una evaluación más detallada y poderla comparar con sus iguales.
Las ventajas de contar con una evaluación precisa sobre el desempeño del niño en esta área y sus dificultades:
• Se pueden plantear con precisión los objetivos de aprendizaje que requiere el niño
• Desarrollar planes de acción.
• Obtener información sobre dónde se pierde el niño en matemáticas con el fin de ajustar los estilos y el proceso de enseñanza-aprendizaje.
• Encontrar alternativas específicas de cómo enseñarle, en lugar de limitarse a la guía de los contenidos correspondientes a su grado escolar.
3.6 Intervención psicopedagógica
Cualquier intervención psicopedagógica que se lleve a cabo debe estar precedida de un diagnóstico diferencial que identifique las causas de las DAM y sus manifestaciones. Con base en éste hay que elaborar un programa seleccionando y organizando las estrategias adaptándolas a las necesidades educativas especiales del niño y tomando en consideración el currículo escolar. Tradicionalmente se consideraba a las DAM como un síndrome unitario, con etiología difusa e incierta, abordada a través de dos formas:
a) Mediante la realización de actividades generales de base psicológica, dirigidos a:
• La adquisición de nociones básicas: conservación, correspondencia, reversibilidad y número.
• El refuerzo de las funciones adquisitivas: atención y memoria.
• A l potenciación de la psicomotricidad: esquema corporal, funciones sensoriales, ritmo, equilibrio y coordinación espaciotemporal.
• La práctica en habilidades de simbolización: expresión oral y escrita.
b) Mediante la realización de actividades específicas para el aprendizaje de las matemáticas:
• La numeración: asociación número-objeto, correcta realización de números. comprensión y utilización de signos matemáticos, sistemas de numeración decimal.
• La resolución de problemas: comprensión, proceso a seguir.
• Nociones específicas como la geometría: relaciones espaciales, mediciones.
Bermejo (2004) afirma que los avances de la investigación cognoscitiva han puesto de manifiesto que una instrucción basada exclusivamente en el aprendizaje de procedimientos resulta estéril si no va acompañada de un aprendizaje conceptual significativo
3.6.1 Principios generales de intervención
Metafóricamente, Rivière (1990) señala que los principios generales en los que se debe basar cualquier estrategia para facilitar el aprendizaje matemático son como un espejo inverso de los factores que lo dificultan, convirtiendo el aprendizaje en algo significativo y motivador para el niño.
Según Hafner (1993) es posible diseñar un perfil de experto en la instrucción de la matemática elemental, utilizando múltiples maneras de representar la información y promover variadas oportunidades para aprender:
• Enfatizar lo conceptual
• Establecer vínculos entre conceptos y organizarlos en patrones o modelos.
• Adoptar una actitud abierta y un enfoque constructivista respecto a esta área.
Las creencias del profesor sobre el pensamiento de sus alumnos afectan el proceso de enseñanza-aprendizaje, por tanto, puede inducir a los aprendices en la construcción del nuevo conocimiento.
En cuanto al entorno de aprendizaje, De Corte (1993), Collins, Brown y Newman (1989), dicen que éste debe permitir la adquisición de aptitudes necesarias para la realización de tareas matemáticas y encaminarse a:
• La transmisión de algoritmos
• Comprensión y construcción de significados
• La enseñanza de estrategias cognoscitivas y metacognoscitivas en un contexto interactivo, como la resolución de problemas en pequeños grupos.
Feliz y González (2002) y Rivière (1990) proponen un decálogo de principios generales para los profesores que deseen lograr una enseñanza de las matemáticas más efectiva y motivadora:
1. Generar expectativas positivas: cuidar las reacciones frente a los errores, los comentarios informales que afectan la autoestima al cuestionar su capacidad y posibilidades de mejora.
2. Atender a la construcción del conocimiento: sobrepasar el simple desarrollo disciplinar y centrarse en un enfoque más global: que el niño investigue, piense, analice, indague, saque conclusiones, etc.
3. La experimentación debe ser la base del aprendizaje: los principios, leyes, pautas, estrategias, etc., se deben introducir a partir de simples experiencias y situaciones significativas que se convertirán en los algoritmos a aplicar.
4. Favorecer y estimular la comprensión: dar tiempo al diálogo, al cuestionamiento, a las consultas, a las dudas, etc. No es adecuado precipitar los resultados. Asegurarse que se ha asimilado lo viejo antes de pasar a lo nuevo.
5. Enseñar paso a paso las estrategias y algoritmos específicos que exige la tarea: utilizar la atención exploratoria del niño como recurso educativo.
6. Asegurarse de que el niño pueda recordar aspectos relevantes de la tarea o problema: ir comprobando que el niño ha procesado la información relevante.
7. La diversidad es un hecho: por tanto, no se puede pretender que todos los niños persigan los mismos objetivos con las mismas actividades y tiempo. Plantear la programación como un espacio flexible y disponer de actividades de diferentes niveles para el refuerzo y la ampliación.
8. La ayuda se debe prestar de forma mutua: utilizar la colaboración entre profesores y alumnos y hacer una coevaluación del trabajo cooperativo con los alumnos.
9. La enseñanza debe seguir una secuencia en espiral ascendente: hay que contextualizar los esquemas matemáticos, esto es un determinado contenido se retoma en niveles sucesivos, superiores y más complejos acordes con los niveles madurativos del niño y valiéndose de otros contenidos que se han ido desarrollando paralelamente.
10.Las tareas de orientación han de ser adecuadas, con procedimientos de análisis profundo y ocasiones frecuentes de aprendizaje incidental: es válido tanto para los que ya están motivados en las matemáticas como para los que no.
3.6.2 Métodos de enseñanza
Bermejo (2004) recomienda aplicar los avances de la investigación cognoscitiva en el aula, en especial las aportaciones de Piaget y Bruner en la didáctica de las matemáticas: un currículo en espiral, el aprendizaje por descubrimiento y el uso de materiales estructurados para construir estructuras abstractas y organizadas.
El esquema de la siguiente página ilustra la secuencia en espiral ascendente de las matemáticas, según Feliz y González (2002)
3.6.3 Los métodos de enseñanza
No todos los métodos de enseñanza producen iguales beneficios, pues depende mucho del aprendiz. Por ejemplo:
a) Capacidad intelectual. los alumnos de capacidad baja necesitan una enseñanza con reglas; los de capacidad media a través del descubrimiento y los de alta capacidad se benefician con cualquiera de los dos procedimientos.
b) Métodos por descubrimiento. Son más eficaces que los de exposición cuando el alumno es extravertido y tiene bajos niveles de ansiedad. Los independientes aprenden más si se les ofrece poca orientación y disponen de material manipulativo; los dependientes requieren orientaciones precisas y de materiales simbólicos.
c) Control interno. Quienes se autorregulan se benefician del trabajo en pequeños grupos; mientras quienes requieren del control externo aprenden por métodos individuales y con la ayuda del profesor.
Víctor Santiuste y Joaquín González-Pérez (2005:293)) sugieren prescripciones de interés complementarias al decálogo de principios generales:
a) Tener en cuenta los conocimientos previos del niño para que los materiales no le resulten demasiado nuevos ni demasiado conocidos.
b) Disponer el tiempo suficiente para que se dé un aprendizaje significativo.
c) Planificar las actividades para que el niño experimente las matemáticas en acción, aclarando los objetivos de estas.
d) Evitar la complejidad de las notaciones, introduciendo la formal y las técnicas pertinentes sólo cuando el niño disponga de suficientes estructuras de conocimiento para asimilarlas y esté adecuadamente motivado.
e) Estimular el aprendizaje de relaciones y la modificación de los puntos de vista, priorizando la comprensión y la resolución de problemas, pero sin descuidar el recuerdo de hechos numéricos, deficitario en el niño con DAM.
f) Aprovechar la matemática inventada por el niño y su interés por el juego.
g) Proporcionar experiencias múltiples, con formas de representación diversas y materiales variados.
h) Emplear la práctica distribuida, breve pero frecuente, en torno a los conceptos más complejos.

3.6.4 Cambio de actitudes
González-Pineda (1998) advierte sobre los factores afectivos que influyen en el niño cuando está resolviendo un problema, por tanto, si tiene una percepción negativa de las matemáticas, generalmente inducidas a través de la instrucción, éste suele inhibirse ante estas tareas, por tanto, hay que romper el círculo vicioso entre las creencias irracionales, ansiedad y conductas de protección, para fomentar creencias constructivas acerca de las matemáticas como, por ejemplo:
• Pobre concepto académico.
• Escasas expectativas de control.
• Patrones de atribución no adaptativos.
• Desconfianza de su capacidad: “yo soy de letras, no sirvo para los números”, “a mí no se me dan los números”.
Para lograr el cambio es indispensable crear un ambiente de confianza en el proceso de enseñanza, y graduar las tareas de manera que el niño logre el éxito de acuerdo con su nivel.
3.6.5 Enseñanza de conceptos y de procedimientos
¿Cuándo surgen las principales dificultades de la enseñanza de las matemáticas?
Comienzan durante la adquisición de conceptos básicos que, según Piaget, son la base de toda actividad matemática.
• Depende del proceso de maduración.
• Enseñar con cuidado nociones de clasificación, correspondencia, valor cardinal, etc.
• Identificar lo relevante de lo irrelevante de cada concepto.
• Ir centrando al niño mediante preguntas, explicaciones breves y claras, ejemplos con las características relevantes más frecuentes.
• Gran variedad de contraejemplos que infrinjan las características relevantes.
¿Por qué Bell recomienda el método de enseñanza diagnóstica?
Bell (1987) recomienda el método de enseñanza diagnóstica, el cual se basa en tareas críticas que exponen las ideas, tanto correctas como equivocadas, del niño, a partir de las cuales se estimula la discusión y uso de muchas técnicas, como diagramas, juegos, invención de preguntas, tareas colectivas, etc. Una vez que el niño descubre el procedimiento correcto de solución, se le plantean problemas similares y se le retroalimenta de inmediato.
¿Qué recomiendan Kelly, Gersten y Carnine respecto a la enseñanza del cálculo y de la resolución de problemas?
Kelly, Gersten y Carnine (1990) señalan que, en el cálculo y resolución de problemas, el niño debe pasar de saber qué a hacer a saber cómo hacerlo con el fin de mitigar concepciones erróneas y lograr un mejor pensamiento estratégico, el cual es la base del funcionamiento metacognoscitivo.
¿Cómo se podría ejemplificar esta recomendación?
El siguiente esquema ejemplifica el proceso de resolución de las ecuaciones: cuál es el procedimiento de despeje de las incógnitas ofrecido por Feliz y González (2002).
¿Cuáles serían los entornos de aprendizaje centrados en la adquisición de capacidades?
De Corte (1993) describe dos entornos de aprendizaje centrados en la adquisición de capacidades:
a) Enseñar problemas verbales de suma y resta a alumnos de primer curso partiendo de la comprensión y representación del conocimiento conceptual subyacente; de este modo se incrementa tanto la cantidad de problemas resueltos como de estrategias utilizadas.
b) Enseñar heurísticos y habilidades metacognoscitivas a alumnos de sexo grado de primaria utilizando el Logo, lo cual facilita la transferencia de dichas habilidades a otros dominios de conocimiento.
Van Haneghan y Barker (1989) intentan enseñar habilidades de monitorización en matemáticas para que el niño determine:
• Si ha dado una respuesta correcta o no.
• Ha elegido una estrategia adecuada o inadecuada.
• Ha comprendido el problema o el concepto.
Cuadro # 10 Habilidades de monitorización.
¿Cuál es el punto de partida que recomienda Derry en las estrategias?
Derry (1989) propone estrategias de resolución de problemas partiendo del reconocimiento de patrones que caracterizan cada tipo de problema y su combinación con las secuencias de acción. Cuenta con el diseño de un programa tutorial para la computadora.

Actividad # 22 Cuento geométrico con tangram


Instrucciones. Diseña tu propio cuento aprovechando el tangram para ilustrarlo. Sube tu propuesta a la plataforma. Aquí cuenta con un ejemplo.
En una bella casa vivía un niño , con su perro , este niño era
muy alegre y le gustaba mucho bailar, pero cierto día su perro se perdió, y el
niño estaba muy triste. Hizo dibujos de su perro y se los enseñó a todos sus
conocidos, alguien le dijo que había visto a su perro cerca del muelle, el muchacho corrió hasta el muelle, el perro al ver a su dueño corrió hacia
él, y los dos felices decidieron realizar un paseo en bote
Fig. # 54. Cuento geométrico con Tangram.






Actividad # 23 Cilindros de operaciones básicas
Instrucciones. Reta a tus compañeros poniendo desafíos que impliquen operaciones básicas Lo pueden jugar en parejas, pequeños grupos o todos. Gana quien coloque los números primero y obtenga la respuesta correcta.



