Chapter_4_Transformations

CHƯƠNG_4_Transformations

52

Sự biến đổi là việc làm cần thiết trong việc model và tạo ra các hình học. Chúng cho phép chúng ta có được các biến thể từ các đối tượng đơn giản ban đầu. Biến đổi giúp chúng ta thay đổi tỉ lệ và định hướng của đối tượng :di chuyển, sao chép, nhân bản, hoặc có thể dẫn đến tổng hợp của các đối tượng. Có nhiều loại biến đổi khác nhau , nhưng để phân loại chúng, chúng ta có thể phân chia thành các nhánh chính, và sự phân chia đầu tiên là biến đổi tuyến tính (linear) và không gian (spatial). Biến đổi tuyến tính thực hiện trong không gian 2D, trong khi biến đổi không gian hiện trong không gian 3D

Cách khác, chúng ta có thể phân loại chuyển đổi theo tình trạng của đối tượng ban đầu, biến đổi như translation, rotation, và reflection giữ hình dạng ban đầu nhưng thay đổi tỉ lệ và làm biến dạng tình trạng ban đầu của đối tượng. Ngoài ra còn có các biến đổi phi tuyến tính. Ngoài translation, rotation, và reflection, chúng ta có các loại biến đổi ti lệ và biến dạng khác nhau và không thống nhất trong không gian 3D như xoắn ốc spiral và xoắn ốc helical .

Để chuyển đổi các đối tượng, chúng ta cần di chuyển và định hướng đối tượng (hoặc một phần của các đối tượng) trong không gian và để làm điều này, chúng ta cần phải sử dụng vector và mặt phẳng là vấn đề cơ bản của các toán học / hình học. Chúng ta sẽ không thảo luận các vấn đề cơ bản của hình học và logic toán học của chúng ở đây, nhưng trước tiên hãy có một cái nhìn sơ lược về vectơ và mặt phẳng vì chúng ta cần chúng để làm việc.

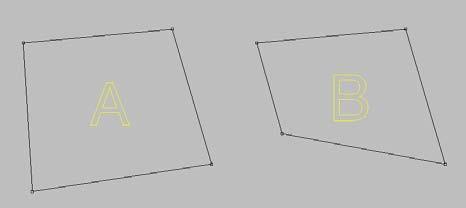
Hình 4.1 Biến đổi có khả năng để tạo ra các hình thức phức tạp từ các cá thể. Thiên nhiên có một số ví dụ tuyệt vời về biến đổi.

53