4_2_On Curves and Linear Geometries

4_2_On Curves and Linear Geometries

Như chúng ta đã thử nghiệm với điểm như là hình học 0 chiều , bây giờ chúng ta có thể bắt đầu suy nghĩ về các đường cong như các đối tượng 1 chiều.Giống như điểm, đường cong có thể là cơ sở xây dựng rất nhiều đối tượng khác nhau.Chúng ta có thể extrude một đường cong cùng nhau và tạo ra một bề mặt, chúng ta có thể kết nối các đường cong khác nhau lại với nhau và tạo ra mặt và khối , chúng ta có thể sắp xếp bất kỳ đối tượng dọc theo một đường cong với những khoảng cụ thể và rất nhiều cách khác để sử dụng một đường cong như là một hình học cơ sở tạo ra các đối tượng khác.

Chuyển vị/ Displacements

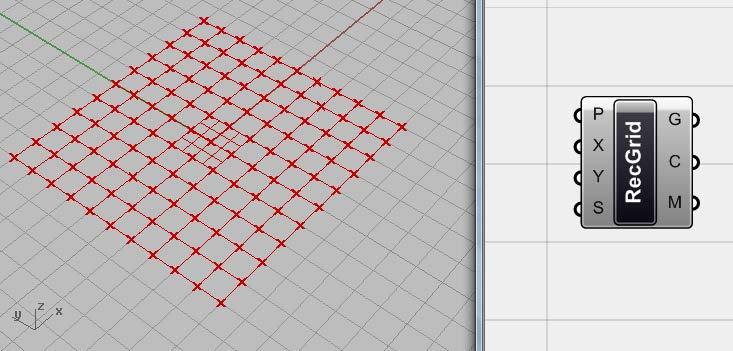
Chúng ta tạo ra lưới điểm trong chương 3 bởi các component <series> và <pt>. Nhưng có một component được gọi <Grid rectangular> (Vector> Point> Grid rectangular) tạo ra một mạng lưới các điểm. Chúng ta có thể kiểm soát số lượng các điểm theo hướng X, Yvà khoảng cách giữa các điểm (tương đương ở cả hai chiều) trong component này.

Hình.4.3. một component <grid rectangular> các giá trị mặc định sẵn của nó

Bạn có thể thay đổi kích thước của lưới bằng <number slider> ở đầu vào (S) của component <grid rectangular>. Bạn cũng có thể thay đổi định hướng của điểm. Để làm điều này, bạn cần một mặt phẳng dính lưới của bạn trên đó. Ở đây, ta giới thiệu một component <XY plane> (Vector> Constants> XY plane) là một phẳng được xác định trước bằng trục X và Y và ta chuyển vị theo trục Z bằng component <Z unit> (Vector > Constants > Z unit) là một vector dọc theo trục Z với chiều dài (độ lớn) bằng 1. Ta có thể thay đổi chiều cao của sự chuyển vị này bởi kích thước của vector thông qua một <number slider>

55

mà ta kết nối với các đầu vào của các component <Z unit>, thay đổi vị trí của <XY plane> dọc theo trục Z sẽ thay đổi vị trí của lưới điểm.

Hình.4.4.điều khiển lưới (lưới được chọn hiện màu xanh lá cây ) với một <number slider> để thay đổi lưới (khoảng cách giữa các điểm) và <Z unit> và <XY plane> khác để thay đổi tọa độ Z của lưới điểm.

Bây giờ nếu bạn nhìn vào out put của <grid rectangular> bạn có thể thấy rằng chúng ta có thể truy cập toàn bộ các điểm cũng như các tế bào lưới và các tế bào trung tâm. Trong ví dụ này, ta đang tìm kiếm một nhóm line bắt đầu từ các điểm trung tâm của các tế bào lưới và mở rộng ra không gian, bằng cách chỉ sử dụng các lưới. Ta chỉ đơn giản là kết nối điểm từ 2 phần M của hai component <grid> cho một component <line>, và tạo ra một nhóm line . Sau đó, thay đổi kích thước của lưới thứ hai sẽ cho kết quả ở hướng của tất cả các line. Ở đây vấn đề là chiều dài của line trong trường hợp này sẽ là khác nhau, nhưng ta muốn vẽ đường có cùng độ dài, và ta cần một chiến lược và đó là lý do tại sao ta sẽ sử dụng một component <line SDL>.

Component <line SDL> vẽ một line với điểm bắt đầu (S), Hướng (D), và Dài (L).Vì vậy, chiều dài của line là điều khiển được.Chính xác những gì ta cần, ta có những điểm bắt đầu (trung điểm của tế bào), và chiều dài line. Hướng?Ta muốn sử dụng lưới tế bào trung điểm thứ hai là điểm thứ hai của line để hướng line của ta là theo hướng của các đường kết nối các điểm giữa lưới tế bào. Để xác định các hướng ở đây ta cần một số vectơ thay vì line.Đó là lý do tại sao ta sẽ tạo ra một tập các vectơ bởi hai bộ điểm này để tạo ra hướng cho component <line SDL>.

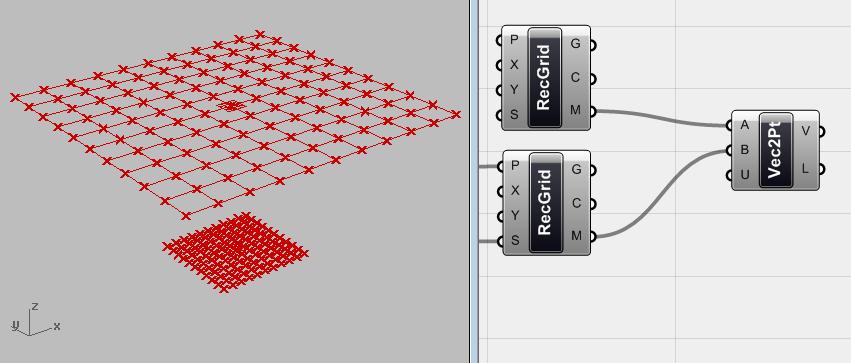
Hình.4.5. Tạo vectơ từ các điểm của lưới đầu tiên hướng tới các điểm của lưới thứ hai của component <vector 2pt> (Vector> Vector> vector 2pt). Component này tạo ra vectơ bằng điểm bắt đầu và điểm cuối của vectơ.

56

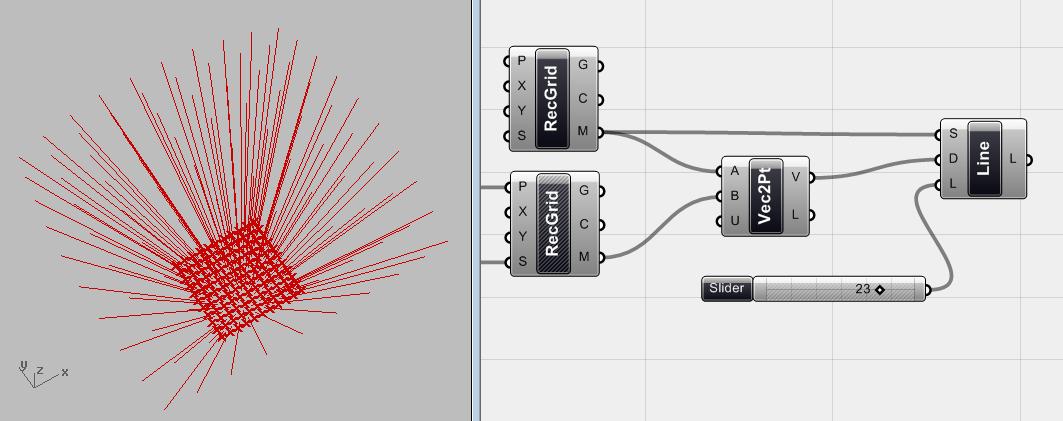
hình.4.6. <line SDL> tạo ra loạt các line từ lưới điểm thứ nhất trải ra vào không gian bởi vì kích thước lớn hơn của lưới thứ hai. Ta có thể thay đổi chiều dài của line bằng <number slider> và ta có thể thay đổi hướng của chúng bằng cách thay đổi kích thước của lưới thứ hai.

Bước tiếp theo, ta muốn thêm một đa giác ở phần cuối của mỗi đường và extrude nó đến điểm bắt đầu của line để cảm nhận tiềm năng sinh ra của các component đường cong.Để tạo ra các đa giác, ta có thêm một mặt phẳng tại điểm cuối của line là mặt phẳng cơ sở để có thể tạo ra các đa giác.

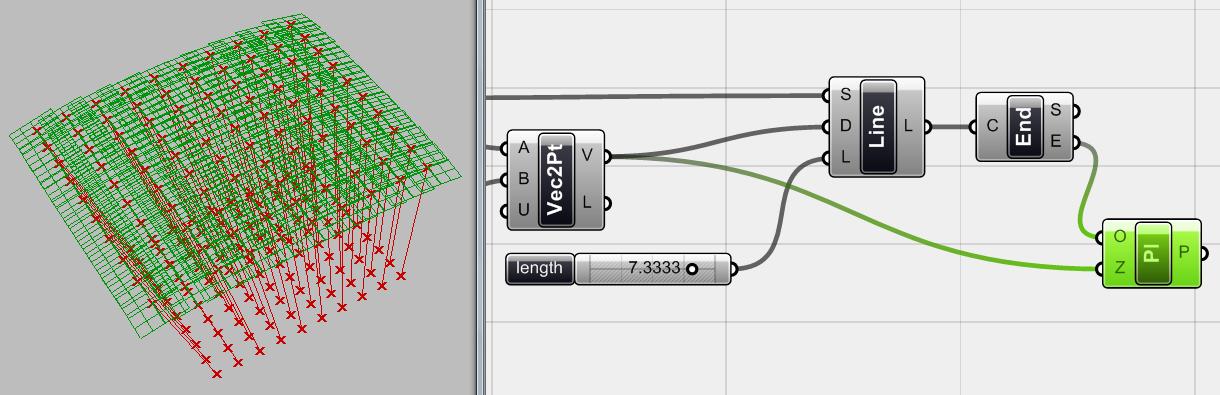
Hình.4.7.bằng cách dung component <end points> (Curve > Analysis> end points) và dung <endpoints> như là gốc toạ độ cho tập hợp các mặt phẳng, ta có thể tạo ra các mặt phẳng cơ sở. Ở đây ta dùng component <Plane Normal> (Vector> Plane) tạo ra các mặt phẳng bằng một điểm gốc và mộ vector theo trục Z cho mặt phẳng(vector pháp tuyến là vector vuông góc với mặt phẳng). ở đây ta dùng những vector của line như là vector pháp tuyến của mặt phẳng.

57

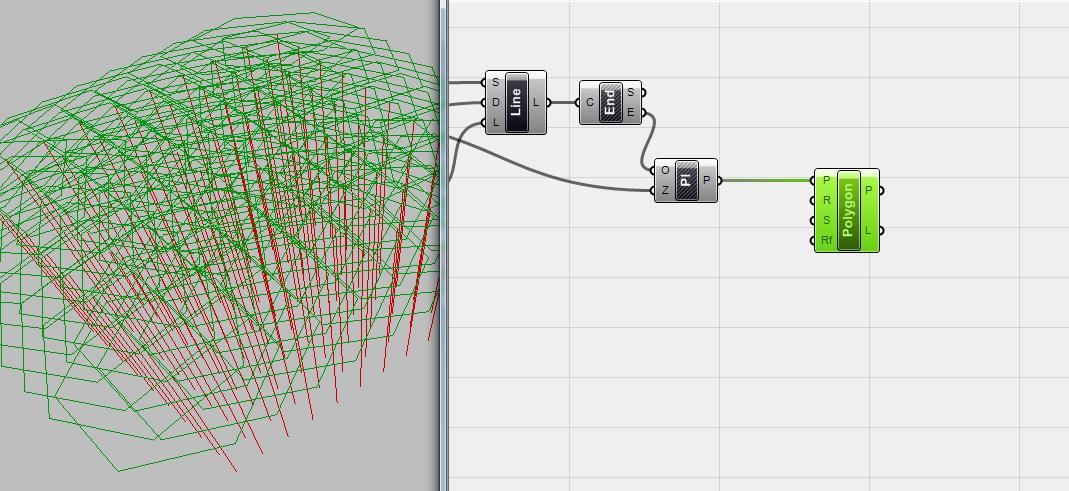
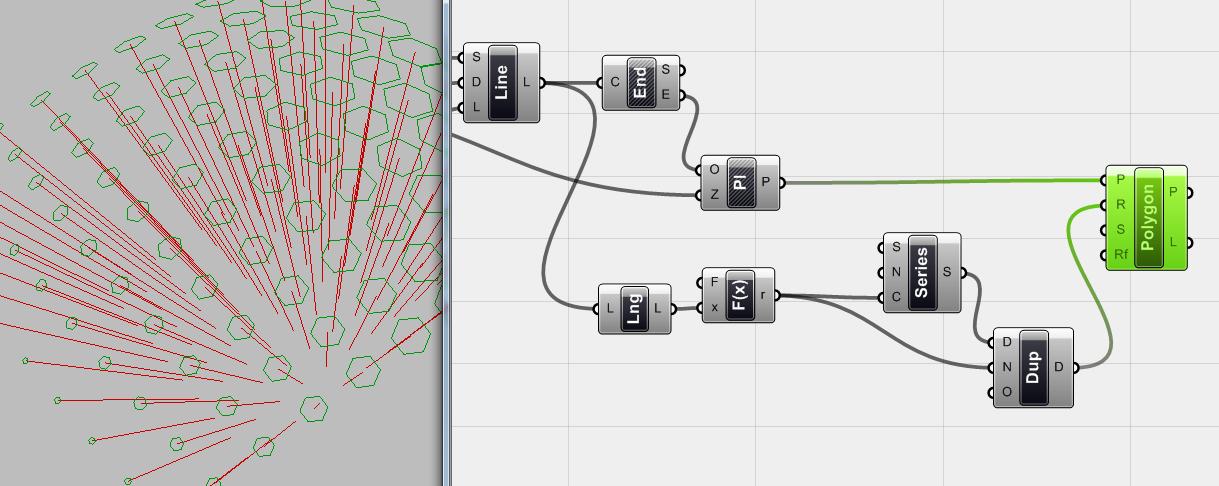
Hình .4.8. thêm vào component <polygon> và dùng các mặt phẳng đã được tạo ra như là mặt phẳng cơ sở cho các lục giác, chúng ta có một tập hợp các lục giác ở điểm cuối và vuông góc với các line đã tạo ra.như các bạn đã thấy, nhưng lục giác này có chung một kích thước nhưng ta muốn có sự thay đổi về kích thước tạo ra một hình dáng mượt mà hơn.

hình.4.9. Với component <List Length> ta nhận được số lượng line và các component <function> tiếp theo đó là căn bậc hai của các đầu vào (F (x) = Sqrt (x)), tính toán số lượng line ở mỗi hàng. Ta sử dụng một component <series> với điểm bắt đầu và kích thước bước (step) = 0,1. Vì vậy, ta tạo ra một danh sách các số từ lớn dần lên bằng số lượng các đa giác ở mỗi hàng. Để có thể sử dụng các giá trị cho tất cả các đa giác, ta nhân đôi các danh sách dữ liệu với số lượng cột (ở đây bằng số lượng hàng) và gắn nó vào

58

đầu vào (R) của đa giác. Như bạn có thể nhìn thấy trong model, mỗi hàng, kích thước của đa giác dần dần thay đổi và mô hình này lặp đi lặp lại đến người cuối cùng.

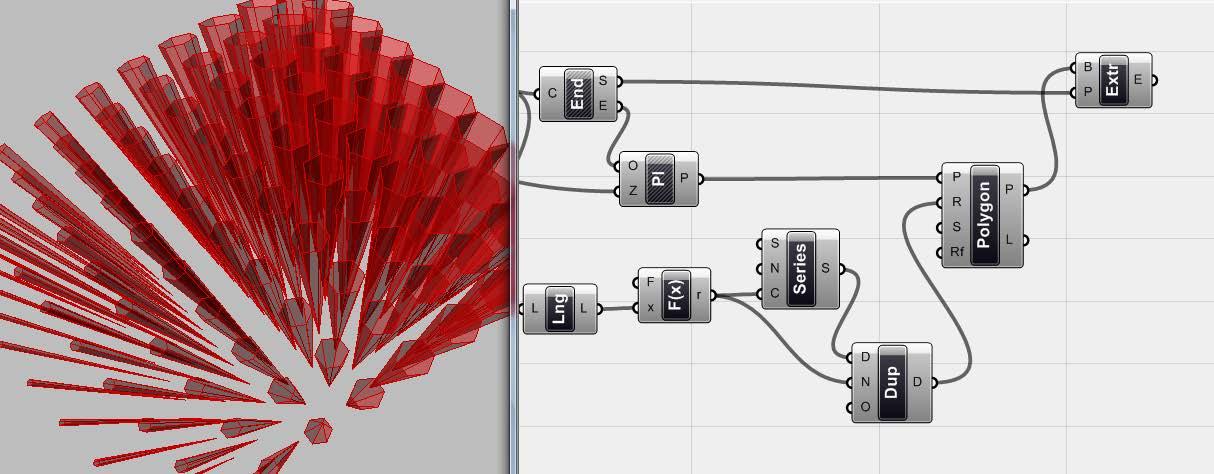
Hình4.10. trong bước cuối cùng, ta dùng component <extrude point> (Surface>Freeform) và ta đã gán điểm bắt đầu của line như là điểm mà ta muốn các luc giác extrude.

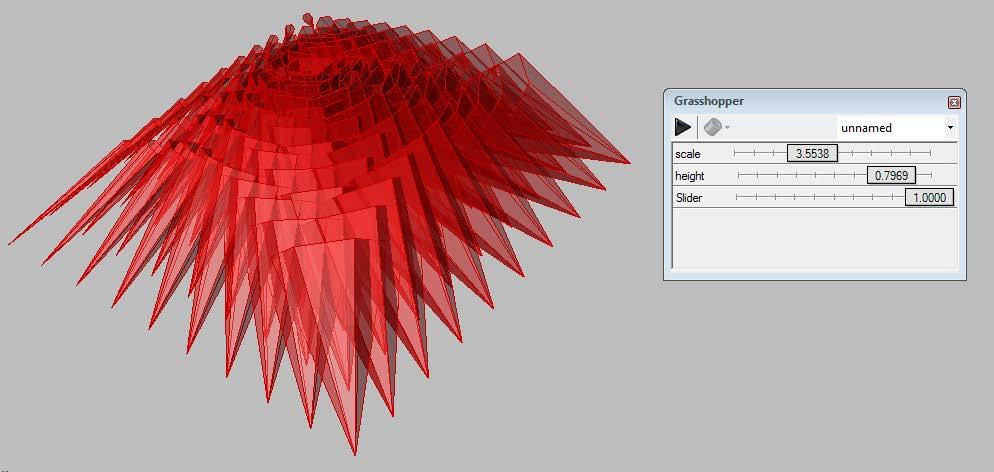
Hình.4.11. Bây giờ sử dụng ‘Remote Control Panel’ từ View menu, bạn có thể thay đổi các giá trị của number slider một cách dễ dàng và chọn cái tốt nhất. Đừng quên bỏ chọn Preview của nhưng d9oi61 tượng không cần thiết đi.

59

Hình.4.12. Final model

60