4_4_On Attractors

4_4_On Attractors

“Attractor một tập hợp các trạng thái của một hệ thống năng lượng vật lý có xu hướng phát triển, bất kể các điều kiện bắt đầu nào của hệ thống. Một điểm hút (point attractor) là một attractor tồn tại ở trạng thái đơn lẻ. Ví dụ, một hòn đá lăn trong một cái tô tròn trơn luôn có xu hướng lăn về điểm thấp nhất là đáy tô, vậy trạng thái cuối cùng và sự bất động là một điểm hút (point attractor).” (Dictionary.com/Science Dictionary)

Hình.4.28. Strange Attractor (Illustration from: http://www.cs.swan.ac.uk/~cstony/research/star/)

70

Trong thiết kế và hình học, những điểm hút sẽ là các component (thường là điểm, đường hoặc bất kỳ dạng hình học nào) ảnh hưởng đến các hình học khác trong không gian, thay đổi trạng thái và làm chúng dịch chuyển, xoay, hay thay đổi kích thước vv.vv… Chúng có thể biểu lộ rõ không gian quanh chúng, và xác định được vùng hoạt động với bán kính ảnh hưởng. Điểm hút có ứng dụng khác nhau trong thiết kế tham số vì chúng có khả năng thay đổi toàn bộ các hình khối thiết kế. Khi xác định được vùng ảnh hưởng, các điểm hút cũng có thể tác động đến hệ thống những tác nhân (agent). Cái cách và độ lớn lực mà những điểm hút tác động lên vật thể khác thì đều có thể điều chỉnh được. Chúng ta sẽ xem xét khái niệm vể điểm hút trong những trường hợp khác nhau, nên trước tiên ta sẽ có một vài ví dụ đơn giản.

Point Attractors

Ta có một hệ những điểm mà tại đó sẽ tạo ra các đa giác. Ta cũng có một điểm đặt tên là <attractor _1> và vẽ một đường tròn <circle> quanh nó để dễ nhận biết. Điểm <attractor_1> này sẽ tác động lên tất cả các đa giác <polygon> trong vùng hoạt động của nó. Điều đó có nghĩa là dựa vào khoảng cách giữa mỗi đa giác và điểm <attractor_1> , và trong phạm vi ảnh hưởng của điểm hút <attractor_1> mỗi đa giác sẽ thay đổi kích thước của nó.

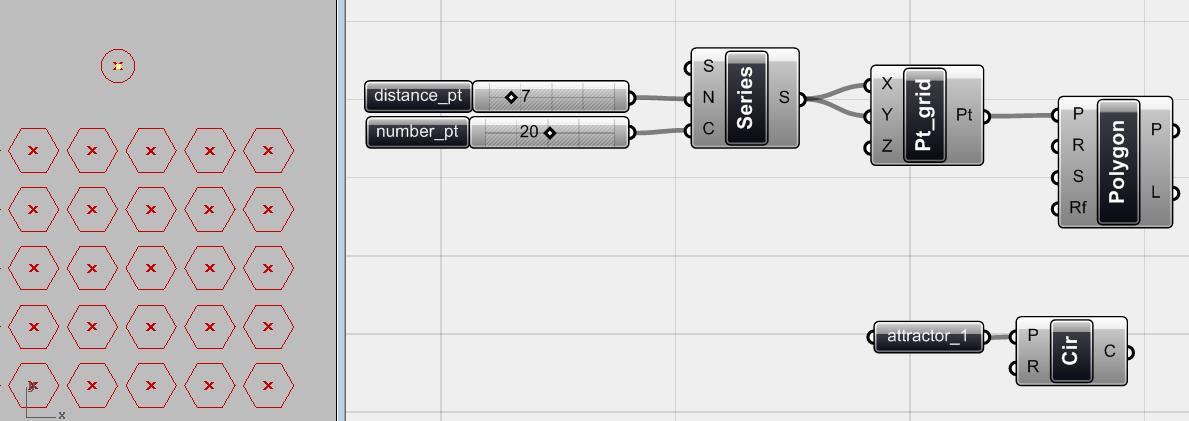
Hình.4.29. Các điểm gốc <point_grid>, các đa giác <polygon> và điểm hút <attractor_1>

Ta có một hệ những điểm mà tại đó sẽ tạo ra các đa giác. Ta cũng có một điểm đặt tên là <attractor _1> và vẽ một đường tròn <circle> quanh nó để dễ nhận biết. Điểm <attractor_1> này sẽ tác động lên tất cả các đa giác <polygon> trong vùng hoạt động của nó. Điều đó có nghĩa là dựa vào khoảng cách giữa mỗi đa giác và điểm <attractor_1> , và trong phạm vi ảnh hưởng của điểm hút <attractor_1> mỗi đa giác sẽ thay đổi kích thước của nó.

71

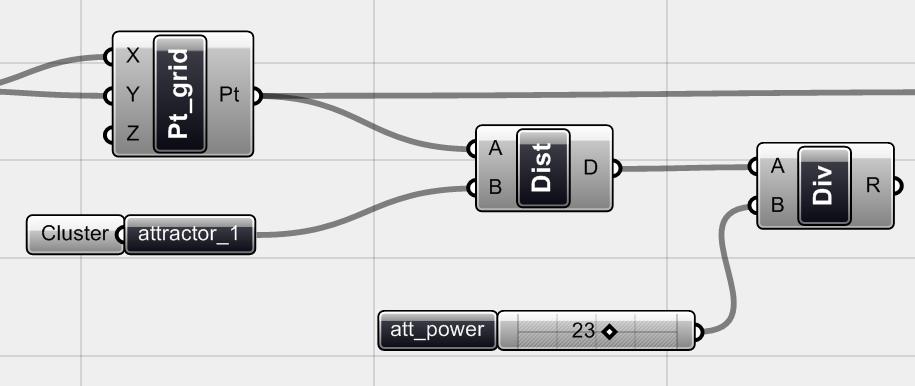
Hình.4.30. Khoảng cách được chia nhỏ để kiểm soát “lực” của <attractor_1>. Ta cũng đã tạo ra một nhóm “cluster” gồm <attractor_1> và <circle> để tạo thành điểm hút. Bạn có thể biến đổi bất kì nhóm hình học nào thành nhóm “cluster” bằng cách chọn chúng và dùng lệnh “ make cluster from selection” từ thanh toolbar của canvas (hoặc Arrange menu hoặc Ctrl+G)

Bây giờ nếu kết nối <div> component với bán kính R của <polygon> ta có thể thấy rằng bán kính của các đa giác tăng lên khi chúng càng xa điểm hút <attractor_1>. Mặc dù điều này có vẻ ổn nhưng chúng ta vẫn cần kiểm soát bán kính tối đa của các đa giác. Mặt khác nếu chúng càng ra xa, chúng sẽ rất lớn và cắt nhau một cách chồng chéo (điều này cũng xảy ra nếu lực hút của <attractor_1> quá lớn). Vì vậy ta phải tự kiểm soát bán kính tối đa của các đa giác.

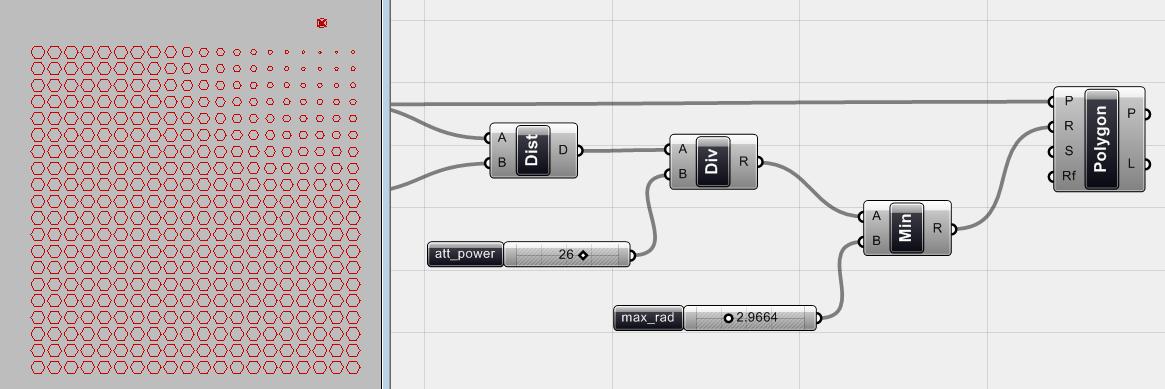
Hình 4.31 Dùng <minimum> component (Scalar > Util > Minimum) vơi một số xác định, ta sẽ có thuật toán chọn ra một giá trị từ <div> component làm bán kính lớn nhất của <polygon>, sao cho giá trị này nhỏ hơn con số ta xác định bởi <number slider>. Như ta thấy trong hình, có những đa giác trong vùng ảnh hưởng của điểm hút thì thay đổi bán kính, trong khi những đa giác khác thì không.

Bây giờ nếu di chuyển vị trí của <attractor_1> trong mặt phẳng làm việc của Rhino, ta có thể thấy rằng các đa giác sẽ thay đổi bán kính tùy theo vị tri của <attractor_1>.

72

Hình 4.32 Tác động của <attractor_1> lên các đa giác. Khi thay đổi vị trí điểm hút thì các đa giác cũng thay đổi theo.

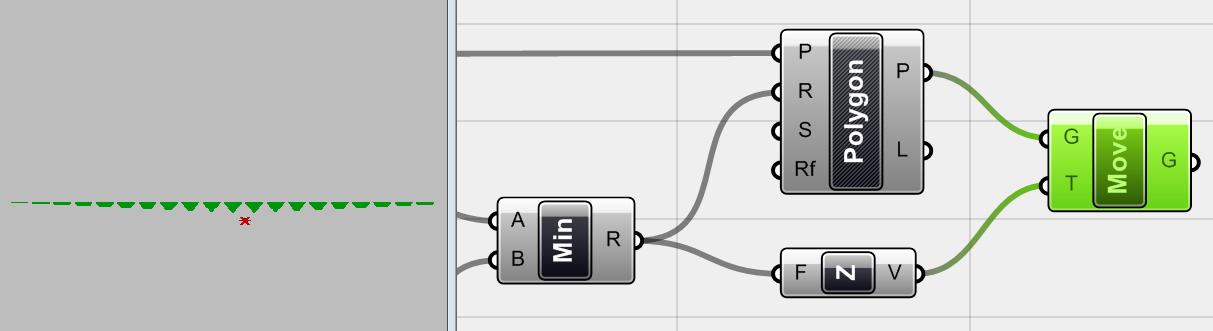
HÌnh 4.33 Với khái niệm tương tự, ta có thể thay đổi các đa giác trong trục Z dựa vào giá trị lấy từ <Min> component hoặc thay đổi nó bằng một hàm số toán học khác.

Ta có thể thực hiện bất kì thuật toán nào với các đa giác này như xoay, thay đổi màu sắc, vv.vv. Nhưng điều gì sẽ xảy ra nếu ta có 2 điểm hút trong cùng một vùng. Ta tạo một nhóm “cluster” khác, tức là một điểm khác trong Rhino đã được gán với nhóm <point> và <circle> trong Grasshopper.

73

Phần đầu tiên của thuật toán thì gần như giống nhau. Ta lại đo khoảng cách giữa điểm <attractor_2> này với tâm của các đa giác hay các điểm lưới <pt_grid>, sau đó tìm <min> của các khoảng cách này và xác định bán kính lớn nhất của đa giác.

Hình 4.34 Thuật toán tương tự đối với điểm hút <attractor_2>

Bây giờ ta đã có 2 bảng dữ liệu khác nhau là khoảng cách từ các đa giác đến mỗi điểm hút. Vì càng gần điểm hút thì các đa giác càng chịu tác động nhiều, nên ta sẽ tìm điểm hút nào gần hơn và dùng nó làm nguồn tác động. Ta sử dụng <min> component để tìm khoảng cách nhỏ nhất hay điểm gần nhất.

Hình 4.35. Tìm điểm hút gần hơn. Sau khi tìm được thì các bước còn lại tương tự như trên. Bây giờ các đa giác đều đã chịu tác động của các điểm hút.

74

Hình 4.36 Thay đổi vị trí điểm hút để thấy tác động của nó đối với các đa giác.

Ta có thể có nhiều điểm hút hơn nữa. Khái niệm này là để tìm điểm hút nào gần với đa giác hơn thì tác động lên đa giác đó. Việc chọn ra cái nào gần hơn được thực hiện bởi <min> component, và chúng ta cũng có những cách chọn khác sẽ được giới thiệu sau.

Có những cách khác để xử lý với các điểm hút như <cull> component (chọn lọc). Với phương pháp này bạn cần có bảng dữ liệu khoảng cách giữa các đa giác và các điểm hút, sau đó lựa chọn khoảng cách ngắn nhất bằng hàm Boolean a>b. Có rất nhiều ví dụ về chủ đề này trên mạng nên ta hi vọng các bạn có thể tự tìm hiểu thêm.

Curve Attractors: Wall project

Chúng ta sẽ hoàn thành cuộc thảo luận này với một ví dụ khác nhưng là về Đường hút vì trong nhiều trường hợp bạn phải xác định rõ trường vật thể bằng đường hút thay vì điểm.

Ở đây mục tiêu của ta là tạo ra một bức tường xốp, lỗ rỗ cho một không gian nội thất để có thể nhìn xuyên sang bên kia. Việc này có thể được cắt từ tấm vật liệu. Trong không gian thiết kế, ta có một tấm phẳng (bức tường), 2 đường cong và những điểm được phân bố tự do. Ta sẽ tạo ra các hình chữ nhật từ những điểm này, dùng nó cắt tấm tường để tạo ra bức tường bị đục lỗ. Ta tổ chức các hình chữ nhật theo 2 đường cong đã cho, để các hình chữ nhật này không lộn xộn mà được phân bố ngẫu nhiên dựa theo những đường cong này.

75

Điều ta cần là tạo ra là một nhóm các điểm ngẫu nhiên và dời chúng đến gần các đường cong dựa vào lực hút của các đường này. Ta sẽ tịnh tiến các điểm này đến cả 2 đường cong nên không cần chọn đường nào gần hơn, ta tịnh tiến các điểm này dựa vào khoảng cách của chúng với các đường cong. Sau đó ta sẽ tạo ra hình chữ nhật từ 3 điểm, cuối cùng ta xác định được kích thước của các hình chữa nhật dựa vào khoảng cách của chúng đến các đường hút.

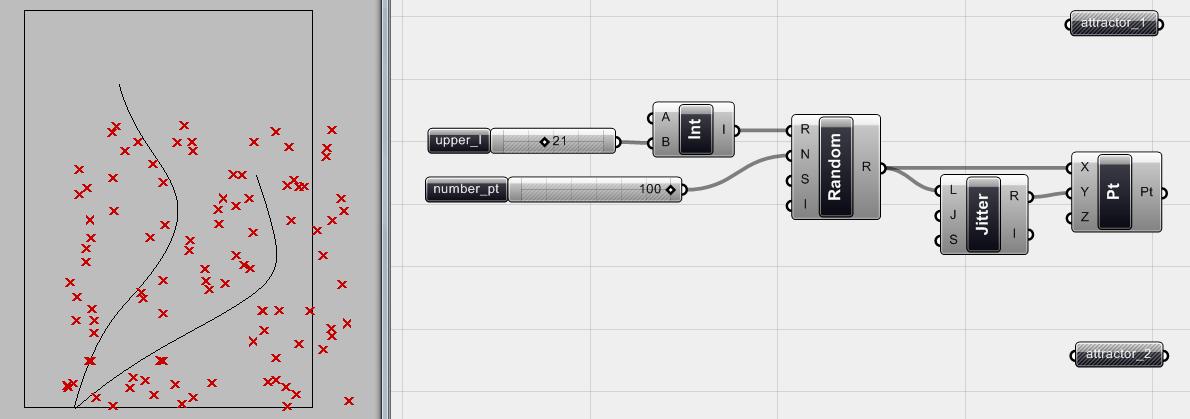
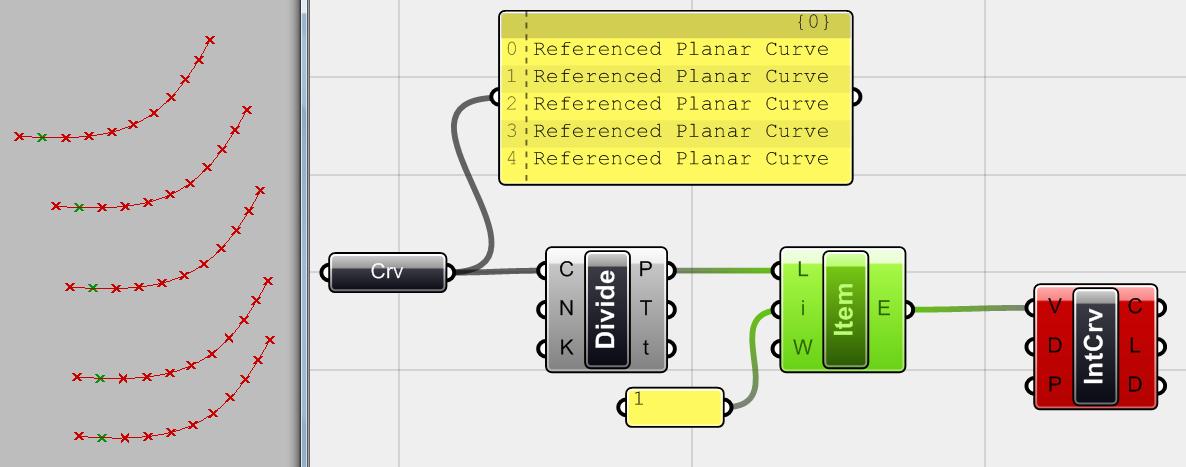
Hình 4.37 Tạo lập một bảng những điểm <point> phân bố ngẫu nhiên và đường hút bằng 2 <curve> component (Params > Geometry > Curve). Ta dùng <interval> component (khoảng, quãng) để xác định số khoảng giữa 0 và giá trị của <number slider> để tìm phạm vi những điểm ngẫu nhiên. Ta sẽ tạo một cluster gồm <interval>, <random>, <jitter>, and <point> để dễ quản lý.

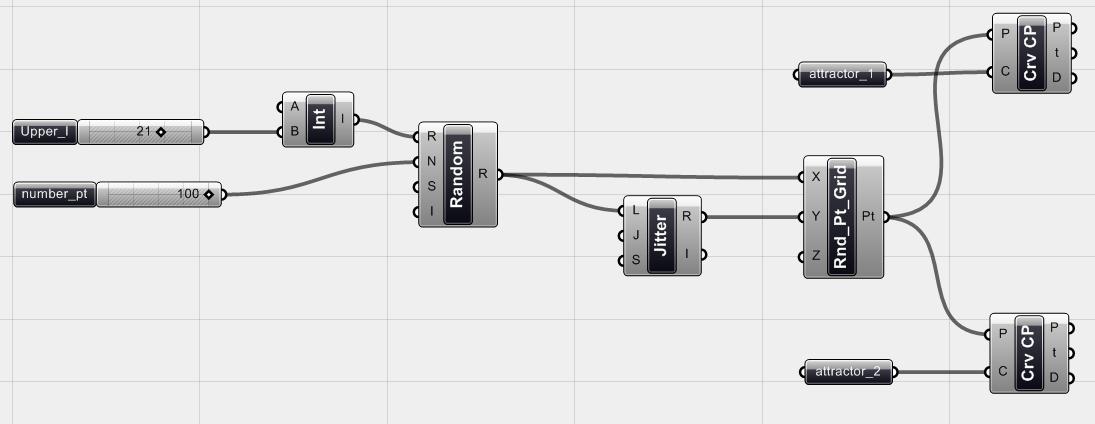
Hình 4.38 Với điểm hút, ta có thể tịnh tiến các hình học khác đến nó một cách đơn giản. Nhưng với đường hút, ta cần tìm một điểm relative và tịnh tiến các điểm <point> khác đến điểm đó. Và điểm này phải là duy nhất đối với mỗi điểm <point> vì đó là mối quan hệ 1-1 giữa đường hút với bất kì hình học nào trong phạm vi ảnh hưởng của nó. Nếu ta xem đường hút (attractor) là một nam châm thì nó sẽ kéo tất cả các điểm các vật về phía nó. Vì vậy về căn bản điều đầu tiên ta cần làm là tìm điểm gần nhất của <Rnd_pt_grid> trên cả 2 đường hút. Đó là những điểm gần nhất trên đường hút đối vối mỗi điểm của < Rnd_pt_grid>. Ta dùng <Curve CP> component (Curve >Analysis >Curve CP) để có được điểm gần nhất tr6en 2 đường hút đối với <Rnd_pt_grid>.

76

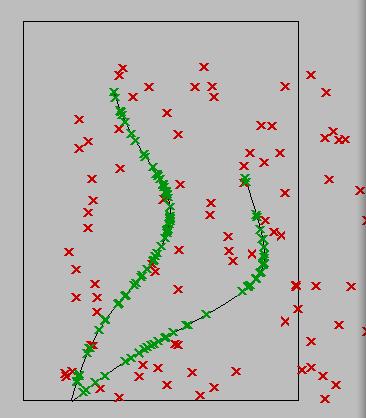
Hình 4.39 Để tịnh tiến các điểm <point> đến các đường hút, ta cần xác định một vector cho mỗi điểm trong <Rnd_pt_grid>, từ điểm đó đến điểm gần nhất của nó trên đường hút. Vì ta đã có điểm bắt đầu và kết thúc của vector nên ta dùng <vector 2pt> component để tạo vector. Điểm thứ 2 của vector < cổng B của component> là điểm gần nhất trên đường hút.

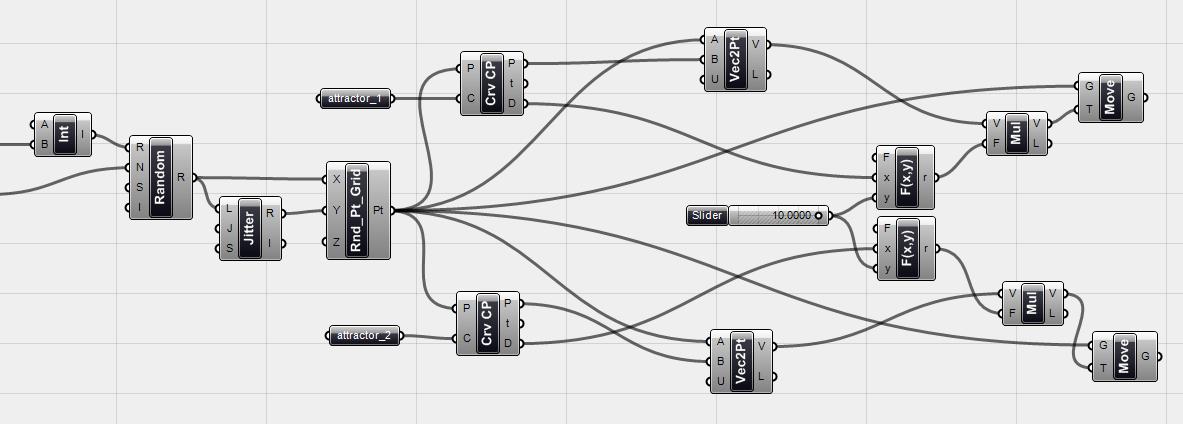
Hình 4.40 Bây giờ ta sẽ liên kết tất cả các điểm <Rnd_pt_grid> với 2 component <move> để dời chúng đến các đường hút. Nhưng nếu ta sử dụng vector đã tạo ở bước trước, tất cả các điểm sẽ bị tịnh tiến đến đường hút và đó không phải điều chúng ta muốn. Ta sẽ dời các điểm liên quan đến khoảng cách của chúng đối với các đường hút. Ta thấy <curve CP> component có một cổng ra (D) cho ta khoảng cách giữa các điểm <point> và điểm gần nhất tương ứng trên đường cong. Chúng ta sẽ không cần phải đo khoảng cách đó bằng một component khác. Ta dùng một <Function 2> component và gán khoảng cách (D) vào cổng X và một <number slider> vào Y để được hàm X/log(Y) để kiểm soát việc tịnh tiến các điểm (Hàm log thay đổi mối quan hệ dạng tuyến giữa khoảng cách và hệ số kết quả của việc tịnh tiến).

77

Ta sử dụng <multiply> component (Vector > Vector > multiply), gán vector <vector 2P> làm vector cơ sở và đổi kích thước của nó bằng hệ số tạo bởi khoảng cách, và ta gàn vector kết quả với <move> component để dời <Rnd_pt_grid> đến các đường hút tùy theo khoảng cách của nó đối với các đường hút.

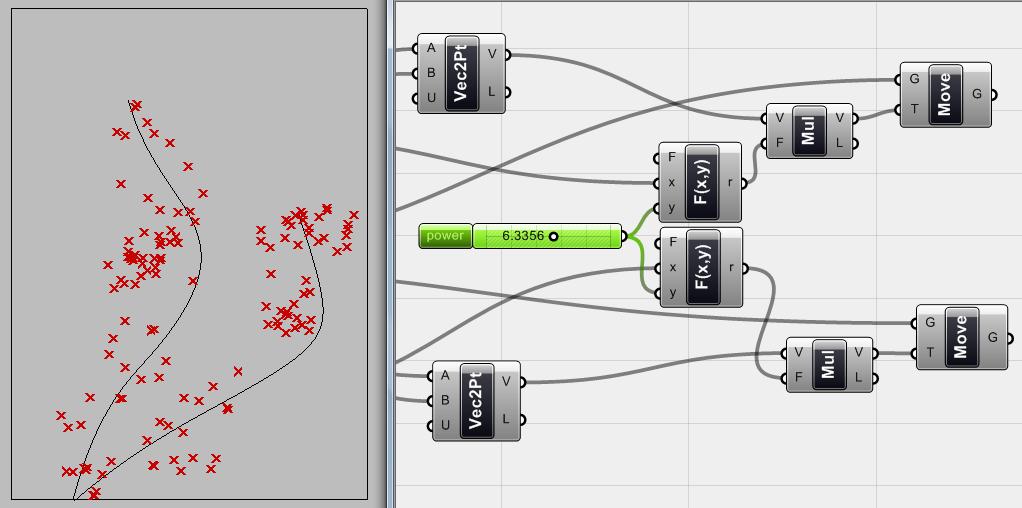
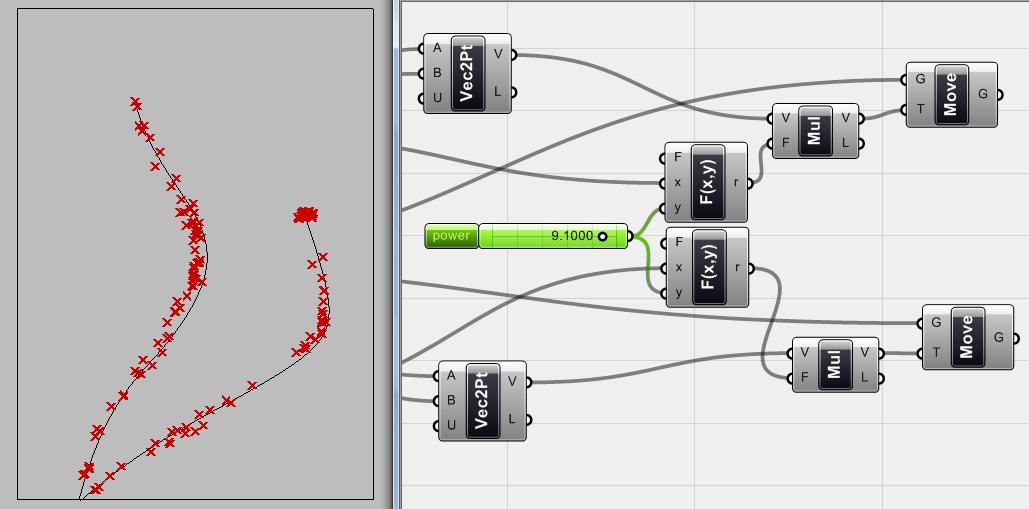
Hình 4.41 <number slider> component thay đổi độ lớn lực mà các đường hút tác động lên các điểm xung quanh để kéo chúng lại gần.

78

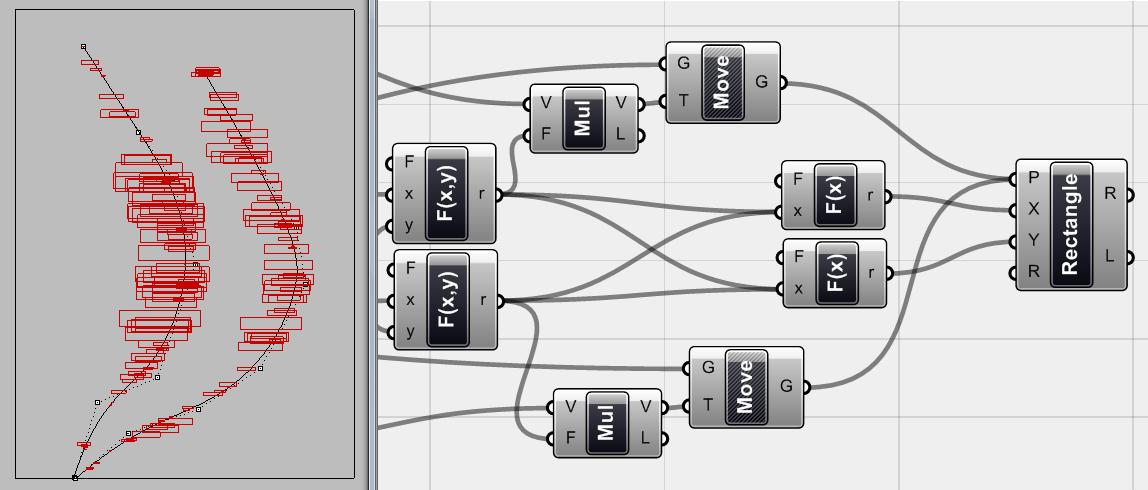
Hình 4.42 Ta dùng <rectangle> component (tạo ra các hình chữ nhật) và gán các điểm đã tịnh tiến <move> (G) với cổng P của <rectangle> để làm điểm cơ sở. Ta sẽ thay đổi kích thước của các <rectangle> dựa vào khoảng cách của chúng đối với các đường hút. Vì vậy ta sẽ dùng giá trị số tương tự như dùng cho vector độ lớn và thay đổi chúng dựa vào 2 hàm. Ta chia giá trị X của những hình chữ nhật cho 5 và chia giá trị Y cho 25. Bạn có thể thấy, các hình chữ nhật có kích thước khác nhau dựa vào khoảng cách ban đầu của chúng đối với đường hút.

Hình 4.43 Thay đổi các biến số sẽ cho kết quả khác nhau.

79

Hình 4.44. Hiệu ứng sau cùng là bức tường bị đục lỗ rỗ.

80