Formule 1 - jaar 4 - leerwerkboek (ed. 2024)

©VANIN

Wiskunde voor het 4de jaar

Arbeidsfinaliteit

Thomas Flamand

Stijn Seys

Jan Vanhee

Hanne Vanveerdeghem

FORMULE 1 ©VANIN

Via www.ididdit.be heb je toegang tot het onlineleerplatform bij Formule 1 voor het 4de jaar Arbeidsfinaliteit. Activeer je account aan de hand van de onderstaande code en accepteer de gebruiksvoorwaarden.

FORMULE 1 ©VANIN

Let op: deze licentie is uniek, eenmalig te activeren en geldig voor een periode van twee schooljaren. Indien je de licentie niet kunt activeren, neem dan contact op met onze klantendienst.

Fotokopieerapparaten zijn algemeen verspreid en vele mensen maken er haast onnadenkend gebruik van voor allerlei doeleinden. Jammer genoeg ontstaan boeken niet met hetzelfde gemak als kopieën.

Boeken samenstellen kost veel inzet, tijd en geld. De vergoeding van de auteurs en van iedereen die bij het maken en verhandelen van boeken betrokken is, komt voort uit de verkoop van die boeken.

In België beschermt de auteurswet de rechten van deze mensen. Wanneer u van boeken of van gedeelten eruit zonder toestemming kopieën maakt, buiten de uitdrukkelijk bij wet bepaalde uitzonderingen, ontneemt u hen dus een stuk van die vergoeding. Daarom vragen auteurs en uitgevers u beschermde teksten niet zonder schriftelijke toestemming te kopiëren buiten de uitdrukkelijk bij wet bepaalde uitzonderingen.

Verdere informatie over kopieerrechten en de wetgeving met betrekking tot reproductie vindt u op www.reprobel.be.

Ook voor het onlinelesmateriaal gelden deze voorwaarden. De licentie die toegang verleent tot dat materiaal is persoonlijk. Bij vermoeden van misbruik kan die gedeactiveerd worden. Meer informatie over de gebruiksvoorwaarden leest u op www. ididdit.be.

© Uitgeverij VAN IN, Wommelgem, 2024

De uitgever heeft ernaar gestreefd de relevante auteursrechten te regelen volgens de wettelijke bepalingen. Wie desondanks meent zekere rechten te kunnen doen gelden, wordt verzocht zich tot de uitgever te wenden.

Fotocredits

p. 19 Scheve toren van Pisa ©Nerthuz/Shutterstock.com, p. 30 puzzel linksboven © Online puzzelen op www.sugurupuzzles. com, p. 30 puzzel linksonder © Copyright Denksport puzzelbladen, p. 30 puzzel rechtsonder © www.davdata.nl, p. 50 parfumflesje Hugo Boss ©Ana Maria Tone/Shutterstock.com, p. 50 Eau de Cologne Versace ©Keith Homan/ Shutterstock.com, p. 50 parfumflesje Chanel N°5 ©Magi Bagi/Shutterstock.com, p. 50 parfumflesje Calvin Klein ©AlenKadr/Shutterstock.com, p. 79 smartphones ©Alexey Boldin/Shutterstock.com, p. 95 iconen Instagram en Snapchat ©Brilliantist Studio/Shutterstock.com, p. 95 icoon Facebook ©rvlsoft/Shutterstock.com, p. 95 icoon WhatsApp ©solomon7/ Shutterstock.com, p. 100 Xbox360 ©Vitor Lando/Shutterstock.com, p. 100 logo’s Adidas, Nike, Puma en Reebok ©Rose Carson/Shutterstock.com, p. 119 Olympisch zwembad ©Paolo Bona/Shutterstock.com, p. 142 scoutsgroep te Chimay ©Thomas Dekiere/Shutterstock.com, p. 172 brandweerwagen ©S-F/Shutterstock.com, p. 192 Marcel Jacobs ©Marco Lacobucci Epp/Shutterstock.com, p. 199 Michael Morkov ©Radu Razvan/Shutterstock.com, p. 203 Ronde van Vlaanderen 2021©Dirk Waem/Belga Image

Eerste druk 2024

Lay-out: Wendy De Haes

ISBN 978-94-647-0580-5 Coverontwerp: KaaTigo D/2024/0078/77

Zetwerk: Alinea Graphics, Crius Group Art. 606325/01 Tekeningen: Dirk Vandamme NUR 120

Inhoudsopgave

Hoe werk je met Formule 1?

Wist je dat je elke dag verschillende soorten getallen gebruikt? En dat je elke dag werkt met cirkels, kubussen of rechthoeken? In dit leerwerkschrift ontdek je hoe je door te tellen en te rekenen, te meten en te tekenen de wereld om je heen beter begrijpt.

Mijn circuit

Titelpagina

Bij het begin van elk hoofdstuk maak je via een leuke cartoon kennis met het onderwerp waarover je iets leert.

Via de ‘Planner’ kun je volgen wat je al gedaan hebt in het hoofdstuk. Kleur het bolletje als je het onderdeel hebt afgewerkt.

Deze pagina biedt een overzicht van de oefeningen op jouw maat en van je resultaten.

Bovendien vind je hier terug bij welke onderdelen je extra oefenmateriaal op iDiddit vindt.

Daarnaast staat in elk hoofdstuk een attitude in de kijker. Zo weet jij waar je tijdens het maken van de oefeningen extra aandacht aan moet besteden.

Aan de slag

©VANIN

Ben ik mee?

In ‘Aan de slag’ krijg je de leerstof met duidelijke voorbeelden aangebracht.

Zie je dit logo in de kantlijn dan maak je zelf een verwerkingsopdracht.

Als dit logo verschijnt mag je je rekentoestel gebruiken. Om je te ondersteunen bij het studeren zie je af en toe ook dit pictogram VIDEO bij de leerstof staan. Open dan de VAN IN Plus-app en scan de pagina. Zo kun je op een handige manier een instructiefilmpje over de leerstof bekijken.

In ‘Ben ik mee?’ ontdek je waar je goed of minder goed in bent. Als je je scores correct invult bij ‘Mijn circuit’, vind je terug welke oefeningen je moet maken in ‘Op mijn maat’.

Op mijn maat

Je resultaat uit ‘Ben ik mee?’ leidt je naar oefeningen op jouw maat, oefeningen die jij aankunt!

Alle oefeningen binnen een onderwerp hebben hetzelfde doel.

Jouw rijstijl bepaalt onder welk metertje je oefent.

Heb je nog veel oefening nodig? Dan rijd je beter op een rustiger tempo. Maak de oefeningen met dit logo.

Heb je gemiddeld gescoord? Dan kun je overgaan op een hoger toerental.

Had je een hoge score? Dan mag je de oefeningen op volle snelheid maken. Die vind je naast dit logo.

Vlieg niet uit de bocht!

ZOEF staat voor Zelfstandig Oefenen.

Hier vind je de oefeningen van ‘Op mijn maat’, maar dan met andere getallen. Je kunt deze telkens opnieuw maken, tot je de leerstof onder de knie hebt.

Even samenvatten

Aan het einde van elk hoofdstuk vind je alles wat je hebt geleerd in een handige samenvatting.

Die kun je gebruiken als hulp bij het studeren.

Gamezone

In de gamezone sluit je elk hoofdstuk af met een puzzel, een spel of een uitdaging. Wiskunde is leuk!

Test op mezelf

Met ‘Test op mezelf’ eindig je het hoofdstuk en meet je jouw vorderingen.

Wedden dat je een versnelling hoger geschakeld bent?

Herhalingsoefeningen

Hier vind je verschillende oefenreeksen terug, telkens aangepast aan jouw niveau. Ga jij de uitdaging aan?

Mijn lesmateriaal

Het onlineleerplatform bij Formule 1

Hier vind je alle inhouden uit het boek, maar ook meer, zoals Excel-bestanden, filmpjes, extra oefeningen ...

Extra materiaal

Bij bepaalde stukken theorie of oefeningen kun je extra materiaal openen, dat je helpt om de leerstof onder de knie te krijgen.

Adaptieve oefeningen

Met adaptieve oefeningen kun je de leerstof inoefenen op jouw niveau. Hier kun je vrij oefenen.

Opdrachten

Hier vind je de opdrachten die de leerkracht voor jou heeft klaargezet.

Evalueren

Hier kan de leerkracht toetsen voor jou klaarzetten.

Resultaten

Wil je weten hoever je al staat met oefenen, opdrachten en toetsen?

Hier vind je een helder overzicht van al je resultaten.

Notities

Heb je aantekeningen gemaakt bij een bepaalde inhoud?

Via je notities kun je ze makkelijk terug oproepen.

Meer weten?

Ga naar www.ididdit.be

Soms is het handig dat je extra lesinformatie of een videofragment kunt bekijken of beluisteren op je smartphone. Als je dit pictogram ziet, open dan de VAN IN Plus-app en scan de pagina.

Schetsen en tekenen

Planner

Aan de slag

1 Hoeken 9

1.1 Benamingen

1.2 Meetinstrumenten

1.3 Hoeken meten

1.4 Hoeken tekenen

2 Evenwijdig en loodrecht 11

2.1 Punt, rechte en lijnstuk

2.2 Evenwijdig, snijdend en loodrecht

2.3 Evenwijdig en loodrecht tekenen met een geodriehoek

3 Vlakke figuren 13

3.1 Benamingen

3.2 Vlakke figuren schetsen en tekenen

4 Ruimtefiguren 15 4.1 Benamingen

4.2 Ruimtefiguren in perspectief schetsen en tekenen

FORMULE 1

Nr.: Klas: Datum: / / 20 / Aan de slag Ben ik mee? Op mijn maat Test op mezelf

©VANIN

1 Hoeken

1.1 Benamingen A hoek benen hoekpunt

1.2 Meetinstrumenten

Notatie: Lees:

a een volledige gradencirkel c een gradenboog op een geodriehoek nulpunt

Meetbereik:

Meetnauwkeurigheid:

Meetbereik:

Meetnauwkeurigheid:

tekenzijde

Meetbereik:

Meetnauwkeurigheid: d een hellingmeter voor een boot

Meetbereik:

Meetnauwkeurigheid:

1.3 Hoeken meten

Meet ^ A

^ A = Je leest:

1.4 Hoeken tekenen

Teken ^ B = 65°.

Stap 1:

Leg je geodriehoek met het nulpunt in het hoekpunt.

Zorg ervoor dat de tekenzijde samenvalt met een been van de hoek.

Stap 2:

Lees het maatgetal van de hoek af bij het andere been.

Let op:

• Soms moet je de benen verlengen om een nauwkeurige meting te doen.

• Er staan telkens twee hoekmaten op je geodriehoek. Denk dus na over ‘scherp’ of ‘stomp’.

Stap 1:

Teken het hoekpunt en een been van de hoek.

Stap 2:

Leg je geodriehoek met het nulpunt in het hoekpunt.

Zorg ervoor dat de tekenrand samenvalt met het getekende been.

Stap 3:

Plaats een punt bij het maatstreepje van 65°.

Stap 4:

Verplaats je geodriehoek. Verbind het hoekpunt met je zelfgetekende punt.

Meet ^ C .

Teken ^ D = 110°.

2 Evenwijdig en loodrecht

2.1 Punt, rechte en lijnstuk

punt rechte lijnstuk

voorstelling A A Ba AB

notatie

Teken een lijnstuk [CD] van 11,5 cm. C

2.2 Evenwijdig, snijdend en loodrecht

evenwijdige rechtensnijdende rechten loodlijnen

De rechten a en b snijden elkaar niet.

Ze hebben geen enkel punt gemeenschappelijk

De rechten a en b snijden elkaar.

Ze hebben één punt gemeenschappelijk

Dat punt noem je het snijpunt

Notatie: a b a b a b

Lees:

De rechte a is evenwijdig met de rechte b.

De rechte a snijdt de rechte b.

De rechte a staat loodrecht op de rechte b.

2.3 Evenwijdig en loodrecht tekenen met een geodriehoek

• Om rechte b evenwijdig met rechte a te tekenen door punt A, gebruik je de evenwijdige hulplijnen van je geodriehoek.

tekenzijde door het punt A

• Om een loodlijn d op een rechte c door een punt B te tekenen, gebruik je de loodlijn van je geodriehoek.

Hulplijn valt samen met de rechte a.

tekenzijde door het punt B

Teken door het punt A de rechte b, zodat de rechte b evenwijdig is met de rechte a.

Loodlijn valt samen met de rechte c.

Teken door het punt B de rechte c, zodat de rechte c loodrecht staat op de rechte d.

3.1 Benamingen

• De cirkel

Vul de ontbrekende benamingen aan.

©VANIN

• De driehoek

Duid aan wat past.

indeling volgens de hoeken

indeling volgens de zijden

scherphoekig rechthoekig stomphoekig

gelijkzijdig gelijkbenig ongelijkbenig

scherphoekig rechthoekig stomphoekig

gelijkzijdig gelijkbenig ongelijkbenig

scherphoekig rechthoekig stomphoekig

gelijkzijdig gelijkbenig ongelijkbenig

Teken in de bovenstaande driehoeken de hoogte op de aangeduide groene basis.

• De vierhoek

Noteer de meest passende benaming van deze vierhoeken.

Duid aan voor welke vierhoek de eigenschap van toepassing is. trapeziumparallellogramrechthoekruit vierkant

De overstaande zijden zijn even lang.

Alle zijden zijn even lang.

De overstaande hoeken zijn even groot.

Alle hoeken zijn even groot.

3.2 Vlakke figuren schetsen en tekenen

Teken met je passer en geodriehoek een gelijkbenige driehoek met basis 4 cm en zijde 5 cm. Maak eerst een schets.

schets uitvoering

Teken met je passer een cirkel met middelpunt M en diameter 6 cm.

Teken met je geodriehoek een rechthoek met zijden van 5 cm en 3 cm.

Teken met je geodriehoek een parallellogram met zijden van 4 cm en 3 cm en een hoek van 50°. Maak eerst een schets.

schets uitvoering

4.1 Benamingen

• Noteer in de kaders de naam van de ruimtefiguren.

• Duid in de kubus een hoekpunt in het rood aan. Duid in de kubus een ribbe in het groen aan.

• Kleur in de balk het grondvlak rood, het bovenvlak groen, een zijvlak blauw.

• Wat betekenen de aangeduide letters? Vul aan.

l = z = b = r = h = d =

4.2 Ruimtefiguren in perspectief schetsen en tekenen

Er zijn verschillende manieren om een ruimtefiguur (3D) voor te stellen in een vlak (2D).

De truc bestaat erin om via enkele welgekozen lijnen diepte te suggereren.

De lijnen die naar achteren lopen, noem je de vluchtlijnen

De vlakke voorstelling van een ruimtefiguur noem je het perspectief.

Isometrisch perspectief

• Teken eerst een opstaande ribbe.

• Teken de vluchtlijnen onder een hoek van 30°.

• Neem steeds de juiste afmetingen van de ruimtefiguur over.

• Alle vluchtlijnen zijn evenwijdig.

• Onzichtbare ribben teken je met een streepjeslijn. 30° 30°

Teken een balk met lengte 3 cm, breedte 2 cm en hoogte 1,5 cm in isometrisch perspectief. Eén hoek van deze balk staat al op het tekenblad. Tip: het tekenblad bestaat uit hoeken van 60°.

Cavalièreperspectief

• Teken eerst het voorvlak.

• Teken de vluchtlijnen onder een hoek van 45°.

• Neem voor de afmeting van de vluchtlijnen de helft van de werkelijke afmeting.

• Alle vluchtlijnen zijn evenwijdig.

• Onzichtbare ribben teken je met een streepjeslijn. 45°

Schets een balk met lengte 4 cm, breedte 3 cm en hoogte 2 cm in cavalièreperspectief. Teken daarna nauwkeurig met je geodriehoek.

schets uitvoering

FORMULE 1

1 Hoeken

Nr.: Klas:

Datum: / / 20 / 20

Meet de gevraagde hoeken nauwkeurig. Verleng indien nodig de benen.

Teken de gevraagde hoeken nauwkeurig.

a De golfspeler slaat de bal omhoog volgens ^ G = 65°.

2 Evenwijdig en loodrecht

Teken door punt K rechte a, zodat a ⊥ m.

b De tennisspeelster slaat de bal omlaag volgens ^ T = 25°.

T

Teken daarna door punt L de rechte b, zodat b // a. Gebruik je geodriehoek.

3 Vlakke figuren

a Schets een gelijkbenige stomphoekige driehoek.

b Schets een rechthoek waarvan de lengte ongeveer dubbel zo lang is als de breedte.

a Teken met je geodriehoek een driehoek met een zijde van 4 cm en een zijde van 3 cm. De hoek tussen die zijden moet 45° zijn.

b Teken met je passer en geodriehoek een ruit met zijde 4 cm en een hoek van 60°.

4 Ruimtefiguren

Vervolledig de balk in cavalièreperspectief. Vergeet de onzichtbare ribben niet.

Schets deze doos in isometrisch perspectief. Vergeet de onzichtbare ribben niet.

1 Hoeken

a Met deze digitale gradenmeter kun je een volledige cirkel meten.

Meetbereik:

Meetnauwkeurigheid:

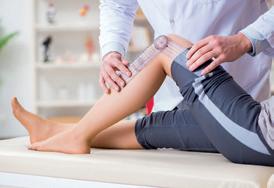
b Met deze goniometer kan de kinesist de beweeglijkheid van je gewrichten meten.

Meetbereik:

Meetnauwkeurigheid:

2 Meet de hoeken nauwkeurig.

1 Bepaal het meetbereik en de meetnauwkeurigheid van deze meettoestellen.

c Deze cirkelzaag kan links en rechts volledig plat.

Meetbereik:

Meetnauwkeurigheid:

d Met deze hoekmeter kun je een hoek overzetten.

Meetbereik:

Meetnauwkeurigheid:

3 Meet nauwkeurig de hoeken tussen het dijbeen en het scheenbeen.

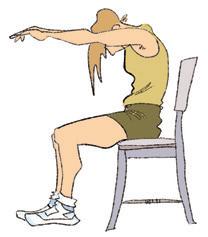
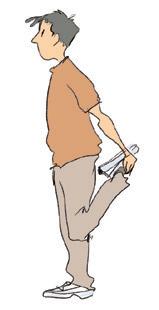
b c d

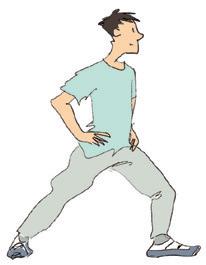
4 Teken de hoeken. Eén been is al getekend.

a ^ A = 30°

b ^ B = 60°

c ^ C = 130° A B C

5 Teken de hoek die de bal maakt met het horizontale been.

a De voetballer trapt de bal omhoog volgens ^ V = 50°.

b De volleybalspeelster smasht de bal volgens ^ B = 25°.

6 Teken een hoek met dezelfde hoekgrootte als de gegeven hoek. Vergeet deze hoek niet te benoemen!

a A b B

7 Teken door het punt C een rechte b die evenwijdig is met de rechte a. Teken door het punt D een rechte c die loodrecht staat op de rechte a. Vul daarna de tabel aan met // of ⊥.

a

8 Vliegtuig A vliegt in een rechte lijn naar Frankfurt. Een tweede vliegtuig stijgt op in Barcelona en volgt een rechtlijnige baan evenwijdig met de baan van vliegtuig A. Boven welke steden vliegt het tweede vliegtuig?

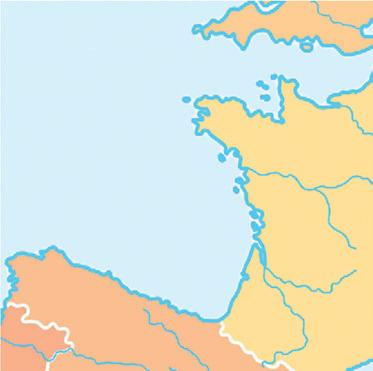
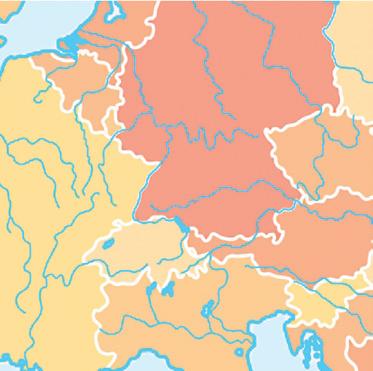
Het tweede vliegtuig vliegt boven

9 Onder een tegel van de badkamer ligt een gouden ketting begraven. Volg de aanwijzingen en vind de ketting.

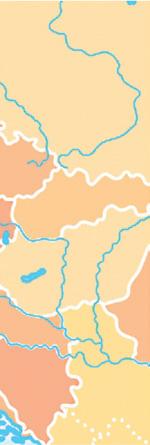
• De rechte a is evenwijdig met de lengte van het bad en gaat door het punt A.

• De rechte b staat loodrecht op de lengte van de kleerkast en gaat door het punt B.

• Het snijpunt van de rechten a en b noem je het punt S.

• De rechte c gaat door het punt C en staat loodrecht op de muur waartegen de wastafel bevestigd is.

• Teken de rechte d door de punten D en S.

• Het snijpunt van de rechten c en d is de tegel waaronder de ketting begraven ligt.

Onder welke tegel ligt de gouden ketting?

De ketting ligt onder tegel: abc

10 Noteer bij elke kleur de juiste benaming.

11 Teken met je passer en geodriehoek:

a een driehoek met zijden 4 cm, 3 cm en 3,5 cm.

b een parallellogram met hoogte 3 cm.

12 Schets eerst. Voer daarna nauwkeurig uit met je geodriehoek.

a Teken een driehoek met zijde 4 cm. De hoeken op die zijde meten 40° en 60°.

b Teken een gelijkbenige driehoek met zijde 3 cm en een hoek van 110°. schets schets

uitvoering uitvoering

13 Schets met de vrije hand.

a een rechthoek die geen vierkant is. b een rechthoekige driehoek.

14 Vervolledig de vierhoek.

a een parallellogram b een trapezium

15 Schets eerst. Voer daarna nauwkeurig uit met je geodriehoek.

a Teken een ruit met zijde 4 cm en een hoek van 130°.

b Teken een driehoek met hoogte 4 cm, basis 5 cm en zijde 4 cm. schets schets

uitvoering uitvoering

16 Kleur van deze ruimtefiguren het grondvlak blauw, het bovenvlak groen en één zijvlak rood.

17 Welke vlakke figuren stellen de gekleurde vlakken van de ruimtefiguren voor?

18 Bepaal de werkelijke lengte, breedte en hoogte van deze balken, die in cavalièreperspectief getekend zijn.

• lengte: mm

lengte: mm • breedte: mm

hoogte: mm

breedte: mm

hoogte: mm

19 Teken de figuur in cavalièreperspectief op ware grootte.

©VANIN

20 Schets met de vrije hand in isometrisch perspectief: a een kubus. b een balk. c een balk die twee keer zo hoog als breed is.

21 In welk perspectief is de figuur getekend? Duid aan.

cavalièreperspectief isometrisch perspectief ander soort perspectief

cavalièreperspectief isometrisch perspectief ander soort perspectief

cavalièreperspectief isometrisch perspectief ander soort perspectief

22 Teken nauwkeurig in cavalièreperspectief. Vergeet de onzichtbare ribben niet.

a een kubus met ribbe 4 cm

b een balk met lengte 4 cm, breedte 3 cm en hoogte 2 cm

23 Een balkvormig appartementsgebouw heeft een hoogte van 40 m, een lengte van 25 m en een breedte van 20 m.

Maak een voorstelling van dit gebouw in cavalièreperspectief op schaal 1 1 000 .

• lengte tekening:

• breedte tekening:

• hoogte tekening:

24 Lena wil dit nestkastje maken.

Noteer de ontbrekende afmetingen.

vooraanzicht linkerzijaanzicht achteraanzicht

rechterzijaanzicht grondaanzicht bovenaanzicht

25 Bekijk de perspectieftekening van de gemetste constructie.

a Vul het juiste aanzicht in.

Kies uit: linkerzijaanzicht, vooraanzicht en bovenaanzicht.

b Vul het overeenkomstige cijfer in.

A in het vooraanzicht = B in het vooraanzicht = C in het vooraanzicht =

A in het linkerzijaanzicht = B in het linkerzijaanzicht = C in het linkerzijaanzicht =

A in het bovenaanzicht = B in het bovenaanzicht = C in het bovenaanzicht =

Vervolledig de onderstaande

Beantwoord de bijbehorende vragen.

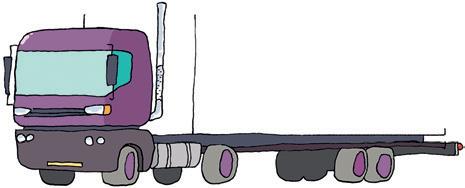
a Als je achter de vrachtwagen rijdt, zie je een

b Als je vlak naast de vrachtwagen rijdt, zie je een

c Als je recht boven de vrachtwagen vliegt, zie je een .

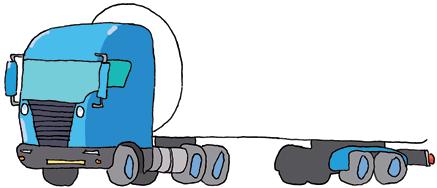
a Als je achter de vrachtwagen rijdt, zie je een

b Als je vlak naast de vrachtwagen rijdt, zie je een .

c Als je recht boven de vrachtwagen vliegt, zie je een

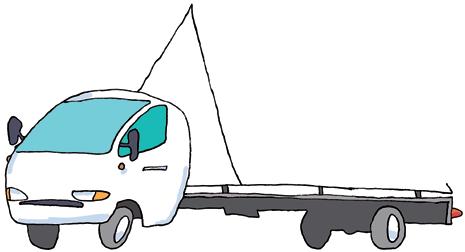
a Als je achter de vrachtwagen rijdt, zie je een

b Als je vlak naast de vrachtwagen rijdt, zie je een

c Als je recht boven de vrachtwagen vliegt, zie je twee .

• Hoeken

A = 50°

• Evenwijdig, snijdend en loodrecht

a is evenwijdig met b a snijdt b a staat loodrecht op b

• Soorten perspectief

isometrisch perspectief cavalièreperspectief

Gamezone

Een cijferblokpuzzel is verdeeld in een of meerdere vormen van een tot vijf vakjes. In die vakjes moet je cijfers schrijven. De kleinste vorm bestaat maar uit één vakje. Daarin vul je altijd het cijfer 1 in. Een vorm met twee vakjes krijgt de cijfers 1 en 2. Een vorm met drie vakjes krijgt de cijfers 1, 2 en 3 enzovoort.

Let op: vakjes met hetzelfde cijfer mogen nooit buren zijn. Ze mogen elkaar dus niet raken, ook niet diagonaal.

Je kunt de vakjes altijd invullen door goed na te denken. Het is geen kwestie van lukraak proberen. Er is telkens maar één juiste oplossing mogelijk.

Test op mezelf FORMULE 1

1 Hoeken

Nr.: Klas:

Datum: / / 20 / 20

Meet de gevraagde hoeken nauwkeurig. Verleng indien nodig de benen.

Teken de gevraagde hoeken nauwkeurig.

2 Evenwijdig en loodrecht

Teken vanuit P het lijnstuk [PK] = 5 cm zodat [PK] ⊥ [AB].

Teken daarna vanuit S het lijnstuk [LS] = 4 cm zodat [LS] // [PB].

3 Vlakke figuren

a Teken met je passer en geodriehoek een gelijkzijdige driehoek met zijde 3,5 cm.

c Teken met je passer en geodriehoek een ruit met zijde 3 cm en een hoek van 60°.

b Teken met je geodriehoek een driehoek met zijde 5 cm. De hoeken op die zijde zijn 45° en 65°.

d Teken met je geodriehoek een parallellogram met een zijde van 4 cm, een zijde van 3 cm en een hoek van 60°.

4 Ruimtefiguren

Teken een kubus met ribbe 2 cm in cavalièreperspectief.

Teken ook de onzichtbare ribben met een streepjeslijn.

Breuken, procenten en decimale getallen

1 Een breuk nemen van een getal

2 3 van 12 eieren = (12 : 3) x 2 = 4 x 2 = 8

Bereken.

a 3 4 van 24 flesjes = = b 3 7 van € 42 = =

2 Gelijke breuken

Vul de ontbrekende teller of noemer aan, zodat er twee gelijke breuken ontstaan. a 2 5 = b

3 Breuken vereenvoudigen

Vervang de breuk door een gelijke breuk met een kleinere teller en noemer. De gelijke breuk met de kleinste noemer is de onvereenvoudigbare breuk

Schrijf als een onvereenvoudigbare breuk.

a 9 21 = b 9 36 = c 14 42 = d 36 54 =

4 Breuken en procenten

4.1 Een procent uit het hoofd berekenen

% = 1 100 = delen door 100

50 % = 50 100 = 1 2 = delen door 2

% = 10

= 1 10 = delen door 10 25 % = 25 100 = 1 4 = delen door 4

= 1 5 = delen door 5

Bereken.

a 20 % van 800 tegels = c 1 % van € 850 = b 25 % van 200 motors = d 10 % van 450 boten =

4.2 Van breuk naar procent

4.3 Van procent naar breuk 44 % == 100

Schrijf de breuk als een procent. Schrijf het procent als een onvereenvoudigbare breuk. a 15 20 == %

24 %

b 12 25 == %

15 % == c 7 50 == %

5 Procenten en decimale getallen

64 % ==

5.1 Van procent naar decimaal getal5.2 Van decimaal getal naar procent

Schrijf het procent als een decimaal getal. Schrijf het decimaal getal als een procent.

6 Breuken en decimale getallen

6.1 Van breuk naar decimaal getal

6.2 Van decimaal getal naar breuk

Schrijf de breuk als een decimaal getal. Schrijf het decimaal getal als een onvereenvoudigbare breuk.

3 5 ==

Centen en procenten 2

Mijn circuit

op mezelf

FORMULE 1

Nr.: Klas: Datum: / / 20 / Aan de slag Ben ik mee? Op mijn maat

©VANIN

Aan de slag

1 Prijsverlagingen en prijsverhogingen

1.1 Dit handige schema helpt je met procenten

D = Deel

P = Procent in kommagetal

B = Beginwaarde

Vul de formules correct aan.

D = P = B =

1.2 Prijsverlagingen

Het zijn solden en er zijn fikse kortingen. De kostprijs wordt verlaagd.

Vul de tabel aan.

a Je krijgt 15 % korting op een T-shirt van € 20. Hoeveel € korting krijg je?

b Je krijgt € 17,60 korting op een broek van € 80. Hoeveel % korting krijg je?

c 18 % korting op een jas komt overeen met € 21,60. Hoeveel kostte de jas eerst?

Korting:

Korting: € 17,60

Korting: € 21,60

Berekening: Berekening: Berekening:

1.3 Prijsverhogingen

Door een prijsstijging van de ingrediënten verhoogt restaurant Puur zijn prijzen. Vul de tabel aan.

a De prijs van de lasagne stijgt met 8 %. Hoeveel euro vraagt Puur nu?

b De zalm kostte € 20, maar wordt € 3 duurder. Met hoeveel % verhoogde de prijs?

c De filet pur wordt 12 % of € 3,60 duurder. Hoeveel kostte de filet pur eerst?

Meerprijs:

Meerprijs: € 3 Meerprijs: € 3,60

Berekening: Berekening: Berekening:

a De prijs van eiken planken was vorig jaar € 1 200 per m³. Dit jaar steeg de prijs met 9 %. Hoeveel kost eik dit jaar?

b De crossfiets die je vorig jaar aan € 1 250 kon kopen, is dit jaar te koop voor € 1 150. Hoeveel procent korting is dat?

Berekening: Berekening:

Antwoordzin: Antwoordzin:

2.1 Sparen

Plaats je geld bij een bank, dan betaalt de bank je een vergoeding (= rente)

In de vakantie werkte je als jobstudent. Je besluit € 1 200 op je spaarrekening te zetten. De bank belooft je na een jaar 1,5 % rente uit te betalen. Bereken hoeveel je na dat jaar op je spaarrekening zult hebben.

Berekening:

Antwoordzin:

2.2 Lenen

Leen je geld bij een bank, dan rekent de bank je daarvoor een kost (= intrest) aan.

Natuurlijk moet je ook nog het geleende geld terugbetalen.

Voor de scooter van je dromen leen je bij een bank € 2 500. Je betaalt die lening in 16 maanden af.

Daarvoor rekent de bank je een intrest van 8 % aan.

a Bereken het totale bedrag dat je aan de bank moet terugbetalen. b Bereken daarna hoeveel je elke maand moet afbetalen gedurende 16 maanden.

Berekening:

Antwoordzin: a b

3.1 Wat is btw?

Btw is de afkorting voor ‘Belasting over de Toegevoegde Waarde’.

De btw is dus een belasting op de verkoop van producten (bv. fruit, laptop, fiets …) en diensten (bv. haar knippen, schilderen, fietsen herstellen …).

Het basistarief in België is 21 %.

Er zijn enkele uitzonderingen:

• 6 % voor basisproducten (zoals melk, groenten en schoolgebouwen).

• 12 % voor sociale goederen en diensten (zoals medicijnen en huisbrandstof).

3.2 Inclusief en exclusief btw

Een prijs inclusief btw betekent dat de btw al in de prijs is inbegrepen.

Een prijs exclusief btw betekent dat de btw nog niet in de prijs is inbegrepen.

a Een trui kost € 18,00 exclusief btw.

Het btw-tarief is 21 %.

Hoeveel is de prijs inclusief btw?

Berekening:

100 %1 %121 %

€ 18,00

Kort:

b Een parfum kost € 42,35 inclusief 21 % btw. Hoeveel is de prijs exclusief btw?

Berekening:

121 %1 %100 %

€ 42,35

Kort:

Antwoordzin: Antwoordzin:

Om de prijs inclusief 21 % btw te berekenen, neem je de prijs exclusief btw x 1,21

Om de prijs exclusief 21 % btw te berekenen, neem je de prijs inclusief btw : 1,21.

a Voor een auto van € 18 600

betaal je een btw-tarief van 21 %.

Bereken de prijs inclusief btw.

Berekening:

b Een schoolgebouw kost € 1 484 000, inclusief 6 % btw. Bereken de prijs exclusief btw.

Berekening:

Antwoordzin: Antwoordzin:

Kans is de mate van waarschijnlijkheid dat een bepaalde gebeurtenis zich zal voordoen.

Kansen worden uitgedrukt in breuken of procenten

Voorbeeld 1

Hoe groot is de kans dat je met één dobbelsteen een drie gooit?

• Hoeveel mogelijke uitkomsten zijn er bij een dobbelsteen?

• Hoeveel mogelijke uitkomsten zijn er om een drie te gooien?

Bereken nu de kans dat je met één dobbelsteen een drie gooit in procent. Rond af op de eenheid.

Berekening:

De kans is dus= %. aantal goede uitkomsten

In een bokaal zitten vier blauwe, vijf rode en elf witte knikkers.

a Hoeveel procent kans maak je, bij één grijpbeurt, om geblinddoekt een rode knikker uit de bokaal te halen?

Berekening: Hoeveel knikkers zijn er in totaal?

Hoeveel rode knikkers zijn er?

De kans is: = %.

Antwoordzin:

b Hoeveel procent kans maak je, bij één grijpbeurt, om geblinddoekt een witte knikker uit de bokaal te halen?

Berekening: Hoeveel knikkers zijn er in totaal?

Hoeveel witte knikkers zijn er?

De kans is: = %.

Antwoordzin:

Voorbeeld 2

Hoeveel procent kans heb je dat je met twee dobbelstenen als som zes gooit?

• Wat is de laagst mogelijke uitkomst voor de som van de ogen van twee dobbelstenen?

• Wat is de hoogst mogelijke uitkomst voor de som van de ogen van twee dobbelstenen?

Vul de som van de ogen van de dobbelstenen aan in het rooster. 7 8

• Hoeveel mogelijke combinaties zijn er? mogelijke combinaties

• Hoeveel combinaties hebben er als som zes? combinaties

• Hoeveel procent kans heb je om met twee dobbelstenen als som zes te gooien? Rond af op de eenheid.

Berekening:

Antwoordzin:

Deze speciale dobbelsteen bevat acht vlakken. Met twee zo’n dobbelstenen kun je dus als som maximaal 16 gooien.

Hoeveel procent kans heb je om als som 11 te gooien?

Rond af op de eenheid.

Berekening:

Antwoordzin:

Naam:

2

FORMULE 1

Nr.: Klas:

1 Prijsverlagingen en prijsverhogingen

Datum: / / 20 / 20

Plaats de D, de P en de B in het schema. Vul daarna de formules aan.

D = Deel

P = Procent in kommagetal

B = Beginwaarde

Korting: Meerprijs:

Berekening: Berekening:

Sparen en lenen

Als jobstudent verdiende je in juli € 2 500. In augustus kreeg je zelfs 7 % meer.

Hoeveel verdiende je in augustus?

Berekening:

3 Btw

Je hebt je zinnen gezet op een e-bike van € 3 200 exclusief btw. Het btw-tarief is 21 %.

Bereken de prijs inclusief btw.

Berekening: Antwoordzin:

De valhelm, passend bij de e-bike, kost € 278,30 inclusief btw. Het btw-tarief is 21 %.

Bereken de prijs exclusief btw.

Berekening:

Antwoordzin:

4 Kansen en procenten

In een pot zitten er 4 rode, 6 groene en 10 witte steentjes.

Hoeveel procent kans maak je, bij één grijpbeurt, om geblinddoekt een groene steen uit de pot te halen?

Berekening:

Antwoordzin:

Hoeveel procent kans heb je om met één dobbelsteen een zes te gooien? Rond af op de eenheid.

Berekening: Antwoordzin:

Hoeveel procent kans heb je om met twee dobbelstenen als som tien te gooien? Rond af op de eenheid.

Berekening:

Op mijn maat

1 Prijsverlagingen en prijsverhogingen

1 Vul eerst het schema aan. Markeer daarna de correcte formules.

2 Vul aan uit het hoofd.

a Op een aankoop van € 200 krijg je 10 % korting.

Korting:

b Je krijgt 25 % korting op je aankoop van € 160.

Korting:

Nieuwe prijs: Nieuwe prijs:

3 Vul aan uit het hoofd.

a Op 150 euro wordt een prijsverhoging van 20 % aangerekend.

Meerprijs:

b Op 80 euro wordt een prijsverhoging van 5 % aangerekend.

Meerprijs:

Nieuwe prijs: Nieuwe prijs:

4 Vul de reclamefolder van de Gummi aan.

a Je krijgt 15 % korting op de verf. b Je krijgt € 21 korting op het tuinmateriaal.

c 15 % korting komt overeen met € 56,25.

Korting:

Berekening:

Korting:

Korting:

5 Door een prijsstijging moet een motorhandelaar zijn verkoopprijzen aanpassen. Vul aan.

a De prijs van een motor die vorig jaar € 8 900 kostte, stijgt met 5 %.

b Een motorbroek kost € 276 na een prijsverhoging van 15 %.

c Handschoenen kosten nu € 119,90. Vorig jaar was de prijs € 110.

Meerprijs: Meerprijs: Meerprijs:

Berekening: Berekening: Berekening:

6 Webwinkel Blue Eyes koopt voor € 4 000 schoonheidsproducten in. De winkel verkoopt de producten met 28 % winst. Hoeveel zal de winkel in kassa hebben als ze alles verkopen?

Berekening: DPB

Antwoordzin:

7 Een flatscreen-tv die je vorige maand aan € 1 100 kocht, is deze maand in promotie voor € 1 023. Hoeveel procent korting heb je gekregen?

Berekening: DPB

Antwoordzin:

8 Op zaterdagnamiddag krijg je bij de bakker 25 % korting op alle taarten. Na 16.00 uur krijg je nog een extra korting van 20 % bovenop die 25 % korting. Bereken de prijs van de afgebeelde taarten als je die om 17.20 uur koopt. Rond af op 5 cent.

Taart 1: kaastaart met rode vruchten Taart 2: perentaart

18,50

Berekening:

12,80

Berekening:

Antwoordzin: Voor taart 1 betaal je om 17.20 uur € en voor taart 2 € .

9 Bereken bij elke aanbieding het kortingspercentage. Rond af op de eenheid. Omcirkel daarna in de tekstballon de actie die het meeste voordeel biedt.

Actie 1

Bij acht repen: 15 % korting

Berekening:

Actie 4

Van € 1,35 per reep naar € 1,05 per reep!

Actie 2 vier plus twee gratis!

Actie 3

Tweede reep aan halve prijs

Actie 5

Acht halen, zeven betalen.

Actie 1Actie 2Actie 3Actie 4Actie 5 kortingspercentage

10 Bereken uit het hoofd.

a Een vriend leent jou 120 euro tegen een forse intrest van 20 %.

Hoeveel moet je in totaal terugbetalen?

Berekening:

b Je leent tegen 5 % rente 500 euro aan je zus.

Hoeveel moet ze in totaal terugbetalen?

Berekening:

Antwoordzin: Antwoordzin:

11 Bereken.

a Je plaatst € 1 500 op een spaarrekening. Na één jaar geeft de bank je 3 % rente.

Hoeveel zul je na één jaar op je spaarrekening hebben?

Berekening:

b Je leent bij de bank € 1 400 tegen een intrest van 7 %.

Hoeveel moet je na één jaar aan de bank terugbetalen?

Berekening:

Antwoordzin: Antwoordzin:

12 Je besluit om op de onderstaande aanbieding op afbetaling in te gaan.

Berekening:

Antwoordzin:

€ 529,95

of € 31,85/maand* *19 maanden

Hoeveel procent intrest rekent de verkoper aan als je op afbetaling koopt? Rond af op de eenheid.

13

Het gezin Coebelle spaart elk jaar € 1 000.

Daarvoor krijgen ze van de bank 2 % rente.

Het gezin Chacoche spaart elk jaar € 10 000.

De bank beloont hen daarvoor met 2,5 % rente.

a Hoeveel spaart het gezin Chacoche meer dan het gezin Coebelle?

Berekening:

Antwoordzin:

b Beide gezinnen sparen vijf jaar na elkaar elk jaar hetzelfde bedrag en ontvangen telkens hun rente.

Vul de tabellen van beide gezinnen aan.

gezin Coebellegespaardtotaaltotaal na intrest 2 %

na 1 jaar€ 1 000 € 1 000

na 2 jaar€ 1 000

na 3 jaar€ 1 000

na 4 jaar€ 1 000

na 5 jaar€ 1 000

gezin Chacochegespaardtotaaltotaal na intrest 2,5 %

na 1 jaar€ 10 000€ 10 000

na 2 jaar€ 10 000

na 3 jaar€ 10 000

na 4 jaar€ 10 000

na 5 jaar€ 10 000

c Hoeveel heeft de familie Coebelle na vijf jaar in totaal gespaard?

d Hoeveel heeft het gezin Chacoche na vijf jaar in totaal gespaard?

e Hoeveel bedraagt het verschil na vijf jaar tussen beide gezinnen?

f Is het verschil groter of kleiner geworden na vijf jaar?

g Geef twee mogelijke verklaringen voor de verandering in het verschil.

• Verklaring 1:

• Verklaring 2:

14 Als jobstudent werk je in een winkel voor schoonheidsproducten.

Je baas gaf je een lijst van producten die je moet voorzien van de prijs inclusief btw. Het btw-tarief bedraagt 21 %.

Vul de correcte verkoopprijzen aan. Rond af op 5 cent.

product prijs excl. btw

lippotlood

€ 3,00

gezichtspoeder€ 10,75

gezichtsreiniging€ 3,80

hydraterende crème

lippenstift

€ 12,50

€ 6,95

15 In de taxfreeshop op de luchthaven kun je sommige producten btw-vrij aankopen. Het voorziene btw-tarief van 21 % valt dus weg.

Bereken voor deze parfums de prijzen exclusief btw. Rond af op 5 cent.

16 Winkelketen Supermercado doet een actie.

Vandaag hoef je de 21 % btw niet te betalen.

Vul de ontbrekende prijzen aan. Rond af op 1 cent.

incl. btw€ 209

excl. btw €

incl. btw €

excl. btw€ 488

incl. btw€ 649

excl. btw €

incl. btw €

excl. btw€ 190

incl. btw€ 216

excl. btw €

17 Door een foutje stonden alle prijzen met een btw-tarief van 6 % vermeld.

Gelukkig zie je direct dat het om producten gaat met een btw-tarief van 21 %. Verbeter de foute prijsaanduidingen. Rond af op 1 cent. prijs incl. 6 % btwprijs excl. btwprijs incl. 21 % btw

18 Bereken tot op één cijfer na de komma.

a Hoeveel procent is de kans dat je met één dobbelsteen een vijf gooit?

b Hoeveel procent is de kans dat je met één dobbelsteen een vier of een vijf gooit?

c Hoeveel procent is de kans dat je met twee dobbelstenen twee van elkaar verschillende cijfers gooit?

19 Deze dobbelsteen telt acht vlakken. Bereken tot op één cijfer na de komma.

a Hoeveel procent is de kans dat je met één dobbelsteen een zeven gooit?

b Hoeveel procent is de kans dat je met één dobbelsteen een drie of een acht gooit?

c Hoeveel procent is de kans dat je met twee dobbelstenen twee van elkaar verschillende cijfers gooit?

20 Je hebt een pot met 5 blauwe, 4 rode en 3 groene knikkers. Bereken de kansen in procent. Rond af op één cijfer na de komma.

a Je neemt willekeurig één knikker.

• Hoeveel procent kans heb je op een blauwe knikker?

• Hoeveel procent kans heb je op een rode knikker?

• Hoeveel procent kans heb je op een groene knikker?

b Bij een eerste beurt haalde je al één rode knikker uit de pot. Je legde hem opzij.

• Hoeveel procent kans heb je bij een tweede beurt op een blauwe knikker?

• Hoeveel procent kans heb je bij een tweede beurt op een rode knikker?

• Hoeveel procent kans heb je bij een tweede beurt op een groene knikker?

21 Een kaartspel telt 52 kaarten.

Er zijn vier soorten: harten, klaveren, ruiten en schoppen.

Bereken de gevraagde procenten tot op één cijfer na de komma.

Hoe groot is de kans in procent dat je bij het blindelings trekken van één kaart:

a een klaveren neemt?

b een aas neemt?

c een hartenaas neemt?

d een heer, vrouw of boer neemt?

22 Je gooit één keer met twee normale dobbelstenen.

Hoe groot is de kans dat het product van de ogen twintig is?

Berekening:

har ten aas, heer, vrouw, boer 10, 9, 8, 7, 6, 5, 4, 3, 2 klaveren aas, heer, vrouw, boer 10, 9, 8, 7, 6, 5, 4, 3, 2 ruiten

©VANIN

aas, heer, vrouw, boer 10, 9, 8, 7, 6, 5, 4, 3, 2

schoppen aas, heer, vrouw, boer 10, 9, 8, 7, 6, 5, 4, 3, 2

Antwoordzin:

23 In een afdeling van de jeugdbeweging zitten 9 jongens en 15 meisjes.

De hoofdleider maakt door middel van loting een groep van vier kinderen.

Hij gooit alle namen van de kinderen van de afdeling in een pot.

Bereken de gevraagde kans in procent.

Rond af op één cijfer na de komma.

a Hoe groot is de kans dat een meisjesnaam als eerste uit de pot komt?

Berekening:

Antwoordzin:

b De hoofdleider trok bij de eerste beurt een jongensnaam.

Hoe groot is de kans dat een meisjesnaam als tweede naam uit de pot komt?

Berekening:

Antwoordzin:

c Bij de tweede loting trok de hoofdleider nog een jongensnaam. Bij de derde trekking een meisjesnaam.

Hoe groot is de kans dat een meisjesnaam als vierde uit de pot komt?

Berekening:

Antwoordzin:

24 De volleybalvereniging bestelt

De trainer noteerde nauwkeurig de maten in een tabel.

a Maak van de bovenstaande tabel een frequentietabel.

b De nieuwe truitjes werden geleverd, maar de maten liggen allemaal door elkaar. Bereken de kans in procent om blindelings een truitje met maat 170 te nemen. Rond af op één cijfer na de komma.

Berekening:

Antwoordzin:

c Bereken de kans in procent om blindelings een truitje met maat 146 of groter te nemen. Rond af op één cijfer na de komma.

Berekening:

Antwoordzin:

25 Je werpt met drie dobbelstenen.

a Hoeveel ogen kun je maximaal gooien?

b Hoeveel ogen kun je minimaal gooien?

c Hoeveel verschillende mogelijke worpen zijn er in totaal?

d Bereken de kans in procent om in één worp samen twaalf ogen te gooien.

• D PB

= P x B

D = Deel

P = Procent in kommagetal

B = Beginwaarde

=

• Om de prijs inclusief 21 % btw te berekenen, neem je de prijs exclusief btw x 1,21

Om de prijs exclusief 21 % btw te berekenen, neem je de prijs inclusief btw : 1,21

• Kansrekenen

Hoe groot is de kans dat je met één dobbelsteen een drie gooit?

aantal goede uitkomsten

De kans is dus 1 6 =17%

aantal mogelijke uitkomsten

D

P

D : B

B = D : P

Gamezone

Een zeeslagpuzzel is een logische puzzel met eenvoudige regels.

• Je moet de locatie van de verborgen schepen vinden in het rooster. Sommige schepen zijn al deels zichtbaar.

• Een schip is een rechte lijn van zwarte vakjes. De grootte van het schip zie je in de legende onder het rooster. Daar vind je ook het aantal schepen.

• Twee schepen mogen elkaar niet raken (ook niet diagonaal).

• De cijfers buiten het rooster tonen aan hoeveel vakjes in die rij of kolom bezet zijn door schepen.

Naam:

Nr.: Klas:

1 Prijsverlagingen en prijsverhogingen

Datum: / / 20 / 20

Plaats de D, de P en de B correct in het schema. Vul daarna de formules aan.

D = Deel

P = Procent in kommagetal

B = Beginwaarde

Korting: Meerprijs:

Berekening: Berekening:

2 Sparen en lenen

Als jobstudent verdiende je in juli € 2 500. In augustus kreeg je 7 % minder. Hoeveel verdiende je in augustus?

Berekening:

Btw

Je hebt je zinnen gezet op een spelcomputer van € 1 800, exclusief btw.

Het btw-tarief is 21 %.

Bereken de prijs inclusief btw.

Berekening: Antwoordzin:

Het toetsenbord, de muis en de headset bij deze pc kosten € 260, inclusief btw.

Het btw-tarief is 21 %.

Bereken de prijs exclusief btw tot op twee cijfers na de komma.

Berekening:

Antwoordzin:

4 Kansen en procenten

In een pot zitten er vijf rode, vijf groene en vijftien witte steentjes.

Hoeveel procent kans maak je, bij één grijpbeurt, om geblinddoekt een groene steen uit de pot te halen?

Berekening:

Antwoordzin:

Hoeveel procent kans heb je om met één dobbelsteen een vijf te gooien? Rond af op de eenheid.

Berekening: Antwoordzin:

Hoeveel procent kans heb je om met twee dobbelstenen als som negen te gooien? Rond af op de eenheid.

Afronden en schatten

1 Afronden

Om een getal af te ronden, kijk je naar het cijfer rechts van de plaats waar je wilt afronden:

• als het volgende cijfer kleiner is dan 5, dan behoud je het vorige cijfer;

• als het volgende cijfer 5 is of groter, dan verhoog je het vorige cijfer met 1.

Voorbeeld: 605,379

afgerond op een honderdste: 605,38 afgerond op een tiende: 605,4 afgerond op de eenheid: 605 afgerond op een tiental:

afgerond op een honderdtal:

Rond elk bedrag af op een tiental.

afgerond op een tiental

Rond elk bedrag af op een euro (zonder komma in de oplossing).

afgerond op een euro

Rond elk bedrag af op een tiende.

afgerond op een tiende

2 Schatten

Vaak is het handig om vooraf te weten hoeveel het resultaat ongeveer zal zijn.

• Rond de getallen af tot getallen waarmee je makkelijker uit het hoofd kunt rekenen.

• Maak de gevraagde bewerking met de afgeronde getallen.

Voorbeeld:

Mira wil graag opbergruimte voor haar tuinmateriaal.

Ze koopt een tuinhuis en een opbergkast.

Schat hoeveel ze moet betalen.

werkelijke prijsafgeronde prijs tuinhuis

opbergkast

Schatten:

€ 2 276

Deze scooter wordt aangeboden met een korting van € 249. Schat in honderdtallen hoeveel de scooter ongeveer zal kosten na aftrek van de korting.

Schatten:

Een ticket voor een concert kost € 38,50.

Een gezin van vijf gaat naar het concert.

Ze kopen elk een drankje van € 2,80.

Schat hoeveel het gezin ongeveer moet betalen.

Schatten:

Schat in honderdtallen hoeveel de tuinaannemer ongeveer moet betalen.

afgeronde prijs bewerkingschatting

a Het bedrijf koopt drie grasmaaiers.

b Ook kopen ze twee nieuwe kettingzagen.

c Daar komen nog vier heggenscharen bij.

d En ten slotte ook nog vijf grastrimmers.

Planner

Mijn circuit

Aan de slag Ben ik mee? Op mijn maat Test op mezelf

FORMULE 1

Nr.: Klas: Datum: / / 20 /

Kijk zeker ook op iDiddit.be

1 Lengtematenp. 63

2 Lengtematen herleiden

3 Omtrek van vlakke figuren

©VANIN

Aantekeningen leerkracht Noteerde ik telkens een eenheid bij mijn antwoord?

Aan de slag

1 Lengtematen

1.1 Benamingen

Lengte druk je uit met een getal en een lengtemaat

De meest gebruikte lengtematen zijn: mm, cm, dm, m en km.

Vul de passende lengtemaat aan.

de breedte van een handpalm de dikte van een bankkaart één kwartier stappen de breedte van een deur de breedte van een duim

1.2 Meetinstrumenten

©VANIN

a Noteer onder elke foto de naam van het meetinstrument. Kies uit: digitale afstandsmeter, lintmeter, meetwiel, schuifmaat.

b Markeer het meetbereik en de meetnauwkeurigheid.

150 mm2 m40 m10 000 m150 mm2 m40 m10 000 m meetnauwkeurigheid meetnauwkeurigheid 0,01 mm1 mm1 dm1 m0,01 mm1 mm1 dm1 m

150 mm2 m40 m10 000 m150 mm2 m40 m10 000 m meetnauwkeurigheid meetnauwkeurigheid 1 mm1 cm1 dm1 m0,01 mm1 mm1 cm2 m

2 Lengtematen

Voordat Mansur begint te schilderen, plakt hij het raam goed af. Het rechthoekige raam is 2,3 m lang en 125 cm breed.

Hoeveel rollen afplaktape heeft Mansur nodig voor zes identieke ramen?

Berekening:

km100 m10 mmdmcmmm

Antwoordzin:

Je zwemt twintig baantjes van 25 m.

Hoeveel kilometer heb je gezwommen?

Berekening:

km100 m10 mmdmcmmm

Antwoordzin:

De kleine broden bij bakkerij Fijnbakkertje zijn 12 cm breed. In de winkel zijn er vijf legplanken van 1,8 m.

Hoeveel kleine broden kan de bakker op de planken leggen?

Berekening:

km100 m10 mmdmcmmm

Antwoordzin:

Welke vlakke figuren herken je in de zwembaden?

Noteer telkens de formule om de omtrek te berekenen.

Duid de gebruikte letter(s) uit de formule aan op de tekening.

Soort figuur:

Formule omtrek:

Soort figuur:

Formule omtrek:

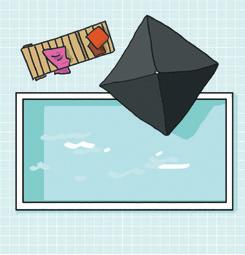
Soort figuur:

Formule omtrek:

Soort figuur:

Formule omtrek:

De boorden van een bureaublad van 110 cm lang en 90 cm breed voorzie je van nieuwe kantfolie.

a Noteer de afmetingen in meter bij de foto.

b Hoeveel meter kantfolie heb je nodig?

Berekening:

Antwoordzin:

4 Lengte in de praktijk

Niels moet voor vijf lampen een kubusvormige armatuur lassen, zoals op de foto. Hoeveel meter metaal heeft Niels minstens nodig?

Berekening:

16 cm

Antwoordzin:

De onderstaande L-vormige living krijgt plinten.

Eén lopende meter plinten kost € 23,95.

a Vul de ontbrekende lengtes aan op de tekening.

b Hoeveel zal het minstens kosten om de woonkamer van plinten te voorzien?

2 m1 m

Berekening:

2 m

4 m

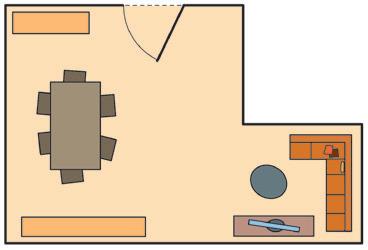
2 m

6 m

Antwoordzin:

Lisette maakt voor haar eindproject in de naaiklas een tent voor haar neefje. Elke ribbe (dus ook van het grondvlak) wil ze met een houten stok verstevigen. De opstaande stokken zijn bovenaan 15 cm langer dan de stof van het tentje.

Hoeveel meter hout moet Lisette kopen?

Antwoordzin:

Berekening:

Naam:

FORMULE 1

1 Lengtematen

Nr.: Klas:

Markeer de passende afmeting.

Datum: / / 20 / 20

39,6 cm39,6 dm39,6 m42,2 mm42,2 m42,2 km55 mm55 cm55 dm

Welk meetinstrument gebruik je het best? Verbind.

a De lengte van de woonkamer. ••meetwiel

b De breedte van een cursusblad. ••meetlat

c De diameter van een houtboor. ••schuifmaat

d De afstand van de kerk tot het cultureel centrum. ••digitale afstandsmeter

2 Lengtematen herleiden

Een touw is 3 m lang.

Hoeveel touwtjes van 25 cm kun je knippen uit dit touw?

Berekening:

Antwoordzin:

Vader legt een pad aan tot achteraan in de tuin. Het pad is 16 m lang.

Hij kiest voor tegels van 90 x 90 cm.

Hoeveel tegels moet vader minstens aankopen?

Berekening:

3 Omtrek van vlakke figuren

Plaats het nummer van de omtrekformule bij de juiste vlakke figuur.

2omtrek = 2 x l + b5omtrek = 2 x l + 2 x b

1omtrek = 4 x z4omtrek = 2 x r x 3,14 driehoek rechthoek vierkant cirkel

3omtrek = 2 x d x 3,146omtrek = z1 + z2 + z3

Bereken de binnenomtrek van deze metalen buizen in mm. Rond af op de éénheid.

Berekening:

Antwoord:

4 Lengte in de praktijk

Berekening:

Antwoord:

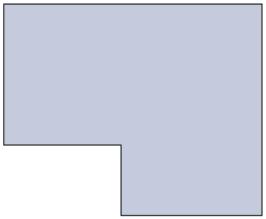
Je wilt deze L-vormige living aan het plafond voorzien van sierlijsten. Eén lopende meter sierlijst kost € 9,85.

Berekening:

Hoeveel zul je minstens betalen voor de sierlijsten? 11 m 5 m 9 m 6 m

Antwoordzin:

Om netjes te kunnen pleisteren, moet je vanuit beide kamers aan de zijkant en bovenkant van de deuropening een profiel plaatsen. De deuropening is 2,5 m hoog en 90 cm breed. Een profiel van 2,5 m kost 2,89 euro.

a Hoeveel profielen moet je kopen?

Berekening:

Antwoordzin:

b Hoeveel moet je betalen voor de profielen?

Berekening:

Op mijn maat

1 Lengtematen

1 Orden van klein naar groot.

Geef de kleinste lengte cijfer 1 en de grootste lengte cijfer 6. de lengte van een olympisch zwembad de lengte van een keukentafel de hoogte van een deur de dikte van een gsm de lengte van een voetbalveld de hoogte van een verdieping

2 Markeer de passende lengte.

4,5 mm4,5 dm 10 mm20 cm 1,05 m3,05 m 4,5 cm4,5 m 25 mm15 dm 2,05 m4,05 m

©VANIN

3

Noteer de letter van het meetinstrument bij de juiste foto.

Markeer het meetbereik en de meetnauwkeurigheid.

A Met een tachymeter meet je de afstand tot aan een vast punt.

B Met een meetmat meet je de lengte van een baby.

C Met een schoenmaatmeter meet je de lengte van een kindervoet.

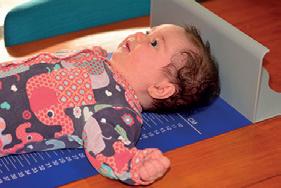
meetbereik meetbereik meetbereik 1 m100 dm1 km20 cm60 cm99 cm99 mm20 cm99 cm

meetnauwkeurigheidmeetnauwkeurigheidmeetnauwkeurigheid 1 mm5 mm1 cm1 mm5 mm1 cm1 mm5 mm1 cm

4 Herleid.

a 4,5 m = cm

e 6 540 m = km

b 250 mm = cm f 0,6 m = mm

c 0,75 km = m g 150 cm = m

d 7,3 cm = mm h 8 400 cm = m

5 Bereken.

a Je last een metalen buis van 38 cm lang aan een buis van 2,8 m.

Hoe lang is de nieuwe buis in meter?

b De nieuwe laptops met een dikte van 21 mm worden geleverd in dozen van 0,5 m hoog.

Hoeveel laptops passen er in een doos?

c Flore wil graag 5 km lopen.

De piste is 1 298 m lang.

Hoeveel rondes moet Flore zeker lopen?

d Je legt zeven planken van 32 mm dik op elkaar in een aanhangwagen met een bakhoogte van 40 cm.

Hoeveel cm hoogte heb je nog over in de bak?

e Elke deelnemer van de rommelmarkt in de straat krijgt een ruimte van 5 m.

Er zijn 214 deelnemers.

Hoeveel km lang moet de straat zeker zijn?

f Een boekenkast is 180 cm hoog en 45 cm breed. Een vrije muur is 3,2 m lang.

Hoeveel kasten kun je tegen de muur plaatsen?

g Op een rol kabel XVB 3 x 1,5 mm² zit 25 m.

Je knipt er 7 stukken van 3,5 m af.

Hoeveel cm blijft er over op de rol?

6 Je hebt in totaal 360 m hout nodig om het tuinhuis te bekleden. Je kocht 140 planken van 2,8 m.

Hoeveel volledige planken heb je te veel aangekocht?

Berekening:

Antwoordzin:

7 Je hangt een kader van 55 cm breed en 85 cm hoog op in het midden van een muur van 2,5 m lang en 2,20 m hoog. Op hoeveel cm van de muurrand hangt het kader?

Berekening:

Antwoordzin:

8 Een leerkracht techniek heeft voor elke leerling twee houten stukken van 35 cm nodig. In de doe-het-zelfzaak kan hij planken kopen van 300 cm lang en 15 cm breed. Hoeveel planken moet hij kopen voor zijn 10 leerlingen?

Berekening:

Antwoordzin:

9 Jan wil alle sierkussens in zijn huis opnieuw bekleden. Voor elk kussen heeft hij 12 dm van een rol stof met breedte 90 cm nodig. Hij vond een rol stof van 10 m x 90 cm met een mooi motief. Hoeveel rollen moet Jan kopen om 16 kussens opnieuw te bekleden?

Berekening: km100 m10 mmdmcmmm

Antwoordzin:

10

Ode wil met haar papa een konijnenren inrichten. Voor welke konijnenren moeten ze het meeste draad kopen?

Soort figuur: Soort figuur: Soort figuur:

Formule omtrek:

Formule omtrek: Formule omtrek:

Berekening: Berekening: Berekening:

Antwoordzin:

11 Een volleybalveld meet 18 m op 9 m.

Als opwarming laat de trainer de spelers 20 toertjes rond het veld lopen.

Hoeveel meter moeten de spelers in totaal lopen?

Soort figuur:

Formule omtrek:

Berekening:

Antwoordzin:

12 Kyenti wil zijn geitenweide omheinen.

Hij schetst zijn weide en schrijft er de afmetingen bij.

Hoeveel zal hij moeten betalen?

Soort figuur:

Formule omtrek:

Berekening:

Antwoordzin:

13 Asmet en Aristo gaan op een reuzenrad met een straal van 17 m.

Hoeveel meter legt het reuzenrad af bij een volledige omwenteling?

Rond af op 1 m.

Soort figuur:

Formule omtrek:

Berekening:

Antwoordzin:

14 Een sleufsilo heeft een lengte van 15 m en een breedte van 9 m.

Hoeveel keerwanden zijn er nodig om deze sleufsilo te bouwen?

Berekening:

Antwoordzin:

15 Om deze constructie te maken heeft men 30 rechtopstaande zijpanelen nodig. De zijpanelen hebben een hoogte van 300 cm en zijn 90 cm breed.

a Hoeveel meter is de omtrek van de constructie?

Berekening:

Antwoordzin:

b Hoeveel meter is de diameter van de constructie?

Rond af tot op twee cijfers na de komma.

Berekening:

Antwoordzin:

16

Hoeveel meter raamprofielen heb je ongeveer nodig om dit raam te kunnen maken?

Rond zinvol af.

Berekening:

Antwoordzin:

900 mm

17 De vierkante doos waarin de kaarsen zitten, heeft telkens een zijde van 4 dm.

Bereken de omtrek van de cirkelvormige kaarsen in centimeter.

b

Berekening:

Antwoordzin:

Berekening:

Antwoordzin:

18 Raf en Mats fietsen elke dag naar school.

a De wielen van Rafs fiets hebben een diameter van 61 cm.

Ze maken 1 566 omwentelingen.

Hoeveel kilometer is het naar zijn school? Rond af op 1 km.

Berekening:

Antwoordzin:

b De wielen van Mats’ fiets hebben een diameter van 71 cm.

Hoeveel omwentelingen maken de wielen van zijn fiets als hij dezelfde afstand fietst als Raf?

Berekening:

Antwoordzin: 2 450 mm

19

Hoeveel meter staal heeft Iwan minimaal nodig om deze bijzettafels te maken? Rond af op één cijfer na de komma. a

Berekening:

120 x 35 x 75 cm b

Antwoordzin:

hoogte 54 cm diameter 60 cm

Berekening:

Antwoordzin:

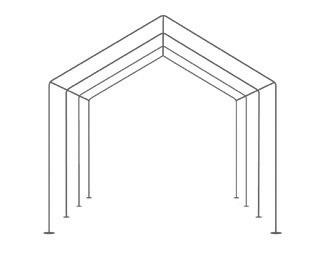
20 Pieter gaat de buizen van zijn partytent vervangen.

De verbindingsstukken van de hoeken zijn nog in goede staat.

Hoeveel meter stalen buizen moet hij kopen om de tent te vernieuwen?

Berekening:

Antwoordzin:

21 Dante renoveert zijn badkamer. Eerst plaatst hij de plinten. Er zitten tien plinten van 45 cm lang verpakt in één doos. Hoeveel dozen plinten heeft hij minimaal nodig voor zijn badkamer?

1 m

Berekening:

2 m

2,5 m

Antwoordzin:

22

Ivana heeft een vierkante tafel gekocht met omtrek 500 cm.

Voor een zitplaats heeft ze 50 cm extra nodig, gemeten vanaf het tafelblad.

Ivana wil de tafel in een vierkante ruimte plaatsen.

Welke minimale zijde moet de ruimte hebben om de tafel met stoelen te kunnen gebruiken?

Soort figuur:

Basisformule omtrek:

Berekening:

Antwoordzin:

23 Simon is met zijn skateboard aan het oefenen op de skateramp. De twee zijkanten van de ramp vormen samen een halve cirkel.

Simon skateboardde 175 keer van de ene naar de andere kant.

Soort figuur:

Basisformule omtrek:

300 cm

Berekening:

Hoeveel meter heeft hij in totaal afgelegd? 400 cm

Antwoordzin:

24 Frans wil voor zijn kleinzoon een vierkante boekenkast bouwen.

a Hoeveel meter hout met dikte 4,5 cm heeft hij minimaal nodig voor het kader?

b Hoeveel meter hout met dikte 2 cm heeft hij minimaal nodig voor de tussenschotten?

Berekening:

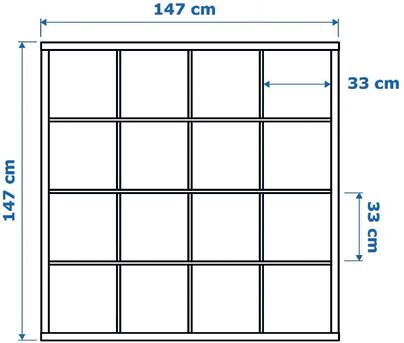
Antwoordzin: a b

Even samenvatten

• Lengtematen herleiden

km100 m10 mmdmcmmm 650 cm 6 5 0 6,5 m

©VANIN

• Omtrek van vlakke figuren

rechthoek vierkant

lengte (l)

breedte (b) zijde (z)

omtrek2 x l + 2 x b of 2 x (l + b) 4 x z

driehoek

omtrek

z1 + z2 + z3 2 x r x 3,14 of d x 3,14

Gamezone

1 Shikaku

Verdeel het rooster in rechthoeken en vierkanten.

In elke rechthoek of elk vierkant mag maar één getal staan.

Het getal in de rechthoek / het vierkant moet overeenkomen met het aantal vakken binnen de rechthoek / het vierkant.

2 Hashiwokakero

De puzzel bestaat uit een aantal eilanden (cirkels) met een nummer.

Je bouwt bruggen (lijnen) tussen de eilanden en let op het volgende:

• Elke lijn verbindt twee eilanden met elkaar, horizontaal of verticaal.

• De lijnen kruisen elkaar niet.

• Tussen twee eilanden trek je maximaal twee lijnen.

• Het aantal lijnen dat van een eiland vertrekt, is gelijk aan het nummer op dat eiland.

• Elk eiland is vanuit elk ander eiland bereikbaar: de eilanden vormen dus samen één groep.

Test

1 Lengtematen

Nr.: Klas:

Markeer de passende afmeting.

Datum: / / 20 / 20

45 mm45 cm45 dm6,5 mm65 mm650 mm140 mm140

Welk meetinstrument gebruik je het best?

Kies uit: meetmat, meetwiel, schuifmaat en tachymeter.

a De afstand in vogelvlucht tot de kerk.

b De lengte van een baby.

c De lengte van een voetbalveld.

d De dikte van een metaalboor.

2 Lengtematen herleiden

De kastmodules zijn 40 cm hoog.

Hoeveel modules kun je op elkaar plaatsen in een ruimte van 2,7 m hoog?

Berekening:km100 m10 mmdmcmmm

Antwoordzin:

Een fles wijn heeft een diameter van 86 mm.

Hoeveel flessen passen naast elkaar in een rek van 1 m?

Berekening:km100 m10 mmdmcmmm

3 Omtrek van vlakke figuren

Een clown wandelt op een speelton. De ton met diameter 50 cm maakt 15 omwentelingen.

Hoeveel meter heeft de clown afgelegd met de ton? Rond af op 1 m.

Soort figuur:

Basisformule omtrek:

Berekening:

Antwoordzin:

Boerin Laura plaatst een omheining rond deze weide. Bereken de lengte van de omheining.

120 m

80 m

Antwoordzin:

4 Lengte in de praktijk

Soort figuur:

Basisformule omtrek:

Berekening:

Jitske wil het bloemperk afboorden zoals op de tekening.

Hoeveel zal de afboording in totaal kosten?

Berekening: Antwoordzin:

t/m 09-11-2024 Online beperkt op voorraad

8 m x 14 cm x 0,7 cm

Optellen en aftrekken

13 noem je de som 9 noem je het verschil 6, 7, 12 en 3 noem je de termen.

1 Handig optellen

Behoud de eerste term.

Splits de tweede term. Tel die in stappen op. + 40 + 7

In een interieurwinkel vind je deze spullen.

Bibi koopt de kandelaar en de vaas. Hoeveel moet ze betalen?

Berekening:

14 + 43 14

Antwoordzin:

Bibi moet euro betalen.

Pieter koopt de vaas en het kussen. Hoeveel moet hij betalen?

Berekening: 43 + 18,90 43

Antwoordzin:

Pieter moet euro betalen.

Bereken handig. Gebruik een kladblad indien nodig.

a 259 + 47 = f 15 + 6,20 = b 152 + 98 = g 19,30 + 7,60 =

c 236 + 234 = h 16,35 + 8,75 = d 196 + 169 = i 23,40 + 18,30 =

e 702 + 447 = j 33,30 + 68,95 = 6 + 7 = 13 12 – 3 = 9

2 Handig aftrekken

Behoud de eerste term. Splits de tweede term. Trek die in stappen af. –

8

Florence krijgt 14 euro korting op deze vaas. Hoeveel moet ze betalen?

43

Berekening:

43 – 14 43

Antwoordzin:

Florence moet euro betalen.

Ingrid betaalt 76,20 euro in de supermarkt. Ze betaalt met twee briefjes van 50 euro. Hoeveel krijgt ze terug?

Berekening:

100 – 76,20 100

Antwoordzin: Ingrid krijgt euro terug.

Bereken handig. Gebruik een kladblad indien nodig.

a 913 – 214 = f 25 – 7,6 =

b 534 – 285 = g 17,4 – 11,5 =

c 172 – 98 = h 9,35 – 3,75 =

d 444 – 234 = i 83,4 – 56,3 =

e 101 – 65 = j 33,3 – 17,45 =

3 Handig optellen en aftrekken

Florian koopt een trui van 59,50 euro en een broek van 79,40 euro. a Hoeveel betaalt hij in totaal?

Berekening:

Antwoordzin:

b Hij betaalt met drie briefjes van 50 euro. Hoeveel krijgt hij terug?

Berekening:

Antwoordzin:

Statistisch onderzoek

Planner

Aan de slag Ben ik mee? Op mijn maat Test op mezelf

FORMULE 1

Nr.: Klas: Datum: / / 20 /

1 Absolute en relatieve frequentie

2 Diagrammen

3 Misleidende diagrammen

4 Handige getallen bij tabellen

©VANIN

Aantekeningen leerkracht Heb ik zinvol afgerond? Leerling:

Leerkracht:

Aan de slag

1 Absolute en relatieve frequentie

1.1 Absolute frequentie

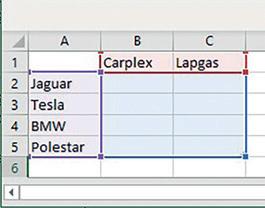
De personeelsleden van het bedrijf Carplex mogen van hun werkgever een bedrijfswagen kiezen.

Ze kunnen kiezen uit de onderstaande merken:

De resultaten van hun keuze vind je in deze tabel:

Om de resultaten overzichtelijk te maken, werk je met een frequentietabel

gegevenaantal

Je noteert alle gegevens

totaal

Beantwoord de vragen.

Je noteert het aantal keer dat het gegeven voorkomt. Dat noem je de absolute frequentie

a Hoeveel personeelsleden mochten een bedrijfswagen kiezen?

b Hoeveel personeelsleden gaven de voorkeur aan een Jaguar?

c Welk merk kozen ze het meest?

1.2 Relatieve frequentie

Ook de personeelsleden van het bedrijf Lapgas mochten uit dezelfde wagens kiezen.

De resultaten van beide bedrijven vind je terug in de frequentietabellen. Vul aan.

Bij welk bedrijf lijkt Polestar het populairst?

Dit antwoord houdt geen rekening met het aantal personeelsleden van elk bedrijf.

Om de resultaten van beide bedrijven te vergelijken, moet je ze procentueel berekenen. Dat noem je de relatieve frequentie.

Beantwoord de vragen.

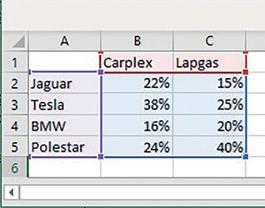
a Vul de frequentietabellen aan.

Je deelt het aantal door het totaal en zet dit om naar procent. Dat noem je de relatieve frequentie.

b Hoeveel procent van de personeelsleden van Carplex kiest voor Polestar?

c Hoeveel procent van de personeelsleden van Lapgas kiest voor Polestar?

d Bij welk bedrijf is Polestar het populairst?

2 Diagrammen

Een frequentietabel kun je omzetten in een diagram.

• Een lijndiagram is een grafiek waarbij je de aantallen van de gegevens (de absolute frequentie) als stippen voorstelt.

De opeenvolgende stippen verbind je met rechte lijnen.

Teken het lijndiagram voor het bedrijf Lapgas.

keuze bedrijfswagen Carplex

• Een staafdiagram is een grafiek waarbij je de aantallen van de gegevens (de absolute frequentie) als staven voorstelt.

Teken de ontbrekende staven.

keuze bedrijfswagen Carplex keuze bedrijfswagen Lapgas

• Een bijzondere voorstelling is een cirkeldiagram.

De grootte van de sectoren komt overeen met de relatieve frequentie.

Hoeveel personeelsleden kozen voor Jaguar?

keuze bedrijfswagen Carplex keuze bedrijfswagen Lapgas

Welk diagram is het meest geschikt om de keuze voor een bedrijfswagen tussen beide firma's onderling te vergelijken?

Een diagram maken met behulp van ICT actie scherm

Open Word.

Klik op Invoegen.

Klik op Grafiek.

Klik op Kolom.

Klik op Gegroepeerde kolom.

Klik op OK.

Maak de frequentietabel op.

Je wilt een grafiek maken die het procentuele resultaat toont. Daarvoor maak je gebruik van: de absolute / relatieve frequentie.

Vul de gegevens in.

Je krijgt de volgende grafiek.

Pas de grafiek aan:

1 Verander de grafiektitel in: ‘keuze bedrijfswagens’.

2 Geef de staven voor Lapgas een groene kleur.

3 Laat de verticale as per 5 % verspringen.

Klik op het staafdiagram.

Klik op Grafiekontwerp.

©VANIN

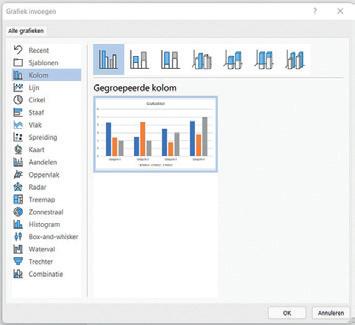
Klik op Ander grafiektype en kies voor Lijndiagram.

Misleidende diagrammen

Let op met diagrammen. Laat je niet vangen. Soms gebruikt men een diagram om een besluit op te dringen of een indruk te versterken.

vermageren met CALORIEVRETER Dit staafdiagram geeft de indruk dat je na vijf keer CALORIEVRETER te gebruiken, spectaculair afvalt.

Kijk goed naar de horizontale as. Wat deed de reclamemaker om het resultaat te versterken?

Schrap wat niet past. Vul aan. Duid aan.

a Het lijkt alsof er tussen 2019 en 2021 een sterke stijging / daling van het aantal verkeersongevallen is.

In werkelijkheid gaat het maar om een stijging / daling met ongevallen.

Het diagram misleidt doordat

 de lijn niet recht getekend is.

 de verticale as niet bij nul begint.

 de horizontale as niet gelijk verdeeld is.

b Het lijkt alsof het aantal leerlingen dat genoeg studeerde, bijna de helft is van het aantal leerlingen dat niet studeerde.

In werkelijkheid is het verschil:

% – % = %.

Het diagram misleidt doordat

 de hoogte van de staven niet in verhouding is.

 de verticale as niet bij nul begint.

 de horizontale as niet gelijk verdeeld is.

c Welke leeftijdscategorie geeft volgens de grafiek het meeste bloed?

Het diagram misleidt doordat

 de staven niet even breed zijn.

 de verticale as niet bij nul begint.

 de horizontale as niet gelijk verdeeld is.

Ik heb genoeg gestudeerd.

van bloedgevers

4.1 Het gemiddelde en de mediaan van een rij getallen bepalen

De tabel geeft je een overzicht van de resultaten die Hanne behaalde voor haar toetsen Frans en Engels, telkens op tien punten.

toets 1toets 2toets 3toets 4toets 5

toets 1toets 2toets 3toets 4toets 5toets 6

Als titularis moet je per vak het gemiddelde en de mediaan van Hannes resultaten berekenen.

Het gemiddelde van een rij getallen berekenen

Het gemiddelde (χ) van een rij getallen is de som van de getallen gedeeld door hun aantal.

Je berekent het gemiddelde tot op een cijfer na de komma meer dan de gegeven getallen.

Berekening: som resultaten aantal toetsen χ

De mediaan van een rij getallen bepalen

De mediaan (Me) van een rij gerangschikte getallen is

• het middelste getal als het aantal getallen oneven is;

• Je rangschikt de gegevens:

• Je telt het aantal gegevens: .

• Is dat even of oneven?

• het gemiddelde van de middelste twee getallen als het aantal even is. even oneven even oneven

• Me =

• Je rangschikt de gegevens:

• Je telt het aantal gegevens: .

• Is dat even of oneven?

• Me =

a Voor welk vak scoorde Hanne gemiddeld het best?

b Voor welk vak laat Hanne haar ouders liever de mediaan zien?

4.2 Het gemiddelde en de mediaan uit een frequentietabel bepalen

Het gemiddelde uit een frequentietabel berekenen

De ouders van Hanne willen weten of ze in vergelijking met de andere leerlingen echt zo slecht scoorde voor toets 2 van Engels.

Daarom willen ze het klasgemiddelde en de mediaan van die toets kennen.

De frequentietabel geeft een overzicht van de klasresultaten van toets 2 voor Engels.

score toets 2012346789 aantal leerlingen221613121

Bereken het gemiddelde voor toets 2. som resultaten aantal leerlingen χ

De mediaan uit een frequentietabel bepalen

Bereken de mediaan voor toets 2.

• Welke leerling is de ‘middelste’?

• Me =

Hanne scoort dus beter / slechter ten opzichte van de mediaan van de klas.

De twee leerlingen die 8 scoorden, hebben gespiekt.

De leraar wijzigt hun punten naar 0.

a Pas de frequentietabel aan.

score toets 2012346789 aantal leerlingen

b Bereken het nieuwe gemiddelde en de nieuwe mediaan. som resultaten aantal leerlingen χ

• Welke leerling is de ‘middelste’?

• Me =

c Vergelijk het nieuwe klasgemiddelde met het vorige klasgemiddelde. Wat merk je?

d Vergelijk de nieuwe mediaan met de vorige mediaan. Wat merk je?

De variatiebreedte (R) is het verschil van het grootste en het kleinste gegeven.

Een ijsmakerij heeft twee vulmachines. Met die machines vullen ze ijsbekers van 150 ml. Het bedrijf doet onderzoek naar de precieze inhoud van de bekers. De tabellen tonen de resultaten.

a Bepaal voor de beide vulmachines de gemiddelde inhoud van de bekers

Berekening:

vulmachine 1: som = aantal = gemiddelde = vulmachine 2: som = aantal = gemiddelde =

Antwoord: χ vulmachine 1 = χ

b Bepaal voor de beide vulmachines de mediaan.

Berekening:

2 =

Antwoord: Me

c Kun je aan de hand van het gemiddelde en de mediaan afleiden welke machine bijgesteld moet worden? Verklaar je antwoord.

d Bepaal voor de beide vulmachines die maat.

Berekening:

Antwoord:

e Welke maat gebruik je beter om te bepalen welke vulmachine bijgesteld moet worden? Duid aan.

gemiddeldemediaanvariatiebreedte

f Welke vulmachine moet bijgesteld worden?

Naam:

FORMULE 1

Nr.: Klas:

1 Absolute en relatieve frequentie

Datum: / / 20 / 15

Een aantal gezinnen werd gevraagd hoe ze hun huis verwarmen. Dit zijn de resultaten. elektriciteitwarmtepompelektriciteitgaswarmtepomp gaselektriciteitgas gas gas gaswarmtepompgaselektriciteitelektriciteit

Vul de frequentietabel aan. Rond af op twee cijfers na de komma.

aantal procent

elektriciteit5 5 : 15 x 100 = 33,33 %

gas warmtepomp

totaal

2 Diagrammen

In vier verschillende leeftijdscategorieën (A, B, C en D) werd aan 60 personen gevraagd: ‘Kijk je naar Familie op VTM?’

Noteer bij elk diagram het nummer van de passende frequentietabel.

A

B

leeftijdscategorie C

3

Misleidende diagrammen

Het diagram stelt de verkoop van de verschillende thema’s van LEGO voor. Wat is er misleidend aan het diagram? Duid aan.

4 Handige getallen bij tabellen

 De staven zijn niet even breed.

 De verticale as begint niet bij nul.

 De hoogtes van de figuurtjes zijn niet gelijk.

 Je weet niet of je de hoogte van de figuur bij de blokjes moet tellen.

 Je kent de betekenis van de getallen bij de verticale as niet.

Het sportmerk AdiNik vraagt aan enkele sprintatleten hun schoenmaat. Dit zijn de resultaten.

Stel

Hoeveel atleten werden ondervraagd?

De hoeveelste atleet is de ‘middelste’?

Op mijn maat

1 Absolute en relatieve frequentie

1 Een onderzoeksbureau stelt enkele jongeren de vraag: ‘Welke van deze apps gebruik je het meest?’

AFRONDEN FacebookInstagram WhatsAppSnapchat

De resultaten van hun keuze vind je in de onderstaande tabel.

Aan een groep senioren stelt het onderzoeksbureau dezelfde vraag.

a Vul de twee frequentietabellen aan. jongeren senioren gegevenaantalprocent

b Beantwoord de vragen.

gegevenaantalprocent

• Hoeveel jongeren werden er in totaal ondervraagd?

• Hoeveel senioren werden er in totaal ondervraagd?

• Hoeveel procent van de jongeren gebruikt Instagram het meest?

• Bij welke doelgroep is Facebook het populairst?

• Welke app gebruiken de senioren helemaal niet?

2 De school vraagt aan de vierdejaars met welk vervoersmiddel ze naar school komen.

a Vervolledig de frequentietabel. Rond af op twee cijfers na de komma. aantal procent te voet 9 fiets/step 21 openbaar vervoer27 wagen 6

bromfiets 17

totaal

b Juist of fout? Omcirkel de passende letters. juistfout

Meer dan de helft van de leerlingen komt te voet, met de fiets of step.TA

Een vierde van de leerlingen komt met de bromfiets of wagen. LT

50 % komt ofwel te voet, ofwel met het openbaar vervoer. SF Er werden 80 leerlingen ondervraagd. SK

17 % van de leerlingen komt met de bromfiets. UA

c Welk woord kun je met de omcirkelde letters vormen?

3 Het Rode Kruis noteert de bloedgroep van een aantal mensen in een tabel.

a Vervolledig de frequentietabel.

b Noteer bij elke staaf de passende bloedgroep.

4

Uit ervaring weet bakker Jos hoeveel broden hij van elke soort moet bakken. Vul de tabel aan.

soort broodprocent aantal wit brood

Berekening: witte broden bruin brood %

25 %

volkorenbrood 15 %

Berekening:

32 bruine broden

Berekening: volkorenbroden

Berekening: meergranenbroden

broden

5 De thuisbatterij van Lieselot is volledig opgeladen door haar zonnepanelen.

Ze beschikt zo over 10 kWh (kilowattuur).

a Lieselot laat haar afwas- en wasmachine werken.

Ze verbruikt daarmee 27 % van de batterij.

Hoeveel kWh heeft ze verbruikt? Rond af op één cijfer na de komma.

Berekening:

Antwoordzin:

b Lieselot kookt op een inductieplaat en laat ook de oven voorverwarmen.

Ze verbruikt 44 % van de resterende energie van de batterij.

Hoeveel kWh heeft ze nu verbruikt? Rond af op één cijfer na de komma.

Berekening:

Antwoordzin:

c Hoeveel % is de batterij nu nog opgeladen?

Berekening:

Antwoordzin:

100 %

6 In vier verschillende leeftijdscategorieën (A, B, C en D) werd aan 90 personen gevraagd: ‘Heb je last van zweetvoeten?’ Noteer bij elk diagram het nummer van de passende frequentietabel.

B

©VANIN

leeftijdscategorie D

7 De grafiek toont je de gemiddelde levensverwachting in België bij de geboorte. Beantwoord de onderstaande vragen. jaarmannenvrouwen 199673,8680,53 200074,5880,92 200576,1481,86 201077,3682,64 201578,5583,16 201678,7883,68 201778,9983,66 201879,2083,69 201979,5884,00 202078,5283,05

a Wat is de levensverwachting van een man geboren in 1996?

b Wat is de levensverwachting van een vrouw geboren in 2020?

c Wat is het verschil in levensverwachting tussen mannen en vrouwen geboren in het jaar 2000?

d Geef een mogelijke verklaring waarom de levensverwachting sinds 1880 stijgt.

e Geef een mogelijke verklaring waarom de levensverwachting van een man lager is dan van een vrouw.

8 Het diagram stelt de hoeveelheid neerslag (N) en de temperatuur (T) per maand in Moskou voor. Beantwoord de onderstaande vragen.

neerslag in mm Klimatologische gemiddelden 1961-1990

a Welke maand is het koudst?

b Hoeveel neerslag valt er in de warmste maand?

c Wat is het verschil in hoeveelheid neerslag tussen de droogste en de natste maand?

d Wat is het verschil in temperatuur tussen de warmste en de koudste maand?

9 Charlotte, Sasha, Sofie en Suzy lopen van huis naar hun trainingscentrum.

Noteer bij elke persoon de letter van het passende diagram. Schrijf kort een mogelijk verhaal voor Sofie.

afstand

tijd A

Charlotte: Ik ben als een pijl vertrokken en was in een mum van tijd in de kleedkamer.

Diagram: afstand

tijd B

©VANIN

Sasha: Ik vertrok goed, maar moest even vertragen doordat het bergop ging.

Diagram: afstand

tijd C

Sofie:

Diagram: afstand

tijd D

Suzy: Ik was snel vertrokken, maar keerde terug om mijn rugzak.

Diagram:

10 De grafiek toont de gemiddelde lichaamslengte van de inwoners van enkele landen.

a Duid de juiste uitspraken aan.

 Je zou denken dat de gemiddelde lichaamslengte van een Canadees veel groter is dan de lichaamslengte van een Indiër.

 Je zou denken dat de gemiddelde lichaamslengte van een Canadees veel kleiner is dan de lichaamslengte van een Indiër.

 Je zou denken dat alle Filipijnen een groeistoornis hebben.

b Vul aan. Schrap wat niet past.

In werkelijkheid is een Canadees cm groter / kleiner dan een Indiër.

c Wat is er misleidend?

 De hoogteverhouding van de mannetjes.

 De verticale as begint niet bij nul.

 De horizontale as is niet gelijk verdeeld.

11 Dit diagram toont de tevredenheid van de gebruikers van twee soorten gameconsoles. Beantwoord.

a Welke fabrikant maakte gebruik van dit misleidende diagram?

 PS5

 Xbox 360

b Wat deed de fabrikant om zijn product in de verf te zetten?

12 Wat is er mis met deze diagrammen? Beschrijf.

Nederland Verenigde StatenCanada Verenigd KoninkrijkIndiaFilipijnen

© Centraal Bureau voor de Statistiek

13

Noteer de letter bij de passende benaming. mediaan gemiddelde variatiebreedte

14 Bereken telkens de mediaan.

a 14 12 17 12 18 19 12 14 17 11 15

• Je rangschikt de gegevens:

• Je telt het aantal gegevens:

• Je bepaalt de mediaan:

b 4 23 20 8 7 8 22 4 21 22 23 20

• Je rangschikt de gegevens:

• Je telt het aantal gegevens:

• Je bepaalt de mediaan:

15 Julia en Gino spelen een dartswedstrijd.

Bij het darten start je met 501 punten.

Je moet zo snel mogelijk eindigen op 0.

a Vul de tabellen aan.

worpen Juliapunten

worp 1

worp 2

worp 3

worp 4

worp 5 JuliaGino

b Bereken het gemiddelde.

c Wie scoorde het hoogste gemiddelde?

d Wie had het minst aantal worpen nodig? even oneven even oneven

worpen Ginopunten

worp 1

worp 2

worp 3

Tijdens het spel gooi ik altijd twee tot negen kegels omver.

Het vrouwelijke jurylid geeft mij een 8 voor uitvoering.

Mijn wedstrijden duren altijd rond de 2 uur.

16

De frequentietabel geeft je een overzicht van een toets wiskunde op tien punten.

punten op 10 012345678910

aantal leerlingen 01041214320

a Bereken het gemiddelde, de mediaan en de variatiebreedte.

Hoeveel leerlingen telt de klas?

De hoeveelste leerling is de ‘middelste’?

Me =

R = – =

b Kevin scoorde maar één op tien. Maar omdat Kevin een tijdje afwezig was, beslist de leerkracht om de toets van Kevin niet mee te laten tellen.

Pas de frequentietabel aan.

Bereken daarna opnieuw het gemiddelde, de mediaan en de variatiebreedte.

punten op 10 012345678910

aantal leerlingen

Hoeveel leerlingen telt de klas?

De hoeveelste leerling is de ‘middelste’?

Me =

R = – =

c Schrap wat niet past. Vul aan.

Het klasgemiddelde stijgt / daalt zo met punten.

De mediaan stijgt / daalt / blijft hetzelfde.

De variatiebreedte stijgt / daalt met punten.

d Heeft Iza, met 6 op 10, een goed resultaat in vergelijking met de klas? Verklaar.

Even samenvatten

• Absolute en relatieve frequentie

Je noteert alle gegevens in de eerste kolom.

Je noteert het aantal keer dat het gegeven voorkomt. Dat noem je de absolute frequentie.

gegevenaantal procent

1212 : 30 = 0,40 = 40 %

1818 : 30 = 0,60 = 60 % totaal30 100 %

Je deelt het aantal door het totaal en zet dit om naar procent. Dat noem je de relatieve frequentie.

• Handige getallen bij tabellen

Gemiddelde

Het gemiddelde (χ) van een rij getallen is de som van de getallen gedeeld door hun aantal.

Mediaan

De mediaan (Me) van een rij gerangschikte getallen is

• het middelste getal als het aantal getallen oneven is;

• het gemiddelde van de middelste twee getallen als het aantal even is.

Variatiebreedte

De variatiebreedte (R) is het verschil van het grootste en het kleinste gegeven.

Gamezone

1 Wat is de waarde van het vraagteken?

2 Wat is de waarde van het vraagteken? 32=7 54=23 76=47 98=79 109=?

3 Welk getal staat er onder de geparkeerde auto?

Naam:

Nr.: Klas:

1 Absolute en relatieve frequentie

Datum: / / 20 / 15

Aan een aantal vrouwen vraagt men waarvoor ze naar de schoonheidsspecialiste gaan. nagels lakkengelaatsverzorgingnagels lakkenvoetmassage gelaatsverzorgingnagels lakkengelaatsverzorgingvoetmassage voetmassagegelaatsverzorginggelaatsverzorgingnagels lakken

Vul de frequentietabel aan. Rond af op de eenheid.

aantal procent nagels lakken gelaatsverzorging voetmassage

totaal

2 Diagrammen

In vier verschillende leeftijdscategorieën (A, B, C en D) werd telkens aan 120 personen de vraag gesteld: ‘Snurk jij in jouw slaap?’

Noteer bij elk diagram het nummer van de passende frequentietabel.

3 Misleidende diagrammen

Op basis van dit diagram beslist de gemeenteraad om € 2 000 te schenken aan de KSA en € 1 000 aan de Chiro.

a Waarom is die beslissing fout?

b Hoe wordt de gemeente misleid? Duid aan.

 De staven zijn niet even breed.

 De verticale as begint niet bij nul.

 Het is niet duidelijk wat de gegevens voorstellen.

4 Handige getallen bij tabellen

KSA en Chiro

De leerlingenraad vraagt aan haar leden hoeveel snoeppakketten ze hebben verkocht ten voordele van het goede doel.

leerlingenraad 1e graad 21213 04322 32344

a Stel de gegevens voor in een frequentietabel.

leerlingenraad 2e en 3e graad 02104 43023

b Bereken het gemiddelde uit de bovenstaande frequentietabellen.

Berekening: leerlingenraad 1e graad: som = aantal leden = gemiddelde = leerlingenraad 2e en 3e graad: som = aantal leden = gemiddelde =

Antwoord: χ leerlingenraad 1e graad = χ leerlingenraad 2e en 3e graad = c Bepaal voor beide leerlingenraden de mediaan.

Berekening:

Antwoord: Meleerlingenraad 1e graad = Me leerlingenraad 2e en 3e graad =

Vermenigvuldigen en delen

1 Handig vermenigvuldigen

• Splitsen

73 x 2 = (70 + 3) x 2 = (70 x 2) + (3 x 2) = 140 + 6 = 146

• Vermenigvuldigen met 4 = tweemaal vermenigvuldigen met 2

3,14 x 4 = 3,14 x 2 x 2 = 6,28 x 2 = 12,56

• Vermenigvuldigen met 10, 100 of 1 000

21 x 10 = 210

37 x 100 = 3 700

48 x 1 000 = 48 000

©VANIN

3,75 x 10 = 37,5

5,76 x 100 = 576

8,37 x 1 000 = 8 370

• Vermenigvuldigen met 5 = vermenigvuldigen met 10 en daarna delen door 2

28,4 x 5 = 28,4 x 10 : 2 = 284 : 2 = 142

Bereken uit het hoofd.

a 4 x 43=

b 24 x 4=

c 9 x 21=

d 167 x 10=

e 7 x 12=

f 5 x 27=

g 7 x 25=

h 16 x 12=

i 55 x 11=

j 3,4 x 100=

k 0,003 x 10=

l 548 x 4=

m 3 x 41,6=

n 7 x 23=

o 42,7 x 5=

p 21 x 14=

q 52,45 x 2=

r 22 x 24=

s 17 x 22=

t 25 x 8=

u 360 x 4=

v 42 x 7=

w 4,2 x 1 000=

x 620 x 5=

2 Handig delen

• Splitsen

86 : 2 = (80 + 6) : 2 = (80 : 2) + (6 : 2) = 40 + 3 = 43

• Delen door 4 = tweemaal delen door 2

24,84 : 4 = 24,84 : 2 : 2 = 12,42 : 2 = 6,21

• Delen door 10, 100 of 1 000

210 : 10 = 21

375 : 100 = 3,75

4 000 : 1 000 = 4

2,75 : 10 = 0,275

5,76 : 100 = 0,057 6

837,5 : 1 000 = 0,837 5

• Delen door 5 = delen door 10 en daarna vermenigvuldigen met 2

63,5 : 5 = 63,5 : 10 x 2 = 6,35 x 2 = 12,70

Bereken uit het hoofd.

a 2 300 : 10= m 10,46 : 2=

b 670 : 5= n 36,24 : 6=

c 132 : 4= o 68,8 : 1 000=

d 165 : 3= p 21,2 : 2=

e 450 : 100= q 0,52 : 4=

f 524 : 4= r 3,35 : 5=

g 96 : 2= s 2,8 : 10=

h 245 : 5 = t 0,9 : 2=

i 3 560 : 10= u 24,64 : 4=

j 8 400 : 100= v 475,5 : 10=

k 144 : 4= w 3,33 : 3=

l 560 : 7= x 8 : 100=

Oppervlakte 5

Planner

Aan de slag 1 Oppervlaktematen en landmaten

1.1 Omtrek of oppervlakte?

1.2 Benamingen

2 Oppervlaktematen en landmaten herleiden112

3 Oppervlakte van vlakke figuren 113

4 Oppervlakte in de praktijk 114

5 Ontwikkeling en oppervlakte van ruimtefiguren115

5.1 Ontwikkeling en oppervlakte van een balk en een kubus

5.2 Ontwikkeling en oppervlakte van een cilinder

Herhalingsoefeningen Handig

Mijn circuit

op mezelf

Aan de slag Ben ik mee? Op mijn maat

FORMULE 1

Nr.: Klas:

Datum: / / 20 /

Oppervlaktematen en landmaten p.

1

2 Oppervlaktematen en landmaten herleiden

3 Oppervlakte van vlakke figuren

4 Oppervlakte in de praktijk

5 Ontwikkeling en oppervlakte van ruimtefiguren

Totaal:

Aantekeningen leerkracht

©VANIN

DE KIJKER Kijk zeker ook op iDiddit.be

Is mijn antwoord realistisch?

Leerling:

Leerkracht:

Aan de slag

1 Oppervlakte en landmaten

1.1 Omtrek of oppervlakte?

Omtrek of oppervlakte? Duid aan.

plinten plaatsen gras zaaien een muur schilderen

omtrek oppervlakte omtrek oppervlakte omtrek oppervlakte

1.2 Benamingen

Oppervlakte druk je uit met een getal en een oppervlaktemaat

De meest gebruikte oppervlaktematen zijn: km2, m2, dm2, cm2 en mm2

De oppervlakte van bouwgrond, landbouwgrond en bosgrond druk je meestal uit in landmaten

De landmaten zijn: ha (hectare), a (are) en ca (centiare). 1 m2 = 1 ca

Vul de passende oppervlaktemaat of landmaat aan.

grootte van twee voetbalvelden

©VANIN

grootte van een halve deur

grootte van een vingernagel

grootte van een speldenkopje

grootte van een blaadje uit een kubusschrijfblok

1 1 of 1 1 1 1

Vul aan met de passende oppervlaktemaat of landmaat.

a De grootte van het scherm van je smartphone is ongeveer 100

b De oppervlakte van de vloer van het toilet thuis is ongeveer 2

c De grootte van een parkeerplaats is ongeveer 10

d De grootte van het natuurdomein in jouw gemeente is 125

Lente en Victor hebben 50 tegels gekocht om hun tuinpad aan te leggen. De tegels hebben elk een oppervlakte van 900 cm2

Hebben ze genoeg tegels om hun pad van 4 m2 aan te leggen?

Berekening: haa ca

Antwoordzin:

Ouassima is van plan een stuk bouwgrond van 23 a 15 ca te verkavelen. Elke kavel moet minstens 300 m2 groot zijn. In hoeveel kavels kan Ouassima de grond verdelen?

Berekening: haa ca

Antwoordzin:

Michelle wil een kartonnen doos met een oppervlakte van 6 dm2 versieren.

Daarvoor gebruikt ze snippers van 2 cm2

Hoeveel snippers heeft Michelle minimaal nodig?

Berekening: haa ca

dm2 cm2 mm2

Antwoordzin:

Pim en Bene mogen op hun tuinbouwbedrijf maar een twintigste van de totale oppervlakte verharden. Het tuinbouwbedrijf is 7 ha groot. Hoeveel vierkante meter mogen ze verharden?

Berekening: haa ca

Antwoordzin:

Welke vlakke figuur herken je in de vorm van de spiegel?

Noteer telkens de formule om de oppervlakte te berekenen.

Duid de gebruikte letter(s) uit de formule aan op de tekening.

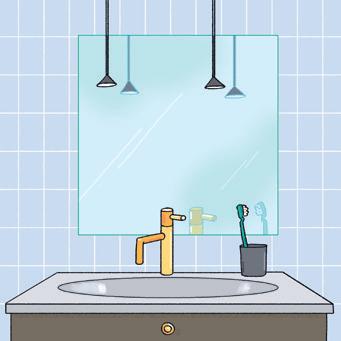
Soort figuur: Soort figuur:

Formule oppervlakte:

Formule oppervlakte:

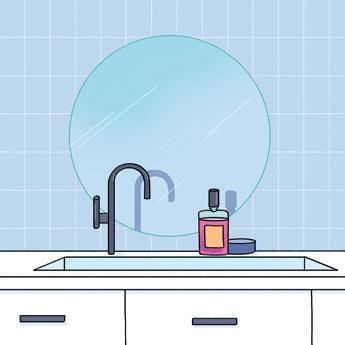
Soort figuur: Soort figuur:

Formule oppervlakte:

Formule oppervlakte:

Lucas en Jara willen hun gazon opnieuw inzaaien.

Het rechthoekige grasveld is 63 m lang en 12 m breed.

Hoeveel dozen graszaad hebben ze nodig?

Berekening:

Antwoordzin:

Oppervlakte

José wil een nieuwe vloer leggen in zijn woonkamer.

• Noteer de ontbrekende lengtes op de tekening. 6 m 3 m 5 m

• Hoeveel zal het minstens kosten om de woonkamer te vloeren?

Tip: verdeel de oppervlakte in herkenbare deeloppervlakten.

Berekening:

mogelijkheid 1

Antwoordzin:

Om krassen te voorkomen moet je een houten vloer lakken.

a Vul de ontbrekende lengtes op de tekening aan.

b Hoeveel liter vloerlak moet je voorzien?

Berekening:

mogelijkheid 2

Antwoordzin:

Een schilder rekent 77 euro aan per vierkante meter.

Hoeveel kost het om deze gevel te laten schilderen?

Berekening:

Antwoordzin:

Ontwikkeling en oppervlakte van ruimtefiguren

5.1 Ontwikkeling en oppervlakte van een balk en een kubus

Een balkvormig doosje is 4 cm lang, 3 cm breed en 1 cm hoog.

Noteer de afmetingen van het doosje bij de afbeelding.

Vouw je het doosje volledig open, dan krijg je de ontwikkeling van de balk.

Die ontwikkeling bestaat uit zes .

• Teken de ontwikkeling van de balk.

©VANIN

• Noteer de afmetingen van het doosje op de ontwikkeling.

• Kleur het voor- en achteraanzicht geel, het linker- en rechterzijaanzicht blauw, het boven- en onderaanzicht rood.

• Wat is de oppervlakte van de balk?

Vul de tabel aan.

oppervlakte rode rechthoeken = 2 x x oppervlakte blauwe rechthoeken = 2 x x

oppervlakte gele rechthoeken = 2 x x

oppervlakte balk = 2 x x + 2 x x + 2 x x

formule balk

Kobe maakt in papier een kubus met een zijde van 2 cm.

• Teken een ontwikkeling van de kubus.

De ontwikkeling bestaat uit zes

• Stel de formule op voor de oppervlakte van de kubus.

oppervlakte kubus =

• Wat is de oppervlakte van de kubus van Kobe?

Berekening:

Antwoordzin:

5.2 Ontwikkeling en oppervlakte van een cilinder

Het blik heeft een diameter van 6 cm en een hoogte van 10 cm.

De ontwikkeling bestaat uit twee en één . r h 2 x r x 3,14

Om de oppervlakte van een cilinder te berekenen,

• neem je twee keer de oppervlakte van de : 2 x r x r x 3,14,

• en tel je daar de oppervlakte van de bij: 2 x r x 3,14 x h.

oppervlakte cilinder = 2 x r x r x 3,14 + 2 x r x 3,14 x h

Hoeveel vierkante centimeter metaal is er nodig om dit blik te maken?

Berekening:

Antwoordzin:

Naam:

FORMULE 1

Nr.: Klas:

1 Oppervlaktematen en landmaten

Markeer de passende afmeting.

Datum: / / 20 / 20

Vul aan met de passende oppervlaktemaat of landmaat.

Kies uit: mm2, cm2, dm2, m2, a of ha

a De oppervlakte van een laptopscherm is 750 .

b De oppervlakte van een zwembad is 250 .

c De oppervlakte van een potloodpunt is 1 .

d De oppervlakte van twee klaslokalen samen is 1 .

2 Oppervlaktematen en landmaten herleiden

De KSA plant een nieuw speelbos van 3 are aan. Per 1,5 m2 mag er een boom staan.

Hoeveel bomen kunnen ze op hun terrein planten?

Berekening:

Antwoordzin:

Tess heeft 29 houten kistjes met een grondoppervlakte van 20 dm2

Heeft Tess genoeg kistjes om een wand van 6,5 m2 te bekleden?

Berekening:

3

Oppervlakte van vlakke figuren

Plaats het nummer van de oppervlakteformule bij de juiste vlakke figuur.

1z x z

2d x 3,14

3r x r x 3,14

42 x l x b

5(b x h) : 2

6l x b

4

Oppervlakte in de praktijk

oppervlakte driehoek

oppervlakte vierkant

oppervlakte rechthoek

oppervlakte cirkel

De kledingwinkel Moleca wordt opnieuw bekleed met tapijt. Het tapijt kost 77,95 euro/m2

Voor de inkomhal van 4 m op 2,5 m wordt geen tapijt voorzien.

Hoeveel zal het vloertapijt in totaal kosten?

Antwoordzin:

Berekening:

5 Ontwikkeling en oppervlakte van ruimtefiguren

Vul de tabel aan.

Welk ontwerp heeft het meeste karton nodig voor de verpakking?

Soort ruimtefiguur

Formule oppervlakte

Berekening oppervlakte

Antwoord Ontwerp 1 / Ontwerp 2 heeft het meeste karton nodig voor de verpakking.

Op mijn maat

1 Oppervlaktematen en landmaten

1 Omtrek of oppervlakte? Duid aan.

afstoffen kaderrandmuren bepleisterenganache over taart doen

omtrek oppervlakte omtrek oppervlakte omtrek oppervlakte

2 Markeer de passende oppervlakte.

3 De onderstreepte delen staan in de verkeerde zin. Schrijf ze naast de juiste zin.

a Het stuk bouwgrond is 1 200 dm2 groot.

b De oppervlakte van het kapsalon is 5 m2

c Het toiletvenster heeft een oppervlakte van 650 cm2

d Het plonsbadje in de tuin is 6,7 a groot.

e Je slaapkamer heeft een oppervlakte van 47 ha.

f Het toetsenbord van je laptop is 81 m2

g Het gemeentebos is maar liefst 49 dm2 groot.

h Het dak van het tuinhuis is 510 000 000 km2 groot.

i De oppervlakte van de aarde bedraagt 8 m2

4 Bereken.

a Omar splitst zijn moestuin van 18 ca op in 6 delen, zodat hij zijn groenten mooi kan verdelen.

Hoe groot is elk deel in m2?

b Het klaslokaal is 30 m2 groot.

Er staan 12 banken in van 1,2 m2

Hoeveel m2 wandelruimte is er over in de klas?

c Een konijn heeft een leefruimte van minimaal 120 dm2 nodig om zich gelukkig te voelen.

Hoeveel konijnen kunnen in een hok van 6 m2?

d Op een pallet liggen in totaal 6 000 mappen met elk een oppervlakte van 7,6 dm2

Hoeveel are kun je met alle mappen bedekken?

5 Elk jaar planten kersverse ouders samen zo'n 700 geboortebomen.

Per boom voorziet de groendienst 1,5 m2 voor een goede groeiontwikkeling.

Dit jaar kocht de gemeente een nieuw perceel aan van 1 ha groot.

Hoeveel jaar kunnen ze dit perceel gebruiken?

Berekening:

Antwoordzin:

6 Friedl en Laurence willen Arne beetnemen door zijn raam vol te kleven met post-its.

Ze hebben in totaal 500 post-its van 58 cm2 groot.

De oppervlakte van Arnes raam is 4 m2

Hebben Friedl en Laurence genoeg post-its?

Indien niet, hoeveel post-its hebben ze te weinig?

Berekening:

Antwoordzin:

7 Welke figuur heeft de grootste oppervlakte?

Rond indien nodig af tot op één cijfer na de komma. 1 2 3

oppervlakte: oppervlakte: oppervlakte:

Formule

Berekening

Antwoordzin:

8 Bakker Tom maakt voor de verjaardag van een vriend een puzzel van 24 stukken uit vanille- en chocoladecake.

De puzzel is 20 cm lang en 10 cm breed. Hoeveel cm2 is elk puzzelstuk? Rond af tot op één cijfer na de komma.

Berekening:

Antwoordzin:

9 Om de bodem van de moestuin te verbeteren gebruik je fossiele zeewierkalk. Per 10 m2 heb je 1,5 kg zeewierkalk nodig.

De rechthoekige moestuin is 10 m lang en 6 m breed. Hoeveel dozen zeewierkalk van 4 kg moet je kopen?

Berekening:

Antwoordzin:

10

Het grondoppervlak van een circustent wordt voorzien van boomschors.

De diameter van de tent is 32 m.

Met één zak boomschors kan de directeur 2,25 m2 bedekken.

Hoeveel zakken boomschors moet de directeur elke keer voorzien?

Berekening:

Antwoordzin:

11

De landingsbaan 07L/25R heeft een lengte van 3,638 km en een breedte van 50 m.

Om de landingsbaan opnieuw te laten asfalteren betaalt de luchthaven 45 euro/m2.

Hoeveel kost het om de landingsbaan opnieuw te laten asfalteren?

Berekening:

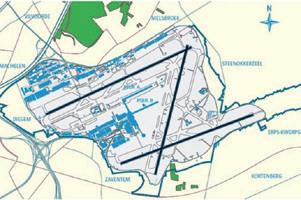
Antwoordzin:

12 Cristina wil zelf een vlieger maken.

De hoogte van het gele stuk is de helft van de hoogte van het blauwe stuk.

Hoeveel cm2 stof heeft ze van elke kleur nodig?

Berekening: 6 dm

72 cm

Antwoordzin:

13

Van het driehoekige grasveld moeten de oude graszoden weg.

Eén vierkante meter graszoden weegt ongeveer 18 kg.

Het containerpark rekent 0,05 euro/kg aan.

Wat kost het om de graszoden in het containerpark bij het groenafval te doen?

Berekening:

Antwoordzin:

©VANIN

14 Marieke beschildert een muur van 4 m lang en 2,5 m hoog met donkergroene verf. Daarbij moet een cirkelvormig vlak niet geschilderd worden.

Een pot donkergroene verf waarmee je 5 m2 kunt schilderen, kost € 19,99.

De muur heeft drie lagen verf nodig.

Hoeveel moet Marieke betalen voor de verf?

Berekening:

Antwoordzin:

15 Javi legt een vijver aan in zijn tuin. De kasseienrand rond de vijver is 40 cm breed. Per vierkante meter kasseien betaalt Javi € 30,21.

Hoeveel moet Javi voor de kasseien rond zijn vijver betalen? 3,2 m

Antwoordzin:

Berekening:

16 Kyenti en Simon willen deze ruimte van hun huis opnieuw betegelen.

De vloerder komt met twee voorstellen. Beide tegels vinden Kyenti en Simon even mooi. Ze besluiten om in te gaan op het goedkoopste voorstel.

voorstel 1

laminaattegels

26,94 euro/m2

20,20 euro/m2

tegellijm per 8 m2

52,79 euro

voorstel 2

laminaattegels

Berekening:

23,10 euro/m2

Welke tegelsoort met bijpassende tegellijm zullen ze kiezen?

Antwoordzin:

tegellijm per 12 m2

59,00 euro

17 Om de huwelijksringen mooi in te pakken, maakt de juweelontwerper een glazen kubusvormig doosje met een ribbe van 3 cm. Hoeveel cm2 glas heeft de juweelontwerper nodig om dit doosje te maken?

Berekening:

Antwoordzin:

18 Een doos Rice Krispies is 28 cm hoog, 21 cm lang en 7 cm breed.

a Teken in het rooster de ontwikkeling van de doos. Tip: de zijden van de vakjes zijn op schaal getekend en stellen 7 cm voor.

schaal 1:7

b Bereken uit hoeveel vierkante decimeter karton zo'n doos minimaal bestaat.

Berekening:

Antwoordzin:

19 Oma wil de poef bekleden met stof. De stof bedekt de onderzijde niet volledig. Daar is er een stofopening met een diameter van 10 cm.

Hoeveel stof heeft oma minimaal nodig om deze poef te bekleden?

Berekening:

Antwoordzin:

20 Louis loopt stage in de tweede kleuterklas met 18 kleuters. Ze knutselen een stoomboot.

De drie losse onderdelen van de boot worden eerst volledig geverfd en daarna samengesteld.

Met een fles van 500 ml verf kun je 60 dm2 verven.

Hoeveel flessen heeft Louis per kleur nodig?

Berekening:

Antwoordzin:

Even samenvatten

• Oppervlaktematen en landmaten herleiden

1 ha = 10 000 m2

• Ken je de formules nog?

rechthoek

lengte (l)

breedte (b)

oppervlakte

zijde (z)

vierkant

hoogte (h) L

basis (b)

oppervlakte (b x h) : 2 r x r x 3,14

• Formules oppervlakte ruimtefiguren

• Oppervlakte van samengestelde figuren

Gamezone

Kleurensudoku

• In een rij mag geen enkele kleur of figuur twee keer voorkomen.

• In een kolom mag geen enkele kleur of figuur twee keer voorkomen.

• In een blok mag geen enkele kleur of figuur twee keer voorkomen.

Tips om de sudoku op te lossen:

©VANIN

• Zoek steeds naar rijen, kolommen en blokken waar maar weinig kleuren of figuren ontbreken.

• Begin met kleuren of figuren die al veel voorkomen.

• Probeer nooit te gokken. Als je één keer fout gokt, kun je de puzzel niet meer oplossen.

Naam:

FORMULE 1

Nr.: Klas:

1 Oppervlaktematen en landmaten

Markeer de passende afmeting.

Datum: / / 20 / 20

5 ca 5 a5 ha 15 cm2 15 dm2 15 m2 0,2 mm2 2 mm2 20 mm2

Vul aan met de passende oppervlaktemaat of landmaat.

Kies uit: mm2, cm2, dm2, m2, a of ha.

a De oppervlakte van België is 3 068,9

b De oppervlakte van een vloertegel is 36 .

c De oppervlakte van een keukeneiland is 5 .

d De oppervlakte van de punt van een dartspijl is 1 .

2 Oppervlaktematen en landmaten herleiden

Alessia wil in haar voortuin bodembedekkers planten. Het tuincentrum adviseert om per 15 dm2 één bodembedekker te planten. Een plantje kost 0,95 euro.

Hoeveel zal Alessia betalen om 3 m2 voortuin aan te planten met bodembedekkers?

Berekening:

Antwoordzin:

In een sporthal met een oppervlakte van 9,24 a wordt een jaarbeurs georganiseerd. Drie vijfde van de oppervlakte moet vrij blijven voor de bar en wandelruimte.

Elke deelnemer krijgt een ruimte van 8 m2

Hoeveel deelnemers kunnen er staan op de jaarbeurs?

Berekening:

3

Oppervlakte van vlakke figuren

Bereken de oppervlakte van de onderstaande figuren. 13 mm

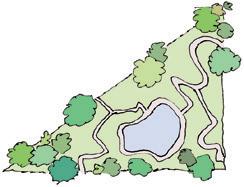
Formule:

Berekening:

Antwoord: De oppervlakte is

4 Oppervlakte in de praktijk

Formule:

Berekening:

Antwoord: De oppervlakte is

Onder het toilet en de wastafel loopt de vloer door. Onder de douche en het bad niet. Wat is de vloeroppervlakte van deze badkamer?

Berekening:

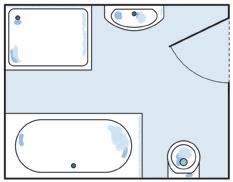
Antwoordzin:

5 Ontwikkeling en oppervlakte van ruimtefiguren

Vul de tabel aan. Duid de passende formule voor de oppervlakte aan. Bereken.

Rekenen met positieve en negatieve getallen

Hiernaast zie je een bankrekeninguittreksel van Stijn.

Het saldo is het bedrag dat op de rekening staat.

Stijn heeft een positief saldo

Vul de rekeninguittreksels aan.

Stijn gaat naar Ikea en geeft daar 138 euro uit.

27/01

credit Ikea

27/01 huidig saldo+ € 1 950

Credit betekent dat er een bedrag afgaat.

Om een creditbewerking uit te voeren moet je dus . vorig saldo+ € 1 950

nieuw saldo

Stijn krijgt 34 euro terug van zijn zus.

27/01

vorig saldo debet zus

nieuw saldo

Debet betekent dat er een bedrag bijkomt.

Om een debetbewerking uit te voeren moet je dus

Stijn moet een voorschot van 2 000 euro betalen op zijn nieuwe elektrische fiets.

27/01

Na die verrichting heeft Stijn een negatief saldo Hij heeft dus schulden bij de bank. vorig saldo voorschot

nieuw saldo

Vul de tabel aan.

beginsaldo € debet + credit

Gilles gaat wandelen in de bergen.

Hij begint op 10 meter boven de zeespiegel

• Op de eerste dag wandelt hij 370 meter omhoog.

Op welke hoogte komt hij aan op dag 1?

Berekening:

Antwoordzin: Gilles komt aan op boven / onder de zeespiegel.

• Op de tweede dag wandelt hij 410 meter omlaag.

Op welke hoogte komt hij aan op dag 2?

Berekening:

Antwoordzin: Gilles komt aan op boven / onder de zeespiegel.

Vul de tabel aan.

Bereken het temperatuurverschil tussen dag 1 en dag 2. dag 1dag 2 bewerking temperatuurverschil

a 5 °C7 °C 7 °C – 5 °C

b –5 °C–2 °C

c –7 °C12 °C

d –1 °C0 °C

Bereken handig. Gebruik een kladblad indien nodig.

a 230 + 56 = f –43 + 23 =

b 130 – 65 = g –55 + 95 =

c 425 – 540 = h –670 – 6 =

d 83 – 84 = i –507 + 800 =

e 45 + 45 = j –67 + 67 =

Bereken handig. Gebruik een kladblad indien nodig. a

Evenredigheden 6

Mijn circuit

Aan de slag Ben ik mee? Op mijn maat Test op mezelf

FORMULE 1

Nr.: Klas: Datum: / / 20 /

Totaal:

Aantekeningen leerkracht

©VANIN

Aan de slag

1 Gelijke verhoudingen

Een verhouding geeft het verband aan tussen twee hoeveelheden. Dat verband stel je meestal met een breuk voor.

PRODUCTFICHE KNAUF PLEISTERGIPS

ONDERGROND

Dient droog te zijn, los van stof en losse delen.

AANMAKEN

25 kg pleister in circa 15 l schoon water strooien.

Na enkele minuten, mixen tot een klontvrije massa.

VERWERKEN

Aanbrengen op ondergrond en vlak zetten.

Na het opstijven de pleister bevochtigen, doorschuren en glad pleisteren.

Noteer de hoeveelheid pleistergips en de hoeveelheid water als een verhouding.

Wil je een grotere of kleinere hoeveelheid maken, dan moeten de verhoudingen gelijk zijn. Voeg je te veel of te weinig van een grondstof toe, dan krijg je niet het gewenste resultaat.

Hoeveel liter water voeg je toe aan 5 kg pleistergips? Schat en duid aan.

3 liter4 liter75 liter

Berekening:

aantal kg pleistergips255

aantal l water 15

Hoeveel pleistergips voeg je toe aan 12 l water? Schat en duid aan. 4 kg 15 kg20 kg

Berekening:

aantal kg pleistergips25 aantal l water 1512

Gelijke verhoudingen noem je evenredigheden. Voorbeeld: 25 15 = 5 3 = 20 12

Duid de verhouding(en) aan die een evenredigheid vormen met de gegeven verhouding.

2.1 Recht evenredige grootheden

Eén ticket voor een zwembeurt kost € 3,00.

Twee tickets kosten € 6,00.

Drie tickets kosten € 9,00.

Hoe meer tickets je koopt, hoe meer / minder je moet betalen.

• Grootheden

Wat zijn de twee grootheden in dit voorbeeld? Vul aan.

De twee grootheden zijn en

• Tabel

Vul de tabel aan.

aantal tickets

• Woordformule Vul de formule aan.

kostprijs (€)0369 kostprijs : aantal tickets = kostprijs =

De verhouding van de grootheden is telkens gelijk.

Het aantal tickets en de kostprijs in euro zijn recht evenredig (RE).

• Grafiek

Teken de punten in het assenstelsel en verbind.

De punten van de grafiek liggen op één rechte lijn door de oorsprong

Lees af op de grafiek of bereken.

a Wat kosten 5 tickets voor een zwembeurt samen?

b Hoeveel betaal je voor een groep van 15 personen?

c Je betaalde 27 euro. Hoeveel tickets kocht je?

2.2 Omgekeerd evenredige grootheden

Door de kraan van één tuinslang volledig open te draaien vul je een zwembad in 48 minuten.

Met een tweede tuinslang met eenzelfde debiet duurt het 24 minuten.

Met nog een derde tuinslang duurt het 16 minuten.

Hoe meer tuinslangen je gebruikt, hoe meer / minder tijd er nodig is.

• Grootheden

Wat zijn de twee grootheden in dit voorbeeld? Vul aan.

De twee grootheden zijn en

• Tabel

Vul de tabel aan.

aantal tuinslangen 1236 tijd (min) 482416

• Woordformule Vul de formule aan.

aantal tuinslangen x tijd = tijd =

Het product van de grootheden is telkens gelijk.

Het aantal tuinslangen en de tijd in minuten zijn omgekeerd evenredig (OE)

• Grafiek

Teken de punten in het assenstelsel en verbind.

tijd (min)

0123456789 10111213

aantal tuinslangen

De punten van de grafiek liggen niet op één rechte lijn.

Lees af op de grafiek of bereken.

a Hoelang duurt het wanneer je 4 slangen aansluit?

b Hoelang duurt het wanneer je 24 slangen aansluit?

c Met hoeveel slangen vul je het zwembad in 12 minuten?

2.3 Grootheden zijn niet altijd evenredig

Een neusklem voorkomt dat er tijdens het zwemmen water in je neus kan.

Als je er twee koopt, krijg je nu tijdelijk de derde gratis.

Voor één neusklem betaal je 4 euro.

Voor twee stuks betaal je 8 euro.

Hoeveel betaal je voor drie neusklemmen?

• Grootheden

Wat zijn de twee grootheden in dit voorbeeld? Vul aan.

De twee grootheden zijn en

• Tabel

Vul de tabel aan.

aantal neusklemmen 01234567 kostprijs (€) 048

Je betaalt dus niet altijd meer als je meer neusklemmen koopt.

De verhouding van de grootheden is niet telkens gelijk.

• Grafiek

Teken de punten in het assenstelsel en verbind.

€ 4,00

Het aantal neusklemmen en de kostprijs in euro zijn niet evenredig (NE)

ko stprijs (€) aantal neusklemmen

0123456789 101112

Zijn de grootheden recht evenredig (RE), omgekeerd evenredig (OE) of niet evenredig (NE)? Duid aan.

a De leeftijd van een persoon en zijn lengte.

b De snelheid waarmee je fietst en de tijd die je nodig hebt om je bestemming te bereiken.

c De tijd waarin je een aquarium vult en de hoogte van het water.

3 Toepassingen op evenredige grootheden

3.1 Toepassingen op recht evenredige grootheden

• Voorbeeld

Met je elektrische step leg je 3 km af in 12 minuten. Hoeveel minuten doe je over een afstand van 5 km als je aan dezelfde snelheid stept?

• Werkwijze

1 Wat zijn de twee grootheden in dit voorbeeld? Vul aan.

De twee grootheden zijn en

2 Zijn de grootheden recht evenredig (RE) of omgekeerd evenredig (OE)? Duid aan. recht evenredig omgekeerd evenredig

3 Vul de tabel aan met de gegevens uit het voorbeeld.

4 Bereken het gevraagde.

©VANIN

• Antwoord

Als je aan dezelfde snelheid stept, doe je er minuten over.

Om voor vijf personen een milkshake te maken heb je 400 ml melk nodig. Hoeveel melk heb je nodig voor acht personen?

Berekening:

Antwoordzin:

Bereken eerst de tijd voor 1 km.

Deze uitkomst hoef je niet telkens te noteren.

3.2 Toepassingen op omgekeerd evenredige grootheden

• Voorbeeld

Je fietst met een snelheid van 18 km/h naar je grootmoeder. Je doet er 20 minuten over. Bij het terugkeren neem je dezelfde weg, maar fiets je aan 12 km/h. Hoelang duurt de terugrit?

• Werkwijze

1 Wat zijn de twee grootheden in dit voorbeeld? Vul aan. De twee grootheden zijn en

2 Zijn de grootheden recht evenredig (RE) of omgekeerd evenredig (OE)? Duid aan. recht evenredig omgekeerd evenredig

3 Vul de tabel aan met de gegevens uit het voorbeeld.

4 Bereken het gevraagde.

• Antwoord

Als je aan 12 km/h fietst, doe je er minuten over.

Een hobbykweker heeft nog voldoende voer om zijn acht konijnen 14 dagen van eten te voorzien. Hij verkoopt zes konijnen. Hoeveel dagen kan hij de overige konijnen nog voederen?

Berekening:

Antwoordzin:

Nr.: Klas:

1 Gelijke verhoudingen

Datum: / / 20 / 20

Welk(e) recept(en) voor chocomousse zijn niet in verhouding met het eerste? Duid aan. INGREDIËNTEN

125 ml room

100 g chocolade

30 g kristalsuiker

ml room

3 › 6 › 9 ›

ml room

200 g chocolade 300 g chocolade

60 g kristalsuiker 90 g kristalsuiker 1,5 eiwitten 3 eiwitten 9 eiwitten

Welk getal ontbreekt in de onderstaande evenredigheden? Vul aan. a 3 4 = b 25 30 = c 15 12 =

2 Evenredige grootheden

Vul de zin aan met een passend woord.

a Hoe duurder de prijs van de tomaten, hoe je er voor 10 euro kunt kopen.

b Hoe groter de terrastegel, hoe je er nodig hebt om een terras van 40 m² te leggen.

Zijn de grootheden recht evenredig (RE), omgekeerd evenredig (OE) of niet evenredig (NE)? Duid aan.

a Het aantal vijzen dat je nodig hebt en de dikte van de plank.

b De waarde van een bankbiljet en het aantal briefjes dat je nodig hebt om aan 200 euro te komen.

c De hoeveelheid deeg en het aantal pistolets dat je van het deeg maakt.

Zijn de grootheden recht evenredig (RE), omgekeerd evenredig (OE) of niet evenredig (NE)? Duid aan.

aantal dozen1249snelheid (km/h)201054 prijs (€) 8163272tijd (h) 1245

Welke woordformule past bij welke tabel? Verbind.

tijd = 30 : aantal •

prijs = massa x 3

3 Toepassingen op evenredige grootheden

Het kookteam had vorig jaar op kamp 24 kg pasta mee voor 120 kinderen. Dit jaar gaan er 90 kinderen mee. Hoeveel kg pasta moet het kookteam voorzien?

Berekening:

Antwoordzin:

Een olijfboomgaard leverde een olijfboer 50 liter olijfolie op. Daar kan hij 100 flessen van 500 ml mee vullen. Hoeveel flessen van 400 ml kan hij vullen?

Berekening:

1 Gelijke verhoudingen

1 Geef de verhoudingen die een evenredigheid vormen dezelfde kleur.

2 Welk getal ontbreekt in de onderstaande evenredigheden? Vul aan.

3 Duid de verhoudingen aan die een evenredigheid vormen.

4 Voor welke verpakking van hotelbroodjes betaal je in verhouding evenveel? Duid aan.

5 Vul de hoeveelheden voor het recept voor pizzadeeg aan. INGREDIËNTENINGREDIËNTENINGREDIËNTENINGREDIËNTEN

6 Vul de zin aan met een passend woord.

a Hoe meer luiers je koopt, hoe je moet betalen.

b Hoe groter de terrastegels, hoe je er nodig hebt om een terras van 100 m² te leggen.

c Hoe groter de muur, hoe verf je moet kopen om die te schilderen.

d Hoe minder gasten een taart opeten, hoe het stuk taart is dat elke gast krijgt.

e Hoe sneller je fietst, hoe tijd je nodig hebt om je bestemming te bereiken.

7 Zijn de grootheden recht evenredig (RE), omgekeerd evenredig (OE) of niet evenredig (NE)? Duid aan.

a Het aantal bouwlagen stenen en de hoogte van het gebouw.

b Het aantal schapen in een wei en de tijd die nodig is om het gras kaal te eten.

c De grootte van het dak en de hoeveelheid opgevangen water.

d De grootte van de tegels en het aantal tegels nodig voor 40 m².

e Het aantal mensen op de bus en de snelheid waarmee de bus rijdt.

8 Vul telkens de tabel van de evenredige grootheden aan.

a aantal stuks1315 d inhoud (l) 12,54 kostprijs (€)515 kostprijs (€) 1016

b aantal pers.50200500 e snelheid (km/h) 202530 inkom (€)205 tijd (min) 1210

c aantal palen101540 f aantal baby’s 61015 omtrek (m)6 24massa (g)9001 500

9 Zijn de grootheden recht evenredig (RE), omgekeerd evenredig (OE) of niet evenredig (NE)? Duid aan.

a aantal 1249 c tijd (min) 201054 oppervlakte (m2) 8163272temperatuur (°C)1245

REOENE REOENE

b aantal stuks2468 d tijd (h) 11,522,5 prijs (€) 6121520afstand (km)24364860

10 Hieronder zie je drie soorten appels.

a Vul voor elke soort de tabel aan. Teken de grafieken.

massa (kg)123

prijs (€)

€ 2,00/kg jonagolds

massa (kg)245

prijs (€)

€ 1,50/kg goldens

€ 2,50/kg granny smiths

massa (kg)023

prijs (€)

b Lees af op de grafiek of bereken.

• Hoeveel kg jonagolds koop je voor 5 euro?

• Hoeveel kg goldens koop je voor 9 euro?

• Hoeveel kg jonagolds kun je met 10 euro meer kopen dan granny smiths?

prijs (€) massa (kg)

012345

11 Mo fietst aan een constante snelheid en legt een afstand van 20 km af in 1 uur. Zijn vriendin Ulrike legt 25 km af in 1 uur.

a Vul de tabel, woordformule en grafiek van Mo en Ulrike aan.

• Tabel • Grafiek Mo af stand (km)

Ulrike

• Woordformule

Afstand Mo =

Afstand Ulrike =

b Lees af op de grafiek of bereken.

• Hoelang doet Mo erover om 100 km af te leggen?

• Welke afstand heeft Mo afgelegd na 90 minuten fietsen?

• Hoeveel km meer dan Mo heeft Ulrike na 4 h afgelegd?

• Ze fietsen allebei 50 km naar hun eindbestemming. Hoelang zal Ulrike op Mo moeten wachten?

tijd (h)

12 Welke grafieken stellen een omgekeerd evenredig verband voor? Duid aan.

13 Welke woordformule past bij welke grafiek? Vul aan met de juiste letter.

a kostprijs = 0,25 x massa

b kostprijs = 1 x massa

c kostprijs = 1,5 x massa

d kostprijs = 2,5 x massa

e kostprijs = 4 x massa

14 Welke woordformule past bij deze tabellen? Vul aan met de juiste letter.

Aaantal personen = oppervlakte : 4,25

Bprijs = aantal x 5,50

Cafstand = tijd : 6

1,539 246 8,51725,5

Doppervlakte = breedte x 4

Emassa = aantal x 0,75

15 Welke grafiek past bij de tabel? Vul aan met de juiste letter.

16 Voor zes blikjes frisdrank betaal je 4,74 euro. Hoeveel betaal je voor 50 blikjes?

Berekening:

Antwoordzin:

17 Om voor vijf personen moussaka te maken heb je deze hoofdingrediënten nodig. Voor een familiefeest wil je dit gerecht voor 18 personen klaarmaken.

Je hebt nog 2,5 kg aardappelen.

Heb je voldoende aardappelen voor dit gerecht?

Berekening:

Antwoordzin:

MOUSSAKA

5 ›

500 g lamsgehakt

580 ml halfvolle melk

625 g aardappelen

1,25 aubergine

500 g tomatenpulp

18 Om 3 500 kWh (kilowattuur) op te wekken met een standaard zonnepaneel van 260 Wp (wattpiek), heb je 16 zonnepanelen nodig. Die nemen een oppervlakte in van ongeveer 27 m2 Een groot gezin heeft tot 4 500 kWh nodig.

Hoeveel panelen moet een groot gezin leggen? Rond zinvol af.

Berekening:

Antwoordzin:

19

Bij een wedstrijd zijn er 12 winnaars. Ze krijgen allemaal 760 euro. Hoeveel krijgt ieder als er maar drie winnaars zijn?

Berekening:

Antwoordzin:

20 Een schapenboer heeft voor de winter hooi gemaaid. Hij kan daarmee zeven weken lang 30 schapen van hooi voorzien. Door een aantal dieren te verkopen, doet hij er nu tien weken mee. Hoeveel schapen heeft hij verkocht?

Berekening:

Antwoordzin:

21 Vier arbeiders hebben nog 5,5 uur nodig om een dakconstructie af te werken. Het is nu 11.30 uur. Er komt één extra arbeider bij. Zullen ze het dak tegen 16 h af hebben?

Berekening:

Antwoordzin:

22

Een 50 inch-televisie heeft een schermdiagonaal van 127 cm.

Wat is de schermdiagonaal in cm van een tv van 65 inch?

Berekening:

Antwoordzin:

23

Op een foto van de voorgevel van een huis is de deur 1,5 cm hoog.

De hoogte van het huis op de foto is 5 cm.

De werkelijke hoogte van de deur is 1,95 m.

Wat is de werkelijke hoogte van het huis?

Berekening:

Antwoordzin:

24 Klas 4A en 4B gaan met de bus op studiereis.

In klas 4A zitten er 10 leerlingen, in klas 4B zitten er 25.

Elke leerling betaalt € 13,40 voor het vervoer.

In klas 4B melden zich ‘s morgens drie leerlingen ziek.

Wat wijzigt er aan de kostprijs per leerling?

Berekening:

Antwoordzin:

Even samenvatten

• Gelijke verhoudingen

Gelijke verhoudingen noem je evenredigheden Voorbeeld: 5 3 = 20 12

• Evenredige grootheden

recht evenredige grootheden omgekeerd evenredige grootheden

Voor één drankje betaal je 2,50 euro.

Hoe meer drankjes je koopt, hoe meer je moet betalen.

Hoe minder drankjes je koopt, hoe minder je moet betalen.

• Tabel

Je verdeelt 120 euro onder elkaar.

Met hoe meer personen je deelt, hoe minder elk krijgt.

Met hoe minder personen je deelt, hoe meer elk krijgt.

• Tabel x 2

REaantal drankjes 0123

OEkostprijs (€)02,557,5 x 2

Dit zijn de grootheden. x 2

Het quotiënt van de grootheden is telkens gelijk.

• Woordformule

kostprijs : aantal drankjes = 2,5 of kostprijs = aantal drankjes x 2,5

• Grafiek

REaantal personen1234

OEbedrag (€) 120604030 : 2

Het product van de grootheden is telkens gelijk.

• Woordformule aantal personen x bedrag = 120 of bedrag = 120 : aantal personen

• Grafiek

De punten van de grafiek liggen op één rechte lijn door de oorsprong

De punten van de grafiek liggen niet op één rechte lijn

Gamezone

1

Chaos Sudoku

Vul de cijfers van 1 tot en met 9 per blok in.

Per rij en per kolom mag dat cijfer maar één keer voorkomen.

2 OXO

Vul het rooster in met X’en en O’s.

• In elke rij of kolom staan evenveel X’en O’s.

• Elke rij en elke kolom is uniek.

• Twee X’en en twee O’s mogen elkaar nooit opvolgen.

Nr.: Klas:

1 Gelijke verhoudingen

Datum: / / 20 / 20

Mortel maak je met vier delen zand, één deel cement en één deel water. Welke bouwvakker maakte geen goede mortel? Duid aan.

5 scheppen cement

5 scheppen water

kg cement

liter water

20 scheppen zand 10 kg zand 2 zakken zand

zak cement

emmer water

Welk getal ontbreekt in de onderstaande evenredigheden? Vul aan.

a 3 5 = b 15 45 = c 25 20 =

2 Evenredige grootheden

Vul de zin aan met een passend woord.

a Hoe groter de oppervlakte van het stuk akkerland, hoe zaad je nodig hebt om maïs te zaaien.

b Hoe groter de inhoud van een glas, hoe glazen je uit één fles kunt halen.

Zijn de grootheden recht evenredig (RE), omgekeerd evenredig (OE) of niet evenredig (NE)? Duid aan.

a Het aantal eieren in de pot en de kooktijd.

b Het aantal afgelegde kilometers en de hoeveelheid brandstof.

c Het kortingspercentage en wat je uiteindelijk moet betalen.

Zijn de grootheden recht evenredig (RE), omgekeerd evenredig (OE) of niet evenredig (NE)? Duid aan.

massa (kg)3458aantal personen60301510 prijs (€)2,403,204,006,40prijs (€)

Welke woordformule past bij de tabel? Noteer de juiste letter. 121518

7,2910,8

Aaantal personen = oppervlakte x 4

Bprijs = aantal : 1,50

Cafstand = tijd x 5

Ehoogte = aantal x 0,6 12930 8620

Dcc haarverf = cc waterperoxide : 2

3 Toepassingen op evenredige grootheden

Met deze hoeveelheid pasta kun je tot 40 personen een portie geven.

Je kookt pasta voor 135 mensen.

Hoeveel verpakkingen van 5 kg heb je nodig? Rond zinvol af.

Berekening:

Antwoordzin:

Een groepje vrienden kan met hun geld 30 drankjes van € 2,20 per stuk kopen. Ze willen graag drankjes van € 2,50 per stuk kopen.

Hoeveel van die duurdere drankjes kunnen ze kopen? Rond zinvol af.

Berekening:

De volgorde van bewerkingen

1 De volgorde van bewerkingen zonder haakjes

1 Vermenigvuldigen en delen van links naar rechts.

2 Optellen en aftrekken van links naar rechts.

Het

veulen draaft op en af!

1.1 Optellen en aftrekken van links naar rechts

1.2 Vermenigvuldigen en delen van links naar rechts 80 : 8 x 4 : 5 a

1.3 De volgorde van bewerkingen zonder haakjes

2 De volgorde van bewerkingen met haakjes

1 Eerst de haakjes uitwerken.

2 Vermenigvuldigen en delen van links naar rechts.

3 Optellen en aftrekken van links naar rechts.

70 + 5 x 12 : (10 – 6)

= 70 + 5 x 12 : 4

= 70 + 60 : 4

= 70 + 15 = 85

Bereken.

Het veulen draaft op en af!

Welk getal komt op de plaats van het vraagteken?

Mijn circuit

op mezelf

FORMULE 1

Nr.: Klas: Datum: / / 20 / Aan de slag Ben ik mee? Op mijn maat

Totaal:

Aantekeningen leerkracht

©VANIN

KIJKER Kijk zeker ook op iDiddit.be

Heb ik telkens een eenheid bij mijn antwoord genoteerd?

Leerling: 12345

Leerkracht: 12345

Aan de slag

1 Volumematen

1.1 Benamingen

Volume (V) druk je uit met een getal en een volumemaat.

De meest gebruikte volumematen zijn: m3, dm3, cm3 en mm3

Ook de inhoudsmaten l, dl, cl en ml geven een volume aan.

Noteer de letter bij de passende volumemaat. 1 m3 1 dm3 1 cm

een watervat

een kaasblokje

1.2 Meetinstrumenten

een brik melk

een korrel rietsuiker

een halfvol glas water

a Noteer onder elke foto de naam van het meetinstrument. Kies uit: maatbeker, maatdop, pipet.

b Markeer het meetbereik en de meetnauwkeurigheid.

meetnauwkeurigheidmeetnauwkeurigheidmeetnauwkeurigheid

Je koopt voor jouw restaurant drie identieke koelkasten. Over welk volume in m3 beschik je om voedsel te bewaren?

Berekening:m3 dm3 cm3 mm3 ldlclml

Antwoordzin:

In één zelfgemaakt ijsje zit een mengsel van 12,5 cl.

Je wilt 50 ijsjes maken.

Hoeveel liter van het mengsel heb je nodig?

Berekening:m3 dm3 cm3 mm3 ldlclml

Antwoordzin:

Berekening:m3 dm3 cm3 mm3 ldlclml

horecakoelkast 600 l

€ 1 070,95

Hade wil voor zes personen pannenkoeken bakken. Daarvoor heeft ze 300 ml melk per persoon nodig. In de koelkast staan twee flessen van 0,75 l. Heeft Hade genoeg melk?

Antwoordzin:

Peter start aan de afbraakwerken van een huis. Hij schat 150 m3 puin en afval te hebben. Eén afvalcontainer heeft een volume van 20 000 l.

Hoeveel containers moet Peter bestellen?

Berekening:m3 dm3 cm3 mm3 ldlclml

Antwoordzin:

Noteer telkens de formule om het volume te berekenen. Duid de gebruikte letter(s) uit de formule aan op de foto.

Vkubus = Vbalk = Vcilinder =

Een kubusvormige bijzettafel heeft een ribbe van 43,5 cm.

De binnenafmeting is 40 cm op 40 cm op 40 cm.

Hoeveel m3 ruimte neemt de bijzettafel in?

Rond af op twee cijfers na de komma.

Berekening: m3 dm3 cm3 mm3 ldlclml

Antwoordzin:

Een vijver is 4 m lang, anderhalve meter breed en 60 cm diep. a Wat is het volume van de vijver in m3?

Berekening:

Antwoordzin:

b Hoeveel liter water is er nodig om de vijver maximaal te vullen?

Berekening:

Antwoordzin:

Na controle met de warmtecamera wil de aannemer twee muren extra isoleren.

De spouwmuren met dikte 8 cm worden opgevuld met isolatie.

a Hoeveel m3 isolatie heeft de aannemer nodig?

Berekening:

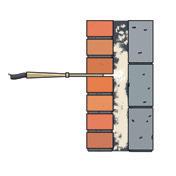
spouwmuur 1: 4 m x 2,5 m

spouwmuur 2: 6 m x 2,3 m

©VANIN

Antwoordzin:

b De prijs per m2 muuroppervlakte vind je terug in de volgende prijzentabel.

Hoeveel moet de klant betalen?

Berekening:

prijzentabel prijs per m2 spouwdikte

18 euro 6 cm

24 euro8 cm

30 euro 10 cm

36 euro 12 cm

Antwoordzin:

Bij een nieuwbouwwoning wordt een cilindervormige regenput geplaatst.

a Hoeveel meter is de binnendiameter van de regenput? 120 cm

Berekening:

Antwoordzin:

b Wat is het volume van de regenput in m3?

Rond af op twee cijfers na de komma.

Berekening:

Antwoordzin:

c Hoeveel liter water kan er in de regenput?

Berekening:

Antwoordzin:

2,8 m 15 cm

Debiet is de hoeveelheid stof die zich per tijdseenheid verplaatst. De meest gebruikte maten voor debiet zijn: m3/h, l/min en l/s.

Deze waterpomp heeft een debiet van 18 m3/h.

Dat betekent dat de pomp 18 m3 water kan oppompen in één uur. Na hoeveel minuten is een zwembad van 2 100 l leeggepompt?

Berekening: inhoudtijd

18 m3 1 h l min

72 beoordelingen

Antwoordzin:

Kacper doucht vijf minuten.

a De douchekraan van Kacper heeft een debiet van 0,15 liter water per seconde. Hoeveel liter water is er uit de kraan gekomen?

Berekening:inhoudtijd

Antwoordzin:

b Kacper koopt een douchekraan met spaarknop. Het debiet wordt zo 3 l/min.

Hoeveel liter water bespaart Kacper op een douchebeurt van 5 minuten?

Berekening:inhoudtijd

Antwoordzin:

c In Vlaanderen betaal je ongeveer € 4,30 voor één kubieke meter water. Hoeveel euro bespaart Kacper met de spaarknop per douchebeurt?

Berekening:

Antwoordzin:

d Het gezin van Kacper telt vijf personen.

Elk gezinslid neemt elke dag één douchebeurt van vijf minuten. Hoeveel bespaart het gezin in één jaar dankzij de spaarknop?

Berekening:

Antwoordzin:

De van een stof drukt uit hoeveel massa van die stof in een bepaald volume aanwezig is. Massadichtheid wordt uitgedrukt in kg/dm

Je zegt dat steen een massadichtheid heeft van 1,8 kg/dm3.

1 dm3 steen weegt 1,8 kg.1 dm3 water weegt 1 kg.

Je zegt dat water een massadichtheid heeft van 1 kg/dm3.

1 dm3 piepschuim weegt 0,03 kg.

Je zegt dat piepschuim een massadichtheid heeft van 0,03 kg/dm3.

Wanneer de massadichtheid kleiner is dan 1 kg/dm3, dan drijft de stof op water.

Markeer in de tabel de stoffen die op water drijven.

aluminium2,7diamant3,5kurk 0,24 arduin 2,6eikenhout0,92lood 11,35 baksteen1,4gietijzer7,21olie 0,9 benzine0,72glas 2,53rubber0,93 beton 2,4goud 19,26zand 1,6 beukenhout0,7ijs 0,93zilver10,47

a Hoeveel weegt 1 dm3 kurk?

b Hoeveel gram weegt 2,5 dm3 kurk?

Berekening:

massavolume

kg 1 dm3

g1 dm3

Antwoord: 2,5 dm3 kurk weegt

c Hoeveel weegt 1 dm3 glas?

d Hoeveel gram weegt 2,5 dm3 beton?

Berekening:

massavolume

kg 1 dm3

g1 dm3

e Hoeveel gram weegt 3 cm3 kurk?

Berekening:

massavolume

kg 1 dm3 g cm3

g

Antwoord: 3 cm3 kurk weegt

f Hoeveel gram weegt 4 cm3 zilver?

Berekening: massavolume

kg 1 dm3 g cm3 g

Antwoord: 2,5 dm3 beton weegt . Antwoord: 4 cm3 zilver weegt .

1 Volumematen

Nr.: Klas:

Datum: / / 20 / 20

Markeer telkens het passende volume. 1 m3 100 l10 m3 10 cl10 cm3 1 l 3 cm3 3 mm3 3 cl

Welk meetinstrument gebruik je het best? Verbind.

a toedienen van oogdruppels • • maatbeker b bouillon toevoegen aan de soep • • pipet c siroop innemen • • pluviometer d de hoeveelheid neerslag bekijken • • maatdop

2 Volumematen herleiden

Berekening:m3

Antwoordzin:

3 Volume van ruimtefiguren

Karen wil haar klanten een bloempot schenken. Welke bloempot heeft het grootste volume? Duid aan.

Hoeveel volle emmers water van 10 l kunnen er in een aquarium van 0,5 m3?

Hoeveel l beton is er nodig om deze trap te gieten?

Berekening:

Antwoordzin:

5 Debiet

Een infuus wordt aangebracht via een katheter met een debiet van 100 ml per uur. De inhoud van het infuus bedraagt 0,5 l.

Na hoeveel uur is het infuus volledig opgenomen in het lichaam?

Berekening: inhoudtijd

Antwoordzin:

6 Massadichtheid

De massadichtheid in kg/dm3 van enkele stoffen vind je in deze tabel. aluminium2,7diamant

a Hoeveel gram weegt 1,5 dm3 lood?

Berekening: massavolume

kg 1 dm3 g1 dm3

b Hoeveel gram weegt 3 cm3 diamant?

Berekening: massavolume

kg 1 dm3 g cm3

Antwoord: 1,5 dm3 lood weegt Antwoord: 3 cm3 diamant weegt

c 2 m3 van een stof weegt 5 400 kg.

Over welke stof gaat het?

1 Volumematen

1 Plaats de letters bij de passende volumemaat.

©VANIN

een druppel water een watervat

een ligbad

2 Markeer het passende volume.

3 Noteer de letter van het meetinstrument bij de passende foto. Markeer het meetbereik en de meetnauwkeurigheid.

A Met een erlenmeyer meng je stoffen in een laboratorium.

B Met een pluviometer meet je de hoeveelheid neerslag.

C Met een waterniveaumeter bepaal je de resterende inhoud van de watertank van een camper.

meetnauwkeurigheidmeetnauwkeurigheidmeetnauwkeurigheid

4 Bereken.

a Je voegt 5 dl room toe aan een saus van 2 l.

Hoeveel liter saus heb je?

b Een container van 20 000 l is maar voor 15 000 l gevuld. Hoeveel m3 kan er nog bij?

c Hilde wil haar zandbak van 0,75 m3 maximaal vullen.

Hoeveel zakken van 25 l moet ze daarvoor kopen?

d Een koe geeft dagelijks 27 l melk.

Hoeveel m3 melk produceren 150 koeien dagelijks?

5 Tuinaannemer Jason staat in voor het onderhoud van het stadspark. Hij gooit al het groenafval in de container.

Hoeveel volle kruiwagens met groenafval kunnen er in de afvalcontainer?

Berekening:

Antwoordzin:

6 Wat heeft het grootste volume?

Markeer telkens de letter die bij de juiste oplossing staat. Maak met de verzamelde letters een woord.

Welk woord kun je vormen met de verzamelde letters?

7 Bereken het volume in cl van de onderstaande vazen. Kies uit: z x z x z of l x b x h of r x r x 3,14 x h.

Berekening

1 2 3

lengtebreedtehoogtestraal diameter hoogtelengtebreedtehoogte 80 mm80 mm120 mm5 cm10 cm18 cm15 cm15 cm15 cm

©VANIN

Antwoord cl cl cl

8 Maison Elle verkoopt potjes met geurstokjes.

Hoeveel potjes van elke soort kan ze vullen met een bidon van 20 l?

Rond zinvol af.

Berekening

1 2 3

lengtebreedtehoogte diameter hoogtelengtebreedtehoogte 60 mm60 mm60 mm 6 cm8 cm 50 mm50 mm15 cm

Antwoord potjes potjes potjes

9 Deze houtkrullen werden samengeperst tot ongeveer 140 liter. Bereken de hoogte in cm. Rond af op één cijfer na de komma.

Berekening:

Antwoordzin:

10 In welke kookpot kan het meeste soep? Duid aan.

kookpot 1: ∅ 18 cm – 20 cm hoogkookpot 2: ∅ 20 cm – 18 cm hoog

Berekening:

Berekening:

11 Visar krijgt de opdracht om vloerisolatie van 10 cm dik te plaatsen bij een klant. De klant wil graag dat Visar de isolatie plaatst in de aangeduide gebieden.

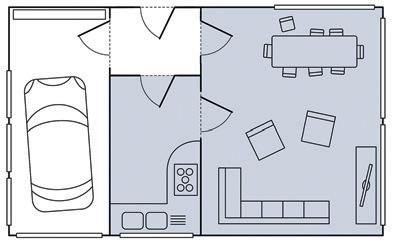
keuken: 7 m x 4 m

woonkamer: 10 m x 8 m

a Hoeveel m3 isolatie moet Visar voorzien?

Berekening:

Antwoordzin:

b Hoeveel zakken isolatiekorrels moet hij voorzien?

Berekening:

EPS HR++ parels 333 liter per zak 29,40 euro per zak

Antwoordzin:

c Hoeveel bedraagt de totale kostprijs van het isolatiemateriaal?

Berekening:

Antwoordzin:

12

Het heeft vorige nacht hevig geregend. De pluviometer geeft aan dat er 15 liter water per m2 is gevallen.

Elines huis heeft een plat dak van 12 m op 15 m.

a Hoeveel liter water is er bijgekomen in de regenput?

Berekening:

Antwoordzin:

b Eline gebruikt ongeveer 65 liter water per douchebeurt.

Hoeveel douchebeurten kan ze nemen met de regenval van vorige nacht?

Berekening:

Antwoordzin:

13 Om drankjes koel te houden maakt Leonie gebruik van herbruikbare ijsblokjes.

a Wat is het volume van één ijsblokje in cm3?

Berekening:

Antwoordzin:

b Wat is de maximale inhoud van het glas in ml?

Rond af op de eenheid.

Berekening:

Antwoordzin:

c Leonie giet het glas halfvol.

Hoeveel ijsblokjes kan Leonie maximaal toevoegen zonder dat het glas overloopt?

Berekening:

Antwoordzin:

14

Brandweerkazerne Oosteroever bekijkt welke methode van blussen zorgt voor het hoogste debiet. Bereken het debiet in liter per uur.

pompwagen: 2 800 liter per minuut

inhoudtijd

hydrant: 120 m3 per uur

inhoud tijd

Antwoord: Antwoord:

15 Tijdens een overstroming is de kelder van Ian voor de helft onder water gelopen. De kelder heeft een afmeting van 3 m op 4 m en is 2,2 m hoog.

a Hoeveel l water staat er in Ian zijn kelder?

Berekening:

Antwoordzin:

b Ian beschikt over een pomp die een debiet heeft van 2 000 l per uur. Hoelang duurt het voor de kelder leeggepompt is?

Berekening:

inhoud tijd

Antwoord: De kelder is leeggepompt na uur minuten.

16 Om de vrachtwagens zoveel mogelijk uit het centrum van Brugge weg te houden, besloot brouwerij De Halve Maan om een ondergrondse pijpleiding aan te leggen.

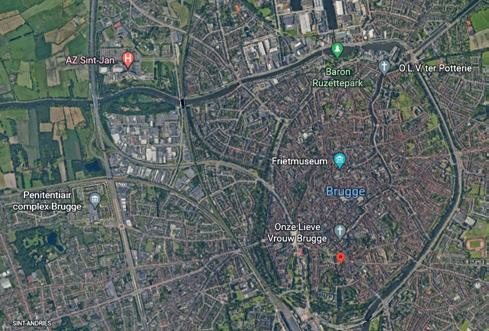
bottelarij aan de rand van de stad

©VANIN

bierbrouwerij in het centrum

a De cilindervormige leiding is 3 km lang en heeft een diameter van 300 mm. Wat is het volume van de pijpleiding in liter? Rond af op twee cijfers na de komma.

Berekening:

Antwoordzin:

b Het duurt 45 minuten om het bier via het centrum te transporteren. Bereken het debiet in liter per uur.

Berekening: inhoud tijd

Antwoordzin:

c Hoeveel flesjes van 33 cl kun je in één uur vullen?

Berekening:

Antwoordzin:

d De flesjes worden in bakken van 24 flesjes verdeeld. Hoeveel volledige bakken kun je vullen per uur?

Berekening:

Antwoordzin:

De massadichtheid in kg/dm3 van enkele stoffen vind je in deze tabel.

aluminium2,7eikenhout0,92kurk 0,24 beton 2,4gietijzer7,21olie 0,9 beukenhout0,7goud 19,26zand 1,6

17 Bereken.

a Hoeveel kilogram weegt 5 dm3 goud?

Berekening:

massavolume

kg 1 dm3

Antwoord: 5 dm3 goud weegt

b Hoeveel gram weegt 2 cm3 olie?

Berekening:

massavolume

kg 1 dm3 g cm3

Antwoord: 2 cm3 olie weegt

18 Welk tafelblad weegt het zwaarst? Duid aan.

eikenhout: 1,3 m x 1,8 m x 0,03 mbeukenhout: 1,2 m x 2,1 m x 0,03 m

Veikenhout = = =

Berekening massa:

massavolume

kg 1 dm3

Vbeukenhout = = =

Berekening massa: massavolume

kg 1 dm3

19 Carolina boort met een boor met een diameter van 3 cm in een balkvormig stuk aluminium.

Hoeveel weegt het blokje in gram nadat ze de boring heeft uitgevoerd?

Rond af op de eenheid.

Berekening:

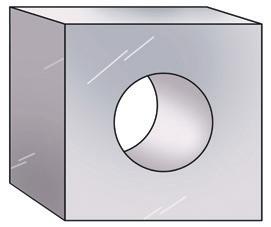
Antwoordzin:

Even samenvatten

• Volumematen herleiden

1 dm3 = 1 l

0,5 m3 05 00 500 dm3

25 cl 0 25 0,25 dm3

• Volume van ruimtefiguren balk kubus cilinder

• Debiet

Debiet is de hoeveelheid stof die zich per tijdseenheid verplaatst.

De meest gebruikte maten voor debiet zijn: m3/h, l/min en l/s.

inhoudtijd

18 m3 1 h : 18 000 18 000 l60 min : 18 000 1l x 2 100 x 2 100 2 100 l7 min

• Massadichtheid

De massadichtheid van een stof drukt uit

Een pomp met een debiet van 18 m3 water per uur pompt in 7 minuten 2 100 l water.

hoeveel massa van die stof in een bepaald volume aanwezig is.

De massadichtheid wordt uitgedrukt in kg/dm3.

massadichtheid kurk = 0,24 kg/dm3

Hoeveel gram weegt 2,5 dm3 kurk?

massavolume

0,24 kg1 dm3 x 2,5

240 g1 dm3 x 2,5

600 g2,5 dm3

Hoeveel gram weegt 3 cm3 kurk?

massavolume

0,24 kg1 dm3 : 1 000 x 3

0,240 g1 cm3

240 g 1 000 cm3 : 1 000 x 3

0,72 g3 cm3

Antwoordzin: 2,5 dm3 kurk weegt 600 g.Antwoordzin: 3 cm3 kurk weegt 0,72 g.

Gamezone

1 Duid de kubus aan waarvan de ontwikkeling gegeven is.

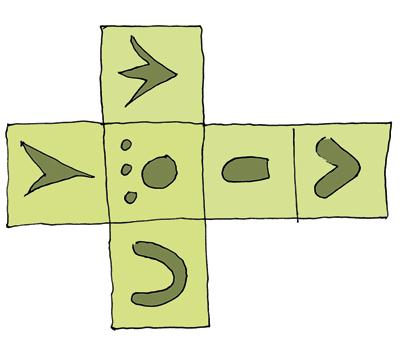
2 Welke kubus voldoet niet aan de gegeven ontwikkeling? Duid aan. a

3 Bachir kleeft zeven dobbelstenen aan elkaar, zoals op de figuur.

Telkens kleeft hij een zijvlak op een zijvlak met hetzelfde aantal ogen.

Hoeveel ogen staan op de buitenkant van deze ruimtefiguur?

Berekening:

Antwoordzin:

1 Volumematen

Nr.: Klas:

Markeer het passende volume.

Datum: / / 20 / 20

Welk meetinstrument gebruik je het best? Verbind.

a de hoeveelheid hoestsiroop

b 550 ml melk

c 150 ml wasmiddel

d een druppeltje kleurstof voor in het taartbeslag

2 Volumematen herleiden

pipet

doseerbol

maatbeker

maatlepel

In de opslagtank van een tankwagen zit 45 m3 dieselbrandstof.

In een wagen kan er gemiddeld 70 l brandstof.

Hoeveel wagens kun je daarmee voltanken?

Antwoordzin:

3 Volume van ruimtefiguren

Welke luidspreker neemt in de rugzak van Gio het meeste plaats in? Duid aan.

4

De cilindervormige fles shampoo heeft een diameter van 6,4 cm en is gevuld tot op een hoogte van 25 cm.

Kapster Faye gebruikt per wasbeurt ongeveer 8 ml shampoo. Hoeveel wasbeurten haalt ze uit één fles?

Berekening:

Antwoordzin:

5 Debiet

Berekening:inhoud tijd

Je wilt je zwembad maximaal vullen. Uit de buitenkraan komt per uur 2,5 m3 water. Je zet de kraan volledig open om 11.20 uur. V = 16 500 l Wanneer zal het zwembad helemaal gevuld zijn?

Antwoord:

6 Massadichtheid

De massadichtheid in kg/dm3 van enkele stoffen vind je in deze tabel.

a Wat is de massa van 1 dm3 lood?

b Hoeveel gram weegt 7 dm3 arduin?

Berekening: massavolume kg 1 dm3 g1 dm3

c Hoeveel gram weegt 1,5 cm3 eikenhout?

Berekening: massavolume kg 1 dm3 g cm3

Rekenen met de tijd en de kalender

1 Rekenen met de tijd

1 h = min 1 min = s 1 h = s

Vul aan.

Een dag telt uren. Een halfuur telt minuten.

Een uur telt minuten. Een kwartier telt minuten.

Een minuut telt seconden. Een uur telt seconden.

Zet om.

3 h = min 120 min = h 1,5 h = min 20 min = s

2 min = s360 s = min 0,5 h = min 10 min = s

4 h = min 15 min = s7 h = min 6 000 s = min

360 min = h 30 min = s2,5 h = min 180 s = min

1 dag = h 1 dag = min 1 week = h7 200 s = h

Raoul en Elena verkopen aardbeien in hun winkel.

a Hoeveel uur is de winkel open op zondag?

b Wanneer kun je op dinsdagmorgen naar de winkel?

c Hoelang is de winkel open op maandagmorgen?

d Hoeveel minuten is de winkel open op donderdagnamiddag?

e Hoeveel uur is de winkel per week open?

OPENINGSUREN WINKEL

MA-VRIJDAG 10.30 - 12.00 u. 16.30 - 19.00 u.

ZATERDAG 9.00 - 12.00 u. 14.00 - 19.00 u.

ZONDAG 9.00 - 12.00 u.

2 Rekenen met de kalender

Eén jaar telt meestal dagen.

Soms telt een jaar dagen. Zo’n jaar noem je een en komt één keer om de vier jaar voor.

In zo’n jaar telt de maand februari dagen.

januari

Op school spreek je ook over trimester en semester

Een trimester duurt maanden. Eén jaar telt trimesters.

Een semester duurt maanden. Eén jaar telt semesters.

Vul aan.

Eén jaar telt maanden. Oktober telt dagen.

Eén jaar telt weken. April telt dagen.

Eén jaar telt dagen. Juni telt dagen.

Eén eeuw telt jaren. Eén jaar telt trimesters.

Eén week telt dagen. Eén semester telt maanden.

Wat is de leeftijd van de familieleden van Farah dit jaar?

geboortejaarleeftijd

©VANIN

geboortejaarleeftijd

Farah 2005 papa 1975

Anaïs 2001 oma 1953

Snelheid 8

Planner

Aan de slag Even herhalen

2 Toepassingen met snelheid

2.1 De afstand berekenen

2.2 De tijd berekenen

3 Diagrammen

3.1 Afstand en tijd in een diagram

3.2 Snelheid en tijd in een diagram

Mijn circuit

op mezelf

Aan de slag Ben ik mee? Op mijn maat

FORMULE 1

Nr.: Klas: Datum: / / 20 /

Aantekeningen leerkracht

©VANIN

Aan de slag

Even herhalen: rekenen met tijd 1 h = min 1 min = s 1 h = s

Vul aan.

0,5 min = s0,25 h = min 3,5 h = min

5 h 03 min = min 4 min 30 s = s10 h 04 min = min

Vul aan.

280 s = h min s905 min = h min s

106 min = h min s1 750 s = h min s

Even herhalen: de reistijd berekenen

Bereken telkens de ontbrekende tijd. vertrekaankomstreistijdvertrekaankomstreistijd 14 : 0515 : 15 h min : 19 : 101 h 45 min : 08 : 1025 min16 : 05 : 2 h 08 min

Even herhalen: recht evenredig (RE) en omgekeerd evenredig (OE)

Moeder rijdt met een constante snelheid van 90 km/h naar Zwitserland.

a Vul de tabel aan

tijd (t) in hafstand (s) in kmsnelheid (v) in km/h

b Markeer wat past.

• Hoe langer moeder rijdt, hoe meer / minder afstand zij aflegt bij dezelfde snelheid. Tijd (t) en afstand (s) zijn recht / omgekeerd evenredig.

• Hoe sneller moeder rijdt, hoe meer / minder tijd zij nodig heeft om dezelfde afstand af te leggen.

Snelheid (v) en tijd (t) zijn recht / omgekeerd evenredig.

• Hoe sneller moeder rijdt, hoe meer / minder afstand zij kan afleggen in dezelfde tijd.

Snelheid (v) en afstand (s) zijn recht / omgekeerd evenredig.

1 Snelheid

Snelheid geeft de verhouding aan tussen de afstand (s) en de tijd (t).

Bereken de snelheden van de vervoersmiddelen in kilometer per uur.

Hoverboard Ninebot Z10 MonowheelSegway Ninebot S snelheid

120 meter per minuut = kilometer per uur 60 kilometer per 1,5 uur = kilometer per uur 45 meter per 10 seconden = kilometer per uur

Amir liep een marathon van 42 km in drie uur.

Wat was de gemiddelde snelheid van Amir in km/h?

Berekening:

s ( )

t ( )

Antwoordzin:

Boris woont op 3,2 km van school. De ochtend van de studiereis heeft hij zich overslapen en haast hij zich met de fiets naar school. Na acht minuten is hij er al.

Wat was de gemiddelde snelheid van Boris in km/h?

Berekening:

s ( )

t ( )

Antwoordzin:

2.1 De afstand berekenen

Ralph vertrok te voet om 12.45 uur. Hij wandelde met een gemiddelde snelheid van 4,5 km/h. Om 15.05 uur kwam hij op zijn bestemming aan.

• Hoelang heeft Ralph gewandeld?

• Hoeveel minuten was hij onderweg?

• Welke afstand heeft hij afgelegd?

Berekening: afstand (km) tijd (min)

Antwoordzin:

Amy skeelerde van 14.00 uur tot 14.42 uur met een snelheid van 14 km/h. Welke afstand heeft ze afgelegd?

Berekening:

s ( )

t ( )

Antwoordzin:

Egels kunnen een snelheid van twee meter per seconde halen. Welke afstand legt een egel af in een halve minuut?

Berekening:

s ( )

t ( )

Antwoordzin:

2.2 De tijd berekenen

Aleksander zwom 3,8 km aan een gemiddelde snelheid van 1,25 m/s. Hoelang zwom Aleksander?

Berekening:

afstand (m)

tijd (s)

s = h min s

Antwoordzin:

Lien vertrekt om 10.30 uur te voet naar de zwemles. Het zwembad ligt op 2,4 km van haar thuis. Ze wandelt aan 4 km/h. Wanneer komt ze bij het zwembad aan?

Berekening:

s ( ) t ( )

Antwoordzin:

De fietssnelweg F310 tussen Brugge en Sluis is 15 km lang.

BRUGGE-SLUIS 15 km F 310 Een speedpedelec haalt snelheden tot 45 km/h. Hoelang doe je ongeveer over de rit Brugge-Sluis?

Berekening:

s ( ) t ( )

Antwoordzin:

3.1 Afstand en tijd in een diagram

Wout fietst aan 15 km/h. Vul de tabel aan.

s (km)051015

Léa fietst aan 20 km/h. Vul de tabel aan.

t (min) s (km) t (min)0306090

Teken aan de hand van de tabellen twee lijndiagrammen die de snelheid van Wout en Léa voorstellen.

©VANIN

Lees de lijn van Riza op het diagram af. Vul aan.

020406080100120140

tijd (min)

Lees de lijn van Abou op het diagram af. Vul aan. s (km) t (min)0102030 s (km) 40 80 t (min)30 90

Riza fietst aan km/h.

Beantwoord de vragen.

a Bij wie is de lijn het steilst?

b Wie rijdt het vlugst?

Abou fietst aan km/h.

c Wie heeft na 100 minuten meer dan 50 km afgelegd?

d Wie fietst niet en staat stil?

e Wie legde op een half uur 10 km af?

Abou

Riza

3.2 Snelheid en tijd in een diagram

Een koerier vertrekt met de bromfiets naar een klant. Het is druk op de weg. Hij kan geen gelijke snelheid aanhouden.

Zijn snelheid is in het lijndiagram hieronder voorgesteld.

Vul in de tabellen telkens de snelheid voor de gegeven tijd aan.

tijd (s)010203040 snelheid (km/h) tijd (s)60708090100 snelheid (km/h)

• Wat is zijn maximumsnelheid?

• Wat is zijn minimumsnelheid?

• Bij welke delen van het diagram versnelt de koerier?

Deze delen van het diagram zijn: stijgenddalendconstant

• Bij welk deel van het diagram vertraagt de koerier?

Dit deel van het diagram is: stijgenddalendconstant

• Bij welke delen van het diagram is de snelheid gelijk?

Deze delen van het diagram zijn: stijgenddalendconstant

Welk deel van het diagram hoort bij de onderstaande zinnen?

Noteer met de juiste letter.

a De koerier rijdt gedurende 10 seconden aan 40 km/h.

b Hij staat voor het rode licht en moet even wachten.

c De verkeerslichten springen op rood. Hij moet remmen.

d Hij vertrekt. Na 20 seconden behaalt hij 40 km/h.

e De wagen voor hem slaat af. Nu kan hij terug versnellen.

f Even kan hij zijn topsnelheid aanhouden.

Naam:

FORMULE 1

1 Snelheid

Vul de tabel aan.

Nr.: Klas:

Wat is de snelheid in km/h?

Datum: / / 20 / 20

afstand (km)60 snelheid tijd (h) 6421 km/h

Je vakantiebestemming ligt op 800 km van je thuis.

Je deed er 7,5 uur over om er te geraken.

Wat was je gemiddelde snelheid in km/h? Rond af op één cijfer na de komma.

Berekening:

afstand (km) tijd (h)

Antwoordzin:

2 Toepassingen met snelheid

Markeer telkens het juiste antwoord.

a Je wandelt met een snelheid van 4 km/h.

Welke afstand heb je na een half uur afgelegd? 2 km8 km30 km

b Een auto rijdt aan een snelheid van 60 km/h. Welke afstand heeft hij na 20 minuten afgelegd? 20 km40 km80 km

Lotte fietste vijf uur aan een gemiddelde snelheid van 36 km/h.

Welke afstand heeft zij afgelegd?

Berekening:

(km) tijd (h)

Je vertrekt om 9.50 uur met de scooter naar de sporthal.

De volleybaltraining start stipt om 10.00 uur.

De sporthal ligt op 2,5 km van je huis.

Met een scooter haal je vlot een snelheid van 18 km/h.

Geraak je nog op tijd op de training?

Berekening:

afstand (km)

tijd (min)

Antwoordzin:

3 Diagrammen

a Vul de tabel aan.

b Teken het lijndiagram dat de snelheid van Mon en Nim voorstelt.

Mon stept aan 12 km/h.

Nim stept aan 16 km/h. s (km)122448

c Beantwoord de vragen.

• Hoeveel km heeft Achiel na twee uur afgelegd?

• Wie rijdt het snelst?

• Wat is de snelheid van Leon?

1 Snelheid

1 Vul de verhoudingstabellen aan.

s (km)60

t (h)10,50,251,5

s (m)1006006 0001 500

t (min)1

2 Vul de verhoudingstabellen aan.

s (km)3015

t (h)2 3

s (m)75

t (s)10603 600

3 Bereken de snelheid in km/h.

s (m)2001005006 000

t (min)2

s (m)0,51 1 000

t (s)1 60

Welke topsnelheid van welk dier past bij de tabel? Noteer de juiste letter.

s (km)1 60

t (min)110

s (m)6 00024 00036 000

t (min)5

afstandtempotijd lopen 1 km? km/h6 min

afstandtempotijd roeien 500 m? km/h2 min

afstandtempotijd schaatsen 250 m? km/h30 s

afstandtempotijd zwemmen 1,5 m? km/h1 s

snelheid km/h snelheid km/h

4

De oma van Mare, Im en Dille woont op 12 km van hun huis.

Mare vertrekt met de elektrische fiets en doet er 20 minuten over. Im ging mee met de wagen en was er in 12 minuten. Dille ging te voet en was 2 h en 30 min onderweg. Wat was hun gemiddelde snelheid in km/h?

Berekening:

Mare s (km) t (min)

Dille s (km) t (min)

De snelheid van Mare was km/h, van Im km/h en van Dille km/h.

5 Je deed er 1 h en 10 min over om van Sint-Niklaas naar Mechelen te fietsen. Je vriend deed er drie kwartier over om van Ieper naar Kortemark te fietsen.

Wie fietste het snelst?

Berekening: s t s t

MECHELEN

KORTEMARK

Antwoordzin:

6 Met de Thalys leg je de afstand van 264 km tussen Brussel en Parijs af in 1 h 22 min.

Wat is de gemiddelde snelheid in km/h? Rond af op de eenheid.

Berekening:

Antwoordzin:

7 Marcell Jacobs won in 2020 goud op de Olympische Spelen.

Hij liep de 100 m spurt in 9,8 s.

Wat was zijn snelheid in km/h? Rond af op één cijfer na de komma.

Berekening:

Antwoordzin:

8 Welke afstand hebben beide wielrenners afgelegd?

Koen Muylle – ochtendrit 04 mei om 06:55 – Staden

Sam Dekeersschieter – middagrit 04 mei om 13:55 – Keiem afstandsnelheidtijd ? km28 km/h30 min afstandsnelheidtijd ? km27 km/h20 min

9 Een wijngaardslak kan tot 8 cm in een minuut afleggen. Kan de slak in een kwartier een druk fietspad van 1,5 m oversteken?

Berekening:

s t Antwoordzin:

10 Kerem vertrekt om 12.10 uur, rijdt gemiddeld 80 km/h en komt om 12.22 uur aan.

Welke afstand heeft hij afgelegd?

Berekening:

s t Antwoordzin:

11 Angela vertrekt om 8.20 uur, roeit gemiddeld 9 km/h en komt om 9.50 uur aan.

Welke afstand heeft ze afgelegd?

Berekening:

Antwoordzin:

12

In welke tijd hebben beide lopers hun afstand afgelegd?

Wim Degrave – middagloop 28 mei 2023 om 21:35 – Heusden

Jurgen Houttekier – ochtendloop 28 mei 2023 om 18:26 – Koolskamp

afstandsnelheidtijd 9 km9 km/h? min afstandsnelheidtijd 3 km12 km/h? min

s (km) t (min)

s (km) t (min)

13 Je gaat te voet naar een feestje. Je wandeltempo is ongeveer 4,5 km/h.

Het feestje is 1,5 km van je thuis. Je moet vóór twee uur ‘s nachts thuis zijn.

Wanneer moet je daar ten laatste vertrekken om op tijd thuis te zijn?

Berekening:

s t

Antwoordzin:

14 Julian vertrok om 11.00 uur voor een tijdrit van 35 km aan 42 km/h.

Wanneer kwam hij aan?

Berekening: s t

Antwoordzin:

15 Bashir loopt aan een gemiddeld tempo van 5,5 minuten per kilometer. Hij liep onlangs een halve marathon van 21 km. Hij vertrok om 14.00 uur.

Bereikte Bashir vóór 16.00 uur de meet?

Berekening: s t

Antwoordzin: 42 km/h

16

Een concert in Brussel van je favoriete band start stipt om 20.00 uur.

De afstand van je thuis naar Brussel is 98 km. Er is veel verkeer, dus je verwacht dat je gemiddeld 90 km/h met de auto kunt rijden.

Wanneer moet je ten laatste met de auto vertrekken?

Berekening:

s

t

Antwoordzin:

©VANIN

17 De IC-trein tussen Poperinge en Kortrijk maakt zes tussenstops en haalt een gemiddelde snelheid van 75 km/h. De afstand tussen beide stations is 52,5 km.

Wanneer komt de IC-trein uit Poperinge in Kortrijk aan?

Berekening:

Antwoordzin:

18 In vogelvlucht ligt de luchthaven van Zaventem 1 064 km van die van Barcelona. Een Boeing 747 heeft een gemiddelde snelheid van 960 km/h.

Hoelang duurt de vlucht van Zaventem naar Barcelona?

Berekening:

Antwoordzin:

19 Tijdens de grand prix van Spa-Francorchamps rijden de F1-piloten 44 ronden van 7 km. De piloten halen tijdens die race vlot een gemiddelde snelheid van 230 km/h.

Hoelang duurt de grand prix ongeveer? Rond af op de eenheid.

Berekening:

Antwoordzin: : 12 : 07

20 Noteer, indien mogelijk, de passende letter bij de uitspraak.

B C D

(km) tijd (h)

a Na 3 uur heeft deze 4 km afgelegd.

b Deze heeft de hoogste snelheid.

c Deze is het traagst.

d Deze gaat 3 km/h.

e Deze heeft 5 km afgelegd in 2,5 uur.

f Deze is 2 km/h sneller dan D.

21 Vul de tabellen aan. Teken telkens het bijbehorende lijndiagram.

s (km)10520 snelheid km/h t (h)2

s (km)10 snelheid km/h t (h)513

s (km)12 snelheid km/h t (h)1,531

22 Beantwoord de vragen.

snelheid( km/h)

(h)

a Wat is de snelheid van opa?

b Wie heeft de grootste snelheid?

c Wie wandelt dubbel zo snel als oma?

(h)

23 Nicolai heeft met zijn vriendin een fietstocht gemaakt. Ze vertrokken om 12 uur. Van zijn uitstap maakte hij een lijndiagram. Beantwoord de vragen.

a Hoeveel kilometer hebben ze die dag afgelegd?

b Hoelang zijn ze onderweg geweest?

c Wat was hun gemiddelde snelheid? Rond af op één cijfer na de komma.

d Tussen welke uren fietsten ze het snelst?

e Wat was hun hoogste snelheid?

f Om hoe laat hebben ze voor het eerst gerust?

g Hoelang hebben Nicolai en zijn vriendin gerust?

h Om hoe laat waren ze halfweg hun fietstocht?

24 Teken het lijndiagram dat past bij de omschrijving.

a Een fietser vertrekt voor een fietstocht met een snelheid van 15 km/h.

b Hij nadert de stad. Het verkeer wordt drukker en hij rijdt een half uur aan 10 km/h.

c Hij rijdt in een spijker en heeft een lekke band. Het duurt een half uur om de band te vervangen.

d Daarna fietst hij met de wind in de rug naar huis aan 20 km/h. 01234 5 10 15 20 af stand (km) tijd (h)

25 De acht diagrammen stellen bewegingen van Ruth voor. Welk diagram past bij welke omschrijving? Vul aan met de juiste letter.

A B C D

E F G H

omschrijving diagram

a Ruth staat aan het stoplicht. Bij groen kan ze terug een stuk rijden en bij het volgende stoplicht moet ze opnieuw wachten.

b Ruth loopt een eindje, rust dan even uit en loopt vervolgens verder.

c Ruth zit eerst op een bankje en vertrekt dan.

d Dit diagram kan niet want je kunt niet terugkeren in de tijd.

e Ruth vertrekt traag, versnelt plots héél erg en loopt dan terug op hetzelfde tempo.

f Ruth vertrekt voor een wandeling, merkt dat er iets uit haar zak is gevallen, keert terug om het op te rapen en zet haar weg verder.

g Ruth gaat bij iemand iets in de bus stoppen en keert dan terug.

h Ruth vertrekt thuis en haast zich om haar kinderen op tijd van school te halen. Daarna wandelen ze samen langzaam naar huis.

26 Hieronder zie je een voorstelling van de snelheid en tijd van twee auto’s. Beantwoord de vragen.

a Wat is de snelheid van de rode wagen na 1 minuut in km/h?

b Wat is de snelheid van de gele wagen na 1 minuut in km/h?

c Na hoeveel minuten rijden ze even snel?

d Wat doet de gele auto tussen minuut 2 en minuut 4?

e Welke auto rijdt na 5 minuten het snelst?

27 Filippo, Wout en Remco nemen het tegen elkaar op in een tijdrit. Beantwoord de vragen. 020406080

a Hoeveel kilometer moeten de renners fietsen?

b Wie wint de tijdrit?

c Wie is na 30 km het snelst?

d Na hoeveel kilometer krijgt Remco een serieuze inzinking?

e Welke renner verandert het vaakst van tempo?

f Wie rijdt aan een gemiddelde snelheid van 40 km/h?

g Wie begint het traagst aan de tijdrit?

©VANIN

28 Hieronder is de snelheid van een lift in een lijndiagram voorgesteld. Duid de passende omschrijving aan.

 De lift begint te stijgen, blijft op een verdieping staan en gaat terug naar beneden.

 De lift vertrekt vanuit stilstand, begint te versnellen, houdt een bepaalde snelheid aan en remt af om te stoppen op een andere verdieping.

29 Tijdens de les lichamelijke opvoeding moest klas 4B touwklimmen. Welke omschrijving past bij welke grafiek? Vul aan.

A B C

(m )

©VANIN

omschrijving diagram

a Elif, een sterke kerel, is in enkele stevige halen onmiddellijk boven.

b Ook Viktor is sportief, maar halfweg het touw verliezen zijn voeten steun en zakt hij even terug. Daarna gaat hij vlot naar boven.

c Roman houdt niet van stoerdoenerij. Hij klimt rustig naar boven.

d Malika begint stoer, maar bereikt uiteindelijk met moeite de top.

e Katia is ook sportief, maar neemt halverwege een rustpauze.

f Lot begint goed aan haar klim maar verliest uiteindelijk haar grip.

Even samenvatten

• Even herhalen 1 h = 60 min 1 min = 60 s 1 h = 3 600 s

• Snelheid

Je loopt aan een tempo van 5 m/s.

Hoeveel km/h is dat? s (m)5 18 000 t (s)13 600

©VANIN

Als je een tempo van 5 m/s hebt, loop je 18 000 m per 3 600 s of 18 km/h.

• Toepassingen met snelheid de afstand berekenen de tijd berekenen

Je fietst 20 minuten aan 80 km/h. Hoe ver heb je gefietst?

Je fietst 15 km aan 18 km/h. Hoelang heb je gefietst? s (km)18 6 t (min)6020 s (km)18115 t (min)60 50

Je hebt 6 km gefietst. Je hebt 50 minuten gefietst.

• Diagrammen afstand en tijd snelheid en tijd af stand (s) tijd (t) snelheid (v) tijd (t) snelheid (v) tijd (t) snelheid (v) tijd (t) constante snelheidversnellenconstante snelheidvertragen x 3 600 x 3 600 : 3 : 3 : 18 x 15 : 18 x 15

Kubussen maken

Welke twee delen vormen samen een kubus van 3 x 3 x 3 of van 2 x 2 x 2 blokken? Noteer de letters van de passende combinaties.

deel 1

deel 2

Test op mezelf

Naam:

FORMULE 1

1 Snelheid

Nr.: Klas:

Vul de verhoudingstabel aan. Wat is de snelheid in km/h?

Datum: / / 20 / 20

afstand (km)0,4 snelheid tijd (min)5253060 km/h

De Ronde van Vlaanderen 2023 werd gewonnen door Tadej Pogacar.

Hij legde 263,7 km af in 6 h 02 min.

Wat was zijn gemiddelde snelheid? Rond af op één cijfer na de komma.

Berekening:

Antwoordzin:

2 Toepassingen met snelheid

Welke afstand legde Pieter af tijdens zijn middagrit? Rond af op één cijfer na de komma.

afstandsnelheidtijd ? km22 km/h1 h 22 min

Berekening: Antwoordzin:

Pieter Van In – middagrit 25 mei om 16:48 – Oostnieuwkerke

Duid telkens het juiste antwoord aan.

a Je fietst met een snelheid van 15 km/h.

Welke afstand heb je na twee uur afgelegd?  7,5 km  17 km  30 km

b Een zwemster haalt een snelheid van 1,5 m/s.

Welke afstand heeft ze na 10 s afgelegd?  15 km  15 m  0,15 km

c Een wedstrijdduif vliegt gemiddeld 80 km/h.

Hoelang doet de duif over 160 km?  2 h  4 h  0,5 h

d Je loopt aan een tempo van 12 km/h.

Hoelang doe je over 4 km?  3 h  60 min  20 min

In de Kattenkoers zitten de renners op 57 km van de finish. Het is nu 15.24 uur.

Je gaat ervan uit dat de renners hun gemiddelde snelheid behouden.

Wanneer komen de renners aan?

Berekening:

38 km/h

Antwoordzin:

3 Diagrammen

Gedurende anderhalve minuut zetten twee fietsers alles op alles op een BMX-parcours.

Beantwoord de vragen.

a Wie had de grootste startsnelheid?

b Wie won de wedstrijd?

c Wat deed rood tussen 30 s en 50 s?

d Wie reed halfweg op kop?

e Hoeveel km/h reed rood bij aankomst?

f Hoeveel keer haalden ze elkaar in?

g Hoeveel km/h reed blauw na 1 minuut?

Formularium

Formules voor procentberekening

D

PB

D = Deel

P = Procent in kommagetal

B = Beginwaarde

Formules voor omtrek en oppervlakte van vlakke figuren

oppervlakte driehoek

z2 z3 z1

hoogte (h) z1+z2+z3(bxh):2

basis (b)

vierkant

rechthoek

zijde (z) 4xzzxz

breedte (b)

cirkel

lengte (l)

straal(r)diameter(d)

d = 2 x r

2xl+2xbof2x(l+b)lxb

2xrx3,14rxrx3,14

Formularium

Formules voor volume en oppervlakte van ruimtefiguren

kubus z z z z x z x z 6 x z x z

©VANIN

balk b l h

cilinder r h

Formule voor schaal

l x b x h2 x l x b + 2 x l x h + 2 x b x h

r x r x 3,14 x h2 x r x r x 3,14 + 2 x r x 3,14 x h

schaal = afmeting op tekening afmeting in werkelijkheid = T W

Lengtematen herleiden

©VANIN

LENGTE Herleidingstabellen

100 kg10 kg kg

©VANIN

g10 g gdg cg mg

g10 g gdg cg mg ton 100 kg10 kg kg

MASSA

©VANIN

Herleidingstabellen

Notities ©VANIN