Pienter 3 - 3u - leerwerkboek (ed. 2024)

©VANIN

Leerjaar 3 3 uur

©VANIN

Philippe De Crock

Dirk Taecke

Thierry Van den Ouwelant

MET MEDEWERKING VAN

Etienne Goemaere

Christophe Gryson

Eddy Magits

Tom Van der Auwera

Martine Verrelst

Via www.diddit.be heb je toegang tot het onlineleerplatform bij Pienter 3.

Activeer je account aan de hand van de onderstaande code en accepteer de gebruiksvoorwaarden.

Kies je ervoor om je aan te melden met je Smartschool-account, zorg er dan zeker voor dat je e-mailadres aan dat account gekoppeld is. Zo kunnen we je optimaal ondersteunen.

Let op: activeer deze licentie pas vanaf 1 september; de licentieperiode start vanaf activatie en is slechts 365 dagen geldig.

3 – 3 u

Fotokopieerapparaten zijn algemeen verspreid en vele mensen maken er haast onnadenkend gebruik van voor allerlei doeleinden. Jammer genoeg ontstaan boeken niet met hetzelfde gemak als kopieën.

Boeken samenstellen kost veel inzet, tijd en geld. De vergoeding van de auteurs en van iedereen die bij het maken en verhandelen van boeken betrokken is, komt voort uit de verkoop van die boeken.

In België beschermt de auteurswet de rechten van deze mensen. Wanneer u van boeken of van gedeelten eruit zonder toestemming kopieën maakt, buiten de uitdrukkelijk bij wet bepaalde uitzonderingen, ontneemt u hen dus een stuk van die vergoeding. Daarom vragen auteurs en uitgevers u beschermde teksten niet zonder schriftelijke toestemming te kopiëren buiten de uitdrukkelijk bij wet bepaalde uitzonderingen. Verdere informatie over kopieerrechten en de wetgeving met betrekking tot reproductie vindt u op www.reprobel.be.

Ook voor het onlinelesmateriaal gelden deze voorwaarden. De licentie die toegang verleent tot dat materiaal is persoonlijk. Bij vermoeden van misbruik kan die gedeactiveerd worden. Meer informatie over de gebruiksvoorwaarden leest u op www.diddit.be.

© Uitgeverij VAN IN, Wommelgem, 2024

©VANIN

De uitgever heeft ernaar gestreefd de relevante auteursrechten te regelen volgens de wettelijke bepalingen. Wie desondanks meent zekere rechten te kunnen doen gelden, wordt verzocht zich tot de uitgever te wenden.

Eerste druk 2024

ISBN 978-94-647-0612-3

D/2024/0078/100

Art. 606358/01

NUR 120

Omslagontwerp: Fikfak

Tekeningen: Dirk Vandamm

Lay-out: Crius Publishing

Pienter

Inhoudsopgave

Hoe werk je met Pienter? 4

Hoofdstuk 1 De stelling van Pythagoras 7

Hoofdstuk 2 De reële getallen 51

Hoofdstuk 3 Driehoeksmeting van een rechthoekige driehoek 81

Hoofdstuk 4 Rekenen met reële getallen 125

Hoofdstuk 5 Beschrijvende statistiek 173

Hoofdstuk 6 Gelijkvormigheid 221

Hoofdstuk 7 Eerstegraadsvergelijkingen, eerstegraadsongelijkheden en formules omvormen 277

Hoofdstuk 8 Vectoren 317

Hoe werk je met Pienter?

Elk hoofdstuk start met een inhoudsopgave en een cartoon. Dat geeft je een eerste indruk van het hoofdstuk.

Bij het begin van elk hoofdstuk maak je aan de hand van een realistische inleiding of een kort onderzoek kennis met het onderwerp dat aan bod zal komen.

Na elk stuk theorie kun je meteen oefenen. Niet alle oefeningen zijn even moeilijk. Ze zijn opgedeeld in drie reeksen:

REEKS A eenvoudige toepassingen

REEKS B basisniveau

REEKS C verdiepingsniveau

Oefeningen zijn genummerd per hoofdstuk en aangeduid met een verticale streep. Op diddit vind je extra oefeningen.

Oefeningen

REEKS A

Stap voor stap kom je meer te weten over wiskunde in het dagelijks leven.

Je leert formuleren in definities, eigenschappen, rekenregels of besluiten.

Je leert ook eigenschappen bewijzen.

22 Plaats de getallen in het venndiagram. a)–12c)1,5e)0,33...g)

23 Noteer de passendste getallenverzameling. Kies uit n, z, q of r

In de marge worden soms pictogrammen gebruikt. Hieronder vind je hun betekenis.

ICT Duidt aan wanneer je een ICT-bestand op diddit terugvindt, bv. Excel of GeoGebra.

Interessante weetjes of achtergrondinformatie herken je aan een kader met vraagteken.

24 Zijn de gegeven getallen rationaal of irrationaal?

R Duidt aan dat je bij het onlinelesmateriaal een remediëringsoefening kunt vinden.

Geeft aan dat je bij het onlinelesmateriaal extra uitdagende leerstof vindt.

Je leraar zal telkens aangeven wat precies voor jou van toepassing is.

Soms is het handig dat je extra lesinformatie via GeoGebra of een videofragment zoals een instructiefilmpje zelf kunt bekijken of beluisteren op je smartphone. Als je dit icoon ziet, open dan de VAN IN Plus-app en scan de pagina.

©VANIN

STUDIEWIJZER De reële getallen

2.1 Decimale voorstelling van rationale getallen

Decimale getallen, zuiver repeterende en gemengd repeterende decimale vormen van elkaar onderscheiden.

De periode en het niet-repeterend deel van een decimale vorm aanduiden.

Decimale schrijfwijze omzetten naar breuk. Breuk omzetten naar decimale schrijfwijze.

2.2 Vierkantswortels

Op het einde van elk hoofdstuk vind je alles wat je moet kennen en kunnen bijeengebracht in een studiewijzer. Dat is een ideale leidraad om je samenvatting te maken.

KENNEN

Een vierkantswortel van een positief getal is een getal waarvan het kwadraat gelijk is aan dat positief getal.

KUNNEN

De vierkantswortels van een positief getal berekenen.

Elk hoofdstuk sluit af met de rubriek ‘Pienter problemen oplossen’ of ‘Problemen uit JWO’ (Junior Wiskunde Olympiade). Het is aan jou om aan de hand van heuristieken en probleemoplossend denken de problemen op te lossen.

2.3 De reële getallen

KENNEN

Sommige onderdelen zijn aangeduid met een groene, blauwe of oranje band. Je leerkracht zal aangeven wat je wel en niet moet kennen.

Een irrationaal getal is een getal met oneindig veel cijfers na de komma en zonder periode.

Een reëel getal is een getal dat rationaal of irrationaal is.

De absolute waarde van een reëel getal is dat getal zonder toestandsteken.

Het tegengestelde van een reëel getal is het reëel getal met dezelfde absolute waarde, maar met een verschillend toestandsteken.

Het omgekeerde van een reëel getal is 1 gedeeld door dat reëel getal.

KUNNEN

Getallen voorstellen in een venndiagram.

Achteraan in het boek zitten twee bladen met een cartoon. Die kun je gebruiken als voorblad voor je eigen notities of voor afgedrukte oefeningen van Pienter Remediëren en voor Extra Leerstof.

De absolute waarde van een reëel getal bepalen.

Het tegengestelde van een reëel getal bepalen.

Het omgekeerde van een reëel getal bepalen.

2.4 Irrationale getallen benaderen

KENNEN

Een wortelvorm is een product van een irrationale vierkantswortel en een rationaal getal.

Een interval in r is een verzameling van opeenvolgende reële getallen.

KUNNEN

Werken met intervallen.

Irrationale getallen afronden in betekenisvolle situaties.

Irrationale getallen benaderen met intervallen.

PIENTER EN DIDDIT

Het onlineleerplatform bij Pienter

Materiaal

Hier vind je het lesmateriaal en de online-oefeningen. Gebruik de filters bovenaan, de indeling aan de linkerkant of de zoekfunctie om snel je materiaal te vinden.

Lesmateriaal

Hier vind je het extra lesmateriaal bij Pienter, zoals remediëringsoefeningen en Excel-bestanden.

Oefeningen

• De leerstof kun je inoefenen op jouw niveau.

• Je kunt hier vrij oefenen.

Opdrachten

Hier vind je de opdrachten terug die de leerkracht voor jou heeft klaargezet.

Evalueren

Hier kan de leerkracht toetsen voor jou klaarzetten.

Resultaten

Wil je weten hoever je al staat met oefenen, opdrachten en evaluaties? Hier vind je een helder overzicht van je resultaten.

E-book

Het e-book is de digitale versie van het leerwerkschrift. Je kunt erin noteren, aantekeningen maken, zelf materiaal toevoegen ...

Meer info over diddit vind je op www.vanin.diddit.be/nl/leerling.

HOOFDSTUK 1 I DE STELLING VAN PYTHAGORAS

©VANIN

1.1 De stelling van Pythagoras formuleren

1.1.1 Op onderzoek

Vul de tabel verder in.

GEOGEBRA

Wat stel je vast als je de laatste twee kolommen vergelijkt?

1.1.2 Benamingen in een rechthoekige driehoek

Een rechthoekige driehoek bestaat uit

• twee rechthoekszijden (vormen een rechte hoek): en

GEOGEBRA

• een schuine zijde of hypothenusa :

1.1.3

De stelling van Pythagoras

Stelling In een rechthoekige driehoek is de som van de kwadraten van de rechthoekszijden gelijk aan het kwadraat van de schuine zijde.

GEOGEBRA

In symbolen: a 2 + b 2 = c 2 waarbij a en b de rechthoekszijden zijn en c de schuine zijde

Drie natuurlijke getallen a, b en c, elk verschillend van 0, a b c die aan de voorwaarde a 2 + b 2 = c 2 voldoen, noem je pythagorische drietallen Het eenvoudigste pythagorisch drietal is 3, 4 en 5.

De stelling van Pythagoras geldt ook omgekeerd.

Stelling Als in een driehoek de som van de kwadraten van de twee kortste zijden gelijk is aan het kwadraat van de langste zijde, dan is de driehoek rechthoekig.

De 3-4-5-regel

Pythagorische drietallen worden gebruikt om een rechte hoek te bepalen.

• Bind op gelijke afstand knopen in een touw. Zo verkrijg je gelijke knoopafstanden.

• Vorm met het touw een driehoek waarvan een zijde drie knoopafstanden heeft; een zijde vier knoopafstanden heeft; een zijde vijf knoopafstanden heeft.

• Zo verkrijg je een rechthoekige driehoek en kun je een rechte hoek uitzetten.

©VANIN

Pythagoras is geboren op het Griekse eiland Samos, vermoedelijk in 569 v.Chr.

In 518 vestigde hij in Zuid-Italië een filosofische school. De leerlingen van die school werden ‘mathematikoi’ of ‘pythagoreeërs’ genoemd en moesten strenge leefregels volgen. Zo moesten ze vegetarisch leven en zweren dat ze geloofden dat alles met getallen te vatten is.

De pythagoreeërs hebben veel verdiensten: ze konden vergelijkingen meetkundig oplossen, ontdekten de irrationale getallen (zie het volgende hoofdstuk) en bestudeerden met succes regelmatige veelvlakken.

De ‘stelling van Pythagoras’ is in elk geval niet door hemzelf of door een van zijn volgelingen bedacht.

De Babyloniërs gebruikten de eigenschap al meer dan 1 000 jaar eerder om de hoogte van muren te bepalen.

De Plimpton-kleitablet, uit 1800 voor Christus, bevat kwadraten die te schrijven zijn als de som van twee andere kwadraten. Die kleitablet is de eerste wiskundige tekst uit de geschiedenis van de mensheid.

Ook in het oude Egypte kende men de 3-4-5-regel al.

Oefeningen

REEKS A

1 Kleur het vak met de passende lengte van de schuine zijde c, zodat de driehoek met zijden a, b en c rechthoekig is.

2 Formuleer bij de driehoeken, indien mogelijk, de stelling van Pythagoras.

3 Onderzoek of de driehoek met zijden a, b en c rechthoekig is. Zet een vinkje. a b c rechthoekig niet rechthoekig

4 Bereken de zijden van de rechthoekige driehoeken. Gebruik een touw met een aantal knopen op gelijke knoopafstand.

knoopafstand lengte van de zijden

a) rechthoekszijde: 3 stukken van 2 cm

rechthoekszijde: 4 stukken van 2 cm

schuine zijde: stukken van 2 cm

b) rechthoekszijde: 3 stukken van 5 cm

rechthoekszijde: stukken van 5 cm schuine zijde: 5 stukken van 5 cm

c) rechthoekszijde: 3 stukken van 15 mm

rechthoekszijde: 4 stukken van 15 mm

schuine zijde: stukken van 15 mm

d) rechthoekszijde: stukken van 7 cm

rechthoekszijde: 4 stukken van 7 cm

schuine zijde: 5 stukken van 7 cm

5 Onderzoek of de driehoek met zijden a, b en c rechthoekig is. Zet een vinkje. a b c rechthoekig niet rechthoekig

©VANIN

6 Onderzoek of nABC rechthoekig is. Zet een vinkje. zijden rechthoekig niet rechthoekig

7 Los op.

a) Om in het park een voetbalpleintje af te bakenen, stapt Stijn twintig passen af in de breedte en zestig in de lengte. Pedro vertrouwt het niet helemaal en vraagt Stijn eens diagonaal over het veld te stappen. Stijn telt 67 passen. Is hun voetbalplein rechthoekig?

Antwoord:

b) Pa wil een tuinhuis achter in de tuin. Hij graaft een rechthoekige kuil van 3,6 m bij 4,8 m voor de grondplaat. Om te controleren of zijn put wel rechthoekig is, meet hij de diagonaal. Die is zes meter. Is de kuil rechthoekig?

Antwoord:

8 Toon aan zonder te meten.

a) Parallellogram PLAK is een rechthoek.

b) Parallellogram KLAP is een ruit.

©VANIN

9 Toon zonder geodriehoek aan dat a ' b

10 Bereken de schuine zijde met de 3-4-5-regel.

a) rechthoekszijde: 60 cm = 3 ? 20 cm

c) rechthoekszijde: 12 dm = rechthoekszijde: 80 cm = 4 20 cm rechthoekszijde: 16 dm = schuine zijde: schuine zijde:

b) rechthoekszijde: 15 m =

d) rechthoekszijde: 90 mm = rechthoekszijde: 20 m = rechthoekszijde: 120 mm = schuine zijde: schuine zijde:

Pythagorische drietallen

1.2 Meetkundige voorstellingen

1.2.1

De stelling van Pythagoras

Neem een driehoek ABC, rechthoekig in C

c b CB A

Je plaatst op elke zijde een vierkant, waarvan de zijde gelijk is aan die zijde van de driehoek.

Je verdeelt de vierkanten in gelijke vierkantjes van 1 cm2.

De vierkanten hebben een oppervlakte van a 2 = cm2, b 2 = cm2 en c 2 = cm2

De oppervlakte van het vierkant op de schuine zijde is

In symbolen:

1.2.2 De Pythagorasboom

1) Teken een willekeurig vierkant.

GEOGEBRA

2) Construeer op dat vierkant een gelijkbenige rechthoekige driehoek waarvan de schuine zijde gelijk is aan de zijde van het vierkant.

3) Construeer daarna een vierkant op elke rechthoekszijde van de driehoek.

4) Op de zijden van die vierkanten kun je opnieuw een gelijkbenige rechthoekige driehoek tekenen met een schuine zijde gelijk aan de zijde van het vierkant.

5) Elke rechthoekszijde van die nieuwe driehoeken is de zijde van een nieuw vierkant.

©VANIN

Als je dezelfde bewerkingen telkens opnieuw uitvoert, verkrijg je de boom van Pythagoras.

De boom van Pythagoras noem je een fractaal.

Het woord ‘fractaal’ is afgeleid van het Latijnse woord fractus, dat ‘gebroken’ betekent. Een fractaal is een meetkundige figuur met bijzondere eigenschappen:

• zelfgelijkvormigheid: binnen een fractaal herhalen bepaalde structuren of patronen zichzelf. Als je een klein detail van een fractaal sterk uitvergroot, zie je steeds dezelfde vorm terug;

• oneindige herhaling van eenzelfde systeem of bewerking.

Oefeningen

REEKS A 11 Bepaal de ontbrekende oppervlakte.

©VANIN

12 Bepaal de lengte van de zijde x.

©VANIN

REEKS C

13 Teken een Pythagorasboom tot je op de tekening 16 gelijke vierkanten verkrijgt.

©VANIN

1.3 De stelling van Pythagoras bewijzen

Stelling

GEOGEBRA

In een rechthoekige driehoek is de som van de kwadraten van de rechthoekszijden gelijk aan het kwadraat van de schuine zijde.

tekening gegeven

• Op de schuine zijde van de driehoek teken je een vierkant met zijde c.

• Daaromheen teken je een vierkant met zijde a + b, zodat de hoekpunten van het vierkant met zijde c op de zijden van het grote vierkant liggen.

©VANIN

een rechthoekige driehoek ABC met rechthoekszijden a en b en schuine zijde c te bewijzen

bewijs

De oppervlakte van de volledige figuur kun je op twee manieren berekenen:

oppervlakte groot vierkant = oppervlakte klein vierkant + oppervlakte vier driehoeken

⇓ definitie oppervlakte vierkant en driehoek

+ 4 ? a b

⇓ merkwaardig product en breuken vereenvoudigen

eigenschappen gelijkheden

besluit

a 2 + b 2 = c 2

De stelling van Pythagoras is een van de meest bewezen stellingen uit de vlakke meetkunde.

Momenteel zijn er meer dan 350 verschillende bewijzen voor die stelling bekend.

Oefeningen

REEKS B

14 Bewijs de stelling van Pythagoras. tekening gegeven

Q RqP r te bewijzen bewijs besluit

REEKS C

15 Bewijs de stelling van Pythagoras.

tekening gegeven

GEOGEBRA

bewijs

©VANIN

te bewijzen

besluit

1.4 Rekenen met Pythagoras

1.4.1 Inleiding

Vader bouwt zelf een tuinhuisje achter in de tuin.

Hij wil balken bestellen om het dakgebinte te maken.

GEOGEBRA

Daarvoor moet hij weten hoe lang die balken minstens moeten zijn.

Om die lengte te berekenen, moet je de stelling van Pythagoras omvormen.

Om in een rechthoekige driehoek een zijde te berekenen, gebruik je de stelling van Pythagoras.

Zo kun je ook een rechthoekszijde berekenen als de schuine zijde en de andere rechthoekszijde gegeven zijn.

1.4.2 Algemeen

1.4.3

©VANIN

De schuine zijde berekenen als de rechthoekszijden gegeven zijn.

Een rechthoekszijde berekenen als de schuine zijde en een rechthoekszijde gegeven zijn.

Voorbeelden

In een rechthoekige driehoek zijn de rechthoekszijden 4 cm en 5 cm lang. Hoe lang is de schuine zijde? (op 0,1 nauwkeurig)

In een rechthoekige driehoek is de schuine zijde 8 cm lang. Een van de rechthoekszijden is 6 cm. Hoe lang is de andere rechthoekszijde? (op 0,1 nauwkeurig)

Oefeningen

REEKS A

16 Bereken, op 0,01 nauwkeurig, de schuine zijde in een rechthoekige driehoek.

rechthoekszijde rechthoekszijde bewerkingen schuine zijde

17 Bereken, op 0,01 nauwkeurig, de rechthoekszijde in een rechthoekige driehoek.

rechthoekszijde schuine zijde bewerkingen rechthoekszijde

18 Bereken, op 0,01 nauwkeurig, de zijde x in de rechthoekige driehoeken.

19 Bereken x op 0,01 nauwkeurig.

©VANIN

20 Bereken, op 0,01 nauwkeurig, de ontbrekende zijde in een rechthoekige driehoek met schuine zijde c

21 Een ladder van 5 meter lang staat tegen een muur. De ladder steunt tegen de muur op een hoogte van 4,80 meter. Hoe ver staat de onderkant van de ladder van de muur?

Antwoord:

22 Een rechthoek heeft een lengte van 10 cm en een breedte van 4 cm. Bereken, op 0,1 cm nauwkeurig, de lengte van de diagonalen van die rechthoek.

Antwoord:

©VANIN

23 Een boom is op een hoogte van 2,30 m afgeknakt door de bliksem. De top van de kruin bevindt zich op 4,85 m afstand van wat er van de stam overgebleven is. Bereken, op 0,01 m nauwkeurig, de oorspronkelijke hoogte van de boom.

Antwoord:

24 Aan de ene kant is een 50 m lang zwembad 1 m diep. Die diepte neemt geleidelijk aan toe tot 3,5 m aan de andere kant van het zwembad. Bereken, op 0,01 m nauwkeurig, de lengte van de bodem van dat zwembad.

Antwoord:

25 Op een terrein staan, op 10 m van elkaar, twee palen met een respectievelijke lengte van 8 m en van 6 m. Je wilt een kabel spannen tussen de toppen van beide palen. Hoe lang moet die kabel minimaal zijn? Bepaal je antwoord op 0,01 m nauwkeurig.

Antwoord: De Babyloniërs hadden een origineel idee om de hoogte van een muur te meten. Ze namen een stok, waarvan de lengte gekend was en die zeker langer was dan de hoogte van de muur, en plaatsten die schuin tot tegen de bovenrand van de muur. Het volstond dan de afstand van de muur tot het onderste punt van de stok te meten.

26 Bereken, op 0,01 m nauwkeurig, de hoogte van de muur, als het onderste punt van een stok van 25 m zich op 10,15 m afstand van de voet van de muur bevindt.

Antwoord:

27 De schuine zijde van een gelijkbenige rechthoekige driehoek is 5 cm. Bereken, op 0,1 cm nauwkeurig, de lengte van de rechthoekszijden.

Antwoord:

©VANIN

28 Bereken, op 0,1 cm nauwkeurig, de hoogte van een gelijkzijdige driehoek met zijden van 6 cm.

Antwoord:

29 Bereken, op 0,1 cm nauwkeurig, de zijden van een ruit waarvan de diagonalen 9 cm en 5 cm lang zijn.

Antwoord:

30 Bereken, op 0,01 cm2 nauwkeurig, de oppervlakte van een vierkant met diagonalen van 3 cm.

Antwoord:

31 Bereken de zijde x in de rechthoekige driehoek. Rond af op 0,01 cm.

32 Een piramide heeft een vierkant grondvlak met een zijde van 6 cm en opstaande ribben van 10 cm. Bereken, op 0,01 cm nauwkeurig, de lengte van het lijnstuk [TE ].

REEKS C

33 Bereken, op 0,01 cm2 nauwkeurig, de oppervlakte van een ruit met zijde 10 cm en een diagonaal van 15 cm.

©VANIN

Antwoord:

34 Bereken, op 0,1 cm nauwkeurig, de rechthoekszijden van een rechthoekige driehoek waarvan de schuine zijde 15 cm is en de ene rechthoekszijde driemaal zo lang is als de andere rechthoekszijde.

Antwoord:

35 Bereken, op 0,01 m nauwkeurig, de omtrek van de cirkel door de hoekpunten van een vierkant met een zijde van 4 m.

4 m

Antwoord:

Extra oefeningen (REEKS C)

1.5 Constructies

1.5.1

Constructie van een schuine zijde

Modeloefening 1: Construeer een lijnstuk c met lengte van 13 cm.

Stel 13 = 4+ 9 = 2+ 3 22 , dan is c = + 22ab met c = 13 cm, a = 2 cm en b = 3 cm.

Stap 1: Teken een lijnstuk a van 2 cm.

Stap 2: Construeer het lijnstuk b van 3 cm loodrecht op a in een grenspunt.

Stap 3: Verbind de vrije grenspunten. Het gevonden lijnstuk c is 13 cm.

1.5.2

Constructie van een rechthoekszijde

Modeloefening 2: Construeer een lijnstuk a met een lengte van 12 cm.

Stel 12 = 16 –4 = 4– 2 22 , dan is a = –22cb met a = 12 cm, b = 2 cm en c = 4 cm.

Stap 1: Teken een lijnstuk b van 2 cm en een loodrechte op b in een van de grenspunten.

Stap 2: Construeer een boog met een straal van 4 cm vanuit het andere grenspunt.

Stap 3: Verbind het vrije grenspunt van b met het snijpunt van de boog met de loodrechte.

Het gevonden lijnstuk a is 12 cm.

Je kunt niet alle lijnstukken met een opgegeven lengte op die manier construeren.

1.5.3 Toepassing

• Construeer een rechthoekige driehoek met rechthoekszijden gelijk aan 1.

• De schuine zijde is dan 1+ 1 22 = 2

• Gebruik de gevonden schuine zijde als rechthoekszijde voor een volgende rechthoekige driehoek.

• De schuine zijde van die driehoek is 2+ 1 2 2 () = 3 .

• Gebruik de gevonden schuine zijde als rechthoekszijde voor een volgende rechthoekige driehoek.

Oefeningen

REEKS A

36 Construeer via de schuine zijde van een rechthoekige driehoek

a) een lijnstuk van 20 cm.

b) een lijnstuk van 10 cm.

37 Construeer via een rechthoekszijde van een rechthoekige driehoek

a) een lijnstuk van 7 cm.

b) een lijnstuk van 5 cm.

REEKS B

38 Construeer

a) een lijnstuk van 11 cm.

b) een lijnstuk van 17 cm.

39 Construeer op twee verschillende manieren een lijnstuk van 8 cm.

a) via de schuine zijde

REEKS C

40 Bereken de andere rechthoekszijde.

b) via een rechthoekszijde

©VANIN

Die eigenschap kun je ook gebruiken om een lijnstuk met een gegeven lengte te construeren.

Construeer

a) een lijnstuk van 5 cm.

b) een lijnstuk van 8 cm.

1.6 Afstand tussen twee punten

1.6.1 Afstand van een punt tot de oorsprong

Het punt A is aangeduid op de tekening.

co(A) = ( , )

GEOGEBRA

Meet de afstand van A tot de oorsprong O

| OA | =

co(B) = (−5, 4)

Stel B voor in het assenstelsel.

Meet de afstand van B tot de oorsprong O

| OB | =

–1–2–3 –4 –5–6–7 234567

Je kunt | OA | ook berekenen.

Je bepaalt het punt S, het snijpunt van de verticale rechte door A en de x-as.

Zo verkrijg je een rechthoekige driehoek AOS.

| OS | = | de x-coördinaat van A | =

| AS | = | de y-coördinaat van A | =

| OA |2 = | OS |2 + | AS |2

| OA |2 = +

| OA |2 =

| OA | =

Bereken | OB |.

Werkwijze De afstand van een punt tot de oorsprong verkrijg je door • de som te berekenen van de kwadraten van de coördinaatgetallen van dat punt en • de vierkantswortel van die som te bepalen.

co(A) = (xA , yA) ⇒ | OA | = xy + 22 AA

1.6.2 Afstand tussen twee punten

Voorbeeld

In een assenstelsel zijn twee punten gegeven:

GEOGEBRA

A met co(A) = ( , ) en B met co(B) = ( , )

• Je kunt de afstand tussen die twee punten meten: | AB | = cm. y

• Je kunt de afstand tussen de twee punten ook berekenen.

Je bepaalt het punt S, dat je verkrijgt als het snijpunt van de horizontale rechte door A en de verticale rechte door B

| AS | = want (verschil van de x-coördinaten)

©VANIN

| BS | = want (verschil van de y-coördinaten)

• Bereken, op 0,01 nauwkeurig, de lengte van de schuine zijde van de rechthoekige driehoek ABS

| AB |2 = | AS |2 + | BS |2

| AB | = || +| | 22 AS BS

| AB | = 4+ 6 22

| AB | = ≈

Algemeen

In een assenstelsel zijn twee punten gegeven:

A met co(A) = (xA , yA) en B met co(B) = (xB , yB).

| CB | = | yB − yA | en

| AC | = | xB − xA |

Je neemt van beide verschillen de absolute waarde omdat afstanden altijd positief zijn.

| AB |2 = | AC |2 + | CB |2

| AB | = || +| | 22 AC CB

| AB | = xx yy BA BA (– )+ (– ) 22 y

Formule Voor A en B met co(A) = (xA , yA) en co(B) = (xB , yB) geldt:

| AB | = (– )+ (– ) 22 xxyy BABA

Voorbeeld 1

Bereken | AB | op 0,01 nauwkeurig, als co(A) = (–2, 4) en co(B) = (3, –5).

| AB | = =

Voorbeeld 2 1234 5 3 C

Bereken | CD | op 0,01 nauwkeurig.

co(C) = co(D) = | CD | = =

Algemeen

Bijzondere gevallen

Afstand van een punt tot de oorsprong 123 45 x 1 y O A –1 –2

co(O) = (0, 0) co(A) = (5, −2)

| OA | = (5 –0)+ (–2– 0) 22

= 5+ (–2) 22

= 25 +4 = 29 ≈ 5,39

Als co(A)= (xA , yA), dan is |OA| = xy22 AA +

Afstand tussen twee punten met dezelfde x-coördinaat 12 34 5 x 1 y O B A –1 –2

co(A)= (2, 1) co(B)= (2, −2)

| AB | = (2 –2)+ (–2– 1) 22 = 0+ (–2– 1) 22 = (–2– 1)2 = |–2 – 1| = |–3| = 3

Algemeen Als de rechte AB verticaal is (dus als xA = xB), dan is | AB | = | yB − yA |.

©VANIN

Afstand tussen twee punten met dezelfde y-coördinaat –1 12 3 –2 x 2 1 O AB y

co(A) = (−2, 1) co(B) = (3, 1)

| AB | = (3– (–2)) + (1– 1) 22 = (3– (–2)) +0 22 = (3– (–2))2 = |3 – (–2)| = |3 + 2| = 5

Algemeen Als de rechte AB horizontaal is (dus als yA = yB), dan is | AB | = | xB − xA |.

Oefeningen

REEKS A

41 Bereken de afstand tussen de gegeven punten op 0,1 nauwkeurig.

a) A en B met co(A) = (2, 5) en co(B) = (5, 7)

I AB I =

b) C en D met co(C) = (4, 12) en co(D) = (3, 5)

I CD I =

c) E en F met co(E) = (4, 7) en co(F) = (6, 3)

I EF I =

42 Bereken de lengte van de lijnstukken op 0,01 nauwkeurig.

a) [AB] met co(A) = (−4, −2) en co(B) = (9, −2)

I AB I =

b) [OC] met co(O) = (0, 0) en co(C) = (2, 7)

I OC I =

c) [DE] met co(D) = (12, −4) en co(E) = (7, 1)

I DE I =

d) [FO] met co(F) = (−8, 4) en co(O) = (0, 0)

I FO I =

e) [GH] met co(G) = (−2, −6) en co(H) = (−4, 0)

I GH I =

f) [IJ] met co(I) = (7, −3) en co(J) = (−7, 3)

I IJ I =

g) [OK] met co(O) = (0, 0) en co(K) = (0, −6)

I OK I =

43 Bereken de afstand tussen de gegeven punten op 0,01 nauwkeurig. Controleer op de figuur.

©VANIN

44 Bereken de afstand tussen de gegeven punten op 0,01 nauwkeurig. Controleer op de figuur.

45 Teken de driehoeken en bereken de omtrek op 0,01 nauwkeurig.

©VANIN

nLAT met co(L) = (4, −2), co(A) = (2, 5) en co(T) = (6, 5)

b) nPEN met co(P) = (−6, 5), co(E) = (−6, −4) en co(N) = (1, −4)

a)

46 De steden Agem, Begem en Cegem worden verbonden door een spoorlijn.

Alle trajecten zijn recht.

De steden hebben in een assenstelsel met ijk 1 km de volgende coördinaatgetallen:

co(A) = (1, 2)

co(B) = (6, 3)

Hoeveel km spoorlijn, op 0,001 km nauwkeurig, is er nodig?

co(C) = (4, 11)

Antwoord:

47 Vanuit de oorsprong bekijk je de punten X, Y en Z met de volgende coördinaatgetallen:

co(X) = (5, 4)

co(Y) = (−6, 2)

Welk punt ligt het dichtst bij de oorsprong?

co(Z) = (−4, −3)

Antwoord:

48 Een full hd-monitor heeft een resolutie van 1 920 bij 1 080 pixels. Een pixel beweegt van positie (50, 50) naar positie (650, 800). Bereken de afgelegde weg op een gehele pixel nauwkeurig.

Antwoord:

49 Een driehoek wordt gevormd door de punten D, E en F met de volgende coördinaatgetallen: co(D) = (1, 3) co(E) = (2, −1) co(F) = (−2, 1)

Onderzoek of de driehoek DEF gelijkbenig en/of rechthoekig is.

Antwoord:

50 De vierkantjes op de figuur hebben een zijde van 12,5 km.

Niels logeert aan de kust. Hoe ver bevindt hij zich van Gent? Hoe ver van Brussel? Rond af op 0,1 km. x y 1 O 1

Niels bevindt zich hier

Brugge

Roeselare

Gent

Aalst

Mons

Turnhout

Antwerpen

Mechelen

Brussel

Hasselt

Liège

Charleroi

Namur

Marche-en-Famenne

Arlon

Antwoord:

1.7 Pythagoras in de ruimte

1.7.1 Modeloefening 1: diagonaal van een kubus

gegeven

een kubus met ribbe 4 cm gevraagd

Bereken de ruimtediagonaal op 0,01 nauwkeurig. oplossing

GEOGEBRA

antwoord

De diagonaal is

1.7.2 Modeloefening 2: hoogte van een piramide

gegeven

een piramide met vierkant grondvlak

Elke ribbe is 4 cm. gevraagd

Bereken de hoogte |EH| op 0,01 nauwkeurig. oplossing

antwoord

De hoogte is

Oefeningen

REEKS A

51 Bereken.

gegeven

een balk met l = 3 cm, b = 2 cm en h = 6 cm

gevraagd

| DF | oplossing

©VANIN

antwoord

| DF | =

52 Bereken op 0,1 cm nauwkeurig.

gegeven

een piramide met vierkant grondvlak met z = 3 cm en h = 5 cm

gevraagd

| AE | oplossing

antwoord

| AE | ≈

53 Bereken op 0,1 cm nauwkeurig.

gegeven

een balk met l = 3 cm, b = 3 cm en h = 5 cm M is het midden van [AE ]. N is het midden van [FG ]. gevraagd

| MN | oplossing

antwoord

| MN | ≈

54 Bereken op 0,1 cm nauwkeurig.

gegeven

een kubus met ribbe 3 cm gevraagd de omtrek van nCEG oplossing

antwoord

De omtrek van nCEG is

55 Bereken, op 0,1 cm nauwkeurig, de hoogte van een piramide met een vierkant grondvlak met zijde 7 cm en opstaande ribbe 11 cm.

Antwoord:

©VANIN

56 Een vrachtwagen heeft een laadruimte met lengte 5,5 m, breedte 3 m en hoogte 2,5 m. Kan een vlaggenmast van 7 m in die laadruimte?

Antwoord:

57 Van een piramidevormige tent hebben alle ribben een lengte van 2,5 m. Milan is 1,82 m groot. Kan Milan rechtop staan in die tent?

Antwoord:

REEKS C

58 Bereken op 0,01 cm2 nauwkeurig.

gegeven

een kubus met ribbe 3 cm gevraagd

de oppervlakte van nBGE oplossing

59 Bewijs.

antwoord

De oppervlakte van nBGE is

gegeven

een balk met ribben l, b en h te bewijzen

| DF | = lb++ 22 2h bewijs

besluit

| DF | = lb++ 22 2h

In een balk is het kwadraat van de lengte van een ruimtediagonaal gelijk aan l 2 + b

STUDIEWIJZER De stelling van Pythagoras

1.1 De stelling van Pythagoras formuleren voor de leerling voor de leerkracht

KENNEN

In een rechthoekige driehoek is de som van de kwadraten van de rechthoekszijden gelijk aan het kwadraat van de schuine zijde.

Omgekeerd: als in een driehoek de som van de kwadraten van de twee kortste zijden gelijk is aan het kwadraat van de langste zijde, dan is de driehoek rechthoekig.

KUNNEN

De stelling van Pythagoras formuleren en toepassen.

1.2 Meetkundige voorstellingen

KUNNEN

Het verband tussen de stelling van Pythagoras en de oppervlakte van de vierkanten op de zijden van een rechthoekige driehoek verduidelijken.

Toepassingen op meetkundige voorstellingen van de stelling van Pythagoras verklaren.

1.3 De stelling van Pythagoras bewijzen

De stelling van Pythagoras bewijzen.

KUNNEN

De stelling van Pythagoras bewijzen in een gewijzigde situatie.

1.4 Rekenen met Pythagoras

KUNNEN

Een onbekende zijde in een rechthoekige driehoek berekenen als twee zijden gegeven zijn.

De stelling van Pythagoras toepassen om vlakke problemen op te lossen.

1.5 Constructies

KUNNEN

Via de stelling van Pythagoras lijnstukken met een bepaalde lengte construeren.

1.6 Afstand tussen twee punten

©VANIN

KENNEN

Voor A en B met co(A) = (xA , yA) en co(B) = (xB , yB) geldt: |AB| = yy xx(– )+ (– ) 22

Afstand van een punt tot de oorsprong.

Als co(A) = (xA , yA), dan is |OA| = + 22 xyAA

Als de rechte AB verticaal is (dus als xA = xB), dan is |AB| = |yB – yA|.

Als de rechte AB horizontaal is (dus als yA = yB), dan is |AB| = |xB – xA|.

KUNNEN

De afstand tussen twee punten, gegeven met hun coördinaten, berekenen in het vlak.

1.7 Pythagoras in de ruimte

KUNNEN

De stelling van Pythagoras toepassen om ruimtelijke problemen op te lossen.

Pienter problemen oplossen

Welke heuristiek(en) gebruik je om de onderstaande problemen op te lossen?

❑ concreet materiaal

❑ schets

❑ schema/tabel

❑ vereenvoudig

❑ gok verstandig

❑ filter

❑ patroon

❑ kennis

❑ logisch nadenken

❑

1. Plaats natuurlijke getallen in de piramide, zodat de som van de getallen in elke twee naast elkaar staande vakjes gelijk is aan het getal in het gemeenschappelijke vakje erboven.

2. Plaats natuurlijke getallen in de piramide, zodat het product van de getallen in elke twee naast elkaar staande vakjes gelijk is aan het getal in het gemeenschappelijke vakje erboven.

HOOFDSTUK 2 I DE REËLE GETALLEN

2.1 Decimale voorstelling van rationale getallen

2.2 Vierkantswortels

2.3 De reële getallen

2.4 Irrationale getallen benaderen

2.5 Reële getallen ordenen

Pienter problemen oplossen

2.1 Decimale voorstelling van rationale getallen

2.1.1 Inleiding

De waarde (in euro) is een rationaal getal Elk rationaal getal kan op twee manieren worden geschreven:

• Voorbeelden:

• Voorbeelden:

2.1.2 Een breuk omzetten naar de decimale schrijfwijze

Om een breuk om te vormen naar de decimale schrijfwijze, deel je de teller van de breuk door de noemer.

24 25 = 17 8 = 17 11 =

2.1.3 Soorten decimale voorstellingen van rationale getallen

decimaal getal

decimale vorm

zuiver repeterend gemengd repeterend 29 20 =

Een decimaal getal is een begrensd kommagetal. 5 11 =

©VANIN

Een zuiver repeterende decimale vorm is een onbegrensd kommagetal waarbij de periode onmiddellijk na de komma begint. 17 6 =

Een gemengd repeterende decimale vorm is een onbegrensd kommagetal waarbij tussen de komma en de periode een niet-repeterend deel voorkomt.

• De periode van een decimale vorm is de cijfergroep na de komma die herhaald wordt.

Voorbeeld: 12,767 6... periode = 76

• Het niet-repeterend deel van een gemengd repeterende decimale vorm is de cijfergroep tussen de komma en de periode.

Voorbeeld: 13,845 210 210... periode = 210 niet-repeterend deel = 845

Afspraken

• Noteer de periode twee keer, gevolgd door drie puntjes.

• Begin de periode zo vroeg mogelijk.

• Houd de periode zo kort mogelijk.

2.1.4 Een decimale schrijfwijze omzetten naar een breuk

Decimale getallen voorbeeld werkwijze

1,65 = 165 100 = 33 20

Stap 1: Noteer het getal als een breuk:

• de teller is het getal zonder komma;

• de noemer is een macht van 10 met zoveel nullen als er cijfers na de komma zijn.

Stap 2: Vereenvoudig, indien mogelijk.

Zuiver repeterende decimale vormen met 0 voor de komma voorbeeld werkwijze

0,454 5... = 45 99 = 5 11

Stap 1: Noteer het kommagetal als een breuk:

• de teller is de periode;

• de noemer is een getal met zoveel negens als er cijfers in de periode zijn.

Stap 2: Vereenvoudig, indien mogelijk.

Zuiver repeterende decimale vormen met een ander getal dan 0 voor de komma voorbeeld werkwijze

2,33...

= 2 + 0,33...

= 2 + 3 9

= 2 + 1 3

= 6 3 + 1 3

= 7 3

Stap 1: Noteer het getal als de som van een aantal gehelen en een getal tussen 0 en 1.

Stap 2: Noteer het getal tussen 0 en 1 als een breuk:

• de teller is de periode;

• de noemer is een getal met zoveel negens als er cijfers in de periode zijn.

Stap 3: Vereenvoudig, indien mogelijk.

Stap 4: Maak het geheel getal en de breuk gelijknamig.

Stap 5: Bepaal de som van de breuken.

Gemengd repeterende decimale vormen

voorbeeld werkwijze

2,161 212...

= 216,121 2... 1 100

= (216 + 0,121 2...) ? 1 100

= 216 + 12 99 ? 1 100

= 216 + 4 33 1 100

= 7 128 33 + 4 33 1 100

= 7 132 33 1 100

= 7132 3300

= 1783 825

Stap 1: Schuif de komma op naar rechts, zodat die juist voor de periode komt te staan, en deel door de passende macht van 10 om de gelijkheid te bewaren.

Stap 2: Noteer het zuiver repeterend kommagetal dat je daardoor vindt als een onvereenvoudigbare breuk.

©VANIN

Stap 3: Vereenvoudig, indien mogelijk.

GEOGEBRA

Om een decimale vorm om te zetten naar een breuk moet je minstens 8 keer de periode ingeven.

Oefeningen

REEKS A

1 Duid het soort decimale schrijfwijze van de rationale getallen aan. decimaal getal zuiver repeterende decimale vorm gemengd repeterende decimale vorm

a) 0,845

b) 0,88...

c) 1,141 4

d) 3,243 624 36...

e) 8,254 4...

f) 16,232 322...

g) 8,07

h) 781,787 8...

i) 0,478 925 925...

j) 18,145 656

2 Vorm de breuken om naar de decimale schrijfwijze.

a) 3 5 = f) 19 12 = k) 210 111 = b) 1 8 = g) 14 37 = l) 17 15 =

c) 2 3 = h) 892 45 = m) 45 33 = d) 80 33 = i) 508 125 = n) 309 125 = e) 14 15 = j) 25 12 = o) 85 72 =

3 Vorm de breuken om naar de decimale schrijfwijze en bepaal telkens de periode. decimale schrijfwijze periode

a) 8 21

b) 7 13

c) 625 7

4 Schrijf de decimale getallen als een onvereenvoudigbare breuk.

a) 0,29 = e) 0,325 =

b) 0,4 = f) 1,18 =

c) 2,7 = g) 0,036 =

d) 1,25 = h) 4,064 =

©VANIN

5 Schrijf de zuiver repeterende decimale vormen als een onvereenvoudigbare breuk.

a) 0,77... =

b) 0,151 5... =

c) 0,090 9... =

d) 0,117 117... =

e) 0,030 030... =

f) 1,55... =

g) 2,181 8... =

h) 4,531 531... =

6 Schrijf de gemengd repeterende decimale vormen als een onvereenvoudigbare breuk.

a) 0,144... b) 1,257 878... c) 18,733...

7 Noteer de rationale getallen in decimale schrijfwijze als een onvereenvoudigbare breuk. a) 2,131 3... d) 72,727 2... g) −0,123 44... b) −1,02 e) −0,212 312 3... h) 50,505 5... c) 17,400... f) 2,757 5... i) −2,969 6...

©VANIN

2.2 Vierkantswortels

2.2.1

Inleiding

2.2.2

Definitie

Een vierkante tegel heeft een oppervlakte van 1 600 cm2 Bereken de lengte van een zijde van een tegel.

Definitie Vierkantswortel van een positief getal

Een vierkantswortel van een positief getal is een getal waarvan het kwadraat gelijk is aan dat positief getal.

In symbolen b is een vierkantswortel van a ⇔ b 2 = a (met a ∈ q+ en b ∈ q)

Opmerking

Waarom kun je de vierkantswortel van een negatief getal niet bepalen?

2.2.3 Positieve en negatieve vierkantswortel van een getal

positieve vierkantswortel negatieve vierkantswortel

• Bepaal een positief getal waarvan het kwadraat gelijk is aan 81.

( )2 = 81

• Besluit: noem je de positieve vierkantswortel van 81.

• Notatie:

81 =

Besluit

• Bepaal een negatief getal waarvan het kwadraat gelijk is aan 81.

( )2 = 81

• Besluit: noem je de negatieve vierkantswortel van 81.

• Notatie: – 81 =

• Elk positief getal a, verschillend van 0, heeft twee vierkantswortels die tegengesteld zijn:

; de positieve vierkantswortel of kortweg de vierkantswortel van a is a

; de negatieve vierkantswortel van a is − a

• 0 heeft juist één vierkantswortel, namelijk 0 zelf.

• Elk negatief getal a, verschillend van 0, heeft geen vierkantswortels.

Oefeningen

REEKS A

8 Bereken zonder rekenmachine.

a) 25 = f) 144 =

b) ––100 = g) 0,25 =

c) 169 = h) ––6 400 =

d) ––1 = i) 0,81 =

e) ––625 = j) 0,04 =

9 Bereken met de rekenmachine op 0,001 nauwkeurig.

a) 5 ≈ f) 98741 ≈

b) ––3 ≈ g) ––158 ≈

c) 490 ≈ h) ––965 ≈

d) ––2 ≈ i) 147,2 ≈

e) 1 258 ≈ j) ––954,26 ≈

REEKS B

10 Bepaal zonder rekenmachine de twee gehele getallen waartussen het resultaat van de vierkantswortels ligt. Controleer achteraf het resultaat met de rekenmachine. ligt tussen de gehele getallen ... verklaring

a) 32 en

b) 250 en

c) ––12 en d) ––184 en

11 Bepaal de gevraagde lengten op 0,001 cm nauwkeurig.

a) de zijde van een vierkant waarvan de oppervlakte 278 cm2 bedraagt

c) de straal van een cirkel met een oppervlakte van 120 cm2

©VANIN

b) de rechthoekszijde van een gelijkbenige rechthoekige driehoek met een oppervlakte van 414 cm2

d) de diameter van een cirkel met een oppervlakte van 845 cm2

12 Los de vergelijkingen op.

a) x 2 – 25 = 0

x 2 = 25

x = –25 of x = 25

x = –5 of x = 5

De oplossingen –5 en 5 noteer je in de oplossingsverzameling V = {–5, 5}.

b) x 2 + 7 = 71

d) 5x 2 = 180

e) 3x 2 – 63 = 300

c) x 7 2 = 28

f) x 3 2 + 14 = 62

De Body Mass Index wordt ook wel eens de queteletindex genoemd, naar de Belgische wiskundige en astronoom Adolphe Quetelet (1796-1874).

Quetelet wordt beschouwd als een van de grondleggers van de moderne sociale statistiek, die zich bezighoudt met het organiseren van volkstellingen en het schetsen van de ‘modale’ mens. Hij was ook heel bedrijvig als sterrenkundige en is de stichter van de Sterrenwacht van Brussel, de voorloper van het Koninklijk Meteorologisch Instituut.

De Body Mass Index (BMI) van een persoon is het getal = 2 BMI m l

Daarbij is m de massa in kilogram en l de lengte in meter. De ‘ideale’ BMI ligt tussen 18,5 en 25. Wie minder dan 18,5 scoort, is te mager. Wie een BMI hoger dan 25 heeft, is te zwaar.

Een BMI hoger dan 30 levert het etiket ‘zwaarlijvig’ op.

13 Bepaal de lengte van een persoon aan de hand van de BMI en de massa van de persoon. Bepaal je antwoord op 0,01 m.

a) BMI = 24 m = 78 kg

b) BMI = 20 m = 60 kg

c) BMI = 28 m = 94 kg

d) BMI = 18 m = 50 kg

Een klassiek probleem van de oude Grieken: ‘Construeer een vierkant met dezelfde oppervlakte als een gegeven cirkel.’

Dat probleem is gekend als de kwadratuur van een cirkel.

Stel: r is de straal van de cirkel. x is de zijde van het vierkant.

Dan: x 2 =  ? r 2

14 Bereken de zijde van een vierkant dat dezelfde oppervlakte heeft als een cirkel met een straal van 5 cm. Bepaal je antwoord op 0,001 cm nauwkeurig.

2.3 De reële getallen

2.3.1 Getallen die je al kent

Definitie Natuurlijk getal

Een natuurlijk getal is een getal dat je verkrijgt bij het tellen van aantallen.

5 is een natuurlijk getal.

Notatie: 5 ∈ n

Lees: 5 is element van n

2.3.2 Uitbreiding getallen

Irrationale lengten

Geheel getal

Een geheel getal is een getal dat je verkrijgt bij het aftrekken van twee natuurlijke getallen.

−3 is een geheel getal.

Notatie: −3 ∈ z

Rationaal getal

Een rationaal getal is een getal dat je verkrijgt bij de deling van twee gehele getallen waarbij het tweede getal niet 0 is.

©VANIN

Lees: −3 is element van z 3 4 is een rationaal getal.

Notatie: 3 4 ∈ q

Lees: 3 4 is element van q

Om een tuinhek te verstevigen, plaats je vier diagonale balken. Bereken de lengte van een diagonale balk aan de hand van de afmetingen op de tekening.

Duid aan welk soort getal het resultaat voor de lengte van de diagonale balk zeker niet is.

❒ natuurlijk getal ❒ geheel getal ❒ rationaal getal

De rekenmachine is ontoereikend om na te gaan of het verkregen resultaat een rationaal getal voorstelt. Ook met de computer, die heel wat meer decimalen kan berekenen, kun je het einde van het getal niet ontdekken (decimaal getal?) en ook geen periode (decimale vorm?).

Irrationale getallen

Er bestaan getallen met oneindig veel cijfers na de komma en zonder periode

Die getallen kun je niet als breuk schrijven en het zijn bijgevolg geen rationale getallen. Je noemt ze irrationale getallen

Definitie Irrationaal getal

Een irrationaal getal is een getal met oneindig veel cijfers na de komma en zonder periode.

Voorbeelden

2 = 1,414 213 562 3...

0,123 456 789...

 = 3,141 592 653 589 793 238 46...

2.3.3 Rationale en irrationale vierkantswortels

rationale vierkantswortels irrationale vierkantswortels

• 121 = • 32 = • 1 4 = • 5 4 =

6,25 = • 10,02 =

Besluit

Een vierkantswortel van een rationaal getal heeft ofwel

• een rationaal getal als uitkomst.

Voorbeelden:

• een irrationaal getal als uitkomst.

Voorbeelden:

2.3.4

Reële getallen

De rationale en de irrationale getallen samen noem je de reële getallen

Definitie

Reëel getal

Een reëel getal is een getal dat rationaal of irrationaal is.

De verzameling van de reële getallen noteer je als r

GEOGEBRA

©VANIN

2 is een reëel getal. Notatie: 2 ∈ r Lees: 2 is element van r Plaats de getallen in het venndiagram.

7,25 37 –2,4 2,345… –7 0,22… –6 3 –12 3 1 3

Enkele bijzondere deelverzamelingen van r:

r0 : de reële getallen zonder 0

r+ : de positieve reële getallen

r - : de negatieve reële getallen

De irrationale getallen bevinden zich in r, maar niet in q:

2.3.5 Absolute waarde van een reëel getal

Definitie Absolute waarde

De absolute waarde van een reëel getal is gelijk aan het getal zonder toestandsteken (plus of min).

Voorbeelden: –3 = 0, 12345 = – =

2.3.6 Tegengestelde van een reëel getal

Definitie Tegengestelde

Het tegengestelde van een reëel getal is het reëel getal met dezelfde absolute waarde, maar met een verschillend toestandsteken.

Voorbeelden: –(–2 ) = –(+) = –(–1,246...) =

2.3.7 Omgekeerde van een reëel getal

Definitie Omgekeerde

©VANIN

Het omgekeerde van een reëel getal is gelijk aan 1 gedeeld door dat getal (verschillend van nul).

Voorbeelden: 1 2 –1 = ()–1 = (–17 )–1 =

Er bestaat een ‘wetenschap’ die zich bezighoudt met technieken om de cijfers van  te onthouden: de piphilologie.

Het bekendste geheugensteuntje komt van de schrijver en biochemicus Isaac Asimov (1920-1992):

'How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics!'

In die zin staat het aantal letters van elk woord voor de opeenvolgende cijfers van het getal  : 3,141 592 653 589 79. Wie liever een Nederlandstalig zinnetje onthoudt, kan volgens hetzelfde systeem de eerste dertien cijfers van het getal  onthouden: 'Ook u kunt u zeker vergissen, uw zwakke brein kan immer verkeerd beslissen.'

In 1897 werd in het parlement van de Amerikaanse staat Indiana een wet aangenomen waarin stond dat het getal  gelijkgesteld moest worden aan 3,2.

Edwin J. Goodwin, een amateurwiskundige, was de opsteller van die wet.

Naast een ‘praktische’ reden had Goodwin er ook financieel belang bij.

Door de ‘uitvinding’ van  = 3,2 kon hij een patent verkrijgen en zo royalty’s ontvangen. De wet werd nadien door de Senaat verworpen dankzij de toevallige aanwezigheid van een wiskundige: deze wees op de fouten die Goodwin gemaakt had om tot  = 3,2 te komen.

Oefeningen

REEKS B

15 Plaats de getallen in het venndiagram.

16 Noteer de passendste getallenverzameling. Kies uit n, z, q of r.

17 Zijn de gegeven getallen rationaal of irrationaal?

18 Duid met een vinkje aan tot welke verzameling(en) het gegeven getal behoort.

19 Is de zijde van het vierkant, waarvan de oppervlakte A gegeven is, een rationale of een irrationale lengte? Zet een vinkje. A (m2) zijde rationaal zijde irrationaal A (m2) zijde rationaal zijde irrationaal

20 Schrijf zonder absolutewaardeteken. a) –7 = c) –3 = e) 1– ,233 = b) 0,85 = d) – –3 7 = f) =

21 Schrijf zo eenvoudig mogelijk. a) –(–8) = c) –() = e) –(+1,455...)= b) –( 2 ) =

22 Bepaal het omgekeerde van de reële getallen. Schrijf je antwoord als een decimaal getal. Rond, indien nodig, af op 0,001 nauwkeurig. a) 4 7 –1 = c) ( 2 )–1 = e) 1,33...–1 = b) (–2)–1 = d) –1 4 –1

2.4 Irrationale getallen benaderen

2.4.1 Inleiding

Bereken 5

Rond af op het gegeven aantal decimalen. Controleer de afgeronde waarde aan de hand van de definitie van een vierkantswortel.

Een irrationaal getal kan nooit exact worden geschreven als decimale vorm. De decimale vorm is enkel een benaderde waarde van dat irrationaal getal.

2.4.2 Afronden

Het afronden van een irrationaal getal gebeurt in functie van de toepassing.

Voorbeeld

2.4.3

Wortelvormen

©VANIN

Koenraad berekent de lengte van het diagonale tussenschot van de afgebeelde tuinomheining. Hij zal de berekende waarde controleren door de meting uit te voeren met een vouwmeter.

Omdat je een irrationale vierkantswortel toch niet exact kunt weergeven door een decimale vorm, kun je als eindresultaat van een opgave de vierkantswortel of een veelvoud ervan noteren.

Definitie Wortelvorm

Een wortelvorm is een product van een irrationale vierkantswortel en een rationaal getal.

Opmerking

• Bij een wortelvorm noteer je het rationaal gedeelte altijd vooraan.

• Bij een wortelvorm mag je het vermenigvuldigingsteken weglaten.

Voorbeelden

3 2 , –7 145 , 1 3 15 ,

Benaderingen van  op 2 decimalen nauwkeurig op 6 decimalen nauwkeurig op 20 decimalen nauwkeurig

2.4.4 Irrationale getallen benaderen met intervallen

Interval

Tijdens een stralende zomerdag rust Fatima tussen 14h en 14h30 op een bank in het park. De tijd tussen 14h en 14h30 noem je een tijdsinterval

Interval in r

Definitie Interval in r

Een interval in r is een ononderbroken verzameling van reële getallen.

Soorten intervallen

Irrationale getallen benaderen

Je kunt een irrationaal getal benaderen door aan te duiden tot welk interval, begrensd door twee rationale getallen, dat irrationaal getal behoort.

Opmerkingen

• Het aantal decimalen van de grenzen van het interval bepaalt de breedte van het interval.

• Om irrationale getallen te benaderen, gebruik je open intervallen.

Voorbeeld

35 ≈ 5,916 079 783

Oefeningen

REEKS B

23 Schrijf de gegeven uitdrukkingen als een wortelvorm.

a) 32 = f) –33(–14) = b) 17 0,5 = g) (– 4) 2,7 3 =

c) –2 8 = h) –0,12 (–12,8 ) =

d) 1 7 (– 4) = i) 1 8 –5 7 = e) –3 4 7 = j) –12 15 –3 8 –1 =

24 Bereken de schuine zijde van de rechthoekige driehoek bij het huisnummer 4. Rond af naargelang het gebruikte meettoestel voor de controlemeting.

2,6 cm

3,2 cm

©VANIN

afronding voor de controlemeting: meettoestel afronding

meetlat op 1 mm

schuifmaat op 0,02 mm

25 Een ring heeft een omtrek van 20 cm. Bereken de diameter van de ring. Rond af naargelang het gebruikte meettoestel voor de controlemeting.

afronding voor de controlemeting: meettoestel afronding

meetlat op 1 mm

schuifmaat op 0,02 mm

omschrijving

a) 3 ⩽ x ⩽ 11

b) –4 < x < 8

c) –1,5 ⩽ x < –0,75

d)

e)

intervalnotatie soort interval

]4 , 16[

[1,7 ; 8,5]

f) – 3 ,

©VANIN

27 In welk open interval met gegeven breedte liggen de volgende irrationale getallen?

irrationaal getal

intervalbreedte interval

a) 7,123 456... 0,1

b) 8 0,01

c) 21 – 1

d) 148 10

e) −4,010 020 003... 0,000 1 f) 1214 – 0,001

REEKS C

28 Bereken de opening van de steeksleutel die je moet gebruiken om de moer los te draaien. 7,5 mm

2.5 Reële getallen ordenen

2.5.1 Inleiding

Symbolen

Voorbeelden

2.5.2

Abscis van een punt op de getallenas

De reële getallen kun je voorstellen op een rechte, die je de reële rechte noemt.

Je doorloopt die rechte van links naar rechts.

Dat noem je de oriëntering van de getallenas en stel je voor met een pijl naar rechts.

Hoe meer je naar rechts gaat, hoe groter de getallen worden.

Op de getallenas kies je twee willekeurige punten, die je de waarde 0 en 1 geeft. Dat noem je de ijk

De afstand tussen die punten is niet noodzakelijk 1 cm.

Als je die ijk verder naar rechts afpast, vind je de volgende natuurlijke getallen.

Plaats de gegeven reële getallen bij de correcte stip op de getallenas.

Definitie Abscis van een punt

De abscis van een punt van de getallenas is het reëel getal dat overeenkomt met dat punt van de getallenas.

Notatie: ab(A) = 0,5 0 1 0,5

Met de rationale getallen kun je nog niet aan elk punt van de getallenas een abscis toekennen. Met de irrationale getallen erbij is dat wel mogelijk.

Besluit Elk punt van de getallenas komt overeen met één reëel getal. Elk reëel getal komt overeen met één punt van de getallenas.

2.5.3 Intervallen voorstellen op een getallenas

Voor het voorstellen van intervallen op een getallenas gelden de volgende richtlijnen:

• De breedte van het interval wordt voorgesteld met een groene of een vetgedrukte lijn.

• De grenzen van het interval worden voorgesteld met een stip: gesloten ● of ● open ● of

• Bijzondere intervallen:

[–1, +∞[ +∞: plus oneindig ]–∞, 2[ −∞: min oneindig

Opmerking

Het interval is altijd open bij –∞ en +∞.

3]

2[

[–2, 0[

[–2, 0[

+ ∞[

∞, 2[

2.5.4 Irrationale getallen voorstellen op een getallenas

Door een natuurlijk getal n te schrijven als een som van kwadraten, kun je n met een aantal rechthoekige driehoeken exact construeren.

1

Stap 1: Schrijf het getal n als een som van een kwadraat van een natuurlijk getal en een tweede natuurlijk getal.

Neem het kwadraat dat het dichtst bij het getal n ligt en kleiner is dan het getal n

Stap 2: Splits dat tweede getal als een som van een kwadraat van een natuurlijk getal en een derde natuurlijk getal.

Stap 3: Doe dat verder tot alle termen kwadraten van een natuurlijk getal zijn.

Stap 4: Teken de nodige rechthoekige driehoeken.

Stap 5: Pas de verkregen lengte n af en plaats het irrationaal getal op de getallenas.

Voorbeeld

Construeer een lijnstuk met een lengte gelijk aan 27 en stel voor op de getallenas.

REEKS B

29 Vul in met <, > of =.

30 Benoem de punten van de getallenas aan de hand van de gegeven abscis.

A) = 2

B) = −1,5

C) = –3

31 Bepaal de abscis van de benoemde punten van de getallenas.

33 Noteer als een interval.

35 n werd met een aantal rechthoekige driehoeken geconstrueerd. Bepaal n.

36 Stel de irrationale getallen voor op de getallenas. Maak daarvoor de nodige constructies met rechthoekige driehoeken.

a) 8 c) –15 8 = 15 =

©VANIN

b) –22 d) 33

37 Construeer een lijnstuk van 38 cm op twee verschillende manieren met twee rechthoekige driehoeken.

38 = 38 = = = = =

38 Verbind je de middens van de zijden van een vierkant, dan verkrijg je een vierkant zoals het groene vierkant op de tekening. De oppervlakte van het grote vierkant bedraagt 4 m2. Bereken de zijde van het kleine vierkant. Bepaal je antwoord op 0,001 m nauwkeurig.

STUDIEWIJZER De reële getallen

2.1 Decimale voorstelling van rationale getallen voor de leerling

KUNNEN

Decimale getallen, zuiver repeterende en gemengd repeterende decimale vormen van elkaar onderscheiden.

De periode en het niet-repeterend deel van een decimale vorm aanduiden.

Decimale schrijfwijze omzetten naar breuk.

Breuk omzetten naar decimale schrijfwijze.

©VANIN

2.2 Vierkantswortels

KENNEN

Een vierkantswortel van een positief getal is een getal waarvan het kwadraat gelijk is aan dat positief getal.

KUNNEN

De vierkantswortels van een positief getal berekenen.

2.3 De reële getallen

KENNEN

Een irrationaal getal is een getal met oneindig veel cijfers na de komma en zonder periode.

Een reëel getal is een getal dat rationaal of irrationaal is.

De absolute waarde van een reëel getal is dat getal zonder toestandsteken.

Het tegengestelde van een reëel getal is het reëel getal met dezelfde absolute waarde, maar met een verschillend toestandsteken.

Het omgekeerde van een reëel getal is 1 gedeeld door dat reëel getal.

Getallen voorstellen in een venndiagram.

KUNNEN

De absolute waarde van een reëel getal bepalen.

Het tegengestelde van een reëel getal bepalen.

Het omgekeerde van een reëel getal bepalen.

2.4 Irrationale getallen benaderen

KENNEN

Een wortelvorm is een product van een irrationale vierkantswortel en een rationaal getal.

Een interval in r is een verzameling van opeenvolgende reële getallen.

Werken met intervallen.

KUNNEN

Irrationale getallen afronden in betekenisvolle situaties.

Irrationale getallen benaderen met intervallen.

2.5 Reële getallen ordenen

KENNEN

Een abscis van een punt op de getallenas is het reëel getal dat overeenkomt met dat punt van de getallenas.

Reële getallen ordenen.

KUNNEN

Irrationale lengten tekenen met behulp van de stelling van Pythagoras.

Reële getallen voorstellen op een getallenas.

De invoering van de verzameling van de reële getallen uitleggen als een vervollediging van de getallenas.

De abscis van een punt op de getallenas bepalen.

Intervallen voorstellen op een getallenas.

©VANIN

Pienter problemen oplossen

Welke heuristiek(en) gebruik je om de onderstaande problemen op te lossen?

❑ concreet materiaal

❑ schets

❑ schema/tabel

❑ vereenvoudig

❑ gok verstandig

Als gelijke afbeeldingen eenzelfde getal voorstellen, welke waarde moet dan onder de vierde kolom staan?

❑ filter

❑ patroon

❑ kennis

❑ logisch nadenken

❑

©VANIN

HOOFDSTUK 3 I DRIEHOEKSMETING VAN EEN

RECHTHOEKIGE DRIEHOEK

©VANIN

3.1 Goniometrische getallen van een scherpe hoek 82

3.2 Rechthoekige driehoeken oplossen 105

Studiewijzer 123

Problemen uit JWO 124

3.1 Goniometrische getallen van een scherpe hoek

3.1.1 Hellingen

Tijdens een fietstocht ziet Wouter een verkeersbord dat een helling van 20 % aangeeft.

GEOGEBRA

Deel telkens het hoogteverschil door de horizontale verplaatsing.

horizontale verplaatsing | AC | = 50 mm | AE | = 70 mm | AG | = 100 mm

hoogteverschil | BC | = 10 mm | DE | = 14 mm | FG | = 20 mm

hoogteverschil horizontale verplaatsing

Wat stel je vast?

De verhouding van het hoogteverschil en de horizontale verplaatsing noem je het hellingsgetal

In het voorbeeld is het hellingsgetal

Het hellingsgetal is de decimale schrijfwijze van het hellingspercentage

In het voorbeeld is het hellingspercentage

Hellingsgetal en hellingspercentage zijn typisch voor een hellingshoek. Als de hellingshoek verandert, veranderen het hellingsgetal en het hellingspercentage.

In de praktijk is het niet zo gemakkelijk om de horizontale verplaatsing en het hoogteverschil te meten. In de landmeetkunde heeft men een speciaal meetinstrument om hellingshoeken te meten: een theodoliet.

Oefeningen

REEKS A

1 Bereken het hellingsgetal.

hoogteverschil horizontale verplaatsing hellingsgetal

2 Bereken het hellingspercentage.

hoogteverschil horizontale verplaatsing hellingspercentage

REEKS B

3 Tijdens een beklimming overwint een fietser een hoogteverschil van 200 m bij een horizontale verplaatsing van 2,5 km.

Bereken het hellingsgetal van de helling die de fietser beklommen heeft.

Antwoord:

4 Jan overwint een hoogteverschil van 30 m bij een horizontale verplaatsing van 400 m. Bereken het hellingspercentage op 0,1 % nauwkeurig.

Antwoord:

3.1.2 Benamingen in een rechthoekige driehoek

Algemeen

Een rechthoekige driehoek heeft twee rechthoekszijden en een schuine zijde. Afhankelijk van de scherpe hoek kun je de rechthoekszijden een specifiekere naam geven.

• De aanliggende rechthoekszijde van een scherpe hoek in een rechthoekige driehoek is de rechthoekszijde die aan de gegeven scherpe hoek ligt.

• De overstaande rechthoekszijde van een scherpe hoek in een rechthoekige driehoek is de rechthoekszijde die tegenover de gegeven scherpe hoek ligt.

©VANIN

Voorbeelden

aanliggende rechthoekszijde van a : [AC ] aanliggende rechthoekszijde van a : overstaande rechthoekszijde van a : [BC ] overstaande rechthoekszijde van a :

aanliggende rechthoekszijde van b : aanliggende rechthoekszijde van b : overstaande rechthoekszijde van b : overstaande rechthoekszijde van b :

Opmerking

In driehoek ABC noem je

| AB | = c de lengte van de schuine zijde (sz) of hypothenusa;

| BC | = a de lengte van de aanliggende rechthoekszijde (arz) van b;

| CA | = b de lengte van de overstaande rechthoekszijde (orz) van b;

| AC | = b de lengte van de aanliggende rechthoekszijde (arz) van a;

| CB | = a de lengte van de overstaande rechthoekszijde (orz) van a.

In wat volgt gebruik je ook de termen schuine zijde, aanliggende rechthoekszijde en overstaande rechthoekszijde als je de lengte van die zijde bedoelt.

REEKS A

5 Vul in.

©VANIN

n KAT n MOL n VIS n REU schuine zijde

aanliggende rechthoekszijde van a overstaande rechthoekszijde van a aanliggende rechthoekszijde van b overstaande rechthoekszijde van b

6 Juist of fout?

a) [AB] is de aanliggende rechthoekszijde van a in n ABC

b) [CD] is de overstaande rechthoekszijde van b in n BCD.

c) [BC] is de schuine zijde in n BCD

d) [CD] is de overstaande rechthoekszijde van a in n ABC

e) [BD] is de aanliggende rechthoekszijde van b in n BCD

f) [AC] is de aanliggende rechthoekszijde van a in n ABC

g) [AC] is de schuine zijde in n ABC

h) [AD] is de aanliggende rechthoekszijde van a in n ACD.

i) [AC] is de overstaande rechthoekszijde van b in n ABC

j) [AB] is de schuine zijde in n ABC

7 In welke driehoek geldt de uitspraak?

1 2 3 1 3 2 uitspraak geldt in driehoek

a) [HE] is de aanliggende rechthoekszijde van ^ H3

b) [AL] is de overstaande rechthoekszijde van ^ H2

c) [CL] is de schuine zijde.

d) [LE] is de aanliggende rechthoekszijde van ^ L2

e) [LH] is de overstaande rechthoekszijde van ^ C

f) [CH] is de overstaande rechthoekszijde van ^ L3

g) [NL] is de schuine zijde.

h) [AH] is de aanliggende rechthoekszijde van ^ H2

i) [NL] is de aanliggende rechthoekszijde van ^ N

j) [HL] is de overstaande rechthoekszijde van ^ N

3.1.3 Verhoudingen in rechthoekige driehoeken

Bij een constante hellingshoek is de verhouding van het hoogteverschil en de horizontale verplaatsing constant. Onderzoek de andere verhoudingen.

GEOGEBRA

Vul de tabel verder in. Rond af op 0,1. sz (mm) arz van a (mm)

n ABC 51 26 44 n DEF 38 19 33 n GHI 83 42 72

Wat stel je vast?

3.1.4 Definities

De verhoudingen van de lengten van de zijden in een rechthoekige driehoek zijn afhankelijk van de scherpe hoek. Je noemt die verhoudingen goniometrische getallen van de scherpe hoek.

Definitie Sinus Cosinus Tangens

De sinus (sin) van een scherpe hoek in een rechthoekige driehoek is de verhouding overstaande rechthoekszijde schuinezijde

De cosinus (cos) van een scherpe hoek in een rechthoekige driehoek is de verhouding aanliggenderechthoekszijde schuinezijde

©VANIN

De tangens (tan) van een scherpe hoek in een rechthoekige driehoek is de verhouding overstaanderechthoekszijde aanliggenderechthoekszijde

Voorbeelden

sos cas toa is een ezelsbruggetje om de definities van sinus, cosinus en tangens van een scherpe hoek te onthouden.

= verstaande chuine s o s

anliggende

Opmerkingen

• In een rechthoekige driehoek is zowel de sinus als de cosinus van een scherpe hoek altijd kleiner dan 1, omdat de schuine zijde de langste zijde is, en dus de noemer altijd groter is dan de teller.

Hoe groter de scherpe hoek, hoe de sinus.

Hoe groter de scherpe hoek, hoe de cosinus.

©VANIN

Hoe groter de scherpe hoek, hoe de tangens

• In een rechthoekige driehoek is de sinus van de ene scherpe hoek gelijk aan de cosinus van de andere scherpe hoek (zijn complement).

sin a = BC AB = cos b

sin b = AC AB = cos a

Het woord sinus is Latijn en betekent ‘gebogen, kromme lijn’. De oudste bekende bron waarin men het heeft over de sinus van een hoek, is een Indisch boek uit de 5e eeuw.

Oorspronkelijk werd de sinus gebruikt als de lengte van een koorde in een cirkel. Leonard Euler (18e eeuw) gebruikte voor het eerst de sinus als verhouding.

De cosinus kwam er om de sinus van de complementaire hoek te berekenen. Edmund Gunter bedacht het woord ‘co-sinus’, dat al vlug vereenvoudigd werd tot ‘cosinus’ door John Newton rond 1660.

Tegen 1675 had Jonas Moore het al afgekort tot ‘cos’.

‘Tangens’ komt van het Latijnse tangere, dat ‘raken’ betekent. Het woord is een idee van de Deense wiskundige Thomas Fincke en werd door hem voor het eerst gebruikt rond 1583.

Andere goniometrische getallen zijn:

Leonard Euler (1707-1783)

3.1.5 Goniometrische getallen van een scherpe hoek berekenen

Zestigdelige graad: onderverdelingen

Hoeken worden uitgedrukt in zestigdelige graden.

GEOGEBRA

Voor nauwkeurigere bepalingen van de hoekgrootte kun je de graad onderverdelen in minuten () en seconden (). Die onderverdeling is gebaseerd op het zestigdelige talstelsel:

Voor de oorsprong van de zestigdelige onderverdeling moet je terug naar de Babylonische tijd, rond 2000 voor Christus.

De Babyloniërs kozen het grondtal zestig omdat het een groot aantal natuurlijke delers heeft, namelijk 12.

Hierdoor kunnen getallen in het zestigtallig stelsel gemakkelijk worden gedeeld in kleinere, gelijkwaardige delen.

Zo kan een graad gemakkelijk worden gedeeld in delen van 30 minuten, 15 minuten, 12 minuten, 10 minuten … Voor de Babyloniërs bestond een jaar uit 360 dagen.

©VANIN

Dankzij de Bruggeling Simon Stevin en zijn werk ‘De Thiende’, in 1585 uitgegeven, gebruiken wij nu het tientallig of decimaal talstelsel. Het zestigtallig talstelsel wordt enkel nog gebruikt voor tijdmeting en hoekmeting.

Goniometrische getallen berekenen met ICT

Met een wetenschappelijke rekenmachine kan je de sinus, de cosinus en de tangens van een scherpe hoek berekenen.

Voorbeelden

Bereken de goniometrische getallen. Rond af op 0,001. • sin 82º

• cos 76º

• tan 43º

cos 38º47

• tan 29º46

GEOGEBRA

REEKS A

8 Vul in.

©VANIN

10 Bereken op 0,001 nauwkeurig.

a) sin 35º ≈ f) tan 80º ≈

b) cos 55º ≈ g) sin 39º ≈

c) tan 62º ≈ h) tan 10º ≈

d) sin 48º ≈ i) cos 82º ≈

e) cos 32º ≈

REEKS B

j) sin 86º ≈

11 Welk goniometrisch getal gebruik je om de onbekende zijde x te berekenen?

a)

x

B 13

©VANIN

Bereken de zijde x op 0,01 nauwkeurig.

14 Bereken op 0,001 nauwkeurig.

a) sin 6º 8 51 ≈

h) cos 14º 58 36 ≈

b) cos 28º 54 22 ≈ i) tan 59º 47 ≈

c) tan 29º 52 38 ≈

j) sin 4 ≈

d) sin 27º 29 ≈ k) sin 89º 57 12 ≈

e) tan 46º 48 ≈ l) tan 58º 38 ≈

f) cos 75º 9 ≈

g) tan 5º 32 55 ≈

©VANIN

m) cos 84º 58 29 ≈

n) sin 79º 52 37 ≈

REEKS C

15 Teken de hoek a.

a) sin a = 3 4

c) cos a = 2 5

b) tan a = 5 15

d) tan a = 3 2

3.1.6 Basiseigenschappen

Verband tussen tangens, sinus en cosinus

Bereken op 0,001 nauwkeurig.

sin 43º ≈ sin43º cos43º ≈ en tan 43º ≈

cos 43º ≈

Wat stel je vast?

Eigenschap = a a a tan sin cos

tekening 16 gegeven

©VANIN

rechthoekige driehoek ABC met ^ C = 90º te bewijzen

tan a = sin cos a a

bewijs

sin a = a c en cos a = b c

⇓ delen van sin a door cos a sin a cos a = a c b c

⇓ rekenen met reële getallen sin a cos a = a c ? c b

⇓ vereenvoudigen

sin a cos a = a b

⇓ definitie tangens

sin a cos a = tan a

besluit

tan a = sin cos a a

De grondformule

Bereken zonder tussendoor af te ronden: (sin 43º)2 + (cos 43º)2 =

Opmerking

(sin a)2 noteer je ook als sin2 a. Analoog voor (cos a)2 en (tan a)2

sin2 25º 47 38 + cos2 25º 47 38 =

Wat stel je vast?

Eigenschap

©VANIN

sin2 a + cos2 a = 1

Die eigenschap noem je de grondformule van de goniometrie.

Opmerking

• sin2 a = 1 - cos2 a ⇒ sin a = 1 - cos2 a

• cos2 a = 1 - sin2 a ⇒ cos a = 1 - sin2 a

tekening gegeven

A CB a b c rechthoekige driehoek ABC met ^ C = 90º

bewijs

te bewijzen

sin2 a + cos2 a = 1

sin a = a c en cos a = b c ⇓

sin2 a + cos2 a = a c 2 + b c 2

⇓ rekenen met reële getallen

sin2 a + cos2 a = a 2 + b 2 c 2

⇓ stelling van Pythagoras

sin2 a + cos2 a = 2 2 c c = 1

besluit

sin2 a + cos2 a = 1

Oefeningen

REEKS A

17 Vul in zonder a te berekenen.

Bepaal je antwoord op 0,001 nauwkeurig.

©VANIN

18 De toets sin van de rekenmachine van Olivia is stuk. Help Olivia om sin 72º te bepalen. Rond af op 0,01 nauwkeurig.

19 Vink de juiste beweringen aan.

REEKS B

20 Vul in zonder a te berekenen. Bepaal je antwoord op 0,01 nauwkeurig.

©VANIN

21 De toetsen cos en tan van de rekenmachine van Joran zijn stuk. Help Joran om cos 33° en tan 33° te bepalen. Rond af op 0,01 nauwkeurig.

REEKS C

22 Waarom is de bewering sin a = 3 4 ⇒ cos a = 1 4 fout?

Goniometrische getallen van een aantal bijzondere hoeken

3.1.7 Een hoek berekenen uit een goniometrisch getal

Bij sin a, cos a en tan a start je vanuit een hoek en verkrijg je een onbenoemd getal. Bij de omgekeerde (inverse) bewerkingen start je vanuit een onbenoemd getal en verkrijg je een hoekgrootte.

Om een hoek te berekenen uit een goniometrisch getal gebruik je ICT. Deze bewerkingen worden op een wetenschappelijke rekenmachine aangeduid met sin-1, cos-1 en tan-1

Voorbeelden

• sin a = 0,75 ⇒ a =

• cos a = 0,3 ⇒ a = • tan a = 2,64 ⇒ a =

GEOGEBRA

Oefeningen

REEKS A

23 Bereken de hoek a

a) sin a = 0,4 a = f) sin a = 0,15 a =

b) cos a = 0,3 a =

c) tan a = 0,2 a =

d) cos a = 3 8 a =

g) cos a = 0,82 a =

h) tan a = 2,74 a =

i) sin a = 2 5 a =

e) tan a = 5 9 a = j) sin a = 1 2 a =

REEKS B

24 Welk goniometrisch getal gebruik je om de hoek a te berekenen?

Antwoord: Antwoord:

Antwoord: Antwoord:

Antwoord: Antwoord:

Het licht plant zich rechtlijnig voort, zolang het in eenzelfde stof blijft. Bij overgang van de ene naar de andere stof buigt de lichtstraal af. Er treedt breking op aan het grensoppervlak van de twee stoffen.

De stralen gaan in een andere richting verder.

De mate waarin een lichtstraal gebroken (afgebogen) wordt, is afhankelijk van de aard van de stof.

Een dichte stof heeft een grote brekingsindex, een ijle stof een kleine.

Bij de overgang van een lichtstraal van stof A naar stof B geldt

©VANIN

waarbij: ^ i = de invalshoek ^ r = de brekingshoek

nA = de brekingsindex van stof A

nB = de brekingsindex van stof B

Die wet staat bekend als de wet van Snellius, naar de Nederlandse wiskundige Willebrord Snell.

Enkele voorbeelden

26 Vul de tabel aan. Bepaal ^ r.

Stel de brekingsindex van lucht gelijk aan 1. ^ i overgang van ... berekeningen ^ r

a) 10º lucht naar water

b) 15º lucht naar glas

c) 20º glas naar diamant

stof A stof B

3.2 Rechthoekige driehoeken oplossen

3.2.1

Inleiding

In een rechthoekige driehoek zijn er zes kenmerkende gegevens:

• de grootte van de drie hoeken (waarvan één hoek 90º is),

• de lengte van de drie zijden.

Omdat je hier alleen met rechthoekige driehoeken werkt, is de rechte hoek altijd gegeven.

Onderzoek welke gegevens nodig zijn om een rechthoekige driehoek volledig te bepalen.

In welke gevallen is het mogelijk om één welbepaalde driehoek te tekenen? Vink aan.

gegeven mogelijk niet mogelijk

a) de rechte hoek en een scherpe hoek

b) de rechte hoek en de schuine zijde

c) de rechte hoek en een rechthoekszijde

d) de rechte hoek en de twee scherpe hoeken

e) de rechte hoek en de beide rechthoekszijden

f) de rechte hoek, een scherpe hoek en de schuine zijde

g) de rechte hoek, een scherpe hoek en een rechthoekszijde

h) de rechte hoek, een rechthoekszijde en de schuine zijde

Hoeveel van de zes kenmerkende gegevens zijn minimaal nodig?

Eigenschap Een rechthoekige driehoek is volledig bepaald door:

©VANIN

In die gevallen kun je de overige elementen van de rechthoekige driehoek berekenen. Dat heet een rechthoekige driehoek oplossen. Daarvoor gebruik je: de som van de scherpe hoeken in een rechthoekige driehoek de stelling van Pythagoras de definities van goniometrische getallen

3.2.2 Rechthoekige driehoeken oplossen

Bij het oplossen van rechthoekige driehoeken gebruik je de volgende formules.

som van de scherpe hoeken

stelling van Pythagoras

©VANIN

Opmerking

Gebruik bij het oplossen van rechthoekige driehoeken bij voorkeur de gegevens, het liefst geen berekende waarde en nooit een afgeronde waarde.

Geval 1: de rechte hoek, een scherpe hoek en de schuine zijde zijn gegeven figuur gegeven oplossing

gevraagd

Geval 2: de rechte hoek, een scherpe hoek en een rechthoekszijde zijn gegeven

figuur gegeven

Geval 3: de rechte hoek, de schuine zijde en een rechthoekszijde zijn gegeven

figuur gegeven oplossing

gevraagd

Geval 4: de rechte hoek en twee rechthoekszijden zijn gegeven

figuur gegeven

gevraagd

b = 4 2,5

= 58º (57º 59 41)

Oefeningen

REEKS A

27 Bereken het gevraagde in de rechthoekige driehoek ABC Rond, indien nodig, de zijden af op 0,1 nauwkeurig.

REEKS B

28 Bereken de ontbrekende elementen van de rechthoekige driehoek ABC. Rond, indien nodig, de zijden af op 0,1 nauwkeurig.

29 Bereken de ontbrekende elementen van de rechthoekige driehoek ABC. Rond de hoeken af op 1º en de zijden op 0,01.

c) a = | AB | ≈

b = 34º | BC | = 20,08 | AC | ≈

©VANIN

a) a = | AB | ≈

b = | BC | = 3,40 | AC | = 6,50

d) a = | AB | = 265,92 b = | BC | = 159,40 | AC | ≈

b) a = 54º | AB | = 8,90 b = | BC | ≈ | AC | ≈

e) a = | AB | ≈ b = 21º | BC | ≈ | AC | = 41,23

30 Bereken de ontbrekende elementen van de rechthoekige driehoek. Rond de hoeken af op 1  en de zijden op 0,01 cm.

a) A ^ = 90º

C ^ = 23º 45 29

| BC | = 46,00

c) C ^ = 90º

| AB | = 8,45

| BC | = 5,10

©VANIN

b) B ^ = 90º

A ^ = 61º 52 14

| AC | = 4,00

d) A ^ = 90º

| AC | = 6,50 | AB | = 7,25

31 Los de vraagstukken op. Rond de afstanden af op 1 cm nauwkeurig.

a) Een boom heeft een schaduw van 12 m.

De zon schijnt onder een hoek van 43º.

Hoe hoog is de boom?

c) Vanaf de top van een torentje wordt een kabel tot op de grond gespannen. Welke hoek maakt de kabel met de grond? 12

25 m 12,6 m

Antwoord:

b) Van een skateramp zijn de lengte van de ramp en de lengte van de constructie gegeven.

Bereken de hellingshoek van die ramp.

Antwoord:

Antwoord:

d) Een ladder steunt tegen een muur op een hoogte van 4,3 m. Op de grond maakt de ladder een hoek van 70º.

Bereken de lengte van de ladder.

Antwoord:

m 43°

4,6 m

6,1 m

4,3 m

70°

32 Los de vraagstukken op. Rond de afstanden af op 1 cm nauwkeurig. Maak telkens eerst een schets.

a) De zon schijnt onder een hoek van 35º op een man van 1,80 m groot. Hoe lang is de schaduw van die man?

c) Tijdens een beklimming moet je 2 400 m fietsen om een hoogteverschil van 700 m te overbruggen. Wat is de hellingshoek?

Antwoord:

b) Een kabelbaan maakt een helling van 35º en overbrugt een hoogteverschil van 1 300 m. Hoe lang is die kabelbaan?

Antwoord:

d) Een vliegertouw is 50 m lang. Hoe hoog bevindt de vlieger zich, als het touw volledig ontrold is en een hoek van 30º met de grond maakt?

Antwoord:

Antwoord:

33 Om de afstand tussen de oevers van een kanaal te berekenen, werden de volgende metingen uitgevoerd. Bereken de afstand op 0,01 m nauwkeurig.

©VANIN

Antwoord:

34 Studies wijzen uit dat een ladder die een hoek van 75º maakt met de grond, het veiligst staat. Een bedrijf dat ramen van hoge gebouwen wast, heeft een nieuw stel schuifladders van 8 m lang aangekocht. Hoe ver moet de onderkant van de ladder van het gebouw verwijderd zijn opdat de ladder het veiligst zou staan? Bepaal je antwoord op 0,01 m nauwkeurig.

Antwoord:

35 Bereken de ontbrekende elementen van de dakconstructie op 1 cm nauwkeurig.

40° x m h m x m 8,30 m

Antwoord:

36 Bereken de hoek a

gegeven

een balk met l = 4 cm, b = 2 cm en h = 12 cm gevraagd de hoek a oplossing

©VANIN

antwoord

De hoek a is

37 Bereken op 0,01 cm2 nauwkeurig. Maak telkens eerst een schets.

a) Bereken de oppervlakte van een vierkant waarvan de diagonalen 12 cm lang zijn.

Antwoord:

b) Bereken de oppervlakte van een ruit met zijden van 24 cm en een stompe hoek van 116º.

c) Bereken de oppervlakte van een parallellogram met zijden 6 cm en 4 cm en een scherpe hoek van 25º.

©VANIN

Antwoord:

d) Bereken de oppervlakte van een gelijkzijdige driehoek met zijden van 13 cm.

Antwoord:

Antwoord:

38 Boven op een gebouw staat een vlaggenmast. Als je op 100 m afstand staat, zie je de top van het gebouw onder een hoek van 21 º en de top van de vlaggenmast onder een hoek van 23 º. Hoe lang is die vlaggenmast op 1 cm nauwkeurig?

Antwoord:

39 Bereken de oppervlakte, op 0,01 cm2 nauwkeurig, van een rechthoek met diagonalen van 17 cm die elkaar onder een hoek van 36º snijden.

Antwoord:

3.2.3 Toepassingen in de ruimte

Modeloefening 1

gegeven

een kubus met ribbe 4 cm gevraagd

Bereken a op 1  nauwkeurig. oplossing

Modeloefening 2

antwoord

De hoek a is

gegeven

een piramide met vierkant grondvlak en ribben van 4 cm gevraagd

Bereken de hellingshoek a op 1  nauwkeurig. oplossing

antwoord

De hellingshoek a is

Oefeningen

REEKS A

40 Bereken de omtrek van n BGE op 0,01 cm nauwkeurig.

gegeven

een balk met l = 5 cm, b = 2 cm en h = 7 cm gevraagd de omtrek van n BGE oplossing

41 Bereken de hoek b op 1  nauwkeurig.

antwoord

De omtrek van n BGE is

gegeven

een balk met l = 3 cm, b = 2 cm en h = 6 cm gevraagd de hoek b oplossing

©VANIN

antwoord De hoek b is

B

42 Bereken de hellingshoek a op 1  nauwkeurig.

gegeven

een piramide met vierkant grondvlak met z = 3 cm en h = 5 cm gevraagd

de hellingshoek a oplossing

antwoord

De hellingshoek a is

43 Een piramide heeft een gelijkzijdige driehoek met zijde 3 m als grondvlak, opstaande ribben van 4 m en een hellingshoek van 65º. Bereken, op 1 cm nauwkeurig, de hoogte van de piramide.

Antwoord:

44 Een kegel heeft een cirkel met diameter 3 m als grondvlak en een hoogte van 5 m. Bereken, op 1  nauwkeurig, de hellingshoek van de kegel.

Antwoord:

©VANIN

45 Pientere Bizon, een indiaan van 1,76 m groot, wil een nieuwe tipi opzetten. Hij vond enkele mooie rechte boomstammen van 2,50 m en sjort ze op 50 cm van de top samen. Wat is de minimale hoek met de grond waaronder hij de stammen moet zetten opdat hij rechtop zou kunnen staan in zijn tent? Bepaal je antwoord op 1  nauwkeurig.

Antwoord:

REEKS C

46 Je plaatst een potlood van 20 cm diagonaal in een cilindervormige houder met een hoogte van 12 cm en een straal van 4 cm.

Hoe ver steekt het boven de rand uit? Onder welke hoek staat het?

Bepaal de hoek op 1  nauwkeurig en de lengte op 0,01 cm nauwkeurig.

Antwoord:

47 Bereken de hoek a op 1  nauwkeurig.

©VANIN

gegeven een balk met l = 3 cm, b = 3 cm en h = 6 cm gevraagd de hoek a oplossing

antwoord De hoek a is

STUDIEWIJZER Driehoeksmeting van een rechthoekige driehoek

3.1 Goniometrische getallen van een scherpe hoek

De sinus (sin) van een scherpe hoek in een rechthoekige driehoek is de verhouding overstaande rechthoekszijde schuinezijde

De cosinus (cos) van een scherpe hoek in een rechthoekige driehoek is de verhouding aanliggenderechthoekszijde schuinezijde

De tangens (tan) van een scherpe hoek in een rechthoekige driehoek is de verhouding overstaande rechthoekszijde aanliggenderechthoekszijde

tan a = sin cos a a

sin2 a + cos2 a = 1 KUNNEN

De sinus, cosinus en tangens van een scherpe hoek berekenen met ICT.

De formules gebruiken om goniometrische getallen te berekenen. Met ICT een hoek berekenen waarvan een goniometrisch getal gegeven is.

3.2 Rechthoekige driehoeken oplossen

Een rechthoekige driehoek is volledig bepaald door:

• twee zijden en de rechte hoek,

• één zijde, één scherpe hoek en de rechte hoek.

©VANIN

KUNNEN

Ontbrekende elementen in een rechthoekige driehoek berekenen met behulp van de sinus, de cosinus, de tangens, de stelling van Pythagoras en de hoekensom.

In vlakke situaties vraagstukken oplossen waarbij ontbrekende elementen van een rechthoekige driehoek berekend moeten worden.

In ruimtelijke situaties vraagstukken oplossen waarbij ontbrekende elementen van een rechthoekige driehoek berekend moeten worden.

Problemen uit JWO

1. Een parallellogram heeft als langste zijde a en als kortste b Verder is het parallellogram samengesteld uit twee gelijkzijdige driehoeken en een parallellogram, die alle drie dezelfde oppervlakte hebben (zie figuur).

De verhouding a b is gelijk aan …

JWO, editie 2010, eerste ronde

2. Onze leerkracht LO daagde onze klas uit om een fietstocht van 125 km af te leggen. We gingen akkoord, op voorwaarde dat er, naast het startpunt, dat ook het eindpunt is, nog vier stopplaatsen zouden zijn onderweg. De leerkracht maakte daarop een plan met verschillende routes die we zouden kunnen volgen. Hiernaast zie je een vereenvoudigde voorstelling van het plan

(startpunt S; stopplaatsen A, B, C, D; afstanden in km).

©VANIN

We mochten met onze klas zelf bepalen welke trajecten we tussen de verschillende stopplaatsen zouden nemen, zolang de totale afstand maar precies 125 km was. Van welk van de volgende trajecten weet je zeker dat het in onze tocht vervat zat?

A) ❒ Van S naar A over 27 km. D) ❒ Van C naar D over 27 km.

B) ❒ Van A naar B over 23 km. E) ❒ Van D naar S over 28 km.

C) ❒ Van B naar C over 26 km.

JWO, editie 2011, eerste ronde

3. Als p + q = 12, dan is p 2 + q 2 + 2p + 2q + 2pq gelijk aan …

JWO, editie 2012, eerste ronde

HOOFDSTUK 4 I REKENEN MET REËLE GETALLEN

4.1 Bewerkingen met reële getallen

©VANIN

4.2 Rekenen met machten van reële getallen

4.3 Rekenen met vierkantswortels van reële getallen 147

4.1.1 Bewerkingen met breuken

Modeloefening 1

2 3 + 3 5 –3 4 1 5 + 2 5 : 3 2

Om breuken op te tellen, maak je de breuken gelijknamig. Daarna tel je de tellers op en behoud je de noemer. 10 15 + 9 15 –3 4 1 5 + 2 5 : 3 2 =

19 15 –3 4 1 5 + 2 5 : 3 2 =

Om breuken te vermenigvuldigen, vermenigvuldig je de tellers met elkaar en vermenigvuldig je de noemers met elkaar.

19 15 –3 20 + 2 5 : 3 2 =

Om een breuk te delen door een andere breuk, vermenigvuldig je de eerste breuk met het omgekeerde van de tweede breuk.

Modeloefening 2

19 15 –3 20 + 2 5 2 3 = 19 15 –3 20 + 4 15 = 76 60 –9 60 + 16 60 = 76 – 9 + 16 60 =

Oefeningen

REEKS A

1 Bereken zonder rekenmachine. Antwoord met een onvereenvoudigbare breuk.

2 Bereken zonder rekenmachine. Antwoord met een onvereenvoudigbare breuk.

3 Bereken zonder rekenmachine. Antwoord met een onvereenvoudigbare breuk. a) 3 4 –6 12 =

4 Werk uit. Antwoord met een onvereenvoudigbare breuk. De letters stellen reële getallen verschillend van 0 voor.

REEKS C

5 Werk uit. Antwoord met een onvereenvoudigbare breuk. De letters stellen reële getallen verschillend van 0 voor.

4.1.2 Eigenschappen van bewerkingen met reële getallen

De eigenschappen van bewerkingen met rationale getallen blijven gelden bij de reële getallen.

optellen vermenigvuldigen

Het optellen en het vermenigvuldigen zijn commutatief.

+ b = b + a (met a, b ∈ r)

? b = b ? a (met a, b ∈ r) 5,3 + 3,2 = 3,2 + 5,3 35 =5 3

Het optellen en het vermenigvuldigen zijn associatief.

Het optellen en het vermenigvuldigen hebben een neutraal element.

Als je bij een reëel getal 0 optelt, verkrijg je opnieuw dat reëel getal.

0 heeft geen invloed op het optellen.

0 is het neutraal element voor het optellen.

a + 0 = a = 0 + a (met a ∈ r)

0 + 6,8

Als je een reëel getal met 1 vermenigvuldigt, verkrijg je opnieuw dat reëel getal.

1 heeft geen invloed op het vermenigvuldigen.

1 is het neutraal element voor het vermenigvuldigen.

a ? 1 = a = 1 ? a (met a ∈ r)

Elk reëel getal heeft een symmetrisch element voor het optellen en het vermenigvuldigen.

Als je een getal en zijn tegengestelde bij elkaar optelt, is het resultaat altijd 0 (neutraal element voor het optellen).

Elk reëel getal heeft een symmetrisch element voor het optellen, namelijk zijn tegengestelde.

Als je een getal en zijn omgekeerde met elkaar vermenigvuldigt, is het resultaat altijd 1 (neutraal element voor het vermenigvuldigen).

Elk reëel getal, verschillend van 0, heeft een symmetrisch element voor het vermenigvuldigen, namelijk zijn omgekeerde.

Het vermenigvuldigen is distributief ten opzichte van het optellen. a ? (b + c) = a ? b + a ? c (met a, b, c ∈ r) 3

Oefeningen

REEKS A

6 Vul het ontbrekende getal in.

a) 3 + = 0

d) 5 + = 0

b) –5,73 + = 0 e) 7 2 + = 0

c) 1 3 + = 0 f) 2 – 3 + = 0

7 Vul het ontbrekende getal in.

a) 4 ? = 1

10 = 1 b) –6 ? = 1

– 3 = 1 c) 3 4 ? = 1

8 Vul het symmetrisch element in.

symmetrisch element voor de optelling

–2 2 = 1

symmetrisch element voor de vermenigvuldiging

a) 8

b) −2

c) 10 3

d) 2,5

e) −0,65

f) 7

g) 5 3

h) –11 3

9 Vul de gebruikte eigenschappen in.

a) 5+ 2+ 7

() =5 +2 +7

() =5 +7 +2

=(5+ 7) +2

=12+ 2

b) 25 (–0,5)

=2()5(–0,5)

=5()2(–0,5)

() =5 2(–0,5)

=5 (–1) = – 5

c) 214+ 514

=(2+ 5) 14

=7 14

d) 5+ 7– 5

=5() +7 –5

=7() +5 –5

() =7 +5 –5

=7 +0

=7

10 Bereken door gebruik te maken van de distributieve eigenschap.

a) 17 ? 99 =

b) 23 102 =

c) 40 ? 8,5 =

11 Werk uit door gebruik te maken van de eigenschappen.

a) 9,32 − 2,17 − 9,32 f) 73 7

©VANIN

b) 5 7 6 1 5 g) –8 23 3 4

c) –3 +7 +8

h) 319+ 7– 219

d) –0,25114 i) 53 52 3

e) 3– 5,63 –3 j) 6 (2– 6 )

4.2 Rekenen met machten van reële getallen

4.2.1

Machten met gehele exponenten

Machten met positieve exponenten

Een macht is een kortere schrijfwijze voor een product van gelijke factoren.

Definitie Macht met een natuurlijke exponent

Opmerking

00 is niet gedefinieerd.

Benamingen

2 5 = 32

2 noem je 5 noem je 32 noem je

Machten met negatieve exponenten

Definitie Macht met een negatieve exponent

Gevolgen

Voorbeelden

Tekentabel voor de machtsverheffing

grondtal exponent teken van de macht voorbeelden

Oefeningen

REEKS A

12 Bereken zonder rekenmachine. a) 24 = c) (–3)3 = e) –2 3 3 = g) 3-3 = b) 140 = d) –61 = f) –2 5 –1 = h) –8 5 –2 =

13 Bereken met de rekenmachine.

() 127 2 =

() 2 6 = e) () –2 4 =

() –3 4 = d) () –5 4 = f) () 7 4 =

14 Bereken met de rekenmachine. Rond, indien nodig, af op 0,001. a) () 2 3 ≈ c) () 6 –5 ≈ e) () –37 4 ≈ b) p 2 ≈ d) –1() 1 4 ≈ f) () –101 –4 ≈

15 Bereken zonder rekenmachine. a) –24 = c) –2–4 = e) –2–3 = b) (–2)4 = d) (–2)–4 = f) (–2)–3 =

16 Bereken zonder rekenmachine. a) () 53 2 = c) –3() 4 2 = e) () 16 2 = b) () –19 2 = d) () 7 2 = f) –2() 8 2 =

17 Bereken zonder rekenmachine. Schrijf het resultaat als een onvereenvoudigbare breuk.

a) 49 56 2 = c) 24 32 –3 =

b) 0,53 = d) 0,012 =

©VANIN

18 Schrijf als een macht. Het grondtal is 2 of 10.

a) 100 000 000 = d) 1 256 =

b) 0,1 = e) 0,000 000 1 =

c) 0,125 = f) 1 024 =

19 Vul de ontbrekende getallen in. a) 2 3 = 1,5 d) –4 3 = 27 g) 8 5 = 0,625 b) 2 = –9 16 e) 4 = 5 2 h) (–5) = 1

20 Schrijf zonder haakjes en met een positieve exponent. De letters stellen positieve getallen verschillend van 0 voor. a) (–a)4 = d) –(–b)–5 = g) –(–b)2 = b) –(–b)7 = e) –a b –3 = h) –a b –3 = c) (–a)–2 = f) ––a b 4 = i) –(–a 3) =

4.2.2 Rekenregels voor machten met gehele exponenten

Product van machten met hetzelfde grondtal

Rekenregel am ? an = am+n (met a ∈ r0,m,n ∈ z)

Bij het product van machten met hetzelfde grondtal moet je het grondtal behouden en de exponenten optellen.

Voorbeelden: a 4 a 3 a –2 = ( ( 3)5 3)-4 =

Quotiënt van machten met hetzelfde grondtal

Rekenregel am an = am – n (met a ∈ r0, m,n ∈ z)

Bij het quotiënt van machten met hetzelfde grondtal moet je het grondtal behouden en de exponenten aftrekken.

Voorbeelden: a 14 a 9 = 7 –4 =

Macht van een macht

Rekenregel (am)n =amn (met a ∈ r0,m,n ∈ z)

Bij de macht van een macht moet je het grondtal behouden en de exponenten vermenigvuldigen.

Voorbeelden: (a 4)3 = (23)2 =

Macht van een product

Rekenregel (a ? b)m =am ? bm (met a,b ∈ r0,m ∈ z)

Om een product tot een macht te verheffen, moet je elke factor tot die macht verheffen.

Voorbeelden: (2ab)3 = (4p)3 =

Macht van een quotiënt

Rekenregel a b m = a m bm (met a, b ∈ r0, m ∈ z)

Om een breuk tot een macht te verheffen, moet je de teller en de noemer tot die macht verheffen.

Voorbeelden:

REEKS A

21 Schrijf de producten als één macht en zonder negatieve exponent. De letters stellen reële getallen verschillend van 0 voor.

22 Schrijf de quotiënten als één macht en zonder negatieve exponent. De letters stellen reële getallen verschillend van 0 voor.

23 Schrijf met één positieve exponent. De letters stellen reële getallen verschillend van 0 voor.

24 Werk de haakjes weg.

a) (3a)3 = c) [(–8) x]–2 = b) (5x)–2 =

25 Bereken zonder rekenmachine.

26 Bereken zonder rekenmachine.

[3 (–a)]4 =

27 Geef telkens drie mogelijkheden.

a) Schrijf 24 16 op drie manieren als een product van twee machten met hetzelfde grondtal 24.

b) Schrijf 24 16 op drie manieren als een macht van een macht met grondtal 24.

c) Schrijf 24 16 op drie manieren als een product van machten met een verschillend grondtal, maar met dezelfde exponent.

28 Bereken zonder rekenmachine door gebruik te maken van de rekenregels voor machten. a)

29 Werk de haakjes weg en schrijf zonder negatieve exponent. De letters stellen reële getallen verschillend van 0 voor.

a) 2b ? (2b)-4 = c) (5t)–2 5t =

b) (7ab)7 (7ab)9 = d) (6a 2b)4 (–3ab3)4 =

Inleiding

a) Als je 11−27 berekent met de rekenmachine, verkrijg je

b) Hoeveel seconden gaan er in 1 000 jaar, als je geen rekening houdt met schrikkeljaren?

Zeer grote en zeer kleine getallen worden zelden voluit geschreven.

Definitie Wetenschappelijke schrijfwijze van een getal

De wetenschappelijke schrijfwijze van een getal is het product van een decimaal getal met één van nul verschillend cijfer voor de komma en de bijbehorende macht van 10.

Van decimale schrijfwijze naar wetenschappelijke schrijfwijze zeer grote getallen zeer kleine getallen

Het aantal rangen dat je de komma naar links moet verschuiven zodat die na het eerste cijfer staat, is de exponent van 10.

73 200 000 = 7,32 10 000 000 = 7,32 107

5 600 000 000 = =

Het aantal rangen dat je de komma naar rechts moet verschuiven zodat die na het eerste cijfer, verschillend van 0 staat, voorzien van een minteken, is de exponent van 10.

0,000 005 2 = 5,2 0,000 001 = 5,2 10–6

0,000 087 = =

Van wetenschappelijke schrijfwijze naar decimale schrijfwijze positieve exponenten negatieve exponenten

Je verkrijgt de decimale schrijfwijze door de komma zoveel rangen naar rechts te verschuiven als de exponent van 10 aangeeft.

2,56 106 = 2,56 1 000 000 = 2 560 000

3,874 108 = =

Je verkrijgt de decimale schrijfwijze door de komma zoveel rangen naar links te verschuiven als de exponent van 10 aangeeft.

7,2 10 –5 = 7,2 0,000 01 = 0,000 072

5,78 10 –9 = =

Bewerkingen met getallen in de wetenschappelijke schrijfwijze

Je kunt rekenen met getallen in de wetenschappelijke schrijfwijze, zonder ze om te zetten in de decimale schrijfwijze. Daarbij maak je gebruik van de rekenregels voor machten.

Voorbeelden 3,5 ? 10−6 ? 2 ? 1011 = (3,5 ? 2) ? (10−6 ? 1011) = 7 ? 10−6+11 = 7 ? 105

©VANIN

(2 ? 10−4)7 = Bij zeer grote en zeer kleine getallen kun je in de war raken wat het aantal nullen betreft. Daarom schrijf je die getallen in de wetenschappelijke schrijfwijze.

kleine getallen grote getallen

10−24 yocto y

deca

Enkel voor de kleine onderverdelingen en veelvouden van de eenheid worden alle gehele getallen als exponent gebruikt. Vanaf de exponenten 3 en −3 zijn de exponenten telkens drievouden. Op die manier kan het aantal namen beperkt blijven.

Om het verschil te laten zien tussen een onvoorstelbaar groot getal en oneindig, voerde Edward Kasner in 1938 de term ‘1 googol’ in. Dat is een getal met waarde 10100 Van die term is ook het woord ‘Google’ afgeleid.

Oefeningen

REEKS A

30 Omcirkel de getallen die in de wetenschappelijke schrijfwijze staan.

2,6 ? 104

−0,3 ? 105 1 ? 10−7

−4,89 ? 105

? 10−2

? 109

? 102

? 10−3

? 106

? 10−6

?

31 Omcirkel de wetenschappelijke schrijfwijze van het gegeven getal. a) b) c) d) 9 300 −40 802

32 Geef de wetenschappelijke schrijfwijze.

decimale schrijfwijze

a) 237 580 000 =

b) 0,000 000 7 =

c) 0,002 374 =

d) 25 147 500 000 000 =

33 Geef de decimale schrijfwijze.

wetenschappelijke schrijfwijze

a) 1,48 ? 108 =

b) 3 ? 10−7 =

c) 8,12 ? 10−9 =

d) 5,034 1012 =

wetenschappelijke schrijfwijze

? 10−3

? 10−2

? 103

? 102

decimale schrijfwijze

34 Tijdens haar vakantiejob stelt Sofie haar baas de volgende deal voor. Ze is bereid om de eerste werkdag van de maand te werken voor één cent per dag, de tweede werkdag voor drie cent, de derde dag voor negen cent ... Haar loon wordt dus elke werkdag verdrievoudigd.

a) Hoeveel zou Sofie verdienen gedurende de eerste werkweek (5 werkdagen)?

b) Hoeveel zou Sofie verdienen op de twintigste werkdag?

35 Geef de wetenschappelijke schrijfwijze van de producten. product wetenschappelijke schrijfwijze

a) 57 108 =

b) 93 10−5 =

c) 8 955 10−4 =

d) 344,124 ? 106 =

36 Bereken zonder rekenmachine. Geef je resultaat in de wetenschappelijke schrijfwijze.

a) 8 : 2 000 000 =

b) 2 500 ? 8 000 000 =

c) 39 000 : 3 000 000 000 =

d) 5 0002 =

e) 3 000 0003 =

f) 123 000 ? 20 000 =

37 Bereken zonder rekenmachine. Geef je resultaat in de wetenschappelijke schrijfwijze.

a) 1,64 104 + 2,3 104 =

b) 210 910 8 –5 =

c) (4 ? 105)3 =

©VANIN

d) (2,3 ? 10−8) ? (3 ? 103)2 =

e) 4,5 10−8 + 8 10−8 =

f) (2 108)−3 =

g) 6,410 1,610 –7 4 =

h) [(1,5 ? 107) ? (2 ? 10−8)]4 =

38 Geef de wetenschappelijke schrijfwijze.

wetenschappelijke schrijfwijze

a) De gemiddelde straal van de aarde bedraagt 6 370 000 m.

b) De snelheid van het licht bedraagt 300 000 km per seconde.

c) De diameter van een uraniumatoom bedraagt

0,000 000 000 25 m.

d) De massa van Jupiter bedraagt 1 898 000 000 000 000 000 000 000 000 kg.

e) De dikte van een rode bloedcel bedraagt

0,000 002 m.

39 In een composthoop van 4 000 liter zitten bacteriën die zich om de zes uur verdubbelen. Bij een onderzoek vindt men in één liter compost 100 000 bacteriën. Hoeveel bacteriën zitten er in de composthoop op dat moment?

Geef je antwoord in de wetenschappelijke schrijfwijze.

Antwoord:

40 De afstand van de aarde tot de zon bedraagt 1,5 108 km. De afstand van Neptunus tot de zon bedraagt 4,5 ? 109 km.

Hoeveel keer staat Neptunus verder van de zon dan de aarde?

Antwoord:

REEKS C

41 De massa van de aarde is ongeveer 5,98 ? 1024 kg. De massa van de zon is 330 000 keer groter. Bereken de massa van de zon.

Geef je resultaat in de wetenschappelijke schrijfwijze.

Antwoord:

42 De massa van een elektron bedraagt 9,11 10−25 g. Hoeveel elektronen gaan er in 1 ton?

Geef je resultaat in de wetenschappelijke schrijfwijze.

Antwoord:

43 Het licht heeft een snelheid van 300 000 km/s. De afstand van de zon tot de aarde bedraagt 1,496 ? 108 km. Hoelang heeft het zonlicht nodig om de aarde te bereiken?

Geef je resultaat in minuten en seconden, op 1 seconde nauwkeurig.

Antwoord:

4.3 Rekenen met vierkantswortels van reële getallen

4.3.1

Som en verschil van vierkantswortels

Gelijksoortige vierkantswortels

525+ 725 = en 12 25 =

79 –2 9 = en 59 =

Je past de distributiviteit toe van het vermenigvuldigen ten opzichte van het optellen en het aftrekken in r

Rekenregel

©VANIN

axbxabx += (+ ) en axbxabx –= (– ) (met a,b ∈ r en x ∈ r+)

713+ 913 = 25 17 –8417 = 29 +8 29 = 2,87 –9,147 =

Niet-gelijksoortige vierkantswortels

9+ 16 = en 9+ 16 =

169– 144 = en 169– 144 =

Besluit

abab +≠ + en abab –≠ – (met a, b ∈ r + 0, a > b)

De driehoeksongelijkheid zegt dat de ‘kortste afstand’ tussen twee punten een rechte lijn is. Er geldt:

• | AD | + | DB | = | AB | omdat A, D en B op één rechte liggen.

DBA

• | AC | + | CB | > | AB | want A, C en B liggen niet op één rechte en vormen dus een driehoek. Die eigenschap is gekend als de ongelijkheid van Minkowski.

In een rechthoekige driehoek met rechthoekszijden a en b a ba2 + b2 is de lengte van de schuine zijde ab + 22 (stelling van Pythagoras).

Volgens de driehoeksongelijkheid is in elke driehoek één zijde altijd korter dan de som van de twee andere zijden. De schuine zijde is dus korter dan de som van de twee rechthoekszijden.

In symbolen:

ab + 22 < a + b of ab + 22 < ab + 22

Oefeningen

REEKS B

44 Werk uit indien mogelijk.

a) 26 +6 = e) 35 –8 35 =

b) 17 21 – 521 = f) 53 +5 =

©VANIN

c) 97 +8 97 = g) –7 3– 83 =

d) 513– 213 = h) () 26 11 +–311 =

45 Werk uit indien mogelijk.

a) 7,37 +8 7 = e) –5 3 +2 =

b) 1 2 5– 25 = f) 5,35,1 –1 2 5,1 =

c) 8,52 –7 3 = g) –2 5 5––5 2 5 =

d) 2,22 –5 2 = h) 1 3 2,4+ –8 9 2,4 =

REEKS C

46 Werk uit indien mogelijk. De letters stellen positieve reële getallen voor.

a) aa2+ 3 = e) ab 2– 2 =

b) xx8– 11 = f) abab + =

c) uu7,2–8 5 = g) ab ba + =

d) bb –4 5 + 3 2 = h) ba – ba =

4.3.2

Product van vierkantswortels

Inleiding

49 = = en 49 = = () 1110 2 = = en () 1110 2 = =

Rekenregel

Het product van de vierkantswortels van twee positieve reële getallen is de vierkantswortel van het product van die twee getallen.

In symbolen: abab = (met a,b ∈ r+)

Bewijs

gegeven

a, b ∈ r + te bewijzen

ab ab =

bewijs

Beide leden van de formule zijn positieve getallen. Het volstaat dus aan te tonen dat hun kwadraten aan elkaar gelijk zijn.

• ab ()2 = ab ()() 22 = a b macht van een product definitie vierkantswortel

• ab ()2 = a ? b definitie vierkantswortel

besluit

ab ab =

Voorbeelden

28 = 312 = 67 =

Vereenvoudigen

Deze rekenregel wordt gebruikt om wortelvormen te vereenvoudigen. In de volgende voorbeelden stellen de letters positieve getallen voor.

18 = 92 = 92 = 32

80 = = = a2b = a 2 b = a 2 b = a b a3 2 = = =

Door wortelvormen te vereenvoudigen, kun je niet-gelijksoortige vormen soms gelijksoortig maken. 2+ 8 = 2+ 42 = 2+ 42 = 2+ 22 = 32

Oefeningen

REEKS B

47 Bereken zonder rekenmachine.

a) 22 = g) 32 2 =

b) 312 = h) 348 =

©VANIN

c) 327 = i) 45 5 =

d) 82 = j) 520 =

e) 218 = k) 624 =

f) 375 = l) 728 =

48 Vereenvoudig.

a) 32 = g) 72 =

b) 104 = h) 45 =

c) 98 = i) 175 =

d) 18 = j) 63 =

e) 90 = k) 153 =

f) 80 = l) 363 =

49 Werk de vermenigvuldigingen

a) 22 32 d) 56 612 = 23 22

b) 22 33 e) 38 254

©VANIN

c) 32 18 f) 28 418

50 Tel de wortelvormen op. a) 6+ 24

51 Tel de wortelvormen op. De letters stellen positieve reële getallen voor.

a) 22 –8 –9 2 aa a =

b) 33 +2 27 –6 48 aa a =

c) 5+ 245– 3180 aa a =

52 Werk de vermenigvuldigingen uit.

a) 53() –2 5

c) () 23 +5 515

b) 36() +2 3

d) () –6 73 14 +21– 27

53 Werk de vermenigvuldigingen uit. De letters stellen positieve reële getallen voor.

a) () 2–aa =

b) () 3+ babb =

c) () –2 –5 xx =

4.3.3 Quotiënt van vierkantswortels

Inleiding 1 4 = = en 1 4 = = 16 100 = = en 16 100 = =

Rekenregel Het quotiënt van de vierkantswortels van twee positieve reële getallen waarbij de noemer niet nul is, is de vierkantswortel van het quotiënt van die getallen.

In symbolen:

Bewijs gegeven

a ∈ r + en b ∈ r + 0 te bewijzen

a b = a b bewijs

Beide leden van de formule zijn positieve getallen.

Het volstaat dus aan te tonen dat hun kwadraten aan elkaar gelijk zijn.

macht van een quotiënt definitie vierkantswortel

a b 2 =

definitie vierkantswortel besluit

a b = a b

Opmerking

Vereenvoudig, indien mogelijk, de breuk met worteltekens. 3 12 = 3 12 = 1 4 = 1 2

Voorbeelden

De noemer wortelvrij maken

Een wortelvorm kun je soms vereenvoudigen door de noemer wortelvrij (rationaal) te maken.

Werkwijze Om de noemer wortelvrij te maken, vermenigvuldig je de teller en de noemer met de vierkantswortel uit de noemer.

In symbolen: a b = ab bb = ab ( b ) 2 = ab b (met a ∈ r en b ∈ r+0)

Vereenvoudig eerst de wortelvormen in de noemer, indien mogelijk.

Voorbeelden

©VANIN

3 5 = 35 55

teller en noemer vermenigvuldigen met de vierkantswortel uit de noemer

5 7 = 5 7 rekenregel quotiënt van vierkantswortels () = 35 5 2 definitie macht = 57 77

teller en noemer vermenigvuldigen met de vierkantswortel uit de noemer = 35 5 definitie vierkantswortel () = 35 7 2 rekenregel product van vierkantswortels en definitie macht = 35 7 definitie vierkantswortel

5 23 = 53 23 3

teller en noemer vermenigvuldigen met de vierkantswortel uit de noemer

5 18 = 5 92 eerst de wortelvorm in de noemer vereenvoudigen = 5 2 ( 3 )2

definitie macht = 5 32 rekenregel product van vierkantswortels = 53 23 definitie vierkantswortel = 52 32 2

teller en noemer vermenigvuldigen met de vierkantswortel uit de noemer = 53 6 rekenen met reële getallen = 52 3 ( 2 )2 definitie macht = 52 32 definitie vierkantswortel = 52 6

rekenen met reële getallen

Oefeningen

REEKS B

54 Bereken zonder rekenmachine.

©VANIN

55 Bereken zonder rekenmachine.

56 Vereenvoudig, schat het resultaat en bereken met de rekenmachine op 0,001 nauwkeurig. vereenvoudigen schatten berekenen

57 Maak de noemer wortelvrij.

a) 7 11 = e) 17 7 = b) 11 6 = f) 8 7 = c) 3 19 = g) 6 13 = d) 2 5 = h) 2 3 =

58 Maak de noemer wortelvrij.

a) 5 36 =

b) –2 22 = c) 27 11 =

d) 53 32 =

e) –2 2 27 =

©VANIN

REEKS C

59 Maak de noemer wortelvrij.

a) 1 3 27 72 = b) 3– 23 3 = c) 34 –5 8 25 =

4.3.4 Macht van een vierkantswortel

Inleiding

() 9 2 = en 92 =

() 4 3 = en 43 =

() 36 –1 = en 36–1 =

Rekenregel De macht van een vierkantswortel van een positief reëel getal is de vierkantswortel van de macht van dat getal.

©VANIN

In symbolen: ( a ) z = az (met a ∈ r + 0 en z ∈ z)

Bewijs

gegeven

a ∈ r + 0 en z ∈ z te bewijzen

( a )z = a z bewijs

Beide leden van de formule zijn positieve getallen. Het volstaat dus aan te tonen dat hun kwadraten aan elkaar gelijk zijn.

• ( a )z 2 = ( a )z 2 = ( a )2 z = a z macht van een macht macht van een macht definitie vierkantswortel

• ( a z )2 = a z definitie vierkantswortel

besluit

( a )z = a z

Voorbeelden

( 2 )6 = ( 3 )–4 =

Opmerking

Deze rekenregel wordt gebruikt om wortelvormen te vereenvoudigen. In de volgende voorbeelden stellen de letters telkens positieve getallen voor.

2 4 = (22 )2 = 22 = 4 35 = 34 31 = 33 2 = 93

a 6 = (a 3 )2 = a 3 b 11 = b 10 b 1 = bb 5

Om de vierkantswortel van een macht met een even exponent te nemen, laat je het wortelteken weg en deel je de exponent door twee.

Om de vierkantswortel van een macht met een oneven exponent te nemen, ontbind je de macht in het grondtal en een even macht ervan en pas je de rekenregels toe.

Oefeningen

REEKS B

60 Bereken zonder rekenmachine.

a) () 2 4 = c) () 11 4 =

b) () 5 6 = d) () 2 10 =

©VANIN

61 Vereenvoudig.

a) 54 = f) 93 = b) 7 3 = g) 108 = c) 83 = h) 45 = d) 65 = i) 36 =

e) 2 11 = j) 115 =

62 Bereken zonder rekenmachine.

a) () 3 –2 = e) 1 3 –4 = b) () –5 –4 = f) () 6 –2 = c) () 10 –6 = g) 1 2 –8 = d) () –3 6 = h) () –7 –4 =

63 Vereenvoudig. De letters stellen positieve reële getallen voor.

REEKS C

64 Vereenvoudig en bereken daarna met de rekenmachine. vereenvoudigen berekenen

65 Vereenvoudig. De letters stellen positieve reële getallen voor. Noteer je resultaat met een positieve exponent.

4.3.5 Bewerkingen met wortelvormen

Meestal zullen er meerdere bewerkingen in een oefening voorkomen. Hier heb je ze nog eens op een rijtje.

Optellen en aftrekken

Rekenregel += axbx(a+b)x en –= axbx(a-b)x (met a,b ∈ r en x ∈ r+)

Voorbeelden: 37 +7 7 = 16 –5 aa =

Opmerking +≠ +b ab a en –≠ –b ab a (met a, b ∈ r + 0, a > b)

Vermenigvuldigen

Rekenregel = abb a (met a,b ∈ r+)

Voorbeelden: 218 = 515 =

Delen

Rekenregel = a b a b (met a ∈ r + en b ∈ r + 0)

Voorbeelden: 2 18 = 96 6 =

Machtsverheffing

Rekenregel () = a z a z (met a ∈ r + 0 en z ∈ z)

Voorbeelden: () 3 4 = () 7 6 =

Afronden

Het heeft meestal geen zin om het resultaat van een bewerking te geven met tien cijfers na de komma. Daarom rond je af.

Voorbeelden

• Bereken op 0,1 nauwkeurig: 10 + 17 ≈

• Bereken op 0,01 nauwkeurig: 5 − 0,2 ≈

• Bereken op 0,001 nauwkeurig: 53 ≈

Opmerking

Rond enkel het eindresultaat af. Elke afronding is immers een afwijking van het exacte resultaat. Door te rekenen met afgeronde waarden, kan de afwijking vergroten.

Dus niet: 26 10 ≈ 26 ? 3,162 = 82,212

Maar wel: 26 10 ≈ 82,219

Schatten

Schat de resultaten van de bewerkingen.

a) 3 + 5

34 – 5

b) –2 15 d) 78 : (–2) 9 < 15 < 16 15 ≈ 16

Toepassingen

Voorbeeld 1

Bereken de oppervlakte van de rechthoek op 0,01 cm2 nauwkeurig.

Schat de oppervlakte.

7 cm 47 cm

Voorbeeld 2

Bereken de oppervlakte.

©VANIN

Bereken het volume van de kubus op 0,001 cm3 nauwkeurig.

Schat het volume.

Bereken het volume.

8 cm

Voorbeeld 3

Bereken de omtrek van de driehoek op 0,1 cm nauwkeurig.

Bereken de schuine zijde.

Schat de omtrek.

4 cm

Bereken de omtrek.

7 cm

Oefeningen

REEKS A

66 Bereken met de rekenmachine op 0,001 nauwkeurig.

a) 2+ 22 ≈ f) –14,3– 101 ≈

b) 5: (–0,3) ≈ g) – 51 : 29 ≈

c) –6 14 ≈

h) – 85 + 0,6 ≈

d) 31 –6,8 ≈ i) – (– 10 ) p ≈

e) –5 (– 23 ) ≈ j) – 11 8 ≈

REEKS B

67 Schat het resultaat.

a) 65 –8 ≈ f) 3,25 –101 ≈ b) –5 +6,3 ≈ g) –17 2 ≈

c) 50 :(–7) ≈ h) 5+ 10 ≈

d) ()–10– 26 ≈ i) () 82 :– 8 ≈

e) –5 48 ≈ j) () 15 p ≈

68 Schat eerst en bereken daarna de oppervlakte op 0,01 nauwkeurig. geschat berekend

a) Een rechthoek waarvan de breedte 5 cm en de lengte 7 cm is.

b) Een cirkel waarvan de straal 5 m is.

c) Een parallellogram waarvan de basis 19 cm en de hoogte 5 cm is.

d) Een cirkel waarvan de diameter 2 cm is.

e) Een driehoek waarvan de basis 11 m en de hoogte 3 m is.

69 Bereken (zonder te meten)

a) de omtrek op 0,1 nauwkeurig. b) de oppervlakte op 0,01 nauwkeurig.

70 Vereenvoudig. De letters stellen positieve reële getallen voor.

a) 4a 9 =

72a 2 =

71 Werk uit.

a) 53 ()2 = e) –215 ()4 =

b) –3 7 ()2 = f) 23 ()3 =

c) 232 ()2 = g) –412 ()–2 =

d) –6 ()4 = h) –2 5 ()5 =

72 Werk uit. De letters stellen positieve reële getallen voor.

a) aa b 2 =

b) ab ab 9 32 3 =

c) ab ba254 33 =

d) ab ab 45 9359 34 =

73 Werk uit. De letters stellen positieve reële getallen voor.

a) aa =

b) () aa3 3 2 =

c) () aa –825 2 =

d) aa33 4 =

e) () aa 8 23 4 =

f) –2ab 3 () =

74 Werk uit en bereken op 0,01 nauwkeurig

a) de inhoud van een kubus met ribben van 5 cm.

c) de inhoud van een cilinder met een straal van 23 cm en een hoogte van 48 cm.

Antwoord:

b) de oppervlakte van een ruit met een grote diagonaal van 263 cm en een kleine diagonaal van 28 cm.

Antwoord:

d) de oppervlakte van een rechthoekige driehoek met rechthoekszijden van 27 cm en 33 cm lang.

Antwoord:

Antwoord:

75 Vereenvoudig. De letters stellen positieve reële getallen verschillend van 0 voor.

a) 5a 4 4a =

b) 32a 2b5 72a =

c) 63ab3 28a 3b =

d) 8a 5 9b6 a 1 2 =

76 Vereenvoudig en werk uit. De letters stellen positieve reële getallen voor.

a) 18a + 98a 50a – =

b) 27a 3 48a + a =

c) 90ab2 40ab2 3 160a – – b =

77 Werk uit. De letter a stelt een positief reëel getal verschillend van 0 voor. Maak de noemer wortelvrij.

4.3.6

Volgorde van de bewerkingen

Wanneer je meerdere bewerkingen uitvoert in een oefening, moet je rekening houden met de volgorde van de bewerkingen.

1) Bewerkingen tussen haakjes ( ) , [ ]

2) Machten en vierkantswortels a n , a

3) Vermenigvuldigen en delen van links naar rechts , :

4) Optellen en aftrekken van links naar rechts + , −

Bij het vierkantswortelteken moet alles wat onder het wortelteken staat, eerst uitgewerkt worden alsof het tussen haakjes staat.

Voorbeelden

Bereken zonder rekenmachine. De letters stellen positieve reële getallen verschillend van 0 voor.

a) 18 + 24 : 6 + 3 d) a ab b b) –1 4 + 4 9 1 2 + 1 16 : 9 4 e) 2+ 3 33aa a c) 5 3 3 –1 2 + 2 3 2 25 7 f) 3+ –2 a 10a –6a 25a

Oefeningen

REEKS B

78 Bereken zonder rekenmachine. Houd rekening met de volgorde van de bewerkingen.

a) 23 – 37 – 4 + 6 8

c) () 817+ 31768 b) 5 2

©VANIN

REEKS C

79 Bereken. De letters stellen positieve reële getallen verschillend van 0 voor.

a) 2– 5 –2 2 4 aa a a b) + 3 a a –() 3 a () 3 3a + a 3 2

STUDIEWIJZER Rekenen met reële getallen

4.1 Bewerkingen met reële getallen

Berekeningen uitvoeren met getallen

• in breukvorm

• in decimale vorm en indien nodig de rekenmachine gebruiken.

De eigenschappen van bewerkingen met reële getallen gebruiken om bewerkingen uit te voeren en te vereenvoudigen.

4.2 Rekenen met machten van reële getallen

©VANIN

KENNEN

a 0 = 1 (met a ∈ r0) a 1 = a (met a ∈ r)

a–n = 1 a n (met a ∈ r0, n ∈ n)

a–1 = 1 a (met a ∈

a m a n = am+n (met a ∈ r0; m, n ∈ z)

Bij het product van machten met hetzelfde grondtal moet je het grondtal behouden en de exponenten optellen.

a m

a n = a m – n (met a ∈ r0; m, n ∈ z)

Bij het quotiënt van machten met hetzelfde grondtal moet je het grondtal behouden en de exponenten aftrekken.

(am)n = am n (met a ∈ r0; m, n ∈ z)

Bij de macht van een macht moet je het grondtal behouden en de exponenten vermenigvuldigen.

(a b)m = am bm (met a, b ∈ r0, m ∈ z)

Om een product tot een macht te verheffen, moet je elke factor tot die macht verheffen.

a b m = a m b m (met a, b ∈ r0, m ∈ z)

Om een breuk tot een macht te verheffen, moet je de teller en de noemer tot die macht verheffen.

De wetenschappelijke schrijfwijze van een getal is het product van een decimaal getal met één van nul verschillend cijfer voor de komma en de bijbehorende macht van 10.

KUNNEN

De rekenregels voor het rekenen met machten toepassen bij het rekenen met getallen en letters.

Omzetten van decimale naar wetenschappelijke schrijfwijze en omgekeerd.

Berekeningen uitvoeren met getallen in wetenschappelijke schrijfwijze.

4.3 Rekenen met vierkantswortels van reële getallen voor de leerling voor de leerkracht

KENNEN –  + –

ax bx ab x += (+ ) en ax bx ab x –= (– ) (met a, b ∈ r, x ∈ r+)

Het product van de vierkantswortels van twee positieve reële getallen is de vierkantswortel van het product van die getallen.

ab a b = (met a, b ∈ r+)

Het quotiënt van de vierkantswortels van twee positieve reële getallen waarbij de noemer niet nul is, is de vierkantswortel van het quotiënt van de grondtallen.

a b a b = (met a ∈ r+ , b ∈ r+0)

Om de noemer wortelvrij te maken, vermenigvuldig je de teller en de noemer met de vierkantswortel uit de noemer. a b ab bb ab b ab b == () = 2 (met a ∈ r, b ∈ r+0)

De macht van een vierkantswortel van een positief reëel getal is de vierkantswortel van de macht van dat getal.

aa z z ) ( = (met a ∈ r+ 0, z ∈ z)

©VANIN

KUNNEN

De rekenregels voor het rekenen met vierkantswortels uitdrukken in woorden.

De rekenregels voor het rekenen met vierkantswortels uitdrukken in symbolen.

Die rekenregels toepassen bij het uitvoeren van bewerkingen.

Bewerkingen met wortelvormen benaderend uitvoeren met behulp van een rekenmachine.

De rekenregels voor het rekenen met vierkantswortels bewijzen.

Oefeningen oplossen, rekening houdend met de volgorde van de bewerkingen.

1. Hoeveel drietallen van opeenvolgende natuurlijke getallen bestaan er zodat een van de getallen een volkomen kwadraat is en de andere twee priemgetallen zijn?

©VANIN

JWO, editie 2020, tweede ronde

2. Kleine zus speelt in een ballenbad met 110 rode, 120 gele en 140 blauwe ballen. Zonder te kijken, neemt ze een aantal ballen uit het bad. Hoeveel ballen moet ze minstens nemen om zeker te zijn dat er 113 van dezelfde kleur bij zijn?

JWO, editie 2019, tweede ronde

3. De volgende staafdiagrammen geven de resultaten van vijf toetsen weer. Welk van de diagrammen stelt gegevens voor waarvan de mediaan groter is dan het gemiddelde?

JWO, editie 2018, tweede ronde

4. De cijfers 1, 2, 3, 4, 5, 6, 7, 8 en 9 worden in die volgorde vervangen door opeenvolgende letters van het alfabet. Als je weet dat uspmru het kwadraat van een natuurlijk getal is, wat is dan dat natuurlijk getal?

JWO, editie 2017, tweede ronde

HOOFDSTUK 5 I BESCHRIJVENDE STATISTIEK

©VANIN

5.1.1 Statistieken

Meestal denk je bij het woord ‘statistiek’ aan tabellen en grafieken. Tabellen en grafieken noem je inderdaad ‘statistieken’.

Je kunt geen krant of weekblad openslaan zonder daarmee geconfronteerd te worden.

Ook de televisie en het internet geven informatie die met statistieken visueel gemaakt wordt.

Sporen van stimulerende middelen in het afvalwater

Top 20 van steden in Europa

Aantal mg per 1.000 inwoners per dag

©VANIN

Antwerpen

Tarragona Amsterdam

Zürich Brussel

Bazel

Genève

Lleida

Lissabon

Valencia

Eindhoven

Utrecht

Kopenhagen

Barcelona

Castellon

Berlijn

Kufstein

Bern

Reykjavik Praag

Bron: EMCDDA

Het gemiddeld aantal doelpunten per wedstrijd

5.1.2 Doel van statistiek

De waaier aan activiteiten die elk statistisch onderzoek met zich meebrengt, kun je in twee grote categorieën verdelen.

beschrijvende statistiek verklarende statistiek

• informatie verzamelen

• informatie verwerken en voorstellen

• informatie analyseren

• verdere analyse

• betrouwbaarheid van de informatie nagaan

• conclusies formuleren

Statistiek is voor de huidige samenleving van groot belang.

Voorbeelden

• Hoe weten confectiebedrijven welke maten ze het meest moeten produceren?

• Hoe plannen fabrikanten van desktops hun productie op lange termijn?

• Hoe weet een land welke accenten het moet leggen in het verkeersbeleid?

• Hoe kun je verschillende prestaties op het gebied van school, sport, arbeid ... met elkaar vergelijken?

Zowel economie, politiek, psychologie, pedagogie, geneeskunde als exacte wetenschappen maken gebruik van de statistiek als werkinstrument.

Al in de oudheid was er sprake van statistische activiteit. Onze voorouders beseften dat de landbouwopbrengst afhankelijk was van de grootte van het stuk land.

Toch heeft het geduurd tot de 16e à 17e eeuw vooraleer regeringen echt nood hadden aan de verwerking van grote hoeveelheden gegevens (sterfte, geboorte, dopen, huwelijken, handel, landbouw ...).

Graunt, Fermat en Pascal gelden daar als de voornaamste figuren.

In de 18e eeuw werden de wiskundige fundamenten van de statistiek gelegd door gebruik te maken van de kansrekening. Bernoulli, Huygens, de Moivre, de Witt, Legendre en Gauss zijn stuk voor stuk wetenschappers die op dat vlak baanbrekend werk geleverd hebben.

©VANIN

In de 19e eeuw vind je naast klinkende namen als Laplace en Galton ook die van een Belg terug. Adolphe Quetelet leverde belangrijk werk in de ‘sociale statistiek’.

Quetelet is vooral bekend omdat hij het begrip Body Mass Index (BMI) introduceerde.

Hij verzamelde ook bevolkingsgegevens en analyseerde die.

In 1841 richtte hij het eerste openbare statistische bureau ter wereld op: de Centrale Commissie voor de Statistiek.

Quetelet is ook de eerste die de grafische weergave van statistische gegevens wetenschappelijk verantwoordde.

In de 20e eeuw was er een verdere ontwikkeling van de mathematische statistiek.

Karl Pearson, Ronald Fisher, Jerzy Neyman en Egon Pearson ontwikkelden de methode van de statistische toetsing. Abraham Wald ontwikkelde de statistische beslissingstheorie.

Met de komst van de computer werd het mogelijk zeer grote hoeveelheden gegevens op korte tijd te verwerken.

Statistiek wordt meer en meer als een aparte wetenschappelijke discipline beschouwd.

5.1.3 Misleidende diagrammen

Soms misbruikt men grafische voorstellingen om een bepaalde conclusie op te dringen of te versterken. •

aantal geboortes in België en Nederland in 2022

20 000 0

Nederland België

Er zijn steeds meer oudere mensen in Europa en steeds minder jonge mensen. Men zegt dat de vergrijzing een probleem is.

De grafische voorstelling toont het aantal geboortes in België en Nederland in 2022.

Het lijkt alsof de vergrijzing in Nederland minder erg is dan in België. Maar is dat zo?

• De evolutie van het aantal klachten over nachtlawaai is op twee manieren voorgesteld.

Op de linkse grafiek zie je een duidelijk dalende tendens. Op de rechtse grafiek lijkt het aantal klachten sterk te stijgen. Welke ingrepen deed men om dat idee te versterken?

Je ziet een voorstelling van de leeftijdsverdeling bij de Vlaamse bloedgevers.

Deze grafische voorstelling wil ons doen geloven dat de meeste bloedgevers tussen de 20 en 40 jaar zijn. Wat heeft men gedaan om dat te tonen?

Oefeningen

REEKS A

1 Waarom zijn deze statistieken misleidend?

a) Ik weet wanneer

ik genoeg gestudeerd heb.

c) vermageren met CALORIEVRETER

b) geoogste hoeveelheid fruit

banaan

appel

kers

d) Bij 'De Lustige Shotters' zijn er de minste blessures bij de 40-plussers.

2 Om aan te tonen hoezeer een stadsbestuur heeft gefaald in zijn beleid om de uitgaven drastisch terug te schroeven, publiceert een oppositiepartij in haar maandblad het onderstaande diagram.

begrotingstekort

a) Welke indruk wil dit diagram wekken?

begrotingstekort

©VANIN

begrotingstekort

begrotingstekort ( × 10 000 euro)

b) Het stadsbestuur nuanceert de kritiek met de nevenstaande voorstelling.

Hoe heeft het stadsbestuur zijn voorstelling verkregen?

3 Aan een aantal leerlingen werd gevraagd naar hun favoriete schoolvak. Hoewel alle vakken even populair bleken te zijn, wekt het diagram toch de indruk dat Nederlands de meeste stemmen kreeg. Hoe komt dat?

4 Omschrijf kort hoe het diagram erin slaagt de indruk te wekken dat het procentuele aantal allochtonen in de VS historisch hoog was op het einde van de twintigste eeuw.

allochtonen in de VS in aantal en percentage aantal in miljoen

REEKS C

5 Het diagram laat uitschijnen dat België zijn best doet om de CO2-uitstoot tegen te gaan. We bevinden ons helemaal onderaan de lijst.

a) Waarom zet dit diagram ons op het verkeerde been?

Landen die het meest CO2 uitstoten (miljoen ton)

China 9.839

VS 5.270

India 2.467

Rusland 1.693

Japan 1.205

Duitsland 799

Iran 672

Saoedi-Arabië 635

Zuid-Korea 616

Canada

573

België 100

Bronnen: EEA, Global Carbon Atlas

b) Welk land is relatief de grootste vervuiler?

©VANIN

6 Verklaar de schijnbare tegenstelling tussen beide grafieken.

Aantal mensen onder de 65 jaar in België

9

Percentage mensen onder de 65 jaar in België

7 Oudere mensen ervaren hun gezondheid slechter dan jongere mensen. Welke ingrepen heeft men gedaan bij het onderstaande diagram om die gedachte nog te versterken?

Hoeveel mensen vinden hun gezondheid (zeer) goed?

5.1.4 Procent en procentpunt

Voorbeeld 1

Stel: je betaalt 20 % belasting. Daarna stijgt de belasting naar 21 %. Hoeveel procent is de belasting gestegen?

• De stijging van 20 % naar 21 % is 1 procentpunt, want 21 % – 20 % = 1 %.

• De stijging van 20 % naar 21 % is 5 procent, want 21 20 = 1,05 = 105 % = 100 % + 5 %.

Definitie Procentpunt

Een procentpunt is een punt op een procentenschaal en is het absolute verschil tussen twee procentuele waarden.

Voorbeeld 2

Stel: op de totale beroepsbevolking van 6 000 000 mensen zijn er 300 000 werklozen.

• Bereken het werkloosheidspercentage.

• De werkloosheid neemt toe met 2 %. Hoeveel werklozen zijn er nu?

• Hoeveel bedraagt het nieuwe werkloosheidspercentage?

• Met hoeveel procentpunt is het werkloosheidspercentage toegenomen?

• Als het werkloosheidspercentage met 2 procentpunt stijgt, hoeveel werklozen zijn er dan?

Oefeningen

REEKS A

8 Bereken het verschil in procentpunt en in procent.

a) Een stijging van het aantal vierdejaars van 15 % naar 20 %.

©VANIN

b) Een stijging van je resultaat voor wiskunde van 73 % naar 81 %.

c) Een daling van het rendement van een aandeel van 2 % naar 1 %.

d) Een daling van het aantal meisjes in een school van 48 % naar 45 %.

e) Voor de vorige toets behaalde je 13/20, voor deze toets 15/20.

f) In 1960 waren er 231 dagen met neerslag. In 2020 waren dat 169 dagen.

REEKS B

9 De consumentenbond publiceert regelmatig een lijst met prijzen van de verschillende supermarkten. Supermarkt A zit, voor de huismerken, op 90 % van de gemiddelde supermarktprijs en supermarkt B op 108 %. A maakt reclame dat ze 18 % goedkoper is dan B. Toon aan dat deze redenering niet klopt.

©VANIN

10 Fatima verdient 5 % meer dan Kevin. Verdient Kevin dan 5 % minder dan Fatima?

REEKS C

11 ‘Wij betalen uw btw: 21 procent korting op alles!’ Klopt die reclame?

12 Het diagram toont de resultaten van de verkiezingen voor het Vlaams Parlement in 2019. De grijze balkjes eronder geven het resultaat van 2014 weer.

Lijst

Open Vld

N-VA

VLAAMS BELANG

CD&V

PVDA

PVDA+

UF

GROEN sp.a Bron: www.hln.be

% van de stemmen

a) Met hoeveel procent is het resultaat van Open Vld gedaald ten opzichte van 2014? Rond af op 0,01 %.

b) Zijn de volgende uitspraken juist of fout?

Het verkiezingsresultaat van N-VA lag in 2019 7,05 procent lager dan in 2014.

Het verkiezingsresultaat van Groen lag in 2014 1,41 procentpunt lager dan in 2019.

juist fout

c) Met hoeveel procent is het resultaat van Vlaams Belang gestegen ten opzichte van 2014?

d) Sp.a en CD&V leden in 2019 allebei verlies. Voor welke partij was dat verlies het grootst ten opzichte van 2014?

5.2 Soorten gegevens

5.2.1 Elementen, kenmerken en gegevens

In de statistiek verzamel je gegevens door kenmerken van elementen te onderzoeken.

De elementen zijn de objecten (personen, dieren, goederen ...) waarover je informatie wenst te verkrijgen.

De kenmerken zijn de eigenschappen van een element. Kenmerken noem je ook variabelen of veranderlijken.

Het geheel van de verkregen gegevens noem je de gegevensverzameling

Voorbeeld

naam aantal puppy's kleur lengte (cm) gehoorzaamheid

Bobby 3 zwart 56 goed

Rex 8 wit 83 zeer goed

Lexy 5 bruin 34 zwak

5.2.2

Soorten gegevens

categorische gegevens

Dat zijn gegevens die een hoedanigheid weergeven. Die gegevens noem je ook kwalitatieve gegevens.

©VANIN

Niet-geordende categorische gegevens hebben geen natuurlijke ordening.

Voorbeeld:

• veranderlijke: kleur

• gegevens: zwart, wit ...

Geordende categorische gegevens hebben een natuurlijke ordening.

Voorbeeld:

• veranderlijke: gehoorzaamheid

• gegevens: goed, zwak ...

De gegevens of data zijn de hoedanigheden of getallen die je verkrijgt na een statistisch onderzoek.

numerieke gegevens

Dat zijn gegevens die het resultaat zijn van tellingen en metingen. Die gegevens noem je ook kwantitatieve gegevens.

Discrete numerieke gegevens beperken zich tot een aantal waarden.

Voorbeeld:

• veranderlijke: aantal puppy's

• gegevens: 3, 8 ...

Continue numerieke gegevens zijn reële waarden tussen bepaalde grenzen.

Voorbeeld:

• veranderlijke: lengte in cm

• gegevens: 56, 83 ...

Oefeningen

REEKS A

13 Welk soort gegevens verkrijg je bij de volgende onderzoeksonderwerpen? categorisch numeriek

onderzoeksonderwerp + gegevens nietgeordend geordend discreet continu

a) de tevredenheid van de leerlingen van onze school over hun leerkracht wiskunde

gegevens: tevreden, ontevreden ...

b) het aantal verkeersboetes in onze stad per jaar tussen 2010 en 2020

gegevens: 215, 190, 307 ...

c) de gemiddelde levensduur van een nieuw soort lampen

gegevens: 2 428 h, 2 369 h, 2 526 h ...

d) de frisdrank die jongeren meestal drinken bij hun middagmaal

gegevens: cola, limonade, fruitsap ...

e) de massa van de boekentas van de leerlingen van het eerste jaar

gegevens: 8,1 kg; 7,6 kg; 6,8 kg ...

f) het onveiligheidsgevoel bij bejaarden in onze stad

gegevens: klein, matig, groot ...

g) de maximale dagtemperatuur in Brussel in de maand mei

gegevens: 18 °C, 22 °C, 19 °C ...

h) het merk van smartphone bij de 18-jarigen van onze school

gegevens: Samsung, iPhone, Huawei ...

i) het aantal huisdieren in een gezin

gegevens: 0, 1, 2, 3 ...

j) het geboorteland van de allochtonen die nu in onze stad wonen

gegevens: Albanië, Italië, Rusland ...

14 Geef drie gegevens die je kunt verkrijgen bij de volgende onderzoeksonderwerpen. Benoem het soort gegevens zo nauwkeurig mogelijk.

a) de favoriete sport van de 15-jarigen van onze gemeente mogelijke gegevens:

soort gegevens:

b) de bakwijze van een steak mogelijke gegevens:

soort gegevens:

c) de snelheid van de wagens op de E313 tussen 22 uur en 23 uur mogelijke gegevens:

soort gegevens:

d) het aantal valpartijen per dag in de vorige Ronde van Frankrijk mogelijke gegevens:

soort gegevens:

e) de schoenmaat van de leerlingen van de klas mogelijke gegevens:

soort gegevens:

f) de hobby’s bij 16-jarigen mogelijke gegevens:

soort gegevens:

g) de massa van de pasgeboren baby’s in Vlaanderen mogelijke gegevens:

soort gegevens:

h) de mate waarin een sporter bijgelovig is mogelijke gegevens:

soort gegevens:

5.3 Statistisch onderzoek

5.3.1

Context

Als je een onderzoek wilt starten, moet je eerst goed nadenken over de context

Zo zul je bij een onderzoek naar ‘de tevredenheid over het openbaar vervoer’ moeten weten welke vragen je zult stellen, aan wie, hoe en wanneer.

Wat zijn de elementen van het onderzoek?

(Wie of wat wordt onderzocht?)

Wat zijn de kenmerken?

(Wat wordt er onderzocht bij de elementen?)

Met welk soort gegevens heb je te maken?

Wat wil je weten?

Waarom voer je het onderzoek?

de tevredenheid over het openbaar vervoer

Hoe, waar en met welke middelen ga je het onderzoek voeren?

5.3.2

Enquête

Om gegevens te verzamelen, neem je een enquête af.

Dat kan op heel wat manieren: schriftelijk, telefonisch, via het internet, een persoonlijk interview ...

De ondervraagde mensen noem je de respondenten

Het aantal mensen dat antwoordt, vormt de respons van de enquête.

5.3.3 Vraagstelling

Je moet goed nadenken over de vragen die je stelt in een enquête.

Ze moeten kort, eenvoudig, duidelijk en begrijpbaar zijn.

Open vragen

Geef je mening over de dienstverlening bij De Lijn.

De respondent mag het antwoord zelf formuleren.

©VANIN

De antwoorden kunnen soms heel verschillend zijn. Ze zijn soms moeilijk samen te vatten en moeilijk te beoordelen. Het is wel mogelijk dat je veel informatie krijgt.

Gesloten vragen

Met welk openbaar vervoer kun je het best vanuit je woonplaats de school bereiken?

❒ bus ❒ trein ❒ tram ❒ geen

De antwoordmogelijkheden zijn beperkt, gemakkelijk samen te vatten en te beoordelen.

Je moet goed nakijken of alle mogelijke antwoorden opgenomen zijn.

5.3.4 Steekproef en populatie

Om de kijkcijfers in Vlaanderen te bepalen, worden uiteraard niet alle tv-kijkers ondervraagd.

Dat is onmogelijk.

Er worden een aantal gezinnen uitgekozen die een schaalmodel vormen voor tv-kijkend Vlaanderen.

Het Centrum voor Informatie over de Media of CIM is een Belgische instelling die gegevens verzamelt en levert voor de reclamemarkt.

De tv-studie van CIM meet op een continue en gestandaardiseerde manier het televisiekijken in Vlaanderen. Daarvoor doet ze een beroep op een panel van 1 500 gezinnen.

Bij elk van die gezinnen is een kijkmeter geïnstalleerd.

Dat toestel registreert het kijkgedrag van de verschillende leden van het gezin en eventuele gasten in Vlaanderen en Brussel.

In totaal staat het panel voor 3 700 personen.

Op die manier hoopt men zicht te krijgen op alle kijkers van vier jaar en ouder.

©VANIN

1THUISVRT125/04/202420:15:0100:26:531.104.819

2HET7UUR-JOURNAALVRT125/04/202419:00:0300:45:29856.893 3NONKELSPLAY425/04/202421:16:1700:33:04783.260 4RESTAURANTMISVERSTANDVRT125/04/202420:44:5700:45:13744.680 5IEDEREENBEROEMDVRT125/04/202419:48:3000:20:32651.625 6EENMAAL,ANDERMAALVTM25/04/202420:44:2100:54:45636.286 7FAMILIEVTM25/04/202420:09:2100:24:53597.933 8NIEUWS19UVTMVTM25/04/202418:59:4700:56:21596.344 9BLOKKENVRT125/04/202418:30:2000:26:59590.056 10AMAIZEGWAUWVRT125/04/202421:32:4500:49:12413.297

Sinds januari 2016 bepaalt men het totaal van het rechtstreekse tv-kijken en het uitgestelde tv-kijken op de dag van uitzending tot zeven dagen na uitzending.

De totale verzameling ‘alle tv-kijkers in Vlaanderen’ noem je de populatie

De kijkers zijn de elementen

In veel gevallen heeft men niet de middelen, de tijd en/of het geld om een volledige populatie te onderzoeken. Daarom bekijkt men een deel van de populatie.

Een deel van de populatie noem je een steekproef.

De steekproef moet een voldoende omvang hebben en representatief zijn voor de populatie, zodat je de vaststellingen kunt veralgemenen.

Soorten steekproeven

100 willekeurig gekozen scholieren van 16 jaar vullen een enquête in over hun studeergewoontes.

In iedere Vlaamse provincie wordt aan 60 stedelingen en 40 plattelandbewoners gevraagd naar hun afkomst.

Elke tiende persoon van een lijst wordt ondervraagd over de vrijetijdsbesteding.

de aselecte steekproef de gerichte steekproef de systematische steekproef

Elk element van de steekproef is bij toeval gekozen en elk element heeft evenveel kans om gekozen te worden.

De populatie wordt onderverdeeld in deelgroepen. Binnen elke deelgroep doe je een aselecte steekproef.

De steekproefelementen worden uit de populatie gekozen volgens een bepaald systeem.

Bron: CIM

5.3.5 Wat er kan mislopen bij een onderzoek

Problemen met de vraagstelling

Bij een onderzoek is de vraagstelling heel belangrijk.

Een vraag moet duidelijk zijn en niet voor interpretatie vatbaar.

Wat is er verkeerd aan de volgende vraag?

Ben je voor of tegen de besparingspolitiek van de regering?

©VANIN

Problemen met de respons

De respons moet groot genoeg zijn. Anders zijn de conclusies niet betrouwbaar.

Een krant doet een onderzoek over ‘voor of tegen het gebruik van kernenergie’.

Uit de onlineantwoorden blijkt dat 70 % voor is.

Is dat cijfer betrouwbaar, als de respons maar 10 % bedraagt?

Problemen met de steekproef

De steekproef moet evenwichtig samengesteld zijn.

Anders krijg je vertekende resultaten.

Om het cultuurprogramma van een stad te bepalen, worden honderd inwoners tussen 30 en 40 jaar bevraagd.

Wat is er fout aan die steekproef?

REEKS A

15 Bepaal de populatie en het soort steekproef. Geef in het geval van een gerichte steekproef vier deelgroepen.

a) de bloedgroep van pasgeborenen in Vlaanderen

populatie:

steekproef:

b) de schoenmaat van de Vlaamse scholier populatie:

steekproef:

c) de favoriete voetbalploeg uit de Jupiler Pro League populatie:

steekproef:

d) de inhoud in ml van melkflessen populatie: steekproef:

e) het aantal uren per week dat de Brusselse scholier studeert populatie:

steekproef:

5.4 Categorische gegevens verwerken

5.4.1

Frequentietabel

Tim vroeg aan een aantal 16-jarigen naar het merk van hun droomauto:

De resultaten van zijn onderzoek heeft hij in een tabel gezet.

Het is niet altijd eenvoudig om uit zo’n tabel ruwe gegevens af te lezen.

Daarom verwerk je de gegevens in een frequentietabel x i n i f i

• Je plaatst de verschillende gegevens in de eerste kolom.

notatie: x i

• Je telt het aantal keer dat elk gegeven voorkomt en noteert dat in de tweede kolom. Dat is de absolute frequentie

notatie: n i

notatie: f i 7 7 60 ≈ 0,116 7 = 11,67 %

Definitie Absolute frequentie

De som van alle absolute frequenties is gelijk aan de omvang n van de steekproef.

• Als je de absolute frequentie deelt door de omvang van de steekproef, verkrijg je de relatieve frequentie

De absolute frequentie ni van het gegeven xi is het aantal keer dat het gegeven voorkomt.

Definitie Relatieve frequentie

De relatieve frequentie fi van het gegeven xifi = n n i is het quotiënt van de absolute frequentie ni en de omvang n van de steekproef.

Voorbeeld 1

Aan een aantal leerlingen werd gevraagd welke dag van de week zij het meest studeren.

Vervolledig de frequentietabel.

xi ni fi

maandag 9

dinsdag 23 woensdag 44

donderdag 29

vrijdag 15

zaterdag 7

zondag 3

• Op welke dag van de week studeren de leerlingen het meest?

• Hoeveel procent van de leerlingen studeert het meest op donderdag?

Voorbeeld 3

Voorbeeld 2

Aan 75 leerlingen werd gevraagd of ze wiskunde een belangrijk vak vinden.

Vervolledig de frequentietabel. xi ni fi

onbelangrijk 4 %

©VANIN

• Hoeveel procent van de leerlingen vindt wiskunde een belangrijk vak?

• Hoeveel leerlingen vinden wiskunde een heel belangrijk vak?

Aan een aantal 16-jarigen werd gevraagd wat ze het liefst doen tijdens hun vrije tijd. Ze konden kiezen tussen vier mogelijkheden. Niets doen was geen optie!

Maak een frequentietabel.

xi ni fi

sport lezen

• Hoeveel leerlingen werden ondervraagd?

• Wat doen de leerlingen het liefst tijdens hun vrije tijd?

• Hoeveel procent van de leerlingen heeft voor sport of lezen gekozen?

• Hoeveel leerlingen kozen niet voor tv-kijken? tv-kijken gamen

5.4.2 Grafische voorstellingen

Staafdiagram

Cirkeldiagram

• Op de horizontale as zie je de verschillende antwoordmogelijkheden.

• De hoogte van de verticale staafjes komt overeen met de (relatieve) frequentie.

©VANIN

• De hoekgrootte van de cirkelsectoren wordt bepaald door de relatieve frequenties. Daarvoor worden die met 360º vermenigvuldigd.

• Een legende toont de verschillende antwoordmogelijkheden.

Categorische gegevens verwerken met ICT

EXCEL

Frequentietabel

Open het bestand ‘DROOM.xlsx’ en ga als volgt te werk.

Staafdiagram

Open het bestand ‘DROOM.frequentietabel.xlsx’ en ga als volgt te werk.

• Selecteer de cellen met de absolute frequentieverdeling.

• Invoegen – Kolom – Gegroepeerde kolom.

• Rechtermuisklik op de horizontale as: Gegevens selecteren – Horizontale aslabels – Bewerken –Aslabelbereik: selecteer de cellen met de waarden van x i

• Grafiek verplaatsen naar een Nieuw Blad: ‘staafdiagram’.

• Grafiekelementen – Grafiektitel en Astitels: typ passende titels in.

• Grafiekelementen – Gegevenslabels – Einde, buitenkant.

De verdere opmaak doe je naar eigen voorkeur.

Cirkeldiagram

Open het bestand ‘DROOM.frequentietabel.xlsx’ en ga als volgt te werk.

• Selecteer de cellen met de relatieve frequentieverdeling.

• Invoegen – Cirkel – Eerste subtype (cirkel).

• Gegevens selecteren – Horizontale aslabels – Bewerken – Aslabelbereik: selecteer de cellen met de waarden van x i

• Grafiek verplaatsen naar een Nieuw Blad: ‘cirkeldiagram’.

• Grafiekelementen – Grafiektitel: typ een passende titel in.

• Gegevenslabels toevoegen.

De verdere opmaak doe je naar eigen voorkeur.

GEOGEBRA

Oefeningen

REEKS A

16 Via een steekproef peilde de directie naar de kwaliteit van de middagmalen op school. De leerlingen konden voor hun oordeel kiezen uit: zeer slecht − slecht − neutraal − lekker − zeer lekker. x

zeer slecht 5

©VANIN

a) Vervolledig de frequentietabel met de relatieve frequentie.

b) Teken met ICT:

• een staafdiagram voor de relatieve frequentie,

• een cirkeldiagram.

c) Hoeveel leerlingen vinden de kwaliteit van het middagmaal slecht of zeer slecht?

d) Hoeveel procent van de leerlingen vindt het eten niet zeer lekker?

17 Van 400 mensen werd de kleur van hun ogen genoteerd.

i n i f i

a) Vervolledig de frequentietabel met de absolute frequentie.

b) Teken met ICT:

• een staafdiagram voor de relatieve frequentie,

• een cirkeldiagram.

c) Hoeveel mensen hebben groene of bruine ogen?

18 Steeds meer mensen schakelen over naar een elektrische wagen. Het staafdiagram toont het aantal ingeschreven volledig elektrische auto’s in 2023.

Aantal elektrische wagens in België

Vlaanderen Brussel Wallonië totaal

©VANIN

a) Hoeveel elektrische wagens zijn er in Brussel ingeschreven?

b) Hoeveel procent van de elektrische wagens vind je in Wallonië?

c) Hoeveel procent van de elektrische wagens zijn er in Vlaanderen en Brussel samen ingeschreven?

d) Teken met ICT een cirkeldiagram.

19 In een Vlaamse stad zijn er 26 749 mensen die een sport beoefenen. Na onderzoek bleken de sportactiviteiten verdeeld zoals in het cirkeldiagram is weergegeven.

a) Vul de frequentietabel in.

b) Teken met ICT een staafdiagram voor de absolute frequentie.

c) Hoeveel ondervraagde mensen beoefenen geen voetbal en geen tennis?

20 Je voert een onderzoek uit naar het merk van smartphone dat de leerlingen van jouw klas bezitten.

a) Stel een frequentietabel op.

merk turven n i f i

b) Teken met ICT:

• een staafdiagram voor de absolute frequentie,

• een cirkeldiagram.

c) Welk merk komt het meest voor?

d) Hoeveel leerlingen van jouw klas hebben dat merk niet?

e) Hoeveel procent van de leerlingen heeft de twee meest voorkomende merken?

f) Denk je dat dit een goede steekproef is die je kunt veralgemenen naar alle leerlingen van een tweede graad in Vlaanderen?

Waarom (niet)?

21 Van 50 mensen werd de bloedgroep in een tabel genoteerd. A AB A O B

a) Maak een frequentietabel. bloedgroep n i f i A B AB O

b) Teken met ICT een cirkeldiagram.

c) Teken met ICT een staafdiagram voor de absolute frequentie.

d) Hoeveel mensen hebben bloedgroep A of B?

e) Hoeveel procent van de mensen heeft een andere bloedgroep dan A of O?

f) Hoeveel keer meer kans heb je om bloedgroep B te hebben dan bloedgroep AB?

22 Van 70 mensen werd de maat van hun T-shirts in een tabel genoteerd. L S M L

Maak een frequentietabel.

b) Teken met ICT een cirkeldiagram.

c) Teken met ICT een staafdiagram voor de relatieve frequentie.

d) Welke maat komt het meest voor?

e) Hoeveel procent van de mensen heeft een T-shirtmaat groter dan M?

f) Hoeveel mensen hebben een T-shirtmaat die kleiner is dan of gelijk aan L?

23 Aan 80 leerlingen wordt bij het invullen van het formulier voor de schooladministratie gevraagd hoe ze naar school komen: te voet (VO), per fiets (FI), met de bus (BU), met de trein (TR), met de wagen (WA), met de bromfiets (BF) of met een ander vervoermiddel (AN).

BU BF FI BF FI BU FI VO

BU BF FI BU FI VO BU FI

FI VO WA BF BU BF BU BU

TR BF FI BF FI BF BU WA

BU FI TR VO BU WA FI TR

FI BF FI BF BU BF WA FI

TR VO BU BF TR VO BU BU

FI BF FI BF AN FI FI BU

AN WA TR WA FI BF BU TR

FI BF TR BF BU VO FI BU

b) Teken met ICT een cirkeldiagram.

c) Teken met ICT een staafdiagram voor de relatieve frequentie.

a) Maak een frequentietabel. vervoermiddel n i f i VO FI BU TR WA BF AN

d) Welk vervoermiddel wordt het meest gekozen om naar school te komen?

e) Hoeveel procent van de leerlingen komt te voet of met de bus naar school?

f) Hoeveel leerlingen komen met de trein of met de fiets naar school?

g) Twee vervoermiddelen maken samen de helft van de steekproef uit. Welke?

24 Aan 60 mensen wordt gevraagd bij welke smartphoneoperator ze aangesloten zijn: Base (B), Orange (O), Proximus (P), Telenet (T) of andere (A).

a) Maak een frequentietabel. operator n i f i andere

b) Teken met ICT een cirkeldiagram.

c) Teken met ICT een staafdiagram voor de absolute frequentie.

d) Hoeveel mensen kiezen niet voor Proximus?

e) Hoeveel procent marktaandeel halen Base en Orange samen?

5.5.1

Niet-gegroepeerde numerieke gegevens verwerken

Frequentietabel

Op een toets wiskunde op 10 behaalden de leerlingen de onderstaande punten:

Naar analogie met de categorische gegevens kun je voor elk gegeven de absolute en relatieve frequentie bepalen.

Om te weten hoeveel leerlingen de helft niet behaalden, moet je de frequenties optellen van de eerste vijf gegevens.

Dat aantal is gelijk aan

2 + 3 + 2 + 4 + 3 = 14

Je zegt dat 14 de cumulatieve absolute frequentie is van het vijfde gegeven.

Je noteert die frequentie als cn 5

Definitie Cumulatieve absolute frequentie

De cumulatieve absolute frequentie cni van het gegeven xi is de som van alle absolute frequenties van het eerste tot en met het i-de gegeven: cni = n 1 + n 2 + . . . + ni

Weten dat er 14 leerlingen zijn die 4 op 10 of minder halen, zegt niet zoveel als je niet weet dat er 36 leerlingen de toets hebben gemaakt. 14 van de 36 leerlingen of 38,89 % noem je de cumulatieve relatieve frequentie van het vijfde gegeven. Je noteert die frequentie als cf 5

Definitie Cumulatieve relatieve frequentie

De cumulatieve relatieve frequentie cfi van het gegeven xi is het quotiënt van de cumulatieve absolute frequentie cni en cfi = cn n i de omvang n van de steekproef.

Hoeveel procent van de leerlingen behaalt minder dan 6 op 10?

Hoeveel leerlingen behalen meer dan 7 op 10?

Hoeveel procent van de leerlingen scoort 6 of 7 op 10?

Voorbeeld 1

Aan 50 leerlingen werd gevraagd hoeveel lestijden lichamelijke opvoeding zij het liefst zouden hebben in de loop van een week. Vervolledig de frequentietabel.

• Hoeveel leerlingen hebben het liefst juist drie lestijden lichamelijke opvoeding?

• Hoeveel leerlingen hebben het liefst meer dan drie lestijden lichamelijke opvoeding?

• Hoeveel procent verkiest hoogstens twee lestijden lichamelijke opvoeding?

• Hoeveel leerlingen verkiezen twee of drie lestijden lichamelijke opvoeding?

©VANIN

Voorbeeld 2

De eigenaar van een boekenwinkel noteerde op een dag het aantal verkochte strips per klant. Vervolledig de frequentietabel.

• Hoeveel klanten telde de eigenaar die dag?

• Hoeveel klanten kochten precies drie strips?

• Hoeveel procent van de klanten kocht precies twee strips?

• Hoeveel procent van de klanten kocht hoogstens drie strips?

• Hoeveel klanten kochten minstens drie strips?

5.5.2 Grafische voorstellingen

Staafdiagram

• De werkwijze is dezelfde als die van categorische gegevens.

• De hoogte van de verticale staven komt overeen met de (relatieve) frequentie.

©VANIN

• Bij niet-gegroepeerde numerieke gegevens worden de staven zo smal mogelijk getekend.

Lijndiagram

• Op de horizontale as zie je de verschillende waarden van x i , in stijgende volgorde.

• De verticale as bevat de frequenties.

• Een gebroken lijn verbindt de punten (x i , n i ) of (x i , f i ).

toets wiskunde punten op 10

Frequentietabel

Open het bestand ‘WISK.xlsx’ en ga als volgt te werk.

Staafdiagram

Open het bestand ‘WISK.frequentietabel.xlsx’ en ga als volgt te werk.

©VANIN

• Selecteer de cellen met de relatieve frequenties en werk naar analogie met paragraaf 5.4.3.

• Om de staven te versmallen:

• Rechtermuisklik op een van de staven.

• Gegevensreeks opmaken: breedte tussenruimte: kies voor 500 %.

Lijndiagram

Open het bestand ‘WISK.frequentietabel.xlsx’ en ga als volgt te werk.

• Selecteer de cellen met de absolute frequentieverdeling.

• Invoegen – 2D-lijn – Lijn met markeringen.

• Gegevens selecteren – Horizontale aslabels – Bewerken – Aslabelbereik: selecteer de cellen met de waarden van x i

• Grafiek verplaatsen naar een Nieuw Blad: ‘lijndiagram’.

• Grafiekelementen – Grafiektitel en Astitels: typ passende titels in.

• De primaire maatstrepen van de horizontale as zet je op de juiste plaats: As opmaken – Aspositie: op maatstreepjes.

De verdere opmaak doe je naar eigen voorkeur.

GEOGEBRA

REEKS A

25 Op een dag in de soldenperiode wordt op straat aan een aantal mensen gevraagd naar het aantal gekochte kledingstukken.

a) Maak een frequentietabel.

b) Hoeveel mensen werden ondervraagd?

c) Hoeveel mensen kochten hoogstens vier kledingstukken?

d) Hoeveel procent van de mensen kocht minstens drie kledingstukken?

e) Hoeveel procent van de mensen kocht twee of drie kledingstukken?

26 In een jeugdbeweging werd de hemdsmaat van een aantal jongens genoteerd.

a) Maak een frequentietabel.

b) Van hoeveel jongens werd de hemdsmaat genoteerd?

c) Hoeveel jongens hebben hoogstens 38 als hemdsmaat?

d) Hoeveel jongens hebben een hemdsmaat kleiner dan 40?

e) Hoeveel procent van de jongens heeft een hemdsmaat groter dan 39?

f) Hoeveel procent van de jongens heeft een hemdsmaat 38 of 39?

27 Tijdens het kamp van de jeugdbeweging wordt naar de leeftijd van de deelnemers gevraagd.

leeftijd deelnemers kamp

a) Maak een frequentietabel.

x i n i cn i

b) Hoeveel deelnemers van het kamp zijn 10 jaar of jonger?

c) Van welke leeftijden zijn er meer dan 10 deelnemers?

d) Teken met ICT een lijndiagram voor de absolute frequentie.

28 Aan de leerlingen van een klas van het derde jaar werd gevraagd hoeveel stukken fruit ze per dag eten.

a) Maak een frequentietabel. x i n i f i cn i cf i

b) Hoeveel leerlingen telt de klas van het derde jaar?

c) Hoeveel leerlingen eten minder dan vier stukken fruit per dag?

d) Hoeveel procent van de leerlingen eet meer dan drie stukken fruit per dag?

e) Teken met ICT een staafdiagram voor de relatieve frequentie.

29 Aan de leerlingen van het derde jaar wordt gevraagd hoeveel Nederlandstalige boeken ze dit jaar al gelezen hebben.

a) Maak een frequentietabel.

b) Teken met ICT:

• een staafdiagram voor de absolute frequentie,

• een lijndiagram voor de relatieve frequentie.

c) Hoeveel leerlingen hebben hoogstens vier boeken gelezen?

d) Hoeveel procent van de leerlingen las drie of vier boeken?

5.6.1 Het gemiddelde

Definitie (Rekenkundig) gemiddelde

Het gemiddelde van een rij getallen is de som van die getallen gedeeld door het aantal getallen.

Formule

Voorbeeld

Het gemiddelde van de rij 2, 4, 2, 4, 7, 4, 4, 9: x = 2+4+2+4+7+4+4+ 9 8 = 36 8 = 4,5

Afspraak

Je rondt het gemiddelde af op één cijfer meer na de komma dan de gegevens.

Opmerkingen

• Het aantal leerlingen dat slechter scoort

dan het gemiddelde is

Verdeelt het gemiddelde de resultaten in twee even grote groepen?

Het gemiddelde heeft de fysische betekenis van een evenwichtspunt.

Anders gezegd: als je alle punten in een pot doet en daarna gelijk verdeelt onder alle leerlingen, dan krijgt elke leerling het gemiddelde.

• Vervang je het resultaat 9 door 50, dan wordt het gemiddelde Dat illustreert dat één resultaat het rekenkundig gemiddelde sterk kan beïnvloeden.

EXCEL

Je gebruikt de Excelfunctie ‘gemiddelde’.

Selecteer de cellen met de gegevens waarvan je het gemiddelde wilt berekenen.

Druk op enter en rond af op één cijfer meer na de komma dan de gegevens.

GEOGEBRA

5.6.2 Het gemiddelde berekenen uit een frequentietabel

De rij 2, 4, 2, 4, 7, 4, 4, 9 kun je ook met een frequentietabel weergeven:

Het gemiddelde kun je dan als volgt berekenen:

©VANIN

Daarbij is k het aantal verschillende gegevens en n = n1 + n2 + … + nk

Voorbeeld

De punten voor een toets wiskunde in het vierde jaar vind je in de tabel.

n i ? x i x =

Niet iedereen kan boven het gemiddelde scoren.

5.6.3 De mediaan

In de gerangschikte rij van 9 getallen 0, 2, 3, 3, 6, 6, 6, 6, 7 is het middelste getal het getal uit die rij. Dat getal noem je de mediaan.

In de gerangschikte rij van 10 getallen 0, 2, 3, 3, 3, 5, 6, 6, 6, 7 zijn er twee middelste getallen, het en het getal uit die rij.

Het gemiddelde van die twee getallen, dus , is de mediaan.

Definitie Mediaan

De mediaan Me van een gerangschikte rij van n getallen is het getal met rangorde n +1 2

De mediaan verdeelt een gegevensrij in twee delen met evenveel elementen. De helft van de gegevens is hoogstens de mediaan, de andere helft minstens de mediaan.

EXCEL

GEOGEBRA

Je gebruikt de Excelfunctie ‘mediaan’.

Selecteer de cellen met de gegevens waarvan je de mediaan wilt bepalen.

De gegevens moeten niet gerangschikt zijn.

5.6.4 De mediaan bepalen uit een frequentietabel

Om de mediaan te bepalen van gegevens die in een frequentietabel gegeven worden, gebruik je de cumulatieve absolute frequentie.

Voorbeeld

De mediaan van getallen is het getal met rangorde

Dus Me =

Betekenis: de helft van de gegevens is hoogstens 5, de andere helft is minstens 5.

5.6.5 De modus

Definitie Modus

De modus Mo is het gegeven met de grootste frequentie.

Voorbeeld

5.6.6 Voor- en nadelen van gemiddelde en mediaan

• Het gemiddelde houdt rekening met alle gegevens. Die centrummaat is heel geschikt bij wetenschappelijk onderzoek.

De tabel toont de punten van een klas van 12 leerlingen voor een eenvoudige toets Frans op 10 punten.

9 10 9 8 9 10 9 10 9 0 10 9 x =

Besluit

©VANIN

Hoeveel leerlingen scoren beter dan het gemiddelde?

Verwijder de ‘uitschieter’ en bereken opnieuw het gemiddelde.

• Bepaal de mediaan voor de punten Frans in de bovenstaande tabel.

Me =

De mediaan is gedefinieerd als het middelste gegeven en is dus niet vatbaar voor uitschieters.

• Dezelfde klas van 12 leerlingen maakte ook een toets wiskunde op 10 punten. Je ziet de resultaten in de onderstaande tabel.

Welke centrummaat geeft het best weer dat in die klas bijna de helft van de leerlingen heel goed heeft gescoord?

Het gemiddelde houdt rekening met alle gegevens, maar is vatbaar voor uitschieters. De mediaan ligt altijd in het midden, maar houdt enkel rekening met de volgorde van de gegevens.

Rond 1980 verwierpen bepaalde natuurvorsers het ontstaan van een gat in de ozonlaag van de atmosfeer boven de Zuidpool op basis van satellietgegevens. Later onderzoek bracht aan het licht dat de ozonmetingen boven de Zuidpool zo laag waren dat de gebruikte computersoftware ze systematisch als fout verwierp. Het systematisch verwijderen van uitschieters is geen goede wetenschappelijke onderzoekshouding.

REEKS A

30 Alle leerlingen van het derde jaar van een school kregen dezelfde oriënterende toets wiskunde. De tabel toont de punten op 20.

©VANIN

i

a) Bepaal de mediaan.

b) Geef de betekenis van de mediaan.

c) Bereken het gemiddelde.

d) Hoeveel procent van de leerlingen haalde meer dan het gemiddelde?

31 Aan een aantal Vlaamse gezinnen werd gevraagd naar het aantal kinderen.

i

a) Bepaal de mediaan.

b) Geef de betekenis van de mediaan.

c) Bereken het gemiddelde.

d) Geef de betekenis van het gemiddelde.

32 Bij een aantal jongeren werd de schoenmaat genoteerd.

x i 36 37 38 39 40 41 42 43

n i 17 12 11 16 15 10 28 16

cn i

a) De helft van de jongeren heeft een schoenmaat kleiner dan

b) Bereken het gemiddelde.

c) Hoeveel procent van de jongeren heeft een schoenmaat kleiner dan het gemiddelde?

33 Aan 85 leerlingen van de tweede graad werd gevraagd hoeveel smartphones ze tot nu toe hadden. De resultaten staan in de frequentietabel. x i 0 1 2 3 4 5 6 n i 1 21 43 10 8 0 2

cn i

a) Bereken het gemiddelde.

b) Bepaal de mediaan.

c) Geef de betekenis van de mediaan.

34 De monitoren van de speelpleinwerking van het gewest Leuven houden een evaluatiedag. Ze noteren hun verbruik van blikjes of flesjes frisdrank.

cn i

a) Bereken het gemiddelde.

b) Bepaal de mediaan.

c) Hoeveel blikjes of flesjes frisdrank zouden alle 542 monitoren van het Vlaamse Gewest samen consumeren?

d) Hoeveel monitoren consumeerden meer frisdrankjes dan het gemiddelde?

35 Van een aantal worpen met twee dobbelstenen werd de som van het aantal ogen genoteerd.

a) Maak een frequentietabel.

b) Teken met ICT een staafdiagram voor de relatieve frequentie.

c) Wat is de meest voorkomende som?

Was dat te verwachten? Waarom (niet)?

d) Bij hoeveel procent van de worpen is de som van het aantal ogen meer dan 9?

e) De helft van de worpen leverde minstens ogen op.

f) Bereken het gemiddelde en geef de betekenis.

36 In het derde jaar van een school wordt een dictee Nederlands afgenomen. De tabel toont hoeveel fouten elk van de leerlingen heeft gemaakt.

a) Maak een frequentietabel.

b) Hoeveel leerlingen deden mee aan het dictee?

c) Teken met ICT een lijndiagram voor de absolute frequentie.

d) Hoeveel leerlingen maakten hoogstens 4 fouten?

e) Welk deel van de leerlingen maakte meer dan 6 fouten?

f) Bepaal de mediaan en geef de betekenis.

g) Bereken het gemiddelde aantal fouten.

37 Gedurende drie maanden werd een verscherpte controle op zwartrijden (rijden zonder geldig vervoerbewijs) uitgevoerd op de trein Oostende – Brussel. Het aantal betrapte zwartrijders per dag vind je in de onderstaande tabel.

a) Maak een frequentietabel.

b) Teken met ICT een staafdiagram voor de absolute frequentie.

c) Teken met ICT een lijndiagram voor de relatieve frequentie.

d) Hoeveel dagen waren er minder dan drie zwartrijders?

e) Hoeveel procent van de dagen was er geen enkele zwartrijder?

f) Hoeveel dagen hadden er vijf of meer mensen geen geldig vervoerbewijs?

g) Als een boete voor zwartrijden 75 euro bedraagt, wat is dan de ‘opbrengst’ bij die verscherpte controle?

38 Aan 45 jongeren werd gevraagd hoeveel dagen per week ze sporten. x i n i f i cn i cf i 0 4

©VANIN

2

a) Vul de frequentietabel verder aan.

b) Hoeveel procent van de jongeren sport vier dagen in een week?

c) Hoeveel jongeren sporten hoogstens drie dagen in een week?

d) De helft van de jongeren sport minstens dagen in een week.

e) Bepaal de modus.

f) Bereken het gemiddelde.

39 De resultaten op 10 voor een toets worden cumulatief voorgesteld.

a) Bepaal de mediaan.

b) Geef de betekenis van de mediaan.

c) Bepaal de modus.

d) Als alle leerlingen evenveel punten hadden, hoeveel zou dat dan zijn?

5.1 Inleiding

Een procentpunt is een punt op een procentenschaal en is het absolute verschil tussen twee waarden uitgedrukt in procenten. KUNNEN

Uitleggen waarom bepaalde statistieken misleidend zijn.

Het verschil tussen de begrippen ‘procent’ en ‘procentpunt’ uitleggen.

5.2 Soorten gegevens

©VANIN

KENNEN

Categorische gegevens zijn gegevens die een hoedanigheid van een kenmerk weergeven.

Geordende categorische gegevens hebben een natuurlijke ordening.

Niet-geordende categorische gegevens hebben geen natuurlijke ordening.

Numerieke gegevens zijn gegevens die het resultaat zijn van tellingen en metingen.

Discrete numerieke gegevens hebben slechts een beperkt aantal waarden.

Continue numerieke gegevens zijn reële waarden tussen bepaalde grenzen.

KUNNEN

Een onderscheid maken tussen elementen, kenmerken en gegevens.

Een onderscheid maken tussen categorische en numerieke gegevens.

Een onderscheid maken tussen geordende en niet-geordende categorische gegevens.

Een onderscheid maken tussen discrete en continue numerieke gegevens.

5.3 Statistisch onderzoek

KENNEN

De populatie is de verzameling van alle elementen van een statistisch onderzoek.

Een deel van de populatie noem je een steekproef.

KUNNEN

Een omschrijving geven van de onderzoeksvraag, de populatie en de steekproef.

Een onderscheid maken tussen een aselecte, een gerichte en een systematische steekproef.

Problemen in verband met de steekproef en de vraagstelling omschrijven.

5.4 Categorische gegevens verwerken

KENNEN

De absolute frequentie n i van het gegeven x i is het aantal keer dat dat gegeven voorkomt.

De relatieve frequentie f i van het gegeven x i is het quotiënt van de absolute frequentie n i en de omvang n van de steekproef: fi = n i n

KUNNEN

De frequenties van categorische gegevens grafisch voorstellen en die voorstelling lezen en interpreteren.

ICT gebruiken om een frequentietabel op te stellen en die grafisch voor te stellen.

5.5 Niet-gegroepeerde numerieke gegevens verwerken voor de leerling voor de leerkracht

KENNEN

De cumulatieve absolute frequentie cn i van het gegeven x i is de som van alle frequenties van het eerste tot en met het i-de gegeven: cn i = n1 + n2 + + ni

De cumulatieve relatieve frequentie cf i van het gegeven x i is het quotiënt van de cumulatieve absolute frequentie cn i en de omvang n van de steekproef: cfi = cn i n

KUNNEN

Een frequentietabel opstellen die de absolute frequentie, de relatieve frequentie, de cumulatieve absolute frequentie en de cumulatieve relatieve frequentie bevat.

De enkelvoudige frequenties van niet-gegroepeerde numerieke gegevens grafisch voorstellen en die voorstelling lezen en interpreteren.

De cumulatieve frequenties van niet-gegroepeerde numerieke gegevens grafisch voorstellen.

ICT gebruiken om een frequentietabel op te stellen en die grafisch voor te stellen.

5.6 Centrummaten

©VANIN

KENNEN

Het gemiddelde van een rij getallen is de som van die getallen gedeeld door het aantal getallen:

Daarbij is k het aantal verschillende gegevens en n = n1 + n2 + … + nk

De mediaan Me van een gerangschikte rij van n getallen is het getal met rangorde n + 1 2

De modus Mo is het gegeven met de grootste frequentie.

KUNNEN

De centrummaten gemiddelde, mediaan en modus bepalen en de informatie die ze bieden, interpreteren.

Pienter problemen oplossen

Welke heuristiek(en) gebruik je om de onderstaande problemen op te lossen?

❑ concreet materiaal

❑ schets

❑ schema/tabel

❑ vereenvoudig

❑ gok verstandig

❑ filter

❑ patroon

❑ kennis

❑ logisch nadenken

❑

©VANIN

1. Een vierkant wordt verdeeld in zestien velden (vier rijen en vier kolommen).

Je moet het vierkant inkleuren en daarbij rekening houden met deze voorwaarden:

• Vier velden moeten blauw zijn.

• Drie velden zijn rood.

• Drie velden zijn wit.

• Drie velden kleuren groen.

• Geen enkele kleur mag meer dan één keer voorkomen in één kolom, één rij en één diagonaal.

Kleur het vierkant in.

Bron: puzzlesite.nl

2. Pa wil iets doen aan zijn buikje en besluit om elke dag sit-ups te doen. Zijn plan bestaat erin dat hij de eerste dag tien sit-ups doet, de tweede dag twaalf, de derde dag veertien … Ma belooft een etentje op de dag dat pa honderd sit-ups kan doen.

Hoelang moet hij wachten op dat etentje?

HOOFDSTUK 6 I GELIJKVORMIGHEID

6.1 Gelijkvormige figuren

6.2 Overeenkomstige hoeken en zijden

6.3 Gelijkvormigheidsfactor

6.4 Omtrek, oppervlakte en volume bij gelijkvormige figuren

6.5 Gelijkvormige driehoeken

6.6 De stelling van Thales

©VANIN

6.1.1 Gelijkvormige vlakke figuren

figuur 1

figuur 2

figuur 3

figuur 4

figuur 5

Vergelijk de logo's met elkaar. Vink de juiste beweringen aan.

figuur 2 ten opzichte van figuur 1

figuur 3 ten opzichte van figuur 1

figuur 4 ten opzichte van figuur 1

figuur 5 ten opzichte van figuur 1

figuur 6

figuur 6 ten opzichte van figuur 1

❒  zelfde vorm ❒  zelfde vorm ❒  zelfde vorm ❒  zelfde vorm ❒  zelfde vorm

❒  vergroting ❒  vergroting ❒  vergroting ❒  vergroting ❒  vergroting

❒  verkleining ❒  verkleining ❒  verkleining ❒  verkleining ❒  verkleining

❒  congruent ❒  congruent ❒  congruent ❒  congruent ❒  congruent

Welke figuren zijn een schaalmodel van figuur 1?

Een pantograaf is een hulpmiddel bij het maken van tekeningen. Het is een verstelbaar parallellogram van hout, metaal of plastic. Een pantograaf wordt gebruikt om afbeeldingen vergroot of verkleind over te nemen.

Je volgt de omtrekken van de na te tekenen afbeelding met een stift. Een potlood, aan het andere uiteinde van het toestel, tekent de figuur vergroot of verkleind na.

6.1.2 Gelijkvormige ruimtefiguren

figuur 1

figuur 2

figuur 4

Vergelijk de balken met elkaar. Vink de juiste bewering(en) aan.

figuur 2 ten opzichte van figuur 1

figuur 3 ten opzichte van figuur 1

figuur 4 ten opzichte van figuur 1

figuur 5

figuur 3

figuur 5 ten opzichte van figuur 1

❒  zelfde vorm ❒  zelfde vorm ❒  zelfde vorm ❒  zelfde vorm

❒  vergroting ❒  vergroting ❒  vergroting ❒  vergroting

❒  verkleining ❒  verkleining ❒  verkleining ❒  verkleining

❒  congruent ❒  congruent ❒  congruent ❒  congruent

Welke figuren zijn gelijkvormig met figuur 1?

©VANIN

6.1.3 Gelijkvormige figuren

Twee figuren zijn gelijkvormig als de ene figuur een schaalmodel is van de andere.

Notatie:

Oefeningen

REEKS A

1 Duid alle gelijkvormige figuren aan. Welke namen van muziekinstrumenten kun je vormen?

©VANIN

Aangeduide letters: Niet-aangeduide letters:

2 Met computertechnieken kun je beelden vervormen. Welke beeldopname is gelijkvormig met de originele beeldopname?

3 Welk venster is gelijkvormig met de deur van het huis?

Antwoord:

4 Vink de meest passende benaming aan. a) c)

©VANIN

❒ gelijkvormig

❒ congruent

❒ geen van beide

❒ gelijkvormig

❒ congruent

❒ geen van beide b) d)

❒ gelijkvormig

❒ congruent

❒ geen van beide

❒ gelijkvormig

❒ congruent

❒ geen van beide

5 Van welke ruimtefiguren zijn het grondvlak en het bovenvlak gelijkvormige figuren? a) b) c) d)

6 Zijn de Daltons gelijkvormige figuren? Verklaar je antwoord.

7 Juist of fout? Zet een vinkje.

a) Alle vierkanten zijn gelijkvormig

b) Alle rechthoeken zijn gelijkvormig.

c) Alle cirkels zijn gelijkvormig.

d) Alle gelijkzijdige driehoeken zijn gelijkvormig.

e) Alle gelijkbenige driehoeken zijn gelijkvormig.

f) Alle ruiten zijn gelijkvormig.

g) Alle rechthoekige driehoeken zijn gelijkvormig.

8 Welke rode balk is gelijkvormig met de blauwe balk? Zet een vinkje.

juist fout

9 Zet een vinkje naast elke juiste uitspraak.

a) Alle balken zijn gelijkvormig. ❒

b) Sommige kegels zijn gelijkvormig. ❒

c) Alle cilinders zijn gelijkvormig. ❒

d) Sommige piramides zijn gelijkvormig. ❒

e) Alle kubussen zijn gelijkvormig. ❒

f) Niet alle bollen zijn gelijkvormig. ❒

10 Gegeven zijn de lengtes in werkelijkheid. Welke gele cilinder is gelijkvormig met de groene cilinder? Zet een vinkje.

11 Gelijkvormige vierhoeken in ruimtefiguren.

a) Welk soort ruimtefiguur herken je?

b) Welke van de gekleurde vlakke figuren zijn gelijkvormig?

c) Hoe liggen de gelijkvormige figuren ten opzichte van elkaar?

12 Verdeel de figuren in twee gelijkvormige figuren.

13 Teken een doorsnede van de ruimtefiguur die het punt A bevat en gelijkvormig is met de doorsnede bepaald door het vlak a.

6.2 Overeenkomstige hoeken en zijden

GEOGEBRA

De twee vierhoeken zijn gelijkvormig. Verbind de overeenkomstige hoeken.

©VANIN

Bekijk de overeenkomstige hoeken.

Wat stel je vast?

Verbind de overeenkomstige zijden.

Bekijk de overeenkomstige zijden.

Bepaal de verhouding van de lengten van de overeenkomstige zijden.

verhouding

Vaststelling In gelijkvormige figuren zijn overeenkomstige hoeken even groot.

Opmerking

Wat stel je vast?

In gelijkvormige figuren zijn overeenkomstige zijden evenredig.

Noteer de figuren volgens de overeenkomstige hoeken: vierhoek vierhoek

Oefeningen

REEKS A

14 Verbind de overeenkomstige hoeken en zijden bij de gelijkvormige vijfhoeken.

©VANIN

15 Noteer de gelijkvormige figuren. Benoem ze volgens afspraak.

figuur is gelijkvormig met figuur

REEKS B

16 nABC en nEFG zijn gelijkvormig. |AB | = 3 cm, |BC | = 4 cm en |AC | = 5 cm. |EF | = 2,5 cm, |FG | = 1,5 cm en |EG | = 2 cm.

a) Verbind de overeenkomstige zijden.

[AB]

[EF] [BC]

b) Bepaal de verhouding van de lengten van de overeenkomstige zijden.

[FG] [AC]

[EG]

17 nABC en nPQR zijn gelijkvormig. |AB | = 2 cm, |BC | = 1,4 cm en |AC | = 3 cm. |QR | = 4,5 cm, |PR | = 3 cm en |PQ | = 2,1 cm.

a) Verbind de overeenkomstige zijden.

[AB] • • [QR]

[BC] • • [PR]

[AC] • • [PQ]

18 Noteer de gelijkvormige rechthoeken.

b) Bepaal de verhouding van de lengten van de overeenkomstige zijden.

figuur is gelijkvormig met figuur

REEKS C

19 Bepaal zonder te meten de lengte van de ontbrekende zijde van de gelijkvormige rechthoek.

©VANIN

6.3 Gelijkvormigheidsfactor

6.3.1

De gelijkvormigheidsfactor

figuur 1

figuur 2

Figuur 2 is gelijkvormig met figuur 1. Bepaal de verhouding van de lengten van de overeenkomstige zijden van figuur 2 ten opzichte van figuur 1. verhoudingen

©VANIN

De verhouding van de lengten van de overeenkomstige zijden van twee gelijkvormige figuren is constant. Die constante noem je de gelijkvormigheidsfactor

Notatie: g = 1 2

figuur 2

figuur 3

figuur 4

Bepaal de gelijkvormigheidsfactor van F2 ten opzichte van F1 F3 ten opzichte van F1 F4 ten opzichte van F1

een vergroting

een verkleining

een congruente figuur

een vergroting

een verkleining

een congruente figuur

een vergroting

een verkleining

een congruente figuur

Besluit

• Bij een verkleining is de gelijkvormigheidsfactor

• Bij een vergroting is de gelijkvormigheidsfactor

• Hoe noem je figuren waarvan de gelijkvormigheidsfactor gelijk is aan 1?

6.3.2 Gelijkvormigheidsfactor en schaal

Een raam op een plan en het raam in werkelijkheid zijn gelijkvormige figuren.

Op een plan lees je de werkelijke afmetingen en de gehanteerde schaal. De schaal is de gelijkvormigheidsfactor van het getekende raam ten opzichte van het werkelijke raam.

delen door de schaal afmeting op tekening werkelijke afmeting vermenigvuldigen met de schaal

©VANIN

Bereken de werkelijke afmetingen van het raam.

Besluit ‘Gelijkvormigheidsfactor’ en ‘schaal’ hebben dezelfde betekenis. Madurodam is een miniatuurstad in Den Haag (Nederland). Alle bouwsels zijn er op schaal 1 25 nagemaakt. Het park bestaat sinds 1952.

Er zijn gebouwen uit historische binnensteden, moderne woonwijken, havengebieden, een luchthaven, kanalen, wegen, landerijen, natuurgebieden en meer.

Oefeningen

REEKS A

20 Duidt de gelijkvormigheidsfactor een vergroting, een verkleining of een congruente figuur aan? g

a) 3

b) 0,25

©VANIN

21 Bepaal de gelijkvormigheidsfactor van vierkant 2 ten opzichte van vierkant 1.

= g = g =

22 Hieronder vind je een kaart op schaal 1 : 5 000 000. Bepaal de werkelijke afstanden.

op tekening in mm in werkelijkheid in km

a) Brussel – Antwerpen

b) Kortrijk – Gent

c) Luik – Hasselt

d) Brugge – Bergen

e) Namen – Bastenaken

23 Bepaal de gelijkvormigheidsfactor van een figuur met zijde [AB] ten opzichte van een figuur met overeenkomstige zijde [AB]. |AB | |AB| verkleining congruent vergroting <

24 Is nABC een vergroting of verkleining van nABC ? Vul daarna de afmetingen van nABC aan. g vergroting verkleining |AB | |

25 Bepaal de gelijkvormigheidsfactor ten opzichte van balk 1. balk 1 balk 2 balk 3 balk 4 g = g = g =

26 Werk de vierhoek ABCD verder af zodat hij gelijkvormig is met de vierhoek ABCD. Wat is de gelijkvormigheidsfactor?

Gelijkvormigheidsfactor: g =

27 Teken een figuur die gelijkvormig is aan de gegeven figuur. Gebruik de gegeven gelijkvormigheidsfactor.

a) g = 4 3 b) g = 3 4

28 Noteer voor de gegeven schaallijnen de gelijkvormigheidsfactor van de tekening op schaal ten opzichte van de werkelijkheid.

b)

29 Madurodam is een Nederlandse miniatuurstad in Den Haag. Alle maquettes in Madurodam zijn op schaal 1 25

a) Het Koninklijk Paleis is een paleis op de Dam in de binnenstad van Amsterdam. Als je weet dat het paleis 52 m hoog is, hoe hoog is het schaalmodel in Madurodam dan?

b) De Erasmusbrug is een brug over de Nieuwe Maas in de haven van Rotterdam. Het schaalmodel in Madurodam heeft een hoogte van 5,56 m. Wat is de werkelijke hoogte van de Erasmusbrug?

©VANIN

c) Een vliegtuig van de Nederlandse luchtvaartmaatschappij KLM meet 2,8 m in Madurodam. Hoe lang is dat vliegtuig in werkelijkheid?

d) Hoe groot zou een maquette van jou in Madurodam zijn?

• Werkelijke lengte: cm

• Lengte in Madurodam: cm

30 Noteer voor het stratenplan de gelijkvormigheidsfactor ten opzichte van de werkelijkheid. Bepaal ook de werkelijke lengte van de Dweersstraat.

a) Gelijkvormigheidsfactor:

b) Werkelijke lengte van de Dweersstraat:

31 In Ieper kun je de Menenpoort, die 40 m breed is, bezichtigen en er dagelijks luisteren naar de Last Post. Blinden en slechtzienden kunnen op een miniatuurversie voelen hoe de Menenpoort eruitziet. De miniatuurversie werd gemaakt in brons en is 80 cm breed. Wat is de schaal van de miniatuurversie?

Antwoord:

32 Bij sommige beeldschermen is de verhouding tussen de breedte en de hoogte 4 : 3. Bij andere beeldschermen is die verhouding 16 : 9.

a) Zijn beide beeldschermen gelijkvormig? Verklaar je antwoord.

❒  ja ❒ nee

b) Bereken in beide gevallen de breedte van het beeldscherm met een hoogte van 36 cm.

©VANIN

REEKS C

33 Om een nieuwe vloer te leggen, gebruikt de tegellegger vier soorten tegels. De tegels worden in een bepaald patroon gelegd, zoals afgebeeld.

a) Noteer voor elke soort tegel de afmeting op de tekening van het legpatroon.

b) Welke tegelsoorten zijn gelijkvormig?

c) Bepaal de gelijkvormigheidsfactor(en) van de gelijkvormige tegels.

34 Op het grondplan hieronder staan de exacte afmetingen in cm vermeld. Volgens welke schaal werd het grondplan getekend? Welke afmeting op de tekening klopt niet met de verkregen schaal?

©VANIN

Een figuur schalen

Heb je een figuur ingevoegd in een Worddocument, dan kun je via Grootte en positie – Formaat die figuur schalen. Let er daarbij op dat de hoogte-breedteverhouding altijd vergrendeld is.

35 Een figuur van 45 mm bij 30 mm wordt in een Worddocument ingevoegd. Je schaalt de figuur, zodat de afmetingen 54 mm bij 36 mm worden. Bepaal de schaal in procent.

6.4.1 Formularium

Omtrek en oppervlakte van vlakke figuren

rechthoek

©VANIN

Volume van ruimtefiguren

6.4.2 Gelijkvormigheidsfactor

Een kubus wordt vergroot met gelijkvormigheidsfactor 4.

Bereken de omtrek (P) van beide voorvlakken.

Formule: P =

Bereken de oppervlakte (A) van beide voorvlakken.

Formule: A =

Bereken het volume (V ) van beide kubussen.

Formule: V =

Bereken de verhouding. Bereken de verhouding. Bereken de verhouding.

omtrek F2

omtrek F1 =

oppervlakte F2 oppervlakte F1

Vergelijk die waarde met g De verhouding is

Vergelijk die waarde met g De verhouding is

Vergelijk die waarde met g De verhouding is

Bij een verkleining of vergroting met factor g wordt de omtrek vermenigvuldigd met factor

Bij een verkleining of vergroting met factor g wordt de oppervlakte vermenigvuldigd met factor

Bij een verkleining of vergroting met factor g wordt het volume vermenigvuldigd met factor

Oefeningen

REEKS A

36 Rechthoek EFGH is gelijkvormig met rechthoek ABCD met gelijkvormigheidsfactor g Vul de ontbrekende afmetingen in de tabel in. g

rechthoek ABCD

rechthoek EFGH

37 De omtrek van het fietswiel van Liezes fiets bedraagt 207 cm.

De omtrek van het fietswiel van de fiets van kleine Jens is 138 cm.

Bepaal de gelijkvormigheidsfactor van het fietswiel van Jens ten opzichte van dat van Lieze.

©VANIN

Antwoord:

38 De omtrek van een minivoetbalveld is 85 meter.

De gelijkvormigheidsfactor van het grote voetbalveld ten opzichte van het minivoetbalveld is 4. Wat is de omtrek van het grote voetbalveld?

REEKS B

39 Een terras is samengesteld uit twee soorten vloertegels die gelijkvormig zijn.

Een tegel van de eerste soort heeft een oppervlakte van 9 dm2

De gelijkvormigheidsfactor van de tweede soort tegels ten opzichte van de eerste soort bedraagt 1 2 .

Bepaal de oppervlakte van een tegel van de tweede soort.

40 De vloer van onze klas en de vloer van de eetzaal zijn gelijkvormig. De vloer van de klas meet 6 m bij 5 m.

Als je de vloer met gelijkvormigheidsfactor 3 vergroot, dan is hij even groot als die van de eetzaal. Bepaal op twee manieren de oppervlakte van de eetzaal.

Lengte eetzaal:

Breedte eetzaal:

Aeetzaal :

Aklas :

Aeetzaal :

41 Een balkvormig flatgebouw met een breedte van 12,5 m, een lengte van 25 m en een hoogte van 50 m wordt nagebouwd op schaal 1 : 25. Vul de tabel verder aan.

flatgebouw in werkelijkheid flatgebouw op schaal lengte breedte hoogte volume

42 Het volume van een balk is 40 cm3.

De gelijkvormigheidsfactor van een andere balk ten opzichte van de gegeven balk is 3. Wat is het volume van de gelijkvormige balk?

©VANIN

43 Het grootzeil van een zeilboot is een rechthoekige driehoek met rechthoekszijden van 9 m en 4 m. Bereken de oppervlakte van het zeil van een miniatuurversie van de zeilboot op schaal 1 : 50.

Antwoord:

44 Een architect tekent het plan van een huis op schaal 1 : 50. Bereken de oppervlakte van het raam op het plan. Bepaal je antwoord op 0,01 cm2 nauwkeurig. a)

b)

©VANIN

45 Een miniatuur van een Egyptische piramide heeft een vierkant grondvlak met een zijde van 184 mm en is 116 mm hoog. De schaal van die miniatuur is 1 1 250 . Bepaal, op 1 m3 nauwkeurig, het volume van de werkelijke piramide in Egypte.

Antwoord:

46 De BMW viercilinder is de hoofdvestiging van BMW in München. Het gebouw is samengesteld uit verschillende cilinders. Een van de cilinders heeft een straal van 12 m en een hoogte van 46 m. Bepaal, op 1 cm3 nauwkeurig, het volume van een miniatuurversie van die cilinder op schaal 1 1 000 .

Antwoord:

C

47 Een olifant heeft gemiddeld een volume van 4 m3. Op het bureau van de directeur van de zoo staat een model op schaal 1 : 20.

Hoeveel liter inhoud heeft het schaalmodel?

©VANIN

48 Hieronder vind je een beelddiagram dat het jaarlijkse verbruik van stookolie van het gezin Pieters voorstelt. Begin 2023 lieten ze hun woning beter isoleren.

De hoogte van de vaten geeft de hoeveelheid stookolie aan die het gezin voor die jaren nodig had.

3 000 l

a) Schat het aantal liter stookolie dat het gezin in 2023 verbruikt heeft:

b) Bereken het aantal liter stookolie dat het gezin in 2023 verbruikt heeft aan de hand van de hoogte van de vaten.

c) Door wie zal zo'n beelddiagram waarschijnlijk opgesteld zijn? Verklaar je keuze.

❒  voorstanders van isolatie ❒  tegenstanders van isolatie

Verklaring:

6.5 Gelijkvormige driehoeken

6.5.1 Inleiding

GEOGEBRA

• Welke driehoeken zijn gelijkvormig?

• Welke hoeken zijn even groot?

• Welke zijden zijn evenredig? = =

• Welke gelijkvormigheidsfactor hoort bij de gelijkvormige driehoeken?

Definitie Gelijkvormige driehoeken

Twee driehoeken zijn gelijkvormig als en slechts als de overeenkomstige hoeken even groot en de overeenkomstige zijden evenredig zijn.

Notatie

Kunstenaars gebruiken vaak gelijkvormige figuren. Zo herken je in het afgebeelde kunstwerkje heel wat gelijkvormige figuren.

Peter Raedschelders is een kunstenaar die vaak gebruikmaakt van gelijkvormige figuren.

Gelijkvormigheidskenmerken voor driehoeken

Op onderzoek

Een driehoek tekenen die gelijkvormig is aan een gegeven driehoek, kun je door gegevens te meten en af te passen. Onderzoek hoeveel gegevens je minimaal nodig hebt.

Gegeven: driehoek PQR

Eén gegeven: = 3 2 PR PR

Teken een driehoek PQR met zijde [PR].

©VANIN

Is de driehoek PQR altijd gelijkvormig met de driehoek PQR?

Twee gegevens: = 3 2 PR PR en ^ P = ^ P 

Teken een driehoek PQR met zijde [PR] en hoek ^ P

Drie gegevens: == 3 2 PQ PQ PR PR en ^ P = ^ P 

Teken een driehoek PQR met zijde [PQ], [PR] en hoek ^ P

Is de driehoek PQR altijd gelijkvormig met de driehoek PQR?

Is de driehoek PQR altijd gelijkvormig met de driehoek PQR?

Door middel van goedgekozen gegevens kun je twee gelijkvormige driehoeken tekenen. Dat is een gelijkvormigheidskenmerk van driehoeken. Zo zijn er drie gelijkvormigheidskenmerken bij driehoeken te onderscheiden.

Gelijkvormigheidskenmerk Z Z H Z Z

Gelijkvormigheidskenmerk Z Z Z Z Z Z

©VANIN

Gelijkvormigheidskenmerk Z Z H Z Z

Twee driehoeken zijn gelijkvormig als en slechts als twee paren overeenkomstige zijden evenredig zijn en de ingesloten hoeken gelijk zijn.

Voor nABC en nABC geldt:

ABC nABC ⇔

Gelijkvormigheidskenmerk

Gelijkvormigheidskenmerk Z Z Z Z Z Z

Twee driehoeken zijn gelijkvormig als en slechts als drie paren overeenkomstige zijden evenredig zijn.

Voor nABC en nABC geldt: nABC nABC ⇔

Gelijkvormigheidskenmerk HH

Twee driehoeken zijn gelijkvormig als en slechts als twee paren overeenkomstige hoeken gelijk zijn.

Voor nABC en nABC geldt:

Gelijkvormigheidskenmerk HH bewijzen

tekening gegeven

te bewijzen

©VANIN

bewijs

1) Constructie:

• Teken het punt D op [AB] zodat |BD | = |BA |.

• Teken een evenwijdige met de zijde [AC] door het punt D

• Het snijpunt van die evenwijdige met de zijde [BC ] noem je E.

2) Bewijs dat nABC ≅ nDBE: kenmerk nABC nDBE verklaring

H ^ A = ^ D DE // AC, overeenkomstige hoeken

Z | AB | = | BD | constructie H ^ B = ^ B gegeven

Volgens kenmerk HZH is nABC ≅ nDBE.

3) Bewijs dat nABC nABC : nDBE is een verkleining van nABC met factor

nABC ≅ nDBE nABC nDBE

ABC nABC

besluit nABC nABC

Oefeningen

REEKS A

49 Zijn de driehoeken gelijkvormig? Als de driehoeken gelijkvormig zijn, vermeld dan het gebruikte gelijkvormigheidskenmerk.

©VANIN

gelijkvormig? ❒ ja ❒ nee

gelijkvormigheidskenmerk:

gelijkvormig? ❒ ja ❒ nee

gelijkvormigheidskenmerk:

gelijkvormig? ❒ ja ❒ nee

gelijkvormigheidskenmerk:

gelijkvormig? ❒ ja ❒ nee

gelijkvormigheidskenmerk:

50 Kun je aan de hand van de gegevens op de tekening besluiten dat de twee driehoeken bij de strijkplank gelijkvormig zijn? Verklaar je antwoord.

51 Zoek de gelijkvormige driehoeken en duid ze in eenzelfde kleur aan. Noteer telkens het gelijkvormigheidskenmerk.

©VANIN

gelijkvormige driehoeken gelijkvormigheidskenmerk

52 Volgens welk gelijkvormigheidskenmerk zijn de driehoeken gelijkvormig?

a) nABC nPBQ: P is het midden van [AB ] en Q is het midden van [BC ]

c) nPQR nAQB: b ⊥

©VANIN

b) nKAT nPAD: a // KT d) nVLO nGUO:

53 Zijn de driehoeken gelijkvormig? Verklaar je antwoord.

Gelijkvormige driehoeken tekenen

Inleiding

• In nABC teken je een evenwijdige met de zijde [AC]. Die evenwijdige snijdt [AB] in D en [BC] in E

• De tabel toont alle hoeken en zijden van nABC en nDBE nABC nDBE

|AB | = 46 mm ^ A = 68º |DB | = 35 mm ^ D = 68º |BC | = 50 mm ^ B = 54° |BE | = 38 mm ^ B = 54° |AC | = 44 mm ^ C = 58° |DE | = 34 mm ^ E = 58°

©VANIN

• Zijn nABC en nDBE gelijkvormig? Verklaar je antwoord.

Gelijkvormigheid van driehoeken bewijzen

Meetresultaten volstaan niet om te besluiten dat twee driehoeken gelijkvormig zijn. Je bewijst de gelijkvormigheid van driehoeken aan de hand van wiskundige eigenschappen en de gelijkvormigheidskenmerken.

tekening gegeven

nABC: DE // AC

D is het snijpunt van [AB] en DE E is het snijpunt van [BC] en DE te bewijzen nABC nDBE

bewijs n en n gelijkvormigheidskenmerk:

besluit

Volgens kenmerk is nABC nDBE

Gelijkheid van hoeken bewijzen

tekening

©VANIN

gegeven |AD | = |DE | = |EF | = |FB | en |AG | = |GH | = |HI | = |IC | te bewijzen ^ D = ^ B

bewijs n en n gelijkvormigheidskenmerk:

besluit

Volgens kenmerk is n n def. n ⇒ ^ D = ^ B

Evenredigheid van lengten bewijzen

tekening gegeven Q aT

PQ ⊥ a en ST ⊥ a R is het snijpunt van PS en a te bewijzen = PQ ST RQ RT

bewijs n en n gelijkvormigheidskenmerk:

besluit

Volgens kenmerk is n n def. n ⇒ = PQ ST RQ RT

REEKS A

54 Bewijs.

tekening

bewijs

n en n

gegeven |AC | = |BC | en |CE | = |CD | te bewijzen nABC nDEC

gelijkvormigheidskenmerk:

besluit

Volgens kenmerk is nABC nDEC

55 Bewijs.

tekening

©VANIN

bewijs

n en n

gegeven rechthoek ABCD: PQ // RS te bewijzen nPBQ nSDR

gelijkvormigheidskenmerk:

besluit Volgens kenmerk is nPBQ nSDR

56 Bewijs.

tekening T U KF L gegeven

bewijs

TL en UK zijn hoogtelijnen in nTUF te bewijzen ^ T = ^ U

©VANIN

besluit

Volgens kenmerk is n n def. n ⇒

57 Bewijs.

tekening

bewijs

besluit

Volgens kenmerk is n n def. n ⇒

gegeven

parallellogram KROM: OP ⊥ KR en KL ⊥ RO te bewijzen | KR | | PR | = | RO | |RL |

Bewijs.

tekening gegeven

parallellogram BOEK: L is het snijpunt van BL en OE S is het snijpunt van OK en BL te bewijzen = OS KS LS BS

bewijs

©VANIN

besluit

Volgens kenmerk is n n

def. n ⇒

REEKS C

59 Twee loodlijnen, elk op een van de benen van een hoek, vormen dezelfde hoek met de deellijn van de hoek. Bewijs.

tekening gegeven te bewijzen

bewijs

besluit

Volgens kenmerk is n n def. n ⇒

6.5.4 Rekenen in gelijkvormige driehoeken

Aan de hand van gelijkvormige driehoeken kun je onbekende zijden in driehoeken berekenen.

Werkwijze

• Bepaal twee driehoeken die gelijkvormig zijn.

• Indien nodig bewijs je de gelijkvormigheid van de driehoeken.

• Stel een evenredigheid op met de onbekende en bekende zijden van de gelijkvormige driehoeken.

• Bereken de onbekende uit de evenredigheid.

Modeloefening 1

• nABC nPQR

• Bereken x en y x 21 = 10 15 ⇔ x = 10 21 15 = 14

Modeloefening 2

Een lantaarnpaal van 4 m heeft een schaduw van 6 m.

Op hetzelfde ogenblik heeft een windmolen

een schaduw van 42 m.

Bepaal de hoogte van de windmolen.

• Bewijs: n en n gelijkvormigheidskenmerk:

Volgens kenmerk is n n

• Berekening:

• Antwoord:

REEKS A

60 Gegeven: nABC ~ nDEF Bereken het gevraagde maatgetal van de lengte van de zijde op 0,01 nauwkeurig.

REEKS B

61 In Tokyo staat een wolkenkrabber met een gevel in de vorm van een rechthoekige driehoek. Het gebouw is 124 m hoog en 85 m breed. Bereken de hoogte van het gebouw in miniatuur als de breedte in miniatuurbouw 17 cm bedraagt. Bepaal je antwoord op 0,1 cm nauwkeurig.

©VANIN

62 Noah wil een driehoekige tafel namaken met dezelfde vorm als de tafel op de foto. Bereken de lengte van de rechthoekszijden van het tafelblad als de schuine zijde 120 cm moet bedragen. Bepaal je antwoord op 0,1 cm nauwkeurig.

63

Gegeven: nABC ~ nDEF

Bereken de ontbrekende maatgetallen van de lengten van de zijden op 0,01 nauwkeurig.

64 Aïda volgt een cursus om kaarsen te gieten.

Ze maakt een kaars in de vorm van een piramide met een driehoekig grondvlak.

De kaars brandt erg gelijkmatig en na een aantal uur is het bovenvlak van de kaars een driehoek die gelijkvormig is met het grondvlak.

De langste zijde van het driehoekige bovenvlak van de kaars meet nu 54 mm.

Bepaal de afmetingen x en y van de overblijvende zijden van het bovenvlak.

Bepaal je antwoord op 1 mm nauwkeurig.

©VANIN

65 Bij de balk zijn twee gelijkvormige doorsneden nABC en nDEF aangeduid.

Bereken de lengten van de zijden [DF] en [EF]. Bepaal de lengte op 0,1 cm nauwkeurig.

Gegeven: |AB | = 18,4 cm | DE | = 6,8 cm | AC | = 16,6 cm | BC | = 14,4 cm

66 Louis is 1,68 m groot en heeft een schaduw van 2,40 m.

Op hetzelfde tijdstip heeft een boom een schaduw van 6,80 m.

Bepaal de hoogte van de boom op 0,01 m. Bewijs eerst de gelijkvormigheid van de driehoeken.

• Bewijs:

• Berekening:

67 Bepaal aan de hand van gelijkvormige driehoeken de ontbrekende lengte x op 0,01 nauwkeurig. Bewijs eerst de gelijkvormigheid van de driehoeken.

• Bewijs:

• Berekening:

REEKS C

68 Een weg stijgt 40 m over een afstand van 1,250 km. Hoeveel meter moet je op die weg afleggen om 15 m te stijgen? Bewijs eerst de gelijkvormigheid van de driehoeken.

• Bewijs:

• Berekening:

69 Loodrecht op de oevers wordt over een 11 m breed kanaal een touw gespannen. Aan het touw is een boei bevestigd. Als Dieter zich aan de ene kant van het kanaal langs de oever 7 m van het touw verwijdert en Ruben verwijdert zich in tegengestelde zin aan de overkant van het kanaal 3 m van het touw, dan ziet Dieter Ruben en de boei op één lijn. Hoe ver is de boei van beide oevers verwijderd? Bepaal je antwoord op 0,1 m nauwkeurig. Bewijs eerst de gelijkvormigheid van de driehoeken.

• Bewijs:

• Berekening:

De stelling van Thales

6.6.1 Evenwijdige projectie

In de zomer is spelen met de frisbee op het strand een populaire activiteit.

De zon zorgt voor een schaduw van de frisbee op het zand. De frisbee wordt als het ware op het zand geprojecteerd.

Als je veronderstelt dat de zonnestralen evenwijdig op de frisbee invallen, kun je dat een evenwijdige of parallelle projectie noemen.

Bij evenwijdige of parallelle projectie worden de punten geprojecteerd op de projectieas (a) evenwijdig met een gegeven rechte (b). Die rechte geeft de projectierichting aan.

Notatie: pa b (A) = A

Lees: Het beeld van het punt A door de evenwijdige projectie volgens de projectierichting b op de projectieas a is het punt A Vul in.

Voer de evenwijdige projecties uit en vul in.

Opmerking

Bij loodrechte of orthogonale projectie worden de punten loodrecht op de projectieas (a) geprojecteerd.

Notatie: pa (A) = A

• Bepaal de gevraagde verhoudingen. Bepaal je antwoord op 0,1 nauwkeurig.

AB

• Wat stel je vast?

Eigenschap Evenwijdige projectie van evenwijdige lijnstukken

©VANIN

Bij evenwijdige lijnstukken die niet evenwijdig zijn met de projectierichting, zijn de verhoudingen van de lengten van de lijnstukken en hun respectievelijke evenwijdige projecties gelijk.

Het is onmogelijk om de bolvormige aarde perfect weer te geven op een kaart in een atlas. Bij de projectie van een bol op een vlak treden altijd vervormingen op.

De eerste poging kwam van onze landgenoot Mercator (16e eeuw). Zijn projectie noem je conform of hoekgetrouw. De oppervlakten zijn echter niet betrouwbaar. Hoe dichter je bij de polen komt, hoe groter de vervormingen.

Na Mercator zijn er nog verschillende methodes ontwikkeld, maar ze hebben allemaal hun nadelen. Afhankelijk van het doel van de kaart is de ene of de andere projectie meer of minder geschikt.

Op onderzoek

De rechten a en b worden gesneden door de evenwijdigen c, d en e Bereken de verhoudingen van de gevraagde lijnstukken.

©VANIN

Wat stel je vast?

Thales’ belangrijkste werk

Thales van Milete werd omstreeks 624 voor Christus geboren. Zijn ouders behoorden in Milete tot de welgestelde en geziene burgerij, waarschijnlijk waren het rijke kooplieden.

Alles wat van Thales bekend is, komt uit ‘tweede hand’, dus afkomstig van mensen die over hem schreven. Thales wordt gezien als de eerste Griekse filosoof, natuurwetenschapper en wiskundige. Een van de grootste verdiensten van Thales was dat hij als eerste niet alleen praktische problemen probeerde op te lossen, maar juist algemene achterliggende principes probeerde te ontdekken.

• Thales voorspelde de zonsverduistering van 585 v.Chr.

• Thales kon de hoogte van de piramides bepalen door de lengte van hun schaduw te meten op het moment dat de zon zo staat dat iemands schaduw gelijk is aan zijn lengte.

• Thales kon de afstand van een schip tot de kust berekenen.

6.6.3 De stelling van Thales formuleren

Stelling

Evenwijdige rechten snijden van twee rechten evenredige lijnstukken af. A B C D E F

In symbolen: AB DE = BC EF

6.6.4 De stelling van Thales bewijzen

©VANIN

tekening gegeven

a en b gesneden door een aantal evenwijdigen (c // d // e): a snijdt de rechten c, d en e in respectievelijk A, B en C ; b snijdt de rechten c, d en e in respectievelijk D, E en F te bewijzen

AB DE = BC EF

bewijs

1) Constructie:

• tAD → ([ AB ]) = [ DG ]

• t BE → ([ BC ]) = [ EH ]

2) Bewijs dat nDEG nEFH:

nDEG en nEFH gelijkvormigheidskenmerk: HH

^ E1 = ^ F overeenkomstige hoeken bij zijn gelijk

^ D = ^ E2 overeenkomstige hoeken bij zijn gelijk een verschuiving behoudt de evenwijdigheid

Volgens kenmerk HH is nDEG nEFH def. n ⇒

3) Bewijs de evenredigheid: |DG | = |DE| |EH | |EF | ⇒ |AB | = |DE | |BC | |EF | (Een verschuiving behoudt de lengte.)

besluit

AB DE = BC EF |DG | = |EH | |DE | |EF |

6.6.5 De stelling van Thales in een driehoek

Teken een rechte a evenwijdig met de zijde [ AC ] van nABC Bereken de verhoudingen.

Verhoudingen:

Besluit

Wat stel je vast?

Een rechte evenwijdig met een zijde van een driehoek verdeelt de andere twee zijden in evenredige lijnstukken.

In symbolen: BD BE = AD CE

6.6.6 Rekenen met de stelling van Thales

Bepaal de onbekende lengte op 0,01 mm nauwkeurig.

©VANIN

6.6.7 De omgekeerde stelling van Thales

Stelling Rechten die van twee rechten evenredige lijnstukken afsnijden, zijn evenwijdig.

Oefeningen

REEKS B

70 Voer de evenwijdige projecties uit en vul in. a b

©VANIN

71 Vul de gegeven evenredigheden in. JB // KC //

Bepaal de onbekende lengte x op 0,01 nauwkeurig als je weet dat a // b // c.

©VANIN

a) pAFAD (B) =

pAD FC ([DE ]) =

pBC AF ( ) = E b) pAB AC (D) =

pAC EF (nDBE) = h) pACBD ( ) = [ AF ] c) pBCAD ([DF ]) =

74 Ga aan de hand van de gegeven lengten na welke rechten evenwijdig zijn.

©VANIN

75 De rechte a is evenwijdig met een zijde van nPQR. Bepaal de lengte x op 0,1 nauwkeurig.

76 Bepaal de onbekende lengten x en y op 0,01 nauwkeurig, als je weet dat a b c d.

77 In welke van de volgende situaties is de rechte p evenwijdig met een zijde van nDAK?

Bepaal je antwoord aan de hand van de gegeven lengten op de tekening.

78 DE AC

Bepaal de lengte van de zijde [ AB ] van nABC op 0,01 nauwkeurig.

79 Een boom heeft een schaduw van 21 m, terwijl een jongen van 1,62 m op hetzelfde moment een schaduw heeft van 2,10 m.

Bepaal de hoogte van de boom op 0,01 m nauwkeurig.

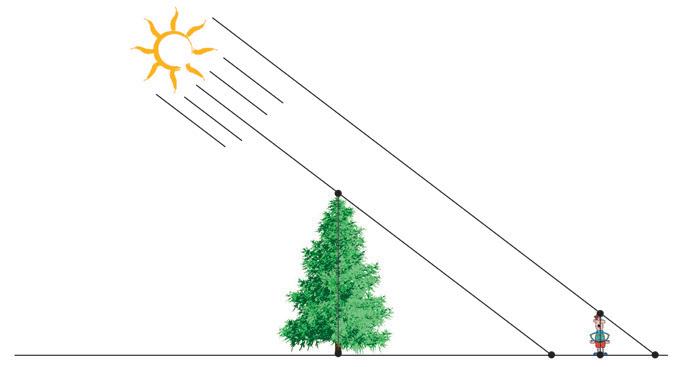
©VANIN

80 Wat is vergankelijker dan een schaduw?

Thales mat de schaduw van de piramide van Cheops ... en werd onsterfelijk.

De vader van Thales was een koopman en soms mocht zijn zoontje mee op reis, bijvoorbeeld naar Egypte. Thales bewonderde daar de piramide van Cheops en een van de priesters vroeg hem: ‘Weet je hoe hoog die piramide is?’ ‘Ik denk het wel’, zei Thales. Hij ging op de grond liggen en maakte twee streepjes in het zand, een aan zijn hoofd en een aan zijn voet.

Daarna stond hij op en verbond beide streepjes door een rechte lijn. ‘Ik zal nu gaan staan aan het uiteinde van deze lijn, die net zo lang is als ik groot ben. Dan zal ik wachten tot mijn schaduw even lang is. Op datzelfde ogenblik zal de schaduw van de piramide even lang zijn als de piramide groot is.’ Wat was de hoogte die Thales op die manier mat, als je weet dat de basis van de piramide 231,92 m en de lengte van de schaduw van de piramide vanaf de voet van de piramide 31,5 m is? b t s h

81 De horizontale planken bij het onderstaande poortje zijn evenwijdig. Bereken de ontbrekende lengte x op 0,01 cm nauwkeurig.

82 Bepaal de onbekende x, als je weet dat a b c.

©VANIN

REEKS C

83 In nPQR is ST // PR. T verdeelt [QR ] in twee stukken die zich verhouden als 2 3 .

Bepaal de lengte van de zijde [PQ ] aan de hand van de gegevens op de tekening.

84 Een piramide wordt gesneden door evenwijdige vlakken.

Bepaal de gevraagde lengten a, b, c en d op de ribben op 0,01 nauwkeurig.

85 Gegeven: | OE | = 4,44, | OF | = 4,95, | EC | = 5,55 en | DB | = 5,71.

Bepaal de lengten | OD | en | AC | op 0,01 nauwkeurig.

Norman Woodland kan als grondlegger van de streepjescode worden beschouwd.

Hij zag het belang in van eenvoudige coderingen om gegevens automatisch te verwerken.

In 1973 stelde hij de twaalfcijferige Universal Product Code (UPC) samen.

©VANIN

De streepjescode wordt gelezen met laserlijnen en de kassa geeft ogenblikkelijk de prijs.

De bundel evenwijdige strepen bepaalt evenredige lengten op de snijlijnen.

Bijgevolg speelt de leesrichting door de laserlijnen geen rol.

Noteer de evenredigheid van lengten bij de afbeelding van de streepjescode.

Middenparallel van een driehoek

Metrische betrekkingen in rechthoekige driehoeken

STUDIEWIJZER Gelijkvormigheid

6.1 Gelijkvormige figuren

KENNEN

Twee figuren zijn gelijkvormig als de ene figuur een schaalmodel is van de andere.

KUNNEN

Gelijkvormige vlakke figuren aanduiden.

Gelijkvormige ruimtefiguren aanduiden.

©VANIN

6.2 Overeenkomstige hoeken en zijden

KENNEN

In gelijkvormige figuren zijn overeenkomstige hoeken even groot.

In gelijkvormige figuren zijn overeenkomstige zijden evenredig.

KUNNEN

Overeenkomstige hoeken en zijden in gelijkvormige figuren aanduiden.

6.3 Gelijkvormigheidsfactor

KENNEN

De verhouding van de lengten van de overeenkomstige zijden van twee gelijkvormige figuren is de gelijkvormigheidsfactor.

Bij een verkleining is de gelijkvormigheidsfactor kleiner dan 1.

Bij een vergroting is de gelijkvormigheidsfactor groter dan 1.

Bij congruente figuren is de gelijkvormigheidsfactor gelijk aan 1.

Gelijkvormigheidsfactor en schaal hebben dezelfde betekenis.

KUNNEN

Uit tekeningen of afmetingen de gelijkvormigheidsfactor bij gelijkvormige figuren bepalen.

Bij een gegeven gelijkvormigheidsfactor de nieuwe afmetingen bepalen.

De werkelijke afmeting van een figuur bepalen wanneer de schaal gegeven is.

6.4 Omtrek, oppervlakte en volume bij gelijkvormige figuren

Bij een verkleining of vergroting met gelijkvormigheidsfactor g wordt de omtrek vermenigvuldigd met factor g

Bij een verkleining of vergroting met gelijkvormigheidsfactor g wordt de oppervlakte vermenigvuldigd met factor g 2

Bij een verkleining of vergroting met gelijkvormigheidsfactor g wordt het volume vermenigvuldigd met factor g 3

Bij een vergroting of verkleining de omtrek, de oppervlakte en het volume van gelijkvormige figuren bepalen.

De werkelijke afmeting van een figuur bepalen wanneer de schaal gegeven is.

6.5 Gelijkvormige driehoeken

Twee driehoeken zijn gelijkvormig als en slechts als de overeenkomstige hoeken even groot en de overeenkomstige zijden evenredig zijn.

Gelijkvormigheidskenmerk Z Z H Z Z

©VANIN

6.6

Twee driehoeken zijn gelijkvormig als en slechts als twee paren overeenkomstige zijden evenredig zijn en de ingesloten hoeken gelijk zijn.

Gelijkvormigheidskenmerk HH

Twee driehoeken zijn gelijkvormig als en slechts als twee paren overeenkomstige hoeken gelijk zijn.

Gelijkvormigheidskenmerk Z Z Z Z Z Z

Twee driehoeken zijn gelijkvormig als en slechts als drie paren overeenkomstige zijden evenredig zijn.

KUNNEN

De gelijkvormigheidskenmerken van driehoeken bewijzen.

De gelijkvormigheid van driehoeken bewijzen aan de hand van de gelijkvormigheidskenmerken.

De gelijkheid van hoeken en de evenredigheid van zijden bewijzen aan de hand van de gelijkvormigheidskenmerken.

De lengte van lijnstukken berekenen aan de hand van gelijkvormige driehoeken.

De stelling van Thales

Bij evenwijdige lijnstukken zijn de verhoudingen van de lijnstukken en hun respectievelijke evenwijdige projecties gelijk.

Evenwijdige rechten snijden van twee rechten evenredige lijnstukken af.

Een evenwijdige projectie uitvoeren.

De stelling van Thales bewijzen.

KUNNEN

De lengte van lijnstukken berekenen aan de hand van de stelling van Thales.

1. In deze vlinder is G de som van de oppervlakten van de twee grote vierkanten en K de som van de oppervlakten van de twee kleinere.

Hoeveel is G K ?

JWO, editie 2020, eerste ronde

2. Een tehuis vangt een aantal weeskinderen op. Het frequentiediagram geeft weer hoeveel kinderen er van elke leeftijd zijn. Wat is de gemiddelde leeftijd van de kinderen?

JWO, editie 2017, eerste ronde

3. De figuur bestaat uit vijf vierkanten. Van vier vierkanten is de oppervlakte gegeven. Wat is de oppervlakte van het gekleurde vierkant?

JWO, editie 2018, eerste ronde

4. Welk van de volgende getallen is geen kwadraat van een natuurlijk getal en ook geen derde macht van een natuurlijk getal?

JWO, editie

eerste ronde

HOOFDSTUK 7 I EERSTEGRAADSVERGELIJKINGEN, EERSTEGRAADSONGELIJKHEDEN EN

FORMULES OMVORMEN

7.1

7.1 Eerstegraadsvergelijkingen

7.1.1 Gelijkheden

Al die uitspraken noem je gelijkheden.

Bij een gelijkheid is de waarde van het deel voor het gelijkheidsteken gelijk aan de waarde van het deel achter het gelijkheidsteken.

Benamingen

Een gelijkheid bestaat uit twee delen.

5 + 7 ⏟ eerste lid linkerlid = 15 – 3 ⏟ tweede lid rechterlid

Eigenschap 1 5 + 7 = 15 – 3 en (5 + 7) + 8 = (15 – 3) + 8

= b ⇔ a + c = b

Eigenschap Gelijkheid met termen

2 = 10 en (5 2) – 7 = 10 – 7

Als je bij beide leden van een gelijkheid eenzelfde getal optelt of aftrekt, dan blijft de gelijkheid bestaan.

Eigenschap 2

6 – 1 = 3 + 2 en (6 – 1)  2 = (3 + 2)  2 17 – 9 = 8 en 17 – 9 4 = 8 4

Eigenschap Gelijkheid met factoren

Als je beide leden van een gelijkheid vermenigvuldigt met of deelt door eenzelfde van nul verschillend getal, dan blijft de gelijkheid bestaan.

Opmerking

5 + 7 = 15 – 3 en 15 – 3 = 5 + 7 18 3 = 3 + 3 en 3 + 3 = 18 3

Vaststelling Bij een gelijkheid mag je beide leden van plaats verwisselen.

7.1.2 Vergelijkingen

Definitie Vergelijking

Een vergelijking is een gelijkheid met een onbekend reëel getal.

Meestal gebruik je de letter x om het onbekende getal voor te stellen.

Een vergelijking oplossen betekent dat je de waarde voor de onbekende x zoekt.

De vergelijking x – 9 = –16 heeft als oplossing x = –7, omdat –7 – 9 = –16.

De oplossing(en) van een vergelijking noteer je als een verzameling. Meestal kies je V Bij vraagstukken met vergelijkingen formuleer je altijd een antwoord.

7.1.3 Even herhalen

Vergelijkingen van de vorm x + a = b (met a, b ∈ r)

Overbrengen van termen

Optellen in het ene lid wordt aftrekken in het andere lid, en omgekeerd.

+ a = b wordt x

Voorbeelden

Na een korting van 15 euro kost je nieuwe T-shirt nog 38 euro. Hoeveel kostte het T-shirt eerst?

• keuze van de onbekende:

• opstellen van de vergelijking:

• oplossen van de vergelijking:

Vergelijkingen van de vorm a x = b (met a ∈ r0, b ∈ r)

Overbrengen van factoren

Vermenigvuldigen in het ene lid wordt delen in het andere lid, en omgekeerd.

 a = b wordt x = b a

Op een fuif krijgt Nabil voor 15 euro zes drankjes. Hoeveel kost één drankje?

• keuze van de onbekende:

• opstellen van de vergelijking:

• oplossen van de vergelijking:

• controle:

• antwoord:

• controle:

• antwoord:

7.1.4 Eerstegraadsvergelijkingen

Definitie

Eerstegraadsvergelijking in één onbekende

Een eerstegraadsvergelijking in één onbekende x is een vergelijking met als standaardvorm ax + b = 0 (met a ∈ r0 en b ∈ r).

Voorbeeld 1

Tijdens een optocht in een safaripark zie je een stoet olifanten. Elke olifant houdt de staart van de vorige vast. In het midden van de stoet is er een bord van 7 m vastgemaakt aan de staart van de ene olifant en de slurf van de volgende.

Elke olifant is 3 m lang. Hoeveel olifanten lopen er mee, als de hele stoet 31 m lang is?

• keuze van de onbekende: x is het aantal olifanten.

• opstellen van de vergelijking:

3 x + 7 = 31

• oplossen van de vergelijking:

3x + 7 = 31

3x = 31 – 7

3x = 24

x = 24 3

x = 8

• controle:

3 8 + 7 = 24 + 7 = 31

Werkwijze

a) Breng de bekende termen naar hetzelfde lid.

b) Reken dat lid uit.

c) Breng de bekende factor naar het andere lid.

d) Bereken de onbekende.

©VANIN

• antwoord: Er lopen 8 olifanten mee in de stoet.

Voorbeeld 2

–5 + x = 7

Voorbeeld 3

6x = –24

Voorbeeld 4

2x + 6 = 12

controle:

controle:

controle:

7.1.5 Vergelijkingen oplossen

Een tuinman krijgt de opdracht een rechthoekig grasperk aan te leggen. De omtrek moet 160 m zijn.

De lengte moet 30 m groter zijn dan de breedte.

Bereken de lengte en de breedte van dat grasperk.

• keuze van de onbekende:

x is de breedte van het grasperk; dan is de lengte van het grasperk x + 30.

• opstellen van de vergelijking:

2  [(x + 30) + x] = 160 of 2  (2x + 30) = 160

• oplossen van de vergelijking:

2  (2x + 30) = 160

Werkwijze

• antwoord: De breedte van het grasperk is m en de lengte is m.

• controle:

• Werk, indien nodig, eerst de haakjes uit.

• Werk de noemers weg door elke term gelijknamig te maken.

• Plaats alle termen met de onbekende in het ene lid en alle andere in het andere lid.

• Werk beide leden uit.

• Deel beide leden door de coëfficiënt van de onbekende, als die niet nul is.

Voorbeelden

Oefeningen

REEKS

A

1 Los de vergelijkingen op.

a) 2x + 7 = 19

f) –1 2 + x = 3 4

©VANIN

b) –x + 8 = –15

g) x –2 3 = 3

c) 3 x = –21

h) 4 x – 2 = 6

d) 5x = 11

i) –6x + 5 = –7

e) 8x – 3 = 17

j) 3 4 x = –21

2 Los de vergelijkingen op. Rond, indien nodig, je resultaten af op 0,000 1 nauwkeurig.

a) 3x + 5 = 7

b) 3,3x – 2,4 = 4,2

c) p – 2p x = 3p

d) 2x – 2 = 1

f) 2 + x = 3

©VANIN

e) –2 5 x + 1 3 = 1 2

g) 0,2x + 1 2 = 3 4

h) 3x – 4 3 = 1

i) px + 0,31 = 0

j) 5 x + 1 = 5

a) 3x + 15 = 22 − 10x

e) 5x + 9 = 2  (x + 3)

©VANIN

b) −2x − 8 = 3x + 7

f) 5x − (2x − 8) = 4x + 23

c) 3x − 9 + 6x = 2x + 12

g) 9  (2x + 7) = 8 − (x + 2)

d) –3 8 x + 1 4 = 4 3 –6 x h) 6 5 x –16 5 = –2 3 x

4 Los de vergelijkingen op. Schrijf je resultaten als een onvereenvoudigbare breuk.

a) 2x + 5 3 = 13

d) 2 3 x 2 + 3 4 = –5 6

©VANIN

b) –9 – 4x 2 = 11 3 e) 2x 2 5 1 3 – –7 2 =

c) 2x + 3 5 = –x + 5 4 f) 4x –x + 1 2 = 3x – 7

7.1.6 Vraagstukken oplossen met vergelijkingen

Werkwijze

• Lees aandachtig het vraagstuk en bepaal de hoofdonbekende. Noteer die als x

• Druk de eventuele nevenonbekenden uit in functie van x.

• Lees opnieuw het vraagstuk en zet de gegevens om in een vergelijking.

• Los de vergelijking op.

• Controleer en formuleer een antwoord.

Voorbeeld 1

Thomas betaalt 5 euro per maand voor een gsm-abonnement. Als dat bedrag verbruikt is, betaalt hij 0,20 euro per minuut die hij extra belt.

In de maand december betaalt hij 7,40 euro.

Hoeveel minuten heeft Thomas in december extra gebeld?

• keuze van de onbekende:

Voorbeeld 2

Om zijn tuin verder af te werken, plaatst Enrico 15 m omheining rond de cirkelvormige waterput en de trapeziumvormige vijver.

Bepaal de straal r van de cirkelvormige waterput op 0,01 m nauwkeurig.

• keuze van de onbekende:

• opstellen van de vergelijking:

• oplossen van de vergelijking:

• opstellen van de vergelijking:

• oplossen van de vergelijking:

• controle:

• controle:

• antwoord: • antwoord:

Oefeningen

REEKS A

5 Los op.

a) Als je het dubbel van een getal aftrekt van 163, krijg je 67. Welk getal is dat?

• keuze van de onbekende:

• opstellen van de vergelijking:

• oplossen van de vergelijking:

• controle:

• antwoord:

b) Een plank van 3,20 m zaag je in zes gelijke stukken. Je houdt nog 2 cm van de plank over. Hoe lang is elk stuk?

• keuze van de onbekende:

• opstellen van de vergelijking:

• oplossen van de vergelijking:

• controle:

• antwoord:

c) In een gelijkbenige driehoek is de tophoek 56º. Hoe groot is elke basishoek?

• keuze van de onbekende:

• opstellen van de vergelijking:

• oplossen van de vergelijking:

• controle:

• antwoord:

d) Een arbeider krijgt per week een vast loon van 190 euro. Daarbovenop krijgt hij 0,85 euro per afgewerkt product. In één week heeft hij 453,50 euro verdiend. Hoeveel artikelen heeft hij die week afgewerkt?

• keuze van de onbekende:

• opstellen van de vergelijking:

• oplossen van de vergelijking:

• controle:

• antwoord:

6 Los op.

a) De som van twee opeenvolgende natuurlijke getallen is 559. Bepaal die twee getallen.

• keuze van de onbekende:

• opstellen van de vergelijking:

• oplossen van de vergelijking:

• controle:

• antwoord:

b) Als je een getal verdubbelt en daarna met 5 vermeerdert, dan is het resultaat gelijk aan het zevenvoud van het oorspronkelijke getal. Bepaal dat getal.

• keuze van de onbekende:

• opstellen van de vergelijking:

• oplossen van de vergelijking:

• controle:

c) Als je een getal vermeerdert met 6 en dan die som vermenigvuldigt met 4, vind je −112. Bereken dat getal.

• keuze van de onbekende:

• antwoord:

• opstellen van de vergelijking:

• oplossen van de vergelijking:

• controle:

• antwoord:

d) Het dubbel van een getal, vermeerderd met 16, is gelijk aan twee derde van het oorspronkelijke getal. Bepaal dat getal.

• keuze van de onbekende:

• opstellen van de vergelijking:

• oplossen van de vergelijking:

• controle:

• antwoord:

7 Van twee flatgebouwen is het hoogste 34 m minder hoog dan het dubbel van het laagste flatgebouw. De gezamenlijke hoogte van de twee gebouwen is 80 m. Bereken de hoogte van het laagste gebouw.

Antwoord:

8 Voor een filmvoorstelling betalen volwassenen 6 euro en kinderen 3,50 euro. Er zitten 192 mensen in de zaal. In de kassa zit 909,50 euro aan inkomsten. Hoeveel kinderen zitten er in de zaal?

Antwoord:

9 Een elektricien knipt een 28 m lange draad in twee stukken, zodat het ene stuk 3 m langer is dan het andere. Bereken hoe lang elk stuk draad is.

Antwoord:

10 De tophoek van een gelijkbenige driehoek is driemaal zo groot als een basishoek.

Bereken de grootte van een basishoek.

Antwoord:

11 De lengte van een rechthoek is 2 cm meer dan het drievoud van de breedte.

De omtrek is 80 cm.

Bereken de breedte van die rechthoek.

Antwoord:

12 De ene scherpe hoek van een rechthoekige driehoek is 9º kleiner dan het dubbele van de andere scherpe hoek. Bereken beide hoeken.

Antwoord:

13 Katja koopt een rokje in de soldenperiode. Ze krijgt 25 % korting en betaalt 52,50 euro. Hoeveel zou het rokje gekost hebben zonder korting?

©VANIN

Antwoord:

14 Oma, moeder en dochter zijn samen 112 jaar oud. Moeder is vijfmaal zo oud als haar dochter en oma is dubbel zo oud als moeder. Hoe oud zijn ze nu?

Antwoord:

15 Boer André heeft enkel kippen en koeien op zijn bedrijf. In totaal heeft hij 136 dieren. Als hij het aantal poten telt, vindt hij er 436. Hoeveel kippen en hoeveel koeien heeft hij?

Antwoord:

16 Een handelsreiziger heeft een vaste maandwedde van 1 100 euro. Daarboven krijgt hij 6 % van de verkoopprijs van de door hem verkochte producten. In oktober verdiende hij 2 709,20 euro. Voor welk bedrag heeft hij verkocht?

Antwoord:

17 Een plank van 6,50 m moet in twee stukken worden gezaagd, zodat het kortste stuk 60 % van het langste stuk is. Bereken de lengte van beide stukken.

Antwoord:

18 De omtrek van een rechthoek, waarvan de lengte 2,5 keer de breedte is, is gelijk aan de schuine zijde van een rechthoekige driehoek met rechthoekszijden van 5 cm en 7 cm. Bereken de afmetingen van die rechthoek. Rond af op 0,01 cm.

Antwoord:

19 Benzine kost op een gegeven moment 1,822 euro per liter. Hassan tankt voor 50 euro benzine. Hoeveel kilometer zal hij kunnen rijden, als het gemiddelde verbruik van zijn auto geraamd wordt op 6 liter per 100 km? Rond af op 1 km.

Antwoord:

REEKS C

20 Een belegd broodje is 18 cm lang. Xavier, Dennis en Lana willen het broodje in drie stukken verdelen, zodat Xavier de helft krijgt van Lana en Dennis drie vierde van Lana. Hoe lang moet elk stuk zijn?

Antwoord:

©VANIN

21 Van drie getallen is gegeven dat het tweede getal 6 minder is dan drie keer het eerste getal. Het derde getal is 2 meer dan twee derde van het tweede. De som van de drie getallen is 172. Bereken die drie getallen.

Antwoord:

22 Een constructiebedrijf krijgt van een grote wijnhandelaar de opdracht een koperen vat te maken, zoals op de figuur is afgebeeld. De straal van het grondvlak moet 0,65 m zijn en de hoogte van het cilindervormige gedeelte moet anderhalve keer de hoogte van het kegelvormige gedeelte zijn. Het vat moet in totaal 2 500 l wijn kunnen bevatten.

Bereken de hoogte van de volledige constructie (op 0,01 m nauwkeurig).

©VANIN

23 Een wijnhandelaar mengt 25 liter wijn van 4,60 euro per liter met 35 liter duurdere wijn. Het mengsel kost 4,95 euro per liter.

Wat is de kostprijs per liter van de duurdere wijn?

24 Een wagen heeft een brandstoftank van 65 l. De wagen verbruikt 7,2 l benzine per 100 km in vlot verkeer en 8,6 l per 100 km in stadsverkeer.

De chauffeur rijdt gemiddeld 2 7 van zijn kilometers in stadsverkeer.

Hoeveel kilometer kan hij afleggen met een volle brandstoftank? Rond af op 1 km.

©VANIN

25 Caroline verdiende vorige maand 20,30 euro meer dan Karel.

Deze maand kregen ze allebei opslag. Caroline kreeg 2,5 % opslag en Karel verdient nu 3 % meer dan vorige maand. Hun gezamenlijke maandelijkse inkomen bedraagt nu 3 983,12 euro. Hoeveel verdienden ze vorige maand elk?

7.2 Eerstegraadsongelijkheden

7.2.1 Definitie

• Zijn de ongelijkheden waar of vals? Vink het goede antwoord aan.

1 3 < 1 2 r  waar r  vals (–6) 2 ⩽ 6 2 r  waar r  vals –2 > –3 r  waar r  vals p ⩾ 22 7 r  waar r  vals

• Zet de zinnen om in symbolen.

a) Een getal is kleiner dan of gelijk aan 5.

b) Het dubbel van een getal is groter dan dat getal verminderd met 7.

c) Een derde van een getal is kleiner dan de helft van dat getal vermeerderd met 2 .

• De waarheidswaarde van de volgende ongelijkheden is afhankelijk van de waarde van x Geef voor elke ongelijkheid één waarde voor x die aan de gegeven voorwaarde voldoet, en één waarde voor x die niet aan de voorwaarde voldoet.

Als een bepaalde waarde van x voldoet aan een ongelijkheid, dan noem je dat getal een oplossing van de ongelijkheid.

Hoeveel oplossingen zijn er voor elk van die ongelijkheden?

Definitie Eerstegraadsongelijkheid in één onbekende

©VANIN

Een eerstegraadsongelijkheid in één onbekende x is een ongelijkheid met als standaardvorm

ax + b > 0;

ax + b ⩾ 0;

ax + b < 0 of ax + b ⩽ 0 (met a ∈ r0 en b ∈ r).

Voorbeeld 1

Een voetbalvereniging huurt een kopieermachine bij een leasingbedrijf. Maandelijks moeten ze daarvoor 125 euro betalen en daarbovenop 1,5 eurocent per kopie. Ze willen niet dat hun jaarlijkse budget voor kopieën meer dan 1 600 euro bedraagt. Hoeveel kopieën mogen ze hoogstens per jaar nemen?

Stel: x is het jaarlijkse aantal kopieën.

• vaste kosten per jaar:

• variabele kosten per jaar:

• totale jaarlijkse kosten:

• op te lossen ongelijkheid:

Voorbeeld 2

Voor welke waarden van x is de omtrek van het trapezium groter dan de omtrek van de driehoek?

• omtrek driehoek:

• omtrek trapezium:

• op te lossen ongelijkheid:

Als je in die ongelijkheid x vervangt door 3, dan verkrijg je , wat juist is. Het reëel getal 3 is een oplossing van de ongelijkheid.

Als je in die ongelijkheid x vervangt door 1, dan verkrijg je , wat fout is. Het reëel getal 1 is geen oplossing van de ongelijkheid.

©VANIN

Zijn er nog andere oplossingen van die ongelijkheid?

Om ongelijkheden van de eerste graad met één onbekende op te lossen, maak je gebruik van de eigenschappen van ongelijkheden.

7.2.2 Eigenschappen van ongelijkheden

Je neemt de ongelijkheid 12 > 11.

Je telt bij beide leden 6 op. Je verkrijgt:

Je trekt van beide leden 13 af. Je verkrijgt:

Eigenschap

Eigenschap

Als je beide leden van een ongelijkheid vermeerdert of vermindert met hetzelfde getal, dan blijft de ongelijkheid gelden.

Je neemt de ongelijkheid 11 ⩽ 12.

Je vermenigvuldigt beide leden met 2. Je verkrijgt:

Je deelt beide leden door 2. Je verkrijgt:

Als je beide leden van een ongelijkheid vermenigvuldigt met of deelt door hetzelfde positieve getal, verschillend van nul, dan blijft de ongelijkheid gelden.

Je neemt de ongelijkheid 11 ⩽ 12.

Je vermenigvuldigt beide leden met −5. Je verkrijgt:

Je deelt beide leden door −2. Je verkrijgt:

Eigenschap Als je beide leden van een ongelijkheid vermenigvuldigt met of deelt door hetzelfde negatieve getal, verschillend van nul, dan keert het ongelijkheidsteken om.

GEOGEBRA

7.2.3 Ongelijkheden oplossen

Voorbeeld 1

Los op: 2x + 3 > 7

2x > 7 − 3

2x > 4 x > 4 2 x > 2

Alle reële getallen groter dan 2 zijn oplossingen van de ongelijkheid. De oplossingsverzameling V van de ongelijkheid is ]2, +∞[ . Die verzameling bevat oneindig veel getallen.

Je kunt die verzameling op de getallenas voorstellen door een open halfrechte.

Voorbeeld 2

Los op: −3x + 6 ⩾ x + 8

Oplossingsverzameling: V =

Voorstelling op de getallenas:

Werkwijze • Werk de haakjes uit.

• Werk de noemers weg door elke term gelijknamig te maken.

• Plaats alle termen die de onbekende bevatten, in het ene lid en alle andere termen in het andere lid.

• Werk beide leden uit.

• Deel beide leden door de coëfficiënt van de onbekende, als die niet nul is. Vergeet het ongelijkheidsteken niet om te keren als de coëfficiënt negatief is.

Oefeningen

REEKS A

26 Los de ongelijkheden op.

x + 7 ⩽ 8

©VANIN

27 Los de ongelijkheden op. Rond, indien nodig, je resultaten af op 0,01 nauwkeurig.

a) 3x + 1 > p

b) 6x – 5 ⩽ 2

c) 2 (–3x + 1) ⩾ x + 9

d) –3 (x + 8) – 5x < 4 (x – 9) + 27

28 Los de ongelijkheden op. Rond, indien nodig, je resultaten af op 0,01 nauwkeurig.

a) 1 4 (5x + 3) > –1 2 (x – 5) V =

b) 8 x + 72 ⩽ 18 x – 50 V =

c) x + 2 4 –4x – 3 8 < x – 1 V =

7.2.4 Vraagstukken

Voorbeeld 1

Een koppel is op reis en wil een auto huren.

Verhuurfirma Carrent vraagt 55 euro per dag voor een onbeperkt aantal kilometers.

Verhuurfirma Rentcar vraagt 38 euro per dag plus 0,20 euro per kilometer.

Vanaf hoeveel kilometer is firma Carrent goedkoper?

• keuze van de onbekende:

Voorbeeld 2

In een squashclub betaal je 75 euro lidgeld per jaar en 3 euro per uur dat je speelt. Ook niet-leden mogen spelen, maar zij betalen 9 euro per uur.

Vanaf hoeveel uur spelen komt het voordeliger uit om lid te worden van de club?

• keuze van de onbekende:

• opstellen van de ongelijkheid:

• opstellen van de ongelijkheid:

• oplossen van de ongelijkheid:

• oplossen van de ongelijkheid:

• antwoord:

• antwoord:

Oefeningen

REEKS A

29 Los op.

a) Bepaal alle reële getallen waarvan het drievoud, verminderd met 8, groter is dan of gelijk is aan het dubbel van dat getal.

• keuze van de onbekende:

• opstellen van de ongelijkheid:

• oplossen van de ongelijkheid:

• antwoord:

REEKS B

30 Los op.

a) Bepaal alle reële getallen waarvan de som van het getal met 15, kleiner is dan het viervoud van het getal.

• keuze van de onbekende:

• opstellen van de ongelijkheid:

• oplossen van de ongelijkheid:

• antwoord:

b) Bepaal alle gehele getallen die je van 17 5 mag aftrekken, opdat het resultaat kleiner is dan 1 8

• keuze van de onbekende:

• opstellen van de ongelijkheid:

• oplossen van de ongelijkheid:

• antwoord:

b) Annemie heeft voor haar drie toetsen wiskunde respectievelijk 91 %, 86 % en 89 % behaald. Ze krijgt morgen een vierde toets. Hoeveel moet ze voor die vierde toets scoren om een gemiddelde van minstens 90 % te behalen?

• keuze van de onbekende:

• opstellen van de ongelijkheid:

• oplossen van de ongelijkheid:

• antwoord:

31 Foto’s afdrukken kost 0,20 euro per foto bij een fotograaf. Een firma die reclame maakt op het internet, ontwikkelt foto’s voor 0,10 euro per foto, maar je moet 2,95 euro betalen voor de verzending. Tot hoeveel foto’s is de fotograaf goedkoper?

©VANIN

Antwoord:

32 Twee handelsvertegenwoordigers worden door hun werkgever als volgt betaald:

• An verdient 1 500 euro per maand + 4 % op het verkoopbedrag.

• Anosh verdient 1 300 euro per maand + 6 % op het verkoopbedrag. Vanaf welk verkoopbedrag (in euro) heeft Anosh een hoger maandinkomen dan An?

Antwoord:

33 Jeroen haalt geld af in het buitenland. Als hij zijn Maestrokaart gebruikt, wordt 3 euro aangerekend plus 0,3 % van het afgehaalde bedrag. Gebruikt hij zijn Visakaart, dan wordt altijd 3,5 % aangerekend. Jeroen wil weten vanaf welk bedrag de Maestrokaart voordeliger is.

Antwoord:

7.3 Formules omvormen

7.3.1

Afhankelijke en onafhankelijke veranderlijke

r De oppervlakte A van een cirkel met straal r bereken je met de formule A = p  r 2

In deze formule is r de onafhankelijke veranderlijke (de input) en A de afhankelijke veranderlijke (de output).

• Uit een gegeven straal kan je de oppervlakte berekenen.

In welke mate verandert de waarde van A als r in waarde verdubbelt?

Verklaar:

• Uit een gegeven oppervlakte kun je de straal berekenen.

A is dan de onafhankelijke veranderlijke en r de afhankelijke veranderlijke.

Als je de formule A = p  r 2 omvormt naar r, dan verkrijg je: r 2 = A

Daaruit volgt: r =

Vul de tabel aan.

7.3.2 Formules omvormen

Voorbeeld 1

De oppervlakte van een rechthoek met lengte l en breedte b kun je berekenen met de formule

A = l  b

Bereken de oppervlakte van de rechthoek hierboven.

©VANIN

Voorbeeld 2

De omtrek van een rechthoek met lengte l en breedte b kun je berekenen met de formule

P = 2  (l + b).

Bereken de omtrek van de rechthoek hierboven.

Wat zijn in die formules de onafhankelijke veranderlijken?

Wat is in die formule de afhankelijke veranderlijke?

• Vorm de formule voor de oppervlakte om naar een formule om de lengte te berekenen.

Wat is in die formule de afhankelijke veranderlijke?

• Vorm de formule voor de omtrek om naar een formule om de lengte te berekenen.

• Vorm de formule voor de oppervlakte om naar een formule om de breedte te berekenen.

• Vorm de formule voor de omtrek om naar een formule om de breedte te berekenen.

• Een rechthoek heeft een oppervlakte van 315 cm2 en een lengte van 45 cm. Bereken de breedte van die rechthoek.

• Een rechthoek heeft een omtrek van 58 cm en een breedte van 12 cm. Bereken de lengte van die rechthoek.

Oefeningen

REEKS A

34 Vorm de formule om naar de opgegeven afhankelijke veranderlijke.

a) F = m  a a = d) V = l  b  h h =

b) U = R  I R = e) s = v  t v =

c) P = W t W = f) p = F A A =

©VANIN

35 De massadichtheid r van een stof is de massa m per volume V Er geldt: r = m V (r is de Griekse letter ‘rho’).

a) Vorm de formule om naar de gegeven afhankelijke veranderlijke m = V =

b) Vul de tabel aan. Bepaal je antwoord op 0,001 nauwkeurig. stof

(kg)

c) De stoffen met een dichtheid kleiner dan 1 blijven drijven op water. Welke stoffen uit de tabel drijven op water?

36 Vorm de formule om naar de opgegeven afhankelijke veranderlijke.

a) A = Dd 2

e) A h = B + b 2

b) r 2 p V = h 3 f) ppAh + 2 r 2 r = 2

©VANIN

c) + b )( I P = 2 b

g) (1 + in) K = k

d) = r v 2 m Fmpz v h) 4 P p I = r 2

37 De gemiddelde snelheid v van een bewegend voorwerp wordt gegeven door de formule v = s t , waarbij s de afgelegde weg is en t de tijd.

a) Wat zijn in die formule de onafhankelijke veranderlijken?

Wat is in die formule de afhankelijke veranderlijke?

b) Vorm de formule om, zodat t de afhankelijke veranderlijke wordt.

c) De afstand tussen Oostende en Dinant bedraagt 205 km.

Jaak rijdt de afstand met een gemiddelde snelheid van 90 km/h. Rozanne rijdt 10 km/h sneller. Hoeveel minuten zal ze eerder in Dinant zijn? Rond af op 0,1 min.

38 De oppervlakte A van een driehoek wordt berekend met de formule A = bh 2 , waarbij b de basis voorstelt en h de hoogte.

a) Wat zijn in die formule de onafhankelijke veranderlijken?

Wat is in die formule de afhankelijke veranderlijke?

b) Hoe verandert de oppervlakte, als je de basis verdubbelt en de hoogte gelijk blijft?

c) Hoe verandert de oppervlakte, als je de hoogte verdrievoudigt en de basis gelijk blijft?

©VANIN

d) Hoe verandert de hoogte, als je de basis verdubbelt en de oppervlakte gelijk moet blijven?

39 De oppervlakte van een vierkant is gelijk aan het kwadraat van de zijde. Een kubus is een zesvlak, waarbij elk vlak een vierkant is.

a) Stel een formule op voor de oppervlakte van een kubus met ribbe r.

b) In welke mate neemt de oppervlakte van een kubus toe, als je de ribbe verdubbelt?

c) Bereken het verschil in oppervlakte van een kubus met ribbe 10 cm en een kubus met ribbe 11 cm.

d) Bereken de ribbe van een kubus met een oppervlakte van 150 cm2

e) Met welke factor moet je de ribbe van een kubus vermenigvuldigen opdat de oppervlakte zou verdubbelen?

40 Je kunt de volgende formule gebruiken om graden Fahrenheit om te zetten naar graden Celsius: c = 5 9  (f − 32). Daarbij is f het aantal graden Fahrenheit (F) en c het aantal graden Celsius (C).

a) Vul de tabel aan.

f (F)

c (C)

b) Vorm de formule om, zodat je C kunt omzetten naar F.

©VANIN

c) In Brugge is het op een gegeven moment 24 C. Een Amerikaan vraagt zich af hoeveel F dat is. Help hem even.

REEKS C

41 Twee weerstanden R1 en R2 die parallel geschakeld zijn, hebben een vervangingsweerstand R die gegeven wordt door de formule RR R 1 = 1 + 1 12 R1 R2

a) Bepaal de formule waarbij R 2 de afhankelijke veranderlijke is.

b) Stel: R 1 = 0,5  en R = 1 6  (ohm: de eenheid van weerstand). Bereken R 2

42 Om te berekenen welke dosis medicijnen aan kinderen toegediend moet worden, wordt de formule van Young gebruikt. Als l de leeftijd is van het kind en d de dosis voor een volwassene, dan geldt m = I d I + 12 , waarbij m de dosis is voor het kind.

a) De meest voorkomende dosis voor een volwassene is 250 mg. Vul de tabel aan voor de gelijkwaardige dosissen voor kinderen. Rond telkens af op 0,001 mg.

leeftijd (jaren) 2 5 9 12 dosis (mg)

b) Vorm de formule om, zodat d de afhankelijke veranderlijke wordt.

c) Vorm de formule om, zodat l de afhankelijke veranderlijke wordt.

©VANIN

d) Rick en zijn pa hebben allebei kiespijn. Pa krijgt pijnstillers voorgeschreven van 600 mg.

De dokter zegt dat Rick dezelfde pijnstillers mag nemen, maar in dosissen die hoogstens 220 mg bedragen. Hoe oud is Rick?

43 In de aerodynamica is het belangrijk om te weten welke massa een stel vleugels kan dragen en welke snelheid er nodig is om te kunnen vliegen.

Als W de massa is in kg, A de vleugeloppervlakte in m 2 , v de kruissnelheid in m/s en d de luchtdichtheid in kg/m 3 , dan geldt de formule W = 0,03 d  v 2 A.

a) Een merel van 90 gram heeft een vleugeloppervlak van 200 cm 2 De vogel vliegt dicht bij de grond, waarbij d = 1,25 kg/m 3. Bereken zijn kruissnelheid (in km/h).

b) In de vliegtuigbouw wordt gewerkt met het begrip ‘vleugelbelasting’; dat is de massa per vierkante meter vleugeloppervlak, dus W A (in kg/m 2). Bereken de vleugelbelasting van een Boeing 747, met een vleugeloppervlak van 511 m 2 en een kruissnelheid van 900 km/h, als hij op een hoogte vliegt waar de luchtdichtheid 0,312 5 kg/m 3 is.

44 Het aantal calorieën K dat een actieve man dagelijks nodig heeft, wordt gegeven door de formule K = 19,18 m + 7 h − 9,52 l + 92,4.

Daarbij is m de massa in kg, h de lengte van de man in cm en l de leeftijd in jaren.

a) Jos is 53 jaar, meet 178 cm en weegt 83 kg. Hoeveel calorieën heeft hij dagelijks nodig? Rond af op een eenheid.

b) Vul de tabel aan. Rond af op een eenheid.

7.1

Eerstegraadsvergelijkingen

Als je bij beide leden van een gelijkheid eenzelfde getal optelt of aftrekt, dan blijft de gelijkheid bestaan.

a = b ⇔ a + c = b + c (met a, b, c ∈ r)

a = b ⇔ a – c = b – c (met a, b, c ∈ r)

Als je beide leden van een gelijkheid vermenigvuldigt met of deelt door eenzelfde van nul verschillend getal, dan blijft de gelijkheid bestaan.

a = b ⇔ a c = b c (met a, b, c ∈ r0)

a = b ⇔ a c = b c (met a, b, c ∈ r0)

Een vergelijking is een gelijkheid met een onbekend getal.

a = b ⇔ b = a (met a, b ∈ r)

Een eerstegraadsvergelijking in een onbekende x is een vergelijking met als standaardvorm ax + b = 0 (met a ∈ r0 en b ∈ r).

Optellen in het ene lid wordt aftrekken in het andere lid, en omgekeerd.

x + a = b wordt x = b – a

x – a = b wordt x = b + a

Vermenigvuldigen in het ene lid wordt delen in het andere lid, en omgekeerd.

x a = b wordt x = b a

x a = b wordt x = b a

©VANIN

KUNNEN

Vergelijkingen van de eerste graad met één onbekende oplossen.

Vraagstukken oplossen die leiden tot een vergelijking van de eerste graad met één onbekende.

7.2 Eerstegraadsongelijkheden

Een ongelijkheid van de eerste graad in één onbekende x is een ongelijkheid met als standaardvorm

ax + b > 0, ax + b ⩾ 0, ax + b < 0 of ax + b ⩽ 0 (met a ∈ r0 en b ∈ r)

Als je beide leden van een ongelijkheid vermeerdert of vermindert met hetzelfde getal, dan blijft de ongelijkheid gelden.

a ⩽ b ⇔ a + c ⩽ b + c (met a, b, c ∈ r)

Als je beide leden van een ongelijkheid vermenigvuldigt met of deelt door hetzelfde positieve getal, verschillend van nul, dan blijft de ongelijkheid gelden.

a ⩽ b ⇔ a  c ⩽ b  c en a ⩽ b ⇔ a c ⩽ b c (met a, b ∈ r en c ∈ r+0)

Als je beide leden van een ongelijkheid vermenigvuldigt met of deelt door hetzelfde negatieve getal, verschillend van nul, dan keert het ongelijkheidsteken om.

a ⩽ b ⇔ a  c ⩾ b  c en a ⩽ b ⇔ a c ⩾ b c (met a, b ∈ r en c ∈ r0)

Vraagstukken oplossen en daarbij

KUNNEN

• in de opgave herkennen welke grootheden aan de orde zijn;

• het probleem vertalen in een wiskundige vorm met algebraïsche bewerkingen;

• verantwoord kiezen tussen schattend of benaderend rekenen en de rekenmachine;

• de oplossing zinvol afronden en interpreteren.

Vraagstukken oplossen die leiden tot een ongelijkheid van de eerste graad met één onbekende, en de oplossing grafisch voorstellen en symbolisch noteren.

7.3 Formules omvormen

KENNEN

In een formule die het verband tussen verschillende veranderlijken weergeeft, noem je

©VANIN

• de veranderlijken waarvan je de waarde kiest, de onafhankelijke veranderlijken;

• de veranderlijke waarvan de waarde berekend wordt, de afhankelijke veranderlijke.

KUNNEN

Een formule omvormen naar een andere veranderlijke.

Vraagstukken oplossen door een gekende of gegeven formule om te vormen naar een andere veranderlijke.

Pienter problemen oplossen

Welke heuristiek(en) gebruik je om de onderstaande problemen op te lossen?

❑ concreet materiaal

❑ schets

❑ schema/tabel

❑ vereenvoudig

❑ gok verstandig

1. Maak met de cijfers 1 tot en met 9 twee getallen. Het product van die twee getallen moet zo groot mogelijk zijn. Alle cijfers moeten precies één keer voorkomen.

❑ filter

❑ patroon

❑ kennis

❑ logisch nadenken

❑

©VANIN

2. Plaats de getallen 1 tot en met 16 in een rij achter elkaar. Zorg ervoor dat de som van elke twee opeenvolgende getallen een kwadraat is.

3. Op een schoolfeest staat een glazen bokaal met knikkers. Wie kan raden hoeveel knikkers er precies in de bokaal zitten, wint een prachtige prijs. Ahmed gokt dat er 90 knikkers in de bokaal zitten, Bette denkt dat het er 97 zijn. Cas is ervan overtuigd dat het er 99 zijn, en Dora gokt dat het er 101 zijn. Alle vier winnen ze niks. Later blijkt dat een van hen er 7 naast zat, iemand 4 en iemand 3. Van de vierde persoon weten we het niet.

Hoeveel knikkers zaten er in die bokaal?

4. Matthijs is groter dan Maya. Lasse is kleiner dan Matthijs. Van slechts een van de onderstaande beweringen weet je met zekerheid dat ze juist is. Welke?

A) Maya is groter dan Lasse.

B) Lasse is groter dan Maya. C) Je kunt niet weten of Maya of Lasse groter is.

HOOFDSTUK 8 I VECTOREN

8.1 Begripsvorming

8.2 Bewerkingen met vectoren

8.3 Toepassingen uit de fysica

©VANIN

8.1.1

Benaming en voorstelling

Een georiënteerd lijnstuk is een lijnstuk waarop een zin is aangeduid door middel van een pijl.

Een lijnstuk [AB] met een zin noteer je als: → AB

De georiënteerde lijnstukken

→

AB, ⟶ PP9 , ⟶ QQ9 en ⟶ RR9 zijn gelijk, want

• ze hebben dezelfde richting

AB⫽PP9⫽QQ9⫽RR9 ;

• ze hebben dezelfde zin (pijl);

• ze zijn even lang

| AB | = | PP9 | = | QQ9 | = | RR9 |

Alle gelijke georiënteerde lijnstukken vormen samen een vector.

Je zegt dat de georiënteerde lijnstukken ⟶ PP9 , ⟶ QQ9 en ⟶ RR9 vertegenwoordigers zijn van eenzelfde vector → AB

Het beeld van driehoek PQR door de verschuiving volgens de vector → AB is de driehoek P9Q9R9

Je noteert: t→ AB (n PQR) = n P9Q9R9

Definitie Vector

Een vector is een grootheid die volledig bepaald wordt door

• een grootte,

• een richting,

• een zin.

Notatie: → AB Je leest dit als: de vector AB

Je kunt een vector ook noteren met een kleine letter met een pijltje erboven: → AB = → v

Bijzonder geval

Een vector met hetzelfde beginpunt als eindpunt noem je een nulvector

De nulvector heeft geen richting en geen zin.

De grootte van de nulvector is 0.

Notatie: → AA = ⟶ BB = = → O

Er bestaan verschillende soorten vectoren.

vrije vector gebonden vector

Een vrije vector wordt gekenmerkt door een richting, zin en lengte.

Een vrije vector kan overal in het vlak of in de ruimte getekend worden; het blijft dezelfde vector.

Scalaire en vectoriële grootheden

Een gebonden vector is een vector die vast(gebonden) is aan een aangrijpingspunt

Een gebonden vector komt overeen met juist één vertegenwoordiger van een vector.

©VANIN

Bij toepassingen wordt een onderscheid gemaakt tussen twee soorten grootheden.

Scalaire grootheden worden volledig bepaald door een maatgetal en een eenheid.

Voorbeelden:

• lengte: 2 m

• massa: 46,2 kg

• temperatuur: 21,0 ºC

Vectoriële grootheden hebben een grootte, richting en zin. Ook het aangrijpingspunt is van belang. Ze worden voorgesteld met behulp van een vector.

Voorbeelden:

• kracht

• snelheid

• versnelling

8.1.2 De norm van een vector

De norm (of de grootte) van een vector → AB is de lengte van het lijnstuk [AB].

Notatie: ‖→ AB‖ Je leest dit als: de norm van vector AB

Definitie Norm van een vector

De norm van een vector → AB is de lengte van het lijnstuk [AB]. ‖→ AB‖ = | AB |

8.1.3

Gelijke vectoren

Definitie Gelijke vectoren

Twee vectoren zijn gelijk als en slechts als ze

• dezelfde grootte hebben;

• dezelfde richting hebben;

• dezelfde zin hebben.

8.1.4 Tegengestelde vectoren

Definitie Tegengestelde vectoren

Twee vectoren zijn tegengesteld als en slechts als ze

• dezelfde grootte hebben;

• dezelfde richting hebben;

• een tegengestelde zin hebben.

Opmerking: de tegengestelde vector van een vector → v noteer je als –→ v Er geldt

Oefeningen

REEKS A

1 Vink de correcte kenmerken aan van vector → AB en vector ⟶ CD.

dezelfde grootte ❒ dezelfde richting ❒ dezelfde zin ❒

dezelfde grootte ❒ dezelfde richting ❒ dezelfde zin ❒

dezelfde grootte ❒ dezelfde richting ❒ dezelfde zin ❒

2 Welke vectoren zijn gelijk en welke zijn tegengesteld? Noteer in symbolen.

Gelijke vectoren: Tegengestelde vectoren:

3 Teken een vector ⟶ CD zodat → AB = ⟶ CD.

©VANIN

4 Teken een vector ⟶ CD zodat → AB = –⟶ CD

Maurits Cornelis Escher (1898-1972) was een Nederlandse graficus. Hij maakte in totaal 448 lithografieën, houtsneden en houtgravures en meer dan 2 000 tekeningen en schetsen. Enkele zeer bekende werken van hem zijn ontworpen rond onmogelijke objecten, zoals de Penrose-trap. Zijn gravures verbeelden vaak onmogelijke constructies, studies van oneindigheid en in elkaar passende meetkundige patronen (vlakverdelingen).

5 Vul telkens het beeld in van de verschuiving volgens de gegeven vector.

1)

(F 11) =

EI ( ) = F 10 g) t→ AC ( ) = F 11

h) t ⟶ DG ( ) = F 10

6 Teken de punten E, F, G en H als je weet dat

7 De figuur is opgebouwd uit vier parallellogrammen met dezelfde basis en hoogte. Vul telkens in met + of –. G D H E F l

©VANIN

a) → AB = → EF

b) → BC = → ED

c) → HI = ⟶ GH

d) ⟶ AD = → CF

e) ⟶ HG = → DE

f) → FC = ⟶ AD

g) → AC = → DF

h) → EH = → FI

i) ⟶ GD = → FI

j) → BA = → BC

8 De figuur is opgebouwd uit gelijkzijdige driehoeken. B is het midden van [AC], D is het midden van [AF] en E is het midden van [CF].

a) Vul aan zodat je een gelijke vector krijgt.

→ AB = → D

⟶ BD = ⟶ E

⟶ DA = ⟶ F

→ CE = → B

b) Vul aan zodat je een tegengestelde vector krijgt.

→ AB = –→ C

→ BE = –⟶ F

→ FE = –→ C

→ DE = –→ B

8.2 Bewerkingen met vectoren

8.2.1

Inleiding

In de lucht ondervindt een valschermspringer verschillende krachten:

• een kracht → FZ gericht naar het middelpunt van de aarde: de zwaartekracht;

GEOGEBRA

• een kracht → F w veroorzaakt door de wind.

8.2.2 De som van vectoren

Formule van Chasles-Möbius

De resulterende kracht kun je voorstellen met behulp van één vector: → F R

Ze heeft hetzelfde effect als de andere twee krachten samen. Om die kracht nauwkeurig te tekenen, leer je in dit onderdeel hoe je vectoren kunt optellen.

Als drie punten in het vlak gegeven zijn, dan kun je, waar je die punten ook legt, altijd de volgende som noteren:

Je noemt vector

Formule Chasles-Möbius

Voor drie punten

van de

De somvector tekenen

Geval 1: het eindpunt van de eerste vector valt samen met het beginpunt van de tweede vector.

Deze methode steunt op de formule van Chasles-Möbius. → AB + → BC = → AC

Geval 2: het eindpunt van de eerste vector valt niet samen met het beginpunt van de tweede vector.

Je tekent een nieuwe vertegenwoordiger van de tweede vector, zodat het eindpunt van de eerste vector samenvalt met het beginpunt van de tweede vector.

AB + ⟶ CD → CD = → BE (gelijke vectoren)

→ AB + → BE formule Chasles-Möbius = → AE

Deze methode heet de kop-staartmethode

Geval 3: de twee vectoren hebben hetzelfde beginpunt

Als de twee vectoren hetzelfde beginpunt hebben, kun je, naast de kop-staartmethode, ook de parallellogrammethode toepassen om de somvector te tekenen.

Je tekent een parallellogram waarvan [AB] en [AC] twee zijden zijn.

De diagonaal [AD] uit het gemeenschappelijk beginpunt A bepaalt dan de somvector ⟶ AD

8.2.3 Het verschil van vectoren

Definitie Verschil van twee vectoren

Het verschil van twee vectoren is de som van de eerste vector met het tegengestelde van de tweede vector.

→ AB –⟶ CD = → AB + (–⟶ CD)

De verschilvector tekenen

Om twee vectoren van elkaar af te trekken, teken je een nieuwe vertegenwoordiger van –⟶ CD, zodat het eindpunt van de eerste vector samenvalt met het beginpunt van deze nieuwe vertegenwoordiger.

C E A → AB –⟶ CD verschil van vectoren

= → AB + (–⟶ CD) –→ CD = → DC (tegengestelde vectoren)

= → AB + ⟶ DC → DC = → BE (gelijke vectoren)

= → AB + → BE

= → AE

Voorbeeld

a) Teken ⟶ PQ –→ RS

formule Chasles-Möbius

b) Vul aan.

PQ –→ RS

⟶ PQ + ( )

8.2.4 Een vector ontbinden in twee componenten

Je kunt elke vector ontbinden in een som van twee of meer vectoren.

Voorbeelden

Ontbind vector → u in twee componenten → v en → w zodat → u = → v + → w

De drager van vector → v is evenwijdig met b

De drager van vector → w is evenwijdig met a

8.2.5 De vermenigvuldiging van een vector met een getal

De vermenigvuldiging van een vector met een reëel getal noem je de scalaire vermenigvuldiging

Definitie Vermenigvuldiging van een vector met een getal

De vector r  → AB (metr ∈ r 0) is een vector waarvan:

• de lengte gelijk is aan het product van de absolute waarde van r en de lengte van → AB ;

• de richting dezelfde is als die van → AB ;

• de zin dezelfde is als die van → AB als r > 0 en tegengesteld als r < 0.

Voorbeelden

a) Gegeven: → AB

Gevraagd: teken 2  → AB

©VANIN

b) Gegeven: → u

Gevraagd: teken –3  → u u

Bijzondere gevallen

0 → AB = → O

r  → O = → O

De formule van Chasles-Möbius is genoemd naar August Ferdinand Möbius (1790-1868) en Michel Chasles (1793-1880). Ondanks het feit dat de formule naar hen werd genoemd, hebben de twee elkaar, naar alle waarschijnlijkheid, nooit ontmoet.

August Möbius was een Duitse wiskundige die in 1815 professor sterrenkunde werd in Leipzig. Later werd hij directeur van de nieuw gebouwde universitaire sterrenwacht. Möbius is onder meer bekend van zijn bijdrage aan de algebraïsche meetkunde en de topologie. Ook de band van Möbius werd naar hem genoemd.

Michel Chasles was een Franse wiskundige die studeerde aan de beroemde Ecole Polytechnique in Parijs, waar hij nadien professor werd. Hij is onder meer bekend van zijn studie van de projectieve meetkunde en de theoretische mechanica.

REEKS A

9 Teken de som van de vectoren en vul aan.

©VANIN

©VANIN

11 Teken de gevraagde vector.

a) ⟶ DC = 2 → AB AA

b) ⟶ CD = –3  → AB

c) → BC = –2 → AB AB

d) → BA = 1 2  ⟶ DC D

©VANIN

REEKS B

12 Vereenvoudig de vectorsommen door gebruik te maken van veelvouden.

a) → AB + → AB + → AB + → AB + → AB =

b) –⟶ CD –⟶ CD =

c) ⟶ PQ + ⟶ PQ + → RS + → RS + → RS =

d) → u + → u –→ v –→ v –→ v =

e) → u + → u + → u + → u + → v –→ v =

13 Vul aan zodat de gelijkheid klopt.

a) ⟶ PQ + = → PR

b) → AB + ⟶ BD + = → AE

c) → DF + = → O

d) –→ AB – = → BC

e) → DF + → FB + → BE =

f) → AA + = → AB

g) ⟶ PQ = → PR –

h) –→ DE = –→ AE +

14 Ontbind vector → u in twee componenten → v en → w

De drager van vector → v is evenwijdig met b.

De drager van vector → w is evenwijdig met a.

15 De figuur bestaat uit vijf even grote gelijkbenige driehoeken. Bepaal telkens de som of het verschil van de vectoren.

a) → AB + → BC =

b) ⟶ AD + → AB =

c) → DF + → DF =

d) → CA + → BC =

e) ⟶ BD –⟶ BD =

f) → EC –⟶ DC =

g) → AF –→ BF =

h) → CF –→ FD =

©VANIN

16 De figuur bestaat uit negen gelijkzijdige driehoeken. Vul in met een vector. A C E

a) → AB + 2 → AC = b) → CJ + 3 ⟶ HD = c) ⟶ HD + 2  → DE = d) 2  → BC + → EH = e) 2 3 → GJ + → IB = f) → HE – 2 ⟶ BD = g) 2  → BE –→ CJ = h) → AC –1 2  → DF =

17 Welke soort vierhoek is ABCD als je weet dat A, B, C en D niet-collineaire punten zijn?

a) → AB = 2  ⟶ CD

b) → AB = –⟶ CD

18 Gegeven is de driehoek ABC. Teken de punten P, Q en R als je weet dat:

a) → AB + → AC = → AP

b) → CA –→ BC = ⟶ CQ

c) → AC + → AC = → AR

©VANIN

19 De volgende figuur bestaat uit vier rechthoeken met een gelijke lengte en gelijke breedte. Schrijf de vector als een som van veelvouden van → u en → v.

a) → DF = b) → GE = c) ⟶ HC = d) ⟶ GA =

e) → GC = f) → FD =

g) → ID =

h) → FH =

20 Teken de som of het verschil van de vectoren.

21 Gegeven is een regelmatige zeshoek. De straal van de omgeschreven cirkel heeft dezelfde lengte als de zijde van de zeshoek. Schrijf de vector als een som van veelvouden van → u en → v

©VANIN

22 Gegeven is een parallellogram ABCD en een willekeurig punt P. Bewijs dat voor elk punt P geldt: → AB + → CP = ⟶ DP

23 In welk vak kom je terecht als je de drie vectoren ⟶ OA, ⟶ OB en ⟶ OC optelt? Laat je werkwijze zien.

©VANIN

24 Gegeven is een kubus. M en N zijn de snijpunten van de diagonalen van de zijvlakken. Schrijf als één vector.

8.3 Toepassingen uit de fysica

8.3.1

Krachtvectoren

Een kracht is een vectoriële grootheid en kan worden voorgesteld met behulp van een gebonden vector.

Een krachtvector wordt bepaald door

• een aangrijpingspunt A,

• een richting AB,

• een zin: van A naar B,

• een grootte: ‖→ AB‖ = | AB |

Als twee krachten → F 1 en → F 2 inwerken op een voorwerp met hetzelfde aangrijpingspunt, dan teken je de resulterende kracht → F R als somvector van → F 1 en → F 2

De krachtvectoren hebben niet dezelfde richting

Tuur en Domien staan ieder aan een kant van een boot. Ze trekken elk aan een touw dat aan de voorkant van de boot werd bevestigd. Tuur trekt met een kracht van 400 N, Domien met een kracht van 550 N.

Teken de resulterende kracht → F R F1

©VANIN

De krachtvectoren hebben dezelfde richting en dezelfde zin

Pieter en Stan duwen aan dezelfde kant een kist horizontaal naar rechts. Ze duwen elk met een kracht van 400 N.

Teken de resulterende kracht → F R

• De richting van de krachten → F 1 en → F 2 is dezelfde.

• De zin van de resulterende kracht → F R is horizontaal naar rechts.

• De grootte van de resulterende kracht vind je als volgt: ‖→ F R ‖ = ‖→ F 1 ‖ + ‖→ F 2‖ = 400 + 400 = 800

De grootte van de resulterende kracht bedraagt 800 N.

De krachtvectoren hebben dezelfde richting en een tegengestelde zin

Pieter en Stan willen zien wie van de twee het sterkst is. Ze duwen elk aan een kant van een kist. Pieter duwt met een kracht → F 1 van 400 N horizontaal naar rechts en Stan duwt met een kracht → F 2 van 500 N horizontaal naar links. Teken de resulterende kracht → F R

©VANIN

• De richting van de krachten → F 1 en → F 2 is dezelfde.

• De zin van de resulterende kracht → F R is horizontaal naar links.

Je kunt besluiten dat Stan het sterkst is.

• De grootte van de resulterende kracht vind je als volgt: ‖→ F R ‖ = ‖→ F 2 ‖ – ‖→ F 1‖ = 500 – 400 = 100

De grootte van de resulterende kracht bedraagt 100 N.

8.3.2 Snelheidsvectoren

Een snelheid heeft altijd een welbepaalde richting, zin en grootte. Als aangrijpingspunt wordt meestal het massazwaartepunt genomen van het voorwerp dat beweegt. Snelheid is daarom ook een vectoriële grootheid.

8.3.3 Versnellingsvectoren

Als de snelheidsvector van een voorwerp verandert, dan zeg je dat het voorwerp ‘versnelt’. Dat woord kan soms wat verwarrend zijn omdat een snelheidsverandering ook een vertraging kan betekenen.

Notatie versnellingsvector: → a

Als de versnellingsvector → a dezelfde zin heeft als de snelheidsvector → v, dan neemt de snelheid in grootte toe.

t = 0 (s)

De auto staat stil. Joris start zijn wagen en drukt op het gaspedaal.

t = 1 (s)

De auto van Joris versnelt.

t = 5 (s)

De auto van Joris versnelt nog altijd.

©VANIN

Als de versnellingsvector → a een tegengestelde zin heeft ten opzichte van de snelheidsvector → v, dan neemt de snelheid in grootte af.

t = 0 (s)

Joris rijdt met zijn wagen en duwt op het rempedaal.

t = 2 (s)

Joris duwt nog steeds op het rempedaal. De auto van Joris vertraagt.

Oefeningen

REEKS B

25 Op de tekening zie je een volle en een halfvolle bus melk.

a) Welke kracht wordt hier telkens voorgesteld?

b) Verklaar waarom de aangrijpingspunten zich op een andere plaats bevinden.

©VANIN

c) Verklaar waarom de krachtvector bij de volle bus melk groter is getekend.

26 Vijf kinderen spelen een spelletje touwtrekken.

De twee jongens trekken samen met een kracht → F 1 van 500 N naar links.

De drie meisjes trekken samen met een kracht → F 2 van 670 N naar rechts.

Stel een grootte van 100 N voor als 1 cm.

a) Teken de krachtvectoren → F 1 en → F 2 op de tekening. Neem als aangrijpingspunt het midden A van het touw. A

b) Teken de resulterende kracht → F R

c) Hoe groot is de resulterende kracht?

d) Wie wint het spelletje touwtrekken?

27 Laura stapt op de bus en gaat achteraan zitten. De bus vertrekt oostwaarts en rijdt tegen een snelheid van 52 km/h.

a) Laura wil de buschauffeur iets vragen.

Ze wandelt met een snelheid van 4,5 km/h oostwaarts.

Hoeveel bedraagt de snelheid van Laura ten opzichte van de grond?

b) Nadien wandelt Laura terug met een snelheid van 4 km/h in de richting van het westen.

Hoeveel bedraagt de snelheid van Laura ten opzichte van de grond?

28 Mil en Margot trekken ieder aan een zware koffer. De zin, de richting en de grootte van de uitgeoefende krachten vind je op de tekening. Teken telkens de resulterende kracht → F R .

Situatie 1:

Situatie 2:

STUDIEWIJZER Vectoren

8.1 Begripsvorming

KENNEN

Een vector is een grootheid die volledig bepaald wordt door

• een grootte,

• een richting,

• een zin.

Notatie: → AB Je leest dit als: de vector AB

De norm van een vector → AB is de lengte van het lijnstuk [AB].

‖→ AB‖ = | AB |

Twee vectoren zijn gelijk als en slechts als ze

• dezelfde grootte hebben;

• dezelfde richting hebben;

• dezelfde zin hebben.

Twee vectoren zijn tegengesteld als en slechts als ze

• dezelfde grootte hebben;

• dezelfde richting hebben;

• een tegengestelde zin hebben.

©VANIN

KUNNEN

Van een gegeven vector een gelijke en een tegengestelde vector tekenen.

Gelijke en tegengestelde vectoren herkennen en benoemen.

8.2 Bewerkingen met vectoren

KENNEN

Voor drie punten A, B en C in het vlak geldt: → AB + → BC = → AC (formule Chasles-Möbius).

Het verschil van twee vectoren is de som van de eerste vector met het tegengestelde van de tweede vector. → AB –⟶ CD = → AB + (–⟶ CD)

De vector r → AB (met r ∈ r 0) is een vector waarvan:

• de lengte gelijk is aan het product van de absolute waarde van r met de lengte van → AB ;

• de richting dezelfde is als die van → AB ;

• de zin dezelfde is als die van → AB als r > 0 en tegengesteld als r < 0.

KUNNEN

Van twee (of meer) vectoren de somvector en de verschilvector definiëren en tekenen.

Het scalair product van een vector en een reëel getal definiëren en tekenen.

Een vector ontbinden in twee (of meer) vectoren.

8.3

Toepassingen uit de fysica

KUNNEN

De resulterende kracht-, snelheids- of versnellingsvector tekenen.

De norm van de resulterende kracht-, snelheids- of versnellingsvector berekenen als de gegeven vectoren dezelfde richting hebben.

Problemen uit JWO

Problemen uit JWO

1. Een rechthoekige puzzel van 1 000 stukjes telt 25 stukjes op elke verticale lijn en 40 op elke horizontale lijn. Hoeveel procent van de stukjes ligt op de rand?

1. Twee vierkanten liggen in een groot vierkant, zoals op de figuur. Wat is de verhouding van de oppervlaktes van vierkant I en II?

JWO, editie 2017, eerste ronde

JWO, editie 2022, eerste ronde

2. In de cirkel zijn een vierkant en vier kwartcirkels getekend. Welk deel van de oppervlakte van de cirkel wordt ingenomen door de vier kwartcirkels?

2. Twee vierkanten liggen in een groot vierkant, zoals op de figuur. Wat is de verhouding van de oppervlaktes van vierkant I en II?

JWO, editie 2022, eerste ronde

JWO, editie 2022, eerste ronde

3. Als (x – 1)  (x + 1) = 4, dan is (x

– x) gelijk aan …

©VANIN

JWO, editie 2021, tweede ronde

4. Toen Pif 15 jaar oud was, was Poef 18. Toen Poef 13 jaar oud was, was Paf 11. Hoe oud was Pif toen Paf 15 was?

JWO, editie 2013, tweede ronde

PIENTER REMEDIËREN

©VANIN

EXTRA LEERSTOF XL

©VANIN

Overzicht Extra Leerstof