











Veelvouden – gemeenschappelijke veelvouden –kleinste gemeenschappelijke veelvoud –gelijknamige breuken

LEERLIJNEN
G 3 breuken
6 delers en veelvouden

MATERIAAL
• werkschrift A blz. 49-51
• een kalender voor klassikaal gebruik, waarop alle dagen van een maand te zien zijn

WISKUNDETAAL
Rekentaal
• het veelvoud

• het (kleinste) gemeenschappelijke veelvoud (kgv)
• gelijknamige breuken
• kleiner of gelijk aan (≤)
Instructie- en contexttaal
• gemeenschappelijk
• de veldloop
• het parcours

LES 14


a Veelvouden van 2 ≤ 20 →
Veelvouden van 3 ≤ 20 →
Het kgv van 2 en 3 is

b Veelvouden van 7 ≤ 100 →
Veelvouden van 8 ≤ 100 →
Het kgv van 7 en 8 is
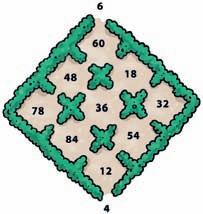
c Veelvouden van 12 ≤ 100 →
Veelvouden van 18 ≤ 100 →
Het kgv van 12 en 18 is

d Veelvouden van 15 ≤ 100 →
Veelvouden van 9 ≤ 100 →
Het kgv van 15 en 9 is
e Veelvouden van 12 ≤ 100 →
Veelvouden van 16 ≤ 100 →
Veelvouden van 24 ≤ 100 →
Het kgv van 12, 16 en 24 is


Noteer van elk getal een reeks veelvouden van klein naar groot.










LESDOELEN
Inoefenen

• Verwoorden wanneer een natuurlijk getal een veelvoud is van een ander natuurlijk getal
• Weten dat elk natuurlijk getal een veelvoud is van 1 en dat elk natuurlijk getal 0 en zichzelf als veelvoud heeft


• Veelvouden opsommen van getallen ≤ 1 000
• De gemeenschappelijke veelvouden vinden van twee natuurlijke getallen ≤ 20 en aangeven welk getal het kleinste gemeenschappelijke veelvoud (kgv) is
• De termen ‘veelvoud, gemeenschappelijk veelvoud en kleinste gemeenschappelijk veelvoud’ gebruiken
• Verwoorden in welke situaties het kgv handig te gebruiken is en dat toepassen


• Breuken gelijknamig maken met behulp van het kgv van de noemers om ze te vergelijken
START
Femke nam vanmorgen een douche. Dat doet ze om de twee dagen. Op welke dagen zal ze deze maand nog douchen?
Laat die dagen op de kalender aanduiden: overmorgen/over twee dagen, over vier, zes ... dagen.
Haar broer Jasper neemt om de drie dagen een douche. Ook hij douchte vanmorgen. Wanneer zullen Femke en Jasper voor het eerst weer op dezelfde dag douchen?
Laat de leerlingen in duo’s naar de oplossing zoeken. Tijdens de bespreking kun je eventueel de dagen waarop Jasper doucht met een andere kleur op de kalender laten aanduiden.
Wie vond het antwoord zonder kalender? Hoe?
Kom tot het besluit dat je het antwoord kunt vinden door op zoek te gaan naar de veelvouden van 2 en 3 en dan te kijken wanneer die het eerst samenvallen: over 6 dagen, dus.
KERN
De veelvouden van een natuurlijk getal
• Wat is een veelvoud van een natuurlijk getal? “Het product van dat getal met een natuurlijk getal.”
Bv. 27 is een veelvoud van 3 want 9 × 3 = 27.
• Hoe vind je alle veelvouden van een getal? “Door het getal te vermenigvuldigen met alle natuurlijke getallen.”
Laat de leerlingen hun werkschrift nemen en maak opgave 1a klassikaal op het bord. De leerlingen werken mee in hun werkschrift.
• Geef de veelvouden van 2 en 3 die kleiner of gelijk zijn aan 20. Laat de veelvouden opnoemen en noteer ze mee op het bord. Gebruik daarbij het symbool ≤ en vestig de aandacht op de betekenis. Veelvouden van 2 ≤ 20 : 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20. Veelvouden van 3 ≤ 20 : 0, 3, 6, 9, 12, 15, 18.
Besteed aandacht aan het feit dat elk natuurlijk getal 0 (0 × getal) en zichzelf (1 × getal) als veelvoud heeft.
Vraag ook welk natuurlijk getal alle andere natuurlijke getallen als veelvoud heeft: 1.
Gemeenschappelijke veelvouden
• Welke veelvouden, komen zowel bij 2 als bij 3 voor? “0, 6, 12 en 18.” Wijs ze aan in de beide reeksen.
• Hoe zou je zulke veelvouden noemen, die bij de beide getallen voorkomen? “Gemeenschappelijke veelvouden.”
Onderstreep de gemeenschappelijke veelvouden op het bord.
Het kleinste gemeenschappelijke veelvoud
Kom terug op de vraag uit de start van de les.
• Over hoeveel dagen douchen Femke en Jasper voor het eerst op dezelfde dag als ze vandaag allebei een douche namen?
“Over 6 dagen.” Omcirkel het getal 6 in de beide reeksen.
• Wat is het getal 6 van 2 en 3? “Het kleinste gemeenschappelijke veelvoud.”
Noteer dat met de afkorting: het kgv van 2 en 3 is 6.
Leg uit dat 0 niet meetelt als kleinste gemeenschappelijke veelvoud, omdat anders alle getallen hetzelfde kgv zouden hebben.
Verkorte werkwijze
Wijs de leerlingen erop:
• dat het volstaat om de veelvouden van één getal te zoeken en te stoppen bij een veelvoud dat deelbaar is door het andere getal.
• dat je daarvoor het best het grootste getal neemt omdat de rij van de veelvouden dan korter is.
les 2 van 4
vorige: les 13
volgende: les 85
Tips
• Let erop dat de leerlingen het begrip ‘veelvoud’ voldoende begrijpen: een aantal keer. Verwijs naar het ‘meervoud’ in taalbeschouwing.
• Vraag hoe ‘groter dan of gelijk aan’ er dan als symbool zal uitzien: ≥.
Tips
• Verwijs bij het begrip ‘gemeenschappelijk’ naar de les over de ggd: wat ze gelijk, hetzelfde ... hebben.
• Wijs op het verschil: bij de delers wordt de grootste gemeenschappelijke deler gezocht, bij de veelvouden het kleinste gemeenschappelijke veelvoud.
• Wijs ook bij de verkorte werkwijze op het verschil: bij de ggd vertrek je het best van het kleinste getal, bij het kgv van het grootste getal.
Pas dat toe op de veelvouden van 2 en 3: 6 is het eerste veelvoud van 3 dat deelbaar is door 2.
Laat die verkorte werkwijze ook eens toepassen op drie getallen, bv. 2, 6 en 9: 18 is het eerste veelvoud van 9 dat ook deelbaar is door 6 en door 2.
Gelijknamige breuken zoeken met behulp van het kgv Op de SVS-scholenveldloop had Alexis na 6 minuten al 5 7 van het parcours afgelegd. Pierre had toen 2 3 van het parcours achter de rug. Wie van de twee liep er op dat moment aan de leiding?
Laat de leerlingen per twee de oplossing zoeken op een blaadje.
5 7 = 15 21 en 2 3 = 14 21 5 7 > 2 3 Alexis liep aan de leiding.
Bespreek achteraf klassikaal:
• Wat heb je gedaan om de breuken te kunnen vergelijken? “Ze gelijknamig gemaakt, op dezelfde noemer gebracht: 21.”
• Hoe heb je die gelijke noemer gevonden? Zien de leerlingen dat 21 het kgv is van 3 en 7?
Besluit dat je bij ongelijknamige breuken op een eenvoudige manier een gelijke noemer vindt door het kgv van de beide noemers te zoeken.
• Waarvoor moet je breuken nog gelijknamig maken? “Om ze op te tellen of af te trekken.”
VERWERKING
Overloop de oefeningen in het werkschrift. Vestig daarbij de aandacht op de tip van de bollobo bij oefening 2.
• De instructiegevoelige leerlingen werken de basisoefeningen in het werkschrift zelfstandig af. Wie klaar is, kan zich (per twee) aan een verdiepende opgave wagen.
• De instructieonafhankelijke leerlingen maken naast (een deel van) de basisoefeningen ook de verdiepende opgaven 1e, 2b en 5 zelfstandig. Je kunt voor hen doorwerktaken voorzien of hen als tutor laten samenwerken met een leerling uit een andere groep. Laat de beide groepen verbeteren met de correctiesleutel.
• Breng de instructieafhankelijke leerlingen samen in een groepje voor verlengde instructie. Zij werken onder begeleiding in het werkschrift of op werkbladen uit de zorgmap. Zie de REDICODIS-maatregelen en tips voor co-teaching op blz. 25.
AFRONDING
Rond de twee lessen over de ggd en het kgv af met een leuk weetje:
Als je de ggd en het kgv van twee getallen met elkaar vermenigvuldigt, is het product gelijk aan het product van die getallen.
Werk een voorbeeld uit aan het bord, bv. met 12 en 18.
• De ggd van 12 en 18 is 6.
• Het kgv van 12 en 18 is 36.
• 12 × 18 = 216 = 6 × 36
Die regel kun je gebruiken om snel het kgv van twee getallen te berekenen als je de ggd kent, bv.
• De ggd van 24 en 30 = 6
• Het kgv van 24 en 30 = (24 × 30) : 6 = 720 : 6 = 120
Laat de leerlingen dat zelf eens per twee uitproberen met twee andere getallen.

Welke groep is het avontuurlijkst?
Op het schoolfeest gaan 9 van de 14 jongens en 5 van de 8 meisjes in de speleobox.
Vul in de verhoudingstabellen de veelvouden aan tot je het kgv van 14 en 8 vindt. jongens 9 14 meisjes


5 8














REDICODIS-MAATREGELEN EN TIPS VOOR CO-TEACHING

REDICODIS-MAATREGELEN EN TIPS VOOR CO-TEACHING in voorbereiding zie voorbeelden bij les 15, 16 en 18


1B-TRAJECT EN TIPS VOOR CURRICULUMDIFFERENTIATIE in voorbereiding zie voorbeelden bij les 15, 16 en 18

Hoofdrekenen: natuurlijke getallen vermenigvuldigen

LEERLIJNEN
B 11 hoofdrekenen: vermenigvuldigen
19 toepassingen
bewerkingen: vraagstukken

MATERIAAL
• werkschrift A blz. 52-54
• de Rekenwijzer
• de bestelbon van kopieerblad 2-2

• de opgaven en de rekenregels van 2-3 en 2-4 (per groepje of per sterke leerling)

















WISKUNDETAAL
Rekentaal
• keer, maal, vermenigvuldigen

• de vermenigvuldiging, de factoren, de vermenigvuldiger, het vermenigvuldigtal, het product, (het) maal(teken)









Instructie- en contexttaal
• de bestelbon, het klantnummer
• het artikel, de code
• de eenheidsprijs, de totaalprijs

• de correctieroller, de perforator, de plakkaatverf


• een set



LESDOELEN
Inoefenen



















• De rekentaal in verband met vermenigvuldigen vlot en correct hanteren
• Op een flexibele manier twee of meer natuurlijke getallen met elkaar vermenigvuldigen naar analogie van en buiten de maaltafels


• Bij vermenigvuldigen flexibel een doelmatige oplossingsmethode toepassen op basis van inzicht in de eigenschappen van de bewerking en in de structuur van de getallen: van plaats wisselen, schakelen, splitsen en compenseren
• Enkelvoudige en samengestelde vraagstukken in verband met vermenigvuldigen met natuurlijke getallen oplossen en daarbij de geleerde begrippen, inzichten en procedures hanteren
• In een vergelijking de ontbrekende symbolen of getallen invullen


Op het einde van het schooljaar geven alle leerkrachten op wat ze aan schoolmateriaal nodig hebben voor het volgende schooljaar, zodat de school alles goed op tijd kan bestellen.
Ze moeten daarvoor een bestelbon invullen, en dat is een hele klus. Deel de bestelbon van kopieerblad 2-2 uit.
Hier zie je de bestelbon voor het zesde leerjaar A van juf Katrien. Bespreek die kort aan de hand van vraagjes als:
• Hoe heet de school van juf Katrien? “De Wijzer.”
• Wat is het e-mailadres van de winkel? “info@paperazie.be”
• Wat betekenen de letters en cijfers in de kolom ‘artikel’? “Het zijn codes die de winkel gebruikt in de catalogus om de artikelen te ordenen.”
• Overloop samen de artikelen die juf Katrien bestelt. Wat betekent de aanduiding ‘SET’? “In deze winkel kun je bijvoorbeeld niet 1 correctieroller apart kopen, je moet altijd een set van 12 correctierollers kopen.”
• Hoeveel latten van 30 cm heeft juf Katrien besteld? “(5 × 5 =) 25 latten.” Vul dat aantal in op de bestelbon.
• Wat wordt bedoeld met ‘eenheidsprijs’? “De prijs per stuk.”
• Wat is de prijs van één lat? “1 euro en 20 cent.” Hoeveel moet de school dan voor die 25 latten betalen? Laat uitrekenen. Noteer de vermenigvuldiging ‘25 × € 1,20 = € 30’ en laat de onderdelen benoemen: vermenigvuldiger, maalteken, vermenigvuldigtal, de factoren, het product.
• In welke kolom hoort die 30 euro? “In de kolom ‘totaalprijs’.”
Noteer ook dat bedrag op de bestelbon.
KERN
Verschillende rekenprocedures
Je kunt deze les op verschillende manieren organiseren.
• Behandel de rekenprocedures klassikaal met de instructiegevoelige en instructieafhankelijke leerlingen. Werk de opgaven uit aan het bord. Maak ook enkele opgaven van oefening 1 tot oefening 4 samen.
• Of verdeel de klas in heterogene groepjes. De leerlingen krijgen ook kopieerblad 2-3 en 2-4. Ze noteren de bewerkingen en koppelen er de rekenregels aan. Als ze dat juist doen, lezen ze van boven naar onder het woord ‘factoren’. Bespreek en verbeter achteraf.
• Of zet instructieonafhankelijke leerlingen zelfstandig aan het werk met de kopieerbladen terwijl jij klassikaal werkt. Ze controleren elkaars oplossing.
Vermenigvuldigen naar analogie van de maaltafels
• Met welke bewerking bereken je hoeveel gommen juf Katrien bestelt? Laat verwoorden en noteer 2 × 30 =.
• Welke opgave uit de maaltafel herken je daarin? “2 × 3 = 6.”
• De vermenigvuldiger is dezelfde, maar het vermenigvuldigtal is 10 keer groter. Het product zal dan ook 10 keer groter zijn. Vul aan: 2 × 3 = 6
× 10 × 10
2 × 30 = 60
• Hoeveel gommen zitten er in 20 dozen? Laat verwoorden en noteer: 20 × 30 =.
• Nu zijn zowel de vermenigvuldiger als het vermenigvuldigtal 10 keer groter.
Hoeveel keer groter zal het product dan zijn? “10 × 10 of 100 keer groter.” Vul aan:
2 × 3 = 6
× 10 × 10 × 100 20 × 30 = 600
volgende: les 40
Tip
Als leerlingen de begrippen niet meer kennen, laat die dan opzoeken in de Rekenwijzer.
Opmerking
In les 40 worden de totaalprijzen op deze bestelbon aangevuld.
Tips
• Je kunt de rekenregel verduidelijken door het vermenigvuldigtal te schrijven met zijn plaatswaardesymbool: 2 × 30 = 2 × 3T = 6T = 60 20 × 30 = 20 × 3T = 60T = 600
• Het kan ook helpen als je de tafeloefening laat onderstrepen.
Merk op Spreek niet over het toevoegen van nullen, want dat is een truc die geen inzicht geeft. Geef dat trucje eventueel enkel als controle mee.
• Je kunt je uitkomst altijd zo controleren: de som van het aantal nullen in de factoren is gelijk aan het aantal nullen in het product.
Maak de eerste drie opgaven van oefening 1 aan het bord. Schakelen en factoren wisselen
• Juf Katrien bestelt 5 sets van 6 zakjes fluostiften. In elk zakje zitten 4 stiften. Hoe bereken je hoeveel stiften dat samen zijn? Laat verwoorden en noteer: 5 × 6 × 4.
• Bij meer dan twee factoren kun je koppels zoeken die het rekenwerk makkelijk maken. Daarbij mag je factoren van plaats wisselen. Vul aan:
Tips
• Duid de factor die je splitst, aanvult of ontbindt duidelijk aan. Gebruik voor elke soort een andere kleur bij leerlingen die daar weinig inzicht in hebben.
• Maak het verschil tussen een factor splitsen of aanvullen (+/–) en een factor ontbinden (×) goed duidelijk.
= 120 = 120 = 120
• Welke manier vind jij het handigst?
Maak een of twee opgaven van oefening 2a aan het bord.
Eén factor splitsen (standaardprocedure)
Hoeveel krijtjes worden er besteld? 3 × 72.
Zien de leerlingen dat ze hier de standaardprocedure kunnen toepassen, namelijk 72 splitsen in 70 en 2 en de beide getallen apart vermenigvuldigen met 3? De oplossing is dan de som van de beide producten. Vul aan:
3 × 72 = (3 × 70) + (3 × 2) = 210 + 6 = 216
70 + 2
Maak de eerste opgave van oefening 3a aan het bord.
Eén factor aanvullen
Hoeveel potloden staan er op de bestelling? 2 × 39.
Zien de leerlingen dat ze hier makkelijk kunnen rekenen als ze van één factor een rond getal maken? Die factor is dan het verschil van twee getallen (39 = 40 – 1). Je vermenigvuldigt ook hier de beide getallen apart. De oplossing is dan het verschil van de beide producten. Vul aan:
2 × 39 = (2 × 40) – (2 × 1) = 80 – 2 = 78
40 − 1
Maak de eerste opgave van oefening 3b aan het bord.
Eén factor ontbinden in een vermenigvuldiging
Hoeveel blauwe balpennen? 3 × 24.
Soms is het handig om één factor te schrijven als een vermenigvuldiging. Dat kan op verschillende manieren. Vul aan:
3 × 24 = (3 × 12) × 2 = 36 × 2 = 72 of = (3 × 3) × 8 = 9 × 8 = 72









Maak de eerste opgave van oefening 3c aan het bord.



Een factor delen door een getal en de andere factor vermenigvuldigen met hetzelfde getal
Hoeveel kosten 5 perforators? (5 × € 18)
De leerlingen hebben geleerd dat het product niet verandert als je één factor met een getal vermenigvuldigt en de andere door dat getal deelt. In dit geval rekent 10 × 9 makkelijker dan 5 × 18.
5 × 18 =
× 2 : 2 10 × 9 = 90
Het kan ook zo: 5 × 18 = (10 × 18) : 2 = 180 : 2 = 90
Maak de eerste kolom van oefening 4 aan het bord.
VERWERKING
• Maak met de instructiegevoelige leerlingen van oefening 1 tot en met 5 telkens (nog) één opgave. Als dat goed lukt, kunnen ze de overige oefeningen zelfstandig afwerken. Oefening 6a kunnen ze in duo uitwerken.
SUGGESTIE
Als je echte bestel- of leveringsbons van klasmateriaal kunt tonen, maakt dat de context voor de leerlingen nog realistischer.


Lees en los op. a Boer Hanssens heeft 50 melkkoeien.
Een koe geeft gemiddeld 23 liter melk per dag. Hoeveel liter melk geeft elke koe gemiddeld per week?
Bewerking:


Antwoord:


Hoeveel liter melk geeft elke koe gemiddeld per jaar (300 dagen)?
Bewerking:

Antwoord:


Hoeveel liter melk geven de 50 koeien gemiddeld per jaar?
Bewerking:
Antwoord:



b Maak zelf een vraagstukje met deze bewerking: 24 × 6 × 5.
c Vermenigvuldig het drievoud van 12 met het dubbel van 15.


Neem 6 keer het vijfvoud van het dubbel van 60.



• De instructieonafhankelijke leerlingen werken meteen zelfstandig en maken ook de verdiepende oefeningen 2b en 6b en c. Daarna kunnen ze de opdrachten op het kopieerblad maken.
• Breng de instructieafhankelijke leerlingen samen in een groepje voor verlengde instructie. Zij werken onder begeleiding. Zie de REDICODISmaatregelen en tips voor co-teaching op blz. 33.
Ze verbeteren allemaal met de correctiesleutel tot en met oefening 5. Verbeter oefening 6 klassikaal en laat de leerlingen verwoorden hoe ze die vraagstukjes opgelost hebben.
AFRONDING
Zoek samen naar gelijkenissen tussen de handige rekenprocedures bij optellen en vermenigvuldigen. Laat voorbeelden bedenken van:
• een term of factor splitsen;
• een term of factor aanvullen tot een rond getal en het verschil compenseren;
• bij optellen bij één term een getal optellen en datzelfde getal van de andere term aftrekken; bij vermenigvuldigen één factor vermenigvuldigen met een getal en de andere factor door hetzelfde getal delen.
• bij optellen en vermenigvuldigen de termen en factoren van plaats wisselen en schakelen.
REDICODIS-MAATREGELEN EN TIPS VOOR CO-TEACHING
oefening 1 Schrijf de oefening 7 × 5 = 35 op het bord. Laat verwoorden welke rekentaal daarbij hoort: factor, product, vermenigvuldiging, vermenigvuldigtal, vermenigvuldiger. Sta erop dat de leerlingen die rekentaal hanteren bij het spreken.
Begin de les met op een speelse manier de maaltafels te herhalen. Laat de leerlingen een zachte bal naar elkaar gooien. Wie de bal vangt, geeft het product. Voer het tempo op.
Laat de leerlingen daarna verwoorden wat er gebeurt met een getal wanneer je het 10 of 100 keer groter maakt. “In het product komen er nullen bij. Het aantal nullen is de som van de nullen bij de factoren”.
Oefen ook dat al spelend met de bal. Zorgleerlingen hebben meestal veel steun aan visuele hulpmiddelen. Gebruik daarom flitskaartjes waarop de oefening visueel is gemaakt.
Het is een hulp om de maaltafel in de oefening te onderstrepen bv. 200 × 700 = oefening 2
Herhaal dat bij een vermenigvuldiging de factoren van plaats mogen gewisseld worden, zonder dat het product verandert.
Schrijf de oefening 5 x 2 x 3 = op het bord.
• Welke factoren zou je eerst samennemen? “5 keer 2.”
• Dat schrijven we zo: (5 × 2) × 3 =. Wat tussen haakjes staat, wordt eerst uitgerekend: (5 x 2) × 3 = 10 × 3 = 30.
Geef ook aandacht aan de andere mogelijkheden: 5 × 3 en 2 × 3. Laat de leerlingen hun denkstappen telkens hardop verwoorden. Opgave b is verdiepend en mag je overslaan.
oefening 3 Zorgleerlingen hebben vaak minder inzicht in de verschillende rekenprocedures. Geef hen steeds de kans om via de standaardprocedure te werk te gaan. In deze les is dat vermenigvuldigen met het splitsen van een van de factoren. Eventueel maak je ook een paar oefeningen met het ‘aanvullen van één factor’ (opgave b).
Geef de leerlingen steeds een uitgewerkt voorbeeld als steun. Dat kan op een onthoudkaart of bord.
Oefening 3c (een factor ontbinden in een vermenigvuldiging) is voor zorgleerlingen heel moeilijk en mag je weglaten.
oefening 4 Maak deze oefening stap voor stap samen met de leerlingen.
oefening 5 Deze oefening is verdiepend en mag je weglaten.
oefening 6 werkblad 1
Laat een leerling het rekenverhaal hardop lezen. Duid een andere leerling aan die de vraagzin herhaalt. Laat de vraag aanduiden met een markeerstift.
Laat alle gegevens opsporen aan de hand van de volgende vragen:
• Welke getallen zijn belangrijk?
• Welke woorden verklappen ons iets meer? Duid alle gegevens aan die we nodig hebben.
• Moeten we optellen (+), aftrekken (-), vermenigvuldigen (x) of delen (:)? Uit welke woorden of zin leid je dat af?
Laat uitrekenen volgens de standaardprocedure van oefening 3. Daarbij splitsen de leerlingen telkens één factor.
Oefening 6b en 6c zijn verdiepend en mag je weglaten.

Leerlingen die bij de oefeningen in deze les ondersteuning nodig hadden, zul je ook tijdens de herhalingsles mogelijk extra moeten begeleiden.
Je vindt daartoe meer verlengde instructie bij toetsdoel 5 ‘Natuurlijke getallen vermenigvuldigen’ in het Evaluatieluik van dit blok.


1B-TRAJECT EN TIPS VOOR CURRICULUMDIFFERENTIATIE
Wat zeggen de eindtermen?
ET 1.13 De leerlingen voeren opgaven uit het hoofd uit waarbij ze een doelmatige oplossingsweg kiezen op basis van inzicht in de eigenschappen van bewerkingen en de structuur van de getallen:
• optellen en aftrekken tot honderd;
• optellen en aftrekken met grote getallen en eindnullen;
• vermenigvuldigen met en delen naar analogie met de tafels.
Strikt genomen vallen oefening 5 (valt buiten ET 1.13) en oefening 6 (verdiepende toepassing) weg.
Vlot naar 1B?
In de praktijk dien je in te zetten op optellen en aftrekken waarbij de som of het aftrektal kleiner of gelijk is aan 1000.
Bij vermenigvuldigen en delen laat je naar analogie met de maal- en deeltafels werken en laat je flexibel een doelmatige oplossingsmethode kiezen op basis van inzicht in de structuur van de getallen en in de eigenschappen van de vermenigvuldiging en de deling.
Aanpak in deze les
Laat de leerlingen die op weg zijn naar 1B mee aansluiten bij de instructieafhankelijke leerlingen om oefening 1 en 2a uit het werkschrift te maken. Volg daarbij de verlengde instructie op de REDICODISpagina.
Oefening 3 en 4 uit het werkschrift worden vervangen door Vlotje 1:
• Opdracht 1: de maaltafels oefenen. Leerlingen die het moeilijk hebben met maaltafels, kun je een tafelkaart laten gebruiken.
• Opdracht 2: vermenigvuldigen met tientallen. Laat de maaltafel in de oefening onderstrepen, als dat een hulp kan zijn. Geef mee dat het aantal nullen in het product de som is van de nullen van de factoren. Dat gebruiken de leerlingen ter controle.
• Opdracht 3: één factor splitsen om handig te rekenen. De leerlingen kijken naar het voorbeeld en vertellen hardop wat ze moeten doen. Ze volgen de lange procedureweg en proberen de stappen zelf te noteren.
Laat eerst de grijs gearceerde oefeningen oplossen en verbeteren met de correctiesleutel. Bepaal op basis van het resultaat bij welke opgaven je ook nog de andere opgaven laat maken.
Oefening 5 en 6 vallen weg.
Als je het digipack comfort hebt, kun je de ‘Vlotjes’ downloaden en afdrukken vanuit bingel voor leerkrachten (via ‘Oefenen en differentiëren’).
