Master Thesis ǀ Tesis de Maestría
submitted within the UNIGIS MSc programme presentada para el Programa UNIGIS MSc

at/en
Interfaculty Department of Geoinformatics- Z_GIS
Departamento de Geomática – Z_GIS
University of Salzburg ǀ Universidad de Salzburg
Sensores Remotos: Evaluación de la amenaza sísmica y efectos cosísmicos en la región de Otavalo, Ecuador.
Remote Sensors:
Assesment of seismic threat and seismic effects in the Otavalo region, Ecuador.
by/por
Carlos Alberto Falconí Gomezjurado
01633541
A thesis submitted in partial fulfilment of the requirements of the degree of Master of Science– MSc
Advisor ǀ Supervisor:
Leonardo Zurita Arthos
Quito - Ecuador, agosto 2022
COMPROMISO DE CIENCIA
Por medio del presente documento, incluyendo mi firma personal certifico y aseguro que mi tesis es completamente resultado de mi propio trabajo. He citado todas las fuentes que he usado en mi tesis y en todos los casos he indicado su origen.
 Quito, 08 de agosto del 2022
Quito, 08 de agosto del 2022
AGRADECIMIENTOS
Mis agradecimientos van dirigidos, en primer lugar, al profesorado de UNIGIS América Latina y de la Universidad de Salzburgo, con quienes compartí períodos académicos y momentos diversos, encaminados a la generación de nuevos conocimientos y capacidades. En segundo lugar, destaco a la persona del Ing. Kervin Chunga PhD, geólogo ecuatoriano con muy alto desarrollo de investigaciones y aplicaciones prácticas en el campo de la Geología de terremotos y tsunamis, quien, a través de su actividad docente en diversas universidades, continúa moldeando generaciones muy prometedoras de ingenieros civiles y geólogos. Fue a partir de mi participación en un curso dictado por el Dr. Chunga, que surgió en mi persona la inquietud de desarrollar una tesis de investigación relacionada con el tema de sismos en el Ecuador. No sabía en lo que incursionaba, a decir verdad; no obstante, la experiencia ha sido muy enriquecedora.
La posibilidad de trabajar en un proceso de consultoría, relacionado con el ordenamiento territorial del cantón Otavalo, me la brindó el Arq. Fabián Gómez C., quien es un profesional muy versado en los temas de planificación del desarrollo económico y de ordenamiento territorial. Fue él quien me invitó a integrar el equipo técnico en la consultoría relacionada con el Plan de Uso y Gestión del Suelo (PUGS) del cantón Otavalo, jurisdicción en la cual pude aplicar los conocimientos adquiridos en el curso de la maestría impulsada desde la Universidad de Salzburgo – Austria.
La ayuda de mi hija Adriana, en la traducción – revisión del Abstract, contribuyó en aclarar a mi persona el orden de las ideas que en aquel resumen expreso. Su hermana mayor, Eliana, también contribuyó al agregar la “chispa” que le caracteriza y, junto con su hermana Adriana, me ayudaron a vencer etapas de agotamiento físico e intelectual.
DEDICATORIA
A mis padres, Gonzalo Falconi H. y Laura Gomezjurado L., quienes, desde el intangible e infinito espacio de la memoria, me guían por caminos de luz y perfeccionamiento personal y profesional;
A mis hijas, Eliana y Adriana Falconí R., dos gemas que el Creador me concedió a través de la vivencia progenitora, junto con su madre Nora Rivadeneira;
A María Idalia, por impulsarme y apoyarme en la incursión y logro de esta experiencia y calificación académica.
RESUMEN
En Otavalo - Ecuador existen fallas geológicas capaces de provocar terremotos de magnitud superior a 5 Mw (momento sísmico). Es una región donde han incidido los mayores terremotos del Ecuador. El Bloque Andino Norte (BNA) es un área geológica presionada entre la placa oceánica de Nazca y la placa continental sudamericana. El BNA limita con la falla regional del Sistema Mayor Dextral (SMD, entre el Golfo de Guayaquil y Caracas).
El objetivo general de esta tesis fue caracterizar la amenaza sísmica y los efectos cosísmicos en el cantón Otavalo. Los objetivos específicos fueron: 1) Zonificar la intensidad, magnitud y aceleración sísmica en la región; 2) Identificar áreas de subsidencia o de desplazamiento del suelo, en la cercanía de fallas geológicas capaces; y 3) Delimitar áreas de pendientes pronunciadas propensas a efectos cosísmicos. Se plantearon las preguntas de investigación: a) ¿Cuánto y por qué varía el error estándar del valor de las magnitudes sísmicas estimadas con técnicas de interpolación espacial Kriging? b) ¿Cuál es el orden de magnitud en que las técnicas de Radar de Apertura Sintética Interferométrico (inSAR) permiten identificar deformaciones en zonas puntuales del territorio cantonal? y, c) ¿Cuánto varía en rango el valor de pendientes en zonas con influencia posible de efectos cosísmicos, de acuerdo con el Análisis de Superposición Ponderada (AHP)?
La revisión de la literatura abordó casos provenientes de varios países, sobre interpolación espacial, interferometría satelital y análisis de superposición ponderada. Algunos casos combinaron técnicas de análisis relacionando a terremotos, deslizamientos de tierra, subsidencias por obras de infraestructura y sobrexplotación de aguas subterráneas.
Los objetivos específicos y las preguntas de investigación arrojaron desarrollos y resultados concretos, contribuyendo al logro del objetivo general. La adaptación del método de Newmark (1965), con las directrices de Jibson et al. (1998), permitió caracterizar los efectos cosísmicos y delimitar las áreas más propensas a estos. El análisis de superposición ponderada fue desarrollado con una capa vector, para el muestreo de datos ráster en las imágenes resultantes de interferometría y en el ráster de aceleración en roca (PGA). Esta decisión obedeció a las limitaciones de la técnica inSAR en áreas con mayor cobertura vegetal (el occidente del cantón). La capa vector integró valores de pendientes, PGA y las estimaciones de la aceleración crítica (ac). Las áreas del cantón más vulnerables a la amenaza sísmica y efectos cosísmicos, se superponen en las parroquias orientales del cantón, con mayor densidad poblacional y dependientes de varios tipos de infraestructura.
Los resultados de la tesis muestran que se puede mejorar investigaciones similares al contar con información geológica y geotécnica de mejor calidad, así como de un registro más detallado y sistemático de deslizamientos de taludes en la región. El desarrollo de investigaciones futuras más detalladas será de gran importancia para la planificación territorial en los municipios ecuatorianos.
Palabras claves Álgebra de mapas, amenaza sísmica, análisis de superposición ponderado, interferometría, mapas isosísmicos
5
ABSTRACT
In Otavalo - Ecuador there are geological faults capable of causing earthquakes of magnitude greater than 5 Mw (seismic moment). It is a region where the biggest earthquakes in Ecuador have affected. The North Andean Block (NAB) is a geological area pressed between the oceanic Nazca plate and the South American continental plate. The NAB limits with the regional fault of the Major Dextral System (MDS, between the Gulf of Guayaquil and Caracas).
The general objective of this thesis was to characterize the seismic hazard and the coseismic effects in the Otavalo canton. The specific objectives were: 1) To zone the intensity, magnitude, and seismic acceleration in the region; 2) To identify areas of subsidence or soil displacement, in the vicinity of capable geological faults; and 3) To delimit areas of steep slopes prone to co-seismic effects. Following research questions were posed: a) How much and why does the standard error of the value of the seismic magnitudes estimated with Kriging spatial interpolation techniques vary? b) What is the order of magnitude in which the Interferometric Synthetic Aperture Radar (inSAR) techniques allow the identification of deformations in specific areas of the cantonal territory? and, c) How much does the value of slopes vary in range in areas with possible influence of co-seismic effects, according to the Weighted Superposition Analysis (AHP)?
The literature review addressed cases from several countries on spatial interpolation, satellite interferometry, and weighted overlay analysis. Some cases combined analysis techniques related to earthquakes, landslides, subsidence due to infrastructure works and overexploitation of groundwater.
The specific objectives and the research questions yielded concrete developments and results, contributing to the achievement of the general objective. The adaptation of the Newmark method (1965), with the guidelines of Jibson et al (1998), allowed characterizing the co-seismic effects and delimiting the areas most prone to them. The weighted overlay analysis was developed with a vector layer, for the sampling of raster data in the resulting images of interferometry and in the raster of acceleration in rock (PGA). This decision was due to the limitations of the inSAR technique in areas with greater vegetation cover (the west of the canton). The vector layer integrated slope values, PGA, and critical acceleration (ac) estimates. The areas of the canton that are most vulnerable to seismic hazard and coseismic effects overlap in the eastern parishes of the canton, with higher population density and dependent on several types of infrastructure.
The results of the thesis show that similar investigations can be improved by having better quality geological and geotechnical information, as well as a more detailed and systematic record of slope slides in the region. The development of more detailed future research will be of great importance for territorial planning in Ecuadorian municipalities.
Keywords
Isoseismic maps, interferometry, map algebra, seismic hazard, weighted overlay analysis
6
7 TABLA DE CONTENIDO 1. INTRODUCCIÓN 14 1.1 ANTECEDENTES 15 1.2 OBJETIVO GENERAL ......................................................................................................... 17 1.3 OBJETIVOS ESPECÍFICOS .................................................................................................. 17 1.4 PREGUNTAS DE INVESTIGACIÓN 17 1.5 HIPÓTESIS 17 1.6 JUSTIFICACIÓN ................................................................................................................. 18 1.7 ALCANCE 18 2. REVISIÓN DE LITERATURA 20 2.1 EL BLOQUE NORANDINO ECUATORIANO (BNA) ............................................................. 20 2.2 SISMOS HISTÓRICOS Y FALLAS GEOLÓGICAS REGIONALES ............................................ 23 2.3 ESTIMACIÓN DETERMINÍSTICA DE MAGNITUDES DE SISMOS Y ACELERACIONES EN ROCA, A PARTIR DE FALLAS CAPACES 24 2.4 INTERPOLACIÓN ESPACIAL .............................................................................................. 25 2.4.1 Estudios en que se ha aplicado Interpolación espacial 28 2.4.1.1 Evaluación de los efectos sísmicos y cosísmicos en Iburi, Hokkaido - Japón 28 2.4.1.2 Grecia: Trazado de mapas isosísmicos 29 2.6 INTERFEROMETRÍA SATELITAL 30 2.6.1 Estudios desarrollados con Interferometría satelital .................................. 35 2.6.1.2 Carta Internacional Espacio y Grandes Desastres: inundaciones del río Paraná 36 2.6.1.3 Terremoto del valle de Napa, California ....................................................... 36 2.6.1.4 Terremoto de Nepal ...................................................................................... 36 2.6.1.5 El terremoto de Pedernales, Manabí - Ecuador ............................................ 36 2.6.1.6 Deslizamientos en el sector de Vallcebre (montes Pirineos – España) .......... 37 2.7 EL MÉTODO DEL BLOQUE DESLIZANTE DE NEWMARK .................................................. 38 2.7.1 La aplicación del método de Newmark (1965) 44 2.7.1.1 Amenaza por deslizamientos en el valle de Aburrá – Colombia. 45 2.7.1.2 Susceptibilidad a deslizamientos en la zona de Sochi. 47
8 2.8 ANÁLISIS DE SUPERPOSICIÓN PONDERADO 48 2.8.1 La aplicación del método AHP 49 2.8.1.1 Beijing, China. Subsidencia del suelo 49 2.8.1.2 Evaluación del riesgo de inundaciones en áreas influenciadas por subsidencia del suelo 49 3. METODOLOGÍA 51 3.1 ÁREA DE ESTUDIO ............................................................................................................ 51 3.2 FLUJOGRAMA................................................................................................................... 58 3.3 DESCRIPCIÓN DE LA METODOLOGÍA 61 3.3.1 Interpolación Espacial .................................................................................. 61 3.3.2 El procesamiento de Interferometría .......................................................... 63 3.3.3 Adaptación del método de Newmark (1965) ............................................... 66 4. RESULTADOS Y DISCUSIÓN ...................................................................................................... 70 4.1 INTERPOLACIÓN ESPACIAL CON KRIGING EMPÍRICO BAYESIANO (EBK) ....................... 70 4.2 RESULTADOS DEL ANÁLISIS DE INTERFEROMETRÍA 77 4.3 ADAPTACIÓN DEL MÉTODO DE NEWMARK (1965) ........................................................ 86 4.4 ANÁLISIS DE LOS RESULTADOS ....................................................................................... 90 4.4.1 Interpolación espacial. 90 4.4.2 Interferometría satelital 91 4.4.3 Adaptación del método de Newmark (1965) 97 4.4.5 Respuestas a las preguntas de investigación 101 4.5 ANÁLISIS CRÍTICO DE LA METODOLOGÍA 105 5. CONCLUSIONES Y RECOMENDACIONES 108 5.1 RESULTADOS DE LA INVESTIGACIÓN .................................................................................... 108 5.2 CONCLUSIONES 111 5.3 RECOMENDACIONES 112 6. REFERENCIAS ......................................................................................................................... 114
ÍNDICE DE FIGURAS
9
ILUSTRACIÓN 1 LA REGIÓN DE OTAVALO Y EL BLOQUE NORANDINO ECUATORIANO 22 ILUSTRACIÓN 2 ESQUEMA SATELITAL DEL SISTEMA SAR. .............................................................................................. 30 ILUSTRACIÓN 3 RELACIÓN ENTRE EL ÁNGULO DE FASE ɸ, LA DISTANCIA INCLINADA R Y LA LONGITUD DE ONDA ʎ DE LA SEÑAL SAR. 31 ILUSTRACIÓN 4 PARÁMETROS GEOMÉTRICOS DE UN SISTEMA SATELITAL SAR. .................................................................. 32 ILUSTRACIÓN 5 MODELO DINÁMICO DEL BLOQUE DESLIZANTE 39 ILUSTRACIÓN 6 REPRESENTACIÓN DE ESFUERZOS PRINCIPALES A PARTIR DE UN ENSAYO DE CORTE EN UNA MUESTRA DE SUELO 40 ILUSTRACIÓN 7 OTAVALO, EVENTOS DE RIESGOS SELECCIONADOS, AÑOS 2010 - 2020. ..................................................... 54 ILUSTRACIÓN 8 OTAVALO, UBICACIÓN, FALLAS CAPACES Y SISMOS IMPORTANTES 57 ILUSTRACIÓN 9 FLUJOGRAMA DE LA METODOLOGÍA UTILIZADA 59 ILUSTRACIÓN 10 MOMENTO SÍSMICO (MW). SEMIVARIOGRAMA OBTENIDO CON INTERPOLACIÓN EBK. ............................... 70 ILUSTRACIÓN 11 INTERPOLACIÓN ESPACIAL EBK PARA MW COMPARACIÓN ENTRE VALORES CALCULADOS Y PREDICHOS 70 ILUSTRACIÓN 12 MOMENTO SÍSMICO, REGIÓN DE OTAVALO 71 ILUSTRACIÓN 13 VARIACIÓN ESPACIAL DE MOMENTO SÍSMICO, REGIÓN DE OTAVALO ........................................................ 71 ILUSTRACIÓN 14 MOMENTO SÍSMICO EN LA REGIÓN DE OTAVALO 71 ILUSTRACIÓN 15 ACELERACIÓN SÍSMICA SEMIVARIOGRAMA OBTENIDO CON INTERPOLACIÓN EBK. 73 ILUSTRACIÓN 16 ACELERACIÓN SÍSMICA. COMPARACIÓN ENTRE VALORES CALCULADOS Y PREDICHOS OBTENIDOS CON INTERPOLACIÓN EBK. 74 ILUSTRACIÓN 17 ACELERACIÓN EN ROCA, REGIÓN DE OTAVALO 75 ILUSTRACIÓN 18 ERROR ESTÁNDAR EN ACELERACIÓN EN ROCA. ..................................................................................... 76 ILUSTRACIÓN 19 MAPA DE PENDIENTES, A PARTIR DEL DEM OBTENIDO POR INTERFEROMETRÍA 78 ILUSTRACIÓN 20 INTERFEROMETRÍA, DESPLAZAMIENTOS EN EL TERRENO ENTRE EL 24 DE MARZO Y EL 17 DE ABRIL DE 2016. 79 ILUSTRACIÓN 21 INTERFEROMETRÍA, MAPA DE ELEVACIÓN. .......................................................................................... 80 ILUSTRACIÓN 22 INTERFEROMETRÍA, MAPA DE COHERENCIA 81 ILUSTRACIÓN 23 DESPLAZAMIENTOS MEDIDOS TRAS EL TERREMOTO DE 16 DE ABRIL DE 2016, OTAVALO 85 ILUSTRACIÓN 24 ACELERACIÓN CRÍTICA ESTIMADA. ..................................................................................................... 87 ILUSTRACIÓN 25 RELACIÓN DE ACELERACIONES EN ROCA RESPECTO A LA ACELERACIÓN CRÍTICA, SECTOR OCCIDENTAL DEL CANTÓN OTAVALO 88 ILUSTRACIÓN 26 RECLASIFICACIÓN DE PENDIENTES, SUSCEPTIBILIDAD A DESLIZAMIENTOS. .................................................. 89 ILUSTRACIÓN 27 CLÚSTERES DE VALORES MEDIDOS DE DESPLAZAMIENTOS, OTAVALO (TERREMOTO ABRIL DE 2016). 93 ILUSTRACIÓN 28 CLÚSTERES DE COHERENCIA EN VALORES MEDIDOS DE DESPLAZAMIENTOS 94 ILUSTRACIÓN 29 ZONIFICACIÓN DE DEFORMACIONES EN LA REGIÓN DE OTAVALO. ............................................................ 96 ILUSTRACIÓN 30 HISTOGRAMA DE DISTRIBUCIÓN DE LOS VALORES DE ACELERACIÓN CRÍTICA ESTIMADOS 99 ILUSTRACIÓN 31 HISTOGRAMA DE DISTRIBUCIÓN DE VALORES PGA/ACRIT 100 ILUSTRACIÓN 32 HISTOGRAMA DE DISTRIBUCIÓN DE VALORES DE PENDIENTES EN TALUDES CON ALTA SUSCEPTIBILIDAD A DESLIZAMIENTOS. ...................................................................................................................................... 103 ILUSTRACIÓN 33 HISTOGRAMA DE DISTRIBUCIÓN DE TALUDES CON SUSCEPTIBILIDAD MODERADA A DESLIZAMIENTOS 104
ÍNDICE DE TABLAS
10
TABLA 1 SELECCIÓN DE SISMOS CON MAGNITUD MAYOR O IGUAL A 5 MW Y PROFUNDIDAD DE EPICENTRO HASTA 20 KM 16 TABLA 2 RESUMEN DE FALLAS CAPACES POR TIPOS Y PROFUNDIDADES DE INFLUENCIA ........................................................ 52 TABLA 3 SELECCIÓN DE EVENTOS DE RIESGO MÁS FRECUENTES EN OTAVALO 53 TABLA 4 OTAVALO, EVENTOS DE RIESGO SELECCIONADOS, AÑOS 2010 - 2020. 55 TABLA 5 OTAVALO. DISTRIBUCIÓN TRIMESTRAL DE EVENTOS DE RIESGO SELECCIONADOS (2010 - 2020). ............................. 56 TABLA 6 COMPARACIÓN ENTRE MÉTODOS DE INTERPOLACIÓN ESPACIAL 62 TABLA 7 DETERMINACIÓN DEL VALOR ADIMENSIONAL C'/(ΓT) 67 TABLA 8 COMPARACIÓN DE PARÁMETROS RESULTANTES DE LA APLICACIÓN DEL MÉTODO DE NEWMARK (1965). ................... 68 TABLA 9 CLASIFICACIÓN DE PENDIENTES (TΑ) DE TERRENO 69 TABLA 10 INFORMACIÓN DE LOS DESPLAZAMIENTOS OBSERVADOS SOBRE FALLAS GEOLÓGICAS CAPACES DE OTAVALO 82 TABLA 11 RESUMEN DE ESTADÍSTICAS DE DESPLAZAMIENTOS DE TERRENO. ...................................................................... 83
TABLA DE ACRÓNIMOS
ACRÓNIMO SIGNIFICADO
2R Distancia de viaje de la señal, ida y vuelta
AHP Analytic Hierarchy Process (superposición ponderada)
AI Area Interpolation, Interpolación de Área
ASF Alaska Satellite Facility
BNA Bloque norandino. Refiere a la sección presionada entre la placa continental sudamericana, la placa oceánica de Nazca y la placa Caribe, determinada además por el Sistema Máximo Dextral de la falla Guayaquil - Caracas.
CEPEIGE Centro Panamericano de Estudios e Informaciones Geográficas
CERESIS Centro Regional de Sismología para América del Sur
CHIS Estación GPS Cerro Chispas
CR Corners Reflectors, reflectores de esquina
DEM Digital Elevation Model, Modelo digital de elevaciones (DEM por sus siglas en Inglés)
DI Difussion Interpolation, Interpolación por Difusión
EBK Empirical Bayessian Kriging, Kriging Empírico Bayesiano
ESA European Space Agency, Agencia Espacial Europea
ESD Enhanced Spectral Diversity, diversidad espectral mejorada
ESMR Estación GPS Esmeraldas
FAHP Fuzzy analytic hierarchy process (proceso de jerarquía analítica difusa)
FS Factor de seguridad para deslizamientos de suelos, determinado por factores geométricos del talud, pendiente, propiedades mecánicas de los suelos y presencia de agua
FSD Factor de seguridad para un valor definido de aceleración
GAD Gobierno Autónomo Descentralizado. Denominación que en la legislación ecuatoriana se da a organismos estatales descentralizados provinciales, municipales, parroquiales.
Gal Unidad de aceleración en el sistema cegesimal (centímetros sobre segundo al cuadrado – cm/s2), llamada así en honor a Galileo Galilei
GEMMA Grupo de Estándares para Movimientos en Masa.
GPS Global Positioning System, Sistema de Posicionamiento Global
GRIB Gridded Bynary,
HDF Hierarchical Data Format,
IDW Inverse Distance Weighted, técnica de interpolación espacial ponderada por el inverso de la distancia
IG - EPN Instituto Geofísico de la Escuela Politécnica Nacional del Ecuador
11
ACRÓNIMO SIGNIFICADO
inSAR Interferometric Synthetic Aperture Radar, Radar de Apertura Sintética Interferométrico
IW Interferometric Wide swath mode, modo de franja interferométrica ancha para adquisición de datos de observaciones sobre la Tierra, en un ancho de 250 Km, resolución espacial 5 m por 20 m (mirada única)
K-Co Kriging Cokriging
KI Interpolación Kernel
KO Kriging Ordinario
LPI Interpolación Polinomial Local m Metro. Unidad básica (de longitud) en el Sistema Internacional (SI) de unidades.
Ma Millones de años
Mw Momento de magnitud de un sismo, se estima proporcional al producto del área del plano de falla (A Km2), la velocidad de deslizamiento de la falla (ú mm/año) y el módulo de deformación de la corteza (μ = 3*1010 Pa
N Newton. Unidad de fuerza en en el SI. Fuerza que aplicada a 1 kilogramo de masa le imparte una aceleración de 1 m/s2
netCDF Network Common Data Form, Pa Pascal, unidad de presión en el SI, equivalente a 1 N/m2.
PF Probabilidad de falla
PGA Aceleración máxima de sismo (en roca). Si el valor es referido al de la gravedad terrestre (9,8 m/s2) se obtiene una magnitud adimensional como una fracción del valor de g.
PMA Proyecto Multinacional Andino
PUGS Planes de Uso y Gestión del Suelo
RBF Radial Base Functions, Funciones de Base Radial
RIOP Estación GPS Riobamba
SAR Synthetic Aperture Radar, Radar de Apertura Sintética
Sentinel-1
Satélite artificial de órbita polar de la ESA, Programa Copérnico, destinado al monitoreo terrestre y de los océanos, puesto en órbita el 3 de abril de 2014
SGMA Servicio Geológico Minero Argentino
SGRE Secretaría de Gestión de Riesgos y Emergencias, Ecuador
SIG Sistemas de Información Geográfica
SLC Simple Look Complex, complejo de mirada única
SMD Sistema Mayor Dextral, arco de fallas entre el Golfo de Guayaquil y Caracas, sistema de falla Guayaquil - Pallatanga
SNAP Sentinel Aplicattion Plataform. Caja de herramientas Sentinel extensible, portable, modular, para abstracción genérica de datos, gestión de memoria y procesamiento de gráficos
12
ACRÓNIMO SIGNIFICADO
TOPSAR Progresive Scans SAR
tα Pendiente de un talud o del terreno, puede ser representada como grados sexagesimales o como porcentaje
USGS United Sates Geological Survey
UTM Universidad Técnica de Manabí
λ Longitud de onda del SAR
τ Retardo, cambio de fase φ entre las señales transmitida y recibida
φ Ángulo de fase
13
1. INTRODUCCIÓN
De acuerdo con la Constitución del Ecuador (Asamblea Constituyente del Ecuador, 2008, art. 264 núm. 1 y 2), en el país la planificación del desarrollo cantonal es competencia exclusiva de los gobiernos municipales. El artículo 241 de la Carta Magna hace mandatorios la planificación y el ordenamiento territorial, promoviendo su carácter equilibrado y equitativo, así como la adopción de políticas públicas relacionadas (Asamblea Constituyente Del Ecuador, 2008, art. 276 y art. 415).
La Ley Orgánica de Ordenamiento Territorial, Uso y Gestión del Suelo (Asamblea Nacional Ecuador, 2016), orienta hacia la urbanización. Se margina el carácter rural de muchos cantones, incluso de las áreas urbanas de sus cabeceras. Introduce definiciones para tratamientos urbanísticos en suelos urbanos y rurales (Asamblea Nacional Ecuador, 2016, art. 4, definiciones 14 y 15) Limita convertir a urbanas áreas de alto valor agro-productivo, a menos que exista una autorización expresa de la autoridad agraria nacional (Asamblea Nacional Ecuador, 2016, art. 19 núm. 3).
El Reglamento de la Ley Orgánica de Ordenamiento Territorial, Uso y Gestión del Suelo (Presidencia de la República del Ecuador, 2019), ofrece lineamientos para la clasificación y subclasificación del suelo, tratamientos, normas urbanísticas y planes complementarios a los Planes de Uso y Gestión del Suelo – PUGS (Presidencia de la República del Ecuador, 2019, art. 15 a 17; art. 18; art. 19 a 29; y art. 30 a 34, respectivamente). No obstante, el componente estructurante de los PUGS se articula en torno a la infraestructura y equipamientos estratégicos, cuya localización puede constituir un factor de vulnerabilidad serio
La planificación y el ordenamiento territorial es excesivamente discursivo. En la práctica actual, los profesionales que incursionan en procesos de consultoría relacionados hacen uso de información secundaria, desactualizada en algunos temas, y no priorizan utilizar técnicas de sensores remotos como un elemento importante para el monitoreo del desarrollo local.
La presente tesis desarrolla un proceso que incluye dichas técnicas para la gestión sostenible del territorio, en particular frente a las amenazas sísmica y cosísmicas latentes.
14
1.1 ANTECEDENTES
En la región del cantón Otavalo, el 15 de agosto de 1868 se suscitó uno de los mayores sismos registrados en esa área y cuyo epicentro fue, precisamente, Otavalo, aunque es más conocido como el terremoto de Ibarra. Otavalo está ubicado en una singularidad tectónica a la cual los especialistas denominan Bloque Norandino Ecuatoriano (BNA), que está presionada entre las placas oceánica de Nazca y la continental sudamericana. Esta gran área ha sido escenario de los mayores sismos registrados en el territorio ecuatoriano, como aquellos de Esmeraldas y Pedernales, con momentos de magnitud sísmica (Mw) de 8,3 y 7,8 Mw en los años 1906 y 2016, respectivamente.
Como aproximación al tema en esta investigación de tesis, se configuró un registro estadístico de sismos con magnitud mayor o igual a 5 Mw, a partir de los Catálogos
Homogenizado 1587 – 2011 del Instituto Geofísico de la Escuela Politécnica Nacional (IG EPN) y 2012 – Actualidad (IG - EPN, 2021) Se filtraron sismos entre las latitudes 1° y -0,3°, y entre las longitudes -80° y -77°, seleccionando 32 más cercanos a la región de estudio. La magnitud más alta registrada es de 8,3 Mw, el promedio simple de la región referida asciende a una magnitud de 5,8 Mw. Los sismos mayores a 5 Mw se producen especialmente a profundidades superficiales (3), a 10 Km de profundidad (3), seguidos por registros a 12 y 8 Km aproximadamente (2 en cada profundidad). 2016 fue el año en que más terremotos corticales se produjeron (11), suscitándose además el sismo de abril en Pedernales. Los registros seleccionados constan en la Tabla 1. El registro de sismos inicialmente escogidos abarcó 118 eventos, incluidos aquellos de los años 1587, 1834, 1859, y 1868. Este último corresponde al conocido como terremoto de Ibarra, que tuvo una magnitud de 7,3 Mw a una profundidad de epicentro de 10 Km (en Otavalo). Es pertinente apreciar que actualmente no se registran eventos sísmicos en la región propuesta de estudio en esta tesis, habiendo transcurrido ya ciento cincuenta y cuatro (154) años del terremoto de 1868. Si bien no existen estudios en Ecuador sobre el período de recurrencia de sismos, sólo se puede presumir que éste habría sido excedido en la región inmediata de Otavalo.
15
16
Fecha Latitud Longitud Profundidad Km Magnitud Fuente Catalogo 31/01/1906 10:22 0,95 -79,37 -20 8,3 Swenson CENTENNIAL 23/10/1944 18:40 0,6 -79,32 -20 6,7 G&R CENTENNIAL 09/04/1976 2:08 0,85 -79,57 -17 6,6 EHB ISC 18/05/2016 11:52 0,44 -79,83 -13,34 5,2 IGEPN IGEPN 05/03/1987 20:54 0,04 -77,67 -12,9 6,4 EHB ISC 03/05/1987 23:10 -0,09 -77,81 -12 7,1 EPNrep ISC 10/09/2014 22:53 0,94 -78,48 -12 6 IGEPN IGEPN 18/05/2016 3:06 0,43 -79,91 -11,21 5 IGEPN IGEPN 19/07/1955 19:00 0,28 -78,39 -10 6,1 IGEPN IGEPN 13/12/1923 18:46 0,88 -77,8 -10 6,1 IGEPN IGEPN 17/12/1926 18:46 0,87 -77,78 -10 6 IGEPN IGEPN 11/05/1994 6:53 0,38 -78,73 -9,5 5,2 FONT IGEPN 31/01/2017 9:22 0,74 -79,77 -9,11 5,7 IGEPN IGEPN 10/07/2016 21:01 0,6 -79,88 -8,67 5,9 IGEPN IGEPN 11/07/2017 7:09 0,76 -79,75 -7,99 5,5 IGEPN IGEPN 17/04/2016 15:24 0,68 -79,99 -7,51 5 IGEPN IGEPN 17/04/2016 15:24 0,68 -79,99 -7,51 5 IGEPN IGEPN 15/12/2018 16:11 0,28 -79,2 -7,21 5 IGEPN IGEPN 19/12/2016 2:11 0,93 -79,84 -6,42 5,8 IGEPN IGEPN 12/08/2014 14:57 -0,05 -78,42 -6,08 5,1 IGEPN IGEPN 06/03/1987 3:14 0,11 -77,87 -6 6 EHB ISC 12/12/2016 10:53 1 -79,95 -5,3 5,1 IGEPN IGEPN 10/08/1990 21:59 -0,04 -78,43 -5 5,3 EPNrep ISC 20/12/2016 12:39 0,96 -79,85 -4,96 5,1 IGEPN IGEPN 20/12/2016 20:04 0,96 -79,82 -4,66 5,1 IGEPN IGEPN 22/05/2018 8:36 0,58 -78,68 -4,06 5,5 IGEPN IGEPN 20/04/2016 16:30 0,53 -79,85 -4 5,4 IGEPN IGEPN 08/10/2000 15:12 0,35 -78,09 -3,9 5,1 FONT IGEPN 01/01/2016 12:15 0,41 -78,97 -2,81 5,3 IGEPN IGEPN 14/04/1958 17:48 0,82 -79,82 0 6,6 ISS ISC 14/04/1958 17:48 0,82 -79,82 0 6,6 ISS ISC 11/05/1955 6:04 -0,2 -77,8 0 6,8 ISS CENTENNIAL A partir de: IG - EPN (2021)
Tabla 1 Selección de sismos con magnitud mayor o igual a 5 Mw y profundidad de epicentro hasta 20 Km.
1.2 OBJETIVO GENERAL
Caracterizar la amenaza sísmica y los efectos cosísmicos en el cantón Otavalo - Ecuador, mediante análisis geoestadístico y de superposición ponderada
1.3 OBJETIVOS ESPECÍFICOS
• Zonificar la intensidad, magnitud y aceleración sísmica en la región
• Identificar áreas de subsidencia o de desplazamiento del suelo, en la cercanía de fallas geológicas capaces.
• Delimitar áreas de pendientes pronunciadas propensas a efectos cosísmicos.
1.4 PREGUNTAS DE INVESTIGACIÓN
• ¿Cuánto y por qué varía el error estándar del valor de las magnitudes sísmicas estimadas con técnicas de interpolación espacial Kriging?
• ¿Cuál es el orden de magnitud en que las técnicas de Radar de Apertura Sintética Interferométrico (inSAR) 1 permiten identificar deformaciones en zonas puntuales del territorio cantonal?
• ¿Cuánto varía en rango el valor de pendientes en zonas con influencia posible de efectos cosísmicos, de acuerdo con el Análisis de Superposición Ponderada (AHP) 2?
1.5 HIPÓTESIS
La utilización de técnicas de Interferometría Satelital, en combinación con técnicas geoestadísticas de Kriging y de Análisis de Superposición Ponderada, permite identificar áreas de riesgo significativo para el ordenamiento territorial del cantón Otavalo en la provincia de Imbabura - Ecuador.
1 inSAR, por sus siglas en Inglés: Interferometric Synthetic Aperture Radar
2 AHP, por sus siglas en Inglés: Analytic Hierarchy Process (AHP)
17
1.6 JUSTIFICACIÓN
Los procesos de planificación urbana y de ordenamiento territorial cantonal se abordan generalmente a partir de información secundaria relacionada con características ambientales, geográficas, hidrológicas y de riesgo. Las aproximaciones que se hacen no contemplan las contingencias derivadas del desarrollo de proyectos extractivos, industriales y agropecuarios en áreas rurales, la localización de infraestructura básica, vial, estratégica, de equipamientos comunitarios urbanos y rurales. Incluso la ampliación del límite urbano hacia áreas rurales y la conversión de éstas en zonas de expansión urbana potenciales resulta muy cuestionable.
Las técnicas de análisis geoestadístico (Kriging), sensores remotos (Interferometría) y superposición ponderada no son utilizadas. En el Ecuador se ha preferido referir a mapas temáticos a gran escala, regionales y hasta nacionales, relacionados con pendientes, amenazas y textura de suelos La generalización de tales representaciones no permite extraer conclusiones relevantes
La información sismológica es muy limitada, como series históricas y en tiempo real. Aún más, información catalogada como de acceso público no se obtiene con facilidad. Tal es el caso del inventario de fallas capaces que, para esta tesis, fue facilitado por el Dr. Kervin Chunga. A partir de esta información se ha hecho una evaluación determinística del riesgo sísmico en la región noroccidental del bloque norandino del Ecuador y, en particular, para el cantón Otavalo.
Los valores de Mw y aceleración de sismos en roca (PGA) bien pueden contribuir a la elaboración de normas locales para la construcción antisísmica de edificaciones e infraestructura en general Estas normas también deben converger para conducir, con criterio técnico – político, la ocupación del espacio geográfico cantonal a fin de prevenir, mitigar o impedir el surgimiento de vulnerabilidades a futuro.
1.7 ALCANCE
Se obtendrán mapas de áreas de subsidencia o de cambios observables mediante plataformas satelitales provistas de sensores inSAR. Esta información está íntimamente
18
relacionada con la microzonificación sísmica cantonal y áreas vulnerables a efectos cosísmicos (deslizamientos, licuefacción de suelos) El análisis proporcionará criterios metodológicos posibles de aplicación con miras a incorporar o reconvertir áreas rurales para el desarrollo urbano cantonal, en resumen, la viabilidad de la expansión del perímetro urbano de la cabecera cantonal en Otavalo. Las escalas de la cartografía a obtener variarán entre 1:250,000 – 1:1,500,000, para acercar hacia Imbabura y la jurisdicción cantonal de Otavalo, o, para extender a la región de las provincias de Imbabura y Carchi, respectivamente. Los resultados que se obtengan podrán ser utilizados por el Gobierno Autónomo Descentralizado (GAD) Municipal de Otavalo en sus planes de desarrollo urbano y ordenamiento territorial cantonal, alimentando a directrices futuras para la construcción de edificaciones sismo – resistentes, así como también a la ubicación óptima de diversos equipamientos cantonales.
19
2. REVISIÓN DE LITERATURA
2.1 EL BLOQUE NORANDINO ECUATORIANO (BNA)
La tectónica de placas terrestres (continentales y oceánicas) provoca sismos cuya intensidad, magnitud y profundidad del epicentro influencian con intensidad variable en un amplio radio de acción (Chunga et al., 2016). Las formaciones geológicas presentan deslizamientos y fracturas. Estas fallas son áreas donde masas de suelos contactan a lo largo de una superficie irregular áspera, con planos de inclinación que dependen de las características mecánicas de los suelos (o rocas). La interacción entre ellas provoca hundimientos o levantamientos del terreno por esfuerzos de tracción o compresión, respectivamente.
De acuerdo con Chunga, K. (conversación telefónica, agosto 2020), hace millones de años (Ma), la acción del flujo de glaciares para el moldeamiento del terreno en la región andina tuvo un efecto similar que se agregó a los procesos tectónicos terrestres a nivel planetario: se produjeron en el territorio fallas geológicas, cuyo carácter de activas las ha hecho merecer el nombre de fallas capaces porque pueden generar sismos corticales de magnitud mayor a 5 Mw.
El Ecuador tiene cuatro regiones morfo estructurales: la insular, la costera, la andina y la amazónica. En la zona costera o litoral colisionan la placa continental sudamericana y la oceánica de Nazca que se subduce bajo la anterior. Esto origina terremotos fuertes de magnitud próxima a 8, ocasionalmente mayor.
En la región continental del Ecuador existe “una franja de colisión intraplaca”, resultado de la interacción entre la placa sudamericana y el bloque norandino (BNA). A esta franja la llaman “Sistema Mayor Dextral (SMD), mega falla de cizalla Guayaquil – Caracas, sistema de falla Guayaquil -Pallatanga” (Chunga, 2016, pág. 6).
Kanamori y McNally (1982) afirman que el BNA está afectado por la zona de subducción entre las costas de Ecuador y Colombia. Witt y Bourgois (2009) sugieren que el BNA “escapó” en tiempos del Pleistoceno inferior (1,8 – 1,6 Ma) de la gran cuenca de antearco 3
3 Antearco. Región entre una fosa oceánica y el arco volcánico asociado, localizado en bordes convergentes y que incluye prismas de acreción y cuencas eventualmente presentes.
20
del golfo de Guayaquil – Tumbes, por el hundimiento o subsidencia que se presentó en una extensión contigua a fallas normales de bajo ángulo, entre 20° y 30° El fenómeno habría contribuido a debilitar la corteza en la cuenca del golfo, impidiendo almacenar energía sísmica y, por lo tanto, a que la zona tenga actualmente una baja recurrencia de sismos: el transporte de sedimentos desde los Andes ecuatorianos también favoreció este proceso (von Huene y Scholl, 1991; Bourgois et al., 2000, citados por Witt y Bourgois, 2009).
La zona del BNA ha sido escenario de terremotos de gran magnitud en el siglo XX: 1906 (8,3 Mw); 1942 (7,9 Mw); 1958 (7,8 Mw); y 1979 (7,7 Mw). En dichos sismos, se rompió aproximadamente el mismo segmento o falla, constituida por una distribución discreta de asperezas. La presencia de una o más zonas débiles entre asperezas adyacentes, puede ocasionar pequeños o grandes terremotos, los cuales implican cierto ancho y cantidad de deslizamiento, menor los primeros, mucho mayor los segundos.
Nocquet, Mothes y Alvarado (2009) establecen que la deformación actual proviene de la subducción de Nazca bajo la placa sudamericana y del movimiento a largo plazo del BNA respecto a la anterior, afectado por la convergencia oblicua de las dos placas. Sus apreciaciones refieren a observaciones efectuadas con la red del Sistema de Posicionamiento Global ecuatoriana (GPS) instalada en 2007.
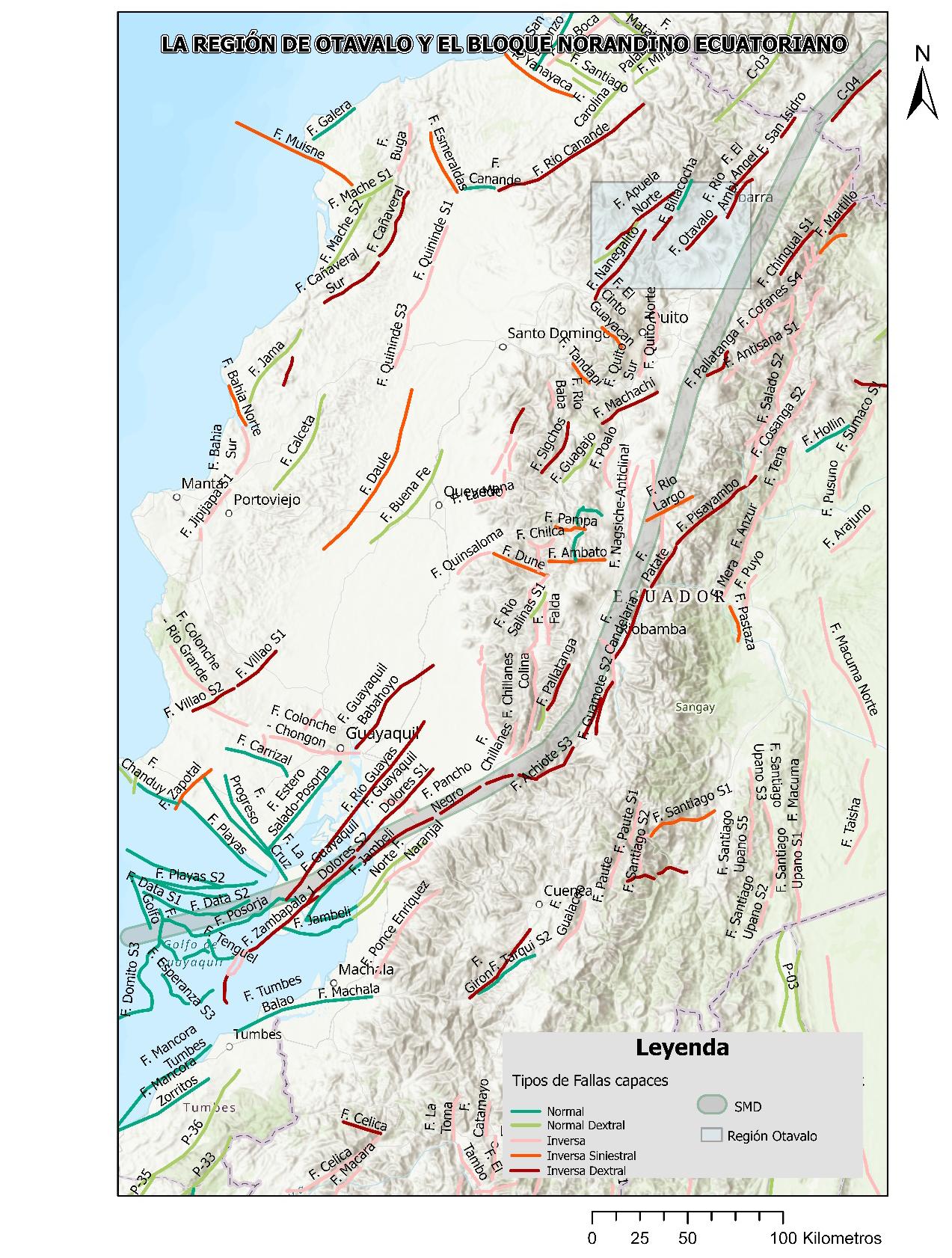
De acuerdo con Nocquet et al. (2009), el movimiento del BNA se evidencia en los sitios de la costa, donde los desplazamientos medidos en las estaciones GPS varían entre 14 – 20 mm/año (Cerro Chispas (CHIS) y Esmeraldas (ESMR)), en dirección N56-60°E. Esto contrasta con sitios en la cordillera, por ejemplo, la estación Riobamba (RIOP) que se desplaza 5 mm/año. Esta diferencia no se explica sólo por la convergencia oblicua Nazca-América del Sur, habiendo estimado los especialistas un vector de rotación del BNA con la tendencia al este respecto de América del Sur. Las predicciones de movimiento del BNA se estiman en 7,3±2,7 mm/año, en dirección N36°E. Este valor podría estar subestimado, por observaciones efectuadas en otros segmentos de fallas, por lo que el movimiento medio del BNA en Ecuador ascendería a 8,7 mm/año en dirección N35°E. La Ilustración 1 representa la trayectoria cualitativa aproximada del SMD (la línea de color gris), que es continua hasta la cuenca del Caribe. El SMD separa arriba y a la izquierda al BNA, y abajo hacia la derecha a la placa sudamericana continental. La región de Otavalo (el rectángulo
21
de color celeste) y las fallas capaces existentes en el Ecuador también se muestran en el mapa
22
Ilustración 1 La región de Otavalo y el bloque norandino ecuatoriano.
2.2 SISMOS HISTÓRICOS Y FALLAS GEOLÓGICAS REGIONALES
El cantón Otavalo es el cantón más austral de la provincia de Imbabura, vasta región que forma parte del BNA en el cual se producen desplazamientos horizontales tipo cizalla además de fallamientos por tracción y compresión. Históricamente, en la región septentrional del SMD se han producido terremotos de magnitud apreciable, en particular aquel conocido como terremoto de Ibarra ciudad muy próxima a Otavalo (16 de agosto de 1868, Mw>6,5). Como dato curioso, el epicentro de dicho sismo fue la ciudad de Otavalo que, para la época del terremoto, había disminuido en importancia respecto a Ibarra: en la época colonial, en Otavalo se estableció un corregimiento. Hay presencia importante de fallas capaces como la Río Ambi (EC-25), la Otavalo (EC-26), las Billacocha – Huayrapungo (EC-27, EC 27a y EC27b), Apuela (EC-28, EC-28a, EC-28b, EC28c), Nanegalito (EC-29). Estas fallas constituyen ramales dispersos de segmentos de fallas como la Guachucal - Cumbal, Tulcán y San Isidro (EC-23) y El Ángel (EC-24), a manera de prolongaciones en cola de caballo del sistema de fallas colombiano Cauca – Patía (Eguez et al. 2003).
La magnitud probable de sismos en la región varía entre 6,3 – 6,6 Mw, más frecuentes que el sismo histórico de 1868. De acuerdo con Soulas et al. (1991), el sistema sinestral Cauca
– Patía – San Isidro presenta sismos de magnitud 6,9 Mw en el segmento Ibarra – El Ángel, con un período de retorno entre 1000 y 2000 años. Dicha magnitud se registró históricamente en el terremoto del 16 de agosto de 1868 (M7), integrado en el Catálogo de intensidades de Ecuador por el Centro Regional de Sismología para América del Sur (CERESIS, 2021). Los nudos sismogénicos identificados en la región de Otavalo están asociados al SMD. La falla Otavalo (EC-26), por ejemplo, tiene una dirección NE-SW y se extiende al sur en Chavezpamba y al norte hasta Atuntaqui (Eguez et al. 2003).
El registro histórico sobre terremotos en Ecuador es corto, lo que hace inviable un análisis de tipo probabilístico. La información sobre fallas geológicas capaces cartografiadas está siendo compendiada por el Proyecto Multinacional Andino PMA─ a través del Grupo de Estándares para Movimientos en Masa GEMMA─ (PMA – GEMMA, 2007) 4. En Ecuador han contribuido a esto los trabajos de Eguez et al. (2003), y de Chunga et al. (2016). De
23
4 SGMA, Servicio Geológico Minero Argentino. PMA, Proyecto Multinacional Andino.
acuerdo con Chunga et al. (2010), en el Ecuador no se han definido parámetros de atenuación de las ondas sísmicas. Chunga et al. (2013) estimaron niveles de sismicidad, a partir de desarrollos matemáticos propuestos por Wells y Coppersmith (1994), para identificar nudos sismogénicos en la costa y los Andes septentrionales del Ecuador. Los terremotos de gran intensidad se producen en la intersección de zonas de fallas (o nudos estructurales), identificadas mediante un proceso determinístico que singulariza nudos sismogénicos incluso en áreas con ausencia de registro de terremotos. Esto supone caracterizar fuentes sísmicas, aplicar relaciones empíricas entre magnitudes de sismos, aceleraciones, desplazamientos máximos respecto a la longitud de la falla (Chunga et al., 2016), para luego generar isolíneas por interpolación y evaluar los efectos cosísmicos de la propagación de las ondas.
2.3 ESTIMACIÓN DETERMINÍSTICA DE MAGNITUDES DE SISMOS Y ACELERACIONES EN ROCA, A PARTIR DE FALLAS CAPACES
De acuerdo con Rivas-Medina et al. (2014), que citan la expresión propuesta por Brune (1968), el momento sísmico se estima proporcional al producto del área del plano de falla (A, Km2), la velocidad de deslizamiento de la falla (ú, mm/año) y el módulo de deformación de la corteza (μ = 3*1010 Pa 5). En puntos editados y distribuidos (como un feature class tipo punto) en las fallas de la región, es posible calcular la magnitud y la aceleración (en roca) de sismos utilizando los procedimientos descritos por Chunga et al. (2016), en particular las expresiones de Wells y Coppersmith (1994) para la magnitud estimada (Mw), y de Fukushima y Tanaka (1990) para la aceleración en roca (PGA):
Ecuación (2.3.1):
�������� =5,08 +1,16 ∗ log (�������� )
Ecuación (2.3.2):
24
������������ = �10�0,41∗��������−���������������������+0,032∗10(0,41∗��������) �� 0,0034 ∗ �������� +1,3� 980
5 Pa, Pascal, 1 N/m2. Se integró estas unidades en la lista de acrónimos.
En las ecuaciones precedentes, Mw es el momento de magnitud estimado, Lf es la longitud de la falla en kilómetros y Hf la profundidad del epicentro del sismo, también en kilómetros. Los cálculos pueden hacerse con Excel y luego ser unidos a la tabla de atributos del archivo geográfico vectorial de puntos para interpolación, mediante la operación Join Aplicando procedimientos geoestadísticos con una de las técnicas de krigeado a seleccionar, es posible obtener resultados en rangos mínimo y máximo de valores para Mw y PGA. Las dos variables son estimadas con criterio determinístico, es decir, considerando a las fallas geológicas capaces como causales de terremotos corticales (profundidad del epicentro Hf próxima a 20 Km).
Existen leyes de atenuación para las ondas sísmicas que han sido estudiadas comparativamente para el Ecuador. Para fallas de tipo cortical como las analizadas en el presente trabajo, Falconí, García y Villamarín (2010) definieron la ecuación que relaciona la aceleración del sismo ah en un lugar diferente del epicentro con el momento de magnitud de sismos Mw, a una distancia D al foco expresada en kilómetros:
Ecuación (2.3.3):
������������(����ℎ )=1,2474 +0,3735 ∗ �������� 0,4383 ∗ ln (���� + 10))
Esta formulación obedece a que, en Ecuador, no se dispone de acelerogramas de sismos que superen el umbral de 0,20g. La expresión anterior obtiene la aceleración en otros sitios distantes del epicentro del sismo. Las unidades de ah son gals (cm/s2).
2.4 INTERPOLACIÓN ESPACIAL
Toda medición ambiental contendrá las coordenadas de los sitios de observación y los valores de los parámetros de las diversas variables medidas en aquellos. Las coordenadas de los sitios pueden ser geográficas o en un sistema cartesiano o proyectado. Los datos pueden ser analizados gráfica o matemáticamente y las observaciones (o registros) pueden ser resumidas en notación matricial.
25
Sichel (1947) desarrolló regresiones matemáticas utilizando mínimos cuadrados, concibiendo una distribución de probabilidad logarítmica normal para predecir la distribución del oro en las minas sudafricanas de Witwatersrand. Puesto que la aproximación de Sichel no consideró el hecho de la distribución asimétrica de las minas y su contenido en el mineral, Krige (1951) propuso la utilización del método de medias móviles. Esta innovación de entonces, se considera en la actualidad que es una aproximación al krigeado simple, cuya formulación orientada al plano de la predicción estuvo a cargo de Matheron (1962).
De acuerdo con Giraldo (2002), el estudio estadístico de información ambiental georreferenciada atañe a múltiples disciplinas y considera variables muy diversas como propiedades fisicoquímicas de suelos, aguas continentales o estuarinas, dispersión de contaminantes en ambientes acuosos, aéreos o hidrogeológicos, distribución de menas de minerales de interés geológico y económico y, así como en el caso presente, la variabilidad espacial de sismos en cuanto a Mw y PGA. El análisis con Kriging ordinario o universal identifica si el valor promedio del parámetro observado en una región es constante o no. Los gráficos de histogramas, diagramas de dispersión, de caja y bigote, sirven para identificar si estas singularidades describen la continuidad de fenómenos naturales (geológicos, climáticos, ecológicos). Por lo tanto, los fenómenos naturales pueden ser modelados espacialmente. También puede hacerse predicciones de valores en sitios donde no se cuente con observaciones. Si la predicción de valores está en la mira, se desarrolla una primera fase de análisis estructural geoestadístico para evaluar la correlación espacial entre puntos, como se describió en el párrafo anterior. Para predecir valores, se calculan promedios ponderados de las observaciones reales.
El análisis estructural geoestadístico implica definir tres funciones: el semivariograma, el covariograma y el correlograma. A mayor cercanía de los sitios de observación en el campo, mayor similitud y correlación espacial (Giraldo, 2002, pág. 21). En ausencia de una estacionariedad, así como de una tendencia (o si éstas son débiles), la varianza de los incrementos de una variable espacial (o regionalizada) es finita. A esta función se denomina variograma (2γ(h)), siendo h el incremento en el valor x de una variable, la “distancia”. La distribución de observaciones registradas no es homogénea. Por ello se toman intervalos de distancia variables, de manera que el semivariograma corresponderá a una distancia
26
promedio entre parejas de sitios en un intervalo. Se utiliza el semivariograma para determinar si existe relación espacial entre datos, porque es la única función que no requiere estimar parámetros.
Kriging es un conjunto de métodos de predicción espacial que minimizan el error cuadrático de una predicción (Giraldo, 2002, pág. 32) La versatilidad radica en que a partir de puntos conocidos (con ubicación geográfica, magnitud de una variable medida) se evalúan o se estiman en otros puntos donde no se conoce su intensidad (expresada como un valor de la variable en referencia). Se obtienen además estimaciones de error e intervalos de confianza de los valores para cada punto en que no se han efectuado mediciones.
De acuerdo con Giraldo (2002), entre los predictores lineales se tiene las variantes de Kriging denominadas Simple, Ordinario, Universal. Como predictores no lineales, surgieron las técnicas de Indicador probabilístico, Log-Normal, Trans-Gaussiano, Disyuntivo. Los lineales son predictores óptimos si hay normalidad multivariada. Los no lineales, en general, son predictores óptimos. Kriging Ordinario (KO) responde a un concepto de krigeado en bloques y puede ser representado mediante un sistema matricial (Giraldo, 2002, pág. 43). Se puede agrupar en cuatro grupos de métodos:
• Geoestadísticos: Kriging Empírico Bayesiano (EBK); Predicción – regresión EBK (EBK RP); Kriging / CoKriging (K-Co); Interpolación de Área (AI);
• Interpolación en tres dimensiones: Kriging Empírico Bayesiano en tres dimensiones;
• Interpolación con barreras: Interpolación Kernel (KI); Interpolación por Difusión (DI);
• Determinísticos: Interpolación Polinomial Local (LPI); Interpolación Ponderada por el inverso de la Distancia (IDW); Funciones de Base Radial (RBF).
Los métodos de interpolación en tres dimensiones y con barreras, no aplican para el presente análisis. Los primeros demandan referir un campo de error de medida, del cual no se dispone en la práctica sismológica actual; los segundos porque los sismos se transmiten por el suelo a grandes distancias atenuando su magnitud conforme se alejan del epicentro y aumenta su profundidad. Algunos otros métodos geoestadísticos y determinísticos tienen sus particularidades. Así, por ejemplo:
27
• EBK R-P combina Kriging con un análisis de regresión de valores de otras variables explicativas (ArcGIS Pro, 2021b).
• AI reagrupa datos a partir de un set de polígonos hacia otro de polígonos objetivo. Es más apropiado para conteo de datos discretos. Incluso el segundo set de polígonos puede ser también utilizado como una variable de cokriging (ArcGIS Pro, 2021c).
• LPI y RBF, son, en el primer caso, un método de interpolación moderadamente rápida y suave (inexactos), y, en el segundo, un método interpolador determinista moderadamente rápido exacto, pero menos flexible que el de Kriging. Ambos métodos no permiten investigar la autocorrelación de los datos, el de LPI si provee con predicciones del error estándar, pero su exactitud es mayor cuanto más se apeguen los datos a una distribución normal (ArcGIS Pro, 2021d)
2.4.1 Estudios en que se ha aplicado Interpolación espacial
2.4.1.1
Evaluación de los efectos sísmicos y cosísmicos en Iburi, Hokkaido - Japón
Zhou et al. (2021) aplicaron técnicas de interpolación Kriging para obtener la distribución del valor de PGA y evaluar los efectos sísmicos y cosísmicos del terremoto de 6,6 Mw que ocurrió a las 3 a.m. el 6 de septiembre de 2018, al oriente de Iburi, Hokkaido (Japón). Los investigadores dispusieron de datos de aceleración horizontal y vertical a partir de acelerómetros.
Esta investigación también consideró aplicar el método de Newmark (1965), pues se investigó el mecanismo de los deslizamientos de tierras regionales, analizando la estabilidad y el desplazamiento permanente de las laderas por el efecto de las lluvias y el movimiento sísmico con criterios bastante similares a los anteriormente expuestos. Se aplicó un análisis de equilibrio límite basado en el método pseudo estático. Luego, se realizó el cálculo de desplazamiento de Newmark basado en el registro de aceleración sísmica. El rango de distribución de los resultados del análisis mostró concordancia con aquellos de casos reales de deslizamientos de tierra. Los resultados verificaron la contribución de la lluvia continua y el fuerte movimiento a la falla de las pendientes regionales.
28
Además de haber provocado 41 muertes humanas e interrupciones del servicio en la ciudad de Sapporo, el sismo desencadenó licuefacción de suelos y cerca de 6.000 deslizamientos de tierra. Entre el 18 y el 24 de septiembre de 2018 se investigaron dichos procesos en campo, a los que contribuyeron la continuidad de lluvias intensas y el tifón: en consecuencia, la superficie del suelo tenía un alto contenido de agua.
2.4.1.2 Grecia: Trazado de mapas isosísmicos
Schenková et al. (2007) utilizaron en Grecia técnicas geoestadísticas para obtener curvas o líneas isosísmicas y representar la distribución espacial de las medidas de terremotos (magnitud, aceleración), dependiendo de factores tales como la geología y la topografía del sitio, las orientaciones de las fallas tectónicas, es decir, diferentes regímenes tectónicos y geomorfológicos. Los investigadores utilizaron la técnica de Kriging y citan además a Gasparini et al. (2003) y De Rubeis et al. (2005), quienes verificaron que, en las técnicas de Kriging, la introducción del semivariograma experimental es útil para filtrar y remover posibles errores resultantes de la interpolación. En sus conclusiones, Schenková et al. (2007) destacaron que la opción de Kriging predeterminado es una herramienta adecuada para cálculos previos orientados al trazado de mapas isosísmicos. Las regiones interiores de los mapas así obtenidos son más confiables que aquellas exteriores de los mismos. En los bordes los campos isosísmicos podrían moldearse de manera incorrecta, debido a las condiciones marginales de la distribución de datos. Añadieron además que los mapas obtenidos con la opción predeterminada de Kriging permiten dibujar mapas isosísmicos en condiciones estándares y homogéneas, pudiendo ser integrados en cualquier atlas de mapas relacionado y utilizarse para evaluar el peligro sísmico vinculando a procesos de planificación territorial.
29
2.6 INTERFEROMETRÍA SATELITAL
El desarrollo teórico de este numeral se basa en la sistematización efectuada por Ferreti et al. (2007), para la Agencia Espacial Europea (European Space Agency, ESA, por sus siglas en Inglés).
De acuerdo con estos autores, un móvil aéreo o espacial provisto con SAR 6 emite y recibe microondas oblicuamente en una distancia inclinada, a lo largo de una trayectoria o azimut.
La recuperación de datos depende de la orientación de la antena, el ángulo de incidencia, el ancho de barrido, la resolución espacial. La topografía local determina otro ángulo de incidencia local.
Las imágenes SAR (maestra y esclava) obtenidas, junto con las matrices complejas dimensionales, contienen información de la amplitud de la dispersión del campo electromagnético y de la diferencia de fase entre las señales transmitida y recibida (interferograma). La interferencia negativa de las imágenes de antes y después de un sismo, provocan al combinarse el oscurecimiento de áreas que se han desplazado en un efecto similar al de arco iris, lo que permite estimar movimientos superficiales hasta de 1 mm/año
Ferreti et al. (2007) destacan que las filas de pixeles de la imagen informan sobre diferentes ubicaciones a lo largo del azimut, mientras que cada columna representa diferentes
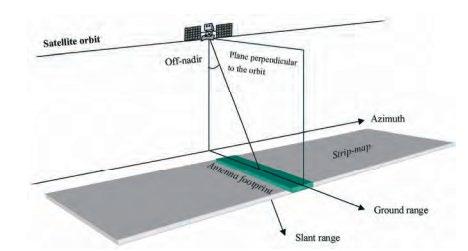
30
Ilustración 2 Esquema satelital del sistema SAR.
6 SAR, por sus siglas en Inglés: Synthetic Aperture Radars
ubicaciones de rango inclinado. Cada pixel está asociado a un área de la superficie terrestre.
Un pixel constituye un número complejo, que integra la amplitud y la información de fase (phase) φ sobre el campo de microondas, dispersado por obstáculos naturales y artificiales.
Los obstáculos que las microondas del radar encuentran generan señales de regreso hacia el sensor, con retardos distintos entre transmisión y recepción, configurando la imagen SAR en una escala de grises. Los pixeles brillantes corresponden a las áreas desde las cuales las microondas del radar se dispersaron de vuelta con mayor amplitud (por ejemplo, formaciones rocosas, áreas urbanas), mientras que los pixeles oscuros corresponden a radiación dispersada de baja amplitud (proveniente de lagos, áreas con mayor vegetación).
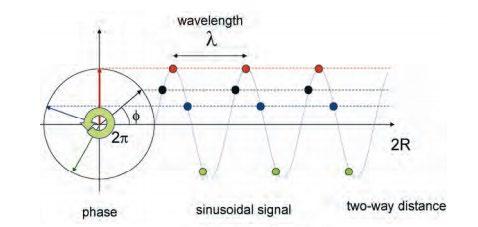
Las microondas transmitidas tienen un comportamiento sinusoidal, con una longitud de onda (wavelength) λ, en la distancia inclinada de ida y vuelta (two-way distance) 2R (ver la Ilustración 3) que determinan la ecuación 2.6.1 correspondiente a φ:
Ecuación (2.6.1):
La función sinusoidal sinφ es periódica con un período 2π radián. La señal transmitida tiene un ángulo de fase φ y está determinado por la relación 2π/λ. El retardo τ equivale al cambio de fase φ entre las señales transmitida y recibida. τ es proporcional al cociente de la distancia 2R recorrida en el viaje de ida y vuelta, respecto de la longitud de onda λ transmitida. La amplitud del interferograma se obtiene multiplicando la amplitud de la
31
Ilustración 3 Relación entre el ángulo de fase ɸ, la distancia inclinada R y la longitud de onda ʎ de la señal SAR.
���� = 2���� ���� (2���� ) = 4���� ���� ∗����
primera imagen por aquella de la segunda; la fase interferométrica es la diferencia de fases entre las dos imágenes (Ferreti et al. 2007, pag. A-17).
La sistematización de Ferreti et al. (2007), establece que la medida de la altitud del terreno se aproxima y simplifica, con un escenario en que dos satélites equipados con SAR orbitan con ángulos de mirada ligeramente distintos y una separación orbital denominada línea de base interferométrica (Bn, perpendicular baseline). La fase interferométrica de cada pixel de imagen SAR dependerá de la diferencia en las rutas de viaje desde cada radar a la celda considerada. Esto genera una diferencia de recorrido (Δr) proporcional al producto de la línea base perpendicular (Bn) y al desplazamiento de las celdas de resolución en la perpendicular al rango inclinado (qs), respecto de la distancia al objetivo desde el radar (ver Ilustración 4 y ecuación 2.6.2).

Ecuación (2.6.2): �������� = 2
Δr es un parámetro que interviene en la definición del aplanamiento del interferograma.
La variación de fase interferométrica Δφ es proporcional a la diferencia de recorrido Δr, dividida por la longitud de onda transmitida. En este análisis, entra en consideración θ, el ángulo de incidencia de las microondas sobre el terreno con respecto a una línea
32
Ilustración 4 Parámetros geométricos de un sistema satelital SAR.
�������� �������� ����
perpendicular imaginaria. �������� es conocida a partir de los datos orbitales, el segundo término de fase es calculado y restado de la fase interferométrica. La variable representada con la letra s representa al rango de inclinación (slant range). Esta operación origina el aplanamiento del interferograma y produce un mapa de fase proporcional a la altitud relativa del terreno. La ecuación 2.6.3 resume la explicación:
Ecuación (2.6.3):
La variación de fase entre dos puntos del interferograma aplanado, provee información de la variación de altitud actual siempre que se haya efectuado el proceso de desenrollado de fase. En este proceso, se obtiene un mapa de elevación en coordenadas SAR del cual se puede extraer un DEM, que posteriormente es referido a un elipsoide y re muestreado en una cuadrícula diferente. Esto se consigue después de desechar valores de altitud de ambigüedad (equivalentes a enteros de los ciclos de fase 2π).
El concepto de altitud de ambigüedad (ℎɑ ) se origina por la diferencia de altitud que genera un cambio de fase interferométrica de 2π luego del aplanamiento del interferograma. Esto ocasiona que la altura de ambigüedad sea inversamente proporcional a la línea base perpendicular, otros términos de la ecuación que prosigue ya están explicados:
Ecuación (2.6.4): ℎɑ = ������������������������ 2��������
Conocidos los parámetros de cada satélite, longitud de onda λ (cm), ángulo de incidencia de la señal θ (°) y la distancia R de travesía satélite - objeto de la onda (Km), es posible desarrollar ecuaciones específicas. Mientras mayor sea la línea base perpendicular más exactitud tendrán las mediciones de altitud. Existe, no obstante, una línea base perpendicular que maximiza la señal (altitud del terreno) respecto a la influencia del ruido, que es también específica de cada plataforma satelital.
33
�������� = 4���� ���� ∗ �������� �������� �������������������� 4���� ���� ∗ �������� ���� ��������������������
Si eventos sísmicos, cosísmicos, hundimientos, o deslizamientos, provocan el desplazamiento entre dos puntos relativos, se produce un intervalo de fase. Por consiguiente, después del aplanamiento del interferograma, la fase interferométrica contiene las contribuciones de la altitud y el desplazamiento. Con un modelo de elevación digital (DEM) disponible, por diferencia respecto de la fase interferométrica se genera el interferograma diferencial.
Según Ferreti et al. (2007), si dos puntos escaneados sobre el terreno cambian su posición relativa entre dos observaciones SAR, aparece en la ecuación de intervalo de fase (Δφ) un término aditivo, independiente de la línea base, afectado por la distancia d del desplazamiento relativo proyectado en el rango de la dirección oblicua (s, slant range).
Ecuación (2.6.5):
Por consiguiente, después del aplanamiento del interferograma, la fase interferométrica contiene las contribuciones de la altitud y el desplazamiento.
Ecuación (2.6.6):
Las condiciones atmosféricas tienen efecto sobre la fase interferométrica de dos tomas SAR no simultáneas. Los mapas de coherencia (γ) permiten estimar con expresiones matemáticas complejas el llamado ruido de fase: existe una expresión simplificada superado un cierto número de vistas satelitales. Los mapas de coherencia son útiles para la segmentación de imágenes.
La relación exacta entre la dispersión de la fase interferométrica y la coherencia γ, obedece a ecuaciones matemáticas complejas. No obstante, con un número de vistas (NL) superior a 4, los pixeles independientes con la misma coherencia son promediados luego de la compensación topográfica (interferograma de vistas múltiples) y aproximado con la ecuación propuesta por Rosen:
34
������������ = 4���� ���� ∗����
�������� = 4���� ���� ∗ �������� �������� �������������������� + 4���� ���� ∗����
Ecuación (2.6.7):
Donde σφ relación de dispersión de la fase interferométrica y la coherencia (los términos restantes están definidos)
En este proceso suele estimarse la dispersión teórica de elevación (����ℎ ) de un DEM generado a partir de Interferometría SAR:
Ecuación (2.6.8):
2.6.1 Estudios desarrollados con Interferometría satelital
La concurrencia de la tecnología de sensores remotos con la utilización de imágenes de los satélites Sentinel-1, tuvo aplicación temprana incluso para preparar a los usuarios a la utilización de estos recursos. Entre el 4 de abril y el 30 de noviembre de 2013, se generaron once imágenes con el sensor Radarsat-2 funcionando en un modo experimental denominado Observación del terreno. Con posterioridad a estas fechas, la aplicación de SAR e inSAR tuvo un desarrollo muy grande.
35
�������� = 1 �2(��������) ∗ �1 −���� 2 ����
����ℎ = �������� ∗ ������������������������ 4������������
2.6.1.2 Carta Internacional Espacio y Grandes Desastres: inundaciones del río Paraná
En junio de 2014, imágenes de Sentinel 1 fueron utilizadas para fotografiar las inundaciones provocadas por el río Paraná, en la frontera entre Paraguay y Argentina, tras la activación de la Carta Internacional Espacio y Grandes Desastres (ESA 2014a)
2.6.1.3 Terremoto del valle de Napa, California
En agosto de 2014 se produjo el terremoto en el valle de Napa, en California, el mayor sismo en 25 años. Dos imágenes de Sentinel-1A (7 y 31 de agosto de 2014) permitieron generar un interferograma que mostró el movimiento del suelo durante el terremoto y registró a la falla geológica cuya activación determinó el sismo, la misma que no había sido identificada como peligrosa con anterioridad al evento (ESA 2014b)
2.6.1.4 Terremoto de Nepal
Una aplicación similar de la Interferometría tuvo lugar cuando se produjo el terremoto en Nepal (25 de abril de 2015). La plataforma GEOHAZARDS brinda acceso a grandes conjuntos de observaciones vinculadas a terremotos y vulcanismo. Las imágenes de radar tomadas sucesivamente en una misma ubicación son combinadas para producir interferogramas con tonos de arco iris, en cuya composición un cambio entre imágenes origina franjas de interferencia distintas similares a las líneas de contorno en un mapa, lo que permite a los usuarios identificar el movimiento del suelo y cambios que pudieren haberse producido entre las tomas (ESA 2015)
2.6.1.5 El terremoto de Pedernales, Manabí - Ecuador
Bejar et al. (2017) refieren que los geólogos establecieron en el pasado el concepto respecto a que los terremotos pueden influir en la activación o colapso de fallas y volcanes vecinos. Esto determina cambios en la corteza terrestre que la geodesia espacial permite registrar en mapas, modelando procesos de deformación crustal, contribuyendo a
36
informar sobre el desplazamiento del suelo, la geometría de la ruptura y la distribución del deslizamiento.
La observación de estos cambios haría posible inferir fallas o volcanes que se acercan al colapso o la activación. La tecnología satelital de Sentinel-1, que incorpora sensores de radar de apertura sintética (SAR), viabiliza medir las deformaciones cosísmicas y post sísmicos para estimar la distribución del deslizamiento, posibilitando generar mapas útiles en procesos de toma de decisiones posteriores a un terremoto.
Con posterioridad al terremoto de Pedernales del 2016 (7,8 Mw, PGA próxima a 0,50g), en Manabí – Ecuador, Cando-Jácome et al. (2020) utilizaron imágenes de Sentinel-1A y desarrollaron el análisis de Interferometría con base a un DEM de 12,5 de tamaño de celda (Proyecto Copernicus) utilizando el software SARPROZ. Adicionalmente, dispusieron de datos geotécnicos obtenidos en pozos de perforaciones practicados por la Universidad Técnica de Manabí (UTM). Con la investigación delimitaron las áreas afectadas por la deformación del terreno (licuefacción cosísmica) en el área cero de la ciudad de Portoviejo y otras aledañas. Por las características sismo tectónicas de la región, las propiedades geotécnicas de los suelos y la magnitud del sismo determinaron que, entre el 2 y el 24 de abril de 2016, la deformación de los suelos varió desde 0,04 hasta 0,920 mm/año, y, que la probabilidad de licuefacción de los suelos del área en estudios aumentó desde 0,24 a 1,07 (de baja a muy alta probabilidad de licuefacción). Las deformaciones del terreno, la geomorfología local que contribuyó a la licuefacción de suelos, determinaron que la mayoría de las edificaciones colapsasen a causa de los daños estructurales sufridos. La investigación fue útil para destacar la importancia de las evaluaciones geotécnicas en la caracterización de los ambientes geológicos, así como también que la tecnología de SAR permite verificar cambios en la deformación del suelo. Los mapas que se generaron contribuirán a la planificación y administración territorial de la ciudad de Portoviejo.
2.6.1.6 Deslizamientos en el sector de Vallcebre (montes Pirineos – España)
Monserrat et al. (2013) refirieron que una aproximación SAR no interferométrica utiliza la geometría de un par de imágenes SAR, y estima la deformación del suelo por la
37
correspondencia de imágenes: los efectos atmosféricos son despreciables. El par de imágenes SAR (maestra y esclava) preprocesadas 7 se compara mediante un algoritmo de coincidencia para detectar un mismo punto de interés y estimar el vector de desplazamiento. El proceso se repite con otros pares de imágenes de la misma zona en una serie de tiempo 8, con lo cual es posible estimar el desplazamiento 2-D, en un rango de dirección o entre rangos de ésta, ubicando reflectores de esquina (CR) 9 en sitios estables, o identificando objetivos naturales fijos de interés para el procedimiento descrito.
2.7 EL MÉTODO DEL BLOQUE DESLIZANTE DE NEWMARK
De acuerdo con Chowdhury et al. (2009), estimar la deformación en taludes que experimentan cambios en las condiciones que controlan su estabilidad, en particular por sismos, ha sido más efectivamente realizado desde la perspectiva de combinar el análisis de equilibrio límite con un análisis dinámico básico. En este sentido se popularizó el método del bloque deslizante propuesto por Newmark (1965), que consideró tres casos:
• Talud con superficie deslizante circular;
• Bloque deslizante de terraplén sobre una superficie horizontal de base;
• Pendiente con superficie de deslizamiento plana.
El método también es llamado como desplazamiento de bloque rígido, en el cual se asume que el factor de seguridad en cualquier ubicación se basa en asumir que el talud es infinito
A criterio de diversos investigadores, puede ser utilizado para aproximarse al desplazamiento provocado por un aumento en la presión de poro del subsuelo ante la infiltración de agua superficial. Los aspectos conceptuales del método de Newmark (1965) se resumen a continuación.
En condiciones de equilibrio, la Ilustración 5 representa un cuerpo en reposo sobre una superficie de cualquier forma. W representa el peso del bloque, el mismo que es
7 Eliminación del ruido y el moteado en las imágenes, este último mediante un filtrado temporal.
8 Serie de tiempo: Definida por fechas de referencia, de interés para el estudio.
9 CR, Corner Reflectors, por sus siglas en Inglés.
38
equilibrado por N (la reacción normal del suelo) y una fuerza tangencial al plano de deslizamiento con dirección contraria al sentido del movimiento. Si un sismo de magnitud, aceleración y tiempo de duración determinados se suscita, la aceleración k(t) provocará el movimiento del cuerpo sólo si alcanza el valor crítico, concepto que involucra la influencia de la geometría del talud, las propiedades y la presión de agua en los poros del suelo.
El Servicio Geológico de los Estados Unidos (United States Geological Survey, USGS) desarrolló una rutina en Java que permite modelar el método de Newmark en sus variantes simplificadas y mediante un análisis riguroso de bloque rígido. El programa es de libre acceso en la plataforma Web del USGS y cuenta con un menú de ayuda del cual se han extraído algunas de las ecuaciones que se exponen (Jibson y Jibson, 2003).
En este sentido, es útil recordar la teoría de Coulomb y su aplicación al concepto de los esfuerzos principales (normal y cortante) y que se aplica a todos los tipos de suelos (Rico Rodríguez y del Castillo Mejía, 2011, pág. 65-67):
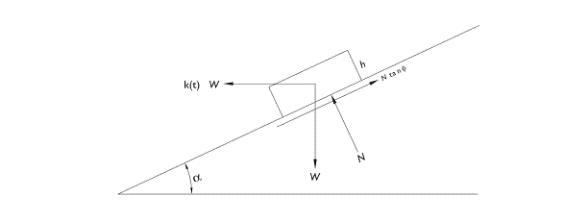
Ecuación (2.7.1), cálculo de la resistencia al corte:
En la ecuación precedente, τ es la resistencia al corte que depende de la cohesión c’ del material, del esfuerzo normal σ y del ángulo φ de fricción del material. Si la misma ecuación se representa en función de los esfuerzos unitarios máximo σ1 y mínimo σ3, se tiene:
39
Ilustración 5 Modelo dinámico del bloque deslizante.
���� = ���� ′ + ��������������������
Si se reemplaza la identidad trigonométrica tanɑ y se eliminan denominadores en las fracciones de la ecuación, se obtiene:
Regularmente, los esfuerzos principales (σ1 y σ3) se interpretan a partir de resultados de laboratorio con muestras de suelo, con ayuda del círculo de Mohr, que se muestra en la Ilustración 6. La figura muestra gráficamente las variables que se deducen del ensayo y que contribuyen a definir parámetros de la ecuación de Coulomb:
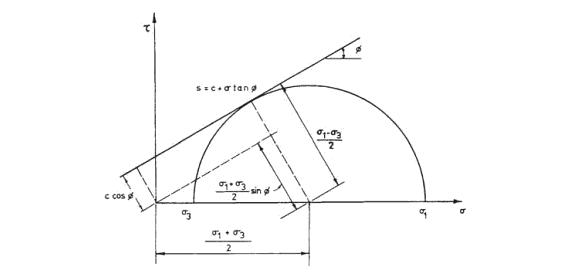
Ilustración 6 Representación de esfuerzos principales a partir de un ensayo de corte en una muestra de suelo.
Sin considerar las fuerzas de presión de poros del agua en el suelo, Newmark simplificó el concepto y estableció que la aceleración crítica ac de un deslizamiento potencial es una función del factor de seguridad (FS) y la geometría del plano o del talud (ángulo de inclinación ɑ):
Ecuación (2.7.2), aceleración crítica
�������� = (�������� 1)����������������ɑ
40 ����1 −����3 2 = ���� ′ + ����1 + ����3 2 ∗ ������������ɑ
����1 −����3 =2���� ′ ∗ ���������������� + (����1 + ����3 ) ∗ ����������������
Durante la breve sacudida de un terremoto, los materiales de los suelos en los taludes se comportan como no drenados, por lo que se utilizan parámetros de resistencia al corte total (de resistencia no drenada o de resistencia total). En esta condición, tanto la fricción y la cohesión del suelo, así como la presión de poros, no se diferencian, por lo que la resistencia total se expresa como una sola cantidad.
De acuerdo con Ambraseys et al. (1995), citados por Chowdhury et al. (2009), los efectos de las fuerzas sísmicas operan en tres etapas:
• La primera es la etapa cosísmica que se produce al instante de ocurrir un terremoto y las deformaciones dependen de la magnitud y duración de aquel;
• El estado inmediato post sísmico es cuando ya no actúan las solicitaciones dinámicas, en el cual las deformaciones y el movimiento dependerán del factor de seguridad y las fuerzas gravitatorias que prevalecen;
• La tercera fase de deformaciones ocurre no necesariamente en forma inmediata a un sismo. Puede transcurrir algún tiempo y depende principalmente de que se generen o migren presiones de poro en el subsuelo, así como también de que se rellenen grietas con agua superficial o subterránea y surjan procesos de fluencia y consolidación del suelo.
Chowdhury et al. (2009) citan a Jibson et al (1998), quienes desarrollaron un método de modelación aplicado al software de sistemas de información geográfica ArcINFO. Jibson y sus colaboradores desarrollaron un análisis riguroso de inestabilidad sísmica de laderas (con aplicación en el cuadrángulo de Oat Mountain 7 ½), a partir de los datos del terremoto de 1994 en Northridge, California. Este fue un caso singular, pues dispusieron de todos los datos necesarios que incluyeron:
• Un inventario detallado de deslizamientos activos,
• Alrededor de 200 registros de movimiento (acelerogramas) del sismo principal,
• Un mapeo geológico de la región a escala 1:24.000,
• Un amplio set de datos sobre las propiedades de las unidades geológicas, y,
41
• Modelos digitales de elevación (DEM) de alta resolución de la topografía (10 m).
Los factores determinantes en esta investigación fueron el inventario preciso de deslizamientos de tierra, el gran detalle del mapa geológico disponible, la compilación de valores de resistencia al corte que hicieron mediante consultas a ingenieros geotécnicos y geólogos expertos, proceso por el cual dispusieron de cientos de resultados de pruebas directas de corte en una gran variedad de unidades geológicas de la región. También consultaron criterios de regulación de valores representativos de la fuerza de cizalladura para condiciones sísmicas, a muchos profesionales de la región. Con respecto a la importancia brindada a la evaluación en los inventarios de deslizamientos en particular, cabe mencionar que Caballero Chaves (2011) documentó y complementó en Colombia una base de datos de deslizamientos inducidos por sismos, incluyendo información de ubicación, identificación y magnitud del sismo, aspectos relacionados con el mecanismo y condición de falla operados, la geología y propiedades de los materiales subyacentes, además de los parámetros sísmicos y las condiciones climáticas en la zona de los deslizamientos. A los datos del inventario así consolidado les sometieron a un análisis de estadística descriptiva, comparación directa y análisis multivariado, llegando a la conclusión de que era difícil establecer relaciones entre las variables del deslizamiento y aquellas del sismo, sugiriendo señalar diferencias entre variables en los modelos de análisis.
Jibson et al. (1998) seleccionaron un DEM con la resolución espacial de 10 m, adoptada para preservar las características topográficas en las que se producen muchos deslizamientos de tierra. Son demasiadas las irregularidades topográficas que se pierden en los DEM de 30 metros más utilizados. Resaltaron, sin embargo, que el DEM es simplemente una representación digital del mapa de curvas de nivel original: cuánto mayor resolución de los DEM, más fielmente reflejan los contornos de los mapas publicados, pero, por supuesto, esto no mejora las limitaciones que el mapa puede tener.
Todos estos datos fueron digitalizados y rasterizados a 10 m de tamaño de celda en la plataforma GIS ArcINFO. Estos datos fueron combinados en un modelo dinámico basado en el análisis de deformación permanente de Newmark (bloque deslizante), para producir en primer término celdas ráster con los valores de aceleración crítica que, de acuerdo con
42
la ecuación 2.7.2, es una función del factor de seguridad y de la geometría de la ladera (el ángulo de la pendiente). Las estimaciones de los desplazamientos cosísmicos de laderas en cada celda fueron comparadas con aquellas del inventario digital de deslizamientos activos por el terremoto de Northridge, para construir una curva probabilística que relacionó los deslizamientos pronosticados con la probabilidad de falla. Con referencia al cálculo del factor de seguridad (FS), Jibson et al. (1998) establecieron que debe ser determinado para cada celda. El FS en estas condiciones está dado por la ecuación
2.7.3:
En esta ecuación φ es el ángulo de fricción efectiva, c’ es la cohesión efectiva, ɑ es el ángulo de la pendiente, γ es peso unitario del material, γw es el peso unitario del agua, t es el espesor del bloque de falla en el sentido normal a la pendiente, y m es la proporción del espesor del bloque que está saturado con influencia del agua. El primer término en el lado derecho es el componente cohesivo de la fuerza, el segundo término representa el componente de fricción, y el tercero la reducción de la resistencia a la fricción debido a la presión del poro. En las condiciones modeladas para la calibración de Oat Mountain, no se incluyó la presión de poro (m=0) porque la mayoría de las fallas en el terremoto de Northridge ocurrieron en condiciones secas (Jibson et al., 1998, pág. 6) 10. De esta manera, el tercer término se eliminó de la ecuación. En esta tesis, por la incertidumbre de cuantificar la influencia de la presión de poro a causa del agua, no se considera este último término en el análisis.
Jibson et al. (1998) desarrollaron una metodología simplificada basada en una ecuación de regresión empírica, para estimar el desplazamiento de Newmark como una función de la intensidad del sismo y la aceleración crítica. La expresión matemática de dicha ecuación incluyó el término de aceleración crítica como logaritmo. A partir del análisis de registros de movimiento (acelerogramas) de 280 estaciones en 13 terremotos, analizaron las componentes horizontales de la aceleración con el fin de estimar la intensidad de Arias
10 El texto original en Inglés dice “no pore-water pressure is included (m=0)”
43
�������� = ���� ′ ��������������������ɑ + �������������������� ����������������ɑ ������������ �������������������� ��������������������ɑ
(1970), única medida numérica de la intensidad del temblor del registro calculada mediante la integración de los valores de aceleración al cuadrado. El análisis con el método de Newmark lo efectuaron para varios valores de aceleración crítica, desde 0.02g a 0.40g. Los desplazamientos de Newmark resultantes fueron luego expresados mediante dos variables predictoras: la aceleración crítica y la intensidad de Arias. La función de probabilidad así obtenida puede ser aplicada para predecir y mapear la variabilidad espacial en la probabilidad de falla, en cualquier condición de interés que sacuda el suelo. Este procedimiento de mapeo puede ser usado para construir mapas de riesgo sísmico a deslizamientos, que podrán contribuir en la preparación de planes de emergencia y en la toma de decisiones racionales, relacionadas al desarrollo y construcción en áreas susceptibles a la falla sísmica de laderas. Puesto que los mapas de riesgo resultantes serán digitalizados, ellos pueden ser actualizados y revisados con datos adicionales que estén disponibles, y mapas personalizados que modelen las nuevas condiciones de interés pueden ser producidos cuando sea necesario.
Khazai y Sitar (2000) refieren a la combinación de los modelos pseudo estático de estabilidad de taludes y de desplazamiento de Newmark (1965), como la aproximación más ampliamente utilizada en varios modelos determinísticos para evaluar los deslizamientos inducidos por sismos. Dependiendo de la magnitud de éstos, el área de pendientes susceptibles y el número de deslizamientos varía en proporción directa. De acuerdo con ellos, los softwares de SIG permiten al usuario modificar y actualizar los parámetros de entrada a los modelos numéricos de estabilidad de taludes, para obtener una evaluación determinística de la susceptibilidad a deslizamientos basada en criterios subjetivos.
2.7.1 La aplicación del método de Newmark (1965)
Además de la aplicación en el cuadrángulo de Oat Mountain 7 ½, a partir de los datos del terremoto de 1994 en Northridge, California, se resumen a continuación otros ejemplos.
44
2.7.1.2 Amenaza por deslizamientos en el valle de Aburrá – Colombia.
Hidalgo Montoya y Vega Gutiérrez (2014) desarrollaron una investigación que integró varios aspectos, entre ellos la topografía, la geología y geotectónica, la hidrología del área de estudio (el valle de Aburrá-Colombia), para calcular la probabilidad de que se suscite un deslizamiento en presencia de un sismo con cierto valor de aceleración.
En su investigación de deslizamientos en el valle de Aburrá-Colombia, estos investigadores se basaron en el cálculo de la aceleración crítica (ac), del factor de seguridad (FS) y de la probabilidad de falla (PF, β1). En el cálculo de FS intervienen factores geométricos del talud o de la pendiente y es posible considerar la influencia del agua en el subsuelo con alguna incertidumbre. En esencia, la ecuación 2.7.4 es similar a la 2.7.3.
Ecuación (2.7.4), Factor de seguridad
El valor de PF o β1 requiere el cálculo previo del factor de seguridad para un valor definido de aceleración (FSD). Las ecuaciones son las siguientes:
Ecuación (2.7.5), Factor de seguridad para una aceleración determinada
En estas ecuaciones, los símbolos tienen los siguientes significados:
�������� Aceleración crítica (expresado como una fracción del valor de g)
H Espesor de la zona que falla (m)
Hw Altura de agua medida desde la superficie de falla (m)
c Cohesión del suelo (kPa)
φ Ángulo de fricción interna del suelo (°)
45
�������� = ���� ���� Hcos ɑ sen ɑ + (�������� −�������� �������� )������������ 2 ɑ���������������� ��������������������ɑ �������� = � ���� ���� Hcos ɑ sen ɑ + (�������� −�������� �������� )������������ 2 ɑ���������������� ��������������������ɑ 1� ����������������ɑ
������������ = � ���� ��������
������������ɑ
������������ɑ
�������� −�������� �������� )������������ɑ���������������� �������� (������������ɑ + ����ℎ ������������ɑ) �
(
+ ����ℎ
) + (
γ Peso unitario del suelo (kN/m3)
γw Peso unitario del agua (kN/m3)
ɑ Ángulo de inclinación del terreno (°)
����ℎ Aceleración producida por el sismo (expresado como una fracción del valor de g)
FSD Factor de seguridad para una aceleración determinada
Si el valor del factor de seguridad para un valor determinado de aceleración (FSD) es menor que la unidad, existe probabilidad de falla (PF). Sin embargo, con fines de aproximación inicial, si el valor de la aceleración crítica (ac) es superada por el valor de la aceleración del sismo (ah), también se puede determinar la probabilidad de falla:
Ecuación (2.7.6), probabilidad de falla
donde ���� �������� es la desviación estándar de la aceleración crítica obtenida del análisis gráfico de acelerogramas sísmicos, habiendo sido ya definidas las otras variables.
La metodología desarrollada por estos investigadores tendría que ser simplificada para el caso ecuatoriano, pues se requiere información meteorológica sobre precipitaciones acumuladas en 3 y 15 días.
Los autores modelaron la estabilidad de taludes utilizando imágenes ráster cuyo tamaño de celda fue de 100 m. En las cuadrículas de la imagen, asignaron parámetros de resistencia y peso unitario de acuerdo con los materiales existentes determinados en el mapa geológico. A partir de la pendiente predominante, valor extraído del DEM, el modelo calculó el factor de seguridad y la aceleración crítica en la celda, ésta última como indicador de la susceptibilidad del terreno a deslizamientos. El efecto de los sismos se evaluó con el método de Newmark (1965), basado en el modelo de talud infinito y adicionó la fuerza ocasionada por el sismo como una fracción del peso de la masa de suelo que falla y experimenta subsidencia.
46
�������� = ����1 = (�������� ����ℎ ) ���� ��������
Los investigadores utilizaron además técnicas para cuantificar el efecto de la incertidumbre, mediante técnicas probabilísticas de confiabilidad que relacionan al método de Montecarlo, así como también el efecto de las precipitaciones. La información meteorológica disponible en Ecuador impide efectuar una aproximación más rigurosa. La principal limitación es la disponibilidad y acceso a información sobre lluvias diarias y su continuidad en períodos, por ejemplo, de tres o hasta quince días, como sugieren algunos criterios internacionales. En la mayoría de las estaciones meteorológicas del Ecuador se dispone de la precipitación total mensual, la lluvia máxima en 24 horas y el número de días en el mes con precipitaciones
Kang et al. (2019) evaluaron, mediante modelos numéricos y correlaciones estadísticas, los valores del factor de seguridad en los taludes de la zona montañosa de Sochi (instalaciones de salto de esquí olímpico), para determinar la susceptibilidad a deslizamientos de tierra.
La zona de Sochi es de alto riesgo sísmico (en la región X, 7,3 Mw). Las fallas activas incluyen aquellas principales de la región del Cáucaso (Bekisheiskii, Krasnopolyanskii, Monastyrskii, Sochinskii), que son aproximadamente paralelas entre sí y corren en dirección este –sureste hacia el noroeste. Los investigadores utilizaron DEM con un tamaño de celda de 5 metros y un error de 0,5 m. Los DEM fueron obtenidos mediante datos de escaneo aéreo utilizados para el análisis topográfico. El procesamiento con ArcGIS permitió generar un mapa de pendientes. Un análisis estadístico de estas últimas caracterizó las áreas con pendientes más pronunciadas permitiendo generar modelos simplificados de aquellas 11 , evaluadas con el software GeoStudio.
En el modelaje de pendientes en Sochi, se consideraron ángulos de pendientes entre 20° y 45°. El factor de seguridad por debajo de 20° fue difícil de evaluar en la región incluso para las condiciones más severas de sismos. Conocidas las características geomecánicas de los suelos de la zona, aplicaron el modelo matemático de Spencer (1967) para evaluar la estabilidad de pendientes. De acuerdo con Khazai y Sitar (2000), el método pseudo estático permite valorar cómo las fuerzas sísmicas de un terremoto pueden ser representadas por
47
2.7.1.3 Susceptibilidad a deslizamientos en la zona de Sochi.
11 La traducción literal del texto sería “modelos simplificados con pendientes de pies de barro”.
aceleraciones horizontal y vertical (coeficientes sísmicos), en el centroide de un talud de deslizamiento: los coeficientes sísmicos son relacionados a la PGA en fracciones variables para las aceleraciones horizontal y vertical, en proporciones que varían de acuerdo con los códigos de construcción locales. El método de Newmark (1965) fue adaptado a condiciones propias de la Federación Rusa y sus regulaciones en el área sísmica, de acuerdo con Medvedev y Sponheuer (1969), permitiendo estimar desplazamientos de suelo considerando diferentes profundidades del epicentro del sismo, para una intensidad conocida del sismo (a partir de 7,3 Mw).
2.8 ANÁLISIS DE SUPERPOSICIÓN PONDERADO
En un sentido netamente matemático, el análisis de superposición ponderada permite incorporar los criterios de paneles de expertos, para generar coeficientes de ponderación que luego son aplicados en la combinación de variables que no necesariamente responden a criterios numéricos, o que, siendo su carácter matemático, las unidades dimensionales no hacen compatible realizar operaciones matemáticas diversas. Los criterios de expertos permiten establecer calificaciones por rangos de cada variable, asignan pesos a cada una, y esto permite efectuar operaciones con álgebra de mapas con archivos geográficos vectoriales y ráster.
Todo conjunto de datos de naturaleza científica responde a un formato optimizado capaz de un almacenamiento multidimensional, como por ejemplo los formatos de archivo Network Common Data Form (netCDF), Hierarchical Data Format (HDF) y Gridded Bynary (GRIB), incorporados en softwares como ArcGIS, de acuerdo con Butler y Ding (2018).
Las imágenes SAR de interferometría contienen, por ejemplo, información de coordenadas geográficas, de tiempo (la fecha y hora en que fueron captadas), así como también de las variables propias del interferograma. Las imágenes de interferometría pueden superponerse con otras generadas a partir de procesos ráster de tipo análisis de superficies, por ejemplo, pendientes en laderas. Algoritmos de selección por atributos facilitan identificar ya sea los sitios más abruptos o los más planos. En uno y otro caso, las imágenes de interferometría pueden converger a identificar eventos de subsidencia, deslizamientos, movimientos del suelo. A estos algoritmos, pueden superponerse rásteres que contengan
48
información complementaria como características geológicas, valores de magnitud y aceleración sísmica generados con técnicas de interpolación espacial Butler y Ding (2018) establecen que los modelos o diagramas de flujo 12 de análisis bidimensionales son incorporados con alguna facilidad o elaboración (según los casos) con ayuda de software de SIG. Sin embargo, con frecuencia es preciso analizar modelos de datos provenientes de múltiples disciplinas científicas como las antes enunciadas.
2.8.1 La aplicación del método AHP
2.8.1.1 Beijing, China. Subsidencia del suelo
Una aplicación del análisis de superposición ponderada (o análisis jerárquico de procesosAHP) fue reportada por Wang et al. (2021), respecto a los problemas de subsidencia del suelo en la ciudad de Beijing - China. La aportación de los investigadores citados en este párrafo refirió a las implicaciones de los hundimientos en los sistemas subterráneos, para lo cual evaluaron el riesgo de inundaciones de estos, utilizando el AHP en combinación con SIG, considerando una zona de amortiguamiento de 500 metros en torno a la línea del metro. Los hundimientos del suelo constituyen un fenómeno geológico inducido por la sobre explotación de recursos subterráneos y la densificación de edificaciones sobre el terreno superior. El ingreso de aguas de escorrentía superficial hacia los sistemas subterráneos opera en estaciones ubicadas en puntos bajos, a través de fisuras y fallas subterráneas.
2.8.1.2 Evaluación del riesgo de inundaciones en áreas influenciadas por subsidencia del suelo
Varios investigadores citados por Wang et al. (2021) utilizaron observaciones de Sentinel1A para monitorear el problema de subsidencia del suelo en el área contigua a la línea del metro, y alguno reportó que dicho fenómeno había sido controlado. En primer término, Wang et al. (2021) seleccionaron veinte variables para establecer un sistema indicador de
49
12 Model Builders
riesgo que abarcó aspectos meteorológicos, hidrológicos, topográficos, cubierta terrestre, geológicos y socio económicos.
Su procesamiento en una plataforma de SIG permitió obtener capas ráster con una resolución espacial de 100 metros. Los porcentajes de ponderación de los indicadores se calcularon con base a los procesos AHP y también de jerarquía analítica difusa (FAHP, Fuzzy Analytic Hierarchy Process). Dichos coeficientes fueron aplicados a los ráster antes obtenidos, para determinar los niveles de riesgo de inundaciones en Beijing. Los resultados de este ejercicio fueron cotejados y validados con información relativa a inundaciones a nivel regional y también registros históricos de eventos relacionados.
Utilizando el análisis de superposición, fueron generados los mapas de riesgo, exposición y vulnerabilidad, considerando además variables como la población, la densidad poblacional, el flujo de pasajeros diario, la densidad y proximidad de líneas del metro y de caminos en torno. Así se identificaron las zonas con más alta vulnerabilidad (Xicheng, Dongcheng, Haidain, Daxin, entre otras), además de identificar los niveles de riesgo de inundaciones de las líneas y las estaciones del metro. El estudio proveyó información útil para la toma de decisiones ante eventos de desastres, para los sistemas subterráneos y para la sostenibilidad del desarrollo de las áreas metropolitanas.
50
3. METODOLOGÍA
El tema de la presente tesis integra el análisis de sismos por la repercusión de fallas tectónicas activas, la topografía obtenida a partir del análisis interferométrico para identificar taludes susceptibles de ser influenciados por efectos sísmicos y cosísmicos, mediante la combinación de álgebra de mapas (vectoriales o ráster) con el método de Newmark (1965) que, en el caso presente, es el eje del análisis jerárquico o de superposición ponderada. Esta aproximación contribuirá a identificar zonas vulnerables y a establecer prioridades de intervención en el cantón Otavalo. A continuación, se describe de manera más detallada el área de estudio.
3.1 ÁREA DE ESTUDIO
La región para la cual se ha caracterizado los sismos históricos mayores a 5 Mw, está comprendida entre 1,00° y 0,20° de latitudes N y S, así como entre 77,67° y 80,20° de longitud W, en su orden. Esta región abarca buena parte del área de las provincias de Esmeraldas, Carchi, Imbabura, Pichincha y Napo.
La atención se concentra luego en el área de influencia del cantón de Otavalo. La zona está comprendida entre 0,5006° y 0,0001° de latitud norte y sur, y entre 77,9996° y 78,7502° de longitud occidental. La superficie que abarca esta micro región es de 4.624,59 Km2. La micro región total seleccionada (refiriendo a Otavalo) involucra a ocho (8) fallas capaces
Esta es el área en la cual se concentran: la interpolación espacial de variables sísmicas; el análisis de interferometría para identificar deformaciones en el territorio; y, la adaptación del método de Newmark (1965) a las condiciones limitadas de información con que se ha trabajado.
El Catálogo de Fallas Capaces en la cordillera de los Andes está siendo integrado por geólogos especializados de instituciones sudamericanas académicas y de investigación. Hasta el momento, se han inventariado 278 segmentos cuya profundidad de falla varía desde superficial hasta los 33 Km. La Tabla 2 muestra un resumen con el número de fallas capaces por tipos (normal, normal Dextral, inversa, inversa siniestral, inversa Dextral) y por rango de profundidad, caracterizadas en el Ecuador:
51
Tabla 2 Resumen de fallas capaces por tipos y profundidades de influencia
La base de datos de la Secretaría de Gestión de Riesgos y Emergencias (SGRE), relacionada con eventos de riesgo registrados en el Ecuador entre los años 2010 y 2020, informa sobre aquellos seleccionados y más frecuentes en el cantón Otavalo que corresponden a deslizamientos, incendios forestales, inundaciones y sismos. A partir de un registro de 464 eventos de riesgo de todo tipo, se filtraron para el cantón Otavalo aquellos más frecuentes y que constan en la Tabla 3.
52
Profundidad Número de fallas capaces por tipo Km Normal Normal Dextral Inversa Inversa Siniestral Inversa Dextral 0 1 5 2 6 1 8 2 5 1 9 1 5 10 1 3 12 2 12 11 2 3 12 9 2 11 4 6 13 1 1 14 2 15 8 2 7 1 9 16 5 1 6 1 3 17 1 18 3 4 16 1 5 19 1 20 12 34 10 3 4 22 1 1 2 23 2 1 2 24 1 25 1 1 10 1 26 1 1 28 12 1 2 30 1 3 33 3 2 3 Total 46 58 108 15 51 Chunga (2010) y Chunga et al. (2010)
Las parroquias en que más se han reportado siniestros son Otavalo (San Luis y Jordán, 116), San José de Quichinche (58), González Suárez (48). Las parroquias que más registran deslizamientos, eventos asociados como cosísmicos, aunque también están inducidos por la acumulación de precipitaciones, son Selva Alegre (19) y San José de Quichinche (9).
La Ilustración 7 muestra la distribución espacial en el territorio cantonal.
53
PARROQUIA Incendio forestal Deslizamiento Inundación Sismo Subtotal Dr. Miguel Egas Cabezas (Peguche) 21 1 1 23 Eugenio Espejo (Calpaquí) 29 2 1 32 González Suárez 46 1 1 48 Jordán 50 3 2 55 Pataquí 1 1 2 San José De Quichinche 48 9 1 58 San Juan De Ilumán 15 1 6 22 San Luis 56 4 1 61 San Rafael 9 3 12 Selva Alegre (Cab. en San Miguel de Pamplona) 6 19 2 2 29 San Pablo del Lago 35 1 1 37 Subtotal 316 32 24 7 379
partir de: SGRE (2020)
Tabla 3 Selección de eventos de riesgo más frecuentes en Otavalo.
A
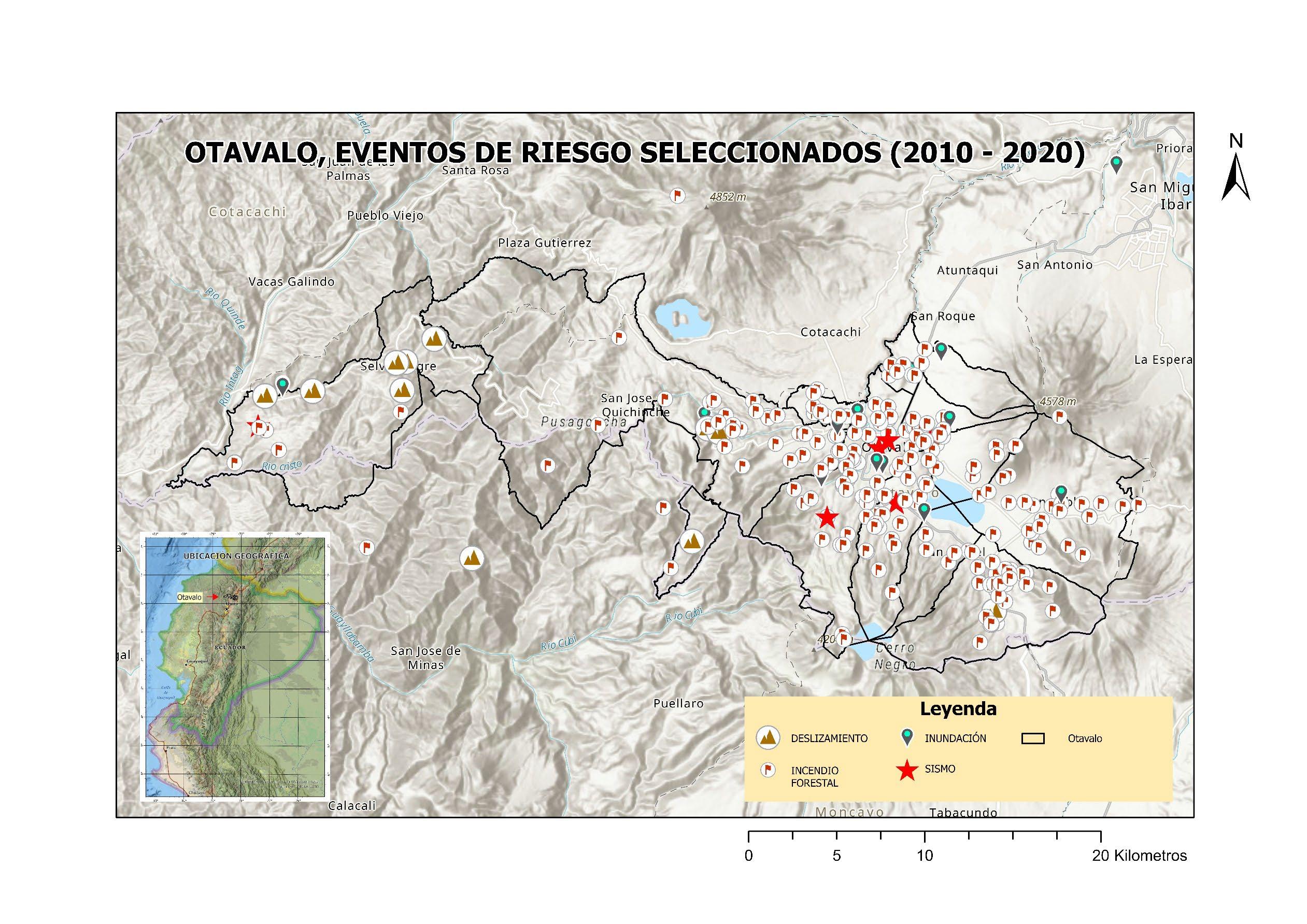
54
Ilustración 7 Otavalo, eventos de riesgos seleccionados, años 2010 - 2020.
Se seleccionaron eventos como incendios forestales, deslizamientos, inundaciones y sismos, un subtotal de 379 distribuidos por parroquias. San Luis y El Jordán corresponden a la jurisdicción de la parroquia matriz Otavalo. La selección se muestra en la Tabla 4
Todas las jurisdicciones parroquiales de Otavalo presentaron a los incendios forestales como el evento de riesgo más frecuente, atribuido a factores antrópicos. Destacan las parroquias San José de Quichinche (48) y González Suárez (46). Las inundaciones fueron más frecuentes en la parroquia matriz (7) y San Juan de Ilumán (6). Las parroquias que registraron mayor cantidad de eventos relacionados con deslizamientos fueron Selva Alegre (19) y San José de Quichinche (9). La distribución temporal de los riesgos que se muestra en la Tabla 5, evidencia que deslizamientos e inundaciones se concentran en el segundo trimestre del año y los incendios forestales en el tercero. De acuerdo con esto, los incendios forestales emergen
55
PARROQUIA Incendio forestal Deslizamiento Inundación Sismo Total Porcentaje San Luis 56 4 1 61 16% San José De Quichinche 48 9 1 59 16% Jordán 50 3 2 56 15% González Suárez 46 1 1 48 13% San Pablo del Lago 35 1 1 38 10% Eugenio Espejo (Calpaquí) 29 2 1 32 8% Selva Alegre (Cab. en San Miguel de Pamplona) 6 19 2 2 31 8% Dr. Miguel Egas Cabezas (Peguche) 21 1 1 24 6% San Juan de Ilumán 15 1 6 23 6% San Rafael 9 3 12 3% Pataquí 1 1 2 1% Total 316 32 24 7 379 100% Porcentaje 83% 8% 6% 2% 100% A partir de: SGRE (2020)
Tabla 4 Otavalo, eventos de riesgo seleccionados, años 2010 - 2020.
en los trimestres con menor cantidad de precipitaciones, los deslizamientos e inundaciones suelen atribuirse a las lluvias, y, los sismos eventuales a las fallas geológicas existentes.
La municipalidad de Otavalo no sistematiza los eventos de riesgos cantonales. La Dirección Municipal de Seguridad Ciudadana atiende emergencias relacionadas con un criterio de apoyo logístico. Su homóloga de Ambiente está relacionada con la gestión de residuos sólidos, el control en la explotación de áridos. En materia de información sobre riesgos, dependen de la información que la SGRE provee. En la Ilustración 8 se tiene una vista general de las fallas geológicas capaces en la región de Otavalo. Se presenta, además, la profundidad en kilómetros que alcanzan estas fallas y una selección de sismos (registrados y catalogados) de siglos anteriores al XX y actuales (siglos XX y XXI). Los sismos seleccionados corresponden a magnitudes mayores o iguales a 5 Mw, con una profundidad de epicentro inferior a 30 Km. En los sismos anteriores al siglo XX, se ha etiquetado el año de su registro. Para los sismos catalogados en los siglos XX y XXI, la etiqueta corresponde a la magnitud del Mw del sismo.
56
Trimestre Deslizamiento Incendio forestal Inundación Sismo Total % relativo Trim.1 9 9 6 24 6% Trim.2 20 8 14 7 49 13% Trim.3 2 246 1 249 66% Trim.4 1 53 3 57 15% Total 32 316 24 7 379 100% % relativo 8% 83% 6% 2% 100%
Tabla 5 Otavalo. Distribución trimestral de eventos de riesgo seleccionados (2010 - 2020).
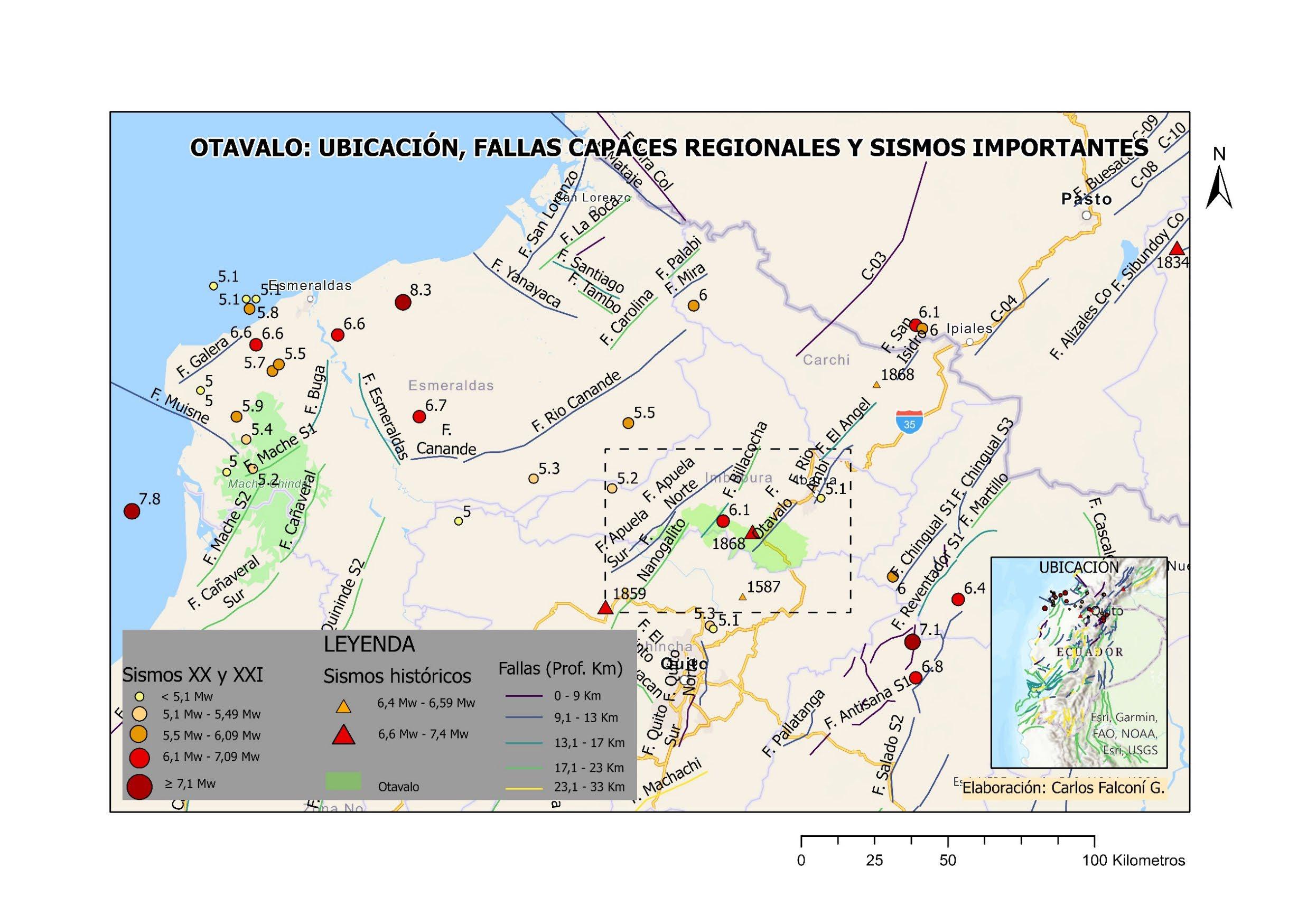
Ilustración 8 Otavalo, ubicación, fallas capaces y sismos importantes
3.2 FLUJOGRAMA
A partir de la revisión de literatura realizada, se puede establecer los siguientes procedimientos metodológicos.
La interpolación espacial Kriging e IDW ha sido aplicada para desarrollar mapas isosísmicos en Grecia (Schenková et al., 2007). En el presente caso, las magnitudes sísmicas de Mw y PGA fueron calculadas previamente, con criterio determinístico, a partir de las expresiones propuestas por Wells y Coppersmith (1994).
Los estudios de interferometría satelital han sido aplicados a la medición de las deformaciones que experimenta la corteza terrestre en el caso de los terremotos en el valle de Napa – California (ESA, 2014b), y en Nepal (ESA, 2015).
Las técnicas de inSAR aplicadas por Cando-Jácome et al. (2020), con posterioridad al terremoto de abril de 2016 en Pedernales – Manabí, evidenciaron que se magnificó la velocidad de desplazamiento de las formaciones geológicas existentes y se acrecentó el coeficiente de licuefacción de los suelos En esta investigación de tesis, a partir de imágenes satelitales en fechas próximas al terremoto de Pedernales, se determinaron subsidencias del suelo en la región de Otavalo como una medida de los efectos cosísmicos observados a una distancia próxima a los 200 Km
Las técnicas de interpolación espacial y del método de Newmark (1965) fueron aplicadas por Zhou et al. (2021) para evaluar efectos cosísmicos y sísmicos en Japón. En el caso del área de esquí en Sochi, el estudio desarrollado por Kang et al. (2019) se basó en el conocimiento de las características geomecánicas de los suelos y aplicó el método de Newmark (1965) en combinación con el de Spencer (1967), previa una adaptación del primero a las condiciones de la Federación Rusa (Medvedev y Sponheuer 1969).
La adaptación de Jibson et al. (1998) del método de Newmark (1965), en el análisis de inestabilidad de laderas en el cuadrángulo de Oat Mountain 7 ½, a partir de los datos del terremoto de 1994 en Northridge, California, resaltan al método como un modelo adaptable a circunstancias diversas que incluye criterios de AHP al considerar las propiedades geotécnicas de los suelos de las formaciones geológicas, la geometría de los taludes de las pendientes obtenidas a partir del DEM obtenido por inSAR y los valores de la aceleración sísmica a partir de la interpolación espacial. Las condiciones limitadas de
58
información en Ecuador fueron salvadas con una generalización de las propiedades geotécnicas, a manera de una aproximación a la adaptación de Jibson et al. (1998). La metodología se resume en la Ilustración 9
INTERPOLACIÓN ESPACIAL: MAGNITUDES DE ACELERACIÓN Y MOMENTO SÍSMICOS.
MÉTODOS GEOESTADÍSTICOS: KRIGING ORDINARIO, KRIGING EMPÍRICO BAYESIANO, INTERPOLACIÓN PONDERADA POR EL INVERSO DE LA DISTANCIA.
MÉTODOS DETERMINÍSTICOS: INTERPOLACIÓN PONDERADA POR EL INVERSO DE LA DISTANCIA.
SELECCIÓN DE MÉTODO MÁS IDÓNEO
INTERFEROMETRÍA ESPACIAL: RADAR DE APERTURA SINTÉTICA DIERENCIAL.
1. DESCARGA 2 IMÁGENES SENTINEL 1 (SLC, IW).
2. SELECCIÓN DE FRANJA Y SUBZONAS DE INTERÉS.
3. PROCESO SINCRÓNICO DE: APLICACIÓN DE ÓRBITA, GEOCODIFICACIÓN, ASIGNACIÓN DE AZIMUT CONSTANTE.
4. OBTENCIÓN DE: DEM, FASE DE INTERFEROGRAMA, MÁSCARA DE COHERENCIA.
5. DESENROLLADO DE FASE. FILTRO DE GOLDSTEIN, EXPORTACIÓN IMAGEN FINAL REF: https://youtu.be/YDkRRvy5RZw
MÉTODO DE NEWMARK (1965):
1. OBTENCIÓN MAPA DE PENDIENTES.
2. SUPERPOSICIÓN CON FALLAS CAPACES Y RÁSTER DE ACELERACIÓN SÍSMICA.
3. VERIFICACIÓN DEFORMACIONES EN TORNO A FALLAS CAPACES.
4. EXTRACCIÓN DE VALORES DE DEFORMACIÓN DEL TERRENO Y COHERENCIA DE LAS MEDICIONES.
5. APLICACIÓN CALCULADORA RÁSTER: SE ASUMEN CONDICIONES HOMOGÉNEAS EN SUELOS
IDENTIFICACIÓN DE ZONAS PROPENSAS A EFECTOS COSÍSMICOS Y SÍSMICOS.
IMPORTANCIA DEL MÉTODO PARA EL ORDENAMIENTO TERRITORIAL EN ECUADOR, LIMITACIONES DE INFORMACIÓN EXISTENTES.
Ilustración 9 Flujograma de la metodología utilizada.
A partir del cálculo determinístico de magnitudes sísmicas, se aplicó interpolación espacial Kriging previa una selección del método más conveniente comparando grupos de técnicas geoestadísticas y determinísticas. Para la variable sísmica de interés, la PGA, se prescindió de afectar por leyes de atenuación respecto a la profundidad del epicentro.
59
El análisis de interferometría se basó en la descarga de dos imágenes Sentinel 1 (S-1), de mirada única (SLC) para interferometría (IW). Las fechas fueron próximas al terremoto del 16 de abril de 2016 en Pedernales (una anterior y otra posterior). De la selección de las franjas y subzonas de interés y procesos de calibración, geocodificación, asignación de azimuth, se procedió a obtener el DEM, la fase del interferograma y la máscara de coherencia. La primera representa las deformaciones ocurridas en el territorio a consecuencia de dicho sismo. La segunda permite identificar si en la región existen zonas en que la información de la fase interferométrica puede ser errónea a consecuencia, por ejemplo, de vegetación natural frondosa. En este caso, se debería efectuar reconocimientos en territorio o recurrir a datos topográficos más precisos de la región en estudio. Se aplicó el filtro de Goldstein para mejorar la imagen y se exportó en archivos ráster y KMZ.
Los resultados de los procedimientos de interpolación espacial y de interferometría satelital se superpusieron en el método de Newmark (1965), adaptando la aproximación efectuada por Jibson et al. (1998). Este método se desarrolla mediante procedimientos de álgebra de mapas (rásteres, vectoriales) y es, en resumen, la clave para aplicar criterios de AHP: superpone la variación espacial de la PGA obtenida por interpolación espacial, la variabilidad de la pendiente del terreno extraída a partir del DEM resultante de interferometría. En el cálculo de la aceleración crítica, el factor de seguridad superpone las características de cohesión, peso específico y ángulo de fricción de los suelos en cada punto, asumidas uniformes como una simplificación; por lo tanto, la pendiente se constituye en el factor discriminante. El cociente de la aceleración crítica con respecto a la PGA permite identificar las zonas propensas a efectos cosísmicos y sísmicos, aún con las limitaciones de información geotécnica, topográfica y de la gran escala de análisis adoptada Este cálculo está referido al valor de la gravedad (g), por lo que se obtienen valores adimensionales. Al superponer la variación espacial de ac/g con el ráster de la PGA expresada como fracción de g, se obtienen valores que de ser superiores a 1 identifican zonas susceptibles a deslizamientos.
60
3.4 DESCRIPCIÓN DE LA METODOLOGÍA
3.4.1 Interpolación Espacial
El archivo shapefile de fallas capaces fue procesado previamente en QGIS con el plugin QChainage, que permite distribuir puntos sobre líneas a intervalos cortos de distancia: fueron ubicados 17.176 puntos entre todas las fallas catalogadas. En cada uno de estos puntos, mediante las ecuaciones de Wells y Coppersmith (1994) para momento sísmico, y de Fukushima y Tanaka (1990) para aceleración sísmica, se calcularon con Excel los valores de las variables sísmicas antes mencionadas: se efectuó una operación de unión espacial de tablas.
Para la interpolación espacial realizada con ArcGIS Pro se utilizó esta red de puntos. Se desarrolló la interpolación espacial de variables sísmicas para todas las fallas capaces caracterizadas en el Ecuador. Se exportó y cortó los rásteres, mediante la herramienta Clip Raster, con una capa de máscara de la región de estudio, que abarca al cantón Otavalo. La interpolación sobre la totalidad de puntos contribuye a minimizar el error estándar de medida, pues todas las fallas son consideradas con toda su potencia, determinada por la longitud. Los procedimientos de interpolación espacial se desarrollaron con base en la capa descrita en este numeral. Se revisó literatura y características de los métodos posibles de aplicación.
En el caso ecuatoriano, la información sismológica es limitada, tanto como serie de tiempo cuanto por la disponibilidad de valores de otras variables sísmicas que contribuyan a explicar el fenómeno, requieren utilizar capas geográficas adicionales (ráster o vector) que se incorporan a manera de variables explicativas o para correlación. Por las consideraciones expuestas, se analizaron ventajas y desventajas de emprender el análisis con EBK, K-Co o IDW En la tabla 6, se presenta un resumen comparativo:
61
Tabla 6 Comparación entre métodos de interpolación espacial.
MÉTODO VENTAJAS DESVENTAJAS REFERENCIA
EBK Automatiza los aspectos más difíciles de la construcción de un modelo Kriging válido. Requiere una mínima interacción con el modelo.
Predice errores estándar más exactos
Realiza predicciones más exactas para datos no estacionarios.
K-Co Utiliza información relacionada con la principal variable de interés autocorrelacionada.
IDW Es exacto. Ofrece una buena primera aproximación a la superficie interpolada a partir de los datos.
Necesita una gran cantidad de puntos de entrada, tamaño del subset y aumento del factor de traslape.
El procesamiento es más lento y correcciones anisótropas o mediante cokriging no están disponibles.
Puede requerir correlaciones cruzadas con otras variables de interés para hacer mejores predicciones del fenómeno.
No arroja medidas ni evaluaciones de errores de predicción. No asume supuestos con respecto a la distribución de los datos.
(ArcGIS Pro, 2021e)
(ArcGIS Pro, 2022a)
(ArcGIS Pro, 2021a)
Se escogió finalmente el método EBK. Las razones para esto es que se contó con un gran número de puntos para la interpolación espacial (más de 17 mil), que en este caso más que ser una desventaja significa lo contrario. En la interpolación inicial, se generó imágenes ráster de las variables sísmicas para la totalidad del shapefile de fallas capaces del Ecuador. A partir de estos rásteres, se exportó imágenes locales enmarcadas en la región inmediata de Otavalo. Por lo tanto, el error estándar es pequeño. A pesar de que IDW se considera un método exacto, no genera resultados para error estándar, lo cual es una desventaja respecto a EBK En cuanto a K-Co, al no contar con una variable adicional para mejorar la predicción, es comparable al método EBK No obstante, EBK tiene las ventajas añadidas de la automatización del variograma y una mínima interacción con el modelo, así como una mayor exactitud en la predicción de errores estándar y de valores de las variables simuladas. A este respecto, para Mw se utilizó la transformación empirical, así como también se seleccionó el semivariograma tipo exponential detrented, para obtener un semivariograma más adecuado a partir de cómo se distribuyen las cruces azules. Para la búsqueda de vecinos cercanos (Nearest Neighbor), se seleccionó la opción estándar circular con un máximo y un mínimo de vecinos cercanos de 15 y 10, respectivamente. En el caso de la PGA, la transformación que se aplicó es log empirical y el semivariograma adoptado el exponential. La transformación log empirical aplica logaritmos a los resultados de la transformación empirical. Esta combina el concepto
62
de Kernel para ajustar los datos a una transformación normal, asegurando la transformación logarítmica que todas las predicciones sean mayores que cero. Con los ajustes antedichos, se obtiene un semivariograma que muestra las cruces azules lo más circunscritas a las líneas del mismo color para Mw y PGA.
3.4.2 El procesamiento de Interferometría
A partir de dos imágenes satelitales, una anterior y otra posterior al 16 abril de 2016 (terremoto de Pedernales), se aplicó el análisis de interferometría con procedimientos desarrollados por la ESA para la plataforma de aplicación Sentinel (SNAP, Sentinel Aplicattion Plataform).
Se identificaron dos imágenes de Sentinel-1A obtenidas con SAR en modo de franja Interferometrica ancha (IW), en un complejo de mirada única (SLC). Cada imagen tiene un ancho de 250 Km con una resolución espacial de 5 por 20 metros, divididas en tres subzonas IW obtenidas mediante radares de escaneo progresivo (TOPSAR, Progresive Scans SAR). El número de ráfagas en cada franja IW es de diez, numeradas de cero a nueve. Las fechas de las imágenes satelitales obtenidas, fueron el 24 de marzo y el 17 de abril de 2016, en órbita ascendente.
Los procedimientos aplicados con la plataforma SNAP facilitaron procesar las dos imágenes simultáneamente. Las etapas sincrónicas del procesamiento incluyeron: aplicación de órbita, geocodificación, asignación de azimut, para obtener la fase de interferometría y la máscara de coherencia, así como también el DEM. Luego, la aplicación del filtro Goldstein permitió eliminar la aparente escisión entre subzonas. La fase del interferograma fue desenrollada para obtener la imagen final georreferenciada, que puede ser exportada como ráster o como archivo KMZ, a ser utilizados en etapas siguientes.
ESA ha desarrollado algunos manuales, de entre los cuales fue particularmente útil consultar a Ferreti et al. (2007) y a Braun y Veci (2021). Existen extensos tutoriales relacionados en la Web, de entre los cuales fue muy relevante estudiar aquel de Sharma (2020; https://youtu.be/YDkRRvy5RZw).
Para la descarga de imágenes satelitales, se alternó entre las plataformas de búsqueda
Copernicus (https://scihub.copernicus.eu/dhus/) y aquella de Alaska Satellite Facility (ASF
63
Data Search (alaska.edu)). Copernicus facilitó el identificador de la imagen, pero las imágenes antiguas suelen no estar disponibles. Con el identificador obtenido en Copernicus, la búsqueda en ASF se facilitó. De esta manera fueron descargadas las imágenes de Sentinel-1A en órbita ascendente de mirada única (SLC) para interferometría (IW), de fechas 24 de marzo y 17 de abril de 2016. En el proceso destacado por Braun y Veci (2021), se abren las imágenes en el explorador y se identifica la región de interés, a fin de seleccionar luego una de las subzonas IWn (subswaths), donde n refiere a una de las tres subzonas (1, 2 y 3, de izquierda a derecha) y las ráfagas (burst, diez numeradas de 0 a 9). Los productos son co registrados (S1 TOPS Coregistration) 13 y a ellos se aplica simultáneamente la información de la órbita (Apply Orbit File) 14. A continuación, se seleccionan aquellas ráfagas de interés de las imágenes (S1 TOPS Split) 15 Cuando se selecciona más de una ráfaga, es recomendable mejorar la calidad del co-registro mediante el operador de diversidad espectral mejorada (S-1 Enhanced Spectral Diversity (ESD)), pues aplica correcciones de desplazamientos de rango y de azimuth a la imagen secundaria (aquella de fecha posterior).
La formación del interferograma y la estimación de la coherencia, procede con los operadores Interferogram Formation 16 y Coherence Estimation 17 . El primer operador relaciona con un DEM, siendo usual escoger entre las opciones SRTM 1SecHGT y SRTM
3SecHGT: el primero ofrece una resolución espacial de 30 m, el segundo de 90 m. Para el desarrollo de esta etapa se escogió SRTM 1SecHGT. Se puede seleccionar que se sustraigan la fase de tierra plana (substract flat-earth phase), la fase topográfica (substract topographic phase) e incluir la estimación de la coherencia (coherence estimation). Se obtienen el interferograma y la coherencia como bandas separadas, cada una de las cuales visibiliza líneas de separación aparente entre las ráfagas. Estas líneas de separación se remueven con el operador S-1 TOPS Deburst 18
Por definición, el interferograma contiene las variaciones provenientes del desplazamiento, la atmósfera y el ruido. Este conjunto de factores se muestra con la
13 Secuencia de comandos: Radar, Coregistration, S1 TOPS Coregistration, S-1 TOPS Coregistration with ESD
14 Secuencia de comandos: Radar, Apply Orbit File
15 Secuencia de comandos: Radar, Sentinel-1 TOPS, S-1 TOPS Split
16 Secuencia de comandos: Radar, Interferometric, Products, Interferometric Formation
17 Secuencia de comandos: Radar, Interferometric, Products, Coherence Estimation
18 Secuencia de comandos: Radar, Sentinel-1 TOPS, S-1 TOPS Deburst
64
apariencia de arco iris, en ciclos de colores arbitrarios que varían de -π a +π 19 . Este patrón de flecos (fringes) representa un ciclo de 2π Cada ciclo representa la mitad de λ (longitud de onda del sensor), por lo que el movimiento relativo del suelo se establece contando las franjas y multiplicando su número por λ/2.
La coherencia puede ser usada para medir la deformación o la topografía, esta última sin remover la fase topográfica. Áreas urbanas, deforestadas o de cultivos presentan altos valores de coherencia (superior a 0,6), mientras que áreas oscuras y forestales con vegetación densa ostentan bajos valores de coherencia (inferior a 0,3). Puesto que la longitud de onda de la banda C de los datos SAR de Sentinel-1 es alrededor de 6 cm, áreas con vegetación densa representan casos de aplicación poco exitosa de interferometría. Los valores de coherencia son útiles para identificar zonas en las que es preciso verificaciones en el terreno o la entrada de datos de fuentes confiables. El plugin Snaphu (Standford University, 2021) debe ser instalado previamente para el desenrollado de la fase del interferograma. Esto se consigue con el operador Unwrapping y sigue tres pasos sucesivos de este submenú: Export, exporta la fase envuelta al Snapu; Unwrapping, Snapu desenrolla la fase; Import, importa la fase desenrollada al SNAP y añade los metadatos de la fase envuelta. La fase desenrollada no tiene una medida métrica, por lo que hay que convertir las unidades de radián a desplazamientos absolutos. Esto se logra con el operador Phase to Displacement 20, que traduce la fase en cambios de superficie a lo largo de la línea de vista (line-of-sight) en unidades métricas. Los valores positivos representan levantamientos y aquellos negativos subsidencias o hundimientos de la superficie, teniendo como referencia la imagen de fecha más temprana.
Finalmente, el operador Terrain Correction 21 geocodificará la imagen corrigiendo las distorsiones geométricas del SAR utilizando un DEM, para producir un mapa proyectado que también puede ser exportado a Google Earth como un archivo KMZ.
19 Letra Phi minúscula, alfabeto griego, con referencia al número Pi (3,14159…)
20 Secuencia de comandos: Radar, Interferometric, Products, Phase to Displacement
21 Secuencia de comandos: Radar, Geometric, Range-Doopler Terrain Correction
65
3.4.4 Adaptación del método de Newmark (1965)
Para los propósitos de un análisis regional, en esta tesis se utilizará el modelo relativamente simple de equilibrio límite referido por Chowdhury et al. (2009), aplicado a una pendiente infinita en un material que tenga resistencia cohesiva y friccional. La aplicación del método de Newmark (1965), de acuerdo con los lineamientos de Jibson et al. (1998), tiene como limitación no contar con las características geomecánicas de los suelos en la región del cantón. Para probar si la metodología es viable, se adoptaron propiedades homogéneas para los suelos.
La adaptación del método se fundamenta en el cálculo del factor de seguridad, que involucra a características de los suelos (ángulo de fricción interna ���� , cohesión c’, peso específico ���� ) y al ángulo ɑ del talud (pendiente). La ecuación 2.7.3 muestra los parámetros referidos de acuerdo con Jibson et al. (1998):
En la ecuación anterior, además de los parámetros cuya simbología se ha explicado, γw es el peso unitario del agua, t es el espesor del bloque de falla en el sentido normal a la pendiente, y m es la proporción del espesor del bloque que está saturado (con influencia del agua).
La metodología propuesta por Jibson et al. (1998) recomienda no considerar el tercer término del segundo miembro de la ecuación (presión de poros). Los investigadores dispusieron de un amplio set de datos, entre ellos acelerogramas de sismos, geología detallada de la zona, información geotécnica relacionada con valores de cohesión, pesos específicos y ángulos de fricción interna de suelos, modelos de elevación digital de alta resolución (10 m).
Estas condiciones no son alcanzables en Ecuador, por lo que en la presente tesis se propone una adaptación respecto al método desarrollado por Jibson et al (1998). Esta adaptación consiste en adoptar un valor único (a manera de promedio regional) para el conjunto de términos c’/(γ*t). Por las razones destacadas, se asumió como valores de las variables antes
66
�������� = ����′ ��������������������ɑ + �������������������� ����������������ɑ ������������ �������������������� ��������������������ɑ
citadas: 5.000 Kg/m2 para la cohesión (c’), 1.700 Kg/m3 para el peso específico de suelos (���� ) y 2,4 metros para el espesor del bloque deslizante (t). Para el ángulo de fricción interna de los suelos se adoptó 28o El ángulo de las laderas en el terreno está determinado por el ráster de pendientes (en grados sexagesimales). Los valores asumidos se resumen en obtener un valor único “promedio regional” para el cociente c’/(γt), como se visualiza en los siguientes cálculos tabulados que definen el procedimiento a seguir con la calculadora ráster presentados en la tabla 7.
En el ejemplo, la intersección entre los valores de cohesión de 3500 Kg/m2 y de peso específico 1600 Kg/m3, arroja un promedio regional de 0,9115. Para propósitos de esta tesis, se asumió suelos franco-arcillo-arenosos, con un peso específico de 1700 Kg/m3. Es decir, el valor del cociente c’/(γt) es de 1,2255 considerando el valor de c’ de 5000 Kg/m2
Mediante álgebra de mapas y calculadora ráster se puede obtener la aceleración crítica de sismos conforme a la ecuación 2.7.2. En esta se reemplaza el FS propuesto por Jibson et al. (1998), prescindiendo del término correspondiente a la presión de poros provocada por la presencia de agua que contribuiría a disminuir su valor:
67
c'/γt Cohesión Kg/m2 2000 2500 3000 3500 4000 4500 5000 Peso específico Kg/m 3 1200 0,6944 0,8681 1,0417 1,2153 1,3889 1,5625 1,7361 1300 0,6410 0,8013 0,9615 1,1218 1,2821 1,4423 1,6026 1400 0,5952 0,7440 0,8929 1,0417 1,1905 1,3393 1,4881 1500 0,5556 0,6944 0,8333 0,9722 1,1111 1,2500 1,3889 1600 0,5208 0,6510 0,7813 0,9115 1,0417 1,1719 1,3021 1700 0,4902 0,6127 0,7353 0,8578 0,9804 1,1029 1,2255 1800 0,4630 0,5787 0,6944 0,8102 0,9259 1,0417 1,1574 1900 0,4386 0,5482 0,6579 0,7675 0,8772 0,9868 1,0965 t 2,4 m
Tabla 7 Determinación del valor adimensional c'/(γt)
�������� = (�������� 1)����������������ɑ �������� ���� = � ����′ ��������������������ɑ + �������������������� ����������������ɑ 1� ������������ɑ
El proceso de cálculo se simuló en Excel y puede adaptarse a la calculadora ráster. En la Tabla 8 se comparan resultados para suelos de baja, mediana y alta cohesión, variando sus pesos específicos y el ángulo de fricción de los suelos en la misma relación:
Como se aprecia, un suelo de baja cohesión (c') y peso específico (γ) presentaría una relación ac/g comparable a la de otro de cohesión y peso específico ligeramente mayores: el ángulo del talud (α) ha aumentado de 30 a 45, el ángulo de fricción de los suelos (φ) ha variado de 22 a 28. Un suelo de c' y γ mayores numéricamente que los anteriores, precisaría que φ sea próximo a 33 y que α aumente de 45 a 75, para que la relación ac/g supere en menos del 10% de variación porcentual (Δ%) a aquella correspondiente al suelo de características medias considerado como referencia.
Con las simplificaciones referidas, los rásteres permitirían visualizar como variarían los valores de aceleración sísmica (ac) y de la relación adimensional ac/g (como fracción de g).
Al ser comparado este ráster con aquel resultante de la zonificación sísmica a partir de fallas capaces, se obtendrían los umbrales a ser superados para contribuir a la incidencia de deslizamientos.
Estas capas y aquella de pendientes obtenida del DEM resultado del análisis de interferometría son objeto de operaciones con álgebra de mapas y calculadora ráster, para identificar las zonas en la región susceptibles a efectos cosísmicos y sísmicos. En este caso, dichos efectos hacen referencia a los efectos cosísmicos del terremoto de Pedernales del 16 de abril de 2016.
68
Parámetro Bajo Medio Alto Unidad Cohesión 3000 3500 5000 Kg/m2 Peso Espec. 1200 1500 1700 Kg/m3 c'/(γt) 1,0417 0,9722 1,2255 φ 22 28 33 ° tanφ 0,4040 0,5317 0,6494 α 30 45 75 ° senα 0,5000 0,7071 0,9659 tangα 0,5774 1,0000 3,7321 FS Newmark 1,74 1,50 1,40 ac/g 0,37 0,36 0,39 Δ% 4,0% 0,0% 8,3% %
Tabla 8 Comparación de parámetros resultantes de la aplicación del método de Newmark (1965).
Aunque la mayoría de software SIG clasifican pendientes (tα) 22 de manera predeterminada, la subdivisión propuesta por Sheng (2010) caracteriza siete clases o categorías y un código de colores, tal como se muestra en la tabla 9.
Tabla 9 Clasificación de pendientes (tα) de terreno. Clase Grados Porcentaje % Color
1 tα < 7 tα<12,3% Amarillo
2 7 ≤ tα <15 12,3% ≤ tα < 26,8% Morado
3 15 ≤ tα <20 26,9% ≤ tα < 36,4% Verde
4 20 ≤ tα < 25 36,4% ≤ tα < 46,6% Marrón
5 25 ≤ tα < 30 46,6% ≤ tα < 57,7% Azul
6 30 ≤ tα < 40 57,7% ≤ tα < 83,9% Rojo
7 tα ≥ 40 tα ≥ 83,9% Naranja
Simbología:
< Menor que, no incluye al valor superior de intervalo, equivale a paréntesis abierto derecho ).
≤ Menor o igual que, sí incluye al valor izquierdo de intervalo, equivale a corchete izquierdo [, constituye un paréntesis cerrado.
≥ Mayor o igual que, sí incluye al valor inferior de intervalo (usualmente, el único) Intervalo: expresión matemática definida por paréntesis abiertos (), cerrados [] o una combinación de ambos
22 Como referencia a tangα de la ecuación del factor de seguridad propuesto por Jibson et al. (1998). Ver ecuación 2.1.3.6.
69
4. RESULTADOS Y DISCUSIÓN
4.1 INTERPOLACIÓN ESPACIAL CON KRIGING EMPÍRICO BAYESIANO (EBK)
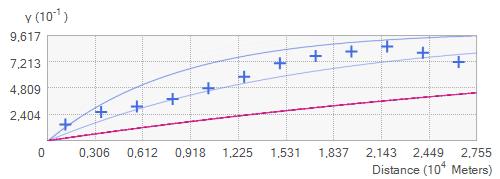
A partir de la interpolación con el método EBK, el semivariograma obtenido para Mw se muestra en la Ilustración 10. Se aprecia las cruces azules se distribuyen en torno a las líneas del mismo color. Así también, la Ilustración 11 hace una comparación entre los valores calculados y aquellos resultantes de la predicción.
Ilustración 11 Interpolación espacial EBK para Mw. Comparación entre valores calculados y predichos.
A continuación, se muestran las superficies ráster para predicción de las magnitudes sísmicas probables de Mw (Ilustración 12) y para error estándar ( Ilustración 13)
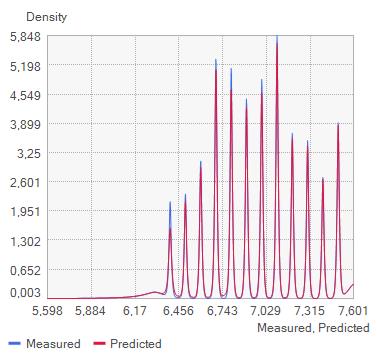
70
Ilustración 10 Momento sísmico (Mw). Semivariograma obtenido con interpolación EBK.
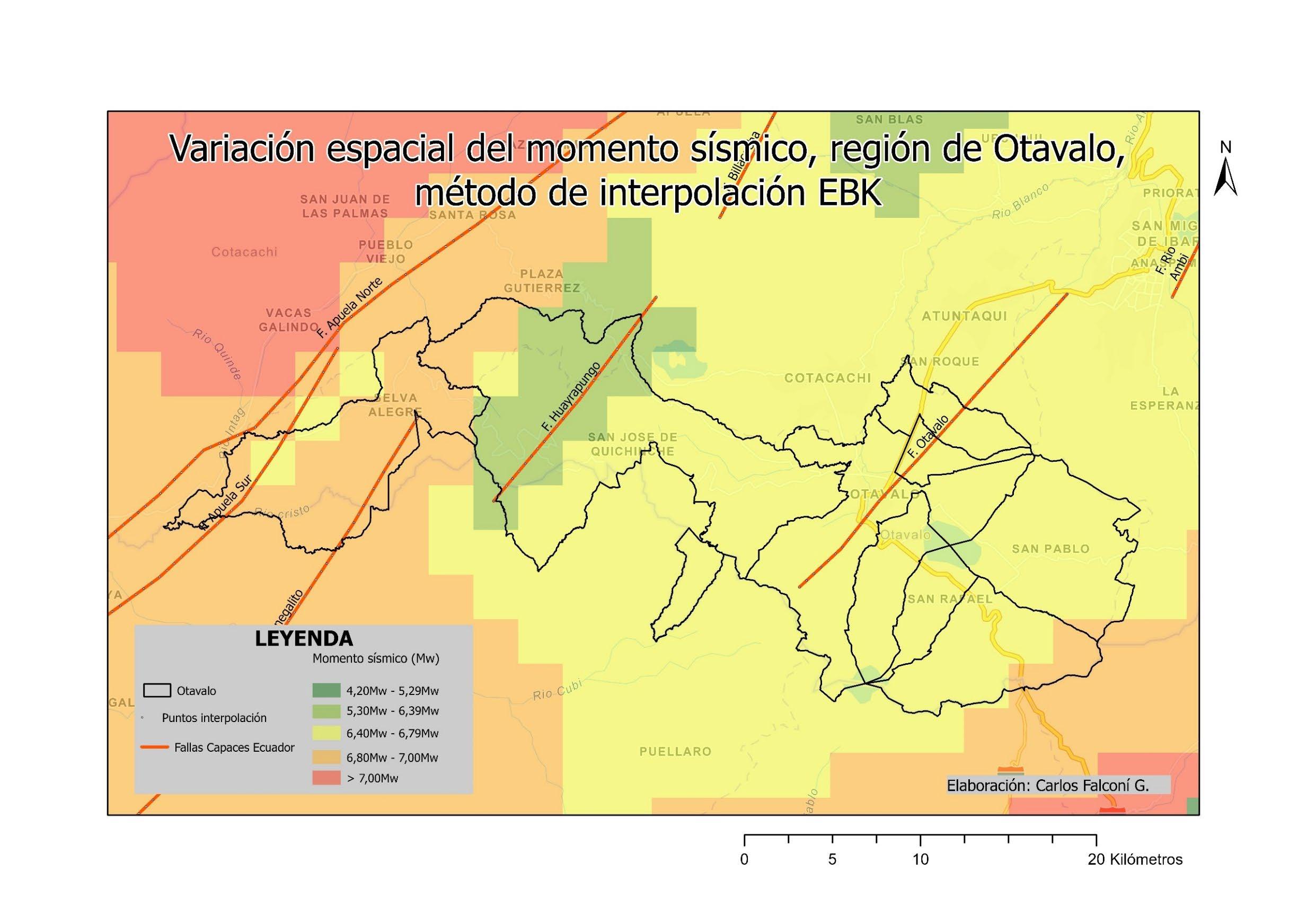
71
Ilustración 12 Momento sísmico, región de Otavalo.
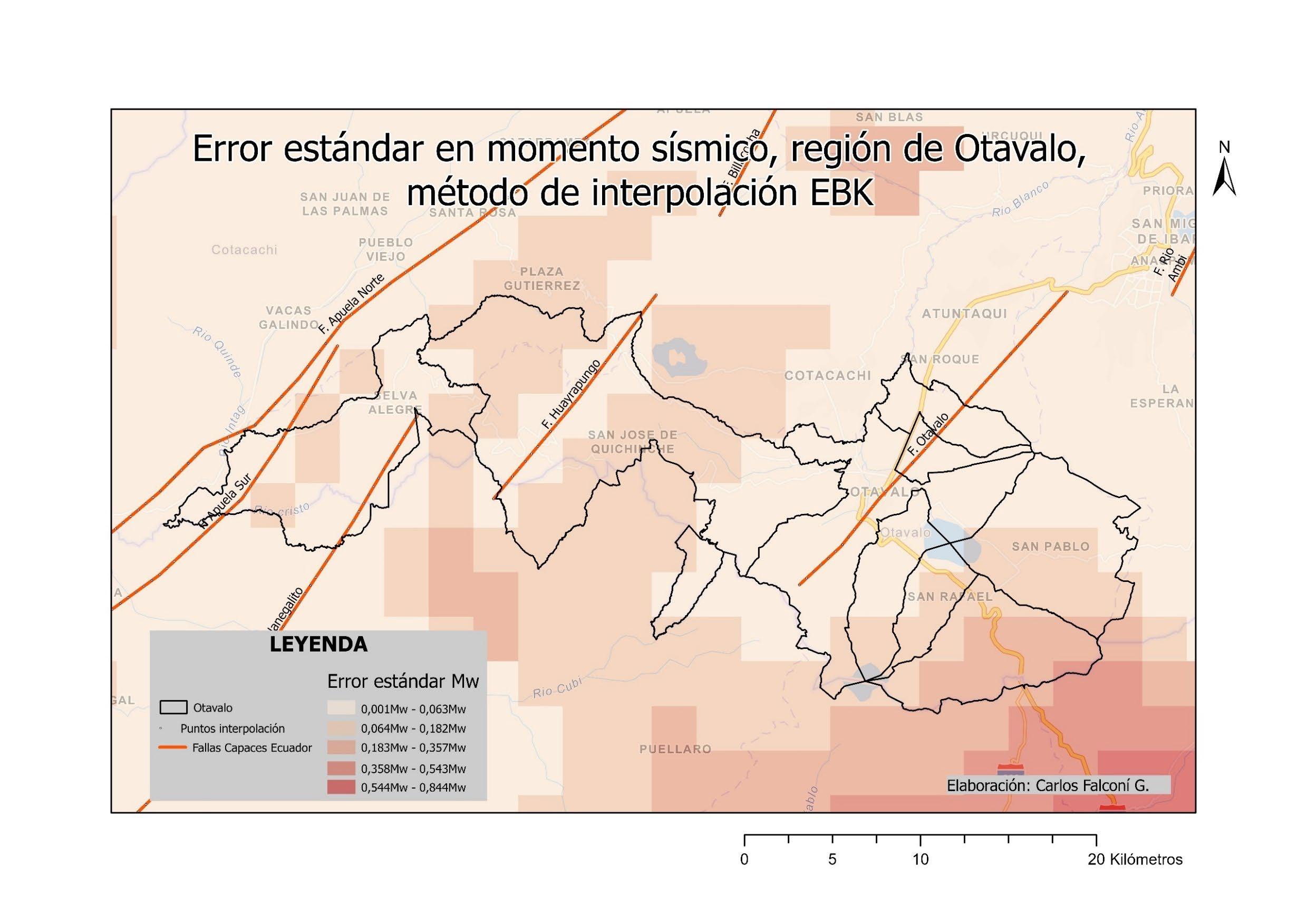
72
Ilustración 13 Error estándar en momento sísmico.
En la región de Otavalo existen fallas geológicas capaces como la Otavalo y la Apuela Sur, con magnitudes potenciales que varían entre 6,6 y 6,8 Mw. Las fallas Nanegalito y Apuela Norte podrían detonar sismos de 7 Mw. Y otras fallas cercanas como la Ambi y El Ángel, podrían presentar sismos con magnitudes próximas a 6,7 Mw. Las fallas Huayrapungo y Billacocha, que se alinean aproximadamente en un eje NNE, presentarían magnitudes de momento sísmico entre 6,4 y 6,5 Mw. Al norte de la región destaca la falla C-03 con magnitudes posibles de 6,9 Mw y, al noroccidente, las fallas Yanayaca y Canandé con un rango entre 6,9 y 7,3 Mw. Al oriente de la región los complejos de fallas Chingual, Reventador y Cascales tiene magnitudes similares a las de la región local de Otavalo antes explicadas.
Para el error estándar de la aceleración sísmica, se aplicaron los mismos parámetros de transformación log empirical y semivariograma exponential, con los mismos resultados de la correlación cruzada para el valor medio y el error estándar. La Ilustración 15 corresponde al semivariograma obtenido para PGA, y la Ilustración 16 a la distribución comparativa de valores calculados y predichos:
Ilustración 15 Aceleración sísmica. Semivariograma obtenido con interpolación EBK.
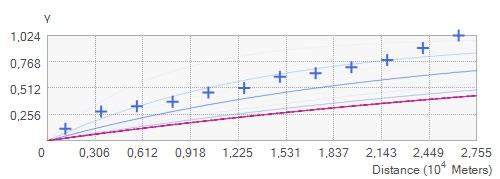
73
Ilustración 16 Aceleración sísmica. Comparación entre valores calculados y predichos obtenidos con interpolación EBK.
En cuanto a la PGA, el conjunto de las fallas Apuela podría inducir sismos con magnitudes de PGA entre 0,36g - 0,41g, las fallas El Ángel, Ambi y Otavalo entre 0,30g - 0,34g. Las fallas Billacocha, Huayrapungo y Nanegalito, a su vez podrían provocar aceleraciones en roca entre 0,21g- 0,28g. El ramal C-03 al norte, es una falla capaz inductora de aceleraciones del orden de 0,44g, ligeramente inferior a la que podría provocar la Canandé que es de 0,45g. Yanayaca al noroccidente y los complejos de fallas Reventador – Cayambe, Cofanes y Chingual al oriente, serían fallas inductoras de sismos con valores de PGA que varían en un orden de magnitud entre 0,36g - 0,39g.
La Ilustración 17 y la Ilustración 18 representan a las superficies rásteres para aceleración sísmica y su error estándar vinculado.
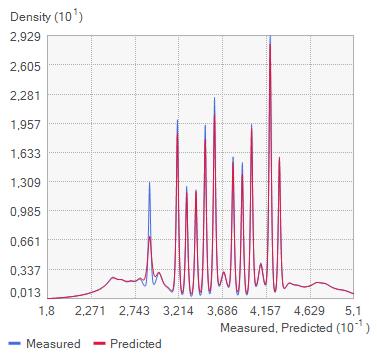
74
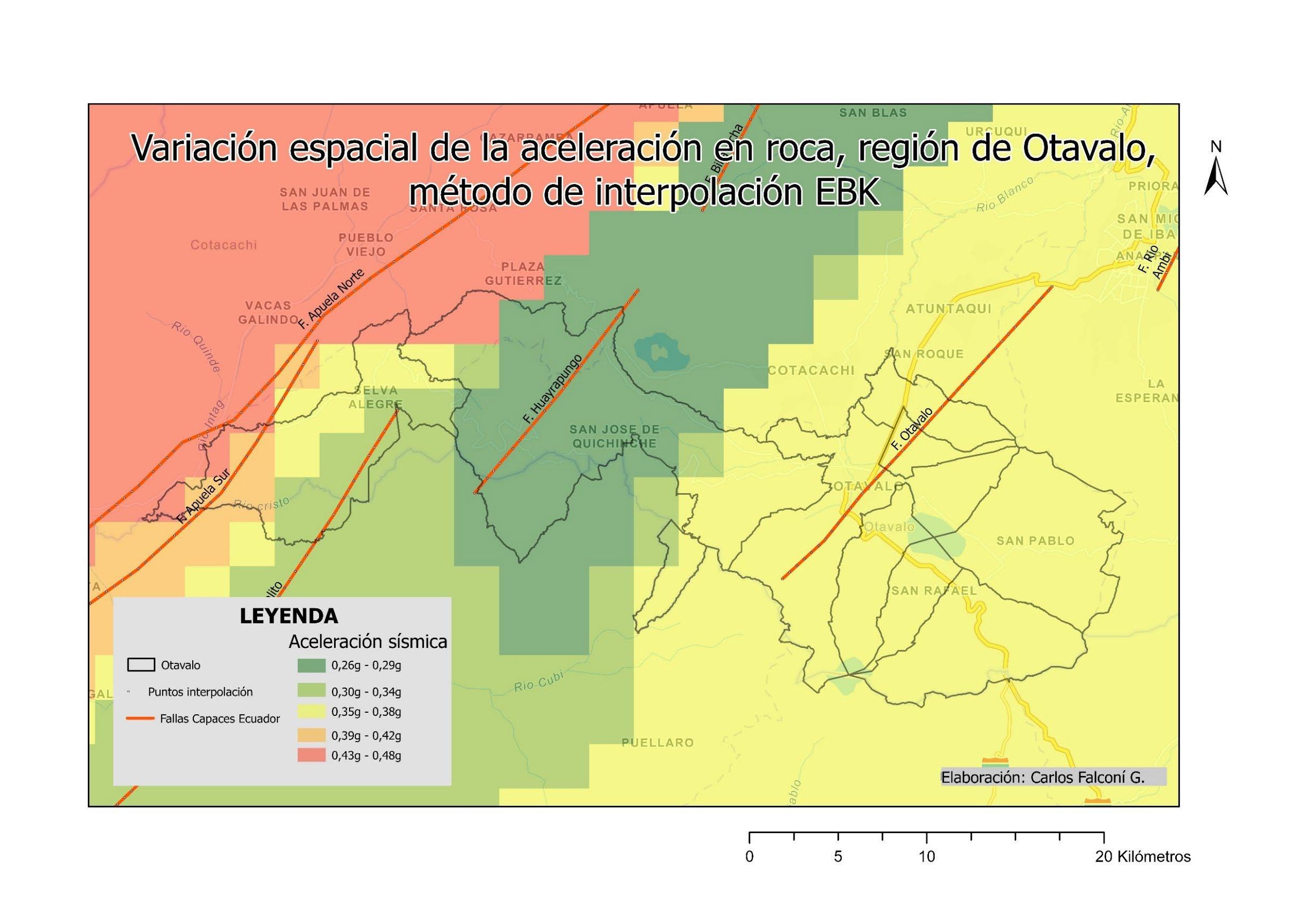
75
Ilustración 17 Aceleración en roca, región de Otavalo.
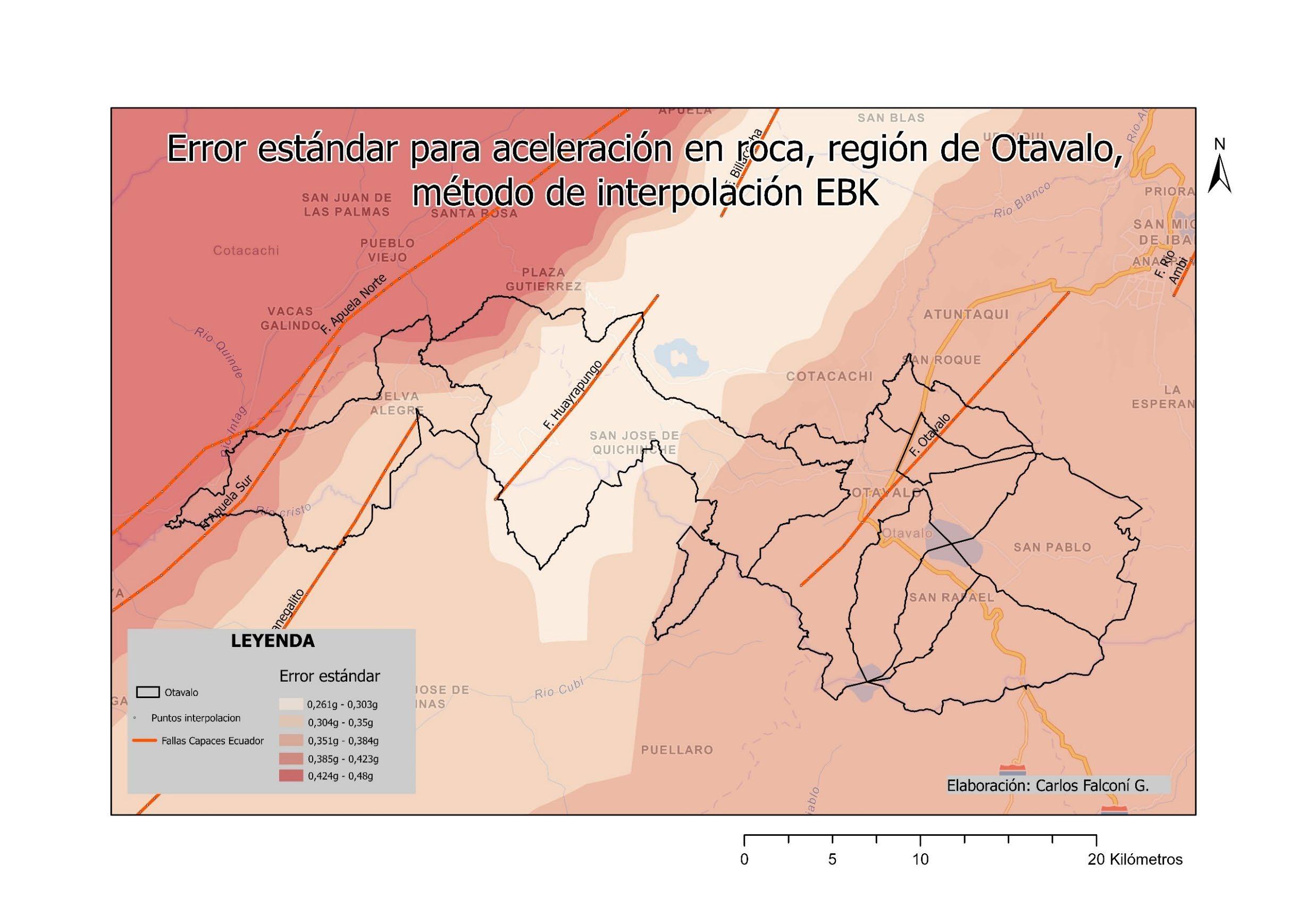
76
Ilustración 18 Error estándar en aceleración en roca.
Los valores medios obtenidos de la interpolación espacial, así como la magnitud del error estándar, son:
• Para Mw: valor medio 0,0002; error estándar promedio de 0,0308.
• Para PGA: valor medio inferior a 0,0001; error estándar promedio de 0,0047.
Los semivariogramas y la comparación de distribuciones entre valores calculados y predichos, son idénticos para el valor medio y el error estándar promedio, tanto para Mw como PGA
4.2 RESULTADOS DEL ANÁLISIS DE INTERFEROMETRÍA
El procesamiento de interferometría con el software SNAP de la ESA permitió obtener un DEM a partir del cual se obtuvo el mapa de pendientes (Ilustración 19). Este mapa responde al criterio metodológico propuesto por Sheng (2010) y que se resume en la Tabla 9 del numeral 3.3.3.
También se generaron imágenes como archivos KMZ para los valores del desplazamiento observado (Ilustración 20), la elevación del terreno (Ilustración 21) y la coherencia en las medidas (Ilustración 22). Esto se hizo a partir del procesamiento de las ráfagas seleccionadas en la subzona de interés en las imágenes de Sentinel-1 para banda ancha interferométrica (IW), complejo de vista simple (SLC) y polarización Vertical-Vertical (VV) En todos los casos, se mantuvo la banda cromática que arrojó el SNAP en el proceso. Al escoger otras paletas de colores, se alteran los valores de mínimos y máximos de las mediciones derivadas a partir de las observaciones satelitales.
77
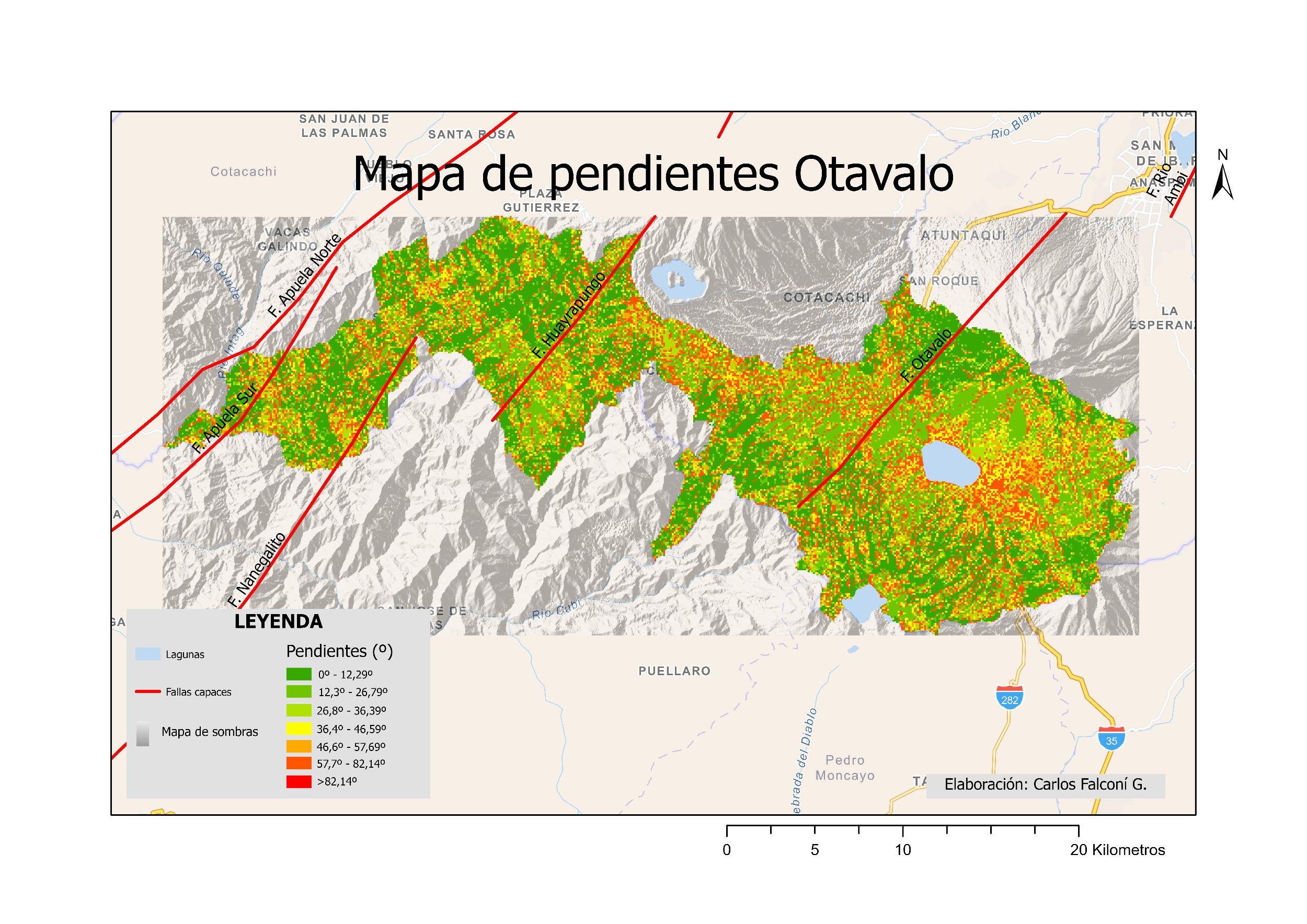
78
Ilustración 19 Mapa de pendientes, a partir del DEM obtenido por interferometría..
Ilustración 20 Interferometría, desplazamientos en el terreno entre el 24 de marzo y el 17 de abril de 2016.
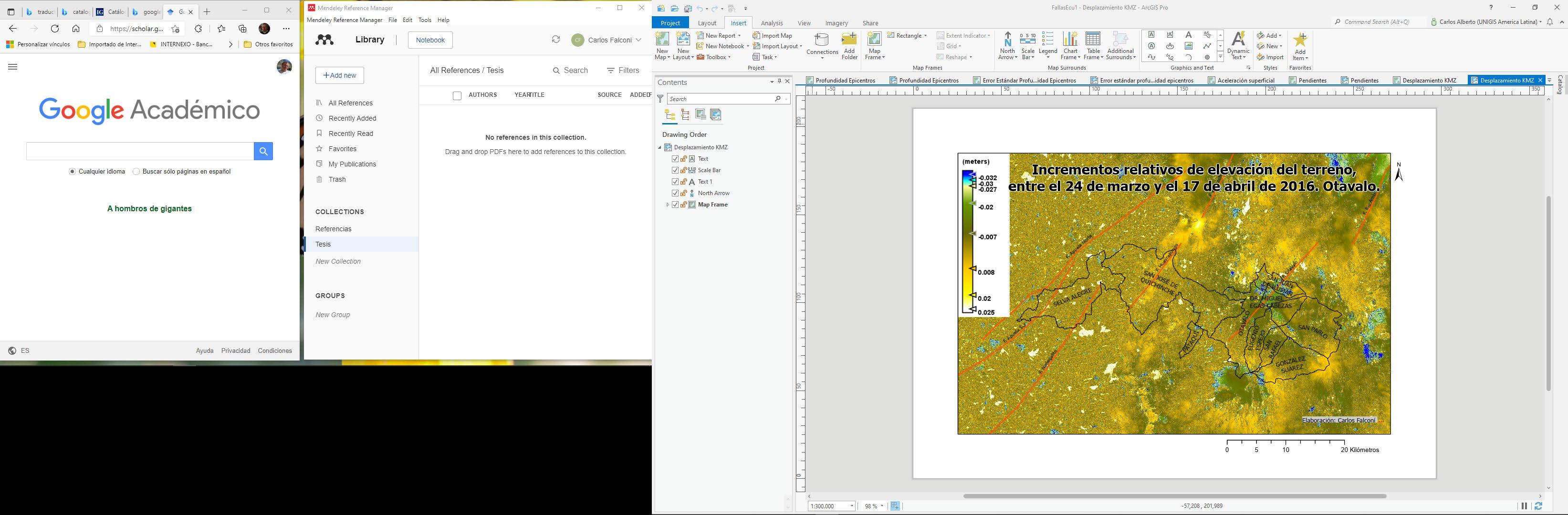
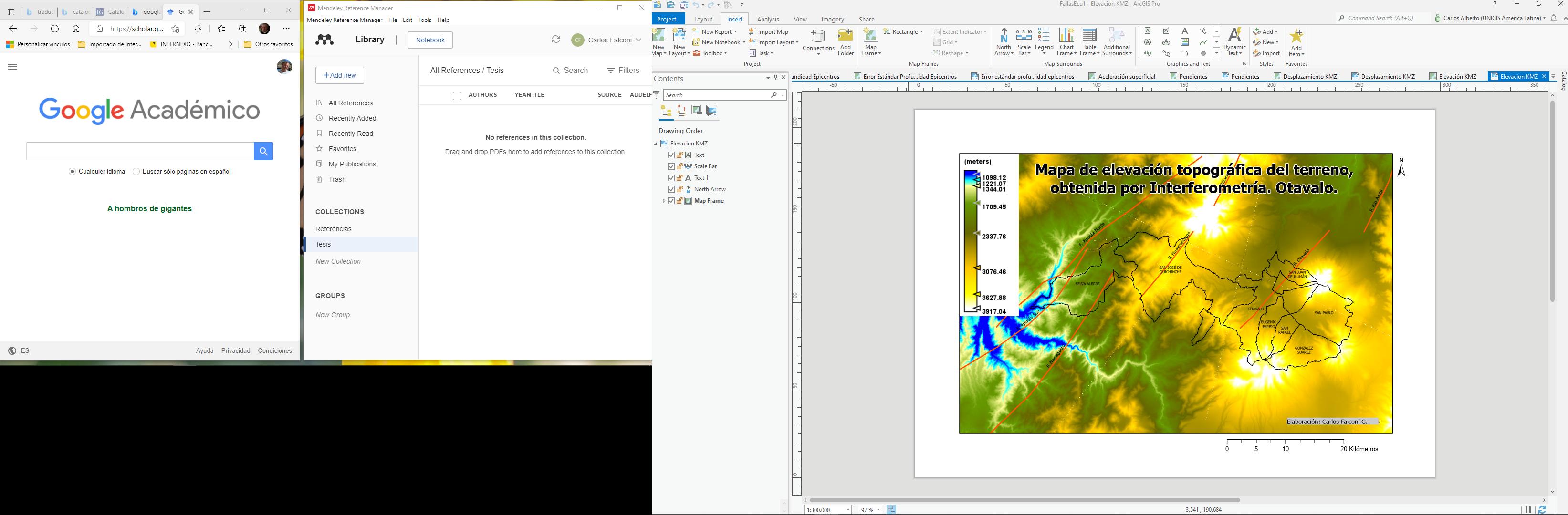 Ilustración 21 Interferometría, mapa de elevación.
Ilustración 21 Interferometría, mapa de elevación.
Ilustración 22 Interferometría, mapa de coherencia.
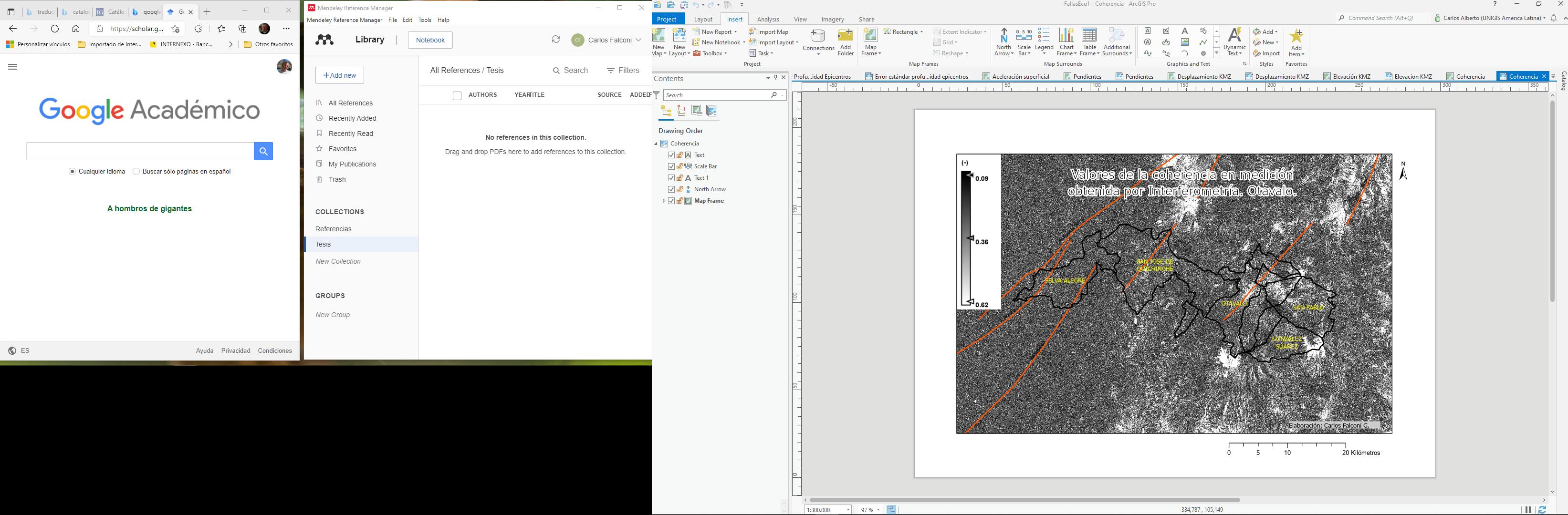
Las imágenes satelitales S-1A del 24 de marzo y 17 de abril de 2016 (productos SLC, IW), fueron escogidas por su proximidad con el evento sísmico del 16 de abril del mismo año, el terremoto de Pedernales en Manabí. La presunción fue poder registrar subsidencias en el terreno a consecuencia del sismo.
Aprovechando los puntos para interpolación espacial que se generaron sobre cada una de las fallas, en aquellas que gravitan directamente sobre Otavalo se hizo un muestreo sistemático de valores. Se extrajo información de los desplazamientos, la coherencia de su medida y la altura topográfica registrada. La Tabla 10 resume por fallas capaces los valores de desplazamiento y coherencia, establecidos luego del procesamiento con SNAP y del muestreo de puntos mediante ArcGIS Pro:
Tabla 10 Información de los desplazamientos observados sobre fallas geológicas capaces de Otavalo
Con excepción de la falla Apuela norte (externa a la jurisdicción de Otavalo), las restantes fallas presentan registros de desplazamientos negativos (hundimientos) en mayor magnitud que los desplazamientos positivos. Esto se registra particularmente en las fallas
82
Rangos de coherencia Falla capaz 0,1-0,35 Apuela norte Apuela Sur Huayrapungo Nanegalito Otavalo Nro. de Puntos 5 17 16 17 Mín. dsp (m) -0,034 -0,007 -0,024 -0,036 Promedio de dsp (m) 0,004 0,001 0,001 -0,010 Máx. dsp (m) 0,034 0,009 0,022 0,003 Desvest de dsp 0,029 0,004 0,009 0,011 0,35-0,6 Apuela norte Apuela Sur Huayrapungo Nanegalito Otavalo Nro. de Puntos 1 6 9 2 2 Mín. dsp (m) 0,021 -0,005 -0,005 -0,009 -0,02 Promedio de dsp (m) 0,021 0,008 0,005 -0,005 -0,015 Máx. dsp (m) 0,021 0,030 0,012 0 -0,009 Desvest de dsp 0,016 0,006 0,006 0,008 0,6-0,85 Apuela norte Apuela Sur Huayrapungo Nanegalito Otavalo Nro. de Puntos 1 6 Mín. dsp (m) -0,01 -0,017 Promedio de dsp (m) -0,01 -0,011 Máx. dsp (m) -0,01 -0,008 Desvest de dsp 0,003 dsp Desplazamiento Min Mínimo Máx Máximo
Apuela sur, Nanegalito y Otavalo para valores de coherencia entre 0,10 – 0,35. Para el rango de coherencia entre 0,60 y 0,85, la falla Otavalo presenta en valor absoluto el mayor hundimiento con respecto a otras. Esto hace intuir que es una de las fallas más peligrosas de la región junto con las Apuela norte y sur. De la Apuela norte sólo se tomó un punto como referencia.
Para facilitar la interpretación de la Ilustración 20 y de la Ilustración 22, se extrajeron puntos de muestreo sistemáticos a partir del ráster generado por interferometría, que integró las variables de desplazamiento, coherencia, altitud. El número de puntos con los que se extrajo información del ráster en mención fue de 200. El análisis estadístico simple efectuado con ArcGIS Pro se resume en la Tabla 11:
Como se aprecia, para los valores de coherencia más altos ubicados en los cuartiles tercero y cuarto (3Q, 4Q), el máximo levantamiento de terreno observado fue de 11 mm y corresponde a una ubicación cercana a la laguna de Mojanda, en las montañas de la parroquia San Rafael (-78°16’; +0°09’09’’). Para valores de coherencia del segundo cuartil (2Q), el máximo levantamiento observado fue de 25 mm, registrado en las elevaciones de la parroquia Quichinche (-78°19’; +0°13’22’’). Se puede apreciar que los valores de
83
Levantamientos (mm) Coh> 0,50 (3Q y 4Q) 0,25 < Coh < 0,50 (2Q) Coh < 0,25 (1Q) Nº Puntos 5 41 38 Promedio 5,4 5,1 5,6 Desv. Estándar 3,8 5,1 6,4 Mínimo ≈ 1 ≈ 0 ≈ 0 Máximo 10,6 25 25 Hundimientos (mm) Coh> 0,50 (3 y 4 Q) 0,25 < Coh < 0,50 (2Q) Coh < 0,25 (1Q) Nº Puntos 14 65 39 Promedio -6,3 -8,5 -7,6 Desv. Estándar 5,7 8,9 7,7 Mínimo ≈ -1 -45,5 -26,6 Máximo ≈ -0 ≈ -0 ≈ -0 Coh Coherencia
Tabla 11 Resumen de estadísticas de desplazamientos de terreno.
desplazamiento positivos tienen un alto coeficiente de variación para los cuartiles referidos de los valores de coherencia: existe mucha dispersión en los valores. En el caso de los desplazamientos negativos, estos tienen una dispersión excesiva. Los valores de coherencia corresponden a los cuartiles primero (1Q) y segundo (2Q). Los máximos hundimientos se registraron en la parroquia Selva Alegre, entre las fallas Apuela sur y Nanegalito (-78°33’02’’; +0°12’52’’) para 2Q, y en la parroquia Pataquí (-78°21’; +0°12’21’’) para 1Q.
El archivo vector obtenido se procesó gráficamente con ArcGIS Pro, obteniendo la Ilustración 23 que clasifica los valores interpolados a partir del ráster de interferometría para las variables desplazamiento y coherencia de las mediciones satelitales.
84
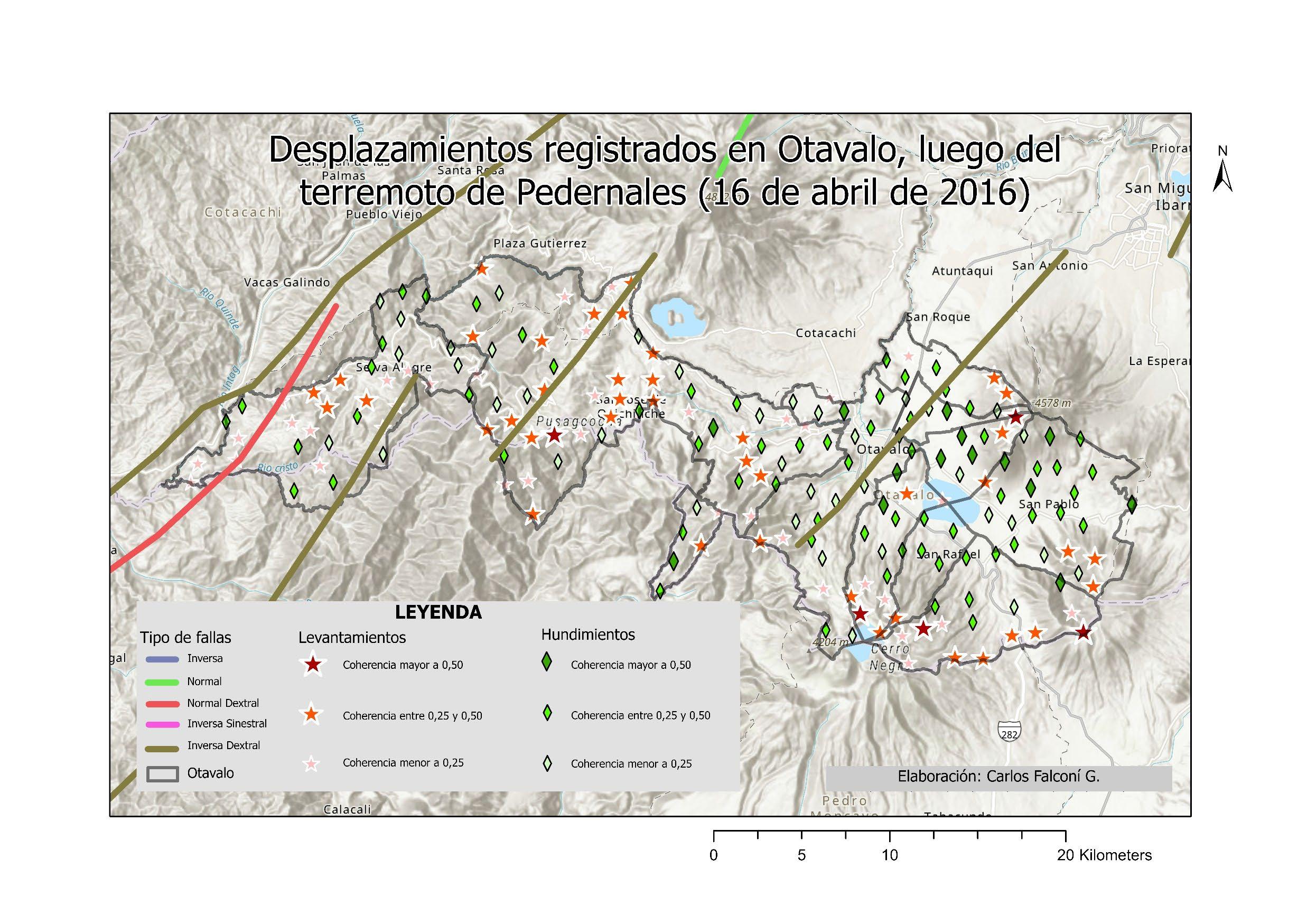
85
Ilustración 23 Desplazamientos medidos tras el terremoto de 16 de abril de 2016, Otavalo.
4.3 ADAPTACIÓN DEL MÉTODO DE NEWMARK (1965)
En la adaptación del método de Newmark (1965), conforme a la aproximación de Jibson et al. (1998), surgieron situaciones imprevistas que motivaron:
• Replicar la interpolación espacial sólo para las fallas y puntos distribuidos sobre éstas en la región de Otavalo,
• Efectuar procesos de generalización de los rásteres de PGA y del DEM,
• Extraer valores a partir de celdas ráster de pendientes y PGA, mediante una capa vectorial de puntos distribuida regularmente cada 100 m dentro de los límites del shapefile de Otavalo
En la Ilustración 24, se muestra el mapa de puntos con la distribución de valores de aceleración crítica, en la cuenca de la laguna de San Pablo por ser la región oriental del cantón Otavalo la más densamente poblada.
La Ilustración 25 visibiliza la variación espacial de los valores de la relación entre PGA/ac. A diferencia de la ilustración anterior, esta última se ha concentrado en el sector occidental del cantón que corresponde a zonas con más cobertura vegetal. El mapa muestra “lagunas” de pixeles sin información, esto a causa de las limitaciones que las técnicas de inSAR tienen particularmente en regiones no deforestadas o con vegetación más densa
Para reclasificar el ráster de pendientes inicialmente definidas en la Ilustración 19, se superpuso mediante selección por atributos las inclinaciones de taludes propuestas por Sheng (2010) con los rangos de ac 0,30g -0,50g, 0,51g – 0,75g, 0,76g – 1,00g, mayor que 1,00g. Estos valores fueron obtenidos del muestreo de valores ráster de ángulos de taludes, el cálculo subsiguiente de ac y su comparación con la PGA. Como resultado de la aplicación del método de Newmark (1965), con la adaptación propuesta por Jibson et al. (1998) sujeta a limitaciones de información, se pudo establecer que los taludes más propensos a los efectos cosísmicos corresponden a los dos primeros rangos de ac: 0,30g -0,50g, 0,51g –0,75g. La Ilustración 26 muestra la imagen obtenida.
86
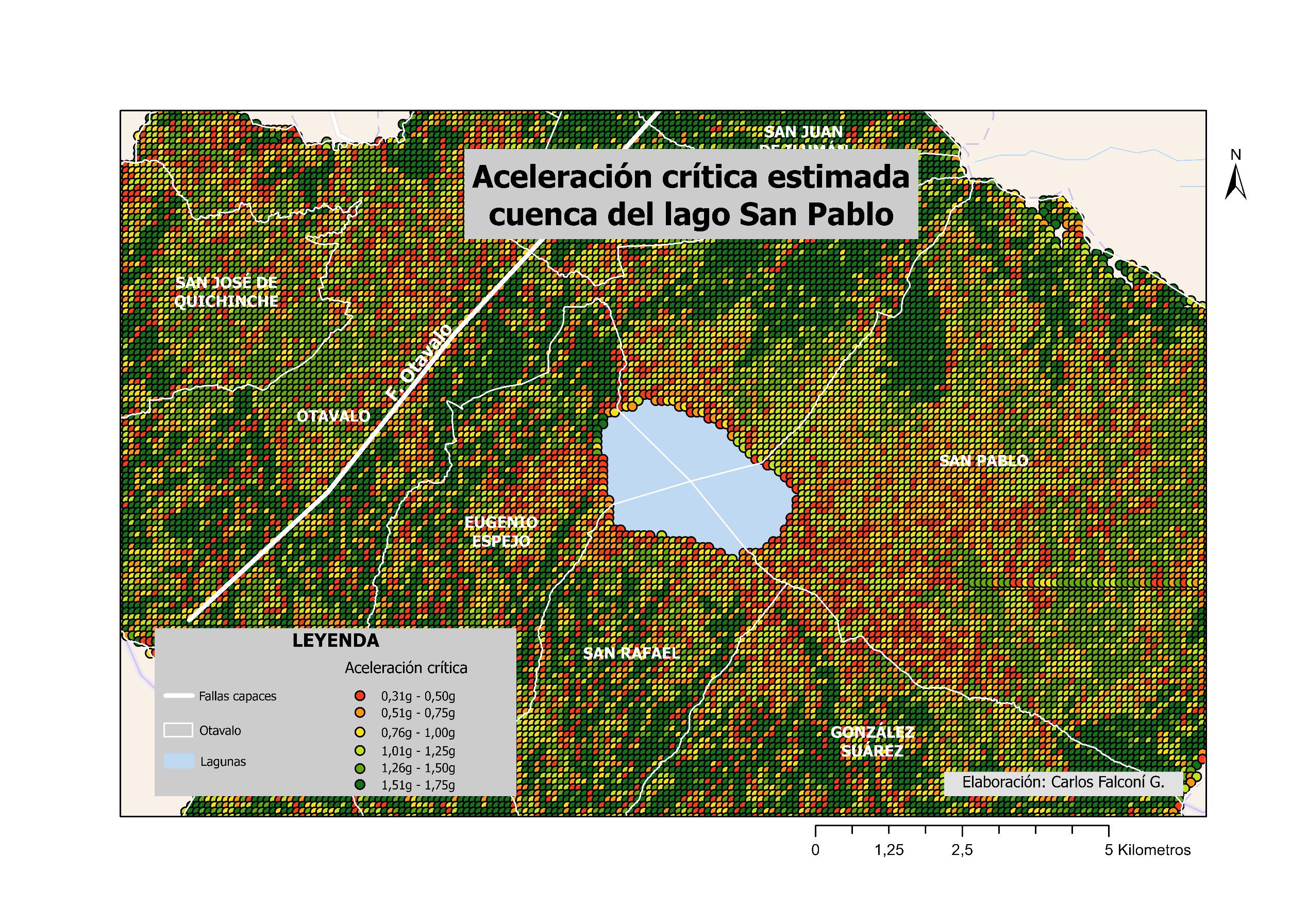
87
Ilustración 24 Aceleración crítica estimada.
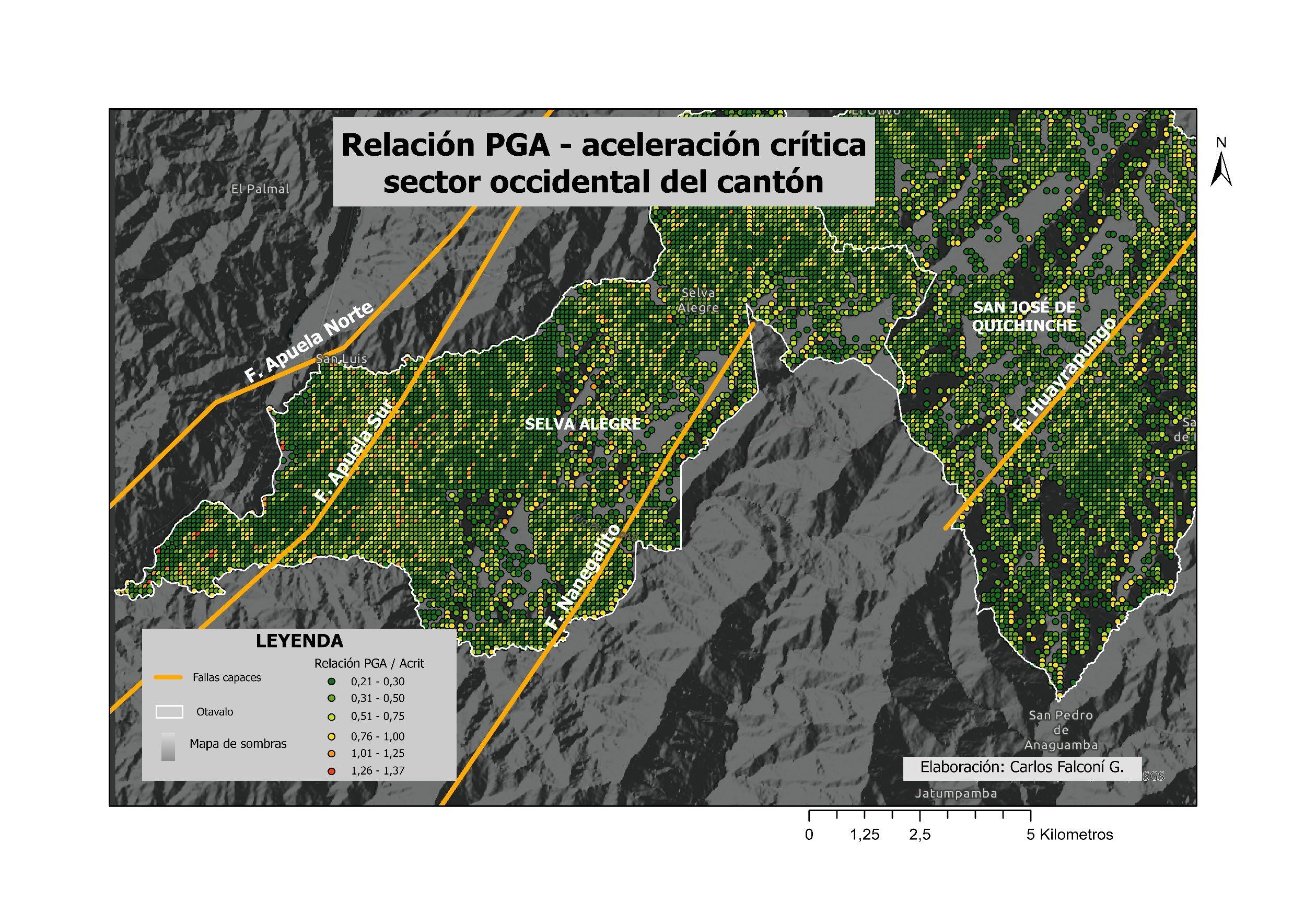
88
Ilustración 25 Relación de aceleraciones en roca respecto a la aceleración crítica, sector occidental del cantón Otavalo.
Ilustración 26 Reclasificación de pendientes, susceptibilidad a deslizamientos.
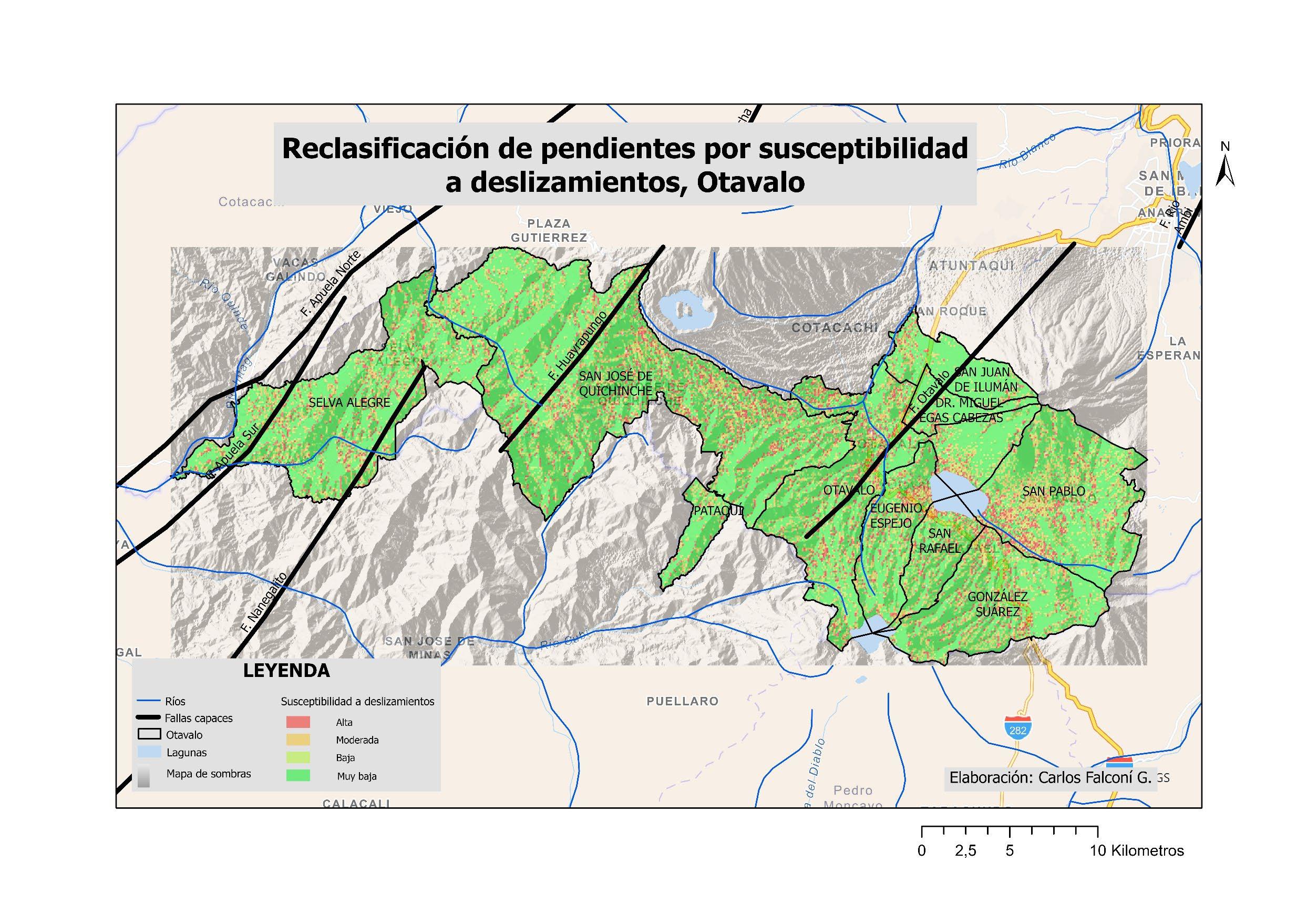
89
4.4 ANÁLISIS DE LOS RESULTADOS
4.4.1 Interpolación espacial.
Es evidente que hacia el occidente de la región de Otavalo las fallas más peligrosas son las Apuela Norte y Sur, y la falla Nanegalito. En medio del área geográfica cantonal está la falla Billacocha; y coincidiendo con la parroquia matriz, gravitan allí las fallas Otavalo y Ambi que se prolongan hacia el norte en las fallas El Ángel y San Isidro. Las superficies ráster de error estándar obtenidas con el método EBK, para Mw y PGA, muestran que la magnitud del error estándar de medición aumenta hacia el noroccidente y hacia el suroriente porque las fallas se alejan de la zona central cantonal. En el noroccidente, la falla Canandé es distante de las Apuela. Al suroriente, la falla Otavalo es lejana del complejo de fallas Chingual y Reventador, incluso de la Quito Norte al sur. De allí la importancia de interpolar en una región mucho mayor a la de estudio en el presente caso. En general, la zona central del cantón Otavalo coincidente con el área de la parroquia San José de Quichinche es la menos expuesta a la amenaza sísmica, considerando los rangos de valores para Mw y PGA. Para momento de magnitud, el valor es próximo a 6,4 Mw en el centro occidente de la parroquia Quichinche. Esta magnitud aumenta hacia el oriente hasta 6,6 Mw. Este sector del cantón corresponde con parte de la parroquia Quichinche y las parroquias Otavalo, Miguel Egas, San Juan de Ilumán, San Pablo del Lago, González Suárez, San Rafael de la Laguna y Eugenio Espejo: el extremo suroriental de González Suárez presenta magnitudes del orden de 6,8 Mw. Hacia el occidente, en dirección hacia la parroquia Selva Alegre, el momento de magnitud aumenta desde 6,8 Mw hasta 7,0 Mw Para PGA, la sección central – occidental de la parroquia San José de Quichinche tiene valores en el orden de 0,30g. El sector oriental de dicha parroquia y el resto del territorio cantonal son áreas en las cuales la PGA es próxima a 0,37g. Esta situación también se reproduce en las parroquias Otavalo, Miguel Egas y San Juan de Ilumán, Eugenio Espejo, San Rafael de la Laguna, González Suárez y San Pablo del Lago. Hacia el occidente, respecto al sector central de la parroquia Quichinche, la aceleración sísmica aumenta hasta ser tan alta como 0,43g.
90
Las fallas capaces Apuela y la Nanegalito (NW) son más peligrosas que las Chingual y Reventador (SE). Al occidente del cantón y hacia el segmento medio del extremo oriental, las fallas capaces están cercanas entre sí (las Apuela, Nanegalito y Billacocha al occidente; la Otavalo y Ambi al oriente). En cuanto más evoluciona la superficie ráster interpolada, hacia el occidente o el oriente, el error estándar aumenta y las tonalidades de rojo son más intensas.
Es evidente que las parroquias más densamente pobladas están al oriente del sector central de Quichinche. Existen más intervenciones antrópicas como infraestructura vial, de servicios básicos, viviendas, equipamientos sociales y estratégicos. La vulnerabilidad surge por la superposición de dichas intervenciones, respecto de la amenaza sísmica subyacente no considerada o quizás ignorada.
Otavalo fue el epicentro del llamado terremoto de Ibarra de 7,3 Mw acontecido en agosto de 1868, famoso por la destrucción de las ciudades en su torno: han transcurrido más de 150 años del hecho. Según Soulas et al. (1991), para el segmento Ibarra – El Ángel del sistema sinestral Cauca – Patía – San Isidro, el período de recurrencia de terremotos en torno a los 6,9 Mw tendría períodos de retorno entre 1000 y 2000 años. En la región de Ibarra – Otavalo, son posibles sismos más frecuentes entre 6,3 y 6,6. En la sierra norte, se reconoce que el período de recurrencia de sismos moderados bordea los cien años.
4.4.2 Interferometría satelital
Aplicando el I de Moran se identificaron clústeres débiles para desplazamientos (Ilustración 27) y valores de coherencia en aquellos (Ilustración 28). Este análisis arrojó como resultado unos pocos y débiles focos de aglomeración de los datos muestreados, tanto para desplazamientos en el terreno como para la coherencia de los valores, es decir su representatividad.
Para desplazamientos, la Ilustración 27 muestra los clústeres más representativos (High –High cluster, H-H). Estos se ubican al occidente del cantón Otavalo en las parroquias Selva Alegre y Quichinche, en las cercanías de las fallas Nanegalito y Huayrapungo, respectivamente. En Selva Alegre, en las coordenadas 78,5053°W y 0,25819°N, se registró un clúster cuyo desplazamiento promedio alcanzó los 21 mm. En Quichinche, las
91
coordenadas 78,3953°W 0,3192°N corresponden al clúster de desplazamientos con un promedio de vecinos cercanos de 7 mm.
Al suroriente del cantón, en la parroquia González Suárez y las coordenadas 78,2472°W 0,1408°N, se verifica el clúster H-H con el mayor valor de desplazamiento, 20 mm. Próximo a este clúster se localiza otro de menor jerarquía, Low-High cluster (L-H), en los altos de la parroquia Otavalo cerca de la laguna de Mojanda (coordenadas 78,2726308°W 0,1407851°N), con un desplazamiento promedio de -22 mm. En la parroquia Ilumán (coordenadas 78,2002°W 0,2728°N) se verifica un High-Low cluster (H-L) con un desplazamiento promedio de 7 mm.
En cuanto a la coherencia de las mediciones, la Ilustración 28 muestra que los clústeres más significativos (H-H) se ubican hacia el nororiente en los límites de las parroquias Otavalo y San Pablo. En Otavalo, el rango de los valores de coherencia está entre 0,36 y 0,77; en San Pablo dichos límites varían desde 0,38 hasta 0,63. Si bien no se ha vinculado a los desplazamientos, un mayor valor de coherencia implica mejor calidad en la señal de retorno hacia el satélite sólo obtenible a partir de áreas urbanas, centros poblados rurales, zonas deforestadas por actividades agrícolas o forestales, o, suelo desnudo de vegetación como el que se verifica en las estribaciones del volcán Imbabura.
Hacia el occidente del cantón, en Quichinche se verifican clústeres H-L de coherencia con un valor próximo a 0,35. En la parroquia Selva Alegre, entre las fallas Nanegalito y Apuela norte (de oriente a occidente), también se verifican clústeres H-L de coherencia cuyos valores varían entre 0,33 y 0,44. Esta parroquia del cantón es la más occidental, tiene mayor cobertura con vegetación pero también es el escenario de intervenciones antrópicas vinculadas a la extracción de minerales para la industria del cemento y a la prospección de metales con interés económico.
92
Ilustración 27 Clústeres de valores medidos de desplazamientos, Otavalo (terremoto abril de 2016).
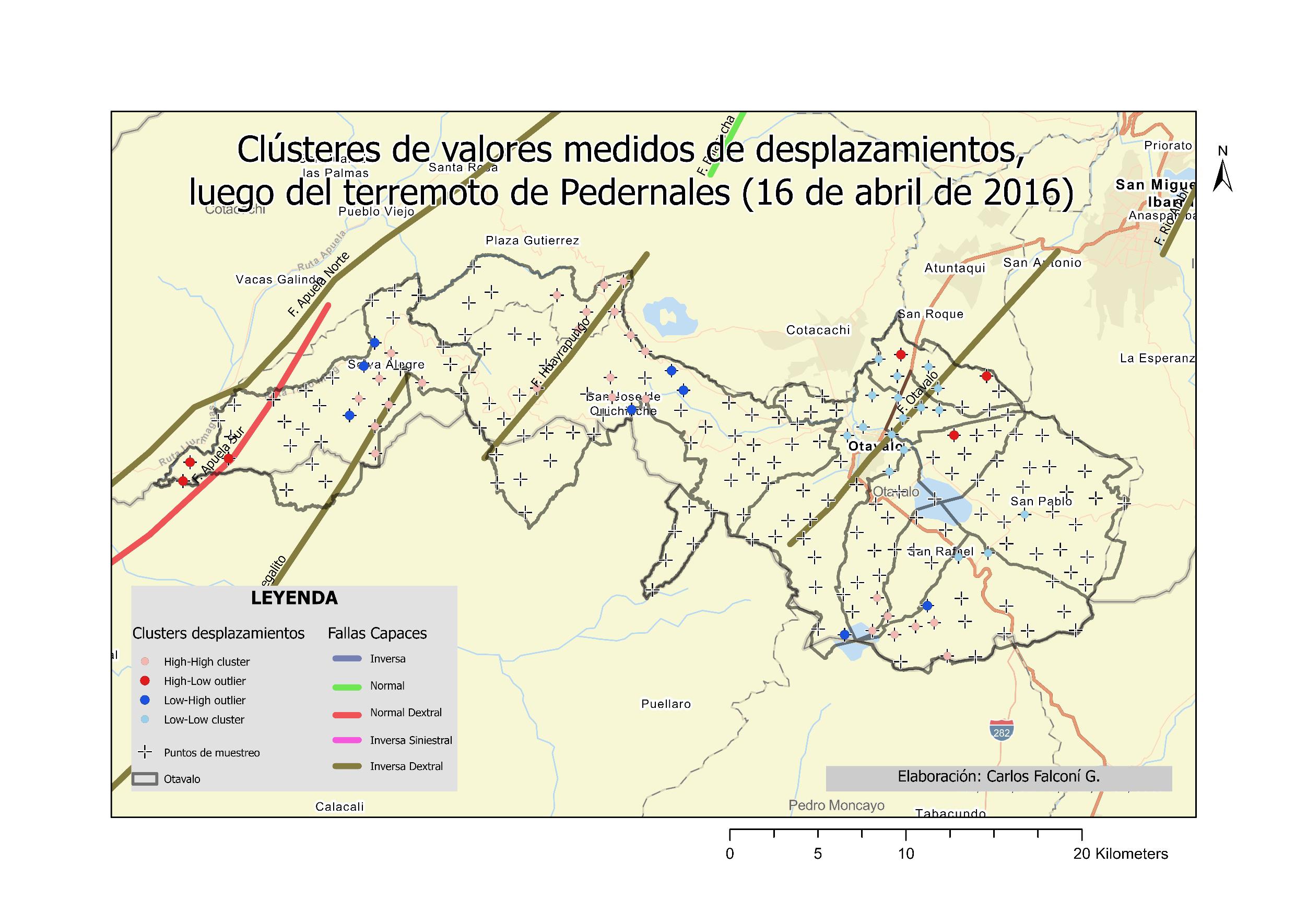
93
Ilustración 28 Clústeres de coherencia en valores medidos de desplazamientos.
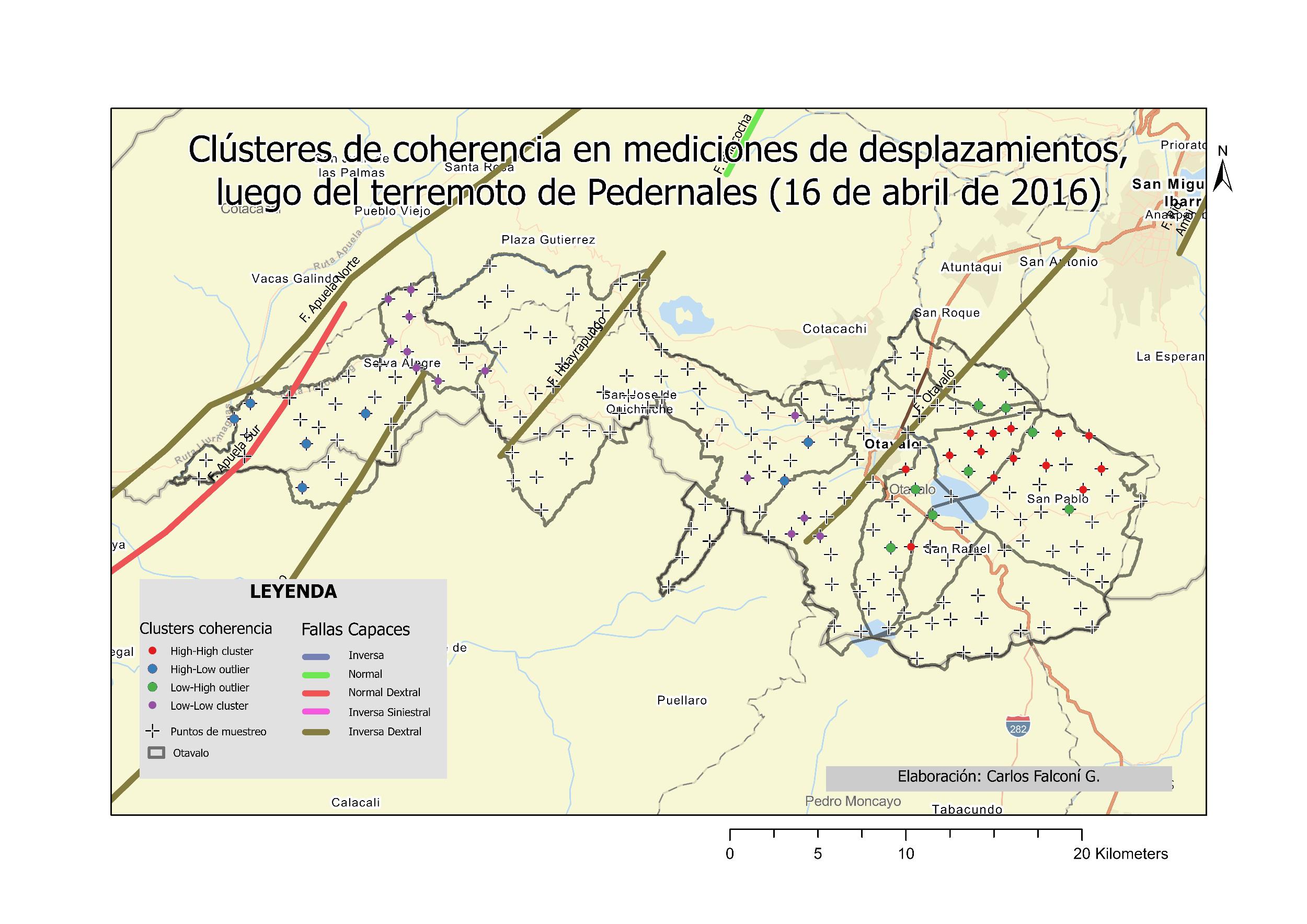
94
Los valores extraídos de deformaciones y de coherencia, tienen un comportamiento muy irregular considerando la jurisdicción cantonal Surge la pregunta: ¿qué resultados ofrecería la región, concentrando el análisis en las deformaciones? Se generó una malla de puntos con los cuales extraer información del ráster de interferometría, se añadió un campo en la tabla de atributos para convertir los valores a milímetros (mm) y luego se rasterizó la malla de puntos aprovechando la herramienta Interpolate Irregular Data de ArcGIS Pro. Se interpoló por Vecinos Cercanos (Nearest Neighbor) y se adoptó un tamaño de celda de 1000 m, para regionalizar alguna continuidad en los valores. Los resultados se muestran en la Ilustración 29. No se optó por métodos de krigeado para la interpolación, puesto que la distribución de los resultados del análisis interferométrico es sumamente irregular.
Se simbolizó mediante una rampa de colores Azul-Blanco-Rojo (Bl-Wh-Re), para representar sucesivamente la variación de levantamientos (+) y hundimientos (-). Lo que la Ilustración 29 muestra es que hacia el noroccidente y el suroriente se presentan levantamientos (color azul), coincidiendo con la cercanía de la falla Río Canandé (la subducción de Nazca) y el volcán Cayambe (la presión de la placa sudamericana). También hay levantamientos contiguos a la falla Quito Norte. Los hundimientos (color rojo) se concentran en la esquina nororiente de la Ilustración 29, y parecen converger en un callejón definido por las fallas C-03, Billacocha, Ambi, El Angel, San Isidro, que confluyen hacia el sistema sinestral Cauca-Patía.
Esta es la zona vinculada al SMD, que define la interacción entre la placa oceánica de Nazca, la continental sudamericana y el BNA. La región estudiada se encuentra en el límite de contacto del BNA con la placa sudamericana y el SMD. Se deduce que el sismo del 16 de abril de 2016, en Pedernales, tuvo la energía suficiente para “empujar al BNA” en dirección
NE. Este fenómeno es coincidente con las apreciaciones de Kanamori y McNally (1982), Nocquet et al. (2009), relacionadas al desplazamiento que se opera en el BNA. En el análisis de resultados de esta tesis, se dedujo que dicho desplazamiento provocó un efecto de hundimiento en el “choque” del BNA con “la franja de colisión intraplaca” (el SMD, ver 2.1) de la placa continental sudamericana.
95
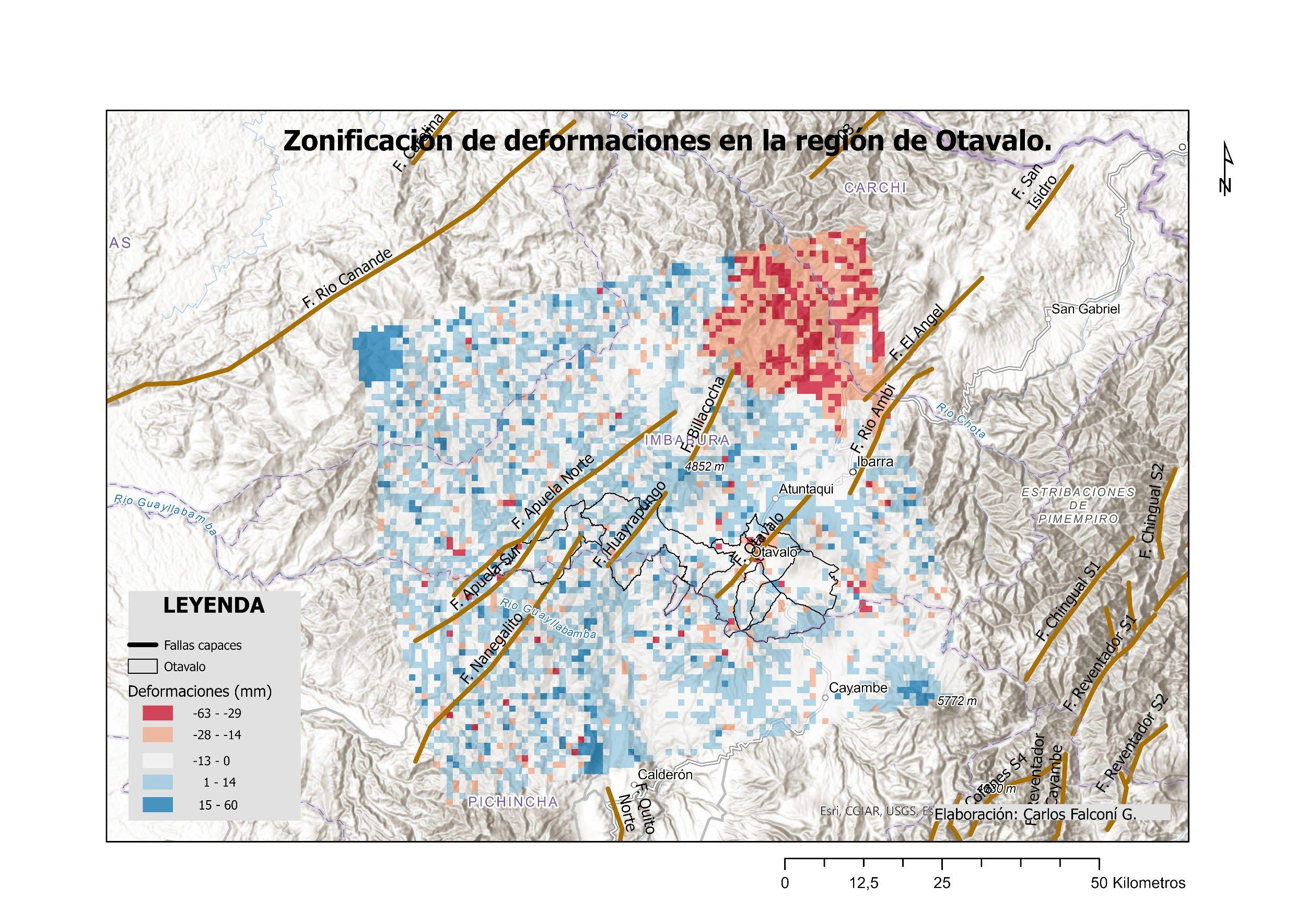
96
Ilustración 29 Zonificación de deformaciones en la región de Otavalo.
De acuerdo con Chunga, K. (conversación telefónica, febrero 2022), los efectos cosísmicos de un terremoto como el que sucedió en abril de 2016, en las costas de Pedernales –Ecuador, pueden tener influencia hasta un radio de 200 Km. La distancia entre las ciudades de Pedernales y Otavalo es de 195 Km en línea recta. La distancia entre Pedernales y la zona con presencia de hundimientos pronunciados (esquina NE de la Ilustración 29), es próxima a 230 Km.
4.4.3 Adaptación del método de Newmark (1965)
Como se destacó en el numeral 4.3, surgieron contingencias que motivaron adoptar estrategias alternativas para lograr el objetivo específico propuesto, la adaptación del método de Newmark (1995) a las condiciones locales.
Para la interpolación espacial, se redujo el área de interpolación de la totalidad de las fallas capaces del Ecuador a la región de Otavalo, pues inicialmente se aplicó una operación de cortado del ráster global. Se siguieron las mismas pautas expuestas en el numeral 4.1, estableciendo el tamaño de la celda ráster en 0,00090° (100 m). Los valores interpolados de la PGA variaron en un rango desde 0,27g y 0,46g, un promedio de 0,36g y una desviación estándar de 0,04g 23 .
Los rásteres obtenidos para DEM y PGA tuvieron celdas de distinto tamaño, por lo que fue preciso generalizar el primero a un tamaño de celda de 100 m: el DEM obtenido por interferometría tenía un tamaño original de celda ráster de 14 m. Adicionalmente, el DEM fue sometido a un relleno de sumideros con el software ArcGIS Pro, con lo cual se generó un ráster de pendientes Las pendientes que se obtuvieron así, solo refiriendo al territorio cantonal de Otavalo, variaron entre 0,42 y 89,74 grados sexagesimales (°), con un promedio de 83,87° y una desviación estándar de 8,44°. No fue viable utilizar la calculadora ráster. La inspección de una u otra imagen (pendientes, PGA) reveló la existencia de valores nulos y ceros. Esta contingencia motivó desechar el análisis con la calculadora ráster. En la fórmula del FS propuesto por Jibson et al. (1998), los denominadores de las fracciones son funciones trigonométricas seno y tangente del
97
23 Verificación efectuada con Raster Functions, Statistics and Histogram Properties
ángulo de la pendiente en cada celda del ráster correspondiente. Si el ángulo del talud es cero (0), sus valores son nulos y por lo tanto cada fracción tiende a un límite infinito desde el punto de vista matemático. En el caso de la función tangente, para el segundo cociente de la expresión de cálculo de FS, si el ángulo del talud es próximo a 90º el valor de la función trigonométrica tiende a un valor infinito; por lo tanto, en el límite dicho sumando de FS tiende a cero.
Por esta razón, sobre el ráster de pendientes se decidió distribuir cada 100 m una capa vectorial de puntos, excluyendo las áreas lagunares de Mojanda y San Pablo. De este proceso, se extrajeron 1.165 valores con registros nulos y cero a partir de una red inicial de 52.419 puntos. Utilizando la red depurada de puntos con valores de pendiente (sin valores cero ni nulos), se extrajeron valores de PGA del ráster correspondiente. Entre los puntos muestreados, se constataron 34 registros con valores nulos de PGA. El total de puntos que se desecharon fue de 1.199, que representa el 2,3% del número de puntos que se distribuyeron inicialmente y con los cuales se consolidó una tabla de atributos. La calculadora de campos permitió establecer los valores de ac y de la relación de la PGA con respecto a la anterior.
Los procesos de extracción de valores a partir de rásteres, la depuración de la red de puntos y el cálculo de variables del método de Newmark (1965), se hicieron con el software QGIS. Con ArcGIS Pro se generaron los mapas de pixeles distribuidos espacialmente, representando con colores contrastantes la variación espacial de los valores de ac y la relación PGA/ac
Para la adaptación del método de Newmark (1965), las variables más relevantes son la aceleración sísmica, las pendientes imperantes y las propiedades geotécnicas de los suelos de un área. Los valores de PGA no fueron afectados por la ley de atenuación propuesta por Falconí et al. (2010), para obtener aceleraciones a nivel del suelo. La profundidad de las fallas corticales en el cantón Otavalo varía entre 10 y 22 Km, con un promedio de 15 Km. El cambio de magnitud en la aceleración atenuada es despreciable. Se optó por un criterio más conservador, del lado de la seguridad, asumiendo el valor de la PGA a la profundidad en que se calculó, correspondiente a la profundidad de cada una de las fallas capaces. Esto también responde a que se prescinde del término correspondiente a la presión de poro (presencia de agua) en el cálculo del FS.
98
La Ilustración 30 muestra el histograma de frecuencias de la aceleración crítica estimada, que en ningún caso corresponde a una distribución normal. Cuanto más cercana sea la aceleración crítica al rango entre 0,26g y 0,47g que corresponde a la variación espacial de la PGA en la región de Otavalo, mayor es el riesgo de que pueda ocurrir deslizamientos. Superado el umbral de 0,47g, se entiende que las características más planas de las pendientes de taludes y las mejores propiedades de suelos requerirán valores de aceleración mucho más altos para inducir efectos cosísmicos como los deslizamientos. El rango de valores de ac varía desde 0,31g hasta 1,74g, con un promedio de 1,17g.
Ilustración 30 Histograma de distribución de los valores de aceleración crítica estimados.
En contraste, si los valores de la relación PGA respecto de ac son próximos a la unidad o superan este valor, mayor será la posibilidad de que en esos lugares un sismo ocasione deslizamientos. La Ilustración 31 muestra la distribución estadística de la relación PGA/ac, cuyos valores extremos varían desde 0,17 hasta 1,37, con un promedio de 0,38. La distribución es asimétrica positiva:
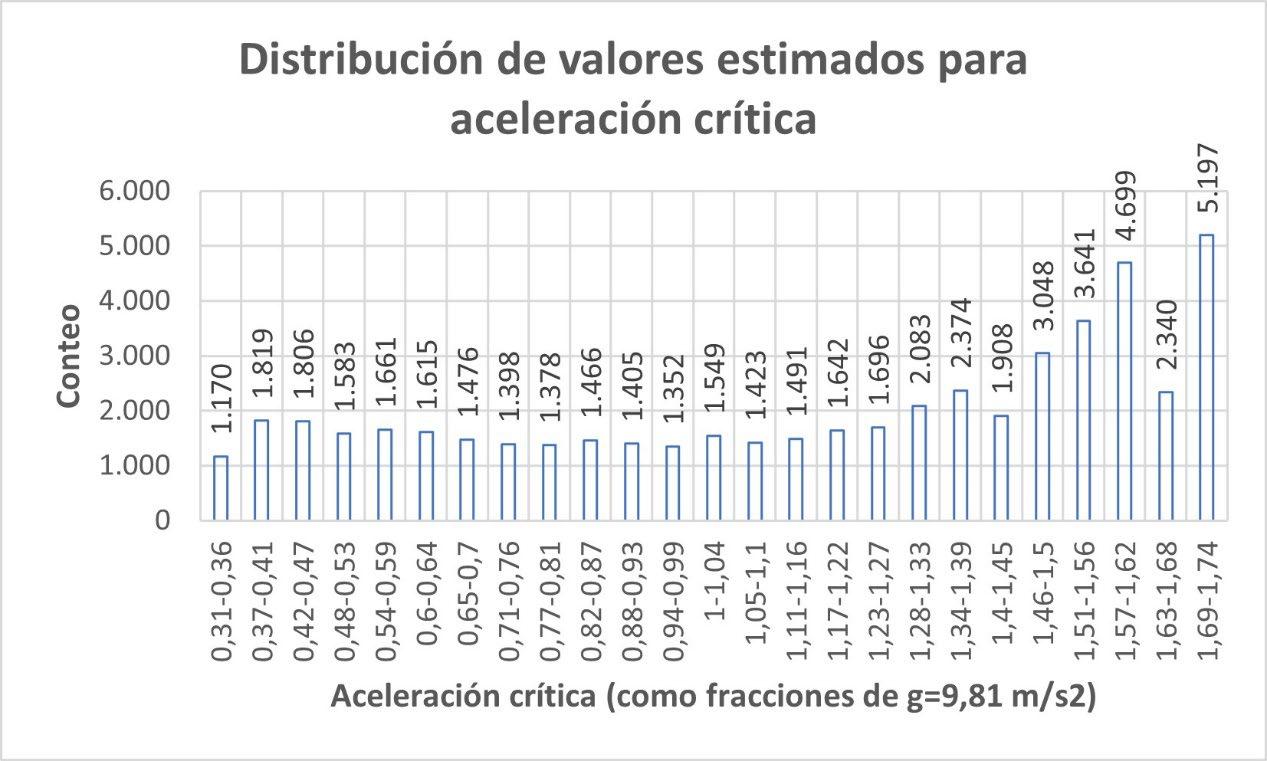
99
Ilustración 31 Histograma de distribución de valores PGA/acrit
El procesamiento desarrollado prueba que SI es posible adaptar el método de Newmark (1965) aproximándose a los lineamientos de Jibson et al. (1998), cuyos requerimientos de información son difíciles de satisfacer en la realidad ecuatoriana. En el caso presente, se asumieron propiedades homogéneas de los suelos en la región lo que, por supuesto, dista de la realidad. Particularmente, en la región occidental del cantón Otavalo los suelos están expuestos a procesos de meteorización y de lixiviación más extremos, lo cual degrada sus propiedades geotécnicas. Esto es a causa de la influencia climática del ecosistema del Chocó que gravita en el suroccidente de Colombia y en el noroccidente del Ecuador.
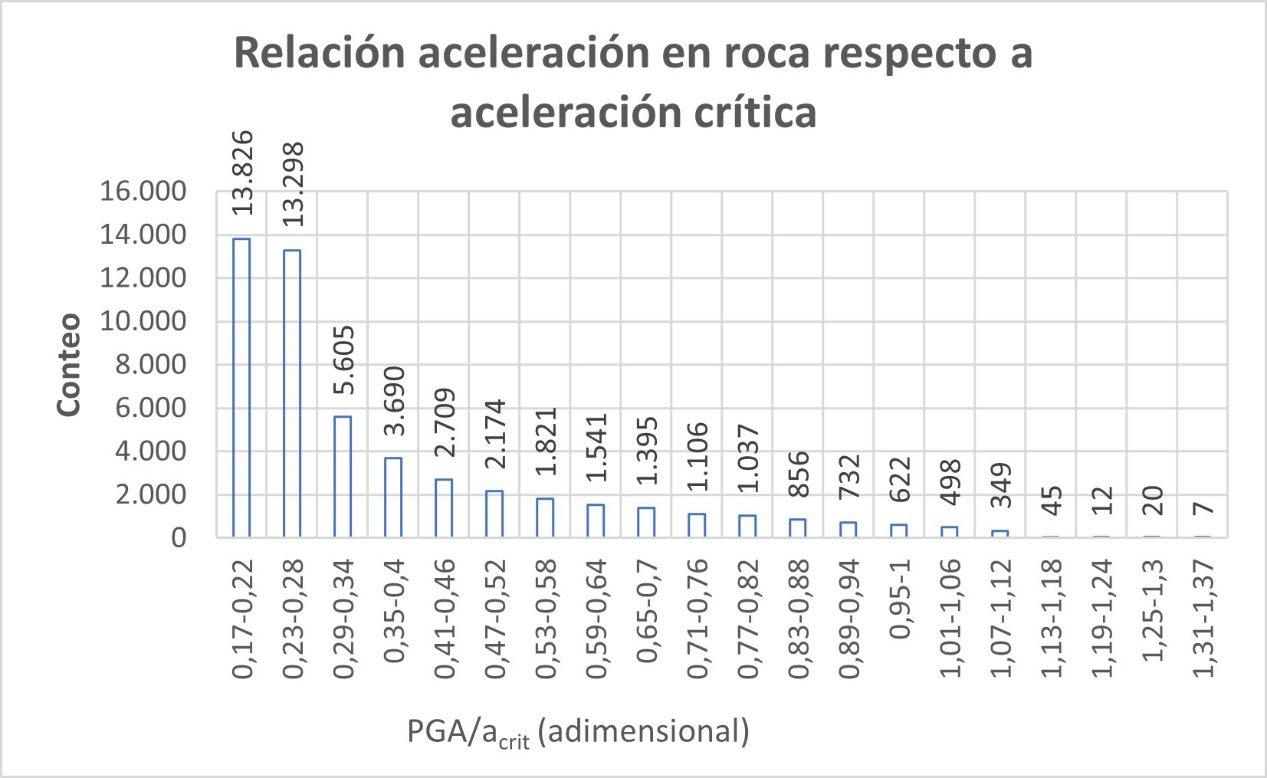
100
4.4.5 Respuestas a las preguntas de investigación
Convergiendo con los objetivos específicos planteados, las preguntas de investigación que se formularon y a las que se dio respuesta son:
• ¿Cuánto y por qué varía el error estándar del valor de las magnitudes sísmicas estimadas con técnicas de interpolación espacial Kriging?
Los errores estándares de Mw en la proximidad a las fallas capaces son pequeños, entre 0,01-0,04, no así en los espacios entre fallas capaces distantes entre sí: por ejemplo, entre las fallas Huayrapungo y Otavalo, y, Huayrapungo y Apuela norte el error estándar de Mw es 0,10. Para PGA, el valor de error estándar en torno a la falla Huayrapungo es de 0,30g. En el sector oriental de la falla Otavalo, el error estándar es del orden de 0,37g. Hacia el occidente del cantón, en la falla Nanegalito el error estándar es 0,33g. Y, entre las fallas Apuela norte y sur, dicha variable varía entre 0,37g – 0,45g.
Lo anterior confirma que cuánto más espaciadas estén las fallas capaces entre sí, mayor será el error estándar en la estimación de valores de las variables sísmicas.
• ¿Cuál es el orden de magnitud en que las técnicas de inSAR permiten identificar deformaciones en zonas puntuales del territorio cantonal?
Las deformaciones medidas en el territorio otavaleño mediante la técnica de inSAR, se clasifican en levantamientos y hundimientos, habiendo asumido como las más representativas aquellas correspondientes a un valor de coherencia igual o mayor que 0,50. Para levantamientos el promedio observado fue de 5 mm, con un rango entre 1 mm y 11 mm. En el caso de hundimientos, el promedio fue de -6 mm.
En el rango de coherencia entre 0,25 y 0,50 se registró mayor número de conteos. Correspondientemente, en el caso de levantamientos el promedio observado fue de 5 mm, y para hundimientos -8 mm. Los máximos valores correspondientes a
101
levantamientos y hundimientos son 25 mm y -46 mm. Estos valores se pueden constatar en la Tabla 11 del numeral 4.4.2
• ¿Cuánto varía en rango el valor de pendientes en zonas con influencia posible de efectos cosísmicos, de acuerdo con el AHP?
Se estableció previamente que el rango crítico más peligroso de ac es aquel entre 0,31g y 0,50g. Además, se asumieron condiciones homogéneas para los suelos con el propósito de explorar la viabilidad de adaptar el método de Newmark (1965). La capa geográfica de puntos de muestreo integró la información de ángulos de talud, PGA, ac y relación PGA/ac. Mediante selección por atributos se determinó que las pendientes de taludes más susceptibles a deslizamientos son aquellas con ángulos superiores o al menos iguales a 66,8°. El rango de pendientes se encuentra entre 67,2° y 82,1°, con un promedio de 73,7° y una desviación estándar de 3,7°. El histograma de frecuencias mostrado en la Ilustración 32 establece que no se trata de una distribución normal, a pesar de que los valores del promedio y la mediana (72,96°) son prácticamente coincidentes. Las pendientes con menores conteos se registran a partir de los 79° y acumulan apenas 128 registros (0,2%) de un subconjunto de 5.320 puntos resultantes de la selección por atributos. El número de puntos seleccionados corresponde al 10,4% del total de puntos de la capa geográfica de puntos de muestreo.
102
Ilustración 32 Histograma de distribución de valores de pendientes en taludes con alta susceptibilidad a deslizamientos.
Es importante destacar que se decidió considerar también a los taludes entre 52,3° y 67,2°, correspondiente al rango de ac entre 0,51g y 0,75g de susceptibilidad moderada a deslizamientos, como otro grupo de sitios de interés. La decisión se basó en los factores que no se pudo valorar, como las diferentes propiedades geotécnicas de los suelos y la incertidumbre que representa la presión de poros. La Ilustración 33 muestra la distribución de valores de este conjunto de datos.
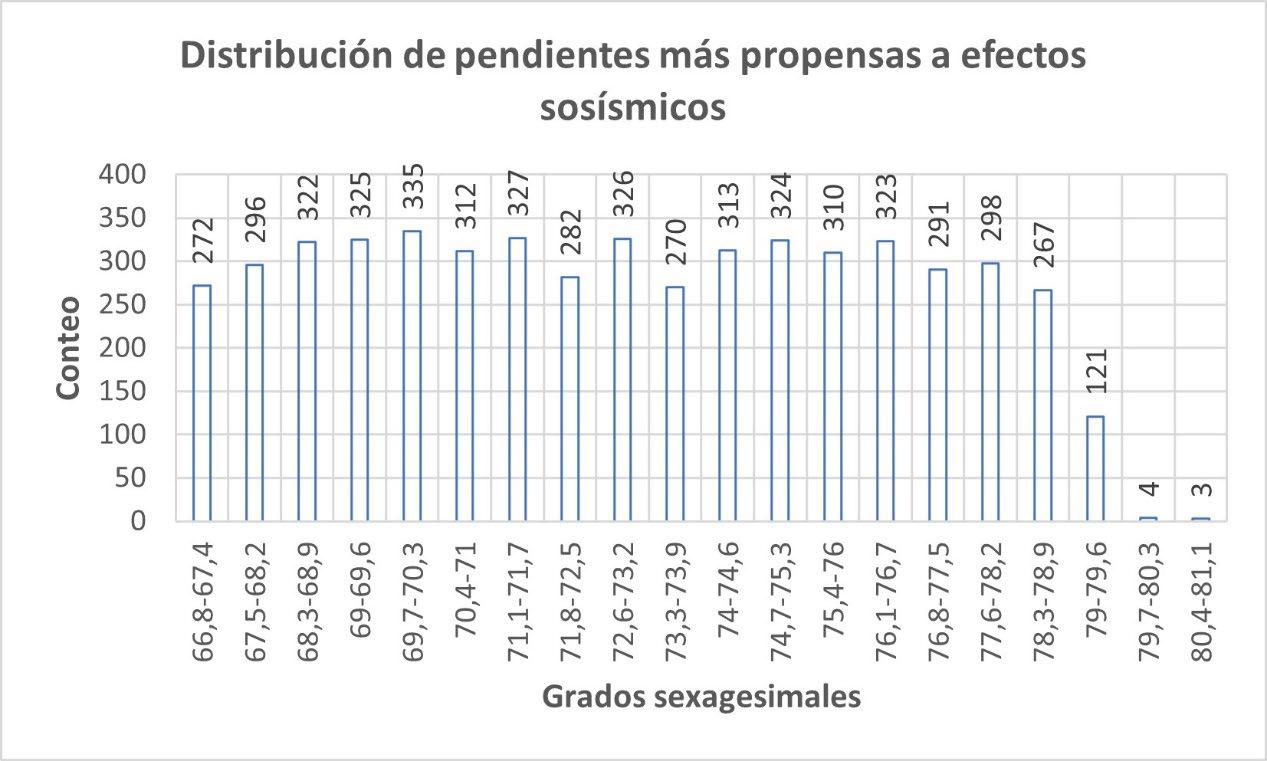
103
El mapa de la Ilustración 26 referido en el numeral 4.3 contiene la reclasificación de pendientes propensas a efectos cosísmicos. A pesar de las limitaciones de información, identifica aquellos taludes más susceptibles a deslizamientos. Particularmente en la cuenca del lago San Pablo, las susceptibilidades alta y mediana se concentran en torno a infraestructura vial contigua a las parroquias más pobladas, al cauce los principales ríos y, por extensión, al de sus quebradas afluentes que propician procesos de socavación del lecho e inducen planos de deslizamientos en taludes cercanos
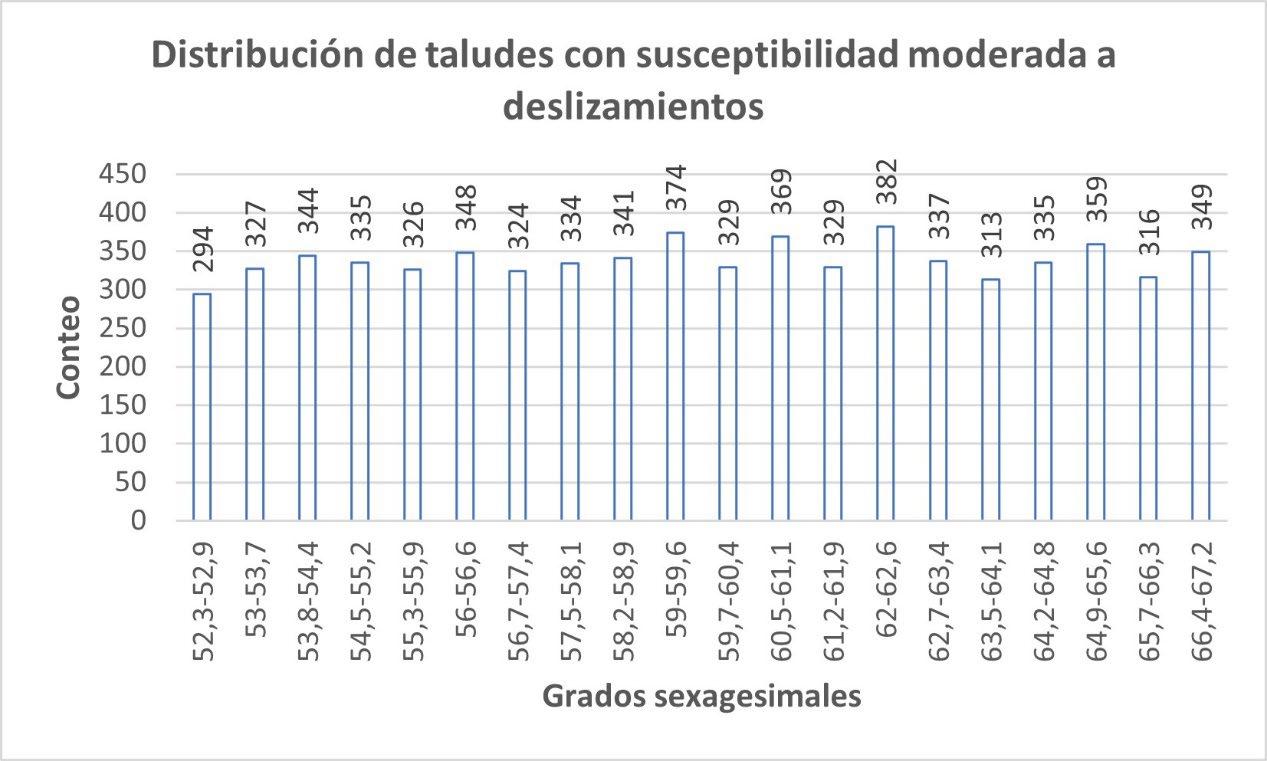
104
Ilustración 33 Histograma de distribución de taludes con susceptibilidad moderada a deslizamientos.
4.5 ANÁLISIS CRÍTICO DE LA METODOLOGÍA
La metodología planteada a partir de la revisión de literatura, y que se esbozó en el numeral 3, fue aplicada con apego a lo previsto para la interpolación espacial y parcialmente para el análisis de interferometría y la adaptación del método de Newmark (1965).
Juzgando con sentido crítico los resultados obtenidos de la interpolación espacial, se pudo establecer que la variación de Mw no presenta mucha dispersión a diferencia de la PGA. Esto determina que los errores estándares de medición sean pequeños en el caso del Mw, y en el orden de las magnitudes medidas para la PGA. La interpolación espacial se realizó a partir de los puntos distribuidos sobre las fallas capaces regionales y, en algunos casos, existen distancias grandes entre una y otra falla, factor que se presume determinante para la mayor dispersión en la medida de la PGA.
En cuanto al análisis de interferometría, se obtuvieron el DEM, la fase desenrollada del interferograma, los archivos KMZ de elevación, deformaciones y coherencia de las mediciones satelitales, el ráster que aglutinó a todas las variables medidas (deformación, coherencia, elevación). Las limitaciones de la aplicación de inSAR en áreas con mayor presencia de vegetación o en zonas de relieves abruptos, determinó que se registraran celdas sin información de las variables de interés.
En torno a la adaptación del método de Newmark (1965) con base a la metodología desarrollada por Jibson et al. (1998), de partida estuvieron claras las limitaciones de información existentes, entre otras, las propiedades mecánicas de los suelos, la carencia de acelerogramas de sismos y datos geológicos con mayor detalle, así como un inventario sistemático de deslizamientos en la región. Esto condujo a generalizar la aplicación de la ecuación del FS (ecuación 2.7.3), convirtiendo a la geometría del talud en el factor discriminante al homogenizar características geotecnicas de los suelos. Las celdas ráster con valores incongruentes o nulos, obtenidas del análisis interferométrico, imposibilitaron efectuar el procedimiento de álgebra de mapas utilizando la calculadora ráster. Por ello, se optó por extraer información del ráster mediante una nube de puntos con los cuales se pudo completar el análisis mediante procedimientos vector, utilizando la herramienta Select by Atributes. De esta manera, se pudo reclasificar las pendientes más susceptibles a deslizamientos superponiendo la información de los rangos de aceleración
105
crítica obtenidos con la adaptación del método de Newmark. Se identificaron clústeres débiles de mediciones de deformaciones y coherencias en el territorio del cantón de Otavalo.
Siempre subyació la inquietud en torno a la distribución de las deformaciones en la región, alternando levantamientos y hundimientos. En el análisis de resultados, se replicó aplicar la nube de puntos para extraer información del ráster en toda la región, no solamente el territorio del cantón otavaleño. Obtenida esta información, se eliminaron valores nulos e incongruentes de desplazamientos, coherencia y elevación, y se convirtió los desplazamientos a milímetros. Prescindiendo de los valores de coherencia de las mediciones satelitales, con ArcGIS Pro la nube de puntos depurada fue rasterizada con la herramienta Interpolate Irregular Data aplicando el método de Nearest Neighbor
El resultado de esta exploración generó la Ilustración 29 que muestra cómo se zonifican las deformaciones en la región y, sobre todo, permitió verificar indirectamente los asertos de geólogos muy especializados respecto al desplazamiento del BNA (Kanamori y McNally, 1982; Nocquet et al. 2009). En cuanto a la hipótesis planteada en esta tesis, el análisis regional de las deformaciones obtenidas con Interferometría permitió verificar su validez. Sobre la aplicación de metodologías similares, en la revisión de literatura destacan los casos de estudio en que se combinaron técnicas de interpolación espacial para desarrollar mapas isosísmicos en Grecia (Schenková et al., 2007). En el Ecuador sólo existen referencias de literatura en torno a una evaluación de la norma ecuatoriana de construcción (orientada al diseño estructural de edificaciones) que no fue considerada para el objeto de esta tesis. Cando-Jácome et al. (2020), en la investigación realizada luego del terremoto de Pedernales en la ciudad de Portoviejo, identificaron a partir de interferometría satelital los desplazamientos operados en la región y, con base a resultados de un intenso plan de exploraciones geotécnicas de los suelos, delimitaron la zona en la cual se magnificaron los desplazamientos y la probabilidad de licuefacción del subsuelo, factores que determinaron que el centro de la urbe portovejense (la zona cero) sea devastado por la onda sísmica del terremoto de abril de 2016 en Pedernales-Ecuador.
En torno al método de Newmark (1965), de la literatura revisada el caso más cercano es aquel del valle de Aburrá en Colombia (Hidalgo Montoya y Vega Gutiérrez, 2014). Estos autores incluyeron en su análisis probabilístico la presión de poros en el suelo, porque
106
consideraron la influencia de las precipitaciones juntamente con los sismos en los deslizamientos de taludes. En el Ecuador, la información meteorológica es limitada haciendo impracticable la metodología seguida por estos investigadores. De allí que la adaptación de Jibson et al. (1998) al método de Newmark (1965) constituyó el acicate para explorar su aplicación en el desarrollo de esta tesis, por supuesto estableciendo las limitaciones de información que se han destacado. La inclusión simultánea de las tres técnicas, interpolación espacial, interferometría satelital y el método de Newmark (1965) que constituye el articulador final para el análisis de superposición ponderada, no fue identificada en la revisión de literatura. El caso más cercano sería el de Zhou et al. (2021) quienes utilizaron técnicas de interpolación Kriging para obtener la distribución del valor de PGA y evaluar los efectos sísmicos y cosísmicos del terremoto de 6,6 Mw ocurrido en septiembre de 2018 cerca de Iburi, Hokkaido (Japón) Los investigadores también aplicaron método de Newmark (1965), para investigar el mecanismo de los deslizamientos de tierra regionales, considerando análisis de estabilidad de las laderas por el efecto de las lluvias y el movimiento sísmico.
Chunga, K. 2022 (conversación telefónica del 25 de mayo de 2022) acota que el análisis de interferometría, orientado a la identificación de áreas con riesgo de deslizamientos, puede ser respaldado con evaluaciones topográficas de campo, por ejemplo, mediante drones de alta precisión en fechas anterior y posterior subsecuentes. Así también, recomienda incluir en los reconocimientos de campo (simultáneos o posteriores) investigaciones geomorfológicas, a fin de caracterizar cambios de curso en el cauce de los ríos, la presencia de escarpes de fallas geológicas
Este trabajo de tesis plantea una línea de investigación prometedora, a nutrirse a futuro con nuevas aportaciones, incluyendo perfiles profesionales multidisciplinarios
107
5. CONCLUSIONES Y RECOMENDACIONES
5.1 RESULTADOS DE LA INVESTIGACIÓN
En la presente tesis, se propuso como objetivo general “Caracterizar la amenaza sísmica y los efectos cosísmicos en el cantón Otavalo, Ecuador”. En tal sentido, se establecieron preliminarmente tres objetivos específicos:
• Zonificar la intensidad, magnitud y aceleración sísmica en la región:
Se utilizó el método de interpolación espacial EBK, adoptando el semivariograma tipo Exponential Detrented, que permite obtener un semivariograma más adecuado. En principio se interpolaron magnitudes sísmicas de Mw y PGA entre puntos distribuidos en todas las fallas capaces del Ecuador. Luego se seleccionó un ráster en la región de Otavalo.
Solamente para la PGA fue necesario luego interpolar nuevamente valores considerando las fallas existentes en la región (Apuela norte, Apuela Sur, Nanegalito, Huayrapungo, Billacocha, Otavalo, Ambi. Fue preferible hacer esto en vista que el tamaño de la celda ráster inicial era mucho mayor que 100 m. Los valores de la PGA variaron hizo entre 0,25g y 0,45g.
Las fallas más peligrosas de la región son las Apuela norte y sur, la Nanegalito y la Otavalo. Las fallas Huayrapungo y Billacocha, en la zona central de la parroquia Quichinche, ostentan los límites inferiores de Mw y PGA. La falla Otavalo gravita sobre el sector oriental del cantón que es el más densamente poblado.
• Identificar áreas de subsidencia o de desplazamiento del suelo, en la cercanía de fallas geológicas capaces.
Se escogieron las imágenes satelitales S-1A SLC IW del 24 de marzo y 17 de abril de 2016, por su proximidad con la fecha del terremoto de Pedernales (16 de abril) Esto aumentaba la probabilidad de medir los desplazamientos (hundimientos y
108
levantamientos) registrados en el territorio cantonal de Otavalo, incluyendo las fallas capaces que lo atraviesan o son aledañas. La Tabla 11, referida en el numeral 4.2, resumió valores de los cuales se considera los más representativos aquellos con una coherencia superior a 0,35.
En las fallas occidentales del cantón (Huayrapungo, Apuela Sur), se registraron levantamientos promedio que varían entre 5 y 8 milímetros, considerando el rango de coherencia entre 0,35 y 0,60. Los valores máximos correspondientes fueron del orden de 12 y 30 mm, respectivamente.
Las fallas Apuela norte, Nanegalito y Otavalo acusan un conteo poco representativo de valores. En el rango de mayor coherencia, 0,60 – 0,85, la falla Otavalo presenta un promedio de hundimientos del orden de -11 mm. Es conveniente destacar que junto con la Nanegalito muestran preferentemente hundimientos en valores de coherencia mayores o iguales a 0,35.
Si bien este par de fallas capaces, Nanegalito y Otavalo, están distantes unas de otra, el particular comportamiento de levantamientos pequeños al occidente (falla Apuela Sur) y hundimientos al oriente (falla Otavalo), apoya la tesis sostenida por Kanamori y McNally (1982), respecto a que el BNA está presionado entre las placas de Nazca y Sudamericana. Esto justificaría por qué en esta región históricamente han ocurrido los sismos más importantes en el Ecuador.
• Delimitar áreas de pendientes pronunciadas propensas a efectos cosísmicos.
Se consideraron 4 rangos de ac para efectuar la reclasificación de pendientes, sujeta no obstante a limitaciones de información geotécnica: 0,30g -0,50g; 0,51g – 0,75g; 0,76g –1,00g; mayor que 1,00g.
Para el rango 0,30g – 0,50g, el ángulo de los taludes asociado varía entre 67,2° – 82,1° (5.580 registros); este es el rango más propenso a deslizamientos para las condiciones simplificadas asumidas. En el rango 0,51g – 0,75g, la variación de pendiente de los taludes se encuentra entre 52,3° - 67,2° (6.765 registros). El tercer rango, 0,76g – 1,00g, refiere a taludes entre 39,5° – 52,3° (5.838 registros). El último rango, mayor que 1,00g, refiere a taludes con pendientes inferiores o iguales a 39,5°.
109
De esta manera, se procedió a reclasificar el ráster de pendientes que se muestra en la Ilustración 19, obteniendo la imagen que consta en la Ilustración 26
La hipótesis refirió a si “La utilización de técnicas de Interferometría Satelital, en combinación con técnicas geoestadísticas de Kriging y de Análisis de Superposición Ponderada, permite identificar áreas de riesgo significativo para el ordenamiento territorial del cantón Otavalo en la provincia de Imbabura - Ecuador”.
En el análisis de resultados interferometría satelital, en esta tesis se contrastaron dos perspectivas:
• Una local, refiriendo al territorio del cantón Otavalo particularmente. En este enfoque, las deformaciones se suceden con aleatoriedad, alternando levantamientos y hundimientos; sin embargo, los hundimientos registrados en torno a la falla Otavalo permitieron intuir la validez de las presunciones de Kanamori y McNally (1982) en torno al BNA
• Otra regional, considerando como tal la totalidad del área cubierta con las franjas y zona seleccionadas de las imágenes satelitales. En esta perspectiva, se hace evidente una zonificación más clara de las deformaciones, destacando los hundimientos hacia la esquina NE de la Ilustración 29. Esto constituye una evidencia indirecta de cómo la pequeña área del BNA analizada se hundió en esa dirección al interactuar con la “franja de colisión intraplaca” de la placa continental sudamericana. Los levantamientos se identifican hacia el sur y suroriente, sobre la falla Quito Norte y el volcán Cayambe, y hacia el noroccidente en la cercanía de la falla Río Canandé por la subducción de la placa de Nazca.
La conclusión a que se pudo llegar en torno a la hipótesis que se planteó, es de que la interferometría satelital, por si sola, SÍ es útil para monitorear riesgos de carácter sísmico y cosísmico.
Las técnicas de interpolación espacial y de análisis de superposición ponderada, contribuyen al propósito al permitir estimar aceleraciones sísmicas con criterio determinístico a partir de fallas capaces, valores que retroalimentan a un análisis de
110
estabilidad de taludes en el contexto del método de Newmark (1965), de acuerdo con la adaptación de Jibson et al. (1998). Por lo tanto, la combinación de las tres técnicas SÍ puede ser aplicada con éxito en el monitoreo de eventos sísmicos y cosísmicos, y, por ende, para identificar áreas probables de riesgo en el ordenamiento territorial no sólo del cantón
Otavalo sino de cualquier otro GAD en el Ecuador, sin perjuicio de su carácter provincial, municipal o parroquial.
5.2 CONCLUSIONES
Como conclusiones de la presente tesis de investigación, se puede resumir lo siguiente:
Fue posible caracterizar la zonificación sísmica del cantón Otavalo, aplicando técnicas de interpolación espacial con el método EBK.
Se pudo desarrollar el análisis de interferometría para la detección de subsidencias en la proximidad de fallas capaces y en el territorio cantonal. Esto contribuyó al logro del objetivo general de la tesis, “Caracterizar la amenaza sísmica y los efectos cosísmicos en el cantón Otavalo, Ecuador”.
El análisis de superposición ponderado se aplicó mediante la adaptación del método de Newmark (1965). El concepto inicial por desarrollar mediante álgebra de mapas ráster tuvo dificultades. Estas se derivaron de las limitaciones de la técnica de interferometría: zonas con mayor cobertura vegetal, cuerpos de agua lagunares, pendientes muy abruptas con paredes cuasi verticales que pueden disminuir la calidad de la señal de retorno al satélite. La solución a esta contingencia fue estructurar un análisis de superposición ponderado con una capa vector de puntos que muestrearon variables de interés en el ráster de interferometría y en el ráster de PGA. En esta capa vector también se calcularon los parámetros del método de Newmark (1995) con los lineamientos de Jibson et al. (1998). Esto hizo posible efectuar un análisis vector de superposición ponderada. Fue posible identificar zonas que potencialmente presentarían efectos cosísmicos como deslizamientos, a partir también de las tres técnicas antes citadas. Pese a las limitaciones de información, el mapa de pendientes reclasificadas en función de la mayor o menor susceptibilidad a deslizamientos de taludes es coherente con la realidad física del cantón y
111
alguna infraestructura existente, que gravita especialmente en las parroquias más pobladas del cantón Otavalo.
5.3 RECOMENDACIONES
La presente tesis exploró una ruta de investigación que se puede seguir y reproducir sin mayores dificultades. Esta se puede mejorar con la convergencia de información geotécnica de buena calidad, para una mejor aproximación al método del bloque deslizante propuesto por Newmark (1965), siguiendo los lineamientos desarrollados por Jibson et al. (1998).
El análisis en su conjunto fue desarrollado a nivel cantonal, evidenciando las limitaciones que la técnica de inSAR tiene para su aplicación en regiones con mayor cobertura vegetal (la zona occidental del cantón). También fue evidente que áreas con pendientes muy abruptas o cuerpos de agua como las lagunas, arrojan inconsistencias en las mediciones
La técnica de SAR, que no incluye interferometría, si permite discriminar áreas lagunares y de ríos, incluso suelos con mayor o menor humedad. En las áreas con pendientes abruptas puede haberse sumado el efecto de una mayor cobertura vegetal o del rebote de la onda de regreso del radar interferométrico en paredes cuasi verticales cercanas. En investigaciones más detalladas, bien puede combinarse las técnicas de SAR e inSAR. En la presente investigación se pretendió cubrir una gran extensión de terreno, surgiendo contingencias diversas que fueron comentadas en los apartados correspondientes. Esto motiva a pensar que el análisis hubiera sido mejor desarrollado en un área pequeña de interés, en la cual contar adicionalmente con información geotécnica y geológica de calidad. Sería recomendable concentrar el análisis en áreas geográficas vinculadas a proyectos viales, de conducción de aguas, de construcción de equipamientos estratégicos, de expansión de zonas urbanas.
En Otavalo existen concesiones para prospección de oro y otros minerales en un sector con la mayor incidencia de la amenaza sísmica (Selva Alegre, occidente del cantón). Las intervenciones antrópicas de este carácter pueden ser eficazmente monitoreadas con interferometría, vinculando a la información geológica, sísmica y geotécnica particular de cada sector.
112
El desarrollo de investigaciones similares en estudios de infraestructura básica, para el trazado y construcción de carreteras, la dotación de equipamientos comunitarios estratégicos o para la ampliación de la mancha urbana son importantes porque permitirían orientar de mejor manera la concepción de proyectos futuros de desarrollo local
También posibilitaría el monitoreo, evaluación de los problemas observados en los proyectos que ya han entrado en operación, pues generalmente se irrumpe en el entorno natural induciendo vulnerabilidades, porque la concepción e implantación de los proyectos desconoció o no consideró las amenazas existentes en la región.
La identificación de áreas con riesgo de deslizamientos mediante interferometría puede ser respaldada en el campo con evaluaciones topográficas de alta precisión (levantamientos con drones), incluyendo reconocimientos geomorfológicos para caracterizar cambios de curso en el cauce de los ríos, la presencia de escarpes de fallas geológicas, la dirección de éstas, con la participación de perfiles profesionales multidisciplinarios
De esta manera, se contribuirá a la prevención y mitigación de riesgos naturales por fenómenos de deslizamientos, hundimientos y licuefacción de suelos. Estas prácticas de prospección del territorio, previas, simultáneas y posteriores a intervenciones antrópicas permitirían hacer más efectivos a los lineamientos legales de ordenamiento territorial, en todas las jurisdicciones político-administrativas del Ecuador.
113
6. REFERENCIAS
ArcGIS Pro (2021a). How inverse distance weighted interpolation works. Accedido 6 de abril de 2021. https://pro. arcgis. com/en/pro-app/help/analysis/geostatisticalanalyst/how-inversedistance-weighted-interpolation-works. htm, 17.
ArcGIS Pro (2021b). What is empirical Bayesian kriging? Accedido 6 de abril de 2021.
https://pro.arcgis.com/es/pro-app/latest/help/analysis/geostatisticalanalyst/what-is-empirical-bayesian-kriging-.htm
ArcGIS Pro (2021c). What is areal interpolation? Accedido 6 de abril de 2021.
https://pro.arcgis.com/es/pro-app/latest/help/analysis/geostatisticalanalyst/what-is-areal-interpolation.htm
ArcGIS Pro (2021d). What are the different kriging models? Accedido 6 de abril de 2021.
https://pro.arcgis.com/es/pro-app/latest/help/analysis/geostatisticalanalyst/what-are-the-different-kriging-models-.htm
ArcGIS Pro (2021e). How local polynomial interpolation works. Accedido el 20 de enero de 2022. https://pro.arcgis.com/es/pro-app/latest/help/analysis/geostatisticalanalyst/how-local-polynomial-interpolation-works.htm
ArcGIS Pro (2022a). Understanding cokriging. Accedido el 20 de enero de 2022.
https://pro.arcgis.com/es/pro-app/latest/help/analysis/geostatisticalanalyst/understanding-cokriging.htm
Arias, A. (1970). Measure of Earthquake Intensity. Massachusetts Inst. of Tech., Cambridge. Univ. of Chile, Santiago de Chile.
Asamblea Constituyente del Ecuador (2008). Constitución de la República del Ecuador. Quito: Tribunal Constitucional del Ecuador. Registro oficial Nro. 449, 79-93.
Asamblea Nacional Ecuador (2016). Ley Orgánica de ordenamiento Territorial, uso y gestión de suelo. QUITO: REPUBLICA DEL ECUADOR/ASAMBLEA DEL ECUADOR.
Braun, A. y Veci, L. (2021). TOPS Interferometry Tutorial. Accedido el 6 de febrero de 2022. http://step.esa.int/docs/tutorials/S1TBX%20TOPSAR%20Interferometry%20with %20Sentinel-1%20Tutorial_v2.pdf
Bejar, M., Álvarez Gómez, J. A., Staller, A., Luna, M. P., Pérez López, R., Monserrat, O., ... y Martínez-Díaz, J. J. (2017). Evaluation of Earthquake-Induced Effects on Neighbouring Faults and Volcanoes: Application to the 2016 Pedernales Earthquake. En AGU Fall Meeting Abstracts (Vol. 2017, pp. S53C-0718).
Brune, J. N. (1968). Seismic moment, seismicity, and rate of slip along major fault zones, Journal of Geophysical Research, 73( 2), 777 – 784, doi:10.1029/JB073i002p00777
114
Butler, K. y Ding, D. (2018). Analysis Patterns for Multidimensional Scientific Data Accedido: 2 de junio 2022. A partir de: https://www.esri.com/about/newsroom/arcuser/analysis-patterns-formultidimensional-scientific-data/
Caballero Chaves, Ó. J. (2011). Base de datos de deslizamientos inducidos por sismos. Pontificia Universidad Javeriana. Facultad de Ingeniería. Departamento de Ingeniería Civil.
Cando-Jácome, M., Martínez-Graña, A., Chunga, K., y Ortiz-Hernández, E. (2020). Satellite radar interferometry for assessing coseismic liquefaction in Portoviejo city, induced by the Mw 7.8 2016 Pedernales, Ecuador earthquake. Environmental Earth Sciences, 79(19), 1-16. http://dx.doi.org/10.1007/s12665-020-09205-x
CERESIS. Centro Regional de Sismología para América del Sur. Catálogo de intensidades de Ecuador (en línea). http://www.ceresis.org/informacion-sismologica/catalogo-deintensidades/ecuador.html (accedido el 10 de marzo de 2021).
Chowdhury, R., Flentje, P., y Bhattacharya, G. (2009). Geotechnical slope analysis, pages 372, 442-444, 458 Crc Press. http://dx.doi.org/10.1201/9780203864203
Chunga, K. (2010). Shallow crustal earthquakes and seismic zonation for Ecuador through the integration of geological, seismological and morphostructural data. University of Insubria (Doctoral dissertation, University of Insubria).
Chunga, K., Michetti, A., Gorshkov, A., Panza, G., Soloviev, A., y Martillo, C. (2010). Identificación de nudos Sismogénicos Capaces de Generar Potenciales Terremotos de M> 6 y M> 6, 5 en la Región Costera y Cadenas Montañosas de los Andes septentrionales del Ecuador. Revista Tecnológica ESPOL–RTE, 23(3), 61-89.
Chunga, K., Pazmiño, N., Martillo, C., Quiñonez, M., y Huaman, F. (2013). Estimación de máximos niveles de sismicidad para el Litoral Ecuatoriano a través de la integración de datos geológicos y sismo-tectónicos. Revista Científica y Tecnológica UPSE, 1(2). http://dx.doi.org/10.26423/rctu.v1i2.17
Chunga, K., Quiñónez, M. F., Huaman, F., Besenzon, D., Mulas, M., Garcés, D., ... y Michetti, A. M. (2016). Geología de terremotos y tsunami. Instituto Panamericano de Geografía e Historia.
Eguez, A., Alvarado, A., Yepes, H., Machette, M. N., Costa, C., Dart, R. L., y Bradley, L. A. (2003). Database and map of Quaternary faults and folds of Ecuador and its offshore regions. US Geological Survey Open-File Report, 3, 289.
ESA, European Space Agency (2014a). Napa Valley quake. Accedido el 20 de enero de 2022, en
115
https://www.esa.int/ESA_Multimedia/Images/2014/09/Napa_Valley_quake#.Ye naku_9plc.link).
ESA European Space Agency (2014b). Paraná river flood. Accedido el 20 de enero de 2022
https://www.esa.int/esearch?q=parana+river+flood
ESA European Space Agency (2015). Nepal earthquake on the radar. Accedido el 20 de enero de 2022.
https://www.esa.int/Applications/Observing_the_Earth/Copernicus/Sentinel1/Nepal_earthquake_on_the_radar#.YenWZCeMnBA.link
Falconí, R. A., García, E., y Villamarín, J. (2010). Leyes de atenuación para sismos corticales y de subducción para el Ecuador. Revista Vol, 13(1), 1-18.
Ferreti, A., Monti-Guarnieri, A., Prati, C., Rocca, F. (2007). inSAR Principles: Guidelines for SAR Interferometry – Processing and Interpretation (Report TM-19). European Space Agency (ESA).
Fukushima, Y., y Tanaka, T. (1990). A new attenuation relation for peak horizontal acceleration of strong earthquake ground motion in Japan. Bulletin of the seismological Society of America, 80(4), 757-783.
Giraldo, R. (2002). Introducción a la geoestadística: Teoría y aplicación. Bogotá: Universidad Nacional de Colombia.
Henao, R. G. (1993). Introducción a la Geoestadística. Universidad Nacional de Colombia.
Hidalgo Montoya, C. y Vega Gutiérrez, J. (2014). Estimación de la amenaza por deslizamientos detonados por sismos y lluvia (Valle de Aburrá-Colombia). Revista Eia, 11(22), 103-117.
IG EPN, Instituto Geofísico de la Escuela Politécnica Nacional (2021). Catálogos Sísmicos. https://www.igepn.edu.ec/catalogos-sismicos (accedido el 10 de marzo de 2021).
Jibson, R. W., Harp, E. L., y Michael, J. A. (1998). A method for producing digital probabilistic seismic landslide hazard maps: an example from the Los Angeles, California, area (p. 98-113). US Department of the Interior, US Geological Survey.
Jibson, R.W. y Jibson, M.W. (2003). Java Programs for Using Newmark's Method and Simplified Decoupled Analysis to Model Slope Performance During Earthquakes. USGS Numbered Series. Open-File Report 2003-5. https://doi.org/10.3133/ofr20035
Kanamori, H., y McNally, K. C. (1982). Variable rupture mode of the subduction zone along the Ecuador-Colombia coast. Bulletin of the Seismological Society of America, 72(4), 1241-1253.
116
Kang, K., Ponomarev, A., Zerkal, O., Huang, S., y Lin, Q. (2019). Shallow landslide susceptibility mapping in Sochi ski-jump area using GIS and numerical Modelling. ISPRS International Journal of Geo-Information, 8(3), 148.
http://dx.doi.org/10.3390/ijgi8030148
Khazai, B. y Sitar, N. (2000). Assessment of Seismic Slope Stability Using GIS Modeling, Geographic Information Sciences, 6:2, 121-128, DOI:10.1080/10824000009480540
Krige, D. G. (1951). A statistical approach to some basic mine valuation problems on the Witwatersrand. Journal of the Southern African Institute of Mining and Metallurgy, 52(6), 119-139.
Matheron, G. (1962). Traité de géostatistique appliquée (No. 14). Editions Technip.
Medvedev, S. V., y Sponheuer, W. (1969, January). Scale of seismic intensity. In Proc. IV World Conference of the Earthquake Engineering, Santiago, Chile, A-2 (pp. 143153).
Monserrat, O., Moya, J., Luzi, G., Crosetto, M., Gili, J. A., y Corominas, J. (2013). Noninterferometric GB-SAR measurement: application to the Vallcebre landslide (eastern Pyrenees, Spain). Natural Hazards and Earth System Sciences, 13(7), 1873-1887. https://doi.org/10.5194/nhess-13-1873-2013, 2013
Newmark, N. M. (1965). Effects of earthquakes on dams and embankments. Geotechnique, 15(2), 139-160. http://dx.doi.org/10.1680/geot.1965.15.2.139
Nocquet, J. M., Mothes, P., y Alvarado, A. (2009). Geodesia, geodinámica y ciclo sísmico en Ecuador. Geología y Geofísica Marina y Terrestre del Ecuador, 83-95.
PMA - GEMMA. Proyecto Multinacional Andino: Geociencias para las Comunidades Andinas – Grupo de Estándares para Movimientos en Masa (2007) Movimientos en Masa de la Región Andina: Una Guía para la Evaluación de Amenazas Servicio Nacional de Geología y Minería. Publicación Geológica Multinacional No. 4, 432 p., 1 CDROM.
Presidencia de la República del Ecuador (2019). Reglamento de la Ley de Ordenamiento Territorial, Uso y Gestión del Suelo. Decreto Ejecutivo 860. Registro oficial Suplemento Nro. 460.
Rico Rodríguez, A. y del Castillo Mejía, H. (2011). La ingeniería de suelos: en las vías terrestres carreteras, ferrocarriles y aeropistas. Editorial LIMUSA.
Rivas-Medina, A., Aguiar, R., Benito, M. B., Gaspar, J., y Parra, H. (2014). Determinación del período de recurrencia y magnitud máxima para el control de las estructuras en el
117
rango elástico ante un sismo asociado a las fallas inversas de Quito. Revista Internacional de Ingeniería de Estructuras, 19, 201-217.
Schenková, Z., Schenk, V., Kalogeras, I., Pichl, R., Kottnauer, P., Papatsimba, C., y Panopoulou, G. (2007). Isoseismal maps drawing by the kriging method. Journal of Seismology, 11(1), 121-129. http://dx.doi.org/10.1007/s10950-006-9023-1
SGRE, Secretaría de Gestión de Riesgos y Emergencias (2020). Base de datos de eventos de riesgo 2010 – 2020.
Sharma, A. (2020). Estimating Subsidence using Sentinel 1 Data in SNAP (Step-by-Step Tutorial). Accedido el 16 de enero de 2022 https://youtu.be/YDkRRvy5RZw
Sheng, T. C. (2010). Manual de campo para la ordenación de cuencas hidrográficas: Estudio y planificación de cuencas hidrográficas (Vol. 13). Food & Agriculture Org.
Sichel, H. S. (1947). Fitting growth and frequency curves by the method of frequency moments. Journal of the Royal Statistical Society, 110(4), 337-347. http://dx.doi.org/10.2307/2981240
Soulas, J. P., Egüez, A., Yepes, H. U. G. O., y Perez, H. (1991). Tectónica activa y riesgo sísmico en los Andes Ecuatorianos y el extremo sur de Colombia. Boletín Geológico Ecuatoriano, 2(1), 3-11.
Spencer, E. (1967). A method of analysis of the stability of embankments assuming parallel inter-slice forces. Geotechnique, 17(1), 11-26.
http://dx.doi.org/10.1680/geot.1967.17.1.11
Standford University (2021) Statistical-Cost, Network-Flow for Phase Unwrapping. Accedido el 19 de mayo de 2022.
https://web.stanford.edu/group/radar/softwareandlinks/sw/snaphu/
Wang, G., Liu, Y., Hu, Z., Zhang, G., Liu, J., Lyu, Y., ... y Liu, L. (2021). Flood Risk Assessment of Subway Systems in Metropolitan Areas under Land Subsidence Scenario: A Case Study of Beijing. Remote Sensing, 13(4), 637.
http://dx.doi.org/10.3390/rs13040637
Wells, D. L., y Coppersmith, K. J. (1994). New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bulletin of the seismological Society of America, 84(4), 974-1002.
Witt, C., y Bourgois, J. (2009). Relaciones entre la evolución de la cuenca del Golfo de Guayaquil-Tumbes y el escape del Bloque Nor-Andino. Geología y Geofísica Marina y Terrestre del Ecuador desde la Costa Continental hasta las Islas Galápagos. Editores: Collot JY, Sallares V., Pazmiño N. Impreso: Argudo & Asociados, Guayaquil-Ecuador, 95-106.
118
Zhou, H., Che, A., Wang, L., y Wang, L. (2021). Investigation and mechanism analysis of disasters under Hokkaido Eastern Iburi earthquake. Geomatics, Natural Hazards and Risk, 12(1), 1-28. http://dx.doi.org/10.1080/19475705.2020.1856201
119


 Quito, 08 de agosto del 2022
Quito, 08 de agosto del 2022


















 Ilustración 21 Interferometría, mapa de elevación.
Ilustración 21 Interferometría, mapa de elevación.











