Tabla 3.1. Operadoras de servicio de transporte de rutas especificadas en el corredor vial E35

Ilustración 3.3. Flujograma de la metodología

En la primera etapa, se obtiene información de registros GPS de velocidad e información proporcionada por la ANT, a fin de estructurar una base de datos de entrada compuesta por una variable espacial y un conjunto de variables no espaciales La variable espacial se obtiene de los registros GPS de velocidad de las unidades de transporte que circulan por distintas rutas del corredor E35. Por otro lado, las variables no espaciales se componen de variables que caracterizan la operación de las empresas de transporte (obtenidas de los mismos registros GPS) y de variables descriptivas obtenidas de información proporcionada por la ANT.

La segunda etapa consta de dos estrategias generales de análisis: espacial y no espacial. El primer análisis general considera la aplicación de un AEDE compuesto por diferentes técnicas que permiten estudiar detalladamente el comportamiento de los datos GPS obtenidos de las empresas de transporte. Estas técnicas son: análisis estadístico espacial, análisis gráfico, autocorrelación espacial, multicorrelación y regresión espacial. Todas ellas son técnicas aplicadas de forma independiente y que aportan información específica para el análisis. El segundo análisis general consiste en la aplicación de un AED convencional (no espacial), en virtud de que se estudian variables no espaciales. Entre las técnicas que componen este análisis se encuentra el análisis estadístico, gráfico, multicorrelación, identificación de atípicos e identificación de grupos. El análisis no espacial tiene como propósito determinar los factores que mayormente influyen en la operación de las empresas de transporte.

Los análisis estadísticos mencionados usan como métricas a: la Media, Distancia Estándar, Desviación Estándar y Elipse para la variable espacial; y la media, desviación estándar, cuartiles, kurtosis y asimetría para las variables no espaciales. Con respecto a los análisis gráficos propuestos, se considera la creación de información ráster para la variable espacial y la creación de diagramas de caja e histogramas de los datos para las variables no espaciales.

Con respecto a la autocorrelación espacial, ésta se determina con base en el Índice de Moran. En el caso de la multicorrelación (correlación entre distintas variables), se utiliza la construcción de la matriz de correlación para el caso de variables espaciales (registros de velocidad de diferentes operadoras) y variables no espaciales.

Posteriormente, para la variable espacial se desarrollan modelos de regresión lineal considerando como variables explicativas a las coordenadas (X, Y) y como variable dependiente a la velocidad. En el caso de las variables no espaciales, el análisis AED correspondiente concluye con la identificación de operadoras atípicas y con la identificación de grupos de operadoras. La identificación de atípicos se efectúa mediante la aplicación del algoritmo del Factor Atípico Local (LOF, por sus siglas en inglés) sobre las variables no espaciales La identificación de grupos se consigue con la técnica clásica de agrupamiento K-means.

En la tercera y última etapa (etapa concluyente), se conjuga el análisis AEDE y AED en concordancia con el tercer objetivo planteado en el presente trabajo para relacionar los datos GPS y los factores no espaciales que influyen en la operación de las empresas de transporte Adicionalmente, en esta etapa se desarrolla la formulación de estrategias de mejora para el control y la planificación del transporte como un aporte de gran valor que surge posterior al diagnóstico de las operaciones de las empresas de transporte elaborado con análisis AEDE y AED

3.3. JUSTIFICACIÓN DE LA METODOLOGÍA

De acuerdo con las secciones que serán explicadas en la siguiente sección, se justifica la metodología considerada en virtud de que los diferentes análisis propuestos permiten cumplir con los objetivos planteados en este trabajo. Por ejemplo, con el procedimiento del análisis exploratorio de datos espaciales y no espaciales se podrá cumplir con el objetivo referente a analizar el comportamiento de los datos GPS de las rutas autorizadas dentro del corredor E35. En este procedimiento se incorporaron: análisis gráfico, estudio de autocorrelación espacial, análisis de grupos, regresión espacial; entre otros. De esta forma, la metodología considera análisis robustos para la identificación del comportamiento de las variables definidas, lo cual tiene concordancia, debido a la complejidad de los sistemas georreferenciados.

Los análisis propuestos se desarrollan a través del software ArcGIS y el lenguaje de programación Python. De este modo, se cuenta con herramientas y códigos complejos y automatizables para una obtención precisa de los análisis indicados.

Por otro lado, la aplicabilidad de la metodología considerada se justifica en que el análisis multivariante de datos es una herramienta fundamental que permite entender las correlaciones existentes entre diferentes variables, lo cual permitió la identificación y el análisis de los factores que influyen en las operaciones de las empresas de transporte, planteado como otro de los objetivos del presente trabajo. En este contexto, es preciso mencionar que la aplicación de técnicas multivariantes es necesaria considerando la complejidad de la información que se está analizando y el enfoque de los objetivos planteados.

Así mismo, la metodología está orientada a obtener la relación espacial existente entre los datos GPS y los factores influyentes identificados, a través del estadístico I de Moran, el cual se obtiene con el procedimiento planteado para la autocorrelación espacial.

Considerando el marco metodológico desarrollado en el capítulo de Revisión de Literatura, se aprecia que los estudios desarrollados incorporan en sus metodologías, un análisis exploratorio de datos en diversos ámbitos con resultados importantes para la interpretación del comportamiento de los mismos, lo cual, en la presente investigación se pretende aplicar para el área de transporte para obtener el diagnóstico de las operaciones, en donde los estudios desarrollados en el país se han enfocado a otros fines.

Finalmente, una vez integrados todos los análisis anteriores en concordancia con los objetivos definidos, la metodología permite el desarrollo y planteamiento de las estrategias de mejora para el control y planificación de transporte. De esta forma, todos los objetivos del presente trabajo pueden ser satisfactoriamente cumplidos.

3.4. DESARROLLO METODOLÓGICO

3.4.1. Obtención de datos para el análisis

En esta sección y en la sección 3.3.2., se presentan y se describen los datos que han sido utilizados para el desarrollo de la presente investigación tanto de carácter espacial como no espacial. De este modo, en la Ilustración 3.4, se presenta el diagrama resumen de la Etapa 1:

Datos analizados.

Obtención de la variables espaciales:

Registros GPS de velocidades.

Obtención de la variables no espaciales:

Registros GPS de operación y variables descriptivas a partir de base de datos ANT.

Ilustración 3.4. Estructura de la Etapa 1

3.4.1.1. Datos analizados

Registros GPS de velocidad de operadoras - Variable espacial

En el portal Transporte Seguro se tiene a disponibilidad datos georreferenciados de velocidad de las unidades vehiculares de las operadoras indicadas en km/h. Los registros GPS de velocidad y coordenadas (X, Y) de posición de las unidades vehiculares se registran con una frecuencia de 1 medición por cada minuto.

La información georreferenciada de velocidad disponible es considerada en este trabajo para desarrollar un diagnóstico de las operaciones de las empresas de transporte público en el corredor vial E35. El diagnóstico se efectúa mediante técnicas de análisis de datos espaciales que se describirán más adelante en la sección 3.4.

Dada la extensión de la información, se consideran registros de GPS de un día completo. El reporte contempla alrededor de 25000 medidas GPS por cada placa y por operadora. Dicho reporte depende de las unidades operativas en el día analizado, por lo que se analiza el registro de medidas según disponibilidad de los datos

En este sentido, cabe mencionar que no necesariamente todas las operadoras transitan en el corredor vial E35 en el mismo día, por lo que es necesario considerar mediciones en diferentes días, de esta manera se consideran registros para los días 13/07/2021 y 20/07/2021.

Además, es importante señalar que en el portal Transporte Seguro no se disponen de registros completos para ciertas operadoras. De acuerdo con la información proporcionada por este portal, se consideran un total de 28 operadoras para el presente estudio En la Tabla 3 2 se muestran las placas de las unidades vehiculares seleccionadas de cada una de estas operadoras y las respectivas rutas a ser analizadas.

Tabla 3.2. Placas operativas de las operadoras bajo estudio

Variables no espaciales

Los datos georreferenciados de velocidad constituyen información valiosa de la operación de una unidad vehicular en particular. A partir de esta información es posible identificar variables que representan detalladamente la operación de una empresa de transporte. Por ejemplo: velocidad media, excesos de velocidad, el tiempo necesario para recorrer su respectiva ruta o el análisis de los puntos en los que una unidad vehicular invade posiciones ajenas a su trayecto (operación fuera de ruta).

En este contexto, con el fin de efectuar un diagnóstico más detallado de las operaciones de las empresas de transporte público, en este trabajo se propone un análisis complementario al análisis espacial de la velocidad. El análisis adicional tiene como propósito principal estudiar la influencia de diferentes factores en las operaciones de las empresas de transporte. Para este análisis se contemplan variables no espaciales.

En el análisis complementario indicado se consideran diferentes variables que se desprenden de los registros GPS de velocidad (Variables de Operación de la Empresa de Transporte) y de información proporcionada por la ANT que describen a las operadoras (Variables descriptivas o características de las operadoras). Debido a que estas variables dejan de estar georreferenciadas, el estudio propuesto para este caso se basa en técnicas de análisis espacial convencional de datos, es decir, análisis no espacial. Las técnicas de análisis que se van a utilizar son descritas en las secciones posteriores.

Las variables no espaciales que se consideran en este análisis particular se indican en la Tabla 3 3

Tabla 3.3. Variables disponibles de las empresas de transporte bajo estudio a) Tiempo de ruta b) Velocidad media

A continuación, se describen distintas particularidades de estas variables.

Se refiere al tiempo de viaje, expresado en segundos, de la ruta autorizada en el Título Habilitante a favor de la operadora de transporte. Para cada operación diaria, el reporte GPS contiene la información de tiempo de ruta por cada placa perteneciente a una operadora de transporte que presta el servicio dentro del área de estudio.

Corresponde al cálculo entre los valores de distancia expresada en kilómetros y el tiempo de ruta; expresada en segundos, detallado en el párrafo anterior. Estas dos variables forman parte del reporte GPS. La ecuación de cálculo es la siguiente:

Velocidadmedia= Distanciaderuta Tiempoderuta (3 1) c) Número de excesos d) Exceso de velocidad

Esta variable define el número de registros con excesos de velocidad que se obtienen para una unidad vehicular en las mediciones GPS. Se considera exceso de velocidad cuando una unidad supera los 90 km/h. Cabe mencionar que en cada reporte GPS disponible del portal de la ANT se muestra el número de excesos según cada placa del vehículo correspondiente.

Corresponde al cálculo del número de excesos de velocidad por placa dividido para el número de registros totales de excesos de velocidad registrados por toda la operadora en el día analizado. La ecuación es la siguiente:

Excesodevelocidad= númerodeexcesos totalderegistrosdeexcesosdelaoperadora (3 2) e) Operación en ruta

La presente variable, obtenida a partir de herramientas de geoprocesamiento en ArcGIS, representa la relación entre el número de registros en los que una unidad se encuentra fuera de la ruta especificada en su título habilitante, es decir, invade una ruta ajena a la permitida y el número de registros totales de esa unidad.

OperaciónenRuta= No.registrosdeunaunidaddentroderuta No.registrostotalesdeunaunidad (3.3) f) Unidades habilitadas g) Cobertura instalación

Cabe mencionar que la invasión de una ruta ajena a la permitida, registrada en GPS, puede obedecer a diversos motivos, por ejemplo, problemas en la calibración y registro de datos desde el GPS, errores de medición o eventualidades que haya atravesado una unidad vehicular.

Corresponde a las unidades vehiculares habilitadas en el Contrato de Operación para cada operadora de transporte, y que operan una determinada ruta y frecuencia autorizada.

Esta variable corresponde a la división del número de kits de seguridad instalados en las operadoras de transporte sobre el total de unidades habilitadas en las mismas.

CoberturadeInstalación= númerodekitsinstalados totalunidadeshabilitadas (3 4) h) Frecuencias en ruta

Se refiere al total de frecuencias autorizadas en Contrato de Operación para cada una de las rutas autorizadas para las operadoras de transporte, para la presente investigación las frecuencias en ruta corresponden a las rutas Quito-Ambato, QuitoLatacunga y Quito-Riobamba; respectivamente i) Total rutas

Corresponde al número total de las rutas autorizadas en Contrato de Operación, esta variable permitirá tener una noción de la dimensión de cada operadora j) Total frecuencias k) Cantón código

Corresponde al número total de las frecuencias autorizadas en Contrato de Operación, esta variable permitirá tener una noción de la dimensión de cada operadora.

Corresponde a la asignación numérica acorde al cantón en el que se encuentra domiciliada la operadora de transporte en análisis, bajo el detalle de la Tabla 3.4.

Adicionalmente, se complementa el conjunto de variables descrito con aquellas referentes a: Gestión Organizacional, Gestión Financiera, Gestión de Conductores y Personal de Apoyo, Gestión de Prestación del Servicio, Gestión Operativa Control y Seguridad, las cuales fueron definidas en la sección 2.1.5.

3.4.1.2. Obtención de variables espaciales

De acuerdo con las descripciones anteriores y a la Ilustración 3 4 presentada en la sección anterior, en este trabajo se utiliza como datos de entrada: registros GPS de velocidad de las operadoras y variables no espaciales compuestas por variables de operación y descriptivas de las operadoras. En esta sección se detalla el proceso para la obtención de esta información.

Obtención de Registros GPS de velocidad

A continuación, se incluye el detalle de la obtención de los registros GPS de velocidad del portal Transporte Seguro. Para el acceso a la plataforma se requiere de la creación de un usuario, al que se asigna un perfil determinado para el uso y aplicación de la información.

La interfaz de la plataforma se muestra en la Ilustración 3.5, la cual presenta como pantalla principal el módulo de Monitoreo, que permite visualizar en tiempo real la operación de una ruta autorizada.

Ilustración 3.5. Interfaz principal de la Plataforma de Transporte Seguro

Para el presente trabajo, se requiere del uso de un módulo denominado Reporte (ver Ilustración 3 6), en el cual se genera toda la reportería referente a vehículos (unidades de transporte) y GPS; entre los principales. El primer reporte generado corresponde a Trayectoria Histórica, el cual contiene los datos de operadora, placa, coordenadas, entre otros.

Ilustración 3.6. Interfaz del Módulo Reporte-Trayectoria Histórica

Con la opción de descarga, se pueden obtener los reportes en formato .xlsx, mismos que fueron cargados en ArcGIS, con la finalidad de obtener la variable Placa, que se encuentra operando las rutas autorizadas dentro del corredor E35; mostradas en la Tabla 3.1.

Otro de los reportes necesarios corresponde a Excesos de Velocidad, tal como se puede apreciar en la Ilustración 3 7. El reporte contiene la información únicamente de la velocidad registrada mayor a 90 km/h categorizada como exceso de velocidad para cada placa, de este modo se genera otra de las variables; denominada asimismo excesos de velocidad, correspondiente a la placa identificada en una de las rutas autorizadas de la zona de análisis, y la variable velocidad máxima.

Por otro lado, se dispone del reporte de Tiempo de Conducción, el que proporciona la información de tiempo (seg) y distancia (km), en la Ilustración 3 8 se muestra el detalle de su interfaz. Con los datos del reporte se generaron las variables de tiempo, distancia y velocidad media.

Ilustración 3.8. Interfaz del Módulo Reporte-Tiempo de Conducción

En la Ilustración 3 9, se muestra el reporte de Resumen de Exceso de Velocidad, mismo que cuantifica los excesos de velocidad por placa dentro de la ruta autorizada, con ello se obtiene la variable número de excesos.

Ilustración 3 9 Interfaz del Módulo Reporte-Resumen de Exceso de Velocidad

Finalmente, de acuerdo con la Ilustración 3.10, para la obtención de la variable espacial de velocidad, se dispone del reporte Actividades por Fecha, en el que existe la información de la velocidad en cada una de las coordenadas registrada por placa perteneciente a la operadora.

Ilustración 3.10. Interfaz del Módulo Reporte-Actividades por Fecha

3.4.1.3. Obtención de variables no espaciales

En este apartado se describe la propuesta de obtención de variables no espaciales a partir de registros GPS de velocidad, considerando la formulación detallada en la sección 3.4.1.1. Adicionalmente, el conjunto de variables no espaciales se compone de variables descriptivas que son proporcionadas directamente por la ANT.

Análisis de operación en ruta

Los datos GPS, obtenidos del portal de Transporte Seguro fueron cargados en el programa ArcGIS, para determinar dos variables necesarias, la placa (unidad vehicular) que operó la ruta del corredor en análisis, exportada a una nueva capa, y la operación en ruta normalizada entre 0 y 1. Con ello, se cuantificó el número de observaciones que se encuentran dentro de la ruta analizada, aplicando como primer paso la herramienta de geoprocesamiento buffer (contorno definido alrededor de una capa) para identificar los puntos que están dentro de dicho buffer. La distancia definida para el buffer se considera como el ancho aproximado de la vía del corredor E35 (30 metros) según se muestra en la Ilustración 3.11.

Ilustración 3.11. Buffer definido a partir de la ruta E35

Con la herramienta selection by location (ver Ilustración 3.12), se identificaron los puntos dentro del buffer definido en el paso anterior, para finalmente obtener la operación en ruta dividiendo la cantidad de observaciones dentro del buffer sobre la cantidad total de observaciones de la unidad vehicular. El valor de operación en ruta forma parte de la matriz de variables para el análisis estadístico posterior.

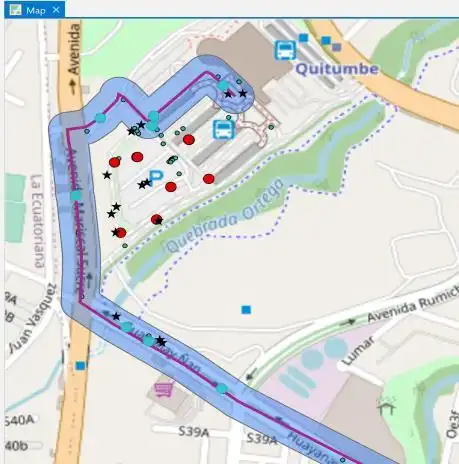
Herramienta de Geoprocesamiento

Capa de entrada: Placa operativa

Buffer

Puntos seleccionados dentro del Buffer

Ilustración 3.12. Selección de observaciones dentro del Buffer definido

En resumen, en la Tabla 3 5 se presenta la matriz de datos de las variables no espaciales descritas. Para esta información se propone el desarrollo de un análisis exploratorio de datos convencional o no espacial.

Tabla 3.5. Matriz de datos de variables de operación y variables descriptivas de las empresas de transporte bajo estudio

3.4.2. Análisis exploratorio de datos espaciales y no espaciales

En este trabajo se propone una diversidad de análisis para estudiar la operación de empresas de transporte. En la Ilustración 3 13 se presenta la estructura de la Etapa 2 que comprende tanto el análisis espacial como el análisis no espacial, la etapa central del presente trabajo que considera la ejecución de los dos primeros objetivos planteados. A continuación, las diferentes propuestas son explicadas, así como el aporte que brinda cada tipo de análisis al diagnóstico total de la operación.

Análisis exploratorio de datos espaciales: Análisis estadístico, gráfico, autocorrelación espacial, multicorrelación y regresión espacial

Análisis exploratorio de datos no espaciales: Análisis estadístico no espacial, gráfico, multicorrelación, identificación de atípicos y de grupos.

Identificación de factores que influyen en las operaciones de las empresas de transporte.

Ilustración 3.13. Estructura de la Etapa 2

3.4.2.1. Análisis exploratorio de datos espaciales

Dentro del ámbito espacial se puede aplicar la media espacial, distancia estándar, desviación estándar y elipse de desviación estándar. La media espacial en un sistema de coordenadas cartesiano corresponde a la ubicación promedio de un conjunto de datos con una característica espacial, esta definición se asemeja también al centro de gravedad de la superficie en donde se encuentran distribuidos los datos y es un indicador de la tendencia central espacial (Marschallinger, 2009)

Está determinada por las siguientes fórmulas:

Donde:

����: Valores en coordenadas x

����: Valores en coordenadas y

��: Total de puntos de la muestra

Por otro lado, la distancia estándar mide la dispersión espacial de un conjunto de datos en torno a su centro de gravedad, por lo que es considerada como una medida para el análisis de patrones. Asimismo, esta variable estadística, indica como los datos se encuentran dispersos de la media espacial. A mayor distancia estándar, será mayor la dispersión y viene dada por la siguiente fórmula:

Donde:

��,��: Media espacial en las direcciones x, y respectivamente.

En complemento, la elipse de desviación estándar es la representación de la tendencia espacial, debido a que la mayoría de los fenómenos espaciales no mantienen una extensión uniforme hacia todas las direcciones. Por lo tanto, se puede definir a la tendencia espacial, como la dependencia de la dirección de las distribuciones espaciales. La elipse de desviación estándar no considera únicamente la dispersión de puntos, sino que además considera la dirección de la extensión de la dispersión. Viene dada con la siguiente fórmula:

Donde ���� 2 ,���� 2 son las desviaciones estándar en las direcciones X, Y, calculadas con la ecuación estadística convencional de desviación estándar de una muestra (ver sección 3.4.2.1).

Análisis gráfico

Con el fin de observar la distribución espacial de la variable velocidad durante el trayecto de una unidad vehicular, es preciso analizar la información georreferenciada desde una perspectiva gráfica. En este sentido, los registros GPS de velocidad son transformados hacia información de tipo ráster De tal manera que la información velocidad durante el trayecto de una unidad vehicular se aprecie mediante capas georreferenciadas en el programa ArcGIS

En la Ilustración 3 14 se muestra un ejemplo de los gráficos que se consideran en este análisis. El principal enfoque consiste en relacionar las diferentes localizaciones del trayecto de una unidad vehicular con los rangos de velocidades que se han registrado. Como se muestra en el ejemplo, el análisis gráfico aporta la posibilidad de identificar patrones y la operación característica de la velocidad de las empresas de transporte de una forma gráfica y sencilla.

Ilustración 3.14. Ejemplo de análisis gráfico a partir de un ráster de datos de velocidad

Para crear un ráster a partir de los registros de velocidad se utilizan las herramientas de ArcGIS de acuerdo con lo indicado en la Ilustración 3.15.

Añadircapade puntos

Capade puntosde velocidad

Herramientade Geoprocesamiento

Capade entrada Campo: Velocidad

Rásterde Interpolación

Ilustración 3.15. Creación de un ráster a partir de registros de velocidad

Análisis de autocorrelación espacial

La autocorrelación espacial en información georreferenciada permite entender el grado en que un elemento es similar a otros elementos cercanos. La autocorrelación permite encontrar patrones que son visualmente apreciables en el espacio. En el caso del presente estudio, el análisis se enfoca en analizar la autocorrelación de la variable velocidad en cada punto (X, Y) de la capa “PUNTOS DE CONTROL” con la finalidad de encontrar el grado de similitud de velocidades entre estos puntos de control y poder hallar patrones en el comportamiento de la trayectoria de una unidad específica.

Una manera ampliamente extendida para medir la autocorrelación espacial de una variable es el índice de Moran (I de Moran). Este índice es considerado en este trabajo para el análisis de autocorrelación espacial. El índice de Moran está dado por la siguiente expresión:

Donde:

��: Número de observaciones o unidades espaciales a ser tomadas en cuenta

��: Valor de una observación

��: Media de todos los valores

������: Variable de peso

La variable de peso para el presente análisis corresponde a la distancia inversa. La interpretación de I de Moran, viene dada de la siguiente manera: valores positivos indica la existencia de grupos de valores similares, es decir una autocorrelación espacial positiva. Valores positivos más altos indican mayor autocorrelación espacial. Un valor negativo significa autocorrelación espacial negativa, valores cercanos a cero indica una falta de dependencia espacial.

Los valores z y p son medidas estadísticas, en donde un valor positivo de z es significativo cuando los valores similares forman agrupamientos espaciales Un valor negativo de z es significativo cuando los valores similares están espacialmente dispersos (Cai y Wang, 2006). Además, en este contexto de análisis, cuando p es menor a 0.05, se puede afirmar que existe algún patrón espacial específico y, por lo tanto, autocorrelación espacial.

El procedimiento para determinar el índice de Moran y las métricas asociadas (z y p) se esquematiza con la Ilustración 3 16

Herramientade Geoprocesamiento Puntos

Capadeentrada

Valordevelocidad Raster

ÍndicedeMoran z p

GráficaGausiana

Ilustración 3.16. Herramienta I de Moran

Análisis de multicorrelación

En este caso se estudia la relación entre los registros GPS de las operadoras consideradas en este trabajo. En este sentido, cabe mencionar que existe un diferente número de registros GPS para cada operadora. Además, estos registros no corresponden a mediciones efectuadas exactamente en las mismas localizaciones. Por estas razones, se crea una base de datos uniforme de velocidades con el mismo número de observaciones y considerando las mismas localizaciones para todas las operadoras. Todo esto con el fin de que el análisis a desarrollarse considere un mismo marco de referencia.

El procedimiento para conseguir una base de datos uniforme (igual número de observaciones e igual localización X, Y de estas) de registros GPS de velocidad es el siguiente:

1. Se genera una capa tipo punto compuesta por puntos distribuidos equidistantemente sobre la carretera de la ruta de análisis. La separación de estos puntos es del 1% de la distancia de la ruta (de este modo se generan 99 puntos sobre la carretera). Estos puntos funcionan como una capa base en la que se proyectan o interpolan los registros GPS de velocidad iniciales.

2. Se utiliza el ráster creado en el análisis gráfico para proyectar o interpolar los valores de los píxeles correspondientes en la capa de puntos base. Estos puntos se denominan en este trabajo como Puntos de Control debido a que simulan puntos de control fijos en la carretera y registran una misma cantidad de datos de velocidad de las empresas de transporte (como si se tratara de fotorradares)

Para generar la capa de puntos base se aplicó la herramienta GeneratePointsAlongLines sobre una capa de tipo línea que traza una ruta de análisis. Esto se desarrolló con el soporte de programación en lenguaje Python, como se indica en el siguiente segmento de código: import arcpy arcpy.env.workspace = 'C:/Users/Usuario/OneDrive/MAESTRIA/TESIS/DATOS/TESIS 21072021/TESIS 21072021.gdb' arcpy.GeneratePointsAlongLines_management('QUITO_AMB', 'percentage_intervals', 'PERCENTAGE', Percentage=1)

De acuerdo con la Ilustración 3 17, una vez ingresado el código se obtiene la capa de puntos de control, sobre la que se calculan las respectivas coordenadas (X, Y).

Puntos de control

Código

Ilustración 3.17. Uso de la herramienta GeneratePointsAlongLines para generación de capa de puntos base

Posteriormente, sobre esta capa de puntos base, se extraen los correspondientes valores de píxel del ráster de interpolación, como se muestra en la Ilustración 3.18. Para la obtención de los valores de velocidad en los puntos de control, se aplica la herramienta extract values to points, aplicado a cada operadora de transporte.

Puntosdecontrol

Rásterde Interpolación

Herramientade Geoprocesamiento

Puntosdecontrol RásterdeInterpolación

Puntosconvalor develocidad extraído

Ilustración 3.18. Extracción de valores de píxel del ráster de interpolación

Una vez efectuadas las acciones descritas antes, se obtiene una base de datos uniforme representada como una matriz con la forma indicada en la Ilustración 3 19 Se aprecia que de esta manera se tienen el mismo número de observaciones o registros (99) para el número de operadoras analizadas y estratificadas de acuerdo con su correspondiente ruta

Ilustración 3.19. Estructura de la Base de Datos uniforme de registros GPS de velocidad

La información de velocidad contenida en la base de datos se expresa como una matriz M de orden nxp de la siguiente forma:

Para la obtención de la correlación entre las diferentes operadoras es necesario definir a la matriz de correlación, la cual describe la correlación entre cada par del total de las operadoras analizadas. La matriz de correlación se define como (Peña, 2002):

Donde cada término rjk de la matriz está dado por:

El término de correlación rjk varía entre -1 y 1 y se calcula como:

En este sentido, el lenguaje de programación de Python cuenta con una herramienta gráfica para visualizar el resultado de la matriz de correlación de una manera más didáctica como un mapa de calor matricial ejemplificado en la Ilustración 3.20. Se considera suficiente estudiar únicamente la diagonal inferior de esta matriz debido a su simetría En cada campo de esta matriz se encuentra el valor calculado de correlación y se asigna también una escala colorimétrica coherente con el valor de esta correlación.

En este análisis, una correlación (positiva o negativa) más cercana a la unidad implica una mayor dependencia lineal (positiva o negativa) entre el par de variables analizadas. Una correlación cercana a 0 implica una menor dependencia lineal, pero no implica que las variables no tienen relación, debido a que puede existir una relación no lineal y más compleja.

Ilustración 3.20. Ejemplo de matriz de correlación

Análisis de regresión espacial

Los análisis descritos anteriormente permiten un diagnóstico detallado de las operaciones de las empresas de transporte. Sin embargo, aún resta el análisis de la relación matemática o cuantitativa entre las coordenadas (X, Y) y la velocidad.

Como un estudio final de la exploración de datos espaciales, se propone el desarrollo de un análisis de regresión considerando como variables explicativas a las coordenadas (X, Y) y como variable dependiente o de salida a la velocidad. En este sentido, el modelo de regresión se debe realizar para cada operadora, utilizando sus correspondientes registros de velocidad como variable de salida.

Este análisis tiene un aporte de gran utilidad, debido a que permite predecir velocidades de una ruta en particular según su ubicación durante el trayecto. Además, esta información sirve para identificar la ubicación de puntos de control o fotorradares una vez que se logren estimar localizaciones altamente susceptibles a que se produzcan excesos de velocidad.

Para este trabajo, se considera un tipo de regresión ampliamente utilizada en análisis de datos (Witten y Frank, 2005): la regresión lineal. Debido a que el detalle formalmatemático de este modelo de regresión escapa del alcance de este trabajo, no se describe la formulación matemática correspondiente

En este sentido, cabe mencionar que el lenguaje Python facilita el uso de este modelo de regresión sin la necesidad de que el usuario conozca en detalle la formulación matemática correspondiente. En Python este modelo se encuentra previamente programado de una manera compacta y lista para ser utilizada en cualquier tipo de problema con el soporte del módulo denominado sklearn.linear_model.LinearRegression (Pedregosa et al., 2012). Por esta razón, se utiliza este modelo de regresión de Python para el desarrollo de este análisis. En la Ilustración 3 21 se esquematiza la metodología considerada para el análisis de regresión.

Ilustración 3.21. Esquema de análisis de regresión con el uso de un modelo de regresión lineal disponible en librerías de Python

3.4.2.2. Análisis exploratorio de datos no espaciales

Este tipo de exploración se concentra en dos tipos de análisis: univariante y multivariante. El análisis univariante contempla el estudio de una sola variable en particular, independientemente de otras, mientras que el análisis multivariante analiza la relación entre múltiples variables (Peña, 2002) El análisis univariante contempla el análisis estadístico no espacial y el análisis gráfico, mientras que el análisis multivariante considera el análisis de multicorrelación, la identificación de atípicos y la identificación de grupos.

En primer lugar, la exploración de datos conlleva al análisis estadístico no espacial, el cual se trata de un análisis univariante. A continuación, se describen diferentes métricas estadísticas utilizadas (Galindo, 2010)

Valor medio o promedio

El promedio, notado como ��, de un conjunto de n mediciones es igual a la suma de sus valores dividido entre n; es decir;

Entre las ventajas del empleo del promedio se puede mencionar que se expresa en las mismas unidades de la variable, en su cálculo intervienen todos los valores de la distribución, es el centro de gravedad de toda la distribución, respetando a todos los valores observados y es único. Entre las desventajas se tiene únicamente que se ve afectado por la presencia de valores atípicos (Galindo, 2010)

Desviación estándar:

La desviación estándar de un conjunto de n mediciones ��1,��2,…,���� es la raíz cuadrada de la suma de los cuadrados de las desviaciones de las mediciones, respecto al promedio ��, dividida entre n-1; es decir:

La desviación estándar es siempre positiva y sus unidades de medida son las mismas que aquellas que corresponden a los datos originales y es única; entre sus principales ventajas.

Los inconvenientes de la desviación estándar es que en su cálculo intervienen todos los valores de la distribución y por ello puede ser complicada su obtención y se ve afectada por los valores atípicos.

Percentiles

Son cada uno de los 99 valores que dividen a la distribución de los datos en 100 partes iguales. Con ellos se pueden encontrar regiones donde se acumulan los datos; así, el 30% de los datos están por debajo del trigésimo percentil.

Cuartiles

Son valores que dividen a la distribución de los datos en 4 partes, cada una de las cuales engloba el 25% de los mismos.

Los cuartiles son tres, el cuartil inferior que deja a su izquierda el 25% de los datos, el cuartil medio que deja a su izquierda el 50% de los datos; coincide con la mediana, y el cuartil superior que deja a su izquierda el 7% de los datos. Por tanto, para calcular los cuartiles solo se deberá tener en cuenta que corresponden a los percentiles de orden 25, 50 y 75; respectivamente.

Kurtosis

En un conjunto de datos es importante analizar la homogeneidad de estos (Peña, 2002). En este sentido, existen diferentes métricas que permiten determinar si existen datos que se separan considerablemente de la media y que por tanto existe alta heterogeneidad. Una medida ampliamente considerada en análisis de datos es la kurtosis, la cual está dada por:

La manera en la que es posible medir la heterogeneidad es la siguiente:

• Cuando existen pocos datos atípicos en los datos la variabilidad será grande, por lo que la kurtosis será elevada (�� >0).

• Cuando los datos se asemejan a una distribución normal, el coeficiente de kurtosis toma un valor de 0.

• Cuando la kurtosis toma valores negativos significa que existen valores atípicos menos extremos que una distribución normal.

Asimetría (skewness)

En análisis de datos es útil el cálculo de coeficientes de asimetría que indiquen el grado de simetría de un conjunto de datos con respecto a su media. El coeficiente de asimetría en este caso puede ser calculado por la expresión dada por Peña (2002) de la siguiente manera:

Cuando se trata de una variable simétrica el coeficiente toma un valor de cero, caso contrario, el coeficiente difiere toma valores grandes a medida que la variable es más asimétrica.

Análisis gráfico

El análisis gráfico en este caso corresponde a la utilización de diagramas de caja e histogramas de las variables no espaciales. Con este tipo de gráficos es posible analizar la estructura de los datos que se analizan, la presencia de observaciones atípicas y la identificación de comportamientos característicos o patrones.

Análisis de multicorrelación

En este caso se analiza la correlación entre pares de variables no espaciales considerando la misma formulación matemática que se explicó en el apartado

3.4.2.1 Cuando se trata de múltiples variables, la multicorrelación permite la búsqueda de relaciones o influencias entre ellas (Witten y Frank, 2005). En este sentido, este tipo de análisis permite identificar los principales factores que influyen en las variables relacionadas con la operación de las empresas de transporte (ver Tabla 3.3).

La manera en la que se identifican estos factores es la siguiente Para cada variable de operación de las empresas de transporte (TIEMPO, VELOCIDAD MEDIA, NÚMERO DE EXCESOS DE VELOCIDAD, EXCESO DE VELOCIDAD Y OPERACIÓN EN RUTA), a través de la matriz de correlación, se determina cual es la variable descriptiva con la que existe una mayor correlación.

En la Ilustración 3.22, se expone la manera en la que se identifica la variable descriptiva con mayor influencia en una variable de operación. En este caso, se considera la variable TIEMPO. Para las variables de operación restantes se sigue el mismo procedimiento. Se debe recalcar que solo una variable descriptiva se considera a la vez.

Ilustración 3.22. Esquema de análisis de mayor influencia de una variable descriptiva sobre una variable de operación

Identificación de atípicos

El análisis propuesto en este caso está orientado a identificar aquellas operadoras que presentan disimilitud con respecto a las demás, con base en la información disponible de las variables no espaciales (ver Tabla 3.5). De esta manera, es posible obtener información adicional relacionada con las empresas de transporte que requieren mayor atención por presentar un comportamiento que se desprende de la tendencia normal que ostentan las demás operadoras.

La identificación de atípicos se desarrolla mediante la aplicación del algoritmo LOF, sobre las variables no espaciales. Este algoritmo se basa en la determinación de la densidad o concentración de datos. De manera que a cada dato se le asigna una ponderación según su distancia relativa con respecto a los datos vecinos o más datos más cercanos Si se supera cierta ponderación umbral (definida a priori en los parámetros del algoritmo), el dato analizado se considera como atípico.

El lenguaje Python cuenta con la librería sklearn.neighbors.LocalOutlierFactor en donde se encuentra implementado el algoritmo LOF. El algoritmo requiere como información de entrada básicamente la matriz de datos de la Tabla 3.5. Se considera la parametrización por defecto del algoritmo.

Identificación de grupos

El análisis de agrupamiento tiene por objeto agrupar elementos en grupos homogéneos en función de las similitudes entre ellos, es decir, la búsqueda de relaciones entre elementos que permitan el agrupamiento según sus características. De esta manera, se encuentra una manera más robusta de encontrar relaciones entre diferentes operadoras, debido a que se considera no sólo pares de variables, como en el caso del análisis de multicorrelación, sino que se considera la relación de una variable con las demás.

El agrupamiento de operadoras en grupos se desarrolla a partir de los datos de las variables de la Tabla 3 5 Se utiliza el algoritmo K-means para el desarrollo del agrupamiento. Este algoritmo divide un conjunto de observaciones (operadoras) en k grupos, de manera que cada observación pertenece al grupo cuyo centroide (valor medio) se encuentra más cercano (Peña, 2002).

El algoritmo requiere que previamente se defina el número de grupos a considerar. Una técnica empírica ampliamente utilizada es monitorear la suma de los cuadrados de las distancias dentro de los grupos de las observaciones hacia el centroide (suma definida con la nomenclatura SCDG). Si se tienen n observaciones, con k=n, SCDG (%) = 0%. Con k=1, SCDG (%) = 100%. De esta forma, se tiene una referencia con la cual se puede plantear el objetivo de definir k grupos para conseguir un SCDG (%) menor a un porcentaje determinado. Porcentajes de 20%, 15% o 10% son usuales en análisis de datos (Pedregosa, et al., 2012)

En la Ilustración 3 23 se presenta un ejemplo de monitoreo del SCDG a medida que se incrementa el número de grupos seleccionados.

Ilustración 3.23. Ejemplo de monitoreo de SCDG (%) para la identificación del número de grupos de operadoras

Fuente: Pedregosa et al. (2012)

Para el presente trabajo, se utiliza el módulo de Python sklearn.cluster.KMeans para el desarrollo de la identificación de grupos de operadoras considerando la matriz de datos de la Tabla 3 5

En este sentido, cabe mencionar que en la Tabla 3 5 se tiene un conjunto de 16 variables. Con el objetivo de que el algoritmo K-means pueda desarrollarse de una manera más precisa, con una matriz de datos más sencilla, se propone la reducción del número de variables mediante una transformación lineal conocida como Componentes Principales.

El análisis de Componentes Principales permite reducir el número de variables de una matriz de datos mediante la extracción de la información más representativa. Por ejemplo, en muchos casos, una matriz de p variables puede reducirse a una matriz de un número menor de variables o componentes, sin una pérdida significativa de información (Peña, 2002).

La reducción en componentes principales se desarrolla con el soporte del módulo de Python sklearn.decomposition.PCA (Pedregosa, et al., 2012) El número de nuevas variables o componentes se define a priori en Python. En este trabajo se considera el uso de 3 componentes principales, debido a que de esta manera se facilita la visualización del número de grupos en un diagrama tridimensional, como se ejemplifica en la Ilustración 3 24

Ilustración 3.24. Ejemplo de identificación de grupos en un conjunto de datos con la técnica K-means (se considera reducción de variables en tres componentes principales)

3.4.2.3. Factores que influyen en las operaciones de las empresas de transporte

Este análisis se reduce a identificar las variables producto del análisis de multicorrelación propuesto en la sección 4.2.3.; referente al análisis exploratorio de datos no espaciales. Los hallazgos son detallados en el siguiente capítulo de Resultados y Análisis en la sección 4.3

3.4.3. Análisis de relación espacial y planteamientos de estrategias

A través de la metodología planteada en la Etapa 2, se puede continuar con el análisis de la Etapa 3, esto en concordancia con los objetivos tres y cuatro planteados en el presente trabajo. En la Ilustración 3.25, se resumen los dos procedimientos considerados en esta etapa.

Relación espacial entre los datos GPS y factores influyentes

Estrategias de mejora para el control y la planificación de transporte

Ilustración 3.25. Estructura de la Etapa 3

3.4.3.1. Relación espacial entre los datos GPS y factores influyentes

Para determinar y lograr el cumplimiento del tercer objetivo, se plantea aplicar un análisis de multicorrelación entre el Índice de Moran; acorde a lo detallado en la sección 3.3.2.1. (Análisis de autocorrelación espacial) y las variables o factores influyentes obtenidos de acuerdo con lo indicado en la sección 3.3.2.3. Los hallazgos son detallados en el siguiente capítulo de Resultados y Análisis en la sección 4.4.

3.4.3.2. Estrategias de mejora para el control y la planificación de transporte

Una vez desarrollada la metodología planteada para el cumplimiento de los tres objetivos anteriores, se han descrito las estrategias a partir de cada resultado obtenido en concordancia al último objetivo definido Cada una de estas estrategias, son detalladas en el siguiente capítulo de Resultados y Análisis en la sección 4.5

Resultados Y An Lisis

En este capítulo se exponen los resultados obtenidos mediante la aplicación de la metodología propuesta, la cual se esquematizó en la Ilustración 3 3 Además, se presenta un análisis de los hallazgos más importantes. A continuación, se desarrolla cada uno de los estudios enmarcados en los enfoques generales del análisis AEDE y AED explicados en el capítulo anterior.

4.1. ANÁLISIS EXPLORATORIO DE DATOS ESPACIALES

4.1.1. Análisis estadístico espacial

En esta sección se analiza estadísticamente las coordenadas (X, Y) de los registros de velocidad de las operadoras de transporte que forman parte de este estudio. En la Tabla 4.1 se presentan los resultados de la media espacial, distancia estándar, desviación estándar de las mediciones y elipse de desviación estándar para el conjunto de registros GPS de velocidad obtenidos de las operadoras bajo estudio.

Tabla 4.1. Estadística descriptiva espacial para los registros GPS de velocidad de las operadoras bajo estudio

En el resultado estadístico mostrado se aprecia que el valor medio de la coordenada X es relativamente cercano para todas las operadoras, lo cual se espera en virtud de que la red vial E35 tiene una localización latitudinal. Con respecto al valor medio de la variable Y, se observan claras diferencias, debido a que existe una diferente dispersión en el conjunto de datos de registros GPS de las operadoras latitudinalmente.

Con respecto a la distancia estándar, se observa que el grado de dispersión es mayor para ciertas operadoras, como: ECUADOR EJECUTIVO, RIOBAMBA

EXPRESS, TRANSVENCEDORES. La interpretación física de este resultado es que las mediciones GPS han registrado localizaciones más dispersas o inclusive información incompleta. Una causa de este efecto son las intermitencias existentes en las mediciones GPS

Por otro lado, en el resultado de desviación estándar y elipse se aprecia cierta similitud en los valores obtenidos entre operadoras, con ligeras diferencias. En este sentido, en la Ilustración 4.1 se observa gráficamente el resultado comparativo del cálculo de la Elipse de desviación estándar para los registros GPS. Esto demuestra que existe consistencia en las observaciones obtenidas de todas las operadoras, es decir, una estructura de datos de los registros GPS similar, lo que permite inferir que estos registros se encuentran dentro de un contexto equiparable. De esta manera, es factible la comparación de operadoras considerando que cada una de ellas ostenta un registro tomado con unidades GPS independientes

Ilustración 4.1. Resultado de Elipse de desviación estándar de registros GPS de velocidad

Un resultado adicional del análisis estadístico mostrado es que no se evidencia la presencia de atípicos en los registros de coordenadas GPS.

4.1.2. Análisis gráfico

En este apartado se obtuvo de una manera gráfica la distribución espacial de los valores de velocidad en km/h de los registros GPS de las diferentes operadoras a través de información ráster. En la Ilustración 4.2, se presenta una muestra de los resultados obtenidos en ArcGIS para las operadoras de la ruta Quito-Ambato

En el resultado mostrado se aprecia la distribución espacial de la información de velocidad que caracteriza el comportamiento de las empresas de transporte. A partir de esta información se desprende información significativa, como las localizaciones en las que las operadoras incurren en excesos de velocidad. En este sentido, es posible identificar zonas comunes en las que se presentan excesos de velocidad. Esta situación puede ocurrir como causa de falta de puntos de control o mecanismos que motiven a las operadoras a mantener regulados sus rangos de velocidad dentro de los límites admisibles en Ecuador.

Quito

Ilustración 4.2. Muestra de resultados del análisis gráfico de operadoras de la ruta Quito-Ambato: a) 22 DE JULIO, b) AMAZONAS, c) AMBATO, d) AMERICA

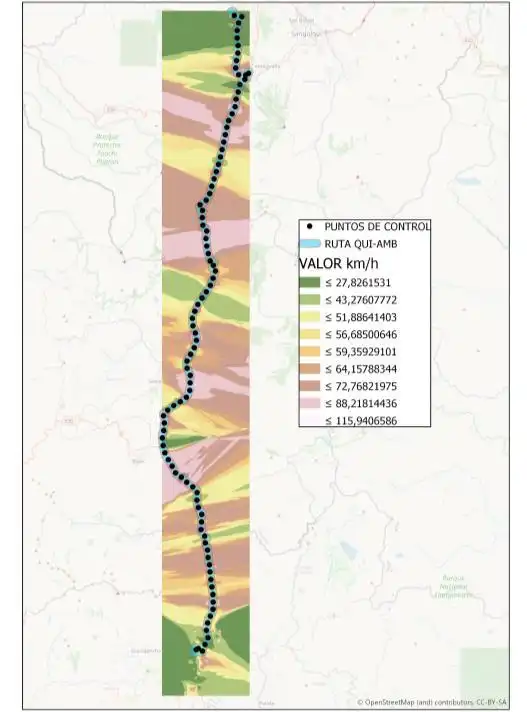
En la información ráster se identifica una cantidad apreciable de veces en las que existen excesos de velocidad. Por otro lado, también se identifican rangos de velocidad bajos, los cuales pueden corresponder a problemas de tráfico durante el trayecto, paradas no autorizadas de las unidades de transporte o eventos fortuitos.

Además, un resultado destacable de este análisis es que el comportamiento de las operadoras es considerablemente distinto, lo cual se evidencia en la información ráster y los patrones gráficos de velocidad que se observan. Esto demuestra claramente que la operación de las empresas de transporte es disímil

En el Anexo 1 se presentan los resultados completos de la Información ráster obtenida para el resto de las operadoras. De manera general, existen diferencias en los patrones que reflejan el comportamiento de la operación de las empresas de transporte. Esto será corroborado más adelante en el análisis de multicorrelación, en donde, en efecto, la correlación entre empresas de transporte es diversa.

4.1.3. Análisis de autocorrelación espacial

En este apartado se identifican patrones del conjunto de registros GPS de velocidad para las diferentes operadoras. Con el uso de la herramienta Autocorrelación espacial (I de Moran) de ArcGIS se miden las autocorrelaciones espaciales para cada operadora de transporte

En la Ilustración 4.3 se presenta una muestra de resultadosgráficos proporcionados por la herramienta ArcGIS sobre el cálculo del Índice de Moran. El gráfico proporcionado por el programa ArcGIS corresponde al resultado de una prueba de hipótesis1 que evalúa la significancia del índice de Moran. Además, se proporcionan los parámetros z y p de dicha prueba estadística.

Como se describió en la sección 3.4.2.1, un valor de z mayor conlleva a una mayor probabilidad de la existencia de grupos en el conjunto de datos. En este sentido, se obtuvo que para la mayoría de las operadoras, existen valores positivos de z elevados, es decir, la existencia de grupos o patrones en la información de velocidad de los registros GPS. a)

Ilustración 4.3. Muestra de resultados autocorrelación Operadoras: a) VAFITUR, b) SANTA, c) TURISMO BAÑOS

El resultado de autocorrelación para todas las operadoras se resume en la Tabla 4 2 La información expuesta indica que en 27 operadoras se obtiene la significancia adecuada (p-value menor a 0.05) para demostrar que existen patrones espaciales específicos en los registros de velocidad. Por lo tanto, en estas 27 operadoras existe con autocorrelación espacial en los datos. Por otro lado, en el caso de la operadora LIDER se aprecia un p-value mayor a 0.05. Esto implica que, para esta operadora, sus registros GPS no presentan ningún patrón espacial específico, es decir, no existe autocorrelación espacial. La interpretación física de este último resultado es que el comportamiento de los datos GPS para esta operadora no obedecen a una tendencia definida y son más cercanos a un comportamiento disperso.

Tabla 4.2. Resultado de autocorrelación del registro GPS de velocidad de operadoras

Con respecto a la operadora LIDER, en la Ilustración 4.4 se presenta el correspondiente resultado ráster En esta información ráster se aprecia la carencia de patrones de velocidad definidos, lo cual se corrobora en el índice de Moran calculado antes.

Ilustración 4.4. Resultado de Información ráster para la operadora LIDER

En el Anexo 2 se presenta el conjunto completo de resultados gráficos de autocorrelación.

4.1.4. Análisis de multicorrelación de la variable velocidad

De acuerdo con la Tabla 3 2, las operadoras bajo estudio recorren diferentes rutas del corredor E35. Por esta razón, para una comparación equitativa, se efectúa el análisis de multicorrelación por separado para las tres rutas posibles de las operadoras: Quito-Ambato, Quito-Latacunga y Quito-Riobamba.

En primer lugar, en la Ilustración 4.5 se presenta el resultado del análisis de multicorrelación de la Variable Velocidad entre Operadores de la ruta QuitoAmbato Se aprecia que existe una correlación significativa entre diferentes operadoras. Por ejemplo, entre las operadoras TOA y 22 DE JULIO se aprecia una correlación de 0.74, siendo el valor más elevado de este análisis. También, se observa una correlación apreciable de 0.72 entre las operadoras TRASANDINA y

AMAZONAS, lo cual implica que existe un comportamiento cercano a una dependencia lineal entre estas operadoras.

Ilustración 4.5. Multicorrelación de la Variable Velocidad entre Operadoras de la ruta Quito-Ambato

Con el propósito de profundizar en este análisis, en la Ilustración 4.6 se muestran gráficos de dispersión entre las cuatro primeras operadoras que recorren la ruta Quito-Ambato. Se incluye la distinción por cantón en el que se localizan las coordenadas correspondientes de cada dato de velocidad. La información mostrada refleja que en localizaciones del cantón Latacunga se presentan los mayores rangos de velocidad.

Ilustración 4.6. Matriz de gráficos de dispersión e histogramas de la Variable Velocidad (km/h) entre una muestra de las Operadoras de la ruta Quito-Ambato Además, en el resultado gráfico se aprecia que existe una mayor dispersión o rango de valores cuando las operadoras transitan en los cantones de Latacunga y Mejía, es decir, que presentan un comportamiento similar en el que ostentan mayor variabilidad en sus velocidades.

Con respecto a la ruta Quito-Latacunga, se obtuvo el resultado de la Ilustración 4 7, considerando que solo tres operadoras transitan en esta ruta. Para este caso, se obtienen valores significativos de correlación entre las tres operadoras, lo que indica un comportamiento lineal entre los registros de velocidad de estas operadoras.

Ilustración 4.7. Multicorrelación de la Variable Velocidad entre Operadoras de la ruta Quito-Latacunga

En este sentido, en la Ilustración 4.8 se expone la relación entre estas operadoras considerando gráficas de dispersión. Se aprecia claramente una tendencia lineal en la relación entre estas operadoras. Además, se obtienen mayores dispersiones cuando las operadoras transitan en Latacunga y Mejía. Se aprecia que en los cantones de Mejía y Latacunga se tienen mayores velocidades que en el caso de las velocidades obtenidas en Quito.

Ilustración

Ilustración 4.9. Multicorrelación de la Variable Velocidad entre Operadoras de la ruta Quito-Riobamba

Finalmente, en la Ilustración 4 9 se muestra el resultado de multicorrelación para las operadoras de la ruta Quito-Riobamba. En este caso se observan bajos valores de correlación entre las operadoras. Este resultado se aprecia de manera gráfica con la Ilustración 4 10, en donde se aprecia una dispersión lejana a una tendencia lineal.

Ilustración 4.10. Matriz de gráficos de dispersión e histogramas de la Variable Velocidad (km/h) entre una muestra de las Operadoras de la ruta Quito-Riobamba

4.1.5. Análisis de regresión espacial

En este caso, con el fin de evitar extender innecesariamente el análisis de este trabajo, se analizaron los modelos de regresión únicamente para las operadoras de la ruta Quito Ambato. En este sentido, en la Ilustración 4 11 se muestra el resultado de los modelos de regresión para las mencionadas operadoras.

Es preciso resaltar que los modelos de regresión desarrollados consideran como variable dependiente a la velocidad y como variables independientes a las coordenadas (X, Y). De esta manera, este análisis aporta con un potencial significativo para la agencia reguladora, debido a que permitiría predecir o estimar un valor de velocidad considerando una coordenada (X, Y) específica.

En el resultado mostrado se aprecia que, para ciertas operadoras, como INTERANDINA, FLOTA_PELILEO, CANARIO o HUAMBALO se obtienen ajustes de la regresión lineal muy aproximados a los registros de velocidad. Para el resto de las operadoras, a pesar de la alta dispersión que presenta el conjunto de datos, el modelo de regresión lineal se muestra como una técnica adecuada para relacionar coordenadas y velocidad.

Con el fin de incluir un criterio cuantitativo en este análisis, se calculó el error medio cuadrático para cada modelo de regresión. En la Tabla 4 3 se presenta el resultado de este error. Un valor menor del mismo indica una mejor aproximación del modelo al comportamiento real de los datos. De esta manera se corrobora que en las operadoras INTERANDINA y FLOTA_PELILEO se obtienen los modelos de regresión más precisos. En la práctica, esto implica que las estimaciones para estas operadoras serán más cercanas a la realidad.

De acuerdo con la gráfica mostrada, se aprecia que la relación entre las coordenadas (X, Y) y la velocidad es más compleja que una relación lineal. No obstante, con fines de simplificación y, de acuerdo con los bajos errores MSE mostrados en la Tabla 4.3, una regresión lineal puede ser suficiente para fines prácticos

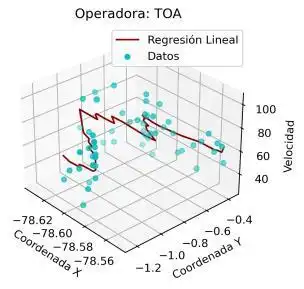
4.2. ANÁLISIS EXPLORATORIO DE DATOS NO ESPACIALES

En esta sección se presentan los análisis no espaciales desarrollados en torno a los datos mostrados en la Tabla 3.5.

4.2.1. Análisis estadístico no espacial

En la Tabla 4.4 se presenta el resultado estadístico descriptivo de las variables analizadas En primer lugar, se aprecia que entre la media y la mediana (Cuartil 50%) existen diferencias considerables para las distintas variables, por ejemplo, en la variable NÚMERO DE EXCESOS En este caso, la media es 3 54 y la mediana es 0. De esta manera, es evidente la presencia de operadoras atípicas considerando solo a la variable de excesos de velocidad, tomando en cuenta que existen operadoras con ningún registro de exceso de velocidad y otras con una cantidad apreciable de excesos (35). Una situación similar ocurre para el caso de las variables EXCESO DE VELOCIDAD y TOTAL DE RUTAS.

La falta de homogeneidad para los datos de las tres variables mencionadas también se aprecia en el cálculo de la kurtosis y la asimetría, en donde se obtienen valores excesivos, lo cual sugiere la presencia de observaciones atípicas en el conjunto de datos.

Para las variables restantes se aprecia que el valor de la media se acerca considerablemente al valor de la mediana, de manera que la distribución de datos puede considerarse como homogénea. Este resultado se corrobora en el cálculo de la kurtosis y el coeficiente de asimetría, en donde se observan valores bajos.