Modelos autorregresivos de serie de tiempo ARIMA

Introducción a las series de tiempo

Las series de tiempo presentan datos de una misma variable que cambia en el tiempo. A diferencia de los datos de corte transversal, las series temporales presentan datos ordenados de forma cronológica. Así, podemos analizar las ventas anuales de las empresas, por ejemplo, desde el año 2000 hasta el año 2021. Los productos terminados transportados a puerto cada trimestre, el número de personas capacitadas por la empresa mensualmente, la rentabilidad de la empresa cada semestre, las exportaciones del Ecuador de forma trimestral (ver Figura N° 1), entre otras variables de interés.

En esta estructura de datos el pasado influye sobre el futuro, pero no a la inversa. Esto debido a que podemos pronosticar una variable gracias a los datos pasados o también denominados rezagos. Por lo cual, siempre es recomendable contar con series largas de datos (se sugiere con más de 30 observaciones). No se pueden tomar muestras en este tipo de datos. Una característica importante de las series temporales es la periodicidad, es decir, la frecuencia con la cual se obtienen o recolectan los datos. La periodicidad puede ser diaria, semanal, mensual, trimestral, semestral, anual. Por ejemplo, las exportaciones de bienes y servicios del Ecuador se registran con periodicidad trimestral y anual.

Muchas series de tiempo económicas presentan un fuerte patrón estacional, por ejemplo, las ventas mensuales de ciertos productos agrícolas presentan cambios simplemente gracias a las condiciones climatológicas. Otro aspecto importante que se puede observar en una serie de tiempo es la tendencia, en el caso de las exportaciones de bienes y servicios del Ecuador (ver Figura N° 1) se puede observar que los datos presentan una tendencia creciente. Las series temporales son útiles para responder preguntas de tipo causal para las que los datos de corte transversal son inadecuados:

¿Cuál es el efecto de un cambio en el personal capacitado en la empresa cuando el cambio se produce en el futuro?

¿Cuál es la mejor predicción de las ventas anuales de la organización en los tres siguientes años?

¿Cuál es la mejor predicción de la rentabilidad anual de la organización en los tres siguientes años?

¿Cuál es la mejor predicción de las exportaciones de bienes y servicios del Ecuador en los tres siguientes años?

Las series de tiempo pueden contribuir a responder preguntas de efectos causales dinámicos y, de predicción o pronóstico. Por lo cual, plantean desafíos particulares y la necesidad de aplicar nuevas técnicas, una de ellas, es la metodología Box Jenkins.

Proceso autoregresivo integrado de promedios móviles ARIMA

Las series de tiempo nos permiten predecir sucesos futuros a partir de valores de la misma variable que sucedieron en el pasado. Este análisis nos lleva a introducir la noción de autoregresivo. Este tipo de modelos nos permite incluir variables predictoras adicionales precisas y fiables que no presentarán interpretación causal.

Por ejemplo, se puede pronosticar las exportaciones trimestrales de bienes y servicios del Ecuador para los próximos trimestres del año 2022. Si el último dato de la serie temporal es el primer trimestre del año 2022, entonces, al partir de este dato Y_t podemos pronosticar el futuro (los tres siguientes trimestres), Y_(t+1) , Y_(t+2), Y_(t+3). Esto solo será posible gracias a que utilizaremos datos del pasado Y_(t-1) , Y_(t-2),…, Y_(t-n), también conocidos como rezagos. Por lo cual, los modelos de series de tiempo toman en cuenta la dependencia existente entre los datos, esto es, cada observación en un momento dado es modelada en función de sus rezagos. Estos modelos se denominan ARIMA (Autoregresiva integrada de promedios móviles) debido a que cuentan con tres componentes AR (Autoregresivo), I (Integrado) y MA (Medias Móviles).

El modelo ARIMA parte del hecho de que una serie de tiempo económico puede ser no estacionaria, es decir, que la media y la varianza de la serie es no constante, por lo cual, la serie es integrada I(d). Por consiguiente, debemos diferenciar la serie temporal d veces para hacerla estacionaria y, luego aplicar el modelo ARMA (p,q). Por lo cual, decimos que la serie es ARIMA (p,d,q). Por lo cual, solo si contamos con una serie estacionaria podemos utilizar la metodología Box Jenkins.

El objetivo de la metodología Box Jenkins es identificar y estimar un modelo estadístico que nos permita pronosticar periodos futuros a partir de datos estacionarios o estables en sí mismo.

Metodología Box Jenkins

Esta metodología distingue 4 pasos para responder a las preguntas ¿cuáles son los valores p,d,q en un modelo ARIMA?

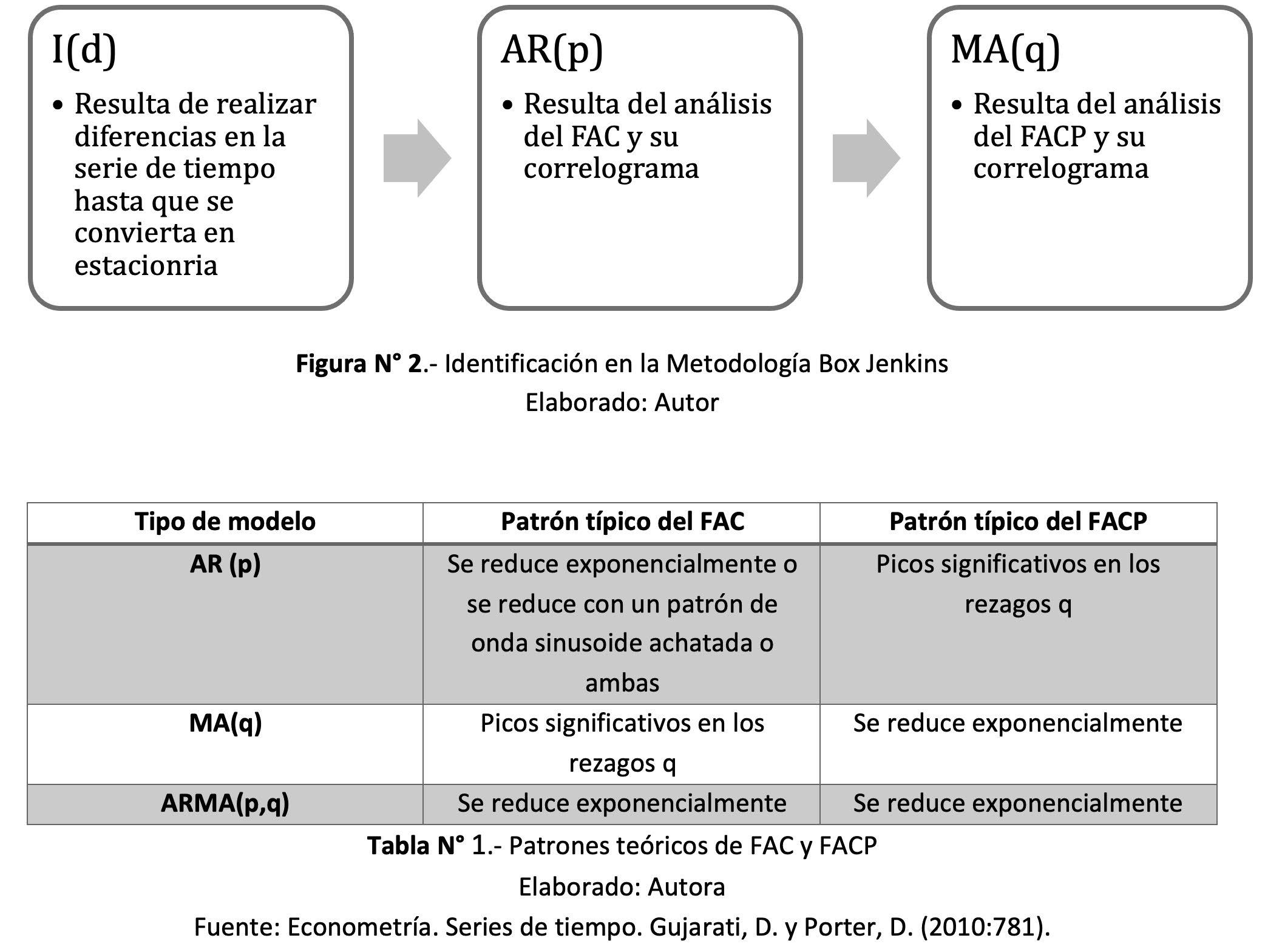
1.- Identificación: se analiza si la serie de tiempo es estacionaria o no a través de las pruebas de raíz unitaria, si no es estacionaria se aplican diferencias en las series hasta que esta se convierta en estacionaria, con ello, obtenemos el orden de integración de la serie (d), y conocemos el componente integrado I(d). Con la serie integrada, analizamos la función de autocorrelación (FAC), la función de autocorrelación parcial (FACP) y los correlogramas para identificar el proceso autoregresivos AR(p) y/o proceso de medias móviles MA(q). Es decir, hemos identificado p,d,q.

2.- Estimación: en esta etapa se estiman los parámetros de los términos autoregresivos (AR) y de promedios móviles (MA) incluidos en el modelo. Esta estimación se puede efectuar a través de mínimos cuadrados ordinarios, pero en otros casos, cuando la estimación es no lineal en parámetros, para lo cual, se utiliza softwares estadísticos.

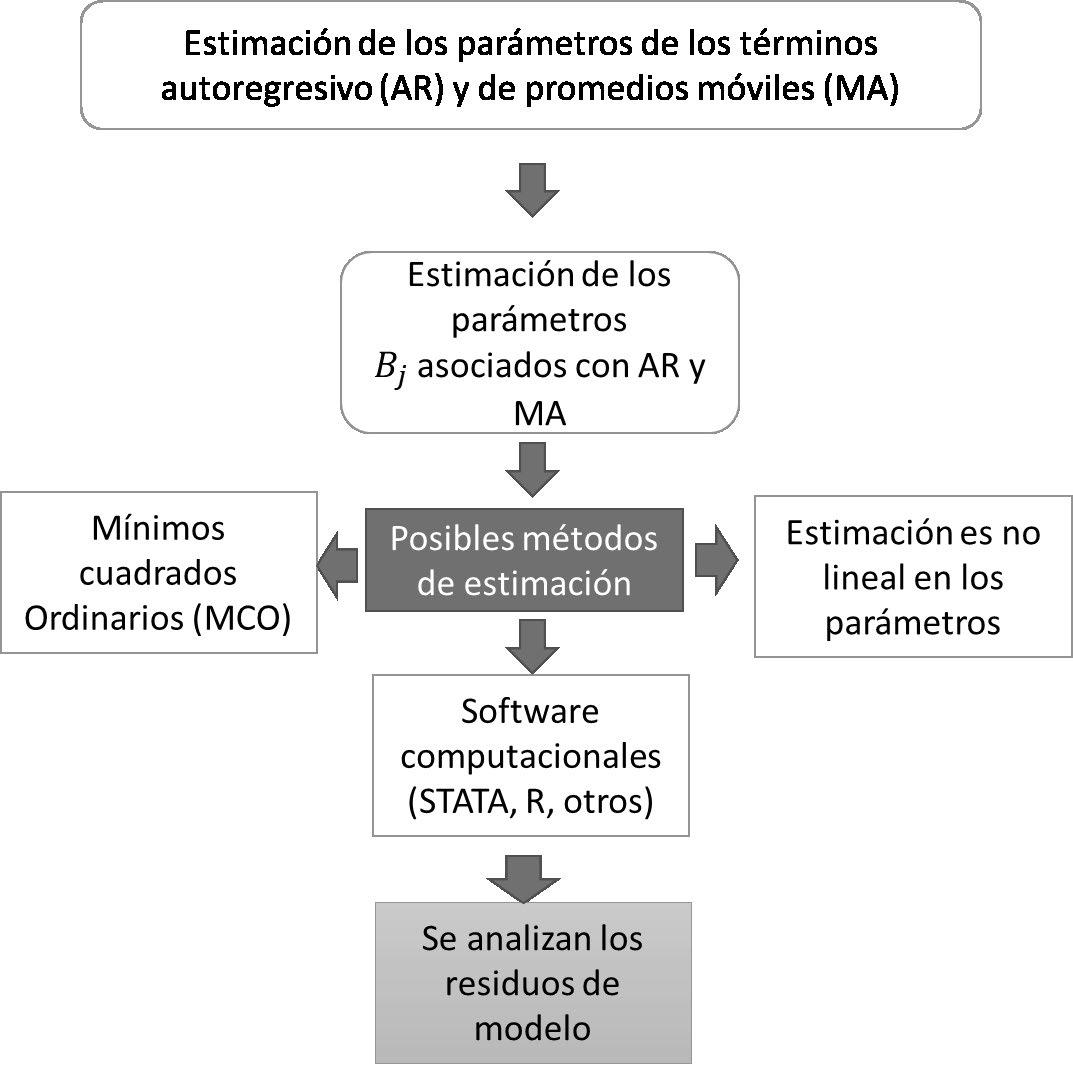
Figura N° 3.- Estimación de los parámetros Autorregresivos y de Medias Móviles

3.- Examen de diagnóstico: una vez identificado el modelo ARIMA y definido los parámetros p,d,q, es necesario evaluar si el modelo presenta un buen ajuste con los datos, ya que es posible que exista otro modelo ARIMA que también se ajuste adecuadamente a los datos. Por lo cual, se debe seleccionar el mejor modelo, para ello, se analizan los residuales del modelo y se identifica si son ruido blanco (es decir, su media es cero y, presentan una varianza constante). En el caso de no serlo es necesario iniciar nuevamente el proceso de identificación del modelo. Por lo cual, se destaca que este proceso es reiterativo hasta identificar el mejor modelo ARIMA.

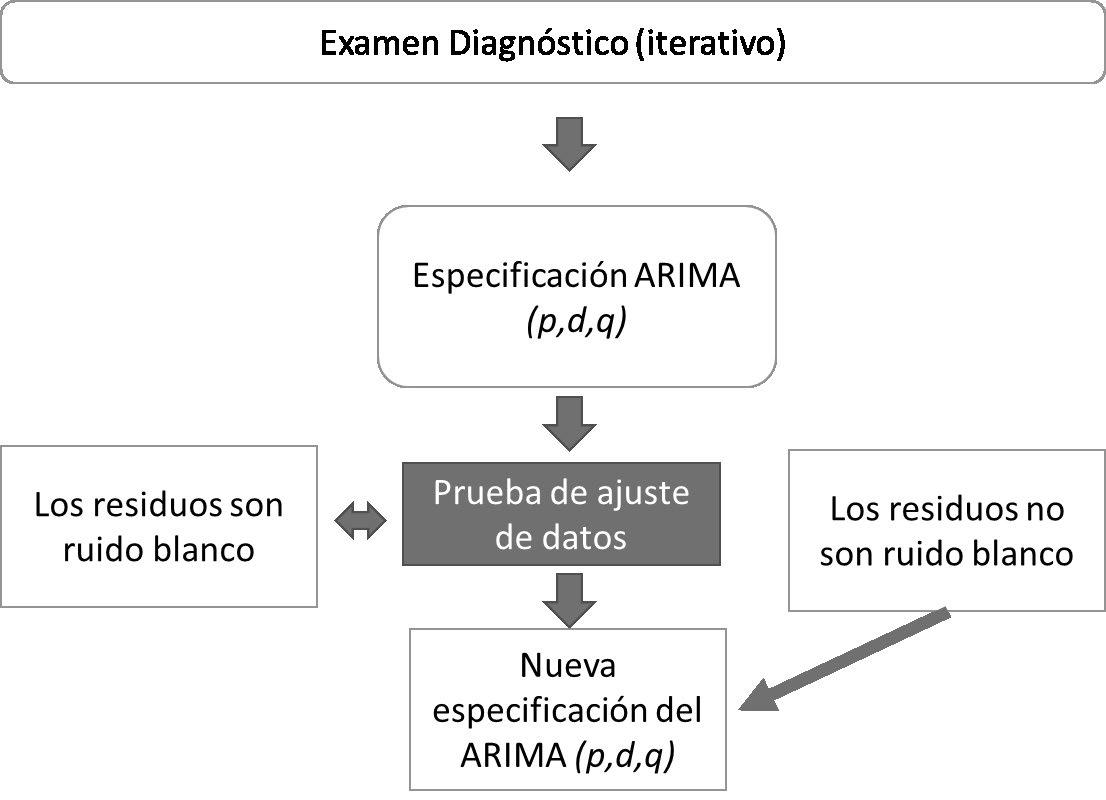
4.- Pronóstico: una vez identificado y especificado el modelo ARIMA (p,d,q) ya se puede realizar una predicción confiable de los datos. La potencia de este modelo es que nos permite obtener pronósticos más confiables que, por ejemplo, utilizando otros métodos, como pronósticos a corto plazo.

Cierre

Las series de tiempo son datos de una misma variable que cambian en el tiempo. Es decir, se encuentran ordenada de forma cronológica. Siempre cuentan con periodicidad, es decir, con la frecuencia con la que se toma los datos: diaria, semanal, mensual, trimestral, semestral, anual. Además, usualmente siempre presentan una tendencia que bien puede ser creciente o decreciente.

Las series de tiempo nos permiten pronosticar una variable para periodos futuros utilizando los datos del pasado, es decir, datos rezagados de la misma variable. Para ello, podemos utilizar el modelo ARIMA y, con ello, el método de estimación Box Jenkins.

El método Box-Jenkins es un método que busca encontrar el mejor modelo ARIMA a través de cual se pueda pronosticar la serie. Para lo cual, cuenta con cuatro pasos que bien pueden ser iterativos: identificación, estimación, examen del diagnóstico y, pronóstico. Recuerde que se requieren al menos 30 observaciones en una serie de tiempo para poder realizar un pronóstico y, que únicamente serán significativos los pronósticos de 2 a máximo 3 años, debido a que el entorno económico es cambiante y presenta incertidumbre.

Bibliografía

Gujarati D, and Dawn Porter C. 2010. Econometría. Madrid (España). McGraw-Hill. México. Quinta Edición