Gabriel Heyvaert
Livre de l’enseignant(e) A
Gabriel Heyvaert
ÉditionsVANIN
Livre-cahier A Livre de l’enseignant(e) A
Carrément MATH
Composition de Carrément math 5
Pour l’élève : 2 livres-cahiers A et B
Pour l’enseignant(e) :
Deux livres de l’enseignant(e) (comprenant le corrigé des livres-cahiers)
Leurs versions numériques sur Wazzou
Les annexes, des exercices supplémentaires et des évaluations disponibles sur Wazzou
Les manuels numériques (A et B) téléchargeables sur Wazzou
Carrément math 5 – Livre de l’enseignant(e) A
Auteur : Gabriel Heyvaert
Illustrations : M-A IZU (Marie-Anne Gueguen) et K'Naye (Karine Nayé-Roy)
Conception graphique : Octopus Creative Communication
Mise en page : NORDCOMPO
Couverture : Kiv'là
Voici le code qui vous donnera accès aux documents reproductibles en ligne liés au présent ouvrage.
Pour activer ce matériel complémentaire, rendez-vous sur www.monactivation.be et suivez-y la procédure d’inscription.
• Une fois votre accès activé, vous pourrez consulter le matériel complémentaire aussi souvent que vous le désirez et aussi longtemps que la version imprimée du présent ouvrage ne sera pas remplacée par une nouvelle édition.
• L’accès au matériel complémentaire ne peut être utilisé que par une seule personne.
• L’accès au matériel complémentaire vous est fourni gratuitement à l’achat de l’ouvrage Carrément Math 5 A Livre de l’enseignant(e). Aucune indemnité ne sera exigible en cas de non-fonctionnement ou d’indisponibilité du site hébergeant le matériel complémentaire ou du matériel complémentaire en lui-même, pour quelque raison que ce soit.
En cas de non-fonctionnement et/ou de question, nous sommes à votre disposition par courriel à l’adresse support@vanin.be.
L’éditeur s’est efforcé d’identifier tous les détenteurs de droits. Si malgré cela quelqu’un estime entrer en ligne de compte en tant qu’ayant droit, il est invité à s’adresser à l’éditeur.
L’orthographe telle que rectifiée le 6 décembre 1990 par le Conseil Supérieur de la langue française est d’application dans la collection. Toutefois, afin de respecter les écrits des auteurs, l’orthographe d’origine y est respectée.
Les photocopieuses sont d’un usage très répandu et beaucoup y recourent de façon constante et machinale. Mais la production de livres ne se réalise pas aussi facilement qu’une simple photocopie. Elle demande bien plus d’énergie, de temps et d’argent. La rémunération des auteurs, et de toutes les personnes impliquées dans le processus de création et de distribution des livres, provient exclusivement de la vente de ces ouvrages. En Belgique, la loi sur le droit d’auteur protège l’activité de ces différentes personnes. Lorsqu’il copie des livres, en entier ou en partie, en dehors des exceptions définies par la loi, l’usager prive ces différentes personnes d’une part de la rémunération qui leur est due. C’est pourquoi les auteurs et les éditeurs demandent qu’aucun texte protégé ne soit copié sans une autorisation écrite préalable, en dehors des exceptions définies par la loi.
Tous droits réservés. En dehors des exceptions définies par la loi, cet ouvrage ne peut être reproduit, enregistré dans un fichier informatisé ou rendu public, même partiellement, par quelque moyen que ce soit, sans l’autorisation écrite de l’éditeur.
1re édition : 2024
© Éditions VAN IN, Mont-Saint-Guibert – Wommelgem, 2024
ISBN 978-94-641-7808-1
D/2024/0078/186
Art. 602856/01
Chapitre 1
Table des matières
Chapitre 2
Chapitre 3
Chapitre 4
Chapitre
Chapitre 6
Chapitre 7
Faut faire le plein ........................................... 149
Attendus par matière ...................................................................................... GXVII
Matières abordées .......................................................................................... GXIX
Corrigé et notes méthodologiques .................................................................. G149
Chapitre 8 Des inventions incroyables ! ......................... 165
Attendus par matière GXXI
Matières abordées GXXII
Corrigé et notes méthodologiques .................................................................. G165
Table des pictos
SO LO
Travail individuel
D U O
Travail en duo
PETIT G ROUPE
Travail en petits groupes COLL ECTIF
Travail en groupe-classe
Documents à télécharger sur Wazzou : exercices supplémentaires, évaluations et annexes
Savoir(s)
Chapitre 1 Nouvelle rentrée
ATTENDUS PAR MATIÈRE
LES NOMBRES
Appréhender le nombre puis la lettre dans tous leurs aspects
Attendus
Utiliser des nombres pour communiquer :
– une quantité ;
– une position ;
– un numéro ;
Des nombres naturels aux nombres réels.
De la comparaison de collections puis de nombres à la relation d’ordre.
Savoir-faire
Dire, lire, écrire et représenter les nombres dans la numération décimale.
Décomposer et recomposer les nombres.
ÉditionsVANIN
Comparer, ordonner, situer des nombres.
Utiliser de manière adéquate les noms des rangs (unité, dizaine, centaine) et les noms des classes (des millions, des mille, des unités simples, des millièmes).
Associer le nom d’un nombre naturel jusqu’aux millions.
Utiliser de manière adéquate les termes liés à la cardinalité :
– égal, le même nombre que, autant que ; – moins que, plus petit que, autant en moins que ;
– plus que, plus grand que, autant en plus que ;
– vaut autant de fois ;
– vaut le dixième, le centième, le millième de…
Associer les symboles d’ordre (<, >, =) aux expressions « est plus petit que », « est plus grand que », « est égal à ».
Utiliser de manière adéquate les termes liés à l’ordinalité des nombres naturels : – avant, après, entre, juste avant, juste après ; – premier, deuxième… dernier.
Attendus
Dire, lire des nombres jusqu’au million et les écrire en chiffres. Expliquer la présence du zéro dans l’écriture des nombres jusqu’au million et dans un nombre décimal.
Décomposer et recomposer des nombres de trois à six chiffres en lien avec la numération décimale.
Utiliser le vocabulaire adéquat et les signes « < », « > » et « = » pour exprimer la comparaison de deux nombres. Exemple :
12,6 = 12,600
12,006 < 12,6
Ordonner des nombres de trois à six chiffres, avec ou sans virgule, de façon croissante ou décroissante.
Placer un nombre, avec ou sans virgule, limité au millième : – sur une portion de droite numérique graduée et sous graduée ; – dans des portions de tableaux numériques.
Exprimer la position d’un nombre, avec ou sans virgule, limité au millième (par encadrement, par approximation selon un degré de précision donné) sur une portion de droite numérique.
Créer des familles de nombres, relever des régularités.
Déterminer la régularité présente dans une suite de nombres donnée.
LES SOLIDES ET FIGURES
(Se) repérer et communiquer des positionnements ou des déplacements
Savoir(s)
Les visions de l’espace.
Savoir-faire
Attendus
Utiliser le vocabulaire exprimant des positions relatives (liées au regard) : devant, derrière, à droite, à gauche, en haut, en bas, au-dessus, en dessous, en face de, de face, de dos, de profil.
Attendus
Déplacer un objet ou soi-même. Tracer un déplacement sur un plan en suivant un enchainement de consignes orales ou écrites.
Situer, placer un objet dans un quadrillage.
Compétence(s)
Lire, interpréter des représentations de l’espace et les confronter au réel.
Savoir(s)
Situer (exprimer la position) un objet dans un quadrillage codé. Placer des objets dans un quadrillage en utilisant le codage.
Attendus
Tracer, sur un plan élaboré selon un quadrillage codé, un itinéraire à partir des points de départ et d’arrivée définis, en respectant au moins quatre points de repère pertinents identifiés.
Appréhender et représenter des objets de l’espace
Les figures, leurs composantes, leurs caractéristiques et leurs propriétés.
Savoir(s)
L’identification et la comparaison de grandeurs d’objets.
Savoir(s)
L’usage des unités conventionnelles.
ÉditionsVANIN
Attendus
Identifier les éléments du plan : droite et segment de droite.
LES GRANDEURS
Concevoir des grandeurs
Attendus
Utiliser de manière adéquate les termes relatifs aux grandeurs : la longueur, la masse, la capacité, le cout, l’aire, le volume.
Utiliser de manière adéquate les termes : longueur, largeur, épaisseur, profondeur, hauteur, périmètre, aire et volume.
Agir sur des grandeurs
Attendus
Utiliser et symboliser : – les unités de longueur ; – les unités de capacité ; – les unités de masse ; – les unités d’aire : le mètre carré (m²), le décimètre carré (dm²), le centimètre carré (cm²), le millimètre carré (mm²) ; – une unité de volume : le centimètre cube (cm³).
Distinguer dans l’expression d’une grandeur mesurée : la grandeur, la mesure et l’unité de mesure.
Savoir-faire
Construire le système des unités conventionnelles.
Attendus
Donner du sens aux unités conventionnelles travaillées en les associant à des objets de l’environnement (un m2 c’est l’aire de…).
Lister des objets de la vie courante dont une grandeur se mesure avec l’unité travaillée.
Donner du sens aux préfixes déci-, centi-, milli-, kilo-, hecto-, déca- dans les unités conventionnelles travaillées.
Compétence(s)
Articuler, en situations significatives, l’estimation d’une grandeur, son mesurage (avec les références et les outils adéquats) et l’appréciation du résultat.
TD
Attendus
Rassembler les instruments de mesure nécessaires et organiser judicieusement les prélèvements de mesures pour comparer des résultats.
LE TRAITEMENT DE DONNÉES
Collecter, organiser, représenter et interpréter des données
Savoir(s) Attendus
L’organisation d’objets, de données.
Compétence(s)
Lire et interpréter des données pour en extraire de l’information.
Résoudre des problèmes en utilisant les données prélevées.
Reconnaitre une représentation de données en : – tableau ; – ensembles ; – arbre (dichotomique) ; – diagramme à bandes.
Attendus
Prélever des informations issues d’une représentation : – d’ensembles incluant des intersections ; – d’un arbre ; – d’un tableau ; – d’un diagramme (à bandes, en bâtonnets et circulaire).
Les nombres
Les solides et figures
Les grandeurs
ÉditionsVANIN
Le traitement des données
Résoudre des problèmes de logique déductive en complétant un tableau à double entrée limité à vingt-cinq cases.
MATIÈRES ABORDÉES
Les nombres jusqu’à 100 000 : – lire – ordonner – classer – situer – écrire
Situer des objets et se déplacer dans un quadrillage Points, lignes et droites
Droites, demi-droites et segments de droite
Les grandes familles de grandeurs : – classement – reconnaissance
Donner du sens aux unités de longueurs, de capacités et de masses
Lecture de tableaux et de graphiques
Activité 1 – Les nombres jusqu’à 100 000
Situation de départ
COLL ECTIF
Introduction :
La voiture fait partie intégrante de notre quotidien. C’est un moyen de transport fort utilisé dans la vie de tous les jours et il n’est pas rare d’en avoir plusieurs par famille. Plusieurs discussions peuvent être lancées sur ce sujet : – le nombre de voitures dans le parc automobile, – la pollution et les carburants, – les énergies « propres »,
Exercice 1
SO LO
Matériel : – Annexes 1 et 2 : Abaques des grands nombres (pp. A1 et A2)
SO LO
SO LO
COLL ECTIF
Un problème est donné aux élèves. Ils (Elles) doivent le lire et répondre aux questions en tenant compte des informations relevées dans le problème.
Chaque élève a sa perception de la voiture idéale. Il (Elle) la dessine dans le cadre et il (elle) annote le dessin avec les informations demandées (prix, année et kilométrage) tout en y donnant du sens et de la crédibilité.
ÉditionsVANIN
Présentation de l’abaque complété aux élèves (annexes 1 & 2). Ils (Elles) l’observent et essaient de le mémoriser dans un laps de temps déterminé par l’enseignant(e).
Ensuite, ils (elles) essaient de compléter l’abaque vierge et de remplir les espaces vides.
Correction et mise en commun.
Remarque : ces abaques peuvent être utilisés tout au long de l’activité pour soutenir les apprentissages chez des élèves qui éprouveraient plus de difficultés.
Prolongement : l’enseignant(e) peut aussi demander aux élèves de mettre leur abaque dans une pochette plastique et, avec des marqueurs pour tableau blanc, d’écrire des nombres qui sont dictés par lui (elle) ou par des élèves.
Chapitre
Nouvelle rentrée 1
1. Les nombres jusqu'à 100 000
Le papa d’Eliot aimerait s’acheter une nouvelle voiture. Pour cela, il se rend dans un garage proche de chez lui afin de trouver le modèle qui conviendrait le mieux à lui et à sa famille de 4 personnes. Il dispose d’un budget de 15 000 €. Autres informations à prendre en compte : il désirerait une voiture avec un faible kilométrage et âgée de moins de 4 ans. Peux-tu l’aider?
12
Réponds aux questions.
Quelle voiture est la plus récente?
Quelle voiture est la plus chère?
La berline noire
Le SUV
Quelle voiture a le plus faible kilométrage?
La berline noire
Et toi, quelle voiture voudrais-tu? Dessine dans ce cadre la voiture de tes rêves et indique les différentes informations (prix, année et kilométrage). 1.
Réponse libre
Classe les voitures dans l’ordre croissant en fonction du prix.
< < < < <
Classe les voitures dans l’ordre décroissant en fonction du kilométrage. >
Lis ces nombres et complète l’abaque.
Classe des millions Classe des mille Classe des unités simples
Dictée de nombres
Exemple de correction
Écris, pour chacun des nombres dictés, sa décomposition.
Exercice 2
SO LO
Les élèves lisent chaque consigne et ils (elles) classent les voitures dans l’ordre croissant en fonction du prix, puis dans l’ordre décroissant en fonction du kilométrage.
Exercice 3
SO LO
COLL ECTIF
SO LO
Lecture collective
SO LO
Laisser aux élèves un temps de lecture pour qu’ils (elles) lisent chaque nombre l’un à la suite de l’autre.
SO LO
En s’aidant d’un exemple, les élèves replacent chaque nombre dans l’abaque, avec sa décomposition dans la colonne de droite.
Exercice 4
ÉditionsVANIN
Cinq nombres sont dictés et les élèves doivent les écrire sur les premiers pointillés, l’un en dessous de l’autre. Attirer leur attention sur les espaces entre les classes des millions, des mille et des unités simples.
Les longues lignes de pointillés seront utilisées pour l’exercice de dépassement. Il consiste à écrire la décomposition des cinq nombres dictés par l’enseignant(e).
Exercice 5
SO LO
Exercice de décomposition qui porte sur chaque chiffre qui compose le nombre.
Insister sur le rôle du zéro, qui indique l’absence d’une quantité dans un rang.
Exemple :
Lorsque j’écris 30 545, cela indique que j’ai 3 DM, 5 C, 4 D et 5 U. Il y a donc absence des unités de mille. Le zéro est indispensable car 30 545 est un autre nombre que 3 545 et ils n’ont donc pas la même valeur.
Exercice 6
SO LO
SO LO
Exercice de décomposition pour lequel un chiffre par nombre a été entouré. Les élèves doivent écrire le rang qu’il occupe dans le nombre.
Les élèves doivent entourer chaque fois le chiffre des centaines.
Exercice 7
SO LO
Exercice inverse.
À partir d’une décomposition, retrouver le nombre. Attention : pour certaines décompositions, l’ordre des rangs n’est pas toujours du plus grand au plus petit.
Petite astuce : placer des points en fonction du nombre de chiffres et combler par des zéros si des rangs sont absents.
Exercice 8
SO LO
ÉditionsVANIN
À présent, il s’agit de voir si chaque élève est capable de faire des décompositions et d’écrire les nombres qui en sont issus.
Bien laisser les élèves travailler seuls et ainsi vérifier si ce point de matière est bien acquis par chacun(e).
D U O
Variante : l’élève invente une décomposition et il (elle) la soumet à son (sa) voisin(e) afin que celui-ci (celle-ci) retrouve le nombre et/ou l’inverse.
Décompose ces nombres.
90 871 = 85 020 =
30 500 = 8 965 = 14 000 =
9 DM + 8 C + 7 D + 1 U
8 DM + 5 UM + 2 D
3 DM + 5 C
8 UM + 9 C + 6 D + 5 U
1 DM + 4 UM
Pour chaque nombre, que représente le chiffre entouré?
17 85 2
8 700
9 9 781
82 0
7 447
les dizaines
les unités de mille
les dizaines de mille
les dizaines
les unités
6 DM + 4 UM + 3 D + 1 U =
2 DM + 4 D =
7 C + 6 UM + 7 DM + 9 U=
3 D + 9 C + 8 U + 9 DM= 7.
1 UM + 8 C + 5 U =
Pour chaque nombre, entoure en orange le chiffre des centaines.
Retrouve les nombres à partir de leur décomposition. Écris-les.
Invente des décompositions et écris le nombre issu de sa décomposition.
4 CM + 3 DM + 4 C + 5 D (Exemple de correction)
Complète le tableau comme l’exemple.
Arrondis à l’unité de mille qui précède.
Arrondis à la centaine qui précède. Nombre
Arrondis à la centaine qui suit.
Arrondis à l’unité de mille qui suit.
Invente.
Complète les pointillés par <, > ou =.
Voici des compteurs kilométriques. Écris les nombres qui précèdent et/ou qui suivent.
Exercice 9
SO LO
Exercice d’encadrement. Encadrer chaque nombre entre la centaine qui le précède et la centaine qui le suit et faire de même avec l’unité de mille.
SO LO
Les élèves doivent inventer des nombres et réaliser l’encadrement pour chacun de ceux-ci.
Exercice 10
SO LO
Les élèves doivent indiquer sur les pointillés si c’est plus grand, plus petit ou égal. Ne pas hésiter à leur demander de transformer les décompositions en nombres entiers afin d’avoir plus facile pour comparer et placer le signe correct.
Exercice 11
ÉditionsVANIN
Premier exercice à réaliser de manière collective. Bien faire attention que l’on fait « +1 km » ou « -1 km » et qu’en fonction du kilométrage donné, il y a des passages.
COLL ECTIF
Suite des exercices : les élèves travaillent individuellement et complètent les différents compteurs kilométriques.
Exercice 12
SO LO
À partir des indices donnés dans chaque morceau de tableau, les élèves doivent compléter les cases grisées.
Au besoin, faire une petite structuration afin de vérifier si la (les) démarche(s) de chaque élève est (sont) correcte(s).
ÉditionsVANIN
Les élèves complètent le reste des cases. Cela permet aussi de vérifier si les réponses de l’exercice initial sont exactes.
COLL ECTIF
Complète les cases vides. 036496
Complète les parties grisées pour chaque morceau de ces tableaux numériques.
Complète les étiquettes de ces droites numériques.
Exercice 13
SO LO
Demander aux élèves de trouver la valeur entre deux graduations pour la première droite.
COLL ECTIF
Mise en commun. L’enseignant(e) fait l’exercice sur la première droite et demande à quelques élèves de verbaliser leur démarche.
SO LO puis COLL ECTIF
SO LO
On procède de la même manière pour la deuxième droite. L’important est de bien faire verbaliser chaque élève pour qu’il maitrise la démarche et puisse la transférer aux autres exercices.
Les autres exercices sont alors réalisés individuellement.
Exercice 14
SO LO
Les élèves doivent écrire le plus grand nombre naturel possible et le plus petit. Attention au(x) plus petit(s) nombre(s) : veiller à ce que les élèves ne placent pas de « 0 » devant car ils seraient alors inutiles.
ÉditionsVANIN
Exercices supplémentaires disponibles en téléchargement. Évaluation disponible en téléchargement.
Activité 2 – Situer des objets et se déplacer dans un quadrillage
Cette partie a pour toile de fond le plan du showroom du garage qui a été quadrillé. Elle est donc en prolongement avec l’activité précédente de ce premier chapitre. Tout d’abord, la première partie (pages 11 et 12) est consacrée à la notion de situer des objets. Quant à la deuxième partie (pages 13 et 14), elle travaille sur les déplacements.
Observer le plan et l’enseignant(e) vérifie la bonne compréhension des différents éléments s’y trouvant.
Exercice 1
SO LO
L’élève doit noter les coordonnées des cases qu’occupent les différents véhicules. Chaque coordonnée est notée en commençant par la lettre puis le nombre.
Exercice 2
SO LO
ÉditionsVANIN
Dans cet exercice, c’est l’inverse. Les coordonnées sont notées et les élèves replacent dans le quadrillage les véhicules avec les couleurs données.
Les élèves ont le choix du placement des deux véhicules tout en conservant bien le nombre de cases et en faisant attention qu’aucun véhicule ne se touche. Ils (Elles) ne doivent pas oublier ensuite de noter, sur les pointillés, les coordonnées de chaque case.
2. Situer des objets et se déplacer dans un quadrillage
Voici un plan du showroom du garage dans lequel le papa d’Eliot s’est rendu.
Écris la position (les coordonnées) des véhicules.
Colorie dans l’espace deux autres véhicules dont voici les coordonnées.
Place ces deux véhicules dans le showroom et note leurs coordonnées. Attention, les véhicules ne peuvent pas se toucher.
Nombreuses réponses possibles
Observe ce réseau et réalise ce que l’on te demande.
– Repère chaque case de la figure et inscris pour chacune les coordonnées.
– Colorie les figures suivantes dans le réseau ci-dessus.
Colorie deux figures de plus sur le réseau et indique leurs coordonnées sur les pointillés. Attention, aucune figure ne peut se toucher.
Figure 1 :
Figure 2 :
Nombreuses réponses possibles
D2
G3
J10
Exercice 3
Chaque élève observe attentivement ce réseau qui est un quadrillage présenté en oblique.
Tout d’abord, ils (elles) doivent repérer les coordonnées, puis les noter sur les pointillés dans les cases de chacune des deux figures, en se référant au réseau.
Pour l’exercice suivant, ils (elles) doivent colorier trois pièces dans le réseau en se basant sur une coordonnée qui leur est donnée pour chaque figure.
ÉditionsVANIN
Dans cet exercice de dépassement, les élèves doivent colorier deux figures qu’ils (elles) inventent, les placer dans le réseau en faisant bien attention qu’aucune figure ne se touche et, pour finir, écrire les coordonnées sur les pointillés.
Exercice 4
SO LO
On arrive dans la partie propre au déplacement.
Le showroom est de nouveau représenté sur cette page et un code écrit au-dessus indique le déplacement qui permet de sortir du showroom.
Le premier déplacement est représenté avec un fond rose. Les élèves doivent donc le continuer en respectant les indications.
Exercice 5
SO
Même exercice. La case verte représente le départ et, en suivant les indications, il faut arriver à la case rouge qui représente l’arrivée.
Au tour des élèves d’inventer un chemin pour rejoindre le point de départ à celui d’arrivée. Une fois leur chemin tracé, ils (elles) peuvent s’inspirer de la consigne de départ pour rédiger les différents déplacements.
Achève le trajet du papa d’Eliot pour sortir du showroom.
À l’aide des indications, trace le trajet demandé.
Légende :
Point de départ
Point d’arrivée
Obstacle
Trouve un autre chemin pour relier les deux cases et écris les différents déplacements.
Nombreuses réponses possibles
Même exercice.
Attention, cette fois-ci, tu dois suivre les lignes du quadrillage.
Légende :
Point de départ
Point d’arrivée
Obstacle
Trouve un autre chemin pour relier les deux cases et écris les différents déplacements.
Nombreuses réponses possibles
Coche le seul déplacement qui ne permet pas de relier les deux points marqués dans le quadrillage ci-dessous.
ÉditionsVANIN
Exercice 6
Le principe est le même ici par rapport à l’exercice précédent, sauf que les déplacements à effectuer se font sur les lignes du quadrillage et non pas de case en case.
Comme pour l’exercice de dépassement précédent, les élèves inventent un déplacement en faisant bien attention de l’effectuer en parcourant les lignes du quadrillage. Ensuite, ils (elles) écrivent les différents déplacements sur les pointillés.
Exercice 7
Bien attirer l’attention des élèves sur la lecture minutieuse de la consigne. Il s’agit de trouver le déplacement qui ne permet pas de relier les deux points.
Les élèves peuvent s’aider en traçant sur le quadrillage les différentes propositions et ainsi déterminer la proposition exacte.
ÉditionsVANIN
Exercices supplémentaires disponibles en téléchargement. Évaluation disponible en téléchargement.
Activité 3 – Que puis-je mesurer ?
Exercice 1
Les grandeurs sont présentes dans notre vie quotidienne sous diverses formes et unités.
Chaque élève y est d’ailleurs confronté en dehors de l’école, et cela à de nombreuses reprises, que ce soit avec le prix d’un achat, la température extérieure, la durée d’un travail, la distance à parcourir pour se rendre à une destination, etc.
Ainsi le point de départ de cette activité sur les grandeurs consiste à partir des représentations mentales des élèves et de leur vécu selon 3 aspects : – l’objet et la grandeur à mesurer, – l’outil pour effectuer la mesure, – la mesure de cette grandeur.
a) L’objet : ce que je peux mesurer comme la largeur du banc, la capacité du vase ou encore la durée de la récré.
b) L’outil pour mesurer : la largeur du banc avec un mètre, la capacité du vase avec un récipient gradué ou la durée de la récré avec un chronomètre.
c) La mesure de cette grandeur : la largeur du banc en cm, la capacité du vase en cl ou la durée de la récré en minutes.
D U O
Les élèves réfléchissent et indiquent quelques exemples sur leur feuille pour chacun des trois cadres.
COLL ECTIF
Mise en commun pour permettre d’exploiter au mieux toute la richesse des élèves.
Prolongement : l’enseignant(e) peut réaliser 3 panneaux reprenant les 3 aspects, avec par exemple une recherche préalable à domicile à effectuer par les élèves : trouver des images représentant une grandeur, un outil pour mesurer…
Remarque : l’écriture sera privilégiée pour les mesures.
Exercice 2
SO LO
Matériel : – Annexe 3 : Les familles de grandeurs (pp. A3-A4)
ÉditionsVANIN
Distribuer l’annexe 3 et observer les images.
SO LO puis
D U O
L’objectif est de faire prendre conscience aux élèves que pour ces 6 familles de grandeurs, il y a plusieurs outils permettant d’effectuer des mesures pour une même famille.
Tout d’abord, essayer de retrouver le nom de ces familles et indiquer l’intitulé de chacune dans les cadres prévus à cet effet. Ensuite, placer les images par famille sur le banc.
3. Que puis-je mesurer?
c) Quelles unités de grandeurs connais-tu? 1.
a) Que peux-tu mesurer dans la vie de tous les jours?
Discutes-en avec ton (ta) voisin(e) et inscris quelques exemples.
b) Avec quoi peux-tu mesurer?
Discutes-en avec ton (ta) voisin(e) et inscris quelques exemples.
Associe chaque image à la famille de grandeurs qui lui correspond (annexe 3).
Longueurs
Masses
Capacités
Monnaies
ÉditionsVANIN
Températures
Temps
Une fois que le classement est effectué, mise en commun. Lorsque le classement est juste, coller les images. Prolongement possible : montrer d’autres images aux élèves afin d’étoffer leur base de données (dynamomètre, planimètre, décamètre, …).
L’enseignant(e) peut même aussi faire découvrir d’autres appareils de mesure qui font référence à d’autres grandeurs tels que le tachymètre, le wattmètre, le manomètre, etc.
ÉditionsVANIN
Exercice 3
SO LO
Des situations sont proposées aux élèves. Ils (Elles) doivent déterminer la ou les famille(s) de grandeurs dont il s’agit.
Permettre aux élèves de partager leurs connaissances et de faire appel à leur vécu en inventant 3 situations et en cochant bien pour chacune la ou les case(s) correspondante(s).
Exercice 4
SO LO
Les élèves doivent à présent relier des unités de mesure avec les grandeurs qui leur correspondent.
COLL ECTIF
Ceci n’est qu’un aperçu de toutes les unités qui existent dans le monde. Ne pas hésiter à faire verbaliser les élèves par rapport à leur vécu et à leurs connaissances.
ÉditionsVANIN
De quelle grandeur s’agit-il?
Colorie les cases adéquates.
Le temps mis pour aller à l’école
La distance entre Liège et Bruxelles
La profondeur de la piscine
La quantité d’eau pour remplir un seau
Le prix de la nouvelle console de jeux
L’eau qui bout
La quantité de farine nécessaire
pour la préparation d’une pâtisserie
Prendre du diesel à la pompe et payer le plein
La hauteur de l’Atomium
La valeur d’une bague en or
Trouve d’autres exemples et coche la case adéquate.
Relie chaque unité de mesure à la grandeur qui lui correspond. 3.
Longueurs Masses (poids) Capacités Monnaies
4.
ÉditionsVANIN
kilo centime
litre
siècle mètre degré minute longueurs gramme masses (poids) centimètre capacités tonne monnaies
franc suisse températures semestre temps
Trouve l’unité adéquate en fonction de la situation.
engbers / Shutterstock.com
Le mont Blanc a une altitude de 4 809
Le Thalys en direction de Paris démarrera à 16 43
Cette pomme pèse 105
Aujourd’hui, le thermomètre affichait 26
Cette baignoire peut contenir 180
DÉCEMBRE 11
Le temps de brossage en moyenne pour les dents est de 2 30
La profondeur de cette piscine est de 90
Cette trottinette coute 45 50
Liège 15 Il faut encore rouler pendant 15
semaines
Dessine l’instrument utilisé pour chaque situation.
Jean pèse 36 kg.
À 10 h, nous prenons notre collation.
La température de l’eau est de 28 °C.
Dans 2 , ce sera le jour de Noël.
ÉditionsVANIN
une balance un pèse-personne un thermomètre un chronomètre
Lors de la dernière course, il a battu son précédent record.
La longueur de la classe est de 9 m.
un mètre un télémètre ou un décamètre une toise ou un mètre une horloge s
5m
Marie mesure 1,40 m.
Écris le nom de l’instrument sur les pointillés.
Exercice 5
SO LO
Dans toute cette multiplicité d’unités, certaines grandeurs se mesurent selon une unité bien précise en fonction d’une situation donnée.
Exemple : l’altitude d’une montagne sera exprimée en mètres et non en centimètres.
Exercice 6
SO LO
Exercice sur les instruments que l’on utilise pour mesurer les grandeurs. Les élèves dessinent l’outil, l’instrument dans le cadre.
Écrire le nom de l’instrument utilisé pour mesurer la grandeur. Les élèves peuvent utiliser le dictionnaire pour éviter les fautes d’orthographe.
ÉditionsVANIN
Exercices supplémentaires disponibles en téléchargement. Évaluation disponible en téléchargement.
Activité 4 – Points, lignes et droites…
Exercice 1
SO LO
COLL ECTIF
Observation d’un tableau de Vassily Kandisky intitulé Rouge-jaune-bleu (1925).
SO LO
L’enseignant(e) demande aux élèves ce qu’ils (elles) voient avec leurs yeux et ce qu’ils (elles) ressentent en eux (elles) quand ils (elles) regardent cette œuvre.
Kandinsky (1866-1944) est célèbre pour son rôle de pionnier de l’art abstrait.
Il s’emploie à inventer un langage de l’émotion : de grandes masses colorées se combinent librement avec des formes et des lignes qui parlent à la sensibilité, à la manière de la musique.
L’art abstrait est un mouvement international qui domine tout le 20e siècle. Il se positionne en rupture avec une conception traditionnelle de l’art comme imitation de la nature. Il ne représente pas des sujets ou des objets du monde naturel, mais des formes et des couleurs pour elles-mêmes. (Source : www.grandpalais.fr)
Prolongement : montrer aux élèves d’autres œuvres de Kandinsky ou même d’autres artistes qui ont marqué l’art abstrait tels que Mondrian, Kupka…
Les élèves doivent repasser sur ce qui leur est demandé en respectant les bonnes couleurs.
D U O puis
PETIT G ROUPE
SO LO
Si l’enseignant(e) remarque des difficultés chez les élèves, il (elle) peut leur proposer de travailler par deux ou en petits groupes.
Attention, il y a beaucoup de possibilités : il faut donc bien respecter les consignes. Mettre en avant que d’un(e) élève à l’autre, les réponses ne seront pas toujours identiques.
Se mettre dans la peau de Kandinsky et réaliser une composition. Importance de montrer d’autres œuvres pour donner des idées aux élèves.
ÉditionsVANIN
1.
4. Points, lignes et droites…
Observe attentivement ce tableau duquel on a enlevé les couleurs. Que vois-tu?
Exemple de correction:
Repasse :
– deux lignes droites en rouge; – deux lignes courbes en vert; – une ligne brisée en orange; – une ligne courbe fermée en bleu.
Vassily Kandinsky, né à Moscou le 16décembre1866 etmort le13décembre 1944, est un peintre et graveur russe. Il est l’un des fondateurs del’art abstrait. Il a peint ce tableau, intitulé Rouge-jaune-bleu, en1925.
À ton tour de jouer à l’artiste! Compose ton œuvre à la manière de Vassily Kandinsky et utilise les couleurs pour faire apparaitre les différentes lignes.
Complète avec les mots proposés et utilise les cadres pour les illustrer.
La ligne brisée – Le point – La ligne courbe – La ligne – La ligne droite est l’intersection de deux droites. On le désigne par une lettre majuscule.
La ligne
Le point A d a e
est un ensemble de points qui se suivent. On la désigne par une lettre minuscule.
Il en existe différents types.
La ligne droite
est le plus court chemin pour se déplacer d’un point à un autre.
La ligne courbe
change de direction sans cesse.
ÉditionsVANIN
La ligne brisée
est composée de segments de droite ayant une extrémité commune.
Exercice 2
Les élèves doivent associer le bon mot avec la définition.
Une fois cela fait, ils (elles) doivent également illustrer la définition en respectant chaque terme qui la constitue.
D U O puis COLL ECTIF
Comparaison avec son (sa) voisin(e) et mise en commun.
ÉditionsVANIN
Exercice 3
SO LO
On passe de la théorie aux exercices…
Les élèves prennent le temps de bien lire les consignes et placent sur le dessin les points demandés en tenant compte des définitions.
Une bonne appropriation des termes devra être assurée pour que les élèves puissent transférer ces notions aux exercices.
D’abord, tracer une ligne droite en tenant compte des informations données, puis placer les points demandés sur le dessin.
Exercice 4
SO LO
Application de la théorie. Les élèves relient chaque étiquette au dessin qui lui correspond.
ÉditionsVANIN
Observe ce dessin et place ces points :
M à l’intersection de la ligne a et b,
N sur la ligne courbe,
O à gauche de la ligne a,
P à l’intersection de la ligne brisée et de b,
Q à droite de la ligne a et en dessous de la ligne b.
Trace une ligne droite c qui coupe a et qui ne coupe pas et ne coupera jamais b.
Place les points suivants :
– R, entre la ligne droite c et la ligne droite b;
– S, à l’intersection de la ligne c et de la ligne a;
– T, à l’intersection de deux lignes qui ne sont pas droites.
Lis chaque étiquette et retrouve le dessin qui lui correspond.
Une ligne droite horizontale
Une ligne courbe fermée
Une ligne brisée ouverte
Une ligne droite verticale
Une ligne courbe ouverte
5.
Rappelle-toi…
Une ligne peut avoir trois directions, elle peut être… horizontale verticale oblique
Reproduis ce dessin.
Combien y a-t-il de…
– lignes horizontales?
– lignes verticales?
– lignes obliques?
Rappelle-toi
COLL ECTIF
Les notions de verticalité, d’horizontalité et d’oblique sont également employées en géométrie et dans d’autres domaines.
Demander aux élèves d’autres exemples de la vie de tous les jours dans lesquels on fait référence à ces trois notions.
Exercice 5
Exercices de reproduction d’une maison constituée de lignes horizontales, verticales et obliques.
ÉditionsVANIN
Les élèves doivent déterminer le nombre de lignes horizontales, verticales et obliques que compte le dessin.
Exercices supplémentaires disponibles en téléchargement. Évaluation disponible en téléchargement.
Activité 5 – Droites, demi-droites et segments de droite
Exercice 1
SO LO
Les élèves complètent les 3 définitions à l’aide des indices.
Attention : une même étiquette peut être utilisée plusieurs fois.
Mise en commun : lecture des définitions et compréhension de celles-ci en s’appuyant sur les illustrations. Bien insister sur le fait de nommer la droite, la demi-droite et le segment de droite et d’utiliser la notation correcte.
Exercice 2
SO LO
ÉditionsVANIN
Application de la théorie. Les élèves colorient la proposition correcte en fonction de ce qui leur est demandé.
COLL ECTIF
1. 2.
5. Droites, demi-droites et segments de droite
À partir des dessins et des indices, complète les différentes définitions.
ni fin
une portion de droite
court chemin une ligne d’un côté par un point par deux points ces deux points par une infinité de points alignés
Une droite est formée les uns après les autres. Elle n’a ni origine, .
On désigne une droite par une lettre minuscule ou par deux lettres majuscules.
Une demi-droite est limitée (son origine).
On désigne une demi-droite par deux lettres majuscules et par un crochet qui indique l’extrémité «[EF».
Un segment de droite est limitée C’est le plus entre
une ligne une portion de droite une portion de droite court chemin ces deu× points par deu× points d’un côté par un point ni fin par une infinité de points alignés
On désigne un segment de droite par deux lettres majuscules mises entre crochets «[AB]».
Colorie la bonne proposition.
Exerce-toi! Attention, pour chaque tracé, n’oublie pas de les nommer.
– Trace une droite c.
–Trace un segment de droite [EF] qui mesure 6cm.
– Trace une demi-droite GH]
– Trace un segment de droite [ST] qui mesure 7,5 cm et une demi-droite [BC ayant comme point d’intersection P.
– Trace deux demi-droites [KL et MN] dont le point d’intersection est Z.
ÉditionsVANIN
Exercice 3
Exercice de traçage. Les élèves tracent ; ils (elles) ne doivent pas oublier de nommer chaque tracé en tenant compte des indications données.
Bien indiquer l’utilité des petits pointillés pour déterminer s’il s’agit d’une demi-droite ou d’une droite et pouvoir ainsi les différencier.
ÉditionsVANIN
Exercices supplémentaires disponibles en téléchargement. Évaluation disponible en téléchargement.
Activité
6 – Donner du sens aux unités de longueur, de capacité et de masse
Exercice 1
SO LO
Les élèves doivent trouver, sur deux tickets de caisse, toutes les grandeurs qui relèvent des masses, des capacités et des longueurs.
Attention à bien respecter les couleurs et de remarquer qu’il y a des grandeurs inutiles, telles que les euros et les watts par exemple.
COLL ECTIF
Mise en commun et confrontation par rapport aux réponses trouvées.
Sur le ticket de caisse de Brico Fou, les élèves doivent calculer le solde de points actuel. Pour cela, ils (elles) doivent additionner le solde des points antérieur avec les points sur le ticket, plus ceux supplémentaires.
Exercice 2
SO LO
COLL ECTIF
À l’aide des différentes unités trouvées à l’exercice précédent et de leur connaissance, les élèves doivent compléter les abaques des trois familles de grandeur.
Mise en commun. Vérifier ses abaques et les compléter si nécessaire.
J’observe
SO LO puis COLL ECTIF
ÉditionsVANIN
Poser la question suivante aux élèves :
→ Par rapport aux trois abaques, que remarquez-vous ?
Dans la vie courante, nous avons recours de façon régulière à ces unités. Cependant, certaines unités sont prises pour références, telles que le m, le l, le g ainsi que le cm et le kg. Par contre, d’autres unités sont très rarement utilisées, comme le dg, le dm ou le q…
Une autre observation à faire par rapport aux trois abaques concerne les préfixes communs. Voir étape suivante avec le « Je retiens ».
6. Donner du sens aux unités de longueur, de capacité et de masse
Relève, sur ces tickets de caisse, les différentes unités de grandeurs.
Entoure les unités de longueur en bleu, les unités de masse en orange, les unités de capacité en vert.
« SPUR »
–Eau plate 6 × 1,5 l 4,99 €
–Pepsi max 24 × 33 cl 9,99 €
–Apéricube Provence 1,99 €
–Pain camp. Blanc coupé 1,79 €
–Heinz tomato ketchup 2,19 €
–Spray après soleil 200 ml 8,09 €
–Olives spécialités 1,59 €
–Cacahuètes 1,30 € 2 × 0,65 €
–Filet de saumon 4 × 175 g 11,99 €
–Huile 125 ml 2,58 €
–Tulipes 10 tiges, 35 cm 3,50 €
–Seau 1 dal 6,70 €
–Ariel poudre 35,23 €
régular 7,150 kg
Total14 art. 91, 93 €
BRICO FOU
–Plan de travail hêtre 75 €
L 200 × l 65 × E 3,8 cm
–Mèche pour foreuse 2,45 €
diam. : 6 mm
–Merlin 3 kg manche en frêne 27,45 €
–Bac potager 100 × 100 × 80 cm 69 €
–Décamètre 10 m 8,45 € –
Dalle terrasse bois 100 × 100 cm 299,85 €
15 × 19,99 €
–Marteau 28 mm manche bois 10,50 €
–Perceuse à percussion 800 W 79,99 €
–Perfax reboucheur 225 ml 7,49 €
–Piscine Prisma 12 m3 849 €
diam. : 366 cm
Total 1 429,18 €
Carte de fidélité
Solde des points antérieur 1 844
Points sur le ticket 719
Points suppl. sur le ticket 48
Solde de points actuel
Calcule le solde de points actuel sur la carte de fidélité de Brico Fou
Replace les unités dans chaque abaque et complète les cases vides.
kl ou m3 ?
Dans la vie courante, on utilise plutôt le terme m3 à la place de kl. 1 m3 = 1 000 l
Que remarques-tu ?
Dans la vie courante, certaines unités (m, kg, cm, g…) sont plus souvent utilisées que d’autres (dag, dg, hl…).
L’abaque des masses à trois unités de plus.
3. 4. 5.
Je retiens
Écris le préfixe des unités.
× 10× 10× 10 : 10: 10: 10 kilohectodéca
gramme mètre litre
× 100 × 1 000 : 100 : 1 000
Préfixe Élément précédant le radical d’un mot et qui en modifie le sens.
Relie
centi- déci: 1 000 : 10 × 100 × 10 : 100 × 1 000
Quelle est l’unité qui est…
– 1 000 fois plus petite que le litre ?
– 10 fois plus grande que le gramme ?
– 100 fois plus grande que le mètre ?
– 1 000 fois plus grande que le gramme ?
– 100 fois plus petite que le litre ?
– 10 fois plus petite que le mètre ?
Construis-toi des repères.
le millilitre
le décagramme
l’hectomètre
le kilogramme
le centilitre
le décimètre
Je retiens
COLL ECTIF
Pour les trois abaques, il y a des points communs qui sont, d’une part, le préfixe et, d’autre part, le rapport entre les différentes unités : – Kilo-, hecto-, déca-, déci-, centi- et milli- ; – Le rapport direct entre ces différentes unités est décimal (× 10 ou : 10).
Exercice 3
SO LO
Exercice de compréhension au niveau des préfixes.
COLL ECTIF
En effet, chaque préfixe correspond à un rapport précis en fonction de l’unité de référence (m, l et g). Donner aux élèves l’abaque vierge avec pour seules références : le m, le l et le kg (annexe 4, p. A5). Les élèves l’observent et essaient de le compléter en remplissant les espaces vides.
Correction et mise en commun.
Remarque : cet abaque peut être utilisé tout au long de l’activité pour soutenir les apprentissages chez des élèves qui éprouveraient plus de difficultés.
Prolongement : demander aux élèves de mettre leur abaque dans une pochette plastique et leur faire utiliser des marqueurs pour tableaux blancs afin de pouvoir le réutiliser par la suite.
Exercice 4
SO LO
Les élèves lisent chaque fois la question et répondent en partant de l’unité de référence. Pour ceux qui éprouveraient des difficultés, ils peuvent s’aider de leur abaque.
Exercice 5
SO LO
COLL ECTIF
Les élèves ont des difficultés avec l’estimation d’une grandeur. Par exemple, prendre une distance entre l’école et un point déterminé. Ensuite, demander aux élèves, selon eux, quelle est la distance.
L’expérience peut être renouvelée en montrant un récipient par rapport à la capacité et un objet par rapport à son poids.
ÉditionsVANIN
Bien faire la vérification pour valider les résultats et faire vivre ces situations aux élèves. Pour cet exercice, juste associer l’unité en fonction du nombre donné. Ce sont essentiellement des objets du quotidien.
Bien faire verbaliser les élèves lors de la correction.
Exercices supplémentaires disponibles en téléchargement. Évaluation disponible en téléchargement.
Activité 7 – Lecture de tableaux et de graphiques
Exercice 1
Cette partie du chapitre 1 porte sur le charbonnage. Le charbon a été l’une des richesses de la Belgique, qui en a produit pendant des siècles. Plusieurs bassins miniers sont répartis le long d’une ligne est-ouest allant de Mons à Liège en passant par la Louvière et Charleroi. Un peu plus au nord, on compte également le bassin de Campine.
Prolongement : c’est l’occasion en abordant cette activité de travailler en parallèle sur la géographie de la Belgique, les villes mais aussi les fleuves.
SO LO
Une situation est donnée aux élèves. Ils (Elles) lisent le problème et essaient d’abord de le résoudre et de démêler les différentes informations en sélectionnant celles qui seront utiles pour sa résolution.
COLL ECTIF
Proposition : l’enseignant(e) peut laisser ses élèves utiliser des couleurs ou fluos pour mettre en évidence certaines informations, ou même utiliser une feuille pour dessiner et visualiser.
Ne pas hésiter à apporter de l’aide si cela est nécessaire pour que chaque élève avance dans la résolution du problème.
La zone de travail permet d’effectuer les calculs et les élèves utilisent l’espace en dessous pour la résolution.
Mise en commun. Bien travailler sur les démarches de résolution des élèves.
Prolongement : on pourrait imaginer que l’enseignant(e) propose à sa classe d’aller faire une excursion à Blegny-Mine et demande aux élèves de calculer le cout en fonction du combiné choisi.
ÉditionsVANIN
7. Lecture de tableaux et de graphiques
Les parents d’Eliot et leurs trois enfants (14, 8 et 6 ans respectivement) ont décidé de partir faire une petite excursion ce weekend. Leur choix s’est porté sur Blegny-Mine. Après avoir pris leurs renseignements sur le site Internet, ils choisissent de descendre dans la mine, descente suivie d’une visite du musée pour terminer avec la découverte du terril et le circuit des arbres.
Résolution 1.
Peux-tu, avec les informations qui te sont données, déterminer le cout de leur excursion et la durée?
■ A.LA MINE (2 h) : il faut descendre pour comprendre
Enfilez votre veste, ajustez votre casque et descendez par la cage de mine à la découverte du travail et de la vie quotidienne des « Gueules Noires ». Découvrez ensuite le processus de triage et de lavage du charbon jusqu’à son expédition.
Visite guidée en FR à 11h, 13h30, 15h30 (+ 14h30 dim. et jours fériés).
•Du 03/07 au 21/08, aussi à 12h30, 14h30 et 16h30
•Autoguides en allemand et en anglais
■ LES COMBINÉS
Combinez en une journée la visite de la mine (2 h) avec une ou plusieurs de ces activités :
– B.LE MUSÉE DE LA MINE (min 1 h) : parcourez librement huit siècles d’exploitation houillère (visite libre). Départ de 11h à 17h.
– C.LA BALADE EN TORTILLARD (50’) : promenez-vous à travers les vergers de la Basse-Meuse. Départ à 13h30, 14h30, 15h30 et 16h30.
!! NOUVEAUX TORTILLARDS ET NOUVEAUX PARCOURS !!
– D.LE BIOTOPE DU TERRIL ET LE « CIRCUIT DES ARBRES » (50’) : circuit pédestre audioguidé présentant la vie sur et autour du terril et jalonné d’œuvres artistiques. Départ de 11h à 17h. Chacune des attractions peut se visiter séparément.
Zone de travail
Situé entre Liège et Maastricht, BlegnyMine est une des quatre authentiques mines de charbon d’Europe dont les galeries souterraines sont accessibles aux visiteurs via le puits d’origine.
Situées à –30 et –60 mètres, elles permettent une découverte complète du processus d’extraction du charbon. Blegny-Mine et les 3 autres sites miniers majeurs de Wallonie (Le Bois du Cazier, Bois-du-Luc et GrandHornu) sont reconnus depuis juillet 2012 comme Patrimoine Mondial par l’UNESCO.
■ TARIFS
Tarif « famille » à partir de 2 adultes et 2 enfants
Adultes Enfants (6-12) Séniors (+60) Jeunes (13-18)
A : La visite de la mine 9,90 €7,00 €8,70 €
A + B + D : Le combiné « Blegny-Mine » 12,10 €8,50 €10,50 €
A + C + D : Le combiné « Dalhem-Blegny » 12,10 €8,50 €10,50 €
A + B + C + D : Le supercombiné (arrivée conseillée avant 11h, au plus tard à 12h30) 15,00 €10,50 €13,00 €
La formule « All-in » : A + B + C + D + plat du jour + 4 boissons 31,00 €24,00 €29,00 €
Formule choisie: A + B + D
Cout de leur excursion: (2 × 12,10 €) + (2 × 8,50 €) + 10,50 € = 51,70 €
Durée: 2 h + 1 h + 50 min = 3 h 50 min
2.
À l’aide du tarif, complète ce tableau.
4 adultes 1 enfant (8 ans) 1 jeune
2 adultes 2 enfants (7 et 5 ans) 1 sénior 1 adulte
Formule A 19,80 € + 17,40 € = 37,20 €
Formules : A + C + D 24,20 € + 21 € = 46,80 €
Zone de travail
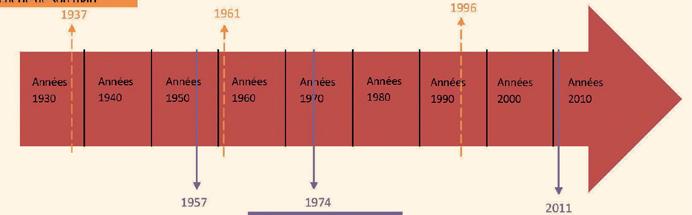
Ce tableau indique le nombre d’ouvriers occupés dans les mines. Essaie de retrouver les données manquantes à partir des informations qui te sont données.
BelgiqueCampineCharleroiLiègeCentre Borinage ou Mons 1948177 17744 06044 50733 31524 05531 180 1952159 54940 75339 14031 31120 16928 176 1957151 89841 01438 34627 98119 94823 918 196188 54133 83023 13816 1176 2029 254 1964 34 55122 35316 0764 6117 400 196940 96121 4689 4605 7171 4642 852 197427 88118 8345 1872 74601 114 197921 220
673
Exercice 2
SO LO
Tableau à double entrée que les élèves doivent compléter. Pour cela, ils (elles) doivent se référer au tableau des tarifs qui se trouve à la page précédente.
Une zone de travail est prévue pour calculer les différents prix de revient.
Exercice 3
Autre tableau présenté aux élèves. Il s’agit d’un relevé du nombre d’ouvriers occupés dans les mines. La 1re colonne reprend le nombre total d’ouvriers en Belgique.
SO LO
COLL ECTIF
Les élèves doivent retrouver les données manquantes en utilisant l’addition et la soustraction. Une zone de travail est à leur disposition.
Correction et mise en évidence des démarches.
ÉditionsVANIN
Exercice 4
Réflexion sur l’utilité et la raison d’un recours à de tels tableaux.
Exercices 5 et 6
Graphique en bâtonnets (histogramme) qui donne la production en tonnes du charbon extrait des mines.
Chaque élève prend le temps de l’analyser et de répondre aux questions.
Remarque : ne pas hésiter à utiliser les termes tels que histogrammes, et même abscisse et ordonnée. Le fait de répéter ces termes tout au long des différentes activités permettra aux élèves de mieux se les approprier.
ÉditionsVANIN
COLL ECTIF
Que constates-tu à la lecture de ce tableau? Discutes-en avec ton (ta) voisin(e).
Nous pouvons constater que le nombre de mineurs a diminué sans cesse alors que les années passaient et que cette tendance ne s’est jamais inversée.
Voici un graphique représentant la production annuelle du charbon en tonnes. Observe-le.
ÉditionsVANIN
Réponds aux questions.
– En quelle année la production a-t-elle été la moins bonne?
– En quelle année la production a-t-elle été la meilleure?
– À partir de quelle année la production de charbon a-t-elle commencé à diminuer ?
– Cite les deux années où la production a été identique : et
Complète ce tableau.
En 1980, c’est la fermeture du charbonnage, 400 personnes y travaillaient encore.
Voici ce qu’il est advenu des 400 personnes :
– 92 personnes sont parties travailler au charbonnage du Roton à Charleroi;
– 13 personnes ont été embauchées dans les charbonnages de Campine;
– 11 personnes se sont reconverties dans un autre secteur;
– 8 personnes ont conservé un emploi à Blegny-Mine;
– 162 personnes ont été pensionnées ou prépensionnées;
– 114 personnes ont été déclarées invalides.
Représente tous ces groupes de personnes avec des couleurs différentes dans le carré ci-dessous.
Compléter le tableau en utilisant les informations du graphique à la page précédente.
COLL ECTIF
En lisant bien attentivement, colorier les différentes parts correspondant aux informations données.
Par exemple : si 92 personnes sont parties travailler ailleurs, il faudra colorier 92 carrés dans le grand carré. Il s’agit de bien organiser les nombres et de colorier l’entièreté du grand carré.
Prendre le temps de s’interroger ensemble sur l’utilité et les avantages du recours à cette représentation.
ÉditionsVANIN
Évaluation disponible en téléchargement.
Exercice 7
Exercice 8
Chapitre 2
Pas à pas…
ATTENDUS PAR MATIÈRE
LES NOMBRES
Opérer sur des nombres et sur des expressions algébriques
Savoir(s)
Les opérations et leurs propriétés.
Les automatismes de base en calcul.
Savoir-faire
Attendus
Associer une opération à ses composantes et son résultat : – addition, termes, somme ; – soustraction, premier terme, deuxième terme, différence ; – multiplication, facteurs, produit ; – division, dividende, diviseur, quotient, reste.
Connaitre de mémoire les décompositions : – de 100 en deux termes ou en deux facteurs ; – de 1, en dixièmes, en deux termes ou en deux facteurs.
Connaitre de mémoire les tables de multiplication jusqu’à T10.
Attendus
Appréhender et utiliser l’égalité. Utiliser l’égalité en termes de résultat : addition, soustraction, multiplication et division.
Utiliser des procédures de calcul mental pour trouver le résultat plus facilement.
Savoir(s)
Le symbolisme spécifique aux objets et relations géométriques.
Savoir-faire
Interpréter et utiliser les symboles géométriques.
Tracer des figures.
ÉditionsVANIN
Utiliser la comparaison des nombres pour effectuer une opération. Exemple : Si 5 × 12 = 60 alors 0,5 × 12 = … et 5 × 1,2 = …
LES SOLIDES ET FIGURES
Appréhender et représenter des objets de l’espace
Attendus
Associer le symbole à sa signification : – A désigne le point A ; – a désigne la droite a ; – [AB] désigne le segment dont les extrémités sont les points A et B ; – // signifie parallèles ; – ⊥ signifie perpendiculaires.
Attendus
Utiliser les symboles spécifiques : A, a, [AB], // et ⊥
Utiliser l’équerre et la latte pour tracer des droites perpendiculaires et parallèles sur papier vierge, avec et sans contraintes.
Savoir(s)
L’identification et la comparaison de grandeurs d’objets.
Savoir(s)
L’usage des unités conventionnelles.
Savoir-faire
Mesurer des grandeurs.
LES GRANDEURS
Concevoir des grandeurs
Attendus
Utiliser de manière adéquate les termes relatifs aux grandeurs : la longueur, la masse, la capacité, le cout, l’aire, le volume.
Agir sur des grandeurs
Attendus
Utiliser et symboliser :
– les unités de longueur ; – les unités de capacité ; – les unités de masse ; – les unités d’aire : le mètre carré (m²), le décimètre carré (dm²), le centimètre carré (cm²), le millimètre carré (mm²) ; – une unité de volume : le centimètre cube (cm³).
Construire le système des unités conventionnelles.
Les nombres
Les solides et figures
ÉditionsVANIN
Les grandeurs
Distinguer dans l’expression d’une grandeur mesurée : la grandeur, la mesure et l’unité de mesure.
Attendus
Effectuer le mesurage d’une grandeur d’un objet de l’environnement et en exprimer le résultat, en utilisant une unité conventionnelle : – de longueur ; – de capacité ; – de masse ; – d’aire : m², dm², cm², mm² ;
– de volume : cm³.
Donner du sens aux unités conventionnelles travaillées en les associant à des objets de l’environnement (un m2 c’est l’aire de…).
Lister des objets de la vie courante dont une grandeur se mesure avec l’unité travaillée.
Donner du sens aux préfixes déci-, centi-, milli-, kilo-, hecto-, déca-, dans les unités conventionnelles travaillées.
Réaliser des conversions significatives (longueur, masse, capacité, aire) en lien avec les unités conventionnelles travaillées, avec ou sans abaques (construits préalablement).
MATIÈRES ABORDÉES
Addition et soustraction jusqu’à 100
Les tables et leur extension
Positions de droites : – parallèles – sécantes – perpendiculaires
Les longueurs
Les capacités
Le traitement des données /
Activité 1 – Addition et soustraction jusqu’à 100
Exercice 1
Il s’agit de commencer ce chapitre par un rappel au niveau des additions et des soustractions jusqu’à 100. Voir si au niveau de ces deux opérations, les calculs au niveau des cent premiers nombres sont acquis.
SO LO
Exercices sur l’addition : compléter des chemins pour lesquels soit la réponse est attendue (la somme), soit l’un des deux termes est à trouver.
Exercice 2
SO LO
Les élèves sont libres d’inventer le chemin de leur choix.
ÉditionsVANIN
Je dépose mes idées
SO LO
Permettre à chaque élève d’expliquer ses démarches pour additionner deux nombres.
COLL ECTIF
Mise en commun afin de partager sur les différentes démarches mises en œuvre par les élèves.
Chapitre
Pas à pas...
1. Addition et soustraction jusqu’à 100
à 100.
À ton tour, invente le chemin de ton choix pour arriver à 100.
Nombreuses réponses possibles
Je dépose mes idées
Résous ces calculs.
14 + 38 =
32 + 45 =
59 + 17 =
23 + 19 + 47 =
5 + 68 =
+ 39 =
42 =
+ 16 =
+ 0 =
+ 18 + 19 =
Colorie d’une même couleur les deux étiquettes qui, en les additionnant, donnent le nombre 100.
Complète ces additions.
15 + 15 + 55 + = 100
80 + + 14 = 100 + 27 + 33 = 100
41 + + 25 = 100 + 10 + 22 + 67 = 100
Relie chaque calcul à sa réponse. Attention, il y a des intrus.
Exercices d’addition. Les élèves résolvent les calculs et notent la somme.
Les élèves doivent trouver deux étiquettes qui, ensemble, donnent la somme de 100.
Additions de plusieurs termes (plus de deux) dont le résultat correspond, dans chaque cas, à 100.
ÉditionsVANIN
Exercice sur la soustraction. Les élèves doivent relier chaque calcul à sa réponse. Attention, il y a de nombreux intrus : toutes les réponses ne seront donc pas forcément reliées à un calcul.
Exercice 3
Exercice 4
Exercice 5
Exercice 6
J’exprime mes idées
SO LO
Permettre à chaque élève d’expliquer ses démarches pour additionner deux nombres.
COLL ECTIF
Mise en commun afin de partager sur les différentes démarches mises en œuvre par les élèves.
SO LO
Les élèves complètent des chemins pour lesquels soit la réponse est attendue (la différence), soit l’un des deux termes est à trouver.
SO LO
Les élèves sont libres d’inventer le chemin de leur choix.
Exercice 7
Exercice 8
Explique comment tu procèdes pour soustraire.
ces chemins.
À ton tour, invente le chemin de ton choix.
réponses possibles
Effectue ces soustractions.
59 – 7 =
87 – 70 =
92 – 85 =
87 – 68 =
61 – 33 =
Résous ces soustractions.
100 – 40 – 20 = 100 – 17 – 31 =
– 61 – 17 =
– 14 – 39 =
– 19 =
– = 75
– = 21
– 17 = 34 – = 16
– 32 =
– = 19
– 56 = 18 – = 0
– 21 =
– 36 – 19 =
– 22 – 66 =
– 45 – 8 =
– 78 – 18 =
Trouve à chaque étiquette sa réponse et relie-la sur la droite des nombres.
Et si on mélangeait un peu ? À toi de jouer…
Exercice 9
SO LO
Exercices de soustraction. Les élèves résolvent les calculs et notent la différence.
Exercice 10
SO LO
Soustractions de deux termes à partir de 100.
Exercice 11
SO LO
Les élèves réalisent chaque calcul. Lorsqu’ils (elles) ont trouvé la réponse, ils (elles) doivent relier l’étiquette au bon endroit sur la droite numérique, en étant le plus précis possible. Une petite aide est donnée au niveau des graduations pour aider les élèves qui éprouveraient des difficultés.
Exercice 12
SO LO
ÉditionsVANIN
Calculs de soustractions et d’additions lacunaires. Les élèves doivent compléter le résultat ou l’un des deux termes du calcul.
Exercices supplémentaires disponibles en téléchargement. Évaluation disponible en téléchargement.
Activité 2 – Les tables et leur extension
Exercice 1
SO LO
On démarre avec un petit rappel des tables qui ont été vues auparavant avant de partir dans leur extension.
Mise en situation : un tableau à double entrée avec des lettres est présenté aux élèves. En multipliant deux facteurs entre eux pour trouver le produit, on obtient une lettre. Chaque lettre trouvée permettra d’obtenir la réponse à la question posée.
COLL ECTIF
Exemple : pour trouver le produit de 36, il y a plusieurs possibilités (4 × 9, 9 × 4 ou 6 × 6), mais dans tous les cas, le produit des facteurs selon les différentes possibilités donne la même lettre.
En partant de l’exemple, confronter la démarche des élèves au fait qu’il y a justement plusieurs possibilités pour y arriver.
Exercice 2
SO LO
Matériel :
– Annexe 5 : Pixel art (les tables et leur extension) (p. A6)
ÉditionsVANIN
Deux tableaux à double entrée, représentant un pixel art, sont à compléter.
Compléter les cases orange.
L’enseignant(e) donne l’annexe 4 aux élèves. À eux (elles) d’inventer un exercice requérant la même démarche que celle de l’exercice qu’ils (elles) viennent de réaliser.
Les plus créatifs (créatives) inventent et ceux (celles) qui éprouvent des difficultés dans les cases blanches reproduisent un pixel art
Ensuite, ils (elles) complètent avec des nombres allant de 0 à 10 les cases grisées. Ne pas aller au-dessus de 10 pour rester dans les tables de multiplication simples. Pour finir, ils (elles) n’auront plus qu’à soumettre leur exercice à l’un(e) de leurs camarades de classe.
Comment appelle-t-on la technique du dessin numérique qui nous vient des débuts de l’informatique et qui consiste à créer des images carré par carré ? Retrouve les bonnes lettres dans le tableau de Pythagore pour obtenir la réponse. Chaque nombre est le résultat d’un calcul des tables de multiplication auquel correspond une lettre.
Effectue ces calculs.
4 × 7 =
400 × 7 000 = 3.
40 × 7 =
400 × 7 =
40 × 70 =
Même exercice !
35 : 5 =
350 : 5 =
3 500 : 50 =
400 × 700 =
4 000 × 70 =
40 × 700 =
J’exprime mes idées
Comment procèdes-tu ?
Tout d’abord, je multiplie 4 et 7.
Ensuite, s’il y a des «0», je les comptabilise pour chaque facteur et je replace le total de «0» à la réponse finale.
3 500 000 : 5 000 = 4.
3 500 : 500 =
35 000 : 5 000 =
35 000 : 50 =
350 000 : 50 =
Comment procèdes-tu ?
Tout d’abord, je divise 35 par 5.
Ensuite, s’il y a des «0», je soustrais les «0» et je replace le total de «0» à la réponse finale.
Relie ces calculs à la bonne réponse.
Exercice 3
SO LO
On part d’une multiplication très simple : 4 × 7
Ensuite, un des deux facteurs ou les deux sont multipliés par 10, 100 ou 1 000, ce qui va impliquer des changements au niveau de la réponse.
Les élèves notent leurs réponses.
D U O
Ensuite, en groupes de deux, les élèves comparent leurs résultats.
J’exprime mes idées
D U O
COLL ECTIF
Les élèves essaient par deux de répondre mentalement à la question en comparant leurs démarches.
Exercice 4
SO LO
D U O
Mise en commun et rédaction d’une démarche collective qui sera transférable par la suite dans les exercices.
On part d’une division très simple : 35 : 5
Ensuite, le diviseur, le dividende ou les deux sont multipliés par 10, 100, 1 000 ou …, ce qui va impliquer des changements au niveau de la réponse.
Les élèves notent leurs réponses.
Pour faciliter les calculs, s’il y a présence de 0 au niveau du dividende et du diviseur, on peut barrer le même nombre de 0 des deux côtés.
Ensuite, en groupes de deux, les élèves comparent leurs résultats.
J’exprime mes idées
D U O
ÉditionsVANIN
Les élèves essaient par deux de répondre mentalement à la question en comparant leurs démarches.
COLL ECTIF
Mise en commun et rédaction d’une démarche collective qui sera transférable par la suite dans les exercices.
Exercice 5
SO LO
Des multiplications sont présentées à gauche et des divisions à droite. Au centre, les réponses. Pour chaque réponse, les élèves doivent associer les bons calculs.
Exercice 6
SO LO
Calculs mettant en pratique ce qui a été vu précédemment. Les élèves résolvent les deux colonnes.
Je retiens
COLL ECTIF
Structuration : garder une trace écrite des démarches à mettre en œuvre pour résoudre une multiplication ou une division au niveau des tables et de leur extension.
Exercice 7
SO LO
ÉditionsVANIN
Un tableau à double entrée dans lequel un dessin en pixel art de voiture a été dessiné. Les élèves complètent les cases.
Compléter le reste des cases.
Résous ces calculs.
8 × 90 000 =
300 × 8 000 =
40 × 500 =
90 × 7 000 =
600 × 90 =
600 000 × 8 =
50 × 40 000 =
Je retiens
320 000 : 8 =
5 600 000 : 700 =
81 000 : 9 =
4 200 : 60 =
4 500 000 : 5 000 =
180 000 : 2 000 =
24 000 : 400 =
Extension de tables multiplication division
500 × 40 = (5 × 4) × (100 × 10) = 20 × 1 000 = 20 000
1) Je multiplie les chiffres différents de 0 : 5 × 4.
2) Je multiplie par 1 000, car : –500 est 100 fois plus grand que 5 ; –40 est 10 fois plus grand que 4.
27 000 : 90 = (27 000 : 9) : 10 = 3 000 : 10 = 300
1) Je divise 27 000 par 9, ce qui me donne 3 000.
2) Je divise 3 000 par 10 et j’obtiens 300.
Complète les cases grises de cette grille.
Complète le reste des cases.
Colorie l’intrus et justifie ton choix.
490 n’est pas un multiple de 9.
32 000 n’est pas un multiple de 6.
420 n’est pas un multiple de 8.
Entoure tous les nombres divisibles par 7.
Complète les calculs suivants.
7 000 × 800 =
6 400 : = 80
40 000 : = 80 × 400 = 24 000
50 000 × 9 = : 300 = 50
2 400 : 80 =
6 000 × 2 000 =
4 900 : 700 =
18 000 : 600 =
6 000 × 70 =
56 000 : = 700
80 × 80 = : 900 = 600
4 000 × = 3 200 000
560 000 : 8 000 = × 6 000 = 4 200 000
90 × = 27 000 × 4 000 = 1 200 000
30 000 : 100 =
Invente des calculs dont le résultat t’est donné. × = 800 : = 20 : = 600 × = 560 000 × = 25 000 × = 6 400 × = 81 000 : = 5 000 : = 7 × = 63 000
Nombreuses réponses possibles
Exercice 8
SO LO
Les élèves identifient le point commun entre les différents nombres d’une même ligne, ce qui leur permettra de trouver l’intrus.
Retrouver tous les nombres qui sont divisibles par 7 (autrement dit, qui sont des multiples de 7).
Exercice 9
SO LO
Calculs lacunaires à résoudre. Multiplications et divisions sont mélangées et la réponse attendue n’est pas forcément le produit ou le quotient.
Exercice 10
SO LO
ÉditionsVANIN
Ici, le résultat est donné aux élèves. Ils (Elles) doivent inventer des multiplications et des divisions qui donnent le résultat escompté.
Exercices supplémentaires disponibles en téléchargement. Évaluation disponible en téléchargement.
Activité 3 – Les longueurs
Exercice 1
SO LO
Travail sur les représentations mentales. Les élèves mobilisent leurs connaissances et écrivent sur les pointillés l’unité qui convient le mieux en tenant compte également du nombre donné.
D U O
Les élèves comparent par deux leurs réponses et réajustent si nécessaire en fonction de leur partage.
COLL ECTIF
Mise en commun et correction. C’est l’occasion également d’élargir à d’autres objets ou êtres vivants.
Je retiens
SO LO
COLL ECTIF
L’exercice 1 permet de mettre en évidence que l’unité de référence est le mètre. Chaque élève va ainsi replacer les différentes unités dans l’abaque sur la première ligne grâce, d’une part, aux unités de l’exercice 1 et, d’autre part, de leurs connaissances, car cela a déjà été travaillé lors de l’année précédente.
Mise en commun. Les unités sont écrites en toutes lettres sur la deuxième ligne de pointillés. Mettre en évidence les préfixes et établir des liens en rapport avec l’unité de référence.
ÉditionsVANIN
3. Les longueurs
Choisis l’unité de longueur adéquate et complète les cases.
Je retiens
Complète les unités sur les pointillés de la synthèse ci-dessous.
Les unités supérieures
Unité de référence
Les unités inférieures
Chaque unité occupe une place bien précise dans l’abaque. Cet outil permet de convertir des longueurs, c’est-à-dire de les transformer selon différentes unités.
À l’aide de ta latte, trace avec la plus grande précision les segments demandés. 48mm 3 4 dm 1,3dm 12mm + 0,5dm
Trace ces deux segments :
a) 0,065m + 3 4 dm b) 2,4dm – 94mm
Place dans l’abaque et convertis selon l’unité demandée.
Exercice 2
SO LO
Tracer avec précision les différents segments demandés. Bien démarrer du point de départ et marquer l’autre extrémité.
Pour faciliter la correction, permettre aux élèves d’utiliser des calques sur lesquels les différents segments ont été tracés. Pour l’exercice de dépassement, il faut d’abord résoudre le calcul. La réponse donnera alors la longueur du segment à tracer.
Exercice 3
SO LO
ÉditionsVANIN
Travail avec l’abaque. Les élèves placent dans l’abaque les différentes longueurs et convertissent suivant l’unité demandée.
Exercice 4
SO LO
Dans cet exercice, travail en deux temps : – Le premier est de transformer toutes les longueurs dans la même unité (en m). Cela facilitera le rangement. – Le deuxième est de ranger les longueurs dans l’ordre croissant (du plus petit au plus grand).
Trouver la longueur qui se rapproche le plus de 11 hm 12 dam et 300 cm. Même démarche : transformer en m et sélectionner la longueur la plus proche.
Exercice 5
SO LO
Il faut transformer les longueurs dans l’unité demandée. Laisser les élèves utiliser l’abaque pour leur permettre de trouver les réponses.
Exercice 6
SO LO
Les élèves complètent les pointillés, puis effectuent les opérations une fois que les différents termes sont dans la même unité.
ÉditionsVANIN
Exercices supplémentaires disponibles en téléchargement. Évaluation disponible en téléchargement.
Range ces grandeurs dans l’ordre croissant.
1 023m1km 3hm 2dam12 300dm120dam 300mm12hm 3m
< < < <
Quelle est, parmi ces longueurs, celle qui se rapproche le plus de 11hm 12dam et 300cm? Entoure-la.
Conseil Transforme toutes les grandeurs dans la même unité.
Convertis.
35,50m = hm
5,030m = cm
9,50m = mm 53,2m = dam
Trouve la réponse dans l’unité demandée.
4. Les capacités
Pour chaque image, trouve l’unité de capacité qui convient.
Les
Complète les unités sur les pointillés de la synthèse ci-dessous.
Unité de référence
Les
inférieures
Activité 4 – Les capacités
Exercice 1
SO LO
Travail sur les représentations mentales. Les élèves mobilisent leurs connaissances et écrivent sur les pointillés l’unité qui convient le mieux en tenant compte également du nombre donné.
D U O
COLL ECTIF
Les élèves comparent par deux leurs réponses et réajustent si nécessaire en fonction de leur partage.
Mise en commun et correction. C’est l’occasion également d’élargir à d’autres objets de la vie quotidienne.
Je retiens
SO LO
COLL ECTIF
L’exercice 1 permet de mettre en évidence que l’unité de référence est le litre. Chaque élève va ainsi replacer les différentes unités dans l’abaque sur la première ligne grâce, d’une part, aux unités de l’exercice 1 et, d’autre part, de leurs connaissances, car cela a déjà été travaillé lors de l’année précédente.
Mise en commun. Les unités sont écrites en toutes lettres sur la deuxième ligne de pointillés. Mettre en évidence les préfixes et établir des liens en rapport avec l’unité de référence.
ÉditionsVANIN
Exercice 2
SO LO
Travail avec les unités. Les élèves lisent attentivement et complètent chaque phrase avec l’unité correcte qu’ils (elles) écrivent sur les pointillés.
Exercice 3
SO LO
D’abord faire compléter l’abaque avec les unités de capacité.
COLL ECTIF
S’assurer que les unités soient correctement placées dans l’abaque.
SO LO
Les élèves placent dans l’abaque les différentes capacités et convertissent suivant l’unité demandée.
ÉditionsVANIN
Complète.
e)Si je remplis un grand tonneau avec 100 seaux de 10l, je suis le 2.
a)Je suis 100fois plus petit que le dl, je suis le
b)Si je verse dans un récipient 10 verres de 10cl, je suis le
c)Je suis 1000fois plus grand que le cl, je suis le
d)Je peux contenir 100l, je suis l’ .
Complète l’abaque et convertis ces grandeurs.
Complète les deux dernières lignes.
Transforme dans l’unité demandée.
0,65l = ml
48 000dl = dal 3 4 hl = dl
2,5l = hl
Range ces grandeurs dans l’ordre décroissant.
0,560dl = ml
0,6m3 = cl 658l = hl 1 5 dal = l
Quelle est, parmi ces capacités, celle qui se rapproche le plus du résultat de ce calcul? Entoure-la.
(0,136hl + 5 140cl) – 3,47dal = l
Complète ces égalités.
= 2 400
Exercice 4
SO LO
Il faut transformer les capacités dans l’unité demandée. Laisser les élèves utiliser l’abaque pour leur permettre de trouver les réponses.
Exercice 5
SO LO
Dans cet exercice, travail en deux temps : – Le premier est de transformer toutes les longueurs dans la même unité (en l). Cela facilitera le rangement. – Le deuxième est de ranger les capacités dans l’ordre décroissant (du plus grand au plus petit).
Trouver la capacité qui se rapproche le plus du résultat du calcul. Même démarche : transformer en l, trouver la réponse du calcul et sélectionner la capacité la plus proche.
Exercice 6
SO LO
ÉditionsVANIN
Dans cet exercice, les conversions sont réalisées, mais il faut compléter par l’unité qui correspond au nombre donné.
Exercice 7
SO LO
Compléter les pointillés avec les signes « < », « > » ou « = ».
Bien insister sur l’importance de comparer les capacités en les mettant dans la même unité.
Exercice 8
SO LO
ÉditionsVANIN
Les élèves complètent les pointillés, puis effectuent les opérations une fois que les différents termes sont dans la même unité.
Compare ces mesures de capacité (<, > ou =).
5 l 8cl 5 080ml
640dal 640 000ml
3 000cl
0,43hl
41hl 36l 41 360cl 6l 39dl 182cl
0,05hl 5 000ml 3,43 kl 14,3hl 200dal
92hl 15dal 9,350m3
Trouve la réponse dans l’unité demandée.
5,8l+32dl+45cl = cl
(2,9dal–70dl)+350cl = dl
dal 100ml
cl cl cl
(360ml+ 1 10 l)–30ml = cl
Conseil
Transforme toutes les grandeurs dans la même unité. Tu y verras plus clair.
Les unités de capacités le plus souvent utilisées sont le millilitre (ml), le centilitre (cl), le litre (l) et le mètre cube (m3).
= l
Quelle est la consommation journalière d’eau en litres et par personne?
Cuisson et boisson
300 cl
Lavage voiture
Autres lavages
Arrosage jardin W.-C.
0,8 dal 1/10 hl
Lavevaisselle
Lavelinge
46 000 ml
Soins du corps
53 l 9 l 170 dl 3 l
Consommation journalière en litres par personne
Zone de travail
Consommation journalière en litres par personne :
3 l + 3 l + 8 l + 9 l + 10 l + 17 l + 46 l + 53 l = 149 l
Résous
Cinq bouteilles de jus d’orange de 30cl valent 2,40€. Quel est le prix au litre?
Zone de travail
Exemple de résolution:
Capacité des 5bouteilles: 30 cl × 5 = 150 cl
Pour trouver le prix au litre: (150 cl : 3) × 2 = 100 cl = 1 l
Prix au litre: (2,40 € : 3) × 2 = 1,60 €/l
Exercice 9
COLL ECTIF
Problème de la vie quotidienne tournant autour de la consommation journalière en eau.
Plusieurs approches possibles :
– Déterminer, avec les élèves, les quantités d’eau nécessaires pour les différents postes. Après affinage des différentes propositions, l’enseignant(e) note, sur les pointillés, les quantités qui se trouvent dans le correctif.
– L’enseignant(e) peut aussi laisser d’abord les élèves faire des estimations par deux, puis procéder lors d’une mise en commun au tri des propositions qui sont analysées, confrontées les unes aux autres et enfin notées sur la feuille.
– Il peut être proposé pour chaque poste plusieurs choix et demander aux élèves de sélectionner la réponse qui leur parait la plus pertinente.
Remarque : les besoins en eau sur le schéma sont rangés dans l’ordre croissant.
Veiller aussi à la bonne compréhension du mot « journalier ».
Une fois que tous les élèves ont les mêmes quantités, les laisser travailler à la résolution du problème. Ils (Elles) peuvent utiliser la zone de travail pour les aider dans leur recherche.
Exercice 10
ÉditionsVANIN
Problème en lien avec la proportionnalité directe. Il peut être résolu de différentes manières. Laisser donc les élèves travailler et le résoudre. COLL ECTIF
Une fois terminé, procéder à une mise en commun afin de mettre à plat les démarches des élèves. Leur permettre de venir les noter au tableau, afin de mieux observer les différentes démarches.
Exercices supplémentaires disponibles en téléchargement. Évaluation disponible en téléchargement.
Exercice 1
Cette activité se déroule en deux temps :
1. Reconnaissance au niveau des droites ;
2. Traçage des droites.
À noter que des traçages seront demandés dans la première partie mais exclusivement en exercices de dépassement.
COLL ECTIF
puis
SO LO
Les élèves observent les lignes et disent ce qu’ils (elles) voient. Les laisser émettre des hypothèses. En effet, ces lignes semblent vouloir se croiser mais il n’en est rien.
Permettre aux élèves de prolonger les lignes et de comprendre ce qu’il se passe. Les droites, même prolongées, gardent un écart constant.
J’observe
COLL ECTIF
C’est une illusion d’optique. Cette illusion célèbre a été observée pour la première fois sur les murs d’une terrasse d’un café. Elle s’appelle « L’illusion du mur du café » et a été décrite par le docteur Richard Gregory en 1979. Pour créer cette illusion, les colonnes de carreaux sombres et clairs sont légèrement décalées à chaque rang pour former des ondulations.
Il est possible de trouver sur Internet des modèles dynamiques (voir par exemple : www.michaelbach.de) qui permettent de mieux comprendre l’illusion.
Mise en commun.
L’espace « J’observe » est complété et le mot « parallèles » est noté en dessous de la deuxième question avec le symbole.
Exercice 2
Démarche assez semblable à celle de l’exercice 1.
COLL ECTIF puis
D
Les élèves observent les lignes et disent ce qu’ils (elles) voient. Les laisser émettre des hypothèses. En effet, ces lignes semblent vouloir se croiser.
ÉditionsVANIN
Permettre aux élèves de prolonger les lignes et de comprendre ce qu’il se passe. En prolongeant les droites, on constate que l’écart diminue ou augmente.
J’observe
COLL ECTIF
Mise en commun.
L’espace « J’observe » est complété et le mot « sécantes » est noté en dessous de la deuxième question avec le symbole.
5. Droites et positions
1.
Observe ces lignes.
2.
J’observe
–Que remarques-tu ? Discutes-en avec ton (ta) voisin(e).
Les lignes semblent «monter» ou «descendre» et vouloir se rencontrer si on les prolongeait. Il n’en est rien.
– Comment appelle-t-on ce type de droites ?
En effet, ce sont des droites qui ne se coupent pas. parallèles (//)
Ce sont des droites .
Observe ces lignes.
J’observe
–Que remarques-tu ? Discutes-en avec ton (ta) voisin(e).
– Comment appelle-t-on ce type de droites ?
Ce sont des droites
Les lignes montent et ou descendent. Si on les prolongeait d’un côté ou de l’autre, elles se couperaient en un point. sécantes ( // )
Repasse sur les pointillés afin d’obtenir une droite parallèle à la droite donnée
a b c
Pour chaque exercice, trace, à l’aide de ton équerre, une autre droite parallèle à celle qui t’est donnée.
Repasse sur les pointillés afin d’obtenir une droite sécante à la droite donnée. a b c
Deux droites sécantes se coupent en formant 4 angles droits.
Retrouve-les et entoure-les en vert.
Ce sont des droites .
5. GR S c T H M f perpendiculaires ( ) e b
Pour chaque exercice, trace, à l’aide de ton équerre, une droite perpendiculaire à celle qui t’est donnée.
Complète avec : //, // ou ⊥. c f [MH c [GR] f [TS] c f [TS]
Trace à l’aide de ton équerre : – une droite e parallèle à la droite f ; – une droite b perpendiculaire à la demidroite HM].
Comment est la droite e par rapport au segment [GR] ?
Perpendiculaire // // //
Exercice 3
SO LO
Exercices mettant en œuvre la notion de parallélisme. Les élèves doivent repasser sur les bons pointillés afin de trouver la droite parallèle à celle donnée.
Les élèves tracent une droite parallèle à celle donnée au moyen de leur équerre Aristo.
Exercice 4
SO LO
SO LO
COLL ECTIF
SO LO
Exercices mettant en œuvre la notion de « sécant ». Les élèves doivent repasser sur les bons pointillés afin de trouver la ou les droite(s) sécante(s) à celle donnée.
Deuxième exercice : parfois les droites peuvent se rencontrer et former 4 angles droits. Aux élèves de retrouver ces deux droites et de les entourer.
Ne pas oublier de compléter le cadre en écrivant le mot « perpendiculaires » et d’écrire son symbole.
Les élèves tracent chaque fois une droite perpendiculaire à celle donnée au moyen de leur équerre Aristo.
5
ÉditionsVANIN
Les élèves complètent avec les trois symboles les pointillés en fonction de la position des droites et des segments de droite.
Tracer ce qui est demandé en tenant compte des informations et ensuite, déterminer la position de la droite e avec un segment de droite.
Exercice
Je retiens
SO LO
Les élèves notent les mots donnés sur la structuration. Attention : le mot « sécantes » doit être écrit deux fois. Ne pas oublier de relier avec la bonne illustration.
COLL ECTIF
Mise en commun et correction collective.
Exercice 6
SO LO
Les élèves travaillent de nouveau avec les 3 symboles des positions sur la base du tracé donné.
ÉditionsVANIN
Placer les points A, B et C qui se trouvent chacun à l’intersection de certaines droites.
Je retiens
Complète avec ces mots : parallèles, sécantes (2), confondues, perpendiculaires, distinctes. nesecoupentpas secoupent neformentpas4anglesdroits c = d l c d l c d l c d l forment4 angles droits l l l l
Deux droites dans un plan
ÉditionsVANIN
parallèles (//) sécantes ( // )
distinctes confondues sécantes ( // )perpendiculaires ( )
Relie ce qui va ensemble.
m = n o p q
Observe, puis complète le tableau.
mnopq m// n// o// p // q //
Place, sur le dessin, les points A, B, C en tenant compte des informations données :
Des élèves doivent tracer deux droites perpendiculaires. Colorie le prénom de ceux qui ont placé correctement leur équerre.
Une fois que tu les as retrouvés, trace pour eux la droite perpendiculaire.
Un des élèves a mal compris la consigne. Il a placé son équerre pour tracer une droite parallèle. De qui s’agit-il ? .
Donne-lui un coup de pouce et trace cette droite parallèle.
Trace à l’aide de ton équerre.
Trace une droite c perpendiculaire à la droite g passant par le point O.
Trace une droite e perpendiculaire à la droite g.
À partir du point S, abaisse la demidroite [SB perpendiculaire à la droite b.
S
Trace une droite d parallèle à la droite b.
Comment est la droite d par rapport à la demi-droite [SB ? .
Eliot perpendiculaire
Eliot
Maxime
Lucie
Julia
Exercice 7
SO LO
À partir de cette page, on va passer au niveau du traçage de droites. Pour cela, il est important de bien placer son équerre et d’en faire prendre conscience les élèves.
SO LO
Un(e) élève a mal compris la consigne et a placé l’équerre de sorte à tracer des droites parallèles. Il faut le (la) retrouver.
COLL ECTIF
Pour vérifier la bonne compréhension du positionnement de l’équerre, l’enseignant(e) demande aux élèves de tracer une droite, une demi-droite ou un segment de droite (l’idée est de réinvestir les notions du chapitre précédent).
Ensuite, il invite les élèves à placer leur équerre en vue de tracer une parallèle, une perpendiculaire ou même une droite sécante. Avant de la tracer, les élèves sont invités à se balader de banc en banc pour vérifier que chacun(e) a bien positionné son équerre.
Discussion et correction éventuelle.
Exercice 8
Exercices de traçage divers avec l’équerre.
Pour chaque exercice, bien lire ce qui est demandé et ne pas oublier de nommer les droites et les points obtenus.
Bien insister sur l’utilisation d’un crayon gris pas trop gras avec une mine bien taillée afin d’être le plus soigneux et le plus précis possible.
ÉditionsVANIN
Exercices de dépassement en prolongement des traçages effectués.
Exercice 9
ÉditionsVANIN
Exercice de traçage d’une forme en trois dimensions. En plus d’être bien précis au niveau des positions des côtés, l’élève devra également respecter les dimensions.
Pour faciliter la correction, prévoir des calques que les élèves peuvent superposer sur leur tracé pour le vérifi er.
Trace les droites a, b, c et d perpendiculaires à la droite j passant respectivement par les points E, F, G et H.
Comment sont les droites a, b, c et d entre elles ?
Trace : m ⊥ a, n // b et p // n.
Nombreuses réponses possibles.
Trace une droite s parallèle à la droite t et passant par le point G.
Trace trois droites parallèles c, d et e espacées d’1 cm.
t
Trace un segment de droite [BC] parallèle à la droite t et distant de 1,5 cm de celui-ci.
Reproduis ce dessin.
ÉditionsVANIN
Trace une droite g confondue avec la droite d.
Trace à l’aide de ton compas.
Abaisse une droite e perpendiculaire à la droite g.
Trace une droite t perpendiculaire à la droite f passant par le point D.
Trace une demi-droite [IJ perpendiculaire à la droite g.
Par le point G, trace la droite i parallèle à la droite j.
Trace un segment de droite [PL] perpendiculaire à la droite f passant par le point C.
Trace une droite b parallèle à la droite c distante de 2,5 cm.
Trace une droite k parallèle à la droite i passant par H.
Construis ce que l’on te demande.
Trace une demi-droite AB] parallèle à la droite b et distante d’1,5 cm de celle-ci.
Utilise avec précision l’équerre et/ou le compas.
b ⊥ a [GD]//b et [GD] mesure 6 cm [ST b c//[ST distante de 2 cm
Complète.
[GD] a c a
Exercice 10
SO LO
Matériel : – Annexe 6 : Tracer des parallèles et des perpendiculaires au compas (pp. A7-A8)
Exercices de traçages divers avec le compas.
Pour préparer les élèves à l’utilisation du compas pour le traçage de droites parallèles et perpendiculaires, utiliser l’annexe 6 : « Tracer des parallèles et des perpendiculaires au compas ».
Pour chaque exercice, bien lire ce qui est demandé et ne pas oublier de nommer les droites et les points obtenus.
Bien insister sur l’utilisation d’un compas à la mine bien taillée.
Exercices de dépassement en prolongement des traçages effectués.
Exercice 11
SO LO
Exercices de traçage au compas et/ou à l’équerre.
ÉditionsVANIN
Attirer l’attention des élèves sur le fait que tout doit être tracé une fois et pas plusieurs fois (par exemple, tracer une fois la droite b, ne pas tracer plusieurs fois la même droite).
Exercices supplémentaires disponibles en téléchargement. Évaluation disponible en téléchargement.
Savoir(s)
Les opérations et leurs propriétés.
Savoir-faire
Construire le sens des opérations.
Chapitre 3 Une nouvelle chambre
ATTENDUS PAR MATIÈRE
LES NOMBRES
Opérer sur des nombres et sur des expressions algébriques
Attendus
Associer une opération à ses composantes et son résultat : – addition, termes, somme ; – soustraction, premier terme, deuxième terme, différence ; – multiplication, facteurs, produit ; – division, dividende, diviseur, quotient, reste.
Attendus
Identifier une opération ou une suite d’opérations à partir d’une situation.
Appréhender et utiliser l’égalité. Utiliser l’égalité en termes de résultat : addition, soustraction, multiplication et division.
Utiliser les propriétés des opérations pour remplacer un calcul par un autre plus simple.
Appliquer un algorithme de calcul écrit pour en comprendre le mécanisme.
Estimer et vérifier.
Utiliser la commutativité de l’addition et de la multiplication.
Utiliser l’associativité de l’addition et de la multiplication.
Effectuer des additions de maximum trois termes (limités au millième).
Effectuer des soustractions limitées au millième (technique de compensation et/ou d’emprunt).
Estimer l’ordre de grandeur du résultat d’une opération (addition, soustraction, multiplication et division), avant de calculer précisément.
Vérifier la plausibilité d’un résultat.
Utiliser les opérations réciproques (+, –) et (×, :) pour vérifier le résultat d’une opération.
Compétence(s) Attendus
Résoudre des problèmes en mobilisant des nombres et des opérations.
Résoudre un problème faisant intervenir des opérations sur les nombres : – en traduisant une situation contextualisée par un dessin, une verbalisation puis l’écriture d’opérations mathématiques (+, –, ×, :) ; – en estimant le résultat ;
en effectuant les calculs ; – en communiquant le résultat avec précision ; – en vérifiant la plausibilité de la réponse et en verbalisant sa démarche.
LES SOLIDES ET FIGURES
(Se) repérer et communiquer des positionnements ou des déplacements
ÉditionsVANIN
Savoir(s) Attendus
Utiliser le vocabulaire exprimant des positions absolues : à côté de, contre, à l’intérieur, à l’extérieur, entre, sous, sur, dans, hors, autour de, face à face, dos à dos.
Les visions de l’espace.
Utiliser le vocabulaire exprimant des positions relatives (liées au regard) : devant, derrière, à droite, à gauche, en haut, en bas, au-dessus, en dessous, en face de, de face, de dos, de profil.
Utiliser le vocabulaire exprimant des positions ordinales : – premier, deuxième, troisième… dernier ; – au début, à la fin, avant, après.
Savoir-faire
Situer, placer un objet ou soi-même.
Savoir(s)
Attendus
Placer un ensemble d’objets/soi-même selon des consignes données ou un modèle observé dans l’espace 2D (photo, plan).
Appréhender et représenter des objets de l’espace
Attendus
Identifier :
Les figures, leurs composantes, leurs caractéristiques et leurs propriétés.
Savoir(s)
L’identification et la comparaison de grandeurs d’objets.
Savoir(s)
L’usage des unités conventionnelles.
Savoir-faire
Mesurer des grandeurs.
Construire le système des unités conventionnelles.
– des quadrilatères : carré, rectangle, losange, parallélogramme, trapèze, trapèze isocèle, trapèze rectangle ; – des triangles : acutangles, rectangles, obtusangles, scalènes, isocèles, équilatéraux ; – un cercle.
LES GRANDEURS
Concevoir des grandeurs
Attendus
ÉditionsVANIN
Utiliser de manière adéquate les termes relatifs aux grandeurs : la longueur, la masse, la capacité, le cout, l’aire, le volume.
Agir sur des grandeurs
Attendus
Utiliser et symboliser :
– les unités de longueur ; – les unités de capacité ;
– les unités de masse ;
– les unités d’aire : le mètre carré (m²), le décimètre carré (dm²), le centimètre carré (cm²), le millimètre carré (mm²) ; – une unité de volume : le centimètre cube (cm³).
Distinguer dans l’expression d’une grandeur mesurée : la grandeur, la mesure et l’unité de mesure.
Attendus
Effectuer le mesurage d’une grandeur d’un objet de l’environnement et en exprimer le résultat en utilisant une unité conventionnelle :
– de longueur ; – de capacité ; – de masse ; – d’aire : m², dm², cm², mm² ; – de volume : cm³.
Donner du sens aux unités conventionnelles travaillées en les associant à des objets de l’environnement (un m2 c’est l’aire de…).
Lister des objets de la vie courante dont une grandeur se mesure avec l’unité travaillée.
Donner du sens aux préfixes déci-, centi-, milli-, kilo-, hecto-, déca-, dans les unités conventionnelles travaillées.
Réaliser des conversions significatives (longueur, masse, capacité, aire) en lien avec les unités conventionnelles travaillées, avec ou sans abaques (construits préalablement).
Compétence(s) Attendus
Résoudre des problèmes dans des situations contextualisées.
Résoudre des problèmes d’achats mobilisant : – des prix exprimés en € et centimes ; – les expressions comme « 1 + 1 gratuit », « le deuxième à moitié prix », « prix à partir de… » ou « jusqu’à 70 % de remise » ; – la notion de bénéfice et de perte.
Résoudre des problèmes dans lesquels deux grandeurs sont en relation de proportionnalité directe.
Exemple : la distance et la durée.
Savoir-faire
Exploiter des situations de proportionnalité directe entre grandeurs.
Mettre en relation des grandeurs
Attendus
Déterminer une quantité dans une situation contextualisée de proportionnalité directe (nombre de… pour…).
Identifier un lien (multiplicatif ou additif) entre deux grandeurs dans un tableau de proportionnalité.
Compléter un graphe fléché ou un tableau de proportionnalité en lien avec une situation de proportionnalité directe.
Compétence(s) Attendus
Résoudre des situations de proportionnalité directe.
Écrire le résultat et sa démarche de résolution d’une situation de proportionnalité directe.
MATIÈRES ABORDÉES
Estimer et arrondir un nombre
L’addition écrite
Les nombres
Les solides et figures
Les grandeurs
Le traitement des données /
La soustraction écrite :
– par emprunt
– par compensation
Les visions dans l’espace
Les polygones
Les masses
La proportionnalité
ÉditionsVANIN
ÉditionsVANIN
Activité 1 – Estimer et arrondir un nombre
Exercice 1
Mise en situation :
Pour refaire la chambre de leur fille, les parents de Lucie vont faire quelques courses dans trois magasins. Ils ont listé ce qu’ils devaient acheter et ont indiqué pour chaque article le prix.
Mission des élèves :
– Déterminer si le budget de 1 300 € est respecté.
SO LO
→ Vous devez estimer le cout total. Est-ce que le budget est respecté ?
D U O
COLL ECTIF
SO LO
COLL ECTIF
SO LO
Donner aux élèves le temps d’en discuter avec leur voisin(e).
Pour cela, pas de calculatrice ni de cahier de brouillon, ils (elles) doivent juste utiliser leur tête : – laisser les élèves chercher en utilisant la technique, la méthode de leur choix ; – l’enseignant(e) peut aider les élèves qui éprouvent des difficultés en leur donnant des indices, tels que arrondir les nombres, utiliser l’associativité…
Ensuite vient la vérification.
Chaque élève s’exprime tant sur le respect du budget que sur le montant qu’il a estimé. L’enseignant(e) note les réponses au tableau.
Mise en commun et correction collective.
ÉditionsVANIN
Travail sur la feuille. Les élèves arrondissent chaque prix de la première liste (Ikéo) et le notent sur les pointillés.
Même démarche pour les deux autres listes. Les élèves travaillent de manière individuelle puis comparent avec leur voisin(e).
L’objectif est de montrer aux élèves l’utilité d’avoir recours à cette technique d’arrondir et d’estimer.
a) Les élèves dessinent des articles pour la chambre de Lucie.
b) Les élèves dessinent des objets et indiquent leur prix. Exercice qui les confronte à la réalité.
1.
Chapitre
Une nouvelle chambre
1. Estimer et arrondir un nombre
Les parents de Lucie ont décidé de refaire la chambre de leur fille. Le budget pour ce projet est de 1 300 €. Voici les listes de courses.
Ikéo
Lit 169 €
Garde-robe 443 €
Bureau 74 €
Bibliothèque 38 €
Table de nuit 24 €
Chaise de bureau 29 €
Estimation :
Brico Buho
Peinture latex pour le plafond 35,90 €
Peinture murale (5 l)
Shady Red (rose pâle) 84,50 €
Peinture murale (2,5 l) Shady Red (rose pâle) 44,50 €
Estimation :
Déco House
Tapis 2 × 79,90 €
Miroir 39,99 €
Housse de couette + taies 24,99 €
Accessoires 55 €
Estimation :
Exemple de solution
Est-ce que le budget est respecté ?Oui. – Non. Zone de travail
a) Dessine, en respectant les listes, la future chambre de Lucie.
b) La mamie de Lucie lui donne un petit bonus de 200 €. Dessine des objets pour sa chambre et indique pour ceux-ci leur prix.
Je retiens
Pourquoi ?
Arrondirdesnombres
On arrondit des nombres pour se simplifier la vie, pour rendre des calculs plus simples ou encore vérifier le résultat d’un calcul par estimation.
Comment ?
Arrondir un nombre, c’est le remplacer par un nombre proche de celui-ci.
Exemples 1 223 est arrondi à 1 220 (nombre arrondi à la dizaine)
Si le chiffre du rang inférieur est 1, 2, 3 ou 4, alors on laisse le chiffre du rang à gauche tel quel et on remplace par des 0 les chiffres des rangs qui suivent.
1 283 est arrondi à 1 300 (nombre arrondi à la centaine)
Si le chiffre du rang inférieur est 5, 6, 7, 8 ou 9, alors on augmente de 1 le chiffre du rang à gauche et on remplace par des 0 les chiffres des rangs qui suivent.
2.
As-tu bien compris ?
Pour arrondir un nombre à l’unité
9
4 526,9 Je regarde le chiffre des dixièmes (rang inférieur) qui est J’augmente de 1 le chiffre des unités et je place un ou des 0 si des chiffres se trouvent à droite.
→ J’obtiens ou .
Pour arrondir un nombre à la dizaine
4 526,9 Je regarde le chiffre des (rang inférieur) qui est J’augmente de le chiffre des et je place un ou des 0 si des chiffres se trouvent à droite.
→ J’obtiens ou .
Pour arrondir un nombre à la centaine
4 526,9 Je regarde le chiffre des (rang ) qui est .
Je laisse tel quel le chiffre des et je place un ou des si des chiffres se trouvent à
→ J’obtiens ou
Je retiens
COLL ECTIF
Deux questions :
Pourquoi arrondir des nombres ?
Les différentes réponses sont notées sur les pointillés.
Comment arrondir ?
Arrondir, c’est remplacer un nombre par un autre proche de celui-ci mais qui peut être arrondit à l’unité, à la dizaine ou…
Ne pas hésiter à faire quelques exercices oralement ou par écrit pour vérifier la bonne compréhension chez les élèves.
Exercice 2
SO LO
COLL ECTIF
Exercices pour vérifier que chaque élève ait bien compris comment arrondir des nombres en fonction du rang demandé (unité, dizaine…).
Plus on avance dans l’exercice, plus il y a de mots à compléter. Travail sur la démarche afin que chaque élève puisse bien se l’approprier.
Prendre le temps de relire avec les élèves et insister sur la démarche en la faisant verbaliser par certains.
ÉditionsVANIN
Exercice 3
SO LO
Les élèves arrondissent chaque nombre à l’unité, à la dizaine, à la centaine et à l’unité de mille.
Exercice 4
SO LO
Des calculs sont écrits les uns en dessous des autres. Pour chacun d’eux, il faut retrouver son estimation sans le résoudre.
Cela implique d’arrondir les nombres afin d’obtenir un calcul plus simple.
Exemple :
312 × 48 = → 300 × 50 = 15 000
ÉditionsVANIN
Calculer la réponse exacte de chaque calcul.
Pour arrondir un nombre à l’unité de mille
inférieur
4 526,9 Je regarde le chiffre des (rang ) qui est J’ de le chiffre des et je place un ou des si des chiffres se trouvent à → J’obtiens ou
Arrondis ces nombres.
À l’unitéÀ la dizaineÀ la centaineÀ l’unité de mille
1 217,8
5 297,1
7 821,2
828,9
Relie chaque calcul à l’estimation de son résultat.
Pour chaque calcul, retrouve la réponse exacte et écris-la sur les pointillés.
Pour chaque calcul, coche la meilleure estimation.
a)5 024 + 6 992 =
5 000 + 6 000
6 000 + 7 000
5 000 + 7 000
d)3 658 + 5 008 =
3 600 + 5 000
3 700 + 5 000
3 600 + 4 900
5. 6. 7. x x x x x x 5 020 + 6 990 = 12 010 6 000 + 800 = 6 800
b)120 560 – 31 504 =
120 600 – 31 500
120 500 – 31 000
120 600 – 32 000
e)258,4 + 2 310,9 =
259 + 2 320
258 + 2 310
258 + 2 311
Donne les estimations et les résultats estimés…
c)5 983 + 789 =
5 990 + 790
5 980 + 790
5 980 + 780
f)256 × 9 632 =
300 × 9 000
250 × 9 630
260 × 9 630
– en arrondissant à la dizaine pour a) : .
– en arrondissant à la centaine pour c) :
– en arrondissant à l’unité de mille pour d) :
4 000 + 5 000 = 9 000
Pour chaque calcul, écris son estimation, puis relie-la au bon résultat.
7 000 –4 500 = 2 500
90 × 30 = 2 700
: 4 =
478 + 6 641 =
8 000: 4 = 2 000
3 500 + 6 600 = 10 100
287,5 × 42,8 = 10 119
300 × 40 = 12 000
Invente un calcul avec son estimation et le résultat.
Nombreuses réponses possibles
Entoure la réponse correcte.
Exercice 5
SO LO
Il faut cocher la meilleure estimation par rapport à un calcul donné.
Les élèves doivent estimer trois des six calculs en arrondissant au rang demandé.
Exercice 6
SO LO
Différents calculs (+, –, × et :) doivent être estimés. Ensuite, grâce à l’estimation, les élèves doivent retrouver le bon résultat.
Même exercice, mais il faut ici inventer un calcul, faire son estimation et indiquer le résultat.
ÉditionsVANIN
Exercice 7
SO LO
Pour entourer la réponse correcte, les élèves doivent estimer chaque calcul.
Exercices supplémentaires disponibles en téléchargement. Évaluation disponible en téléchargement.
Activité 2 – Les visions dans l’espace
Exercice 1
SO LO
Double tâche pour les élèves :
1. Tracer (utilisation de la latte obligatoire) trois meubles suivant les informations données. Ces dernières permettent de travailler le vocabulaire exprimant des positions absolues et relatives. Les dimensions sont données à l’échelle pour faciliter le travail.
2. Dessiner différents éléments. Certains éléments seront dessinés à main levée, mais parfois la latte peut être aussi de la partie. Laisser les élèves libres pour cette partie.
COLL ECTIF
SO LO
Permettre aux élèves de se déplacer dans la classe afin de voir la production de leurs condisciples. Si besoin, prévoir un moment de réajustement par la suite.
Laisser l’imagination des élèves faire son œuvre. Ils (Elles) doivent agrémenter la chambre de Lucie en dessinant d’autres objets. Pour les objets placés sur le plan, il faudra, en parallèle, rédiger une phrase pour décrire leur position.
ÉditionsVANIN
1.
2. Les visions dans l’espace
Observe le plan de la chambre de Lucie.
Trace et dessine ce que l’on te demande sur le plan de la chambre.
Échelle : 1 50
Trace :
– un bureau (3 cm sur 1,5 cm) contre le mur en face du lit;
– à droite du bureau, une bibliothèque (3 cm sur 1 cm) collée contre le bureau;
– à gauche, quand tu rentres dans la chambre, une garde-robe (4 cm sur 1,5 cm) contre le mur pour que Lucie puisse y ranger ses vêtements.
Dessine :
ÉditionsVANIN
– une table de nuit à droite du lit;
– à gauche du lit se trouve un tapis ;
– sur le tapis, il y a les pantoufles de Lucie;
– devant le bureau, une chaise ;
– au-dessus du lit, un oreiller ;
– sur le bureau, le Carrément Math en haut à gauche.
Trace ou dessine d’autres objets pour agrémenter la chambre de Lucie et écris leur position.
Voici la bibliothèque de Lucie. Complète les phrases avec les mots suivants : 2.
dans – dos à dos – à l’intérieur – sous – hors – sur – entre – face à face – contre – à côté
a) Le dictionnaire est ........................... la coupe.
b) Les crayons sont ............................. le gobelet.
c) Le cadre photo est ........................... la coupe et la casquette.
d) Les deux peluches sont ......................... .
e) La console est ................................. des peluches.
f) La coupe est ................................... le dictionnaire.
ÉditionsVANIN
g) La mallette est ................................... la bibliothèque.
h) Les pièces sont .............................. de la boite.
i) Une pièce est ................................. de la boite.
j) Les statuettes sont .......................... l’une de l’autre.
Tout en bas de la bibliothèque, dessine une troisième statuette. sous dans entre dos à dos à côté sur contre à l’intérieur hors face à face
Sur la 1re étagère, dessine à gauche de la pièce un objet que tu aimerais ranger.
Exercice 2
Utilisation du vocabulaire propre aux positions relatives. En effet, c’est le regard de l’élève qui détermine la position des objets. Les élèves replacent donc les termes donnés sur les pointillés.
Les élèves comparent avec leur voisin(e) afin de vérifier leurs réponses et de réajuster si nécessaire.
ÉditionsVANIN
L’exercice de dépassement fait appel au talent artistique de l’élève. Il (Elle) doit donc dessiner ce qui lui est demandé en tenant compte des informations.
Exercice 3
SO
SO
Exercice exploitant davantage le vocabulaire exprimant des positions ordinales : – premier, deuxième, troisième… dernier ; – au début, au milieu, avant, après.
Le vocabulaire permet d’identifier les tranches des livres sur lesquelles il faut écrire le titre demandé.
À partir des données, les élèves colorient les tranches dans la couleur demandée.
ÉditionsVANIN
Appel à l’imagination des enfants en inventant des titres de livres sur les tranches restantes. Il faut également rédiger une phrase pour écrire leur position.
Exercice 4
Lis attentivement et complète les tranches des livres demandés sur le dessin.
Sur la troisième étagère, Lucie a rangé ses livres et ses bandes dessinées. Petit problème : beaucoup de titres sur les tranches se sont effacés. Aide-la à les compléter.
– Le titre du premier livre est une BD qui s’appelle «Ziteuf» et le titre, c’est : «La bande des copains».
– Juste avant «Le voyage d’Émilie» se trouve le livre « Les Aristochiens ».
– Le dernier livre est «Les aventures du P’tit André».
– Au milieu des livres, Lucie a rangé son «Carrément Math».
– Juste après «1001 Histoires», c’est «Jack et la tomate magique».
– Le 8e livre a pour titre «Le Petit Chaperon bleu».
Colorie les tranches des livres demandés sur le dessin ci-dessus. 4.
Colorie la tranche du livre :
– qui se trouve entre «Jack et la tomate magique» et «Artchi au pays des Minitoys » en bleu ;
– qui est en avant-dernier en rouge;
– qui est en 10e position en vert;
– qui est juste après «Le voyage d’Émilie» en jaune;
– qui est au début de l’étagère en orange.
Pour les tranches restées vides, trouve un titre et écris où il se situe.
Observe cette partie de Stratego. 5.
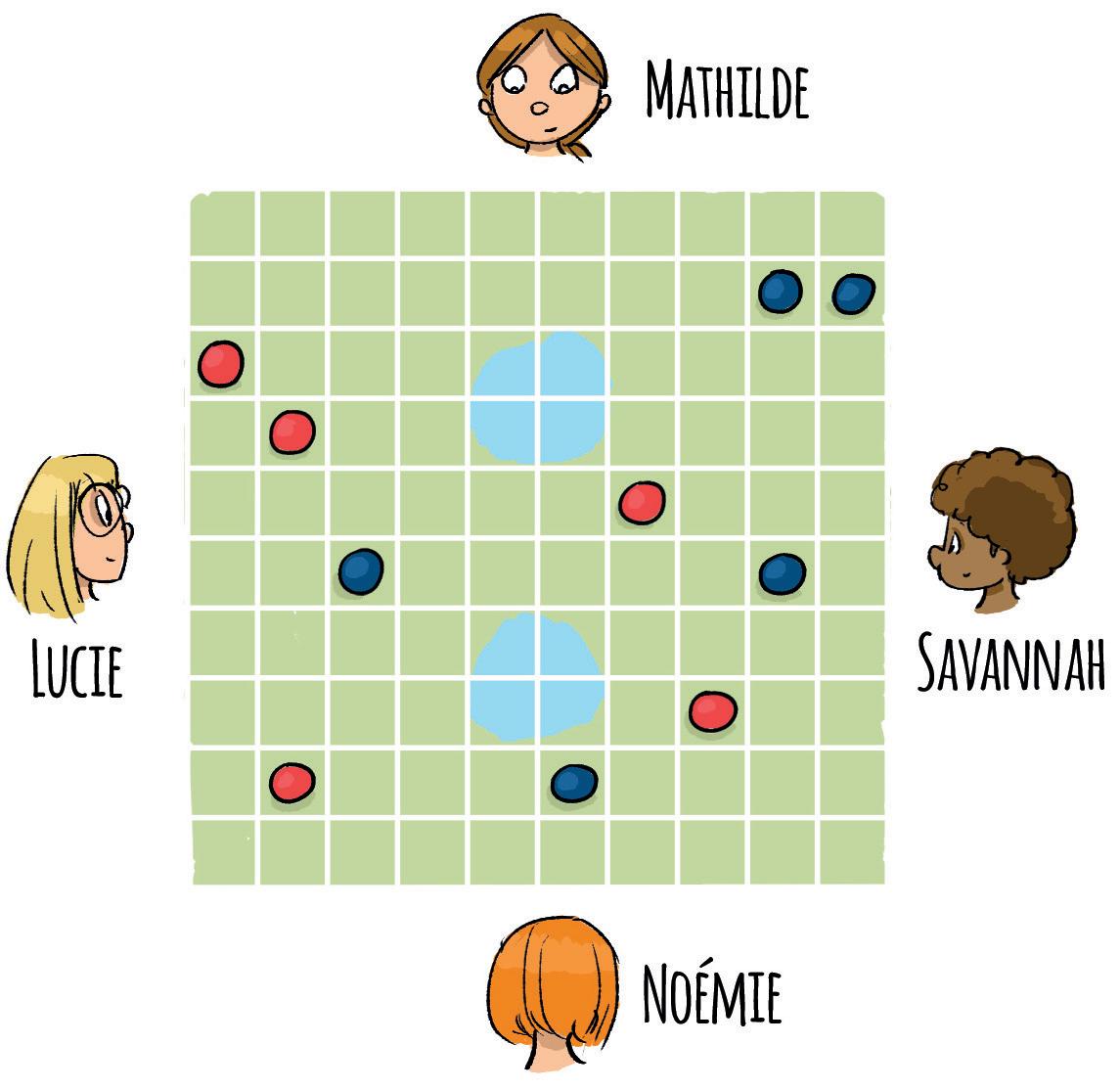
– Que voit Noémie?
– Que voit Lucie?
– Dessine ce que voit Savannah.
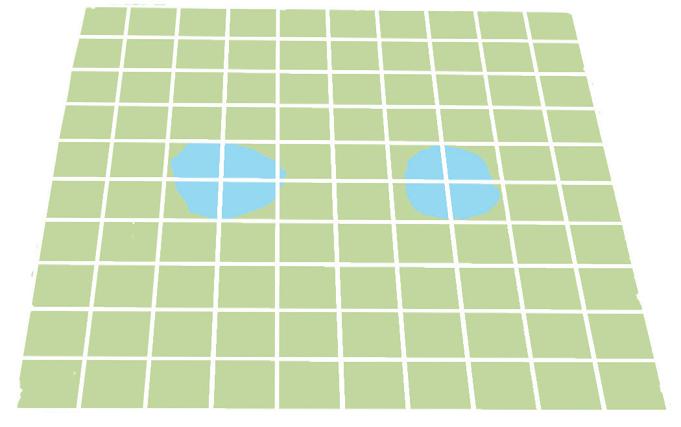
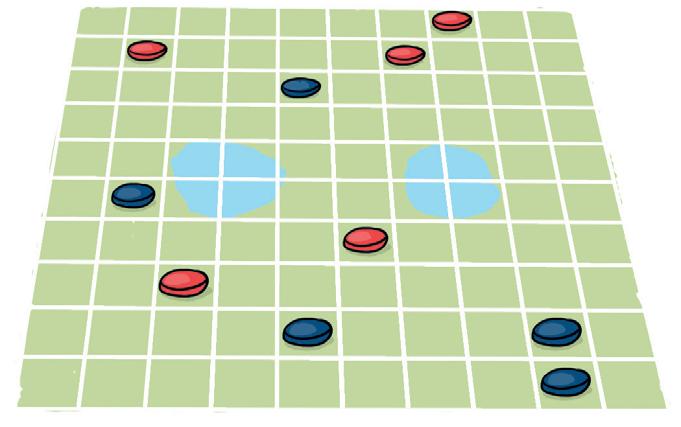
Les élèves doivent se mettre à la place de trois personnes qui font une partie de Stratego. Pour les deux premières (Noémie et Lucie), ils (elles) ont trois choix et doivent donc sélectionner la bonne réponse. Pour la troisième, il faut redessiner ce que Savannah voit. Les élèves doivent ainsi se mettre à sa place et dessiner les pions bleus et rouges.
ÉditionsVANIN
Activité
3 – L’addition écrite
Mise en situation :
La famille Beckers fait le tour du monde. L’itinéraire de ce tour du monde est illustré sur la carte géographique qui est à la page suivante.
SO LO puis COLL ECTIF
Les élèves observent la carte.
Sont mis en commun : – l’échelle, – les continents, les pays par où ils vont passer, – la légende, – etc.
Faire verbaliser également le fait que certains déplacements se font par cargo pour rejoindre différents points de l’itinéraire.
SO LO
À chacun(e) de trouver le nombre total de kilomètres parcourus sur les routes par la famille Beckers.
COLL ECTIF
Mise en commun des différentes démarches effectuées par les élèves.
Proposition : permettre aux élèves de se déplacer de banc en banc pour jeter un coup d’œil sur le travail de leurs condisciples.
→ Discussion sur les observations de chacun(e).
Objectif : arriver à mettre en évidence l’emploi et la pertinence de l’addition écrite avec plusieurs termes dans ce cas-ci.
Correction au tableau. Bien insister sur le respect de la position de chaque chiffre par rapport au rang qu’il occupe.
Calculer la totalité des kilomètres parcourus par la famille.
Exercice 1
Carte géographique sur laquelle l’itinéraire du tour du monde est illustré.
Les différentes distances parcourues sur les continents et les océans sont notées en km.
3. L’addition écrite
Le tour du monde des Beckers’Trotters
Les Beckers sont une famille de Bruxelles, ils ont décidé de partir faire le tour du monde en camping-car. Ils avaient envie de découvrir d’autres pays, de voir de magnifiques paysages et d’aller à la rencontre des gens dont la culture est parfois bien différente.
Observe bien la carte à la page suivante et calcule le nombre total de kilomètres parcourus sur les routes par la famille Beckers.
Zone de travail
ÉditionsVANIN
Exemple de démarches
La réponse peut-être trouvée en effectuant plusieurs calculs écrits.
Distance totale effectuée sur les routes: 63 497 km
Calcule la totalité des kilomètres parcourus par la famille Beckers (sur terre et sur mer).
Sur terre: 63 497 kmSur mer: 19 727 kmTotal: 83 224 km
ÉditionsVANIN
ÉditionsVANIN
Je retiens
COLL ECTIF
Synthèse sur l’addition écrite qui comporte 4 points :
1. Estimation : prolongement de la 1re partie du chapitre 3 qui va donc être utile aux élèves.
2. Faire attention à bien aligner les chiffres et à bien les positionner selon leur rang. Ne pas hésiter à laisser de l’espace entre les chiffres.
3. Réaliser l’addition et utiliser les termes propres à l’addition écrite (report(s), terme(s), somme).
4. Vérifier que la somme obtenue est bien proche de l’estimation qui avait été réalisée au départ.
Prolongement : donner deux additions écrites que les élèves vont devoir résoudre en mettant en pratique les 4 points de la synthèse.
Par exemple :
2 508 + 94 309 + 981 = 90 374 + 99 + 4 784 =
ÉditionsVANIN
Je retiens
1
4
Je vérifie que le résultat se rapproche bien de mon estimation de départ.
2 791 = ± 2 800
Je fais une estimation 816 + 1 975 800 + 2 000 = 2 800
2
3
Addition écrite
J’additionne les chiffres de chaque rang. Si la somme est plus grande que 9, alors je reporte le chiffre de la dizaine au rang suivant.
les reports les termes la somme
J’aligne correctement chaque chiffre de chaque rang les uns en dessous des autres
UM C D U 81 6 1 +9 75
! N’oublie pas de bien écrire le signe de l’opération !
J’explique avec mes mots
Estime, effectue cette addition écrite et explique tes démarches.
Estimation
J’additionne le report avec 7 C et 2 C.
J’obtiens ainsi 10 centaines. J’écris 0 et je reporte 1 qui représente une unité de mille au niveau du rang suivant.
Coche chaque fois la bonne proposition. 111 56813 +7408 64221
Le chiffre 8 du 2e terme vaut...
8 unités
8 dizaines
8 centaines
Le chiffre 9 représente...
9 unités
9 dizaines
9 centaines
Le 2 du report vaut...
2 unités
2 dizaines
2 centaines
J’additionne 2 et 4 unités. Cela donne 6unités. x x x
Impossible à dire
Impossible à dire
Impossible à dire
Invente une question que tu pourras soumettre par la suite à ton (ta) voisin(e).
Nombreuses réponses possibles
J’explique avec mes mots
SO LO
Il s’agit de réaliser une addition écrite puis de se centrer sur des étapes bien précises.
Ces étapes sont entourées par un ovale dont part une flèche qui renvoie à un espace pour écrire ce qu’il se passe au niveau mental.
Ce travail de métacognition permet de comprendre toute la subtilité de l’opération écrite.
Par exemple : un report « 1 » en fonction de la position n’est pas forcément une unité comme le disent trop souvent les élèves.
D U O puis COLL ECTIF
Laisser les élèves comparer leurs réponses entre eux (elles) et passer ensuite à la correction.
Exercice 2
SO LO
Exercice en prolongement de l’étape précédente.
Les élèves doivent cocher la bonne réponse à ce qui leur est demandé.
SO LO
Attention : bien vérifier qu’aucune des propositions ne peut convenir avant de cocher « Impossible à dire ».
ÉditionsVANIN
L’idée est de donner une petite fiche vierge et de permettre aux élèves de concevoir une addition, de la résoudre et d’ensuite cibler une étape de cette opération en soumettant la réponse dans un choix multiple.
Prolongement : ces fiches pourraient être projetées ou plastifiées pour pouvoir passer dans la main de chaque élève et permettre à l’enseignant(e) d’interroger un plus grand nombre.
Exercice 3
SO LO
Les élèves doivent d’abord estimer puis effectuer des additions écrites.
SO LO
Additions écrites supplémentaires de deux ou trois termes.
Exercice 4
SO LO
Il faut chaque fois modifier une addition en fonction de ce qui est demandé pour répondre à la consigne.
ÉditionsVANIN
Exercices supplémentaires disponibles en téléchargement. Évaluation disponible en téléchargement.
Estime, puis effectue les additions écrites.
8 452 + 782 = Estimation :
34 875 + 69 705 = Estimation :
6 057 + 15 961 = Estimation :
Effectue ces additions sur une feuille. 8 452 +
Modifie cette addition en fonction de la consigne demandée.
Modifie un seul chiffre afin de ne plus avoir aucun report.
Exemple de correction
Ajoute un troisième terme pour avoir un report de 2 C sans toucher aux deux autres termes.
4. La soustraction écrite
À la fin du périple de la famille Beckers, le compteur kilométrique du campingcar indiquait 84 328 km. À combien était-il lorsque les Beckers ont démarré leur tour du monde ?
Zone de travail
Estimation :
au départ
Compare avec ton (ta) voisin(e).
Quel était le kilométrage du camping-car lorsqu’ils sont arrivés en Afrique ?
Utilise une feuille pour effectuer tes opérations écrites.
Exemple de correction à réaliser en calculs écrits.
84 328 km – (19 834 km + 20 678 km) = 43 816 km 40 512 km
Je retiens
Complète les pointillés dans la synthèse ci-dessous. Voici les mots à remplacer : vérifie – estime – soustrais – aligne. 3 Je les chiffres de chaque rang.
C
–les termes
différence ! N’oublie pas de bien écrire le signe de l’opération ! 2 724 – 891 = – = 1 J’ en arrondissant les termes. UM C D U 7 22 4 – 891 2 J’ correctement chaque chiffre de chaque rang les uns en dessous des autres 4 Je que le résultat se rapproche bien de mon estimation de départ. = ± Soustraction écrite 84 000 –63 000 = 21 000
Activité 4 – La soustraction écrite
Exercice 1
Mise en situation :
Toujours dans le cadre du tour du monde de la famille Beckers, les élèves doivent déterminer le kilométrage de départ du camping-car.
SO LO
Pour ce faire, ils (elles) doivent aller chercher au début de la partie 2 l’information du kilométrage effectué sur les routes lors du tour du monde et soustraire ce nombre au kilométrage donné.
Les élèves utilisent la zone de travail pour trouver la solution.
COLL ECTIF
Mise en commun des différentes démarches des élèves.
COLL ECTIF
C’est peut-être l’occasion de voir si la méthode est l’emprunt ou la compensation ou encore si les deux méthodes ont été utilisées.
Proposition : permettre aux élèves de se déplacer de banc en banc pour jeter un coup d’œil sur le travail de leurs condisciples.
→ Discussion sur les observations de chacun(e).
Objectif : arriver à mettre en évidence l’emploi et la pertinence de la soustraction écrite.
Correction au tableau. Bien insister sur le respect de la position de chaque chiffre par rapport au rang qu’il occupe.
Il faut calculer le kilométrage du camping-car lorsque la famille est arrivée en Afrique. Les élèves ont plusieurs possibilités quant à la résolution du problème. Plusieurs étapes sont nécessaires pour trouver la réponse.
Je retiens
COLL ECTIF
Synthèse sur la soustraction écrite qui comporte 4 points. Pour celle-ci, les élèves doivent replacer les termes proposés.
1. Estimation : prolongement de la 1re partie du chapitre 3 qui va donc être utile aux élèves.
ÉditionsVANIN
2. Faire attention à bien aligner les chiffres et à bien les positionner selon leur rang.
Ne pas hésiter à laisser de l’espace entre les chiffres.
3. Réaliser la soustraction et utiliser les termes propres à la soustraction écrite (emprunt(s), terme(s), compenser, différence).
4. Vérifier que la différence obtenue est bien proche de l’estimation qui avait été réalisée au départ.
Prolongement : donner deux soustractions écrites que les élèves vont devoir résoudre en mettant en pratique les 4 points de la synthèse.
SO LO
Par exemple : 90 000 – 3 874 = 47 381 – 963 =
Exercice 2
SO LO
Cette étape doit être l’occasion de prendre le temps de s’arrêter pour revoir les deux méthodes de soustraction :
– la soustraction par emprunt : lorsqu’on ne peut pas soustraire deux chiffres d’un même rang, il faut alors emprunter dans le rang qui suit directement à gauche pour rendre la soustraction possible.
– la soustraction par compensation : lorsqu’on ne peut pas soustraire deux chiffres d’un même rang, on agit sur le chiffre du premier terme en ajoutant « 10 » (aux dizaines par exemple) et sur le deuxième terme en ajoutant « 1 » (aux centaines) pour équilibrer.
COLL ECTIF
SO LO
COLL ECTIF
Voir les deux exemples dans le manuel. Laisser les élèves les observer et, ensuite, prendre le temps de les faire au tableau pour bien montrer les méthodes de l’emprunt et de la compensation.
Pour conclure, les élèves doivent résoudre deux exercices afin que l’enseignant(e) puisse vérifier qu’ils (elles) ont bien compris et sont capables de trouver la réponse par eux(elles)-mêmes.
Correction et verbalisation des emprunts et de la compensation.
Exercice 3
SO LO
Les élèves doivent d’abord estimer puis effectuer des soustractions écrites.
ÉditionsVANIN
Soustractions écrites supplémentaires.
L’enseignant(e) peut imposer la/les méthode(s) à utiliser.
Pour résoudre une soustraction écrite, il y a deux possibilités.
Observe et résous.
La soustraction par emprunt
Ce n’est pas possible de faire « 1 moins 5 », car 1 est plus petit que 5.
Donc, il faut emprunter 1 centaine qui devient 10 dizaines et qui rend ainsi la soustraction possible.
La soustraction par compensation
Ce n’est pas possible de faire « 1 moins 5 », car 1 est plus petit que 5.
Donc, il faut ajouter 10 dizaines au premier terme et compenser avec 1 centaine au deuxième pour rendre la soustraction possible.
Tu agis seulement sur le plus grand terme. Tu agis sur les deux termes. À toi…
Estime, puis effectue ces soustractions écrites.
678 – 4
Effectue ces soustractions sur une feuille.
Retrouve les chiffres manquants.
Effectue ces calculs écrits.
Fais les preuves sur une feuille pour vérifier si tu as trouvé la bonne réponse.
Pour vérifier un calcul écrit, le résultat trouvé doit être
Exercice 4
Exercices sur l’addition et la soustraction écrites en calculs lacunaires. Ici, il ne s’agit pas de trouver la somme ou la différence mais de compléter les « trous » au niveau des termes ou de la réponse.
Exercice 5
SO LO
Exercices en deux temps : – réaliser les estimations portant sur les deux opérations ; – faire la preuve pour vérifier le résultat de chaque opération.
ÉditionsVANIN
Exercices supplémentaires disponibles en téléchargement. Évaluation disponible en téléchargement.
Activité 5 – Les masses
Exercice 1
SO LO
Travail sur les représentations mentales. Les élèves mobilisent leurs connaissances et écrivent, sur les premiers pointillés, l’estimation qui conviendra le mieux pour chaque objet.
Les deuxièmes pointillés sont prévus pour la correction. Ce sont d’ailleurs les réponses de l’exercice 4 qui permettront aux élèves de confronter les bonnes réponses à leurs estimations.
COLL ECTIF
En attendant l’exercice 4, mettre en place un moment de discussion collective pour permettre aux élèves de donner leurs estimations et de déterminer les représentations de chacun, les écarts ou les rapprochements entre celles-ci.
Je retiens
SO LO
L’exercice 1 met en évidence l’unité de référence qu’est le gramme. Chaque élève peut ainsi replacer les différentes unités dans l’abaque sur la première ligne grâce, d’une part, aux unités de l’exercice 1 et, d’autre part, de leurs connaissances, car cela a déjà été travaillé lors de l’année précédente.
COLL ECTIF
Mise en commun. Correction des unités de l’abaque. Mettre en évidence les préfixes et établir des liens en rapport avec l’unité de référence.
Exercice 2
SO LO
Pour chaque chiffre souligné, les élèves doivent indiquer l’unité qui lui correspond.
1.
5. Les masses
Estime la masse de chacun de ces objets. Tu pourras vérifier tes estimations grâce aux réponses trouvées à l’exercice 4.
Estimation :
Correction :
Estimation :
Correction :
Estimation :
Correction :
Estimation :
Correction :
Je retiens
Complète les pointillés de la synthèse ci-dessous.
Les unités supérieures
Estimation :
Correction :
Estimation :
Correction :
Les
Indique, pour chaque chiffre souligné, l’unité qui lui correspond.
4864,55 kg 9700,561 g 853260,5 cg
Convertis ces grandeurs à l’aide de l’abaque. 3.
4.
Résous ces calculs. Chaque réponse est le poids d’un des objets de l’exercice 1, que tu devras replacer. Compare-les à tes estimations.
3 g − 0,2 dag = g 5 q + 1 000 kg = t
5. Complète.
6. 1 2 kg + 10 000 cg = kg
Range ces grandeurs dans l’ordre décroissant.
Exercice 3
SO LO
Travail avec l’abaque. Les élèves placent dans l’abaque les différentes longueurs et convertissent suivant l’unité demandée.
Exercice 4
SO LO
COLL ECTIF
Voici donc l’exercice qui est en lien avec l’exercice 1. Les élèves résolvent les calculs, leur réponse étant également une des réponses de l’exercice 1 qu’ils (elles) replacent sur les premiers pointillés.
En effet, les réponses de l’exercice 4 ne sont pas dans le même ordre que les réponses de l’exercice 1. Bien insister auprès des élèves afin qu’ils donnent du sens en les plaçant.
Mise en commun pour clôturer les échanges précédents, afin de corriger les mauvaises représentations et affiner celles des élèves.
Exercice 5
SO LO
Dans cet exercice, travail en deux temps : – transformer toutes les masses dans la même unité (cela facilitera le rangement) ; – ranger les masses dans l’ordre décroissant (du plus grand au plus petit).
Exercice 6
SO LO
ÉditionsVANIN
Divers calculs lacunaires mélangeant les 4 opérations mathématiques (+, –, × et :). Tenir compte du résultat et compléter les pointillés pour arriver à la réponse.
Exercices supplémentaires disponibles en téléchargement. Évaluation disponible en téléchargement.
Activité 6 – Polygones à gogo…
Exercice 1
SO LO
Avec les indices (les mots mais aussi les images des figures) qui leur sont donnés, les élèves doivent compléter les définitions.
Attention : certains mots doivent être utilisés plusieurs fois.
COLL ECTIF
Mise en commun et lecture des définitions. L’enseignant(e) veille à la bonne compréhension des élèves.
Exercice 2
SO LO
Application de la théorie dans cet exercice. Les élèves doivent trouver d’abord les polygones et, ensuite, les non-polygones.
Petite explication sur l’origine du mot « polygone ».
ÉditionsVANIN
1.
6. Polygones à gogo…
À l’aide des mots et des figures, complète les définitions. Attention : certains mots doivent être utilisés plusieurs fois.
droite – un – côtés – des – segment – les – plane – tous – fermée – segments – surface – de
Un polygone, c’est une dont sont
touslescôtés des segments surface plane fermée un des côtés unsegment de droite de droite
Un non-polygone, c’est une dont au moins n’est pas .
Colorie les bonnes réponses. polygone non-polygone 2.
ÉditionsVANIN
Le nom polygone vient du grec ancien : de « poly- » et de « -gone ». = plusieurs = angle Le savais-tu ? surface plane fermée
4.
Voici un réseau de lignes. Repasse sur celles-ci afin d’obtenir les figures demandées.
Exemple : un polygone qui a 4 côtés en rouge.
– Un polygone qui a 7 côtés en vert
– Un non-polygone, qui n’a pas de côté droit, en orange
– Un polygone qui a 5 côtés en bleu foncé
– Un non-polygone, avec trois côtés droits, en mauve
– Un polygone qui a 8 côtés en noir
Repasse ensuite pour obtenir…
– un polygone qui a 4 côtés, parallèles 2 à 2, en brun.
– un non-polygone avec 2 côtés droits en jaune.
– un polygone de ton choix en gris.
– un non-polygone de ton choix en bleu clair.
Voici des polygones réguliers.
Attention, une erreur s’est glissée dedans. Retrouve-la.
Complète la série à droite et trace un polygone régulier.
Coche la bonne définition.
C’est un polygone qui a ses angles de différentes amplitudes et ses côtés isométriques.
C’est un polygone qui a ses angles de même amplitude et ses côtés isométriques.
Exemple de correction x
C’est un polygone qui a ses angles de même amplitude et ses côtés de différentes longueurs.
Exercice 3
SO LO
Repasser sur les lignes pour obtenir les polygones et les non-polygones demandés.
Même consigne. Faire attention à bien respecter les caractéristiques demandées pour certaines figures.
Exercice 4
SO LO
Parmi les polygones, il existe des polygones particuliers qui sont les polygones réguliers.
D U O
COLL ECTIF
SO LO
Les polygones réguliers sont des polygones dont tous les côtés sont isométriques et tous les angles de même amplitude.
Deux consignes pour l’exercice 4 : – trouver l’erreur qui s’est glissée parmi les polygones réguliers ; – cocher la bonne définition.
Comparaison avec le voisin ou la voisine.
Mise en commun et verbalisation des observations (les côtés, les angles, les amplitudes…).
ÉditionsVANIN
4 figures données, dont 3 polygones réguliers, sont tracées. Les élèves disposent d’un espace sur la droite pour tracer un polygone régulier.
Comme le losange a été éliminé, on peut se poser la question de savoir si un polygone régulier de 4 côtés existe.
Évidemment que oui… Le carré peut donc être tracé. Cependant, les élèves peuvent également essayer de tracer un octogone, par exemple.
Prolongement : les différents noms des polygones réguliers constituent une grande richesse au niveau du vocabulaire.
L’enseignant(e) peut par exemple proposer de tracer des polygones réguliers inscrits dans des cercles, et mettre ainsi les élèves au défi de tracer un octogone. Il (Elle) peut aussi suggérer l’utilisation du compas.
Exercices supplémentaires disponibles en téléchargement.
Évaluation disponible en téléchargement.
Activité 7 – La proportionnalité
Exercice 1
SO LO
Mise en situation :
Observation de plusieurs photos de Jimmy, un élève. Ces photos ont différents formats.
D U O puis COLL ECTIF
Mise en commun :
→ Que constatez-vous lorsque vous regardez ces photos ?
→ Discutez-en avec votre voisin(e).
Les photos n’ont pas toutes les mêmes proportions. Certaines présentent des déformations et d’autres conservent les bonnes proportions.
SO LO
L’enseignant(e) peut demander aux élèves de colorier toutes les photos qui ont conservé leurs proportions.
COLL ECTIF
Compléter le cadre « J’ai observé ».
Exercice 2
SO LO
Pour bien comprendre ce que signifie la conservation des proportions, les élèves doivent reproduire le visage d’un(e) élève.
Attention de bien mettre l’accent sur l’utilisation du quadrillage pour être le plus précis possible.
COLL ECTIF
Si l’enseignant(e) constate que des élèves ont des difficultés à démarrer l’exercice, il (elle) peut alors, collectivement, le commencer et insister sur le quadrillage.
COLL ECTIF
Permettre aux élèves de circuler dans les bancs ou afficher des productions de certains élèves pour mettre en évidence ce qui est correct et ce qui ne l’est pas.
Faire verbaliser les élèves pour que les erreurs identifiées ne puissent pas se reproduire par la suite.
7. La proportionnalité
Le photographe est venu faire les photos individuelles à l’école. Lorsqu’on les a distribuées aux élèves, Jimmy a fait une drôle de tête… 1. Qu’en penses-tu ? Discutes-en avec tes camarades.
J’ai observé
Certaines photos sont déformées au niveau de la longueur et/ou de la largeur. Elles n’ont pas toutes les mêmes proportions.
ÉditionsVANIN
À toi de jouer ! Reproduis ce visage en veillant à garder les proportions. 2.
Je retiens
Deux grandeurs sont proportionnelles si, quand l’une est multipliée ou divisée par deux, trois…, l’autre est également multipliée ou divisée par deux, trois…
Exemple : Si1 paquet de biscuits coute3 €, alors3 paquets de biscuits coutent9 €. × 3 × 3
Complète le tableau. 3.
4.
de jeux vidéos
Voici une recette de cuisine pour la préparation de crêpes. Les ingrédients sont prévus pour 6 personnes. Trouve les quantités pour 3 personnes et pour une classe de 24 élèves.
Ingrédients pour 6personnes 20 crêpes
•6 œufs
•500g de farine
•1litre de lait
• 2cuillères à soupe d’huile
Ingrédients pour 3personnes crêpes
• œufs
• .................... g de farine
• .................... cl de lait
• .................... cuillère(s) àsoupe d’huile
Calcule les quantités pour 15 personnes.
50 crêpes: 15 œufs, 1,250 kg de farine, 2,5 l de lait, 5 cuillères.
Ingrédients pour 24 personnes crêpes • œufs
• .................... kg de farine • .......... litres de lait
cuillère(s) àsoupe d’huile
5.
Le prix des tomates au kilo est de 2,20 €.
À combien cela reviendrait-il si j’en achète 3 kg ?
Pri× pour 3 kg: 2,20 € × 3 = 6,60 €
Je retiens
COLL ECTIF
Lecture du cadre « Je retiens ».
À la suite de la lecture de l’exemple, demander aux élèves de donner d’autres exemples et les partager avec l’ensemble de la classe.
Exercice 3
SO LO
Exercice mettant en application la théorie.
Des liens peuvent être établis que l’enseignant(e) mettra en évidence : – si je multiplie par 2 puis par 4, je peux directement multiplier par 8 ; – entre les lignes, le rapport est toujours le même.
Exercice 4
SO LO
Même principe mais avec une présentation différente.
Une liste d’ingrédients pour confectionner des crêpes a été déterminée en fonction du nombre de personnes. Les élèves doivent trouver les réponses pour 3 et 24 personnes.
L’enseignant(e) peut faire calculer les quantités d’ingrédients pour le nombre d’élèves présents dans sa classe. Et pourquoi ne pas réaliser la recette ?
ÉditionsVANIN
Calculer les quantités pour 15 personnes.
Exercice 5
SO LO
Petit problème basé sur une situation de proportionnalité.
Exercice 6
SO LO
Les situations de proportionnalité peuvent aussi être représentées sous la forme de graphiques. Observation de deux graphiques dont l’un des deux représente une situation de proportionnalité.
D U O
→ Avec votre voisin(e), déterminez quel graphique représente une situation de proportionnalité et expliquez votre choix.
COLL ECTIF
Chacun(e) peut donner son avis et interagir à propos des avis émis.
Exercice 7
SO LO
Compléter le tableau et le graphique qui lui correspond.
COLL ECTIF
SO LO
Mise en commun. L’enseignant(e) peut aussi poser des questions sur le graphique. Par exemple : → D’après le graphique, quel sera le bénéfice réalisé si 60 paquets de gaufres sont vendus ?
Insister sur la continuité de la ligne qui est représentative d’une situation de proportionnalité.
ÉditionsVANIN
Calculer le bénéfice pour 343 paquets de gaufres vendus.
Observe ces deux graphiques.
L’un des deux représente une situation de proportionnalité, lequel ? Discutes-en avec ton (ta) voisin(e).
C’est le graphique A car les points sont alignés sur une droite tandis que pour le graphique B, la ligne est brisée et le rapport n’est pas le même.
Complète le tableau puis le graphique.
La classe de Mme Sophie a décidé de faire une vente de gaufres. Ce sont des paquets de 4 gaufres vendus au prix de 4 €/pièce. Pour chaque paquet, le bénéfice est d’1,50 €.
343 paquets de gaufres ont été vendus au final. Quel a été le bénéfice ?
9.
Est-ce que la situation qui t’est présentée est une situation de proportionnalité ?
Colorie la bonne réponse.
DVD12614
Prix 12 €24 €72 €168 € Situation de proportionnalité ? oui non
Pommes de terre
Variété : Nicola
Origine : Belgique
Prix au kilo : 0,90 €
Martine en a pris 5 kg et elle a payé 4,50 €.
Croissance d’un chêne
Situation de proportionnalité ? oui non
(en mètres)
Situation de proportionnalité ? oui non
20406080 âge (en années)
Complète le tableau.
À la boucherie, Jean doit acheter 600 g de saucisses. Il constate que le prix au kilo est de 10 €. Combien va-t-il payer ?
Il payera pour 600 g: (10 €: 5) × 3 = 6 €
Combien payera-t-il s’il prend 450 g ?
Il payera: (10 €: 10) × 4,5 € = 4,5 €
Exercice 8
SO LO
Plusieurs situations de la vie courante sont données. Les élèves doivent déterminer s’il s’agit ou non de situations de proportionnalité.
D U O
Mise en commun avec le (la) voisin(e) et échange si les réponses ne correspondent pas.
Exercice 9
SO LO
Tableau à compléter. Les élèves doivent ensuite déterminer le rapport entre la longueur d’un côté et le périmètre.
Exercice 10
SO LO
ÉditionsVANIN
Problème de proportionnalité. Les élèves doivent trouver le prix qu’un client payera s’il achète 600 g de saucisses. Ils (Elles) doivent trouver le prix s’il prend 450 g.
Exercices supplémentaires disponibles en téléchargement. Évaluation disponible en téléchargement.