Carrément Math - Livre de l'enseignant 1A - Edition PACTE

Livre de l’enseignant(e) A

1

Christelle Collard

Livre de l’enseignant(e) A

1

Carrément MATH

Composition de Carrément math 1

Pour l’élève : 2 livres-cahiers A et B

Pour l’enseignant : - Deux livres de l’enseignant (comprenant le corrigé et les annexes des livres-cahiers)

- Leurs versions numériques disponibles sur Wazzou

- Des exercices supplémentaires et des évaluations disponibles sur Wazzou

- Les manuels numériques (A et B) téléchargeables sur Wazzou

Carrément math 1 – Livre de l’enseignant(e) A

Auteur : Christelle Collard

Illustrations : Lisa-Marie Figuès (Lymut)

Conception graphique : Octopus Creative Communication

Mise en page : Octopus Creative Communication – Softwin

Couverture : Kivlà!

Voici le code qui vous donnera accès aux documents reproductibles en ligne liés au présent ouvrage.

Pour activer ce matériel complémentaire, rendez-vous sur www.vanin.be/myvanin et suivez-y la procédure d’inscription.

• Une fois votre accès activé, vous pourrez consulter le matériel complémentaire aussi souvent que vous le désirez et aussi longtemps que la version imprimée du présent ouvrage ne sera pas remplacée par une nouvelle édition.

• L’accès au matériel complémentaire ne peut être utilisé que par une seule personne.

• L’accès au matériel complémentaire vous est fourni gratuitement à l’achat de l’ouvrage Carrément MATH 1 – Guide de l’enseignant(e). Aucune indemnité ne sera exigible en cas de non-fonctionnement ou d’indisponibilité du site hébergeant le matériel complémentaire ou du matériel complémentaire en lui-même, pour quelque raison que ce soit.

• En cas de non-fonctionnement et/ou de question, nous sommes à votre disposition par courriel à l’adresse support@vanin.be.

L’éditeur s’est efforcé d’identifier tous les détenteurs de droits. Si malgré cela quelqu’un estime entrer en ligne de compte en tant qu’ayant droit, il est invité à s’adresser à l’éditeur.

L’orthographe telle que rectifiée le 6 décembre 1990 par le Conseil Supérieur de la langue française est d’application dans la collection. Toutefois, afin de respecter les écrits des auteurs, l’orthographe d’origine y est respectée.

Les photocopieuses sont d’un usage très répandu et beaucoup y recourent de façon constante et machinale. Mais la production de livres ne se réalise pas aussi facilement qu’une simple photocopie. Elle demande bien plus d’énergie, de temps et d’argent. La rémunération des auteurs, et de toutes les personnes impliquées dans le processus de création et de distribution des livres, provient exclusivement de la vente de ces ouvrages. En Belgique, la loi sur le droit d’auteur protège l’activité de ces différentes personnes. Lorsqu’il copie des livres, en entier ou en partie, en dehors des exceptions définies par la loi, l’usager prive ces différentes personnes d’une part de la rémunération qui leur est due. C’est pourquoi les auteurs et les éditeurs demandent qu’aucun texte protégé ne soit copié sans une autorisation écrite préalable, en dehors des exceptions définies par la loi.

Tous droits réservés. En dehors des exceptions définies par la loi, cet ouvrage ne peut être reproduit, enregistré dans un fichier informatisé ou rendu public, même partiellement, par quelque moyen que ce soit, sans l’autorisation écrite de l’éditeur.

1re édition : 2022

© Éditions VAN IN, Mont-Saint-Guibert – Wommelgem, 2022

ISBN 978-94-641-7659-9

D/2022/0078/22

Art. 601276/01

Table des matières

Chapitre 1 En avant… chez « les grands » 7

Attendus par matière .......................................................................................................... GXXV

Matières abordées GXXV

Corrigé et notes méthodologiques G7

Chapitre 2 Comme les 5 doigts de la main 17

Attendus par matière GXXVI

Matières abordées ............................................................................................................ GXXVII

Corrigé et notes méthodologiques G17

Chapitre 3 À la ferme 27

Attendus par matière ....................................................................................................... GXXVIII

Matières abordées GXXIX

Corrigé et notes méthodologiques G27

Chapitre 4 Au pays de Blanche-Neige 41

Attendus par matière GXXX

Matières abordées ............................................................................................................. GXXXI

Corrigé et notes méthodologiques G41

Chapitre 5 Une drôle de découverte pour Tao et Élisa 51

Attendus par matière ........................................................................................................ GXXXII

Matières abordées GXXXIII

Corrigé et notes méthodologiques G51

Chapitre 6 Au pays de 9 65

Attendus par matière GXXXIV

Matières abordées ............................................................................................................ GXXXV

Corrigé et notes méthodologiques G65

Chapitre 7 Au pays de 10 77

Attendus par matière ....................................................................................................... GXXXVI

Matières abordées GXXXVII

Corrigé et notes méthodologiques G77

Chapitre 8 L’arrivée de Xia 89

Attendus par matière ..................................................................................................... GXXXVIII

Matières abordées GXXXIX

Corrigé et notes méthodologiques G89

Table des pictos

Travail individuel

Travail en duo

Travail en petits groupes

Travail en groupe-classe

Documents à télécharger sur Wazzou : exercices complémentaires, évaluations et annexes

Introduction

Nouveau référentiel ? Nouveau Carrément Math !

Dès la rentrée 2022, le nouveau référentiel de mathématiques développé dans le cadre du Pacte pour un Enseignement d’excellence entre en application. Notre collection Carrément Math s’adapte donc à cette mise à jour, dont les principales lignes directrices et changements majeurs sont détaillés cidessous.

TABLEAUX SYNOPTIQUES

CHAMP 1 – De l’arithmétique à l’algèbre1

1. Appréhender le nombre puis la lettre dans tous leurs aspects

Savoir

Des nombres naturels aux nombres réels.

Utiliser des nombres pour communiquer :

une quantité ;

– une position ;

– un numéro…

Utiliser, de manière adéquate, les dix chiffres utiles à l’écriture des nombres.

Associer le nom d’un nombre (naturel jusqu’à 39) à son écriture en chiffres.

Reconnaitre les nombres de 1 à 20 en s’appuyant sur :

des schèmes structurés mettant en évidence les nombres 2, 5 ou 10 ;

des collections différentes de même quantité ;

– des variations des positions des objets d’une même collection (invariance/conservation) ;

– des variations de l’origine et du sens de comptage des objets d’une même collection (indépendance du cardinal).

Savoir Des nombres naturels aux nombres réels.

Utiliser des nombres pour communiquer :

une quantité ;

– une position ;

– un numéro…

Utiliser, de manière adéquate, les noms des rangs (unité, dizaine).

Associer le nom d’un nombre (naturel jusqu’à 100) à son écriture en chiffres.

Reconnaitre les nombres de 1 à 100 en s’appuyant sur :

des schèmes structurés mettant en évidence les nombres 2, 5 ou 10 ;

des collections différentes de même quantité ;

– des variations des positions des objets d’une même collection (invariance/conservation) ;

– des variations de l’origine et du sens de comptage des objets d’une même collection (indépendance du cardinal) ;

– des représentations en dizaines et unités. Utiliser, de manière adéquate, les mots « pair » et « impair ».

Savoir

Les chaines numériques.

Dire les nombres dans l’ordre stable jusqu’à minima 39.

Compter par 2 et par 5 jusqu’à 20.

Savoir

Les chaines numériques.

Dire les nombres dans l’ordre stable jusqu’à minima 100.

Compter par 2 jusqu’à 20 et par 5 jusqu’à 50 et par 10 jusqu’à 100.

1 Correspond au domaine Nombres et opérations des Socles de compétences.

Savoir

De la comparaison de collections puis de nombres à la relation d’ordre.

Utiliser, de manière adéquate, les termes liés à la cardinalité :

– égal à, le même nombre que, autant que ;

moins que, plus petit que ; – plus que, plus grand que.

Associer les symboles d’ordre (<, >, =) aux expressions « est plus petit que », « est plus grand que », « est égal à ».

Utiliser, de manière adéquate, les termes liés à l’ordinalité des nombres naturels :

avant, après, entre, juste avant, juste après ; – premier, deuxième… dernier.

Savoir-faire

Dire, lire, écrire et représenter les nombres dans la numération décimale.

Dire, lire les nombres jusqu’à 20 et les écrire en chiffres.

Expliquer la présence du zéro dans l’écriture de 10 et de 20.

Représenter les nombres jusqu’à 20 : – avec du matériel de comptage ;

– en dizaines et unités ;

– à l’aide de schèmes.

Savoir-faire

Dénombrer des collections à organiser.

Dénombrer des collections (jusqu’à 20) en comptant par 1, par 2, par 5 à l’aide de matériel et cardinaliser la totalité.

Savoir-faire

Décomposer et recomposer les nombres.

Décomposer et recomposer des nombres de 1 à 20 en lien avec la numération décimale.

Ex. : 17, c’est 1 D et 7 U.

Décomposer et recomposer les nombres jusqu’à 20 :

– en deux termes, de manière non ordonnée ;

en plusieurs termes dont l’addition réitérée.

Décomposer et recomposer les nombres jusqu’à 20 multiplicativement sous forme de nombre de paquets de…

Savoir

De la comparaison de collections puis de nombres à la relation d’ordre.

Utiliser, de manière adéquate, les termes liés à la cardinalité :

– égal à, le même nombre que, autant que ;

moins que, plus petit que, autant en moins que ;

plus que, plus grand que, autant en plus que ;

– vaut le double de, la moitié de…

Associer les symboles d’ordre (<, >, =) aux expressions « est plus petit que », « est plus grand que », « est égal à ».

Utiliser, de manière adéquate, les termes liés à l’ordinalité des nombres naturels :

avant, après, entre, juste avant, juste après ;

– premier, deuxième… dernier.

Savoir-faire

Dire, lire, écrire et représenter les nombres dans la numération décimale.

Dire, lire des nombres jusqu’à 100 et les écrire en chiffres.

Expliquer la présence du zéro dans l’écriture des dizaines et de 100.

Représenter les nombres de 20 à 100 : – avec du matériel de comptage ;

– à l’aide de schèmes ;

– en dizaines et unités.

Savoir-faire

Dénombrer des collections à organiser.

Dénombrer des collections (jusqu’à 100) en comptant par 1, par 2, par 5, par 10 à l’aide de matériel et cardinaliser la totalité.

Savoir-faire

Décomposer et recomposer les nombres.

Décomposer et recomposer des nombres de 1 à 100 en lien avec la numération décimale.

Ex. : 76, c’est 7 D et 6 U.

Décomposer et recomposer des nombres jusqu’à 100 en deux termes, de manière non ordonnée.

Décomposer et recomposer multiplicativement les nombres :

12, 24, 48, et les lier ;

– 12, 36, 72 et les lier ;

12, 60 et les lier ;

15, 45 et les lier.

Savoir-faire

Comparer, ordonner, situer des nombres.

Utiliser le vocabulaire adéquat et les signes

« < », « > » et « = » pour exprimer la comparaison de deux nombres.

Ordonner des nombres (de 1 à 20) du plus petit au plus grand ou inversement.

Placer un nombre donné jusqu’à 20 sur une bande numérique.

Exprimer la position d’un nombre jusqu’à 20 (par encadrement, par approximation) sur une bande numérique.

Décomposer et recomposer le nombre 100

additivement :

• en deux termes ;

• en plusieurs termes dont l’addition réitérée ;

Ex. : 100, c’est 80 et 20 ; 100, c’est 25 et 25 et 25 et 25.

multiplicativement.

Ex. : 100, c’est 2 fois 50.

Savoir-faire Comparer, ordonner, situer des nombres.

Utiliser le vocabulaire adéquat et les signes « < », « > » et « = » pour exprimer la comparaison de deux nombres.

Ordonner des nombres (de 1 à 100) du plus petit au plus grand ou inversement.

Placer un nombre donné jusqu’à 100 :

sur une bande numérique ;

– dans un tableau.

Exprimer la position d’un nombre jusqu’à 100 (par encadrement, par approximation selon un degré de précision donné) sur une bande numérique. Compléter des portions d’un tableau numérique où sont donnés quelques nombres (jusqu’à 100).

Savoir-faire

Créer des familles de nombres, relever des régularités.

Représenter les tables de multiplication par 2, par 5 et par 10 (T2, T5, T10) :

– à partir de situations ;

avec des dessins ;

– en mots ;

– en calculs (additions réitérées et multiplications).

Exprimer, de diverses manières, les régularités observées au sein de T2, T5, T10 et les lier.

2.

Savoir

Les opérations et leurs propriétés.

Associer une opération à son symbole :

– addition, « + » ;

soustraction, « - ».

Associer le symbole « = » à l’expression « est égal à » et le symbole « ≠ » à l’expression « n’est pas égal à ».

Savoir

Les opérations et leurs propriétés.

Associer une opération à son symbole :

– addition, « + » ;

soustraction, « - » ;

– multiplication, « x ».

Associer le symbole « = » à l’expression « est égal à » et le symbole « ≠ » à l’expression « n’est pas égal à ».

Opérer sur des nombres et sur des expressions algébriques

Savoir

Les automatismes de base en calcul.

Connaitre de mémoire :

les additions dont le résultat vaut 10 ;

– les additions dont le résultat vaut maximum 10 ;

les soustractions dont le premier terme est maximum 10.

Savoir-faire

Construire le sens des opérations.

Utiliser, en situations concrètes, le vocabulaire familier lié aux quatre opérations.

Ex. :

Ajouter, avancer de, monter de, mettre en plus…

Regrouper, rassembler, mettre ensemble, mettre avec…

Reculer, enlever, retirer, cacher, perdre…

– Faire des tas, des paquets, des piles de…

Partager, répartir en… tas, distribuer à…

Savoir-faire

Appréhender et utiliser l’égalité.

Montrer et verbaliser ce qui est le même ou pas, ce qui est égal ou pas, entre deux collections d’objets ou deux représentations d’objets.

Utiliser l’égalité en termes de résultat : addition et soustraction jusqu’à 20.

Savoir Les automatismes de base en calcul.

Connaitre de mémoire :

les tables d’addition des dix premiers nombres ;

les doubles jusqu’à 20 et les moitiés des nombres pairs jusqu’à 20.

Connaitre de mémoire les tables de multiplication T2, T5 et T10.

Savoir-faire

Construire le sens des opérations.

Utiliser, en situations concrètes, le vocabulaire familier lié aux quatre opérations.

Ex. :

Ajouter, avancer de, monter de, mettre en plus…

– Regrouper, rassembler, mettre ensemble, mettre avec…

– Reculer, enlever, retirer, cacher, perdre…

Chercher l’écart entre, la différence…

– Faire des tas, des paquets, des piles de…

– Partager, répartir en… tas, distribuer à…

Savoir-faire

Appréhender et utiliser l’égalité.

Montrer et verbaliser ce qui est le même ou pas, ce qui est égal ou pas, entre deux collections d’objets ou deux représentations d’objets.

Utiliser l’égalité en termes de résultat : addition, soustraction jusqu’à 100, multiplication en lien avec les tables et les nombres étudiés.

Utiliser l’égalité en termes d’équivalence : nombres jusqu’à 20.

Ex. :

12 + 7 = 19

19 = 12 + 7

12 + 7 = 20 - 1

15 + 5 = 4 x 5

Savoir-faire

Utiliser les propriétés des opérations pour remplacer un calcul par un autre plus simple.

Utiliser la commutativité de l’addition.

Savoir-faire

Utiliser les propriétés des opérations pour remplacer un calcul par un autre plus simple.

Utiliser la commutativité de l’addition et de la multiplication.

Utiliser l’associativité de l’addition et de la multiplication.

Savoir-faire

Utiliser des procédures de calcul mental pour trouver le résultat plus facilement.

Utiliser la technique de décomposition pour effectuer une addition ou une soustraction.

Effectuer des multiplications spécifiques par 10 et par 20.

Compétence

Résoudre des problèmes en mobilisant des nombres et des opérations.

Résoudre un problème faisant intervenir des opérations sur les nombres :

– en traduisant une situation contextualisée par un dessin, une verbalisation, puis l’écriture d’une opération mathématique (+, -) ;

– en effectuant les calculs ;

– en communiquant le résultat avec précision.

Savoir-faire Estimer et vérifier.

Vérifier la plausibilité d’un résultat.

Utiliser les opérations réciproques (+, -) pour vérifier le résultat d’une opération.

Compétence

Résoudre des problèmes en mobilisant des nombres et des opérations.

Résoudre un problème faisant intervenir des opérations sur les nombres :

– en traduisant une situation contextualisée par un dessin, une verbalisation, puis l’écriture d’une opération mathématique (+, -, x) ;

– en effectuant les calculs ;

– en communiquant le résultat avec précision, et verbaliser sa démarche.

Imaginer une situation en partant de la communication du résultat.

Ex. : maman a payé 12 euros.

CHAMP 2 – Des objets de l’espace à la géométrie2

1. (Se) Repérer et communiquer des positionnements ou des déplacements

Savoir

Les visions de l’espace.

Utiliser le vocabulaire exprimant des positions absolues : à côté de, contre, à l’intérieur, à l’extérieur, entre, sous, sur, dans, hors, autour de.

Savoir

Les visions de l’espace.

Utiliser le vocabulaire exprimant des positions absolues : à côté de, contre, à l’intérieur, à l’extérieur, entre, sous, sur, dans, hors, autour de, face à face, dos à dos.

Utiliser le vocabulaire exprimant des positions relatives (liées au regard) : devant, derrière, à droite, à gauche, en haut, en bas, au-dessus, en dessous, en face de.

Utiliser le vocabulaire exprimant des positions ordinales :

premier, deuxième, troisième… dernier ;

– au début, à la fin, avant, après.

Savoir

Les déplacements.

Utiliser le vocabulaire décrivant un déplacement, tel que : monter, descendre, avancer, reculer, s’éloigner, se rapprocher, faire demi-tour…

Utiliser le vocabulaire exprimant des positions ordinales :

premier, deuxième, troisième… dernier ;

– au début, à la fin, avant, après.

Savoir

Les déplacements.

Utiliser le vocabulaire décrivant un déplacement, tel que : monter, descendre, avancer, reculer, s’éloigner, se rapprocher, faire demi-tour…

Savoir

Les systèmes de repérage : du quadrillage au repère orthonormé.

Utiliser le vocabulaire lié aux quadrillages : colonnes, lignes et cases.

Savoir-faire

Situer, placer un objet ou soi-même.

Situer (exprimer la position absolue ou ordinale) un objet ou soi-même avec le vocabulaire adéquat dans l’espace 3D (réel, vécu, miniaturisé).

Placer un objet/soi-même selon des consignes données ou un modèle observé dans l’espace 3D (réel, vécu, miniaturisé).

Savoir-faire

Déplacer un objet ou soi-même.

Se déplacer ou déplacer un objet dans l’espace 3D (réel, vécu, miniaturisé) en suivant deux consignes orales consécutives.

Expliquer oralement un déplacement vécu, à l’aide du vocabulaire adéquat, en identifiant au moins deux points de repère.

Savoir-faire

Situer, placer et déplacer un objet ou soi-même sur une bande orientée.

Situer (exprimer la position absolue ou ordinale) un objet sur une bande orientée.

Placer un objet sur une bande orientée. Ex. : jeux de parcours.

Déplacer un objet ou soi-même d’une quantité donnée, sur une bande orientée.

Savoir-faire

Situer, placer un objet ou soi-même.

Situer (exprimer la position absolue, relative ou ordinale) un objet ou soi-même avec le vocabulaire adéquat :

– dans l’espace 3D (réel, vécu, miniaturisé) et 2D (dessin, croquis, photo) ;

– selon le point de vue de l’élève.

Placer un objet/soi-même selon des consignes données ou un modèle observé dans l’espace 3D (réel, vécu, miniaturisé) et 2D (dessin, croquis, photo).

Savoir-faire

Déplacer un objet ou soi-même.

Se déplacer ou déplacer un objet dans l’espace 3D (réel, vécu, miniaturisé) en suivant à minima trois consignes orales consécutives.

Expliquer oralement un déplacement vécu, à l’aide du vocabulaire adéquat, en identifiant au moins trois points de repère.

Savoir-faire

Situer, placer et déplacer un objet ou soi-même sur une bande orientée.

Situer (exprimer la position absolue ou ordinale) un objet sur une bande orientée.

Placer un objet sur une bande orientée. Ex. : jeux de parcours.

Déplacer un objet ou soi-même d’une quantité donnée, sur une bande orientée.

Savoir-faire

Situer, placer un objet dans un quadrillage.

Situer (exprimer la position) un objet dans un quadrillage non codé.

Placer un objet dans un quadrillage non codé, selon des consignes données ou un modèle observé.

Compétence

Lire, interpréter des représentations de l’espace et les confronter au réel.

Réaliser dans un espace connu un agencement spatial de minimum quatre objets correspondant à une photo donnée (vue de face).

Compétence

Lire, interpréter des représentations de l’espace et les confronter au réel.

Réaliser dans un espace connu, un agencement spatial de minimum six objets correspondant à une vue du dessus donnée.

Savoir

Les figures, leurs composantes, leurs caractéristiques et leurs propriétés.

Identifier un carré, un rectangle, un triangle, un disque.

Les figures, leurs composantes, leurs caractéristiques et leurs propriétés.

Identifier un carré, un rectangle, un triangle, un disque, un cercle.

Désigner des composantes des figures travaillées : côtés (longueur, largeur), sommets, angles (droits).

2. Appréhender et représenter des objets de l’espace Savoir

Savoir

Les solides, leurs composantes, leurs caractéristiques et leurs représentations planes.

Désigner un cube, un parallélépipède rectangle, un cylindre, une sphère.

Énoncer des caractéristiques des figures travaillées : le nombre de côtés, les côtés isométriques et le nombre d’angles droits.

Savoir

Les solides, leurs composantes, leurs caractéristiques et leurs représentations planes.

Désigner un cube, un parallélépipède rectangle, un cylindre, une sphère.

Identifier les composantes des solides travaillés : faces, arêtes, sommets.

Désigner un objet courant correspondant à un solide similaire (cube, parallélépipède rectangle, cylindre, sphère).

Savoir-faire

Construire des solides et des figures avec du matériel varié.

Reproduire des solides à partir de modèles 3D donnés, avec du matériel varié (pâte à modeler, blocs ou boites à assembler…).

Reproduire des figures par découpage, par pliage et avec du matériel varié.

Savoir-faire

Tracer des figures.

Utiliser la latte pour tracer, sur papier vierge, une droite sans contrainte.

Tracer des figures à main levée en repassant sur des « segments de droite » formés par des faisceaux de droites donnés.

Énoncer des caractéristiques des solides travaillés : nombre de faces, forme des faces, des faces de même empreinte.

Savoir-faire

Construire des solides et des figures avec du matériel varié.

Reproduire des solides à partir de modèles 3D donnés, avec du matériel varié (pâte à modeler, blocs ou boites à assembler…).

Reproduire et construire des rectangles et des carrés par découpage, par pliage et avec du matériel varié.

Savoir-faire

Tracer des figures.

Utiliser la latte pour tracer, sur papier vierge, une droite en passant par un, puis deux points donnés.

Tracer des quadrilatères et/ou des triangles à la latte, en repassant sur des « segments de droite » formés par des faisceaux de droites donnés.

Tracer un rectangle, un carré à la latte sur papier tramé, avec et sans contraintes.

Savoir-faire

Tracer des axes de symétrie, des diagonales, des médianes et des hauteurs.

Matérialiser un axe de symétrie d’un dessin ou d’une image symétrique par pliage.

Produire une forme symétrique par découpage, à partir d’une feuille pliée en deux.

Savoir-faire

Comparer des figures.

Comparer les caractéristiques d’un carré et d’un rectangle selon les côtés et les angles.

Savoir-faire

Établir des relations entre des objets en 3D et leurs représentations en 2D.

Associer les empreintes produites par les faces d’un solide aux figures géométriques (carré, rectangle, disque, triangle).

Savoir-faire

Établir des relations entre des objets en 3D et leurs représentations en 2D.

Associer une empreinte produite à une des faces d’un solide.

Dessiner le contour de toutes les faces d’une boite parallélépipédique ou cubique donnée.

Compétence

Articuler, en contexte, les caractéristiques puis les propriétés des solides et des figures, les procédés de construction et de traçage.

Construire un carré, un rectangle en assemblant deux figures données (rectangles, carrés, triangles).

Dessiner le contour de toutes les faces d’une boite parallélépipédique ou cubique donnée.

Compétence

Articuler, en contexte, les caractéristiques puis les propriétés des solides et des figures, les procédés de construction et de traçage.

Construire un carré, un rectangle en assemblant des figures données (rectangles, carrés, triangles).

CHAMP 3 – Des grandeurs à la relation entre variables3

1. Concevoir des grandeurs P1 P2

Savoir

L’identification et la comparaison de grandeurs d’objets.

Utiliser de manière adéquate les termes relatifs aux grandeurs : la longueur, la masse, le cout.

Énoncer la comparaison de deux objets selon une de leurs grandeurs (plus/moins/aussi) :

– en général : petit/grand ;

– selon leur longueur : court/long ;

selon leur masse : léger/lourd.

Savoir

L’identification et la comparaison de grandeurs d’objets.

Utiliser de manière adéquate les termes relatifs aux grandeurs : la longueur, la masse, la capacité, le cout.

Énoncer la comparaison de deux objets selon une de leurs grandeurs (plus/moins/aussi) :

– selon leur longueur : court/long ;

– selon leur masse : léger/lourd ;

selon leur capacité : vide/plein, rempli.

Utiliser de manière adéquate les termes : longueur, largeur, épaisseur, profondeur, hauteur, le contour de.

Savoir

La notion de durée et la comparaison de durées. Utiliser, en situation, le vocabulaire en référence à la durée en utilisant des expressions telles que « le temps utilisé pour… », « telle activité dure… », « la durée de… ».

Savoir-faire

Comparer des objets selon une de leurs grandeurs.

Comparer des objets donnés par rapport à un objet de référence (plus/moins) selon la longueur, la masse, la capacité

Classer des personnes selon leur taille, des objets donnés selon leur longueur.

Savoir-faire

Comparer les durées d’évènements, d’actions.

Savoir-faire

Comparer des objets selon une de leurs grandeurs.

Comparer des objets donnés par rapport à un objet de référence (plus/moins/aussi) selon la longueur, la masse, la capacité.

Classer des objets donnés selon la masse.

Savoir-faire

Comparer les durées d’évènements, d’actions.

Trier des situations données évoquant des durées subjectives (ressenties) ou objectives.

Comparer la durée de situations vécues par rapport à une durée de référence (plus/moins) : un sablier, une chanson…

Comparer la durée de situations vécues (dure moins longtemps/plus longtemps que…) en référence à la minute, à plusieurs minutes (5 minutes, 10 minutes…).

Compétence

Choisir, en situations significatives, des démarches pertinentes de comparaisons de grandeurs d’objets.

Choisir une action concrète pertinente pour comparer des longueurs (regarder, juxtaposer…), verbaliser son action et expliquer son choix.

2. Agir sur des grandeurs

Savoir

L’usage des unités conventionnelles.

Utiliser et symboliser l’euro (€).

Compétence

Choisir, en situations significatives, des démarches pertinentes de comparaisons de grandeurs d’objets.

Choisir une action concrète pertinente pour comparer des masses (regarder, juxtaposer, soupeser…), verbaliser son action et expliquer son choix.

Savoir

L’usage des unités conventionnelles.

Utiliser et symboliser :

le mètre (m), le centimètre (cm) ;

– le kilogramme (kg) ;

– le litre (l) ;

l’euro (€).

Distinguer dans l’expression d’une grandeur mesurée : la grandeur, la mesure et l’unité de mesure.

Savoir

Le mesurage des durées.

Utiliser et symboliser l’heure (h), la minute (min), la seconde (s).

Énoncer la relation de durée : 1 minute = 60 secondes.

Savoir-faire

Mesurer des grandeurs.

Effectuer le mesurage d’une longueur à l’aide d’un étalon non conventionnel choisi (corporel, familier et commun à la classe) et en exprimer le résultat approximatif.

Savoir-faire

Mesurer des grandeurs.

Effectuer le mesurage d’une masse/d’une capacité à l’aide d’un étalon non conventionnel choisi (familier et commun à la classe) et en exprimer le résultat approximatif.

Effectuer le mesurage de la masse d’objets de l’environnement, en utilisant la balance à plateaux et des kilogrammes étalons et en exprimer le résultat approximatif.

Effectuer le mesurage de la capacité d’objets de l’environnement par transvasement d’un récipient de 1 litre et en exprimer le résultat approximatif.

Effectuer le mesurage d’une longueur d’objets de l’environnement et en exprimer le résultat en utilisant l’unité conventionnelle adéquate (m, cm).

Savoir-faire

Utiliser des instruments, des supports pour exprimer un instant dans le temps et mesurer des durées.

Savoir-faire

Utiliser des instruments, des supports pour exprimer un instant dans le temps et mesurer des durées.

Lire l’heure sur un support – analogique : en heures ;

digital : en heures et minutes.

Utiliser une durée de référence (sablier, chanson…) comme indicateur de temps pour déterminer la durée d’une action vécue.

Utiliser une horloge analogique avec trotteuse pour déterminer la durée d’une action courte (moins de 3 minutes).

Savoir-faire

Choisir une grandeur et justifier son choix.

Choisir, parmi plusieurs estimations d’une longueur (en m ou en cm), d’une masse (en kg), celle qui est la plus plausible et justifier son choix. Choisir, parmi plusieurs estimations de durées d’actions données en secondes, celle qui est la plus plausible et justifier son choix.

Savoir-faire

Construire le système des unités conventionnelles.

Donner du sens aux unités conventionnelles travaillées, en les associant à des objets de l’environnement.

Ex. : un litre, c’est la contenance de… ; un kilogramme, c’est lourd comme… ; 10 euros, c’est le prix de…

Lister des objets de la vie courante dont une grandeur se mesure avec l’unité travaillée.

Savoir-faire

Donner du sens à des unités usuelles de durées. Associer la seconde, la minute, quelques minutes, 15 minutes à la durée de situations vécues.

Compétence

Articuler, en situations significatives, l’estimation d’une grandeur, son mesurage (avec les références et les outils adéquats) et l’appréciation du résultat.

Établir une collection d’au moins cinq objets de référence d’une mesure de grandeur donnée (longueur, masse) en estimant, en mesurant ou en cherchant l’information pour se créer des images mentales de ces mesures.

Estimer la longueur d’un objet en référence à une unité conventionnelle choisie (le mètre, le cm) avant d’effectuer le mesurage.

Estimer, en soupesant, la masse d’un objet en référence à une unité conventionnelle choisie (le kilogramme) avant d’effectuer le mesurage sur une balance.

Compétence

Recourir à divers outils et stratégies pour anticiper, représenter, planifier, gérer le temps en fonction de divers buts.

Estimer en secondes la durée d’une activité à vivre ou vécue.

Quantifier la durée nécessaire à la réalisation d’une activité connue et régulièrement vécue (de la seconde à 15 minutes) pour en vérifier la faisabilité dans le laps de temps défini ou imparti.

Compétence

Résoudre des problèmes dans des situations contextualisées.

Résoudre des problèmes d’achats mobilisant :

maximum deux articles ;

des prix entiers jusqu’à 20 €.

Compétence

Résoudre des problèmes dans des situations contextualisées.

Résoudre des problèmes d’achats mobilisant :

maximum trois articles ;

des prix entiers jusqu’à 100 €.

3. Opérer sur des grandeurs – Périmètres, aires et volumes

Savoir

Les périmètres et les aires de figures, les volumes de solides.

Montrer le contour d’une figure.

Montrer la surface d’une figure.

Savoir

Les périmètres et les aires de figures, les volumes de solides.

Énoncer que le périmètre d’une figure est la longueur de son contour.

Montrer la surface d’une figure.

Savoir-faire

Construire et utiliser des démarches pour calculer des périmètres, des aires de figures et des volumes de solides.

Tracer dans un quadrillage le contour déplié d’un rectangle ou d’un carré, en identifiant chaque côté.

4. Agir puis opérer sur des grandeurs – Fractions

Savoir

La notion de fraction partage en lien avec des grandeurs d’objets (réels, représentés).

Utiliser de manière adéquate les expressions : un demi de…, la moitié de…, un quart de…

Savoir-faire

Exploiter des fractions partages et des pourcentages.

Fractionner des objets en demis et en quarts au départ de matériels variés.

Recomposer l’unité à partir de deux demis ou de quatre quarts.

Savoir

La notion de fraction partage en lien avec des grandeurs d’objets (réels, représentés).

Utiliser de manière adéquate les expressions : un demi de…, la moitié de…, un quart de…, deux quarts de…, trois quarts de…

Savoir-faire

Exploiter des fractions partages et des pourcentages.

Fractionner des objets, selon leur longueur, leur capacité, leur aire, en demis et en quarts, au départ de matériels variés.

Recomposer l’unité à partir de demi(s) et de quarts.

Représenter des fractions partages plus petites ou égales à l’unité : ⋅ 2 , ⋅ 4 de…

Reconnaitre des représentations de fractions partages plus petites ou égales à l’unité : ⋅ 2 , ⋅ 4 de…

5.

Savoir-faire

Exploiter des situations de proportionnalité directe entre grandeurs.

Déterminer une quantité dans une situation (vécue et manipulée) de proportionnalité directe (nombre de… pour…).

Savoir-faire

Exploiter des situations de proportionnalité directe entre grandeurs.

Déterminer une quantité dans une situation (vécue et manipulée) de proportionnalité directe (nombre de… pour…).

Représenter une situation vécue et manipulée de proportionnalité directe de manière figurative.

Mettre en relation des grandeurs

CHAMP 4 – De l’organisation de données à la statistique4

Collecter, organiser, représenter et interpréter des données

Savoir

L’organisation d’objets, de données.

Utiliser les mots :

trier : « a ou n’a pas… » (selon le critère défini) ;

Ex. : la couleur.

– classer (selon des caractéristiques définies au sein d’un critère) ;

Ex. : rouge, jaune, bleu…

Savoir L’organisation d’objets, de données.

Utiliser les mots :

trier : « a ou n’a pas… » (selon le critère défini) ;

Ex. : la couleur.

– classer (selon des caractéristiques définies au sein d’un critère) ;

Ex. : rouge, jaune, bleu…

Reconnaitre une représentation de données en :

tableau ;

– ensembles ;

arbre (dichotomique) ;

– diagramme à bandes.

Savoir-faire

Recueillir des informations.

Collecter des informations à partir d’une question exigeant une réponse par oui ou par non.

Savoir-faire

Recueillir des informations.

Collecter des informations à partir d’une question :

– exigeant une réponse par oui ou par non ;

permettant un classement des données récoltées.

Savoir-faire

Trier, classer des objets ou des données.

Organiser des objets réels ou représentés :

par tri selon un critère déterminé ;

– par classement selon maximum trois caractéristiques déterminées, au sein d’un critère.

Déterminer le critère appliqué dans l’organisation d’objets réels ou représentés.

Choisir un critère à appliquer pour trier des objets réels ou représentés.

Savoir-faire

Trier, classer des objets ou des données.

Organiser des objets réels ou représentés :

par tri selon un critère déterminé ;

– par classement selon des caractéristiques déterminées, au sein d’un critère.

Déterminer le critère appliqué dans l’organisation d’objets réels ou représentés.

Choisir, pour organiser des objets réels ou représentés :

– un critère à appliquer à un tri ;

un critère et au moins deux caractéristiques à appliquer à un classement.

Savoir-faire

Présenter des données.

Compléter le support donné, en fonction de la situation, pour représenter un tri ou un classement :

des ensembles disjoints ;

– un tableau à double entrée.

Savoir-faire

Présenter des données.

Compléter le support donné, en fonction de la situation, pour représenter un tri ou un classement :

– des ensembles disjoints ;

– un arbre dichotomique (un seul critère) ;

– un tableau à double entrée ;

un diagramme à bandes horizontales ou verticales.

4 Correspond au domaine Traitement de données des Socles de compétences.

Compétence

Lire et interpréter des données pour en extraire de l’information.

Prélever des informations issues d’une représentation :

– d’ensembles disjoints ;

d’un tableau à double entrée.

Compétence

Résoudre des problèmes en utilisant les données prélevées.

Résoudre des problèmes de logique déductive, en complétant un tableau à double entrée limité à neuf cases.

Compétence

Lire et interpréter des données pour en extraire de l’information.

Prélever des informations issues d’une représentation :

– d’ensembles disjoints ;

d’un arbre dichotomique (un seul critère) ;

– d’un tableau à double entrée ;

– d’un diagramme à bandes horizontales ou verticales.

Compétence

Résoudre des problèmes en utilisant les données prélevées.

Résoudre des problèmes de logique déductive, en complétant un tableau à double entrée limité à neuf cases.

Sommaire

Vous retrouverez ici dans le détail les n° de page des livres-cahiers A et B permettant à l’élève de construire les attendus du nouveau référentiel. Les attendus suivis d’un astérisque* doivent particulièrement faire l’objet de nombreuses manipulations et être vécus physiquement par l’élève (au cours de psychomotricité, par exemple), pour être ensuite oralisés. Ils ne se retrouvent donc pas systématiquement dans les livres-cahiers en tant que tels, mais sont mentionnés dans les notes méthodologiques en lien avec certaines activités.

CHAMP 1 – De l’arithmétique à l’algèbre

1. Appréhender le nombre puis la lettre dans tous leurs aspects

Savoir

Des nombres naturels aux nombres réels.

Utiliser des nombres pour communiquer :

– une quantité ;

une position ;

– un numéro…

Utiliser, de manière adéquate, les dix chiffres utiles à l’écriture des nombres.

Associer le nom d’un nombre (naturel jusqu’à 39) à son écriture en chiffres.

Reconnaitre les nombres de 1 à 20 en s’appuyant sur :

– des schèmes structurés mettant en évidence les nombres 2, 5 ou 10 ;

des collections différentes de même quantité ;

– des variations des positions des objets d’une même collection (invariance/ conservation)* ;

– des variations de l’origine et du sens de comptage des objets d’une même collection (indépendance du cardinal).

Savoir

Les chaines numériques.

10-11 ; 16 ; 18 ; 20 ; 30-34 ; 42 ; 52 ; 69-70 ; 83

51 ; 65

Dire les nombres dans l’ordre stable jusqu’à minima 39. 22 Compter par 2 et par 5 jusqu’à 20. 21

Savoir

De la comparaison de collections puis de nombres à la relation d’ordre. Utiliser, de manière adéquate, les termes liés à la cardinalité :

égal à, le même nombre que, autant que ;

– moins que, plus petit que ;

– plus que, plus grand que.*

Associer les symboles d’ordre (<, >, =) aux expressions « est plus petit que », « est plus grand que », « est égal à ».

Utiliser, de manière adéquate, les termes liés à l’ordinalité des nombres naturels :

– avant, après, entre, juste avant, juste après ; – premier, deuxième… dernier.

Savoir-faire

Dire, lire, écrire et représenter les nombres dans la numération décimale.

Dire, lire les nombres jusqu’à 20 et les écrire en chiffres.

Expliquer la présence du zéro dans l’écriture de 10 et de 20.

Représenter les nombres jusqu’à 20 :

avec du matériel de comptage ; – en dizaines et unités ; – à l’aide de schèmes.*

Savoir-faire

Dénombrer des collections à organiser.

Dénombrer des collections (jusqu’à 20) en comptant par 1, par 2, par 5 à l’aide de matériel et cardinaliser la totalité.*

Savoir-faire

Décomposer et recomposer les nombres.

Décomposer et recomposer des nombres de 1 à 20 en lien avec la numération décimale.

Ex. : 17, c’est 1 D et 7 U.

Décomposer et recomposer les nombres jusqu’à 20 : – en deux termes, de manière non ordonnée ;

en plusieurs termes dont l’addition réitérée.

92-96 8-13 ; 31 ; 43-45 ; 75-76 ; 86-87 ; 95

12 ; 15 ; 35-38 ; 41 ; 43-46 ; 53 ; 54-58 ; 68 ; 70 ; 7984 ; 94

50 ; 60 ; 62 ; 7071 ; 73 ; 81-82 ; 85 ; 88 ; 94 ; 98

Décomposer et recomposer les nombres jusqu’à 20 multiplicativement sous forme de nombre de paquets de… 34-35 ; 48 ; 5669 ; 74 ; 83-84 ; 96

Savoir-faire

Comparer, ordonner, situer des nombres. Utiliser le vocabulaire adéquat et les signes « < », « > » et « = » pour exprimer la comparaison de deux nombres. 24 ; 34 ; 61 ; 75

Ordonner des nombres (de 1 à 20) du plus petit au plus grand ou inversement. 67 33 ; 80 Placer un nombre donné jusqu’à 20 sur une bande numérique. 42 80

Exprimer la position d’un nombre jusqu’à 20 (par encadrement, par approximation) sur une bande numérique.

20 ; 24 ; 53 ; 67

52 ; 69 ; 93

2. Opérer sur des nombres et sur des expressions algébriques

Savoir

Les opérations et leurs propriétés.

Associer une opération à son symbole : – addition, « + » ;

– soustraction, « - ».

Associer le symbole « = » à l’expression « est égal à » et le symbole « ≠ » à l’expression « n’est pas égal à ».

Savoir

Les automatismes de base en calcul.

Connaitre de mémoire :

– les additions dont le résultat vaut 10 ;

les additions dont le résultat vaut maximum 10 ;

– les soustractions dont le premier terme est maximum 10.

Savoir-faire

Construire le sens des opérations.

Utiliser, en situations concrètes, le vocabulaire familier lié aux quatre opérations.

Ex. :

– Ajouter, avancer de, monter de, mettre en plus…

– Regrouper, rassembler, mettre ensemble, mettre avec…

Reculer, enlever, retirer, cacher, perdre…

– Faire des tas, des paquets, des piles de…

Partager, répartir en… tas, distribuer à…*

Savoir-faire

Appréhender et utiliser l’égalité.

Montrer et verbaliser ce qui est le même ou pas, ce qui est égal ou pas, entre deux collections d’objets ou deux représentations d’objets.

85-88 7 ; 14 ; 72

23 ; 61

22 ; 29 ; 55

Utiliser l’égalité en termes de résultat : addition et soustraction jusqu’à 20. 96 32 ; 36 ; 4647 ; 49

Savoir-faire

Utiliser les propriétés des opérations pour remplacer un calcul par un autre plus simple.

Utiliser la commutativité de l’addition.* 92-96

Compétence

Résoudre des problèmes en mobilisant des nombres et des opérations.

Résoudre un problème faisant intervenir des opérations sur les nombres :

en traduisant une situation contextualisée par un dessin, une verbalisation, puis l’écriture d’une opération mathématique (+, -) ;

en effectuant les calculs ;

en communiquant le résultat avec précision.

7 ; 83

CHAMP 2 – Des objets de l’espace à la géométrie

1. (Se) Repérer et communiquer des positionnements ou des déplacements

Savoir

Les visions de l’espace.

Utiliser le vocabulaire exprimant des positions absolues : à côté de, contre, à l’intérieur, à l’extérieur, entre, sous, sur, dans, hors, autour de. 78 ; 92

Utiliser le vocabulaire exprimant des positions ordinales : – premier, deuxième, troisième… dernier ;

au début, à la fin, avant, après.

Savoir

Les déplacements.

Utiliser le vocabulaire décrivant un déplacement tel que : monter, descendre, avancer, reculer, s’éloigner, se rapprocher, faire demi-tour…*

Savoir-faire

Situer, placer un objet ou soi-même.

Situer (exprimer la position absolue ou ordinale) un objet ou soi-même avec le vocabulaire adéquat dans l’espace 3D (réel, vécu, miniaturisé).*

Placer un objet/soi-même selon des consignes données ou un modèle observé dans l’espace 3D (réel, vécu, miniaturisé).*

Savoir-faire

Déplacer un objet ou soi-même.

Se déplacer ou déplacer un objet dans l’espace 3D (réel, vécu, miniaturisé) en suivant deux consignes orales consécutives.*

Expliquer oralement un déplacement vécu, à l’aide du vocabulaire adéquat, en identifiant au moins deux points de repère.*

Savoir-faire

Situer, placer et déplacer un objet ou soi-même sur une bande orientée. Situer (exprimer la position absolue ou ordinale) un objet sur une bande orientée. 97-100

22 ; 77

Placer un objet sur une bande orientée. Ex. : jeux de parcours. 98 ; 100 78

Déplacer un objet ou soi-même d’une quantité donnée, sur une bande orientée.* 75-76

Compétence

Lire, interpréter des représentations de l’espace et les confronter au réel.

Réaliser dans un espace connu un agencement spatial de minimum quatre objets correspondant à une photo donnée (vue de face).*

Savoir

Les figures, leurs composantes, leurs caractéristiques et leurs propriétés.

Identifier un carré, un rectangle, un triangle, un disque. 25

Savoir

Les solides, leurs composantes, leurs caractéristiques et leurs représentations planes.

Désigner un cube, un parallélépipède rectangle, un cylindre, une sphère. 29 Désigner un objet courant correspondant à un solide similaire (cube, parallélépipède rectangle, cylindre, sphère).

Savoir-faire

Construire des solides et des figures avec du matériel varié.

Reproduire des solides à partir de modèles 3D donnés, avec du matériel varié (pâte à modeler, blocs ou boites à assembler…).*

Reproduire des figures par découpage, par pliage et avec du matériel varié.* 90

Savoir-faire

Tracer des figures.

Utiliser la latte pour tracer, sur papier vierge, une droite sans contrainte. 64 Tracer des figures à main levée en repassant sur des « segments de droite » formés par des faisceaux de droites donnés.

Savoir-faire

63

Établir des relations entre des objets en 3D et leurs représentations en 2D. Associer les empreintes produites par les faces d’un solide aux figures géométriques (carré, rectangle, disque, triangle). 30

Dessiner le contour de toutes les faces d’une boite parallélépipédique ou cubique donnée. 26

Compétence

Articuler, en contexte, les caractéristiques puis les propriétés des solides et des figures, les procédés de construction et de traçage.

CHAMP 3 – Des grandeurs à la relation entre variables

1. (Se) Repérer et communiquer des positionnements ou des déplacements

Savoir

L’identification et la comparaison de grandeurs d’objets.

Utiliser de manière adéquate les termes relatifs aux grandeurs : la longueur, la masse, le cout.

Énoncer la comparaison de deux objets selon une de leurs grandeurs (plus/ moins/aussi) :

– en général : petit/grand ;

selon leur longueur : court/long ;

– selon leur masse : léger/lourd.

Savoir-faire

Comparer des objets selon une de leurs grandeurs.

Comparer des objets donnés par rapport à un objet de référence (plus/moins) selon la longueur, la masse, la capacité.

Classer des personnes selon leur taille, des objets donnés selon leur longueur.

Savoir-faire

Comparer les durées d’évènements, d’actions.

Comparer la durée de situations vécues par rapport à une durée de référence (plus/moins) : un sablier, une chanson… 39-40

Compétence

Choisir, en situations significatives, des démarches pertinentes de comparaisons de grandeurs d’objets.

Choisir une action concrète pertinente pour comparer des longueurs (regarder, juxtaposer…), verbaliser son action et expliquer son choix.*

Savoir

L’usage des unités conventionnelles.

62 59

Utiliser et symboliser l’euro (€). 28 ; 53-54

Savoir-faire

Mesurer des grandeurs.

Effectuer le mesurage d’une longueur à l’aide d’un étalon non conventionnel choisi (corporel, familier et commun à la classe) et en exprimer le résultat approximatif.

Savoir-faire

59-61

Utiliser des instruments, des supports pour exprimer un instant dans le temps et mesurer des durées.

Utiliser une durée de référence (sablier, chanson…) comme indicateur de temps pour déterminer la durée d’une action vécue. 39-40

Compétence

Résoudre des problèmes dans des situations contextualisées. Résoudre des problèmes d’achats mobilisant :

maximum deux articles ; – des prix entiers jusqu’à 20 €.

Les périmètres et les aires de figures, les volumes de solides.

La notion de fraction partage en lien avec des grandeurs d’objets (réels, représentés). Utiliser de manière adéquate les expressions : un demi de…, la moitié de…, un quart de…

Exploiter des fractions partages et des pourcentages.

des objets en demis et en quarts au départ de matériels variés.*

l’unité à partir de deux demis ou de quatre quarts.

Exploiter des situations de proportionnalité directe entre grandeurs.

Déterminer une quantité dans une situation (vécue et manipulée) de proportionnalité directe (nombre de… pour…).*

CHAMP 4 – De l’organisation de données à la statistique

Collecter, organiser, représenter et interpréter des données

Savoir

L’organisation d’objets, de données.

Utiliser les mots :

trier : « a ou n’a pas… » (selon le critère défini) ; Ex. : la couleur.

classer (selon des caractéristiques définies au sein d’un critère) ;

Ex. : rouge, jaune, bleu…

Savoir-faire

Recueillir des informations.

25 ; 65 ; 92

Collecter des informations à partir d’une question exigeant une réponse par oui ou par non. 25

Savoir-faire

Trier, classer des objets ou des données.

Organiser des objets réels ou représentés :

– par tri selon un critère déterminé ;

par classement selon maximum trois caractéristiques déterminées, au sein d’un critère.

Déterminer le critère appliqué dans l’organisation d’objets réels ou représentés.*

Choisir un critère à appliquer pour trier des objets réels ou représentés.*

Savoir-faire

Présenter des données.

Compléter le support donné, en fonction de la situation, pour représenter un tri ou un classement :

des ensembles disjoints ;

– un tableau à double entrée.

Compétence

Lire et interpréter des données pour en extraire de l’information.

Prélever des informations issues d’une représentation :

d’ensembles disjoints ;

– d’un tableau à double entrée.

Compétence

Résoudre des problèmes en utilisant les données prélevées.

47-48 26 ; 66 ; 94 ; 99

92

Résoudre des problèmes de logique déductive, en complétant un tableau à double entrée limité à neuf cases. 100

Comparatif des tables des matières

Les livres-cahiers de première année ont donc été mis à jour selon les nouveaux prescrits, et leurs tables des matières adaptées comme suit.

Nombres et opérations Solides et figures Grandeurs Traitement de données

*Supprimé (pas dans le référentiel « Pacte d’excellence ») · Ajouté (intégré dans le référentiel « Pacte d’excellence »)

2018 2022 (Pacte)

Chapitre 1 – En avant… chez « les grands »

1. Je reconnais et je dénombre 1, 2 et 3

2. Je fais de la correspondance terme à terme

3. Je décompose 2 et 3

4. Je découvre la quantité « rien »

5. Je fonce entre 0 et 5

1. Je reconnais et je dénombre 1, 2 et 3

2. Je fais de la correspondance terme à terme

3. Je décompose 2 et 3

4. Je découvre la quantité « rien »

5. Je fonce entre 0 et 5

Chapitre 2 – Comme les 5 doigts de la main

1. Je dénombre, je situe, j’ordonne et je compare jusqu’à 5

2. Je comprends les successions chronologiques

3. Je connais les moments de la journée*

4. Je reconnais les formes géométriques

5. Je fais des empreintes

Chapitre 3 – À la ferme

1. Je joue avec mes doigts jusqu’à 6

2. J’ajoute les dés et les dominos

3. Je m’arrête et je dépose mes idées

4. J’ajoute les dés et les dominos

5. Je connais les maisons de Tao jusqu’à 6

6. Je connais les maisons d’Élisa jusqu’à 6

7. Gauche ou droite ?*

1. Je dénombre, je situe, j’ordonne et je compare jusqu’à 5

2. Je comprends les successions chronologiques

3. J’organise différents moments

4. Je reconnais les formes géométriques

5. Je fais des empreintes

1. Je joue avec mes doigts jusqu’à 6

2. J’ajoute les dés et les dominos

3. Je m’arrête et je dépose mes idées

4. J’ajoute les dés et les dominos

5. Je connais les maisons de Tao jusqu’à 6

6. Je connais les maisons d’Élisa jusqu’à 6

7. Je compare des durées

Chapitre 4 – Au pays de Blanche-Neige

1. Je reconnais, je situe et je décompose 7

2. Je comprends le tableau à double entrée

3. Je connais les jours de la semaine*

1. Je reconnais, je situe et je décompose 7

2. Je comprends le tableau à double entrée

3. Je découvre le contour et la surface

Chapitre 5 – Une drôle de découverte pour Tao et Élisa

1. Je voyage dans le pays de 8

2. Je m’entraine à compléter et à lire la droite des nombres

3. Je reconstruis 8

4. Je joue avec les dés et je groupe pour faire 8

5. Je verbalise (en route vers l’addition)

6. Je reporte un étalon quelconque

7. Je mesure avec mes pas…

8. Je compare des objets entre eux

9. Je trace à main levée

10. Je trace avec ma latte

Chapitre 6 – Au pays de 9

1. Je dénombre, je situe, j’ordonne et je décompose 9

2. Je plonge dans un « bain » de 0 à 9

3. Je raconte des histoires (soustractions)

4. Je compare et je classe

5. Je me déplace dans un quadrillage

Chapitre 7 – Au pays de 10

1. Je travaille avec le nombre 10

2. Je me souviens de la soustraction

3. Je mélange les additions et les soustractions

Chapitre 8 – L’arrivée de Xia

1. Je m’entraine à lire les nombres

2. Je me repère dans un quadrillage (grâce aux cases)

3. Je me repère dans un quadrillage (grâce aux nœuds)

1. Je voyage dans le pays de 8

2. Je m’entraine à compléter et à lire la droite des nombres

3. Je reconstruis 8

4. Je joue avec les dés et je groupe pour faire 8

5. Je verbalise (en route vers l’addition)

6. Je reporte un étalon quelconque

7. Je mesure avec mes pas…

8. Je compare des objets entre eux

9. Je trace à main levée

10. Je trace avec ma latte

1. Je dénombre, je situe, j’ordonne et je décompose 9

2. Je plonge dans un « bain » de 0 à 9

3. Je raconte des histoires (soustractions)

4. Je compare et je classe

5. Je me déplace dans un quadrillage

1. Je travaille avec le nombre 10

2. Je me souviens de la soustraction

3. Je mélange les additions et les soustractions

1. Je m’entraine à lire les nombres

2. Je me repère dans un quadrillage (grâce aux cases)

3. Je me repère dans un quadrillage (grâce aux nœuds)

Chapitre 9 – Sohan achète du chocolat

1. Je m’exerce au passage par la dizaine

2. Dizaines et unités : je me souviens

3. J’additionne et je soustrais

4. Je joue à peser des objets du quotidien

5. Je pèse avec des mesures naturelles

1. Je m’exerce au passage par la dizaine

2. Dizaines et unités : je me souviens

3. J’additionne et je soustrais

4. Je joue à peser des objets du quotidien

5. Je pèse avec des étalons naturels

Chapitre 10 – Une journée sous la pluie > Xia découvre un nouveau sport

1. Je découvre la multiplication*

2. Je construis mes premières tables de multiplication*

3. Je découvre le mètre*

4. Le temps qui passe*

1. Je connais le contour et la surface

2. Je m’entraine aux comptages

3. Je m’entraine : <, >, =, ≠

4. Je trie

5. Je compare

6. Je représente des objets dans l’espace

Chapitre 11 – Il est l’heure !

1. Je découvre 12 sous toutes ses formes

2. Je découvre le double de…

3. Je découvre la symétrie*

4. J’apprends à lire l’heure exacte*

1. Je découvre 12 sous toutes ses formes

2. Je découvre le double de…

3. Je découvre la moitié de…

4. Je découvre le quart de…

5. Je connais le quart de…, la moitié de…

Chapitre 12 – Je joue avec les nombres jusqu’à 14

1. Je sais faire tous les calculs jusqu’à 14

2. Je sais trouver la suite logique

3. Je fais mes achats

Chapitre 13 – Au verger

1. Je partage… sans faire de jaloux

2. Je découvre la moitié de…*

3. Je complète tous les arbres de 15*

4. Je sais faire tous les calculs jusqu’à 15

5. Le litre*

Chapitre 14 – En route !

1. Je m’occupe des préparatifs du voyage

1. Je sais faire tous les calculs jusqu’à 14

2. Je sais trouver la suite logique

3. Je fais mes achats

1. Je partage… sans faire de jaloux

2. Je sais faire tous les calculs jusqu’à 15

3. Je découvre les capacités

4. J’organise des objets

1. Je m’occupe des préparatifs du voyage

2. J’organise des objets

Chapitre 15 – Le tournoi « 3 contre 3 » de Sohan

1. Je connais 18

2. Je découvre le kilogramme (kg)*

Chapitre 16 – Un étang à l’école…

1. Je voyage entre 10 et 20

1. Je connais 18

2. J’agence des objets et je construis des formes

1. Je voyage entre 10 et 20

2. J’interprète des données et je résous des problèmes

Suggestion de planification

Autre bouleversement : à partir de la rentrée 2022, le nouveau calendrier scolaire alternera 5 blocs de 6 à 8 semaines et pauses de 2 semaines. Vous trouverez ci-dessous une proposition de répartition des chapitres selon cette nouvelle organisation du rythme scolaire en « blocs ».

Chaque enseignant se chargera d’adapter/modifier cette suggestion en fonction de son groupeclasses et des réalités de son agenda.

Rentrée BLOC 1 Congés d’automne BLOC 2 Vacances d’hiver BLOC 3 Congé de détente BLOC 4 Vacances de printemps BLOC 5 Vacances d’été

Chapitre 1 – En avant… chez « les grands »

Chapitre 2 – Comme les 5 doigts de la main

Chapitre 3 – À la ferme

Chapitre 4 – Au pays de Blanche-Neige

Chapitre 5 – Une drôle de découverte pour Tao et Élisa

Chapitre 6 – Au pays de 9

Chapitre 7 – Au pays de 10

Chapitre 8 – L’arrivée de Xia

Chapitre 9 – Sohan achète du chocolat

Chapitre 10 – Xia découvre un nouveau sport

Chapitre 11 – Il est l’heure !

Chapitre 12 – Je joue avec les nombres jusqu’à 14

Chapitre 13 – Au verger

Chapitre 14 – En route !

Chapitre 15 – Le tournoi « 3 contre 3 » de Sohan

Chapitre 16 – Un étang à l’école…

BLOC 1

BLOC 2

BLOC 3

BLOC 4

BLOC 5

Savoir

1

En avant… chez « les grands »

ATTENDUS PAR MATIÈRE

LES NOMBRES

Appréhender le nombre puis la lettre dans tous leurs aspects

Des nombres naturels aux nombres réels.

Utiliser des nombres pour communiquer :

– une quantité ;

– une position ;

– un numéro ; – …

Utiliser de manière adéquate les dix chiffres utiles à l’écriture des nombres. Reconnaitre les nombres de 1 à 20 en s’appuyant sur :

– des schèmes structurés mettant en évidence les nombres 2, 5 ou 10 ;

– des collections différentes de même quantité ;

– des variations de positions des objets d’une même collection (invariance/conservation) ;

– des variations de l’origine et du sens de comptage des objets d’une même collection (indépendance du cardinal).

Savoir-faire

Dire, lire, écrire et représenter les nombres dans la numération décimale.

Dénombrer des collections à organiser.

Décomposer et recomposer les nombres.

LES NOMBRES

Dire, lire les nombres jusqu’à 20 et les écrire en chiffres. Représenter les nombres jusqu’à 20 : – avec du matériel de comptage ; – à l’aide de schèmes.

Dénombrer des collections (jusqu’à 20) en comptant par 1, par 2, par 5, à l’aide de matériel, et cardinaliser la totalité.

Décomposer et recomposer les nombres jusqu’à 20 en deux termes, de manière non ordonnée.

MATIÈRES ABORDÉES

1, 2, 3 : décompositions, reconnaissance, dénombrements Découvrir la quantité « rien » Bain de 0 à 5 : dénombrer, recomposer, décomposer, ordonner Correspondance terme à terme LES SOLIDES

Notes méthodologiques

Situation de départ

En avant… chez « les grands » !

Lire l’histoire aux élèves. Engager avec eux une conversation sur leurs craintes de ce grand jour de rentrée chez « les grands », leurs angoisses, les choses qui les rassurent en ce premier jour d’école. Présentation des personnages principaux : Tao et Élisa qui vont accompagner les élèves tout au long de l’année.

Chapitre

En avant… chez « les grands » !

Qu’allons-nous faire à la récré ?

Et en classe ?

Suis-je bien habillée ?

On y va !

Qui veux-tu retrouver ?

Je reconnais et je dénombre 1, 2 et 3

1. C’est la rentrée ! La cour est en désordre ! À toi de vite ranger tous les jouets dans les bons bacs de rangement.

1 2 3

Lorsque tout est bien rangé, oralise ce que tu as fait.

Activité 1

Je reconnais et je dénombre 1, 2 et 3

Exercice 1

Avant l’activité, prévoir des classements d’objets à faire en classe. Créer avec eux les boites de 1, 2 et 3. Y déposer les objets amenés par l’enseignant(e). Laisser les élèves classer eux-mêmes les collections dans les boites.

Exercice 2

Activité disponible pour les plus rapides.

Faire l’exercice en collectif avec les élèves afin de bien repérer ce qu’il y a au sein de votre classe (le nombre de porte(s), d’horloge(s), de calendrier(s)). L’activité peut être étendue oralement à d’autres objets de la classe.

Exercice 3

Par des petits jeux, bien vérifier en classe que la notion « le plus » est acquise. Si cette notion reste floue, proposer des petits jeux aux élèves.

è Qui a le plus de crayons dans son plumier ?

è Qui a le plus de lignes sur son pull ?

Proposer des séries d’objets aux élèves et leur demander où il y en a le plus.

Exercices complémentaires

2. Observe ta classe, compte et relie.

Autres réponses possibles en fonction des classes

3. Où y en a-t-il le plus ? Entoure.

Je fais de la correspondance terme à terme 2.

1. Relie chaque crayon à son cahier.

D’autres possibilités seront acceptées par l’enseignant.

2. Relie pour que chaque enfant puisse avoir un bureau et une chaise. Dessine ce qui manque.

Activité 2

Je fais de la correspondance terme à terme

Exercice 1

Lire la consigne aux élèves. Les laisser travailler seuls.

Exercice 2

Bien préciser aux élèves qu’ils vont devoir dessiner ce qu’il manque.

Exercice 3

Bien préciser aux élèves qu’ils vont devoir, cette fois-ci, barrer ce qu’il y aura en trop.

Exercices complémentaires

3. Relie chaque garçon à un ballon puis à un goal de football. Barre ce qu’il y a de trop.

Je décompose 2 et 3 3.

1. Après avoir manipulé en classe, dessine les billes quand elles arrivent dans les assiettes.

2. Je m’arrête et je dépose mes idées…

Activité 3

Je décompose 2 et 3

Exercice 1

Beaucoup de manipulations en classe sont nécessaires. Prévoir des rouleaux vides d’essuie-tout, des balles de ping-pong et des boites vides. Faire manipuler les élèves à faire descendre des balles dans les rouleaux et voir ce qui arrive dans la boite si je fais descendre une balle dans le tuyau de gauche et deux balles dans le tuyau de droite (cf. les dessins). Ne pas dépasser un total de 3.

Exercice 2

Construire ensemble les maisons de 2 et 3. Bien expliquer que les « briques » de la maison se posent dans un certain ordre et que cet ordre doit être respecté. Obtenir ainsi :

Exercices complémentaires

Évaluations

Activité 4

Je découvre la quantité « rien »

Exercice 1

Lire la consigne aux élèves.

Exercice 2

Exercice collectif oral dans un premier temps. Prendre le temps d’analyser chaque idée des élèves et voir ce qui est correct ou non. En discuter ensemble.

Dans un second temps, laisser les élèves dessiner la situation qu’ils préfèrent.

Je découvre la quantité « rien » 4.

1. Colorie la situation où il y a zéro.

2. Discute avec tes amis et trouve une situation (en classe, à la maison…) où il n’y a « rien » et représente-la ici.

Je fonce entre 0 et 5 5.

1. Colorie :

- en bleu tout ce qui parle de 0, - en jaune tout ce qui parle de 1, - en vert tout ce qui parle de 2, - en rouge tout ce qui parle de 3, - en orange tout ce qui parle de 4, - en rose tout ce qui parle de 5.

1 0 5

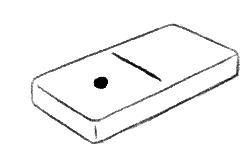
4 3 2

Activité 5

Je fonce entre 0 et 5

Exercice 1

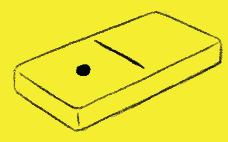
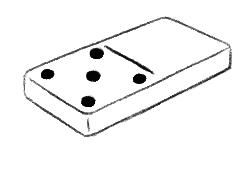
Donner aux élèves une couleur à la fois. Leur faire prendre le crayon bleu et leur faire colorier toutes les situations qui parlent de 0, puis leur faire prendre le jaune, …

Ou, au tableau, inscrire tous les nombres et les couleurs correspondantes et laisser travailler seuls les élèves sur toutes les quantités en même temps.

Exercice 2

Faire des exercices semblables en collectif avant de laisser travailler seuls les élèves.

Exercice 3

Expliquer aux élèves que les points peuvent être dessinés où ils veulent sur le dos de la coccinelle. Toute la quantité à gauche, toute la quantité à droite ou toute la quantité répartie sur les deux ailes. Bien préciser qu’il ne faut pas dessiner la quantité sur l’aile de gauche et la même sur l’aile de droite. La quantité doit représenter le nombre de points que l’on doit retrouver au total sur la coccinelle.

2. Recompositions jusqu’à 5 : dessine le nombre de points dans les dominos et écris le nombre total de points.

3. Décompositions jusqu’à 5 : dessine le nombre de points manquants sur le dos des coccinelles.

4. Ordonne jusqu'à 5.

Driiiiiiiing ! La récré est terminée. Les enfants sont rangés. Peux-tu indiquer leur place dans la file ?

5. Et s’ils sont rangés dans l’autre sens pour sortir ?

6. Continue les frises.

Exercices 4 et 5

Faire vivre ces exercices dans la cour, à plusieurs reprises.

Exercice 6

Les élèves effectuent l’exercice individuellement.

Exercices complémentaires Évaluations ................................................................................................................................................... ...................................................................................................................................................

Savoirs

Comme les 5 doigts de la main !

ATTENDUS PAR MATIÈRE

LES NOMBRES

Appréhender le nombre puis la lettre dans tous leurs aspects

Des nombres naturels aux nombres réels.

Utiliser des nombres pour communiquer : – une quantité ; – une position ; – un numéro.

Utiliser de manière adéquate les dix chiffres utiles à l’écriture des nombres.

Reconnaitre les nombres de 1 à 20 en s’appuyant sur : – des schèmes structurés mettant en évidence les nombres 2, 5 ou 10 ; – des collections différentes de même quantité.

De la comparaison de collections puis de nombres à la relation d’ordre.

Savoir-faire

Dire, lire, écrire et représenter les nombres dans la numération décimale.

Utiliser de manière adéquate les termes liés à la cardinalité : – égal à, le même nombre que, autant que ; – moins que, plus petit que ; – plus que, plus grand que.

Dire, lire les nombres jusqu’à 20 et les écrire en chiffres. Représenter les nombres jusqu’à 20 : – avec du matériel de comptage ; – en dizaines et unités ; – à l’aide de schèmes.

Décomposer et recomposer les nombres.

Comparer, ordonner, situer des nombres.

Décomposer et recomposer les nombres jusqu’à 20 en deux termes, de manière non ordonnée.

Exprimer la position d’un nombre jusqu’à 20 (par encadrement, par approximation) sur une bande numérique.

Opérer sur des nombres et sur des expressions algébriques

Savoir-faire

Appréhender et utiliser l’égalité.

Montrer et verbaliser ce qui est le même ou pas, ce qui est égal ou pas, entre deux collections d’objets ou deux représentations d’objets.

Savoir

LES SOLIDES ET FIGURES

Appréhender et représenter des objets de l’espace

Les figures, leurs composantes, leurs caractéristiques et leurs propriétés.

Savoir-faire

Établir des relations entre des objets en 3D et leurs représentations en 2D.

Identifier un carré, un rectangle, un triangle, un disque.

LES NOMBRES

LES SOLIDES ET FIGURES

LES GRANDEURS

Dessiner le contour de toutes les faces d’une boite parallélépipédique ou cubique donnée.

MATIÈRES ABORDÉES

Dénombrer, situer, ordonner et comparer jusqu’à 5

Reconnaitre les formes géométriques (triangle, rectangle, carré, disque)

Comprendre les successions chronologiques

Organiser différents moments

LE TRAITEMENT DES DONNÉES /

Notes méthodologiques

Situation de départ Comme les 5 doigts de la main !

Laisser les élèves observer la BD. Les laisser verbaliser. Lire ensuite la BD entière aux élèves. S’arrêter sur l’expression « s’entendre comme les 5 doigts de la main ». Insister sur les éléments de la BD (pots de peinture, crayons, nounours, ballons). Insister également sur le mot « empreintes ».

Activité disponible pour les plus rapides.

Faire le tour des élèves et leur demander : è Et toi ? Avec qui t’entends-tu comme les cinq doigts de la main ? Noter chaque réponse au tableau afin que chaque élève puisse écrire lui-même dans le chemin d’écriture le prénom de son meilleur ami.

Comme les 5 doigts de la main

Nous nous entendons et nous sommes amis « comme les 5 doigts de la main ».

Avec votre instituteur(trice), discutez ensemble de l’expression : « s’entendre comme les 5 doigts de la main ».

Et toi ? Quel est le prénom de celui ou celle avec qui tu t’entends « comme les 5 doigts de la main » ?

Écris son prénom ici :

Je

1. Compte les objets.

4 1

3

Il y a ........ crayons sur la table. Il y a ........ ballons sur la table.

Il y a boite de mouchoirs sur la table. Il y a livres à colorier sur la table.

2 4 5

Il y a nounours sur la table. Il y a pots de peinture sur la table.

Retrouve tous ces objets dans la BD de la page précédente et entoure-les.

dénombre, je situe, j’ordonne et je compare jusqu’à 5 1.

2. Relie.

Activité 1

Je dénombre, je situe, j’ordonne et je compare jusqu’à 5

Exercice 1

Faire vivre la situation en réel avant le passage sur feuille.

Laisser ensuite les élèves travailler en individuel.

Activité disponible pour les plus rapides.

Quelles sont les collections où il y en a le plus ?

Entoure.

Exercice 2

Expliquer la consigne aux élèves : relier le nombre d’objets à la main correspondante.

Activité disponible pour les plus rapides.

Quelles sont les collections où il y en a le plus ?

Entoure.

Dessine une main et numérote chaque doigt.

Exercice 3

Manipuler énormément avant l’activité. Imaginer de dessiner dans la cour des droites à la craie et faire placer des étiquettes. Autre activité possible : donner les étiquettes numérotées aux élèves et leur demander de se placer dans une file. Attention : toujours insister sur le sens de la droite.

Activité disponible pour les plus rapides.

Exercice 4

Lire la consigne aux élèves. Travail en individuel. Il convient ici de faire verbaliser au maximum les élèves pour qu’ils intègrent les termes liés à la cardinalité (« égal à », « le même nombre que », « autant que » / « moins que », « plus petit que » / « plus que », « plus grand que »), en déclinant notamment cet exercice avec d’autres collections à manipuler. L’élève pourra alors indiquer, par rapport à des schèmes ou dominos et en manipulant un maximum, quelles sont les collections qui sont plus petites, plus grandes ou égales.

Exercice 5

Lire la consigne aux élèves. Travail en individuel.

Exercice 6

Lire la consigne aux élèves. Travail en individuel.

Entoure 4 feuilles. Dessine 5 bougies sur le gâteau.

Colorie 3 poissons.

4. Entoure, dessine ou colorie.

5. Entoure les collections qui sont plus petites que le domino.

6. Entoure les collections qui sont plus grandes que le domino.

7. Entoure les collections qui sont égales au domino.

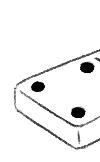
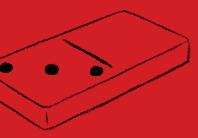
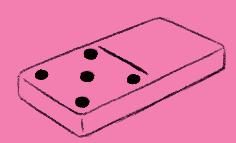
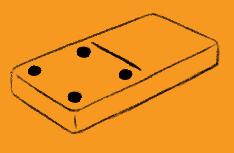
8. Complète les dominos pour faire toujours

5.

Exercice 7

Lire la consigne aux élèves. Travail en individuel.

Exercice 8

Pour cette activité, faire prendre aux élèves leur domino de 5 et l’afficher également au tableau. Au préalable, des jeux identiques en collectif au tableau sont vivement conseillés.

Exercices complémentaires

Évaluations

Activité 2. Je comprends les successions chronologiques

Travailler en collectif. Faire verbaliser les élèves.

è Que se passe-t-il dans ces histoires ?

è Par quoi commencer ?

Attention : l’histoire de la bougie : elle se consume, elle ne grandit pas. Bien faire verbaliser les élèves sur cette différence par rapport aux autres histoires. Ensemble et oralement, faire verbaliser les élèves sur chaque histoire en utilisant les termes : « en premier, il se passe ceci », « en deuxième, cela »… Bien passer en revue chaque histoire et ne pas hésiter à en ajouter d’autres. Il est important de ne pas sauter cette étape et de vérifier que chacun puisse verbaliser les successions chronologiques.

Exercices complémentaires

2.

Je comprends les successions chronologiques

Numérote les images dans l’ordre chronologique.

J'organise différents moments 3.

1. Colorie en bleu la première étape, en vert la deuxième étape et en rouge la dernière étape des histoires.

Décris ensuite oralement ces étapes en utilisant « au début », « au milieu » et « à la fin ».

2. Écris en rouge le chiffre se situant avant et en vert celui qui se trouve après.

Activité 3. J’organise différents moments

Exercice 1

Cet exercice se passe en deux temps : un premier temps où l’élève colorie les différentes étapes et un deuxième temps où il faut verbaliser en utilisant les termes « au début », « au milieu », « à la fin ». Ces deux étapes peuvent tout à fait être réalisées dans le sens inverse : d’abord verbaliser ensemble si les élèves éprouvent des difficultés à établir un ordre chronologique, puis passer à la version coloriage.

Exercice 2

Compléter les droites de nombres. Bien expliquer aux élèves les couleurs à prendre. Avant de passer à la version cahier, faire plusieurs exercices en collectif au tableau.

Activité 4. Je reconnais les formes géométriques

Matériel : Annexe 1 - Formes géométriques (pp. A1-A5)

Travailler en collectif avant d’ouvrir le livre. Utiliser l’annexe 1 et mettre la tête de Tao et d’Élisa en grand au tableau. Avoir différentes formes : carrés, rectangles, disques et triangles à pouvoir coller sous Élisa (rectangles et carrés) ou Tao (disques et triangles).

Laisser ensuite les élèves travailler dans le livre en individuel.

Exercices complémentaires Évaluations

Je reconnais les formes géométriques 4.

Tao et Élisa dessinent des formes. Peux-tu rendre à chacun ses dessins ? Tao adore les triangles et les disques. Élisa, elle, préfère les rectangles et les carrés. À toi de jouer !

Colorie les formes dans la même couleur que le teeshirt de chacun.

Je fais des empreintes 5.

À toi de t’amuser comme Tao et Élisa ! Avec de la peinture, fais des empreintes de différentes boites apportées en classe. Tu peux laisser tes traces ici. Essaie de respecter les couleurs de Tao et d’Élisa comme sur la page précédente.

Activité 5. Je fais des empreintes

Exercices de manipulation : sur de grands panneaux, faire les empreintes des boites apportées par les élèves et les classer. Dans le livre, permettre aux élèves de laisser une trace de l’activité. Tenir à l’œil que l’activité principale doit se dérouler hors du livre de l’élève.

N-O

Savoirs

À la ferme

ATTENDUS PAR MATIÈRE

LES NOMBRES

Appréhender le nombre puis la lettre dans tous leurs aspects

Des nombres naturels aux nombres réels.

Utiliser des nombres pour communiquer : – une quantité ; – une position ; – un numéro.

Utiliser de manière adéquate les dix chiffres utiles à l’écriture des nombres.

Reconnaitre les nombres de 1 à 20 en s’appuyant sur : – des schèmes structurés mettant en évidence les nombres 2, 5 ou 10 ; – des collections différentes de même quantité.

De la comparaison de collections puis de nombres à la relation d’ordre.

Savoir-faire

Dénombrer des collections à organiser.

Décomposer et recomposer les nombres.

Utiliser de manière adéquate les termes liés à la cardinalité : – égal à, le même nombre que, autant que ; – moins que, plus petit que ; – plus que, plus grand que.

Dénombrer des collections (jusqu’à 20) en comptant par 1, par 2, par 5, à l’aide de matériel, et cardinaliser la totalité.

Décomposer et recomposer les nombres jusqu’à 20 en deux termes, de manière non ordonnée.

Opérer sur des nombres et sur des expressions algébriques

Savoir-faire

Appréhender et utiliser l’égalité.

Montrer et verbaliser ce qui est le même ou pas, ce qui est égal ou pas, entre deux collections d’objets ou deux représentations d’objets.

Savoir-faire

Comparer les durées d’évènements, d’actions.

Savoir-faire

Utiliser des instruments, des supports pour exprimer un instant dans le temps et mesurer des durées.

LES GRANDEURS

Concevoir des grandeurs

Comparer la durée de situations vécues par rapport à une durée de référence (plus/moins) : un sablier, une chanson…

Agir sur des grandeurs

Utiliser une durée de référence (sablier, chanson…) comme indicateur de temps pour déterminer la durée d’une action vécue.

LES NOMBRES

Connaitre les décompositions jusqu’à 6 et les maisons Représenter 0 à 6 par les dominos, les dés ou les doigts Dénombrer jusqu’à 6

LES SOLIDES ET FIGURES / LES GRANDEURS

Comparer des durées

LE TRAITEMENT DES DONNÉES /

Situation de départ À la ferme

Raconter la BD aux élèves. Une journée à la ferme. Tao ramasse les œufs de poule tandis qu’Élisa ramasse ceux de canard. De retour à l’école, l’institutrice demande : « Combien d’œufs de poule y avait-il ? Et combien d’œufs de canard ? » Tao et Élisa montrent, chacun à sa manière, la quantité 6. Les élèves se rendent compte qu’ils montrent 6 de manières différentes. L’institutrice en profite pour expliquer que c’est pareil et qu’ils ont raison tous les deux.

Jouer en classe :

è Qui préfère montrer comme Tao ?

è Qui préfère montrer comme Élisa ?

è Pourrait-il y avoir d’autres manières de montrer 6 ?