Auswirkungen von Verkehrsschwingungen auf den erhärtenden Beton

Schwingungsprognose am Beispiel eines Brückentragwerks an der A 23 in Wien Auswirkungen von Verkehrsschwingungen auf den erhärtenden Beton

von Alois Vorwagner, Michael Kleiser, Marian Ralbovsky, Thomas Kozakow

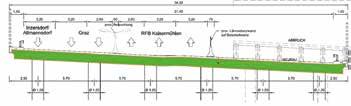
Baumaßnahmen an Brücken im Bestandnetz nehmen einen immer höheren Anteil am Infrastrukturbauvolumen als Neubauten auf der »grünen Wiese« ein. Diese müssen in der Regel unter Aufrechterhaltung des Verkehrs durchgeführt werden. Der Maßnahmenumfang umfasst unter anderem geringfügige Erneuerungen von Randkappen samt Kragplattenenden, kann jedoch auch Verbreiterungen für weitere Fahrstreifen zur Kapazitätserweiterung bis hin zu gänzlichen Neuerrichtungen von Stahlbetontragwerken in halbseitiger Bauweise beinhalten (Bild 1). Das Anbetonieren an Bauteile, die durch laufenden Verkehr dynamisch beansprucht werden, ist in solchen Fällen unvermeidbar und wirft in regelmäßigen Abständen die Frage des Einflusses auf den Erhärtungsprozess als auch auf die Verbundeigenschaften in der Fuge und der Anschlussbewehrung auf. Insbesondere durch den Umstand, dass dynamische Einwirkungen auf den erhärtenden Beton umfangreiche Konsequenzen auf den Bauablauf haben können, ist ein frühzeitiges Wissen der Kritikalität schon in der Ausschreibungsphase von hoher Wichtigkeit. Am Beispiel der neuen Bendabrücke im Zuge der A 23 »Hochstraße Inzersdorf« wird diese Fragestellung erörtert und werden Abschätzungsmethoden für allgemeine Betrachtungen abgeleitet.

1

Bauen im Bestand mit unterschiedlichen Verkehrs- und Betonierphasen © ASFiNAG

1 Schwingungseinwirkung auf den erhärtenden Beton Der Effekt von Vibrationen auf den erhärtenden Beton ist schon lange bekannt. In der Frühphase der Erhärtung wirken sich Schwingungen positiv auf die Materialverdichtung und somit auf die erzielbare Festigkeit aus. Ab einem kritischen Aushärtungsgrad des Zementgefüges können aber intensive Schwingungen das Gefüge und damit die Verbindungen des Zementleims nachhaltig stören, womit die Betoneigenschaften wie Dichtheit oder Festigkeit abnehmen. In der Baudynamik hat sich die Schwinggeschwindigkeit als eine charakterisierende Größe vor allem im Erschütterungsschutz etabliert. Die Empfehlungen für dessen Grenzwert wurden von vielen Autoren untersucht und sind sehr uneinheitlich. Zur detaillierten Diskussion bezüglich des Grenzwertes wird auf [1] verwiesen. Für die folgenden Betrachtungen wurde als Kompromiss ein Grenzwert von 20 mm/s herangezogen. 2 Brückentragwerk Hochstraße Inzersdorf Rund 145.000 Kfz/d benützen die A 23 Südost-Tangente als kürzeste, jedoch meistbefahrene Autobahn Österreichs. Die Brückenkonstruktion der Hochstraße Inzersdorf befindet sich am Südende der A 23 und wurde in den Jahren 1968–1970 als Firmenalternative errichtet. Aufgrund von massiven Schäden wurde in den Jahren 2015–2018 die sechsstreifige Brücke unter der Grundvoraussetzung der Aufrechterhaltung sämtlicher Fahrstreifen und Relationen rück- und neugebaut (Bild 2). Der Neubau speziell der Bendabrücke als Plattentragwerke mit einer Regelspannweite von 19,50 m und einer Plattendicke von 90 cm erfolgte mit Hilfe einer provisorischen Verbreiterung in Etappen, wobei der Anschluss der Fahrbahnplatte in der zweiten Etappe unter aufrechtem Verkehr betoniert werden musste (Bild 4).

Da die tatsächlich auftretende maximale Schwinggeschwindigkeit vorab nicht ermittelt werden konnte, wurde zur Schwingungsreduktion eine Unterstellung entlang der Arbeitsfuge ausgeschrieben. Daraus entwickelte sich ein Forschungsprojekt der ASFiNAG, um während der Bauphase die verkehrsinduzierten Schwingungen zu evaluieren mit dem Ziel, den genannten Grenzwert einzuhalten und somit die Unterstellungen einzusparen [1] [2] [6]. Im Anschluss daran wurde eine Parameterstudie durchgeführt, welche die Einflussfaktoren auf das Schwingverhalten einer Brücke untersucht und eine Schwingungsprognose für allgemeine Platten- und Plattenbalkentragwerke schon in der Planungsphase ermöglicht.

3 Dynamische Interaktion Zur Ermittlung der Schwinggeschwindigkeiten wurden einerseits Messungen in der ersten Etappe am Tragwerk durchgeführt und andererseits das Tragwerk als Finite-Elemente-(FE-)Modell dargestellt. Mit gezielten Verkehrsüberfahrten am Bauwerk mit dem AIT- Messfahrzeug RoadStar® unter bekannten Achslasten wurde das Berechnungsmodell an die Messergebnisse kalibriert. Das FE-Modell wurde mit zahlreichen Überfahrtsvarian ten aus einem Mehrkörpermodell eines Lkw-Modells belastet, um die dynamische Interaktion bestmöglich im Vorfeld zu erfassen. Um auch den Einfluss der Oberflächenbeschaffenheit der Fahrbahn im Modell optimal abzubilden, wurde diese während der Überfahrt mit dem Messfahrzeug gescannt, die Daten in das Modell implementiert und somit die gemessene Fahrbahnunebenheit berücksichtigt.

2

Übersicht des betrachteten Bauabschnittes im Bauzustand © Aus [1]/ASFINAG

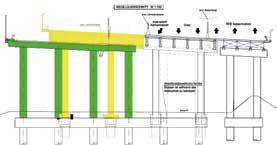
3 Querschnitt des neuen Tragwerks der Bendabrücke © ASFiNAG

Die Ergebnisse zeigten erwartungsge mäß, dass die Durchbiegungen und Dehnungen des untersuchten Tragwerks hauptsächlich durch die Fahrzeugmasse beeinflusst werden, während die dynamischen Schwinggeschwindigkeiten primär vom Straßenprofiltyp, der Profiltiefe sowie von der Fahrgeschwindigkeit und der Wahl der Fahrspur (Mitte oder Rand) abhängig sind. Im Zuge der Dauermes sungen wurde erkannt, dass die Einzelüberfahrten nachts die größeren Schwinggeschwindigkeiten als der Mischverkehr tagsüber lieferten. Durchführung und

Ergebnisse sind umfassend in [1] und [6] beschrieben. Auch die Wirkungsweise einer Tragwerksunterstellung zur vorgesehenen Schwingungsminimierung wurde in Varianten untersucht. Dabei zeigte sich, dass sich eine Unterstellung generell schwingungsmindernd auswirkt, die Wirksamkeit wiederum aber stark vom Straßenprofil und von der Fahrzeuggeschwindigkeit abhängig ist. Gestützt auf diese Ergebnisse, konnte die Unterstellung schlussendlich eingespart und ein Konzept mit angepasster Verkehrsführung umgesetzt werden [1] [2].

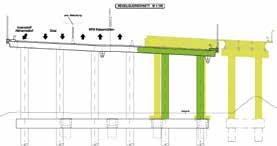
Etappenweise Herstellung der neuen Bendabrücke und kritische Arbeitsfuge © ASFiNAG

5

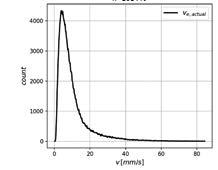
Berechnete maximale Geschwindigkeiten v max der 181.440 Konfigurationen der Plattenbrücken © ASFiNAG 6

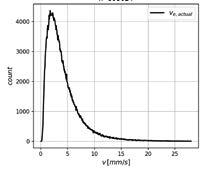
Errechnete maximale Geschwindigkeiten v max der 393.024 Konfigurationen der Plattenbalkenbrücken © ASFiNAG

4 Abschätzung der Schwinggeschwindigkeit als Planungswerkzeug Um eine Einschätzung der verkehrsinduzierten Schwingungen schon in der Planungsphase zu ermöglichen, wurden verschiedenste Überfahrtskombinationen im Zuge von Großrechenserien anhand von zwei Brückengrundtypen, einer Platten- und Plattenbalkenbrücke, durchgeführt. Mit dem am AIT entwickelten parametrisierten FEM-Solver konnten die dynamischen Einzelüberfahrten eines 45-t-Lkw-Mehrkörpermodells (Vierachser) am Hochleistungssimulationsrechner simuliert werden. In Summe wurden dabei für 574.000 unterschiedliche Kombinationen von Brückenabmessungen die Fahrbahn- und Überfahrtseigenschaften berechnet und die Auswirkungen auf die auftretende maximale Schwinggeschwin digkeit v max ausgewertet. Die variierten Parameter waren: – Überfahrtsparameter: – Straßenprofilklassen A+, A und B nach [5] sowie lokale Unstetigkeits- stellen – Überfahrtsgeschwindigkeit: v car (30–100 km/h) – Spurführung: Brückenrand und -mitte – Tragwerkspezifische Parameter: – Spannweite L, Breite B – Schlankheit als Verhältnis zur Tragwerkshöhe H: L/H – Statisches System Einfeld / Mehrfeld – Kreuzungswinkel 75° oder 90° – Trägersteifigkeiten wie Träger- schlankheit, Anzahl, Abstände sowie Zustand (gerissen oder ungerissen) Die Ergebnisse der Großrechenserie sind als Histogramme in Bild 5 für die Plattenbrücke und in Bild 6 für den Plattenbalken dargestellt. Bei der Plattenbrücke wurde der Wert von 20 mm/s in 31,80 % der Berechnungen überschritten, bei der Plattenbrücke waren dies nur 5,30 % der Berechnungen, was jedoch darauf zurück zuführen ist, dass die Platte im Modell nicht enthalten ist und durch einen Überhöhungsfaktor noch zusätzlich berücksichtigt werden muss. Gesetzmäßigkeiten und Zusammenhänge konnten nur als Tendenzen gefunden werden, womit die Ermittlung von analytisch ableitbaren Abschätzungsformeln erschwert wurde. Zur Lösung dieses Problems wurde auf die Metamodell-Technik zurückgegriffen. Damit lassen sich zum einen die Ergebnisse besser interpretieren und zum andern Einflüsse besser erheben und schlussendlich eine Abschätzungsformel für die Planung von Bauphasen ermitteln. Metamodelle dienen, mathematisch ausgedrückt, dem Zweck, die Beziehung von mehreren Eingangsvariablen zu einer oder mehreren Ergebnisvariablen zu approximieren. Sie beruhen nicht auf physikalischen Gesetzen, sondern auf mathematischen Modellen, die Eingangsparametern in einem vorgegebenen Wertebereich die gleichen Ergebnisse wie das physikalische Modell zuordnen. v max,assess = k ∙ (c 0 + c 1,L ∙ L + c 2,B ∙ B + c 3,v ∙ v car + c 4,SL ∙ SL ) Gl 1 Konkret wurden die im FEM- Ergebnisdatensatz der Großrechenserien (Eingangsvariablen) vorhandenen Antwortvariablen für die Metamodelle angepasst, welche auf einfachen Brückenparametern basieren. Metamodelle ersetzen somit die mechanisch-physikalischen Modelle in definierten Eingangs-parameterbereichen. In diesem Fall dient als Anpassung ein Polynomansatz, welcher durch multivariable Regressionsanalyse bestmöglich gefittet wird. Dabei wurden die Koeffizienten c i des gewählten Polynoms ermittelt, welche auf die Parameter L = Länge, B = Brückenbreite, V car = Überfahrtsgeschwindigkeit, SL = Schlankheit Bezug nehmen. Eine Unterteilung auf mehrere Gruppen entsprechend dem statischen System (Ein-, Mehrfeld), der Fahrbahnrauigkeit (Klassen nach ISO 8606 [5]) und Position der Überfahrt (Mitte oder Rand) verbesserte die Ergebnisse zusätzlich. Für jede Gruppe wird ein eigenes Set an Koeffizienten c i ermittelt, anhand dessen die maximale Schwinggeschwindigkeit v max,assess entsprechend Gleichung 1 einfach abgeschätzt werden kann. Ein Korrekturterm k ermöglicht generell eine bessere Anpassung der Abschätzungsformeln an die Berechnungsergebnisse.

Die Methodik sowie die gefundenen Anpassungsformeln sind umfassend in [4] beschrieben und dort zusammen mit den entsprechenden Koeffizienten dargestellt.

VORANKÜNDIGUNG zum Symposium BRÜCKEN IN DER STADT Tagungsort und Tagungsdatum: Mannheim 2020

Mit BRÜCKEN IN DER STADT wollen wir viele Anfragen insbesondere aus Städten und Kommunen beantworten, wann die nächste Veranstaltung vorgesehen ist, die nicht nur Geh- und Radwegbrücken thematisiert, sondern auch größere Bauwerke in den Innenstädten.

2020 werden wir, und zwar in Mannheim, dieses Thema aufgreifen und nicht nur große Querungen über Gleisanlagen oder innerstädtische Brückenzüge und Überführungen vorstellen, sondern natürlich ebenso Geh- und Radwegbrücken. Am Beispiel zweier großer Wettbewerbe werden zudem herausragende Vorschläge internationaler Planungsbüros und Architekten präsentiert.

Und da für die Akzeptanz bei der Bevölkerung Voraussetzung ist, dass die Beleuchtung, dem Anlass entsprechend, ausreichend und harmonisch gestaltet ist, kommt ihrer Konzeption genau wie der des Lärmschutzes eine hohe Bedeutung zu.

Viele Vorschläge liegen uns bereits vor, weitere erwarten wir gerne.

Wir freuen uns, wenn Sie sich dafür interessieren.

mit MixedMedia Konzepts VERLAGSGRUPPE WIEDERSPAHN

1/2 . 2020 | BRÜCKENBAU Biebricher Allee 11 b 65187 Wiesbaden Tel.: +49/611/98 12 920 Fax: +49/611/80 12 52 kontakt@verlagsgruppewiederspahn.de www.verlagsgruppewiederspahn.de www.mixedmedia-konzepts.de www.symposium-brueckenbau.de

7

Abmessungen des Anwendungsbeispiels: Plattenbrücke mit L = 19,50 m, H = 0,90 m und B = 20,70 m © ASFiNAG

5 Anwendungsbeispiel Um die Vorgangsweise der möglichen Abschätzung in der Vorplanung zu illustrieren, wird die Bendabrücke der A 23 hier als Anwendungsbeispiel (Bild 7) präsentiert. Für dieses Tragwerk liegen ebenso die Messdaten der Schwingge schwindigkeiten während der Bauphase wie detaillierte Ergebnisse vor. Die Eingangsparameter in Gleichung 1 sind: Plattenbrücke mit einer Regelspannweite von L = 19,50 m, eine Plattendicke von H = 0,90 m, ergo eine Schlankheit SL = 21,60. Die Brückenbreite B = 20,70 m ist damit größer, als in der Großrechenserie mit B max = 16,00 m durchgeführt wurde. Als Straßenprofil wird als Klasse Typ A entsprechend [5] gewählt, um die im Bauzustand lokalen Unebenheiten ebenfalls abzudecken. Unterschieden werden kann nun, ob die Brücke in der Mitte oder am Rand überfahren wird, ebenso wurde die Fahrzeuggeschwindigkeit v car zwischen 30 km/h und 100 km/h schrittweise variiert. Die Koeffizienten c 0 –c 4 wurden entsprechend den zugehörigen Gruppen nach [4] erhoben und mit Gleichung 1 die Schwinggeschwindigkeit v max,assess abgeschätzt:

v max,assess = k ∙ (c 0 + c 2,L ∙ 19,5 + c 2,B ∙ 16,00 + c 3,v ∙ 16,66 + c 4,SL ∙ 21,66 ) Der gemessene Wert von v max mess = 13,30 mm/s stimmt sehr gut mit der abgeschätzten Schwinggeschwindigkeit bei Einzelüberfahrt am Rand mit v car = 65 km/h überein. Bei einer Überfahrt in Brückenlängsmitte würde dieser Wert bei gleicher Geschwindigkeit auf v max, assess = 7 mm/s nahezu halbiert werden. Der Einfluss der Überfahrtsgeschwindigkeit sowie das Zeitsignal des Messwerts sind in Bild 8 dargestellt.

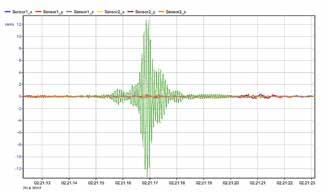
Ergebnis der Abschätzungsformel der Schwinggeschwindigkeit als Einfluss der Verkehrsführung © ASFiNAG

9 Messwert V max mess = 13,33 mm/s nach [6] © ASFiNAG

6 Zusammenfassung und Schlussfolgerungen In einem Forschungsprojekt im Zuge des Neubaus der Bendabrücke in Wien wurden die maßgeblichen Schwinggeschwindigkeiten evaluiert und, darauf aufbauend, Einflussfaktoren auf die Schwinggeschwindigkeit bei Verkehrsüberfahrten mittels einer Parameterstudie untersucht, um kritische dynamische Einwirkungen auf die Betonerhärtung auszuschließen. Es wurden neben einer detaillierten Tragwerksanalyse Großrechenserien durchgeführt. Die Ergebnisse zeigen, dass erwartungsgemäß Mehrfeldtragwerke weniger anfällig sind als einfeldrige, was im Zuge der Großrechenserie bestätigt wurde. Ebenso nehmen mit schlankeren Bauteilen oder höheren Überfahrtsgeschwindigkeiten die Schwingungen zu. Die Verkehrsführung kann die Schwingungsbelastung verbessern, wenn das Tragwerk in der Mitte statt am Rand überfahren wird. Eine verbesserte Straßenrauigkeit, insbesondere in Spannweitenmitte, wirkt sich positiv auf die Schwingungsminderung aus, tendenziell wirkt auch die Überfahrtsgeschwindigkeit reduzierend. Mithilfe eines Metamodells ließen sich einfach anwendbare Abschätzungsformeln [4] mit einem linearen Polynomansatz und Korrekturfaktor für die Streubreite finden. Damit können Richtgrößen für auftreten de Schwinggeschwindigkeiten für allgemeine Platten- und Plattenbalkentragwerke in der Planungsphase ermittelt und somit gezielte Maßnahmen zur Vermeidung kritischer Schwinggeschwindigkeiten ausgeschrieben werden.

Literatur [1] Ralbovsky, R.; Vorwagner A.; Kleiser, M.; Kozakow,T.; Geier R.: Verkehrsschwingungen bei Betonierarbeiten auf bestehenden Straßenbrücken; in: Beton- und Stahlbetonbau (noch nicht erschienen). [2] Ralbovsky M., Vorwagner A., Kozakow T., Geier R.: Einflüsse auf die Amplitude verkehrsinduzierter Schwingungen bei Arbeiten auf Bestandbrücken; in: Tagungsband des 3. Brückenkolloquium »Beurteilung, Ertüchtigung und Instandsetzung von Brücken«, Wien, 2018, S. 499–505. (Publikation erscheint in der März 2020.) [3] Kozakow, T.: Abbruch und Neubau unter vollem Verkehr. Hochstraße Inzersdorf und Neilreichbrücke; in: Brückenbau, 9. Jg., 2017, Heft 1/2, S. 116–123. [4] Ralbovsky, R.; Vorwagner A.; Kleiser, M.; Kozakow, T.: Abschätzung von verkehrsinduzierten Schwingungen von Straßenbrücken vor anstehenden Bauarbeiten. Bildung eines Meta-Modells zur Erstabschätzung des Risikos einer negativen Beeinflussung auf den erhärtenden Beton beim Betonieren unter Verkehr, (eingereicht). [5 ISO/TC 108/SC 2: ISO 8608:2016 Mechanical Vibration, Road surface profiles. Reporting of measured data. [6] ASFiNAG Endbericht zum Forschungsprojekt »Untersuchung von Brückenschwingungen während der Bauzeit«. 31.05.2019, unveröffentlicht.

7 Danksagung Die vorgestellte Arbeit wurde mit finanzieller Unterstützung der ASFiNAG Bau Management GmbH durchgeführt. Die Autoren möchten an dieser Stelle ihren Dank für die erfolgreiche Kooperation zum Ausdruck bringen.

Autoren: Dipl.-Ing. Dr. Alois Vorwagner AIT Austrian Institute of Technology GmbH, Wien, Österreich Dipl.-Ing. Dr. Michael Kleiser ASFiNAG Bau Management GmbH, Wien, Österreich Dipl.-Ing. Dr. Marian Ralbovsky AIT Austrian Institute of Technology GmbH, Wien, Österreich Ing. Thomas Kozakow ASFiNAG Bau Management GmbH, Wien, Österreich Bauherr ASFiNAG Baumanagement GmbH, Wien, Österreich

Ausführungsplanung Thomas Lorenz ZT GmbH, Graz, Österreich IBBS ZT GmbH, Wien, Österreich IKK ZT GmbH, Wien, Österreich

Prüfingenieur Dipl.-Ing. Bernhard F. Otto, Wien, Österreich

Schwingungsmessung Schimetta Consult ZT GmbH, Wien, Österreich

F&E-Projekt AIT Austrian Institute of Technology GmbH, Wien, Österreich

Bauausführung Strabag AG, Wien, Österreich Habau Hoch- und Tiefbaugesellschaft mbH, Wien, Österreich Porr Bau GmbH, Wien, Österreich

HEICO FASTENING SYSTEMS

HEICO-LOCK ® HLK-SCHEIBEN

Das Sicherungssystem für HV-Garnituren

HEICO Befestigungstechnik GmbH

Z-14.4-702

Fraunhofer MVO08

 speziell zur Sicherung von HV- Schraubengarnituren nach DIN EN 14399  zertifiziertes und überwachtes Bauprodukt  geregelt über die allgemeine bauaufsichtliche Zulassung Z-14.4-702

 hoher Korrosionsschutz durch Zinklamellenbeschichtung

HEICO-LOCK ® KEILSICHERUNGSSYSTEME

Qualitativ hochwertige Sicherungen für anspruchsvolle Schraubenverbindungen

Mitglied Deutscher Stahlbau-Verband