4. ELASTIC GRID SHELLS

4. ELASTIC GRID SHELLS

The proposed task aims to continue research into applications of resistant membrane structures. We will create virtual and subsequent real models creatively by physically searching for a form and applying numerical methods based on finding the shape and modelling the equilibrium state of geometric nonlinear shapes. Static shapes are often straight with horizontal lines and may appear quiet and active shapes are diagonal with orthogonal lines. This behavior of traditional interpretation of geometrical design was caused by a lack of the existence of computational and material characteristic tools. The principles behind this “computation” have also been computationally recreated and are now in principle available to designers. We will aim to free constructions from shapes that are based on straight lines. As it is known, the basic elements of standard shapes are line and plane, positive-curved line guides the spherical geometry, while a negative-curved line guides hyperbolic geometry. The "Form Finding" method allows searching for shapes regardless of traditional compositional, static, or constructional principles using a virtual, so-called trans-architecture. Evolution in nature, which optimized natural structures, has also become a major source of inspiration for the shapes of structures in construction and architecture. However, the "Free Form" shapes have no analogy in nature, and it is impossible to describe them exactly mathematically. We want to choose our approach to the issue of shape search and optimization of the so-called free-form membrane constructions of synclastic and anticlastic shapes. This problem requires designers to understand and analyze sets of relationships between parameters and components. One of the useful tools for producing architectural designs is to convert aims into abstract shapes. In its long history, algorithmic plan as a form-finding strategy, permitted designers to oversee complex non-standard associative geometries, recommending a move from the computerized representation of frame to its efficient representation into a parametric demonstration through code. Modern geometry became more attractive in the architectural design process with great innovations from form-finding stages to the final fabrication. An elastic geodesic grid (EGG) is one of the subgroups of lightweight structures that can be freely used to unfold the free-form spaces and make the application of the grid movable. Furthermore, their installation does not need complicated instructions. Lightweight grid constructions are especially needed for realization where large spans and low weight are required and do not have to be straight, at the same time the satisfactory curved shape for the designer is based on iteration.

Our goals are to analyze how the virtual design of such a structure becomes real according to elastic deformation and to use it in different scaling for public spaces. As we show the structure in Fig. 4.1, the grid system is 2d, with the dimensions x,y including spaces between the strips in u,v distances. The transformation of this flat surface in 2d to 3d we achieve via induced curvature to the structure, applying to bend or twisting the grid elements. The materials used for this type of construction are available and common ones are available on the market. The new position of the form-finding grid system is usually found geometrically, which is the function of networks of elastic grid geodesic curves. This elastic-kinematic mechanism for Set up the free-form finding substructure offers a non-Euclidian form simply call it a curved shape surface during the installation of geometry, therefore we realize the boundary conditions of the anchors. Yet we used a small physical model with a small budget for a better understanding of the kinematic behavior of such free form finding substructure, to serve for further development and their easy installation, and expansion at various scales in the future. This setup procedure makes the doubly curved surface more easy, quick, and more material efficient. The creation of such constructions is aesthetic, functional, and special, in addition, they are nice because the form finding of the surface is curved, which brings us closer to nature and gives us a sense of freedom with its parametric design. The creativity of elastic geodesic grids is the transformation analysis of the structure that the input data come for the planar surface design, where the output data are achieved from a 3d curved surface grid, this can be set up simply by pulling at least the two corners at the planar state with applying some additional bending. To create a spatial surface, we select a simple way using sheet plat for its perfect characteristics, which is closely related to the Japanese art of origami. Recently besides architecture diagrams, there has been developed digital graphic investigation support with visual programming such as grasshopper inside rhino using the kangaroo solver plug-in for parametrizing the geometry of the folding structure. An elastic grid shell is a system “consisting of flexible members”. The required geometry is achieved through the progressive elastic bending of originally in-plane grid members Fig. 4.1. The erection process can be completed on initially plane flat grid disposition or through gradually bent of single members (gradually erected). The main purpose of this presentation is to build a regulation method for elegant temporary structures, which can be realized shortly by inexperienced builders or workers. The variety of a geodesic dome and elastic grid shell structural system is motivated by its amazing budget, clearness of structure and high install ability potential, continue the ongoing research in the

field of their structure concept, design, and analysis, set up the work procedures and Potential development are still open.

Fig.4.1: Plane flat Elastic flat grid plan members (models created by the authors) The reason for the creation of our EGG was based on cutting plastic lamellas in the width of 2cm, the thickness of 2mm, and in 1m length for both directions x, y, while the lamellas will be mounted at a distance of 100mm in both directions u, v, which will eventually create an area of 1m x1m Fig. 4.1. Practical lamellas are deformable but after the creation of curved shape based on curvature in both directions which controls the shape and therefore ensures the stability and safety of the entire structure. In all nodes, we have created notches in the x, y-axis directions, for ease of node movement in the x-direction and y-direction, respectively, so that the design will be able to provide us with different types of shapes in the form-finding process which is the function of iteration.

Fig. 4.2: Elastic deformation, reversible deformations, and form finding of E.G.SH, (models created by the authors)

We try to understand the conceptual design of elastic grid shells in all its difficulties, and we try to find a solution for their theoretical, structural, and technical concepts. An elastic grid shell is a freeform non-Euclidean structure, generally doubly curved, but formed out through the reversible deformation of a normal and originally flat structural grid. This type of grid shell, known as an elastic grid shell, offers a very elegant method to create freeform shapes from an originally flat and proper grid Fig. 4.2, which indeed has many practical advantages: planar initial geometry, ordinary connection nodes, modular cross-sections, and so on. Note that the term rigid shell is often opposed to the term elastic grid shell to indicate net structures that behave like shells but are not formed in an active-bending process. Elastic grid shell is one of the subgroups of lightweight structure that can be freely used to unfold the free-form spaces and make the application of the grid flexible as well as movable. Furthermore, their installation does not need complicated installation. Lightweight grid constructions are especially needed for realization where large spans and low self-weight are required and do not have to be straight, at the same time the satisfactory curved shape for the designer is based on iteration during the state of the form-finding process. Our goals are to analyze how the virtual design of such a structure becomes real according to elastic deformation Figure 4.2 and to use it in reality with different scaling for public spaces. As we show the initial grid flat plan in Fig. 4.1, the grid system is 2d, with the dimensions x,y including spaces between the strips in u, and v distances. The transformation of this flat surface in 2d to 3d we achieve via induced curvature to the structure, applying to bend the grid elements. The materials used for this type of construction are available and common ones are available on the market.

The new position of the form-finding grid system is usually found geometrically, which is the function of networks of elastic grid geodesic curves. This elastic-kinematic mechanism for Set up the free-form finding substructure offers a non-Euclidian form simply call it a curved shape surface during the installation of geometry, therefore we realized the boundary conditions of the anchors. Yet we used a small physical model with a small budget for a better understanding of the kinematic behavior of such free form finding substructure, to serve for further development and their easy installation, and expansion at various scales in the future. This setup procedure makes the doubly curved surface more easy, quick, and more material efficient. The creation of such constructions is aesthetic, functional, and special, in addition, they are nice because the form finding of the surface is curved, which brings us closer to nature and gives us a sense of freedom with its parametric design. The creativity of elastic grid shells is the transformation analysis of the structure that the

input data come for the planar surface design, where the output data are achieved from a 3d curved surface grid, this can be set up simply by pulling at least the two corners at the planar state with applying some additional bending. The bending and twisting behavior of the strips can be analyzed by using different characteristics of materials and cross-sections. A parametric model is special not for what it does but rather for how it was made.

In this way, the utilization of parametric models in the computerized plan permits architects to depict the geometry of their model with adaptability and make conditions between the components of the model, using particular rules and limitations. To make parametric models, designers utilize algorithmic editors that ordinarily consolidate visual programming dialects (like Grasshopper inside Rhino3d,), to overcome the imperatives of the interface, and to design specifically, overseeing not the form (with the plan devices given by common program packages), but the code that produces the shape. In this way, the designer can define the associations of the parts of the parametric model into code, so that an alteration within the parameters that depict it'll, cause a facilitated general upgrade in this way by watching the varieties of the created comes about. Visual programming involves representing programs not as text but rather as diagrams.

Both Grasshopper and Generative Components are based around graphs (a mathematical name for a type of flowchart) that map the flow of relations from parameters, through userdefined functions, usually concluding with the generation of geometry. Changes to parameters or the model’s relationships cause the changes to propagate through the explicit functions to automatically redraw the geometry. Usually, we use the Kangaroo tool when a quick form-finding procedure is needed in conceptual design. First, a simple NURBS surface has been divided in u,v grid, and then used as the reference geometry for a formfinding test. In the setup of the model we start to constrain and anchor the number of points at corners, and the simulation of a hanging model will be run by a kangaroo solver plug-in.

Parametric models, using grasshopper inside Rhino using kangaroo plugin to find physical

Form finding, which is one of the most powerful designs in contemporary architecture today, leads to creating forms, gravity, tension, minimal surfaces, compression, relaxation, and optimization are known in the realm of physics Fig. 4.3.

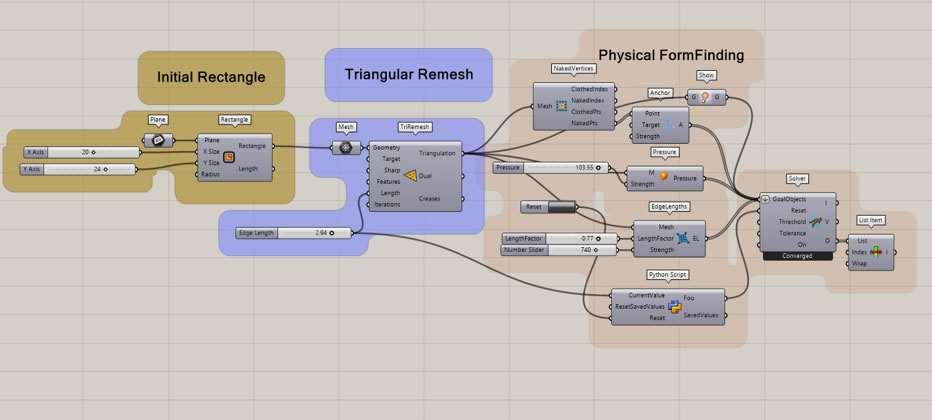
Fig. 4.3: Grasshopper Script created by the author, physical form finding

As we observe from Fig. 4.3, how the code produces the shape, changing the parameters of an initial rectangle or in Triangular remesh of the model relationships cause the changes of the entire form of physical form finding. In this way, the designer can define the associations of the parts of the parametric model into code. These relationships between the parameters and the components offer one useful tool for producing architectural designs converting aims into abstracted shapes, this modern geometry became more attractive in the architectural design process with great innovations from form-finding stages to the final fabrication.

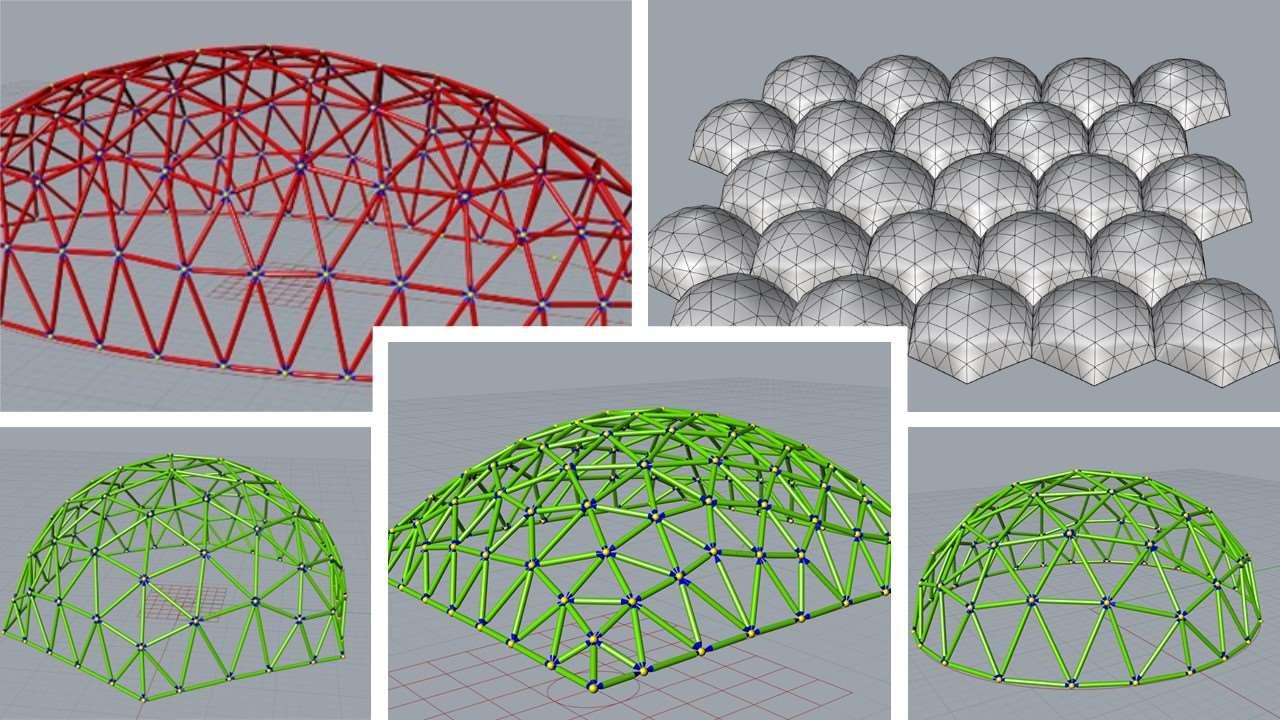
Fig. 4.4: Form Finding of the elastic geodesic dome using grasshopper inside Rhino, (models created by the authors)

Fig. 4.5.: Parametric Physical Form-Finding of EGG Shells (models created by the author)