7. MÖBIUS BAND

7. MÖBIUS BAND

In 1858, the astronomer and mathematician August Ferdinand Möbius was the first to define a surface in three-dimensional space at the Paris Academy of Sciences, a surface we know today as the Moebius band. But history reveals that the true discoverer was Johann Benedict Listing, who came across this surface in July 1858 (I. Peterson, 2001). The strip twisted is called a ribbon of Möbius or Möbius strip, also Mobius or Moebius band. Non-orientability of the Möbius strip means that in the process of motion of a plane not- symmetrical figure inside a Möbius strip, this figure, having returned to the initial point, transforms into its own mirror image. The well-known single-sided Möbius strip has inseparable properties that can be expressed in architectural form, surface, and space. Analyzing the way of transforming the 2D of the Möbius band into 3D enables the creation of a new property for architectural space based on the human scale.

Thanks to the development of computer technology and available professional programs that consider the non-linear properties of materials in the process of our thought and design, we can analyze and investigate parametric surfaces to realize long-span’s structures based on pure mathematical descriptions. This modern way allows us to easily design unimaginably mathematical curves to create real architectural spaces (V. Petresin, and R. Laurent-Paul, 2002). The so-called fluid topological architecture is the result of a set of new ideas of space. In topology, there is no longer difference between two places, you can move from one space to the other space using a continuous deformation with neither leap, tear nor cut. This is the case of Möbius geometry which plays an important role in modern architecture and design. Topology is a mathematical study of the properties that are preserved through the deformation, twisting, and stretching of objects. Its relatively recent discovery by architects led to an interesting transformation of the art of understanding and building space. The Möbius band or strip is a structure that represents the progress of a two-dimensional plane into a three-dimensional space. By integrating the inside space with the outside surface, it creates a single continuously deformed curved surface.

The interest of the authors in applying topology to virtual architecture led to the creation of a project called the Observatory based on the Möbius band. The outside of the structure becomes the inside, where horizontal bearing members become vertical members and then they transform into the horizontal again.

The introduction of the Möbius strip into architecture is a unique phenomenon by which we can achieve the spatial feeling of a person walking and still twisting, without having to walk up or down. The Möbius strip offers new possibilities for design space, where the interior of the building becomes external and vice versa just as the horizontal elements of the space become vertical elements, it becomes a horizontal element again or where the space is turned into another space. However, the shape creation of the Möbius band has great potential as an architectural form that is difficult to visualize and investigate without the aid of digital technologies (I. Peterson, 2001). The creation of architectural space as well as an understanding of the idea of space within a walk inside the building resulted in two projects: First, the realization of multi Möbius strip Fig. 7.1 and second, as a single Möbius band. Both objects were designed to be located on the banks of the river Danube Fig. 7.2.

Fig. 7.1. Möbius Strip Rotations of Other Geometric Shapes (models created by the authors)

Fig. 7.2. Möbius Strip Structure of Rectangle Geometric Shape

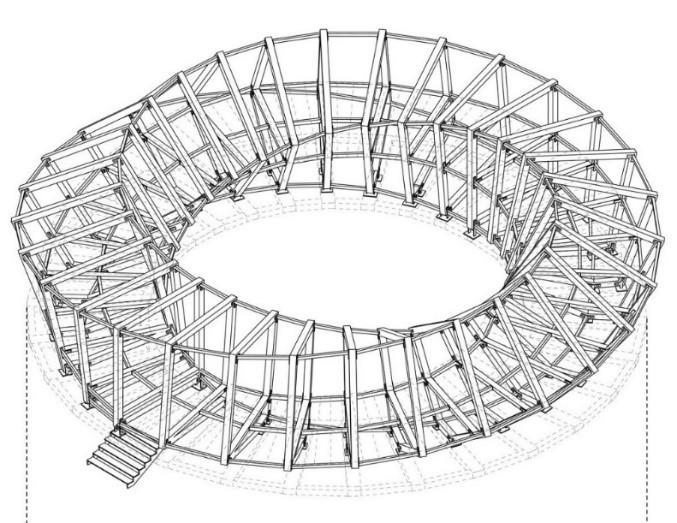
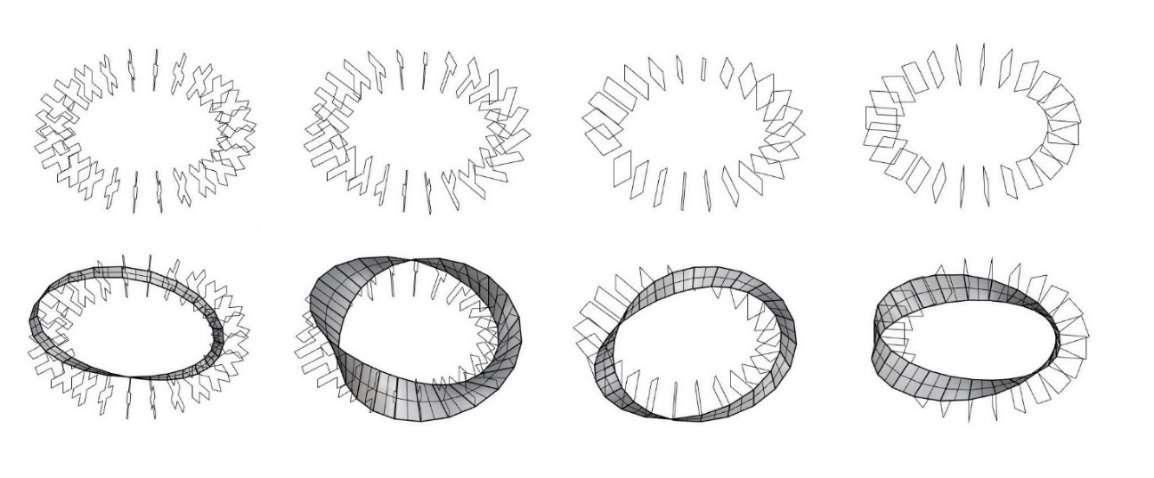
Fig. 7.3. Mobius Band with Various Degrees of Twist

Imagine surfaces or spaces with continuous rotations without interruption along the entire length of a certain material resulting in a new form with completely different properties. Our construction design depicted in Fig. 7.2 consists of 30 timber frames in a shape of a square 4 x 4 meters. Each one of them rotates on a circle every 12 degrees and on its axis - 6 degrees. On top of these two kinds of frame rotation, the wooden floor gradually elevates, starting from 0.60 m and reaching a height of 2.15 meters, which is why the visitors enter the observatory’s ramp by 6 stairs. When the frame concludes it is 90-degree rotation, the floor rises by 1.5 meters compared to the beginning of the walkway, thus creating a different volume and height of space within each frame, ranging from 2 meters to 3.6 meters. From this height is derived the width of the walking part of the ramp, which adjusts its width so that the height of the space is never less than the mentioned 2 meters, allowing fluid movement through the space. The ramp is therefore 4 meters at the widest point and 2.76 meters at the narrowest. The volume of the space thus gradually decreases, but even in its smallest configuration, it is large enough for a comfortable transition. This space created by the rotation allows the visitors to enjoy unique vistas, thanks to the continual change of heights and widths of space. As for the construction details, a solution to all joints is steel plates, which are visible on purpose, so that the visitors can better understand how the structure works. There are two types of foundations possible – the first one is the concrete footing for permanent placement of the observatory and the second solution is full wooden frame foundations, which add mobility and variability of placement. The second variant is located on a supported concrete podium raised above the river Fig. 7.2.

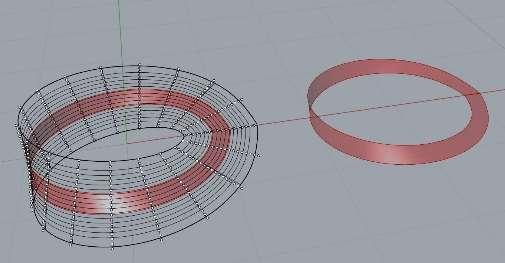
7.1 FORMS, DEFORMATIONS AND ANIMATION As we know, the Möbius strip is the simplest geometric shape which has only one surface and only one edge. It can be created by taking a strip of paper, giving it a half twist along it, and then joining the two narrow ends together. If the curved profile of the structure following the path of the Möbius surface has a positive concavity direction at the starting point of the translation, it will have a negative convexity direction after having completed the path and revolving to the starting point. Creating the Möbius strip is a complicated task when using a physical model, but the current technology such as using Grasshopper, which is virtual visual programming Inside Rhino, enables us to create several different models and reconfigure them in a digital environment (J. Thulaseedas and R. J. Krawczyk). This virtual tool shows the power of parametric modeling for the design phase of the project and integrates it with Rhino. The following explanation shows the process of creating the Möbius strip structure in different ways. Creating the Möbius Strip due to Mathematical Equations Here we investigate the basic mathematical equations of the Möbius Band and its extension to a geometry. If we slit a Möbius strip along its long axis, then we shall have an oriented strip twisted at 2π. Fig. 7.1.2 and Fig. 7.1.3 demonstrate the usual elliptical Möbius strip, when the value of the integer equals 1. The Möbius strip in 3 dimensions can be represented parametrically f (����, ����) as follows:

Parametrical equations: ����� ���� ����� =

⎡������������(����)+����∗����������������� �����∗������������(����)⎤ ⎢ ⎢ ������������ (����)+����∗����������������� �����∗������������ (����)⎥ ⎥where  ranges from 0 to ⎣ ����∗������������ (����/����) ⎦ 2*π and  ranges typically from - 0.4 to 0.4

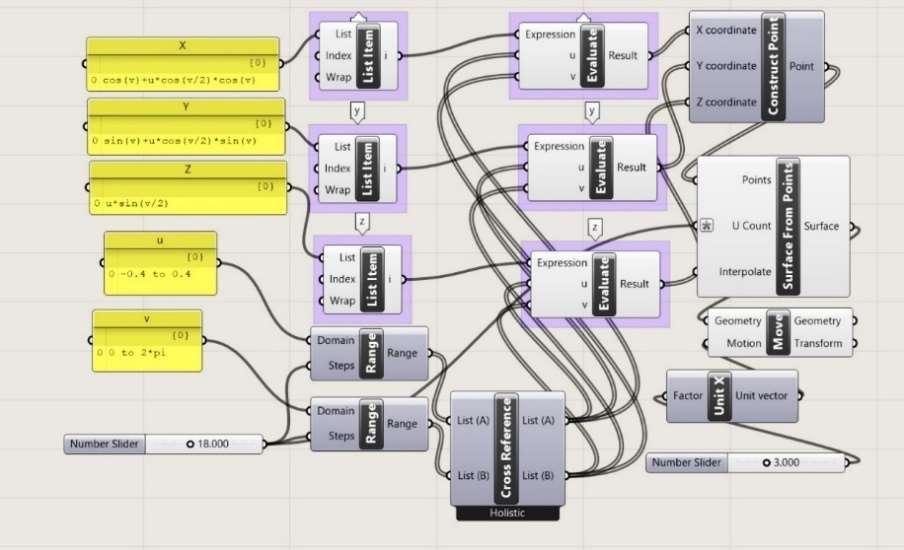
Fig. 7.1.1. Process of Thinking in the Grasshopper Programme (Variant a)

Fig. 7.1.2. Deformations and Animation of Möbius Band ( = - 0.1 to 0.1)

7.1.3a 7.1.3b

Fig. 7.1.3a, b. Deformations and Animation of Möbius Band, for a  = - 0.1 to 0.1, for b = - 0.3 to 0.3 (Variant a) a. Using Curve for Creating Mobius Band The generation of a curve representing the path of an ellipse or circle form is determined by the number of segments which will be distributed uniformly at equal distances, inclinations, and the center of the individual segments defining the axes of rotation from which the edge points are calculated. Connecting the edges of the segments to each other generates the shape of the Möbius band.

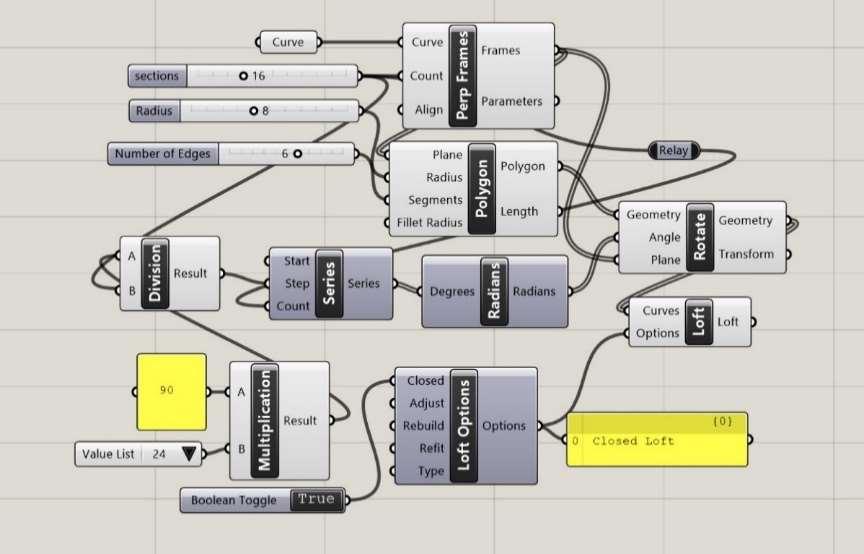
Fig. 7.1.4. Process of Thinking in the Grasshopper Programme (Variant b)

Fig. 7.1.5. Möbius Bands with Various Degrees of Twist with Constant Floor Level (Variant b) b. Using Circle for Creating Mobius Band

The Parametric form of the definition of a Möbius strip this an elliptical plan that shows the

Möbius strip twisted several times when the value of the integer is more than 1 Fig. 7.1.7.

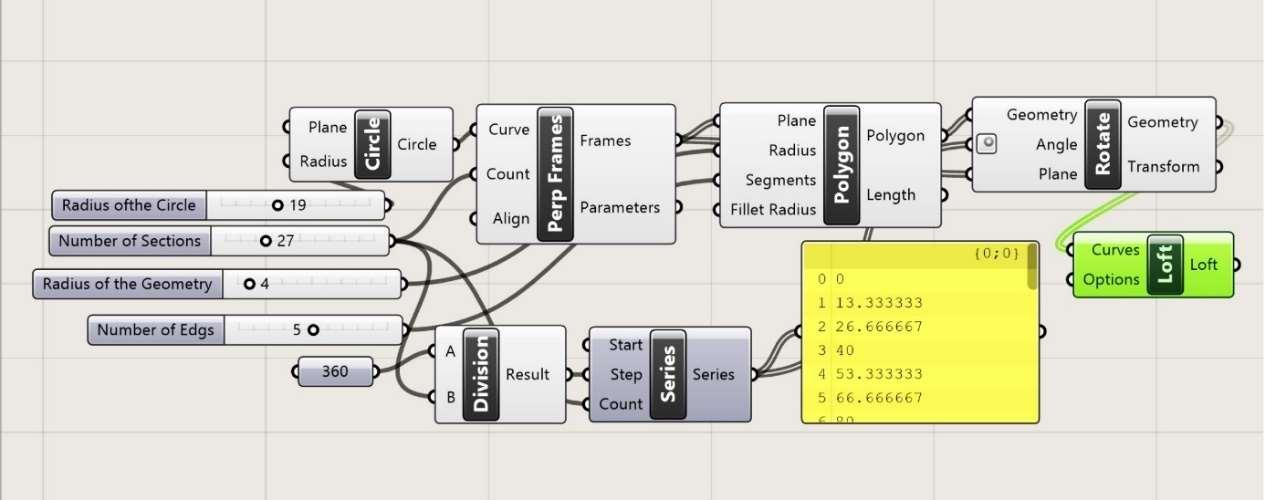
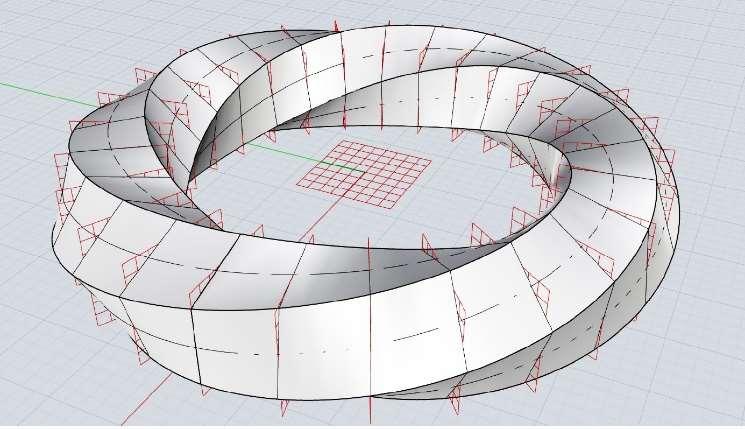
Fig. 7.1.6. Process of Thinking in the Grasshopper Programme (Variant c)

Fig.7.1.7. Möbius Bands with Various Degrees of Twist with Constant Floor Level (Variant c)

Grasshopper inside Rhino is the newest technology that seems to have the potential of finally solving the compatibility issues with Rhino, as we mentioned before in the example of virtual designing of Möbius strip by parametric modeling. In our short example, we have explained in detail the process of thinking with a step-by-step approach, so as to better understand the process of creating the conceptual form improvement of the Möbius band in different ways. We used the perp frames tool that allow us to create our structure, this comprehensive plugin helped us to fulfill our purpose in a simple way. Once we have finished the overall shape in Grasshopper, we baked the geometry and continued with the creation of details directly in Rhino. In the end, we sorted the geometry based on layers and materials. To conclude, the conceptual design of structures is a specific part of the design process when the most fundamental and influential decisions are made. It is an area where all the parameters such as experience, intuition, tradition, and technical skills of designers come together.  Process of thinking according to program GH, for creating Mobius strip Fig. 7.1.8: Drawing the basic curve of Rhino, Loading geometry from Rhino to GH  Input parameters, side length, number of profiles, rotation angle, floor height  Divide the curve into equal parts  Create a geometry that will rotate around the curve at 180 degrees  Sequences of frames, parallel to rotation around the curve  Creating a surface from frames, the function of connecting curves and lines  Baking-exporting geometry from GH back to Rhino

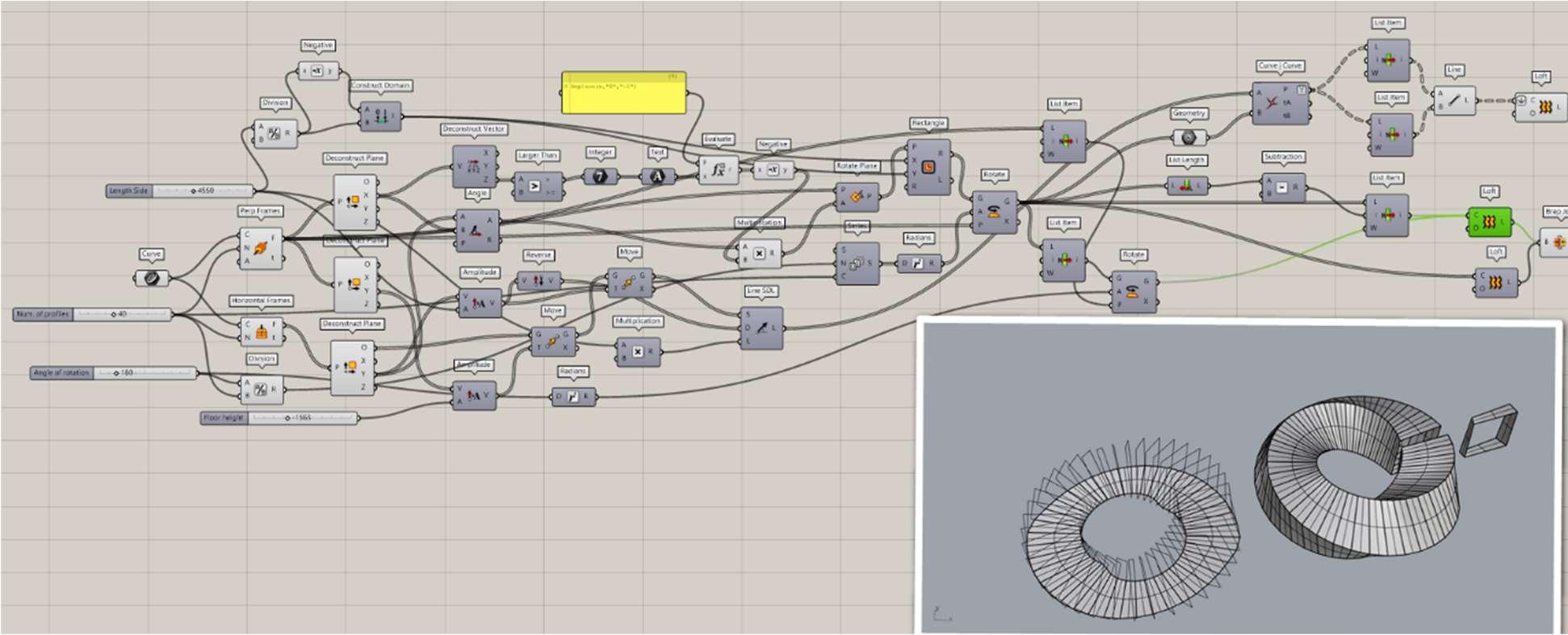
Fig. 7.1.8. Process of Thinking in the Grasshopper Programme (Variant d)