EdiblE infra struC turEs
OrganisatiOnal

PattErns fOr
EdiblE infrastruCturEs
Organisational Patterns for Urban-Agricultural Landscapes
DarrickBorowski (MArch) JeroenJanssen (MArch)
Part I research was done with Nikoletta Poulimeni (MSc)
Emergent Technologies & Design Architectural Association, London, 2010-2012
 Above: Settlement Simulation Rules
Cover Image: The City of Brooklyn, 1879; by Currier & Ives, Library of Congress public domain
Above: Settlement Simulation Rules
Cover Image: The City of Brooklyn, 1879; by Currier & Ives, Library of Congress public domain
ABSTRACT
Edi B l E i nf RASTR u CT u RES is an investigation into an urbanism which considers food as an integral part of a city's metabolic infrastructure. Working within this mode, we explore the generative potential of such a system to:
• Create an urban ecology that provides for its residents within the given boundaries of the system via local, multi-scalar, distributed food production
• Enhance agricultural production by reconnecting the traditional waste-nutrient cycle which was lost with industrial farming
• De-couple food/energy costs from fossil fuels by limiting transport at all levels, from source to table
Our research is conducted via the building up of a sequence of algorithms, beginning with a Settlement Simulation, which couples consumers to productive surface area within a cellular automata type computational model. Based on precedent research, this relationship forms the basis for meeting urban and productive metrics while exploring emergent patterns in the distribution of dwellings and agriculture within a given territory.
Through topological analysis and interpretation of the simulation output, we explore the hierarchical components for a new Productive City. These patterns and resulting networks inform:
• the structure and programming of the urban circulatory network
• an emergent morphological organisation based around productive urban blocks
• opportunities for new architectural typologies
The resulting prototypical Productive City questions the underlying mechanisms that shape modern urban space and shows how agricultural production can also serve a social role, in the reintroduction of public space into the city.
We see our research as a small step in demonstrating the architectural potential of mathematical modelling and simulation in addressing complex urban spatial and programmatic challenges facing future generations.
Urban Ecologies & Agriculture, Metabolism of Cities, Food Systems, Simulation & Algorithmic/ Procedural Design Methods
AC knowl E dg E m E n TS
We are deeply indebted to Mike and George, under whose guidance the ideas in this book were born and encouraged to take form.
We also thank Wolf, Toni & Suryansh for hours of discussion and strengthening of the work.
And of course, thank you to Nikoletta for continuing to help us advance the project, even after her phase was complete.
Jeroen dedicates this work to his Mom. Thanks to Filiz for her wonderful support, to Dad and his family (Cesar & Sebastian included) and all the EmTech friends for their contributions and the wonderful time in and outside of the AA.
Darrick is deeply grateful to his parents and sisters for their faith and support, his wife Betsy for steering the ship while on this adventure, and his daughters, Berrit & Astrid, for forgiving him for the story-times missed.
Cities & Food: seleCted dAtA & stAtistiCs
World population 2010: 6,908.7 million.
Projected population 2050: 9,150.0 million.
Average growth rate: 1.2%, of which in more developed countries: 0.3% and in the least: 2.3%.
Percentage of the world's population living in cities in 2010: approx 50%.
Percentage by which the world's urban population is expected to increase by 2050: 200%
For the more developed countries 75% of the people live in urban areas with a growth rate of 1.9% (between 2005 and 2010). 29% of the population of the least developed countries are urban, with a growth rate of 4.0%.
Total fertility rate for the world in 2010: 2.52%.
For least developed countries: 4.23% and for more developed countries: 1.65%.
(All numbers from UNFPA, 2010)
Population Density of some European and North American Cities:
Paris 208 / ha
Barcelona 160 / ha
New York 106 / ha
Athens 77 / ha
London 49 / ha
Berlin 39 / ha
Amsterdam 35 / ha
Rome 21 / ha
In the US, 87 calories of fuel are typically expended to transport one calorie of food. (Burke; in: White, 2010).
17% of the US national energy use is expended in agricultural sector, but only a fifth of that is growing and harvesting, the rest is transport, packaging + storage.
In 2007 the average farm size in US - 449 acres (182 Hectares).
75% of UK produced strawberries are of a single variety, Elsanta. Not because they taste particularly good, but because of good characteristics while being transported and a long shelf life. (Paxton; in: Viljoen, 2005. CPULs)
The average item of food consumed in the US travelled 1500 miles from source to table (2414 km).
The average consumer spends 06 - 12 cents of every food dollar on transport costs. (Burke; in: White, 2010. Bracket: On Farming).
The area of land required to feed New York City is approx the size of the UK.
At the current rate of growth, we will need to cultivate a new land area the size of Brazil to feed the world’s population.
In 1968 already for every joule of energy provided by eating food, 5 joules were needed to produce that food. (Leach, 1976. Energy and Food Production)
The Ecological Footprint of a typical US citizen in 2007 was 8,0 hA per capita. This includes 1.08 hA for cropland and 5.57 hA for dissolving the carbon dioxide again. (Ewing, 2010. The Ecological Footprint Atlas 2010)
This carbon footprint can be reduced by 28.8% (1.60 hA) when food is produced organically, consumed locally and eaten when in season. (Stanley, 2007. Sustainability in practice)

Average worldwide internet search traffic (top) and news reference volume (bottom) for the term "urban agriculture" for the period 2004-2011, by Google Trends.




Food Crisis
As urban sprawl continues to weave a lowdensity ex-urban condition between the cities of the world's mega-regions, agricultural production is driven further from urban consumers while claiming more and more of our forests and natural habitats. Food is produced in distant lands using cheap labour and imported using relatively cheap fossil fuels. This increased separation of urban populations from their food sources has had considerable social, environmental and economic ramifications which, until recent times, have been overlooked as the economies of the current food system continued to produce increasing convenience and lower prices.
S o C i A l Eff ECTS
This estrangement is unprecedented in biological and ecological systems and the consequences of the global predominance of such system are beginning to become clear. The world's population marked a turning point recently with over half of the world’s population living in cities for the first time in our history.1 Over 3 billion people are now urbanites, many of whom leave behind generations of knowledge of growing and gathering food, relying instead on an anonymous supply of food managed by commercial interests. This growing alienation from where our food comes from and how it is produced is arguably a root cause for the rise in many dietary linked health problems, as many urbanites consider food as little more than a necessary fuel, disregarding its sources, means of production and quality.
Envi R onm E n TA l E ff ECTS
The increased production requirements to feed this population are taxing our available land resources. The UN estimates that by 2050 the population of the world’s cities will have doubled, requiring a land area the size of
Brazil to feed these new urbanites. Not only are we running out of land to grow on, but the remaining vegetation that is being cleared for agriculture would be our primary defence against the accumulation of greenhouse gases. As urban regions grow to accommodate the influx of people, their food will be grown on our currently undeveloped and unprotected regions. Already “an estimated 1.7 million hectares of Amazonian rainforest are lost to farmland every year”2 contributing to our inability to manage carbon levels and slow the rate of climate change.
E Conomi C E ff ECTS
Worldwide food riots in 2007-2008, and the more recent uprisings in Northern Africa in 2011, foreshadow that the system is perilously close to a tipping point as well. Relying on fossil fuels for storage, transport, fertilizer, pesticides and industrial processes, food prices spiked recently as the world approaches (or has already surpassed) peak oil3. The UN forecasts that food prices will continue to rise by 70% by 2050, attributing rising energy prices and climate change among the key factors4 .
1. UNFPA, 2010. The State of world population 2010.
2.
Countries with food riots in 2007-2008 (indicated in red), FAO.
3. OECD, 2011. OECDFAO Agricultural Outlook 2011-2020.
4. OECD, 2011. OECDFAO Agricultural Outlook 2011-2020.


1960 to 2000, World market prices for agricultural commodities, World Bank.
1990 to 2011, Food Price Index, OECD, September 2011
P R o P o SA l
The problems with the current food system are rooted in, as Caroline Steel suggests, "a longtime undervaluing of the economic costs of natural capital"5. As the underlying resources that enabled our current food system become scarcer we can begin to see that the founding assumptions that have led to the spatial separation of production and consumption are flawed. Taking a long-term view paves the way for a reexamination of this model. While historically, moving agriculture to the bounds of available transport seemed inevitable in light of urban land values, when viewed through the lens of the coming crisis these economic assumptions can no longer be considered a given.
We are proposing a systems-based model for urban growth which considers food as an integral part of the energy infrastructure. In contrast to the current urban model where food is an input and waste is an output, ours is an integrated approach considering the urban region as an ecological system with the potential for a closed loop of energy, nutrient and waste cycles. There is a long history of agriculture benefitting from the waste of the pre-industrialized city and while some research has begun into modern techniques our primary focus is on the spatial organization of such a system.
In the development of our system, we consider the agricultural and the urban as an extensible system of cellular units which organize themselves into an interdependent network of ‘production cells’ and ‘consumer cells’. The model takes local conditions as inputs, tailoring the output to accommodate for the varying land use requirements within urban, suburban and
ex-urban contexts. At the macro scale, the result is a gradient of production intensities, allowing for a heterogeneous distribution of productive surfaces and built densities, able to meet a variety of productive and urban metrics.
We explore, in the interaction of these spatially competing but functionally interdependent programmes, opportunities for new urban spaces and typologies which address the competing demands for urban land as well as the large amounts of surface area required to feed urban populations.
Local production of food will result in significant reductions in transport costs and environmental impacts and benefits from the overlaps in energy-waste cycles. The resulting new urban spaces will reacquaint urban consumers with their food sources, providing new opportunities for work and recreation.
We see the potential of our work in the development of new kinds of procedural/ algorithmic design tools for planning our future cities. The ability of our system to generate a variety of solutions (in the form of urban morphologies) in response to the given inputs is key to the successful future implementation.

dOmain: CitiEs, fOOd & COmPutatiOn
Cities And FArms - A VerY BrieF HistorY oF Food And its eFFeCt on PAtterns oF HumAn settlement
In our polarized society which insists on positing ‘city’ as separate and opposite to ‘country’, it may be difficult for many to imagine that the emergence of cities was enabled, sustained and even necessitated by the invention of agriculture. In fact, several of the features we still consider characteristic of urban settlement appeared early on in an effort to manage the flows of agricultural output for the collective.
It is believed that around ten thousand years ago, the organized management of seeds from wild grasses in the fertile crescent gave humans the security to begin settling permanently. Prior to this, humans were nomadic hunter-gatherers, constantly on the move following their food sources. By 3500BC in Sumeria we see several new ‘urban’ innovations aimed at facilitating agricultural productivity, including: a city administration and writing system for keeping records and managing agricultural lands, and the first public infrastructure projects, undertaken in an effort to take advantage of the flooding of the Tigris and Euphrates for irrigation.6
As settlements grew larger and more sophisticated, the complexity of the systems needed to feed them increased. Like the Sumerians 3000 years earlier, Greek and Roman settlements were surrounded by agricultural suburbs, which were seen as continuous extensions of their cities. However in the GrecoRoman systems we begin to recognize new land use economics arising. Rich landowners on the outskirts of the Greek ‘polis’ produced oil and wine, while around Rome, the ‘ager,’ described as ‘an endless sprawl of commercial farms’7, produced fruits and vegetables, all highcost luxury items at the time. The staples that actually fed the citizens were imported from abroad, leading to the establishment of large militaries and expansionist empires.
A thousand years later, the cities of preindustrial Europe were still organized by a similar land use model which was described
in more detail by Johann von Thünen in “The Isolated State.” Von Thunen posited that the market value of land together with the price of agricultural commodities and cost of transport, leads to a general spatial distribution of a land uses around a city. The Thunen model is a series of concentric rings, with the city in the middle followed by 1.) dairy and market gardens 2.) wooded area for fuel, 3.) grains, 4.) grazing land for livestock and finally 5.) wilderness where agriculture is no longer profitable due to distance to market.
Until the railroads, the size, location and organization of cities was limited by food transportation logistics - the distances and means by which food could affordably and safely travel. Fish and grain went by boat. Livestock walked into town. Fruits and vegetables were grown in or as close to the city as possible to take advantage of waste from city dwellers, and to avoid damaging the produce during transport. London bears witness to this history in its many neighbourhoods and streets shaped and named after the roles they filled when food filled the public life of a city.8
Once the railroad was introduced, cities were liberated from the limits of traditional transport. With the ability to move products from much further afar, the agricultural belts which once bounded cities was released and urban populations and geographical area exploded. The automobile again served to dramatically decentralize our cities and privatize the spaces where we bought our food, further isolating the consumer from food producers.





The earliest known cities evolved around 3500 BC in Mesopotamia / Sumeria and helped facilitate the management of agricultural lands.
Many Roman landholders operated suburban farms in the 'Ager'
Evidence of food flows into and throughout the preindustrial city remain embedded in the built forms and networks of the modern city
Thünen’s model of land use in the preindustrial city: the black dot = a city; 1 (white) dairy and market gardening; 2 (green) forest for fuel; 3 (yellow) grains and field crops; 4 (red) ranching; the outer, dark green area represents wilderness where agriculture is not profitable;
Johann Heinrich von Thünen , The Isolated State (1826)
10. Waldheim, C., 2010. Notes Toward a History of Agrarian Urbanism.
20tH CenturY reACtions to industriAlizAtion: Visions For An AgrAriAn urBAnism
At the turn of the 20th century critics of the modern industrial city began to conceptualize new models for growth which, as Charles Waldheim observes “proposed... a radical decentralization and dissolution of the urban figure into a productive landscape... render[ing] the classical distinction between city and countryside irrelevant.”9
gAR d E n Ci T i ES of To- m o RR ow
Ebenezer Howard’s Garden City concept was a socialist utopia comprising of a collection of interconnected city-states. Each city-state would be 6000 acres (2430 ha), only 1000 acres (400 ha) of which would be built, leaving the rest to be cultivated. All lands were owned by the collective with profits going back to the community. The communities would be connected via rail. Citizens would have the advantages of urban living (albeit more on the scale of 30,000 person towns) while never being far from the country.
In Howard’s original scheme the towns would be built compactly, with densities comparable to London at the time (200 ppl/ha), however, as Caroline Steel points out, his ideas were grossly misinterpreted and in implementation, it was widely viewed as a justification for suburban sprawl.
B R oA dACRE Ci T y / uS oni A
9. Waldheim, C., 2010. Notes Toward a History of Agrarian Urbanism.
Like Howard’s Garden Cities, Frank Lloyd Wright’s Broadacre City was widely considered his critique of urbanization in his country as well as a direct refutation of his contemporary Corbusier’s Ville Contemporaine. Wright proposed "an indigenous organic model for North American settlement across an essentially boundless plain of cultivated landscape."10
Each resident had a full acre to live and garden on. Retail, civic centers, factories, etc... were
scattered throughout this vast decentralized landscape and all of it was accessed via the automobile and highway.
Th E nE w R E gion A l PATTER n / Th E nE w Ci T y
Ludwig Hilberseimer's urbanism model, like Wright's was a low-density horizontal regional system composed of settlement units, connected by a highway system.
Unlike Broadacre however, The New City's form was in large part, a response to the natural environment, being informed by topography, hydrology, vegetation, and wind patterns and could be considered an early attempt at an ecologically informed urbanism. However once again we see a decentralized response to the highly compact industrial city of the day.
Con C lu S ion S
There was a political, moral and social implication common to each of these proposals which was a reaction to the runaway growth and density brought on by the industrialization of the times. Howard, Wright and Hilberseimer took as their starting point that the new tendency toward decentralization, afforded by the automobile and railroad, was both inevitable and good for its inhabitants.
In contrast today, the realities of global population growth and a new understanding of the limits on the carrying capacity of our planet, demand we reconsider the role of density in planning for a new agrarian urbanism.






ContemPorArY ProPosAls: CentrAlisAtion, meCHAnisAtion & Food FACtories
As it is becoming widely understood that the boundaries of our current food systems are being reached, we see multiple proposals from different fields of expertise to deal with the topic. From architecture firms to greenhouse technologists try to find an answer for the future.
Pig Ci T y By mv R dv
MVRDV's concept for Pig City proposes to concentrate all pork farming in the Netherlands in highly productive towers. Inside these towers also space is allocated to grow all the required grain to feed the pigs and thus use waste as fertilizer for the crops. The towers reduce the land area needed for pork farming nowadays and minimize the needs for transportation and distribution.11
vERT i CA l fAR m
Dr. D Despommier, professor of environmental sciences and microbiology at Columbia University, developed a concept for vertical farms. 150 of these self sustaining towers could feed the population of New York City, and act as net producers of clean water and energy.
The circular design and glass facade allows light to penetrate as deep as possible in the building. Runoff water is collected for filtration and irrigation. The controlled interior environment could grow fruit, vegetables, grains and even fish, poultry and pigs. Waste is being treated to make it usable again as drinking water, fertilizer for crops or heat energy. Control of breed and harvesting is highly mechanized.12
Su
STA in AB l E Ci T i ES
High on the international agenda are new sustainable towns, like Masdar in Saudi-Arabia or Dongtan near Shanghai in China. For as they claim to be sustainable for the environment and as far as the current state of the global food
network is considered, one would expect that these cities need a strategy to deal with food production.
In the design stage highly productive plant factories were proposed for Dongtan. 9 hA of these advanced technological and enclosed spaces would produce the food for it's 800.000 inhabitants, while generating it's own energy needs with solar panels. Apparently the sustainability of the Dongtan stops at the city gate, because the developer decided not to incorporate the design and food production is not covered in the final built environment. All consumptive needs will be shipped into town.
Con C lu S ion
The proposals discussed here show a promising shift in attention to a discussion about the world's production-consumption model. Action is needed to keep food security at a manageable level. As we stated before it is important to remain and even increase the biodiversity of our food production, to be able to cover single failures or diseases possible somewhere in the food chain. The vertical farms by Despommier have a high level of technology and therefore will need a high amount of capital investment. The yields they are supposed to produce are very promising to introduce within the boundaries of the city. A negative aspect of the towers is that most likely they will be owned by one large company dominating the food production of the whole of New York City. In our model to preserve biodiversity we see distributed production as key. The same arguments can be applied to the Pig City model of MVRDV.






ContemPorArY ProPosAls: Continuous ProduCtiVe urBAn lAndsCAPes (CPuls)
A more promising model to introduce in small scale urban environment will be the CPUL model, mainly because it is based on a thorough research to the impacts of food production inside cities. Viljoen and Bohn propose a model for continuous productive landscape embedded in the urban context. The system should be introduced incrementally and could supply up to 25% of the fruit and vegetables required for the urban population.
The model is funded in an extensive research to the impacts of food production in history, how to implement it in the urban context and what yields could be expected. CPULs are intended to lay out a continuous open space in the urban environment, formed by a network of planted open space, linear parks or inter-connected open patches. Space is reserved for organic urban agriculture, leisure space and natural environment to absorb pollution or cool the city.
Following, the model is implemented to gradually change the urban tissue of London.13
Con C lu S ion
For as we see food as an integral part of the urban experience and the level of scale we want to explore with this new model, the CPULs will be very close to our intention. The research shows successful precedents and references like urban agriculture in Havana which we will address later on.
However, for our research as well we feel being influenced by the science of metabolism, landscape or urban ecology and the importance of mathematical simulations in the design process. In the next sections we will draw parallels between these fields of research and the development of our own model.


LeisurESCAPE, concept for CPULs, Viljoen and Bohn, 2005







urBAn metABolism & eCologiCAl FootPrint
As the urbanisation of the world increases and cities continue to grow, it is important to understand the systems for the movement of people, food, water, energy, waste and other supplies.
uRBA n mETAB oli S m
In all living forms metabolism is considered as the system that captures energy and materials from the environment, transforms it into fuels, transports it to every cell and finally disposes its waste back into the environment as nutrients for another cycle and another organism. Biological metabolism operates through surfaces and branching networks that, from the smallest to the largest species, exhibit identical mathematical parameters. Metabolism is also of importance in determining the behaviour of individuals and populations and how they act in their local environment.14
In comparison, urban metabolism has been defined as the entire input of resources and energy used by people and the built environment, and the subsequent output of wastes. As said before, in nature, waste materials are absorbed beneficially back into the local environment. Modern cities don’t do that, they tend to have a lineair rather than a circular metabolism. This needs to change, as we reach the boundaries of how much nature can take.
Em ER g E n CE of T h E C i T y
Around 5,000 years ago cities started to emerge from dispersed settlements condensing into nuclei, which amplified the flow of materials, energy and information, and increased social and cultural complexity. Climatic and ecological stresses drove populations to ecologically favourable locations, for example towards river valleys. Over time systems of cities show several collapses when growing beyond their critical size. After dispersal and reversion to simpler systems of linked
settlements, new cities emerge again, this time with a higher level of complexity.15 Cities are considered as principal engines of innovation and economic growth.
mETAB oli C SCA l E & food S u PP ly
Before the industrial revolution, the critical size of cities was largely bound by agriculture and how to control the food supplies to the city. In modern times this is largely decoupled and mostly driven by economical systems. As cities continue to grow, and the need for supplies keep increasing, scaling principles show a remarkable resemblance with biological metabolic systems.
Biology shows an extraordinary simplicity and universality in scaling key structural and dynamical processes. Across an immense range of energy and mass and in a broad spectrum of phenomena, similar behaviour is being discovered. Almost all physiological characteristics of biological organisms scale with body mass as a power law. For example metabolic rate scales with an exponent of 3/4, meaning that the metabolic rate decreases with body size. These scaling principles constrain the dynamics and geometry of distribution networks within organsims, and therefore the pace of life.
Exploring scaling relations for cities, Bettencourt poses that:
"Despite the enormous complexity and diversity of human behavior and extraordinary geographic variability, we have shown that cities belonging to the same urban system obey pervasive scaling relations with population size, characterizing rates of innovation, wealth creation, patterns of consumption and human behavior as well as properties of urban infrastructure."16
As we see, as cities grow, requirements in supplies increase sublineair. Still, cities have a large impact on the surrounding ecosystems.
LN[Walking Speed (m/s)]

LN[Mammalian Heart Rate (beats/min)]

Diagram showing relations between in and outputs in the city's food production, consumption and waste cycles.
The pace of urban life increases with population size, while pace of biological life decreases with body size.
E Cologi CA l fooTPR in T
In order to stress out the pressure city dwellers have on the environment, the ecological footprint has been developed. The calculation shows the relationship between the caloric intake of a person and the waste he produces and how much land area is needed to absorb the waste and generate new resources. It distinguishes different categories to differentiate human impact on different territories:
1. Built-up land
This is the area of land which has been physically occupied by human activities.
2. Cropland
Reflects the amount of land area required to grow all crops consumed by humans and livestock.
3. Grazing land
Reflects the land area required for grazing land to feed livestock and in traded goods.
4. Forest land
Human demand on the world's forest, used for fuel and timber.
5. Fishing grounds
Represents fisheries' demand on aquatic ecosystems.
6. Carbon footprint
The area of forest land needed to take up anthropogenic carbon dioxide emissions.
These numbers sum up to the land area needed per capita, to regenerate earth's surface. As shown in the diagram, the average Ecological Footprint of a US citizen in 2007 was 8.0 hA, where there is only 3.9 hA available within the boundaries of the USA.17
A large proportion of this number is required for the Carbon footprint (5.57 hA in the example). Research pointed out that 28.8% of the world's CO 2 output is directly related to food transport, packaging and processing18
Ecological footprint (USA, 2007) 8.0 hA per capita (200 x 400 m.)
0.07 hA Built up land vs. 1.08 hA Cropland Source: Global Footprint Network, 2010

Comparison of the Ecological Footprint of a typical American male with Bedford Square, in London.
lAndsCAPe eCologY & urBAn eCologY



As one of our goals is to create a closed loop of energy in our system, the understanding of how the spatial organisation of the landscape elements, either natural or human, effects the flows of energy in their ecosystems and vice versa was potential for the development of our system.
PATC h ES , Co RR ido RS & mATR ix
According to Richard T.T. Forman19, the basic spatial elements of any pattern on land are patches, corridors and matrix, each of them constituting an ecosystem. These elements can vary in shape, size and function.
Patch is defined as "a relatively homogeneous nonlinear area that differs from its surrounding".
Corridor as "a strip of a particular type that differs from the adjacent land on both sides".
Matrix as the background ecosystem or land-use type in a mosaic, characterized by extensive cover, high connectivity, and/or major control over dynamics.
They can be categorised according to the level of human activity into natural, semi-natural or intensive-use green-space, and built areas.
The proportion of these elements and their arrangement within a landscape informs the flows of energy, materials and species which in turn modify the patterns that were created.
Different kind of patches emerges in various proportions and sizes within landscapes having a wide range of ecological implications for productivity, biodiversity, soil and water.
CoARSE & f in E gRA in
Forman is using grain (the coarseness in texture or granularity of spatial elements composing an area) as an attribute of evaluating the different size configurations. An aggregation of large patches is defined as coarse-grain while an intermixture of different small land uses as finegrain.
Forman suggests that a coarse-grain region with some fine-grain areas is the optimum design for nature and people. Claiming that in a fine grain the negative effect of people in nature is so significant that it cannot maintain its integrity, large patches of nature are most likely to be present in the outer urban-region ring.
Con C lu S ion S
The learnings from ecology is not contributing in indicating the exact types and locations of the elements but suggests (from experiments/ observations from the relations in different configurations) the perhaps-optimum relations and proportions in order to exhibit the highest suitability for natural processes, agricultural production or the built human community.


Portland, USA urban region
London, United Kingdom urban region
Source: Forman R.T.T. (2008). Urban Regions: Ecology and Planning Beyond the city.
Major city
Metropolitan area
(continuous biult land)
Urban region
Inner satellite city
Outer satellite city
Wedge (greenspace)
Lobe (built land)
Bulge

Urban-region ring (green space mosaic with scattered buildings, villages, towns and satellite cities)
Green space composed of landscapes, large patches, small patches, major corridors, narrow corridors (cropland, forest, desert, grassland)
Suburbs
Sprawl (if present)
Nearby major city Metropolitan area Urban-region ring

Five Priorities for nature conservation illustrated with patch-corridormatrix model.
Patches and corridors are natural or seminatural vegetation and the backround matrix is less suitable land use.
AlgoritHms, simulAtion, ProCedurAl design For Cities
Several computational models developed from different disciplinary backgrounds address the concept of how a set of local rules dominates the behaviour of a system. Many of these models are used in landscape and urbanism science exploring the causes and consequences of land use dynamics.
Cellular automata, neutral models, percolation theory and geometric models are some of the simulation methods that enables the bottomup emergence of complex patterns from the interactions among proximal entities.
dl A C i T y Agg RE g AT ion S imul AT ion
Michael Batty has used computer simulation to study the larger scale patterns of cities and the mathematical relationships between scale and form resulting from the self-organizing nature of cities. The Diffuse Limited Aggregation experiments (shown right) have been able to reproduce patterns resembling urban growth using simple computation rules.
These studies have been primarily analytical in nature although we propose to develop our own algorithms which could be used in a generative ends.
STEP h E n mARS h A ll' S Ci T i ES A nd Evolu T ion
Stephen Marshall's work deals more directly with the smaller scale organization of built forms and networks within a city and attempts to understand the basic underlying processes that lead to material organizations. Again, the goals here have been to dissect and analyse, but we feel we can build upon these basic experiments to inscribe new spatial relationships necessary for food production and study their effects on urban form.
Tool S
For the development of the system we will make use of generic notebook computers running McNeel's Rhinoceros with the Grasshopper plugin. In this software we will be scripting in VB.net language. All the work shown here will be produced within this environment.





Diffuse Limited Aggregation experiments
Hierarchical neutral model produce maps that vary in the abundance and dispersion (clumping) of habitat : - Random - Slightly Clumped - Highly Clumped





Percolation in 2d square lattices with system size LL=150x150. Occupation probability p = 0:45; 0:55; 0:59; 0:65; and 0:75, respectively.
The largest cluster percolates through the lattice from top to bottom in this example when p = 0:59.
ProduCtiVe surFACe AreA reQuirements
We believe that current schemes for the implementation of urban agriculture in the United States are, while well-intended, limited in their potential performance by being retroactive and reactionary. Designers, planners and urbanites seek out under-utilized land and building surfaces within an existing urban fabric which was conceived in a post-industrial model. This model presumed that urban growth was unlimited because food will always be able to be imported from an infinite countryside via mechanized transportation methods.
Our proposal, in contrast, is based on contemporary research that suggests:
a. rural productive land is not unlimited, especially if we consider the need to preserve uncultivated forested regions for consuming carbon.
b. 'acceptable' transportation distances will be limited by the economic and environmental costs of fossil fuel use in the near future.
Confronted with this reality, cities will once again need to plan for the productive surfaces required to feed them to be within the extent of a reasonable transportation radius. We see acknowledgement of this concept in the growing ‘locavore’ movement, which suggests consumption being limited to foods produced within a 100 mile or even 30 mile radius20 . While we acknowledge the efficacy of setting such hard and fast rules may be disputed21, we propose that travel distances are considered as part of a larger system which seeks to reduce energy inputs at all points in the supply chain.
To meet this challenge we must answer the question 'how much productive area is required to feed a given population?' We will do this by looking at caloric intake for a typical North American diet, equating this to kilograms of edible biomass, then looking at yields from various precedents which may be applicable in our model.
C A lo R i C i n TA kE
The United States Food & Drug Administration puts typical US calorie consumption in the year 2000 as 3700 calories per day, 1100 calories of which are lost to spoilage, plate waste, and cooking/other losses. So consumed calories is just under 2700 calories per person per day.22
Edi B l E Biom ASS P R odu CT ion
Following on the next pages are data on yields from various agricultural techniques. In order to set out a model for productive plots within the urban context, it is important to find out how much land is needed to feed the population. To do that we will look at existing precedents on urban farming and techniques how to increase production of the agricultural plots. Scale and size of plots will be considered as an important factor in our model.
Based on research by Viljoen and Bohn23, we set a first relation between the urban household and the required productive area of 100 m2 per person. In an urban environment this will provide for the annual consumption of fruits and vegetables, which mainly because of the scale are best suitable to cultivate in urban productive areas.
E Cologi CA l fooTPR in T
Current models of food production and distribution are heavily dependent on cheap labour, fossil fuels and large scale efficiency. As we have seen they have a gigantic impact on the way we 'consume' our planet. We believe that with a new model of urban agriculture with local seasonal production a large contribution can be met to shrink our 'Ecological Footprint'24
Area of Fruits &Vegetables
Household / Annum (259sq m)





Typical New York household with 259 m2 Productive Surface required.
Examples of urban farming precedents in London, Brooklyn NYC and Havana.
Cuba, and Havana in particular, exhibit one of the most innovative and comprehensive models present nowadays supporting food production within the boundaries of its cities. The system was developed after an urgent need to improve the national food supply.
Since the early 1800’s agriculture in Cuba has been fully dominated by sugar production, being the world’s largest producer. The main trade partner was the former Soviet Union. Agriculture and food industry was almost completely dependent on imports, going up in 1989 to 100% of wheat, 90% of beans, and also 94% of fertilizers and 97% of animal feedstocks.25
After the collapse of the Soviet Union in 1989 and the severe strengthening of the US trade embargo the country suffered under an intense economical crisis. Imports reduced drastically, electricity generation was reduced, fuel and parts for maintaining the transport vehicles became scarce. The agricultural system went towards a critical disruption, with a subsequent impact on the availability on nationally produced food.
Cuba is highly urbanized, more than 75% of the 11.22 million people live in cities. These regions were hardest hit by the crisis, because it was difficult to transport the food to the consumers. Vacant lots started to be taken over to farm and this initiated a novel type of urban agriculture. Families started to cultivate patios, rooftops and empty side plots in order to feed themselves.
The government responded to support the new situation with knowledge and resources. There was a major lack of farming experience by the people, specifically about the organic techniques necessary for urban cultivation. Urban land use rights were restructured to give better access to land. The Ministry of Agriculture’s Urban Agriculture Department set up a large network of extension officers, training services and seed houses to support the farmers. In order to make it easier to distribute the produce from the farm to the consumers, the
government allowed food to be sold at farmers markets and on-site stands throughout the city. This means there were no costs for transport or storage and the food is always fresh.
Since 1990 a national alternative agricultural model has been developed that aims to replace high levels of imported agricultural inputs with alternative methods for organic use of pest and disease control, soil fertility and other innovative issues. Early in this process there was a distinctive place for scientific knowledge based development in agricultural biotechnology and biological control.
Viljoen and Bohn26 identify a number of distinct categories of agricultural plots, according to their size, location, users and yield:
1. Small urban gardens, cultivated by families size smaller then 1000 m2 yields 8 to 12 kg/m2*yr.
2. Medium size urban gardens, cultivated by families but produce for trade size between 1000 and 3000 m2 yields 8 to 12 kg/m2*yr.
3. Urban community gardens, cultivated by collectives of farmers. size between 1000 and 3000 m2 yields 20 kg/m2*yr.
4. Large state farms, voluntary cultivators size larger then 1 hA yields 0.6 kg/m2*yr.
5. Large commercial farms size larger then 1 hA yields 25 kg/m2*yr.
Specific for the situation in Havana are the high productive gardens in category 3. These ‘Organopónicos Populares’ are highly embedded in the residential areas of cities and can produce up to 30% of the caloric intake of the urban dwellers.27 Most of these plots selling the crops from the gate.



Two Examples of ‘Organopónicos Populares’ in Havana.
Sizes, configurations and management types of urban gardens and commercial farms found in Havana, Cuba (Viljoen, 2005):
1. Small urban gardens
2. Medium sized single family gardens
3. Urban community gardens
4. Large state farms
5. Large commercial farms
Burke, E., 2010. Farm Plus. in: White, M. Bracket: On Farming
Giacomelli, G., 2011. Personal interview.
A primary challenge to retrofitting existing cities with agriculture on a commercial scale has been one of space. Food production as a livelihood requires a certain scale and minimum yields, which is specific to the crop and context1.
In developing our model, we will need to ensure that adequate production area is allocated for commercial urban farmers. These productive areas will need to meet certain criteria, such as minimum continuous size, to be profitable.
In order to understand the requirements for a commercially viable small to medium sized farm in an urban region, we set out to find some working models as a reference.
With an increased consumer interest in food sources and greater awareness of industrial agriculture techniques in the US, locally grown and organic food growing has been attracting a new breed of farmer and new type of farms.
The following three farms are all located within the suburbs of major US metropolitan regions. All are between 1-10 hectares and sell direct primarily to urban consumers via farmer's markets, on-site sales, and CSA (Community Supported Agriculture) subscriptions.
SA ndhill oR g A ni CS
Greyslake, IL (Chicago suburbs)
Part of a masterplan for Prairie Crossing, a nature preserve and suburban development with 400 homes and 142 hectares (350 acres) of protected lands.
6.5 hectares (16 acres) leased to 1 farmer by the developer. Employs 3 year-round + 7 more seasonal employees.
Distribution via on-site market, city farmer's markets, and 280 CSA (Community Supported Agriculture) subscribers.
Notes:
Boundary design: topography + plantings provide physical separation of agriculture from residential; homes are raised above farm
providing views; walking trails around fields create opportunities for hybrid recreation spaces.
Sunol Ag PAR k
Sunol, CA (San Francisco suburbs) Developed by SAGE (non-profit) which has a long-term lease on a public utility easement.
7.3 hectares (18 acres) leased to 6 farmers; each leases from 0.8-2.8 hectare (2-7 acre) plots, separated by rows of sunflowers.
Distribution via local farmer's markets, and subscriptions by area families.
Notes:
This model, an area subdivided into smaller parcels, is good for farms near urban areas which are typically smaller scale, start-up farmers allowing them to start on smaller plots, sharing resources with neighbouring tenants farmers. Basic infrastructure is provided for, including irrigation, deer fencing, and a small shared office. Also serves as a recreational park.
A
PP l ETon fAR m
S CSA
Ipswich, MA (Boston metro region)
Part of land trust, totalling 283 hectares (700 acres) of primarily recreational land.
10 hectares (25 acres) Trust runs farm, employing farmers directly.
Distribution via CSA subscriber pick-ups at onsite market and pick-your-own. Supplies to 530 families (fully-subscribed). Self-sufficient after 4 yrs.
Notes:
On-site pickups and pick-your-own encourage strong links with public.








6.5 hectares leased to single farmer
7.3 hectares leased to 6 farmers (0.8-2.8 ha ea.)
10 hectares operated as single farm by land trust
Sandhill Organics
6.5 hectares leased to single farmer sells to subscribers at on-site market and city farmers' markets
Sunol Ag Park
7.3 hectares leased to 6 farmers (0.8-2.8 ha ea.)
Appleton Farms
10 hectares single farm operated by land trust sells direct to subscribers
PreCedent: greenHouses & HigHer Yields
g REE nhou SES
Greenhouses create a controlled interior climate by enclosing a productive area with glass. The growing season is being stretched, up to year round production, providing higher yields then possible on open-air plots. The Netherlands show some of the world largest commercial farms and a large amount of related research is carried out by Wageningen University.
Important factors in regulating the climate and therefore increasing the production numbers is the control of temperature, irrigation and the CO 2 concentration. During summer interior temperature easily gets too hot and cooling needs to take place. Traditionally this was done by opening the windows in the roof but as nowadays the interior concentration of CO2 is artificially increased and highly controlled, this can cause a loss of up to 85%28 of the CO 2 put into the system. During the night and in the winter heating the interior environment demands a lot of fossil fuel energy.
i n CREAS ing PR odu CT ion
Where regular fields show yeilds around 30 to 35 kg/m2*yr, a high quality greenhouse could produce around 70 to 80 kg/m2*yr29. Increasing the interior CO 2 concentration will make it possible to increase the yields by 120% and up to 140% compared to contemporary greenhouses. To make these techniques economical viable, the minimum area of continuous greenhouse needs to be between 1 to 2 hA.
Different techniques already exist to increase the concentration of CO 2 and others are being researched, specifically different ways to retrieve CO 2 from biomass:
1. Natural digestion
Leaving organic waste material inside the greenhouse to digest in a natural way
2. Composting
Add composted matter to the soil to naturally release CO2
3. Fermentation
By means of water purification and fertilizer fermentation waste processes can be utilized.
4. Combustion
By combustion of biomass the exhaust fumes can be caught to supply a higher CO2 concentration.
5. Pyrolysis
A low-oxygen heating process where CO2 is being produced on a molecular level. This process needs further development, but show some promising results to implement on smaller scale and to combine with urban waste cycles.
6. Other large scale techniques
Derive CO 2 from power plants or industries is a means of receiving high amounts of CO 2 emissions, but not suitable for our purpose, for as the aim is to apply the greenhouses on a small urban scale.
h yd R o P oni C TEC hniqu ES
Another possibility to increase yields is the use of hydroponic technologies to produce crops. Instead of regular soil, hydroponics utilizes nutrient solutions for growing plants, with or without the use of an artificial medium to provide mechanical support.
The technology is highly productive, requires less use of water and land, and protective for the environment. Combined with greenhouses, it asks for high end technology and intensive capital investments. Since regulating the aerial and root environment is a major concern in such agricultural systems, production takes place inside enclosures designed to control air and root temperatures, light, water, plant nutrition, and adverse climate.30




Typical large scale greenhouses in Westland, the Netherlands.
Highly technological Hydroponic farm system
31. Patterson, R and Giacomelli, G., 2008. Resource and Production Model for the South Pole Food Growth Chamber.
32. Sadler, P., Giacomelli, G. et al., 2009
Prototype BLSS Lunar Greenhouse
33. Numbers derived from: Giacomelli, G., 2011. Personal interview.




Sou T h Pol E Ch A m
BER
Research by Gene Giacomelli, combined with the University of Arizona and NASA, has been carried out to develop production facilities for extreme climates like on the moon and Antarctica.31 32
In one of the most extreme and remote environments fresh vegetables are grown in the 'South Pole Food Growth Chamber', to support the crew of the NASA South Pole Station during their annual eight-month period of isolation. Semi-automated hydroponic technology and extensive data monitoring is utilized to grow multiple salad crops. Current production numbers are around 50 kg/m2*yr with everyday production during the eight month stay, but can be improved significantly to reach numbers comparable to greenhouse technology.33
lun AR gREE nhou SE
Another research by Giacomelli is the Lunar Greenhouse study. It demonstrates a closed system for maximum biomass generation, food production within a poly-culture cropping system, water recycling and revitalization of interior atmosphere. It is designed to produce all of the fruit and vegetables needed by a crew member on 28 to 40 m2 crop production. This would generate 50% of the caloric intake required. The design is furter adapted to meet the requirements of NASA and to be able to be sent to the lunar surface.
Small urban gardens Less than 1000 m2
Medium size urban gardens
Urban community gardens
Between 1000 and 3000 m2
Between 2000 and 5000 m2
Urban or periurban
Urban or periurban
Vacant urban sites, cultivation in containers of imported soil
One person or familyTo supply cultivator or family 8 - 12 kg/ m2*yr Havana, Cuba
Family or small cooperative
Collectives of farmers, with institutional technical support and advice
Large state farms Larger then 1 hAPeri-urbanVoluntary cultivation by workers
High yield commercial farms Larger then 1 hAGoverment alloted vacant urban sites
Commercial suburban farms
Commercial suburban farms
6.5 hectaresGreyslake, IL (Chicago suburbs)
7.3 hectaresSunol, CA (San Francisco suburbs)
Commercial suburban farms 10 hectaresIpswich, MA (Boston metro region)
GreenhousesTypical larger then 2 hA
Greenhouses with high CO2 Typical larger then 2 hA
Westland, the Netherlands
Westland, the Netherlands
Commercially viable work centres or cooperatives
Farms are leased to a single farmer
Leased to 6 farmers (0.8 - 2.8 hA each)
Feed producers and for trade 8 - 12 kg/ m2*yr Havana, Cuba
Produce for trade and small-scale consumption by producers 20 kg/m2*yrHavana, Cuba
Feed state workers and institutions 0.6 kg/m2*yrHavana, Cuba
Produce for sale25 kg/m2*yrHavana, Cuba
Sells to subscribers at on-site market and city farmers' markets 8 - 12 kg/ m2*yr (app.) Sandhill Organics
Distribution via local farmer's markets, and subscriptions by area families 8 - 12 kg/ m2*yr (app.) Sunol Ag Park
Single farm operated by land trust
Commercial highly industrialized farms
Commercial highly industrialized farms
HydroponicsCan be grown on small scale Not climate dependent Most likely commercial, as capital investment is high.
South Pole Chamber 22 m2
Lunar Greenhouse
NASA South Pole Station
28 - 40 m2 Moon NASA
Sells direct to subscribers Growing produce for 530 families Appleton Farms
Produce for sale70 - 80 kg/ m2*yr Giacomelli, 2011
Produce for sale80 - 110 kg/ m2*yr Vermeulen, 2010
Primarily produce for sale up to 75 kg/ m2*yr Giacomelli, Jensen, 1997
kg/m2*yrPatterson, 2008
2009
and the pace of life in cities.
QuAntiFYing sPAtiAl CHArACteristiCs oF A CitY
(or wHAt we meAn wHen we tAlK ABout ‘urBAn’)
In presentations and discussions, we’ve found that the suggestion that cities could and should grow their own food within their boundaries raises strong reactions. It seems what is feared might be lost is the notion of ‘urbanity.’
Of prime concern for us is that our system produces aggregations of human settlement that could be characterized as urban.
We recognize the social, economic and environmental benefits of a rapidly urbanizing world and ‘cities as principal engines of innovation and economic growth’.34
So, while we will provide opportunities for urbanites who would prefer to keep a garden, we are not proposing a return to agrarian society.
Therefore it was critical that we identify what we believe are the key qualities of urbanity and extract techniques for quantitative evaluations fo these. These will serve as fitness criteria for evaluating our generated tissues.
dE n S i T y
Population Density will be a key metric used in the generation of our new urban tissue. Therefore we need to:
a. determine what is the appropriate range of population densities for a new productive urban morphology and then
b. ensure that we can meet various targets within that range while still accommodating for the productive surface area required.
The following are population densities for some European and North American cities widely regarded as archetypal of Western urbanism:
Paris 208 ppl / ha
Barcelona
New York
London
160 ppl / ha
106 ppl / ha
50 ppl / ha
Amsterdam 35 ppl / ha
One approach might be to use these numbers as a reference for wwgenerating tissues of similar character. However these numbers are misleading for two reasons.
First, measuring density is highly dependant on sample size. So although the density of New York City is 106 ppl/ha, that number is largely meaningless as it is the gross density for all five boroughs. When one thinks of New York, they likely have an image of Manhattan in mind. If you were to take a density measure for Manhattan, you would find something closer to 280 ppl / ha, already higher than Paris or any other city on our list. However this still is not the whole story. The population density of the Upper East Side is 552 ppl/ha and if you were to take a measure of a few blocks on the Upper East Side, you'd get a density measure of over 1000 ppl/ha. With each zoom level, we get a more accurate measure of a specific urban morphology. In contrast, the larger the sample, the more 'averaged' it is and therefore, less descriptive of any particular place.
The second problem is in relating population density to a perceived spatial experience. In practice, two largely similar urban spaces can have radically different population densities depending on household size and dwelling area, which are both cultural and income related. However since our productive plots will be population dependant, we will need to make some assumptions about household size and dwelling size for the given area.
Berghauser Pont and Haupt35 suggest that a multi-variable approach is necessary in order to use density meaningfully as a way of describing urban form. In their book Space Matrix, they identify three descriptors of urban space:
1. 'Building Intensity’ (FSI) or FAR
2. ‘Coverage’ (GSI) and
3. ‘Network Density’ (N)








STok E n E wingTon - london
(D) London: 50 ppl / hA
(D) Stoke Newington: 142 ppl / hA
FAR: 0.64
Coverage: 0.33
OSR: 1.06
Source: 2001 Census, Office for National Statistics.
B R ooklyn hE igh TS - nyC
(D) New York City: 106 ppl / hA
(D) Brooklyn Heights: 205 ppl / hA
FAR: 2.0
Coverage: 0.53
OSR: 0.38
Source: New York City Department of City Planning
dE P ij P - A m STER dA m
(D) Amsterdam: 35 ppl / hA
(D) De Pijp: 216 ppl / hA
FAR: 1.78
Coverage: 0.47
OSR: 0.30
Source: Berghauser Pont, M. and Haupt, P. (2010). SpaceMatrix Space, Density and Urban Form.
g RAC i A - B ARCE lon A
(D) Barcelona: 160 ppl / hA (D) Gracia: 287 ppl / hA
FAR: 1.92
Coverage: 0.57
OSR: 0.22
Source: Berghauser Pont, M. and Haupt, P. (2010). SpaceMatrix Space, Density and Urban Form.
PATTERN
The path systems of early humans
Generalised graphic representation of a port town's hinterlands' development, making use of an imagined situation.
Source: Otto F. (2009).







HIERARCHY
Historic and modern settlement structures.
(a) The market square in the centre, the intensity of circulation dissipates outward from this core.
(b) The main flows and highest standard routes on the national network outside the town.
Dunbar in 1830. The high street is the widest street and the most significant urban space.
(a) Traditional arterial street combining traffic movement and frontage access. (b) Distributor road - dedicated to traffic movement. (c) Access road - combines traffic and pedestrian movement with access to buildings.
Source: Marshall S. (2005)





Cov ERAg E & oPE n S PACE
For our purposes Coverage and Open Space Ratio will be used to describe the building intensity and amount of open space relative to the given floor area.
Coverage describes the amount of land area built-up compared to unbuilt. While OSR can be described as "the amount of non-built space at ground level per square meter of gross floor area... this figure provides an indication of the pressure on non-built space."36
As a value to compare different tissues and to relate the simulations to existing built environment Open Space Ratio can be defined as:
OSR = (1 - C) / FAR. where:
Coverage (C) = Foot print / Sample Area
Floor Area Ratio (FAR) = Gross Floor Area / Sample Area.
Therefore a high OSR means a relatively open urban experience (Stoke Newington, London has a OSR = 1.06) relative to the amount of built up area and a low value talks about a highly densified environment (Gracia, Barcelona shows a OSR = 0.22).
nET wo R kS
Another key component of how one experiences the city is the network of public spaces that connects it. We've determined two characteristics of the network which will be addressed: pattern formed, and hierarchy.
nET wo R k PATTER n
In his book Occupying and Connecting Frei Otto's explains how path networks were formed in early human occupations. He proposes that path layouts were driven by function and scale and identifies three main types.
1. At the regional scale, searches for food resulted in the generation of direct minimal routes by which destinations were reached with the least effort and minimal detours.
2. Within a settlement on the other hand, the primacy of the need for settler communication resulted in more redundancy with a higher density of paths and connections, the formation of closed loops and an allowance for larger detours.
3. Meanwhile the links between neighbouring settlements were achieved by paths of optimum length.
37
In all of these cases a branching pattern can be found in which the toleration of detours and energy expended travelling is balanced with the overall network length. A hybrid between the two criteria is considered a minimized detour network which blends direct connections with minimal paths.
nET wo R k hi ERARC hy
The focal point of these early human occupations was typically a food or the water source. As the population of settlements increased, the focal point converted into a market square with urban activities taking place on the streets around it. Traditionally the intensity of "circulation dissipated outward from this core." In this way, the market square served as an attractor for more settlers.
In contrast, modernist urban layouts proposed road systems optimised for traffic circulation, breaking down the relationship between movement and urban place-making. The main streets were converted into high traffic routes distributing urban activities around the periphery.
36. Berghauser Pont, M. and Haupt, P. (2010). SpaceMatrix Space, Density and Urban Form.
37. Otto F. (2009). Occupying and Connecting.
sYstem dYnAmiCs modeling
SySTE m dyn A mi CS
In nature many self regulating systems are found, including local or global ecosystems and population learning processes. Systems dynamics is a method to understand the dynamic behaviour of these complex systems over time.
Some characteristics of system dynamics are:
1. Fundamental to the method is the recognition that the structure of any system is often just as important in determining its behaviour as the individual components themselves. Many circular, interlocking and time-delayed relationships among its components build up a complex system, and therefore the behaviour of the whole cannot be explained in terms of the behaviour of the parts.
2. All systems, whether electrical, biological or social, have common patterns, behaviours and properties that can be understood and used to develop greater insight into the behaviour of complex phenomena and to move closer toward a unity of science.
m od E l l ing A nd S imul AT ion
The real power of system dynamics is utilised through mathematical simulation. These models are based on:
1. Stocks and Flows
A stock is an entity that accumulates or depletes over time. A flow is a rate of change in a stock.
2. Feedback loops
Feedback loops inform stocks or flows about how much they will be reinforced by different actions in the system.
3. Equations
Mathematical equations determine the size of flows, dependent on constant parameters, feedback loops, and time steps.
While running the simulations the behaviour of the system over time can be observed and analysed. An example of a simple model could be a predator-prey system where the population of prey will feed the predators, but when the prey starts to die out, this will decrease the population of the predators until a stable point where it will grow again. The model will show a cyclic diagram of growing and shrinking populations.
Applied to our system, we could model an urban simulation where internal or external food production influences the use of energy and resources required to produce. Benefits can be measured for the combination of production and consumption within the boundaries of the city.
Con C lu S ion
While the potential application of system dynamics modelling software like Stella as an evaluation tool is promising, we propose to further develop this Stella model in the MArch phase of our research, focusing for this phase on a Rhino/Grasshopper/VB.Net script which has more generative potential.
System Dynamics Model in software Stella.
1. Graphical representation of simulation model
2. Model behaviour over time: While increasing internal (1) and decreasing external production (2), Total city waste (3) will decrease and use of Reusable energy (4) will grow.
Diagram showing relations between in- and outputs in the city's food production, consumption and waste cycles.
CITY
FOOD: INTERNAL PRODUCTION
AGRICULTURAL WASTE > URBAN: HEAT SERVES THE CITY LESS TRANSPORT DECREASES CO2 PRODUCTION METHANE GAS USED AS FUEL
CITY CONSUMPTION
FOOD: EXTERNAL PRODUCTION WASTE:
>
rEsEarCh
initial ExPErimEnts
CouPling dwellings And ProduCtiVe surFACe
ov ERvi E w
In order to start coupling dwellings to the productive surface required we first need to establish the relationship between them. How much is the caloric intake of a person and how much land does it take to support him? What do we expect to grow in cities and how much of this problem can we expect to address?
Rul ES
From data concerning typical households in New York City we derived that the average size of a town house apartment is 72 m2, which is inhabited by 2.59 persons in average.
Taking the caloric consumption of a US citizen as a reference and considered that we can grow fruit and vegetables on productive plots within the urban context, the land area needed to feed a person is set to 100 m2.
This would provide enough land to grow all the fruit and vegetables needed in the average diet. Looking at previous research and precedents on urban farming, it seems that fruit and vegetables are excellent crops to introduce within the urban tissue. They can be grown in fairly small amounts, whereas grains, cereals and livestock need much larger continuous landscape (multiple hectares connected) to become economically viable.
Ex PER im E n TS
With these numbers considered, next we will develop some small experiments to understand the relationships between them and start to establish some geometrical implications of this data.
The learnings and conclusions of the excersices will lead us to develop the organisational algorithm to couple consumers to producers again.

Area of Fruits &Vegetables
The first experiment aims to investigate the effect of the horizontal mode of development versus the vertical on the population density and the required surface area.
Com P u TAT ion A l Rul ES
The experiment begins with one dwelling of 72m2 (6m x 12m) and the required ‘farmed’ area of 259m2 attached to it. The number of units can be increased by rising the number of dwellings either in X-axis, leading to a horizontal expansion or in Z-axis enabling a vertical growth. The surface area of cultivated land is increasing respectively to the number of dwellings added.
PARA m ETERS
(Nx) Number of Dwellings in X-axis (horizontal)
(Nz) Number of Dwellings in Z-axis (vertical)
(PI) Production Intensity: 1 person = 100m2
(Dw) Dwelling/Household size: 72 m2 = 2.59 persons
q uA li T i ES mEAS u RE d
(Dp) Population Density: Number of people to the surface area.
Con C lu S ion S
We observed that the density remains stable when we rise the number of dwellings horizontally and it increases when we alter the vertical expansion. It seems to be obvious that the vertical mode of development will increase the density, nevertheless, because for every added dwelling there is an additional need of 259 m2 of productive land, there is a critical point, which lies around 5 to 6 storeys, after which the increase in density trades off. HorizontAl



PAtH lengtH: distriButed Vs VertiCAl growtH
ov ERvi E w
This experiment examines the travel distance involved to gather your food if you distribute the same number of housing units over the required surface area by breaking them from a single vertical tower into multiple shorter ones.
Com P u TAT ion A l Rul ES
The experiment begins with a number of dwelling units (Nd) stacked in a multi-storey tower and the ‘farmed’ area attached to it. The tower is then broken into multiple shorter towers spread around the perimeter of the surface, while keeping the number of units the same.
PARA m ETERS
(Nd) Number of Dwellings units
(Q) Quantity of Towers
(PI) Production Intensity: 1 person = 100m2
(Dw) Dwelling/Household size: 72 m2 = 2.59 persons
q uA li T i ES mEAS u RE d
(A) Average Path Length (m.)
Con C luSion S
While increasing the quantity of towers, the average path length between the urban units and the agricultural plots is decreasing. The graph shows that after a certain point the benefits to spread out trail off and there is no significant difference in average path length. Reason for this is that the distribution reaches a state where there is a horizontal organization of units, without the spatial benefits of stacking floors.








mAximizing ProduCtiVe
ov ERvi E w
Here we start to manipulate the surface in order to provide more growing area for crops, on a constant land area.
The surface will be divided into growing strips with a critical width, derived from planting beds utilized in precedents, and oriented towards the sun. These strips are elevated, where the sun angle will determine how far the beds can be extended.
Com P u TAT ion A l Rul ES
The experiment starts with a planting depth (L) divided in (P) number of segments. The segments of planting beds are elevated by increasing the height between them. Then the individual segments are extended until the point where the sun ray reaches.
PARA m ETERS
(P) Number of Segments that we divide the field
(L) Inital planting depth (m.)
(A) Sun angle
(E) Elevation per segment (m.)
q uA li T i ES mEAS u RE d
(Dp) Total Depth of planting beds (m.)
Con C lu S ion S
Starting from a single plane with an initial planting depth of 30m., the depth increases to 47m. when elevated to a segment height of 3m. As can be expected the increase in surface will be linear with the height. Other factors will then be restrictive to what is possible. For example one can think of adjacencies in the urban tissue, or how to reach the elevated plots.

AggregAtion
ov ERvi E w
The aggregation logic showed on this page is based on the adjacency of two land uses (one urban and one productive). Local agent rules and a time sequential logic determine the outcome how these individuals will aggregate and show different possible patterns.
Com P u TAT ion A l Rul ES
As a start the dwelling is tied with three plots of productive land connected linearly. When the next dwelling aggregates it will try to connect with another dwelling either in a perpendicular or in a parallel way, choosing randomly. To ensure that the required agricultural area is available in the aggregation, the plots should never intersect with previously aggregated cells.
PARA m ETERS
(Dw) Dwelling/Household size: 72m2 = 2.59 persons
(PI) Production Intensity: 1person = 100m2 (Ct) Connection Type
Con C luSion S
Within this simple set up defined by local aggregation rules some interesting patterns are emerging and a first sense of settlements can be detected.
When only one particular connection is chosen, different separated zones of urban and productive land emerge where growth is strongly directed.
When chosen randomly, more compact and complex patterns grow over time, with small scale aggregations of urban tissue.




i ni T i A l Ex PER im E n TS RE vi E w: EvA luAT ion & Con C lu S ion S
The experiments presented in this section gave us an understanding of the relationships and geometrical implications of certain formal rules. We set targets for size of dwelling units and productive area required to feed these people. We found relationships between density, floor heights and required surface area to produce the fruit and vegetables to feed the population. The first geometrical tests were carried out to increase the productivity of a plot by altering the geometrical properties. With the results of these exercises we proceed and start to construct an algorithmic logic to organise the consumptive and productive landscapes.
The last aggregation shown on the left page, will form the starting point for the further development of the organisational system into a model informed by local rules and adjacencies. With the input values established and the results of the experiments in mind, the next section will focus on the application of the system on a neighbourhood scale, while simulating the aggregation patterns emerging.
systEm dEvElOPmEnt:
i. settlement simulAtion ii. networK toPologies
iii. reView & FurtHer worK
SETTLEMENT SIMULATION
COUPLING DWELLINGS & FARMS
PRODUCTION INTENSITY & DENSITY
NETWORK TOPOLOGIES
IDENTIFY CLUSTERS PLACE DISTRIBUTION NODES
FARMS DWELLINGS WHOLESALE RETAIL
NETWORK REINFORMS SETTLEMENT
ROUTE HEIRARCHY
PATHS CONNECT NODES
FOOD DISTR.
SOCIAL
BUILT FORMS ATTRACT TO NETWORK
m.ArCH. PHAse
SEASONAL/ CLIMATE VARIATIONS
WATER & WASTE LOOPS
LOCATING ADDITIONAL PROGRAMS
COMMERCIAL INSTITUTIONS
SYSTEM SCALING (MACRO)
INFORMING NEIGHBOUR TISSUES
REGIONAL PATTERNS
sYstem deVeloPment oVerView
ARCHITECTURAL DEVELOPMENT
BUILDING TYPOLOGIES
URBAN-AGRI. PUBLIC SPACE


To begin growing our system we looked to build upon the most basic processes which drive the human tendencies toward urbanization and agriculture and the opposing forces that have resulted in the current state of city vs country. Our research suggests both that urbanization and agriculture result from the very basic tendency of life to organize itself into ever increasing complexity in order to take advantage of the increasing cost-benefits of cooperation.
Just as in the origins of life, where simple polymers joined in symbiotic relationships to form the first basic metabolisms38, cities have emerged and flourished due to economies created in what are essentially higher scale metabolic circuits39. Our system development begins with modelling this process of cooperative settlement, allowing agents to ‘choose’ to live adjacent to another, or to live remotely - this tendency being weighted with a user-defined variable.
However just as densities in predator populations put stress on their prey and
subsequently the ecology that sustains them, the very success of cities are stressing their sustainability. This causality becomes evident when the drive toward density pushes agricultural production to the hinterland and increases the energetic costs of obtaining this fuel.
Once these basic processes are modelled, we will introduce and explore parameters which could steer the system dynamics towards a more stable state, as previously defined. These parameters, once identified and understood, will provide the means with which to implement intelligent controls to enable implementation and adaptation to specific environmental and political contexts.

settlement simulAtion:
CouPling dwelling And AgriCulturAl ProduCtion

ov ERvi E w
The Settlement Simulation is a computational model based on a multi-state cellular automata. The model uses simple behavioural rules to recreate the aggregation logic of dwellings and small subsistence farms in a given area via an ‘unplanned’ vernacular methodology. The goal of the simulation was to investigate the sorts of distributions and collective form that might result without the oversight of a top-down ‘planner’.
Com P u TAT ion A l Rul ES
40. Pont, Meta Berghauser, 2010. Space Matrix: Space, Density and Urban Form.
41. Typical Household size for New York City based on US Census Bureau statistics, 2000
42. Based on an urban productive area required to provide the household with their annual consumption of fruits and vegetables. Viljoen, Andre, 2005. CPULS
The simulation begins with the first ‘settler’ arriving on site placing his/her dwelling and farming the land around it. The dwelling has a footprint of 72 m2 (6m x 12m), based on a typical urban townhouse in the northern latitudes40 The household size is considered to be 2.59 persons41. The ‘farmed’ area attached to the dwelling is 100 m2/person (259 m2/household)42
A second settler arrives and ‘randomly’ chooses to build either adjacent to the first or to build remotely. Should they build adjacent, they need to relocate any farm land displaced by their dwelling. If remote, they will potentially begin a new settlement. This process is repeated until the field is full.
In the computational model these dwellings and farms are broken into modular units. The dwelling area is represented as one unit while the associated productive area required is approximately equal to the area of three dwelling units. Therefore, with every one dwelling placed, three productive units must be placed.
The likelihood for a new settler to build remote or adjacent is weighted by a ‘Friendliness Factor’ (F), a number between 0 and 1. F = 0 means all units will try to build remote, while F = 1 means all units will try to be attached. An F of 0.3 results in a 30% chance that a unit will choose to build remotely.
Vertical growth is triggered when a settler ‘chooses’ to build on an existing dwelling in a settlement which is sufficiently dense. In computational terms, this means that when the ‘state’ of the selected cell is already set as a dwelling, the neighbouring cells are checked to see how many surrounding cells are also dwellings. If the count of neighbour dwellings is above the given vertical growth threshold (v), a dwelling is added to that cell (presumably another flat above the existing). If the number of neighbours is less than (v), the agent chooses one of the unbuilt cells to build on.
PARA m ETERS
(F) Friendliness Factor: variable from 0 to 1
Controls likelihood of dwellings to cluster and therefore size of resulting dwelling clusters
(A) Field Size: 1 km2
The simulation was run on an area of 1 km2 in order to limit the distribution of dwellings and farms to an area considered ‘walkable’.
(v) Vertical Growth threshold: 8 (range: 0 - 8) Number of surrounding dwellings needed to trigger vertical growth
(PI) Production Intensity: 1 person = 100m2
(Dw) Dwelling/Household size: 72m2 = 2.59 persons
q uA li T i ES mEAS u RE d
(Dp) Population Density:
Density measured of the overall tissue.
(H) Floor Height:
Both maximum and average floor heights are measured in each tissue generated.
(OSR) Open Space Ratio:
The ratio of unbuilt ground area to built volume.
(F) Frequency:
The distribution of dwellings in the field.
DWELLING & PRODUCTION CELLS
Productive Surface (100 m2 /person) 259 m2
Dwelling
2.59 persons
m2

SETTLEMENT SIMULATION RULES

Production and Dwelling areas are broken into cellular units to be reconfigured.
1st Settler puts down dwelling and farms around it
2nd chooses to build adjacent to first or remote
When a built unit replaces a farm, the farm must be relocated to next nearest undeveloped cell.
VERTICAL GROWTH RULE
Unit to be placed
Target cell Neighbour check

If a selected cell is already built, but has unbuilt neighbours it does not meet vertical growth threshold, and therefore the dwelling must be built on an adjacent unbuilt cell.

If the selected cell is built and all neighbours are also built, a new dwelling unit may be placed above the existing unit.



f = 0

Dwelling units: 2500
Productive units: 7500
(D) Population Density: 64.75 ppl/hA (OSR) Open Space Ratio: 4.56
Average # of Floors: 1
Frequency Distribution of Dwellings:
f = 0.3

Dwelling units: 2506
Productive units: 7518
(D) Population Density: 64.91 ppl/hA (OSR) Open Space Ratio: 4.55
Average # of Floors: 1.01
Frequency Distribution of Dwellings:
f = 0.6

Dwelling units: 2558
Productive units: 7674
(D) Population Density: 66.25 ppl/hA (OSR) Open Space Ratio: 4.52
Average # of Floors: 1.10
Frequency Distribution of Dwellings:
(11) tissues were generated, starting with an F value of 0 and increasing in steps of 0.10 with each run. Population density distribution was measured in each tissue using a scan-line analysis. For every scanned line of cells (1 cell wide in x-direction, 100 cells long in y-direction)
the number of dwelling units are counted and divided by the overall total. This gives us the percentage of dwellings in each row. Frequencies were plotted and used to compare how Friendliness affects the heterogeneity of the generated tissues.



f = 0.9

Dwelling units: 2723
Productive units: 8169
(D) Population Density: 70.53 ppl/hA
(OSR) Open Space Ratio: 4.47
Average # of Floors: 1.55
Frequency Distribution of Dwellings:
f = 0.95

Dwelling units: 2820
Productive units: 8460
(D) Population Density: 73.04 ppl/hA
(OSR) Open Space Ratio: 4.40
Average # of Floors: 1.90
Frequency Distribution of Dwellings:
‘Friendliness’ = 0 resulted in a relatively homogeneous distribution of dwellings and farms as agents try to distance themselves from each other by choosing random positions in the field. The resulting tissue resembled a suburban settlement typology where distancing is the predominant spatial characteristic.
f = 1

Dwelling units: 2917
Productive units: 8751
(D) Population Density: 75.55 ppl/hA (OSR) Open Space Ratio: 4.57
Average # of Floors: 5.31
Frequency Distribution of Dwellings:
‘Friendliness’ = 1 resulted in one large cluster of dwellings with agriculture constantly being pushed outwards and eventually becoming one large productive area surrounding a single dwelling cluster. This resembles a low resolution model of the current urban/ agriculture dynamic whereby intensive development in cities pushes food production


out of any land within a desirable travel distance to the city centre.
As we moved incrementally from F=0 to F=1 we observed the dwelling clusters growing in density and size, allowing for larger identifiable agricultural areas to form in the field.
When F=0.7 to F=0.9, we see dwellings primarily tending to cluster with the occasional ‘loner’ breaking from the group to become a seed for a new dwelling cluster. The earlier in the simulation the dwelling is placed, the larger the resulting cluster. The resulting tissue contains a range of cluster sizes resembling a distribution of settlements in an urban region. Christopher Alexander suggests that settlement sizes will follow Zipf’s law resulting in varying sizes.
Population Density ranges from 64.75 when F = 0 to 75.55 when F = 1. This is to be expected as the total number of people that can live in the

given area is limited by the production capacity of a plot which is set at 1 person / 100 m2
luAT ion & Con C lu S ion S
The aggregation patterns that emerge from the Settlement Simulation suggest human settlement patterns at several scales higher than explicitly intended in the setting out of the model rules.
This suggests that perhaps by limiting the distance to which a community is allowed to relocate its agriculture, we might introduce a fractal nature to the organization of our urban area where the pattern at the neighbourhood scale is similar to the pattern at the regional scale.
We may take advantage of the increasing
F = 0.9

heterogeneity of the tissues of increasing F values in order to work between various scales. Perhaps higher F values tissues may be more appropriate as a low resolution pattern for a larger scales while the more homogenous lower F values might be better suited to create higher resolution tissues to be used at the neighbourhood scale.
In subsequent development we will introduce (D) Population Density targets. This will require increasing productivity of agricultural plots as well as incorporating area for infrastructure and public space within the simulation. In order for it to be meaningful (D) should be measured as a gross density as opposed to a net density.
A PPE ndix: A lgo R i T hmS
SETTLEMENT SIMULATION
1. Initialize at the start:
• Pick a random empty cell.
• Place a dwelling.
• Select the 8 neighbours of the cell.
• From these pick randomly 3 empty cells.
• Convert each cell into an open productive plot.
For every iteration:
2. Decide if the next dwelling is clustering or building remotely, according to the Friendliness Factor (F).
• To do this, generate a random number between 0 and 1 and compare to F;
• If larger than F, build remotely.
• Select a random empty cell somewhere in field.
• If smaller than F, build adjacent.
• Pick one of the build cells.
• Then select one of the 8 neighbours.
3. Check what type the selected cell belongs to. It can either be a dwelling, a productive plot or empty.
• If the cell is built:
• Check the 8 neighbours, and pick the ‘lowest’.
• Which means pick in order:
• First empty cells, then productive, lastly built.
• If all 8 cells are built:
• Select the cell with the fewest dwellings as new target cell.
• If the cell is built, add an extra dwelling to the number of dwellings in that cell.
• If the cell is productive, place the dwelling and replace the productive plot to the closest possible empty cell (see step 4).
• If the cell is empty, place a dwelling.
4. Place 3 productive plots as close as possible to the modified cell.
• To do this, find the 8 neighbours.
• From these pick randomly 3 empty cells.
• Convert each cell into an open productive plot.
• If there are not enough empty spots:
• Check a second ring of 16 neighbours.
• From these pick randomly empty cells until the required 3 cells are selected.
• If there are still not enough cells converted:
• Pick randomly empty cells until the required 3 cells are converted.
5. While the field is not full:
• Continue to the next time step and start at step 2 again.
• If the field is full:
• End the simulation.

ovERvi E w
By coupling dwellings to the area of production required to support the inhabitants, we introduce a new limit to the achievable population density within a given urban area.
From the previous experiment we concluded that even as the dwellings aggregate into denser clusters by growing vertically into taller units, the population density achievable by our current production intensity is limited to 75.55 ppl/ha. As local density increases, the overall density approaches 76 ppl/ha. Using the rooftops would allow us to achieve the maximum of 100 ppl/ha. Therefore in order to achieve population densities that compare to our reference cities, we will need to increase production intensity.
P R odu CT ion i n TE n S i T y
As previously shown, our research suggests that increased productivity from a given area of land can be accomplished in a number of ways. We have broken these into four categories which we will call the productivity gradient with values according:
1. Innovative Agricultural Techniques
2. Manipulated Production Surface (to increase surface area - includes folding, terracing, vertical/hanging plantings)
3. Enclosures which primarily use natural light (typical greenhouses) and minimally extend the growing season.
10. Highly Industrialized Enclosures which rely on artificial light and energy and can be planted year round, extending the number of harvests.
However these categories correspond to a jump in necessary capital investment and ongoing running costs associated with each type, limiting commercial viability to economic conditions. Also the higher startup costs would likely pose a barrier to entry for small farmers /
entrepreneurs and lead to further consolidation of the food industry. Therefore, in order to encourage a decentralized food source system, a range of solutions is desirable.
Com P u TAT ion A l Rul ES
Two additional rules were introduced to allow the model to accommodate for increased population densities. Firstly, when the field is full, the algorithm allows agents to increase the production intensity of existing cells. Therefore, a settler can still build, but his/her productive needs must be met by either: an increase of yields from an existing agricultural plot, or a neighbouring built cell must introduce production, introducing ‘hybrid’ types.
Production Intensity (PI) is allowed to increase in steps of one, corresponding to number of people who’s annual fruit and vegetable needs are met per 100m2. Therefore a cell having PI = 3 means three people are provided for on that 100m2 plot.
More work needs to be done to correlate the Production Intensity values to real world implementations, however our research has indicated that PI=3 could be achieved with readily available greenhouse technology, PI=5 is achievable with highly specialized greenhouse technology, and PI=10 could achieved by a two level high-tech energy intensive greenhouse.
The second rule relates to ‘Aggressiveness of Development’ (AD) and is implemented to allow the user to adjust the likelihood that each built cell be adjacent to at least one productive cell. Therefore when Density and Friendliness are high, setting AD = 0 ensures that all inhabitants live adjacent to at least one agricultural plot.
Innovative Agricultural Techniques Increase Yield/ m2

Manipulate Surface to Increase Productive Surface Area

Enclosure (Greenhouse) using natural light
As production intensity (crop yield from a given land area) increases beyond a certain point, the capital investment and energy requirements increase as well, creating a barrier to entry for smaller farmers, therefore a mix of production types is needed.
Multi-Level ‘Vertical Farm’ Enclosure using artificial light


People fed / 100 m2 (Fruits and Vegetables)
NOTE : HYBRIDS ARE NOW SHOWN WITH GREEN ROOFTOPS
Plan
Section

PARA m ETERS
(F) Friendliness Factor: F= 0.3 , 0.6, 0.9
(D) Population Density: D= 140, 220, 280
(PI) Production Intensity = 0-10 ppl/ha
(AD) Aggressiveness of Development = 0 to 1 (variable)
(PC) Productivity Ceiling = 10 pp/ha
(HC) Height Ceiling (Allowable # of Floors) = 6
q uA li T i ES mEAS u RE d
(PG) Productivity Gradient: Frequency Distribution of Production Intensities from 0 to 9.
(OSR) Open Space Ratio: OSR = (1 - C) / FAR where: Coverage (C) = Footprint / Sample Area and Floor Area Ratio (FAR) = Gross Floor Area / Sample Area.
1km.

1km.
mET hod
The revised Settlement Simulation was run for a variety of parameter settings to compare the combined effects of Friendliness, Density and Aggressiveness on Production Intensity and urban qualities such as Open Space Ratio.
Thirty tissues were generated using three Density targets each run with ten F values and AD=0. Nine were selected and with those F and D values run again with AD=1.
Population Densities used were based on sample tissues studied. 280 ppl/ha is the density of Gracia neighbourhood in Barcelona, 220 ppl/ha relates to Brooklyn Heights in
F = 0.85 | D=220
Brooklyn, NY and 140 ppl/ha corresponds to Stoke Newington in London.
Generated tissues were studied for the resulting Productivity Gradient. Frequency distributions were plotted for the resulting productivity values giving us an idea of what the population density threshold might be for a system which is more conducive to small farmers and entrepreneurs.



















Tissues were generated employing Production Intensity rules to meet density targets. Images show three Density settings and three ‘Friendliness’ factors.


f = 0.45 | d =140
Dwelling units: 5406
Productive units: 5008
(OSR) Open Space Ratio: 0.84
Average # of Floors: 1.08
Frequency Distribution of PI: f = 0.85 | d =140
Production Intensity (ppl/100m2)
Dwelling units: 5406
Productive units: 6426
(OSR) Open Space Ratio: 1.16
Average # of Floors: 1.51
Frequency Distribution of PI:
Production Intensity (ppl/100m2)
f = 0.95 | d =140
Dwelling units: 5406
Productive units: 7357
(OSR) Open Space Ratio: 1.39
Average # of Floors: 2.05
Frequency Distribution of PI:
Intensity (ppl/100m2)
f = 0.45 | d =220
Dwelling units: 8495
Productive units: 3832
(OSR) Open Space Ratio: 0.32
Average # of Floors: 1.38
Frequency Distribution of PI:
f = 0.45 | d =280
Dwelling units: 10811
Productive units: 3768
(OSR) Open Space Ratio: 0.27
Average # of Floors: 1.73
Frequency Distribution of PI:
F = Friendliness Factor
D = Population Density Target
AD = Agressiveness of Development = 1
f = 0.85 | d =220
Dwelling units: 8495
Productive units: 5092
(OSR) Open Space Ratio: 0.43
Average # of Floors: 1.73
Frequency Distribution of PI:
f = 0.85 | d =280
Dwelling units: 10811
Productive units: 4656
(OSR) Open Space Ratio: 0.27
Average # of Floors: 2.02
Frequency Distribution of PI:
f = 0.95 | d =220
Dwelling units: 8495
Productive units: 6221
(OSR) Open Space Ratio: 0.56
Average # of Floors: 2.25
Frequency Distribution of PI:
f = 0.95 | d =280
Dwelling units: 10811
Productive units: 5538
(OSR) Open Space Ratio: 0.33
Average # of Floors: 2.42
Frequency Distribution of PI:
Red arrows and curves above indicate anomalies in the distribution of Production Intensities. In certain combinations of input values, higher intensities accumulate at a faster rate.



















Developer Aggressiveness was introduced and set to 0 so that all built cells are adjacent to min one prod cell. Images show three Density settings and three ‘Friendliness’ factors.


f = 0.45 | d =140
Dwelling units: 5406
Productive units: 5060
(OSR) Open Space Ratio: 0.83
Average # of Floors: 1.10
Frequency Distribution of PI:
f = 0.85 | d =140
Dwelling units: 5406
Productive units: 6085
(OSR) Open Space Ratio: 1.04
Average # of Floors: 1.38
Frequency Distribution of PI:
f = 0.95 | d =140
Dwelling units: 5406
Productive units: 6940
(OSR) Open Space Ratio: 1.26
Average # of Floors: 1.77
Frequency Distribution of PI:
F = Friendliness Factor
D = Population Density Target
AD = Agressiveness of Development = 0
f = 0.45 | d =220
Dwelling units: 8495
Productive units: 4133
(OSR) Open Space Ratio: 0.33
Average # of Floors: 1.45
Frequency Distribution of PI:
f = 0.45 | d =280
Dwelling units: 10811
Productive units: 4133
(OSR) Open Space Ratio: 0.27
Average # of Floors: 1.84
Frequency Distribution of PI:
f = 0.85 | d =220
Dwelling units: 8495
Productive units: 4835
(OSR) Open Space Ratio: 0.39
Average # of Floors: 1.64
Frequency Distribution of PI:
f = 0.85 | d =280
Dwelling units: 10811
Productive units: 4503
(OSR) Open Space Ratio: 0.27
Average # of Floors: 1.97
Frequency Distribution of PI:
f = 0.95 | d =220
Dwelling units: 8495
Productive units: 5675
(OSR) Open Space Ratio: 0.52
Average # of Floors: 1.96
Frequency Distribution of PI:
f = 0.95 | d =280
Dwelling units: 10811
Productive units: 5073
(OSR) Open Space Ratio: 0.31
Average # of Floors: 2.19
Frequency Distribution of PI:
Red arrows and curves above indicate anomalies in the distribution of Production Intensities. In certain combinations of input values, higher intensities accumulate at a faster rate.
When Population
Density is high and Friendliness is low Production Intensity is not distributed gradually but instead exhibits disproportionately more high-intensity cells.



The introduction of Production Intensity rules allowed us to achieve the desired Density targets while meeting productivity requirements for that population.
The effects of Density and Friendliness work as opposing forces; Density fills the field by increasing the amount of material that can be ‘poured’ in. Without the effect of Friendliness (F=0) the simulation results in a uniform distribution of material.
Friendliness then acts much as a centripetal force, pulling the dwellings into tightly packed ‘piles’ at certain attractor points, the locations of which are determined by the first few dwellings that are placed. (The earliest placed dwellings create the largest aggregations.)
In this way, Friendliness has the effect of introducing differences in spacial intensities in an otherwise uniform state.
As these clusters are created production cells are pushed out of the dwelling clusters, but
the algorithm dictates that they stay close. Therefore large clusters of dwellings result in large aggregations of high intensity production gathered around the perimeter of their volumes.
While ‘D’ is high and ‘F’ is low, we see anomolies in the distribution of Production Intensities.
In the PI distributions for sample tissues: F=0.45|D=220, F=0.45|D=280, and F=0.85|D=280 we see a drop in the frequency of PI=3 units, then disproportionately more high-intensity cells compared with the other samples. As the friendliness is increased for each of these density values, the distributions return to a pattern of diminishing frequencies, similar to the other tissues.
We believe this is likely attributed to low Open Space Ratios, which result from high D with low F. In these tissues, dwelling clusters overwhelm open plots and settlers begin aggregating highintensity productive units around themselves, placing their own production atop their neighbours. Therefore, when an economical
distribution of production intensities is considered desirable, the following thresholds should be considered.
For D=140 use F > 0.45
For D=220 use F > 0.85
For D=280 use F > 0.95
Aggressiveness of Development (AD) has little effect on the distribution of Production Intensity types.
OSR is similar in both sets of samples, although the size of ‘continuous’ open plots is reduced slightly. The compromise here could be weighed against the benefits resulting from the dwelling clusters having more direct access to small agricultural plots. This could be considered advantageous in a scenario which calls for a greater percentage of the population ‘growing their own’ while still requiring high densities. This can be studied in greater detail once cluster sizes can be identified in the samples (see following sections).
In addition, ‘livability’ of the dwelling clusters could be considered improved when AD=0, by ensuring better light, ventilation and views by the penetration of agricultural cells within the large dwelling clusters.
ADDING PRODUCTION INTENSITY & POPULATION DENSITY TARGETS
• While the field is not full:
• Calculate the Settlement Simulation as shown in the previous section.
• When the field is full and the Target Density (D) is not met:
• Changes made in Step 3:
• If the target cell is productive, place the dwelling and keep the productive capacity in the cell.
• If the target cell is empty, place a dwelling and add 1 production equivalent (PI) to the same cell.
• Replace Step 4 and 5 with:
• Increase the intensity of 3 productive plots with 1 PI (when the target cell was empty, change only 2 plots).
• To do this, find the 8 neighbours.
• From these pick randomly 3 productive plots.
• Increase the intensity of each cell with 1 PI.
• If there are not enough empty spots:
• Check a second ring of 16 neighbours.
• From these pick randomly productive plots
until the required 3 cells are selected.
• If there are still not enough cells converted:
• Pick randomly from the productive cells
in the field until the required 3 cells are converted.
• While D is not met:
• Continue to the next time step and start at step 2 again.
• If D is reached:
• End the simulation.
settlement simulAtion: reFerenCe tissue ComPArisons
In the tissues generated through a bottom up approach we examine how local spatial interaction produces different patterns. So far we were evaluating the spatial patterns that emerged, using quantitative measurements such as Density and Open space ratio.
At this point we consider it important to relate these generated tissues to sample ones from reference cities. Our aim was not to compare the generated tissues with these real-world ones but to reference their visual form to the urban characteristics of existing inhabited places. This gave us a rough estimation of the possible urban qualities that can correspond to these measurements.

F = Friendliness Factor
D = Density Target
AD = Agressiveness of Development = 0
FAR: 0.64
Coverage: 0.33
OSR: 1.06
Source: 2001 Census, Office for National Statistics.





f = 0.45 | d =140
Dwelling units: 5406
Productive units: 5060
(OSR) Open Space Ratio: 0.83
Average # of Floors: 1.10
Distribution of Dwellings:



f = 0.85 | d =220
Dwelling units: 8495
Productive units: 4835
(OSR) Open Space Ratio: 0.39
Average # of Floors: 1.64


RE f ERE n CE T i SS u E : Brooklyn Heights - Brooklyn, NY
(D) New York City: 106 ppl / hA
(D) Brooklyn: 140 ppl / hA
(D) Brooklyn Heights: 205 ppl / hA
FAR: 2.0
Coverage: 0.53
OSR: 0.38
Source: New York City Department of City Planning




f = 0.45 | d =280
Dwelling units: 10811
Productive units: 4133
(OSR) Open Space Ratio: 0.27
Average # of Floors: 1.84
FAR: 1.92
Coverage: 0.57
OSR: 0.22
Source: Berghauser Pont, M. and Haupt, P., 2010. SpaceMatrix Space, Density and Urban Form.

Food Distribution




Once the producer and consumer cells are distributed in our simulation space, they need to be connected in a network typology that facilitates the circular movement of food, water, waste and people between the producers and consumers with the lowest energy requirements.
For this phase of the research, we will initially focus on the:
1. Movement / distribution of food from source to consumer
2. Social movement of inhabitants
In the subsequent MArch phase, we will look to incorporate:
3. Collection of drainage and rain water from the urban surfaces and redistribution for the irrigation of productive plots.
4. Collection, processing and reuse of waste nutrients from dwelling units to fertilize productive plots.
Once the topologies for each of these network functions is addressed in isolation, strategies will be discussed for overlaying the four networks and where there might be opportunities for combining them.
In addition as these networks are constructed, their topology will be used to re-inform and further develop the morphology and distribution of the built forms.
Com P u TAT ion
At this point, the data set locating cell types and intensities generated by the Settlement Simulation component will be sent as input into the Network Building component which will place network nodes and connect them.


networK: Food distriBution identiFYing Clusters & loCAting distriBution nodes
ovERvi E w: n od E Ty PES
Adjacencies in our urban-agricultural landscapes are only as performative as our food distribution system. Network performance will be evaluated on the energy expended linking consumers to their food sources.
To begin structuring the movement of food from source to consumer we identified three distribution types:
Wholesale Nodes:
Farmers will take advantage of their urban locations by setting up on-site Farm Shops which sell to retailers as well as direct to consumers via subscription services such as a CSA(Community Supported Agriculture) programmes and ‘veg-boxes’. (open dailyvisited weekly)
Retail Nodes:
Small grocers and convenience stores will be distributed throughout the neighbourhood with a high level of redundancy. These retailers purchase direct from farmers and offer consumers ease of access and longer hours. (open daily - visited daily)
Wholesale Cooperative Markets:
Farmer’s Markets where several farmers come together to sell in a market setting where consumers are offered ‘one stop shopping.‘ These should be located in the densest dwelling clusters in order to serve the largest audience and reduce travel barriers to those inhabitants. Farmers markets also serve to activate other commercial activity therefore they should be located on a high-use route within the network structure. (weekly event - visited weekly)
Com P u TAT ion A l Rul ES
Therefore, wholesale farm-stands will be located on large areas of productive surface (minimum of 1-2 hectares).
Retail nodes will be distributed throughout dwelling clusters such that any dwelling should be within a one minute radius of a retail node which at 5km/hr is equivalent to 83m.
Retail nodes will be connected back to farmstands using a branching structure.
Farmers Markets (wholesale cooperatives) will be located at a later stage once network topology is established and highly trafficked branches of the network are identified as ‘market streets’.
In order to begin locating these nodes, we must first identify the clusters of dwellings and commercial sized aggregations of productive cells.
NODE TYPES:

Example Distribution of All Node Types


Wholesale Nodes: (On-site Farm Shops) - open daily - visited weekly or twice weekly - all residents can access within 5-10 min walk

Retail Nodes: (Small scale grocers, convenience stores and specialty shops) - open daily, - visited daily or every other day - 1 min walk

Wholesale Cooperative: (Centrally located Farmer’s Markets) - weekly event - visited weekly - 10 min walk max
People's choice of transport method (and subsequent fossil fuel energy use) is influenced by the distance to be travelled.
Cluster Identification:
1. Pick a cell.
2. Check neighbours for correct type.
3. Add to cluster and check next ring.

Retail Node Placement:
Step1: Place a Retail Node in the center of the cluster.
Step2: Select one of the cells at distance 2*W.
Step3: Place the next Retail Node and select one of the cells at 2*W.
Step 4:
Continue with step 3 until there are no cells available anymore in the cluster.
Served cells by Retail Node
Served cells by Retail Node
Cells within selecting range
Cells within selecting range
Cells most likely to be picked
Cells most likely to be picked
Possible Retail Nodes
Possible Retail Nodes
Remaining cells in cluster
Remaining cells in cluster
Node
C lu STER d ETECT ion
After the algorithm distributes the consumer and producer cells, clusters need to be defined in order to place the Wholesale and Retail Nodes . Different thresholds define how many of each will be present in the tissue. These nodes will be placed after the different clusters are defined.
Com P u TAT ion A l Rul ES
Recognition of clusters for urban or productive cells slightly differ from each other. The rules are as follows:
1. To select the productive clusters:
- From all the productive cells, the algorithm picks a central cell in a cluster, meaning the cell with the lowest production intensity.
- From there it crawls outwards to find connected cells. Productive cells need to share a common edge to belong to the same cluster. Therefore only four neighbours are checked if they are productive.
- From these neighbours, it looks for the next ring of neighbours to join to the cluster.
- If there are no connected neighbours anymore, switch to the next cluster, by looking for the next cell to start the search.
2. To select the dwelling clusters:
- From all the dwelling cells, the algorithm picks the tallest cell available to start crawling outwards to find connected cells.
- If there are dwellings available within the eight neighbours, these cells are added to the current cluster.
- From these neighbours, it will look for the next ring of neighbours to join to the cluster.
- If there are no connected neighbours present anymore, the algorithm switches to the next cluster, by looking to the next tallest cell available.
PARA m ETERS
(A1) Minimum Area of productive cluster: 1 hA. Threshold for placing a Wholesale Node when a farm cluster is ought to be commercially viable.
(A2) Area of a large-size commercial farm: 7 hA.
(W) Maximum walking distance: 1 min. = 83 m. Used as a threshold to place the Retail Nodes.
Pl ACE w hol ESA l E n od ES
When the algorithm finished the search for productive clusters, it will add a Wholesale node when the cluster is larger then A1. When the farm cluster is larger then A2, it will be subdivided in sectors of A2 and nodes will be added for each sector.
Pl ACE R ETA il n od ES
When the dwelling clusters are defined and Wholesale Nodes are present, Retail Nodes are distributed throughout the cluster. If there are no Wholesale Nodes present, the urban tissue generated is of such fine grain, that there is no reason to exist for a food distribution network and therefore no Retail Node will be placed.
When the cluster is large enough, which means that there are dwellings further away from the central node then W, Retail Nodes are placed. The algorithm looks for the central cell to add the first node. From this node it looks for a hexagonal pattern to place nodes in order to ensure that all the cells in the cluster are within the set range W. The steps are more precisely described in the diagrams on the left page.
q uA li T i ES mEAS u RE d
(N) Number of Nodes: Shows how many nodes are present in the tissue.
(Ar) Area distribution of productive plots. The distribution shows how large the farms are.









Tissues were scanned for continuous agricultural clusters. Plots > 1 ha, considered viable for commercial production, are identified above in green. Large plots (> 7 ha) are further subdivided into min. 7ha plots with a wholesale node placed for each.
Area Distribution of productive
Area Distribution of productive plots:
Area Distribution of productive plots:
mET hod
Productive and Dwelling Clusters are identified for the previous 9 tissues. Wholesale and Retail Nodes are then placed according to the given parameters. Area Distribution of Productive Plots is measured to define how each category of farm is represented in the tissue. For the dwelling clusters trip time to the nearest Retail Node is calculated to measure how successful the placement of the retail nodes was.
oBSERvAT ion S : w hol ESA l E fAR m S
The most extreme tissue is generated by F=0.95 and D=140, where there is primarily one large farm. Here the productive area was divided in 9 7ha sectors each with a Wholesale Node.
The other end shows tissues with only plots smaller than 1 hA and no Wholesale Nodes. This means that by current economics, the productive plots are likely not large enough to be viable, requiring a higher level of participation in individual production on the part of the population.
When we look at the diagonal from top left to bottom right, we see the threshold where the tissues generate farms larger than 1 hA allowing for Wholesale Nodes. Around 50% of the plots here are small urban gardens, between 300 and 3000 m2. The distribution of categories show a mix of categories which could be compared with the situation we have seen before in Havana.
F = Friendliness Factor
D = Density Target
Categories of productive plots in graphs:
1. < 300 m2: personal allotments.
2. between 300 and 3000 m2: small urban gardens.
3. between 3.000 and 10.000 m2 (1 hA): communal urban farms.
4. between 1 and 7 hA: small commercial farms.
5. > 7 hA: large commercial farms.









oBSERvAT ion S : R ETA il S ho PS
Compared to the farm clusters, the dwelling clusters are working inverse. The tissue for F=0.95 and D=140 shows only a few clusters large enough to contain Retail Nodes, with more than 50% of the dwellings further then 1 minute away from the closest Retail Node.
The tissues on the other end of the matrix, like F=0.45 | D=280, show one continuous built cluster. Because no Wholesale Nodes are present in these tissues, the algorithm in the next step will not produce a network to distribute food from producer to consumer. Therefore no Retail Nodes are placed. Again we see a situation in which the inhabitants would
Trip time from Dwelling to Retail Node:
be producing the majority of their own fruits and vegetables.
Con C lu S ion S & d i SC u SS ion
What we see in the previous two sets of experiments is that varying combinations of the parameters Density (D) and Friendliness (F) result in radically different distribution structures with social implications.
When the Density is high and Friendliness is low, we lack the continuous productive surface required for commercial-scale growers. Instead productive area is fragmented into small urban gardens.
F = Friendliness Factor
D = Density Target
Categories of trip time in graphs:
1. < 0.5 min. walk = 83 m. radius (at average of 5 km/h).
2. between 0.5 and 1 min. 3. between 1 and 1.5 min.
4. between 1.5 and 2 min.
5. > 2 min. walk






This type of pattern may not be politically feasible in a contemporary western city, where urban dwellers have come to rely on retailers for their food supply.
*These novel implementations of the system are outside of the scope of Phase I but we are interested in exploring these kinds of scenarios in the forthcoming MArch phase.
However, One could imagine a social situation in which such an arrangement could be implemented; for example a new city for climate refugees, in which the displaced population arrives with agrarian skills and the desire to maintain this cultural knowledge in an urban environment.*
For our next step of development, we will take forward two of our tissues (F=0.85 | D=220 and F=0.95 | D=220) shown above, which are similar in input values but demonstrating distinctly different distributions of large continuous productive areas.
Distribution paths will be generated for each, connecting Wholesale Nodes and Retail Nodes while evaluating relative energy expenditures.
RECOGNIZE CLUSTERS
1. For each cell check the type.
• If the cell is a dwelling, add the cell to the dwelling list.
• If the cell is a productive plot, add the cell to the productive list.
2. Recognize clusters for both types.
• If the type is a dwelling:
• Find the tallest cell in the field.
• If the type is productive:
• Find the lowest productive cell in the field.
• From this cell start to look for connected cells.
• If the type is a dwelling:
• Select the 8 neighbours.
• For each of the neighbour cells check:
• If the cell is a dwelling:
• Add the cell to the cluster.
• Remove the cell from the list of available cells.
• If the type is productive:
• Select the 4 directly adjacent neighbours.
• For each of the adjacent neighbour cells check:
• If the cell is productive:
• Add the cell to the cluster.
• Remove the cell from the list of available cells.
• For Each of the neighbours, select the next ring of neighbours.
• For Each neighbour neighbour check for coincidence with the existing cluster.
• For Each selected cell that is not coincident check the type.
• If this corresponds with the cluster:
• Add the cell to the cluster.
• Remove the cell from the list of available cells.
• While there are still valid neighbours added to the cluster:
• Keep selecting the next ring of neighbours and perform the previous checks again.
• If there are no valid neighbours anymore:
• Return the cluster.
• Start at step 2 again to select the next cluster from the list of available cells.
• If there are no available cells left:
• Return the list of clusters and end the function.
PLACE WHOLESALE NODES
For Each productive cluster place the required wholesale nodes:
• If the area of the cluster is larger the threshold (A1) of a viable commercial farm:
• Add Wholesale Nodes:
• Calculate how many nodes (Wh) are needed to support the production, dependent on threshold A2.
• Find the central cell.
• If Wh = 1
• Place the node in the central cell.
• If Wh > 1 And Wh <= 5
• Distribute the nodes in a circular pattern on a distance of 2/3 of the radius from the center.
• For each node find the closest cell to ensure that all nodes are located in a productive plot.
• If Wh > 5
• Place the first node in the central cell.
• Distribute the remaining nodes in a circular pattern
on a distance of 2/3 of the radius from the center.
• For each node find the closest cell to ensure that all nodes are located in a productive plot.
• If Wh is reached switch to the next cluster.
PLACE RETAIL NODES
For Each dwelling cluster place the required retail nodes:
• If the cluster is larger then the threshold (TH) of 1 minute walking distance:
• Add Retail Nodes:
• Find the central cell.
• Place the first node.
• Remove all the cells that are within the TH from the list of available cells.
• For each already placed node:
• While there are available cells left:
• Find all the cells that are within a range of 2 * TH to each node.
• Add the distance from each of the selected cells towards every node together to get a sum of distance.
• Select the cell with the largest sum.
• Place the next node in this cell.
• Remove all the cells that are within the TH from the list of available cells.
• If there are no available cells left:
• Switch to the next cluster.

networK: Food distriBution ConneCting distriBution nodes
ov ERvi E w
Connecting the newly generated distribution points back to their source nodes requires constructing a graph which weighs energy expenditure in two urban processes via their correlated network properties:
1. Average Path (Trip) Length - which measures the average distance to move material from a particular source to each distribution node attached to it, and as a result influences the likeliness that the trip be taken on foot or via the use fossil fuel based transportation.
2. Total Network Length - which reflects the cost for the construction and ongoing maintenance of city streets.
Unfortunately, these properties are inversely proportional to each other. Direct connection of each distribution node to its source node provides the shortest possible average trip length. However the resulting network structure fails to take advantage of node adjacencies and is therefore highly wasteful of material and maintenance. The overall network length of such a network is significantly longer than say a minimum spanning tree which instead links each vertex to its closest (or lowest weighted) neighbour. Such a network uses the least material to connect all vertices however results in an extremely high percentage of detour between nodes as measured by comparing the direct path length, to the newly constructed path length.
Com P u TAT ion A l Rul ES
To construct a network topology that would provide the highest benefit for cost, we require a hybrid which identifies a range of solutions within which the trade-offs are reasonableneither trip lengths nor total network length are dramatically increased by decreasing the other.
Our solution is a parametric tool which allows a user to step by step increase the amount of
allowable detour and measure the effect on characteristic trip length and overall network length.
Allowable detour is controlled by the measure of the angle drawn between:
L1 - The already existing connection between source and the closest neighbour.
L2 - The possible direct connection between the source and the new node to connect.
If the angle α < the threshold, the new node is allowed to connect through the neighbour, otherwise the connection will be direct. If not it checks the next closest node and repeats until cycling through all the nodes.
PARA m ETERS
(αd) Detour Angle, variable between 0° and 90°.
m EAS u RE m E n TS
(T) Average Trip Time, in minutes. Trip time from every Retail Node to the closest Wholesale Node.
(N) Total Network Length, in m. Total length of all the generated network paths.
mET hod
A Network Path algorithm was written which takes the set of source and distribution points generated in the simulation as inputs and connects them with a branching network with the wholesale node at the 'source' and retail nodes at the branching junctions. Topology of the paths was varied by adjusting the Detour Angle. Two sample tissues were selected for testing the effects of the Network Paths component: D=220 | F=0.85 and D=220 | F=0.95. These were selected in order to compare the difference in networks required to connect tissues of the same density but with very different spatial characteristics.
Existing Retail Node
Existing Retail Node
Wholesale Node Retail Node to connect
1.
Retail Node to connect
Wholesale Node
Wholesale Node
Detour Angle = 0°
Detour Angle = 15°
Existing Retail Node
2.
Retail Node to connect
Wholesale Node
Detour Angle = 30°
Building the Food Distribution Network.
Check:
Measure angle a between L1 and L2.
Option 1:
If a < Detour Angle and also L1 < L2, then connect through the existing Retail Node.
Option 2:
If a > Detour Angle and also L1 < L2, then connect directly to the Wholesale Node
Different Detour Angles produce different branching patterns.
Detour Angle = 55°

f = 0.85 | d =220
3 Wholesale nodes, 54 Retail Nodes
Dwelling cluster (W > 1 min.) Commercial Farm
Node Wholesale Node cluster (> 1 hA)
Range of input values:
Corresponding output range as plotted in the graph:
(m.) 17,400 to 7,411 T (min.) 4.02 to 6.15
oBSERvAT ion S
When αd is set between 00 and 300 , there is a major reduction of N (56% decrease: from 17,400m to 7,653m) and minimal increase of T (17% increase: from 4.02 to 4.85 min.).
When αd is set between 300 and 900 , there is almost no reduction of N (0,03% dicrease: from 7,653m to 7,411 m), while there is a considerable increase of T (21% increase: from 4.85 to 6.11 min.).
contraints (yellow zone)
(m)
Average Trip Time (T) plotted against Total Network Length (N) for various Detour Angles (αd).





f = 0.95 | d =220
12 Wholesale nodes, 50 Retail Nodes
Range of input values:
Corresponding output range as plotted in the graph: N (m.) 6,946 to 5,770 T (min.) 1.64 to 2.42
oBSERvAT ion S
When αd is set between 00 and 300 , there is a minor reduction of N (12% decrease: from 6,946m to 6,055m) and almost no increase of T (0.08% increase: from 1.64 to 1.79 min.).
When αd is set between 300 and 900 , there is almost no reduction of N (0,05% dicrease: from 6,055m to 5,770m), while there is a considerable increase of T (26% increase: from 1.79 to 2.42 min.).
budget contraints (yellow zone)
Average Trip Time (T) plotted against Total Network Length (N) for various Detour Angles (αd).





= 0.85 | d =220 | α d=30 °

= 0.95 | d =220 | α d=30 °
EvA luAT ion & Con C lu S ion S
What we see is that by increasing the Detour Angle, N decreases in overall length while T, Average Trip Time, increases. We are interested in the rate of change of these values and for which inputs the trade-offs are reasonable. This should be evident in the graph where it exhibits a high degree of curvature or a sudden steep drop-off in the slope.
In the first tissue (F= 0.85 | D=220) shows only a few sources of food and large size dwelling clusters around. The Detour Angle affects significantly the measured values for the built network. The angle of 30° is considered as a critical value where there is a significant change in numbers. Below this value, a small change in αd will commence a jump in N. Above the critical angle, a small change will inform a major change in T.
The second tissue (F= 0.95 | D=220) is more clustered and therefore more commercially viable productive area is present. This produces more distribution trees with less branching
depth then the other evaluated tissue. The fragmented network, causes that the ranges of values for both the overall network length and the average trip time are much narrower, therefore changing the detour angle has less effect on the outcome. This is directly related to the generated tissue and accounted by the fact that the number of Wholesale Nodes is considerably larger than in the first case while the number or Retail Nodes (related to the people to feed) remains almost the same.
As the numbers show, the produced networks are highly suitable for distribution of food throughout the tissue. In order to move people in the city with other destinations then reaching their food, for example for more general purposes, these networks are not very effective and a high percentage of detours can be expected. Therefore, in the next section, we add another layer of information to the algorithm in order to provide the ability for social movement across the settlements.
A PPE ndix: Algo R i T hm
NETWORK TOPOLOgy
If there are Retail Nodes (R) and Wholesale Nodes (Wh) present build a network to connect them.
• For each target Wh:
• Select the R’s to connect to
• For each R:
• Measure the target distance from target Wh to R. • For each Wh:
• Measure the distance to R. • Sort the distances from small to large.
• Select R as valid if the target Wh is the closest.
• Sort the selected R’s according to the shortest distance to the target Wh.
• For Each selected R:
• Build a connection:
• Define Wh as start point of the new connection.
• Define R as end point of the new connection.
• Check the detour angle (A):
• Define a vector between Wh and R.
• For each selected R check:
• If there is a line connected to this selected R:
• Define a vector between Wh and this R.
• If the angle between the two vectors <= A:
• Select this R as possible connection point.
• Measure the distance to Wh.
• If there are possible R’s within the range of A:
• Sort the possible R’s according to their shortest distance.
• Define the closest of these R’s as new start point.
• Make a line between the start and end point.
• Add this line to the network.
• When there are no selected R’s available anymore, continue to the next Wh.
• Check for coincident lines in the network and delete them.

ConneCting ACross settlements
ov ERvi E w
The previous step in the algorithm generated a network which prioritized the distribution of food as main characteristic. The resulting patterns were 'tree-like' graphs, with a strong emphasis on the 'producer to consumer' route topology.
In this experiment we aim to create a model which facilitates the social movement of people. In that case the routes do not have a specific designation but they are indented to enhance the movement through the tissue eliminating the number of cul-de-sacs or dead ends. Therefore an increase in continuity of the network and the possible occurrence of loops can be expected.
Com P u TAT ion A l Rul ES
The previously generated layout is only able to connect Retail Nodes in a single shortest direction to its closest source. This generates shallow trees with a high number of discontinuous routes.
The parametric model we will propose here makes it possible for Retail Nodes to connect to multiple Wholesale Nodes, while using the existing food distribution network already present. This will essentially connect the open ends of the separate tree patterns, allowing for continuous routes throughout the tissue.
Input will be the Overlap percentage, ensuring that each Retail Node will connect to the Wholesale Nodes that are within the overlap range. The closest Node is taken as reference distance, where the overlap is added to that distance in order to select the valid Wholesale Nodes.
PARA m ETERS
(Ov) Overlap Percentage variable between 0% and 100%.
m EAS u RE m E n TS
(Cn) Connectivity, varies from 0 to 1.
The degree to which all nodes are connected.
(Cr) Circuity, varies from 0 to 1.
The to which loops and circuits are present in the network.
(N) Total Network Length, in m.
Total length of all the generated network paths.
mET hod
The algorithm for the network building will be slightly adjusted. Instead of connecting each Retail Node to only one single Wholesale Node, the algorithm will check if it should connect to multiple Nodes, by checking if they are within the Overlap Range.
For the two proceeded tissues (F= 0.85 | D=220 | αd=30° and F= 0.95 | D=220 | αd=30°) the Overlap Percentage will be tested in 11 different steps from 0 to 100%. While varying the input, the effect on Connectivity and Circuitry of the network will be compared to the changes in Total Network Length. The results of the tests are shown on the next page.
Evaluation for Connectivity (Cn) and Circuitry (Cr) according to the following equations38:
number of linkages
maximum possible number of linkages
Cn = = number of circuits or loops maximum possible number of circuits
Cr = = where:
L = number of linkages
V= number of nodes
L 3(V-2)
L-V+1 2V-5
Wholesale Node to connect
ReferenceWholesale Node
Building the Social Movement Network.
Check:
Measure distances L1 and L2 and check against the Overlap Percentage.
L1 L2 Ov
Retail Node
ReferenceWholesale Node
Wholesale Node to connect
Retail Node
Option 1.
Overlap Percentage = 0 %
Option 2. Check
ReferenceWholesale Node
Overlap Percentage = 50 %
Wholesale Node to connect
Retail Node
Option 1: If Ov > (L2 - L1)/L1 where L1 is the closest distance, connect to both Wholesale Nodes.
Option 2: If Ov < (L2 - L1)/L1 then do not connect to a second Wholesale Node
Different Overlap Percentages produce different patterns.
Overlap Percentage = 75 %
D=220 F=0.85 A=30 57 Nodes

|
Dwelling cluster (W > 1 min.)
Commercial Farm
Network Length (m)
Connectivity (Cn) and Circuitry (Cr) plotted against Total Network Length (N) for various Overlap Percentages (Ov).
D=220 F=0.95 A=30 62 Nodes
Wholesale Node cluster (> 1 hA)
Range of input values:
Corresponding output range as plotted in the graph: N (m.) 7,653 to 10,908 Cn 0.32 to 0.44
Cr 0 to 0.15
oBSERvAT ion S
When Ov is varied from 0 to 100%, N increases with 30% to 10,908 m. At the same time both Connectivity and Circuitry increase steadily, as could be expected. Cn grows with 27% from 0.32 to 0.44 and Cr rises from 0 to 0.15.




D=220 F=0.95 A=30 62 Nodes

f = 0.95 | d =220 | α d=30 °
Range of input values:
Corresponding output range as plotted in the graph:
oBSERvAT ion S
When Ov is varied from 0 to 100%, N explodes with 141% to 14,200 m. At the same time both Connectivity and Circuitry increase considerably more then the tissue on the left page. Cn doubles from 0.27 to 0.54 and Cr rises from 0 to 0.3. Again this is completely dependent on the amount of Wholesale Nodes and Retail Nodes and how well they are distributed in the field.
ChartTitle
Connectivity (Cn) and Circuitry (Cr) plotted against Total Network Length (N) for various Overlap Percentages (Ov).

Overlap= 20%

Overlap= 70%

Overlap= 50%

Overlap= 100%

Reference tissue: 1 km2 of Fort Green, a typical residential neighbourhood in Brooklyn, NY.
Graph of reference tissue network (above)
N = 18,300 m
Cn = 0.60
Cr = 0.39
Connectivity (orange) Circuitry (blue)
Generated tissue
Total Network Length (m)
Comparison between Connectivity (Cn) and Circuitry (Cr) of the generated tissue and Fort Green in Brooklyn, NY.

F= 0.95 | D=220 | α d=10° | Ov=0.20
N = 5968 m
Cn = 27%
Cr = 0%
EvA luAT ion & d i SC u SS ion
The results show a steady increase in the measured Connectivity and Circuitry when the Overlap Percentage grows. This behaviour can easily be explained because the previous experiment generates separated tree-like graphs, where they become interconnected by the introduced Overlap Percentage. The most clustered tissue (F= 0.95 | D=220 | αd=10°) shows the largest difference in data, due to the presence of a large number of commercial

F= 0.95 | D=220 | α d=10° | Ov=1
N = 14200 m
Cn = 54%
Cr = 30%
farms and the fragmented network it generates. At the same time the Overall Network Length for this tissue increases enormously.
In order to place the results in a context, we compare these to a 1 km2 reference tissue from Fort Green, Brooklyn, NYC which is a typical example of the New York - Brooklyn grid network. Connectivity and Circuitry were measured and plotted against each other in the graph above.
The data shows that the Brooklyn grid, which can be accounted for its high level of Connectivity and Circuitry, provides slightly higher values then the generated network, while the latter approaches the Brooklyn values but at the same time exhibits efficiency in connecting the nodes with a much shorter Overall Network Length. It shows that the algorithm produces a path system that could start to inform the flow of people between the settlements.
A PPE ndix: Algo R i T hm
NETWORK TOPOLOgy WITH OVERLAP
Calculate the Network as described in the previous section, but replace:
• Select the R’s to connect to
• For each R:
• Measure the target distance from target Wh to R.
• For each Wh:
• Measure the distance to R.
• Sort the distances from small to large.
• Define if R is valid to connect to.
• Define a range according to the given overlap percentage.
• Multiply the shortest distance with this percentage.
• If the target distance <= range:
• Select this R as valid to connect with the target Wh.






sYstem deVeloPment:
iii. reView & FurtHer worK
The computational model developed thus far has the capacity to distribute dwellings and required productive surfaces.
• It can adjust production intensity of plots in order to accommodate population density targets.
• That pattern can then be analysed for the placement of source and distribution nodes.
• Those nodes can then be connected with branching path networks.
• These individual path networks can be connected into a continuous urban fabric which facilitates social movement of residents.
However some aspects of our initial goals have not been addressed:
• The geometry of cells in the tissues produced are still tied to the initial grid. The morphology of the tissue should now be reinformed by the networks produced.
• A network for water and waste collection, processing and reuse needs implementing in order to take advantage of the waste-nutrient cycle which is typical of ecological systems.
• The algorithm is only allocating production area for fruits and vegetables, which was determined to be the appropriate crops for inner urban zones.
• The system is currently limited to a scale of approximately 1km2. In order to reasonable affect the food system for a population, the system needs to be considered at least on a regional scale.
In the following pages, we sketch out an initial approach to dealing with these issues in the future development.
sYstem deVeloPment: ConClusion
Having built a computational model which appears to be meeting the goals set out for our research, we will now apply the methodology to a test site to see how contextual inputs could inform the initialization of the model.
Additionally, we will explore one of our sample tissues produced for its potential to produce new kinds of public urban space and new typologies which accommodate urban programs while providing for productive surfaces.
systEm dEvElOPmEnt
tEst CasE: brOOklyn navy yard
sYstem test CAse: BrooKlYn nAVY YArd

PR oj ECT BR i E f
We propose as a contextual test case the redevelopment of a site currently situated between neighbourhoods in Brooklyn, New York. This will be a new neighbourhood type, a working community that will illustrate by example how the food system could be reimagined via a new urban morphology which:
a.) Creates an ecology which can provide for its residents within the walk-able boundaries of the system via local, multiscalar, distributed food production
b.) Enhances agricultural production by reconnecting the traditional waste-nutrient cycle which was lost with industrial farming
c.) De-couples food costs from fossil fuels by limiting food transportation at all levels, from source to table
In addition, we will make a first attempt at identifying a potential high street for the area and subsequently locating a cultural institution, A Centre for Urban Farming, to serve as an attractor to the neighbourhood.
More than a neighbourhood, our proposal will serve as a prototype; an algorithmic procedural model for urban growth which could be implemented throughout the city and larger region. The results of each implementation would be different and specific to the context within which it was situated.
Con TE x T uA l in P u TS
New inputs, which will need to be addressed when implementing on a specific site, will be:
• Area and Topography of the site.
• Boundary Conditions, which include: Adjacent Communities
Existing Network: Through-Routes to Maintain Entry/ Exit points into new tissue
• Urban Character desired, which includes:
Population / Density
OSR Open Space
Network Density / Connectivity
Sociological / Political considerations
Si TE An A lyS i S
The new neighbourhood will connect the highly desirable neighbourhoods of DUMBO to the north and west, and Fort Greene to the south, as well as the converted warehouses of the Navy Yard to the east. It sits at a critical junction in transportation networks, easily accessible from Manhattan, Brooklyn and the rest of New York City. Our internal network should link to and provide continuity between these neighbouring communities.
Currently the site is home to a automobile tow-pound lot and low-income public housing projects. We propose replace these with quality low cost housing integrated into a neighbourhood of mixed incomes and mixed uses. Adjacency to the Navy Yard will provide easy access to work space for small businesses and new food related jobs. The York St subway stop (linking directly to downtown Manhattan) is located at the western end of the site and within a 5 min walk to the centre of the new neighbourhood.
dE n S i T y & fR i E ndlin ESS
Brooklyn, NY has an overall population density is 140 ppl / ha. Manhattan overall by comparison is 280 ppl/ ha. When we examine smaller samples of residential blocks in the vicinity of our site, we find densities between as high as 538ppl/ha. However at the neighbourhood scale, we find that around 200ppl/ha is not uncommon for desirable residential areas. Brooklyn Heights for example, an attractive terraced neighbourhood to the west, with a mix of single-family and multifamily townhouses and some apartment blocks, has a population density of 205 ppl/ ha.








Above: Samples of street patterns from neighborhoods adjacent to the selected site in Brooklyn, NY
Left: Typical building typologies in adjacent neighbourhoods.

f = 0.3 | d = 200
Dwelling units: 2380
Productive units: 1302
(D) Population Density: 200 ppl/hA (OSR) Open Space Ratio: 0.29
Frequency Distribution of Dwellings:

f = 0.8 | d = 200
Dwelling units: 2380
Productive units: 1797
(D) Population Density: 200 ppl/hA
(OSR) Open Space Ratio: .33
Frequency Distribution of Dwellings:

f = 0.97 | d = 200
Dwelling units: 2380
Productive units: 2469
(D) Population Density: 200 ppl/hA
(OSR) Open Space Ratio: 0.57
Frequency Distribution of Dwellings:
Frequency Distribution of PI:
Frequency Distribution of PI:
Intensity (ppl/100m2)
Intensity (ppl/100m2)
Frequency Distribution of PI:
(D) Population Density Target: 200 ppl / ha
(F) Friendliness Factor: tested 0.3 - 0.97, selected 0.9
(PI) Production Intensity: 100m2 / person
Base value for area of production required for fruits / vegetables per person per annum.
Intensity (ppl/100m2)
(Dw) Dwelling/Household size: 72m2 = 2.59 persons (Brooklyn’s average household size per the US Census 2010.)
nE w i n P u TS
Addition inputs implemented for the first time as a trial in this test case:
• A custom input mesh was drawn to match the boundary/area of the site.
• An attractor function was written to accept physical inputs as influences to the


settlement distribution. Main through routes that need to be maintained and connection nodes to surrounding streets were input as curves and points.
• Buildings around the boundary of the site were also input as attractors in order to populate the boundary streets and create a continuous extension of the existing fabric.
mET hod
The simulation was run with D=200, but with several (F) Friendliness settings. Several
Opposite page: The images show different runs of the settlement simulation varying (F) Friendliness values on the chosen site followed by analysis of resulting tissues.
Left: The final tissue selected based on its: OSR, heterogeneity of densities and capacity to generate a mixture of large and small scale productive plots.
f = 0.9 | d = 200
Dwelling units: 2380
Productive units: 1857
(D) Population Density: 200 ppl/hA (OSR) Open Space Ratio: 0.43
Frequency Distribution of Dwellings:
Frequency Distribution of PI:
selected sample outputs are shown above/ opposite page.
After evaluating the tissues, checking for a heterogeneity of density distribution, OSR's comparable to reference tissues, and the ability of the pattern to produce viable large-scale (>1ha) commercial farms while maintaining a continuous urban fabric, D=200 | F=0.90 was selected to build a network on.
Identify clusters of large (>1 ha) agricultural plots and place wholesale nodes

f = 0.9 | d =200
4 Wholesale Nodes
Area of Commerical Farms = 8.9 hA
Area Distribution of productive plots:
BrooKlYn nAVY YArd: nodes And PAtHs
PARA m ETERS
Identify clusters of dwellings and place retail nodes

17 Retail Nodes
1 Retail Node serves 140 Dwellings Trip times from Dwelling to Retail Node:
Category of distances f = 0.9 | d =200
(W) Maximum Walking Distance to Retail Node = 83 m./ 1 minute (at typical 5km/hr)
(A) Detour Angle = 40°
(O) Overlap Percentage = 30%
mET hod
The D=200 | F=0.9 Simulation output was fed into the network builder function.
The algorithm first detected clusters of dwellings and productive cells.
Continuous Productive plots of larger than 1 ha were identified and wholesale nodes placed.
Retail Nodes were placed throughout the dwelling clusters, based on the (W) Maximum Walking Distance parameter.
Connect wholesale nodes to retail nodes with Network Paths Function: ad=40°

Average trip time plotted against total network length for various Detour Angle values:
From every Wholesale Node towards the closest Retail Nodes a distribution network is built, using several Detour Angles as inputs. 40deg was selected for its balance of low trip time and low overall network cost.
In order to facilitate a continuous social movement individual distribution trees were connected changing the Overlap values. Unlike our sample tissues in the previous experiments, we were unable to generate connectivity and circuitry values to approach the Brooklyn
Connect internal 'trees' and boundary nodes with Network Overlap Function: Ov=30%

Comparison of Connectivity and Circuitry of the generated tissue, to reference tissue in Brooklyn, NY:
(orange) Circuitry (blue)
reference tissue. We believe that our test network is too small and this aspect of the network function should be tested again on a larger scale in the future.
The images above show the output from each step of the network algorithm, with evaluations.



Network becomes an attractor. Built forms pack along routes and provide clear continuous farm clusters. The diagram shows the steps to get the final result.
BrooKlYn nAVY YArd:
PARA m ETERS
(S) Street Width, between 6 and 12 m. Local street width dependent on the hierarchy.
(R) Range of Repulsion from Network, 6 - 12 m. Defines how far cells move away from network.
(At) Attractiveness of Network = 30%
Relative distance attracted to network.
(D) Relative Distance to Neighbour = 10 m.
mET hod
To start forming urban tissue with space for movement of food, people and production, a few steps have been developed for the purpose of this case study.
Shown on the left page are the different stages how to use the generated network as an attractor and a first attempt how this network informs the urban space in the neighbourhood. First the network is used as a repeller to clear space for streets. This algorithm takes the outcome of the simulation and the network

builder as a start. If the cells are within the Range of Repulsion, they are moved away from the network path.
Next step is the attractiveness of the Network. All the cells are pulled towards the closest branch of the Network, with a certain percentage relative to their distance to the Network.
The image at the bottom of the left column shows how then the cells are rotated and orientated according to the direction of the
closest branch of the generated Network. This will produce street facades aligned with each other.
The Last step of this algorithm is to make sure that the individual cells are not intersecting with each other. If they are closer then the set distance, they move away from their neighbours to maintain this distance. This ensures that on each cell there is enough space to actually build the number of dwellings that the settlement simulation calls for.



BrooKlYn nAVY YArd: networK HierArCHY
Thus far the paths of our generated network have no hierarchy. They are all treated equally by the algorithm. There is no way to distinguish between quieter residential streets and high streets for example, in order to start locating our weekly neighbourhood farmers market and cultural programs.
On routes most likely to get large amounts of traffic, widths will be allocated to accommodate larger flows as well as convertible space for the weekly farmer's market. These events will even generate more traffic and therefore attract more commercial activity. It is most likely that adjacent to these streets new shops will open and cultural program will develop. The addition of these functions will inform new residents to settle as close as possible and therefore densify the generated urban tissue once more.
These kinds of feedback loops will be further developed in the subsequent Part II of this research.

A first attempt was made here at an informal analysis of the network flows for the potential high streets and cultural centre of the neighbourhood.
The central north-south corridor which connects Fort Greene to the south and DUMBO to the north and west, will likely be a source of flows in and out of our site.
The midpoint of that route has quite a few paths connecting through it and one could imagine a high level of internal network traffic passing through this point therefore the cultural program, The Centre for Urban Farming, has been located here.
Of course in the future development, this first informal analysis should be replaced with a mathematical analysis of the network using Space Syntax or a similar algorithm.


Overview of neighbourhood showing cultural centre (left), high street (centre) and wholesale farm shop location (foreground).

Research, Education & Public Programs are integrated into the landscape and serve as a community hub


Urban-Agricultural Landscapes provide opportunities for new kinds of public spaces and experiences
BrooKlYn nAVY YArd: test CAse eVAluAtion
Implementation of our computational model on a test site in the Brooklyn Navy Yard validated some conclusions from the theoretical experiments in the previous chapter and called into question some computational steps as needing further development.
Settlement distribution was shown to work within a custom mesh boundary. Boundary conditions were implemented as attractors fairly successfully as the simulation was able to generate a tissue which seems to function as an extension of the surrounding urban fabric. The network function identified wholesale supplier locations, distributed shops and connected them with efficient distribution
trees. The adequacy of the overlap function in creating continuous and circuitous networks for social movement was hard to evaluate due to small sample size.
This problem of the social network was further amplified after adapting the built forms to the network morphology. We can see 'deep' aggregations of dwelling units without connection to primary network routes. These need to be connected in future development. Additionally, the visualizations show that this last algorithm operates in a 'broad stroke'. The output generated requires further refinement before proceeding to detail design. Environmental parameters could inform this next step in the future.
FurtHer worK: wAter And wAste looPs

ov ERvi E w
In evaluating the path system used for moving food throughout the system, path / trip length was a primary consideration because the movement of the resource requires the energy input of an individual going to the source, retrieving the materials and returning to the origin point.
In contrast, when planning for the movement of water or waste, gravity and pressure supply the energy to move the resource, and the primary cost is in the construction and maintenance of the network. In this case a minimum spanning tree, which connects all the nodes in the 'cheapest' way, is the most efficient topology, however locating the pipes is ideally done in conjunction with the street network for maintenance reasons.
Another important input in the system will be storage. The collection of rain water and waste, but also the use for irrigation will be discontinuous flows and probably not matching in time. Therefore the system needs to be able to store the supplies. Important in biological and ecological models is storage of resources on a local level, so that they can be utilized locally again and no energy is lost in transportation. For this reason our model will have a preference for local small scale storage.
Com P u TAT ion A l Rul ES
To construct a network topology that would cover water and waste loops, it is important to understand the flows of input and output, but also the capacities of storage facilities within the network. A model needs to be set out that organises these parameters, while building a geometry linked to the already generated street network.
For our purposes, we've set out a schematic approach to the problem, to suggest how this might be approached in future development.
Sewage water collection system
Rain water collection from rooftops
Rain water collection through porous street surface
Sewage water clean facility
Temporary stock irrigation water
Fine grained network provides for productive plots
Fine grained tap network for enclosed production
Irrigation network
Collection Distribution

systEm
EvaluatiOns & COnClusiOns








We set out to explore spatial patterns for the reintroduction of food production into the urban environment.
We asked how might we incorporate the productive surface area required to feed the population of a given area within a certain distance of the consumer, reducing the energetic requirements of transportation at all levels of the supply chain.
BUILT FORMS ORIENT TO NETWORK
We aimed to do this while maintaining characteristics of urbanity which we believe afford cities their vibrancy, make them 'livable' and create the conditions for social mobility and infrastructural efficiencies that come with density and the metabolic scaling of cities.
Our method of exploration was to build a computational model which begins by creating settlement patterns and concludes by connecting these patterns via path networks. Functionality was added to the algorithm step by step, building upon previous outputs. Each of these steps was evaluated quantitatively and qualitatively to assess their potential to achieve our stated ambitions.



sYstem deVeloPment eVAluAtions: QuAntitAtiVe Assessments

m EET ing PR odu CT ivi T y RE qui RE m E n TS
Our system produces neighbourhood scale urban tissues (approximately one km2) which contain adequate productive surface area to supply that population with a typical fruit and vegetable diet per annum (comparable to a North American, European, or industrialized nation's diet.)
Additional dietary requirements such as cereals, grains and meats need to be addressed at the regional scale.




m EET ing u RBA n m ETR i CS
Parameters can be adjusted which result in changing measurable urban characteristics in the generated tissues such as homogeneity, local density, FAR, coverage and open space. Tissues were shown to be comparable, by several measurements, to neighbourhoods in New York, London, Amsterdam and Barcelona.
PR odu CT ion in TE n S i T y & P o P. d E n S i T y
The computational model allows us to set density targets for the area and calculates the necessary increases in and distribution of production intensity which would be required to feed that population size in a site of that density.
SCA l ES of PR odu CT ion :
Productive surface areas generated were shown to be comparable to viable growing areas for: small-medium sized vegetable farmers, communal gardens, and individual allotments.


di STR i B u T ion nod ES
A food distribution system is generated for the tissue, to connect producer and consumer cells. Distribution networks consist of on-site farm shops, small local retailers, and farmer's markets.
Within our system, all residents are within roughly a one minute walk to a small grocer, convenience store or specialty shop for their daily or every other day shops.
We were able to show that all residents and retailers could be within a 10 minute walk of a farm-shop (wholesaler) for their weekly/ bi-weekly purchases and CSA/veg-box subscription services.
In our next phase, we will identify network hierarchy and suggest a location for the main retail corridor for the neighbourhood which also serves as the location for the weekly farmer's market. This would be within a 10-12 minute walk of all dwellings for a weekly shop.

di STR i B u T ion n ET wo R k
The distribution types are connected via branching systems, from source to retailer, the topologies of which can be adjusted to balance energy / cost criteria; weighing average trip time versus overall network length.

S o C i A l n ET wo R k
Social movement across the tissue is provided for by controlling the 'range of overlap' in distribution networks, allowing them to connect across trees and create a higher degree of connectivity and circuitry.
It was shown that our tissue can achieve similar, although admittedly not as high, connectivity and circuitry as a grid system typical in cities such as New York, but with lower total network costs.
sYstem deVeloPment ConClusions
uRBA n-Ag R i C ulT u RA l lA ndSCAPES
By ensuring agricultural production remains within our system boundaries, the adjacencies and hybrid types introduced into the urban environment suggest to us the potential for new types of urban public space.
In Part II we explore this potential in range of typologies which situate themselves at various positions in the gradients between public and private, agricultural and urban:
P R odu CT ivi T y gRA di E n T
When Density is high and Friendliness is low, dwelling clusters overwhelm open plots and ‘settlers’ begin aggregating production into high-intensity units around themselves, resulting in an uneven distribution of Production Intensities. In our experiments, an economical distribution of Production Intensities is best achieved with the following thresholds:
For D=140 use F > 0.45
For D=220 use F > 0.85
For D=280 use F > 0.95
d i STR i B u T ion of P R odu CT iv E
AREA A nd i TS E ff ECT on food
d i STR i B u T ion SySTE m S
PATTER n S A nd SCA l E
Changing the input value for (F) Friendliness results in spatial patterns which suggest human settlements viewed at different scales.
We propose that perhaps by limiting the distance to which a community is allowed to relocate its agriculture, we may introduce a fractal dimension to the organization of our urban tissue, where the pattern at the neighbourhood scale is similar to the pattern at the regional scale but with different crops at each scale.
dE n S i T y & fR i E ndlin ESS
Density and Friendliness work as opposing forces, the former filling the space, the latter compacting the aggregate material into localized clusters. The resulting differences in spatial intensities translate to heterogeneous urban tissues providing a rich and varied urban experience.
Our experiments revealed a threshold at which the food distribution system shifts from the familiar producer-consumer model, to one that relies on distributed production by the population.
When D is high and F is low, productive plots are likely not large enough to be commercially viable (by current techniques and economics). Instead, in this scenario, the productive area is distributed in smaller plots throughout the tissue.
Interesting, this threshold is at roughly the same values identified earlier for efficient distributions of Production Intensities: D=140/ F>0.45, D=220/ F>0.85, D=280/ F>0.95.
S o C i A l C i RC ul ATo Ry n ET wo R k
Social movement across the generated tissues, is achieved by connecting the individual distribution trees with an overlap percentage. In Part II we'll look at how dwellings connect back to this primary network and how the distribution of open spaces in our tissues can suggest a secondary circulatory network.
R E fin E m E n TS RE qui RE d AT T h E
A RC hi TECT u RA l SCA l E
While the test cases highlighted a lack of resolution achieved by the algorithm at the architectural and street-scape level, they did suggest exciting new possibilities for a finer level of development. In Part II, Environmental parameters, agricultural requirements and urban programs provide more detailed inputs for further resolution at this scale.
The units produced by the Settlement Simulation are considered to be diagrammatic. In place of these volumes, the many varieties of urban surfaces should be considered for their potential for production. Sectional variation will be employed to exploit this potential.
Th E limi TAT ion S of u S ing Po P ul AT ion dE n S i T y
Using population density has historically proven an unreliable metric in analysing urban form. Household size varies greatly with economic conditions and changes in demographics of an area. As Berghauser Pont and Haupt showed in their book Space Matrix, areas of Amsterdam have experienced extreme fluctuations in population density within the same built environment over the last 400 years. For our purposes, agricultural production must be tied to number of people and not FAR or GSI or other more formally consistent density evaluation tools. Therefore our experiments have been run with household sizes typical of Brooklyn, NY and similar cities of the US and Western Europe. However, the model has the ability to be re-scaled for different household sizes for application to various communities.
R E gion A l S CA l E
Working at the regional scale will allow us to address crops not incorporated in the neighbourhood model. We propose that the regional model might be implemented by working at a lower resolution, incorporating these additional production types as well as natural preserves and recreation areas and topographical features. The calculations made at this lower resolution would provide the inputs (Density, Friendliness, etc..) for the neighbourhood-scale simulations, much like climate models which use a variable scale grid.
d i STR i B u TE d vS Com PACT Ci T i ES
Contemporary theories of urban growth hold that compactness, density and vertical growth are the route to lowering the ecological footprint of cities. Studies of transportation usage in cities of increasing densities seem to support this, citing lower fossil fuel consumption in hyper-compact Asian metropolises44
This argument however, fails to acknowledge the agricultural footprint of city dwellers. Once productive lands, grazing areas, and related fossil fuels use is factored in, it becomes clear that compacting our living spaces is a small part of the work needed to be done to alleviate the pressure humans put on our planet.
Our work suggests that there is a limit to the effectiveness of vertical growth and density alone, and that approaches to urbanism must consider the city's inputs and outputs and metabolic processes as a whole.
Part ii: S P a tial develo P ment


Spatial Development: tranSlating Data to Space
While in Part I our primary concern was the development of a system which would distribute people and plants in such a way as to meet the urban and productive ambitions set out in the beginning of our research, Part II attempts to develop and illustrate the spatial potential of the generated data-set. We will look at the emergent structures - patterns and relationships - resulting from our algorithms and offer strategies and tactics for architectural interpretation of the data.
We hope to show that the distribution patterns and resulting networks can suggest:
• The programming and character of the urban circulatory network
• A spatial organisation for our city driven by a new type of productive urban block
• The development of new architectural typologies
Throughout our investigation of this new prototypical city, we see our critical opportunity in how we allocate the resources available in a
given territory - land, sky/air and sun/energy. And in how we separate, join or blur boundaries between Public and Private, Agricultural and Urban.
Public space will be the primary focus for intervention in our urban project. Urban public space is a result of where you place your thresholds - how you slice the private off from the public - and what you choose to enclose and separate. In developing a design for a city, we see agriculture as a mechanism for the reintroduction of new kinds of public space into this city. This is not a new idea. Commons were originally shared lands for grazing, providing social structure and places to meet or trade within settlements.
We'll look at how these kinds of spaces can be returned and integrated into modern urban environments.
Sample tiSSue For Spatial Development (1 km2) D=220 | F=0.95 | α D=30° | ov=0.7

Settlement Simulation Output with D=220, F=0.95

Continuous Productive Areas & Wholesale Nodes identified
For our exploration of spatial opportunities, we will use our 1km2 sample tissue developed in the previous phase, with the parameters D=220 | F=0.95 | α d =30° | Ov=0.7.We will work at various scales. Our method, at each scale, will consist of:

Retail Nodes placed in dwelling clusters, within 1 minute walks
1. Topological analysis of the output generated (studying properties appropriate at each scale)
2. Extraction of rules based on characteristics of the properties studied
3. Exploration of the potential application of these rules in the context of the 1 km2 sample tissue.


Retail Nodes find nearest Wholesale nodesDistribution Trees are constructed with αd=30°

Distribution Trees connect with Overlap = 0.7
SITE CONDITIONS
TARGET DENSITY
FRIENDLINESS FACTOR

SETTLEMENT SIMULATION
PATTERN OF DWELLINGS & PRODUCTION
WALKING DISTANCE
DETOUR ANGLE
PLACE DISTRIBUTION NODES
URBAN CIRCULATORY NETWORK PROGRAM REQUIREMENT
BUILD NETWORK
CIRCULATORY
ATTRACT GEOMETRY TO PATHS AND NODES
PLACE PARK/ RECREATION NODES
BUILD SECONDARY NETWORK GENERATE PRODUCTIVE VALLEYS
PRODUCTIVE BLOCKS
DIFFERENTIATE GREENHOUSE TYPES
COMBINATORIAL DEVELOPMENT
DETECT TOPOLOGICAL TYPES ASSIGN ACCESS & ASPECT TYPES THE PRODUCTIVE CITY
PRODUCTIVE TYPES
the Productive network


the proDuctive network programming urBan Space
Overview
What we have called our 'distribution network', will in practice become the streets and sidewalks of our city, or the urban circulatory network. These paths, together with the convex open spaces along them or where several paths meet, make up most of what we think of when we think of urban space.
In addition, the private & semi-private built spaces that bound this circulation network, giving form to the open space, when successful as attractors of activity, become an extension of the public realm and contribute the to the urban experience.
While in our system, our network was generated with the intention of moving food from production cells and wholesale shops to retailers and consumers, these paths will of course take on all kinds of urban circulation, and will need to support the full complement of programmes that make a vibrant city.
We have identified four categories of public urban programmes, to be accommodated:
• Social Mixing Programmes
• Circulation
• Recreational/ Leisure / Gathering places
• Agricultural Infrastructure
In this section we will look at a strategy for reading the characteristics of the generated networks and how this might inform the distribution of public urban programmes.
S O cial Mixing Pr O gra MM e S
These are places where people meet and where goods and ideas are produced and exchanged. This includes shops & entertainment, workspaces, studios & offices and institutions. Social Mixing Spaces benefit from accessibility, exposure to sidewalk/street traffic and transparency of materials for communication to this traffic. These spaces extend the public realm of the street into the bounding architectural volumes enriching the experience of movement through the streets.


S O cial Mixing Pr O gra MM e S
Shops & Entertainment
Workspaces - Studios/Offices
Institutions - Museums, Educational, Civic, etc..
In the interest of avoiding the pitfalls of traditional zoning, we will not differentiate between these various uses but instead encourage a diverse mix, resulting in neighbourhoods that accommodate living, working and leisure and more consistent occupancy throughout the different times of day.44
c irculati O n
In the interest of reducing fossil fuel dependence, our city will encourage movement primarily by foot, bicycle and public transport. However, we acknowledge that automobiles, or


c irculati O n
Pedestrian paths
Bicycles - paths and racks
Public (Bus, Train, Tram) - routes & stops
Personal Transport Vehicle - streets & parking
an evolution of that form, are likely to remain a part of modern life. Therefore space will be allocated for some sort of personal transport vehicle, whatever that might become in the next 10, 20 or 30 years.
Therefore priority will be given to pedestrian paths and bicycles. Bicycles will require paths and parking racks. Public transport (Bus, Tram, Train) will require appropriately sized routes with adequate coverage & stops/stations at walk-able (5 min) intervals. Personal Transport Vehicles will require streets with some sort of protection for pedestrians and finally parking.


agricultural i nfraStructure
Food shops, storage, seed banks, nurseries, labs, education, administrative
Water & Waste Systems - collection, treatment, storage & distribution


r ecreati O nal/g athering SPace S
Hardscapes - urban squares
Green Spaces - parks, playgrounds, playing fields
agricultural i nfraStructure
In addition to gardens, greenhouses and shops, agricultural production will require facilities for product storage, seed banks, nurseries, etc.. New specialised networks for water and waste collection, treatment, storage and distribution will be needed in order to take advantage of city water runoff and waste and redirect it for irrigation.
r ecreati O nal/ g athering P lace S
Finally, no city would be desirable for habitation without public spaces for gathering, sitting, relaxing, playing or simply people watching. We will look for opportunities to create loosely speaking, two kinds of recreational gathering spaces - Hardscapes, like urban squares and Green spaces like playing fields and parks.


the proDuctive network noDeS & pathS
Meth O d
We'll want to take advantage of the characteristics of the emergent structure of our network to inform how we might distribute our public urban programmes.
We'll focus on the connectivity of the nodes and paths. For the paths, we'll use the space syntax algorithm developed by Bill Hillier45 and colleagues at UCL as it measures connectivity but weighting it with certain other parameters such as centrality, and has been shown to be a more accurate representation of how people use a network.
Connectivity can help us to determine likely concentrations of flows within a network. Highly connected nodes and paths will be more likely to be used in the course of a typical user's travels through a network.46
Therefore, placing infrastructures at these nodes and paths, we will be able to serve larger percentage of the population than lesser connected network components.
Likewise, these highly used network components will be attractors for private investment, or social mixing programmes, such as retail, food, drink and entertainment uses, as these uses benefit from exposure to traffic.
These social mixing programmes will in turn again amplify the attractivity of the highly connected nodes and paths, resulting in the potential for large concentrations of people and a vibrant street life.
We'll want to plan for this eventuality by developing a methodology for providing adequate space for these activities in the appropriate locations throughout our urban fabric.
In this section, we'll begin with an analysis of the distribution network generated from our sample tissue. We will examine the nodes and paths of the network, ranking them by their level of connectivity and integration, respectively.

Wholesale Nodes
Frequency Distribution of Wholesale Nodes:
Rank Qty.

Sample Wholesale nodes extracted and categorized according to number of connections
w h O le Sale nO de S
Wholesale nodes were identified and categorised according to the number of connections from W1 (one connection) to W6+ (for six or more connections).
Our sample tissue does not contain 1's or 2's. This is a result of the networking algorithm, which connects many retail nodes to a single wholesale node.
Our lowest ranked wholesale node is a W3, of which there are two, both at the perimeters of the tissue and would likely become W4 or W5 when the city expands. W4's are most commonly occurring, which we will call 'Minor Hubs'
Nodes beyond W4, we classify as 'Major Hubs.' Our sample tissue generated (3) W5's, (1) W6, and (1) W7.
The distribution of node types is a result of the αd and Ov parameters used in the network building steps (p. 98-109).
r etail n Ode S
In the same way, Retail nodes were identified and categorised according to their number of connections, from R1 to R6+.
Retail nodes tend to connect only to the neighbours before or after them on route towards a Wholesale node. The range of what is considered 'on route' is a determined by the angle of detour (αd ) value.
R2's were most frequent (22), which are essentially points along a continuous path. These will likely serve the immediate connected blocks.
R3's were next most frequent (16). These, as well as the R4's (of which there are only 4) will have a larger draw, so we'll call these 'Local Nuclei'.
Although there are no R5's, we have an aberrant occurrence of an R6, which due to its highly connected nature, would likely function as a hub, similar to a W5 or W6, although without the wholesale function, which might limit its initial global draw.

Sample Retail nodes extracted and categorized according to number of connections
3
OPEN SPACE [M2]
Unprogrammed Open Space
Circulation Space
Production
Outdoor Eat / Drink
ENCLOSED SPACE [M2]
Food Shop / Market
Food Infrastructures
Social / Mixing-public / Semi-public
Social / Mixing-public / Semi-private
Train Route / Station
Bus Route / Stop
Bicycle Rack
w h O le Sale nO de S
Programme space was allocated relative to the connectivity rating of the node. Highest connected nodes are designated a total open space of 10,000 m2, which is comparable to Leicester Square (8000 m2) or Bedford Square (13000m2) in London, UK. This area is from facade to facade and so is further broken down into circulation, production, outdoor eating/ drinking and finally an unprogrammed open
1,0002,5005,00010,000 1005001,0002,500 7001,5003,0005,000 1002505001,500 1002505001,000 300400450600 300400450600 1,5005,0009,00017,000 7002,5004,5008,500 280083001440026700
space is reserved. These areas are then scaled down and adjusted for each node type.
Space is also allocated for complementary programmes in the bounding architectural volumes. Each node requires a food shop and supporting infrastructure, as well as social mixing spaces, each scaled according to node rank and expected volume of people. To calculate the area available for these, the perimeter of the circle with an area = assigned
Programme areas allocated according to Wholesale node connectivity
OPEN SPACE [M2]
Unprogrammed Open Space
Circulation Space
Production Space
Outdoor Eat / Drink
ENCLOSED SPACE [M2]
Food Shop / Market
Food Infrastructures
Social / Mixing-public / Semi-public
Social / Mixing-public / Semi-private
5001,0002,5004,000 --
Train Route / Station
Bus Route / Stop
Bicycle Rack
open space was taken as a frontage length, a depth was added for a typical urban shop footprint, and number of floors designated. The total was then broken into the various categories of enclosed programmes.
These initial numbers should be further refined with a more in depth analysis of projected people flows.
r etail nO de S
Programme space in retail nodes was allocated in a similar method although scales are more modest relative to the wholesale nodes. While Wholesale nodes are by nature global attractors within our network, Retail nodes are expected to have a local draw, and so are expected to serve a smaller population.
programme on additional floors
programme on additional floors
programme on additional floors
programme on additional floors
Programme areas allocated according to Retail node connectivity
Node Programming assigned throughout tissue
nO de Pr O gra MM e S aPP lied
In applying the programme areas to the nodes throughout the tissue according to rank, we can begin to see a differentiation in public spaces across our prototypical city. The distribution of scales, with a higher concentration of larger, highly connected 'major hubs' near the centre, and smaller 'local nuclei' scattered throughout, suggests a hierarchy of spaces, with varying intensities of use driven by the inherent characteristics of the network.
Next we'll look at how the paths can be similarly informed by the likely flows suggested by their connectivity.
aP Pendix: a lg O rith M S
Define programme allocations of noDes
• for each Wholesale node:
• rank the number of connections (nr.):
• for each retail node:
• rank the number of connections (nr.)
• assign area for programmes according to the rank of the node and the requirements in the table:
• open space
• circulation
• production
• outdoor eat/drink
• food/shop market
• food infrastructure
• social mixing space - semi-public
• social mixing space - semi-private
a nalyS i S Overview
Paths in the generated network are analysed by their connectivity and integration within the tissue. Integration here is taken from the method developed by Bill Hiller / Space Syntax47. This measures the accessibility for destination of trips for each space or path. Each path is ranked from the least to the most integrated by a percentage ranging from 0 to 100%.
Path r ating S
Following, the paths are divided in three categories of integration(i). These will be used to apply programmes resulting in different path characteristics throughout the whole tissue:
• The low integrated paths (i < 50%). These are emerging at the outskirts of the tissue and most likely to change when new paths are added.
• The medium integrated paths (50% >= i < 85%). These paths are connecting the low with the high paths and connect mostly to the major hubs in the tissue.
• The high integrated paths (i >= 85%). This category represents the most integrated paths and therefore the most likely paths where activity concentrates. These streets will become the high streets in the tissue with commercial frontages and farmers’ markets located within the urban space.
Paths are analysed for connectivity and integration, and ranked from 0% to 100%.
1. Paths called out with low integration: i < 50%
2. Paths called out with medium integration: 50% >= i < 85%
3. Paths called out with high integration: i >= 85%
network pathS
Sectional programming
Overview
Path programmes can be divided into linear/ routes and points/nodes that serve those routes. A bus route for example requires a bus lane for movement and a shelter, or at minimum standing space, for a stop.
Therefore we will address the paths primarily in section, allocating widths for routes and positions for nodes relative to those routes. These sectional locations we will call programme zones.
Each path will be allocated space for four types of programme zones, these are as follows:
Public/Private t ran S iti O n
This is the area directly adjacent to the building facade. We will encourage a ‘soft’ transition between public/private by allocating space for and encouraging:
• Sidewalk retail and seating with transparent/ opening facades
• Front porches and small gardens for residential buildings
Pede Strian Path S
Ample space allocation for pedestrian circulation should make it clear that people will be the priority on our paths. This zone should also be buffered from transit/transport but by soft means, allowing mutability between zones and allowing the whole path to function as an event space at times.
i nfraStructure
This zone will accommodate both traditional and 'edible' infrastructures. Included is space for food production, most likely lower maintenance crops, like fruit trees and berry bushes, but will also include space for bus stops, street furniture and lighting.
t ran SPO rt/ t ran S it
Each path will include space for bicycle traffic and public transit, either bus or tram. Limited space will also be provided for some sort of personal transport vehicle.
The range of widths and relative location of the zones will be determined by the path integration ranking, which we have previously broken into 3 categories - low, medium, and high.
Secti O nal cOMPO nentS
Sectional Components are suggested for the four different zones defined in the previous section. These give actual program and activity to the public space. A library of these components could be implemented and populated over the rated circulatory paths. The examples shown on this page are the first attempt to start building a library and can easily be expanded and change according to, for example, local climatic inputs, technological development or political choices.
Sidewalk Fruit/veg Stand
Semi-private Garden
Cafe / Restaurant Outdoor Seeting News Stand
Semi-enclosed Covered Market/ Greenhouse
Overview
The materiality of our public spaces should further our intention of directing flows of energy and resources through the system.
In addition to rainwater runoff and latent heat and solar energy, the urban environment offers opportunities for exchange of information - that is, communication between inhabitants.
We propose that material choices are considered in the interest of harnessing these latent resources.
e xa MP le r ule S
Path surfaces should be permeable, not paved, and have a dedicated system for the collection of rainwater runoff at street level.
Facade transparency should be relative to path integration. Higher ranked paths should have more transparent facades at street level. Continuity of glazed facades is encouraged, minimising solid opaque facades on highly trafficked streets.
Our intention is to extend the experience of public urban space into the built volumes which line our paths. Glazing will providing exposure for the social/mixing program and encourage communication between public open space and semi-public enclosed programmes.
On the other hand, thick masonry walls with high thermal mass have long been used as heat sinks in traditional greenhouses. We would encourage then, as a material strategy, building envelopes be driven in response to the energetic and information requirements of the programmes.


walls trap and release heat within greenhouses in the winter months.


Permeable surfaces are proposed for the circulatory paths, reducing heat island effect and allowing rain water runoff to filter through for collection and reuse.


Transparent facades at street level encourage communication between public open space and semi-public enclosed programmes.
Path Components applied on a low-integration rated path (typical example)
Path Components applied on a medium-integration rated path (typical example)
Secti O nal cOMPO nentS aPP lied
In applying the sectional programme components, emphasis should be on walkable, ‘edible’ streets with a priority given to pedestrian and plantings. Pedestrian paths
should be protected from traffic by a permeable boundary of infrastructural components. Street levels should remain continuous to encourage mutability between different uses at different times of day (shown in diagram on right page).
The direction of the sun should be considered when placing infrastructure zones, keeping these to the sunny side of the street (where applicable, on primarily East-West streets.)
Example of changing programmes on the same path shown during morning commute (top) and noon market (bottom), on a highly integrated path (typical example)
Programme and size allocated to the paths in the tissue.
Path Pr O gra MM e S aPP lied
When the programmatic zones are assigned to the different categories of circulatory paths, we can see, like the node programmes, a distinct hierarchy of streets results.
The highly integrated paths, near the centre of the tissue, with their wider sectional properties, suggest a high street or retail core. However, our streets will prioritise pedestrians and integrate agricultural production. Lower integrated streets generate less intense and narrower streets, suggesting more residential streets.
Pendix: a lg O rith M S
Define geometry of paths:
• for each path:
• evaluate for integration and rank between 0 and 100% integration
• if integration < 50% then total streetwidth = 9-17m.
• if integration >= 50% and < 85% then total streetwidth = 17-25m.
• if integration >= 85% then total streetwidth = 25-34m.
• according to the streetwidth:
• Define programmatic properties.
• orientate edible infrastructures on the sun side of the path
Overview
With the information of the previous sections, where size, areas and programmatic zones are assigned to the nodes and paths, now it’s time to adapt the built morphology to this data. Starting with the distribution of dwellings and greenhouses generated by the settlement simulation, here we define rules for adaptation.
rule
S
The transformations in this section are applied to the dwellings and greenhouses only. Therefore these need to be identified and called out first.
• These cells are then checked for proximity to the network paths and nodes. If they are within the assigned clear area, for those specific nodes and paths, then the cells are repelled from them and circulatory space starts to appear.
• The next step is to attract all the volumes back to the network with a factor relative to the distance. This ensures continuous open productive space between the dwellings.
• Following the built volumes are oriented towards the network to create coherent facade envelopes.
• As a last step occurring intersections of volumes are resolved by a recursive process of dispersal and attraction. A minimum distance to each other can be set, according to the final size of the dwelling units.
Para M eter S
(W) Sectional width of paths based on the hierarchy of paths and the allocation of sectional programme zones, widths are defined
(A) Clear area of nodes based on the character of the wholesale and retail nodes the required clear area is provided
(At) Factor of attraction factor defining how much the dwellings and greenhouses are attracted to the network
(Dir) Orientation of network
Direction of network path defining the alignment of the morphology
(D) Minimum distance between dwellings Distance set to resolve intersections
ResultingCorridor
1. Move away from the network when closer then W to generate corridors.
2. Move towards the network with factor At to increase adjacency to the network.
3. Rotate cells to align to Dir, the closest path of the network.
4. Distribute the cells in an equal distance of D from each other to avoid intersections.
Morphological adaptation rules


Dwellings & Greenhouses (Built volumes) identified

allocated programme space


1.) Built volumes are repelled from network edges and nodes

4.) Intersections of volumes are resolved by recursive dispersal and attraction
Built morphology steps applied to our sample tissue
Resulting morphology , shown after adaptation to programme allowances in network edges and nodes. Scale = 1 : 5000
the proDuctive network programme implementation
Overview
With the circulatory space defined and programme zones assigned, now it’s time to actually insert the additional programmes in the tissue and give volume to these. The nodes act as intense insertions of programme with a range of influence on the paths. On these pages we will talk about the implementation to the nodes. The final location and size of the volumes will be dependent on the adapted morphology proceeded from the previous section.
rule S
To begin with the required open space is cleared according to the node category defined before. A range of influence can be defined how far the programme is introduced onto the network paths. With this information and the required areas from the table, volumes are inserted on the lower floors of the built morphology. The final step is to put the dwellings and greenhouses back, lifted above. The urban tissue will be like a carpet laid over the programmes, without loosing any of the dwellings or productive units.
Para M eter S
(C) Node category the category of the node is defined by the number of connected network edges
(T) Character and types of social mixing programmes list of programme to be allocated to the specific node
(A) Allocated areas and open space corresponding areas for the different types of programme defined by the node category
(R) Range of influence the node category defines how influential the social/mixing program will be for the whole urban tissue, meaning how far can it grow along the paths
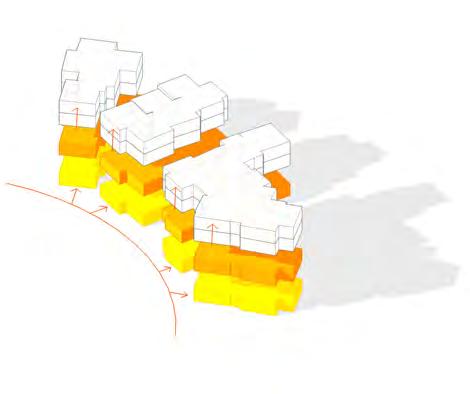
Space for social mixing programmes is created by inserting floors under dwellings and greenhouses
1. Clear required open space according to node category

2. Check range of influence for where to add social mixing programmes

3. Social Mixing Programmes are inserted as new floors (below dwelling units)

4. Dwellings and greenhouses are placed above the inserted programmes
nO de Pr O gra MM e S iMP le M ented e xa MP le
When all the rules and data for the additional programmes are defined and allocated, this page shows a possible implementation at a highly connected wholesale node (W6).
Multiple strategies are possible with the rule set, chosen here is to lift the centre area of the node in order to provide a continuous market
space for pedestrians. The circulatory routes are lowered at the boundary of the node. The section shows tunnels for vehicles to connect underneath the undulating landscape.
The high connectivity of the node suggests a stop for public transport, here implemented as a underground connection.


An urban circulatory corridor and node, after built morphology is adapted to network programming


the proDuctive network concluSion
Using connectivity to suggest node and path hierarchy results in a circulatory network with differentiated spatial characteristics.
Further development is required on a growth strategy. How will wide open, highly ranked nodes and streets work when the city is just starting? It may feel desolate if they are too large and the population is still small. How we deal with this depends on how quickly it is expected to be populated. Also, when the city expands beyond the initial 1km2 tissue, the ranking of the paths and nodes will change relative to the larger network. We’ll need a strategy to address this change over time.
We have not specifically designated lowerintegrated streets as residential or higher-rated as commercial. In contrast, we will ensure that dwelling units are distributed throughout the city, however, the use at street level will likely be a factor of the path's Integration value. We have not resolved whether provisions for storefront space would be implemented in the planning stages with an algorithm or whether this would be left to market forces.
Either way, the distribution of dwellings determined by the Settlement Simulation would be maintained. The point of responsibility for inserting of the social mixing programmes below these dwellings requires further investigation.
Pendix:
built morphology aDapts to informeD netWork
• for each dwelling and each greenhouse:
• locate the centre point:
• if the point is too close to a node:
• then move away from it.
• if the point is too close to a path:
• then move away from it
• if the dwelling is within the range of programming:
• assign the additional program
• move the point towards the closest path by a factor relative to the distance
• apply the building footprint (convert the data-cell to geometry)
• align the building towards the network
• solve the intersections between dwellings:
• check the distance to the other points
• if closer then the minimum distance (d):
• move both points away from each other to create d
• continue to the next point
• continue the steps untill all the points have a minimal d to each other.
the Productive Block

proDuctive Block the organiSing component oF the proDuctive citY
As a result of the previous steps, the basic unit of organisation of our urban tissue emerges; that is the Productive Block.
Our new type of urban block is result of a series of generative operations which are driven by the production and distribution of food, and the subsequent programming of the urban circulatory corridors. This intention is fundamentally different from that of the dominant western model, which prioritises the maximisation of profits from land values for individuals and developers. Analysis of our generated tissue will expose the effects of this intentionality and reveal new opportunities created for the mutual benefit of the urban community at large.
A quick scan of our tissue reveals:
• Blocks varying in size/area based on the density of nodes and their connected edges.
• Each block contains concentrations of productive area
• As well as a ring of built clusters, including dwellings and greenhouses
• The aggregation of these blocks results in urban corridors, enclosed by built form, which provide the space for public mixing programmes in the kind of densities we have come to associate with urban environments
• This density of social mixing opportunities, supported by the productive infrastructures distributed within, begins to suggest how we might meet our stated goal of meeting both urban and productive metrics in a new type of Productive City.
In this section we’ll look at how our block can be optimised for productivity and what kinds of public spaces and programmes might take advantage of this new kind of organisation.

Typical Manhattan Blocks & Parcels (1934, Bromley Insurance Maps, NY Public Library)
It is useful now to compare our block side by side to scale next to a Manhattan block in order to extract some essential differences between the urban fabric generated by our system and that of the modern land ownership driven model.
The New York City block is typically 270m x 80m. The long thin rectangle maximizes perimeter length (storefront exposure) at the sacrifice of interior area. The performance of this form can be evaluated in the context of real estate market demands, as exposure is what
you lease when you lease space in New York, exposure to mass flows of people and traffic moving through the city’s circulatory network.
Our sample block in comparison, is similar in area to 2-3 NY blocks, however with much less surface area devoted to circulation. Instead
of maximizing street-frontage, our system generates largely convex polygonal blocks which result in large open spaces within, concentrating productive open space into continuous workable plots.
Edible Infrastructures Productive Block
Taking a prototypical section through our block, we see a thickened boundary layer of built form which delimits an agricultural common from the urban circulatory corridors.
In effect each block provides three layers of spatial experience - we have our (relatively) familiar Urban Corridors, but in place of a
wall of storefronts, there is a permeable zone of dwellings, greenhouses and public mixing spaces, through which we enter the Productive Commons.






the proDuctive Block analYSiS oF BlockS anD reSulting open Space
Overview
In our system, a block is defined as a unique area enclosed by a closed loop of linked network edges. Loops are generated in our system as a result of the Overlap Parameter (Ov), shown previously (p.104-105). A larger Ov (from a possible range of 0 to 1) results in more redundancy in distribution paths and a more highly connected network overall.
In our pursuit of a highly connected, highly social urban fabric, like that found in our reference cities, like New York, we showed that higher Overlaps were preferable (p.108). It was also shown however, these higher values result in escalating infrastructural investment costs (p106-107). Additionally, these loops occasionally include terminal points of distribution trees, which, in effect, become ‘dead ends’ or ‘cul-de-sacs.’ A higher Ov would result in fewer of these dead ends however would also result in smaller blocks, which, as we can see now, would diminish the size of continuous productive plots. Therefore we recognise, in the implementation of our system, several tissues will need to be generated using different values, and the various benefits will need to be weighed in choosing the fittest output.
Our sample tissue, generated with Ov = 0.7, shows a diverse distribution of sizes of productive commons, accommodating different scales of production and a good balance of network cost and connectivity relative to our reference cities.
Block morphology (white) and resulting open space (grey)
Scale = 1 : 5000
Identification of productive blocks in the generated tissue.
Individuals are called out and categorized according to their number of edges
of Area and Nr of Blocks in the tissue
nalyS i S
Closed loops, or Blocks, were identified in the sample tissue sorted be number of edges. Various properties were measured, including areas of production, dwelling and open space.
BLOCK GEOMETRIES EXTRACTED AND SORTED BY NUMBER OF EDGES
Comparing the properties of the blocks revealed:
• number of edges corresponds to the relative area of the block. Blocks with fewer sides are smaller and visa versa.
1514147,300
• Of the 24 blocks, half have 4 edges. However, 46% of the total surface area of all the blocks, is delivered by the blocks with 6 or more edge components, which are only 5 blocks.
• Also, when the size of the blocks increases, the area of production grows, from 25% for the smaller blocks to a maximum of 53.5% for the larger ones. This suggests that the larger blocks are more suitable to be used for commerial farms.

ew yO rk b lO ck
Area of Block:
Area of Open space:
Area of Productive Common:
Total area of Production:
Area of Greenhouses:
Area of Rooftop Greenhouses:
• Lastly, we can see that the average built space (coverage) for all the blocks is 61% of the area. The different blocks show a range from 41.9% to 73.4%, providing different densities of built morphology throughout the tissue. This will inform further differentiation in the urban experiences in the neighbourhoods.
• The large edges may require intersections with a secondary path network to provide more choice for social movement.
Nr. of Dwellings:
Nr. of People: 1854
Average Production Intensity: 0 ppl/hA
PerfO r M ance O f the Pr O ductive b lO ck
To understand these figures, relative to our reference cities, we can compare these findings again to the Manhattan block.
As mentioned before, the area of the Manhattan block is 43% of the size of our sample Productive Block shown here. Therefore numbers should be considered as percentages, not compared directly.
t he Pr O ductive b lO ck
Total Area of Block:
Total Area of Open space:
m2
m2 Area of Productive Common:
Total area of Production:
Area of Greenhouses:
m2
Area of Rooftop Greenhouses: 8.600 m2
Potential Productive Roofs:
Footprint of Dwellings:
of Dwellings:
Average Production Intensity: 2.2 ppl/hA
The built area in Manhattan is with 60%, slightly larger then the coverage of 58% in our block showed here.
the key difference however is in use of the open space between the two tissues.
In New York the remaining open space is nearly completely devoted to circulation (with almost double the length of cirulatory perimeter, 1.7x when compared to the same area); whereas in our new Productive Block, a considerable
amount of open space has been generated for Edible Infrastructures, in all three spatial zones; on the circulation paths, within the built clusters, and within the Productive Common.
Resulting Networks delimited by architectural form - Urban Circulatory System and Productive Commons
Productive Commons
Built Clusters
Urban Circulatory Network
t wO t y P e S O f O P en S Pace
We’ve seen how the emergent structure of our Productive Block organises open space into an interior Productive Common and an Urban Circulatory Corridor bounding its edges.
Next we’d like to look at how the two open space types are related, how they might connect, and look for opportunities to facilitate flows of people across both, making the productive areas accessible to public. We can see the two systems clearly across the tissue by identifying the urban voids, and sorting the spaces into: those within a given range of network edges, and those outside that range, and in the 'interiors' of the blocks.
A survey of the resulting diagram shows that in a few cases these different types of open spaces connect, but more often the productive commons are isolated into islands, trapped within an enclosure of built form. While this structure serves to facilitate production by concentrating open space into continuous workable plots, it denies much of the inhabitants access to one of the primary resources treasured by most urbanites, access to open green space. Furthermore, it continues the long standing separation of consumers from their food sources. In the next section we'll look at how we might link these islands of open space into a new kind of urban network.

proDuctive commonS recreational noDeS/ network
Overview
In order to connect the two types of open space we propose to place parks and recreational programme within the productive commons. These recreational nodes are then linked back to the primary network with paths going through the built form of dwellings and greenhouses. The allocated areas and secondary paths will give children access to green space without the need of crossing circulatory routes and everyone will have access to a quieter secondary circulatory system for bikes and pedestrians only.
assumptions mentioned above.
With the area and number of nodes defined, now the nodes need to be placed inside of the productive common. To do that, we find the centre of mass of the open space cluster. When one node is required it is placed on this centre point. When more nodes are to be placed, a circle is drawn to locate the nodes at a maximum walking distance of 3 minutes. From this theoretical location, the actual location of the recreational node is ensured within the space. At last the required area is allocated.
Para M eter S
48. Alexander, C., et. al., 1977. A Pattern Language: Towns, Buildings, Construction.
r ecreati O nal nO de S g enerative r ule S
To find the area required for the recreational spaces the number of residents in the block were counted and estimated that 30% of these will be children. We allocate 1 m2 of space per child to be required as playground (this number can be adjusted for different community demographics). The area is then broken up to serve between 500 and 1000 residenΩts each.
As a reference, Christopher Alexander48 describes the required open spaces in urban tissue as 15 to 30 m2 per person. Assuming that 1/50 of the total number of people is in the space at the same time, and providing a space for 500-1000 people, the minimum area would be app. 150 m2 which complies with our
(Nr) Nr of people per block count the number of people connected to a specific open space
(P) Percentage of children determines the amount of children in order to define the size of the recreational node
(A) Catchment area defines what is the maximum number of people served by one recreational node
(D) Maximum walking distance sets the maximum distance between two nodes within a cluster.
1. Detect centroid of productive common area
2. Determine # of Nodes for a max three minute walking distance
3. Locate within and allocate required area
Rules applied to various sized Productive Commons, resulting in placement of 1, 2, and 4 Recreational Greens respectively Rules for the allocation of Recreation Green Spaces
Small Productive Common (2,744 m2)
1 node generated - 218 m2 for 723 residents
Large Productive Common (31,115 m2)
4 nodes generated - 1,289 m2 for 4,248 residents
Medium size Productive Common (8,698 m2)
2 nodes generated - 530 sq meters for 1744 residents
Parks & Recreational Green Network resulting in a secondary low-intensity circulatory system. The numbers indicate the # of people served by that specific Recreational Node.
Primary Network Path New Secondary Circulatory System Productive Commons
Recreational nodes connect to the primary network through built clusters, creating paths which utilise all three spatial zones.
The resulting network of paths and nodes activates the Productive Commons as a public green space.
a SecO ndary r ecreati O nal n etwO rk
Recreational Nodes were then connected by finding paths through the built clusters back to the primary network.
The resulting recreational network is composed of three types of paths:
• Green paths through the productive commons
• Semi-enclosed/covered paths through the built clusters utilizing public greenhouses and social mixing spaces
• Primary urban circulatory paths
These paths will also serve to provide access to dwellings within the cluster, but as yet but without access to the primary circulatory paths.

proDuctive valleYS maXimiZing Solar eXpoSure For proDuction
Overview
Having identified an emergent organisational structure within our blocks, with clear concentrations of production, we can now begin to prioritise these areas for solar exposure.
The previous algorithms have lacked local rules for regulating building heights, only an overall cap. By introducing a post-processing step at this point we can ensure that the building heights are distributed according to their proximity to productive surfaces. Buildings that are nearer to a productive common will have a lower maximum height. As buildings get further from the common, their maximum height will be higher. Building heights will be highest at the perimeters of the blocks, along the urban circulatory corridors, adding to the different characters of the two spatial zones.
b uilding h eight r ule S
The building height redistribution algorithm steps are as follows:
• First identify the productive commons within each block
• Set the obstruction angle, according to the local climate and the corresponding sun height
• For each dwelling, check the proximity to the productive common, and the elevation of the dwelling
• Check if this data corresponds with the allowable height, dependent on the obstruction angle
• If the position of the dwelling is too high, look outwards of the productive common to find the first location that matches the criteria. Relocate the dwelling to this new found position
• Continue the steps for all the dwellings, until all are inside of the obstruction envelope
1. Buildings check location relative to Productive Common
2. Allowable Height is identified based on relative position (obstructing dwellings are indicated in red)
3. Obstructing dwellings are moved toward network edges creating ‘Productive Valleys’
Sections extracted showing before and after redistribution of building heights.
Block Before Building Height Redistribution

Para M eter S
(a) Obstruction Angle climatic input how steep the Valleys can be build, to not obstruct the sun
(p) Position of dwelling location of the dwelling according to the closest productive common
(H) Allowable Height according to the obstruction angle and the position of the dwelling, a maximum allowable height can be defined

Block After Building Height Redistribution
r e S ultS
The effect is terraced setbacks around the commons on the interiors of the blocks and tall volumes lining the edges: creating Productive Valleys which have a clear agricultural character and Urban Canyons/Corridors which emphasise a more urban spatial character.
Furthermore, these setbacks can be utilized to provide private outdoor space or greenhouses for residents which will be explored in the typological development chapter.
April 1 - Solar Exposure Before Redistribution
April 1 - After Redistribution
June 21 - Solar Exposure Before Redistribution
June 21 - After Redistribution
partial shade - 3 to 6 h. of solar radiation
partial sun - 6 to 8 h. of solar radiation
full sun - 8+ h. of solar radiation
Growing zone
Area Distribution of Solar Exposure June 21:
P lanting ZO ne S by SO lar ex POS ure
Solar analysis of our prototypical Productive Block, before and after, shows the changes as a result of our redistribution of building heights.
Analysis was run for two dates, using London as the location. Outdoor planting usually begins after last frost, usually in April for London, therefore the first analysis was run for April 01. At the other extreme we show the solar exposure for summer solstice, June 21, to see how if and what kind of effect we have when the sun is high.
April 1
Area Distribution of Solar Exposure April 1: Page 4
Before Redistribution
After Redistribution
June 21
Results are mapped in three categories of solar exposure, corresponding to the three categories of solar requirements most cultivated crops can be fit into49. These are:
Zone 1 - Full Sun (8+ hrs) - tomatoes, peppers, most vegetables.
Zone 2 - Partial Sun (6-8 hrs) - root vegetables
Zone 3 - Partial Shade (3-6 hrs) - leafy greens
Results show that in April, we have reduced the amount of Partial Shade area by 36%, with a slight increase in Partial Sun (+22%) but a dramatic increase in the amount of Full Sun (+157%).
Meanwhile, as expected, the results in June are not as dramatic, but with a still considerable increase in Full Sun (+87%). Partial Sun/Shade zones have been compromised in exchange for this additional Full Sun area as a majority of vegetables fit into the latter category. However these areas can always be re-balanced later with shade trees if more shade area is required for growing leafy greens and root vegetables.
We can use the maps of the solar zones of each block to begin to develop a planting strategy.
Density of the block (and hence the resulting building heights) as well as overall block area are both factors that will ultimately determine the hours of solar exposure and the type of plants appropriate for planting. Smaller denser blocks will of course result in less sun and therefore be more appropriate for root vegetables and leafy greens.
As a result, each block may choose to specialise in a particular crop or group of crops based on sunlight available to their plot. A kind of trade may develop between blocks each with their particular product to offer.

The Productive Common after building height redistribution.

the proDuctive Block concluSion
As a result of the steps in our algorithmic process, we've seen the emergence of three spatial zones, organised as layers within a new type of Productive Block. We've seen how this block compares in performance with a typical New York block and the new kinds of open space afforded with our block type.
Around the perimeter of the block is the Urban Corridor which was dealt with in the previous section. Within the interior of the block is the Productive Common. We looked at how we might optimise the building height distribution for solar access to this area. We also saw how we might take advantage of this open space to create a secondary network of recreational nodes and paths.
Once these interior patches are linked back to the primary network, it becomes clear that these concentrations of production are serving another role beyond food production. By placing production back into the urban environment, we can see agriculture acting as mechanism for the reintroduction of public space back into the city, fighting back against the continuing privatisation of our cities.
Delimiting the inside (common) from outside (corridor) is the cluster of built form, consisting of dwellings, greenhouses, and social mixing spaces. In the next section we will zoom in to this level, and turn our attention to these aggregations.
aP Pendix: a lg O rith M S
place recreational noDes
• for each productive common:
• assign the adjacent dwellings belonging to that common
• count the number of people
• assign 1 node for 500 and 1 extra node for every increment of 1000 people
• select the children in the block (0.3*ppl) and assign 1 m2 per child
• for each node:
• Define the location:
• 1 in the centre, 2 or more on a circle, with the radius of the circle defined by 3min walking distance between the nodes
• find the closest meshfaces to ensure the physical location inside of the productive commons
• find adjacent meshfaces until the area requirements are met.
seconDary netWork
• for each node:
• connect them all together as an 'ideal' network regardless of the existing geometry
• Detect greenhouses and open space that are available for semi-public circulation
• make the shortest route possible through those spaces:
• following the direction of the 'ideal' paths as guides.
• connect recreational nodes back to primary network
reDistributing DWellings for solar access
• for each dwelling:
• extract the centre point of the geometry
• check its proximity to the open space,
• check the height of the dwelling
• if the height of the dwelling is above the obstruction angle (climate input):
• then remove the dwelling
• find the next empty spot outwards that lies below the obstruction angle.
• replace the dwelling in this spot
• continue until all the dwellings are not obstructing the productive commons.
Productive tyPologieS


proDuctive tYpologieS overview
Having first investigated the outside of our blocks - that is the urban circulatory network, and then the interior - the productive commons, we need to now zoom in and focus our attention on the collection of built form around the perimeter of the block, which delimits the two systems from one another. These clusters display distinct internal and external characteristics which differ from our typical urban model which we will want to explore for their architectural opportunities.
Internally, that is within the clusters, we have a mix/distribution of dwellings, greenhouses and public mixing spaces generated by the algorithms thus far. This mix, and the adjacencies created, show the potential for a variety of unexpected new typologies which mix urban programmes and intensive greenhouse production with a variety of public/privateness of each.
Externally, the clusters have a unique position in a new kind of urban environment. They border two distinct public open space types. In landscape ecology50, these types of edge
conditions are typically dense thriving systems that benefit from the resources of both ecologies they border. In a forest, the canopy thrives due its ability to extract resources from both ground below and the sun above. In a water ecology, the shoreline is often teaming with life, as the organisms that live there have evolved to utilise the resources of both the land and water systems they are situated between. Our inhabitants will likewise see the benefits of living on this kind of edge condition which will have access to both their beloved urban environment and the new productive commons which are woven into the urban fabric.
Our intention in this section, it should be clarified, is not to design in detail, or to dictate an over-arching formal mandate for the city’s typologies. Our aim, instead is to investigate the patterns generated by our system and extract some strategies and tactics (in the form of components and rules) to be employed for the development of a new type of Collective Form.51

50. Forman, R.T.T. and Godron, M., 1986. Landscape Ecology.
51. Maki, F. 2008. Nurturing Dreams
GEOMETRICAL TACTICS
Private terraces
SECTIONAL DIFFERENTIATION OF USE
Lift dwellings over social/mixing
Landscape building
greenhouse dwelling retail/ commercial
VERTICAL CIRCULATION
Interior circulation
Exterior via greenhouse
We are interested in a Collective Form approach, as defined by the Metabolist architect, Fuhimiko Maki52, for its expand-ability, flexibility, and a composition being a result of component parts - the parts of which retain their individual identity in the whole.
We position this approach in contrast to one which would try to envelope the individual units into a monolithic landscape or megaform, where individuality is sacrificed in the interest of a unified formal character. We've seen the negative effects of this approach in the early
Public/semi-public gathering spaces at di erent levels vertical circulation
MATERIAL STUDIES
1/3 of the unit must be transparant the rest will be brick/concrete/stone/etc.
modernist housing experiments across both the US and Europe.
We propose that the potential for a new activated public life will emerge from the unique social interactions made possible in the organisation of public programming and agricultural activity within our productive city. Within this overall structure, private spaces can still be allowed to differentiate and encourage personal ownership and identity.
The result of which will be a diverse and unexpected public space envelope which is a
GREENHOUSE INTEGRATION
Street-to-private transition
glass roof infill
Courtyards Enclosed terraces
‘infill’/cover remaining spaces inside with glass roofs, connecting di erent levels where possible
Generate infill-roof:
- locate dwelling edges - find low spine in center - ‘loft’ surface between
greenhouse layer on facade
result of the dynamic between public & private, productive & urban.
Overview O f tactical OPPO rtunitie S
A quick scan of the morphology generated thus far, some potential opportunities for architectural development have suggested themselves. We'll look at how we might systematise an approach for exploiting these tactical opportunities, such as:
Interior view of enclosed space
• Greenhouse integration, including various degrees of public/private production
• Communal greenhouses serving as circulation, both horizontal and vertical, encouraging a continuity of flows through the clusters, connecting interior of the blocks to exteriors
• Social mixing spaces distributed within the clusters.
• Differentiation of types of dwelling units
each resident decides how much and how intensively to grow.
cluSter analYSiS
c lu Ster analyS i S rule S
Dwellings and greenhouses in the tissue are detected and sorted in clusters. When the units are within a radius smaller then (D), the neighbour distance (in the analysis of out 1km2 sample tissue, shown on the right, D is set to 12 m.), then they are determined to belong to the same cluster. Inside the cluster connections are made between the units. The units are saved in a list of clusters to further categorise into distinct types.
Para M eter S (Nd) Neighbour Distance maximum radius to search for units to join in the same cluster.
System-wide Dwelling & Greenhouse Cluster Topology
Scale = 1 : 5000
Linear Chains
Single Unconnected Cells Linear & Branching Chains
eM ergent tOPO lO gical t y P e S
Study of the topology of the dwellings and greenhouse clusters in our sample tissue reveals a range of possible relationship structures between adjacent units.
Five unique types of relationship were identified as representative of the variations within the tissue.
We call these our 'topological types'. They can be summarised as:
• Single Unconnected Cells
• Linear Chains
• Linear Branching Chains
• Loops
• Double Chains
Most of the continuous connected structures within the tissue can not be described as being solely one of these types, but rather are a combination of these.
These combinations will inform the development of the new combinatorial types.
Direct Connection
Corridor type Connection
Loops via shared Connection Perpendicular Secondary Path
Semi-enclosed loops
linear/parallel 2-sides enclosed ‘L’ 3-sides enclosed ‘U’ 4-sides enclosed
combinations
r elati O n S hi P O f dwelling S tO g reenh O u S e S
Another emergent property in the tissue is the relationship of dwelling and greenhouse units. Instead of only looking at the individual units and their connections, we also have to look at the relationships between these types.
A few typical relationships can be extracted, from parallel clusters aligned side by side, to different degrees of enclosure, up to fully enclosed loops.
As with the previous exploration, within single clusters many different combinations were found, where one cluster for instance, can have multiple enclosed neighbouring clusters.
This data will suggest tactics for differentiation of public, semi-public(communal), and private greenhouses in further steps.
Perpendicular Secondary Path
Semi-enclosed loops
Direct Connection Corridor type Connection
Combinations of corridor access and direct access
acce SS tO c irculatO ry netwO rk
In addition to their topological type and the relationships between production and dwelling units, the individual units can be further classified by their connections back to the primary network.
This further characterisation of dwelling units can be defined according to:
• Topological type of the containing cluster.
• Relationship to greenhouses and public-ness of access ways.
Combinatorial Cluster
Loops via shared Connection
• Proximity and orientation to the network.
• Relative depth within the larger dwelling clusters.

tYpologY ruleS
tranSlating Data into tYpeS
With the topological data extracted from the tissue, we can translate our cells and clusters into typological components.
These building blocks will each bring with them rules for combination which will suggest access and aspect, public/private character, circulation, and sectional differentiation.
Public and private spaces will be allocated providing different spatial character to the clusters. Greenhouses and newly formed communal spaces will be exploited for both access and production.
The rules developed in this section should be seen as part a master planning tool, to be put into the hands of individual architects and designers in the interest of the collective manifestation of the Productive City.

Single Node
Linear Chain
Linear Chain
Single Node
Linear Branching Chain
Linear & Branching Chains
Rowhouse Type

Linear Branching Chain
Dual aspect with direct access to public space
Linear Chain
Loop/cluster
Loop/cluster
Linear Branching Chain
Double Chain
Double Chain
Loop/cluster
Combinations
Combinations
Double Chain
Combinations
b aS e cOMPO nentS
Our typological types inform the differentiation of dwelling units that will form the base components of our new combinatorial typologies. These base components can be related to familiar dwelling types found in most urban environments.
Courtyard Type
Dual aspect with shared access via communal space


Apartment / Block Type
Single Aspect units accessible via internal circulation
Single cells, Linear and Linear Branching Chains suggest individual direct access, and dual aspect, that is light and air from two sides, most likely front and back, resembling what we might call a rowhouse type.
Double chains are more likely to provide access through internal corridors with single aspect units, such as those found in apartment/block type buildings.

Rowhouse Type
Dual aspect with direct access to public space

Courtyard Type
Dual aspect with shared access via communal space
Loops suggest a courtyard type, but can be further differentiated as single or dual aspect units arranged in a courtyard configuration. The difference being that access is via a semiprivate communal space, which is distinct from access directly from the circulatory network.
Apartment / Block Type
Single Aspect units accessible via internal circulation

Relationships can be plotted on a gradient between:
• Urban/Agricultural
• Private/Public
r elati O n S hi P tO Pr O ducti O n
When productive units are added to these base types, further differentiation is generated. Production units can be classified as public, communal (semi-private) or private based on scale, topology, and adjacency to the circulatory networks.
When public or communal production is situated between the dwellings and circulatory networks, these can serve as a semi-public/ private gradient and suggest social-mixing spaces for residents in these clusters.
Providing circulatory space within these units creates opportunities for flows of people between dwellings and the two circulatory networks, the primary urban network on the outside of the blocks, and the secondary green/ recreational network on the interiors.
TOPOLOGY
Semi-enclosed Forecourt
Courtyard Component with Productive Embedded within Rowhouses Accessed via Private Productive Units
Apartment / Block Component Accessed via Productive

DWELLING TOPOLOGY
Vertical Circulation Within Apartment/block
S ecti O nal O PPO rtunitie S
These same relationships can be exploited in section as well. Corridor access can be accommodated within the dwelling clusters, with the introduction of new communal spaces providing the buffer between the semi-private corridor and the connection to the public urban space. On the other hand, direct access, dual aspect units can circulate vertically in tall public/semi-public atrium-like greenhouse volumes.
The terracing generated by our building height redistribution provides opportunities for private productive spaces on the adjacent roofs. These can manifest as small private, or communal outdoor spaces or greenhouses. Alternatively, some climates, such as those in higher colder latitudes, might suggest large greenhouse envelopes. These might be constructed as temporary structures which are seasonal, or might be used to transition a territory longer term, from a colder climate to a warmer one as is projected due to global warming.
Vertical Circulation Within Greenhouse
ARCHITECTURAL TACTICS



proDuctive tYpologieS eXampleS oF implementation in Situ
Overview
To illustrate how these rules might be deployed in context, we've extracted two sample clusters from our tissue for development, one medium density (491 ppl/ha) and another high density (1023 ppl/ha).
The medium density cluster is equivalent to roughly one half the area of a typical New York block with a density similar to blocks in the Brooklyn Heights neighbourhood. Meanwhile the high density is comparable in density to blocks in Manhattan's Upper East Side.
r ule S
1. Architectural development of a cluster begins with identification of the topological types, and establishment of the base components.
2. Next greenhouses are analysed for their scale, relationship to dwellings, and proximity to the primary network. Public and communal greenhouses are identified, and access to dwellings through greenhouses is established.
3. Communal mixing spaces are located.
4. Vertical circulation is resolved
5. Envelope is developed, including implementation of productive facades and large scale greenhouses.
Example of implementation in medium density cluster:
1. Identify the dwelling components and define access and aspect
meDium DenSitY cluSter
2. Identify public and private character of greenhouses.
3. Locate common access spaces and assign greenhouses used for circulation.
4. Define vertical access in dwelling clusters.
Dwelling with corridor access
Dwelling with individual access
Public greenhouse, for circulation
Semi-public greenhouse, for access Private greenhouse
Common access under dwellings
Vertical circulation


Example implementation of a medium density typology
Section - North-South
Scale: 1:500
meDium DenSitY tYpologY
Overall Footprint of Cluster: 11,700 m2
Footprint of Dwellings: 5,600 m2
Nr. of Dwellings: 222
Nr. of People: 575
Population Density: 491 ppl/ha
Total Productive Area: 10,000 m2
Area of Greenhouses: 6,300 m2
Area of Rooftop Greenhouses: 3,700 m2
Overall Production Intensity: 5.8 ppl/100 m2
Example of implementation in a high density cluster:
1. Identify the dwelling components and define access and aspect
high DenSitY cluSter
2. Identify public and private character of greenhouses.
3. Locate common access spaces and assign greenhouses used for circulation.
4. Define vertical access in dwelling clusters.
Dwelling with corridor access
Dwelling with individual access
Public greenhouse, for circulation
Semi-public greenhouse, for access
Private greenhouse
Common access under dwellings
Vertical circulation


Example implementation of a high density typology
Section - North-South
high DenSitY tYpologY
Overall Footprint of Cluster: 6,400 m2
Footprint of Dwellings: 4,000 m2
Nr. of Dwellings: 253 Nr. of People: 655
Population Density: 1023 ppl/ha
Total Productive Area: 3,100 m2
Area of Greenhouses: 2,600 m2
Area of Rooftop Greenhouses: 500 m2
Overall Production Intensity: 21.1 ppl/100 m2




proDuctive tYpologieS concluSion
The generated tissue exhibits a diverse variety of topological clusters. When we read these and categorise them according to the relations shown in this section, rules can be extracted which can lead to an architectural language of the Productive Typologies.
Our aim has been to extract rules or guidelines. The final implementation of these is still the work for the individual architect, and therefore these should be understood as a procedural set of design guidelines.
In our example implementation, we were particularly in a highly articulated Collective Form, purposefully diagrammatic, where each unit maintains its identity. However, we do not suggest that this is the inevitable outcome of the data-set.
In dealing only with relationships, we believe that the extracted rules are flexible enough that it's possible to imagine that, with another interpretation of the rules, one can have a very different architectural form than the ones shown.
What should be evident however, in comparing several architectural interpretations, is a likeness in the experience of sequential spaces, the relative density and production intensity.
the Productive city
teSt caSe: kungSängen (Stockholm region)


the proDuctive citY new territorieS - new inputS
Overview - e x Panding the catalO gue O f i n P utS
So far we've seen how our system performs on a small site, grafted into an existing urban fabric. We've also explored in more depth, the emergent spatial characteristics of a 1 km2 prototypical tissue generated without a context.
Now we'd like to turn our attention to a largely undeveloped rural site within the greater Stockholm urban region to test how the system adapts to new contexts and populations, how it will perform on larger sites, and what sorts of new inputs will be needed for implementation in new territories.
StO ckh O l M
Stockholm is actively pursuing progressive policy efforts to both mitigate and prepare for the effects of climate change54, including a goal to be fossil fuel free by 2050 and the adaptation of building codes for a warmer wetter climate. Within the next 50-100 years, Stockholm is
expecting a 4-6 deg C. increase in average temperature (comparable to Barcelona today), 0.5m sea level rise and, most interesting to us, a 1-2 months extended growing season.
Additionally, within the next 20-30 years the city is expecting 150,000 new residents53. By then, some projections are that the earth's mid-latitudes will be nearly uninhabitable, precipitating unprecedented migrations. Scandinavian countries are preparing for an influx of environmentally displaced peoples.
However, nowhere in Stockholm's climate strategy, that we have found, do they address agriculture or food policy, one of the largest contributors to greenhouse gas emissions.
Therefore we propose to a build a new city for 150,000 people, on an agricultural peninsula near Kungsängen, 30 min from Stockholm by commuter rail. This new community will serve as a prototype, mixing urban commuters from Stockholm, with climate refugees arriving with agrarian skills, creating a working model for a new Productive City.

53. Stockholm municipality website
54. Rosenzweig, C. et al. 2011. Climate Change and Cities. p. 241
teSt caSe: kungSängen
initialiSation oF the Site
Site i n P utS
Initialisation for a new site involves establishing: site boundaries, landscape components and whether they are developable, or to be protected, and attractors which will influence the distribution of local densities.
Site Extent/Boundaries:
The proposed site is on a 12 km2 peninsula, bounded on the north by a commuter train line and the existing town of Kungsängen. The eastern boundary is waterfront, while south and west is primarily wooded waterfront.
Landscape Features:
1. Agricultural & Pasture land (Matrix)9 km2 total area to be developed into our new Productive City.
2. Waterfront/Shoreline (Edge) - will serve as an attractor for development. Densities will increase in proximity to waterfront. We will want to preserve public access to this resource.
3. Wooded lands (Patches) - to be protected and may potentially serve as low-intensity recreational areas.
4. Settlement/Town (Patch) - will initially be an attractor. As our new settlement begins it will use the resources of the existing town to the south. However over time, the old town will be allowed to redevelop using the rules of the new productive city.
Other Attractors:
5. Kungsängen Train Station - a new commuter station in the old town of Kungsängen will link our settlement to downtown Stockholm in 30min. a dditi O nal cO n S iderati O n S fO r future S ite S
Topography - Although the terrain on this site is fairly flat, future sites will likely encounter highly varied and sloped terrains. A preprocessing algorithm should be developed which evaluates the grade of slopes within the site and hours of solar exposure. This data would then be used to inform the land available for settlement or cultivation in Settlement Simulation.





teSt caSe: kungSängen
Simulation Scaling StrategY
Ov erview
The Kungsängen site is 9 km2. The Settlement Simulation was developed to run on a 1km2 field size ensuring all production for those residents is within a walk-able distance.
While the simulation will run on larger sites, (a test for this site was run on a 2 km2 field) we found that large continuous productive plots, and associated Wholesale Nodes, begin to aggregate away from the denser dwelling clusters, which form around the attractor seeds. Also, computation time grows considerable with each km2 added, as the various evaluations that are done across the simulation field must check more and more cells at every run count.
r ule
S
Therefore, our strategy for scaling will be to tile the site, sequentially adding 1 km2 tiles, taking initialization data from the boundary of each previous tile.
Working in tiles will ensure that the required production capacity and associated Wholesale Nodes are distributed within 15min walking distances of residents.
On our Kungsängen site, tiles will be assigned different Density (D) and Friendliness (F) values providing residents a choice of 'neighbourhoods' with varying spatial characters city-wide. The most compact neighbourhoods will be nearest the train station and another at the south end of the shoreline with views back to the city of Stockholm. The western-most tiles near the wooded patches will be the most dispersed.
f urther d evelOPM ent
The distribution of Densities and Friendliness values across the tiles should really be negotiated by the tiles as they develop, in a larger scale cellular automata type calculation (as happens cell by cell within the simulation.)
Also to be investigated is how the outputs of the early tiles may be re-informed by the results of the latter tiles.
D80/F.85
D80/F.85
D120/F.70
D120/F.70
D80/F.85
D140/F.70
D180/F.85
D140/F.70 1 km 1 km
D100/F.60
D80/F.85
D140 / F.70
D180/F.85
D120/F.60
D140/F.70
teSt caSe: kungSängen Settlement Simulation
P OP ulati O n/ S O cial i n P utS
Parameter settings for the Settlement Simulation are determined by the intended population, including number of people, as well as social and cultural factors.
As shown in the system development, Density and 'Friendliness' together determine the compactness of the dwelling typologies and the distribution of production sizes.
Commuters typically prefer not to live too dense, although our target audience will be attracted to the 'walk-able' lifestyle promoted by our city so we will attempt to strike a balance.
Our second intended social group, environmentally displaced peoples, will likely arrive with agrarian skills, so we will aim to provide for more distributed smaller scale production.
Para M eter S :
(D) Population Density: 180 ppl / ha (initial tile) based on sodermalm, a desirable, medium density neighbourhood in central stockholm.
(F) Friendliness Factor: 0.85 (initial tile)
0.6-0.85 tested, 0.85 selected for desirable distribution of production sizes
(PI) Production Intensity: 120m2 / person area for basic production for fruits / vegetables per annum - slightly higher than previous to account for shorter growing season.
(Dw) Dwelling/Household size: 80m2 /2.29 ppl average values for stockholm, from municipally published figures
(A) Field Size: 1 km2 extent of initial settlement, a 'walk-able' site
(v) Vertical Growth threshold: 4 number of surrounding dwellings needed to trigger vertical growth
(AD) Aggressiveness of Development = 1 required adjacent productive cells
(PC) Productivity Ceiling = 9 pp/ha
(HC) Height Ceiling (Allowable # of Floors) = 6
M e th O d
The simulation was run on 12 tiles successively, each roughly from 0.5 to 1.5 km2
a dditi O nal cO n S iderati O n S
Climate - Our initial system was developed for deployment in temperate biomes. The Stockholm region, while still within the temperate zone, is bordering on the Boreal forest. This challenge was interesting to us as an opportunity to tune our implementation or the system and perhaps suggest new inputs.
One potential change, due to the shorter growing season, is that productive cells will likely require more greenhouse enclosures and energy production to achieve previous values.






Settlement Simulation Output Shown as Phased Growth:
Left:
Phase 1, initial 1km2 tile D180 | F.85
Right: Phase 2, with second tile added D140 | F.70
Growth continues, Phases 3 & 4: Left: D120 | F.70 & D180 | F.85
Right: D100 | F.60 & D120 | F.60
Phases 5 & 6, including the redevelopment of old town Kungsängen: Left: D80 | F.85
Right: D140 | F.70


Settlement Simulation on a 9 km2 field, showing a high density compact district around the bay to the NE and dispersed district with detached dwellings in productive fields to the SW
Kungsängen
0 1 5km
i nternal & e xternal factO r S

In our sample tissues, the network was generated from internal inputs, connecting concentrations of production to dwellings, varying the detour and degree of connectivity. The Brooklyn test showed how this internal network could link to surrounding urban fabric.
The Kungsängen site presents a new scenario. Here our development will serve as a satellite city to Stockholm, the region's metropolitan core, therefore the commuter link is of prime importance. We'll look at how this link affects the internal network organisation.
Para M eter S
(A1) Minimum Area of productive cluster: 1 hA. threshold for placing Wholesale node
(A2) Max. size of a commercial farm: 7 hA. threshold for splitting a farm into a multiple Wholesale nodes
(W) Walking Distance (max) to a Retail Node: 83 meters/ 1 minute (at typ. pace 5km/hr)
(αd) Detour Angle: 30°
(Ov) Overlap Percentage: 50% (30, 50, 70, 90 tested - 50 selected)
new i n P utS / rule S
The combined site was scanned for Wholesale and Retail nodes. Two new network inputs / rules were implemented for testing. First a transit spine was placed, linking our site to the commuter train station with stops every 400m (5 min walks) Transit nodes checked for nearby Wholesale nodes, and if within range, they were merged.
Secondly a waterfront path was input with nodes for public space every 2 min. These nodes checked for retail nodes nearby and similarly merged if within range.
9 km2 tissue scanned for Retail & Wholesale Nodes (left)
New Inputs (right)
• Transit line & stops at 5min walks linking to existing commuter station (dark blue)
• Waterfront path with nodes at 2 min walks (light blue)
New Nodes are integrated into the distribution network:
1. Transit Nodes check for Wholesale Nodes within attraction range. If found, the Wholesale Node is integrated into the Transit Node.
2. Waterfront nodes are likewise joined with Retail Nodes.
Integration Map (left): shows most highly connected and integrated paths, ie, those most likely to be destinations for inhabitants of the city
Choice Map (right) shows most likely through routes to those destinations for network wide trips.
All nodes were subsequently linked in distribution trees and overlapped as per previous steps.
cO nnectivity a nalyS i S
The resulting paths and nodes were analysed for connectivity and ranked. These ratings were then used to generate the pubic space programme areas on the paths and nodes and built morphology was adapted to accommodate these public spaces.
a dditi O nal cO n S iderati O n S
Choice maps should inform a path widths in terms of establishing primary routes through a city. We currently use the integration measure as it tells us about most likely destinations for trips within the network.
Working with existing street patterns - in Brooklyn we took a tabula rasa approach, sweeping away the existing urban fabric within our site. It would be interesting to see how our system could work less aggressively in existing fabrics, perhaps suggesting subtle changes to a street network
Additionally, one critique that could be levelled against our emergent street patterns is poor navigability. This could be addressed architecturally, with what Kevin Lynch55 would call 'monuments', interventions which establish unique identities to different places/nodes providing cues for mapping a city. However, there still may be a scenario where a more easily navigable pattern be demanded, something more grid-like. We believe that our system could be adapted to achieve these ambitions.
Overall 9 km2 Network Map showing Wholesale, Retail, Transit, and Waterfront Nodes and Paths rated by Integration value
Built Morphology adapts to rated network generating Productive Blocks, with Urban Corridors & Productive Commons.


teSt caSe: kungSängen
proDuctive BlockS & recreational network
Overview
With the network generated, and built morphology adapted to the network programming, we turn our attention to the Productive Blocks.
Blocks across the different tiles exhibit much more variation in size than in our 1km2 tissue, resulting from the varying sizes of continuous productive areas generated by the different combinations of Density and Friendliness values. These larger blocks are also lower in population density and provide a different dwelling character than those within our denser more central tiles.
r ecreati O nal nO de S / n etwO rk
With landscape elements as inputs, we can look to the natural features of the site to complement our recreational network.
Recreational Nodes within the blocks can connect to protected forests and the public waterfront, creating more varied recreational environments for city dwellers accessible by a low-intensity path network.
Also, the sides of blocks that front wooded patches will be particularly desirable.
S O lar e x POS ure O P ti M i Sati O n
Northern latitudes will require lower sun obstruction angles and therefore terracing within the blocks will be more gradual. This will also mean that some blocks will not be able to meet the requirements of the building height algorithm if the density is too high. A rule could be implemented which allows dwellings to move to adjacent blocks if this situation arises.



Waterfront Nodes create public spaces along a coastal path
Recreational Nodes connecting back to native wooded patches
Productive Valleys optimised for solar exposure to the Commons
teSt caSe: kungSängen tYpologieS
t y PO lO gie S infO r M ed by cl i M ate
The Kungsängen test site suggests new challenges in the interpretation of the 'Production Intensities' set out in the Settlement Simulation.
In a colder climate with a shorter growing season, it will be expected that there will be a heavier reliance on greenhouses, potentially including covering the productive common.
In order to maintain the public nature of our production areas, this would suggest the inclusion of the recreational green spaces within that enclosure, as well as the secondary circulatory network. This leads to the further question of whether access to our dwellings will likewise open into the communal greenhouse or whether it is a separate self-contained structure.
We propose for Kungsängen, the development of a 'Greenhouse Block' type, with an enclosure continuing to the extent of block perimeter. Implementation of greenhouse blocks would be based on the collective Production Intensity of the block, as determined in the Settlement Simulation, the date for which is stored in each cell of the model.
S eaSO nality and cl i M ate c hange
The materiality and structure of the greenhouse block would need to consider whether these are intended as:
• Year-round greenhouse skins with adjustable levels of permeability and ventilation based on seasonality
• Or temporary enclosures which are erected (or perhaps simply skinned) when the temperature drops below the crop's tolerance threshold. This 'event' could be celebrated as a seasonal festival.
Also at play in the greenhouse strategy, is the role of climate change in a region's long-term productivity potential.
It may be found, for a certain territory, that a greenhouse is required for the next 20-30 years, but that with the manifestation of expected temperature increases, the greenhouse will be no longer necessary.
Certain crops, such as leafy greens and root vegetables, have long been grown in unheated winter greenhouses in climates such as the New England region of the US. Others, if desired, would require heat and are probably not feasible at the moment but could subject of further development. For example, the surrounding dwellings, built of thick masonry walls could act as heat sinks to temper fluctuations in temperature.


56. Alexander, C. et.al. 1977. A Pattern Language: Towns, Buildings, Construction.
Overview teSt caSe: kungSängen
Further work: citY & regional Scale
So far, a model has been built to produce tiles whose dimensions are considered “walk-able.”
For our experiments we’ve used a 1km2 as most of points in this field could be walked to from any other in 12-15 min. This scale could be correlated to say, a district.
A rudimentary strategy for tiling was implemented which, upon further development, could pass parameter inputs from one tile to the next. This requires identifying what role each neighbourhood fills in the larger system, thereby the types of neighbourhoods that are needed and what information each neighbourhood should pass ‘up’ to the larger model to inform adjacencies in the collective.
We believe this scaling can be addressed using the logic similar to that of global climate modelling where the grid resolution is scaled to switch between a large generalized model and higher resolution local models. In a 'lower resolution' regional model each cell would represent a 1km2 plot of our current simulation.
The results of the regional simulation would provide the inputs (Density, Friendliness, etc..) for the neighbourhood-scale Settlement Simulation allowing specific cells to be generated at this higher resolution.
regi O nal Pr O ductivity ty P e S
Working at this larger scale, also allows us to consider elements of the food system which were excluded from the city/district scale, such as:
• Grains & Cereals
• Livestock Grazing Areas
• Timber Production Lands
• Preserved Natural & Recreation Areas
These products require larger continuous land areas and will need to be implemented as new cellular components in the regional model. Per
capita production area requirements will need to be established and incorporated into the regional model.
n ew i n P utS / c riteria
Existing topography and landscapes will need to be considered and new metrics will need to be introduced for the preservation of ‘natural’ areas for CO2 absorption, watershed preservation and recreation.
Subsequently the network strategy will require revisiting, as the larger scale network will have new cell types. Grains, cereals and livestock will need to be processed and transported into the distribution nodes within the dwelling clusters. New fitness criteria for travel distances will also need to be considered.
Para M eter S
(AR) Area (of Region)
(DR) Overall Density (of Region)
(FR) Compactness (Friendliness)
(T) Travel Distance
Qualitie S MeaS ured
(PG) Productivity Gradient
frequency Distribution of production intensities
Distribution of Sizes/Densities of Settlements (compared to Zipf's law and c alexander's suggested patterns56)





Cells in the regional model will represent portions of tissue at the neighbourhood scale. The regional simulation will inform input values for 1km scale models.
Additional Production Types are required at the regional scale, including: grains and cereals, grazing land for livestock, and timber production.
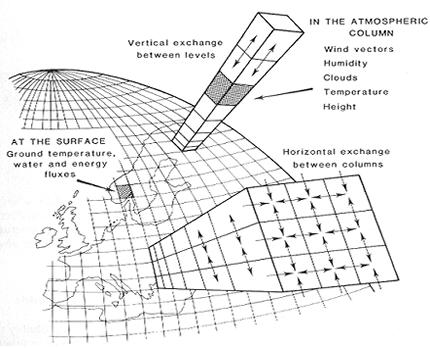
Climate modelling at increasing resolutions using a variable scale grid.
SPatial develoPment evaluationS & concluSionS
SITE CONDITIONS
TARGET DENSITY
FRIENDLINESS FACTOR

SETTLEMENT SIMULATION
PATTERN OF DWELLINGS & PRODUCTION
WALKING DISTANCE
DETOUR ANGLE
PLACE DISTRIBUTION NODES
URBAN CIRCULATORY NETWORK
ATTRACT GEOMETRY TO PATHS AND NODES
BUILD NETWORK
REC. SPACE RATIOS
PLACE PARK/ RECREATION NODES
BUILD SECONDARY NETWORK GENERATE PRODUCTIVE VALLEYS
DIFFERENTIATE GREENHOUSE TYPES
COMBINATORIAL DEVELOPMENT
PRODUCTIVE TYPES
Spatial Development goalS & proceSS
In Part I we developed a Settlement Simulation for distributing dwellings and production, and a networking strategy for connecting the two.
Our aim in Part II was to show how analysis of the generated patterns and resulting networks informs the translation into urban space and new typologies.
We began with a network analysis of a sample tissue generated in Part I and showed how connectivity of the nodes and paths informs their public programmes.
As a result of the programming and aggregation of built forms along the network, we found a new organisational structure for our city emerges, the Productive Block, which differentiates urban space into Productive Commons, Urban Corridors and a thick but permeable zone of dwellings and greenhouses delimiting the two. The two spatial types were re-connected with a secondary recreational network and the block morphology was optimised to provide maximize solar radiation to the Productive Common.
The clusters of built volumes within this boundary layer were analysed for their own emergent organisation and rules were proposed for the development of new combinatorial typologies, or Productive Types.
The total effect, is the Productive City, productive at multiple hierarchies.
Spatial Development evaluationS &
Pr O gra MM ing u rban S Pace
Four categories of urban programmes were addressed throughout the Urban Circulatory Network: Social Mixing, Circulation, Agricultural, and Recreational/ Gathering spaces. These were distributed based on analysis of network characteristics.

rban nO de S
ode connectivity informed type and size of programme space allocated. A distribution of node connectivity and types resulted in a differentiation of urban gathering spaces, with nodes ranging in function from ‘Major Hubs’ to ‘Local Nuclei.’
Higher connected nodes, such as the Major Hubs, were considered higher-level attractors and therefore assigned more open space and more floor area dedicated to social mixing spaces.
u rban Path S
Paths were likewise analysed for their connectivity/integration and ranked. Path sections were then broken into four programme zones, Public/Private Transition, Pedestrian Paths, Infrastructure, and Transport/Transit. Sectional Components were proposed for the four zones.
S Patial h ierarchy
In applying the scaled programme areas to nodes and paths throughout the sample, differentiation in public spaces across the tissue began to suggest a spatial hierarchy, at a city district scale (1km2). Further work is required to resolve how a hierarchy might emerge when multiple districts are combined.
Pr O ductive b lO ckS
We saw how our system organizes the urban fabric into Productive Blocks with novel spatial characteristics. The blocks are enclosed by dwellings and greenhouses with Productive Commons inside and Urban Corridors outside.
Comparison of our blocks with New York showed how the morphology of our blocks prioritises interior area for production, compared to a Manhattan block which is optimised for perimeter length (storefront exposure.)
recreati O nal netwO rk
Recreational green spaces were located and scaled according to block population and open space, creating parks accessible to each block without crossing an urban corridor. These were then connected with a lower intensity secondary network for pedestrians and bicycles.
Pr O ductive cOMMO n S O P ti M i S ed fO r S O lar e x POS ure
Solar Analysis of a typical Productive Common showed that our block morphology generates productive space which can be planted in three solar zones, corresponding to the three categories of crop sun needs.
A building height redistribution algorithm was implemented to maximize available sun hours which resulted in a 157% increase of ‘full sun’ in April and an 87% increase in July.
Spatial Development evaluationS & concluSionS
eM ergent t y PO lO gie S
Studying the adjacencies generated by our algorithms, strategies and tactics were extracted for the development of new architectural typologies. The new typologies differentiate spatial experiences by taking advantage of their relationships to urban circulatory corridors and productive areas.




t y PO lO gical cOMPO nentS
Topological analysis of the dwelling and greenhouse units revealed a diverse population of connected clusters, reducible to essential topological types. These suggested base dwelling components based on familiar urban typologies.
Through their collective organisation, location in a cluster relative to the primary network and their relationship to productive units, its was shown how these base components and their associated rules informs translation into new typologies.

g reenh O u S e differentiati O n
The characteristics of greenhouse units, such adjacency to circulatory networks, cluster size, and relationship to dwelling components, informed their function in the cluster.
This included public/privateness of greenhouse units, and suggested which clusters might serve as circulation between dwelling units and circulatory networks.
l andS ca P e ele M entS aS in P utS
We saw in the Kungsängen test case how landscape elements can act as inputs, serving as attractors for settlement, informing new types of network nodes, and connecting to the internal recreational network.
Further development is needed on how a more challenging terrain will inform plant-able and buildable areas, water strategies and solar access to crops.
r egi O nal netwO rk in P utS
We also saw how the presence of a metropolitan core in the settlement region can influence the network strategy. In a satellite city like Kungsängen, the commuter train link became a unique and vital node and can reorganize an internal network.
Our initial test demonstrated how transit links might be integrated however further development might look at how to the scale transit linked nodes accordingly.

Scaling Strategy
Kungsängen provided an opportunity to test our system on a larger territory. Our tiling strategy showed that much more work is needed on how information is passed between each stage of growth; for example how simulation parameters for each tile could be determined algorithmically and how successive growth can re-inform already established districts.
The question remains as our population grows, and increasingly urbanises how will we colonise the new territories that will become available.
(site: eastern edge of Greenland Ice Sheet, 10m thick as surveyed in Jan 2011)




And how will we feed that population when we run out of land?
(site: Ijmeer, Amsterdam, NL)




city aS Pr O ce SS
Approaching the city as a process suggests a different strategy for planning. One that is capable of handling problems of complexity, of which the city is surely one, as Jane Jacobs57 identified half a century ago.
This was our starting point for using an algorithmic design approach. At the core of our system, is a relationship between population and the surface area required to feed them followed by the movement of energy/resources through a system.
In place of planning maps, we a working towards a procedural model for development which respects the relationships required to sustain a city. This method acknowledges a multiplicity of solutions and allows for individuals to act on their own motivations, while providing a framework that maintains those key relations.
b uilding t he SySte M
In considering the various ways to structure an algorithmic design tool, we have chosen to build our system in a series of sequential 'layers', each building on the last.
Each step involves, identifying the key relationships at the various scales and hierarchies, testing various parameters for their effects, and evaluating.
The strength of this approach lies in the ability to focus each step on one problem, isolating the variables involved in solving that problem, and building on emergent properties from the layer below.
a PP licati O n /de P lOy M ent O f the SySte M
We see potential in the application of our work as an interactive planning tool. Ultimately, the deliverable of the tool should be not a 2D drawing or 3D model, but an interactive solver, maintaining a set of strategic relations but adaptable to changing urban conditions.
The tool is not complete, of course, but we believe it will be enriched by experimental deployment in a variety of contexts and territories.
The major piece of work that remains is in the tailoring of a diverse catalogue of inputs for adaptation to new environments and in the growth/phasing strategy - how do you seed a new city, and change the ‘plan’ according to the actual growth that materialises and unexpected changes that arise. Some of these changes may be changing climate, population and cultural changes, changes in the flows of people and materials between neighbouring cities, and new technologies in agriculture and energy production.
utati O n a l l i M itati O n S
All scripts have been run on a standard laptop computers in individual components and range in computation time from 3 minutes to 3 hours. The Settlement Simulation itself computes a 1 km2 field of Population Density 200 ppl/ha in approximately 20 minutes.
We believe initial implementation will require a skilled operator and designer/interpreter. Once the initial model is setup for a territory, it could seen how an interface might be developed which allows changes in parameters to be explored by the client/municipality.
Also, at the moment, we are limited in the number of parameters that can be calculated in one run. Additional inputs will likely require additional 'layers' of algorithm which would be strategically inserted in the process. Some inputs, such as regional and topographical considerations, will need to be built in another resolution - whether finer grain or courser dependant on the challenge to be addressed.
agriculture & the city
We hope to have shown that by considering the problem of agricultural production as part a system, including the energy inputs, production, consumption and waste cycles in our schema, we can turn the current crisis into an opportunity.
Agriculture benefits from proximity to consumers. Urban waste products can be turned into energy. Water runoff, can be reused. Meanwhile the city also benefits from local production which: removes transportation and storage costs, reduces greenhouse gas emissions, creates jobs, and provides new types of urban spaces which re-connect city dwellers with their food sources.
The obstacle to implementation of such a system is the current political-economic value system which prioritises land speculation and private development, and down-plays the actual cost of natural resources. This kind of myopic thinking has long driven the separation of our cities and farmlands, only accelerated by industrial technologies.
It will take visionary municipalities to question the value of their land as it is currently framed, repositioning it as a vital energy source worth protecting and managing.
We've demonstrated one prototype for how this aim might be achieved. We hope we've shown that it is not only feasible, but a novel and provocative future for cities and city dwellers.
Mathe M atical M O delling fO r a ddre SS ing urban de S ign P r O ble MS
At the outset of our research, our interest was in tackling one specific challenge facing our increasingly urbanizing planet, however through the exploration of solutions to urban agricultural, we believe we’ve developed a methodology which could be adapted to a address a number of urban spatial challenges. The core of our method involves identifying essential systemic relationships and building a computational model for exploring the possibility space implicit in those relationships.
The resulting spatial patterns are then analysed and interpreted for their emergent organisational forms which likely would not be apparent in the initial setting out of the local rule-set.
Adapting this methodology to address new challenges likewise involves:
• the identification of the fundamental relationships
• parameters and rules which explore the possible variations of the relationship
• analysis of the emergent phenomena
• interpretation and extraction of strategies and tactics for implementation
We see our research as a small step in demonstrating the potential of mathematical modelling and simulation in addressing the complex urban spatial and programmatic challenges facing us in the future, many of which we are now only beginning to get a glimpse of.
'Steering' the M O del: lO cal rule S , glO bal effectS , t endencie S
We’ve shown how by putting in place a framework of simple rules, then varying the degree of intensity of certain parameters we can generate urban tissues which exhibit gradients of concentration of various properties.
Just as mathematical models used in physics are correlated with physical processes, we have attempted to base our rules on basic human behaviours that produce tendencies in the built environment. The result is that we can see a degree of isomorphism between our model and certain patterns in human settlement.
This allows us the opportunity to experiment and study the effects of changes in parameters of the system and make certain observations as to the potential effects on urban environments.
These parameters are likewise correlated to physical world relationships. By fixing some constants, such as the area of productive surface required per capita, we can ensure that criteria
is met, while allowing the designer to compare the remaining range of viable configurations. This flexibility to operate within a space of possible solutions allows for implementation within a variety of contexts.
In evaluating the generated tissues, we once again compare back to observed metrics to make fitness evaluations. Certain criteria are fairly rigid. Existing agricultural techniques for example, have established limits to their productivity per given area while remaining economically viable. We can set this relationship as a constant for the time being and adjust it in the future as economic conditions and technologies evolve.
Others are in the realm of value judgements and have sociopolitical consequences. For example as the ‘fineness’ of the grain of our urban tissue increases in response to raising the (D) Density and lowering the (F) Friendliness settings, the maximum size of productive plots decreases are the continuous space desired by commercial growers is squeezed out. This allows us to find the threshold at which a community can
expect to rely on commercial growers within a certain type of urban morphology. Beyond this point, the community must be prepared to increasingly ‘grow their own’ or become part of a collective which contributes back into the local food system.
This may be a desired effect as this sort of system could create jobs should the desire for agricultural jobs exist as does in certain migrant worker communities. These possibilities are allowed for within the framework of the model and it is through analysis of the particular social and political context that we would determine the fitness of each scheme. What remains constant is that the global footprint of the community would remain within the limits established in building the model.
auth O r S hi P
This type of procedural approach opens up questions of the role of designer and degrees of control. As we built up the computational model, we consciously made an effort to avoid deterministic tendencies, trying instead set up boundaries of a system within which solutions could emerge.
We are interested in the changes this has introduced into our mode of operation. There is a temptation to believe that in setting up the most precise set of inputs and rules extracted from the design problem, an obvious 'solution' would be offered by the algorithm, however, it has been our experience that even in this framework, there are decisions that remain firmly in the realm of the designer.
The following pages show the script used to generate the settlement simulation, detectclusters and build the network.
The software environment used was McNeel's Rhinoceros 4.0 with the Grasshopper plugin version 0.8.0051.
Settle M ent S i M ulati O n
Private Sub qRunScript(ByVal w1 As Double, ByVal d As Integer, ByVal w As Double, ByVal M As Mesh, ByVal C1 As Integer, ByVal int As List(Of Double), ByVal NM As Boolean, ByVal DE As Boolean, ByVal X As Boolean, ByVal w3 As Double, ByVal C0 As Integer, ByVal vu As Boolean, ByVal crvs As List(Of Curve), ByVal range As Double, ByRef intList As Object, ByRef chk As Object)
If X OrElse runcount = 0 Then ResetValues If NM = True Then initAttractMesh(M, crvs, w, range, intL) Else
UseBorder(M, int, intL) End If End If
Dim popDens As Double = (BldgCount * 2.59) / (AreaMassProperties.Compute(M).Area / 10000) If (DE = True AndAlso popDens >= d) OrElse (DE = False AndAlso EndCount > M.Faces.Count - 1) Then FinalOutput(M, intL) intList = intL Exit Sub End If
NextGeneration(M, w, intL, DE, w1, w3, C0, C1)
'=== OUTPUT ===
If vu Then intList = intL
'=== PRINT IN READ OUT === print(" ") print("Dwellings = " & BldgCount) print("Production Capacity = " & FarmCount) print("Population Density = " & (BldgCount * 2.59) / (AreaMassProperties.Compute(M).Area / 10000) & " ppl / hA")
runcount += 1 print(" ") print("RC=" & runcount) print("EC=" & endcount) End Sub
'<Custom additional code>
Dim runcount As int32 = 0
Dim endcount As int32 = 0
Dim BldgCount As int32 = 0
Dim FarmCount As int32 = 0
Dim HybridCount As int32 = 0
Dim Greenhouse As int32 = 0
Dim BldSpots As int32 = 0
Dim No_Farms As int32 = 0
Dim intL As New List(Of Double)
Dim rand As New Random ()
'=======Reset All Values to start the simulation====
Private Function ResetValues As Boolean runcount = 0 endcount = 0 BldgCount = 0 FarmCount = 0 HybridCount = 0 Greenhouse = 0 BldSpots = 0 No_Farms = 0 intL.Clear
Return True End Function
'=======Final Output================================
Private Function FinalOutput (ByVal M As Mesh, ByVal intL As List(Of Double)) As Boolean print("Field Full or Reached Desired Density") print("Dwellings = " & BldgCount) print("Production Capacity = " & FarmCount) print("Population Density = " & (BldgCount * 2.59) / (AreaMassProperties.Compute(M).Area / 10000) & " ppl / hA") runcount += 1 print(" ") print("RC=" & runcount) print("EC=" & endcount)
Dim maxH As int32 = int32.MinValue
Dim maxP As int32 = int32.MinValue
For i As int32 = 0 To M.Faces.Count - 1
Dim P As int32 = ProductionValue(intL.item(i)) If P > maxP Then maxP = P If intL.item(i) >= 2 AndAlso intL.item(i) < 3 Then
Dim h As int32 = Height(intL.item(i))
If h > maxh Then maxh = h End If Next
print("Max Floors = " & maxH) print("Max Production Intensity = " & maxP) Return True End Function
'=======NextGen Function============================
Private Function NextGeneration (ByVal M As Mesh, ByVal w As Double, ByRef intL As List (Of Double), ByVal DE As Boolean, ByVal w1 As Double, ByVal w3 As Double, ByVal C0 As int32, ByVal C1 As int32) As Boolean
Dim r As Double = rand.NextDouble print("random =" & r) If r > w Then Print("Loner")
'R E M O T E S E T T L E R
Dim EmptL As New List (Of int32)
Dim EmptyType As int32 = 0
Dim UBound As int32 = 1
If EndCount >= M.Faces.Count - 1 Then EmptyType = 1
For i As int32 = 0 To M.Faces.Count - 1 If intL.item(i) >= EmptyType AndAlso intL. item(i) < EmptyType + UBound Then EmptL. Add(i)
Next
Dim NewBLD As int32 = EmptL.item(rand. Next(EmptL.Count))
Dim Place As Boolean = PlaceBLDGS(M, w, NewBLD, intL, DE, w1, w3, C0, C1)
Else
Print("Friendly")
'F R I E N D L Y S E T T L E R
Dim BuildL As New List (Of int32) For i As int32 = 0 To M.Faces.Count - 1 If intL.item(i) = 0.5 OrElse (intL.item(i) >= 2 AndAlso intL.item(i) < 3) Then BuildL. Add(i)
Next
Dim Friendly As int32 = BuildL.item(rand. Next(BuildL.Count))
Dim NList As List (Of int32) = NeighbourList(M, Friendly)
Dim NewBLD As int32 = NList.item(0)
Dim Place As Boolean = PlaceBLDGS(M, w, NewBLD, intL, DE, w1, w3, C0, C1)
End If
Return True
End Function
'========Pick a cell to Place New Building and define STATE of SIM========================================
Private Function PlaceBLDGS (ByVal M As Mesh, ByVal w As Double, ByRef NewBLD As int32, ByRef intL As List(Of Double), ByVal DE As Boolean, ByVal w1 As
Double, ByVal w3 As Double, ByVal C0 As int32, ByVal C1 As int32) As Boolean
Dim Pr As Double = rand.NextDouble
Dim agr As Double = rand.NextDouble If DE = False Then
Print("High Tech Factor = " & Pr) End If
Dim State As Int32 = 0
'DECIDE WHICH TYPE OF FARMING IS BEING PICKED '0 MEANS ONLY USE OPEN FARM PLOTS '1 MEANS THE USE OF HIGHER PRODUCTIVE LANDSCAPES If DE = True Then If EndCount > M.Faces.Count - 1 Then State = 1
ElseIf DE = False Then If Pr < w1 OrElse EndCount > M.Faces.Count - 1 Then State = 1
End If print("State: " & State)
If intL.item(NewBLD) >= 2 AndAlso intL. item(NewBLD) < 3 Then NewBLD = CheckBuiltNeighbours(M, NewBLD, intL)
'MAKE SURE THAT A CELL IS ALWAYS CONNECTED TO A GREENSPACE If intL.item(NewBLD) < 2 AndAlso agr > w3 Then
Dim Faces() As int32 = M.Faces.
AdjacentFaces(NewBLD)
For Each F As int32 In Faces
Dim FFaces() As int32 = M.Faces.
AdjacentFaces(F)
Dim Build As int32 = 0
For i As int32 = 0 To FFaces.Length - 1 If intL.item(FFaces(i)) >= 2 AndAlso intL. item(FFaces(i)) < 3 Then Build += 1 Next If Build >= 3 Then print("It's too busy here and I want to stay next to this Productive Plot!")
Return False Exit Function End If Next End If
ChangeCell(M, w, State, NewBLD, intL, DE, C0, C1)
Return True End Function
'=======Change Cell According to State And Discovered Type=====================================
Private Function ChangeCell (ByVal M As Mesh, ByVal w As Double, ByVal State As int32, ByVal NewBLD As int32, ByRef intL As List (Of Double), ByVal DE As Boolean, ByVal C0 As int32, ByVal C1 As int32) As Boolean
Dim MaxFloors As Double = 2 + C0 / 100
Dim type As Int32 = 0
If intL.item(NewBLD) >= 1 AndAlso intL. item(NewBLD) < 2 Then type = 1
If intL.item(NewBLD) >= 2 AndAlso intL. item(NewBLD) < 3 Then type = 2
If type = 0 Then Print("(0) WeeWhoa! I'm a Zero. Do your whatever you like!.")
If type = 1 Then Print("(1) What Fun! I'm a One! Make a bldg and MOVE a farm or increase the Productivity.")
If type = 2 Then Print("(2+) WooHoo i'm a TWO! SEE How Dense it is and place a dwelling!.")
If type = 0 Then
If State = 0 Then intL.item(NewBLD) = 2.01
If State = 1 Then intL.item(NewBLD) = 2.0101
BldSpots += 1
ElseIf type = 1 Then
If intL.item(NewBLD) >= 1.0003 Then print("This plot is to valuable to convert into a Dwelling, continue the search!")
Return False
Exit Function
End If
If State = 0 Then intL.item(NewBLD) = 2.01 If State = 1 Then intL.item(NewBLD) += 1.01
BldSpots += 1
ElseIf type = 2 Then If intL.item(NewBLD) >= MaxFloors Then print("This Building is too high, continue the search!")
Return False
Exit Function
End If
intL.item(NewBLD) += .01
End If
Dim n As int32 = 0
If State = 0 Then n = 3
If type = 1 Then n = 4
ElseIf State = 1 Then n = 3
If type = 0 Then n = 2
End If
If State = 0 Then
BuildAdjacentProduction(M, NewBLD, 0, n, 0, w, intL, C1)
No_Farms += 3
ElseIf State = 1 Then If FarmCount >= n + 3 Then
BuildAdjacentProduction(M, NewBLD, 1, n, 1, w, intL, C1)
Else
BuildAdjacentProduction(M, NewBLD, 0, n, 0, w, intL, C1)
EndCount += n
End If End If
BldgCount += 1 FarmCount += 3
If State = 0 Then EndCount += 3 If type = 0 OrElse type = 1 Then EndCount += 1
ElseIf State = 1 Then If type = 0 Then EndCount += 1
End If
Return True End Function
'=======Build Production Landscape (farms or hybrids) around urban===============================
Private Function
BuildAdjacentProduction (ByVal M As Mesh, ByVal NewBLD As int32, ByVal type As Double, ByVal n_farms As int32, ByVal State As int32, ByVal w As Double, ByRef intL As List (Of Double), ByVal C1 As int32) As Boolean Dim ProductionCeiling As Double = 1 + (C1 / 10000)
Dim NList As List (Of int32) = NeighbourList(M, NewBLD)
Dim okList As New List (Of int32) For i As int32 = 0 To NList.Count - 1 If State = 1 AndAlso intL.item(NList.item(i)) >= ProductionCeiling Then Continue For If intL.item(NList.item(i)) >= type AndAlso intL.item(NList.item(i)) < type + 1 Then okList.Add(NList.item(i))
Next okList.Sort
If okList.Count < n_farms Then Print("Expanding the search - looking for neighborNeighbors!")
Dim NNList As New List (Of Int32) For i As int32 = 0 To NList.Count - 1 NNList.AddRange(NeighbourList(M, NList. item(i)))
Next
Dim NNList_ok As New List(Of Int32) For i As int32 = 0 To NNList.Count - 1
Dim coincident As int32 = 0
If NNList.item(i) = NewBLD Then coincident += 1
For j As int32 = i + 1 To NNList.Count - 1
If NNList.item(i) = NNList.item(j) Then coincident += 1
Next
For j As int32 = 0 To okList.Count - 1 If NNList.item(i) = okList.item(j) Then coincident += 1 Next
If coincident = 0 Then NNList_ok.Add(NNList. item(i))
Next
Dim NNList_0 As New List (Of Int32) For i As int32 = 0 To NNList_ok.Count - 1 If State = 1 AndAlso intL.item(NNList_ ok.item(i)) >= ProductionCeiling Then Continue For If intL.item(NNList_ok.item(i)) >= type AndAlso intL.item(NNList_ok.item(i)) < type + 1 Then NNList_0.Add(NNList_ok.item(i))
Next NNList_0.Sort okList.AddRange(NNList_0)
End If For i As int32 = 0 To Math.Min(n_farms - 1, okList.Count - 1)
If State = 0 Then intL.item(OkList.item(i)) += 1.0001 If State = 1 Then intL.item(OkList.item(i)) += .0001 Next
If okList.Count < n_farms Then Print("No neighborNeighbors Found! Picking a random spot")
Dim TestL As New List (Of int32) For j As int32 = 0 To M.Faces.Count - 1 If State = 1 AndAlso intL.item(j) >= ProductionCeiling Then Continue For If intL.item(j) >= type AndAlso intL.item(j) < type + 1 Then TestL.Add(j) Next
TestL = Shuffle(TestL)
If TestL.Count > n_farms - okList.Count Then For j As int32 = okList.Count To n_farms - 1
If State = 0 Then intL.item(TestL.item(jokList.Count)) += 1.0001
If State = 1 Then intL.item(TestL.item(jokList.Count)) += .0001 Next Else
Print("No Available Plots Found! Picking a random build spot")
Dim TestL2 As New List (Of int32) For j As int32 = 0 To M.Faces.Count - 1
If State = 1 AndAlso intL.item(j) >= ProductionCeiling Then Continue For If intL.item(j) >= type + 1 AndAlso intL. item(j) < type + 2 Then TestL2.Add(j) Next
TestL2 = Shuffle(TestL2)
If TestL2.Count > n_farms - okList.Count Then For j As int32 = okList.Count To n_farms - 1
intL.item(TestL2.item(j - okList.Count)) += .0001 Next Else
print("HELP, the Field is Full! What to do?!")
print("Alarm! Make more farms: " & (n_ farms - okList.Count))
End If End If End If Return True End Function
'=======Find Neighbours for specific type============
Private Function FindNeighbours (ByVal M As Mesh, ByVal intL As List (Of Double), ByVal type As int32, ByVal TestList As List (Of int32)) As List (Of int32)
Dim TestBLD As int32 = TestList.item(rand. Next(TestList.Count))
Dim N_List As List (Of Int32) = NeighbourList(M, TestBLD)
Dim ok_List As New List (Of int32)
For i As int32 = 0 To N_List.Count - 1 If intL.item(N_List.item(i)) >= type AndAlso intL.item(N_List. item(i)) < type + 1 Then ok_List.Add(N_List. item(i))
Next
Ok_List = Shuffle(ok_List)
Return Ok_List End Function
'=======Check how many Neighbours are built=========
Private Function CheckBuiltNeighbours (ByVal M As Mesh, ByVal NewBLD As int32, ByRef intL As List (Of Double)) As int32
Dim OutPut As int32 = NewBLD
Dim NList As List (Of int32) = NeighbourList(M, NewBLD)
Dim HList As New List (Of Double)
Dim h As Double = intL.item(NewBLD)
Dim counter As int32 = 0
For i As int32 = 0 To NList.Count - 1
HList.Add(intL.item(NList.item(i)))
If intL.item(NList.item(i)) >= 2 AndAlso intL. item(NList.item(i)) < 3 Then counter += 1 Next
Dim NArr() As int32 = NList.ToArray
Dim HArr() As Double = HList.ToArray
Array.Sort(HArr, NArr)
If HArr(HArr.Length - 1) < h OrElse counter <= 3 Then
OutPut = NArr(0)
End If
Return OutPut End Function '=======Neighbourpicking (8 Neighbours)=============
Private Function NeighbourList (ByVal M As Mesh, ByVal r As int32) As List (Of int32)
Dim ptL As New List (Of Point3f)
Dim NeigList As New List (Of int32)
Dim ptA, ptB, ptC, ptD As New Point3f
M.Faces.GetFaceVertices(r, ptA, ptB, ptC, ptD)
ptL.Add(ptA)
ptL.Add(ptB)
ptL.Add(ptC)
ptL.Add(ptD)
For i As int32 = 0 To M.Vertices.Count - 1
Dim TMPpt As Point3f = M.Vertices.item(i)
For j As int32 = 0 To 3 If TMPpt = ptL.item(j) Then NeigList.Add(i)
End If Next
Next
Dim faceL As New List (Of int32)
Dim faceL_ok As New List (Of int32)
For i As int32 = 0 To NeigList.Count - 1
Dim vertF() As int32 = M.Vertices. GetVertexFaces(NeigList.item(i)) faceL.AddRange(vertF)
Next
For i As int32 = 0 To faceL.Count - 1
Dim counter As int32 = 0
If faceL.item(i) = r Then counter += 1
For j As int32 = i + 1 To faceL.Count - 1 If faceL.item(i) = faceL.item(j) Then counter += 1
Next If counter = 0 Then faceL_ok.Add(faceL.item(i)) End If Next
Dim ShufList As List (Of int32) = shuffle(faceL_ ok)
Return ShufList End Function
'=======Shuffle List Function========================
Private Function shuffle (ByVal indexL As List (Of int32)) As List (Of Int32)
Dim indexL_ok As New List (Of int32)
Dim li As List (Of int32) = indexL
For i As int32 = 0 To li.count - 1
Dim rInd As Int32 = rand.Next(li.Count)
Dim pick As Int32 = li.item(rInd)
indexL_ok.Add(pick)
li.RemoveAt(rInd)
Next
Return indexL_ok End Function
'=======Calculate Height Of Plot====================
Private Function Height (ByVal type As Double) As Double
Dim h_st As String = type.toString
If h_st.Length > 4 Then
Dim h_st2 As String = h_st.Remove(4) h_st = h_st2
End If
Dim h_ar() As String = h_st.Split(".")
Dim h As Double = h_ar(1)
Return h End Function
'=======Calculate Production Value Of A Plot========
Private Function ProductionValue (ByVal type As Double) As Double
Dim P_st As String = type.toString
If P_st.Length > 4 Then
Dim P_st2 As String = P_st.Remove(0, 4)
P_st = P_st2
Else
Return 0
Exit Function
End If
Return P_St End Function
d etect c lu Ster S and P lace nO de S
Private Sub RunScript(ByVal intL As List(Of Double), ByVal M As Mesh, ByVal ONOFF As Boolean, ByVal th As Integer, ByVal Ar As Integer, ByRef chk As Object, ByRef Mrkt As Object, ByRef FSt As Object, ByRef Bldgs As Object)
Dim PlotArea As Double = AreaMassProperties. Compute(M).Area / M.Faces.Count
Dim BuildingCluster, FarmCluster As New DataTree (Of int32)
Dim RetailNodes, Farmstands As New List (Of Point3d) If ONOFF Then print("Calculate the Clusters")
CheckClusters(M, intL, BuildingCluster, FarmCluster, RetailNodes, Farmstands, Ar, PlotArea, th) End If
'Last Check to remove overlapping Retail Circles
Dim RetailN As New List (Of Point3d) For i As int32 = 0 To RetailNodes.Count - 1
Dim dL As New List (Of Double)
Dim MinD As Double = Double.PositiveInfinity For j As int32 = i + 1 To RetailNodes.Count1
Dim d As Double = RetailNodes.item(i). DistanceTo(RetailNodes.item(j)) If d < MinD Then MinD = d Next If MinD >= .9 * th Then RetailN. Add(RetailNodes.item(i)) Next
Mrkt = RetailN FSt = FarmStands Bldgs = BuildingCluster chk = FarmCluster
End Sub
'<Custom additional code>
'============Evaluate Clusters======================
Public Function CheckClusters (ByVal M As Mesh, ByVal intL As List (Of Double), ByRef BuildingCluster As DataTree (Of int32), ByRef FarmCluster As DataTree (Of int32), ByRef RetailNodes As List (Of Point3d), ByRef Farmstands As List (Of Point3d), ByVal Ar As int32, ByVal PlotArea As Double, ByVal th As int32) As Boolean
Dim Buildings, Farms As New List (Of int32) For i As int32 = 0 To intL.Count - 1 If intL.item(i) >= 1 AndAlso intL.item(i) < 2 Then Farms.Add(i) If intL.item(i) >= 2 AndAlso intL.item(i) < 3 Then Buildings.Add(i)
Next
GetClusterTree(M, intL, 2, Buildings, BuildingCluster, Farmstands, RetailNodes, Ar, PlotArea, th)
GetClusterTree(M, intL, 1, Farms, FarmCluster, Farmstands, RetailNodes, Ar, PlotArea, th)
Return True End Function
'========Get a Tree of Clusters=====================
Public Function GetClusterTree (ByVal M As Mesh, ByVal intL As List (Of Double), ByVal type As int32, ByVal TestList As List (Of int32), ByRef ClusterTree As DataTree (Of int32), ByRef Farmstands As List (Of Point3d), ByRef RetailNodes As List (Of Point3d), ByVal Ar As int32, ByVal PlotArea As Double, ByVal th As int32) As Boolean
Dim p As int32 = 0
Dim counter As int32 = 0
While TestList.Count > 0
Dim path As New GH_Path (0, p)
'DEFINE CLUSTERS STARTING WITH TALLEST FACE OR A RANDOM SPOT
Dim TallestFace As int32 = FindTallestFace(intL, TestList, type)
Dim Cluster As List (Of int32) = GetCluster(type, M, intL, TallestFace, TestList, Ar, PlotArea, FarmStands, RetailNodes, th) ClusterTree.AddRange(Cluster, Path)
p += 1 counter += 1
If counter = M.Faces.Count Then Exit While End While Return True End Function '===========Define Cluster And Output Data===========
Public Function GetCluster (ByVal type As int32, ByVal M As Mesh, ByVal intL As List (Of Double), ByVal TallestFace As int32, ByRef TestList As List (Of int32), ByVal Ar As int32, ByVal PlotArea As Double, ByRef FarmStands As List (Of Point3d), ByRef RetailNodes As List (Of Point3d), ByVal th As int32) As List (Of int32)
Dim Cluster As New List (Of int32) Cluster.Add(TallestFace) TestList.Remove(TallestFace)
Dim N0_List As New List (Of int32) If type = 1 Then
Dim N_Faces() As int32 = M.Faces. AdjacentFaces(TallestFace)
N0_List = New List (Of int32) (N_Faces) ElseIf type = 2 Then N0_List = NeighbourList(M, TallestFace) End If
Dim NList As New List (Of int32) For i As int32 = 0 To N0_List.Count - 1 If intL.item(N0_List.item(i)) >= type AndAlso intL.item(N0_List.item(i)) < type + 1 Then NList.Add(N0_List.item(i)) Next
Dim counter As int32 = 0
While NList.Count > 0
Dim NNList As New List (Of int32) For i As int32 = 0 To NList.Count - 1 Cluster.Add(NList.item(i)) TestList.Remove(NList.item(i))
Dim NN_Faces0 As New List (Of int32) If type = 1 Then
Dim NN_F() As int32 = M.Faces. AdjacentFaces(NList.item(i))
NN_Faces0 = New List (Of int32) (NN_F)
ElseIf type = 2 Then NN_Faces0 = NeighbourList(M, NList. item(i))
End If
Dim NN_Faces As New List (Of int32) For j As int32 = 0 To NN_Faces0.Count - 1 If intL.item(NN_Faces0.item(j)) >= type AndAlso intL.item(NN_Faces0.item(j)) < type + 1 Then NN_Faces.Add(NN_Faces0. item(j))
Next
For j As int32 = 0 To NN_Faces.Count - 1
Dim coincident As int32 = 0
For Each Face As int32 In Cluster If NN_Faces.item(j) = Face Then coincident += 1
Next
For Each Face As int32 In NList If NN_Faces.item(j) = Face Then coincident += 1
Next
For Each Face As int32 In NNList If NN_Faces.item(j) = Face Then coincident += 1
Next
If coincident = 0 Then NNList.Add(NN_Faces.item(j))
End If Next
Next NList = NNList counter += 1 If counter = M.Faces.Count Then Exit While End While If type = 1 Then FarmStands. AddRange(AddFarmStand(M, Cluster, Ar, PlotArea)) If type = 2 Then RetailNodes. AddRange(AddRetailNodes(M, Cluster, th))
Return Cluster End Function
'==========Add Retail Nodes to Build Cluster========
Public Function AddRetailNodes(ByVal M As Mesh, ByVal Cluster As List (Of int32), ByVal th As int32) As List (Of Point3d)
Dim TestList As New List (Of int32)
For i As int32 = 0 To Cluster.Count - 1 TestList.Add(Cluster.item(i))
Next
Dim MarketTH1 As int32 = (th ^ 2 * math.PI) / 100
Dim minX As Double = Double.PositiveInfinity
Dim maxX As Double = Double.NegativeInfinity
Dim minY As Double = Double.PositiveInfinity
Dim maxY As Double = Double.NegativeInfinity
For i As int32 = 0 To Cluster.Count - 1
Dim Pt As Point3d = M.Faces.
GetFaceCenter(TestList.item(i))
If minX > Pt.X Then MinX = Pt.X
If maxX < Pt.X Then MaxX = Pt.X
If minY > Pt.Y Then MinY = Pt.Y
If maxY < Pt.Y Then MaxY = Pt.Y
Next
Dim RetailN As New List (Of Point3d)
Dim Cpt As New Point3d (MinX + (MaxX - MinX) / 2, MinY + (MaxY - MinY) / 2, 0)
If TestList.Count / MarketTH0 >= 1 Then
Dim dL As New List (Of Double)
For j As int32 = 0 To TestList.Count - 1
dL.Add(Cpt.DistanceTo(M.Faces. GetFaceCenter(TestList.item(j))))
Next
Dim Clust() As int32 = TestList.ToArray
Dim dArr() As Double = dL.ToArray
Array.Sort(dArr, Clust)
RetailN.Add(M.Faces.GetFaceCenter(Clust(0)))
For j As int32 = 0 To Clust.Length - 1
If dArr(j) <= th Then TestList. Remove(Clust(j))
Next
End If
Dim counter As int32 = 0
While TestList.Count > 0
Dim dL As New List (Of Double)
For j As int32 = 0 To TestList.Count - 1
Dim dCl As Double = 0
For Each pt As Point3d In RetailN
Dim d As Double = pt.DistanceTo(M.Faces. GetFaceCenter(TestList.item(j)))
If d <= 2 * th Then dCl += d
Next
dL.Add(dCl)
Next
Dim Clust() As int32 = TestList.ToArray
Dim dArr() As Double = dL.ToArray
Array.Sort(dArr, Clust)
If dArr(dArr.Length - 1) >= th Then RetailN. Add(M.Faces.GetFaceCenter(Clust(Clust.Length - 1)))
For j As int32 = 0 To Clust.Length - 1 For i As int32 = 1 To RetailN.Count - 1
If RetailN.item(i).DistanceTo(M.Faces. GetFaceCenter(Clust(j))) <= Math.Sqrt(2) * th Then TestList.Remove(Clust(j))
Next Next counter += 1
If counter >= M.Faces.Count Then Exit While End While
Return RetailN End Function
'=========Add FarmStand to Farm Cluster=============
Public Function AddFarmStand (ByVal M As Mesh, ByVal
Cluster As List (Of int32), ByVal Ar As int32, ByVal PlotArea As Double) As List (Of Point3d) Dim minX As Double = Double.PositiveInfinity
Dim maxX As Double = Double.NegativeInfinity
Dim minY As Double = Double.PositiveInfinity
Dim maxY As Double = Double.NegativeInfinity
For i As int32 = 0 To Cluster.Count - 1
Dim Pt As Point3d = M.Faces.
GetFaceCenter(Cluster.item(i))
If minX > Pt.X Then MinX = Pt.X If maxX < Pt.X Then MaxX = Pt.X If minY > Pt.Y Then MinY = Pt.Y
If maxY < Pt.Y Then MaxY = Pt.Y
Next
Dim FarmPts As New List (Of Point3d)
Dim Cpt As New Point3d (MinX + (MaxX - MinX) / 2, MinY + (MaxY - MinY) / 2, 0)
Dim vec As New Vector3d (0, (MaxY - MinY) / 3, 0)
Dim no As int32 = Cluster.Count / (7 * Ar / PlotArea)
If no = 0 AndAlso Cluster.Count / (Ar / PlotArea) >= 1 Then no = 1
For i As int32 = 0 To no - 1
If no = 1 Then
FarmPts.Add(CPt)
ElseIf no >= 2 AndAlso no < 6 Then
Dim FPT As Point3d = Cpt + vec vec.Rotate((2 * Math.PI) / no, vector3d. ZAxis)
FarmPts.Add(FPT)
ElseIf no >= 6 Then If i = 0 Then
FarmPts.Add(CPt) Else
Dim FPT As Point3d = Cpt + vec vec.Rotate((2 * Math.PI) / (no - 1), vector3d.ZAxis)
FarmPts.Add(FPT) End If End If Next
Dim FarmShops As New List (Of Point3d) For i As int32 = 0 To FarmPts.Count - 1
Dim dL As New List (Of Double) For j As int32 = 0 To Cluster.Count - 1 dL.Add(FarmPts.item(i).DistanceTo(M.Faces. GetFaceCenter(Cluster.item(j)))) Next
Dim Clust() As int32 = Cluster.ToArray Array.Sort(dL.ToArray, Clust) FarmShops.Add(M.Faces.GetFaceCenter(Clust(0))) Next
Return FarmShops End Function
b uild n etwO rk
Private Sub RunScript(ByVal MarketPoints As List(Of Point3d), ByVal FarmShops As List(Of Point3d), ByVal Angle As Integer, ByVal Overlap As Integer, ByVal ONOFF As Boolean, ByRef NW As Object, ByRef EV As Object, ByRef TL As Object, ByRef TAV As Object, ByRef WL As Object)
If ONOFF Then
Dim Net As List (Of Line) = Network(MarketPoints, FarmShops, Angle, Overlap)
NW = Net
End If End Sub
'<Custom additional code>
'==============Build the Network From Farmstands to Inner-Cluster-Markets==============================
Private Function Network (ByVal Markets As List (Of Point3d), ByVal FarmShops As List (Of Point3d), ByVal Angle As int32, ByVal Overlap As int32) As List (Of Line)
Dim Netw As New List (Of Line)
Dim MarketsUsed As New List (Of Point3d)
If Markets.Count > 0 AndAlso FarmShops.Count > 0 Then
For i As int32 = 0 To FarmShops.Count - 1
Dim Net As New List (Of Line)
Dim MarketsOk As New List (Of Point3d) For j As int32 = 0 To Markets.Count - 1
Dim d0 As Double = Markets.item(j). DistanceTo(FarmShops.item(i))
Dim d1L As New List (Of Double) If FarmShops.Count > 1 Then For k As int32 = 0 To FarmShops.Count1
If k = i Then Continue For d1L.Add(Markets.item(j). DistanceTo(FarmShops.item(k))) Next
If d1l.Count > 0 Then d1L.Sort
If d0 <= (Overlap / 100 + 1) * d1L. item(0) Then MarketsOk.Add(Markets. item(j))
End If Else
MarketsOk.Add(Markets.item(j))
End If Next
Dim dL As New List (Of Double)
For j As int32 = 0 To MarketsOk.Count - 1
dL.Add(FarmShops.item(i). DistanceTo(MarketsOk.item(j))) Next
Dim M_Arr() As Point3d = MarketsOk.ToArray Array.Sort(dL.ToArray, M_Arr) MarketsOk = New List (Of Point3d) (M_Arr)
For j As int32 = 0 To MarketsOk.Count - 1
Dim ptFrom As Point3d = FarmShops.item(i) Dim PtTo As Point3d = MarketsOk.item(j) PtFrom = FindNewPoint(MarketsOk, ptTo, ptFrom, Angle, Net) MarketsUsed.Add(PtTo)
Dim ln As New Line (ptFrom, ptTo) Net.Add(ln)
Next
Netw.AddRange(Net)
Next End If
Dim NetwFIN As New List (Of Line) For i As int32 = 0 To Netw.Count - 1
Dim ln0 As Line = Netw.item(i)
Dim coincident As int32 = 0 For j As int32 = i + 1 To Netw.Count - 1
Dim ln1 As Line = Netw.item(j)
If ln0.From = ln1.From AndAlso ln0.To = ln1. To Then coincident += 1
If ln0.From = ln1.To AndAlso ln0.To = ln1. From Then coincident += 1
Next
If coincident = 0 Then NetwFIN.Add(ln0)
Next
Return NetwFIN End Function
a da P t built MO r P h O lO gy tO netwO rk
Private Sub RunScript(ByVal int As List(Of Double), ByVal M As Mesh, ByVal Netw As List(Of Line), ByVal MOVE As Boolean, ByVal ROTATE As Boolean, ByVal RAND_ANGLE As Boolean, ByVal Dwelling As List(Of Polyline), ByVal GEOM As Boolean, ByVal ATTR As Boolean, ByVal RelAttr As Double, ByVal RESET As Boolean, ByVal DISP As Boolean, ByVal VU As Boolean, ByVal PRGEO As Boolean, ByVal OffsetCrv As List(Of Line), ByVal TRIM As Boolean, ByVal PRODVOL As Boolean, ByVal Streetwidths As List(Of Double), ByVal RetailN As List(Of Point3d), ByVal WholeSaleN As List(Of Point3d), ByRef BldgsPT As Object, ByRef Farms As Object, ByRef BldgsM As Object, ByRef GreenH As Object, ByRef chk As Object, ByRef TopoLineList As Object, ByRef ProdPT As Object, ByRef RoofGreenH As Object, ByRef RoofTOP As Object, ByRef BldgsFLOOR As Object)
If RESET OrElse RC = 0 Then RC = 0 PtList.Clear TypeList.Clear Offset.Clear RetailOffset.Clear WholesaleOffset.Clear Offset = UseSpaceSyntax(StreetWidths) SetNodeOffsets(RetailN, WholesaleN, Netw, RetailOffset, WholesaleOffset)
InitializePoints(M, int, Netw, MOVE, ROTATE, ATTR, RelAttr, RAND_ANGLE, Offset, PtList, typeList, RetailN, WholesaleN, RetailOffset, WholesaleOffset)
End If
Dim ColFarm As New List (Of Mesh)
Dim RoofTFarm As New List (Of Mesh)
Dim BldgsFL As New List (Of Mesh)
Dim BLD As New List (Of Point3d) Dim PPT As New List (Of Point3d)
If DISP Then ptList = BuildingDispersion(typeList, ptList, Netw)
Dim PtEndList As New List (Of Point3d) For i As int32 = 0 To ptList.Count - 1 PtEndList.Add(PtList.item(i))
Next
If MOVE Then PtEndList = ClearStreets(PtList, Netw, Offset, MOVE, RetailN, WholesaleN, RetailOffset, WholesaleOffset)
If VU Then
Dim TopoLines As New List (Of line)
Visualize(M, int, ptEndList, typeList, BldgsM, BldgsFL, Netw, RAND_ANGLE, ROTATE, GEOM,
Dwelling, MOVE, BLD, ColFarm, RoofTFarm, PRGEO, RoofGreenH, GreenH, TopoLines, PPT)
TopoLineList = TopoLines
BldgsPT = BLD
ProdPt = PPT
BldgsFLOOR = BldgsFL
If PRGEO Then For i As int32= 0 To M.Faces.Count - 1 ColFarm.Add(ColorFarm(M, int, i, ProductionValue(int.item(i)), Netw, OffsetCrv, TRIM, PRODVOL))
Next
End If
Farms = ColFarm RoofTOP = RoofTFarm End If
RC += 1 print(“RC: “ & RC)
End Sub
‘<Custom additional code>
Dim RC As int32 = 0
Dim PtList As New List (Of Point3d)
Dim TypeList As New List (Of int32)
Dim Offset As New List (Of Double)
Dim RetailOffset As New List (Of Double)
Dim WholesaleOffset As New List (Of Double)
‘============Detect Offsets of Streets==============
Public Function UseSpaceSyntax (ByVal StreetWidths As List (Of Double)) As List (Of Double)
Dim Offset As New List (Of Double)
Dim dMinNew As Double = 0
Dim dMaxNew As Double = 1
Dim dMin As Double = Double.PositiveInfinity
Dim dMax As Double = Double.NegativeInfinity
For Each d As Double In StreetWidths
If d < dMin Then dMin = d
If d > dMax Then dMax = d
Next
For Each d As Double In StreetWidths
d = ((d - dMin) / (dMax - dMin)) * (dMaxNewdMinNew) + dMinNew
Dim O As Double = 8
If d >= .85 Then O = 14
If d >= .5 AndAlso d < .85 Then O = 10 Offset.Add(O)
Next
Return Offset
End Function
‘============Set Clear Areas of Nodes==============
Public Function SetNodeOffsets (ByVal RetailN As List (Of Point3d), ByVal WholesaleN As List (Of Point3d), ByVal Network As List (Of Line), ByRef RetailOffset As List (Of Double), ByRef WholesaleOffset As List (Of Double)) As Boolean
Dim OffsetRet As New List (Of Double)
Dim OffsetWhole As New List (Of Double) For i As int32 = 0 To RetailN.Count - 1
Dim Retail As Point3d = RetailN.item(i)
Dim count As Int32 = 0 For Each N As Line In Network
If N.To = Retail OrElse N.From = Retail Then count += 1
Next
Dim area As Double = 250 If count = 3 Then area = 500
If count = 4 Then area = 1000
If count = 5 Then area = 2500
If count >= 6 Then area = 5000
Dim Off As Double = math.Sqrt(area / math.PI) OffsetRet.Add(Off)
Next
For i As int32 = 0 To WholesaleN.Count - 1
Dim WholeSale As Point3d = WholesaleN.item(i)
Dim count As Int32 = 0 For Each N As Line In Network If N.To = WholeSale OrElse N.From = WholeSale Then count += 1
Next
Dim area As Double = 1000
If count = 4 Then area = 2500
If count = 5 Then area = 5000
If count >= 6 Then area = 10000
Dim Off As Double = math.Sqrt(area / math.PI) OffsetWhole.Add(Off)
Next
RetailOffset = OffsetRet WholesaleOffset = OffsetWhole
Return True End Function
‘=============Clear the Streets as Last Step========
Public Function ClearStreets (ByVal StartList As List (Of Point3d), ByVal Network As List (Of Line), ByVal Offset As List (Of Double), ByVal MOVE As Boolean, ByVal RetailN As List (Of Point3d), ByVal WholesaleN As List (Of Point3d), ByVal RetailOffset As List (Of Double), ByVal WholesaleOffset As List (Of Double)) As List (Of Point3d)
Dim PtList As New List (Of Point3d)
For i As int32 = 0 To StartList.Count - 1
Dim pt As Point3d = StartList.item(i)
‘CHECK DISTANCE TO NETWORK AND MOVE AWAY FROM IT If MOVE Then
Dim dL As New List (Of Double)
Dim pL As New List (Of Point3d)
For j As int32 = 0 To Network.Count - 1
Dim testPt As Point3d = Network.item(j). ClosestPoint(pt, True)
Dim d As Double = pt.DistanceTo(testPt)
dL.Add(d)
pL.Add(testPt)
Next
If dL.Count > 0 Then
Dim dist() As Double = dL.ToArray
Dim PTS() As Point3d = pL.ToArray
Dim NW() As Line = Network.ToArray
Dim Off() As Double = Offset.ToArray
Array.Sort(dist, PTS)
Array.Sort(dL.ToArray, Off)
Array.Sort(dL.ToArray, NW)
Dim v1 As New Vector3d (0, 0, 0)
For j As int32 = 0 To dL.Count - 1 If dist(j) <= Off(j) Then Dim v2 As Vector3d = pt - PTS(j) If dist(j) <= .1 Then v2 = NW(j).Direction
v2.Rotate(-Math.PI / 4, vector3d. ZAxis)
End If v2.Unitize
v2 *= Off(j)
v1 = v2
pt += v1
Else
Exit For End If Next
‘pt += v1
End If
‘CHECK DISTANCE TO NODES AND MOVE AWAY FROM THEM
For j As int32 = 0 To RetailN.Count - 1
Dim d As Double = pt.DistanceTo(RetailN. item(j))
If d < RetailOffset.item(j) Then
Dim c As New Circle (pt, RetailOffset. item(j))
Dim ptproj As Point3d = c.ClosestPoint(pt)
Dim v As Vector3d = ptProj - pt
Dim l As Double = v.Length v.Unitize
v *= l
pt += v
End If Next
For j As int32 = 0 To WholesaleN.Count - 1
Dim d As Double = pt.DistanceTo(WholesaleN.item(j))
If d < WholesaleOffset.item(j) Then
Dim c As New Circle (pt, WholesaleOffset.item(j))
Dim ptproj As Point3d = c.ClosestPoint(pt)
Dim v As Vector3d = ptproj - pt
Dim l As Double = v.Length v.Unitize
v *= l
pt += v End If Next End If PtList.Add(pt) Next
Return PtList End Function ‘===========Building Packing Code===================
Public Function BuildingDispersion (ByRef typeList As List (Of int32), ByVal ptList As List (Of Point3d), ByVal Network As List (Of Line)) As List (Of Point3d)
Dim dL As New List (Of Double)
Dim maxD As Double = Double.NegativeInfinity
For i As int32 = 0 To ptList.Count - 1
Dim minD As Double = Double.PositiveInfinity
For j As int32 = 0 To Network.Count - 1
Dim d As Double = ptList.item(i). DistanceTo(Network.item(j). ClosestPoint(ptList.item(i), True)) If d < minD Then minD = d Next
dL.Add(minD) If maxD > minD Then MaxD = minD Next
Dim pts() As Point3d = PtList.ToArray
Dim types() As int32 = TypeList.ToArray Array.Sort(dL.ToArray, Pts)
Array.Sort(dL.ToArray, types)
Dim PtLL As New List (Of Point3d)
PtLL.AddRange(pts)
Dim typeLSORT As New List (Of int32) typeLSort.AddRange(types)
Dim bb As New BoundingBox (ptList)
Dim Cpt As Point3d = bb.Centre
For i As int32 = 0 To PtLL.Count - 2
Dim pti As Point3d = PtLL.item(i)
For j As int32 = i + 1 To PtLL.Count - 1
Dim ptj As Point3d = PtLL.item(j)
Dim delta As Double = pti.DistanceTo(ptj)-9 If delta > 0 Then Continue For Dim v1 As Vector3d = pti - ptj
v1.Unitize
v1 *= Math.Abs(delta) / 2
pti += v1 ptj -= v1
ptLL.item(i) = pti
ptLL.item(j) = ptj
Next
Next
For i As int32 = 0 To PtLL.Count - 1
Dim ptTMP As Point3d = PtLL.item(i)
Dim dL1 As New List (Of Double)
Dim ptL1 As New List (Of Point3d)
For j As int32 = 0 To Network.Count - 1
Dim TestPt As Point3d = Network.item(j).
ClosestPoint(ptTMP, True)
Dim d1 As Double = ptTMP.DistanceTo(TestPt)
dL1.Add(d1)
ptL1.Add(TestPT)
Next
Dim DST() As Double = dL1.ToArray
Dim PTS1() As Point3d = ptL1.ToArray
Array.Sort(DST, PTS1)
If PTS.Length > 0 AndAlso DST.Length > 0 Then
Dim v2 As Vector3d = ptTMP - PTS(0)
v2.Unitize
v2 *= DST(0) / ((RC + 1) * DST(0))
ptTMP += v2
ptLL.item(i) = ptTMP
End If Next
typeList = typeLSort
Return ptLL End Function
S O rt tOPO lO gical c lu Ster S
Private Sub RunScript(ByVal PR As DataTree(Of Point3d), ByVal linePR As DataTree(Of Line), ByVal BL As DataTree(Of Point3d), ByVal lineBL As DataTree(Of Line), ByRef PR_ptloner As Object, ByRef PR_ptlinear As Object, ByRef PR_lnlinear As Object, ByRef PR_ptbranch As Object, ByRef PR_lnbranch As Object, ByRef PR_ptloop As Object, ByRef PR_lnloop As Object, ByRef PR_ptcombi As Object, ByRef PR_ lncombi As Object, ByRef DW_ptloner As Object, ByRef DW_ptlinear As Object, ByRef DW_lnlinear As Object, ByRef DW_ptbranch As Object, ByRef DW_lnbranch As Object, ByRef DW_ptloop As Object, ByRef DW_lnloop As Object, ByRef DW_ptcombi As Object, ByRef DW_ lncombi As Object)
SortClusters(PR, linePR, PR_ptLoner, PR_ptLinear, PR_lnLinear, PR_ptBranch, PR_lnBranch, PR_ptLoop, PR_lnLoop, PR_ptCombi, PR_lnCombi)
SortClusters(BL, lineBL, DW_ptLoner, DW_ptLinear, DW_lnLinear, DW_ptBranch, DW_lnBranch, DW_ptLoop, DW_lnLoop, DW_ptCombi, DW_lnCombi) End Sub
‘<Custom additional code>
Public Function SortClusters (ByVal Points As DataTree (Of Point3d), ByVal Lines As DataTree (Of Line), ByRef ptLoner As DataTree (Of Circle), ByRef ptLinear As DataTree (Of Circle), ByRef lnLinear As DataTree (Of Line), ByRef ptBranch As DataTree (Of Circle), ByRef lnBranch As DataTree (Of Line), ByRef ptLoop As DataTree (Of Circle), ByRef lnLoop As DataTree (Of Line), ByRef ptCombi As DataTree (Of Circle), ByRef lnCombi As DataTree (Of Line)) As Boolean
Dim ptLon, ptLin, ptBra, ptLoo, ptCom As New DataTree (Of Circle)
Dim lnLin, lnBra, lnLoo, lnCom As New DataTree (Of Line)
Dim l, l1, l2, br, cb As New int32
For i As int32 = 0 To Points.BranchCount - 1
Dim Path As GH_Path = Points.Path(i)
Dim pL As List (Of Point3d) = Points. Branch(Path)
If pL.Count <= 1 Then
Dim lonPath As New GH_path (0, l) ptLon.Add(New Circle(pL.item(0), 2.5), lonPath)
l += 1
Else
Dim lL As List (Of Line) = Lines. Branch(Path)
If pL.Count - lL.Count = 1 Then
Dim CirL As New List (Of Circle)
Dim linear As Boolean = True
For Each p As Point3d In pL
Dim count As int32 = 0
For Each Ln As Line In lL
If Ln.From = p OrElse Ln.To = p Then count += 1
Next
If count > 2 Then linear = False
CirL.Add(New Circle(p, 2.5))
‘ptLin.Add(New Circle(p, 2.5), linPath)
Next
If linear Then
Dim linPath As New GH_Path (0, l1)
lnLin.AddRange(lL, linPath)
ptLin.AddRange(CirL, linPath)
l1 += 1
Else
Dim braPath As New GH_Path (0, br)
lnBra.AddRange(lL, braPath)
ptBra.AddRange(CirL, braPath) br += 1
End If
ElseIf lL.Count - pL.Count >= 0 AndAlso lL.Count - pL.Count <= 2 Then
Dim looPath As New GH_Path (0, l2)
For Each p As Point3d In pL
ptLoo.Add(New Circle(p, 2.5), looPath)
Next
lnLoo.AddRange(lL, looPath)
l2 += 1
ElseIf lL.Count - pL.Count > 2 Then
Dim comPath As New GH_Path (0, cb)
For Each p As Point3d In pL
ptCom.Add(New Circle(p, 2.5), comPath)
Next
lnCom.AddRange(lL, comPath)
cb += 1
End If End If Next
ptLoner = ptLon
ptLinear = ptLin
ptBranch = ptBra
ptLoop = ptLoo
lnLinear = lnLin
lnBranch = lnBra
lnLoop = lnLoo
ptCombi = ptCom
lnCombi = lnCom
Return True
End Function
b uilding h eight r edi Stributi O n
Private Sub RunScript(ByVal VALBoundary As DataTree(Of Polyline), ByVal DWEL As List(Of Point3d), ByVal angle As Double, ByVal RESET As Object, ByVal VIS As Boolean, ByVal Network As List(Of Line), ByVal NetOffset As List(Of Double), ByRef DW As Object, ByRef DEL As Object, ByRef newL As Object, ByRef chk As Object) If RESET OrElse RC = 0 Then RC = 0 change = 0
DwTree.Clear DistTree.Clear PolyList.Clear
DwTree = InitializeTree(VALBoundary, DWEL, DistTree, PolyList) Offset.Clear Offset = UseSpaceSyntax(NetOffset)
End If Dim moved As Boolean = AgriculturalValleys (DwTree, DistTree, Removed, NewLocation, change, notreloc, angle)
If moved = False Then Stopping = True
If VIS Then
DW = DwTree DEL = Removed NewL = NewLocation chk = DistTree
End If print(“Nr of relocated Dwellings: “ & change) print(“RC = “ & RC)
RC += 1
End Sub
‘<Custom additional code>
Dim RC As int32 = 0
Dim change As int32 = 0
Dim notreloc As int32 = 0
Dim Stopping As Boolean = False
Dim DwTree As New DataTree (Of Point3d)
Dim DistTree As New DataTree (Of Double)
Dim PolyList As New List (Of PolyLine)
Dim Removed As New List (Of Point3d)
Dim NewLocation As New List (Of Point3d)
Dim Offset As New List (Of Double)
‘======RELOCATE DWELLINGS - AGRICULTURAL VALLEYS====
Public Function AgriculturalValleys(ByRef DwTree As DataTree (Of Point3d), ByRef DistTree As DataTree (Of Double), ByRef Removed As List (Of Point3d), ByRef NewLocation As List (Of Point3d), ByRef change As int32, ByRef notreloc As int32, ByVal angle As Double) As Boolean
Dim int As int32 = 0
Dim moved As Boolean = False
Dim DwTreeCopy As New DataTree (Of Point3d)
(DwTree)
Dim DistTreeCopy As New DataTree (Of Double) (DistTree)
For i As int32 = 0 To DwTree.BranchCount - 1
Dim pt As Point3d = DwTree.Branch(i). item(DwTree.Branch(i).Count - 1)
Dim d As Double = DistTree.Branch(i). item(DistTree.Branch(i).Count - 1)
If pt.Z > (d + 4) * math.Tan(math.PI * angle / 180) Then ‘OrElse tooclose Then Dim relocated As Boolean = False For j As int32 = i+1 To DwTree.BranchCount-1
Dim pt1 As Point3d = DwTree.Branch(j). item(DwTree.Branch(j).Count - 1)
Dim d1 As Double = DistTree.Branch(j). item(DistTree.Branch(j).Count - 1)
Dim pt2 As New Point3d (pt1.X, pt1.Y, pt1.Z + 4)
If pt2.Z <= (d1 + 4) * math.Tan(math.PI * angle / 180) Then DwTreeCopy.Branch(j).Add(pt2) DistTreeCopy.Branch(j).Add(d1) NewLocation.Add(pt2) change += 1 relocated = True
Exit For End If Next If relocated Then DwTreeCopy.Branch(i).Remove(pt) DistTreeCopy.Branch(i).Remove(d) Removed.Add(pt) int = i moved = True
print(“Last removed index: “ & int) Else notreloc += 1 print(“I can’t place this nr of dwellings! nr.: “ & notreloc)
End If If DwTreeCopy.Branch(i).Count < 1 Then DwTreeCopy.RemovePath(DwTreeCopy.Path(i)) If DistTreeCopy.Branch(i).Count < 1 Then DistTreeCopy.RemovePath(DistTreeCopy. Path(i))
Exit For End If Next
DwTree = DwTreeCopy DistTree = DistTreeCopy If Moved Then Return True
Else Return False End If End Function
literature citeD
Alexander, C. Ishikawa, S. Silverstein, M. with Jacobson, M. Fiksdahl-King, I. Angel, S., 1977. A Pattern Language: Towns, Buildings, Construction. New York: Oxford University Press.
Ball, P., 2004. Critical Mass: How one thing leads to another. New York: Farrar, Straus and Giroux.
Berghauser Pont, M. and Haupt, P., 2010. SpaceMatrix Space, Density and Urban Form. Rotterdam: NAi Publishers.
Delanda, M., 2011. Philosophy and Simulation: The Emergence of Synthetic Reason. New York: Continuum.
Ewing B., D. Moore, S. Goldfinger, A. Oursler, A. Reed, and M. Wackernagel, 2010. The Ecological Footprint Atlas 2010. Oakland: Global Footprint Network
FAO (Food and Agriculture Organization of the United Nations), 2011. 2010-11 The State of Food and Agriculture. Rome: United Nations.
Flake, G.W., 1998. The Computational Beauty of Nature: Computer Explorations of Fractals, Chaos, Complex Systems, and Adaptation. Cambridge, MA : MIT Press.
Forman, R.T.T., 1995. Land Mosaics: The ecology of landscapes and regions. New York: Cambridge University Press.
Forman, R.T.T., 2008. Urban Regions: Ecology and Planning Beyond the City. New York: Cambridge University Press.
Forman, R.T.T. and Godron, M., 1986. Landscape Ecology. New York: John Wiley and Sons, Inc.
Forman, R.T.T., 2010. Urban Ecology and the Arrangement of Nature in Urban Regions. In: Mostafavi, M. Ecological Urbanism. Baden: Lars Muller, pp. 312-323.
Gottmann, J., 1961. Megalopolis. The urbanized northeastern seaboard of the United States. New York: The Twentieth Century Fund.
Jacobs, J., 1961. The Death and Life of Great American Cities. New York: Random House.
Leach, G., 1976. Energy and food production. Guildford: IPC Bussiness Press Ltd.
Lin, Z., 2010. Kenzo Tange and the Metabolist Movement, Urban Utopias of Modern Japan. London: Routledge.
Lynch. K., 1960. The Image of the City. Cambridge: MIT Press.
Maki, F. 2008. Nurturing Dreams. Cambridge: MIT Press.
Marshall, S., 2008. Cities, Design & Evolution. Munich: Prestel.
Marshall, S., 2005. Streets & Patterns. London: Spon Press.
Mollison., B. 1991. Introduction to Permaculture. Tasmania: Tagari Publications.
OECD (Food and Agriculture Organization of the United Nations), 2011. OECD-FAO Agricultural Outlook 2011-2020. New York: OECD Publishing
Otto,F., 2009. Occupying and Connecting: Thoughts on Territories and Spheres of Influence with Particular Reference to Human Settlement. Stuttgart: Edition Axel Menges
Pearson, S. and Gardner, R. [1997] Neutral Models: useful tools for understanding landscape patterns. In: Bissonette, J. ed. Wildlife and Landscape Ecology: Effects of pattern and scale. New York: Springer. pp. 215-230
Rosenzweig, C. et al. 2011. Climate Change and Cities. Cambridge: Cambridge University Press.
Steel, C., 2008. Hungry City: How Food Shapes Our Lives. London: Vintage
UNEP, 2008. Kick The Habit, A UN Guide to Climate Neutrality. New York, United Nations.
UNFPA (United Nations Population Fund), 2010. The State of world population 2010. New York: United Nations
USDA (United States Food & Drug Administration), 2002. Profiling Food Consumption in America, Agriculture Fact Book. Washington D.C.: USDA
Viljoen, A. Bohn, K. and Howe, J., 2005. Continuous Productive Urban Landscapes: Designing Urban Agriculture for Sustainable Cities. Oxford: Elsevier Ltd.
Weinstock, M., 2010. The Architecture of Emergence: The Evolution of Form in Nature and Civilisation. West Sussex: John Wiley & Sons Ltd.
White, M. and Przybylski, M., 2010. Bracket: On Farming. Barcelona: Actar
a rticle S
Alexander, C., 1965. A City is Not a Tree. Architectural Forum. 122, pp. 58-62
Batty, M., 2009. A Digital Breeder for Designing Cities. AD Magazine, 79 (4), pp. 46-49
Bettencourt, L. et al., 2007. Growth, innovation, scaling, and the pace of life in cities. – Proc. Natl Acad. Sci. USA 104: 7301–7306.
Bettencourt, L. et al., 2006. Growth, innovation, scaling and the pace of life in cities. PNAS, 104 (17), pp. 7301-7306.
Bourque, M. and Canizares, K., 2000. Urban Agriculture in Havana, Cuba. Food production in the community by the community and for the community, Urban Agriculture Magazine. 1(1).
Burke, E., 2010. Farm Plus: Hybrid Agricultural Landscapes. Bracket: On Farming, Barcelona: Actar.
Budiansky, S., 2010, Math Lessons for Locavores, New York Times. Aug 19, 2010
Chamberlain, L., 2007. Skyfarming., New York Times, April 1, 2007
Christensen, K. 2002. Percolation Theory
Doron, G., 2005. Urban Agriculture: Small, Medium, Large. AD Magazine, 75 (3), pp. 52-59
Hillier, B. and Vaughan, L. 2007. The City as One Thing.
Howard, M., 2007. My Empire of Dirt., New York Magazine, Sept 10, 2007
Jensen, M., 1997. Hydroponics. Hort Science, 32 (6).
Patterson, R and Giacomelli, G., 2008. Resource and Production Model for the South Pole Food Growth Chamber.
Rosset, P. and Benjamin, M., 1994. Two steps back, one step forward: Cuba’s National Policy for Alternative Agriculture. Gatekeeper, series No. 46.
Sadler, P., Giacomelli, G. et al., 2009. Prototype BLSS Lunar Greenhouse.
Stanley, D., 2007. Sustainability in practice. Achieving the UK’s climate change commitments and the efficiency of the food cycle. e3 Consulting.
Sukkel, W. Stilma, E. and Jansma, J.E. 2010. Verkenning van de milieueffecten van lokale productie en distributie van voedsel in Almere. Wageningen: Stichting Dienst Landbouwkundig Onderzoek (DLO)
Vermeulen, P. and van der Lans, C., 2010. CO2 dosering in de biologische glastuinbouw.
Waldheim, C., 2010. Notes Toward a History of Agrarian Urbanism. Design Observer, November 2010
Weinstock, M., 2011. The metabolism of the city. AD Magazine, 81 (4), pp. 102-107
photoS, illuStrationS & other SourceS
Cover page
Currier & Ives. 1879. The City of Brooklyn. [lithograph]. Library of Congress public domain. Available at: <http://en.wikipedia. org/wiki/History_of_Brooklyn> [Accessed 22 September 2011]
p. 9
Google Trends. 2011. [digital image] Available at: <http://trends.google.com/trends/viz?q=u rban+farming&date=all&geo=all&graph=week ly_img&sort=0&sa=N> [Accessed 23 September 2011]
p. 10.
1. Degginger Photography. 2010. [photograph] Available at: <http://www.degginger. com/Professional/Aerial-Photography/ ContainerYardAerialNewJersey1/918953563_ p23a4-L.jpg> [Accessed 22 September 2011]
2. Greenmap. 2008. [photograph] Available at: <http://www.myninjaplease.com/green/?cat=24> [Accessed 22 September 2011]
3. NY Times. 2008. [photograph] Available at: <http://www.nytimes. com/2008/06/15/weekinreview/15mcneil. html?scp=2&sq=2008/06/15%20food&st=cse> [Accessed 22 September 2011]
4. BuelahMan's Revolt. 2011. [digital image] Available at: <http://buelahman.files.wordpress. com/2011/02/riot-map1.gif> [Accessed 23 September 2011]
p. 11.
1. OECD (Food and Agriculture Organization of the United Nations), 2011. [digital image] Available at: <http://www.fao.org/docrep/004/ y3557e/y3557e07.gif> [Accessed 23 September 2011]
2. OECD (Food and Agriculture Organization of the United Nations), 2011. [digital image] Available at: <http://www.fao.org/fileadmin/ templates/worldfood/images/home_graph_3. jpg> [Accessed 23 September 2011] p. 19.
1. The Ancient Near East. 2008. [digital image] Available at: <http://nobler.us/AAA%20DATA/ History%20Project/The%20History%20Project/ index_img3.gif> [Accessed 22 September 2011]
2. Comenzar Juego. 2009. [photograph] Available at: <http://comenzarjuego.com/wpcontent/uploads/2009/05/civitas_001.jpg> [Accessed 22 September 2011]
3. Steel, C. 2009. How food shapes our cities. [video still] Available at: < http://www.ted.com/ talks/carolyn_steel_how_food_shapes_our_ cities.html> [Accessed 25 September 2011]
4. Absolu Living. 2010. [digital image] <http:// www.absoluliving.com/jpg/%7Bid:1505%7Cw: 350%7Ch%7Ctb:m%7Cq:90%7D/image-ppourbouton-paris-a-l-epoque-gallo-romaine.jpg> [Accessed 22 September 2011]
5. von Thünen, J. 1826. Three Magnets. [digital image] Available at: <http://en.wikipedia.org/ wiki/Von_thunen> [Accessed 23 September 2011]
p. 21.
1. Howard, E. 1898. Three Magnets. [digital image] Available at: <http://en.wikipedia. org/wiki/Ebenezer_Howard> [Accessed 22 September 2011]
2. Howard, E. 1902. The Garden City Concept. [digital image] Available at: <http://en.wikipedia. org/wiki/Ebenezer_Howard> [Accessed 22 September 2011]
3. Wright, F.L. 1950. Broadacre City. [digital image] Available at: <http://places.
designobserver.com/feature/notes-toward-ahistory-of-agrarian-urbanism/15518/> [Accessed 22 September 2011]
4. Wright, F.L. 1950. Broadacre City. [photograph] Available at: <http://www.alamo. edu/sac/honors/main/papers%2004/Campos/ BROACRE_FRANK.JPG> [Accessed 22 September 2011]
5. Hilbersheimer, L. 1944. The City in the Landscape. [digital image] Available at: <http:// places.designobserver.com/feature/notestoward-a-history-of-agrarian-urbanism/15518/> [Accessed 22 September 2011]
6. Hilbersheimer, L. 1944. Bird's-eye view of commercial area and settlement unit. [digital image] Available at: <http://places. designobserver.com/feature/notes-toward-ahistory-of-agrarian-urbanism/15518/> [Accessed 22 September 2011]
p. 23.
1. 2. 3. MVRDV. 2000. [digital image] Available at: < http://www.mvrdv.nl/#/news/181pigcity> [Accessed 25 September 2011]
4. 5. 6. Jacobs. C. 2007. [digital image] Available at: < http://nymag.com/news/features/30020/> [Accessed 25 September 2011]
p. 25
1. Viljoen, A. Bohn, K. and Howe, J., 2005. Continuous Productive Urban Landscapes: Designing Urban Agriculture for Sustainable Cities. Oxford: Elsevier Ltd., Plate 6.
2. Viljoen, A. Bohn, K. and Howe, J., 2005. Continuous Productive Urban Landscapes: Designing Urban Agriculture for Sustainable Cities. Oxford: Elsevier Ltd., Plate 8.
p. 27.
1. 2. Bettencourt, L. et al., 2007. Growth,
innovation, scaling, and the pace of life in cities. – Proc. Natl Acad. Sci. USA 104: p. 7304.
p. 30.
1. Wikipedia. 2001. [digital image] Available at: <http://upload.wikimedia.org/wikipedia/ en/1/13/NLCD_landcover_MSN_area.png> [Accessed 23 September 2011].
2. Wikipedia. 2001. [digital image] Available at: <http://upload.wikimedia.org/wikipedia/ en/e/e0/NLCD_impervious_MSN_area.png> [Accessed 23 September 2011].
3. Wikipedia. 2001. [digital image] Available at: <http://upload.wikimedia.org/wikipedia/en/a/ ab/NLCD_canopy_MSN_area.png> [Accessed 23 September 2011].
p. 31.
Forman, R.T.T., 2008. Urban Regions: Ecology and Planning Beyond the City. New York: Cambridge University Press.
1. Color Figure 28
2. Color Figure 21
3. p. 6
4. p. 38 p. 33.
1. 2. Batty, M., 2009. A Digital Breeder for Designing Cities. AD Magazine, 79 (4), p. 47
3. 4. 5. Pearson, S. and Gardner, R. [1997] Neutral Models: useful tools for understanding landscape patterns. In: Bissonette, J. ed. Wildlife and Landscape Ecology: Effects of pattern and scale. New York: Springer. pp. 221
6. 7. 8. 9. 10. Christensen, K. 2002. Percolation Theory, p. 4
All efforts have been made to credit photos and illustrations where possible.
p. 37.
1. Food Mapping. 2008. [photograph] Available at: <http://foodmapper.files.wordpress. com/2008/05/city-farming2.png> [Accessed 23 September 2011]
2. Urban Times. 2011. [photograph] Available at: < http://static.theurbn.com/wp-content/ uploads/2011/05/urban-farm-brooklyn-42.jpg> [Accessed 26 September 2011]
3. Sarah Griffiths Design. 2011. [photograph] Available at: <http://sarahgriffithsdesign. files.wordpress.com/2011/05/img_6634.jpg> [Accessed 23 September 2011]
4. Sarah Griffiths Design. 2011. [photograph] Available at: <http://sarahgriffithsdesign. files.wordpress.com/2011/05/img_6769.jpg> [Accessed 26 September 2011]
p. 39.
1. Flickr, IPES.org. 2011. [photograph] Available at: <http://www.flickr.com/photos/ipesorg/5355248486/sizes/l/in/photostream/> [Accessed 15 September 2011].
2. Viljoen, A. Bohn, K. and Howe, J., 2005. Continuous Productive Urban Landscapes: Designing Urban Agriculture for Sustainable Cities. Oxford: Elsevier Ltd., Plate 5.
p. 41.
1. Flickr, teacherbarbct. 2008. [photograph]
Available at: <http://farm4.static.flickr.com/318 8/2758107605_00d5d37199_b.jpg> [Accessed 23 September 2011].
2. Flickr, teacherbarbct. 2008. [photograph]
Available at: <http://farm4.static.flickr.com/313 8/2758941626_82ce254567_b.jpg> [Accessed 23 September 2011].
3. Sage. 2009. [photograph] Available at: <http://www.sagecenter.org/wp-content/ uploads/2009/06/iumien-stawberry-stand5-
muang-and-warn1-300x168.jpg> [Accessed 23 September 2011].
4. Sage. 2009. [photograph] Available at: <http://www.sagecenter.org/wp-content/ uploads/2009/06/090t2.jpg> [Accessed 23 September 2011].
5. Flickr, MFNHouse. 2010. [photograph] Available at: <http://farm5.static.flickr. com/4119/4827647032_a7c84a28e2.jpg> [Accessed 23 September 2011].
6. Flickr, MFNHouse. 2010. [photograph] Available at: <http://farm5.static.flickr. com/4094/4827653856_f7d653fb57_b.jpg> [Accessed 23 September 2011].
7. Flickr, MFNHouse. 2010. [photograph] Available at: <http://farm5.static.flickr. com/4142/4827510414_db74f75cf0_b.jpg> [Accessed 23 September 2011].
p. 43.
1. Wikipedia. 2005. [photograph] Available at: <http://upload.wikimedia.org/wikipedia/ commons/0/09/Westland_s-gravenzande_2. jpg> [Accessed 14 September 2011].
2. Wikipedia. 2005. [photograph] Available at: <http://upload.wikimedia.org/wikipedia/ commons/2/21/Westland_kassen.jpg> [Accessed 14 September 2011].
3. Wikipedia. 2002. [photograph] Available at: <http://upload.wikimedia. org/wikipedia/commons/c/c7/ TomateJungpflanzenAnzuchtNiederlande.jpg> [Accessed 14 September 2011].
4. Evergreen Garden Solutions. 2010. [photograph] Available at: <http://www. evergreenhydro.net/hydroponicsmachines.jpg> [Accessed 14 September 2011].
p. 44.
1. Antarctica. 2007. [photograph] Available at: <http://antarctica.kulgun.net/SouthPole/ Diary2007/Pics/IMG_5884.jpg> [Accessed 15 September 2011]
2. OnOrbit. 2011. [photograph] Available at: <http://onorbit.com/node/3062> [Accessed 15 September 2011]
3. Tech News Arizona. 2011. [photograph] Available at: <http://www.technewsarizona.com/ ArticleImage.aspx?d=20110412&t=0600&f=1&s=m ain> [Accessed 15 September 2011]
4. OnOrbit. 2011. [photograph] Available at: <http://onorbit.com/node/3062> [Accessed 15 September 2011]
p. 47.
1. Local local history. 2011. [photograph] Available at: <http://www.locallocalhistory.co.uk/ schools/william-patten/walk1/dumont%20rd%20 2_1137.jpg> [Accessed 23 September 2011]
2. Bluesky. 2011. [aerial photograph] Available at: <maps.google.com> [Accessed 10 September 2011]
3. Geolocation.ws. 2009. [photograph] Available at: <http://v2.cache7.c.bigcache.googleapis.com/ static.panoramio.com/photos/original/47090113. jpg?redirect_counter=2> [Accessed 23 September 2011]
4. Google. 2010. [aerial photograph] Available at: <maps.google.com> [Accessed 10 September 2011]
5. Panoramio. 2010. [photograph] Available at: <http://static.panoramio.com/photos/ original/35155306.jpg> [Accessed 23 September 2011]
6. Aerodata International Surveys. 2011. [aerial photograph] Available at: <maps.google.com> [Accessed 10 September 2011]
7. Janssen, J. 2010. Barcelona [photograph].
8. Google. 2010. [aerial photograph] Available at: <maps.google.com> [Accessed 10 September 2011]
p. 48.
Otto,F., 2009. Occupying and Connecting: Thoughts on Territories and Spheres of Influence with Particular Reference to Human Settlement. Stuttgart: Edition Axel Menges
1. p. 55
2. 3. 4. 5. 6. 7. p. 107
Marshall, S., 2005. Streets & Patterns. London: Spon Press.
8. p. 4
9. p. 5
10. 11. 12. p. 51
p. 64.
1. Janssen, J. 2011. View over Plaka, Athens [photograph].
2. Wikipedia. 2001. [aerial photograph] Available at: <http://upload.wikimedia.org/ wikipedia/commons/e/e4/Crops_Kansas_ AST_20010624.jpg> [Accessed 25 September 2011].
p. 65. / p. 66 / p. 72.
LITSe. 2010. [photograph] Available at: <http:// litse.files.wordpress.com/2010/11/farmhousesoverlooking-fertile-valley-la-pas-to-potosi.jpg> [Accessed 23 September 2011]
p. 73.
1. Food Mapping. 2008. [photograph] Available at: <http://foodmapper.files.wordpress. com/2008/05/city-farming2.png> [Accessed 23 September 2011]
2. Oregon Live. 2009. [photograph] Available at: <http://media.oregonlive.com/business_impact/
photo/doug-beghteljpg-201fcd6d05b59380_ large.jpg> [Accessed 23 September 2011]
3. Sarah Griffiths Design. 2011. [photograph] Available at: <http://sarahgriffithsdesign. files.wordpress.com/2011/05/img_6634.jpg> [Accessed 23 September 2011]
4. Amazing Data. 2009. [digital image] Available at: <http://www.amazingdata.com/Image/ amazing_fun_ecology_29013000801023479 75S600x600Q85_200907231602492229.jpg> [Accessed 15 September 2011]
p. 83.
Bluesky. 2011. [aerial photograph] Available at: <maps.google.com> [Accessed 10 September 2011]
p. 84.
Google. 2010. [aerial photograph] Available at: <maps.google.com> [Accessed 10 September 2011]
p. 85.
Google. 2010. [aerial photograph] Available at: <maps.google.com> [Accessed 10 September 2011]
p. 86.
1. Marshall, S., 2005. Streets & Patterns. London: Spon Press. p. 158
2. Dirty 30’s. 2011. [digital image] Available at: <http://www.paper-dragon.com/1939/images/ manhattan_lower.jpg> [Accessed 23 September 2011].
3. Otto,F., 2009. Occupying and Connecting: Thoughts on Territories and Spheres of Influence with Particular Reference to Human Settlement. Stuttgart: Edition Axel Menges
4. Flickr, Abram VanElswyk. 2010. [aerial photograph] Available at: <http://farm5.static. flickr.com/4034/4439153189_70869c1762.jpg> [Accessed 23 September 2011]
p. 87. / p. 88.
Arquitectura 4. 2011. [digital image] Available at: <http://www.ub.edu/geocrit/sn-63-3.gif> [Accessed 23 September 2011]
p. 89.
1. A Gardener’s World. 2010. [photograph] Available at: <http://66.209.177.99/ gardenersworld.ca/wp-content/ uploads/2010/04/FruitStand1-300x225.jpg> [Accessed 23 September 2011]
2. Google. 2010. [streetview photograph] Available at: <maps.google.com> [Accessed 22 August 2011]
3. Borowski, D. 2011. Broadway Market [photograph]
p. 98. / p. 104. - see reference for p. 87.
p. 108.
Google. 2011. [aerial photograph] Available at: <maps.google.com> [Accessed 11 September 2011]
p. 116.
Wikipedia. 2010. [photograph] Available at: <http://upload.wikimedia.org/wikipedia/ commons/thumb/3/3a/New_York_City_ location_Brooklyn.svg/500px-New_York_ City_location_Brooklyn.svg.png> [Accessed 23 September 2011].
117.
1. Wikipedia. 2007. [photograph] Available at: <http://upload.wikimedia.org/wikipedia/en/ thumb/e/eb/Willow_Street.jpg/450px-Willow_ Street.jpg> [Accessed 23 September 2011].
2. Geolocation.ws. 2009. [photograph] Available at: <http://v2.cache7.c.bigcache.googleapis.com/ static.panoramio.com/photos/original/47090113. jpg?redirect_counter=2> [Accessed 23 September 2011]
3. Wikipedia. 2009. [photograph] Available at: <http://upload.wikimedia.org/wikipedia/ commons/7/79/Smith_Union_Bk_N_snow_jeh. JPG> [Accessed 23 September 2011].
4. 5. 6. 7. 8. Google. 2011. [aerial photograph] Available at: <maps.google.com> [Accessed 21 June 2011]
p. 130.
Wikipedia. 1859. [technical drawing] Available at: <http://upload.wikimedia. org/wikipedia/commons/9/9b/CerdaavantprojecteEixample-1955.jpg> [Accessed 25 September 2011].
p. 142.
Currier & Ives. 1879. The City of Brooklyn. [lithograph]. Library of Congress public domain. Available at: <http://en.wikipedia. org/wiki/History_of_Brooklyn> [Accessed 22 September 2011]
p. 150.
1. Hawkes, J. 2008. Old Street, Shoreditch and Hoxton, looking East. [photograph]
2. A scientist in the kitchen. 2008. [photograph] Available at: < http://ascientistinthekitchen.net/ to-market/to-market-to-market%E2%80%A6-theround-up/> [Accessed 3 February 2012]
p. 152.
1. Ramparts of Civilization. 2011. [photograph] Available at: <http://www.rampartsofcivilization. com/?p=2435> [Accessed 3 February 2012]
2. Cbus Cycle Chic. 2011. [photograph] Available at: <http://cbuscyclechic.wordpress. com/> [Accessed 3 February 2012]
3. Redmond Pie. 2011. [photograph] Available at: < http://www.redmondpie.com/iphone-5-eventto-be-streamed-live-at-covent-garden-applestore-in-london/> [Accessed 3 February 2012]
4. Wikipedia. 2008. [photograph] Available at: <http://en.wikipedia.org/wiki/File:ULTra_001. jpg> [Accessed 3 February 2012]
p. 153.
2. Wikipedia. 2006. [photograph] Available at: <http://it.wikipedia.org/wiki/File:Venezia_ piazza_s.Marco_2.JPG> [Accessed 3 February 2012]
3. FLI Brightwater. 2005. [photograph] Available at: <http://www.brightwaterfli. com/files/20050331052246_BAFF-002.JPG> [Accessed 3 February 2012]
4. The Brow. 2009. [photograph] Available at: <http://uptowndowntownnyc.files.wordpress. com/2009/04/washington_square_park_chess_ players_by_david_shankbone.jpg> [Accessed 3 February 2012]
p. 154.
1. Nicholls, S. 1720. General view of Covent Garden looking north. [Engraving] Available at: <http://en.wikipedia.org/wiki/File:Covent_ garden_c1720.jpg> [Accessed 3 February 2012]
2. SF.Streetblog. 2009. [photograph] Available at: <http://sf.streetsblog.org/wp-content/ uploads/2009/04_02/Picture_18.png> [Accessed 3 February 2012]
p. 156.
A Gardener’s World. 2010. [photograph] Available at: <http://66.209.177.99/ gardenersworld.ca/wp-content/ uploads/2010/04/FruitStand1-300x225.jpg> [Accessed 23 September 2011]
p. 157.
Google. 2010. [streetview photograph] Available at: <maps.google.com> [Accessed 22 August 2011]
p. 179.
1. Criterium Cincinnati Engineers. 2009. [photograph] Available at: <http:// criteriumincincinnati.files.wordpress. com/2009/12/imgp02021.jpg> [Accessed 6 February 2012]
2. The High Line. 2009. [photograph] Available at: <http://www.serpentinegallery.org/High%20 Line%20PHASE%201%2009-06%205054%20 press%20page.jpg> [Accessed 6 February 2012]
3. Alexander Studios. 1937. [photograph] Available at: <http://taylorempireairways. com/wp-content/uploads/2009/11/Window_ shopping_Eatons_01.jpg> [Accessed 6 February 2012]
4. The London Sightseeing Guide. 2009. [photograph] Available at: <http://londonsightseeing.net/wp-content/uploads/2011/03/ OxfordStreet-selfridges.jpg> [Accessed 6 February 2012]
5. Soepsmuller, A. 2010. [photograph] Available at: <http://www.flickr.com/photos/35158370@ N03/5297529833/sizes/l/in/photostream/> [Accessed 6 February 2012]
6. Scays. 2009. [photograph] Available at: <http://www.flickr.com/photos/ scays/3869940227/> [Accessed 6 February 2012]
p. 190./ p. 192.
Bromley , G.W.. 1934. plate 58. New York: Manhattan Land Book. [map] Avaliable at: <http://library.gc.cuny.edu/34th_st/items/ show/897> [Accessed 22 August 2011]
p. 195.
1. Wayfaring. 2008. [photograph] Available at: <http://www.wayfaring.info/wp-content/ uploads/2008/10/takayama-hida-folk-village-5. JPG> [Accessed 22 August 2011]
2. Borowski, D. 2011. France [photograph]
3. Wikipedia. 2009. [photograph] Available at: <http://upload.wikimedia.org/wikipedia/ commons/7/79/Smith_Union_Bk_N_snow_jeh. JPG> [Accessed 23 September 2011].
p. 200. - see reference for p. 190.
p. 204.
The Brow. 2009. [photograph] Available at: <http://uptowndowntownnyc.files.wordpress. com/2009/04/washington_square_park_chess_ players_by_david_shankbone.jpg> [Accessed 3 February 2012]
p. 222.
1. Brooklyn New York. 2007. [photograph]
2. Wayfaring. 2008. [photograph] Available at: <http://www.wayfaring.info/wp-content/ uploads/2008/10/takayama-hida-folk-village-5. JPG> [Accessed 22 August 2011]
p. 223. / p. 233.
Pierrepapierciseaux. 2012. [photograph] Available at: <http://pierre-papier-ciseaux. blogspot.com/2012_01_05_archive.html> [Accessed 22 August 2011]
p. 258.
1. Google. 2011. [aerial photograph] Available at: <maps. google.com> [Accessed 16 January 2012]
2. Bilmark, C. J. 1868. Stockholm Panorama. [lithography] Available at: <http://en.wikipedia.org/wiki/File:Stockholm_ panorama_1868.jpg> [Accessed 6 February 2012]
p. 259.
Google. 2011. [aerial photograph] Available at: <maps.google. com> [Accessed 28 December 2011]
p. 279.
1. Bullseye Creative. 2010. [photograph] Available at: < http:// bullseyedan.files.wordpress.com/2010/09/centralparkskyline. jpg> [Accessed 25 September 2011]
2. Natural World Museum. 2011. [photograph] Available at: < http://artintoaction.org/wp-content/uploads/2011/05/cowsgrazing.jpg> [Accessed 25 September 2011]
3. Jungle Jen's Journal. 2011. [photograph] Available at: < http://1.bp.blogspot.com/-b74xjomM7Fk/Tmlr3VdkRdI/ AAAAAAAAA2A/w5bvbvdTW-4/s1600/wheatfields.jpg> [Accessed 25 September 2011]
4. Li, L. 2011. A review on recent efforts of the Mediterranean regionale climate modelling. [conference lecture] Available at: < http://www.medclivar.eu/Final_Conference/.%5Cprese ntazioni%5CConference%5C7june%5Cplenary%5CLLi.pdf> [Accessed 25 September 2011]
5. Marshall Institute. 2000. [digital image] Available at: < http://www.marshall.org/article.php?id=71> [Accessed 25 September 2011]
Other S O urce S
Giacomelli, G. 2011. Discussion on greenhouse technology and research conducted by University of Arizona (Personal interview with Dr. Gene Giacomelli, Professor of Agriculture and Biosystems Engineering, and Director of the Controlled Environment Agriculture Program, University of Arizona, 1 September 2011)
Brooklyn Typology - http://typology.fakeisthenewreal.org/ list/density/
Wageningen University Greenhouse Horticulture - http:// www.glastuinbouw.wur.nl/UK/
Stockhom - http://international.stockholm.se/FutureStockholm

