Acknowledgements
Without the contribution of certain people, we would not have been able to realize this work. First we would like to express our gratitude to Mike Weinstock and George Jeronimidis; with their guidance and support we were able to explore new dimensions in our personal and professional development. Evan Greenberg and Mehran Garleghi for providing us with advice, inspiration and encouragement during the entire EmTech course. Specially, we would like to thank Olga Kravchenko (MSc), without whose contribution and friendship this thesis could not have come true.
Additionally we would like to thank our families and friends for supporting and inspiring us throughout this time. And last but not least we would like to thank each other for this exciting time full of new discoveries.
Acknowledgements
Symbiotic aggregations
Abstract
The thesis proposes an urban infill system as an alternative model for urban growth in Istanbul. The proposed model compliments the two existing ones currently used. The infill system should be capable of adding density to existing urban areas by adapting to the local conditions, while adding a much needed, and recently neglected, quality public space that is based on traditional values.
The two current growth models in Istanbul, namely suburban sprawl and urban redevelopment are challenged. From the lacks of these models the complimentary alternative is formed. The proposal is an Infill system that interacts symbiotically with the existing urban tissue, growing in the residual spaces of the city and adding diverse programmes, morphological variations and public space to the area. In order to inform the system, key existing public areas, along with vernacular architectural typologies were researched; their social, architectural and environmental qualities abstracted.
A sequence of experiments were developed to generate and evaluate the performance-driven infill strategy. The experiments are conducted on Cihangir, a central area of Istanbul; and the results are evaluated and discussed at every stage. The experiments are conducted on two scales: urban neighbourhood and cluster scale. The final growth model, formed by an iterative design process was finally tested according to environmental, architectural and urban performance. A design proposal driven by the generated information serves as a demonstration of the system’s robustness and flexibility; concluding with an overview of the potential of this model as an alternative growth strategy.
Abstract
Symbiotic aggregations
Contents
1 Introduction............................................. 2
1.1 Urban growth
Istanbul and urban growth
Current growth models
1.2 Infill
1.3 Public Space
1.4 Research questions
2 Domain................................................12
2.1 Urban infill
2.2 Public space integrated to architecture
3 Methods............................................... 18
3.1 General process
3.2 Generative methods
Parametric modelling
Genetic algorithms (GA)
Cellular automata (CA)
Cellular automata controlled by a GA
3.3 Evaluation methods
Space Syntax (network)
Shading analysis
Solar access analysis
Sky View Factor Visibility
CFD
4 Case studies........................................... 32
4.1 Element of public space in Istanbul Pedestrian street Sidewalk Passage Courtyard Square Arcade Stairs
4.2 Mardin
4.3 Cihangir
5 Design development.................................... 50
5.1 Objectives
General objectives map
Population
Public space Environmental
5.2 Design development process overview
5.3 Infill growth Aim
Methods
Setup: environmental boundary
Setup: context
Initial tests
Implementation
Iteration
Contents Results Conclusion
Open spaces Aim Methods / Setup Initial tests Implementation Results Conclusion
Base network and secondary nodes Aim Methods / Setup Initial tests Implementation Results Conclusion
Network morphology (public space) Aim Methods / Setup Initial tests Implementation Results Conclusion
Environmental (wind) Aim Methods / Setup Initial tests Implementation Results Conclusion 5.8 Programmatic distribution Aim Setup Implementation Results Local distribution Aim Setup Implementation Results Conclusion 6 Design............................................... 140 6.1 Design Translation 6.2 Design Proposal 7 Results & conclusion.................................. 150 7.1 Results 7.2 Conclusions & further development Urban system Environmental conclusions Computational conclusions 8 References & bibliography.............................. 158 9 Appendix............................................. 164
5.4
5.4
5.6
5.7
Symbiotic aggregations
01 Introduction
1.1 Urban growth
Istanbul and urban growth
Current growth models
1.2 Infill
1.3 Public space
1.4 Research questions
3 Introduction
1.1 Urban growth
Istanbul and urban growth
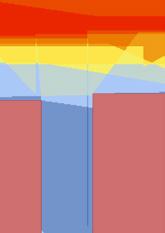
Istanbul is located in the north-western part of Turkey between Europe and Asia. The city is found in a mild climate zone, where long hot summers and short humid winters are the norm. With 13.85 million inhabitants, Istanbul is Turkey’s largest city. Its particular condition, as the only Sea route between the Black Sea and the Mediterranean, has made it one of the major ports in Europe. As a result the city accommodates 30% of the country’s foreign trade, making it a very attractive destination for inland migration (Columbia University, Urban Planning Program, 2011). These circumstances result in a rapidly growing population that is expected to increase by 2.17 million inhabitants in ten years and 5.15 million in thirty.
Assuming the propagation of the current urban growth models, the city will increase its size by 217.1 km2 in 10 years in order to accommodate the projected population growth. This number will rise up to 414.5 km2 in 30 years. The current growth trends add the greatest pressure in the periphery of Istanbul. This uncontrolled expansion of Istanbul has caused a decrease of the city’s environmental and agricultural resources, along with pollution issues such as the water crises in 1993/94 caused by sewerage flow into one of its major water sources: Elmali (P. Hlavinekin Risk Management of Water Supply and Sanitation System P.220). In addition, its potential to expand horizontally is reaching its limits since its already merging with neighbouring cities such as Gebze.
10 years 20 years 30 years
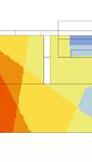
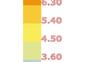
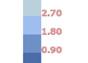
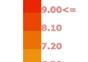
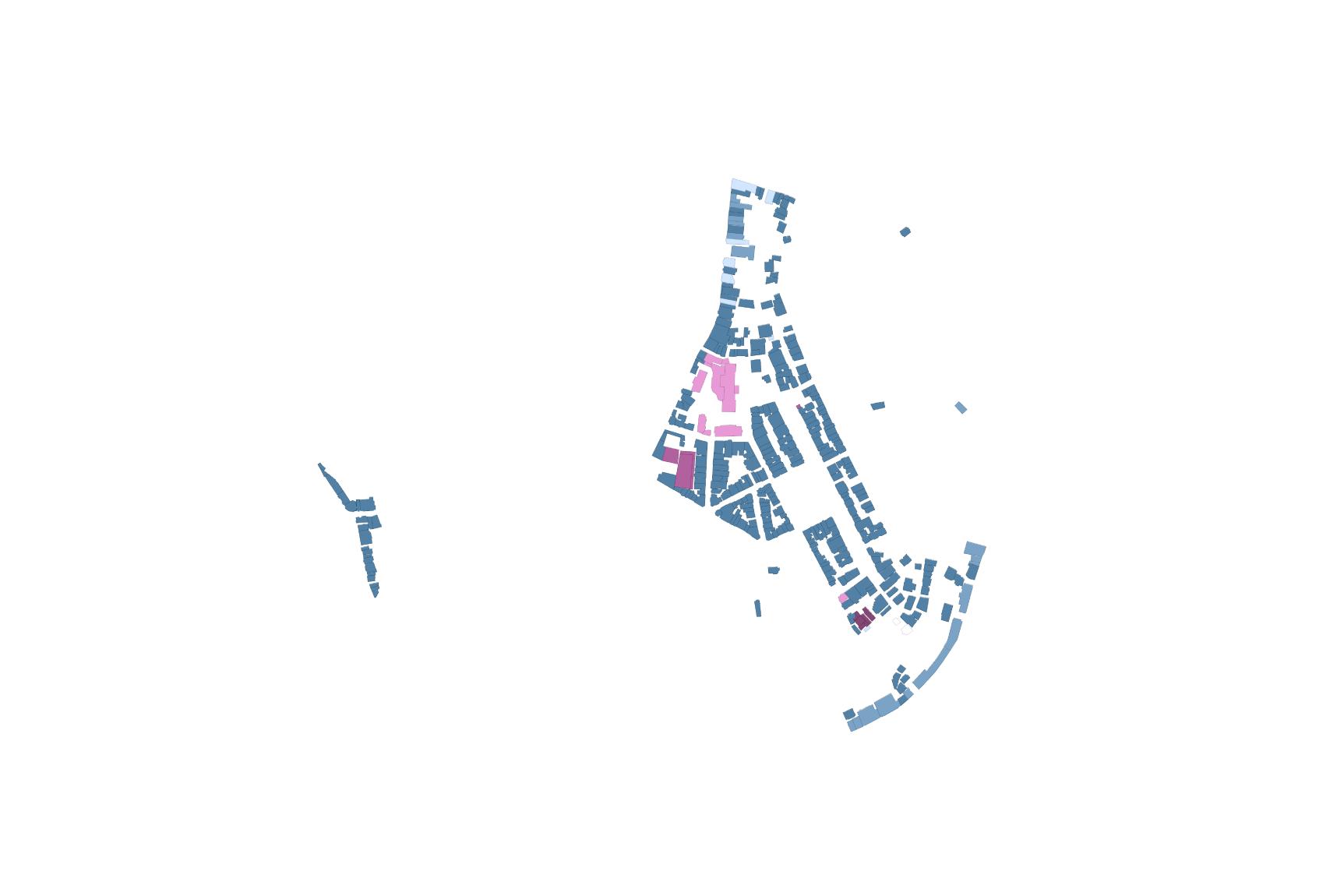
Map showing Istanbul’s population density (point colour gradient) overlapped with the current urban footprint of Istanbul. If Istanbul’s population keeps growing and building following the current models, it would need to add an area of 217.1km2 in 10 years, 312.6km2 in 20 and 412.4km2 in 30.
Symbiotic aggregations
20,000 - 25,000 15,000 - 20,000 10,000 - 15,000 5,000 - 10,000 500 - 5,000 0 - 500 40,000 - 50,000 habitants / km2 35,000 - 40,000 30,000 - 35,000 25,000 - 30,000 12,500 h/km2 15,700 h/km2 172.9 km2 217.1 km2 2,713,760 hab 248.9 km2 312.6 km2 3,907,714 hab 328.3 km2 412.4 km2 5,155,010 hab 4
Figure 1.1.1
low pressure on urban pressure on urban pressure on rural
low pressure on rural
5 Introduction represents the areas of greater change smaller change larger change
a d p q r s t e u b c f g h j l k n o m i
Figure 1.1.2 (above)
The areas with the greatest growth pressure lie in the periphery, where agriculture and forest land is under pressure to be developed.
Figure 1.1.3 (below) Map showing the gradient of population change in Istanbul. The largest population increase is in the periphery.
According to the current predictions for the coming years, more than 80% of Istanbul’s population will be living in apartments; specifically, 65% will live in peripheral apartment tower blocks, and 15% in other type of apartment buildings. Only 8% of the population will live single houses and an additional 8% in gated communities (Turkish Statistical Institute TUIK). Within central areas, the number of people living in apartments is even larger at 95%.

Current growth models
Great urban spaces posses a unique sense of place that is experienced by the city dwellers every day. The central and traditional areas of Istanbul portray these rich urban textures that were formed as a palimpsest of centuries of urban evolution, refinement, combination and alteration. The richness of this fabric is most strongly characterized and conveyed by the public spaces – side streets, open markets, public squares, terraces, and passages – that are disappearing from the contemporary Turkish building practices.
The current strategies for addressing the housing deficit for Istanbul’s growing population can be divided into two main groups. The first one, and currently the most widespread, is the unchallenged building expansion towards the periphery, either in sprawling suburban housing projects, tower blocks or even some attempts to reproduce ‘villa-type developments’ or ‘traditional neighbourhood architecture’ (Bozdogan,
6 Symbiotic aggregations
Figure 1.1.4
“The unchallenged building towards the periphery, either in sprawling suburban housing projects, tower blocks or even some attempts to reproduce ‘villa-type developments’” (Image: Aksoz).
1996) (emphasis added). Many of these developments take advantage of the peripheral undeveloped land, such as the case of the Kemer Country suburb: perhaps a spin-off from León Krier’s new-urbanism within gated communities. The second strategy, and one that is being observed in cities around the world, is the process of redeveloping land within city’s centres. Independent of its scale, the territory is being transformed by urban renewal; this is the demolition of existing structures for redevelopment and adaptive reuse of formerly uninhabitable structures – a process that is colloquially referred to as gentrification.
This second practice, although less economically viable than the former, particularly in places where land is readily available at low prices in the periphery, is understandable when one considers the benefits of centrality. As Lefebvre states in The Production of Space, “[…] the centre continues effectively to concentrate wealth, means of action, knowledge, information and ‘culture’. In short, everything.” (Lefebvre, 1974) However, given the high demand for available space in central areas, the prices of available land and space rise, segregating populations according to their economical means. In Istanbul this process is exemplified, by the case of the Sulukule neighbourhood, amongst others, where the local Romany population has been dispersed in a process that resulted in the “appropriation of existing land for the use of higher-status groups” (Isam, 2010).

7 Introduction
Figure 1.1.5
‘Demolition of existing structures for redevelopment’, currently occurring in central Istanbul. (Image: Zaldivar).
Furthermore, in 1974 Lefebvre, both observing and predicting urbanization trends, argues that “countries in the throes of rapid development blithely destroy historic spaces – houses, palaces, military or civil structures. If advantage or profit is to be found in it […] Later, however, perhaps towards the end of the period of accelerated growth, these same countries are liable to discover how such spaces may be pressed into the service of cultural consumption, of ‘culture itself’” (Lefebvre, 1974). Stressing the economical and technical challenge that is to recover them from years of neglect.
The two current growth models can therefore be challenged. By understanding the shortcomings of the two existing models, and the virtues of indigenous settlements, this work argues for the possibility a third model as a viable growth alternative. One that could alleviate the pressure on territorial expansion by increasing the supply of space in central areas; addressing the loss of meaningful public space and, consequently, of public life. The work proposes a design strategy that exploits the distinct architectural qualities that have been developed indigenously over the years, and applies them in central areas by means of an infill system.
8 Symbiotic aggregations
1.2 Infill
Urban infill is generally defined as the development of vacant or under utilized land within the city’s built-up area (Brooks, Donaghy and Knaap, 2011). The construction is done either in open spaces, deserted plots, half-built plots, or vacant buildings; all within urban neighbourhoods that area already somewhat developed.
This strategy is proposed as an alleviatory substitute to urban sprawl and its negative impact on the community as it has the possibility to densify and articulate existing urban tissues. Urban sprawl is characterized by spread out development patterns which demonstrate poor land use, increased infrastructural load and unconnected communities, which, due to the long distances to public services and between one another, create isolated car-dependent societies. On the other hand, urban infill does not require reclamation of new land or the building of entirely new infrastructure, and facilities and features may be proposed to improve the life of the existing community. Infills are often (but not always) built in central areas, offering shorter commuting times than from the suburbs and reducing traffic congestion and pollution.
To the local population of the neighbourhood, urban infill may sometimes seem as a threat due to the loss of open space associated with it and the additional traffic load (McConnell and Wiley, 2010). But these issues can be successfully addressed.
In Japan, the historical lack of space within dense cities, like Tokyo, has forced the population and architects to work within highly restrictive physical spaces. Residual spaces are by-products of systems that compartmentalize land, such as transport and infrastructure ones, along with top-down planning and zoning. These residual spaces are occupied with great creativity as is lucidly exemplified in Atelier Bow-Wow’s Pet Architecture Guidebook 4. In turn, the aggregated characteristics of this type of architecture generates a site-specific and adapted infill system. Similarly, other cities have developed their own kind of Pet Architecture, not always driven by the geographical lack of land, but rather by the central lack of space. Large north American cities, such as New York or San Francisco have employed infill strategies that maximize the occupation of three-dimensional space within a legal framework; but settlements in developing countries exemplify this appropriation of space in a more creative and diverse, albeit poorly planned, manner.
In Istanbul, as a result of centuries of urban overlay and growth, hundreds of these residual spaces have been formed within its traditional urban fabric. These spaces emerge by the imposition of urban systems over previous ones over time. And it is within these rarely occupied spaces that it is proposed to densify the city and add much needed spaces.

9 Introduction
Figure 1.1.6 Infill corner shop in Tokyo. Image from Atelier Bow-Wow’s Pet Architecture Guide Book - Living Spheres Vol. 2.
1.3 Public space
Public space is a defining feature of Istanbul’s urban life. The aforementioned growth scenarios show a clear neglect for public space. In the case of the apartment towers – like the ones shown on the section below from the suburban area of Atasehir – the main areas of public interaction have been relegated to mere parking spaces or driveways. The central re-development projects, on the other hand, have been keen on privatising public space and turning public street life into a private commodity. It is not difficult to argue that the rich public life that characterises Istanbul is being jeopardised by the newer developments, ever further from busy centres; and the promise of a ‘modern’ lifestyle deprives people from an architecture that is better suited to its social and natural environment.
The section in the opposite page shows Hazzopulo: a small courtyard that is surrounded by nine interacting building blocks near to Istiklal Avenue. The courtyard connects its surroundings through two large gateways and one passage. The surrounding buildings are connected by a perimeter arcade that links the separate volumes and relates them to the courtyard; also, the arcade generates environmentally comfortable areas for seating and walking. The entrance arch acts like a transition portal from the busy public streets to an equally public, but qualitatively different space. The variety and diversity of these public spaces and transitions that coexist on such a small scale exemplify the architectural richness that is being lost. The different morphologies are matched by and equally diverse programme: there are coffee shops, restaurants, businesses and residences that share common service areas and public paths. And they all seem intricately linked to morphology of the public space.

10 Symbiotic aggregations
Figure 1.1.7
Cross section of Atasehir, an affluent new neighbourhood in Istanbul.
1.4 Research questions
The research questions revolve around the problematic of building within very specific conditions. The project necessarily has to adapt to its highly restrictive immediate physical environment composed of streets, stairs, plazas and buildings, but also to its socioeconomic and environmental context.

The main research question, then, would be: can the residual spaces in Istanbul, within the borders of the built urban space, be systemically used as generators for a growth that responds to its context? And is the system robust enough to function as a viable third model?

Can a significant network of public spaces based on traditional values be successfully formed within the rigid constrains of an already built environment? And if so, what are the limitations of an infill system before it negatively affects quality of the existing spaces?
Finally, to what extent can a urban-scale, or at least neighbourhood-scale system, be algorithmically detailed, in effect deleting the boundaries between urban and architectural system. Does it make sense to keep the project at an urban level, or push towards the architecture detail. To what extent can this growth be seen as an urban strategy – is it a global strategy or does it remain local (architectural or urban proposal)?
11 Introduction
Figure 1.1.8
Traditional open space for pedestrians in Istanbul.
Figure 1.1.9
Cross section of Hazzopulo, near Istiklal avenue in Istanbul. The richness of the architecture and the open spaces is evident.
12 Symbiotic aggregations
02 Domain
2.1
2.2
13 Domain
Urban infill strategy
Public space integrated to architecture
2.1 Urban infill strategy
The overall advantage of infill buildings, and the stress for generating new habitable space in an efficient yet comfortable way in dense city centres, has driven many architects and developers towards infill proposals.
New York, with population of 8,405,837 million (www.nyc.gov), an estimated annual population growth of 3%, and density rates that vary between 40,000 and 20,000 hab/km2, has many areas with high demand for new housing projects and little space available. This creates a fertile ground for new architectural solutions. Two examples from New York city are SHoP architects’ Porter House at 66 9th and OMA’s peeka-boo tower at 23 East and 22nd. They are examples of contemporary adaptive-reuse and infill buildings.
The Porter house by SHoP architects, is an expansion of 1,858m2 on top of an old (1905) warehouse. This project almost doubles the habitable area of the existing building and its material-efficient zinc façade has turned it to an iconic building within its neighbourhood. A former abandoned industrial warehouse was re-used, which is seen as a big improvement for the neighbourhood, where deserted buildings seem to foster urban decadence. In this case no open spaces were lost, since the entire addition was done on top of the existing building, and cantilevering 2.5m over the neighbouring one.

14 Symbiotic aggregations
Figure 1.1.7
The Porter house by SHoP Architects. Image from SHoP Architects.
OMA designed a tower at 23 East and 22nd, nicknamed the peek-a-boo tower in response to a clients desire to exploit a rather small terrain in prime location as much as possible. The tower rises from a 300m2 plot, and cantilevers over 9 meters above the neighbouring buildings. A diagonal shape was chosen in order not to block the view to One Madison Park, and to gain valuable views to the park. In addition, the floor heights vary in size, higher at the narrow sections and lower at the wider parts, adapting to the rare site and envelope conditions.

The tower was designed taking into consideration the challenge of building in existing dense urban environments: the limited plot size, the neighbouring buildings and existing vistas. Finally, it manages to add a substantial amount residential and commercial space without compromising the comfort conditions for the existing buildings.
Conclusion
From these examples, valuable lineaments can be extracted for the project. The Porter house example shows that it is feasible to add a significant amount of space not top of a century old building. And that a contemporary structure can interact symbiotically with an old unused one.
OMA’s tower shows that plot size is not as much as fundamental constraint as could be thought. Furthermore, it exemplifies a way in which the local conditions can inform the architecture, in terms of environment, views and economy. And that architecture in this scale can achieve a benefit for client and local population alike. It also shows clever ways in which rare geometric configurations can be occupied.
Along with these considerations, it can be concluded from these examples that successful infill buildings offer a good growth alternative for dense cities, and can be beneficial for the existing environment. Thus, infill can be viewed as a symbiotic alternative, rather than a parasitic one. On the other hand, the current architectural trends for infill show isolated projects that function independently from one another. But given the large increases in urban populations around the world, a more systemic approach would be needed to address large populations.
15 Domain 107m 9.2m 10m
Figure 1.1.8
23 East and 22nd Street by OMA. Image source by Luxigon/OMA Architects.
Figure 1.1.9 Section from the peek-a-boo tower (recreated).
2.2 Public space integrated to architecture
Block / Tower (Stan Allen & Rafi Segal)
Block/Tower proposes a new mixture of living and working environment, using an existing conventional office building in Manhattan as a base structure. This approach proposes the reuse of existing urban buildings by altering them; thus adapting to the urban necessities and changes.

The traditional tower that portrays the commercial and speculative architectural approach that is becoming obsolete in today’s urbanism is merged with the idea of the urban block. The repetitiveness of the tower is broken by the integration of a public space that extends from the street level, spiralling around the core to the higher levels of the tower. In this way, it is expected to extend the urban experience of open space into its vertical dimension.
To achieve this goal, a spiral pathway of continuous public space is generated by carving out the exterior of the building while the central vertical connections are kept. The pathway that extends through the entire building satisfies different public functions, interacting with the adjacent private spaces. The generated heterogenous section of the building allows different spatial configurations to coexist, permitting distinct social communities to occupy the space to their desire.
16 Symbiotic aggregations
Figure 2.1.4
Block / Tower Stan Allen and Rafi Segal (Allen and Segal, 2014).
TEK Building (BIG)
The TEK building in Taipei is proposed 57m cubic structure that is perforated by a spiralling public space that extends from the ground to the rooftop garden of the building. The extension of the urban space into the large volume generates a three dimensional street that is surrounded by social functions. The changing size of the spiral controls the penetration of light inside the volume.

17 Domain
Figure 2.1.5
TEK Building BIG (Big.dk, 2015).
18 Symbiotic aggregations
03 Methods
3.1 General process
3.2 Generative methods
Parametric modelling
Genetic algorithms (GA)
Cellular automata (CA)
Cellular automata controlled by a GA
3.3 Evaluation methods
Space Syntax (network)
Shading analysis
Solar access analysis
Sky View Factor
Visibility
CFD
19 Methods
3.1 General process
The general process flow diagram shown opposite provides a basic overview of the methodology followed throughout the thesis. The generative process will be explained in detail in the design development chapter, but the layout serves here as a reference in order to show what methods are being used at each stage. Some of the methods were selected after a first set of experiments proved the inadequacy of the first ones tried; the full reasoning for this will be elaborated in the appropriate section.
The process begins with a general research on Istanbul and on local urban strategies focused on public space. But in order to understand the nature of public open space and its adaptation to the local climatic and geographic conditions in traditional settlements in the region, a vernacular settlement was analysed: Mardin. To complement this understanding, other contemporary examples from Istanbul itself were investigated – ranging from late XIX century built neighbourhoods to contemporary ones. The analysis of these case studies results in values that can be translated into parameters for the project development, or as information for the design logic. These results are fully explained on the case studies chapter.
For the design development, a test site for the experiment was analysed utilizing mapping and tissue sampling techniques. In this site a generative process that consists of six experiments will be run iteratively. Different criteria will be evaluated at every stage in order to re-inform the process, in this sense, the experiment learns from itself. For the morphology generation process it is important to note that several experiments were carried out before settling on the totalistic cellular automaton with varying neighbourhoods, which rules’ thresholds are controlled by a genetic algorithm.
20 Symbiotic aggregations
Table 3.1.1
The general process flow diagram showing the experiments where the specific methods are employed.
Methods relationship to Experiments
Methods used
Cellular automata (CA)
Genetic algorithms (GA)
Experiment / process desigend
6 3 Infill growth
Aim
Methods
Population
CA and GA [1]
Parametric modelling
[2]
Parametric modelling
Public space GA
Shading analysis
Solar access analysis
[3]
Parametric modelling
Public space GA
Space Syntax
Setup: environmental boundary
Setup: context
Initial tests
Implementation
Iteration
Results
Conclusion
6 4 Open spaces
Aim
Methods / Setup
Initial tests
Implementation
Results
Conclusion
6.5 Base network
Aim
Methods / Setup
Initial tests
Implementation
Results
Conclusion
Solar access analysis [4]
Public space
Environmental [5]
Population / Functions [6]
Sky View Factor
Parametric modelling Visibility
6 6 Network morphology (public space)
Aim
Methods / Setup
Initial tests
Implementation
Results
Conclusion
Associative modelling
CFD
Shading analysis
Solar access analysis
6 7 Environmental (wind)
Aim
Methods / Setup
Initial tests
Implementation
Results
Conclusion
6.8 Programmatic distribution
Generative and evaluation
Associative modelling
Aim
Setup
Results
21 Methods
3.2 Generative methods
Parametric modelling
Parametric modelling, sometimes referred to as associative modelling, is a design technique where a set of base parameters or variables, through algorithmic relationships, determine a specific outcome. The result is directly informed, transformed or affected by the base parameters. Diverse information parameters can be weaved together; any criteria that can be quantified and brought together into a cohesive environment can be used to inform the model. The challenge lies in the quantification of diverse values (if possible), and the evaluation of the results.
Popular software packages that are currently used for parametric modelling include Grasshopper for Rhino, Autodesk Revit, Autodesk Dynamo and Catia amongst many others. Each software has its own limitations and advantages; within this thesis, the use of Grasshopper was preferred for its broad and active support community, the many user-made plug-ins available and the facility to implement scripting languages such as Python, Visual Basic or C#. The possibility to use scripting languages outside a specific software adds a lot of flexibility and scope to a model.
Genetic Algorithms
Genetic Algorithms (GAs) are a subset of Evolutionary Computation, which is a subfield of Natural Computing. ‘The first glimpses of the ideas
22 Symbiotic aggregations
Actively transcribed DNA
‘Christ-
tree’ structures. The trunk of the Christmas tree is a strand of coding DNA that serves as a template from which hundreds of identical RNA molecules are produced simultaneously.

Genetic algorithms derive their logic from natural processes such as natural selection and evolution, DNA, genotype and phenotype.
Image source: http://bio3400.nicerweb.com/Locked/ media/ch13/christmas_tree_rRNA.html.
underlying genetic algorithms (GAs) are found in [John H.] Holland’s papers in the early 1960s’ (Back, Fogel and Michalewicz, 1997). They were further popularized by Holland in 1975, and have since been utilized and developed in diverse fields.
The logic of genetic algorithms mimics natural evolutionary processes. Solutions are evolved by a process derived from natural selection within a computational environment. A series of controlling parameters –genes – form the genetic pool for the algorithm. An initial population is generated using a genotype made from a collection of genes from this gene pool; subsequently the emerging phenotype is evaluated for predefined fitness criteria. From the original population, a subgroup will be selected depending on their fitness ranking, and then they will breed by recombining their genotype; other factors such as mutation and elitism also play a role. Usually the selected group will have desirable characteristics and be generally fit (although there can be exemptions) and the process will start generating a population with fitter individuals.
GAs are mostly used as optimization algorithms or as search algorithms, where the search can be executed within a fixed database or a mathematical space of possibilities with a variable fitness landscape. It’s important to note that there are also many limitations to GAs, especially with more complex problems, and sometimes other optimization algorithms will yield better results. Within the context of this thesis they are used as a mechanism to find the rules and thresholds that govern a Cellular Automata and as a multi- objective optimization algorithm.
23 Methods
Figure 3.2.1
visualized under an electron microscope. Transcriptional units appear as
mas
Cellular Automata
Cellular Automata (CA) is a model formed by a regular grid of cells that contain a finite amount of information or ‘states’. Each cell lies within a neighbourhood of adjacent cells that determine its state over time. The initial grid configuration in time t=0 is thus altered when time t=(t+1) depending on the states of the neighbouring cells at t=0. Traditionally the state of a given cell can be either developed or non developed, and the cells within the neighbourhood determine its potential for further development in time t=(t+1).
The concept of computing automata, and hence of cellular automata was introduced by John von Neumann (von Neumann, 1963) in the 1940’s and developed along with Sanislaw Ulam. The ideas were further developed and popularized by John Conway’s ‘Game of Life’ and later approximated in three dimensions (Bays, 1987) The application of CA models as a tool to understand cities by urbanists and architects has come a long way. Recently it has been applied as a modelling tool at an urban scale for predicting land use (Krawczyk, 2002), however calibrating these models seems very problematic, mostly descriptive and arguably not predictive. Their use as city models can be contested.
Within the thesis, CA was chosen to model growth within heterogeneous boundary conditions, and simultaneously to propose an initial morphology at a building and block scale. Previously, Robert J. Krawczyk has carried out experiments at this scale of architecture, where he proposes different ways to interpret architectural forms resulting from CA models (Krawczyk, 2002). Furthermore, some work has shown how vernacular-like architectural structures can be modelled using a 2D totalistic CA, where each new configuration in time is superimposed above the previous one on a third dimension (Situngkir, 2010).
24 Symbiotic aggregations
Figure 3.2.2
Recreated time frame from J. Conway’s ‘game of life’, cellular automata model.
Cellular Automata controlled by a GA
An altered totalistic CA model is the one used, for after several experiments it proved to be the most beneficial for a morphology generation, however the rules that proved most beneficial were still hard to determine for each situation, for this reason an attempt is made to control the development by using a GA. There have been some cases where a totalistic cellular automaton model has been controlled by a GA, particularly for the modelling of urban systems (M. Batty, 2005) (R. Breukelaar, T. Bäck, 2005). Only a few of these are documented, and as far as the research time permitted, no cases were found where a model like this was used to generate architectural morphologies.


The idea to control the CA model rules’ threshold variables and neighbourhood sizes emerged from the necessity to spawn a large number of architectural types that could occupy multifarious boundary conditions. Totalistic CA models are very deterministic, and probabilistic ones are hard to predict and control. So in order to use a CA model as a morphology generator, a way to reverse engineer the rules that produce desirable results was developed by implementing a genetic algorithm. There have been previous examples that show promising results for using this method as the ones shown below (A. Chavoya, Y. Duthen, 2006). Here, a CA with changing rules successfully produced close approximations to basic geometric shapes.
For the final experiment, a complex model was used, where the rules and the neighbourhood for each cell could be altered at each time step. The neighbourhood type and range, the rule threshold for development and the total time became the phenotype of the genetic algorithm. The genotype is expressed as the final configuration of the developed cells. The precise mechanisms for the tuning of this model will be explored in the design development section.
25 Methods
Figure 3.2.3
“2D shapes. Desired shapes (upper row), and shapes obtained with the Moore (middle row), and the 2D Margolus (lower row) models.
[The figure] shows results for 2D shapes. For ease of visualization, cells that fall outside the desired shape are shown in light gray [...]”
Figure 3.2.4
“3D shapes. Desired shapes (upper row), and shapes obtained with the 3D Margolus model (lower row).”
From A. Chavoya et al. 2006.
3.3 Evaluation methods
Space Syntax
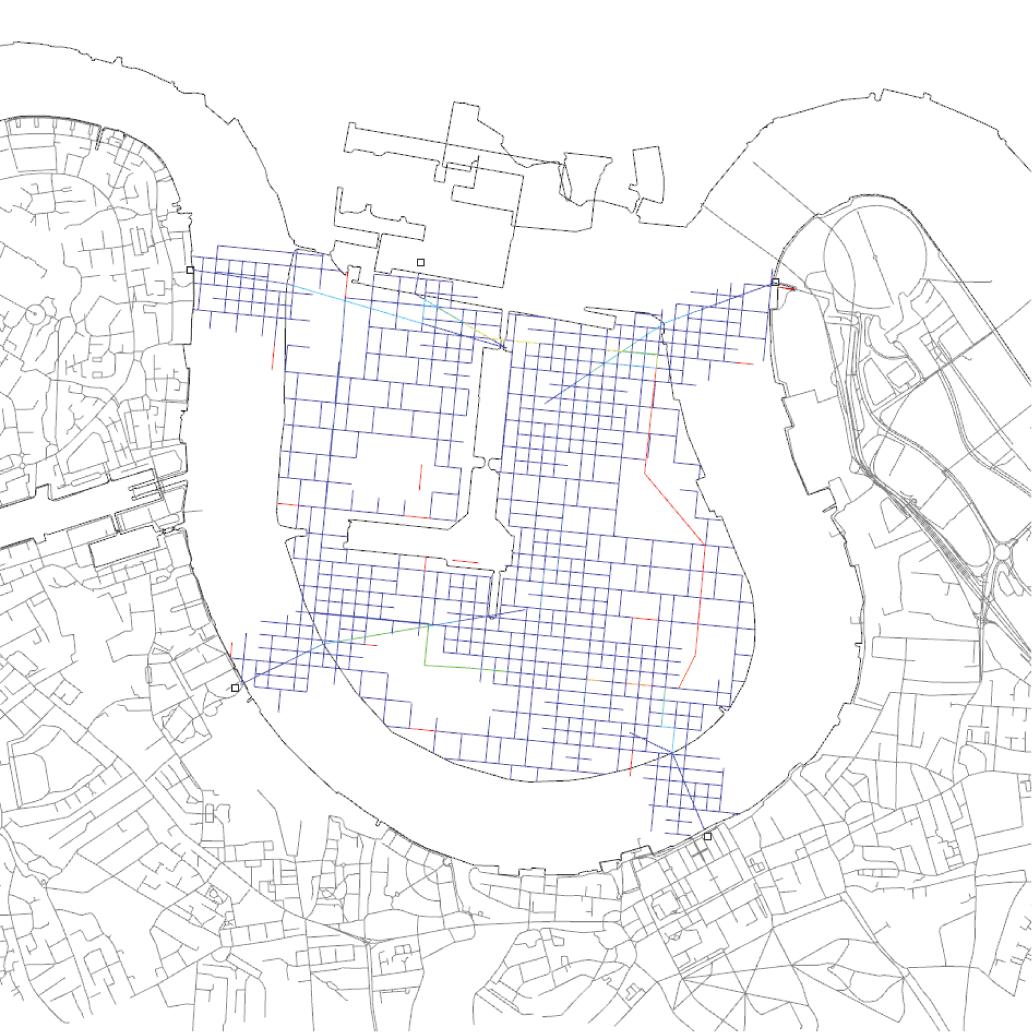
Network theory reduces complex interacting systems into a graph of nodes connected by edges. Such a method enables the evaluation of the interactions regardless any additional information that the network may possess.
Based on Network Theory, Space Syntax provides several evaluation methods that address the urban street networks and the influence of the urban form on pedestrian movement and car circulation. Space Syntax theory suggests that the urban form determines the activity of certain areas, and these areas become more or less attractive for specific functions. The reduction of the urban form into a graph liberates the traditional evaluation of urban systems from aesthetical considerations, and enables a quantification therefor relying on the network logic.
There are several analysis methods within Space Syntax theory that can be used to evaluate the urban form. The three most popular techniques used are Integration, Choice and Depth Distance or Betweenness Centrality. (Hiller and Stonor, 2010)
Integration calculates the angular distance in a system. It measures the number of turns that have to be made in order to get from one node to another through the shortest path. The paths with less turns are evaluated as more integrated ones.
Choice measures the probability of the traffic flow on any given edge. Where each segment is selected as a starting point with a certain load and this load is divided at each intersection.
The depth distance calculates the metric distance from the centre point of each segment within the network to the centre point of each other segment. The streets with lowest depth value are the ones which are nearest to all the other streets.
Additionally to the analysis of the streets, the intersection nodes can also be evaluated. One of these evaluation methods is the Betweenness Centrality Analysis. This analysis evaluates the importance of a node, and its influence on others by measuring how many times the node is travelled through in the shortest path from any node to all other nodes.
The assumption is made that the shortest path is always preferred; however, within Space Syntax, the evaluation can be biased towards paths that have the smallest angular deviation as well. Therefore, there are two options for this evaluation: the Betweenness Metric and the Betweenness Angular.
26 Symbiotic aggregations
Figure 3.3.1
Example of a shortest path analysis for two given points within a street network.
Betweeness Angular
Figure 3.3.2
Example of a Betweenness analysis using Space Syntax for Isle of Dogs, London.
Shadow hours analysis
It is imperative to calculate the amount of shadow casted on a given place during the day. In hot climates, shading at street level during the hot seasons is crucial in order to allow open public spaces such as parks, courtyards or plazas to function. Non-shaded open areas are rarely used for they become very uncomfortable. Large exposed surfaces with a high albedo can greatly increase an undesirable heat gain, making it almost impossible for people to utilize these spaces during daytime.
Urban open spaces are usually surrounded by buildings that block some or all of the sun rays, thus generating different shadows at different times of the day. A sun vector occlusion calculation was performed in order to understand what percentage of these sun rays are blocked by a given geometry. Essentially, the amount of hours the sun is blocked for an area equals to the amount of shadow hours during the day.
The hottest season for Istanbul, according to the yearly weather data, range from June 1st to August 31st between 11:00am and 4:00pm (average business hours coincide with the setting sun at 8pm). The sun vectors for each hour on the first and last day of this period are calculated, and this creates a range of sun vectors for the hot season.
This analysis was performed to evaluate the new open spaces created within the existing built environment at a cluster scale. The evaluation of acceptable shading values was done with respect to the current existing conditions and will be further explained in the targets section.

27 Methods
Figure 3.3.3
Grid representation of the existing buildings to inform the model of the existing conditions.
>6 shade hours <1 shade hours
Solar access analysis
Appropriate solar access is necessary for buildings to function. It improves the life quality of the occupants, reduces the energy consumption for artificial lightning and, pared with material albedo, determines the heat gain of the building, which is desirable during winter, but a disadvantageous during summer in Istanbul.
The orientation and geometry of a building, i.e. the number and size of faces exposed to direct and indirect sunlight, affects the heat gain, which is the absorbed thermal radiation of the building that accumulates during the day and is released during the night. The most affected faces are the ones that get direct solar exposure as opposed to the ones hit by indirect light. Indirect light refers to the rays scattered from the surfaces that are directly exposed to the sun, and which have less energy and therefore produce less heat.
The analysis was preformed for the winter period of Istanbul based on annual weather data. The results were used in consideration of a potential detrimental effect on the quality of life for the existing residents, and to evaluate the generated volumes and public spaces. Finally, a mapping of the solar access on the surfaces of buildings is used as a design guideline that helps to define the surface treatment.



28 Symbiotic aggregations
Figure 3.3.4
<1
>6
perspective 1 perspective 2 top view
Example of a solar access analysis performed on for an analysis period of 6 hours.
sun hours
sun hours
View Factor
The sky view factor (SVF) is a ratio that measures the amount of the sky dome that is visible from a given point. This point, typically set at one meter above the ground, becomes the center of a hemisphere’s equator. The hemisphere represents the full 360° vision from the given point. The portion of the sky that is visible from this point, i.e. the amount that is not blocked by a structure or physical object, is remapped to a ratio ranging from 0 to 1, where a ratio of 1 indicates a full view of the sky.
This commonly used factor is adapted within the first experiment of this thesis. In this case, it is to be understood as the portion of the sky that can be seen from within a building. Only facades with windows are considered, and the base points are set within the buildings at a distance of 1m from the facade at every floor. An average sky view factor for the site was constructed and the resulting percentage became the SVF that was to be kept for the existing buildings.
On the subsequent experiments, the SVF was used in a traditional manner to evaluate the generated networks and open spaces. The results are compared to existing spaces that were previously evaluated using the same method and setup.
29 Methods
Figure 3.3.5 Adapted sky view factor (SVF). Sky
d1 α β b a a d2 w = 2a + b
Visibility Analysis
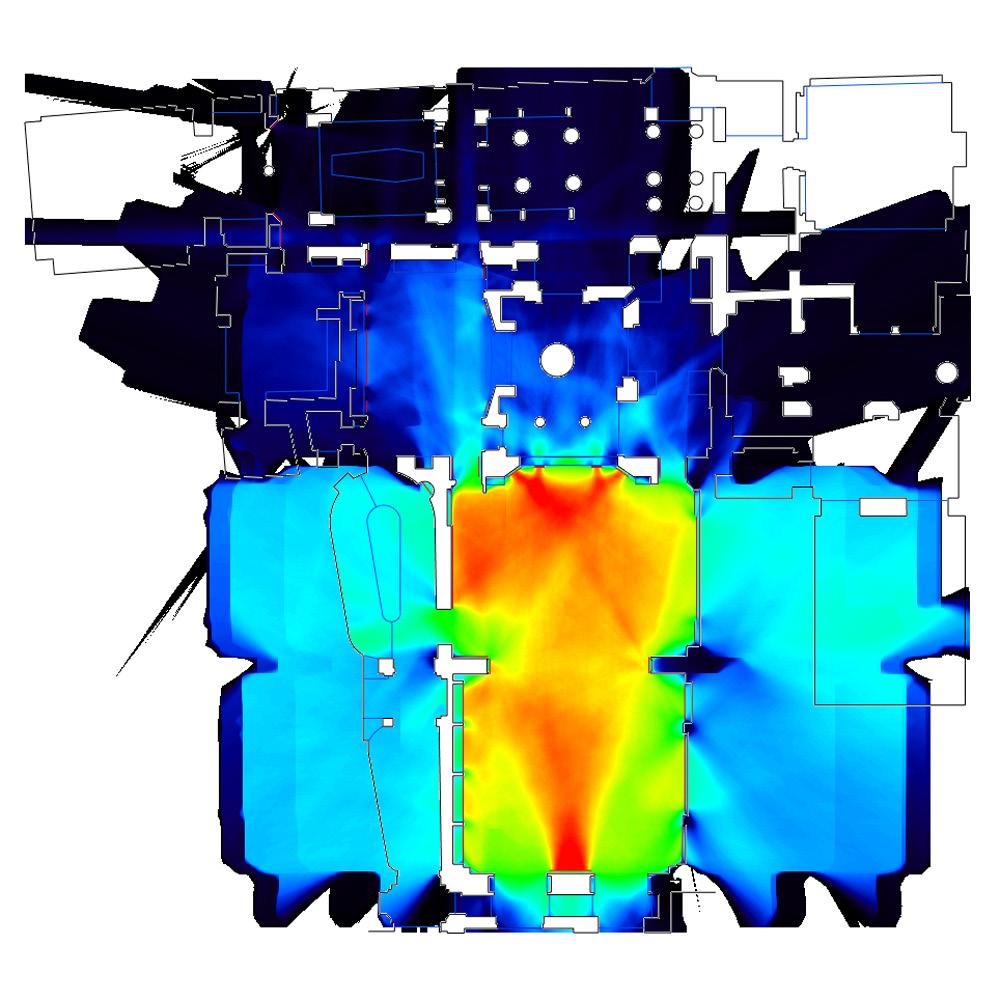
Space Syntax theory argues that the urban geometry influences the movement patterns of the users. Bill Hillier states that there is a direct relation between the visible perception and the movement patterns of people. (Hillier, 2014)
The navigation patterns of the user depend on the spotting of the strategical points that perform as the references for orientation or as destinations of the movement. The way-finding in a complex environment depends highly on these points of reference, as the movements towards or from these points is determined by the user’s possibility of visualizing the one from the other.
The visibility analysis provides a quantification of the visible relationships between certain urban areas and observer points. In the urban analysis visibility is the visible area of an urban location that is directly visible from several observer points. The quantification of the visible area is conducted by dividing the analysed area into a cellular or point grid; then, the observer points will be connected to these cells by straight lines if there are no obstacles between the cell and the observer point. Each one of the surface’s cells receives a value according to their visibility from the preselected set of observer points. As a result a view shed will be obtained that displays a colour gradient of visible to invisible points on the surface. This view shed is also called the isovist.
30 Symbiotic aggregations
Figure 3.3.6 Isovist analysis.
Computational Fluid Dynamics (CFD) Analysis

Computational fluid dynamics (CFD) is a virtual simulation environment that provides qualitative and, sometimes, quantitative predictions about the behaviour of fluids within closed or open spaces. Under the definition of fluid flows one can consider the meteorological phenomena, environmental hazards, interaction of the objects with the surrounding air, water or other fluids, combustion in propulsion systems etc. Due to its wide scope of analytic possibilities and its inexpensive implementation, as opposed to wind tunnels or other physical models, these simulations have become widely used bye naval engineers and mechanical engineers; in the automotive design industry, aviation and architecture.
However, CFD simulations can not replace the physical models and measurements; their implementation is understandable at early design stages, where many inexpensive design options or sketches can be evaluated. The predictions have to be validated through meticulously calibrated physical experiments. Scale is an important factor. Predictions within controlled and enclosed environments are more reliable than larger ones. Open systems, in particular, are very hard to predict bye means of a mathematical model.
A CFD setup requires several analytic steps to start the simulation. First, the problem must be stated. It should be decided on which physical conditions are directly related to the flow problem. The goal of the CFD simulation should be determined and specific: is the goal to improve the performance through shape optimization or to observe the velocities and vectors in the model? After the statement of the problem, a mathematical model will be prepared that determines the resolution of the input information. The obstacles with minor or no influence on the solution will be eliminated to increase the computational efficiency. The boundary conditions and their rugosity, the type and the velocity of the flow will be defined. Boundary conditions can be explained as the surrounding volumes that obstruct or conduct the fluid, and inlet and outlet faces. According to the properties of the boundary faces, i.e. the pressure values the fluid type and the flow velocity the CFD will provide the behavioural prediction of the fluid within the boundary volume. The mesh discretisation helps to define the zones in the analysis mesh where a higher resolution of information has to be provided. However, the resolution of the mesh can increase the computing time. The simulation is an iterative process. The more iterations result in an increase of solution’s accuracy at the expense of computing time (Anon, 2015).
In order to conduct the wind flow test two softwares were tested: Autodesk Flow Design and Autodesk Simulation CFD. Both packages were selected due to the ease of the file exchange and information flow between the Rhino modelling engine and the CFD solver. Although flow design has a very user friendly interface, Simulation CFD provided more control options and detail; therefore all the simulations were conducted in Simulation CFD.
31 Methods
Figure 3.3.6 Wind velocity analysis in simulation CFD.
32 Symbiotic aggregations 04 Case studies
Pedestrian street
Sidewalk Passage Courtyard Square Arcade Stairs
33 Case studies
4.1 Element of public space in Istanbul
4.2 Mardin
4.1 Elements of public space in Istanbul

The quality of public space can be numerically evaluated by rating the intensity of social activities. The activities that occur in public can be classified in two types: necessary activities that occur in everyday life and the recreational activities that are more optional. (Gehl, 2009) The necessary activities such as commuting between places, habitation, work and grocery shopping, necessarily happen regardless the built environment. However, the recreational activities such as sitting outside or going for a walk are directly related to the composition and the environmental properties of the built environment. The relation of the recreational activities to their surrounding varies depending on the sociocultural values of each society. Therefore, in order to quantify the qualities of a public space it is necessary to understand some of the cultural habits of the Turkish society.
The importance of social interaction that takes place in the public spaces of Istanbul is vanishing. The new growth scenarios that use regularly dispersed urban models, that neglect the public exposure that is embedded in Turkish tradition, are becoming the norm. Since these models only respond to the population growth; they lack any architectural intentions for a recreational or leisure activities. For this reason, the central areas of the city, that respond to the social needs of the population, remain as the main global attractors within the urban area of Istanbul.
When the urban areas with high historical and cultural value are observed,
34 Symbiotic aggregations
Figure 4.1.1
French Street, Istanbul. Image source: Beyoglu entry in Wikipedia website.
it can be noted that these show spaces that foster social interaction and a vivid social life. The vibrant social life in Istanbul is projected on the public spaces. With an origin from the open semi-public spaces in vernacular Turkish architecture, the contemporary street is reclaimed by the surrounding businesses as a space of exhibition that fosters random social encounters and interaction. The reclamation of the street blurs the boundaries between inside and outside; it transforms the street from a transit zone into a habitable one. The result is a continuous public space that extends from streets through passages that connect larger plazas with smaller courtyards. This densely interconnected public space is host to diverse architectural typologies that create several micro-climates within the urban fabric, that increase flexibility of the public spaces, for they form a conglomerate of open, semi-open and closed areas that are able to accommodate many activities.
In order to generate a new urban model that addresses the social idiosyncrasies of the Turkish population, it is necessary to understand what drives the social interactions that are related to the composition of the public spaces. Typically, the evaluation of the public spaces depends on a subjective perception of the user, but the intention of evaluating their existing qualities and enhancing them, can only be achieved through an objective understanding of the urban conglomerate of Istanbul. Understanding the relationships between the different types of public space and their key urban features will help to develop a set of parameters for the experiments. The various elements of the public space will be often referred to, in the text, as typologies, traditional values or traditional morphologies.
35 Case studies
Figure 4.1.2
3D axonometric presentation of Tunnel Square in Istanbul. This square was essential in order to understand the continuity of the public space within the morphologically changing built environment. It is a composition of narrow streets, passages, plazas that connect to the terraces in upper levels of the buildings. Therefore it also represents the multi- levelled nature of the public space in Istanbul.
Pedestrian street































The street is the centre of social and commercial activities in Turkish culture. The extension of the surrounding amenities to the street converts it from being a zone of transitional movement into a space of interaction. In Istanbul the pedestrian streets are usually surrounded by buildings of 15-20m height, which provide shadow for the pedestrians during the day. The usually unidirectional composition of the pedestrian street provides an almost equally distributed direct visual access to the surrounding functions.
The pedestrian street branches out in the urban composition and forms other urban typologies. Therefore it can be considered as a distributor, that connects the different urban formations. Therefore street can be described as the most public urban space. This property makes the street an important attractor, therefore usually the pedestrian streets are very busy places in Istanbul. The intense activity overloads the urban space and decreases the user comfort.

36 Symbiotic aggregations 10-15 m 3-6 m sunlight hours analysis high low 0 >9 high low visibility analysis sky view factor
Figure 4.1.3 (above)
Istiklal Avenue, the busiest pedestrian street in Turkey, has 2 million visitors per day (Wikipedia, 2015).
Figure 4.1.4 (above right)
Diagram showing a pedestrian street. From top to bottom: plan view, sunlight hours analysis, visibility analysis and SVF.
Sidewalk






The limited open area in the dense urban tissue results in absence of semi private courtyards which are important values of the traditional Turkish architecture. In traditional Turkish architecture, the semi private courtyards serve as a habitable space during the hot summer months, due to the environmental comfort they provide.
The demand for a semi open ventilated space leads to reclamation of the sidewalk and privatization of it by placing private goods. Accordingly the street becomes a semi private zone to receive guests, observe the passengers and spend hot summer days.







The reclamation of the sidewalk can be mostly observed in the narrow streets, since the densely built environment provides shading and increases the environmental comfort on the sidewalk.

The sidewalks are usually reclaimed by small amenities in the locality. The lack of any physical or visual boundary keeps these areas from being private, therefore these spaces can be considered as a semi public zones within the public space.
37 Case studies sunlight hours analysis high low 0 7 high low visibility analysis sky view factor 3-5 m 1-2 m
Figure 4.1.5 (above) Streets are reclaimed by the surrounding small businesses as semi private space.
Figure 4.1.6 (above left) Diagram showing the reclaimed areas of the sidewalk. From top to bottom : plan view, sunlight hours analysis, visibility analysis and SVF.
Passage
















































A mixture of indoor and outdoor elements composes the traditional public space in Istanbul. The streets extend to the indoors in order to creating protected shortcuts to other outdoor areas. Instead of building a boundary between indoor and outdoor areas, these extensions also categorized as passages, distract the pedestrian movement from the outdoor streets and generate a diverse urban movement. The protected microclimate of the passages also makes them to favourable branches of the street network during the cold winter months.

The passages usually attract the retail and small businesses which do not necessarily have to be exposed to streets. Compared to the big indoor shopping malls passages create a small microcosmos in the urban fabric. The passageway serves as a gathering place by the shop owners, while waiting for the customers. It is also regained as a space for exhibiting the goods in order to attract the customer inside the shops. This properties converts the passage from being a connection between two places into a own value of the Turkish public space, which creates its own microcosmos.

38 Symbiotic aggregations sunlight hours analysis 0 9 high low high low visibility analysis sky view factor 4-6 m 15-20 m
Figure 4.1.7 (top): Avrupa Passage on Mesrutiyet Avenue. Image source (Listemis, 2012).
Figure 4.1.8 (above): Axonometric representation of the public space in Flower Passage Istanbul.
Figure 4.1.9 (right): From top to bottom: plan view, sunlight hours analysis, visibility analysis, SVF.
Courtyard




















































The urban courtyard can be compared to the semi-private courtyards in the traditional Turkish house. Similar to the Turkish house, these places filter the visitors from busy pedestrian areas. Courtyards also create a semi-public zone between the private residential buildings that surround it.





Courtyards are usually hidden in the dense urban fabric of Istanbul. They branch out from the public zones through hidden passages. The boundaries can be a dark entrance or a stairway, so the squares appear to be a cull-de-sacs. Users require a local knowledge to find the access. The restricted accessibility helps to maintain the local atmosphere, and forms a recreational zone for the inhabitants of the area. The accessibility for the local communities produces a vigorous social interaction by the locals. The users are usually from the neighbourhood and have a close relationship with the inhabitants of the area. The sizes of the courtyards can vary, but the ones smaller than 20m2 tend to remain private given their constrained size. It is important to be connected from more than one point to the network to induce a pedestrian flow.

39 Case studies sunlight hours analysis 0 9 high low high low visibility analysis sky view factor 2-3 m 4-5m
Figure 4.1.10 (top) Hazzopulo Courtyard. Image source (görüntüle, 2012).
Figure 4.1.11 (above) Axonometric view of the courtyard at Hazzopulo.
Figure 4.1.12 (left) From top to bottom : plan view, sunlight hours analysis, visibility analysis, SVF.
Square




























Public squares are extensions of pedestrian streets, they contribute to the orientation and breaking the linear character of pedestrian paths. Squares generate hubs that connect the pedestrian street to others. Basically these are junctions of pedestrian paths.

A plaza is one of the main elements for any social activity. Without having any solid boundaries to the surrounding areas, it is accessible by everyone and therefore an important point for public gathering. It can be surrounded by semi-public functions with the terraces oriented towards the plaza. Since the observation is the first stage of public interaction, these terraces are usually occupied first. The desirability of the plazas changes according to their size and location, with emphasis on the latter.
The plazas that are directly connected to important urban paths are larger attractors for the public. However, some plazas such as Taksim square do not follow this rule, even though it is in a very well connected area, due to its large size (almost 200m by 200m) the square remains only a zone of transition and a space for political events and proselytism, but is very rarely used by the public as a gathering point. A busy car street detaches the surrounding functions from the square, therefore the vibrant atmosphere cannot be extended towards the it. Looking at this particular problematic of Taksim square, it can be concluded that the size and the barriers have a big influence on the quality of a public square. Learning from this situation, in order to calculate the upper limit in the size of a square, keeping a certain urban density should be taken into consideration. Spreading out the density results in a loss of perception that leads to disorientation and urban desertification.
40 Symbiotic aggregations sunlight hours analysis high low 0 >7 high low visibility analysis sky view factor 20-30 m 10-15 m
Figure 4.1.15 (above)
Axonometric representation of a public square.
Figure 4.1.16 (right)
From top to bottom: plan view, sunlight hours analysis, visibility analysis and SVF.
Figure 4.1.17 (opposite)
Pictures of Taksim square (above) and Galata Tower square (below)


41 Case studies
Arcade





















Arcades are constructed in order to avoid over heating of the building surfaces during the hot summer days and protect the surface from humidity that is caused by precipitation.






















Arcades create semi-open spaces that provides sight protection from the street. The climatic comfort and sight protection that it provides makes the arcade a desirable semi-private space for inhabitants.

42 Symbiotic aggregations sunlight hours analysis high low 0 >7 high low visibility analysis sky view factor 2-3 m 2-3 m
Figure 4.1.18 (above) Arcade way of Rustem Pasa Mosque Istanbul (Wikipedia, 2015)
Figure 4.1.19 (top right) Axonometric representation of a arcade way
Figure 4.1.20 (right) From top to bottom: plan view, sunlight hours analysis, visibility analysis and SVF.
Stairs





















Istanbul’s extremely diverse topography makes the stair a desirable urban solution. In areas where the inclination brutally changes, many streets have been adapted into stairs. This network system requires high physical activity from the user, therefore many of the stairs have small shaded flat zones where the user can stop and relax for a while. The staircases connect the entrances of many buildings. The shaded zones at the building entrances are used as semi private spaces by the inhabitants of the building, who appropriate the public space for their personal use. The generated atmosphere is quite unique, where the street becomes a natural extension of the house or office.

43 Case studies sunlight hours analysis high low 0 >7 high low visibility analysis sky view factor 2-4 m 1-1.5 m
Figure 4.1.21 (above) Arcade way of Rustem Pasa Mosque Istanbul (Wikipedia, 2015).
Figure 4.1.22 (top left) Axonometric view of a street with stairs.
Figure 4.1.23 (left) From top to bottom : plan view, sunlight hours analysis, visibility analysis and SVF.
44
sizes number of connections ranking functions privacy value w = 4 m-10 m h = 6 m -12 m area = 500 - 2000 m2 2- 6 w = 2 m-10 m h =3 m - 6 m area = 2 - 50 m2 paralell to street w = 1 m-2m h = depends on the canteliever area = 0.5 - 5 m2 parallel to street w = 10 m-20 m h = open air area = 200-500 m2 2-5 w = 15 m-60 m h = open air area = 500 - 2000 m2 from every corner accessible w = 8 m-16 m h = open air depends on crossing streets 1 retail leisure 3 4 2 5 6 semi private space amenities semi private space small business leisure small business retail leisure semi public retail leisure semi public w = 3m -5m h = open air 2-3 6 semi private pedestrian street square stair sidewalk arcade courtyard passage private public
Symbiotic aggregations
The analysis of different typologies that comprise the traditional urban space in Istanbul ended up in an evaluation of these types regarding their environmental and social qualities.
The evaluation concluded that the people prefer smaller protected areas for longer stays. Therefore, the socially active public zones of stay do not necessarily provide higher visibility; rather, people seem to be drawn to corners or protected areas, where at least to walls form a corner. On the other hand, the places of transit such as streets are more active when the visibility is high.
Due to the privacy that they provide, the smaller public spaces such as sidewalks, courtyards, stairs and passages were more desirable. These zones support the emergence of the instant social interaction without directly relating to it. The indirect relation to function attaches an adaptive property to these types of spaces, where the shape of built environment is not dictated by the function, but rather it attracts different functions. The relation of the typologies to the functions was carried further to develop a logic for functional distribution.
45 Case studies
Table 4.1.1 (opposite)
The chart shows the properties and the ranking of typologies that compile the public space in Istanbul.
4.2 Mardin
Values are obtained from positive and negative cases, certain areas in Istanbul were investigated, but so should nearby vernacular settlements which share similarities in geography, topography or climate, because “[c]ity forms emerged within different topographies and ecological systems, evolving from regional variations [...]” and “[their] forms expanded and developed, strongly coupled to the dynamic changes of climate and ecology within which they were situated.” (Weinstock, 2010) It makes sense, then, to extract specific information from vernacular architecture that shares similar conditions to the site. The design logic obtained can be translated into parameters or target values for the project. It was important to select a tissue that displays the vernacular properties of Turkish housing and the relation of these to the urban fabric.
As one of the oldest urban settlements in Turkey, Mardin offers detailed information about vernacular architecture in relation to a high dense urban fabric. The city displays a particular relationship to the ground, which takes its origins from the nomadic settlements (Hensel, 2010). The interaction between the ground and the built environment is one of the most particular. The two dimensional projection of the figure ground does not provide an information on the complex three dimensional maze-

46 Symbiotic aggregations
Figure 4.2.1 Landscape of Mardin (kalemsizdergi.com/mardin/ mardin-tathevler-miniaturk).
Figure 4.2.2 (opposite) Defining urban features in Mardin.
like structure of the city. Originating from the nomadic organization of the settlements, the city’s plan has a distinct relationship to the ground. The densely built structure anchors itself to the topography by creating terraced houses overlapping each other and connected to the neighbours through the rooftops and bridges.
The particular location on a steep hill is a defining parameter for the urban fabric. The streets are often parallel to the terrain to avoid large inclinations; though perpendicularly the inclination determines the orientation of the houses and allows them not to cover the views of each other, while the south facing façades minimise exposure to sun. The climate has a big influence on the density of the urban structure. Large openings are avoided to reduce solar access and heat gain, and creating bridges between roofs over the streets below increases the shadow during hot summers (up to 42°C) and to helps hinder cooling in the winter months (-13°C). In addition, a large amount of shaded arcades can be observed and their function has been discussed in the traditional typologies in Istanbul.
The introverted organization of the houses separates the living space into layers of privacy. The semi-private courtyard is accessible to the visitors and provides an area for social interaction. Arcades that surround the courtyard create a microclimate that serves for the cooling of the courtyard in the hot summer months. These covered arcades are used as social areas in the hot summer days. The interior of the house is divided into two spaces with different climatic conditions. The larger areas, which are located right next to the arcades exterior, are spaces that are used in summer months; smaller rooms, which are mostly exposed to sun, are occupied in the winter months.
47 Case studies
courtyards semiopen spaces
private spaces
4.3 Cihangir
Cihangir is one of Istanbul’s most lively neighbourhoods where modern habits fusions with the traditional elements of Turkish culture. Even though it is located in the very centre of Istanbul, the area could preserve traditional neighbourhood characteristics. The reason for the preservation is that neighbourhood is slightly isolated from the busy Taksim square and it’s continuation to Istiklal Street which is argued to be the busiest street in Turkey with almost 2 million passengers a day.
Contrasting the busy structure of Istiklal, Cihangir inhabits a more local social structure. The visitor number decreases dramatically in contrast to Istiklal This decrease can rely on two reasons; the topographic properties of the area filter the accessibility. The inclination from the waterfront towards Taksim forces the passengers that arrive in Kabatas to take the underground that directly connect to Taksim square. Secondly the distribution of the leisure functions are mainly concentrated on the plateau zones of the area, therefore these zones are more attractive for the visitors from outside the neighbourhood, whereas the actual neighbourhood keeps its tranquillity.
However the strong effect of the topography over the functional distribution creates an inequality within the patch. The inhabitants that live in the lower end of the inclination still need to climb a whole hill to arrive to a leisure area.
The goal was set as keeping these properties of neighbourhood, while densifying the area. Therefore the public activities and elements of the Turkish public space were the most important to analyse in order to carry the understanding of a neighbourhood further in a high dense urban structure.
A central area of 0.12 km2 within this neighbourhood was selected as the site to perform the experiment at. Having many different possibilities for urban infill allowed to explore the system’s limits. Also, being low on leisure function turned it to a good site to test addition of multiple public facilities.

48 Symbiotic aggregations
Figure 4.3.1 Typical landscape in Cihangir neighbourhood. (Image: Aksoz)
n
residential office mixed commercial residential
abandoned health mixedcommercialeducationparking office
religious open public
Case studies
Figure 4.1.17
Selected area for the experiment in Cihangir.
education parking health open public religious abandoned
05 Design development
50 Symbiotic aggregations
5.1 Objectives
General objectives map
Population
Public space
Environmental
5.2 Design development process overview
5.3 Infill growth
Aim
Methods
Setup: environmental boundary
Setup: context
Initial tests
Implementation
Iteration
Results
Conclusion
5.4 Open spaces
Aim
Methods / Setup
Initial tests
Implementation
Results
Conclusion
5.4 Base network and secondary nodes
Aim
Methods / Setup
Initial tests
Implementation
Results
Conclusion
5.6 Network morphology (public space)
Aim
Methods / Setup
Initial tests
Implementation
Results
Conclusion
5.7 Environmental (wind)
Aim
Methods / Setup
Initial tests
Implementation
Results
Conclusion
5.8 Programmatic distribution
Aim Setup
Implementation Results
Local distribution
Aim Setup
Implementation
Results
Conclusion
51 Design development
5.1 Objectives
General objectives map
In order to set up the complex series experiments, it was important to define the physical boundaries. A 12.2ha area in Cihangir, in central Istanbul was selected. Questioning the qualitative and quantitative drivers for the urban composition, it was decided to separate the targets into three categories: population targets, public space targets and environmental targets. Where the population targets sets the limits to the growth, the public space and environmental targets intend to enhance the existing qualities of the urban tissue through architectural diversification and improving the environmental comfort conditions.
Population
Limiting the population to a specific target would predefine the boundaries of the growth system. Instead, setting a population target beyond the expected conditions adds pressure on the system and forces it to grow as a competing criterion.
The population projections made by the Turkish Statistical Institute (TUIK) was taken as an base outline (turkstat.gov.tr, 2014). From the three population growth scenarios predicted by TUIK, the most extreme prediction shows a population increase of 5.2 million inhabitants in 30 years; this scenario was selected to calculate the population target. The population increase was distributed, keeping the recent density gradient and adding up the population in direct relation to the density
52 Symbiotic aggregations
Table 5.1.1
The objectives map shows the link between the particular objectives set out to achieve the global ambition and the specific parameters that are related to them.
Objectives map
Different objectives
specific parameters parameters
existing population
proposed population
composition
total area required
[2]
Population
demographics functions [1]
existing programme
proposed programme
requirements
total area required
total area
characteristics connectivity
Public space performance
visibility
sky view factor
surface inclination
network betweenness
inclination
accesibility
beaufort scale
Environmental [3]
comfort range
solar access
shading wind
human comfort scale
indirect sunlight albedo
direct sunlight
beaufort scale
53 Design development
gradient. This calculation resulted in an addition of 13,200h/km2 in the district of Beyoglu, where the selected patch in the neighbourhood of Cihangir is located. This population density was multiplied times the size of the selected patch which is 12.2ha; therefore, the target is 1,741 additional inhabitants within the site.
The population target determines the target volume and the set up for the functional distribution. The total population was set up as a driver to calculate the target area of the open spaces.
Public space
Public space provides a stage for social activity and interaction. Therefore it represents one of the essential aspects of urban design. The intensity of social activity in an urban area is directly related to the quality and diversity of the public spaces it consists. The quality of public space depends on the sociocultural habits of the certain society. Designing high quality public spaces requires a comprehension of the certain cultural habits.
In case of Istanbul urban life exposes itself on the street. The urban articulation results in emergence of a high spatial diversity,that provides various relations to the public realm and different environmental qualities. These emerging spaces are reclaimed by the inhabitants and converted into the public or semi public spaces. It can be concluded that the quantity and diversity of the public space is one of the main drivers of Istanbul’s vivid public life.
In order to generate a socially active urban growth this diversity was classified in different types. In order to fully explore the potential of the infill system and to be able to generate new typologies as well as traditional ones, the target in general was set to generate as many morphological types as possible without setting a target number for each.
The target area for open spaces were set as 9m2 per person for the new population (1,741 people) and the existing (3,615 people). This standard was set according to World Health Organization (WHO) that recommends that cities should provide a minimum of 9m2 of green space per capita. Although the parks were generated according to this target, the emerging typologies such as passages and courtyards were not respected in this target. The target area for open spaces was used to evaluate the overall area of the emerging and generated public spaces.
Environmental
The quality of an urban composition is related to the environmental properties. The environmental properties influence the user comfort and therefore influence the activity in the certain urban area. Evaluation of environmental properties can be an aid in quantification of the urban quality of the urban space.
54 Symbiotic aggregations
Table 5.1.2 (opposite) Projections for Istanbul’s population in 10, 20 and 30 years. The results show the population that would need to be added to Cihangir if Istanbul were to stop expanding.
population growth projection for 10 years
population growth projection for 20 years
population growth projection for 30 years
*1 3.6 is the average number of habitants per housing unit
*2 225m2 is the average amount of area (including all services except public space) for a housing unit
55 Design development
12.72 km2 12.72 km2 26.32 km2 59.28 km2 132.16 km2 123.89 km2 106.59 km2 115.62 km2 451.18 km2 47.31 km2 20,000 - 25,000 15,000 - 20,000 10,000 - 15,000 5,000 - 10,000 500 - 5,000 0 - 500 40,000 - 50,000 1.17% 1.17% 2.42% 5.45% 12.15% 11.39% 9.80% 10.63% 41.48% 4.35% 10.18 km2 10.18 km2 21.06 km2 47.42 km2 105.72 km2 99.11 km2 85.27 km2 92.50 km2 360.94 km2 37.85 km2 23,655 2,255,900 1,156,200 1,598,850 2,477,800 3,304,000 1,778,400 921,200 508,800 636,000 habitants / km2 * Istanbul’s urban area 870,159 km2 Istanbul’s area 1,087,699 km2 - 20% not buildable ‘density-area’ (x) coefficient 4,378.6 hab 417,574.0 hab 214,016.2 hab 295952.0 hab 548,648.4 hab 611,580.5 hab 329,187.3 hab 170,516.9 hab 94,180.4 hab 117,725.6 hab x * 2,713,760 14,660,805 remap each x additional population for 2023 2,713,760 35,000 - 40,000 30,000 - 35,000 25,000 - 30,000 329,187.3 hab 47.42 km2 6,941.95 hab 3.6 = 6,941.95 hab / km2 * 225m2 = 433,871.9 m2 ∑14,660,806 1,087.699 km2 12.72 km2 12.72 km2 26.32 km2 59.28 km2 132.16 km2 123.89 km2 106.59 km2 115.62 km2 451.18 km2 47.31 km2 10.18 km2 10.18 km2 21.06 km2 47.42 km2 105.72 km2 99.11 km2 85.27 km2 92.50 km2 360.94 km2 37.85 km2 870,159 km2 Istanbul’s area 1,087,699 km2 - 20% not buildable 20,000 - 25,000 15,000 - 20,000 10,000 - 15,000 5,000 - 10,000 500 - 5,000 0 - 500 40,000 - 50,000 1.17% 1.17% 2.42% 5.45% 12.15% 11.39% 9.80% 10.63% 41.48% 4.35% 23,655 ∑14,660,806 2,255,900 1,156,200 1,598,850 2,477,800 3,304,000 1,778,400 921,200 508,800 636,000 habitants / km2 * Istanbul’s urban area 1,087.699 km2 ‘density-area’ (x) coefficient 6,305.0 hab 601,291.1 hab 308,175.4 hab 426,160.0 hab 660,436.7 hab 880,653.4 hab 474,017.5 hab 245,538.1 hab 135,616,4 hab 169,520.4 hab x * 3,907,714 14,660,805 remap each x additional population for 2033 3,907,714 35,000 - 40,000 30,000 - 35,000 25,000 - 30,000 474,017.5 hab 47.42 km2 9,996.15 hab 3.6* = 9,996.15 hab / km2 * 225m2 = 624,759.5 m2 12.72 km2 12.72 km2 26.32 km2 59.28 km2 132.16 km2 123.89 km2 106.59 km2 115.62 km2 451.18 km2 47.31 km2 10.18 km2 10.18 km2 21.06 km2 47.42 km2 105.72 km2 99.11 km2 85.27 km2 92.50 km2 360.94 km2 37.85 km2 870,159 km2 Istanbul’s area 1,087,699 km2 - 20% not buildable 23,655 ∑14,660,806 20,000 - 25,000 15,000 - 20,000 10,000 - 15,000 5,000 - 10,000 500 - 5,000 0 - 500 40,000 - 50,000 1.17% 1.17% 2.42% 5.45% 12.15% 11.39% 9.80% 10.63% 41.48% 4.35% 2,255,900 1,156,200 1,598,850 2,477,800 3,304,000 1,778,400 921,200 508,800 636,000 habitants / km2 * Istanbul’s urban area 1,087.699 km2 ‘density-area’ (x) coefficient 8,317.5 hab 793,216.1 hab 406,541.3 hab 562,185.2 hab 871,240.3 hab 1,161,747.5 hab 625,318.3 hab 323,910.9 hab 178,903.5 hab 223,629.4 hab x * 5,155,010 14,660,805 remap each x additional population for 2043 5,115,010 35,000 - 40,000 30,000 - 35,000 25,000 - 30,000 625,318.3 hab 47.42 km2 13,186.81 hab 3.6* = 13,186.81 hab / km2 * 225m2 = 824,175.3 m2
According to Köppen climate classification, Istanbul has a Mediterranean climate characterized by dry hot summers and relatively cold winters. During the summer (June, July August) there is almost no precipitation and average high temperature of 29 degrees and during the coldest month (February) the temperature drops to an average low of 3 degrees (Koeppen-geiger.vu-wien.ac.at, 2015).
Due to the climate change between summer and winter moths it was important to set the targets that address the user comfort in both seasons. Accordingly the targets for environmental properties were classified in three categories; solar access, shading and wind.
To accommodate the growth without compromising the conditions in which the residents live in, the recent solar access and sky view factors were respected by the growth system. The growth system intended to keep a certain solar exposure for the generated public spaces for the winter moths and provide shading for the summer.
Wind was used to bring a certain user comfort into the system, where shading could not be achieved. The prevailing wind direction with the during the summer (NNE) average wind speed (6m/s) was taken as an input for the evaluation of the experiments. The targets for wind speed was set relying on user comfort vs. wind speed calculations of Isumov and Davenport.
There was not a numeric target that was set for shading rather the results were compared to the case studies of well functioning urban areas and evaluated accordingly.
5.2 Design development process overview
The design development consists of six sequential experiments that aim to address the objectives previously laid out. The series of experiments is additive, and necessarily build up on the results of the previous ones. The experiments were carried out in two different scales as shown opposite. Some were conducted on the entire neighbourhood scale, and, for computational ease, others were carried out in each sub-patch area (yellow). In some cases several tests compose a single full experiment, for this reason the process was designed in a way such that the necessary feedback loops became embedded within. A few of the experiments were iterated several times, since the results prompted a necessary modification or adaptation of the process. Finally, it’s important to mention that the final scheme shown in the design development map is the distilled result of a trial and error process filled with dead ends and mistakes.
The aim of the infill growth experiment is to build a specific infill morphology that responds to its context; the result should provide the framework where an urban and architectural character can be
56 Symbiotic aggregations
Figure 5.1.1 (opposite) Axonometric view of the patch in Cihangir. The subpatches are divided by yellow lines.

57 Design development
subsequently developed. The experiment addresses the volumetric qualities and character of the proposed infill. Demographic and programmatic constraints are taken into account.
The open spaces experiment forms open spaces that are highly articulated and connected amongst themselves and to the existing network. The experiment aims to add public space on different vertical datums that can relate to the existing topography and buildings. The result is a group of three-dimensionally placed open spaces.
The base network experiment aims to build a comfortable network that weaves the generated open spaces, the emerged open spaces, and the existing network. The experiment relies on the previous results, and deforms the open spaces to satisfy regulations and comfort parameters.
The network morphology (public space) experiment seeks to refine the previous result and relate it to comfort and environmental criteria. The link between morphology and sky view factor, visibility, solar access and shading is established and evaluated. The result is a detailed public space network generated by performance data and a body plan design.
The environmental(wind)experiment works on the premise of perforating volumes to permit wind access to achieve specific comfort levels. It takes into account the previous experiment’s resulting solar access and shading parameters and builds up on them. Based on a comfort scale for winter and summer, wind becomes a mediating factor that can be utilised to increase comfort where needed. The expected result should show an increase of public areas where the comfort criteria is met, while keeping as much of the original volumes as possible.
Finally, theprogrammaticdistribution assigns functions to the volumes according to the architectural characteristics of the space. This makes the experiment particular for it is both an information generative process and an evaluation tool. By working on the premise that people will use spaces based on their characteristics, rather than an imposed programme, this experiment algorithmically distributes functions depending on the local architectural conditions. As a result a public gradient is generated, which is then translated into design information. Ideally the distribution should match the initial expected targets for a given population, so the closer the match is, the more successful the whole process is; it is in this sense that this experiment is also an evaluation method.
58 Symbiotic aggregations
Table 5.2.1 (opposite)
The design development map shows the link between the particular objectives set out to achieve the global ambition and the specific steps (or experiments) in the process.
The left column refers to the objectives map, and the right column to specific chapters in this section.
Design development map
Link to objectives
total volume
[2]
Population
total area characteristics
6 3 Infill growth
Aim
Methods
Experiment / process desigend demographics functions [1]
Setup: environmental boundary
Setup: context
Initial tests
Implementation
Iteration
Results
Conclusion
6 4 Open spaces
Public space performance
[3]
Public space performance
characteristics connectivity total area
characteristics [4]
Public space performance environmental sky view factor visibility solar access shading
Environmental [5]
characteristics connectivity total area solar access
comfort range zone shading wind
Aim
Methods / Setup
Initial tests
Implementation
Results
Conclusion
6.5 Base network
Aim
Methods / Setup
Initial tests
Implementation
Results
Conclusion
6 6 Network morphology (public space)
Aim
Methods / Setup
Initial tests
Implementation
Results
Conclusion
6 7 Environmental (wind)
Aim
Methods / Setup
Initial tests
Implementation
Results
Conclusion
Population / Functions [6]
characteristics
morphology total area distribution
6.8 Programmatic distribution
Generative and evaluation
Aim
Setup
Results
59 Design development
5.3 Infill growth
In order to prove that an infill strategy can be used to add density to existing urban tissues, the infill growth experiment was proposed. The infill growth experiment lies at the heart of this dissertation for it forms the basis for the rest of the work. In order not to be so deterministic from the onset, three results will be selected on which to experiment further; they are evaluated for multiple criteria, some of which are competing, so the results will show high variation as well.
The experiment is set within a specific context, and is highly constrained by physical and environmental factors. Further parameter and constrains will be added on the subsequent experiments. On a second iteration of the experiment, the growth will be split into areas of distinct architectural and structural character, adding a necessary logic of structure and connectivity that is highly dependant on the immediate context.

The method selection will be thoroughly discussed, for this infill morphology generative process can be achieved by different means, but only one is finally selected and carried forward. Associative modelling, and Cellular Automata (CA) are considered as possible base modelstheir advantages and disadvantages will be discussed.
Aim
The aim of this experiment is to test whether it is possible to generate, by using evolutionary computation, a specific infill morphology that
60 Symbiotic aggregations
Figure 5.3.1
‘These areas are conformed by a collection of empty plots, parking lots, side-walls, residual spaces or generally neglected areas’. (Image: Aksoz)
recognises and meaningfully occupies residual, neglected and potential spaces within an existing urban fabric, considering the physical and environmental constrains. Particularly, the generated infill should begin to sketch specific architectural types and morphologies that are deemed desirable.

Methods
An infill growth strategy is proposed to occupy the viable space within a specific buildable envelope. In order to generate a logic material growth strategy, a variation on a cellular automata model was chosen; the idea behind is to have a basic set of growth rules that make sense within the locality, so that a logical global form can emerge. As explained in the methods section, several experiments in the literature point towards a possible implementation of CA as a morphology generator, particularly where the boundary conditions are diverse and rather strict.
It is in the nature of cellular automata and agent based models to produce complex forms resulting from local interactions and rules. The results, although deterministic, are hard to predict after several time steps, particularly on a three-dimensional grid space. For instance, the rules can be formalized as follows: ‘[d]efine environment E as the number of living neighbours required to prevent a currently living cell from expiring, with Ei ≤ E ≤ Eu. Fertility F is the number of neighbours required to create a new living cell, Fi ≤ F ≤ Fu. Define the transition rule R as the 4-tuple (EiEuFiFu).” In the game of life model, the rule 2333 produces the famous ‘life-like’ result capable of programming itself (Bays, 1987) and in 3d life the rule 4555 yields similar results. In 3d life, the three-dimensional variant of the game of life, the total possibilities of transition rules R is finite, defined by [Ei ≤ E ≤ Eu] and [Fi ≤ F ≤ Fu] considering all the possible permutations for Ei, Eu, Fi, Fu where 0 ≤ E ≤ 26, and 0 ≤ F ≤ 26. (Bays, 1987)
The total number of possibilities is a rather small finite number (26^4 or 456,976) but only a few yield ‘life-like’ results. By determining a small set of axioms that describe ‘life-like’ behaviour, most rules can be discarded as useless (not meeting the criteria). After a set of experiments, the best set of rules for a given criteria (i.e. the possibility to produce gliders) can be selected. (Bays, 1987) Following a similar approach for our system, the intensity and range of the rules can be used as genes in a genetic algorithm, which changes the extent on which the growth logic is carried out and generates a vast array of results which can be evaluated for different criteria, instead of seeking ‘life-like’ results, the experiments focuses on finding fixed states in time where the fixed morphology is performing desirably.
By using this two-fold method of pairing cellular automata and genetic algorithms, it is expected that the fittest overall morphology will be selected, while remaining useful in the local level. The cellular automata’s local logic ensures that whatever growth is selected it is never in contradiction with the local rules set beforehand; while the
61 Design development
Figure 5.3.2
‘These areas are conformed by a collection of empty plots, parking lots, side-walls, residual spaces or generally neglected areas’. (Image: Aksoz)
Sky View Factor subtraction process
genetic algorithm will try to find what combination of these rules, in what order and with which intensity will provide the best results. In effect, since there are three global criteria, the genetic algorithm is exploring a three-dimensional space of morphological possibilities formed by the CA’s rules that act on a local scale and define a global form.
Setup : Environmental boundary
The CA operates on a three-dimensional point array that occupies the entirety of the negative space in the patch. A maximum of 15.0m above the highest building is considered as an upper limit for the negative volume, while the topography and the buildings constitute the remaining borders.
The resolution of the point cloud determines the size of the cells, and although subsequent volumetric transformations will be performed, their original size is quite defining. The morphology will grow from the point cloud, so - for computational ease - the original Cartesian orientation of the point cloud is preset. It is important to align the array with the urban grid as much as possible, while negotiating an environmentally-driven orientation as well. Three similarly oriented regions were recognized within the patch, and the tessellation operation was performed for each one separately. Once this is done, the result is a patch with a potential volume of 1,131,435m3, for comparison, the ‘shard’ building in London has an estimated volume of 624,000m3
In order not to compromise the existing conditions at the site, an
62 Symbiotic aggregations
Figure 5.3.3
Logic of evaluating the Sky View Factor for the existing buildings façades, and the generated envelope.
Existing buildings are selected for analysis.
Only the façades with windows and openings are kept for analysis.
Existing buildings
Façades with windows
Degree of SVF
Boolean difference volume
A volume is extruded from each of the façades following a vector defined by the SVF angle. This angle ensures a minimum sky visibility from every point.
SVF
Any point within the generated volumes will be deleted in order not to permit CA growth to occur within it.
environmental boundary was set up. The boundary was produced by taking the entire three dimensional point cloud of the negative space, and subtracting from it points within the crucial volumes that need to remain unobstructed in order to maintain solar access and sky view for the existing buildings. This resulted in a reduced but complex point cloud in which the CA could grow.
The important areas that need to remain unobstructed for solar access are determined by the sun vectors that affect building’s faces that receive 4 hours or more of sunlight during the winter period which is December 1st to February 28th between 9:00 am to 5:00 pm. After these faces were identified and isolated, a volumetric envelope is extruded from them, following the relevant sun vectors, and every point within this volume is removed.
A similar process was carried out in order to maintain a base sky view factor. For this, only the façades that have windows were considered. The lowest conditions observed in the site is 20% sky visibility at the narrowest streets, therefor this was set as the minimum boundary to maintain.
The resulting point cloud has a potential floor area of 377,145m2
Considering 20m2 per person is for residential use and programmatic distribution at its maximum area per function, a 105,749m2 will be needed. According to this calculation, even if 28% of the potential point cloud were used, it would be possible to reach the projected target in terms of area and environmental conditions.
63 Design development
Figure 5.3.4 Logic of evaluating the solar radiation for the existing buildings façades, and the generated envelope.
Existing buildings are selected for analysis.
Solar radiation 75.0% Solar radiation 64.7% Solar radiation 69.9%
Only the façades that are subject to high solar radiation during winter are selected for the analysis.
Existing buildings
Winter sun vectors
Exposed faces
Winter solar access considering self shading
A volume is extruded from each of the façade’s sections. The extrusion vector corresponds to the reversed sun vector for each hour that the façade is exposed.
Generators
First, the areas that present an opportunity to be used as terrains for infill were identified. These areas are conformed by a collection of empty plots, parking lots, side-walls, residual spaces or generally neglected areas; they are referred to as the unbuilt or negative space in a figure-ground diagram. Flat roofs were also identified in order to recognize possible space for expansion, for it was an original ambition not to affect inclined roofs, and flat roofs are easier to appropriate. The identification and mapping process of these areas were manually done; site mapping and surveying techniques were used.
Once the zones of opportunity were identified, they were translated into the 3d point cloud model previously developed. The points are then fed into the CA model as generators: this is the cells that will be developed at time t=0, or in the case of a probabilistic CA model, as the cells that have a specific high potential for development. For flat roofs the potential of development is also increased, but are not necessarily generators. For the python code see the appendix.
64 Symbiotic aggregations
Figure 5.3.5
On the left the map shows the deterioration of the buildings rated from 1-10, 1 being the worst. On the right the two main building typologies are mapped: type ‘a’ is the traditional type where buildings cantilever over the street and type ‘b’ are generally modernist buildings.
Figure 5.3.6 (opposite)
Illustration of the remaining point cloud, after the substraction of SVF and Solar Radiation volumes generated previously. On this point cloud the CA experiments will run.
n 1 10 type b type a


65 Design development
weighting: For a Moore neighbourhood where the CA grows above.
Implementation
Neighbourhoods
Each cell in the CA model has a neighbourhood of adjacent cells. The relationships of one cell to its neighbours are dictated by the geometry and extent of its neighbourhood, which can range from one adjacent cell to very large ones that mimic ‘action at a distance’. For this experiment, traditional neighbourhoods are used. These are the Moore neighbourhood and the von Neumann neighbourhood, only their extension is controlled as one of the parameters used by the GA.
Local rules
Once the generators are identified and set as 3d points, the CA is set up. The model operates on two different neighbourhoods following three distinct rules. Each rule is intended to produce specific growth patterns that were identified as probable generators of relevant morphologies. These are vertical growth, horizontal spread and passage/cantilever generation (see fig 7.1).
66 Symbiotic aggregations
Figure 5.3.7
Cellular Automata logic for producing diverse architectural types.
Set generators GA 1 1 1
Vertical growth Horizontal growth Passages/ cantilevers
d
Extended von Neumann neighbourhood is set with a variable ‘d’.
Topographical advantage: where the topography allows, the CA connects different elevations.
Variable
0 0 0 1 1 1 0*0*0* - - - 0 0 0
Generators are given different values depending on their initial (t=0) condition.
Vertical growth
The vertical growth modelling is approximated by a CA building method where the cell to be developed is informed by the status of the cells in the Moore neighbourhood below it, i.e. the cell directly beneath it and the eight cells that surround it. The cells that share a face with the bottom one are the face-connection cells and the remaining four are vertex-connection cells. Each of these subsets of cells can have a differential weighting for the transition rule R that is controlled by the GA in either the probabilistic or totalistic model.
67 Design development
Figure 5.3.8
Cellular Automata logic for producing vertical growth by using a 2D Moore neighbourhood.
Direct face connection
Total connections on moore neighbourhood
cell above
Corner connection 2d space
vertical growth
Horizontal growth
The horizontal growth modelling is approximated by a CA building method where the entire 3d Moore neighbourhood of a given cell is taken into account. Every cell that has at least one face connection with a developed cell is evaluated. So if ‘face connections’ ≥ 1 the cell is evaluated for its entire Moore neighbourhood. The total state of each cell determines the potential of weather the central cell is developed or not: this results in cantilevers and horizontal expansion where appropriate. The transition rule R is then controlled by a GA and can have a value x, where 1 ≤ x ≤ 26.
The 3D Moore neighbourhood is tested to find any cells with a face connection to a developed one. There are 26 neighbouring cells within this neighbourhood.
68 Symbiotic aggregations
Figure 5.3.9
Cellular Automata logic for producing horizontal growth by using a 3D Moore neighbourhood.
horizontal growth
Total connections 3d Moore neighbourhood
3d space Face connections Edge connections Vertex connections
Passages | cantilevers
The production of desirable morphologies and connections in the general growth is fostered by a rule that can detect specific opportunities within the 3d point cloud. An extended von Neumann neighbourhood is used to inform the development of a given cell, and all the cells that stretch through the von Neumann neighbourhood’s ‘arm’ that have potential for development will be develop too.
First, for any given developed cell, its variable-extension von Neumann neighbourhood is analysed, if within the neighbourhood there is a cell with potential, such as ‘flat roof’ cells, then the entire arm of such neighbourhood becomes developed; finally if any cell below the newly developed cells is developable, and the one below it as well, then the intermediate cells become developed too at time t=t+1. For each cell that is developed, the passages/cantilever criterion in the genetic algorithm is given one point. The GA’s genes control the extent ‘d’ of the von Neumann neighbourhood, but not its transition rule R, for if even one cell has potential, development will occur.
69 Design development
Figure 5.3.10
Cellular Automata logic for producing cantilevers and passages by using an extended von Neumann neighbourhood.
passages
d d
| cantilevers
2d space
d = extension of von Neumann
Extended
1 1 1 0 0 0 1 1 1 0*0*0* - - - 0 0 0
3d space: if there is enough space for passages underneath, these are consolidated
von Neumann neighbourhood
Genetic algorithm
A multi-objective genetic algorithm was set up to explore the CA’s possibilities. The fitness criteria chosen are three: first, the total volume is to be maximized; second, a certain regularity of the form was aimed for by dividing the total number of contours by the number of floors; and lastly, whenever the passage/cantilever rule was performed by the CA a point was awarded, the aim was to foster the development of these morphologies. The initial experiments are shown opposite.
The algorithm was tested on two modalities: probabilistic and totalistic. In the probabilistic model, the algorithm is able to determine the probability of a cell being developed based on the conditions of its neighbours; while in the totalistic, the development of a cell is directly determined by the state of its neighbours. The results are compared on the next two spreads, where it becomes evident why a totalistic model was preferred. Furthermore, given the random aspect of a probabilistic model; it was impossible to replicate a given experiment twice with identical results. And given the sensitivity of CA models to initial conditions, a probability change at the initial time would have a cascading effect on the whole model, since a GA would not be able to understand the direct relation of genotype to phenotype (unless, perhaps, if hundreds of generations were carried out, where the probabilities tended to converge).
70 Symbiotic aggregations
Figure 5.3.11
First experiments on a small patch, exemplifying the three fitness criteria.
Figure 5.3.12 (opposite)
Initial experiments showing the evaluation criteria for the GA pared with CA growth.
V C P V C P V C P V- total volume P- total passages C- contours / levels 25,245m3 28 3. 42 G10 - 03 V- total volume P- total passages C- contours / levels G10 - 04 4,590m3 2 2.63 V- total volume P- total passages C- contours / levels G10 - 08 24,651m3 43 3.82
71 Design development Volume tests Contours
levels
Morphology
V- total volume 1,215m3 V - 01 C- contours / levels C - 01 4.63 P- total passages P - 01 0 V- total volume 2,268m3 V - 02 C- contours / levels C - 02 1.54 P- total passages P - 02 12 V- total volume 7,245m3 V - 03 C- contours / levels C - 03 1.00 P- total passages P - 03 28 V- total volume 9,828m3 V - 04 C- contours / levels C - 04 1.00 P- total passages P - 04 6 8 10 10 10 3 4 10 13 9 0 10 10
/
tests per mass
tests
72
V- total volume P- total passages C- contours / levels 4,320m3 45* 3.33 V C P G10 - 05 V- total volume P- total passages C- contours / levels G10 - 03 4,617m3 13* 2.53 V C P V- total volume P- total passages C- contours / levels 4,941m3 13* 2.60 V C P G10 - 02 V- total volume P- total passages C- contours / levels G10 - 01 5,886m3 12* 2.41 V C P V- total volume P- total passages C- contours / levels-V C P Base patch V- total volume P- total passages C- contours / levels G10 - 04 11,799m3 52* 3.76 V C P
Symbiotic aggregations
73 Design development V- total volume P- total passages C- contours / levels 11,259m3 31* 3.05 V C P G10 - 06 V- total volume P- total passages C- contours / levels G10 - 07 7,452m3 26* 2.93 V C P V- total volume P- total passages C- contours / levels G10 - 08 (selected for comparison) 12,123m3 43* 3.20 V C P V- total volume P- total passages C- contours / levels G10 - 09 10,611m3 38* 3.17 V C P V- total volume P- total passages C- contours / levels G10 - 10 10,341m3 30* 3.0 V C P V- total volume P- total passages C- contours / levels G10 - 11 11,299m3 48* 3.50 V C P
74
V- total volume P- total passages C- contours / levels-V C P Base patch V- total volume P- total passages C- contours / levels G10 - 01 1,647m3 0 1.5 V C P V- total volume P- total passages C- contours / levels G10 - 02 (selected) 29,754m3 40 3.37 V C P V- total volume P- total passages C- contours / levels 25,245m3 28 3.42 V C P G10 - 03 V- total volume P- total passages C- contours / levels G10 - 04 4,590m3 2 2.63 V C P V- total volume P- total passages C- contours / levels G10 - 05 22,248m3 27 3.06 V C P
Symbiotic aggregations
75 Design development V- total volume P- total passages C- contours / levels 24,597m3 33 3.33 V C P G10 - 06 V- total volume P- total passages C- contours / levels G10 - 07 2,592m3 0 2.0 V C P V- total volume P- total passages C- contours / levels G10 - 08 24,651m3 43 3.82 V C P V- total volume P- total passages C- contours / levels 6,750m3 8 2.75 V C P G10 - 09 (selected) V- total volume P- total passages C- contours / levels G10 - 10 1,593m3 0 1.5 V C P V- total volume P- total passages C- contours / levels G10 - 11 (selected) 22,680m3 37 3.43 V C P
Iteration
The obtained volumes after the first iteration showed a high range of spatial variation, but new issues regarding the structure and network system were encountered. Due to the selective growth system that was only growing from the predefined generators on the floor towards the flat roofs of the existing buildings, dense aggregations on the flat rooftops were occurring. Considering the low structural quality of the existing buildings, it was assumed that the structural system of the existing buildings were exposed to high pressures. To avoid this problem it was decided to revise the growth scenario and the generators.
A survey of the selected patch and tissue sampling provided a detailed analysis of the existing buildings. The buildings were evaluated according to their functional and cultural importance, combined with their structural stability. Hence, during this state of the project this evaluation can be considered quite detailed. However, this information was used to develop a demolition strategy of the existing buildings. This way the implementation of the structural elements to existing would provide the required extra support for the existing and proposed new growth.
Due to the general ambition, a demolish/rebuild model was not accepted as the target solution, since it was transforming the patch entirely. Therefore a partial demolition model was selected as a solution. In order to generate a partial demolition strategy, the buildings with low ranking were digitally recreated as cells. This permitted a direct interface with the developed cellular model.
The structural cells were sub-classified into multiple groups, starting from cells connecting to the floor and cells on the rooftops. The cells that share a vertical connection to floor were classified as vertical structural cells. These can take higher structural pressures, therefore any additional pressure above these cells was considered acceptable. These vertical connections determine whether adjacent cells are acceptable or not; cells within a 3m to 6m range area allowed, for a cantilever of this size was considered acceptable. The case studies shown at the domain chapter have cantilevers of up to 12m.
All the remaining cells, which are concentrated on the building tops are classified into two distinct groups according to the pressure that is applied on the existing building. If less than two levels are added, these can become lightweight structures, but any structure higher than two floors added too much pressure and had to be solved by adding additional vertical structural connections.
After the highlighting of the problem areas, the classification of the existing building dictated the further steps. If it was qualified as a demolishable building, the cells under the problem area were chosen to be demolished and rebuilt as structurally stronger elements that are anchored to the ground. This approach also serves as structural
76 Symbiotic aggregations
Figure 6.3.13 and Figure 6.3.14 (previous spreads) Catalogue of results for the genetic algorithm using a probabilistic model and a totalistic one, respectively.
Figure 6.3.15 (opposite)
The buildings that were qualified as demolishable were rebuilt as cellular data in order to be integrate them to the CA’s coordinate system.

77 Design development
reinforcement for the existing building.
John Frazer has demonstrated the feasibility of a CA with architectural implications that does not only vary on a state of being alive or not (0 or 1), but that can rather carry many possible states of being. In a particular experiment he proposed a cell that had 8 possible states – each representing an architectural quality – that depended on the states of the adjacent cells with equally 8 possible states each. The resulting combination is exponentially rich. In a similar way, but also affected by the local existing context, the generated growth was separated into distinct areas with different architectural or structural character. These distinct characters, in turn, will inform the final design and subsequent experiments. The differentiated states of the cells add order and structure to the growth process.
Due to the time constraints it was decided to treat this process as an iteration on the initial results; however, in a further step this process should be implemented within the CA generation.
78 Symbiotic aggregations
Figure 5.3.16 Result section of the Infill Growth and Iteration processes.
Figure 5.3.17 (opposite)
Pseudo Code diagram for classification of the generated cells.
low density
high density
Structural cells (cores)
Regular cells (anchored) Lightweight cells Cantilever cells Demolished buildings
Controll growth scenario
Growth from the ground Growth on the roof
Controll the amount of pressure
number of additional floors � 2
number of additional floors > 2
Controll the ground condition
demolishable buildings not demolishable buildings
Further vertical connections distance to street � 6m distance to street > 6m
keep the cells vertical structure
demolish the cells below and reconstruct them as structural elements
create vertical connections to the street
only lightweight structures
79 Design development
Results
The results table shown above compares the Infill-growth experiment and the Infill-Iteration to the original patch. The resulting 152,410m3 of volume generated on the iteration is a good partial result, but within this volume the network and public spaces still remain to be generated, and they will remove usable space. Considering this partial result, 43,545.7m2 of usable floor-area would be generated if a generous 3.5m floor height is considered. This would be enough area for 2,903 new inhabitants if we consider an average floor-area per person of 15-20m, and exclusively a residential use.
We consider that, since the growth only occurs within an environmental boundary, it is of no use to evaluate the affectation on the existing patch at this point. However, at the conclusion of the thesis, it will be evaluated by using an analysis that takes into account the entirety of the process.
Two buildings are demolished on the sub-patch, but the gain is also considerable. By demolishing the 4,177m3 of the building’s volume in bad conditions, we are replacing it by an equal amount that will be able to support the cells generated at higher levels. The economical soundness could be contested, but it can be justified by the selection of damaged buildings that meet specific criteria.
80 Symbiotic aggregations
Experiment Category Before experiment After experiment Infill-growth Generated volume (total) Area used (total) Generated volume (sub-patch) Building comparison (sub-patch) Area used (sub-patch) n/a 1,280m2 (residual/open space) n/a n/a n/a 142,757m3 11,346m2 12,200m3 120m2 8 * 6 level buildings† Generated volume (total) Area used (total) Generated volume (sub-patch) Building comparison (sub-patch) Area used (sub-patch) n/a 1,280m2 (residual/open space) n/a n/a n/a 154,485m3 1,679.3m2 16,377m3 288m2 10 * 6 level buildings† Demolished buildings (sub-patch) n/a 2 Infill Iteration Demolished volume (sub-patch) n/a 4,177m3 Table
Results table
5.3.1
Comparison of Infill Growth and Infill Iteration results, before and after the experiment was carried out.
Conclusion
Even though the results of this experiments are partial, and would not make sense unless placed in the context of the entire work, if the environmental conditions are met, the generated growth is promising. Several results meet the basic criteria for selection, so a few options can be carried along to the next stage to experiment further.
The information generated regarding the differentiation of the cells into different categories (shown in the diagram on the previous spread) can be kept to inform the final design. The character of each cell will be complemented with other properties, but this first step of differentiation already adds a significant amount of variation. Each of the cells’ states being determined by their location and relation to other cells and to the ground and existing buildings.

81 Design development
Figure 5.3.18 Result section of the Infill Growth and Iteration processes.
5.4 Open spaces
The definition of open spaces used here encompasses every delineated space, whether public, semi-public or private, that is exposed to the outside. They can be parks, patios, plazas, private courtyards, gardens or terraces; and, except for terraces that form part of a building, their footprint is referred to as the negative space in figure ground theory.

In Turkish architecture open spaces have a particular way of occupation and generation. The climate and social patterns have forged public space and life through hundreds of years. The richness of forms, sizes and patterns of open spaces is admirable, so it results almost tantalising to try to understand and parametrically reproduce their logic. Working on the thesis’ aim to provide highly articulated public spaces based on traditional values, it follows that the characteristics that make the existing spaces so successful should be mimicked to some extent, albeit in a contemporary manner. On the case studies section and objectives introduction to this chapter the series of parameters that can be abstracted and evaluated is presented: from morphological traits to environmental or social ones.
This experiment will be considered successful to the extend that desirable open spaces can be generated within the strict geometrical and spatial constrains of the ‘infill growth’ developed. It is important to stress that, by setting the generation of open spaces high on the priority list, they will become one of the main drivers of the final morphology.
82 Symbiotic aggregations
Figure 5.4.1
Semi-public open space, where the small corridors connect different buildings to the main street network. There are no gates blocking the path. (Image: Zaldivar)
Although in many existing examples the open spaces seem to be the result of a system with a different hierarchy, were buildings are the priority, we artificially reverse this in accordance to the initial ambition. Secondary nodes and open spaces do arise, somewhat haphazardly, from the interaction between generated volumes, existing ones and the network. In these half-planned accidents, we find the beauty of the system.
Aim
This experiment is composed of two linked processes. In this section the first one is addressed, but is intimately linked to the next. The aim is to generate a target open area that presents desirable environmental qualities and morphological traits.
In order to evaluate the success of the experiment, spaces will be analysed for sunlight access and shading throughout the year, and subsequently compared to existing successful ones.
Setup / Methods
The setup consists of the digital model for the developed morphology obtained from the previous experiment. The centre point of each cell within the growth is selected, however, the cell’s specific status has no relevance within this section. Every operation is carried out using the cells and their centre point. Associative modelling techniques within the Grasshopper environment of Rhino are used, pared with a genetic algorithm (GA) script. The genetic algorithm is used to generate
83 Design development
three-dimensionally located open spaces within the ‘infill growth’. The selection criteria is the performance of the open spaces evaluated for environmental performance and total area generated.
Initial tests
The initial tests, developed independently from the actual site, were carried out to identify the morphological parameters that could be used to determine the envelope of the open space. The volume above open spaces (if any) is deleted by performing a boolean difference operation with a defined geometry, much like carving a hole in plaster. The subtracting geometry’s form is dependant on existing morphologies and environmental factors; the intent is to generate shaded open areas during summer and illuminated areas for winter. Although direct sunlight increases heat gain, indirect illumination has a psychological effect on the perceived temperature.
In order to develop a subtracting envelope that sculpts the open space, a flexible body plan was produced. First, the immediate volume above the open space, varying from 3.0 to 5.0 meters in height, is formed into a right prism, above this prism, a truncated pyramid is formed. The pyramid’s base can be of any size equal or smaller to open space’s, and must lie within its planar boundary; the tip of the pyramid can be placed anywhere on the positive z direction, while its x and y coordinates cannot be further than 2l from the base plane’s centre, where l is the longest side of the open-space base rectangle. Using these simple variables, the pyramid’s vertical angle and opening size can change. The expected result is a body plan that can generate spaces with arcades, passages
84 Symbiotic aggregations
environmental envelope ‘a’ environmental envelope ‘b’ environmental envelope ‘c’ environmental envelope ‘d’
Figure 5.4.2 Variations of the open spaces’ environmental envelopes.
and openings optimised for the aforementioned environmental criteria. The initial tests, shown opposite demonstrate that a desirable solar exposure and shading can be achieved; the reduction of deleted volume and total area are left to the genetic algorithm to optimise.
Implementation
The general process was carried out on the entire patch, although for computational ease this was subdivided into five separate areas. The areas were selected so that most intense network connections developed within each one, and the connectivity between one another happened through the existing street network only. Once each section had been selected, the following algorithm was carried out:
Process:
1] The point cloud formed by the centres of the growth’s cells is used to find every elevation datum possible.
2] The overall contours of the cells at each datum is generated, and within this boundaries a point p is selected to become the centre point of an open space.
3] An N number of open spaces with a centre point p are generated; their length and width are l and w respectively, where neither l or w is greater than 1/3 of the square root of the corresponding level’s contour total area.
4] Once each rectangle is generated, a prism of variable height h
85 Design development
Figure 5.4.3
N number of spaces 1] 2] 3] 4] 5] p c l w p area c 3 l ≤ area c 3 w ≤ GA
Diagramatic Pseudo Code for the placement of the open spaces.
cell centre points contours at each elevation w·l rectangle environmental envelope ‘Boolean Difference’
is formed by extruding the rectangle on the positive z axis. The previously mentioned (initial tests) truncated pyramid is formed above the prism, with a variable base, and a variable tip point.




5] N, p and each l and w for each point become the variables or genes for the genetic algorithm, along with the parameters that define the subtracting volume. Each resulting open space rectangle generated is evaluated for solar exposure and shading in winter and summer. The total volume deleted is evaluated against the area produced.
Initially a genetic algorithm was set up so that it tried to maximise the total area of the open spaces and minimise shading. The results showed many small parks being placed all over the ‘infill growth’. Two corrections were made: first, the target became to maximise the average area of the open spaces generated and to minimise the deleted volume. This strategy proved to be more successful, and the resulting individuals dialogued between smaller spaces at the bottom of the growth where more shading was possible, and larger spaces at the top where more room was available by using rooftops and cantilevers.
The GA ran for 20 generations for each of the three growth options extracted from the previous experiment. From each test, three individuals were selected from the elite and Pareto front, resulting in nine distinct options based on three different growths. The thought behind was not to lose variation in the early experiments that, from the linear nature of their hierarchy, already have a deterministic influence on the whole process. Out of the nine individuals generated, three are selected that produce the more ‘usable’ architectural spaces. These are then sorted according to the total building depth (above 3.0m) and its geometric characteristics.
86 Symbiotic aggregations
Figure 5.4.4
Generation and evaluation of an open space, from left to right: the original volume, the substraction, and the shading analysis.
Figure 5.4.5 (opposite)
Evaluation of an open space. From a single selected growth morphology, three possible options are generated. The selected options are marked with a grey dot on the left.
G10 - 11 A,B,C
87 Design development
- 11 A (G20 -03) G10 - 11 B (G20 -09) G10 - 11 C (G20 -13) V- total volume P- total passages C- continuity (contours / levels) S- shaded area A- area of open spaces 22,680m3 37 3.43 15% 850 V- total volume P- total passages C- continuity (contours / levels) S- shaded area A- area of open spaces 22,680m3 37 3.43 58% 225 V- total volume P- total passages C- continuity (contours / levels) S- shaded area A- area of open spaces 22,680m3 37 3.43 27% 780 V- total volume P- total passages C- continuity (contours / levels) S- shaded area A- area of open spaces 22,680m3 37 3.43 15% 850 V- total volume P- total passages C- continuity (contours / levels) S- shaded area A- area of open spaces 22,680m3 37 3.43 58% 225 V- total volume P- total passages C- continuity (contours / levels) S- shaded area A- area of open spaces 22,680m3 37 3.43 27% 780
G10
V C P S A V C P S A V C P S A
V- total volume
P- total passages
C- continuity (contours / levels)
S- shaded area A- area of open spaces

88
22,680m3 37 3.43 15% 850 22,680m3 37 3.43 58% 225 V- total volume P- total passages C- continuity (contours / levels) S- shaded area A- area of open spaces
- 11
V C P S A
Symbiotic aggregations
G10
(selected)
V C P S A
G10 - 11



89 Design development 22,680m3 37 3.43 27% 780 V- total volume P- total passages C- continuity (contours / levels) S- shaded area A- area of open spaces G10 -
(selected) V C P S A V- total volume P- total passages C- continuity (contours / levels) S- shaded area A- area of open spaces 6,750m3 8 2.75 52% 315
V C P S A
11
G10 - 09 (selected)
Results table
Results
The results show that it is possible to generate enough viable open spaces by using this method. The total area generated for the whole patch is 8,849m2, out of which 61.3% is shaded more than 6 hours during summer. An additional 30,433m2 of open space were generated as emergent terraces and roofs, out of which only 23.7% is shaded more than 6 hours during summer. A simple comparison between the existing conditions and the generated ones shows that the increment in open spaces is quite significant, originally there were 1,280m2 of open space (not including vehicular streets), the total for the patch is 11,346m2. Considering the 140,094m3 of usable volume remaining after the subtraction of open spaces, or 40,036.8m2 of floor space if a floor height of 3.5m is considered, a good ratio between open-space to volume is achieved, roughly 1:4.
Additionally, the table shows a comparison of percentage of shaded areas during summer and winter for an average tower development in the periphery of Istanbul, and for Tünel Pasaji, a very live and successful urban space. The values achieved are quite similar to the ones existing in the Tünel Pasaji neighbourhood, thus corroborating the suitability of the spaces generated.
The solar exposure achieved for open spaces during winter is 3,601 sunlight-hours, and 4,764 during summer. The overall distribution of shading is quite uneven. This can be easily explained, because some of the generated spaces appear on the lower levels, increasing their
90 Symbiotic aggregations
Experiment Category Before experiment After experiment Open space generation
towers) Generated open space
during summer (>6hr)
during winter (>4hr)
during summer (>6hr)
during winter (>4hr) Emerged open space Growth volume n/a n/a n/a n/a n/a n/a 152,410m2 8,449m2 61.3% 43.5%* 30,433m2 23.7% 78.2% 140,094m2 Ground solar exposure 45.74% 45.97% 30% n/a % n/a % n/a % n/a Shaded during summer (>6hr)
during winter (>4hr)
during summer (>6hr)
during winter (>4hr)
Compariosn 2 (periferal
Shaded
Shaded
Shaded
Shaded
Shaded
Shaded
Shaded
Compariosn 1 (Tünel pasaji)
Figure 5.4.6 (previous srepads) Four results, including the three selected, for the subpatch’s generated growth and open spaces.
Table 5.4.1
Results of the open spaces experiment, comparing before and after.
shading, while some are practically roof-tops.

Conclusion
The overall distribution of shaded areas and exposed ones is quite definitive. The probable outcome, for the over-exposed spaces, is that they will become practically unusable during summer. On the other hand, the variation and ranges of shading on the public space is quite satisfactory. Arguably, this variation will permit the open spaces to function, and become appropriated by the local population. The resulting distribution is not definitive, for emergence of new open spaces and the network opening will drastically change their character. For this reason, at this point, a full evaluation is still not possible and three options will be carried forward. The three selected options are shown on the previous spread, marked with a ‘selected’ caption and a grey dot; the remaining ones are shown in the appendix.
The resulting morphologies around the public space are quite promising. Arcade-like and light accesses start to bring typological variation into the growth, without compromising too much of the generated volume.
Regarding the computational performance, the genetic algorithm worked well, although the calculation of solar exposure and the Boolean difference operation were quite expensive. These operations drastically reduced the amount of generations and population we could run on an average laptop setup. On further development the algorithm could be simplified to reduce running time.
91 Design development
Figure 5.4.7
Result section of second experiment showing the substraction performed with the environmental envelope of the open spaces.
5.5 Base network and secondary nodes
Inclined and winding pedestrian and vehicular networks are indigenous to Istanbul and other Mediterranean cities with similar water-front topographies. Over the centuries cities have developed specific patterns of adaptation to the topography, generating distinctive and useful architectural and urban solutions. The ground figure is ‘overridden’ by many of these settlements, where networks occupy different elevations, taking advantage of rooftops, and differentiated building heights as part of their path and as public space (e.g. Mardin or Catal Huyuk [Çatalhöyük]). Given the restrictive space where infill systems can grow and the existing topography - both natural and artificial (i.e. existing buildings) - the generated network will not be conditioned to a single layer, rather it will be generated in a way in which it weaves different heights to the existing network.
On an initial run a tree like branching system was used. This could hardly be considered a network and for that reason a net pattern was preferred, instead of the initial branching one. It is expected that the modifications will yield a richer tissue, one that the habitants will be more likely to use, both locally and as secondary pedestrian routes. The pedestrian network will link every generated open space, and occupy flat rooftops if possible. The resulting morphology (generated in the next step) will hopefully succeed in surpassing the performance of existing models.

92 Symbiotic aggregations
Figure 5.5.1
Multilayered pedestrian connections in Istanbul. (Image: Zaldivar)
Space syntax methodologies are used to test if this model is better, and also to analyse the relative impact on the existing tissue. It is expected that highly connected centres, that vigorously interact with the local tissue, will be generated. These centres of connectivity won’t have a major impact on the overall system (provided the scale of the interaction); and, by following the local infill strategy logic, a semi-island effect should produce local nodes of interaction as opposed to regional centres such as Taksim square or Istiklal avenue. These centres should be an active part of the network, providing shortcuts or more ‘central’ nodes, otherwise one could predict their dismal underutilisation.
The diagrams above show the representation of existing network paths in Istanbul, Lisbon and Hong Kong. Their ill assortment is intended to show the flexibility of public paths that humans have been able to generate, adapting to and transforming the landscape with each intervention. Steep one-meter wide corridors connect the buildings of medieval Lisbon, in Alfama. Similar adaptations can be seen in contemporary Hong Kong, where technological advances have been implemented to tame the harsh topographical and environmental conditions. There is no reason to suppose that Istanbul could not be subject to this kind of interventions, particularly in the light of the existing solutions that may well be improved upon.
93 Design development
Hong Kong Istanbul Lisbon
Figure 5.5.2
Diagrams of existing stair connections in Hong Kong, Istanbul and Lisbon.
Aim
The experiment’s aim is to generate secondary nodes within (and on top of) the growth - connecting to the previously generated open spaces and to the existing urban network of vehicular and pedestrian streets - and to prove that a viable internally connected network can be achieved. The topography and existing building datums should inform the algorithm that generates the connections, for their inclination is a main factor.
Network theory, a part of the more general graph theory, on which space syntax is built, will be used to evaluate whether the evaluated network is sufficiently connected to attract pedestrian flow, while an inclination analysis will be embedded in the algorithm to produce regulated ramps and stairs.
Setup / Methods
The linear diagram presented above and opposite (fig 6.XX), show the general setup for the experiment. The first and second stages show what has been achieved by the previous experiments, while the third and fourth show how the setup will be used. Following is a basic explanation:
1] Use the previously generated open spaces as fixed nodes in the network. Then, find a fixed ‘seed’ connection to an existing street.
Key:
94 Symbiotic aggregations 4 connections node 3 connections node 2 connections node 1 connections node 0 connections node Fixed open space Vertical connection Generated network Existing network 1 2
Figure 5.5.3 (above and opposite) Geographical and topological network generation process.
2] Assuming the results of the first two experiments, find the natural connections to the existing network i.e. places where the volumes connect to the ground, accesses to public space, vertical connections and demolished buildings that can presumably be used as vertical cores. These connections are represented as red vertical arrows.
3] Generate secondary nodes: A GA will control the position of these variable secondary nodes along with the network edges that connect them to other nodes.
4] Take into account the existing network in order to evaluate the global network in terms of its centrality and connectivity. The system should form a single network that can be evaluated both locally and globally.
The topological network diagram is made by taking into account the existing streets, the generated network and nodes, and the possible vertical connections from the ground to the building. The topography is not built into this model, but the physical network used by the GA is highly dependant on the terrain, trying to minimise the inclination of the edges.
95 Design development 3 4
This experiment builds on the open spaces generated by the first experiment. Out of the nine selected individuals three were tested. Ideally all of them should be analysed, but time constrains did not permit this. The setup consists of the digital model of the generated open spaces as well as the initial cells. The same computational environment is used for ease of information transfer and speed.
Initial tests
There are different parameters for which to optimise a network whilst only considering its inclination i.e. the total rise and run of ramps and stairs. The local conditions are deformed as the global configuration changes; but, as a general rule, it is desirable to keep the local rise and run of each set equal throughout the length of the network; or, in the case of public space, from node to node. Given the high amount of possibilities that exist – from a mere technical point of view –for connecting to given nodes by using standard stairs and ramps, the network has enough flexibility to respond to the information of neighbouring conditions such as shading and sun access or adjacency to specific functions.
Initial tests were carried out to see the general connectivity of the existing patch (above), and to be able to compare it to the intervention. Given the scale of action of the intervention, it is expected that areas with higher internal connectivity will arise, while the global network will not be significantly altered.
Since the open spaces lie at different elevations, and the topography is a key feature of the area, tests were carried out to determine different ways to optimise the inclination of a network. Ramps are preferred over stairs. Single layers that work within separate topographical elevation datums are also preferred; so stairs are used only where the inclination is too steep, and are terraced out to increase comfort.
The initial experiments show at least five different ways in which a single connection between two points can be optimised using stairs and ramps (shown opposite). The basic possibilities are the following:
1] Maximise flat area (single). By forcing a small segment of the network to negotiate the height differential between start and finish, the rest of the network can be flattened out, yielding the maximum flat surface area.
2] Maximise flat area (distributed). Similarly to the previous one, the height differential is negotiated in the least possible length of the network; these inclined areas are evenly distributed along the full length of the network, however.
3] Minimiseanglea. Minimise the total average angle of the network; given the limitations set by the maximum ramp inclination possible,
96 Symbiotic aggregations
Figure 5.5.4 (opposite) Graphs showing the legal limits of stairs and ramps.
maximum inclination (stairs and ramp) maximum inclination (stairs by regulation with landings)
for a ramp and stairs without landings.
The total rise for each segments is 3.60m while the landing’s run is 1.20m.
1:16 and 1:20 ramps with corresponding landings
comfortable inclination (stairs by regulation with landings)
The total rise difference betweek a 1:20 ramp and a 1:16 ramp, over a 100m total run is ~1.00m. This difference, for the scale of the clusters, is negligible.
The total run for each segments is 4.00m while the landing is 2.00m.
97 Design development
Maximum (theoretical) inclination
0 0 10 20 30 40 50 60 70 80 90 100 50 40 30 20 total rise (meters) total run distance (meters) 10 60 0 0 10 20 30 40 50 60 70 80 90 100 50 40 30 20 total rise (meters) total run distance (meters) 10 60 29.8° max 24.2° average angle 3.58° max
0 0 10 20 30 40 50 60 70 80 90 100 50 40 30 20 total rise (meters) distance (meters) 10 60 0 0 10 20 30 40 50 60 70 80 90 100 50 40 30 20 elevation (meters) distance (meters) 10 60
1:20 1:16 ramp stairs
and minimum stair rise (shown opposite), this form of optimization may not be possible for some segments. The result is a continuous homogenous rise.
4] Maximise landings of fixed length ‘l’. For any given landing size, it is possible to find which is the maximum number of these that can happen in a single segment of the network.
Network overlaid results
5] Maximise continuous surface length. If a large extent of continuous surface is desired, the ramp section of the network segment could be maximised.
Any combination of these parameters within a single network is possible, and their physical characteristics will become evident later. The richness in a varied selection can be contradictory to specific comfort criteria, but as will be shown, it can also increase the diversity of spatial morphologies generated.
Implementation
The pseudo code for the algorithm is shown on the following spread. It becomes evident that the algorithm is quite a simple one, making it computationally inexpensive. The genetic algorithm has three targets: to reduce the total inclination of the network, to generate avoid the overlaying of two open spaces and the generated one and to make sections of invariant inclination (least mean average deviation). The topography plays an important role here, for it affects the length and
Inclination
Is the summation of the inclination angle for each segment of the network: S = {α1, α2, ... , αn}. total inclination = αi |S|
Deviation
It is the average absolute deviation of the network’s inclination where each section’s angle is a member of the set: S = {α1, α2, ... , αn}.
Overlap
98 Symbiotic aggregations
Figure 5.5.5 (opposite)
Graphs showing the different ways of optimizing the inclination of a path when considering its rise and run.
Table 5.5.1
Network’s inclination optimization parameters: Inclination, deviation and overlap.
∑ 1 n n i = 1 |xi - m(x)|
i = 1 ∑
Fixed nodes
b c d f
Avoids overlapping on the cartesian xy plane of two open space polygons.
maximise flat area (single)
Maximise the flat area in a continuous surface.
maximise flat area (distributed)
The total flat area is the same as in the ‘maximise flat area (single)’ graph; however, in this case, the area is distributed equally.
minimise angle α maximise landings (of fixed length ‘l’)
The angle alpha is calculated by averaging all of the rise angles in the network.
maximise continuous surface length
The landing length l = 6.00m. The maximum amount of landings possible over a 100m run is 11.
multi-parameter (example)
If large extents of continuous surfaces are required, the ramp legth section of the run could be maximized.
When working with different segments, the network can be differentialy optimized depending on the desired local and global effects.
99 Design development
0 0 10 20 30 40 50 60 70 80 90 100 50 40 30 20 total rise (meters) total run distance (meters) 10 60 0 0 10 20 30 40 50 60 70 80 90 100 50 40 30 20 total rise (meters) total run distance (meters) 10 60
0 0 10 20 30 40 50 60 70 80 90 100 50 40 30 20 total rise (meters) distance (meters) 10 60 0 0 10 20 30 40 50 60 70 80 90 100 50 40 30 20 elevation (meters) distance (meters) 10 60
1:20 1:16
0 0 10 20 30 40 50 60 70 80 90 100 50 40 30 20 total rise (meters) distance (meters) 10 60 0 0 10 20 30 40 50 60 70 80 90 100 50 40 30 20 elevation (meters) distance (meters) 10 60
1:20 α
Pseudo code for GA:
Find the nodes and sub-nodes from developed open spaces and emergent ones. Generate a topological network between the nodes depending on distance and node hierarchy within the network. Give each node an area.
Generate quadrilateral with the specified area and connect the nodes.
Make the line connections reach a point on the closest edges of two connected quadrilaterals.
Let the genes for the GA control the position of the open spaces and the length of their sides with a constant area and always over the original node. Detect areas where open spaces overlap and penalize them in the fitness evaluation.
Find the places, if any, where the connection lines or the area lines intersect with existing buildings. Each intersection is highly penalized in the fitness evaluation.
Let the genes for the GA control the t point on the edges of two connected quadrilaterals that form the connection line. The connection lines will be optimised for length and gradient depending of the specified fitness criterion.
Save resulting network for evaluation.
100 Symbiotic aggregations b c d f
b c d f b c d f b d1 d2 d3 c d f b c d f b c d f b c d f
GA
inclination needed by an edge to connect to an existing street.
The algorithm was executed separately for each section of the patch. Since the information used was only point coordinates and lines formed between two points, the computation time was small (<100ms per iteration in an average 2014 laptop setup). This allowed for the experimentation with different Genetic Algorithm setups regarding the population size, the total generations and mutation probabilities.
Out of several tests, three were selected, for they best illustrate the results. The first experiment conducted ran for 40 generations and had a population of 40 individuals, the second had a population 120 and ran for only 15 generations and the final one was ran with a population of 150 individuals for only 10 generations.
Finally, a betweenness centrality analysis was carried out on the unaltered patch and on the generated one to test the effect on the global network. Also, the betweenness for the generated areas was evaluated to test if they integrated to the network or not.
101 Design development
Deviation
is the average absolute deviation of the network’s inclination where each section’s angle is a member of the set: S = {α1, α2, ... , αn}. ∑ 1 n n i = 1 |xi - m(x)| Inclination Is the summation of the inclination angle for each segment of the network: S = {α1, α2, ... , αn}. total inclination = αi |S| i = 1 ∑ Fixed nodes Overlap Avoids overlapping on the cartesian xy plane of two open space polygons. b c d f
It
Network overlaid results
Figure 5.5.6 (opposite)
Diagrammatic Pseudo Code for the optimization of the base network and the placement of open spaces. Figure 5.5.7 (above)
Overlay of several results from the iterations of the genetic algorithm.
102 Symbiotic aggregations crash inclination deviation average inclination 0 E1-G1.11 E1-G1.32 E1-G1.34 E1-G10.3 E1-G10.13 E1-G10.18 E1-G20.4 E1-G20.29 E1-G20.37 E3-G10.139 E3-G10.107 E2-G15.73 E2-G15.71 E1-G40.28 E1-G40.21 E1-G40.7 E1-G30.36 E1-G30.19 E1-G30.13 500 400 300 200 fitness individual 100 600 700 800 Experiment 1,2 & 3 comparison of fittest individuals 0 100 120 80 60 40 average inclination (degrees) Experiment - Generation (fittest individual for the given criterion) 20 E1-G1 E1-G10 E1-G20 E1-G40 E2-G15 E1-G30 Average inclination - E1, E2 adn E3 200 180 160 300 280 260 240 Mean Average Deviation (MAD) Experiment - Generation (fittest individual for the given criterion) 220 E1-G1 E1-G10 E1-G20 E1-G40 E2-G15 E3-G10 E3-G10 E1-G30 Deviation optimization - E1, E2 adn E3 200 180 160 300 280 260 240 Crash events (divide by 10) Experiment - Generation (fittest individual for the given criterion) 220 E1-G1 E1-G10 E1-G20 E1-G40 E2-G15 E3-G10 E1-G30 Crash optimization - E1, E2 adn E3 460 440 560 540 520 500 Summation of inclination (degrees) Experiment - Generation (fittest individual for the given criterion) 480 E1-G1 E1-G10 E1-G20 E1-G40 E2-G15 E3-G10 E1-G30 Inclination optimization - E1, E2 adn E3
Results
The results for the three experiments selected are compared in the graphs shown opposite. For experiment one (E1), four cross sections are shown, at the 10th, 20th, 30th and 40th generations; for E2 and E3 only the final generation in shown, G15 and G10 respectively. It is evident that E2 was the most successful one at optimising every parameter. The average inclination achieved was of 24°, generally comfortable stairs lie somewhere between 30° - 45°, meaning that we have ample room for designing ramps and continuous surfaces. This angle can be further reduced in the next part of the process by including the open spaces as part of continuous surfaces that negotiate the rise of the network.
Crash events, where open spaces overlap or hit an existing building were not completely eliminated. If they collide with a building, they will be modelled so they adapt to the context. If they overlap on top of each other, an individual assessment is manually carried out and sometimes they are merged. This will be further shown when the open spaces are translated into designed surfaces. On hindsight, this manual discrimination of ‘clashing’ surfaces could be integrated as a strict exclusion from the algorithm; a Boolean function could ensure that only acceptable results are kept in the GA for breeding.
103 Design development
Figure 5.5.8 (opposite) Charts showing the progressive improvement in the optimization of the network. Experiment E1 is shown at four cross-sections, while for experiments E2 and E3 only the final generations are shown.
I - inclination C- crash D- deviation E2 - G15.73 457.65 198 200.37 I - inclination C- crash D- deviation E2 - G15.71 494.37 168 175.01 I D C I D C I D C E1 - G1.34 I - inclination C- crash D- deviation 547.53 240 241.42
Figure 5.5.9 (above) Evaluation diagram of three elite individuals. E2G15.71 is selected.
Regarding the connectivity of the network, the betweenness centrality analysis (shown below) demonstrates that by tightly weaving a network in a small area, a high degree of internal connectivity is achievable. In some cases, the proposed network has a higher centrality value than adjacent streets; this can be explained because some of the generated routes are obvious shortcuts between nodes. For the entire neighbourhood, however, given the scale of the generated networks in comparison to the existing ones – almost one order of magnitude smaller – it is hard to have a big impact on the overall structure.
Conclusion
The results achieved seem promising, and are corroborated in the next part of the process. There is enough information generated to continue the process, and the inclination achieved is definitely acceptable.
The simplicity of the algorithm proved to be of great benefit when trying to determine which strategy worked better to optimise the network. We can hypothesise, from these results, that the previous GAs carried out for the cellular growth and the open space generation might not have been following the best strategy. Retrospectively, the two previous
*Note:
There is a bias on the second image (right) used to appreciate the effect on the generated network. These results were not validated and should be considered tentative at best.
104 Symbiotic aggregations n 1.0 0 1.0 0
Figure 5.5.10 Space Syntax’s Betweenness Centrality (Metric) analysis for the selected patch. Before and after images are shown.
algorithms could’ve been simplified to permit the same number of iterations and population sizes; otherwise, a strategy testing might have been done separately to find an appropriate one, but it is hard to determine, within the scope of the thesis, whether this approach would’ve been appropriate or not.
On further development, it is possible to imagine interventions on existing streets, making some strictly pedestrian. The effect this would have on the general connectivity could bias the results positively; potentially increasing the pedestrian flow through the generated tissues. Although the inclination is included in the generative process, it is not part of the betweenness centrality analysis, if this could be embedded in the evaluation, the results would be more accurate and the predictions more reliable.

105 Design development
Figure 5.5.11 Result cross section with the overlay of open spaces and network.
5.6 Network morphology (public space)
The morphology of public spaces and networks in existing parts of Istanbul are the result of hundreds of years of architectural and urban development. Every so often, a new layer is formed. Each one informs and deforms the subsequent one, in the way that underlying sediments in rivers determine the growth pattern of subsequent depositions. The resulting space mediates between urbanism and architecture, between environment and functionality. From these formations there are key features that can be abstracted, such as the morphology, the proportions, the visibility and intelligibility. In existing cities, years of occupation patterns have moulded the public space, in a computational environment, time can be accelerated by an algorithm developed to accomplish the synchronised dance that weaves all of these parameters together. The algorithm proposed is a translation one: it takes the input information, finds parametrical relationships between geometry and performance, and yields a specific result which can then be evaluated. The variation comes from the specific context and the iterations of previous experiments; otherwise, by itself, this experiment is deterministic and each result depends solely on the given input.

Aim
The aim of this experiment is to test wether a proposed translation algorithm can reproduce (some of) the rich values and patterns present in traditional public space networks, and if so, to what extent?
Parameters will be added methodically to increase complexity.
106 Symbiotic aggregations
Figure 5.6.1
Terraces and a winding public stair in Cihangir. (Image: Zaldivar)
Setup
After developing a line network that connects primary and secondary nodes with the existing rooftops and public networks, an algorithm was developed that was able to translate information into an actual network morphology. The result is informed not only by the result of the previous experiments, but by specific contextual information derived from the existing buildings and the environment. The views to the Bosphorus, and the sky view factor begin to play a role on the way that open spaces are formed; hopefully, the result will be a rich dialogue between a varied array of parameters.
The algorithm needs to be informed by several parameters and perform various evaluations. This means that there’s certain information that needs to be available in the digital model, including the general location of sights (mainly the Bosphorus), the model of the existing topography and buildings along with the generated cells, and the evaluation of the existing and proposed network - namely, the betweenness and centrality.
In addition to the base information, several evaluation tools are set to inform the development (or not) of the network. The parameters to be measured are the sky view factor, the visibility, the solar access, and the binary condition of adjacency to a highly connected segment of the network or an open space. This set of tools informs the development of the network in real-time.
107 Design development
Symbiotic aggregations
data: v1 v2 v3 v4
Input Betweenness centrality:
Variable width:
Variation of the nodes’ elevation:
The inclination of each edge segment can be varied by changing the elevation of the nodes. They can vary by +/- 1.00m, so that the height differential can be mediated by the open space.
landing length ‘n’ is a function of the total run and rise of each segment.
n = 1.25m n = 1.25m n = 1.25m n = 0.90m n = 0.90m n = 0.60m n = 1.40m n = 1.40m n = 0.60m w=3.5 w=2.0 1.5 ≤ w ≤ 6.0 1.5 ≤ w ≤ 6.0 w=2.0 w=3.0 1.5 ≤ w ≤ 6.0 1.5 ≤ w ≤ 6.0 w=3.5 1.5 ≤ w ≤ 6.0 w=4.0 1.5 ≤ w ≤ 6.0
108
z = 5.70 z = 5.85 z = 5.70 z = 6.30 z = 5.00 z = 7.00 z = 6.00 z = 6.00 area: 100m2 x: 0.0 y: 0.0 z: 0.0 area: 100m2 x: 0.0 y: 15.0 z: 6.0 area: 100m2 x: 0.0 y: 25.0 z: 9.0 ±1.00m ±1.00m b a c
Variation of landings: ∑ CB(v) = n σst(v) σst s≠v≠t
The width depends on the betweenness centrality of the two nodes that form an edge. The higher the betweenness value, the wider the path will be.
Terrace logic:
As part of the setup, there needs to be a flexible body plan for the network. It has to be robust enough to handle very diverse initial conditions, and needs to be flexible enough to allow for variation. Every edge connecting a pair of vertices has a specific length and inclination. These two parameters determine the rise and run of the network, and whether it becomes a ramp or a stair. Also, the size of the landings can vary depending on these conditions. The width of the path is directly related to the betweenness centrality value for the given edge in the network, where the higher the centrality value, the wider the path. Finally, the network path tends to become flatter (if possible) when it is adjacent to a public space, and the size of the public space, linearly determines the influence on the path’s inclination. A similar relationship can be found in many existing urban areas in Istanbul.
When the network’s path morphology is generated, terraces will be formed in tandem by following the predetermined body plan. The plan controls the formation of terraces that extend from the stairs’ landings, parallel to the network, and they are partitioned at every landing to form discrete elements at different heights. The terraces are only formed if they meet the required criteria. First, the terraces are only generated if there is enough area available to expand that is not obstructed by a building volume. The size of the terraces depends on the physical boundary of their surrounding, and on the proposed width of the network. The high and low boundary limits for this parallel extension is anywhere from 1.00m to 4.00m, since terraces larger than this are rare in the existing urban tissue, and smaller ones are deemed useless.
109 Design development
Figure 5.6.2 (opposite and above) Parameters used for the generation of the network’s morphology, and their corresponding modifications.
The formation of terraces is initially informed by the size of the landing, so that a comfortable connecting path can be established. Then, the terraces extend as much as they can, unless they collide with a volume.
Connectivity path. Smaller landings inhibit the formation of terraces. Variable terrace size. Variable terrace size.
Once the group of terraces is generated in their positions with their appropriate size and geometry, the second set of criteria come into play. It is understood that for small semi-public or semi-private areas, such as terraces, to be appropriated they require certain characteristics. Generally, a medium permeability or view percentage along a medium to high sky view factor (SVF) are consider as good conditions for they form desirable environments. Finally, the SVF is coupled with an overall shading criteria that permits a comfortable occupation throughout the seasonal change.


From the path’s surface an envelope is generated that is 2.5m - 3.5m in height; it subtracts volume from the cells and, where the evaluation shows very low solar exposure, generates light shafts. These shafts, that have a specific truncated-pyramid shape determined by the sun vectors, are subtracted from the volumes. This environmental envelope, similar to the one from the pubic spaces, forms a series of tunnels and openings that perforate the volume. The actual position of the network has a direct effect on the depth and solar exposure of the buildings.


The expected result is a pedestrian network, such as the ones already existing in the area, where small open spaces appear to be formed in a seemingly natural process. They should appear where conditions are desirable for the appropriation of space by local residents, and where the topography and streets permit. The difference is that by understanding the conditions which originally permitted the formation of these spaces, the undesirable or residual ones can be filtered out. In this way the neighbours can benefit from all the formed terraces, for private or commercial purposes. If the algorithm is successful, the terraces should only appear as events in an otherwise ordered network, adding meaningful diversity to the path.
Visibility, Sky View Factor and sunlight hours analysis from existing stairs and terraces in Istanbul. These terraces are widely occupied.














Diagrams showing the process by which the generation of terraces is determined. The formation of terraces depends on the area available, the SVF, the Visibility and the solar exposure. At the bottom an environmental envelope is shown; it will be used to perform a geometric substraction from the generated infill volumes.



110 Symbiotic aggregations
Figure 5.6.3
Figure 5.6.4 (opposite)
sunlight hours analysis high low 0 high low visibility analysis sky view factor sunlight hours analysis high low 0 >7 high low visibility analysis sky view factor 2-4 m 1-1.5 m


111 Design development > 80% SVF < 30% SVF high permeability low permeability svf = 0.62 svf = 0.37 svf = 0.87 svf = 0.33 svf = 0.00 svf = 0.00 p = 0.98 p = 0.91 p = 0.79 p = 0.23 p = 0.00 p = 0.00
Initial Tests
To test the suitability and performance of the algorithm, initial tests were carried on a single section of the path. Parameters were gradually added to see the individual effect of each one. The first algorithm tested was quite robust, but was too flexible, for each segment – divided at every landing – was individually formed. The result was a very rich path, but quite broken one. This generated oddly shaped volumes, many of which were quite unsuitable; although, one could argue, rather similar to the existing streets.
On the second iteration some flexibility was removed by not allowing each segment to be further fragmented and rotated. The resulting volumes were mostly orthogonal. This setting was preferred for it meant that the architectural spaces remaining were geometrically simpler, and probably easier to occupy.
Finally, the initial tests pointed to the fact that the algorithm had to be developed linearly, where an ordered set of paths had to be followed for the algorithm to work. This is because each open space is necessarily informed by the adjacent and following edges in the network; and because compiling the whole network on a single run would require a lot of computing power causing our meek computers to crash.
The initial tests, with a crooked network plan, generate weird volumes once the subtractive operation is carried out. For this reason, an orthogonal network was preferred.
Initial tests show how the open spaces can negotiate the height differential of the network’s edges, thus averaging the overall inclination.
112 Symbiotic aggregations
Figure 5.6.5
Figure 5.6.6 (opposite)
Intital test - 01 Intital test - 02 Intital test - 03 Intital test - 04
Nodes a,b,c - test 01
Node ‘a’ is fixed, whiled node ‘b’ is the variable open space in the middle. Node ‘c’ is generated on the next iteration (expansion) of the network.
Nodes a,b,c - test 02
Nodes a,b,c - test 03
The total rise for each segments is 3.60m while the landing’s run is 1.20m.
The total rise difference betweek a 1:20 ramp and a 1:16 ramp, over a 100m total run is ~1.00m. This difference, for the scale of the clusters, is negligible.
Nodes a,b,c - test 04
The total run for each segments is 4.00m while the landing is 2.00m.
113 Design development 0 0 2 4 6 8 10 12 14 16 18 20 22 24 10 8 6 4 elevation (meters) distance (meters) 2 12 14 0 0 2 4 6 8 10 12 14 16 18 20 22 24 10 8 6 4 elevation (meters) distance (meters) 2 12 14 0 0 2 4 6 8 10 12 14 16 18 20 22 24 10 8 6 4 elevation (meters) distance (meters) 2 12 14 0 0 2 4 6 8 10 12 14 16 18 20 22 24 10 8 6 4 elevation (meters) distance (meters) 2 12 14
Implementation
Following the cues from the initial tests, the translation algorithm was progressively performed on successive sections of the network. Although the result is a broken topography that resembles hundreds of steps, many sections have such a small inclination that they’ll eventually become part of a continuous surface. Once the initial conditions, the evaluation tools and the parametric relationships are set in place – as described in the previous sections – the implementation is carried out progressively. It could be remarked that the process is a slow one, and takes over a day to perform for a single area (sub-patch). The analysis and evaluation follows.
Results
Opposite is shown a diagram containing all of the ‘genetic’ information that is needed to construct the network’s envelope. An evaluation at this stage seems redundant, for the generation of the network strictly depends on previously evaluated parameters such as Sky View Factor, visibility or solar access. The results are considered positive without further evaluation, as a network morphology was successfully translated from the existing parameters. On subsequent stages, a more thorough evaluation will be done for specific characteristics, such as the environmental comfort (wind) and the public-space surface’s performance; since they are incomplete at this stage, they’ll remain untested.
Conclusion
The algorithm is an intricately constructed one. The amount of information that is embedded on a single path of the network is remarkable, but it also turns the implementation process into a slow and clumsy one. If, after running the algorithm once, it is discovered that a relationship or parameter is not appropriate, it would require a long time to rerun the process; so, computationally, it is not the most successful method developed.
On the other hand, the generated morphology is an existing one. The richness of the patterns that are formed are surprising. The interplay of terraces, stairs and open spaces forms a rich tapestry that adapts to its immediate context, whether it is an existing one or a proposed one.
114 Symbiotic aggregations
Figure 5.6.6 (opposite) Different envelopes used to perform a boolean difference operation on the volumes above the network and open spaces. The characteristics of each envelope are described by the numerical parameters shown.

115 Design development N = 02 p =x- 1,185.7 y- 971.2 z- 39.0 l = 15.0m w= 8.5m N = 03 p =x- 1,195.2 y- 968.1 z- 49.0 l = 15.0m w= 8.5m N = 04 p =x- 1,203.3 y- 988.7 z- 25.0 l = 18.0m w= 15.0m N = 05 p =x- 1,178.5 y- 898.7 z- 35.0 l = 12.0m w= 6.0m N = 06 p =x- 1,165.8 y- 899.1 z- 33.0 l = 12.8m w= 8.5m N = 07 p =x- 1,099.9 y- 865.0 z- 15.0 l = 26.0m w=20.0m N = 15 p =x- 1,099.9 y- 865.0 z- 15.0 l = 26.0m w=20.0m N = 15 p =x- 1,099.9 y- 865.0 z- 15.0 l = 26.0m w=20.0m N = 21 p =x- 1,099.9 y- 865.0 z- 15.0 l = 26.0m w=20.0m N = 15 p =x- 1,099.9 y- 865.0 z- 15.0 l = 26.0m w=20.0m N = 16 p =x- 1,099.9 y- 865.0 z- 15.0 l = 26.0m w=20.0m N = 22 p =x- 1,099.9 y- 865.0 z- 15.0 l = 26.0m w=20.0m N = 22 p =x- 1,109.9 y- 865.0 z- 12.0 l = 26.0m w=20.0m N = 22 p =x- 1,109.9 y- 865.0 z- 12.0 l = 26.0m w=20.0m N = 14 p =x- 1,099.9 y- 865.0 z- 15.0 l = 26.0m w=20.0m N = 14 p =x- 1,099.9 y- 865.0 z- 15.0 l = 26.0m w=20.0m N = 11 p =x- 1,099.9 y- 865.0 z- 15.0 l = 26.0m w=20.0m N = 12 p =x- 1,099.9 y- 865.0 z- 15.0 l = 26.0m w=20.0m N = 01 p =x- 1,203.3 y- 988.7 z- 52.0 l = 6.0m w= 6.0m
5.7 Environmental (wind)
Introduction
Due to the extreme hot climate of Istanbul in the summer months the buildings and the open urban areas should not be exposed to high amounts of sun. Solar exposure increases the surface temperature and the radiation that is absorbed heats up the open spaces around them. The dense urban fabric builds obstacles and stops the wind from penetrating deep into the urban tissue, trapping the heat between the buildings.
The user comfort is directly related to the environmental properties of the public spaces. One of the environmental elements that determines the comfort for pedestrians is wind flow. Wind flow has a direct influence on user comfort. In the next paragraphs, the speeds of wind that are considered comfortable for pedestrians will be discussed.
The Beaufort scale provides a description for the mechanical forces of various wind velocities, however to understand the physical action of wind in built up urban areas, the wind speed should be related to pedestrian activity. The urban wind flow is not constant, the wind speed is influenced by the changing urban morphologies and meteorological factors. Therefore, the urban environment shows fluctuations in wind speed even within a small area. Different morphological conditions of built landscape can increase or decrease the wind speed locally. In 1975, Isumov and Davenport proposed a pedestrian wind comfort criteria that relates the intensity of the user activity to the frequency of given wind speeds throughout the year. Accordingly, with the increase of the user activity, the desirable wind speed increases as well. From these calculations a wind speed of 4-6m/s were considered as desirable.
The distribution of wind direction in Istanbul throughout the year (Windfinder.com, 2015)
The distribution of wind direction in Istanbul in August (Windfinder.com, 2015)
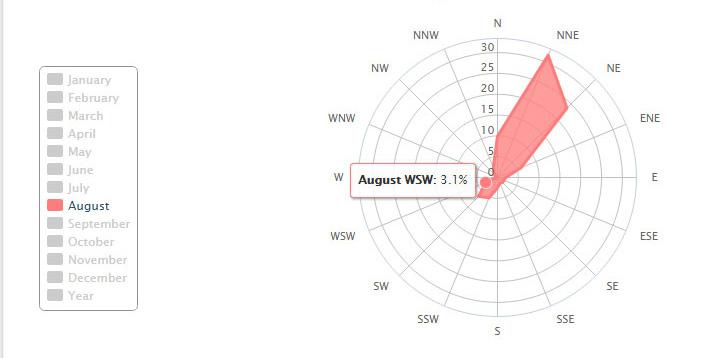
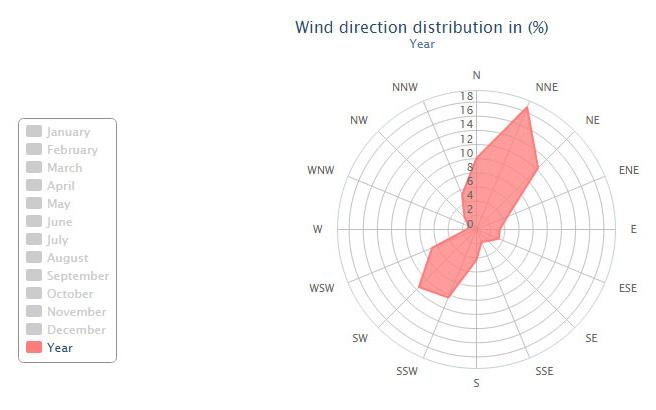
The distribution of wind direction in Istanbul in January (Windfinder.com, 2015)

116 Symbiotic aggregations
Figure 5.7.1 (above left)
Figure 5.7.2 (above top)
Figure 5.7.3 (above bottom)
Descriptive Term
Specification for Estimating Speed

0 Calm Smoke rises vertically
1 Light Air 2 – 5
2 Light Breeze
3 Gentle Breeze
4 Moderate Breeze
5 Fresh Breeze
6 Strong Breeze
7 Near Gale
8 Gale
9 Strong Gale
10 Storm
Direction of wind shown by smoke drift but not by wind vanes.
Wind felt on face; leaves rustle; ordinary vane moved by wind.
Leaves and small twigs in constant motion; wind extends light flag
Raises dust and loose paper; small branches are moved
Small trees in leaf begin to sway; crested wavelets form on inland waters.
Large branches in motion; whistling heard in telegraph wires; umbrellas used w ith difficulty
Whole trees in motion; inconvenience felt in walking against the wind.
Breaks twigs off trees; generally impedes p ro g ress.
Slight structural damage occurs e.g. to roofing shingles, TV antennae, etc.
Seldo m experienced inland; trees uprooted; considerable structural damage occurs
Very rarely experienced; accompanied by widespread damage 12
11
117 Design development
Number
(m/s)
Beaufort
Violent Storm
Hurricane 6 – 11 Speed 12 – 19 20 – 29 Less than 2 30 – 39 40 – 50 51 – 61 60 – 74 75 – 87 88 – 102 103 – 116 Above 116
Figure 5.7.4
The graph shows the relation between the intensity of the wind speed to the user comfort relying on the intensities of the activities. (adapted)
Figure 5.7.5 (below) Beaufort Scale. (adapted)
Aim
The high temperatures can be avoided by forcing the wind into the urban fabric. The morphological properties of the built environment relate directly to the velocity of the wind flow that penetrates between the buildings.
The aim is to control the wind speed on the open spaces by manipulating the morphology of the surrounding buildings. Public spaces with different micro climatic properties will be generated that respond to changing climatic conditions throughout the year.
In order to evaluate these experiments, the results will be simulated in CFD and compared to the wind conditions of the previous experiment.
Targets
The environmental targets were selected relying on the previous research on the relation between the pedestrian comfort and environmental qualities. The entire system was divided into sections that were classified according to the intensity of the activities. Sections with stairs and high inclination were considered as high activity areas whereas the public spaces were considered as areas of lower activity. Predefined environmental quality criteria for standing and sitting activities were set as targets. This leads to a target wind speed of 5m/s on more than 50% of the exposed public space during summer activities.
The areas that are more optimised for winter months were designed to be exposed to the sun as much as possible and protected from the SSE wind which is the prevailing wind direction during the winter months. It was decided that, as a maximum, 50% of the public space could be designed as winter public spaces.
Setup /Methods
The digital model obtained from the previous experiment is accepted as initial condition for the CFD analysis. The result of the initial CFD simulation shows the public areas that are poorly exposed to wind. A generative algorithm within the Grasshopper plug-in for Rhino was used to make perforations around the selected areas by manipulating the building morphologies. The results were later analysed and evaluated in Autodesk Simulation CFD.
118 Symbiotic aggregations
Initial Tests
Given the complexity of the generated urban aggregation, not every public space displays the same morphological relation to its surrounding volumes. Some public spaces are surrounded by built volumes on three edges of the public space, whereas some are only surrounded on two edges. Due to this condition every kind of public space had to be perforated in a different way. Meaning that a ventilation strategy had to be developed, that considers the specific morphology of the public space.
Public spaces were divided into three cases. Perforation strategies on these cases were tested in an isolated environment. The results were evaluated in CFD simulation and the selected strategies were implemented on the sub-patch scale.
The three cases can be listed as 75% enclosure, 50% 25% enclosure and dense aggregation around the public space. The geometries were manipulated by performing Boolean difference operations. The morphology of the perforation was varied and evaluated according to the velocity and the spread of the wind flow
public space.
119 Design development
on the
case(1) 75% enclosure case(2) 25% enclosure case(3) depth > 15m perforation type a perforation type b perforation type b case(1) 75% enclosure case(2) 25% enclosure case(3) depth > 15m perforation type a perforation type b perforation type b
5.7.6
Figure
Diagrams that explain the different types of enclosure around the public spaces and the perforation strategies that will be tested using CFD.
Strategy 1 : Perforation Along the Wind Direction
The tests were carried depending on an initial setting of a wind tunnel along the wind direction with a 3m width. The morphology of the tunnel was modified in 5 steps. These strategies were then analysed in CFD simulation. It was observed that even in the initial condition through the reduction of the wind area in the wind tunnel, a ventouri effect was achieved, accordingly wind speed was increased up to 6.5 to 7m/s in the tunnel. However this increase was dropped to 5m/s at the wind outlet arriving at the public space. Although the wind speed was increased and a certain wind flow was achieved on the public space it was observed that the dominant wind speed on the public space still remained under 3 m/s which is considered as a low wind flow for the summer months. Therefore further morphological manipulations were tested in order to increase the speed of the wind flow and spread it more equally on the public space.
To increase the wind exposed area on the public space different funnel morphologies with an outlet of 6m width and 9m width with a funnel length of 4.5m was tested. In another test the outlet of the funnel was kept in 6m and the length of the funnel was increased to 7.5m. Relying on the results of these tests it was concluded that a funnel morphology with an extension of the width towards wind outlet was spreading the wind on the public space and generating a higher wind distribution with higher speeds. However decreasing the length of the funnel has a negative effect on the wind velocity, since it increased the path of the spread, and therefore wind starts to spread already in the tunnel and slows down when it achieved the public space.
In following tests funnel morphology at the wind inlet of the wind tunnel was tested. These tests also guided to the conclusion that a funnel at the inlet does not increase the wind speed dramatically but lengthens the path of the wind with higher speeds on the public space, creating a drag effect.
120 Symbiotic aggregations
Figure 5.7.7 (opposite)
Perforations along the wind direction was tested by varying the tunnel morphology. The funnel morphology at the wind outlet edge of the tunnel performed most effectively in these tests, since it spread the accelerated wind speed in the tunnel on the public space.

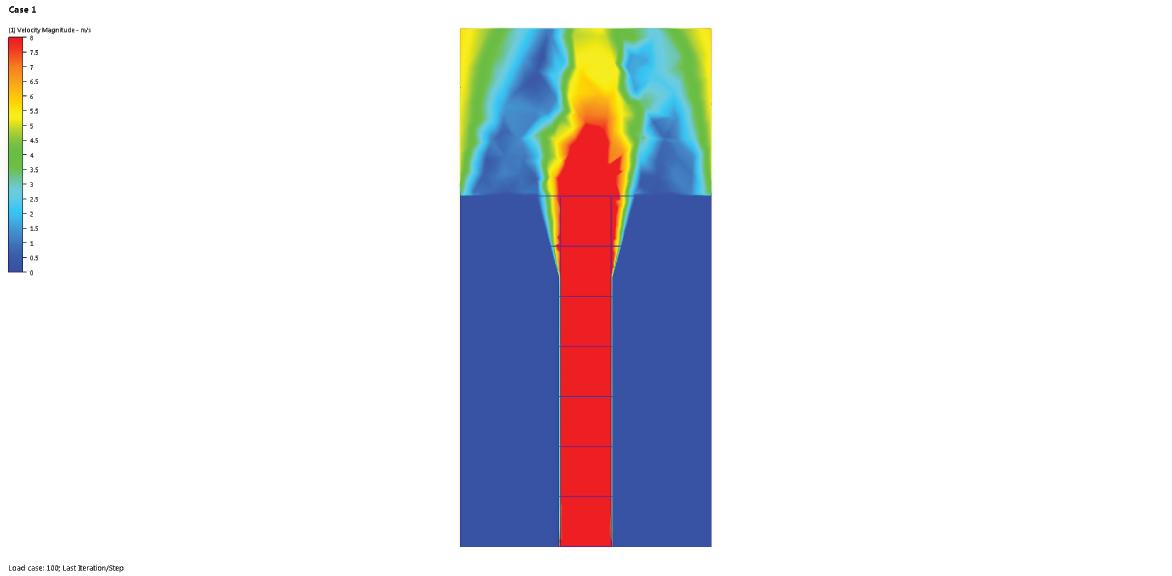



121 Design development volume reduction 20% area exposed to > 4m/s 26% volume reduction 22% area exposed to > 4 m/s 60% volume reduction 23 % area exposed to > 4 m/s 60% volume reduction 25 % area exposed to > 4 m/s 33% volume reduction 25 % area exposed to > 4 m/s 40%
Strategy 2 : Perforation on the public spaces with 75% enclosure
Former tests were performed on a public space with 25% enclosure. These tests helped to develop an understanding on the relation between the obstacle morphology and the distribution of the wind on the public space. However wind flow behaves differently in an enclosure of 75%, since the wind is trapped by the surrounding volumes on the public space the lack of drag on the not perforated edges ends up in a deceleration of the wind velocity on the public space.
Aiming to observe the wind behaviour on the public space which is enclosed on 75 % of the surroundings, relations between the perforations at the surrounding edges were investigated. Strategies were tested basing on a initial condition of a 9m x 15m public space with an opening at the not wind facing edges. Different compositions of the perforations were tested starting from 50% perforation on the one edge varying to 50% perforation on three edges. The placement of the perforations were observed in symmetrical and diagonal compositions. Another tests were investigating the funnel morphology in order to decrease the volume loss by perforation keeping the same area of accelerated wind flow on the public space.
As results of these tests it was observed that there are several possibilities to distribute the wind evenly on public space. The diagonal placement of perforation was generating a diagonal drag and therefore a large area of the public space could be exposed to accelerated wind flow. A third perforation on the side edge was also generating an alternative drag and therefore increasing the flow distribution area. The funnel was performing as a spread mechanism and this way the volume reduction could be decreased.
Perforations along the wind direction was tested also tested on a 75% enclosed public space. Here the perforations on 3 enclosed edges of the public space generated a cross ventilation effect, therefore the wind entering from the windward edge was dragged towards the perforations. This way the wind flow spread on a large area of the public space.
122 Symbiotic aggregations
Figure 5.7.8 (opposite)
volume reduction 11 % area exposed to > 4 m/s = 13 %
volume reduction 23 % area exposed to > 4 m/s = 33 %
volume reduction 23 % area exposed to > 4 m/s = 60 %
volume reduction 29 % area exposed to > 4 m/s = 66 %
volume reduction 19 % area exposed to > 4 m/s = 53 %
volume reduction 20 % area exposed to > 4 m/s = 60 %

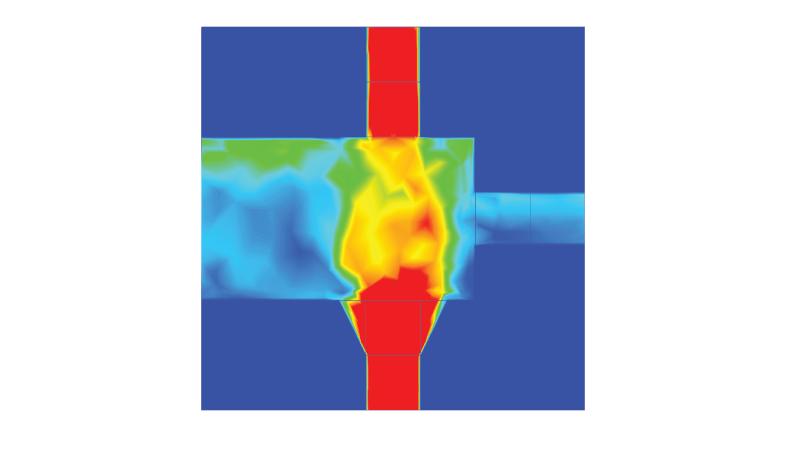
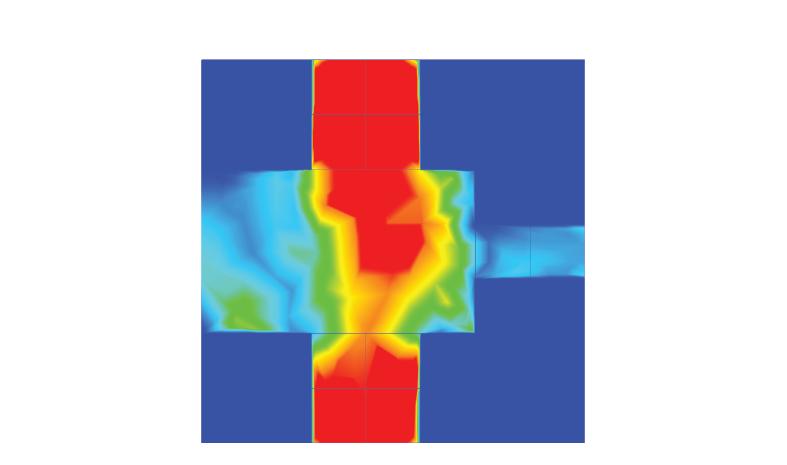

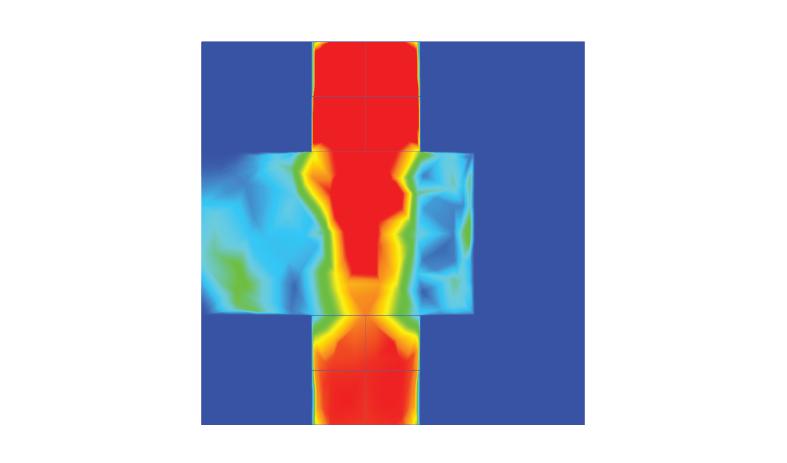
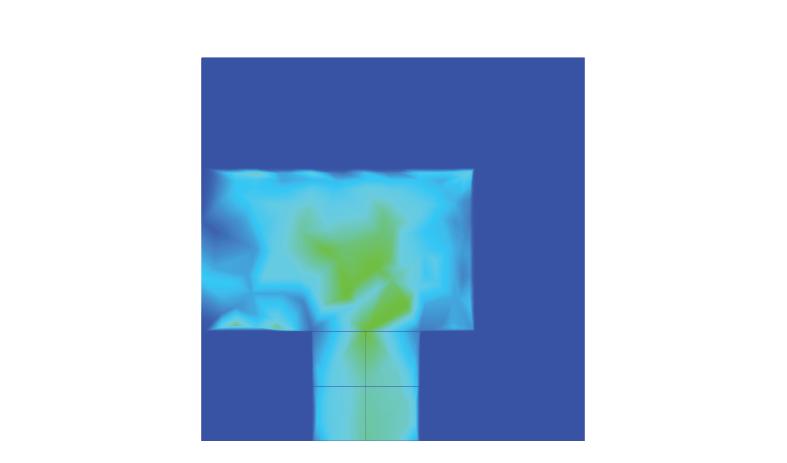






123 Design development
Strategy 3 : Perforations Deviating From Wind Direction
Due to the variation of the volumetric aggregation some public spaces were neighbouring dense areas with a depth larger than 15m. Since the prevailing wind was not always perpendicular to urban grid perforations larger than 15m depth, perforations along the wind direction resulted in emergence of volumes with narrow corner angles. In order to prevent such a problem another strategy with perforations deviating from the prevailing wind direction was tested.
In these tests the limitations of the deviation from the prevailing wind direction was investigated. Starting from a setting with a branching perforation that is perpendicular to wind direction, wind inlets were deviated between 90 and 60 degrees from the wind direction. 60 degrees deviation from the wind direction performed a small increase in the wind flow on the public space but any of these changes were not considered as perceivable therefore this strategy was not carried further in the implementation.
124 Symbiotic aggregations
Figure 5.7.9
Branching perforations were tested for the cases where the probability of a perforation along the wind direction was low.




125 Design development volume
area exposed to
2.5m/s = 25% volume reduction 30 % area exposed to >2.5 m/s = 33% volume
area exposed
m/s
volume
area
m/s
reduction 23 %
>
reduction 24 %
to > 2.5
= 25%
reduction 16 %
exposed to > 2.5
= 75%
Implementation
The geometry that was obtained from the previous experiment was analysed in CFD simulation. The isolation of the wind simulation on the generated public spaces displayed the areas that are poorly exposed to wind. These open spaces were selected to carry the wind perforation process.
Since each public space was on a different level, perforations were carried on the same level as the public space. To not penetrate into another open space, the perforations were not higher than 3m. The pseudocode for perforations is as following:
1] Classify the public space according to enclosure ( 25%, 75%).
2] Find the wind ward edges of the public spaces.
3] Place the mid point of the wind outlet calculating the quantity of the volumes to be penetrated).
4] Define the size of perforation according to intensity of the activity (public space 30% perforation, stairs 40% perforation) .
5] Generate a wind tunnel with a funnel morphology at the wind outlet face.
6] Boolean the wind tunnel from the cellular aggregation.
However in this pseudo code the third step was not generating a desirable wind tunnel since it was looking for least number of volumes
126 Symbiotic aggregations α3 α4 α2 α1
If the angle α between the edge of the public space a and the wind direction is ≥ 90° edges face the wind
selection of the edges facing wind classification of the public spaces according to enclosure
perforation of the volumes
Figure 5.7.10
Diagram shows the pseudo code for the generation of the wind perforations.
to be penetrated. As a result instead of perforating the code was only manipulating the edges of surrounding volumes. All though this manipulation was helping the wind to penetrate in the public space due to the lack of a wind tunnel, the speed of the wind was not increasing. Therefore in the second iteration a lower limitation of minimum 2 cells to penetrate was implemented into this step.
To generate a ventilation effect on the public space it was necessary to perforate the volumes opposite the wind inlet. However here the morphology of the perforation did not play an important role on the wind speeds. Therefore these perforations were intended to be as short as possible in order to prevent the high loss of the volumes and generation of not useful spaces. The algorithm was set to find the closest counterpoint of the next cell to the perforation and generate the wind outlet between these two points.
In former experiments another morphology methodology was tested. In this method, the volumes around the public spaces were treated as data. A generative algorithm was scaling, merging and perforating the surrounding volumes. There were two reasons why this method was not carried further. Firstly the through independent scale factors, some very narrow faces were emerging when the volumes were merged. All though an extension of the algorithm was cleaning these faces, this way the control over entire geometry was getting harder. Another problem occurred due to the separation of the network generation from morphology generation. In the step of symbiosis both branches of the system were displaying very individual rules, that ended up in clashes in the system.
127 Design development
Results

All though the perforations were applied to all the public areas regarding the intensities of the activities, for a detailed comparison 5 public spaces were selected and compared to initial case. The selected spaces were in various sizes and had different relations to the surroundings within the cluster.
As a general result all the public spaces increased in the size through the perforation. In four of the five cases the distribution of the wind on the public space increased however on one of the cases it dropped. While the wind flow higher than 4m/s could not be observed on the entire public spaces, the perforations generated zones on the public space that is exposed to wind. This ended up in environmental variety on each public space.
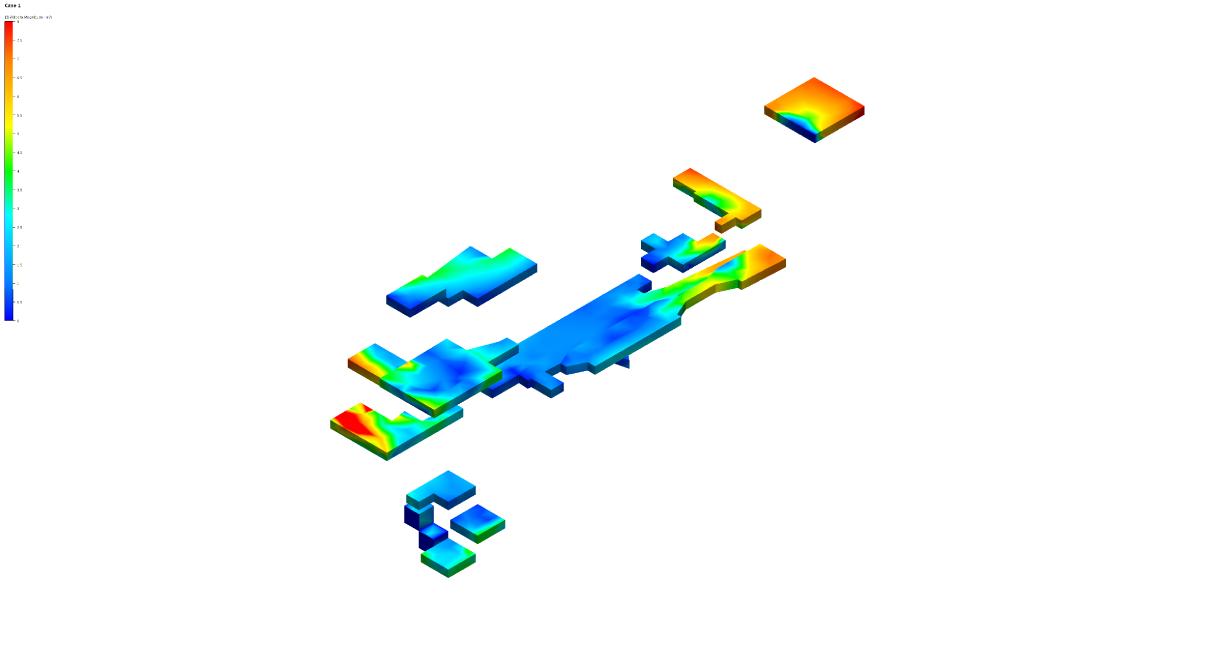
128 Symbiotic aggregations
p s 1 i n i t a l p s 2 i n i t i a l p s 3 i n i t a l p s 4 i n i t i a l p s 5 i n i t a l p s 1 f n a l p s 2 f i n a l p s 3 f n a l p s 4 f n a l p s 5 f n a l
Figure 5.7.11 (top)
The diagram shows the positions of the selected public spaces for the result comparison before and after the experiment.
Figure 5.7.12 (above)
The CFD simulations show the wind velocity on the public spaces before and after the experiment.
Figure 5.7.12 (opposite)
The comparison on of the wind speed before and after the experiment on selected public spaces.








area exposed to > 4 m/s.....0% name.........................................ps 1 initial name.........................................ps 1 final name.........................................ps 2 initial
m² area exposed to > 4 m/s..................= 45%
m² area exposed to > 4 m/s..................= 27%
m² area exposed to > 4 m/s..................42%
area......................................................198
area......................................................324
area......................................................63
Conclusions
The generation of perforations around the public space resulted in increase in partial increase in the perceived comfort. 65% of the public spaces displayed a higher performance compared to the initial condition.
The entire area of the public space could not be exposed to higher velocities of wind flow but each public space was displaying areas with wind exposed and wind protected zones within itself. This differentiation of the micro climate within the public space could result in a all year around use of public space, with a dominated use of different zones within the public space according to the season.

Through the perforations public spaces were extended in area and new typologies of public spaces were emerged. The emerging extension through perforations were displaying high amounts of wind flow. Therefore these perforations also improved the overall performance of the generated cluster by introducing ventilation tunnels. These spaces can influence the placement of the windows on the building facade due to the high potential of ventilation. Also the high wind exposure and low solar exposure can convert these areas to socially active zones in the summer months related to the comfort they provide.
This approach was only concentrating on the prevailing wind direction,

130
Figure 5.7.13
The final result after the experiment with the projected CFD simulation on the public spaces.
and taking this wind into account. The perforations were only oriented to this direction. Could there be another approach that also takes the other winds in account? The size and the location of the public spaces were dictating the placement of the perforation holes. How would another public space setting with smaller public space formations perform.
131 Design development
5.8 Programmatic distribution
The quality of a certain urban setting is highly related to the distribution of the functions within. Urban functions display different attraction values according to the necessity in the daily life and enhance in the social activity of inhabitants. Therefore urban areas with a high functional diversity is mostly qualified as high quality urban zones.
Istanbul constitutes multiple centres. The centres of historical and cultural importance display a homogeneous functional distribution compared to the newly developments. The reason for that matter lays in the growth trends that based on functional zoning, which were integrated in the urban planning approaches in ‘80s and remained the same till now. This approach generates a growth scenario that clearly separates the functional diversity by generating function oriented building typologies. Such an approach results in building typologies that are not adaptable to the future changes. The conglomeration of the same typology in a urban area generates a functional zoning in urban tissue that lack functional diversity. Accordingly urban pedestrian experience diminishes in the car oriented urban setting.
132 Symbiotic aggregations District: .......................................................Fener Population Density:..................26 734 inh/km² Recreational Functions:.................................15 Amenities:.........................................................91 Retail:...................................................................5 District: ...................................................Kadikoy Population Density:..................12 591 inh/km² Recreational Functions:.................................39 Amenities:.........................................................60 Retail:................................................................35 50 000 50 000 50 50 100 100 50 50 District: ...................................................Kadikoy Population Density:..................15 692 inh/km² Recreational Functions:...................................5 Amenities:...........................................................0 Retail:..................................................................1 50 000 50 50
Figure 5.8.1
The analysis of different urban patches in Istanbul informed the global distribution logic, that is developed for the experiment.
residential office mixed commercial
n/a clinic service bank
restaurant artisanshop shop convenience pharmacy other
Figure 5.8.2 (left) Functional distribution in the sub-patch in Cihangir.
Aim
Functional distribution will be used to enhance the certain qualities of the aggregated urban area, without generating high values of functional conglomeration. It is aimed to enhance the functional qualities of the locality, rather than generating an attraction area for the global image of Istanbul.
Setup
The functional distribution in urban patches from different parts of Istanbul will be analysed by tissue sampling. These areas will be compared to each other relying on the statistics of TUIK, which provide a social image for different districts of Istanbul. Accordingly ideal numbers of distribution for each function will be extracted and implemented to selected urban patch. This experiment will be carried in the global scale. A second experiment will be conducted in the local scale relying on the result of the certain experiment.
Implementation
1km2 area from three different districts of Istanbul was selected as case studies. Each studied tissue was selected according to the age of the tissue, the location in the urban fabric and intensity of public activity throughout the day.
133 Design development
education parking health openpublic religious abandoned n
Figure 5.8.3 (right) Functional distribution at ground level in the sub-patch in Cihangir.
The functions to be analysed were classified in three groups. Functions such as small commerce, pharmacies, grocery shops and artisan shops were classified as amenities. Larger retail functions such as shopping malls and supermarkets were classified as commercial. The functions related to social activities such as restaurants, bars and coffee shops were classified as recreational functions.
Two socially active patches Kadikoy and Fener displayed a high functional diversity, where in Kadikoy the distribution of leisure functions were higher compared to Fener which had a high amount of amenity distribution. Atasehir being one of the new developmental zones in Istanbul was very inactive and the functional distribution was concentrated in shopping malls. Accordingly this model was eliminated.
The distribution values were based on the average model of Kadikoy and Fener since both were stronger in distribution of different functions which were important for the social life. The amenities in Fener was not just serving the neighbourhood but also creating a social atmosphere, since the owners of these small shops were also inhabitants of the neighbourhood. Small commerce reclaimes the street and extends their goods to the street. This way the street was becoming a place of communication and interaction. Therefore it was decided take Fener as a model for the calculation of amenity distribution. In Kadikoy district a high amount of recreational and commercial functions were observed. Also this district is noted as one of the areas with the most social activity in Istanbul. Therefore for the calculation of recreational functions Kadikoy was taken as the base model, whereas the commercial functions were kept lower than Kadikoy. Since these were attracting the crowds, it was avoided to distribute high numbers of commercial functions.
The extracted numbers were calculated according to the relation of these districts to the population density. This numbers were then projected to the preset target population in the selected urban patch. These numbers were than distributed in the clusters regarding the relation of the cluster volume to the total generated volume.
Results
As a result of previously mentioned calculations, 226 amenities , 170 recreational functions and 27 retail functions were distributed within a overall volume of 125,985m3. These functions were assigned to each cluster according to size. Since the larger and smaller clusters are equally distributed in the entire patch there was no functional conglomeration in any of the areas. Although each cluster had at least one of each function, larger clusters were more self-sufficient.
134 Symbiotic aggregations
Figure 5.8.4 (opposite)
The global distribution of the functions for the entire patch.
v =583 m3, amenities 1, leisure 1, retail 1
v =1050 m3, amenities 2, leisure 1, retail 1
v=2915 m3, amenities 5, leisure 3, retail 1
=3868 m3, amenities 6, leisure 5, retail 1
v =2991 m3, amenities 5, leisure 4, retail 1
v =18486 m3, amenities 33, leisure 25, retail 3
v = 52967 m3, amenities 93, leisure 70, retail 9a
v = 2106 m3, amenities 4, leisure 3, retail 1
v =6068 m3, amenities 10, leisure 8, retail 1
v =6766 m3, amenities 12, leisure 9, retail 1
v =11559 m3, amenities 20, leisure 15, retail 2
v =4233 m3, amenities 7, leisure 5, retail 1
135 Design development
Local Distribution
The case studies on typologies of urban space displayed a direct relation between the functional distribution and the type of public space. There are two drivers that influence this relation. Firstly the environmental qualities of the urban typology dictate the intensity of the activities therefore functions linked to more intense activities require higher environmental comfort. Another driver is the relation of the function to the most public spaces. A value of privacy was given for each type of public space according to their relation to public. Same evaluation was also considered for the functions.
Aim
Instead of dictating the building typologies relying on the functions, it was aimed to distribute the functions relying on the emerging typologies in the system. Such an approach extends the adaptability of the system by not limiting the building morphology by predefined function.
The numbers for functional distribution for each cluster were obtained in the previous experiment. This experiment will distribute these functions within the cluster.
Setup/Methods
The 3 dimensional model obtained from the previous experiment was analysed through an algorithm that provides a quantification of generated typologies of public space. The functions will be then distributed according to the matching privacy value of each type.
136 Symbiotic aggregations
amenities proximity to street betweenness privacy size artisan shop grocery shop small commerce supermarket retail commercial 80-200 m2 10-25 m2 10-100 m2 2-15 m2 reataurant coffee/pub recreational open semi public open public residential p r i va t e public r el a ti v e p r o ximi t y r el a ti v e p r o ximi t y high be t w eeness l o w be t w eeness
Figure 5.8.5
The relation between the functions and allocation of these within the urban fabric.
Implementation
The types of public spaces were classified in groups regarding the enclosure. Accordingly the types were classified as open space, arcades, passages and courtyards in 4 groups.
The developed geometry was very complex to analyse the types manually. Therefore an algorithm was developed to extract the places and number of each typology. The pseudo code for this algorithm is as follows
Distinguishing between covered and not covered spaces:
1] Project a 3m by 3m point grid on the geometry.
2] Draw straight lines from each point in z axis in length of 30m.
3] Trim the lines with the generated volume.
4] Calculate the length of the lines and separate the ones that have a length < 30m in a different group (these are considered as covered spaces).
Discovering the two-dimensional morphology of the space.
5] in both groups of points draw straight lines in -x,+x and -y,+y directions of 15m length.
137 Design development
Figure 5.8.6
Diagrammatic Pseudo Code for the local distribution. An algorithm was generated to allocate and quantify the different typologies that are generated as a result of the previous steps.
6] Trim the lines with the generated volume
7] Calculate the length of the lines and separate them into different groups
The classification of the types is as follows:
In the list of covered zones.
If the line in one of -x,+x or -y,+y directions remains untrimmed this space is considered as an arcade.
If positive and negative directions of the same axis is trimmed the space is considered as a passage.
In the group of covered areas:
If the sum of the length of a line in - and + directions is >10m the space is considered as open space.
If the length is < 10m the space will be considered as a courtyard.

138 Symbiotic aggregations
Figure 5.8.7
A privacy gradient was applied to volumes, depending on the proximity of each volume to the generated urban type.
Results
The typology navigation resulted in allocation of 14 parks, 13 courtyards, 21 arcades, 6 passages. A five step gradient from public to private was applied on the cells relying on the allocation of the types. This gradient informed the placement of the function within the cluster regarding relation to privacy gradient. The functions were not directly distributed, rather the information for the functional distribution was generated. The selection of the size and how many cells will be occupied with a certain function can be decided in an extra step.
Conclusions
The algorithm provided a deeper insight in the generated system by analysing it morphologically. It was finding the predicted typologies and additionally it decided to classify some areas in certain types depending on system intrinsic logics. This resulted in classification of some areas as semi private courtyards. The emergence of this areas were related to the high articulation of the generated volumes.
139 Design development
140 Symbiotic aggregations 06
Design
141 Design
6.1 Design proposal
6.2 Design translation

142 Symbiotic aggregations
6.1 Design translation
The aim of the design translation was to use the information obtained from the evaluation process to inform a final design.
The public spaces obtained in the previous experiments were previously analysed according to solar exposure, visibility, wind flow and sky view factor. The information obtained from these analysis was overlaid and used to inform the design a three-dimensional surface topography.

The public spaces were analysed as flat surfaces. The information that was obtained from this analysis resulted in zones with different environmental values on the surface. These zones were classified according to environmental conditions. The factors such as wind and shading defined the function of the public space in that area, whereas the values of visibility and sky view factor informed the morphology of a specific function.
The general topography of the surface is already determined by the open-spaces generation algorithm, and the network morphology one. The design process occurs within the boundary permitted by the preliminary results.
The outlines for the design proposal were as following:
The shaded wind perforations will be designed as continuous
143 Design
Figure 6.1.1 (opposite)
The information provided by the sunlight hours analysis, wind speed simulation, visibility analysis and sky view factor was used to develop a design proposal.
Figure 6.1.2 (above)
The final result of the design proposal for the public space surface.
Symbiotic aggregations
Cellular density
Cellular differentiation
Regular cells (anchored)
Lightweight cells
Cantilever cells

Demolished buildings
Structural cells (cores)
Programmatic differentiation
Solar analysis for the entire year
6.0 hours
0.0 hours
144
Low density High density Public Private
seating elements that allow wind flow while serving as open areas.
The shaded areas will be partly designed as a seating landscape when matched to an appropriate adjacent programme – public to semi-public activities.
The areas with low visibility values will be designed as an ascending amphitheatre to provide views to users; ideally towards iconic cityscapes.
A similar approach is proposed for the building morphology. From previous experiments, some very specific characteristics have already been obtained for each cell. This information can be overlaid and placed in a design matrix, where each set of conditions correspond to an equivalent material or surface treatment. The programme ‘dials’ shown above relate specific programmatic functions to their desired environmental conditions throughout the day – this information would serve as the translator that gives the matrix.
On the one side of the matrix there would be the informing parameters: solar exposure, building density, cellular quality and programme. On the other axis there would be the design lineaments that could define the surface’s porosity, reflectivity, roughness, transparency and albedo. Then, a suitable material and colour choice could be made.
145 Design residential work services ammenities open public space 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
Figure 6.1.3 (opposite)
Each cell has a diverse vocation and characteristics, this information, along with the environmentalprogrammatic necessities shown above, serve as the base information for a final design.
Figure 6.1.4 (above)
Five dials showing the solar requirements for winter and summer for different programmes.
6.2 Design proposal
As a result a three-dimensional landscape was designed, that connected public spaces to each other. However this proposal is one possibility of many and it is evaluated by the aesthetical assessment of the designer. Therefore this section can be open to a wider discussion and further proposals.

Once the cells are translated into their corresponding type, and a continuous public space is formed, the results are matched. The integration of both designs forms a symbiotic morphology that productively relates to its environment.
The sections show opposite illustrate the integration of the design proposal to the existing network of buildings, streets and stairs. Light shafts appear in section ‘b’; while lightweight cells appear as canopies on sections ‘a’ and ‘b’. Also in section ‘a’, there appear two bridges that is connecting the rooftops of two exisitng buildings and a generated one: the first is shown in section on the left side, and the other one is corssing from left to right on the right side of the drawing. Section ‘c’ is the most interesting, for it shows an area where the developed network naturally integrates to the existing one. The stairs take advantage of the existing topography and rise towards the upper leves of the growth. If one is to be places on the back street (right) the is almos an equal distance to the existing lower street as there is to the higher levels, where the second network elevation datum is found.
146 Symbiotic aggregations
Figure 6.2.1 Diagram showing where the sections are from.
Figure 6.2.2 (opposite) Sections ‘a’, ‘b’ and ‘c’ through the design proposal.
section ‘c’ section ‘b’ section ‘a’
147 Design
Section ‘c’
Section ‘b’
Section ‘a’

148 Symbiotic aggregations
Figure 6.2.3 Render view.

149 Design
Figure 6.2.4 Render view.
07 Results & conclusions
150 Symbiotic aggregations
7.1 Results
7.2 Conclusions & further development
Urban system
Environmental conclusions
Computational conclusions
151 Results & conclusions
Symbiotic aggregations











152
Volume: FAR: Public Area: Volume: FAR: Public Area: Volume: FAR: Public Area: Green Area: 3,888m3 6.1 90m2 5,670m3 4.2 261m2 61,236m3 3.3 1,420m2 1,080m2 Volume: Public Area: Green Area: 28,114m3 5.3 1,350m2 1,134m2 Volume: FAR: Public Area: Green Area: FAR: Public Area: Green Area: FAR: Public Area: Green Area: 5.6 108m2 90m2 4.2 189m2 90m2 42,326m3 2.7 2,505m2 1,350m2
7.1 Results
The proposed urban system increased the habitable capacity of a 120,000m2 urban patch by adding 126,094m3 volume on an area of 11,346m2 residual spaces. A demolish rebuild model occupying this area with an average of 18m height (which is 6 floors) would add 204,228m3 volume. However, this system would not provide any additional public space and over-crowd the existing public space by the addition of the proposed population. The intervention enabled a population growth of 2,800 inhabitants, which is 60% higher than the set target population.
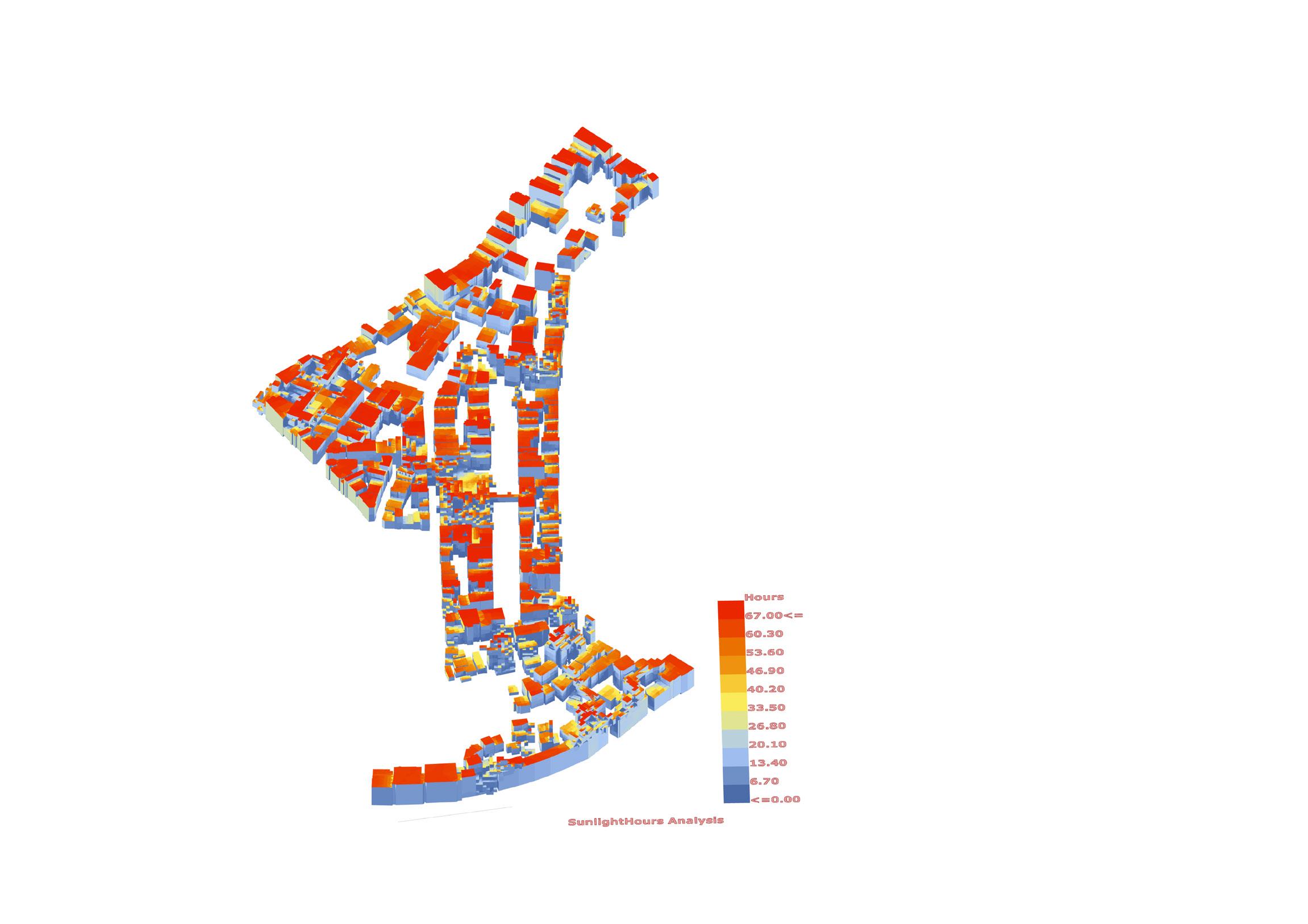
The area of the public spaces were increased by 38,882m2 in total, from which 30,433m2 are emerging public spaces. To draw up a comparison 38,882m2 equals to 3.8 times the size of the Bedford Square. Considering the size of the patch, of 12.2ha, this is quite a respectable result.
The existing patch was affected by a 12.13% decrease in the sky view factor on the streets and an 18% decrease in sunlight hours throughout the year. However, the shading on the ground was only changed, surprisingly, by 0.48% which means that the existing conditions were not severely affected, while the generated ones are good.

153
Figure 7.1.1 (opposite) Catalogue of diverse morphologies, adapted to their unique locations, generated by the ‘infill growth’ and ‘open spaces’ experiments.
Figure 7.1.2 (above)
Comparison of solar hours on the building surfaces for the whole patch. Before (left) and after the experiment (right).
7.2 Conclusions & further development

Relying on the previously mentioned results several questions arise regarding the urban system, generative (computational) process, environmental results and further steps.
Urban System

The system was tested on a small dense patch in Istanbul. And resulted in increase of habitable and public spaces within this patch. The preset population targets were achieved. Therefore it can be concluded that this system can accommodate the population growth in Istanbul within the next 30 years, by keeping and enhancing the qualities of the public life.
The selected process provided a generative growth that act on the local properties of generators. Therefore the emerging urban growth displayed a highly differentiated aggregation that depend on the same generative logics. Due to this property, the system appears as a local intervention although it is controlled in an urban scale.
The major contributor of this result was the different site conditions of the selected residual spaces, that is already consisted within the urban fabric. Therefore the generative system responds differently in
154 Symbiotic aggregations
Figure 7.2.1
Comparison of SVF on the ground for the whole patch. Before (left) and after the experiment (right).
n
each locality. This brings up the question of the selection of an urban system that is growing within a built urban condition in comparison to selection of an unbuilt urban site to generate an urban system. Since the built environment already inherit a vast differentiation, the system responds in every selected generator differently, therefore a highly differentiated form emerges. However, applying the same system on an unbuilt area might end up in more regular formations due to the lack of differentiation that only exist within the built context. The system’s diversity depends on its context’s richness.
Environmental Conclusions
The generative system aimed to respect the existing environmental qualities of the built environment. Accordingly the generated volume was trying to keep the minimum existing sky view factor, and prevent from extra shading on the street level. Due to the already dense urban fabric, the intervention did not increase the ground shadow dramatically. However a minor decrease in the sky view factor and solar access could be observed.
The generative methods for the environmental targets were tested in isolated environments and applied further into the generative process. Although the solar manipulations succeeded relatively, wind perforations displayed different results than predicted in the CFD simulation. The

155
Figure 7.2.2
Comparison of shading for the entire year on the ground for the whole patch. Before (left) and after the experiment (right).
n
answer to this problem may lie in the complex behaviour of the wind within an urban environment. The dense existing tissue generates urban wind flows that cannot be predicted entirely. Therefore the strategies that take the prevailing wind as the main wind direction and generate the system accordingly do not entirely succeed. A further suggestion for this problem can be the detailed implementation of the existing wind vectors into the generative design process that can be extracted from the CFD analysis.
Another criteria that was not taken into account was the combination of the temperature with the wind flow. This calculation can help to evaluate the user comfort in a higher detail and inform the design proposal further, creating an outline for the construction materials in relation to their albedo effects.

Computational conclusions
This thesis is only a part of a larger learning process that encompasses the entirety of the course, and even more. It is understandable that many of the experiments or processes presented are not optimal, on hindsight, they can be considered only our best attempts at the time. As the thesis work progressed, we renewed our understanding and mastery of earlier techniques and computational skills, so quite evidently, there is a disparity between the first and latter tests.
156 Symbiotic aggregations high low evaluation of surface inclination
Figure 7.2.3
Evaluation of the public space inclination, where yellow to orange has an acceptable inclination, and red became stairs.
The first algorithms written were quite inefficient. Without previous knowledge on sieves and other methods for reducing computational expenses, it was difficult to achieve optimum results. More importantly, the skills and rigour with which the algorithms were evaluated also improved over time. Perhaps the best example is the detailed analysis carried out for the results of the genetic algorithm for the base network and secondary nodes experiment. Had we been as rigorous on the initial ones, we would’ve developed a much more solid platform from which to defend the results.
It can be argued, however, that as architects we are not to be so concerned with computational efficiency as with the urban and architectural results. But, if one is to be as objective as possible, it is impossible to separate form from content, meaning that the cleverness and elegance with which the algorithms are devised and implemented are directly related to the cleverness and elegance of the results. Architecture cannot mask the underlying logics and drivers if a solid argument is to be made for the superiority of this methodology. A long trail remains ahead, and expertise is by no means an easy goal: but one that is worth striving for.
Overall, the amount of work produced would not have been possible without the algorithmic power of computers. And to understand their true value for architecture is of utmost importance today.
On modelling
Models are abstractions of an aspect of the real world. They are used to analyse, understand or predict specific information, and are only as good as the accuracy of the information that can be derived from them. To corroborate a model produced by a computer simulation, physical testing and empirical information would be needed.
CFD results are only good as a starting point, and on further development they should be physically tested. Other computer simulations regarding solar access and shading are more accurate, but any model that tries to predict human behaviour can always be contested. Sociology and anthropology have argued on both sides of the reductionism line for a long time, and it is not within the scope of this thesis to discuss their findings.
157 Results & conclusions
158 Symbiotic aggregations
08 References & Bibliography
159 References & bibliography
References and bibliography
A. Chavoya and Y. Duthen. Using a genetic algorithm to evolve cellular automata for 2D/3D computational development. In GECCO ’06, pages 231-232, 2006.
Allen, S. and Segal, R. (2014). Block/Tower: A Vertical Landscape in Midtown Manhattan.Architectural Design, 84(5), pp.60-65.
Atelier Bow-Wow, Pet Architecture Guide Book, Living Spehere Vol. 2, World Photo Press, 2001
Batty, Michael, Cities and Complexity, The MIT Press, 2005
Bays, Carter, Candidates for the Game of Life in Three Dimensions. Complex Systems 1, University of South Carolina, 1987
R. Breukelaar and T. Bäck. Using a genetic algorithm to evolve behaviour in multi dimensional cellular automata: emergence of behaviour. In GECCO ’05, pages 107–114, 2005.
Bozdogan, Sibel, Vernacular Architecture and Identity Politics: The case of the “Turkish House”, Traditional Dwellings and Settlements Review, Volume VII, Number II, 1996
Brooks, N., Donaghy, K. and Knaap, G. (2012). The Oxford handbook of urban economics and planning. 1st ed. New York: Oxford University Press.
Christenson, M. (2010). Registering visual permeability in architecture: isovists and occlusion maps in AutoLISP. Environment and Planning B: Planning and Design, 37(6), pp.1128-1136.
Hensel, Michael, Turkey at the threshold, AD Architectural Design, Jan/ Feb 2010 Profile No. 203, pp. 2010
Gehl, J. (2011). Life between buildings. 1st ed. Washington, DC: Island Press.
Hillier, B. (2014). The Generic City and its Origins. Architectural Design, 84(5), pp.100-105.
Holland, J.H., Adaptationinnaturalandartificialsystems:anintroductory analysis with applications to biology, control, and artificial intelligence Ann Arbor, MI: University of Michigan Press, 1975
Istanbul Studio: ‘Planning for Transparency and Inclusion, Columbia University Urban Planning Program, 2011
160 Symbiotic aggregations
Krawczyk, Robert J., Architectural Interpretation of Cellular Automata. Generative Art, College of Architecture, Illinois Institute of Technology, 2002 Kuzmin, D. (n.d.). Introduction to Computational Fluid Dynamics.
Lefebvre, Henri, The Production of Space, Blackwell publishers Inc, 1974
Îslam, Tolga, Current Urban Discourse, Urban Transformation and Gentrification in Istanbul, Architectural Design, Turkey At the Threshold Jan/Feb 2010 Profile No. 203
T. Back, D. Fogel, Z. Michalewicz, Handbook of Evolutionary Computation, IOP Publishing and Oxford University Press, 1997.
Von Neumann, J., TheGeneralandLogicalTheoryofAutomata, in J. Von Neumann, Collected Works, edited by A. H. Taub Volume V, Design of Computers, Theory of Automata and Numerical Analysis. Pergamon Press, 1963
Situngkir, H.Exploring Ancient Architectural Designs with Cellular Automata,BFI Working Paper Series WP-9-2010, Bandung Fe Institute, Indonesia, 2010.
Stathopoulos, T. (2009). Wind and Comfort. In: EACWE 5. Florence, Italy.
Weinstock, M. The Architecture of Emergence: The evolution of form in nature and civilization, John Wiley & Sons Ltd, 2010
Onur Özsoy, Hasan Sahin,Housing price determinants in Istanbul, Turkey: An application of the classification and regression tree model, International Journal of Housing Markets and Analysis, Vol. 2 Iss: 2, pp.167 – 178, 2009
Virginia McConnell and Keith Wiley, Infill Development: Perspectives and Evidence from Economics and Planning, Discussion paper, May 2010.
2013, Attractiveness Survey, Ernst Young and Partners, ITO
Bill Hillie, Tim Stonor, Space Syntax: Strategic Urban Design, City Planning Institute of Japan, 25 Jun. 2010
Vicky Cheng and Edward Ng, WindforComfortinHighDensityCities, Department of Architecture, University of Cambridge, Cambridge, UK, Department of Architecture, The Chinese University of Hong Kong, Hong Kong, PLEA 2008 –25th Conference on Passive and Low Energy Architecture, Dublin, 22nd to 24th
October 2008
Mohammad Rahim Rahnama, Mohammad Hossein, HeraviTorbati, Study of Physical-Spatial Effects of High-Rise Building, American Journal of Engineering Research (AJER) Volume-03, Issue-01, pp-233-244, 2014
161 References & bibliography
Symbiotic aggregations
Websites: World Health Organisation (WHO). http://www.who.int/
Turkish Institute of Statistics (TUIK). http://www.tuik.gov.tr/ http://weather.sg.msn.com/
New York City government website. http://www.nyc.gov/
Big.dk, (2015). BIG | Bjarke Ingels Group. [online]
Available at: http://www.big.dk/#projects-tek [Accessed 26 Jan. 2015].
Görüntüle, P. (2012). fashionist: Beyoglu’nda bir gün... [online] Cansansalmoda.blogspot.co.uk.
Available at: http://cansansalmoda.blogspot.co.uk/2012/03/ beyoglunda-bir-gun.html [Accessed 3 Feb. 2015].
Turkstat.gov.tr, (2015). ..::Welcome to Turkish Statistical Institute(TurkStat)’s Web Pages::... [online]
Available at: http://www.turkstat.gov.tr/PreTablo.do?alt_id=1027
[Accessed 30 Jan. 2015].
http://www.coolgeography.co.uk/
City Population Statistics city. http://www.population.de/
Koeppen-geiger.vu-wien.ac.at, (2015). World Maps of Köppen-Geiger climate classification. [online]
Available at: http://koeppen-geiger.vu-wien.ac.at/present.htm [Accessed 3 Feb. 2015].
(Windfinder.com, 2015) Windfinder.com, (2015). Windfinder.com - Wind and weather statistic Yesilköy/Istanbul. [online]
Available at: http://www.windfinder.com/windstatistics/istanbul [Accessed 3 Feb. 2015].
Google Earth geographical imaging.
http://www.wikimedia.com/images
http://www.Yandex.maps.com/
162
163 References & bibliography
164 Symbiotic aggregations 09 Appendix
165 Appendix
These two maps, along with a few others presented throughout the book, form a collection of data abstracted from the patch. Most of the information was used to inform the system’s development at one point or another. The roof type allows us to see what buildings have a possibility of being built on top of, and the building height map was used to build the 3D model of the patch.
166 Symbiotic aggregations n 3m +40m flat roof inclined
Building height and roof type mapping Chapter 4.3 Cihangir.
Results for the generation of open spaces
Chapter 5.4 Open spaces.
Out of the three results from the infill growth experiment, three options were developed and selected for each one, so a total of nine options were produced to be further evaluated at the open spaces generation experiment. The following diagrams show the options that were not selected and, consequently, not carried forward.

167 Appendix V- total volume P- total passages C- continuity (contours / levels) S- shaded area A- area of open spaces 29,754m3 40 3.37 33% 765 G10 - 02 V C P S A


168
V- total volume P- total passages C- continuity (contours / levels) S- shaded area A- area of open spaces 29,754m3 40 3.37 43% 819m2 G10 - 02 V C P S A V- total volume P- total passages C- continuity (contours / levels) S- shaded area A- area of open spaces 29,754m3 40 3.37 39% 657 G10 - 02 V C P S A
Symbiotic aggregations


169 Appendix V- total volume P- total passages C- continuity (contours / levels) S- shaded area A- area of open spaces 6,750m3 8 2.75 72% 300 G10 - 09 V C P S A V- total volume P- total passages C- continuity (contours / levels) S- shaded area A- area of open spaces 6,750m3 8 2.75 91% 81 G10 - 09 V C P S A
Genetic Algorithm optimization
Chapter 5.5 Base network and secondary nodes. Chapter 7.2 Conclusions & further development.
The graphs on the following three pages the results for every individual at different generations for all three experiments of the bese network generation. Argualbly, this kind of detailed anlayses and tests should’ve been conducted for every genetic algorithm used, as is discussed in the ‘computational conclusions’ of Chapter 7.2.
The image on page 173 shows the logic by which these results were evaluated and generated. It was not included in the text body because there is a more comprehensive pseudo code diagram availabe.
170 Symbiotic aggregations crash inclination deviation average inclination 0 1 2 3 4 5 6 7 8 9 39 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 40 500 400 300 200 fitness individual 100 600 700 800 Experiment 1 - G1 0 1 2 3 4 5 6 7 8 9 39 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 40 500 400 300 200 fitness individual 100 600 700 800 Experiment 1 - G10 *3rd place
171 Appendix crash inclination deviation average inclination 0 1 2 3 4 5 6 7 8 9 39 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 40 500 400 300 200 fitness individual 100 600 700 800 Experiment 1 - G20 0 1 2 3 4 5 6 7 8 9 39 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 40 500 400 300 200 fitness individual 100 600 700 800 Experiment 1 - G30 0 1 2 3 4 5 6 7 8 9 39 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 40 500 400 300 200 fitness individual 100 600 700 800 Experiment 1 - G40
Symbiotic aggregations
172
crash inclination deviation average inclination 1 2 3 4 5 6 7 8 9 39 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 40 individual Experiment 2 - G15 (1 to 40) 0 500 400 300 200 fitness 100 600 700 800 41 42 43 44 45 46 47 48 80 79 78 77 76 75 74 73 72 71 70 69 68 67 66 55 54 53 52 51 50 49 56 57 58 65 64 63 62 61 60 59 individual Experiment 2 - G15 (41 to 80) 0 500 400 300 200 fitness 100 600 700 800 88 87 86 85 84 83 82 81 89 90 91 92 93 94 95 96 97 120 119 118 117 116 115 114 113 112 111 110 109 108 107 106 105 104 103 102 101 100 99 98 individual Experiment 2 - G15 (81 to 120) 0 500 400 300 200 fitness 100 600 700 800
test area as nodes
If each node is considered as a fix point, then the network is highly constrained. In reality, each node should be represented as an extension of the network, for it is public space.
In this case the yellow lines represent the actual geometry that each platform has, providing room to vary and optimize the network.
public space deformation (constant area)
network deformation (increases total distance)
As public space depends only on a fixed area and a node that lies within the polygon, the network can deform in order to optimize the slope degree.
Finally, the network can deform, taking a longer broken path. This effectively increases the linear distance between nodes, permitting a lower gradient.
173 Appendix 0 0 10 20 30 40 50 60 70 80 90 100 50 40 30 20 elevation (meters) distance (meters) 10 60
0 0 10 20 30 40 50 60 70 80 90 100 50 40 30 20 total rise (meters) total run distance (meters) 10 60 0 0 10 20 30 40 50 60 70 80 90 100 50 40 30 20 total rise (meters) total run distance (meters) 10 60 translation of nodes into flat areas b c d f b c d f
0 0 10 20 30 40 50 60 70 80 90 100 50 40 30 20 total rise (meters) distance (meters) 10 60
b c d f b c f d b c b c d f b c d f d f b c d f
Python script for CA controlled through GA
Chapter 5.3 Infill growth.
Chapter 7.2 Conclusions & further development.
The following python code corresponds to the script that finds the generators and developes a CA logic. Not all scripts are shown in the appedinx, but this one is important to include for in developes in detail the logics that govern the CA growth. Hopefully, the results can be elaborated on and pushed forward.
One of the final jurors of this thesis proposed the idea of having variable generators as well, that could be controlled by the genetic algorithm’s genes. Due to lack of time it is not possible to carry out this test; but it remains an open avenue for further development.
174
Symbiotic aggregations
SETTING GENERATORS AND FLAT ROOFS
import Rhino import scriptcontext import ghpythonlib.components as gh import itertools
import math
# switch script context to use Rhino scriptcontext.doc = Rhino.RhinoDoc.ActiveDoc # for accesssing GH classes import clr clr.AddReference("Grasshopper") from Grasshopper.Kernel.Data import GH_Path from Grasshopper import DataTree
layerTree = DataTree[Rhino.Geometry.GeometryBase]() for i in range(len(layernames)): objs = scriptcontext.doc.Objects.FindByLayer(layernames[i]) if objs:
geoms = [obj.Geometry for obj in objs] path = GH_Path(i)
layerTree.AddRange(geoms, path)
a = layerTree
# Setting generators
# this code is executed within the grasshopper environment for Rhino as shown bottom right # it takes a topographic model as a surface, a point cloud of negative space and generators as layers in rhinoceros
# Transform a string (x,y,z) into a list of [[x,y,z][x1,y1,z1]]
def KeyToPts(key):
Pts=[] if isinstance(key,list or tuple) == True: for each in key:
split = each.split(', ')
split2=[] for j in split:
newj = j.replace("(", "")
newj = newj.replace(")", "")
coord=int(newj)
split2.append(coord)
Pts.append(split2)
else:
split = key.split(', ')
split2=[]
for
j in split:
newj = j.replace("(", "")
newj = newj.replace(")", "")
coord=int(newj)
split2.append(coord)
Pts.append(split2)
return Pts
# Transforms a set of [x,y,z] coordinates into a string (x,y,z)
def PtsToKey(pts):
keyN=[]
if isinstance(pts[0],list) == True: for each in pts:
j=str(each)
newstr = j.replace("[", "")
newstr = newstr.replace("]","")
newstr = newstr.replace("(","")
newstr = newstr.replace(")","")
keyN.append(newstr)
else:
j=str(pts)
newstr = j.replace("[", "")
newstr = newstr.replace("]","")
newstr = newstr.replace("(","")
newstr = newstr.replace(")","")
keyN.append(newstr)
return keyN
def FindCellBelow (key):
Pt1 = KeyToPts(key)
PtBelow = Pt1[0][0],Pt1[0][1],Pt1[0][2]-3
keyN = PtsToKey(PtBelow)
return keyN
curves = Generator
175 Appendix
Symbiotic aggregations
bottom_cells={}
for i in range (0,len(x)):
keyName = (x[i],y[i])
strKey = str(keyName)
strKey = strKey.replace("(", "")
strKey = strKey.replace(")", "")
bottom_cells[strKey]=[]
for i in range (0,len(x)):
keyName = (x[i],y[i])
strKey = str(keyName)
strKey = strKey.replace("(", "")
strKey = strKey.replace(")", "")
bottom_cells[strKey].append(z[i])
x=[]
y=[]
z=[] for each in bottom_cells:
low_point = KeyToPts(each)[0]
low_point.append(min(bottom_cells[each]))
x.append(low_point[0])
y.append(low_point[1])
z.append(low_point[2])
grid={}
for i in range (0,len(x)):
keyName=x[i],y[i],z[i]
strKey=str(keyName)
strKey = strKey.replace("(", "")
strKey = strKey.replace(")", "")
boolean=0
grid[strKey]=boolean
for strKey,boolean in grid.items():
newKey = FindCellBelow(strKey)
if newKey[0] in grid:
grid[strKey] = 0
else:
pts=[]
grid[strKey] = 1
for strKey,boolean in grid.items():
if boolean == 1:
split = strKey.split(', ')
pt = gh.ConstructPoint(split[0],split[1],0)
boolean_inside = gh.PointinCurves(pt,curves)
if boolean_inside[0] == 2:
pt1 = gh.ConstructPoint(split[0],split[1],split[2])
pts.append(pt1)
a=[] for pt in pts:
brep_cp = gh.BrepClosestPoint(pt,Brep) if brep_cp[1] < 3.1:
a.append(pt)
del grid
del bottom_cells
### Flat roofs
def Find_Cell_Below (key):
Pt1 = KeyToPts(key)
PtBelow = Pt1[0][0],Pt1[0][1],Pt1[0][2]-3
keyN = PtsToKey(PtBelow)
return keyN
def Find_Cell_Above (key):
Pt1 = KeyToPts(key)
PtAbove = Pt1[0][0],Pt1[0][1],Pt1[0][2]+3
keyN = PtsToKey(PtAbove)
return keyN curves = Generator
grid={}
for i in range (0,len(x)):
keyName=x[i],y[i],z[i]
strKey=str(keyName)
strKey = strKey.replace("(", "")
strKey = strKey.replace(")", "")
176
boolean=0
grid[strKey]=boolean

a=grid
for strKey,boolean in grid.items():
new_key = Find_Cell_Below(strKey) if new_key[0] in grid:
grid[strKey] = 0
else:
grid[strKey] = 1
new_key_2 = Find_Cell_Above(strKey) if new_key_2[0] in grid:
grid[new_key_2[0]] = 1
pts=[] for strKey,boolean in grid.items(): if boolean == 1:
split = strKey.split(', ')
pt = gh.ConstructPoint(split[0],split[1],0)
boolean_inside = gh.PointinCurves(pt,curves) if boolean_inside[0] == 2:
pt1 = gh.ConstructPoint(split[0],split[1],split[2])
pts.append(pt1)
a=[] for pt in pts:
brep_cp = gh.BrepClosestPoint(pt,Brep) if brep_cp[1] < 6.1:
a.append(pt)
CELLULAR AUTOMATA CONTROLLED BY A GA
Takes in several genes as shown to the right Yields a cellular automata model import ghpythonlib.components as gh import itertools
import math
grid_size = 3
### Transforms a set of [x,y,z] coordinates into a string (x,y,z) def PtsToKey(pts):
keyN=[]
if isinstance(pts[0],list) == True: for each in pts:
j=str(each)
newstr = j.replace("[", "")
newstr = newstr.replace("]","")
newstr = newstr.replace("(","")
newstr = newstr.replace(")","")
keyN.append(newstr)
else:
j=str(pts)
newstr = j.replace("[", "")
newstr = newstr.replace("]","")
newstr = newstr.replace("(","")
newstr = newstr.replace(")","")
keyN.append(newstr)
return keyN
### Transform a string (x,y,z) into a list of [[x,y,z][x1,y1,z1]] def KeyToPts(key):
Pts=[]
if isinstance(key,list or tuple) == True: for each in key:
split = each.split(', ')
split2=[] for j in split:
newj = j.replace("(", "")
newj = newj.replace(")", "")
coord=int(newj)
split2.append(coord)
Pts.append(split2)
else:
split = key.split(', ')
split2=[]
for j in split:
newj = j.replace("(", "")
177 Appendix
Symbiotic aggregations
newj = newj.replace(")", "") coord=int(newj)
split2.append(coord)
Pts.append(split2) return Pts
### Adj_Coord takes a list of coordinates and returns the nearby cells as [x,y,z] def Adj_Coord(pts): adjCoords=[]
test_length = [-grid_size,0,grid_size]
if isinstance(pts[0], list) == True: for each in pts:
temp_points = [(each[0]+x1,each[1]+y1,each[2]+z1) for x1 in test_length for y1 in test_length for z1 in test_length \ if abs(x1)+abs(y1)+abs(z1) != 0]
adjCoords.append(temp_points)
adjCoords = list(itertools.chain.from_iterable(adjCoords))
else:
temp_points = [(pts[0]+x1,pts[1]+y1,pts[2]+z1) for x1 in test_length for y1 in test_length for z1 in test_length \ if abs(x1)+abs(y1)+abs(z1) != 0]
adjCoords.append(temp_points)
return adjCoords
### Takes a list of coordinates and returns same level near cells as [x,y,z]
def AdjFaceCoord(pts):
adjCoords1=[]
test_length = [-grid_size,0,grid_size]
if isinstance(pts[0], list) == True:
for each in pts:
temp_points = [(each[0]+x1,each[1]+y1,each[2]) for x1 in test_length for y1 in test_length if abs(x1)+abs(y1) != 0] adjCoords1.append(temp_points)
adjCoords1 = list(itertools.chain.from_iterable(adjCoords1))
else:
temp_points = [(pts[0]+x1,pts[1]+y1,pts[2]) for x1 in test_length for y1 in test_length if abs(x1)+abs(y1) != 0] adjCoords1.append(temp_points)
return adjCoords1
### Direct Face Coord (total 4) as [x,y,z] def Face_Coord(pts):
adjCoords1=[]
test_length = [-grid_size,0,grid_size]
if isinstance(pts[0], list) == True:
for each in pts:
temp_points = [(each[0]+x1,each[1]+y1,each[2]) for x1 in test_length for y1 in test_length if abs(x1)+abs(y1) == 3] adjCoords1.append(temp_points)
adjCoords1 = list(itertools.chain.from_iterable(adjCoords1))
else:
temp_points = [(pts[0]+x1,pts[1]+y1,pts[2]) for x1 in test_length for y1 in test_length if abs(x1)+abs(y1) == 3] adjCoords1.append(temp_points)
return adjCoords1
### Corner Coord (total 4) as [x,y,z]
def Corner_Coord(pts): adjCoords1=[]
test_length = [-grid_size,0,grid_size]
if isinstance(pts[0], list) == True: for each in pts:
temp_points = [(each[0]+x1,each[1]+y1,each[2]) for x1 in test_length for y1 in test_length if abs(x1)+abs(y1) == 6] adjCoords1.append(temp_points)
adjCoords1 = list(itertools.chain.from_iterable(adjCoords1))
else:
temp_points = [(pts[0]+x1,pts[1]+y1,pts[2]) for x1 in test_length for y1 in test_length if abs(x1)+abs(y1) == 6] adjCoords1.append(temp_points)
return adjCoords1
### Takes [x,y,z]. Find out how many adjacent face cells are 1 and return total value (int)
def FaceValue(coords):
value=0 for each in coords:
key = PtsToKey(each) if key[0] in grid: if grid.get(key[0]) == 1:
value=value+1
else:
else:
value=value+0
value=value+1
return value
#Finds whether cells are in different places
def Find_Cell_Above(key):
pt1 = KeyToPts(key)
PtAbove = pt1[0][0],pt1[0][1],pt1[0][2]+grid_size
keyN = PtsToKey(PtAbove)
return keyN
178
def Find_Cell_Below(key):
pt1 = KeyToPts(key)
pt_below = pt1[0][0],pt1[0][1],pt1[0][2]-grid_size
keyN = PtsToKey(pt_below)
return keyN
### drop the ball
def Drop_Ball(key,dict):
pt_below = Find_Cell_Below(key)
pt_below_1 = Find_Cell_Below(pt_below)
if pt_below[0] in dict:
if pt_below_1[0] in dict:
if grid[pt_below[0]] == 0:
dict[pt_below[0]] = 3
elif grid[pt_below[0]] == 2:
dict[pt_below[0]] = 1
### cantilevers
def Cantilever(key,dict,temp_dict):
pt1 = KeyToPts(key)
von_neumann = Face_Coord(pt1) for i in von_neumann:
key_i = PtsToKey(i)
pt_below = Find_Cell_Below(key_i)
if key_i[0] in dict and pt_below[0] in dict:
if dict[key_i[0]] != 1:
near_cells_a = Adj_Coord(i)
print near_cells_a[0]
near_c_value = FaceValue(near_cells_a[0])
print near_c_value if near_c_value > 8 and near_c_value < 10:
dict[key_i[0]] = 1
temp_dict[key_i[0]] = 1
#Find the lowest ground points in a generator
### create a dictionary with each coordinate as key
### create a parallel dictionary with the same coordinates for iterations class find_cells(object):
def __init__(self, key, dict, initial_status=0):
self.status = initial_status
self.key = key
def find(self,key,x,y,dict):
Pt1 = KeyToPts(key)
PtAbove = Pt1[0][0]+x,Pt1[0][1]+y,Pt1[0][2]
keyN = PtsToKey(PtAbove)
if keyN[0] in dict:
self.key = keyN[0] if dict[keyN[0]] == 2:
self.status = 1
### x or y must == 0
def Grow_Horizontal(key,dict,dict_temp,x,y):
if x == 0 or y == 0 and abs(y)+abs(x) >= 1:
y1=y*grid_size
my_key = find_cells(key,dict,0)
my_key.find(key,x1,y1,dict)
if my_key.key in dict:
if my_key.status == 1:
dict[my_key.key] = 1
counter = abs(x)+abs(y)
if x > 0:
while counter > 0:
Pt = KeyToPts(my_key.key)
Pt1 = Pt[0][0]-(grid_size*counter),Pt[0][1],Pt[0][2]
key1 = PtsToKey(Pt1) if key1[0] in dict:
dict_temp[key1[0]] = 1
grid[key1[0]] = 1
else:
grid[key1[0]] = 1
counter = counter-1
elif x < 0:
while counter > 0:
Pt = KeyToPts(my_key.key)
Pt1 = Pt[0][0]+(grid_size*counter),Pt[0][1],Pt[0][2]
key1 = PtsToKey(Pt1) if key1[0] in dict:
dict_temp[key1[0]] = 1
grid[key1[0]] = 1
else:
grid[key1[0]] = 1
counter = counter-1
179 Appendix
x1=x*grid_size
Symbiotic aggregations
elif y > 0:
while counter > 0:
Pt = KeyToPts(my_key.key)
Pt1 = Pt[0][0],Pt[0][1]-(grid_size*counter),Pt[0][2]
key1 = PtsToKey(Pt1)
if key1[0] in dict:
dict_temp[key1[0]] = 1
grid[key1[0]] = 1
else:
grid[key1[0]] = 1 counter = counter-1
elif y < 0:
while counter > 0:
Pt = KeyToPts(my_key.key)
Pt1 = Pt[0][0],Pt[0][1]+(grid_size*counter),Pt[0][2]
key1 = PtsToKey(Pt1)
if key1[0] in dict:
dict_temp[key1[0]] = 1
grid[key1[0]] = 1
else:
grid[key1[0]] = 1 counter = counter-1
### Run the code
grid={}
gridP={} for i in xrange(0,len(x)):
keyName=x[i],y[i],z[i]
strKey = str(keyName)
strKey = strKey.replace("(", "")
strKey = strKey.replace(")", "")
boolean=0
grid[strKey]=boolean
gridP[strKey]=boolean
### Set generator points to 1 coordinates=[]
testPts=[] for each in inputPt:
coor = gh.Deconstruct(each)
coordinates.append(coor) for each in coordinates:
round=gh.Round(each)
testPts.append(round[0])
keyList = PtsToKey(testPts)
for keyE in keyList:
intEach = KeyToPts(keyE)
if keyE in grid:
grid[keyE] = 1
gridP[keyE] = 1
del coordinates
del testPts
del keyList
### Set flat roof points to 2 coordinates=[]
testPts=[] for each in roofPt:
coor = gh.Deconstruct(each)
coordinates.append(coor) for each in coordinates:
round=gh.Round(each)
testPts.append(round[0])
keyList = PtsToKey(testPts) for keyE in keyList:
intEach = KeyToPts(keyE)
if keyE in grid:
grid[keyE] = 2
gridP[keyE] = 2
del coordinates del testPts
del keyList
### Run the code II
temp_grid = dict(grid) temp_grid2 = {} for n in range(Generations): for strKey,boolean in temp_grid.items():
if boolean == 2:
temp_grid2[strKey] = 2
if boolean == 1:
180
coords = KeyToPts(strKey)
near_cells = AdjFaceCoord(coords)
corner_cells = Corner_Coord(coords)
face_cells = Face_Coord(coords) for each in near_cells:
key1 = PtsToKey(each) if key1[0] in temp_grid: if temp_grid[key1[0]] == 2:
temp_grid2[key1[0]] = 1
grid[key1[0]] = 1
total_value = ((FaceValue(corner_cells))*corner_value)+((FaceValue(face_cells))*face_value) if total_value >= threshold[n]:
cell_above = Find_Cell_Above(strKey) if cell_above[0] in grid:
else:
grid[cell_above[0]] = 1
temp_grid2[cell_above[0]] = 1
cell_above = Find_Cell_Above(strKey) if cell_above[0] in grid:
grid[cell_above[0]] = 0
temp_grid2[cell_above[0]] = 0
temp_grid2[strKey] = 1
Grow_Horizontal(strKey,grid,temp_grid2,s,0)
Grow_Horizontal(strKey,grid,temp_grid2,0,s)
Grow_Horizontal(strKey,grid,temp_grid2,-s,0)
Grow_Horizontal(strKey,grid,temp_grid2,0,-s)
Grow_Horizontal(strKey,grid,temp_grid2,t,0)
Grow_Horizontal(strKey,grid,temp_grid2,0,t)
Grow_Horizontal(strKey,grid,temp_grid2,-t,0)
Grow_Horizontal(strKey,grid,temp_grid2,0,-t)
Drop_Ball(strKey,grid)
if toggle[n] == 1: Cantilever(strKey,grid,temp_grid2)
del temp_grid
temp_grid = dict(temp_grid2)
del temp_grid2
temp_grid2 = {}
### Final step: build cells from points count=0
buildCells=[] for each in grid:
if grid[each] == 1 or grid[each] == 3: cells = KeyToPts(each) merged = list(itertools.chain.from_iterable(cells)) buildCells.append(merged)
if grid[each] == 3: count = count + 1
points=[] for each in buildCells:
point = gh.ConstructPoint(each[0],each[1],each[2])
points.append(point)
181 Appendix