John Engeseth
Odd Heir
Håvard Moe
Tea Toft Norderhaug
Sigrid Melander Vie
Forhold
Forholdet mellom 2 og 3 er 2 3 eller 2 : 3.
ProsentBrøkDesimaltall
== 23 % 23 100 0, 23
Potens og kvadratrot
=⋅44 4 2 = 42
for yrkesfag P
Vekstfaktor
Ny verdi= gammelverdi vekstfaktor =⋅NG V
Endring i flere perioder =⋅ Ny verdigammelverdi vekstfaktor antall perioder
NG V t
Proporsjonale størrelser
x og y er proporsjonale hvis y x = k, der k er proporsjonalitetskonstanten.
1020304050
Omvendt proporsjonale størrelser x og y er omvendt proporsjonale hvis xy er konstant.
John Engeseth
Odd Heir
Håvard Moe
Tea Toft Norderhaug
Sigrid Melander Vie for yrkesfag
Bokmål
Læreboka Matematikk for yrkesfag P følger læreplanen i matematikk 1P-Y for Vg1 i yrkesfaglige utdanningsprogram (LK20).
© H. Aschehoug & Co. (W. Nygaard) 2020 2. utgave / 4. opplag 2024
Materialet er vernet etter åndsverkloven. Uten uttrykkelig samtykke er eksemplarfremstilling, som utskrift og annen kopiering, bare tillatt når det er hjemlet i lov (kopiering til privat bruk, sitat o.l.) eller i avtale med Kopinor (www.kopinor.no).
Utnyttelse i strid med lov eller avtale kan medføre erstatnings- og straffansvar.
Redaktører: Cathrine Frydenlund og Line Holst
Grafisk formgiving: Marit Jakobsen
Ombrekking: ord & form, Gudbrand Klæstad
Omslag: Basta Illustrasjon & Design, Victor Paiam
Bilderedaktør: Hege Rødaas Aspelund
Tekniske tegninger: Framnes Tekst & Bilde AS, Eirek Engmark
Grunnskrift: Frutiger LT Std 45 Light 10/14
Papir: 100 g G-print 1,0
Trykk: Merkur Grafisk AS
Innbinding: Bokbinderiet Johnsen AS, Skien
ISBN 978–82-03-40759-8 www.aschehoug.no
SVANEMERKET
Om Matematikk for yrkesfag P
Matematikk for yrkesfag P følger fagfornyelsens læreplan i matematikk 1P-Y som gjelder fra august 2020, og består av lærebok og digitale ressurser på Aunivers.no
Læreboka
Vi presenterer matematikken på en strukturert og forståelig måte. Vi følger opp teori og eksempler med innlæringsoppgaver. I eksemplene legger vi vekt på gode forklaringer og framgangsmåter, også med GeoGebra og regneark der det er relevant. I tillegg har vi UTFORSK-oppgaver som får elevene til å se sammenhenger i faget, og SNAKK-oppgaver som gir elevene muligheten til å kommunisere matematikk.
Hvert underkapittel inneholder differensierte oppgaver:
Røde oppgaver er en naturlig fortsettelse av innlæringsoppgavene. Blå oppgaver gir større utfordringer.
Til slutt i hvert kapittel finner du Blandede oppgaver som gir både mengdetrening og dybdelæring. Oppgavene i boka er i stor grad praktisk rettet. Siste kapittel i boka er et eksamenstreningskapittel, der oppgavene er delt inn i Uten hjelpemidler og Med hjelpemidler
Digitale ressurser på Aunivers.no
Her finner du teori og praktiske oppgaver som er tilpasset ditt utdanningsprogram
– bygg- og anleggsteknikk
– design og tradisjonshåndverk
– elektrofag
– frisør, blomster- og interiørdesign
– helse- og oppvekstfag
– IKT og medieproduksjon
– naturbruk
– restaurant- og matfag
– salg, service og reiseliv
– teknikk og industriell produksjon
I tillegg finner du:
regneark
Som lærer får du også tilgang til:
opplegg og tips til hvordan du kan variere undervisningen
Vi håper at Matematikk for yrkesfag P møter dine forventninger til et komplett læreverk. Vi setter stor pris på kommentarer og innspill, så send oss gjerne en e-post til: matematikkforyrkesfag@aschehoug.no.
Vi ønsker deg lykke til med faget!
Hilsen forfatterne John Engeseth, Odd Heir, Håvard Moe, Tea Toft Norderhaug, Sigrid Melander Vie, og redaktørene Line Holst og Cathrine Frydenlund.
Innhold
1 Verktøykassen
1A Tallregning 8
1B Overslagsregning 16
1C Avrunding 19
1D Likninger 22
1E Grafisk framstilling 26
Sammendrag 37
Kapitteltest 38
2 Forhold og prosent
2A Veien om 1 42
2B Forhold 45
2C Prosent og promille 50
2D Prosentregning 55
2E Prosentregning med vekstfaktor 61
2F Prosentendring i flere perioder 68
Sammendrag 76
Kapitteltest 77
3 Måleenheter
3A Prefikser 80
3B Måleenheter for lengde, masse og volum 84
3C Arealenheter 89
3D Flere volumenheter 94
3E Tidsenheter 98
3F Sammensatte enheter 101
Sammendrag 112
Kapitteltest 113
4 Tolke og bruke formler
4A Regning med formler 116
4B Proporsjonalitet 126
4C Omvendt proporsjonalitet 130
4D Formler fra geometrien 134
Sammendrag 142
Kapitteltest 143
5 Økonomi
5A Lønn 146
5B Sparing 151
5C Lån 158
5D Hva skal jeg velge? 166
5E Budsjett og regnskap 168
5F Merverdiavgift 172
5G Anbud 176
Sammendrag 183
Kapitteltest 184
6 Eksamenstrening
Uten hjelpemidler 187
Med hjelpemidler 192
Fasit 203
Register 219
Bildeliste 221
GeoGebra i 1P-Y 222
Verktøykassen
KAPITTELINNHOLD
1A Tallregning 8
1B Overslagsregning 16
1C Avrunding 19
1D Likninger 22
1E Grafisk framstilling 26
Hva blir svaret på regnestykket 8 + 4 ⋅ 3?
Du er vel enig i at det bare kan være ett riktig svar her?
Hva det riktige svaret er, og hvilke regler vi må følge for å finne det riktige svaret, det skal du lære om i dette kapitlet sammen med mye annet som er nyttig å kunne.
Tallregning
–4 –3 –2–10123456789
Tallene som er merket av på tallinja ovenfor, er hele tall.
Tallet 5 står til høyre for tallet 2 på tallinja. 5 er et større tall enn 2. Det skriver vi slik: 5 > 2.
Tegnet > betyr større enn
Tallet 4 står til venstre for tallet 2 på tallinja. 4 er et mindre tall enn 2. Det skriver vi slik: 4 < 2.
Tegnet < betyr mindre enn.
Tallene blir større jo lenger mot høyre på tallinja vi kommer.
1.1 U
a Skriv to tall som er større enn 3 og mindre enn 1.
b Skriv tre tall som er større enn 8 og mindre enn 2.
11,11,21,31,41,51,61,71,81,9
Det er uendelig mange tall på tallinja. På figuren ovenfor har vi tatt en del av tallinja og forstørret den. Pila peker mot desimaltallet 1,2.
Tallet 1,2 har to sifre. Det har én desimal.
Tallet 1,25 har tre sifre. Det har to desimaler.
Tallene 1,2 og 1,20 har samme plass på tallinja.
Lars måler lengden av et bord. Lars sier at bordet er 1,20 m langt. Johnny måler det samme bordet og sier at bordet er 1,2 m langt.
Lars har målt bordet med større nøyaktighet enn Johnny fordi Lars oppgir lengden av bordet med flere sifre enn det Johnny gjør.
1.2 U
Hvor mange sifre og hvor mange desimaler er det i
a 2,8 b 17,56 c 240,3 d 2500,7
1.3 U
Skriv tallene i stigende rekkefølge.
4 1 3
1.4 U
Skriv av og sett inn >, < eller = riktig i rutene. a 53 b 2,552,5 c
Regning med positive og negative tall
5(2)523 +−=−=
Å legge til et negativt tall er det samme som å trekke fra det tilsvarende positive tallet. Legg merke til at vi setter parentes rundt negative tall når de kommer etter et regnetegn.
5(2)527 −−=+=
Å trekke fra et negativt tall er det samme som å legge til det tilsvarende positive tallet.
Når vi ganger, er fortegnet på svaret avhengig av hvor mange negative faktorer det er. En faktor er et tall som står foran eller bak et gangetegn, eller foran eller bak et deletegn.
3(2)6
(3)(2)6
(3)(2)(1)6
Ganging med negative tall
Når det er 1, 3, 5,… negative faktorer, blir svaret negativt. Når det er 2, 4, 6,… negative faktorer, blir svaret positivt.
Tilsvarende regel gjelder når vi deler med negative tall.
( 6) : 2 = 3
( 10) : ( 5) = 2
1.5 U
Regn ut. a 3 6 b 2 ( 4) + 6 c ( 2) ⋅ ( 4) d ( 2) ⋅ 3 ⋅ 4 e 12 : ( 3) f ( 12) : ( 2)
Potenser
Eksponent 23
Grunntall
1.6 U
Til nå (2019) er den laveste målte temperaturen i Norge 51,4 °C (Karasjok 1886). Den høyeste målte temperaturen er 35,6 °C (Nesbyen 1970).
Hvor stor er temperaturforskjellen mellom den laveste og den høyeste målte temperaturen?
1.7 U
En dag er temperaturen 8,0 °C. Hva blir temperaturen hvis den a øker med 5,0 °C
b minker med 10,5 °C
c først øker med 4,0 °C, deretter minker med 5,5 °C
23 er eksempel på en potens. Tallet 2 er grunntallet i potensen og 3 er eksponenten.
23 er det samme som 2 2 2.
Grunntallet i en potens kan være både positivt og negativt.
23 er en potens med 2 som grunntall og 3 som eksponent.
23 = 2 2 ⋅ 2
Eksponenten forteller hvor mange ganger grunntallet skal stå som faktor.
Regner vi ut potensen 23, får vi: 2
1.8 U
Skriv og regn ut en potens med a 3 som grunntall og 4 som eksponent b 2 som eksponent og 5 som grunntall
1.9 U
Regn ut. a 62 b 92 c 43 d 53 e 13
SNAKK
Kvadratrot
25 er eksempel på en kvadratrot. Kvadratroten av 25 er det positive tallet som ganget med seg selv blir 25. Fordi 5 ⋅ 5 = 25, er 255
Å finne kvadratroten av et tall betyr å finne det positive tallet som ganget med seg selv gir tallet.
Uten hjelpemidler er det lettest å ta kvadratroten av et tall hvis tallet er et kvadrattall: 1, 4, 9, 16, 25, 36, 49,…
Vi kan ikke ta kvadratroten av negative tall.
1.10 U
Regn ut.
a 36 b 49 c 81 d 144 e 225
a Læreren utfordrer Ronny til å finne en omtrentlig verdi for 14
Ronny sier at 14 er mer enn 3,5 men mindre enn 4. Hvordan tror du Ronny har tenkt?
b Finn en omtrentlig verdi for 40
I GeoGebra kan du enten bruke kommandoen sqrt() eller hurtigtasten Alt + r for få finne kvadratroten av et tall. Sqrt er forkortelsen for square root, som er det engelske ordet for kvadratrot.
gir eksakt verdi:
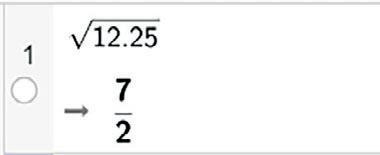
gir tilnærmet verdi:
Kubikkrot
8 3 er eksempel på en kubikkrot. 82 3 fordi 2228 ⋅⋅=
Legg merke til at vi ikke kan ta kvadratroten av negative tall, men at vi kan ta kubikkroten av negative tall.
82 3 −=− fordi ( 2) ( 2) ( 2) = 8.
EKSEMPEL 1
1.11 U
Regn ut.
a 27 3 b 64 3 c 27 3
I GeoGebra finner vi kubikkroten med kommandoen nrot.
Skjermbildet nedenfor viser hvordan du finner 15 3
Regnerekkefølge
Hva blir svaret på regnestykket 8 + 4 ⋅ 3?
Det kan ikke være mer enn ett riktig svar på et regnestykke, altså må vi ha regler som bestemmer rekkefølgen vi skal gjøre utregningene i.
Regnerekkefølge:
❶ Parenteser
❷ Potenser og kvadratrøtter
❸ Ganging og deling
❹ Pluss og minus
Vi bruker reglene, og regner ut stykket ovenfor slik: 84381220 +⋅=+=
Legg merke til hvilke ord som betyr det samme: multiplisere: gange dividere: dele addere: legge sammen subtrahere: trekke fra
Regn ut 52(31)2 +⋅+ uten hjelpemidler.
52(31)524 22+⋅+=+⋅
5216=+⋅ 532=+ = 37
Parentesen
Potensen
Ganger sammen
Legger sammen
SNAKK
Digitale verktøy skal være programmert til å følge regnerekkefølgen.
Du må være nøye med hva du skriver inn, for verktøyet gjør bare det du gir det beskjed om!
1.12
Regn ut uten hjelpemidler. Kontroller med hjelpemidler.
a 1534 b 2342 ⋅+⋅ c 4 (3 + 5) d 4 + 2 (3 + 4) e 4 2 + 32 f 52 3 4
1.13
Regn ut uten hjelpemidler. Kontroller med hjelpemidler.
a 32 42 b 91649 +− c 3 (4 + 5) (2+4) 2 d 2532 e 56 3 f 8 2 43 6 + ⋅
Gange/dele med 10, 100, 1000
Bruk kalkulatoren til å kontrollere disse utregningene: 3,75 10 = 37,5 3,75 100 = 375 3,75 1000 = 3750 865 : 10 = 86,5 865 : 100 = 8,65 865 : 1000 = 0,865
Ser du systemet?
Å gange med 10 er det samme som å flytte kommaet
én plass mot høyre.
Å gange med 100 er det samme som å flytte kommaet to plasser mot høyre.
Osv.
Å dele med 10 er det samme som å flytte kommaet
én plass mot venstre.
Å dele med 100 er det samme som å flytte kommaet to plasser mot venstre.
Osv.
Lars og Bilal studerer huskereglene ovenfor. Bilal sier:
«Å dele med 10 er det samme som å gange med 0,1, å dele på 100 er det samme som å gange med 0,01 og å dele på 1000 er det samme som å gange med 0,001.»
Det skjønner ikke Lars.
Hvordan vil du forklare dette for Lars?
EKSEMPEL
2
EKSEMPEL 3
Regn ut.
a 4,5 ⋅ 100 b 8,5 : 100
a 4,5 100 = 450
Du skal gange med 100, altså skal du flytte kommaet to plasser mot høyre.
Når du har flyttet kommaet én plass, står det bak 5-tallet. Du skal flytte kommaet én plass til, det er det samme som å legge til én 0 bakerst.
b 8,5 : 100
Du skal dele med 100, altså flytte kommaet to plasser mot venstre.
Vi skriver noen nuller foran 8-tallet. Da blir det lettere å flytte kommaet.
00008,5 : 100
8,5 : 100 = 0,085
1.14 U
Regn ut.
a 2,65 10 b 4,3 100 c 5,0 1000
d 645,8 : 100 e 12,7 : 10 f 35,8 : 1000
1.15 U
Regn ut.
a 75,8 : 100 b 0,12 : 100
c 0,06 1000
d 0,5 : 10 e 0,045 100 f 0,12 10
Regn ut 65 : 1000
Når det ikke står noe komma i et tall, kan du alltid «late som om» det står et komma og null bak det bakerste sifferet.
65 : 1000 = 65,0 : 1000
Så bruker vi «knepet» fra eksempel 2 med å skrive noen nuller foran 6-tallet.
Da blir det lettere å flytte kommaet tre plasser mot venstre.
000 065,0 : 1000 = 0,065
65 : 1000 = 0,065
1.16 U
Regn ut.
a 8 : 10 b 65 : 100
c 95 : 1000
d 6 : 1000 e 25 : 1000 f 8 : 1000
RØDE OPPGAVER
1.17 U
Du har tallene 3 og 4. Bruk pluss, minus, gange og dele for å lage et regnestykke slik at svaret a blir størst mulig b blir minst mulig
1.18 U Regn ut.
a 16 ( 2) b 5 3
1.19 U Regn ut.
a 2342 ⋅+⋅ b 6:223 +⋅ c 23432 ⋅− d (35):(75)2 +−
1.20 U Regn ut.
a 3,65 ⋅ 10 b 45 : 100 c 3,5 ⋅ 100 d 0,23 : 10 e 2,654 ⋅ 100
1.21 U Regn ut. a 53 b 26 c 104
BLÅ OPPGAVER
1.22 U
Skriv av og sett inn riktige tall i rutene. (Det kan være flere tall som passer.) a ⋅= 12 b :=−3 c ⋅=−8 d ⋅= 0,50
1.23 U
Skriv av og sett inn < eller >, eller = i rutene. a −⋅−+− 2(1)6(4) b 0,121001200:100 c 0,00310300:1000
1.24 U Sorter tallene i stigende rekkefølge.
80 23 0,007 1000 65 32
1.25
Skriv av figuren til venstre. Plasser tallene 2, 4 og 10 i rutene på figuren slik at svaret blir a størst mulig b minst mulig
1.26
Skriv det tallet som er halvparten så stort som 44. Kan dette tallet skrives som en potens med et helt tall som grunntall?
Overslagsregning 1B
Helena er i kiosken og vil kjøpe et ukeblad til 68 kr og en bagett til 54 kr. Hun lurer på hvor mye det omtrent vil koste til sammen.
Det kan Helena finne ut ved å gjøre et overslag.
Når hun gjør et overslag, bytter hun ut tallene med andre tall som det er lettere å regne med i hodet.
Helena bytter ut 68 kr med 70 kr, og 54 kr med 50 kr.
70 kr + 50 kr = 120 kr. Det vil koste omtrent 120 kr til sammen.
Når vi gjør et overslag, bytter vi ut tallene med andre tall som det er lettere å regne raskt med i hodet.
Omtrent hvor mye blir 34,50 + 97?
Vi bytter ut 34,50 med 30 og 97 med 100.
30 + 100 = 130
34,50 + 97 er omtrent 130. (Uten overslag: 131,50)
Legg merke til at vi byttet ut 34,50 med et mindre tall og 97 med et større tall.
Merk!
Overslag er ikke det samme som avrunding.
I eksempel 4 byttet vi ut 34,50 med 30, og 97 med 100 for å få tall som det er lettere å regne i hodet med.
Hvis vi i stedet hadde byttet ut 34,50 med 40 og 97 med 90, hadde vi fått det samme svaret: 40 + 90 = 130.
EKSEMPEL 5
EKSEMPEL 6
Omtrent hvor mye blir 8,6 7,4?
Vi bytter ut 8,6 med 9 og 7,4 med 7.
9 7 = 63
8,6 7,4 er omtrent 63. (Uten overslag: 63,64)
Legg merke til at vi byttet ut 8,6 med et større tall og 7,4 med et mindre tall.
Slik bør vi bytte ut tallene når vi skal gjøre et overslag:
Legge sammen og gange:
Vi bytter ut det ene tallet med et større tall og det andre tallet med et mindre tall. Har vi flere enn to tall, fortsetter vi å bytte ut på denne måten.
Trekke fra og dele:
Vi bytter ut med tall som alle er større eller alle er mindre.
a Omtrent hvor mye blir 633 225?
b Omtrent hvor mye blir 814 : 220?
a Vi bytter ut 633 med 600 og 225 med 200.
600 200 = 400 633 225 er omtrent 400. (Uten overslag: 408)
b Vi bytter ut 814 med 800 og 225 med 200.
800 : 200 = 4 814 : 225 er omtrent 4. (Uten overslag: 3,7)
Legg merke til at vi både i oppgave a og i oppgave b i eksempel 6, byttet ut begge tallene med mindre tall.
1.27 U
Bruk overslagsregning til å finne et svar som er omtrent riktig.
a 215 + 97 b 37,5 + 17,5
c 8,2 6,8 d 22,4 4,3
1.28 U
Bruk overslagsregning til å finne et svar som er omtrent riktig.
a 8,3 + 7,8 + 9,1 b 42,5 : 7,4
c 12,5 20,4 d 24,5 + 31,5 + 12,3
1.29 U
Håvard skal til Berlin og finner et hotellrom til 82 euro per natt.
Omtrent hvor mye er dette i norske kroner når én euro koster 9,89 kr?
1.30 U
Sigrid er ute og spiser på en restaurant i København. Regningen kommer på 480 danske kroner. Omtrent hvor mye er dette i norske kroner når 100 danske kroner koster 128,80 norske kroner?
Vi kan også bruke overslag til å vurdere om svaret på en utregning kan være riktig.
EKSEMPEL 7
Maria regnet ut 1,8 ⋅ 2,8 ⋅ 9,5 med kalkulatoren. Hun fikk 64,296. Kan dette være riktig?
Vi bytter ut 1,8 med 2, 2,8 med 3 og 9,5 med 10. 2 ⋅ 3 ⋅10 = 60
Vi byttet ut tallene i det opprinnelige regnestykket med større tall.
Svaret på regnestykket 1,8 2,8 9,5 må altså bli mindre enn 60. 64,296 kan derfor ikke være et riktig svar.
1.31 U
a Per regnet ut 7,8 8,8 og fikk 73,2. Kan dette være et riktig svar?
b Olav regnet ut 3,9 3,8 1,7 og fikk 25,194. Kan dette være et riktig svar?
1.32 U
Hvilke av regnestykkene nedenfor gir et svar som er omtrent 20?
a 8,5 ⋅ 2,4 b 8,5 : 2,4 c 38 : 1,89 d 38 : 0,57
Avrunding
En pakke med 11 skiver ost veier 150 gram.
Hvor mye veier én skive ost?
Vi bruker kalkulatoren og regner ut 150 : 11. 150 : 11 = 13,63 636 364
Vi velger å runde av vekten av én skive til et helt tall.
Én skive ost veier ca. 14 gram.
Hvis vi hadde valgt å runde av vekten til én desimal, ville vi ha sagt at én skive ost veier ca. 13,6 gram.
Hvis det første sifferet vi sløyfer er 0, 1, 2, 3 eller 4, runder vi av nedover.
Hvis det første sifferet vi sløyfer er 5, 6, 7, 8 eller 9, runder vi av oppover.
1,34 ≈ 1,3 1,37 ≈ 1,4
1.33 U
a Rund av tallet 7,92 til et tall med én desimal.
b Rund av tallet 4,345 til et tall med tre sifre.
c Rund av tallet 0,99 til et tall med én desimal.
d Rund av tallet 30,67 til et helt tall.
1.34 U
Rund av tallet 4358,85 til
a et helt tall
b nærmeste hundre
c nærmeste tusen
Mmega1 000 000million kkilo1000tusen hhekto100hundre
Odd Heir har i en årrekke vært lærer, lærebokforfatter og kursholder i matematikk for videregående skole.
dadeka10 ti ddesi0,1tidel ccenti0,01hundredel
John Engeseth har bred undervisningspraksis og underviser til daglig ved Elvebakken videregående skole. Han har vært forfatter av matematikkbøker for videregående skole i mange år.
mmilli0,001tusendel
Håvard Moe har bred realfaglig utdanning og har skrevet lærebøker i matematikk i flere år.
μmikro0,000 001milliondel
Omgjøring av enheter
Lengde
Han er lærer ved Sandnessjøen videregående skole og underviser i matematikk, fysikk og kjemi.
Sigrid Melander Vie er utdannet sivilingeniør fra NTNU. Hun jobber som lærer ved Rud videregående skole og underviser i matematikk og fysikk. Sigrid har i flere år bidratt til Aschehougs læreverk i matematikk for videregående skole.
Matematikk for yrkesfag P følger fagfornyelsens læreplan i Matematikk 1P-Y og består av lærebok og digitale ressurser på Aunivers.no
Læreboka
:10 :10 :10 :1000 :1000 :1000
Læreboka inneholder teori, eksempler og innlæringsoppgaver samt differensierte oppgaver til hvert underkapittel. I tillegg har vi UTFORSK-oppgaver som får elevene til å se sammenhenger i faget, og SNAKK-oppgaver som gir elevene muligheten til å kommunisere matematikk. Slutten av hvert kapittel inneholder blandede oppgaver.
24 60 60
:60 :60 :24
Sammensatte enheter
= Fart strekning tid
Eksempler på enheter: km/h og m/s
= Massetethet masse volum
Eksempler på enheter: kg/m3 og g/L
=⋅ Energi effekt tid
Eksempler på enheter: MJ og kWh
Tea Toft Norderhaug har mastergrad i matematikk fra NTNU. Hun er lærer ved Bjørknes privatskole og underviser i matematikk, kjemi og naturfag. Tea har i flere år bidratt til Aschehougs læreverk i matematikk for videregående skole.
Aunivers.no inneholder blant annet:
•Lærestoff tilpasset de ti utdanningsprogrammene –bygg- og anleggsteknikk –design og tradisjonshåndverk
–elektrofag
–frisør, blomster- og interiørdesign –helse- og oppvekstfag
–IKT og medieproduksjon –naturbruk
–restaurant- og matfag –salg, service og reiseliv –teknikk og industriell produksjon
•Fullstendige løsninger til alle oppgavene
•Opplæringsressurser til GeoGebra og regneark
•Interaktive oppgaver
•Eksamensløsninger
Som lærer får du også tilgang til:
•Lærerveiledning
•Kapittelprøver
•Terminprøver
•Aktivt klasserom