Matemagisk
Asbjørn Lerø Kongsnes
Kristina Markussen Raen
Martin Sørdal
Matemagisk GRUN N BOK B
Asbjørn Lerø Kongsnes
Kristina Markussen Raen
Martin Sørdal
Bokmål
Bli kjent med Matemagisk 6 Hva betyr sporene?
SPILL
AKTIVITET
KOPIARK tilgjengelig
på Aunivers.no.
SNAKKE MATTE
Oppgaver som viser spesielt viktige ideer og tenkemåter.
Oppgaver der dere skal snakke matte med hverandre.
Her trener dere på å forklare hvordan dere tenker.
Jeg gjør noen ganger «toppturen», men jeg gjør alltid «terrengløypa» først.
Noen ganger jobber jeg litt i «følg stien» og litt i «terrengløypa».
FØLG STIEN
Oppgaver der du får trent mer på det klassen har arbeidet med i fellesskap. Her trener du på én ting om gangen.
TERRENGLØYPA
Oppgaver som bygger videre på det klassen har arbeidet med i fellesskap. Her kan du få sammensatte utfordringer, også fra flere temaer på en gang.
TOPPTUR
Oppgaver som er svært utfordrende. Jobb med toppturen hvis du mestrer oppgavene i terrengløypa godt.
Noen få ganger jobber jeg bare i «terrengløypa».
Noen ganger jobber jeg bare i «følg stien».
5 Vinkler og parallelle linjer
Samtalebilde:
1 Hva ser dere på bildet?
2 Kan dere navn på noen triks der man snur rer rundt?
3 Kommer dere på andr e aktiviteter der man snurrer rundt?
4 Hva tror der e tallene i navnet på triksene betyr?
Begreper:
Spiss vinkel
Stump vinkel
Rett vinkel
Vinkelrett Parallelle linjer
Oppstart
Dette er en aktivitet for to elever.
Elev 1 bruker blyant og linjal og tegner et enkelt hus i skriveboka si.
Med ryggen til elev 2 skal elev 1 forklare hvordan huset ser ut.
Elev 2 tegner hvordan han tror huset ser ut.
Sammenlikn de to husene og diskuter resultatet.
Bytt roller og gjenta aktiviteten.
SNAKKE MATTE
Hvilken vinkel er størst?
SNAKKE MATTE
a Hvem har størst vinkel mot målet?
b Hvem har minst vinkel mot målet?
c Hvilken spiller tror dere har størst sjanse for å skåre mål?
Hvilken vinkel er størst?
To linjer som møtes i et punkt, danner en vinkel. De to linjene kalles vinkelbeina til vinkelen. Punktet linjene møtes i, kalles toppunktet.
Vi måler vinkler i grader. Grader skrives med tegnet °. Det fins tre hovedtyper av vinkler:
Spiss vinkel:
Mindre enn 90°
Rett vinkel: 90°
Vi markerer vanligvis vinkelen med en bue, men når vinkelen er rett (90°), bruker vi alltid et lite kvadrat for å markere vinkelen.
Stump vinkel: Mellom 90° og 180°
SNAKKE MATTE
Se deg rundt i klasserommet.
a Finn eksempler på vinkler som er spisse, rette og stumpe.
b Velg en rett vinkel i klasserommet. Hvordan ville det sett ut hvis den var spiss eller stump i stedet?
SNAKKE MATTE
Gi eksempler på vinkler i klasserommet som
a har en fast størrelse
b kan endre størrelse
SNAKKE MATTE
Hvor mange vinkler ser dere her?
2 Hvor kan romskipet bevege seg uten å kunne bli sett av UFO-en? Tegn av og tegn inn området der romskipet ikke kan bli sett.
Du trenger ikke å tegne av helt nøyaktig.
3 Hvilken vinkel er størst?
4 Hvilken vinkel er størst?
5 Har vinkelen fast størrelse, eller kan den endre størrelse?
6 Sorter vinklene fra minst til størst.
7 Sorter vinklene fra minst til størst.
8 Tegn minst to vinkler som er
a spisse
b stumpe
c rette
d Sorter vinklene fra minst til størst.
a Finn minst tre eksempler på vinkler som er rette.
b Finn minst tre eksempler på vinkler som er spisse.
c Sorter vinklene fra minst til størst.
d Finn minst tre eksempler på vinkler som er stumpe.
e Sorter vinklene fra minst til størst.
10 Hvor mange stjerner kan UFO-en se?
11 Marta og Emily står i et rom. De svarte strekene viser vegger. Kan Marta og Emily se hverandre? Begrunn svaret. a b
c Tegn av situasjonen fra oppgave b.
En ny person, Andrine, kommer inn i rommet. Fargelegg området der Andrine kan plassere seg for at alle tre skal kunne se hverandre.
Du trenger ikke å tegne av situasjonen helt nøyaktig.
12 Se på kartene, tegn av veiene og marker vinklene. a b
Emily
Marta
Emily
Marta
Vei
Vinkler som en del av en sirkel
Når vi skal måle størrelsen på en vinkel, kan vi bruke en gradskive.
1 Legg midtpunktet til gradskiva på toppunktet til vinkelen.
2 Juster gradskiva slik at det ene vinkelbeinet ligger langs linja som viser 0°.
3 Bruk det andre vinkelbeinet til å lese av størrelsen på vinkelen.
toppunkt vinkelbein
vinkelbein
Denne vinkelen er 60°.
SNAKKE MATTE
Hvem har rett? Begrunn svaret.
Vinkelen er 80°.
Vinkelen er 100°.
Gjett vinkelen
Dette er et spill for to spillere.
Utstyr: Linjal og gradskive
Hvordan spille?
1 Tegn tre vinkler hver.
2 Bytt vinkler og gjett på hvor store vinklene til den andre spilleren er.
3 Mål vinklene til den andre spilleren nøyaktig med gradskive.
4 For hver vinkel, regn ut differansen mellom gjettet og målt vinkelstørrelse.
Differanse betyr det samme som forskjell.
5 Legg sammen de tre differansene. Summen er spillerens poengsum.
Spilleren med lavest poengsum vinner spillet.
En tabell som dette kan være til hjelp.
Vi kan tenke på en vinkel som en del av en sirkel. En hel sirkel er 360°.
SNAKKE MATTE
Hvor stor er den ukjente vinkelen?
SNAKKE MATTE
Hvor mange vinkler ser dere her?
13 a Tegn hva du tror blir resultatet av å kjøre programmet.
Speed 0 betyr at vi velger den høyeste tegnehastigheten.
b Kjør programmet, og sjekk om du gjettet riktig.
Vi utvider programmet ved å legge til noen nye blokker.
c Hva tror du blir resultatet av å kjøre programmet?
d Kjør programmet, og sjekk om du gjettet riktig.
Endre programmet slik at du får disse resultatene:
e f g
14 Gjett først hvor stor vinkelen er. Mål deretter nøyaktig med gradskive. a b c d
15 Se på illustrasjonen.
a Finn tre vinkler som er spisse. Mål vinklene med gradskive.
b Finn tre vinkler som er stumpe. Mål vinklene med gradskive.
c Finn tre vinkler som du tror er rette. Mål vinklene med gradskive.
16 Tegn en vinkel som er a 90° b 45° c 50° d 120°
17 Hvor stor er den ukjente vinkelen? a b c d
18 Hvor stor er den ukjente vinkelen?
Parallelle linjer
SNAKKE MATTE
Under ser dere tre par med linjer. Hvilket par skal ut? Begrunn svaret.
To linjer er parallelle hvis avstanden mellom dem er den samme overalt.
Parallelle linjer vil aldri krysse hverandre, uansett hvor lange de er.
Parallelle linjer
Ikke-parallelle linjer
SNAKKE MATTE
Forklar hvorfor de to linjene til høyre i eksemplet ikke er parallelle.
19 Skriv alle linjestykkene på figuren som er parallelle.
Det nederste linjestykket heter AB fordi det går fra A til B
FØLG STIEN
20 a Tegn to linjer som ikke er parallelle.
b Forklar hvordan du kan se at linjene ikke er parallelle.
c Tegn to linjer som er parallelle.
d Forklar hvordan du kan se at de to linjene er parallelle.
21 Hvilke linjer er parallelle?
22 Hvilke linjer er parallelle?
23 Hvilke linjestykker er parallelle?
Å finne fram i byen
Anders jobber som taxisjåfør i byen. Han må ha god kjennskap til gatene rundt jernbanestasjonen for å finne fram.
Ia Forklar hva det vil si at to gater er parallelle.
b Hvilke gater er parallelle med Storgata?
c Hvilke gater står vinkelrett på Storgata?
d Hvilke gater er ikke parallelle med Storgata og står heller ikke vinkelrett på Storgata?
Vinkelrett betyr at vinkelen mellom gatene er en rett vinkel, altså 90°.
II
Anders kjører ut fra taxiholdeplassen og tar til høyre på Parkalleen.
Deretter svinger han 90° til høyre ved første mulighet. Til slutt svinger han 90° til venstre og ender opp ved kirka.
a Skriv hvilke gater Anders har kjørt i.
b Anders skal kjøre videre fra kirka til båten ved Havnegata. Beskriv den korteste ruta Anders kan kjøre.
III
Anders er på parkeringsplassen ved torget. Han har en passasjer som skal til krysset mellom Parkveien og gata som går parallelt med Storgata.
Anders oppdager at flere strekninger er stengt for biltrafikk på grunn av veiarbeid.
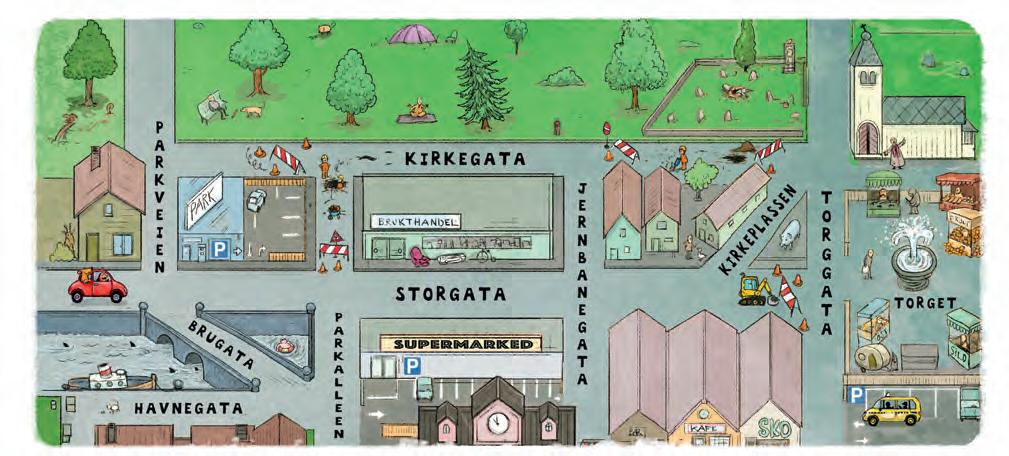
Beskriv ruta Anders må kjøre for å komme fram til rett sted.
Frode er på vei ut fra kirka. Han oppdager røyk 30 grader mot høyre.
Petter er på vei ut fra bruktbutikken. Han ser røyk 60 grader mot venstre. Hvor brenner det?
TERRENGLØYPA
Noen ganger kan det være uklart hvilken vinkel vi mener hvis vi skriver ∠A. Da bruker vi tre bokstaver i en bestemt rekkefølge for å navngi vinkelen.
Første bokstav Endepunktet på det første vinkelbeinet
Andre bokstav Toppunktet til vinkelen
Tredje bokstav Endepunktet på det andre vinkelbeinet
Toppunktet til vinkelen står alltid i midten.
Denne vinkelen får navnet ∠BAC.
Denne vinkelen får navnet ∠CAD.
Vi navngir alle vinklene mot klokka. Det vil si at det er forskjell på ∠BAD og ∠DAB
Denne vinkelen får navnet ∠BAD.
24 a Gjett hvor store ∠BAC og ∠CAB er i hver av figurene.
Mål deretter vinklene nøyaktig med gradskive.
b Regn ut ∠BAC + ∠CAB for hver av figurene over. Hva oppdager du?
c Tegn tre punkter, A, B og C. Tegn linjestykker fra A til B og fra A til C.
Forklar hvorfor ∠BAC + ∠CAB = 360°.
Her er AC et rett linjestykke og ∠CBD = 45°.
Vi skal finne ut hvor stor ∠DBA er.
Siden AC er en rett linje, er ∠DBA + ∠CBD = 180°.
Dermed er ∠DBA + 45° = 180°.
Da er ∠DBA =
=
25 a ∠CBD = 70°. Hvor stor er ∠DBA?
b ∠CBD = 132°. Hvor stor er ∠DBA?
26 a ∠DBE = 100°. ∠CBD = ∠EBA.
Hvor stor er ∠EBA?
b ∠CBD = 32°. Hvor stor er ∠DBA?
Hvor stor er ∠DBE?
27 Kunstverket er laget av ulike geometriske figurer.
Skriv minst fem vinkler som er
a spisse
b rette
c stumpe
d mellom 180° og 360°
e Velg minst fem av vinklene fra oppgave a, c eller d. Mål deretter nøyaktig med gradskive.
28 Hvor mange vinkler ser du her som er
a mindre enn 180°
b mindre enn 360°
29 Jøran skal plassere et 360-graders overvåkningskamera på et museum.
Under ser du ulike forslag til hvor han kan plassere kameraet. Den grønne trekanten viser plasseringen av overvåkningskameraet. De markerte punktene er spesielt kritiske punkter som det er ønskelig at overvåkningskameraet skal fange opp.
a Hvilke kritiske punkter er synlige for kameraet?
b Hvilke kritiske punkter er synlige for kameraet?
c Er det mulig å plassere overvåkningskameraet slik at det overvåker alle de kritiske punktene? Begrunn svaret.
Oppsummering
HVA ER EN VINKEL?
To linjer som møtes i et punkt, danner en vinkel De to linjene kalles vinkelbeina til vinkelen.
Punktet linjene møtes i, kalles toppunktet.
Vi måler vinkler i grader. Grader skrives med tegnet °.
Det fins tre hovedtyper av vinkler: toppunkt
Spiss vinkel:
Mindre enn 90°
Rett vinkel: 90° Stump vinkel: Mellom 90° og 180°
Vi markerer vanligvis vinkelen med en bue, men når vinkelen er rett (90°), bruker vi alltid et lite kvadrat for å markere vinkelen.
VINKLER SOM EN DEL AV EN SIRKEL
Vi kan tenke på en vinkel som en del av en sirkel. En hel sirkel er 360°.
Å MÅLE VINKLER MED GRADSKIVE
Når vi skal måle størrelsen på en vinkel, kan vi bruke en gradskive.
1 Legg midtpunktet til gradskiva på toppunktet til vinkelen.
2
3
Juster gradskiva slik at det ene vinkelbeinet ligger langs linja som viser 0°.
Bruk det andre vinkelbeinet til å lese av størrelsen på vinkelen.
Denne vinkelen er 60°.
PARALLELLE LINJER
To linjer er parallelle hvis avstanden mellom dem er den samme overalt.
Parallelle linjer vil aldri krysse hverandre, uansett hvor lange de er.
Parallelle linjer Ikke-parallelle linjer
toppunkt vinkelbein
vinkelbein
TOPPTUR
På denne toppturen skal vi utforske hvor mange vinkler mellom 0° og 360° som dannes når vi tegner 1, 2, 3, 4, … linjestykker fra et bestemt startpunkt.
Vi starter med to linjestykker, AS og BS
Det kan for eksempel se ut som på figuren til høyre.
Disse to linjestykkene danner to vinkler som er mellom 0° og 360°.
Vinklene er ∠ASB og ∠BSA.
T1 Tre linjestykker møtes i punktet S.
Vi kaller linjestykkene AS, BS og CS.
a Tegn to mulige skisser som viser hvordan dette kan se ut.
b Disse tre linjestykkene danner seks vinkler som er mellom 0° og 360°. Navngi alle seks vinklene.
T2 Fire linjestykker møtes i punktet S.
Vi kaller linjestykkene AS, BS, CS og DS.
a Tegn to mulige skisser som viser hvordan dette kan se ut.
b Hvor mange vinkler mellom 0° og 360° dannes av disse fire linjestykkene?
c Navngi alle vinklene.
På denne toppturen skal alle linjestykkene starte i samme punkt S, og ingen linjestykker skal ligge oppå hverandre.
Du kan utvide skissene fra oppgave T1 eller tegne nye skisser.
T3 Vi har noen linjestykker, AS, BS, CS, DS, …
a Fyll ut tabellen.
b Tenk deg at du har n slike linjestykker, der n er et hvilket som helst positivt heltall. Forklar hvordan du kan regne ut hvor mange vinkler mellom 0° og 360° som dannes av disse n linjestykkene.
T4 Vi utforsker nå ikke lenger antallet vinkler totalt, men utforsker i stedet antallet vinkler med ulik vinkelstørrelse.
Gi eksempler på tilfeller der antallet vinkler med ulik vinkelstørrelse er mindre enn antallet vinkler totalt.
T5 Vi har fire linjestykker, AS, BS, CS og DS
a Hva er det minste antallet ulike vinkelstørrelser mellom 0° og 360° som kan dannes av disse fire linjestykkene?
b Tegn en skisse som viser hvordan det er mulig.
T6 Vi har n linjestykker, AS, BS, CS, DS, …, der n er et hvilket som helst tall.
a Hva er det minste antallet ulike vinkelstørrelser mellom 0° og 360° som kan dannes av disse n linjestykkene?
b Forklar hvordan det er mulig.
Matemagisk 6 B GRUN N BOK
Matematikk for 5.–7. trinn
Matemagisk følger fagfornyelsen (LK20) og stimulerer elevene til å utforske og diskutere fra første stund. Lærebokas struktur ivaretar fellesskapet i klassen slik at elevene lærer sammen. Elevene får individuelle tilpasninger gjennom en unik differensieringsmodell.
Matemagisk 6 består av
• grunnbok 6A
• grunnbok 6B
• parallellbok 6A
• parallellbok 6B
• oppgavebok 6
• Matemagisk 1–7 Aschehoug Univers
• Matemagisk 6 Digitalbok
• digital lærerveiledning
På Aunivers.no finner du Aschehougs digitale læremidler.