







Inger-Lise Fritzen
Erling Kvistad Nilsen
Margareth Nilsen
Sindre Nyborg









Matemagisk 2 Lærerveiledning er en del av læreverket Matemagisk 1–10. Læreverket følger læreplanen i matematikk for 1.–10. årstrinn (LK20).
© H. Aschehoug & Co. (W. Nygaard) 2020
2. utgave / 1. opplag 2020
Materialet er vernet etter åndsverkloven. Uten uttrykkelig samtykke er eksemplarfremstilling, som utskrift og annen kopiering, bare tillatt når det er hjemlet i lov (kopiering til privat bruk, sitat o.l.) eller i avtale med Kopinor (www.kopinor.no). Kopiering fra engangsbøker er ikke tillatt etter Kopinor-avtalen.
Utnyttelse i strid med lov eller avtale kan medføre erstatnings- og straffansvar.
Redaktør: Rebekka Næss
Grafisk formgiving: ord & form, Gudbrand Klæstad
Omslagsdesign: Marit Jacobsen
Omslagsillustrasjon: Erik Ødegård, Basta Tekniske tegninger: Espen Skevik Baklid
Illustrasjoner: Erik Ødegård, Basta og Kai Lützenkirchen
Grunnskrift: Avenir
Papir: 115 g G-Print Trykk og innbinding: Livonia Print
ISBN 978-82-03-40967-7
Aunivers.no
Forfatterne har mottatt støtte fra Det faglitterære fond.
Matemagisk 1–4 (2. utgave) er nyskrevet til fagfornyelsen og nye læreplaner fra 2020. Deler av læremiddelet bygger på ideer og elementer fra Kroknes, Kavén, Persson: Matemagisk 1–4 (1. utgave, Aschehoug)
Palovaara, Kavén, Persson: Uppdrag Matte: Mattedetektiverna (Liber AB, Stockholm)
Kavén: Mattedetektiverna Lärarboken, Liber AB
Matematikk kan oppleves som vakkert og engasjerende og skape nysgjerrighet dersom en mestrer og liker faget. Det kan også oppleves som vanskelig, kjedelig og lite relevant. Det er sjelden manglende matematiske evner som er grunnen til at noen elever synes at matematikk er vanskelig. Ofte er det grunnlaget for å forstå, eller ferdighetene til å mestre, som ikke er lært godt nok. Det vil i sin tur skape negative assosiasjoner til faget og hindre engasjement.
I Matemagisk legger vi derfor opp til å gi elevene dette nødvendige grunnlaget for å lære og forstå matematiske begreper og ferdigheter. Gjennom en systematisk og helhetlig innføring av grunnleggende begreper og ferdigheter legger vi til rette for god forståelse og mestring allerede fra starten av. Dette grunnlaget kan elevene ta med seg videre og bruke i all annen læring.
I et stadig mer digitalisert samfunn blir behovet for og etterspørselen etter digitale løsninger større. Mange lærere foretrekker likevel å kunne variere
Vennlig hilsen forfatterne
digitale løsninger med tradisjonelle elevbøker. Vi legger derfor til rette for at dere selv kan variere og bruke de løsningene som passer best for dere og for elevenes behov. Vi tilbyr komplette digitale læringsløp, med filmer, spill og adaptive oppgaver, på Aunivers.no, i tillegg til tradisjonelle grunnbøker og oppgavebøker. I kombinasjon med lekpregede aktiviteter, matematiske mysterier og samtaler vil elevene ha gode forutsetninger for å legge et solid og godt grunnlag for å meste matematikk.
Vi håper at dere vil ha stor glede av det fantastiske universet til Matemagisk. Vi håper at Pi og Luringen, og alle de andre skapningene dere finner i Matemagisk, kan være med på reisen og legge det grunnlaget elevene trenger for å mestre matematikken og oppleve matematikk som relevant, spennende og lærerik.
Takk til alle våre elever, som er grunnen til at vi har skrevet denne boka.
Lykke til på reisen! Vi ønsker dere mange magiske øyeblikk underveis!
Inger-Lise Fritzen, Erling Kvistad Nilsen, Margareth Nilsen og Sindre Nyborg




Matemagisk – enkelt for læreren, bra for eleven
I Matemagisk får du læringsløp til hvert tema. Læringsløp er fullstendige undervisningsopplegg fra begynnelse til slutt. Du kan selvfølgelig selv velge om du vil bruke læringsløpene våre slik de er, eller plukke ut de delene du mener passer for deg og dine elever. Læringsløpene til sidene i grunnboka finner du beskrevet i lærerveiledningen. Digitale læringsløp til tavle og læringsbrett finnes på Aunivers.no.
Læringsløpene inneholder alt du trenger, blant annet
• læringsmål og viktige begreper
• systematisk begrepsinnlæring
• aktiviteter til oppstart
• aktiviteter til underveisvurdering
• tips til videre arbeid
Matemagisk ønsker å skape mestringsfølelse, engasjement og verdifulle matematiske oppdagelser.
Det skal være inspirerende og gøy å lære. Barn er nysgjerrige og ønsker å oppdage og skape. For de yngste elevene i skolen er lek nødvendig for trivsel og utvikling, men også i opplæringen gir leken mulighet til kreativ og meningsfylt læring. Med Matemagisk får elevene utforske matematikk aktivt, både sammen og alene.
Elevene vil gjennom arbeidet
• utforske og eksperimentere
• stille spørsmål
• argumentere for egne og forstå andres løsninger
I lærerveiledningen er det gode tips til utforskende og lekende aktiviteter som stimulerer elevenes nysgjerrighet, samtidig som de har tydelig faglig fokus og støtter opp under arbeidet med grunnboka. Aktivitetene i lærerveiledningen og oppgavene i grunnboka hjelper elevene med å sette nye ideer og begreper i sammenheng med tidligere kunnskap og erfaringer. Steg for steg bygger elevene sin kompetanse, slik at det dannes en solid matematisk grunnmur.
Gjennom detaljerte forslag til oppstart av øktene, «matemagiske mysterier», utforskende aktiviteter og samarbeidsoppgaver kan du enkelt legge til rette for at elevene kan «snakke matte» med hverandre. Når elevene får tid til å tenke, reflektere, stille spørsmål og oppleve at faget er relevant, utvikles matematisk kreativitet og nysgjerrighet.
Matemagisk ønsker å stimulere til elevenes utvikling av matematisk begrepsforståelse.
Matemagisk bygger på en systematisk og gjennomtenkt innlæring av grunnleggende matematiske begreper, med utgangspunkt i det som kalles systematisk begrepsundervisning, etter tidligere professor i kognitiv læringspsykologi ved Universitetet i Oslo, Magne Nyborg. Ved å legge til rette for god begrepsinnlæring helt fra starten av hjelper vi elevene til å legge et godt grunnlag for videre matematisk forståelse og gode ferdigheter i problemløsing og regning.
Nyborg definerte et begrep slik: «Viten om en gruppe av fenomener, hva de er like i, men også hva som skiller dem. Omfatter også viten om hva som skiller dem fra forvekslingslike grupper.» Et fenomen kan være konkrete objekter/ting, men også noe abstrakt, for eksempel en følelse eller en situasjon. Det vil si at for å få et godt begrep om noe, må en se mange og ulike eksempler på det som skal læres. En må lære seg å se etter felles egenskaper og forskjeller i de ulike fenomenene, men også kunne skille dem fra grupper som er så like at de kan forveksles. Dette er læringsprosesser som skjer automatisk og intuitivt fra barna er små, men ved bevisst å følge disse naturlige læringsprosessene i undervisningen legger vi til rette for god begrepsdannelse hos elevene.
Begrepsundervisningsmodellen har tre faser. I den første, den selektiv assosiasjonsfasen, viser vi mange og ulike eksempler på det som skal læres, samtidig som vi setter ord på hvilke typiske egenskaper de har. I den selektive diskriminasjonsfasen sammenlikner vi fenomenet med andre fenomener som er så like at de kan forveksles, og finner de som hører med i den gruppa vi lærer om. I den siste fasen, den selektive generaliseringsfasen, setter vi ord på hva alle de ulike fenomenene vi lærer om, har til felles. De deler minst én felles egenskap, som gjør at de hører med i den samme gruppa av fenomener.
I Matemagisk jobber vi først med det Nyborg kaller grunnleggende begrepssystemer, for eksempel form, plass, retning, stilling, mengde, antall og symboler, for disse danner grunnlaget for å forstå mer abstrakte og komplekse matematiske begreper senere. Ved språklig å bevisstgjøre elevene til å finne likheter og forskjeller hjelper vi dem til å styre oppmerksomheten sin. Samtidig kan elevene overføre det de har lært til å analysere og stadig lære nye begreper. Elevene lærer å strukturere begrepene i begrepshierarkier, og slik kan de bygge på sin begrepskunnskap videre oppover i trinnene og i alle fag.
Matemagisk lar kjerneelementene gjennomsyre matematikkundervisningen.
Utforsking og problemløsing
Utforsking i matematikk handler om at elevene leter etter mønster, finner sammenhenger og diskuterer seg fram til en felles forståelse. Arbeidet i Matemagisk skal være utforskende ved at elevene ved hjelp av en solid begrepsforståelse og gode ferdigheter finner sammenhenger og bruker kjente begreper til å forklare tenkemåtene sine og forstå hvordan andre elever tenker.
Den algoritmiske tankegangen er viktig for å kunne løse problemer. Vi må bryte ned problemet i delproblemer som kan løses systematisk. Hvordan vi kommer fram til løsningene, hva vi tenkte, og hvilke strategier vi brukte, er viktigere enn selve svaret. Det viktigste er at elevene kan sette ord på og forklare hvorfor de valgte å bruke de strategiene de gjorde. Da kan vi sammen se på de ulike valgene som er gjort, og få en dypere forståelse for hvorfor noen strategier fører fram til riktig svar og noen ikke gjør det. De gale svarene kan gjerne løftes fram. La elevene forstå at et galt svar ofte kan lære oss mer matematikk enn et riktig.
Modellering og praktisk bruk
En modell i matematikk er en beskrivelse av virkeligheten i matematisk språk. Elevene skal gradvis forstå hvordan ulike modeller i matematikk blir brukt for å beskrive hverdagen og samfunnet, og de skal selv lage modeller som beskriver egne tanker. I Matemagisk knyttes begreps- og ferdighetsundervisningen tett opp mot hverdagslivet og elevenes erfaringsverden. Undervisningen vil derfor oppleves som virkelighetsnær og relevant, og bygges på elevenes tidligere erfaringer.
Resonnering og argumentasjon
Resonnering i matematikk handler om å kunne følge, vurdere og forstå matematiske tankerekker. Det innebærer at elevene skal forstå at matematiske regler og resultater ikke er tilfeldige, men har klare begrunnelser. Elevene skal utfor me egne resonnementer både for å forstå og for å løse et problem. Argumentasjon i matematikk handler om at elevene begrunner framgangsmåter, resonnementer og løsninger og beviser at de er gyldige.
Matemagisk har en rekke aktiviteter og oppgaver som handler om å finne like egenskaper ved elementer i en mengde, og å argumentere for sin løsning. Et eksempel er denne sorteringsoppgaven:

Elevene velger selv en egenskap å sortere etter. De må kunne argumentere for sin løsning og forklare hvorfor denne måten å sortere på er gyldig. Ved å bli presentert for oppgaver med flere riktige svar fra første dag på skolen, vil det bli en naturlig tenkemåte for elevene. Elevene spør hverandre hvordan de har tenkt, og diskuterer validiteten i ulike løsninger. De blir således tidlig vant til å kunne følge, vurdere og forstå matematiske tankerekker.
Representasjon og kommunikasjon
Representasjoner i matematikk er måter å uttrykke matematiske begreper, sammenhenger og problemer på. I arbeidet med oppgaver i Matemagisk er det viktig at elevene har tilgang til konkreter og halv-konkreter, slik at de opplever en gradvis overgang fra konkrete representasjoner til symbolske. Elevene i småskolen lærer at tall, bokstaver, regnetegn og så videre er symboler som står for noe annet enn seg selv. «3» kan bety antallet tre i en mengde; «+» er et symbol som betyr «å legge sammen». For å kunne lage egne modeller og forstå andres er det helt avgjørende å ha felles symboler og god symbolforståelse. Tre epler og to epler vil alltid være fem epler, uavhengig av hvem som legger sammen mengdene. Hvordan vi skriftlig uttrykker det som skjer når mengdene legges sammen, kan være ulikt fra person til person. Én elev vil tegne tellestreker, en annen vil skrive med bokstaver og en tredje vil skrive regnestykket 3 + 2 = 5. Alle representasjonene krever symbolforståelse. I Matemagisk oppfordres elevene til å vise løsningene sine med ulike representasjoner og forklare løsningene sine til medelever. Man må ha et felles språk for å kunne sette ord på egne tanker og forstå andres tanker.
Abstraksjon og generalisering
Abstraksjon i matematikk innebærer at elevene gradvis utvikler tanker, strategier og matematisk språk. Utviklingen går fra konkrete beskrivelser til formelt symbolspråk og formelle resonnementer. I Matemagisk tar vi små steg og bygger stein på stein, slik at elevene får tid til å fordype seg og utvikle tanker, strategier og matematisk språk.
Generalisering i matematikk handler om at elevene oppdager sammenhenger og strukturer som kan anvendes i nye og ukjente situasjoner og oppgaver. Matemagisk har generaliseringsoppgaver under hvert tema. Disse oppgavene hjelper elevene til å finne felles egenskaper, se sammenhenger og systematisere kunnskapen sin.
Matematiske kunnskapsområder
De matematiske kunnskapsområdene er tall og tallforståelse, algebra, funksjoner, geometri, statistikk og sannsynlighet. I Matemagisk begynner vi på begynnelsen, slik at elever ikke starter skoleløpet med misoppfatninger og «hull» i kunnskapen sin. Elevene trenger for eksempel god mengdeforståelse for å utvikle god tallforståelse, de må forstå symbolbruk for å kunne utvikle gode regnestrategier, og de må vite hva en enhet er for å forstå brøk eller måle lengder. Matemagisk 1–4 legger til rette for at elevene skal kunne utvikle et godt begrepsapparat og en verktøykasse bugnende av strategier.
Matemagisk hjelper læreren i vurderingsprosessen.
Vurdering av elevenes faglige kompetanse skal gi et bilde av hva elevene kan, men også fremme læring og utvikling. God vurdering, der forventningene er tydelige og eleven deltar og blir hørt underveis i læringsarbeidet, er en nøkkel når det gjelder å tilpasse undervisningen.
• Oppstartsaktivitetene åpner for å vurdere elevenes forkunnskaper.
• Nøkkelhullsoppgavene i grunnboka gir læreren mulighet til å vurdere elevenes forståelse underveis, uten å måtte rette alle oppgavene elevene har gjort i boka.
• «Snakke matte» gir læreren mulighet til å vurdere elevenes resonnementer og begrepsbruk.
• Vurderingsaktivitetene ved slutten av hvert tema hjelper læreren å vurdere om elevene er klare for å bygge ut kunnskapen sin.
Læreren kan således hjelpe elevene ved å bruke forslagene til læringssamtaler, de forskjellige oppstartsoppgavene og tips til ulike vurderingsaktiviteter som finnes i lærerveiledningen. Disse aktivitetene gir læreren mulighet til å vurdere elevene
uten at de opplever det som en vurdering. Ved bruk av nøkkelhullsoppgavene kan læreren enkelt se hvilke elever som har forstått, og hvilke elever som trenger mer trening.
Matemagisk gjør det enkelt å tilpasse opplæringen.
Matemagisk legger opp til at elevene skal jobbe over lengre tid med temaene, slik at alle elever får tid til å forstå og mestre. La gjerne elevene arbeide sammen om oppgavene i boka, slik at de kan snakke sammen, lese sammen og lære av hverandre underveis.
• Mange oppgaver har flere riktige svar, slik at elevene kan arbeide med den samme oppgaven, men på sitt eget nivå.
• Til hvert oppslag finner læreren «Arbeid med sidene», der det finnes tips til hvordan man kan jobbe med oppgavene i grunnboka i klasserommet.
• Spor-oppgavene i slutten av hvert kapittel i grunnboka gir elevene oppgaver med ulik vinkling. Alle elevene kan begynne på rødt spor, der de minst komplekse oppgavene finnes, og så jobbe seg nedover siden til gult og eventuelt blått spor.
Kompetansemål
Mål for opplæringa er at eleven skal
• måle og samanlikne storleikar som gjeld lengd og areal, ved hjelp av ikkje-standardiserte og standardiserte måleiningar, beskrive korleis og samtale om resultata
Barn begynner tidlig med å sammenlikne det de ser. De kan sammenlikne farger, former og størrelser. Ting kan være store eller små, ha ulik høyde, lengde og vekt. Men vi kan ikke vite sikkert om en ting er liten eller stor uten å ha noe å sammenlikne med. Størrelse er et relativt begrep, for størrelsen må sammenliknes med noe annet for å gi mening.
I dette kapitlet skal vi blant annet jobbe med å måle lengder ved hjelp av ulike ikke-standardiserte målenheter, blant annet kroppsmål. Etter hvert er hensikten å rette oppmerksomheten mot behovet for standardiserte målenheter, slik at målingene kan bli helt nøyaktige. I læreplanen står det at elevene skal lære å måle og sammenlikne størrelser som gjelder lengde og areal. Vi velger derfor først å introdusere elevene for de overordnede begrepene stor og liten størrelse, for så å introdusere lengde, bredde, høyde og areal.
Elevene må lære å velge den målenheten som er mest hensiktsmessig i forhold til størrelsen på den lengden som skal måles. Størrelsen angis da som et antall av den målenheten som det er plass til mellom startpunktet og sluttpunktet for målingen.
Til de voksne hjemme
I dette kapitlet skal vi lære om måling. Vi skal måle blant annet lengder, bredder og flater ved hjelp av ulike ikke-standardiserte målenheter. Dette er mål som ikke er standardiserte, blant annet kroppsmål. I tidligere tider var det vanlig å ta utgangspunkt i kroppsdeler når man skulle måle lengder. Dette var praktisk, siden lengdemålet alltid var tilgjengelig der man var, men det gav usikre mål. De varierte fra person til person og fra land til land. Derfor meldte behovet seg for standardiserte målenheter, slik at målingene kunne bli helt nøyaktige. Nøyaktige målenheter som vi skal jobbe med nå, er centimetre (cm) og kvadratcentimetre (cm2). Men før vi måler nøyaktig med standardiserte målenheter, jobber vi med de overordnede størrelsesbegrepene: stor og liten størrelse, stor og liten lengde, stor og liten høyde. Størrelse er et relativt begrep, for størrelsen må sammenliknes med noe annet for å gi mening. En ting kan ikke kalles stor eller liten før vi sammenlikner den med noe som er mindre eller større.
Begreper vi øver på
• Stor størrelse – stor
• Liten størrelse – liten
• Stor lengde – lang
• Liten lengde – kort
• Stor høyde – høy
• Liten høyde – lav
• Å sammenlikne og måle lengder
• Lengde og bredde
• Centimeter – cm
• Å sammenlikne og måle flater
• Kvadrat
• Kvadratcentimeter – cm2
Når vi måler, sammenlikner vi en lengde, eller en størrelse, med noe annet og teller antallet enere av målenheten. Vi sammenlikner da lengder og bredder med centimeteren på en linjal og teller antallet centimetre. Vi sammenlikner ulike flater med en kvadratcentimeter og teller antallet kvadratcentimetre.
Aktiviteter dere kan gjøre hjemme
• Sorter sko, blyanter, bøker, leker, steiner, greiner o.l. etter størrelse, fra minst til størst, samtidig som dere bruker begrepene liten, mindre, minst og stor, større, størst.
• Sammenlikn ting ved middagsbordet etter høyde. Saftmuggen har stor høyde i forhold til saftglasset. Saftglasset har liten høyde i forhold til kasserollen. Vannmuggen er høyest. Tallerkenen er lavest.
• Mål lengden og bredden av rommet ved hjelp av antallet musesteg. Sammenlikn med et annet rom. Hvilket rom er størst?
• Bygg hus eller tår n av duplo, lego eller klosser og sammenlikn størrelser.
• Lag slanger med modell-leire og sammenlikn lengder.
• Mål flaten av kjøkkenbordet ved hjelp av A4-ark. Hvor mange ark trenger vi for å fylle bordet? Sammenlikn med et annet bord. Hvilket bord har størst areal?
• Les og dramatiser «Eventyret om Gullhår».
• Les og dramatiser «Bukkene Bruse».
• Syng «Oppe på fjellet der bor det tre trolle».
• Mål høyden til familiemedlemmene. Marker høyden på en dørlist med blyant, og mål antallet centimetre.
Hvis dere har flere språk hjemme, kan dere bruke både norsk og andre språk når dere snakker om måling.
Lykke til!
Bruk en hyssing og finn ut hvor langt tauet til Hilde er.
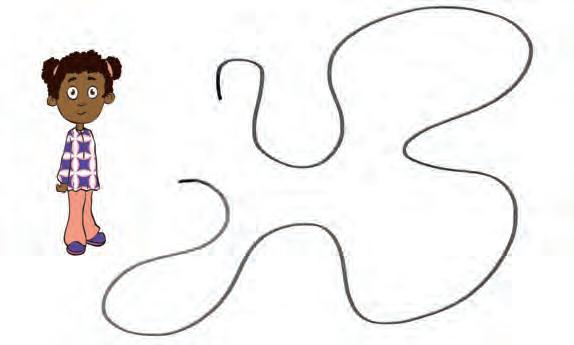
Tegn et tau som er lengre enn Hildes.
Tegn et tau som er kortere enn Hildes.
Hvor mange tomler langt er tauet til Hilde?
Svar:
Tegn et tau som er tre tomler kortere enn Hildes tau.
Bruk ein hyssing og finn ut kor langt tauet til Hilde er.

Teikn eit tau som er lengre enn Hilde sitt.
Teikn eit tau som er kortare enn Hilde sitt.
Kor mange tomlar langt er tauet til Hilde?
Svar:
Teikn eit tau som er tre tomlar kortare enn Hilde sitt tau.
Bruk målebånd og mål kroppsdelene på hverandre.
Rundt hodet er det cm.
Armen er cm lang.
Overarmen er cm lang.
Underarmen er cm lang.
Beinet er cm langt.
Rundt håndleddet er det cm.
Foten er cm lang.
Kroppen er cm lang.
Anna vil sette på to kroker på planken. Det skal være like langt mellom krokene som til kantene. Hvor langt må det være mellom krokene?
Svar:
Bruk måleband og mål kroppsdelane på kvarandre.
Rundt hovudet er det cm.
Armen er cm lang.
Overarmen er cm lang.
Underarmen er cm lang.
Beinet er cm langt.
Rundt handleddet er det cm.
Foten er cm lang.
Kroppen er cm lang.
Anna vil setje på to krokar på planken. Det skal vere like langt mellom krokane som til kantane. Kor langt må det vere mellom krokane?
Svar:

Før dere begynner: Be elevene peke og fortelle hva de ser på bildet.
Repeter begrepene elevene lærte i første klasse (linjefor mer, flateformer, plass, retning, stilling, mengde, enhet og antall).
Analytisk koding (AK): Still spørsmål, for eksempel: «Kan du peke på og sette ord på noe du har lært tidligere?», «Hvilken linjefor m har den?», «Er det størst antall av gule eller røde blomster?»
Underveis i kapitlet
Elevene kan gjer ne komme med flere egenskaper når dere ser på myldrebildet. Løft fram alle egenskaper som elevene kommer med. Avslutt med en oppsummering der du framhever begrepet dere har arbeidet med.
Stor og liten
• Kan du peke på geita som har stor størrelse?
• Hvilken størrelse har Pi i forhold til Luringen?
Lang og kort
• Hvilket målebånd er lengst?
• Kan du peke på sagen som er kortest?
Høy og lav
• Hvilken høyde har den midterste geita i forhold til de to andre?
Å sammenlikne og måle lengder
• Hvorfor ser Luringen så forskrekket ut?
Lengde og bredde
• Hvor lang og bred er den planken Pi og Luringen måler?
Centimeter – cm
• Ser du noen centimetre på bildet?
Å sammenlikne og måle flater
• Hvilket av hjulene har størst flate?
Kvadrat
• Ser du noen kvadrater på bildet?
Kvadratcentimeter – cm2
• Hvordan kan Pi og Luringen finne antallet kvadratcentimetre på planken sin?
La elevene stille hverandre spørsmål til bildet.
Aktiviteter før vi jobber i boka
Leker og sanger for å vekke elevenes bevissthet rundt egne forkunnskaper om størrelse og sammenlikning av størrelser:
Lek:
• Sorter sko, blyanter, bøker, leker, steiner, greiner eller liknende etter størrelse.
• Les og dramatiser «Eventyret om Gullhår».
• Les og dramatiser «Bukkene Bruse».
Syng:
• «Oppe på fjellet der bor det tre trolle»
Læringsmål
Eleven skal
• forstå og gjøre seg forstått når dere snakker om størrelse
• vite at ingenting er stort eller lite i seg selv, bare når vi sammenlikner med noe annet
Viktige begreper
Størrelsesbegreper er relative begreper. Det vil si at vi alltid må angi størrelsen i relasjon til noe annet.
• stor
• større
• størst
• liten
• mindre
• minst
Størrelse er et relativt begrep fordi størrelsen må sammenliknes med noe annet for å gi mening. Når vi skal sammenlikne og tydeliggjøre relasjoner mellom ting, bruker vi uttrykket i forhold til. I forhold til er synonymt med sammenliknet med. En kopp er stor i forhold til en fyrstikkeske, men liten sammenliknet med en sykkelveske. Ting kan også være like i størrelse.
Ulike bøyningsfor mer for størrelsesbegreper kan vi også introdusere nå. Det kan vi gjøre ved å legge fram en rekke ting i økende eller minkende størrelse: stor –større – størst og liten – mindre – minst.
Vær klar over at noen elever kan blande størrelse med alder. Ikke sammenlikn elevenes høyde, vekt eller fysiske størrelse.
Utstyr
• ting som kan rangeres etter størrelse, for eksempel klær, sko, kjøkkenredskaper, verktøy, leker, baller, lekedyr, lekebiler eller treklosser
1 Tegn noe som er større enn denne sykkelen.

2 Fargelegg ballene som er større enn golfballen.

3 Tegn tre ting du ser i klasserommet, som har ulik størrelse. Tegn strek til riktig tegning.
Tips til oppstart
Siden stor og liten er relative begreper, må vi alltid presentere eksemplene parvis – da blir det samtidig både assosiasjons- og forskjellslæring. For å hjelpe elevene med å sortere begrepene er det lurt å bruke det overordnede begrepet størrelse nå i innøvingsfasen. Si derfor «stor størrelse», ikke bare «stor».
Assosiasjon/forskjellslæring: Størrelse er et relativt begrep, og derfor må størrelse ses i forhold til noe annet. Vi sammenlikner derfor stor og liten størrelse i samme oppgave. Bruk åtte–ti ting som kan måles eller sorteres etter
størrelse. Ha for eksempel baller i ulike størrelser. Vis for eksempel fram en fotball og spør: «Er denne ballen stor eller liten?» Du kan få ulike svar. For å vite om noe er stort eller lite må man ha noe å måle eller sammenlikne med. Ta så fram en håndball og vis begge ballene samtidig. Elevene vil se at fotballen er stor sammenliknet med håndballen. Fotballen har stor størrelse i forhold til håndballen, og håndballen har liten størrelse i forhold til fotballen. Ta fram en tennisball og sammenlikn den med håndballen. Hvilken ball er stor eller liten nå? Elevene vil oppdage at håndballen har liten størrelse
Hvilke egenskaper har du fargela, felles?
4 Tegn noe som er mindre enn denne sykkelen.

5 Fargelegg ballene som er mindre enn badeballen.
Hvilke egenskaper har ballene du fargela, til felles?

6 Tegn tre ting som har ulik størrelse. Tegn strek til riktig tegning.
liten mindre minst
sammenliknet med tennisballen. Du kan fortsette med å sammenlikne størrelsen til ulike baller, store og små. Let fram andre ting med stor og liten størrelse, og gjenta øvelsen.
Generaliseringsfasen: Lag tre mengder der det er to ting med ulik størrelse i hver mengde. Pek på den største tingen i hver mengde. Spør hvilken egenskap disse tingene har til felles. Til slutt kan dere legge tingene ved siden av hverandre og sortere dem etter størrelse: stor, større, størst og liten, mindre, minst.
Arbeid med sidene
La elevene arbeide sammen, og les oppgavene høyt.
1 Dette er en assosiasjons-/forskjellsoppgave. Hensikten med oppgaven er å bruke ordene «stor størrelse» og «stor –større» for å si noe om størrelse i forhold til noe annet. Underveis kan du spørre: «Hvilken størrelse har tegningen din i forhold til sykkelen?»
2 Denne forskjellslæringsoppgaven skal trene elevene i å skille stor og liten størrelse. Still spørsmål, for eksempel: «Her har du gjort helt riktig, men kan du fortelle meg hvor-
for du har fargelagt akkurat disse ballene?»
3 Denne oppgaven kan brukes til underveisvurdering. Her skal elevene tegne tre valgfrie ting og sammenlikne størrelsene.
4 Dette er en assosiasjons-/ forskjellsoppgave. Hensikten med oppgaven er å bruke ordene «liten størrelse» og «liten» for å si noe om størrelse i forhold til noe annet.
Underveis kan du spørre: «Hvilken størrelse har tegningen din i forhold til sykkelen?»
5 Denne forskjellslæringsoppgaven skal trene elevene i å skille mellom stor og liten størrelse. Still spørsmål, for eksempel: «Her har du gjort helt riktig, men kan du fortelle meg hvorfor du har fargelagt akkurat disse ballene?»
6 Denne oppgaven kan brukes til underveisvurdering. Her skal elevene tegne tre valgfrie ting og sammenlikne størrelsene. Tegner eleven ting med ulike størrelser og kobler dem til riktig begrep?
Tips til videre arbeid
Gi elevene praktiske oppgaver:
• Finn noe som er større enn matboksen din.
• Finn noe som er mindre enn pennalet ditt.
• Finn noe som er like stort som hånda di, osv
• Når elevene har funnet flere ting, kan de sortere dem etter størrelse: stor – større – størst, liten – mindre – minst.
• Gå på jakt etter ulike størrelser! La elevene finne og sammenlikne ulike størrelser. Dere kan også gå på jakt i minnet: «Har dere noe hjemme som har stor størrelse?»
Vurderingsaktiviteter
• Sorter ulike ting fra minst til størst og fra størst til minst.
Læringsmål
Eleven skal
• forstå og gjøre seg forstått når dere snakker om lengde
• vite at ingenting er langt eller kort i seg selv, bare når vi sammenlikner med noe annet
Viktige begreper
Størrelsesbegreper er relative begreper. Det vil si at vi alltid må angi størrelsen i relasjon til noe annet.
lang
lengre
lengst
kort
kortere
kortest
Det finnes flere ulike typer størrelser. Når vi tenker at noe har stor størrelse, kan det være at vi tenker at noe er langt i forhold til noe annet. Lengde måles i en linje fra et punkt til et annet, ofte mellom ytterpunktene på en gjenstand. Linjen trenger ikke å være rett. Vi kan for eksempel måle omkretsen til en figur eller kjøreavstanden mellom to byer. Vi kan også̊ måle etter tenkte rette linjer, som når vi skal finne avstand i luftlinje, høyden til et fjell, dybden til en innsjø eller diameteren til et rør.
Gradbøying av lengdebegreper introduseres også. Det kan vi gjøre ved å legge fram en rekke ting i økende eller minkende lengde: lang – lengre – lengst, kort – kortere – kortest.
Utstyr
• ting som kan rangeres etter lengde, for eksempel blyanter, pennaler, bøker, piperensere, hyssing, hoppetau, cuisenaire-staver eller stearinlys
Tips til oppstart
Siden kort og lang er relative begreper, må vi alltid presentere eksemplene parvis – da blir det
7 Tegn tre blyanter som er lengre enn Luringens blyant.
Hvilke egenskaper er like for alle blyantene du har tegnet?


8 Tegn strek til riktig bestikk. lang lengre lengst

Hvilken slange er lengst?

samtidig både assosiasjons- og forskjellslæring.
Assosiasjons/forskjellslæring: Bruk åtte–ti ting som kan måles eller rangeres etter størrelsen lengde. Her bruker vi linjaler som eksempel. Ha linjaler i ulike størrelser tilgjengelig ute av elevenes synsvidde. Vis fram én linjal. Spør: «Har denne linjalen stor eller liten lengde?» Du kan få ulike svar. Vis deretter fram to linjaler med ulik lengde. Spør elevene igjen: «Har denne linjalen stor eller liten lengde i forhold til denne?» Gjenta med flere eksempler.
Generaliseringsfasen: Lag tre grupper med to ting i hver gruppe. De to tingene i hver gruppe skal ha ulik lengde. Be elevene peke ut den tingen i hver gruppe som har stor lengde i forhold til den tingen som ligger ved siden av Elevene skal kunne svare: «De er like ved at de har stor lengde i forhold til den tingen de ligger ved siden av.» Gjør det samme med liten lengde.
Til slutt kan dere legge tingene ved siden av hverandre og sortere dem etter størrelse: lang – lengre – lengst, kort – kortere – kortest.
10 Tegn tre blyanter som er kortere enn Luringens blyant.
Hvilke egenskaper er like for alle blyantene du har tegnet?

11 Tegn strek til riktig bestikk


kortere kortest
12 Slangen på tegningen er kort. Tegn en slange som er enda kortere.

Hvilken slange er kortest?

Arbeid med sidene
La elevene arbeide sammen, og les oppgavene høyt.
7 Dette er en assosiasjons-/ forskjellsoppgave der elevene skal tegne noe som er lengre enn noe annet. Hensikten med oppgaven er å bruke ordene «stor lengde» og «lang – lengre» for å sette noe i forhold til noe annet. Underveis kan du spørre: «Hvilken lengde har blyantene dine i forhold til blyanten i boka?»
8 Denne forskjellslæringsoppgaven skal trene elevene i å skille stor og liten lengde. Still spørsmål, for eksempel: «Her har du gjort helt riktig, men
kan du fortelle meg hvorfor du har tegnet strek her?»
9 Denne oppgaven er mer kompleks og kan brukes til underveisvurdering. Her skal elevene tegne en slange som er lengre enn slangen på bildet og sammenlikne størrelsene. Hvordan måler vi når noe har buet form? Bruk gjerne en hyssing for å sammenlikne.
10 Dette er en assosiasjons-/ forskjellsoppgave der elevene skal tegne noe som er kortere enn noe annet. Hensikten med oppgaven er å bruke ordene «liten lengde» og «kort – kortere» for å sette noe i forhold
til noe annet. Underveis kan du spørre: «Hvilken lengde har blyantene dine i forhold til blyanten i boka?»
11 Denne forskjellslæringsoppgaven skal trene elevene i å skille stor og liten lengde. Still spørsmål, for eksempel: «Her har du gjort helt riktig, men kan du fortelle meg hvorfor du har tegnet strek her?»
12 Denne oppgaven er mer kompleks og kan brukes til underveisvurdering. Her skal elevene tegne en slange som er kortere enn slangen på bildet og sammenlikne størrelsene. Hvordan måler vi når noe har buet form? Bruk gjerne en hyssing for å sammenlikne.
Tips til videre arbeid
• Gi elevene praktiske oppgaver:
– Finn den lengste blyanten i pennalet.
– Finn den korteste blyanten i pennalet.
– Finn to blyanter som er like lange.
– Sorter blyantene etter lang – lengre – lengst og kort – kortere – kortest.
– Gå på jakt etter ulike lengder! Dere kan også gå på jakt i minnet: «Har dere noe hjemme som har stor lengde?», «Hvor langt er rommet ditt?», «Hvor lang er sykkelen din?»
• Brett papirfly. Hvilket flyr lengst?
Vurderingsaktiviteter
• Lag tre mengder der det er to ting med ulik lengde i hver mengde. Spør: «Kan du peke på den tingen som er lang i forhold til den andre tingen i mengden?» Gjør det samme med kort.
• Sorter ulike ting fra kortest til lengst og fra lengst til kortest.
Læringsmål
Eleven skal
• forstå og gjøre seg forstått når dere snakker om høyde
• vite at ingenting er høyt eller lavt i seg selv, bare når vi sammenlikner med noe annet
Viktige begreper
Størrelsesbegreper er relative begreper. Det vil si at vi alltid må angi størrelsen i relasjon til noe annet.
• høy
• høyere
• høyest
• lav
• lavere
• lavest
Når vi måler i loddrett stilling oppover, kalles lengdemålet som regel høyde. Lengdemålet kalles dybde når vi måler i loddrett stilling nedover fra for eksempel havoverflaten. Vi peker tilbake på det elevene har lært om vannrett og loddrett stilling. Ulike bøyningsformer for lengdebegreper kan vi også introdusere nå. Det kan vi gjøre ved å sette fram en rekke ting i økende eller minkende høyde: høy – høyere –høyest, lav – lavere – lavest.
Utstyr
• ting som kan rangeres etter høyde, for eksempel maler, legofigurer, duplofigurer, støvler, brusflasker, melkekartonger, legotårn, klosser, eller cuisenaire-staver
Tips til oppstart Høy og lav er relative begreper, så vi må vi alltid presentere eksemplene parvis – da blir det samtidig både assosiasjons- og forskjellslæring.

Assosiasjons/forskjellslæring: Bruk åtte–ti ting som kan måles eller rangeres etter størrelsen høyde. Her bruker vi lego- og duplofigurer som eksempler. Ha figurer i ulike størrelser tilgjengelig ute av elevenes synsvidde. Vis fram én figur. Spør: «Har denne figuren stor eller liten høyde?» Du kan få ulike svar. Vis deretter fram to figurer med ulik høyde. Spør elevene igjen: «Har denne figuren stor eller liten høyde i forhold til denne?» Gjenta med flere andre eksempler.
Generaliseringsfasen: Lag tre mengder med to ting i hver gruppe. De to tingene i hver gruppe skal ha ulik høyde. Be elevene peke ut den tingen i hver gruppe som har stor høyde i forhold til den tingen den ligger ved siden av Elevene skal kunne svare: «De er like ved at de har stor høyde i forhold til den tingen de ligger ved siden av.» Gjør det samme med liten høyde.
Til slutt kan dere sette tingene ved siden av hverandre og sortere dem etter høyde: høy – høyere – høyest, lav – lavere – lavest.
16 Tegn tre ting som er lavere enn lyset.

17 Fargelegg husene som er lavere enn Luringens hus.

18 Tegn tre ting med ulik høyde. Tegn strek til riktig tegning.
Arbeid med sidene
lav lavere lavest
La elevene arbeide sammen, og les oppgavene høyt.
13 Dette er en assosiasjons-/ forskjellsoppgave der elevene skal tegne noe som er høyere enn noe annet. Hensikten med oppgaven er å bruke ordene «stor høyde» og «høy – høyere» for å sette noe i forhold til noe annet. Underveis kan du spørre: «Hvilken høyde har lysene dine i forhold til lyset i boka?»
14 Denne forskjellslæringsoppgaven skal trene elevene i å skille mellom stor og liten høyde. Still spørsmål, for eksempel: «Her har du gjort helt riktig, men kan du fortelle meg hvorfor du har fargelagt disse husene?»
15 Denne oppgaven er mer kompleks og kan brukes til underveisvurdering. Her skal elevene tegne ting med ulike høyder og sammenlikne størrelsene. De skal også koble tegningene til begrepene høy – høyere – høyest.
16 Dette er en assosiasjons-/ forskjellsoppgave der elevene skal tegne noe som er lavere enn noe annet. Hensikten med oppgaven er å bruke ordene «liten høyde» og «lav – lavere» for å sette noe i forhold til noe annet. Underveis kan du spørre: «Hvilken høyde har lysene dine i forhold til lyset i boka?»
17 Denne forskjellslæringsoppgaven skal trene elevene i å skille stor og liten høyde. Still spørsmål, for eksempel: «Her har du gjort helt riktig, men kan du fortelle meg hvorfor du har fargelagt disse husene?»
18 Denne oppgaven er mer kompleks og kan brukes til underveisvurdering. Her skal elevene tegne ting med ulike høyder og sammenlikne størrelsene. De skal også koble tegningene til begrepene lav – lavere – lavest.
Tips til videre arbeid
• Gi elevene praktiske oppgaver:
– Bygg tår n med klosser eller lego og sammenlikn høydene.
– Hopp og sett strek med kritt på veggen ute, eller på tavla.
Vurderingsaktiviteter
• Lag tre mengder der det er to ting med ulik høyde i hver mengde. Spør: «Kan du peke på den tingen som er høy i forhold til den andre tingen som er i den samme mengden?» Gjør det samme med lav.
• Sorter ulike ting fra lavest til høyest og fra høyest til lavest.
Læringsmål
Eleven skal
• kunne sammenlikne og måle lengder
• kunne velge hensiktsmessige målenheter
Viktige begreper
Størrelsesbegreper er relative begreper. Det vil si at vi alltid må angi størrelsen på noe i relasjon til noe annet.
• måle
• sammenlikne
• enhet
• målenhet
I tidligere tider var det vanlig å ta utgangspunkt i kroppsdeler når man skulle måle lengder. Dette var praktisk, siden lengdemålet da alltid var tilgjengelig der man var, men det gav usikre mål. De varierte fra person til person og fra land til land. Derfor meldte behovet seg for standardiserte målenheter. Når vi måler, sammenlikner vi en lengde med noe annet og teller antallet enere av målenheten. I dette kapitlet bruker vi blant annet tommel, fot og fingerspenn for å sammenlikne lengder. Elevene bør oppfordres til å reflektere rundt hvilken målenhet de mener er best egnet til å måle ulike lengder.
Eksempler på gamle lengdemål:
• Steinkast – avstanden man kunne kaste en nevestor stein
• Pilskudd – avstanden man kunne skyte en pil med en bue
• Dagsreise – avstanden man kunne ro eller seile en båt i løpet av en dag
Utstyr
Ikke-standardiserte målenheter:
• binderser, blyanter, fyrstikker, viskelær, hoppetau, kladdebøker osv
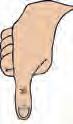
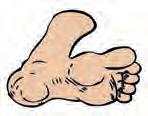
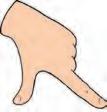
tommel fot fingerspenn
19 Hvor lang er kanten på matboksen din?
Før i tiden målte folk ved hjelp av kroppen. Føtter, tomler og fingerspenn ble brukt til å måle med.

Kanten på matboksen er like lang som tomler.
Kanten på matboksen er like lang som føtter.
Kanten på matboksen er like lang som fingerspenn.
20 Hvor lang er vinduskarmen i klasserommet?
Vinduskarmen er like lang som tomler.
Vinduskarmen er like lang som føtter.
Vinduskarmen er like lang som fingerspenn.
21 Hvor langt er klasserommet ditt?
Klasserommet er like langt som tomler.
Klasserommet er like langt som føtter.
Klasserommet er like langt som fingerspenn.
Kroppsmål:
• tomme – tverr målet av tommelfingeren målt ved roten av neglen
• fot – avstanden mellom hælen og tuppen av stortåa
• fingerspenn – avstanden mellom tommelspissen og spissen av lillefingeren når fingrene er spent ut
Tips til oppstart
Å måle er en ferdighet og må undervises i på en litt annen måte enn et begrep.
Kognisjons/modelleringsfasen:
Ta med en planke til klasserommet, eller vis planken til Pi og Luringen på myldrebildet. Du sier
at denne planken er perfekt som begynnelse på en liten trehytte, men at du trenger flere like lange planker. Legg fra deg planken og lat som om du går til butikken. Der sier du at du vil ha mange planker som er like lange som den du har liggende hjemme. Den ansatte i butikken skjønner ingenting, for han vet jo ikke hvor lang planken som ligger hjemme hos deg er, og det vet jo egentlig ikke du heller. Dermed går du hjem og måler med forskjellige ikke-standardiserte målenheter. Eksempler på enheter: tomme, fot, fingerspenn, håndsbredd, binderser, blyanter, fyrstikker, viskelær o.l. I klasserommet kan dere sammen finne ut hva som
tiden hjelp av tomler og brukt til med.
Kan jeg bruke foten min til å måle denne esken? Kan jeg bruke foten min til å måle klossen? Kan jeg bruke klossen til å måle esken?
Det vi bruker til å sammenlikne lengde med, kaller vi måleenhet.



22 Snakk sammen. Finn en måleenhet som passer.
Jeg skal måle hvor lang en blyant er.
Da kan jeg måle med
en kloss
Jeg skal måle hvor lang en sko er.
Da kan jeg måle med
måleenhet
Jeg skal måle hvor lang en fotballbane er.
Da kan jeg måle med
egner seg best til å vise lengden med når du går i butikken igjen. Svaret er: Det du får mest effektiv og presis måling med.
Øvefasen: Elevene får deretter gjøre egne erfaringer med å måle med ulike målenheter og her me etter det de har sett du har gjort. Noen elever kan være unøyaktige når de måler. Da er det viktig at læreren er observant og tett på, slik at disse elevene får rask støtte og hjelp til å måle nøyaktig.
Automatiseringsfasen: Når elevene er trygge på å måle og de måler nøyaktig, kan de øve mer på egen hånd.
Arbeid med sidene
La elevene arbeide sammen, og les oppgavene høyt.
19 I denne øvingsoppgaven bruker elevene ulike målenheter for å måle den samme lengden. Snakk med elevene om hvilken målenhet de bruker, og hvilken de synes er best. Det kan være lurt å legge de ulike målenheten etter hverandre. Bruk for eksempel begge tomlene og flytt én og én mens dere teller antallet enheter.
20 Dette er en øvingsoppgave der elevene bruker ulike målenheter for å måle den samme lengden. Snakk med elevene om hvilken målenhet de bruker, og hvilken de synes er best.
21 Dette er en øvingsoppgave der elevene bruker ulike målenheter for å måle den samme lengden. Snakk med elevene om hvilken målenhet de bruker, og hvilken de synes er best.
22 I denne vurderingsoppgaven skal elevene vurdere hvilken målenhet som passer best. Dere kan gjerne vurdere andre ikke-standardiserte målenheter i tillegg til kroppsmålene. Hvilken målenhet egner seg best?
Tips til videre arbeid
• Gi elevene praktiske oppgaver:
– La elevene tippe hvor langt ti meter er ute i skolegården. Mål deretter med meterstokk. Stemte det?
– Hvor mange skritt er det rundt skolen?
– Mål diameteren rundt et tre i skolegården. Hvilken målenhet kan vi bruke i dette tilfellet?
Vurderingsaktiviteter
• Når dere skal gå ut av klasserommet: Be elevene måle avstanden fra pulten sin til døra med føttene sine og fortelle deg lengden i antall føtter.
Eleven skal
• vite forskjellen på lengde og bredde
• kunne velge hensiktsmessige målenheter
Viktige begreper
• lengde
• bredde
• målenhet
Vi fortsetter å måle med ikke-standardiserte målenheter.
Når vi måler linjer eller kanter i vannrett stilling, kaller vi lengdemålet som regel for lengde eller bredde, alt etter om det er den lengste eller korteste siden av en gjenstand vi måler. Vi kaller den korteste siden for bredde og den lengste siden for lengde. Når vi måler lengde og bredde, pleier vi å holde måleutstyret slik at vi måler i retning fra venstre mot høyre (leseretningen). Det gjør det enklere når vi skal måle med linjal seinere.
Utstyr
• rektangulære ting i ulike størrelser, som bøker, papplater og liknende
Vi kaller den korteste siden for bredde og den lengste siden for lengde.
23 Hvor lang er Matemagisk-boka di?
Velg måleenhet selv.
Lengden til boka er lik
måleenhet
24 Hvor bred er Matemagisk-boka di?
Velg måleenhet selv.
Bredden til boka er lik
måleenhet
25 Mål en annen bok.
Lengden til boka er lik
måleenhet
Bredden til boka er lik
måleenhet



Tips til oppstart
Assosiasjonsfasen: Vis fram Matemagisk-boka, før fingeren over og tell antallet kanter. Spør om de synes at kantene er like lange. Fortell at vi kaller de lengste sidene for lengde og de korteste sidene for bredde. Vis fram enda en flateform som har tydelig lengde og bredde, og sett ord på de lengste sidene, lengde, og de korteste sidene, bredde. Gjenta med flere ting (ark, esker, viskelær, fyrstikkeske, klassebilde o.l.).
Forskjellslæring: La elevene få peke ut lengde og bredde på ting i klasserommet (pulten, kateteret, plakater, vinduer, dører, gulvflaten, bøker, viskelær o.l.). Hold til slutt fram ulike ting og still sant/usant-spørsmål: «Er det sant at dette er lengden/bredden?»
Generalisering: Pek på ulike bredder og spør hva de har til felles. Gjør det samme med lengder. Til slutt snakker dere om hva alle bredder/lengder har til felles. Hvilke egenskaper er like?
Lengden
Bredden
Lengden
Bredden
Lengden
Bredden
26 Hvor lang er bredden og lengden? Velg måleenhet.
Lengden til firkanten er lik
Bredden til firkanten er lik
Lengden til flagget er lik
Bredden til flagget er lik
Lengden til esken er lik
Bredden til esken er lik
Arbeid med sidene
La elevene arbeide sammen, og les oppgavene høyt.
23 Dette er en øvingsoppgave der elevene velger en målenhet og teller antallet enheter. Hvilken enhet egner seg best?
24 Dette er en øvingsoppgave der elevene velger en målenhet og teller antallet enheter. Snakk med elevene om hvilken enhet de bruker
25 Dette er en øvingsoppgave der elevene velger en målenhet og teller antallet enheter. Snakk med elevene om bredde og lengde.
26 Dette er en oppgave for underveisvurdering. Velges det relevante målenheter? Har eleven begrep om lengde og bredde? I den nederste oppgaven må vi ikke forveksle lengde/bredde med høyde. Styr oppmerksomheten mot stillingen.
Tips til videre arbeid
Gi elevene praktiske oppgaver:
• Mål lengden og bredden til ulike bøker, nettbrett, bokser, kasser, melkekartonger o.l.
• Mål lengden og bredden av klasserommet.
• Når dere skal gå ut av klasserommet: Be elevene peke ut lengden og bredden på ulike bøker, bokser, kasser, melkekartonger og liknende.
– Spør: «Hva har alle lengder til felles?»
– Spør: «Hva har alle bredder til felles?»
Matemagisk følger fagfornyelsen (LK20) og vekker nysgjerrigheten til elevene. Med Matemagisk får elevene utforske matematikk aktivt, både sammen og alene.
Matemagisk skaper mestringsfølelse, engasjement og verdifulle matemagiske oppdagelser.
Matemagisk 1 består av:
• grunnbok 1
• oppgavebok 1
• Lærerveiledning 1
• Matemagisk 1–7 Aschehoug Univers
På Aunivers.no finner du Aschehougs digitale læremidler.