Asbjørn
Matemagisk



Asbjørn Lerø Kongsnes
Hedda Louise Lang-Ree
Gaute Nyhus
Matemagisk

APARAL L E LLBOK

Bli kjent med Matemagisk 5 Hva betyr sporene?




SNAKKE MATTE
SPILL
AKTIVITET
Oppgaver som viser spesielt viktige ideer og tenkemåter.
Oppgaver der dere skal snakke matte med hverandre. Her trener dere på å forklare hvordan dere tenker.
Henviser til tilsvarende oppgave i grunnboka. Det matematiske innholdet er bevart, men oppgaven kan være justert i parallellboka.
FØLG STIEN
Oppgaver der du får trent mer på det klassen har arbeidet med i fellesskap. Her trener du på én ting om gangen.
TERRENGLØYPA
Oppgaver som bygger videre på det klassen har arbeidet med i fellesskap. Her kan du få sammensatte utfordringer, også fra flere temaer på en gang.









0
Vårt matemagiske klasserom4
1 Å utforske brøk ..........19
Bli kjent med brøk .................22
Brøkdelen
Brøkdelen
2
2 Likeverdige brøker ........53 En halv .........................55
3 Addisjon og subtraksjon med brøk .....87

4
4 Desimaltall og brøk på tallinja






















SNAKKE MATTE

a Hva ser dere på bildet?
c Hvor langt tror dere toget er?
b Hvor tror dere bildet er tatt?
d Hvor mange containere tror dere det er plass til på toget?
SNAKKE MATTE
Hvor mange personer er det mulig å få plass til i deres klasserom?
Svar med
• et tall dere er ganske sikker på at er for høyt
• et tall dere er ganske sikker på at er for lavt
• et tall dere tror er omtrent riktig
SNAKKE MATTE
Hvor mange blyanter bruker klassen deres i løpet av et år?
Svar med
• et tall dere er ganske sikker på at er for høyt
• et tall dere er ganske sikker på at er for lavt
• et tall dere tror er omtrent riktig
Bildet til høyre viser noen prikker. Vi skal finne ut hvor mange prikker det er, uten å telle alle sammen.
Her ser du hvordan fire elever har sett for seg prikkene.
Finner du andre måter å se prikkene på? Tegn alle måtene du finner.
OPPGAVE 002
Lag tegninger som viser ulike måter å se prikkene. Tegn så mange måter du klarer.
OPPGAVE 003
Lag tegninger som viser ulike måter å se prikkene. Tegn så mange måter du klarer.
Lag tegninger som viser ulike måter å se prikkene. Tegn så mange måter du klarer.
Spill : Treff tallet
DEL 1
Dette er et spill for to spillere.
Hvordan spille?
Spiller A begynner med å velge tallet 1, 2 eller 3.
Spiller B legger til 1, 2 eller 3 til tallet spiller A valgte.
Spiller A legger til 1, 2 eller 3 til summen av de forrige tallene.
Slik fortsetter det.
Vinneren er den som legger til et tall slik at summen blir måltallet 13.
Eksempel
Spiller A velger tallet 2.2
Spiller B legger til 3.2 + 3 = 5
Spiller A legger til 1.5 + 1 = 6
Spiller B legger til 2.6 + 2 = 8
Spiller A legger til 2.8 + 2 = 10
Spiller B legger til 3.10 + 3 = 13
Det er viktig å spille spillet mange ganger!


Siden spiller B la til et tall slik at summen ble måltallet 13, vinner spiller B.
DEL 2
a Diskuter ulike strategier i spillet Treff tallet. Hvordan bør vi tenke for å vinne?
b Er det best å være spiller A eller spiller B?
DEL 3
a Spill Treff tallet med måltallet 12. Er det best å være spiller A eller B nå?
b Hva med måltallet 14? Måltallet 15? Måltallet 16? Ser dere noe mønstre?

Hvor mange svarte flekker er det på leoparden?
Svar med
• et tall dere er ganske sikker på at er for høyt
• et tall dere er ganske sikker på at er for lavt
• et tall dere tror er omtrent riktig
SNAKKE MATTE
a Hvilke tall er tegnet på tallkartet?
b Se nøye på tallene. Hvilke mønstre oppdager dere?
Beskriv mønstrene fra Snakke matteoppgaven her.

Tallet 12 kan tegnes på ulike måter.
a Hva er felles for alle måtene?
b Hvilke av tallene under kan tegnes på ulike måter? Du må dele tallene i like store grupper.
Vis hvordan du tenker ved å tegne tallene på ulike måter.



OPPGAVE 006
Hvilke av tallene fra tallkartet kan tegnes på flest ulike måter? Du må dele tallene i like store grupper.
SNAKKE MATTE
a Kan dere dele tallet 7 i ulike deler slik at det er like mange i hver del?
b Hvilke tall er tegnet som én sirkel på tallkartet. Hva er felles for disse tallene?
SNAKKE MATTE
Bildene viser en del av et tall fra tallkartet. Hvilke tall kan det være?
SNAKKE MATTE

Hvor mange containere tror dere det er på bildet?
Svar med
• et tall dere er ganske sikker på at er for høyt
• et tall dere er ganske sikker på at er for lavt
• et tall dere tror er omtrent riktig
Froskehopp
Utstyr:
•Brikker (frosker) i to farger
MÅL:
De røde og blå froskene skal bytte plass på så få trekk som mulig.
Når du har løst oppgaven, ser det slik ut:
Regler:
•En frosk kan gå ett steg til siden hvis sidefeltet er ledig.
•En frosk kan hoppe over én annen frosk hvis landingsfeltet er ledig.
•Det kan bare stå én frosk på hvert felt.
a Hvor mange trekk trenger du for å bytte plass på froskene?
Svar: trekk
b Hva hvis det er 3 frosker på hver side?
Svar: trekk
c Hva hvis det er 4 frosker på hver side?
Med to frosker på hver side klarte jeg det på 8 trekk.

Svar: trekk
Hiyanna har skrevet opp hvor mange ganger hun flytter røde og blå frosker etter hverandre når det står to frosker på hver side. Hun bruker så få trekk som mulig.
2froskerpåhverside:12221
d Skriv opp på liknende måte hvor mange ganger du flytter røde og blå frosker når det er 3 frosker på hver side. Bruk så få trekk som mulig.
e Gjenta oppgave d for 4 frosker på hver side.
f Ser du noe mønster?












1 Å utforske brøk
Samtalebilde:
1Hva ser dere på bildene?
2Hva har tingene på bildene til felles?

3Hva er likt, og hva er ulikt med appelsinene?
Begreper: Tenk med:




Oppstart
Her er sirkler delt i én, to, tre, fire, fem, seks, åtte, ti og tolv like store biter.
Utfordring 1
Hvor mange biter trengs for å dekke en hel sirkel?
GråOransjeMørkeblå
1bitbiter 2biter
GrønnBrunRød
biterbiterbiter
LillaGulLyseblå
biterbiterbiter
Utfordring 2
Sett strek mellom brøksirkelen og riktig forklaring.
1 firedel av en hel sirkel
Utfordring 3
Sant eller usant?
1 seksdel av en hel sirkel
a En oransje bit er større enn tre røde biter.
b Tre røde biter er like stort som to grønne biter.
c En grønn bit er halvparten av en oransje bit.
Tre røde biter dekker en oransje bit.
En rød bit er 1 tredel av en oransje bit. =
Utfordring 4
Sant eller usant?
a En grønn bit er 1 todel av en oransje bit.
b En gul bit er 1 todel av en brun bit.
c En lilla bit er 1 åttedel av en oransje bit.
Utfordring 5
Hvilken bit er
1 tredel av en hel sirkel
SantUsant

SantUsant
a 1 todel av en mørkeblå bitSvar:
b 1 todel av en rød bitSvar:
c 1 firedel av en mørkeblå bitSvar:
kjent med brøk
Hvor stor del av sirkelen er fargelagt?
FigurBeskrivelseBrøkdel med ordBrøkdel med symbol
1 av 2 like store deler er fargelagt.

1 av 4 like store deler er fargelagt.
1 av 12 like store deler er fargelagt.
Figuren må være delt inn i like store deler.
SNAKKE MATTE
1 todel av sirkelen er fargelagt.
1 firedel av sirkelen er fargelagt.
1 tolvdel av sirkelen er fargelagt.
1 2 av sirkelen er fargelagt.
1 4 av sirkelen er fargelagt.
1 12 av sirkelen er fargelagt.
Tallet på toppen kalles teller og tallet nede kalles nevner
Teller Nevner Brøkstrek 1 2

Hvor stor del av figuren er fargelagt? Hvordan skriver vi det med symboler? a b
SNAKKE MATTE
Sammenlikn figurene. Hva er likt, og hva er ulikt?
OPPGAVE 101
Hvor stor del av figuren er fargelagt? Skriv med ord og som brøk.
g Skriv brøkene over fra minst til størst.
h Hvordan tenkte du da du sorterte brøkene?



SNAKKE MATTE
Tuva og Yonas har bakt hver sin kake til skoleavslutningen. Når de drar hjem, er halvparten av hver kake spist opp.
a Hvor stor brøkdel av kaka si får Tuva med hjem?
b Hvor stor brøkdel av kaka si får Yonas med hjem?
c Hvem får mest kake med hjem?




Å brette papirstrimler
DEL 1
Du trenger en papirstrimmel.

Brett papirstrimmelen i to like store deler.

Gjett hvor mange like store deler papirstrimmelen er brettet i nå.
Brett så den doble strimmelen i to like store deler.

Brett ut og se om du gjettet riktig.
Brett sammen papirstrimmelen igjen. Brett i to like store deler enda en gang.



6 Hvor mange like store deler er papirstrimmelen brettet i nå?
6 Forklar med dine egne ord hvordan du kan brette en papirstrimmel i åtte like store deler.
DEL 2
Begynn med en ny papirstrimmel.
Brett papirstrimmelen i tre like store deler.


Hold papirstrimmelen sammenbrettet.

3 4 DEL 3

Jeg tenker jeg skal lage en S når jeg skal brette i tre like store deler. er.


Brett i to like store deler på nytt. Hvis du har gjort riktig, er papirstrimmelen nå brettet i seks like store deler.


Er det mulig å brette en papirstrimmel i seks like store deler på andre måter?
Begynn med en ny papirstrimmel.
Brett papirstrimmelen i to like store deler.
Brett ut og fargelegg én av de to delene.

Forklar at du har fargelagt 1 2 av papirstrimmelen.
Lag tre nye papirstrimler der du fargelegger 1 3 , 1 4 og 1 6 av papirstrimmelen.
Vis med papirstrimler hvilken brøk som er størst av
OPPGAVE 102
a Tre venner deler én pizza likt. Hvor mye får de hver?
Skriv som brøk:
b Fem venner deler én pizza likt. Hvor mye får de hver?
Skriv som brøk:
c Ti venner deler én pizza likt. Hvor mye får de hver?
Skriv som brøk:
d Alle pizzaene er like store. Sett ring rundt vennegruppa som får mest pizza per person.



OPPGAVE 103


a Sorter brøkene fra minst til størst.
b Hvilke mønstre oppdager du når du sorterer brøker der telleren er 1?
OPPGAVE 104
En venn har gått glipp av de første mattetimene dere har hatt om brøk. Lag en plakat som vennen din kan se på. Tegn og skriv hva du har lært om brøk fram til nå. Bruk gjerne eksempler.
FØLG STIEN
OPPGAVE 105
Hvor stor del av figuren er fargelagt? Skriv med ord og som brøk.


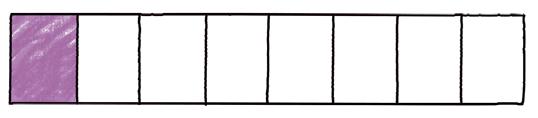


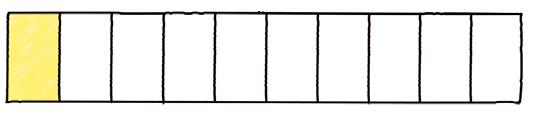
OPPGAVE 106
Noen barn deler én stor pizza likt mellom seg. Tegn og skriv hvor stor brøkdel hvert barn får hvis de er
MinstStørst e Skriv brøkene fra minst til størst.
OPPGAVE 107
Hvor stor del av figuren er fargelagt?
a b c d
e Brett en papirstrimmel til hver av figurene, og fargelegg like stor del.
OPPGAVE 108
Hvilken bit er
a 1 2 av en oransje bit
Svar:
b 1 4 av en oransje bit
Svar:
c 1 5 av en oransje bit
Svar:
d 1 3 av en oransje bit
Svar:
e 1 2 av en mørkeblå bit
Svar:
f 1 4 av en mørkeblå bit
Svar:
Brøksirkler
GråOransjeMørkeblå
GrønnBrunRød
LillaGulLyseblå
g 1 2 av en brun bit
Svar: h 1 2 av en rød bit
Svar:
Brøkdelen av en figur
Nevneren viser antall deler figuren er delt inn i. Telleren teller antall deler vi har.

3 firedeler er fargelagt.
7 sjudeler er fargelagt.


Vi skriver 3 4 .
SNAKKE MATTE
Vi skriver 7 7 .
Dette er det samme som én hel.
Alle delene i figuren må være like store!
Hvilke figurer og brøker hører sammen?
SNAKKE MATTE
a Hvilken brøk er størst av 3 6 og 4 6 ?
b Hvordan kan dere tenke når dere sammenlikner to brøker med lik nevner?
c Hvilken brøk er størst av 6 9 og 4 9 ?
Nevneren viser antall deler figuren er delt inn i. Telleren teller antall deler vi har. Teller Nevner Brøkstrek 6 9





a Hvilken brøk er størst av 2 3 og 2 6 ?
b Hvilken brøk er størst av 3 8 og 3 4 ?
c Hvordan kan dere tenke når dere sammenlikner to brøker med lik teller?
d Hvilken brøk er størst av 5 7 og 5 8 ?
OPPGAVE 109 Fyll ut tabellen.
Matemagisk 5 APARAL L ELLBO K
Matematikk for 5.–7. trinn
Matemagisk følger fagfornyelsen (LK20) og stimulerer elevene til å utforske og diskutere fra første stund. Lærebokas struktur ivaretar fellesskapet i klassen slik at elevene lærer sammen. Elevene får individuelle tilpasninger gjennom en unik differensieringsmodell.
Matemagisk 5 består av:
• grunnbok 5A
• grunnbok 5B
• parallellbok 5A
• parallellbok 5B
• oppgavebok 5
• Matemagisk 1–7 Aschehoug Univers
• ØveMatematikk
• Matemagisk 5 Digitalbok
• digital lærerveiledning
På Aunivers.no finner du Aschehougs digitale læremidler.
