Matemagisk
Asbjørn Lerø Kongsnes
Kristina Markussen Raen
Matemagisk
PARAL L E LLBOK
Asbjørn Lerø Kongsnes
Kristina Markussen Raen
Martin Sørdal
Bli kjent med Matemagisk 7 Hva betyr sporene?
SNAKKE MATTE
SPILL
AKTIVITET
Oppgaver som viser spesielt viktige ideer og tenkemåter.
Oppgaver der dere skal snakke matte med hverandre. Her trener dere på å forklare hvordan dere tenker.
2
Henviser til tilsvarende oppgave i grunnboka. Det matematiske innholdet er bevart, men oppgaven kan være justert i parallellboka.
FØLG STIEN
Oppgaver der du får trent mer på det klassen har arbeidet med i fellesskap. Her trener du på én ting om gangen.
TERRENGLØYPA
Oppgaver som bygger videre på det klassen har arbeidet med i fellesskap. Her kan du få sammensatte utfordringer, også fra flere temaer på en gang.
0 Vårt matemagiske klasserom4
1 Statistikk ..............13
Søylediagram .....................15
Linjediagram .....................23
Sektordiagram ....................32
Sentralmål .......................37
Oppsummering ...................51
2 Regning med brøk ........53
Grunnleggende brøk ...............56
Addisjon og subtraksjon med brøk .....63
Brøkdelen av et tall ................70
Oppsummering ...................83
3 Brøk, desimaltall og prosent85
Grunnleggende om brøk, desimaltall og prosent ..............88 Hvor mange prosent? ...............96 Tall med mange desimaler ..........108 Oppsummering ..................117
4 Regning med prosent .....119 10 %, 20 %, 25 % og 50 % .........121 Andre prosenter ..................130 Oppsummering ..................152
Hvor mange brune flekker er det på en sjiraff?
Svar med
•et tall dere er ganske sikker på at er for høyt
•et tall dere er ganske sikker på at er for lavt
•et tall dere tror er omtrent riktig
OPPGAVE 001
En trapp har 4 trappetrinn. Noah kan gå ett trinn om gangen eller to trinn om gangen når han skal opp trappa.
a På hvor mange ulike måter kan Noah gå opp trappa?
Én måte å gå opp trappa er: 1 steg
2 steg 1 steg
Hvor mange ulike måter er det hvis trappa har
b 6 trappetrinn
c 8 trappetrinn
Rammedomino
Dette er et spill for tre lag med to spillere på hvert lag.
Utstyr: 28 dominobrikker dere får fra læreren deres.
Mål:
Hver spiller skal lage en ramme med fire brikker. Sidene som ligger inntil hverandre, må passe sammen. Laget som først fullfører sine to rammer, vinner spillet.
Forberedelser:
•Del ut 4 brikker til hver spiller. Legg brikkene synlig på bordet med forsiden opp.
Jeg har fullført rammen min.
•Legg de 4 siste brikkene i fellesområdet midt på bordet, med forsiden opp.
Hvordan spille?
I hver runde velger laget én av sine spillere som skal gjøre én av disse handlingene:
A Gi én av brikkene dine til medspilleren din.
B Legg én av brikkene dine i fellesområdet.
C Ta én brikke fra fellesområdet.
Ingen spillere kan ha mer enn 4 brikker foran seg. Derfor er den første handlingen i spillet å legge en brikke i fellesområdet.
Fellesområde
Hiyanna har bestemt seg for en regel tre tall skal følge.
TallFølger tallene regelen?
1, 3, 5Ja 2, 4, 6Ja 1, 2, 3Nei 7, 9, 11Ja 12, 8, 4Ja
a Seks elever prøver å finne ut hva regelen kan være. Hvilke elever har rett om hva regelen kan være?
Tallene øker med 2 for hver gang.
Tallene øker med det samme for hver gang.
Summen av tallene er større enn 10.
Tallene er enten bare partall eller bare oddetall.
b Fins det andre muligheter for hva regelen kan være?
Tallene øker med det samme for hver gang, men øker ikke med 1.
Forskjellen mellom hvert av tallene er mer enn 1.
c Lag din egen regel. La en medelev prøve å finne ut hva regelen din er, ved å si tre tall. Du må si om tallene følger regelen din eller ikke.
DanielMathilde
KimMina
IsmahilDanielle
Magiske kvadrater
Utstyr:
•Brikker med tallene fra 1 til 16
•Tomme kvadrater i størrelse 3 × 3 og 4 × 4
Et magisk kvadrat er et kvadrat der summen av tallene i hver rad, hver kolonne og langs hver diagonal blir den samme.
DEL 1
Vi skal undersøke om kvadratet under er et magisk kvadrat.
168 357 249
Rader er vannrette og går bortover.
Kolonner er loddrette og går nedover.
a Regn ut summen langs hver diagonal.
b Vis at summen langs hver rad blir 15.
c Regn ut summen langs hver kolonne.
d Forklar hvorfor dette ikke er et magisk kvadrat.
DEL 2
a Lag et magisk 3 × 3 kvadrat med tallene fra 1 til 9. Hvert tall kan bare brukes én gang.
Tallet 5 må stå i midten.
b Er det mulig å lage det magiske kvadratet på ulike måter?
Skriv alle måtene du finner.
DEL 3
Lag et magisk 4 × 4 kvadrat med tallene fra 1 til 16. Hvert tall kan bare brukes én gang.
Statistikk
Samtalebilde:
1Hva ser dere på bildet?
2Hvordan kan kjøretøyene deles inn i grupper? Kandet gjøres på ulike måter?
3Omtrent hvor mange biler tror dere det er på bildet?
4Omtrent hvor mange motorsykler tror dere det er på bildet?
5Omtrent hvor lang tror dere en typisk bil er?
Begreper:
Søylediagram
Linjediagram
Sektordiagram
Førsteakse Andreakse Frekvenstabell
Sentralmål
Gjennomsnitt
Median
Oppstart
Nidarosdomen er 98 m høy. Omtrent hvor høye er de andre bygningene? Begrunn svarene.
Nidarosdomen Frihetsgudinnen
Eiffeltårnet
Empire State Building Burj Khalifa
98 m
Søylediagram
SNAKKE MATTE
Søylediagrammet viser hvor mange elever som deltar på ulike fritidsaktiviteter i klasse 7A.
Antall elever
Fritidsaktiviteter i klasse 7A
FotballHåndballOrienteringSvømmingDansingBand
a Hvilken fritidsaktivitet er mest populær?
b Hvor mange kategorier viser diagrammet?
c Hvor mange elever deltar på svømming?
d Hvor mange flere elever deltar på dansing enn på svømming?
e Hvor mange elever tror dere det er i klassen? Begrunn svaret.
Kategoriene er her de ulike fritidsaktivitetene. Håndball er ett eksempel på en kategori.
OPPGAVE 101
Se på diagrammet i Snakke matte-oppgaven. Sant eller usant? SantUsant
Det er flere som deltar på svømming enn på håndball.
Det er flere som deltar på ballspill enn på de andre aktivitetene til sammen.
SNAKKE
Under ser dere 12 flagg. På hvilke måter er det mulig å sortere flaggene?
DanmarkPeru
Norge
Sameland Syria Somalia
Frankrike
PolenRussland
Island
Jemen EU
a Sett strek mellom flagg og riktig kategori.
Flagg med 2 farger Flagg med 3 farger Flagg med 4 farger
b Fyll ut tabellen.
KategoriAntall flagg
Flagg med 2 farger
Flagg med 3 farger
Flagg med 4 farger
c Lag et søylediagram som viser resultatet.
Antallflagg
Observere og systematisere
1 Velg noe dere vil undersøke i klassen. Det skal være noe dere kan observere. Det vil si at dere skal måle eller telle noe.
2 Sorter informasjonen i kategorier, og lag en frekvenstabell.
KategoriTellestreker Frekvens (antall)
Det kan være farge på klær, fargeblyanter, farge eller lengde på håret, hvilke biler som kjører forbi skolen, lengde på navnene i klassen, osv. en, osv.
Frekvensen er det samme som antallet observasjoner av en kategori. Dette er et eksempel på en frekvenstabell:
FremkomstmiddelFrekvens (antall)
3 Lag et søylediagram som viser resultatet.
Frekvens(antall)
Sykkel3 Bil5 Lastebil1
SNAKKE MATTE
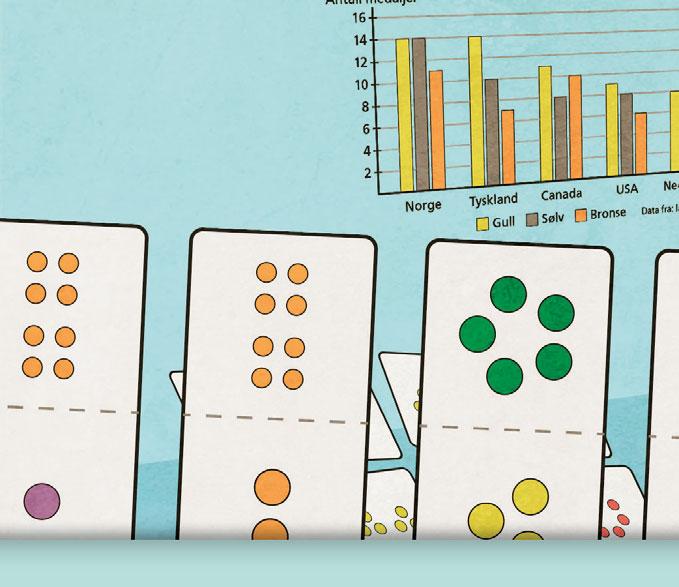
Søylediagrammene viser hvor mange medaljer de fem beste landene vant under vinter-OL i Pyeongchang i 2018. Begge søylediagrammene er laget med utgangspunkt i det samme datasettet.
Antall medaljer
Land med flest medaljer i vinter-OL 2018
NorgeTysklandCanadaUSANederland
Land med flest medaljer i vinter-OL 2018
NorgeTysklandCanadaUSANederland
GullSølvBronse Data fra: langrenn.com
a Forklar hva diagrammene viser.
b Hvor mange gullmedaljer vant Nederland?
c Hvor mange medaljer vant Norge?
d Sammenlikn diagrammene. Hva er likt, og hva er ulikt?
e Hvilket diagram synes dere er best? Begrunn svaret.
Et datasett er den informasjonen vi for eksempel kan samle inn ved en spørreundersøkelse eller ved observasjon.
FØLG STIEN
OPPGAVE 103
Tabellen viser hvor mange elever som syklet til skolen en dag på Åsen skole. Lag et søylediagram som viser informasjonen fra tabellen.
Antallelever
KlasseAntall elever 7A20 7B20 7C10 7D15
OPPGAVE 104
Diagrammet viser antall innbyggere i ulike fylker i 2020.
Agder Antall innbyggere i ulike fylker i 2020
Innlandet
Møre og Romsdal
Nordland
Oslo
Rogaland
Troms og Finnmark
Trøndelag
Vestfold og Telemark
Vestland
Viken
Antall innbyggere
a Omtrent hvor mange innbyggere var det i Vestland?
Svar:
Jeg ser at det var litt mer enn 300 000 innbyggere i Agder i 2020.
Data fra: ssb.no
b Omtrent hvor mange flere innbyggere var det i Oslo enn i Rogaland?
Svar:
Til høyre ser du 20 figurer.
a Fyll ut tabellen.
KategoriAntall
Trekant
Firkant
Sirkel
Kryss
Hjerte
Stjerne
b Lag et søylediagram som viser resultatet.
Antallfigurer
c Sorter figurene på en annen måte og lag et søylediagram som viser resultatet.
Antallfigurer
OPPGAVE 106
I 2020 ble verden rammet av en pandemi (covid-19). Diagrammet viser antall påviste tilfeller i Norge etter kjønn og ulike aldersgrupper.
Antall påviste tilfeller av covid-19 i Norge (Tall per mars 2021)
0–910–1920–2930–3940–4950–5960–6970–7980–8990+
a Hva viser diagrammet?
KvinnerMenn
b I hvilken aldergruppe hadde flest personer fått påvist covid-19 per mars 2021?
Svar:
c Omtrent hvor mange kvinner i aldersgruppa 50–59 år hadde fått påvist covid-19 per mars 2021?
Svar:
d Omtrent hvor mange personer i aldersgruppa 30–39 år hadde fått påvist covid-19 per mars 2021?
Svar:
e Var det stor forskjell på antall kvinner og antall menn som hadde fått påvist covid-19 per mars 2021?
Linjediagram
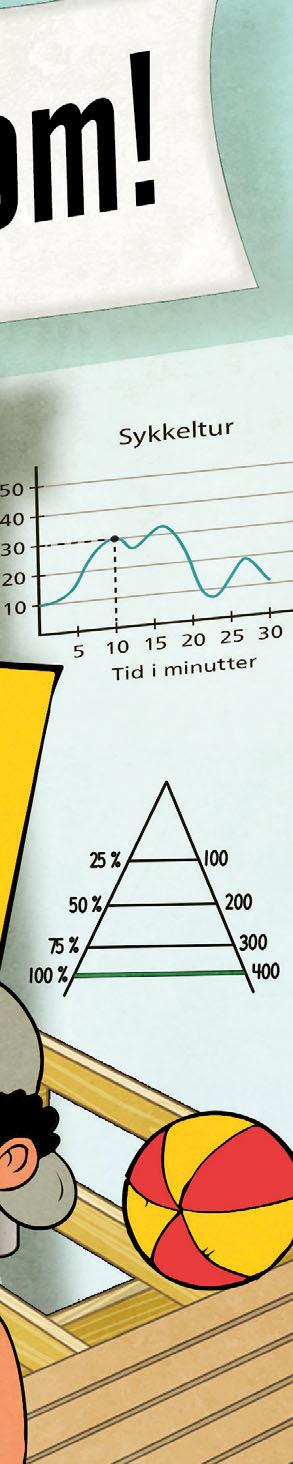
Marta har vært på sykkeltur. Linjediagrammet viser informasjon om turen. Langs førsteaksen måler vi tid i minutter. Langs andreaksen måler vi syklistens høyde over havet.
OPPGAVE 107
Det svarte punktet viser at etter 10 minutter var Marta 30 meter over havet.
Førsteaksen er vannrett og kan også kalles x-aksen. Andreaksen er loddrett og kan også kalles y-aksen.
Det er lurt å bruke linjediagram når vi vil vise utvikling over tid.
Se på eksemplet over. Omtrent hvor høyt over havet var Martha etter 20 minutter?
Svar: meter over havet.
SNAKKE MATTE
Linjediagrammet viser temperaturen gjennom et døgn i Stavanger.
Temperatur gjennom døgnet
a Hva viser førsteaksen? Hva viser andreaksen?
b Når på dagen var temperaturen høyest?
c Hva var temperaturen på det høyeste?
d Beskriv hvordan temperaturen endret seg i løpet av døgnet.
e Når på året tror du målingen er gjort? Begrunn svaret.
SNAKKE MATTE
Kaja aker ned en bakke. Hvilket diagram tror dere passer best til situasjonen?
Begrunn svaret.
SNAKKE MATTE
Sylvester bygger et legotårn. Hvilket diagram tror dere passer best til situasjonen?
Begrunn svaret.
SNAKKE MATTE
Her ser dere tre linjediagrammer som viser temperaturen en dag fra kl. 09 til kl. 12.
a Sammenlikn diagrammene. Hva er likt, og hva er ulikt?
b Er alle diagrammene tegnet på riktig måte? Begrunn svaret.
Ta pulsen
I denne aktiviteten skal dere undersøke hvordan pulsen endrer seg over tid etter en løpetur.
1 Øv på å finne og måle pulsen.
For å finne antall pulsslag per minutt kan dere telle antall pulsslag i løpet av 15 sekunder og deretter gange med 4.
Da er pulsen min 4 30 = 120. nder ag.
I løpet av 15 sekunder telte jeg 30 pulsslag.
2 Løp en eller to runder rundt skolen så fort dere kan.
3 Mål pulsen når dere er ferdige med å løpe. Mål etter 0, 1, 2, 3 og 4 minutter.
4 Fyll ut tabellen. Antall
5 Lag et linjediagram som viser hvordan pulsen endrer seg over tid etter løpeturen.
Pulsens endring over tid etter en løpetur
Antall minutter etter at dere er ferdige med å løpe
Nora og Betina har svømt om kapp. De har svømt fra den ene siden til den andre siden av bassenget, og tilbake igjen.
Svømmekonkurransen
a Hvor lang tid brukte Betina?
b Hvem kom først til mål?
c Hvor langt er bassenget?
d Hvor langt svømte de?
e Hvor lang tid hadde Betina brukt da hun snudde?
f Hvem snudde først?
g Beskriv konkurransen mellom Nora og Betina så nøyaktig dere klarer.
h Omtrent hvor mange meter ledet Betina med på det meste?
FØLG STIEN
OPPGAVE 108
Diagrammet viser hvordan temperaturen i Oslo varierte gjennom en måned i 2020.
1.3.5.7.9.11.13.15.17.19.21.23.25.27.29.31.
Dato
a Hva viser førsteaksen?
b Hva viser andreaksen?
c Hvilken dag var kaldest?
Svar:
d Hva var temperaturen den kaldeste dagen?
Svar: °C
Data fra: yr.no
Diagrammet viser hvordan temperaturen i Oslo varierte gjennom en måned i 2020.
1.3.5.7.9.11.13.15.17.19.21.23.25.27.29.31. Dato
Data fra: yr.no
a Beskriv hvordan temperaturen utviklet seg fra starten av måneden til slutten av måneden.
b Hvilken måned kan dette være? Begrunn svaret.
c Hva var temperaturforskjellen mellom den varmeste og kaldeste dagen?
Svar: °C
d Hvor mange dager i løpet av måneden var temperaturen mellom 6 °C og 12 °C?
Svar:
OPPGAVE 110
Maja og Lea er i en fornøyelsespark og skal ta tømmerrenna. Diagrammet viser hvor mange meter tømmerrenna er over startpunktet på ulike tidspunkter.
En tur med tømmerrenna
Antall meter over startpunktet Tid i sekunder
a Hvor høyt over startpunktet er tømmerrenna på sitt høyeste?
Svar:
b Hvor lenge varer en tur med tømmerrenna?
Svar:
c Beskriv Maja og Leas tur med tømmerrenna.
Storm har løpt 3 km. Tabellen viser pulsen hans på ulike tidspunkter.
Avstand han har løpt 0 m500 m1000 m1500 m2000 m2500 m3000 m
Puls, slag i minuttet 75150140155150145170
a Lag et linjediagram som viser dataene fra tabellen.
Puls under Storms løpetur
Det er lurt å måle avstanden langs førsteaksen og pulsen langs andreaksen.
Pulsslag per minutt
Avstand han har løpt i meter
b Beskriv utviklingen i Storms puls.
Diagrammet viser antall scorede mål for Bodø/Glimt og Molde i Eliteserien i fotball 2020.
Scorede mål i Eliteserien 2020
123456789101112131415161718192021222324252627282930
Kampnummer
a Hvor mange mål scoret Bodø/Glimt på de første 11 kampene?
Svar: mål
b Hvor mange kamper brukte Molde på å passere 60 mål?
Svar: kamper
c Sant eller usant?
1 Molde har scoret flere mål enn Bodø/Glimt.
2 Etter 20 kamper, hadde Bodø/Glimt scoret 20 flere mål enn Molde.
3 Forskjellen i antall scorede mål mellom Bodø/Glimt og Molde øker gjennom hele sesongen.
SantUsant
Molde
Bodø/Glimt
Sektordiagram
Et sektordiagram er en sirkel delt inn i ulike sirkelsektorer
Hver sirkelsektor hører til en kategori. Sirkelsektoren viser hvor stor del kategorien utgjør av helheten.
FavorittmatFrekvensDel av helheten
Taco1050
SNAKKE MATTE
Er diagrammet i avisartikkelen under et godt diagram? Begrunn svaret.
Nikolay har skrevet en artikkel i skoleavisa:
Sjokkerende mange favorittmiddager i 7C
I de siste mattetimene har vi undersøkt hvilke favorittmiddager elevene i 7C har. Resultatene vises i tabellen og sektordiagrammet. I klassen er det så mange som 12 ulike favorittmiddager. Det var overraskende!
FavorittmatFrekvens
Pasta bolognese 4
Pasta carbonara 1
Pizza margherita 3
Pizza med ost og skinke 5
Pizza med pepperoni 2 Taco 5 Hamburger 2
3 Sushi 2 Laks 1
1 Fiskepinner 1
Til sammen30
Favorittmat i 7C
Fiskepinner
Fiskekaker
Laks
Sushi
Cheeseburger
Hamburger
Taco
Skrevet av Nikolay 12 år
Pasta bolognese
Pasta carbonara
Pizza margherita
Pizza med ost og skinke
Pizza med pepperoni
Emilie og Milla synes diagrammet i avisartikkelen er uoversiktlig. De har derfor gruppert observasjonene i ulike kategorier.
a Forklar hvordan Emilie har gått fram for å lage diagrammet.
b Sammenlikn Emilies diagram med diagrammet i avisartikkelen. Hva er likt, og hva er ulikt?
c Sammenlikn Emilies diagram med diagrammet i avisartikkelen. Hvilket diagram er mest oversiktlig? Begrunn svaret.
Milla har gruppert observasjonene på en annen måte.
d Hvordan tror dere Milla har tenkt da hun lagde diagrammet?
Både Emilies og Millas diagram er laget ut fra resultatene i klasse 7C. Diagrammene viser de samme resultatene som i avisartikkelen, men på to andre måter.
e Sammenlikn diagrammene til Emilie og Milla. Hva er likt, og hva er ulikt?
f Liker dere Emilies eller Millas diagram best? Begrunn svaret.
Når dere diskuterer oppgaven over, kan du skrive noen notater her.
Pizza med ost og skinke
Millas diagram
Taco
Pasta bolognese Pizza margherita
Cheeseburger
Andre
Pasta Pizza Taco Fisk Burger Emilies diagram
SNAKKE MATTE
Tuva har tatt tiden hun brukte på å gå til skolen hver dag i løpet av en uke.
UkedagTid i minutter
Mandag7 Tirsdag8
Onsdag10
Torsdag8
Fredag10
Tuva vil lage et diagram som viser resultatet. Hvilket diagram bør hun velge? Begrunn svaret.
FØLG STIEN
OPPGAVE 113
Hvilket diagram hører til hvilken tabell? Sett strek fra diagram til tabell.
Tabell 1
FargeAntall
Blå25 Oransje25
Grønn25 Gul25
Tabell 2 FargeAntall
Blå30 Oransje10
Grønn10 Gul10
Tabell 3
Blå600 Oransje200
Grønn300 Gul100
Tabell 4
Blå120 Oransje 60 Grønn 85 Gul 35
OPPGAVE 114
Sektordiagrammet viser favorittisen til elevene i 7A. Det er 20 elever i klassen. Fyll ut tabellen.
Favorittis i klasse 7A
KategoriBrøkdel av klassenAntall elever Saftis
Softis
Diagram A Diagram B Diagram C Diagram D
Matemagisk 7 APARAL L ELLBO K
Matematikk for 5.–7. trinn
Matemagisk følger fagfornyelsen (LK20) og stimulerer elevene til å utforske og diskutere fra første stund.
Lærebokas struktur ivaretar fellesskapet i klassen slik at elevene lærer sammen. Elevene får individuelle tilpasninger gjennom en unik differensieringsmodell.
Matemagisk 7 består av:
• grunnbok 7A
• grunnbok 7B
• parallellbok 7A
• parallellbok 7B
• oppgavebok 7
• Matemagisk 1–7 Aschehoug Univers
• ØveMatematikk
• Matemagisk 7 Digitalbok
• digital lærerveiledning
På Aunivers.no finner du Aschehougs digitale læremidler.