Matemagisk 9 Parallellbok by Aschehoug Utdanning

Matemagisk Parallellbok

Asbjørn Lerø Kongsnes

Anne Karin Wallace

Matemagisk

Parallellbok

Asbjørn Lerø Kongsnes

Anne Karin Wallace

Matemagisk 9 Parallellbok er en del av læremiddelet Matemagisk 1–10.

Læremiddeletfølger læreplanen i matematikk for 1.–10. årstrinn.

1. utgave / 1. opplag 2023

Materialet er vernet etter åndsverkloven. Uten uttrykkelig samtykke er eksemplarfremstilling, som utskrift og annen kopiering, bare tillatt når det er hjemlet i lov (kopiering til privat bruk, sitat o.l.) eller i avtale med Kopinor (www.kopinor.no).

Utnyttelse i strid med lov eller avtale kan medføre erstatnings- og straffansvar.

Redaktør: Kari Kleivdal og Trine Alnæs

Grafisk formgiving: Marit Jakobsen og Type-it AS

Omslag: Marit Jakobsen

Bilderedaktør: Nina Hovda Johannesen

Tekniske tegninger: Arnvid Moholt og Trine Alnæs

Illustrasjoner: Erik Ødegård, Kari Sortland, Martin Hvattum

Ombrekking: ord og form, Gudbrand Klæstad

Grunnskrift: Frutiger LT Std, 10/14 pkt.

Papir: 100 g G-print 1,0

Trykk: Merkur Grafisk AS Innbinding: Bokbinderiet Johnsen AS, Skien

ISBN 978-82-03-41236-3 Aunivers.no

Foto

s. 6 Bartosz Hadyniak/iStock , s. 40 johnnorth/iStock, s. 62 Yusufozluk/iStock, s. 88 NTB Scanpix / Sipa Asia, s. 112 Caroline Brundle Bugge/iStock, s. 144 Shuoshu/iStock

www.aschehoug.no

Forfatterne har mottatt stipend fra det faglitterære fond.

Innhold

11 Figurtall og tallmønster

11A Å multiplisere to parenteser ......12

11B Figurtall .....................21

11C Tallmønstre ..................30

12 Statistikk

12A Tabeller og diagrammer .........44

12B Sentralmål og spredningsmål .....52

13 Sannsynlighet

13A Grunnleggende sannsynlighet ....64

13B Store talls lov.................74

13C Sammensatte forsøk . . . . .

. 80

14 Linjer, figurer og vinkler

14A Definisjoner og egenskaper ..... 90

14B Vinkler i mangekanter .........102

15 Areal og omkrets

15A Arealenheter ................117

15B Areal og omkrets av mangekanter................121

15C Areal og omkrets av sirkler og sirkelsektorer .............134

16 Pytagoras’ setning og formlikhet

16A Pytagoras’ setning ............147

16B Spesielle trekanter ............160

16C Formlikhet og kongruens.......164

17 Volum og overflate

17A Volum .....................178

17B Volum og overflate av noen tredimensjonale figurer ........184 Fasit ..........................200

Velkommen til Matemagisk 9

Matemagisk 9 legger til rette for at dere som elever får være aktive, utforske og oppdage matematiske sammenhenger. Vi ønsker at dere skal snakke matte med hverandre, utvikle forståelse og bli gode problemløsere. Boka legger opp til at dere kan samarbeide om matematikken. I boka finner dere varierte oppgaver knyttet til virkeligheten som gjør matematikken meningsfull og relevant. Boka kan brukes alene eller i kombinasjon med Matemagisk 8–10 Elevhåndbok

Fellesløypa

I hvert delkapittel er det en fellesløype. Denne er designet for arbeid i fellesskap i klassen. Den består av teori, eksempler, utforskende oppgaver, Snakke matte-oppgaver, spill, aktiviteter og andre varierte oppgaver. Programmering og andre digitale verktøy er integrert i delkapitlene der det er relevant.

Nøkkelhull

Oppgaver som viser spesielt viktige ideer og tenkemåter.

Oppgaver der dere skal snakke matte med hverandre. Her trener dere påå forklare hvordan dere tenker.

Følg stien

Oppgaver der du får trent mer på det klassen har arbeidet med i fellesskap. Her trener du på én ting om gangen. Følg stien dekker det mest sentrale faginnholdet og finnes i slutten av hvert delkapittel.

Vi legger gunnlaget

Eksempler, forklaringer og oppgaver som repeterer fagstoff som du har arbeidet med på tidligere trinn. Dette trenger du for å løse de neste oppgavene.

Henviser til tilsvarende oppgave i grunnboka. Det matematiske innholdet er bevart, men oppgaven kan være justert i parallellboka.

Henviser til tilsvarende eksempel i grunnboka. Det matematiske innholdet er bevart, men eksemplet kan være justert i parallellboka.

SNAKKE MATTE

Skriv ryddig og oversiktlig. Da blir også matematikken enklere.

Ikke gi opp selv når det blir vanskelig.

Samarbeid gjerne med hverandre!

Tren på å stille spørsmål om det du faktisk lurer på.

Hiyanna

Henrik

Tuva

Yonas

Figurtall og tallmønster 11

1Hva ser dere på bildet?

2 Oppdager dere noen mønstre?

3 Beskriv mønstrene dere oppdager.

Vi legger grunnlaget

En variabel er et symbol som står for et tall. Verdien av variabelen kan variere. Vi bruker ofte små bokstaver som variabler, for eksempel a, b, n, t eller x

Et algebraisk uttrykk er et regneuttrykk med en eller flere variabler.

OPPGAVE 1

Eksempler på algebraiske uttrykk er 4 + x 12 ⋅ a 5 a + 3 b

a Hva er verdien av det algebraiske uttrykket 6 x hvis x = 3?

b Hva er verdien av det algebraiske uttrykket 6 x + 4 hvis x = 2?

c Hva er verdien av det algebraiske uttrykket y + 6 ⋅ x hvis x = 5 og y = 1?

Å forenkle et algebraisk uttrykk vil si å skrive om det algebraiske uttrykket til et annet, enklere uttrykk. Det forenklede uttrykket skal alltid ha samme verdi som det opprinnelige uttrykket, uansett hvilke tall vi setter inn for variablene.

Vi forenkler uttrykket a + a + a + a til 4a. Uansett hvilket tall vi setter inn for a, er verdien av a + a + a + a og verdien av 4a den samme.

a = 3, så er

a + a + a = 3 + 3 + 3 + 3 = 12 4 ⋅ a = 4 ⋅ 3 = 12

Vi trenger ikke skrive gangetegn mellom tallet og variabelen. 4a betyr 4 ⋅ a Hvis +

OPPGAVE 2

Skriv så enkelt som mulig.

a a + a + a + a + a = b y + y + y =

c n + n + n + n + n + n = d k + k + k k =

e 3b + 4b = f 2a + 9a =

g 11x 5x =

h 4n + 2n 3n =

2x og 5x er ledd av samme type.

5x og 5 er ikke ledd av samme type.

3x og 3y er ikke ledd av samme type. e.

EKSEMPEL 1

Skriv uttrykket 5a 3 + 7 2a så enkelt som mulig.

Løsning

5a 3 + 7 2a = 5a –3+7 –2a

= 5a –2a 3 + 7

= 3a +4

Vi fargelegger ledd av samme type med samme farge for å skape oversikt.

Vi endrer rekkefølgen på leddene (pass på at fortegnene følger med riktig ledd).

Vi trekker sammen de røde leddene for seg, og de blå leddene for seg.

OPPGAVE 3

Skriv så enkelt som mulig.

a 4a + 3a + 5 8

Å GANGE ET TALL MED EN PARENTES

Figuren viser et rektangel. Vi kan regne ut arealet av rektanglet på to ulike måter.

1 Ved å gange antall ruter i hver kolonne med antall ruter i hver rad.

I hver rad er det 4 ruter.

I hver kolonne er det 2 + 3 = 5 ruter.

Til sammen er det 4 (2 + 3) = 4 5 = 20 ruter.

2 Ved å legge sammen antall blå og røde ruter.

Det er 4 2 = 8 blå ruter.

Det er 4 3 = 12røde ruter.

Til sammen er det 4 ⋅ 2 + 4 ⋅ 3 = 8 + 12 = 20 ruter.

Vi ser at de to måtene å regne på gir samme svar.

Vi kan skrive 4 (2 + 3) = 4 2 + 4 3

Det var ingenting spesielt med tallene vi valgte i dette eksemplet.

Denne måten å regne på fungerer uansett hvilke tall vi bruker.

For alle tall a, b og c er a(b + c) = ab + ac a

OPPGAVE 4

a Regn ut arealet av rektanglet på to ulike måter.

1 Gang antall ruter i hver kolonne med antall ruter i hver rad.

2 Regn ut arealet av det blå rektangelet. Regn ut arealet av det røde rektanglet. Legg sammen de to arealene.

b Forklar hvorfor regninga ovenfor viser at 3 (5 + 2) = 3 5 + 3 2.

Skriv uttrykket 5a + 2(a + 3b) så enkelt som mulig.

Løsning

5 2( 3 )5 22 3 526 76 ++=+⋅+⋅ =++ =+

a a b a a b aab ab

OPPGAVE 5

Skriv så enkelt som mulig.

a 4 + 2(a + 1)

c 2a + 6(a + 2)

Vi løser opp parentesen ved å gange faktoren 2 med begge leddene inni parentesen.

Vi trekker sammen ledd av samme type.

b 3 + 5(x + 4)

d 3(a + 2b) + 4a

Løs opp parentesen i uttrykket 4(a – 3).

Løsning

4(a 3) = 4 a + 4 ( 3)

= 4a + ( 12) = 4a 12

OPPGAVE 6

Løs opp parentesene.

a 4(n 2)

Vi løser opp parentesen ved å gange 4 med a og 3.

Vi regner ut 4 a og 4 ( 3).

Å legge til 12 er det samme som å trekke fra 12.

b 4(y 5)

EKSEMPEL 2

EKSEMPEL 3

11.1

11A Å multiplisere to parenteser

Utforske og begrunne hvordan vi multipliserer to parenteser. Multiplisere to parenteser og trekke sammen uttrykk.

OPPGAVE 7

Her ser du et regneark.

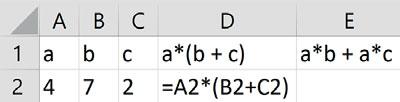
a Kopier regnearket og lag en formel i celle E2 som regner ut ab + ac

b Endre tallene i celle A2, B2 og C2. Sammenlikn svaret i celle D2 med svaret i celle E2. Hva oppdager du?

c Prøv flere ulike endringer av tallene i celle A2, B2 og C2. Prøv med negative tall og desimaltall også. Sammenlikn svaret i celle D2 med svaret i celle E2. Hva oppdager du?

OPPGAVE 8

Regn ut på to forskjellige måter.

a 3 (5 + 2)

b 8 (3 5)

c 3 (3 13)

d 6 (2 + 8)

OPPGAVE 9

Bruk tallene fra regnestykkene i oppgave 8 i regnearket du laget i oppgave 7. Sammenlikn svarene du fikk da du regnet for hånd og da du brukte regnearket.

OPPGAVE 10

a Nedenfor ser du to ulike rektangler. Du skal regne ut arealet av hvert av rektanglene på to måter.

1 Regn direkte ut totalt antall ruter.

2 Regn ut hvor mange ruter det er av hver farge og legg sammen til slutt.

b La a, b, c og d være positive tall. Bruk de samme tenkemåtene som i oppgave a, og lag to algebraiske uttrykk for arealet av rektanglet uttrykt ved a, b, c og d

Uttrykk 1:

Uttrykk 2:

OPPGAVE 11

I hver av deloppgavene skal du regne ut svaret på to forskjellige måter. Del også opp rektanglene og sett på tall, slik at de viser hvordan du tenker når du regner på de to ulike måtene.

(4 + 1) (2 + 2)

(3 + 2) (1 + 1)

Se gjerne på det du gjorde på forrige side.

OPPGAVE 12

Lag et regneark eller et pythonprogram som kan brukes til å undersøke om (a + b)(c + d) = ac + ad + bc + bd for tall a, b, c og d

Du skal sjekke om venstre side og høyre side av likhetstegnet har samme verdi. Prøv gjerne med tilfeller der noen av tallene er desimaltall eller negative tall.

Er (a + b)(c + d) = ac + ad + bc + bd for tall a, b, c og d?

Nei

Martin er glad i å løpe og løper både morgenøkter og kveldsøkter. Morgenøktene er 6 km lange, mens kveldsøktene er 3 km lange. Martin løper både morgen- og kveldsøkter 4 hverdager og 1 helgedag hver uke. Han lurer på hvor langt han løper til sammen hver uke.

1 2

Henriks løsning

Martin løper 4 + 1 = 5 dager i løpet av en uke. Hver dag løper han 6 + 3 = 9 km.

Til sammen løper han (4 + 1) (6 + 3) = 5 9 = 45 km i uka.

Hiyannas løsning

Martin løper 4 6 = 24 km til sammen på morgenen på hverdagene.

Han løper 4 3 = 12 km til sammen på kvelden på hverdagene.

Han løper 1 ⋅ 6 = 6 km til sammen på morgenen i helgene.

Han løper 1 3 = 3 km til sammen på kvelden i helgene.

Til sammen løper han 4

Forklar hvordan Henrik og Hiyannas løsning illustrerer at vi kan multiplisere to parenteser med hverandre på følgende måte:

(a + b)(c + d) = ac + ad + bc + bd

SNAKKE MATTE

EKSEMPEL 4

Regn ut (a + 5)(a + 2) og trekk sammen så mye som mulig.

(a + 5)(a + 2) = a a + a 2 + 5 a + 5 2

= a2 + 2a + 5a + 10 = a2 + 7a + 10 ⋅= aaa2

OPPGAVE

Regn ut og trekk sammen så mye som mulig.

a (a + 4)(a + 3)

a 3 a 4

b (2 + x)(4 + x)

c (a + 3)(5 + a) d (x + y)(x + 3)

Følg stien

OPPGAVE 14

Løs opp parentesene.

a 5(x + 2) b 3(a + 4)

c (n + 4)(n + 3) d (t + 1)(t + 1) 11.9 11.10 11.11

c 6(y 8)

OPPGAVE 15

Regn ut og trekk sammen så mye som mulig.

a 12 + 3(x 4)

c 4 + 6(3 + n)

5(7 − n)

b 10 2(a 5)

d 4(x + 2) + 4(x − 1)

OPPGAVE 16

Regn ut og trekk sammen så mye som mulig.

a (x + 2)(x + 3) b (a + 5)(a + 1)

Vi legger grunnlaget

OPPGAVE 17

Her ser du de tre første figurene i et mønster.

Figur nr. 1Figur nr. 2Figur nr. 3

a Fargelegg figurene slik at det kommer fram hvordan mønstret vokser.

b Forklar hvordan mønstret vokser.

c Forklar hvordan figur nr. 20 ser ut.

Nedenfor ser du forenklede tegninger som viser hvordan figur nr. 10, 50 og 100 ser ut.

Figurene ser jo egentlig ikke sånn ut, men våre tegninger gjør at vi kan forstå hvordan de ser ut.

Figur nr.

d Lag tilsvarende tegninger som viser hvordan figur nr. 30 og 200 ser ut.

Nedenfor ser du hvordan figur nr. n ser ut.

Figur nr. n n n 1 nn

e Bruk figurene og fyll ut den systematiske tabellen.

FigurnummerRegneuttrykk som viser antall brikker i figuren

f Forklar hvorfor det er 1 + 4 n brikker i figur nr. n

OPPGAVE 18

Her ser du de tre første figurene i et mønster.

Figur nr. 1Figur nr. 2Figur nr. 3

a Tegn figur nr. 4 og figur nr. 5.

b Hvor mange brikker trenger du totalt for å lage figur nr. 4? Svar: brikker

c Hvor mange brikker trenger du totalt for å lage figur nr. 5? Svar: brikker

d Lag forenklede tegninger som viser hvordan figur nr. 20, 50 og n ser ut.

e Fyll ut tabellen.

FigurnummerRegneuttrykk som viser antall brikker i figuren

1 2 3 20 50 n

Regneuttrykket på den nederste raden i tabellen, kaller vi det algebraiske uttrykket for antall brikker i figur nr. n

11B Figurtall

Utforske og beskrive mønstre i arbeid med figurtall. rektangeltall og kvadrattall n når figuren er sammensatt av ulike deler.

På 8. trinn brukte vi følgende strategier i arbeid med figurtall:

OPPGAVE 19

a Tegn figur nr. 5.

b Hvor mange brikker trenger du for å lage figur nr. 5?

c Forklar hvordan figur nr. 10 ser ut.

Svar: brikker

d Fyll ut tabellen.

FigurnummerRegneuttrykk som viser antall brikker i figuren Antall brikker i figuren

Figur nr.

11.23 OPPGAVE 20

På hver figur er det kvadratiske fliser som danner et stort kvadrat. La n være antall fliser langs en av kantene.

n = 5

a Fyll ut tabellen.

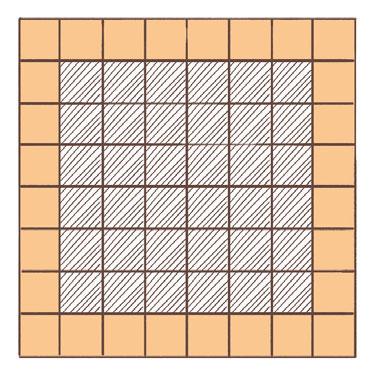
n = 8

Antall fliser langs kanten (n)Antall oransje fliser på figuren

Nedenfor ser du rammen på figur nr. 5 og figur nr. 8 med andre farger.

n = 5

b Fyll ut tabellen.

n = 8

Antall fliser langs kanten (n)Regneuttrykk som viser antall brikker i rammen på figuren 5 8

c Lag forenklede tegninger som viser hvordan rammen ser ut når det er 20 og 50 brikker langs kanten.

d Fyll ut tabellen.

Antall fliser langs kanten (n)Regneuttrykk som viser antall brikker i rammen på figuren 5 8 20 50 n

e Fargelegg figurene på en annen måte og lag forenklede tegninger som viser hvordan rammen ser ut når det er 40 og 100 brikker langs kanten.

n = 5

n = 8

f Fyll ut tabellen.

Antall fliser langs kanten (n)Regneuttrykk som viser antall brikker i rammen på figuren 5 8 40

n Her skal du komme fram til andre regneuttrykk enn i oppgave d

OPPGAVE 21

Her ser du de tre første figurene i et mønster.

a Tegn figur nr. 4.

c Fyll ut tabellen.

FigurnummerAntall brikker i hver rad Antall brikker i hver kolonne

Kvadrattall

nr. 3

De første kvadrattallene er 1, 4, 9, 16, 25, 36, … Algebraisk uttrykk: n2

Tallene som viser antall brikker i disse figurene kalles ofte rektangeltall

b Lag en forenklet tegning som viser figur nr. 50.

Regneuttrykk som viser antall brikker i figuren

Figur

Figur nr.

Figur nr. 2

Figur nr. 1

Figur nr. 3

Figur nr. 2

Her ser du de fire første figurene i et mønster.

Figur nr. 1

Figur nr. 2

Figur nr. 3

nr. 4

For å skape mer oversikt kan vi dele opp figurene i mindre enheter.

Figur nr. 1

Figur nr. 2

Figur nr. 3

Vi lager en forenklet tegning av figur nr. 100 og n

Figur nr. 4

100 · 100 n · n n

100

Figur nr. 100

Figur nr. n

Figur nr. n er en illustrasjon av n + kvadrattall nr. n

Et algebraisk uttrykk for antall brikker i figur nr. n blir derfor n + n2

OPPGAVE 22

Se på eksemplet ovenfor. Bruk det algebraiske uttrykket, og regn ut hvor mange brikker det er i figur nr. 10.

Figur

OPPGAVE 23

Her ser du de tre første figurene i et mønster.

nr. 1 Figur nr. 2 Figur nr. 3

a Vis med farger hvordan du kan dele opp figurene i mindre enheter.

b Lag et algebraisk uttrykk for antall brikker i figur nr. n

Skriv uttrykket så enkelt som mulig.

OPPGAVE 24

Lag en figurtallsoppgave. Bytt oppgave med en annen elev, og løs hverandres oppgave.

Figur

Følg stien

OPPGAVE 25

Her ser du de tre første figurene i et mønster.

a Forklar hvordan mønstret vokser.

b Forklar hvordan figur nr. 50 ser ut.

c Lag forenklede tegninger av figur nr. 10, 30 og n

d Fyll ut tabellen.

Figur nr. 3

Figur nr. 2

Figur nr. 1

Lag et algebraisk uttrykk for antall brikker i figur nr. n

Figur nr. 3

Figur nr. 2

Figur nr. 1

Figur nr. 3

Figur nr. 2

Figur nr. 1

OPPGAVE 27

Her ser du de tre første figurene i et mønster.

a Fargelegg figurene slik at du deler figurene opp i mindre enheter.

b Forklar hvordan figur nr. 10 ser ut.

c Lag forenklede tegninger som viser hvordan figur nr. 10, 100 og n ser ut.

d Lag et algebraisk uttrykk for antall brikker i figur nr. n

Figur nr. 3

Figur nr. 2

Figur nr. 1

11CTallmønstre

Utforske tallmønstre.

Systematisere og beskrive tallmønstre med ord, tegninger og algebraiske uttrykk.

Begrunne hvilke tall tallmønstrene gjelder for.

EKSEMPEL 6

I en fotballserie skal alle lagene møte hverandre én gang. Vi lurer på hvor mange kamper som må spilles i hele serien til sammen.

Stille spørsmål: Hvor mange kamper blir det hvis det er 3 lag i serien?

Skape oversikt: Vi setter opp en systematisk oversikt med logoene til tre lag.

Vi ser at det blir 3 kamper.

Lage en hypotese:

Tegne figurer: Vi lager en figur som viser hvilke lag som skal møte hverandre.

Når det var 3 lag ble det 3 kamper i serien. Vi lager derfor hypotesen om at det blir like mange kamper som det er lag.

Teste med andre tall:

Vi sjekker antall kamper hvis det er 4 lag i serien.

Vi ser at det blir 6 kamper hvis det er 4 lag. Vi må derfor forkaste hypotesen og gå tilbake til å lete og oppdage et mønster.

Vi må fortsette å lete etter mønstre til vi finner et mønster vi er ganske sikker på at stemmer. En hypotese er et forslag til en sammenheng.

Vi ser at med 4 lag blir det 1 + 2 + 3 = 6 kamper.

Vi ser fra mønstret over at det blir 1 + 2 + 3.

Vi ser fra fargene på linjene på figuren til venstre at det blir 1 + 2 + 3.

Vi tenker oss nå at det er 5 lag i serien. Da blir det 1 + 2 + 3 + 4 = 10 kamper.

EKSEMPEL 6 forts.

Vi kan regne ut antall kamper ved å ta 1 + 2 + 3 + ... der det siste tallet i regnestykket er én mindre enn antall lag.

Matematikk for 8.–10. trinn

Matemagisk oppfordrer elevene til å utforske og diskutere fra første stund. Læremiddelets struktur ivaretar fellesskapet i klasserommet. Fellesdelene i hvert kapittel er laget for at elevene skal lære sammen. Dette gjør de gjennom «Snakke matte», spill, aktiviteter og utforskende samarbeidsoppgaver.

Den unike differensieringsmodellen i Matemagisk gir elevene individuelle tilpasninger innenfor samme tema. Slik lærer elevene matematikk på sitt nivå, men likevel i takt med hverandre.

Matemagisk er utviklet av fagpersoner og lærere med nærhet til klasserommet.

Matemagisk 9 består av:

• Lærebok

• Parallellbok

• Matemagisk 8–10. Elevhåndbok

• Matemagisk 8–10 Digital, med elevressurser og lærerveiledning

Digitale ressurser ﬁnner du på Aunivers.no