Макаренко А. А., Винокуров Л. А

ISSN 2413–9599 (Print) ISSN 2541–870Х (Online)

DOI: 10.21778/2413-9599-2020-30-3-75-85 УДК 621. 397.6

www.radioprom.org

Алгоритмы цифровой обработки изображений в задачах визуальной навигации беспилотного воздушного судна

А.А. Макаренко 1, 2 , Л.А. Винокуров 2

1 АО «Научно-производственное предприятие «Радар ммс», Санкт-Петербург, Россия 2 ФГАОУ ВО «Национальный исследовательский университет информационных технологий, механики и оптики», Санкт-Петербург, Россия

В статье изложены алгоритмы цифровой обработки изображения в визуальной навигационной системе беспилотного воздушного судна и представлены результаты работы программы, реализующей эти алгоритмы. В соответствии с изложенными алгоритмами выполняется оценка спектра пространственных частот изображения. Вид и структура двумерного амплитудного пространственного спектра изображения позволяет выделить наличие вертикальных и горизонтальных границ и линий на изображении и дать общее представление об их пространственной ориентации. Для ускорения расчетов корреляционной функции также используется спектральное представление сравниваемых изображений. По результатам цифровой обработки амплитудного двумерного пространственного спектра изображения, наблюдаемого бортовой телевизионной камерой, формируются данные, позволяющие уточнить пространственные координаты беспилотного воздушного судна и оценить состояние и положение посадочной площадки. Метод основан на численном анализе двумерного амплитудного спектра изображения. Представлены результаты работы описанных алгоритмов.

Ключевые слова: навигационная система, корреляционно-экстремальная система, цифровая обработка изображения, амплитудный спектр, дискретное преобразование Фурье

Для цитирования: Макаренко А. А., Винокуров Л. А. Алгоритмы цифровой обработки изображений в задачах визуальной навигации беспилотного воздушного судна // Радиопромышленность. 2020. Т. 30, № 3. С. 75–85. DOI: 10.21778/2413-9599-2020-30-3-75-85

© Макаренко А. А., Винокуров Л. А., 2020

Digital image processing algorithms for visual navigation of an unmanned aircraft

A.A. Makarenko 1, 2 , L.A. Vinokurov 2

1 Research and Production Enterprise Radar mms JSC, Saint Petersburg, Russia 2 National Research University of Information Technologies, Mechanics and Optics, Saint Petersburg, Russia

The algorithms of digital image processing in the unmanned aerial vehicle (UAV) visual navigation system are stated and the program realization of the method is presented in the article. Assessment of a range of spatial frequencies of the image is carried out using the stated algorithms. The look and structure of a two-dimensional amplitude spatial spectrum of the image allow allocating existence of vertical and horizontal borders and lines on the image and giving a general idea about their spatial orientation. The spectral submission of the compared images is also used for the acceleration of correlation function calculations. Using the results of digital processing of an amplitude two-dimensional spatial range of the image observed by the onboard TV camera the data allowing to specify the spatial UAV coordinates and to estimate a condition and position of the airfield are formed. The method is based on the numerical analysis of a two-dimensional amplitude spectrum of the image. Results of operation that confirm efficiency of the stated algorithms are presented.

Keywords: navigation system, correlation-extremal system, digital image processing, amplitude spectrum, discrete Fourier transform

For citation: Makarenko A. A., Vinokurov L. A. Digital image processing algorithms for visual navigation of an unmanned aircraft. Radio industry (Russia), 2020, vol. 30, no. 2, pp. 75–85. (In Russian). DOI: 10.21778/2413-9599-2019-30-3-75-85

Введение

В настоящее время большинство беспилотных воздушных судов (БВС) оснащены различными системами навигации, в том числе визуальными. Также широко используются системы автоматического возврата в точку взлета. Данные системы используются для облегчения пилотирования летательного аппарата либо активируются при возникновении внештатных ситуаций. Визуальная (или оптическая) система навигации может применяться для более точного позиционирования БВС в пространстве, а также использоваться как резервная при отказе основной навигационной системы.

Существует два основных класса визуальных навигационных систем: основанные на методе одновременной локализации и построения карты (simultaneous location and mapping, SLAM), а также корреляционно-экстремальные системы навигации (КЭСН).

SLAM-системы основаны на группе методов, позволяющих определять местоположение объекта по изображению с бортовой телевизионной камеры (или стереопары) и одновременно строить трехмерную карту местности, которая попадает в поле зрения телевизионной камеры. Алгоритмы, реализующие такие методы, в настоящее время находят применение в самоуправляемых автомобилях, домашних роботах [1].

Алгоритмы SLAM эффективно работают на глубоких рельефах, однако при использовании для работы над плоской подстилающей поверхностью они часто не обеспечивают требуемой точности. Также они крайне требовательны к точности калибровки ТВ-камеры и вычислительным ресурсам платформы.

Принцип работы КЭСН основан на сравнении изображения земной поверхности или совокупности ориентиров (текущего изображения) с эталонным изображением, сформированным заранее. Рассогласование положения этих изображений в принятой системе координат позволяет сформировать команду для удержания объекта управления на заданной траектории [2].

Информативным признаком, позволяющим визуальной системе навигации беспилотного воздушного судна определять величину тангажа, крена и/или рыскания этого БВС по величине угла наклона или поворота наблюдаемого бортовой телевизионной камерой изображения, является амплитудный пространственный двумерный спектр. Научная новизна работы заключается в применении амплитудного пространственного двумерного спектра наблюдаемого изображения не только в качестве информативного признака при корреляционном сопоставлении изображений (как, например, в [2]), но и в качестве источника информации, применяемой для определения направления перемещения БВС в пространстве.

Для расчета спектра используется преобразование Фурье [3]. Для дискретного двумерного случая преобразование Фурье всегда существует и может быть выражено следующим равенством:

F(u,v) = 1 MN u=0 M-1 ∑ v=0 N-1 ∑ f(x, y)e −i2π ⎛ ⎝ ⎜ ux M + uv N ⎞ ⎠ ⎟ , (1)

где f (x, y) – массив значений яркости текущего кадра изображения – функция двух переменных размерами M×N, x = 0, 1, 2,…, M – 1, y = 0, 1, 2,…, N – 1, u = 0, 1, 2,…, M – 1, v = 0, 1, 2,…, N – 1. Данное выражение должно быть вычислено для всех u и v. Переменные x и y называются пространственными переменными или переменными изображения, переменные u и v – переменными преобразования или частотными переменными. При работе с изображениями гармонические составляющие, из которых состоит спектр, принято называть пространственными частотами. Их значения численно характеризуют количество периодов повторения изменяющихся по синусоидальному закону значений яркости элементов изображения на единицу длины.

Вид и структура двумерного амплитудного пространственного спектра изображения позволяет выделить наличие вертикальных и горизонтальных границ и линий на изображении и дать общее представление об их пространственной ориентации. Как видно из рис. 1, ориентация двумерного амплитудного пространственного спектра изображения характеризует в локальной системе координат направление границ и линий на исходном изображении. Таким образом, определив направление максимального сосредоточения спектральных составляющих спектра, можно в локальной системе координат найти угол поворота всего изображения и расположенных на нем объектов.

Полет над протяженным объектом

Важной областью применения математического аппарата спектрального анализа, относящейся к визуальной навигации беспилотного воздушного судна, является исследование наблюдаемой с борта БВС подстилающей земной поверхности. Такое исследование позволяет уточнить координаты места нахождения летательного аппарата и наземных объектов и скорректировать, если это необходимо, параметры. Эти действия обычно проводятся посредством корреляционного анализа [2, 3], скорость осуществления которого значительно повышается при реализации корреляционной процедуры в области пространственных частот [3].

Математический аппарат корреляционного анализа применяется для определения степени связи между двумя сигналами. Мерой корреляции двух сигналов является коэффициент корреляции.

Исходное / Original

Фурье-спектр / Fourier spectrum

Исходное / Original а)

Фурье-спектр / Fourier spectrum

Исходное / Original б)

Фурье-спектр / Fourier spectrum

в)

Рисунок 1. Изображения прямоугольника и их пространственные спектры: а – наклон 0°, б – наклон 45°, в – наклон 60° Figure 1. Images of a rectangle and their spatial spectra: a – tilt of 0°, б – tilt of 45°, в – tilt of 60°

В общем случае, корреляция эталона w(x, y) размерами n×m (n и m – нечетные числа) с изображением f (x, y) размерами M × N (рис. 2) задается выражением

c(x, y) = ∑∑ w(s,t) f(x + s, y + t), s t

где s = –(n – 1)/2, …, –1, 0, 1, …, –(n – 1)/2, t = –(m – –1)/2, …, –1, 0, 1, …, –(m– 1)/2 и суммирование ведется по области пересечения w и f. Это выражение так вычисляется для всевозможных значений переменных сдвига x и y, чтобы каждый элемент эталона w в какой-то момент попадал на каждый пиксель изображения f, в предположении, что размеры

изображения больше размеров эталона [3]. Такое предположение справедливо, поскольку его всегда можно обеспечить содержанием полетного задания БВС, указав в задании высоту полета и сформировав эталон соответствующего масштаба.

Коэффициент корреляции выражается следующим равенством:

γ(x, y) =

∑∑ [w(s,t) − w][ f(x + s, y + t) − f xy ] ∑ s ∑ [ t w(s,t) − w] 2 ∑∑ [ f(x + s, y + t) − f xy ] 2 , (3) s t s t

где суммирование ведется по всем парам координат, общим для f и w, w – среднее значение элементов маски w (вычисляемое только один раз), а f xy – среднее значение элементов изображения f по области, совпадающей с текущим положением w. Маску w часто называют эталоном, а вычисление корреляции – сопоставлением с эталоном. Коэффициент корреляции γ(x, y) изменяется в диапазоне от –1 до 1. Максимальное значение γ(x, y) достигается при наибольшем сходстве нормализованного (вычитанием среднего значения) эталона и соответствующей области в f (также нормализованной). Минимум достигается, когда обе нормализованные функции имеют наименьшее сходство.

Рис. 2 демонстрирует выполнение описанной процедуры корреляции. Функция f дополняется нулевыми элементами для ситуаций, когда центр w оказывается вблизи границы f.

На рис. 2 показан эталон w размерами m × n с центром в произвольной точке (x, y) изображения f. В этой точке с помощью формулы (4) производится расчет коэффициента корреляции, следующим шагом эталон смещается в соседнюю точку, и процедура повторяется. Полное множество

Начало координат / Origin of coordinates

n

m

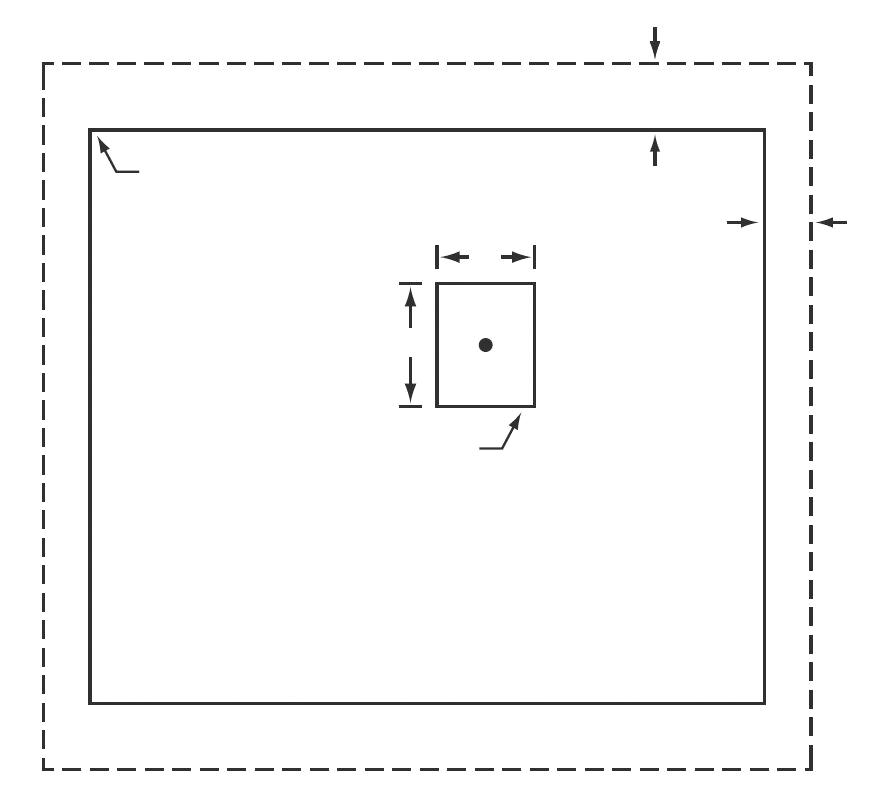
(x, y)

Эталон w с центром в произвольной точке (x, y) / Standard w centered at an arbitrary point (x, y) (m – 1)/2

(n – 1)/2

Изображение, f / Image, f

Расширение / Extension

Рисунок 2. Схема корреляционного сопоставления с эталоном Figure 2. Scheme of correlation comparison with the standard коэффициентов корреляции γ(x, y) находится путем перебора значений x и y при условии, что центр эталона w проходит по всем значениям f. После этого находится максимальное значение коэффициента корреляции γ(x, y), координаты найденной точки (x, y) являются координатами максимального совпадения изображения f с эталоном w.

Описанный выше алгоритм требует большого количества вычислений. Поэтому целесообразно определить способ ускорения расчетов, чтобы обеспечить возможность реализации процедуры корреляционного поиска в бортовой аппаратуре БВС.

Пространственная корреляция связана с преобразованием Фурье согласно теореме о корреляции: COR( f,w) ⇔ F * (u,v)W(u,v), (4)

где F и W – Фурье-образы функций f и w соответственно, а символ * означает комплексное сопряжение. Однако при расчете пространственной корреляции по формуле (4) требуется равенство размеров функций f и w. Для этого функцию w дополняют нулями до размеров изображения f.

Как правило, для упрощения вычислений применяются алгоритмы с использованием быстрого преобразования Фурье [2], так как данное действие позволяет заменить операции умножения на операции сложения.

В соответствии с формулой (4) коэффициент корреляции (3) можно вычислить с помощью следующего равенства: γ(x, y) = COR( f,w) , COR( f,q) (5)

где оператор COR– вычисление корреляции по формуле (2), f– изображение размерами x × y, w – эталон размерами m × n, q – изображение размерами m × n, заполненное единицами (таким путем ограничивается область, в которой вычисляется корреляция).

Пользуясь теоремой о корреляции (4) выражение (5) принимает следующий вид: γ(x, y) = IFFT[F(u,v)W * (u,v)] IFFT[F(u,v)Q * (u,v)] , (6)

где IFFT – оператор обратного преобразования Фурье, F, W и Q – Фурье-образы функций f, w и q соответственно, * – символ комплексного сопряжения.

Следует отметить, что при использовании выражения (6) изображения w и q дополняются нулевыми значениями до размеров изображения f. В данном случае значения коэффициентов корреляции будут лежать в диапазоне от 0 до 255, для нормировки значений необходимо воспользоваться следующим выражением:

γ(x, y) ÌÓÏ = γ( γ x, y max ) , (7)

где γ max – максимальное значение функции γ(x, y). Данное выражение рассчитывается для всех пар координат (x, y). Таким образом, коэффициент корреляции будет изменяться в диапазоне от 0 до 1, где 1 – полное совпадение эталона w с изображением f. Координаты точки γ(x, y) = γ max соответствуют координатам точки (x, y) изображения f, в которой оно максимально совпадает с эталоном w. При использовании равенства (6) нет необходимости вычислять коэффициент корреляции в каждой точке изображения f, т. к. расчет производится параллельно. Рис. 3 иллюстрирует пример расчета коэффициентов корреляции γ(x, y) (6) с использованием выражения (7).

Как следует из рис. 3в, координаты максимального коэффициента корреляции соответствуют координатам положения эталона на изображении. Таким приемом можно осуществлять поиск объектов на изображении, а также сравнивать изображения между собой. Рис. 4 демонстрирует результаты поиска эталонных изображений на реальных изображениях протяженных объектов.

На незашумленных изображениях координаты расположения эталонов представлены в табл. 1.

Для анализа возможностей практического применения разработанного алгоритма проведена его проверка на устойчивость к шумам на изображении. Для этого к исходным изображениям

а)

б)

Нормированные коэффициенты корреляции / Normalized correlation coefficients 1

500

, pix . y y , пикс. / 1000

1500

2000

2500

3000

500 1000 1500 2000 2500 3000 3500 x, пикс. / x, pix

4000 4500 5000

в)

0,98

0,96

0,94

0,92

0,9

0,88

0,86

0,84

0,82

Рисунок 3. Иллюстрация результатов поиска эталона в изображении: а – изображение, б – эталон, в – график нормированных коэффициентов корреляции γ(x, y) норм Figure 3. Illustration of the standard search results in the image: a – image, б – standard, в – graph of normalized correlation coefficients γ(x, y) norm

а)

б)

в)

г)

SNR = –6,8774 дБ / SNR = –6,8774 dB

д)

SNR = –1,218 дБ / SNR = –1,218 dB

е)

Рисунок 4. Иллюстрация результатов поиска эталона на изображении протяженного объекта: а, б – эталоны, в, г – найденные эталоны на незашумленных изображения подстилающей поверхности, д, е – найденные эталоны на зашумленных изображениях подстилающей поверхности Figure 4. Illustration of the results of the search for the standard on the image of an extended object: a, б – standards, в, г – found standards on non-noisy images of the underlying surface, д, е – found standards on noisy images of the underlying surface

добавлялся гауссовский белый шум с различными параметрами дисперсии D и математического ожидания M. Рис. 4д и 4е демонстрируют результаты работы алгоритма при наличии на исходном изображении гауссовского белого шума и соотношениях объект/фон (сигнал/шум) –6,8774 и –1,218 дБ соответственно.

На зашумленных изображениях координаты расположения эталонов представлены в табл. 2.

Сопоставляя содержание табл. 1 и 2, можно сделать вывод о том, что разработанный алгоритм позволяет находить положение эталона в исходном изображении даже при уровне шумов, превышающем уровень полезного сигнала.

Пользуясь вышеописанными зависимостями, можно синтезировать алгоритм информационного обеспечения бортовой навигационной системы беспилотных воздушных судов для решения задачи автоматического полета БВС от одного пункта до другого и обратно над железнодорожными путями, автомобильными дорогами или трубопроводами. Двумя основными частями такого алгоритма являются:

1.

2. Вычисление параметров ориентации объекта, находящегося на подстилающей поверхности. В рамках данной задачи объектами являются шоссейные дороги или железнодорожные пути. Нахождение пункта разворота БВС. По введенному в полетное задание эталонному изображению пункта разворота летательный аппарат должен в автоматическом режиме определить область, в которой нужно совершить разворот и полететь в обратном направлении вдоль того же протяженного объекта до пункта старта, эталонное изображение которого также введено в полетное задание.

Определение угла поворота объекта

Для нахождения угла поворота объекта, расположенного на наблюдаемой подстилающей поверхности, используется наличие связи между ориентацией амплитудного пространственного двумерного спектра изображения и ориентацией изображения, которому этот спектр соответствует. Процедуру

Таблица 1. Координаты расположения эталонов на незашумленных изображениях Table 1. Coordinates of the location of standards on non-noisy images

Изображение / Image x, пикс. / x, pix. y, пикс. / y, pix.

Рис. 4в / Fig. 4в Рис. 4г / Fig. 4г 533

621 1492

2228 вычисления угла поворота объекта можно разделить на три шага (для наглядности в качестве примера взято изображение черного прямоугольника на случайном фоне):

1.

2.

3. Шаг I – вычисление пространственного спектра изображения. Результат вычисления представлен на рис. 5. Шаг II – вычисление сумм амплитуд всех гармоник пространственного спектра по направлениям, соответствующим в локальной системе координат углам поворота в диапазоне от 0° до 180° с шагом в 1° (на рис. 6 продемонстрировано только несколько направлений суммирования). Определение направления, по которому сумма амплитуд гармоник имеет максимальное значение (рис. 7). Зная, какому углу наклона соответствует направление с максимальной суммой гармоник, можно судить об угле поворота объекта.

Линия, соответствующая максимальной сумме амплитуд гармоник, отклонена от вертикальной оси локальной системы координат на 26°. На такой угол поворачивалось изображение прямоугольника при создании тестового изображения поворота, то есть программа, работающая по изложенному алгоритму, корректно определила положение повернутого в плоскости изображения объекта.

Алгоритм вычисления угла поворота объекта также был проверен на устойчивость к шумам на изображении. Для этого к исходному изображению (рис. 5а) добавлялся гауссовский белый шум с различными параметрами дисперсии D и математического ожидания M. Рис. 8 демонстрирует результаты работы алгоритма вычисления угла поворота объекта при соотношении объект/фон 12,6 дБ на изображении.

Устойчивость алгоритма к воздействию шумов объясняется тем, что энергия спектральных составляющих широкополосного шума в спектре рассредоточена по всей ширине спектра и изменение уровня шума изменяет только амплитуды всех спектральных составляющих, практически не изменяя рельефную структуру амплитудного спектра,

Таблица 2. Координаты расположения эталонов на зашумленных изображениях Table 2. Coordinates of the location of standards in noisy images

Изображение / Image x, пикс. / x, pix. y, пикс. / y, pix.

Рис. 4д / Fig. 4д Рис. 4е / Fig. 4е 534

621 1493

2228

а)

б)

Рисунок 5. Результат вычисления пространственного спектра – шаг I: а – исходное изображение, б – пространственный спектр Figure 5. Result of calculating the spatial spectrum – step I: a – original image, б – spatial spectrum

Рисунок 6. К пояснению процедуры вычисления сумм амплитуд гармоник – шаг II; в выделенном круге показаны линии, по которым производится суммирование амплитуд гармоник спектра Figure 6. To an explanation of the procedure for calculating the sums of harmonic amplitudes – step II; the highlighted circle shows the lines along which the amplitudes of the spectrum harmonics are summed

определяемую объектами, находящимися на бражении. изо

Пример работы алгоритмов

Для иллюстрации работы данного алгоритма в составе имитационной модели полета БВС использовано схематичное (рис. 9) и реальное (рис. 10) изображение автомобильной дороги. Для передвижения вдоль линии необходимо с некоторой частотой, обусловленной размером шага, определять угол поворота линии, которая попадает в область

Рисунок 7. Результат вычисления направления, по которому сумма амплитуд гармоник имеет максимальное значение, соответствующего углу поворота объекта – шаг III; черным цветом показана линия, соответствующая вычисленному направлению Figure 7. The result of calculating the direction along which the sum of the amplitudes of the harmonics has a maximum value corresponding to the angle of rotation of the object – step III; black color shows the line corresponding to the calculated direction

интереса. Перемещение в следующую точку должно происходить с таким шагом, чтобы область интереса смещалась не более, чем на 30%. То есть при размерах окна 512×512 пикселей шаг смещения должен быть меньше 153 пикселей. Такая величина смещения позволит распознать ситуацию, при которой протяженный объект, вдоль которого осуществляется полет, изменит свое направление (например, дорога повернет на 90° в сторону) или протяженный объект частично «исчезнет» под каким-либо препятствием (под мостом или густыми

а)

б)

Рисунок 8. Иллюстрация результатов работы алгоритма при наличии шумов на изображении: а – исходное изображение, б – угол наклона 26° Figure 8. Illustration of the results of the algorithm in the presence of noise in the image: a – the original image, б – tilt of 26°

зарослями деревьев). Поскольку предложенный алгоритм оперирует не с конкретными объектами на изображении, как себя обычно ведет визуальная система сопровождения, а с целым изображением, представленным в виде спектра, то спектральные составляющие резко изменившего ориентацию протяженного объекта или сохранившейся на изображении части этого протяженного объекта позволят определить степень изменения этого объекта и не нарушить его сопровождение (здесь можно допустить некоторую аналогию с голографическим представлением объекта).

Из представленных результатов исследования можно сделать вывод, что данный алгоритм позволяет отслеживать путем перемещения область интереса вдоль кривой линии.

Нахождение пункта разворота беспилотного воздушного судна

Нахождение пункта разворота БВС выполняется на основе корреляционно-экстремального анализа последовательности изображений. Предварительно формируется изображение области, содержащей пункт разворота. Для этого могут

а)

б)

в)

Рисунок 9. Использование алгоритма нахождения угла поворота для движения вдоль кривой линии: а – первый шаг, б – n-й шаг, в – заключительный шаг Figure 9. Using the algorithm for finding the angle of rotation for movement along the curved line: a – first step, б – n-th step, в – the final step

а) б) в) Рисунок 10. Иллюстрация работы алгоритма для случая полета над автомобильной дорогой: а – начало автоматического полета, б – прохождение беспилотного воздушного судна вдоль дороги, в – остановка беспилотного воздушного судна (пункт разворота для полета в обратном направлении) Figure 10. Illustration of the algorithm operation for the case of flight over a road: a – the beginning of an automatic flight, б – the passage of an unmanned aircraft along the road, в – a stop of an unmanned aircraft (turning point for the opposite direction flight)

быть использованы доступные аэрофотоснимки земной поверхности или специально произведенные снимки местности, где предполагается осуществить полет БВС.

Алгоритм нахождения места разворота включает в себя следующие шаги:

1. Получение эталонного изображения. Для получения эталонного изображения, с которым в дальнейшем будут сравниваться текущие кадры, делается снимок в точке старта. Рассчитывается значение корреляции по формуле (6) и определяется максимальное значение результирующей функции γ max . В данном случае эталоном w(x, y) и изображением f(x, y) будет являться один и тот же кадр, т. е. данным действием производится расчет автокорреляции. Полученное значение принимается за полное совпадение (100%). 2. Сравнение последовательности кадров с эталоном. При каждом шаге смещения области интереса, обусловленном перемещением БВС, получаемый кадр сравнивается с эталоном с помощью равенства (6). В этом случае f(x, y) – текущий кадр, w(x, y) – эталон. Затем вычисляется максимальное значение функции корреляции в данный момент γ(x, y) Результаты имитационного моделирования полета беспилотного

БВС позволили сделать вывод о том, что если текущее значение корреляции γ(x, y) меньше, чем 96% от γ max , область интереса смещается в следующую точку согласно выбранному шагу.

Значение корреляции γ(x, y), равное или превышающее 96%, в 200 экспериментах с различными изображениями и эталонами обеспечило безошибочное нахождение эталона на наблюдаемом изображении. 3. Сравнение с изображением области, содержащей точку разворота. Если совпадение отсутствует, текущий кадр принимается за новый эталон и продолжается движение. 4. Остановка в пункте разворота. Если регистрируется совпадение с изображением области, содержащей пункт разворота (при выполнении неравенства γ(x, y)≥0,96γ max ), движение прекращается и выполняется разворот для движения к пункту старта.

Результаты полунатурного моделирования разработанных алгоритмов продемонстрировали возможность их практического применения.

Выводы

Авторами разработаны алгоритмы цифровой обработки изображения в визуальной навигационной системе беспилотного воздушного судна и представлены результаты работы программной реализации разработки, входящей в имитационную модель полета БВС. В соответствии с изложенными алгоритмами выполняется оценка спектра пространственных частот изображения. По результатам цифровой обработки амплитудного двумерного пространственного спектра изображения,

наблюдаемого бортовой телевизионной камерой, формируются данные, позволяющие уточнить пространственное положение БВС.

Результаты полунатурных испытаний представленных в статье алгоритмов определения углов поворота объекта и полета над протяженным объектом, проведенных на имитационной модели полета беспилотного воздушного судна с вертикальным взлетом и посадкой, показали возможность применения этого алгоритма для обеспечения полета БВС вдоль трубопровода, шоссейной дороги или железнодорожных путей и локализации места разворота для полета в обратном направлении после достижения конечного пункта полета.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1.

2.

3. Глаголев В. М., Ладонкин А. В. Оптическая система навигации летательных аппаратов // Известия ТулГУ. Технические науки. 2016. Вып. 10. С. 186–194. Баклицкий В. К. Корреляционно-экстремальные методы навигации и наведения. Тверь: ТО «Книжный клуб», 2009. 360 с. Гонсалес Р., Вудс Р. Цифровая обработка изображений. М: Техносфера, 2012.1104 с.

REFERENCES

1.

2.

3. Glagolev V. M., Ladonkin A. V. Optical navigation system of aircrafts. Izvestiya TuLGU. Tekhnicheskie nauki, 2016, iss.10, pp. 186–194. (In Russian). Baklitskii V. K. Korrelyatsionno-ehkstremalnye metody navigatsii i navedeniya [Correlation-extreme methods of navigation and guidance]. Tver, TO Knizhnyi kluB Publ., 2009, 360 p. (In Russian). Gonsales R., Vuds R. Tsifrovaya obrabotka izobrazhenii[Digital image processing]. Moscow, Tekhnosfera Publ., 2012,1104 p. (In Russian).

СВЕДЕНИЯ ОБ АВТОРАХ

Макаренко Александр Александрович, к. т.н, доцент, АО «Научно-производственное предприятие «Радар ммс», 197375, Санкт-Петербург, ул. Новосельковская, д. 37, лит. А, тел.: +7 (911) 920-37-89, e-mail: makarenko_aa_el@radar-mms.com. Винокуров Лев Александрович, магистрант, Национальный исследовательский университет информационных технологий, механики и оптики, 197101, Санкт-Петербург, Кронверкский пр., д. 49, тел.: +78 (911) 119-21 -13, e-mail: levka.vin@ gmail.com.

AUTHORS

Aleksandr A. Makarenko, Ph.D. (Engineering), associate professor, Research and Production Enterprise Radar mms JSC, 37A, ulitsa Novoselkovskaya, Saint Petersburg, 197375, Russia, tel.: +7 (911) 920-37-89, e-mail: makarenko_aa_el@radar-mms.com. Lev A. Vinokurov, master’s degree student, National Research University of Information Technologies, Mechanics and Optics, 49, Kronverksky prospekt, Saint Petersburg, 197101, Russia, tel.: +7 (911) 119-21 -13, e-mail: levka.vin@gmail.com.

Поступила 14.07.2020; принята к публикации 23.07.2020; опубликована онлайн 07.09.2020. Submitted 14.07.2020; revised 23.07.2020; published online 07.09.2020.