El proceso termodinámico
Un sistema termodinámico existe en un estado particular descrito por las propiedades del sistema en un tiempo específico. Si el sistema experimenta un cambio de estado, se somete a un proceso termodinámico. Un proceso termodinámico es la acción de cambiar un sistema termodinámico de un estado a otro, y se describe como la serie de estados termodinámicos que un sistema experimenta a medida que se transforma del “estado inicial” al “estado final”. Esta es una definición muy formal de lo que intuitivamente es un concepto muy sencillo. En esencia, un proceso es lo que le ocurre a un sistema cuando se le agrega o se le retira masa o energía, o conforme la masa o la energía dentro del sistema experimentan una transformación interna. Algunos ejemplos de procesos son el sistema enfriador o calentador, la compresión de un sistema o su expansión, y los cambios en un sistema a medida que la electricidad fluye dentro de él. Un objeto que acelera conforme cae desde cierta altura es un ejemplo de un proceso que implica una transformación interna de energía, como se describirá en el capítulo 2. Por lo general, se muestra la progresión de un proceso termodinámico mediante un diagrama que ilustre la forma en que dos de las propiedades del sistema varían durante el proceso. Por ejemplo, en la figura 1.13 se muestra el proceso termodinámico de calentar aire en un contenedor rígido (volumen fijo) ilustrando la relación entre la presión y la temperatura de este proceso.
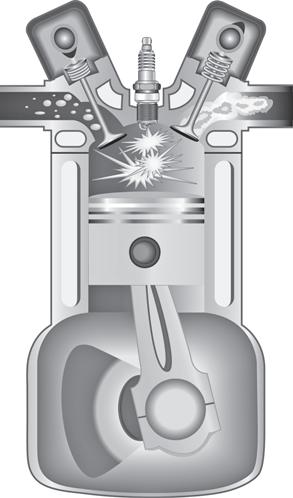
A menudo, los sistemas pasan por una serie de procesos. Como ejemplo, considere los gases dentro del ensamblaje del pistón-cilindro en un motor automotriz con las válvulas de entrada y de escape cerradas. Estos procesos se muestran en la figura 1.14. Primero, el pistón comprime el aire y la mezcla de combustible. Después se usa una chispa para encender la mezcla, lo que causa un rápido incremento en la temperatura y la presión. El aumento en la presión empuja el pistón a medida que los
(a)(b)(c) P
1
2
P T
FIGURA 1.13 Diagrama de presión contra temperatura (P-T ) de un proceso termodinámico.
1 2 3
(d) V
11 1.1 Conceptos básicos:
sistemas, procesos y propiedades
FIGURA 1.14 Tres procesos durante la operación del motor de un automóvil: (a) carrera de compresión, (b) proceso de combustión y (c) carrera de expansión. (d) Los procesos se muestran en un diagrama de presión contra volumen (P-V ).
Generador de vapor
ENTRADA de calor ENTRADA de electricidad
1 2
de electricidad 4
SALIDA de calor
Condensador
gases atraviesan por un proceso de expansión. A partir de esta descripción se aprecia que los gases experimentan una serie de tres procesos con las válvulas cerradas.
Un caso especial de una serie de procesos ocurre cuando el estado inicial del primer proceso es el mismo que el estado final del último proceso. Si el estado inicial y el estado final de un sistema son idénticos antes y después de una serie de procesos, se dice que los procesos completaron un ciclo termodinámico. Los ciclos representan un papel importante en la termodinámica, tanto en el desarrollo teórico de varios conceptos como en la aplicación práctica de la termodinámica en sistemas cotidianos. Un ejemplo de ciclo es una planta simple de electricidad de vapor, como se muestra en la figura 1.15. Aquí se envía agua líquida a través de una bomba, lo cual incrementa la presión del agua líquida. El agua líquida a alta presión se calienta y evapora para producir un vapor de alta presión que pasa a través de una turbina que genera electricidad. Después, el vapor de baja presión se envía a través de un condensador que utiliza agua de enfriamiento externa de baja temperatura para retirar el calor del vapor y, por lo tanto, permitir que se condense en un líquido de baja presión que después se envía a la bomba y el ciclo se repite. Para que el ciclo se repita continuamente, el agua debe entrar a la bomba en el mismo estado cada vez que completa una fase a través de los procesos. Así, el agua pasa por cuatro procesos, en donde los estados inicial y final son iguales.
1.1.3 Concepto de equilibrio termodinámico
En general, el equilibrio se describe como un estado de balance debido a la cancelación de las acciones de fuerzas opuestas. Existen muchos tipos de equilibrios, algunos de los cuales seguramente conoce. El equilibrio mecánico es el estado que existe cuando un sistema no experimenta aceleración porque las fuerzas mecánicas que actúan sobre él están balanceadas. En la termodinámica, a menudo se verá el equilibrio mecánico como el estado en el cual la presión en un sistema
Capítulo1 Introducción a la termodinámica y la energía 12
FIGURA 1.15 Diagrama esquemático de un ciclo de Rankine básico para las plantas eléctricas de vapor.
Bomba
3 Turbina SALIDA
básicos: sistemas, procesos y propiedades
es uniforme. El equilibrio térmico es el estado en el que dos o más sistemas están a la misma temperatura, o cuando un solo sistema tiene una temperatura uniforme.
El equilibrio termodinámico es el estado que existe cuando un sistema está en una combinación de equilibrios térmico, mecánico, químico y de fase. Un sistema en equilibrio termodinámico no tiene la capacidad de cambiar su estado de manera espontánea; para que su estado cambie debe experimentar una fuerza impulsora proveniente de fuera del sistema.
En este libro se estudiará la termodinámica del equilibrio. Existe otra rama de la termodinámica, conocida como termodinámica del no equilibrio, que está fuera del alcance de esta obra y que no tiene muchas aplicaciones prácticas para la mayoría de los ingenieros. En la termodinámica del equilibrio se asume que los sistemas están en un estado de equilibrio termodinámico. Sin embargo, vea que a medida que un sistema procede de un estado al otro durante un proceso, puede no estar en equilibrio a cada momento. Por ejemplo, si se calienta en la estufa un contenedor de agua, el agua que está al fondo del contenedor, cerca de la fuente de calor, puede estar más caliente que el agua que está en la parte de arriba del contenedor. Si se le da tiempo suficiente, todo el sistema estará a la misma temperatura, pero en un instante determinado técnicamente el sistema no estará en equilibrio térmico. En tales situaciones se suele considerar que el sistema pasa por una serie de estados de casi equilibrio. Aunque dichos estados no están estrictamente en equilibrio, las desviaciones del equilibrio experimentadas son insignificantes en términos del análisis general del problema, y la desviación solo existe por periodos relativamente cortos. Si bien estas desviaciones del equilibrio pueden causar errores en un análisis muy detallado de un sistema, por lo general no provocan errores significativos en un análisis de ingeniería o en el diseño de un sistema.
1.1.4 Propiedades termodinámicas
Es necesario encontrar una forma de describir el estado de un sistema termodinámico. Las propiedades termodinámicas de un sistema son las herramientas para describir el estado de un sistema. Una propiedad termodinámica es una cantidad cuyo valor numérico es independiente de la forma en que se alcanzó el estado de un sistema, y solo depende del estado del equilibrio termodinámico local del sistema. Esta es una distinción importante, porque significa que cualquier cosa cuyo valor dependa de un proceso específico atravesado por el sistema no es una propiedad del sistema en sí, sino más bien una descripción del proceso.
Sin duda, usted ya conoce muchas propiedades, como temperatura, presión, masa, volumen y densidad. Como un ejemplo de la forma en que la temperatura se ajusta a la definición de propiedad, considere el aire en una habitación. Si el aire de la habitación está a una temperatura en particular, la descripción del sistema no necesita explicar cómo se logró dicha temperatura (por calefacción o enfriamiento); el sistema simplemente está a esa temperatura. Otras propiedades notables son viscosidad, conductividad térmica, emisividad y muchas más que se presentarán en este libro cuando sea pertinente. El color también entra en la definición de una propiedad, porque el color de un sistema puede describirse numéricamente mediante un espectro que describa las longitudes de onda de la luz que componen el color.
Algunas propiedades se consideran extensivas y otras, intensivas. Una propiedad extensiva es aquella cuyo valor depende de la masa del sistema, mientras que una propiedad intensiva es aquella cuyo valor es independiente de la masa del sistema. Un método rápido para determinar si una propiedad es extensiva o intensiva es dividir mentalmente el sistema a la mitad y determinar si el valor de la propiedad en la mitad del sistema cambiaría. Esto debe arrojar el resultado de que la temperatura, la presión y la densidad son propiedades intensivas, porque un sistema de la mitad de tamaño tendrá el mismo valor en esas propiedades que el sistema original (es decir, dividir el sistema a la mitad no afecta su temperatura). Sin embargo, la masa y el volumen son propiedades extensivas porque cada una tendrá valores diferentes en un sistema de la mitad de tamaño del sistema inicial (es decir, el volumen de un sistema de la mitad de tamaño que el sistema inicial claramente será la mitad del volumen inicial).
13 1.1
Conceptos
Las propiedades extensivas se transforman en propiedades intensivas al dividir la propiedad extensiva entre la masa del sistema. Tales propiedades transformadas se denominan “específicas”. Por ejemplo, el volumen de un sistema, V , se divide entre la masa, m, para dar el volumen específico, v:
v 5 Vym
(1.1)
Se puede notar que el volumen específico es el inverso de la densidad, , la cual se define como la masa dividida entre el volumen ( 5 myV ).
Como se verá más adelante, por lo general es más fácil trabajar con las propiedades intensivas de un sistema en un análisis termodinámico y después multiplicar el valor de la propiedad por la masa del sistema para obtener el valor total de la cantidad extensiva de ese sistema en particular. Trabajar con propiedades intensivas permite evitar la necesidad de realizar cálculos para cada masa posible de un sistema que atraviesa un proceso. Se resuelve el proceso en una base intensiva (por unidad de masa) en general y después se aplica la solución a cualquier masa específica que pase por el proceso.
Las propiedades de una sustancia están relacionadas entre sí mediante ecuaciones de estado Como se verá, algunas ecuaciones de estado son relaciones muy sencillas, mientras que otras son tan complicadas que se calculan mejor con programas de computadora. Un ejemplo de una ecuación de estado simple que probablemente conoce es la ley de los gases ideales:
PV 5 mRT (1.2)
donde P es la presión, T es la temperatura y R es la constante de gas específica del gas ideal, la cual es igual a la constante universal del gas ideal, R –, dividida entre la masa molecular del gas, M. La ley de los gases ideales también se escribe en términos de un volumen específico:
Pv 5 RT (1.3)
Más adelante se explorará la ley de los gases ideales con más detalle.
En la ecuación (1.3) se ve que para un gas en particular hay tres propiedades relacionadas mediante la ecuación de estado dada. Dos de estas propiedades pueden establecerse en forma independiente, y la tercera se calcula al conocer las otras dos. Las propiedades que pueden elegirse arbitrariamente para un sistema en particular se denominan propiedades independientes, mientras que las propiedades cuyos valores se determinan de manera subsecuente mediante una ecuación de estado se conocen como propiedades dependientes. En la ecuación (1.3), si la presión, P, y el volumen específico, v, se eligen como las propiedades independientes, la temperatura, T, es una propiedad dependiente cuyo valor se determina mediante la ley de los gases ideales. En forma similar, si P y T se conocen como las propiedades independientes, entonces v será la propiedad dependiente.
Las ecuaciones (1.2) y (1.3) proporcionan también un ejemplo concreto del beneficio de usar propiedades específicas. Suponga que le piden compilar una lista de información para encontrar el volumen total ocupado por un gas en particular para un conjunto de presiones y temperaturas. Si calculara directamente el volumen total con la ecuación (1.2) tendría que compilar una lista para cada posible masa del gas. Sin embargo, con la ecuación (1.3) podría preparar una lista de volúmenes específicos y después pedir al usuario de los datos que multiplicara el número dado por la masa particular del sistema. Es claro que el segundo enfoque es más simple.
Más adelante se introducirán formalmente las propiedades básicas y de fácil medición con que se suele describir un sistema. Pero primero se debe comentar la naturaleza de los sistemas de unidades en la termodinámica.
1.1.5 Una nota sobre las unidades
Generalmente se usan dos amplios sistemas de unidades en la práctica de la ingeniería. Un sistema, conocido como Sistema Internacional (SI), es común en casi todo el mundo, mientras que el otro, conocido como sistema inglés de ingeniería (EE, English Engineering) está limitado en su mayor
Capítulo1
a la
14
Introducción
termodinámica y la energía
1.1 Conceptos básicos: sistemas, procesos y propiedades
parte a Estados Unidos, aunque el SI cada vez es más común ahí también. El sistema de unidades SI se basa en principios científicos y favorece el sistema numérico decimal. El sistema EE se desarrolló aleatoriamente con el tiempo con medidas de conveniencia que a menudo carecen de estándares universales consistentes. Aunque desde entonces se han desarrollado estándares, las unidades de conversión en el sistema EE a menudo son nominativas y en la actualidad parecen tener asignados valores arbitrarios.
Aunque se puede estar más familiarizado en la vida cotidiana con las unidades del sistema EE, el sistema SI es mucho más fácil para realizar cálculos científicos o de ingeniería. Así, este libro se concentrará en el sistema SI, porque hacerlo así le permitirá centrarse en la comprensión de los principios termodinámicos en lugar de quedar atrapado en el aprendizaje de conversión de unidades. Se utilizará el sistema EE para algunos ejemplos y problemas en aras de la familiaridad.
Para ilustrar la sencillez intuitiva del sistema SI se pueden comparar las unidades de los sistemas para una medición de longitud. El sistema SI utiliza el metro, m, como unidad base de longitud. Si un sistema es sustancialmente mayor o menor que un metro, se aplica uno de los prefijos que se muestran en la tabla 1.1 para el sistema SI. Así, 1 milímetro (mm) es igual a una milésima parte de un metro: 1 mm 5 0.001 m. Un kilómetro (km) equivale a mil metros: 1 km 5 1 000 m. En la práctica común también se utiliza el centímetro (cm), que es igual a una centésima parte de un metro: 1 cm 5 0.01 m.
En el sistema EE, la unidad base de longitud es el pie (ft, foot). Para convertir a tamaños más grandes o más pequeños se emplean factores de conversión como 1 pie 5 12 pulgadas y 1 milla 5 5 280 ft. Aunque tales conversiones son posibles, pueden introducir una complejidad innecesaria a los cálculos y causar errores más fácilmente que las conversiones de unidades SI.
La unidad de tiempo de los sistemas de unidades SI y EE es el segundo (s). Ambos sistemas emplean conceptos como milisegundos (ms) para 0.001 s. Además, consideran que 1 minuto es igual a 60 segundos y 1 hora equivale a 3 600 segundos. Estas conversiones son las únicas situaciones en las que el sistema de unidades SI no se ocupa exclusivamente de factores de 10 en conversiones de unidades.
PREGUNTA PARA REFLEXIÓN O DISCUSIÓN
En la mayor parte del mundo se usa el sistema de unidades SI, mientras que Estados Unidos suele emplear el sistema de unidades EE. ¿Sería buena idea que Estados Unidos adoptara el sistema SI? ¿Qué se necesitaría para que esto ocurriera?
Recuerde que una vez que se aprenden los principios termodinámicos, se aplican en la misma forma sin importar el sistema de unidad que se emplee. Es importante, en ambos sistemas de unidades, estar seguro de que las unidades en las ecuaciones se cancelen adecuadamente para dar las unidades finales correctas. TABLA
15
Prefijos comunes en el sistema de unidades SI. PrefijoFactorSímbolo Pico 10 12 p Nano 10 9 n Micro 10 6 Mili 10 3 m Centi 10 2 c Kilo103 k Mega106 M Giga109 G Tera1012 T
1.1
T = 100 ºC T = 0 ºC T = 50 ºC
Partición removida
(a)(b)
FIGURA 1.16 (a) Caja partida a la mitad con algunas moléculas a 100 y a 0 °C. (b) Después de que las moléculas calientes colisionan con las moléculas frías, todas las moléculas están a 50 °C.
1.2 INTRODUCCIÓN A ALGUNAS PROPIEDADES COMUNES
Como se mencionó, algunas propiedades termodinámicas son conocidas, se encuentran comúnmente y son (muy) fáciles de medir. Estas son las propiedades con que a menudo se describe un sistema. En esta sección se analizarán algunas de estas propiedades comunes y las unidades asociadas con ellas.
1.2.1 Temperatura
Cuando se piensa en conceptos como “calor”, la primera propiedad que suele venir a la mente es la temperatura. Y aunque las temperaturas se analizan sin problema, puede ser difícil definir la palabra temperatura. La temperatura es una medida del movimiento molecular y la energía asociada con el movimiento dentro de un sistema. Los sistemas con bajas temperaturas tienen movimientos relativamente lentos asociados con sus átomos y moléculas, mientras que los sistemas con altas temperaturas tienen un movimiento relativamente rápido de sus átomos y moléculas. En cierto sentido, esta es la razón de que un sistema caliente tienda a enfriarse cuando entra en contacto con un sistema frío (y por qué el sistema frío se calienta). Las moléculas de movimiento rápido en el sistema caliente colisionan con aquellas de movimiento lento en el sistema frío, transfiriendo un poco de energía a las moléculas que se mueven con más lentitud. Esto causa que las moléculas de movimiento rápido se ralenticen (lo que lleva a una disminución de la temperatura en el sistema caliente) y que las de movimiento lento se aceleren (lo que causa un aumento de la temperatura para el sistema frío); este proceso se ilustra en la figura 1.16
Hay muchos métodos para medir la temperatura de un sistema, pero el más común es el termómetro (vea la figura 1.17). Si observa un termómetro, verá una escala que muestra una serie de marcas que indican los “grados” de la sustancia. En el sistema de unidades SI, la unidad de temperatura es el grado Celsius (°C). Este sistema da puntos de referencia científicos y lógicos para definir la escala:
0 °C corresponde al punto de congelación del agua a presión atmosférica.
100 °C corresponde al punto de ebullición del agua a presión atmosférica.
FIGURA 1.17 Termómetro común para medir la temperatura.
Capítulo1 Introducción a la termodinámica y la energía 16
© TAGSTOCK1/Shutterstock.com
En el sistema de unidades EE, la unidad de temperatura es el grado Fahrenheit (°F). Los puntos de ajuste para definir esta escala son los siguientes, y se comparan con la escala de Celsius en la figura 1.18:
32 °F corresponde al punto de congelación del agua a una presión de 1 atmósfera (atm).
212 °F corresponde al punto de ebullición del agua a una presión de 1 atmósfera.
Es claro que estos valores no tienen mucho sentido científico. Sin embargo, la escala de temperatura es muy conveniente para las descripciones cotidianas de la temperatura. Si se considera la mayor parte del mundo, un rango de temperatura de 0 a 100 °F es adecuado para describir el rango de temperaturas que es probable que se experimente. Aunque algunas personas se encuentran en temperaturas fuera de esta gama, la mayoría de la gente vive casi todo el año en temperaturas dentro de este rango.
Ambas escalas tienen temperaturas fijas en los mismos puntos físicos, así que se puede derivar una relación entre estas dos escalas:
T(8C) 5 5 9 [T(8F) 32](1.4)
o, en forma equivalente, T(8F) 5 9 5 T(8C) 1 32(1.5)
FIGURA 1.18 La imagen de la izquierda muestra la temperatura en grados Celsius y Fahrenheit del agua helada, mientras que la imagen de la derecha muestra lo mismo del agua hirviendo a 1 atm.
Ambas escalas de temperatura se basan en un punto 0 (punto cero) establecido arbitrariamente que las hace escalas relativas. Aunque las escalas relativas son adecuadas para comparar temperaturas de diferentes sistemas y para determinar un cambio de temperatura, las escalas relativas pueden causar problemas significativos al realizar cálculos que involucren una temperatura específica. Considere la ley de los gases ideales, ecuación (1.2), escrita en una forma para resolver la masa de un sistema:
m 5 PVyRT
Ahora suponga que desea determinar la masa de un sistema cuya temperatura es la del punto de congelación del agua a presión atmosférica. Si utiliza el sistema de unidades SI y grados Celsius obtendría una masa infinita para el sistema, mientras que el sistema de unidades EE y grados Fahrenheit daría una masa finita. Es evidente que hay un problema si se pueden calcular una masa infinita y una masa finita para el mismo sistema solo por las unidades con que se mide la temperatura. Del mismo modo, si la escala de temperatura da una temperatura por debajo de cero, la masa del sistema sería negativa. Para evitar los problemas que pueden resultar del uso de una escala de temperatura relativa se utiliza una escala de temperatura absoluta.
Si se retoma la idea de lo que es la temperatura, una medida del movimiento molecular en un sistema, entonces es posible crear un concepto de una escala de temperatura que no se base en un punto cero arbitrario. Si se enfría un sistema, sus moléculas en el sistema se ralentizan. Mientras más frío se vuelva el sistema, más lentamente se moverán las moléculas. En algún momento cesará todo el movimiento de nivel molecular. En el punto donde cesa todo movimiento se puede definir una escala para tener una temperatura de cero. Dicha escala se denomina escala de temperatura absoluta, porque se basa en una verdadera definición de movimiento cero. No es posible tener una temperatura más baja que este “cero absoluto” porque el movimiento no puede ser más lento una vez que las moléculas se han detenido.
17 1.2 Introducción a
algunas propiedades comunes
32 ºF 0 ºC 212 ºF 100 ºC
La escala de temperatura absoluta en el sistema de unidades SI es la escala Kelvin (K). Un Kelvin (1 K) es igual en magnitud a 1 °C. El cero absoluto ocurre en −273.15 °C, y esto corresponde a 0 K. Por lo tanto, la relación entre las escalas de temperatura de Celsius y Kelvin es
T(K) 5 T(°C) 1 273.15 (1.6)
En la práctica, el 273.15 a menudo se redondea a 273. El tamaño de un grado Celsius y el tamaño de un kelvin son idénticos, por lo que la diferencia de temperatura es idéntica numéricamente en las escalas de Kelvin y Celsius, como se muestra en el ejemplo 1.1.
c EJEMPLO 1.1
Determine la diferencia de temperatura en °C y K entre un sistema a 30 °C y un sistema a 70 °C.
Dado que: TA 5 30 °C, TB 5 70 °C
Encuentre: DT en °C y K
Solución: Se considerarán dos sistemas, A y B, con las temperaturas dadas indicadas: TA 5 30 °C, TB 5 70 °C. La diferencia de temperatura es ΔT 5 TB – TA
En grados Celsius, la diferencia de temperatura es igual a DT 5 70 8C 30 8C 5 40 8C
Cada una de las temperaturas puede convertirse a la escala Kelvin.
TA 5 30 1 273.15 5 303.15 K 5 303 K TB 5 70 1 273.15 5 343.15 K 5 343 K
La diferencia de temperatura en Kelvin es DT 5 343 K 303 K 5 40 K
Análisis: Numéricamente, la diferencia en temperatura es la misma porque el tamaño de cada unidad es igual. En la práctica, esto significa que se puede usar cualquiera de las escalas cuando se consideran diferencias en temperatura. Además, si el valor de alguna cantidad tiene unidades de “unidad/K”, el valor es el mismo en términos de “unidad/°C” y viceversa.
En el sistema de unidades EE, la escala de temperatura absoluta es la escala Rankine (R). Como en el sistema SI, la magnitud de la unidad 1 R es igual a la magnitud de 1 °F. Se produce cero absoluto en −459.67 °F, que corresponde a 0 R. Por lo tanto, la relación entre las escalas de temperatura Fahrenheit y Rankine es
T(R) 5 T(8F) 1 459.67 (1.7)
En la práctica, 459.67 se redondea a menudo a 460. Los mismos conceptos de las escalas de temperatura SI respecto de las implicaciones del tamaño de las unidades aplican también para las escalas de temperatura para Rankine y Fahrenheit.
Cabe señalar que la temperatura en Kelvin y la temperatura en Rankine se relacionan mediante T(K) 5 5 9 T(R) (1.8)
c EJEMPLO 1.2
Un sistema tiene una temperatura de 25 °C. Determine el valor de esta temperatura en °F, K y R.
Dado que: T(°C) 5 25 °C
Encuentre: T(°F), T(K), T(R)
Solución: Con T(°C) 5 25 °C, se puede utilizar la ecuación (1.5) para encontrar la temperatura del sistema en °F: T(8F) 5 9 5 T(8C) 1 32 5 9 5 (25) 1 32 5 77 8F
Capítulo1
18
Introducción a la termodinámica y la energía
Con la ecuación (1.6) se encuentra la temperatura del sistema en Kelvin:
T(K) 5 T(8C) 1 273.15 5 25 1 273.15 5 298.15 K 5 298 K
Con la ecuación (1.8), reescrita para despejar T(R), se encuentra la temperatura del sistema en Rankine:
T(R) 5 9 5 T(K) 5 9 5 (298.15) 5 536.67 R 5 537 R
Estos distintos valores se ilustran en la figura 1.19.
25 ºC 77 ºF298 K537 R
FIGURA 1.19 Cuatro termómetros muestran la misma temperatura en cuatro escalas diferentes.
Hoy en día, las escalas de temperatura absoluta se definen a través del punto 0 absoluto y el punto triple del agua. (El punto triple del agua es la temperatura a la que coexisten las fases sólida, líquida y de vapor). Esta temperatura es de 0.01 °C, y por lo tanto el tamaño de una unidad de K en la escala de temperatura Kelvin se especifica a través del punto 0 absoluto y el punto triple del agua a una temperatura de 273.16 K (hay 273.16 unidades Kelvin de tamaño uniforme entre el 0 absoluto y el punto triple del agua).
PREGUNTA PARA REFLEXIÓN O DISCUSIÓN
Piense en algunos escenarios posibles que darían un resultado sin sentido si divide entre la temperatura con una escala de temperatura relativa. ¿Cómo se puede utilizar esto para recordar a otros que utilicen solo las temperaturas absolutas al multiplicar por o dividir entre una temperatura?
1.2.2 Masa, moles y fuerza
La propiedad conocida como masa especifica la cantidad de una sustancia. La masa se representa con la letra m. Un poco como la temperatura, la masa representa un concepto fácil de entender pero difícil de definir. La unidad SI para la masa es el kilogramo (kg), y la unidad EE para la masa es la libra-masa (lbm).
Un mol representa la cantidad de átomos o moléculas que contiene una sustancia, relacionándolos con el número de Avogadro igual a 6.022 3 1023. De manera más formal, el número de Avogadro se define como el número de átomos de carbono presentes en 0.012 kg de carbono-12. El
19 1.2 Introducción
a algunas propiedades comunes
Introducción a la termodinámica y la energía
número de moles de una sustancia se representa con la letra n. La masa molecular o masa molar, M, de una sustancia es la masa de un mol de esa sustancia: M 5 myn
Sin embargo, debido a que con frecuencia se utiliza la masa en kilogramos, por lo general la preocupación mayor es por el número de kilomoles (kmol) de una sustancia; en tal caso, la masa molecular representa la masa en kg de 1 kmol (mil moles) de la sustancia. En este libro se tratará principalmente la masa más que los moles, hasta que se comience a tratar sobre mezclas de gases y sistemas de reacción química.
De la segunda ley del movimiento de Newton, la fuerza, F, que ejerce una masa que experimenta una aceleración, a, es igual a F 5 ma (1.9)
La unidad de fuerza del SI es el newton (N), y por definición 1 N 5 1 kg · m/s2. Entonces, en el sistema de unidades SI, la unidad de fuerza se deriva directamente de la definición de fuerza, porque las unidades de aceleración son m/s2. Debe tener en cuenta que el peso, W, de un objeto es la fuerza que ejerce la masa del objeto en un campo gravitacional con una aceleración igual a g: W 5 mg. Al nivel del mar en la Tierra, la aceleración debida a la gravedad, g, es de 9.81 m/s2 en unidades SI, y de 32.17 ft/s2 en unidades EE. En lugar de conocer un valor diferente para la aceleración debida a la gravedad en otras ubicaciones, estos son los valores que se deben utilizar por defecto. Tenga en cuenta que el peso de un objeto puede cambiar, pero la masa del objeto se mantiene constante sin importar dónde se encuentre. Así, si un objeto se mueve en un campo gravitacional diferente, su peso va a cambiar, por eso los objetos pesan menos en la Luna que en la Tierra aunque tengan la misma masa.
Hay una complejidad adicional en el sistema de unidades EE respecto de la fuerza. La unidad de fuerza en el sistema EE es la libra-fuerza (lbf). Conforme se desarrollaron el uso de las unidades y el concepto de masa, fue conveniente que la masa y el peso de un objeto en libras fueran numéricamente iguales en el nivel del mar en la Tierra a pesar de que la masa y el peso se representan con unidades diferentes. Por lo tanto, si un objeto tiene una masa de 50 lbm, debe tener un peso de 50 lbf en el nivel del mar. Sin embargo, al tener en cuenta que la aceleración debida a la gravedad es de 32.17 ft/s2, esto claramente no ocurrirá con la ecuación W 5 mg. Para considerar esto, en el sistema de unidades EE se introduce un factor de conversión de unidades, gc: gc 5 32.174 lbm ? ft/(lbf ? s2)
A su vez, esto cambia la ecuación (1.9) a F 5 maygc para unidades EE. De hecho, en toda ecuación donde haya que convertir entre lbm y lbf debe introducirse el factor de conversión gc; esta es una de las complicaciones de aprender termodinámica con unidades EE. En unidades SI, gc 5 1. En este libro, y como se hace hincapié en las unidades SI, se ignorará gc en las ecuaciones, pero sin perder de vista que será necesario convertir unidades en los cálculos de unidades EE.
c EJEMPLO 1.3
Un objeto en un planeta distante tiene un peso de 58.5 N. La aceleración debida a la gravedad en el planeta es de 31.5 m/s2. Determine la masa del objeto.
Dado que: W 5 58.5 N g 5 31.5 m/s2
Encuentre: m
Solución: Como W 5 mg, se tiene m 5 58.5 Ny31.5 m/s2 5 58.5 kg m/s2y31.5 m/s2 5 1.86 kg
20
Capítulo1
c EJEMPLO 1.4
En la Tierra a nivel del mar, un bloque de metal tiene un peso de 295 lbf. El bloque se coloca en un cohete y se envía a la Luna, donde la aceleración debida a la gravedad es de 5.32 ft/s2. Determine el peso del bloque de metal en la Luna.
Dado que: Tierra: W e 5 295 lbf, ge 5 32.17 ft/s2
Luna: gm 5 5.32 ft/s2
Encuentre: W m (peso en la Luna)
Solución: Al incorporar el factor de conversión de la unidad, gc, la masa del objeto se determina a partir de la información dada sobre el peso del bloque en la Tierra.
m 5 W e gc yge 5 (295 lbf) (32.17 lbm ? ft/lbf ? s2)y(32.17 ft/s2) 5 295 lbm
La masa es constante, por lo que, con la aceleración debida a la gravedad en la Luna, se encuentra el peso del bloque en la Luna:
W m 5 mgm ygc 5 (295 lbm)(5.32 ft/s2)y(32.17 lbm ft/lbf s2 ) 5 48.8 lbf
En la figura 1.20 se ilustran estos diferentes pesos.
295 lbf Luna
48.8 lbf
FIGURA 1.20 Escalas que muestran el peso del mismo objeto en la Tierra y en la Luna.
1.2.3 Volumen y volumen específico
El volumen, V, de un sistema es el espacio físico que ocupa dicho sistema. El volumen representa una región espacial tridimensional, así que la unidad SI del volumen es el metro cúbico: m3. La unidad EE del volumen es el pie cúbico: ft3
Como se mencionó, los cálculos termodinámicos se realizan en general con propiedades intensivas, y el resultado se escala al multiplicar por la masa del sistema. El volumen es una propiedad extensiva, mientras que el volumen específico, v, es la propiedad intensiva correspondiente. El volumen específico es el volumen total del sistema dividido entre la masa del sistema: v
Las unidades para el volumen específico en el sistema SI son m3/kg, y en el sistema EE son ft3/lbm. Como se ha señalado, el volumen específico es el inverso de la densidad, : v 5 1y
1.2.4 Presión
La última de las propiedades comunes de un sistema que se miden fácilmente es la presión, P, con que a menudo se describe un sistema. La presión es la fuerza ejercida dividida entre el área, A, sobre
21 1.2 Introducción a algunas propiedades comunes
Tierra
5 Vym
Gas
la cual actúa esa fuerza. En un punto particular en el espacio, la presión se encuentra como el límite de la fuerza dividido entre el área conforme el área se aproxima al área de un punto:
P 5 lím A S A9
F A (1.10)
donde A9 es el área del punto. En la práctica, la presión ejercida sobre un sistema o por un sistema será uniforme en la superficie, de modo que en general la presión se calcula simplemente como
P 5 FyA (1.11)
En unidades SI, la unidad de presión es el pascal (Pa), donde 1 Pa 5 1 N/m2. Sin embargo, si considera el tamaño de esta unidad verá que es igual al peso en la Tierra de un objeto de aproximadamente 0.1 kg repartido en un metro cuadrado de espacio: esta es una unidad de presión muy pequeña. Así, en termodinámica se suelen considerar las unidades de presión en kilopascales (kPa) (1 000 Pa) y megapascales (MPa) (106 Pa). En ocasiones encontrará unidades de presión en “bares”, donde 1 bar 5 100 kPa 5 105 Pa. La razón de esta unidad se verá en breve. La unidad estándar de presión en las unidades EE es la libra-fuerza por pie cuadrado: lbf/ft2. A menudo se utilizará también la libra-fuerza por pulgada (in, inch) cuadrada (lbf/in2 o psi), donde 1 lbf/ft2 5 144 lbf/in2 debido a que hay 12 pulgadas en un pie.
Si se supone que un sistema está en equilibrio, el equilibrio mecánico requiere que la presión ejercida sobre el exterior de un sistema sea igual a la que el sistema ejerce desde el interior. Por lo tanto, la presión dentro de un sistema se determina como la presión neta ejercida sobre el sistema por fuerzas externas. Tenga en cuenta que estas fuerzas pueden incluir las paredes que rodean al sistema y que empujan hacia atrás en su interior; por lo tanto, puede ser más fácil medir la presión dentro del sistema en lugar de añadir las presiones externas ejercidas sobre él.
La presión atmosférica es la fuerza que ejerce el aire por encima de alguna ubicación (el peso del aire) dividida entre el área sobre la cual se distribuye. La presión atmosférica estándar, P0, se define como la presión media del aire a nivel del mar y es igual a
P0 5 101.325 kPa 5 14.696 lbf/in2 5 2 116.2 lbf/ft2
A menudo la presión atmosférica estándar se designa como 1 atm, y las presiones pueden reportarse en términos de cierto número de atmósferas. Como se ve, la presión atmosférica estándar es aproximadamente de 100 kPa, lo que indica que una presión expresada en bares es más o menos igual al número de atmósferas. La presión atmosférica local, Patm, suele ser diferente de la presión atmosférica estándar, en particular a una altitud significativa por encima del nivel del mar. La presión del aire en las zonas montañosas es mucho menor que la del nivel del mar; la diferencia es lo bastante significativa para que su efecto en las propiedades de ebullición del agua altere los tiempos de cocción de algunos alimentos.
L
Atmósfera
FIGURA 1.21 Manómetro calibrado para medir la presión al interior de un tanque de gas.
Medir una diferencia de presión es una tarea relativamente fácil. Para ello se utilizan manómetros u otros medidores de presión sencillos. Como se muestra en la figura 1.21, en un manómetro, un tubo que contiene un líquido se coloca entre los dos sistemas cuyas presiones deben compararse; en este caso, un cilindro que contiene un gas y la atmósfera. El cilindro contiene gas presurizado, lo cual ejerce una fuerza mayor en un lado del fluido en comparación con la fuerza ejercida por la atmósfera en el otro lado. Esto causa una diferencia en la altura, L, del líquido entre los dos tubos el manómetro. Al multiplicar L por la densidad del líquido y la aceleración local
Capítulo1
22
Introducción a la termodinámica y la energía
debida a la gravedad se obtiene la diferencia de presión entre ambos sistemas. Esta diferencia en la presión se denomina presión manométrica, P g :
P g 5 gL (1.12)
La presión manométrica también se mide de otras maneras. Considere el estado del manómetro si el gas dentro del cilindro tiene una presión igual a la de la atmósfera local. En este caso, ambos extremos del tubo experimentan la misma fuerza y no habrá diferencia de altura entre el fluido en ambas patas del manómetro. Esto indica que la presión manométrica es de cero. Pero, ¿la presión dentro del cilindro es igual a cero? No, la presión es igual a la presión atmosférica. Por lo tanto, para obtener la presión real del sistema se deben combinar la presión manométrica y la presión atmosférica local para obtener la presión absoluta, P:
P 5 P g 1 P atm (1.13)
La presión absoluta es la presión necesaria para los cálculos que implican ecuaciones de estado con las que se determinan otras propiedades de un sistema.
Otra manera de comprobar la necesidad de la presión absoluta es considerar el problema de determinación de la masa de aire dentro de un neumático desinflado de bicicleta, cuya presión de aire es idéntica a la presión atmosférica local: un medidor de neumáticos daría cero para un neumático desinflado. ¿Todavía hay aire dentro del neumático? Sí, todavía hay aire dentro del neumático porque no se ha dado una condición de vacío en el caso de un neumático que pierde su aire. Recuerde la ley de los gases ideales [reescrita a partir de la ecuación (1.2)]: m 5 PVyRT
Es claro que la presión manométrica de cero no se puede utilizar como la presión del aire dentro del neumático porque eso llevaría a una masa de cero. En cambio, se requiere la presión absoluta en este cálculo; en este caso, la presión absoluta es igual a la presión atmosférica local. Como se mencionó, la presión atmosférica local no es necesariamente igual a la presión atmosférica estándar, aunque se puede utilizar la presión atmosférica estándar como una buena aproximación si no se dispone de otra información. Medir la presión atmosférica local tiende a ser más difícil y costoso. Un dispositivo habitual para dicha medición es el barómetro, y por lo tanto la presión atmosférica local se llama a menudo presión barométrica.
PREGUNTA PARA REFLEXIÓN O DISCUSIÓN
¿Qué ocurriría si coloca un neumático de bicicleta bien sellado y completamente inflado en una cámara con una presión de 15 atm?
c EJEMPLO 1.5
Un medidor de presión en un tanque lleno de helio comprimido indica que la presión dentro del tanque es de 352 kPa. Un barómetro en la habitación donde está el tanque, indica que la presión barométrica local es de 100.2 kPa. Determine la presión absoluta del helio dentro del tanque.
Dado que: P g 5 352 kPa (el manómetro indica la presión manométrica en el tanque). P atm 5 100.2 kPa (el barómetro proporciona la presión atmosférica local). Encuentre: P
Solución: La presión absoluta es la suma de la presión manométrica y la presión atmosférica: P 5 P g 1 P atm 5 352 kPa 1 100.2 kPa 5 452.2 kPa 5 452 kPa
23 1.2 Introducción
a algunas propiedades comunes
FIGURA 1.22
Diagrama que muestra las presiones ejercidas sobre el gas en un dispositivo pistón-cilindro.
c EJEMPLO 1.6
Un pistón circular en un cilindro tiene un diámetro de 5 cm. El cilindro contiene aire. Un manómetro dentro del cilindro da una presión de 300 kPa. El pistón está al nivel del mar, donde la aceleración debida a la gravedad es de 9.81 m/s2. Determine la masa del pistón.
Dado que: D 5 5 cm 5 0.05 m, Pg 5 300 kPa, g 5 9.81 m/s2
Encuentre: m
Solución: Como se muestra en la figura 1.22, la presión absoluta dentro del cilindro es igual a la presión ejercida por el peso del pistón más la presión atmosférica local. Por lo tanto, la diferencia de presión entre el aire dentro y fuera del cilindro (es decir, la presión manométrica) es resultado del peso del pistón. Así, no es necesario encontrar la presión absoluta en el tanque para calcular la masa del pistón; solo se debe equiparar la presión manométrica a la producida por el pistón:
P g 5 FyA 5 mgyA
El área del pistón es la de un círculo:
A 5 D2y4 5 (0.05 m)2y4 5 0.00196 m2
Tenga en cuenta que la unidad de presión que se deriva naturalmente de una fuerza en newtons es el pascal. Por lo tanto, P g 5 300 kPa 5 300 000 Pa.
m 5 P g Ayg 5 (300 000 Pa)(0.00196 m2)y(9.81 m/s2)
5 (300 000 N/m2)(0.00196 m2)y(9.81 m/s2) 5 60.0 N · s2/m
5 60.0 (kg · m/s2)(s2/m) 5 60.0 kg
Análisis: Este problema es una buena ilustración del beneficio de hacer un seguimiento de las unidades durante el cálculo. Realizar el seguimiento de las unidades y cancelarlas de manera adecuada permite evitar errores por descuido. Por ejemplo, si se hubiera mantenido la presión de calibración en kPa, la respuesta final habría sido incorrecta, porque las unidades no se habrían cancelado correctamente para dar una masa en kilogramos.
Los dos ejemplos anteriores ilustran el uso de la “precisión de ingeniería” en las respuestas para los cálculos termodinámicos. En general, la precisión de ingeniería considera de tres cifras significativas en el valor. Una cifra significativa es un número 0 que no marca posición en una respuesta. Los números 10 300, 431, 2.04 y 0.00352 tienen tres cifras significativas. En general, se considera que la mayoría de las cantidades puede medirse con tres cifras significativas de precisión, y que casi todos los objetos se pueden construir con tales especificaciones sin una cantidad excesiva de esfuerzo. Es claro que algunas aplicaciones necesitan más precisión y otras menos. Pero en este curso se buscará en general dar respuestas a tres cifras significativas de precisión y se asumirá que las cantidades dadas se conocían con esa precisión, aunque no se den en ese nivel (como el diámetro de “5 cm” en el ejemplo 1.6).
Hay algunos procesos termodinámicos especiales que tienen una propiedad constante. Un proceso de temperatura constante también se conoce como proceso isotérmico, mientras que un proceso de presión constante se denomina también proceso isobárico. Con menor frecuencia, a un proceso de volumen constante a veces se le llama proceso isocórico.
1.3 LEY CERO DE LA TERMODINÁMICA
Ahora que se presentaron algunos conceptos y propiedades básicos en la termodinámica es hora de considerar una de las cuatro leyes que rigen la termodinámica. La ley se conoce como ley cero de la termodinámica, como se le denominó formalmente en referencia a la primera ley de la termodinámica, pero después se le consideró una ley fundamental.
Capítulo1
24
Introducción a la termodinámica y la energía
Pg Patm Pg
1 Patm
Considere tres sistemas: A, B y C. La ley cero de la termodinámica establece que si el sistema A está en equilibrio térmico (es decir, si tiene la misma temperatura) con el sistema B, y el sistema B está en equilibrio térmico con el sistema C, entonces el sistema A está en equilibrio térmico con el sistema C. Esta ley debe parecer lógica, y como es tan evidente no se estableció de manera formal tan pronto como otras leyes científicas. Sin embargo, como se verá, la ley cero está en el centro de la medición de la temperatura, y ya se ha considerado aquí que la temperatura es una propiedad muy importante en termodinámica. Por lo tanto, se declaró formalmente la ley cero, y las otras leyes de la termodinámica se apoyan en ella y dependen de ella para proporcionar una base para las mediciones correctas de temperatura.
Como ejemplo de un dispositivo de medición de temperatura considere el termómetro de mercurio que se muestra en la figura 1.23. El termómetro se coloca en un vaso que contiene agua y está hecho de vidrio que contiene mercurio. Una vez que el termómetro alcanza una temperatura constante, se supone que está midiendo la temperatura del agua. Pero en realidad está indicando la temperatura del mercurio dentro del vaso. Para asumir que se determina la temperatura del agua se debe suponer que la temperatura del mercurio (THg ) es igual a la temperatura del vidrio (T g ), que a su vez es igual a la temperatura del agua (T w ). Para que este sea el caso, el mercurio debe estar en equilibrio térmico con el vidrio, y el vidrio debe estar en equilibrio térmico con el agua. Por la ley cero se puede afirmar que el mercurio está en equilibrio térmico con el agua, y de hecho la medición de la temperatura del mercurio es igual a la medición de la temperatura del agua: THg 5 T g y T g 5 T w de modo que THg 5 T w
Observe que alcanzar el equilibrio térmico es un requisito para que funcione este concepto de medición de temperatura. Si se almacena el termómetro de mercurio en un refrigerador y luego se le saca y se le coloca en un vaso de agua hirviendo, indicar la temperatura del mercurio como se mostró en el termómetro inmediatamente después de colocarlo en el agua no dará la temperatura del agua. El equilibrio térmico entre los tres sistemas no habría alcanzado ese punto, y la ley cero indica que la temperatura del mercurio no será igual a la temperatura del agua hasta que se cumplan las condiciones de equilibrio térmico.
1.4 FASES DE LA MATERIA
Una sustancia pura es una sustancia químicamente homogénea, es decir, una sustancia que tiene una composición química uniforme en todo momento. Una sustancia pura puede ser una sustancia de una sola molécula (como agua, nitrógeno y oxígeno) o bien, una mezcla de sustancias con una composición constante siempre (como el aire, que es una mezcla de gases que tiene la misma composición a lo largo de un sistema de tamaño razonable). Una fase de la materia es una cantidad de materia de una sustancia pura que es físicamente homogénea. Así, una fase es química y físicamente uniforme en todo momento. Hay un número relativamente pequeño de fases de la materia, tres de las cuales son de primordial interés para los ingenieros: sólida, líquida y gaseosa. La fase plasma es importante en algunas aplicaciones, y fases como un condensado de Bose-Einstein son de interés sobre todo en un nivel científico pero no necesariamente práctico.
La fase sólida se caracteriza por una cantidad de materia cuyos átomos o moléculas están en una estructura de retícula fija. Los átomos o moléculas están muy separados entre sí y se mantienen en su lugar por la acción de fuerzas de atracción intermoleculares. Un sólido mantiene su forma sin ayuda de un contenedor. Conforme un sólido se calienta, las moléculas oscilan cada vez más dentro de la estructura de retículo y, al final, tendrán suficiente energía para liberarse de la red. Este será un proceso de fusión si las moléculas pasan a la fase líquida, y un proceso de sublimación si las moléculas se mueven a la fase gaseosa.
FIGURA 1.23 Un termómetro de mercurio mide la temperatura del agua. Los tres sistemas (el mercurio, el vidrio y el agua) están en equilibrio térmico, así que la temperatura del mercurio (que es aquella que se determina) es la misma que la temperatura del agua.
25 1.4 Fases de la materia
Tg THg TW
En la fase líquida, las moléculas todavía están muy separadas entre sí, pero no están en una estructura de retícula fija. Las moléculas son libres de moverse dentro de la fase y no están obligadas a estar en una posición al lado de otra molécula en particular: las moléculas pueden desplazarse y girar. Las fuerzas intermoleculares no son tan fuertes como en la fase sólida, pero son lo bastante fuertes para mantener a las moléculas en un entorno ordenado y estructurado. A medida que se añade más energía al líquido, las moléculas ganan bastante energía para superar las fuerzas intermoleculares que mantienen el líquido unido y se produce así el proceso de ebullición a un gas.
La fase gaseosa se caracteriza por átomos o moléculas libres que se desplazan en direcciones aleatorias sin estar sujetos a otras moléculas. El espaciamiento entre las moléculas es grande y las fuerzas intermoleculares son muy pequeñas. Las interacciones entre las moléculas en un gas se producen sobre todo mediante colisiones a medida que las moléculas se mueven en diferentes direcciones. A veces, la fase gaseosa se denomina fase de vapor. Estas fases son idénticas, aunque el término vapor suele aplicarse a las sustancias que están relativamente cerca de su punto de ebullición/ condensación en la fase líquida. El término “gas” se reserva con más frecuencia para las sustancias que comúnmente se experimentan como un gas, a pesar de que se sabe que podrían existir en otras fases. Por lo tanto, es común referirse a gases de hidrógeno, nitrógeno o dióxido de carbono, pues en la vida cotidiana estas sustancias suelen experimentarse solo en la fase de gas. Sin embargo, la fase gaseosa del agua a menudo se llama “vapor de agua” porque el agua se suele experimentar en sus formas líquida y gaseosa (y sólida).
Las fases también cambian como resultado de la eliminación de energía del material. Un gas se condensa en un líquido (o directamente en un sólido en las condiciones apropiadas) y un líquido se congela en un sólido. Si se agrega energía al material, los cambios de fase ocurren en la dirección opuesta. Para una sustancia, las temperaturas a las que se producen estos procesos dependen de la presión del sistema y no de la dirección del cambio de fase. Por lo tanto, a una presión de 1 atm, el agua pura cambia de la fase sólida (hielo) a la fase líquida al derretirse a 0 °C, y el agua líquida cambia a hielo por la congelación a 0 °C también. Del mismo modo, el agua líquida a 1 atm hierve a la fase de gas (vapor de agua) a 100 °C, y el vapor de agua se condensa en agua líquida a 100 °C. Estas temperaturas son diferentes a distintas presiones, como se ilustra en la figura 1.24 Por ejemplo, la temperatura de ebullición/condensación del agua a 200 kPa es de 120.2 °C, y a 1 000 kPa es de 179.9 °C.
Capítulo1
26
Introducción a la termodinámica y la energía
FIGURA
0 250 500 750 1 000 1 250 1 500 1 750 Presión
0 Temperatura
20406080100120140160180200
1.24 Presión de ebullición del agua como función de temperatura.
de ebullición (kPa)
(°C)
Como se verá con mayor detalle en el capítulo 3, una sustancia pura puede existir en un sistema en más de una fase. Un ejemplo común de esto es un vaso de agua helada, que contiene agua líquida y hielo a la misma temperatura si se ha alcanzado el equilibrio térmico entre ambos. Cuando existen múltiples fases de una sustancia dentro de un sistema y las masas de cada fase son inmutables, el sistema se considera en equilibrio de fase. El equilibrio de fase es un requisito para que un sistema se considere en equilibrio termodinámico.
PREGUNTA PARA REFLEXIÓN O DISCUSIÓN
¿Cuáles son dos formas en que se puede evitar que hierva el agua líquida a 1 atm y 100 °C?
Resumen
En este capítulo se estableció la importancia de la energía en el mundo y la necesidad de que haya ingenieros para entender la ciencia que describe la energía: la termodinámica. Se describieron algunos conceptos fundamentales del análisis termodinámico, como el sistema, el proceso y el concepto de propiedades termodinámicas. Se introdujeron los sistemas de unidades SI y EE, y cabe señalar que la mayor parte del enfoque de este libro se centra en las unidades SI. Se analizaron las propiedades básicas con que normalmente se describen sistemas, como la temperatura y la presión. Se presentó la ley cero de la termodinámica y se exploró su aplicación en los sistemas de medición de temperatura. Por último, se presentó la idea de una fase de la materia.
Todos estos son conceptos fundamentales, muchos de los cuales tal vez ya conozca por otros cursos. Sin embargo, el resto de este libro se basa en estos conceptos, y usted debe estar seguro de entender a fondo estos principios antes de seguir adelante. Algunos principios se mencionarán explícitamente en futuros puntos del libro, pero otros conceptos (como equilibrio termodinámico o la ley cero) se asumirán implícitamente como un componente fundamental del desarrollo de los principios de la termodinámica.
ECUACIONES CLAVE
Conversiones de escalas de temperatura:
T(8C) 5 5 9 [T(8F) 32] (1.4)
T(8F) 5 9 5 T(8C) 1 32 (1.5)
T(K) 5 T(8C) 1 273.15 (1.6)
T(R) 5 T(8F) 1 459.67 (1.7)
Fuerza: F 5 ma/gc (1.9) donde gc = 1 (unidades SI) o gc 5 32.174 lbm · ft/(lbf · s2) (unidades EE) Presión absoluta: P 5 P g 1 P atm (1.13)
27 Ecuaciones clave
PROBLEMAS
1.1 En los siguientes sistemas, determine si el sistema descrito se modela mejor como un sistema aislado, cerrado o abierto:
(a) vapor que fluye a través de una turbina (b) una bombilla incandescente (c) una bomba de combustible en un automóvil en movimiento (d) un ancla de un barco hundido que descansa 3 000 m bajo la superficie del océano (e) el techo de una casa
1.2 En los siguientes sistemas, determine si el sistema descrito se modela mejor como un sistema aislado, cerrado o abierto:
(a) un árbol que crece en un bosque (b) un televisor (c) una computadora portátil (d) la nave espacial Voyager 2 en su estado actual (e) la nave espacial Messenger cuando se puso en órbita alrededor de Mercurio
1.3 En los siguientes sistemas, determine si el sistema descrito se modela mejor como un sistema aislado, cerrado o abierto:
(a) un neumático inflado (b) un aspersor de césped en uso activo (c) una taza llena de agua líquida (d) el radiador de un motor (e) una formación rocosa a 200 m por debajo de la superficie de la Tierra
1.4 En los siguientes sistemas, determine si el sistema descrito se modela mejor como un sistema aislado, cerrado o abierto:
(a) una bomba que suministra agua a un edificio (b) una tetera con agua hirviendo (c) un volcán activo (d) una barra de oro macizo colocada dentro de una caja muy bien aislada (e) una silla
1.5 En los siguientes sistemas, determine si el sistema descrito se modela mejor como un sistema aislado, cerrado o abierto:
(a) una polea en un ascensor (b) una bañera (c) un ser humano
(d) una pieza de metal que se moldea en un torno (e) un cometa que orbita el Sol en la nube de Oort (la nube de cometas inactivos ubicada mucho más allá de las órbitas de los planetas)
1.6 Considere una botella cerrada medio llena de agua y colocada en un refrigerador. Trace diagramas que muestren el sistema más adecuado para un análisis termodinámico que: (a) solo considera el agua (b) considera solamente el agua y el aire dentro de la botella (c) toma en cuenta el agua y el aire dentro de la botella, y la propia botella (d) considera solo la botella y no el contenido (e) contempla todo el contenido del refrigerador, pero no el refrigerador físico
Capítulo1 Introducción a la termodinámica y la energía 28
1.7 Considere una manguera de incendios con agua que fluye a través de ella y después a través de una boquilla al final de la manguera. Trace diagramas que muestren el sistema más apropiado para un análisis termodinámico que:
(a) toma en cuenta solamente el agua en la boquilla del sistema (b) considera el agua que fluye a través de la manguera y la boquilla (c) contempla tanto el agua que fluye a través de la boquilla como la propia boquilla
1.8 Una pelota de baloncesto está a punto de salir de la mano de un jugador para un tiro. Trace diagramas que muestren el sistema más adecuado para un análisis termodinámico que:
(a) considera solamente el aire dentro de la pelota (b) toma en cuenta solamente el material que compone la pelota y no el aire dentro de ella (c) considera la pelota y el aire en el interior (d) contempla la pelota, el aire interior y la mano del jugador (e) considera todo el estadio en donde se encuentra la pelota
1.9 Para condensar un flujo de vapor, el agua de refrigeración líquida se envía a través de una tubería y el vapor pasa por encima del exterior de la tubería. Trace diagramas que muestren el sistema más adecuado para un análisis termodinámico que:
(a) considera solo el agua que fluye a través de la tubería (b) toma en cuenta solo el vapor de condensación en el exterior de la tubería (c) considera solo la tubería (d) contempla la tubería, la refrigeración interna y el vapor de condensación externo
1.10 Trace un diagrama esquemático del lugar donde vive. Identifique cualquier sitio donde la masa o la energía puedan entrar o salir de la habitación o del edificio.
1.11 Delinee un diagrama esquemático de un motor de automóvil. Identifique cualquier lugar donde la masa o la energía puedan entrar o salir del motor.
1.12 Trace un diagrama esquemático de una computadora de escritorio. Identifique cualquier lugar donde la masa o la energía puedan entrar o salir de la computadora.
1.13 Esboce un diagrama esquemático de un puente de autopista sobre un río. Identifique cualquier mecanismo que pueda hacer que la masa o la energía fluyan hacia o desde el sistema del puente.
1.14 Trace un diagrama esquemático de un avión en vuelo. Identifique cualquier lugar donde la masa o la energía puedan entrar o salir de la aeronave.
1.15 Un sistema cerrado se somete a un proceso de volumen constante (isocórico) a 0.25 m3/kg conforme la presión cambia de 100 kPa a 300 kPa. Esboce este proceso en un diagrama P-v (presión vs. volumen específico).
1.16 Un sistema se somete a un proceso isotérmico a 30 °C a medida que el volumen específico cambia de 0.10 m3/kg a 0.15 m3/kg. Trace este proceso en un diagrama T-v (temperatura vs. volumen específico).
1.17 Un sistema se somete a un proceso isobárico de 50 a 30 °C, a una presión de 200 kPa. Esboce este proceso en un diagrama P-T (presión vs. temperatura).
1.18 Un sistema se somete a un proceso descrito por Pv 5 constante, desde un estado inicial de 100 kPa y 0.25 m3/kg hasta un volumen específico final de 0.20 m3/kg. Determine la presión final y trace este proceso en un diagrama P-v (presión vs. volumen específico).
29 Problemas
1.19 Esboce en un diagrama P-v los tres procesos secuenciales siguientes por los que pasa un sistema:
(a) una expansión de presión constante desde un estado inicial de 500 kPa y 0.10 m3/kg hasta un volumen específico de 0.15 m3/kg
(b) una despresurización de un volumen específico constante a una presión de 300 kPa (c) un proceso que acompañe a Pv 5 constante a una presión final de 400 kPa
1.20 Trace un diagrama T-v de los siguientes tres procesos secuenciales que experimenta un sistema:
(a) un calentamiento de volumen específico constante de 300 K y 0.80 m3/kg a una temperatura de 450 K
(b) una compresión isotérmica a un volumen específico de 0.60 m3/kg (c) un enfriamiento isocórico a 350 K
1.21 Trace un diagrama P-T de un sistema sometido a los dos procesos secuenciales siguientes: (a) una compresión isotérmica de 500 K y 250 kPa a una presión de 500 kPa (b) un enfriamiento isobárico a una temperatura de 350 K
1.22 Delinee un diagrama P-v de un sistema cerrado sometido a los cuatro procesos secuenciales siguientes:
(a) una compresión isobárica de 200 kPa y 0.50 m3/kg a un volumen específico de 0.20 m3/kg (b) una expansión de volumen constante a un volumen específico de 0.30 m3/kg (c) una despresurización de volumen constante a una presión de 125 kPa (d) una expansión de presión constante a un volumen específico de 0.30 m3/kg
1.23 Un ciclo termodinámico consiste en los tres procesos siguientes. Esboce el ciclo en un diagrama T-v
(a) un calentamiento de volumen constante de 0.10 m3/kg y de 300 K a 500 K (b) una expansión isotérmica a un volumen específico de 0.15 m3/kg (c) un proceso lineal que devuelve el proceso a su estado inicial
1.24 Un ciclo termodinámico consiste en los tres procesos siguientes. Trace el ciclo en un diagrama P-v
(a) una compresión isobárica de 300 kPa y 1.20 m3/kg a un volumen específico de 0.80 m3/kg (b) un proceso para el que Pv 5 constante a un volumen específico de 1.20 m3/kg (c) un proceso de volumen constante que produce una presión de 300 kPa
1.25 Un ciclo termodinámico implica los cuatro procesos siguientes. Esboce el ciclo en un diagrama P-T.
(a) un calentamiento isobárico de 500 K y 400 kPa a una temperatura de 700 K (b) una compresión isotérmica a una presión de 800 kPa (c) un enfriamiento isobárico a una temperatura de 500 K (d) una expansión isotérmica adecuada
1.26 El punto de fusión del plomo a presión atmosférica es de 601 K. Determine esta temperatura en °C, °F y R.
1.27 El punto de fusión del oro a presión atmosférica es de 2 405 R. Determine esta temperatura en °C, °F y K.
1.28 A una presión de 5.1 atm, el dióxido de carbono se condensa en un líquido a −57 °C. Determine esta temperatura en °F, K y R.
Capítulo1
30
Introducción a la termodinámica y la energía
1.29 La temperatura “normal” de un ser humano es de 98.6 °F. Determine esta temperatura en °C, K y R.
1.30 El punto de ebullición del amoniaco a presión atmosférica es de 239.7 K. Determine esta temperatura en °C, °F y R.
1.31 El punto de fusión del aluminio a presión atmosférica es de 1 220 °F. Determine esta temperatura en °C, K y R.
1.32 A presión atmosférica, el punto de ebullición del metanol es de 337.7 K y el del etanol es de 351.5 K. Convierta ambas temperaturas a grados Celsius y determine la diferencia entre ellas en K y °C.
1.33 A presión atmosférica, el punto de fusión del platino puro es de 2 045 K y el de la plata es de 1 235 K. Convierta ambas temperaturas a grados Celsius y determine la diferencia entre ellas en K y °C.
1.34 Usted desea agregar un cubo de hielo en una taza de agua caliente para enfriar el agua. La temperatura del cubo de hielo es de −10 °C y la temperatura del agua es de 92 °C. Convierta ambas temperaturas a Kelvin y determine la diferencia entre ellas en K y °C.
1.35 El oxígeno, O2, tiene una masa molecular de 32 kg/kmol. ¿Cuántos moles representan 17 kg de O2?
1.36 Usted determina que 1.2 kmoles de una sustancia tienen una masa de 14.4 kg. Determine la masa molecular de la sustancia.
1.37 Se le pregunta si desea tener una caja que contiene 3.5 kmoles de oro. La única condición de la oferta es que usted debe llevarse la caja solo con su propia fuerza. ¿Cuál es la masa del oro en la caja si la masa molecular del oro es de 197 kg/kmol? ¿Cree que podrá aceptar este trato?
1.38 Suponga que un kilomol de cualquier sustancia gaseosa a una temperatura y presión dadas ocupa un volumen de 24 m3. La densidad de un gas determinado en estas condiciones es de 1.28 kg/m3 ¿Cuánta masa del gas está presente si usted tiene un contenedor de 2.0 m3 lleno de gas a la temperatura y presión dadas, y cuál es la masa molecular del gas?
1.39 La quema de un combustible de hidrocarburos convertirá el carbono del combustible en dióxido de carbono. Para quemar cada kmol de carbono se necesita 1 kmol de oxígeno (O2). Esto produce 1 kmol de CO2. Si originalmente tiene 2 kg de carbono para quemar, ¿cuál es la masa de CO2 que se producirá? La masa molecular del carbono es de 12 kg/kmol, la del oxígeno es de 32 kg/kmol y la del CO2 es de 44 kg/kmol.
1.40 Una roca en el nivel del mar en la Tierra (donde g 5 9.81 m/s2) tiene una masa de 25 kg. ¿Cuál es el peso de la roca en newtons?
1.41 En un planeta distante, la aceleración debida a la gravedad es de 6.84 m/s2. El peso de un objeto en ese planeta es de 542 N. ¿Cuál es la masa del objeto? Si ese objeto se lleva a la Tierra, donde g 5 9.81 m/s2, ¿cuál es el peso del objeto?
1.42 ¿Cuánta fuerza se necesita para acelerar una pelota con una masa de 0.5 kg a una velocidad de 25 m/s2?
1.43 ¿Cuánta fuerza se necesita para acelerar un bloque con una masa de 1.59 lbm a una velocidad de 35 ft/s2?
1.44 Un objeto tiene una masa de 145 lbm. Este objeto se envía al espacio y se coloca en la superficie de un planeta donde la aceleración debida a la gravedad es de 25 ft/s2. ¿Cuál es el peso del objeto en lbf en el otro planeta?
31 Problemas
1.45 La aceleración debida a la gravedad en Marte es de 12.17 ft/s2. En el nivel del mar en la Tierra, un astronauta puede levantar un objeto que pesa 125 lbf. ¿Cuál es la masa de un objeto que el astronauta podría levantar en Marte?
1.46 Un palo de golf aplica una fuerza de 12 lbf a una pelota de goma que tiene una masa de 1.5 lbm. ¿Cuál es la aceleración experimentada por la pelota cuando se encuentra con la fuerza?
1.47 ¿Qué fuerza se requiere para acelerar una roca de 5.0 lbm a una velocidad de 35 ft/s2?
1.48 El volumen específico del vapor a 500 °C y 500 kPa es de 0.7109 m3/kg. Usted tiene un contenedor cuyo volumen es de 0.57 m3, y está lleno de vapor a 500 °C y 500 kPa. Determine la masa del vapor en el contenedor.
1.49 Un bloque sólido de composición desconocida tiene dimensiones de 0.5 m de longitud, 0.25 m de ancho y 0.1 m de altura. El peso del bloque en el nivel del mar (g 5 9.81 m/s2) es de 45 N. Determine el volumen específico del bloque.
1.50 Una mezcla de agua líquida y vapor de agua ocupa un tubo cilíndrico cuyo diámetro es de 0.05 m y cuya longitud es de 0.75 m. Si el volumen específico del agua es de 0.00535 m3/kg, determine la masa del agua presente.
1.51 La densidad de varios metales es la siguiente: plomo: 11 340 kg/m3, estaño: 7 310 kg/m3 y aluminio: 2 702 kg/m3. Se le da una caja pequeña (0.1 m 3 0.1 m 3 0.075 m) y se le dice que está llena con uno de estos metales. La caja no se puede abrir ni se puede leer su etiqueta. Usted decide pesar la caja para determinar el metal que contiene. Encuentra que el peso de la caja es de 53.8 N. Determine la densidad y el volumen específico de la caja, y elija al probable metal que está en el interior.
1.52 Una persona con una masa de 81 kg se para sobre una pequeña plataforma cuya base es de 0.25 m 3 0.25 m. Determine la presión ejercida por la persona sobre el suelo bajo la plataforma.
1.53 Una pared de 2.5 m2 de área es golpeada por una ráfaga de viento. La fuerza ejercida por el viento en la pared es de 590 kN. Determine la presión ejercida por el viento sobre la pared.
1.54 Una prensa aplica una presión de 800 kPa uniformemente sobre un área de 0.025 m2. ¿Cuál es la fuerza total aplicada por la prensa?
1.55 Se utiliza un manómetro para determinar la diferencia de presión entre la atmósfera y un depósito de líquido. El fluido en el manómetro es agua, con una densidad de 1 000 kg/m3. El manómetro se encuentra en el nivel del mar, donde g 5 9.81 m/s2. La diferencia de altura entre el líquido en las dos patas del manómetro es de 0.25 m. Determine la diferencia de presión.
1.56 Con un manómetro de mercurio (r 5 13 500 kg/m3) se mide la diferencia de presión entre dos tanques que contienen fluidos. La diferencia en la altura del mercurio entre los dos tubos es de 10 cm. Determine la diferencia de presión entre los tanques.
1.57 Usted elige utilizar un manómetro de mercurio (r 5 13 500 kg/m3) para verificar la precisión de un manómetro en un tanque de nitrógeno comprimido. El manómetro se coloca entre el tanque y la atmósfera, y la diferencia de altura del mercurio entre los dos tubos es de 1.52 m. El medidor de presión por verificar señala una presión de 275 kPa en la presión del medidor del tanque. ¿El medidor de presión es preciso?
1.58 Los tanques de gas comprimido a menudo tienen presiones de calibración de al menos 1 MPa. Suponga que desea utilizar un manómetro para medir la presión de un depósito de aire comprimido cuya presión fue de al menos 1 MPa. El manómetro se colocaría entre el tanque y la atmósfera. ¿Cuál es la longitud mínima del tubo necesaria para tal medición si el líquido en el manómetro es (a) mercurio (r 5 13 500 kg/m3), (b) agua (r 5 1 000 kg/m3) y (c) aceite de motor (r 5 880 kg/m3)? ¿Parecen prácticos estos dispositivos para esta medición?
Capítulo1
a la
y la
32
Introducción
termodinámica
energía
1.59 Se configura un manómetro que utiliza un líquido con una densidad de 625 lbm/ft3 para medir la diferencia de presión entre dos ubicaciones en un sistema de flujo. La altura del líquido del manómetro es de 0.52 ft. ¿Cuál es la diferencia de presión entre las dos ubicaciones?
1.60 El manómetro de un tanque de nitrógeno comprimido indica 785 kPa. Un barómetro indica que la presión atmosférica local es de 99 kPa. ¿Cuál es la presión absoluta en el tanque?
1.61 El medidor de presión en un tanque de aire comprimido indica 120 psi. La presión atmosférica local se mide como 14.5 psi. ¿Cuál es la presión absoluta en el tanque?
1.62 Se mide la presión del aire dentro de un dispositivo de pistón-cilindro con un manómetro. El diámetro del cilindro es de 8 cm. Mientras el pistón está en reposo, el manómetro señala una presión de 40 kPa. Un barómetro mide la presión atmosférica hasta 100 kPa. Se coloca un peso con una masa de 20 kg en la parte superior del pistón y el pistón se mueve hasta que llega a un nuevo punto de equilibrio. ¿Cuál es la nueva presión de calibración y la nueva presión absoluta del aire en el cilindro cuando se alcanza este nuevo equilibrio?
1.63 La presión absoluta del aire en un dispositivo de pistón-cilindro es de 220 kPa. La presión atmosférica local es de 99 kPa. Si la aceleración debida a la gravedad es de 9.79 m/s2 y el diámetro del cilindro es de 0.10 m, ¿cuál es la masa del pistón?
1.64 Hay aire en un dispositivo de pistón-cilindro. El diámetro del cilindro es de 12 cm, la masa del pistón es de 5 kg y la aceleración debida a la gravedad es de 9.80 m/s2. La presión atmosférica local es de 100.5 kPa. Determine la masa de un conjunto de pesos que debe añadirse a la parte superior del pistón para que la presión absoluta del aire en el cilindro sea de 250 kPa.
1.65 Un depósito de líquido ejerce una presión de 300 kPa sobre un tapón situado en el fondo del depósito. La presión atmosférica local es de 99 kPa. El diámetro del tapón circular es de 2.5 cm. ¿Cuál es la fuerza adicional que debe aplicarse al tapón para mantenerlo en su lugar?
1.66 ¿Cuál es la presión absoluta del aire situado en un dispositivo de pistón-cilindro para un cilindro de 0.5 ft de diámetro, con una masa de pistón de 150 lbm y una presión atmosférica local de 14.65 psi? El dispositivo se encuentra en el nivel del mar en la Tierra.
1.67 Considere un dispositivo de pistón-cilindro inicialmente en equilibrio donde la presión de aire dentro del cilindro es de 150 kPa. Se desea elevar la presión del aire a 300 kPa añadiendo aire al cilindro sin cambiar la ubicación del pistón. Si el pistón tiene un diámetro de 8 cm, ¿cuál es la cantidad de masa que debe añadirse al pistón para mantenerlo en el mismo lugar con la presión más alta? Suponga una aceleración estándar debido a la gravedad en el nivel del mar en la Tierra.
33 Problemas