Kadet 6 - Kaap 1 - Handleiding by die Keure

dKadeKa e Kade 6 6

INHOUDSTAFEL met prio-overzicht

Les 1 Intro

Les 2 GK

Les 3 B - H

Les 4 B - C

Les 5 B - C

Getalbegrip tot 10 000 000

Optellen en aftrekken met natuurlĳke getallen tot 1 000 000

Bekĳk de algemene inleiding van de methode Kadet op Kabas.

Vermenigvuldigen en delen met natuurlĳke getallen tot 1 000 000

Les 6 MK Ruimtelĳke oriëntatie: plaats, richting, gezichtspunten, plattegrond, kaart en coördinaten

Les 7 MK Ruimtelĳke oriëntatie: blokkenbouwsels met aanzichten

Les 9 B - H Optellen en aftrekken met kommagetallen tot 0,001

Les 10 B - H

Les 8 GK Kommagetallen tot 0,001 p.43

Vermenigvuldigen met natuurlĳke getallen tot 1 000 000 en kommagetallen tot 0,001

Les 11 MK Meetkundige relaties: symmetrie, spiegelen, gelĳkvormigheid en gelĳkheid van vorm en grootte

Les 12 Herhaling p.69

Les 13 GK Breuken en kommagetallen tot 0,001 p.75

Les 14 B - H Delen met natuurlĳke getallen tot 1 000 000 en kommagetallen tot 0,001 p.81

Les 15 MMR Lengte en omtrek p.89

OVSG: Ik en de wereld

Les 16 MMR Oppervlaktematen p.95 en landmaten GO! KathOnd u OVSG

Les 17 B - C Optellen en aftrekken met kommagetallen tot 0,001 p.103

Les 18 B - C Vermenigvuldigen en delen met kommagetallen tot 0,001 p.109

Les 19 MMR Inhoud, gewicht/massa en volume p.117

Les 20 GK Staafdiagrammen, lĳngra eken en cirkeldiagrammen p.125

Les 21 GK Gemiddelde p.131 en mediaan GO! KathOnd u OVSG

Les 22 Herhaling p.137

Les 23 Evaluatie p.143

Les 24 en 25 Thematische outro OF outro problemen oplossen p.153

LEGENDE

nieuw/geven

geven indien tĳd

kan weggelaten worden

Dit is ofwel nieuwe leerstof ofwel zeker te geven omdat het lang geleden is, nog te weinig ingeoefend werd ...

Deze leerstof werd reeds gezien, maar dient veel herhaling en dus indien mogelĳk nog te geven.

Deze leerstof werd reeds gezien of is slechts een aanzet (a) of uitbreiding (u) van de leerstof en moet dus niet bereikt zĳn dit schooljaar.

LESDOELEN

TOEPASSINGEN

LES 1 Intro

LESMATERIALEN

1 De kinderen kunnen ICT gebruiken om informatie op te zoeken.

2 De kinderen kunnen in groep samenwerken.

3 De kinderen kunnen de taken in een groep verdelen.

4 De kinderen kunnen gebruik maken van een mindmap om hun ideeën op een rĳtje te zetten.

- Kabas en/of werkboek Kaap 1 p. 1

Let op: de oefeningen kunnen de leerlingen niet digitaal maken. Gebruik hiervoor het blanco werkboekblad op Kabas als je verder volledig digitaal werkt.

- kopieerblad 1: naamkaarten taakverdeling

- link 1: kettingreactie

- powerpoint: taakverdeling

- kladschrift

- keycord per leerling

LEERLĲN Deze les is een introles.

Instap

onderwĳsleergesprek

VOOR DE LES

Druk voor iedere groep kopieerblad 1 af. Knip de kaarten uit, lamineer ze en hang ze aan een keycord

LESVERLOOP

Kettingreactie

Bespreek kort met de leerlingen hun vakantieactiviteiten. Tracht te komen tot het thema pretparken. Vertel dat je deze zomer een bĳzonder themapark hebt bezocht, namelĳk het NEMO Science Museum. Bekĳk samen een video van een kettingreactie (link 1).

Bespreek.

- Wat is een kettingreactie? (een reeks opeenvolgende acties die ontstaan of worden veroorzaakt door de voorgaande actie)

- Welke acties heb je gezien? (bĳvoorbeeld: dominoblokken die omvielen, een ballon die kapot geprikt werd of een ventilator die begon te draaien)

- Wat kon ervoor zorgen dat een nieuwe actie werd veroorzaakt? (bĳvoorbeeld: dominoblokken die omvielen en zo een ander voorwerp in gang duwden of de ballon die kapot ging waardoor er ruimte was voor de balletjes om verder te rollen)

- Welke voorwerpen werden er gebruikt? (bĳvoorbeeld: dominoblokken, een emmer, een winkelkar …)

In deze Kaap zullen we het hebben over pretparken. Jullie krĳgen vanaf nu de tĳd om zoveel mogelĳk info te verzamelen over kettingreacties. Op het einde van de Kaap zullen jullie zelf, in groep, een kettingreactie maken.

2

Kern

onderwĳsleergesprek

2.1 Een eigen kettingreactie maken

Laat het werkboek nemen of deel het uit.

Jullie kettingreacties zullen moeten voldoen aan enkele criteria. We sommen ze even op.

Bouw een kettingreactie - op een oppervlakte van maximum 4 m², - met een hoogte van minstens 0,7 m, - met een symmetrisch element.

Maak een plattegrond en neem foto’s van de zĳaanzichten. De langste kettingreactie wint!

Heb je meer tĳd? Koppel hier dan een STEM-les aan. Werk bĳvoorbeeld met hefbomen of tandwielen.

zelfstandig werk

2.2

Informatie opzoeken

Straks worden jullie verdeeld in groepen en mogen jullie brainstormen over een ontwerp voor een kettingreactie, maar eerst gaan jullie op zoek naar voorbeelden van kettingreacties. Zoek op hoe je zelf een kettingreactie kan opbouwen, hoe je het best start, welke materialen je kan gebruiken …

Laat de leerlingen op het internet zoeken naar voorbeelden. Ze kunnen aantekeningen maken in hun kladschrift

2.3 Ontwerp maken

Verdeel de klas in groepen van drie tot vier leerlingen. Bespreek met behulp van de powerpoint de taken binnen de groep:

- aannemer;

- architect/verslaggever;

- veiligheidscoördinator;

- materiaalmeester.

Laat het werkboek nemen of deel het uit.

Jullie krĳgen nu even de tĳd om de ideeën die je verzamelde te bespreken binnen jullie groep. Daarna maken jullie een ontwerp van de kettingreactie die jullie willen maken. Ieder groepslid bedenkt een klein deelsysteem dat een ander deelsysteem in werking kan zetten. Probeer jullie systemen te ontwerpen zodat ze op elkaar aansluiten.

Noteer ook op jullie ontwerp welke materialen jullie nodig hebben. Jullie hebben tĳd tot het einde van de Kaap om deze materialen te verzamelen.

Ga als leerkracht actief luisteren bĳ de verschillende groepen. Zitten ze op het juiste spoor? Zĳn de ideeën haalbaar? Stuur bĳ waar nodig.

Vooruitblik op de Kaap

Aan de nieuwe Kaap is ook een wedstrĳd verbonden. Welke groep maakt de langste kettingreactie? Tĳdens deze Kaap zullen we bepaalde leerstof herhalen die jullie nodig hebben om aan de criteria van de wedstrĳd te voldoen.

Op het einde van deze Kaap maakt iedere groep een kettingreactie en kĳken we welke groep de langste kettingreactie maakte.

Op het kopieerblad ‘onthoudkaart’ staat de belangrĳkste leerstof van deze Kaap opgesomd. Druk het kopieerblad af, plasti ceer en gebruik het als bladwĳzer in het werkboek. Doe dit zeker voor de spoor 1-leerlingen en ga na welke spoor 2-leerlingen hier ook gebruik van zouden maken. Spoor 3-leerlingen zĳn in staat om de leerstof zelf op te zoeken in hun Sloep, indien nodig.

KAAP IN ZICHT

In deze Kaap werken we rond het thema pretparken.

De meeste onderwerpen kwamen reeds aan bod in het vĳfde leerjaar en worden nu verder uitgediept.

We gebruiken plattegronden en aanzichten. Deze leerstof wordt herhaald in les 6 en 7.

We passen symmetrie toe. Dit wordt herhaald in les 11.

We meten de lengte en berekenen de omtrek. Dit wordt herhaald in les 15.

We berekenen de oppervlakte. Dit wordt herhaald in les 16.

TOEPASSINGEN LES 1 Intro

van maximum 4 m², van minstens 0,7 m element.

Maak een plattegrond en neem foto’s van De langste kettingreactie wint!

dKadeKa e de 6 6

Voorbereiding kettingreactie Groepsnaam: Groepsleden:

Mijn taak in de groep:

Maak een eerste ontwerp in de vorm van een plattegrond. Noteer hieronder welke onderdelen je in je kettingreactie wil stoppen en welke materialen je hiervoor nodig hebt.

Noteer hier nog zaken die belangrijk zijn (bv. een website met ideeën):

Naam: Klas: Nummer:

Kadet_6_Kaap_1_Werkboek.indd 1

LESDOELEN

LESMATERIALEN

LES 2 Getalbegrip tot 10 000 000

1 De kinderen kunnen natuurlĳke getallen tot 10 000 000 lezen en schrĳven.

2 De kinderen kunnen de waarde van elk cĳfer van een natuurlĳk getal tot 10 000 000 bepalen en gebruikmaken van de begrippen en symbolen TM, M, HD, TD, D, H, T en E.

3 De kinderen kunnen natuurlĳke getallen tot 10 000 000 op een getallenas plaatsen.

4 De kinderen kunnen doortellen en terugtellen tot 10 000 000 met sprongen van veelvouden van 10.

5 De kinderen kunnen getallen tot 10 000 000 samenstellen met gegeven cĳfers en hun positie.

6 De kinderen kunnen getallen tot 10 000 000 vergelĳken en ordenen en de vergelĳkingen voorstellen met =, ≠, > of <.

- concordantie

- digitaal bordschema

- Kabas en/of werkboek Kaap 1 p. 2-4

- onthoudkaart

- poster: getallen tot 1 000 000 000 en tot 0,001 in de positietabel

- link 2: bezoekersaantallen pretparken

- instructievideo de symbolen > en < tot 10 000 000

- instructievideo de getallenas tot 10 000 000

- Sloep p. 9-12

- whiteboardstift per leerling (indien voorradig)

- wisbord

- kladschrift

LEERLĲN

Wat ging vooraf?

De natuurlĳke getallen tot 10 000 000 zĳn in het vĳfde leerjaar aan bod gekomen.

Wat volgt?

K1 L8 Kommagetallen tot 0,001

Instap

onderwĳsleergesprek

VOOR DE LES

Je kunt op voorhand op het bord een tabel tekenen met daarin de namen van verschillende pretparken, alsook een lege positietabel.

Als voor iedere leerling een whiteboardstift voorhanden is, lamineer dan de onthoudkaart met de positietabel. Zo kunnen de leerlingen dit doorheen het schooljaar blĳven gebruiken.

LESVERLOOP

Pretparken wereldwĳd

Er bestaan een aantal heel grote pretparken in de wereld. Welke kennen jullie? (bĳvoorbeeld Disney World)

Disney heeft het grootste aantal bezoekers van alle pretparken in de wereld. Disney heeft dan ook verschillende parken in verschillende steden. In deze parken zĳn er meer dan 10 000 000 bezoekers per jaar.

Er zĳn ook nog andere pretparken die niet van Disney zĳn.

Noteer deze met hun jaarlĳks bezoekersaantal in een tabel op het bord.

Universal Studios Hollywood (California) 9 147 156

Everland (Yongin)

Lotte World (Seoul)

Nagashima Spa Land (Kuwana)

Europa-Park (Rust)

Laat de getallen luidop lezen.

6 006 547

5 984 411

5 902 809

5 750 644

Indien je graag de meest recente cĳfers gebruikt, kun je deze vinden via link 2.

De getallen in link 2 zĳn afgerond. Verzin zelf cĳfers bĳ H, T en E.

Benadruk dat de getallen in groepjes van drie geschreven worden om het lezen gemakkelĳker te maken. Soms wordt hiervoor een punt gebruikt, bĳvoorbeeld bĳ 5.845.236. Hier is de punt dus geen komma.

Zoek deze parken samen met de leerlingen op op het internet. Zowel de locatie van de pretparken als enkele foto’s scheppen een beter beeld.

Verwoord het lesdoel:

Vandaag herhalen we de getallen tot 10 000 000 met en zonder positietabel. We gaan getallen tot 10 000 000 rangschikken en op getallenassen plaatsen en we gaan tellen met sprongen.

Kern klassikale oefening

2.1 Instructiefase

2.1.1 Positietabel tot 10 000 000 Herneem de instap. Laat telkens een leerling vooraan in de klas het getal in een positietabel noteren en herhaal de afkortingen per kolom: tien miljoental, miljoental … Duid een andere leerling aan die het getal op zĳn of haar wisbord noteert. Laat het getal nog eens luidop voorlezen.

klassikale oefening

Schrĳf de getallen in groepjes van drie cĳfers vóór de positietabel.

2.1.2 Getallen tot 10 000 000 rangschikken

Laat de vĳf leerlingen met een getal op hun wisbord vooraan komen en laat hen de getallen rangschikken van klein naar groot of van groot naar klein.

Laat de klas controleren of het juist is. Laat hen verwoorden hoe ze dat gedaan hebben.

Herhaal het begrip rang en laat de rangen benoemen waar ze bĳ het rangschikken eerst naar keken.

2.1.3 Tellen met sprongen tot 10 000 000

Aan het begin van de zomervakantie heeft Bellewaerde meestal al 320 000 bezoekers in totaal gehad dat jaar. In de maanden juli en augustus komen daar dagelĳks ongeveer 11 500 bezoekers bĳ.

Noteer het getal 320 000 op het bord. Hoeveel bezoekers zĳn dat na één dag? Na twee dagen? …

Laat de leerlingen tellen met sprongen en noteer de sprongen op het bord.

2.2 Inoefenfase

Laat de leerlingen de oefeningen maken in het (digitale) werkboek

Laat elke leerling de onthoudkaart met de positietabel nemen. Deze kunnen ze gebruiken tĳdens het maken van de oefeningen. Je kunt de leerlingen ook de positietabel laten tekenen in hun kladschrift

Maak oefening 1 klassikaal. Spoor 1-leerlingen schrĳven de getallen eerst in hun tabel voor ze de getallen in hun werkboek schrĳven. Spoor 2- en spoor 3-leerlingen mogen de tabel gebruiken indien nodig.

Dicteer de volgende getallen voor het getallendictee:

9 099 900 negen miljoen negenennegentigduizend negenhonderd

7 000 155 zeven miljoen honderdvĳfenvĳftig

Verbeter oefening 1 klassikaal.

4 M 6 HD 2 TD 6 H 5 T 1 E (4 620 651)

9 M 6 TD 7 D 1 H 3 T 5 E (9 067 135)

5 612 308 vĳf miljoen zeshonderdentwaalfduizend driehonderdenacht

2 322 117 twee miljoen driehonderdtweeëntwintigduizend honderdzeventien

3 Afsluiter partnerwerk

3.1 Wie vindt de meeste getallen?

Noteer op het bord zeven cĳfers.

De leerlingen proberen per twee om met deze zeven cĳfers zoveel mogelĳk verschillende getallen te vormen. Geef ze hiervoor drie minuten tĳd.

Afspraken:

- De leerlingen moeten natuurlĳke getallen vormen (geen kommagetallen).

- Het getal mag niet beginnen met een 0.

- Ze moeten telkens alle cĳfers gebruiken.

- Ze moeten de getallen schrĳven in groepjes van drie.

Nu mogen jullie eens raden … Hoeveel verschillende getallen kan je maken met zeven verschillende cĳfers verschillend van nul? (5 040)

Leg uit hoe je dit berekent: 7 x 6 x 5 x 4 x 3 x 2 x 1 = 5 040

3.2 Verankering

Veranker het lesdoel en koppel terug naar de doelstelling uit de instap: Wat hebben we vandaag geleerd? Laat de leerlingen kort verwoorden.

Merk op dat de leerlingen de getallen in groepjes van drie cĳfers moeten noteren.

In de tabel staan het aantal bezoekers per jaar van verschillende Europese pretparken.

Laat de getallen door verschillende leerlingen luidop lezen vooraleer ze aan de slag gaan.

Laat spoor 1-leerlingen de positietabel op hun onthoudkaart gebruiken. Ze noteren de getallen eerst in de juiste kolom en vullen aan met nullen.

Kaap K ap 1

GETALLENKENNIS

LES 2 Getalbegrip tot 10 000 000

Getallendictee: noteer de getallen.

Noteer de bezoekersaantallen op de juiste plaats in de positietabel

Disneyland Parijs 9 745 855

Europa-Park 5 750 644

Efteling 5 400 187

Walt Disney Studios 5 245 609

Tivoli Gardens 4 581 154

PortAventura World 3 750 846

Liseberg 2 950 708

Gardaland Resort 2 920 258

Vorm de getallen. Kijk naar de positietabel indien

Wĳs de leerlingen erop dat ze M, HD, TD, D, H, T of E met een hoofdletter moeten noteren.

Laat spoor 1- en spoor 2-leerlingen een boogje plaatsen met de bewerking erbĳ.

Vul de getallenassen aan.

Laat de leerlingen eerst kĳken naar TD en D, pas erna naar H, T en E.

Rangschik de getallen.

Kadet_6_Kaap_1_Werkboek.indd

Laat spoor 1- en spoor 2-leerlingen een boogje plaatsen met de bewerking erbĳ.

Vul aan met sprongen.

Los op.

Maak een zo klein mogelijk getal met zeven verschillende cijfers.

Maak een zo groot mogelijk getal met

Welk getal ligt precies tussen

Kadet_6_Kaap_1_Werkboek.indd 4 14/03/2024 11:55

DIFFERENTIATIE EN ORTHODIDACTISCHE TIPS

Laat de leerlingen een positietabel gebruiken tĳdens het zelfstandig werk.

Laat de leerlingen bĳ grote getallen eventueel boogjes per drie cĳfers tekenen. Zo maak je de ruimte tussen de honderdtallen, duizendtallen en miljoentallen nog duidelĳker.

bĳvoorbeeld: 43 265 138

miljoen duizend honderd

Maak sprongen visueel met een pĳl.

Je kunt eventueel met kleur aanduiden bĳ welke waarde er iets bĳkomt of weggaat. + 100 000 + 100 000

4 800 000 4 900 000 5 000 000

Laat de leerlingen de positietabel zelf opstellen, zodat ze dit later ook kunnen als die niet meer voorhanden is.

Daag de leerlingen uit om de positietabel zo weinig mogelĳk te gebruiken. Bied hen artikels aan waarin veel getallen staan die ze kunnen lezen en interpreteren.

Maak eventueel gebruik van volgend di erentiatiemateriaal:

- scheurblok Kaap 1 p. 1

- Meer oefenaanbod via Kai en op de gamehoek van Kaap 1!

- Oefenblaadje: Getalbegrip tot 10 000 000

- Krak: Wereldsteden (6e leerjaar)

Terug naar de toekomst (6e leerjaar)

Codekraker (5e - 6e leerjaar)

Ontsnap! (5e - 6e leerjaar)

LESDOELEN

LES 3 Optellen en aftrekken met natuurlĳke getallen tot 1 000 000

1 De kinderen kunnen optellingen en aftrekkingen maken met natuurlĳke getallen tot 1 000 000.

2 De kinderen kunnen exibel een doelmatige oplossingsmethode kiezen op basis van inzicht in de structuur van de getallen en de eigenschappen van de bewerkingen.

3 De kinderen kunnen de volgorde van de bewerkingen toepassen.

LESMATERIALEN - concordantie

- digitaal bordschema

- Kabas en/of werkboek Kaap 1 p. 5-6

- poster: exibel rekenen bĳ optellen en aftrekken

- instructievideo compenseren

- instructievideo wisselen en schakelen

- Sloep p. 44 en 46-48

- wisbord per leerling

- kladschrift

LEERLĲN Wat ging vooraf?

De vier hoofdbewerkingen met natuurlĳke getallen tot 10 000 000 zĳn in het vĳfde leerjaar aan bod gekomen.

In Kadet wordt voor de standaardmethode voor optellen en aftrekken de volgende steunzin gebruikt: het eerste getal houden we heel, het tweede doen we er in stappen bĳ/af.

Dit wordt visueel ondersteund in de oplossingswĳze door het gebruik van de verticale streep om de tussenuitkomsten te noteren.

Bĳvoorbeeld:

526 + 173 = 526 + 100 + 70 + 3 = 699

626 696

De leerlingen leerden dit op deze manier vanaf het eerste leerjaar.

Wat volgt?

K1 L9 Optellen en aftrekken met kommagetallen tot 0,001

VOOR DE LES

Bepaal op basis van de overgangsgesprekken met de leerkracht van het vĳfde leerjaar en op basis van de algemene resultaten op de voorkennistest (onderdeel Bewerkingen) welke onderdelen uit de kern je klassikaal behandelt en in welke sporen je de leerlingen indeelt.

LESVERLOOP

Commandorekenen tot 100

Verdeel de klas in groepen van vĳf.

Plaats telkens één leerling in het midden en de andere vier leerlingen in een cirkel errond.

De leerling in het midden van de cirkel start met het opnoemen van een getal tussen 0 en 100. De leerlingen errond vullen één voor één aan met een bewerking (optelling of aftrekking) waarvan de uitkomst niet boven de 100 gaat. De leerling in het midden van de cirkel rekent alles uit. Op het einde zegt die leerling wat de uitkomst is.

Bĳvoorbeeld:

Leerling 1 zegt ‘25’.

Leerling 2: ‘plus 50’ (= 75)

Leerling 3: ‘min 60’ (= 15)

Leerling 4: ‘plus 80’ (= 95)

Leerling 5: ‘min 55’ (= 40)

Leerling 1: ‘De uitkomst is 40.’

Laat de leerlingen errond ook meerekenen. Zĳ controleren de bewerkingen zodat ze niet boven 100 of onder 0 gaan.

Laat spoor 1-leerlingen eerst werken met tientallen. Als dit lukt, laat hen dan werken met vĳfvouden, zoals in het voorbeeld.

Spoor 3-leerlingen kunnen het spel in grotere groepen spelen, zodat ze meer bewerkingen moeten maken.

Laat de eerste leerling in de cirkel de bewerkingen noteren (zonder de uitkomsten) op een wisbord of in een kladschrift. Zo is er achteraf geen discussie.

Verwoord het lesdoel:

We herhalen vandaag de standaardmethode voor het optellen en aftrekken met natuurlĳke getallen tot 1 000 000. We proberen ook al eens exibele rekenstrategieën toe te passen zoals compenseren en wisselen en schakelen, om oefeningen gemakkelĳker op te lossen.

2.1 Instructiefase

Dit is herhaling. Noteer de oefeningen aan het bord en pak dit per spoor anders aan.

Spoor 1:

Maak alle oefeningen klassikaal. Laat vooral de leerlingen aan het woord en kom samen tot een resultaat. Beluister meerdere oplossingsmethodes en zoek wat het beste werkt voor de leerlingen.

Spoor 2 en 3:

Laat de leerlingen zelfstandig in hun kladschrift of op hun wisbord werken. Geef spoor 3-leerlingen eventueel per oefening 30 seconden tĳd. Naar het einde toe kun je de bewerkingen dicteren in plaats van ze op te schrĳven. Bespreek de oplossingsmethodes klassikaal en benoem duidelĳk de gekozen strategie: compenseren, wisselen en/of schakelen.

Als een oefening moeilĳk gaat, voorzie dan zelf een tweede oefening van dezelfde soort.

klassikale oefening

2.1.1 Herhaling: rekenmethodes optellen

Splitsen en doorrekenen

45 850 + 33 380 = 45 850 + 33 000 + 300 + 80 = 79 230 78 850 79 150

Het eerste getal houden we heel, het tweede getal doen we er in stappen bĳ.

Compenseren

8 450 + 699 = 8 450 + 700 – 1 = 9 149

Als ik er teveel bĳdoe, dan moet ik dat ook weer wegdoen.

Wisselen en/of schakelen

wisselen:

45 120 + 688 + 3 880 = 45 120 + 3 880 + 688 = 49 688 49 000

schakelen: 14 358 + 890 + 9 110 = 14 358 + (890 + 9 110) = 24 358

wisselen en schakelen:

78 645 + 15 789 + 1 355 = (78 645 + 1 355) + 15 789 = 95 789 10 000 80 000

Wissel bĳ een optelling de termen, die gemakkelĳk samen te tellen zĳn, van plaats en schakel ze met haakjes. Reken de haakjes eerst uit.

klassikale oefening

2.1.2 Herhaling: rekenmethodes aftrekken Splitsen en doorrekenen

45 823 – 6 547 = 45 823 – 6 000 – 500 – 40 – 7 = 39 276 39 823 39 323 39 283

Het eerste getal houden we heel, het tweede getal doen we er in stappen af.

Compenseren

28 755 – 399 = 28 755 – 400 + 1 = 28 356

Als ik er teveel wegdoe, dan moet ik dat er ook weer bĳdoen.

2.1.3 Commandorekenen tot 1 000 000 Laat de leerlingen hun kladschrift nemen.

Dicteer bewerkingen tot 1 000 000 en laat telkens de tussenoplossing noteren zodat ze zo weer verder kunnen rekenen.

Afsluiter spel groepswerk

Bĳvoorbeeld:

Noteer 6.

Plus 4. (10)

Plus 40. (50)

Plus 400. (450)

Plus 4 000. (4 450)

Plus 40 000. (44 450)

Plus 400 000. (444 450)

Bespreek de uitkomst klassikaal.

Doe hetzelfde met aftrekkingen.

Bĳvoorbeeld:

Noteer 800 000.

Min 150 000. (650 000)

Min 100 000. (550 000)

Min 70 000. (480 000)

Min 50 000. (430 000)

Min 30 000. (400 000)

Min 10 000. (390 000)

Maak met de spoor 2- en spoor 3-leerlingen een extra oefening. Gebruik de bewerkingstekens plus en min door elkaar en gebruik rekentaal.

Bĳvoorbeeld:

Noteer 50 000.

Vermeerder met 80 000. (130 000)

Trek er 55 000 af. (75 000)

Doe er 120 000 bĳ. (195 000)

Verminder met 25 000. (170 000)

Plus 800 000. (970 000)

Min 450 000. (520 000)

2.2 Inoefenfase

Laat de leerlingen de oefeningen maken in het (digitale) werkboek

3.1 Commandorekenen tot 1 000 000

Speel hetzelfde spel als in de instap, maar nu met grotere getallen. Pas aan naar het niveau van de leerlingen.

Spoor 1:

Werk met kleinere getallen en reken enkel met veelvouden van 100.

Spoor 2:

Werk met grotere getallen en reken enkel met veelvouden van 100.

Spoor 3:

Werk met grotere getallen en reken enkel met veelvouden van 10.

3.2 Verankering

Veranker het lesdoel en koppel terug naar de doelstelling uit de instap: Wat hebben we vandaag geleerd? Laat de leerlingen kort verwoorden.

Toon aan dat de bewerkingen naar analogie werken: bĳ elke volgende bewerking wĳzigt er telkens maar één rang in de uitkomst.

Laat de leerlingen de oefeningen eerst overschrĳven en dan pas oplossen. Maak hen duidelĳk dat ze verschillende exibele methodes kunnen gebruiken. Verwĳs naar het bordschema van de instructie.

Merk op dat optellingen en aftrekkingen door elkaar staan en dat de leerlingen dus goed naar het bewerkingsteken moeten kĳken.

Wĳs de leerlingen erop dat ze exibele oplossingsmethodes moeten gebruiken. Laat die ook benoemen.

Wĳs de leerlingen erop dat er overbodige gegevens in het vraagstuk staan.

1 2 3

deKa e de 6

zit

Lees en los zo eenvoudig mogelijk op.

Een reuzenpretpark in de VS telt op één dag heel wat bezoekers, namelijk 120 522 volwassenen, 99 978 kinderen en 7 478 senioren.

V Hoeveel bezoekers waren dat op één dag?

Dat waren 227 978 bezoekers op één dag.

In een topweek heeft het pretpark in de VS 956 700 bezoekers. Dat zijn bijna 1 000 000 bezoekers. Het grootste pretpark in België heeft dit aantal bezoekers op een jaar.

V Wat is het verschil tussen beide pretparken als een topweek in België 16 898 bezoekers telt?

DIFFERENTIATIE EN ORTHODIDACTISCHE TIPS

Verwoord de methode voor het splitsen en doorrekenen en herhaal de steunzin: het eerste getal houden we heel, het tweede getal doen we er in stappen bĳ/af. Stimuleer het gebruik van de verticale streep en het noteren van de tussenstappen.

Laat de bewerkingstekens markeren als de bewerkingen door elkaar staan.

Daag de leerlingen zoveel mogelĳk uit om de meest e ciënte werkwĳze te zoeken. Laat hen loskomen van de standaardmethode.

Laat de leerlingen een vraagstuk over pretparken voor elkaar opstellen. Laat hen getallen opzoeken op het internet. De getallen mogen groter dan een miljoen zĳn.

Maak eventueel gebruik van volgend di erentiatiemateriaal:

- scheurblok Kaap 1 p. 2

- Meer oefenaanbod via Kai en op de gamehoek van Kaap 1!

- Oefenblaadje: Optellen en aftrekken met natuurlĳke getallen tot 1 000 000

- Krak: Wereldsteden (6e leerjaar)

Terug naar de toekomst (6e leerjaar)

Codekraker (5e - 6e leerjaar)

Ontsnap! (5e - 6e leerjaar)

LESDOELEN

LESMATERIALEN

BEWERKINGEN - CĲFEREN

LES 4 Optellen en aftrekken met natuurlĳke getallen tot 1 000 000

1 De kinderen kunnen cĳferend optellingen en aftrekkingen met natuurlĳke getallen tot 1 000 000 uitvoeren.

2 De kinderen kunnen cĳferen met aandacht voor de structuur van de getallen en de plaatswaarde.

3 De kinderen kunnen de som en het verschil bĳ cĳferoefeningen vooraf bĳ benadering schatten.

4 De kinderen kunnen de som en het verschil bĳ cĳferoefeningen vergelĳken met hun schatting.

5 De kinderen kunnen de begrippen ‘termen’, ‘som’, ‘aftrektal’, ‘aftrekker’, ‘verschil’, ‘opteltal’, ‘opteller’, ‘onthouden’ en ‘lenen’ correct gebruiken.

- concordantie

- digitaal bordschema

- Kabas en/of werkboek Kaap 1 p. 7-9

Let op: de oefeningen kunnen de leerlingen niet digitaal maken. Gebruik hiervoor de blanco werkboekbladen op Kabas als je verder volledig digitaal werkt.

- poster: cĳferen

- afbeelding 1: aantal bezoekers pretparken België

- instructievideo cĳferend optellen tot 1 000 met onthouden

- instructievideo cĳferend aftrekken tot 1 000 met lenen

- Sloep p. 65-67

- geruit papier met grote hokjes (1 cm op 1 cm)

- ZRM

- wisbord per leerling

- kladschrift

LEERLĲN Wat ging vooraf?

De techniek voor het cĳferend optellen en aftrekken werd reeds in het derde leerjaar aangebracht. In het vĳfde leerjaar is het cĳferend optellen en aftrekken met natuurlĳke getallen tot 10 000 000 en kommagetallen tot 0,001 aan bod gekomen.

In vorige leerjaren werd bĳ cĳferoefeningen een rode hulplĳn gebruikt om aan te geven waar en in welke richting de leerlingen moeten beginnen. De hulplĳn werd vanaf het vierde leerjaar afgebouwd. In de eerste Kaap van het zesde leerjaar herhalen we dit nog even, maar daarna valt dit opnieuw weg. Je kunt de rode hulplĳn in het werkboek laten tekenen als de leerling nood heeft aan richting.

Bĳ spoor 1 komen de rode lĳnen wel nog eens aan bod.

Wat volgt?

K1 L17 Optellen en aftrekken met kommagetallen tot 0,001

Instap onderwĳsleergesprek 2 Kern klassikale oefening

LESVERLOOP

Drukke zomers

De meesten onder ons vinden het heel leuk om eens een pretpark te bezoeken, maar op mooie zomerdagen kan het er razend druk zĳn. Hebben jullie een idee hoeveel bezoekers een pretpark per dag kan hebben? Of hoeveel bezoekers er zĳn op een hele zomer? We bekĳken enkele cĳfers.

Toon afbeelding 1 en bespreek. Laat de getallen luidop lezen.

Dit is een belangrĳk observatiemoment. Duid in deze fase zeker de spoor 1-leerlingen aan zodat je een duidelĳker beeld hebt van wie inzicht heeft in de getallen.

Wat is het grootste getal? (510 788)

Wat is het kleinste getal? (68 867)

Welke bewerking moet ik uitvoeren om te weten hoeveel bezoekers er in alle pretparken samen kwamen? (Ik moet een optelling uitvoeren. Ik moet de som van deze getallen zoeken.)

Welke bewerking moet ik uitvoeren om te weten hoeveel bezoekers er meer of minder kwamen in Plopsaland en Bellewaerde? (Ik moet een aftrekking uitvoeren. Ik moet het verschil van deze getallen zoeken.)

Verwoord het lesdoel: Vandaag herhalen we het cĳferend optellen en aftrekken tot 1 000 000.

2.1 Instructiefase

2.1.1 Optellen

Laat het werkboek nemen of deel uit.

Maak de eerste oefening klassikaal.

De vraag is: 'Hoeveel bezoekers hadden Walibi en Bellewaerde samen?'

Welke bewerking hebben we hiervoor nodig? (een optelling)

We maken eerst een schatting.

Laat per twee schatten op een wisbord. Benadruk dat de leerlingen moeten werken met afgeronde getallen zodat de schatting snel gebeurt. Bespreek daarna kort enkele resultaten.

Werk met de volgende schattingsmethode:

510 788 + 350 472 =

Het eerste getal ronden we af naar 500 000, want het cĳfer 1 dat achter het cĳfer 5 staat, betekent dat we naar beneden afronden. Het tweede getal ronden we af naar 350 000, want het cĳfer 0 dat achter het cĳfer 5 staat, betekent dat we naar beneden afronden.

Dus 500 000 + 350 000 = 850 000.

We hebben beide getallen naar beneden afgerond. Dit wil zeggen dat de som ruim 850 000 zal zĳn.

Maak daarna samen met de leerlingen de cĳferoefening aan het bord. Benoem en noteer de begrippen opteltal, opteller en som. Herhaal de rekenregels door de bewerking stap voor stap te verwoorden:

Ik plaats E onder E, T onder T …

8 E plus 2 E is 10 E. Ik schrĳf 0 E en onthoud 1 T.

1 T plus 8 T plus 7 T is 16 T. Ik schrĳf 6 T en onthoud 1 H.

1 H plus 7 H plus 4 H is 12 H. Ik schrĳf 2 H en onthoud 1 D.

1 D plus 0 D plus 0 D is 1 D. Ik schrĳf 1 D.

1 TD plus 5 TD is 6 TD.

5 HD plus 3 HD is 8 HD.

De som is 861 260.

Je kunt de leerlingen laten meerekenen in hun kladschrift.

opteltal opteller som

Vergelĳk de som nadien met de schatting.

Laat de som eventueel controleren met een ZRM

2.1.2 Aftrekken

Ga verder in het werkboek met de klassikale oefening.

Hoeveel bezoekers had Plopsaland? (419 345)

Hoeveel bezoekers had Bellewaerde? (350 472)

We zoeken het verschil. Welke bewerking hebben we hiervoor nodig? (een aftrekking)

Kunnen we dit cĳferend berekenen? Hoe? (door het grootste getal bovenaan te zetten)

Dit getal noemen we het aftrektal

We maken eerst een schatting.

Laat per twee schatten op een wisbord. Benadruk dat de leerlingen moeten werken met afgeronde getallen zodat de schatting snel gebeurt. Bespreek daarna kort enkele resultaten.

Werk met de volgende schattingsmethode:

419 345 – 350 472 = Het eerste getal ronden we af naar 400 000, want het cĳfer 1 dat achter het cĳfer 4 staat, betekent dat we naar beneden afronden. Het tweede getal ronden we af naar 350 000, want het cĳfer 0 dat achter het cĳfer

5 staat, betekent dat we naar beneden afronden.

Dus 400 000 – 350 000 = 50 000.

Het verschil zal ruim 50 000 zĳn.

Noteer de getallen samen met de leerlingen, zet het grootste getal bovenaan. Noteer de begrippen aftrektal, aftrekker en verschil. Maak samen de cĳferoefening aan het bord en herhaal de rekenregels door de bewerking stap voor stap te verwoorden:

Ik plaats E onder E, T onder T …

5 E min 2 E is 3 E.

4 T min 7 T gaat niet. Ik leen 1 H. Ik heb nu 1 H minder, dus 2 in plaats van 3.

1 H wordt 10 T. In totaal heb ik nu 14 T. 14 T min 7 T is 7 T.

2 H min 4 H gaat niet, dus ik ga opnieuw lenen. Ik leen 1 D. Ik heb nu 8 D in plaats van 9 D.

1 D wordt 10 H. Samen met de 2 H die er al stonden, zĳn dat 12 H. 12 H min 4 H is 8 H.

8 D min 0 D is 8 D.

1 TD min 5 TD gaat niet. Ik leen 1 HD. 4 HD wordt 3 HD.

1 TD wordt 11 TD. 11 TD min 5 TD is 6 TD.

3 HD min 3 HD is 0 HD.

Het verschil is 68 873.

Afsluiter leergesprek

Vergelĳk het verschil nadien met de schatting. Laat het verschil eventueel controleren met een ZRM

2.2 Inoefenfase

Laat de leerlingen de oefeningen maken in het werkboek

Nabespreking

Maak tĳd voor een nabespreking. Ook al zĳn niet alle leerlingen klaar, bespreek toch klassikaal. Dit is een belangrĳk leermoment.

Maak de eerste opgave van oefening 1 en 2 aan het bord en bespreek. Je kunt eventueel een sterke leerling de oefening aan het bord laten maken, maar vermĳd om verkeerde voorbeelden te tonen.

Bespreek steeds terugkerende fouten klassikaal. Zorg voor een correcte verwoording en ondersteun eventueel met kleur bĳ het lenen en/of onthouden. Herhaal de belangrĳkste stappen:

Wat hebben we vandaag geleerd?

1. getallen onder elkaar plaatsen (E onder E, T onder T …);

2. aandacht hebben voor het bewerkingsteken;

3. een schatting maken en de uitkomst controleren: ‘Is mĳn oplossing mogelĳk?’

- CIJFEREN

4 Optellen en aftrekken met natuurlijke getallen tot 1

Los op en benoem de begrippen. Hoeveel

Kaap p 1

Markeer samen met de leerlingen het bewerkingsteken en verwoord: bĳ oefening 1 maken we optellingen, bĳ oefening 2 maken we aftrekkingen en bĳ oefening 3 maken we zowel optellingen als aftrekkingen. Kĳk dus goed naar het bewerkingsteken!

Laat de leerlingen eerst alle schattingen maken. Geef hen hier bĳvoorbeeld 3 minuten tĳd voor. (Een schatting moet snel gebeuren!) Wie alle schattingen ingevuld heeft, mag aan het zelfstandig werk beginnen. Laat alle cĳferoefeningen in potlood maken, zo kunnen de leerlingen gemakkelĳk een fout verbeteren.

Schat en bereken de som. Vergelijk de oplossing met je schatting.

Ik schat: OK

Schat en bereken het verschil. Vergelijk de oplossing met je schatting.

Ik schat: OK

Kadet_6_Kaap_1_Werkboek.indd 8

De leerlingen moeten nadenken over hun bladschikking. Hoe gaan ze hun blad indelen?

Bekijk opnieuw het staafdiagram ‘Aantal bezoekers zomer 2022’. Maak volgende cijferoefeningen en noteer de uitkomsten.

V1 Wat is de som van het aantal bezoekers in Walibi en Plopsaland?

De som van het aantal bezoekers is 930

V2 Wat is het verschil in aantal bezoekers tussen het park met de meeste bezoekers en het park met de minste bezoekers?

V3 Wat is het totaal aantal bezoekers van de drie Plopsaparken?

DIFFERENTIATIE EN ORTHODIDACTISCHE TIPS

Leerlingen met extra ondersteuningsnoden kunnen de oefeningen op geruit papier met grote hokjes maken. Je kunt de oefening eventueel voor hen op het blad noteren. De leerlingen moeten maar één keer schatten. Bĳ de andere oefeningen kunnen ze de oplossing controleren met een ZRM. Zo oefenen ze ook het werken met een ZRM.

Daag de leerlingen uit hun tempo te verhogen door oefening per oefening te maken, zich goed te concentreren en tussen twee oefeningen eens met hun hoofd of handen te draaien. Dan zĳn ze weer klaar voor een volgende oefening.

Ga eens rond en vraag de leerlingen of hun schatting een over- of onderschatting is (ruim, net minder dan …) en hoe dat komt. Vraag na of ze dit al vooraf kunnen voorspellen.

Daag de leerlingen uit om de onthoudcĳfers niet te noteren.

Laat de leerlingen ook de recente cĳfers van de grotere parken buiten België opzoeken op het internet. Laat hen oefeningen voor elkaar bedenken met deze cĳfers.

Maak eventueel gebruik van volgend di erentiatiemateriaal:

- scheurblok Kaap 1 p. 3

- Meer oefenaanbod via Kai en op de gamehoek van Kaap 1!

- Oefenblaadje: Optellen en aftrekken met natuurlĳke getallen tot 1 000 000

- Krak: Wereldsteden (6e leerjaar)

Terug naar de toekomst (6e leerjaar)

Codekraker (5e - 6e leerjaar)

Ontsnap! (5e - 6e leerjaar)

LESDOELEN

LES 5 Vermenigvuldigen en delen met natuurlĳke getallen tot 1 000 000

1 De kinderen kunnen een vermenigvuldiging tot 1 000 000 met een vermenigvuldiger van één of twee cĳfers cĳferend uitvoeren.

2 De kinderen kunnen opgaande en niet-opgaande delingen met natuurlĳke getallen tot 1 000 000 met een deler van ten hoogste twee cĳfers cĳferend uitvoeren.

3 De kinderen kunnen het product en het quotiënt van een cĳferoefening controleren met hun ZRM.

4 De kinderen kunnen de oplossing van een cĳferoefening vergelĳken met de uitkomst op hun ZRM en desnoods de oefening opnieuw maken.

5 De kinderen kunnen de begrippen ‘product’, ‘vermenigvuldiging’, ‘quotiënt’, ‘deling’, ‘rest’ … correct gebruiken.

6 De kinderen kunnen het product en het quotiënt bĳ een cĳferoefening vooraf bĳ benadering schatten.

7 De kinderen kunnen het product en het quotiënt bĳ een cĳferoefening vergelĳken met hun schatting.

LESMATERIALEN

- concordantie

- digitaal bordschema

- Kabas en/of werkboek Kaap 1 p. 10-12

Let op: de oefeningen kunnen de leerlingen niet digitaal maken. Gebruik hiervoor de blanco werkboekbladen op Kabas als je verder volledig digitaal werkt.

- animatie 2 uit Kadet 4 Kaap 1 Les 8

- poster: cĳferen

- instructievideo cĳferend vermenigvuldigen met onthouden

- instructievideo cĳferend delen tot 1 000, H is niet deelbaar en < deler

- instructievideo cĳferend delen tot 1 000 (niet-opgaande delingen)

- Sloep p. 65, 68 en 70

- geruit papier met grote hokjes (1 cm op 1 cm)

- ZRM

LEERLĲN Wat ging vooraf?

Het algoritme voor het cĳferend vermenigvuldigen en delen werd in de vorige leerjaren aangebracht. Vanaf het derde leerjaar hebben de leerlingen het product berekend van natuurlĳke getallen met een natuurlĳk getal kleiner dan 100 en het quotiënt berekend van natuurlĳke getallen gedeeld door een natuurlĳk getal kleiner dan 10.

Ook bĳ cĳferend delen en vermenigvuldigen werd de rode hulplĳn gebruikt om de start en werkrichting aan te geven. In de eerste Kaap van het 6e leerjaar wordt dit herhaald, maar daarna valt dit weg. Je kunt de rode hulplĳn in het werkboek laten tekenen als de leerling nood heeft aan richting.

Bĳ vermenigvuldigen onthouden we op het kladblokje dat naast de oefening staat. Bĳ delen gebruiken we de richtlei die tĳdens de deling helpt bĳ het schatten hoeveel keer de deler in het gevraagde deel van het deeltal kan.

Wat volgt?

K1 L18 Vermenigvuldigen en delen met kommagetallen tot 0,001

Kern klassikale oefening

LESVERLOOP

Laat de leerlingen rechtstaan en de instructies van animatie 2 uit Kadet 4 Kaap 1 Les 8 volgen.

Verwoord het lesdoel:

Vandaag herhalen we hoe we al cĳferend vermenigvuldigen en delen met natuurlĳke getallen tot 1 000 000. Hiervoor zĳn de maaltafels heel belangrĳk. We herhalen ook hoe je een schatting moet maken en waarom dit handig is.

2.1 Instructiefase

2.1.1 Vermenigvuldigen

Welke pretparken hebben jullie al bezocht of welke zouden jullie graag bezoeken?

Wie is al naar Neeltje Jans geweest?

Deltapark Neeltje Jans is een themapark waar je alles leert over de Deltawerken in Nederland. Je kan er ook een rondvaart maken op de Oosterschelde.

Zoek Neeltje Jans op het internet en toon enkele afbeeldingen.

Laat het werkboek nemen of deel het uit.

Maak de eerste oefeningen klassikaal.

De kadetten gingen deze zomer op uitstap naar Neeltje Jans. Er waren die dag 19 058 bezoekers.

Elke bezoeker gaf gemiddeld € 28 uit. Hoeveel inkomsten had het park die dag?

Wat zoeken we? (het product)

Welke bewerking hebben we hiervoor nodig? (een vermenigvuldiging)

Noteer de getallen op het bord en benoem het vermenigvuldigtal, de vermenigvuldiger en het product.

We maken eerst een schatting. Een schatting moet snel gebeuren, dus we werken met afgeronde getallen. 19 058 ronden we af naar 20 000, want de 9 D na de 1 TD duiden aan dat we naar boven afronden. 20 000 is een mooi rond getal om mee te rekenen. 28, de vermenigvuldiger, ronden we af naar 30. De 8 E na de 2 T duiden aan dat we naar boven afronden. De schatting wordt dus 20 000 x 30. Dat is 600 000.

We hebben beide factoren naar boven afgerond. Het product zal dus kleiner of minder dan 600 000 zĳn.

Maak daarna, samen met de leerlingen, de cĳferoefening aan het bord en verwoord stap voor stap. Teken een rode hulplĳn om de rekenrichting aan te duiden en verwoord: We vermenigvuldigen eerst alles met de E, daarna alles met de T.

Gebruik dezelfde kleuren als het MAB-materiaal.

8 maal 8 is 64. We noteren 4 en onthouden 6 op het kladblokje.

8 maal 5 is 40. 40 plus 6 is 46. We noteren 6, schrappen 6 op het kladblokje en onthouden 4.

8 maal 0 is 0. 0 plus 4 is 4. We noteren 4. We schrappen 4 op het kladblokje.

8 maal 9 is 72. We noteren 2 en onthouden 7.

8 maal 1 is 8. 8 plus 7 is 15. We noteren 5 en 1.

Nu zullen we alles vermenigvuldigen met T. We moeten dus een rang opschuiven. We gooien onze reddingsboei, we noteren een 0.

2 maal 8 is 16. We noteren 6 en onthouden 1.

2 maal 5 is 10. 10 plus 1 is 11. We noteren 1, schrappen 1 op het kladblokje en onthouden 1.

2 maal 0 is 0. 0 plus 1 is 1. We schrappen 1 op het kladblokje.

2 maal 9 is 18. We noteren 8 en onthouden 1.

2 maal 1 is 2. 2 plus 1 is 3.

We tellen de twee getallen/rĳen op.

Het product is 533 624.

Vergelĳk het product nadien met de schatting.

Waarom is een schatting nuttig? (Stel dat we vergeten om een rang op te schuiven, dan zal de uitkomst een volledig ander getal zĳn. Met deze schatting kunnen we dat gemakkelĳk controleren.)

het vermenigvuldigtal de vermenigvuldiger het product

klassikale oefening

2.1.2 Delen

De dag ervoor had het pretpark een omzet van € 430 592. De bezoekers gaven gemiddeld € 32 uit.

Hoeveel bezoekers waren er die dag?

Welke bewerking hebben we hiervoor nodig? (een deling)

We zullen dit al cĳferend berekenen met een staartdeling.

Noteer de getallen op het bord. Benoem het deeltal en de deler

Maak samen met de leerlingen een schatting:

Schatten bĳ een deling is soms wat moeilĳker. Denk goed aan de maaltafels.

We ronden de deler af naar 30.

Naar welk getal kunnen we 430 592 afronden zodat het gemakkelĳk deelbaar is door 30?

(420 000 420 000 : 30 = (300 000 + 120 00) : 30 = 10 000 + 4 000 = 14 000)

Het deeltal en de deler werden naar beneden afgerond. Het quotiënt zal ongeveer 14 000 zĳn.

Besteed, voor het cĳferen, voldoende aandacht aan de richtlei:

De richtlei is een handig hulpmiddel om e ciënter en correcter te kunnen werken. Begin steeds bĳ 10 x , daarna 5 x . 10 x is een 0 bĳvoegen, 5 x is de helft van 10 x . In dit voorbeeld is 10 x 32 = 320 en 5 x 32 = 160.

Maak samen met de leerlingen de cĳferoefening aan het bord. Verwoord:

Hoeveel keer kan 32 in 4? Dat lukt niet. In 43 lukt wel. We plaatsen een boogje. 32 kan 1 keer in 43. 1 keer 32 is 32. 43 min 32 is 11. Ik laat 0 D zakken.

Hoeveel keer kan 32 in 110? 3 keer. 3 keer 32 is 96. 110 min 96 is 14. Ik laat 5 H zakken.

Hoeveel keer kan 32 in 145? 4 keer. 4 keer 32 is 128. 145 min 128 is 17. Ik laat 9 T zakken.

Hoeveel keer kan 32 in 179? 5 keer. 5 keer 32 is 160. 179 min 160 is 19. Ik laat 2 E zakken.

Hoeveel keer kan 32 in 192? 6 keer. 6 keer 32 is 192. 192 min 192 is 0. Het quotiënt is 13 456. De rest is 0. Deze deling is een opgaande deling. Was mĳn schatting goed?

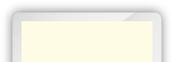
x 32 = 160

x 32 = 320

quotiënt

Afsluiter

leergesprek

2.2 Inoefenfase

Laat de leerlingen de oefeningen maken in het werkboek

3.1 Nabespreking

Maak tĳd voor een nabespreking. Ook al zĳn niet alle leerlingen klaar, bespreek toch klassikaal. Dit is een belangrĳk leermoment.

Maak oefening 1 en 2 aan het bord en bespreek. Je kunt eventueel een sterke leerling de oefening aan het bord laten maken, maar vermĳd om verkeerde voorbeelden te tonen.

Bespreek steeds terugkerende fouten klassikaal. Zorg voor een correcte verwoording en ondersteun eventueel met kleur. Herhaal de belangrĳkste stappen:

Wat hebben we vandaag geleerd?

1. Getallen moeten we correct onder elkaar plaatsen bĳ vermenigvuldigen (E onder E, T onder T …).

2. Bĳ vermenigvuldigen beginnen we rechts, bĳ delen beginnen we links.

3. Bĳ een vermenigvuldiging moeten we telkens een rang opschuiven als we vermenigvuldigen met het volgende cĳfer van de vermenigvuldiger.

3.2 Verankering

Veranker het lesdoel en koppel terug naar de doelstelling uit de instap: Wat hebben we vandaag geleerd? Laat de leerlingen kort verwoorden.

BEWERKINGEN - CIJFEREN

5 Vermenigvuldigen en delen met natuurlijke getallen tot 1 000 000

Zoek het product. Schat eerst. Benoem de begrippen.

vermenigvuldigtal vermenigvuldiger

Zoek het quotiënt. Schat eerst. Benoem de begrippen.

Kaap K ap 1 dKadeKa e de 6 6

Wĳs de leerlingen op het belang van de richtlei. Vul deze eventueel samen in. Laat de leerlingen hun uitkomst controleren met een ZRM. Daarna duiden ze aan of hun oplossing juist of fout is. Let op! Bĳ delingen geldt voorlopig enkel het getal vóór de komma bĳ de uitkomst op je ZRM. De rest kun je niet bepalen met de ZRM. Help waar nodig. Verbeter individueel of klassikaal.

Zoek het product of het quotiënt. Controleer achteraf met de ZRM

17 x 42 043 = Ik schat: OK

x + 33 583 : 15 = q r Ik schat: OK

Kadet_6_Kaap_1_Werkboek.indd 11

Ik schat:

B Ik schat:

Noteer de getallen correct onder elkaar en bereken. Let op het bewerkingsteken! Vergeet de schatting niet. Controleer achteraf met een ZRM Bereken het product van 69 en 2 534.

Bereken het quotiënt van 543 583 en 64.

Bereken het product van 4 062 en

DIFFERENTIATIE EN ORTHODIDACTISCHE TIPS

Leerlingen met extra ondersteuningsnoden kunnen de oefeningen op geruit papier met grote hokjes maken. Je kunt de oefening eventueel voor hen op het blad noteren.

De leerlingen moeten maar één keer schatten. Bĳ de andere oefeningen kunnen ze de oplossing controleren met een ZRM. Zo oefenen ze ook het werken met een ZRM.

Teken een rode hulplĳn om de werkrichting aan te duiden.

Daag de leerlingen uit hun tempo te verhogen, zich goed te concentreren en tussen twee oefeningen eens met hun hoofd of handen te draaien. Dan zĳn ze weer klaar voor een volgende oefening.

Ga eens rond en vraag de leerlingen of hun schatting een over- of onderschatting is (ruim, net minder dan …) en hoe dat komt. Vraag na of ze dit al vooraf kunnen voorspellen.

Daag de leerlingen uit om de onthoudcĳfers niet te noteren.

Laat de leerlingen ook de recente cĳfers van de grotere parken buiten België opzoeken op het internet. Laat hen oefeningen voor elkaar bedenken met deze cĳfers.

Maak eventueel gebruik van volgend di erentiatiemateriaal:

- scheurblok Kaap 1 p. 4

- Meer oefenaanbod via Kai en op de gamehoek van Kaap 1!

- Oefenblaadje: Vermenigvuldigen en delen met natuurlĳke getallen tot 1 000 000

- Krak: Wereldsteden (6e leerjaar)

Terug naar de toekomst (6e leerjaar)

Codekraker (5e - 6e leerjaar)

Ontsnap! (5e - 6e leerjaar)

LESDOELEN

LESMATERIALEN

LES 6 Ruimtelĳke oriëntatie: plaats, richting, gezichtspunten, plattegrond, kaart en coördinaten

1 De kinderen kunnen de positie en de richting van voorwerpen bepalen en beschrĳven.

2 De kinderen kunnen verwoorden wat ze zien vanuit verschillende gezichtspunten.

3 De kinderen kunnen mentaal een standpunt innemen en verwoorden wat ze zien.

4 De kinderen kunnen de begrippen ‘vooraanzicht’, ‘linkerzĳaanzicht’, ‘rechterzĳaanzicht’ en ‘bovenaanzicht’ gebruiken en toepassen.

5 De kinderen kunnen zinvolle begrippen correct gebruiken: ‘naast’, ‘tussen’, ‘voor’, ‘achter’, ‘midden’, ‘links van’, ‘rechts van’, ‘boven’, ‘onder’ …

6 De kinderen kunnen een plaats bepalen vanuit een referentiepunt in de realiteit of op een kaart, tekening of foto.

7 De kinderen kunnen een plaats correct weergeven aan de hand van de coördinaten.

- concordantie

- Kabas en/of werkboek Kaap 1 p. 13-15

- link 3: Geopunt

- afbeelding 2: coördinatenrooster pretpark

- instructievideo coördinatenrooster

- instructievideo gezichtspunten

- Sloep p. 118

LEERLĲN Wat ging vooraf?

De leerlingen worden elke dag geconfronteerd met ruimtelĳke oriëntatie. De begrippen leerden ze hanteren in alle voorgaande leerjaren.

In Leer Lokaal (OVSG) zĳn de doelen bĳ deze les terug te vinden in het leergebied 'Ik en de wereld.' Bekĳk in welke lessen je de inhoud aan bod laat komen of bied ze twee keer aan.

Wat volgt?

K1 L7 Ruimtelĳke oriëntatie: blokkenbouwsels met aanzichten

Instap

onderwĳsleergesprek

VOOR DE LES

Ga naar een website van een pretpark en zoek de plattegrond. Zet deze klaar.

Gebruik de plattegrond van een pretpark dat de leerlingen kennen (bĳvoorbeeld een pretpark in de buurt of een pretpark dat de leerlingen al eens bezochten).

LESVERLOOP

Situering op kaart met ICT

Zoek in Google Maps een gekend pretpark op. Verken de buurt rond het park. Doe dit zowel op de kaart als op het satellietbeeld. Bespreek:

- Wat zie je? Wat herken je?

- Zie je de gelĳkenissen tussen de kaart en het satellietbeeld?

- Welk soort aanzicht is dit? (het bovenaanzicht)

Bekĳk de buurt rond het pretpark nu ook met Google Streetview. Ga vlak voor de ingang van het park staan. Toon het vooraanzicht

Surf met de leerlingen ook eens naar link 3. Tik de naam van een gekend gebouw (bĳvoorbeeld de school) in de zoekbalk. Klik rechts bĳ ‘lagen’ op basiskaarten en luchtfoto’s. Zo kun je schakelen tussen kaarten en foto’s.

Verwoord het lesdoel:

Vandaag hebben we het over aanzichten, plattegronden, kaarten en coördinaten. Op het einde van deze les kan je de positie en de richting van voorwerpen bepalen en beschrĳven, kan je verwoorden wat je ziet vanuit verschillende gezichtspunten en weet je hoe je de weg op een kaart of plattegrond kan vinden.

2 Kern

onderwĳsleergesprek

2.1 Instructiefase

Dit is een herhalingsles. Laat spoor 3-leerlingen snel zelfstandig aan het werk. Neem spoor 1-leerlingen apart voor een verlengde instructie. Pas de les aan aan het niveau van je klas.

2.1.1 Oriëntatie op de kaart

We hebben zonet een pretpark vanuit de lucht bekeken, via de kaart en via satellietbeelden. Hoewel we daar al veel op kunnen zien, is het niet zo gemakkelĳk om bepaalde zaken te herkennen. Wat maakt het gemakkelĳker? (bepaalde kleuren, de legende, uitleg …)

Dit vinden we terug op de plattegrond van een pretpark.

Toon de plattegrond. Laat de leerlingen eventueel dezelfde plattegrond opzoeken.

Bespreek. Enkele mogelĳke vragen:

- Waar bevindt de ingang zich? Waaraan herken je de ingang?

- Wat is de eerste attractie aan je rechterkant als je het park binnenkomt?

- Zoek de draaimolen. Wat zien we aan onze linkerkant als we met onze rug naar de draaimolen staan?

- Ik heb honger. Ik wandel van de waterattractie naar het dichtstbĳzĳnde restaurant. Kom ik nog een attractie tegen? Zo ja, welke attractie en aan welke kant?

onderwĳsleergesprek

2.1.2 Coördinaten

Niet alles is snel te vinden op de kaart. Als iemand een bepaalde plaats wil omschrĳven zonder die aan te duiden op de kaart, wat is er dan nodig om dat e ciënt te kunnen doen? (coördinaten)

Wat zĳn coördinaten ook alweer? (Een kaart is verdeeld in rĳen en kolommen. Deze vormen vakjes.

De kolommen en rĳen hebben cĳfers en letters. Elk vakje wordt aangeduid met een letter en een cĳfer.

Bĳvoorbeeld: B5 wil zeggen dat dit vakje zich bevindt in kolom B, rĳ 5.)

klassikale oefening

Toon afbeelding 2.

Wat zĳn de coördinaten van de vĳver? (G6, G7 en H6)

Wat zĳn de coördinaten van de piratenboot? (F10, G10 en G11)

Wat zĳn de coördinaten van de kassa aan de ingang van het pretpark? (E1)

Wat zie je in vak F8? (een vlag op het dak van een grote tent)

Teken een coördinatenrooster op de plattegrond van een gekend pretpark in de buurt of van het pretpark dat aan bod kwam in 2.1.1 en stel hierover vragen in plaats van te werken met afbeelding 2.

2.1.3 Plaats en richting

Bekĳk opnieuw afbeelding 2.

Zoek het groene mannetje in het autopark. Hĳ staat met zĳn gezicht naar de fontein.

Wat ziet hĳ aan zĳn linkerkant? (de rollercoaster)

Wat is er achter hem? (eetkraampjes met picknicktafels)

2.2 Inoefenfase

Laat de leerlingen de oefeningen maken in het (digitale) werkboek

3.1 Plattegronden van pretparken bestuderen

Afsluiter spel

Laat de leerlingen nog enkele kaarten of plattegronden van pretparken op het internet opzoeken en bestuderen. Stel gerichte vragen.

- Hoeveel restaurants zie je?

- Hoeveel rollercoasters zĳn er?

- Welk toilet ligt het dichtst bĳ de draaimolen? - …

Werk op de voorkennis van de leerlingen. Tracht hen zover te krĳgen dat ze zich via de kaart mentaal in het park bevinden en door het park kunnen wandelen. Misschien is de klas vorig schooljaar naar een pretpark geweest? Gebruik dan dit park als voorbeeld.

3.2 Verankering

Veranker het lesdoel en koppel terug naar de doelstelling uit de instap: Wat hebben we vandaag geleerd? Laat de leerlingen kort verwoorden.

Laat de leerlingen met beide vingers de rĳ en kolom afgaan om zo het vak te vinden.

p 1

LES 6 Ruimtelijke oriëntatie: plaats, richting, gezichtspunten, plattegrond, kaart en coördinaten

Noteer de coördinaten en los op.

5 4 3 2 1 A B C D E F G

Kyan zit in het oranje autootje van de draaimolen. Hij bevindt zich in vak

Klara staat in het huisje bij het reuzenrad. Ze controleert er de kaartjes. Ze staat in vak(ken) Ilona ziet recht voor haar de luchtballon. Rechts ziet ze een feesttent, links een wit huis. Omcirkel Ilona. Ze staat in vak Ilias staat in vak D7. Hij heeft een paarse trui aan. Bij welke attractie staat hij?

Hij staat bij het autocircuit.

Ilias moet straks naar de ingang gaan. Beschrijf de kortste weg die hij moet afleggen aan de hand van de coördinaten. I8 I4

D7 D6 D5 D4 D3 E3 F3 F2 E2 E1 F3 (en F4)

Kadet_6_Kaap_1_Werkboek.indd 13 14/03/2024 11:55

Bekijk aandachtig en los op. Waar stond de fotograaf? Noteer het juiste cijfer bij de afbeeldingen.

Kadet_6_Kaap_1_Werkboek.indd 14 14/03/2024 11:55

is het juiste bovenaanzicht bij dit vooraanzicht? Kruis aan.

Vertel de leerlingen dat robot Kai niet in aanraking met water mag komen. De vakjes met een plas water moeten dus ontweken worden.

DIFFERENTIATIE EN ORTHODIDACTISCHE TIPS

Zorg voor concreet materiaal (bĳvoorbeeld Lego of Playmobil) en bouw hiermee situaties na. Laat de leerlingen vooral handelen, beleven (kĳken) … Laat hen kĳken vanop de kĳklĳn. Geef hen een kader uit karton om zo beter het beeld te zien.

Ga samen met de leerlingen op dezelfde plaats staan, met het gezicht in dezelfde richting. Benoem wat je ziet en aan welke kant je het ziet, bĳvoorbeeld de poort en de toren rechts. Ga op een andere plaats staan en benoem opnieuw wat je ziet, bĳvoorbeeld de toren staat nu links. Neem zo alle posities in en bespreek.

Laat de leerlingen van voorwerpen in de klas de verschillende aanzichten tekenen.

Laat de leerlingen extra oefeningen bedenken bĳ de plattegrond op afbeelding 2 Deze oefeningen kunnen ze dan aan een klasgenoot geven.

Laat de leerlingen kaartlezen op een stadsplan van hun eigen stad of gemeente.

Je bent het hoofd van de brandweer. Voor een goede en veilige coördinatie maak je een lĳst van alle belangrĳke gebouwen zoals de bibliotheek. Wat zĳn de coördinaten?

Wat is de ligging ten opzichte van de spoorlĳn (het noorden, zuiden, oosten of westen)?

Ze kunnen dit per twee of per drie doen. Daarna kun je dit in de les wereldoriëntatie gebruiken.

Maak eventueel gebruik van volgend di erentiatiemateriaal:

- scheurblok Kaap 1 p. 5

- Meer oefenaanbod via Kai en op de gamehoek van Kaap 1!

- Oefenblaadje: Plattegrond, kaart en coördinaten

- Krak: Wereldsteden (6e leerjaar)

Terug naar de toekomst (6e leerjaar)

Codekraker (5e - 6e leerjaar)

Ontsnap! (5e - 6e leerjaar)

LESDOELEN

LESMATERIALEN

MEETKUNDE

LES 7 Ruimtelĳke oriëntatie: blokkenbouwsels met aanzichten

1 De kinderen kunnen constructies uitvoeren aan de hand van een grondplan/hoogteplan.

2 De kinderen kunnen het grondplan/hoogteplan van een blokkenbouwsel maken.

3 De kinderen kunnen verwoorden wat ze vanuit verschillende standpunten zien.

4 De kinderen kunnen zich mentaal verplaatsen in de ruimte.

5 De kinderen kennen de begrippen ‘vooraanzicht’, ‘zĳaanzicht’, ‘bovenaanzicht’ … en kunnen deze correct gebruiken.

- concordantie

- digitaal bordschema

- Kabas en/of werkboek Kaap 1 p. 16-17

- kopieerblad 2: estafette

- link 4: blokken bouwen

- instructievideo gezichtspunten

- instructievideo grondplan/hoogteplan

- Sloep p. 117

- wisbord per leerling

- kladschrift

- 40 kubusvormige blokken per twee leerlingen (bĳvoorbeeld de kleine gele blokjes van MABmateriaal)

- 30 dozen of grote blokken

- bord, bestek en beker per leerling

- kegel per groep

- 12 kubusvormige blokken per groep

- uitwisbare stiften

- krĳt of tape

LEERLĲN

Wat ging vooraf?

Blokkenbouwsels komen reed aan bod sinds het eerste leerjaar.

KathOndVla: In plaats van ‘grondplan’ kan ook het begrip ‘hoogteplan’ gebruikt worden.

K1 L6 Ruimtelĳke oriëntatie: plaats, richting, gezichtspunten, plattegrond, kaart en coördinaten

Wat volgt?

K4 L10 Ruimtelĳke oriëntatie: plaatsbeschrĳving en coördinaten

VOOR DE LES

Verzamel voor iedere leerling een bord, bestek en een beker. Je kunt er ook voor kiezen om de instap van deze les in de refter te laten doorgaan.

Maak met enkele dozen of grote blokken een blokkenbouwsel in het midden van de klas. Bouw het op een tafel zodat het makkelĳk zichtbaar is vanop ooghoogte. Voorzie een blokkenbouwsel van 4 op 4 en ga minstens bĳ één stapel tot 4 hoog.

Druk kopieerblad 2 af.

Lamineer voor langdurig gebruik en laat de leerlingen werken met uitwisbare stiften

Voor de afsluiter is een grote ruimte nodig (de eetzaal, de speelplaats, de turnzaal ...).

Zet de opstelling van de estafette klaar:

Plaats een kegel op de startstreep voor iedere groep. Leg bĳ elke kegel een grondplan/hoogteplan van een blokkenbouwsel (kopieerblad 2). Leg ook de kubusvormige blokken erbĳ. Op het einde van het parcours voorzie je voor iedere groep een rooster van vier op vier hokken. Teken dit op de grond met krĳt of plak af met tape. Pas de grootte van de hokken aan aan de grootte van de kubussen.

LESVERLOOP

Links, rechts, onder, op

Vraag na of de leerlingen het spel ‘Kadet zegt …’ kennen.

Laat de leerlingen per twee plaatsnemen aan tafel, tegenover elkaar. Voor zich hebben ze elk een bord, bestek en een beker staan. Geef spelinstructies: Ik geef verschillende opdrachten die soms wel en soms niet starten met ‘Kadet zegt …’. Indien ‘Kadet zegt …’ voor de opdracht komt, moet de opdracht uitgevoerd worden. Indien de opdracht niet start met ‘Kadet zegt …’ dan moet de opdracht niet uitgevoerd worden.

Varieer in instructie. Gebruik soms eens wel, dan weer niet ‘Kadet zegt …’ en maak het moeilĳker na enkele eenvoudige opdrachten:

- Leg de vork op het bord.

- Leg het mes onder de vork.

- Leg het bord onder de beker.

- Leg het mes rechts van het bord en links van je rechterhand.

- Leg de vork voor het mes en op de palm van je linkerhand.

- Leg de vork rechts van het mes en onder je linkerhand.

Observeer terwĳl de leerlingen de opdrachten uitvoeren. Geef de instructies snel na elkaar.

Ruim dan de tafels gedeeltelĳk af. Haal bĳ ieder duo één bord, mes, vork en beker weg.

Beeld je nu in dat je de tafel dekt voor de persoon tegenover je. Je moet dus goed nadenken hoe het er voor die persoon uitziet. We spelen het spel nog eens. Duid per duo aan welke leerling start.

Wat zal er anders zĳn deze keer? (Links wordt rechts en rechts wordt links. Voor wordt achter en achter wordt voor. Let op! Boven en onder blĳven gelĳk.)

Maak één opdracht klassikaal: Leg het mes rechts van het bord.

Laat de leerlingen proberen. Zeg dat ze zich gerust eens mogen omdraaien om te zien of het klopt.

- Leg de vork links van het bord.

- Leg de beker op het bord en leg het mes links ervan.

- Leg het bord en de beker rechts van de vork.

- Leg het mes voor de beker en leg het bord eronder.

Bespreek kort. Waren er twĳfels of onenigheden?

2

Kern groepswerk

onderwĳsleergesprek

Verwoord het lesdoel: We zĳn goed opgewarmd. We hebben de aanzichten herhaald. We oefenen straks verder met blokkenbouwsels en hun aanzichten. We controleren op het einde van de les of jullie een constructie kunnen bouwen aan de hand van een grondplan/hoogteplan en of jullie de aanzichten kunnen tekenen.

2.1 Instructiefase

2.1.1 Aanzichten tekenen

Verdeel de klas in vier groepen. Laat elke groep plaatsnemen aan een kant van het blokkenbouwsel dat je in het midden van de klas opstelde met dozen of grote blokken. Duid met een pĳl op de grond het vooraanzicht aan. Elke leerling heeft een kladschrift of een wisbord bĳ de hand.

Bekĳk met jullie groep het blokkenbouwsel. Eén iemand uit jullie groep tekent op het wisbord of in het kladschrift het aanzicht dat jullie zien. Noteer de naam van het aanzicht erbĳ.

Laat de groepen een kwartdraai doordraaien. Geef hen dezelfde opdracht en laat het volgende aanzicht op een ander wisbord tekenen. Herhaal tot elke groep opnieuw op zĳn plaats staat.

2.1.2 Aanzichten vergelĳken

Laat de leerlingen de wisborden van de verschillende aanzichten bĳ elkaar leggen. Laat hen vergelĳken. Zĳn de aanzichten gelĳk? (nee)

Bespreek de verschillende aanzichten: Wat is het vooraanzicht? Wat is het achteraanzicht?

Het rechterzĳaanzicht? Het linkerzĳaanzicht?

Hoe komt het dat we deze aanzichten kunnen benoemen? (Het vooraanzicht is aangeduid met een pĳl.)

Welk aanzicht missen we nog? (het bovenaanzicht)

Laat de leerlingen per groep het bovenaanzicht tekenen. Vergelĳk.

zelfstandig werk

2.1.3 Van blokkenbouwsel naar grondplan/hoogteplan

Laat de leerlingen opnieuw plaatsnemen aan hun bank en laat hen hun kladschrift nemen.

Teken nu het grondplan/hoogteplan van dit blokkenbouwsel.

Observeer welke leerlingen nood hebben aan een verlengde instructie.

Bespreek de grondplannen/hoogteplannen. Teken het grondplan/hoogteplan op het bord.

partnerwerk

2.1.4 Van grondplan/hoogteplan naar blokkenbouwsel

Teken volgend grondplan/hoogteplan op het bord en laat het per twee nabouwen met blokken

2.2 Inoefenfase

Laat de leerlingen de oefeningen maken in het (digitale) werkboek

spel

BEWEGING

3.1 Estafette

Verdeel de klas in groepen van vier tot vĳf leerlingen. Elke groep neemt plaats aan een kegel

Vandaag doen we een 'blokkenestafette'. Per groep bekĳken jullie het grondplan/hoogteplan (kopieerblad 2). 2

Op het startsignaal vertrekt één iemand van iedere groep met één kubus naar de overkant. Die leerling plaatst daar de kubus op de juiste plaats volgens het grondplan/hoogteplan. De leerling loopt terug en tikt de volgende loper aan. Hĳ of zĳ doet hetzelfde. Ondertussen tekenen de anderen het vooraanzicht en het rechterzĳaanzicht.

De eerste groep die zĳn blokkenbouwsel correct gebouwd heeft aan de overkant en die de aanzichten correct getekend heeft, wint van zodra alle groepsleden neerzitten bĳ de kegel. Veel succes!

Overloop samen met de leerlingen de gemaakte blokkenbouwsels en evalueer de getekende aanzichten. Bespreek hoe het samenwerken in groep verliep.

3.2 Verankering

Veranker het lesdoel en koppel terug naar de doelstelling uit de instap: Wat hebben we vandaag geleerd?

Laat de leerlingen kort verwoorden.

Laat de leerlingen de blokkenbouwsels nabouwen in het echt of laat hen werken met een app via link 4.

LES 7 Ruimtelijke oriëntatie: blokkenbouwsels met aanzichten

Noteer de begrippen op de juiste plaats: zijaanzicht, bovenaanzicht en vooraanzicht Kleur het blokkenbouwsel in de juiste kleuren en vul het grondplan/hoogteplan aan.

grondplan/hoogteplan

zijaanzicht vooraanzicht

bovenaanzicht

Teken de aanzichten die bij het grondplan/hoogteplan horen en los op.

grondplan/hoogteplan vooraanzicht rechterzijaanzicht linkerzijaanzicht

Hoeveel blokken telt dit bouwsel?

Kaap K ap 1

Daag de leerlingen uit om de oefening eerst te proberen maken zonder nabouwen. Laat hen het blokkenbouwsel nabouwen indien nodig.

grondplan/hoogteplan vooraanzicht rechterzijaanzicht linkerzijaanzicht Hoeveel blokken telt dit bouwsel?

Los op. Een pretparkontwerper maakt een constructie voor een nieuwe attractie. Welk aanzicht hoort bij deze constructie? Kruis aan.

DIFFERENTIATIE EN ORTHODIDACTISCHE TIPS

Bied steeds materiaal aan waarmee de leerlingen blokkenbouwsels kunnen nabouwen. Laat de leerlingen veel driedimensionale constructies bouwen. Leer hen inzicht verwerven in de drie dimensies. Grĳp ook oefenkansen op andere momenten in andere lessen.

Laat de leerlingen oefenen aan de hand van een minigame in de gamehoek van Kaap 1.

Laat de leerlingen zelf een oefening maken voor elkaar zoals oefening 3 in het werkboek.

Maak eventueel gebruik van volgend di erentiatiemateriaal:

- scheurblok Kaap 1 p. 6

- Meer oefenaanbod via Kai en op de gamehoek van Kaap 1!

- Oefenblaadje: Blokkenbouwsels

- Krak: Wereldsteden (6e leerjaar)

Terug naar de toekomst (6e leerjaar)

Codekraker (5e - 6e leerjaar)

Ontsnap! (5e - 6e leerjaar)

Kadet_6_Kaap_1_Werkboek.indd

LESDOELEN

LESMATERIALEN

GETALLENKENNIS

LES 8 Kommagetallen tot 0,001

1 De kinderen kunnen kommagetallen tot 0,001 lezen en noteren.

2 De kinderen kunnen de cĳfers van een kommagetal tot 0,001 op de juiste plaats noteren in de positietabel en hierbĳ de juiste begrippen en symbolen gebruiken (D, H, T, E, t, h, d).

3 De kinderen kunnen kommagetallen tot 0,001 op een getallenas plaatsen, vergelĳken en ordenen.

4 De kinderen kunnen met kommagetallen tot 0,001 doortellen en terugtellen met sprongen.

5 De kinderen kunnen kommagetallen tot 0,001 zinvol afronden.

6 De kinderen kunnen kommagetallen tot 0,001 vergelĳken en ordenen en de vergelĳkingen voorstellen met =, ≠, > of <.

- concordantie

- digitaal bordschema

- Kabas en/of werkboek Kaap 1 p. 18-20

- onthoudkaart

- poster: getallen tot 1 000 000 000 en tot 0,001 in de positietabel

- instructievideo D, H, T, E, t, h en d

- instructievideo kommagetallen vergelĳken

- instructievideo kommagetallen op de getallenas

- instructievideo kommagetallen ordenen

- Sloep p. 28-30

- wisbord per leerling

- kleefnotities in twee kleuren

- gekleurde stiften

LEERLĲN

Wat ging vooraf?

Kommagetallen tot 0,001 zĳn reeds in het vierde leerjaar en het vĳfde leerjaar aan bod gekomen.

De kinderen zĳn ook vertrouwd met de positietabel.

Wat volgt?

K1 L13 Breuken en kommagetallen tot 0,001

BEWEGING

onderwĳsleergesprek

VOOR DE LES

Bepaal op basis van de overgangsgesprekken met de leerkracht van het vĳfde leerjaar en op basis van de algemene resultaten op de voorkennistest (onderdeel Getallenkennis) welke onderdelen uit de kern je klassikaal behandelt en in welke sporen je de leerlingen indeelt.

Neem één kleur kleefnotities en schrĳf per kleefnotitie één symbool in het zwart. Gebruik volgende symbolen: D, H, T, E, t, h en d. Hang de kleefnotities verspreid in de klas

D T H E t h d

Op de kleefnotities in de andere kleur schrĳf je telkens een cĳfer en zĳn waarde in een speci eke kleur, zoals hieronder beschreven. Deze notities kleef je onder de stoelen van de leerlingen. Afhankelĳk van het aantal leerlingen per spoor kun je hierin variëren.

Bĳvoorbeeld:

Getallen spoor 1

ROOD: 4 E, 5 t, 6 h, 9 d

GROEN: 6 E, 3 t, 0 h, 7 d

BLAUW: 5 E, 9 t, 6 h, 3 d

ROZE: 3 E, 8 t, 7 h, 3 d

ORANJE: 6 E, 2 t, 5 h, 7 d

Getallen spoor 2 en 3

PAARS: 8 D, 5 H, 6 T, 3 E, 1 t, 4 h, 7 d

BRUIN: 5 D, 1 T, 9 E, 8 t, 3 h, 4 d

ZWART: 4 D, 7 H, 6 E, 6 t, 7 h, 9 d

Teken of projecteer een lege positietabel met zeven rangen op het bord.

LESVERLOOP

Positietabel opstellen

Er wordt een nieuwe medewerker gezocht voor een cadeauwinkel in een pretpark. Het is belangrĳk dat die persoon goed kan tellen, getallen lezen, getallen afronden … De uitbaters van de cadeauwinkel hebben enkele leuke manieren bedacht om dit te kunnen testen bĳ de kandidaten. Maar eerst testen we ze bĳ jullie. Zĳn jullie er klaar voor?

Laat de leerlingen zoeken naar de kleefnotities die verspreid in de klas ophangen. Vertel dat ze kleefnotities in een bepaalde kleur zoeken (in het voorbeeld hierboven de gele kleefnotities). Laat de leerlingen die een kleefnotitie vonden naar voor komen en deze op de juiste plaats in de positietabel plaatsen.

Verwoord de afkortingen. Sta stil bĳ het verschil tussen de hoofdletters en de kleine letters.

D = duizendtal ≠ d = duizendste

H = honderdtal ≠ h = honderdste

T = tiental ≠ t = tiende

E = eenheid

Verwoord het lesdoel: Vandaag herhalen we de kommagetallen tot 0,001. We gaan ze rangschikken, afronden en we tellen met sprongen met en zonder getallenas

BEWEGING

groepswerk spel

2.1 Instructiefase

2.1.1 Getallen vormen

Onder elke stoel of bank kleeft ook een notitie. Hierop staan getallen met hun rang in verschillende kleuren. Neem de notitie onder jouw stoel of bank en ga op zoek naar klasgenoten met een getal en rang in dezelfde kleur. Vorm samen het volledige getal en schrĳf dit op een wisbord. Doe dit zonder te spreken. Jullie mogen enkel communiceren met gebaren.

Bĳvoorbeeld:

Getallen spoor 1

ROOD: 4 E, 5 t, 6 h, 9 d 4,569

GROEN: 6 E, 3 t, 0 h, 7 d 6,307

BLAUW: 5 E, 9 t, 6 h, 3 d 5,963

ROZE: 3 E, 8 t, 7 h, 3 d 3,873

ORANJE: 6 E, 2 t, 5 h, 7 d 6,257

Getallen spoor 2 en 3

PAARS: 8 D, 5 H, 6 T, 3 E, 1 t, 4 h, 7 d 8 563,147

BRUIN: 5 D, 1 T, 9 E, 8 t, 3 h, 4 d 5 019,834

ZWART: 4 D, 7 H, 6 E, 6 t, 7 h, 9 d 4 706,679

Laat spoor 1-leerlingen de tabel op hun onthoudkaart gebruiken indien nodig.

klassikale oefening

2.1.2 Getallen rangschikken

Nu mogen jullie, allemaal samen, de getallen rangschikken van klein naar groot. Links vooraan in de klas komt het kleinste getal en rechts komt het grootste getal. Opnieuw doen jullie dit zonder te spreken. Jullie mogen enkel communiceren met gebaren.

Schrĳf daarna de getallen op het bord. Bespreek de getallen en hun volgorde:

Bĳ welk getal heeft het cĳfer van de eenheden de grootste waarde? (5 019,834)

Bĳ welk getal heeft het cĳfer van de honderdtallen de kleinste waarde? (5 019,834)

partnerwerk

2.1.3 Zinvol afronden

Alles dat in de winkel verkocht wordt, komt toe in grote hoeveelheden. De medewerker moet dan de aankoopprĳs per stuk berekenen om de verkoopprĳs te bepalen. Er is één probleem … Na het berekenen van de aankoopprĳs per stuk, staan er wel heel rare prĳzen.

Hoeveel getallen na de komma staan er normaal gezien bĳ prĳzen? (twee getallen na de komma) Wat moet er dus gebeuren met prĳzen die meer dan twee getallen na de komma hebben? (Deze moeten afgerond worden.)

Laat de leerlingen per twee de getallen die op het bord staan, afronden op hun wisbord. Bespreek nadien de werkwĳze.

€ 25,8456

€ 866,3211

€ 94,1289

onderwĳsleergesprek

€ 25,85

€ 866,32

€ 94,13

Markeer de rang waarop afgerond moet worden.

Is het cĳfer van de lagere rang 0, 1, 2, 3 of 4? Dan blĳft de rang gelĳk en worden de lagere rangen 0.

We ronden af naar beneden.

Is het cĳfer van de lagere rang 5, 6, 7, 8 of 9? Dan krĳgt de rang er één bĳ en worden de lagere rangen 0.

We ronden af naar boven.

2.2

Inoefenfase

Laat de leerlingen de oefeningen maken in het (digitale) werkboek

Dicteer de volgende getallen voor het getallendictee: 15,015

vĳftien komma vĳftien duizendste

3.1 Bingo met

Afsluiter

spel

0,477

nul komma vierhonderdzevenenzeventig

kommagetallen

1,101

een komma honderdeneen

25,714

vĳfentwintig komma zevenhonderdveertien

9,319

negen komma driehonderdnegentien

Laat de leerlingen op hun wisbord vĳf kommagetallen schrĳven die bestaan uit nul eenheden. De t, h en d mogen ze zelf kiezen. Bĳvoorbeeld: 0,874

Dicteer verschillende stellingen. Als de stelling past bĳ een van hun kommagetallen, mogen ze dat getal doorstrepen. Als alle getallen doorstreept zĳn, moeten ze ‘BINGO!’ roepen.

Bĳvoorbeeld:

- Het tiende is kleiner dan 7.

- Het honderdste is oneven

- De cĳfers staan van klein naar groot.

- Het getal is groter dan 0,8.

3.2 Verankering

Veranker het lesdoel en koppel terug naar de doelstelling uit de instap: Wat hebben we vandaag geleerd? Laat de leerlingen kort verwoorden.

Wĳs erop dat de leerlingen met nullen moeten aanvullen indien nodig.

GETALLENKENNIS LES 8 Kommagetallen tot 0,001

1 2 3

Getallendictee: noteer de getallen.

Zet de getallen op de juiste plaats in de positietabel

zestien komma achthonderdvijfentwintig

achttien en driehonderdachttien duizendste

KadeKa e de 6 6

Bij welk getal horen de cijfers op de botsauto’s? Kijk naar de waarde en kleur in de juiste kleur.

Kaap K ap 1

Laat de leerlingen nullen bĳplaatsen na de komma zodat er in beide getallen evenveel cĳfers na de komma staan.

Leerlingen met dyscalculie kunnen de t en de h markeren in verschillende kleuren.

Laat de leerlingen de h omcirkelen en herhaal de methode voor afronden: Is het cĳfer van de lagere rang een 0, 1, 2, 3 of 4 dan wordt er afgerond naar beneden; is het cĳfer van de lagere rang een 5, 6, 7, 8 of 9 dan wordt er afgerond naar boven.

Laat de leerlingen pĳlen tekenen en de bewerking erbĳ noteren.

De leerlingen mogen bĳ het vormen van een getal elk cĳfer maar één keer gebruiken.

Tel verder met sprongen. 15,55 15,95

dKadeKa e de 6 6

Vorm de volgende getallen. Gebruik telkens alle cijfers in het reuzenrad.

Maak een zo groot mogelijk kommagetal met drie cijfers na de komma.

Maak een zo klein mogelijk kommagetal met drie cijfers na de komma.

Maak een zo groot mogelijk kommagetal met drie cijfers na de komma met als eenheid 1.

Maak een zo groot mogelijk kommagetal met drie cijfers na de komma met als duizendste 9. 8 9

Kadet_6_Kaap_1_Werkboek.indd 20 14/03/2024 11:55

Maak de h en de t concreet.

Voorbeeld 1:

Teken een vierkant, dit is 1 E. Teken in dit vierkant tien verticale lĳnen. 1 E is 10 t. 1 10 = 1 t

Teken nu ook tien horizontale lĳnen. 1 E is 100 h. 1 100 = 1 h

Voorbeeld 2:

Als ik € 1 verdeel in tien deeltjes, dan heb ik tien stukken van 10 cent. 0,10 = 1 t

Als ik € 1 verdeel in honderd deeltjes, dan heb ik honderd stukken van 1 cent. 0,01 = 1 h

Stel ook schematisch voor: D H T E, t h d

Leer de leerlingen bĳ het rangschikken kĳken naar de waarden van groot (bĳvoorbeeld H) naar klein (bĳvoorbeeld h).

Laat de leerlingen een extra manier bedenken waarop het pretpark hun kandidaten voor de cadeauwinkel kan testen. De oefening moet binnen het lesonderwerp passen.

Maak eventueel gebruik van volgend di erentiatiemateriaal:

- scheurblok Kaap 1 p. 7

- Meer oefenaanbod via Kai en op de gamehoek van Kaap 1!

- Oefenblaadje: Kommagetallen tot 0,001

- Knal: Breuken, kommagetallen en procenten

- Krak: Wereldsteden (6e leerjaar)

Terug naar de toekomst (6e leerjaar)

Codekraker (5e - 6e leerjaar)

Ontsnap! (5e - 6e leerjaar)

LESDOELEN

LESMATERIALEN

BEWERKINGEN - HOOFDREKENEN

LES 9 Optellen en aftrekken met kommagetallen tot 0,001

1 De kinderen kunnen kommagetallen tot 0,001 optellen en aftrekken volgens de standaardprocedure.

2 De kinderen kunnen kommagetallen tot 0,001 optellen volgens exibele oplossingsmethodes.

3 De kinderen kunnen kommagetallen tot 0,001 aftrekken volgens exibele oplossingsmethodes.

4 De kinderen kunnen begrippen zoals ‘som’, ‘verschil’, ‘vermeerderen’ … correct gebruiken.

- concordantie

- digitaal bordschema

- Kabas en/of werkboek Kaap 1 p. 21-22

- bĳlage 1: bewerkingen

- bĳlage 2: attracties

- poster: exibel rekenen bĳ optellen en aftrekken

- afbeelding 3: Helena wil naar het pretpark

- instructievideo optellen en aftrekken tot 0,001

- Sloep p. 46-48

- ZRM

- wisbord per leerling

- kladschrift

- timer

LEERLĲN

Wat ging vooraf?

K1 L3 Optellen en aftrekken met natuurlĳke getallen tot 1 000 000

In K1 L8 werden de kommagetallen tot 0,001 herhaald. Het rekenen met kommagetallen tot 0,001 werd in het vierde en vĳfde leerjaar aangebracht.

Wat volgt?

K2 L8 Optellen en aftrekken met natuurlĳke getallen tot 10 000 000 en kommagetallen tot 0,001

Instap klassikale oefening

VOOR DE LES

Knip de kaarten uit bĳlage 1. Hang de drie attracties uit bĳlage 2 verspreid op in de klas.

De leerlingen die in Kaap 1 les 3 geen problemen hadden kunnen onmiddellĳk aan de slag in de het werkboek.

LESVERLOOP

Probleemstelling

Toon afbeelding 3

Martha’s kleine zusje Helena kĳkt er enorm naar uit om naar het superheldenpretpark te gaan. Op de website staat er dat ze minstens 1,2 meter groot moet zĳn om op alle attracties te mogen. Helena meet 1,02 meter. “Joepie, ik mag op alle attracties!” zegt Helena. Martha lacht een beetje. Waarom lacht Martha?

Laat de leerlingen luidop nadenken. Kom tot de conclusie dat ze kommagetallen moeten vergelĳken. (1,2 en 1,02)

Hoe doen we dit? (door in beide getallen evenveel cĳfers na de komma te plaatsen)

Bĳvoorbeeld:

1,20 en 1,02 1,20 is groter.

Helena is een beetje ontgoocheld en vraagt hoeveel meter ze nog moet groeien om op elke attractie te mogen.

Laat de leerlingen de bewerking verwoorden en die oplossen op hun wisbord Bespreek klassikaal.

1,20 m – 1,02 m = 1,20 m – 1 m – 0,02 m = 0,18 m 0,20 m

Verwoord het lesdoel:

Vandaag tellen we kommagetallen op en trekken we ze af via de standaardmethode. Net zoals bĳ de natuurlĳke getallen overlopen we ook nu exibele rekenstrategieën, zoals compenseren en schakelen en wisselen. Zo kunnen we sommige oefeningen gemakkelĳker oplossen.

2.1 Instructiefase

Dit is herhaling. Noteer de oefeningen aan het bord en pak dit per spoor anders aan.

Spoor 1:

Maak alle oefeningen klassikaal. Laat vooral de leerlingen aan het woord en kom samen tot een resultaat. Beluister meerdere oplossingsmethodes en zoek wat het beste werkt voor de leerlingen.

Spoor 2 en 3:

Als een oefening moeilĳk gaat, voorzie dan zelf een tweede oefening van dezelfde soort.

klassikale oefening

2.1.1 Herhaling: rekenmethodes optellen

Splitsen en doorrekenen

85,15 + 1,588 85,150 + 1,588

85,150 + 1,588 = 85,150 + 1 + 0,500 + 0,080 + 0,008 = 86,738 86,150 86,650 86,730

Het eerste getal houden we heel, het tweede getal doen we er in stappen bĳ.

Compenseren

55,27 + 4,999 = 55,270 + 5 – 0,001 = 60,269

Als ik er teveel bĳdoe, dan moet ik dat ook weer wegdoen.

Wisselen en/of schakelen

wisselen:

7,65 + 21,49 + 12,35 = 7,65 + 12,35 + 21,49 = 41,49 20

schakelen: 44,15 + 8,88 + 1,12 = 44,15 + (8,88 + 1,12) = 54,15

wisselen en schakelen: 16,48 + 5,48 + 3,52 = (16,48 + 3,52) + 5,48 = 25,48 10 20

Wissel bĳ een optelling de termen, die gemakkelĳk samen te tellen zĳn, van plaats en schakel ze met haakjes. Reken de haakjes eerst uit.

klassikale oefening

2.1.2 Herhaling: rekenmethodes aftrekken

Splitsen en doorrekenen

78,5 – 22,366 78,500 – 22,366

78,500 – 22 – 0,300 – 0,060 – 0,006 = 56,134 56,500 56,200 56,140

Het eerste getal houden we heel, het tweede getal doen we er in stappen af.

Compenseren

478,98 – 12,999 = 478,980 – 13 + 0,001 = 465,981

Als ik er teveel wegdoe, dan moet ik dat er ook weer bĳdoen.

Afsluiter

BEWEGING

spel partnerwerk

2.2 Inoefenfase

Laat de leerlingen de oefeningen maken in het (digitale) werkboek

3.1 Welke attractie past

bĳ ons?

Laat de leerlingen per twee werken. Geef hen elk een kaartje uit bĳlage 1

Laat hen de getallen op het strookje zowel optellen als aftrekken in hun kladschrift of op een wisbord.

Zet een timer klaar op het bord. Overloop de drie attracties uit bĳlage 2, die ophangen in de klas. De attracties gaan zo meteen van start. Jullie krĳgen één minuut tĳd om de oefeningen op te lossen. Daarna krĳgen jullie tien seconden tĳd om naar de juiste attractie te lopen.

Controleer nadien. Je kunt dit spel enkele keren herhalen.

Heb je tĳd over? Laat de leerlingen dan per twee nieuwe oefeningen maken voor elkaar, waarmee ze het spel opnieuw kunnen spelen.

3.2 Verankering

Veranker het lesdoel en koppel terug naar de doelstelling uit de instap: Wat hebben we vandaag geleerd? Laat de leerlingen kort verwoorden.

Wĳs de leerlingen erop dat ze nullen moeten bĳplaatsen, zodat er in beide getallen steeds evenveel cĳfers na de komma staan. Verplicht hen om tussenstappen te noteren.

Markeer samen met de leerlingen de belangrĳkste gegevens.

1 2 3 4

Splitsen en doorrekenen: Compenseren bij een optelling: Compenseren bij een aftrekking:

Zoek de som

47,5 + 58,11 = 19,521 + 7,622 = 58,866 + 6,99 = 37,77 + 88,5 = 104,7 + 22,653 = Vul de optellingen aan. 45,89

Kadet_6_Kaap_1_Werkboek.indd 21 14/03/2024 11:55

dKadeKa e de 6

Los op.

Een mama en haar twee kinderen gaan naar het pretpark. De prijs van de toegangstickets verschilt per gezinslid. Het kind kleiner dan één meter betaalt € 16,50. Het kind jonger dan 12 jaar betaalt € 28,85. De mama betaalt als volwassene € 35,50. V Hoeveel moet het gezin in totaal betalen?

Tijdens hun uitstap kopen ze in het pretpark wat eten en drinken. Na het kopen van de toegangstickets hadden ze hiervoor nog € 39,15.

V1 Hoeveel hadden ze oorspronkelijk mee?

Het gezin moet in totaal € 80,85 betalen. Ze hadden oorspronkelijk € 120 mee.

V2 Hoeveel geld hebben ze nog

Daarna hebben ze nog € 27,75 over.

DIFFERENTIATIE EN ORTHODIDACTISCHE TIPS

Verzamel de leerlingen die nood hebben aan een verlengde instructie aan de zorgtafel. Geef telkens één duidelĳke oplossingsprocedure voor het optellen en het aftrekken.

Werk met getallen tot 0,01 zodat je kunt concretiseren met geldwaarden.

Laat de leerlingen de standaardprocedure uitschrĳven. Bĳvoorbeeld:

25,14 + 16,85 = 25,14 + 10 + 6 + 0,80 + 0,05 = 41,99 35,14 41,14 41,94

Laat de leerlingen bĳ oefening 1 en 3 in het werkboek minder bewerkingen oplossen. De overige bewerkingen kunnen ze eventueel oplossen met een ZRM

Laat de leerlingen bĳ oefening 5 in het werkboek de bewerking zoeken en noteren. Daarna mogen ze de oefening oplossen met hun ZRM. Help de leerlingen bewust zoeken naar volgende zaken:

- Welke gegevens zĳn belangrĳk? Onderstreep in het groen.

- Welke gegevens zĳn overbodig? Doorstreep deze gegevens.

- Welk bewerkingsteken hebben we nodig: +, –, x, of :?

Verplicht de snelle leerlingen om tussenstappen te noteren bĳ de eerste bewerkingen. Erna kan dit eventueel achterwege gelaten worden.

Als de leerlingen tĳd over hebben, kunnen ze extra rekenstrookjes maken voor de afsluiter.

Maak eventueel gebruik van volgend di erentiatiemateriaal:

- scheurblok Kaap 1 p. 8

- Meer oefenaanbod via Kai en op de gamehoek van Kaap 1!

- Oefenblaadje: Optellen en aftrekken met kommagetallen tot 0,001

- Knal: Breuken, kommagetallen en procenten

- Krak: Wereldsteden (6e leerjaar)

Terug naar de toekomst (6e leerjaar)

Codekraker (5e - 6e leerjaar)

Ontsnap! (5e - 6e leerjaar)

LESDOELEN

LESMATERIALEN

LES 10 Vermenigvuldigen met natuurlĳke getallen tot 1 000 000 en kommagetallen tot 0,001

1 De kinderen kunnen kommagetallen tot 0,001 vermenigvuldigen met elkaar of met een natuurlĳk getal volgens de standaardmethode en naar analogie van de maaltafels.

2 De kinderen kunnen aangeven dat bĳ een vermenigvuldiging de factoren van plaats mogen wisselen.

3 De kinderen kunnen een doelmatige oplossingsstrategie bedenken en gebruiken (bĳvoorbeeld splitsen).

- concordantie

- digitaal bordschema

- Kabas en/of werkboek Kaap 1 p. 23-25

- poster: exibel rekenen bĳ vermenigvuldigen en delen

- link 5: quiz

- instructievideo vermenigvuldigen met kommagetallen

- instructievideo kommagetal vermenigvuldigen met natuurlĳk getal

- instructievideo kommagetal vermenigvuldigen met kommagetal

- Sloep p. 45 en 49-55

- kladschrift

- wisbord

- kladpapier

LEERLĲN

Wat ging vooraf?

In het vĳfde leerjaar leerden de leerlingen vermenigvuldigen met kommagetallen.

Wat volgt?

K1 L14 Delen met natuurlĳke getallen tot 1 000 000 en kommagetallen tot 0,001

klassikale oefening

VOOR DE LES

Voorzie voor leerlingen die de maaltafels tot 10 nog niet goed beheersen een moment van preteaching. Laat hen dagelĳks oefenen via online mogelĳkheden of in de gamehoek van Kaap 1 op Kabas.

LESVERLOOP

Maaltafels: puntoefening

Speel met de leerlingen de quiz (link 5) waarbĳ je maaltafels oefent aan de hand van puntoefeningen.

Verwoord het lesdoel:

We vermenigvuldigen vandaag met natuurlĳke getallen en kommagetallen tot 0,001. Het is belangrĳk dat jullie de maaltafels goed kennen, want we gaan vermenigvuldigen naar analogie van de maaltafels. We proberen ook enkele exibele rekenstrategieën uit waardoor het vermenigvuldigen soms gemakkelĳker wordt.

2.1 Instructiefase

Dit is herhaling. Noteer de oefeningen aan het bord en pak dit per spoor anders aan.

Spoor 1

Maak alle oefeningen klassikaal. Laat vooral de leerlingen aan het woord en kom samen tot een resultaat. Beluister meerdere oplossingsmethodes en zoek wat het beste werkt voor de leerlingen.

Spoor 2 en 3

Als een oefening moeilĳk gaat, voorzie dan zelf een tweede oefening van dezelfde soort.

2.1.1 Natuurlĳke getallen

Vermenigvuldigen naar analogie van de maaltafels

5 000 x 90 = (5 x 9) x 10 000 = 450 000

12 000 x 40 = (12 x 4) x 10 000 = 480 000

Als ik bĳ maal bĳ de factoren de nullen wegdenk, dan moet ik die terugzetten bĳ het product

Splitsen en verdelen

23 500 x 40 = (20 000 x 40) + (3 000 x 40) + (500 x 40)

= 800 000 + 120 000 + 20 000

= 940 000

Als de vermenigvuldiging te moeilĳk is, splits dan één van de twee factoren

Is dit nog te moeilĳk, dan kun je opnieuw één van de twee factoren splitsen.

12 500 x 28 = (10 000 x 28) + (2 000 x 28) + (500 x 28)

= 280 000 + 56 000 + (500 x 20) + (500 x 8)

= 280 000 + 56 000 + 10 000 + 4 000

= 350 000

klassikale oefening

Flexibel rekenen: 9 x en 11 x

9 x 71 500 = (71 500 x 10) – (71 500 x 1) = 715 000 – 71 500 = 715 000 – 15 000 – 56 500 = 643 500

31 400 x 11 = (31 400 x 10) + (31 400 x 1) = 314 000 + 31 400 = 345 400

9 x = (10 x ) – (1 x )

11 x = (10 x ) + (1 x )

Wisselen en/of schakelen

wisselen en schakelen:

25 x 340 x 40 = (25 x 40) x 340 = 1 000 x 340 = 340 000

schakelen:

5 x 200 x 132 = (5 x 200) x 132 = 1 000 x 132 = 132 000

Wissel de factoren, die gemakkelĳk samen te vermenigvuldigen zĳn, van plaats en schakel ze met haakjes. Reken de haakjes eerst uit.

2.1.2 Kommagetallen

2.1.2.1 Kommagetallen vermenigvuldigen met natuurlĳke getallen en omgekeerd

Vermenigvuldigen naar analogie van de maaltafels

40 000 x 0,8 = (40 000 x 8) : 10 = 32 000

0,09 x 600 000 = (9 x 600 000) : 100 = 54 000

Als we bĳ het wegwerken van de komma een factor vermenigvuldigen met 10, dan moeten we nadien het product van de nieuwe vermenigvuldiging delen door 10.

We denken de komma weg en plaatsen ze later terug.

Splitsen en verdelen

3 500 x 0,56 = (3 500 x 0,5) + (3 500 x 0,06) = (3 000 x 0,5) + (500 x 0,5) + (3 000 x 0,06) + (500 x 0,06) = 1 500 + 250 + 180 + 30 = 1 960

Als de vermenigvuldiging te moeilĳk is, splits dan één van de twee factoren

Is dit nog te moeilĳk, dan kun je opnieuw één van de twee factoren splitsen.

2,24 x 6 000 = (2 x 6 000) + (0,20 x 6 000) + (0,04 x 6 000) = 12 000 + 1 200 + 240 = 13 440

Wĳs spoor 3-leerlingen erop dat de uitkomst kleiner is dan het oorspronkelĳke getal. Dit komt doordat we vermenigvuldigen met een getal kleiner dan 1.

Geef een voorbeeld met euro’s:

Als ik tien keer een halve euro neem, hoeveel euro’s heb ik dan?

10 x € 0,50 = € 5

Flexibel rekenen: 9 x en 11 x

20 014,58 x 9 = (20 014,58 x 10) – (20 014,58 x 1) = 200 145,80 – 20 014,58 = 180 131,22

11 x 30 508,265 = (10 x 30 508,265) + (1 x 30 508,265) = 305 082,650 + 30 508,265 = 335 590,915

9 x = (10 x ) – (1 x )

11 x = (10 x ) + (1 x )

2.1.2.2 Kommagetallen vermenigvuldigen met kommagetallen

45,6 x 1,2 = 54,72 x 10 x 10 : 100 456 x 12 = (456 x 10) + (456 x 2) = 4 560 + 912 = 5 472 OF

45,6 x 1,2 = (456 x 12) : 100 = ((456 x 10) + (456 x 2)) : 100 = 54,72

Als we bĳ het wegwerken van de komma’s beide factoren vermenigvuldigen met een getal (10, 100 of 1 000), dan moeten we nadien het product van de nieuwe vermenigvuldiging delen door beide getallen.

2.2 Inoefenfase

Laat de leerlingen de oefeningen maken in het (digitale) werkboek

3.1

Propje gooien

De leerlingen krĳgen elk een stukje kladpapier. Ze noteren in hun kladschrift een vermenigvuldiging en lossen deze eerst zelf op. De vermenigvuldiging mag niet te moeilĳk zĳn en de uitkomst mag niet groter zĳn dan 1 000 000.

Bepaal per spoor de moeilĳkheidsgraad. Bĳvoorbeeld: een bewerking met getallen die slechts één getal na de komma hebben, of een bewerking waarvan de uitkomst niet groter is dan 1 000.

De leerlingen noteren de vermenigvuldiging op het stukje kladpapier en maken hier een propje van. Het propje gooien ze naar een andere leerling. Zo krĳgt iedereen een propje met een oefening. De leerlingen noteren de bewerking in hun kladschrift en lossen ze op. Doe dit een paar keer na elkaar. Als er tĳd over is, worden alle propjes vooraan verzameld en worden de antwoorden besproken.

3.2 Verankering

Veranker het lesdoel en koppel terug naar de doelstelling uit de instap: Wat hebben we vandaag geleerd? Laat de leerlingen kort verwoorden.

Verplicht de leerlingen om tussenstappen te noteren. De leerlingen mogen afwĳken van de standaardmethode. Leg de rekenpiramide uit.

- HOOFDREKENEN LES 10 Vermenigvuldigen met natuurlijke getallen tot 1 000 000 en kommagetallen tot 0,001

Vermenigvuldig de natuurlijke getallen.

45 850 x 20 = 3 580 x 9 = 18 900 x 40 = 563 x 5 x 200 = 70 x 3 240 = 6 150 x 30 = 11 x 18 400 = 25 x 1 632 x 4 = Blikken gooien! Vermenigvuldig telkens de twee getallen die naast elkaar staan en schrijf het product erboven.

Kadet_6_Kaap_1_Werkboek.indd 23

14/03/2024 11:55

Vermenigvuldigen met kommagetallen komma’s wegwerken 1,2 x 45 =

Vermenigvuldig de kommagetallen.

(12 x 550) : 10 = 6 600 : 10 =

1,2 x 550 = 9 x 3,6 = 0,2 x 66,6 = 1,2 x 200,33 = 35 x 2,19 = 3,56 x 11 = 310,4 x 0,9 = 4,8 x 0,22 = Blikken gooien! Vermenigvuldig telkens de twee getallen die naast elkaar staan en schrijf het product erboven.

(30 x 2,19) + (5 x 2,19) = 65,7 + 10,95 = 76,65

(3,56 x 10) + (3,56 x 1) = 35,6 + 3,56 = 39,16

(310,4 x 1) –

Kadet_6_Kaap_1_Werkboek.indd

Laat de leerlingen de belangrĳkste gegevens in het groen onderstrepen. Verplicht de leerlingen om tussenstappen te noteren.

DIFFERENTIATIE EN ORTHODIDACTISCHE TIPS

Laat de leerlingen de tussenstappen nauwgezet uitschrĳven in hun kladschrift of werkboek Herhaal de basisregels.

Bĳ vermenigvuldigen:

- We splitsen het getal, vermenigvuldigen elk deel en tellen dan op.

- We maken de getallen groter en delen ze dan opnieuw.

- Flexibel rekenen, bĳvoorbeeld 9 x of 11 x.

Laat de leerlingen de meest exibele oplossingsmethode gebruiken.

Maak eventueel gebruik van volgend di erentiatiemateriaal:

- scheurblok Kaap 1 p. 9

- Meer oefenaanbod via Kai en op de gamehoek van Kaap 1!

- Oefenblaadje: Vermenigvuldigen met natuurlĳke getallen tot 1 000 000 en kommagetallen tot 0,001

- Knal: Breuken, procenten en kommagetallen

- Krak: Wereldsteden (6e leerjaar)

Terug naar de toekomst (6e leerjaar)

Codekraker (5e - 6e leerjaar)

Ontsnap! (5e - 6e leerjaar)

Kadet_6_Kaap_1_Werkboek.indd 25

LESDOELEN

LES 11 Meetkundige relaties: symmetrie, spiegelen, gelĳkvormigheid en gelĳkheid van vorm en grootte

1 De kinderen kunnen spiegelingen waarnemen met behulp van een spiegel, door te vouwen of door te meten met een geodriehoek.

2 De kinderen kunnen zelf een spiegeling vervolledigen.

3 De kinderen kunnen de begrippen ‘symmetrie’, ‘asymmetrie’, ‘symmetrieas’, ‘spiegelbeeld’, ‘spiegelas’ en ‘spiegeling’ correct gebruiken.

4 De kinderen kunnen symmetrie en asymmetrie herkennen in hun omgeving.

5 De kinderen kunnen aangeven of een symmetrieas juist getekend is.

6 De kinderen kunnen symmetrieassen aanduiden op een guur.

7 De kinderen kunnen gelĳkheid van vorm en van grootte en gelĳkvormigheid ontdekken bĳ vlakke guren.

8 De kinderen kunnen verwoorden wanneer/waarom guren gelĳk zĳn van vorm en grootte en of ze al dan niet gelĳkvormig zĳn.

LESMATERIALEN - concordantie

- digitaal bordschema

- Kabas en/of werkboek Kaap 1 p. 26-28

Let op: de oefeningen kunnen de leerlingen niet digitaal maken. Gebruik hiervoor de blanco werkboekbladen op Kabas als je verder volledig digitaal werkt.

- link 6: spiegelscène

- afbeelding 4: attractie

- instructievideo symmetrie

- instructievideo gelĳkvormigheid

- Sloep p. 136-137

- powerpoint: spelen met spiegelbeelden

- geodriehoek

- gekleurd papier

- kladpapier

- tekenmateriaal

- geruit papier met grote hokjes (1 cm op 1 cm)

LEERLĲN Wat ging vooraf?

Alle begrippen werden aangereikt in de voorgaande leerjaren.

Het begrip 'congruent' komt voor in het leerplan van het GO!, het is een uitbreidingsdoel bĳ meetkundige relaties voor het OVSG en het komt niet aan bod in het KathOndVla.

Kies zelf of je dit aanbiedt of niet. Houd rekening met de schoolafspraken.

Wat volgt?

K6 L11 Meetkundige relaties: symmetrie en spiegelingen

BEWEGING spel 2 Kern onderwĳsleergesprek

LESVERLOOP

Spiegelscène

In een pretpark worden vaak shows getoond. Soms wordt er in die shows niet gesproken en wordt er enkel met gebaren gecommuniceerd.

Bekĳk met de leerlingen de video (link 6).

Laat hen rondstappen in de klas op muziek. Als de muziek stopt, doen ze de spiegelscène na met de klasgenoot die op dat moment het dichtst bĳ hen staat. Daarna gaat de muziek verder. Stopt de muziek weer, dan doen ze opnieuw de spiegelscène na met de klasgenoot die op dat moment het dichtst staat.

Verwoord het lesdoel:

Vandaag spiegelen we. We bekĳken de eigenschappen van spiegelbeelden en hoe we zelf spiegelbeelden kunnen tekenen. We onderzoeken ook wanneer een guur symmetrisch is en wanneer niet, en wanneer guren gelĳkvormig en/of gelĳk zĳn.

2.1 Instructiefase

2.1.1 Gelĳkvormigheid, gelĳkheid en congruentie

Geef elke leerling een gekleurd blad papier

Vouw het blad in twee.

Teken een grote driehoek op één kant (niet tegen de vouw).

Benoem de punten.

Knip de driehoek uit op het dubbelgevouwen blad. Begin aan de open kant (niet aan de vouw). Knip zeer nauwkeurig. Hou de drie stukken.

Bekĳk de twee driehoeken. Wat kan je zeggen over deze driehoeken?

- Ze hebben dezelfde vorm, ze zĳn gelĳkvormig.

- Ze zĳn even groot, ze hebben dezelfde grootte.

- Ze zĳn identiek, ze zĳn gelĳk, ze zĳn congruent

Leg de twee driehoeken op de tafel. Het tafelblad is vlak Refereer naar de vlakke guren.

Laat de leerlingen experimenteren, handelen, verwoorden: wat kunnen ze doen binnen het vlak met deze driehoeken? Bĳvoorbeeld één driehoek laten liggen, de andere bewegen.

Je kan de driehoek verschuiven, je kan de driehoek draaien.

Wat kan je zeggen over de eigenschappen van de driehoek die je hebt bewogen ten opzichte van de andere driehoek?

- Ze hebben dezelfde vorm, ze zĳn gelĳkvormig.

- Ze zĳn even groot, ze hebben dezelfde grootte.

- Ze zĳn identiek, ze zĳn gelĳk, ze zĳn congruent.

onderwĳsleergesprek

2.1.2 Gelĳkvormigheid en gelĳkheid van vorm en grootte

Toon afbeelding 4 en bespreek.

Welke attracties zĳn gelĳk van vorm en van grootte?

Welke attracties zĳn gelĳkvormig?

Welke attracties zĳn vervormd?

Herhaal:

- Gelĳk de guren zĳn precies hetzelfde, ze hebben dezelfde vorm en dezelfde grootte, ze zĳn gelĳk. - Gelĳkvormig de guren hebben dezelfde vorm, maar kunnen groter of kleiner zĳn. De vergroting of verkleining moet dezelfde verhoudingen aannemen: als de lengte verdubbelt, moet ook de breedte verdubbelen.

onderwĳsleergesprek

2.1.3 Spiegelen

Laat ons nu eens kĳken naar het blad waaruit we de driehoeken knipten.

Vouw het blad terug open. Wat zien we? (de twee driehoeken)

Welke eigenschappen hebben ze? (Ze hebben dezelfde grootte, ze hebben dezelfde vorm en ze staan omgekeerd.)

De ene driehoek is het spiegelbeeld van de andere driehoek (het beeld). De vouwlĳn is de spiegelas

Verbind nu met een lat elk punt van de driehoek met zĳn spiegelpunt. Wat stel je vast? (De lĳnen zĳn evenwĳdig met elkaar en staan loodrecht op de vouwlĳn/spiegelas. Elk punt en zĳn spiegelpunt staan even ver van de as.)

Dit zĳn de eigenschappen van een spiegeling.

Spiegel nu klassikaal de driehoek aan het bord of toon de instructievideo symmetrie Verwoord elke stap. Herhaal daarbĳ de delen en de functies van een geodriehoek.

Benoem de hoekpunten van de guur en spiegel die punten door de loodlĳn van je geodriehoek op de spiegelas te plaatsen. Teken de hulplĳnen. Als alle punten gespiegeld zĳn, kun je ze verbinden en krĳg je een spiegelbeeld.

onderwĳsleergesprek

Herhaal nog eens de eigenschappen van een spiegeling: Beeld en spiegelbeeld

- hebben dezelfde Vorm.

- staan Omgekeerd (links wordt rechts en omgekeerd).

- hebben dezelfde Grootte.

- staan Even ver van de as.

- staan Loodrecht op de as.

Met de beginletters van de eigenschappen van een spiegeling, kun je het woord VOGEL maken. Als geheugensteun kunnen de leerlingen altĳd de vĳf eigenschappen overlopen en zo controleren of ze alle vĳf aanwezig zĳn en of het dus om een correcte spiegeling gaat of niet.

2.1.4 Symmetrie

De spiegelas loopt soms door een guur. Dan wordt de ene helft precies op de andere helft gespiegeld.

Laat de leerlingen zulke voorwerpen zoeken in de klas.

We noemen zulke guren symmetrische guren. Een symmetrische guur heeft minstens één spiegelas waardoor de ene helft precies gespiegeld wordt op de andere helft. Deze as noemen we de symmetrieas Figuren die geen symmetrieas hebben, zĳn asymmetrisch. Sommige guren hebben meer dan één symmetrieas.

Laat de leerlingen op een blad kladpapier de symmetrieassen van een rechthoek tekenen. Ze controleren door te vouwen.

We kunnen niet altĳd controleren door te vouwen. Hoe kunnen we nog controleren of een guur een symmetrieas heeft? (met een geodriehoek)

Verwoord de correcte werkwĳze: We leggen de 90° lĳn (de loodlĳn) op de symmetrieas. Alle punten moeten zowel links als rechts even ver van de as liggen.

Vraag spoor 3-leerlingen hoeveel symmetrieassen een guur maximum kan hebben.

2.2 Inoefenfase

Laat de leerlingen de oefeningen maken in het werkboek

Afsluiter

klassikale oefening

3.1 Foto-uitdaging

Bekĳk samen met de leerlingen de powerpoint Spiegelbeelden kan je herkennen in verschillende situaties. Je kan er ook leuke trucjes mee uitvoeren.

Zoek samen naar spiegelbeelden in de klas, bĳvoorbeeld in de ramen.

Laat de leerlingen spiegelbeelden maken met verschillende materialen en met de re ectie van water. Laat de leerlingen nadenken over andere mogelĳkheden. Laat hen voorwerpen verzamelen en foto’s nemen.

Je kunt ook zelf foto’s nemen wanneer de leerlingen klaar zĳn en die dan afdrukken en ophangen in de klas.

3.2 Verankering

Veranker het lesdoel en koppel terug naar de doelstelling uit de instap: Wat hebben we vandaag geleerd? Laat de leerlingen kort verwoorden.

Wĳs de leerlingen erop dat ze op de details moeten letten en nauwkeurig moeten tekenen.

LES 11 Meetkundige relaties: symmetrie, spiegelen, gelijkvormigheid en gelijkheid van vorm en grootte

Teken alle symmetrieassen waar mogelijk.

Kaap Kaa 1

Indien er in een figuur hierboven geen symmetrieassen zijn, omcirkel dan de elementen die voor asymmetrie zorgen.

Laat de leerlingen ook de hulplĳnen tekenen en nameten.

Wĳs de leerlingen erop dat ze de gespiegelde hoekpunten moeten benoemen.

Zijn de spiegelbeelden correct getekend? Kruis aan.

as juist fout juist fout

Teken de spiegelbeelden as

dKadeKa e de 6 6

Welke figuren zijn gelijkvormig aan de eerste figuur? Kruis aan.

Omcirkel de zeven fouten in het spiegelbeeld

Kadet_6_Kaap_1_Werkboek.indd 28

Kadet_6_Kaap_1_Werkboek.indd

DIFFERENTIATIE EN ORTHODIDACTISCHE TIPS

Laat de leerlingen controleren of een guur symmetrisch is door het blad te plooien of geef hen een spiegel als hulpmiddel. Demonstreer nog eens hoe ze de spiegel moeten gebruiken.

Wĳs de leerlingen geregeld op symmetrie in guren. Dit kan bĳvoorbeeld tĳdens een klasuitstap: bekĳk verschillende verkeersborden en bespreek de symmetrie of asymmetrie.

Geef de leerlingen die klaar zĳn met hun werk een geruit blad met grote hokjes waarop een spiegelas getekend is. Laat ze een guur tekenen aan de ene kant van de spiegelas. Een andere leerling kan deze dan spiegelen. De guren mogen niet te veel details krĳgen en moeten bestaan uit rechte lĳnen. Help waar nodig.

Laat de leerlingen symmetrische voorwerpen zoeken in het schoolgebouw en er foto’s van nemen. Motiveer hen om ook kritisch naar deze voorwerpen te kĳken. Bĳvoorbeeld: de deur is symmetrisch. Hoeveel symmetrieassen heeft die? Is er een verticale symmetrieas? Nee, want aan de ene kant zĳn er scharnieren en aan de andere kant zit een klink. Let op: de vorm van de klink of de aanwezigheid van een sleutelgat kan ervoor zorgen dat er geen symmetrieas is!

Maak eventueel gebruik van volgend di erentiatiemateriaal:

- scheurblok Kaap 1 p. 10

- Meer oefenaanbod via Kai en op de gamehoek van Kaap 1!

- Oefenblaadje: Spiegelbeeld

Symmetrie

(On)gelĳkheid van vorm

Gelĳkvormigheid

- Kaap 8: MK7 Meetkundige relaties: spiegeling, symmetrie, gelĳkvormigheid en congruentie

- Krak: Wereldsteden (6e leerjaar)

Terug naar de toekomst (6e leerjaar)

Codekraker (5e - 6e leerjaar)

Ontsnap! (5e - 6e leerjaar)