LEERBOEK
Functies
D-finaliteit 5 uur
Philip Bogaert
Filip Geeurickx
Marc Muylaert
Roger Van Nieuwenhuyze
Erik Willockx
CARTOONS
Dave Vanroye

D-finaliteit 5 uur
Philip Bogaert
Filip Geeurickx
Marc Muylaert
Roger Van Nieuwenhuyze
Erik Willockx
CARTOONS
Dave Vanroye
Dit boek bevat drie hoofdstukken.
Elk hoofdstuk is opgebouwd uit verschillende paragrafen met aan het einde een handige samenvatting.
Definities vind je op een rode achtergrond. Eigenschappen vind je op een groene achtergrond. Methodes, rekenregels en formules vind je op een zachtblauwe achtergrond. 1.4
Wiskunde is een eeuwenoude wetenschap. De geschiedenis van de wiskunde en de herkomst van bepaalde begrippen worden zachtpaars afgedrukt. Wiskunde kent veel links met andere vakken We tonen zo’n link in een paarsgekleurd kadertje.
De nummers van de oefeningen hebben een gele kleur. Een sterretje duidt op een extra uitdaging.
De wiskunderugzak staat bij oefeningen waarbij je verder moet denken dan de net geziene leerstof.
Achteraan in dit boek vind je de oplossingen



Heel veel opdrachten kun je uitvoeren met ICT. Bij dit boek hoort een webpagina van GeoGebra, gevuld met heel wat digitale oefeningen en applets.
Die vind je terug via www.polpo.be.
Na elk hoofdstuk wordt een wiskundige vaardigheid in de kijker gezet.
Wat moet je kennen en kunnen?
Je krijgt ook een handig overzicht van wat je moet kennen en kunnen na het geziene hoofdstuk.
Wanneer je wiskunde studeert, maak je uiteraard heel wat oefeningen opnieuw en maak je oefeningen die je in de klas niet maakte. Elk hoofdstuk sluit af met enkele herhalingsoefeningen
Een ideale test voor jezelf om te zien of je de leerstof beheerst.










Tijd voor een nieuwe reeks wiskundige uitdagingen die (waar mogelijk) een link zullen leggen met de realiteit. Wiskunde is immers geen saaie wetenschap, maar een boeiende en levendige materie. En laat dat nu net het vertrekpunt zijn van de schrijvers van dit boek. Tweedegraadsfuncties en elementaire functies waren zeker nodig bij The Ride to Happiness by Tomorrowland, een achtbaan in Plopsaland De Panne. Wat zal de wiskundige vergelijking zijn van de weg die de wagentjes afleggen op deze achtbaan ? Hoe hoog moeten de stellingen zijn bij een welbepaalde stijging (of daling) van de weg ? In dit boek maak je ook kennis met algebraïsch rekenen, waar vooral de euclidische deling en de deelbaarheid in � [x] besproken worden. Een (heel) exacte wetenschap is dus onontbeerlijk om veiligheid en fun te combineren. Veel plezier !




Wiskunde is overal.
De boog van de Tyne Bridge in Newcastle heeft de vorm van een (deel van een) parabool. Daardoor loopt een horizontale rechte, die voetgangers en auto’s naar de overkant brengt. Als je de coördinaten van enkele punten kent, kun je de vergelijking van de parabool terugvinden. Die leidt dan weer naar andere berekeningen zoals de hoogte van de brug en de afstand tussen de twee pijlers. In dit hoofdstuk lossen we tweedegraadsvergelijkingen en tweedegraadsongelijkheden op en illustreren we ze met een waaier aan realistische toepassingen.


1Reële functies
Hieronder vind je de grafische voorstelling van een aantal verbanden tussen twee variabele grootheden.
Zijn deze verbanden functies? Hoe kun je dit grafisch onderzoeken ?
reële functie
Een functie is een verband tussen twee variabelen x en y waarbij voor elke x -waarde hoogstens één y -waarde bestaat. We noemen y de afhankelijke variabele en x de onafhankelijke variabele. Een reële functie is een functie waarbij de variabelen x en y reële getallen zijn. Er zijn verschillende representaties van een functie mogelijk: verwoording, tabel, letterformule (voorschrift) en grafiek.
Voor reële functies gebruiken we de letters f , g , h ... of f 1, f 2, f 3
De formule die de functie bepaalt, is het functievoorschrift
Zo spreken we over de functie f met voorschrift f ( x ). De y -waarden noemen we ook de functiewaarden of beelden.
Voorbeeld :
Elk reëel getal heeft juist één tweevoud, dus is dat verband een functie f 1 met voorschrift f 1( x ) = 2x
f 1( 3) = 2 3 = 6
( 3, 6) ∈ f 1
f 1(– 2) = 2 ( –2) = –4
dom f 1 = R
ber f 1 = R
Het domein van een functie f is de verzameling van de x -waarden waarvoor de functiewaarde bestaat.
Notatie : dom f
Merk op :
Het domein van een functie kun je grafisch vinden door de grafiek van de functie loodrecht te projecteren op de x -as.
Het bereik (of beeld) van een functie f is de verzameling van de y -waarden waarvoor er een x -waarde bestaat zodat y = f ( x )
Notatie : ber f
Merk op :
Het bereik van een functie kun je grafisch vinden door de grafiek van de functie loodrecht te projecteren op de y -as.
Een nulwaarde van een functie is een x -waarde waarvoor de functiewaarde nul is.
in symbolen:
α is een nulwaarde van f ⟺ f ( α) = 0
⟺ de grafiek van f snijdt of raakt de x -as in ( α, 0)
Merk op :
De nulwaarden van f zijn de oplossingen van de vergelijking y = f ( x ) = 0.
– Een functie kan meer dan één nulwaarde hebben.
– De nulwaarden zijn de eerste coördinaatgetallen van de snijpunten van de grafiek van de functie met de x -as.
Voorbeelden :
Wanneer je de stand van je zicht- of spaarrekening regelmatig bijhoudt, dan merk je dat de stand van je rekening wijzigt door stortingen of afnamen, met andere woorden de grafiek stijgt of daalt. Ook bij temperatuurmetingen merken we dat de temperatuur stijgt, daalt of constant blijft aan de hand van de grafiek.
Beschouw de grafiek van volgende willekeurige functie f
De bovenstaande grafiek is de grafiek van een functie f . Hierbij is dom f = ]–∞, 11] en ber f = ]–∞, 3].
Dit is een waardetabel van de functie f
x –5 –4 –3 –2 –1
0123456789 1011
f ( x ) –10 –5 –2 –1 –2 –5 –3 –1
↓ de functiewaarden worden groter als de x -waarden groter worden
13333210 –1
↓ de functiewaarden worden kleiner als de x -waarden groter worden ↓ de functiewaarden worden groter als de x -waarden groter worden
Uit de grafiek en de tabel kunnen we het volgende afleiden :
↓ de functiewaarden blijven constant als de x -waarden groter worden
↓ de functiewaarden worden kleiner als de x -waarden groter worden
– In het interval ] –∞, –2[ stijgt de grafiek, de functiewaarden worden groter naarmate de x -waarden groter worden.
–
In het interval ] –2, 0[ daalt de grafiek, de functiewaarden worden kleiner naarmate de x -waarden groter worden.
– In het interval ] 0, 4[ stijgt de grafiek, de functiewaarden worden groter naarmate de x -waarden groter worden.
– In het interval ] 4, 7[ stijgt noch daalt de grafiek, de functiewaarden blijven constant (nl. 3) naarmate de x -waarden groter worden.
– In het interval ] 7, 11[ daalt de grafiek, de functiewaarden worden kleiner naarmate de x -waarden groter worden.
Een functie is stijgend in een interval als de functiewaarden in dat interval groter worden bij toenemende x -waarden.
Een functie is dalend in een interval als de functiewaarden in dat interval kleiner worden bij toenemende x -waarden.
Een functie is constant in een interval als de functiewaarden voor alle x -waarden in dat interval gelijk blijven.
Extreme waarden van een functie
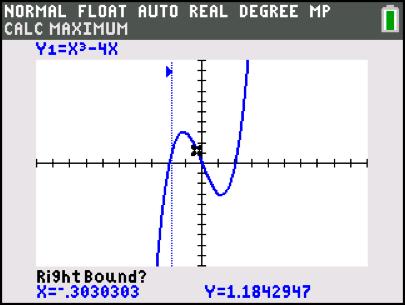
Gegeven : de functie f met f ( x ) = x 3 – 4x

Deze functie stijgt in het interval ]–∞; –1,15[ en gaat bij x = –1,15 over in een dalende functie.
Hierbij is f ( –1,15) = 3,08.
We zeggen dat 3,08 een maximum is van de functie voor x = –1,15.
Deze functie daalt in ]–1,15; 1,15[ en gaat bij x = 1,15 over in een stijgende functie.
Hierbij is f ( 1,15) = –3,08.
We zeggen dat –3,08 een minimum is van de functie voor x = 1,15.
We kunnen dit ook in een overzichtelijke tabel plaatsen.
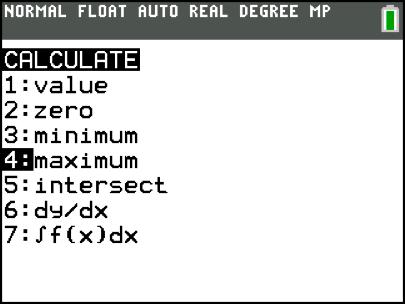


Maxima en minima noemen we de extreme waarden van de functie.
Merk op dat een extreme waarde een functiewaarde is en geen x-waarde.
extreme waarden
Als een functie overgaat van stijgen naar dalen in ( a , f ( a )), dan zeggen we dat de functie een maximum f ( a ) heeft voor x = a .
Als een functie overgaat van dalen naar stijgen in ( a , f ( a )), dan zeggen we dat de functie een minimum f ( a ) heeft voor x = a
Opmerking :
Een functie kan meerdere maxima en/of minima hebben.

Tekenverloop van een functie
Bij bovenstaande grafiek merken we dat :
• –6, 0 en 4 de nulwaarden van deze functie f zijn, met andere woorden f ( –6) = f ( 0) = f ( 4) = 0 ;
• als x ∈ ]–∞, –6[ bevindt de grafiek zich boven de x -as, met andere woorden f ( x ) > 0 ;
• als x ∈ ]–6, 0[ bevindt de grafiek zich onder de x -as, met andere woorden f ( x ) < 0 ;
• als x ∈ ]0, 4[ bevindt de grafiek zich boven de x -as, met andere woorden f ( x ) > 0 ;
• als x ∈ ]4, +∞[ bevindt de grafiek zich onder de x -as, met andere woorden f ( x ) < 0.
We kunnen dit in een overzichtelijke tabel plaatsen.
x –∞ –6 0 4 +∞
f ( x ) + 0 – 0 +0 –
Algemeen :
De grafiek van een functie f bevindt zich onder de x -as ⟺ f ( x ) < 0.
De grafiek van een functie f bevindt zich boven de x -as ⟺ f ( x ) > 0.
De grafiek van een functie f snijdt of raakt de x -as in ( a , 0) ⟺ f ( a ) = 0.
f
f
Gegeven: de grafiek van een functie f
In de intervallen ] –4, –2[ en ] –2, 0[ daalt de functie telkens. We merken echter op dat de daling in ] –4, –2[ groter is dan in ] –2, 0[, want voor dezelfde toename van de x -waarden is de afname van de y -waarden het grootst in ] –4, –2[.
Algebraïsch kunnen we dat vaststellen als :
• in [ 4, 2] is ∆ y ∆ x = y2 y1 x 2 x 1 = 0 8 2 ( 4) = 4
• in [ 2,0] is ∆ y ∆ x = y2 y1 x 2 x 1 = 4 0 0 ( 2) = 2
In de intervallen ] 2, 4[ en ] 4, 6[ stijgt de functie telkens. We merken echter op dat de stijging in ] 4, 6[ groter is dan in ] 2, 4[, want voor dezelfde toename van de x -waarden is de toename van de y -waarden het grootst in ] 4, 6[.
Algebraïsch kunnen we dat vaststellen als :
• in [2,4] is ∆ y ∆ x = y2 y1 x 2 x 1 = 0 ( 4) 4 2 = 2
• in [4,6] is ∆ y ∆ x = y2 y1 x 2 x 1 = 8 0 6 4 = 4
Wenoemen ∆ y ∆ x hetdifferentiequotiëntvan eenfunctieovereeninterval.
differentiequotiënt
AlsA a , f (a ) enB b , f ( b ) tweepuntenzijnvan degrafiekvaneenfunctie f ,dannoemenwe
∆ y ∆ x = f ( b ) f (a ) b a het differentiequotiënt of de gemiddeldeverandering van f over hetinterval [a , b ]
Als ∆ y ∆ x > 0,danstijgtdiefunctieoverdatinterval; als ∆ y ∆ x < 0,dandaaltdiefunctieoverdatinterval.


Toename van x : Dx = x 2 – x 1
Toename van y :
Dy = y 2 – y 1 y
Vorig jaar bestudeerde je de eerstegraadsfuncties (of lineaire functies). We herhalen kort.
eerstegraadsfunctie
Een eerstegraadsfunctie is een functie die elk reëel getal x afbeeldt op ax + b met a ∈ R0 en b ∈ R
Het functievoorschrift ax + b is een veelterm van de eerste graad in x . in symbolen:
f is een eerstegraadsfunctie ⇐⇒ f ( x )= ax + b met a ∈ R 0 en b ∈ R
Andere notaties : f : x → ax + b of : y = ax + b
• dom f = ber f = R
• De nulwaarde van f is b a
• Grafiek en tekentabel : de grafiek van f is een rechte met richtingscoëfficiënt a die gaat door het punt met coördinaat ( 0, b )
a > 0
De functie is stijgend.
a < 0
De functie is dalend.
constante functie
Een functie f is een constante functie ⟺ f ( x ) = b met b ∈ R
De grafiek van een constante functie is een rechte evenwijdig met de x -as door het punt met coördinaat ( 0, b )
De richtingscoëfficiënt van de grafiek is nul.
Taak :
Teken de grafieken van de functie f met voorschrift f ( x ) = 2x – 1 en de functie g met voorschrift g ( x ) = –2x + 5. Bepaal daarna voor elke functie het domein, het bereik, de nulwaarden, de snijpunten van de grafiek met de assen, de richtingscoëfficiënt van de grafiek, het stijgen/dalen en het tekenverloop. x
• Je weet dat een functie een verband is tussen twee variabelen x en y waarbij voor elke x -waarde hoogstens één y -waarde bestaat. We noemen y de afhankelijke variabele en x de onafhankelijke variabele. De representaties van een functie zijn: verwoording, tabel, letterformule en grafiek.
• Je weet dat een reële functie een functie is waarbij de variabelen x en y reële getallen zijn.
• Je weet wat bedoeld wordt met een functievoorschrift. De ‘formule’ die de functie bepaalt, noemen we het functievoorschrift. We spreken van de functie f met voorschrift f ( x ). We noemen y de functiewaarde van f in x als f ( x ) = y
Notatie: y = f ( x )
• Je kent de betekenis van domein, bereik en nulwaarde van een functie. Het domein van een functie f is de verzameling van de x -waarden waarvoor de functiewaarde bestaat.
Notatie: dom f (grafisch: projecteer de grafiek van de functie loodrecht op de x -as)
Het bereik van een functie f is de verzameling van de y -waarden waarvoor er een x -waarde bestaat zodat y = f ( x )
Notatie: ber f (grafisch: projecteer de grafiek van de functie loodrecht op de y -as)
Een nulwaarde van een functie is een x -waarde waarvoor de functiewaarde nul is. Een nulwaarde is het eerste coördinaatgetal van een snijpunt of raakpunt van de grafiek van de functie met de x -as. in symbolen : α is een nulwaarde van f ⟺ f ( α) = 0
⟺ de grafiek van f snijdt of raakt de x -as in ( α, 0)
• Je kunt een grafiek construeren en je kunt bepalen of de grafiek al dan niet de grafiek van een functie voorstelt.
Een grafiek is de grafiek van een functie als en slechts als elke rechte evenwijdig met de verticale as hoogstens één gemeenschappelijk punt heeft met de grafiek.
• Je kunt op de grafiek van een functie het domein, het bereik, de nulwaarden, het stijgen en dalen en de extrema bepalen.
Een functie is stijgend in een interval als de functiewaarden in dat interval groter worden bij toenemende x -waarden.
Een functie is dalend in een interval als de functiewaarden in dat interval kleiner worden bij toenemende x -waarden.
Een functie is constant in een interval als de functiewaarden voor alle x -waarden in dat interval gelijk blijven.
Als een functie overgaat van stijgen naar dalen in ( a , f ( a )), dan zeggen we dat de functie een maximum f ( a ) heeft voor x = a .
Als een functie overgaat van dalen naar stijgen in ( a , f ( a )), dan zeggen we dat de functie een minimum f ( a ) heeft voor x = a
• Je kent de betekenis van het differentiequotiënt of de gemiddelde verandering van f over het interval [ a , b ]
AlsA a , f (a ) enB b , f ( b ) tweepuntenzijnvandegrafiekvaneenfunctie f ,dannoemenwe
∆ y
∆ x = f ( b ) f (a ) b a hetdifferentiequotiëntofdegemiddeldeveranderingvan f over hetinterval [a , b ]
Als ∆ y
∆ x > 0,danstijgtdiefunctieoverdatinterval;als ∆ y ∆ x < 0,dandaaltdiefunctieoverdatinterval.
• Je weet dat een functie f een eerstegraadsfunctie is als en slechts als f ( x ) = ax + b met a ∈ R0 en b ∈ R
• Je weet dat een functie f een constante functie is als en slechts als f ( x ) = b met b ∈ R
Is de grafiek een grafische voorstelling van een functie? Zo ja, neem de letter(s) mee en maak hiermee een woord. a d g
Hieronder vind je de voorschriften van de functies f , g , h , m en k . Bepaal telkens : – het domein en het bereik ; – de nulwaarde ; – het snijpunt van de grafiek met de assen ; – de richtingscoëfficiënt van de grafiek ; – het stijgen en dalen ; – het tekenverloop.
Bepaal het domein, het bereik, de nulwaarden, het tekenverloop en het stijgen/dalen van volgende functies. a
In deze Finse saunablokhut midden in het bos kun je je favoriete temperatuur opzoeken. Er zijn immers banken op verschillende hoogten. De temperatuur bovenaan kan meer dan 100°C bedragen, terwijl het aan de grond maar 20°C kan zijn. Op deze grafiek lees je de temperatuur af in functie van de hoogte in de blokhut. Gebruik de grafiek om volgende vragen op te lossen.

a Stel: je zit op de onderste bank en gaat één bank (= 50 cm) hoger zitten. Met hoeveel °C stijgt de temperatuur ?
b Noteer het functievoorschrift dat hoort bij de grafiek.
c Een man (met een lengte van 1,75 m) staat recht in de blokhut. Wat is het temperatuurverschil tussen zijn hoofd en zijn tenen ?
Wanneer je een elastisch balletje op de grond gooit en je zou de weg die het balletje volgt kunnen tekenen, dan krijg je een baan die er als volgt uitziet :

Wanneer een speerwerper zijn speer werpt en je zou de baan van de speer in slow motion weergeven, dan zou je volgende figuur te zien krijgen.

Het kwadratisch verband tussen s (horizontale verplaatsing in meter) en h ( s ) (hoogte in meter) wordt weergegeven door :
h ( s )= 3 50 s 2 + 6 5 s
– De baan van de bal wordt bepaald door de tweedegraadsfunctie h met voorschrift h ( s )= 3 50 s 2 + 6 5 s
– De grafiek van die functie is een parabool
– Uit de grafiek leiden we af dat de maximumhoogte van de bal 6 m is bij een horizontale verplaatsing van 10m. Het hoogste punt T( 10, 6) wordt de top van de parabool genoemd.
De grafiek is symmetrisch t.o.v. de rechte r ⟷ x = 10. Die rechte r wordt de as van de parabool genoemd.
Als de bal niet tegengehouden wordt, zal hij de grond raken op 20 m van zijn vertrekpunt. We noemen 0 en 20 de nulwaarden van de tweedegraadsfunctie h
tweedegraadsfunctie
Een tweedegraadsfunctie is een functie f met voorschrift f ( x ) = ax 2 + bx + c waarbij a , b en c gegeven reële getallen zijn (met a ≠ 0). Die functie noemen we ook een kwadratische functie of een functie van de tweede graad
Voorbeelden :
f ( x ) = 2x 2
g ( x ) = –x 2 + 4x – 3
Tegenvoorbeelden :
k ( x ) = 2x 3 – 2x + 8
l ( x ) = –x + 3
h ( x ) = 6x 2 – 9x m ( x ) = 6
Verklaar waarom de functies k , l en m geen tweedegraadsfuncties zijn.
In wat volgt behandelen we de verschillende gevallen die kunnen voorkomen. We starten met het eenvoudigste geval, waarbij a = 1 en b = c = 0.




2Grafiek
de functie f met f ( x) = x2
Om de grafiek van de tweedegraadsfunctie f met voorschrift f ( x ) = x 2 te tekenen, bepalen we een aantal koppels van f in een visgraatdiagram. We kiezen een aantal x -waarden en we zoeken voor elk van die waarden het beeld of de functiewaarde.
Wanneer we de punten uitzetten in een georthonormeerd assenstelsel (dat is een assenstelsel waarbij de x -as en de y -as loodrecht op elkaar staan en de lengten van de eenheden op beide assen gelijk zijn) en ze door een vloeiende lijn verbinden, zien we een kromme ontstaan, die we een parabool noemen.
De grafiek van f met f ( x ) = x 2 is een parabool.
Kenmerken :
aDomein van de functie
Het domein van een functie f is de verzameling van de x -waarden waarvoor de functiewaarde bestaat.
Grafisch vinden we het domein van een functie door de grafiek van de functie loodrecht te projecteren op de x -as.
Het domein van de functie f is R.
We noteren dom f = R
bHet bereik van de functie
Het bereik van een functie f is de verzameling van de y -waarden waarvoor er een x -waarde bestaat zodat
y = f ( x ). Grafisch vinden we het bereik van een functie door de grafiek van de functie loodrecht te projecteren op de y -as.
Het bereik van de functie is [ 0,
De nulwaarden van een functie f zijn de x -waarden waarvoor de functiewaarde nul wordt, m.a.w. de nulwaarden zijn de oplossingen (ook wel de wortels genoemd) van de vergelijking f ( x ) = 0.
Grafisch vinden we de nulwaarden als de eerste coördinaatgetallen van de snijpunten van de grafiek met de x -as.
Hierhebbenweéénnulwaarde,nl.0want f ( x )= x 2 = 0
x = 0
De grafiek van de functie ligt steeds boven de x -as want ∀ x ∈ R : f ( x ) = x 2 ⩾ 0. In de nulwaarde is de functiewaarde gelijk aan 0. In een tekentabel geeft dat :
x –∞ 0 +∞
f ( x ) + 0 +
We zien duidelijk dat deze functie eerst daalt, een minimum bereikt en nadien weer stijgt. Het punt van de grafiek waarin de functie de minimumwaarde bereikt, noemen we de top T van de parabool. In dit geval is de top T( 0, 0)
De opening van de parabool is naar boven gericht (hol). We noemen die parabool een dalparabool
De grafiek is symmetrisch t.o.v. de y -as. Dat blijkt trouwens ook al uit het visgraatdiagram, want f ( –x ) = f ( x ). Daarom noemen we de functie een even functie. De y -as noemen we de symmetrieas van de parabool (of korter: de as van de parabool). Het snijpunt van de parabool met zijn symmetrieas is precies de top van de parabool.
f is een even functie ⟺
de y -as is de symmetrieas van de grafiek van f ⟺
∀ x ∈ dom f : f ( x ) = f ( –x )




We tekenen in één assenstelsel de grafieken van de functies met voorschrift :
Kenmerken :
Degrafiekvandefunctie f 2 met f 2 ( x )= 2 x 2 endegrafiekvandefunctie f 3 met f 3 ( x )=
algemenekenmerkenalsdegrafiekvan f 1 met f 1 ( x )= x 2
Deopeningvandegrafiekvan f 2 met f 2 ( x )= 2 x 2 issmallerdandievandegrafiekvan f 1 met f 1 ( x )= x 2
Deopeningvandegrafiekvan f 3 met f 3 ( x )= 1 2 x 2 isbrederdandievandegrafiekvan f 1 met f 1 ( x )= x 2 .
Degrafiekvan f 2 met f 2 ( x )= 2 x 2 heeftdevolgendekenmerken:
• dom f 2 = R
• ber f 2 = [0, +∞[
• T (0,0) isdetop.Heteerstecoördinaatgetalisdenulwaardevandefunctie.Hettweedecoördinaatgetalis hetminimumvandefunctie.Deopeningvandeparaboolisnaarbovengericht(hol).Wesprekenvaneen dalparabool.
• Deasisde y -as.
• f 2 iseenevenfunctie.
Diekenmerkengeldenookvoor f 3
Merk op :
–
Als a ( a > 0) groter wordt, dan wordt de opening van de parabool smaller. We noemen a de openingscoëfficiënt van de parabool. We zeggen dat de grafiek van f uitgerokken is volgens de y -as met factor a
– Grafische betekenis van a :
als T( 0, 0) de top is van de grafiek, dan zijn A( 1, a ) en B( –1, a ) punten van de grafiek.
We tekenen in één assenstelsel de grafieken van de functies met voorschrift :
Kenmerken :
De grafiek van de functie f 2 met f 2( x ) = –x 2 is het spiegelbeeld t.o.v. de x -as van de grafiek van f 1 met f 1( x ) = x 2 .
Voor dezelfde x -waarden krijgen we immers tegengestelde y -waarden.
De grafiek van f 2 met f 2( x ) = –x 2 heeft de volgende kenmerken :
• dom f 2 = R
• ber f 2 = ] –∞, 0]
•T( 0, 0) is de top. Het eerste coördinaatgetal is de nulwaarde van de functie. Het tweede coördinaatgetal is het maximum van de functie. De opening van de parabool is nu naar onderen gericht (bol), we spreken van een bergparabool
• De as is de y -as.
• f 2 is een even functie.
Die kenmerken gelden ook voor f 3 en f 4
Besluit :
De grafiek van de functie f met f ( x ) = ax 2 is een parabool waarvan de opening wordt bepaald door het teken van a
– Is a > 0, dan is de opening naar boven gericht; we hebben een dalparabool.
Is a < 0, dan is de opening naar onderen gericht; we hebben een bergparabool. We noemen a de openingscoëfficiënt van de parabool.
– Als | a | groter wordt, dan wordt de opening van de parabool smaller. Als | a | kleiner wordt, dan wordt de opening van de parabool breder.
We tekenen in één assenstelsel de grafieken van de functies met voorschrift :
Kenmerken :
De grafiek van de functie f 2 met f 2( x ) = ( x + 2)2 is congruent met de grafiek van f 1 met f 1( x ) = x 2. Ze wordt verkregen door die laatste twee eenheden naar links te verschuiven. De as is de rechte met vergelijking x = –2 en het punt T( –2, 0) is de top. Om dezelfde functiewaarden te bekomen, moeten we x -waarden nemen die twee eenheden kleiner zijn.
f 1( 3) = f 2( 1) = 9
De grafiek van f 3 is congruent met de grafiek van f 1. Ze wordt verkregen door die laatste 3 eenheden naar rechts te verschuiven. De as is de rechte met vergelijking x = 3 en het punt T( 3, 0) is de top. Om dezelfde functiewaarden te bekomen, moeten we x -waarden nemen die drie eenheden groter zijn.
f 1( 3) = f 3( 6) = 9
Besluit :
De grafiek van f met f ( x ) = ( x – α)2 is congruent met de grafiek van g met g ( x ) = x 2
Ze wordt verkregen door die laatste te verschuiven evenwijdig met de x -as :
Is α > 0, dan verschuiven we horizontaal naar rechts met α eenheden ;
Is α < 0, dan verschuiven we horizontaal naar links met | α | eenheden.
De as is de rechte met vergelijking x = α en het punt T( α, 0) is de top.
We tekenen in één assenstelsel de grafieken van de functies met voorschrift :
Kenmerken :
De grafiek van de functie f 2 met f 2( x ) = x 2 + 3 is congruent met de grafiek van f 1 met f 1( x ) = x 2. Ze wordt verkregen door die laatste 3 eenheden naar boven te verschuiven. De as is de y -as en het punt T( 0, 3) is de top.
Het bereik van de functie is [ 3, +∞[
Merk op dat bij dezelfde x -waarden de functiewaarden bij f 2 drie eenheden groter zijn. Merk ook op dat er geen snijpunten met de x -as zijn. De functie heeft dus geen nulwaarden.
De grafiek van f 3 met f 3( x ) = x 2 – 2 is congruent met de grafiek van f 1 met f 1( x ) = x 2. Ze wordt verkregen door die laatste twee eenheden naar onderen te verschuiven. De symmetrieas is de y -as en het punt T( 0, –2) de top.
Het beeld van de functie is [ –2, +∞[
Merk op dat bij dezelfde x -waarden de functiewaarden bij f 3 twee eenheden kleiner zijn. Merk ook op dat er twee snijpunten met de x -as zijn. De functie heeft dus twee nulwaarden.
Besluit :
De grafiek van f met f ( x ) = x 2 + b is congruent met de grafiek van g met g ( x ) = x 2
Ze wordt verkregen door die laatste te verschuiven evenwijdig met de y -as :
Is b > 0, dan verschuiven we verticaal naar boven met b eenheden ;
Is b < 0, dan verschuiven we verticaal naar onderen met | b | eenheden.
De as is de y -as en het punt T( 0, b) is de top.
ber f = [ b, +∞[
Voorbeeld 1 : f ( x ) = ( x – 2)2 + 3
Kenmerken:
– de coördinaat van de top T is ( 2, 3);
– de as gaat door de top en heeft als vergelijking x = x T of x = 2 ; – dom f = R ; – ber f = [ y T, +∞[ = [ 3, +∞[ ; – de grafiek van f met f ( x ) = ( x – 2)2 + 3 ontstaat door die van f 1 met f 1( x ) = x 2 horizontaal twee eenheden te verschuiven naar rechts, gevolgd door een verticale verschuiving van drie eenheden naar boven (of omgekeerd).
Voorbeeld 2 : f ( x ) = 2( x + 4)2 – 1
+
f( x) = 2( x + 4)2 – 1
Kenmerken :
– de coördinaat van de top T is ( –4, –1);
– de as gaat door de top en heeft als vergelijking x = x T of x = –4;
– dom f = R ;
– ber f = [ y T, +∞[ = [ –1, +∞[ ; – de grafiek van f met f ( x ) = 2( x + 4)2 – 1 ontstaat door die van f 1 met f 1( x ) = x 2 verticaal uit te rekken met factor 2 en daarna te verschuiven, eerst horizontaal naar links met vier eenheden en daarna verticaal naar onderen met één eenheid.
7Grafiek van de functie f met f ( x) = ax2 + bx + c
Voorbeeld 1 : f ( x ) = x 2 – 6x + 8
We herschrijven het voorschrift van de functie f : f ( x ) = x 2 – 6x + 8
⟺ f ( x ) = ( x 2 – 6x + 9) – 1
⟺ f ( x ) = ( x – 3)2 – 1
De grafiek van de functie f wordt dus bekomen door de grafiek van f 1 met f 1( x ) = x 2 tweemaal te verschuiven. Eerst horizontaal naar rechts met drie eenheden en daarna verticaal naar onderen met één eenheid, of omgekeerd.
Kenmerken: – de coördinaat van de top T is ( 3, –1); – de as gaat door de top en heeft als vergelijking: x = x T of x = 3 ; – dom f = R ; – ber f = [ y T, +∞[ = [ –1, +∞[ ; – snijpunt met de y -as : x = 0
f (0)= 02 6 · 0 + 8 = 8
A( 0, 8) is dus het snijpunt van de grafiek van f met de y -as.
Voorbeeld 2 : f ( x ) = –x 2 + 2x + 8
Taak : toon aan dat je dit functievoorschrift kunt herschrijven tot f ( x ) = –( x – 1)2 + 9.
Geef de kenmerken van deze functie f
Voorbeeld 3 : f ( x ) = –2x 2 + 4x – 3
We herschrijven het voorschrift van de functie f : f ( x ) = –2x 2 + 4x – 2 – 1
⟺ f ( x ) = –2( x 2 – 2x + 1) – 1
⟺ f ( x ) = –2( x – 1)2 – 1
De grafiek van f wordt dus bekomen door de grafiek van f 1( x ) met f 1( x ) = x 2 achtereenvolgens : – te spiegelen t.o.v. de x -as: f 2( x ) = –x 2
– te versmallen met factor 2: f 3( x ) = –2x 2
– één eenheid horizontaal naar rechts te verschuiven : f 4( x ) = –2( x – 1)2
– één eenheid verticaal naar onderen te verschuiven : f ( x ) = – 2( x – 1)2 – 1
f4( x) = –2( x – 1)2
Kenmerken : – de coördinaat van de top T is ( 1, –1); – de as heeft als vergelijking x = 1 ; – dom f = R ; – ber f = ] –∞, –1]; – snijpunt met de y -as: A( 0, –3).

f ( x) = –2( x – 1)2

Algemeen : Berekening van α en β in functie van a , b en c :
f ( x )= ax 2 + bx + c en f ( x )= a ( x α)2 + β zijngelijkwaardigwant:
f ( x )= a ( x α)2 + β
f ( x )= a ( x 2 2αx + α2 )+ β
f ( x )= ax 2 2a αx + a α2 + β
2aα = b en aα2 +β = c
f ( x )= ax 2 + bx + c
f ( x )= ax 2 + bx + c en f ( x )= a ( x α)2 + β zijngelijkwaardigals α = b 2a en β = b 2 + 4ac 4a
De grafiek van de functie f met f ( x ) = a ( x – α)2 + b ontstaat uit de grafiek van de functie f 1 met f 1( x ) = x 2 in maximaal vier stappen : – Is a negatief, spiegel dan de grafiek t.o.v. de x -as.
– Versmal of verbreed de parabool, naargelang | a | > 1 of | a | < 1. Zo bekom je de grafiek van f 2 met f 2( x ) = ax 2 – Verschuif de parabool evenwijdig met de x -as over een afstand | α | Zo bekom je de grafiek van f 3 met f 3( x ) = a ( x – α)2. Als α > 0 verschuif je de grafiek naar rechts, als α < 0 verschuif je de grafiek naar links.
– Verschuif de parabool evenwijdig met de y -as over een afstand | b | Zo bekom je de grafiek van f met f ( x ) = a ( x – α)2 + b. Als b > 0 verschuif je de grafiek naar boven, als b < 0 verschuif je de grafiek naar onderen.
Kenmerken :
a Grafiek
De grafiek van de functie f met f ( x ) = ax 2 + bx + c is een parabool p waarvan de as evenwijdig is met de y -as. y = ax 2 + bx + c wordt de vergelijking van de parabool genoemd.
Als a > 0, dan is p een dalparabool. Als a < 0, dan is p een bergparabool.
b Top T α, β = T b 2a , b 2 + 4ac 4a = T b 2a , f b
c As x = α of x = b 2a
d Domein dom f = R
e Bereik Als a > 0,danisber f = β , +∞ = b 2 + 4ac 4a , +∞ = f b 2a , +∞
Als a < 0,danisber f = −∞, β = −∞, b 2 + 4ac 4a = −∞, f b 2a
f Nulwaarden De nulwaarden zijn de oplossingen van de vergelijking ax 2 + bx + c = 0 (zie 1.4).
g Stijgen en dalen Als a > 0
Als a < 0
Bespreek de kenmerken van de tweedegraadsfunctie f met f ( x ) = x 2 + 2x – 8.
– Omdat a = 1 ( > 0), is de grafiek van de tweedegraadsfunctie een dalparabool.
– Top T( α, b): α = b 2a = 2 2 · 1 = 1
β = b 2 + 4ac 4a = 4 + 4 · ( 8) 4 = 4 32 4 = 36 4 = 9
m.a.w.decoördinaatvandetopTis ( 1, 9)
controle: β = f ( 1) = ( 1)2 + 2 ( 1) 8 = 9
As : x = α ⇐⇒ x = 1
–
– Visgraatdiagram
Om de grafiek te kunnen schetsen, berekenen we nu enkele punten van de grafiek aan de hand van een visgraatdiagram. Hierbij maken we dankbaar gebruik van de symmetrieas.
f ( 1)=( 1)2 + 2 · ( 1) 8 = 9
f
f
f (0)= 02 + 2 0 8 = 8 f ( 2)=( 2)2 + 2 ( 2) 8 = 8
1)= 12 + 2 1 8 = 5 f ( 3)=( 3)2 + 2 ( 3) 8 = 5
2)= 22 + 2 · 2 8 = 0 f ( 4)=( 4)2 + 2
( 4) 8 = 0
f (3)= 32 + 2 3 8 = 7 f ( 5)=( 5)2 + 2 ( 5) 8 = 7
f
4)= 42 + 2 · 4 8 = 16 f ( 6)=( 6)2 + 2 · ( 6) 8 = 16
x –6 –5 –4 –3 –2 –1 01234
f ( x ) 16 70 –5 –8 –9 –8 –5 07 16 top
– dom f = R
– ber f = [ b, +∞[ = [ –9, +∞[
Nulwaarden

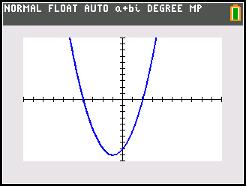


De nulwaarden zijn de x -waarden waarvoor de functiewaarde nul wordt. Blijkbaar kunnen we in dit geval de nulwaarden aflezen uit het visgraatdiagram (dat is niet steeds mogelijk). nulwaarden: –4 en 2 – Stijgen en dalen – Grafiek
x –∞ –1 +∞
f ( x ) +∞ ↘ –9 ∥ min ↗ +∞
De functie heeft een minimum –9 voor x = –1.
– Snijpunt met de y -as: A( 0, –8) x
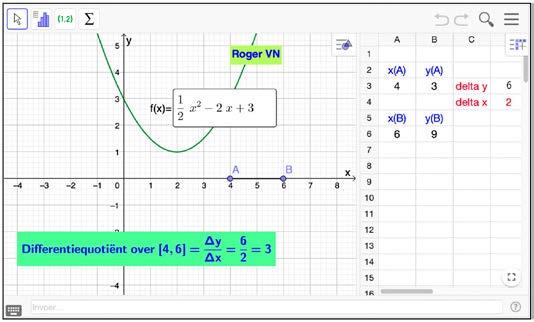
Gegevenisdefunctie f met f ( x )= 1 2 x 2 2 x + 3. Bekijkenweevendegemiddeldetoenamevan defunctieoverhetinterval [0,6].
f (0)= 3
f (6)= 9 ∆ f ( x )= 9 3 = 6 Degemiddeldetoenamevan f over [0,6] :
f ( x )
x [0,6] = ∆ f ( x ) ∆ x = 6 6 = 1
Die gemiddelde toename of de verhouding van de toename van de afhankelijke variabele ten opzichte van de toename van de onafhankelijke variabele noemen we het differentiequotiënt
Dat de toename geen constante toename is, blijkt duidelijk als we het interval [ 0, 6] opsplitsen in drie deelintervallen.
Degemiddeldetoenamevan f over [0,2]
ofhetdifferentiequotiëntvan f over [0,2] :
f (0)= 3
f (2)= 1
∆ f ( x )= 1 3 = 2
∆ f ( x )
∆ x [0,2] = ∆ f ( x ) ∆ x = 2 2 = 1
Degemiddeldetoenamevan f over [2,4] of hetdifferentiequotiëntvan f over [2,4] :
f (2)= 1
f (4)= 3
∆ f ( x )= 3 1 = 2
∆ f ( x )
∆ x [2,4] = ∆ f ( x )
∆ x = 2 2 = 1
Degemiddeldetoenamevan f over [4,6] of hetdifferentiequotiëntvan f over [4,6] :
f (4)= 3
f (6)= 9
∆ f ( x )= 9 3 = 6
∆
6 2 = 3
• Je kent de definitie van een tweedegraadsfunctie.
Een tweedegraadsfunctie is een functie f met f ( x ) = ax 2 + bx + c waarbij a , b en c gegeven reële getallen zijn (met a ≠ 0). Dit noemen we ook een kwadratische functie of een functie van de tweede graad.
• Je weet dat de grafiek van de functie f met f ( x ) = a ( x – α) 2 + b ontstaat uit de grafiek van de functie f1 met f1( x ) = x 2 in maximaal vier stappen :
– Is a negatief, spiegel dan de grafiek t.o.v. de x -as.
– Versmal of verbreed de parabool naargelang | a | > 1 of | a | < 1.
Zo bekom je de grafiek van f 2 met f 2( x ) = ax 2
– Verschuif de parabool evenwijdig met de x -as over een afstand | α | .
Zo bekom je de grafiek van f 3 met f 3( x ) = a ( x – α)2
Als α > 0 verschuif je de grafiek naar rechts, als α < 0 verschuif je de grafiek naar links.
– Verschuif de parabool evenwijdig met de y -as over een afstand | b |
Zo bekom je de grafiek van f met f ( x ) = a ( x – α)2 + b
Als b > 0 verschuif je de grafiek naar boven, als b < 0 verschuif je de grafiek naar onderen.
• Je kunt het voorschrift van f ( x ) = ax 2 + bx + c omvormen tot
f ( x )= a ( x α)2 + β met α = b 2a en β = b 2 + 4ac 4a
• Je kunt een tweedegraadsfunctie f met f ( x ) = ax 2 + bx + c als volgt onderzoeken.
a Grafiek
De grafiek is een parabool met vergelijking y = ax 2 + bx + c en waarvan de as evenwijdig is met de y -as.
b Top T α, β = T b 2a , b 2 + 4ac 4a = T b 2a , f b 2a
c As x = α of x = b 2a
d Domein dom f = R
e Bereik Als a > 0,danisber f = β , +∞ = b 2 + 4ac 4a , +∞ = f b 2a , +∞ Als a < 0,danisber f = −∞, β = −∞, b 2 + 4ac 4a = −∞, f b 2a
f Nulwaarden De nulwaarden zijn de x -waarden van de snijpunten van de grafiek met de x -as.
g Stijgen en dalen Als a > 0 Als a <
h Snijpunt met de y -as A( 0, c )
• Je weet dat het differentiequotiënt van functie f over het interval [ a , b ] gelijk is aan de gemiddelde toename van de afhankelijke variabele t.o.v. de onafhankelijke variabele over het interval.
Notatie: ∆ f ( x ) ∆ x [a , b ]
Gegeven zijn de functies met onderstaande voorschriften.
Welke zijn eerstegraadsfuncties? Welke zijn tweedegraadsfuncties ?
a f 1 ( x )= 2 x 1
b f 2 ( x )= 1 3 x
c f 3 ( x )= x 3 x
Gegeven : de grafieken van de tweedegraadsfuncties f , g , h en i
Gevraagd : bepaal grafisch het domein, het bereik, de nulwaarden, het tekenverloop en het stijgen/dalen van die tweedegraadsfuncties.
Gegeven zijn de functies met onderstaande voorschriften.
f 1 ( x )= 2 x 2 3 x + 1 f 2 ( x )= x 2 + 4 x + 5 f 3 ( x )= x 3 x 2 f 4 ( x )=
a Van welke functie is de grafiek een dalparabool ?
b Van welke functie is de grafiek een bergparabool ?
c Welke parabool is het breedst, welke het smalst ?
x 2 + 4 x 8
Vul aan :
a De grafiek van de functie g met g ( x ) = ( x – 4)2 verkrijg je door de grafiek van de functie f met f ( x ) = x 2 naar… te verschuiven met … eenheden volgens de …-as.
b De grafiek van de functie g met g ( x ) = ( x + 1)2 verkrijg je door de grafiek van de functie f met f ( x ) = x 2 naar… te verschuiven met … eenheden volgens de …-as.
c De grafiek van de functie g met g ( x ) = x 2 – 4 verkrijg je door de grafiek van de functie f met f ( x ) = x 2 naar… te verschuiven met … eenheden volgens de …-as.
d De grafiek van de functie g met g ( x ) = x 2 + 1 verkrijg je door de grafiek van de functie f met f ( x ) = x 2 naar… te verschuiven met … eenheden volgens de …-as.
Noteer per opgave op welke waarde de schuifknoppen geplaatst moeten worden.
a De top van de grafiek is T( 4, –5).
b De openingscoëfficiënt is –0,5.
c De vergelijking van de grafiek is y = x 2 – 10x + 30.
d De openingscoëfficiënt is 4 en de top van de grafiek is T( –2, 3)

Onderstaande grafieken zijn ontstaan door de grafiek van f met f ( x ) = x 2 te spiegelen om de x -as en/of horizontaal te verschuiven en/of verticaal te verschuiven. Bepaal het voorschrift van de tweedegraadsfuncties g , h , i en j .
Bepaal het voorschrift van de tweedegraadsfuncties f , g , h en i
Stel het voorschrift op van de functie g waarvan je de grafiek bekomt als je de grafiek van de functie f met
f ( x ) = x 2 :
a twee eenheden verschuift naar links volgens de x -as.
b vier eenheden naar onderen verschuift volgens de y -as.
c drie eenheden verschuift naar rechts volgens de x -as en één eenheid verschuift naar boven volgens de y -as.
d eerst spiegelt t.o.v. de x -as en daarna twee eenheden verschuift naar links volgens de x -as en drie naar boven volgens de y -as.
e eerst vier eenheden naar rechts verschuift volgens de x -as en twee naar onderen volgens de y -as om daarna te spiegelen t.o.v. de x -as.
f eerst versmalt met openingscoëfficiënt 3 en daarna één eenheid naar links verschuift volgens de x -as en één eenheid naar onderen volgens de y -as.
Zet de volgende voorschriften om in de vorm van f ( x ) = a ( x – α)2 + b en teken de grafiek van de bijbehorende functies. Controleer jouw antwoord met behulp van ICT en noteer achtereenvolgens de transformaties die de grafiek van de functie g met g ( x ) = x 2 ondergaat.
a f 1 ( x )= x 2 + 6 x + 9
b f 2 ( x )= x 2 + 6 x + 2
c f 3 ( x )= x 2 + 4 x 1
d f 4 ( x )= 2 x 2 + 5
e f 5 ( x )= 2 x 2 8
f f 6 ( x )= 2 x 2
g f 7 ( x )= 1 4 x 2 + 2 x
h f 8 ( x )= 1 4 x 2 + x
i f 9 ( x )= x 2 4 3 x
j f 10 ( x )= 3 2 x 2 3 x + 12
k f 11 ( x )= 3 2 x 2 3 x 12
l f 12 ( x )=
Onderzoek de tweedegraadsfuncties met onderstaande voorschriften.
– Ga na of de grafiek een berg- of dalparabool is.
– Geef de coördinaat van de top.
– Geef de vergelijking van de symmetrieas.
– Bepaal het domein en het bereik.
– Teken de grafiek.
– Bepaal de nulwaarden.
– Geef aan waar de functie stijgt of daalt.
– Controleer je antwoorden met ICT.
a f ( x )= x 2 + 2 x + 3
b f ( x )= 4 x 2 + 4 x 1
c f ( x )= x 2 + 4 x 5
d f ( x )= 3 x 2 + 6 x
e f ( x )= 4 x 2 9
f f ( x )= 0,5 x 2 x 4
Vergelijk de ligging van de toppen van de grafieken van de functies f , g en h als :
f ( x )= 2 x 2 4 x + 6 g ( x )= x 2 2 x + 3 h ( x )= x 2 3 + 2 3 x 1
Gegeven is grafiek p van de functie f met f ( x ) = ( x – 2)2 + 4.
Bepaal het voorschrift van de grafiek van de tweedegraadsfunctie g waarvan je de grafiek verkrijgt door de grafiek van de functie f :
a te spiegelen om de x -as.
b te spiegelen om de y -as.
c te spiegelen om de oorsprong.
Bepaal het voorschrift van de functie g waarvan de grafiek ontstaat door de grafiek van de functie f met f ( x ) = x 2 te spiegelen om :
a de rechte met vergelijking x = –1. b de rechte met vergelijking y = 3. c het punt P( 2, –1).
Bepaal het voorschrift van de functie g waarvan de grafiek ontstaat door de grafiek van de functie f met
f ( x ) = 2x 2 – 4x + 5 te spiegelen om :
a de rechte met vergelijking x = –2. b de rechte met vergelijking y = 2. c het punt P( 2, 0)
Bepaal m ∈ R opdat de top van de grafiek van f met f ( x ) = x 2 + 3x + m op de x -as ligt.
Gegeven : f met f ( x ) = – 2x 2 – bx + 3 met b ∈ R de symmetrieas van de grafiek is de rechte r met vergelijking x = –2
Gevraagd : bepaal b ( ∈ R ).
Gegeven : f met f ( x ) = 2x 2 + bx + c met b , c ∈ R
T( –1, 2) is de top van de grafiek van f
Gevraagd : bepaal b en c
Gegeven : de functie f met f ( x ) = –x 2 – 2x + 4
Gevraagd : bereken het differentiequotiënt van de functie over het gegeven interval.
a [ –3, 3] c [ –3, 1]
b [ –3, –1] d [ 1, 2]
Gegeven : de functie f met f ( x ) = 2x 2 – 12x + 5
Gevraagd : bereken het differentiequotiënt van de functie over het gegeven interval.
a [ 0, 8] c [ 0, 4]
b [ 0, 6] d [ 0, 2]
Gegeven : de functie f met f ( x ) = x 2 – 4x + 6
Gevraagd : bereken het differentiequotiënt van de functie over het gegeven interval.
a [ 3, 4]
b [ 3 ; 3,1]
c [ 3 ; 3,01]
d [ 3 ; 3,001]
Gegeven zijn de functies met onderstaand voorschrift. Welke van deze functies zijn even? Illustreer dit grafisch met ICT. Toon dit ook algebraïsch aan.
a f ( x ) = 3x 2 – 4x
b f ( x ) = x 3 – 4x 2 + 3
c f ( x ) = ( x 2 – 3)2
d f ( x ) = x 2 – x 4
Vier van de volgende figuren zijn stukken van de grafiek van eenzelfde tweedegraadsfunctie. Welke is geen stuk van diezelfde grafiek ?
De tweedegraadsfunctie f ( x ) = ax 2 + bx + c voldoet aan f ( x ) = f ( 1 – x ). Waaraan is a + b gelijk ?
In de figuur zie je de parabool met vergelijking
y = 1 2 x 2 3 x + 4
De coördinaten van P zijn :
(A) ( –2, –1) (B) 3, 5 2 (C) ( –4, –2) (D) 5, 5 2 (E) ( –6, –3)
VWO 2020 eerste ronde, vraag 12 © Vlaamse Wiskunde Olympiade vzw
Alle toppen van de parabolen met vergelijking y = x 2 + bx , met b ∈ R, liggen op
(A)een rechte(B)een cirkel(C)een hyperbool(D)een bergparabool(E)een dalparabool
VWO 2020 eerste ronde, vraag 23 © Vlaamse Wiskunde Olympiade vzw
De parabolen met vergelijking y = a x 2 4 en y = a x 2 4 snijden de x-as en de y-as (van een orthonormaal assenstelsel) in vier verschillende punten. Als die vier punten de hoekpunten zijn van een vierkant, dan is | a | gelijk aan:
(A) 1 4 1 2 (B) 1 4 1 2
VWO 2023 tweede ronde, vraag 17 © Vlaamse Wiskunde Olympiade vzw
Onderstaande figuur toont een kromme in het xy-vlak met vergelijking y = ax2 + bx + c, met a, b, c ∈ R. Bepaal de tekens van (a, b, c).
(A) ( +, –, –) (C) ( –, +, +)
(B) ( +, –, +) (D) ( –, –, +)
IJkingstoets burgerlijk ingenieur augustus 2022, oefening 2
Parabolen
Parabolen werden al in de oudheid bestudeerd. De Griekse wiskundige Apollonius van Perga (derde eeuw voor Christus) gaf de naam parabool aan de doorsnede van een kegel met een vlak dat evenwijdig is aan een beschrijvende van de kegel (zie figuur). De grote natuurkundige Galileo Galilei (1544–1642) ontdekte 2000 jaar later dat projectielen afgevuurd met een kanon een parabolische baan volgen (met verwaarlozing van luchtweerstand). Ook spoorwegtunnels en bruggen zijn soms parabolisch. De lob van een voetbalspeler, de worp van een speerwerper of een kogelstoter zijn parabolen als er niet te veel wind staat… Laat je een parabool wentelen rond zijn as, dan ontstaat er een omwentelingsparaboloïde. Een voorbeeld daarvan is een schotelantenne.
Een veelterm ontbinden in factoren is die veelterm schrijven als een product van zo veel mogelijk factoren. Dat is nuttig om algebraïsche vormen te vereenvoudigen en vergelijkingen van hogere graad op te lossen.
Bij het ontbinden in factoren is dit steeds de eerste vraag die je je moet stellen: kun je een gemeenschappelijke factor afzonderen ?
Wat kun je afzonderen ?
Een getal? Bekijk alle coëfficiënten en neem hiervan de grootste gemene deler.
Een letter ? Bekijk de letters die je in elke term terugvindt en kies voor de laagst voorkomende exponent.
Wat komt er dan binnen de haakjes ?
Het quotiënt van de gegeven veelterm met wat je buiten de haakjes noteerde.
Voorbeelden :
Bij het afzonderen van gemeenschappelijke factoren pas je dus de distributieve eigenschap toe.
Afzonderen van gemeenschappelijke factoren
in symbolen : ab + ac = a · ( b + c )
in woorden : Om gemeenschappelijke factoren af te zonderen, noteer je voor de haakjes : de factoren die in elke term van de veelterm voorkomen : – de ggd van de gehele coëfficiënten ; – alle gemeenschappelijke letters, elk met hun kleinst voorkomende exponent. tussen de haakjes : het quotiënt van de gegeven veelterm met de afgezonderde eenterm.
Opmerkingen :
– Je kunt je ontbinding controleren door je resultaat weer uit te werken. Je past dan de distributieve eigenschap van de vermenigvuldiging t.o.v. de optelling in R toe en je krijgt weer de opgave.
– Staan er in de opgave meer mintekens dan plustekens, dan zonder je ook het minteken af.
– Probeer de opgave steeds zo ver mogelijk te ontbinden. Begrijp je de volgende voorbeelden?
Herinner je je het merkwaardig product waarbij je twee toegevoegde tweetermen vermenigvuldigde ?
( a – b ) ⋅ ( a + b ) = a 2 – b 2
Als je een verschil van twee kwadraten hebt, kun je die ontbinden in factoren door de formule in omgekeerde zin toe te passen.
a 2 – b 2 = ( a – b )( a + b )
Voorbeelden : 16a 2 81 = (4a 9)(4a + 9) 0,25 x 6 = 0,5 x 3 0,5 + x 3 4a 9 49
Merkwaardige tweeterm ontbinden in symbolen : a 2 – b 2 = ( a – b ) · ( a + b )
Opmerkingen :
• Je kunt de ontbinding controleren door je resultaat weer uit te werken. Je past dan de formule toe en je krijgt weer de opgave.
• Een som van twee kwadraten zoals 25a 2 + 1 kun je niet ontbinden.
• Als het minteken bij het eerste kwadraat staat, herschrijf je de opgave :
– 16x 2 + 9 = 9 – 16x 2
= ( 3 – 4x )( 3 + 4x )
• Ga steeds eerst na of je een gemeenschappelijke factor kunt afzonderen.
2a 4 – 8a 2 = 2a 2( a 2 – 4)
= 2a 2( a – 2)( a + 2)
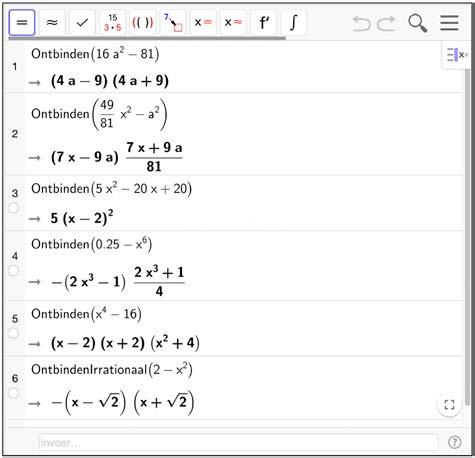
Herinner je je het merkwaardige product waarbij je het kwadraat van een tweeterm berekende ?
( a + b )2 = a 2 + 2ab + b 2
( a – b )2 = a 2 – 2ab + b 2
Als je een drieterm hebt van de vorm a 2 + 2ab + b 2 of van de vorm a 2 – 2ab + b 2 kun je die ontbinden in factoren door de formule in omgekeerde zin toe te passen.
Hoe vind je de grondtallen terug?
Zeker twee van de drie termen zijn kwadraattermen. Stel jezelf de vraag: waarvan is de term het kwadraat ?
Zo vind je de twee grondtallen terug. Controleer zeker dat de derde term wel degelijk het dubbel product is van de twee grondtallen.
:
Merkwaardige drieterm ontbinden
in symbolen : a 2 ± 2ab + b 2 = ( a ± b )2
Opmerkingen :
• Je kunt je ontbinding controleren door je resultaat weer uit te werken. Je past dan de formule toe en je krijgt weer de opgave.
• Als de drie termen kwadraattermen zijn, zul je de vierkantswortels zoeken van de termen met de grootste en de kleinste exponent.
Zois x 4 + x 2 + 1 4 = x 2 + 1 2 2 .
• Ga steeds eerst na of je een gemeenschappelijke factor kunt afzonderen.
Voorbeelden : 5x 2 – 20x + 20 = 5 ( x 2 – 4x + 4)
= 5 ⋅ ( x – 2)2
49a 5 + 126a 3 + 81a = a ( 49a 4 + 126a 2 + 81)
= a ⋅ ( 7a 2 + 9)2
• Ontbind steeds zo ver mogelijk.
x 4 – 2x 2 + 1
= ( x 2 – 1)2
= ( x – 1)2( x + 1)2

• Je weet dat een veelterm ontbinden betekent dat je de veelterm schrijft als een product van zo veel mogelijk factoren.
• Je kunt een veelterm ontbinden in factoren door de volgende werkwijze toe te passen.
Zonder alle gemeenschappelijke factoren af door de distributieve eigenschap in R toe te passen.
Voor de haakjes noteer je de factoren die in elke term voorkomen (de ggd van de coëfficiënten en alle gemeenschappelijke letters, elk met hun kleinst voorkomende exponent).
Tussen de haakjes noteer je het quotiënt van de gegeven veelterm met de afgezonderde eenterm.
Pas indien mogelijk één van de formules van de merkwaardige producten toe.
ab + ac = a ( b + c )
a 2 – b 2 = ( a – b ) ( a + b )
a 2 ± 2ab + b 2 = ( a ± b )2


Ontbind in factoren door alle gemeenschappelijke factoren af te zonderen.
a 30 x 2 + 25 x + 15
b a + a 2 + a 3
c 16 x 12
d 14 x 3 + 21 x 2
e 48a 3 + 32a 2 + 16a
f 14 x 3 21 x 2 + 7 x
g 9 2 a 3 + 3 2 a 2
h 1 2 a 3 + 1 3 a 2
i √2 x 2 + x
j3 ( x 1)2 2 ( x 1)
k (3 x 4)2 6 x + 8
l ( x + π)2 π ( x + π)
Ontbind in factoren door het merkwaardig product a 2 – b 2 = ( a + b )( a – b ) toe te passen.
a x 2 16
b 100 y 2
c 1 25 a 2
d a 4 36
e x 2 4 y 2
f b 4 4a 2
g 25a 2 + 9 b 4
h0,25 x 4 25 y 2
i b 2 3
j x 4 1
k ( x 1)2 (2 x 3)2
l a 2m 1
Ontbind in factoren door het merkwaardig product a 2 ± 2ab + b 2 = ( a ± b )2 toe te passen.
a x 2 + 8 x + 16
b 25 x 2 40 x + 16
c 25 x 2 40 xy + 16 y 2
d x 2 + x + 1 4
e 25 x 6 + 9 30 x 3
f25a 2 10a + 1
Ontbind, indien mogelijk, in factoren.
a 7 x 2 6 x
b 4 x 2 9
c x 2 4 xy + 4 y 2
d 3 x 2 + 6 xy + 3 y 2
e 5 x 2 80
f xy 2 2 xyz + xz 2
g 25 x 2 + 20 x 4
g x 2 + 14 x 49
h a 2 4 a 1
i ( x 1)2 + 4 ( x 1) + 4
j2 x 2 + 6√2 x + 9
k6 xy 1 9 x 2 y 2
l a 2m 2a m + 1
h6 x 1 9 x 2
i x 4 4
j5 x 5 20 xy 4
k x 2 ( x 1) 4 ( x 1)
l x 2 8 + x 6 1 18
m a 2m + 2a m + 1
n a 5m 2a 3m + a m
Wie hoort niet thuis in het rijtje? Verklaar. a
Draai maar rond !

Als a 2 + a = b 2 + b en a ≠ b , dan is a + b gelijk aan :
JWO 2021 eerste ronde, vraag 21 © Vlaamse Wiskunde Olympiade vzw
Als ( x – 1)( x + 1) = 4, dan is ( x 3 + x )( x 3 – x ) gelijk aan :
JWO 2021 tweede ronde, vraag 16 © Vlaamse Wiskunde Olympiade vzw
Welk van de volgende getallen is een deler van 316 – 1 ? (A)37 (B)41 (C)43 (D)47 (E)53
JWO 2019 tweede ronde, vraag 18 © Vlaamse Wiskunde Olympiade vzw