LEERBOEK
Matrices en stelsels
D-finaliteit economie en wetenschappen
Philip Bogaert
Filip Geeurickx
Marc Muylaert
Roger Van Nieuwenhuyze
Erik Willockx
CARTOONS
Dave Vanroye
Dit boek bevat twee hoofdstukken.
Elk hoofdstuk is opgebouwd uit verschillende paragrafen met aan het einde een handige samenvatting.
Definities vind je op een rode achtergrond. Eigenschappen vind je op een groene achtergrond. Methodes, rekenregels en formules vind je op een zachtblauwe achtergrond.
Wiskunde is een eeuwenoude wetenschap. De geschiedenis van de wiskunde en de herkomst van bepaalde begrippen worden zachtpaars afgedrukt.


Hoe gebruik je VBTL ? 5 Een matrix vermenigvuldigen met een reëel getal (scalair) Veronderstel dat de productie bij de firma gedurende opeenvolgende maanden steeds gelijk blijft. De maandproductie (in duizendtallen) wordt gegeven door de volgende tabel. A(arhus) C(harleroi) D(ortmund) Wat is de totale productie van elk model in elk filiaal gedurende die zes maanden 6 19 6 54 6 15 90 13 78 SM 15 90 10 60 6 20 120 12 72 We noemen de matrix S het product van het getal 6 met de matrix M en we noteren dit als M product van een matrix met een reëel getal Het product van een -matrix met een reëel getal (ook scalaire vermenigvuldiging genoemd) een matrix met dit reële getal. ij James Joseph Sylvester (1814 –1897) Sylvester was de eerste die het woord ‘matrix’ gebruikte. Hij duidde er een rechthoekig Cambridge en werd er tweede van zijn jaar. Hij kreeg zijn diploma niet, want hij weigerde zijn geloof te verloochenen en een religieuze eed af te leggen voor de Anglicaanse Kerk. Hij werkte eerst een paar jaar als professor in Londen en trok daarna naar de universiteit van Virginia, in de Verenigde Staten. Maar … na enkele maanden moest hij al terugkeren. Hij nam er namelijk de benen nadat hij een leerling had geslagen die in zijn les de krant zat te lezen en hem beledigde. De student bleef roerloos liggen en Sylvester dacht dat hij hem gedood had. Terug in Engeland werkte hij eerst een tiental jaren als boekhouder en later als advocaat. Zo leerde hij Arthur pensioenleeftijd van 55 bereikt had. Hij hield zich een tijdje bezig met een andere passie, poëzie, maar de wiskunde liet hem niet los: hij trok opnieuw naar de VS, nu voor een zestal jaren. Hij werd professor in Baltimore en startte er het eerste wiskundige tijdschrift op, The American Journal of Mathematics. Na zijn terugkeer werd hij dan weer professor in Oxford. Hij stierf op 82-jarige leeftijd in Londen.
1 insymbolen: O R A R A O A O A 00 0 0 heefteensymmetrischelementvoorhetoptellenin namelijkzijntegengesteldematrix insymbolen: tegengestelde matrix =[ =[ 00 00 insymbolen: ∀A B R B B A Immers b + b + b b + b + groep Het woord ‘groep’ is afkomstig (1830) van de Franse wiskundige Galois (1811–1832). De eerste definitie van 1 Matrices 1.1 Terminologie en bewerkingen Eigenschappen van de bewerkingen met matrices 28 Matrixvoorstelling van een graaf 2 Stelsels van eerstegraadsvergelijkingen Willekeurige stelsels oplossen Toepassingen Inverse matrix van een vierkante Oplossingen 107 Trefwoordenregister 117 Matrices en stelsels
De nummers van de oefeningen hebben een gele kleur.
Een sterretje duidt op een extra uitdaging.
Maak ook kennis met voorbeeldvragen uit ijkingstoetsen en toelatingsexamens.
Achteraan in dit boek vind je de oplossingen
ICT is een ideaal hulpmiddel.
Bij dit boek hoort een webpagina van GeoGebra, gevuld met heel wat digitale oefeningen en applets.
Die vind je terug via www.polpo.be.
Wat moet je kennen en kunnen ?
op het einde van elk hoofdstuk zie je een handig overzicht van wat je moet kennen en kunnen







WAT MOET JE KENNEN EN KUNNEN Matrices 1 pagina -matrix en kan een matrix noteren met de juiste symbolen. Ik ken de definitie van enkele bijzondere matrices. 10 Ik kan bewerkingen op matrices uitvoeren met en zonder ICT. 13 Ik kan een matrix vermenigvuldigen met een reëel getal. Ik weet wanneer twee matrices met elkaar vermenigvuldigbaar zijn en kan die vermenigvuldiging uitvoeren. 15 Ik ken de eigenschappen van de optelling van matrices. Ik ken de eigenschappen van de vermenigvuldiging van een matrix met een scalair. Ik ken de eigenschappen van de vermenigvuldiging van vierkante matrices. Ik ken de eigenschappen van de transpositie van een matrix. 34 Ik weet wat idempotente, nilpotente en involutorische matrices zijn. Ik ken het verband tussen een gewogen graaf en een matrix. Ik weet wat overgangsmatrices, populatiematrices en verbindingsmatrices zijn en kan die in concrete situaties toepassen.
Oplossingen 1.1 Terminologie en bewerkingen 1 1613107 2a 3, b 4, 1, 2, 2, 5 274 7 36 466 + 0 23 202 3 20 6a 911 10 dnietzinvol 18 119 fnietzinvol 462837 69 48 93 84 2489 enietzinvol hnietzinvol 10875 7617 18 24 45 154 221550 70799 gnietzinvol p 3, 2, 1 b Oplossingen
2 *
1
3 Eigenschappen van de vermenigvuldiging van vierkante matrices Het vermenigvuldigen is niet intern in R als ≠ Het is immers onmogelijk om bijvoorbeeld een 3-matrix met een 2 × 3-matrix te vermenigvuldigen. Verklaar. Voor het onderzoeken van eigenschappen van de vermenigvuldiging van matrices beperken we ons tot de vierHetvermenigvuldigenisinternin insymbolen: b b b b + + Hetvermenigvuldigenin insymbolen: )=( We illustreren de eigenschap aan de hand van een cijfervoorbeeld. De berekening kun je herhalen voor willekeurige × 2-matrices of nog algemener – voor willekeurige 3 1 50 32 )= 18156 A B C 624 07 We vinden dezelfde uitkomst
In dit boek krijg je een mooie portie lineaire algebra voorgeschoteld, want je maakt kennis met matrices en stelsels.
In het eerste hoofdstuk zie je de terminologie, de bewerkingen en de eigenschappen van matrices. Vaak worden ze gebruikt om de evolutie van een toestand in een zekere periode te beschrijven. Je komt matrices tegen in de economie (voorraadmatrices, productiematrices, prijzenmatrices, Markovketens), de geografie (verbindingsmatrices, directewegenmatrices), de sociale wetenschappen (migratiematrices), de biologie (Lesliematrices) …
In het tweede hoofdstuk leer je stelsels van eerstegraadsvergelijkingen oplossen vanuit concrete problemen. Een stelsel is een wiskundige vertaling van enkele concrete voorwaarden. Hier maak je kennis met het oplossingsalgoritme van Gauss(-Jordan).
Ook in dit boek is ICT onontbeerlijk. Een grafische rekenmachine en GeoGebra zullen je een aanzienlijk tijdsvoordeel opleveren die je kunt gebruiken om te leren mathematiseren.








Inhoud
1
2
Matrices 1.1 Terminologie en bewerkingen 9 1.2 Eigenschappen van de bewerkingen met matrices 28 1.3 Matrixvoorstelling van een graaf 42
Stelsels van eerstegraadsvergelijkingen 2.1 Willekeurige stelsels oplossen 67 2.2 Toepassingen 89 2.3 Inverse matrix van een vierkante matrix 98 Oplossingen 107 Trefwoordenregister 117 Matrices en stelsels




Matrices 1





Een matrix is een schematische voorstelling van getallen, netjes geordend tussen twee grote blokhaakjes. Eenmaal je de basisbeginselen onder de knie hebt, leer je er al snel mee rekenen en bestudeer je ook de eigenschappen van matrices. Het mooie eraan is dat ze multi-inzetbaar zijn, zowel in de economie, de geografie als de sociale wetenschappen, maar ook in de biologie.
Ga even met ons mee naar het Amazonewoud: een ornitholoog bestudeerde er bijvoorbeeld jarenlang een vogelsoort. Hij kwam tot de conclusie dat slechts 40% van de eitjes uitkomt, dat de kans dat ze een volgend levensjaar halen 60% is en dat geen enkel vogeltje het vijfde levensjaar haalt. In het derde en vierde levensjaar legt elke vogel gemiddeld twee eitjes en in het vijfde levensjaar is dat er slechts één. Giet je al die gegevens in matrices, dan kun je aantonen dat de vogelsoort met uitsterven bedreigd is.


Matrices
1.1
1.2
1.3
8
Terminologie en bewerkingen 1 Definities 9 2 Bijzondere matrices 10 3 Matrices transponeren 12 4 Matrices optellen 13 5 Een matrix vermenigvuldigen met een reëel getal (scalair) 14 6 Matrices vermenigvuldigen 15 7 Macht van een matrix 17 8 Samenvatting 18 9 Oefeningen 19
Eigenschappen van de bewerkingen met matrices 1 Eigenschappen van de optelling van matrices 28 2 Eigenschappen van de vermenigvuldiging van een matrix met een scalair 30 3 Eigenschappen van de vermenigvuldiging van vierkante matrices 32
Distributiviteit van de vermenigvuldiging t.o.v. de optelling bij matrices 33 5 Eigenschappen van de transpositie van een matrix 34 6 Nuldelers 35 7 Idempotente, nilpotente en involutorische matrices 36 8 Samenvatting 37 9 Oefeningen 38
4
Matrixvoorstelling
een graaf 1 Overgangsmatrices 42 2 Populatiematrices of Lesliematrices 46 3 Verbindingsmatrices 51 4 Samenvatting 52 5 Oefeningen 53 Wat moet je kennen en kunnen? 64 1
van
1.1 Terminologie en bewerkingen
1 Definities






Inleidend voorbeeld:
Een fabrikant van plooifietsen heeft momenteel 3 modellen lopen. Een lowbudgetmodel (LM), een klassiek model (KM) en een sportief model (SM). De firma heeft 4 productielijnen in Europa : één in Aarhus (A), één in Braga (B), één in Charleroi (C) en één in Dortmund (D).
Het aantal fietsen (in duizendtallen) dat deze maand van de productieband liep in elk filiaal, vind je terug in het onderstaande schema.
In dit productieschema zijn vooral de getallen belangrijk. De labels bovenaan en links kunnen we gerust weglaten als je de volgorde kent. Wat nog overblijft, noteren we tussen grote vierkante haken.
We verkrijgen een matrix met 3 rijen en 4 kolommen, een 3 × 4-matrix.
A =
17131114
87910
13101511
matrix
Voor a 11, a 12, … , a mn ∈ R noemen we
A =
a m 1 a m 2 a m 3 a mj a mn
De matrix A noteren we soms in de volgende verkorte notatie : A = [ a ij ].
De verzameling van alle m × n -matrices duiden we aan met Rm × n
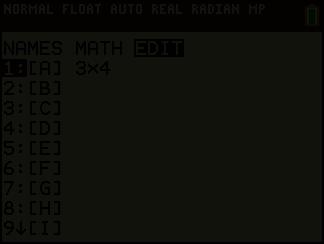




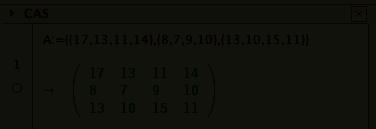
Een matrix wordt aangegeven met een hoofdletter. We spreken hier van de 3 × 4-matrix A of van een matrix A met dimensie (of orde) 3 × 4. De 12 getallen in de matrix zijn de elementen. De elementen van een matrix stellen we voor door kleine letters, meestal voorzien van twee indices: een eerste index voor de rij en een tweede index voor de kolom. Zo staat het getal 9 op de tweede rij (2), derde kolom (3). We noteren dit als volgt : a 23 = 9. Bepaal zelf a 31 en a 13. De verzameling van alle 3 × 4-matrices noteren we als R3 × 4
Andere notatie :
|| || : Cayley (1858)
( ) : Bôcher (1907)
een matrix met m rijen en n kolommen, een matrix met dimensie m × n of kortweg een m × n -matrix.
De reële getallen a ij met i ∈ {1, 2, … , m } en j ∈ {1, 2, … , n } noemen we de elementen van de matrix.
9 1 Matrices
A(arhus) B(raga) C(harleroi) D(ortmund) LM 17 13 11 14 KM 8 7 9 10 SM 13 10 15 11
a
a 2n . . . . . . . . .
in .
.
a 11 a 12 a 13 a 1 j a 1n
21 a 22 a 23 ··· a 2 j ···
a i 1 a i 2 a i 3 a ij a
. . .
gelijke matrices
Twee m × n -matrices noemen we gelijk als elke twee overeenkomstige elementen gelijk zijn.
Voorbeeld :
Algemeen in Rm × n : [a ij ]=[ bij ] ⇐⇒∀i , j : a ij = bij
Dubbele indices komen al voor bij de Duitse wiskundige Leibniz (1646–1716) in 1700.
2 Bijzondere matrices
rijmatrix
Een rijmatrix is een matrix met slechts één rij.
Voorbeelden :
258
8390
a
kolommatrix
Een kolommatrix is een matrix met slechts één kolom.
Voorbeelden :
2 4 0
nulmatrix
Een nulmatrix is een matrix waarvan alle elementen gelijk zijn aan nul.
Voorbeelden :
10
a 11 a 12 a 21 a 22 = b11 b12 b21 b22 ⇐⇒ a 11 = b11 a 12 = b12 a 21 = b21 a 22 = b22
11
12
a
a 13 ··· a 1n
a 11 a 21 a 31 . a m 1
7 √2 0 1
O 2×3 = 000 000 O4×2 = 00 00 00 00
vierkante matrix
Een vierkante matrix is een matrix waarvan het aantal rijen gelijk is aan het aantal kolommen.
Voorbeelden :
2 1 30
nevendiagonaal
hoofddiagonaal
Het aantal rijen (of kolommen) noemen we de orde van de vierkante matrix.
Zo is de orde van de bovenstaande voorbeelden respectievelijk 2, 3 en n
De elementen a 11, a 22, … , a nn liggen op de hoofddiagonaal van de vierkante matrix.
In het eerste voorbeeld zijn dat de elementen 2 en 0, in het tweede voorbeeld zijn het de elementen 2, 11 en 12.
De elementen a 1n , a 2n –1, … , a n 1 liggen op de nevendiagonaal van de vierkante matrix.
In het eerste voorbeeld zijn dat de elementen –1 en 3, in het tweede voorbeeld zijn het de elementen –1, 11 en 0. symmetrische matrix
Een symmetrische matrix is een vierkante matrix waarvan de elementen a ij en a ji , die symmetrisch liggen t.o.v. de hoofddiagonaal, gelijk zijn aan elkaar.
in symbolen:
A =[a ij ] ∈ R n ×n issymmetrisch ⇐⇒∀i , j ∈{1,2,..., n } : a ij = a ji
Voorbeelden :
scheefsymmetrische matrix
Een scheefsymmetrische matrix is een vierkante matrix waarvan de elementen a ij en a ji , die symmetrisch liggen t.o.v. de hoofddiagonaal, tegengesteld zijn aan elkaar.
in symbolen:
A =[a ij ] ∈ R n ×n isscheefsymmetrisch ⇐⇒∀i , j ∈{1,2,..., n } : a ij = a ji
Voorbeeld :
012 103 2 30 Merk op dat de elementen op de hoofddiagonaal 0 zijn.
driehoeksmatrix
Een driehoeksmatrix is een vierkante matrix waarvan alle elementen beneden of boven de hoofddiagonaal nul zijn.
Voorbeelden
21 03
500 8 10 738
Het eerste voorbeeld is een bovendriehoeksmatrix (alle elementen onder de hoofddiagonaal zijn nul), het tweede voorbeeld een onderdriehoeksmatrix (alle elementen boven de hoofddiagonaal zijn nul).
11 1 Matrices
25 1
a 11 a 12 ··· a 1n a 21 a 22 ··· a 2n . . . . . a n 1 a n 2 ··· a nn
5117 0612
.
1 5 8 5 3 2 8 2 7 15 86 53110 8117 2 60 24
:
boven- en onderdriehoeksmatrix
A =[a ij ] ∈ R n ×n iseen bovendriehoeksmatrix ⇐⇒ ∀i , j ∈{1,..., n } : i > j =⇒ a ij = 0
A =[a ij ] ∈ R n ×n iseen onderdriehoeksmatrix ⇐⇒ ∀i , j ∈{1,..., n } : i < j =⇒ a ij = 0
diagonaalmatrix
Een diagonaalmatrix is een vierkante matrix waarvan alle elementen die niet tot de hoofddiagonaal behoren, nul zijn.
in symbolen:
A =[a ij ] ∈ R n ×n iseendiagonaalmatrix ⇐⇒ ∀i , j ∈{1,..., n } : i = j =⇒ a ij = 0
Voorbeelden
We noteren dit ook als diag(5, –3, 6).
scalaire matrix
Een scalaire matrix is een diagonaalmatrix waarvan alle elementen op de hoofddiagonaal gelijk zijn.
Voorbeelden
eenheidsmatrix
Een eenheidsmatrix is een diagonaalmatrix waarvan alle elementen op de hoofddiagonaal gelijk zijn aan 1.
Voorbeelden
3 Matrices transponeren
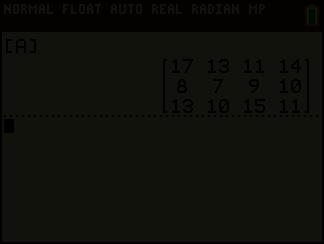
Wanneer we in een matrix A de rijen als kolommen schrijven en de kolommen als rijen, waarbij we de volgorde van de elementen behouden, bekomen we een nieuwe matrix die we de getransponeerde (of gespiegelde) matrix A T noemen. We voeren een matrix-transpositie uit.
Voorbeeld :
De getransponeerde van een m × n -matrix is een n × m -matrix. [ a ij ]T = [ a ji ]
Taak : toon aan dat ( A T )T = A .


12
5
0 3
0 0 6 1000
= diag (1,2,3,4)
:
0 0
0
0200 0030 0004
50 05 200 0 20 00 2
:
: I 2 = 10 01 I 3 = 100 010 001 I n = 10 ··· 0 01 . . . . . 0 0 01
A = 123 456 =⇒ A T = 123 456 T = 14 25 36
4 Matrices optellen
We bekijken de productie (in duizendtallen) bij de plooifietsenfabrikant voor twee opeenvolgende maanden.


Productie voor de maand november :








Productie






De totale productie van de twee maanden samen wordt gegeven door :
som van matrices
[a ij ]+[ bij ]=[a ij + bij ] met i ∈{1,..., m } en j ∈{1,..., n }
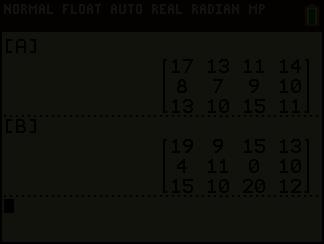

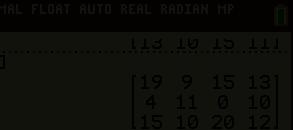


We noemen de matrix S de som van de matrices N en D en we noteren dit als S = N + D
De som van twee m × n -matrices is een m × n -matrix waarvan elk element gelijk is aan de som van de overeenkomstige elementen van de gegeven matrices.
Merk op dat twee matrices slechts kunnen worden opgeteld als ze dezelfde dimensie hebben !
Matrices
Het woord ‘matrix’ betekent in het Latijn fokdier of moederdier, maar ook baarmoeder. Een andere betekenis van het woord is holle gietvorm. Denk maar aan het Franse woord ‘matrice’ of aan het Nederlandse woord ‘matrijs’.
Die laatste betekenis brengt ons dichter bij de wiskundige betekenis van het woord. Matrix wordt ook in de biologie gebruikt. Daar betekent het kiemlaag. Met die term wordt ook het omhulsel van chromosomen aangeduid. Ook in de natuurkunde, de economie en de geografie worden matrices gebruikt.
13 1 Matrices
A(arhus) B(raga) C(harleroi) D(ortmund) LM 17 13 11 14 KM 8 7 9 10 SM 13 10 15 11 N = 17131114 87910 13101511
A(arhus) B(raga) C(harleroi) D(ortmund) LM 19 9 15 13 KM 4 11 0 10 SM 15 10 20 12 D = 1991513 411010 15102012
voor de maand december :
A(arhus) B(raga) C(harleroi) D(ortmund) LM 17 + 19 = 36 13 + 9 = 22 11 + 15 = 26 14 + 13 = 27 KM 8 + 4 = 12 7 + 11 = 18 9 + 0 = 9 10 + 10 = 20 SM 13 + 15 = 28 10 + 10 = 20 15 + 20 = 35 11 + 12 = 23
=
= 17 + 1913 + 911 + 1514 + 13 8 + 47 + 119 + 010 + 10 13 + 1510 + 1015 + 2011 + 12
S
36222627 1218920 28203523
5 Een matrix vermenigvuldigen met een reëel getal (scalair)
Veronderstel dat de productie bij de firma gedurende 6 opeenvolgende maanden steeds gelijk blijft. De maandproductie (in duizendtallen) wordt gegeven door de volgende tabel.
1991513
Wat is de totale productie van elk model in elk filiaal gedurende die zes maanden ?
1991513
906012072
15102012
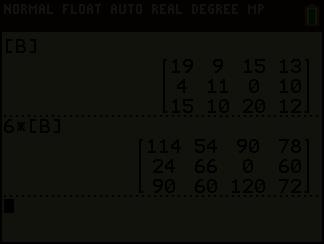
We noemen de matrix S het product van het getal 6 met de matrix M en we noteren dit als S = 6 M
product van een matrix met een reëel getal
Het product van een m × n -matrix met een reëel getal (ook scalaire vermenigvuldiging genoemd) is een m × n -matrix waarvan elk element gelijk is aan het product van het overeenkomstige element van de gegeven matrix met dit reële getal.
r [ a ij ] = [ r a ij ]
James Joseph Sylvester (1814 –1897)
 J.J. Sylvester
J.J. Sylvester
J. J. Sylvester was de eerste die het woord ‘matrix’ gebruikte. Hij duidde er een rechthoekig getallenschema mee aan in een werk dat hij rond 1850 publiceerde. Sylvester, geboren in Londen, had een bijzonder rijkelijk gevuld cv. Hij studeerde wiskunde in Cambridge en werd er tweede van zijn jaar. Hij kreeg zijn diploma niet, want hij weigerde zijn geloof te verloochenen en een religieuze eed af te leggen voor de Anglicaanse Kerk. Hij werkte eerst een paar jaar als professor in Londen en trok daarna naar de universiteit van Virginia, in de Verenigde Staten. Maar … na enkele maanden moest hij al terugkeren. Hij nam er namelijk de benen nadat hij een leerling had geslagen die in zijn les de krant zat te lezen en hem beledigde. De student bleef roerloos liggen en Sylvester dacht dat hij hem gedood had. Terug in Engeland werkte hij eerst een tiental jaren als boekhouder en later als advocaat. Zo leerde hij Arthur Cayley kennen, een wiskundige met wie hij goed bevriend raakte en vaak samenwerkte. Sylvester werd weer professor in 1855, aan de militaire academie van Woolwich. Hij werkte er 14 jaar, tot hij de pensioenleeftijd van 55 bereikt had. Hij hield zich een tijdje bezig met een andere passie, poëzie, maar de wiskunde liet hem niet los: hij trok opnieuw naar de VS, nu voor een zestal jaren. Hij werd professor in Baltimore en startte er het eerste wiskundige tijdschrift op, The American Journal of Mathematics. Na zijn terugkeer werd hij dan weer professor in Oxford. Hij stierf op 82-jarige leeftijd in Londen.
14
A(arhus) B(raga) C(harleroi) D(ortmund) LM 19 9 15 13 KM 4 11 0 10 SM 15 10 20 12 M =
411010
15102012
A(arhus) B(raga) C(harleroi) D(ortmund) LM 6 · 19 = 114 6 · 9 = 54 6 · 15 = 90 6 · 13 = 78 KM 6 · 4 = 24 6 · 11 = 66 6 · 0 = 0 6 · 10 = 60 SM 6 · 15 = 90 6 · 10 = 60 6 · 20 = 120 6 · 12 = 72 S =
114549078 2466060
= 6 ·
411010
6 Matrices vermenigvuldigen
Voorbeeld 1:
De productie van plooifietsen van de voorbije maand bedraagt (in duizendtallen) :
De verkoopprijs van de fietsen bedraagt :
V = 7009501100
Bereken de totale omzet van elk filiaal (in duizenden euro’s) :
Z = 33800267503275031400
We noemen matrix Z het product van matrix V met matrix M en we noteren dit als Z = V M
Voorbeeld 2:
Een onderhoudsfirma levert aan elk van de 4 filialen maandelijks 2 soorten onderhoudsartikelen.
Op het einde van elk kwartaal maakt de firma een overzicht van wat ze maandelijks voor elk filiaal aan onderhoudsartikelen moet betalen.
De prijzen (in euro) van de onderhoudsartikelen van het afgelopen kwartaal vind je terug in de volgende tabel.
We bekomen de volgende prijzenmatrix :
15 1 Matrices
A(arhus) B(raga) C(harleroi) D(ortmund) LM 17 13 11 14 KM 8 7 9 10 SM 13 10 15 11 M = 17131114 87910 13101511
LM KM SM
euro 950
1100 euro
700
euro
A(arhus) B(raga) C(harleroi) D(ortmund) 700 17 700 13 700 11 700 14 + 950 · 8 + 950 · 7 + 950 · 9 + 950 · 10 + 1100 13 + 1100 10 + 1100 15 + 1100 11 = 33 800 = 26 750 = 32 750 = 31 400
maand
januari 23,00 17,00 februari 23,20 17,30 maart 23,40 17,40
artikel 1 artikel 2
P = 23,0017,00 23,2017,30 23,4017,40
De maandelijks geleverde hoeveelheden bedragen :
We bekomen de volgende leveringsmatrix:
L =
145120187156
De maandelijkse kost in euro aan onderhoudsartikelen per filiaal noteren we in de volgende tabel.

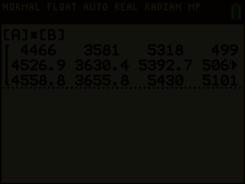
Merk op dat het product van een 3 × 2-matrix met een 2 × 4-matrix, een 3 × 4-matrix is.
Het element 5392,70 wordt verkregen door de som van de producten 23,20 93 en 17,30 187 te maken. We zeggen dat het element 5392,70 (dat op de 2e rij 3e kolom van de productmatrix staat) bekomen wordt door de som van de producten te nemen van de elementen van de 2e rij van de eerste matrix met de overeenkomstige elementen uit de 3e kolom van de tweede matrix
product van matrices
Het product van een m × n-matrix A = [ aij] met een n × p-matrix B = [ bij] is een m × p-matrix C = [ cij] waarbij het element cij van de i-de rij j-de kolom verkregen wordt door de som te nemen van de producten van de elementen van de i-de rij van de matrix A met de overeenkomstige elementen van de j-de kolom van de matrix B.
Hetproductvaneen m × n -matrix A =[a ij ] meteen n × p -matrix B =[ bij ] iseen m × p -matrix C =[ c ij ] waarbijhetelement c ij vande i -derij j -dekolomverkregenwordtdoordesomtenemenvan deproductenvandeelementenvande i -derijvandematrix A metdeovereenkomstigeelementen vande j -dekolomvandematrix B
Merk op :
Om twee matrices A en B te kunnen vermenigvuldigen, moet het aantal kolommen van matrix A gelijk zijn aan het aantal rijen van matrix B
16
A(arhus) B(raga) C(harleroi) D(ortmund) artikel 1 87 67 93 102 artikel 2 145 120 187 156
876793102
A(arhus) B(raga) C(harleroi) D(ortmund) januari 23,00 87 + 17,00 145 = 4466,00 23,00 67 + 17,00 120 = 3581,00 23,00 93 + 17,00 187 = 5318,00 23,00 102 + 17,00 156 = 4998,00 februari 23,20 · 87 + 17,30 145 = 4526,90 23,20 · 67 + 17,30 120 = 3630,40 23,20 · 93 + 17,30 187 = 5392,70 23,20 · 102 + 17,30 156 = 5065,20 maart 23,40 87 + 17,40 · 145 = 4558,80 23,40 67 + 17,40 · 120 = 3655,80 23,40 93 + 17,40 · 187 = 5430,00 23,40 102 + 17,40 · 156 = 5101,20 Schematisch geeft dit : 876793102 145120187156 = L P = 23,0017,00 23,2017,30 23,4017,40
4526,903630,405392,705065,20 4558,803655,805430,005101,20 = P · L
4466,003581,005318,004998,00
A
c ij = a i 1 · b1 j + a i 2 · b2 j + + a in · bnj = n k =1 a ik · bkj
· B = C met
Schema:
••
a i 1 a i 2 a in
met
7 Macht van een matrix
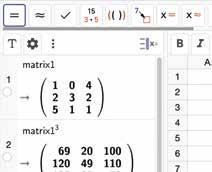
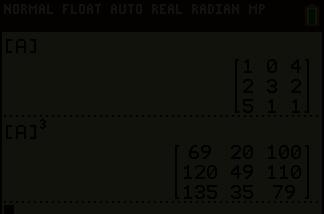
Is A een vierkante n × n -matrix en p ∈ N0, dan definiëren we een macht van A als volgt. macht van een matrix
A p = A A A (p factoren)
Voorbeeld :


















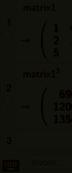
































17 1 Matrices
••···•
••···•
••···• ••···•
••
j •• ||||| |||||
bnj •• = ••••• •••••
b1 j
•• b2
••
•• ••••• •••••
m
p
•• c ij
m × n n × p
×
nj
c ij = a i 1 · b 1j + a i 2 · b 2j + … + a in · b
104 232 511 3 = 104 232 511 104 232 511 104 232 511 = 2148 181116 12423 104 232 511 = 6920100 12049110 1353579
8 Samenvatting
• Je kent de betekenis, de definitie en de terminologie van matrices.
Voor a 11, a 12, … , a mn ∈ R noemen we A =
a 11 a 12 a 13 a 1 j a 1n
a 21 a 22 a 23 a 2 j a 2n
. . . . .
a i 1 a i 2 a i 3 ··· a ij ··· a in
. . . . . . . . . .
a m 1 a m 2 a m 3 a mj a mn
een matrix met m rijen en n kolommen, een matrix met dimensie m × n of kortweg een m × n -matrix. De reële getallen a ij met i ∈ {1, 2, … , m } en j ∈ {1, 2, … , n } noemen we de elementen van de matrix.
Twee m × n -matrices noemen we gelijk als elke twee overeenkomstige elementen gelijk zijn.
[ a ij ] = [ b ij ] ⟺ ∀i , j : a ij = b ij
• Je kent de benamingen en de betekenis van enkele bijzondere matrices.
– Een rijmatrix is een matrix met slechts één rij.
– Een kolommatrix is een matrix met slechts één kolom.
– Een nulmatrix is een matrix waarvan alle elementen gelijk zijn aan nul.
– Een vierkante matrix is een matrix waarvan het aantal rijen gelijk is aan het aantal kolommen.
– Een symmetrische matrix is een vierkante matrix waarvan de elementen a ij en a ji , die symmetrisch liggen t.o.v. de hoofddiagonaal, gelijk zijn aan elkaar.
– Een scheefsymmetrische matrix is een vierkante matrix waarvan de elementen a ij en a ji , die symmetrisch liggen t.o.v. de hoofddiagonaal, tegengesteld zijn aan elkaar.
– Een driehoeksmatrix is een vierkante matrix waarvan alle elementen beneden of boven de hoofddiagonaal nul zijn.
– Een diagonaalmatrix is een vierkante matrix waarvan alle elementen die niet tot de hoofddiagonaal behoren, nul zijn.
– Een scalaire matrix is een diagonaalmatrix waarvan alle elementen op de hoofddiagonaal gelijk zijn.
– Een eenheidsmatrix is een diagonaalmatrix waarvan alle elementen op de hoofddiagonaal gelijk zijn aan 1.
– Wanneer we in een matrix A de rijen als kolommen schrijven en de kolommen als rijen, waarbij we de volgorde van de elementen behouden, bekomen we een nieuwe matrix die we de getransponeerde (of gespiegelde) matrix A T noemen.
[ a ij ]T = [ a ji ]
• Je kunt bewerkingen uitvoeren met matrices.
De som van twee m × n -matrices is een m × n -matrix waarvan elk element gelijk is aan de som van de overeenkomstige elementen van de gegeven matrices.
[a ij ]+[ bij ]=[a ij + bij ] met i ∈{1,..., m } en j ∈{1,..., n }
Het product van een m × n -matrix met een reëel getal is een m × n -matrix waarvan elk element gelijk is aan het product van het overeenkomstige element van de gegeven matrix met dit reële getal. r [ a ij ] = [ r a ij ]
Hetproductvaneen m × n -matrix A =[a ij ] meteen n × p -matrix B =[ bij ] iseen m × p -matrix C =[ c ij ] waarbijhetelement c ij vande i -derij j -dekolomverkregenwordtdoordesomtenemenvan deproductenvandeelementenvande i -derijvandematrix A metdeovereenkomstigeelementen vande j -dekolomvandematrix B
Het product van een m × n -matrix A = [ a ij ] met een n × p -matrix B = [ b ij ] is een m × p -matrix C = [ c ij ] waarbij het element c ij van de i -de rij j -de kolom verkregen wordt door de som te nemen van de producten van de elementen van de i -de rij van de matrix A met de overeenkomstige elementen van de j -de kolom van de matrix B
A B = C met c ij = a i 1 b1 j + a i 2 b2 j + ... + a in bnj = n k =1 a ik bkj
Is A een vierkante n × n -matrix en p ∈ N0, dan definiëren we een macht van A als volgt: A p = A · A · … · A (p factoren)
18
9 Oefeningen
A is een 3 × 4-matrix waarvoor a ij = 2i 2 – 3j + 1. Schrijf de matrix voluit.
Bepaal u , v , w ∈ R zodat de volgende gelijkheden waar zijn.
a 2 u 14 u + v 13 = 52 v 13 u 2 v
b 32 u + v uv 3 w 10 = v w 3 w v 4 7
v + w 0
aGegeven: A =
xx 2 40
0 2 y 1 y 2 002 .Bepaal x , y ∈ R zodat A eenscalairematrixis.
bGegeven: B =
cGegeven: C =
2 q p 1 532q
3 + pq + 3 2p .Bepaal p , q ∈ R zodat B eensymmetrischematrixis.
0 v 5 v 3 v 4 uu + v
51 2 v 0
.Bepaal u , v ∈ R zodat C eenscheefsymmetrischematrixis.
Als je weet dat A een 3 × 4-matrix is, K een 5 × 4-matrix en L een 2 × 6-matrix, bepaal dan de dimensie van de matrices B , C , D , E en F .
K = ( A T C + 2B )T
L = D A E + ( E T F )T
Schrijf
A = 257 9 38 146 als een som van een symmetrische en een scheefsymmetrische matrix.
Gegeven zijn de volgende matrices:
Welke van de volgende sommen zijn zinvol en welke niet ?
Bereken de zinvolle sommen.
a A + B d A C
b A + D T e2 B 3 C T
c A T 2 (C 2 D ) f A 3 ( B T + D )
1 19 Matrices
45 60 1 3 B = 56 4 2 30 C = 7 810 1 92 D = 51 2 356
A =
1 2 3 4 5
6
Gegeven zijn de volgende matrices:
Welke producten zijn zinvol en welke niet ? Bereken de zinvolle producten.
a A · C h B · C
b C A i C B
c A B j D C
d B T A k C T D
e A D l B 2 f B · D m A 2
g D B
Gegeven:
Bepaal p , q , r ∈ R zodat P + Q = 2R
Gegeven:
Bepaal u , v , w ∈ R zodat U 2V = 3W
Gegeven :
Gevraagd:
a Bereken M N
b Bereken N M
Gegeven:
A = 3 57
Gevraagd : Welke van de volgende uitdrukkingen is zinvol ? A T C A of B T C B Bereken die.
Gegeven:
Indien zinvol, bereken :
a
b
2
20
A = 215 6 34 708 B = 9 1 115 02 C = 103 5410 D = 117 9 12
n D 2
Q
1
R
P = pp 1 p + 26
=
q 72q
= 2 rr r 7
.
2 V
v
2 vv W
U = u 2 2 u + 2 1 u
=
+ 11
= ww + 1 3 w
N = 3 2 4 8
M = 2 573
B
2 5 8 C = 100 0 20 003
=
A = 217 32 1 842 B = 10 1 1 01 C = 1 2 3 D = 45 E = 7 3 21 24
A C – B T E – D
ICT. 7
10 11 12
A
B – C D – 4 E Werk dit ook uit met
8 9
Gegeven :
Indien zinvol, bereken :
a A B T C – E D
b A C – D E
Werk dit ook uit met ICT.
Gegeven :
Gevraagd :
Bereken indien zinvol : ( A + I 3) B – B ( C – I 3) + ( D – I 3) ( D + I 3)
Controleer met ICT.
Gegeven :
A = 37 1
Gevraagd :
Bereken A 6 + A 4 + A 3 + A.
B = [ b ij ] is een 3 × 2-matrix waarvoor b ij = i 2 – j + 3 en C = [ c ij ] is een 2 × 4-matrix waarvoor c ij = 5i – 3j + i
Bereken D = B C
Bepaal
1 21 Matrices
A = 145 7 96 B = 79 6 3 210 485 C = 13 80 31 D = 17 E = 9 6
A = 123 304 2 4 1 B = 201 030 104 C = 1 11 20 2 033 D = 11 1 1 11 111
2
j
x , y , z , a , b , c ∈ R als : 2 y 1 z 0 3 3 1 x · 230 041 1 67 = 5 b 3 8323 a 21 c T
a , b en c zodat de volgende uitdrukkingen zinvol zijn. a 2 a 3 1 · 41 50 = 7a 2 7 a 2 · I 2 c 4 2 13 · 3a 2 0 a 83a bc T = 47 011 b 2a 3 · 41 + 7 b 210 = 230 3a + b 13 d 12a b 2 a 3 0 c 2a b · 4 1 01 = 4 1 5a + 31 + a 0 1 13 14 15 16 17 18
Bepaal
Bereken en controleer met ICT.
Gegeven : A =
Los de volgende matrixvergelijkingen op.
a 2 X – A B = C
b D – X = A – B C
c X T – 4 · I 2 = D 2 – 3 · B + 2 · A · C
Gegeven: A iseen2 × 2-matrixwaarvoor A 0 1 = 7 5 en A 2 + A = I 2 .
Gevraagd:Bepaal A .
Los op :
4
Toon aan :
Gegeven : In deze tabel vind je de verkoopcijfers van een eetkraampje op een kerstmarkt.


De gehanteerde prijzen zijn :



Gevraagd : Bereken V P T en interpreteer die matrix.




















22
102 a 30 214 2 210 a 23 0 1 a · 301 014 1 a 2 T + 100 a 5a 5 a 94aa
2
5 6 7
48 0 9 D
11 12 1516
3 10 B =
2 C =
=
2 X 3 Y =
112 00 2 003
+ Y = 100
21 1
3 X
1862
a
0
c
f =
0
b
c
a 00
b 0 00
d 00 0 e 0 00
ad 00
be 0 00 cf
a 00 0 b 0 00
3 =
a 3 00 0 b 3 0 00 c 3
pizza hamburger pita pastabeker V = donderdag 87 55 65 43 vrijdag 146 78 172 92 zaterdag 155 173 201 124 69 93 91 108
pizza hamburger pita pastabeker P = € 6 € 5 € 7 € 9
19 20 21
* 23 24
* 22
Een camping niet ver van Dinant ontvangt deze zomer in de maand juli heel wat scoutsverenigingen. Ze komen uit West-Vlaanderen, Limburg en Antwerpen. De verdeling per leeftijdsgroep zoals momenteel geboekt, ziet er als volgt uit :
Bereken per leeftijdsgroep hoeveel scouts er tijdens elke periode op de camping aanwezig zijn .
M = 1 – 10 juli
11 – 20 juli
21 – 30 juli
De camping weet uit ervaring dat er tijdens die periode heel wat gesnoept wordt. Als richtlijn voor een kampperiode hanteert de campinguitbater volgend schema :














1 Matrices
Vanuit
kapoenen welpen jongverkenners givers W = 1 – 10 juli 53 76 47 28 11 – 20 juli 47 55 33 19 21 – 30 juli 62 68 41 22 Vanuit Limburg kapoenen welpen jongverkenners givers L = 1 – 10 juli 34 42 22 15 11 – 20 juli 45 51 27 20 21 – 30 juli 29 32 16 9 Vanuit
kapoenen welpen jongverkenners givers A = 1 – 10 juli 41 53 31 24 11 – 20 juli 36 44 27 17 21 – 30 juli 23 39 27 16
West-Vlaanderen
Antwerpen
kapoenen welpen jongverkenners
givers
kapoenen welpen jongverkenners givers S = fruit 7 6 5 4 chips 6 6 4 4 ijsjes 4 5 4 6 Bereken S M
25
T en interpreteer die matrix.
Een handelaar mag deze zomer zijn mocktails promoten op het strand in drie strandbars. Er zijn vijf verschillende mocktails, elk op basis van een andere fruitsoort. De fruitsoorten zijn mango, ananas, passievrucht, framboos en kiwi.
In volgende tabel staan het aantal verkochte mocktails gedurende de eerste helft van juli:
Het aantal verkochte mocktails gedurende de tweede helft van juli:
Prijs per mocktail:
Met welke bewerking kan de handelaar onmiddellijk de opbrengst (Q) van de mocktails gedurende de hele maand juli per strandbar berekenen? opbrengst










strandbar B
Q = strandbar A
strandbar C

























24
strandbar A strandbar B strandbar C K = mango 122 156 111 ananas 145 189 126 passievrucht 135 161 106 framboos 129 178 102 kiwi 111 150 154
strandbar A strandbar B strandbar C L = mango 145 163 143 ananas 186 191 155 passievrucht 173 175 167 framboos 159 162 153 kiwi 144 144 148
prijs P = mango € 5,50 ananas € 5,20 passievrucht € 6,10 framboos € 5,70 kiwi € 5,10
26
In St Mary Mead, een gezellig ouderwets Engels dorpje, levert melkboer Hercule wekelijks een aantal producten aan de plaatselijke pensions : Hotel Bertram (HB), Agatha Cottage (AC) en Maples House (MH).
De wekelijkse levering voor deze maand (= 4 weken) bedraagt :










a Noteer de bovenstaande gegevens in matrixvorm (matrix WL).
b Bereken de matrix die de levering van deze maand weergeeft (ML).
De prijzen van de verse producten variëren van week tot week.
Deze maand bedroegen de weekprijzen (in shilling) :

























c Schrijf de bovenstaande gegevens in matrixvorm (matrix P ).
d Wanneer Hercule op het einde van de maand zijn factuur wil maken voor de plaatselijke pensions, welke matrices moet hij dan met elkaar vermenigvuldigen ?
Vermenigvuldig die matrices, maar opgelet : hou rekening met het feit dat 12 pence = 1 shilling en 20 shilling = 1 pond.
De onderstaande matrix geeft informatie over de voedingswaarde per 100 gram van enkele producten :
kip
22527120
3638,20,579,3
2608,5252 7160,6810,4
363,50,14,8
3687,136,92
15812,811,50,7
580,30,415
401,10,29,1
versetonijn rijst
witbrood boter
mageremelk
halfoudekaas ei appels wortelen
a Welke dimensie heeft de bovenstaande matrix ?
b Omschrijf de betekenis van het element v 43
c Tel de elementen van de derde kolom op. Heeft die som zin ? Waarom (niet) ?
d Sidi nuttigt op een dag de volgende maaltijden : ontbijt : 2 sneetjes brood (60 gram), 1 eitje (60 gram), 20 gram boter en een glas melk (2 dl) middagmaal : 150 gram kip, 200 gram rijst, 150 gram wortelen tussendoor : 1 appel (200 gram)
avondmaal : 2 sneetjes brood (60 gram), eentje met verse tonijn (100 gram) en eentje met halfoude kaas (50 gram)
Zet die gegevens om in een matrix en bereken de hoeveelheid calorieën, proteïnen, vetstoffen en koolhydraten die Sidi vandaag binnenkreeg.
1 25 Matrices
HB AC MH melk 16 liter 22 liter 24 liter boter 9 kg 7 kg 11 kg kaas 17 kg 13 kg 5 kg eieren 4 dozijn 8 dozijn 14 dozijn
1e week 2e week 3e week 4e week melk 3 3,5 3,5 4 boter 4 4 5 4,5 kaas 5,5 5,5 5 6 eieren 4 4,5 4 5
V =
18520110
calorieënproteïnenvetstoffenkoolhydraten
27 28
Een fabriek telt twee productielijnen voor het maken van zetels. Op productielijn A zijn dat 24 zetels per dag, op productielijn B 20 zetels per dag. In het productieschema zie je dat op beide productielijnen drie types zetels gemaakt worden.
Aantal geproduceerde zetels per dag :
lijnAlijnB 129 78 53
type eenzit tweezit driezit
a Geef de bijbehorende productiematrix P



































b Productielijn A is 4 dagen per week in gebruik, productielijn B 5 dagen. Schrijf die gegevens in een 2 × 1-matrix T
c Bereken P T en interpreteer die gegevens.
Een winkelier heeft drie filialen : U, V en W. Gedurende één week is bijgehouden hoeveel koelkasten van de merken A, B, C en D verkocht zijn. De gegevens zijn verwerkt in de volgende matrix.
De inkoopprijs van een koelkast van merk A is 460 euro, van merk B 650 euro, van merk C 880 euro en van merk D 500 euro. De verkoopprijs van een koelkast is respectievelijk 820 euro, 990 euro, 1340 euro en 860 euro.
a Verwerk de gegevens over inkoopprijs en verkoopprijs in een matrix P zodat P M betekenis heeft. Bereken ook N = P M
b Bedenk een matrix K zodat N · K informatie geeft over het totale inkoop- en verkoopbedrag van de drie filialen samen.
c Bereken de totale winst die de drie filialen deze week samen gemaakt hebben op de koelkasten.
De families Janssens (vader, moeder, zonen Xander en Kasper en dochter Ellen) en Moors (twee vaders, zoon Thomas en de honden Rik en Rak) gaan samen een paar weken kamperen naar het zuiden. De familie Janssens heeft drie tenten, de familie Moors één. In totaal verbleven ze op drie campings : 5 dagen camping A, 4 dagen camping B en 7 dagen camping C. De dagtarieven (in euro) van elke camping staan in onderstaande tarievenmatrix.
volw.kinddiertent
3,001,401,102,10
3,901,800,802,50
2,101,200,801,70
a Vul volgende matrices aan.
G = J M
campingA campingB campingC
volw. kind dier tent A B C
D =



































b Bereken de matrix H = T G en geef een betekenis aan die matrix.
c Welke camping was voor de familie Moors het voordeligst ?
d Welke informatie geeft de matrix K = D · H ?
26
M = UVW 856 342 7101 9123 A B C D
T =
29 30 31
In het eethuisje om de hoek hebben ze heerlijke wafels. Je kunt er vandaag kiezen uit 3 soorten.
W 1 : een wafel met ijs en slagroom
W 2 : een wafel met fruit en slagroom
W 3 : een wafel met fruit en ijs
De wafels kennen een vaste samenstelling. Zo krijg je als je een wafel met ijs en slagroom bestelt, een wafel van 80 gram met 140 gram ijs en 20 gram slagroom.
Een wafel met fruit en slagroom bestaat uit een wafel van 80 gram, 100 gram fruit en 20 gram slagroom.
Een wafel met fruit en ijs bestaat uit een wafel van 80 gram, 60 gram fruit en 120 gram ijs.
De samenstelling van die soorten kunnen we weergeven in een matrix, waarbij de hoeveelheden zijn weergegeven in kg.
wafelijsfruitslagroom
0,080,1400,02
M =
0,0800,100,02
0,080,120,060






W1 W2 W3












Verder is een inkoopprijzenmatrix I gegeven die de prijs (in euro) per kg geeft van de ingrediënten, een matrix A die de aantallen wafels weergeeft die deze dag verkocht zijn en een matrix V die de prijs per wafel geeft. I =
3,78 2,95 8,22 2,40
wafel ijs fruit slagroom A = W1 W2 W3
a Waarom kun je het product M · A niet uitrekenen ?
b Bereken G = A · M . Welke betekenis hebben de getallen in G ?
c Bereken K = G · I . Wat stellen de getallen in K voor ?
d Bereken P = M · I . Wat stellen de getallen in P voor ?
e Leg uit waarom je de matrix K ook kunt berekenen met K = A · P .
f Bereken de winst (in euro) die het eethuisje vandaag maakte met de drie soorten wafels.
Voordematrix A = ab 1 a 0 met a en b reëlegetallengeldtdat A A = A
Welkeuitspraakiswaar?
(A) er is geen enkel koppel (a, b) dat hieraan voldoet
(B) a = b = 0
(C) a = 0 en b is willekeurig
(D) a = 1 en b is willekeurig
Toelatingsexamen arts 2019, vraag 8
Dereëlegetallen a en b voldoenaan
Bepaalhetproduct ab
(A) –4 (B) –2 (C) 2 (D) 4
Toelatingsexamen arts 2023, vraag 7
1 27 Matrices
784685 V = W1 W2 W3 4,755,255,75
a 1 4 8 b · a 1 4 8 b = a 1 4 8 b
32 33
34
1.2 Eigenschappen van de bewerkingen met matrices
1 Eigenschappen van de optelling van matrices
Het optellen van matrices komt grotendeels neer op het optellen van reële getallen. We moeten immers de overeenkomstige elementen van de matrices optellen. Het is dan ook niet verwonderlijk dat we de eigenschappen van de optelling in R terugvinden in de optelling in R
Om aan te tonen dat Rm × n , + een commutatieve groep is, moeten we 5 eigenschappen aantonen. Om het rekenwerk wat te vereenvoudigen, beperken we ons tot 2 × 2-matrices. Je kunt de berekeningen steeds herhalen voor willekeurige m × n -matrices.
We werken met de volgende matrices.
[1] Deoptellingisinternin R m ×n . insymbolen:
∀ A , B ∈ R m ×n : A + B ∈ R m ×n
Immers :
[2] Hetoptellenin R m ×n isassociatief. insymbolen:
∀ A , B , C ∈ R m ×n : ( A + B )+ C = A +( B + C )
Immers :
( A + B )+ C =
=
R isassociatief.
=
=
= A +( B + C )
28
m × n , +.
A = a 11 a 12 a 21 a 22 B = b11 b12 b21 b22 C = c 11 c 12 c 21 c 22
A + B = a 11 a 12 a 21 a 22 + b11 b12 b21 b22 = a 11 + b11 a 12 + b12 a 21 + b21 a 22 + b22 ∈ R 2×2
a 11 a 12 a 21 a 22 + b11 b12 b21 b22 + c 11 c 12 c 21 c 22
a 11 + b11 a 12 + b12 a 21 + b21 a 22 + b22 + c 11 c 12 c 21 c 22
(a 11 + b11 )+ c 11 (a 12 + b12 )+ c 12
a 21 + b21 )+ c 21 (a 22 + b22 )+ c 22
=
(
+( b11 + c 11 ) a 12 +( b12 + c 12
*Hetoptellenin
∗ = a 11
)
21 + c 21
22 +( b22 + c 22 )
(a 21 +( b
) a
21 a 22 + b11 + c 11 b12 + c 12 b21 + c 21 b22 + c 22
a 11 a 12 a
a 11
12 a 21 a 22 + b11 b12 b21 b22 + c 11 c 12 c 21 c 22
a
[3] Denulmatrixishetneutraalelementvoorhetoptellenin R m ×n . insymbolen:
O ∈ R m ×n en ∀ A ∈ R m ×n : A + O = A = O + A
Immers :
A + O = a 11 a 12
[4] Elkematrix A van R m ×n heefteensymmetrischelementvoorhetoptellenin R m ×n , namelijkzijntegengesteldematrix A insymbolen:
∀ A ∈ R m ×n , ∃! A ∈ R m ×n : A +( A )= O =( A )+ A
tegengestelde matrix
A =[a ij ]
A =[ a ij ]
Immers :
[5] Hetoptellenin R m ×n iscommutatief. insymbolen:
∀ A , B ∈ R m ×n : A + B = B + A
Immers :
A + B = a
*Hetoptellenin R iscommutatief.
= B + A
Besluit : Rm × n , + is een commutatieve groep
Het woord ‘groep’ is afkomstig (1830) van de Franse wiskundige Galois (1811–1832). De eerste definitie van een groep wordt echter pas aangetroffen bij de Engelsman Cayley in 1854.
29 1 Matrices
a
= a 11 +
a 12 +
a 21 +
a 22 +
= a 11
12 a 21 a 22 =
21 a 22 + 00 00
0
0
0
0
a
A
A
a 21 a 22 + a 11 a 12 a 21 a 22 = a 11 a 11 a 12 a 12 a 21 a 21 a 22 a 22 =
+( A )= a 11 a 12
00 00 = O
a 21 + b21
22 + b22
11 a 12 a 21 a 22 + b11 b12 b21 b22 = a 11 + b11 a 12 + b12
a
12 + a 12 b21 + a 21 b22 + a 22 =
b21 b22 +
a 21 a 22
∗ = b11 + a 11 b
b11 b12
a 11 a 12
2 Eigenschappen van de vermenigvuldiging van een matrix met een scalair
[6] Descalairevermenigvuldigingvaneenreëelgetalmeteenelementvan R m ×n , levertopnieuweenelementvan R m ×n op. insymbolen:
∀ r ∈ R , ∀ A ∈ R m ×n : r · A ∈ R m ×n
Immers : r · A =
[7] Descalairevermenigvuldigingvanreëlegetallenmeteenelementvan R m ×n is gemengdassociatief. insymbolen:
∀ r , s ∈ R , ∀ A ∈ R m ×n : r · ( s · A )=( rs ) · A
Immers : r ( s A )=
*Hetvermenigvuldigenin R isassociatief.
[8] Descalairevermenigvuldigingisdistributieft.o.v.deoptellingin R m ×n . insymbolen:
∀ r ∈
Immers :
,
,
30
r · a 11 a 12 a 21 a 22 = ra 11 ra 12 ra 21 ra 22 ∈ R m ×n
r s a 11 a 12 a 21 a 22 = r sa 11 sa 12 sa 21 sa 22 = r ( sa 11 ) r
sa 12 ) r ( sa 21 ) r ( sa 22
∗
=( rs
· a 11 a 12 a 21 a 22 =( rs
(
)
= ( rs )a 11 ( rs )a 12 ( rs )a 21 ( rs )a 22
)
) · A
R
∀ A
B ∈ R m ×n : r ( A + B )= r A + r B
r
r · a 11 a 12 a 21 a 22 + b11 b12 b21 b22 = r · a 11 + b11 a 12 + b12 a 21 + b21 a 22 + b22
r (a 11 + b11 ) r (a 12 + b12 ) r · (a 21 + b21 ) r · (a 22 + b22 ) ∗ = ra 11 + rb11 ra 12 + rb12 ra 21 + rb21 ra 22 + rb22
= ra 11 ra 12 ra 21 ra 22 + rb11 rb12 rb21 rb22 = r a 11 a 12 a 21 a 22 + r b11 b12 b21 b22
r
r · B
· ( A + B )=
=
*Devermenigvuldigingisdistributieft.o.v.deoptellingin R
=
· A +
[9] Descalairevermenigvuldigingisdistributieft.o.v.deoptellingin R . insymbolen:
∀ r , s ∈ R , ∀ A ∈ R m ×n : ( r + s ) A = r A + s A
Immers :
*Devermenigvuldigingisdistributief t.o.v.deoptellingin R .
[10] Hetproductvanhetreëelgetal1meteen m × n -matrix A isgelijkaandematrix A . insymbolen:
1 ∈ R en ∀ A ∈
Immers :
Matrixrekenen
Matrixrekenen is een vrij jonge tak in de wiskunde. Alhoewel er sporen van verre voorlopers gevonden kunnen worden bij de Babyloniërs (4e eeuw voor Christus) en bij de Chinezen (2e eeuw voor Christus), is het toch vooral in de 19e eeuw dat de Britten Cayley en Sylvester zich op de studie van matrices gaan toeleggen.
In 1850 is James Sylvester (1814–1897) de eerste die de term ‘matrix’ gebruikt. In 1858 publiceert zijn vriend en collega Arthur Cayley (1821–1895) ‘Memoir on the Theory of Matrices’ waarin de theorie volledig uitgewerkt wordt. Later wordt er ook nog belangrijk onderzoek verricht door Frobenius, die in zijn werk in 1878 het woord ‘matrix’ nog niet gebruikt, maar in zijn latere werken wel.
Het begrip (reële) vectorruimte, dat al in 1846 optrad bij Cayley en Grassmann (1809–1877), werd pas axiomatisch gedefinieerd (1888) door de Italiaan Peano (1858–1932).
31 1 Matrices
( r +
A =( r + s ) a 11 a 12 a 21 a 22 = ( r + s ) a 11 ( r + s ) a 12 ( r + s ) · a 21 ( r + s ) · a 22 ∗ = ra 11 + sa 11 ra 12 + sa 12 ra 21 + sa 21 ra 22 + sa 22
s )
= ra 11 ra 12 ra 21 ra 22 + sa 11 sa 12 sa 21 sa 22 = r a 11 a 12 a 21 a 22 + s a 11 a 12 a 21 a 22 = r A +
s A
R m ×n : 1 · A = A
1 A = 1 a 11 a 12 a 21 a 22 = 1 a 11 1 a 12 1 · a 21 1 · a 22 = a 11 a 12 a 21 a 22 = A
3 Eigenschappen van de vermenigvuldiging van vierkante matrices
Het vermenigvuldigen is niet intern in Rm × n als m ≠ n .
Het is immers onmogelijk om bijvoorbeeld een 2 × 3-matrix met een 2 × 3-matrix te vermenigvuldigen. Verklaar.
Voor het onderzoeken van eigenschappen van de vermenigvuldiging van matrices beperken we ons tot de vierkante matrices.
[11] Hetvermenigvuldigenisinternin R n ×n insymbolen:
n
∀ A , B ∈ R n ×
Immers :
[12] Hetvermenigvuldigenin R n ×n isassociatief. insymbolen:
∀ A , B , C ∈ R n ×n : A ( B C )=( A B ) C
We illustreren de eigenschap aan de hand van een cijfervoorbeeld. De berekening kun je herhalen voor willekeurige 2 × 2-matrices of – nog algemener – voor willekeurige n × n -matrices .


We vinden dezelfde uitkomst !




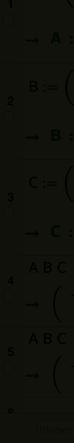




32
A
B ∈
n :
·
R n ×
A B = a 11 a 12 a 21 a 22 b11 b12 b21 b22 = a 11 · b11 + a 12 · b21 a 11 · b12 + a 12 · b22 a 21 b11 + a 22 b21 a 21 b12 + a 22 b22 ∈ R 2×2
A = 3 1 24 B = 50 16 C = 32 07 A · ( B · C )= 3 1 24 · 50 16 · 32 07 = 3 1 24 1510 344 = 42 14 18156 ( A B ) C = 3 1 24 50 16 32 07 = 14 6 624 32 07 = 42 14 18156
[13] Deeenheidsmatrixiseenneutraalelementvoordevermenigvuldigingin R n ×n . insymbolen:
I n ∈ R n ×n en ∀
Immers :
[14] Hetvermenigvuldigenin R n ×n isnietcommutatief. insymbolen:
∃ A , B ∈ R n ×n : A B = B A
We illustreren dit met enkele cijfervoorbeelden.
Dus : A B ≠ B A A en B noemen we niet-commuterende matrices
Dus : C · D = D · C C en D noemen we commuterende matrices
4 Distributiviteit van de vermenigvuldiging t.o.v. de optelling bij matrices
[15] Devermenigvuldigingisin R n ×n linksenrechtsdistributieft.o.v.deoptelling. insymbolen:
∀
Omdat de vermenigvuldiging van matrices niet commutatief is, kunnen we niet kortweg spreken van distributiviteit, wel van linkse en rechtse distributiviteit van de vermenigvuldiging t.o.v. de optelling.
We illustreren de eigenschap aan de hand van een cijfervoorbeeld.
We bekomen in beide gevallen hetzelfde resultaat. Toon nu zelf aan de hand van een voorbeeld de tweede eigenschap aan.
33 1 Matrices
A
R
: A · I n = A = I n · A
∈
n ×n
A I 2
a 11 a 12 a 21 a 22 10 01 = a 11 a 12 a 21 a 22 = A
=
A = 3 1 24 B = 50 16 C = 32 07 D = 12 011 A · B = 14 6 624 B · A = 15 5 923 C · D = 316 077 D · C = 316 077
(
+ C )= A B + A C
A , B , C ∈ R n ×n : ( A + B ) · C = A · C + B · C
A , B , C ∈ R n ×n : A
B
∀
A = 3 1 24 B = 50 16 C = 32 07 A · ( B + C )= 3 1 24 · 50 16 + 32 07 = 3 1 24 · 22 113 = 5 7 048 A · B + A · C = 3 1 24 · 50 16 + 3 1 24 · 32 07 = 14 6 624 + 9 1 624 = 5 7 048
5 Eigenschappen van de transpositie van een matrix
Degetransponeerdevandesomvantweematricesisgelijkaandesomvandegetransponeerdematrices. insymbolen:
∀ A , B ∈ R m ×n : ( A + B )T = A T + B T
Bewijs voor m = n = 2 :
( A + B )T = a
Algemeen bewijs :
Stel A =[a ij ]
B =[ bij ]
Danis:
A + B =[a ij + bij ]
( A + B )T =[a ji + b ji ]
( A + B )T =[a ji ]+[ b ji ]
( A + B )T = A T + B T
= A T + B T
Degetransponeerdevanhetproductvaneenscalairmeteenmatrixisgelijkaan hetproductvandiescalairmetdegetransponeerdematrix.
insymbolen:
∀ r ∈ R , ∀ A ∈ R m ×n : ( r A )T = r A T
Bewijs voor m = n = 2 :
( r A )T = r a
34
a 12 a
11 b12 b21 b22
12 + b12
22 + b22
21
b22
11
21 a 22 + b
T = a 11 + b11 a
a 21 + b21 a
T = a 11 + b11 a 21 + b
a 12 + b12 a 22 +
21
12 b22
21
22 T + b11 b12 b21 b22 T
= a 11 a 21 a 12 a 22 + b11 b
b
= a 11 a 12 a
a
11 a 12 a 21 a 22 T = ra 11 ra 12 ra 21 ra 22 T = ra 11 ra 21 ra 12 ra 22 = r a 11 a 21 a 12 a 22 = r A T
Taak : geef een algemeen bewijs.
Degetransponeerdevanhetproductvantweematricesisgelijkaanhetproductvan degetransponeerdevandefactoreninomgekeerdevolgorde.
insymbolen:
∀ A ∈ R m ×n , ∀ B ∈ R n ×p : ( A B )T = B T A T
Bewijs voor m = 3, n = p = 2 :
( A · B )T = a 11 a 12 a 21 a 22 a 31 a 32 · b11 b12 b21 b22 T
=
a 11 b11 + a 12 b21 a 11 b12 + a 12 b22
a 21 · b11 + a 22 · b21 a 21 · b12 + a 22 · b22 a 31 b11 + a 32 b21 a 31 b12 + a 32 b22
T
= a 11 b11 + a 12 b21 a 21 b11 + a 22 b21 a 31 b11 + a 32 b21
a 11 b12 + a 12 b22 a 21 b12 + a 22 b22 a 31 b12 + a 32 b22
B T A T = b11 b12 b21 b22 T a 11 a 12 a 21 a 22 a 31 a 32 T
= b11 b21 b12 b22 · a 11 a 21 a 31 a 12 a 22 a 32
= b11 a 11 + b21 a 12 b11 a 21 + b21 a 22 b11 a 31 + b21 a 32
b12 a 11 + b22 a 12 b12 a 21 + b22 a 22 b12 a 31 + b22 a 32
= a 11 b11 + a 12 b21 a 21 b11 + a 22 b21 a 31 b11 + a 32 b21
a 11 b12 + a 12 b22 a 21 b12 + a 22 b22 a 31 b12 + a 32 b22
We bekomen in beide gevallen hetzelfde resultaat.
6 Nuldelers
Indien A B = O of B A = O terwijl A ≠ O en B ≠ O , dan noemen we A en B nuldelers
Voorbeeld :
A =
320 15 17 415
A · B =
000 000 000
= O
B = 242 3 6 3 1 2 1
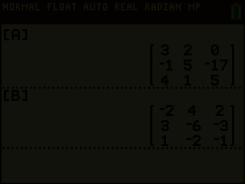
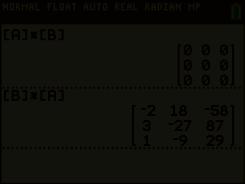
B · A =
218 58 3 2787 1 929

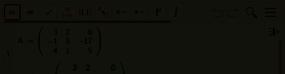





35 1 Matrices
7 Idempotente, nilpotente en involutorische matrices
idempotente matrix
Indien voor een vierkante matrix A ( ≠ O) geldt dat A 2 = A , dan noemen we A een idempotente matrix.
Voorbeeld :

nilpotente matrix
Voorbeeld


involutorische matrix
Een
Voorbeeld






Indien voor een vierkante matrix A ( ≠ O) een van nul verschillend natuurlijk getal n bestaat waarvoor A n = O , dan noemen we A een nilpotente matrix met index n .









36
A = 2 2 4 134 1 2 3 iseenidempotentematrixwant A 2 = 2 2 4 134 1 2 3
: A = 12 1 000 12 1 iseennilpotentematrixmetindex2want A 2 = 000 000 000 B = 2 23 2 23 5 50 iseennilpotentematrixmetindex3want B 2 = 15 150 15 150 000 maar B 3 = 000 000 000
I
vierkante matrix A is involutorisch indien A 2 =
: A = 01 1 5 45 4 45 isinvolutorischwant A 2 = 100 010 001 = I
8 Samenvatting
• Jekuntaantonendat R m ×n , + eencommutatievegroepis.
Deoptellingisinternin R m ×n
∀ A , B ∈ R m ×n : A + B ∈ R m ×n
Hetoptellenin R m ×n isassociatief.
∀ A , B , C ∈ R m ×n : ( A + B )+ C = A +( B + C )
Denulmatrixishetneutraalelementvoorhetoptellenin R m ×n
O ∈ R m ×n en ∀ A ∈ R m ×n : A + O = A = O + A
Elkematrix A van R m ×n heefteensymmetrischelementvoorhetoptellenin R m ×n , namelijkzijntegengesteldematrix A .
∀ A ∈ R m ×n , ∃! A ∈ R m ×n : A +( A )= O =( A )+ A
Hetoptellenin R m ×n iscommutatief.
∀ A , B ∈ R m ×n : A + B = B + A
• Jekentdeeigenschappenvandescalairevermenigvuldigingenkuntzeaantonen.
Descalairevermenigvuldigingvaneenreëelgetalmeteenelementvan R m ×n , levertopnieuweenelementvan R m ×n op.
∀ r ∈ R , ∀ A ∈ R m ×n : r A ∈ R m ×n
Descalairevermenigvuldigingvanreëlegetallenmeteenelementvan R m ×n isgemengd associatief.
∀ r , s ∈ R , ∀ A ∈ R m ×n : r ( s A )=( r s ) A
Descalairevermenigvuldigingisdistributieft.o.v.deoptellingin R m ×n
∀ r ∈ R , ∀ A , B ∈ R m ×n : r ( A + B )= r A + r B
Descalairevermenigvuldigingisdistributieft.o.v.deoptellingin R
∀ r , s ∈ R , ∀ A ∈ R m ×n : ( r + s ) A = r A + s A
Hetproductvandescalair1meteen m × n -matrix A isgelijkaandezematrix A
1 ∈ R en ∀ A ∈ R m ×n : 1 A = A
• Jekentdeeigenschappenvandevermenigvuldigingvanvierkantematricesenkuntzeaantonen.
Hetvermenigvuldigenisinternin R n ×n .
∀ A , B ∈ R n ×n : A B ∈ R n ×n
Hetvermenigvuldigenin R n ×n isassociatief.
∀ A , B , C ∈ R n ×n : A · ( B · C )=( A · B ) · C
Deeenheidsmatrixiseenneutraalelementvoordevermenigvuldigingin R n ×n .
I n ∈ R n ×n en ∀ A ∈ R n ×n : A · I n = A = I n · A
Hetvermenigvuldigenin R n ×n isnietcommutatief.
∃ A , B ∈ R n ×n : A · B = B · A
• Jeweetdat A en B nuldelerszijnals A B = O of B A = O (en A = O , B = O ) .
• Jekentdedefinitiesvanidempotente,nilpotenteeninvolutorischematrices.
Indienvooreenvierkantematrix A (= O ) geldtdat A 2 = A ,dannoemenwe A eenidempotente matrix.
Indienvooreenvierkantematrix A (= O ) eenvannulverschillendnatuurlijkgetal n bestaat waarvoor A n = O ,dannoemenwe A eennilpotentematrixmetindex n .
Eenvierkantematrix A isinvolutorischindien A 2 = I
37 1 Matrices
9 Oefeningen
A = a 6 1 2 B = 2 b 33 1 2 3 4 5 6 7
Gegeven: A = 32 4 3 en B = 32 53
Toonaandat ( A + B )2 = A 2 + B 2 .Hoekunjeditverklaren?
De n × n -matrices A en B commuteren met elkaar enkel en alleen indien de matrices A + B en A – B met elkaar commuteren.
Bewijs dit.
Toonaandatallematricesvandevorm ab ba commuteren.
Welke van de volgende beweringen zijn waar ? Verklaar.
a ∃ A , B ∈ R n ×n : A · B = B · A
b ∀ A , B ∈ R n ×n : ( A + B )( A B )= A 2 B 2
c ∀ A , B ∈ R n ×n : A · B = O ⇐⇒ A = O of B = O
d ∀ A ∈ R n ×n : A 2 = O =⇒ A = O
e ∀ A ∈ R n ×n : A 2 = O =⇒ A 3 = O
f ∀ A , B ∈ R n ×n : A B = O =⇒ B A = O
Gegevenisdematrix M = abcd efgh .
aBedenkeenmatrix A waarvoorgeldt: M · A = M
bBedenkeenmatrix B waarvoorgeldt: B M = M
Bepaal x en y zodat de matrices A en B commuteren.
a A = 5 4 63 ; B = 7 6 x 4
b A = 12 x y 7 ; B = 1 9 46
c A = 11 x 35 ; B = 02 y 9
d A = 87 71 ; B = 5 x 2 y
Bepaal a en b zodat A en B idempotent zijn.
38
10
Toonaandatals bc = a a 2 ,dematrix M = ab c 1 a idempotentis.
Bepaal c en d zodat C en D involutorisch zijn.
C = 54 c 5 D = 67 5 d
Toonaandatals bc = 1 a 2 ,dematrix M = ab c a involutorischis.
11
Bepaal e en f zodat E en F nilpotent met index 2 zijn.
E = e 8 2 4
F = 1216 f 12
12
Toonaandatals bc = a 2 ,dematrix M = ab c a nilpotentmetindex2is.
Gegeven :
K = 84 pq L = 87 rs M = 8 4 tu
K 2 = KL 2 = IM 2 = O
Gevraagd :
Bepaal p , q , r , s , t , u ∈ R.
Tip : maak gebruik van de oefeningen 8, 10 en 12.
Gegeven: A = ab cd waarbij a , b , c , d ∈ R
Gevraagd:Toonaandat A 2 =(a + d ) A (ad bc ) I 2 . WerkditookuitmetICT.
Gegeven: P = 1 5 k lm
Gevraagd:Bepaal k , l en m zodat P = P 2 en P P T 2 = O
Gegeven: Q = kl m 0
Gevraagd:Bepaal k , l en m zodat Q 2 = I en Q = Q T
1 39 Matrices
8 9
13 14 * 15 16
Bewijs : als A B = A én B A = B , dan zijn A en B idempotent.
Gegeven : A is een vierkante matrix
Gevraagd : Bewijs de volgende uitspraken.
a De matrix A + A T is een symmetrische matrix.
b De matrix A – A T is een scheefsymmetrische matrix.
c De matrix A A T is een symmetrische matrix.
A en B zijn 3 × 3-matrices waarvoor geldt : A B = B A .
Bereken ( A + B ) ( A 2 – AB + B 2).
Bewijs : ( A B C )T = C T B T A T
Als A een nilpotente matrix is met index 3, B idempotent is en C involutorisch, vereenvoudig dan volgende uitdrukking (m.a.w. bepaal X ) :
X = A 4 – B 3 + C 2 – I
Gegeven :
A is een nilpotente matrix met index 3.
is een idempotente matrix.
C en D zijn nuldelers.
Gevraagd : Bereken indien mogelijk (indien niet mogelijk, verklaar dan waarom):
a (G (3 A 4
Bereken A en B als M = A · B
40
A = 482 2 4 1 120 B = 2 2 4 134 1 2 3 C = 123 010 246 D = 3 6 3 000 121 F = 200 030 00 1 G = 321 40 1
B
C D ))T ( B 2 F 3 ) (G I 3 )T
+(2CD )T ( F 3 B 2 ) ( I 3 G )T M = 12 3 325 453 A = 100 .10 ..1 B = 0.. 00.
2
b G T G 2 A 3
17 * 18 * 19 20 21 22 23 *
Welke van de volgende uitspraken is juist ? Verklaar je antwoord.
a A ∈ Rn ×n is idempotent ⟹ 2A – I is involutorisch
b A ∈ Rn ×n is idempotent ⟹ 2A – I is idempotent
c A ∈ Rn ×n is idempotent ⟹ 2A – I is nilpotent
d A ∈ Rn ×n is idempotent ⟹ A en A – I zijn nuldelers
Wenoemen A ∈ R n ×n orthogonaal indien A A T = I n .
aToonaandat A =
√2 2 √2 2 √2 2 √2 2
eenorthogonalematrixis.
bToonaandat B = 01 10 eenorthogonalematrixis.
cToonaandat C = cos α sin α sin α cos α eenorthogonalematrixis.
dToonaandat D =
1 9 8 9 4 9
1 9 4 9
ControleerditmetICT.
eenorthogonalematrixis.
Veronderstel α ∈ R enbeschouwdematrix A = 01 α 00 α 001
Welk getal staat op de tweede rij, derde kolom van de matrix A25 ?
(A) –α (B) α (C) α24 (D) –α25
IJkingstoets burgerlijk ingenieur juli 2023, oefening 5
1 41 Matrices
4 9 4 9 7 9 8 9
24 * 25 26
1.3 Matrixvoorstelling van een graaf
1 Overgangsmatrices
Voorbeeld 1 : de amateurmeteoroloog
Thomas wil later meteoroloog worden. Nu al houdt hij zorgvuldig alle gegevens over het weer bij. Zo onderscheidt hij voor de weersgesteldheid voor een dag in april drie situaties : warm weer (W), bewolkt (B) en regen (R).
Na de bestudering van een groot aantal statistieken komt Thomas tot de volgende uitspraken.
– Is het vandaag warm weer, dan zijn de kansen voor morgen :
warm weer 0,6 ; bewolkt 0,3 ; regen 0,1
– Is het vandaag bewolkt weer, dan zijn de kansen voor morgen :
warm weer 0,3 ; bewolkt 0,4 ; regen 0,3
– Is het vandaag regenachtig, dan zijn de kansen voor morgen :
warm weer 0,1 ; bewolkt 0,5 ; regen 0,4
Het regent vandaag. Youssef heeft echter voor overmorgen een barbecue georganiseerd en hij vraagt aan Thomas wat de kans is dat die kan plaatsvinden. M.a.w. wat is de kans dat, als het op een dag in april regent, dat het twee dagen later mooi weer is ?
Dit probleem kunnen we natuurlijk oplossen door gebruik te maken van een kansboom :
Antwoord : 0,06 + 0,15 + 0,04 = 0,25. M.a.w. er is 25% kans dat de barbecue kan plaatsvinden met mooi weer. Meteorologisch hebben we te maken met drie toestanden (W, B en R) die in elkaar kunnen overgaan. Schematisch voorgesteld geeft dit de volgende figuur :




















42
R vandaag morgen overmorgen B R B W 0,6 0,3 0,5 0,1 0,4 0,1 R W 0,1 · 0,6 = 0,06 0,5 0,3 = 0,15 0,4 · 0,1 = 0,04 B R W B R W
R W B 0,4 0,4 0,6 0,5 0,3 0,3 0,3 0,1 0,1
Zo’n schema noemen we een gewogen graaf. De punten (knooppunten) van de graaf zijn de weersituaties. De getallen bij de pijlen zijn de kansen op de mogelijke overgangen tussen de weertypen.
Die kansen kunnen we nu samenbrengen in een matrix A . van
A =
WBR
0,60,30,1 0,30,40,5 0,10,30,4
W B R naar
Die matrix A noemen we een overgangsmatrix. Bij afspraak zetten we steeds het woordje ‘van’ bovenaan.
Bekijken we opnieuw de kansboom. Daar werd de gevraagde kans verkregen door de som van de volgende producten :
0,6 · 0,1 + 0,3 · 0,5 + 0,1 · 0,4
Je maakt dezelfde berekening als je het element a 13 van de matrix A 2 wil bepalen.
W B R W ......0,1
B ......0,5 R ......0,4
A = naar
= A
W B R
0,60,30,1
Regent het vandaag, dan geeft het element a 13 van A 2 blijkbaar de kans dat het twee dagen later mooi weer is. Geeft A de kansen op de overgangen voor één dag, dan geeft A 2 de kansen per twee dagen.
Analoog geeft A 3 de overgangen per drie dagen en A n de kansen per n dagen.
Taak:
– Bereken A 2 en bereken de kans dat het overmorgen regent.
– Door omstandigheden wordt de barbecue een dag verlaat. Bereken de kans dat het dan mooi weer is.
 Arthur Cayley
Arthur Cayley
Arthur Cayley (Richmond 1821 – Cambridge 1895)
Als zoon van een koopman bracht de Brit Arthur Cayley de eerste acht jaren van zijn leven door in Rusland (Sint-Petersburg). Nadien keerden zijn ouders terug naar Engeland. Ondanks zijn talent voor wiskunde slaagde Cayley er niet in om na zijn studie in Cambridge als wiskundige aan de slag te gaan. Hij koos ervoor om als advocaat aan het werk te gaan om in zijn levensbehoeften te kunnen voorzien. In de 14 jaar dat hij dit beroep uitoefende, schreef hij wel zo’n 250 à 300 artikels over wiskunde. Dit maakte indruk en in 1863 werd hij toch benoemd als professor in Cambridge.
Alhoewel hij nu veel minder verdiende, was hij er gelukkig want hij had nu een baan waarop hij zich met hart en ziel kon toeleggen. Zijn productiviteit nam in alle hevigheid toe. Er volgden zeker 1000 artikels waarin de matrixrekening ruim de aandacht kreeg. Bijna 70 jaar na de dood van Cayley herkende de Duitse natuurkundige Werner Heisenberg (1901-1976) hierin het perfecte gereedschap om de kwantummechanica verder te ontwikkelen. In 1881 werd Cayley gedurende een semester gasthoogleraar aan de John Hopkins University in de Verenigde Staten. Elke les werd bijgewoond door Sylvester, die van 1876 tot 1883 hoogleraar was aan die universiteit. Zijn naam is verbonden met Cayleytafels, die vaak in de groepentheorie worden gebruikt.
43 1 Matrices
van
W
B ......... R
......0,25 .........
= A 2
Voorbeeld 2 : migratie
Ergens in een bepaalde regio in Zuid-Amerika verhuist jaarlijks 15% van de plattelandsbewoners ( P ) naar de steden ( S ), terwijl in diezelfde periode 10% van de stedelingen terug naar het platteland trekt.
Schematisch kunnen we dit met behulp van een graaf als volgt voorstellen :
Dit schema is nochtans niet correct, omdat het geen rekening houdt met de eventuele aangroei of inkrimping van de totale bevolking. Houden we nu rekening met het feit dat in diezelfde regio het bevolkingsaantal elk jaar met 4% toeneemt, dan krijgen we het correctere schema :
Net zoals in de vorige gevallen hoort bij die graaf een matrix. Dergelijke overgangsmatrix wordt ook wel migratiematrix genoemd.
Stel je voor dat er in 2022 in stedelijk gebied 68 000 mensen en op het platteland 82 000 mensen wonen, dan wonen er één jaar later :
0,936 · 68 000 + 0,156 · 82 000 = 76 440 in stedelijk gebied en 0,104 68 000 + 0,884 82 000 = 79 560 op het platteland.
De berekening gaat sneller wanneer je de bevolkingscijfers in matrixvorm noteert en je de matrixvermenigvuldiging uitvoert met je grafische rekenmachine.
Hoe zien de bevolkingcijfers in het stedelijk gebied en op het platteland er in 2030 uit ?


44
0,15 0,1 0,85 0,9 S P
0,156 0,104 0,884 0,936 S P
van M
0,1040,884
= SP 0,9360,156
S P naar
B2023 = M B2022 = 0,9360,156 0,1040,884 68000 82000
79560
= 76440
Voorbeeld 3 : Markovmodel
In een provinciestadje, niet zo ver hiervandaan, beconcurreren vier schoenwinkels (die we gemakshalve A, B, C en D noemen) elkaar. Er is dan ook heel wat verloop onder de klanten.
Dit verloop zouden we (op jaarbasis) kunnen voorstellen door de volgende graaf:












of de volgende overgangsmatrix : van
M =
35%15%20%5%
15%30%15%20%
20%35%45%15%
30%20%20%60%
Als momenteel 40% van het klantenpotentieel in schoenwinkel A koopt, 30% in B, 20% in C en 10% in D, kunnen we ons de volgende vraag stellen : Indien de overgangscijfers juist zijn, wat is dan de evolutie in de tijd en treedt er stabilisatie op ?
Stellen we de huidige verdeling van het klantenpotentieel
is de situatie na één jaar :
De evolutie in de loop der jaren
A
We hebben de indruk dat er inderdaad na verloop van tijd een stabiele verdeling van het klantenpotentieel is.
Namelijk 16% voor schoenwinkel A, 19,8% voor B, 28,2% voor C en 36% voor D.
Dit voorbeeld is een typisch voorbeeld van een Markovmodel.
Markovmodel
Een Markovmodel is een matrixmodel waarbij alle elementen van de matrix M positief of nul zijn en waarbij alle kolomsommen gelijk zijn aan 1 (of 100%).
45 1 Matrices
A B C D 20% 20% 35% 45% 60% 30% 20% 20% 15% 15% 20% 15% 30% 5% 35% 15%
ABCD
A B C D naar
voor door A 0 = 40% 30% 20% 10% dan
A 1 = M · A 0 = 0,350,150,200,05 0,150,300,150,20
· 0,40 0,30 0,20 0,10 = 0,23 0,20 0,29 0,28 = 23% 20% 29% 28%
0,200,350,450,15 0,300,200,200,60
:
is
n = M n · A 0 =
0,150,300,150,20 0,200,350,450,15 0,300,200,200,60 n · 0,40 0,30 0,20 0,10 of : nu na 1 jaar na 2 jaar na 3 jaar na 4 jaar na 5 jaar na 6 jaar na 7 jaar na 8 jaar A 40% 23,00% 18,25% 16,74% 16,25% 16,09% 16,04% 16,02% 16,02% B 30% 20,00% 19,40% 19,59% 19,70% 19,74% 19,76% 19,76% 19,76% C 20% 29,00% 28,85% 28,45% 28,29% 28,24% 28,22% 28,22% 28,22% D 10% 28,00% 33,50% 35,23% 35,76% 35,93% 35,98% 36,00% 36,00%
0,350,150,200,05
2 Populatiematrices of Lesliematrices
Voorbeeld 1 : tropische vogels
Twee ornithologen hebben een nieuwe vogelsoort ontdekt in het tropische Amazonegebied. Na jaren observatie komen ze tot de volgende conclusies :
– slechts 40% van de eieren komt uit en bereikt de leeftijd van één jaar ;
– de kans om het volgende levensjaar te halen is steeds 60% ;
– geen enkele vogel wordt ouder dan vijf jaar ;
– in het derde en vierde levensjaar legt elke vogel gemiddeld twee eieren, in het vijfde levensjaar is dat gemiddeld slechts één ei.
De populatie telt momenteel 80 eenjarigen, 50 tweejarigen, 30 driejarigen, 20 vierjarigen en 180 eieren (of nuljarigen).
Toon aan dat de soort met uitsterven bedreigd is en dat de populatie om de 16 jaar halveert.
Oplossing :
Om voorspellingen te kunnen doen over de samenstelling van bepaalde populaties dieren, maakte de Engelse zoöloog Leslie omstreeks 1945 gebruik van grafen en matrices.
De populatie vogels bestaat uit vijf generaties : nuljarige (= in hun eerste levensjaar), eenjarige, tweejarige, driejarige en vierjarige vogels. De gegevens hierboven zijn in een graaf weer te geven :
Die graaf kunnen we ook weergeven met een zogenaamde Lesliematrix of populatiematrix.




























De Lesliematrix beschrijft de overgang van de ene generatie vogels naar de andere en heeft in dit geval dus een overgangsperiode van 1 jaar, de duur van een generatie vogels. Op de eerste rij van de matrix L vind je de geboortecijfers van de populatie vogels. In de volgende rijen staan de overlevingskansen. De nullen op de tweede tot en met de vijfde rij geven aan dat zo’n overgang niet mogelijk is. Een populatiematrix is eigenlijk een speciale overgangsmatrix.
46
1 2 2 0,4 0 nuljarig 1 eenjarig 2 tweejarig 3 driejarig 4 vierjarig 0,6 0,6 0,6
van L = 0j1j2j3j4j 00221 0,40000 00,6000 000,600 0000,60 0j 1j 2j 3j 4j naar
De huidige populatie vogels kunnen we ook weergeven in de vorm van een matrix.
Na één jaar ziet de populatie vogels er als volgt uit :
Schetsen we de evolutie van het aantal vogels in de tijd, dan krijgen we de volgende populatietabel.






Hieruit blijkt overduidelijk dat, als er geen speciaal kweekprogramma wordt opgezet, de vogelsoort zal uitsterven. We zien ook dat de populatie om de 16 jaar halveert.
P. H. Leslie (1900 –1972)
P. H. Leslie was een Engels bioloog die in 1945 een model introduceerde dat het mogelijk maakte voorspellingen te doen over de samenstelling van populaties. Hij werkte op een afdeling van de universiteit van Oxford, waar ze zich bezighielden met het bestuderen van dierenpopulaties.
De matrices die naar hem genoemd zijn, worden vaak gebruikt in de demografie. Naar zijn werk ‘On the Use of Matrices in Certain Population Mathematics’ wordt in de vakliteratuur vaak verwezen.
47 1 Matrices
P0 = 180 80 50 30 20
P1 = L P0 = 180 72 48 30 18
P0 P4 P8 P12 P16 P20 P24 P28 P32 0 j 180 156 131 110 92 77 64 54 45 1 j 80 65 55 46 38 32 27 23 19 2 j 50 42 34 29 24 20 17 14 12 3 j 30 26 22 18 15 13 11 9 7 4 j 20 16 13 11 9 8 7 6 5 totaal 360 305 255 214 178 150 126 106 88
Voorbeeld 2 : red de okapi
De okapi is naaste familie van de giraf, maar is veel kleiner en zijn nek is niet zo lang. De okapi is pas door wetenschappers ontdekt in 1901. Hij komt alleen voor in de regenwouden in het noordoosten van Centraal-Afrika.
op 1-1-2022
op 1-1-2023


Een onderzoeksteam observeert de okapi in het wild om meer te weten te komen over zijn leefomgeving en behoeftes. In de volgende tabel staat informatie over de populatie okapi’s in de streek van Wamba.









Verder weten we dat 15% van de eenjarigen binnen het jaar sterft en dat alleen de volwassen exemplaren nakomelingen krijgen.





– Hoeveel nakomelingen heeft een volwassen okapi gemiddeld per jaar ? Wat zou een bioloog hieruit kunnen besluiten ?
– Wat is het sterftepercentage bij de kalveren ?
– Hoeveel procent van de volwassen dieren stierf in 2022 ? Als je aanneemt dat een volwassen okapi en een eenjarige evenveel kans hebben om te overleven, hoeveel procent van de okapi’s stierf er dan door ouderdom? Kun je hieruit de gemiddelde leeftijd van een okapi raden ?
– Wanneer we aannemen dat de populatie okapi’s zich na 2022 net zo ontwikkelt als in de tabel, hoeveel kalveren, eenjarigen en volwassenen zijn er dan op 1-1-2024? En op 1-1-2025 ?
– Toon aan dat het totale aantal okapi’s na 9 jaar met 25% verminderd is.
Oplossing:
– De 740 volwassen okapi’s zorgden voor 148 nieuwe kalveren. Dit is een gemiddelde van 0,2 per okapi. In de veronderstelling dat er evenveel mannetjes als wijfjes zijn, is dat een gemiddelde van 0,4 per wijfje of één kalf om de tweeënhalf jaar.
– Van de 140 kalveren bereiken er 126 de leeftijd van één jaar. M.a.w. het sterftepercentage bij kalveren is 10%.
– Als 15% van de eenjarigen sterft, dan worden er 0,85 · 120 = 102 eenjarigen volwassen. Het aantal volwassenen zou dus 102 + 740 = 842 moeten zijn. Vergelijken we dit met de waargenomen 694, dan moeten er 842 – 694 = 148 volwassen dieren gestorven zijn. Dit is 20%.
Als we veronderstellen dat de overlevingskans van een eenjarige en een volwassen okapi gelijk is (15%), dan sterft 5% van de volwassen okapi’s door ouderdom. D.w.z. dat de gemiddelde leeftijd van een okapi ongeveer ( 2 + 20) jaar = 22 jaar moet zijn.
– We stellen de gevonden percentages schematisch voor door een graaf.
De bijbehorende Lesliematrix en populatiematrix P 2022 zijn de volgende:
De evolutie van de populatie in de tijd kunnen we nu berekenen.
Hieruit kunnen we de antwoorden op de gestelde vragen afleiden.
Taak: stel een exponentiële functie op die het aantal okapi’s geeft in functie van de tijd. (t = 0 op 1-1-2022)

48
aantal
aantal
kalveren (0-1 jaar) 140 148 eenjarigen 120 126 volwassenen (2 jaar of ouder) 740 694
van L = KEV 000,2 0,900 00,850,8 K E V naar P = 140 120 740
P2022 P2023 P2024 P2025 P2026 P2027 P2028 P2029 P2030 P2031 kalveren 140 148 139 132 129 124 120 115 111 107 eenjarigen 120 126 133 125 119 116 112 108 104 100 volwassenen 740 694 662 643 621 598 577 556 536 517 totaal 1000 968 934 900 869 838 809 779 751 724
0,2 0,85 0,9 0,8
eenjarig kalf volwassen
Voorbeeld 3 : olifanten
Afrikaanse olifanten leven in groepjes, families of kuddes van wijfjes met hun jongen van verschillende leeftijden, onder leiding van een matriarch. De draagtijd is ongeveer 22 maanden, waarna er één jong geboren wordt.
Tweelingen komen voor, maar zijn uiterst zeldzaam. Een baby wordt 2 jaar gezoogd. Meestal baart een wijfje eens in de 4 jaar een jong.









Een Afrikaanse olifant is volwassen na 10 jaar. De jonge bull verlaat rond die leeftijd de kudde en zwerft dan solitair rond. De gemiddelde leeftijd van een olifant in het wild is 60 jaar. Elk jaar wordt, ondanks een totaal jachtverbod, minstens 5% van de populatie door stropers gedood. Een natuurreservaat bevat momenteel 80 olifanten : 10 baby’s (jonger dan 2 jaar), 20 jongen (die tussen 2 en 10 jaar zijn) en 50 volwassenen (ouder dan 10 jaar).
Hoe verlopen de aantallen binnen die populatie onder de gegeven voorwaarden ?
Oplossing:
We verdelen de olifanten in klassen, bijvoorbeeld :
– klasse I = baby’s = jonger dan 2 jaar
– klasse II = de jongen = 2- tot 10-jarigen
– klasse III = de volwassenen = +10-jarigen
Als tijdseenheid nemen we twee jaar.
We verwerken de gegevens :
– Een babyolifant evolueert eerst naar een jong ; omdat 10% van een kudde (ongeacht de leeftijd) wordt weggestroopt, evolueert 90% van de baby’s naar een jong.
–
1 4 van de jongen wordt volwassen, 3 4 blijft jong. Dus 3 4 van 90% van de jongen blijft in klasse II (= 67,5%) en 1 4 van 90% van de jongen wordt volwassen (= 22,5%) ; hiervan verlaat de helft (= de bulls) de kudde (maar die blijven wel in het reservaat).
4% van de volwassenen sterft van ouderdom, 10% wordt gestroopt ; de overlevingskans is dus ongeveer 86%.
–
– Om de vier jaar wordt er één baby per volwassen (vrouwelijke) olifant geboren : dat geeft 1 4 baby per olifant om de twee jaar.
Samengebracht in een Lesliematrix en bijbehorende graaf geeft dat :
van
L =
IIIIII 000,25 0,90,6750
00,2250,86
I II naar III
49 1 Matrices






50 I III II 0,25 0,22 0,86 0,67 0,9
START NA 1 JAAR NA 2 JAAR NA 3 JAAR NA 4 JAAR NA 5 JAAR NA 6 JAAR NA 7 JAAR NA 8 JAAR NA 9 JAAR NA 10 JAAR I 10 13 12 11 11 11 11 12 12 12 12 II 20 23 26 29 30 30 31 31 31 32 32 III 50 48 46 45 45 46 46 47 47 47 48 80 84 84 85 86 87 88 90 90 91 92
Verwachte evolutie van de populatie :
Met GeoGebra :
3 Verbindingsmatrices
Voorbeeld : directewegenmatrix
Jonas is reisleider voor het agentschap Blitz. Volgens de reisbrochure moeten de toeristen vijf bezienswaardigheden bezoeken in een bergachtige streek waar niet zoveel wegen voor busvervoer beschikbaar zijn.
De vijf bezienswaardigheden en hun onderlinge berijdbare verbindingswegen worden weergegeven door volgende graaf.





Er zijn twee directe wegen van E naar D. Eén daarvan is een eenrichtingsweg.
Omgekeerd is er maar één directe weg van D naar E. Er is een directe weg van C naar C. Zo’n weg heet een lus.

In een verbindingsmatrix (horend bij een graaf) staan enen en nullen. Een 1 geeft aan dat er een rechtstreekse verbinding is tussen de twee punten van de graaf. Een 0 geeft aan dat er geen rechtstreekse verbinding is.
In een directewegenmatrix staat het aantal rechtstreekse wegen tussen elk tweetal punten.
51 1 Matrices
A C D E B
van V = ABCDE 01100 10000 11101 10001 00110 A B C D E naar
van W = ABCDE 01200 10000 21101 10002 00110 A B C D E naar
Bij een gegeven directewegenmatrix W geeft de matrix W 2 informatie over het aantal tweestapswegen, dat zijn wegen met één tussenstop, tussen elk tweetal punten van de graaf.
van
ABCDE
52202
01200
W 2 =
33611
01420
31103
Zo blijkt uit W 2 dat je via één tussenstop van E naar A kunt, maar niet van E naar D.
Uit V blijkt dat je wel rechtstreeks van E naar D kunt.
Om te weten op hoeveel manieren je van de ene bezienswaardigheid naar de andere kunt met ten hoogste één tussenstop, maken we gewoon de som van de matrices W en W 2
van
ABCDE
53402
11200
W + W 2 =
54712
11422
31213
Analoog geeft W 3 het aantal driestapswegen tussen de punten van de graaf, of algemener geeft W n het aantal
n -stapswegen tussen de punten van de graaf.
W 2 , W 3, … noemen we meerstapsmatrices
4 Samenvatting
• Je kunt problemen oplossen die steunen op :
– grafen
– overgangsmatrices
– populatiematrices of Lesliematrices
– verbindingsmatrices
52
A B C D E naar
A B C D E naar
5 Oefeningen
Opmerking vooraf: bewerkingen met matrices in onderstaande oefeningen kun je uitvoeren met ICT.
De dagen in de maand juni zou je kunnen onderverdelen in vier categorieën. De dagen met een gemiddelde temperatuur onder de 20 °C noemen we fris (F), de dagen met een temperatuur tussen de 20 °C en 25 °C zijn normaal voor de tijd van het jaar (N), dagen tussen de 25 °C en 30 °C noemen we zomers (Z) en de dagen boven de 30 °C zijn heet (H).
– Na een frisse dag zijn de kansen voor de volgende dag :
fris 0,3 ; normaal 0,55 ; zomers 0,1 ; heet 0,05
– Na een normale dag zijn de kansen voor de volgende dag :
fris 0,15 ; normaal 0,6 ; zomers 0,2 ; heet 0,05
– Na een zomerse dag zijn de kansen voor de volgende dag :
fris 0,1 ; normaal 0,4 ; zomers 0,4 ; heet 0,1
– Na een hete dag zijn de kansen voor de volgende dag : fris 0,05 ; normaal 0,35 ; zomers 0,45 ; heet 0,15
a Vervolledig de onderstaande graaf . N Z F H
b Vandaag, dinsdag, is de gemiddelde temperatuur 24 °C. Wat is de kans dat het vrijdag op de sportdag een zomerse dag wordt ?
De meeneempizzazaak op de hoek verkoopt pizza’s met verschillende bodems. Je hebt de klassieke bodem licht en krokant (A), de pizza’s met een korstje gevuld met kaas (B) en de panpizza waarbij het deeg goudbruin gebakken is in de pan (C). Over een periode van een kwartaal blijven de meeste klanten hun pizzabodem trouw, maar sommigen stappen nadien over naar een andere bodem. (Zie hiervoor overgangsmatrix P ) van
a Hoeveel procent van de klanten die dit kwartaal een klassieke pizza gekocht hebben, doen dat volgend kwartaal opnieuw ?
b Op dit ogenblik koopt 45% van de klanten een klassieke pizza, 25% een kaaspizza en 30% een panpizza. Bereken de procentuele verdeling van de klanten voor het volgende kwartaal, na twee kwartalen en na drie kwartalen.
c Hoeveel procent van de klanten koopt volgend kwartaal dezelfde soort pizza als op dit ogenblik ?
Op een stuk landbouwgrond worden graangewassen (G), kolen (K) en bieten (B) verbouwd. Uit volgende graaf blijkt dat niet elk jaar de verdeling van die teelten over de grond dezelfde is.
a Stel de bijbehorende overgangsmatrix op.
b Dit jaar wordt 40% van de grond gebruikt voor graangewassen. De rest wordt gelijkmatig verdeeld voor de kolen en de bieten. Hoe ziet de verdeling er de komende twee jaren uit ?
c Op hoeveel procent van de grond wordt twee jaar later hetzelfde verbouwd als dit jaar
1 53 Matrices
P =
ABC 0,800,150,07 0,120,750,03 0,080,100,90
A B C naar
? B G K 0,2 0,15 0,45 0,4 0,15 0,35 0,15 0,5 0,65 1 2
3
Op een Thais eiland wonen op een zeker tijdstip 8000 mensen.
In het enige dorp van het eiland wonen op dat tijdstip 3000 mensen, de overige wonen op het platteland.
Per jaar trekt 18% van de dorpsbewoners naar het platteland, terwijl 24% van de plattelandsbewoners naar het dorp trekt.
De omvang van de bevolking van het eiland is constant, geboorte en sterfte houden elkaar in evenwicht.
a Geef het migratiepatroon op het eiland weer met een graaf en met een matrix.
b Bereken hoe de bevolking verdeeld zal zijn over dorp en platteland na 1, 2 en 3 jaar.












c Hoe zou de bevolking over dorp en platteland verdeeld moeten zijn opdat de aantallen dorpsbewoners en plattelandsbewoners zich door migratie niet meer zouden wijzigen ? M.a.w. welke verdeling over dorp en platteland is stabiel ?
Een gebied ergens in Midden-Amerika kun je demografisch indelen in drie deelgebieden :
– de kuststreek (K) waar momenteel 25% van de bevolking woont;
– de plaatselijke dichtstbijzijnde stad (S) die 15% van de bevolking huisvest;
– het binnenland (B) met de overige 60% van de bevolking.
Dit gebied kent het volgend migratiepatroon :
– 6% van de binnenlandse bevolking trekt naar de kust, 10% naar de stad;
– 10% van de kustbewoners trekt naar de stad, 2% keert terug het binnenland in;
– 10% van de stadsbewoners kiest voor de kuststreek, 4% keert terug naar het binnenland.
Gevraagd :
a Stel dit migratieproces grafisch voor m.b.v. van een graaf.
b Stel de bijbehorende migratiematrix op.
c Ga na of die migratiematrix een Markovmodel is.
d Hoe verloopt de verdeling van de bevolking op lange termijn ?

Een zwemclub deelt zijn leden in naar zwemervaring en leeftijd.
Na de zwemschool (Z) word je waterduivel (W) om vervolgens aan competitiezwemmen (C) te doen en ten slotte een senior (S) te worden.
Uit ervaring weten we dat de jaarlijkse overgang van de leden beschreven wordt door de volgende overgangsmatrix A
a Hoe kun je uit de overgangsmatrix aflezen dat alleen de waterduiveltjes volledig binnen de club blijven ?
b De samenstelling van de club bestaat uit 60 leden in de zwemschool, 30 waterduivels, 30 competitiezwemmers en 20 senioren. Bereken de samenstelling van de club na drie jaar.
c Volgens dit model vermindert het aantal leden in de zwemschool. Nu schrijft de zwemschool jaarlijks nieuwe leden in, zodat het aantal leden steeds 60 blijft. Hoe ziet de nieuwe overgangsmatrix er dan uit ? Bereken met die matrix de verdeling na drie jaar.
54
4
van A = ZWCS 0,5000 0,30,600 00,40,70 000,20,8 Z W C S naar
5 6
Op een Bloso sportkamp kunnen de deelnemers elke dag kiezen uit vier soorten activiteiten : gevechtssporten (GS), balsporten (BS), watersporten (WS) en survival (SV). Uit ervaring weet de leiding dat sommige deelnemers graag elke dag veranderen van activiteit, sommige kiezen dan weer elke keer hetzelfde. Ze zouden dit kunnen voorstellen door volgende graaf :
Stel dat het kamp begint op een maandag. Op die dag kiezen 10 deelnemers voor gevechtssporten, 25 voor balsporten, 40 voor watersporten en 15 voor survival. Hoe is dan de verdeling op vrijdag?
















































Een houtzagerij koopt in Canada
1000 ha bosrijke grond en besluit het volgende systeem te hanteren :
–3 5 2 5 1 10 van de open ruimte (= niet bebost of ontbost gebied) wordt aangeplant;
–3 5 2 5 1 10 van de oudere kaprijpe bomen wordt gerooid.
Verder is gegeven dat jaarlijks 3 5 2 5 1 10 van de jonge bomen kaprijp is en het gebied momenteel de volgende verdeling kent : 20% open ruimte (O), 40% jonge bomen (J), 40% kaprijpe bomen (K).
Gevraagd :
a Stel dit proces van rooien en aanplanten grafisch voor m.b.v. van een graaf.
b Stel de bijbehorende evolutiematrix op.
c Ga na of die matrix een Markovmodel is.
d Hoe verloopt de verdeling van het gebied op lange termijn ?



































1 55 Matrices
GS BS WS SV 0,35 0,20 0,20 0,40 0,30 0,40 0,10 0,25 0,20 0,10 0,20 0,30 0,25 0,30 0,25 0,20
7 8
Leden van een scoutsvereniging worden onderverdeeld in verschillende leeftijdsgroepen, takken genaamd. Elke tak is verschillend, de activiteiten zijn aangepast aan de leeftijd. De meeste takken hebben een driejarige werking. Op die manier krijgen de leden elk jaar een andere functie in de tak. Als eerstejaars moeten ze nog veel leren, als derdejaars kunnen ze zelf al eens verantwoordelijkheid opnemen. We onderscheiden vijf takken :
– 7 tot 8 jaar : kapoenen (K)
– 9 tot 11 jaar : welpen en kabouters (W)
– 12 tot 14 jaar : jonggivers (giver is een samentrekking van gids en verkenner) (JG)
– 15 tot 17 jaar : givers (G)
– 18+ : jins (J)
Uit ervaring weten ze dat de jaarlijkse overgang van de leden beschreven wordt door de volgende overgangsmatrix : van






A
KWJGGJ 10000 0,40,65000 00,350,500 000,30,50 0000,250,4
K W JG G J naar


















a Hoe kun je aan de matrix zien dat er elk jaar nieuwe kapoenen worden ingeschreven ?
b Stel de matrix voor d.m.v. een graaf.
c Momenteel zijn er 45 kapoenen, 70 welpen, 55 jonggivers, 35 givers en 20 jins. Hoeveel zijn dat er van elke groep volgend jaar ?
d Stijgt het ledenaantal op termijn of daalt het ?
e Is er (volgens dit model) stabilisatie op langere termijn ? Zo ja, hoe ziet de verdeling van de leden er dan uit ?
De drie vrienden Aad, Mitch en Jente gaan geregeld uit. Telkens is het een van hen die de andere twee trakteert.
– De kans dat nadat Mitch trakteert, Aad, Jente of Mitch opnieuw trakteert, is even groot.
– Aad trakteert nooit tweemaal na elkaar. De kans dat Jente na een traktatie van Aad trakteert, is dubbel zo groot als de kans dat Mitch trakteert.
– Jente trakteert nooit tweemaal na elkaar. De kans dat Aad na een traktatie van Jente trakteert, is driemaal zo groot als de kans dat Mitch trakteert.
Gevraagd :
a Stel dit traktatieproces grafisch voor m.b.v. van een graaf.
b Stel de bijbehorende matrix op.
c Ga na of die matrix een Markovmodel is.












d Wie heeft na verloop van tijd het meest getrakteerd, en wie het minst ? Hoe liggen de verhoudingen ?
56
=
9 10
13
De groei van een populatie vissen wordt vaak gekenmerkt door hoge vruchtbaarheidscijfers en door een lage overlevingskans voor pasgeboren exemplaren. Van een populatie vissen zijn de volgende gegevens bekend :
– slechts 0,5% van de eitjes komt uit en haalt het eerste levensjaar ;
– eenjarigen hebben 40% kans om het jaar te overleven ;
– tweejarigen hebben 70% kans om drie jaar oud te worden ;
– geen van de vissen haalt de leeftijd van 4 jaar ;
– alleen driejarige vissen kunnen nakomelingen hebben, gemiddeld legt zo’n vis 800 eitjes.
Een bioloog vangt duizend visjes (500 eenjarigen, 300 tweejarigen en 200 driejarigen) en 100 000 eitjes en laat die weer vrij in een nieuwe omgeving. Hoe verloopt die populatie de komende 8 jaar ?
De levensloop van een bepaald soort knaagdier wordt weergegeven door de volgende graaf.
14 *
a Stel de bijbehorende populatiematrix op.
b Ga uit van 50 nuljarigen, 40 eenjarigen en 30 tweejarigen en ga na hoe de totale populatie zich zal ontwikkelen.
c Toon aan dat, als ze erin slagen om de overlevingskans van de eenjarigen van 70% naar 77% te brengen, de populatie na een aantal jaren stabiel wordt.
























Stel je een bepaalde soort kevers voor die maximaal zo’n drie jaar oud worden. Door statistisch onderzoek is het volgende gebleken :
– 30% van de kevers overleeft gemiddeld het eerste levensjaar ;
– in het eerste levensjaar heeft een kever gemiddeld 0,7 nakomelingen ; – 6% van de kevers overleeft gemiddeld het tweede levensjaar ; – in het tweede levensjaar heeft een kever gemiddeld 1,6 nakomelingen ; – geen enkele kever wordt ouder dan drie jaar en in het derde jaar krijgt een kever geen nakomelingen.
Stel de gegevens voor door een graaf en stel de bijbehorende populatiematrix op.
Een chemische reactor is voor 30% gevuld met stof A, voor 50% met stof B en voor 20% met stof C. Die stoffen reageren onderling. Uit berekeningen blijkt dat na een dag het volgende gebeurd zal zijn : van stof A blijft 60% behouden, 30% wordt omgezet in stof B en 10% in stof C ; van stof B blijft 50% behouden, 40% wordt omgezet in stof A en 10% in stof C ; van stof C blijft 40% behouden, 40% wordt omgezet in stof A en 20% in stof B. Breng de gegevens over in een schema en bereken de situatie na 1, 2 en 3 dagen.Treedt er op lange termijn stabilisatie op ?
1 57 Matrices
1,1 0,4 0 j 1 j 2 j 3 j 0,7 0,8 0,1
11 800 0,7 0,005 0,4 eenjarig tweejarig driejarig eitjes
12
In de lente van 2019 en in de lente van 2021 brachten biologen de populatie tijgers in kaart van een welbepaald gebied. De tijgers zijn daarbij ingedeeld in vier leeftijdsklassen. Iedere leeftijdscategorie bevat evenveel mannetjes als vrouwtjes.


















Op grond van die gegevens gaan biologen ervan uit dat de verandering in de aantallen tijgers per leeftijdscategorie beschreven kan worden met een 4 × 4-matrix T , een zogeheten tijgerpopulatievoorspellingsmatrix.
– Neem aan dat alle vrouwelijke tijgers in de klassen II, III en IV jongen krijgen en wel evenveel per twee jaar, ongeacht de klasse waarin zij zich bevinden.
– Neem verder aan dat de overlevingskans voor tijgers in klasse III even groot is als voor de tijgers in klasse II.
a Stel de matrix T op.
b ‘Er zijn zoveel jonge tijgers dat een tijgerplaag dreigt’, zegt de Perzische overheid. De boswachter zegt : ‘Welnee, de tijgers dreigen juist uit te sterven’. Wie heeft gelijk ? Motiveer je antwoord.
Gegeven :
Ergens in de Braziliaanse jungle vertoont een kolonie dwergaapjes een bepaald sociaal gedrag. De kolonie kan opgesplitst worden in drie duidelijke deelgroepen (A, B en C) die min of meer zelfstandig leven. Het eigenaardige is dat er tussen de groepen een vast verloop van aapjes is. Om de twee maanden verlopen 15% van de aapjes uit groep A naar groep B en 10% van de aapjes uit groep A trekt naar groep C. Analoog verlopen tweemaandelijks 8% van de aapjes uit groep B naar groep A en 20% van groep B naar groep C.
Van groep C vind je twee maanden later 12% in groep A en 5% in groep B.
Gevraagd :


a Stel dit migratieproces grafisch voor met behulp van een graaf.
b Stel de bijbehorende migratiematrix op.
c Ga na of die migratiematrix een Markovmodel is.
d Hoe verloopt de verdeling van de aapjes in de drie groepen op lange termijn ?



58
klasse lente 2019 lente 2021 I (0- en 1-jarigen) 150 315 II (2- en 3-jarigen) 150 90 III (4- en 5-jarigen) 150 90 IV (6-jarig en ouder) 150 150
15 16
Julie weet nooit welk vervoermiddel te kiezen om van de ene kant van de stad naar de andere kant te gaan. Neemt ze de tram, neemt ze de bus of gaat ze met de metro ? Ze heeft het volgende ingenieuze plan bedacht.
In de zitkamer staan drie vazen : een rode, een blauwe en een gele. In de rode vaas legt ze drie rode, twee blauwe en één gele bal, in de blauwe vaas twee rode, drie blauwe en één gele bal en in de gele vaas één rode, één blauwe en vier gele ballen.




















Ze trekt een bal uit de rode vaas en legt hem terug. Is de getrokken bal rood, dan gaat ze met de tram en neemt ze de volgende keer opnieuw een bal uit de rode vaas. Is de bal blauw, dan neemt ze de bus en neemt ze de volgende keer een bal uit de blauwe vaas. Is de bal geel, dan gaat ze met de metro en neemt ze de volgende keer een bal uit de gele vaas. Dezelfde regels gelden bij het nemen van een bal uit een andere vaas.
Gevraagd :
a Stel dit ingenieuze systeem grafisch voor m.b.v. van een graaf.
b Stel de bijbehorende matrix op.
c Ga na of die matrix een Markovmodel is.
d Welk vervoermiddel neemt Julie na verloop van tijd het meest en welk het minst ?
Hoe liggen de verhoudingen ?
Een autoverhuurbedrijf heeft vestigingen in Antwerpen, Brugge en Dinant.
Op t = 0, met t in maanden, zijn er 100 auto’s in de vestiging in Antwerpen, 90 in de vestiging in Brugge en 80 in de vestiging in Dinant. Na afloop van de huurperiode mag de huurder zelf beslissen in welke vestiging hij de auto aflevert.
Onderzoek wijst uit dat 10% van de auto’s uit Antwerpen na een maand in Brugge terechtkomt en 5% in Dinant.
20% van de auto’s uit Brugge wordt in Antwerpen afgeleverd en 15% in Dinant.
15% van de auto’s uit Dinant staat één maand later in Antwerpen, 10% in Brugge.
a Stel die situatie voor d.m.v. een graaf.
b Geef de bijbehorende overgangsmatrix.
c Ga na of die matrix een Markovmodel is.
d Na verloop van tijd stabiliseert de situatie. Geef de stabiele situatie.
























1 59 Matrices
17 *
18
Een kweker van taxusplantjes heeft 5 klassen van plantjes in voorraad.
klasse lengte aantal
I kleiner dan 40 cm 1457
II van 40 cm tot 60 cm 1214
III van 60 cm tot 80 cm 694
IV van 80 cm tot 1 m 397
V groter dan 1 m 238
Een plantje groeit per jaar maximaal 20 centimeter. Een plantje blijft dus in dezelfde klasse of gaat over naar de volgende klasse. Indien de kweker alle plantjes zou laten staan, zouden we dit schematisch als volgt kunnen weergeven.
Het is natuurlijk niet de bedoeling van de kweker om de plantjes te laten staan, hij wil zo veel mogelijk verkopen. Plantjes van klasse I worden niet verkocht en voor elk verkocht plantje van klasse II tot V wordt een nieuw taxusplantje geplant in klasse I.
Zoek een schema zodat de taxuskweker jaar in jaar uit evenveel plantjes kan blijven verkopen. M.a.w. hoeveel plantjes uit klasse II tot V mag hij jaarlijks te koop aanbieden ? Of bereken a , b , c en d in het volgend schema.
In het moestuintje (2 are groot) kweekt tuinman Alfred verse groenten. Momenteel staan er in het moestuintje 60 m2 tomaten, 35 m2 sla, 50 m2 wortelen en 55 m2 boontjes.
Om de grond niet te veel uit te putten, plant hij nooit twee keer hetzelfde op dezelfde plaats. Hij gebruikt volgend schema om te bepalen wat er het volgende jaar waar komt .















a Hoe ziet de verdeling van de vier groenten in de moestuin er volgend jaar uit ?
b Hoe ziet de verdeling van de vier groenten in de moestuin eruit binnen vijf jaar ?
c Is er op lange termijn een vaste verdeling ?
60
0,25 0,75 I II III IV V 0,2 0,2 0,15 0,8 0,8 0,85 1
d c b a 0,25 0,75 0,8 – a 0,8 – b 0,85 – c 1 – d I II III IV V 0,2 0,2 0,15
Zo ja, welke ? W T S B 0,20 0,45 0,45 0,35 0,40 0,35 0,30 0,25 0,40 0,30 0,30 0,25 19 20
De graaf hieronder geeft de situatie weer van een skigebied. Vanuit het dal D gaan twee skiliften naar K en L. Vanuit K en L vertrekken dan weer skiliften naar M. Vanuit de verschillende toppen starten verschillende afdalingen (zie de cijfers naast de desbetreffende weg).

a Hoeveel tweestapswegen zijn er van D naar M ?
b Hoeveel tweestapswegen zijn er van M naar D ?
c Hoeveel tweestapswegen zijn er van K naar K ?
d Hoeveel tweestapswegen zijn er van K naar L ?




e Op hoeveel verschillende manieren kan een skiër van M naar D, al dan niet met een tussenstop?
Ergens in de Stille Oceaan bevindt zich een kleine eilandengroep. Tussen de verschillende eilandjes vaart op regelmatige tijdstippen een veerboot, zoals aangeduid op onderstaand schema.
Is het mogelijk om via ten hoogste één tussenstop van om het even welk eiland naar om het even welk ander eiland te gaan ?
Een vliegtuigmaatschappij vliegt over enkele Europese steden volgens het schema hiernaast.
a Stel dit vliegschema voor door een graaf.
b Geef de bijbehorende overgangsmatrix.
c Van waar naar waar kun je niet vliegen met hoogstens één tussenstop ?
d Kun je van elke stad naar elke stad met hoogstens twee tussenstops ?
van naar
Pristina Chisinau
Chisinau Podgorica
Podgorica Pristina
Chisinau Vaduz
Vaduz Vilnius
Vilnius Pristina
Pristina Vilnius
Vilnius Valletta
Valletta Pristina
Podgorica Valletta
Valletta Podgorica
1 61 Matrices
L D K M 2 3 2 4 2 1 1 2 3
Alfa
Jota
Omega
Epsilon
Utopia
21
22 23
24
Een vliegtuigmaatschappij vliegt over enkele Centraal-Amerikaanse steden volgens onderstaand schema.
a Stel dit vliegschema voor door een graaf.
b Geef bijbehorende verbindingsmatrix.
c Van welke stad naar welke stad kun je niet vliegen met hoogstens één tussenstop?
d Kun je van elke stad naar elke stad met hoogstens twee tussenstops?
25
Een busmaatschappij heeft busverbindingen zoals weergegeven in volgende graaf.
a Geef bijbehorende verbindingsmatrix.
b Van waar naar waar kun je een bus nemen met hoogstens één tussenstop?
c Kun je vanuit elke bushalte elke andere bushalte bereiken met hoogstens twee tussenstops?
Gegeven is de volgende verbindingsmatrix tussen acht treinstations.
van naar
Iquitos
Iquitos
Bogota
Caracas
a Stel de verbindingsmatrix voor door een graaf.
b Van waar naar waar kun je een trein nemen met hoogstens één tussenstop?
c Kun je vanuit elke treinhalte elke andere treinhalte bereiken met hoogstens twee tussenstops?
Bogota
Panama
Caracas
San José
San José Iquitos
San José Quito
Quito
Quito
Panama
Bogota
San José
Caracas
Panama Quito
62
van V = ABCDEFGH 01000101 10110000 01011000 01101110 00110010 10010010 00011101 10000010 A B C D E F G H naar
A B C D E F G
A B D C E G F H
26
Zes volleybalploegen (A, B, C, D, E en F) spelen een toernooi.
A wint van B, D en E
B wint van D, E en F
C wint van A, B en D
D wint van E en F
E wint van C en F
F wint van A en C
a Bij dit probleem kun je een gerichte graaf tekenen met pijlen van winnaar naar verliezer. Stel de directewegenmatrix V op die bij de graaf hoort. Hoe volgt uit de matrix V dat A, B en C gelijk zijn geëindigd?
b Omdat er slechts één beker beschikbaar is, telt de jury het aantal ‘tweestapsoverwinningen’ mee. Om die tweestapsoverwinningen in de eindbeoordeling niet te laten doorwegen, wordt de eindstand bepaald door V + 0,5 · V 2. Geef de eindstand van het toernooi.
In de bossen van Twin Peaks worden maandelijks het aantal uilen en het aantal muizen geteld. Als we met Un het aantal uilen in maand n noteren en met Mn het aantal muizen uitgedrukt in 1000 in maand n, dan blijkt de volgende gelijkheid een goed wiskundig model te zijn voor de evolutie van de populaties: voor elk natuurlijk getal n is
Un +1 M n +1 = 0,50,4 0,1041,1 Un M n
In een maand zonder uilen zouden de muizen een belangrijke natuurlijke vijand kwijt zijn. Met hoeveel procent zou de muizenpopulatie in zo’n maand groeien?
IJkingstoets basiskennis wiskunde handelsingenieur 2020, vraag 22
1 63 Matrices
gewonnen verloren A 3 2 B 3 2 C 3 2 D 2 3 E 2 3 F 2 3
(A) 0,1% (B) 10% (C) 110% (D) 700%
27 * 28
Matrices 1
64 WAT MOET JE KENNEN EN KUNNEN ?
pagina Ik ken de definitie van een m × n-matrix en kan een matrix noteren met de juiste symbolen. 9 Ik ken de definitie van enkele bijzondere matrices. 10 Ik kan een matrix transponeren. 12 Ik kan bewerkingen op matrices uitvoeren met en zonder ICT. 13 Ik kan matrices optellen. 13 Ik kan een matrix vermenigvuldigen met een reëel getal. 14 Ik weet wanneer twee matrices met elkaar vermenigvuldigbaar zijn en kan die vermenigvuldiging uitvoeren. 15 Ik kan een vierkante matrix tot een macht verheffen. 17 Ik ken de eigenschappen van de optelling van matrices. 28 Ik ken de eigenschappen van de vermenigvuldiging van een matrix met een scalair. 30 Ik ken de eigenschappen van de vermenigvuldiging van vierkante matrices. 32 Ik ken de eigenschappen van de transpositie van een matrix. 34 Ik weet wat nuldelers zijn. 35 Ik weet wat idempotente, nilpotente en involutorische matrices zijn. 36 Ik ken het verband tussen een gewogen graaf en een matrix. 42 Ik weet wat overgangsmatrices, populatiematrices en verbindingsmatrices zijn en kan die in concrete situaties toepassen. 42 Ik kan met behulp van matrices de evolutie van een blok gegevens beschrijven. 46



Stelsels van eerstegraadsvergelijkingen 2
















Een van de oudste bekende wiskundige werken heet het Jiǔzhāng Suànshù, wat het vaakst vertaald wordt als de negen hoofdstukken van rekenkunde. Eeuwenlang schreven verschillende generaties geleerden hieraan mee, het werd gepubliceerd rond het jaar 100 v.Chr. De methodiek is erg oplossingsgericht. In elk hoofdstuk worden concrete problemen aangekaart, daarvoor worden dan algemene methoden aangereikt om die op te lossen. Het achtste hoofdstuk gaat over stelsels van eerstegraadsvergelijkingen met twee of drie onbekenden. Je vindt er bijvoorbeeld dit vraagstuk terug. Je kunt het oplossen nadat je dit hoofdstuk onder de knie hebt.


Bij de verkoop van 2 buffels en 5 schapen en de aankoop van 13 varkens, krijg je 1000 munten. Bij de verkoop van 3 buffels en 3 varkens kun je precies 9 schapen kopen. Bij de verkoop van 6 schapen en 8 varkens en de aankoop van 5 buffels moet je 600 munteenheden extra betalen. Hoeveel kost 1 buffel, 1 schaap en 1 varken?





Stelsels van eerstegraadsvergelijkingen
2.1
2.2
2.3
66
Willekeurige stelsels oplossen 1 Inleiding 67 2 Definities 69 3 Oplossingenverzameling van een stelsel 70 4 Gelijkwaardige stelsels 72 5 Homogene stelsels 74 6 Elementaire rijoperaties op een matrix 74 7 Methode van Gauss-Jordan: eerste vorm 76 8 Methode van Gauss-Jordan: tweede vorm (spilmethode) 80 9 Verband tussen oplosbaarheid, rang en uitgebreide matrix 84 10 Samenvatting 85 11 Oefeningen 86
Toepassingen 1 Hotel Bertram 89 2 Het spelprogramma 90 3 Oefeningen 92
Inverse
matrix 1 Definitie 98 2 Berekenen van A-1 99 3 Eigenschappen 101 4 Toepassing: oplossen van een stelsel met de methode van de inverse matrix 102 5 Samenvatting 103 6 Oefeningen 104 Wat moet je kennen en kunnen? 106
matrix van een vierkante
2


























































 J.J. Sylvester
J.J. Sylvester
































































































































































































































































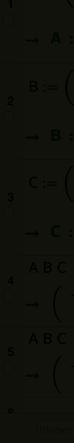







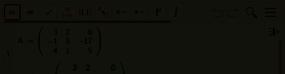
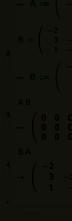











































 Arthur Cayley
Arthur Cayley
































































































































































































































































































































































