VBTL 6 - Leerboek Analyse 4 - inkijk & materiaal 3e graad by die Keure

LEERBOEK

Analyse 4 i Integraalrekening

D-ﬁnaliteit gevorderde wiskunde

Philip Bogaert

Filip Geeurickx

Marc Muylaert

Roger Van Nieuwenhuyze

Erik Willockx

CARTOONS

Dave Vanroye

Hoe gebruik je VBTL ?

Dit boek bevat vier hoofdstukken. Elk hoofdstuk is opgebouwd uit verschillende paragrafen met aan het einde een handige samenvatting.

Deﬁnities vind je op een rode achtergrond. Eigenschappen vind je op een groene achtergrond. Methodes, rekenregels en formules vind je op een zachtblauwe achtergrond.

Wiskunde is een eeuwenoude wetenschap. De geschiedenis van de wiskunde en de herkomst van bepaalde begrippen worden zachtpaars afgedrukt.

1 2 *

De nummers van de oefeningen hebben een gele kleur. Een sterretje duidt op een extra uitdaging. Maak ook kennis met voorbeeldvragen uit ijkingstoetsen en toelatingsexamens.

Achteraan in dit boek vind je de oplossingen

Oplossingen

ICT is een ideaal hulpmiddel.

Bij dit boek hoort een webpagina van GeoGebra, gevuld met heel wat digitale oefeningen en applets. Die vind je terug via www.polpo.be.

Wat moet je kennen en kunnen ?

Op het einde van elk hoofdstuk zie je een handig overzicht van wat je moet kennen en kunnen

Tussen 1665 en 1685 vonden Isaac Newton (1642 – 1727) en Gottfried Wilhelm Leibniz (1646 – 1716) onafhankelijk van elkaar de differentiaalrekening uit. Hiermee konden ze raaklijnen aan krommen en graﬁeken van functies bepalen. Daarover leerde je al in de vorige boeken.

Newton ontdekte kort daarna dat het omgekeerde van differentiëren kon worden toegepast op het berekenen van oppervlakten en volumes van ﬁguren (vlakke en ruimtelijke) die worden begrensd door krommen of gekromde oppervlakken.

Al vanaf de oudheid probeerden wiskundigen de oppervlakte onder een kromme te berekenen. Voor de oppervlakte van een cirkelschijf werkte de geniale Griek Archimedes (3e eeuw v.Chr.) met ingeschreven regelmatige veelhoeken en leidde hij zo de formule πr 2 af. In dit boek leer je zelf een methode om de oppervlakte onder een kromme te benaderen met rechthoekjes. Ook maak je kennis met een manier om de oppervlakte exact te berekenen. Daarbij ga je functies integreren. Je zult merken dat er een eenvoudig verband bestaat tussen integreren en differentiëren.

Als je ooit oppervlakten moet berekenen in Parc Güell (Barcelona), neem dan zeker dit boek mee als hulp.

Inhoud

Analyse 4 i Integraalrekening

Bepaalde integralen

1.1 Het ontstaan van de integraalrekening – het integraalbegrip 9

1.2 Riemannsommen 13

1.3 Deﬁnitie van de bepaalde integraal 16

1.4 Oppervlakten met een toestandsteken (of georiënteerde oppervlakten) 17

1.5 Praktische werkwijze voor het berekenen van een bepaalde integraal 19

1.6 Optelbaarheid van de bepaalde integraal 24

1.7 Oppervlakte van het gebied begrensd door de graﬁek van een functie en de x-as 26

1.8 Oppervlakte van het gebied begrensd door de graﬁeken van twee functies 28

1.9 Hoofdstelling van de integraalrekening 30

1.10 Toepassingen op oppervlakteberekening 37

1.11 Oneigenlijke integralen 42

Integratiemethoden

2.1 Fundamentele integralen 69

2.2 Integratie door substitutie 77

2.3 Integratie van elementaire rationale functies – splitsen in partieelbreuken 91

2.4 Partiële integratie 99

Toepassingen van de integraalrekening

3.1 Oppervlakte van bijzondere vlakke ﬁguren 119

3.2 Zwaartepunt van een vlakke ﬁguur 127

3.3 Volume van omwentelingslichamen 132

3.4 Booglengte van een vlakke kromme 158

3.5 Manteloppervlakte van een omwentelingslichaam 165

Toepassingen van integralen in andere disciplines

4.1 Snelheid en afgelegde weg 179

4.2 Versnelling en snelheid 181

4.3 Kracht en arbeid 183

4.4 Marginale kostprijs 186

4.5 Gini-coëfﬁciënt en Lorenzcurve van de inkomensverdeling 188

4.6 Elasticiteit van de vraag 190

Bepaalde integralen 1

Deze ﬁets- en wandelbrug, die meer dan 20 miljoen euro heeft gekost, kun je in haar volle glorie bezichtigen in het Engelse Stockton-on-Tees. Ze werd de inﬁnity bridge genoemd omdat ze (samen met de weerspiegeling in het water) het symbool voor oneindigheid vormt.

Als het wandel- en ﬁetsplatform mooi horizontaal is en je kent de functie om de bogen te beschrijven, dan kun je de oppervlakte tussen kromme en rechte berekenen (en daarbij heb je integralen nodig …).

In Dubai (Verenigde Arabische Emiraten) is er trouwens een brug met dezelfde naam die we hier ook hadden kunnen plaatsen, zoek die gerust eens op.

Bepaalde integralen

1 Het ontstaan van de integraalrekening – het integraalbegrip 9

2 Riemannsommen 13

3 Deﬁnitie van de bepaalde integraal 16

4 Oppervlakten met een toestandsteken (of georiënteerde oppervlakten) 17

5 Praktische werkwijze voor het berekenen van een bepaalde integraal 19

6 Optelbaarheid van de bepaalde integraal 24

7 Oppervlakte van het gebied begrensd door de graﬁek van een functie en de x-as 26

8 Oppervlakte van het gebied begrensd door de graﬁeken van twee functies 28

9 Hoofdstelling van de integraalrekening 30

10 Toepassingen op oppervlakteberekening 37

11 Oneigenlijke integralen 42

Wat moet je kennen en kunnen? 66

1 Het ontstaan van de integraalrekening – het integraalbegrip

Enkele voorbeelden :

De grootste wiskundige van de hele oudheid was ongetwijfeld de Griek Archimedes (287 – 212), die in Syracuse op Sicilië woonde als adviseur van koning Heroon.

Zijn belangrijkste prestatie is de uitvinding van de integraalrekening, tweeduizend jaar voordat Newton en Leibniz de differentiaalrekening ontdekten.

Hij leverde belangrijke bijdragen die behoren tot het gebied dat we nu de integraalrekening noemen : de bepaling van de oppervlakte van vlakke figuren en het volume van lichamen.

In Archimedes’ boek ‘De kwadratuur van een parabool’ vinden we de volgende stelling : de oppervlakte van een parabolisch segment met de koorde a als basis is gelijk aan 4 3 maal de oppervlakte van de ingeschreven driehoek met basis a en top in dat punt van de parabool waar de raaklijn evenwijdig is aan a

oppervlakteparaboolsegmentOAB = 4 3 maaloppervlakte ∆OAB

Een bewijs m.b.v. integralen vind je op blz. 37.

In het boek ‘Over de bol en de cilinder’ vinden we de volgende uitdrukkingen:

De oppervlakte van een bol is het viervoud van de oppervlakte van een grote cirkel ( A bol = 4πr 2 )

Het volume van een bol is gelijk aan 2 3 van het volume van de omgeschreven cilinder

Een bewijs van die eigenschappen m.b.v. integralen vind je op blz. 139.

De aanpak van de oude Grieken had echter een belangrijke beperking: voor de berekening van de oppervlakte van elke nieuwe figuur was een nieuwe aanpak nodig, meestal gebaseerd op de meetkunde van die tijd. Ze hadden geen algemene methode waarmee de berekeningen konden worden uitgevoerd.

Pas in de zeventiende eeuw ontwikkelden Newton en Leibniz, onafhankelijk van elkaar, een algemene methode om oppervlakten van kromlijnige figuren te berekenen : de integraalrekening. Newton vond namelijk, kort nadat hij de differentiaalrekening had bedacht, dat de omgekeerde bewerking van differentiëren de methode van de integraalrekening is.

We geven eerst enkele voorbeelden van grootheden die als oppervlakten voorgesteld kunnen worden. Newton

Archimedes

a Oppervlakten

In de vlakke meetkunde heb je al de oppervlakte van een aantal figuren bestudeerd. We frissen je geheugen even op.

b Afgelegde weg

In de volgende grafiek wordt de snelheid die een sprinter ontwikkelt, uitgezet in functie van de tijd.

(m/s)

– Kun je berekenen hoeveel afstand hij heeft afgelegd in 10 seconden?

De afstand kun je op de grafiek zichtbaar maken in de vorm van een oppervlakte. Welke ?

c Nitraatgehalte in water

Een bedrijf, gelegen aan een rivier die uitmondt in de Schelde, loost regelmatig nitraatafval. Het heeft een vergunning gekregen van de overheid voor het lozen van 1 ton per week.

De stroomsnelheid van de rivier wordt verondersteld constant te zijn met een debiet van 40 000 m3 water per dag. Stroomafwaarts wordt eenmaal per dag (op de middag) een watermonster gemeten. Voor deze week geeft dit :

Via deze meetresultaten kun je de hoeveelheid nitraten schatten die het meetstation passeert. Met een debiet D = 40 000 m3/dag en de gemeten concentratie c is de totale hoeveelheid nitraten n die gedurende een dag (een tijdsinterval ∆t ) passeert, te schatten met de formule : n = D · c · ∆t

Voor de hele week ( ∆t = 1) wordt dat :

D ( c 2 + + c 7) · ∆t = 40 000 m3 · 21,9729 g/m3 = 878,916 kg.

Wegens het grote debiet is er ook een snelle verandering in concentratie. De enige manier om nauwkeuriger de lozing van de fabriek te controleren is vaker meten. In plaats van eenmaal per dag besluit men viermaal daags (0.00 u., 6.00 u., 12.00 u. en 18.00 u.) te meten. Dat geeft het volgende resultaat.

In een week tijd zijn dat dus 28 metingen (c1 to c 28). Vooral tijdens de weekdagen zijn de resultaten van de metingen in de voormiddag opvallend hoger dan in de namiddag.

Voor de totale hoeveelheid nitraten in de loop van deze week geldt ∆ t = 1 4 : n = D ( c 1 + c 2 + ... + c 28 ) 1 4 = 40000m3 92,0332g/m3 1 4 = 920,332kg

Het verschil van meer dan 40 kg nitraat gemeten bij een nauwkeurige waarneming leidde tot de plaatsing van een sensor in het water, die continu stalen neemt. De sensor geeft een signaal dat wordt doorgegeven aan een penschrijver, die een directe grafische weergave levert van het gemeten signaal. De uitvoer van de penschrijver is een grafiek van het gemeten nitraatgehalte (in g/m3) als functie van de tijd (in dagen).

De totale hoeveelheid nitraat in een week is evenredig met de oppervlakte onder de grafiek.

Oplossing :

De oppervlakte bedraagt 23,0085 eenheden. Dat resulteert in 920,34 kg nitraat per week.

In veel situaties waarbij je met grafieken werkt, heeft de oppervlakte tussen de grafiek en de x -as een betekenis. De gezochte oppervlakte kun je schatten door het gebied op te delen in rechthoekjes en de oppervlakte van die laatste op te tellen.

In dit boek leer je hoe je zo’n oppervlakte nauwkeurig kunt verkrijgen als de vergelijking van de grafiek bekend is. Je berekent dan een bepaalde integraal.

2 Riemannsommen

We vragen ons af wat de oppervlakte is van het gebied in het eerste kwadrant dat ingesloten wordt door de grafiek van de functie f met f ( x ) = –x 2 + 2x + 3, de x -as en de y -as.

Hiertoe verdelen we het interval [ 0, 3] in 3 gelijke deelintervallen met breedte ∆x = 1. We beschouwen nu twee soorten rechthoeken.

De ondersom s3 van de oppervlakten van de eerste soort rechthoeken is kleiner dan de gevraagde oppervlakte.

s 3 = 1 3 + 1 3 + 1 0 = 6

De bovensom S3 van de oppervlakten van de tweede soort rechthoeken is groter dan de gevraagde oppervlakte.

S 3 = 1 4 + 1 4 + 1 3 = 11

Hoe meer deelintervallen, hoe fijner de rechthoeken (Riemannfrietjes genaamd), en hoe dichter de ondersom en bovensom de werkelijke oppervlakte benaderen.

voor n = 6 (∆x = 0,5) krijgen we :

Om de oppervlakte exact te bepalen, berekenen we s n en S n voor steeds groter wordende waarden van n en proberen we de limieten te berekenen voor n → +∞

We vermoeden dat lim n → +∞ sn = lim n → +∞ Sn = 9, zodat de exacte oppervlakte van het gebied 9 (oppervlakte-eenheden) groot is. Later zullen we berekenen dat dat inderdaad zo is.

Bernhard Riemann (1826–1866)

Georg Friedrich Bernhard Riemann werd op 17 september 1826 geboren in Breselenz (niet ver van Hannover) als tweede kind in een gezin met zes kinderen.

Zijn vader, een lutherse dominee, onderwees zijn kinderen zelf, maar toen Bernhard 10 was, ging hij naar de school in het dorp.

In 1840, hij was toen 14, ging hij naar het lyceum in Hannover. Hij woonde in die tijd bij zijn grootmoeder, die hem ﬁnancieel steunde. Toen die in 1842 overleed, ging hij naar het gymnasium van Lüneburg. Hij was een zeer verlegen en teruggetrokken jongen met een zwakke gezondheid, waar hij heel zijn leven de gevolgen van droeg.

De schooldirecteur merkte snel het wiskundige talent van Riemann op en gaf hem het boek ‘Théorie des nombres’ van Legendre. Nauwelijks 6 dagen later had de jonge Riemann dit bijna 900 bladzijden tellende leerboek over getaltheorie ingestudeerd. Zijn commentaar: “Dit was een prachtig boek, ik heb het onder de knie.”

In 1846 schreef hij zich in als student aan de universiteit van Göttingen. Aanvankelijk volgde hij les aan de faculteit theologie om te voldoen aan het verlangen van zijn vader, die van hem een dominee had willen maken. Vrij vlug gaf hij die richting op om zich toe te leggen op de wiskunde.

Na een jaar verhuisde hij naar de universiteit van Berlijn, waar hij les kreeg van Jacobi, Steiner, Dirichlet en Eisenstein. Het was Dirichlet die Riemann het meest beïnvloedde en hem vroeg om zijn medewerker te worden. In 1849 keerde Riemann naar Göttingen terug om zijn doctoraat voor te bereiden. In 1851 promoveerde hij onder Gauss met zijn proefschrift ‘Grundlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse’. In 1854 moest Riemann nog een proefschrift schrijven, een zogenaamd Habilitationsschrift, om een aanstelling te krijgen aan de universiteit van Göttingen. In dat proefschrift gaf hij een precieze deﬁnitie van integreerbaarheid, die tegenwoordig bekendstaat als de Riemannintegraal en een verbetering was van de deﬁnitie van Cauchy en Dirichlet. Pas in 1902 ontwikkelde de Franse wiskundige Henri Lebesgue (1875 – 1941) de zogenaamde Lebesgue-integraal, een nog ruimer begrip, dat voor veel doeleinden beter bleek.

In 1857 werd Riemann assistent-professor aan de universiteit van Göttingen. In 1859 overleed Dirichlet, die Gauss had opgevolgd. Riemann werd benoemd tot zijn opvolger. In datzelfde jaar werd hij ook verkozen tot corresponderend lid van de Berlijnse academie van wetenschappen. Hij was door zijn ontdekkingen beroemd geworden in Europa.

Dankzij zijn baan als professor ging het Riemann op ﬁnancieel gebied een stuk beter en in 1862 huwde hij met Elise Koch. Nauwelijks een maand later kreeg hij pleuritis en werd hij ernstig ziek.

Hij reisde regelmatig naar Italië om te herstellen. In 1863 werd zijn dochter Ida geboren in Pisa. Bernhard Riemann stierf op 20 juli 1866 aan het Lago Maggiore ten gevolge van tuberculose.

Bernhard Riemann

3 Deﬁnitie van de bepaalde integraal

Op dezelfde manier kun je de oppervlakte van het gebied tussen de grafiek van een positieve, continue functie f en de x -as in het interval [ a , b ] bepalen.

1 Verdeel [ a , b ] in n gelijke deelintervallen met breedte ∆ x = b a n .

2 Bereken in elk ( i -de) deelinterval het minimum van de functiewaarden ( f min( x i ) = m i ) en het maximum van de functiewaarden ( f max( x i ) = M i ). Aangezien f continu is in [ a , b ] zijn dat minimum en dat maximum steeds te vinden (stelling van Weierstrass).

3 Bereken de ondersom sn

en de bovensom Sn

4 Bereken lim n → +∞ sn enlim n → +∞ Sn

We kunnen bewijzen dat voor functies die continu zijn in [ a , b ] de limieten bestaan en gelijk zijn.

5 De gemeenschappelijke waarde van de limieten noemen we de bepaalde integraal van a tot b van de functie f

We noteren : lim n → +

Opmerking :

De Duitse wiskundige Bernhard Riemann heeft aangetoond dat het niet nodig is om het maximum of het minimum van de functiewaarden te nemen. Je krijgt ook hetzelfde resultaat als je de breedte vermenigvuldigt met een willekeurige functiewaarde f ( xi) die in het deelinterval aangenomen wordt.

De Riemannsom noteer je dan als

i -de deelinterval met breedte

Kiezen we nu in elk deelinterval een willekeurige x i , dan geldt : m i f ( x i ) M i

De Riemannsom ligt dus altijd tussen de ondersom en de bovensom. Laat je nu n oneindig groot worden, dus Dx → 0, dan benaderen de ondersom, de bovensom en de bovenstaande Riemannsom elkaar.

Immers : lim

Volgens de insluitstelling van de limieten geldt dus (zie VBTL 5 Analyse 2) :

4

Oppervlakten

met een toestandsteken (of georiënteerde oppervlakten)

Een buitenhuisje wordt van energie voorzien door een accumulator, verbonden met een tiental zonnepanelen. Anderzijds wordt er ook heel wat energie verbruikt door allerlei toestellen. Het nettoresultaat van deze toe- en afname van energie (gisteren) wordt weergegeven door de volgende grafiek.

Oppervlakten van de gebieden boven de x -as betekenen een toename van energie. Oppervlakten van gebieden onder de x -as betekenen een afname van energie.

Het is dus zinvol om aan de oppervlakte van een gebied een teken toe te kennen. We maken de volgende afspraak. Oppervlakten van gebieden boven de x -as hebben een positieve waarde en die onder de x -as hebben een negatieve waarde.

Het nettoresultaat van de energietoename/-afname is de som van de oppervlakten met hun teken. We definiëren de bepaalde integraal voor de energiefunctie f over [ 0, 24] als de som van de (georiënteerde) oppervlakten van de gebieden tussen : – de grafiek van de energiefunctie f ; – de x -as ; – de rechten x = 0 en x = 24.

Notatie : 24

We beschouwen de tekentabel van de functie f in [ 0, 24]

Hieruit volgt dat :

Als de functiewaarden negatief zijn, wordt ook de integraal van de functie negatief. We moeten dan rekenen met de tegengestelden van die functiewaarden.

Bijgevolg geldt :

Meetkundige betekenis van de bepaalde integraal

Gegeven is de functie f , die continu is in het interval [ a , b ].

De bepaalde integraal van a tot b van de functie f is de som van de oppervlakten met teken (georiënteerde oppervlakten) van de gebieden tussen : – de grafiek van f ; – de x -as ; – de rechten x = a en x = b (evenwijdig met de y -as).

Notatie : b a f ( x ) dx

Merk op dat de bepaalde integraal enkel bepaald wordt door de functie f en de grenswaarden a (beneden- of ondergrens) en b (bovengrens).

Voorbeeld :

Opmerkingen : ① De naam van de variabele speelt geen rol. Dus

② Als f ( x ) zowel positieve als negatieve waarden aanneemt in [ a , b ], dan moet je dat interval zo splitsen dat er gebieden ontstaan waarin f ( x ) uitsluitend positief (of 0) of uitsluitend negatief (of 0) is.

③ Uit het voorgaande blijkt dat de functies die continu zijn in een gesloten interval, in dat interval ook integreerbaar zijn.

5 Praktische werkwijze voor het berekenen van een bepaalde integraal

Om bepaalde integralen te berekenen, volgen we de werkwijze die gegeven werd op blz. 16.

De integraal van een functie f over het interval [ a , b ] is het getal dat je als volgt bekomt :

1 Verdeel [ a , b ] in n gelijke deelintervallen met breedte ∆ x = b a n .

2 Bereken de functiewaarde f ( x ) van een willekeurig getal x i uit elk deelinterval.

3 Bepaal de som : ∆

( x 1 )+

4 Bereken de limiet van die som voor n → +∞ , dat is voor Dx → 0.

In symbolen :

Voorbeelden :

Dat is de oppervlakte van een rechthoek met afmetingen

en 1.

b Integraal van x

We verdelen [ a , b ] in n deelintervallen met breedte ∆ x = b a n . Als x i nemen we de linkergrens van elk interval. INTERVAL

[

We nemen a < b .

desomvandeeerste n termen vaneenrekenkundigerijis: s = u 1 + u n 2 n

Dat is de oppervlakte van een rechthoekig trapezium met als grote basis b , als kleine basis a en als hoogte b – a

Integraal

De benaming ‘integraal’ komt van het Latijnse ‘integrare’, wat ‘volledig maken’ betekent. Die benaming werd door Leibniz vermoedelijk gekozen om uit te drukken dat het getal de ‘integratie’ of volledige oppervlakte weergaf tussen de kromme en de x-as.

De notatie van de bepaalde integraal is als volgt ontstaan. De plaats van het somteken (∑) werd ingenomen door een ouderwetse S, de eerste letter van ‘summa’ (Latijn voor som). a is de ondergrens en b is de bovengrens van het hele interval. f(x) is de integrand, d.w.z. het voorschrift van de te integreren functie. De notatie dx zegt dat je de lengte van een deelinterval zo klein kunt kiezen als je zelf wilt : D x → 0.

c Integraal van x 2

over het interval [ 0, b ] met b > 0

We verdelen [ 0, b ] in n deelintervallen met breedte ∆ x = b a n . Als xi nemen we de rechtergrens van elk interval.

[

(*) Stelindeformule (k + 1)3 = 1 + 3k + 3k 2 + k 3 k achtereenvolgensgelijkaan1,2,..., n .Danbekomje:

23 = 1 + 3 1 + 3 12 + 13

33 = 1 + 3 2 + 3 22 + 23

43 = 1 + 3 · 3 + 3 · 32 + 33 n 3 = 1 + 3 (n 1)+ 3 (

(1 + n )3 = 1 + 3n + 3n 2 + n 3

Tellenwerespectievelijkderechterledenendelinkerledenbijelkaarop,enschrappenwelinksen rechtsdegelijketermen(= gelijkederdemachten),dankrijgenwe: (1 + n )3

Taak : bewijs deze eigenschap opnieuw door volledige inductie. over het interval [ a , b ] met 0 < a < b

over het interval [ a , b ] met a < b ⩽ 0

b a x 2 dx = a b x 2 dx symmetrie = ( a )3 3 ( b )3 3 = b 3 a 3 3 y –b b –a a O y = x 2 x

Besluit :

b a x 2 dx = b 3 a 3 3

Opmerking :

Je merkt vast de regelmaat in de 3 formules die we tot nu toe gezien hebben. We kunnen dus vermoeden dat algemeen geldt :

b a x n dx = b n +1 n + 1 a n +1 n + 1 n ∈ N

Het algemeen bewijs geven we later. Het is duidelijk dat deze methode alleen maar voor zeer eenvoudige functies snel tot een resultaat leidt. Voor de andere gevallen is het nodig dieper in te gaan op de eigenschappen van bepaalde integralen.

Aanvullende definities (uitbreiding van het integraalbegrip) :

In b a f ( x )dx noemen we a de ondergrens en b de bovengrens.

De definitie van blz. 17 geldt alleen voor a < b

• a = b Voor een functie f die integreerbaar is in a geldt : a a f ( x )dx = 0

We kunnen die integraal dus opvatten als een grensgeval in de formule. Als we in de Riemannsom aannemen dat Dx = 0, dan zijn de som zelf en haar limiet gelijk aan nul.

• a > b Voor een functie f die integreerbaar is over [ b , a ] geldt : b a f ( x )dx = a b f ( x )dx

Die definitie wordt aannemelijk als we in de Riemannsom van blz. 17 aanvaarden dat Dx < 0. Het teken van de som en van haar limiet wordt dan gewijzigd.

6 Optelbaarheid van de bepaalde integraal

Op de bovenstaande tekening lezen we af :

f ( x )dx = A 1 A 2 + A 3

Hieruit blijkt de eigenschap

Als a , b en c behoren tot een interval waarin f integreerbaar is, dan hebben we voor elke ligging van a , b en c :

Bewijs :

We zullen ervan uitgaan dat a , b en c drie verschillende getallen zijn. Gerangschikt in stijgende orde zijn er dan 6 mogelijkheden voor a , b en c : abc , acb , bac , bca , cab , cba . We geven voor het geval abc een bewijs. We nemen een verdeling van [ a , b ] en een verdeling van [ b , c ]. De vereniging van beide is dan de verdeling van [ a , c ]. Voor de Riemannsommen horend bij die verdelingen schrijven we de grenzen bij het somteken.

Dus : c

Als we deze verdelingen onbeperkt verfijnen, dan krijgen we door een limietovergang : c a f ( x )dx = b a f ( x )dx + c b f ( x )dx

⇒ b a f ( x )dx = c a f ( x )dx c b f ( x )dx

⇒ b a f ( x )dx = c a f ( x )dx + b c f ( x )dx

Merk de gelijkenis op met de bekende formule van Chasles-Möbius voor vectoren in het vlak of in de ruimte.

Taak: ➀ Bewijs de stelling als twee van de drie getallen a , b en c aan elkaar gelijk zijn.

➁ Bewijs de stelling als alle drie de getallen a , b en c gelijk zijn.

➂ Geef een bewijs van de stelling voor het geval bac

Enkele verdere eigenschappen :

1 Lineariteit

Als f en g integreerbaar zijn over een interval en als k een gegeven reëel getal is, dan zijn ook f + g en k · f integreerbaar over dit interval en dan geldt :

Bewijs van (1) :

Taak: geef een analoog bewijs van eigenschap 2.

Opmerking :

De eigenschappen (1) en (2) kunnen we als volgt samenvatten.

Alsdefuncties f en g integreerbaarzijnin [a , b ],dangeldtvoorelke

in woorden: de integraal van een lineaire combinatie van functies is een lineaire combinatie van de integralen.

Voorbeeld :

2 Ongelijkheden

Als f en g integreerbaarzijnin [a , b ],dangeldt:

Bewijs : We veronderstellen dat

7 Oppervlakte van het gebied begrensd door de graﬁek van een functie en de x-as

Inhetvoorbeeldvanvorigeblz.vondenwedat

Meetkundiggezienbetekentditdat 4 3 degeoriënteerdeoppervlakteisvanhetgebiedbegrensddoordegraﬁek

Willen we de werkelijke oppervlakte van gebieden I en II samen berekenen, dan moeten we de twee opper vlakten apart berekenen.

– We onderzoeken eerst waar de grafiek van f boven of onder de x -as ligt. x

grafiek onder de

– In [ 0, 1] ligt de grafiek van f onder de x -as. Hier is de georiënteerde oppervlakte negatief en dus gelijk aan het tegengestelde van de gevraagde oppervlakte.

– In [ 1, 2] ligt de grafiek van f boven de x -as. De georiënteerde oppervlakte is positief en dus gelijk aan de gevraagde oppervlakte.

– De totale (werkelijke) oppervlakte bedraagt dus :

Opmerking :

We kunnen ook zeggen dat de gevraagde oppervlakte A gelijk is aan

Geef hiervoor een verklaring.

Dus : A = A I + A II =

0 | 2 x 2 + 2 x 4 | dx = 6

Regel :

Om de oppervlakte te bepalen van het gebied begrensd door de grafiek van de functie f en de x -as in het interval [ a , b ] op de x -as, ga je als volgt te werk.

1 Bereken de nulwaarden van f die in [ a , b ] gelegen zijn en bepaal het teken van f in elk deelinterval.

2 Bepaal de oppervlakte in elk deelinterval.

Is f ( x ) ⩾ 0, dan is de oppervlakte over dat deelinterval gelijk aan de integraal van f over dat interval. Is f ( x ) ⩽ 0, dan is de oppervlakte over dat deelinterval het tegengestelde van de integraal van f over dat deelinterval.

3 Tel de bekomen oppervlakten op.

Opmerking :

We kunnen ook zeggen dat de gevraagde oppervlakte gelijk is aan

| f ( x ) | dx

Door de absolute waarde van f ( x ) als integrand te nemen, worden de gebieden die bij f onder de x -as liggen, gespiegeld om de x -as, zodat ze boven de x -as liggen.

Taak : toon aan dat de oppervlakte van het gebied dat ingesloten wordt door de grafiek van f met f ( x ) = –x 2 + 2x + 3, de x -as en de y -as, gelijk is aan 9.

8 Oppervlakte van

het gebied begrensd door de graﬁeken van twee functies

Voorbeeld :

Bereken de oppervlakte A van het gebied tussen de grafieken van de functies f en g met

in het interval [ –3, 2]

– We onderzoeken eerst waar de grafiek van f of de grafiek van g het meest naar boven ligt.

Hiertoe onderzoeken we het teken van v

• In [ 3, 2] geldt:

In [ 2,0] geldt:

• In [0,2] geldt: v ( x ) 0of f ( x ) g ( x )=⇒

Opmerking :

We kunnen ook zeggen dat A

Geef een verklaring.

Toegepastophetvoorbeeldwordt

Regel :

Om de oppervlakte te bepalen van het gebied begrensd door de grafieken van twee functies f en g in het interval [ a , b ] gaan we als volgt te werk.

1 We berekenen de nulwaarden van v = f – g die in [ a , b ] gelegen zijn en bepalen het teken van v ( x ) = f ( x ) – g ( x ) in elk deelinterval.

2 We bepalen de oppervlakte in elk deelinterval. Is v ( x ) ⩾ 0, dan is de oppervlakte over dat deelinterval gelijk aan b a v ( x ) dx . Is v ( x ) ⩽ 0, dan is de oppervlakte over dat deelinterval gelijk aan b

3 We tellen de bekomen oppervlakten op.

Opmerking :

We kunnen zeggen dat de gevraagde oppervlakte gelijk is aan b a | v ( x ) | dx of b a | f ( x ) g ( x ) | dx

v ( x ) dx .

9 Hoofdstelling van de integraalrekening

1 Integraalfuncties

Uit (5) volgt : b 1 x 2 dx = b 3 3 13 3 = b 3 3 1 3

Met elke bovengrens b stemt een b 1 x 2 dx overeen.

Zoontstaateenfunctie I 1 ,met I 1 ( x )= x 3 3 1 3

We noemen ze de integraalfunctie van f met f ( x ) = x 2 en ondergrens 1.

schrijven we I a ( x )= x a f ( t ) dt . x y 1 O 1 x f ( x ) = x 2 I 1( x )

De functie I 1 laat met elke x de oppervlakte I ( x ) overeenstemmen onder de grafiek van f in het interval [ 1, x ]

Algemeen zouden we door I a met I a ( x )= x a f ( x ) dx de integraalfunctie van f met ondergrens a kunnen voorstellen.

Omdat in die notatie x in twee betekenissen voorkomt,

Volgens opmerking 1 (blz. 18) speelt de naam van de variabele geen rol.

Er geldt dus : b a f ( x ) dx = b a f ( t ) dt = b a f ( u ) du = ...

integraalfunctie

Defunctie I a met I a ( x )= x a f ( t )dt

noemen we de integraalfunctie van f met ondergrens a I a ( x ) stelt de veranderlijke oppervlakte voor onder de grafiek van f in [ a , x ] x y y = f (x) 0 a x Ia(x)

Voorbeelden :

We kunnen dus vermoeden dat algemeen geldt : D ( I a ( x ))= D

) Met andere woorden : de afgeleide van een integraalfunctie is opnieuw de oorspronkelijke functie.

Die eigenschap noemen we de hoofdstelling van de integraalrekening. Om de stelling te bewijzen, hebben we eerst een hulpstelling nodig.

2 Middelwaardestelling van de integraalrekening middelwaardestelling

Als f continuisin [a , b ],danbestaatereen c ∈ [a , b ] : b a f (

Bewijs :

1 a < b

We verdelen [a , b ] in n gelijke deelintervallen met lengte ∆ x = b a n xi is een willekeurig getal in het i -de deelinterval.

Stellen we nu m = inf[ f [ a , b ]] dan geldt : M = sup[ f [ a , b ]]

n deelintervallen

) < n i =1 f ( x i ) ∆ x < M ( b a )

)

Aangezien f continu is, bestaat er in [ a , b ] een r zodat f ( r ) = m en een s zodat f ( s ) = M (stelling van Weierstrass).

Volgens de tussenwaardestelling bereikt f ( x ) in [ r , s ] alle waarden tussen m en M Dus bestaat er in [ r , s ] en bijgevolg in [ a , b ] minstens één c zodat

f ( c )= 1 b a · b a f ( x ) dx ,waaruitvolgt: ∃

2 a = b

Danis b a f ( x )dx = 0 =( b a ) f ( c )

3 a > b

Uit 1 volgtdan:

)

Meetkundige betekenis van de middelwaardestelling Is f continu in [ a , b ], dan bestaat er een c in [ a , b ] zodat de oppervlakte van de rechthoek met b – a als basis en f ( c ) als hoogte gelijk is aan de oppervlakte onder de grafiek van f in [ a , b ]

( b a ) · f ( c )= b a f ( x ) dx of f ( c )= 1 b a b a f ( x ) dx y O a x y = f (x ) c b

gemiddelde waarde

Het getal 1 b a b a f ( x ) dx noemen we de gemiddelde waarde van f over [ a , b ]

Opmerking :

f ( c )= 1 b a b a f ( x ) dx met c ∈ ]a , b [ kunnenweookschrijvenals

f ( c )= 1 n ∆ x lim n → +∞ n i = 1 f ( x i ) ∆ x met ∆ x = b a n

≈ n i = 1 f ( x i ) n

We kunnen dit interpreteren als de uitbreiding van het rekenkundig gemiddelde van de functiewaarden f ( x 1), f ( x 2), …, f ( x n ).

Daarom noemen we f ( c ) de gemiddelde waarde van f in [ a , b ]

Voorbeeld :

3 Hoofdstelling van de integraalrekening hoofdstelling integraalrekening

Bewijs :

4 Primitieve functies

De integraalfunctie I a met I a ( x )= x a f ( t ) dt is een primitieve functie van f , want volgens de hoofdstelling is DIa( x ) = f ( x )

primitieve functie

F iseen primitievefunctie van f

DF = f of F = f f ( x ) f ′( x )

Voorbeelden :

differentiëren primitiveren

• F met F ( x )= x 3 iseenprimitievefunctievan f met f ( x )= 3 x 2 want Dx 3 = 3 x 2 .

Andereprimitievefunctiesvan f hebbenalsvoorschrift x 3 1, x 3 + 2, x 3 + 8 3 ,...

Wezullenaantonendatalleprimitievefunctiesvan f eenvoorschrifthebbenvandevorm x 3 + C ,met C eenwillekeurigreëelgetal.

• F met F ( x )= sin x iseenprimitievefunctievan f met f ( x )= cos x want D (sin x )= cos x .

Andereprimitievefunctiesvan f hebbenalsvoorschriftsin x 1 2 ,sin x + 1,sin x + 5 3

Wezullenaantonendatalleprimitievefunctiesvan f eenvoorschrifthebbenvandevormsin x + C ,met C eenwillekeurigreëelgetal.

stelling

Twee primitieve functies F 1 en F 2 van f verschillen slechts in een constante term.

Bewijs :

F 1 is een primitieve functie van f

F 2 is een primitieve functie van f

DF 1 = f en DF 2 = f

DF 2 = DF 1

DF 2 DF 1 = 0

D ( F 2 F 1 )= 0

F 2 F 1 = C met C ∈ R

Besluit :

F 2 = F 1 + C met C ∈ R

Een functie heeft oneindig veel verschillende primitieve functies, die onderling slechts een constante verschillen. Daarom wordt vaak de volgende notatie gebruikt.

Als f een functie is met f ( x ) = 3x 2, dan is F met F ( x ) = x 3 + C een primitieve functie van f

Bij het bepalen van een primitieve functie van f ga je dus op zoek naar een functie F waarvan de afgeleide f is.

Voorbeelden :

• Deprimitievefunctiesvan f met f ( x )= sin x zijndefuncties F met F ( x )= cos x + C

want D ( cos x )= sin x

• Deprimitievefunctiesvan f met f ( x )= x 2 zijndefuncties F met F ( x )= x 3 3 + C

want D x 3 3 = x 2

• Deprimitievefunctiesvan f met f ( x )= 1 x 2 zijndefuncties F met F ( x )= 1 x + C

want D 1 x = 1 x 2

• Meeralgemeenzijndeprimitievefunctiesvan f met f ( x )= x n met n = 1defuncties F met F ( x )= x n +1 n + 1 + C

want D x n +1 n + 1 = (n + 1) · x n n + 1 = x n

• Deprimitievefunctiesvan f met f ( x )= 1 x zijndefuncties F met F ( x )= ln | x | + C

want D ln | x | = 1 x

• Deprimitievefunctiesvan f met f ( x )= a x zijndefuncties F met F ( x )= a x ln a + C

• Deprimitievefunctiesvansinhzijndefunctiescosh + C

want D (cosh x )= sinh x

• Deprimitievefunctiesvan f met f ( x )= 1 √ x 2 + k zijndefuncties F met F ( x )= ln | x + √ x 2 + k | + C

want D (ln | x + √ x 2 + k |)= 1

Taak :

Vul nu zelf de volgende tabel aan. Raadpleeg de rekenregels van afgeleiden in het boek Analyse 3. functie

5 Berekenen van bepaalde integralen d.m.v. primitieve functies

We zoeken nu een methode om de integraal b a f ( x ) dx te berekenen van een willekeurige continue functie f

We weten dat I a met I a ( x )= x a f ( t ) dt een primitieve functie van f is. Als F een willekeurige primitieve functie

van f is, dan hebben we I a ( x )= x a f (

) dt = F ( x )+ C

• Stellen we x = a , dan vinden we : a a f ( t ) dt = F (a )+ C

0 = F (a )+ C C = F (a ) endus: I

• Stellen we x = b , dan vinden we : I a ( b )= b

) dt = F ( b ) F (a )

Het verschil F ( b ) – F ( a ) wordt kort genoteerd als [ F ( x )] b a

We hebben nu volgende eigenschap bewezen :

Als f continu is in [ a , b ] en F is een willekeurige primitieve functie van f in [ a , b ], dan geldt : b a f ( x ) dx =[ F ( x )] b a = F ( b ) F (a )

Praktische berekening : Om een bepaalde integraal b a f ( x ) dx te berekenen, gaan we als volgt te werk.

1 We berekenen een willekeurige primitieve functie F van f

2 We berekenen F ( a ) en F ( b ).

3 We berekenen F ( b ) – F ( a )

Voorbeelden :

We vinden hier de formule terug van blz. 23.

10 Toepassingen op oppervlakteberekening

1 Oppervlakte van een paraboolsegment

We zoeken de oppervlakte A van het deel van het vlak begrensd door de parabool met vergelijking y 2 = 2px en de rechte met vergelijking x = a Uit de symmetrie van deze figuur om de x -as volgt :

Hieruit volgt dat

Dit laatste resultaat was al door Archimedes gekend (zie blz. 9).

Opmerking : Uit het vorige volgt ook dat

2 Oppervlakte van een hyperboolsegment

We zoeken de oppervlakte A van het deel van het vlak begrensd door de hyperbool met vergelijking xy = k , de x -as en de rechten met vergelijking x = a en x = b ( a , b > 0)

We vinden :

3 Oppervlakte van het gebied tussen de graﬁeken van f met f ( x) = sin x en g met g( x) = cos x in π

We onderzoeken eerst het teken van v ( x )= sin x cos x in

De gevraagde oppervlakte :

4 Oppervlakteberekening met y als onafhankelijke variabele

Voorbeeld : Bereken de oppervlakte A van het gebied begrensd door de parabool met vergelijking y 2 = 4x en de rechte met vergelijking y = 2x – 4.

We zoeken eerst de snijpunten :

De snijpunten zijn dus S1 (1, –2) en S2 (4, 4).

De oppervlakte A is eenvoudiger te berekenen door y in plaats van x te beschouwen als onafhankelijke variabele.

y 2 = 4 x ⇐⇒ x = y 2 4 = f ( y )

y = 2 x 4 ⇐⇒ x = y + 4 2 = g ( y )

5 Praktische toepassing

Een poort is parabolisch van vorm en kan beschreven worden door de vergelijking y = 6x – x 2

De poort is de oppervlakte van het gebied begrensd door de kromme met vergelijking y = 6x – x 2 en de x -as.

• Hoe breed is de poort (breedste punt) ?

Hoe hoog is de poort ? (1 eenheid = 1 meter)

• De poort is dringend aan een likje verf toe. Eén liter verf kost € 15. Met 1 liter verf schilder je 4 m2. Hoeveel verf heb je nodig en wat kost je dat, als je weet dat de verf steeds per liter wordt verkocht ?

• Tijdens het schilderen ben je van plan tweemaal te pauzeren.

Je doet dat telkens nadat je 1 3 van de poort hebt geverfd.

Als je van links naar rechts schildert, op hoeveel meter van de linkerkant pauzeer je dan telkens ?

Oplossing :

• Snijpunten van de parabool met de x -as : A( 0, 0) en B( 6, 0)

• Top van de parabool : C( 3, 9)

Breedte van de poort : ( 6 – 0) m = 6 m

Hoogte van de poort : 9 m

• Oppervlakte van de poort : A = 6

De oppervlakte van de poort bedraagt 36 m2. Je hebt dus 9 liter verf nodig en dat kost je € 135.

• Eerste pauze.

Je pauzeert de eerste maal nadat je 1 3 van de oppervlakte hebt geverfd.

De vraag is nu : bij welke bovengrens is het resultaat van de bepaalde integraal gelijk aan 12 ?

Stellen we die bovengrens gelijk aan a , dan krijgen we de volgende ‘integraalvergelijking’. a 0 (6 x x 2 )dx = 12

3 x 2 x 3 3 a 0 = 12

3a 2 a 3 3 = 12

a 3 9a 2 + 36 = 0

Die laatste vergelijking in a lossen we op met behulp van ICT.

Antwoord :

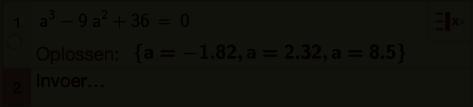
Op 2,32 meter van de linkerkant pauzeer je een eerste maal.

• Tweede pauze.

Je pauzeert een tweede maal nadat je 2 3 van de oppervlakte hebt geverfd. Dat is nadat je 24 m2 hebt geverfd.

Een analoge redenering als de vorige geeft : a 0 (6 x x 2 )dx = 24

3 x 2 x 3 3 a 0 = 24

3a 2 a 3 3 = 24

a 3 9a 2 + 72 = 0

Met behulp van ICT :

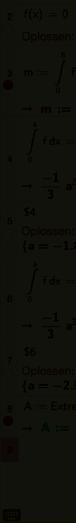
Antwoord :

Je pauzeert een tweede maal op 3,68 m van de linkerkant.

Opmerking :

Na het berekenen van de grens van de eerste pauze kun je de grens van de tweede pauze ook als volgt vinden :

6 – 2,32 = 3,68

11 Oneigenlijke integralen

Bij de definitie van de bepaalde integraal b a f ( x ) dx hebben we verondersteld dat de integratiegrenzen

reële getallen zijn en dat de integrand binnen het interval [ a , b ] begrensd is.

Wanneer we de definitie uitbreiden tot het geval waarbij minstens een van de grenzen oneindig groot wordt, spreken we van een oneigenlijke integraal van de eerste soort.

Wanneer we de definitie uitbreiden tot het geval waarbij de integrand niet begrensd is binnen de integratiegrenzen, spreken we van een oneigenlijke integraal van de tweede soort.

Oneigenlijke integralen van de eerste soort

Een oneigenlijke integraal van de eerste soort is een integraal waarvan minstens een van de grenzen oneindig groot wordt.

Notaties :

Voorbeeld 1 :

Bereken de oppervlakte van het gebied begrensd door de grafiek van de functie f met f ( x )= 1 x en de x -as rechts van de rechte met vergelijking x = 1.

M.a.w.bereken

Oplossing :

De oppervlakte van het onbegrensde gebied G is dus oneindig. We zeggen dat de oneigenlijke integraal divergent is.

Voorbeeld 2 :

Bereken de oppervlakte van het gebied begrensd door de grafiek van de functie f met f ( x )= 1 x 2 en de x -as links van de rechte met vergelijking x = –1.

M.a.w.:bereken

Oplossing :

Ondanks het feit dat het gebied G onbegrensd is, is de oppervlakte eindig ( = 1) We zeggen dat de oneigenlijke integraal convergent is.

Voorbeeld 3 :

Bereken de oppervlakte van het deel van het vlak begrensd door de grafiek van de functie f met f ( x )= 1 1 + x 2 en de x -as.

M.a.w.:bereken

Oplossing :

zodat

Algemeen

Op voorwaarde dat deze limieten bestaan.

Is deze limiet eindig, dan noemen we de oneigenlijke integraal convergent; is deze limiet oneindig, dan noemen we de oneigenlijke integraal divergent

Oneigenlijke integralen van de tweede soort

Een oneigenlijke integraal van de tweede soort is een integraal waarbij de integrand niet begrensd is binnen de integratiegrenzen.

Voorbeeld 1 :

Bereken de oppervlakte van het gebied begrensd door de grafiek van de functie f met f ( x )= 1 x 2 en de x -as, en dat voor x ∈ [ 0, 1].

M.a.w.:bereken 1 0 1 x 2 dx .

Oplossing :

De oppervlakte van het onbegrensde gebied G is dus oneindig. De oneigenlijke integraal is divergent.

Omdat lim x →0 > 1 x 2 =+∞ is de functie f niet begrensd in [ 0, 1]. Merk op dat 0 een pool is van f We definiëren de gevraagde integraal als volgt:

Voorbeeld 2 :

Bereken de oppervlakte van het gebied begrensd door de grafiek van de functie f met f ( x )= 1 2√ x en de x -as, en dat voor x ∈ [ 0, 4]

M.a.w.:bereken 4 0 1 2√ x dx

Oplossing :

Omdatlim

∞ is f nietbegrensdin [0,4].Wedeﬁniërendegevraagdeintegraalalsvolgt:

Ondanks het feit dat het gebied G onbegrensd is, is de oppervlakte eindig. De oneigenlijke integraal is convergent.

Voorbeeld 3 :

Bereken de oppervlakte van het gebied begrensd door de grafiek van de functie f met f ( x )= 1 3 √ x 2 en de x -as, en dat voor x ∈ [ –1, 1]

M.a.w.:bereken 1

Oplossing :

Omdatlim

.Wedeﬁniërendegevraagdeintegraalalsvolgt:

Algemeen :

Is f nietbegrensdin a enis f integreerbaarover ]a , b ],danis b a f ( x ) dx = lim t →a > b t f ( x ) dx

Is f nietbegrensdin b enis f integreerbaarover [a , b [,danis

b a f ( x ) dx = lim

t a f ( x ) dx

Is f nietbegrensdin c ∈ ]a , b [ enis f integreerbaarover [a , c [ ∪ ] c , b ],danis

b a f ( x ) dx = lim t → c < t a f ( x ) dx + lim t → c > b t f ( x ) dx .

Is deze limiet eindig, dan noemen we de oneigenlijke integraal convergent ; is deze limiet oneindig, dan noemen we de oneigenlijke integraal divergent.

12 Samenvatting

• Je kent de definitie van een bepaalde integraal.

– De gemeenschappelijke waarde van de limieten van de bovensom S n en de ondersom s n noemen we de bepaalde integraal van a tot b van de continue functie f :

: integraalteken

a : ondergrens

– Riemanndefinitie :

b : bovengrens

f ( x ): integrand

dx : lengte van een deelinterval

• Je kent de meetkundige betekenis van de bepaalde integraal.

De bepaalde integraal van a tot b van een functie f die continu is in [ a , b ] is de som van de georiënteerde oppervlakten van de gebieden tussen de grafiek van f , de x -as en de rechten met vergelijking x = a en x = b

Oppervlakten van gebieden boven de x -as hebben een positieve waarde en die onder de x -as hebben een negatieve waarde.

• Je kent de volgende eigenschappen van de bepaalde integraal.

a f ( x ) dx = 0

• Je kent de methode om de oppervlakte te bepalen van het gebied begrensd door de grafiek van een functie f en de x -as in het interval [ a, b ] op de x -as.

( x ) | dx

• Je kent de methode om de oppervlakte te bepalen van het gebied begrensd door de grafieken van de functies f en g in het interval [ a, b ].

A =

a | f ( x ) g ( x ) | dx

• Je weet wat een integraalfunctie is.

De functie Ia met I a ( x )= x a f ( t ) dt noemen we de integraalfunctie van f met ondergrens a .

• Je kent de middelwaardestelling van de integraalrekening en je kunt ze bewijzen.

f iscontinuin [a , b ]=⇒∃ c ∈ [a , b ] : b a f ( x ) dx =( b a ) f ( c )

Hetgetal 1 b a b a f ( x ) dx noemenwedegemiddeldewaardevan f over [a , b ]

• Je kent de hoofdstelling van de integraalrekening en je kunt ze bewijzen.

Als f continuisin [a , b ],dangeldtin [a , b ] : I a ( x )= D

• Je weet wat een primitieve functie is.

F is een primitieve functie van f ⟺ DF = f of F ′ = f

x a f ( t ) dt

= f ( x )

Twee primitieve functies van f verschillen slechts in een constante term.

• Je kunt een bepaalde integraal berekenen met behulp van primitieve functies.

Als f continu is in [ a , b ] en F is een willekeurige primitieve functie van f , dan is : b a f ( x ) dx =[ F ( x )] b a = F ( b ) F (a )

• Je weet wat oneigenlijke integralen van de eerste soort en van de tweede soort zijn en je kunt ze berekenen.

– Een oneigenlijke integraal van de eerste soort is een integraal waarvan minstens een van de grenzen naar oneindig nadert. +

)

x ) dx

f ( x ) dx = lim t →−∞ b t f ( x ) dx

f ( x ) dx = lim

t f ( x ) dx

op voorwaarde dat die limieten bestaan.

Is de limiet eindig, dan noemen we de oneigenlijke integraal convergent. Is de limiet oneindig, dan noemen we de oneigenlijke integraal divergent.

– Een oneigenlijke integraal van de tweede soort is een integraal waarbij de integrand niet begrensd is binnen de integratiegrenzen.

Is f nietbegrensdin a enis f integreerbaarover ]a , b ],danis

b a f ( x ) dx = lim t →a > b t f ( x ) dx .

Is f nietbegrensdin b enis f integreerbaarover [a , b [,danis

b a f ( x ) dx = lim t

t a f ( x ) dx

Is f nietbegrensdin c ∈ ]a , b [ enis f integreerbaarover [a , c [ ∪ ] c , b ],danis

b a f ( x ) dx = lim t → c < t a f ( x ) dx + lim t → c > b t f ( x ) dx

Is de limiet eindig, dan noemen we de oneigenlijke integraal convergent. Is de limiet oneindig, dan noemen we de oneigenlijke integraal divergent.

13 Oefeningen

Beschouw de functie f met functievoorschrift f ( x )= x 1 2

a Bereken de ondersom van deze functie over het interval [ 1, 8] bij zeven (gelijke) deelintervallen.

0 b Bereken de bovensom van deze functie over het interval [ 1, 8] bij zeven (gelijke) deelintervallen.

c Bereken met behulp van oppervlakteformules de exacte oppervlakte van het vlakdeel begrensd door de grafiek van deze functie en de x -as over het interval [ 1, 8]

Gegeven is de functie g met functievoorschrift g ( x ) = x + 1.

a Bereken de ondersom en de bovensom van de functie over het interval [ –4, 4] bij acht (gelijke) deelintervallen.

b Bereken met behulp van oppervlakteformules de exacte oppervlakte van het gebied tussen de grafiek van de functie en de x -as over het interval [ –4, 4]

Gegeven is de functie h met functievoorschrift h ( x ) = 4 – 2x.

a Bereken de ondersom en de bovensom van de functie over het interval [ –4, 1] bij tien (gelijke) deelintervallen.

b Bereken met behulp van oppervlakteformules de exacte oppervlakte van het gebied tussen de grafiek van deze functie en de x -as over het interval [ –4, 1]

Gegeven is de functie f met functievoorschrift f ( x )= 3 8 ( x 3 8 x 2 + 16 x )

Bereken de ondersom en de bovensom van de functie over het interval [ 0, 4] bij respectievelijk 4, 8 en 16 (gelijke) deelintervallen.

Toon aan dat b a x 3 dx = b 4 4 a 4 4 met behulp van Riemannsommen (zie blz. 16).

Tip : n i =1 i 3 = n 2 (n + 1)2 4 (bewijs deze formule met volledige inductie.)

Bereken 6 0 f ( x ) dx

Bereken de oppervlakte van het gebied onder de parabool met vergelijking y = x 2 en boven het interval [ 0, 3] op de x -as als volgt :

a Verdeel het interval [ 0, 3] in 6 ( = n ) gelijke deelintervallen met lengte ∆ x = 1 2 en bereken de ondersom sn en de bovensom Sn

b Bereken met ICT de ondersom en de bovensom voor n = 20, 50, 100, 500 en 999.

Leid hieruit lim n →+∞ sn enlim n →+∞ Sn af.

c Toon aan dat voor een willekeurige n (met n Dx = 3) geldt : sn = 3(3 ∆ x )(6 ∆

Bepaallim n →+∞ (∆ x →0) sn enlim n →+∞ (∆ x →0) Sn .

Aanwijzing: n i =1 i 2 = n (n + 1)(2n + 1) 6

d Bereken nu de gevraagde oppervlakte. Controleer je antwoord met ICT.

Bereken volgende bepaalde integralen. a 4 0 f ( x ) dx met f ( x )= 2als0 x 2 1als2 < x 4

x als0 x < 3

f ( x ) dx met f ( x )=

3als x 1 2 x + 5als1 < x < 3 x 4als3 x 4

0als x > 4

3als3 x < 6 x 3als6 x 8

De debietgrafiek van de wekelijkse wasbeurt van de heer Albert E. ziet er ongeveer uit zoals op onderstaande figuur.

a Bedenk een voorschrift bij het debiet D in functie van de tijd t

b Hoeveel liter is er in de badkuip na 5, 10, 20, 25 en 30 minuten ?

c Beschrijf het watervolume in de badkuip in functie van de tijd en teken de bijbehorende volumegrafiek. d Bereken de afgeleide van de volumefunctie. Vergelijk met de debietfunctie en formuleer je bevindingen.

In de volgende grafiek wordt de snelheid van een jogger in meter per minuut uitgezet in functie van de tijd.

tijd(min.) snelheid(m/min.)

a Bereken de afgelegde afstand na 30 minuten.

b Bereken de gemiddelde snelheid (in km/h).

Bereken de volgende integralen.

Bereken de oppervlakte van het lichtgroen gekleurde gebied.

Bereken de oppervlakte van het gebied begrensd door de grafiek van de functie f , de x -as en de gegeven verticale lijnen als :

a f ( x )= 2 x 4 x = 1, x = 1

b f ( x )= x 2 + 2 x + 3 x = 0, x = 3

c f ( x )= x 2 4 x = 2, x = 3

d f ( x )= x 3 + 4 xx = √3, x = √2

e f ( x )=( x 2)( x 2 1) x = 1, x = 2

Bereken de oppervlakte van het gebied ingesloten tussen de grafiek van de functie f en de x -as (tussen de snijpunten met de x -as) als :

a f ( x )= x 2 + 4 x

b f ( x )= x 2 + 5 x 4e f ( x )= x 4 10 x 2 + 9

c f ( x )= x 3 3 x + 2

Bereken de oppervlakte van het blauw gekleurde gebied.

f ( x ) = 5x – x 2

g ( x ) = x 2 – 3x + 6 x y

Bereken de oppervlakte van het gebied begrensd door de grafieken van f en g met onderstaande voorschriften en de gegeven verticale lijnen.

a f ( x )= 2 x 2 g ( x )= x 2 + 1, x = 0, x = 1

b f ( x )= x 2

( x )= 2 x , x = 0, x = 2

c f ( x )= x 3 3 x 2 + 2 g ( x )= x 1, x = 2, x = 3

d f ( x )= x 3 + 2 x 2 4 g ( x )= x 2 + 4 x , x = 3, x = 2

Bereken de oppervlakte van het gebied begrensd door de grafieken van f en g als :

a f ( x )= 2 x x 2 g ( x )= x

b f ( x )= x 2 2 g ( x )= x 2 7 x + 12

c f ( x )= 6 x x 2 g ( x )= x 2 2 x

d f ( x )= x 3 3 x 2 + 3 x 1 g ( x )= x 1

e f ( x )= x 3 + 8 g ( x )= x 2 + 2 x + 8

Bepaal de oppervlakte van het gekleurde gebied.

k 1 ↔ y = x 2 6 x + 5

k 2 ↔ y = x 2 + 6 x 5 r ↔ y = 5

Bepaal de oppervlakte van het gebied ingesloten door de grafiek van de functie f met f ( x ) = 3x 2 – x 4 en de rechte met vergelijking y = –4

Gegeven zijn de functies f en g met f ( x ) = ( x + 2)3 en g ( x ) = 8 + 4x . a Bereken de oppervlakte van het gebied ingesloten door de grafieken van f en g b Bereken de oppervlakte van het gebied ingesloten door de grafieken van f en g en de rechte met vergelijking x = 1.

c Bereken de oppervlakte van het gebied ingesloten door de grafieken van f en g en de rechte met vergelijking y = 27

Bepaal de oppervlakte van het gebied begrensd door de parabool met vergelijking y 2 = 4x en de rechte door de punten P( 1, 2) en Q( 4, –4).

Bereken de oppervlakte van het gebied ingesloten door de grafiek van f met f ( x ) = x 4 – 12x 2 en de verticale lijnen door de buigpunten van de grafiek.

Bereken de oppervlakte van het gebied ingesloten door de parabool met vergelijking 4y = x 2 en de rechten met vergelijking 2y = x en y = x

De grafiek van f met f ( x ) = x 3 + 3x 2 sluit met de raaklijn in P( 2, f ( 2)) en de x -as een gebied in. Bereken de oppervlakte van dat gebied.

Een poort is parabolisch van vorm en kan beschreven worden door de vergelijking y = 3( 4 – x 2) (de poort is de oppervlakte van het gebied tussen de parabool en de x -as).

Gevraagd :

a Bereken de oppervlakte van de poort.

b Hoeveel hoger moet je de poort maken (zelfde breedte op de x -as en nog steeds parabolisch van vorm) opdat de oppervlakte zou verdubbelen ?

c Hoeveel breder moet je de poort maken (zelfde hoogte en nog steeds parabolisch van vorm) opdat de oppervlakte zou verdubbelen ?

De spanten van deze sporthal hebben de vorm van een parabool met vergelijking y = x x 2 25 .

De vloer is een rechthoek van 25 bij 35 meter.

Bereken het volume van de hal.

Bepaal k ( ∈ R) zodat :

Los de volgende vergelijkingen op.

a x 2 tdt + 1 x dt = 0

b 1 x (5 u 4 16) du + x 1 (5 u 4 16) du = 0

De oppervlakte van het gebied ingesloten door de grafiek van f met f ( x ) = x 3, de x -as en de rechte met vergelijking x = k ( k > 0) is 324. Bereken k .

De oppervlakte van het vlakdeel ingesloten door de grafiek van f met f ( x ) = x 2 – 4x + 3, de x -as, de y -as en de rechte met vergelijking x = k ( k ∈ R+) is 4. Bereken k .

Bepaal de oppervlakte van het gebied ingesloten door de grafiek van de functie f met f ( x ) = –5x 4 + 10x 3 + 14x 2 + 2x + 3 en de x -as.

Bepaal nu k (nauwkeurigheid 3 decimalen) zodat de rechte met vergelijking x = k die oppervlakte in twee gelijke delen verdeelt.

Als f continu is in [ a , b ], bewijs dan :

b a f ( x ) dx b a | f ( x ) | dx

Hint : bewijs eerst dat voor elke x ∈ dom f geldt : – |

Verklaar waarom a a f ( x ) dx = 0 (a > 0) als de functie f een oneven functie is.

Bepaal de integraalfunctie I a met I a ( x ) = y = x x 2 25 van de functies met onderstaande voorschriften.

Toon telkens aan dat I ′ a ( x ) = f ( x )

a f ( t )= 5

b f ( t )= 2 t + 1

volgende bepaalde integralen.

Bepaal een primitieve functie van de functies met onderstaande voorschriften.

a f ( x )= 4 3 x 3 + 2 3 x

b f ( x )= 1 x 2 1 + 2 x 2

c f ( x )= 1 √ x + 2

d f ( x )= 2 x · ln2 e f ( x )= 2sin x 3cos x

Gegeven zijn de functies f , g en h met f ( x ) = sin 2

, g ( x ) = –cos 2x en h ( x ) = 2sin x cos x

a Toon aan dat f en g beide primitieve functies van h zijn.

b Toon aan dat f en g slechts een constante verschillen en geef die constante.

Bereken de volgende bepaalde integralen.

Bereken de oppervlakte van het gebied begrensd door de grafiek van de functie f , de x -as en de gegeven verticale lijnen als :

a f ( x )= 3 √ xx = 0, x = 8c f ( x )= 1 x 2 x = 1, x = 2

b f ( x )= e x x = 2, x = 2d

Gegeven is de functie f met f ( x )= 1 2 x

A ( p ) is de oppervlakte van het gebied ingesloten door de grafiek van f , de x -as, de y -as en de rechte met vergelijking x = p met p > 0.

a Bereken A ( p ).

b Bereken de waarde van p waarvoor geldt : A (p )= 3

Gegeven is de functie f met f ( x )= 2√ x

De rechte t raakt aan de grafiek van f in het punt P( …, 4)

a Geef een vergelijking van t .

b Bereken de blauw gekleurde oppervlakte.

Bereken de oppervlakte van het gebied begrepen tussen de krommen met vergelijking :

a y = 8 x 6 x 2 ; y = 2 x

b y = x 2 ; y = 16 x 2 ; x = 4; y = 0

c y = 1 + cos x ; y = 1 sin x ; x = 3π 4 ; x = 7π 4

d y = x 2 2 ; y = 1 x 2 + 1

e y 2 = 2 x ; x 2 = 2 y

f y 2 = x ; y = x 2

g y 2 = 8 x ; y = x

h y 2 = 4 x ; x = 0; y = 2

i y 2 = 2 x 1; y = x 2

j y = ln x ; x = 0; y = 1; y = 2

Hint: Neem y als onafhankelijke variabele (zietoepassing4 blz.38-39)

Bereken in het aangeduide integratie-interval het getal c , waarvan sprake in de middelwaardestelling, voor de volgende integralen.

Bereken de gemiddelde waarde van de functie f over het interval [ a , b ] als : a f (

Bereken de volgende oneigenlijke integralen van de eerste soort.

Bereken de volgende oneigenlijke integralen van de tweede soort.

Is de volgende uitspraak juist ? Verklaar.

Kun je de volgende integraal berekenen ? Verklaar.

Bepaalde integralen

De parabool in deze figuur heeft vergelijking y = x 2. De waarden a en b op de y -as voldoen aan 0 < a < b

De gearceerde oppervlakte wordt gegeven door

Toelatingsexamen arts 2021, vraag 7

Op bijgaande figuur worden de parabolen met vergelijking y = ( x – 1)2 en y = ( x + 1)2 en de rechte met vergelijking y = 9 afgebeeld. Bepaal de oppervlakte van het ingekleurde deel in de figuur.

IJkingstoets burgerlijk ingenieur september 2019, oefening 30

De figuur toont de grafiek van een oneven functie f

Toelatingsexamen arts 2023, vraag 8

Welke van de onderstaande integralen geeft de oppervlakte van het gekleurde gebied als resultaat ?

Waaraan is de oppervlakte van het gekleurde gebied op de figuur gelijk ?

IJkingstoets basiskennis wiskunde handelsingenieur 2022, vraag 36

Wat is de oppervlakte van het gebied begrensd door de y -as, de kromme y = e x en de rechte y = 2 ?

IJkingstoets basiskennis wiskunde handelsingenieur 2023, vraag 36

Op bijgaande figuur zijn de parabool met vergelijking y = x 2 en het punt A( 2, 4) afgebeeld. Wat is de vergelijking van de rechte door de oorsprong die het ingekleurde gebied begrensd door de y -as, de parabool en de horizontale rechte y = 4 in twee even grote delen verdeelt ?

Oefenmodules ijkingstoets 2022-2023, faculteit ingenieurswetenschappen KU Leuven, oefening 7.12

Beschouw het gebied tussen de parabool met vergelijking y = x 2 – 2x + 2, de raaklijn aan de parabool in het punt ( 3, 5) en de coördinaatassen. De oppervlakte van dit gebied is gelijk aan :

Oefenmodules ijkingstoets 2022-2023, faculteit ingenieurswetenschappen KU Leuven, oefening 7.14

Gegeven de functie : R → R : x → x = max{m ∈ Z : m x }. Dat is de functie die elk reëel getal x afbeeldt op het grootste geheel getal kleiner of gelijk aan x , bijvoorbeeld π = 3. Wat is de waarde van de bepaalde integraal

x dx ?

IJkingstoets burgerlijk ingenieur juli 2022, oefening 28

Veronderstel dat f : R → R een continue functie is die voldoet aan f ( x ) = f ( –x ) voor alle x ∈ R. Er is gegeven dat 1

IJkingstoets burgerlijk ingenieur augustus 2020, oefening 22

De oppervlakte van het gebied ingesloten door de krommen met vergelijking y = x 2 en y = √ x is gelijk aan :

Typevragen ijkingstoets industrieel ingenieur, standaardvragen oefening 9

Bepaalde integralen 1

Ik kan een oppervlakte onder de grafiek van een functie benaderen met behulp van een ondersom of bovensom van rechthoeken.

Ik ken de definitie van de bepaalde integraal als limiet van een som.

Ik ken de betekenis van de bepaalde integraal als georiënteerde oppervlakte tussen de grafiek en de horizontale as in een bepaald interval.

Ik kan een bepaalde integraal berekenen.

Ik ken de optelbaarheid en lineariteit van de bepaalde integraal.

Ik kan met behulp van een bepaalde integraal de oppervlakte berekenen die begrensd is door de grafieken van twee functies.

Ik ken de middelwaardestelling en kan ze bewijzen.

Ik ken de hoofdstelling van de integraalrekening en kan ze bewijzen.

Ik ken de betekenis van een primitieve functie.

Ik kan de oppervlakte berekenen van een gebied met y als onafhankelijke veranderlijke.

Ik ken de definitie van oneigenlijke integralen en weet hoe ik die moet berekenen.

2Integratiemethoden

Wanneer een ingenieur voor zijn berekeningen eenmalig een bepaalde integraal moet berekenen, volstaat meestal een benadering tot op een zekere nauwkeurigheid van het resultaat. Hij zal zich ook tevreden stellen met numerieke integratiemethoden, geleverd door zijn rekenmachine of door computersoftware.

Wanneer een wetenschapper een bepaald proces in zijn algemeenheid wil beschrijven, maakt hij dikwijls gebruik van onbekenden en parameters. Het rekenen met symbolische letternotaties is hierbij nodig. Omdat ICT hier soms tekortschiet, blijft een minimale kennis van integratiemethoden zelfs in het huidige computertijdperk vereist.

Integratiemethoden

2.1 Fundamentele integralen

1 Onbepaalde integraal 69

2 Fundamentele integralen 71

3 Opeenvolging van operatoren 71

4 Lineariteit van de onbepaalde integraal 72

5 Onmiddellijke integratie 72

6 Integratie door splitsing 73

7 Toepassingen 73

8 Samenvatting 74

9 Oefeningen 75

2.2 Integratie door substitutie

1 Stelling 1 : aanpassing van de differentiaal 77

2 Toepassing : vier belangrijke formules 78

3 Stelling 2 : algemene substitutieregel 78

4 Stelling 3 : gevolg van de substitutieregel 80

5 Stelling 4 : de teller is de afgeleide van de noemer 81

6 Toepassing : twee belangrijke formules 81

7 Substitutie bij bepaalde integralen 82

8 Toepassing 83

9 Samenvatting 84

10 Oefeningen 85

2.3 Integratie van elementaire rationale functies – splitsen in partieelbreuken

1 Integralen van het type

2 Integralen van het type

3 Integralen van het type

4 Toepassing

5 Samenvatting

6 Oefeningen

2.4 Partiële integratie

1 Principe 99

2 Integralen met een integrand waarvoor geen onmiddellijke integratie bestaat 100

3 Integralen met als integrand een gemengde functie – verlaging van de macht 101

4 Integralen met als integrand een gemengde functie – terugkeer van de integrand 102

5 Integratie van elementaire kwadratische wortelvormen 103

6 Partiële integratie bij bepaalde integralen 105

7 Toepassing 106

8 Recursieformules 108

9 Samenvatting 109 10 Oefeningen 110

Wat moet je kennen en kunnen? 116

2.1 Fundamentele integralen

In het vorige hoofdstuk hebben we aangetoond dat de bepaalde integraal b a f ( x ) dx eenvoudig berekend kan worden op voorwaarde dat we een primitieve functie F van f kunnen vinden.

Er geldt immers : b a f ( x ) dx = F ( b ) F (a )

In dit hoofdstuk gaan we op zoek naar technieken om primitieve functies te bepalen.

1 Onbepaalde integraal

Gegeven : De functie f met f ( x ) = 2x

Dan is F met F ( x ) = x 2 een primitieve functie van f

Immers : DF ( x ) = Dx 2 = 2x = f ( x )

We weten dat alle primitieve functies van f slechts van elkaar verschillen door een constante. Zo zijn de volgende functies ook primitieve functies van f

F 1 met F 1 ( x )= x 2 + 2

F 2 met F 2 ( x )= x 2 √2

F 3 met F 3 ( x )= x 2 + π

De verzameling van alle primitieve functies van f is dus

{ F c met F c ( x ) = x 2 + C en C ∈ R}

Die verzameling noemen we de onbepaalde integraal van f met f ( x ) = 2x en stellen we voor door

2 xdx (lees:integraalvan2 xdx )

Dus: 2 xdx = x 2 + C

Algemeen :

Het zoeken naar een primitieve functie F met een functie f heet primitiveren of integreren. In dit verband spreken we van de onbepaalde integraal van f . Hiervoor is een apart teken ingevoerd, het integraalteken

f ( x ) dx = F ( x )+ C

Omdat deze integraal slechts op een constante na gedefinieerd is, spreken we van de onbepaalde integraal. De constante C noemen we de integratieconstante. Het functievoorschrift f ( x ) achter het integraalteken noemen we de integrand. Het is het voorschrift van de functie f waarvan de primitieve functies worden gezocht. Achter de integrand staat dx , wat aangeeft dat x de variabele is waarnaar we integreren. Omdat f ( x ) meestal expliciet als functie van x geschreven is, lijkt dit overbodig. Later zul je echter zien dat het nuttig kan zijn dat de variabele aangegeven is. De variabele x noemen we de integratievariabele.

Dus : f ( x ) dx = F ( x )+ C ⇐⇒ DF ( x )= f ( x )

Voorbeelden

• sin xdx = cos x + C want D ( cos x )= sin x

• 1 x 2 dx =

• dx √ x 2 + k = ln | x + √ x 2 + k | +C

• dx cos2 x = tan x + C want D tan x = 1 cos2 x

• sinh xdx = cosh x + C want D cosh x = sinh x

• e at dt = 1 a e at + C

(zieVBTL5/6Analyse3)

Primitieve functies

In 1676 heeft Newton als eerste een lijst van primitieve functies gepubliceerd. In de meeste gevallen schreef Newton zijn primitieve functies als machtreeksen.

De notatie ∫ f(x) dx is afkomstig van Leibniz en wordt algemeen gebruikt.

2 Fundamentele integralen

De formules voor het afleiden van functies geven aanleiding tot een aantal basisintegralen. We noemen ze ook wel fundamentele integralen, omdat elke integraal op de een of andere manier herleid kan worden tot een van die integralen.

)

Het bewijs van de formules volgt uit 1.

Voorbeeld :

Bewijs van formule (2) : D x n +1 n + 1 + C = (n + 1) x n n + 1 + 0 = x n

3 Opeenvolging van operatoren

• D f ( x )dx = f ( x )

Want: D f ( x )dx = D ( F ( x )+ C )= DF ( x )= f ( x )

• d f ( x )dx = f ( x )dx

Want: d f ( x )dx = D ( f ( x )dx dx = f ( x )dx

• df ( x )= f ( x )+ C

Want: df ( x )= f ( x )dx = f ( x )+ C

Differentiaalvaneenfunctie df ( x )= Df ( x ) · dx of df ( x )= f ( x ) · dx (zieVBTL5/6Analyse3)

4 Lineariteit van de onbepaalde integraal

stelling

af ( x )+ bg ( x ) dx = a f (

) dx +

( x ) dx (a en b nietbeidenul)

Bewijs :

We moeten dus (volgens 1) aantonen dat de afgeleide van het rechterlid gelijk is aan de integrand van het linkerlid. We gebruiken volgende rekenregels : afgeleide van een som : D ( f + g ) = Df + Dg constante factor bij het afleiden : D ( k f ) = k Df

Hieruitvolgtdat:

Omdat f ( x )dx en g ( x )dx eenintegratieconstantebevatten,mogenweschrijven:

af (

)+ bg (

5 Onmiddellijke integratie

Hierbij gebruiken we uitsluitend de basisformules (fundamentele integralen).

Voorbeelden :

6 Integratie door splitsing

Bij integratie door splitsing wordt gebruikgemaakt van de basisformules en van de lineariteit van de onbepaalde integraal.

Voorbeelden :

•

Merk op dat we slechts één integratieconstante schrijven !

= dx 2 1 x 2 + 1

= x 2Bgtan x + C

• (sin x + cos x )dx = sin xdx + cos xdx = cos x + sin x + C

• tan2 xdx = sin2 x cos2 x dx = 1 cos2 x cos2 x dx = dx cos2 x dx

= tan x x + C

Inditvoorbeeldkunnenweookonmiddellijktan2 x vervangendoorsec2 x 1.

7 Toepassingen

Toepassing 1 :

Ga via integraalrekening na of de gemiddelde waarde van de functie f met f ( x ) = 3sin x + 5 over één periode gelijk is aan 5.

Oplossing :

De periode van f met f ( x ) = 3sin x + 5 is dezelfde als de periode van de functie g met g ( x ) = sin x , de periode is dus gelijk aan 2p. De gemiddelde waarde van f in [ 0, 2p] wordt :

Toepassing 2 :

1 2 3 4 5 6 7 8 0 0 f ( x )= 3sin x + 5

Bereken f ( x ) als gegeven is dat f ( x )= 1 √ x en f ( 4) = 2.

Oplossing :

• Uit het gegeven volgt dat f ( x )= 1 √ x dx = x 1 2 dx = x 1 2 1 2 + C = 2√ x + C .

• f (4)= 2 ⇐⇒ 2√4 + C = 2 ⇐⇒ C = 2

Dus: f ( x )= 2√ x 2

8 Samenvatting

• Je kent de definitie van de onbepaalde integraal van een functie f f ( x )dx = F ( x )+ C ⇐⇒ DF ( x )= f ( x ) (integratieconstante C ∈ R )

• Je kent de volgende eigenschappen en je kunt ze bewijzen.

D f ( x )dx = f ( x )

d f ( x )dx = f ( x )dx

df ( x )= f ( x )+ C

[af ( x )+ bg ( x )]dx = a f ( x )dx + b g ( x )dx (a en b nietbeidenul)

• Je kunt de onbepaalde integraal van een functie f bepalen door uitsluitend de fundamentele (basis)integralen en de basiseigenschappen van de integraalrekening te gebruiken.

• Je kunt ook integreren door splitsing. Hierbij wordt gebruikgemaakt van de lineariteit van de onbepaalde integraal.

9 Oefeningen

Bereken de volgende integralen.

3 x √ xdx

Bereken de volgende integralen.

Bereken de volgende integralen. a (a sin t + b cos t )dt

Bereken de volgende bepaalde integralen.

aBereken D tanh x en D coth x enleidhieruitaf:

7 * 8 9 10 11

Bereken f ( x ) als gegeven is :

a f ( x )= 2 x 3; f ( 1)= 5 2

b f ( x )= 2 x 2 + x ; f (2)= 10 3

Beschouw een functie f waarvoor geldt : f (1)= 1en

Bereken de gemiddelde waarde van de functie f

met voorschrift f ( x )= 1 4 x 4 9 4 x 2 + x + 3

over het interval [ –3, 2]

Kun je de volgende integraal berekenen ? Verklaar.

2 dx ( x + 1)2

Welkevanonderstaandeﬁgurenkandegraﬁekvoorstellenvandefunctie f

Oefenmodules ijkingstoets 2022–2023, faculteit ingenieurswetenschappen KU

Bereken

Oefenmodules ijkingstoets 2022–2023, faculteit ingenieurswetenschappen KU Leuven, oefening 7.17

2.2 Integratie door substitutie

Taak : Wewetendat cos xdx = sin x + C .Mogenwehieruitaﬂeidendat cos5 xdx = sin5 x + C ?

• Toonaandatditniethetgevalisdooreenprimitievefunctievan f met f ( x )= cos5 x tezoeken.

• Vulnuaan: cos5 xdx = + C

1 Stelling 1 : aanpassing van de differentiaal

stelling 1

Bewijs :

+ b )

Hieruit volgt dat

Praktisch gebruik : om vlot te werken, schrijf je meestal nog een tussenstap bij het gebruik van deze stelling. Eerst pas je de differentiaal dx aan, om nadien de stelling toe te passen.

+ b )dx =

Voorbeelden

2 Toepassing : vier belangrijke formules

• Twee veel voorkomende integralen van goniometrische functies zijn cos2 xdx en sin2 xdx .

xdx = 1 +

( x + sin x · cos x )+ C

Taak : bereken sin2 xdx doorsin2 x tevervangendoor 1 cos2 x 2 .

We onthouden :

• Twee veel voorkomende integralen met betrekking tot de cyclometrische functies zijn

We onthouden :

3 Stelling 2 : algemene substitutieregel

stelling 2

Bewijs

Merk op :

Deze stelling is in de integraalrekening de tegenhanger van de kettingregel uit de theorie van de afgeleiden.

Praktisch gebruik :

De formule is soms vlotter hanteerbaar wanneer je g ( x ) gelijkstelt aan een nieuwe variabele t

Dan is dg ( x ) = g ′( x )dx = dt . De stelling wordt dan :

stelling 2

Als f ( x )dx = F ( x )+ C en g met g ( x )= t eenaﬂeidbarefunctieis,danis f ( t )dt = F ( t )+ C .

Dit noemen we de substitutieregel

De bedoeling van die regel is voornamelijk de gegeven integraal door een gepaste substitutie te herleiden tot een fundamentele integraal. Alle fundamentele integralen kunnen nu uitgebreid worden door x te vervangen door t = g ( x ).

Zo bekom je bijvoorbeeld :

• t n dt = t n +1 n + 1 + C (n = 1)

• dt t = ln | t | +C

• dt cos2 t = tan t + C

Voorbeelden :

• I = x x 2 + 1 dx

• I = cos x (1 + sin x )2 dx

Stel x 2 + 1 = t ,danis d ( x 2 + 1)= 2 xdx = dt ,zodat

= √ t + C = x 2 + 1 + C

Stel1 + sin x = t ,danis d (1 + sin x )= cos xdx = dt ,zodat I = cos xdx (

Opmerking :

Je kunt de voorbeelden van stelling 1 ook berekenen door t expliciet op te schrijven. We tonen dit aan voor voorbeeld 2.

• I = (2 x 3)4 dx

Stel2 x 3 = t ,danis d (2 x 3)= 2dx = dt ,zodat

4 Stelling 3 : gevolg van de substitutieregel

stelling 3

f n ( x ) · f ( x )dx = f n +1 ( x ) n + 1 + C (n = 1)

Bewijs : D f n +1 ( x ) n + 1 = 1 n + 1 D ( f n +1 ( x )) = 1 n + 1 (n + 1) f n ( x ) Df ( x ) = f n ( x ) f ( x )

Opmerking :

Integralenvandevorm f n ( x ) · f ( x )dx wordendoordesubstitutie t = f ( x ) herleidtotdefundamentele integraal t n dt .

Voorbeelden :

• I = ( x 2 3 x + 1)4 (2 x 3)dx Stel f ( x )= x 2 3 x + 1,danis f ( x )= 2 x 3,zodat I = ( x 2 3 x + 1)4 d ( x 2 3 x + 1) = ( x 2 3 x + 1)5 5 + C Ofstel x 2 3 x + 1 = t ,danis d ( x 2 3 x + 1)=(2 x 3)dx = dt ,zodat I = t 4 dt

• I = ln3 x x dx Stel f ( x )= ln x ,danis f ( x )= 1 x ,zodat I = ln3 xd (ln x )= ln4 x 4 + C • I = sin x cos3 x dx Stelcos x = t ,danis d (cos x )= sin xdx = dt ofsin xdx = dt ,zodat

• I = x · 3 √ x 2 + 1 · dx Stel f ( x )= x 2 + 1,danis f ( x )= 2 x ,zodat

5 Stelling 4 : de teller is de afgeleide van de noemer

stelling 4

f ( x ) f ( x ) dx = ln | f ( x ) | + C

Bewijs :

D (ln | f ( x ) |)= 1 f ( x ) · Df ( x )= f ( x ) f ( x )

Opmerking :

Integralenvandevorm f ( x ) f ( x ) dx wordendoordesubstitutie t = f ( x ) herleidtotdefundamentele

integraal dt t .

Voorbeelden :

• I = x 2 x 3 + 1 dx

• I = dx x · ln x

Stel f ( x )= x 3 + 1,danis f ( x )= 3 x 2 ,zodat I = 1 3 3 x 2 x 3 + 1 dx = ln | x 3 + 1 | + C

Ofstel x 3 + 1 = t ,danis d ( x 3 + 1)= 3 x 2 dx = dt of x 2 dx = dt 3 ,zodat I = 1 3 dt t = 1 3 ln | t | + C = 1 3 ln | x 3 + 1 | + C

Stel f ( x )= ln x ,danis f ( x )= 1 x ,zodat I = 1 x ln x dx = ln | ln x | + C

• I = tan xdx of: I = sin x cos x dx

• I = e x e x + 1 dx

Stel f ( x )= cos x ,danis f ( x )= sin x ,zodat I = sin x cos x dx = ln | cos x | + C

Stel f ( x )= e x + 1,danis f ( x )= e x ,zodat I = ln | e x + 1 | + C = e x +1 > 0 ln( e x + 1)+ C

6 Toepassing : twee belangrijke formules

tan xdx = sin x cos x dx

Stel f ( x )= cos x ,danis f ( x )= sin x zodat

tan xdx = sin x cos x dx = ln | cos x | +C = ln | sec x | +C

cot xdx = cos x sin x dx

Stel f ( x )= sin x ,danis f ( x )= cos x zodat

cot xdx = cos x sin x dx = ln | sin x | +C

7 Substitutie bij bepaalde integralen

Voorbeeld

Methode 1 Bereken eerst de onbepaalde integraal.

Methode 2 Aanpassen van de integratiegrenzen.

(1)

Aanpassing van de grenzen : ondergrens : als x = –2, dan is t = 1 zie (1) bovengrens : als x = 2, dan is t = 3

8 Toepassing

De wekelijkse opbrengst van een recente film kan beschreven worden door de functie d met voorschrift d ( t )= 40 t t 2 + 25 met d ( t ): opbrengst in miljoenen dollars en t : tijd in weken.

Gevraagd :

• Rond welke periode is de weekopbrengst het grootst ?

• Hoeveel bedraagt de opbrengst na 1 jaar ?

Oplossing :

• We maken eerst de grafiek van de functie d met t ⩾ 0.

d ( t )

• Berekenen van het maximum van d : d ( t )= D 40 t t 2 + 25

+ 25)

Rond het einde van de vijfde week kent de opbrengst van de filmproductie zijn hoogtepunt met een opbrengst van ongeveer 4 miljoen dollar per week.

• De opbrengst na 1 jaar (= 52 weken) is de som van de opbrengsten gedurende de periode van de lancering van de film tot het einde van de 52e week.

Dit betekent : jaaropbrengst =

Stel t 2 + 25 = y , dan is 2tdt = dy

Als t = 0, dan is y = 25.

Als t = 52, dan is y = 522 + 25 = 2729.

Bijgevolg : jaaropbrengst = 2729 25 20 y dy = y > 0 20[ln y ]2729 25 = 93,856294...

Antwoord :

De opbrengst van de film gedurende het eerste jaar is 93 856 294 dollar.

9 Samenvatting

• Je weet dat de substitutiemethode bij onbepaalde integralen bestaat uit de volgende stappen.

– We vervangen de variabele x door de variabele t door een betrekking tussen x en t op te geven, de zogenaamde substitutieformule.

– De gegeven integraal wordt dan herleid tot een fundamentele integraal.

– De gevonden primitieve functie heeft t als variabele. We vervangen t in functie van x met behulp van de substitutieformule.

• Je weet dat de aard van de substitutie afhangt van de vorm van de integrand. Je kunt de volgende stellingen toepassen.

– Stelling 1 (aanpassing van de differentiaal)

Als f ( x ) dx = F ( x )+ C , danis f (ax + b ) dx = 1 a

Met behulp van die stelling verkregen we de volgende belangrijke formules.

– Stelling 2 (substitutieregel)

Als f ( x )dx = F ( x )+ C en g eenaﬂeidbarefunctieis,danis f (g ( x )) g ( x )dx = F (g ( x ))+ C

ofals f ( x )dx = F ( x )+ C en g met g ( x )= t eenaﬂeidbarefunctieis,danis f ( t )dt = F ( t )+ C

– Stelling 3

f n ( x ) f ( x )dx = f n +1 ( x ) n + 1 + C (n = 1)

– Stelling 4

f ( x ) f ( x ) dx = ln | f ( x ) | +C

• Je kunt de substitutieformule toepassen bij bepaalde integralen.

– Je stelt de substitutieformule op om over te gaan van de variabele x naar een variabele t en je past de integratiegrenzen aan, die voor de nieuwe integratievariabele t moeten gelden.

– Je kunt ook eerst afzonderlijk de onbepaalde integraal bepalen en pas daarna de bepaalde integraal berekenen. In dit geval moeten de integratiegrenzen niet gewijzigd worden.

10 Oefeningen

Bereken de volgende integralen.

a 1 73 x 2 dx l x + 7 1 x 2 dx

b x · e x 2 dx m x 3 · 1 + x 4 dx

c 3 sin 2 x + π 7 dx n 3 x 3 x 2 + 3 dx

d e x 1 e 2 x dx o 1 √ x (1 √ x ) dx

e 2 5 x + 3 dx

sin8 x 9 + sin4 4 x dx f 2 9 x 2 7 dx

g lnn x x dx

(4 x 3 + 1) ( x 4 + x )7 dx

5 x 5 x + 3 x dx

h 12 x ln x dx s 1 sin2 3 x dx

i 5 (2 x )2 dx t 1 csc x + cot x dx

j x 7 + x 4 dx u 1 sin2 x 2 x + cos2 x dx

k 1 2 x + 2 x dx v dx cos2 x √tan x 1

Bereken de volgende integralen. a 1 x (1 + ln2 x ) dx

b e 1 x x 2 dx

1 x 2 + 4 dx

6 9 4 x 2 dx

c 1 ln x x dx n 1 2 x 2 + 1 dx

d 2 x +2 2 x + 2 dx o dx ( x + 1)2 + 1

e 3 42 x 1 5 x +2 dx p xdx √ x + 1 4 √ x + 1

f ( x + π)e dx q sin x cos xdx g 1 cot(7 x 3) dx

h (1 + x )2 √ x dx

i x 2 1 + x 6 dx

2 x + 1 x 2 + x + 2 dx

Bgtan x 1 + x 2 dx

x · 2 x 2 + 1dx

j 3 x e 2 x dx u 3 x 4 + 3 x dx

k 1 4 x 2 + 1 dx v sin2 x (2 + sin x )2 dx

Bereken de volgende bepaalde integralen.

de volgende oneigenlijke integralen.

Bereken de volgende bepaalde integralen.

Bepaal het voorschrift van de primitieve functie

Los op in R :

x 0 (3 t 2 4 t + 1)dt = x 1 (4 t 3 6 t )dt

1 t 2 = Bgsin x b 2 x 1 (2 t 3 t )dt = 1 x (2 t + 3)dt

Berekendeoppervlaktevanhetgebiedbegrensddoorde x -asendegraﬁek vandefunctie f met f ( x )= x √1 x 2 .

Bereken de oppervlakte van het gebied begrepen tussen de grafieken van f en g als

a f ( x )= sin x ; g ( x )= sin2 x met x ∈ [0,2π]

b f ( x )= tan x ; g ( x )= cot x ende x -asmet x ∈ 0, π 2

c f ( x )= x 2 4 ; g ( x )= 8 x 2 + 4

Bereken de oppervlakte van het ingekleurde gebied.

a Gegeven is de grafiek van f met f ( x ) = 5 sin 3x

b Gegeven zijn de grafieken van f en g met f ( x ) = cos x + 1 en g ( x ) = –3 – 3 cos x .

( x )= 3 3cos

f ( x )= 5sin3 x

Bereken de oppervlakte van het deel van het vlak begrensd door de lus van de kromme met vergelijking y 2 = x 4 – x 5 .

A is het maatgetal van de oppervlakte van het deel van het vlak begrensd door de krommen met vergelijking y = 1 + cos x y = 1 + cos

Bewijs : A = A ′

aBereken I =

sin x 1 + cos2 x dx

bBewijsdatvoorelke f ,continuverondersteldin [0, a ],geldt:

cGebruik a en b om J =

x sin x 1 + cos2 x dx teberekenen.

Vraag uit de toenmalige toelatingsexamens burgerlijk ingenieur

A ′ is het maatgetal van de oppervlakte van het deel van het vlak begrensd door de krommen met vergelijking y = 1 + cos

integraal

Toelatingsexamen arts 2022, vraag 4

Waaraan is de volgende integraal gelijk ? (

IJkingstoets basiskennis wiskunde handelsingenieur 2022, vraag 37

Voor welke positieve waarde van a is : a

IJkingstoets basiskennis wiskunde handelsingenieur 2022, vraag 38

Oefenmodules ijkingstoets 2022–2023, faculteit ingenieurswetenschappen KU Leuven, oefening 4.12

Bepaal de waarde van de bepaalde integraal e 1 dx x 1 + ln( x ) . (A) ln

Oefenmodules ijkingstoets 2022–2023, faculteit ingenieurswetenschappen KU Leuven, oefening 4.13

(B) 2 (C)

Oefenmodules ijkingstoets 2022–2023, faculteit ingenieurswetenschappen KU Leuven, oefening 1.29

Oefenmodules ijkingstoets 2022–2023, faculteit ingenieurswetenschappen KU Leuven, oefening 1.31 Bereken I = 4 1 ln x x dx (A) ln 4 (B) 1 2

Oefenmodules ijkingstoets 2022–2023, faculteit ingenieurswetenschappen KU Leuven, oefening 7.15 Bereken de integraal

Waaraan is de volgende integraal gelijk ?

0 x sin (1 x 2 ) dx

–

IJkingstoets burgerlijk ingenieur augustus 2022, oefening 4

Waaraanis 2 0 3 x 2 24 2 x 3 7 dx gelijk? (A) –212 (B) –26 (C) 222 (D) 228

IJkingstoets burgerlijk ingenieur juli 2023, oefening 6

Over een continue functie f : R → R is gegeven dat

0 f ( x ) dx = 8, 2 1 f ( x ) dx = 2,

Waaraanis 2 0 f (2 x ) dx dangelijk?

) dx = 4.

7 (B) 8 (C) 14 (D) 20

IJkingstoets burgerlijk ingenieur juli 2023, oefening 11

Bepaal het natuurlijk getal n waarvoor geldt dat

(A) 50 (B) 100 (C) 150 (D) 200

IJkingstoets burgerlijk ingenieur augustus 2023, oefening 18

Deonbepaaldeintegraal ( x 2 + 1)2 dx isgelijkaan(waarbijtelkens c ∈ R )?

geen van voorgaande

IJkingstoets basiskennis wiskunde handelsingenieur 2023, vraag 35

Gegeven zijn een continue functie g : R → R en de functie f : R → R met f ( x ) = g ( x + 1) voor alle x ∈ R

Verder zijn twee reële getallen a en b gegeven met a < b < 0. Welke van de volgende beweringen is als enige altijd waar ?

IJkingstoets burgerlijk ingenieur juli 2019, oefening 30

2.3 Integratie van elementaire rationale functies – splitsen in partieelbreuken

1 Integralen van het type

∫ px + q ax2 + bx + c dx met D = b2 – 4ac > 0

Voorbeeld 1 :

x 5

2 x 2 + x 1 dx

Omdat de noemer van de integrand ontbindbaar is, proberen we de integrand te schrijven als de som van twee partieelbreuken waarvan de noemers van de eerste graad zijn.

Aangezien2 x 2 + x 1 =(2 x 1)( x + 1),stellenwe x 5 2 x 2 + x 1 = A 2 x 1 + B x + 1 (*) waarin A en B nognadertebepalenconstantenzijn.

De onbepaalde coëfficiënten A en B vinden we door de teller van de som van de partieelbreuken gelijk te stellen aan de teller van de gegeven breuk.

Als we het rechterlid van (*) op gelijke noemer plaatsen, dan bekomen we : x 5

2 x 2 + x 1 = A ( x + 1)+ B (2 x 1) 2 x 2 + x 1 = ( A + 2 B ) x +( A B ) 2 x 2 + x 1

Hieruit volgt :

( A + 2 B ) x +( A B )= x 5

⇐⇒ A + 2 B = 1

A B = 5

⇐⇒ A = 3 B = 2

Zodat : x 5 2 x 2 + x 1 = 3 2 x 1 + 2 x + 1

Algemeen :

En bijgevolg : x 5 2 x 2 + x 1 dx = 3 2 x 1 + 2 x + 1 dx = 3 2 x 1 dx + 2 x + 1 dx = 3 2 d (2 x 1) 2 x 1 + 2 d ( x + 1) x + 1 = 3 2 ln | 2 x 1 | +2ln | x + 1 | +C

Als de tweedegraadsvorm in de noemer van de integrand ontbindbaar is in twee verschillende factoren, m.a.w. als de tweedegraadsvorm in de noemer twee verschillende nulwaarden x 1 en x 2 heeft, dan kun je de integrand altijd schrijven als px + q ax 2 + bx + c = A x x 1 + B x x 2

Voorbeeld 2 : 2 x 2 3 x 16 2 x 2 5 x 3 dx

Voer eerst de euclidische deling uit. Je vindt als quotiënt 1 en als rest 2x – 13. (Ga dit na !)

2 x 2 3 x 16

2 x 2 5 x 3 dx = 1 + 2 x 13 2 x 2 5 x 3 dx = dx + 2 x 13 2 x 2 5 x 3 dx

Aangezien2 x 2 5 x 3 =(2 x + 1)( x 3),stellenwe 2 x 13 2 x 2 5 x 3 = A 2 x + 1 + B x 3 (*) waarin A en B nognadertebepalenconstantenzijn.

Als we het rechterlid van (*) op gelijke noemer plaatsen, dan bekomen we :

2 x 13

2 x 2 5 x 3 = A ( x 3)+ B (2 x + 1) 2 x 2 5 x 3 = ( A + 2 B ) x +( 3 A + B ) 2 x 2 5 x 3

Hieruit volgt : ( A + 2 B ) x +( 3 A + B )= 2 x 13 ⇐⇒ A + 2 B = 2 3 A + B = 13 ⇐⇒ A = 4 B = 1

Zodat : 2 x 13 2 x 2 5 x 3 = 4 2 x + 1 + 1 x 3

En bijgevolg :

2 x 2 3 x 16 2 x 2 5 x 3 dx = dx + 4 2 x + 1 dx + 1 x 3 dx = dx + 4 2 d (2 x + 1) 2 x + 1 d ( x 3) x 3 = x + 2ln | 2 x + 1 |− ln | x 3 | +C = ln (2 x + 1)2 x 3 + x + C

2 Integralen van het type

Voorbeeld 1 : 4 x + 5 x 2 6 x + 9 dx

Oplossing :

4 x + 5

+ q ax2 + bx + c dx met D = b2 – 4ac = 0

4 x + 5 x 2 6 x + 9 dx = 4 x + 5 ( x 3)2 dx

x 2 6 x + 9 dx = 4 x + 5 ( x 3)2 dx

= 4( x 3)+ 17 ( x 3)2 dx

= 4 x 3 + 17 ( x 3)2 dx

= 4 1 x 3 dx + 17 1 ( x 3)2 dx

= 4 d ( x 3) x 3 + 17 d ( x 3) ( x 3)2

= 4ln | x 3 |− 17 x 3 + C

Algemeen :

Als de tweedegraadsvorm in de noemer van de integrand ontbindbaar is in twee gelijke factoren, m.a.w. als de tweedegraadsvorm in de noemer slechts één nulwaarde x 1 heeft, kun je de integrand altijd schrijven als px + q ax 2 + bx + c = A x x 1 + B ( x x 1 )2

Voorbeeld 2 : 4 x + 3 4 x 2 4 x + 1 dx

Oplossing :

4 x + 3 4 x 2 4 x + 1 dx = 4 x + 3 (2 x 1)2 dx

= 2(2 x 1)+ 5 (2 x 1)2 dx = 2 2 x 1 + 5 (2 x 1)2 dx = 2 1 2 x 1 dx + 5 1 (2 x 1)2 dx = d (2 x 1) 2 x 1 + 5 2 d (2 x 1) (2 x 1)2

= ln | 2 x 1 |− 5 2(2 x 1) + C

Algemeen :

Aangezien x 2 6 x + 9 =( x 3)2 ,stellenwe 4 x + 5 x 2 6 x + 9 = A x 3 + B ( x 3)2 waarin A en B nog nadertebepalenconstantenzijn.

Alswehetrechterlidopgelijkenoemerplaatsen, bekomenwe: 4 x + 5 x 2 6 x + 9 = A ( x 3)+ B ( x 3)2 = Ax +( 3 A + B ) ( x 3)2

Hieruitvolgt:

Ax +( 3 A + B )= 4 x + 5 ⇐⇒ A = 4 3 A + B = 5 ⇐⇒ A = 4 B = 17

zodat: 4 x + 5 x 2 6 x + 9 = 4 x 3 + 17 ( x 3)2

Bijgevolg: 4 x + 5 x 2 6 x + 9 dx = 4 x 3 dx + 17 ( x 3)2 dx = 4 d ( x 3) x 3 + 17 d ( x 3) ( x 3)2 = 4ln | x 3 |− 17 x 3 C

3 Integralen van het type

Voorbeeld 1 : 4 x 1 x 2 + 2 x + 3 dx

px + q ax2 + bx + c dx met D = b2 – 4ac < 0

Bevat de teller de onbepaalde x , dan splits je de teller in een som van twee termen, waarbij de eerste term een veelvoud is van de afgeleide van de noemer en de tweede term een constante (eventueel nul).

4 x 1 x 2 + 2 x + 3 dx = A (2 x + 2)+ B x 2 + 2 x + 3 dx

Uit4 x 1 = A (2 x + 2)+ B = 2 Ax +(2 A + B ),volgt A = 2 B = 5

zodat 4 x 1 x 2 + 2 x + 3 dx = 2(2 x + 2) 5 x 2 + 2 x + 3 dx

) ( x + 1)2 + 2 = 2ln | x 2 + 2 x + 3 |− 5 √2 Bgtan x + 1 √2 + C

Algemeen :

Heeft de kwadratische vorm ax 2 + bx + c = 0 geen nulwaarden, dan bestaan er constanten A en B zodat px + q ax 2 + bx + c = A (2ax + b )+ B ax 2 + bx + c px + q ax 2 + bx + c dx (met p = 0)kanzoherleidwordentotéénintegraalvandevorm f ( x ) f ( x ) dx = ln | f ( x ) | + C enéénvandevorm p ax 2 + bx + c dx

Voorbeeld 2 : 3 x + 5 x 2 + x + 1 dx

3 x + 5 x 2 + x + 1 dx

3 x + 5 x 2 + x + 1 dx = A (2 x + 1)+ B x 2 + x + 1 dx

Uit3 x + 5 = 2 Ax +( A + B ),volgt

A = 3 2 B = 7 2

Zodat :

4 Toepassing

In een dierenpark wordt via sensoren aan de in- en uitgang het aantal bezoekers constant op- en afgeteld.

Het aantal aanwezigen in het park gedurende de dag wordt grafisch in kaart gebracht en blijkbaar kan dat beschreven worden door het wiskundige model a (

t de tijd in uren (t = 0 is het openingsuur van het park, d.i. om 10 uur).

Gevraagd :

• Ga na of op het sluitingsuur, d.i. 20.00 u., alle bezoekers weer weg zijn.

• Hoeveel bezoekers telt het park gemiddeld per uur in de loop van de dag ?

• Als je weet dat het park vandaag 1226 bezoekers telde, hoelang bleven ze dan gemiddeld ?

Oplossing :

• Om 8 uur ’s avonds is t = 10 en a ( 10) = 0, m.a.w. om 8 uur ’s avonds hebben alle bezoekers het park verlaten.

• Gemiddeld aantal bezoekers per uur : 1 10 10 0 a ( t )dt = 1 10 10 0 5800 t 2 10 t + 29 200 dt

= 580 10 0 d ( t 5) ( t 5)2 + 4 20 10 0 dt

= 580 1 2 Bgtan t 5 2 10 0 200

≈ 490,368

Het gemiddelde aantal bezoekers per uur is ongeveer 490.

• Gemiddelde tijd dat een bezoeker in het park vertoefde : totaalaantalbezoekuren totaalaantalbezoekers = 4903,68 1226 ≈ 4

Elke bezoeker bleef gemiddeld ongeveer 4 uur in het dierenpark.

5 Samenvatting

• Je kunt een integraal berekenen van het type px + q ax 2 + bx + c dx met D = b 2 – 4ac > 0.

px + q

ax 2 + bx + c = A x x 1 + B x x 2

• Je kunt een integraal berekenen van het type

px + q

ax 2 + bx + c

dx met D = b 2 – 4ac = 0.

px + q

ax 2 + bx + c = A x x 1 + B ( x x 1 )2

• Je kunt een integraal berekenen van het type

px + q

ax 2 + bx + c dx met D = b 2 – 4ac < 0.

Heeft de tweedegraadsvorm ax 2 + bx + c = 0 geen nulwaarden, dan bestaan er constanten A en B zodat

ax 2 + bx + c = A (2ax + b )+ B

ax 2 + bx + c .

px + q

ax 2 + bx + c dx (met p = 0)kanzoherleidwordentotéénintegraalvandevorm

f ( x )

f ( x ) dx = ln | f ( x ) | + C enéénvandevorm p

ax 2 + bx + c dx .

6

Oefeningen

Bereken de volgende integralen.

a 10 5 x 2 x 2 + 3 x 2 dx j 5 2 x 4 x 2 4 x + 1 dx

b 17 x + 1 3 x 2 5 x 2 dx k 3 x 2 + 2 x + 2 dx

c 14 x 5 4 x 2 1 dx l 2 x 2 2 x + 3 dx d 6 x 10 x 2 + 2 x 3 dx

4 x 2 + 4 x + 5 dx e x 4 x 2 + 6 x + 8 dx

f 2 (5 x 38) x 2 11 x + 18 dx

1 x 2 4 x + 8 dx

x 2 x 2 2 x + 1 dx g 22 x 15 4 x 2 3 x dx p 2 x + 1 4 x 2 + 12 x + 11 dx

h 5 2 x ( x 1)2 dx q 2 x + 7 x 2 + 6 x + 18 dx

i 3 x + 7 x 2 + 4 x + 4 dx r 4 x + 1 x 2 6 x + 13 dx

Bereken de volgende integralen. a

x 2 + 5 x 8 x 2 x 2 dx

3 x 3 + 29 x 2 + 66 x 21 x 2 + 10 x + 25 dx b x 3 x 2 4 x + 9 x 2 x 6 dx g 27 x 2 + 30 x + 4 9 x 2 + 12 x + 4 dx

c 2 x 3 9 x 2 + 10 x + 1 x 2 4 x + 3 dx h x 4 3 x 3 + 11 x 2 9 x 3 x 2 2 x + 9 dx d 2 x 4 + 7 x 3 8 x 2 7 x + 9 2 x 2 + 7 x 4 dx i 2 x 3 x 2 + 6 x + 16 x 2 2 x + 5 dx

e x 3 2 x 2 x + 3 ( x 2)2 dx j x ( x + 4) x 2 + 4 dx

In een kustdorpje, ergens in Normandië, verloopt het bevolkingsaantal nogal seizoengebonden. Het aantal inwoners wordt door de plaatselijke overheid voorgesteld door het volgende wiskundige model :

a ( t )= 9990

t 2 12 t + 37 t ∈ [0,12]

met t : de tijd in maanden (t = 0 is 1 januari)

a ( t ): het aantal inwoners

De plaatselijke burgemeester moet, als antwoord op een vraag van de overheid in verband met de veiligheid, op een formulier het aantal inwoners van zijn dorp vermelden. De burgemeester is van plan om het gemiddelde aantal inwoners op zijn formulier te vermelden. Welk getal vult de burgemeester in ?

Gegeven is de grafiek van de functie f met voorschrift f

Bereken de oppervlakte van het ingekleurde gebied.

Bereken de oppervlakte van het gebied begrensd/ingesloten door de krommen met vergelijking y = f ( x ) en y = g ( x ).

( x )= 5 x

( x )= 4 x

( x )= 1 2 (11 x + 21)

( x )= 0 Bereken a ∈ ] 0, 6[ zodat a a 12 x 2 36 dx = 2,2

2.4 Partiële integratie

1 Principe

Deafgeleidevanhetproductvantweefuncties f en g wordtgegevendoor:

[ f ( x ) g ( x )] = f ( x ) g ( x )+ f ( x ) g ( x ) (zieAnalyse2)

Weintegrerenbeideleden:

Hieruitvolgt: f ( x ) g ( x ) dx = f ( x ) g ( x ) dx f ( x ) g ( x ) dx of f ( x ) g ( x ) dx = f ( x ) g ( x ) f ( x ) g ( x ) dx

Besluit : Formule:

Andereschrijfwijzen:

Deze methode wordt dikwijls toegepast bij het integreren van producten en quotiënten. We spreken van partiële integratie omdat in het rechterlid van de formule nog een integraal voorkomt.

Voorbeeld : x · sin x · dx = x · d ( cos x ) = P.I. x · ( cos x ) ( cos x ) · dx = x cos x + cos x dx

= x cos x + sin x + C

Taak : Ganadoortedifferentiërenof x sin x dx = x cos x + sin x + C

2 Integralen met een integrand waarvoor geen onmiddellijke integratie bestaat

Voorbeeld 1 :

Bereken ln xdx .

Stel : u = ln x

dv = dx ⟹ v = x (eigenlijk is v = x + C ; we kiezen C = 0 want het volstaat dat we één primitieve v hebben)

ln xdx P.I. = x · ln x xd ln x

= x ln x x 1 x dx

= x ln x dx

= x ln x x + C

= x (ln x 1)+ C

Voorbeeld 2 :

Bereken Bgtan2 xdx .

Stel : u = Bgtan2x dv = dx ⟹ v = x

Bgtan2 xdx P.I. = x · Bgtan2 x xd Bgtan2 x = x · Bgtan2 x x · 1 1 + 4 x 2 · 2dx = x Bgtan2 x 2 x 1 + 4 x 2 dx = x Bgtan2 x 1 4 d (1 + 4 x 2 ) 1 + 4 x 2

= x · Bgtan2 x 1 4 ln(1 + 4 x 2 )+ C

3 Integralen met als integrand een gemengde functie –verlaging van de macht

Voorbeeld 1 :

Bereken x cos xdx .

Stel : u = x

dv = cos xdx = dsinx ⟹ v = sinx

x cos xdx = xd sin x

P.I. = x sin x sin xdx

= x · sin x + cos x + C

Taak : ga na of bij de keuze u = cosx en dv = xdx de integrand niet eenvoudiger, maar ingewikkelder wordt.

Voorbeeld 2 :

Bereken ( x 2 + 3 x ) e x dx .

Stel : u = x 2 + 3 x

dv = e x dx = de x =⇒ v = e x

( x 2 + 3 x ) e x dx = ( x 2 + 3 x ) de x

P.I.=( x 2 + 3 x ) e x e x d ( x 2 + 3 x ) =( x 2 + 3 x ) e x (2 x + 3) e x dx

Stel : u = 2 x + 3

dv = e x dx = de x =⇒ v = e x

( x 2 + 3 x ) · e x (2 x + 3) e x dx

P.I.=( x 2 + 3 x ) e x (2 x + 3) e x e x d (2 x + 3)

=( x 2 + 3 x ) e x (2 x + 3) e x + 2e x dx

=( x 2 + 3 x ) · e x (2 x + 3) e x + 2e x + C

=( x 2 + 3 x 2 x 3 + 2) · e x + C

=( x 2 + x 1) e x + C

Taak : ga na of bij de keuze u = e x en dv = ( x 2 + 3x )dx de integrand niet eenvoudiger maar ingewikkelder wordt. De graad van de veeltermfunctie wordt niet lager maar hoger.

4 Integralen met als integrand een gemengde functie –terugkeer van de integrand

Voorbeeld :

Bereken e 2 x sin3 xdx .

Stel : u = sin3 x

Stel : u = cos3 x

In het rechterlid verschijnt opnieuw de te zoeken integraal.

Bijgevolg :

Taak : Ga na of bij de keuze u = e

en dv = sin

de onbepaalde integraal eveneens berekenbaar is en tot dezelfde oplossing leidt.

5 Integratie van elementaire kwadratische wortelvormen

Integralenvanhettype x 2 + kdx en k x 2 dx :

Voorbeeld 1 :

Bereken I = x 2 + 5 dx .

Oplossing :

I = x 2 + 5 dx

P.I. = x x 2 + 5 xd x 2 + 5

= x x 2 + 5 x 2 x 2 x 2 + 5 dx

= x x 2 + 5 x 2 x 2 + 5 dx

= x x 2 + 5 x 2 + 5 5 x 2 + 5 dx

= x x 2 + 5 x 2 + 5 x 2 + 5 + 5 1 x 2 + 5 dx

= x x 2 + 5 I + 5ln x + x 2 + 5 1 x 2 + k dx = ln | x + x 2 + k | + C

In het rechterlid verschijnt opnieuw de te zoeken integraal.

Bijgevolg :

2 I = x x 2 + 5 + 5ln x + √ x 2 + 5 + C

⇐⇒ I = 1 2 x x 2 + 5 + 5 2 ln x + x 2 + 5 + C

Voorbeeld 2 :

Bereken I = 4 x 2 dx

Oplossing :

I = 4 x 2 dx

P.I. = x 4 x 2 x d 4 x 2

= x 4 x 2 x 2 xdx 2 4 x 2

= x 4 x 2 x 2 dx 4 x 2

= x 4 x 2 x 2 + 4 4 4 x 2 dx

= x 4 x 2 4 x 2 dx + 1 4 x 2 dx

= x 4 x 2 I + 4Bgsin x 2

In het rechterlid verschijnt opnieuw de te berekenen integraal.

Bijgevolg :

2 I = x 4 x 2 + 4Bgsin x 2 + C

I = x 2 4 x 2 + 2Bgsin x 2 + C

6 Partiële integratie bij bepaalde integralen

Omeenbepaaldeintegraalvandevorm b a udv teberekenen,zijnertweemogelijkheden.

(1) Webepaleneerstdeonbepaaldeintegraal udv = F ( x )+ C enweberekenendanhetgetal F ( b ) F (a ).

(2) Uitdeformule udv = uv vdu volgtonmiddellijk

Wegebruikenbeidemethodenbijdeberekeningvan e 1 ln x x 2 dx .

(1) Weberekeneneerst ln x x 2 dx .

Stel u = ln x dv = dx x 2 = d 1 x =⇒ v = 1 x ln x x 2 dx P.I. = ln x x + 1 x d ln x = ln x x + dx x 2 = ln x x 1 x + C Dus : e 1 ln x x 2 dx = ln x x 1 x e 1 = 1 e 1 e + 1 = e 2 e (2) e 1 ln x x 2 dx P.I. = ln x x e 1 + e 1 dx x 2 = ln e e + ln1 + 1 x e 1 = 1 e 1 e + 1 = e 2 e

7 Toepassing

Een kaasmaker houdt zelf één geit thuis ; hij gebruikt de melk om geitenkaas te maken. Door omstandigheden graasde de geit op een weide waarvan de ondergrond sterk verontreinigd was met een toxische stof. Het gif wordt in de vetreserves opgeslagen en verlaat het lichaam weer via de melk. Elke dag komt de veearts langs om de concentratie gif in de melk te meten. De waargenomen concentraties in milligram/liter zijn te vatten in het voorschrift

c ( t ) = 10te –0,3t

waarbij t de tijd is in dagen na het eten van het verontreinigde gras. Het geitje levert 2 liter melk per dag.

G ( t ) geeft de totale hoeveelheid uitgescheiden gif (in milligram) in functie van de tijd.

Gevraagd :

a Na hoeveel dagen is de concentratie van de toxische stof het grootst ?

b Na hoeveel dagen is de concentratie kleiner dan 2 mg/l ?

c Wat is de waarde van G (0) ?

d Wat is de toename van G ( t ) per dag ? (M.a.w. : bepaal G ′( t ) )

e Bepaal G ( t )

f Bereken lim t →+∞ G ( t ) . Wat is de totale hoeveelheid gif die het geitje heeft binnengekregen ?

g Wanneer is 95 % van het gif verdwenen ?

Oplossing :

We maken eerst de grafiek van de waargenomen concentraties.

c ( t )

a Na hoeveel dagen is de concentratie van de toxische stof het grootst ? Berekenen van c ′( t ) Bepalen van de nulwaarden van c ′( t ) c ′( t ) = 10e –0,3t + 10te –0,3t ( –0,3) c ′( t ) = 0 ⟺ e –0,3t ( 10 – 3t) = 0

Tekenverloop van c ′( t ) t –∞ 10 3 +∞

c ′( t ) + 0 –

c ( t ) ↗ 12,26 ‖ maximum ↘

De concentratie toxische stoffen in de melk is het grootst in de loop van de vierde dag ( t = 3,33) en bedraagt 12,26 mg/l.

b Na hoeveel dagen is de concentratie kleiner dan 2 mg/l ?

c ( t )= 2

⇐⇒ 10 te 0,3 t = 2

⇐⇒ te 0,3 t = 0,2

Die vergelijking is oplosbaar met ICT.

Antwoord : op de 15e dag (dus na veertien dagen) is de concentratie gif in de melk lager dan 2 mg/l.

c Wat is de waarde van G ( 0)?

In het begin is er nog geen gif afgescheiden. Bijgevolg is G ( 0) = 0.

d Wat is de toename van G ( t ) per dag?

G ( t ) = de hoeveelheid gif die vandaag werd afgescheiden

= hoeveelheid melk, concentratie gif in de melk

= 2 10te –0,3t = 20te –0,3t

e Bepaal G ( t )

G ( t )= t

9 10 (3 t +

f Bereken lim t →+∞ G ( t ) . Wat is de totale hoeveelheid gif die het geitje heeft binnengekregen?

lim t →+∞ G ( t )= lim t →+∞ 200 9 10 (3 t + 10) e 0,3 t ∗ = 2000 9 ≈ 222,22

Het geitje heeft in totaal ongeveer 222,22 milligram gif binnengekregen.

g Wanneer is 95 % van het gif verdwenen ?

G ( t )= 95% 2000 9 = 1900 9

⇐⇒ 200 9 10 (3 t + 10) e 0,3 t = 1900 9

⇐⇒ (3 t + 10) e 0,3 t = 1 2

Ga via ICT na dat t ≈ 15,8.

Antwoord: na 16 dagen is meer dan 95 % gif uit het lichaam van het geitje verdwenen.

8 Recursieformules

Voorbeeld : Bereken I n = sinn xdx

n = 1: I 1 = sin xdx = cos x + C

n = 2: I 2 = sin2 xdx = 1 2 ( x sin x cos x )+ C

We zullen dan I n kunnen vinden voor elke n ∈ N0 als we een betrekking opstellen tussen I n en I n –1 of tussen I n en I n –2. Een dergelijke betrekking noemen we een recursieformule (recurrere = teruglopen).

I n = sinn 1 x sin xdx

Stel u = sinn 1 x dv = sin dx = d (cos x )=⇒ v = cos x I n = P..I sinn 1 x cos x + cos x d (sinn 1 x ) = sinn 1 x cos x + cos x (n 1) sinn 2 x cos xdx = sinn 1 x cos x +(n 1) sinn 2 x cos2 xdx = sinn 1 x cos x +(n 1) sinn 2 x (1 sin2 x )dx

= sinn 1 x cos x +(n 1) sinn 2 xdx (n 1) sinn xdx = sinn 1 x cos x +(n 1) I n 2 (n 1) I n =⇒ (1 + n 1) · I n = sinn 1 x · cos x +(n 1) · I n 2 I n = 1 n · sinn 1 x · cos x + n 1 n · I n 2 ❶

Toepassingen :

• Om sin3 xdx teberekenen,stellenwein ❶ n = 3.Wekrijgen

I 3 = 1 3 sin2 x cos x + 2 3 I 1

=⇒ sin3 xdx = 1 3 sin2 x cos x + 2 3 sin xdx of sin3 xdx = 1 3 sin2 x · cos x 2 3 cos x + C

• sin4 xdx = 1 4 sin3 x cos x + 3 4 sin2 xdx

∗ = 1 4 sin3 x cos x + 3 8 ( x sin x cos x )+ C = 1 4 sin3 x cos x + 3 8 x 3 8 sin x cos x + C

Taak : bereken op dezelfde manier sin5 xdx en sin6 xdx

9 Samenvatting

• Je kent de formule van partiële integratie. f ( x )g ( x )dx = f ( x )g ( x ) f ( x )g ( x )dx of f ( x )dg ( x )= f ( x )g ( x ) g ( x )df ( x ) of udv = uv vdu met f ( x )= u en g ( x )= v

Deze methode wordt dikwijls toegepast bij het integreren van producten.

• Overzicht : bepalen van u en dv

Na het toepassen van de formule blijft in het rechterlid nog een integraal staan. Daarom zeggen we dat hier een partiële integratie uitgevoerd is. Of een partiële integratie succes heeft, hangt af van de aard van de integraal in het rechterlid. Is die integraal gecompliceerder dan de gegeven integraal, dan moeten we de berekening op die wijze opgeven. Hieronder volgen enkele tips. integrand u dv effect

veeltermfunctie · exponentiëlefunctie

bv. x 2 e x dx

veeltermfunctie sinus-ofcosinusfunctie

bv. x cos xdx

veeltermfunctie logaritmischefunctie

bv. x 3 ln xdx

veeltermfunctie cyclometrischefunctie

bv. x Bgtan xdx

exponentiëlefunctie sinus-ofcosinusfunctie

bv. e x cos xdx

veeltermfunctie

u = x 2 ⟹ du = 2xdx

veeltermfunctie

u = x ⟹ du = dx

logaritmischefunctie

u = ln x =⇒ du = dx x

cyclometrischefunctie

u = Bgtan x =⇒ du = dx 1 + x 2

vrije keuze

exponentiële functie

dv = e x dx ⟹ v = e x

sinus- of cosinusfunctie

dv = cos xdx ⟹ v = sinx

veeltermfunctie

dv = x 3 dx =⇒ v = x 4 4

veeltermfunctie

dv = xdx =⇒ v = x 2 2

verlaging van de graad van de veeltermfunctie

logaritmische functie verdwijnt, de integrand wordt een rationale functie

cyclometrische functie verdwijnt

vrije keuze terugkeer van de integrand na tweemaal partiële integratie

• Je kunt ook partiële integratie bij bepaalde integralen toepassen. b a udv =[ uv ] b a b a vdu

• Je kunt recursieformules opstellen met behulp van partiële integratie.

10 Oefeningen

Bereken de volgende integralen.

a Bgsin xdx

b Bgcos2 xdx

c ln( x 2 + 2)dx

d ln x 2 dx

Bereken de volgende integralen.

a 2 xe x dx

b x sin2 xdx

c x 2 e 3 x dx

d x

e 3 x dx

e ln x x 2 dx

Bereken de volgende integralen.

a x 2 1 dx

b 9 x 2 dx

c x 2 + 8 dx

e ln2 xdx

f Bgtan √ xdx

g Bgsin2 xdx

h ln( x + x 2 + 5)dx

f x sin x cos xdx

g x 3 ln xdx

h x Bgsin xdx

i x 2 x dx

j x sin2 xdx

d 3 x 2 dx

e 4 x 2 + 6 dx

f 16 9 x 2 dx

Bereken de volgende integralen.

a e 2 x cos3 xdx

b sin x e x dx

c cosh x sin2 xdx

d e x (1 + e x ) sin xdx

e e ax cos bxdx

Bereken de volgende bepaalde integralen.

0 ( x 2 + 1) sin xdx b e 1 ln x x dx

x cos2 x dx d 2 1 ln(2 x )dx e +∞ 0 e x cos xdx

f x Bgsin x 1 x 2 dx

g sin(ln x )dx h x sin2 x dx

i ln(tan x ) cos2 x dx

j x e x (1 + x )2 dx

1 xe √1 x 2 dx

e x cos xdx

8 *

a Bereken de oppervlakte ingesloten door de grafieken van de krommen met vergelijking : y = 2 · Bgcot x ; y = π 3 en x = √3.

b Bereken de oppervlakte van het gebied begrepen tussen de grafiek van f met f ( x )= x · sin2 x ende x -asmet

Bereken de oppervlakte van het gebied ingesloten door de grafiek van de functie f met f ( x ) = ln( 1 + x 2), de x -as en de verticalen door de buigpunten van de grafiek van f . Stel de gevraagde oppervlakte grafisch voor en controleer je antwoord.

Bereken de oppervlakte van het gebied begrensd door de grafieken van f met f ( x ) = x ln x en g met g ( x )= 16ln x x . Stel de gevraagde oppervlakte grafisch voor en controleer je antwoord met ICT.

Herneem het probleem van blz. 106 met c ( t ) = 4t 2 e–0,5t

Bewijs de volgende recursieformules.

a π 2 0 cosn xdx = n 1 n π 2 0 cosn 2 xdx

d tann xdx = 1 n 1 · tann 1 x tann 2 xdx

e dx sinn x = cos x (1 n ) sinn 1 x + n 2 n 1 dx sinn 2 x

∈ N0 \{1}

11 12

Bereken de oppervlakte van het gebied :

a dat ingesloten is door de krommen met vergelijking y = e x , y = ln x , x = 0 en y + x = 1 + e

b tussen de kromme met vergelijking y = 4 4 + x 2 en haar asymptoot.

c dat begrensd is door de krommen met vergelijking y =

, y = 0 en x = 0 (voor x ⩾ 0).

Een speciale functie…

De gammafunctie, die in heel wat wetenschappelijke toepassingen voorkomt, is gedefinieerd als volgt :

Γ ( x + 1)= +∞ 0 t x e t dt

a Toon aan dat G( 1) = 1.

b Bepaal met partiële integratie G( 2)

c Toon aan met behulp van partiële integratie dat voor een willekeurige x geldt G( x + 1) = x G( x )

d Toon aan dat voor elk natuurlijk getal n geldt G(n + 1) = n !

e Gegeven is dat Γ 1 2 = √π

Bereken G( 6, 5).

I n = 1 0 x n · √1 xdx (n ∈ N )

a Bewijs : I 0 = 2 3

b Bewijs de volgende recursieformule door middel van partiële integratie.

I n = 2n 2n + 3 I n 1

c Bewijs enkel met wat voorafgaat dat I 2 = 16 105

Vraag uit de toenmalige toelatingsexamens burgerlijk ingenieur

We definiëren de energie van een functie f in een interval [ a , b ] als

Gegeven : de functie g met g ( x ) = x .

a f ( x ) 2 dx

Gevraagd : de parameter c bepalen in de functie h met h ( x ) = c sin( px ), zodanig dat de energie van de verschilfunctie f = g – h minimaal is in het interval [ –1, 1]

Vraag uit de toenmalige toelatingsexamens burgerlijk ingenieur

Bereken de volgende integralen, die door partiële integratie of door een substitutie worden omgezet in integralen van rationale functies.

a dx √ x 2 4 √ x 3

b x 2 · ln ( x 2 + 4) dx

c Bgtan ( x + 1) dx d e t e 2 t 16 dt

Bereken de volgende integralen met behulp van ICT.

a 2 x + 3

x 2 + x + 1 2 dx

b 4 x + 5

x 2 + 10 x + 26 3 dx

c e x

e 2 x + 4e x + 5 2 dx

d x Bgtan x 1 + x 2 2 dx

e x 3 + 2 x 6 x 2 + 2 x + 5 2 dx f x 2 x 2 + 1 3 dx g t 6 dt t 4 + 2 t 2 + 1 h e 1 ln x √ x ln x 1 + ln2 x 2 dx

Herhalingsoefeningen – gemengde reeks

Alle methoden die in de theorie vermeld zijn, komen in de volgende reeks voor. Bereken volgende integralen. Controleer met ICT.

Integratiemethoden

Ik weet dat primitiveren de inverse operatie is van afleiden.

Ik ken de definitie van een primitieve functie en van een onbepaalde integraal.

Ik ken de formules van fundamentele integralen.

Ik kan opeenvolgende operatoren na elkaar toepassen.

Ik ken de lineariteit van de onbepaalde integraal en kan die toepassen.

Ik kan met behulp van de fundamentele integralen onmiddellijke integratie toepassen.

Ik kan integralen berekenen door aanpassing van de differentiaal.

Ik weet wat integratie door substitutie is en kan dat toepassen.

Ik kan elementaire rationale functies integreren door ze te splitsen in partieelbreuken.

Ik weet wat partiële integratie is en kan dat toepassen.

Toepassingen van de integraalrekening 3

Omwentelingslichamen zijn ruimteﬁguren die ontstaan door een vlakdeel rond een as te omwentelen (die as noemen we dan ook de omwentelingsas).

Zo krijg je een bol als je een cirkelschijf laat draaien rond een middellijn van de cirkel.

In dit hoofdstuk krijg je een mooie reeks omwentelingslichamen voorgeschoteld. De meeste ken je al (de cilinder, de kegel, de bol …) en sommige zijn stukjes van gekende lichamen (een afgeknotte kegel, een bolschijf …). Maar er zijn ook leuke nieuwkomers. De torus bijvoorbeeld heeft een lichaam dat je krijgt nadat je een cirkel laat wentelen om een rechte die in het vlak van de cirkel is gelegen maar de cirkel niet snijdt. De vorm van de torus kom je vaak tegen, bv. bij de bakker (donuts) of in dit zwembad.

Om volumes, booglengten en (mantel-) oppervlakten te berekenen, hebben we onze kennis van integralen nodig.

Toepassingen van de integraalrekening

3.1 Oppervlakte van bijzondere vlakke ﬁguren

1 Oppervlakte van een cirkel 119

2 Oppervlakte van een cirkelsegment 121

3 Oppervlakte van een cirkelsector 122

4 Oppervlakte van een ellips 123

5 Oppervlakte van een parameterkromme 124

6 Samenvatting 124

7 Oefeningen 125

3.2 Zwaartepunt van een vlakke ﬁguur

1 Zwaartepunt van puntmassa’s 127

2 Zwaartepunt van vlakke ﬁguren 128

3 Algemene methode 129

4 Samenvatting 130

5 Oefeningen 131

3.3 Volume van omwentelingslichamen

1 Volume van omwentelingslichamen 132

2 Toepassingen 137

3 Regel van Pappus-Guldin 145

4 Volume van een lichaam begrensd door twee loodvlakken op de x-as 147

5 Toepassingen 148

6 Praktische toepassing 151

7 Samenvatting 152

8 Oefeningen 153

3.4 Booglengte van een vlakke kromme

1 Booglengten berekenen 158

2 Toepassingen 160

3 Samenvatting 162 4 Oefeningen 163

3.5 Manteloppervlakte van een omwentelingslichaam

1 Manteloppervlakte 165

2 Toepassingen 169

3 Samenvatting 172

4 Oefeningen 173

Wat moet je kennen en kunnen? 176

3.1 Oppervlakte van bijzondere vlakke

ﬁguren

1 Oppervlakte van een cirkel

Probleemstelling :

Bereken de oppervlakte van een cirkel met straal r

Oplossing :

De vergelijking van een cirkel met straal r en middelpunt in de oorsprong is :

2 + y 2 = r 2

Vanwege de symmetrie t.o.v. beide assen volstaat het de oppervlakte van het deel van de cirkel gelegen in het eerste kwadrant te berekenen en nadien het gevonden resultaat te vermenigvuldigen met 4.

De vergelijking van de cirkel in het eerste kwadrant is :

Methode 1 : partiële integratie

I = r 2 x 2 dx

P.I. = x · r 2 x 2 xd r 2 x 2

= x r 2 x 2 x 2 x 2 r 2 x 2 dx

= x r 2 x 2 x 2 r 2 x 2 dx

= x r 2 x 2 r 2 x 2 r 2 r 2 x 2 dx

= x r 2 x 2 r 2 x 2 r 2 x 2 dx + r 2 r 2 x 2 dx

= x · r 2 x 2 r 2 x 2 dx + r 2 Bgsin x r

= x r 2 x 2 I + r 2 Bgsin x r

=⇒ I = 1 2 x r 2 x 2 + r 2 2 Bgsin x r + C

zodat: A = 4 r 0 r 2 x 2 dx = 4 1 2 x r 2 x 2 + r 2 2 Bgsin x r r 0 = 4 0 + r 2 2 Bgsin1 (0 + 0) = 2 r 2 π 2 = π r 2

Methode 2 : een bijzondere substitutie

Stel x = r sin t en t ∈ π 2 , π 2 ,danis dx = r cos tdt en r 2 x 2 = r cos t .

Als x = 0,danis r sin t = 0of t = 0.

Als x = r ,danis r sin t = r of t = π 2

zodat: A = 4 π 2 0 r cos t r cos tdt

= 4 r 2 · π 2 0 cos2 tdt

= 2 r 2 t + sin t cos t π 2 0

= π r 2

A cirkel = pr 2

2 Oppervlakte van een cirkelsegment

Probleemstelling :

Bereken de oppervlakte van een cirkelsegment met straal r en middelpuntshoek ‡ (in radialen !).

Oplossing :

De vergelijking van een cirkel met straal r en middelpunt in de oorsprong is :

x 2 + y 2 = r 2

Vanwege de symmetrie om beide assen volstaat het de oppervlakte van het deel van het segment gelegen in het eerste kwadrant te berekenen en nadien het gevonden resultaat te vermenigvuldigen met 2.

De vergelijking van de cirkel in het eerste kwadrant is : y = r 2 x 2

Oppervlakte van het cirkelsegment

Stel x = r cos t en t ∈ [0, π], danis dx = r sin tdt en r 2 x 2 = r sin t

Als x = a ,danis a = r cos t of t = Bgcos a r = ϑ 2

Als x = r ,danis r = r cos t of t = Bgcos1 = 0

zodat: A

tdt

3 Oppervlakte van een cirkelsector

Probleemstelling :

Bereken de oppervlakte van een cirkelsector met straal r en middelpuntshoek ‡ (in radialen).

Oplossing :

Methode 1 :

A = oppervlaktesectorOABC = oppervlaktedriehoekOAC + oppervlaktesegmentABCD

Methode 2 : Regel van drie

Gevolg : Een cirkel is een cirkelsector met middelpuntshoek ‡

4 Oppervlakte van een ellips

Probleemstelling :

Bereken de oppervlakte van een ellips met halve assen a en b

Oplossing :

De vergelijking van een ellips met halve assen a en b en middelpunt in de oorsprong is : x 2

a 2 + y 2 b 2 = 1

Vanwege de symmetrie t.o.v. beide assen volstaat het de oppervlakte van het deel van de ellips gelegen in het eerste kwadrant te berekenen en nadien het gevonden resultaat te vermenigvuldigen met 4.

De vergelijking van de ellips in het eerste kwadrant is : y = b a a 2 x 2

Oppervlakte ellips : A = 4 a 0 b a a 2 x 2 dx

Stel x = a sin t en t ∈ π 2 , π 2 , danis dx = a cos tdt en a 2 x 2 = a cos t .

Als x = 0,danis a sin t = 0of t = 0.

Als x = a ,danis a sin t = a of t = π 2

zodat: A = 4 b a π 2 0 a cos t a cos tdt

= 4ab · π 2 0 cos2 tdt

= 2ab t + sin t cos t π 2 0 = πab

A ellips = pab

5 Oppervlakte van een parameterkromme

Probleemstelling :

Bereken de oppervlakte van het deel van het vlak begrensd door de x -as en door een tak van de cycloïde met stelsel parametervergelijkingen

x = R ( t sin t )

y = R (1 cos t ) t ∈ [0,2π]

Oplossing :

A = b a ydx = b a R (1 cos t )d (Rt sin t )

= R 2 2π 0 (1 cos t )2 dt = R 2 

2π 0 dt 2 2π 0 cos tdt + 2π 0 cos2 tdt

= R 2 t + 1 2 ( t + sin t · cos t ) 2π 0 = 3πR 2

6 Samenvatting

cirkel

• Je kunt de oppervlakte van een vlakke figuur berekenen met behulp van een bepaalde integraal.

cirkelsegment met straal r en middelpuntshoek ‡ (in rad)

cirkelsector met straal r en middelpuntshoek ‡ (in rad)

• Je kunt de oppervlakte berekenen van een parameterkromme.

ellips met halve assen a en b

2 3 4 5 6 7

7 Oefeningen

Bereken de oppervlakte van dit gekleurde deel van een cirkelschijf.

0 y = r 2 x 2 a b r

De cirkel met vergelijking x 2 + y 2 = 9 wordt gesneden door twee verticalen met vergelijking x = a en x = b Bepaal a en b zodanig dat de cirkel in drie gelijke delen wordt verdeeld.

Bereken de oppervlakte van het oppervlak gelegen binnen de ellips met vergelijking 4x 2 + 9y 2 = 36 en buiten de cirkel met vergelijking x 2 + y 2 = 4.

Bereken de oppervlakte van het oppervlak begrepen tussen de cirkels met straal 1 en respectieve middelpunten M( 0, 0) en M′( 1, 0)

Bereken de oppervlakte van het deel van het vlak tussen de parabool met vergelijking y 2 = 2x en de cirkel met vergelijking x 2 + y 2 – 4x = 0 (uitwendig t.o.v. de parabool).

Bereken de oppervlakte van een cirkel met behulp van een stelsel parametervergelijkingen van de cirkel : x = r · sin t y = r · cos t t ∈ [0,2π]

Bereken de oppervlakte van een ellips met behulp van een stelsel parametervergelijkingen van de ellips : x = a sin t y = b cos t t ∈ [0,2π]

Bereken de oppervlakte van het deel van het vlak begrensd door de regelmatige astroïde met stelsel parametervergelijkingen : x = 2cos3 t y = 2sin3 t t ∈ [0,2π]

Bereken de oppervlakte van het lemniscaat van Gerono met stelsel parametervergelijkingen

x = cos t y = sin t cos t t ∈ [0,2π]

3.2

Zwaartepunt van een vlakke ﬁguur

In de sterkteleer moet je bij de belastingsgevallen op buiging, wringing en knik heel vaak het zwaartepunt van vlakke figuren bepalen.

Daarbij heb je het begrip moment nodig.

moment

Het moment M van een puntmassa ten opzichte van een punt A is het product van de kracht die op de massa werkt en de afstand van de massa tot het punt A.

1 Zwaartepunt van puntmassa’s

In de figuur hiernaast bevinden zich op de x -as drie puntmassa’s. De afstanden zijn uitgedrukt in meter.

– We berekenen eerst het totale moment M van deze puntmassa’s t.o.v. de oorsprong.

M = 1 3 + 2 1 + 3 5 = 20

– Die drie puntmassa’s kunnen worden vervangen door 1 puntmassa waarop een kracht werkt van 9 N (resultante) in het zwaartepunt. Dat zwaartepunt ligt op de x -as op een afstand a van de oorsprong, zodanig dat die puntmassa hetzelfde moment M oplevert.

Dus:20 = 9 a of a = 20 9

Taak :

Toon door berekening aan dat de plaats van het zwaartepunt gelijk blijft als de momenten uitgerekend worden t.o.v. het punt met coördinaat ( –1, 0)

2 Zwaartepunt van vlakke ﬁguren

We beschouwen de vlakke figuur L met constante massa m per oppervlakte-eenheid. De totale massa van L is dus 9 m en de kracht F die op de massa inwerkt, is gelijk aan 9 m g

De figuur bestaat uit de 3 rechthoeken R 1, R 2 en R 3.

De zwaartepunten van de rechthoeken zijn de middelpunten

Z1( 1,5 ; 4,5), Z2( 0,5 ; 2,5) en Z3( 1,5 ; 0,5)

We mogen dus aannemen dat de kracht F 1 van R 1 aangrijpt in Z1, de kracht F 2 van R 2 aangrijpt in Z2, de kracht F 3 van R 3 aangrijpt in Z3

Hieruit volgt dat

F 1 = 1 3 m g

F 2 = 1 3 m g

F 3 = 1 3 m g .

De drie puntmassa’s Z1, Z2 en Z3 kunnen worden vervangen door 1 puntmassa waarop een kracht werkt van 9 m g ( = F ) in het zwaartepunt Z( a , b ). Het zwaartepunt Z ligt zodanig dat het moment van de puntmassa’s gelijk is aan het totale moment van de figuur.

We beschouwen de momenten t.o.v. de x -as.

M x (F )= M x (F 1 )+ M x (F 2 )+ M x (F 3 )

9m g b = 3m g 4,5 + 3m g 2,5 + 3m g 0,5 b = 5 2

– We beschouwen de momenten t.o.v. de y -as.

M y (F )= M y (F 1 )+ M y (F 2 )+ M y (F 3 )

9m g a = 3m g 1,5 + 3m g 0,5 + 3m g 1,5 a = 7 6

HetzwaartepuntisdusZ 7 6 , 5 2 .

Het moment M ℓ van een puntmassa t.o.v. een rechte ℓ is het product van de kracht die op de massa werkt en de afstand van de massa tot de rechte ℓ.

3 Algemene methode

We beschouwen de figuur begrensd door de parabool met vergelijking y = 4x – x 2 en de x -as. Om het zwaartepunt te bepalen verdelen we het interval [ 0, 4] in n gelijke delen met midden x i en bouwen we een Riemannsom op.

De oppervlakte van een willekeurige rechthoek is dan f ( x i ) ∆x

Hierop werkt een kracht F i = m · g · f ( x i ) · ∆x , die aangrijpt in het zwaartepunt Zi x i , f ( x i ) 2 .

We berekenen nu de som van de momenten van de rechthoeken t.o.v. de x -as.

– Het moment van de figuur t.o.v. de x -as is de limiet van die uitdrukking.

– Op analoge manier vinden we : M

– Is Z( a , b ) het zwaartepunt, dan geldt :

Bij homogene vlakke figuren begrensd door een continue functie f en de x -as geldt dat het zwaartepunt gegeven wordt door Z( x Z , y Z ) waarbij :

x Z = M y A yZ = M x A

A = b a f ( x )dx

M x = 1 2 b a f ( x ) 2 dx

M y = b a x · f ( x ) dx

Voorbeeld :

Bepaal de coördinaat van het zwaartepunt van een halve cirkel met straal 4 en middelpunt O.

Oplossing :

f ( x )= √16 x 2

A = 1 2 π42 = 8π

M x = 1 2 4 4 16 x 2 dx = 1 2 16 x x 3 3 4 4 = 128 3

M y = 4 4 x √16 x 2 dx = 0 onevenfunctietussensymmetrischegrenzen

waaruit volgt :

x Z = 0en yZ = 1 8π 128 3 = 16 3π Dus:co (Z)= 0, 16 3π

4 Samenvatting

f ( x )= 16 x 2

• Je weet dat het moment M van een puntmassa ten opzichte van een punt A het product is van de kracht die op de massa werkt en de afstand van de massa tot het punt A.

• Je kunt het zwaartepunt van een vlakke figuur berekenen. De figuur kan vervangen worden door een puntmassa waarop dezelfde totale kracht werkt. Het zwaartepunt ligt zodanig dat het moment van de puntmassa gelijk is aan het totale moment van de figuur.

5 Oefeningen

Bepaal het zwaartepunt van deze figuur.

Bepaal de zwaartepunten van de figuren begrensd door :

a y = 4 x 2 , x = 0, y = 0

b y = x 2 8 , y = 0, x = 4

c y = x 2 , y = x ,

d y = x 2 + 3, y = x 2 3, x = 0, x = 6

e x = y 2 , x 2 = 8 y ,

f y = sin3 x , y = 0, x = 0, x = π 3

Bepaal het zwaartepunt van het deel van de cirkel met vergelijking x 2 + y 2 = a 2 dat gelegen is in het eerste kwadrant.

Bepaal het zwaartepunt van het deel van de ellips met vergelijking 9x 2 + 16y 2 = 144 dat gelegen is in het eerste kwadrant.

3.3 Volume van omwentelingslichamen

1 Volume van omwentelingslichamen

cilinder afgeknotte kegel kegel bol

Bovenstaande lichamen zijn omwentelingslichamen. Ze ontstaan door het wentelen van een vlakdeel rond een rechte : de omwentelingsas

We nemen de x -as van een georthonormeerd assenkruis als omwentelingsas. De omwentelingslichamen die we zullen beschouwen, ontstaan door het deel van het xy -vlak dat begrensd wordt door de x -as, twee evenwijdigen met de y -as en de grafiek van de functie f , te laten wentelen om de x -as.

De oppervlakte van een vlakke figuur kun je benaderen met rechthoekjes. Het volume van ruimtefiguren kun je benaderen met cilindertjes. Omdat je het volume van een cilinder kunt berekenen met de formule :

V = oppervlakte grondvlak hoogte = pr 2h

waarin r de straal en h de hoogte is, kun je het volume van zo’n ruimtefiguur benaderen door het volume van alle cilinderdeeltjes op te tellen.

dbrnjhrj - stock.adobe.com h r

Toepassingen van de integraalrekening

Inleidend voorbeeld :

Hieronder staat een kegel afgebeeld. Het is een omwentelingslichaam, bepaald door het wentelen rond de x -as van het vlakdeel begrensd door de x -as, de y -as, de rechte met vergelijking x = 15 en de grafiek van de functie f met f ( x )= x 3 .

( x )= x 3

We berekenen het volume van de kegel met hoogte 15 en met als straal van het grondvlak 5 met een methode die helemaal analoog is met die van de oppervlakteberekening.

Op de figuur rechts zie je hoe de kegel door vijf cilinders kan worden benaderd. De som van de vijf volumes is groter dan het volume van de kegel, maar dat is niet echt belangrijk. Onder- en bovensommen benaderen toch dezelfde waarde als je oneindig veel cilinders gebruikt, m.a.w. als de hoogte van elke cilinder (die ligt langs de x -as) naar 0 nadert.

Welke integraal bij deze berekening hoort, wordt duidelijker als je de hoogte in n gelijke stukken verdeelt en het volume van een willekeurige cilinder bekijkt.

– Als je n even hoge cilinders gebruikt, dan wordt de hoogte

van elke cilinder gelijk aan 15 n

Dus ∆ x = 15 n

– Bekijk nu de k -de cilinder. Het volume van die cilinder is :

π · x k 3 2 · ∆ x , waarbij xk een willekeurige x -waarde in het k -de deelinterval is.

De som van de volumes van alle deelcilinders is

Vn = n k = 1 π x k 3 2 ∆ x

– Als Dx → 0 ( of n → +∞), dan benadert die som steeds beter het volume van de kegel. Het gevraagde volume V is dan :

V = lim n → + ∞ n k = 1 π x k 3 2 15 n

– De Riemannsom benadert zo een integraal die eenvoudig te berekenen is.

V = 15 0 π · x 2 9 dx = π 9 · x 3 3 15 0 = 125π

Veralgemening :

Stel dat f een continue functie is in [ a , b ]

We berekenen het volume V van het omwentelingslichaam dat is ontstaan door het wentelen rond de x -as van het vlakdeel begrensd door de x -as, de grafiek van f en de rechten met vergelijkingen x = a en x = b .

Hoe onregelmatig die lichamen ook zijn, toch kunnen we hun volume berekenen met behulp van integralen. We gaan als volgt te werk.

– We verdelen het interval [ a , b ] in n gelijke deelintervallen met breedte ∆ x = b a n

– In elk deelinterval [ xi –1, xi ] kiezen we een willekeurige x -waarde ci

Op elk deelinterval bouwen we een rechthoekje met breedte Dx en hoogte | f ( ci )|

Bij wenteling rond de x -as beschrijft elk rechthoekje een cilinder met volume Dx p · [ f ( ci )]2.

– We nemen de som Vn van de volumes van al die cilindertjes.

Vn = n i = 1 b a n · π · f ( c i ) 2 –

Na onbeperkt verfijnen van de verdeling in [a , b ] wordt het gevraagde volume

V = lim n → + ∞ n i =1 b a n π f ( c i ) 2 (1)

Aangezien f continu is in [a , b ], is ook de functie pf 2 continu in [ a , b ]. Volgens de definitie van bepaalde integralen wordt (1) :

V = π b a f ( x ) 2 dx

Besluit :

Als f continu is in [ a , b ], dan is het volume van het omwentelingslichaam ontstaan door het wentelen rond de x -as van het vlakdeel begrensd door de grafiek van f , de x -as en de rechten met vergelijkingen

x = a en x = b , gelijk f ( c i ) f ci xi– 1 xi x y z a b y = f ( x ) 0 aan V = π b a f ( x ) 2 dx of V = π b a y 2 dx

Voorbeeld 1:

Hieronder staat een champagneglas afgebeeld. Het is een omwentelingslichaam bepaald door het wentelen rond de x -as van het vlakdeel begrensd door de x -as, de y -as, de rechte met vergelijking x = 10 en de grafiek van de functie f met f ( x )= √1,2 x (in cm).

a Wat is de inhoud (in cl) van het champagneglas ?

b Hoeveel champagne bevat het glas als het tot 8 cm hoog is gevuld ?

c Hoeveel glazen kun je zo schenken uit een magnumfles van 1,5 l ?

Oplossing :

De inhoud van het champagneglas is dus 188,4956 cm3

Als het glas tot op een hoogte van 8 cm gevuld is, dan bevat het ongeveer 12,06 cl champagne.

c Uit een magnumfles van 1,5 l kun je 12 glazen champagne schenken.

Voorbeeld 2 :

Bereken het volume van het omwentelingslichaam dat is ontstaan door omwenteling om de y -as van het gebied ingesloten door de kromme met vergelijking y = 4 – x 2, de positieve x -as en de positieve y -as.

Oplossing :

Analoog als bij de wenteling van een vlakdeel om de x -as geldt bij de wenteling om de y -as :

Als f continu en inverteerbaar is in [ a , b ], dan is het volume van het omwentelingslichaam dat ontstaat door het wentelen rond de y -as van het vlakdeel begrensd door de grafiek van f , de y -as en de rechten met vergelijking y = c en y = d , gelijk aan :

In dit voorbeeld wordt het volume :

Voorbeeld 3 :

Bereken het volume van het omwentelingslichaam dat is ontstaan door wenteling om de x -as van het gebied ingesloten door de parabool met vergelijking y = x 2 en de rechte met vergelijking y = 4.

Oplossing :

Het te wentelen vlakdeel is nu niet begrensd door een grafiek en de x -as, maar door twee grafieken.

We bekomen het volume door de vlakdelen begrensd door de respectievelijke grafieken afzonderlijk te laten wentelen en de bekomen volumes van elkaar af te trekken.

f ( x ) = 4

g ( x ) = x 2

2 Toepassingen

Volume van een cilinder

We beschouwen een cilinder met hoogte h en met r als straal van het grondvlak, beschreven door het wentelen rond de x -as van de rechthoek ORQP.

De vergelijking van de rechte k is : y = r .

Bijgevolg is het volume van de cilinder :

We vinden dus inderdaad ons uitgangspunt van blz. 132 terug als bijzonder geval.

Als Ag de oppervlakte van het grondvlak voorstelt, dan is : Vcilinder = Ag h

Volume van een kegel

We beschouwen een kegel met hoogte h en met r als straal van het grondvlak, beschreven door het wentelen rond de x -as van de driehoek OQP.

De rechte k heeft als vergelijking y = r h x

Bijgevolg is het volume van de kegel

Als Ag de oppervlakte van het grondvlak voorstelt, dan is : V

Volume

van een afgeknotte kegel x O h P Q (h , b)

R(0, a ) b k y z 0 a y = b a h x + a

We beschouwen een afgeknotte kegel met hoogte h en met a en b als stralen van het respectievelijke bovenvlak en grondvlak.

De afgeknotte kegel wordt beschreven door het wentelen rond de x -as van het rechthoekig trapezium ORQP.

De rechte k heeft als vergelijking y a = b a h 0 · ( x 0) ⇐⇒ y = b a h x + a .

Bijgevolg is het volume van de afgeknotte kegel : π h 0 b a h x + a 2 dx

We gebruiken de substitutie : b a h x + a = t b a h dx = dt dx = h b a dt

Voor x = 0 is t = a

Voor x = h is t = b

volume afgeknotte kegel = π b a t 2 · h b a · dt = πh b a t 3 3 b a = πh b a b 3 a 3 3 b 3 a 3 =( b a )( b 2 + ab + a 2 ) = πh 3 ( b 2 + ab + a 2 )

Als Ag en Ab de oppervlakte van respectievelijk het grond- en het bovenvlak voorstellen,

dan is : Vafgeknottekegel = h 3 A g + A b + A g A b

Volume van een bol

We beschouwen een bol met straal r , beschreven door het wentelen rond de x -as van een halve cirkel met straal r (zie oranje deel).

De halve cirkel boven de x -as heeft als vergelijking y = r 2 x 2

Bijgevolg is Vbol

Uitgedrukt in functie van de diameter d vinden we r =

d 3 8 = πd 3 6 Vbol = πd 3 6 met d = 2 r

Volume van een bolschijf

Een bolschijf is het lichaam dat ontstaat door een bol te snijden met twee evenwijdige vlakken. De doorsneden van die vlakken met het boloppervlak zijn cirkels met stralen r 1 en r 2 ; ze zijn respectievelijk het grond- en bovenvlak van de bolschijf. De afstand tussen de vlakken is de hoogte h van de bolschijf.

y z O

Als x 2 + y 2 = r 2 de vergelijking is van de cirkel die de bol beschrijft na wenteling om de x -as, dan is : Vbolschijf =

Pythagoras

Het volume van een bolschijf is gelijk aan de som van de volumes van twee cilinders en het volume van een bol, waarbij : – de cilinders respectievelijk het grond- en het bovenvlak van de bolschijf als grondvlak hebben en de halve hoogte van de bolschijf als hoogte ; – de bol de hoogte van de bolschijf tot middellijn heeft.

Volume van een bolsegment

Een bolsegment kan beschouwd worden als een bolschijf waarvan het bovenvlak een puntcirkel is ( r 2 = 0).

Bijgevolgishetvolumevaneenbolsegmentgelijkaan:

DoortoepassingvandestellingvanPythagorasvindenwe r

)

h 2 (2) (2) in (1) geeft : Vbolsegment = π (2 rh h 2 ) h 2 + πh 3 6 = π rh 2 πh 3 2 + πh 3 6 = πh 2 3 (3 r h )

Opmerking :

Vbol = 1 3 π4 r 2 (3 r 2 r ) of Vbol = 4 3 π r 3

Stellen we in de formule van het volume van het bolsegment h = 2r , dan bekomen we opnieuw het volume van de bol.

Volume van een torus

Een torus is een lichaam dat ontstaat door een cirkel te laten wentelen om een rechte die in het vlak van de cirkel gelegen is, maar die niet snijdt.

Devergelijkingvandecirkel

Het volume van de torus is gelijk aan het verschil van de volumes van twee omwentelingslichamen.

Het volume van een torus is dus gelijk aan het product van de oppervlakte van de wentelende cirkel en de lengte van de weg die het middelpunt bij wenteling doorloopt ( zie regel van Pappus-Guldin, blz. 145).

Volume van een paraboloïde

We zoeken het volume van een paraboloïde ontstaan door het wentelen van de parabool met vergelijking y 2 = 2px rond zijn symmetrieas en begrensd door een loodvlak op de wentelingsas.

Vomgeschreven cilinder = π 2

Bijgevolg is het volume van een paraboloïde de helft van het volume van de omgeschreven cilinder.

Opmerking :

Een radiotelescoop heeft de vorm van een omwentelingsparaboloïde omdat alle invallende stralen die evenwijdig zijn met de as, naar één punt (= brandpunt) teruggekaatst worden.

Volume van een omwentelingsellipsoïde

Een omwentelingsellipsoïde ontstaat door het wentelen van de ellips met vergelijking

x -as.

Volume van een eenbladige omwentelingshyperboloïde

Een eenbladige omwentelingshyperboloïde ontstaat door wenteling om de y -as van de hyperbool met vergelijking x 2 a 2 y 2 b 2 = 1

We berekenen het volume voor y ∈ [ –k , k ].

Uit x

eenbladige hyperboloïde

Bijwentelingomde y -asgeldt:

Opmerking :

De koeltorens van een kerncentrale zijn meestal in de vorm van een eenbladige omwentelingshyperboloïde gebouwd.

3 Regel van Pappus-Guldin

regel van Pappus-Guldin

Het volume van een omwentelingslichaam is gelijk aan de oppervlakte van de te omwentelen figuur maal de omtrek van de cirkel die door het zwaartepunt van die figuur wordt beschreven.

volume van een cilinder

oppervlakterechthoekORQP: r · h

zwaartepuntrechthoekORQP:Z h 2 , r 2

Vcilinder = oppervlakterechthoek maal omtrekvandecirkel beschrevendoorhetzwaartepunt = rh 2π r 2 = π r 2 h

volume van een kegel

oppervlaktedriehoekOQP: r h 2

zwaartepuntdriehoekOQP:Z 2h 3 , r 3

Vkegel = oppervlaktedriehoek maal omtrekvandecirkel beschrevendoorhetzwaartepunt

= rh 2 2π r 3

= 1 3 π r 2 h

volume van een bol

oppervlaktehalvecirkel:

zwaartepunthalvecirkel:Z 0, 4 r 3π Vbol = oppervlaktehalvecirkel maal omtrekvandecirkel beschrevendoorhetzwaartepunt

oppervlaktecirkel c : π r 2

zwaartepuntcirkel c :Z (0, R )

Vtorus = oppervlakterechthoek maal omtrekvandecirkel beschrevendoorhetzwaartepunt

= π r 2 (2π R ) = π r 2 · 2πR

4 Volume van een lichaam

begrensd door twee loodvlakken op de x-as

Instap –

In de formule van het volume van omwentelingslichamen

V = b a π[ f ( x )]2 dx

is A ( x )= π[ f ( x )]2 de oppervlakte van de doorsnede van het lichaam met een vlak in het punt met abscis x en loodrecht op de x -as.

Dus: V =

A ( x )dx

– Om het volume van een aardappel te bepalen, wordt die in schijfjes gesneden en van elke doorsnede wordt de oppervlakte bepaald.

Het volume van zo’n schijfje is (bij benadering) de oppervlakte van de ene rand vermenigvuldigd met de hoogte. De som van al die volumetjes is een goede benadering voor het volume van de aardappel. Hoe dunner de schijfjes, hoe beter de benadering. De gevonden benaderingen

zijn ook benaderende sommen voor

A ( x )dx ,

zodat deze integraal het volume van de aardappel voorstelt.

Veralgemening

We kunnen bewijzen dat het volume van elk lichaam dat begrensd wordt door twee loodvlakken op x (in a en b ) wordt gegeven door b a A ( x )dx , waarbij A ( x ) de oppervlakte is van de loodrechte doorsnede op de x -as, aangebracht in het punt met abscis x .

Besluit :

Als A ( x ) het voorschrift van een continue functie is in [ a , b ], dan is het volume van het ruimtelichaam dat begrensd wordt door twee loodvlakken op de x -as met vergelijkingen x = a en x = b gelijk aan b a

A ( x )dx waarbij A ( x ) de oppervlakte voorstelt van de doorsnede van het lichaam met een vlak in het punt met abscis x en loodrecht op de x -as.

5 Toepassingen

Volume van een prisma

We plaatsen een prisma zo dat het grondvlak O bevat en de x -as loodrecht op het grondvlak staat.

Alle doorsneden van een prisma die evenwijdig zijn met het grondvlak zijn congruent en hebben dus dezelfde oppervlakte. Is Ag de oppervlakte van het grondvlak, dan hebben we A ( x ) = Ag

Bijgevolg is het volume van het prisma :

Dat geeft ons de klassieke regel : Vprisma = oppervlaktegrondvlak · hoogte = A g h

Die formule geldt ook voor het volume van een parallellepipedum, een balk en een kubus.

Volume

van een piramide

We plaatsen de top van een piramide (met hoogte h ) in O en het grondvlak loodrecht op de x -as.

Ag is de oppervlakte van het grondvlak en A ( x ) de oppervlakte van de doorsnede, op een afstand x van de top en loodrecht op de x -as. De doorsnede is het beeld van het grondvlak door een homothetie met centrum O en factor k = x h

Elke homothetie met factor k beeldt een veelhoek met oppervlakte A af op een veelhoek met oppervlakte k 2 A (zie VBTL 3 meetkunde).

Bijgevolg : A ( x ) A g = x 2 h 2 of A ( x )= x 2 h 2 A g

Volumevandepiramide: h 0 x 2 h 2 A g dx = A g h 2 · x 3 3 h 0 = A g h 3

Dat geeft ons de klassieke regel :

Volume van een afgeknotte piramide

De hoogte van de afgeknotte piramide is h . Ag en Ab zijn de oppervlaktes van respectievelijk het grond- en bovenvlak.

We vinden het volume van de afgeknotte piramide als het verschil van de volumes van 2 piramides.

Volume van de afgeknotte piramide :

We berekenen eerst a

Uit de vlakke meetkunde weten we het volgende. A b A g = a 2 (h + a )2

A b A g = a h + a

afgeknottepiramide

Volume van een ellipsoïde met vergelijking

Op de figuur hiernaast zie je dat a , b en c de halve lengten zijn van de drie assen van de ellipsoïde

Hierin is A ( x ) de oppervlakte van een doorsnede van het lichaam met een vlak in het punt met abscis x en loodrecht op de x -as. y x z c a b O

Elke vlakke doorsnede is een ellips.

Volume ellipsoïde = a a A ( x )dx (1)

De doorsnede is een ellips met vergelijking

Bijgevolg is A ( x )= π b a a 2 x 2

(2) in (1) : volume van de ellipsoïde :

oppervlakte ellips = pab

π bc a 2 a a (a 2 x 2 )dx

= π bc [ x ]a a π bc a 2 x 3 3 a a = π bc 2a π bc a 2 2a 3 3 = 4πabc 3

Opmerkingen : –

Volumevaneenellipsoïdemetvergelijking

Is a = b = c , dan is de ellipsoïde een bol

Vbol = 4 3 πa 3 (zie blz. 146)

Is b = c ≠ a , dan is de ellipsoïde een omwentelingsellipsoïde.

Vomwentelingsellipsoïde = 4 3 πab 2 (zie blz. 143)

6 Praktische toepassing

Inhoud van een stookolietank

Een horizontaal geplaatste cilindervormige tank heeft een lengte L = 300 cm en een straal R = 75 cm. Met een meetstok stelt men vast dat er in de tank nog tot op 60 cm hoogte stookolie is. Hoeveel liter stookolie bevat de tank ?

Oplossing:

Deinhoudisgelijkaan: oppervlaktecirkelsegment L cm3 .

Deinhoudisgelijkaan: oppervlaktecirkelsegment · L cm3

Deinhoudisdusgelijkaan

met

uitgedruktinradialen.

Deinhoudisdusgelijkaan R 2 2 · (α sin α) · L met α debijbehorendemiddelpuntshoek uitgedruktinradialen.

InderechthoekigedriehoekMCBgeldt:

Hieruitvolgtdatsin

Deinhoudvandetankisbijgevolg

Detankbevatdusnog1980,246literstookolie.

Deinhoudvandetankisbijgevolg

Detankbevatdusnog1980,246literstookolie.

7 Samenvatting

• Als f continu is in [ a , b ], dan is het volume van het omwentelingslichaam ontstaan door het wentelen om de x-as van het vlakdeel begrensd door de grafiek van de functie f , de x-as en de rechten met

vergelijkingen x = a en x = b , gelijk aan V

Als de as van de omwenteling de y -as is, dan is V

• Je kent de regel van Pappus-Guldin.

Het volume van een omwentelingslichaam is gelijk aan de oppervlakte van de te omwentelen figuur maal de omtrek van de cirkel die door het zwaartepunt van die figuur wordt beschreven.

• Als A( x ) het voorschrift is van een continue functie in [ a , b ], dan is het volume van het ruimtelichaam dat begrensd wordt door twee loodvlakken op de x-as met vergelijkingen x = a en x = b , gelijk aan b a A ( x )dx , waarbij A( x ) de oppervlakte voorstelt van de doorsnede van het lichaam met een vlak

in het punt met abscis x en loodrecht op de x-as.

V = b a A ( x )dx

2 3 4

8 Oefeningen

Bereken het volume van het omwentelingslichaam ontstaan door wenteling om de x -as van de kromme met de gegeven vergelijking in het aangegeven interval.

Bereken met behulp van oneigenlijke integralen het volume van het lichaam dat ontstaat bij wenteling om de x -as van de kromme met de gegeven vergelijking in het gegeven interval.

a y = e x , x ∈ [0, +∞[ c y = 1 x 2 , x ∈

Bereken het volume van het lichaam dat ontstaat bij wenteling van het vlakdeel ingesloten door de kromme met vergelijking y = x 2, de x -as, de y -as en de rechte met vergelijking x = 2 om de as met vergelijking :

Bereken het volume van het lichaam dat ontstaat bij wenteling van het vlakdeel ingesloten door de kromme met vergelijking y = x 3, de x -as, de y -as en de rechte met vergelijking x = 1 om de as met vergelijking :

a y = 0

b x = 0 c x = 1

Beschouw het vlakdeel begrensd door de parabool met vergelijking y = 4x – x 2 en de x -as.

Bereken het volume van het lichaam dat ontstaat door dit vlakdeel te laten wentelen om de rechte met vergelijking y = 6.

Bereken het volume van het lichaam dat ontstaat bij wenteling rond de x -as van de vlakke figuur begrensd door de krommen met de gegeven vergelijkingen.

a y = 4 x x 2 ; y = x f y 2 = 2 x ; x 2 = 2 y

b y = x 2 ; y 2 = 8 x g x 2 + y 2 = 25; x + 7 y 25 = 0

e y = 4 x 2 ; y = 4 x 2 ; x = 2; y = 0

Het vlakdeel begrensd door een boog van de ellips met vergelijking x 2 9 + y 2 5 = 1, de x -as en de loodlijnen op de x -as in de brandpunten F( 2, 0) en F′( –2, 0), wentelt rond de x -as.

Bereken het volume van het ontstane lichaam.

Bereken het volume van het lichaam dat ontstaat door het wentelen om de x -as van de cycloïdeboog met stelsel parametervergelijkingen :

x = R ( t sin t ) y = R (1 cos t ) t ∈ [0,2π]

Bereken het volume van het lichaam dat ontstaat bij wenteling om de x -as van het deel van de hypocycloïde met stelsel parametervergelijkingen :

x = 2cos t + cos2 t y = 2sin t sin2 t t ∈ [0, π]

Toepassingen van de integraalrekening

Bereken het volume van het lichaam dat ontstaat bij wenteling om de x -as van het deel van een regelmatige astroïde met stelsel parametervergelijkingen :

 x = 2cos3 t y = 2sin3 t t ∈ [0, π]

a Schets de kromme k met stelsel parametervergelijkingen :

x = t 2

y = 4 t t 3 t ∈ R

b Bereken het volume van het lichaam dat ontstaat door het lusvormige deel van k om de x -as te laten wentelen.

Bereken het volume van het lichaam dat ontstaat door wenteling rond de x -as van het vlakdeel ingesloten door de kromme met gegeven vergelijking in het gegeven interval. Maak eerst een schets van het gevraagde lichaam met ICT.

a x 2 y 2 = x 4 , x ∈ [ 1,1]

b y 2 = x 4 x 5 , x ∈ [0,1]

c y 2 = x 2 (2 + x ) 2 x , x ∈ [ 2,0]

d y 2 = 1 x 2 3 , x ∈ [ 1,1]

De buitenwand van een koeltoren kan worden gemodelleerd door een kromme te wentelen.

Als we de toren in gedachten kantelen, dan kunnen we die bekomen door de grafiek van de functie f met f ( x )= 20 x + 2 ,en0 x 8, rond de x -as te wentelen. De meeteenheid langs de x -as en de y -as is meter.

Bereken het volume van die toren (in liter).

Bereken de parameter a y x

Als we de parabool met vergelijking y = ax 2 tussen x = –25 cm en x = + 25 cm om de y -as wentelen, dan ontstaat een paraboloïde.

Het volume van de parabolische schotel moet 28 liter worden.

Bereken het volume van het lichaam begrensd door de elliptische paraboloïde met vergelijking x 2 + 4y 2 = z en het vlak met vergelijking z = 4.

Bepaal het volume van een rechte elliptische kegel met top T( 0, 0, 5) en met als grondvlak de kromme met stelsel vergelijkingen :

Maak eerst een schets van het gevraagde lichaam met ICT.

De voorkant van een evenementenhal is een deel van de grafiek van de functie f met f

De vloer is een rechthoek van 20 m bij 40 m. Om een gepaste luchtverversingsinstallatie te kunnen plaatsen, moet het volume van de hal berekend worden. Hoeveel bedraagt dit volume (in m3) ?

Hiernaast staat een borrelglaasje. De bovenkant heeft een diameter van 4 cm. Het glas is 4 cm diep. Het vooraanzicht van het glas heeft de vorm van een parabool.

Op de hoogte h (in cm) is de straal van de doorsnede (= cirkel) r (in cm).

Hierbijgeldtdat r = h

a Bereken de inhoud van het glas in cm3.

b Hoeveel van dit soort glaasjes kun je vullen met een fles van een liter ?

De assen van twee omwentelingscilinders met straal r zijn loodrecht snijdend. Bereken de inhoud van het deel van de ruimte dat binnen de twee cilinders ligt.

Aanwijzing : t.o.v. een orthonormaal assenstelsel, dat hier afgebeeld staat, hebben de twee cilinders de volgende vergelijkingen : C 1 ↔ x 2 + z 2 = r 2 ; C 2 ↔ y 2 + z 2 = r 2

Toon aan dat de doorsnede van het gemeenschappelijke deel van een vlak, loodrecht op de z -as, een vierkant is.

Toepassingen op de in dit hoofdstuk verkregen formules (zie formuleblad blz. 197-198). Op te lossen zonder integralen !

Bereken het volume van een regelmatig viervlak als een ribbe ervan 6 cm meet.

Een cirkel is ingeschreven in een gelijkzijdige driehoek met zijde r . De volledige figuur wentelt om de hoogtelijn van de driehoek.

Bewijs dat de verhouding van het volume van de verkregen bol tot het volume van de verkregen kegel gelijk is aan 4 9

Van een afgeknotte kegel K weet je dat de oppervlakte van het grondvlak viermaal zo groot is als de oppervlakte van het bovenvlak. Bovendien is in de afgeknotte kegel een bol B ingeschreven. (Die bol raakt het bovenvlak, het grondvlak en de mantel.)

Bewijs dat volume B volume K = 4 7

Een kegel is ingeschreven in een bol met straal r . Bepaal de hoogte van de kegel zodat het volume zo groot mogelijk wordt.

Beschouw in deze figuur de cirkelsector OPQ.

Als de sector wentelt om de x -as, dan ontstaat er een bolsector

De lengte van de loodrechte projectie op de x -as van de beschrijvende boog PQ is de hoogte h van die bolsector. Bereken het volume van de bolsector in functie van h en r (= de straal van de bol).

Een bolschil is het deel van een bolvolume dat ontstaat door het wentelen van een cirkelsegment om een middellijn die buiten het segment loopt. De lengte van de koorde van het segment is k en de projectie ervan op de as van wenteling is h . Bereken het volume.

Een horizontaal geplaatste cilindervormige olietank heeft een diameter van 126 cm en kan 3000 liter olie bevatten. Met de meetstok stel je vast dat de tank nog gevuld is tot een hoogte van 28 cm. Hoeveel olie (tot op 1 cl nauwkeurig) zit er nog in die tank ?

Er werd een olietank geplaatst met de afmetingen die vermeld staan op de onderstaande figuur. De tank is cilindervormig (m.a.w. als je in het punt A een vlak loodrecht op AB brengt, dan verkrijg je een cirkel als doorsnede).

Met een meetstok stel je vast dat de tank nog gevuld is tot een hoogte van 68 cm. Hoeveel liter stookolie bevat de tank (tot op 1 cl nauwkeurig) ?

3.4 Booglengte van een vlakke kromme

1 Booglengten berekenen

Instap :

Gegeven : De functie f met f ( x )= x √ x 2

Gevraagd : Bereken de lengte van het deel van de grafiek van f begrensd door de punten O( 0, 0) en A( 4, 4), m.a.w. de booglengte of lengte van de boog OA

Oplossing : Een eerste ruwe benadering van de booglengte is de lengte van de bijbehorende koorde | OA |. | OA | = √16 + 16 ≈ 5,66 x y 3 2 1 1 2 3 4 5 6

Een betere benadering bekomen we door de som te maken van de lijnstukken [OB], [BC], [CD] en [DA].

Toon aan dat | OB | + | BC | + | CD | + | DA |≈ 5,74.

De exacte lengte van de boog OA kunnen we slechts via integraalberekening vinden.

Berekening van booglengten f is een continue functie in [ a , b ]

We berekenen de lengte L van de grafiek van f begrensd door de punten met a en b als abscis

t.o.v. een georthonormeerd assenstelsel. We lossen dit probleem op door de gevraagde booglengte te benaderen door een som van lengten van lijnstukken. x y

Toepassingen van de

• Verdeel [ a , b ] in n even lange deelintervallen met lengte Dx De deelpunten zijn x 0 = a , x 1, x 2, …, x i –1, x i, …, x n – 1, x n = b .

• Verbind de punten Pi – 1 ( x i – 1, f ( x i – 1)) en Pi ( x i , f ( x i )) door een lijnstuk.

• In elk deelinterval benaderen we de lengte van de boog Pi 1 Pi door de lengte van de koorde | Pi 1 Pi |

| Pi 1 Pi | = ( x i x i 1 )2 +[ f ( x i ) f ( x i 1 )]2 =( x i x i 1 ) · 1 + f ( x i ) f ( x i 1 ) x i x i 1 2 ( x i > x i 1 )

We veronderstellen dat de gegeven functie f ook afleidbaar is in [ a , b ] f is dus continu in [ x i –1, x i ] en afleidbaar in ] x i –1, x i [ .

Volgens de middelwaardestelling van Lagrange geldt dan :

∃ c i ∈] x i 1 , x i [ : f ( c i )= f ( x i ) f ( x i 1 ) x i x i 1 (zie Analyse 2)

Bijgevolg is | Pi 1 Pi | = ∆ x 1 +[ f ( c i )]2

• De som L n van de lengten van alle koorden | Pi 1 Pi | is een benadering van de gevraagde booglengte :

L n = n i = 1 ∆ x · 1 +[ f ( c i )]2

• Na onbeperkt verfijnen van de verdeling van [ a , b ] wordt de gevraagde booglengte :

L = lim n → +∞ n i = 1 1 +[ f ( c i )]2 · ∆ x

• Is f ′ continu in [ a , b ], dan is ook 1 +( f )2 continu in [ a , b ] en is volgens de definitie van de bepaalde integraal :

L = b a 1 +[ f ( x )]2 dx

Besluit :

Als f afleidbaar is in [ a , b ] en de afgeleide functie f ′ is continu in [ a , b ], dan is de booglengte van de grafiek van f over [ a , b ] gelijk aan :

L = b a 1 +[ f ( x )]2 dx of :

L = b a 1 + y 2 dx 1 1 0 O a b L y = f ( x ) x y

Voorbeeld : We kunnen nu de exacte lengte van de boog OA uit de instap berekenen. L = | OA | = 4

+ f ( x )

+ 9 x

2 Toepassingen

Lengte van een cirkelboog

Gegeven : Een cirkelboog | ACB | met straal r en met middelpuntshoek α in een georthonormeerd assenstelsel

Gevraagd : | ACB |

Oplossing : De figuur is symmetrisch t.o.v. x . Daarom voeren we de berekening uit voor de boog AC met vergelijking

We bekomen, als we de middelpunthoek α in radialen meten :

lengte cirkelboog = straal middelpuntshoek =

Gevolg : als we α = 2p stellen, dan vinden we de omtrek van een cirkel met straal r .

Lengte van een kettinglijn

Hangen we een ketting op in de punten P en Q, dan neemt die ketting onder invloed van haar eigen gewicht de vorm aan van een kromme met vergelijking y = a 2 e x a + e x a = a cosh x a . We noemen die kromme een kettinglijn.

We berekenen de lengte van de kromme in het interval [ –a , a ]. L = 2 a 0 1 + sinh2 x a dx y = a cosh x a

y = sinh x a = 2 a 0 cosh2 x a dx cosh2 x a sinh2 x a = 1 = 2a a 0 cosh x a d x a = 2a sinh x a a 0 = 2a sinh1 ≈ 2,35a

Lengte van een parameterkromme

Voor een kromme gegeven door een stelsel parametervergelijkingen

x = f ( t ) y = g ( t ) met t ∈ [ t 1 , t 2 ] en y = dy dt dx dt is de booglengte gelijk aan L =

Voorbeeld :

Bereken de lengte van een cycloïde met stelsel parametervergelijkingen

x = R ( t sin t ) y = R (1 cos t ) met t ∈ [0,2π]

L = 2π

0 [R (1 cos t )]2 +(R sin t )2 · dt

= 2π

0 R 2 2R 2 cos t + R 2 cos2 t + R 2 sin2 t dt

= 2π

0 √2R 2 2R 2 cos t dt

= 2π

0 2R 2 (1 cos t ) · dt 1 cos t = 2sin2 t 2

= 2π

0 4R 2 sin2 t 2 dt

= 2R · 2 2π 0 sin t 2 d t 2

= 4R cos t 2 2π 0 = 4R (1 + 1)= 8R

3 Samenvatting

• Je kunt de lengte bepalen van een boog (een deel van een grafiek, begrensd door 2 punten).

Als f afleidbaar is in [ a , b ] en de afgeleide functie f ′ continu is in [ a , b ], dan is de booglengte van de grafiek van f over [ a , b ] gelijk aan

L = b a 1 + f ( x ) 2 dx of : L = b a 1 + y 2 dx

Voor een kromme ↔ x = f ( t ) y = g ( t ) met t ∈ [ t 1 , t 2 ] is de booglengte gelijk aan L = t 2 t 1 dx dt 2 + dy dt 2 dt

• Je weet dat de lengte van een cirkelboog gelijk is aan het product van straal r en middelpuntshoek α L = r · α

• Je kent de formule voor de omtrek van een cirkel.

p = 2pr 1 1 0 O a b L y = f ( x ) x y

2 3

4 Oefeningen

Bereken de booglengte van de grafiek van f als : a f ( x )= 2 3 x √ x

( x )= ( x 1)3

d f ( x )= x 4 + 3 6 x

Bereken de booglengte voor x ∈ [ 1, 4] en y ∈ R+ van de semikubische parabool met vergelijking 27y 2 = 8 ( x – 1)3.

Bereken de booglengte van de lus in [ 0, 3] van de kromme met vergelijking 9y 2 = x ( 3 – x )2.

Een kabel is op 20 m hoogte aan twee verticale palen bevestigd.

Bij die kabel hoort de formule y = 8 cosh ( 0,125x )

a Hoe ver staan de palen uit elkaar ?

Geef je antwoord in dm nauwkeurig en controleer het gevonden resultaat aan de hand van de grafiek.

b Bereken de lengte van de kabel in dm.

Bereken de omtrek van de regelmatige astroïde met vergelijking x 2 3 + y 2 3 = a 2 3 .

Bereken met de formule van blz. 161 de booglengte van de kromme met het gegeven stelsel parametervergelijkingen.

x = 2 1 + t 2 y = 2 t 1 + t 2 met t ∈ 1, √3 d

= R ( t sin t ) y = R (1 cos t ) met t ∈ [0,2π] b x = 4 t 2 y = 8 t 3 met t ∈ [0,1] e x = e t · sin t y = e t · cos t met t ∈ [0,2π]

c x = 2cos3 t y = 2sin3 t met t ∈ [0,2π]

Eenellipswordtbepaalddoorhetstelselparametervergelijkingen x = 3cos t y = 2sin t met t ∈ [0,2π]

Bereken de omtrek van die ellips.

De voorkant van een koekjestrommel is een deel van een parabool met vergelijking y = x 2 5 + 2 x . De bodem is een rechthoek van 10 cm bij 20 cm.

Hoeveel cm2 blik heb je nodig om deze trommel te maken ?

3.5 Manteloppervlakte van een omwentelingslichaam

1 Manteloppervlakte

Voor de berekening van het volume van een omwentelingslichaam stellen we ons tevreden met een benadering door cilinders.

Voor de manteloppervlakte volstaat een dergelijke benadering niet. We moeten werken met afgeknotte kegels.

volume manteloppervlakte

We stellen daarom eerst een formule op voor de manteloppervlakte (of zijdelingse oppervlakte) van een afgeknotte kegel.

Manteloppervlakte van een kegel r a a ‡ 2pr ontwikkeling

We beschouwen een kegel met straal r en apothema a . Het manteloppervlak van de kegel is een cirkelsector met straal a en booglengte 2pr (= omtrek van het grondvlak van de kegel).

Is ‡ het maatgetal (in radialen) van de hoek van die sector, dan geldt : 2pr = a ‡ (zie blz. 160) (1)

We weten dat de oppervlakte van een cirkelsector met straal a en middelpunt ‡ gelijk is aan a 2 2 ϑ (zie blz. 122).

Bijgevolg : manteloppervlakte kegel of zijdelingse oppervlakte kegel

manteloppervlakte kegel = halve omtrek van het grondvlak apothema = pra

Manteloppervlakte

van een afgeknotte kegel

We beschouwen een kegel met straal r 1 en apothema a 1 Als we een vlak aanbrengen, evenwijdig met het grondvlak, dan ontstaat een afgeknotte kegel met stralen r 1 en r 2 en apothema a = a 1 – a 2

De manteloppervlakte van de afgeknotte kegel is gelijk aan het verschil van de manteloppervlakten van twee kegels.

Manteloppervlakte afgeknotte kegel :

Construeer PU ⫽ TN in het vlak TNQ.

Dan is

We brengen (2) in (1) en we bekomen :

manteloppervlakte afgeknotte kegel = pr 1a + pr 2a

Bijgevolg :

manteloppervlakte afgeknotte kegel = p( r 1 + r 2)a (3)

Opmerking :

Is R de straal van de cirkel op halve hoogte, dan wordt formule (3) : manteloppervlakte afgeknotte kegel = 2pRa

Manteloppervlakte van een omwentelingsoppervlak

Gegeven : De kromme met vergelijking y = f ( x ) in een georthonormeerd assenstelsel. Op die kromme nemen we de punten A [ a , f ( a )] en B [ b , f ( b )].

We veronderstellen dat f differentieerbaar is in [ a , b ] en dat de afgeleide functie f ′ continu is in [ a , b ] en dat f enkel positieve waarden aanneemt in [ a , b ]

Gevraagd : De manteloppervlakte van het lichaam dat ontstaat door wenteling van AB om de x -as.

f (ci ) y = f (x ) ci

Oplossing : x y O z B A a b xi xi – 1 Pi Pi – 1

• Verdeel [ a , b ] in n even lange deelintervallen met lengte Dx . De deelpunten zijn x 0 = a , x 1, x 2, … x i –1, x i , … , x n = b

• Verbind de punten Pi –1( x i –1, f ( x i –1)) en Pi ( x i , f ( x i )) door een lijnstuk.

• Benader in elk deelinterval [ x i –1, x i ] de boog Pi 1 Pi door de koorde [ Pi –1 Pi ]. Bij het wentelen om de x -as beschrijft die koorde een afgeknotte kegel met stralen f ( x i –1) en f ( x i ). Het apothema is [ Pi –1 Pi ]

| Pi 1 Pi | = ∆ x 1 + f ( c i ) 2 met c i ∈ ] x i 1 , x i [ (zie blz. 159)

• De manteloppervlakte van de afgeknotte kegel is dan :

A i = π f ( x i 1 )+ f ( x i ) 1 + f ( c i ) 2 ∆ x

Hoe kleiner we de deelintervallen kiezen, hoe dichter x i –1, x i en ci naderen naar eenzelfde x -waarde x ′ i zodat f ( x i –1) ≈ f ( x i ) ≈ f ( x ′ i ) en f ′( ci ) ≈ f ′( x ′ i )

• De som n i =1 2π f ( x i ) 1 + f ( x i ) 2 ∆ x is te beschouwen als een benaderende waarde voor de manteloppervlakte A van het lichaam dat ontstaat door wenteling van de boog AB om de x -as. We krijgen ook de indruk dat we de nauwkeurigheid van de benadering kunnen verbeteren door de verdeling [ a , b ] onbeperkt te verfijnen.

A = lim n → +∞ n i =1 2π f ( x i ) 1 + f ( x i ) 2 ∆ x

Omdat 2π f · 1 +( f )2 continu is in [ a , b ] ( f en f ′ zijn immers continu in [ a , b ]),

wordt A = b a 2π f ( x ) 1 + f ( x ) 2 dx of A = 2π b a f ( x ) · 1 + f ( x ) 2 · dx (1)

Opmerking :

Als f niet positief is, maar in een eindig aantal punten van [ a , b ] van teken verandert, dan breiden we formule (1)

uit tot A = 2π

f ( x ) 1 + f ( x ) 2 dx

Besluit : –

Als de functie f afleidbaar is in [ a , b ] en de afgeleide functie continu is in [ a , b ], dan is de manteloppervlakte van het omwentelingslichaam beschreven door de grafiek van f bij wenteling om de x -as, gelijk aan A = 2π

f ( x ) 1 + f ( x ) 2 dx of A = 2π

| y |· 1 + y 2 · dx

– Als de as van de wenteling gelijk is aan de y -as, dan is A =

Voorbeeld :

Gegeven : hiernaast is een rugbybal van 28 cm lengte getekend. De bovenste helft van de bal heeft de vorm van de grafiek van de functie f met f ( x )= 0,53 √ x (28 x ) met x in cm en x = 0 aan de linkerzijde van de bal.

Gevraagd : bereken de oppervlakte van de bal (in cm2).

Oplossing :

De oppervlakte van de bal is de manteloppervlakte van het omwentelingslichaam dat ontstaat door de grafiek van f te laten wentelen rond de x -as.

Antwoord :

De oppervlakte van de rugbybal is ongeveer 1125

2 Toepassingen

Manteloppervlakte van een cilinder

We nemen een omwentelingscilindervlak met straal r en hoogte h t.o.v. een georthonormeerd assenstelsel.

De manteloppervlakte ontstaat door wenteling om de x -as van de grafiek van f met f ( x ) = r voor x ∈ [ 0, h ]

Hiervoor is f ′( x ) = 0 en dus :

Bijgevolg : manteloppervlakte cilinder = omtrek grondvlak hoogte = 2prh

Opmerking :

De totale oppervlakte van de cilinder = 2prh + 2pr 2. Verklaar.

Manteloppervlakte van een kegel

We nemen een omwentelingskegelvlak met straal r en hoogte h t.o.v. een georthonormeerd assenstelsel.

De manteloppervlakte ontstaat door wenteling om de x -as van de grafiek van f met f ( x )= r h x voor x ∈ [ 0, h ].

Hiervoor is f ( x )= r h zodat :

We vinden de formule terug die op blz. 165 als uitgangspunt is gebruikt.

Opmerking :

De totale oppervlakte van de kegel = pra + pr 2 .

Oppervlakte van een bolzone

Een bolzone is een deel van een boloppervlak begrepen tussen twee evenwijdige vlakken. De afstand tussen die vlakken noemen we de hoogte van de bolzone.

Beschouw een bolzone met straal r en hoogte h in een georthonormeerd assenstelsel.

De oppervlakte van de bolzone wordt voortgebracht door wenteling om de x -as van de grafiek van f met f ( x )= r 2 x 2 voor x ∈ [ a , a + h ]

Hiervooris f ( x )=

Bijgevolg:

oppervlakte van een bolzone = omtrek van een grote cirkel hoogte = 2prh

Opmerking :

Een bolschijf (zie blz. 140) is het deel van een bolvolume dat begrensd is door een bolzone en het grond- en bovenvlak hiervan.

Oppervlakte van een bolkap

Een bolkap is het deel van een boloppervlak dat aan één kant van het snijvlak met de bol ligt. Je kunt een bolkap beschouwen als een bolzone waarvan het bovenvlak een puntcirkel is.

Op analoge wijze als bij de vorige toepassingen vinden we A bolkap = 2prh .

Opmerking :

Een bolsegment is het deel van het bolvolume dat begrensd is door een bolkap en door het grondvlak hiervan.

Gevolg :

De bol is een bijzonder geval van de bolzone of de bolkap met h = 2r oppervlakte bolkap = 2prh

Merk op dat dit gelijk is aan viermaal de oppervlakte van een grote cirkel van het boloppervlak.

(Mantel)oppervlakte van een torus

Een torus is een ruimtefiguur die ontstaat door een cirkel te laten wentelen rond een rechte die in het vlak van de cirkel gelegen is, maar die niet snijdt.

r c y

O ( 0, R)

De vergelijking van de cirkel c is :

De manteloppervlakte van de torus is gelijk aan de som van de manteloppervlakten van twee omwentelingslichamen.

De manteloppervlakte van de torus wordt :

De manteloppervlakte van een torus is dus gelijk aan het product van de omtrek van de wentelende cirkel en de omtrek van de cirkel die het middelpunt bij wenteling doorloopt.

Toepassing :

Bepaal de oppervlakte van het deel van de aarde dat gezien kan worden van op 10 000 m hoogte. We veronderstellen dat het aardoppervlak bolvormig is, met als straal r = 6378 km.

Uit (1) volgt : A = 2

We drukken de oppervlakte A van de waarneembare bolkap uit in functie van de aardstraal r en hoogte h A = 2pr · | CD | (1)

Omdat WA raakt aan de aarde, en dus een raaklijn is aan een meridiaancirkel, geldt : WA ⊥ MA.

In de rechthoekige driehoek MAW geldt : | AM |2 = | WM |·| MD |

3 Samenvatting

Als we hierin r = 6378 km en h = 10 km stellen, dan vinden we A = 400 114,224 km2. Ter vergelijking : de oppervlakte van de aarde is 4pr 2 km2 = 511 185 932,5 km2

• Je kunt de manteloppervlakte van een omwentelingslichaam berekenen. – Als de functie f afleidbaar is in [ a , b ] en de afgeleide functie continu is in [ a , b ], dan is de manteloppervlakte van het omwentelingslichaam beschreven door de grafiek van f bij wenteling om de x -as, gelijk aan

– Als de as van de wenteling de y -as

2 3 4

4 Oefeningen

Bereken de manteloppervlakte van het omwentelingsoppervlak beschreven door de grafiek van f als :

a f ( x )= 2 x + 1 over [2,6] enbijwentelingom x

b f ( x )= x 3 3 over [0,1] enbijwentelingom x

c f ( x )= x 2 9 over 0,3√2 enbijwentelingom y

d f ( x )= 3 √ x over [0,2] enbijwentelingom y

e f ( x )= √6 x over [0,4] enbijwentelingom x

f f ( x )= ln x over [1,4] enbijwentelingom y

g f ( x )= e x over [0, +∞] enbijwentelingom x

h f ( x )= sin x over [0, π] enbijwentelingom x

i f ( x )= tan x over 0, π 4 enbijwentelingom x

j f ( x )= acosh x a over [ a , a ] enbijwentelingom x

(Bijwentelingvandielaatstekettinglijnrondde x -asontstaateen catenoïde.)

Bereken met integralen de oppervlakte van de torus die ontstaat door het wentelen van de cirkel

c ↔ ( x – 5)2 + y 2 = 9 rond de y -as.

Bereken de manteloppervlakte van het lichaam dat ontstaat door wenteling van de kromme K met

a K ↔ x 2 + ( y – 6)2 = 9 en bij wenteling om x

b K ↔ y 2 = –4x over [ –4, 0] en bij wenteling om x

c K ↔ 4x 2 + 9y 2 = 36 en bij wenteling om y

Bereken de manteloppervlakte van het lichaam dat ontstaat door wenteling om x van de lus in [ 0, 3] van de kromme met vergelijking 9y 2 = x ( 3 – x )2

Bereken de manteloppervlakte van het lichaam dat ontstaat door wenteling om x van het deel van het vlak begrensd door de parabolen met vergelijking y 2 = 4x en y 2 = 5 – x

Als we de parabool met vergelijking x 2 = 4y rond de y -as wentelen, ontstaat een paraboloïde (x en y in dm).

Bepaal de waarde van y zodat de oppervlakte van de parabolische schotel 16√3 dm2 bedraagt.

Voor de kromme die gegeven wordt door een stelsel parametervergelijkingen

x = f ( t )

y = g ( t ) met t ∈ [ t 1 , t 2 ]

en die wentelt om de x -as, is de manteloppervlakte van het verkregen omwentelingsoppervlak

gelijk aan A = 2

Bereken met die formule de manteloppervlakte van het lichaam dat ontstaat bij wenteling om x van de krommen met onderstaande parametervoorstelling :

x = R ( t sin t )

y = R (1 cos t ) met t ∈ [0,2π] c

b x = 2cos3 t y = 2sin3 t met t ∈ [0, π]

x = 2cos t cos2 t y = 2sin t sin2 t met t ∈ [0, π]

x = e t cos t y = e t sin t met t ∈ 0, π 2

Toepassingen op de in dit hoofdstuk verkregen formules (zie formuleblad blz. 197-198).

Op te lossen zonder integralen !

Een cirkel is ingeschreven in een gelijkzijdige driehoek met zijde r . De volledige figuur wentelt om de hoogtelijn van de driehoek.

Bewijs dat de verhouding van de oppervlakten van de verkregen bol tot de totale oppervlakte van de verkregen kegel gelijk is aan 4 9

Een satelliet wordt gelanceerd in een (cirkelvormige) baan rond de aarde (een bol met straal 6378 km).

Bereken de hoogte van de baan opdat je steeds een vierde deel van het aardoppervlak zou zien.

Bepaal de afmetingen van een cilinder met maximale manteloppervlakte ingeschreven in een bol met straal 30 cm.

Toepassingen van de integraalrekening

Een omwentelingskegel is omgeschreven aan een halve bol met straal r . Het grondvlak van de kegel ligt in het vlak dat de halve bol begrenst. Bepaal de straal en de hoogte van de kegel waardoor de manteloppervlakte extremaal wordt.

Onderzoek de aard van het extremum.

Vraag uit de toenmalige toelatingsexamens burgerlijk ingenieur

We beschouwen een dubbelbolle lens met dikte d . De zijvlakken van de lens behoren tot twee bollen met respectieve stralen r en r ′ Bepaal de totale oppervlakte van de lens.

B M P Q S

Het glazen reservoir van een thermosfles heeft de volgende binnenafmetingen (in millimeter).

a Bereken de oppervlakte van het reservoir (in cm2).

b Bereken de inhoud van het reservoir (in cl).

Gegeven : De cirkels c en d

De cirkels snijden elkaar in A en B en vormen als het ware een maantje

Gevraagd : a Bereken de oppervlakte A van het maantje.

b Bereken het volume V en de manteloppervlakte M van het lichaam beschreven door het maantje bij wenteling om de x -as.

Toepassingen van de integraalrekening 3

Ik kan de oppervlakte van een vlakke figuur berekenen met behulp van een bepaalde integraal.

Ik kan het zwaartepunt van een vlakke figuur berekenen met behulp van een bepaalde integraal.

Ik kan het volume van een omwentelingslichaam berekenen met behulp van een bepaalde integraal.

Ik kan de booglengte van een vlakke kromme berekenen met behulp van een bepaalde integraal.

Ik kan de manteloppervlakte van een omwentelingslichaam berekenen met behulp van een bepaalde integraal.

119

127

132

158

165

pagina

Toepassingen van integralen in andere disciplines 4

Bij de lancering van deze spaceshuttle werd arbeid verricht door de twee raketten. Om die arbeid te bepalen heb je integralen nodig.

Het gebruik van integralen tref je trouwens in nog een pak andere voorbeelden aan : als je de afgelegde afstand wilt berekenen van een raceauto als de snelheidsfunctie bekend is of als je de arbeid moet bepalen van een voorwerp dat wordt voortgetrokken. Ook een econoom kan niet zonder integralen als hij de kostprijs berekent wanneer de dagproductie met één eenheid stijgt.

Ook om de inkomensongelijkheid te meten binnen een bepaalde bevolkingsgroep zijn er integralen nodig.

Toepassingen van integralen in andere disciplines

1 Snelheid en afgelegde weg 179

2 Versnelling en snelheid 181

3 Kracht en arbeid 183

4 Marginale kostprijs 186

5 Gini-coëfﬁciënt en Lorenzcurve van de inkomensverdeling 188

6 Elasticiteit van de vraag 190

7 Samenvatting 192

8 Oefeningen 193

Wat moet je kennen en kunnen?

1 Snelheid en afgelegde weg

a We weten dat, als een voorwerp beweegt met een constante snelheid v gedurende het tijdsinterval [ t 1, t 2], de afgelegde weg gelijk is aan v · ( t 2 – t 1)

De afgelegde weg wordt immers voorgesteld door de oppervlakte onder de snelheidsgrafiek.

Dus :

v ( t 2 – t 1)

b Als een voorwerp gedurende het tijdsinterval [ t 1, t 2] beweegt met een veranderlijke snelheid v ( t ), dan kunnen we de afgelegde weg als volgt berekenen.

– Verdeel het interval [ t 1, t 2] in n gelijke deelintervallen met als lengte ∆t .

– Veronderstel dat in elk deelinterval de snelheid constant blijft en gelijk is aan v i (= snelheid in het midden van het deelinterval).

De afgelegde weg in het deelinterval is dan v i · ∆t

– De afgelegde weg in het tijdsinterval [ t 1, t 2] is dan bij benadering gelijk aan v 1 · ∆t + v 2 · ∆t + … + v n · ∆t

(

)

afgelegde weg = snelheid maal tijd of s = v t

Dus: s = lim ∆ t →0 ( v1 · ∆ t + v2 · ∆ t + + vn · ∆ t )

– De correcte afgelegde weg vinden we door de limiet van die som te nemen, waarbij we ∆t naar 0 laten naderen (of n → + ∞). (1)

of: s = lim n →+∞ n i =1 vi · ∆ t of: s = t 2 t 1 v ( t )dt deﬁnitievandebepaaldeintegraal

Opmerking :

In het boek Analyse 2 hebben we gezien dat :

v ( t )= Ds ( t )= ds ( t ) dt

De functie s van de afgelegde weg is dus een primitieve functie van de snelheidsfunctie v

Voorbeeld :

Welke afstand legt een voertuig in 8 seconden af als v ( t ) = 3t 2 + 2t (met v ( t ) in m/s) ?

Oplossing :

De gevraagde afstand s = 8 0 (3 t 2 + 2 t )dt

=[ t 3 + t 2 ]8 0 = 512 + 64 = 576

Het voertuig legt 576 m af.

2 Versnelling en snelheid

Stel dat een voorwerp gedurende het tijdsinterval [ t 1, t 2] beweegt met een veranderlijke versnelling a ( t ).

Wat is dan de snelheid v tussen de tijdstippen t 1 en t 2 ?

Toon op een analoge manier als op blz. 179 aan dat :

a ( t )dt (2)

Opmerking :

In het boek Analyse 2 hebben we gezien dat : a ( t )= Dv ( t )= dv ( t ) dt

De snelheidsfunctie v is dus een primitieve functie van de versnellingsfunctie a . Hieruit volgt dat t

)dt

Zo vinden we formule (2) terug.

Voorbeeld 1 :

Als een massa van een bepaalde hoogte naar beneden valt, dan werken er op de vallende massa twee krachten : de zwaartekracht en de wrijvingskracht.

Opmerking :

De zwaartekracht is steeds naar de aarde gericht en dicht bij het aardoppervlak is ze constant. De grootte van de zwaartekracht is m g . Hierin is g de gravitatieversnelling. Die is bij benadering gelijk aan 9,81 m/s2 Als je de wrijvingskracht verwaarloost, dan is de resulterende kracht de zwaartekracht.

Volgens de wet van Newton geldt dan :

m g = m a ( t )

Dus : a ( t ) = g is in dit geval constant.

De snelheid na t seconden is :

v ( t )= t 0 gdy = g [ y ] t 0 = g t

De afgelegde weg na t seconden is :

s ( t )= t 0 gydy = g y 2 2 t 0 = g t 2 2

Een valbeweging over niet al te grote afstanden kan door de vergelijking s ( t )= g · t 2 2 beschreven worden.

Voorbeeld 2 :

Bepaal het voorschrift s ( t ) van de plaatsfunctie s van een motorfiets (bewegend op een rechte baan) als je weet dat het voorschrift van de versnellingsfunctie a wordt gegeven door a ( t ) = 6t + 2.

Bovendien is ook gegeven dat s ( 0) = 0 en v ( 0) = 4.

Oplossing :

• We bepalen eerst het voorschrift van de snelheidsfunctie v :

v ( t )= a ( t )dt

= (6 t + 2)dt

= 3 t 2 + 2 t + C 1

Uit v (0)= 4volgtdat C 1 = 4

zodat v ( t )= 3 t 2 + 2 t + 4.

• s ( t )= v ( t )dt

= (3 t 2 + 2 t + 4)dt

= t 3 + t 2 + 4 t + C 2

Uit s (0)= 0volgtdat C 2 = 0

zodat s ( t )= t 3 + t 2 + 4 t .

3 Kracht en arbeid

a Als op een systeem een constante kracht F inwerkt en dit verplaatst (in de richting van F ), dan zeggen we in de fysica dat de kracht een arbeid W = F s verricht, waarbij F de grootte van de kracht voorstelt en s de afgelegde weg (verplaatsing) van het systeem. Arbeid wordt uitgedrukt in joule (J), 1 Nm = 1 J.

Voorbeeld :

Een wagentje wordt voortgetrokken over een recht spoor met een kracht van 1,8 N (newton) en over een afstand van 4 m (meter).

We berekenen de arbeid die hiervoor vereist is.

W = F · s = 1,8 · 4 = 7,2

De nodige arbeid bedraagt 7,2 J (joule)

Grafische betekenis :

We stellen vast dat de arbeid gelijk is aan de oppervlakte van het rechthoekige gebied R

Hieruit volgt :

1,8ds = 1,8 [ s ]4 0 = 1,8 · (4 0) = 7,2

b In veel gevallen is de kracht niet constant gedurende de verplaatsing van een systeem.

In de figuur zie je een veer.

PLAFOND

0,15 m

Links is de veer in rust. Als je die veer 0,15 m uitrekt en vervolgens loslaat, dan wordt de veer door de veerkracht teruggetrokken. De veerkracht is volgens de wet van Hooke recht evenredig met haar uitrekking. Hoe groter de uitrekking, hoe meer kracht er nodig is.

F v = k u met F v : de veerkracht

u : de uitrekking

k : de veerconstante

Neem k = 2 N/m.

In de onderste stand is de veerkracht dan 2 0,15 N = 0,30 N. Maar even

Fveer = k · u later, op 0,05 m afstand, is de veerkracht nog maar 2 0,05 N = 0,10 N.

Hoe groot is de door de veerkracht verrichte arbeid tijdens die periode ?

Net zoals bij de bepaling van de afgelegde weg (blz. 179) kun je de arbeid benaderen door de weg in kleine stukjes te verdelen. De afgelegde weg s vanaf u = 0,15 m tot u = 0,05 m heeft een lengte van 0,10 m.

Als u = 0,15 m, dan is s = 0 m.

Als u = 0,05 m, dan is s = 0,10 m.

( s ) s

1 s 0

• We verdelen het interval [ s 1, s 2] = [ 0; 0,10] in n ( = 5) gelijke deelintervallen met lengte ∆s ( = 0,02 m).

• We nemen aan dat in elk i -de deelinterval de kracht constant blijft en gelijk is aan F i (F i is de minimale kracht in elk deelinterval). De arbeid in dat deelinterval is dan F i · ∆s .

• De arbeid W over het interval [ s 1, s 2] is dan bij benadering gelijk aan

F1 ∆ s + F2 ∆ s + ... + Fn s = n i =1 Fi ∆ s

Voor n = 5 is W = 0,02 ( 0,26 + 0,22 + 0,18 + 0,14 + 0,10) = 0,018

• De correcte arbeid vinden we door de limiet van die som te nemen waarbij we ∆s naar 0 laten naderen (of n → +∞)

Dus: W = lim n →+∞ n i =1 Fi ∆ s of: W = s2 s1 F ( s )ds deﬁnitiebepaaldeintegraal

In het voorbeeld van de veer is F = 2u en u = –s + 0,15.

Hieruit volgt dat F = –2s + 0,3.

Voor de arbeid die de veerkracht verricht, geldt : W = 0,10 0 ( 2 s + 0,3)ds = s 2 + 0,3 s 0,10 0 = 0,02

Je kunt ook zeggen dat de arbeid gelijk is aan de oppervlakte van het gebied onder de grafiek van F , waarbij de kracht afhankelijk is van de afgelegde weg.

Taak :

Toon aan dat de door de veerkracht verrichte arbeid ook berekend kan worden met de formule : W = 0,15

0,05 2 udu

Hierbij is u de uitrekking t.o.v. het evenwichtspunt.

Voorbeelden :

Arbeid verricht door een raket die verticaal opstijgt tot een hoogte h

Taak :

We houden geen rekening met de luchtweerstand en met de rotatiebewegingen van de aarde. We veronderstellen verder dat de aarde een homogene bol is (zwaartepunt in het middelpunt) en dat het massaverlies van de raket te verwaarlozen is. De fysica leert ons dat de gravitatiekracht F op een massa m , op een afstand x van het middelpunt van de aarde gelegen, wordt gegeven door :

F = G · m · M x 2 met m :massavanderaket

M :massavandeaarde = 5,977 1024 kg

G :gravitatieconstante = 6,67 · 10 11 m3 kg · s 2

R = 6,378 · 106 m

De gevraagde arbeid is dus :

W = R +h R G m M x 2 dx = GmM · 1 x R +h R = GmM

Bereken met die formule de arbeid die nodig is om een raket met een massa van 1000 kg op een hoogte van 500 km te brengen.

Arbeid die nodig is om een raket buiten de aantrekkingskracht van de aarde te brengen

W = +∞ R G · m · M x 2 dx = lim h →+∞ GmM 1 R 1 R + h = GmM R

Laten we even ‘idealistisch’ doordenken. We veronderstellen dat de raket bij het vertrek een eenmalige stoot krijgt en er verder geen kracht op wordt uitgeoefend, afgezien van de zwaartekracht. Wat moet dan de vertreksnelheid zijn om te ontsnappen aan de aantrekkingskracht van de aarde ?

De kinetische energie die de raket met beginsnelheid v 0 meekrijgt, is mv0 2 2 . Die moet gelijk zijn aan de te leveren arbeid.

Daaruit volgt dan : mv0 2 2 = GmM R ⇐⇒ v0 = 2GM R ≈ 11181

De ontsnappingssnelheid van de raket bedraagt dus 11 181 m/s of ongeveer 11,2 km/s.

Foto: ESA

4 Marginale kostprijs

Een marginale kostenfunctie geeft aan hoeveel de dagelijkse kosten stijgen als de dagproductie stijgt van x naar x + 1 eenheden. In het boek Analyse 2 hebben jullie het volgende geleerd.

De totale kostenfunctie van een product wordt gegeven door :

K ( q ) = 1,5q 3 – 20q 2 + 100q + 50 met q : de te produceren hoeveelheid.

De fabrikant wil weten hoe de totale kosten veranderen bij toename van de productie. De gemiddelde kostenstijging bij een productietoename van 10 naar 14 producten is :

K (14) K (10) 14 10 = 1646 550 4 = 274 De gemiddelde kostenstijging is 274 euro.

Grafische interpretatie :

De gemiddelde kostenstijging is de richtingscoëfficiënt van de rechte door de punten ( 10, 550) en ( 14, 1646) In de economie spreken we ook van de marginale kost. Die geeft de helling weer in een punt van de kostengrafiek. Het is de limiet van de gemiddelde kostenstijging bij steeds kleinere productietoenamen en dus niets anders dan de afgeleide functie van de kostenfunctie.

Grafische interpretatie :

De marginale kost is, net zoals de ogenblikkelijke snelheid, de helling (rico) van de raaklijn. De marginale kostenfunctie wordt gegeven door :

M (q )= 4,5q 2 40q + 100 = dK (q ) dq Voor q = 14 zal de marginale kost 422 euro zijn.

Grafieken van de totale kostenfunctie en de marginale kostenfunctie :

K (q )= 1,5q 3

q 2 +

q +

M (q )= 4,5q 2 40q + 100

Bij volkomen concurrentie (bv. de grondstoffenmarkt, de beurs …) maximaliseert de verkoper zijn winst als de marktprijs van zijn producten gelijk is aan de marginale kost.

W = O – K (winstfunctie = omzetfunctie – kostenfunctie)

W ismaximaalals dW dq = 0of dO dq = dK dq .

Toepassingen

Als de marktprijs van een product 150 euro (dus O ( q ) = 150q ) bedraagt, hoeveel stuks zal deze aanbieder dan op de markt brengen zodat de winst maximaal is ? dO dq = dK dq ⇐⇒ 4,5q 2 40q + 100 = 150

4,5q 2 40q 50 = 0

D = 1600 + 900 = 2500 q1 = 40 + 50 9 = 10

q2 = 10 9

De aanbieder zal dus 10 stuks op de markt brengen.

Besluit : de marginale kostenfunctie is niets anders dan de afgeleide van de totale kostenfunctie : M ( q ) = K ′( q ).

Omgekeerd is de totale kostenfunctie dus een primitieve functie van de marginale kostenfunctie.

Voorbeeld :

De kostprijs om 100 exemplaren per week van een bepaald product te maken is 400 000 euro.

De marginale kostprijs is gegeven door de formule : M ( q ) = 40 + 100q – 0,01q 2 .

a Wat is de kostprijs om 300 stuks per week te maken ?

b Bepaal de marginale kostprijs bij een weekproductie van 300 stuks (d.w.z. de stijging van de kostprijs bij een productieverhoging van 300 naar 301).

c Bepaal de stijging van de kostprijs bij een productieverhoging van 300 naar 350 stuks.

Oplossing : a

M (q )= K (q )= dK (q ) dq =⇒ K (q )= M (q ) dq = (40 + 100q 0,01q 2 ) dq = 40q + 50q 2 0,01 3 q 3 + c

Wewetendat K (100)= 400000 ⇐⇒ 40 (100)+ 50 (100)2

Dusdetotalekostenfunctie K heeftalsvoorschrift K (q )= 40q + 50q 2 0,01 3 q 3 302000 3

K (300) = 4 321 333,333

De kostprijs om 300 stuks per week te maken bedraagt 4 321 333,333 euro.

b M (300) = 40 +100 · 300 – 0,01 · (300)2 = 29 140. De marginale kostprijs bij een weekproductie van 300 stuks is 29 140 euro.

c K (350) K (300)= 350 300 (40 + 100q 0,01q 2 ) dq = 1574083,33. De kostprijs stijgt met 1 574 083,33 euro.

5 Gini-coëfﬁciënt en Lorenzcurve van de inkomensverdeling

De Lorenzcurve is de grafische weergave van de verdeling van het inkomen of vermogen van een bevolking. Op de grafiek kun je aflezen hoe groot de inkomensongelijkheid van een bevolking is.

Hieronder zie je als voorbeeld de grafiek van de verdeling van de gezinsinkomens van een bepaalde stad.

proportievanhettotaleinkomen(cumulatief)

I IIgelijkeverdeling l ( x )= 1 3 x + 2 3 x 3 ongelijkeverdeling

proportievandegezinnenmetdelaagsteinkomens(cumulatief)

Op de x -as worden de percentages van de gezinnen met de laagste inkomens geplaatst. Op de y -as zie je de percentages van het totale inkomen van alle gezinnen. Dikwijls worden in plaats van percentages de proporties in het interval [ 0, 1] weergegeven.

De grafiek van de functie l met l ( x ) = 1 3 x + 2 3 x 3 heet de Lorenzcurve van de bijbehorende inkomensverdeling.

Op die grafiek kun je bijvoorbeeld aflezen dat 25% van de gezinnen met de laagste inkomens gezamenlijk slechts 9% van het totale inkomen verdienen. De 50% van de gezinnen met de laagste inkomens verdient 25% van het totale inkomen.

Bij volstrekte gelijkheid van inkomen zou moeten gelden : l ( x ) = x voor alle x [ 0, 1]. Naarmate de ongelijkheid tussen de inkomens toeneemt, zal de Lorenzcurve dieper doorzakken.

De oppervlakte tussen de eerste bissectrice met vergelijking y = x en de Lorenzcurve met vergelijking y = l ( x ) is een maatstaf voor de ongelijkheid.

Max Otto Lorenz (1876 – 1959)

De Lorenzcurve werd in 1905 ontwikkeld door Max Otto Lorenz (1876 – 1959), een Amerikaanse econoom en statisticus. Zijn ouders waren Duitse emigranten, zijn vader was een succesvolle zakenman. Hij publiceerde zijn bekendste paper (over deze curve) toen hij nog aan het doctoreren was. Hij gaf les, publiceerde papers en werkte ook geregeld voor Amerikaanse overheidsinstanties zoals de U.S. Bureau of Statistics.

De Gini-coëfficiënt of Gini-index G wordt in de economie gebruikt om de inkomensongelijkheid in een samenleving te meten.

Ze wordt als volgt gedefinieerd : G = A I A

De waarde ligt steeds tussen 0 en 1, waarbij :

• 0 staat voor een absolute gelijkheid van inkomens: iedereen heeft hetzelfde inkomen.

• 1 staat voor absolute ongelijkheid van inkomens: één persoon krijgt het volledige inkomen, de anderen krijgen niets.

Voorbeeld :

We berekenen de Gini-coëfficiënt bij de Lorenzcurve van de inkomensverdeling uit het voorbeeld van vorige bladzijde.

Corrado Gini (1884 – 1965)

De Gini-coëfﬁciënt werd door de Italiaanse statisticus Corrado Gini (1884 – 1965) in 1912 gepubliceerd in zijn werk

Variabilità e mutabilità .

Income inequality: Gini coefficient, 2023

Op de weergave hieronder zie je de inkomensongelijkheid in onze wereld van 2023. Voor het Vlaamse Gewest lag de index op 0,22. Dat was iets lager dan het Waalse Gewest (0,25) en serieus lager dan het Brussels Hoofdstedelijk Gewest (0,32). Het Europees gemiddelde was in 2023 iets meer dan 0,29.

The Gini coefficient¹ measures inequality on a scale from 0 to 1. Higher values indicate higher inequality. Depending on the country and year, the data relates to income measured after taxes and benefits, or to consumption, per capita².

6 Elasticiteit van de vraag

a Als een artikel verhoogt in prijs ( p ), dan loopt de gevraagde hoeveelheid ( q ) meestal terug. Ook het omgekeerde is waar. Vaak kun je het verband tussen p en q vastleggen in een zogenaamde vraagfunctie met voorschrift p = f ( q ). De grafiek van deze functie is de zogenaamde vraagcurve.

Bij een prijsverhoging zijn er dus twee tegengestelde invloeden op de opbrengst ( O = p q ): p stijgt, q daalt.

Welke van de twee overweegt ? Dat hangt af van de vraagfunctie en wordt uitgedrukt door de elasticiteit E .

In de economie werd daarom het begrip elasticiteitscoëfficiënt E als volgt ingevoerd :

= E (1)

Het minteken zorgt ervoor dat E ⩾ 0 ; dp en dq hebben immers een verschillend teken.

Voorbeeld :

Devraagfunctieheeftalsvoorschrift p = q 4 + 10

Dus: dp dq = 1 4

Uit (1) volgtdat E = p q · dp dq = 4p

– Voor bijvoorbeeld q = 10 is E = 3.

Dat betekent dat bij 1% prijsverhoging, q met 3% en de opbrengst met 2% achteruitgaat. De afnemers reageren fel op de prijsveranderingen. De vraag wordt ‘elastisch’ genoemd. –

Voor bijvoorbeeld q = 30is E = 1 3 .

Dat betekent dat bij 1% prijsverhoging q met slechts 1 3 % omlaag gaat en de opbrengst 2 3 % groter wordt. De afnemers reageren zwak : de vraag is niet elastisch.

– Voor bijvoorbeeld q = 20 is E = 1.

Bij een prijsverhoging van 1% daalt q met 1% en blijft de opbrengst hetzelfde. De vraagelasticiteit is gelijk aan 1.

Taak :

Toon aan dat de opbrengst maximaal is bij q = 20 en p = 5.

b Als we werken in een omgeving van ( q , p ) waar E constant is, dan is (1) een differentiaalvergelijking van de eerste orde en de eerste graad die we oplossen door scheiding van de variabelen.

(1) dp p = 1 E dq q dp p = 1 E dq q

ln | p | = 1 E ln | q | + c p > 0en q > 0

ln p = 1 E ln q + ln e c

ln p = ln e c q 1 E p = e c q 1 E p = k q 1 E met k = e c (2)

De oplossing geeft een verband tussen p en q in de omgeving ( q , p ) waar E constant is.

In het algemeen zal E verschillende waarden aannemen in verschillende delen van de vraagcurve. Daarom is (2) in het algemeen niet de vergelijking van de volledige vraagcurve.

7 Samenvatting

Toepassingen van integralen in de fysica

• Je kunt de afgelegde weg s berekenen als je de snelheid v ( t ) kent in het tijdsinterval [ t 1, t 2].

s = t 2 t 1 v ( t )dt

• Je kunt de snelheid v berekenen als je de versnelling a ( t ) kent in het tijdsinterval [ t 1, t 2].

v = t 2 t 1 a ( t )dt

• Je kunt de arbeid W berekenen die verricht wordt door een veranderlijke kracht F ( s ) bij een verplaatsing van een systeem over een afstand s ∈ [ s 1, s 2].

W = s2 s1 F ( s )ds

Toepassingen van integralen in de economie

• Je weet dat de Lorenzcurve de grafische weergave is van de inkomensverdeling van een bevolking. Je weet dat de Gini-coëfficiënt G in de economie gebruikt wordt om de inkomensongelijkheid in een samenleving weer te geven.

proportievanhettotaleinkomen(cumulatief)

I II

gelijkeverdeling

ongelijkeverdeling

proportievandegezinnenmetdelaagsteinkomens(cumulatief)

• Je weet dat de totale kostenfunctie K een primitieve functie van de marginale kostenfunctie M is, want K ′( q ) = M ( q )

K (q )= M (q )dq

• Je weet dat de stijging van de kostprijs bij een productieverhoging van q 1 naar q 2 bepaald wordt door q2

M (q ) dq G = A I A I + A II

8 Oefeningen

Een voorwerp beweegt op een rechte lijn met een gegeven snelheid v ( t )

Op het ogenblik t = 0 is s = 0. Schrijf s in functie van t en bereken de afgelegde weg na 10 seconden.

a v ( t )= 3 t + 1

b v ( t )= t 2 5 + 6 t

c v ( t )= √ t + 2

Een voorwerp beweegt op een rechte lijn met een gegeven versnelling a ( t ) en beginsnelheid v 0

Op het ogenblik t = 0 is s = 0. Schrijf s in functie van t en bereken de afgelegde weg na 5 seconden.

a a ( t )= t + 1; v0 = 2

b a ( t )= t 3 ; v0 = 2

c a ( t )= 1 √ t ; v0 = 3

Bepaal het voorschrift s ( t ) van de plaatsfunctie s van een puntmassa (begrensd op een rechte baan) als je weet dat het voorschrift van de versnellingsfunctie a wordt gegeven door a ( t )= 3√ t . Bovendien is s ( 0) = 2 en v ( 4) = 10.

Een bal rolt over een baan met een beginsnelheid van 8 m/s.

Door de wrijving zal de snelheid verminderen met 2 m/s2 Hoe ver rolt de bal ?

Een automobilist rijdt met een snelheid van 108 km/h en remt af met een vertraging van 3 m/s2

a Schrijf v en s in functie van t

b Hoeveel bedraagt de remweg ?

Een voorwerp wordt op een hoogte van 1500 m losgelaten. Voor de snelheid v na t seconden geldt de formule : v = 20t – t 2

Die formule geldt tot het tijdstip waarop de snelheid niet meer toeneemt. Daarna blijft de snelheid constant.

a Bereken het tijdstip waarop de maximale snelheid is bereikt.

b Bereken hoeveel meter het voorwerp is gevallen tot het moment waarop de snelheid maximaal wordt.

c Bereken na hoeveel seconden het voorwerp op de grond komt.

Een parachutist met een massa van 60 kg springt uit een vliegtuig met een snelheid van 2 m/s. De snelheid v ( t ) wordt in dit systeem beschreven door de differentiaalvergelijking

v ( t )= 10 v ( t ) 3

a Toon aan dat v ( t )= 30 28 e t 3

b Hoeveel bedraagt de snelheid van de parachutist na 10 seconden vrije val ?

c Bereken de grenswaarde van de valsnelheid van de parachutist.

Een komeet met massa 20 ton vliegt recht naar de aarde. Bereken de arbeid die verricht wordt door de gravitatiekracht van op een hoogte van 10 000 km tot op het aardoppervlak.

Een veer heeft in ruststand een lengte van 0,30 m. De kracht F nodig om de veer uit te rekken over een afstand van x meter is F = 25 000 x newton.

a Bereken de arbeid die nodig is om de veer uit te rekken van 0,30 m tot 0,35 m.

b Bereken de arbeid die nodig is om de veer uit te rekken van 0,35 m tot 0,40 m.

Een treinstel remt iets te laat af, waardoor het stootblok 25 cm wordt ingedrukt.

De buffers van het stootblok hebben een veerconstante van 3 106 N/m.

Bepaal bij hoeveel cm het stootblok twee keer zoveel energie kan opnemen als bij 25 cm.

Een buigzame kabel heeft een lengte van 15 m. Je wilt de kabel 10 m ophijsen. Hoeveel arbeid kost dat als je weet dat de kabel 15 N per meter weegt ?

Een last met een gewicht van 1000 N wordt aan een kabel 20 m opgehesen. De kabel weegt 20 N per meter en wordt op een haspel gewikkeld.

a Hoeveel arbeid wordt er verricht om alleen al het voorwerp op te hijsen ?

b Hoeveel arbeid is er nodig om de kabel te hijsen ?

c Hoeveel arbeid is er in totaal nodig ?

Bereken de arbeid die nodig is om 500 kg steenkool vanuit een 500 m diepe mijn naar boven te trekken met behulp van een kabel die 30 N/m weegt.

In de fysica bewijst men dat de arbeid die door gas geleverd wordt bij een constante druk p , wanneer het volume uitzet van V 1 naar V 2, gegeven wordt door : W = p · (V 2 – V 1).

Als p veranderlijk wordt, kom je vrij gemakkelijk tot de algemene formule : W = V2 V1 p dV (Hierbijis p eenfunctievan V )

Bij het uitzetten van gas is V 2 > V 1. – Bij het samendrukken ( V 2 < V 1) bekom je de compressiearbeid.

1,5 m3 ideaal gas met een begindruk van 2 · 105 Pa drukt men samen zonder warmte-uitwisseling met de omgeving tot een eindvolume van 0,5 m3. De compressie gebeurt volgens de formule p V 1,4 = c (= constante).

Bereken de compressiearbeid.

Toepassingen van integralen in andere disciplines

De stroomsterkte I van een wisselstroom is veranderlijk en wordt op elk ogenblik t gegeven door I = I 0 sin ω t met ω = 2π T I 0 :maximalestroomsterkte T :periode

ω :pulsatie

De effectieve stroomsterkte I e van een wisselstroom is per definitie de stroomsterkte van een gelijkstroom die in dezelfde tijd en met dezelfde weerstand warmte ontwikkelt.

Als tijd nemen we een volledige periode T . De weerstand stellen we voor door R . Volgens de wet van Joule is het kwadraat van de effectieve stroomsterkte I e het gemiddelde van I 2 in het tijdsinterval 0, T = 2π

Toon nu aan dat I e = I 0 √2 2 .

De marginale kostprijs in een bedrijf wordt gegeven door de functie M met : M ( q ) = 0,03q 2 – 30q + 7000 (euro)

a Bepaal de marginale kostprijs bij een dagproductie van 300 stuks.

b Bepaal de stijging van de kostprijs bij een productieverhoging van 300 naar 350 stuks.

De kostprijs om 100 exemplaren van een bepaald product te maken, is 50 000 euro.

De marginale kostprijs wordt gegeven door : M ( q ) = – 20 + 10q – 0,01 q 2 .

a Bepaal het voorschrift van de kostenfunctie K .

b Wat is de kostprijs om 250 stuks van dat product te maken ?

c Bepaal de stijging van de kostprijs bij een productieverhoging van 250 naar 300 stuks.

Bepaal het voorschrift van de kostenfunctie K als de marginale kostprijs M ( q ) en de vaste kosten K 0 gegeven zijn.

a M ( q ) = 1,5q + 2 ; K 0 = 100

b M ( q ) = 0,15q 2 – 30q + 20 ; K 0 = 1200

Het verband tussen de prijs ( p ) en de gevraagde hoeveelheid ( q ) van een artikel wordt vastgelegd door log p = – 4 – 0,8 log q

a Bepaal de elasticiteitscoëfficiënt E .

b Als de prijs 10% verhoogt, met hoeveel procent neemt dan de gevraagde hoeveelheid toe?

Bereken de Gini-coëfficiënt bij de Lorenzcurven met vergelijking :

a l ( x )= 1 4 x + 3 4 x 3

b l ( x )= 4 5 x 3 1 5 x 2 + 2 5 x

Toepassingen van integralen in andere disciplines 4

Ik kan de afstand uit de snelheid berekenen met behulp van bepaalde integralen.

Ik kan de snelheid uit de versnelling berekenen met behulp van bepaalde integralen.

Ik kan arbeid uit kracht berekenen met behulp van bepaalde integralen.

Ik kan de marginale kostprijs berekenen met behulp van bepaalde integralen.

Ik weet dat de Lorenzcurve de grafische weergave is van de inkomensverdeling en ik kan ze tekenen.

Ik kan de Gini-coëfficiënt berekenen van de inkomensverdeling van een samenleving.

Ik ken de prijselasticiteit als toepassing op bepaalde integralen.

179

181

183

186

188

189

190

Overzicht van de formules voor oppervlakte en volume van belangrijke ruimteﬁguren

Manteloppervlakte

Totaleoppervlakte

bolkapbolsegment

Manteloppervlakte

Totaleoppervlakte

Bolzone = deelvanhetboloppervlakgelegentussen tweeevenwijdigesnijvlakken.

Bolschijf = deelvanhetbolvolumebegrensddooreen bolzoneenhetgrond-enbovenvlakhiervan.

Volumebolschijf

Oppervlaktebolzone

Bolkap = deelvanhetboloppervlakdataan éénkantvaneensnijvlakmetdebolligt.

Bolsegment = deelvanhetbolvolumebegrensddoor eenbolkapenhetgrondvlakhiervan.

Volumebolsegment = 1 3 πh 2 (3 r h )

Oppervlaktebolkap = 2π rh

bolschil r h k

bolsector

Bolschil = deelvanhetbolvolumedatontstaatdoor hetwentelen(over360 ◦ )van eencirkelsegmentomeenmiddellijn diebuitendatsegmentloopt.

Volumebolschil = 1 6 πhk 2 (zieoefening21blz.157)

Bolsector = deelvanhetbolvolumedatbegrensdis dooreenbolkapeneenkegel.Vandie kegelligtdetopinhetmiddelpuntvan debolenhetgrondvlakvaltsamenmet hetgrondvlakvandebolkap.

Volumebolsector = 2 3 π r 2 h (zieoefening20blz.157) r h

Een n -zijdigprismaiseenlichaambegrensddoor tweeevenwijdigecongruenteveelhoeken(grond-en bovenvlak)en n zijvlakkenmetevenwijdigesnijlijnen.

Volume = A g h

Oppervlakte = somvandeoppervlaktenvanhetgrondvlak,hetbovenvlakendezijvlakken

Eenbalkiseenrechtprismawaarvanhetgrondvlak eenrechthoekis.

Volume = A g · h = l · b · h

Oppervlakte = 2 · (l · b + l · h + b · h ) l b h

Eenkubusiseenbalkwaarvanalleribbenevenlangzijn.

Volume = z 3

Oppervlakte = 6 z 2

Eenpiramideiseenlichaambegrensddoor eengrondvlak(eenveelhoek)endriehoekige zijvlakkendieineenpunt(detop)samenkomen.

Volume = 1 3 A g h

Oppervlakte = somvandeoppervlaktenvan hetgrondvlakendezijvlakken

Eenafgeknottepiramideiseendeelvaneenpiramide gelegentussenhetgrondvlakeneendoorsnedeevenwijdigmethetgrondvlak.

Volume = 1 3 h ( A g + A b + A b · A g )

Oppervlakte = somvandeoppervlaktenvanhetgrondvlak,hetbovenvlakendezijvlakken

Oplossingen

1 Bepaalde integralen (blz. 50)

1 a 10,5

b 14

c 12,25

2 a ondersom = 13 ; bovensom = 21

b exacte oppervlakte = 17

3 a ondersom = 32,5 ; bovensom = 37,5

b exacte oppervlakte = 35

4 n ondersom bovensom

6 18

s6 = 6,875; S6 = 11,375

b s20 = 8,3363; S20 = 9,6863

s50 = 8,7318; S50 = 9,2718

s100 = 8,8655; S100 = 9,1355

s500 = 8,973; S500 = 9,027

s999 = 8,9865; S999 = 9,0135 clim n → +∞ sn = lim n → +∞ Sn = 9 d9

8 a 2 b 21,5 c 10,5

12als5 < t 10

0als10 < t 20

9als20 < t 30

0als t > 30

bna5minuten:30l na10minuten:90l na20minuten:90l na25minuten:45l na30minuten:0l

12 t 30als5 < t 10

90als10 < t 20

9 t + 270als20 < t 30

0als t > 30 d V ( t )= D ( t ) 10 a 4225 m b 8,45 km/h 11 a4 b 375 2 c 26 3 d4 e 255 4 f 242 5

13 a8 b9 c13 d 53 4 e 37 12

14 a 32 3 b 9 2 c 27 4 d 2459 288 e 784 15

15 8 3

16 a 2 3 b3 c 57 4 d 63 4

17 a 1 6 b 250 3 c 64 3 d 1 2 e 37 12 18 44 3 19 96 5

20 a8 b 25 4 c 275 8

21 9 22 72√2 5

23 7 3

24 11 3

25 a 32

b dubbel zo hoog

c tweemaal zo breed

26 3645,83 m3

27 a k = 4of k = 3

b k = 2of k = 2

c k = 1 4 of k = 1 2

28 a x = 1 √3of x = 1 + √3 b x = 2of x = 0of x = 2

29 6

30 4

31 1,917

34 a I a ( x )= 5( x a )

b I a ( x )= x 2 + x a 2 a

c I a ( x )= 2 x 3 3 + x + 2a 3 3 a

d I a ( x )= x 4 x 2 a 4 + a 2 4

35 a90 b x 2 5 x + 6 c 15 2 d9 e 45 2

36 a 13 2 b16 c 4 d 23 2 e 10 3 f2 g3 h 15 2

37 a x 4 + x 2 3

b 1 x x + 2 x 3 3

c2√ x + 2 x

d2 x

e 2cos x 3sin x f 1 2 x ln 1 2

g 3 4 x · 3 √ x 2Bgtan x

hln | x | + Bgsin x

39 a 14 3 b2

c2 d1 e1 f π 6 g2ln 1 + √2 h9 6√2

40 a12

b e 2 1 e 2 c 1 2 d1

41 a 1 1 2 p ln2

42 a x 2 y + 4 = 0 b 4 3

43 a 8 6ln3 3

b 20 3

c2√2

d 3π 2 6 e 4 3 f 9 2 g 32 3 h 2 3 i 16 3 j e 2 e

44 a 1 2 b 0,88of0,88 c 1 √3 2 d √3

45 a 4 3 b6 c 2 π d π 4 eln3 f 4 3ln3 46 a 1 2 b 1 2 c 1 n 1 d 1 3 e +∞ f3 47 a +∞ b +∞ c0 d6

48 niet juist (oplossing = +∞)

49 neen, de limiet bestaat niet

50 A

2.1 Fundamentele integralen (blz. 75)

1 a 2 x 5 5 + C

b 6 5 x 2 √ x + C

c 1 6 x 6 + C

d 6 17 x 2 6 x 5 + C

etan x + C

f 2 x 3 3 + 3 x 2 2 2 x + C

g 4 x 3 3 6 x 2 + 9 x + C h 3 x 2 2 5ln | x | + C i 1

7 x · ln7 + C

j2ln | x + x 2 + 3 | + C

k x + C

l 4 3 x √ x + 2√ x + C

mtan x + C

n 4 5 x 2 √ x + 10 3 x √ x + C

o 1 2ln 8 5 · 8 5 x + C

p tan x + C q x 2√3+1 2√3 + 1 + C

r x Bgtan x + C

s cot x x + C

t 4 9 x 2 4 √ x + C

utan x cot x + C

2a cot x + cos x + C b 12 ln 1 2 · ln 1 2 x 8 ln 3 4 · 3 4 x + C

c2Bgtan x x + C d cot x 2 + C e 60 119 x 60 x 59 5 8 x · 5 x 3 + C f 2cos x + C

3a a · cos t + b · sin t + C b 2e t + C c x 2 2 + x sin y + C d x y cos y + C e x 2 · e y + C

f2 x e y + C 4a π 2 b 135 4

c2 + √2 d0 e8 ln2 5 f 9 ln 2 3

6a f ( x )= x 2 3 x 3 2

b f ( x )= 2 x 3 3 + x 2 2

c f ( x )= 2 x 1 sin x

d f ( x )= 1 2 x + 2 x 7 67 5

8 0 9 +∞ 10 B 11 A

2.2

Integratie door substitutie (blz. 85)

1 a 72 3 x 3ln7 + C

b e x 2 2 + C

c 3 2 cos 2 x + π 7 + C

dBgsin e x + C

e 2 5 ln | 5 x + 3 | + C

f 2 3 ln | 3 x + 9 x 2 7 | + C

g (ln x )n +1 n + 1 + C

h12ln | ln x | + C

i 5 2 x + C

j 1 2√7 Bgtan x 2 √7 + C

k Bgtan2 x ln2 + C

l 1 x 2 + 7 · Bgsin x + C

m (1 + x 4 ) 1 + x 4 6 + C

n 9 4 3 x 2 + 3 2 + C

o 2ln | 1 √ x | + C p Bgtan sin2 4 x 12 + C

q x 4 + x 8 8 + C

r ln 5 3 x + 1 ln 5 3 + C

s cot3 x 3 + C

t ln | 1 + cos x | + C

u ln | 2 x + cos2 x | 2 + C

v2√tan x 1 + C

2aBgtan(ln x )+ C

b e 1 x + C

cln | ln x | + C d 4ln | 2 x + 2 | ln2 + C e 3 16 5 x 100ln 16 5 + C

f ( x + π)e +1 e + 1 + C g ln | cos(7 x 3) | 7 + C

h2√ x + 4 x √ x 3 + 2 x 2 √ x 5 + C i Bgtan x 3 3 + C

j 3 x · e 2 x 2 + ln3 + C k Bgtan2 x 2 + C l Bgtan x 2 2 + C

m3Bgsin 2 x 3 + C

n ln | x √2 + 2 x 2 + 1 | √2 + C

oBgtan( x + 1)+ C p 2( x + 1) √ x + 1 3 + 4( x + 1) 4 √ x + 1 5

+( x + 1)+ 4 · 4 ( x + 1)3 3 + C

q cos2 x 4 + C

rln( x 2 + x + 2)+ C

s Bgtan x 2 2 + C

t (2 x 2 + 1) 2 x 2 + 1 6 + C

u ln | 4 + 3 x | ln3 + C

v2ln | 2 + sin x | + 4 2 + sin x + C

3 a 1383 5

b π 4

d π2 16 e ln3 2 f 27 3 √9 3 8 g 9 2 hln2 i 4 π 2 j ln3 2 k1 ln2 l e π π + 1

4 a +∞ b1 c0 d 1 2 e12 f2

5a0 b4 c0 d4 e π f π

6 a x 3 2 x 2 + x + 3 b 1 2 sin 2 x + π 2 + 1 2

c e 2 x 3 + e

d 3 8 (2 x 1) 3 √2 x 1 3 8

7 3 e 2 1 2e

8 a {1;1,5214} b {−1;0,735} c √3 2 d {6 e } 9 2 3 10 a4

bln2

c2π 4 3 11 a 10π 3 b8π 12 32 105 13 A = A = 1 √3 2

2.3 Integratie van elementaire

rationale functies – splitsen in partieelbreuken (blz. 97)

1 a 3 2 ln | 2 x 1 |− 4ln | x + 2 | + C

b 2 3 ln | 3 x + 1 | + 5ln | x 2 | + C

c 1 2 ln | 2 x 1 | + 3ln | 2 x + 1 | + C

d7ln | x + 3 |− ln | x 1 | + C

e4ln | x + 4 |− 3ln | x + 2 | + C

f2ln | x 8 | + 8ln | x 2 | + C

g 1 2 ln | 4 x 3 | + 5ln | x | + C

h 2ln | x 1 |− 3 x 1 + C

i3ln | x + 2 |− 1 x + 2 + C

j 1 2 ln | 2 x 1 |− 2 2 x 1 + C

k3Bgtan( x + 1)+ C

l √2 · Bgtan x 1 √2 + C

m4Bgtan( x + 2)+ C

n 1 2 Bgtan x 2 2 + C

o ln | 2 x 2 2 x + 1 | +2Bgtan(2 x 1) 4 + C

p 1 4 ln | 4 x 2 + 12 x + 11 |− 1 √2 Bgtan 2 x + 3 √2 + C

qln | x 2 + 6 x + 18 | + 1 3 Bgtan x + 3 3 + C

r2ln | x 2 6 x + 13 | + 13 2 Bgtan x 3 2 + C

2a x + 2ln | x 2 | + 4ln | x + 1 | + C b x 2 2 + 3ln | x 3 |− ln | x + 2 | + C

c x 2 x + 2ln | x 3 |− 2ln | x 1 | + C d x 3 3 2 x + 1 2 ln | 2 x 1 | + 3ln | x + 4 | + C e x 2 2 + 2 x + 3ln | x 2 |− 1 x 2 + C f 3 x 2 2 x + ln | x + 5 | + 1 x + 5 + C g3 x 2 3 ln | 3 x + 2 | + 4 3(3 x + 2) + C h x 3 3 x 2 2 3 2√2 Bgtan x 1 2√2 + C i x 2 + 3 x + ln | x 2 2 x + 5 | + 3 2 Bgtan x 1 2 + C j x + 2ln | x 2 + 4 |− 2Bgtan x 2 + C

3 2340

4 8,928513

5a7,5 8ln2 ≈ 1,9548

b5,25 + 16ln2 ≈ 16,34035

c4 2ln3 ≈ 1,8028 d2√2 + 2ln √2 1 ≈ 1,06568

6 a = 3,0031

2.4 Partiële integratie (blz. 110)

1 a x · Bgsin x + 1 x 2 + C

b x Bgcos2 x 1 4 x 2 2 + C

c x ln( x 2 + 2) 2 x + 4 √2 Bgtan x √2 + C

d2 x ln x 2 x + C

e x · ln2 x 2 x · ln x + 2 x + C

f x · Bgtan √ x √ x + C

g x Bgsin2 x + 2 1 x 2 Bgsin x 2 x + C

h x ln x + x 2 + 5 x 2 + 5 + C

2a 2e x ( x + 1)+ C

b x · cos2 x 2 + sin2 x 4 + C

c e 3 x 9 x 2 6 x + 2 27 + C

d e 3 x (3 x + 1) 9 + C

e ln( x + 1) x + C

f sin2 x 2 x cos2 x 8 + C

g x 4 (4ln x 1) 16 + C

h 2 x 2 1 · Bgsin x + x · 1 x 2 4 + C

i 2 x ( x · ln2 1) (ln2)2 + C

j 2 x 2 2 x · sin2 x cos2 x 8 + C

3a 1 2 x x 2 1 1 2 ln | x + x 2 1 | + C

b 1 2 x 9 x 2 + 9 2 Bgsin x 3 + C

c 1 2 x x 2 + 8 + 4ln | x + x 2 + 8 | + C

d 1 2 x 3 x 2 + 3 2 Bgsin x √3 3 + C

e 1 2 x 4 x 2 + 6 + 3 2 ln | 2 x + 4 x 2 + 6 | + C

f 1 2 x 16 9 x 2 + 8 3 Bgsin 3 x 4 + C

4a e 2 x (3sin3 x 2cos3 x ) 13 + C

b e x (sin x + cos x ) 2 + C

c sin2 x · sinh x 2cos2 x · cosh x 5 + C

e x (sin x cos x ) 2 + e 2 x (2sin x cos x ) 5 + C

e e ax (a · cos bx + b · sin bx ) a 2 + b 2 + C

f x Bgsin x 1 x 2 + C

g x sin(ln x ) cos(ln x ) 2 + C

h x · cot x + ln | sin x | + C

itan x ln(tan x ) 1 + C

j e x 1 + x + C

5a π2 2 b 1 2 c π 2ln2 4

d3 ln2 1

e 1 2

f 1 g

e b (sin b cos b ) e a (sin a cos a ) 2 h 96ln2 28 9 i π 2 2 j 1

7 0,52789

8 8,03414

9 • nadevierdedag

• opheteindevandetiendedag

• G (0)= 0

• G ( t )= 8 t 2 e 0,5 t

• G ( t )= 16 8 e 0,5 t ( t 2 + 4 t + 8)

• 128mg

• nadertiendagen

a e 2 + 2e 3 2

c = 2 π

15 a2√ x + 8 · 4 √ x + ln | 4 √ x + 1 | + 27 | 4 √ x 3 | + C

b x 3 ln( x 2 + 4) 3 2 x 3 9 + 8 x 3 16 3 Bgtan x 2 + C

c ( x + 1) Bgtan( x + 1) 1 2 ln | x 2 + 2 x + 2 | + C

d 1 8 ln e t 4 e t + 4 + C 16 a 4 x 1 3( x 2 + x + 1) + 8√3 9 Bgtan 2 x + 1 √3 + C

b 45 8 Bgtan( x + 5) 45 x 3 + 675 x 2 + 3450 x + 6008 8( x 2 + 10 x + 26)2 + C c Bgtan( e x + 2) 2 + e x + 2 2( e 2 x + 4 · e x + 5) + C d x +( x 2 1) Bgtan x 4( x 2 + 1) + C

e 1 2 ln( x 2 + 2 x + 5) 21 16 Bgtan x + 1 2 + 3 x 1 8( x 2 + 2 x + 5) + C f Bgtan x 8 + x ( x 2 1) 8( x 2 + 1)2 + C g 5Bgtan t 2 t 2( t 2 + 1) + t 3 3 2 t + C h π 2 8 ≈ 0,142699

Herhalingsoefeningen - gemengde reeks (blz. 115) 1 20 20 x 3 3 5 x 2 5 x 2 12 + C 2 3 6 (5 4 x )5 10 + C 32 x 3 + 2 x 2 √ x 5 x 2 2 + C 4 4 x 3 + 4 x + 1 + C

5 ± cos4 x 4 + C 6 e 2 x 2 4 + C 7 2ax · 5 bx a ln2 + b ln5 + C

3.1 Oppervlakte van bijzondere vlakke

figuren (blz. 125)

1 r 2 Bgsin b r Bgsin a r + b r 2 b 2 a r 2 a 2

2 a = –0,794796 ; b = 0,794796

3 2p 4 2π 3 √3 2

5 2π 16 3

6 pr 2

3.2 Zwaartepunt van een vlakke figuur (blz. 131)

1 co (Z)= 67 34 ,5

2 aco (Z)= 3 4 , 8 5

bco (Z)= 3, 3 5

cco (Z)= 1 2 , 2 5 dco (Z)= 21 5 ,0 eco (Z)= 9 5 , 9 10 fco (Z)= π 6 , π 8

3.3 Volume van omwentelingslichamen (blz. 153)

Booglengte van een vlakke kromme

3.5 Manteloppervlakte van een omwentelingslichaam (blz. 173)

1 a72π√5 b π 2√2 1 9

c π 17√17 27 2 d13,29

e 49π 3

f π 4√17 √2 · ln 4 + √17 1 + √2 ≈ 51,181

g π √2 + ln 1 + √2 ≈ 7,212

h2π √2 + ln 1 + √2 ≈ 14,424

i π √5 √2 + ln √5 1 2√2 2 ≈ 3,84

j π2 a 2 (2 + sinh2)

2 60p2

3a72π2 b 8π 5√5 1 3 c 6π√5 3√5 + 4ln 3 + √5 2 5 ≈ 89

4 3p 5 π 32√2 17 + 17√17 6

6 1,65 dm

7 a 64πR 2 3 b 48π 5 c 128π 5 d 2π√2(2e π + 1) 5

9 6378 km

10 straal = 15√2cm;hoogte = 30√2cm

11 straal = r √6 2 cm;hoogte = r √3cm; extremum:minimum

12 πd 4 rr d ( r + r ) r + r d

13 a 488,78 cm2 b 62,48 cl

14 a 0,71 b 4p2 – 8p ; 45,95

4 Toepassingen van integralen in andere disciplines (blz. 193)

1a s ( t )= 3 t 2 + 2 t 2 ; s (10)= 160

b s ( t )= t 3 + 45 t 2 15 ; s (10)= 700 3

c s ( t )= 2 t √ t 3 + 2 t ; s (10)= 20 3 + √10 3

2a s ( t )= t 3 + 3 t 2 + 12 t 6 ; s (5)= 130 3

b s ( t )= t 2 40 t 20 ; s (5)= 585 4

c s ( t )= 4 t √ t + 9 t 3 ; s (5)= 5 4√5 + 9 3

3 s ( t )= 4 5 t 2 √ t 6 t + 2

4 16 meter

5a v ( t )= 3 t + 30; s ( t )= 3 t 2 2 + 30 t b150meter

6a t = 10 b 2000 3 m ≈ 666,667m c 55 3 s ≈ 18,33 s

7 b 29 m/s c 30 m/s

8 7,6 ⋅ 1011 J

9 a 31,25 J b 93,75 J

10 √2 4 m ≈ 35,36cm

11 750 J

12 a 20 000 J

b 4000 J

c 24 000 J

13 6 202 500 J

14 413 884,18 J

16 a 700 euro b 21 250 euro

17 a K (q )= q 3 300 + 5q 2 20q + 16000 3

b260750euro

c98583,33euro

18 a K( q ) = 0,75q 2 + 2q + 100

b K( q ) = 0,05q 3 – 15q 2 + 20q + 1200

19 a E = 1,25

b q neemt toe met 12,5%

20 a 3 8 b 1 3

Trefwoordenregister

A afgeknotte kegel 138, 166 afgeknotte piramide 149 arbeid 183

B bepaalde integraal 16 bol 139 bolkap 170 bolschijf 140 bolsegment 141 bolzone 170 booglengte 158 bovensom 14

C cilinder 137 cirkel 119 cirkelboog 160 cirkelsector 122 cirkelsegment 121 constante snelheid 179 convergent 44

D divergent 44

E elasticiteit 190 ellips 123 ellipsoïde 149

F fundamentele integralen 71

G gemiddelde waarde 32

Gini 189

Gini-coëfficiënt 189

Gini-index 189

H hoofdstelling van de integraalrekening 31, 33 hyperboolsegment 37

I integraalfunctie 30 integraalrekening 9 integrand 70 integratie door splitsing 73 integratie door substitutie 77 integratieconstante 70 integratievariabele 70 integreren 69

K kegel 137, 165 kettinglijn 161 kracht 183

L lemniscaat van Gerono 126 Lorenz 188 Lorenzcurve 188

M manteloppervlakte 165 marginale kost 186 middelwaardestelling 31 moment 127

O omwentelingsas 132 omwentelingscilindervlak 169 omwentelingsellipsoïde 143 omwentelingshyperboloïde 144 omwentelingskegelvlak 169 omwentelingslichaam 132 onbepaalde integraal 69 ondersom 14 oneigenlijke integraal van de eerste soort 42 oneigenlijke integraal van de tweede soort 42

Pappus-Guldin 145 paraboloïde 143 paraboolsegment 37 parameterkromme 124 partiële integratie 99 prijselasticiteit 190 primitieve functie 34 primitiveren 69 prisma 148

R recursieformule 108 regel van Pappus-Guldin 142, 145 Riemann 15 Riemannsommen 13, 16

S stelling van Weierstrass 32 substitutieregel 79

T torus 142, 171

V veranderlijke snelheid 179 versnelling 181

W Weierstrass 32

Z zwaartepunt van puntmassa’s 127