
METHODECONCEPT / REDACTIE
Boom voortgezet onderwijs
AUTEURS
Sjef Buil
Marcel Eijkelkamp
Freek Hoogeveen
Peter Koopmans
Maarten Mies
Dirk-Jan van de Poppe
Donald Staal
Arjen Wielemaker


METHODECONCEPT / REDACTIE
Boom voortgezet onderwijs
Sjef Buil
Marcel Eijkelkamp
Freek Hoogeveen
Peter Koopmans
Maarten Mies
Dirk-Jan van de Poppe
Donald Staal
Arjen Wielemaker
Inhoud
1 Beweging
1.1 Plaats en snelheid 8
1.2 Rekenen aan snelheid 14
1.3 Plaats-tijddiagram 20
1.4 Versnelling 26
1.5 Snelheid-tijddiagram 32
Toetsvoorbereiding 38
2 Elektriciteit 1
2.1 Spanning en stroomsterkte 42
2.2 De wet van Ohm 48
2.3 Weerstand 54
2.4 Serie- en parallelschakelingen 60
2.5 Gemengde en sensorschakelingen 66
Toetsvoorbereiding 72
3 Kracht en beweging
3.1 Eigenschappen van krachten 76
3.2 De eerste wet van Newton 82
3.3 De tweede wet van Newton 88
3.4 De derde wet van Newton 94
3.5 Weerstandskrachten 100
Toetsvoorbereiding 106
4 Trillingen en golven
4.1 Trillingen 110
4.2 Massa-veersysteem 116
4.3 Resonantie 122
4.4 Lopende golven 128
4.5 Staande golven 134
Toetsvoorbereiding 140
5 Radioactiviteit
5.1 Het atoommodel 144
5.2 Radioactief verval 150
5.3 Halveringstijd 156
5.4 Activiteit 162
5.5 Doordringend vermogen en dracht 168
Toetsvoorbereiding 174
6 Stoffen en materialen
6.1 Warmte en temperatuur 178
6.2 Warmtetransport 184
6.3 Gas- en vloeistofstromen 190
6.4 Functionele materialen (schoolexamen) 196
Toetsvoorbereiding 202
Naslag
A Rekenen
A1 Machten van tien 206
A2 Significantieregels 206
A3 Rekenen met formules 208
B Systematisch opdrachten oplossen 209
C Diagrammen
C1 Diagrammen maken 210
C2 Informatie uit diagrammen 211
C3 Raaklijn aan de grafiek 212
C4 Oppervlakte onder de grafiek 213
D Practicum
D1 Bereik en nauwkeurigheid 214
D2 Onderzoek 215
D3 Ontwerp 217
D4 Videometen 219
Verantwoording illustraties 220 Numerieke antwoorden 222 Register van begrippen 230
3.1 Eigenschappen van krachten 76
3.2 De eerste wet van Newton 82
3.3 De tweede wet van Newton 88
3.4 De derde wet van Newton 94
3.5 Weerstandskrachten 100
Toetsvoorbereiding 106
DOeL Je leert wat het effect van een kracht is.
Eigenschappen van krachten De honkbalspeler in figuur 3.1 slaat de bal terug. Als hij de bal raakt, oefent de knuppel een kracht uit op de bal. De bal deukt hierdoor in en verandert van snelheid en van richting. Een kracht die op een voorwerp werkt, kan dus:
de vorm van het voorwerp veranderen;
de snelheid van het voorwerp veranderen;
de richting van het voorwerp veranderen.
Kracht is een grootheid. Het symbool van kracht is F en de eenheid is newton (N). Kracht is een vector. Een vector is een grootheid die niet alleen een grootte heeft, maar ook een richting.
Een kracht teken je met een pijl (figuur 3.2). De drie kenmerken van een krachtvector zijn:
Het aangrijpingspunt is het punt waar de kracht op het voorwerp werkt. Hier begint de pijl.
De richting van de pijl geeft de richting van de kracht weer.
De lengte van de pijl geeft de grootte van de kracht weer. Hoe groter de kracht, hoe langer de pijl. De krachtenschaal geeft aan hoeveel newton overeenkomt met 1 cm (figuur 3.2).
Zwaartekracht Op alle voorwerpen met een massa werkt de zwaartekracht F z. De grootte van de zwaartekracht hangt af van de massa (m) van het voorwerp en van de valversnelling ( g). Op aarde is de waarde van g gemiddeld 9,81 m s–2
De zwaartekracht grijpt aan in het zwaartepunt van een voorwerp en is altijd recht naar beneden gericht. Je berekent de zwaartekracht met de formule:
F z = mg
F z zwaartekracht in N
m massa in kg
g valversnelling in m s−2

3.1 De knuppel oefent een kracht uit op de honkbal.
m = 1,90 kg
aangrijpingspunt
F z = 18,5 N
3.2 Zwaartekracht op een voorwerp, getekend als vector met krachtenschaal 1 cm ≙ 5,0 N
Veerkracht Als je een veer uitrekt, voel je de tegenwerkende kracht van de veer. Deze tegenwerkende kracht is de veerkracht (figuur 3.3), die gelijk is aan de kracht waarmee je aan de veer trekt. Hoe verder je de veer uitrekt, hoe groter de veerkracht is. De veerkracht is recht evenredig met de uitrekking van de veer, waarbij de uitrekking u het lengteverschil is tussen de uitgerekte veer en de niet-uitgerekte veer. Rek je de veer twee keer zo ver uit, dan wordt de veerkracht dus twee keer zo groot. Zet je de veerkracht in een diagram uit tegen de uitrekking, dan is de grafiek een rechte lijn door de oorsprong.
Voor het verband tussen de veerkracht en de uitrekking van een veer geldt:
F v = Cu
F v veerkracht in N C veerconstante in N m−1 u uitrekking in m
Dit verband staat bekend als de wet van Hooke. C is hierin de veerconstante van de veer. De veerconstante is de kracht die nodig is om de veer 1 m uit te rekken. Hoe groter de veerconstante, hoe meer kracht je nodig hebt en dus hoe stugger de veer.
Voorbeeld [1] De veer in figuur 3.3 heeft een lengte van 12 cm.
Je trekt de veer met een kracht van 40 N naar beneden, zodat de lengte van de veer 30 cm wordt. Bereken de veerconstante van de veer.
Gegeven: F v = 40 N beginlengte = 12 cm eindlengte = 30 cm
Gevraagd: C in N m−1
Bereken: 1 Bereken de uitrekking: u = 30 – 12 = 18 cm = 0,18 m 2 Bereken de veerconstante:
F v = Cu → C = F v u → C = 40 0,18 = 222 N m−1
Antwoord: De veerconstante is 2,2 102 N m−1
3.3 Uitrekking van een veer
1 a Noteer de drie effecten van een kracht op een voorwerp. R
b Wat zijn de drie kenmerken van een vectorpijl? R
c Een vectorpijl met een lengte van 12,2 cm is getekend met een krachtenschaal van 1 cm 50 N. Bereken de grootte van de kracht die de vectorpijl weergeeft. T1
d Een kracht van 138,4 N wordt getekend met een krachtenschaal van 1 cm 20 N. Bereken de lengte van de vectorpijl. T1
e Teken een pijl die de zwaartekracht op jou weergeeft. Bedenk zelf een krachtenschaal. T2
2 Afbeelding A
In afbeelding A staan de krachten die werken op een gewichtheffer en op de gewichten.
a Bepaal de grootte van de krachten aan de hand van de krachtenschaal. T1
b Bereken hoeveel kilogram de gewichtheffer tilt. T2
c Bereken de massa van de gewichtheffer. T2
3 In figuur 3.3 is een veer getekend die naar beneden wordt getrokken.
a Bereken hoe groot de veerkracht is als de veer 10 cm is uitgerekt. T1
b Bereken de lengte van deze veer als de veerkracht 30 N bedraagt. T1
c Een andere veer rekt twee keer zo ver uit bij dezelfde veerkracht. Beredeneer hoe groot de veerconstante van deze veer is. T2
4 In een experiment wordt gekeken naar de uitrekking van twee veren en een elastiekje. Van de resultaten van dit experiment is een tabel gemaakt.
a Maak van de gegevens in de tabel een (F,u)- diagram. Kies zelf geschikte eenheden en verhoudingen. T1
b Leg uit hoe je aan de grafiek kunt zien welke van beide veren de grootste veerconstante heeft. T2
c Bepaal van beide veren de veerconstante. T2
d Leg uit welke veer het stugst is. T1
e Leg uit of de wet van Hooke geldt voor het elastiekje. I
5 Afbeelding B / Werkblad 3.5
In een experiment wordt de veerconstante van een veer bepaald. Daarvoor is bij verschillende krachten de uitrekking van de veer gemeten. In afbeelding B zijn de meetgegevens uitgezet in een (F,u)- diagram.
a Hoe noem je het verband tussen F v en u? R
b Bepaal de veerconstante van de veer met behulp van het (F,u) -diagram. T2
c Bereken de uitrekking van de veer bij een veerkracht van 15 N. T1
d Teken op het werkblad de grafiek van een veer met een twee keer zo kleine veerconstante. T1
6 Je schiet een bal tegen een ruit. De bal kaatst terug en op de ruit zie je een ronde vlek met een diameter van de helft van de bal.
a Welke kracht zorgt ervoor dat de bal terugkaatst? T1
b Op welk effect van een kracht wijst de ronde vlek? T1
c Beschrijf de effecten van de kracht van de ruit op de bal. T1
d De bal oefent ook een kracht uit op de ruit. Welk effect heeft deze kracht? T2
e Maak een schets met daarin de kracht op de bal en de kracht op de ruit, op het moment dat de ronde vlek ontstaat. I
7 Afbeelding C / Werkblad 3.7
Twee ballen van ongelijke massa worden vanaf een flat losgelaten. In afbeelding C zie je het (v,t)- diagram van de beweging van beide ballen.
a Hoe bepaal je uit een (v,t)-diagram de versnelling op een tijdstip? R
b Toon met een bepaling aan dat bij het loslaten van de ballen de versnelling overeenkomt met de valversnelling op aarde T1
c Leg uit welke bal de grootste versnelling heeft op t = 1,0 s. T2
d Verklaar waardoor de eindsnelheid van bal 1 groter is dan die van bal 2. I
8 Afbeelding D
Het wereldrecord voor de deadlift (een onderdeel van gewichtheffen) staat op naam van Hafþór Júlíus Björnsson, die het in mei 2020 presteerde om een gewicht met een massa van 501 kg op te tillen. Bereken de maximale massa die Björnsson zou kunnen optillen als hij niet op aarde stond, maar op de maan (gebruik je tabellenboek). T2

9 Afbeelding E
In afbeelding E zie je vier veren van gelijke lengte die naast elkaar zijn opgehangen. De veren vormen zo een samengesteld veersysteem. Elke individuele veer heeft een veerconstante van 20 N m−1. Aan dit systeem wordt een massa van 1,5 kg gehangen.
a Bereken de kracht die op elke veer wordt uitgeoefend. T1
b Bereken de uitrekking van het veersysteem. T2
c Bereken de veerconstante van het veersysteem. T2
De vier veren worden nu onder elkaar gehangen. Aan de onderste veer wordt een massa van 1,5 kg gehangen.
d Toon aan dat de veerconstante van dit nieuwe veersysteem gelijk is aan 5,0 N m−1 De massa van de veren zelf mag je verwaarlozen. I
Heb je het leerdoel bereikt?
R Ik ken de betekenis van de volgende begrippen:
Kracht
Vector
Zwaartekracht
Massa
Valversnelling
Veerkracht
Uitrekking
Wet van Hooke
Veerconstante
T1 Ik kan rekenen met de formules voor de zwaartekracht en de veerkracht.
T2 Ik kan uitleggen wat het effect van een kracht op een voorwerp is.
I Ik kan veersystemen analyseren.
Examentraining
10 Afbeelding F en G
Een leerling doet een aantal proeven met een elastiek dat postbodes vaak gebruiken. Zie afbeelding F.
Allereerst bepaalt zij de veerconstante van het elastiek. Ze knipt het elastiek door en trekt eraan met een krachtmeter. Ze meet de lengte l van het elastiek als functie van de kracht F. In het diagram van afbeelding G zijn de resultaten van de metingen weergegeven.
l (cm)
45,0
40,0
35,0
30,0
25,0
20,0 0,0
a Leg uit of het elastiek voldoet aan de wet van Hooke. T2
b Toon met behulp van het diagram aan dat de veerconstante van het elastiek 25 N m –1 is. I
Voor de veerconstante van een elastiek dat niet al te ver wordt uitgerekt, geldt:
C = EA 0 l 0
Hierin is:
C veerconstante (N m –1)
E een constante
l 0 lengte van het onbelaste elastiek (in m)
A 0 doorsnede van het onbelaste elastiek (in m 2)
c Toon met behulp van de formule aan dat de eenheid van E gelijk is aan N m−2 T2
De doorsnede van het onbelaste elastiek is een rechthoek met de afmetingen 1,0 mm × 7,5 mm.
d Bereken de waarde van de constante E. T2
Naar voorbeeldexamen natuurkunde havo 2015, opgave 2

DOeL Je leert wat het betekent als een snelheid niet verandert.
Evenwicht van krachten De bergbeklimmer uit figuur 3.4 hangt aan een veiligheidstouw. Op de klimmer werken twee krachten: de zwaartekracht (Fz) en de spankracht (Fs) van het touw. Als er verschillende krachten op een voorwerp werken, is de som van deze krachten de resulterende kracht (Fres). Krachten die in dezelfde richting werken, tel je bij elkaar op. Krachten in tegengestelde richting trek je van elkaar af. De twee krachten op de bergbeklimmer zijn even groot, maar tegengesteld gericht. De resulterende kracht is dus gelijk aan 0 N. Is de resulterende kracht nul, dan spreek je van evenwicht (F res = 0 N).
Normaalkracht Op een boek dat op tafel ligt, werkt de zwaartekracht (figuur 3.5). Toch ligt het boek stil. Er werkt dus nóg een kracht op het boek, die even groot is en tegengesteld gericht is aan de zwaartekracht. Alleen dán is de resulterende kracht gelijk aan nul. Deze kracht die de tafel in opwaartse richting uitoefent op het boek, is de normaalkracht (FN). De normaalkracht staat altijd loodrecht op het vlak dat de kracht uitoefent.
Voorbeeld [2] Een blok met een massa van 5,2 kg hangt stil aan een veer. De veer rekt 7,1 cm uit. Zie figuur 3.6. Bereken de veerconstante van de veer in N m –1
Gegeven: m = 5,2 kg
u = 7,1 cm = 0,071 m
g = 9,81 m s–2
Gevraagd: C in N m –1
Berekening: De massa is in evenwicht, dus de resulterende kracht op de massa is gelijk aan nul, oftewel F z = F veer
Voor de zwaartekracht geldt: F z = mg
Voor de veerkracht geldt: F v = Cu
Invullen van F z en F v in F z = F v levert:
mg = Cu → C = mg u = 5,2 × 9,81 0,071 = 718 N m −1
Antwoord: C = 7,2 102 N m –1 F z F s
3.4 Krachten op een bergklimmer: F z = F s FN FZ
3.5 De zwaartekracht en de normaalkracht in evenwicht u F v F z
3.6 Massa aan een veer
De eerste wet van Newton Als op een voorwerp de resulterende kracht 0 N is, blijft het voorwerp stilstaan. Dat klinkt logisch. Maar hetzelfde geldt voor een voorwerp dat met een constante snelheid in een rechte lijn beweegt. Zolang de snelheid en de richting niet veranderen, is de resulterende kracht op het voorwerp 0 N.
De Engelse wis- en natuurkundige Isaac Newton (1642−1727) beschreef dit belangrijke natuurkundige inzicht in 1687. Sindsdien staat dit bekend als de eerste wet van Newton:
Als op een voorwerp geen resulterende kracht werkt, veranderen de snelheid en de richting van het voorwerp niet.
In symbolen kun je dit als volgt kort weergeven: F res = 0 → ∆v = 0.
Een voorwerp dat stilstaat, blijft dus stilstaan. Een voorwerp dat snelheid heeft, behoudt dus die snelheid en richting.
De eerste wet van Newton wordt ook wel de wet van de traagheid genoemd.
Bewegen met een constante snelheid Als je op je fiets of scooter zit, moet je kracht leveren om met een constante snelheid te blijven rijden. Stop je met trappen of laat je het gas los, dan neemt je snelheid af. Om dit te begrijpen, moet je kijken naar alle krachten die op de fiets of de scooter werken. Behalve de voorwaartse kracht zijn er ook tegenwerkende krachten, zoals de luchtweerstandskracht. Om met een constante snelheid te blijven rijden, moet je deze tegenwerkende krachten compenseren. De resulterende kracht is dan nul (figuur 3.7). Volgens de eerste wet van Newton verandert de snelheid dan niet.
In de ruimte zijn er geen weerstandskrachten. Een ruimteschip kan er zonder aandrijfkracht met constante snelheid bewegen.
3.7 F res = 0 N, de scooter houdt dezelfde snelheid.
11 Afbeelding A
De student in afbeelding A zit stil op een stoel.
a Welke krachten werken er op de student? R
b Hoe groot is de resulterende kracht op de student? R
c Leg uit dat de eerste wet van Newton van toepassing is. T1
13 Drie personen duwen tegen een kast. Persoon
A duwt met een kracht van 120 N, persoon B duwt met 85 N en persoon C duwt met 35 N. Bereken de resulterende kracht als: T1
a alle personen in dezelfde richting duwen.
b persoon B tegen de richting van A en C in duwt.
c persoon A tegen de richting van B en C in duwt.
14 Afbeelding B
Met de weeghaak uit figuur B kun je de massa van een zak aardappelen meten. In de weeghaak zit een veer met een veerconstante van 2000 N m−1 .

12 Geef voor de onderstaande voorbeelden aan of de beschreven bewegingen voldoen aan de eerste wet van Newton.
a Een fietser trekt op nadat hij het stoplicht op groen heeft zien springen. T1
b Een persoon duwt tegen een zware kist, zonder dat die in beweging komt. T1
c Een piano wordt met constante snelheid omhooggehesen door een takel. T1
d Een satelliet beweegt met constante snelheid in een baan om de aarde. T2
e Een bal wordt recht omhoog gegooid en ‘hangt’ even stil op zijn hoogste punt. I
a Bereken de uitrekking als je er een zak met aardappelen van 5 kg aan hangt. T2
b Bereken wat de weeghaak op de maan zou aangeven. Maak gebruik van je tabellenboek. I
15 Twee personen trekken samen in horizontale richting aan het touw van een slee. Op de slee zitten twee kinderen. De slee beweegt met een constante snelheid.
a Hoe groot is de resulterende kracht die op de slee werkt? T1
b De massa van de slee met de kinderen is 40 kg. Bereken de normaalkracht die de grond op de slee uitoefent. T1
c De slee ondervindt van de sneeuw een weerstandskracht, waarvoor geldt:
F w = 0,1 FN. Bereken de weerstandskracht. T2
d De ene persoon trekt met een kracht van 20 N. Bereken de kracht waarmee de andere persoon trekt. T1
16 Afbeelding C
Een paperclip is vastgemaakt aan een touwtje. De andere kant van het touwtje is bevestigd aan een tafel. Je houdt een magneet boven de paperclip, waardoor deze wordt aangetrokken.
In afbeelding C zie je dat de paperclip het touwtje heeft strakgetrokken en net onder de magneet ‘zweeft’.
a Welke twee krachten werken op de paperclip omlaag? T1
b Welke kracht werkt op de paperclip omhoog? T1
c Leg uit welke van de drie krachten het grootst is. T2
17 Afbeelding D, E en F / Werkblad 3.17
In de afbeeldingen D, E en F zijn verschillende krachten getekend met een gegeven krachtenschaal. Niet alle aanwezige krachten zijn getekend. Met een cirkel is weergegeven waar deze ontbrekende krachten aangrijpen.
a Teken de ontbrekende kracht die nodig is om de lamp in afbeelding D in evenwicht te brengen. T1
b Teken de ontbrekende kracht die nodig is om de fiets in afbeelding E een resulterende kracht van 200 N naar links te geven. T2
c Teken de ontbrekende krachten die nodig zijn om de container in afbeelding F in evenwicht te brengen. I
18 Buiten de atmosfeer van de aarde ondervinden ruimteschepen geen weerstandskrachten.
a Leg met behulp van de eerste wet van Newton uit dat het ruimteschip zonder gebruik van de motoren zijn snelheid kan behouden. T1
b Leg uit hoe een ruimteschip kan afremmen. I
Door slim gebruik te maken van de beweging van de planeten is het mogelijk om een ruimteschip in de juiste richting te sturen, zonder dat daarvoor extra brandstof nodig is.
c Welke kracht stuurt bij zo’n manoeuvre het ruimteschip in de juiste richting? I
d Waarom zijn de krachten op het ruimteschip tijdens zo’n manoeuvre niet in evenwicht? T2
19 Afbeelding G
In afbeelding G zie je het (v,t)- diagram van een auto die van een helling rolt.
a Leg uit vanaf welk moment de auto in evenwicht is. T1
b Leg uit welke kracht de auto laat versnellen. T2
c Leg uit waarom de versnelling van de auto afneemt. I
Onderaan de helling rijdt de auto weer op een horizontaal oppervlak.
d Leg uit dat de automobilist gas zal moeten geven om met een constante snelheid te blijven rijden. T2
Heb je het leerdoel bereikt?
R Ik ken de betekenis van de volgende begrippen:
Spankracht
Resulterende kracht
Evenwicht
Normaalkracht
Eerste wet van Newton
T1 Ik kan de eerste wet van Newton toepassen.
T2 Ik kan uitleggen of een voorwerp in evenwicht is.
I Ik kan analyseren hoe de beweging van een voorwerp verandert als gevolg van een resulterende kracht. g
Examentraining
20 Afbeelding H
Marloes heeft een wieg gekocht voor haar baby. De wieg hangt aan een veer en kan zachtjes op en neer trillen (afbeelding H).
Op de verpakking van de wieg staat:
C veer = 1,3 kN m –1 en mwieg = 12,2 kg.
Bereken hoe ver de veer is uitgerekt als de wieg aan de veer hangt. T1
Naar examen natuurkunde havo 2016-II, opgave 2
21 Afbeelding I / Werkblad 3.21
Een verkeersvliegtuig vliegt op 11 km hoogte met een constante snelheid van 950 km h−1. Er werken vier krachten op het vliegtuig. Twee van die krachten zijn in afbeelding I getekend: de naar voren gerichte motorkracht en de naar boven gerichte liftkracht. De liftkracht is groter naarmate de snelheid van het vliegtuig groter is.
a Teken op het werkblad de twee andere krachten met de juiste lengte. Zet erbij hoe de krachten heten. T1
De massa van het vliegtuig is 65 ton.
b Bepaal met behulp van afbeelding I de grootte van de motorkracht. T2
c Leg uit waarom het voordelig is om op grote hoogte te vliegen. T2
Als het vliegtuig op de startbaan aan het versnellen is, werken er drie krachten in verticale richting op het vliegtuig.
d Welke drie krachten zijn dit? I

DOeL Je leert wat het verband is tussen kracht en versnelling.
De tweede wet van Newton Volgens de eerste wet van Newton veranderen de snelheid en de richting van een voorwerp niet als er geen resulterende kracht op dat voorwerp werkt. Hieruit volgt dat als de snelheid of de richting van een voorwerp wel verandert, er dus een resulterende kracht moet werken op dat voorwerp.
Als een auto optrekt, wordt de snelheid steeds groter. Hiervoor is een resulterende kracht naar voren nodig. De motorkracht moet dus groter zijn dan de weerstandskrachten op de auto (figuur 3.8a).
De auto krijgt dan een versnelling in de richting van de resulterende kracht. Als de motorkracht even groot is als de weerstandskrachten (figuur 3.8b), is er geen versnelling. Als de motor stopt met kracht leveren, blijven alleen de weerstandskrachten over (figuur 3.8c).
De resulterende kracht is nu tegengesteld gericht aan de beweging, zodat de auto zal vertragen.
De versnelling die een voorwerp krijgt, hangt niet alleen af van de resulterende kracht op dat voorwerp, maar ook van de massa.
De versnelling is recht evenredig met de resulterende kracht en omgekeerd evenredig met de massa. Het verband tussen deze drie grootheden staat bekend als de tweede wet van Newton:
F res = ma
F res resulterende kracht in N m massa in kg a versnelling in m s−2
Om een massa van 1 kg een versnelling van 1 m s−2 te geven, is dus een resulterende kracht van 1 N nodig. Bij een versnelling werkt de resulterende kracht in de richting van de beweging. Bij een vertraging is de versnelling negatief. De resulterende kracht is dan tegengesteld gericht aan de beweging.
3.8 a Versnelling: F res in de richting van de beweging
b Constante snelheid: F res gelijk aan nul
c Vertraging: F res tegengesteld gericht aan de beweging
Voorbeeld [3] De motor van de auto in figuur 3.8a levert een kracht van 2,6 kN in de richting van de beweging. Het totaal aan weerstandkrachten op de auto is gelijk aan 1,9 kN. De massa van de auto is 1200 kg. Bereken de versnelling van de auto.
Gegeven: Fmotor = 2,6 kN = 2600 N
F w = 1,9 kN = 1900 N
m = 1200 kg
Gevraagd: a
Berekening: 1 Bereken de resulterende kracht:
F res = Fmotor – F w → F res = 2600 – 1900 = 700 N
2 Bereken de versnelling:
F res = ma → a = F res m = 700 1200 = 0,583 m s−2
Antwoord: De versnelling van de auto is 0,58 m s−2 .
Voorbeeld [4] Een scooter versnelt. In figuur 3.9 zie je het (v,t)-diagram van de scooter. De massa van de scooter met berijder is 150 kg. De totale weerstandskracht is gelijk aan 85 N. Bereken de kracht die de scooter moet leveren voor deze versnelling. Geef je antwoord in twee significante cijfers.
Gegeven: (v,t)-diagram
m = 150 kg
F w = 85 N
Gevraagd: Fscooter
Berekening: 1 Bepaal de versnelling uit de helling van de grafiek:
∆v = 14,0 – 8,0 = 6,0 m s–1
∆t = 10 s
a = Δv Δt → a = 6,0 10 = 0,60 m s–2
2 Bereken de resulterende kracht:
F res = ma → F res = 150 × 0,60 = 90 N
3 Bereken de kracht van de scooter:
F res = Fscooter – F w →
Fscooter = F res + F w = 90 + 85 = 175 N
Antwoord: De scooter levert een kracht van 1,8 102 N.
(m s–1)
3.9 (v,t)-diagram van de scooter
22 a Maak de juiste keuze: de versnelling is recht evenredig / omgekeerd evenredig met de resulterende kracht. R
b Maak de juiste keuze: de versnelling is recht evenredig / omgekeerd evenredig met de massa. R
c De resulterende kracht op een scooter is tegengesteld gericht aan de rijrichting. Wat gebeurt er met de snelheid van de scooter? R
d Leg uit dat bij een eenparig versnelde beweging de resulterende kracht constant is. T1
23 De auto uit voorbeeld 3 remt met een kracht van 2,6 kN. Op dat moment zijn de weerstandskrachten op de auto 1,8 kN. Bereken de versnelling van de auto op dat moment. T1
24 De Mercedes 200i levert bij het wegrijden een motorkracht van 1,5 kN. De auto heeft een massa van 1200 kg. Een bijbehorende trailer heeft een massa van 1000 kg als deze maximaal beladen is.
a Bereken de maximale versnelling bij het wegrijden van de auto zonder trailer. T1
b Bereken de maximale versnelling bij het wegrijden van de auto met trailer. T1
c Waarom is het belangrijk dat de trailer zelf ook voorzien is van een remsysteem? T2
25 Een trein trekt in 70 s eenparig op van 0 tot 130 km h−1. De massa van de trein is 250 ton. Bereken de resulterende kracht op de trein tijdens het optrekken. T2
26 Een fietser met een massa van 79 kg trekt vanuit stilstand in 5,0 s eenparig op tot een snelheid van 24 km h –1. De massa van de fiets is 18 kg. De totale weerstandskracht is 40 N.
a Bereken de versnelling van de fietser. T1
b Bereken de trapkracht van de fietser. T1
27 Een motorrijder trekt eenparig op van 0 naar 100 km h –1 bij een motorkracht van 1,5 kN. De massa van de motor met bestuurder is 250 kg.
a Bereken hoelang dit minimaal duurt. T2 b waarom staat er bij vraag a ‘minimaal’? I
28 Afbeelding A
In afbeelding A zie je het (v,t)-diagram van een testrit van een nieuwe elektrische fiets. De massa van de fiets, inclusief bestuurder, is 103 kg. Verwaarloos eerst de weerstandskrachten.
a Tussen t = 0,0 s en t = 4,0 s levert de elektromotor een constante kracht van 85 N. Bereken de kracht die de fietser zelf moet uitoefenen tijdens het optrekken. T1
b Bereken de kracht waarmee geremd wordt tussen t = 55 s en t = 60 s. T1
Tussen t = 20 s en t = 30 s oefent de grond een constante weerstandskracht van 74 N uit op de fiets.
c Bereken de grootte van de kracht die de fietser en de elektromotor dan samen moeten leveren. T2
29 Afbeelding B / Werkblad 3.29
Bij een botsproef wordt een auto met hoge snelheid tegen een barrière gereden, om metingen te verrichten die de veiligheid van de auto in kaart brengen. De geteste auto heeft een massa van 1100 kg en is voorzien van een kreukelzone. Het (v,t)- diagram van deze botsproef is uitvergroot weergegeven op het werkblad.
a Bepaal de maximale kracht waarmee de auto wordt afgeremd. T2
b Wat gebeurt er op tijdstip t = 0,17 s? T2
c Beredeneer dat het vergroten van de kreukelzone van de auto de remkracht zal verkleinen. I
30 Een auto remt eenparig af van 104 km h –1 naar 85 km h –1. De massa van de auto is gelijk aan 1,45 103 kg. De remkracht is 3,3 103 N. Verwaarloos de weerstandskracht.
Bereken hoelang het afremmen duurt. T2
31 Afbeelding C
In afbeelding C is de stuwkracht van een vuurpijl uitgezet tegen de tijd. De massa van de vuurpijl is 420 g. Verwaarloos alle weerstandskrachten.
a Bereken de zwaartekracht op de vuurpijl. T1
b Bepaal de maximale versnelling van de vuurpijl. T1
c Leg uit dat de vuurpijl versnelt tot het tijdstip t = 1,65 s. I
d Welk soort beweging heeft de vuurpijl op t = 2,0 s? T2
32 Straaljagers die landen op een vliegdekschip hebben maar een heel korte remweg. Om de straaljager snel af te remmen, wordt een speciale kabel gebruikt, die aan het begin van de landingsbaan is gespannen. Tijdens de landing grijpt de straaljager de kabel met een haak die aan de staart van het toestel vastzit. Een straaljager met een massa van 27 000 kg en een aanvliegsnelheid van 225 km h –1 wordt door de kabel in 2,9 s afgeremd.
a Bereken de gemiddelde remkracht die de kabel levert tijdens het afremmen van de straaljager. Neem aan dat de straaljager eenparig vertraagt. T2
b Waarom staat bij vraag a ‘gemiddelde’ remkracht? I
c Bereken de remweg van de straaljager. T2
De startbaan op het vliegdekschip heeft een lengte van slechts 75 m. Daarom wordt bij het opstijgen een katapultsysteem gebruikt. De motoren van de straaljager kunnen bij het opstijgen een maximale stuwkracht leveren van 155 kN.
d Bereken de extra kracht die de katapult moet leveren om de straaljager van 0 naar 250 km h –1 te versnellen. Neem aan dat de versnelling van de straaljager eenparig is. I
33 Elke lift is beveiligd met een automatisch remsysteem, dat in werking treedt als de snelheid van de lift groter wordt dan 15 m s–1
Bij een keuring moeten de liften binnen 3,0 m stilstaan. Er worden drie verschillende liften getest:
Lift A heeft een massa van 1000 kg en een maximale remkracht van 40 kN.
Lift B staat altijd stil na 0,5 s en heeft een massa van 1700 kg.
Lift C heeft een massa van 1400 kg en komt binnen 0,38 s tot stilstand.
a Leg uit welke liften door de keuring komen. Licht je antwoord toe met een berekening. T2
b Laat zien dat lift C de grootste remkracht kan uitoefenen. T2
c Leg uit waarom lift B voor de gebruikers ervan als minst intens wordt ervaren bij een noodstop. I
Heb je het leerdoel bereikt?
R Ik ken de betekenis van het volgende begrip:
Tweede wet van Newton
T1 Ik kan rekenen met de tweede wet van Newton.
T2 Ik kan informatie uit bewegingsgrafieken combineren met de tweede wet van Newton.
I Ik kan de eerste en de tweede wet van Newton gebruiken om de beweging van een voorwerp te analyseren.
Examentraining
34 Afbeelding D en E
Met een auto is een testrit gemaakt op een horizontale weg. Afbeelding D is het (v,t)-diagram van deze rit.
Volgens de specificaties is de auto in staat om in 10 s van 0 tot 80 km h−1 te versnellen. De massa van de auto is 1500 kg.
a Laat met een berekening zien of daar tijdens de testrit aan is voldaan. T1
b Bepaal de resulterende kracht op de auto op t = 0 s. T1
In de grafiek zie je drie momenten waarop de chauffeur schakelt. Na het schakelen versnelt de auto weer.
c Leg uit hoe uit de grafiek blijkt dat de versnelling na het schakelen kleiner is dan vóór het schakelen. T2
Tijdens het schakelen wordt de motor ontkoppeld. Op de auto werken dan alleen de weerstandskrachten. In afbeelding E is het gedeelte van de snelheidsgrafiek tussen t = 5,0 s en t = 7,0 s vergroot weergegeven. In die periode schakelt de chauffeur voor de tweede maal.
d Bepaal de grootte van de weerstandskrachten op de auto tijdens het schakelen. T2
Tussen t = 17 s en t = 20 s rijdt de auto met constante snelheid. De automotor levert dan een kracht van 8,0 102 N.
e Hoe groot zijn dan de weerstandskrachten op de auto? T1
Naar examen natuurkunde havo 2007-I, opgave 1
DOeL Je leert dat krachten altijd in paren voorkomen.
Krachtenparen In figuur 3.10 duwt schaatser A schaatser B van zich af. Beide schaatsers bewegen dan versneld achteruit. Hebben beiden dezelfde massa, dan is de versnelling van de schaatsers gelijk. Blijkbaar oefent dan niet alleen schaatser A een kracht uit op schaatser B, maar oefent schaatser B tegelijkertijd een even grote, maar tegengestelde, kracht uit op schaatser A. Krachten blijken altijd in paren voor te komen. De twee krachten zijn even groot, tegengesteld gericht, en werken op verschillende voorwerpen. Deze wisselwerking van krachten werd voor het eerst beschreven door Newton en staat bekend als de derde wet van Newton.
Oefent een voorwerp A een kracht uit op voorwerp B, de actiekracht, dan oefent voorwerp B tegelijkertijd een even grote, maar tegengesteld gerichte kracht uit op voorwerp A, de reactiekracht. In symbolen kun je dit als volgt kort weergeven: FAB = −FBA
Hierin is FAB de kracht die A op B uitoefent en FBA de kracht die B op A uitoefent.
Het minteken geeft aan dat de krachten in tegengestelde richting werken.
De drie wetten vergeleken Als je tegen een bal trapt, oefen je een kracht uit op de bal (figuur 3.11). Tegelijkertijd voel je dat de bal ook een reactiekracht op jouw voet uitoefent (derde wet). Als je naar de figuur kijkt, lijkt het misschien alsof deze twee krachten elkaar opheffen, omdat ze even groot en tegengesteld gericht zijn. Volgens de eerste wet zou de snelheid dan niet veranderen. Echter: beide krachten werken op verschillende voorwerpen, namelijk op de voet en op de bal. Op beide werkt dus wel degelijk een resulterende kracht. Het effect is dat de bal door de kracht van je voet (FAB) versnelt en dat tegelijkertijd je voet door de kracht van de bal (FBA) vertraagt. De versnelling van de bal bereken je vervolgens met de tweede wet.
3.10 Schaatsers die elkaar duwen: FAB en FBA vormen een krachtenpaar. Je geeft de krachten een verschillende kleur om aan te geven dat ze op verschillende voorwerpen werken.
3.11 Krachten bij het trappen tegen een bal
Gewicht en gewichtloos De zwaartekracht die op jou werkt, zorgt ervoor dat je een even zo grote neerwaartse kracht op de ondergrond uitoefent. Deze kracht op de ondergrond noem je het gewicht Fgewicht (figuur 3.12). Als reactie oefent de ondergrond een even grote, maar tegengestelde, kracht uit op jou. Deze kracht staat loodrecht op de ondergrond en is de normaalkracht FN (zie ook paragraaf 3.2). Het gewicht en de normaalkracht vormen dus een krachtenpaar.
Als je van een tafel springt, is er geen kracht op de ondergrond meer. Er is daarom geen gewicht en dus ook geen normaalkracht tijdens de sprong. Je bent dan gewichtloos.
Voorbeeld [5] De jongen in figuur 3.13a oefent een kracht uit op de kast en op de vloer. De kast en de jongen komen niet van hun plaats. Teken deze krachten en de krachten die daar volgens de derde wet van Newton bij horen.
Uitwerking: 1 De jongen duwt tegen de kast. Dit is Fduw in figuur 3.13b. Om te kunnen duwen, zet de jongen zich met z’n rechtervoet af tegen de vloer. Dit is Fafzet
2 Volgens de derde wet vormt elke kracht een krachtenpaar met een reactiekracht. De reactiekracht van de duwkracht is de kracht van de kast op de jongen (Fkast op jongen). Deze is even groot als Fduw. De reactiekracht van de afzetkracht is de weerstandskracht van de vloer op de jongen (Fvloer op jongen). Deze kracht werkt naar voren en is even groot als Fafzet
3 De jongen staat stil, dus moeten de twee horizontale krachten die op de jongen werken even groot zijn en tegengesteld gericht: Fvloer op jongen
= − Fkast op jongen. Alle vier de krachten zijn dus even groot.
Antwoord: De twee krachtenparen zijn getekend in figuur 3.13b.
3.12 Gewicht en normaalkracht als krachtenpaar
3.13a Tegen een kast duwen
duw Fkast op jongen
Fvloer op jongen
3.13b Krachtenparen bij het duwen tegen een kast
Fafzet
35 Bij een honkbalwedstrijd wordt vaak met grote kracht tegen een bal geslagen.
a Welke kracht is het grootst: de kracht van de knuppel tegen de bal of de kracht van de bal tegen de knuppel? R
b Maak een schets van de knuppel en de bal en teken beide krachten. T1
c Leg uit wie de grootste versnelling krijgt: de bal of de knuppel. T1
d Een speler in het veld vangt de bal op in zijn hand. Wat zijn hierbij de actiekracht en de reactiekracht? T1
e Waarom zijn de termen ‘actiekracht’ en ‘reactiekracht’ ongelukkig gekozen? I
36 In figuur 3.12 zijn drie krachten getekend.
a Welke twee krachten vormen een krachtenpaar? R
b Welke twee krachten heffen elkaar op? T1
37 Afbeelding A / Werkblad 3.37
In afbeelding A zie je een hardloper die wegsprint. Hij zet zich daarbij met een kracht van 600 N af tegen de grond.
a Teken de reactiekracht. Let op het aangrijpingspunt van deze kracht. T1
b Leg uit dat beide krachten elkaar niet kunnen opheffen. T1
c Bereken de versnelling van de sprinter als zijn massa 70 kg is. T1
38 Bekijk nog eens voorbeeld 5. Op de kast werkt behalve de duwkracht ook een weerstandskracht F w
a In welke richting wijst deze weerstandskracht? T1
b Leg uit dat deze weerstandskracht even groot is als de duwkracht van de jongen. T1
De weerstandskracht op de kast vormt samen met een andere kracht een krachtenpaar.
c Geef aan waar deze andere kracht op werkt en hoe deze gericht is. T2
Als de jongen harder duwt, komt de kast in beweging.
d Welke uitspraken over de krachten op dat moment zijn juist? Licht je antwoord toe. I
a Fduw = F w
b Fduw > F w
c Fduw > Fkast op jongen
D Fduw = Fkast op jongen
39 Afbeelding B / Werkblad 3.39
Bij een touwtrekwedstrijd trekt persoon P via een touw met 500 N aan persoon Q. Dit is Ftrek in afbeelding A. Beide personen staan stil.
a Leg uit of de kracht van persoon Q op persoon P groter dan, kleiner dan of gelijk is aan 500 N. T1
b Teken de krachten waarmee beide personen zich afzetten tegen de grond en teken de bijbehorende reactiekrachten. Let op dat je ze de juiste lengte geeft. T2
c Leg uit wat de rechter persoon moet doen om te winnen. Tip: welke kracht moet groter worden? I Ftrek Q P b

40 Afbeelding C / Werkblad 3.40
Twee magnetische ringen worden rondom een cilinder geplaatst. De bovenste magneet blijft zweven. De massa van elke ring is 100 g.
a Welke twee krachten werken op de bovenste magneet? T1
b Leg uit dat de twee krachten uit vraag a even groot zijn. T1
c Welke drie krachten werken op de onderste magneet? T1
d Teken de vijf krachten. Geef daarbij duidelijk het aangrijpingspunt aan en de grootte van de krachten. T2
e Welke twee van de vijf getekende krachten zijn elkaars krachtenpaar? T2
f Hoe groot is het gewicht van de onderste magneet? I
g Je haalt de bovenste magneet weg. Hoe groot is nu het gewicht van de onderste magneet? T2
41 Afbeelding D
Een leerling staat in een lift op een weegschaal. Op de weegschaal kan ze aflezen dat haar massa 65 kg is. Als de lift in beweging komt, ziet ze dat de weegschaal (tijdelijk) een andere waarde aangeeft.
a Welke grootheid meet de weegschaal? T1
In afbeelding E zie je de massa die de weegschaal aangeeft tijdens de beweging van de lift naar boven. Op t = 2,0 s start de lift. De leerling oefent een kracht uit op de weegschaal. Dit is het gewicht.
b Wat is de naam van de reactiekracht van het gewicht? R
c Bereken het gewicht van de leerling op t = 3,0 s. T1
d Welke twee krachten werken op de leerling? T1
e Bereken de versnelling van de lift en de leerling op t = 3,0 s. Tip: bereken eerst de resulterende kracht op de leerling. I
f Leg uit wat er op t = 7,0 s gebeurt en verklaar waarom de weegschaal nu een lagere waarde aangeeft. T2
42 De aarde oefent op elk voorwerp op aarde een aantrekkende kracht uit: de zwaartekracht. Volgens de derde wet van Newton oefent dan elk voorwerp ook een kracht op de aarde uit. Stel je laat een bal met een massa van 800 g vallen.
a Bereken de kracht die de bal op de aarde uitoefent. T2
b Leg uit dat je het effect van die kracht op de aarde niet ziet. I
43 Afbeelding E
In de ruimte doen astronauten experimenten bij gewichtloosheid. Om ze aan de gewichtloosheid te laten wennen, worden zogenaamde paraboolvluchten uitgevoerd. Daarbij stijgt een vliegtuig in korte tijd naar een grote hoogte. Op een bepaald moment worden de kleppen aan de vleugels in een zodanige stand gezet dat er geen liftkracht meer werkt. De versnelling die het vliegtuig dan ondervindt, is gelijk aan de valversnelling. Afbeelding E laat het verloop zien van zo’n paraboolvlucht.
a Leg uit wat er in afbeelding F wordt bedoeld met ‘1g’, ‘1,8g’ en ‘0g’. I
b Leg uit dat de astronauten gewichtloos zijn vanaf het moment dat alleen de valversnelling op het vliegtuig werkt. I
Heb je het leerdoel bereikt?
R Ik ken de betekenis van de volgende begrippen:
Derde wet van Newton
Actiekracht
Reactiekracht
Gewicht
Gewichtloos
T1 Ik kan de aanwezige krachtenparen in beschreven situaties herkennen.
T2 Ik kan uitleggen hoe je van snelheid of richting verandert in de ruimte.
I Ik kan uitleggen wanneer er gewichtloosheid optreedt.
Examentraining
44 Afbeelding F en G / Werkblad 3.44
Om satellieten in een baan om de aarde te brengen of het International Space Station te voorzien van goederen, wordt gebruikgemaakt van raketten. Een van deze raketten is de Ariane-5. Door het uitstoten van verbrandingsgassen wordt de raket voortgestuwd.
a Leg dit uit met een natuurkundige wet. T2
De beweging tijdens de start van de Ariane-5-raket wordt onderzocht aan de hand van een video-opname. Van de eerste honderd seconden is een (v,t)-diagram gemaakt (afbeelding G).
De totale massa van de Ariane-5-raket bij de start is 7,14 105 kg.
b Bereken de stuwkracht die de raket ondervindt op t = 0 s. Bepaal daarvoor eerst de resulterende kracht op de raket op t = 0 s met behulp van afbeelding G. I
Zelfs als de raket buiten de atmosfeer van de aarde is, ondervindt hij de zwaartekracht van de aarde.
c Wat is de reactiekracht van de zwaartekracht en waarop werkt deze reactiekracht? T2
In het International Space Station (ISS), dat in een baan om de aarde beweegt, zijn de astronauten gewichtloos.
d Geef hier een verklaring voor. I
(m s–1)

DOeL Je leert wat het effect van weerstandskrachten op een beweging is.
Luchtweerstandskracht Een parachutist in vrije val bereikt in een paar seconden een snelheid van ongeveer 180 km h−1. Aanvankelijk is de versnelling gelijk aan de valversnelling g, maar deze neemt snel af tot 0 m s–2. Dat komt doordat de parachutist een steeds grotere weerstand ondervindt van de lucht. Dit is de luchtweerstandskracht (Fw,l). Als de snelheid verdubbelt, wordt de luchtweerstandskracht vier keer zo groot. Deze neemt dus kwadratisch toe met de snelheid. De luchtweerstandskracht hangt ook af van de dichtheid van de lucht, van het frontale oppervlak van de parachutist, en van de luchtweerstandscoëfficiënt. De luchtweerstandscoëfficiënt hangt onder andere af van de vorm van het voorwerp. Hoe gestroomlijnder het voorwerp, hoe kleiner de luchtweerstandscoëfficiënt.
Voorbeeld [6] In figuur 3.14 zie je een deel van het (v,t)-diagram van de sprong van een parachutist. Op het tijdstip t = 62 s is de parachute volledig open en bedraagt de luchtweerstandskracht 6600 N. Bepaal de grootte van de luchtweerstandskracht op het tijdstip t = 70 s.
Gegeven: Fw,l op t = 62 s is 6600 N
Gevraagd: Fw,l op t = 70 s
Berekening: 1 Lees de snelheid af op t = 62 s:
v (t = 62 s) = 25 m s−1
2 Lees de snelheid af op t = 70 s:
v (t = 70 s) = 12,5 m s−1. De snelheid is 2,0 keer zo klein geworden. De luchtweerstandskracht is evenredig met de snelheid in het kwadraat, en is dus 2,02 = 4,0 keer zo klein geworden.
Fw,l = 6600 4,0 = 1650 N
Antwoord: Fw,l = 1,7 103 N
v (m s–1)
3.14 (v,t)-diagram van een parachutesprong
Schuifwrijvingskracht Het is veel gemakkelijker om een lichte kast over een gladde vloer te verschuiven dan een zware kast over vloerbedekking. De tegenwerkende kracht is hier de schuifwrijvingskracht (Fw,s) Zolang de kast blijft staan, is de schuifwrijvingskracht gelijk aan de duwkracht (figuur 3.15a). Immers, volgens de eerste wet van Newton is de resulterende kracht op een voorwerp dat stilstaat gelijk aan nul. Op het moment dat de kast gaat schuiven, is de maximale schuifwrijvingskracht (Fw,s,max) bereikt (figuur 3.15b). Volgens de tweede wet van Newton krijgt het voorwerp nu een versnelling.
De maximale schuifwrijvingskracht is recht evenredig met de normaalkracht die het oppervlak op het voorwerp uitoefent.
Deze hangt ook af van de ruwheid van beide oppervlakken.
Rolweerstandskracht Rollende voorwerpen die niet slippen, ondervinden een rolweerstandskracht (figuur 3.16). Hoe harder de wielen en de ondergrond, hoe kleiner de rolweerstandskracht.
De rolweerstandskracht hangt niet af van de snelheid.
Voorbeeld [7] Een slee met een kind erop heeft een massa van 51 kg. De slee versnelt met 1,2 m s–1 bij een duwkracht van 240 N. Een tweede kind met een massa van 33 kg gaat ook op de slee zitten. Leg uit of de slee nu nog van zijn plaats komt als de duwkracht gelijk blijft.
Gegeven: m1 = 51 kg, Fduw = 240 N, a = 1,2 m s–2 , m 2 = 33 kg
Gevraagd: Is Fduw groter dan F w,s,max ?
Berekening: 1 Bereken de resulterende kracht op de slee:
F res = ma = 51 × 1,2 = 61,2 N
2 Bereken de maximale schuifwrijvingskracht:
F res = Fduw − F w,s,max → → F w,s,max = Fduw − F res = 240 − 61,2 = 178,8 N
3 Bereken de maximale schuifwrijvingskracht met beide kinderen op de slee:
De normaalkracht die de grond op de slee uitoefent, wordt, net als de zwaartekracht, 51 + 33 51 = 1,65 × zo groot. De maximale schuifwrijvingskracht wordt dan ook 1,65 × zo groot. F w,s,max = 178,8 × 1,65 = 295 N. Dit is groter dan de duwkracht van 240 N.
Antwoord: De slee komt met dezelfde duwkracht niet van zijn plaats.
duw
F w, s
3.15a Schuifwrijvingskracht als het voorwerp in evenwicht is (F res = 0 N)
duw
3.15b Wanneer er geduwd wordt met een kracht die groter is dan F w,s,max , komt het voorwerp in beweging (F res ≠ 0 N).
Fw, rol
3.16 Rolweerstandskracht
45 a Welke vier grootheden bepalen de luchtweerstandskracht? R
b Waar hangt de maximale schuifwrijvingskracht van af? R
c Op grote hoogte in de atmosfeer ondervinden vliegtuigen minder luchtweerstandskracht. Wat is hier de belangrijkste oorzaak van? T1
d Leg uit of de luchtweerstandscoëfficiënt van een racewagen groter of kleiner is dan de luchtweerstandscoëfficiënt van een personenauto. T1
e Je fietst van een asfaltweg een zandpad op. Wat gebeurt er met de rolweerstand? T1
46 Bekijk het (v,t)-diagram van de sprong van een parachutist in figuur 3.14. De massa van de parachutist met parachute is 85 kg.
a Leg uit hoe groot de luchtweerstandskracht op t = 0 s is. T1
b Waarom is de val van de parachutist geen eenparig versnelde beweging? T1
c Beredeneer met welke factor de luchtweerstandskracht toeneemt als de snelheid van de parachutist van 10 m s−1 tot 30 m s−1 toeneemt. T1
d Bepaal de luchtweerstandskracht op t = 10 s. Tip: bepaal eerst de versnelling op dit tijdstip. T2
e Vlak voor het opengaan van de parachute bereikt de parachutist een maximale constante snelheid. Leg uit hoe groot de luchtweerstandskracht dan is. T2
f Leg uit of de luchtweerstand op t = 100 s groter is dan, even groot is als of kleiner is dan bij de maximale snelheid. I
47 Een slee met een massa van 10 kg is beladen met 70 kg aan dozen. Om de slee in beweging te krijgen, moet er horizontaal aan getrokken worden met een minimale kracht van 170 N.
a Hoe groot is de schuifwrijvingskracht als er niet aan de slee wordt getrokken? T1
b Je trekt horizontaal met een kracht van 100 N aan de slee. Leg uit hoe groot de schuifwrijvingskracht op de slee dan is. T1
c Bereken de versnelling van de slee als je horizontaal trekt met een kracht van 400 N. T1
d Beredeneer hoe groot de maximale schuifwrijvingskracht is als je de slee zonder de dozen erop trekt. T2
48 Afbeelding A
Bij een bandschuurmachine wordt er met hoge snelheid een stuk schuurpapier rondgedraaid. Tijdens het schuren legt Astrid een blok hout op het frame van de bandschuurmachine voordat ze duwt. Het schuurpapier beweegt van boven naar beneden.
a Leg uit in welke richting de schuifwrijvingskracht staat. T2
b Leg uit dat de normaalkracht die het frame op het blok hout uitoefent tijdens het schuren groter is dan normaal. I
49 Afbeelding B
Een vrachtwagen ondervindt weerstandskrachten tijdens het rijden. De grootte van deze krachten bij verschillende snelheden is weergegeven in afbeelding B.
De motor van de vrachtwagen kan maximaal 8,0 kN leveren.
(N)
luchtweerstandskracht
rolweerstandskracht
a Bij welke snelheid is de rolweerstandskracht even groot als de luchtweerstandskracht? T1
b Welke motorkracht moet de vrachtwagen leveren om met een constante snelheid van 60 km h−1 te rijden? T1
c Bepaal de maximale snelheid van de vrachtwagen. T2
Voor de luchtwrijvingskracht geldt:
Fw,l = kv2
Hierin is k een constante en v de snelheid.
d Van welke grootheden hangt de constante k af? T1
e Bepaal de waarde van k met behulp van het diagram. T2
Bij een snelheid van 80 km h−1 laat de chauffeur het gas los zonder te remmen. De massa van de vrachtwagen is 8,0 ton.
f Bereken de versnelling van de vrachtwagen op dat moment. T2
50 Een kast met een massa van 60 kg staat op een horizontale ondergrond. Voor de maximale schuifwrijvingskracht geldt:
F w,s,max = fFN
Hierin is f de schuifwrijvingscoëfficiënt, die afhangt van de materialen waarvan het voorwerp en het contactoppervlak gemaakt zijn. De schuifwrijvingscoëfficiënt van de kast op de grond is 0,9.
a Leg uit dat f geen eenheid heeft. T1
b Leg uit dat een zwaardere kast moeilijker te verschuiven is dan een lichtere kast. T1
c Bereken de maximale grootte van de schuifwrijvingskracht op de kast. T1
Er is minder kracht nodig om de kast in beweging te houden dan om hem bij stilstand in beweging te krijgen. De waarde van f bij een bewegende kast is 0,5.
d Bereken de resulterende kracht op de bewegende kast als je met een kracht van 400 N duwt. T2
51 Schuifwrijving is hinderlijk als je bijvoorbeeld een zware kist wilt verschuiven. Maar in sommige gevallen is schuifwrijving onmisbaar. Zonder schuifwrijvingskracht zou je bijvoorbeeld niet kunnen lopen. Als je loopt, oefen je met je voeten een kracht naar achteren uit op de grond. Als reactie oefent de grond een even grote, naar voren gerichte schuifwrijvingskracht op je uit.
a Leg uit wat er gebeurt als je over een spiegelgladde weg probeert te rennen. T2 b Voorzichtig lopen lukt dan vaak nog wel. Leg dat uit. I
52 Afbeelding C
Het is een misverstand dat kogels tot een grote diepte in water kunnen doordringen. Vanwege de hoge snelheid is de weerstandskracht dan namelijk dusdanig groot dat de kogel een enorme vertraging ondervindt.
De weerstandskracht van water gedraagt zich op dezelfde manier als de luchtweerstandskracht.
Een kogel van 25 g raakt het water met een snelheid van 720 m s−1. De weerstandskracht is op dat moment gelijk aan 4,9 kN.
a Bereken de vertraging die de kogel zal ondervinden bij het raken van het water. T1
b Leg uit dat de weerstandskracht na het raken van het water zal afnemen. T2
c Bereken na hoeveel meter de kogel in het water tot stilstand komt. Neem daarbij aan dat de kogel eenparig vertraagt met een gemiddelde remkracht van 2,0 kN. T2
d De kogel vervormt als hij het water raakt. Leg uit of de kogel dan dieper of minder diep doordringt in het water. I

53 Afbeelding D
Op een grasveld vindt een touwtrekwedstrijd plaats tussen twee leerlingen. Leerling A is zwaarder dan leerling B.
a Leg uit welke leerling in het voordeel is. I
b Welke factoren spelen nog meer een rol? I
Heb je het leerdoel bereikt?
R Ik ken de betekenis van de volgende begrippen:
Luchtweerstandskracht
Schuifwrijvingskracht
Rolweerstandskracht
T1 Ik kan redeneren met de luchtweerstandskracht en de schuifwrijvingskracht.
T2 Ik kan weerstandskrachten toepassen in combinatie met de wetten van Newton.
I Ik kan beredeneren hoe weerstandskrachten het evenwicht van een voorwerp beïnvloeden.
Examentraining
54 Afbeelding E, F en G / Werkblad 3.54
Skydiven is een sport waarbij men uit een vliegtuig springt en een groot deel van de tijd richting de aarde valt zonder de parachute te openen. Na enige tijd is de snelheid van de skydiver constant. Afbeelding E is het (v,t)-diagram van het begin van zo’n sprong. In de eerste twee seconden is de luchtweerstand vrijwel te verwaarlozen.
a Toon dit aan met behulp van het diagram in afbeelding E. T1
In de eerste 20 s valt de skydiver over een afstand van 0,90 km.
b Hoe kun je dit met behulp van het diagram in afbeelding E aantonen? T1
De skydiver springt op een hoogte van 3,0 km uit het vliegtuig. Op een hoogte van 0,80 km opent hij zijn parachute.
c Bepaal de tijd tussen het verlaten van het vliegtuig en het openen van de parachute. T2
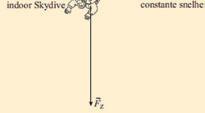
Bij Indoor Skydive te Roosendaal kun je zelf het unieke gevoel van vrijheid ondervinden van een skydiver die uit een vliegtuig is gesprongen. In een grote schacht met glazen wanden wordt lucht met een hoge snelheid omhooggeblazen. Als je in deze windtunnel horizontaal op de luchtstroom gaat ‘liggen’ (afbeelding F), kun je blijven zweven. Bij zweven heffen de kracht van de omhoogstromende lucht en de zwaartekracht elkaar op (afbeelding G). Naast de skydiver is een andere skydiver getekend, die uit een vliegtuig is gesprongen en met een constante snelheid verticaal naar beneden valt.
d Teken op het werkblad de vector van de luchtweerstandskracht voor deze situatie. Let daarbij op de richting en de lengte van de vector. Licht je tekening toe. T1
Karel zweeft in de windtunnel van Indoor Skydive. De kracht die de luchtstroom op hem uitoefent, is recht evenredig met zijn frontale oppervlakte. Zijn massa, inclusief windpak en helm, is 82 kg. In zwevende positie strekt Karel zijn armen en benen uit, waardoor zijn frontale oppervlakte met 10% toeneemt. Hij schiet op dat moment omhoog, omdat er dan wel een resulterende kracht op hem werkt.
e Bereken de grootte van deze resulterende kracht. l
Naar examen natuurkunde havo 2013-I, opgave 2



Controleer bij elke paragraaf van dit hoofdstuk of je de leerdoelen hebt bereikt. Zo niet, lees dan de uitleg nog eens goed door of bekijk de uitlegvideo’s. Maak daarna de volgende opdrachten.
1 a Wat zijn de drie effecten van een kracht? R
b Een auto rijdt met een constante snelheid. Wat geldt er dan volgens de eerste wet van Newton? R
c Wat is de eenheid van de veerconstante? R
d Welke drie kenmerken heeft een krachtvector, getekend als pijl? R
e Wordt de luchtweerstandscoëfficiënt groter of kleiner als de stroomlijn van een voertuig verbeterd wordt? T1
f Leg uit dat de twee krachten die een krachtenpaar vormen elkaar nooit kunnen opheffen. T1
2 Afbeelding A
Een liftkooi met een massa van 1200 kg is aan zestien kabels opgehangen. In afbeelding A zie je het (h,t)-diagram van de lift. De lift versnelt eenparig in de eerste 5 s.
a Toon met behulp van het (h,t)-diagram aan dat de lift een versnelling heeft van 0,64 m s–2 T1
b Bereken de spankracht in elke kabel tijdens de versnelling. T2
c Leg uit dat de spankracht in de kabels tussen t = 5 s en t 10 s geleidelijk aan afneemt. I
3 Afbeelding B
Een fietser heeft zowel last van de luchtweerstandskracht als van de rolweerstandskracht. In afbeelding B is de luchtweerstandskracht die een fietser ondervindt, uitgezet tegen de snelheid. De rolweerstandskracht is 8,0 N. De fietser kan een maximale trapkracht van 60 N uitoefenen op de fiets. De massa van fietser en fiets samen is 85 kg.
a Laat met behulp van het diagram in afbeelding B zien dat de luchtweerstandskracht kwadratisch toeneemt met de snelheid. T2
b Bepaal de trapkracht van de fietser bij een constante snelheid van 20 km h−1 . T1
De fietser versnelt als hij met een snelheid van 25 km h−1 fietst. De trapkracht is 50 N.
c Bepaal de versnelling van de fietser. T2 d Bepaal de maximale snelheid die de fietser kan behalen. I
4 Verklaar de volgende gebeurtenissen met de wetten van Newton.
a Je stopt met trappen en komt tot stilstand met je fiets. T1
b Een blad valt met een constante snelheid van een boom. T1
c Je schiet naar voren als de bus plotseling hard remt. T1
d Je zakt door het ijs. T2
e Je zit bij iemand achter op de fiets en duwt die persoon in de rug, maar je gaat daardoor niet harder. I
5 Een parachutist met een massa van 90 kg springt uit een vliegtuig. Na korte tijd bereikt hij een zeer hoge constante valsnelheid.
a Waarom geldt de eerste wet van Newton niet bij het begin van de sprong? T1
b Bereken de grootte van de weerstandskracht bij de hoge constante valsnelheid. T2
c Leg uit met welke factor de snelheid toeneemt als de luchtweerstandskracht met een factor 2 toeneemt. I
6 Afbeelding C / Werkblad T3.6
Een stalen blok A met een massa van 500 g ligt op een aluminium plaat en is via een koord en een katrol verbonden met een massa m
7 Een motorfiets heeft vier veren. Elke veer draagt een vierde deel van de massa van de motor. Een motorrijder heeft een massa van 70 kg. Als de motorrijder op de motorfiets stapt, zakt de motor 1,7 cm in. Bereken de veerconstante van elke veer. T2
8 Afbeelding D
Bij een noodremtest wordt bij hoge snelheid zo hard mogelijk geremd. Hierbij blokkeren de wielen volledig.
In afbeelding D is het (v,t)- diagram van zo’n noodremtest te zien. De gebruikte auto had een massa van 1400 kg. Verwaarloos de luchtweerstandskracht.
a Bepaal met welke remkracht er is geremd. T1
Naarmate de banden vaker worden gebruikt, zal de remkracht afnemen.
b Beredeneer dat de remtijd tweemaal zo groot wordt als de remkracht halveert. T2
(km h–1)
a Schets de vier aanwezige krachten op blok A als het in rust is. Geef daarbij aan welke krachten even groot zijn. T1
b Schets de twee krachten op m in de juiste verhouding. T1
c Welke van de zes getekende krachten vormen een krachtenpaar? T1
©
2023 Boom voortgezet onderwijs, Meppel, The Netherlands
Derde druk, 2023
Behoudens de in of krachtens de Auteurswet van 1912 gestelde uitzonderingen mag niets uit deze uitgave worden verveelvoudigd, opgeslagen in een geautomatiseerd gegevensbestand, of openbaar gemaakt, in enige vorm of op enige wijze, hetzij elek tronisch, mechanisch door fotokopieën, opnamen of enig andere manier, zonder voorafgaande schriftelijke toestemming van de uitgever.
Voor zover het maken van kopieën uit deze uitgave is toegestaan op grond van artikelen 16h t /m 16m
Auteurswet 1912 jo. besluit van 27 november 2002, Stb 575, dient men de daarvoor wettelijk verschuldigde vergoeding te voldoen aan de Stichting Reprorecht te Hoofddorp (postbus 3060, 2130 kb , www.reprorecht.nl) of contact op te nemen met de uitgever voor het treffen van een rechtstreekse regeling in de zin van art. 16l, vijfde lid, Auteurswet 1912. Voor het overnemen van gedeelte(n) uit deze uitgave in bloemlezingen, readers en andere compilatiewerken (artikel 16, Auteurswet 1912) kan men zich wenden tot de Stichting PRO (Stichting Publicatie en Reproductierechten, postbus 3060, 2130 kb Hoofddorp, www.stichting pro.nl).
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, recording or otherwise without prior written permission of the publisher.
isbn 978 94 9322 408 7 www.boomvoortgezetonderwijs.nl

Polaris is een RTTIgecertificeerde methode en onderscheidt vier soorten vragen:
r Reproductievragen
t1 Trainingsgerichte toepassingsvragen
t2 Transfergerichte toepassingsvragen
i Inzichtvragen
Voor meer informatie over de RTTIsystematiek, zie www.docentplus.nl.
Boekontwerp & omslag René van der Vooren, Amsterdam
Tekstredactie
Charlotte Journée tekstredactie, Nijmegen
Opmaak & technische tekeningen PPMP, Wolvega