Volum 5A Elevbok BM (9788211029492)

VOLUM

Audun

Helene

GRATULERER MED DIN NYE

VOLUM 5A MATEMATIKKBOK!

Nå har du gått 4 år på skole, og du har helt sikkert oppdaget at matematikk kan brukes til mange forskjellige ting i hverdagen din. Når du bruker klokke, lager mat etter oppskrifter, handler med penger, leser fotballtabeller eller prøver å forstå værvarsel, bruker du matematikkunnskapene dine.

Vi som har laget denne læreboken har lagt vekt på at du som elev skal få tid til å forstå og bruke det du lærer. Vi tror på at læring skjer når elever får samarbeide, undre seg sammen og prøve ut nye løsninger. Med hjelp fra læreren din gir Volum matematikkbok deg en mulighet til å utforske, resonnere og generalisere matematikk – du får kompetanse i utforsking og problemløsning.

Boken har en oppbygning som du vil kjenne igjen på de ulike leksjonene. Hver leksjon er lagt opp slik at du starter med å bygge videre på noe du har arbeidet med tidligere, før du skal tilegne deg ny kunnskap.

De grønne sidene i begynnelsen av boken er repetisjon fra småtrinnet.

En leksjon er bygget opp på denne måten:

er utforsking og problemløsingssider. Her arbeider du med oppgaver som er laget slik at du kan oppdage sammenhenger og løse matematiske problemer i kjente og ukjente situasjoner.

er øvingssider. Her blir det presentert nytt stoff, og du arbeider med ulike øvingsoppgaver og problemløsingsoppgaver. Det er ikke meningen at du skal gjøre alle oppgavene. Oppgavene varierer i vanskelighetsgrad og hensikt. Hva passer best for deg? Dette finner du ut gjennom samtaler med læreren din eller i samarbeid med andre elever.

Røde sider

inneholder aktiviteter. Her får du repetere og anvende det du har lært på lilla og gule sider gjennom spill, lek og samarbeidsoppgaver.

Lykke til i arbeidet med matematikk. Vi håper at du får «den gode matematikkfølelsen» når du arbeider med lærestoffet i Volum 5A.

Gule sider

Lilla sider

Bøkene på mellomtrinnet består av leksjoner som følger en fast rytme. Hver leksjon består av en lilla utforskende økt, to gule økter med teori og øvingsoppgaver og røde sider med varierte aktiviteter. De grønne sidene i 5A er repetisjon og anvendelse.

I utforskende økter oppfordres elevene til å utforske og undersøke matematiske problemstillinger. De skal planlegge løsningsmetoder, forklare og begrunne løsningene, og oppmuntres til å stille nye spørsmål som de skal prøve å finne svar på.

Teori, noe nytt sto . Mer konkret og visuell støtte på de to første sidene. Åpne, rike og utfordrende oppgaver på side tre.

Samarbeid i lek, spill og aktiviteter for å variere arbeidsmetodene og øke forståelsen av leksjonenes tema.

Øvrige leksjoner

Repetisjonssidene i starten av boka inneholder tilbakeblikk fra småtrinnet. Samtalebilder på side 1, øvingsoppgaver på side 2 og 3, og utforsking, problemløsing eller aktiviteter på side 4.

Presentasjon av en problemløsingsstrategi på side 1. Øvelsesoppgaver på side 2. Strategiene er generelle og brukes i arbeid med andre problemløsingsoppgaver i boka.

Oppsummering og anvendelse fra foregående leksjoner. De mest grunnleggende oppgavene kommer først, deretter mer sammensatt og problemløsende oppgaver.

LILLA SIDER GULE SIDER RØDE SIDER

Studer bildet med fugler og fugleunger.

2.1 Hvor stor brøkdel?

Ina og Lars ser på de svarte fuglene og finner ut at én er fugleunge og tre er voksne.

De prøver å skrive dette som brøk.

Ina skriver:

3 4 av de svarte fuglene er voksne.

Lars skriver: 1 4 av de svarte fuglene er fugleunger.

a) Hvordan kan Ina og Lars ha tenkt for å komme fram til svarene sine?

Lars ser at det er i alt 24 fugler, og at 8 er gule. Han skriver 8 — 24 av fuglene er gule.

Læreren spør Lars: «Hvor stor brøkdel av fuglene er da ikke gule?».

b) Hjelp Lars med å finne løsningen. Finnes det flere måter å løse det på?

2.2 Studer bildet og skriv påstander som passer til brøkene.

1 4 4 24 12 24

2.3 Hvor stor brøkdel?

a) Hvor mange har brunt nebb av alle fuglene? Skriv svaret som brøk.

b) Vurder hvilke av disse påstandene som stemmer:

3

4 av de blå fuglene er voksne.

8 24 av fuglene er gule.

3

4 av de brune fuglene har blå øyne.

4 24 av fuglene er svarte. 1 24 av fuglene er svart med blått øye.

6 av 2 fugler med brunt nebb er gule.

c) Gjør om de usanne påstandene slik at de stemmer.

Definisjon av brøk som del av en mengde.

brøk = teller nevner

Telleren forteller hvor mange av enhetene vi har. Den teller det aktuelle antallet. nevneren forteller hvor mange enheter det er totalt.

2 5 av fuglene er røde.

3 5 av fuglene er blå.

2.4 Skriv brøkene.

Vi sier: «To femdeler av fuglene er røde.»

Vi sier: «Tre femdeler av fuglene er blå.»

a) Teller er 1 og nevner er 6.

c) Fire syvdeler.

b) Nevner er 5 og teller er 6.

d) Tretten trettideler.

e) Teller er a og nevner er b. f) Én todel.

2.5 Hvor stor brøkdel?

a) Hvor stor brøkdel av fugleungene i hvert rede er grå?

b) Hvor stor brøkdel av fugleungene i hvert rede er ikke grå?

2.6 Hvor stor brøkdel?

a) Hvor stor brøkdel av eggene er blå?

b) Hvor stor brøkdel av eggene er brune?

c) Hvor stor brøkdel av eggene er ikke hvite?

2.7 Hvilke av brøkene passer til mengden nedenfor? Begrunn svaret ditt.

2.8 Skriv to brøker til hver av mengdene.

2.9 Regn ut.

a) Du har fire viskelær, og 1 4 av dem er røde. Hvor stor brøkdel er ikke røde?

b) Du har seks sirkler og fargelegger to røde og tre gule. Hvor stor brøkdel av sirklene er ikke fargelagt?

c) 2 6 av alle kjolene er røde, og 1 6 av alle kjolene er blå. Hvor stor brøkdel av kjolene er verken rød eller blå?

2.10 Drøft påstandene med en medelev.

a) Dersom jeg har 3 blå og 4 røde blyanter, så er 3 4 av blyantene blå.

b) Jeg spiste 4 4 av en løk, og broren min spiste 1 4 av den samme løken.

c) 5 6 av eggene i et rede er blå. Da har 1 6 av eggene en annen farge.

a) b) c)

2.11 Hvor stor brøkdel av alle fuglene er

a) inne i rektangelet?

c) inne i sirkelen?

b) inne i både rektangelet og sirkelen?

d) utenfor rektangelet og sirkelen?

2.12 Brøkdel av rutene.

a) Hvor stor brøkdel av rutene er blå? Rød? Gul?

b) Hvor stor brøkdel av rutene er rød?

Fig. 1

Fig. 1

Fig. 2

Fig. 2

Definisjon av brøk som del av en lengde.

brøk = teller nevner

Telleren forteller hvor mange av de like lange delene vi har. Den teller det aktuelle antallet. nevneren forteller hvor mange like lange deler en lengde er delt opp i totalt.

Rødt linjestykke er 5 cm. Grønt linjestykke er 2 cm. Hele linjestykket er 5 cm + 2 cm = 7 cm.

5 7 av hele linjestykket er rødt. 2 7 av hele linjestykket er grønt. Hele linjestykket er

2.13 Hvor stor brøkdel av linjestykket er rødt? Hvor stor brøkdel er grønt? a) b)

2.14 Hvilken brøk skal stå der pilen peker?

=

= 1.

2.15 Hvor stor del av hver brøkstav er gul?

2.16 Hvor stor brøkdel av brøkstavene utgjør hver farge?

a) b) c) d)

2.17 Tegn et linjestykke der

a) 3 5 av linjestykket er blått

b) 1 3 av linjestykket er blått og 1 3 er rødt

c) 3 7 av linjestykket er blått og 4 7 er rødt

2.18 like lange deler?

To elever har forsøkt å fargelegge 5 7 av et linjestykke som er 14 cm langt:

a) Hvorfor ble ikke lengden av de to fargelagte delene like?

b) Hvordan kan du rette opp denne feilen?

2.19 Hvor stor brøkdel er lengden av hver farge i forhold til hele lengden?

Ikke gi deg før du har lært deg forskjellen på teller og nevner.

Skriv riktig brøk for rød, blå, gul og grønn del. Begrunn svaret.

2.20 Tegn et linjestykke og marker disse brøkene:

2.21 Hvilken brøk hører til hvilken figur?

2.22 Vinn så mange skjold som mulig.

Bruk tallene til høyre, og lag en brøk til hvert skjold. Tallene skal bare brukes én gang.

Dersom brøken blir større eller lik halve skjoldet, er skjoldet ditt. Klarer du å vinne alle?

Figur A

Figur B Figur C

Figur D Figur E

2.23 Brøkstrimler.

Arbeid sammen to og to. Klipp av hver deres strimmel fra langsiden på et A4-ark.

1) Brett strimmelen slik at du får to like deler. Fargelegg den ene delen blå.

2) Brett strimmelen igjen, og fargelegg feltet rødt.

3) Brett strimmelen for tredje gang, og fargelegg feltet gul.

Brett ut strimmelen igjen og legg den foran deg, slik at du ser alle fargene.

a) Skriv med brøk hvor stor del av strimmelen hver farge dekker. Begrunn svarene deres.

En familie har brukt papirstrimlene til å måle føttene sine. Her er resultatene:

Mor: tre røde

Far: to blå

Daniel: syv gule

Lillian: tre gule

Helene: seks gule

Krister: to røde

b) Skriv lengden på føttene til alle i familien som brøk.

c) Hvem har lengst føtter? Hvem har nest lengst? Og hvem har de korteste føttene? Vis hvordan du tenker.

Du kan bruke resten av A4-arket som hjelp til å finne løsningene. Du kan tegne, klippe og skrive.

2.24 Brettspill.

For 2–3 spillere

Dere trenger

• en terning

• små spillebrikker

Mellom hver fugl på spillbrettet er summen av brøkene én hel. De ulike banefargene er delt inn i ulike brøklengder.

Slik spiller dere:

• Spillerne velger hver sin banefarge.

• Dere slår terningen etter tur.

• Hver gang dere passerer en fugl, har dere kommet 1 hel lengde, som gir 1 poeng.

• Brikkene kan bare flyttes til egg eller fugl.

• Når dere kommer til START må dere stoppe, og velge en annen banefarge på neste kast.

• Førstemann til 20 poeng har vunnet.

Har du oransje bane, kan du flytte når du får

Har du grønn bane, kan du flytte når du får

Har du gul bane, kan du flytte når du får

Har du blå bane, kan du flytte når du får

Hvis du får for høyt antall, blir du stående.

BRØKDEL AV ET AREAL

3.1 Markedsplassen.

På markedsplassen skal de sette opp salgsboder, matsteder og lignende til en festival. Fram til nå har fem ulike bedrifter holdt av plass. Alle som leier en plass, må betale ut fra hvor stor del av markedsplassen de bruker. Bruk kopioriginal 3.1.

a) Hvor stor del av hele markedsplassen har hver bedrift holdt av? Skriv som brøk.

b) Hvordan fant du teller og nevner? Tegn og forklar.

c) Eieren leier ut hele markedsplassen for 24 000 kr. Vurder om leieprisene i tabellen er rettferdige.

Brages brød og pizza

1 av 6 deler er fargelagt. Den fargelagte delen er 1 6 av hele figuren.

5 — 6 av figuren er ikke fargelagt.

5 av 8 deler er fargelagt. Den fargelagte delen er 5 8 av hele figuren.

3 8 av figuren er ikke fargelagt.

Telleren forteller hvor mange av de aktuelle delene vi har, den teller antallet. Nevneren forteller hvor mange like store deler figuren er delt opp i.

3.2 Hvor stor brøkdel er fargelagt? Hvor stor brøkdel er ikke fargelagt?

3.3 skriv brøken.

a) Telleren er 1, og nevneren er 5.

c) Telleren er 3, og nevneren er 9.

3.4 Tegn brøkene som del av et areal.

b) Telleren er 4, og nevneren er 8.

d) Nevneren er 2, og telleren er 6.

3.5 Hvor stor brøkdel av kaken er

a) lilla?

b) turkis?

c) gul?

Hvor stor del av kaken er ikke

d) lilla?

e) turkis?

f) gul?

3.6 Hvilken brøk tilhører hvilken tekst

1) Telleren er to, og nevneren er seks.

2) Når jeg har to deler av noe som er delt i fem like store deler, kan jeg skrive at jeg har …

3) Telleren er fem, og nevneren er to.

4) Hvis noe er delt i tre like deler og jeg mangler to av delene for å ha det hele, da har jeg …

5) Telleren er tre, og nevneren er en.

3.7 Hver figur er del av en større figur. Tegn hele figuren.

3.8 Hvem har fargelagt figurene?

Mette har fargelagt 3 8 av sin figur gul.

Knut har fargelagt like deler grønn og gul. 1 2 av Elisabeths figur er gul.

På Einars figur er fargene

a) b) 4 5 6

c) d) 1 2 3

Ser du noen sammenheng mellom figurene på hver linje?

LAG LIK STØRRELSE PÅ DELENE

Figuren er delt i 3 deler, men de er ikke like store.

Ved hjelp av et stiplet linjestykke kan figuren deles i 4 like store deler.

3.10 Hvilke figurer har 1 — 4 fargelagt?

Figuren har 2 grønne deler av totalt 4 like deler.

2 4 av figuren er grønn.

3.11 Hvor stor del av figuren er fargelagt?

3.12 Hvor stor brøkdel er fargelagt?

3.13 ola utvider på markedsplassen.

Ola åpner utsalg av fruktdrikk også, og må leie større plass.

Hvor mye må han regne med å betale i leie nå?

Se informasjonen i 3.1.

Ragnarok lys og scene

Olas fruktdri kk

Olas sjokoladebar Olas sjokoladebar

Oli nes butikk Idas smykker

Oli nes butikk

Brages brød og pizza

3.14 Hvilke av påstandene er sanne?

a) 1 2 av teppet er rosa.

b) Mer enn 1 4 av teppet er lilla.

Oli nes butikk

c) Rosa og lilla dekker like store brøkdeler av teppet.

d) Bitene som er merket med 1 og 2, utgjør 1 4 av hele teppet.

e) Den grønne delen kan være 1 10 av hele teppet.

3.15 Hvor stor brøkdel er fargelagt?

a) De tre figurene nedenfor består av en trekant inni en firkant. Hvor stor brøkdel av firkantene er fargelagt?

b) De tre figurene nedenfor består av en trekant inni et kvadrat. Hvor stør brøkdel av kvadratene er fargelagt?

c) Undersøk om dette gjelder for figurene i oppgave a og b:

areal av trekant 1 + areal av trekant 2 2 areal av trekant 3 =

3.16 Bingo med brøksirkel.

Dere trenger

• et bingobrett til hver spiller, se kopioriginal 3.16

• fargeblyanter

• to terninger

Antall spillere:

• Hele klassen eller mindre grupper

Spilleregler:

• Hver elev får utdelt et bingobrett, og læreren (eller lederen for spillet) kaster terningene.

• De to tallene blir teller og nevner i en brøk. Telleren kan ikke være større enn nevneren. Læreren noterer brøken og leser den høyt.

• Elevene ser etter en sirkel med riktig nevner på spillebrettet, og fargelegger brøkdelen som ble lest opp.

• Når en elev har fargelagt fem fulle brøksirkler vannrett eller loddrett, sier han eller hun «bingo»!

• Spillet kan for eksempel avsluttes når en elev har fylt ut hele brettet.

Eksempel:

• Læreren slår 2 og 4. Telleren kan ikke være størst, så brøken blir 2 4

• Spillerne finner en sirkel som er delt i fire, og fargelegger 2 4 .

• De kan også fargelegge 1 — 2 i en sirkel som er delt i to, siden den har samme verdi som 2 4 .

3.17 Arbeid med tangram.

Bildet under viser et tangram. Det er et puslespill som består av 7 brikker som til sammen danner et kvadrat.

a) Hvor stor brøkdel utgjør hver farge av hele kvadratet?

1 4 5 6 7

LEKSJON X

OPPSUMMERING LEKSJON

4.1 skriv som brøk.

Hvor stor del er blå?

Hvor stor del er gul?

4.2 Hvor stor del av alle fiskene er …

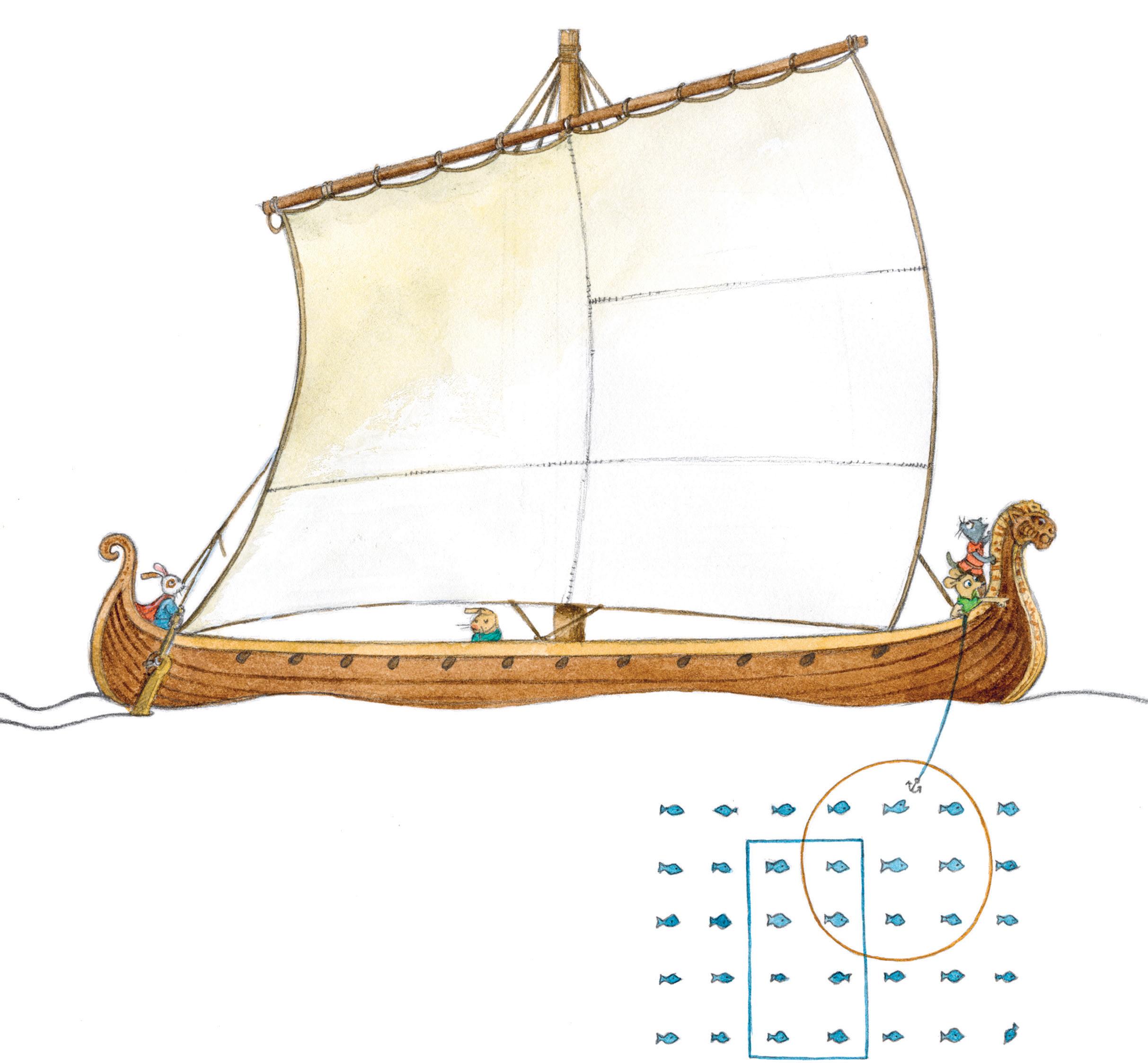
a) inne i sirkelen?

b) inne i firkanten?

c) inne i både firkanten og sirkelen?

d) inne i firkanten og sirkelen til sammen?

e) verken i sirkelen eller i firkanten? Skriv som brøk.

4.3 sant eller usant?

a) En måned er én tolvdel av et år.

b) En dag er én syvdel av en uke.

c) En uke er én femdel av en måned.

d) En uke er 1 52 av et år.

4.4 Hva mangler i setningen?

a) 1 kr er ■ ■ av 10 kr.

c) 5 kr er ■ ■ av 100 kr.

b) 5 kr er ■ ■ av 20 kr.

d) 20 kr er ■ ■ av 100 kr.

4.5 Tegn en strek slik at tekst og bilde samsvarer.

a) 2 4 av figuren er grønn.

b) 1 3 av figuren er grønn.

4.6 Hvor stor brøkdel er fargelagt grønn?

a)

b)

c)

4.7 Hvor stor brøkdel av målene i kampen skåret hjemmelaget?

a) Liverpool–ManU 3–1

c) Rosenborg–Brann 5–3

b) ManU–Liverpool 1–2

d) Brann–Rosenborg 1–0

4.8 Formasjonen til Rosenborg er 4 – 3 – 3.

Hvor stor brøkdel av spillerne er

a) forsvarsspillere?

b) angrepsspillere?

c) verken forsvarsspillere eller angrepsspillere?

4.9 landslaget i fotball har 5 — 11 av spillerne på midtbanen.

Hvor stor brøkdel av spillerne tenker du spiller

a) i forsvar?

b) i angrep?

c) som målvakt?

Sammenlign spilleoppsettet ditt med noen medelever.

4.10 Betaler du riktig beløp?

a) Fire personer deler en regning likt. Du betaler 40 kr av totalt 160 kr.

b) Fem personer deler en regning likt. Du betaler 30 kr av 120 kr.

c) Fem personer deler en regning likt. Du betaler 50 kr, og de andre fire betaler til sammen 200 kr.

4.11 Vilde og Mina har sommerjobb.

Vilde tjener 120 kr per time og Mina tjener 150 kr per time.

Mina sier: Jeg tjener 1 4 mer enn det du tjener.

Vilde sier: Jeg tjener 1 5 mindre enn det du tjener.

Hvem har rett?

4.12 lag brøkoppgaver med disse figurene. Bytt oppgaver med en annen elev.

SAMMENLIGNE ENKLE BRØKER

5.1 I butikken Idas smykker skal en vegg dekkes med bokhyller.

Her ser vi fire skisser av ulike hyller med inndeling som passer akkurat i bredden til veggen:

Hele veggen

a) Hvor stor brøkdel av veggen dekker hver hylle? Skriv brøkene i stigende rekkefølge, fra den minste til den største.

b) Se på tellerne og nevnerne i brøkene i oppgave a. Hva er likt, og hva er forskjellig?

5.2 Ida vil fylle hyllene med gjennomsiktige bokser. Hun har kjøpt pakker med fire bokser i ulike størrelser.

a) Hvor stor brøkdel av hver hylle har hun fylt opp?

b) Hvilken brøk i oppgave a er størst, og hvilken er minst? Hva er likt og hva er ulikt i de to brøkene?

c) Hvilken sammenheng ser du mellom størrelsen på nevnerne og verdien av brøkene?

5.3 Hvordan finner vi ut hvilken brøk som er størst, når tellerne er like?

Formuler en regel. Vis gjerne med brøkstaver.

ekstraoppgave

Lag forslag til kombinasjoner av hyller som passer akkurat til veggens bredde. Det skal være minst to typer bokhyller i hvert forslag. Bruk brøkstaver.

LIK TELLER ELLER LIK NEVNER

Vi ser at 3 3 > 2 3 > 1 3

Dersom nevnerne er like, er brøken med størst teller størst. Figurene er delt opp i like mange og like store deler.

Vi ser at 1 — 4 > 1 — 6 > 1 — 10

Dersom tellerne er like, er brøken med minst nevner størst. Figurene er like store, men delt opp i ulikt antall og dermed ulike størrelser.

5.4 Forklar for en medelev hvorfor 1 2 er større enn 1 6 .

5.5 Alle i familien bestilte én pizza hver. Her er det som er igjen:

a) Hvor stor brøkdel har hver av dem igjen?

b) Hvor stor brøkdel av pizzaen har hver av dem spist?

5.6 Hvilken brøk er størst?

Her kan det være nyttig å bruke brøkstavene. 1 — 3 2 — 3 3 — 3 74 leksjon 5 / Sammenligne enkle brøker

Anne Håvard

Alma Madeleine

5.7 Fire søsken kjøper en like stor sjokolade hver. Alle tar én bit.

Her ser du hvor mye de har igjen:

Skriv brøkdelen sjokolade hver av dem har spist, i stigende rekkefølge.

5.8 skriv to ulike brøker som er

5.9 skriv brøkene og sett inn <, > eller =.

5.10 skriv brøkene i stigende rekkefølge, fra minst til størst.

Amira Sebastian Philip Emma

5.11 Ingen figurer skal ha hvite felt.

Tegn figuren, og fargelegg slik at teksten stemmer.

a) b) c)

Differansen mellom gul og grønn er 2 16

12 18 er ikke rød.

Grønn er 2 12 .

Summen av gul og rød er 5 6

Differansen mellom gul og rød er 2 36

5.12 Hvilken brøk?

a) Skriv en brøk som er mindre enn 2 15 .

b) Skriv en brøk som er mindre enn den du fant i oppgave a, og deretter en brøk som er mindre enn den igjen.

c) Hva tror du er den minste brøken som er større enn 0?

5.13 Den algebraiske regelen for å sammenligne brøker med lik teller ser slik ut:

a b > a c dersom b < c

a) Sjekk om den algebraiske regelen stemmer ved å sette inn tall for a, b og c.

b) Sjekk hvordan det blir om c < b.

c) Stemmer regelen om b = c?

d) Stemmer regelen om brøkene blir snudd: b a > c a dersom b < c?

e) Stemmer regelen om brøkene blir snudd: b a > c a dersom b > c?

Hvilken brøk er størst av 5 — 9 og 7 — 15 ?

Halvparten av 9 er 4,5 så 5 9 er mer enn halvparten.

Halvparten av 15 er 7,5 så 7 15 er mindre enn halvparten.

Derfor er 5 — 9 > 7 — 15 .

5.14 skriv av og sett inn <, > eller =.

5.15 skriv tre brøker med ulike nevnere til hver oppgave.

Brøkene skal ha verdi

a) lik en halv

b) større enn en halv

c) mindre enn en halv

5.16 skriv av og sett inn <, > eller =.

5.17 sammenligning av brøker.

Hvilken regel passer til hvilken oppgave? Sett sammen tall og bokstav.

1: Hvis brøkene har like tellere, er brøken med minst nevner størst.

2: Hvis brøkene har like nevnere, er brøken med størst teller størst.

3: Hvis de andre reglene ikke kan brukes, kan vi prøve å sammenligne med en halv.

5.18 Hvilken brøk er størst?

A: Hva er størst av 14 — 20 og 8 — 20 ?

B: Hva er størst av 8 14 og 9 20 ?

C: Hva er størst av 3 9 og 3 6 ?

5.19 skriv tre brøker til hver oppgave.

Den ene skal være mindre enn en halv, den andre større enn en halv og den tredje like stor som en halv.

a) med 8 som nevner

b) med 40 som nevner

c) med 100 som nevner

5.20 sett inn tall for a.

a) Sett inn a = 2, og vurder hvilken brøk som er størst. a – 1 2 • a a + 1 2 • a

b) Prøv det samme med a = 3 og a = 4.

c) Hvilken sammenheng finner du?

5.21 nærmest halvparten.

a) I hvilket av disse to rektanglene er det fargelagt nærmest halvparten av arealet? Begrunn svaret ditt.

b) I hvilket av disse to kvadratene kan du fargelegge nærmest halvparten av arealet? Du kan bare fargelegge hele ruter. Begrunn svaret ditt.

5.22 Velg verdier for x og y.

5.23 Terningspill – den største brøken.

2–4 spillere

Dere trenger

• tre terninger

• notatark

• blyant Slik spiller dere:

• Spiller 1 kaster terningene og får tre tall. Velg ett av tallene som teller og ett som nevner, og skriv en brøk. Nevneren må være større enn telleren. Kaster spilleren tre like tall, blir det omkast.

• Spiller 2 kaster terningene og gjør det samme.

• Spillerne sammenligner brøkene. Den med størst brøk får 1 poeng.

• Spillerne fortsetter å kaste terningene annenhver gang.

• Førstemann til 10 poeng har vunnet.

Tenk gjennom!

• Hva er det lurt å tenke på når du skal plassere tallene?

• Finnes det et triks for å lage høyest mulig tall?

• Hva er de beste tallene å få?

Prøv terningspillet en gang til. Du kan også velge denne versjonen:

Variant

Alle tre terningene skal brukes for å lage en brøk. To av tallene summeres og brukes som nevner, og det tredje blir teller. Nevneren må være større enn telleren.

a) Hvilken brøk hører til hvilken figur?

b) Sorter figurene i oppgave a i stigende rekkefølge fra den minste brøken til den største.

c) Er det figurer dere ikke klarer å avgjøre brøkverdien på? Hvorfor?

d) Hvilke strategier brukte dere for å finne brøkverdier?

5.24 Vurder størrelsen på de fargede sektorene.

– et nytt læreverk i matematikk for barneskolen etter fagfornyelsen 2020.

Verket har en tydelig og forutsigbar struktur, og et stort og variert oppgavemangfold.

Når elevene får undre seg, diskutere og utforske sammen over tid, tror vi på at alle kan oppleve matematikk som engasjerende og meningsfylt.

VOLUM legger til rette for at elevene får god tid til å øve på å forstå, anvende og utfordre ferdighetene sine i forskjellige matematiske sammenhenger.

I et trygt og raust læringsfellesskap kan elevene argumentere og dele ideer – og på den måten bidra til å utvikle et felles, presist og hensiktsmessig matematisk språk.

Sammen med hver elevbok følger konkreter til bruk i undervisningen.

Les mer om verket på www.fagbokforlaget.no