Global Thinkers: Physics and Chemistry 2. Secondary (sample)

SECONDARY EDUCATION

Chemist2 ryPhysics sample

Contents Basic knowledge in the course

The scientific method

The hypothesis of a madman or a Pioneer?

1. Scientific knowledge

2. Physical and chemical changes

3. Physical quantities. Units and measurement

4. Scientific language

5. Laboratory equipment. Safety guidelines

6. Science, technology and society

Recreational science Scientific report. The snowman

errors

1 Matter

Decanting in Roman times

1. The properties of matter

2. Pure substances and mixtures

3. Liquid solutions

4. Techniques for separating mixtures

5. Suspensions and colloids

Recreational science Solid or viscous liquid?

Practical work Solution, colloid or suspension?

2 States of aggregation

1. Characteristics of states of aggregation

2. The kinetic theory of matter, KTM

3. Pressure and temperature

4. Gas laws

5. Changes of state

6. Change of state graphs

Recreational science Cubitos de aceite

Practical work Boiling a mixture

Understand, reflect and test your skills

12

3 The atom

Atoms: from ancient Greece to the modern day

1. Matter is made up of atoms

2. The characteristics of atoms

3. Atomic number and mass number

4. Ions

5. Can we see atoms?

4 Chemical

Naming chemical substances

of matter

70

96

1. The periodic table of the chemical elements

2. Simple substances and compounds

3. Molecules and crystals

4. Applications of chemical elements

5. Chemical formulas

6. Industrial, biomedical and technological applications

Recreational science Memorising the chemical elements

Practical work Discontinuity of matter II

Understand, reflect and test your skills

5 Chemical reactions

Modern agriculture

1. Changes in material systems

2. Chemical reactions

3. Characteristics of chemical reactions

4. Chemicals of natural and artificial origin

5. Sustainable chemistry and commitments

6. Chemical reactions and the environment

Recreational science Homemade glue

Practical work Chemical reactions

Understand, reflect and test your skills

130

6 Forces and motion

9 Energy sources

The correct path

1. Energy sources

2. Main uses of energy

3. Problems due to energy use

4. Possible solutions to the energy problem

5. Sustainable development

7 Energy. Mechanical energy

8 Thermal energy

188

THE SCIENTIFIC METHOD

THE HYPOTHESIS OF A MADMAN OR A PIONEER?

In 1846, Ignaz P. Semmelweis began work as an assistant doctor at the Vienna General Hospital. This hospital was divided into two wards: one for doctors, where Semmelweis worked, and another for midwives. Johann Klein, the medical director in charge of the doctors’ ward, was the first person to have his students examine cadavers at the hospital. This meant the obstetrics students were both performing autopsies on cadavers and attending mothers giving birth.

After the implementation of the new training system, the cases of puerperal fever in women who gave birth in the doctors’ ward increased significantly in comparison with the midwifery ward. After weeks of observation, Semmelweis proposed a hypothesis that the student doctors were transmitting the puerperal fever. He saw that they were performing autopsies on cadavers, then exploring the pregnant mothers without washing their hands. At first, he was accused of being mad and was

even fired from his job. However, Semmelweis then made it obligatory for anyone examining cadavers to wash their hands afterwards and disinfect them with a calcium chloride solution. With this new rule in place, the cases of puerperal fever dropped dramatically, confirming Semmelweis’ hypothesis. Nevertheless, several years passed before the scientific community recognised the value of this great doctor’s observations and contributions.

READING AND LISTENING

1 What do the following words mean:

a) Unconventional.

b) Pioneer.

c) Obligatory.

d) Implement.

2 Use the words in the previous activity to write a summary of the text.

3 Why was Semmelweis treated like a lunatic?

Discussing in pairs: Creating a hypothesis

4 Look at the following pictures. What can you notice? Discuss with a classmate the different colours of the sky and the time of day.

LEARNING SITUATION CHALLENGES THAT LEAVE AN IMPRINT

LEARNING SEQUENCE

GAME 1. TYPE A. THE SCIENTIFIC METHOD

1.1 Propose a hypothesis related to a scientific or pseudoscientific piece of news that can be resolved through a simple investigation on the Internet.

1.2 Design the physical card that will contain the hypothesis and where the players will enter the result (if it is correct, they will mark value 1; if incorrect, value 0), and contains the address of the website where they should consult the news item.

GAME 2. TYPE B. MAGNITUDES AND MEASURES

2.1 Think of an activity in which you have to measure a physical quantity with a measuring instrument.

2.2 Players must calculate the relative error that is made and express the complete result in scientific notation. The exponent of the power of 10 will be the digit sought.

Once you have a clear idea on the reason behind the different colours, create a hypothesis on the colour of the sky and the ocean in pairs.

Instructions on handwashing

5 Nowadays, washing and disinfecting hands is a general practice. Especially in times of a pandemic, it is extremely important to wash your hands thoroughly. Even though most people are used to washing their hands before and after carrying out activities, such as before cooking or after using the toilet, not many people know how to wash their hands properly.

Write a short paragraph where you explain, step by step, how to properly wash your hands.

Then, describe the relationship between washing and disinfecting your hands and the 3.3 and 3.8 SDG targets.

2.3 Design the card with the clues for the players, write on it the measured result and leave it next to the measuring instrument.

CREATE AN EQUATION

The escape room cannot be solved until the first three units have been finished, but now the keys that help solve the enigma will be determined:

3.1 The digits 1 and 0 obtained in the type A games of the three units of the book will make a binary number that corresponds to the first two numbers of the padlock combination.

3.2 The equation that will give the last two digits of the combination will come out.

SAFETY STANDARD SHEETS

For more each type B game, a card will be designed with the essential safety regulations to be able to carry it out. Players will find those tokens next to each of the microgames.

+ for guidelines, go to anayaeducacion.es

SCIENTIFIC KNOWLEDGE

Scientific knowledge comes from the need to solve a problem or explain a phenomenon using facts.

However, we need to ensure that the conclusions reached match reality. If we do not, the knowledge we find would not be scientific.

The figure below shows a simplified diagram of these methods, which we call the ‘scientific method.’

Scientific knowledge is what emerges from studying phenomena with the scientific method.

Scientific knowledge adheres to the following criteria:

• It is a human construction to which many people have contributed over history.

Analyse

• What is a hypothesis?

• What must a hypothesis do to become scientific knowledge?

• It develops through rigorous working methods based on the scientific method.

• It is based on experiment; it can never be based on beliefs, intuitions or assumptions.

• It must match reality and it must be possible to replicate as many times as necessary.

Sciences and pseudosciences

Sometimes people try to pass off non-scientific knowledge as scientific. These ideas are called pseudoscience (false science. One example is astrology, which has no scientific basis or predictive power.

PHYSICAL AND CHEMICAL CHANGES

Physics and Chemistry are scientific disciplines that have the purpose of explaining the world in which we live. Since in it, everything is constant change, its main objective is to explain these changes.

Both focus their study on matter. If matter has well-defined boundaries, then we refer to it as an object or a body. The atmosphere is a material system, since it does not have well-defined limits. A piece of iron, or your pencil, are objects, since they do.

Matter can be so small as to need a microscope to see it, or as large as the entire universe. In either case, it can undergo two types of change.

Understand, think, investigate...

1 The text says that scientific knowledge is the work of many people. Name two of those people and search the Internet for other scientists whose work was used to advance science.

2 Round table. Given the properties of scientific knowledge, explain why horoscopes are not scientific knowledge.

3 What is the origin of scientific knowledge? What do we do if a hypothesis fails?

4 Discuss whether the statement ‘everything in the world is in constant change’ is true or false.

5 Indicate whether the following changes are physical or chemical and why: an object falls, we crumple paper and then burn it, we dissolve salt in water, a cloud forms, fruit ripens.

■ Physical changes

If we raise the temperature of a piece of iron until it melts, we still have iron. At the beginning it was in a solid state and afterward it was in a liquid state. It is the same when an ice cube melts.

Physical changes are those in which after the change, we still have the same substance.

■ Chemical changes

However, if we leave a piece of iron in the open air, it will eventually rust and the final substance is different from the original.

Chemical changes are those in which the substances at the end differ from those at the beginning.

Normally, chemical changes are accompanied by physical changes that help us recognise them. For example, a gas emission, colour change or bubbling.

Physical and chemical changes: examples

Iron melts when it reaches a temperature of 1 540 °C. When this happens, a new substance is not formed, but the substance does change state. This is a case of a physical change. When there is a change of state, these cases are physical changes.

However, when iron rusts, it forms a new substance, iron oxide, with very different properties. Unlike iron, iron oxide is not a good conductor of electrical current for example. These cases, in which the final substances differ from the originals, are chemical changes.

Melted iron

Rusted iron

PHYSICAL QUANTITIES. UNITS

AND MEASUREMENT

3.1 Physical quantity

To check whether a hypothesis matches reality, we must know the properties involved in the phenomenon we are interested in and how they influence it. This is the concept of physical quantities.

Physical quantities are the properties of phenomena that we can measure objectively.

If someone tells us that they will take 10 minutes to arrive, we can measure the time with a stopwatch and, done correctly, it will not matter who takes the measurement. Time, just like mass and length, is a physical quantity since it can be measured objectively.

Then, when we deal with justice, love, or beauty, we are no longer dealing with physical quantities. How would we measure, for example, the beauty of an object? Would we all agree?

3.2 Units and measurement

In the previous example, we could say 600 seconds instead of 10 minutes, since each minute is 60 seconds. Generally, a physical quantity can be written using different units.

The unit of a physical quantity is the definite magnitude used to measure the amount of quantity.

Once we decide on a unit, we can proceed with measuring the quantity. Therefore, when we say that something is two metres long, it means that the chosen unit (the metre) fits twice in the length that we are measuring.

Measuring consists of comparing the quantity measure with a specific unit.

A number without a unit has no physical meaning. In physics and chemistry, every value needs a unit. Imagine that someone tells you they will take 7 to arrive. You might ask: 7 what? Minutes? Hours? Days?

Unit symbols

Each unit is written with a symbol made of one or more letters. You can consult the tables on the next page.

The symbols of the units are written in lower case, unless they come from a proper name, in which case the first letter is in upper case. We never add an ‘s’ for plural to a symbol. For example: write twenty grams as 20 g and not 20 gs.

3.3 Fundamental and derived quantities. International system of units (SI)

There are many physical quantities, but all can be expressed in terms of the so-called magnitudes básicas. The rest, which can be obtained from the first, are derived quantities.

There are also different units for the same quantity and it is necessary to agree on which to use. The international system of units (SI), a set of units for international use, emerged from the XI General Conference on Weights and Measures in 1960.

The table on the right shows the fundamental quantities and their SI units. The table below shows some derived quantities.

Some derived quantities and their units

Understand, think, investigate...

6 Discuss whether the following traits of a person are physical quantities:

a) Height.

b) Curiosity.

b) Honour.

d) Weight.

En los casos afirmativos, indica si se trata de una magnitud fundamental o derivada, y sus unidades SI.

7 Where possible, indicate whether it is a fundamental quantity or a derived one, and its SI units.

8 Logic wheel. Why are density and energy measured using derived units? What is their relationship to fundamental quantities?

9 Search for information on the Internet about quantities and units that appear in the tables on this page that you don’t know and briefly define them. Consult the table of contents of this book and think about whether you are going to use all the magnitudes and quantities this year.

3.4 Scientific notation

In Physics and Chemistry, sometimes we need to work with very large or very small numbers. For example, the distance between the Earth and the Sun is around 150 million kilometres (150 000 000 000 m) and the size of a grain of pollen is of the order of a thousandth of a millimetre (0.000001 m). We use powers of 10 to write these values. For example:

With these powers, the Earth-Sun distance is 1.5 · 1011 m, and the size of the pollen grains is of the order 10–6 m.

This way of writing numbers, with a whole number followed, or not, by decimals and the correct power of ten, is known as scientific notation.

3.5 Multiples and submultiples

It is also common to use multiples or submultiples of the SI units, adding them as prefixes (table below). With these, the Earth-Sun distance is 150 Gm and the size of a pollen grain is of order 1 μm.

1 The radius of the Earth is some 6 380 km. Write it in scientific notation and in SI units.

First, we write the radius in SI, keeping in mind that the ‘kilo’ prefix is equal to 103:

RE = 6 380 km = 6 380 · 103 m = 6 380 000 m

To leave just one whole digit, we must divide by 1 000 000 (106). So to keep the value from changing, we will have to multiply by 106

In scientific notation it is:

RE = 6.38 · 106 m

2 A motorcycle moves at 90 km/h. Write its velocity in SI units.

To change units, we use conversion factors for all the units we must convert:

We write the conversion factors necessary such that the desired units remain.

So, for the opposite conversion, we would write as follows:

There is a resource on multiples and submultiples on anayaeducacion.es

3.6 Measuring instruments

We measure physical quantities with instruments designed for the task.

The choice of the appropriate instrument is crucial. For example, you could not measure your own mass with a kitchen scale, since they cannot usually measure such large masses.

Therefore, it is worth knowing the properties of measuring instruments. This year, we will focus on just two:

• Minimum value and maximum value. These are the smallest and largest values, respectively, that the instrument can measure. The difference between them is the measurement scale.

• Sensibility. This is the instrument’s ability to detect changes in the quantity measured. It is related to the smallest division on its scale.

The photo on the right shows two graduated cylinders. Both make measurements with the same unit of volume, the millilitre, mL (a thousandth of a litre). But they have different properties:

• Left-hand graduated cylinders:

– Minimum value: 5 mL

– Maximum value: 50 mL

– Sensibility: 1 mL

• Right-hand graduated cylinders:

– Minimum value: 2.5 mL

– Maximum value: 25 mL

– Sensibility: 0.5 mL

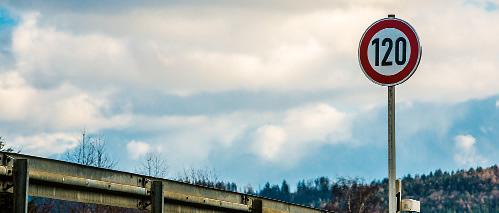
Understand, think, investigate...

10 Answer the following questions:

a) What is the measurement scale of graduated cylinders in the picture?

b) With which one could you measure 15.5 mL? 60 mL? 75.5 mL?

11 The speed limit on the motorway is 120 km/h. Write it in SI units.

Properties of measuring instruments

12 Find the sensibility of the stopwatch on a mobile phone.

13 Analyse the traits of a bathroom scale and a kitchen scale. Discuss the differences.

14 The density of distilled water is 1 g/cm3. What is its value in SI units? Hint: 1 m = 100 cm = 102 cm, where (1 m)3 = 1 m3 = (102 cm)3 = 106 cm3

15 The distance between the Moon and the Earth is 384 000 km. Write it in scientific notation with SI units and with the multiple and submultiple prefixes for the units.

16 Work with the interactive unit conversion application on anayaeducacion.es

SCIENTIFIC LANGUAGE

To communicate the results of scientific research, we use very rigorous language, which is usually accompanied by physical equations, data tables and graphs.

4.1 Physical equations

A physical equation is a mathematical formula that relates physical quantities.

For example, mean velocity is the distance an object travels in a given unit of time. Its equation is:

Relaciones de proporcionalidad

Direct proportion

When two quantities, A and B, are directly proportional, their mathematical relationship is:

Ak B =

Inverse proportion

When two quantities, A and B, are inversely proportional, their mathematical relationship is:

A B k =

In both equations, k is a constant.

This formula is not read ‘v is equal to d divided by t’. Instead, the letter ‘v’ represents average velocity, ‘d’ the distance travelled, and ‘t’ the time required to travel it. The letters in physical equations are symbols used to represent physical quantities and, since they have physical meaning, they are measurable properties.

Apart from calculating the value of quantities, physical equations are also useful for finding the proportionality of quantities. Two of the most common relationships are direct and inverse proportionalities.

Two quantities are directly proportional when you can multiply one by a number to obtain the other and they are inversely proportional when a number is divided by a quantity and you obtain the other one.

The box below shows the mathematical equations of these types of proportionality. Practise analysing them every time you see a physical equation.

Problem solved

3 Study the proportionality between the mean velocity, the distance travelled and time.

Supposing the distance travelled was 6 m and the time taken was 3 s, the mean velocity would be:

v = 3 6 s m = 2 m/s

If we double the distance to 12 m, but keep the time constant at 3 s, the velocity also doubles:

v = 3 12 s m = 6 m/s

If we keep the distance at 6 m and double the time to 6 s, the velocity halves:

v = 6 6s m = 1 m/s

This tells us that mean velocity is directly proportional to the distance travelled, and inversely proportional to the time employed.

4.2 Tables and graphs

To study the relationship between two quantities, we design experiments in which we change the values of one of them (the independent variable) and measure the values of the other (the dependent variable). Then we organise these measurements in data tables, from which we can make graphs. To do so:

• We trace the coordinates, or axes.

• We label each one with the quantity it represents and the units in which we measured it. We put the independent variable on the abscissa (X axis) and the dependent variable on the ordinate (Y axis).

• We select a scale for each axis such that it contains the entire range of values of the variable it represents.

• We plot one point for each data pair in the table.

• We join the points with a line.

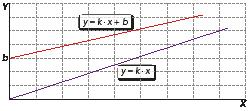
• From the data table and the graphs, we can deduce the proportionality of the quantities. The figure on the right shows the graph of the proportionalities studied. The graphs on the right show the proportional relationships you have studied.

Problem solved

4 We measure how a spring lengthens when we hang a mass on it and obtain the following data:

Common graphs

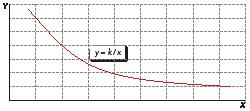
Direct linear proportionality

Does not intersect the origin.

Intersects the origin.

Inverse proportionality

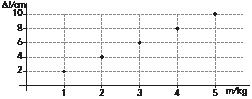
Represent the data in a graph and find the relationship between mass and length.

In this case, the mass is the independent variable (it is what we are changing) and the length is the dependent variable (what we are measuring). The graph is shown on the right.

Understand, think, investigate...

17 Pressure is defined as the force exerted per unit of surface area (p = F/S). Study the proportionality between the given quantities.

18 In Problem solved 4, write the relationship between the quantities: length and mass, in words. What is k? What is its unit

We observe a directly proportional relationship, so Δl = k · m. From the data in the table, we can deduce that k = 2. So Δl = 2 · m, where Δl is measured in cm, and m in kg.

19 We measure the volume of a mineral fragment as a function of its mass. We obtain:

Draw the graph and study the V-m relationship.

LABORATORY EQUIPMENT. SAFETY GUIDELINES

5.1 Basic laboratory equipment

You can find a wide range of equipment in a laboratory, some of which we show on the following pages. Throughout the year, we will describe how to use each piece of equipment and explain any new equipment needed.

5.2 Safety guidelines in the laboratory

You should follow these safety guidelines in the laboratory. In the event of an accident, tell the nearest teacher.

• Wear safety glasses and latex gloves if necessary.

• Do not wear clothing or objects that restrict your movement.

• Do not move around unless you have a reason and do not run.

• Cover any open wounds.

• Wash your hands with soap afterwards.

• Do not sniff, taste or ingest laboratory products.

• Handle acids and bases with caution, since most are corrosive.

• If you must mix an acid with water, add the acid to the water, not the other way around.

• Clean any spills with abundant water.

• Note any warning signs on chemical products (figure below).

5.3 Waste management

Laboratory work generates waste. Some can be disposed of in the usual way (organic, paper, plastic, glass).

Other waste, however, may damage the environment and must be packaged, stored and classified according to its properties and risks, so that it can be delivered to specialist companies for treatment and disposal (see the picture below).

Before throwing waste into the bin or pouring something down the drain, ensure that you are putting it in the right place.

It is very important to conserve nature and every action, however small, helps.

Laboratory waste management

20 With your parents’ supervision, examine your home cleaning products and identify some of the labels shown on this page. Make a table with the name of the product, the meaning of the label and the chemical formula of the product (if it appears).

21 Waste management can involve incineration, encapsulation, confinement, or use as an alternative fuel. Search for information about these terms and write a brief report about the types of waste handled by each method.

LABORATORY EQUIPMENT. SAFETY GUIDELINES 5

Basic laboratory equipment

Beaker

Graduated cylinder

Funnel

Erlenmeyer flask

Distillation flask

Round bottom flask

Wire gauze Scale

Double clamps

Wooden clamps

Wash bottle

Test tubes

Evaporating dish

Ring stand

SCIENCE, TECHNOLOGY AND SOCIETY

It is easy to confuse science and technology, but they have many differences. Some of these are:

• Purpose. The purpose of science is to explain the world around us; technology is for manufacturing devices.

• Starting point. Science comes from the need to answer a question; technology helps us satisfy our needs.

• Procedure. Science seeks answers by testing hypotheses that must describe reality; technology consists of the design and fabrication of products that must work.

• Final product. The product of science is universal knowledge; the product of technology is a particular object.

Finding information

Would you like to be a top technician in a clinical diagnostics lab? In the anayaeducacion.es resource bank you’ll find more information on this job.

Despite these differences, science and technology are closely related. They shape society, which in turn makes decisions about the future direction of scientific and technology research.

All of these relationships make it difficult to refer individually to science, technology or society, since they are almost inseparable. Science, technology, and society (STS) refers to the study of STS relationships (figure below).

The following page shows some examples of the relationships between science, technology and society, with which you live every day.

Science influences society, allowing us to know the world in which we live and improve our living conditions. Society, for its part, may decide what to research and influence science via subsidies.

Science needs technology to improve instruments for observations and measurement, which are possible due to scientific advances.

Technology improves or harms our lives depending on how we use it. At the same time, society shapes the development of technology through demand.

Science, technology and society are closely related

Pharmaceutical industry

Some examples of STS relationships

Textile industry

The pharmaceutical industry has increased our life expectancy. Scientific research is involved in determining the active ingredients of medicines, and the technology industry manufactures the medicine.

Automotive industry

Para fabricar un coche se necesitan entre 70 000 y 90 000 piezas, y todas ellas se diseñan con relación a la investigación científico-tecnológica. Una vez fabricado, facilita nuestros desplazamientos.

Understand, think, investigate...

22 Despite the fact that medicine and clothing are produced in mass quantities, there are many people who do not have access to such goods and cannot even meet their basic water and food needs. Look up SDG targets 2.1 and 6.7 and reflect on this. Summarise your opinion so that you may debate it with your classmates.

23 When do you think mobile phones were invented? What were mobile phones from 15 years ago like? After answering, search for information on the Internet and check your answers.

Each year there are more and more people on the planet and therefore more need for clothing. This means we require more research into more durable textiles with better thermal properties.

Communications

When mobile phones were first invented, they required a lot of scientific and technological research. This now enables us to speak with people all over the planet with handheld devices.

24 Today almost all cars run on gasoline or diesel, though some prototypes use other fuels. In small groups, search for information about these prototypes and prepare a slideshow about one of them.

25 Making mobile phone batteries requires coltan, a mineral from columbite and tantalite. Search for information about the ‘coltan war’ and, keeping in mind the data from targets 8.7 and 8.8, write a brief report. Share your conclusions with the rest of the class..

SCIENCE WORKSHOP

Recreational science

Scientific report. The snowman

All scientific research starts with a need to respond to a problem, or fact, that requires explanation.

To find the answer, we must form a hypothesis and check it against reality. If it passes our tests, the hypothesis becomes part of scientific knowledge. Otherwise, we must form a new hypothesis.

To check a hypothesis, we normally use experiments. They can be done in many ways, but must always be replicable by other researchers. Scientific communication of the results helps make that possible.

A scientific report must have at least the parts listed on the right.

• Cover

• Contents

• Problem statement

• Hypothesis

Reflect

• Method

• Results

• Conclusions

• References

One snowy winter day, you are making a snowman with some friends. When you finish, someone suggests putting a jacket on it so that it takes longer to melt.

Is that right? Would it take longer to melt with a jacket on?

Form small groups and tackle the problem using the scientific method. To communicate your results, write a report in poster format, as shown on the following page.

Writing a scientific report

We must clearly specify the problem we confront. In this case, for example, it could be: Does a snowman melt faster with a jacket, or without it?

We must specify the hypothesis, or possible answer, explaining why we think it might be true. There may be more than one. Then, we must indicate the process followed to check the hypothesis, specifying the materials used and the way they were used.

For each hypothesis, we must obtain the results obtained using verbal, mathematical or graphical language.

The conclusions must be based on the obtained results. If these conclusions support the hypothesis, we will have an answer to the problem; if not, we will have to generate a new hypothesis.

Practical work

Writing the measurement

Surely you will have noted that the values obtained from a measurement depend on the instrument you use and that even with the same instrument, you may obtain different values. We accept that all measurements have errors or uncertainty

There are methods for finding the error of a measurement, but always recall that the measurement error will be at least equal to the sensibility of the instrument

Once we know the error, we write the measurement as:

Measurement errors

Objective

The goal of this exercise is to learn that whenever you make a measurement, you will make errors that you must report, together with the measurement itself.

Your proposal

Is there a way of checking that all measurements include errors? If so, explain how you would do it.

Our proposal

The measurement of a quantity is influenced, among other things, by the properties of the instrument used and how it is used. We will check it with some measurements of two fundamental quantities: length and time.

What you will need

• Ruler

• Measuring tape

• Stopwatch

• Mobile phone

Guidelines

Measuring length

• Measure the width and height of a mobile phone, first with a ruler and then with your measuring tape. Write the results and, next to them, the precision of the instrument used.

This means that the time measured could be between 3.63 s and 3.65 s, giving us a range of possible values instead of one specific value. That said, if you had to use this time to do a calculation, you would use the value 3.64 s.

• If the end of the mobile is between two tick marks on the scale, take the lesser value (we always do this for graduated scales).

Measuring time

• Let an object fall from 1 metre high (use the measuring tape to measure the height) and measure the time it takes to fall to the ground. First, use the laboratory stopwatch, and then, use the stopwatch application on the mobile phone.

• Take two measurements with each stopwatch, write down the results, and write down the precision of each stopwatch next to them.

Once you have the data, review the following information and do the proposed activities.

Draw conclusions…

1 Did you get the same width and height measurements for the mobile with the ruler and the measuring tape? What about the falling time with the two stopwatches? If there was a difference, calculate it for each case.

2 For which quantity, length or time are the differences greatest? Explain why you think that is.

3 Write the measurements and their related uncertainties and check whether for each quantity the values fall within the same range.

4 Search for information about ‘random and systematic errors’ and summarise it in a few lines, giving examples.

CHALLENGES THAT LEAVE THEIR MARK

UNDERSTAND

Organise your ideas

concept map

1 Summarise information in a drawing. Make a drawing to scale of an instrument used to measure length. Indicate its minimum height, maximum height, measurement interval and sensitivity. Give examples of measurements taken with it.

2 Conceptual map. Copy and complete the following concept map. Following the example, create one that summarizes the purpose of scientific knowledge and the types of language used to communicate the results of scientific inquiry.

Remember that you can find the answers to all calculation activities on anayaeducacion.es

Scientific knowledge

1 We all contribute. Explain in your own words what the scientific method is. Can you recall a situation in your everyday life in which you have used it, with or without knowing it?

2 What is your horoscope? Search on several horoscope websites for what they say will happen for someone with your horoscope tomorrow. Decide whether what you have read is scientific knowledge.

Physical and chemical changes

3 Physics and Chemistry are, among others, called experimental sciences. Why do you think that is? With what properties of scientific knowledge can you relate that fact?

4 Apart from the physical and chemical changes, there are other changes we can observe in nature: nuclear changes. Research them and write a definition. Then, create a table with the different types of nuclear changes and an example of each.

5 Classify the following changes as physical or chemical and explain your reasoning

a) Vinegar reacting with marble.

b) An egg frying.

c) Formation of steam when water boils.

d) Dilation of a metal beam.

e) Iron heated until red hot.

f) Digestion of an apple.

Physical quantities. Units and measurement

6 Give two examples of physical quantities and two other properties or traits that are not physical quantities and justify your answer. For each physical quantity, list at least two units other than SI units.

7 How wide is your desk? How tall are you? What is the distance between Madrid and Berlin? Why did you use the units you did for each case? Write the lengths in scientific notation and SI units.

8 In astronomy, distances are enormous and astronomers have defined appropriate units for them:

– Astronomical unit (AU). This is defined as the mean Earth-Sun distance. It is 150 000 000 km.

– Light year. This is the distance light travels in a vacuum in a year at 300 000 km/s. It is 9.5 · 1012 km.

– Parsec (pc). This is 3.2616 light years. Write these units in SI, first without and then with scientific notation. Write parsecs and light years in AU.

9 What physical quantity could you measure with this instrument and what are the instrument’s properties?

11 Which lengths are written wrong? Why?

a) 10 ms.

b) 25 m.

c) 42 mt.

12 Thinking hats. Design a method for measuring the radius of the cylindrical base of a lamp post. Estimate the values and write the measurement.

Scientific language

13 From the following graph, which represents the distance travelled by a vehicle as a function of time:

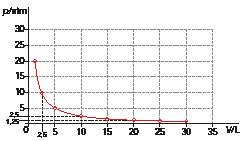
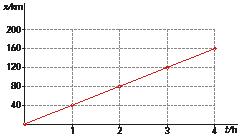
a) Make a table with at least five data pairs.

b) Examine the relationship between the quantities and write in verbal and mathematical language.

c) Find the mean velocity of the vehicle.

10 An airplane flies at 2 000 feet above sea level at 400 miles per hour (mph). Find the conversion factors you need to write this data in SI.

14 Shared interpretation. Write the relationship between the quantities plotted on the following graph in both verbal and mathematical language.

15 Newton’s second law, which you will study in future years, relates the force acting on an object with the acceleration it imparts. Its mathematical formula is:

F = m · a

where m is the mass of the object. Write it in words, specifying the proportionality relationships you observe.

MATTER 1

DECANTING IN ROMAN TIMES

Romans certainly knew a thing or two about matter and its related concepts. They used their knowledge of pressure effects, different densities of mixtures, and separation techniques, such as decantation, very effectively. This is clear to see in their incredible constructions, such as the Segovia aqueduct and the Nimes aqueduct (France).

For a long time, people thought the large Roman reservoirs built at the ends of aqueducts, and the cisterns for collecting rainwater — such as the Monturque cistern (Córdoba) and the Theodosius cistern (Istanbul) — were only for storing water. However, recent studies have shown that they had a very different purpose. These enormous reservoirs probably acted as decanters, separating out the solid particles suspended in the water. Together with the red paint on the inner walls

of the aqueduct (recent hypotheses suggest this acted as a bactericide and a fungicide), this demonstrates that water purification was very important for the Romans.

READING AND LISTENING

1 What determines the characteristics of an object?

a) Colour.

b) Material.

c) Shape.

2 According to Aristotle, how was matter formed?

3 What was the main contribution of alchemists to the current understanding of matter?

4 Explain what it means that Robert Boyle came back to Democritus’ idea.

LANGUAGE BANK

SPEAKING

5 Look at the two images and describe what you observe. Then, compare them.

LEARNING SITUATION CHALLENGES THAT LEAVE AN IMPRINT

LEARNING SEQUENCE

RESEARCH GROUPS.

1.1 Get into groups of 4 or 5.

1.2 The first challenge is to brainstorm ideas about what a volcano is. In your group, create a mind map to show everything you know about this natural phenomenon. Try to answer the following questions: What does a volcano have to do with physics and chemistry?

• Are there any pure substances or mixtures in lava?

Next, research on the Internet how people are working to improve the quality of water in your city, or measures they are taking to reduce the amount of pollution in lakes, rivers or oceans. Finally, look up targets 6.1 and 6.3. How do they relate to the images and your research?

WRITING

In the history of science, even though a person was on the right track to find something meaningful, many times other theories and ideas imposed on the correct one. For instance, when Gregor Mendel (1822-1884) explained how the laws of genetic inheritance work, nobody listened to him and he died without being recognised. It wasn’t until the next century that his ideas were accepted.

The following shows other three similar cases. Use the word prompts to create sentences that describe the ideas of each of them. In each case, you must write at least two sentences in past simple by conjugating the underlined verbs in that tense.

1 Ignaz Semmelweis, handwashing, discover, infection, doctor, hospital, reduce.

2 Gregor Mendel, inherit, experiments, plants, peas, carry out, genes

3 Aristarchus, the Sun, mathematician, the Earth, is, orbit, propose

• What properties of matter do the materials expelled by the volcano have?

WHAT COMES OUT OF A VOLCANO?

It’s time to organise your ideas and search for any missing information.

• What is a volcano?

• What does a volcano expel?

• Is the material in solid, liquid or gas form?

• What happens when the mass of magma reaches the sea? Have you heard of neutralisation?

• What is the chemical composition of lava?

• What about gases? What gases does a volcano expel?

Do some research.

SCIENTIFIC POSTER.

Use the online tool to create a poster to explain your model. Create an outline with all the information from activities 1 and 2. Don’t forget that the information has to be related to the volcano you are going to design.

+ for guidelines, go to anayaeducacion.es

THE PROPERTIES OF MATTER

As you already know, we are surrounded by matter and it can be found in different states.

Matter is anything that has a fundamental property called mass and which occupies space, or volume.

When we refer to matter with precise limits, we use the term object or body. The body may be regular (with a known geometric shape like a sphere, cylinder or cube), or irregular (like a stone). To refer to matter that has no definite limits, we typically use the term ‘material system’. For example, fluids or a sand dune are material systems.

To describe an object or material system, we need to know its properties. We can distinguish between:

• General properties. These are properties that we can use to distinguish matter from non-matter, but are insufficient for telling apart different types of materials. This includes length, mass, volume, surface area and temperature.

• Characteristic or specific properties. These are properties that enable us to distinguish between one type of matter and another. They include density, phase change temperatures, electrical conductivity, thermal conductivity and many others.

1.1 General properties: mass and volume

As we will study in the future, mass is related to different variables, such as the amount of substance, the force of attraction that the Earth exerts on the object (the weight) or the difficulty in changing a state of movement (stop or change direction).

Mass related to the quantity of matter an object or material system has. It is a basic or fundamental quantity.

We measure mass with a balance and its SI unit is the kilogram, kg.

Types of scales

To measure the mass of an object, the object is placed on one pan and weights are placed on the other, from highest to lowest value, until the scales are balanced. The mass of the object is the sum of the masses of the weights used.

In this case, the object is placed on the pan, and the weights on the guides are moved, from the higher to the lower values, until the scales are balanced. The mass of the object is the sum of the values indicated in the weights’ position.

Its operation is much simpler than that of analogue scales. The object is placed on the pan and, by means of sensors, its mass is measured by the action of the weight force. The measured value is shown on the digital display.

Two-arm scales

One-arm scales

Digital or electronic scales

The other general property of matter is volume, i.e., the space it occupies. This is a derived quantity. Its SI unit is the cubic metre, m3

Volume is the space occupied by a body or a material system.

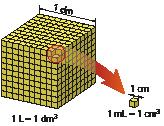
To measure the volume of a liquid, it must be placed in a container. The maximum volume that a container can hold is known as its capacity; the unit of capacity is the litre (L).

A litre is the maximum volume that a cubic container with a side length of 1 dm can hold. We often use multiples and submultiples of the litre:

1 L = 1dm3; 1 mL = 1 cm3; 1 kL = 1m3

To measure different volumes of liquids, we use graduated instruments, such as graduated cylinders, pipettes or burettes; however, to measure specific volumes of liquids, we use volumetric instruments, such as volumetric flasks and pipettes whose capacity corresponds to the volume measured.

Find out more about lab equipment for measuring volumes of liquids in the presentation on anayaeducacion. es

Understand, think, investigate...

1 Think and share in pairs. Is light matter? Answer this question by giving arguments based on the general properties of matter.

2 Which quantity has been measured in the picture above, and is the measurement expressed in SI units? If your answer is no, write the value of that measurement in SI units.

The volume of an irregular solid Is the same as the volume of water it displaces; it is obtained by subtracting the volumes of water with and without the solid introduced. The volume of a regular solid is obtained by measuring its dimensions and applying the corresponding mathematical expression; for example, the volume of a cylinder of radius r and height h is:

3 Not all glassware in the laboratory is used to measure volumes. Identify in the left photograph the glassware containers that have other uses, draw them, and explain what they are used for.

4 A common mistake is to confuse the centilitre, cL, with the cubic centimetre, cm3. Using the equivalences we have seen, indicate the relationship between these units.

Measurement of volumes of liquids and solids

DENSITY OF SOME TYPES OF MATTER

1.2 A specific property: density

The value of this property, which is a derived quantity, allows us to distinguish between substances.

Density is the relationship between the mass of an object or fluid and the volume it takes up.

In mathematical terms, we write this relationship as a ratio (quotient):

In the formula above, m is the mass, which has units of kg in SI, and V is the volume expressed, in m3, so d is the density, which has SI units of kg/m3

In everyday language we tend to misuse the concept of density; for example, when we say that “something floats on water because it weighs little” we are only indicating that it has a low mass. This is incorrect, because for one material system to float on another, the mass to volume ratio of the former must be less than that of the latter, i.e., the former must be less dense than the latter.

1 Design a way to determine the material of which two objects are made, if we suspect that one of them is made of iron and the other of lead.

Data:

Object A: mass = 36.2 g; volume = 3.20 mL

Object B: mass = 33.8 g; volume = 4.30 mL

One way is to calculate the density of each and compare the results with the densities of iron and lead.

To obtain the density in SI units, we must express the mass and volume in their corresponding SI units, kg and m3, respectively.

To obtain the mass in kg, divide by 103:

mA = 36.2 g = 0.036 2 kg = 3.62 · 10–2 kg

mB = 33.8 g = 0.033 8 kg= 3.38 · 10–2 kg

Understand, think, investigate...

5 Use the conversion factors and scientific notation to change the units of the measurements given in the previous exercise.

6 Circle of points of view. Indicate how you would measure the volume of the objects of the Problem solved. Why do you think this data is expressed in mL?

7 Could you store 8 kg of ethanol in a 7 L cylinder? Will there be too much or too little ethanol?

We know that 1 mL = 1 cm3. To express the volume in cm3, we will have to divide by 106:

VA = 3.20 mL = 3.20 · 10–6 m3

VB = 4.30 mL = 4.30 · 10–6 m3

Dividing mass by volume, we obtain the density:

Comparing these results with the table, we can see that material A corresponds to lead and B to iron.

8 Revolving sheet. Balsa wood (Ochroma piraminade) is a highly sought-after wood, as it is not very dense (d = 160 kg/m3) and yet it is very strong. What applications do you think this type of wood has?

9 Calculate the mass of a surfboard with a volume of approximately 60 dm3 using the data from the previous activity.

1.3 Measuring density

Direct measurement of density

The density of a liquid can be measured directly using a density meter: a glass instrument consisting of a hollow cylinder with a weighted bulb at one end that can float vertically. To measure the density value, place it vertically in the liquid and allow it to float freely. When it is still, read the value on the measuring paper.

Indirect measurement of density

Density is a derived quantity, so it can be calculated from the values of the quantities that define it, mass and volume. To do this, measure the values of the mass and volume of the body independently, and calculate the value of their quotient to obtain a value for the density.

To measure mass, a balance is used. To measure volume, we will need different instruments depending on whether we are dealing with a regular solid, an irregular solid, or a liquid.

• Guidelines for using a balance

We can use analogue scales (one or two arms) or digital scales. Their use has already been described above. The zeroing error must be avoided: when the pans are empty, the balance must read zero. There are screws at the ends of the arms to adjust them. In the case of electronic scales, they must be set to zero each time a weighing is performed.

• Guidelines for using a cylinder

When using graduated instruments, such as a cylinder, it is important to avoid the parallax error (see picture below).

Investigating the densimeter

Experimental method

Look at the photo. What property is the density measurement based on? Research buoyancy and share your findings with your group.

Maths

CREATE

Create a visual reminder of the rounding off rules when dividing.

m = 24 g = 0,024 kg

V = 8 mL = 0,000 008 m3

Using a balance, measure the mass of the object whose density we want to know.

Using a measuring cylinder, calculate its volume (you will find instructions on anayaeducacion.es)

Finally, we divide the mass of the object by its volume, and apply the rounding off rules.

PURE SUBSTANCES AND MIXTURES

When we study fluids, we can find two different situations: pure substances, substances that aren’t mixed with other substances, or a mix of several pure substances.

A pure substance is a type of matter that cannot be decomposed into simpler ones by physical methods. A mixture is a fluid formed of several pure substances that we can separate using physical methods.

2.1 Pure substance: simple and compounds

There are two types of pure substances: simple (or elementary) substances, and substances that we call compounds:

• Simple substances are substances that are made up of atoms of the same chemical element, so they cannot be broken down by chemical change (no new ones are formed).

For example, O2 is a simple substance made up of only the chemical element oxygen, O.

• Compounds are substances that can be broken down into other substances by chemical methods.

The specific case of water is explained in the following table.

Pure

Simple substance

Gold is a simple substance, so its characteristic properties are constant. Moreover, it does not decompose upon chemical change.

Compound substance

Many medicines are compound substances that break down into more simple substances when they are swallowed, injected, etc. To ensure they work properly, we must always follow the doctor’s instructions.

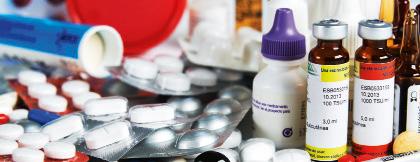
During the process of electrolysis (which you will study later), the action of an electric current breaks down water, H2O, into two simple substances: hydrogen, H2, and oxygen, O2. This is a chemical change.

2.2 Heterogeneous mixtures

The substances that make up this type of mixture are sometimes distinguishable at first glance. Their physical properties vary from one part to another, which is why they are called heterogeneous. Heterogeneous mixtures exist in the solid state (figure below) as well as in liquid and gaseous states. Some of these mixtures are suspensions, which will be discussed later.

2.3 Homogeneous mixtures

Such mixtures are also called solutions. At first glance, we cannot tell the difference between a pure substance and a homogeneous mixture, as their properties are the same in every place. Solutions can be in solid, liquid and gaseous states (the box below shows an example of each case).

In order to know whether we are dealing with a solution or a pure substance, we must somehow cause the separation of the substances that form the mixture, or we must know their composition beforehand.

In order to achieve the separation of the components of the mixture, the change of state of one of them is usually caused by heating the mixture.

Types of mixtures

Understand, think, investigate...

10 Round table. Bottled water usually has a chemical analysis on the label that gives information about the substances present. Can we say that it is a pure substance? Explain your answer.

11 Chain of consequences. Is milk a pure substance? Design a method to test your answer and represent its stages and conclusions.

12 The mirror. Explain the difference between a mineral and a rock. Which is a pure substance and which is a mixture? Give an example of each.

13 Find out about the origin of the word “electrolysis” and relate it to the picture on the previous page. What are the applications of the electrolysis of water?

Sand: heterogeneous mixture

Steel: alloy (solid solution)

As can be seen at a glance, the different materials that make up the sand can be distinguished, as they have different sizes, textures, colours, etc.

Drinking water: liquid solution

Drinking water is a liquid solution of salts and water. If we were to ingest pure water, this would cause an imbalance in our body.

Air: gaseous solution

Air is a mixture of gases. It is a gaseous solution. Its composition is approximately 79% nitrogen and 21 % oxygen.

Steel is a solid solution of iron and carbon. Solid metal solutions are called alloys. Their properties are different to those of their components. For example, they are tougher and lighter.

The different properties of alloys mean they are commonly used in the construction and automobile industries, and in implants and prosthetics, among many other things.

People have used some alloys since ancient times and they are still found in everyday objects. These include:

• Bronze: a mixture of copper and tin.

• Brass: a mixture of copper and zinc.

• Nickel silver: a mixture of copper, nickel and zinc.

LIQUID SOLUTIONS

3.1 Dissolutions

As we have already seen, homogeneous mixtures of several pure substances are also known as solutions. In all solutions, the components that make up the solution are given the following names:

• Solvent, which is the substance that is in the greatest proportion in a solution. If we are dealing with a solution in which water is present, known as aqueous solutions, we always consider water as the solvent, even if it is in a smaller proportion.

• Solute, which is the substance that is dissolved in the solvent. It is usually found in smaller proportions than the solvent. We can have more than one solute in a solution.

There are solid, liquid and gaseous solutions. The table on the left shows examples of solid, liquid and gaseous solutions; in the rest of the section, we will study the preparation and characterisation of liquid solutions. In the resource bank on anayaeducacion.es you will find an informative presentation on the lab equipment you need to prepare a liquid solution.

Method for preparing a solution

A four-step method is used to prepare a solution of a solid in a liquid in the laboratory. For example, consider the preparation of a solution of 4 g of solute in 100 mL of solution:

1. Measure the mass of solute using a balance, trying to be as accurate as possible.

2. Pour the solid into a beaker, and dissolve it using distilled water.

3. Transfer the solution from the beaker to the volumetric flask using the funnel.

4. Finally, using a wash bottle and a dropper, add distilled water up to the mark.

3.2 Concentration of a solution

We can find solutions that have the same substances but in different proportions. So we say that they have different concentrations.

The concentration of a solution is the amount of solute in a certain amount of solution.

In the example we have just seen on the previous page, the concentration is written as mass/volume and we can calculate it as follows:

14 Air consists mainly of nitrogen (79 %); the major solute is oxygen. Does air contain more solutes?

15 Work with the concentration simulation available on anayaeducacion.es. Calculate the concentration, expressed in g/L, of the solution in the photographs on the previous page.

where m s is the mass of the solute in grams, VT is the total volume in the solution in litres, L, and C is the concentration in grams per litre, g/L.

3.3 Diluted, concentrated, and saturated solutions

If a solution has a higher concentration than another, we say that the first one is a more concentrated solution and the second is more diluted.

If a solution has the maximum possible concentration, the addition of more solute causes it to no longer dissolve; we will then have a saturated solution. If we add more solute to a saturated solution, we will obtain a precipitate, which is solute that cannot dissolve.

The solubility is the concentration of the saturated solution. The value of this concentration depends on the solute, the solvent and the temperature.

16 Compare the mathematical expression of density with that of concentration. What similarities and differences do you find? Are they the same quantity? Draw a Venn diagram with your answer.

If the concentration of a solution is much less than the solubility, the solution is diluted.

When the concentration approaches the solubility, we call it a concentrated solution.

When it reaches the solubility, the solution stops dissolving solute and the solute precipitates.

It isn’t possible to dissolve more solute at that temperature and in that volume of solvent. The solute precipitates

TECHNIQUES FOR SEPARATING MIXTURES

4.1 For heterogeneous mixtures

There are a variety of techniques that allow separating the components of a heterogeneous mixture. They are all physical methods based on the different value of a property of the components of the mixture, such as whether they are in the same or a different state of aggregation, their density, or their size. Some of them are shown in the box below, although there are many others that you will learn about later.

Techniques for separating heterogeneous mixtures

This consists in the separation of the components of a heterogeneous mixture if they have different densities. It may be a mixture of immiscible liquids (which do not dissolve, such as water in oil), or of a solid suspended in a liquid or gas.

For two immiscible liquids, pour the mixture into the separating funnel, as in the figure. After a certain time, the less dense liquid floats. Then, open the tap to separate the denser liquid, which can be collected in a beaker.

If we have a mixture of a solid and a liquid, it will be possible to separate the larger particles of the solid using a filter, or a filter medium.

The filter paper in the image retains the solid particles, while the water passes through it.

The separation is obtained because the components of the mixture have different densities.

In this case, the mixture goes through the action of a centripetal force, caused by a high-speed rotary motion.

This technique is used to separate heterogeneous mixtures for which decanting or filtration is not sufficient, e.g., to separate plasma from blood.

4.2 For homogeneous mixtures

Separation techniques for homogeneous mixtures allow the solvent to be separated from the solute or solutes. The two most commonly used ones are described below.

This technique is indicated when we have a solid solute, such as a salt, dissolved in water.

It consists of evaporating the solvent to obtain a saturated solution, in which the solid will begin to precipitate. To do this, pour the solution into a crystalliser. Once the solvent has evaporated, we will have salt crystals.

DISTILLATION

Distillation allows separating a solution consisting of two liquids with different boiling temperatures.

Place the solution in a round-bottomed flask and heat it. When the boiling temperature of the most volatile substance is reached, it changes to a gaseous state. The vapours generated pass into the inner tube of the coolant, where they condense and are collected in the collector. Cooling water flows through the outer coolant tube, which cools the vapours without coming into direct contact with them.

Review the presentation on anayaeducacion. es again to remind yourself how to use the lab equipment.

Understand, think, investigate

17 Make a hierarchical diagram with the classification of mixtures and the separation techniques that can be used in each case according to the state of aggregation of the substances that form the mixture and the property on which each separation technique is based. Use the diagram on the right.

18

Thinking heads. You have a sample of a residue consisting mainly of sand and water. You also observe a viscous liquid in this mixture that appears to be oil. You are asked to determine whether there are also dissolved salts. How would you go about separating the components of this mixture?

Types

SUSPENSIONS AND COLLOIDS

We have seen that a homogeneous mixture is one in which it is not possible to distinguish its components with the naked eye. However, sometimes we may mistakenly think that a mixture is homogeneous when, in fact, we are dealing with a suspension or a colloid.

5.1 Suspensions

Consider, for example, a finely divided solid (powder), which is dispersed in a liquid or gas. In the absence of agitation, and given enough time, the solid settles and falls.

In this case, it is a heterogeneous mixture known as a suspension. The most common suspensions are of solids in gases or liquids. The phase in which the dispersion occurs is called the dispersing phase and the solid that is suspended is known as the phase separation.

5.2 Colloids

A mixture with intermediate characteristics between a suspension (heterogeneous) and a solution (homogeneous) is known as a colloid.

In this case, the particles do not settle at the bottom after some time. These are particles smaller than 100 nm, which are very difficult to separate from the dispersing phase.

Strictly speaking, a colloid is neither a solution nor a heterogeneous mixture. However, in many cases, the terminology used for solutions is used for colloids. For example, we speak of solute to refer to the substance that is in the smallest proportion in this mixture.

There are colloids formed by the dispersion of a solid or liquid in a gas or liquid, or by condensation of a gas in another gas phase, as in the case of clouds.

Everyday examples of suspensions and colloids

Antibiotics for children are not soluble in water. They are prepared by making a suspension of the medicine in water, so that they can be administered in liquid form.

An example of a colloid is homemade gelatine. There are many examples of colloids in the kitchen, as not all substances dissolve in the solvent.

Suspension

Colloid

Designing an experiment

Based on what you have learnt about the Tyndall effect, can you design an experiment to demonstrate that jelly is really a colloid? Describe your experiment.

The solid particles that form a colloid are larger than those of the solute that is dissolved in a solution. These particles are therefore able to change the direction of propagation of light, scattering it. This is because each of the small particles that make up the scattered phase acts as a light emitter, causing its direction to change, so that the light rays can be seen. This phenomenon is known as the Tyndall effect. It can be observed clearly in partly cloudy skies, as clouds are an example of a colloid.

Understand, think, investigate

19 Check. Which technique would you use to separate the components of these mixtures? Are they solutions, suspensions or colloids?

a) Salt water.

b) Dust cloud.

c) Milk.

d) A blood sample.

e) Wall painting.

20 Write a definition for the following terms: suspension and colloid. Look up the term ‘emulsion’ and explain its meaning in your own words. Give an example of each using material systems that are present in your home.

21 Assembly of ideas. Mayonnaise, like milk, is an emulsion. One version of this sauce is made from milk and olive oil. Why do you think it is necessary to whisk the mixture to obtain the sauce? What happens when we say that the sauce has been “curdled”?

22 Find the following materials at home and classify them as homogeneous, heterogeneous or colloid mixtures:

a) Juice made from concentrate.

b) Whole milk.

c) Deodorant spray.

d) Chamomile tea.

e) Hydrogen peroxide.

f) Body lotion.

g) Cream.

How to differentiate a colloid from a solution

SCIENCE WORKSHOP

Recreational science

Solid

or viscous liquid?

Analyse

• If we pour water, oil or honey on a surface, what happens? You can see that their behaviour is quite different: water, when poured, spreads more than oil and honey. This is because water is less viscous.

• If you have played with green slime, you may have noticed that it behaves differently from liquids and solids.

Introduction

One of the characteristics that allows us to recognise the three states of aggregation is viscosity, i.e., the resistance to flow of a gas or liquid. In the following experiment we will learn how to identify it.

Materials

• Starch powder • White glue • Food colouring • Water • A spoon • A glass • A bowl • A self-sealing bag.

Build

We are going to make homemade green slime.

• In half a glass of warm water, dilute a teaspoon of starch.

• In a bowl, add one tablespoon of this solution and two tablespoons of white glue. A few drops of food colouring can be added.

• Stir the mixture, first with a spoon and then with your fingers. Place the resulting paste in the self-sealing bag and put it in the refrigerator.

Experiment

• Does the paste flow more or less easily than honey? And compared to oil? Is it a liquid or is it a solid? Is viscosity the same as density?

• Pour the paste carefully into a glass and make it slide. Measure the time it takes to reach the edge. Do the same with the oil and the water; in this way, we can compare the viscosity of these materials.

• Knead the paste with your hands and roll it into a ball. We observe that the more force that is applied, the less it behaves like a liquid, i.e., its viscosity increases.

Conclusions

The paste we have prepared behaves like a very viscous liquid. Moreover, its viscosity increases when we subject it to some kind of stress, such as tensions, torsion, or if we hit it. This is why we say that some fluids, such as the one we have made, can behave like solids. These fluids are called non-Newtonian fluids, and they are very common. Look up information on everyday non-Newtonian fluids, and relate it to the behaviour of ketchup and chocolate.

Practical work

Solution, colloid or suspension?

Statement of the problem

The aim of this practice is to classify mixtures of everyday substances into solutions, colloids and suspensions.

Your proposal

How can we distinguish a suspension from a solution? And a solution from a colloid? What tests can we use to determine whether we are dealing with one of these types of mixture?

Our proposal

We will look at some properties that allow us to differentiate between suspensions, solutions and colloids:

• If the mixture separates into layers when not stirred for a certain time.

• If the complete mixture passes through filter paper, or instead part of it remains unfiltered.

• Whether it is transparent to the light of a laser pointer or whether, on the contrary, it causes this light to be scattered and can then be observed.

Materials

• Water

• Flour

• Cylinder

• Coffee

• Beakers

• Milk

• Filter paper

• Laser pointer or torch.

• Funnel

• Balance

Preparation of the mixtures

Prepare three different mixtures: one of water and flour, one of water and coffee, and one of water and milk. For the latter two, use only a few drops of coffee or milk.

Sequence of tests

• Filtration. First, pass the mixtures through the filter paper, using the funnel (set-up shown in section 4). Observe whether there are differences between the appearance of the original mixture, the filtrate, and the part retained on the filter paper.

• Sedimentation. Then allow the samples to stand, each in a different container, for several hours. Observe if there are any differences before and after the standing time.

• Tyndall effect. Shine the light of a laser pointer through the mixtures. To see it better, turn off the lights in the laboratory. Observe whether or not the light beam is visible as it passes through the mixture.

Were the components separated by filtration?

Did we observe the Tyndall effect?

1 Using the diagram above, draw conclusions about the experiments you performed.

2 Explain why it is possible to see the light beam through a colloid and a suspension.

Water and flour (separate)

Water and coffee

Water and milk

CHALLENGES THAT LEAVE THEIR MARK

UNDERSTAND

Organise your ideas Hierarchical concept map General properties

1 Work with the diagram. Copy the diagram in your notebook and include new branches and boxes based on these ideas:

• Include three examples of simple substances and compounds.

• From the table “Homogeneous mixtures or solutions”, include a branch to describe the particularities of aqueous solutions and another with the concept of concentration and the types depending on the amount of solute present.

• Mass

• Volume

•

•

• Decanting

• Filtration

• Distillation

Remember that you can find the answers to all calculation activities on anayaeducacion.es

Properties of matter

1 Indicate whether the following are measures of mass, density, volume or none of the above:

a) 3 kg b) 4 cL c) 27 m3 d) 3 g/L e) 690 mm

2 How many 7 L bottles are needed to fill a 3 m3 swimming pool? Could we install it on a terrace supporting a maximum mass of 1 500 kg? Water density = 1 kg/L.

3 Bearing in mind that the thermal conductivity of wood is much lower than that of metals, explain why frying pans are made of metal, while their handles are usually made of wood. Is thermal conductivity a characteristic property?

4 Logic wheel. We have two rods of different materials, both of the same length and volume. If one of them has more mass than the other, can we know which material it is made from? Assume we are given the values of the quantities mentioned in the statement of the problem.

Pure substances and mixtures

5 Classify these materials according to whether they are pure substances, homogeneous mixtures or heterogeneous mixtures:

a) Air b) Quartz

c) Iron d) Orange juice

6 1-2-4. Indicate the difference between a chemical substance and a chemical element.

Solutions

7 In the laboratory, we prepared a solution containing 70 g of alcohol in 100 mL of water. Indicate which is the solute and which is the solvent.

8 Calculate the concentration of the solution of the previous exercise, expressed in g/L.

9 If we prepare another solution, but in this case using 20 g of alcohol, will it be a more concentrated or more dilute solution than the previous one?

10 Circle of viewpoints. Do mixtures exist in the solid state? Are they homogeneous or heterogeneous mixtures?

11 What laboratory equipment do you need to prepare an aqueous solution of 10 g of salt per 250 mL of solution? What is the concentration of this solution?

12 Nominal group. Can we compare the solubility of two salts in water? Design a method for testing which of the two salts is more soluble.

13 When we prepare homemade lemonade with sugar, sometimes, when we refrigerate it, we notice that there is a large deposit of sugar at the bottom of the container containing the lemonade. Can you explain this? Remember that solubility varies with temperature.

LEARNING SITUATION

REFLECT

14 The solubility of gases decreases with increasing temperature. Use this to explain why fish are killed by warm water spills.

Separation techniques for mixtures

15 Indicate the names of these materials and whether they are used in separation techniques for homogeneous or heterogeneous mixtures. a) b)

16 Design a method for separating a mixture of oil, vinegar and salt. Explain the material you would use, the steps you would follow and the purpose of each step.

17 On what property is separation by decantation based? Could we separate water from salt using this technique? Explain your answer.

18 We have a suspension of a solid, whose particles have a very small size (powder), in water. We place this suspension in a container and observe that it takes a long time for the particles to settle to the bottom. Which separation technique would you use to speed up the process?

You have created the first part of your poster, so you can start to think about how to improve your skills. Do the self-assessment on anayaeducacion.es and ask at least two people from other teams to assess you as well. When you assess another person, you can indicate their level, but also offer them ideas to improve certain areas.

Aspects Yes With help Not yet

I was able to make a thorough and detailed study of a volcano.

TEST YOUR SKILLS

Carry out the competency assessment included at anayaeducacion.es

© GRUPO ANAYA, S.A., 2023 - C/ Valentín Beato, 21 - 28037 Madrid.

All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior permission of the publishers.