Butlletí de la Societat Catalana de Matemàtiques

BUTLLETÍ

DE LA SOCIETAT CATALANA DE MATEMÀTIQUES

Institut d’Estudis Catalans

Volum 37 • Número 2 • Desembre 2022

BARCELONA 2022

© dels autors dels articles

Editat per la Societat Catalana de Matemàtiques filial de l’Institut d’Estudis Catalans Carrer del Carme, 47 08001 Barcelona

Text original revisat lingüísticament per la Unitat d’Edició del Servei Editorial de l’IEC Compost per Rosa M. Rodríguez

Imprès a Ediciones Gráficas Rey, SL

ISSN: 0214-316-X

Dipòsit Legal: B 19272-1987

Els continguts del Butlletí de la Societat catalana de MateMàtiqueS estan subjectes —llevat que s’indiqui el contrari en el text, en les fotografies o en altres il lustracions— a una llicència Reconeixement - No comercial - Sense obres derivades 3.0 Espanya de Creative Commons, el text complet de la qual es pot consultar a http://creativecommons.org/licenses/by-nc-nd/3.0/es/deed.ca. Així, doncs, s’autoritza el públic en general a reproduir, distribuir i comunicar l’obra sempre que se’n reconegui l’autoria i l’entitat que la publica i no se’n faci un ús comercial ni cap obra derivada..

ButlletídelaSocietatCatalanadeMatemàtiques Vol.37,núm.2,2022.Pàg.101–136. DOI:10.2436/20.2002.01.104

Polinomis,polítopsipuntsd’equilibridexarxes dereaccions

ElisendaFeliu

Resum: Enaquestarticlefemunaintroduccióalateoriadel’estudidelspunts d’equilibridexarxesdereaccions,totcentrant-nosenexemplesqueprovenendelmón delabiologiamolecular.Elspuntsd’equilibrisónlessolucionspositivesd’unsistema d’equacionspolinòmiquesqueconténombrososparàmetres.Undelsobjectiusdela teoriaésestudiarelspuntsd’equilibricomafunciódelsparàmetres,ienparticular determinar-neelnombre.Aquestsproblemestrobensolucionseneinesprovinentsde lageometriaalgebraica(real)il’àlgebracomputacional,peròlesparticularitatsdels sistemesqueprovenendexarxesenspermetensovintobtenirresultatsmésprecisos. Enaquestarticleexplicaremalgunsresultatsefectiusrecentsenaquestaàrea,enquè l’estudidelsistemaidelesregionsdeparàmetreséspossiblegràciesal’estudidela geometriad’unpolítopassociatalsistema.

Paraulesclau: xarxadereaccions,multiestacionarietat,biestabilitat,polítopdeNewton, positivitat,geometriaalgebraicareal.

ClassificacióMSC2020: 92C45,34E15,80A30,13P10.

1Introducció

Elspolinomismultivariatssónfuncionsqueapareixenfreqüentmentenestudismatemàticsienaplicacionscoml’estudidefenòmensrealsomodels enenginyeria.Ensónexemplesdestacableselsmodelsenrobòtica,enquèla configuracióespacialdelscomponentsdelrobotespotdescriuremitjançant polinomis,encriptografia,enl’estudidepuntsd’equilibridesistemesdinàmics descritsperpolinomis,oenestadística,enquèmodelscomunsesbasenen,o espodenreescriurecomaexpressionspolinòmiques.

Dinselmóndelesmatemàtiques,l’estudidelconjuntdelessolucions desistemespolinòmicsdonallocala geometriaalgebraica,enquèaquests conjuntss’anomenen varietatsalgebraiques.Trobemresultatsmoltbonics iconcisossobrelessolucionscomplexes,iresultatsencaraméspotentssi passemal’anomenat espaiprojectiu,ontenimsolucionsal’infinit.L’exemple clàssicéselteoremafonamentaldel’àlgebra,queensdonaelnombreexacte

d’arrelsd’unpolinomi,comptadesambmultiplicitat,nomésmirantelgraudel polinomi.Endiversesvariables,tenimelteoremadeBézoutperasistemesamb unnombrefinitdesolucionsal’espaiprojectiucomplex[65,capítol2],que ensdiuqueaquestnombreéselproductedelsgraustotalsdelspolinomisdel sistema.Sobre C \{0},elteoremadeBernsteinensdonaunacotadelnombre desolucions,tottenintencomptelaconfiguracióespacialdelsexponentsdels polinomisdelsistema[6].Lacotaés,amésamés,elnombregenèricde solucions.

Perexemple,peralsistema

entindrem2ambcoordenadescomplexesnonul.les.

Quanpassemalsnúmerosreals,aquestateoriatansenzillad’enunciar(però nodedemostrar)esdesmunta.Janomésambunavariableveiemquelahistòria vaperunaaltrabanda:elpolinomi xm 1té m arrelscomplexes,perònomés unaoduesdereals,depenentdelaparitatde m.Engeneral,esdedueixde laregladelssignesdeDescartes[25, 72]queelnombred’arrelsrealsnonulleséslinealenelnombredemonomis.Endiversesvariablestrobemtambé cotescomplicadesquefanreferènciaalsmonomis.Enaquestscasos,però,no existeixlanociódegenericitat:elssistemesdepolinomisreals,enprincipi, notenenunnombredesolucionsconstantperaquasitotselsvalorsdels coeficients.Tenim,alcontrari,regionsonelnombredesolucionsésconstant,i lafronteradelesregionsvedonadaperl’anomenatdiscriminant.Perexemple, unpolinomidegraudostindràzerooduesarrelsreals,depenentdelsigne deldiscriminant,iaixòpassaenregionsdel’espaidecoeficientsobertesenla topologiaeuclidiana.

Peracabardecomplicarlahistòria,sielsnostrespolinomismodelenabundàncies,comsovintpassaambsistemesdinàmicspolinòmics(ienaquest article),aleshoresensinteressenlessolucionsrealsipositives.Perexemple, sienelsistema (1) enscentremnomésenlessolucionspositives,aleshores, independentmentdelsvalorsdelsparàmetres,entindremuna.Enaquesta situaciótenimalgunescotessobreelnombredesolucionstambé[10],algunes debasadesengeneralitzacionsdelaregladesignesdeDescartes[7, 57].Tenim,però,principalmentalgoritmesqueensdonencertainformaciósobreel possiblenombredesolucionsdelsistemavariantelscoeficients.Elsalgoritmes generalsesbasen,entrealtres,enmètodesd’eliminaciódequantificadorsi descomposicióalgebraicacilíndrica[4].

Comquel’estudidesolucionspositivessorgeixdel’interèsenlesaplicacions,s’hananatdesenvolupantmètodesespecíficsperacadaaplicació,a vegadessensedetectarqueelsmètodessónvàlidsperasistemesmésgenerals queelsqueestrobenenl’aplicació.Aquestarticlesecentraenl’aplicació

al’estudidepuntsd’equilibridexarxesdereaccions.Enaquestcas,tenim unsistemad’equacionsdiferencialspolinòmiques,ielspuntsd’equilibrisón lessolucionspositivesdelsistemadonatpelspolinomis.Aquestsistemaés paramètric,ambparàmetresprovinentsdelesparticularitatsdelaxarxa.Per exemple,lesequacionsenlaprimeracolumnade (1) corresponenaunsistemadepuntsd’equilibrid’unaxarxa.Lesequacionsalasegonacolumna de (1) defineixenunafamíliad’espaislinealsafinsparal.lelsquecontenenla dinàmicadelsistemaambelnivelldeterminatperlacondicióinicial.

L’estudidexarxesdereaccions,demaneraformal,esremuntaalsanys setantaambelstreballsseminalsdeFeinbergiHorniJackson[29, 30, 49], enquèl’interèsestavaprincipalmentenxarxesdereaccionsquímiques.Va serl’origendel’anomenada teoriadexarxesdereaccionsquímiques (CRNT enanglès)[34].Aqueststreballs,continuatsprincipalmentperFeinbergiel seugrupdurantlesdècadessegüents,estudienpropietatsdelesxarxesque esmantenenperatotselsvalorsdelsparàmetresapartird’invariantsde laxarxasenzillsdecalcular[31, 33].Tambétrobemalgoritmesmoltpotents quesóncapaçosdedecidirsilaxarxapotteniralmenysdospuntsd’equilibri positiusenalgundelsespaislinealsafins[32, 51].Aquestsalgoritmesexploren l’estructuraconcretadelsistemaisónmoltmésefectiusqueelsalgoritmes genèrics,quesóncecsaaquestespropietats.

Al’inicidelsegle xxi esvadonarlaconfluènciadedosfactors.Peruna banda,lacomunitatdematemàticsdedicatsal’àlgebraaplicadavacréixer substancialment,ivanaparèixernousmètodescomputacionalsacompanyats d’ordinadorsméspotents.Perl’altra,duesbranquesdelabiologiamolecular vanagafarméspes(labiologiadesistemesilabiologiasintètica),gràciesa lesnovestecnologiesquepermetienrecopilarmoltesmésdadesialeseines experimentalsdesintetitzacióbioquímica.Aixòvaferquel’interèsperl’estudi delspuntsd’equilibridexarxesrevifésis’expandís,araambnovesaplicacions ipreguntesprovinentsdelmónbioquímic.Lesxarxesdereaccionss’estudien desdelpuntdevistaalgebraic,peròtambéanalíticiestocàstic;vegeuper exemple[1,12,13,16,17,23,24,52,61,66].

Unabonapartd’aquestarticles’ocupad’introduirelsobjectespropisde l’estudidexarxesdereaccions,bàsicamentcentrant-nosenquèésunaxarxa, icoms’estudialavariaciódelesconcentracionsdelessevescomponentsen eltemps.Introduiremmodelsimportantsensenyalitzaciócel.lular,queens serviranperail lustrarlateoria,itambéperaplantejarpreguntesobertes.En lasegonapartdel’articleenscentremenl’estudidela multiestacionarietat, ésadir,l’existènciadevalorsdelsparàmetresperalsqualshihaalmenys dospuntsd’equilibri.Enparticular,veuremalgunsresultatsperentendrela regiódeparàmetresonaixòpassa.Aquestaqüestióestàllunydeserresolta demaneraefectiva,iperaxarxessenzillesaquestaregióencaranoesconeix. Recentment,s’haproduïtunimpulsgràciesal’úsderesultatsquerelacionen propietatsdepolinomisambobjectespolièdrics(comaraelpolítopdeNewton). Enaquestarticleenscentremenalgunsd’aquestsresultats,quecomptenamb lacontribuciódel’autora.

2Xarxesdereaccionsilasevadinàmica

2.1Xarxesdereaccions

Començaremintroduintelsobjectesprincipalsd’aquestarticle,quesónels sistemesd’equacionspolinòmiquesquedescriuenelspuntsd’equilibrid’una xarxadereaccions.Unaxarxadereaccionsésinformalmentunacol.leccióde reaccionsentrecertes espècies.Perexemple,si X1 i X2 sónduesespècies,una xarxa(fictícia)dereaccionspodriaser

X1 X2 2X2 2X1 X1 + X2 2X2 (2)

Segonslaxarxa, X1 esconverteixen X2 mitjançantlaprimerareacció,dues unitatsde X2 interaccionenperproduir-neduesde X1,ifinalment X1 i X2 interactuenperformarduesunitatsde X2.

Lesespèciespodenser«qualsevolcosa»queinteraccionaambaltres.Per exemple,podemtenirunaxarxadereaccionsbioquímiques,onlesespècies sónproteïnes,RNAoaltresmacromolècules.Aquestesxarxessovintestan involucradesensistemesdesenyalitzaciócel lular,isónlesquefaremservir d’exempleenaquestarticle.Unmecanismehabitualapareixenlaxarxa

A + K AK Ap + K, (3)

on s’usaperarepresentarduesreaccionsendireccionsoposades.En aquestaxarxa,tenimunaproteïna A (anomenada substrat)queinteractuaamb unaaltraproteïna K (anomenada quinasa),ifruitdelainteracció,ungrup fosfat(marcatambelsubíndex p)s’adjuntaalaproteïna A.Aquestprocés esdiu fosforilaciócatalitzadaperunaquinasaviaelmecanismedeMichaelisMenten;anàlogament,trobemelprocésdedesfosforilació.Aquestmecanisme defosforilacióésmoltcomúeneucariotes.Unmecanismesimilar,habitualen bacteris,consisteixenungrupfosfatque«salta»d’unaproteïnaaunaaltra fruitd’unainteracció.Unmodelmoltsimpled’unmecanismeambaquestes característiquesvindriadonatperlaxarxa

onveiemque HK passaelgrupfosfata RR.Laproteïna HK ésuna quinasa histidina,iRRésun reguladorderesposta.

Peròlesespèciespodenserdemoltsaltrestipus.Trobemxarxesdereaccionsentrepersones,perexemple,enmodelsepidemiològics,moltconeguts arapopularmentdegutalapandèmiaglobalrecentdecovid-19.Elsistemamés clàssicésl’anomenat SIR,onhihatresespècies: S (personessusceptiblesde serinfectades); I (personesinfectades); R (personesrecuperadesomortes).La xarxaenaquestcasés:

Lesespèciestambépodenseranimals,comenelsmodelsd’interaccióentre espèciesqueinclouenelmodelclàssicdeLotka-Volterra:

0 CC + G 2GG 0.

Enaquestmodel,la C representaunapresa(C deconill)ila G unpredador(G deguineu).Segonslaxarxa,elsconillsilesguineusesreprodueixen iesmorenrespectivamentdeformaexponencial.Lesguineusmengenconillsperreproduir-seid’aquestamaneratenimreduccióicreixementdels conillsilesguineus,respectivament.

Finalment,noensoblidemdemencionarquelesxarxespodenserentre espèciesquímiques!Unareacciómoltconegudaéslaformaciódelesmolècules d’aigua 2H +

Arajapodemdefinirdemaneraformalquèentenemperunaxarxade reaccions.D’araendavant,peraunconjuntfinit X={X1,...,Xn},elselementsde ZX ≥0 elsidentificaremambcombinacionslinealsformalsde X1,...,Xn ambcoeficientsa Z≥0,ésadir,elementsdelaforma a1X1 +···+ anXn amb a1,...,an ∈ Z≥0 oambvectors (a1,...,an) ∈ Zn ≥0 segonsconvingui.

Definició 1. Una xarxadereaccions sobreunconjunt X={X1,...,Xn} ésun subconjuntfinit R⊆ ZX ≥0 × ZX ≥0.Elselementsde X s’anomenen espècies.Un element (y,y) ∈R s’anomena reacció iesdenotanormalmentcom y y.

Els complexos delaxarxasónelselementsdelconjunt

C={y | y y ∈R obé y y ∈R peraalgun y ∈ ZX ≥0}.

Si y y ∈R ,diemque y ésel reactant delareacció,i y el producte

Peralaxarxa(2),elconjuntdecomplexosés

C={X1,X2, 2X1, 2X2,X1 + X2}.

Entreells, X1,2X2, X1 + X2 sónreactants,i X2,2X1,2X2 sónproductes.Enla notacióvectorial,escriuremelconjuntdecomplexoscom

{(1, 0),(0, 1),(2, 0),(0, 2),(1, 1)}

Unaxarxadereaccions(osimplement xarxa)admetunarepresentacióen formade graf dirigit,enquèelsnodessónelscomplexosilesarestessónles reaccions.Perexemple,laxarxa(2)espotrepresentarambelgraf

quetécincnodes,tresarestesdirigidesiduescomponentsconnexes.L’estudidepropietatsdeladinàmicadelaxarxaapartirdecaracterístiquesdel grafhatingutunrolimportantenlateoriadexarxesdereaccions,sobretot enelstreballsoriginalsdeFeinberg[30, 32, 33].Quanintroduïmlesxarxesen elsexemples,faremservirlarepresentacióengrafocomacol.lecciódereaccionsindistintament.Addicionalment,enelsexemplesconcretsderellevància biològica,lesespèciesesdenotenambelssímbolsqueindiqueneltipusde proteïna,inousant Xi

Totseguitenscentraremenl’estudidela dinàmica delaxarxa,ésadir, encomlesabundànciesdelesespèciescanvienamesuraquetenenllocles reaccions.Unaprimeraobservacióquefareméslasegüent.Cadavegadaque unareaccióocorre,lesabundànciesdelesespèciescanvienrestantelnombre demolèculesdelreactantisumantlesdelproducte.Perexemple,perala xarxa (2),sielnombredemolèculesde X1, X2 és a1, a2,respectivament,si laprimeraolatercerareaccionstenenlloc,tindrem a1 1, a2 + 1molècules de X1, X2

Engeneral,cadareacció y y donallocaunvector y y ∈ Zn,i quanlareacciótélloc,alnombreactualdemolèculescalafegir-li y y.Això indicaque,sienuninicitenimuncòmputdemolècules a = (a1,...,an),a mesuraquelesreaccionsvantenintlloc,latupladelnombredemolèculesviu enl’espaiafílineal

a + y y | y y ∈R

Aquestaobservaciódonallocaladefiniciósegüent:

Definició 2. Donadaunaxarxadereaccions R sobreunconjuntd’espècies X={X1,...,Xn}, l’espaid’estequiometria éselsubespaivectorialde Rn:

S= y y | y y ∈R .

La dimensiódelaxarxa ésperdefinicióladimensióde S iladenotaremamb s.

Enl’exemple(2),lestresreaccionsdonenllocalsvectors

( 1, 1),(2, 2),( 1, 1) (5)

i,pertant,l’espaid’estequiometriaés S= ( 1, 1) .Laxarxatédimensió s = 1.

2.2Dinàmica

Donadaunaxarxa,l’estudideladinàmicadelesabundànciesdelesespèciesde laxarxarequereix,comperatotatascademodelatge,ferhipòtesisiprendre decisionssobreleseinesmatemàtiquesquevolemusariques’escauenenla situacióqueintentementendre.Lesxarxesdereaccionss’estudienambmodels deterministesoestocàstics,entempscontinuoentempsdiscret.Elsmodelsestocàsticss’ajustenseguramentmilloralarealitat,peròtenenunacomplexitat moltsuperioralsmodelsdeterministes,sobretotalsmodelsdeterministes

Polinomis,polítopsixarxesdereaccions 107

ambtempscontinu.Ésperaixòquesovints’usenmodelsdeterministes,amb equacionsdiferencials,enquèhihamolteseinesdisponiblesperalseuestudi. Labonanotíciaésquealgunscomportamentsdelsmodelsestocàsticsespoden deduirapartirdemodelsdeterministesassociats[2, 55].Enaquestarticle enscentraremenunsmodelsbasatsenequacionsdiferencialsordinàriesi autònomes,queaméssónpolinòmiques.

Denotaremamb xi(t) laconcentraciódel’espècie Xi eneltemps t iconsiderarem x(t) = (x1(t),...,xn(t)) elvectordeconcentracions.Enmoltes ocasionslareferènciaaltemps t s’ometrà.Enelsmodelsdeterministes,la variaciódelaconcentració xi(t) eneltempséslasumaponderadadelavelocitatdelesreaccionsqueinvolucren Xi,ambelspesosdonatsperlaproducció netade Xi enlareacció,ésadir,per yi yi silareaccióés y y .Obtenim aixíl’equaciódiferencial

dxi(t) dt = y y ∈R (yi yi)vy y (x(t)),i = 1,...,n,

on vy y (x(t)) éslavelocitatdelareacció y y, quedepèndelaconcentracióactual.

Sisuposemqueelconjunt R={b1 b1,...,br br } estàordenat, podemconstruirlamatriu N ∈ Zn×r ambcolumneselsvectorsdelesreaccions: b1 b1,...,br br .Aquestamatrius’anomena matriud’estequiometria.Llavors, podemescriureelsistemaenformavectorial

onhemomèsl’escripturaexplícitade t ion vi(x) és vbi bi (x).Observeuque lesderivadesviuenenl’espaivectorialgeneratperlescolumnesde N,queés precisamentl’espaid’estequiometria S.

Enl’exemple (2) tenimtresreaccions,iordenemelconjunt R segonsl’ordre enquèapareixena(2).Obtenimelsistema

onlamatriudecoeficientsestàformadapelsvectorsde (5).Equivalentment, tenim

Encaraensfaltaindicarquinaformatenenlesvelocitatsdelesreaccions vi(x),ienaquestpuntcalfernoveshipòtesis,depenentdelmecanismeques’estudiailescondicionsd’ambient.Enaquestarticleassumim

queescompleixla lleid’acciódemasses,introduïdaperGuldberg(químic) iWaage(matemàtic)el1864[46]ienarticlessubsegüents.Segonslallei,se suposaquelesmolèculesestanrepartideshomogèniamentiquelavelocitat reflecteixlaprobabilitatqueduesmolèculesestrobinperatzar.Aquestes condicionsnosolendonar-seenunambientcel.lular,però,totiaixí,aquests modelscontinuenusant-seilesconclusionstenenuncertgraudevalidesa. Addicionalment,altresmodelsmoltcomunsenprocessosenzimàticsixarxes metabòliques,comelsobtingutsapartirdevelocitatsdeMichaelis-Menten, sorgeixendeprocessosdereduccióisimplificaciódemodelsamblalleid’acció demassesatravésdemecanismescoml’anomenat quasiequilibri [21].

Explícitament,segonslalleid’acciódemasses,lavelocitatd’unareaccióés proporcionalalproductedelesconcentracionsdelesespèciesenelreactant.A

i > 0.Comquelesvelocitatssónmonomis,elsistemad’equacions diferencialsresultantconsisteixenpolinomisiaixòensportaaintroduir notacióhabitualprovinentdel’àlgebraenl’estudidepolinomismultivariats.

ConsideremaddicionalmentelproductedeHadamard(componentacomponent):

Sidenotemamb B ∈ Zn×r ≥0 la matriudereactants,ambcolumnes b1,...,br dereactantsdelesreaccionsi κ = (κ1,...,κr ) ∈ Rr >0 elvectordeconstantsde reacció,aleshoreselmonomi (9) s’escriucom κixbi ,iconsiderantles r reaccions,elvectordevelocitatsésprecisament κ ◦ xB .Aixídoncs,elsistema (6) d’equacionsdiferencialsambla lleid’acciódemasses és

dx

dt = N(κ ◦ xB ). (10)

Observemunaparticularitatimportantdelamatriu N:sil’entrada (i,j) és negativa,ésperquè Xi formapartdelreactantdelareacció j-èsima,i,pertant, lavelocitatdereaccióésmúltiplede xi.Aixòimplicaquetotselstermesnegatiusdel’equacióde dxi/dt sónmúltiplesde xi.Consegüentment,si xi(t0) = 0 enalgunmoment t0 d’unatrajectòria,llavors dxi(t0)/dt ≥ 0i,pertant,la concentració xi noesdevindrànegativa.Apartird’aquestaobservacióespot deduirunaspectemoltimportant(iesperable)deladinàmicad’aquestssistemes:sielvectordeconcentracionsinicialpertanya Rn ≥0 (resp. Rn >0),aleshores lesconcentracionsesmantenennonegatives(resp.positives),alllargdetotala trajectòria[70].Enaquestcasdiemqueelsortantspositiusinonegatiussón invariants(entempspositiu).

Elscoeficientsdelsistema (10) sóncombinacionslinealsdelesconstants dereacció κ.Aquestesconstantssónnormalmentdesconegudes,difícilsde mesurar,i,amésamés,hihavariabilitatentreindividusidepenendeles condicionsambientals.Ésd’interès,pertant,estudiarelsistemaperavalors arbitrarisdelesconstantsdereacció.Aixídoncs,enstrobemdavantlatasca d’estudiarunsistemad’equacionsdiferencialsparamètric.

Engeneral,quans’introdueixunaxarxadereaccions,etiquetemlesreaccionsamblasevaconstantdereacciói,d’aquestamanera,quanaquestes sóndesconegudes,esfixal’ordreconsideratpelconjuntdereaccionsambel subíndexdelaconstant.Perexemple,introduiremlaxarxa(2)com

Enaquestcas,lamatriudereactantsés:

i,pertant, x1(t) + x2(t) ésconstantalllargdelestrajectòries,ésadir,al llargdelessolucionsde (8).Aquestarelacióvedonadapelfetque (1, 1) és unvectordelnucliesquerrede N,o,ditambaltresparaules,delcomplement ortogonaldel’espaid’estequiometria S

Engeneral,peracadavector ω ∈S⊥,tenim ω · dx dt = 0(aquí · denotael producteescalar)jaque ω N = 0.Deduïmque ω · x ésconstantalllargde lestrajectòriesiobtenim,d’aquestamanera,integralsprimereslineals.Enel contextdexarxesdereaccions,lesequacions

ω · x = c

són lleisdeconservació,i c s’anomena concentraciótotal.Siconsideremara unamatriu W ∈ Rd×n lesfilesdelaqualformenunabasede S⊥ (pertant,de rang d = n s,on s ésladimensiódelaxarxa),obtenimquelestrajectòries delsistema(10)estanconfinadesenespaisafinslinealsambequacions

Wx = c, on c ∈ Rd ésaraunvectoridepèndelacondicióinicial.Totamatriu W d’aquestescaracterístiquess’anomena matriudelleisdeconservació.

Cadaconjuntdelaforma

Pc ={x ∈ Rn ≥0 | Wx = c}, amb c ∈ Rd s’anomena classed’estequiometria.Comaobjectematemàtic,es tractad’unpolíedre,jaqueestàdefinitperequacionsidesigualtatslineals. Variant c obtenimpolíedresenespaisafinslinealsparal.lelsquecontenenla dinàmica,talcoms’il.lustraalafigura1.

Unresultatimportantésquelesclassesd’estequiometriasóncompactes siinoméssi S⊥ contéunvectorambtoteslescoordenadespositives[5].En aquestcasdiemquelaxarxaés conservativa.Quanaixòpassa,ladinàmicaestà confinadaenunespaicompacte,ienparticularlestrajectòriesestandefinides peratottempspositiu.

Peralaxarxa (2),tenim s = d = 1ipodemconsiderarlamatriudelleisde conservació W = [11].Comquetoteslescoordenadessónpositives,laxarxa ésconservativa.

Figura 1: Classesd’estequiometriaperaunaxarxaambtresespèciesi dimensió2,perexemple,donadesperlesequacions x1 + x2 + x3 = c, variant c

2.3Puntsd’equilibriibiestabilitat

L’estudid’unaxarxaescorresponadeterminarlespropietatsmatemàtiques delsistemad’equacionsdiferencials (10).Enestudisquantitatius,enquètenim informaciódelesconcentracionsdelesproteïnesendiferentspuntsdeltemps, l’objectiuésaproximarelsvalorsdelsparàmetresi,normalmentmitjançant simulacionsnumèriques,entendreladinàmicadelaxarxaipredirelcomportamentdelesconcentracionseneltemps.Enestudisqualitatius,esbusca entendreladinàmicadelaxarxaengeneral,peratotselsvalorsdelsparàmetres.Elsobjectiussónmésgenèricsisecerca,perunabanda,determinar quinescaracterístiquesdinàmiquesespodenaconseguirescollintadequadamentelsvalorsdelsparàmetres,iperl’altra,volemtrobarpropietatsdelaregió deparàmetresonelsistema (10) mostralacaracterísticad’interès.Enaquest article,enscentraremenl’existènciademésd’unpuntd’equilibri,propietat ques’anomena multiestacionarietat

Els puntsd’equilibri delaxarxa,uncopfixatsunsvalorsdelesconstantsde reacció κ,sónlesconcentracionsperlesqualselcostatdretde (10) s’anul.la, ésadir,lessolucionsdelsistema

Observemquenomésensinteressenlessolucionsnonegatives,jaquelesaltres solucionsnosónrealistes.Defet,enscentraremenlessolucionspositives,és adir,a Rn >

:

Elsistema (11) l’anomenarem sistemadepuntsd’equilibri.Elconjunt Eκ és laintersecciódelavarietatalgebraicareal(ocomplexa)donadapertotesles solucionsdelsistema (11) ambl’ortantpositiu.L’anomenarem varietatdepunts d’equilibripositius

Comjahemobservatanteriorment,ladinàmicadelaxarxatéllocalesclassesd’estequiometria,i,pertant,elspuntsd’equilibrideladinàmicas’estudien restringitsaaquestesclasses.Aquestsestrobencomasoluciódelsistema d’equacionspolinòmiques

0 = N(κ ◦ xB ),c = Wx,x ∈ Rn ≥0 (12)

Elsegonconjuntd’interèsperanosaltresés,doncs,elconjuntdesolucions de(12)ambconcentracionspositives:

Tκ,c ={x ∈ Rn >0 | N(κ ◦ xB ) = 0,Wx = c}.

Aquestconjuntdepèndedostipusdeparàmetres.Perunabanda,tenimles constantsdereacció κ ∈ Rr >0,queapareixencomacoeficientsenunapartde lesequacions,iperl’altra,lesconcentracionstotals c ∈ Rd,quedefineixenel nivellambquètraslladem S⊥.Unamanerageomètricad’entendrelafamília Tκ,c ésqueintersequemunafamíliadevarietatsalgebraiquesquevariensegons κ

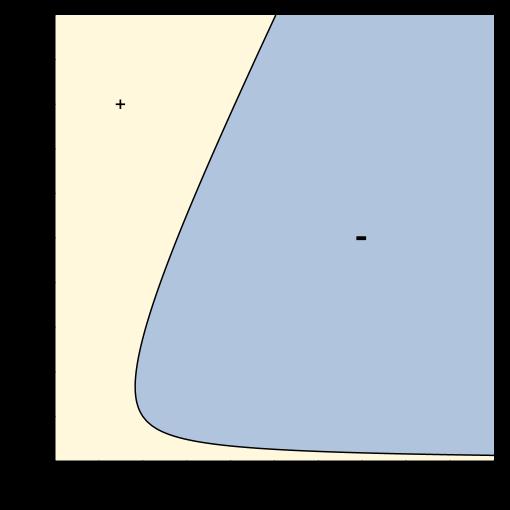
ambunacol.lecciódevarietatslinealsambelmateixespaivectorialdefinidor.A lafigura2s’il.lustraaquestainterpretació.Lescorbescontínuescorrespondrien alasolucióde (11),ésadir,sónpuntsd’equilibri.Cadacorbacorresponauna elecciódelparàmetre κ.Lesrectesdiscontínuessónclassesd’estequiometria perdiferentsconcentracionstotals.Laintersecciód’unacorbacontínuaamb unarectadiscontínuaésunpuntd’equilibrienunaclassed’estequiometria.

Figura 2: Duesil.lustracionsenduesvariablesdelafamíliadevarietats Eκ obtingudesvariant κ (líniescontínues)juntamentamblesclasses d’estequiometria(líniesdiscontínues).

Lasegonaigualtatsorgeixdelfetquelesduesprimeresequacionssónlinealmentdependents,ientreure’nunadelesdues,ensquedemambunsistema d’equacionsambduesvariablesiduesequacions.Aixònoéscasual:comque leslleisdeconservaciócorresponenacombinacionslinealsdedependència delesequacionsdelsistemadepuntsd’equilibri,sempretenim d equacions redundants.Entreure-les,obtenimunsistemaambelmateixnombred’equacionsquedevariables.Diemqueelsistemaésquadrat.Perasistemesquadrats ambcoeficientsarbitraris,calesperarqueelnombredesolucionssiguifinit,i elmateixéscertperalssistemesquedefineixen Tκ,c .Ésadir,ambhipòtesis

moltpocrestrictivesenlaxarxa,elconjunt Tκ,c seràfinitperaquasitotsels valorsdelsparàmetres[35].

Totiserunconjuntfinit,el nombre d’elementsdelconjuntpotdependre del’elecciódelsparàmetres.Perexemple,alafigura2(b),podemescolliruna corbacontínuaiunadediscontínuaquenoméss’intersequenenunpunt,però tambépodemferaltreseleccionsitrobarduescorbesques’intersequenen trespunts.Peraaquestaxarxa,hihaclassesd’estequiometriaquetenenuno méspuntsd’equilibri,depenentdel’eleccióde κ.Peraltrabanda,alafigura2(a) totparelldecorbescontínuaidiscontínuas’intersequenexactamentenun punt.Enaquestcas,peratotselsvalorsdelsparàmetres,toteslesclasses d’estequiometriatenenunpuntd’equilibri.Aquestesobservacionsensporten alasegüentdefiniciócentrald’aquestarticle.

Definició 3. Unaxarxadereaccionsadmet multiestacionarietat si,peraalgun valordelsparàmetres κ ∈ Rr >0 i c ∈ Rd,elconjunt Tκ,c téalmenysdos elements.

Si,amésamés, Tκ,c téalmenysdoselementsquesónpuntsd’equilibri estables(relatiusalaclassed’estequiometria),aleshoresdiemquelaxarxa admet biestabilitat.

Elconjuntdeparàmetres

Ω

∈ Rr >0 × Rd | #Tκ,c ≥ 2} s’anomena regiódemultiestacionarietat

Ladeterminaciódesiunaxarxaadmetmultiestacionarietato,mésconcretament,biestabilitat,ésuntemadegraninterès,degutaltipusdecorbes senyal-respostaassociadesaaquestescaracterístiques.Elsenyaléstípicament unparàmetredelsistemaquevariapercausesexternes,ilarespostaésla concentraciód’unaproteïnainvolucradaenl’activacióodesactivaciód’algun mecanismecel.lular(perexemple,latranscripciód’ungen)apartirdesila concentracióésaltaobaixa.Elssistemesbiestablestenenelpotenciald’oferir respostesrobustes,quenodepenendepetitesfluctuacionsdelparàmetre,i, pertant,sóncomunsidesitjablesensenyalitzaciócel.lular.

2.4Exemplesdexarxesdesenyalitzaciócel.lular

Duesxarxesqueamplienelsdosexemplesdefosforilació (3) i (4) tindranun rolimportantenaquestarticle.Enprimerlloc,trobemelcicledefosforilaciói desfosforilacióendiversosllocsseguintelmecanismedeMichaelis-Menten[21, 48].Enaquestcas,trobemunaproteïna A queadmetgrupsfosfatenmés d’unlloc,posem .Unpossiblemecanismepreveuquehihaunaquinasaque catalitzalafosforilaciód’aquests llocsdemaneradistributivaiseqüencial,és adir,elsllocsesfosforilenenunordredeterminat,icadacontactequinasasubstratdonallocalafosforilaciód’unsolgrupfosfat.Ladesfosforilació procedeixambelmateixmecanisme,peròenl’ordreinversicatalitzatperun enzimanomenat fosfatasa

Perexemple,pera = 1,tenimlaxarxa

on K éslaquinasa,i F éslafosfatasa.Enaquestaxarxatenimsisreaccions,sis espèciesisiscomplexos X={

.

Recordemquelanotació y y indicaunareaccióreversible,quevoldir quetenimlesreaccions y y i y y .

Pera = 2,tenimel cicledualdefosforilació:

Engeneral,peracada ,anomenemaquestaxarxa cicledefosforilaciói desfosforilacióamb llocs.Pera = 1,laxarxanotémultiestacionarietat, peròpera ≥ 2sí.Defet,sesapquelaxarxatécomamolt2 1punts d’equilibriencadaclassed’estequiometria,isesapquehihaclassesperales qualsenté + 1si ésparelli si éssenar[68, 71].S’haconjecturatquela xarxaadmetels2 1puntsd’equilibrienalgunaclassed’estequiometriasi s’escullenles κ adequadament,peròlaconjecturanoméss’hapogutdemostrar finsa = 4[42].Sesaptambéquepera ≥ 2lesxarxessónbiestables[38].

Aquestafamíliadexarxess’haconvertitenelbancdeprovesdenous mètodesiidees.Perunabanda,tégranimportànciabiològica,iperunaaltra, encarahihamoltespreguntesobertes.Perexemple,pera = 2nosesapsi elsistema (10) tésolucionsperiòdiques(oscil lacions)niesconeixlaregióde multiestacionarietatexplícitament.

Elsegonexempled’importànciaesconstrueixapartirdelmecanisme (4),tot introduintfosforilacióenmésd’unlloc,talcomhemfetambl’exempleanterior. Unmodelsenzilldetransmissiódelsenyalenbacterisambunaanomenada quinasahistidinahíbrida éslaxarxa

Enaquestmodel,laquinasahistidina HK tédosllocsdefosforilació.Quan elsegonllocestàfosforilat,independentmentdelasituaciódelprimer,elgrup fosfatpotpassaralaproteïnareguladoraderesposta RR.Laprimerailatercera reaccionscorresponenalafosforilaciódelprimerllocambelsegonlloclliure oocupat,respectivament.

Sesapqueaquestaxarxaadmetmultiestacionarietatibiestabilitat,i,addicionalment,esconeixambgrandetalllaregiódemultiestacionarietat,com veuremmésendavant[54].

2.5Parametritzacions

Al’horad’estudiarelspuntsd’equilibrid’unaxarxa,ésmoltútilteniruna descripcióexplícitadelavarietatdepuntsd’equilibripositius Eκ mitjançant parametritzacions.Siladimensiódelaxarxaésmàxima,ésadir, n,llavors nohihalleisdeconservacióis’esperaque Eκ siguifinit.Enaquestcas,una parametritzacióequivaldriaatrobaraquestspuntsexplícitament,cosaqueés raramentpossible(ambles κ comaparàmetres).Siladimensiódelaxarxa noésmàxima,aleshores Eκ tédimensiópositiva(genèricament, d = n s),i sovint(sorprenentment)espodentrobarparametritzacions.

Perexemple,consideremlaxarxa (4),onafegimquelasegonareacciósigui reversible,iusemnomsdelesespèciesmésadientsaltractamentmatemàtic:

dimensió2.Enparticular,elsistemadepuntsd’equilibritéduesequacions linealmentindependents(observemqueéselsistema(1)delaintroducció):

Engeneral,diremqueunaxarxaadmetuna parametritzacióracionalpositiva siexisteixunaaplicaciócontínuaiexhaustiva

Rd >0 φ Eκ ⊆ Rn >0,ξ

ambtoteslesentradesracionalsen ξ1,...,ξd ienlescomponentsde κ.N’és unexemplelaparametrització(16)amb ξ1 = x1, ξ2 = x2.

Queunavarietatalgebraicaadmetiunaparametritzacióracionalnoéselmés habitual:genèricament,unavarietatalgebraicanoadmetràunaparametrització! Peròentrelesvarietatsquesorgeixenapartirdesistemesdepuntsd’equilibris dexarxes realistes,sovintpodemtrobar-neuna.Aixòesdeuprincipalmental fetquelesxarxesrealsnosóngenèriques,i,enparticular,hihamoltalinealitat enelssistemesdepolinomis:elgraudelsmonomiscorresponalnombrede molèculesqueinteractuen,ienelmóndelabiologiamolecular,onlesespècies sónmacromolècules,noesdonaelcasquetresomésproteïnesinteractuïn simultàniament.

Quanelsistematémoltalinealitat,llavorséspossiblequepuguemresoldre elsistemadepuntsd’equilibriperunesvariablesenfunciódelesaltres,talcom hemfetamblaxarxa (15).Aquestaestratègiadetrobarparametritzacionsvia eliminaciólinealhaestatmoltexplorada.Vegeu,perexemple,[40,41,47,63].

Unaparametritzacióracionalpositivade Eκ enspermetrà avaluar funcions alspuntsd’equilibri,i,comveuremmésendavant,aixòenspermetràtreure conclusionssobrelaregiódemultiestacionarietat.Detotesmaneres,nosempre tindremal’abastunaparametrització.Siampliemlavarietat Eκ demaneraque κ tambésiguiunavariable,llavors sempre podemtrobarunaparametrització. Perdremlainformacióquedonal’especialitzacióaun κ determinat,però podremestudiarl’existènciadedeterminadespropietatsperaalgunvalorde κ.

Considerem,doncs,la(partpositivadela)varietat

Lademostracióconsisteixaprovarquel’aplicació ψ queenvia (κ,x) a (κ ◦ xB ,x 1) éslainversade ϕ.Ellema4ensindicaque,peraestudiar E, éssuficientestudiar (ker(N) ∩ Rr

Pertant,existeixunnombrefinitdegeneradors, e1,...,e ( nohadeser necessàriamentladimensiódeker(N))talque

Aquestaparametritzaciójuntamentambellema4ensdonaunaparametritzacióde

on E éslamatriudecolumnes e1,...,e .Aquestaparametritzacióconsisteix enfuncionsracionalsen λ, h

Existeixendiversosalgoritmesperatrobarelsgeneradorsd’unconpolièdric, ambimplementacionscomperexemplea SAGE [64]i Polymake [45].Aixídoncs, aquestaparametritzacióde E espottrobaralapràctica.

Peralaxarxa (15),onhemtrobatunaparametritzacióde Eκ a (16),la parametritzaciódelavarietatd’incidència E s’obtédelamanerasegüent. Primer,enscaltrobarelsgeneradorsdelconpolièdric ker(N) ∩ R4 ≥0,iobtenim

x, κ,aquestaparametrització perdinformaciódelcomportamentdeles κ concretesinomésserveixpera explorarlavarietat E.Ésadir,nopodemespecialitzaraquestaparametrització aun κ concret.

3Multiestacionarietat

Arajatenimtotselsingredientsperaendinsar-nosenelsresultatssobreel comportamentdelspuntsd’equilibridelaxarxa.Enaquestaseccióderesultats enscentremadecidirsiunaxarxaadmetmultiestacionarietati,siéselcas,a donarinformacióparcialdelaregiódemultiestacionarietat.

Lapreguntaqueensplantegemés,doncs,determinarsiexisteixen κ, c tal queelconjunt Tκ,c téalmenysdoselementsi,siesdonaaquestcas,trobarel

conjuntdeparàmetresperalsqualsaixòpassa.Ambxarxesproupetites,com perexemple (2), (14) o (15),podemmanipularlesequacionsideduirsilaxarxa témultiestacionarietatono.Peralaxarxa (15),jahavíemvista (16) queels

Elspuntsd’equilibriestanencorrespondènciaamblesarrels

d’aquestpolinomi.Uncàlculsenzillensdiuqueelpolinomiéspositiuquan x1 = c1.Comqueeltermeindependentésnegatiu,concloemqueelpolinomi téunaúnicaarrelenl’intervald’interès,i,pertant,laxarxatéexactament unpuntd’equilibripositiuperatotaelecciódeparàmetres.Laxarxanoté multiestacionarietat.

D’unamanerasimilar,peròinvocantresultatssobrearrelspositivesmés avançats,espotconclourequelaxarxa (14) admetmultiestacionarietat.En aquestcas,elspuntsd’equilibris’estudienapartird’unpolinomicúbic.Addicionalment,usantseqüènciesdeSturm,espotdeduirquelaxarxatétres puntsd’equilibripositiussiinoméssi

Aquestexempleésmoltinteressant,jaqueespottrobarlaregiódemultiestacionarietat,però,alavegada,noentenimgaireinformació.Quinaforma té?Ésconnexa?Quèensdiudelsaspectesbiològicsquedonenllocamultiestacionarietat?Iaquíésonhemderecordarquetreballemambsistemesde polinomisqueprovenendexarxesd’interèsiquevolemsercapaçosd’interpretariexplorarelsresultatsmatemàticsobtinguts.

Noméslesxarxessenzillesiambmoltalinealitatinherentpermetenmanipulacionsperreduirl’estudidelspuntsd’equilibrial’estudidelesarrels

d’unpolinomienunintervaldeterminat.Enprincipi,lareduccióaunpolinomi enunavariable z quasisempreéspossiblegràciesalateoriadelesbases deGröbneriel«lemadelaforma»(shapelemma)[22].Aquestateoria,però, noensretornaelconjuntenquèhemdebuscarlesarrels z pertalqueles solucionsdelsistemasiguinpositives.Ésperaixòquelateoriadexarxesde reaccionsdurantcinquantaanyshaestatdesenvolupantresultatsperadeterminarmultiestacionarietat.S’hanexploratmoltesdireccions,ifer-neunallista exhaustivaésimpossible,peròl’article[53]contéunbonresumdelesestratègiesactualsidonaunbonnombredereferències.Lamajoriadelsresultats enspermetendecidirsilaxarxaadmetmultiestacionarietat,perònoensdiuen gaireressobrelaregiódemultiestacionarietat.

Enaquestarticleexpliquemunmètodeque,amésdedecidirsobrela multiestacionarietat,ensdonainformaciósobreelsparàmetres.Elmètodees basaenelteoremacentraldelareferència[15](aquíenpresentemunaversió simplificada).Perapoderenunciarelteorema,necessitemintroduirlafunció següent.Consideremunamatriudelleisdeconservació W ∈ Rd×n isuposem queestàreduïdaperfiles.Siguin ω1,...,ωd lesfilesde W i i1 < <id els índexsdelaprimeraentradadiferentdezeroenlesfiles ω1,...,ωd.Consideremlafunció fκ (x) donadapelspolinomisaladretade (10),iconstruïm lafunció ˜ fκ (x) totsubstituintl’entrada ij de fκ (x) per ωj · x cj .Perala xarxa (15),lamatriuassociadaaleslleis (18) ésreduïdaperfilesitenim i1 = 1, i2 = 3.D’aquíobtenimlafunció

Observemqueelconjuntdesolucionspositivesdelsistema fκ (x) = 0és exactament Tκ,c .

Teorema 5 ([15]). Consideremunaxarxaconservativaambconstantsdereacció κ ∈ Rr >0,iconsideremlafunció ˜ fκ donadaperunaelecciódematriudellei deconservació W reduïdaperfiles.

Suposemque Eκ ∩Pc ⊆ Rn >0 peratotaclassed’estequiometria Pc ,ésa dir,totselspuntsd’equilibridelesclassestenentoteslescoordenadespositives. Consideremeldeterminantdelajacobianade fκ (x)

pκ (x) = ( 1)s det(Jfκ (x)),

on s ésladimensiódelaxarxa.Aleshoresescompleix:

(a) Si

sign(pκ (x)) =+1 peratot x ∈Eκ ,

aleshores #Tκ,c = 1 peratot c ∈ Rd .

(b) Si

sign(pκ (x)) =−1 peraalgun x ∈Eκ , aleshores #Tκ,c ≥ 2 pera c = Wx∗

ElisendaFeliu

Laprovad’aquestresultatesbasaenlateoriadel’índexdeBrouwer,ies demostraquelafunció ( 1)s fκ téíndex1alpunt0respectedel’ortantpositiu. Elfetquelaxarxasiguiconservativas’usaperagarantirquelestrajectòriesdel sistemad’equacionsdiferencialsestanfitades,iapartird’aquíespotconstruir unahomotopiaentre ˜ fκ iunafunciódelaqualconeixemelgrau.

Vegemcompodemusaraquestteorema.Laxarxa (15) ésconservativa,ies potveurefàcilmentquecompleixlacondiciódelteoremasobrel’absènciade puntsd’equilibrialafronteradel’ortantpositiuintersecatambcadaclasse d’estequiometria.Usant(21), pκ (x) és

Senseavaluar pκ

Aquestpolinomitéexactamentuncoeficientnegatiu,i,pertant,nopodem saberasimplevistasiassoleixvalorsnegatius.Perpoderaplicarelteorema5, hemd’avaluar pκ (x) alspuntsd’equilibri,iaixòhopodemfergràciesala parametrització

x1, x2, x3, x6.Avaluant pκ (x) a ψ iconsiderantnoméselnumerador(eldenominadorés positiu),obtenimelpolinomi

Veiemclaramentque,si κ1 ≥ κ3,aleshores qκ (ξ) éspositiuperatot ξ ∈ R2 >0 i elteorema5ensindicaque#Tκ,c = 1peratot c. Si,alcontrari, κ1 <κ3,aleshores,posant ξ1 = ξ2 = α, qκ (ξ) esconverteix enunpolinomien α degrau3ielcoeficientprincipalésnegatiu.Així,per a α> 0suficientmentgran, qκ (ξ) serànegatiu.Elteorema5ensdiuaraque #Tκ,c ≥ 2peraalgun c i,pertant,laxarxaadmetmultiestacionarietat.

Polinomis,polítopsixarxesdereaccions 121

Concloemquelaxarxaésmultiestacionària,i,amésamés,tenimlacondició quehandecomplirles κ pertalqueaixòsiguipossibleperaalgun c.Enaltres paraules,hemtrobatlaprojecciódelaregiódemultiestacionarietatenl’espai delesconstantsdereacció κ.Recordemqueperaaquestaxarxahavíemtrobat laregióa (19),ilainterpretacióbiològicanoeraclara.Ara,larelacióenles κ esredueixa κ3 >κ1.Mirantelroldelesreaccionsquetenenaquestesdues constantsdereaccióa (14),veiemquecorresponenalafosforilaciódelprimer llocde HK:pera κ1 elsegonllocestàlliure,ipera κ3 elsegonllocestàocupat. Deduïmque,pertalqueespuguidonarmultiestacionarietat,ésnecessarique lafosforilaciódelprimerllocsiguimésràpidaquanelsegonllocjaestàocupat. Iaquestainterpretaciótésentitbiològic.

Alternativament,siensimaginemlasituacióenquènohaguéssimpogut trobarunaparametritzacióde Eκ ,podemusarlaparametritzaciódelavarietat d’incidència E de (17).Peraaquestaxarxaamblahistidinaquinasahíbrida,el con ker(N)

6

0

(24)

Elpolinomi q(λ,h) tédinoutermes,dosdelsqualstenencoeficientnegatiu. Compodemdecidirsiaquestpolinomiassoleixvalorsnegatiusquantotes lesvariablessónpositives?Sabemquehauriadeserpossibleperquèjahem vistqueaquestaxarxaadmetmultiestacionarietat,peròhihaalgunamanera sistemàticadedetectar-ho?Aquestapreguntaseràeltemadelasecciósegüent.

Recapitulant,gràciesalteorema5,hemcanviatlaqüestiódedecidirsi elconjunt Tκ,c tédosoméselementsperladedecidirsiunpolinomipren valorsnegatiusquanésavaluatal’ortantpositiu.Aquestapreguntaestàmolt relacionadaambl’estudidepolinomisnonegatius,ésadir,polinomisquemai nopodensernegatiussobreelsreals,quealavegadatéimplicacionsdirectes enproblemesd’optimitzacióienelproblema17èdeHilbert[11].

Sipartimd’unaparametrització,elpolinomitécoeficientsparamètricsila preguntaconsisteixadecidirsielpolinomiparamètricpotsernegatiupera algunvalordelsparàmetres.Enaquestcasensplantegemlapregunta:

D’aquestamaneraobtenimlaprojecciódelaregiódemultiestacionarietaten l’espaideles κ.Asimplevistapotsemblarqueaquestanovapreguntatéles mateixesdificultatsqueentendreelsconjunts Tκ,c .Enambdóscasos,estracta deproblemesdegeometriasemialgebraicaambquantificadors,iqueespoden resoldreenprincipiambmètodespropisd’eliminaciódequantificadors[4]. Aquestsmètodes,però,sónaltamentcostosos,iperalssistemesrealistes d’interès,nosónefectius.

Alapràctica,però,hihadiversosresultatsquerelacionenelssignesqueun polinomipotprendreenl’ortantpositiuamblescaracterístiquesd’unpolíedre associatalpolinomi.Elsalgoritmesdegeometriapolièdricasónmoltmenys costososjaqueesbasenentècniquesdeprogramaciólineal.Comveuremala secciósegüent,aquestsmètodesenspermetranrespondrelanostrapregunta iestudiarl’espaideles κ quedonenllocamultiestacionarietatdemanera satisfactòriaperadiversesxarxes.

4Signesdepolinomisieinespolièdriques

4.1ElpolítopdeNewton

Perpoderaplicarelteorema5alpolinomiparamètric qκ (ξ) obtingutapartir delnumeradorde pκ (x) avaluatenunaparametrització,comencemexplorant elssignesdelscoeficientsdelpolinomi,talcomhemfetamblesxarxes (14) i (15).Elfetqueunpolinomitinguiuncoeficientnegatiunoimplica,però, quepuguiprendrevalorsnegatiusenl’ortantpositiu.Unexempleclàssicésel polinomi

x2 2xy + y 2 = (x y)2 ≥ 0, quemaiésnegatiutotiteniruncoeficientnegatiu.Decidirsiunpolinominomés prenvalorsnonegatiusnoésunatascagenstrivial.Aquíenscentraremens algunscasosconcrets,iellectorpotllegirméssobreelproblemaal’article[3].

Observemqueamblaxarxa (14) ielpolinomi (23),hempogutdeduirqueel fetqueelcoeficientfosnegatiuerasuficientperaconcloureque qκ (x) també podiasernegatiu.Aixídoncs,hihacoeficientsquesón«mésimportants» qued’altresperarespondrelanostrapregunta.Perentendrequinssónels coeficientsimportants,introduïmelpolítopsegüent(vegeutambé[27]).

Definició 6. Consideremunpolinomimultivariat f(x) = v∈A αv xv ∈

amb αv ∈ R \{0} i

polítopdeNewton NP(f) de f ésl’envolventconvexade A:

Donadaunacara τ de NP(f),denotemamb fτ larestriccióde f alsmonomis contingutsalacara:

Laclauaraestrobaenelresultatclàssicsegüent(enpodeutrobaruna demostracióa[37]).

Proposició 7 Consideremunpolinomimultivariat f(x) ∈ R[x1,...,xn] iuna cara τ delpolítopdeNewton NP(f).Aleshores,peraqualsevol y ∗ ∈ Rn >0, existeix x∗ ∈ Rn >0 talque

sign(f(x∗)) = sign(fτ (y ∗)).

Enparticular,peratotvèrtexde NP(f),existeix x∗ ∈ Rn >0 talque

sign(f(x∗)) = sign(αv ).

Peralpolinomi

1,i,pertant,elpolítopdeNewtonésl’envolventconvexadelspunts

Unail.lustracióde NP(qκ ) latrobemalafigura3.L’exponent (1, 2),quecorresponalcoeficientnegatiu,ésunvèrtexdelpolítopdeNewton,i,pertant,el fetqueelcoeficientsiguinegatiujaimplicaque qκ (ξ) assoleixvalorsnegatius gràciesalaproposició7.

Quantalpolinomi (24) amblesvariables λ, h,jahemcomentatquetenim dinoumonomis.ElpolítopdeNewtontécatorzevèrtexs,entreellselsdos termesambcoeficientnegatiu!Aixídoncs,elpolinomi q(λ,h) prenvalors negatiusal’ortantpositiuilaxarxaadmetmultiestacionarietat.

Siaraconsideremelcicledualdefosforilacióintroduïta (13) ambels paràmetres λ, h,ésadir,considerantlaparametritzacióde E de (17),obtenim unpolinomiamb400monomis,112delsqualstenencoeficientnegatiu.Entre ellstrobemexponentsquesónvèrtexsdelpolítopdeNewton.Pertant,el polinomiassoleixvalorsnegatiusperlaproposició7,ielteorema5ensportaa conclourequelaxarxa (13) admetmultiestacionarietat.Siconsideremlaxarxa ambtresllocsdefosforilació,llavorselpolinomité5096monomis,delsquals 1536sónnegatius,iunaltrecopalgunsd’ellscorresponenavèrtexsdelpolítop deNewton.Deduïmaixíquelaxarxaadmetmultiestacionarietat(remarquem quejasesapquelaxarxaadmetmultiestacionarietatquanelnombredellocs defosforilacióésalmenysdos).

Figura 3: PolítopdeNewtondelpolinomi(23).

ElisendaFeliu

Aquestaestratègiafuncionaperamoltesxarxes,tantamblaparametrització de E,illavorspodemdecidirsilaxarxaadmetmultiestacionarietatono, comambunaparametritzacióde Eκ (siexisteix),iaixípodemtrobarvalors deles κ quepermetenlamultiestacionarietat.Enelsexemples,hemobviat comprovarqueleshipòtesisdelteorema5escompleixen.Peraaixòtenim einescomputacionalsdisponibles,talcomestandescritesa[15].

4.2Polinomiscircuit

Tornantalcicledualdefosforilacióintroduïta (13),podemdiralgunacosa sobrelaregiódemultiestacionarietatusantunaparametritzacióde Eκ ?Pera laxarxa (14) hempoguttrobarlaprojeccióexactadelaregiódemultiestacionarietat,peròamblaxarxa(13)lasituacióésbastantméscomplicada.

on K1,K2,K3,K4 > 0depenende κ isónlesanomenades constantsdeMichaelisMenten.Hihasiscoeficientsquepodensernegatius,ilarestasónpositius.El signed’aquestscoeficientsdepèndelsigned’und’aquestsdospolinomis:

1 + K4).

Si b1(κ) ≥ 0i b2(κ) ≥ 0,aleshoreselteorema5ensdiuquelaxarxatéun únicpuntd’equilibriacadaclassed’estequiometria.Si b1(κ)< 0,aleshores undelsmonomisqueacompanyenelcoeficientcorresponaunvèrtexdel polítopdeNewton,i,pertant,amblaproposició7ielteorema5concloemque laxarxaadmetmultiestacionarietatenalgunaclassed’estequiometria.Ésadir, elconjuntdeparàmetrespelsquals b1(κ)< 0pertanyalaprojecciódelaregió demultiestacionarietatenles κ.Aquestresultatapareixperprimercopa[19].

Iquèpassasi b2(κ)< 0i b1(κ) ≥ 0?Enaquestcas,elmonomi ξ2 1 ξ2 2 ξ2 3 queacompanya b2(κ) nocorresponacapvèrtexdelpolítopdeNewton.És elpuntdestacatal’interiordelacarahexagonalil lustradaenprimerterme alafigura4;pertant,nopodemafirmardirectamentqueelpolinomipugui prendrevalorsnegatius.Detotesmaneres,laproposició7enspermetreduirla

determinaciódesi qκ (ξ) admetvalorsnegatiusalpolinomirestringitalacara hexagonal,jaquetotselsaltrescoeficientssónpositius.

Figura

: PolítopdeNewtondelpolinomi (25).Elpuntdestacatalacara hexagonalenprimerplacorresponauncoeficientqueésnegatiupera algunsvalorsde κ

Lacarahexagonalviualpla x1 + x2 = 4i,pertant,multiplicantelpolinomi per ξ4 1 ,ensquedaunpolinomien ξ2/ξ1 i ξ3.Redefinint ξ2 = ξ2/ξ1,totes redueixaestudiarelpolinomi:

Enaquestcas,saberelsignedelcoeficientnoéssuficientinecessitemusar lainformaciódelvalorconcretdelscoeficients.Perexemple,jahemvistque elpolinomi x2 2xy + y 2 noadmetvalorsnegatius,però,incrementantel coeficientnegatiu,perexemple x2 3xy + y 2,aleshoresjasíqueassoleix valorsnegatius(amb (x,y) = (1, 1)).

Lesrelacionsexplícitesentreelscoeficientsquefanqueunpolinomisigui nonegatiunoesconeixenengeneral,peròhihauncasparticularenquètenim unaexpressiósimple.

Definició 8 Un polinomicircuit en n variablesésunpolinomidelaforma

talque v0,...,vm formenunsímplex m-dimensional ∆ a Rn i u pertanya l’interiorrelatiude ∆ (respectelatopologiainduïdaalmínimsubespailineal queconté ∆).

4

ElisendaFeliu

Peraunpolinomicircuit, u s’escriudeformaúnicaencoordenadesbaricèntriquescom u = m i=0 γivi amb γi > 0peratot i i m i=0 γi = 1.

Elteoremasegüentdonalarelacióexactaque β ielsaltrescoeficients α han decomplirpertalqueelpolinomisiguinonegatiu.Aquestteoremaapareixen diferentstreballsambdiferentnotació[50, 60, 62].Aquíusemelformalisme de[50].

Teorema 9. Consideremunpolinomicircuiten n variables

l’interiordelsímplexs’escriuencoordenadesbaricèntriquescom

Tornantalnostreproblemaambelcicledualdefosforilacióielpolinomi (26),elsexponentsdelsonzemonomiselsindiquemambunpuntala

figura6.Elpolinominoésunpolinomicircuit,peròespotdescompondre comlasumadequatrepolinomiscircuit:dosd’ellsambsuportsobreunsímplex2-dimensional(triangles),ielsaltresdosambsuportsobreunsímplex 1-dimensional(segments).Considerantlasumadelsquatrenúmerosdecircuit ielteorema9,deduïmque,si

Addicionalment,usanttècniquessimilarsalesdelpolítopdeNewton,però araconsiderantalgunsdelsparàmetresde gκ comavariables,podemveure queexisteixenparàmetres κ amb b1(κ) ≥ 0, b2(κ)< 0ialavegada gκ pren valorsnegatiussobrel’ortantpositiu.Enparticular,podemsaberque b2(κ)< 0 noerasuficientperadecidirlamultiestacionarietat.Vegeu[37]peralsdetalls. Encaranos’haobtingutcapexpressióexplícitadelaprojecciódelaregióde multiestacionarietatenles κ.Unestudimésgeneralperalaxarxaamb llocs defosforilacióespottrobara[36].

Figura 6: PolítopdeNewtonambtotselsexponentsmarcatspelpolinomide gκ (ξ2,ξ3) de (26).Elsdostrianglesdevèrtexs {α1,α3,α5} i {α2,α4,α6},respectivamentielsdossegmentsmarcatsamblínia discontínuail.lustrenelspolinomiscircuitenquè gκ (ξ2,ξ3) espotdescompondre.

Observació. Elsresultatsd’aquestesduesúltimessubseccionsil.lustrencom l’estudid’unsobjectespolièdricsilaconfiguraciódelsexponentsal’espaiens doneninformaciósobrelaregióonelsparàmetresdelaxarxadonenllocamultiestacionarietat.Alaliteraturatrobemaltresresultatsqueexplorenaquestes relacionsdesdepuntsdevistadiferents.Elsdosresultatsmésdestacatssón elssegüents.Perunabanda,s’hanobtingutprojeccionsdelaregiódemultiestacionarietatenlesconcentracionstotalsialgunesdeles κ [8].Elmètoderau enestudiarsubdivisionsdelpolítopdeNewtonambdeterminadescaracterístiques,ialavegadaesbasaentreballsanteriors[9].Elsegonresultattroba projeccionsdelaregiódemultiestacionarietatenl’espaidelesconcentracions totals,peraxarxesqueadmetenunaparametritzaciómonomial[18].

4.3Laregiódemultiestacionarietaticonnectivitat Comjas’hacomentat,trobarlaregiódemultiestacionarietatexplícitament ésunatascaforadel’abastdelestècniquesactuals.Enlesduessubseccions anteriorshemil.lustratcomobtenirinformaciódelaprojecciódelaregióen les κ

Lapreguntasegüentqueenspodemplantejaréssipodem«entendre»laregiósensetrobar-laexplícitament.Perexemple,ensagradariadeduirpropietats topològiquesdelaregió.Laconnectivitatdelaregiónohaestatgaireexplorada ifinsfapocesteniennomésestudisnumèricsfetsconsideranttècniquesde l’estudidenúvolsdedadescombinadesamblageneraciódemoltspunts d’equilibri[58].Cadacomponentconnexadelaregiódemultiestacionarietat espotinterpretarcomunmecanismediferentperaassolir-la,i,pertant,el nombredecomponentsconnexesensdonaunaideadelacomplexitatdels mecanismesqueindueixenamultiestacionarietat.

Perconcloureaquestaseccióonrelacionemqüestionsdemultiestacionarietatitècniquespolièdriques,consideremunresultatmésrecentenquèl’estudi delaconfiguracióespacialdelsexponentsdelpolinomi q(λ,h) enspermetde maneramoltsenzillaconclourequelaregiódemultiestacionarietatésconnexa, sensetrobar-la.

Peraentendreelresultatprincipald’aquestasecció,hemd’introduirla nociód’hiperplàseparadordelsexponentspositiusielsnegatius.

Definició 10 Consideremunpolinomimultivariat

amb αv ∈ R \{0} i A ⊆ Zn ≥0 finit.Diemque f admetun hiperplàseparador estricte siexisteixunhiperplà ω y = a a Rn talque ω v<a peraalmenysun exponent v ∈ A ambcoeficientnegatiu,i,amésamés,peracadaexponent v ∈ A escompleix:

• Si ω · v>a,aleshoreselcoeficientde xv éspositiu.

• Si ω · v<a,aleshoreselcoeficientde xv ésnegatiu.

(Al’hiperplàhipodemtenirsimultàniamentexponentsambcoeficientpositiui ambcoeficientnegatiu.)

Perexemple,peralpolinomi

f(x,y) =−4x2y + 2xy 2 xy + 5x + 3y + 1

existeixunhiperplàseparadorestricte,talcomesmostraalafigura7.Pels resultatsde[39],sesapquequantenimunhiperplàseparadorestricte,l’antiimatgedelasemirectarealnegativa, f 1((−∞, 0)),éscontràctil,ienparticular arc-connexa.Aquestfets’il.lustraalafigura7.Apartird’aquestresultat,juntamentambelteorema5,espotdemostrarelteoremasegüent.

Teorema 11 ([67]). Consideremelpolinomi q(λ,h) obtingutapartirde pκ (x) ilaparametritzaciódelavarietatd’incidència E de (17).Si q admetunhiperplà separadorestricte,aleshoreslaregiódemultiestacionarietatenelsparàmetres (κ,c) ésarc-connexa.

Enelmateixesperitqueelproblematractatenlesduessubseccionsanteriors,hemtraduïtunapreguntacomplexaadecidirsobrel’existènciad’un hiperplà,cosaqueespotdeterminarambprogramaciólineal.

7: Al’esquerras’il.lustraelpolítopdeNewtonde

= 4x2y + 2xy 2 xy + 5x + 3y + 1juntamentambelsexponents,i unhiperplàseparadorestrictedonatperlarecta x = 1.Elsexponents ambcoeficientpositius’indiquenambuncercleple,ielsdecoeficient negatiu,ambuncerclebuit.Aladretail lustremelsignede f al’ortant positiu.Alaregiómésfosca,elpolinomiésnegatiu,alamésclara éspositiu,ilacorbaéslavarietat f(x) = 0.Veiemqueambduesregions sónarc-connexes.

Elteorema11enspermetdeduirque,peranombrosesxarxes,laregióde multiestacionarietatésarc-connexa.Perexemple,aquestéselcasdelaxarxa amblaquinasahistidinahíbrida (14) ielcicledualdefosforilacióambdos itresllocs.Peramésexemples,vegeu[67].Enparticular,peraunaxarxa desenyalitzacióqueinvolucralaproteïnaERK,enquèelpolinomi q(λ,h) té quasi20000monomis,podemconclourequelaregiódemultiestacionarietat ésarc-connexa.Totiquenoespotaplicarelteorema11atoteslesxarxes ambregiódemultiestacionarietatarc-connexa,veiemqueelmètodeadmetel tractamentdexarxesambpolinomisrealmentgrans.Almateixtemps,s’han introduïtmètodesperarebaixarelcostcomputacionalbasatsenlareducció delaxarxa[67].

5BiestabilitatibifurcacionsdeHopf

Perconcloureaquestarticle,comentarembreumentques’apliquenestratègiessimilarsperadecidirsobrelabiestabilitatitambésobrebifurcacionsde Hopf.Recordemqueunpuntd’equilibri x∗ és(asimptòticament)establesila jacobianadelsistema (10) avaluadaa x∗ té s = rang(N) valorspropisamb partrealnegativa;siund’ellstépartrealpositiva,aleshores x∗ ésinestable. LesbifurcacionsdeHopfsorgeixenquan,envariarunparàmetredelsistema, unparelldevalorspropisambpartimaginàrianonul.lapassadetenirpart

Figura

f(x,y)

realpositivaatenir-lanegativa,oviceversa.Enparticular,peraunvalorconcretdelparàmetretindremunaparellaconjugadadevalorspropispurament imaginaris.

L’ingredientessencialperaestudiaraquestespropietatsquantenimparàmetresdesconegutssónelsdeterminantsdeHurwitz,querelacionenelsigne delapartrealdelesarrelsd’unpolinomireal(enelnostrecasseràelpolinomicaracterísticdelajacobiana)ambelsigned’unsaltrespolinomisenels coeficientsdelpolinomioriginal.

Mésconcretament,consideremunpolinomiambcoeficientsreals

Pera i = 1,...,n,el determinantdeHurwitz Hi éselmenorprincipal i-èsimde lamatriu H.

El criterideRouth-Hurwitz [43]ensdiuque,si Hi > 0peratot i = 1,...,n, aleshorestoteslesarrelsde p tenenpartrealnegativa.El criterideLiu ([56]; vegeutambé[26])ensdiuque p téunaparellaconjugadad’arrelspurament imaginàriesilarestatépartrealnegativasiinoméssi

Consideremelpolinomicaracterísticdelajacobianade (10),desprésde dividirpelfactor zn s (provenintdelfetqueladimensióde (10) és s).Comhem fetanteriorment,peraavaluar-loalspuntsd’equilibri,podemobéusaruna parametritzacióde Eκ ,iobtenimunpolinomien z ambcoeficientsen κ i ξ,o bélaparametritzacióde E de (17),iobtenimunpolinomien z ambcoeficients en λ, h.ConstruintelsdeterminantsdeHurwitzobtenimpolinomis H1,...,Hs obéen κ, ξ obéen λ, h,ipodemprocediraestudiarelspossiblessignes combinantl’estudisimultanidelspolítopsdeNewtondetotsells.

Unexemplemoltsenzillvedonatperunaxarxaquemodelaeltransport enzimàticd’ionsdecalci[44]:

on X1 éslaconcentraciódecalcicitosòlic [Ca++], X2 éslaconcentracióde calcialreticleendoplasmàtic, X3 éslaconcentraciódel’enzimcatalitzantel transporti X4 representaunaespècieintermediària.

Elsistemad’equacionsdiferencialsamblalleid’acciódemassesés

quetéunalleideconservació x3 + x4 = c (enparticularlaxarxanoésconservativa).Lavarietatdepuntsd’equilibripositius Eκ admetunaparametrització enlavariable

= x4 ∈ R>0 donadaper

ElsdeterminantsdeHurwitzdelpolinomicaracterísticdelajacobianadel sistemad’equacionsdiferencialsdividitper z iavaluataaquestaparametritzaciósón(amb a1(κ),...,a

UsantelcriterideLiu(icomprovantapartqueelparàmetre c ensserveixcom aparàmetredebifurcació),concloemquelaxarxaadmetunabifurcacióde Hopfperaalgunvalorde c siinoméssiescompleix(27).

AquestaestratègiaperaestudiarlabiestabilitatilesbifurcacionsdeHopf ésmoltméselaboradacomparadaambl’estudidemultiestacionarietatde lasecció3,jaqueelsdeterminantsdeHurwitzfàcilmentesdevenenmolt grans,ambmilionsdetermespelfetqueprovenendedeterminantsenels coeficientsdelpolinomicaracterístic,quealavegadaprovenendelasuma demenors!Totiaixí,aquestaestratègiaenspermetconclourebiestabilitati estudiarbifurcacionsdeHopfensituacionsfavorables.Ellectorpotllegirmés sobreaquestaestratègiaperabiestabilitatibifurcacionsdeHopfa[28, 69]i enmoltsdelsestudisdexarxesconcretesenquès’hanaplicataquesteseines, perexemplea[14,20,59].

Alllargdel’articlehemanatindicantquehihaencarabastantespreguntes obertessobreelsciclesdefosforilacióen llocs.Perunabanda,nosabem elnombremàximdepuntsd’equilibriquepodemobtenir(esconjecturaque són2 1),noconeixemlaregiódemultiestacionarietatperalcicledual,nitan solslaprojeccióal’espaideles κ,i,finalment,nosabemsielcicledualadmet bifurcacionsdeHopf!ElcriterideLiuenaquestcasésdifícildecomprovar, jaquetant αn com Hn 1 tenencoeficientsdelsdossignes,isónmoltgrans,i nos’hapogutdecidirsisimultàniament Hn 1 espotanul.lar,mentreque αn esmantépositiu.Enresum,encarahihamoltespreguntesinteressantsper contestarsobreelsciclesdefosforilació,tantdesdelpuntdevistamatemàtic combiològic.Resoldrelespreguntesimplicaintroduireinesmatemàtiques noves,queseguramentseranrellevantsperal’estudid’altressistemes.Ushi animeu?

Agraïments

Aquestarticleharebutelsuportdel’IndependentResearchFunddeDinamarca idelaUnióEuropeaatravésdelprojecteERC-2021-COG-101044561,POSALG. Lesopinionsexpressadesenaquestarticlesóndel’autorainoreflecteixen necessàriamentlesdelaUnióEuropea.

Referències

[1] Anderson,D.F. «Globalasymptoticstabilityforaclassofnonlinear chemicalequations». SIAMJ.Appl.Math.,68(5)(2008),1464–1476.

[2] Anderson,D.F.;Craciun,G.;Kurtz,T.G. «Product-formstationary distributionsfordeficiencyzerochemicalreactionnetworks». Bull.Math. Biol.,72(8)(2010),1947–1970.

[3] Andradas,C. «Polinomispositiusidesigualtatspolinomials». Butlletíde laSocietatCatalanadeMatemàtiques,20(1)(2005),7–18.

[4] Basu,S.;Pollack,R.;Roy,M.-F. AlgorithmsinRealAlgebraicGeometry 2aed.Berlín:Springer-Verlag,2006.(AlgorithmsandComputationin Mathematics;10)

[5] Ben-Israel,A. «Notesonlinearinequalities.I.Theintersectionofthe nonnegativeorthantwithcomplementaryorthogonalsubspaces». J.Math. Anal.Appl.,9(1964),303–314.

[6] Bernstein,D.N. «Thenumberofrootsofasystemofequations». Funkcional.Anal.iPriložen.,9(3)(1975),1–4.[Enrus]

[7] Bihan,F.;Dickenstein,A.;Forsgård,J. «OptimalDescartes’ruleof signsforsystemssupportedoncircuits». Math.Ann.,381(3-4)(2021), 1283–1307.

[8] Bihan,F.;Dickenstein,A.;Giaroli,M. «Lowerboundsforpositiveroots andregionsofmultistationarityinchemicalreactionnetworks». J.Algebra, 542(2020),367–411.

[9] Bihan,F.;Santos,F.;Spaenlehauer,P.-J. «Apolyhedralmethodfor sparsesystemswithmanypositivesolutions». SIAMJ.Appl.Algebra Geom.,2(4)(2018),620–645.

[10] Bihan,F.;Sottile,F. «NewfewnomialupperboundsfromGaledual polynomialsystems». Mosc.Math.J.,7(3)(2007),387–407.

[11] Blekherman,G. «Nonnegativepolynomialsandsumsofsquares».A: SemidefiniteOptimizationandConvexAlgebraicGeometry.Filadèlfia,PA: SIAM,2013,159–202.(MOS-SIAMSer.Optim.;13)

[12] Boros,B. «Ontheexistenceofthepositivesteadystatesofweaklyreversibledeficiency-onemassactionsystems». Math.Biosci.,245(2)(2013), 157–170.

[13] Cappelletti,D.;Wiuf,C. «Product-formPoisson-likedistributionsand complexbalancedreactionsystems». SIAMJ.Appl.Math.,76(1)(2016), 411–432.

[14] Conradi,C.;Feliu,E.;Mincheva,M. «OntheexistenceofHopfbifurcationsinthesequentialanddistributivedoublephosphorylationcycle». Math.Biosci.Eng.,17(1)(2020),494–513.

[15] Conradi,C.;Feliu,E.;Mincheva,M.;Wiuf,C. «Identifyingparameterregionsformultistationarity». PLoSComput.Biol.,13(10)(2017),e1005751.

[16] Conradi,C.;Flockerzi,D. «Switchinginmassactionnetworksbasedon linearinequalities». SIAMJ.Appl.Dyn.Syst.,11(1)(2012),110–134.

[17] Conradi,C.;Flockerzi,D.;Raisch,J.;Stelling,J. «Subnetworkanalysis revealsdynamicfeaturesofcomplex(bio)chemicalnetworks». Proc.Nat. Acad.Sci.,104(49)(2007),19175–19180.

[18] Conradi,C.;Iosif,A.;Kahle,T. «Multistationarityinthespaceoftotal concentrationsforsystemsthatadmitamonomialparametrization». Bull. Math.Biol.,81(10)(2019),4174–4209.

[19] Conradi,C.;Mincheva,M. «Catalyticconstantsenabletheemergenceof bistabilityindualphosphorylation». JournalofTheRoyalSocietyInterface, 11(95)(2014).

[20] Conradi,C.;Mincheva,M.;Shiu,A. «Emergenceofoscillationsina mixed-mechanismphosphorylationsystem». Bull.Math.Biol.,81(6)(2019), 1829–1852.

[21] Cornish-Bowden,A. FundamentalsofEnzymeKinetics.3aed.Londres: PortlandPress,2004.

[22] Cox,D.;Little,J.;O’Shea,D. Ideals,Varieties,andAlgorithms.AnIntroductiontoComputationalAlgebraicGeometryandCommutativeAlgebra 3aed.NovaYork:Springer,2007.(UndergraduateTextsinMathematics)

[23] Craciun,G.;Dickenstein,A.;Shiu,A.;Sturmfels,B. «Toricdynamical systems». J.SymbolicComput.,44(11)(2009),1551–1565.

[24] Craciun,G.;Pantea,C. «Identifiabilityofchemicalreactionnetworks». J. Math.Chem.,44(1)(2008),244–259.

[25] Descartes,R. LaGéométrie.1637.

[26] ElKahoui,M.;Weber,A. «DecidingHopfbifurcationsbyquantifiereliminationinasoftware-componentarchitecture». J.SymbolicComput.,30(2) (2000),161–179.

[27] Elizalde,S. «Combinatòriaibiologia:funcionsd’inferènciaialineació deseqüències». ButlletídelaSocietatCatalanadeMatemàtiques,21(1) (2006),39–52.

[28] Errami,H.;Eiswirth,M.;Grigoriev,D.;Seiler,W.M.;Sturm,T.;Weber,A. «DetectionofHopfbifurcationsinchemicalreactionnetworks usingconvexcoordinates». J.Comput.Phys.,291(2015),279–302.

ElisendaFeliu

[29] Feinberg,M. «Onchemicalkineticsofacertainclass». Arch.Rational Mech.Anal.,46(1972),1–41.

[30] Feinberg,M. «Complexbalancingingeneralkineticsystems». Arch.RationalMech.Anal.,49(1972),187–194.

[31] Feinberg,M. «Chemicalreactionnetworkstructureandthestabilityof complexisothermalreactors—I.Thedeficiencyzeroanddeficiencyone theorems». ChemicalEngineeringScience,42(10)(1987),2229–2268.

[32] Feinberg,M. «Chemicalreactionnetworkstructureandthestability ofcomplexisothermalreactors—II.Multiplesteadystatesfornetworksof deficiencyone». ChemicalEngineeringScience,43(1)(1988),1–25.

[33] Feinberg,M. «Theexistenceanduniquenessofsteadystatesforaclass ofchemicalreactionnetworks». Arch.RationalMech.Anal.,132(4)(1995), 311–370.

[34] Feinberg,M. FoundationsofChemicalReactionNetworkTheory.Cham: Springer,2019.(AppliedMathematicalSciences;202)

[35] Feliu,E.;Henriksson,O.;Pascual-Escudero,P. «Dimensionanddegeneracyinpolynomialsystemscomingfromreactionnetworks».En preparació(2023).

[36] Feliu,E.;Kaihnsa,N.;deWolff,T.;Yürük,O. «Parameterregionfor multistationarityin n-sitephosphorylationnetworks».Preprint(2022). arXiv:2206.08908.

[37] Feliu,E.;Kaihnsa,N.;deWolff,T.;Yürük,O. «Thekineticspaceofmultistationarityindualphosphorylation». J.Dynam.DifferentialEquations,34 (2)(2022),825–852.

[38] Feliu,E.;Rendall,A.D.;Wiuf,C. «Aproofofunlimitedmultistabilityfor phosphorylationcycles». Nonlinearity,33(11)(2020),5629–5658.

[39] Feliu,E.;Telek,M.L. «OngeneralizingDescartes’ruleofsignstohypersurfaces». Adv.Math.,408(2022),partA,articlenúm.108582,29p.

[40] Feliu,E.;Wiuf,C. «Variableeliminationinchemicalreactionnetworks withmass-actionkinetics». SIAMJ.Appl.Math.,72(4)(2012),959–981.

[41] Feliu,E.;Wiuf,C. «Variableeliminationinpost-translationalmodification reactionnetworkswithmass-actionkinetics». J.Math.Biol.,66(1-2)(2013), 281–310.

[42] Flockerzi,D.;Holstein,K.;Conradi,C. «n-sitephosphorylationsystems with2n 1steadystates». Bull.Math.Biol.,76(8)(2014),1892–1916.

[43] Gantmacher,F.R. TheTheoryofMatrices.Vol.1,2.NovaYork:Chelsea PublishingCo.,1959.[TraduïtperK.A.Hirsch]

[44] Gatermann,K.;Eiswirth,M.;Sensse,A. «Toricidealsandgraphtheory toanalyzeHopfbifurcationsinmassactionsystems». J.SymbolicComput., 40(6)(2005),1361–1382.

[45] Gawrilow,E.;Joswig,M. «polymake:aframeworkforanalyzingconvexpolytopes».A: Polytopes–CombinatoricsandComputation.Basilea: Birkhäuser,2000,43–73.(DMVSem.;29)

[46] Guldberg,C.;Waage,P. «Studiesconcerningaffinity». Forhandlingeri Videnskabs-SelskabetiChristiania (1864),35.

[47] Gunawardena,J. «Alinearframeworkfortime-scaleseparationinnonlinearbiochemicalsystems». PLoSOne,7(5)(2012),e36321.

[48] Gunawardena,J. «SomelessonsaboutmodelsfromMichaelisandMenten». Mol.Biol.Cell,23(4)(2012),517–519.

[49] Horn,F.;Jackson,R. «Generalmassactionkinetics». Arch.RationalMech. Anal.,47(1972),81–116.

[50] Iliman,S.;deWolff,T. «Amoebas,nonnegativepolynomialsandsumsof squaressupportedoncircuits». Res.Math.Sci.,3(2016),articlenúm.9, 35p.

[51] Ji,H. «Uniquenessofequilibriaforcomplexchemicalreactionnetworks». Tesidemàster(2011).

[52] Joshi,B.;Shiu,A. «Atomsofmultistationarityinchemicalreaction networks». J.Math.Chem.,51(1)(2013),153–178.

[53] Joshi,B.;Shiu,A. «Asurveyofmethodsfordecidingwhetherareaction networkismultistationary». Math.Model.Nat.Phenom.,10(5)(2015), 47–67.

[54] Kothamachu,V.B.;Feliu,E.;Cardelli,L.;Soyer,O.S. «UnlimitedmultistabilityandBooleanlogicinmicrobialsignalling». JournalofTheRoyal SocietyInterface,12(108)(2015),20150234.

[55] Kurtz,T.G. «Therelationshipbetweenstochasticanddeterministicmodelsforchemicalreactions». J.Chem.Phys.,57(7)(1972),2976–2978.

[56] Liu,W.M. «CriterionofHopfbifurcationswithoutusingeigenvalues». J. Math.Anal.Appl.,182(1)(1994),250–256.

[57] Müller,S.;Feliu,E.;Regensburger,G.;Conradi,C.;Shiu,A.;Dickenstein,A. «Signconditionsforinjectivityofgeneralizedpolynomialmaps withapplicationstochemicalreactionnetworksandrealalgebraicgeometry». Found.Comput.Math.,16(1)(2016),69–97.

[58] Nam,K.-M.;Gyori,B.M.;Amethyst,S.V.;Bates,D.J.;Gunawardena,J. «Robustnessandparametergeographyinpost-translationalmodification systems». PLoSComput.Biol.,16(5)(2020),e1007573.

[59] Obatake,N.;Shiu,A.;Tang,X.;Torres,A. «Oscillationsandbistability inamodelofERKregulation». J.Math.Biol.,79(4)(2019),1515–1549.

[60] Pantea,C.;Koeppl,H.;Craciun,G. «Globalinjectivityandmultiple equilibriainuni-andbi-molecularreactionnetworks». DiscreteContin. Dyn.Syst.Ser.B,17(6)(2012),2153–2170.

ElisendaFeliu

[61] PérezMillán,M.;Dickenstein,A.;Shiu,A.;Conradi,C. «Chemical reactionsystemswithtoricsteadystates». Bull.Math.Biol.,74(5)(2012), 1027–1065.

[62] Reznick,B. «Formsderivedfromthearithmetic-geometricinequality». Math.Ann.,283(3)(1989),431–464.

[63] Sáez,M.;Wiuf,C.;Feliu,E. «Nonnegativelineareliminationforchemical reactionnetworks». SIAMJ.Appl.Math.,79(6)(2019),2434–2455.

[64] TheSageDevelopers. «SageMath,theSageMathematicsSoftwareSystem (Version9.2)».(2021). https://www.sagemath.org.

[65] Shafarevich,I.R. BasicAlgebraicGeometry.NovaYork-Heidelberg: Springer-Verlag,1974.(DieGrundlehrendermathematischenWissenschaften;213)[TraduïtdelrusperK.A.Hirsch]

[66] Shiu,A.;Sturmfels,B. «Siphonsinchemicalreactionnetworks». Bull. Math.Biol.,72(6)(2010),1448–1463.

[67] Telek,M.L.;Feliu,E. «Topologicaldescriptorsoftheparameterregionof multistationarity:decidinguponconnectivity». PLoSComput.Biol.,19(3) (2023),1–38.

[68] Thomson,M.;Gunawardena,J. «Unlimitedmultistabilityinmultisite phosphorylationsystems». Nature,460(2009),274–277.

[69] Torres,A.;Feliu,E. «Detectingparameterregionsforbistabilityinreactionnetworks». SIAMJ.Appl.Dyn.Syst.,20(2020),1–37.

[70] Vol’pert,A.I. «Differentialequationsongraphs». Math.USSR-Sb.,17 (1972),571–582.

[71] Wang,L.;Sontag,E. «Onthenumberofsteadystatesinamultiplefutile cycle». J.Math.Biol.,57(1)(2008),29–52.

[72] Wang,X. «AsimpleproofofDescartes’sruleofsigns». Amer.Math. Monthly,111(6)(2004),525–526.

DepartmentofMathematicalSciences, UniversityofCopenhagen

Universitetsparken 5, 2100 København,Danmark efeliu@math.ku.dk

ButlletídelaSocietatCatalanadeMatemàtiques Vol.37,núm.2,2022.Pàg.137–172. DOI:10.2436/20.2002.01.105

Oscil.ladorsenressonància

DavidRojas

Resum: Unoscil ladorésunsistemaenelqualtotselsmovimentspossiblessón periòdics.Siaquestperíodeéscomúperatotselsmoviments,esdiuquel’oscilladorésisòcron.Quanelsistemaésforçatperunapertorbacióperiòdicaambel mateixperíode,ladinàmicapotcanviardràsticamentielfenomenderessonànciapot aparèixer.Enaquestarticleestudiaremquinespropietatshandecompliraquestes pertorbacionsperobtenirsolucionsnoacotades.Consideraremdiferentsoscil.ladors, desdel’harmònicfinsageneralitzacionsnolineals,ifaremuntastdelconceptede ressonànciaautoparamètrica.

Paraulesclau: oscil.lador,ressonància,pertorbació,isocronia.

ClassificacióMSC2020: 34C10,34C15,34D05,34D10,34D23.

1Introducció

Ésabrilde1831.Unabrigadadesoldatsdel’armadabritànicamarxenapassobreelpontpenjantdeBroughtonpercreuarelriuIrwellaBroughton,propde Manchester.Desobte,elponts’ensorraiunadotzenadesoldatsacabena l’aiguadelriu.Pocdesprés,l’armadabritànicacomunicaatotselsseussoldats que,apartird’ara,ésobligattrencarelpasdelamarxaencreuarunpontllarg.

ElcantantderockJaimeVendera,l’any2005,alprograma MythBusters de DiscoveryChannel,esmicolaunacopadevidrefentservirnoméslasevaveu, ambuncritde105decibels.Se’npotveureunarepresentacióalseucanalde Youtube[41].

SegonsJosuè6:1-27,l’armadaisraelitavacreuarelriuJordàivaenvoltarla ciutatemmuralladadeJericó.DurantsisdiesJosuèfamarxarlessevestropes alvoltantdelaciutatialsetèfasonarelscornsdebanyesdemoltó.Llavors,el murcauielsisraelitescremenlaciutat.

Unnendemanaserempèsalgronxadordelparcdelaplaça.Elsseuspares, deformasincronitzada,lidonenpetitsimpulsosque,apocapoc,fanquevagi agafantaltura.

Totesaquesteshistòriestenenuncomúdenominador.Entotselscasos, unsistemavibratoriesveuafectatperunaforçaperiòdicaexterna.Enelcas

enquèlafreqüènciadelaforçaexternacoincideixambladelsistema,aquest experimentauncreixementdel’amplituddelseuestat,quemoltprobablement produiràelseucol.lapse.Aquestfenomenésconegutcoma ressonància.

Elconceptederessonànciaesfaservirendiversoscampsiambdiferents sentits.Elsexemplesanteriorscorresponenalconceptederessonàncialligatala pertorbacióperiòdicadesistemesoscil latoris,comtambéhosónlaressonància acústicadelsinstrumentsmusicals(vegeul’articledeTomásSanz-Perelaen aquestmateixnúmero),laressonànciademareadelabadiadeFundyila dinàmicadeltubdeRubens,unarepresentaciódelfuncionamentdelquales potveurealcanaldeYoutube SteveMould [27].Quanparlemderessonància, intuïtivamentpensemendosfenòmensquesucceeixenalhora:lacoincidència deduesfreqüències(ladelsistemailadelapertorbació)iuncreixementde l’amplituddelsistemaqueacabaproduintinestabilitat.Avegades,però,el conceptederessonànciaesfaservirnoméslligatalprimerdelsfenòmens.Per exemple,laressonànciaorbitalpotdonarlloctantalainestabilitatdelsistema, talcommostrenelsforatsdel’anelldeSaturn,comtambéal’estabilitat,comen elcasdelaressonància1:2:4delesllunesdeJúpiter,Io,EuropaiGanimedes.

Enaquesttreballenscentraremenlaressonànciaqueprovocainestabilitat. Mésconcretament,faremunrecullderesultatssobreressonànciad’oscil.ladors pertorbatsperiòdicamentientendrem,durantpràcticamenttoteltext,el conceptederessonànciacomelfetquetoteslessolucionsdelsistemasón noacotades.Veuremelsdosexemplesmecànicsméssenzills:l’oscil.lador harmònicil’oscil ladorasimètric,icontinuaremambexemplesmésgenerals fugintdelalinealitat.

Al’últimasecciótractaremunconceptederessonànciasubtilmentdiferent, laressonànciaautoparamètrica.Encomptesd’unaforçaexterna,considerarem modelsambdosmodesvibratorispropis.Veuremcomelfetqueelsistema estiguienressonància,ésadir,quelesfreqüènciesdelsdosmodessiguin commensurables,provocaqueelsistemamostriinestabilitat.

Unlectorambconeixementsderessonànciatrobaràafaltarenaquesta introduccióelqueseguramentésl’exemplemésparadigmàtic:elcol.lapsedel pontdeTacoma-Narrows.Aquestexemples’haomèsintencionadament.Primer, perlafaltad’unanimitatsobreelmotiudelcol.lapsei,segon,perquèestudis recentssuggereixenqueelfenomenderessonàncianoésproduïtpelventcom aforçaexterna,sinóperlaressonànciaentreelsmodesvibratorisverticalide torsiódelpont.Veuremunmodelqueintentaexplicaraquestfetaladarrera secció.

2Pertorbacionsexternes

Elfetdeconsiderarequacionsdiferencialsdesegonordreautònomesper descriuremodelsfísicsnoéscircumstancial.Alamecànicaclàssica,lasegona lleideNewtonrelacional’acceleraciód’unapartículaamblesforcesquehi interactuen,lesqualsdepenen(normalment)delasevaposicióivelocitat.En electrònica,lalleideKirchhoffrelacionalaintensitatdecorrentamblaseva derivadatemporalilasevaprimitiva.Enambdóscasos,imoltsaltres,la

dinàmicadelsistemavedescritaperunaequaciódiferencialdesegonordre. Perexemple,enelcasd’uncircuitRLCensèrie,quanelvoltatgedelafontés constant, V(t) = V0,laintensitatdecorrent I(t) satisfàl’equaciódiferencialde segonordrelineal

LI(t) + RI(t) + 1 CI(t) = 0,

on L, R i C sónlainductànciadelabobina,laresistènciailacapacitatdel condensador,respectivament.Enl’equacióanterioriduranttoteltreball, usarem f(t) i f(t) perdenotarladerivadaprimeraisegonadelafunció f(t), respectivament.Quan,encanvi,lafontésuncorrentaltern,lafunció V(t) és periòdicailaintensitatdecorrentsatisfàunaequaciódiferencialforçada periòdicament,

LI(t) + RI(t) + 1 CI(t) = d dtV(t).

Aquestfetmotival’estudidepertorbacionsperiòdiquesdesistemesautònoms. Unaltreexempleelpodemtrobaralamecànicaceleste.Quandoscossos interactuensegonslalleidelagravitació,elmovimentdelprimercosvedescrit perl’equaciódeKepler

on x(t) éslaposiciódelamassa m1 suposantqueelcentredemassesdel problemaésl’origen,i m2 éslamassadelsegoncos.Estracta,enefecte,d’una equaciódiferencialautònomadesegonordre.Quanméscossosentrenenjoc,el problemaesdevémoltméscomplicat.Enocasionsésinteressantconsiderar comafectenl’equacióanteriorforcesexercidesperaltresastresdemanera periòdicai,pertant,esconsiderenpertorbacionsperiòdiquesdel’equacióde Kepler,

Comhemcomentatalaintroducció,l’efectederessonànciapotaparèixer quanunsistemaautònomquepresentasolucionsperiòdiqueséspertorbat periòdicament.Duranttotalaseccióconsideraremsistemesautònomsen elsqualstoteslessolucionssónperiòdiquesd’unmateixperíode.D’aquesta manera,diremqueelsistemaésunoscil ladorielperíoded’aquestoscil lador éselperíodecomúdetoteslessevessolucions.Quanunsistemaenaquestes condicionsésforçatambunapertorbacióperiòdicaexternaambelmateix períodequeeldel’oscil.lador,elfenomenderessonànciapotaparèixer.En aquestcontext,entendremressonànciacomlapropietatquetoteslessolucionsdelsistemapertorbatsónnoacotades.Mésconcretament,si x(t) ésla soluciódelsistemapertorbat,aleshores

peraalgunasuccessió {tn}.Enaquestaseccióestudiaremaquestfenomenen diferentsmodels,començantpelcaslineal,l’oscil.ladorharmònic,passantper

lasevaversióasimètricaicompletantambalgunesgeneralitzacionsd’ambdós casos.Peraunresumméscompletd’algunsdelsresultatssobreressonància, existènciad’òrbitesperiòdiquesisolucionsnoacotadesdesistemespertorbats periòdicamentquepresentarem,vegeueltreballdeMawhin[25].

2.1L’oscil.ladorharmònic

Comencemaquestaseccióambunaderivaciódel’oscil ladorharmònicque,tot iserelemental,ensserviràdeguiaalllargd’aquesttreball.

Consideremunamollaambconstantderigidesa k> 0penjadadelsostre (vegeulafigura1).Commésgranéslaconstant k,mésrígidaéslamollai,en conseqüència,més«difícil»ésestirar-la(oestrènyer-la).Perevitarproblemesde xocambelsostre,suposaremqueaquestestà«infinitament»llunydel’extrem delamollad’onpengemunamassa m> 0.Enpenjarlamassa,elseupes desplaçalamollaunacertadistància d0 > 0respectedelaposiciód’equilibri inicial,iassoleixunaaltraposiciód’equilibri.SegonslaprimeralleideNewton, enequilibrilasumatotaldeforcesqueintervenenenelsistemamecànic hadesernul.la.Enaquestcas,observemduesforcesquemantenenaquest equilibri.Enprimerlloc,elpesdelamassapenjadadel’extremdelamolla,amb magnitud mg,on g ésl’acceleraciódelagravetatallloconestrobalamassa. Ensegonlloc,laforçaquelamollaexerceixperevitarquelamassacaiguii que,segonslalleideHooke,témagnitud kd0.Fixemqueelsentitpositiudel movimentéselmarcatpelpes.Llavors,laprimeralleideNewtondiu:

Figura 1: Representaciód’unoscil.ladorharmònicamblesforcesinternesquehiinteractuen.

Denotemamb x(t) eldesplaçamentdelamassarespectedelaposició d’equilibri.Ara,laforçadelamollaés k(d0 + x(t)),mentrequeelpesroman constant.Tenim,doncs,undesequilibrideforcesi,enconseqüència,moviment. SegonslasegonalleideNewton,

mg k(d0 + x(t)) = mx(t), on ˙ x(t) éslavelocitatdel’objectei ¨ x(t) lasevaacceleració.Observemque l’anteriorigualtatesredueix,fentservirl’equació(1),al’expressió

x(t) + ω2x(t) = 0, (2) amb ω := k m .L’equació (2) ésl’oscil.ladorharmònic (o oscil.ladorlineal)ité comafreqüèncianatural ω,degutalfetquetoteslessolucionssóndelaforma

x(t) = A cos(ωt + ϕ), ésadir,totestenenperíodemínim T = 2π ω .Enl’expressióanterior, A denota l’amplituddel’oscil lació x(t) i ϕ éslafase.Lafreqüència ω i,pertant,el període T nomésdepenendelsparàmetresdelsistema(k i m)isóncomunsa toteslessolucions,independentmentdelescondicionsdeposicióivelocitat inicialsdelamassa.Enparticular,esdiuquel’equació (2) téuncentreisòcron al’origen.

Unequilibriésuncentresitoteslessolucionsambcondicionsinicials properessónperiòdiques.Si,amésamés,elperíodeéscomúatotesles solucions,elcentreesdiuisòcron.Enelcasdel’oscil ladorharmònic,lasolució constant x(t) = 0ésunequilibrii,comhemvist,toteslesaltressolucions de(2)sónperiòdiquesdeperíode T = 2π ω .

Consideremaral’oscil ladorharmònic (2) forçatexternamentperunafunció contínuai2π -periòdica p(t), x(t) + ω2x(t) = p(t). (3)

Femnotarqueprendre p(t) ambperíode2π noésrestrictiu.Enefecte,un canviproporcionaldetempséssuficientperobtenir p(t) ambelperíode desitjatacanvidemodificar ω.Enaquestpuntésnaturalpreguntar-secomes comportenlessolucionsdel’equació(3).

Totafunciócontínua2π -periòdicatéundesenvolupamentensèriede Fourier

p(t) ∼ p0 + ∞ n=1 (pn cos(nt) + qn sin(nt)).

LaconvergènciadelasèriedeFourierdepèndelaregularitatdelafunció p(t) Perobtenirconvergènciapuntualéssuficienttenirdiferenciabilitatambderivadacontínua,mentrequelacontinuïtatasseguraconvergència gairebépera tot t.Donatquel’objectiud’aquestadiscussiónorecauenlaregularitatdela pertorbació,ellectorpotassumir-nemésquecontinuïtatperconvèncer-sede ferservirlaigualtat = encomptesdel’aproximació ∼ enlaidentitatanterior.

Lalinealitatdel’equació (3) permettrobarlasoluciócomasumadeles solucionsdelesequacions

xn(t) + ω2xn(t) = pn cos(nt) + qn sin(nt),n = 0, 1, 2,... (4)

detalformaque x(t) = ∞

=0 xn(t).L’equacióanteriorespotresoldre,perexemple,fentservirlatransformadadeLaplace.Denotantamb Xn(s) =L{xn(t)}(s),

Elprimersumanddel’expressiócorrespon,desprésdeferlatransformada inversadeLaplace,alasoluciódelaparthomogèniade (4).Enelsegonterme ésonelfenomenderessonànciaentraenacció.Observemquel’expressió de xn(t) variasignificativamentsi

cas

xn(t) = An cos(ωt) + Bn sin(ωt) + pn cos(nt) + qn sin(nt)

, amb An = xn(0)(ω2 n2) p

)

nn).Observemque enelcas ω ≠ n lessolucionssóngenèricamentquasiperiòdiquesiacotades, iexisteixnomésunasolucióambelmateixperíodequelapertorbacióexterna p(t):aquellaqueanul.laelscoeficients An i Bn.Quan ω = n,lessolucions sóndelaforma

xn(t) = (2n2xn(0) nqnt) cos(nt) + (2xn(0) + qn + npnt) sin(nt) 2n2 .

Enaquestcas,lessolucionssóngenèricamentnoacotadesexcepteelcasen què pn i qn s’anul len.Aquestraonamentésclàssiciesresumeixenelresultat següent.

Proposició 1. Sigui p(t) unafunciócontínua 2π -periòdica,aleshores:

(a) Si ω ≠ n ∈ N,toteslessolucionsdel’equació (3) sónquasiperiòdiquesi acotadesexcepteuna,queés 2π -periòdica.

(b) Si ω = n ∈ N i p2 n + q2 n ≠ 0,toteslessolucionsdel’equació (3) sónno acotades.

(c) Si ω = n ∈ N i p2 n + q2 n = 0,toteslessolucionsdel’equació (3) són 2π -periòdiques.

Hemobservatqueperobtenirelfenomenderessonànciaésnecessariqueel períodedelapertorbacióexternasiguielmateixqueelperíodedel’oscil.lador harmònic,perònoéssuficient.Necessitemlacondicióextra p2 n + q2 n ≠ 0que, totisergenèrica,evidentmentnosempresesatisfà.Comaexempled’aquest fenomen,considereml’oscil.ladorharmònicambperíodemínim2π pertorbat perunafunció2π -periòdica p(t), ¨ x + x = p(t). (5)

Enaquestcas, ω = 1.Lafunció p(t) = cos(t) + cos(2t) és2π -periòdica amb p1 = p2 = 1, pn = 0pera n ≠ 1, 2i qn = 0peratot n ≥ 1.Enparticular, p2 1 + q2 1 = 1i,enconseqüència,lapertorbacióprovocaressonància(vegeu lafigura2esquerra).Encanvi,lafunció p(t) = cos(2t) + cos(3t) tambéés

2π -periòdicaamb p2 = p3 = 1, pn = 0pera n ≠ 2, 3i qn = 0peratot n ≥ 1. Donatque p2 1 + q2 1 = 0,aquestaforçaexternanoprovocaressonància(vegeula figura2dreta).

Figura 2: Solucióde (5) ambcondicionsinicials x(0) = 1, ˙ x(0) = 0amb p(t) = cos(t) + cos(2t) (esquerra)i p(t) = cos(2t) + cos(3t) (dreta).

Lacondició p2 n + q2 n ≠ 0potescriure’sdemaneraequivalentfentservirla notaciócomplexadelasèriedeFourier.Enefecte,

Éslegítimanomenar-la condicióderessonància del’oscil.ladorharmònic.

Ésimportantobservarquetotaladiscussióanteriorésindependentde l’amplituddelaforçaperiòdicaexterna.Ésadir,elfenomenderessonància apareixtotiquelapertorbaciósiguipetita.Enaltresparaules,podemescriure l’equació(3)com

ilacondicióderessonànciaimplicaràquetoteslessolucionssónnoacotades peratot0 < 1.Aixòsubratllaqueelfetd’obtenirsolucionsnoacotadesno provédelaquantitatd’energiaquelaforçaafegeixalsistema,sinódelmoment enelqualaquestaenergias’estàintroduint.Elterme«energia»utilitzatprovéde lafísicaifareferènciaalhamiltoniàdelsistema,interpretatcoml’energiatotal

delmodel.Enelcasdel’oscil.ladorharmònicsensepertorbar,l’energiatotales conservaalllargdelestrajectòries.Ésadir,si x0(t) éssolucióde(2),

peratot t ∈ R i E0 depènnomésdelescondicionsinicialsde x0(t).Encanvi, quanelsistemaésforçatperiòdicamentperunapertorbació p(t),aleshores l’energiadelsistemacanviaalllargdeltempscom E(t)

p(t), on x(t) éssoluciódel’equació (7).D’aquestaúltimaexpressióesderivael concepted’energiaintroduïda.

Demaneranatural,l’exempleanteriormotival’estudidelaressonància peraoscil.ladorsisòcronsmésgenerals.Lesproperesseccionsestandedicades aestudiarcomlacondicióderessonànciavariaenmodelsmecànicsque generalitzenl’oscil.ladorharmònic.Abans,però,vegemqueaquestproblematé sentitnomésenmodelssensedissipacióenergètica.

2.1.1Ladissipaciód’energiaesmorteeixlaressonància Elsistemaque hemconsideratinicialmental’equació (2) notédissipacióijustamentaquest éselfetpelquallaforçaexternaambfreqüènciaressonantfaquetotesles solucionssiguinnoacotades.Siconsideremqueelmodelpresentafriccióamb elmedi,al’equaciódelmovimenthemd’afegirunaforçadefriccióoposadaal moviment,queenlamajoriadelssistemesvibratorisesconsideraproporcional alavelocitat, cx(t),amb c> 0.Siincloemaquestterme,l’equaciódel movimentespotescriurecom

s’anomena coeficientdissipatiu.Lessolucionsdelmodelamb dissipaciódistenqualitativamentdelessolucionsperiòdiquesdelcasnodissipatiu.Enaquestcasobtenimtrestipusdesoluciódepenentdecomdeforta siguilaforçadefricció.Sidenotemamb X(s) =L{x(t)}(s) latransformada deLaplacede x(t),del’equació(8)deduïm

Sisesatisfàque ξ ≥ 1,aleshoreslesarrelsdelpolinomi s2 + 2ξω+ω2 sónreals ilasolució x(t) de (8) s’escriucomunacombinaciód’exponencials.Enaquest casesdiuqueelsistemaestà sobreesmorteït inohihamovimentoscil latori. Quan0 <ξ< 1,aleshoreslesarrelsdeldenominadorsóncomplexesila solució x(t) prenlaforma

x(t) = Ae ξωt cos( t + ϕ),

amb = ω 1 ξ2.Observemque,totiseroscil.latòria,lasolucióanterior tendeixal’equilibrienavançareltempsperlapresènciadeladissipació,i s’obtenenelques’anomenen oscil.lacionsesmorteïdes.

Demaneranatural,sorgeixlapreguntadecomescomportenlessolucionsdelmodelambfriccióquanafegimenergiaalsistemademaneraperiòdica.Podemconsiderarelsistema (8) pertorbatperunafunciócontínuai

,

(9)

Seguintunprocedimentsimilaraldelcasnodissipatiu,obtenimquelessolucionsde(9)espodenescriurecom

=

,on

Lessolucionsde (9) tenenduespartsbendiferenciades.Laprimeraconsisteix enunaparttransitòria,l’associadaalaparthomogèniadel’equació,ique ambelpasdeltempstendeixazeroacausadeltermeexponencial.Lasegona part, z

(t),apareixacausadelapertorbacióperiòdica.Observemqueestracta d’unafunció2π -periòdica,igualqueenelcasnodissipatiu,ambamplitud

Figura 3: Amplituddelapartestacionàriadelasoluciódel’oscil lador harmònicambparàmetres p2 1 + q2 1 = 1i pn = qn = 0pera n ≠ 1.Pera cadavalorde ξ,elmàximdel’amplitud Zn s’assoleixen ω = ωr .

Enaquestcaslaressonància,però,s’enténdemaneradiferent.Lesfuncions zn(t) (i,pertant,lasolució x(t))sónacotades.Detotesmaneres,observanteldenominadordel’amplitud Zn,podemveurequeaquestaésmàxima quan ω = ωr := n 1 2ξ2 (vegeulalocalitzaciódelmàximencadascuna delescorbesdelafigura3).Aquestvalorrepelnomde freqüènciaderessonància,pelfetdeserlafreqüènciaenquèl’amplituddelasolucióésmàxima. Unaobservacióevidentésqueaquestafreqüènciaderessonànciatendeixala del’oscil.ladorharmònicsensefriccióquan ξ → 0.Però,adiferènciadelcas nodissipatiu,aquesta«amplitudgran»delasoluciónoésindependentde lamagnituddelaforçaperiòdicapertorbativa.Enefecte,siconsideremuna pertorbaciópetita p(t),alnumeradordelscoeficientsde zn(t) elstermes pn i qn passenaser pn i qn,ipodemreduirl’amplituddelasoluciótantcom vulguem.Aquestfetéscomúenelssistemesdissipatiusiésperaixòqueno elsconsideraremalarestadeltreball.

2.2L’oscil.ladorasimètric

Unaprimerageneralitzaciódel’oscil.ladorlinealésl’oscil.ladorasimètric.Per alasevadeducció,seguiremlaconstrucciód’unmecanismeproposatperOrtega[31].Comenelcasharmònic,consideremunamassa m penjadad’una mollaambconstantderigidesa k1 desd’unsostrefinsal’infinit.Denotem amb x(t) eldesplaçamentdelamassarespectealaposiciód’equilibri.Ara, consideremunasegonamolla,sensemassa,ambconstantderigidesa k2 de talmaneraquelalongituddelamollacoincideixiamblaposiciód’equilibri delaprimera,ésadir, x = 0.Aquestasegonamollanoestàancoradaala massa,peròconsideremlamassa m detalmaneraque,pera x ≤ 0,lamassa técontacteambambduesmollesdeconstants k1 i k2,mentrequepera x> 0, noméslaprimeramollaambconstant k1 exerceixforçasobrelamassa(vegeu lafigura4).Perdeduirl’equaciódelmovimentdelamassasotaaquestartefacte mecànic,hemdeconsiderarlesduesdisposicionsquepottenir.Si x(t)> 0, l’equaciódelmovimentesdevélamateixaqueperal’oscil ladorharmònicamb constantderigidesa k1.Aixídoncs,

0,sobrelamassaactuenambduesmollesalhora. DonatquelalleideHookeéslinealrespectealaconstantderigidesa,obtenim

maneraméscompactaposant x+ = max{0,x} i x = max{0, x},iobtenim aixíl’equaciódelmovimentdel’oscil.ladorasimètric

onhemomèsladependènciatemporalpersimplicitat.Essencialment,estracta d’unoscil.ladorharmònicambconstantderigidesadiferentpera x< 0iper a x> 0.

Llunydesemblarunartefacteacadèmic,l’oscil.ladorasimètrichamostratla sevapresènciasubjacentenmodelsmecànicsméscomplexos.N’ésunexemple elmodelproposatperLazeriMcKennaa[20]peraunpontensuspensió. Consideremunpontdellargada L i x ∈ [0,L] lavariablequeparametritzala posicióhoritzontalalllargdelpont.Eldesplaçamentverticaldelpont u(t,x) respecteal’horitzontal u = 0(amb u> 0enladirecciósotal’horitzontal)al punt x enfunciódeltemps t satisfàl’equaciódiferenciald’Euler-Bernoullide l’elàstica

(13)

ambcondicionsalafrontera u(t, 0) = u(t,L) = d2 dx2 u(t, 0) = d2 dx2 u(t,L) = 0 Enl’equacióanterior,observemqueelfactor au+ estàmotivatpelfetque,en unpontensuspensió,elscablesqueelsubjectennomésinteractuen(ambuna forçalinealsegonslalleideHooke)quanlaposicióverticalestàpersotade l’horitzontal u = 0(ésadir, u> 0).Lafunció f modelalesforcesexternes alesqualséssotmesacadapartdelpontalllargdeltempsi,essencialment, estàcompostaperdoscomponents f = f1 + f2.Elmésgran, f1,corresponal mateixpesdelpont,mentrequeelsegon, f2,ésméspetitaitéaveureambels efectespertorbatiusexternsacausadefactorscomlafricciódelvent.Donada lasimetriadelpontil’ancoratgeaterraalspunts x = 0i x = L,lafunció f es potmodelardemanerasimplificadacom

f(x,t) = (1 + p(t)) sin πx L .

Aquestfetmotivalacercadesolucionsdelaforma u(t,x) = v(t) sin πx L .En efecte,substituint u(t,x) enl’equació(13)s’obté

v(t) + π L 4 v(t) + av +(t) = 1 + p(t).

Figura 4: Representaciód’unoscil.ladorasimètric.

Finalment,pera v(t) = v +(t) v (t),trobemque v(t) hadesatisferl’equació diferencialdel’oscil.ladorasimètricpertorbat v(t) + ω2 1v +(t) ω2 2v (t) = 1 + p(t),

Comentàvemal’inicidelaseccióquel’oscil ladorasimètric (12) ésuna generalitzaciódel’oscil.ladorharmònic.Perunabanda,aquestfetésclar jaquecoincideixambl’oscil ladorharmònicquan ω2 1 = ω2 2.Però,totiser unoscil.ladordefinitatrossos,l’oscil.ladorasimètricresultasertambéun oscil.ladorisòcron.Aixòesdeualfetqueacadascunadelesduesregions separadesper x = 0l’oscil.ladorasimètricéslineal.Considerem x(t) lasolució de (12) ambcondicionsinicials x(0) = 0, ˙ x(0)> 0.Llavors,inicialment,la dinàmicade x(t) estàdescritaperl’equació (10).D’aquesta,sabemquetrigarà exactamentuntemps t1 = π ω1 atornara x = 0.Precisament, x(t1) = 0i ˙ x(t1) =

x(0)< 0.Ambaquestesnovescondicionsinicials,ladinàmicade x(t) està descritaaraperl’equació (11) itrigaràexactamentuntemps t2 = π ω2 desdel temps t1 asatisfer x(t1 + t2) = 0i x(t1 + t2) =−x(t1) = x(0).Aquestfetno ésnomésindependentdelavelocitatinicial,sinódelaposicióinicial,imostra quetotasolucióésperiòdicadeperíodemínim

solucióde (12) ambcondicionsinicials x(0) = A, x(0)

forçatexternamentperunafunciócontínuai

L’equació (14) vaserconsideradainicialmentperDancer[10, 11]iFuˇcík[14, 15],interessatsperl’existènciadesolucionsperiòdiquesiambcondicionsde fronteradeDirichlet.Consideremlafamíliadecorbes

Observemque (ω1,ω2) ∈ σ siinoméssitoteslessolucionsde (12) són 2π -periòdiques.Ésadir, (ω1,ω2) ∈ σ generalitzalacondició ω ∈ N enel contextdel’oscil ladorharmònic.Defet, (n,n) ∈ σ .Elresultatsegüentés degutaFuˇcík[14]imostral’absènciaderessonànciadel’equació (14) quan (ω1,ω2)

Teorema 2. Si (ω1,ω2) ∉ σ ,aleshoresl’equació (14) téunaòrbita 2π -periòdicaperaqualsevol p(t)

Continuantambl’analogiaambelcaslineal,homesperariaque,si (ω1,ω2)∈ σ ,aleshoreselfenomenderessonànciaaparegués.Dancer([10])vadonar exemplesdepertorbacions p(t) talsquel’equació (14) notésolucions2π -periòdiquesquan (ω1,ω2) ∈ σ .Aquestresultatpotsemblaranecdòticenel queensocupasinofospelresultatsegüent,conegutcoma segonteoremade Massera [23].Sigui

x = X(t,x),x ∈ R2 , (15) uncampvectorial X : R × R2 → R2,2π -periòdicen t iambregularitatsuficient persuposarexistènciaiunicitatdesolucions.Denotemamb x(t,x0) lasolució de(15)ambcondicióinicial x(0,x0) = x0 ∈ R2

Teorema 3 (SegonteoremadeMassera). Sitoteslessolucionsde (15) estan definidesenelfuturiunad’ellesésacotadaenelfutur,aleshoresexisteixuna solució 2π -periòdica.

Aquestenunciatésmésfortquel’original,quenomésdemanaexistènciaen elfuturperasolucionsdefinidesa t0 = 0.Defet,lahipòtesidel’existència d’unasolucióacotadaenelfuturespotrelaxardemanantl’existènciad’una solucióquesatisfaciqueellímitinferiordelasevanormaestiguiacotatenel futur.Ambaixòs’obtélavariantdelsegonteoremadeMasserasegüent.

Teorema 4 Sitoteslessolucionsde (15) estandefinidesenelfuturinoexisteixen òrbites 2π -periòdiques,aleshores

lim t→+∞ x(t,x0) =∞ peratot x0 ∈ R2 .

AquestúltimresultatensmostraqueDancer([10])trobapertorbacions p(t) talsquel’equació (14) ésressonantquan (ω1,ω2) ∈ σ .TambéaDancer[10] apareixperprimeravegadalafunció1

Ψp(θ) := 2π 0 p(t)C(θ + t)dt,θ ∈ R (16)

Aquestafuncióresultaessencialperentendreelfenomenderessonànciade l’oscil.ladorasimètric.Definim

A(p) :={θ ∈ R : Ψp(θ) = 0}.

AlonsoiOrtega([1])provenelresultatsegüentsobrel’existènciadesolucions noacotades.

Teorema 5. Si (ω1,ω2) ∈ σ i p ∈ L1(R/2π Z) éstalque A(p) ésnobuiti Ψp(θ) ≠ 0 peratot θ ∈A(p),aleshoresexisteix R> 0 talquetotasolució x(t) del’equació (14) amb x(t0)2 + x(t0)2 >R peraalgun t0 ∈ R ésnoacotadaen elfuturoenelpassat.

1 Lafuncióoriginalmentesdenotaamb Φp ,peròalesproperesseccionsesfaràserviraquesta notacióperaunaaltrafunciósimilari,ambelpropòsitdecomparar-les,s’haescollitcanviar-la per Ψp

Lanotació R/2π Z al’enunciatanteriorienresultatssubsegüentsfareferènciaal’espaiquocient {x + 2π Z : x ∈ R} ondoselements x, y estanidentificats siinoméssi x y = 2πn peraalgun n ∈ Z.Unafunció p : R/2π Z → R és, pertant,unarepresentaciód’unafunció2π -periòdicaenundominiacotatde longitud2π .Aquestanotacióprovédel’anàlisiharmònicapersolucionarla divergènciadelesintegralsinvolucradesenelcàlculdeconvolucions.Així, p ∈ L1(R/2π Z) ésl’espaidefuncions2π -periòdiquesintegrablesa [0, 2π].És

Tornemalresultatdelteorema5.Permotivarlaconnexióambelcas harmònic,notemque,si

(12) esdevé C(t) = cos(nt).

(6) de l’oscil.ladorharmònic, | ˆ pn| > 0.Tanmateix,lafunció Ψp(θ) notéelmateix paperque ˆ pn enelcaslineal.Liu([21])iKunze([18])mostrenenelresultat següentque,si Ψp nocanviadesigne,aleshorestoteslessolucionsde (14) són acotades.

Teorema 6 Si (ω1,ω2) ∈ σ i p ∈ C 6(R/2π Z) talque A(p) =∅,aleshores toteslessolucionsdel’equació (14) sónacotades.Ésadir,si x(t) ésunasolució, llavorsestàdefinidaperatot t ∈ R isatisfà

Per C k(R/2π Z) enteneml’espaidefuncions2π -periòdiquesamb k derivadescontínues.Ésrellevantmencionarquelahipòtesi C 6 esdevéunacondició necessàriaperalestècniquesempradesalaprovaiésunproblemaobertla veracitatdelresultatperaclassesdefuncionsmenysregulars.

Observemqueenelcaslinealladicotomiaprovocadaperl’anul.lacióde | ˆ pn| determinaqueobétoteslessolucionssónnoacotadesobésón2π -periòdiques (i,pertant,acotades).Totidesconèixersi Ψp éslafuncióapropiadaque generalitza ˆ pn enelcasasimètric,AlonsoiOrtegaprovena[1]queelsdos tipusdesolucionspodencoexistir,comperexemplesotalapertorbació p(t) = cos(rt) amb r ≥ 1,trencantaixílasimilitudambelcascontinu.

2.3Potencialsisòcronsnolineals

Seguintamblaideadegeneralitzarl’oscil.ladorharmònic,enaquestasecció suposaremunoscil.ladornolinealisòcron

¨

x + V (x) = 0,x ∈ R, (17) definitatotalarectareal.Ésadir,suposemque x = 0ésl’únicequilibride l’equacióitoteslessolucionssónperiòdiquesdeperíode2π .Enlamateixa direccióquealesseccionsanteriors,volemestudiarcomescomportenles solucionsdel’oscil.ladornolinealquanafegimunaforçaexternapetitaamb elmateixperíode.Mésconcretament,volemsabercomhadeser p(t) talque toteslessolucionsdel’equació

x + V (x) = p(t) (18) siguinnoacotadesperatot ≠ 0petit.

Consideremelcilindre C = (R/2π Z) × [0, +∞) ambcoordenades (θ,r) i denotemamb ϕ(t,r) lasoluciódel’equació (17) ambcondicionsinicials x(0) = r , x(0) = 0.Denotemamb ψ(t,r) lasoluciócomplexadel’equacióvariacional y + V (ϕ(t,r))y = 0,y(0) = 1, ˙ y(0) = i.

Llavorsdefinimlafunció Φp : C → C,

Enaquestasecciódemostraremquelafunció Φp téunpaperanàlegalde ˆ pn peral’oscil ladornolineal.Primer,veuremquetoteslessolucionsde(18)són noacotadessilacondició inf C |Φp(θ,r)| > 0(20)

sesatisfà.Després,veuremque,si Φp téunzeronodegenerat,aleshores l’equació (18) téunaòrbitaperiòdica.Aquestsresultats,juntamentambaltres consideracionssobreoscil.ladorsisòcronsnolineals,espodentrobara[33].

Abansdedonarelsenunciatsilesprovesd’aquestsresultats,faremdues observacions.Laprimeraésque,efectivament,lacondició (20) ésequivalenta lacondicióderessonàncialineal | ˆ pn| > 0peral’oscil.ladorharmònic.Siprenem

= 1 2 n2x2,lasoluciócomplexadel’equacióvariacionalésindependent de r ,

donatsexplícitament.Hompodriaserescèpticipensarquenohihaoscil ladors isòcronsnolineals.Elresultatsegüentespottrobara[32]iésunaversió globaldelateoriadepotencialsisòcronselaboradaperUrabe[39, 40],que, originàriament,eradecairelocal.

Donatuninterval I = (α,β) amb −∞≤ α< 0 <β ≤+∞,esdefineixla classed’Urabe U(I) comelconjuntdefuncions u : I → R quesatisfan u(0) = 0, u ∈ C 0(I) i v ∈ C 1(I),on v(x) = xu(x).

Teorema 7 (teoremad’Urabe). Suposemque V ∈ C 2(I) satisfà

V(0) = V (0) = 0,xV (x)> 0 si x ≠ 0

iqueexisteix V ∈ (0, +∞] talque lim x→α+ V(x) = lim x→β V(x) = V.

Amés,suposemqueexisteix T> 0 talque,peracada x0 ∈ I, x0 ≠ 0,el problemadeCauchy x + V (x) = 0,x(0) = x0, x(0) = 0, téunasolucióambperíodemínim T .Aleshoresexisteixunafunciósenar S ∈

U(J) amb J = ( (2V) 1 2 , +(2V) 1 2 ) i |S(X)| < 1 pera X ∈ J talquelasolució X(x) del’equació

dX dx = 2π T 1 1 + S(X),X(0) = 0,

estàdefinidaal’interval I,onsatisfà V(x) = 1 2 X(x)2

Elrecíprocd’aquestresultattambééscert.Donadaunafunció S(X) amb lescondicionsdelteoremaiunnúmero T> 0,lafunció V(x) definidaperles identitatsdelteoremasatisfàlescondicionsdel’enunciati,pertant,produeix unoscil ladorisòcron.Unexempled’isòcronnolinealdefinitatotalarectareal éseldonatper S(X) = α arctan X, |α| < 2 π proposatperOrtega[30].

Unasegonacaracteritzaciódelspotencialsisòcronsésladonadademanera independentperZampieri[42]iperCima,MañosasiVilladelprat[9]entermes d’involucions.Enaquestcassesuposaquelafunciópotencial V(x) ésanalítica a R.Diemque σ ésuna involucióestricta siésunafuncióanalíticaa R diferent delaidentitatquesatisfà σ(0) = 0i σ(σ(x)) = x peratot x ∈ R.

Teorema 8. L’origendel’equació x + V (x) = 0 ésuncentreisòcrondeperíode T siinoméssiexisteixunainvolucióestricta σ quesatisfà V(x) = π 2 2T 2 (x σ(x))2 peratot x ∈ R

2.3.1Ressonànciadel’oscil.ladornolinealglobal Elresultatsegüentmostraque,silafunciópotencial V(x) del’oscil.ladorisòcron (17) tésegona derivadaacotadai p(t) ésunafunció2π -periòdicailocalmentintegrableque satisfàlacondicióderessonància (20),aleshoresl’equació (18) ésressonant peratot ≠ 0petit.

Teorema 9. Sigui V ∈ C 2(R) definidaatotalarectarealiquesatisfà V(0) = 0, xV (x)> 0 si x ≠ 0.Amés,suposemquetoteslessolucionsde (17) són 2πperiòdiques.Suposemque V (x) ésacotadaperatot x ∈ R iquelacondició (20) sesatisfàperaalgun p ∈ L1(R/2π Z).Aleshorestotasolució x(t) del’equació (18) satisfà

(|x(t)|+|x(t)|) =+∞.

Prova. Perprovarelresultatfaremservirlavariantdelsegonteoremade Masseraenunciatalteorema4.L’estratègiaseràprovarquenoexisteixen òrbites2π -periòdiquesquesiguinsolucióde (18) pera ≠ 0petit.Abans,però, necessitemestudiarunparelldepropietatsdel’equaciólineal

+ a(t)y = b(t), (21)

(i) Siguin u(t) i v(t) lesduessolucionsfuncionalmentindependentsde l’equació (21) amb b ≡ 0ambcondicionsinicials u(0) = v(0) = 1i u(0) = v(0) = 0.Aleshoresexisteixunaconstant C> 0,depenentnomés de

(ii) Sigui y(t) lasoluciódel’equació (21) ambcondicionsinicials y(0) = ˙ y(0) = 0.Aleshores |y(t)|≤

[0, 2π]

Enefecte,perprovar(i)observemquelamatriu Φ(t) = uv u v ésunasolució delsistemalineal ˙ Y = A(t)Y amb A(t) = 01 a(t) 0 .Perladesigualtatde Gronwall, Φ(t) ≤ exp t 0 A(s) ds , on · denotalanormadematriusinduïdaperlanormadelsupremde R2.És adir,donadaunamatriu A = (aij

, A = max{|a11|+|a12|, |a21|+ |a22|}.Donatque a L∞(0,

K,

max{1,K}= M.Llavors, Φ(t) ≤ e2πM peratot t ∈ [0, 2π],laqualcosaprova(i).Perveure(ii),aplicantla fórmuladevariaciódeconstants,esté

= 1 0 (v(t)u(s) v(s)u(t))b(s)ds.

UtilitzantladesigualtatdeCauchy-Schwarzjuntamentamb(i)obtenim

Amblaintenciód’arribaracontradicció,suposemqueexisteixunasuccessió { n} amb n ≠ 0i n → 0talquel’equació (18) téunasolució2πperiòdica xn(t) pera = n.Denotemamb Xn(t) lasoluciódel’oscil lador isòcron (17) amblesmateixescondicionsinicialsque xn(t) a t = 0.Ésadir, Xn(0) = xn(0) i ˙ Xn(0) = xn(0).Observemqueaixòéspossiblejaquel’isòcron (17) ésglobal.Consideremladiferència yn(t) = xn(t) Xn(t).Peruna banda,lafunció yn(t) éssoluciódel’equaciólineal y + a(t)y = b(t),y(0) = y(0) = 0, amb a(t) = 1 0 V ((1 λ)xn(t) + λXn(t))dλ,b(t) = np(t).

Enefecte,espotcomprovardirectamentfentservirque Xn(t) éssolucióde (17), xn(t) éssolucióde(18)i,pelteoremadelvalormitjà, V (xn(t)) V (Xn(t)) yn(t) = a(t).

Perlapropietat(ii)deduïmque

onfemservir K = supx∈R |V (x)|.

Peraltrabanda,lafunció yn(t) tambééssolució2π -periòdicadel’equació lineal ¨ y + V (Xn(t))y = np(t) qn(t), amb

Calobservarqueelscoeficientsd’aquestaequaciósón2π -periòdicsperquè l’oscil.lador (17) ésisòcron.Toteslessolucionsde (17) sóndeltipus ϕ(t θ,r).Enparticular, Xn(t) = ϕ(t θn,rn) peraalgun θn ∈ [0, 2π] i rn ≥ 0. Lafunció ψ(t θn,rn) ésunasolució2π -periòdicanotrivialdel’equació homogènia y + V (Xn(t))y = 0.Aleshores,perl’alternativadeFredholm,

Fentservirlacota (22) iladefinicióde qn(t),elteoremadeconvergència dominadaimplica

Fentservirdenoulaconvergènciadominada, Φp(θn,rn) → 0quan n →+∞.Aixòésincompatibleamblacondicióderessonància(20)iprovaelteorema. ✷

Elteorema9ésunacondiciósuficientperalaressonànciadel’equació (18), però,defet,noestàgairellunyd’éssertambénecessària.Elresultatsegüent mostralavalidesad’unrecíprocparcialdelresultatanterior:unasolucióperiòdicaexisteixquanlafunció Φp téunzeronodegenerat.Aquestacondició denodegeneracióésenelsentitdelateoriadegraudeBrouwer.Sigui Ω unsubconjuntobertiacotatde Rd i f : Ω → Rd unafunciócontínuaqueno s’anul.laalafronterade Ω.Primersuposemque f ∈ C 1(Ω) itéunnombrefinit dezeros x1,...,xn ∈ Ω amb det f (xi) ≠ 0peracada i = 1,...,n.Aleshores elgraudeBrouwerde f en Ω és deg(f, Ω) = n i=1 signdet f (xi).

Si f éscontínua,potseraproximadaperfuncions fk enlescondicionsanteriors idefinim

deg(f, Ω) = lim k→+∞ deg(fk, Ω).

Diem,doncs,queunzero x ∈ Ω de f és nodenegerat siexisteixunobert U de x ∈ Ω talque f(y) ≠ 0peratotpunt y ∈ U\{x} ielgraudeBrouwer deg(f, U) nos’anul.la.

UnapropietatimportantdelgraudeBrouweréslasevainvariànciaper homotopiaitéunpaperclauenlaprovadelresultatsegüent.

Teorema 10 Sigui V enlescondicionsdelteorema9isuposemque Φp téun zeronodegenerat (θ∗,r∗) amb r∗ > 0.Aleshoresl’equació (18) téunasolució 2π -periòdicaperatot petit.

Prova. Denotemamb x(t; x0,v0, ) lasoluciódel’equació (18) ambcondicions inicials x(0) = x0, x(0) = v0

Peracada ∈ R considereml’aplicacióalpla F : R2 → R2 definidaper

Laidead’aquestaprovaésveureque F0 téunzeronodegeneratenelsentit delateoriadegraudeBrouwer.Aquestfetimplicaquepera ≠ 0petitl’aplicació F tambétéunzero.Observemque,peracada ,unzerodel’aplicació F corresponaunasolució2π -periòdicadel’equació(18).

Comquel’equació (17) ésisòcronadeperíode2π ,totasoluciónotrivialté períodemínim 2π n peraalgun n ∈ N.Lafunció ψ(·,r),soluciódel’equació variacional,téperíode 2π n il’aplicació

Φp(θ,r) := Φp θ n ,r estàbendefinidaalcilindre C .L’aplicació (θ,r) (nθ,r) ésundifeomorfisme localenelcilindreobert C = (R/2π Z) × (0, ∞).Sigui (θ∗,r∗) elzerono degeneratde Φp deleshipòtesisdelteorema.Aleshores (nθ∗,r∗) ésunzero nodegeneratde ˜ Φp perladefiniciódelgraudeBrouwer.

Consideremeldifeomorfisme

η : (θ,r) ∈ C ϕ θ n ,r ,

,r

R2 \{(0, 0)}

Lafunció y(t) = ∆(t; η(θ,r), 0) éslasoluciódelproblemadevalorinicial y + V ϕ t θ n ,r y = p(t),y(0) = y(0) = 0.

Aleshores,perlafórmuladevariacionsdeconstants,

∆(t; η(θ,r), 0)

∆(t; η(θ,r), 0) = M t θ

on M = v u v u i u(t,r) = Re ψ(t,r), v(t,r) = Im ψ(t,r),amb ψ(t,r) la soluciódel’equacióvariacional ¨ y + V (ϕ(t,r))y = 0, y(0) = 1, ˙ y(0) = i.En conseqüència,

(F0 ◦ η)(θ,r) = 2πM θ n ,r ˜ Φp(θ,r).

Notemqueaquíestemidentificant C i R2,detalmaneraque ˜ Φp prenvalorsa R2

Lamatriu M tédeterminant1i,enconseqüència,elszerosdelesfuncions F0 ◦η i Φp coincideixen.Peracada λ ∈ [0, 1] definim Hλ : C → R2 com

Hλ(θ,r) = M λθ n ,r ˜ Φp(θ,r).

2.3.2L’oscil.ladordePinneycomaprototipambsingularitat Tantl’equaciódel’oscil.ladorlinealcomlesdel’asimètricielnolinealques’hanconsiderat estavendefinidesatotalarectareal.Enparticular,elseuespaidefaseéstot R2 Existeixen,però,centresisòcronsproduïtsperpotencialsambsingularitatsque estandefinitsenunasemirectapròpiai,pertant,l’espaidefaseésunsemiplà. Unexemplebenconegutésl’oscil.ladordePinney[34](vegeulafigura5),

Figura 5: Al’esquerra,lafunciópotencialdePinneyambsingularitat a x =−1.Aladreta,elretratdefasedelsistemapotencial.Lazonaombrejadacorresponal’anelldeperíodes,enaquestcaselsemiplà x> 1.

L’equaciódePinneyéstambéconegudacomaequaciód’Ermakov-Pinneyper seruncasparticulard’unafamíliamésgeneraldesistemesintegrablesdonats perErmakov[12],totique,perserjustos,laprimeraapariciód’aquestaequació ésd’unarticledeSteenendanèspublicatl’any1874.Esrecomanallegir[35] peraunresumhistòricdel’equació.TornantaPinney,a[34]esdonauna expressióexplícitadelessolucionsambcondicionsinicials x(0) = r , ˙ x(0) = 0.

Enparticular,

Observemquetoteslessolucionssónperiòdiquesdeperíode2π .L’equació (23) resultanosernomésunexemple:ChalykhiVeselova[8]demostrenquel’oscilladordePinneyil’oscil.ladorlinealsónelsúnicsisòcronsracionalsllevat detranslació,sumad’unaconstantirescalat.Peraquestmotiu,ésnatural

preguntar-noscomescomportenlessolucionsde (23) quanhiafegimuna pertorbacióexterna2π -periòdica.

Elresultatsegüentresponaaquestapregunta.Denotemamb ψ(t,r) la soluciócomplexadel’equacióvariacional

Teorema 11. Sigui p ∈ L1(R/2π Z) unafuncióquesatisfàlacondicióderessonància (20) amb ψ(t,r) definidaa (24).Aleshorestoteslessolucionsdel’equació

sónnoacotadesperatot ≠ 0 petit.

Engeneral,comprovarlacondicióderessonàncianolineal (20) peraun oscil ladorisòcronqualsevolpotsermoltdifícil.Enelcasdel’oscil ladorde Pinney,aixòéspossiblequanlapertorbacióperiòdicaéslinealen sin(t) i cos(t)

Corol.lari 12. Si p(t) = a0 + a1 cos(t) + b1 sin(t),l’equació (25) ésressonant quan a2

2.3.3Ressonànciad’unisòcronacotat Finsaratotselsoscil.ladorstractats hanestatisòcronsglobals.Ésadir,toteslessolucionsdelesequacionssón bendefinidesi2π -periòdiques.Unfenomennogairecomúperòpossible éselcasd’oscil ladorsisòcronsacotats.Engeneral,uncentreacotatalpla acostumaaestarconfinatalaregiódelimitadaperunaòrbitahomoclínica oheteroclínica.Aquestasituacióésincompatibleamblaisocronia,jaqueen ambdóscasosalmenysunequilibriestrobaalafronteradel’anelldeperíodes i,percontinuïtat,elperíodedelessolucionsproperesaaquestafronteraha decréixercapal’infinit.Malgrataixò,éspossibleconstruircentresisòcrons acotatsfentservirfuncionspotencialsambsingularitats.Pertaldediferenciarhodelcasdel’oscil ladordePinney,aquestasingularitathadeserintegrable.

Ésadir,l’equació

x + V (x) = 0 hadesersingular,peròelhamiltonià H(x, ˙ x) = 1 2 ˙ x2 + V(x) hadeserregular. Enaquestcasesdiuquel’equaciódiferencialtéunasingularitatdèbil.

Enprimerainstància,l’existènciad’oscil.ladorsisòcronsacotatspodria semblarestranya.Tanmateix,lacaracteritzaciód’isòcronsd’Urabepresentada

alteorema7ésunamoltbonaeinapercrear-ne.Defet,segonsaquestresultat, hihatantsoscil.ladorsisòcronsacotatscomfuncionssenars S ∈ C(I) ∩ C 1(I \ {0}) amb I = (α,β), α< 0 <β,quesatisfan S(α) + 1 = 0.L’exemplemés senzillquesatisfàaquestescaracterístiqueséslafuncióidentitat, S(X) = X,la qual,fentservirelteorema7,produeixl’oscil.ladorisòcronacotat

Figura 6: Al’esquerra,funciópotencialambsingularitatdèbila x = α. Aladreta,retratdefasedelsistemapotencial.Lazonaombrejada corresponal’anelldeperíodes.Lasevafronteraestàemfatitzadaen negreta.

L’anteriorexempleésunamostrad’oscil ladorisòcronacotat,peròdurant larestadelaseccióconsideraremelcasgenèric.

Suposemque V ∈ C 2(I) ésunafunciópotencialdefinidaal’interval I = (α, +∞) amb −∞ <α< 0quesatisfà V(0) = V (0) = 0i xV (x)> 0si x ≠ 0. Amés,suposemque lim x→α+ V(x) = lim x→β V(x) = V< +∞, ilim x→α+ V (x) =+∞, amb0 <β< +∞.Sotaaquestescondicions,l’equació x + V (x) = 0,x ∈ I, téuncentreal’origenambanelldeperíodes P acotat(vegeulafigura6).És importantobservarquelessolucionsforade P noestandefinidesglobalment jaquepresentenunacol.lisióamblasingularitat x = α entempsfinit.

Suposemquetoteslessolucionsperiòdiquescontingudesa P són2πperiòdiquesi,peracada > 0,denotemamb ϕ(t,(x0,x0)) lasolucióde l’isòcronacotatpertorbatperiòdicament

x + V (x) = p(t),x(0) = x0, x(0) = x0, (27) amb (x0,x0) ∈ P.Amés,denotemamb

ϕ(t, U) :={ϕ(t,(x0,x0)) : (x0,x0) ∈U}

elconjuntdetoteslessolucionsdel’equació (27) ambcondicionsinicialsal subconjunt U⊂ P.Enaquestcas,elcilindresobreelqualesdefineixla funció Φp introduïdaa (19) ésacotat.Enefecte,considerem C = (R/2π Z) × [0,β) ambcoordenades (θ,r).Larestadefuncionssóndefinidesdelamateixa maneraqueenelcasglobal.Elresultatderessonànciaperal’isòcronacotatés elsegüent.

Teorema 13. Suposemque V satisfàlescondicionsanteriorsisigui p ∈ L1(R/2π Z) quesatisfàlacondicióderessonància (20).Aleshores,peracadasubconjuntcompacte K⊂ P ambinteriornobuiti d> 0 existeix ∗ > 0 tal que,si 0 < < ∗,llavorstotabolaobertadecondicionsinicials B ⊂K amb diàmetre d satisfà ϕ(t,B) ⊂K peraalguntemps t> 0

Observemqueaquestresultatésbastantdiferentdelsobtingutsfinsara quantaressonància.Elfetquel’anelldeperíodes,enquèlessolucions2πperiòdiquesestandefinidesglobalment,siguiacotatfaqueelresultatderessonànciaenaquestcass’hagid’entendrecomunresultatd’escapadadel’anell. Mésconcretament,elques’afirmaésl’existènciad’algunmomentenelqual s’abandonal’anelldeperíodes.Peròaixònotreuquelessolucionspuguin tornareventualment.

Tantenelteorema9,enquèestractalaressonànciadel’oscil ladorno linealglobal,comenelteorema11,enquèestractal’oscil.ladordePinney, l’einaclauperprovarelsresultatséslavariantdelsegonteoremadeMassera presentadaalteorema4.Enaquestcas,talcoms’hacomentatabans,nototes lessolucionsestandefinidesenelfutur.Aixòimpossibilitaferservirlamateixa estratègiaqueenelscasosanteriors.EncomptesdelsegonteoremadeMassera, l’einaclauenaquestresultatéselsegüentteoremadepuntfixdeMontgomery (vegeu[31,secció3.9]).

Teorema 14 (teoremadepuntfixdeMontgomery). Siguin ∆ ⊂ R2 unsubconjuntobertisimplementconnexambmesurafinitai h : ∆ → ∆ unhomeomorfismequepreserval’orientacióil’àrea.Aleshores h téunpuntfix.

Laprimerapartdelaprovadelteorema13ésanàlogaaladelteorema9: consisteixaprovarlanoexistènciad’òrbites2π -periòdiques.Enaquestcas,en comptesdenoexistènciaglobal,lanoexistènciaesdonaperacompactesdins l’anelldeperíodes.

Proposició 15 Sotaleshipòtesisdelteorema13,peratotsubconjuntcompacte K⊂ P ambnointeriorbuitnoexisteixcapsolució 2π -periòdicade l’equació (27) contingudaa K pera ≠ 0 petit.

Noésrestrictiupensarque K ésunsubconjuntcompactesimplement connex.Consideremlafamíliad’aplicacionsdePoincaré

P : K→ (α, +∞) × R

definidesper P((x0,x0)) = ϕ(2π,(x0,x0)).Comquepera = 0toteslessolucionsdel’equació (27) ambcondicionsinicialscontingudesa P sóndefinides globalment,podemassegurarl’existènciade ∗∗ > 0talque,si0 < < ∗∗ , aleshorestoteslessolucionsdel’equació (27) ambcondicionsinicialscontingudesa K estanbendefinidespera t ∈ [0, 2π].

Perprovarelteorema13procedimperreduccióal’absurdisuposemque existeixunasuccessió { n}n≥0, n → 0,quesatisfà0 < n < ∗∗ talquepera cada = n existeixunabolaobertadecondicionsinicials Bn ⊂K ambdiàmetre d> 0queesmantédinsde K sotal’acciódelfluxpositiudel’equació (27). Ésadir, ϕ n (t,Bn) ⊂K peratot t> 0.Enparticular, P m n ⊂K peratot m ≥ 1. Donatquel’aplicaciódePoincaré P n convergeixalaidentitatuniformementsobresubconjuntscompactesquan n →+∞ i,donatqueeldiàmetredelabola Bn ésfix,existeix0 < ∗ < ∗∗ talque,si0 < n < ∗,aleshores P n (Bn) ∩ Bn ≠ ∅. Amés,comque P n ésinjectiva,tenimque P m+1 n (Bn) ∩ P m n (Bn) ≠ ∅ peracada enter m ≥ 0.Enparticular,launiódetotselsiteratsdel’aplicaciódePoincaré de Bn, Bn := m≥0 P m n (Bn), ésunsubconjuntobertsimplementconnexipositivamentinvariantsotal’acció del’aplicació P n .Ésadir, P n (Bn) ⊂Bn (vegeulafigura7esquerra).

Pertald’aplicarelteoremadepuntfixdeMontgomery,necessitemqueel conjunt ∆ siguiinvariantperl’homeomorfisme h.Enaquestcas,seguint[31, lema17],veiemquelainvariàncialapodemobtenirprenentelconjunt int(Bn),

Figura 7: Al’esquerra,representaciódelconjunt Bn.Aladreta,representaciódelconjunt Bn.

on int(U) denotal’interiordelsubconjunt U.Elconjuntobert int(Bn) ésconnexiinvariantperl’accióde P n ,perònoésnecessàriamentsimplementconnex. Persuperaraquestobstacle,considerem Bn elconjuntobertsimplementconnexformatper int(Bn) ielsseuspossiblesforatsplens(vegeulafigura7 dreta).

Ambaquestaconstrucció, Bn ésunsubconjuntobertsimplementconnex invariantsotal’acciódel’aplicació P n .Amés, Bn témesurafinitajaqueestà contingutdinsdelcompacte K,queéssimplementconnex.Podem,doncs, aplicarelteoremadelpuntfixdeMontgomeryperconcloureque P n téun puntfixa Bn.Aquestpuntfixclaramentcorresponal’existènciad’unasolució 2π -periòdicade (27) pera = n contingudaa K,laqualcosacontradiula proposició15iproval’enunciatdelteorema13.

Demanerasimilaralcasdel’oscil.ladordePinney,elteorema13espotaplicarefectivamentenl’exemple (26) quanespertorbaambunafuncióperiòdica linealensin(t) icos(t).

Corol.lari 16 Suposantque p(t) = a0 + a1 cos(t) + b1 sin(t),l’equació (26) ésressonantensubconjuntscompactessi

on Jν (x) denotalafunciódeBesseldeprimertipus.

2.4Generalitzaciódel’oscil.ladorasimètric:elcasnolineal Delamateixamaneraqueelsresultatsanteriorsgeneralitzenlacondició deressonànciadel’oscil.ladorharmònic,semblanaturalpreguntar-sesiel mateixsucceeixambl’oscil ladorasimètric.MañosasiTorresa[22]proven l’existènciad’oscil.ladorsasimètricsnolineals.Siguin F(x) = a 2 x2 + O(x3)

i G(x) = b 2 x2 + O(x3), a,b> 0,funcionsanalítiquesdefinidesaunentorn de x = 0.Esdefineixelsistemaatrossos2

x + F(x) = 0si x ≥ 0,

x + G(x) = 0si x< 0. (28)

Teorema 17. Sigui F(x) = a 2 x2 + O(x4) unafuncióparellaianalíticaa x = 0.

Aleshores,peracada b> 0 existeixunaúnicafunció G parellaianalítica

a x = 0 talque G(x) = b 2 x2 + O(x4) ielsistema (28) téuncentreisòcrona l’origendeperíode

τ = π 1 √a + 1 √b .

2 Elsistemaoriginala[22]estàdefinitatrossosrespectealavelocitat x = 0,encomptesdela posició x = 0quehemfetservira (28).Enaquestarticles’haconsideratl’escripturarespecte a x = 0perpoderferunacomparacióméssenzillaambl’oscil ladorasimètriclineal (10)-(11).El teorema17sesegueixdelamateixaprovadelsistemaoriginala[22].

Observemque,enefecte,elresultatanteriorgeneralitzal’existènciade l’oscil.ladorasimètric (12) enelcasnolinealprenent a = ω2 1 i b = ω2 2.Fins onl’autord’aquestarticleconeix,elproblemaderessonànciaenl’oscil.lador asimètricnolinealencaranohaestatabordat.Semblaraonableque,adequant lestècniquesques’hanfetservirperal’oscil.ladorasimètriclineal,espogués arribararesultatssimilarsalsd’aquest.

2.5Resultatsderessonànciaperahamiltoniansmésgenerals

Elssistemespotencialstractatsfinsarasóncasosparticularsdesistemes hamiltonians.Tantelfenomend’isocroniacomelproblemaderessonànciano sónexclusiusdelssistemespotencialsialgunsdelsresultatsques’hanvist finsarapodenestendre’sahamiltoniansmésgenerals.

Considerem H : R2 → R declasse C 1,positivaipositivamenthomogèniade grau2.Ésadir,peratot u ∈ R2 i λ> 0, H(λu) = λ2H(u) i min u =1 H(u)> 0.Amés,suposemqueelgradient ∇H ésLipschitzcontinu.Enaquestes condicions,elsistemahamiltonià

u = J∇H(u), (29)

amb J = 0 1 10 ,téuncentreisòcronal’origen.Denotemamb τ elperíode delcentreisòcroniconsiderem,ambl’esperitdegeneralitzarelsescenaris anteriors,elsistemahamiltoniàpertorbatperiòdicament

u = J∇H(u) + p(t), (30)

amb p : R → R2 contínuai2π -periòdica.Fonda,a[13],prova,sotalesanteriors condicions,que,si 2π τ ∉N,aleshoreselsistema (30) téunasolució2π -periòdica peraqualsevolpertorbació p(t).Amés,provaque,si 2π τ ∈ N,aleshoresexisteix unapertorbació2π -periòdica p(t) talquetoteslessolucionsdelsistema (30) sónnoacotades.

Ambl’esperitdecaracteritzarlespertorbacionsqueprodueixenressonància, Fondaintrodueixlafunció3 deressonància Ψp : R2 → R associadaa (30) definida per

Ψp(θ) := 2π 0 p(t)|ϕ(t + θ) dt,θ ∈ R, (31)

on ϕ éslasoluciódelsistemaisòcron (29) talque H(ϕ(t)) = 1 2 .Lafunció Ψp éscontínuai τ-periòdicaiserveixcomacriterideressonànciadelsistema (30), comesmostraalsdosresultatssegüents.

Teorema 18. Sigui p ∈ C 6(R/2π Z).Suposemque 2π τ ∈ N ique Ψp nocanvia designe.Aleshores,toteslessolucionsde (30) sónacotades.

Teorema 19. Sigui 2π τ ∈ N isuposemque Ψp canviadesignealmenysquatre vegadesal’interval [0,τ),ambtotselszerossimples.Aleshores,elsistema (30) té unasolució 2π -periòdica,mentrequetoteslessolucionsambcondicionsinicials prougranssónnoacotades.

3 Denous’hacanviatlanotacióoriginalperevitarconfusióal’horadecomparar-laamb Φp definidaa(19).

Notemlasimilitudd’aquestsdosdarrersenunciatsambelsteoremes5i6 peral’oscil.ladorasimètric.Amés,lafunció Ψp a (31) estàdefinidasobreuna soluciódelsistemaisòcron,talcomesdefineixlafuncióderessonànciapera l’oscil ladorasimètric (16).Aquestsfetsmotivenl’elecciódelamateixanotació peraambdues.

Finsonarribenelsconeixementsdel’autor,nohiharesultatsderessonància perahamiltoniansenlescondicionsdel’inicidelasecciófentserviruna funcióderessonànciaanàlogaaladefinidaperal’oscil.ladornolineal (19). Ésadir,fentservirlasoluciódelesequacionsvariacionalsencomptesdela soluciódel’isòcron.Semblariapossibletrobargeneralitzacionsdelsresultats deressonànciadelspotencialsnolinealsenelmarcdelshamiltoniansisòcrons.

3Ressonànciaautoparamètrica

Enaquestaseccióvisitaremunconceptederessonànciaunamicadiferentdels anteriors.Finsarahemfetservirelconceptederessonànciaassociatalfet quetotesounagranquantitatdelessolucionsd’unmodelsónnoacotades iprodueixengransoscil.lacions.Aquestfetanavadelamàdelacongruència entrelafreqüènciadel’oscil.ladoriladelapertorbacióperiòdicaexterna. Moltesvegades,elmateixfetd’aquestacongruènciarepelnomde ressonància, independentmentdelcomportament(localoglobal)delessolucions.Enaquesta seccióveuremquehihamodelsenelsqualstenimdosmodesd’oscil.lació (ésadir,dostipusd’oscil laciópropis)ielsistemapotpresentarressonància intrínsecamentsensenecessitatdeforcesexternes.

Unexempleclàssicéselpèndoldelongitudvariable(opèndol-molla), presentatperOlssona[29].Quanlamassadelpèndol-mollas’esculldetal maneraquelamollas’estiraunterçdelasevalongitudsensemassaper assolirlaposiciód’equilibri,petitesoscil lacionsverticalsdelamollaestornen inestablesil’oscil.ladorpassadevibrarenelmodeharmònicavibrarenel modepèndol.Aquestfetesconeixcoma ressonànciaautoparamètrica iesdevé conseqüènciadelainestabilitatd’undelsmodesd’oscil.lació.Aquestfenomen espotvisualitzar,perexemple,alvídeo[28]delcanaldeYoutube SteveMould Alesproperesseccionsvisitaremaquestexempleielrelacionaremambun modeldelpontdeTacoma-NarrowspresentatperArioliiGazzolaa[3].

3.1Pèndolamblongitudvariable

Consideremunamolladelongitud 0 enrepòsancoradaalsostreihipengem unamassa m del’extreminferior.Talcomvamveurealasecció2.1,lamolla s’estiraacausadelpesdelamassaiassoleixunanovalongitudd’equilibri

z0 = 0 + mg k (32)

Denotemamb x(t) i z(t) lesdesviacionshoritzontalivertical,respectivament, delaposiciód’equilibritalcomesmostraalafigura8.

Lesenergiescinèticaipotencialdelsistemavenendonadesperlesexpressions

on (t) = (z0 z(t))2 + x(t)2 éslalongituddelamollaacadainstantde temps.L’energiatotalconservadadelsistemas’escriucom

Ometremapartird’araladependènciatemporalpersimplicitat.Definim ω2 s := k/m i

:= g/z0 i,ambl’esperitdesuposarquelesdesviacionsdesde l’equilibrisónpetites,desenvolupemelhamiltonià H pera x i z petitfinsa ordrecúbic,iobtenimelhamiltoniàaproximat

ω

2 0 .Observemqueelsdosprimerstermesdelhamiltoniàcorresponenamovimentsharmònicsenlesposicionshoritzontalivertical,respectivament.Eltercertermefad’acoblamententreelsdosmodesvibratorisi permetlatransferènciad’energiadel’unal’altre.L’últimtermeésconstantino contribueixaladinàmica.Delhamiltoniàaproximat H deduïmlesequacions delmoviment,

Figura 8: Representaciód’unpèndoldelongitudvariable.

Entermesgenerals,petitesdesviacionsdelaposiciód’equilibricorresponen amovimentsharmònicsindependents.Aixòéselqueesdedueixdelstermes linealsdelesequacions (33),jaqueeltermed’acoblamentésdegrausuperior. Però,comveuremacontinuació,unaressonànciaentrelesfreqüènciesdels dososcil.ladors(horitzontalivertical)potcausarquepetitesvariacionscreixin ràpidamentenamplitud.

Suposemquelavibracióverticalésdominantrespecteal’horitzontal,de talmaneraque x z.Delasegonaequacióde (33) obtenimqueelmoviment vertical,ambcondicionsinicials z(0) = a, z(0) = 0,espotaproximarperla solucióharmònica

z(t) = a cos(ωs t).

Substituintaquestaalaprimeraequacióde (33),obteniml’equaciódiferencial desegonordre

(34)

Aquestaequacióésunfamóscasparticulard’equaciódeHillconegudacoma equaciódeMathieu[24,26,38].

Engeneral,l’equaciódeMathieu

x + (δ + cos(t))x = 0(35)

haestatmoltestudiadai,enparticular,s’handeterminatcompletamentles regionsd’estabilitatdel’equilibri x(t) = x(t) = 0alpladeparàmetres (δ, ) ∈

R2.Alafigura9podemveurelesregionsestables(zonesombrejades)iles

Figura 9: Regionsestablesiinestablesdel’equaciódeMathieu.Figura extretade[38,figura4.1].

regionsinestables(zonesenblanc),anomenades,també, llengüesd’Arnold.Les regionsestablesesconnectenalspuntsdelaforma (δ, 0) amb δ = n2 4 per a n ∈ N.Aquestspunts,enparticular,sóninestablesiésd’on«neixen»les zonesd’inestabilitatpera ≠ 0.Ambuncanviapropiatdetemps,podem relacionarl’equació (34) amblaformanormaldel’equaciódeMathieuiobtenir queaquestspuntsd’inestabilitatcorresponenalarelació

ωs ωp = 2 n ,n ∈ N. (36)

Pera n = 1aixòestradueixa ωs = 2ωp,unaressonànciadetipus2:1 entrelesfreqüènciesdelsdososcil.ladorsharmònicsde (33).Reprenentla notació ω2 s = k/m i ω2 p = g/z0,observemquelaigualtat ωs = 2ωp es tradueixa mg k = z0 4 .

Imposantaquestaigualtata(32),obtenim z0 = 4 3 0

Ésadir,laressonànciaesprodueixjustamentquanlalongitudd’equilibrien penjarlamassadelamollaés1/3mésgranquelalongituddelamollaenrepòs. Ésimportantobservarqueaquestfenomencorresponalaressonància2:1 entrelesfreqüènciesjaquesatisfàlaidentitat (36) amb n = 1.Larestade ressonànciespossibles, n ≥ 2,sónincompatiblesambelproblemadelpèndol delongitudvariableacausadelarestriccióelemental z0 > 0.

3.2ModeldelpontdeTacoma-Narrows

Nopodríemacabaruntextqueparlasobreelfenomendelaressonànciasense mencionar,d’algunamanera,undelsexemplesmésparadigmàticsd’aquest fet.Jasiguiperlasevaespectacularitatoperlasevarellevànciaarquitectònica, l’esdevenimentquevasucceirel7denovembrede1940haacabatsentun referentdel’efectedelaressonància.

Sónmoltselsmodelsproposatsperdonarexplicacióalcol lapsedelpont deTacoma-Narrows[4, 5, 36].Moltsd’ellsestanbasatsenl’efectedelventila creaciódevòrtexsatravésdeladinàmicadefluids.Perexemple,Amman,von KármániWoodruff([2])atribueixeneldesastrealaressonànciadelpontambel ventbasant-seensimulacionsdinsdetúnelsdevent.Malgrataixò,Scanlan([37]) iGreeniUnruh([16])neguenquelacreaciódevòrtexsfosrellevantenl’augment delesvibracionsdetorsió.Mésrecentments’hacomençataposardemanifestla relaciód’aquestfenomenambelcomportamentnolinealdelesestructures[19]. Enaquestaseccióvisitaremunmodelenquèesproposaqueelcol.lapse delpontdeTacoma-Narrowsésdegutaunaressonànciainternaentreles freqüènciesdedosmodesvibratorisdelsistema:lesoscil.lacionsverticalsdel pontilesdetorsió.

ElmodelqueproposenArioliiGazzola[3]consideraunpontensuspensió formatperunnombrefinitdebarresparal.lelesconnectadesmitjançantforces linealsd’atracció.Alafigura10podemveure’nunarepresentació,onlesbarres estanressaltadesennegretaiestanunidesalstensorsverticals,ilesàrees transversalsrepresentenlesconnexionsentrelesdiferentsbarres.Totiqueel modelproposatconsideraunnombrearbitraridebarresacoblades,tantper aladescripciódelmodelcomperaextreure’nlaconclusiód’inestabilitatdel problema,n’hihaproudeconsiderarnomésunabarra.

Consideremunabarrademassa m ilongitud2 sostingudaperdoscables alsextrems.Laposiciódelabarraespotdescriurepelseudesplaçament vertical y(t) respectealaposiciód’equilibriil’anglederotació θ(t),talcom esmostraalafigura11.Lesforcesdesuspensiódelscableslaterals C1 i C2 són denotadesamb f(y + sin θ) i f(y sin θ),respectivament.Denotantamb F(s) :=− s 0 f(u)du,l’energiapotencialdelmodelvedonadaperl’expressió

V = F(y sin θ) + F(y + sin θ), mentrequel’energiacinèticaés

Observemqueelprimertermedel’energiacinèticacorresponal’energiacinèticaprovinentdelmovimentvertical,mentrequeelsegontermeésl’energiacinèticadetorsió.Delaconservaciódel’energia,obtenimelhamiltonià H = V + T i,pertant,deduïmlesequacionsdelmoviment

Clarament,lamassa m notécappaperenelsistemaanteriori,pertant, considerarem m = 1apartird’ara.Elsautorsde[3]suggereixen f(s) := (s + s2 + s3) comamodeldelaforçadelscables.Fentservirl’aplicacióde

Figura 10: Discretitzaciód’unpontensuspensió.Figurainspiradaen[3, figura2].

Poincaréalpla (θ,θ),observenquel’equilibri (θ,θ) = (0, 0) (corresponenta unaòrbitaperiòdicaalpla (y,y))passadeserestableainestablequanl’energia passauncertllindar.Encomptesdeseguirelsautors,enaquestaseccióveurem comelmodelanteriorestàrelacionatambl’equaciódeMathieu(35).

Seguintelspassosdelaseccióanterior,consideremquelavibracióvertical ésdominantrespectealadetorsió,demaneraque θ y.Assumint,a més,queeldesplaçamentverticaléspetit,laprimeraequacióde (37) espot aproximarperl’oscil.ladorharmònic ¨ y + 2y = 0i,pertant,podemaproximarel movimentverticalper y(t) = a cos(√2t), a> 0.Substituintaquestaexpressió enlasegonaequacióde (37) iprenentnoméseltermelinealen θ del’equació, obteniml’equaciódiferencial

Fentservirelcanvidetemps τ = √2t ipropietatstrigonomètriqueselementals, obtenimlasegüentformageneralitzadadel’equaciódeMathieu

L’augmentdel’energiaa[3]espotinterpretarcoml’augmentdel’amplitud a en l’equacióanterior.L’equació (38) télaformad’unageneralitzaciódel’equació Mathieuclàssica,donadaper x + [δ + (cos(t) + α cos(2t))]x = 0.

Observemquelesduesfreqüènciesinvolucradessóncommensurables.Broer iSimó([7])estudiencomeldiagramaderegionsd’estabilitatdel’equacióde Mathieuvariaquan α ésconsideratunparàmetrepetit.Fentservir,perexemple, elsmecanismesquepresentenJordaniSmitha[17],basatsenl’existènciade solucions2π -periòdiquesomètodespertorbatius,éspossibleconstruirun diagramaderegionsd’estabilitatsimilaraldelafigura9quan α = α( ),comés elcasdel’equació (38).Defet,lasoluciótrivial x(t) = ˙ x(t) = 0pera δ = 3i

Figura 11: Representaciód’unabarraensuspensió.

i α petitsésestable.Lainestabilitatprovédelasortidadelaregiód’estabilitat enaumentar i α.Aixòesdeualfetque δ = 3noésunpuntdenaixementde lesregionsd’inestabilitatdel’equaciódeMathieu.Semblaraonablepensarque elsresultatsd’estabilitatpresentatsa[3]espodenrelacionaramblesregions d’estabilitatdel’equaciódeMathieuambduesfreqüènciescommensurables.

Agraïments

L’autoragraeixaArmengolGasull,RafaelOrtegaiJordiVilladelpratperla lecturadelmanuscritielssuggerimentsquesensdubtehanservitpermillorar aquestarticle.

L’autorésmembredelgrupderecercafinançat2021SGR00113iaquest treballhaestatproduïtsotaelfinançamentdelprojectePID2020-118281GBC31.

Referències

[1] Alonso,J.M.;Ortega,R. «Rootsofunityandunboundedmotionsofan asymmetricoscillator». J.DifferentialEquations,143(1)(1998),201–220.

[2] Amman,O.H.;vonKármán,T.;Woodruff,G.B. «Thefailureofthe TacomaNarrowsBridge».FederalWorksAgency(1941).

[3] Arioli,G.;Gazzola,F. «Anewmathematicalexplanationofwhattriggered thecatastrophictorsionalmodeoftheTacomaNarrowsBridge». Appl. Math.Model.,39(2)(2015),901–912.

[4] Bleich,F. «Dynamicinstabilityoftruss-stiffenedsuspensionbridgesunder windaction». TransactionsoftheAmericanSocietyofCivilEngineers,114 (1)(1949),1177–1222.

[5] Bleich,F.;McCullough,C.B.;Rosecrans,R.;Vincent,G.S. TheMathematicalTheoryofVibrationinSuspensionBridges.WashingtonDC:U.S. GovernmentPrintingOffice,1950.

[6] Bonheure,D.;Fabry,C.;Smets,D. «Periodicsolutionsofforcedisochronousoscillatorsatresonance». DiscreteContin.Dyn.Syst.,8(4)(2002), 907–930.

[7] Broer,H.;Simó,C. «ResonancetonguesinHill’sequations:ageometric approach». J.DifferentialEquations,166(2)(2000),290–327.

[8] Chalykh,O.A.;Veselov,A.P. «Aremarkonrationalisochronouspotentials». J.NonlinearMath.Phys.,12(2005)179–183.

[9] Cima,A.;Mañosas,F.;Villadelprat,J. «Isochronicityforseveralclasses ofHamiltoniansystems». J.DifferentialEquations,157(2)(1999),373–413.

[10] Dancer,E.N. «Boundary-valueproblemsforweaklynonlinearordinary differentialequations». Bull.Austral.Math.Soc.,15(3)(1976),321–328.

[11] Dancer,E.N. «OntheDirichletproblemforweaklynon-linearelliptic partialdifferentialequations». Proc.Roy.Soc.EdinburghSect.A,76(4) (1976/77),283–300.

[12] Ermakov,V.P. «Second-orderdifferentialequations:conditionsofcompleteintegrability». Appl.Anal.DiscreteMath.,2(2)(2008),123–145.[Traduït del’originalrus,de1880,perA.O.HarinieditatperP.G.L.Leach.]

[13] Fonda,A. «PositivelyhomogeneousHamiltoniansystemsintheplane». J. DifferentialEquations,200(1)(2004),162–184.

[14] Fuˇcík,S. «Boundaryvalueproblemswithjumpingnonlinearities». ˇ Casopis Pˇest.Mat.,101(1)(1976),69–87.

[15] Fuˇcík,S. SolvabilityofNonlinearEquationsandBoundaryValueProblems. Dordrecht-Boston,Mass.:D.ReidelPublishingCo.,1980.(Mathematicsand itsApplications;4)[AmbunpròlegdeJeanMawhin]

[16] Green,D.;Unruh,W.G. «ThefailureoftheTacomabridge:aphysical model». Amer.J.Phys.,74(8)(2006),706–716.

[17] Jordan,D.W.;Smith,P. NonlinearOrdinaryDifferentialEquations.An IntroductiontoDynamicalSystems.3aed.Oxford:OxfordUniversityPress, 1999.(OxfordTextsinAppliedandEngineeringMathematics;2)

[18] Kunze,M. «Remarksonboundednessofsemilinearoscillators».A: NonlinearAnalysisanditsApplicationstoDifferentialEquations.Boston,MA: BirkhäuserBoston,2001,311–319.(Progr.NonlinearDifferentialEquations Appl.;43)

[19] Lacarbonara,W. NonlinearStructuralMechanics.Theory,Dynamical PhenomenaandModeling.NovaYork:Springer,2013.

[20] Lazer,A.C.;McKenna,P.J. «Large-amplitudeperiodicoscillationsin suspensionbridges:somenewconnectionswithnonlinearanalysis». SIAM Rev.,32(4)(1990),537–578.

[21] Liu,B. «Boundednessinasymmetricoscillations». J.Math.Anal.Appl.,231 (2)(1999),355–373.

[22] Mañosas,F.;Torres,P.J. «Isochronicityofaclassofpiecewisecontinuous oscillators». Proc.Amer.Math.Soc.,133(10)(2005),3027–3035.

[23] Massera,J.L. «Theexistenceofperiodicsolutionsofsystemsofdifferentialequations». DukeMath.J.,17(1950),457–475.

[24] Mathieu,É. «Mémoiresurlemouvementvibratoired’unemembranede formeelliptique». J.Math.PuresAppl.,13(1868),137–203.

[25] Mawhin,J. «Resonanceandnonlinearity:asurvey». UkrainianMath.J.,59 (2)(2007),197–214.

[26] Minorsky,N. IntroductiontoNonlinearMechanics.AnnArbor:Edwards, 1947.

[27] Mould,S. «Abetterexplanationofresonance». https://youtu.be/ dihQuwrf9yQ

[28] Mould,S. «Whatifswingshadspringsinsteadofropes:Autoparametric Resonance». https://youtu.be/MUJmKl7QfDU.

[29] Olsson,M.G. «Whydoesamassonaspringsometimesmisbehave?». Amer.J.Phys.,44(1976),1211–1212.

[30] Ortega,R. «Periodicperturbationsofanisochronouscenter». Qual.TheoryDyn.Syst.,3(1)(2002),83–91.

[31] Ortega,R. PeriodicDifferentialEquationsinthePlane.ATopological Perspective.Berlín:DeGruyter,2019.(DeGruyterSeriesinNonlinear AnalysisandApplications;29)

[32] Ortega,R.;Rojas,D. «AproofofBertrand’stheoremusingthetheoryof isochronouspotentials». J.Dynam.DifferentialEquations,31(4)(2019), 2017–2028.

[33] Ortega,R.;Rojas,D. «Periodicoscillators,isochronouscentersandresonance». Nonlinearity,32(3)(2019),800–832.

[34] Pinney,E. «Thenonlineardifferentialequation y + p(x)y + cy 3 = 0». Proc.Amer.Math.Soc.,1(1950),681.

[35] Redheffer,R.;Redheffer,I. «Steen’s1874paper:historicalsurveyand translation». AequationesMath.,61(1-2)(2001),131–150.

[36] Rocard,Y. DynamicInstability:Automobiles,Aircraft,SuspensionBridges Londres:CrosbyLockwood,1957.

[37] Scanlan,R.H. «Developmentsinlow-speedaeroelasticityinthecivil engineeringfield». AIAAJ.,20(6)(1982),839–844.

[38] Stoker,J.J. NonlinearVibrationsinMechanicalandElectricalSystems. NovaYork,N.Y.:IntersciencePublishers,Inc.,1950.

[39] Urabe,M. «Potentialforceswhichyieldperiodicmotionsofafixedperiod». J.Math.Mech.,10(1961),569–578.

[40] Urabe,M. «Thepotentialforceyieldingaperiodicmotionwhoseperiodis anarbitrarycontinuousfunctionoftheamplitudeofthevelocity». Arch. RationalMech.Anal.,11(1962),27–33.

[41] Vendera,J. «VocalCoachJaimeVenderaShattersGlass#85». https:// youtu.be/Jy8js2FmGiY.

[42] Zampieri,G. «Ontheperiodicoscillationsof x = g(x)». J.Differential Equations,78(1989),74–88.

Departamentd’Informàtica,MatemàticaAplicadaiEstadística UniversitatdeGirona

C/delaUniversitatdeGirona, 6,CampusdeMontilivi, 17003 Girona

david.rojas@udg.edu

ButlletídelaSocietatCatalanadeMatemàtiques Vol.37,núm.2,2022.Pàg.173–204. DOI:10.2436/20.2002.01.106

Perquèensagradalamúsica?

Unarespostamatemàtica

TomásSanz-Perela

Resum: Perquèensagradalamúsica?Perquèenssemblaqueelsoqueprodueix unaodiversesteclesd’unpianoésmúsicai,encanvi,consideremqueelsoquefaun gotencaureaterraéssoroll?Perquèquand’unclarinetid’unaflautasonalamateixa notalasentimdiferent?Iquinaéslaraóperlaqual,sensehaverestudiatmúsica,som capaçosdedistingirunapersonaquetotjustacabadecomençaratocarelviolíiens semblaquedesafinad’unaquetémésexperiènciaidiemqueafina?

Enaquestarticledonaremrespostaaaquestespreguntesfentservirlesmatemàtiquescomaeinaprincipal.Perfer-ho,prendremcomapuntdepartidal’equaciód’ones, queenspermetràcomprendrelescaracterístiquesprincipalsdelsodelsinstruments musicals.Apartird’aquestsconeixementspodrementendrelesideesques’hanfet serviralllargdelahistòriaperconstruirlesescalesmusicals,quesónlabasedegran partdelamúsicaqueconeixem.Finalment,estudiaremelsconceptes dissonància i consonància d’unamaneramatemàticaientendremmillorperquèalgunssonsens resultenmésagradablesqued’altres.

Paraulesclau: equaciód’ones,espectreharmònic,sèriesdeFourier,escalesmusicals, dissonància.

ClassificacióMSC2020: 00A65,35L05,74K05.

1Conceptespreliminars

1.1Onesiso

Elsoésunaimpressióproduïdaal’oïdacausadaperlesvibracionselàstiques d’uncosqueespropaguenperl’aire(oaltresmedismaterials)enformad’ones. Moltsovint,però,tambéenshireferimcomlaformad’energiaqueprodueix aquestasensació.Mentrequelaprimeraconcepció,méssensorial,esrelaciona ambunaperspectivamésartística,lasegona,mésfísica,éslaqueprenemquan volemferunaanàlisimésobjectivad’aquestfenomen.

Lesfuncionstrigonomètriquessónelsobjectesmatemàticsmésbàsicsque serveixenperdescriureonesivibracions.Elssonsquesóntransmesosen formad’onasimpleelsanomenem tonspurs o simples ielsrepresentemdela manerasegüent:

Al’expressióanterior, t representaeltemps; A ésl’amplituddel’ona; φ,la fase,1 i f ,la freqüència (queindicaquantesoscil.lacionshihaenunsegonies mesuraenHz).Enalgunscasos,ensreferiremaunafunciócomaquestacoma senyal.

Enelnostrediaadia,però,mainotrobemtonspurs;qualsevolsoque sentimestransmetenformad’onamoltméscomplexaqueuntopur.Un delsgransdesenvolupamentsdelesmatemàtiquesdelsegle xix,l’anàliside Fourier,éselqueavuienspermetanalitzarelsocomplexentermesdetons simplesifuncionstrigonomètriques.Comveurem,lapropietatmésrellevant delsodelsinstrumentsmusicalsésqueestàformatperunasuperposicióde tonssimpleslesfreqüènciesdelsqualsestandistribuïdesd’unamaneramolt concreta.Aquestfetnonomésdiferenciaunsomusicald’unsoqualsevol,sinó queéselpuntdepartidad’unaanàlisiprofundadelsfenòmensdeconsonància idissonància.

1.1.1Lescaracterístiquesdelso Ladualitatentrelapercepciósensorialiel fenomenfísicdelsotambéesveureflectidaquanparlemdelescaracterístiques delso.Totseguitdescrivimlescaracterístiquesmésimportantsperaaquest text,desd’unpuntdevistasensorialiexplicitant-nelacorrespondènciaamb magnitudsfísiques:

• Altura: qualitatdelsoquepermetdistingir-neund’unaltreipoder-los ordenarenunaescalaquevadelsmésgreusalsmésaguts.Nototsels sonstenenunaalturadefinida,però,enelcasdetonssimples,l’altura escorresponamblasevafreqüència.Pelquefaalesnotesmusicals produïdesperuninstrument,l’alturaescorresponamblafreqüènciamés baixadetoteslesquecomponenelso(comveuremmésendavant).

• Sonoritat: graudesensaciósonoraproduïdaperunsod’unadeterminada intensitatacústica.Peratonspurs,estàdirectamentrelacionadaamb l’amplitudd’ona.D’unamaneramenysprecisa,s’anomena volum.

• Timbre: qualitatdelsoquepermetdistingir-nedosquetenenlamateixa alturaisonoritat.Depèndirectamentdel’espectre (delqualparlaremala subsecció2.5).

1.2Unaprimeranociódeconsonància

Podríemconsiderarquelarelacióentrelesmatemàtiquesilamúsicacomença al’antigaGrècia,alsegle vi aC.,alvoltantdel’escolapitagòrica.Aquesta societatfilosòficaireligiosavaserfundadaperPitàgores,unafiguraclauenel desenvolupamentdelesmatemàtiques,sempreenvoltadademisteriillegenda. Ésaaquestpersonatge—ilasevaescola—aquis’atribueixenlesprimeres anàlisissobrelaconsonància.

1 Enaquestarticlenoentraremadiscutiraquestamagnitudisempreveuremexpressions amb φ = 0.Noteuque,fentuncanvidevariableseneltemps,podemconsiderar φ = 0.

Elmonocord

Peranalitzarelsod’unacorda envibrar,elspitagòricsfeien servirunmonocord,uninstrumentrudimentarid’unasola cordaambunacaixaderessonànciaquepermetiamodificar lalongituddelacordamitjançantundiapasó.

Elspitagòricsvanobservarquedues cordesdelesmateixescaracterístiques, sotmesesalamateixatensió,ensertocadessimultàniament,produïenunso agradablesileslongitudsdelesdues estavenenraonsd’enterspetits,com ara2:1,3:2,4:3,etc.Aquestésun exemple,potserelmésantic,delleide lanaturalesaregidaperl’aritmèticadels enters,undelspilarsdeladoctrinapitagòrica,segonslaqualelmónqueensenvoltaestàgovernatcompletamentpels números.

Aquestfetobservatpelspitagòricséspossiblementl’origendel’escala musicalquetotsconeixemavuidia(vegeulasubsecció3.2.1)ilabasesobrela qualestàconstruïdalagranmajoriadelamúsicaoccidental.Undelsobjectius d’aquestarticleésdonarunaexplicacióaaquestfetresponentunapregunta general:quèfaqueduesnotestocadesalhoraensagradinmésomenys?

2Anàlisimatemàticadelsoapartirdel’equaciód’onesiles sèriesdeFourier

L’objectiud’aquestaseccióésentendreelsoqueprodueixuninstrument musicaldesd’unaperspectivamatemàtica.Perfer-ho,estudiaremundels modelsméssenzillsquehiha:l’equaciód’onesunidimensional.Totiquees tractad’unmodelsimplificat,aquestaequacióensproporcionaunadescripció forçaprecisadelmovimentd’unacordaenvibrar,comaralad’unviolíouna guitarra.Enconseqüència,enspermetentendreelsoqueprodueix.

Aquestaexposiciótécomafilconductorlahistòriaquehihaaldarrere delaresoluciódel’equaciód’ones(perainformaciómésdetallada,podeu consultar[15, 2, 3]).Percomençar,presentareml’equaciód’onesiladeduirem ambargumentssenzillsapartirdelasegonalleideNewton.Totseguit,comentaremunesprimeressolucionsobtingudesperd’AlembertiEuleramitjansdel segle xviii.Continuaremlahistòriaesmentantdemanerabreualgunesdeles aportacionsmésimportantsdematemàticscomBernoullioLagrangefinsa arribaralesideesdeFourier,jaaprincipisdelsegle xix,queenspermetran resoldrel’equaciód’onesientendreelsoqueprodueixunacorda.Lateoria deFourierensdonaràunajustificaciómatemàticaalfetqueunacordapugui vibraramésd’unafreqüènciaalhora,o,ditd’unaaltramanera,alfetqueun socomplexespuguidescompondreenunasuperposiciódetonssimples.A més,amesuraqueresoleml’equaciód’onesveuremquelamateixaestructura del’instrumentfaqueaquestasuperposiciódetonsnosiguiarbitrària,sinó quesegueixiunpatrómoltclar:toteslesfreqüènciesdevibraciód’unacorda

sónmúltiplesenterspositiusd’unafreqüènciafonamental.Aquestfetésclaua l’horad’entendrelamúsicaoccidental,comveuremenlesseccionssegüents. Acabaremaquestasecciódefinintelconcepted’espectre ipresentantalgunes aplicacionsdelateoriadeFourieraltractamentilasíntesidelso.

Aquestaéslapartdeltextambcontingutmatemàticmésavançat.Toti quefaremserviralgunsconceptesbàsicsd’anàlisiid’equacionsdiferencials, ambunsconeixementselementalssobrederivacióiintegración’hihaprou perentendrelamajoriadelsargumentsquedescriurem.Lesconclusionsmés importantspercomprendrelarestadeltextsónalasubsecció2.4ialaprimera partdelasubsecció2.5.

2.1L’equaciód’ones

L’equaciód’onesésunadelesequacionsenderivadesparcialsmésfamosesi antiguesdelafísicamatemàtica.Ensserveixcomamodelsenzillperexplicar elmovimentd’unacordaenvibrar.

Elmodeléselsegüent:perdescriureelmovimentd’unacordadelongitud L envibrar,consideremunafunciódeduesvariablesquedenotemamb u:

Elvalor u(x,t) representaeldesplaçamentdelacordaenelpunt x respectea lasevaposiciód’equilibrial’instantdetemps t.

Aquestafunció u satisfàl’equacióenderivadesparcialssegüent:

on c2 ésunaconstantpositivaqueinvolucralescaracterístiquesfísiquesdela corda.Enefecte, c2 = ρ/τ,on ρ representaladensitatlinealdelacordai τ,la tensió.

Notació. Enalgunspuntsdel’articlefaremservir utt i uxx perdenotarles segonesderivadesde u respectealtempsil’espai,respectivament.

2.1.1D’onsurtl’equaciód’ones? L’equaciód’onesésessencialmentlasegonalleideNewtonaplicadaaunpuntdelacordaaescalainfinitesimal. Recordemqueaquestalleiinvolucratresmagnituds:força,massaiacceleració. Analitzemlaprimeradelestresaescalainfinitesimal.Perfer-hoensajudarem del’esquemasegüent,querepresentaeldesplaçamentverticaldelacorda enunpetitinterval (x,x + h) enuninstantdetempsconcret t,ésadir,la funció u(,t):

Lesfletxesqueapareixenenaquestesquemarepresentenlaforçaqueactua sobreelsextremsd’aquestsegmentacausadelfetquelacordaestàseparada delasevaposicióderepòs.Aquíestemsuposantquelacordaésperfectament flexible,cosaquepermetmodelitzarlaforçadetensióentotpuntcomuna forçatangencial.Comqueensinteressaanalitzarelmovimentverticaldela corda,nomésensocuparemdelacomponentverticaldelaforçaqueactua enelsegment (x,x + h),queanomenarem Fh.Elmòduld’aquestamagnitud vindràdonatperladiferènciadelescomponentsverticalsdelesforcesals extremsdesegmentdecorda,ésadir,

Fh = T(x + h) sin(θ(x + h,t)) T(x) sin(θ(x,t)).

Noteuqueestemnegligintaltresforcescomlagravetatoelfregament.2 Enun primermodelsenzillpodemsuposarquelatensióésuniformeatotalacorda, ival τ.Aleshores,podemescriure

Fh = τ(sin(θ(x + h,t)) sin(θ(x,t))).

Sipensemenlacordad’unviolíounaguitarra,ésclarqueeldesplaçamenttransversaldelacordaésmoltpetitenrelacióamblalongituddela corda.Pertant,podemsuposarque θ(x,t) ésmoltpetiti,enconseqüència, cos(θ(x,t)) ≈ 1. Així,doncs,teniml’aproximaciósegüent:

sin(θ(x,t)) = tan(θ(x,t)) cos(θ(x,t)) = ∂u ∂x(x,t) cos(θ(x,t)) ≈ ∂u ∂x(x,t).

Pertant,laforçavertical Fh vedonada,essencialment,perladiferènciadeles primeresderivadesenelspunts x + h i x.

Siarapassemaescalainfinitesimal(perfer-hodemanerarigorosa,cal dividirentre h iprendreellímit h → 0),obtenimquelacomponentverticalde laforçaésproporcionalalasegonaderivadade u respectea x,concretament

F(x,t) = τ ∂2u ∂x2 (x,t).

2 Afegiralmodelunaforçacomelfregamentnoafectal’anàlisiquefaremalasubsecció2.3, nomésafegeixundecaïmentexponencialentempsdel’amplituddelmoviment,senseafectar-ne lafreqüènciademanerarellevant.

SegonslalleideNewton,aquestaforça F hadeserigualalamassaper l’acceleració.Notem,però,que,aescalainfinitesimal,enllocdelamassa hemdeconsiderarladensitatdelacorda,queanomenem ρ (intuïtivament, ladensitatéslamassaquetéun«punt»concretdelacorda).D’altrabanda, recordemquel’acceleració(vertical)d’un«punt»delacordaéslasegona derivadarespectealtempsde u(x,t),queéslaposiciód’aquest«punt».Per tant,enaquestcas,lasegonalleideNewtons’escriucom

2.2Primeressolucionsdel’equaciód’ones

2.2.1Lafórmuladed’Alembert Espodriadirquel’estudidelmovimentde lescordesenvibrarmitjançantequacionsenderivadesparcialsvacomençara mitjansdelsegle xviii.L’any1747,elmatemàticfrancèsJeanleRondd’Alembertvadeduiriresoldreunaprimeraequaciód’onesperaunacordasotaunes certescondicionsdeperiodicitat,simetriairegularitat[4].Méstard,Leonhard Eulertambévapresentaruntreballenquèdeduïaunaequaciód’onesunamica mésgeneral[5].

Elfruitd’aqueststreballsésunafórmulaexplícitaperresoldrel’equació d’onesa R (comsiconsideréssimunacordadelongitudinfinita).L’expressió, queavuiesconeixcoma fórmuladed’Alembert,éslasegüent:

on g i h representenlescondicionsinicials(a t = 0)delproblema.Enefecte,sicalculemlaposicióinicialdelacorda,trobem u(x, 0) = g(x).Dela mateixamanera,sideriveml’expressióanteriorrespectealtemps,obtenim ∂u/∂t(x, 0) = h(x),querepresentalavelocitatinicial.Noteuque,sicalculem lessegonesderivadesentempsiespaide u apartirdelafórmula (1),obtindrem efectivamentque u resoll’equaciód’onesa R.

Apartird’aquestafórmulatambéespotresoldreelproblemadelacorda vibrantambelsextremsfixats,siesconsiderenunessimetriesadientsde lescondicionsinicialsdelproblema(podeuconsultar-neelsdetallsa[14]). Tanmateix,enaquestcasl’expressióqueobtenimapartirde (1) noserveixper comprendredemaneraprofundaelsoqueprodueixunacordaenvibrar,a diferènciadelsargumentsquepresentaremalasubsecció2.3.

2.2.2Continualahistòria:debaticontrovèrsia Pocdesprésdelstreballs ded’Alembertid’Euler,untercermatemàticvaentrareneldebatsobrela resoluciódel’equaciód’ones.DanielBernoullivaproposarunasolucióde lamanerasegüent:

Enaquellaèpocaencaranoesconeixiaelprincipidesuperposició(ésadir,que peraunaequaciólineal,coméselnostrecas,lasumadesolucionstambéés unasolució),iBernoullivaserincapaçdesuggerircapmètodepertrobaruna fórmulaperalscoeficients A1,A2,... (apartirdelaposicióidelavelocitat inicials).

Enaquestpuntdelahistòriavasorgirundebatintensentred’Alembert, EuleriBernoulli(vegeu[15]).Enprimerlloc,d’Alembertestavaconvençutque lessolucionsdel’equaciód’oneshaviendeserdiferenciablesarreu,mentre queEulersuggeriaestudiar,també,funcionsamb«punxes»,comlaquees mostraalafigura1.D’Alembertargumentavaqueallàonlesfuncionsnofossin

diferenciablesnoespodiacalcularlasegonaderivada(enespai).Pertant,enaquestspuntsl’equaciód’onesnoteniasentit.Eulerargumentavaque, atèsquel’equacióeraunmodelperavibracions ambamplitudmoltpetita,elfetdeconsiderar aquestesfuncionsnointroduïaunerrorsignificatiual’horaderesoldre-les.Detotamanera, semblaqueenaquellaèpocalesmatemàtiquesno estavenproudesenvolupadesperresoldreaquestaqüestió.

Ensegonlloc,tantd’AlembertcomEulertenienmoltsdubtessobrelasolució proposadaperBernoulli.D’unabanda,d’Alembertnocreiaqueunacorda poguésvibrarambmésd’unafreqüènciai,pertant,ladescomposició (2) no teniacapsentit.D’altrabanda,Eulerpensavaqueaquestadescomposiciónoera prougeneralperinclourefuncionsnodiferenciables.3

Enaquestpuntdeladiscussió,l’any1759unaquartapersonavaentraral debat:elmatemàticJoseph-LouisLagrange.Enunextenstreball[10],vaconsiderarunadiscretitzaciódelacordacomunconjuntfinitdemassespuntuals. D’aquestamanera,l’equaciód’onesesconvertiaenunsistemad’equacions diferencialsordinàriesqueespodiaresoldre.Finalment,Lagrangevaobtenir unasoluciódel’equaciód’onesenfertendirainfinitelnombredemasses puntuals.Així,vaobtenirlasolució

3 Comesveuriaméstard,totsdosestavenequivocats:lateoriadeFourierdemostraque qualsevolfunciócontínua(ifinsitotmésirregular)espotexpressarcomunasumainfinitade funcionstrigonomètriques.

Figura 1: Condicióinicial nodiferenciableperòperfectamentadmissibledesd’un puntdevistafísic.

on g i h són,respectivament,laposicióilavelocitatinicialsdelacorda. AquestaexpressióvaportarLagrangemoltapropdelqueavuidiaesconeix coma sèriesdeFourier,delesqualsensocuparemalasecciósegüent.No obstantaixò,semblaqueenaquellmomentaquestatroballanovaserprou satisfactòria:Lagrangebuscavaunasolucióintegralal’equaciód’onesi,enlloc d’això,vatrobarunasoluciócomasèrieinfinita.Amés,comEuler,Lagrange consideravaquenoespodiarepresentarunafuncióarbitràriaapartird’una sumadefuncionstrigonomètriquesperquèaquestesnoerenprougenerals. SemblaqueaquestessónalgunesdelesraonsperlesqualsLagrangenova descobrirlessèriesdeFourier.Calnotar,però,que,totinoestard’acordamb lessolucionsproposadesperBernoulli,lasoluciódeLagrangeaportavauna maneradecalcularelscoeficients A1,A2,... de (2) entermesd’expressions integralsqueinvolucravenfuncionstrigonomètriquesilescondicionsinicials.

ApartirdelapublicaciódeLagrange,eldebatentorndel’equaciód’ones esvaapagardurantuntemps.Perveuretancataquestdebatvanhaverde passarunamicamésdecinquantaanys,durantelsqualslateoriadefuncions ialtresqüestionsmatemàtiquesvanevolucionar.Enefecte,novaserfinsal començamentdelsegle xix queJean-BaptisteJosephFouriervadonar,de maneraindirecta,unasoluciósatisfactòriaalproblemadel’equaciód’ones.

Fourierestavainteressataresoldrel’equaciódelacalor,

queserveixcomunmodelsenzillperdescriurel’evoluciódelacalorenuna varetadelongitud L.Finsaaquellmomentningúnohaviaestatcapaçdedonar unasolucióaaquestaequació,llevatd’algunscasosconcrets,enquèlesdades delproblema(perexemple,lescondicionsinicials)involucravenfuncionstrigonomètriques.LaidearevolucionàriadeFouriervaserconsiderarsituacionsmés complexesapartirdesuperposaraquestessolucionsdecasossenzills,laqual cosaelvaportaralproblemad’anàlisisegüent:podemexpressar«qualsevol» funciócomasumainfinitadefuncionstrigonomètriques?

L’any1807,Fouriervapresentaral’AcadèmiadeCiènciesfrancesaelsseus primersestudis,enelsqualsexposavaaquestesideesiafirmavaque,efectivament,lessèriestrigonomètriquespodienexpressarunafuncióarbitrària. EltreballdeFouriernovatenirunabonarebudaperpartdel’Acadèmia(el presidentdelaqualeraLaplace,que,comhemcomentat,pensavaqueuna generalitzaciócomaquestanoerapossible).Noobstantaixò,Fourieresva dedicaraestudiaraquestaqüestióivaculminarelseutreballl’any1822amb lapublicacióde Théorieanalytiquedelachaleur [6],onvadesenvoluparla teoriadelessèriesdeFourier.4

4 Desdelpuntdevistaactual,elsresultatsdeFouriernosóntotalmentrigorosos,jaque enaquellmomentnoestavadeltotperfiladalanociódefunciónilateoriad’integració.Peter GustavLejeune-Dirichlet,unsanysméstard,vadonarunademostraciómésrigorosadequines condicionsgarantienlaconvergènciadelessèriesdeFourier[11].

LesideesdeFourier,totiquevansermoltcontrovertidesenelsseus inicis(comhemvist,lacomunitatmatemàtica«desconfiava»d’aquestessèries trigonomètriques),vanrevolucionarlesmatemàtiquesd’aquellaèpocaiavui sónunaeinafonamental.Enelproblemaqueensocupa,eldelacordavibrant, lessèriesdeFouriersónlabaseteòricaquejustificalesprimeresideesde Bernoulli(itambélesexpressionsqueelmateixLagrangehaviatrobat).Ala secciósegüentensdedicaremaresoldrel’equaciód’onesambl’ajudadeles sèriesdeFourier,laqualcosaenspermetràentendred’unamaneramoltmés profundaelsoqueprodueixuninstrumentmusical.

2.3Resoluciódel’equaciód’ones

Enaquestaseccióensocuparemderesoldrel’equaciód’onesquemodelitza unacordadelongitud L fixadaalsextrems.Perfer-ho,seguiremelmètodede separaciódevariables,queenspermetràtrobarels modesdevibració delacorda.Acontinuació,seguintlesideesdeFourier,consideraremqueelmoviment delacordaésunasuperposiciódelsseusmodesdevibració.D’aquestamanera, lateoriadelessèriesdeFourierensserviràpertrobarl’expressióadequada delasolucióal’equaciód’onesambcondicionsinicials.

2.3.1Modesdevibració Donadaunacordaambelsextremsfixats,elnostre primerobjectiuéstrobarunseguitdesolucions(ésadir,maneresdevibrarde lacorda)«bàsiques»o«simples».Comquenoensinteressaunproblemaconcretambunesdeterminadescondicionsinicials,nomésconsiderareml’equació enderivadesparcialsjuntamentamblescondicionsdevora,ésadir,

on L éslalongituddelacordai u,elseudesplaçamentrespectealaposició d’equilibri.

Elmètodede separaciódevariables consisteixabuscarsolucionsdela forma u(x,t) = X(x)T(t),ésadir,devariablesseparades.Siimposemque aquestafunció u resolguil’equaciód’ones,obtenim XT = c2X T,

on denotaladerivadad’unafuncióunidimensionalrespectealasevavariable. Dividintconvenientmentl’equacióanteriorentre c2XT ,arribema

Enaquestaigualtat,lapartdel’esquerranomésdepènde t ilapartdeladreta, nomésde x.Pertant,(3)hadeserunaconstant,queanomenarem λ:

D’aquíobtenim,d’unabanda,l’equaciódiferencial

Recordemquelacondició X(0) = X(L) = 0descriuelfetqueelsextremsdela cordaestansemprefixos.

Unaprimeraobservacióimportantésque,si X ≡ 0,laconstant λ hadeser positiva.Enefecte,simultipliqueml’equació (5) per X,laintegrema (0,L) i femservirlafórmulad’integracióperparts,obtenim

onhemfetservirque X(0) = X(L) = 0ique X noésconstant(noteuque,si X fosconstant,lescondicionsdevorafarienque X ≡ 0).

Peròelfetrealmentinteressant(lesconseqüènciesdelqualveuremmés endavant)ésque,sivolemobtenirunasoluciónotrivialde (5) —ésadir, X ≡ 0—,laconstant λ nopotserqualsevolnúmero.Nomésperaunsvalors concretsde λ obtindremunasoluciódiferentdezero,comveuremtotseguit.

Comque λ> 0,podemescriure λ = ω2 ilessolucionsde X + ω2X = 0 sóndelaforma

X(x) = A cos (ωx) + B sin (ωx), amb A,B ∈ R.

Siimposemque X(0) = 0,necessàriament A = 0i,pertant, X(x) = B sin (ωx) amb B ≠ 0.Siaraimposemque X(L) = 0,obtenim sin (ωL) = 0,il’única maneraqueaquestaigualtatsesatisfaciésque ωL siguiunmúltipleenter de π .Ésadir, ωL = nπ amb n ∈ Z.Comque λ = ω2,nomésenscalconsiderar enterspositius,iperacada n = 1, 2,... obtenimunasoluciódelaforma

Xn(x) = Bn sin

Uncoptrobatselspossiblesvalors λn,elspodemsubstituiral’equació temporal (4),queresulta T + c2(nπ/L)2T = 0ilasevasolucióésdelaforma Tn(x) = αn cos

sin

, amb αn,βn ∈ R.

Enconclusió,peracada n = 1, 2,...

tenimunasoluciódel’equaciód’ones quesatisfàlescondicionsdevoraiqueésdelaforma

= a

cos

x , (6) amb an,bn ∈ R constantsarbitràries.

Ésadir,peracada n tenimuna«formadelacorda» Xn,queesmouamb movimentharmònicivarial’amplitudal llargdeltemps.Aquestes«formes»(osolucions) Xn s’anomenen modesdevibració.Alafigura2podemveureelsquatre primersmodesdevibraciód’unacorda. Enaquestcas,lacordapassadelaposiciórepresentadaamblalíniacontínua alaposicióoposada,representadaamb lalíniadiscontínua,ambmovimentharmònicdonatperlafunció Tn(t).Veiem queelmodedevibració Xn té n ventres (puntsdemàximadistànciaalaposició d’equilibri)i n + 1 nodes (puntsonno hihamoviment).Lesonesambaquesta formas’anomenen onesestacionàries.

2.3.2L’equaciód’onesambcondicionsinicials.SèriesdeFourier Finsara enshempreocupatd’entendrealgunespossiblessolucionsdel’equaciód’ones sotacertescondicionsdevora,quecorresponenafixarelsextremsd’unacorda. Hemobtingutunasèriedesolucions un(x,t) —devariablesseparades, (6) qued’algunamaneraensexpliquencompotvibrarlacorda.

Elnostreobjectiuaraésresoldreelproblema

on g(x) éslaposicióinicialdelacordai h(x),lavelocitatinicial.Aixòens permetràafirmarquepodemdescompondrequalsevolsoluciódel’equació d’onescomacombinaciódelessolucions un trobadesanteriorment.

Elquevolemésobtenirunasolucióde (7) apartirdelesfuncions un Talcomhemcomentatabans,comquel’equaciód’oneséslineal,qualsevol combinaciólineal(finita)deles un tambéresoll’equaciód’onesisatisfàles condicionsdevora.Així,doncs,volemferunacombinaciólinealadequadade solucions(trianta (6) lesconstants an i bn demaneraadient)perquèlescondicionsinicialstambésesatisfacin.Si t = 0,obtenim un(x, 0) = an sin nπ L x i, pertant,sivolemqueunacombinaciólinealdeles un siguisolució,necessitempoderexpressar g(x) comunacombinaciólineal(finita)de sin nπ L x .No obstantaixò,aquestfetnosemblaevidentperaunafunció g arbitrària.Tenim elmateixproblemaamb h(x)

Figura 2: Els4primersmodesdevibraciód’unacordafixadapelsextrems.

Perintentarresoldreaquestimpediment,ensplantegem,doncs,feruna combinaciólineal infinita desolucions un:

Observemqueaquestaexpressiósatisfàlescondicionsdevorairesolformalmentl’equaciód’onesenderivar-latermeatermeisensetenir-neencomptela convergència.Siimposemlescondicionsinicials,obtenim

pelquefaalavelocitatinicial.D’aquestamanera,elproblemaapareixal’hora dedeterminaruns an i bn adequatsperquèlesexpressions (9) i (10) siguin certes.Ésenaquestpuntenquèsorgeixlaqüestiósegüent:

«Donadaunafuncióarbitrària5 ϕ,espodentrobarunscoeficients cn tals quel’expressió

siguicerta?I,enaquestcas,elspodemtrobardemaneraexplícita?»

Comhemexplicatmésamunt,unproblemamoltsimilaralnostre,provinent del’equaciódelacalor,vaconduirFourierainiciarlateoriahomònima:l’anàlisideFourier.Elresultatmésimportantd’aquestateoriaresponafirmativament lapreguntaanteriori,entermesd’aquestarticle,elpodemenunciardela manerasegüent: Teorema

5 Enaquestcas,contínua,jaquevolemquerepresenti,perexemple,laposicióiniciald’una cordareal.

6 Engeneral,aquestaigualtats’had’entendrecomunlímita L2 (l’espaidefuncionsdequadrat integrable).Defet,ésenaquestespaionesdesenvolupademaneranaturaltotalateoriade lessèriesdeFourier.Noobstantaixò,peralsobjectiusd’aquestarticlen’hihaproudesuposar queaquestaigualtatéscertasensepreocupar-nosgairedelaconvergència(detotamanera, si,perexemple,suposemque ϕ éscontínuaidiferenciableatrossos—comalafigura1—,la convergènciaésuniforme).

Sifemservirelteoremaanteriora(9)i(10),obtenimlesexpressions

l’expressió(8),obtindremlasoluciódelproblema(7).

2.4Quèensdiul’equaciód’onessobreelsodelsinstruments?

Alaseccióanteriorhemvistque,siconsideremunacordafixadapelsextrems, podemdescriure’nlamaneradevibrarmitjançantunasumainfinitadesolucionsperiòdiqueseneltemps.Ésadir,podemdescompondrequalsevol vibraciócomplexaenelementsméssenzillsd’analitzarid’entendre,els modes devibració.Aixòhaestatpossiblegràciesadosingredients:

1. L’equaciód’onesjuntamentamblescondicionsdevora.7 Aquestsdos elementsdeterminennonoméselsmodesdevibració(ésadir,les«formes bàsiques»amblesqualsunacordapotvibrar),sinótambélesfreqüències alesqualsvibracadamode—vegeu(13)i(14).

2. LateoriadeFourier,queensgaranteixquesemprepodemdescriure qualsevolmovimentdelacordavibrantapartirdelsmodesdevibració. Ditd’unaaltramanera,enspermetdescompondrequalsevolcondició inicialenelsmodesdevibració,estudiarelmovimentdecadamodeper separat(cadascundelsqualsvibraràambunafreqüènciacaracterística, comhemvist)isuperposaraquestsmovimentsperobtenirelmoviment complexdelacorda.

Enresum,podemdescriureelmovimentd’unacordavibrant(fixadapels extrems)apartirdel’expressió

7 Lescondicionsdevoratenenunpaperfonamentalal’horadedescriurel’espectrede freqüènciesd’uninstrument(vegeulanotaalpeu10).

Comafinaruninstrument decorda

Fixem-nosquelasoluciód’ones ensexplicacompodemafinarun instrumentdecorda,comarauna guitarraounvioloncel. Afinar un instrumentdecordavoldir«ajustarlafreqüènciafonamentald’una nota».Apartirde (14),veiemque enelcasd’unacordavibrantlafreqüènciafonamentalés f

Elsparàmetres L i ρ,quecorresponenalalongitudiladensitatlineal delacorda,respectivament,estanfixatsperlescaracterístiques del’instrument.Encanvi,lamajoriad’instrumentsdecordadisposendeclausquepermetenmodificarlatensió τ alaqualestàsotmesacadacorda.Pertant,lasolució del’equaciód’onesensmostraque, sivolemaconseguirunanotamés aguda(ambunafreqüènciamésalta),elquehemdeferésaugmentar latensiódelacorda.

on L éslalongituddelacorda, τ és latensiói ρ ésladensitatlinealde lacorda(vegeulasubsecció2.1).És adir,lacordavibra alhora enles diferentsfreqüències fn,quesón totesmúltiplesentersde f1,ésa dir, fn = nf1.Aquestasuperposiciódefreqüèncieséselquearribaa travésdel’aireal’orellad’unapersonaqueestàescoltant,laqualho percepcomunsomusical.

Elsnúmeros fn s’anomenen freqüènciesdevibració ielprimerde tots, f1, freqüènciafonamental,ja queapartird’aquestvalorpodem obtenirtoteslesaltresfreqüències, comesveua (14).Defet,aquestaestructuratanregulardelesfreqüènciesapareixalamajoriad’instrumentsmusicalsiésunfactor clauqueenspermetdistingirunso musical(comelquefalacordad’un violoncel)d’unsoqualsevol(per exemple,eld’unobjectequecau aterra).Amés,podríemdirque aquestadistribuciódefreqüències éselpilarenquèesbasalamajoria delamúsicaqueconeixemavuidia, peròparlaremd’aquestaqüestióde maneradetalladaalasecció3.

2.5L’espectreharmònicdelsodelsinstruments

Alesseccionsanteriorss’explicademaneramatemàticacomunacordapot vibraralhoraamúltiplesfreqüènciesi,pertant,compotproduirunsoquesigui launiódediversostonspurs(onessinusoidalssimples),cadascundelsquals ambunafreqüènciaiunaamplitudconcretes.Enmúsicasesolenanomenar harmònics cadascund’aqueststonssimplesenelsqualsesdescomponelso queprodueixuninstrument.Elvolumdecadaharmònicestàdeterminatper l’amplituddecadaonasimple,quedepèndirectamentdelscoeficients an i bn al’expressió(13),ésadir,delescondicionsinicials8 —recordeu(11)i(12).

Donatunsoqualsevol,nonecessàriamentd’uninstrumentmusical,ens podempreguntarperquinesfreqüènciesestàformat.Perobteniraquestainformacióesfaservirunaeinamatemàticaanomenada transformadadeFourier,

8 Aquestes,alseutorn,depenendedosfactors:d’unabanda,delamaneradetocarde l’intèrpret,i,del’altra,delescaracterístiquesfísiquesdel’instrument.

delaqualparlaremtotseguit.Noobstantaixò,engeneral,elmésprobableés queobtinguemunasèriedetonssimplesambfreqüènciesarbitràries,queno segueixincapmenadepatró.9 Enaquestcasgeneral,elsanomenarem parcials i nomésfaremservirelterme harmònic quanlesfreqüènciessegueixinunpatró delaforma fn = nf1,amb n = 1, 2,...

Anomenem espectre elconjuntdelsparcialsd’unso(ésadir,lesfreqüènciesdevibraciójuntamentamblesamplitudscorresponents).Encasqueles freqüènciessiguintotesmúltiplesentersd’unafreqüènciafonamental,farem servirelterme espectreharmònic.

L’espectreésundelsfactorsprincipalsquedeterminenel timbre decada instrument.Ésadir,enspermetdistingir-neund’unaltreencaraquetoquinla mateixanotaalhora.Així,doncs,siunaflautaiunviolítoquenlamateixanota (ésadir,produeixenunsoamblamateixafreqüènciafonamental),totique ladistribuciódefreqüènciesdelsharmònicséslamateixa,elvolumdecada harmònicdelviolí(ésadir,l’amplitudambquèoscil lacadamodedevibració) seràdiferentdeldel’harmòniccorresponentalaflauta.Finsitothihacasos enquèlescaracterístiquesfísiquesdel’instrumentfanquecertsharmònicsno siguinpresentsenelso.Unamostrad’aixòéselclarinet,l’espectredelqual estàformatperfreqüènciesquesónmúltiplesenters senars d’unafreqüència fonamental.10

Figura 3: L’espectrededosinstrumentsqueestantocantlamateixa nota,un do d’aproximadament130Hzdefreqüència(C2ennotació anglosaxona).L’eixhoritzontaldelsgràficsrepresentalesfreqüències enescalalogarítmica;l’inicidecadaoctavaestàmarcatambleslínies verticals.L’eixverticalrepresental’amplitudmesuradaendecibels.Enel segongràficespotveurequenomésapareixenelsharmònicssenars.

9 Ésnomésensituacionsmoltconcretes(comperexemplepassaambelsinstruments,però nonomésenaquestcas)enquètenimunaeinaextraalanostradisposició:l’equaciód’ones (oalgunaaltraequacióqueregeixilavibraciód’unmaterial).L’equaciód’ones,ditdemanera informal,«força»elmaterialavibrarnomésambunescertesfreqüències(comara fn = nf1, amb n = 1, 2,... ,enelcasdel’equaciód’onesendimensió1).

10 L’equaciód’onestambéserveixperdescriureelsod’unclarinet,peròenaquestcasles condicionsdevoracanvienihemdeconsiderar ∂x u(L,t) = 0enllocde u(L,t) = 0(vegeu[1]).

Elproblemaespotresoldretalcomhohemfetenelcasdelacorda,peròelsmodesdevibració sóndiferents:a (5) hemdeconsiderarlescondicionsdevora X(0) = X (L) = 0,laqualcosafa quelesfreqüènciesdel’espectresiguin fn = (2n 1)c/(4L),ésadir,nomésapareixenmúltiples senarsdelafreqüènciafonamental f1 = c/(4L)

2.5.1LatransformadadeFourier Donadaunafunció u(t) d’unavariable real t,laseva transformadadeFourier ésunafunció [Fu](ν) d’unavariablereal ν definidaperl’expressió [Fu](ν) :

Elpropòsitdel’articlenoésestudiardemanerarigorosaaquestobjectematemàtici,peraquestmotiu,nomésensocuparemdedonar-neunadefinició intuïtivaiesmentar-nealgunesaplicacions.

ElpuntdepartidaperentendreelsignificatdelatransformadadeFourier d’unafuncióéselcàlculheurísticsegüent:

Enelcas α ≠ 0hemfetservirlafórmulad’Euler(eiθ = cos θ + i sin θ)ihem suposatquelessimetriesdelesfuncionstrigonomètriquesfanqueaquestes integrin0a (−∞, ∞) (d’aquíl’úsdelaigualtatentrecometes).

Consideremaralafunció u(t) = cos(2πt),quepodementendrecomun senyalsenzilldefreqüència1,percalcular-nelatransformadadeFourier.Per fer-ho,mitjançantlafórmulad’Eulerpodemexpressar u(t) = (e2πit +e 2

)/2 i,utilitzant(15),tenim11

Ditdemaneraintuïtiva,totalamassade Fu estrobaconcentradaa |ν|= 1. Ésadir,latransformadadeFourierde u ha«detectat»quel’únicafreqüència presentalsenyal u és1.

Sifemelmateixcàlculambunsenyalméscomplex,delaforma u(t) = a1 cos(2πf1t) + a2 cos(2πf1t) +··· ,obtindremque [Fu](ν) = 0arreuexceptesi |ν|= fj .Enaquestcas, [Fu](fj )«=»aj · (+∞/2).Ésadir, Fu detecta nonoméslesfreqüènciesde u(t),sinótambéenquinaproporcióapareixenal senyal.Ditd’unaaltramanera,descriul’espectredelsenyal u(t)

Peraunafunció u(t) general,lasevatransformadadeFourierenunvalor ν espotentendre,demanerainformal,comunamesuradelaproporcióenquè lafreqüència ν apareixa u(t).Encertamanera, F «trenca»unsenyal u(t) en toteslespossiblesfreqüènciesiensdiuenquinaproporcióestrobacadascuna a u(t).Pertant,ésunaeinaessencialperanalitzarl’espectred’unso.

Comque Fu ésunafuncióqueprenvalorscomplexos,elméshabitualés representarl’espectred’unsenyal u apartirdelgràficde |Fu|.Alapràctica,

11 Selipotdonarunsentitrigorósaaquestcàlculdinslateoriadedistribucions.Enaquest cas,si u(t) = cos(2πt),tenim Fu(ν) = (δ0(ν 1) + δ0(ν + 1))/2,on δ0 ésladeltadeDirac.La distribució δ0 representa,demaneraintuïtiva,unamassaunitàriaconcentradaenunsolpunt,0.

encaraqueconsideremunsoambespectreharmònic,mainoveuremelsvalors +∞ quehemtrobatenelnostreargumentheurístic,jaquetotselssenyals tenenunaduradafinita.Totiaixò,elqueveiemalarealitatquanconsideremun soambespectreharmònicésungràficqualitativamentsemblant,ésadir,amb «pics»alspuntsoneslocalitzenlesfreqüències fn (comesveualafigura3).

2.5.2Aplicacions:síntesiitractamentdeso Laveritablepotènciadela transformadadeFourier,però,ésqueespotdesfer.Ésadir,existeixuna operacióinversa,anomenada transformadadeFourierinversa,queesdefineix com

Així, [F 1[Fu]](t) = u(t).

Aquestfetofereixunmuntdepossibilitatsalmóndeltractamentdigital delso,comlesquepresentemtotseguitsenseentrar-hiafons:

• Síntesideso:podemcrearunsoambl’espectrequevulguemapartirde triarunesfreqüènciesiamplitudsi,després,aplicar-hilatransformada deFourierinversa.

• Compressiód’arxiusdeso:podemanalitzarlatransformadadeFourier d’unsenyalperidentificar-nelespartsmésimportantsieliminar-nela resta.Latransformadainversaenspermetobtenirelsenyalsimplificat.

• Filtres,equalització,eliminaciódesoroll:gràciesalatransformadadeFourierpodemaplicarunseguitd’operacionsaunapartconcretadel’espectre delso(comaraeliminarfreqüènciespersobred’uncertvaloroaugmentar elvolumdelesgreus).Aplicantlatransformadainversaobtenimelso modificat.

3Elproblemadel’afinaciódelsinstruments

Alaseccióanteriorhemfetservirlesmatemàtiquesperentendrelespropietats bàsiquesdelsodelsinstrumentsmusicals.Hementèsperquinmotiupodem descriureelsocomunasuperposiciódetonssimplesihemvistqueladistribuciódefreqüènciesd’aqueststonsnoésarbitrària,sinóquesegueixunpatró moltparticular:toteslesfreqüènciessónmúltiplesentersd’unafreqüència fonamental.Concretament,hemobservatquelesfreqüènciesproduïdesper unacordavibrantsegueixenl’expressió

L, τ i ρ representen,respectivament,lalongitud,latensióiladensitatlineal delacorda(vegeulasubsecció2.1).Unsoquecompleixaquestescaracterístiquess’anomena notamusical.Sidosinstrumentsprodueixenunanotaambla mateixafreqüènciafonamental,esconsideraquetotsdossonssónlamateixa nota,encaraquel’espectredecadascunsiguidiferent.

Finsaraenshemcentrataentendreafonsl’elementmésbàsicdelamúsica: lesnotesmusicals.Arabé,unanotapersimateixanofamúsica:lesmelodies,lescançonsolesobresmusicalsengeneralconsisteixenenunseguitde notes,potserdediversosinstruments,interpretadesalllargd’untempsiamb unescertescaracterístiques.I,sibél’oïdahumanaéscapaçdedistingirun granventalldefreqüències,elméshabitualésquelesnotesqueconstitueixen unamelodiaforminunconjuntfinitproureduït,laqualcosahaestataixíenla majoriadelamúsicaoccidentaldesdelsseusinicis.

Perentendre-hodemaneraméssenzilla,pensemenelfuncionamentd’un piano.Enaquestinstrument,cadateclaaccionaunmartell,elqualcolpeja unacorda.12 Lanotaproduïdadepènúnicamentdelatensió,ladensitati lallargàriadelacorda,comhemvista (16),i,pertant,comqueaquestes magnitudsnoespodenmodificarmentreestocal’instrument,ambunatecla noméspodemfersonarunanota.Ésadir,siesvolproduirunaaltranota,cal tocarunaaltratecla,laqualfavibrarunaaltracordaambunalongituditensió diferents.Pertant,elnombredenotesquepotferunpianoestàlimitatal nombredetecles,habitualment88,i,enconseqüència,qualsevolmúsicacreada ambaquestinstrumentconsistiràenunacombinaciómésomenyscomplexa d’aquestes88notes.

Continuantambaquestexemple,imaginemquevolemconstruirunpiano perfermúsica.Abandadeqüestionstècniques,lapreguntamésbàsicaque enspodemferéscomhemdetriarlafreqüènciafonamentaldecadanota, laqualcosanomésdepèndelescaracterístiquesfísiquesdelacorda—com hemvista (16).Enaquestcontext,s’anomena afinació l’eleccióconcretade lesfreqüènciesfonamentalsdelesnotesd’uninstrument(od’unaescala,com veuremmésendavant).

Comhemcomentat,jadesdelsinicisdelamúsicas’haviaobservatque,si femsonarsimultàniamentduescordesamblesmateixescaracterístiques(pel quefaadensitatitensió),aquestesprodueixenunsoagradablesileslongituds detotesduesestrobenenunaraód’enterspetits.Gràciesa (16),aixòequival alfetquelesfreqüènciesfonamentalsdelesnotesquesonenformenunaraó d’enterspetits.Pertant,idealment,l’afinaciódelpianohauriadeconstarde freqüènciesquesegueixinaquestapremissa.Tanmateix,aconseguir-hopera toteslesnotesésunatascacomplicada,comveuremtotseguit.

Alllargdelahistòrias’hanfetdiversespropostesperintentardonaruna soluciósatisfactòriaalproblemadel’afinaciódelsinstruments.Enaquestaseccióenpresentaremtresquesintetitzenl’evolucióhistòricacapal’afinacióque femserviravuidia:l’afinaciópitagòrica,l’afinaciójustail’afinaciótemperada. Perfer-hod’unamaneramésclara,introduiremprimerelsconceptesd’escala i d’interval

12 Aixòésunasimplificació.Enrealitat,lamajoriadelesnotesdelpianoconstendetrescordes quesónaccionadesalhoraperunmartell(que,defet,vibrenambfreqüènciesfonamentalsmolt properesperònoigualsperaportarriquesatímbricaalsodel’instrument).Noméslesnotesmés greusdelpianoconstend’unaoduescordes.Entotal,unpianotéalvoltantde230cordes.

3.1Escalesiintervals

Anomenem escala unconjuntfinitdenotesordenadessegonslasevafreqüència fonamental.Bonapartdelamúsicaoccidentalfaservirl’escalacromàtica,que constadedotzenotes: do, do , re, re , mi, fa, fa , sol, sol , la, la i si,lesquals corresponenadotzeteclesconsecutivesdelpiano.13 L’escalacromàticaésuna extensiódel’escaladiatònicamajor,formadaperlesnotes do, re, mi, fa, sol, la i si,lesqualsescorresponenambsetteclesblanquesconsecutivesdelpiano. Aquestesescalessónlesquehandeterminattradicionalmentelnomde lesnotesmusicals.Unpianoestàformatperdiversesescalescromàtiques successives,lesnotesdelesqualsrebenelnomenfunciódelaposicióque ocupenal’escala.Així,doncs,desprésdel si,queésl’últimanotad’unaescala cromàtica,velaprimeranotadel’escalasegüent,ques’anomenanovament do, comesmostraalafigura4.Aquestarepeticióesdeuaunfenomenanomenat equivalènciad’octaves,delqualparlaremmésendavant.

Ladiferènciad’alturaentreduesnotess’anomena interval iespotmesurar apartirdelafreqüènciafonamentaldecadascuna,talcomtambéveuremmés endavant.Enuncontextpuramentmusical,elsintervalsdel’escalacromàtica s’acostumenaexpressarmitjançantunordinalseguitd’unadjectiu.Així,doncs, donadesduesnotes a i b,l’ordinaldel’intervalqueformenésdefinitpel nombredenotesquehihaentre a i b (totesduesincloses)al’escaladiatònica. Perexemple,entreun re iun sol hihaquatrenotes, re, mi, fa i sol,i,per tant,formenunintervaldequarta.Pelquefaal’adjectiu,eldeterminenaltres qualitatssonoresdel’interval—enlesqualsnoentrarem—,totiqueenuna escalatemperada(vegeulasubsecció3.2.3)vedeterminatpelnombrede semitonsquehihaentreduesnotes.Unintervalespotdescriureambels adjectius major, menor, just o justa, disminuït o disminuïda o augmentat o augmentada (perexemple, intervalmajor, sextamenor, quartajusta o sèptima disminuïda),totiqueavegadesl’adjectiuespotometre(especialmentquan parlemdelsintervalsd’octava,quartaoquinta,enquè,sinos’especificares,es consideraquesónjustos).

3.1.1L’equivalènciad’octaves Enlamúsicaoccidental,l’intervalmésimportantésl’octava,queestàformatperduesnoteshomònimesdeduesescales consecutives.Persimplificarl’exposicióconsiderareml’intervalformatentre

13 Lesnotesambelsímbol ,anomenat sostingut o diesi,tambéespodenanomenarpelnom delanotasegüentambelsímbol ,anomenat bemoll.Així,podemescriurel’escalacromàtica d’aquestamanera: do, re , re, mi , mi, fa, sol , sol, la , la, si i si

la

la si do

do re

re mi fa

fa sol

sol la

la si do

do re

re mi fa

fa sol ...

sol

Figura 4: Representacióparcialdelesnotesdelpiano.

laprimeranotad’unaescala,queanomenem do,ilaprimeranotadel’escala següent,queanomenem do’.

Lapeculiaritatdel’intervald’octavaésquelafreqüènciafonamentaldela notamésaguda, do’,éseldobledelafreqüènciafonamentaldelanotagreu, do. Pertant,sianalitzeml’espectredefreqüènciesd’aquestesduesnotes,veurem elpatrósegüent:

Espectre(do) ={f, 2f, 3f, 4f,... } iEspectre(do’) ={2f, 4f, 6f, 8f,... }, on f éslafreqüènciafonamentaldel do.Ésadir,l’espectredefreqüències del do’ coincideixexactamentamblameitatdel’espectredel do.Aquesta coincidènciafaquepercebemtotesduesnotescomlamateixa(totiquela segonalasentimmésaguda)i,consegüentment,querebinelmateixnom.

Enefecte,lamajoriadepersonesreconeixduesnotesseparadesperun intervald’octavacomsifossinlamateixanota.Perexemple,quanunhomei unadonacantenlamateixamelodia,l’homesovintlacantaunaoctavamés greuacausadelessevescaracterístiquesfísiques.Totiaixò,lamajoriad’oients acostumenapercebre-hocomunasolamelodia.Comhemdit,aixòesdeua lacoincidènciadelsharmònics:sianalitzeml’espectreconjuntdeduesnotes separadesperunaoctava,trobaremquetoteslesfreqüènciessónmúltiples entersd’unadefonamentali,pertant,percebemaquestsocomunasolanota. Ditd’unaaltramanera,afegirl’octavanoalteraladistribuciódel’espectre,sinó noméslesamplitudsdelsharmònicsparellsi,pertant,percebemunasolanota ambuntimbrelleugeramentdiferent.

Així,doncs,apartird’unasolaescalacromàticaquecomençaal do,en podemdefinirunaaltrasimplementdoblantlesfreqüènciesdelesnoteso dividint-lesentredos.Qualsevold’aquestesescalessonaràigualquel’escala cromàticainicial(peròmésagudaomésgreu).Aquestprocésespotrepetir infinitamentfinsalslímitsdelapercepcióhumana.Elpiano,undelsinstrumentsambregistre(rangdenotesqueespodentocar)mésampli,consta habitualmentdesetoctavesmésunaterceramenor,ielrangdefreqüències fonamentalsvadels27.5Hzals4186.01Hz.

Notació. Enlarestadeltextindiqueml’octavaalaqualpertanyunanota mitjançantunsubíndex,iprenemcomareferènciael la ambunafreqüència de440Hzcoma la4.D’aquestamanera,el do centraldelpianoés do4 iel do mésgreudelpiano, do1

3.1.2Comesmesurauninterval Comhemdescritmésamunt,l’interval ésladiferènciad’alturaentreduesnotes,laqualvolemmesurarentermes defreqüènciesfonamentals.Lapercepcióauditivahumanadelafreqüència éslogarítmica:sentimquehihalamateixadistànciaentreel la4 iel la5 que entreel la5 iel la6,peròentreelsdosprimershihaunadiferènciade440Hz, mentrequeentreelsdossegonsladiferènciaésde880Hz.Pertant,donades duesnotesambfreqüènciesfonamentals f1 i f2,nopodemsimplementdefinir ladiferènciad’alturacoma |f1 f2|,jaque,sicanviemd’octavamultiplicant totesduesfreqüènciesper2k,on k ∈ Z,ladiferènciad’alturaesveuràalterada pelfactor2k .

Engeneral,donadesduesfreqüències f1 i f2 amb f1 >f2,expressem l’intervalqueformencomlaraó r = f1/f2 (obé f1 : f2).Aquestaescalaés multiplicativa,ésadir,per«sumar»dosintervalshemdemultiplicar-neles raonsiper«restar-los»,dividir-les.Perexemple,enunaescalaambafinació justa(vegeulasubsecció3.2.2),l’intervalentre do i mi ésderaó6/5ientre mi i sol,de5/4.Pertant,l’intervalentre do i sol ésderaó3/2.Delamateixamanera, perdividiruncertintervalderaó r en m partsiguals,hemdeconsiderar l’interval r 1/m,jaque,si«sumem» m intervalsd’aquestaraó,obtenim r

3.2L’evoluciódel’afinaciódel’escalacromàtica

Totseguitpresentaremd’unamaneramoltresumida14 l’evolucióquevapatir l’afinaciódel’escalacromàticafinsaarribaral temperamentigual,elsistema d’afinacióestàndardques’utilitzaavuidia.Aquestaevolucióvaestarmarcada perl’objectiud’aconseguirqueelsintervalsdel’escalafossinconsonants,ésa dir,agradablesal’oïda.

Comjahemesmentat,laconcepciómésbàsicadeconsonànciadedues notesestrobaenlaraódelessevesfreqüènciesfonamentals.Unaexplicació senzillad’aquestfetéslasegüent:siduesnotesestrobenenunaraóde p/q, aleshoreslafreqüènciadel q-èsimharmònicd’unacoincidiràambladel pèsimharmònicdel’altra;amés,aquestacoincidènciaesrepeteixdemanera periòdica.Perexemple,pensemenlesnotes do i sol afinadesdemaneraque forminunintervaldequintajusta(ésadir,formantunaraóde3/2).Enaquest cas,elsegonharmònicdel sol coincidiràambeltercerdel do;elquartdel sol, ambelsisèdel do,iaixísuccessivament.Lapartmésimportantdel’espectre sónelsprimersharmònics,jaqueéslapartmésaudible.Pertant,commés petitssiguinelsentersquedefineixenlaraód’uninterval,méscoincidències trobaremalapartaudibledel’espectrei,pertant,percebremmésconsonància.

Totiqueelsconceptesde consonància i dissonància sónmoltméscomplexos(enparlaremalapròximasecció),araperaraenslimitaremaassociar-losa lacoincidènciadelsharmònics,jaqueelssistemesd’afinacióquepresentarem totseguitestanbasatsenaquestprincipi.

3.2.1L’afinaciópitagòricail’espiraldequintes Desprésdel’octava,la raód’entersmésimportantenlamúsicaoccidentalés3:2.Aquestinterval s’anomena quintajusta.Elspitagòricscreienqueunaescalamusicalhavia d’estarformadanomésperintervalsd’octavaidequinta.Totseguit,veiem comesconstrueixaquestaescala.

Posempercasunanotaambunacertafreqüènciafonamental,comara el do4.Laquintadel do4 ésel sol4,laquals’obtémultiplicantper3/2les freqüènciesdelaprimeranota.Mitjançantaquestaoperacióobtenimdues notesdel’escala.Apartirdel sol4,enbusquemlaquintafentelmateixiobtenim el re5,queestrobaal’octavasegüent.Sidividimlesfreqüènciesdel re5 entre dos,obtenimunanotamésperal’escala: re4,al’octavainicial.Repetimaquest procési,buscantlaquintaapartirdel re4,aconseguimel la4 i,posteriorment, 14Podeutrobarexplicacionsmésextensessobrelaconstrucciód’escalesmusicalsa[1,7,13].

el mi5,quepodembaixarunaoctavadividintentredoslessevesfreqüències. Continuantaquestprocés,dividintentredosquancalgui,hemconstruïtuna successiódequintesascendentsapartirdel do4.Perfer-hocapavall,calfer elmateix.Dividintentre3/2lesfreqüènciesdel do4 obtenimel fa3 (al’octava inferior),quecol.loquemal’escalaprincipalcoma fa4 multiplicantperdosles freqüènciesd’aquestanovanota.D’aquest fa4 baixemal si 3;després,al mi 3, iaixísuccessivament.Observeuque,perobtenirlesnotesdel’octavaoriginal, calmultiplicarperdoslesfreqüències.

Espodriapensarque,siapartirdel do4 repetimaquestprocéssuficients cops,enalgunmomenttornaremal do4 itancaremelcicle,laqualcosaequivaldriaatrobarunnúmeronatural n> 0talque,enmultiplicar3/2persi mateix n cops,obtinguéssimunapotènciade2,diguem-ne,2m amb m natural. Observem,però,que

= 3

iaquestaúltimaequaciónotésolució,atèsqueequivaldriaatrobarduesdescomposicionsd’unnúmeroenfactorsprimers.Pertant,elprocésdecrearnotes apartirdel’intervaldequintanoespottancarmaiidonallocaunasuccessió infinitadenotesquesesolrepresentarambunaespiral(vegeulafigura5).

L’escalapitagòricaconstruïdad’aquestamaneranoésconsistent,jaque nomésvolemdefinirdotzenotesperaunaescalaienteniminfinites.Per resoldreaquestproblemacalcanviarlafreqüènciad’unadelesnotesde l’espiralperladelseu enharmònic. 15 D’aquestamaneraestancal’espirali s’obtéel cicledequintes.Vegem-neunexemple:

del’esquerra)perobtenirelcicledequintes(panelldeladreta,on hemfetexplíciteslesraonsdelsintervalsrespecte do).Enaquestcas, lafreqüènciadel sol (ambraó6561:4096)baixapertaldeserigual alafreqüènciadel la (ambraó128:81).

15 Enharmoniaclàssica,esdiuqueduesnotessónenharmòniquessitenennomdiferent peròsonenigual,perexemple mi i re o la i si .Aquestsparellsdenotestenenlamateixa freqüènciaenunaescalatemperada.

Figura 5: Alafiguras’observacomtancarl’espiraldequintes(panell

Engeneral,estriaunadelesquintesiesredueixunamica,iaixíesforma elques’anomena quintadelllop.Aquestintervaldifereixd’unaquintajustaen unaraóde312/219,laquals’anomena comapitagòrica icorresponagairebé unquartdesemitòtemperat(vegeulasubsecció3.2.3).Pertant,hihauràuna quintaquesempreenssonaràdesafinada:aquestaéslalimitaciómésgrande l’afinaciópitagòrica.

3.2.2Afinaciójusta Lesescalesd’afinaciójustasónl’evoluciónaturalde l’afinaciópitagòricaiesbasenenlamateixapremissa:definirelsintervalscom unaraód’enterspetits.Tanmateix,enaquestcasesconsiderentotesaquestes raonsapartird’unanotainicial,comara do.Així,doncs,laquintacontinuasent deraó3:2ielseucomplementarirespecteal’octava,laquarta,de4:3.La terceramajortéunaraóde5:4ilasextamenor,de5:3.Finalment,lasegona majorcorresponalaraó9:8ilasèptimamajor,a15:8.Aquestsintervals s’anomenen purs.Uncopafinadeslesnotesdel’escaladiatònicamajor,calfer elmateixamblarestadenotesdel’escalacromàtica,peralaqualcosahiha diversespropostes,lesqualsnoexposaremaquí.

Calferunincísenaquestadiscussió:totsaquestsintervalsestancalculats respecteaunanotafonamental,comara do,peròaixònovoldirque,per exemple,toteslesquintestinguinraó3:2.Siconsideremlaquintaformada entre re i la,téunaraóde40:27 ≈ 1 48,quecorresponadividirlaraódel la, 5:3,entrelaraódel re,9:8.Enaquestcas,aquestaquintaésmésbaixaque laformadaentre do i sol,queésjusta,ambraó3:2 = 1.5.Aquestfetfaque, sibéapartirde do totselsintervalssónmoltmésconsonantsqueenl’escala pitagòrica,apartird’altresnotesnohosón.D’aquestamanera,sitoquemuna obraqueestàescritaenlatonalitat16 de do major,hihauràmésintervalsque sonaranconsonantsquesientoquemunaen re major,enquèlaquintanoés justa,comjas’havistenl’exempleanterior.Comquenoésfactibleteniruna afinacióperacadatonalitati,amés,unamateixaobrapotcanviardetonalitat alllargdeldiscursmusical,sorgeixenelques’anomenen temperaments,que sónmodificacionsdelsintervalsdel’escalad’afinaciójustapertaldemillorarnel’afinació.Undelsexemplesmésconegutséseltemperamentigual,que descriuremtotseguit.

3.2.3Temperamentigual Elconcepte temperamentigual apareixperdefinirunaescalaquepuguiserutilitzadaenqualsevoltonalitat.Peraconseguir-ho, esdivideixl’octavaendotzepartsigualsi,apartird’aquí,escreentotsels intervals.

Enefecte,sipartimdel’octava,deraó2,iladividimendotzepartsiguals, obtenimel semitòtemperat,deraó21/12.Apartird’aquestintervalconstruïmtoteslesnotesdel’escalatemperada,quetenenraons2k/12,amb k = 0, 1,..., 11, respectealaprimeranotadel’escala(k = 12corresponal’octava,laprimera notadel’escalasegüent).

16 Enmúsica,elconceptede tonalitat fareferènciaaunaorganitzaciójeràrquicadelesnotes d’unaescalaenrelacióambunanotadereferència.Perdenominarunatonalitatesfaservirel nomdelanotadereferènciaseguitd’unadjectiu(típicament major o menor enfunciódels intervalsambmésimportànciaharmònica).

Enaquestcas,laquintadeixadetenirraó3/2perpassaratenirraó27/12 Pelquefaaaltresintervals,passaunacosasemblant.L’afinaciótemperada sacrificalesquintesjustesenrebaixar-leslleugeramentitambéaltresintervals purs,comaralesterceres,quequedenmésafectades.Acanvi,s’obtéuna afinacióacceptableperatoteslestonalitats.Aquestésunsistemad’afinació proubo,jaqueésrelativamentproperalsintervalsjustosipermettocar enqualsevoltonalitatsenseperdrequalitatenl’afinació(alasecciósegüent veuremcompodemmesuraraixò).Pertotplegat,actualmentesconsideraque elsistemad’afinacióestàndardéseltemperamentigual.

4Teoriadeladissonància

Alesseccionsanteriorshemvistquelapropietatfonamentalquedefineix unsomusicalésquelesfreqüènciesdel’espectresónmúltiplesentersd’una freqüènciafonamental.Amés,hemanalitzatquinesconseqüènciestéaquest fetsiconsideremunanocióbàsicadeconsonància(associadaaintervalsenraó d’enterspetits),icomaixòestéencompteal’horad’escollirunconjuntfinit desonsperformarl’escalacromàtica,queéslabasedelagranmajoriadela músicaoccidental.

Enaquestaseccióintroduiremlateoriadeladissonància,queenspermetrà ferunaanàlisidemaneramésprofundadeperquèunsintervalssonende maneramésagradablequealtres,icomespotquantificaraquestaqualitat. Aixòenspermetràjustificarquel’escalatemperadaésunabonaelecciópel quefaaladissonànciai,d’aquestamanera,podremdonarunarespostamés completaaperquèensagradalamúsicaquefaservireltemperamentigual. Peraunaexposicióméscompleta,podeuconsultar[13].

4.1Superposiciódeduesonessimples.Batecsiaspror

Alllargdelahistòriadelamúsica,elstermes consonància i dissonància s’han definitdediversesmaneres,algunesdelesqualssónimprecises.Novaserfins alsegle xix queHermannvonHelmholtz([9])vadonarunaexplicaciócientífica imésrigorosadelconceptede dissonància apartirdel’anàlisideduesones simplessuperposades.ComHelmholtzvaobservar,quansentimalhoradues onessimplesamblamateixafreqüència,silafreqüènciad’unavaaugmentant progressivament,passemdesentirbatecsaasprori,després,percebemles duesonescomatonsdiferents.Totseguit,desenvoluparemaquestesidees.

Consideremunaonasimple v0(t) = sin (2πf0t) ambunafreqüència f0 fixada.Volemestudiarelresultatdesuperposaraquestaonaiunaaltradelaforma v(t) = sin (2πft),ambunafreqüència f quefaremvariar.Perfer-ho,hem deconsiderarlasumadetotesduesi,mitjançantidentitatstrigonomètriques, obtenimquel’onaresultantés:

Enaquestcas, V(t) espotinterpretarcomunaonasimplequevibraamb freqüència f +f0 2 iambunaamplitudquevariaambfreqüència f f0 2 ,comespot veurealafigurasegüent:

Silafreqüència f ésprouproperaa f0,percebremuntodefreqüència f0+f 2 ≈ f0 ambunvolumqueoscil la.Aquestavariacióenl’amplitudésel queesconeixcoma batecs,lafreqüènciadelsqualsés fb = |f f0| 2 ,ésadir,se senten fb batecspersegon.Comqueelvalorde f éspropera f0, fb éspetit ielsbatecsespodensentirclarament.Sifemvariar f ,amesuraqueaquesta freqüèncias’allunyade f0,elvalorde fb esfaràmésgranisentirembatecs cadacopmésràpids.D’aquestamanera,elsoéscadacopmenysagradablei provocaunasensaciód’aspror queaugmentafinsaunpuntmàximapartir delqualcomençaadesaparèixeripercebemelsocomadostonsdiferentsde freqüències f0 i f

Apartird’aquestfetpodemdonarunanociómésprecisadelconceptede dissonància entredostonspurs:lamàximaconsonànciaescorresponamb l’absènciadebatecs,mentrequelamàximadissonànciaescorresponambel puntmàximd’aspror.Compodemveure,niladissonàncianilaconsonància sónaspectesabsolutsdelso;ésadir,unparelldesonsnopotsernomés consonantodissonant,sinóquepotsermésconsonantomésdissonantque d’altres.

Aquestanociódedissonànciaexplicaperquèduesnotessonenmésconsonantssil’intervalqueformenésunaraód’enterspetits:comquecoincideixen moltsharmònics,nohihabatecsniaspror.Amés,enspermetentendrecom, finsitotsensetenirestudismusicals,lespersonessóncapacesd’identificar quanalgúafinaono.Imaginemunapersonaqueestàcantantis’acompanya ambunpianoperfectamentafinat.Silapersonacantaunanotalafreqüència delaqual«xoca»amblesfreqüènciesdel’instrument,lanostraoïdapercebrà asprorienssemblaràqueestàdesafinant.Si,encanvi,lapersonacantauna notaambunafreqüènciaquenointerfereixamblesfreqüènciesdelpiano,no sentiremasproriconsideraremqueestàafinant.

4.2Commesurarladissonància

Alsanysseixanta,ReinierPlompiWillemJohannesMariaLeveltvandura termeunexperimentpertaldemesurarladissonància[12].Vanfersentir parellsdetonspursadiversespersones,queelshaviend’associaraunnúmeroentre0i1,fentcorrespondre0amblamàximaconsonànciai1amb

Figura 6: Duesonessimplessuperposades.

lamàximadissonància.Ambaquestesdadesvolienobtenirungràficqueillustrésladissonànciadedostonsenfunciódeladiferènciadelesseves freqüències.Elresultatvaserunacorbacomladelafigura7.Esvaobservar queelpuntmàximdedissonànciaeraalvoltantdemigsemitòtemperat.

Apartirdelesdadesobtingudesespot construirunafuncióques’ajustiprou béaaquestacorbaiquepermetimesurarquantitativamentladissonànciaentre tonspurs.Ésadir,podemdefiniruna funcióque,donatsdostonssimples,calculiladissonànciaquehihaentretots dos.L’anomenarem funciódedissonància.Perdescriure-lad’unamaneramés formal,consideraremunto t comunparell t = (f,a),on f éslafreqüènciadelto i a,l’amplitud.Tenintencompteaquesta definició,donatsdostons t1 i t2,endenotaremladissonànciacom d(t1,t2).En aquesttreballnoensinteressal’expressióconcretad’aquestafunció,noméscal entendrequèrepresenta;podeutrobarfórmulesexplícitesperalafuncióque interpolalacorbadelafigura7ipera d a[13,apèndixE].

Arabé,l’objectiudePlompiLevelteraanalitzarladissonànciadetons complexos,comlesnotesproduïdesperinstruments,queestanformadesper lasuperposiciódetonssimples.Perfer-ho,vansuposarqueladissonànciaera additivaique,enconseqüència,lasumadelesdissonànciesentreelsdiferents harmònicsdeduesnoteseraladissonànciatotal.Engeneral,donatunconjunt detonspurs T={t1,t2,... },laseva dissonànciatotal ésdefinidaper:

Enaquestcas,donadesduesnotes N={t1,t2,... } i N={t1,t2,... }, definidesapartirdelseuespectre(queestàformatperlesfreqüènciesi amplitudsdelstonsdequèescomponlanota),definimladissonànciaentre lesduescom

Ésadir,permesurarladissonànciaentreduesnotesconsideremlauniódels dosespectresiencalculemladissonànciatotal.

Compodemcomprovar,aquestadefinicióde dissonànciad’uninterval està directamentrelacionadaambl’espectredelesnotesqueelformen.Vegem,tot seguit,lainformacióqueensaportalafunciódedissonànciaperaunespectre harmòniciquinarelaciótéambelssistemesd’afinaciódefinitsanteriorment.

Figura 7: Dissonànciadedostonspurs comafunciódelasevadistància(mesuradaentonstemperats).

4.3Corbesdedissonància

Consideremunanotadefreqüènciafonamental f ambunespectreharmònic.Ésadir, N={(f,a1),(2f,a2),(3f,a3),... },onlesamplitudsdecada freqüènciaestandeterminadesperlescaracterístiquesdel’instrumentque produeixilanota.Enconsiderarunintervalderaó r apartird’aquestanota, obtenimunanotanovaenquètoteslesfreqüènciesdel’espectreestanmultiplicadesper r : N (r) ={(rf,a1),(2rf,a2),(3rf,a3),... }.Sifixemlafreqüència fonamental f ielsvalors aj ,podemconsiderarlafunciósegüent:

D : [1, 2] → R r → D(N , N (r)).

Noteuqueaquestafuncióenscalculaladissonànciad’unintervalderaó r ,on r vadesd’1,quecorrespondriaal’uníson,finsa2,quecorrespondriaal’octava.Si representemlafunció r D(r) enunagràfica,obtenimla corbadedissonància:

Elsmínimsd’aquestagràficarepresentenintervalsdedissonànciamínima. Sielscomparemambelsintervalspursderaons5:4,6:5,4:3,3:2,5:3 i2:1(quecorresponen,respectivament,alsintervalsdeterceramenor,tercera major,quartajusta,quintajusta,sextamajorioctava),observemelsegüent:

Figura 8: Corbadedissonànciaperanotesambsisharmònics(tots amblamateixaamplitud).

Figura 9: Disposiciódelsintervalspursalagràficadedissonància.S’observaquecoincideixenambelsmínimsdelafunciódedissonància.

Veiem,doncs,quel’afinaciójustas’adaptaperfectamentaaquestgràfic ienredueixladissonància.Elfetd’obteniraquestacorbaiobservarque encaixavaambelsintervalsqueclàssicamentesconsideravenconsonantsva serprecisamentelresultatmésimportantdel’articledePlompiLevelt[12].

Comjahemcomentat,l’afinaciójustatédiversosinconvenientsquefan queenmoltscasosnosiguiadequatfer-laservir.Vegemaralarelacióentre l’afinacióatemperamentigualilagràficadedissonància,enlaqualhemmarcat lesdotzenotesdel’escala:

Podemobservarque,totiquel’escalatemperadanoassoleixexactamentels mínimsdelagràficadedissonància,ensendonaunamoltbonaaproximació. Ésperaquestaraóquelamúsicafetaambaquestaescala(que,comhemdit, avuidiaesconsideral’afinacióestàndard)ensresultaagradableal’oïda.

Enconclusió,lateoriadeladissonànciaestàbasadaenexperimentsdirectamentrelacionatsamblanostraoïdaiensproporcionaunaeinapermesurar ladissonànciadelssons.Aquestamesurapermetdonarunajustificaciómés precisadelaconsonànciadelsintervalsjustosimesurarlaqualitatdel’afinació temperada.

4.4Mésenllàdel’espectreharmònic Comhemvist,l’espectredelesnoteséselquedeterminaquinssónelsintervalsdemínimadissonància.Enelcasdelesnotesmusicals,elseuespectre (formatperfreqüènciesquesónmúltiplesentersd’unaaltrafreqüència)té unadistribuciótancaracterísticaquefaqueelsintervalsformatsperunaraó d’enterspetitssiguinmínimsdelafunciódedissonància.Peraquestmotiu, quansentimaquestsintervalstenimunasensaciómésagradableal’oïda.

Arabé,lafunciódedissonànciaquehemconstruïtalaseccióanterior tambéespotferservirperanalitzarsonsambqualsevolmenad’espectre.I,tot iquelamajoriadelsinstrumentsqueconeixemtenenunespectreharmònic(o quasi),n’hihaqueno.Enaquestcas,éspossiblequenotinguisentitferservir

Figura 10: Disposiciódelesnotesdel’escalatemperadaalagràficade dissonància.

l’afinaciótradicionaliquen’hihagiunaaltraelsintervalsdelaquals’ajustin mésalsmínimsdelagràficadedissonànciaperaaquestespectrenoharmònic.

Unexempled’aquestfets’observaenl’afinaciódelpiano.Adiferència delquepassaambunviolíounaguitarra,lescordesdelpianotenenuna rigidesaquenoésnegligible.Pertant,siesvolferunaanàlisiacuradadel movimentdelescordesdelpiano,calafegiruntermeal’equaciód’ones quetinguiencompteaquestacaracterística.Enaquestcas,siresolemlanova equació,espotcomprovarquel’espectredefreqüènciessegueixunadistribució delaforma

fn = nf◦ 1 + Bn2 , amb n = 1, 2,..., on f◦ = c/2L (elsparàmetres c i L estandefinitsalasecció2)i B ésun paràmetrequedepèndelarigidesadelacorda.Ésadir,tenimunespectre lleugerament«dilatat»respecteal’harmònic.Siconsideremaquestespectrea l’horaderepresentarlagràficadedissonància,veuremqueelsmínimsestan lleugeramentdesplaçatsenrelacióamblagràficad’unespectreharmònic.

Figura 11

harmònic(líniadiscontínua)idel’espectred’unacordaambrigidesa comladelpiano(líniacontínua).Leslíniesgrisesverticalsmarquenla distribuciódelesnotesd’unaescaladetemperamentigual;laquinta justail’octavaleshemmarcatamblíniesverticalsmésgruixudesperquè espuguindistingirmésbé.

Aquestfetsuggereixunaafinaciódiferentdel’estàndard,amblesoctaves unamicapersobredelaraó2:1,encasqueelparàmetre B nosiguinegligible, comperexemplepassaalregistreagutdelpiano.Enefecte,simesuremles freqüènciesd’unpianoquehaestatafinatperunafinadorprofessional,veurem que,amesuraqueensallunyemdelapartcentraldelpiano,l’afinació«s’estira» lleugerament.Podeutrobarunaexplicaciómésdetalladad’aquestfeta[8],on, abandad’analitzarl’espectredelpiano,esfaunapropostad’afinacióbasada enlateoriadeladissonància.

Peracabar,fixem-nosquelateoriadeladissonànciatambéensdonauna einacreativamoltútil.Imaginemquehemsintetitzatunsoambunespectre concretqueensagradaperlessevescaracterístiquessonores.Elméshabitual

: Comparacióentrelescorbesdedissonànciad’unespectre

Perquèensagradalamúsica?Unarespostamatemàtica 203

seriaafinarlesfreqüènciesfonamentalsambl’afinacióestàndardi,apartir d’aquí,fermúsica.Noobstantaixò,sil’espectredelsonoésharmònic,és moltpossiblequeobtinguemintervalsdissonants.Permilloraraquestaspecte, podemrepresentarlagràficadedissonànciai,apartirdelsmínims,construir unaescalaalmàximdeconsonantpossibleperaaquestsosintetitzat.

Agraïments

L’autorésmembredelgrupderecerca2017SGR01392iharebutfinançament delsprojectesMTM2017-84214-C2-1-P,RED2018-102650-TiEP/S03157X/1. L’autoragraeixaAlbaPérezelssuggerimentspermillorarlaqualitatlingüística deldocument.

Referències

[1] Benson,D. Music:AMathematicalOffering.Cambridge:CambridgeUniversityPress,2007.

[2] Boyer,C.B.;Merzbach,U.C. AHistoryofMathematics.Hoboken,NJ:John Wiley&Sons,2011.

[3] Cajori,F. AHistoryofMathematics.AmericanMathematicalSoc.,1999. (AMSChelseaPublishingSeries;303)

[4] d’Alembert,J.leRond. «Récherchessurlacourbequeformeunecorde tenduëmiseenvibration». Memoiresdel’Academieroyaledesscienceset belleslettres.Classedemathematique.Tom3(1747),214–219.

[5] Euler,L. «Surlavibrationdescordes». Mémoiresdel’académiedessciences deBerlin,4(1750),69–85.

[6] Fourier,J.-B.J. Théorieanalytiquedelachaleur.París:ChezFirminDidot, PereetFils,1822.

[7] Girbau,J. «Lesmatemàtiquesilesescalesmusicals». ButlletídelaSocietat CatalanadeMatemàtiques,18(1985),3–28.

[8] Gràcia,X.;Sanz-Perela,T. «Thewaveequationforstiffstringsandpiano tuning». Reports@SCM,3(1)(2017),1–16.

[9] vonHelmholtz,H. OntheSensationsofTones.DoverPubs.,1877.

[10] deLagrange,J.-L. «Recherchessurlanatureetlapropagationduson».A: ŒuvresdeLagrange.PublicadesperJ.-A.Serret.Vol.I.39–148.14v.[Obra originalmentpublicadaa MiscellaneaTaurinensia.Vol.I,1759]

[11] Lejeune-Dirichlet,P.G. «Ontheconvergenceoftrigonometricseries whichservetorepresentanarbitraryfunctionbetweentwogivenlimits». J.ReineAngew.Math.,4(1829),157–169.

[12] Plomp,R.;Levelt,W.J.M. «Tonalconsonanceandcriticalbandwidth». ThejournaloftheAcousticalSocietyofAmerica,38(4)(1965),548–560.

[13] Sethares,W.A. Tuning,Timbre,Spectrum,Scale.Londres:SpringerLondon,2005.

[14] Strauss,W.A. PartialDifferentialEquations:AnIntroduction.2aed.Hoboken,NJ:JohnWiley&Sons,2007.

[15] Wheeler,G.F.;Crummett,W.P. «Thevibratingstringcontroversy». Amer. J.Phys.,55(1)(1987),33–37.

DepartamentodeMatemáticas UniversidadAutónomadeMadrid

CiudadUniversitariadeCantoblanco, 28049 Madrid,España

tomas.sanz@uam.es

ButlletídelaSocietatCatalanadeMatemàtiques Vol.37,núm.2,2022.Pàg.205–206

Englishsummaries

ElisendaFeliu

Polynomials,polytopes,andsteadystatesofreactionnetworks

Inthispaperweintroducethetheoryofthestudyofsteadystatesofreaction networks,andwefocusonexamplesfrommolecularbiology.Steadystates arethepositivesolutionstoasystemofpolynomialequationscontaining numerousparameters.Oneoftheobjectivesofthetheoryistostudysteady statesasafunctionofparameters,and,inparticular,todeterminetheirnumber. Theseproblemscanbesolvedusingtoolsfromrealalgebraicgeometryand computationalalgebra,butthespecificcharacteristicsofthesystemsstemming fromreactionnetworkshaveallowedmorein-depthfindingstobeobtained.In thisarticleweexplainsomeoftherecenteffectiveresultsinthisarea,where thestudyofthesystemandoftheparameterregionsispossiblethankstothe examinationofthegeometryofanassociatedpolytope.

Keywords: reactionnetwork,multistationarity,bistability,Newtonpolytope, positivity,realalgebraicgeometry.

MSC2020SubjectClassification: 92C45,34E15,80A30,13P10.

DavidRojas

Oscillatorsatresonance

Anoscillatorisisochronousifallmotionsareperiodicwithacommonperiod. Whenthesystemisforcedbyatime-dependentperiodicperturbationwith thesameperiod,thedynamicsmaychangedrasticallyandthephenomenon

ofresonancecanappear.Inthisarticlewewillstudywhichpropertiesthe perturbationsmustfulfilinordertoobtainunboundedsolutions.Wewill considerdifferentoscillators,fromharmonictononlineargeneralizations,and wewillsetoutanumberofremarksabouttheconceptofauto-parametric resonance.

Keywords: oscillator,resonance,perturbation,isochrony.

MSC2020SubjectClassification: 34C10,34C15,34D05,34D10,34D23.

TomásSanz-Perela

Whydowelikemusic?Amathematicalanswer

Whydowelikemusic?Whydowefeelthatthesoundproducedbyoneor morepianokeysismusicandyetwecallthesoundthataglassmakeswhen fallingtothegroundnoise?Whydowehearthesamenoteplayedbyafluteor aclarinetdifferently?Andwhy,withouthavingstudiedmusic,areweableto distinguishapersonwhohasjuststartedstudyingtheviolinandplaysoutof tunefromanexperiencedone?

Inthisarticle,wegiveanswerstothesequestionsusingmathematicsas themaintool.Todoso,ourstartingpointwillbethewaveequation,which willallowustounderstandthemainpropertiesofthesoundproducedby musicalinstruments.Basedonthisknowledgewewillbeabletounderstand theideaswhich,throughouthistory,havebeenbehindtheconstructionof musicalscales,whichformthebasisofmostofthemusicweareacquainted withnowadays.Finally,wewillstudytheconceptsof dissonance and consonance fromamathematicalperspective,andwewillgainabetterunderstandingabout whysomesoundsaremorepleasantthanothers.

Keywords: waveequation,harmonicspectrum,Fourierseries,musicalscales, dissonance.

MSC2020SubjectClassification: 00A65,35L05,74K05.

Instruccionsperalsautors

Elsarticlessotmesosapublicaciós’hand’enviaralseditorsoaqualsevol membredelcomitèeditorialpercorreuelectrònic,preferentmentenformat PDF.Elsoriginalshandecontenirlaversióanglesadeltítol,unresumbreuen catalàienanglès,paraulesclauencatalàienanglèsielscodisdelaclassificació permatèriesMSC2020.

Lesversionsdefinitivesdelsarticlesacceptatss’handepresentarencodiTEX, preferentmentenl’estilLATEXpropidel Butlletí.Aquestestilespotobtenira lespàgineswebdelaSocietatCatalanadeMatemàtiques(SCM).Esrecomana unaextensiód’entre15i35pàgines.Femnotarqueenaquestapublicació s’utilitzapreferentmentelpuntperaseparardecimals,enllocdelacoma recomanadaperl’IEC,perapoderfacilitarlacomprensiódelesexpressions matemàtiques.Pertald’accelerarelprocésdeproducció,espregaalsautors quesegueixinlesindicacionscontingudeseneldocumentd’exemple.

Laversióenpaperdel Butlletí s’imprimeixenblancinegre.Quanun articlecontinguifiguresencoloriesconsidericonvenient,l’autorproporcionarà unaversiódelsgràficssubstituintelcolorpertonsdegrisosilíniesdegruix variable.Aixímateix,modificaràelscomentarisquefacinreferènciaalcolorde lesfigures.Enqualsevolcas,el Butlletí publicaràl’originalencolorenelseu formatelectrònic.

Lapropietatintel lectualdelsarticlesésdelsrespectiusautors.

Elsautors,enelmomentdelliurarelsarticlesal Butlletí perasol.licitar-ne lapublicació,acceptenelstermessegüents:

—ElsautorscedeixenalaSCM(filialdel’Institutd’EstudisCatalans)els dretsdereproducció,comunicaciópúblicaidistribuciódelsarticlespresentats peraserpublicatsal Butlletí.

—ElsautorsresponendavantlaSCMdel’autoriail’originalitatdelsarticles presentats.

—Ésresponsabilitatdelsautorsl’obtenciódelspermisosperalareproducciódetotelmaterialgràficinclòsenelsarticles.

—LaSCMestàexemptadetotaresponsabilitatderivadadel’eventual vulneraciódedretsdepropietatintel.lectualperpartdelsautors.

CadaautorrebràunacòpiaenPDFd’altaqualitatdelaversiódigitaldelseu articleiunexemplarimprèsdelnúmerodel Butlletí enelqualespubliqui.

Lacorrespondènciaadministrativarelacionadaambel Butlletí s’had’adreçaralaSCM.

Pelquefaalaprotecciódedadespersonals,l’Institutd’EstudisCatalans(IEC) compleixelqueestableixelReglamentgeneraldeprotecciódedadesdelaUnió Europea(Reglament2016/679,del27d’abrilde2016).Deconformitatamb aquestanorma,s’informaque,ambl’acceptaciódelesnormesdepublicació, elsautorsautoritzenquelessevesdadespersonals(nomicognoms,dadesde contacteidadesdefiliació)puguinserpublicadesenelcorresponentvolum del Butlletí.

Aquestesdadesseranincorporadesauntractamentqueésresponsabilitat del’IECamblafinalitatdegestionaraquestapublicació.Únicaments’utilitzaranlesdadesdelsautorsperagestionarlapublicaciódel Butlletí ino serancedidesatercers,niesproduirantransferènciesatercerspaïsosoorganitzacionsinternacionals.Uncoppublicatel Butlletí,aquestesdadeses conservarancomapartdelregistrehistòricd’autors.Elsautorspodenexercir elsdretsd’accés,rectificació,supressió,oposició,limitacióeneltractament iportabilitat,adreçant-seperescrital’Institutd’EstudisCatalans(carrerdel Carme,47,08001Barcelona),obéenviantuncorreuelectrònical’adreça dades.personals@iec.cat,enquès’especifiquidequinapublicacióestracta.

Comitèeditorial

AntoniGuillamon(editorencap) DepartamentdeMatemàtiques UniversitatPolitècnicadeCatalunya antoni.guillamon@upc.edu

CarmeCascante

Dep.deMatemàtiquesiInformàtica UniversitatdeBarcelona cascante@ub.edu

BartomeuColl Dep.deMatemàtiquesiInformàtica UniversitatdelesIllesBalears tomeu.coll@uib.cat

NúriaFagella

Dep.deMatemàtiquesiInformàtica UniversitatdeBarcelona fagella@maia.ub.es

ArmengolGasull DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona armengol.gasull@uab.cat

GáborLugosi

ICREAiDepartamentd’Economia UniversitatPompeuFabra gabor.lugosi@upf.edu

RosaCamps(editoraadjunta) DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona rosa.camps@uab.cat

MarcNoy

DepartamentdeMatemàtiques UniversitatPolitècnicadeCatalunya marc.noy@upc.edu

FrancescPlanas DepartamentdeMatemàtiques UniversitatPolitècnicadeCatalunya francesc.planas@upc.edu

JoanSaldaña Dep.d’Informàtica,Mat.AplicadaiEstadística UniversitatdeGirona joan.saldana@udg.edu

MartaSanz-Solé Dep.deMatemàtiquesiInformàtica UniversitatdeBarcelona marta.sanz@ub.edu

GilSolanes DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona gil.solanes@uab.cat

SocietatCatalanadeMatemàtiques

La SocietatCatalanadeMatemàtiques(SCM) ésunasocietatfilialdel’Institutd’EstudisCatalans,quecontinualesactivitatsdelaSecciódeMatemàtiques delaSocietatCatalanadeCiències,quefoufundadaperl’Institutl’any1931. Lesfinalitatsdela SCM són:elconreudelesciènciesmatemàtiques,l’extensió delseuconeixementenlasocietatcatalana,elfomentdelseuensenyament idelasevainvestigacióteòricaiaplicada,aixícomlapublicaciódetotamena detreballsques’adeqüinaaquestsobjectius.La SCM desenvolupalesseves activitatsenlesterresdellenguaiculturacatalanes.Elcatalàés,doncs,la llenguapròpiadela SCM ilaqueésusadanormalmententotselsseusactesi publicacions.

La SCM editalespublicacionsperiòdiques SCM/Notícies, ButlletídelaSocietatCatalanadeMatemàtiques, NouBiaix (encol.laboracióamblaFEEMCAT)i Reports@SCM.Elssocisdela SCM reben,gratuïtament,aquestespublicacions.

La SCM téconvenisdereciprocitatambdiversessocietatsmatemàtiques d’arreudelmón,mitjançantelsqualselssocisdela SCM obtenenunareduccióenlaquotadesocid’aquestessocietats.Aixímateix,elssocisdela SCM podenfer-sesocisdelaSocietatMatemàticaEuropeapagantunaquota complementària.

LaJuntaDirectivadela SCM estàconstituïdaperlespersonessegüents:

Presidenta:MontserratAlsinaiAubach

Vicepresidents:JoanPortiiPiqué,JosepVivesiSanta-Eulàlia

Secretària:MargaridaMitjanaiRiera

Tresorer:AlbertGranadosiCorsellas

Vocals:ClaraMateoCampo,DavidVirgiliCorreas

Delegatdel’IEC:JoaquimBrunaiFloris

L’adreçadela SCM éscarrerdelCarme,47,08001Barcelona.Telèfon: 933248583.Fax:932701180.Correuelectrònic: scm@iec.cat.Adreçaweb: http://scm.iec.cat.