Assembly, pattern and reciprocity

almost infinite integration possibilities and a break with the economy of scale. Finally, digital manufacturing is a standardized tool that needs to be standardized, like the suitcase described by Carpo. It legitimizes collaborative work and the sharing of intellectual resources. Copying is not necessarily negative, especially with an algorithmically generated element that has the advantage of containing both its result and its process. It can thus be readjusted and reintegrated from one project to another. This mode of production of architecture is neither simpler nor more efficient, but different. However, the outcome should still remain linked to the architect’s style and not to a predefined style as Parametricism might suggest.

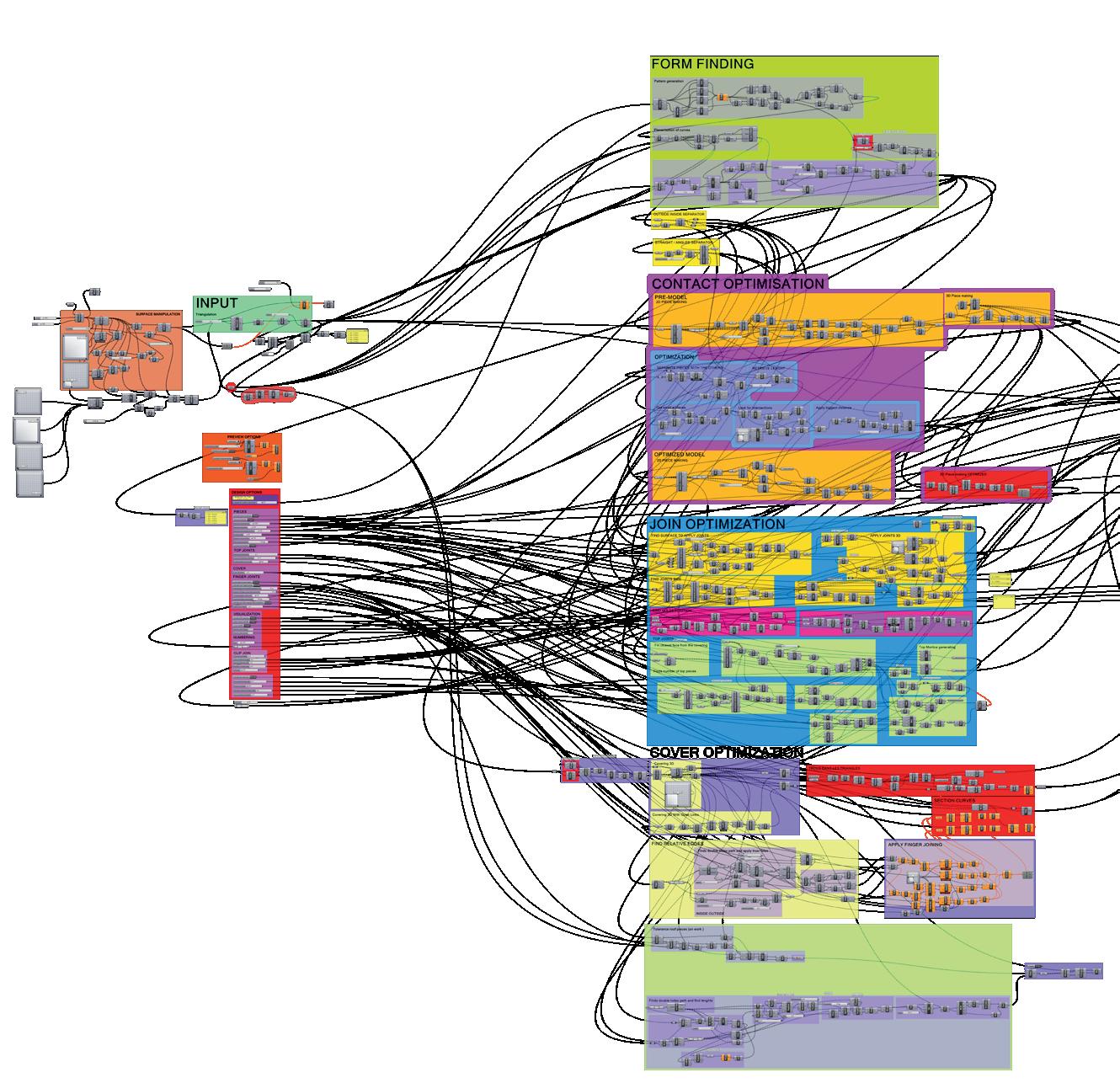
a. Assembly, pattern and reciprocity In order to deepen the subject, I spent a semester studying the integrative computational approach. For this reason, I have examined many projects and pavilions from the point of view of their assembly, shape and accessibility. I then set up a project similar to the project Wikihouse - in its construction principle - by aiming to transform any surface, complex or not, into a network of parts to be assembled without nails or screws. Although a little more theoretical, my research also aims to manufacture using cut-to-size boards with standard and affordable technology. My objective is to evaluate how easily such a technology is accessible and to see if it is possible to approach a construction concept in a personal way, to take control of the design and manufacturing process. I was particularly interested in woodworking, for reasons generally equivalent to those mentioned above. To propel such research, it is essential to target a certain technique, we will approach the study of what are called reciprocal structures in order to revisit their application. We will therefore see what it is about in the second part of the brief, but it is important to understand the reasons for this choice. This technique, traditionally used in self-construction, has the particularity of presenting a structural deficit for ease of installation. It takes the form of patterns necessary to induce reciprocity between the elements, all the elements support and are supported in a circle of forces. These patterns, with their singular aesthetics, can give rise to an original archetype of architecture. This practice also conveys cultural values that I was interested in using and revisiting. Assembly, pattern and reciprocity can be algorithmically recomposed in as many ways as possible as the algorithmic architecture will enjoy exploring.

48

RECIPROCAL STRUCTURES OR NEXORADS

Principle of reciprocal structure where each person supports and is supported by another in a closed circle.41

2.12. The architecture of reciprocal structures

Before going any further, it is essential to clearly define what the socalled reciprocal structures, reciprocal frames or nexorades. These terms are very unknown in the world of architecture although more and more articles are trying to popularize the subject. Executive structures are already a concept the important thing is to visualize what it means to add reciprocity.

Reciprocal structures or reciprocal frames are a three-dimensional structural grid configuration composed of at least three elements. The simplest nexorade arrangement is to place the beams in a closed circuit where each part is supported by its predecessor at one end and fixed on the other side. In their more complex arrangements, they compose structures whose interest is to be able to form double curved surfaces.

The mutually supported elements are placed tangentially around a central point and form an inner polygon. The other end of the parts therefore constitutes an external polygon. This system is often used because it does not require internal columns, it is suitable for creating covers. In the case of a hemispherical roof, the central polygon can be used as a zenithal light.

The visual and structural expression of these assemblies can be greatly varied by changing the number of elements, their lengths and the internal and external radii defining their location. It is possible, and this will be developed further, to multiply the reciprocal frames to form a grid, even more flexible, freed by its reduced need for supports.

The name « Reciprocal frames » also called reciprocal frames comes from designer Graham Brown, who deployed this type of structure in England, designating by the reciprocal word the way in which the elements support each other. The geometric characteristics of such structures produce architectures with circular or polygonal patterns which, when regular, have the advantage of requiring only one and the same length for all fragments.

The functional organization and division of the internal spaces of the architecture into RF1 differ fundamentally from traditional rectangular plans. Without the need for structures within the form, the result is a free and flexible architectural volume. This method also differs from traditional cylindrical structural systems (such as yurts), as the elements do not meet in a specific central point. This creates a spiral visual effect that brings a considerable aesthetic impact which, combined with this free space, creates a specific architecture with reciprocal frames.

One of the major potentials of these structures is that they are able, if the beams are adapted, to travel small or large distances without adding any particular complexity. By multiplying these frames, it is possible to obtain a wide variety of structural configurations while crossing large spans. Although reciprocal structures have been used in many countries and have endorsed different denominations: (Serliotype ceiling; Reciprocal frames,, Svastica structures, Nexorades, Lever-arch structures, etc.,), they are poorly represented in current architectural production.44

1 reCiproCAl frAme - reCiproCAl frAme the AbbreviAtion rf is Commonly used in teXts thAt desCribe them to Avoid redundAnCy. this is Also the CAse for rfs : reCiproCAl frAme system whiCh refers to An Assembly of reCiproCAl frAmes.

Tipi Sioux structure 42

2.13. Brief history of reciprocal structures

It is difficult to trace the very origin of this process, as it is very poorly documented or differently named. This technique being mainly composed of wood, has not withstood well over time and has not transferred any physical impressions. However, the transmission of this method can be observed in temporary structures such as tipis or the hogans Navajos, that leads us to believe that they have been around for a long time. The reciprocal frameworks would have developed in all continents in parallel, although the oldest sources would come from Asia. Towards the end of the 12th century, a Buddhist monk named Chogen (1121-1206) allegedly made a system of spiral joists in temple construction. These structures would have brought a mystical value to it because of their aesthetics. Unfortunately, there is no tangible remains of such monuments today, although it is possible to identify this technique in the current Japanese framework.

They are also found in medieval Europe, where architecture and particularly landings were shaped using wooden beams. As buildings became more and more voluminous, it became necessary to find elements of longer lengths. The contracting authority, if it had the means, could import larger logs from abroad, otherwise alternatives had to be considered to cover the required spans. In the Middle Ages, some floors were made from four joists placed one on top of the other, as seen above, but in a planar composition. Between 1225-1250, the architect Villard de Honnecourt studied some configurations to « build with elements that are too short ». This indicates a prior knowledge of these structures was therefore already in use for a long time, even if it is not possible to determine their exact origin.

Structural grid for medieval bearing. (Drawing of A. E. Piroozfar.)44 Planar assembly of Honnecourt. (Drawing of A. E. Piroozfar.)45

A little later, Leonardo da Vinci (1452-1519) continued to explore it by proposing the first complex frames composed of a series of reciprocal frames. His research aimed to create a structural system using a multitude of small elements. He also studied a bridge based on the principles of reciprocity, but in another area, already tested in China, this bridge nevertheless remains a reference in terms of selfsupporting structures today.45

In 1537, Sebastiano Serlio (1475-1554) published the sketch of a mesh quite similar to that of Honnecourt where he showed how to compose a landing where the joists were slightly too short. The objective is to work on a 4.5 m square floor with 4.2 m long beams. It is noticeable that it cuts the material in order to fit them into each other. This is a clear difference from previous sketches where the elements had only one point of contact.

Serlio planar assembly . (Drawing of A. E. Piroozfar.)47

John Wallis (1616-1703) then presented in 1695, in his Opera Matematica, a new version of this bearing composition. He claims to be the first to discover this kind of plot, and he « would be unlikely to have been aware of work previously done by Honnecourt or da Vinci ».46 He would have built one of these structures at Oxford in 1649 and would have been the first to propose a structural analysis, although incomplete, of these systems in 1670.47

It can be seen that research on RFs are mainly driven by the need to cross combined with the lack of means to do so. This technique was already a major economic challenge and we will see that it will continue to do so, at least in Europe. The technical limitations of the time maintained the configurations in the form of a repeated grid or a simple curvature. It is now interesting to observe the architectural production of the last century and more particularly the effervescence of pavilions resulting from the encounter between reciprocal frames and algorithmic architecture.

Planar assembly of da vinci and selfsupporting bridge. (Drawing of A. E. Piroozfar.)46

Illustration des analyses de structures réciproques de John Wallis48