Method of Gauss Orbital Determination of Near-Earth Asteroid 2015 HH10

Novel Research.

Method of Gauss Orbital Determination of Near-Earth Asteroid 2015 HH10

by Evan J., Jacqueline M., Milenka M. (VI)1

1Summer Science Program and Sommers-Bausch Observatory, University of Colorado Boulder, Boulder, CO, 80309, USA

Abstract

Near-Earth asteroids, a subset of near-Earth objects (NEOs), are characterized by their close approach to the Sun. By definition, an astronomical body is considered an NEO if it comes within 1.3 AU of the Sun at its closest point. If a NEO is believed to make an approach close enough to the Earth to cause significant damage, it is assessed as a potentially hazardous object (PHO). We observed the NEO 2015 HH10 over the course of four nights to determine its orbit. Using observational data and the orbital determination Python program that we developed, we determined its orbital elements and generated an ephemeris of its future trajectory and position. Our methods and procedures are shown to be more precise than the JPL Horizons database.

There is a multitude of different space objects floating around the Solar System, including both natural and artificial space debris. Artificial or manmade debris includes old machinery or dead satellites left behind by human space missions. Natural space debris consists of asteroids and comets which break up into smaller meteoroids. While both asteroids and comets formed early on in the universe about 4.5 billion years ago [1], comets and asteroids differ in composition. Comets are usually made of ice, dust, and other rocky material, populating the Kuiper Belt in the outer edges of the Solar System or even beyond the Solar System in the Oort Cloud [2]. Asteroids are small bodies that orbit the sun, primarily residing in the asteroid belt between Mars and Jupiter. They are usually around 1,000 km or less in diameter and are composed of metals and other rocky materials, such as iron or nickel, as well as elements abundant in the Earth, such as oxygen and silicon [3]. An asteroid must pass within 1.3 AU of the Sun at its closest approach to be considered a near-Earth asteroid [1]. Some Mars-crossing asteroids which lie between the main asteroid belt and the near Earth asteroid population fit within the parameters of NEOs if their perihelion (point in the orbit when the object is closest to the Sun) is less than 1.3 AU. There are several types of near-Earth asteroids, classified by their orbits and locations: Atira asteroids, Atens Asteroids, Apollo asteroids, and Amor asteroids [2]. 2015 HH10 is categorized as an Apollo asteroid which means its orbit crosses Earth’s orbit and it has a semi-major axis greater than Earth’s. Its perihelion is less than the Earth’s aphelion (point in the orbit when the object is farthest from the Sun). Since Apollo asteroids are Earth-crossing, they are interesting targets to study as potentially hazardous objects (PHO). For example, in 2013, the Chelyabinsk meteor (an Apollo asteroid) exploded over rural Russia, injuring an estimated 1,500 people [4]. The Apollo asteroid population forms the majority of currently known PHOs. In order to expand the search for NEOs and predict possible PHO behavior, the International Astronomical Search Collaboration provides amateur astronomers with data so they can make scientific discoveries, often focusing on month-long Asteroid Search Campaigns in which teams search for asteroids [5]. Search campaigns such as those run by the International Astronomical Search Collaboration encourage international cooperation and the involvement of citizen scientists in real-time astronomical discoveries. In order to determine the orbit of an asteroid, there are several necessary components, known as the six Keplerian elements: semi-major axis, eccentricity, inclination, longitude of the ascending node, argument of perihelion, and mean anomaly. The semi-major axis measures half of the longer axis in an ellipse, generating the ”long radius” that defines the size of the orbit. The eccentricity is used to describe the elongation of an ellipse; a perfectly circular ellipse has an eccentricity of 0. The inclination is the angle between the asteroid’s plane and the Earth’s plane (ecliptic plane). The longitude of the ascending node is the angle between the Vernal Equinox and the ascending node, the point at which the orbital and ecliptic planes intersect. The argument of perihelion is the angle between the asteroid’s ascending node and perihelion, the point where the asteroid is closest to the Sun. The three angles—inclination, longitude of the ascending node, and argument of perihelion—are known as the Euler angles as they describe the asteroid’s orbit orientation relative to the original reference plane. The mean anomaly is a convenient approximation for the angular position of the object, calculated from specific times of observation, that varies linearly with time. These six orbital elements are the foundation for finding and predicting the trajectory of an asteroid. In addition to the main elements, the time of perihelion (date and time at which an object is closest to the Sun) can be derived. The orbital state vectors (Cartesian vectors of position and velocity) produced by the Method of Gauss (MoG) are used to find the six orbital elements in conjunction with observational data taken over at least three separate nights, roughly equally-spaced in time.

Figure 1. Diagram of orbital elements

II. OBSERVATIONS AND IMAGE PROCESSING

A. Data Acquisition

Observations occurred at Sommers-Bausch Observatory (SBO-463) in Boulder, Colorado. We utilized the PlaneWave CDK20 optical tube telescope and STF-8300 for imaging. The PlaneWave CDK20 optical telescope has two fused silica mirrors: one at 7.5 in (191 mm) and one at 20 in (508 mm) [6]. It has a focal length of 3454 mm and focal ratio of F/6.8. The STF8300 uses the KAF-8300 CCD, with a total of 8.3 million pixels [6]. SkyX software was used for telescope navigation. Each night we took three sets of lights using the UV/IR cut-off filter with 10-minute intervals in between each series. We also acquired darks and flats for every night of observation. The darks were taken with the same exposure time as the lights. The apparent magnitude of 2015 HH10 shifted each night, which dictated our exposure times accordingly. Table 1 lists the dates and times for our four successful observations. B. Image Processing

Astrometry was first performed on the acquired data from observation. AstroImageJ was used to detect 2015 HH10 across data from each night. The first task after every observation was to find 2015 HH10 throughout the series we took. We generated master darks and master flats. We then subtracted and divided our light series by the darks and flats to adjust for systematic error in the camera and telescope. In order to identify the movement of 2015 HH10 from the many stars in the frame, we cycled through the series and looked for movement. The best frame from each series was then uploaded into nova.astrometry.net to determine the transformations from pixel coordinates to celestial coordinates and to download the files containing the errors of these transformations. Once reopened in AstroImageJ, we selected our asteroid using the measurement tool and recorded the right ascension (RA) and declination (DEC) of our asteroid. We next performed photometry on our data to determine the magnitude of 2015 HH10 using SAOImageDS9 and data from the AAVSO Photometric All Sky Survey (APASS). A trend line was generated from chosen star targets’ magnitudes and signals (average noise in the sky). The signal of the asteroid was input into the line of best fit to produce its magnitude. Astrometry and photometry results were formatted and sent to the Minor Planet Center for review and consideration.

To go from x and y pixel values to RA and DEC values, we must use a coordinate transformation. Least Squares Plate Reduction (LSPR) uses stars with known RAs and DECs to create a least squares fit for this transformation. LSPR is a statistical procedure that approximates the best fit for a set of data points by minimizing the sum of the residuals for the points from the curve. This method can be used to predict certain dependent variables. We used nova.astrometry.net to conduct LSPR on our images since the site allowed us to find the RAs and DECs of our asteroid during our observations. Table 2 lists the RA and DEC of 2015 HH10 across all four observations and individual series taken. C. Results

III. ORBIT DETERMINATION

A. Methods

As previously stated, we utilized the Method of Gauss (MoG) and data from our last three observations to determine a preliminary orbit for 2015 HH10. There are numerous steps to MoG, beginning with finding an initial asteroid vector guess using the scalar equation of Lagrange an inputting Gaussian time intervals gathered from the time of observation. These Lagrange scalars are used to calculate an initial position magnitude. We can use the position magnitude and a truncated Taylor series expansion of r about the central value to determine the Lagrange coefficients, f and g. These Lagrange coefficients can be used to find the position and velocity vectors. After adjusting the times by accounting for the travel time of light, new Lagrange coefficients are found. This process is iterated to produce increasingly accurate values for the asteroid’s position and velocity vectors at the middle observation. The final position and velocity vectors are used as inputs in addition to the time of observation to find the orbital elements for 2015 HH10. The entire process requires data from three separate observations to predict the position at a fourth separate time. To calculate the orbital elements, first the angular momentum (h) of 2015 HH10 was calculated at the middle observation time by taking the cross product of the position (r2) and velocity (.r2) vectors produced by MoG.

The semi-major axis (a) was then calculated by using the middle observation’s position and velocity.

Eccentricity (e) of the asteroid was calculated with the previously determined angular momentum (h) and the semi-major axis (a).

The inclination (i) was calculated using the angular momentum (h).

The longitude of the ascending node (Ω) was calculated from inclination (i) and angular momentum (h).

To find the argument of perihelion (ω), the angular distance from the ascending node to the asteroid and true anomaly needed to be calculated first. We calculated angular distance from the ascending node to the asteroid (U) from the central position vector (r2), inclination (i), and longitude of the ascending node (Ω).

The true anomaly (ν) was calculated from eccentricity (e), semi-major axis (a), central position (r2) and velocity vectors (.r2), and angular momentum (h). The true anomaly (ν) and the angular distance (U) from the ascending node to the asteroid were used to find the argument of perihelion. Then the eccentric anomaly (E) was calculated.

The mean anomaly (M) was found using the eccentric anomaly (E).

Last of all, the time of perihelion (T) was determined using the current time and the mean anomaly (M).

Constant k is the factor needed to convert from regular days to Gaussian days. This was calculated through our Python orbital determination code. We compared our resulting ephemeris derived from the computed orbital elements to the online JPL Horizons database to determine our accuracy. We conducted Monte Carlo simulations to visualize the full range of values for each of our orbital elements, factoring in the RA and DEC uncertainty provided by nova.astrometry.net. For each Monte Carlo iteration, we chose RA and DEC values from Gaussian distributions with the mean as the average values of RA and DEC and the standard deviation as the uncertainty in RA and DEC. These values were run through the code to produce orbital elements. The results were plotted onto histograms, one for

each orbital element. We ran 100,000 total iterations of our Monte Carlo simulations. To assess the consistency of our ephemeris generation program, we inputted orbital elements from the middle observation in addition to the date of the last observation to calculate the expected RA and DEC of the last observation. The expected RA and DEC was then compared to the actual observed value. IV. DISCUSSION

The Monte Carlo simulations produced orbital elements that had somewhat small error bars and values close enough to JPL Horizon’s predicted values that they fell well within those error bars, around one standard deviation away. The generated ephemeris using data from three of our observations and the orbital elements we found using the MoG yielded RAs and DECs very close to the measured values even on the observation nights we didn’t use as our MoG input data. The errors between the MoG ephemeris values and the astrometry measurements are consistently lower than the JPL Horizon predictions (Table 3), sitting under 0.02% for all RAs and DECs. While JPL Horizon’s results

Figure 2. Orbit Visualization; 2015 HH10 is the blue orbit and Earth is the green orbit

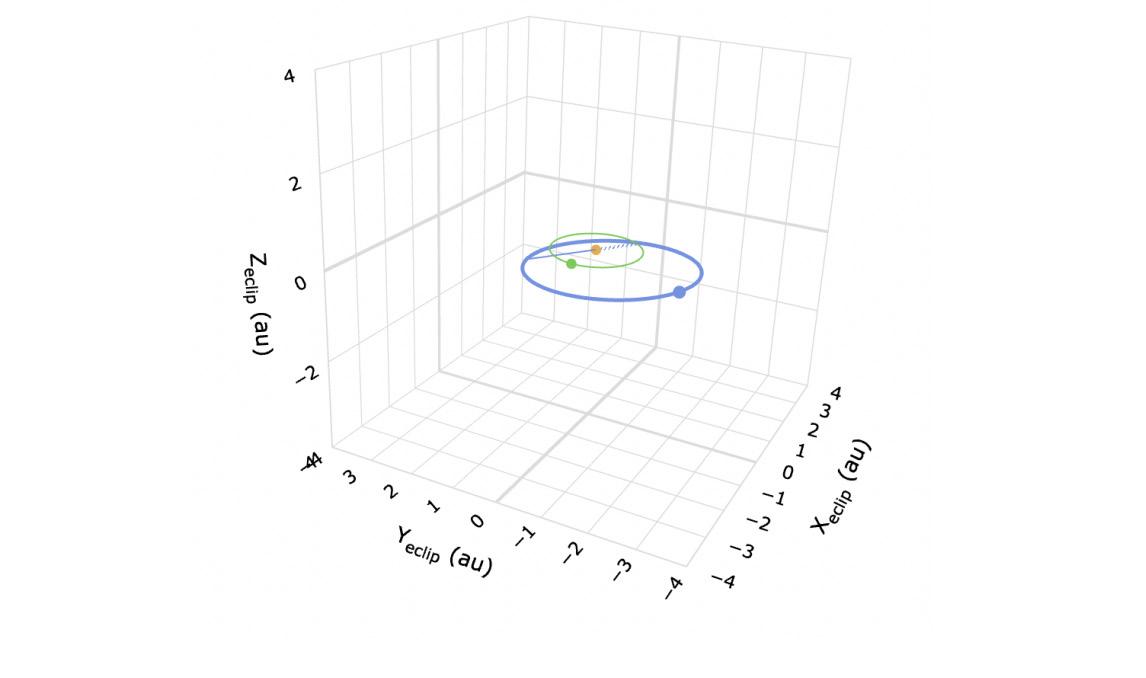
Figure 3. Semi-major Axis (AU) (left), Eccentricity (right) Figure 4. Time of Perihelion Passage (JD) (left), Inclination (DEG) (right)

Figure 5. Longitude of Ascending Nodes (DEG) (left), Argument of Perihelion (EG) (right)

are also relatively accurate, their percent errors are greater than what MoG produced. JPL Horizons has a particularly higher error in DEC calculations than RA. In general, the JPL Horizons database seems to less accurate, followed by the Monte Carlo simulations. All in all, our self-generated MoG ephemeris produces the most accurate predictions for the position of 2015 HH10 at a specific time. The minuscule percent errors, even for the observation night which was not included in our method of Gauss data, indicate a high level of accuracy in our methods and procedures. Certain complications arose throughout the process. When assessing data from observation one to calculate the position (r2) and velocity ( ̇r2) vectors, the r2 values did not converge, so the first observation was neglected for our final orbital determination. In addition, noise and star interference prevented the analysis of every series. In the third series of observation one, the asteroid was too faint to detect, preventing the AstroImageJ program from detecting it for proper measurements. In the second series of observation three, the asteroid passed in front of a star, making it impossible to take measurements of its RA, DEC, and Source. More observations and more data would increase the accuracy of our orbital determination. Instead of just taking one set of orbital elements from a single observation date, it would be more precise to average the values of several sets of observations and use those averages to predict 2015 HH10’s future position.

V. ACKNOWLEDGMENTS

We would like to thank Dr. Michael Dubson and Dr. Donovan Domingue, our professors, for guiding us through the conceptual foundation of our research and providing us support with the real-time application and creation of our project. We would also like to thank all the TAs, including Peter Lande, Jessica Dong, Mia Liang, and Grace Edwards for their help and patience with helping us debug our code, and supervising late-night observations. We’d like to recognize the University of Colorado Boulder for providing us with the facilities and technology to conduct our research at the Sommers-Bausch Observatory. Last, but not least, thank you to the Summer Science Program for providing us with this opportunity.